» Задачи на построение сечений» ( 10 класс)

РЕШЕНИЕ ЗАДАЧ

НА ПОСТРОЕНИЕ СЕЧЕНИЙ

Цель урока: учить решать задачи на построение сечений тетраэдра и параллелепипеда.

Планируемые результаты:

Личностные УУД

— аргументировано оценивать свои и чужие поступки;

— ответственное отношение к учению на основе мотивации к учению и познанию

Предметные УУД

— знать понятия секущей плоскости, сечения тетраэдра и параллелепипеда;

— строить сечения тетраэдра и параллелепипеда.

Метапредметные УУД познавательные

— анализировать и обобщать;

— классифицировать;

— устанавливать аналогии (создавать модели объектов).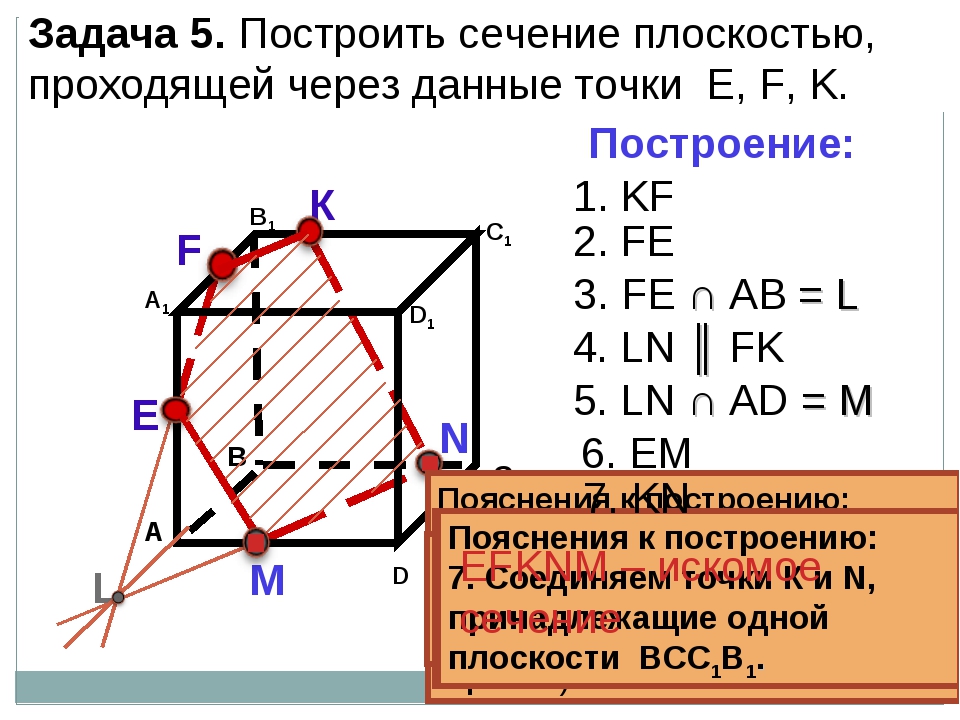

ХОД УРОКА

1. Организационный этап.

Готовность к уроку.

2. Постановка цели и задач. Мотивация учебной деятельности.

— Здравствуйте, дети. Какие фигуры мы рассматривали на прошлом уроке?

О: На прошлом уроке мы рассматривали тетраэдр и параллелепипед. Учились изображать эти многогранники на плоскости.

— Сегодня мы будем учиться решать задачи на построение сечений тетраэдра и параллелепипеда. Для этого сначала узнаем, что такое сечение, как строить сечения и параллельно проведём небольшую классификацию возможных сечений тетраэдра и параллелепипеда.

На листочках (раздаточный материал) запишем число, классная работа и тема урока – Задачи на построение сечений.

2. Актуализация знаний

Рассматривая чертёж ответьте на вопросы:

1. (тетраэдр) Назовите прямую, по которой пересекаются плоскости

АВС и АDС; АВК и СDB.

2. Точки пересечения DК и АВС; КSи АВС.

3. Каким граням принадлежит точка К.

4. (Параллелепипед) Пересечение плоскостей АА₁В₁ и АСD; РВС и А₁D₁С₁

5. Точки пересечения РМ и АВС; СМ и А₁D₁С_1.

6. Каким граням принадлежит точка М.

3. Первичное усвоение новых знаний.

— Что же такое сечение? Проведём секущую плоскость, т.е. плоскость, по обе стороны от которой есть точки многогранника.

— Эта секущая плоскость пересекает грани тетраэдра по каким фигурам?

О: секущая плоскость пересекает грани по отрезкам

— Многоугольник, сторонами которого являются эти отрезки, называется

сечением тетраэдра (параллелепипеда).

Многоугольник. А у нас на модели четырёхугольник. Что это значит? – значит в зависимости от того, сколько граней многогранника пересечёт секущая плоскость, столько сторон будет у многоугольника в сечении.

У тетраэдра сколько граней? Значит, в сечении могут получиться только треугольник и четырёхугольник.

У параллелепипеда шесть граней значит, в сечении может получиться только треугольник, четырёхугольник, пятиугольник и шестиугольник.

Давайте рассмотрим все возможные случаи построения. Перейдём к изображениям.

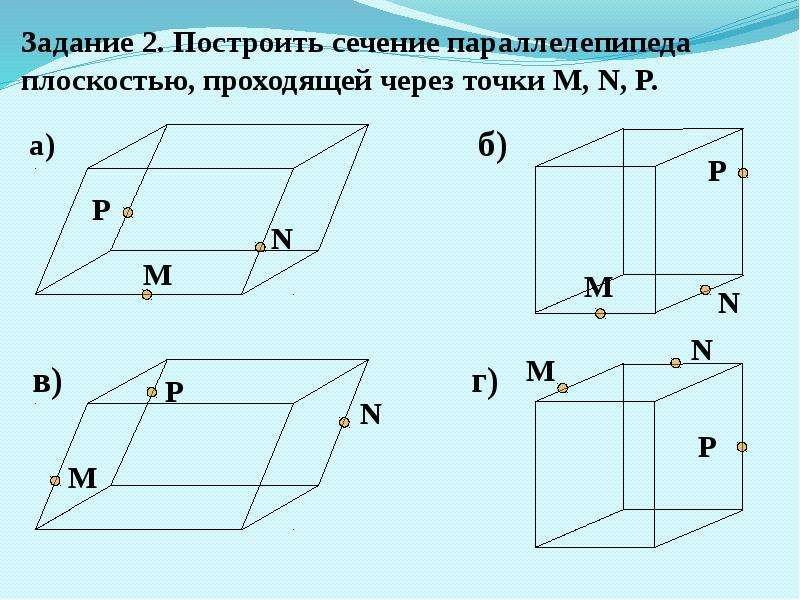
Ф1. Даны три точки. Построить сечение тетраэдра плоскостью.

— Достаточно ли данных для построения?

О: Да, через три точки, не лежащие на одной прямой …

Знаем, что секущая плоскость пересечёт эту грань по отрезку. Две точки этого отрезка известны. Как построить линию пересечения?

О: соединить точки.

NB: две точки сечения лежат в одной грани, значит соединяем их отрезком.

Наш треугольник изображён некорректно.

Как изображаются отрезки, лежащие на невидимых гранях?

О: Они изображаются пунктирными линиями.

Ф2. Параллелепипед. Даны три точки. (Ученик у доски. Проводит аналогичные рассуждения).

Ф4. Провести сечение через три точки. Точка Р лежит в нижней невидимой грани параллелепипеда.

Точка Р и отрезок ОК лежат в параллельных плоскостях. Т.е. секущая плоскость пересекает две параллельные плоскости. Что произойдёт?

О: Секущая плоскость пересечёт параллельные плоскости по параллельным отрезкам. Получили по две точки в каждой грани. Их можно соединить.

Ф5. Соединяем точки А и С, А и В. Надо построить ещё одну точку, принадлежащую двум граням, содержащим точки и плоскости сечения. Эта точка лежит на линии пересечения граней. Продолжаем…

Ф6. При построении сечений параллелепипеда помним всегда свойство линий пересечения параллельных плоскостей с секущей плоскостью. В нашем случае это секущая плоскость. Найдём ещё одну точку пересечения секущей

плоскости и нижней грани. Эти точки лежат в одной плоскости. Соединяем

их…

Физминутка. Поухаживаем за своим зрением.

Посмотреть на переносицу и задержать взор на счёт 1-4. До усталости глаза не доводить. Затем открыть глаза, посмотреть вдаль на счёт 1-6. Повторить ещё раз.

Ф7. Аналогичные рассуждения.

5. Первичная проверка понимания и закрепление.

Ф3. Провести сечение через ребро АВ и точку С. Достаточно ли данных для построения? Выполняют самостоятельно.

— Какой теоретический материал поможет строить сечения тетраэдра и параллелепипеда?

О: аксиома стереометрии об общей точке двух плоскостей;

свойстве линий пересечения параллельных плоскостей с секущей плоскостью.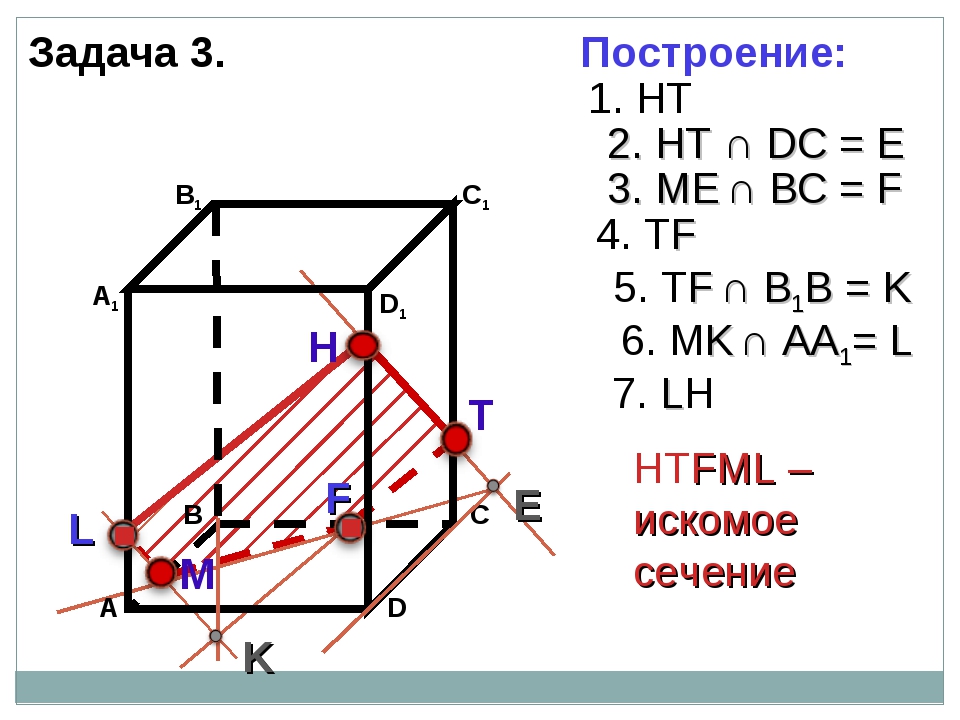

— какие многоугольники могут получиться в сечении тетраэдра и параллелепипеда?

О: треугольники, четырёхугольники. А у параллелепипеда ещё пятиугольник и шестиугольник.

4. Информация о домашнем задании, инструктаж.

— На следующем уроке продолжим работать над этой темой.

— Д.З. п.14, № 69, 82 (1)

7. Рефлексия.

Анализ анкеты карты рефлексии. Подведение итогов урока.

РАЗДАТОЧНЫЙ МАТЕРИАЛ

Задачи на построение сечений

Материал урока.

Прежде чем мы приступим к решению задач на построение сечений, давайте вспомним, какие фигуры называются тетраэдром и параллелепипедом.

Повторим основные аксиомы стереометрии.

Первая аксиома звучит так: Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Вторая аксиома звучит так: Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.

Третья аксиома звучит так: Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.

Очень часто при решении задач необходимо строить сечение тех или иных пространственных фигур. На уроке мы рассмотрим задачи на построение сечений тетраэдра и параллелепипеда.

Прежде всего, давайте уточним, что мы будем понимать под сечением тетраэдра или параллелепипеда.

Секущей плоскостью тетраэдра или параллелепипеда мы назовем любую плоскость, по обе стороны от которой имеются точки данного тетраэдра или параллелепипеда. Секущая плоскость пересекает грани тетраэдра или параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра или параллелепипеда.

Мы знаем, что у тетраэдра четыре грани, значит, его сечениями могут быть треугольники или четырехугольники. У параллелепипеда 6 граней, поэтому его сечениями могут быть треугольники, четырехугольники, пятиугольники и шестиугольники.

При построении сечений параллелепипеда мы не забываем, что если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны.

То есть, если секущая плоскость пересекает две противоположные грани по каким-то отрезкам, то эти отрезки будут параллельны.

 

На рисунках нетрудно убедиться в этом. Секущая плоскость пересекает левую и правую грани по отрезкам AB и CD, а переднюю и заднюю грани по отрезкам АЕ и BC. Поэтому можно записать, что АB параллельно CD и АЕ параллельно BC.

На втором рисунке АB параллельно ЕD, AF параллельно CD, BC параллельно EF.

Для построения сечения тетраэдра или параллелепипеда достаточно построить точки пересечения секущей плоскости с рёбрами пространственного тела, а после этого соединить каждые две построенные точки, которые лежат в одной грани.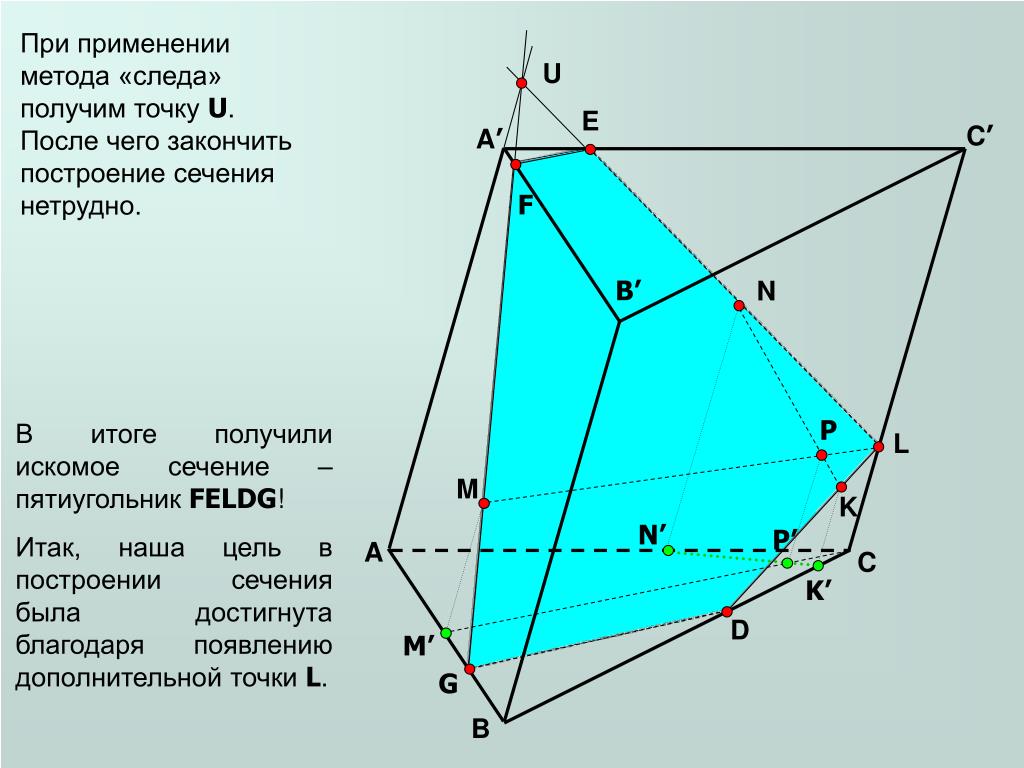

Перейдем к решению задач.

Сначала рассмотрим задачу, в которой секущей плоскостью тетраэдра будет треугольник.

Задача. Построить сечение тетраэдра плоскостью, которая проходит через точки , , .

Построение.

 

Поскольку каждые две точки лежат в одной грани, значит, секущая плоскость пересекает грани по прямым МК, НК, МН. Значит, треугольник МНК – искомое сечение.

Рассмотрим аналогичную задачу для параллелепипеда.

Задача. Построить сечение параллелепипеда плоскостью, которая проходит через точки , , .

Построение.

 

Решим еще несколько задач.

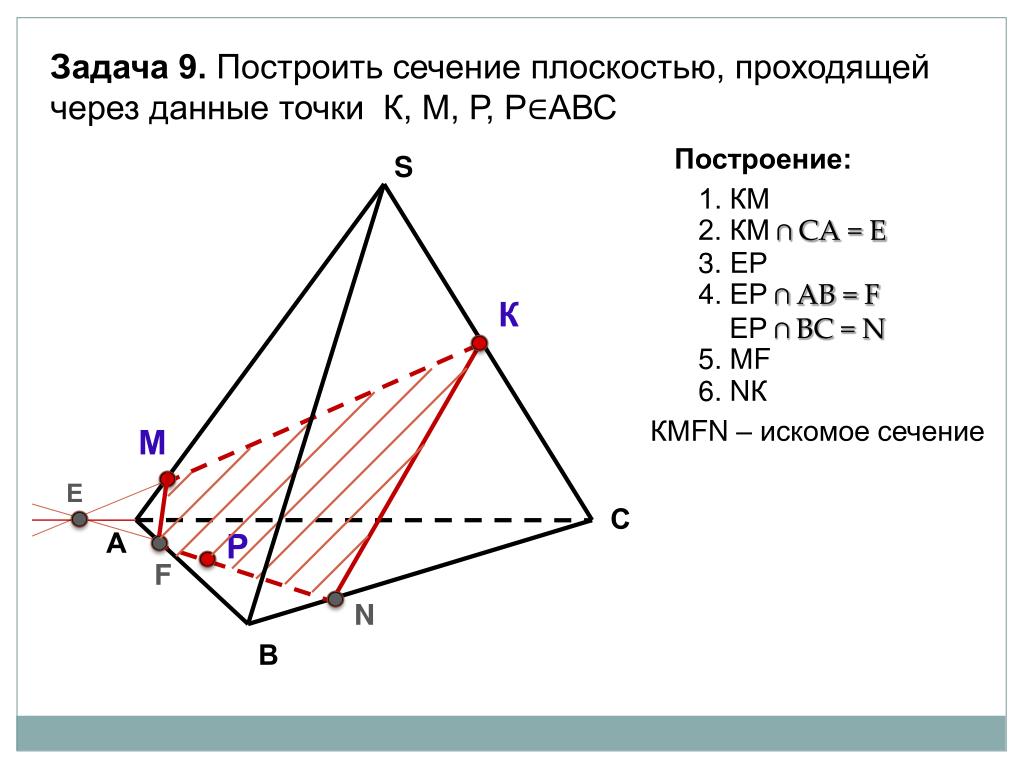
Задача. Построить сечение тетраэдра плоскостью, которая проходит через точки , , , лежащие соответственно на рёбрах , , .

Построение.

Теперь давайте вернемся на несколько шагов назад и построим такую дополнительную точку, которая будет лежать в грани DBC и DAB.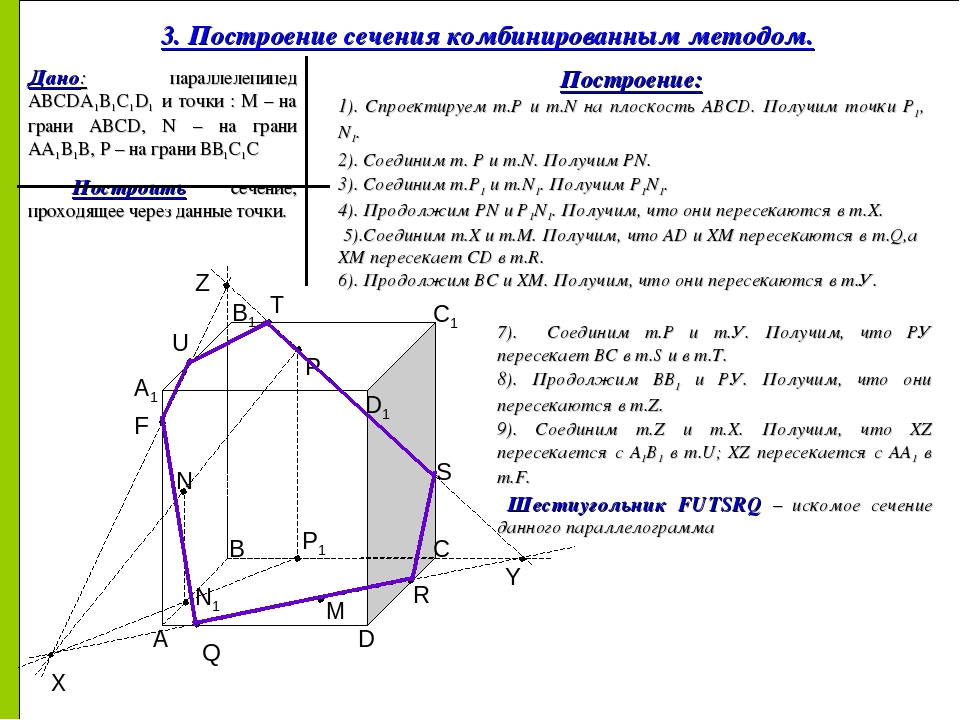

Для этого продлим до пересечения прямые EF и DB. Эта точка лежит в грани DBC, значит, ее можно соединить с точкой К. Обозначим за точку M точку пересечения этой прямой с ребром BC. Тогда получим, что секущая плоскость пересекает грань DBC по прямой NK. Точка N лежит в плоскости ABC, значит, ее можно соединить с точкой F. Значит, секущая плоскость пересекает грань ABC по прямой FN.

То есть получили, что еще одним вариантом сечения тетраэдра плоскостью, которая проходит через тоски F, Е, К будет четырехугольник FEKN.

Задача. Построить сечение прямого параллелепипеда плоскостью, которая проходит через точки , , .

Построение.

Решим еще одну задачу.

Задача. Построить сечения куба плоскостью, проходящей через точки , , .

Построение.

Метод построения сечения, при котором находят след секущей плоскости на каждой грани, называется методом следов.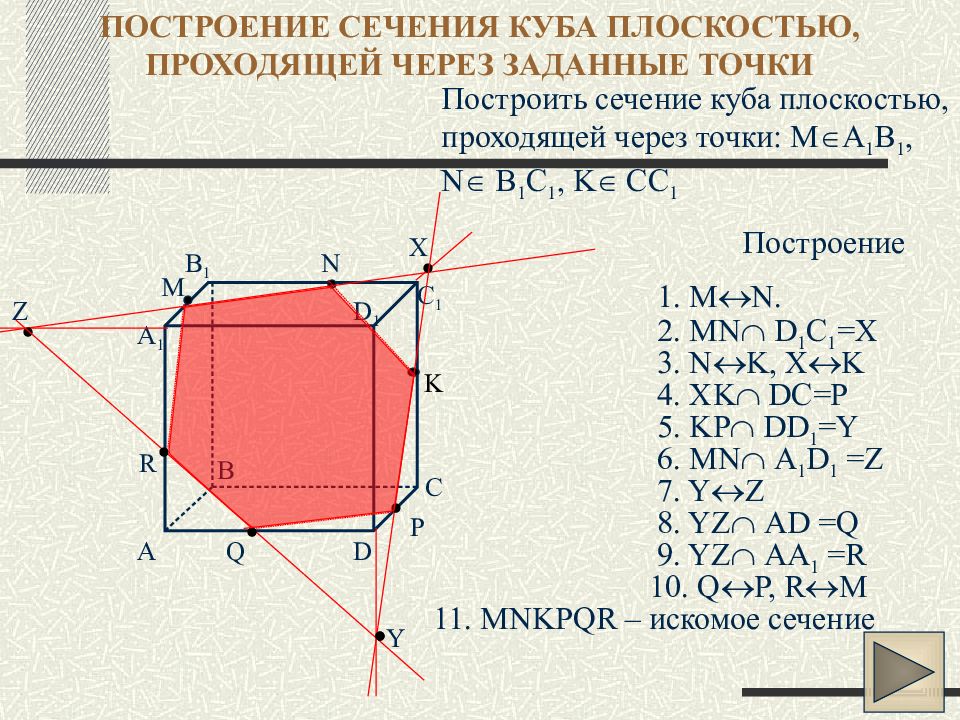

Решим еще одну задачу.

Задача. Построить сечение прямого параллелепипеда плоскостью, которая проходит через точки , , .

Построение.

Подведем итоги урока. Сегодня на уроке мы определили, что секущей плоскостью тетраэдра или параллелепипеда называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра или параллелепипеда.

Показали, что в сечении тетраэдра может получиться треугольник или четырехугольник.

В сечении параллелепипеда может получиться треугольник, четырехугольник, пятиугольник или шестиугольник.

Урок геометрии по учебнику Геометрия 10 под редакцией Л.С. Атанасяна. Тема Задачи на построение сечений. 10-й класс

Урок геометрии по учебнику «Геометрия 10» под редакцией Л.С. Атанасяна.

Тема: «Задачи на построение сечений».

10-й класс

Цель урока:

• Знакомство с понятием сечения многогранника.
• Определение видов многоугольников, являющихся сечениями тетраэдра и параллелепипеда.
• Классификация задач на построение сечений по способу задания секущей плоскости.
• Рассмотрение примеров решения задач на построение сечений тетраэдра и параллелепипеда.

Ход урока

Изложение нового материала.

Назовем секущей плоскостью многогранника плоскость, по обе стороны от которой имеются точки данного многогранника. Секущая плоскость пересекает грани многогранника по отрезкам. Многоугольник, сторонами которого являются эти отрезки называется сечением многогранника. Поскольку тетраэдр имеет четыре грани, его сечением могут быть только треугольники и четырехугольники (учитель показывает Слайд 1 из презентации 1). Параллелепипед имеет шесть граней, поэтому его сечениями могут быть только треугольники, четырехугольники, пятиугольники и шестиугольники (Слайд 2 из презентации 1).

Типы задач на построение сечений.

(Слайд 3 из презентации 1)

В задачах на построение сечений секущая плоскость может быть задана:

• Двумя пересекающимися прямыми.
• Двумя параллельными прямыми.
• Прямой и точкой, не лежащей на этой прямой.
• Тремя точками, не лежащими на одной прямой.

Поскольку прямая задается двумя точками, то все задачи на построение сечений можно свести к построению сечения плоскостью, проходящей через три точки, не лежащие на одной прямой.

Эти точки могут быть расположены: А) в вершинах; Б) на ребрах; В) на гранях.

В соответствии с вышесказанным можно сформулировать следующие типы задач, в зависимости от того где расположены три точки, задающие секущую плоскость:

1) ААА; 2)ААБ; 3)ААВ; 4)АББ; 5)АБВ; 6)АВВ; 7)БББ; 8)ББВ; 9)БВВ; 10)ВВВ.

Для построения сечения достаточно построить точки пересечения секущей плоскости с ребрами многогранника, после чего останется провести отрезки соединяющие каждые две построенные точки, лежащие в одной и той же грани.

Рассмотрим решение задачи 1 из текста учебника. (Презентация 2, ученики выполняют построение в тетрадях.)

На ребрах AB, BD и CD тетраэдра ABCD отмечены точки M, N и P. Построить сечение тетраэдра плоскостью MNP.

Решение.

Построим сначала прямую, по которой плоскость MNP пересекается с плоскостью грани АВС. Точка М является общей точкой этих плоскостей. Для построения еще одной общей точки продолжим отрезки NP и BC до их пересечения в точке Е, которая и будет второй общей точкой плоскостей MNP и ABC. Следовательно, эти плоскости пересекаются по прямой МЕ. Прямая МЕ пересекает ребро АС в некоторой точке Q. Четырехугольник MNPQ искомое сечение.

Закрепление нового материала.

Решение задачи Т-ББВ (один из учеников решает на доске, остальные решают в тетради).

Постройте сечение тетраэдра ABCD плоскостью, проходящей через точки Е и F, лежащие на ребрах DC и BD соответственно, и точку G, лежащую на грани ABC.

Решение задачи П-ББВ (один из учеников решает на доске, остальные решают в тетради).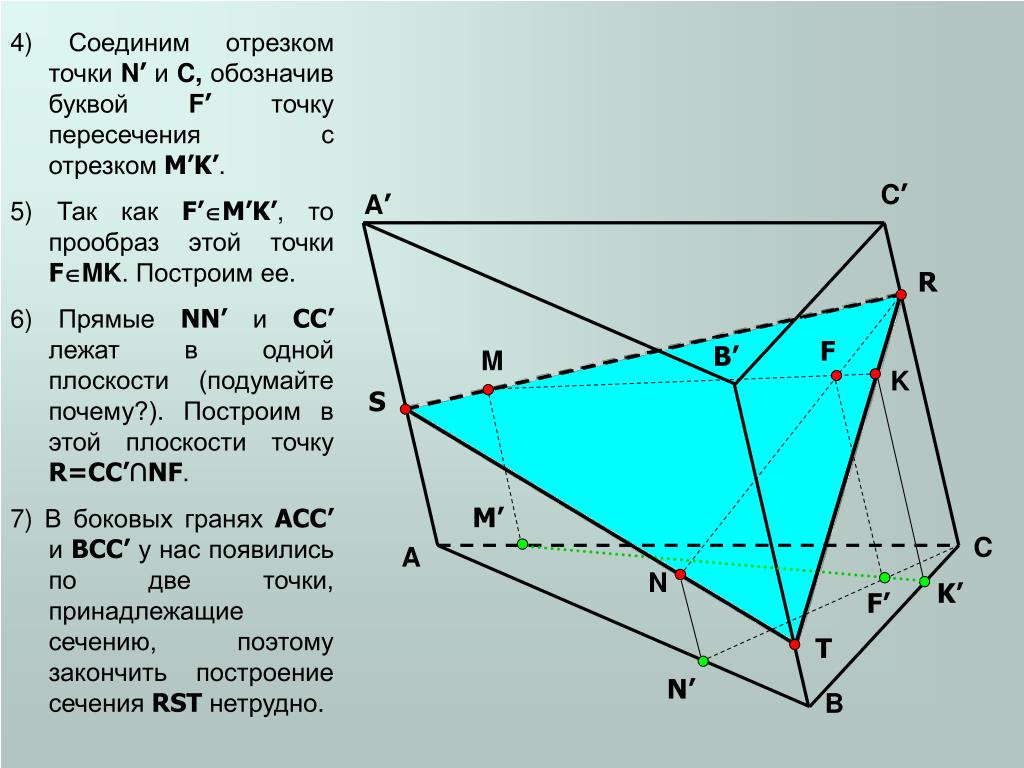

Постройте сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки Е и F, лежащие на ребрах АВ и DD₁ соответственно и точку G, лежащую на грани BCC₁.

Домашнее задание.

Задачи Т-ААБ, Т-АБВ, П-ААА, П-БББ

(Учитель раздает распечатки с текстом задач из Приложения 1.)

 

Скачано с www.znanio.ru

Урок математики «Построение сечений многогранника»; 10-11 класс — К уроку — Математика, алгебра, геометрия

Матлашевская Лилия Петровна

Учитель математики

МАОУ «Гимназия № 2» г.Перми

Построение сечений многогранника

Цели и задачи урока:

• Закрепление навыков построения сечений на примере пирамиды.

• Обобщение учебного материала по теме через формирование умения применять приёмы построения сечений в новой ситуации (сечение параллелепипеда).

• Формирование навыков исследовательской работы; в том числе умения синтезировать и анализировать, обобщать, выделять главное.

• Формирование специальных умений и навыков, в том числе навыков использования математического языка.

• Развитие технического, логического, образно-пространственного мышления учащихся.

• Воспитание культуры графического труда.

Материалы и оборудование:

Для учащихся:

• Рабочая тетрадь.

• Ноутбук с презентационными и иными материалами к уроку.

• Ручка, карандаш, резинка.

• Раздаточный материал.

Модуль №5 материалов заочной естественно — научной школы при КрасГУ. Приложение1

Карточки для индивидуальной работы. Приложение2

Для учителя:

• Слайдовая презентация PowerPoint «Сечение многогранников плоскостью». Приложение3. Flash-презентация. Приложение6

• Проектор

• Компьютер

• CD диск. Виртуальная школа Кирилла и Мефодия, уроки геометрии 10 класс, 2005г.

Педагогические средства для решения поставленных задач:

1. Тип урока: закрепление знаний.

2. Материал, изучаемый на уроке, представлен, развернуто, введена научная терминология.

3. Для повышения эффективности урока и подачи нового материала в более доступной динамичной форме, использованы слайдовая презентация (разработанные для урока учителем).

4. Для изложения нового материала применены приемы фронтальной работы со слайдом, задана самостоятельная проблемная работа по построению сечений многогранников, стимулирующая саморазвитие учащихся и мотивирующая учащихся на изучение темы «Сечения многогранников» (задачи ЕГЭ).

Ход урока:

1. Организационный момент.

2. Проверка д/з (фронтально, ответы на доске)

3. Актуализация прежних знаний (повторение аксиом планиметрии, стереометрии и теорем о существовании плоскости), методы построения сечений.

(слайды №1,2,3)

Перед учащимися ставится задача, в ходе решения которых повторяются основные аксиомы и теоремы. Осуществляется пошаговая проверка построения сечения.

На данном этапе отрабатывается умение аргументировать свое решение.

4. Закрепление навыка построения сечений и запись алгоритма (сл.№4)

Два ученика выполняют данную задачу у доски с последующей проверкой с помощью презентации. Этап позволяет проконтролировать сформированность навыков грамотной математической записи.

5. Обобщение полученных знаний при построении сечений куба (слайд №7- работа на ноутбуках).

Ученики выполняют задание самостоятельно в тетради с последующей самопроверкой (материалы к уроку). В случае затруднения при работе ученики могут использовать подсказку в презентации «Для самостоятельного изучения» Приложение4, а также модуль №5 материалов заочной естественно — научной школы при КрасГУ или материалы CD — Виртуальная школа Кирилла и Мефодия, уроки геометрии 10 класс, 2005г.

6. Применение полученных знаний при решении задачи из сборника ЕГЭ (Пример 12, 2005 год – учебно-тренировочные задания для подготовки к ЕГЭ). На уроке рассматривается только построение сечений. Рассмотрим задачу:

Дан куб ABCDA₁B₁C₁D₁. Через точки С, D₁ и середину ребра АА₁ проведена плоскость. Найдите площадь сечения, если ребро куба равно 4.

7. Обсуждение и проверка полученного результата.( слайд №8)

На данном этапе усиливается мотивация изучения данной темы, как необходимость для успешной сдачи ЕГЭ.

8. Подведение итогов урока и домашнее задание с комментариями к нему. (слайды №№24,25,26). Приложение5

Домашняя работа

• на «3» — построить сечение на бумажном носителе без описания;

• на «4» — построить сечение с пошаговым описанием построения (см.слайд 4)

• на «5» – построить сечение с полным обоснованием (пошаговым описанием построения и ссылками на аксиомы и теоремы).

Геометрия | 10 класс Математика

Резюме курса

---

В Fishtank Math Geometry учащиеся углубляют свое понимание геометрических отношений и учатся формулировать формальные математические аргументы в отношении геометрических ситуаций.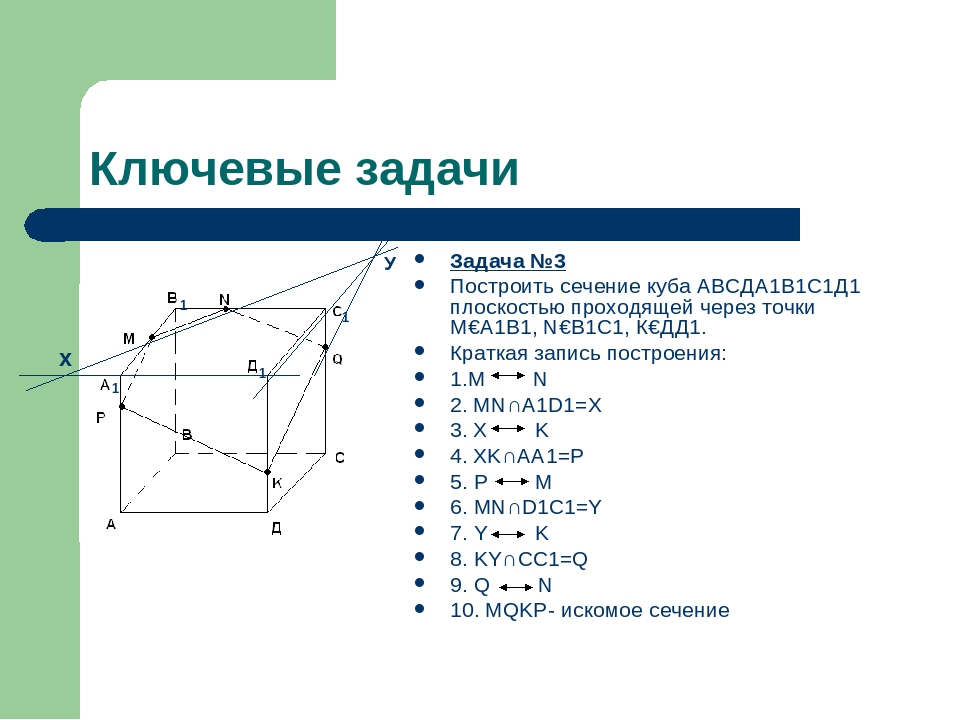 Этот курс, который следует стандартам Common Core для геометрии и основам учебной программы штата Массачусетс, использует подход, несколько отличающийся от более традиционных занятий по геометрии, в котором особое внимание уделяется преобразованию. Преобразования используются, чтобы помочь учащимся понять и доказать конгруэнтность и другие геометрические отношения.Также большое внимание уделяется доказательствам: студенты учатся доказывать концепции и идеи, которые они изучали годами. Время занятий сосредоточено на шести основных темах: 1) установление критериев конгруэнтности треугольников на основе жестких движений; (2) установление критериев подобия треугольников на основе расширений и соображений пропорциональности; (3) неформальное объяснение формул окружности, площади и объема; (4) применение теоремы Пифагора к координатному плану; (5) доказательство основных геометрических теорем; и (6) расширение студенческой работы с вероятностью.(См. Структуры учебной программы штата Массачусетс. ) Поскольку Fishtank Math стремится предложить учащимся путь к изучению исчисления на старшем курсе, этот курс по геометрии также охватывает продвинутые стандарты, которые иногда рассматриваются в курсах продвинутой математики и предварительного исчисления.

Основы успеха:

Геометрия в старших классах основывается на обучении геометрии, которое проводилось в начальной и средней школе, но с ключевым отличием в том, что учащиеся должны доказывать и объяснять понятия, которые они изучили в предыдущие годы.В начальной школе учащиеся узнали об атрибутах фигур, сравнили и классифицировали эти атрибуты, а также научились составлять и разбирать фигуры. В средней школе учащиеся развили концептуальное понимание взаимосвязей углов на диаграммах с параллельными линиями и взаимосвязей углов внутри и снаружи треугольников. Они также научились описывать геометрические элементы, измерять длину окружности и площадь кругов, а также делать наблюдения и делать предположения о геометрических формах, используя здравые рассуждения и доказательства. Учащиеся узнали, как «построить» треугольник, используя разные длины сторон, и узнали, что свойства треугольника основаны на соотношении между длинами сторон и величинами внутренних углов. Эти фундаментальные знания будут иметь важное значение для успеха студентов в этом курсе, поскольку они строят цепочки рассуждений для объяснения, моделирования и доказательства геометрических отношений и ситуаций.

Читать далее F9F71AAC-D645-4DB6-8B51-DCD6337664FD Читать меньше F9F71AAC-D645-4DB6-8B51-DCD6337664FD

Математические стандарты | Common Core State Standards Initiative

В течение более десяти лет исследования математического образования в странах с высокими показателями пришли к выводу, что математическое образование в Соединенных Штатах должно стать значительно более целенаправленным и последовательным, чтобы улучшить успеваемость по математике в этой стране.Чтобы выполнить это обещание, математические стандарты призваны решить проблему учебной программы, которая «шириной в милю и глубиной в дюйм».

Эти новые стандарты основаны на лучших математических стандартах высокого качества, принятых в штатах по всей стране. Они также опираются на наиболее важные международные модели математической практики, а также на исследования и материалы из многочисленных источников, включая государственные департаменты образования, ученых, разработчиков оценивания, профессиональные организации, педагогов, родителей и учащихся, а также представителей общественности.

Математические стандарты обеспечивают ясность и конкретность, а не общие утверждения. Они стараются следовать замыслу, предложенному Уильямом Шмидтом и Ричардом Хуангом (2002), не только подчеркивая концептуальное понимание ключевых идей, но и постоянно возвращаясь к организационным принципам, таким как позиционное значение и законы арифметики, для структурирования этих идей.

Кроме того, «последовательность тем и представлений», изложенная в своде математических стандартов, должна соответствовать тому, что уже известно о том, как учащиеся учатся.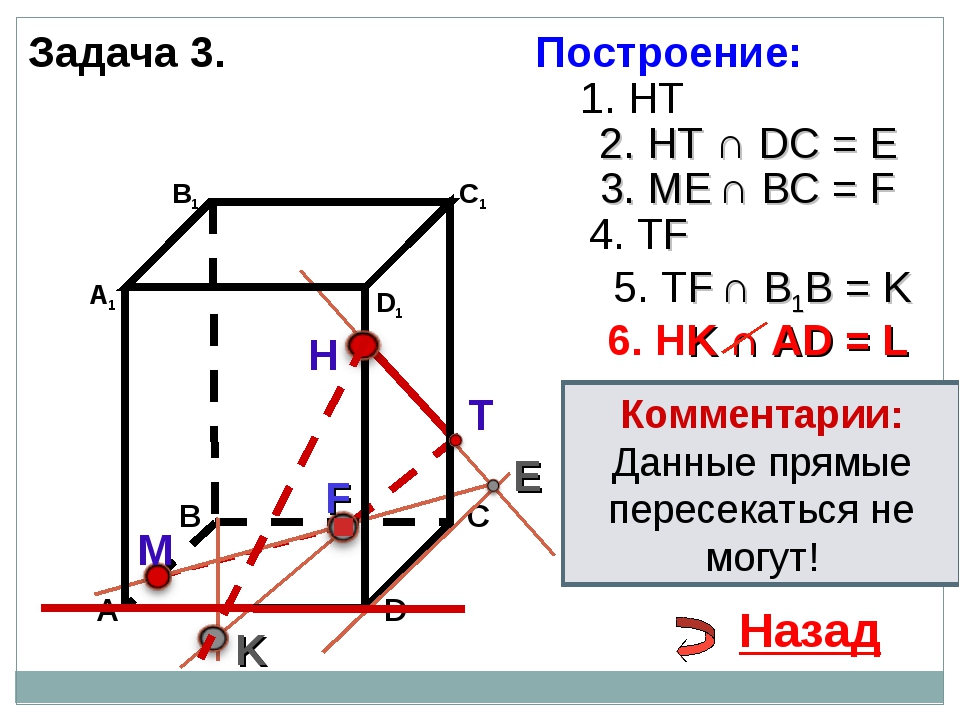 Как отмечает Конфри (2007), разработка «последовательности препятствий и задач для учащихся… без понимания смысла, вытекающего из тщательного изучения обучения, было бы неудачным и неразумным». Таким образом, разработка стандартов началась с исследований, основанных на исследованиях, в которых подробно описывалось то, что известно сегодня о том, как математические знания, навыки и понимание учащихся развиваются с течением времени. Знания и навыки, которые учащиеся должны подготовить к математике в колледже, карьере и жизни, пронизаны стандартами по математике.Они не включают отдельные якорные стандарты, подобные тем, которые используются в стандартах ELA/грамотности.

Common Core концентрируется на четком наборе математических навыков и понятий. Учащиеся будут более организованно изучать концепции как в течение учебного года, так и в разных классах. Стандарты побуждают учащихся решать реальные проблемы.

Понимание математики

Эти стандарты определяют, что учащиеся должны понимать и уметь делать при изучении математики. Но просить ученика понять что-то означает также просить учителя оценить, понял ли это ученик. Но как выглядит математическое понимание? Один из способов сделать это для учителей — попросить учащегося обосновать, в соответствии с его математической зрелостью, почему конкретное математическое утверждение верно или откуда взялось математическое правило. Математическое понимание и процедурные навыки одинаково важны, и оба они поддаются оценке с помощью математических задач достаточной сложности.

10 лучших способов улучшить свои оценки по математике

Многие учащиеся и родители просят дать советы и методы для лучшего изучения математики. Вот мой список топ-10, который применим к любому уровню математики.

1) Если вы чего-то не понимаете, сосредоточьтесь на освоении этой темы, прежде чем переходить к следующей теме.  Звучит просто, но это абсолютно необходимо. Допустим, студент изучает алгебру, например. Кроме того, скажем, ему или ей трудно понять, как складывать и вычитать отрицательные и положительные числа.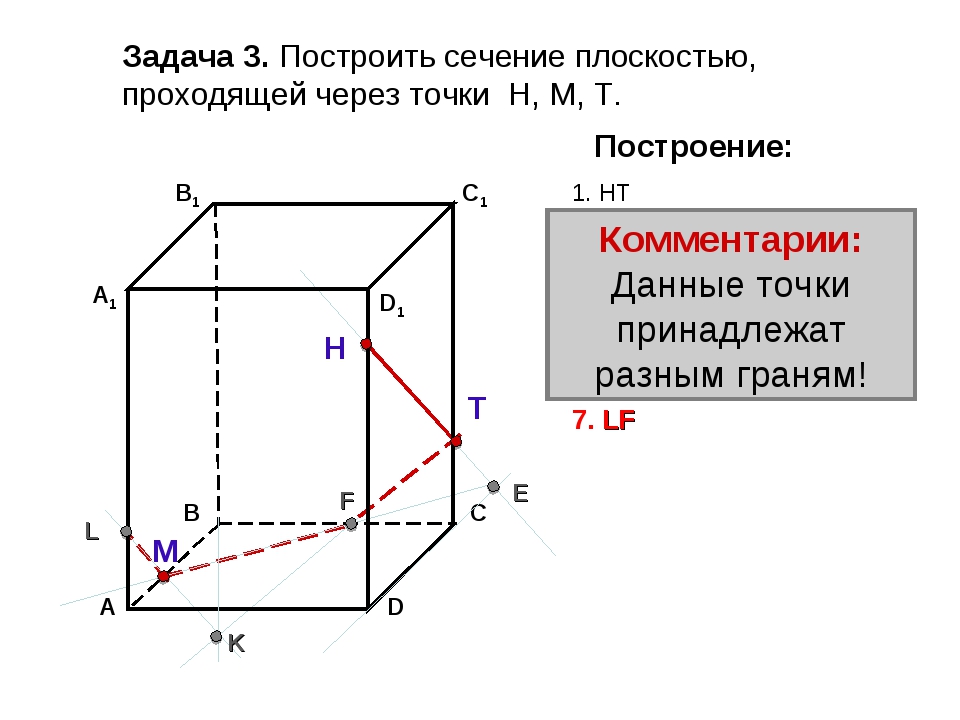 Все мы боремся с этим в начале, так как это неприятный момент для большинства студентов. Некоторые ученики в такой ситуации, разочарованные тем, что они «не могут» выучить эту тему, переходят к следующему уроку в надежде, что смогут понять этот.

Это прямой путь к катастрофе.

Математика очень похожа на обучение чтению. Если вы не знаете, как звучит ваша буква, то у вас нет надежды произнести слова вслух, конечно же, вы не сможете прочитать книгу.Все математические курсы преподаются в определенной последовательности, потому что каждая тема основывается на предыдущей теме. Если у вас возникли проблемы с темой, продолжайте работать с ней, пока не поймете ее и не сможете успешно решать проблемы. Просмотрите раздел DVD еще раз, посетите мастер-класс, прочитайте книгу и примеры во второй раз или даже возьмите совершенно другую книгу, чтобы объяснить ее по-другому … но что бы вы ни переворачивали страницу и не занимались следующей темой. Если вы это сделаете, вы еще больше разочаруетесь и, по всей вероятности, начнете терять надежду.

2) Работайте с примерами задач и проверяйте свои ответы, чтобы практиковаться на каждом уроке.  Суть всей серии DVD состоит в том, чтобы «учиться на примерах», и это самый простой способ выучить математику. После просмотра раздела на DVD и прочтения раздела в учебнике приступайте к рабочим примерам с конца главы. Обязательно решайте задачи, ответы на которые есть в конце книги, и проверяйте каждую. Всегда начинайте с самой простой задачи в книге, даже если вам кажется, что решить ее будет слишком «легко».Очень очень важно укрепить вашу уверенность. Вот почему уроки DVD начинаются с более простых задач, которые никто не поймет. Постепенно решайте все более и более сложные задачи из вашей книги и проверяйте свой ответ для каждой из них. После решения дюжины или более задач из раздела (лучше двух десятков) вы готовы перейти к следующему разделу. Многие ученики хотят пропахать урок, чтобы добраться до следующего. Вы не можете просто прочитать раздел в учебнике по математике и стать экспертом в этом разделе. Вы должны работать проблемы. Если вы не можете работать с проблемами, значит, вы не готовы двигаться дальше. Хорошей новостью является то, что рабочие задачи укрепят вашу уверенность, а уверенность — это 100% главное в математике.

3) Приступая к решению математической задачи, не прокладывайте в голове путь от задачи к ответу, прежде чем что-либо записывать.  Я вижу это почти каждый день. Очень часто, когда кто-то смотрит на математическую задачу, он пытается «решить ее» в уме, прежде чем что-то записать.Возьмем, к примеру, алгебру. Когда начинающий ученик смотрит на уравнение, у него возникает соблазн решить уравнение в уме и ничего не записывать. Студенты склонны делать это чаще всего с помощью текстовых задач. Поскольку словесная задача записывается в виде предложения, принято думать, что вы можете «думать свой путь к ответу». Я скажу вам, что я никогда, никогда не решу какую-либо математическую задачу, не записав ее. Всегда.

Что вам нужно сделать, так это начать с того, что сначала запишите проблему. Затем вы начинаете решать ее шаг за шагом. Записывайте даже самые простые вещи. Вам нужно убедиться, что каждый шаг, который вы записываете, является совершенно законным. Другими словами, если вы, например, решаете уравнение и вычитаете «10» из обеих частей… запишите это. Затем на СЛЕДУЮЩЕМ шаге сделайте это вычитание. Затем, если вам нужно разделить обе части на «2», запишите ЭТО… затем на СЛЕДУЮЩЕМ шаге фактически выполните деление. Это дает вам бумажный след для проверки вашей работы, а также позволяет разбить проблему на небольшие куски.Если вы можете быть уверены, что каждый маленький шаг является законным, тогда вы будете в хорошей форме. Если вы попытаетесь сделать слишком много дел одновременно, что является обычным делом, вы, вероятно, попытаетесь сделать что-то незаконное и попадете в беду.

4) Когда вы учитесь и делаете домашнее задание, постарайтесь найти для этого тихое место.  Я был самым злостным преступником в этом, когда учился в школе. Раньше я слушал музыку все время, пытаясь сделать домашнее задание. Я также слушал телевизор как «фоновый шум» во время учебы.Со временем я понял, что если бы у меня было тихое место без фонового шума, я мог бы сосредоточиться намного лучше. Что я обнаружил, так это то, что при чтении, например… мне пришлось бы прочитать что-то, возможно, 3 или 4 раза, если бы я слушал что-то еще, но только один раз, если бы я немного помолчал. Люди любят слушать музыку во время учебы, но я убежден, что это гораздо эффективнее, если вы этого не делаете. Постарайтесь найти тихое место в своем доме или в библиотеке, чтобы закончить школьные дела, и вы сделаете свою работу намного быстрее, потому что сможете сосредоточиться и усвоить больше.

5) Если кто-то попросит вас о помощи, постарайтесь как можно лучше объяснить ему тему.  Этот пункт может показаться немного странным для этого списка… но есть одна универсальная истина. Те, кто может учить других, правильно понимают материал. Много раз при обучении в группах будет один член группы, который отстает и не «понимает». Попытайтесь помочь этому человеку, даже если ваша собственная работа займет больше времени. Вы не только почувствуете, что помогаете кому-то другому добиться успеха, но процесс перефразирования информации для кого-то еще и разбиения информации на небольшие куски улучшит ваше собственное понимание.Это поможет вам понять на фундаментальном уровне, какие камни преткновения есть в этой теме, что поможет вам, когда вы будете продвигаться в изучении математики.

6) Никогда, никогда не решайте математические задачи ручкой.  Это довольно просто. Вы сделаете ошибку; это только вопрос времени. Когда вы это сделаете, вы захотите полностью стереть свою ошибку и написать поверх нее. Вы никогда, никогда не захотите что-то выцарапывать и писать рядом с выцарапанным. Это приведет к тому, что статью будет трудно читать, а вычеркивания фактически увеличат ваше беспокойство по поводу решения этих проблем.Вы хотите чистую и аккуратную бумагу с чистым, хорошо продуманным решением.

7) Попробуйте использовать механический карандаш с отдельным ластиком, если можете.  Механические карандаши имеют более четкие линии, а отдельный ластик позволяет стирать более аккуратно. Нет ничего хуже, чем совершить ошибку и попытаться что-то стереть, а затем просто размазать это по всей странице. Дешевые ластики сделают это и усложнят вам жизнь. Купите хороший механический карандаш и хороший отдельный ластик.

8) Делайте свои решения аккуратными и построчными.  Всегда работайте над задачами вертикально, с одним шагом в каждой строке. Никогда не работайте горизонтально. Это может занять больше бумаги, но вам будет намного легче следовать своим шагам. Что еще более важно, учитель сможет намного лучше следить за вашей работой, что позволит ему/ей дать вам частичный балл. Если шагов всего 2, а их должно быть 10, баллы за мыслительный процесс вы не получите. Шаги, которые вы записываете, сообщают учителю, о чем вы думаете и как вы решаете проблему.

9) Не работайте над проблемами очень поздно ночью.  Я знаю, что все студенты колледжа будут смеяться над этим, но это правда.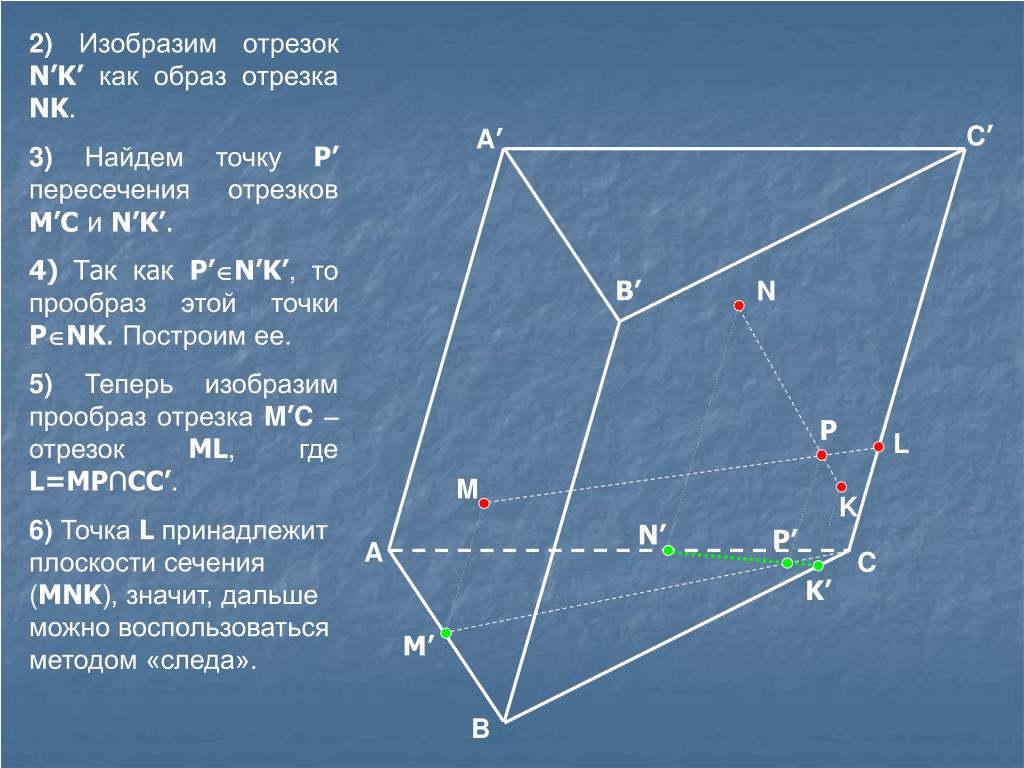 Я много, много раз пытался заниматься вычислениями или физикой поздно ночью, после 12 или часа ночи, но вы просто оказываете себе медвежью услугу. Я часами смотрел на проблемы, потому что я просто не мог уснуть, пока не знал, как их решить… затем я, наконец, заснул от крайней усталости… но когда я проснулся, мне показалось так просто, как продолжить проблема.Кроме того, я работал над задачами по ночам и получал неправильный ответ, и я знал, что должен допустить глупую ошибку в решении. Обычно я пытался найти ее, но часто, когда вы устали, вы просто не можете найти глупую ошибку. На следующее утро примерно через 5 минут я мог обнаружить простую ошибку со знаком или даже простую ошибку умножения, которая вызвала проблему.

10) Если проблема поддается этому, нарисуйте картину проблемы.  Это наиболее применимо для студентов, изучающих тригонометрию, исчисление и физику, но также применимо к любой текстовой задаче по базовой математике или алгебре.Пожалуйста, сделайте себе одолжение и нарисуйте изображение того, что описывает проблема, даже если ваше изображение простое. Мы визуальные существа… процесс рисования ситуации заставляет нас усвоить то, чего на самом деле требует проблема. Это помогает понять, как действовать дальше. Если вы изучаете физику, вы должны нарисовать картинку для каждой задачи, которую решаете. Если вы занимаетесь исчислением, обязательно нарисуйте картинки для всех связанных с ним задач. Если вы занимаетесь исчислением 2 или исчислением 3, обязательно нарисуйте все свои трехмерные задачи (трехмерные интегралы).Если вы изучаете основы математики, и Дженни дает Бобу 2 карандаша, а Боб отдает 1 карандаш, нарисуйте эту ситуацию. Это действительно поможет вам понять, как действовать дальше.

Помните, что в изучении математики нет панацеи. Это приходит с шаг за шагом и с практикой. Приведенные выше советы помогут вам в изучении математики и придадут вам уверенности. А уверенность — это 100% залог успеха в изучении математики любого уровня.

---

Джейсон Гибсон — основатель MathTutorDVD.ком. Вы можете ознакомиться с его обширным опытом и образованием здесь.

11 Математические приложения и онлайн-инструменты, рекомендуемые учителями для PreK-12

Для некоторых учителей математики цифровые инструменты, которые помогают учащимся визуализировать математические концепции, такие как Desmos, или веб-сайты, поощряющие математические дискуссии, такие как Fraction Talks, уже были частью их репертуара до пандемии. Но других учителей дистанционное обучение впервые подтолкнуло к изучению математических приложений и онлайн-ресурсов.

Мы поговорили с сотнями педагогов и просмотрели более 500 комментариев, чтобы узнать, какие математические инструменты они сочли полезными и бесполезными во время дистанционного обучения этой весной, а какие сократили для использования в новом учебном году.

Практика математических навыков

Ряд математических приложений и онлайн-инструментов могут помочь учащимся развить необходимое базовое понимание арифметических операций, которые им понадобятся в качестве основы для решения более сложных математических задач позже, рассказали нам учителя математики.

Чтобы помочь младшим школьникам практиковать такие навыки, как счет, сложение и вычитание, Эшли Блэквелдер, координатор Elementary STEAM в Южной Каролине, настоятельно рекомендует бесплатное приложение Moose Math для iPhone и iPad.В Moose Math учащиеся играют в математические игры, которые приносят им очки, чтобы помочь построить город. Блэквелдер говорит, что детям легко ориентироваться в этом формате, и он отлично подходит для кратковременной концентрации внимания.

Разработчик учебных программ и учебных пособий Кэсси Табризи порекомендовала веб-сайт Happy Numbers (дошкольный – 5-й класс) по подписке (14,50 долл. -порядок математических понятий. Чтобы использовать его, ученики превращаются в персонажей динозавров и решают математические задачи, чтобы вылупить яйца динозавров.Табризи сказала, что веб-сайт полезен, но рекомендует использовать его умеренно: ученикам может показаться утомительным, если они будут заниматься более 10 минут в день.

Учащиеся сражаются с монстрами в образе волшебника в Prodigy (1–8 классы), бесплатном игровом веб-сайте (также доступен в виде приложения для iPhone, iPad, iPod Touch и Android). Prodigy нравится детям, но не педагогам, потому что он больше основан на игре. Бритни Пейдж, учительница пятого класса из Сиэтла, говорит, что, хотя это больше похоже на игру, ей нравится, что она автоматически нацелена на математические понятия, с которыми учащиеся сталкивались во время предварительного оценивания, и отслеживает, какой прогресс они добились в целевых областях.Большинство учителей предлагают Prodigy в качестве опции для студентов, если они заканчивают задание раньше срока.

Предоставлено Prodigy

Успешно решив математическую задачу, питомец студента произносит заклинание в бою.

Zearn (1–5 классы), бесплатная веб-программа для самостоятельного изучения, согласованная с Eureka Math — бесплатным учебным планом по математике от PreK до 12, — начинается обычный урок с веселых разминочных упражнений, таких как сложение сколько яблок съедает мультяшная лиса, заинтересовать учащихся. Работая по программе, учащиеся решают арифметические задачи на время, смотрят обучающие видеоролики по новым понятиям и решают практические задачи.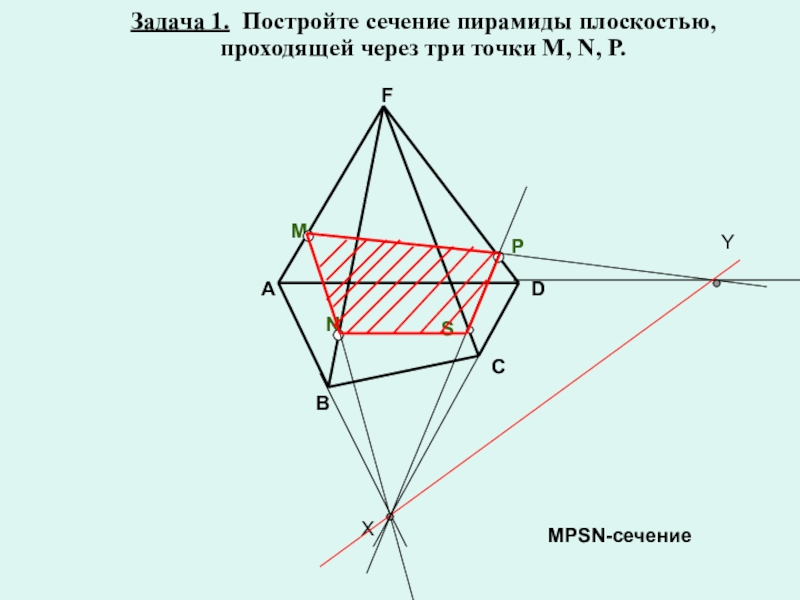 Шеннон Макграт, преподаватель из Вестерн-Спрингс, штат Иллинойс, говорит, что Zearn — это хорошая «концептуальная практика высокого уровня» и дает хорошие отзывы как учителям, так и ученикам, но иногда может слишком медленно прогрессировать для детей, которые быстро осваивают концепции.

Открытые математические задачи

Открытые математические задачи — задачи, которые обычно имеют более одного ответа — помогают учащимся развивать концептуальное понимание математики, а не зацикливаться на запоминании фактов, сказали преподаватели математики, с которыми мы разговаривали, которые постоянно упоминали три бесплатных веб-сайта, которые можно использовать для открытых математических задач. .

Open Middle (дошкольный – 12-й класс) оставляет части уравнения пустыми и просит учащихся заполнить их, чтобы оно стало верным. «Мне нравится Open Middle для удаленного обучения, особенно в сочетании с Google Jamboard, — говорит МакГрат. «Задачи вдохновляют на исследовательское мышление, игровые игры, творчество и настойчивость».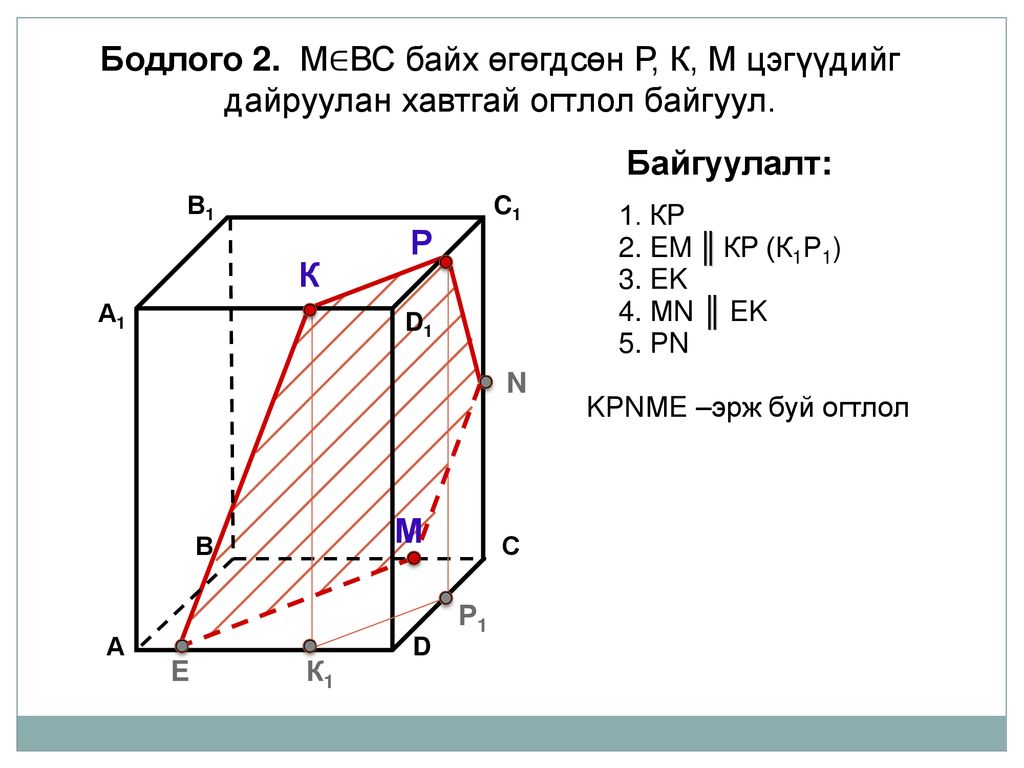

Предоставлено Мэри Бурасса/Который не принадлежит

Использование «Какому не принадлежит?» Студенты Мэри Бурасса, изучающие математику, приводят математический аргумент, почему каждый график лишний.

МакГрат также любит математику (дошкольный – 12-й класс) для создания сообщества. При использовании сайта учащиеся выбирают между двумя примерами из реальной жизни — например, коробкой конфет с пятью рядами и 14 столбцами или коробкой конфет с семью рядами и девятью столбцами — и должны привести математический аргумент, чтобы подтвердить свой выбор.

Какой из них не принадлежит? (pre-K–12 класс), аналогичный сайт, демонстрирует четыре фигуры, числа или графики и просит учеников описать, какая из них не принадлежит, используя математический словарь.«Это отлично подходит для начала синхронного обсуждения, поскольку считается задачей с низким уровнем пола и высоким потолком», — говорит Джозеф Манфре, специалист по математике из Департамента образования Гавайев.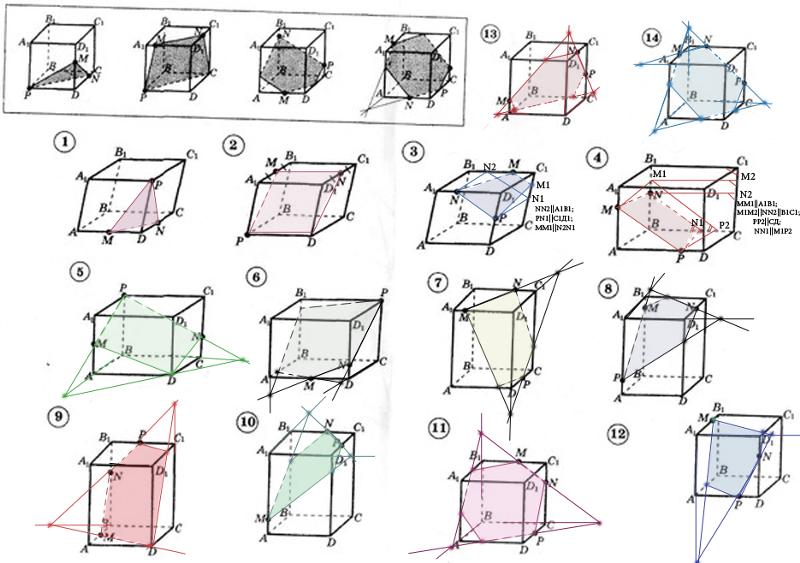 Учительница математики средней школы Мэри Бурасса просит своих учеников, изучающих математику, определить причины, по которым каждый график в наборе из четырех не принадлежит, указывая характеристики графика, такие как асимптоты и недифференцируемые точки, а позже ее ученики создают свои собственные наборы WODB.

Богатые математические задачи

Для сложных математических задач — задач, которые поддаются строгости, сотрудничеству и концептуальному мышлению — преподаватели математики отметили пару веб-сайтов.

Предоставлено Брайаном Пенфаундом/Fraction Talks

Учащиеся используют это изображение из Fraction Talks, чтобы попрактиковаться в сложении и умножении дробей. Нижняя угловая часть представляет собой ½ x ¼ = ⅛.

Fraction Talks (1–12 классы) — это веб-сайт, заполненный изображениями фигур — например, треугольников внутри треугольников, — которые поощряют математические дискуссии. Просто спрашивая студентов: «Что вы наблюдаете?» может подсказать им, что и сколько фигур они заметили, спрашивая: «Сколько фигур красных или заштрихованных?» побуждает учащихся изучать и понимать дроби. Как только учащиеся получат базовое представление о дробях, они смогут приступить к изучению более сложных понятий. Предлагая учащимся смотреть на части фигуры и на то, какие дроби они получают при объединении, Брайан Пенфаунд помог своим ученикам седьмого и восьмого классов визуализировать сложение и умножение дробей.

Visual Patterns (K – класс 12) показывает начало шаблона, например, несколько клеток в сетке, а затем просит учащихся составить уравнение, соответствующее шаблону. «Несмотря на то, что есть только один ответ, — говорит Манфре, — вы можете задавать более глубокие вопросы с помощью таких задач и вовлекать учащихся в математику в ее более естественной, наглядной форме.

Предоставлено Visual Patterns

Учащиеся должны определить уравнение для этого шаблона.

Инструменты моделирования

По словам учителей математики, симуляции, такие как манипулирование выражением и просмотр изменений на графике, являются отличными инструментами, помогающими учащимся визуализировать математические концепции.

Предоставлено Эшли Таплин

Эшли Таплин, специалист по математике средней школы, попросила своих учеников нарисовать, как они себя чувствовали в течение первой недели дистанционного обучения.

Апплеты — простой код с определенной целью — были упомянуты несколькими учителями как хороший ресурс. Студенты-статистики Эммы Чьяппетта используют апплеты с сайта RossmanChance.com, например, для манипулирования и определения шаблонов распределения выборки на графиках. Она создает базовое руководство о том, как использовать апплет, какие значения следует изменить, а затем задает вопросы, чтобы заставить учащихся критически осмыслить эти шаблоны. Кьяппетта также использует апплеты Массачусетского технологического института для своих студентов, изучающих линейную алгебру.

Desmos (6–12 классы), веб-сайт с интерактивными математическими заданиями и графическим калькулятором (также доступен в виде приложения для iPhone, iPad, iPod Touch и Android) — еще один бесплатный инструмент, пользующийся популярностью среди учителей, как мы слышали. Хотя социальное и эмоциональное обучение (SEL) и математика могут показаться несовместимыми, учителя интегрировали SEL в уроки математики с помощью Desmos. Например, в первую неделю дистанционного обучения Эшли Таплин, специалист по математике средней школы из Сан-Антонио, штат Техас, попросила своих учеников составить график своего самочувствия.Таплин говорит, что ей особенно нравится, что учителя могут выполнять свои собственные задания, например, о параболах и сортировке карточек, где учащиеся сопоставляют карточки с именем, соответствующим уравнением и правильным графическим представлением функции.

Вопросы и решения по математике для 10 класса

Консорциум Smarter Balanced Assessment Consortium (SBAC) — это стандартизированный тест, который включает множество новых вопросов, улучшенных с помощью технологий.

Некоторые из них: Множественный выбор — один правильный ответ, Множественный выбор — несколько правильных ответов, Сопоставление таблиц, Перетаскивание, Горячий текст, Заполнение таблицы, Графики, Уравнения / числа, Расширенный построенный ответ, Короткий ответ и многое другое.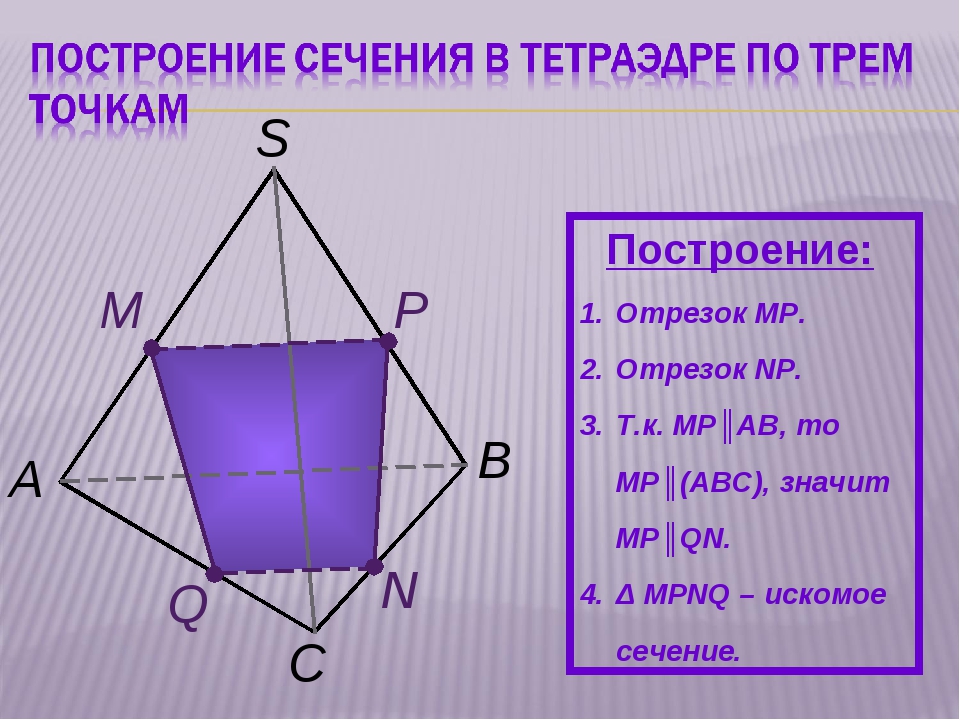

Эта страница содержит несколько примеров вопросов, а также ссылки на практические тесты по математике для 10 класса, которые дают вам представление о вопросах, которые ваши учащиеся, скорее всего, увидят на тесте. После каждого примерного вопроса следует объяснение ответа. Объяснение включает в себя важные аспекты задачи, которые вам, возможно, потребуется рассмотреть для навыков, процессов и информации, которые должны знать ваши студенты.

Домен: 10 класс >> Число и количество — система реальных чисел

Пример вопроса: Оценка 9 ^150/300

1. 18
2. 9
3. 3
4. 81

Объяснение ответа: 9 ^150/300 = 9 ^1/2 = квадратный корень из 9 = 3.В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Однако в этой задаче показатель степени можно уменьшить, поэтому сначала мы должны уменьшить его. Показатель степени 150/300 = 1/2. Таким образом, проблема становится 9 в степени 1/2. Знаменатель равен 2, поэтому мы извлекаем квадратный корень из 9, что равно 3. Числитель равен 1, поэтому мы возводим 3 в 1-ю степень, и ответ равен 3.

Стандарты: HSN.RN.A.1

Нажмите здесь, чтобы попрактиковаться: число и количество – вопросы системы действительных чисел по математике для 10 класса

Домен: 10 класс >> Количество и количество — количество

Пример вопроса: Перепишите x ^1/2 в подкоренной форме.

1. √х
2. √х ²
3. 1/√x
4. -√x

Объяснение ответа: В задаче с рациональным показателем степени числитель указывает степень, а знаменатель — корень. Поскольку проблема в том, x ^1/2 , знаменатель равен 2, что указывает на то, что мы должны извлечь квадратный корень, а числитель равен 1, поэтому мы должны возвести это в первую степень, иначе не будет показателя степени, поскольку показатель степени 1 редко встречается. использовал. Таким образом, ответ представляет собой квадратный корень из x, записанный как √x.

Стандарты: HSN.RN.A.1

Нажмите здесь, чтобы попрактиковаться: 10 класс Количество и количество – Количество Вопросы

Домен: 10 класс >> Число и количество – Комплексная система счисления

Пример вопроса: Полностью упростить i(7−i)

1. 7i-i ²
2. 1+7i
3. 6и
4. −1+7i

Объяснение ответа: i(7−i)=i*7−i*i=7i−i ² =7i−(−1)=7i+1=1+7i

Начните с использования метода распределения.Теперь упростим −i ² =1 по определению. Теперь переставьте и поставьте действительную часть первой, а мнимую последней, чтобы она выглядела как a+bi.

Стандарты: HSN.CN.A.2

Нажмите здесь, чтобы попрактиковаться: 10 класс Математика числа и количества – Вопросы по комплексной системе счисления

Домен: 10 класс >> Число и количество — векторные и матричные количества

Пример вопроса: Вектор в стандартной форме имеет компоненты . Что такое начальная точка?

1. (0, 0)
2. (3, 10)
3. (6, 20)
4. Недостаточно информации

Ответ Объяснение: Поскольку вектор находится в стандартном положении, мы знаем, что начальная точка (0, 0) или начало координат.

Стандарты: HSN.VM.A.2

Щелкните здесь, чтобы попрактиковаться: число и количество – векторные и матричные величины Вопросы для 10 класса по математике

Домен: 10 класс >> Алгебра – Видение структуры в выражениях

Пример вопроса: Какое выражение эквивалентно 9x ² – 16y ² ?

1. (3x – 4 года) (3x – 4 года)
2. (3x + 4г) (3x + 4г)
3. (3x + 4 года) (3x – 4 года)
4. (3x – 4 года) ²

Объяснение ответа: Студент должен распознать выражение как разность двух полных квадратов

Стандарты: HSA.SSE.A.2

Нажмите здесь, чтобы попрактиковаться: Алгебра – Структура выражений Вопросы для 10 класса по математике

Домен: 10 класс >> Алгебра — арифметика с многочленами и рациональными выражениями

Пример вопроса: Вычислить f(x)=−a ³ +6a−7 при a = – 1 и указать остаток.

1. -14
2. -12
3. 14
4. 12

Объяснение ответа: студент должен подставить – 1 в функцию следующим образом −(−1) ³ +6(−1)−7=−12 и найти значение, чтобы получить остаток

Стандарты: HSA.АПР.Б.2

Щелкните здесь, чтобы попрактиковаться: Алгебра — арифметика с многочленами и рациональными выражениями Вопросы для 10 класса по математике

Домен: 10 класс >> Алгебра – Создание уравнений

Пример вопроса: Соотношение персонала и гостей на гала-вечере было 3 к 5. Всего в бальном зале находилось 576 человек. Сколько гостей было на гала?

1. 276
2. 300
3. 360
4. 216

Объяснение ответа: Установите пропорцию гостей к общему количеству людей, 8/5 = x/576.Решите перекрестным умножением. 8x = 2880. Разделите обе части на 8. Таким образом, x = 360.

Стандарты: HSA.CED.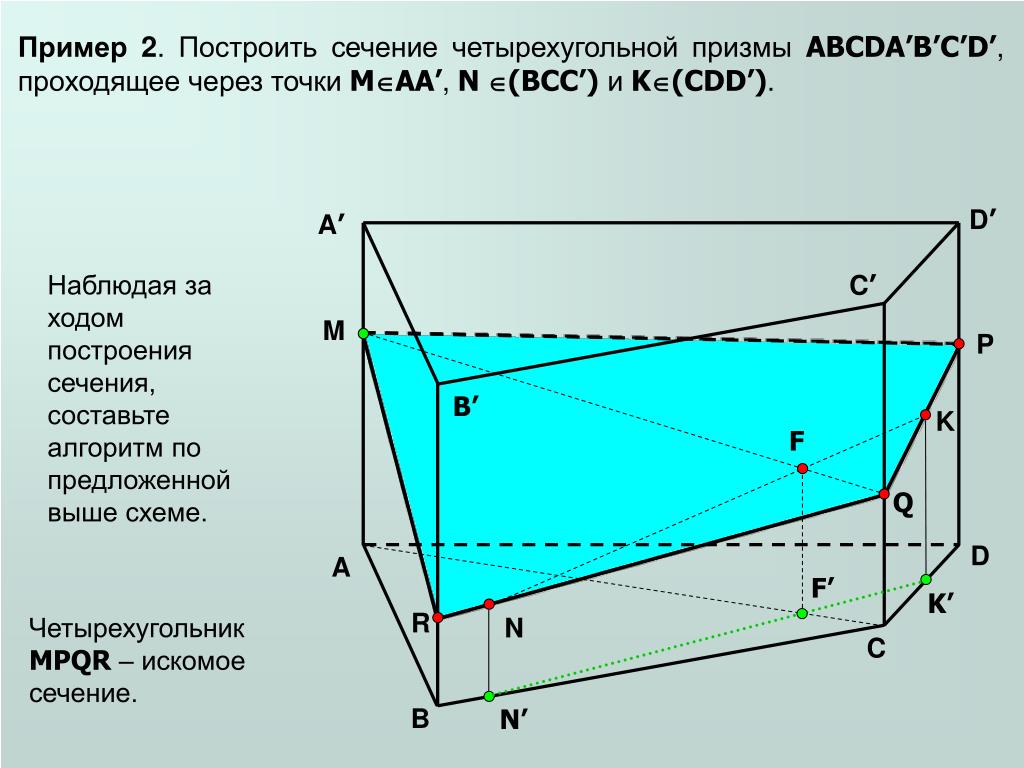 A.3

Нажмите здесь, чтобы попрактиковаться: Алгебра – Создание уравнений Вопросы для 10 класса по математике

Домен: 10 класс >> Алгебра – рассуждения с уравнениями и неравенствами

Пример вопроса: Решите квадратное уравнение x ² +10x=−25.

1. -10
2. 10
3. 5
4. -5

Объяснение ответа: Эту задачу можно легко решить, переставив уравнение так, чтобы оно решалось относительно нуля, а затем разложите на множители, как показано:

x ² +10x=−25

х ² +10х+25=0

(х+5)(х+5)=0

Поскольку оба фактора абсолютно одинаковы, у вас будет только одно решение этой проблемы.

х+5=0

х=-5

Стандарты: HSA.REI.B.4

Нажмите здесь, чтобы попрактиковаться: Алгебра – Рассуждения с помощью уравнений и неравенств Вопросы для 10 класса по математике

Домен: 10 класс >> Функции — интерпретация функций

Пример вопроса: Какой график может представлять график функции f(x)=sin(x)?

Ответ Объяснение: График функции sin всегда выглядит как волна. Единственная, которая может быть функцией sin, это D.

.

Стандарты: HSF.IF.C.7

Щелкните здесь, чтобы попрактиковаться: Функции – интерпретация функций. Вопросы по математике для 10 класса

Домен: 10 класс >> Функции — Построение функций

Пример вопроса: Опишите, как график g(x)=x ³ – 5 может быть получен сдвигом f(x) = x ³ + 2,

1. Сдвиг вправо 7 шт.
2. Сдвиг влево 7 единиц
3. Сдвиг вверх на 7 единиц
4. Сдвиг вниз на 7 единиц

Объяснение ответа: Единственное, что изменилось в двух уравнениях, это точка пересечения с осью y, которая управляет сдвигом по вертикали (вверх или вниз).Чтобы получить график g(x), сдвинув график f(x), вы должны сдвинуть f(x) вниз на 7 единиц, чтобы измениться с +2 на -5.

Стандарты: HSF.BF.B.3

Щелкните здесь, чтобы попрактиковаться: Функции. Вопросы построения функций для 10 класса по математике

Домен: 10 класс >> Функции — интерпретация функций

Пример вопроса: Решите 3 ^x =12, используя логарифмическую форму.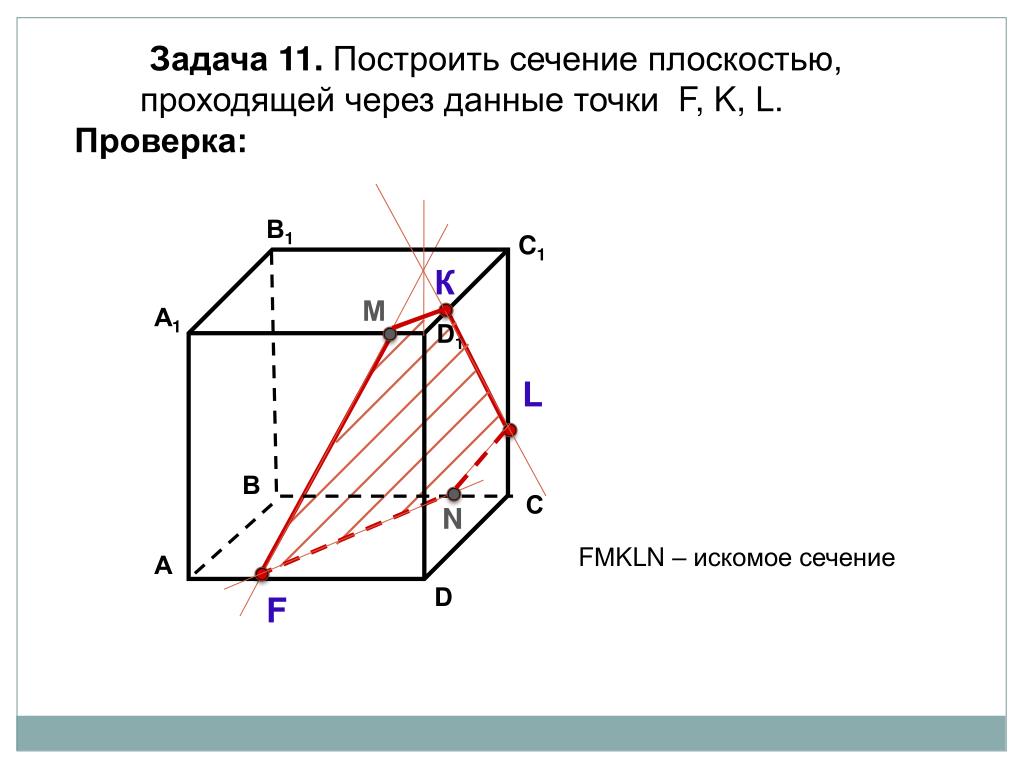

1. х = ln12/ln3
2. х = пер(4)
3. х = пер(9)
4. Ни один из этих

Объяснение ответа:
Решите с помощью журналов следующим образом:
3 ^x =12
x=log(основание 3) 12
x=ln12/ln3

Стандарты: HSF.LE.A.4

Щелкните здесь, чтобы попрактиковаться: Функции – интерпретация функций. Вопросы по математике для 10 класса

Домен: 10 класс >> Функции — Тригонометрические функции

Пример вопроса: В единичном круге видно, что tan(5π/4)=1 . Каково значение cos(5π/4)?

1. −√2/2
2. не определено
3. √2/2
4. -1

Объяснение ответа:
Тригонометрическое отношение косинуса равно отношению длины прилежащей стороны к длине гипотенузы.Длина смежной стороны — это значение x в точке на единичной окружности. Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения косинуса любого угла в единичной окружности — это значение x точки на единичной окружности, соответствующей этому углу. Тригонометрическое отношение тангенса равно длине противолежащей стороны, деленной на длину прилежащей стороны. Длина противоположной стороны — это значение y в точке единичной окружности, а длина соседней стороны — это значение x в точке единичной окружности.Гипотенуза — это радиус единичной окружности, поэтому гипотенуза равна 1. Таким образом, значение отношения тангенсов любого угла в единичной окружности — это отношение yx от точки на единичной окружности, соответствующей этому углу. В этом вопросе тангенс(5π/4)=1. Это отношение берется из точки (−2/√2, −2/√2), которая соответствует углу величиной 5π/4 радиана. Таким образом, используя приведенную выше информацию, значение cos(5π4) совпадает со значением x в точке (−2/√2, −2/√2). Следовательно, значение cos(5π/4) =-2/√2.

Стандарты: HSF.TF.A.2

Нажмите здесь, чтобы попрактиковаться: Функции – Тригонометрические функции. Вопросы по математике для 10 класса

Домен: 10 класс >> Геометрия – конгруэнтность

Пример вопроса: Какими будут координаты точки S после применения следующего правила: (x+3, y -2)?

1. (1, -4)
2. (-2, -2)
3. (2, -2)
4. (3, -2)

Объяснение ответа: Ответ: B
Объяснение: Данное правило преобразования состоит в том, чтобы переместить точку на 3 единицы вправо и на 2 единицы вниз, как показано на следующей диаграмме:

Стандарты:

Щелкните здесь, чтобы попрактиковаться: Геометрия – вопросы на соответствие для 10 класса по математике

Домен: 10 класс >> Геометрия — подобие, прямоугольные треугольники и тригонометрия

Пример вопроса: По какому свойству углы BAX и TSX равны?

1. Соответствующие уголки
2. Вертикальные уголки
3. Альтернативные внутренние уголки
4. Равные углы

Объяснение ответа: Ответ: A

Хотя это конгруэнтные углы, вопрос касается свойства. Поскольку они находятся в соответствующих местах с поперечной (AX), правильный ответ A

.

Стандарты: HSG.SRT.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия — вопросы о подобии, прямоугольных треугольниках и тригонометрии для 10 класса по математике

Домен: 10 класс >> Геометрия – Круги

Пример вопроса: Каковы правило перевода и масштабный коэффициент расширения, когда Окружность F→Окружность F′ ?

1. (х, у)→1/4(х, у+10)
2. (х, у)→4(х, у+10)
3. (х, у)→1/4(х+10,у)
4. (х, у) → 1/4 (х, у-10)

Ответ Объяснение: Исходный круг F имеет центр в точке (−5,−6) с радиусом 4 единицы.Перемещенный/расширенный круг F’ имеет центр в точке (−5,4) с радиусом 1 единица. Это означает, что центр был перемещен вверх на 10 единиц. В качестве преобразования этот перевод записывается как (x,y)→(x,y+10). Окружность F также расширилась в 1/4 раза, потому что радиус был уменьшен с 4 единиц до 1 единицы. В качестве преобразования это расширение записывается как (x, y) → 1/4 (x, y). Соединяя перевод и расширение вместе, правило (x, y) → 1/4 (x, y + 10).

Стандарты:

Нажмите здесь, чтобы попрактиковаться: Геометрия – круги. Вопросы по математике для 10 класса

Домен: 10 класс >> Геометрия – выражение геометрических свойств с помощью уравнений

Пример вопроса: Какое значение на числовой прямой на рисунке ниже делит отрезок EF на две части с отношением длин 3:1?

1. -5
2. -3
3. -2
4. -1

Объяснение ответа: Точка E находится в точке -7 на числовой прямой на рисунке, а точка F находится в точке 1.Таким образом, длина отрезка EF равна 8. Чтобы разделить отрезок на две части с отношением их длин 3:1, измените отношение на 3x:1x, чтобы разрешить варьирование положения на числовой прямой. Затем установите сумму двух частей равной 8 и найдите x. 3x+1x=8;4x=8;x=2. Теперь, когда вы знаете, что x=2, найдите 3x, равное 6. Найдите значение на числовой прямой, прибавив 6 к позиции точки E. −7 +6=-1. Значение на числовой прямой, которая делит отрезок EF в отношении 3:1, равно -1.

Стандарты: HSG.GPE.B.6

Нажмите здесь, чтобы попрактиковаться: Геометрия – Выражение геометрических свойств с помощью уравнений Вопросы для 10 класса по математике

Домен: 10 класс >> Геометрия — геометрические измерения и размеры

Пример вопроса: Каков объем показанной ниже призмы?

1. 1350 см ³
2. 1350 см
3. 675 см ³
4. 675 см

Объяснение ответа: Используйте формулу объема пирамиды:

В=1/2.а.к.х

В данном случае длина 15 см, длина основания 10 см, а высота 9 см. Следовательно:

V=1/2.15.10.9=675 см ³

Стандарты: HSG.GMD.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия – геометрические измерения и вопросы по математике для 10 класса

Домен: 10 класс >> Геометрия – Моделирование с помощью геометрии

Пример вопроса: Компания отправляет сферические пресс-папье в кубических коробках. Окружность пресс-папье 9π см. Если коробка соответствует сфере точно так, что стороны сферы касаются коробки, каков объем наименьшей коробки, которую компания может использовать для доставки?

1. 81 см ³
2. 81 см ³
3. 729 см ³
4. 1009 π см ³

Объяснение ответа:

Обратите внимание, что диаметр сферы будет таким же, как сторона куба.Используя значение окружности, можно определить диаметр пресс-папье.
C = πd9π
см = πd9
см = d
Так как диаметр равен сторонам {\dots}
V=s ³
V=(9 см) ³
V=729 см ³

Стандарты: HSG.MG.A.3

Нажмите здесь, чтобы попрактиковаться: Геометрия – Моделирование с помощью геометрии Вопросы для 10 класса по математике

Домен: 10 класс >> Статистика и вероятность – интерпретация категориальных и количественных данных

Пример вопроса: Учитывая приведенную ниже диаграмму рассеяния, какой тип функции выражает корреляцию между двумя переменными?

1. Линейный
2. Экспоненциальный
3. Квадратичный
4. Полярный

Ответ Объяснение: Обратите внимание, что тренд графика (красный) между точками данных образует линию.

Стандарты: HSS.ID.A.4

Щелкните здесь, чтобы попрактиковаться: Статистика и вероятность – интерпретация вопросов по категориальным и количественным данным для 10-го класса по математике

Домен: 10 класс >> Статистика и вероятность – выводы и обоснование выводов

Пример вопроса: В исследовательском проекте о поведении домашних животных была выбрана случайная выборка из 400 кошек. Исследование показало, что 60% кошек предпочитают спать внутри дома.Курица была любимой едой для 35% этих кошек. Исследование также показало, что у 85% кошек, которые предпочитали спать вне дома, было другое любимое блюдо. Сколько кошек в выборке больше всего любили курицу и предпочитали спать внутри?

1. 84
2. 56
3. 160
4. 156

Объяснение ответа: Если в выборке 400 кошек и 60% кошек предпочитают спать внутри, то 400.0.60=240 кошек предпочитают спать внутри, а 160 кошек предпочитают спать снаружи. Далее, если любимым блюдом 35% тех кошек, которые предпочли спать внутри, была курица, то 240,0,35=84 кошки в выборке предпочли спать внутри и имели курицу в качестве своего любимого блюда.

Стандарты: HSS.IC.B.6

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Делать выводы и обосновывать выводы Вопросы для 10 класса по математике

Домен: 10 класс >> Статистика и вероятность – условная вероятность и правила вероятности

Пример вопроса: В студенческом совете открыта одна вакансия.Школа проводит выборы и имеет восемь равновероятных кандидатов. Класс статистики AP хочет смоделировать результаты выборов, поэтому учащиеся должны выбрать подходящий метод моделирования. Они намерены провести испытания с симуляцией. Какой из этих методов будет наиболее подходящим?

1. Вращение колеса с восемью равными ячейками
2. Подбросьте монету восемь раз за каждые выборы
3. Бросить кости
4. Бросьте четыре кубика

Объяснение ответа: В вопросе говорится, что существует восемь равновероятных кандидатов. Это означает, что каждый кандидат имеет одинаковые шансы на победу на выборах. Только вращающееся колесо с восемью равными ячейками может имитировать эту ситуацию, потому что у колеса есть равные шансы приземлиться на каждой ячейке.

Стандарты: HSS.IC.A.1

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность – Условная вероятность и правила вероятности Вопросы для 10 класса по математике

Домен: 10 класс >> Статистика и вероятность — использование вероятности для принятия решений

Пример вопроса:

Используя приведенную выше диаграмму Венна, найдите P(C или E).

1. 1/3
2. 7/24
3. 5/24
4. Ни один из этих

Объяснение ответа: Просто подсчитайте точки данных в кругах C и E. Их 8 из 24 общих точек данных, и, уменьшая, мы получаем 8/24=1/3.

Стандарты: HSS.CP.B.7

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность: использование вероятности для принятия решений Вопросы для 10 класса по математике

Домен: 10 класс >> Статистика и вероятность — использование вероятности для принятия решений

Пример вопроса: Статистик, работающий в Sweet Shop USA, получил задание выяснить, какова вероятность того, что машина для помадки выйдет из строя и в процессе работы будет испорчена целая партия помадки. Каждая неисправность машины обходится компании в 250 долларов. Статистики подсчитали, что вероятность того, что 1 из 20 партий помадки будет потеряна из-за неисправности машины, составляет 1. Какова ожидаемая величина этих убытков за один месяц, если компания производит 20 партий помадки каждый день?

1. 3750 $
2. 150 000 долларов США
3. $7500
4. 375 $

Объяснение ответа: Поскольку в большинстве месяцев 30 дней, будем считать, что в месяце 30 дней. Мы можем использовать E(x)=x1p1+x2p2+…+xipi или просто вычислить следующим образом
E(X)=.05*250*30=375$

Стандарты: HSS.MD.A.4

Нажмите здесь, чтобы попрактиковаться: Статистика и вероятность: использование вероятности для принятия решений Вопросы для 10 класса по математике

Учебная программа по математике

Учебная программа по математике

Единицы в рамках учебной программы по математике предназначены для преподавания в том порядке, в котором они представлены в детском саду до двенадцатого класса. Существует логическая и соответствующая уровню развития последовательность стандартов, при этом большое внимание уделяется представленным основным, вспомогательным и дополнительным стандартам контента, поскольку большинство концепций основаны друг на друге.В рамках единиц округа могут выбирать, в каком порядке представлять стандарты. Стандарты основного, вспомогательного и дополнительного контента имеют цветовую маркировку, чтобы школьные округа понимали, какому приоритету отдать предпочтение. Целью стандартов является интеграция основных, вспомогательных и дополнительных стандартов. Порядок, в котором стандарты и математические методы сгруппированы в единицах, является предполагаемой интеграцией.

Цели уровня обучения и концепции приоритетов

Основная, вспомогательная и дополнительная группы стандартов содержания математики основаны на Стандартах обучения студентов штата Нью-Джерси.Не все содержание данного класса одинаково подчеркивается в стандартах. Некоторые кластеры требуют большего внимания, чем другие, в зависимости от глубины идей, времени, необходимого для освоения или моделирования, и/или их важности для будущих уровней обучения. Стандарты в структуре имеют цветовую кодировку: основной (зеленый), вспомогательный (синий) и дополнительный (желтый). Предлагаемые стандарты математической практики перечислены в каждом разделе и должны регулярно включаться в ежедневные занятия по математике. Важно отметить, что основные стандарты (зеленые) специально помещены в тестируемые классы, чтобы обеспечить время для формального обучения этим стандартам.

Свободное владение языком в классах K-5

Начальные блоки от детского сада до второго класса рассчитаны на то, чтобы больше времени уделить фундаментальным математическим понятиям, необходимым для будущих блоков, чтобы достичь свободного владения математикой. Например, раздел 1 детского сада начинается с «Названия чисел и последовательность счета», которые необходимо преподавать перед «Основами с моделями сложения и вычитания» в Разделе 2. Другие разделы в классах с третьего по пятый также следуют той же логической последовательности стандартов. обеспечение достаточного времени для формального обучения основным стандартам, при этом встраивая стандарты вспомогательного и дополнительного контента, а также стандарты математической практики.Также важно отметить, что требование беглости речи от детского сада до пятого класса имеет решающее значение для освоения учащимися.

Разговоры по математике

После изучения структуры и понимания того, как организованы стандарты и навыки, школы/округи должны загрузить структуру и переименовать ее как свою собственную. Педагоги должны продолжать совместные обсуждения учебной программы и инструкций, которые начинаются с обсуждения оценивания.Начав таким образом строить разговоры, вы тесно увязываете доказательства с обучением учащихся. Структура позволяет направлять и фиксировать основные компоненты, которые строятся на учебной программе. Структуру можно рассматривать как предварительную работу перед тем, как школы/округи составят или пересмотрят свои собственные учебные документы.

Обзоры курсов

12 упражнений для отработки поперечных сечений трехмерных фигур в стиле ниндзя

Нахождение формы, полученной в результате разрезания трехмерной фигуры, — забавная тема.Студентам очень нравится эта тема. Когда вы ищете идеи для преподавания этой темы, вы неизбежно найдете вводное задание с использованием пластилина. Учащиеся делают трехмерные фигуры из пластилина, а затем вырезают их с помощью какой-либо веревки. Но есть и другие способы помочь учащимся увидеть и понять эту тему, поэтому сегодня я делюсь 12 другими заданиями (но вы можете увидеть несколько разных версий этого пластилина здесь и здесь).

Одна вещь, которая мне кажется интересной в преподавании этой темы, заключается в том, что речь идет о трех измерениях, но учащиеся должны понимать ее в двухмерном пространстве на бумаге или на экранах компьютеров.Это то, что делает эту тему уникальной.

В моем классе мы много практикуемся как с бумажными, так и с онлайн-играми и заданиями. В этом посте я хотел бы поделиться с вами некоторыми из этих идей. У студентов есть много практических занятий, и они действительно увлекаются этой деятельностью. Вы увидите, что этот список действий предлагает широкий спектр практики.

Вот список:

Крестики-нолики

Карточки с заданиями

Модели Geogebra онлайн

Кубическая игра

Игра «Соответствие»

Органайзер для графических сечений БЕСПЛАТНО

Рабочий лист с фигурами

Флаер с поперечными сечениями

Задача производительности

PBS Видео

Рабочий лист множественного выбора

Кахут

 

Кажется, людям действительно нравится эта игра в крестики-нолики.Он включает в себя четыре разных карты крестики-нолики. Три карты имеют простые старые формы, а на последней изображены настоящие объекты. Вы можете использовать это упражнение в качестве упреждающего набора. Кроме того, это очень хорошо работает для быстрого финишера с партнером. Особенно мне нравятся примеры из реального мира. Студенты играют с партнерами и в конечном итоге много говорят о формах, которые они изучают, и их поперечных сечениях. В целом, эта игра дает учащимся некоторую практику визуализации трехмерных фигур на бумаге и размышления о том, как выглядят поперечные сечения.

Мне нравится универсальность карточек заданий. Вы можете выполнять множество различных действий, таких как Scoot, партнерская работа, весь класс с досками или билеты на выход. Этот набор карточек с заданиями включает 27 карточек. На первых 9 карточках рассматриваются названия трехмерных фигур, а на остальных 18 карточках указывается форма, полученная в результате трехмерного среза. Эти карточки с заданиями идеально подходят для легкой и быстрой практики.

У

Geogebra есть довольно крутые онлайн-инструменты. Без сомнения, мой фаворит — их инструмент поперечных сечений и твердых тел для этой темы.Это дает детям такой классный интерактивный взгляд на то, что мы подразумеваем под поперечными сечениями трехмерных фигур.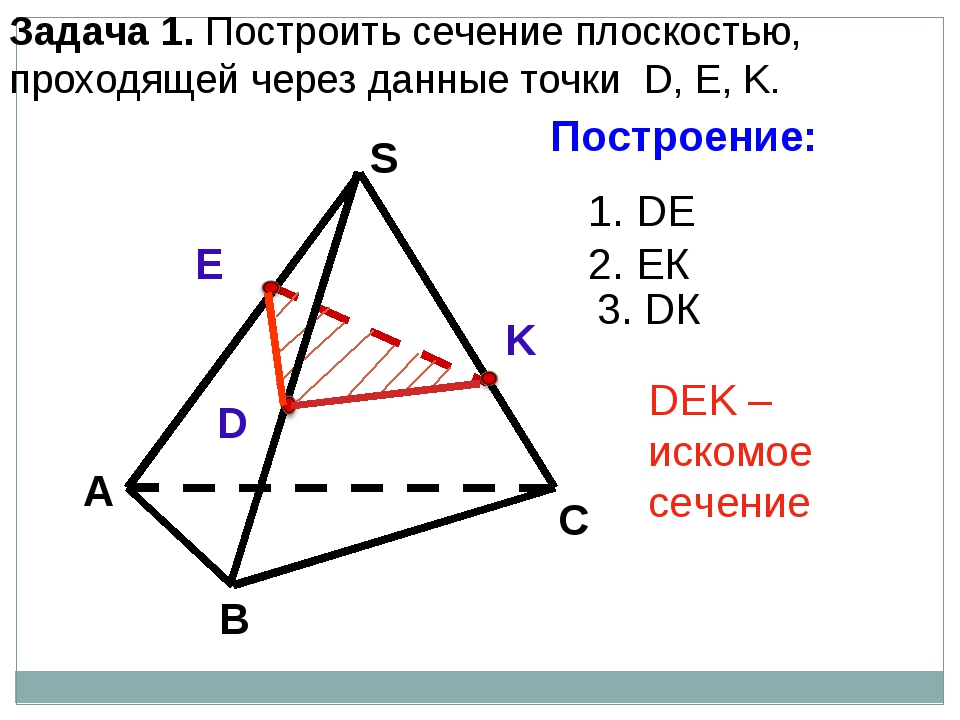 В этом инструменте есть множество форм, и вы можете манипулировать нарезкой по-разному. Вы можете соединить это с нашим графическим органайзером ниже, и тогда учащимся не придется просто снимать в темноте при работе с этими фигурами. Вы определенно захотите смоделировать, как его использовать, и показать учащимся различные функции. Им нравится работать с такими инструментами на компьютере.

Если вы ищете занятие, которое поможет учащимся выйти из режима рабочего листа, вы можете попробовать эту игру с кубиками.Он включает в себя два разных способа игры и дает учащимся много повторений с определением поперечных сечений. В одном из вариантов этого задания с кубом используется графический органайзер, и в него играют всем классом. Вы катите куб, а затем определяете различные характеристики трехмерных фигур. Другая версия игры предназначена для партнеров или небольших групп и использует карты и кубики. Учащиеся выбирают карточку, а затем бросают кубик, на котором изображены различные вопросы. Они должны ответить на вопросы.Моим детям нравится играть в эту игру, потому что она социальная, а мне нравится, потому что они получают так много повторений за такой короткий промежуток времени.

Задания на сопоставление дают учащимся новый взгляд на понятия. В этом упражнении на сопоставление учащимся дается форма, и они должны найти поперечные сечения, параллельные основанию, перпендикулярные основанию и диагональные к основанию. Они используют рабочий коврик и кладут на него маленькие кусочки бумаги. Мои ученики сказали, что им нравится вырезать и перемещать бумагу.Вы можете повторно использовать набор (в качестве центра и т. д.) или попросить учеников склеить его и поместить в свою интерактивную тетрадь.

Хотите больше идей и ресурсов для веселых игр для средней школы, в том числе БЕСПЛАТНЫЙ математический лабиринт, который каждый месяц будет приходить прямо на ваш почтовый ящик? Присоединяйтесь к клубу «Лабиринт месяца», и вы в игре!

Да! Запишите меня в клуб «Математический лабиринт месяца»!

Не могу дождаться, когда увижу тебя там.

Я люблю графические органайзеры. Когда я только начинала работать учителем, у меня были 4-часовые блочные занятия со студентами ELL.Мы работали над изучением английского языка большую часть дня. Я использовал много графических органайзеров, подобных этому, и с тех пор я был одержим ими. В этом графическом органайзере учащиеся отвечают на один и тот же вопрос несколько раз, используя разные формы. Это отличный инструмент, помогающий учащимся говорить о поперечных сечениях в академической манере. Все, что им нужно сделать, это взять свой ответ и превратить его в предложение. Это особенно хорошо работает с ELL и учащимися специального образования. Загрузите его бесплатно здесь.

В этом рабочем листе есть несколько замечательных иллюстраций, которые помогут учащимся увидеть срезы в поперечных сечениях. Вы можете предложить учащимся поработать над этим заданием с партнером и начать разговор о математике. Кроме того, вы можете использовать его как занятие для всего класса и показывать учащимся по одному примеру за раз.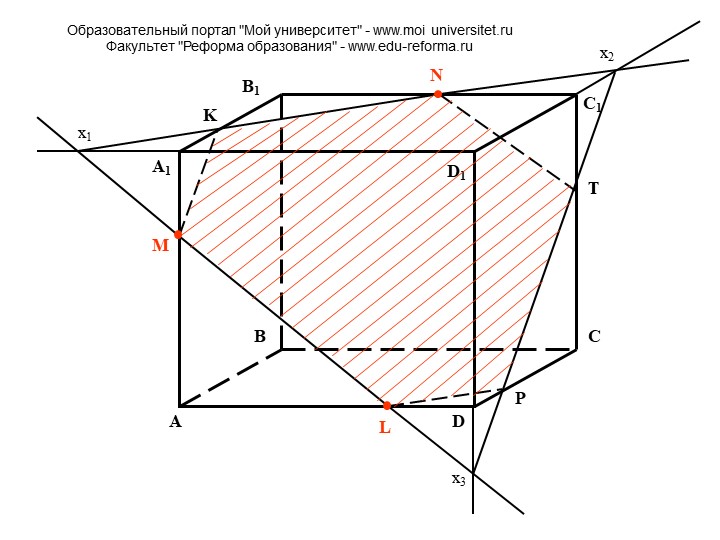 Затем я предлагал учащимся отвечать на вопросы на своих досках или SmartPal. Вот несколько вопросов, которые вы могли бы использовать:

1. Какая двухмерная форма получается из среза, показанного на рисунке?
2. Как он изменится, если разрезать его в другом направлении?
3. Каково основание этой фигуры и сколько у нее граней?

Есть много способов сделать рабочие листы чем-то большим, чем просто рабочими листами.Как вы можете видеть выше, один из простых способов улучшить его — просто продвинуться немного дальше с вопросами и иллюстрациями из рабочего листа.

Мне нравится, когда дети могут манипулировать математикой на своих условиях и пытаться что-то понять. Это делает математику более реальной, а не просто списком шагов. Этот флаер отлично подходит именно для этого. Студенты могут видеть различные формы, такие как конус, цилиндр, пирамида и призма. Кроме того, они могут менять основание и перемещать поперечное сечение. Прежде чем предложить им попробовать что-то конкретное с помощью этого инструмента, я даю учащимся несколько минут, чтобы просто поиграть с ним.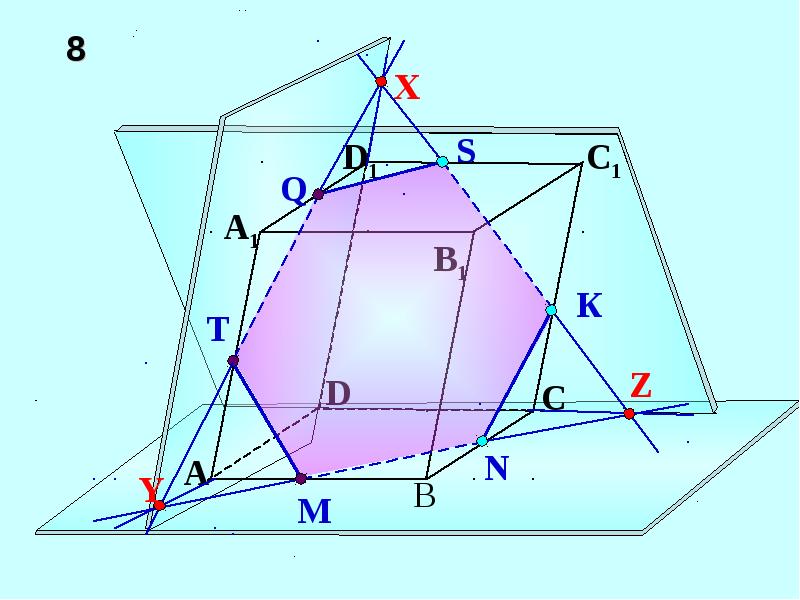 Вам понравится слушать, как говорят ваши ученики, используя этот онлайн-инструмент.

Это задание на производительность от Illustrative Mathematics представляет собой задание на производительность, в котором учащиеся должны взять то, что они узнали о поперечных сечениях, и применить это на практике. Задание называется Cube Ninjas, которое мне нравится, потому что я думаю, что детям нравится все, что содержит слово ниндзя. Если вам нравится хамить, вы можете сделать целую рутину ниндзя, когда вводите это занятие. Я мог бы сделать это, если бы я был в правильном настроении!

В самом задании учащимся предлагается проанализировать различные срезы куба.Они должны нарисовать диаграмму и использовать точный математический язык для описания того, что происходит. Если у вас мало времени (как у меня большую часть времени), вы можете раздать разные кусочки разным группам и собрать что-то вроде головоломки. По истечении времени позвольте каждой группе сделать краткую презентацию своих выводов.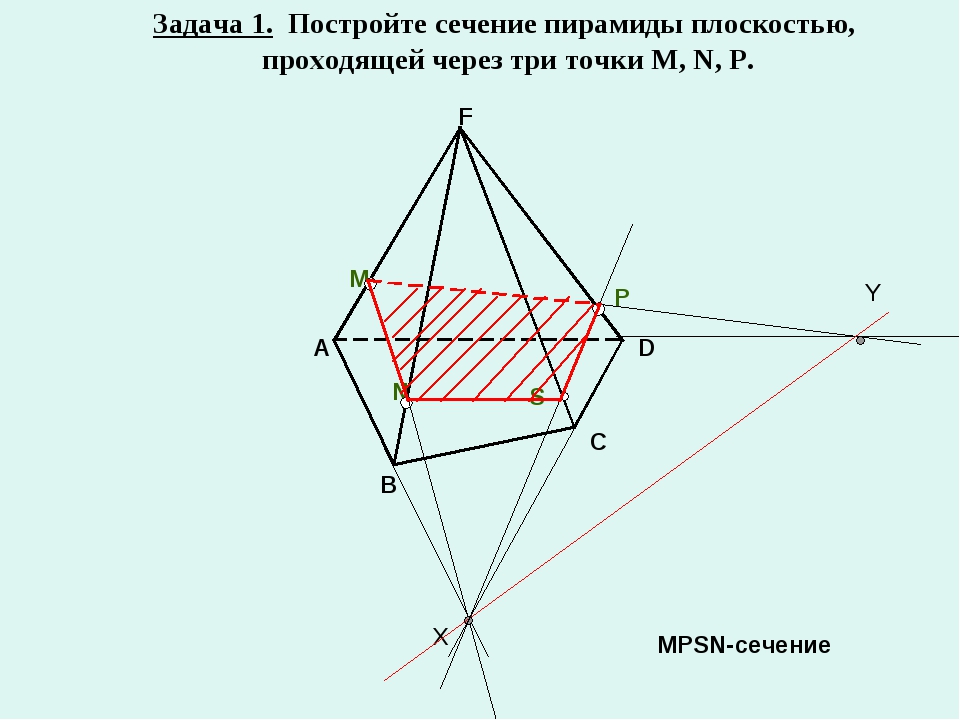

Это видео от PBS Video очень забавное и прекрасно работает в качестве упреждающего набора во время этого модуля. У них есть группа детей, которые разыгрывают рекламный ролик, продающий вещи, которые делают кусочки разных продуктов.Мне это нравится, потому что это дает всем реальные примеры этих кусочков. К тому же, это запоминающееся. Когда мы все смотрим что-то запоминающееся, например это видео, оно дает нам что-то, на что мы можем ссылаться через устройство. После того, как учащиеся посмотрят видео, обязательно предложите им поговорить об этом с партнером. Дайте им возможность переварить то, что они видели в видео.

Этот рабочий лист даст вам немного практики для ваших учеников в форме, похожей на тест, с множественным выбором.Мне нравится использовать игры с рабочими листами. Игра, которую я использовал с этим рабочим листом, называется «Выбери их из 4 карт». Учитель ставит задачу на видеокамеру, а ученики решают ее на доске. Когда все закончат, учитель задает вопросы по задаче, и тот, кто ответит, берет карту из колоды.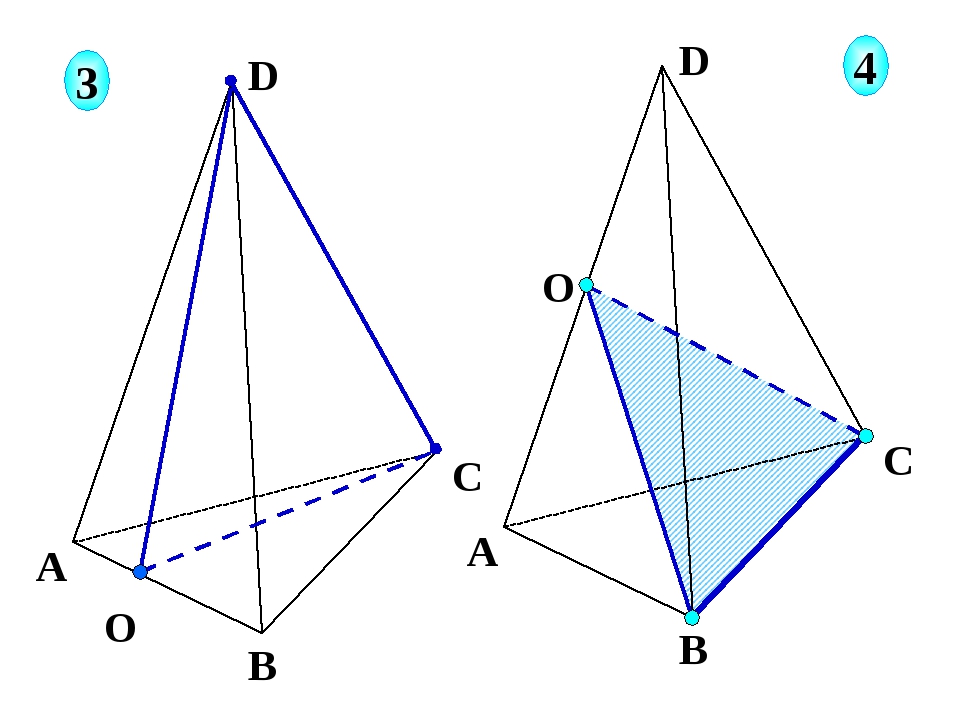 Как только каждый из четырех учеников выбрал карточку, остальные ученики записывают имя одного из учеников, которое, по их мнению, будет иметь самую высокую карточку. Студент с самой высокой картой получает 4 очка, следующий по величине получает 3 очка, следующий по величине получает 2 очка, а самая младшая карта получает 1 очко.Остальной класс получает количество баллов, которое заработал выбранный ими ученик. Эта простая игра просто добавляет немного веселья к ответам на некоторые вопросы.

Рабочие листы по этой ссылке содержат подробные изображения некоторых поперечных сечений и спрашивают, какое поперечное сечение получается из них. Кроме того, вы можете спросить об основании, названии фигуры или количестве граней. Эти рабочие листы помогают укрепить некоторые основы этой концепции.

Kahoot — это компьютерная игра, которая вовлекает весь класс в практику поперечных сечений трехмерных фигур.В этом Kahoot есть 27 вопросов, которые заставят детей задуматься. Если 27 вопросов кажутся вам слишком большими, помните, что вы можете загрузить игру в свою учетную запись и редактировать ее. Вы можете удалить некоторые вопросы и сделать игру более быстрой. Иногда дети слишком увлекаются Kahoot, и вам нужно напомнить им, что мы тренируемся, а не просто играем в игру.

Вопросы в этом Kahoot касаются либо того, какая форма получается в результате определенного поперечного сечения, либо какая форма может иметь определенное поперечное сечение.Разнообразия вопросов не так уж и много, но практика довольно быстро нарабатывается. Кроме того, помните, что результаты игр Kahoot можно загрузить на свой Google Диск, что делает их хорошей формирующей оценкой.

Попробуйте что-нибудь

Мы просмотрели множество заданий, но у вас, вероятно, нет времени на их все. Мой вызов вам, чтобы попробовать одну новую вещь и посмотреть, как она работает. Если все пойдет хорошо, вы можете добавить это упражнение или инструмент в набор приемов учителя.