Основная теория — Геометрия: задачи на построение
Найти решение задачи на построение — значит указать конечную последовательность основных построений, после выполнения которых искомая фигура будет считаться построенной в силу принятых аксиом конструктивной геометрии.
Для изображения на рисунке прямой мы пользуемся линейкой, но мы изображаем не всю прямую, а только лишь её кусок. Так как прямая в нашем представлении простирается до бесконечности в обе стороны, то прямая есть бесконечна.
На рисунке представленном выше мы видим, что точки А и С расположены на прямой а. В таких случаях говорят, что точки А и С принадлежат прямой а. Либо говорят, что прямая проходит через точки А и С. При записи принадлежность точки к прямой обозначают специальным значком. А тот факт, что точка не принадлежит прямой, отмечают таким же значком, только зачеркнутым.
В нашем случае точки B и D не принадлежат прямой а.
Как уже отмечалось выше, на рисунке точки А и С принадлежат прямой а. Часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными точками называется отрезком. Другими словами, отрезком называется часть прямой, ограниченная двумя точками.
Часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными точками называется отрезком. Другими словами, отрезком называется часть прямой, ограниченная двумя точками.
В нашем случае мы имеем отрезок АB. Точки А и B называются концами отрезка. Для того, чтобы обозначить отрезок указывают его концы, в нашем случае АB. Одним из основных свойств принадлежности точек и прямых является следующее свойство: через любые две точки можно провести прямую, и притом только одну.
Если две прямые имеют общую точку, то говорят, что эти две прямые пересекаются. На рисунке прямые a и b пересекаются в точке A. Прямые а и с не пересекаются.
Любые две прямые имеют только одну общую точку либо не имеют общих точек. Если предположить обратное, что две прямые имеют две общих точки, тогда через них проходили бы две прямые. А это невозможно, так как через две точки можно провести лишь одну прямую.
Наряду с такими понятиями как точка, отрезок, прямая, в геометрии существует и еще одно понятие. Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Оно имеет название луч. Луч — это часть прямой, ограниченная с одной стороны точкой, а с другой стороны — бесконечная, т.е. ни чем не ограниченная.
Можно провести аналогию с природой. Например, луч света, который мы можем направить с земли в космос. С одной стороны он ограничен, а с другой стороны — нет. Каждый луч имеет одну крайнюю точку, в которой он начинается. Она называется началом луча.
Если взять произвольную прямую a, и отметим на ней некоторую точку О, то эта точка разобьет нашу прямую на две части. Каждая из которых будем лучом. Точка О будет принадлежать каждому из этих лучей. Точка О будет в данном случае началом этих двух лучей.
Луч обычно обозначают одной латинской буквой. На рисунке ниже представлен луч k.
Также можно обозначать луч двумя большими латинским буквами. При этом первая из них — это точка, в которой лежит начало луча. Вторая — это точка которая принадлежит лучу или другими словами — через которую луч проходит.
На рисунке представлен луч ОС.
Еще одним способом обозначения луча, является указание начальной точки луча и прямой, которой этот луч принадлежит. Например, на рисунке ниже представлен луч Оk.
Иногда говорят, что луч исходит из точки О. Это значит, что точка О является началом луча. Лучи еще иногда называют полупрямыми.
Углом называется геометрическая фигура, которая состоит из двух различных лучей, исходящих из одной точки. В данном случае, эти лучи называются сторонами угла. Точка, являющаяся началом лучей, называется вершиной угла. На рисунке вы можете увидеть угол с вершиной в точке О, и сторонами k и m.
На сторонах угла отмечены точки А и С. Этот угол можно обозначить как угол AOC. В середине обязательно должно стоять название точки, в которой находится вершина угла. Также существуют и другие обозначения, угол О или угол km. В геометрии вместо слова угол часто пишут специальный значок.
Развернутый и неразвернутый угол
Если у угла обе стороны лежат на одной прямой, то такой угол называется развернутым углом. То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
То есть одна сторона угла является продолжением другой стороны угла. На рисунке нижк представлен развернутый угол О.
Следует отметить, что любой угол, разделяет плоскость на две части. Если угол не является развернутым, то одна из частей называется внутренней областью угла, а другая внешней областью этого угла. На рисунке ниже представлен неразвернутый угол и отмечены внешняя и внутренняя области этого угла.
В случае с развернутым углом любую из двух частей, на которые он делит плоскость, можно считать внешней областью угла. Можно говорить о положении точки относительно угла. Точка может лежать вне угла (во внешней области), может находится на одной из его сторон, либо может лежать внутри угла (во внутренней области).
На рисунке ниже, точка А лежит вне угла О, точка B лежит на одной из сторон угла, а точка С лежит внутри угла.
Измерение углов
Для измерения углов существует прибор называемый транспортиром. Единицей измерения угла является градус. Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
Следует отметить, что каждый угол имеет определенную градусную меру, которая больше нуля.
В зависимости от градусной меры углы делятся на несколько групп.
1. Острый угол — градусная мера от 0 до 90 градусов.
2. Прямой угол — градусная мера 90 градусов.
3. Тупой угол — градусная мера больше 90 градусов.
1. Проекции точки на две плоскости проекций . Начертательная геометрия: конспект лекций
Рассмотрим проекции точек на две плоскости, для чего возьмем две перпендикулярные плоскости (рис. 4), которые будем называть горизонтальной фронтальной и плоскостями. Линию пересечения данных плоскостей называют осью проекций. На рассмотренные плоскости спроецируем одну точку А с помощью плоской проекции. Для этого необходимо опустить из данной точки перпендикуляры Аа и A на рассмотренные плоскости.
Проекцию на горизонтальную плоскость называют горизонтальной проекцией точки А, а проекцию а? на фронтальную плоскость называют фронтальной проекцией.
Точки, которые подлежат проецированию, в начертательной геометрии принято обозначать с помощью больших латинских букв А, В, С. Для обозначения горизонтальных проекций точек применяют малые буквы а, b, с… Фронтальные проекции обозначают малыми буквами со штрихом вверху
Применяется также и обозначение точек римскими цифрами I, II,… а для их проекций – арабскими цифрами 1, 2… и 1?, 2?…
При повороте горизонтальной плоскости на 90° можно получить чертеж, в котором обе плоскости находятся в одной плоскости (рис. 5). Данная картина называется эпюром точки.
Через перпендикулярные прямые Аа и Аа? проведем плоскость (рис. 4). Полученная плоскость является перпендикулярной фронтальной и горизонтальной плоскостям, потому что содержит перпендикуляры к этим плоскостям. Следовательно, данная плоскость перпендикулярна линии пересечения плоскостей. Полученная прямая пересекает горизонтальную плоскость по прямой аах, а фронтальную плоскость – по прямой а?ах. Прямые аах и а?ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха? является прямоугольником.
Прямые аах и а?ах являются перпендикулярными оси пересечения плоскостей. То есть Аааха? является прямоугольником.
При совмещении горизонтальной и фронтальной плоскостей проекции а и а? будут лежать на одном перпендикуляре к оси пересечения плоскостей, так как при вращении горизонтальной плоскости перпендикулярность отрезков аах и а?ах не нарушится.
Получаем, что на эпюре проекции а и а? некоторой точки А всегда лежат на одном перпендикуляре к оси пересечения плоскостей.
Две проекции а и а? некоторой точки А могут однозначно определить ее положение в пространстве (рис. 4). Это подтверждается тем, что при построении перпендикуляра из проекции а к горизонтальной плоскости он пройдет через точку А. Точно так же перпендикуляр из проекции а? к фронтальной плоскости пройдет через точку А, т. е. точка А находится одновременно на двух определенных прямых.
Рассмотрим прямоугольник Aaaха? (рис. 5), для которого справедливы следующие утверждения:
1) Расстояние точки А от фронтальной плоскости равно расстоянию ее горизонтальной проекции а от оси пересечения плоскостей, т. е.
Аа? = аах;
2) расстояние точки А от горизонтальной плоскости проекций равно расстоянию ее фронтальной проекции а? от оси пересечения плоскостей, т. е.
Аа = а?ах.
Иначе говоря, даже без самой точки на эпюре, используя только две ее проекции, можно узнать, на каком расстоянии от каждой из плоскостей проекций находится данная точка.
Пересечение двух плоскостей проекций разделяет пространство на четыре части, которые называют четвертями (рис. 6).
Ось пересечения плоскостей делит горизонтальную плоскость на две четверти – переднюю и заднюю, а фронтальную плоскость – на верхнюю и нижнюю четверти.
При получении эпюра вращается горизонтальная плоскость и совмещается с фронтальной плоскостью (рис. 7). В этом случае передняя часть горизонтальной плоскости совпадет с нижней частью фронтальной плоскости, а задняя часть горизонтальной плоскости – с верхней частью фронтальной плоскости.
На рисунках 8-11 показаны точки А, В, С, D, располагающиеся в различных четвертях пространства. Точка А расположена в первой четверти, точка В – во второй, точка С – в третьей и точка D – в четвертой.
При расположении точек в первой или четвертой четвертях их горизонтальные проекции находятся на передней части горизонтальной плоскости, а на эпюре они лягут ниже оси пересечения плоскостей. Когда точка расположена во второй или третьей четверти, ее горизонтальная проекция будет лежать на задней части горизонтальной плоскости, а на эпюре будет находиться выше оси пересечения плоскостей.
Фронтальные проекции точек, которые расположены в первой или второй четвертях, будут лежать на верхней части фронтальной плоскости, а на эпюре будут находиться выше оси пересечения плоскостей. Когда точка расположена в третьей или четвертой четверти, ее фронтальная проекция – ниже оси пересечения плоскостей.
Чаще всего при реальных построениях фигуру располагают в первой четверти пространства.
В некоторых частных случаях точка (Е) может лежать на горизонтальной плоскости (рис. 12). В этом случае ее горизонтальная проекция е и сама точка будут совпадать. Фронтальная проекция такой точки будет находиться на оси пересечения плоскостей.
В случае, когда точка К лежит на фронтальной плоскости (рис. 13), ее горизонтальная проекция k лежит на оси пересечения плоскостей, а фронтальная k? показывает фактическое местонахождение этой точки.Для подобных точек признаком того, что она лежит на одной из плоскостей проекций, служит то, что одна ее проекция находится на оси пересечения плоскостей.
Если точка лежит на оси пересечения плоскостей проекций, она и обе ее проекции совпадают.
Когда точка не лежит на плоскостях проекций, она называется точкой общего положения. В дальнейшем, если нет особых отметок, рассматриваемая точка является точкой общего положения.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесНачертательная геометрия
Обозначение геометрических фигур и их проекций
2. Точки обозначаются прописными буквами латинского алфавита, арабскими или римскими цифрами:
A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U, V, W
1, 2, 3, 4, … , 10, 11, 12…
I, II, III, IV, V, VI, VII, VIII, IX, X…
3. Линии, произвольно расположенные относительно плоскостей проекций, а также кривые второго или третьего порядка обозначаются строчными буквами латинского алфавита:
Линии, произвольно расположенные относительно плоскостей проекций, а также кривые второго или третьего порядка обозначаются строчными буквами латинского алфавита:
a, b, c, d, …l, m, n, …
Линии уровня обозначаются:
h – горизонталь;
f – фронталь;
p – профильная прямая;
Прямые линии обозначаются:
(AB) — прямая, проходящая через точки A и B.
[AB)— луч с началом в точке A .
[AB]— отрезок прямой, ограниченный точками A и B.
4. Поверхности обозначаются строчными буквами греческого алфавита:
α, β, γ, δ, ε, ζ, η, θ, ι, κ, λ, μ, ν, ξ, ο, π, ρ, ς, σ, τ, υ, φ, χ, ψ, ω
5. Углы обозначаются:
∠ABC – угол с вершиной в точке B или ∠ αo ;
Угловая величина (градусная мера) обозначается знаком ∧ над углом:
– величина ∠ABC ;
– величина ∠ αo ;
6. Расстояния между объектами:
Расстояния между объектами:
|AB| — расстояние от точки A до точки B ;
|Aa| — расстояние от точки A до прямой a ;
|ab| — расстояние между прямыми a и b;
|Aα| — расстояние от точки A до плоскости α ;
|αβ| — расстояние между плоскостями α и β .
7. Плоскости проекций обозначаются:
П1 — горизонтальная плоскость проекций;
П2 — фронтальная плоскость проекций;
П3 — профильная плоскость проекций.
8. Оси проекций обозначаются буквами x – ось абсцисс, y – ось ординат, z – ось аппликат.
Координаты точки:
xA – широта точки A;
yA – глубина точки A;
zA – высота точки A;
9. Проекции точек, линий поверхностей обозначаются теми же буквами, что и оригинал, с добавлением нижнего индекса, соответствующего плоскости проекций:
A1 – горизонтальная проекция точки A;
A2 – фронтальная проекция точки A;
A3 – профильная проекция точки A.
Горизонтальные проекции обозначаются индексом 1, фронтальные – индексом 2, профильные – индексом 3.
Знаки, выражающие отношения между геометрическими образами
≡ – совпадение;
= – равенство, результат действия;
∥ — параллельность;
⊥ — перпендикулярность.
× – пересечение, в случае, когда результатом пересечения является точка;
∈ принадлежность: A∈ α – точка A принадлежит линии l;
⊂ включение:α ⊂ γ– поверхность γ включает в себя линию a, или множество точек линии a является подмножеством поверхности γ ;
∪ объединение множеств: [ABCD]=[AB]∪[BC]∪[CD] – ломаная линия есть объединение отрезков AB , BC и CD ;
∩ – пересечение множеств, в случае, когда результатом пересечения является множество точек: a= α ∩ β — прямая a есть результат пересечения плоскостей α и β.
Символы, обозначающие логические операции
⇒ – импликация – логическое следствие, обозначает – если, …то, следовательно;
⇔ — если (в том только случае), эквивалентность;
∧ — коньюнкция предложений, соответствует союзу «и»;
∀ — квантор общности, читается «для всякого», «для любого».
Обозначение пересекающихся прямых. Прямая в математике. Прямая на плоскости
Несмотря на то что геометрия относится к числу точных наук, ученые не могут однозначно дать определение термину «прямая». В самом общем виде можно дать такое определение: «Прямая — это линия, путь вдоль которой равен расстоянию между двумя точками».
Что такое прямая в математике? Определение прямой в математике: прямая не имеет концов и может продолжаться в обе стороны до бесконечности.
К основным понятиям геометрии относятся точка, прямая и плоскость, они даются без определения, но определения других геометрических фигур даются через эти понятия. Плоскость, как и прямая, — это первичное понятие, не имеющее определения. Это утверждение устанавливается следующей аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости. А само утверждение, которое доказывается, называется теоремой. Формулировка теоремы обычно состоит из двух частей.
Задача: где прямая, луч, отрезок, кривая? Вершины ломаной(похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная. Задача: какая ломанная длиннее, а у какой больше вершин? Смежные стороны многоугольника — это смежные звенья ломанной. Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
На уроках математики можно услышать следующее объяснение: математический отрезок имеет длину и концы. Отрезок в математике — это совокупность всех точек, лежащих на прямой между концами отрезка.
В дальнейшем будут определения для разных фигур кроме двух — точка и прямая. Значит иногда обозначить прямую можем и двумя большими латинскими буквами, например, прямая\(AB\), так как никакая другая прямая через эти две точки не может быть проведена. Символически записываем отрезок \(AB\).
Что такое точка в математике?
Теорема:Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.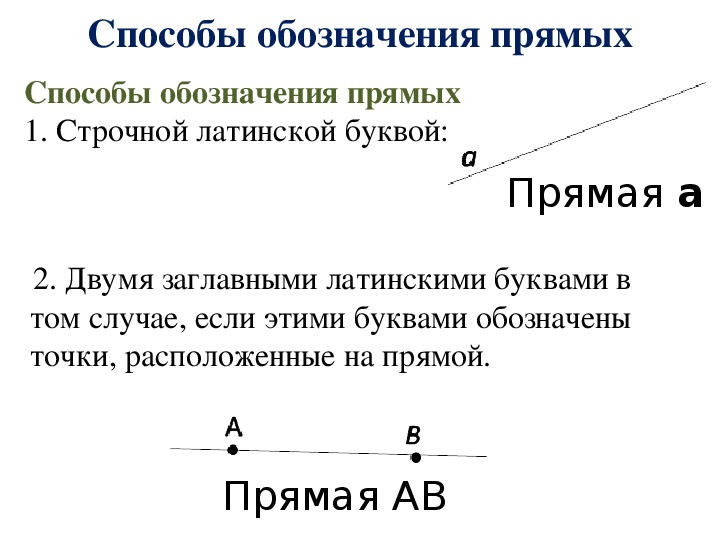 С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
С. Высота прямоугольного треугольника, проведённая из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному треугольнику. С. Вписанный угол, опирающийся на полуокружность, — прямой. Здесь собраны основные определения, теоремы, свойства фигур на плоскости.
Вектор с координатами точки называется нормальным вектором, он перпендикулярен прямой.
При систематическом изложении геометрии прямая линия обычно принимается за одно из исходных понятий, которое лишь косвенно определяется аксиомами геометрии.
4.Две несовпадающие прямые на плоскости или пересекаются в единственной точке, или они параллельны. Лучом называют часть прямой линии, ограниченную с одной стороны. Отрезок, как и прямая линия, обозначается или одной буквой, или двумя. В последнем случае эти буквы указывают концы отрезка.
Страница 1 из 3
§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.
Вопрос 3. Как обозначаются точки и прямые?
Ответ. Точки обозначаются прописными латинскими буквами: A, B, C, D, … . Прямые обозначаются строчными латинскими буквами: a, b, c, d, … .
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую a на рисунке 4 можно обозначить AC, а прямую b можно обозначить BC.
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
Ответ. Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: «отрезок AB», то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
В этой статье мы подробно остановимся на одном из первичных понятий геометрии – на понятии прямой линии на плоскости. Сначала определимся с основными терминами и обозначениями. Далее обсудим взаимное расположение прямой и точки, а также двух прямых на плоскости, приведем необходимые аксиомы. В заключении, рассмотрим способы задания прямой на плоскости и приведем графические иллюстрации.
Навигация по странице.
Прямая на плоскости — понятие.
Прежде чем дать понятие прямой на плоскости, следует четко представлять себе что же представляет собой плоскость. Представление о плоскости позволяет получить, к примеру, ровная поверхность стола или стены дома. Следует, однако, иметь в виду, что размеры стола ограничены, а плоскость простирается и за пределы этих границ в бесконечность (как будто у нас сколь угодно большой стол).
Если взять хорошо заточенный карандаш и дотронуться его стержнем до поверхности «стола», то мы получим изображение точки. Так мы получаем представление о точке на плоскости .
Так мы получаем представление о точке на плоскости .
Теперь можно переходить и к понятию прямой линии на плоскости .
Положим на поверхность стола (на плоскость) лист чистой бумаги. Для того чтобы изобразить прямую линию, нам необходимо взять линейку и провести карандашом линию на сколько это позволяют сделать размеры используемой линейки и листа бумаги. Следует отметить, что таким способом мы получим лишь часть прямой. Прямую линию целиком, простирающуюся в бесконечность, мы можем только вообразить.
Взаимное расположение прямой и точки.
Начать следует с аксиомы: на каждой прямой и в каждой плоскости имеются точки.
Точки принято обозначать большими латинскими буквами, например, точки А и F . В свою очередь прямые линии обозначают малыми латинскими буквами, к примеру, прямые a и d .
Возможны два варианта взаимного расположения прямой и точки на плоскости : либо точка лежит на прямой (в этом случае также говорят, что прямая проходит через точку), либо точка не лежит на прямой (также говорят, что точка не принадлежит прямой или прямая не проходит через точку).
Для обозначения принадлежности точки некоторой прямой используют символ «». К примеру, если точка А лежит на прямой а , то можно записать . Если точка А не принадлежит прямой а , то записывают .
Справедливо следующее утверждение: через любые две точки проходит единственная прямая.
Это утверждение является аксиомой и его следует принять как факт. К тому же, это достаточно очевидно: отмечаем две точки на бумаге, прикладываем к ним линейку и проводим прямую линию. Прямую, проходящую через две заданные точки (например, через точки А и В ), можно обозначать двумя этими буквами (в нашем случае прямая АВ или ВА ).
Следует понимать, что на прямой, заданной на плоскости, лежит бесконечно много различных точек, причем все эти точки лежат в одной плоскости. Это утверждение устанавливается аксиомой: если две точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Множество всех точек, расположенных между двумя заданными на прямой точками, вместе с этими точками называют отрезком прямой или просто отрезком . Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А
и В
являются концами отрезка, тогда этот отрезок можно обозначить АВ
или ВА
. Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Точки, ограничивающие отрезок, называются концами отрезка. Отрезок обозначают двумя буквами, соответствующими точкам концов отрезка. К примеру, пусть точки А
и В
являются концами отрезка, тогда этот отрезок можно обозначить АВ
или ВА
. Обратите внимание, что такое обозначение отрезка совпадает с обозначением прямой. Чтобы избежать путаницы, рекомендуем к обозначению добавлять слово «отрезок» или «прямая».
Для краткой записи принадлежности и не принадлежности некоторой точки некоторому отрезку используют все те же символы и . Чтобы показать, что некоторый отрезок лежит или не лежит на прямой пользуются символами и соответственно. К примеру, если отрезок АВ принадлежит прямой а , можно кратко записать .
Следует также остановиться на случае, когда три различных точки принадлежат одной прямой. В этом случае одна, и только одна точка, лежит между двумя другими. Это утверждение является очередной аксиомой. Пусть точки А
, В
и С
лежат на одной прямой, причем точка В
лежит между точками А
и С
. Тогда можно говорить, что точки А
и С
находятся по разные стороны от точки В
. Также можно сказать, что точки В
и С
лежат по одну сторону то точки А
, а точки А
и В
лежат по одну сторону от точки С
.
Тогда можно говорить, что точки А
и С
находятся по разные стороны от точки В
. Также можно сказать, что точки В
и С
лежат по одну сторону то точки А
, а точки А
и В
лежат по одну сторону от точки С
.
Для полноты картины заметим, что любая точка прямой делит эту прямую на две части – два луча . Для этого случая дается аксиома: произвольная точка О , принадлежащая прямой, делит эту прямую на два луча, причем две любые точки одного луча лежат по одну сторону от точки О , а две любые точки разных лучей – по разные стороны от точки О .
Взаимное расположение прямых на плоскости.
Сейчас ответим на вопрос: «Как могут располагаться две прямые на плоскости относительно друг друга»?
Во-первых, две прямые на плоскости могут совпадать .
Это возможно в том случае, когда прямые имеют по крайней мере две общие точки. Действительно, в силу аксиомы, озвученной в предыдущем пункте, через две точки проходит единственная прямая. Иными словами, если через две заданные точки проходят две прямые, то они совпадают.
Во-вторых, две прямые на плоскости могут пересекаться .
В этом случае прямые имеют одну общую точку, которую называют точкой пересечения прямых. Пересечение прямых обозначают символом «», к примеру, запись означает, что прямые а и b пересекаются в точке М . Пересекающиеся прямые приводят нас к понятию угла между пересекающимися прямыми . Отдельно стоит рассмотреть расположение прямых на плоскости, когда угол между ними равен девяноста градусам. В этом случае прямые называются перпендикулярными (рекомендуем статью перпендикулярные прямые, перпендикулярность прямых). Если прямая a перпендикулярна прямой b , то можно использовать краткую запись .
В-третьих, две прямые на плоскости могут быть параллельными.
Прямую линию на плоскости с практической точки зрения удобно рассматривать вместе с векторами. Особое значение имеют ненулевые векторы, лежащие на данной прямой или на любой из параллельных прямых, их называют направляющими векторами прямой . В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
В статье направляющий вектор прямой на плоскости даны примеры направляющих векторов и показаны варианты их использования при решении задач.
Также следует обратить внимание на ненулевые векторы, лежащие на любой из прямых, перпендикулярных данной. Такие векторы называют нормальными векторами прямой . О применении нормальных векторов прямой рассказано в статье нормальный вектор прямой на плоскости .
Когда на плоскости даны три и более прямых линии, то возникает множество различных вариантов их взаимного расположения. Все прямые могут быть параллельными, в противном случае некоторые или все из них пересекаются. При этом все прямые могут пересекаться в единственной точке (смотрите статью пучок прямых), а могут иметь различные точки пересечения.
Не будем подробно останавливаться на этом, а приведем без доказательства несколько примечательных и очень часто используемых фактов:
- если две прямые параллельны третьей прямой, то они параллельны между собой;
- если две прямые перпендикулярны третьей прямой, то они параллельны между собой;
- если на плоскости некоторая прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую прямую.

Способы задания прямой на плоскости.
Сейчас мы перечислим основные способы, которыми можно задать конкретную прямую на плоскости. Это знание очень полезно с практической точки зрения, так как на нем основывается решение очень многих примеров и задач.
Во-первых, прямую можно задать, указав две точки на плоскости.
Действительно, из аксиомы, рассмотренной в первом пункте этой статьи, мы знаем, что через две точки проходит прямая, и притом только одна.
Если в прямоугольной системе координат на плоскости указаны координаты двух несовпадающих точек, то есть возможность записать уравнение прямой, проходящей через две заданные точки .
Во-вторых, прямую можно задать, указав точку, через которую она проходит, и прямую, которой она параллельна. Этот способ справедлив, так как через данную точку плоскости проходит единственная прямая, параллельная заданной прямой. Доказательство этого факта проводилось на уроках геометрии в средней школе.
Если прямую на плоскости задать таким способом относительно введенной прямоугольной декартовой системы координат, то есть возможность составить ее уравнение. Об этом написано в статье уравнение прямой, проходящей через заданную точку параллельно заданной прямой .
В-третьих, прямую можно задать, если указать точку, через которую она проходит, и ее направляющий вектор.
Если прямая линия задана в прямоугольной системе координат таким способом, то легко составить ее каноническое уравнение прямой на плоскости и параметрические уравнения прямой на плоскости .
Четвертый способ задания прямой заключается в том, что следует указать точку, через которую она проходит, и прямую, которой она перпендикулярна. Действительно, через заданную точку плоскости проходит единственная прямая, перпендикулярная данной прямой. Оставим этот факт без доказательства.
Наконец, прямую на плоскости можно задать, указав точку, через которую она проходит, и нормальный вектор прямой.
Если известны координаты точки, лежащей на заданной прямой, и координаты нормального вектора прямой, то есть возможность записать общее уравнение прямой .
Список литературы.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Позняк Э.Г., Юдина И.И. Геометрия. 7 – 9 классы: учебник для общеобразовательных учреждений.
- Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б., Киселева Л.С., Позняк Э.Г. Геометрия. Учебник для 10-11 классов средней школы.
- Бугров Я.С., Никольский С.М. Высшая математика. Том первый: элементы линейной алгебры и аналитической геометрии.
- Ильин В.А., Позняк Э.Г. Аналитическая геометрия.
Copyright by cleverstudents
Все права защищены.
Охраняется законом об авторском праве. Ни одну часть сайта www.сайт, включая внутренние материалы и внешнее оформление, нельзя воспроизводить в какой-либо форме или использовать без предварительного письменного разрешения правообладателя.
Точка — это абстрактный объект, который не имеет измерительных характеристик: ни высоты, ни длины, ни радиуса.
 В рамках задачи важно только его местоположение
В рамках задачи важно только его местоположениеТочка обозначается цифрой или заглавной (большой) латинской буквой. Несколько точек — разными цифрами или разными буквами, чтобы их можно было различать
точка A, точка B, точка C
A B Cточка 1, точка 2, точка 3
1 2 3Можно нарисовать на листке бумаги три точки «А» и предложить ребёнку провести линию через две точки «А». Но как понять через какие? A A A
Линия — это множество точек. У неё измеряют только длину. Ширины и толщины она не имеет
Обозначается строчными (маленькими) латинскими буквами
линия a, линия b, линия c
a b cЛиния может быть
- замкнутой, если её начало и конец находятся в одной точке,
- разомкнутой, если её начало и конец не соединены
замкнутые линии
разомкнутые линии
Ты вышел из квартиры, купил в магазине хлеб и вернулся обратно в квартиру. Какая линия получилась? Правильно, замкнутая. Ты вернулся в исходную точку. Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб, зашёл в подъезд и разговорился с соседом. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.
Ты вышел из квартиры, купил в магазине хлеб. Какая линия получилась? Разомкнутая. Ты не вернулся в исходную точку.- самопересекающейся
- без самопересечений
самопересекающиеся линии
линии без самопересечений
- прямой
- ломанной
- кривой
прямые линии
ломанные линии
кривые линии
Прямая линия — это линия которая не искривляется, не имеет ни начала, ни конца, её можно бесконечно продолжать в обе стороны
Даже когда виден небольшой участок прямой, предполагается, что она бесконечно продолжается в обе стороны
Обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами — точками, лежащими на прямой
прямая линия a
aпрямая линия AB
B AПрямые могут быть
- пересекающимися, если имеют общую точку.
 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.- перпендикулярными, если пересекаются под прямым углом (90°).
- параллельными, если не пересекаются, не имеют общей точки.
параллельные линии
пересекающиеся линии
перпендикулярные линии
Луч — это часть прямой, которая имеет начало, но не имеет конца, её можно бесконечно продолжать только в одну сторону
У луча света на картинке начальной точкой является солнце
солнышко
Точка разделяет прямую на две части — два луча A A
Луч обозначается строчной (маленькой) латинской буквой. Или двумя заглавными (большими) латинскими буквами, где первая — это точка, с которой начинается луч, а вторая — точка, лежащая на луче
луч a
aлуч AB
B AЛучи совпадают, если
- расположены на одной и той же прямой,
- начинаются в одной точке,
- направлены в одну сторону
лучи AB и AC совпадают
лучи CB и CA совпадают
C B AОтрезок — это часть прямой, которая ограничена двумя точками, то есть она имеет и начало и конец, а значит можно измерить её длину.
 Длина отрезка — это расстояние между его начальной и конечной точками
Длина отрезка — это расстояние между его начальной и конечной точкамиЧерез одну точку можно провести любое число линий, в том числе прямых
Через две точки — неограниченное количество кривых, но только одну прямую
кривые линии, проходящие через две точки
B Aпрямая линия AB
B AОт прямой «отрезали» кусочек и остался отрезок. Из примера выше видно, что его длина — наикратчайшее расстояние между двумя точками. ✂ B A ✂
Отрезок обозначается двумя заглавными(большими) латинскими буквами, где первая — это точка, с которой начинается отрезок, а вторая — точка, которой заканчивается отрезок
отрезок AB
B AЗадача: где прямая , луч , отрезок , кривая ?
Ломанная линия — это линия, состоящая из последовательно соединённых отрезков не под углом 180°
Длинный отрезок «поломали» на несколько коротких
Звенья ломаной (похожи на звенья цепи) — это отрезки, из которых состоит ломанная. Смежные звенья — это звенья, у которых конец одного звена является началом другого. Смежные звенья не должны лежать на одной прямой.
Смежные звенья не должны лежать на одной прямой.
Вершины ломаной (похожи на вершины гор) — это точка, с которой начинается ломанная, точки, в которых соединяются отрезки, образующие ломаную, точка, которой заканчивается ломанная.
Обозначается ломанная перечислением всех её вершин.
ломанная линия ABCDE
вершина ломанной A, вершина ломанной B, вершина ломанной C, вершина ломанной D, вершина ломанной E
звено ломанной AB, звено ломанной BC, звено ломанной CD, звено ломанной DE
звено AB и звено BC являются смежными
звено BC и звено CD являются смежными
звено CD и звено DE являются смежными
A B C D E 64 62 127 52Длина ломанной — это сумма длин её звеньев: ABCDE = AB + BC + CD + DE = 64 + 62 + 127 + 52 = 305
Задача: какая ломанная длиннее
, а у какой больше вершин
? У первой линии все звенья одинаковой длины, а именно по 13см. У второй линии все звенья одинаковой длины, а именно по 49см. У третьей линии все звенья одинаковой длины, а именно по 41см.
Многоугольник — это замкнутая ломанная линия
Стороны многоугольника (помогут запомнить выражения: «пойти на все четыре стороны», «бежать в сторону дома», «с какой стороны стола сядешь?») — это звенья ломанной. Смежные стороны многоугольника — это смежные звенья ломанной.
Вершины многоугольника — это вершины ломанной. Соседние вершины — это точки концов одной стороны многоугольника.
Обозначается многоугольник перечислением всех его вершин.
замкнутая ломанная линия, не имеющая самопересечения, ABCDEF
многоугольник ABCDEF
вершина многоугольника A, вершина многоугольника B, вершина многоугольника C, вершина многоугольника D, вершина многоугольника E, вершина многоугольника F
вершина A и вершина B являются соседними
вершина B и вершина C являются соседними
вершина C и вершина D являются соседними
вершина D и вершина E являются соседними
вершина E и вершина F являются соседними
вершина F и вершина A являются соседними
сторона многоугольника AB, сторона многоугольника BC, сторона многоугольника CD, сторона многоугольника DE, сторона многоугольника EF
сторона AB и сторона BC являются смежными
сторона BC и сторона CD являются смежными
сторона CD и сторона DE являются смежными
сторона DE и сторона EF являются смежными
сторона EF и сторона FA являются смежными
A B C D E F 120 60 58 122 98 141Периметр многоугольника — это длина ломанной: P = AB + BC + CD + DE + EF + FA = 120 + 60 + 58 + 122 + 98 + 141 = 599
Многоугольник с тремя вершинами называется треугольником, с четырьмя — четырёхугольником, с пятью — пятиугольником и т. д.
д.
Понимание логики геометрии представлений—Справка | ArcGIS for Desktop
Доступно с лицензией Standard или Advanced.
Поскольку геометрические эффекты изменяют конфигурацию, а иногда и тип геометрии, понимание того, какой логике геометрии следуют правила представлений, очень важно. Геометрические эффекты выполняются последовательно. Результат одного геометрического эффекта становится исходным материалом для следующего, таким образом, вы можете построить цепочку геометрических эффектов, чтобы достичь соответствующей логики геометрии. Независимо от того, как геометрия динамически изменилась в ходе цепочки геометрических эффектов, результат последнего эффекта должен соответствовать типу геометрии слоя символов. Если в заголовке слоя символов появляется предупреждающий символ, это означает разъединение в логике геометрии. Только что добавленный слой символов не имеет никакой геометрии для обозначения..
Корректная и некорректная геометрия для комбинаций слоев символов| Полигональная геометрия | Линейная геометрия | Точечная геометрия | |
|---|---|---|---|
Слой символов заливки | Символы для внутренних частей полигона | Вызывает ошибку логики геометрии поскольку отсутствует геометрия полигона для заполнения | Вызывает ошибку логики геометрии поскольку отсутствует геометрия полигона для заполнения |
Слой линейных символов | Символы для границ полигона | Символы для линий | Вызывает ошибку логики геометрии поскольку отсутствует геометрия линии для отрисовки |
Слой маркерных символов | Размещает маркеры в полигонах с учетом стиля размещения маркеров | Размещает маркеры на линиях с учетом стиля размещения маркеров | Размещает маркеры на точках с учетом стиля размещения маркеров |
Например, добавление слоя заливок к линейному правилу представления приведет к появлению предупреждения, поскольку для заливки нет полигональных объектов. Чтобы восстановить логику, добавьте геометрический эффект линии-к полигону к каждому слою заливок или части глобальных эффектов к правилу. Однако обратное действие (добавление линейного слоя символов к полигональному правилу представления) предупреждение не создает, поскольку линейный символ будет применен к отображению границ полигональной геометрии.
Чтобы восстановить логику, добавьте геометрический эффект линии-к полигону к каждому слою заливок или части глобальных эффектов к правилу. Однако обратное действие (добавление линейного слоя символов к полигональному правилу представления) предупреждение не создает, поскольку линейный символ будет применен к отображению границ полигональной геометрии.
| Чтобы изменить входящую геометрию | На итоговую геометрию | Использовать | Пример |
|---|---|---|---|
Точка | Точка |
|
|
Точка | Линия |
|
|
Точка | Полигон |
|
|
Линия | Точка |
|
|
Линия | Линия |
|
|
Линия | Полигон |
|
|
Полигон | Точка |
|
|
Полигон | Линия |
|
|
Полигон | Полигон |
|
|
Связанные темы
Отзыв по этому разделу?| Элементы начертательной геометрии | Обозначения |
|---|---|
| Плоскости проекций: горизонтальная фронтальная профильная дополнительные, вводимые при замене плоскостей | П1 П2 П3 П4, П5 … |
| Оси проекций – линии пересечения плоскостей проекций горизонтальной и фронтальной горизонтальной и профильной фронтальной и профильной | x y z |
| Начало координат | O |
| Коэффициенты искажений в аксонометрии: по оси x по оси y по оси z | u v w |
| Проецируемые точки | A, B, С . .. .. |
| Вспомогательные точки | 1, 2, 3 … |
| Проекции точек на плоскостях проекций: горизонтальной фронтальной профильной | A1 или A′ A2 или A″ A3 или A′″ |
| Проекции точек на осях: x y z | Ax Ay Az |
| Прямые в пространстве | a, b, c … |
| Прямые в пространстве, заданные точками | AB, CD … |
| Проекции прямых на плоскостях проекций: горизонтальной фронтальной профильной | a1 a2 a3 |
| Проекции прямых, заданных точками, на плоскостях проекций: горизонтальной фронтальной профильной | А1B1 А2B2 А3B3 |
| Следы прямой и их проекции: горизонтальный фронтальный профильный | Н (Н1, Н2) F (F1, F2) P (P1, P2) |
| Углы наклона прямой к плоскостям проекций | α, β, γ . .. .. |
| Плоские фигуры | ABC, ABCD … или Ф1, Ф2 … |
| Проекции фигур на плоскостях проекций: горизонтальной фронтальной профильной | А1B1C1 А2B2C2 А3B3C3 |
| Плоскости | α, β, γ … |
| Следы плоскости и ее проекции: горизонтальный фронтальный профильный | αП1 или hα αП2 или fα αП3 или pα |
| Точки схода следов плоскости: горизонтальный фронтальный профильный | xα yα zα |
| Линии уровня: горизонталь фронталь профильная | h f p |
Векторные данные
Цель: | Ознакомиться с моделями векторных данных, используемыми в ГИС. | |
Основные понятия: | вектор, точка, полилиния, полигон, вершина, геометрия, масштаб, качество данных, символика, источник данных |
Обзор
Vector data provide a way to represent real world features within the GIS environment. A feature is anything you can see on the landscape. Imagine you are standing on the top of a hill. Looking down you can see houses, roads, trees, rivers, and so on (see figure_vector_landscape). Each one of these things would be a feature when we represent them in a GIS Application. Vector features have attributes, which consist of text or numerical information that describe the features.
Глядя на ландшафт, мы можем выделить основные объекты, например дороги, дома и деревья.
A vector feature has its shape represented using geometry. The geometry is
made up of one or more interconnected vertices. A vertex describes a position
in space using an X, Y and optionally z axis. Geometries which have
vertices with a Z axis are often referred to as 2.5D since they describe
height or depth at each vertex, but not both.
A vertex describes a position
in space using an X, Y and optionally z axis. Geometries which have
vertices with a Z axis are often referred to as 2.5D since they describe
height or depth at each vertex, but not both.
Когда геометрия объекта состоит из одного узла, это точечный объект (см. рисунок figure_geometry_point). Когда геометрия состоит из двух и более узлов, причем первый и последний узел не совпадают, это линейный объект (см. рисунок figure_geometry_polyline). Если объект образован тремя или более узлами, причем первый и последний узел совпадают, то это полигональный объект (см. рисунок figure_geometry_polygon).
Точечный объект описывается координатами X, Y и, опционально, Z. Атрибуты точки описывают её, например, что это дерево или фонарный столб.
Полилиния это последовательность соединённых узлов. Каждый узел имеет координаты X, Y (и, опционально, Z). Описывают полилинию её атрибуты.
Описывают полилинию её атрибуты.
Полигон, как и полилиния, явялется последовательностью узлов. Однако, в полигоне первый и последний узел всегда совпадают.
Возвращаясь к рисунку ландшафта, показаному выше, вы теперь должны суметь распознать на нем различные типы геометрий, используемых в ГИС (см. рисунок figure_geometry_landscape).
Объекты ландшафта и их представление в ГИС. Реки (голубые) и дороги (зелёные) представляются линиями, деревья — точками (красными) и дома — полигонами (белыми).
Точечные объекты в деталях
Первое, что необходимо понять, когда речь идет о точечных объектах, что, их использование зависит от масштаба. Рассмотрим это на примере городов. Если у нас есть мелкомасштабная карта (которая охватывает большую область), города лучше обозначать точками. Однако, при увеличении карты и переходе к более крупным масштабам, границы городов лучше отображать как полиногы.
Выбор точек для представления объектов реального мира зависит от используемого масштаба (как далеко вы находитесь от объекта), удобства (создание точечных объектов занимает меньше времени) и типа объектов (некоторые вещи, например телефонные будки, нет смысла хранить в виде полигонов).
Как было показано на рисунке figure_geometry_point, точечный объект имеет координаты X, Y, и опционально Z. Координаты X и Y зависят от используемой системы координат (Coordinate Reference System, CRS). Системы координат будут рассмотрены немного позже. Сейчас для простоты будем считать, что система координат это способ точно указать где именно находится объект на поверхности земли. Одной из наиболее распространенных систем координат является широта-долгота. Линии долготы идут от Северного полюса к Южному. Линии широты идут с Востока на Запад. Вы можете точно описать свое местонахождение, сообщив кому-либо свою долготу (X) и широту (Y). Если сделать такие же измерения для дерева или телефонной будки, а затем отметить их на карте, вы получите точечный объект.
Так как мы знаем, что Земля не плоская, полезно добавлять к точкам и координату Z. Она описывает высоту объекта над уровнем моря.
Полилинии в деталях
Точечный объект это один узел, полилиния же состоит из двух и более узлов. Полилиния это путь, проходящий через каждый узел, как показано на рисунке figure_geometry_polyline. Когда соединяется два узла, создаётся линия. При соединении нескольких таких линий, они образуют «линию линий» или полилинию.
Полилиния это путь, проходящий через каждый узел, как показано на рисунке figure_geometry_polyline. Когда соединяется два узла, создаётся линия. При соединении нескольких таких линий, они образуют «линию линий» или полилинию.
Полилинии используются для отображения линейных объектов, таких как дороги, реки, горизонтали, тропинки, авиамаршруты и т.д. Иногда к полилиниям предъявляются дополнительные требования помимо основных требований к геометрии. Так, горизонтали могут соприкасаться (например, на скалах) но не должны пересекаться. Аналогично полилинии, используемые для хранения дорожной сети, должны быть соединены на перекрестках. В некоторых ГИС-приложениях вы можете задавать такие специальные правила для объектов и ГИС будет следить за тем, чтобы полилинии соответствовали им.
Если узлы изогнутой полилинии находятся на большом расстоянии друг от друга, она может выглядеть зубчатой или неровной в зависимости от масштаба (см. рисунок figure_polyline_jagged). Поэтому важно выполнять оцифровку полилиний с расстоянием между узлами, которое будет достаточным для масштаба, в котором данные будут использоваться.
рисунок figure_polyline_jagged). Поэтому важно выполнять оцифровку полилиний с расстоянием между узлами, которое будет достаточным для масштаба, в котором данные будут использоваться.
Полилинии на мелких масштабах (1:20000 слева) выглядят сглаженными. При увеличении масштаба (1:500 справа) они становятся ломаными.
Атрибуты полилинии описывают её свойства или характеристики. Например, полилиния дороги может иметь атрибуты, описывающие тип поверхности, количество полос и направления движения и т.д. ГИС могут использовать эти атрибуты для отображения полилинии подходящим цветом или стилем.
Полигоны в деталях
Полигональные объекты это замкнутые области такие как плотины, острова, границы стран и подобные. Как и полилинии, полигональные объекты создаются из ряда узлов, соединенных линией. Однако, так как полигон всегда описывает замкнутую область, первый и последний узел всегда должны совпадать! Полигоны часто имеют общую геометрию — границы, общие для нескольких соседних полигонов. Многие ГИС-приложения могут следить за тем, чтобы границы смежных полигонов совпадали. Более подробно это рассматривается в разделе Топология этого руководства.
Многие ГИС-приложения могут следить за тем, чтобы границы смежных полигонов совпадали. Более подробно это рассматривается в разделе Топология этого руководства.
Как точки и полилинии, полигоны имеют атрибуты. Атрибуты описывают каждый полигон. Например, плотина может иметь атрибуты со значениями глубины и качества воды.
Векторные данные в слоях
Now that we have described what vector data is, let’s look at how vector data is
managed and used in a GIS environment. Most GIS applications group vector features
into layers. Features in a layer have the the same geometry type (e.g. they
will all be points) and the same kinds of attributes (e.g. information about what
species a tree is for a trees layer). For example if you have recorded the
positions of all the footpaths in your school, they will usually be stored
together on the computer hard disk and shown in the GIS as a single layer. This
is convenient because it allows you to hide or show all of the features for that
layer in your GIS application with a single mouse click.
Редактирование векторных данных
ГИС-приложения позволяют создавать и редактировать геометрии объектов слоя — этот процесс называется оцифровка и будет подробно рассмотрен позже. Если слой содержит полигоны (например, здания), ГИС-приложение позволит вам создать новые полигоны в этом слое. Аналогично, если вы захотите изменить форму объекта, приложение разрешить сделать это только в том случае, если измененная геометрия будет оставаться корректной. К примеру, вы не сможете отредактировать линию так, чтобы она состояла только из одного узла — вспомните предыдущий материал: линия должна иметь как миниму два узла.
Создание и редактирование векторных данных является важной функцией ГИС, т.к. это один из основных способов получить необходимые данные. Например, вы занимаетесь мониторингом загрязнений в речке. Вы можете использовать ГИС для оцифровки всех стоков ливневых вод (в виде точечного слоя). Также вы можете оцифровать саму речку (как линейный объект). И, наконец, можно снять показания уровня кислотности (pH) вдоль реки и нанести эти места на карту (тоже в виде точечного слоя).
И, наконец, можно снять показания уровня кислотности (pH) вдоль реки и нанести эти места на карту (тоже в виде точечного слоя).
Помимо создания собственных данных можно использовать существующие свободные векторные данные. Так, вы можете получить данные, используемые на картах масштаба 1:50000 в Управлении геодезии и картографии.
Масштаб и векторные данные
Масштаб является важной характеристикой векторных данных при работе в ГИС. Данные обычно получают либо путем оцифровки существующих карт, либо обработкой данных от устройств системы глобального позиционирования. Карты имеют различные масштабы, поэтому при переносе векторных данных с карты в ГИС (например, путем оцифровки бумажной карты), цифровые данные будут иметь тот же масштаб, что и исходная карта. Этот эффект демонстрируется на рисунках figure_vector_small_scale и figure_vector_large_scale. Выбор неправильного масштаба может стать источником многих проблем. Например, при использованиии векторных данных, показанных на рисунке figure_vector_small_scale, в планировании мероприятий по охране водно-болотных угодий может привести к тому, что важные части болот просто не будут учтены! С другой стороны, если вы создаёте карту региона, использование данных оцифрованных в масштабе1:1000 000 будет разумным и поможет сэкономить время и силы при оцифровке.
Векторные данные (красные линии), оцифрованные с мелкомасштабной (1:1000000) карты.
Векторные данные (зелёные линии), оцифрованные с крупномасштабной (1:50000) карты.
Символика
При добавлении векторных слоёв в ГИС они будут отображены базовыми символами со случайной расцветкой. Одно из преимуществе ГИС состоит в том, что вы легко можете создавать персонализованные карты. ГИС позволяет задать цвета, наилучшим образом отвечающие типу объектов (например, можно отображать водные объекты голубым цветом). Кроме того, ГИС позволяет задавать условные знаки. Так, если у вас есть точечный слой с информацией о деревьях, положение каждого дерева можно обозначить значком дерева, вместо стандартного кружка, который используется ГИС при первом открытии слоя (см. рисунки figure_vector_symbology, figure_generic_symbology и figure_custom_symbology).
В ГИС можно использовать диалог (похожий на приведенный здесь) для настройки отображения вашего слоя.
Когда слой (например, слой деревьев) загружается первый раз, ГИС отображает его обычным знаком.
После настройки отображения понять, что слой представляет деревья, намного легче.
Символика это удобный инструмент, делающий карты наглядными и упрощающий работу с ГИС-данными. В следующих главах ((Атрибуты векторных данных) мы более подробно рассмотрим как символика может помочь в понимании ГИС-данных.
Что можно делать в векторными данными в ГИС?
В самом простом случае использовать векторные данные в ГИС можно точно так же, как и обычную топографическую карту. Настоящая сила ГИС проявляется когда нам потребуется получить ответы на вопросы вида: «какие дома попадали в зону затопления на протяжении 100 лет?», «где разместить больницу, чтобы она была доступна наибольшему числу пациентов?», «кто из учащихся проживает в заданном районе?». ГИС является отличным инструментом для получения ответов на подобные вопросы при помощи векторных данных. Обычно процесс получения ответов на такие вопросы называют пространственным анализом. В последующих разделах он будет рассмотрен подробнее.
Проблемы векторных данных
При работе с векторными данными могут возникать некоторые проблемы. Мы уже упоминали о проблемах, связаных с оцифровкой данных в различных масштабах. Кроме того, векторные данные требуют обслуживания и доработки, чтобы быть уверенными в их точности и надежности. Неточные векторные данные могут быть получены при использовании неправильно настроенных инструментов оцифровки; когда люди, выполняющие оцифровку, недостаточно аккуратны; когда на процесс сбора и подготовки данных выделено недостаточно средств и т.д.
Если ваши векторные данные низкого качества, это часто заметно при просмотре данных в ГИС. Например, «щели» могут возникать в случае, если ребра двух соседних полигонов не соприкасаются (см. figure_vector_slivers).
Щели возникают, когда вершины двух полигонов на общих границах не совпадают. На мелких масштабах (например, 1 слева) вы можете не заметить ошибок. На крупных масштабах щели выглядят как белые полосы между полигонами (2 справа).
Overshoots can occur when a line feature such as a road does not meet another road exactly at an intersection. Undershoots can occur when a line feature (e.g. a river) does not exactly meet another feature to which it should be connected. Figure figure_vector_shoots demonstrates what undershoots and overshoots look like.
Недоводы (1) возникают при оцифровке линий, которые должны быть соединены, но не смотря на это не соприкасаются. Перехлесты (2) возникают когда линия пересекает другую линию, с которой она должна была быть соединена.
Чтобы подобные ошибки не возникали, важно выполнять оцифровку данных очень внимательно и аккуратно. В разделе, посвященном топологии, мы рассмотрим некоторые из этих ошибок более подробно.
Что мы узнали?
Подведём итоги:
Векторные данные использутся для отображения объектов реального мира в ГИС.
Векторные объекты имеют геометрию одного из типов: точка, линия или полигон.

Каждый объект имеет атрибуты, описывающие его.
Геометрия объекта состоит из набора узлов.
Точечная геометрия состоит из одного узла (X, Y и, необязательно, Z).
Линейная геометрия состоит из двух и более узлов, формирующих линию.
Полональная геометрия состоит как минимум из четырёх узлов, описывающих замкнутую область. Первый и последний узел всегда одинаковы.
Выбор того или иного типа геомерии зависит от масштаба, удобства и целей использования данных в ГИС.
Большинство ГИС-приложений не позволяют хранить различные типы геометрий в одном слое.
Оцифровка это процесс создания цифровых векторных данных, путем их рисования в ГИС.
Векторные данные могут иметь проблемы с качеством, такие как перехлесты, недоводы и щели, о которых необходимо помнить.

Векторые данные могут использоваться для пространственного анализа в ГИС, например, для поиска ближашей больницы или школы.
Концепция векторных данных показана на рисунке figure_vector_summary.
Эта диаграмма показывает, как ГИС-приложение работает с векторными данными.
Попробуйте сами!
Вот некоторые идеи для заданий:
Используя топографическую карту района (похожий на рисунок figure_sample_map), проверьте, что учащиеся могут идентифицировать различные типы векторных данных.
Подумайте, как вы будете создавать векторные объекты, соответвствующие объектам школьного двора, в ГИС. Создайте таблицу различных объектов, расположенных вокруг школы и попросите учащихся определить какой тип геометрии лучше всего использовать для этих объектов в ГИС. В качестве примера используйте таблицу table_vector_1.
Можете ли вы идентифицировать два точечных и один полигональный объект на этой карте?
Реальный объект | Подходящий тип геометрии |
|---|---|
Флагшток | |
Футбольное поле | |
Тропинки вокруг школы | |
Места расположения кранов | |
И т. |
Table Vector 1: Создайте аналогичную таблицу (оставив поле с типом геометрии пустым) и попросите учащихся определить подходящий тип геометрии.
Стоит учесть
Если у вас нет компьютера, можно использовать топографическую карту и прозрачную пленку, чтобы рассказать о векторных данных.
Дополнительная литература
Подробную информацию о работе с векторными данными в QGIS можно найти в Руководстве пользователя QGIS.
Что дальше?
В следующем разделе мы познакомимся с атрибутивными данными и узнаем как использовать их для описания векторных объектов.
Обозначения и символы в планиметрии — видео и расшифровка урока
Линейные отношения
Параллельные линии — это линии, которые никогда не пересекаются и не пересекаются. Перпендикулярные линии пересекаются под прямым углом. Вместо того, чтобы выписывать слова «параллельно» и «перпендикулярно», мы используем геометрическую запись.
Две параллельные линии обозначаются двумя вертикальными линиями.
Символ двух перпендикулярных линий — перевернутая буква T.
Части линии
Отрезок линии — это участок линии между двумя конечными точками. Чтобы пометить сегмент линии, определите две конечные точки и поместите над ними символ сегмента.
Другая часть линии называется лучом. Луч имеет одну конечную точку и всегда продолжается в одном направлении. Чтобы выразить это, используйте первую букву как конечную точку, а вторую букву как любую точку дальше по лучу.
На этом изображении луч AB не совпадает с лучом BA , потому что у них две разные конечные точки.
Геометрические фигуры
Плоскость — это плоская поверхность, существующая в пространстве. Думайте о плоскости как о потолке, полу или стене комнаты. Плоскости могут пересекаться друг с другом, а могут никогда не соприкасаться. Плоскость названа с использованием трех не лежащих на одной прямой точек , что означает, что невозможно провести линию через точки.
Думайте о плоскости как о потолке, полу или стене комнаты. Плоскости могут пересекаться друг с другом, а могут никогда не соприкасаться. Плоскость названа с использованием трех не лежащих на одной прямой точек , что означает, что невозможно провести линию через точки.
Углы образованы двумя лучами с одинаковыми концами. Все углы имеют вершину , которая является конечной точкой двух лучей. Если в вершине есть только один угол, мы можем идентифицировать угол, используя одну заглавную букву, где точка вершины — это имя угла. Мы также можем определить угол, используя три заглавные буквы, где первая и третья буквы — это точки на лучах, образующих углы, а вторая буква — это вершина.Третий способ определить угол — вставить число внутрь угла.
Следующий угол можно определить четырьмя различными способами, но мы всегда помещаем символ угла перед буквами-идентификаторами.
Чтобы идентифицировать треугольник, нарисуйте треугольник перед тремя вершинами треугольника.
Единицы измерения
Когда речь идет о единицах измерения, длина сегмента может быть выражена как две конечные точки сегмента без символа над ним.
При обсуждении меры угла поставьте m перед символом угла, чтобы показать меру.
Конгруэнтные фигуры имеют одинаковый размер и одинаковую форму. Меры углов двух конгруэнтных треугольников равны. Пока углы равны, меры равны. Конгруэнтность относится к формам, а равенство — к числам.
Обратите внимание, что символ конгруэнтности имеет волнистую линию над знаком равенства.
Символ равенства — это просто знак равенства.
Длины сторон двух равных треугольников равны. Однако стороны не равны; вместо этого стороны конгруэнтны.
Однако стороны не равны; вместо этого стороны конгруэнтны.
Итоги урока
Давайте повторим.Целью геометрической нотации является определение геометрических фигур или форм и мер этих фигур, таких как их длина или размеры. Вот список всех геометрических обозначений, обсуждаемых в этом уроке.
Точки и линии — определение, примеры, часто задаваемые вопросы
В геометрии точка – это место, представленное точкой. У точки нет длины, ширины, формы или размера, у нее есть только положение.Когда две отдельные точки соединяются, они образуют линию.
Что такое точка и линия?
Понятие точек и линий важно для понимания геометрических фигур. С помощью точек мы можем обозначать и идентифицировать геометрические фигуры, а с помощью линий мы можем рисовать фигуры.
Точка
Точка определяется как местоположение в любом пространстве и представляется точкой ( . ). У него нет ни длины, ни высоты, ни формы, ни размера.Он знаменует собой начало рисования любой фигуры или формы и помечен заглавными буквами.
Строка
Ряд точек, соединенных прямым путем, определяется как линия. Линия обычно определяется двумя точками. Он может быть обозначен одной буквой в нижнем регистре или двумя заглавными буквами. Линия не имеет толщины и может бесконечно простираться в обоих направлениях. Длина линии не определена, и она может иметь бесконечное количество точек. Обратите внимание на следующий рисунок, чтобы узнать разницу между точкой и линией.
Типы точек и линий
В геометрии есть разные типы точек. Давайте обсудим их, чтобы идентифицировать их легко.
Коллинеарные и неколлинеарные точки
Если три или более точек лежат на одной прямой, то такие точки называются коллинеарными. Если группа точек не лежит на одной прямой, эти точки называются неколлинеарными.
Если группа точек не лежит на одной прямой, эти точки называются неколлинеарными.
Копланарные точки и некомпланарные точки
Если группа точек лежит в одной плоскости, то они называются компланарными точками.Множество точек, не лежащих в одной плоскости, являются некомпланарными точками.
Обратите внимание на следующий рисунок, на котором показаны различные типы точек.
Типы линий
Так же, как и различные типы точек, существуют различные типы линий, которые можно легко отличить на основе их уникальных свойств.
- Горизонтальная линия – Линия, которая отображается слева направо или справа налево и параллельна оси x на плоскости, называется горизонтальной линией.
- Вертикальная линия . Линия, которая отображается сверху вниз или снизу вверх и параллельна оси Y на плоскости, называется вертикальной линией.
- Пересекающиеся линии . Когда две линии пересекаются и встречаются в одной точке, они называются пересекающимися линиями.
 Точка, в которой они встречаются, называется точкой пересечения.
Точка, в которой они встречаются, называется точкой пересечения. - Перпендикулярные линии . Когда две линии пересекаются точно под углом 90°, они называются перпендикулярными линиями.
- Параллельные прямые – Две прямые называются параллельными, если они не пересекаются ни в одной точке и равноудалены друг от друга.
Обратите внимание на приведенный ниже рисунок, на котором показаны различные типы линий.
Советы по точкам и линиям
- Точка не имеет длины, ширины, формы или размера.
- Когда две отдельные точки соединяются, они образуют линию.
- Линия бесконечно простирается в обоих направлениях.
- Параллельные линии не пересекаются.
- Линии, которые пересекаются друг с другом под углом 90°, называются перпендикулярными линиями.
- Две или более точек, лежащих на одной прямой, являются коллинеарными.
- Две или более точек, лежащих в одной плоскости, являются точками в одной плоскости.

Связанные статьи о точках и линиях
Ознакомьтесь с этими интересными статьями, чтобы узнать больше о точках и линиях.
Часто задаваемые вопросы по пунктам и линиям
Сколько точек требуется для определения линии?
Линия идентифицируется и определяется двумя точками, которые соединяются, образуя линию.Вот почему название строки обычно состоит из двух заглавных букв.
Сколько конечных точек в линии?
Линия не имеет конечной точки, так как она может продолжаться бесконечно в обоих направлениях.
Что мы называем точками, которые не лежат на одной линии?
Точки, не лежащие на одной прямой, называются неколлинеарными.
Каковы реальные примеры точек и линий?
Несколько реальных примеров точек — это кончик карандаша, кончик иглы или местоположение места на карте.Несколько реальных примеров линий — это провод или край стола.
Какие бывают типы линий в геометрии?
В геометрии существуют различные типы линий, которые можно идентифицировать на основе их свойств, например, горизонтальные линии, вертикальные линии, параллельные линии, перпендикулярные линии и пересекающиеся линии.
Система обозначения инструмента ASA
Геометрия режущего инструмента в основном относится к некоторым конкретным углам, относящимся к режущим кромкам.Определенные признаки режущего инструмента, написанные определенным и стандартизированным образом, используются для обозначения этого инструмента. Существуют различные стандартные системы обозначения токарного инструмента с одной точкой; у каждого есть определенные преимущества и недостатки. Обычно используемые системы для обозначения токарного инструмента включают систему ASA, систему ORS, систему NRS и т. д., как указано ниже.
СистемаПолная форма ASA — Американская ассоциация стандартов.
Американской ассоциации стандартов (ASA) использует три взаимно перпендикулярные плоскости в качестве эталона для измерения различных углов токарного инструмента с одной точкой (SPTT).Эти три самолета и их основные характеристики перечислены ниже.
- Опорная плоскость (π R ) — это плоскость, перпендикулярная вектору скорости резания (V c ).

- Продольная плоскость станка (π X ) — это плоскость, перпендикулярная базовой плоскости (π R ) и вдоль направления продольной подачи для внешней прямой токарной обработки.
- Поперечная плоскость станка (π Y ) — это плоскость, перпендикулярная базовой плоскости (π R ) и вдоль направления поперечной подачи для внешней прямой токарной обработки.Таким образом, все три плоскости взаимно перпендикулярны.
ASA определяет два разных передних угла, два разных задних угла, два разных угла режущей кромки и значение радиуса вершины в дюймах. Различные функции одноточечного токарного инструмента (SPTT), отображаемые системой ASA, представлены ниже.
- Боковой передний угол (γ X ) — это угол ориентации передней поверхности инструмента от базовой плоскости (π R ), измеренный в продольной плоскости станка (π X ).

- Задний передний угол (γ Y ) — это угол ориентации передней поверхности инструмента от базовой плоскости (π R ), измеренный на поперечной плоскости станка (π Y ).
- Боковой задний угол (α X ) — это угол ориентации главной боковой поверхности инструмента от вектора скорости резания (V c ) и измеренный в продольной плоскости станка (π X ).
- Задний задний угол (α Y ) — это угол ориентации главной боковой поверхности инструмента от вектора скорости резания (V c ) и измеренный на поперечной плоскости станка (π Y ).
- Угол подхода (Φ s ) — это угол между главной режущей кромкой и поперечной плоскостью станка (π Y ), измеренный на опорной плоскости (π R ).
- Угол торцевой режущей кромки (Φ e ) — это угол между вспомогательной режущей кромкой и продольной плоскостью станка (π X ), измеренный на опорной плоскости (π R ).

- Радиус носа (r)— Это не что иное, как кривизна на кончике инструмента.Следует отметить, что в системе ASA значение радиуса носа выражается в дюймах.
Все вышеупомянутые семь функций токарного инструмента указаны в определенной последовательности, как показано ниже. Такая спецификация также называется номенклатурой инструмента или сигнатурой инструмента. Последовательность обозначения должна соблюдаться строго. Однако разные люди могут использовать разные обозначения для разных углов, сохраняя исходную последовательность неизменной.
Для примера номенклатуры инструментов следует учитывать несколько моментов.Прежде всего, это значение углов просвета. Углы просвета всегда положительны — они не могут быть нулевыми или отрицательными. Обычно он колеблется в пределах 3º – 15º. Передний угол может иметь положительное, отрицательное или даже нулевое значение. Один пример системы обозначения инструмента ASA и интерпретации углов инструмента из такой номенклатуры показан на следующем рисунке.
Рассмотрим другой пример. Скажем, типичный токарный инструмент может быть указан в системе ASA как:
–8º, 6º, 5º, 10º, 15º, 30º, 1/8 (дюйм)
Следовательно, при интерпретации мы можем написать:
- Задний передний угол (γ Y ) = –8º
- Боковой передний угол (γ X ) = 6º
- Задний задний угол (α Y ) = 5º
- Угол бокового просвета (α X ) = 10º
- Угол торцевой режущей кромки (Φ и ) = 15º
- Угол подхода (Φ с ) = 30º
- Радиус носа (r) = 1/8 дюйма
- Книга: Принципы машиностроения С.Сингх (С. Шанд).
- Книга: Механическая обработка и станки А. Б. Чаттопадхьяя (Wiley).
- Книга: Резка металла: теория и практика А. Бхаттачарьи (Новое центральное книжное агентство).
- Книга: Производственные процессы Дж. П. Каушиша (PHI).
- Книга: Производственная наука М. И.
 Хака и С. Хана (PHI).
Хака и С. Хана (PHI).
Мы не можем найти эту страницу
(* {{l10n_strings.REQUIRED_FIELD}})
{{l10n_strings.CREATE_NEW_COLLECTION}}*
{{l10n_strings.ADD_COLLECTION_DESCRIPTION}}
{{l10n_strings.COLLECTION_DESCRIPTION}} {{addToCollection.description.length}}/500 {{l10n_strings.TAGS}} {{$элемент}} {{l10n_strings.ПРОДУКТЫ}} {{l10n_strings.DRAG_TEXT}}{{l10n_strings.DRAG_TEXT_HELP}}
{{l10n_strings. LANGUAGE}}
{{$выбрать.выбранный.дисплей}}
LANGUAGE}}
{{$выбрать.выбранный.дисплей}}{{article.content_lang.display}}
{{l10n_strings.АВТОР}}{{l10n_strings.AUTHOR_TOOLTIP_TEXT}}
{{$выбрать.выбранный.дисплей}} {{l10n_strings.CREATE_AND_ADD_TO_COLLECTION_MODAL_BUTTON}} {{l10n_strings.CREATE_A_COLLECTION_ERROR}}Определение дуги в геометрии | Примеры и как определить
Круги просты, но у них есть части. Одна часть — это дуга, отрезок круга, кусок его окружности.Сами дуги бывают разных типов, например, большие дуги, полуокружности и малые дуги.
Одна часть — это дуга, отрезок круга, кусок его окружности.Сами дуги бывают разных типов, например, большие дуги, полуокружности и малые дуги.
Содержание
- Окружности и окружности
- Полукруги и дуги
- Идентификация дуг
- Измерительные дуги
Окружности и окружности
Окружность — это множество всех точек, равноудаленных от данной точки. Окружность это расстояние по окружности.
[вставьте рисунок круга с изогнутой стрелкой вокруг него, чтобы показать длину окружности]
Круги могут иметь углы, образованные двумя радиусами.Это 90 207 центральных углов 90 208, и они почти всегда обозначаются либо их точным измерением угла (или радиана), либо греческой буквой тета, ϴ:
.[вставить чертеж окружности с центральным углом ϴ]
Окружности также могут иметь углы, образованные двумя хордами (отрезками прямой с концами на окружности) с общей конечной точкой на окружности. Эти углы называются вписанными углами :
Эти углы называются вписанными углами :
[вставить чертеж вписанного угла]
Как центральные углы, так и вписанные углы образуют большую и малую дуги.
Полуокружности и дуги
Дуга — это часть окружности, которая меньше всей окружности. Поскольку это допускает почти все возможные части, математики разбивают дуги следующим образом:
- Второстепенная дуга — Дуга с углом, меньшим или равным 180° или π радианам
- Полуокружность — Дуга, имеющая размер ровно 180° или π радиан, что исключает обозначение какой-либо части окружности как большой или малой
- Большая дуга — дуга, размер которой больше или равен 180° или π радианам
[Вставьте два рисунка: на одном изображен круг, разделенный на малую и большую дуги, а на другом — круг, разделенный на два полукруга]
Идентификация дуг
В типичном рисунке круга читатель понимает, что речь идет о малой дуге. На этом рисунке нас интересует малая дуга, определяемая центральным углом ϴ:
На этом рисунке нас интересует малая дуга, определяемая центральным углом ϴ:
[вставить рисунок окружности с центральным углом ϴ, образующим острый угол, с выделенной малой дугой этого угла]
Для маркировки малой дуги требуются только ее конечные точки на окружности. Вот малая дуга GO:
[вставить рисунок окружности с малой дугой GO, помеченной и выделенной]
Если вам нужна главная дуга, выберите и пометьте обе конечные точки дуги и случайную точку между ними.Здесь у нас есть главная дуга FUN:
[вставить рисунок окружности с тремя точками F, U, N на большой дуге]
Дуги обычно обозначаются в письменной форме с помощью их точек (две для малой дуги, три для большой дуги), а затем рисуется крошечная короткая дуга, проведенная над буквами:
Измерительные дуги
Дуги имеют два размера:
- Уголок
- Длина
Одним из способов измерения дуги является центральный угол окружности. Это угол дуги . Вы помещаете строчную букву m перед письменной формой дуги, например:
Это угол дуги . Вы помещаете строчную букву m перед письменной формой дуги, например:
Таким образом, вы могли бы написать mFUN = 45° и сказать: «Большая дуга FUN измеряет 45 градусов».
Другой способ измерения дуг — их расстояние по окружности окружности. Это длина дуги . Чтобы написать длину дуги словами, вы ставите маленькую букву l перед письменной формой, например:
.[см. рисунок 2, отправленный по электронной почте, и поместите графическую дугу над lGO ниже]
Таким образом, вы можете написать lGO = 13.4 см, и вы сказали бы: «Длина дуги GO составляет 13,4 сантиметра».
Следующий урок:
Как найти длину дуги
7.6: Правила последовательности — обозначение E, Z
Когда каждый атом углерода в двойной связи присоединен к водороду и неводородному заместителю, геометрические изомеры могут быть идентифицированы с использованием номенклатуры цис-транс , обсуждаемой в предыдущий раздел. Однако, когда двойная связь присоединена к трем или четырем неводородным заместителям, есть несколько примеров, когда цис-транс номенклатура неэффективна для описания ориентации заместителей в геометрических изомерах.В этих ситуациях используется строгая система ИЮПАК для обозначения изомеров алкенов, называемая системой E/Z. Система E/Z анализирует два заместителя, присоединенных к каждому атому углерода в двойной связи, и присваивает каждому высокий или низкий приоритет. Если группа с более высоким приоритетом на обоих атомах углерода в двойной связи та же самая сторона , то говорят, что алкен имеет изомер Z (от немецкого zusammen = вместе). Вы можете думать о Z как о Zame Zide, чтобы запомнить его. Если группа с более высоким приоритетом находится на противоположных сторонах , то алкен имеет изомер E (от немецкого entgegen = противоположный).
Однако, когда двойная связь присоединена к трем или четырем неводородным заместителям, есть несколько примеров, когда цис-транс номенклатура неэффективна для описания ориентации заместителей в геометрических изомерах.В этих ситуациях используется строгая система ИЮПАК для обозначения изомеров алкенов, называемая системой E/Z. Система E/Z анализирует два заместителя, присоединенных к каждому атому углерода в двойной связи, и присваивает каждому высокий или низкий приоритет. Если группа с более высоким приоритетом на обоих атомах углерода в двойной связи та же самая сторона , то говорят, что алкен имеет изомер Z (от немецкого zusammen = вместе). Вы можете думать о Z как о Zame Zide, чтобы запомнить его. Если группа с более высоким приоритетом находится на противоположных сторонах , то алкен имеет изомер E (от немецкого entgegen = противоположный).
Обратите внимание: если оба заместителя и углерод с двойной связью одинаковы, изомеризация E/Z невозможна. Кроме того, если возможна изомерия E / Z, замена заместителей, присоединенных к углероду с двойной связью, превращает один изомер в другой.
Кроме того, если возможна изомерия E / Z, замена заместителей, присоединенных к углероду с двойной связью, превращает один изомер в другой.
Приоритет заместителей для системы E,Z назначается с использованием правил последовательности Кана-Ингольда-Прелога (CIP). Это те же самые правила, которые используются для назначения конфигураций R/S хиральным центрам в Раздел 5.5 . Здесь представлен краткий обзор использования правил CIP для определения конфигурации алкена, но более подробно правила CIP обсуждаются в разделе 5 стандарта .5 .
Правило 1) Правило «первой точки различия»
Во-первых, определите два закрепителя на каждом углероде с двойной связью отдельно. Ранжируйте эти заместители на основе атома , который непосредственно присоединен к углероду двойной связи. Заместитель, атом которого имеет более высокий атомный номер, имеет преимущество перед заместителем, атом которого имеет более низкий атомный номер.
Что имеет более высокий приоритет по правилам CIP: C с прикрепленными к нему O и 2 H или C с тремя C? Первый C имеет один атом высокого приоритета, но также два атома низкого приоритета.Как они «уравновешиваются»? Ответ на этот вопрос требует четкого понимания того, как выполняется ранжирование. Простой ответ заключается в том, что первое отличие имеет значение; О выигрывает.
Чтобы проиллюстрировать это, рассмотрим молекулу слева. Двойная связь здесь E или Z ? На левом конце двойной связи Br > C. А вот правый конец двойной связи требует тщательного анализа.
На правом конце первый атом, присоединенный к двойной связи, представляет собой C в каждом положении.Галстук, поэтому смотрим, что присоединено к этому первому С. Для верхнего С это ССС (поскольку тройная связь считается трижды). Для более низкого C это OHH — перечислено в порядке от атома с высоким приоритетом к низкому. OHH имеет более высокий приоритет, чем CCC, из-за первого атома в списке. То есть О нижней группы превосходит С верхней группы. Другими словами, O является атомом с наивысшим приоритетом среди всех атомов в этом сравнении; таким образом, O «побеждает».
То есть О нижней группы превосходит С верхней группы. Другими словами, O является атомом с наивысшим приоритетом среди всех атомов в этом сравнении; таким образом, O «побеждает».
Таким образом, группы с высоким приоритетом находятся «вверху» на левом конце (-Br) и «внизу» на правом конце (-CH 2 -O-CH 3 ).Это означает, что показанный изомер противоположен = entgegen = E . И какое имя? Функция «название» ChemSketch говорит, что это (2 E )-2-(1-бромэтилиден)пент-3-инилметиловый эфир.
Правило 2)
Если первый атом у обоих заместителей одинаковый, то действуйте по обеим цепочкам заместителей, пока не будет определена первая точка различия.
Правило 3)
Помните, что атомы, участвующие в множественных связях, рассматриваются по определенному набору правил.Эти атомы рассматриваются так, как если бы они имели такое же количество атомов с одинарными связями, какое они присоединили к атомам с множественными связями.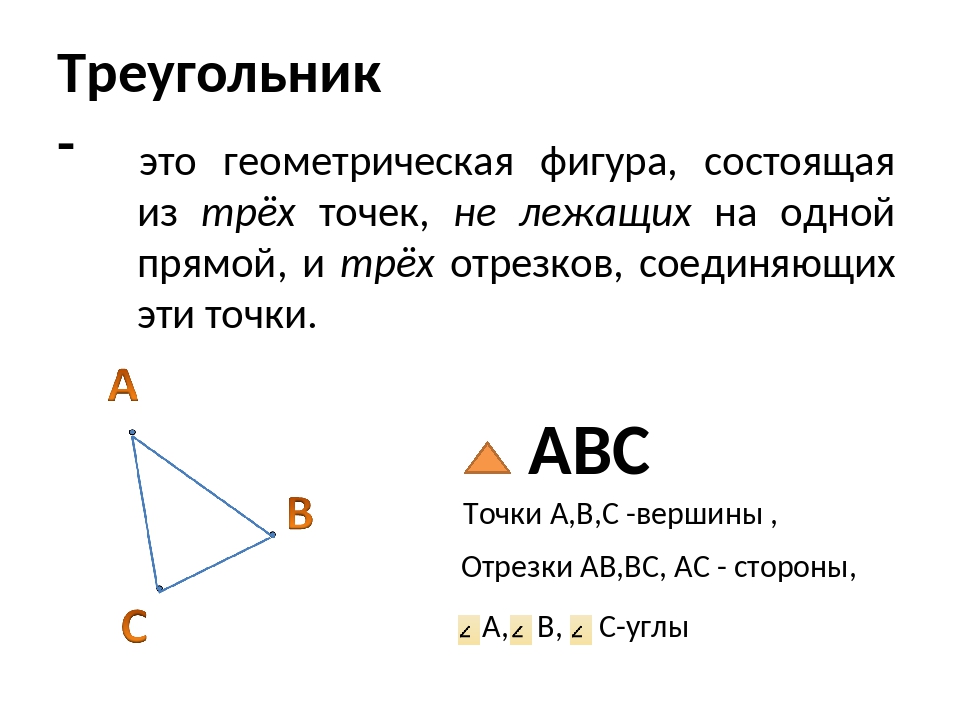
Простым примером, показывающим необходимость системы E/Z, является алкен, 1-бром-2-хлор-2-фтор-1-иодэтен, который имеет четыре разных заместителя, присоединенных к двойной связи. На рисунке ниже показано, что для этой молекулы существует два совершенно разных геометрических изомера, ни один из которых не может быть назван с использованием системы цис-транс .
Рассмотрим левую структуру.На углероде с двойной связью слева два атома, присоединенные к двойной связи, представляют собой Br и I. Согласно правилам приоритета CIP, I имеет более высокий приоритет, чем Br (более высокий атомный номер). Теперь посмотрите на углерод справа. Присоединенными атомами являются Cl и F, причем Cl имеет более высокий атомный номер и более высокий приоритет.
При рассмотрении относительного положения групп с более высоким приоритетом группа с более высоким приоритетом находится «внизу» по левому углероду двойной связи и «внизу» по правому углероду двойной связи.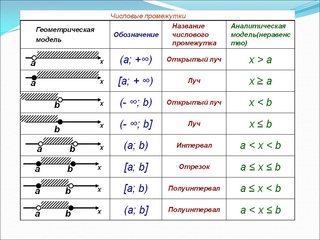 Поскольку обе группы с более высоким приоритетом находятся на одной и той же стороне двойной связи («внизу» в данном случае), они zusammen = вместе.Следовательно, это изомер (Z). Точно так же правая структура (E).
Поскольку обе группы с более высоким приоритетом находятся на одной и той же стороне двойной связи («внизу» в данном случае), они zusammen = вместе.Следовательно, это изомер (Z). Точно так же правая структура (E).
Пример 7.5.1: Бутен
| цис -2-бутен | транс -2-бутен |
На рисунке выше показаны два изомера 2-бутена. Вы должны узнать их как цис и транс .Давайте проанализируем их, чтобы увидеть, являются ли они E или Z . Начните с левой структуры (цис-изомера). На C2 (левый конец двойной связи) к двойной связи присоединены два атома C и H. Согласно правилам приоритета CIP, C имеет более высокий приоритет, чем H (более высокий атомный номер). Теперь посмотрите на C3 (правый конец двойной связи). Точно так же атомы C и H, причем C имеет более высокий приоритет. Мы видим, что группа с более высоким приоритетом находится «внизу» на С2 и «внизу» на С3. Поскольку обе приоритетные группы находятся на одной и той же стороне двойной связи («внизу» в данном случае), они zusammen = вместе.Следовательно, это ( Z )-2-бутен.
Мы видим, что группа с более высоким приоритетом находится «внизу» на С2 и «внизу» на С3. Поскольку обе приоритетные группы находятся на одной и той же стороне двойной связи («внизу» в данном случае), они zusammen = вместе.Следовательно, это ( Z )-2-бутен.
Теперь посмотрите на правую структуру ( транс-изомер ). В этом случае приоритетная группа находится «внизу» на левом конце двойной связи и «вверху» на правом конце двойной связи. Поскольку две приоритетные группы находятся на противоположных сторонах двойной связи, они entgegen = противоположные. Следовательно, это ( E )-2-бутен.
Инициативы суперинтенданта / Обозначения диплома
Учащиеся, получившие аттестат о среднем образовании, также могут получить печать диплома: звание ученого или звание за заслуги.Учащиеся также будут иметь возможность получить звание ученого продвинутого уровня в школах округа Пинеллас. Студенты могут получить любое или все эти обозначения, но они не обязаны это делать.
В дополнение к требованиям для получения стандартного диплома учащиеся, претендующие на статус стипендиата штата, должны соответствовать определенным требованиям к курсу и тестированию:
- Математика
- Заработайте один балл по алгебре II
- Заработайте один балл по статистике или по столь же строгому курсу
- Учащиеся, поступившие в 9-й класс в 2014-2015 учебном году или позднее, также должны будут сдать стандартизированный экзамен по геометрии в масштабе штата.
- Наука
- Пройти стандартизированную оценку EOC по биологии I в масштабе штата
- Заработайте один балл по химии или физике
- Заработайте один балл по курсу, одинаково строгому с химией или физикой
- Учащийся, зачисленный на курс Advanced Placement, International Baccalaureate или Advanced International Certificate of Education Biology, который сдает соответствующий экзамен по биологии AP, IB или AICE и набирает минимальный балл, необходимый для получения кредита колледжа, будет соответствовать требованиям без необходимости сдавать оценка биологии I EOC.

- Общественные науки
- Пройти стандартизированную оценку EOC по истории США в масштабе штата
- Учащийся, зачисленный на курс AP, IB или AICE, который включает темы по истории Соединенных Штатов, сдавший соответствующую оценку AP, IB или AICE и набравший минимальный балл, необходимый для зачета колледжа, будет соответствовать этому требованию без необходимости сдавать экзамен United States Оценка EOC по истории штатов.
- Иностранный язык
- Получите два кредита на одном иностранном языке
- Факультативы
- Заработайте хотя бы один кредит в программе Advanced Placement, International Baccalaureate, Advanced International Certificate of Education или на курсе с двойным зачислением.
Учащиеся, претендующие на звание за заслуги перед штатом, должны получить один или несколько отраслевых сертификатов из списка, утвержденного штатом.

 Две прямые могут пересекаться только в одной точке.
Две прямые могут пересекаться только в одной точке.

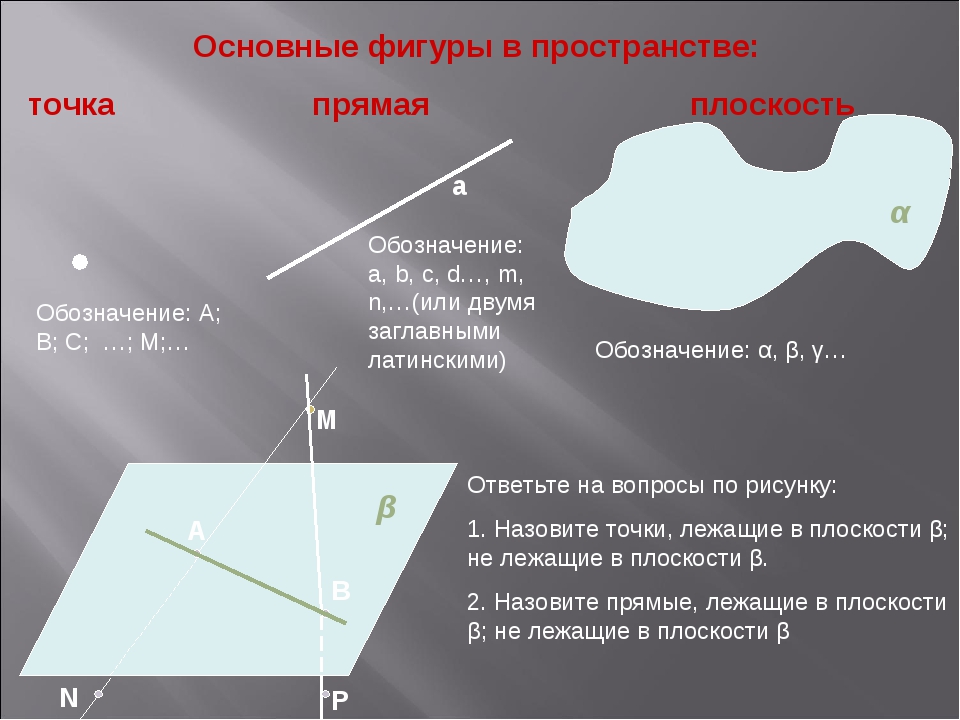

 д.
д.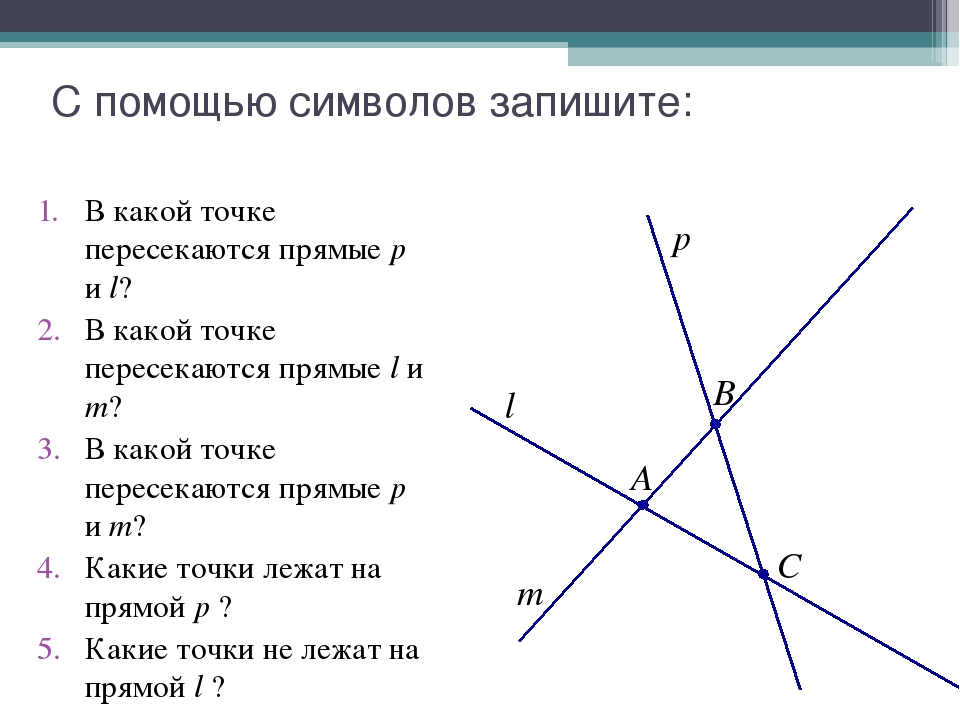 Точка, в которой они встречаются, называется точкой пересечения.
Точка, в которой они встречаются, называется точкой пересечения.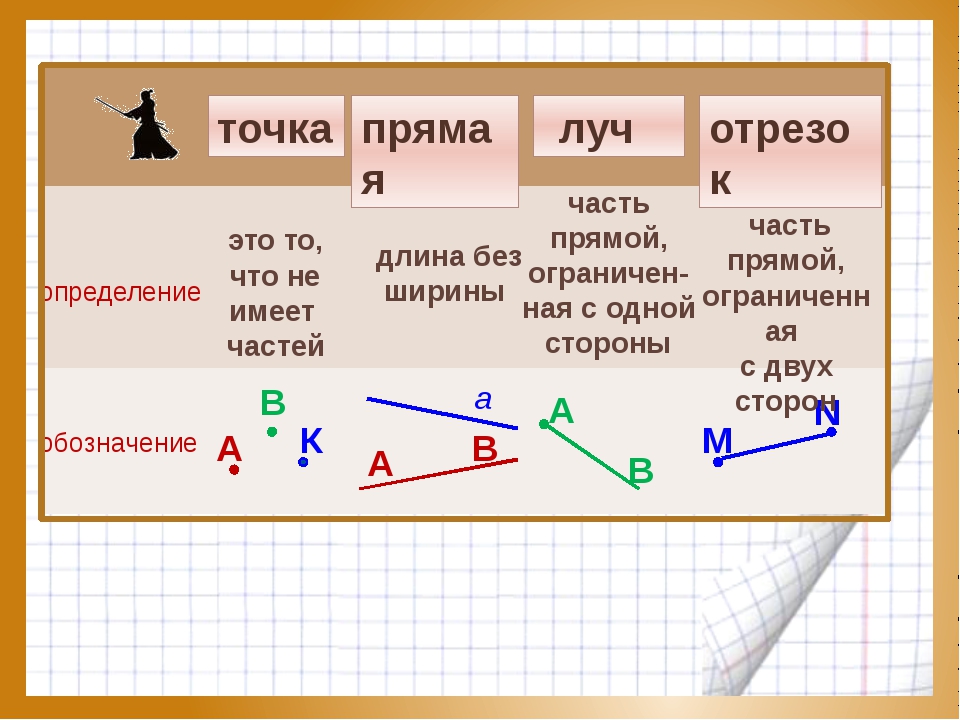


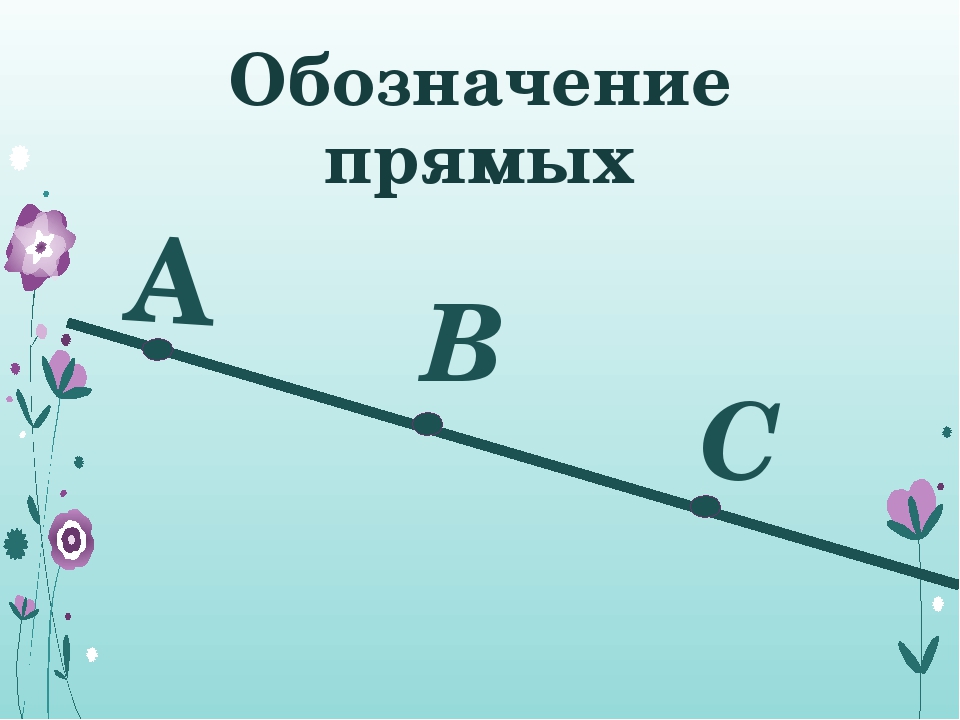
 Хака и С. Хана (PHI).
Хака и С. Хана (PHI).