Построение сечений призмы — Электронный образовательный ресурс «Построение сечений многогранников и тел вращения»
Задача №1: Построить сечение призмы ABCDEA1B1C1D1E1. Точка М принадлежит верхнему основанию, прямая d лежит в плоскости нижнего основания
1) Через точку M проведем прямую n||d;
2) Прямая n пересекает ребро B’C’ в точке S и ребро E’D’ в точке Q;
3) Так как прямая d принадлежит плоскости нижнего основания, d пересекает ребра CB, BA, DE в точках X, Y, Z соответственно;
4) Так как точки S и X лежат в плоскости грани BCC’B’, соединим эти точки. Прямая SX пересекает ребро BB’ в точке N;
5) Так как точки Q и Z лежат в плоскости грани EDD’E’, соединим эти точки. Прямая QZ пересекает ребро EE’ в точке T;
6) Так как точки N и Y лежат в плоскости грани ABB’A’, соединим эти точки. Прямая NY пересекает ребро AA’ в точке P.
7) Соединим последовательно точки S, N, P, T, Q. Получим искомое сечение SNPTQ.
Задача №2: Построить сечение призмы ABCDEA1B1C1D1E1. Точка М принадлежит боковому ребру, прямая d лежит в плоскости нижнего основания.
Построение:
1) Так как прямая d принадлежит плоскости нижнего основания, d пересекает ребра CB, EA, DE, BA в точках X, Y, Z, H соответственно;
2) Так как точки M и Z лежат в плоскости грани EDD’E’, соединим эти точки. Прямая MZ пересекает ребро EE’ в точке N и ребро DD’ в точке T соответственно;
3) Так как точки N и Y лежат в плоскости грани AEE’A’, соединим эти точки. Прямая NY пересекает ребро AA’ в точке G;
4) Так как точки G и H лежат в плоскости грани ABB’A’, соединим эти точки. Прямая GH пересекает ребро BB’ в точке P;
5)
Так как точки P и X лежат в плоскости грани BB’C’C, соединим эти точки.
6) Соединим последовательно точки P, S, T, N, G. Получим искомое сечение PSTNG.
Анимация построения:Сечения призмы — презентация онлайн
1. Сечения призмы
Выполнила Иванова ВероникаСтудентка группы 12-э-16
Для решения многих геометрических
задач, необходимо уметь строить
сечения призмы различными
плоскостями
3. Плоская фигура, образовавшаяся при пересечении какой-либо плоскости с пространственной фигурой, называется плоским сечением или просто с
Плоская фигура,образовавшаяся
при пересечении
какой-либо
плоскости с
пространственной
фигурой,
называется
плоским сечением
или просто
сечением этой
фигуры.
Назовем секущей плоскостью призмы любую
плоскость , по обе стороны от которой имеются
точки данной призмы
Многоугольник, сторонами которого являются эти
отрезки, называется сечением призмы.
5. Сечением призмы является многоугольник, вершины которого расположены на ребрах, а стороны целиком лежат на гранях.
6. Вид сечения зависит от расположения плоскости
Сечения призмы плоскостями, параллельнымибоковым ребрам, являются параллелограммами
В частности параллелограммами являются диагональные
боковых ребра, не принадлежащей одной грани.
Построить сечение призмы плоскостью –
означает:
В плоскости каждой пересекаемой грани
многогранника указать 2-е точки,
принадлежащие сечению;
Соединить их прямой;
Найти точки пересечения прямой с ребрами
призмы.
9. Методы построения сечений призм
Метод следовМетод внутреннего
проектирования
или
метод вспомогательных
сечений
Комбинированный метод
10. Метод следов
Если плоскостьпересекает
плоскость
по прямой S, то
прямую S называют следом
плоскости
на плоскость
11.
Метод следов Метод следов включает триважных пункта:
Строится линия пересечения (след)
секущей плоскости с плоскостью
основания многогранника.
Находим точки пересечения
секущей плоскости с ребрами
многогранника.
Строим и заштриховываем сечение.
Построить сечение призмы, проходящее через
данную точку и след секущей плоскости если
точка находится на одной из боковых граней
Построим призму
Проведем след секущей плоскости на
плоскости основания призмы
А
Пусть точка А принадлежащая сечению
находится на боковой грани
А
Сначала строится отрезок, по которому
сечение призмы пересекает грань, на которой
находится данная точка А.
А
Для этого построим прямую, по которой
плоскость данной грани
А
Для этого построим прямую, по которой
плоскость данной грани
пересекает плоскость основания
А
D
пересекает
Эта прямая пересекает след секущей
плоскость основания
плоскости в точке D.
А
D
Проведем прямую через точку А и D.
Эта прямая пересекает след секущей
плоскости в точке D.
А
С
В
D
Проведем прямую через точку А и D.
Отрезок ВС прямой АD на рассматриваемой
грани и есть пересечение этой грани с секущей
плоскостью.
А
В
D
Концы отрезка ВС принадлежат и соседним
граням. Поэтому описанным способом можно
построить пересечение и остальных граней с
нашей секущей плоскостью.
Построить сечение призмы, проходящее через
данную точку и след секущей плоскости если
данная точка находится на верхнем
основании
Пусть точка принадлежащая сечению находится на верхнем
основании
Тогда линия пересечения секущей плоскости с верхним основанием
будет параллельна следу секущей плоскости
Проведем след секущей плоскости призмы
25. Задача для самостоятельного решения. Призма ABCDA1B1C1D1. Построить сечение, проходящее через точки M, N, L.
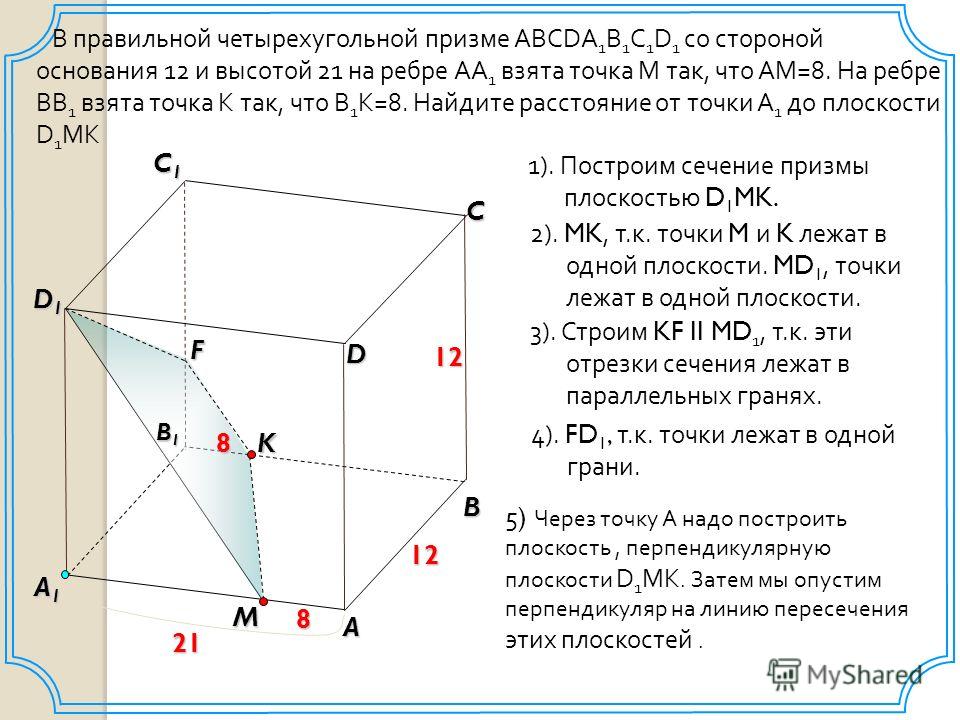MKNTPL — искомое сечение.N
B1
X2
C1
K
T
X1
D1
A1
B
C
P
M
A
L X3
D
Найдите площадь поверхности прямой
призмы, в основании которой лежит ромб с
диагоналями, равными 25 и 60, и боковым
ребром, равным 25.
Найдите боковое ребро правильной
четырехугольной призмы, если
сторона ее основания равна 15, а
площадь поверхности равна 930.
30. Решение
Спасибо за внимание!Сечения многогранников
СЕЧЕНИЯ МНОГОГРАННИКОВ
Если многогранник лежит по одну сторону от данной плоскости, то он может: а) не иметь с плоскостью ни одной общей точки; б) иметь одну общую точку – вершину многогранника; в) иметь общий отрезок – ребро многогранника; г) иметь общий многоугольник – грань многогранника.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Если у многогранника имеются точки, лежащие по разные стороны от данной плоскости, то общ ая часть многогранника и плоскости называе тся сечением многогранника плоскостью .
Диагональные сечения
Сечение призмы плоскостью, проходящей через диагональ основания и два прилежащих к ней боковых ребра, называется диагональным сечением призмы.
Сечение пирамиды плоскостью, проходящей через диагональ основания и вершину, называется диагональным сечением пирамиды.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Пусть плоскость пересекает пирамиду и параллельна ее основанию. Часть пирамиды, заключенная между этой плоскостью и основанием, называется усеченной пирамидой. Сечение пирамиды также называется основанием усеченной пирамиды.
Упражнение 1
Какой фигурой может быть сечение многогранника плоскостью?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Многоугольником или объединением нескольких многоугольников.
Упражнение 2
Сколько диагональных сечений имеет n -угольная: а) призма; б) пирамида?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) ;
б) .
4
Упражнение 3
Может ли в сечении куба плоскостью получиться:
а) треугольник ?
б) правильный треугольник ?
в) равнобедренный треугольник ?
г) прямоугольный треугольник ?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
д) тупоугольный треугольник ?
Ответ: а) Да;
в) да;
г) нет;
д) нет.
б) да;
Упражнение 4
Может ли в сечении куба плоскостью получиться:
а) квадрат;
б) прямоугольник;
в) параллелограмм;
г) ромб;
д) трапеция;
е) прямоугольная трапеция?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Да;
б) да;
в) да;
е) нет.
г) да;
д) да;
6
Упражнение 5
Может ли в сечении куба плоскостью получиться:
а) пятиугольник;
б) правильный пятиугольник?
Ответ: а) Да;
б) нет. У пятиугольников, которые получаются в сечении куба, имеются две пары параллельных сторон, а у правильного пятиугольника таких сторон нет.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 6
Может ли в сечении куба плоскостью получиться:
а) шестиугольник;
б) правильный шестиугольник;
в) многоугольник с числом сторон больше шести?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Да;
в) нет.
б) да;
Упражнение 7
Может ли в сечении правильного тетраэдра плоскостью получиться : а) остроугольный треугольник; б) прямоугольный треугольник; в) тупоугольный треугольник ?
Ответ: а) да;
б) да.
Пусть ABCD – единичный тетраэдр. Точка E на ребре AD отстоит от вершины A на расстояние ¼ . Точка F на ребре AB отстоит от вершины A на расстояние x . Найдем x
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
По теореме косинусов находим CE 2 = 13/16, CF 2 = x 2 + 1 – x , EF 2 = 1/16 + x 2 – x /4. Используя теорему Пифагора находим x = 1/6.
в) да. Если точку G на ребре AB взять между A и F , то угол CEF будет тупой.
9
Упражнение 8
Может ли в сечении правильного тетраэдра плоскостью получиться квадрат?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Да. Если сечение проходит через середины ребер.
Упражнение 9
Может ли в сечении тетраэдра плоскостью получиться четырехугольник, изображенный на рисунке ?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: Нет.
Упражнение 10
Какие многоугольники можно получить в сечении четырехугольной пирамиды плоскостью?
Ответ: Треугольник, четырехугольник, пятиугольник.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 11
Может ли в сечении октаэдра плоскостью получиться:
а) треугольник;
б) четырехугольник;
в) пятиугольник;
г) шестиугольник;
д) семиугольник;
е) восьмиугольник?
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Ответ: а) Нет;
б) да;
в) нет;
г) да;
д) нет;
е) нет.
Построение сечений
При построении сечений многогранников, базовыми являются построения точки пересечения прямой и плоскости, а также линии пересечения двух плоскостей.
Если даны две точки A и B прямой и известны их проекции A’ и B’ на плоскость, то точкой С пересечения данных прямой и плоскости будет точка пересечения прямых AB и A’B’
Если даны три точки A , B , C плоскости и известны их проекции A’ , B’ , C’ на другую плоскость, то для нахождения линии пересечения этих плоскостей находят точки P и Q пересечения прямых AB и AC со второй плоскостью. Прямая PQ будет искомой линией пересечения плоскостей.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Упражнение 1
Постройте сечение куба плоскостью, проходящей через точки E , F , лежащие на ребрах куба и вершину B .
Решение. Для построения сечения куба, проходящего через точки E , F и вершину B ,
Соединим отрезками точки E и B , F и B .
Через точки E и F проведем прямые, параллельные BF и BE , соответственно.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученный параллелограмм BFGE будет искомым сечением.
Упражнение 2
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P её точку пересечения с AD .
Обозначим Q точку пересечения прямых PG и AB .
Соединим точки E и Q , F и G .
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученная трапеция EFGQ будет искомым сечением.
Упражнение 3
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P её точку пересечения с AD .
Обозначим Q , R точки пересечения прямой PG с AB и DC .
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Обозначим S точку пересечения FR c СС 1 .
Соединим точки E и Q , G и S .
Полученный пятиугольник EFSGQ будет искомым сечением.
Упражнение 4
Постройте сечение куба плоскостью, проходящей через точки E , F , G , лежащие на ребрах куба .
Решение. Для построения сечения куба, проходящего через точки E , F , G ,
найдем точку P пересечения прямой EF и плоскости грани ABCD .
Обозначим Q , R точки пересечения прямой PG с AB и CD .
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Проведем прямую RF и обозна — чим S , T её точки пересечения с CC 1 и DD 1 .
Проведем прямую TE и обозначим U её точку пересечения с A 1 D 1 .
Соединим точки E и Q , G и S , U и F .
Полученный шестиугольник EUFSGQ будет искомым сечением.
Упражнение 5
Постройте сечение куба плоскостью, проходящей через точки E , F , G , принадлежащие граням BB 1 C 1 C , CC 1 D 1 D , AA 1 B 1 B , соответственно.
Решение. Из данных точек опустим перпендикуляры EE’ , FF’ , GG’ на плоскость грани ABCD , и найдем точки I и H пересечения прямых FE и FG с этой плоскостью.
IH будет линией пересечения искомой плоскости и плоскости грани ABCD .
Обозначим Q , R точки пересечения прямой IH с AB и BC .
В режиме слайдов построение производится по шагам, кликаньем мышкой.
Проведем прямые PG и QE и обозначим R , S их точки пересечения с AA 1 и CC 1 .
Проведем прямые SU , UV и RV , параллельные PR , PQ и QS .
Полученный шестиугольник RPQSUV будет искомым сечением.
Упражнение 6
Постройте сечение куба плоскостью, проходящей через точки E , F , лежащие на ребрах куба , параллельно диагонали BD .
Решение. Проведем прямые FG и EH , параллельные BD .
Проведем прямую FP , параллельную EG , и соединим точки P и G .
Соединим точки E и G , F и H .
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Полученный пятиугольник EGPFH будет искомым сечением .
20
Постройте сечение двух кубов плоскостью, проходящей через точки K , L , M , лежащие на ребрах куба .
Упражнение 7
Решение. Сначала построим сечение верхнего куба. Это будет шестиугольник LNMPKQ.
Продолжим MN , PK и QL. Соответствующие точки обозначим R , S и U , V .
Проведем прямые RX и VY , параллельные UV и SR , соответственно.
В режиме слайдов построение сечение производится по шагам, кликаньем мышкой
Искомое сечение состоит из двух шестиугольников LNMPKQ и RSUVYX.
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E , F , G .
Упражнение 8
Решение. Соединим точки E и F .
Проведем прямую FG и ее точку пересечения с CC 1 обозначим H .
Проведем прямую EH и ее точку пересечения с A 1 C 1 обозначим I .
Соединим точки I и G .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный четырехугольник EFGI будет искомым сечением .
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E , F , G .
Упражнение 9
Решение. Проведем прямую EG и обозначим H и I ее точки пересечения с CC 1 и AC .
Проведем прямую IF и ее точку пересечения с AB обозначим K .
Проведем прямую FH и ее точку пересечения с B 1 C 1 обозначим L .
Соединим точки E и K , G и L .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный пятиугольник EKFLG будет искомым сечением .
Постройте сечение призмы ABCA 1 B 1 C 1 плоскостью, параллельной AC 1 , проходящей через точки D и D 1 .
Упражнение 1 0
Решение. Через точку D проведем прямую параллельную AC 1 и обозначим E ее точку пересечения с прямой BC 1 . Эта точка будет принадлежать плоскости грани ADD 1 A 1 .
Проведем прямую DE и обозначим F ее точку пересечения с ребром BC .
Соединим отрезком точки F и D .
Через точку D проведем прямую параллельную прямой FD и обозначим G точку ее пересечения с ребром A 1 C 1 , H – точку ее пересечения с прямой A 1 B 1 .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую DH и обозначим P ее точку пересечения с ребром AA 1 .
Соединим отрезком точки P и G .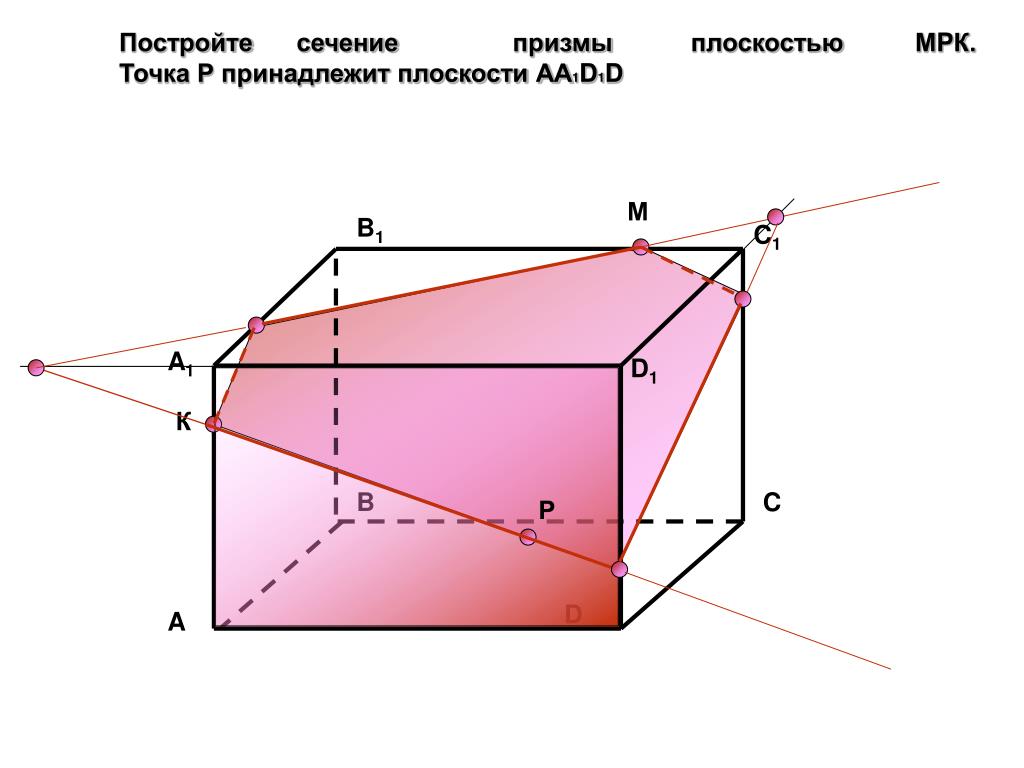
Полученный четырехугольник EFIK будет искомым сечением .
Построить сечение призмы ABCA 1 B 1 C 1 плоскостью, проходящей через точки E на ребре BC , F на грани ABB 1 A 1 и G на грани ACC 1 A 1 .
Упражнение 1 1
Решение. Проведем прямую GF и найдем точку H ее пересечения с плоскостью ABC .
Проведем прямую EH , и обозначим P и I ее точки пересечения с AC и AB .
Проведем прямые PG и IF , и обозначим S , R и Q их точки пересечения с A 1 C 1 , A 1 B 1 и BB 1 .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки E и Q , S и R .
Полученный пятиугольник EQRSP будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A , B , D 1 .
Упражнение 1 2
Решение. Заметим, что сечение будет проходить через точку E 1.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую AB и найдем ее точки пересечения K и L с прямыми CD и FE .
Проведем прямые KD 1 , LE 1 и найдем их точки пересечения P , Q с прямыми CC 1 и FF 1 .
Шестиугольник ABPD 1 E 1 Q будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки A , B’ , F’ .
Упражнение 1 3
Решение. Проведем отрезки AB’ и AF’ .
Через точку B’ проведем прямую, параллельную AF’ , и ее точку пересечения с EE 1 обозначим E’ .
Через точку F’ проведем прямую, параллельную AB’ , и ее точку пересечения с CC 1 обозначим C’ .
Через точки E’ и C’ проведем прямые, параллельные AB’ и AF’ , и их точки пересечения с D 1 E 1 и C 1 D 1 обозначим D’ , D” .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки B’ , C’ ; D’ , D” ; F’ , E’ .
Полученный семиугольник AB’C’D”D’E’F’ будет искомым сечением .
Построить сечение правильной шестиугольной призмы плоскостью, проходящей через точки F’ , B’ , D’ .
Упражнение 1 4
Решение. Проведем прямые F’B’ и F’D’ , и найдем их точки пересечения P и Q с плоскостью ABC .
Проведем прямую PQ . Обозначим R точку пересечения PQ и FC .
Точку пересечения F’R и CC 1 обозначим C’ .
Соединим точки B’ , C’ и C’ , D’ .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Через точку F’ проведем прямые, параллельные C’D’ и B’C’ , и их точки пересечения с AA 1 и EE 1 обозначим A’ и E’ .
Соединим точки A’ , B’ и E’ , D’ .
Полученный шестиугольник A’B’C’D’E’F’ будет искомым сечением .
Построить сечение пирамиды ABCD плоскостью, параллельной ребру AD и проходящей через точки E , F .
Упражнение 1 5
Решение. Соединим точки E и F .
Через точку F проведем прямую FG , параллельную AD.
Соединим точки G и E .
Полученный треугольник EFG будет искомым сечением.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Построить сечение пирамиды ABCD плоскостью, параллельной ребру CD и проходящей через точки E , F .
Упражнение 1 6
Решение. Через точки E и F проведем прямые EG и FH , параллельные CD.
Соединим точки G и F , E и H .
Полученный четырехугольник EGFH будет искомым сечением.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Построить сечение пирамиды ABCD плоскостью, проходящей через точки E , F , G .
Упражнение 17
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G ,
проведем прямую EF и обозначим P её точку пересечения с BD .
Обозначим Q точку пересечения прямых PG и CD .
Соединим точки F и Q , E и G .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Полученный четырехугольник EFQG будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, проходящей через точки A , E , F .
Упражнение 18
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G , проведем прямую EF и обозначим G её точку пересечения с DB .
Проведем прямые AG и CB . Обозначим P их точку пересечения.
Проведем прямую PF и обозначим Q её точку пересечения с SC .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки A и F , A и E , E и Q .
Полученный четырехугольник AFQE будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, проходящей через точки E , F , G .
Упражнение 19
Решение. Для построения сечения пирамиды, проходящего через точки E , F , G ,
проведем прямую FG и обозначим P её точку пересечения с SB .
Проведем прямую PE и обозначим Q её точку пересечения с AB .
Проведем прямую GQ и обозначим R её точку пересечения с AD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую RE и обозначим T её точку пересечения с SD .
Соединим точки T и F .
Полученный пятиугольник ETFGQ будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, параллельной AS и проходящей через точки E , F .
Упражнение 2 0
Решение. Соединим точки E и F .
Через точку F проведем прямую, параллельную AS , и обозначим G ее точку пересечения с AC .
Проведем прямую EG и обозначим H ее точку пересечения с AD .
Через точку H проведем прямую, параллельную AS , и обозначим I ее точку пересечения с SD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки I и F .
Полученный четырехугольник EFIH будет искомым сечением.
Построить сечение пирамиды SABCD плоскостью, параллельной BD и проходящей через точки E , F .
Упражнение 2 1
Решение. Проведем прямую EF и обозначим Q ее точку пересечения с AC .
Проведем прямую SO и обозначим P её точку пересечения с EF .
Через точку P проведем прямую GH , параллельную BD .
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Соединим точки F , G , E , H .
Полученный четырехугольник FGEH будет искомым сечением.
Построить сечение пирамиды SABCDEF плоскостью, проходящей через точки A 1 , C 1 , E 1 .
Упражнение 2 2
Решение. Найдем точку пересечения P прямой A 1 C 1 с плоскостью основания.
Найдем точку Q пересечения прямой E 1 C 1 с плоскостью основания.
Прямая PQ будет линией пересечения плоскости сечения и плоскости основания.
В режиме слайдов построение сечения производится по шагам, кликаньем мышкой
Проведем прямую ED и обозначим R , её точку пересечения с прямой PQ .
Проведем прямую E 1 R и обозначим D 1 её точку пересечения с SD .
Аналогичным образом находятся точки F 1 и B 1 .
Шестиугольник A 1 B 1 C 1 D 1 E 1 F 1 будет искомым сечением.
Графическая работа №4 «Сечение призмы плоскостью» — Студопедия
Задание:
1. Построить три проекции шестиугольной призмы, усечённой плоскостью Р
2. Построить натуральную величину сечения.
3. Построить развёртку усечённой шестиугольной призмы.
4. Построить прямоугольную изометрическую проекцию усечённой шестиугольной призмы.
5. Нанести размеры на чертеже.
6. Заполнить основную надпись.
Примечание:
7. Данная работа выполняется индивидуально, согласно варианта. (см. таблицу).
8. Масштаб 1:1.
9. Угол наклона между осями в прямоугольной изометрической проекции 1200.
10. Если развёртка и изометрическая проекция усеченной шестиугольной призмы не помещаются на одной стороне листа, то можно их разместить на обороте.
| № варианта | α,град | А, мм | № варианта | α,град | А, мм |
| 45 | 90 | 45 | 100 | ||
| 60 | 90 | 25 | 100 | ||
| 40 | 90 | 30 | 100 | ||
| 30 | 90 | 35 | 100 | ||
| 35 | 90 | 40 | 100 | ||
| 50 | 90 | 35 | 100 | ||
| 48 | 75 | 45 | 80 | ||
| 45 | 75 | 40 | 80 | ||
| 35 | 75 | 35 | 80 | ||
| 30 | 75 | 25 | 80 | ||
| 25 | 75 | 30 | 80 | ||
| 28 | 75 | 25 | 80 |
Графическая работа «Сечение призмы плоскостью»
Сечение — призма — Большая Энциклопедия Нефти и Газа, статья, страница 3
Сечение — призма
Cтраница 3
Развертку боковой поверхности с основанием и фигурой сечения призмы строят следующим образом.
Проводят прямую, на которой откладывают пять отрезков, равных длинам сторон пятиугольника, лежащего в основании призмы.
[31]
На рис. 63 приводятся построения истинной величины сечения призмы, рассеченной по линии Т — Т плоскостью, перпендикулярной фронтальной плоскости проекции. [33]
На рис. 2.50 изображен ход луча в главком сечения призмы MAN ( в плоскости, перпендикулярной преломляющему ребру) с преломляющим углом в, расколэжеяпой а воздухе. [35]
Возьмем точку М на середине ребра AAY и изобразим сечение призмы плоскостью Р, проходящей через точки В, М и D. Для этого соединим точки В, и D. [36]
На рис. 269 изображены: прямоугольный треугольник ABC — сечение призмы плоскостью V и Blt Вг — сечения грузов той же плоскостью. Применяем объединенный принцип Даламбера — Лагранжа. [37]
Заметим, что заштрихованная часть плоскости ADB не является сечением призмы. [38]
К двум шарам на этом треугольнике, который представляет собой сечение призмы, Стевин добавляет двенадцать других одинаковых с ними шаров. Соединим их друг с другом равными нитями, образовав из них ожерелье, в котором наши четырнадцать шаров находятся на равных расстояниях друг от друга. [39]
Аналогично этому представляются относительные температуры и для других характерных точек сечения призмы, а также и в параллелепипеде. [40]
Это определенное уравнение, которое удовлетворяется во всех точках контура сечения призмы. [41]
Какое наибольшее число сторон может иметь многоугольник, получающийся в сечении 10-угольной призмы плоскостью.
Сколько у него может быть пар параллельных сторон.
[42]
Значение К — увеличение тензометра — зависит от длины диагонали d сечения призмы и расстояния D между зеркальцем и линейкой. [44]
Страницы: 1 2 3 4
1
Первый слайд презентации: Сечение призмы плоскостью
Изображение слайда
2
Слайд 2: Задание
Выполнить чертеж усеченной призмы Найти действительную величину контура сечения
Изображение слайда
3
Слайд 3
Варианты Татаренко Лякишев Махнач Пассар Печеницына Присяжнюк Уткина Черепанова Щербакова Щукин Юрищева Ядонист Шиверских
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
4
Слайд 4
На чистом формате выполните рамку, основную надпись Построение выполняется в центре листа – по данным варианта выполнить три проекции шестигранной призмы с высотой h и основанием d
Изображение слайда
Изображение для работы со слайдом
5
Слайд 5
Обозначать точки пересечения.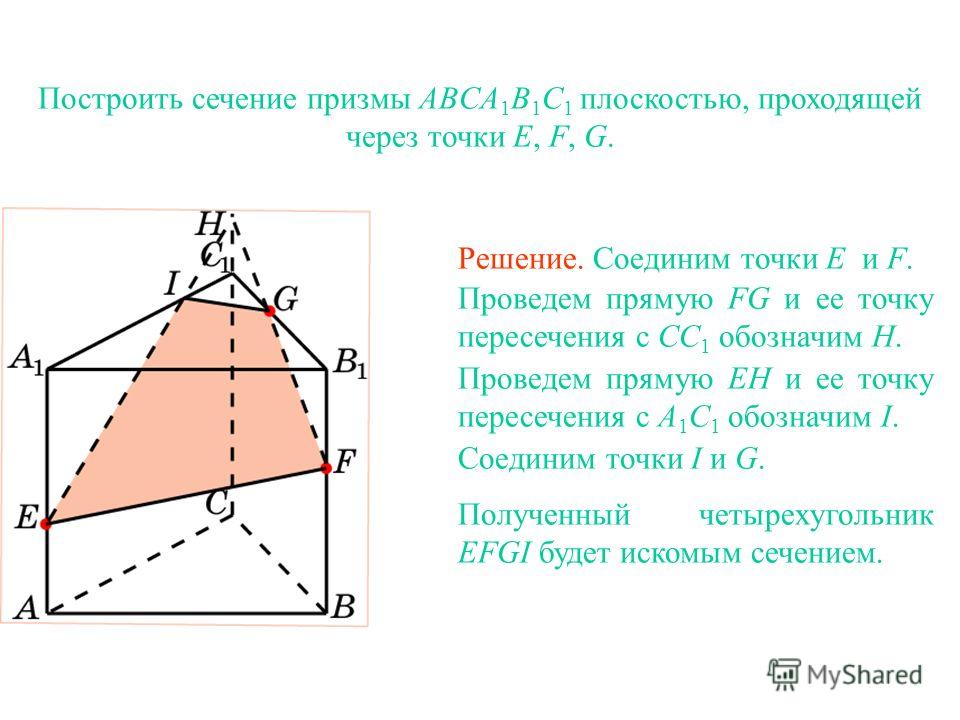
Учитываем, что у призмы есть два задних, невидимых ребра, т.е. точек будет 6
Изображение слайда
Изображение для работы со слайдом
6
Слайд 6
Из-за того, что все точки лежат на ребрах призмы, на виде сверху они совпадут с углами основания
Изображение слайда
Изображение для работы со слайдом
7
Слайд 7
Для построения точек пересечения на виде слева проводим горизонтальные линии проекционных связей
Изображение слайда
Изображение для работы со слайдом
8
Слайд 8
Обозначаем полученные точки и соединяем их – должен получиться неправильный шестигранник
Изображение слайда
Изображение для работы со слайдом
9
Слайд 9
При выполнении обводки чертежа отсеченную часть (верхнюю) не обводим, если при последующих построениях отсеченная часть будет мешать – ее можно убрать
Изображение слайда
Изображение для работы со слайдом
10
Слайд 10
Строим натуральную величину сечения В свободном месте листа над видом прямо проводим три линии, параллельные плоскости сечения, расстояние между которыми равно расстоянию между гранями шестигранника и центрально горизонтальной линией на виде сверху
Изображение слайда
Изображение для работы со слайдом
11
Слайд 11
Из точек пересечение секущей плоскости и призмы проводим перпендикуляры (угол 90 0 )
Изображение слайда
Изображение для работы со слайдом
12
Слайд 12
Отмечаем и соединяем точки пересечения секущей плоскости и ребер шестигранника на натуральной величине сечения
Изображение слайда
Изображение для работы со слайдом
13
Слайд 13
Маркируем натуральную величину сечения, проставляем размеры (вы вместо букв ставите цифры и условные обозначения)
Изображение слайда
Изображение для работы со слайдом
14
Слайд 14
Оформляем основную надпись
Изображение слайда
Изображение для работы со слайдом
15
Последний слайд презентации: Сечение призмы плоскостью
Окончательный вид работы
Изображение слайда
Изображение для работы со слайдом
Задача по математике — 1151
2015-11-02Правильная треугольная призма $ABCA_{1}B_{1}C_{1}$ пересечена плоскостью, проходящей через середины ребер $AB, A_{1}C_{1}, BB_{1}$.
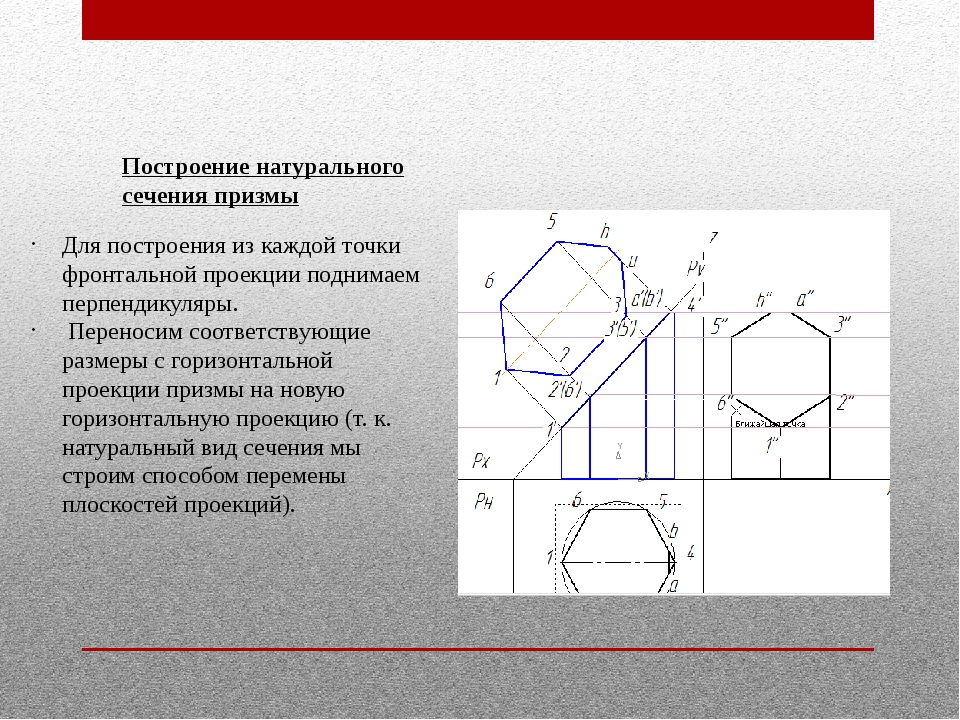{2} \sqrt{3}}{4} = \frac{13 \sqrt{3}}{6}$;
откуда $\sigma = \sigma_{1} \sqrt{ \frac{3}{2}} = \frac{13 \sqrt{2}}{4}$.
сечений прямоугольной призмы
Пересечение — это точка или набор точек, общих для двух или более геометрических фигур. Плоскость — это плоская поверхность, которая простирается во всех направлениях.
Поперечное сечение — это пересечение трехмерной фигуры и плоскости. Представьте себе плоскость, пересекающую показанную пирамиду, конус или призму.
На приведенном ниже рисунке показано пересечение конуса и плоскости. Поперечное сечение — круг.
На приведенном ниже рисунке показано пересечение треугольной призмы и плоскости. Поперечное сечение — треугольник.
Трехмерная фигура может иметь несколько различных поперечных сечений в зависимости от положения и направления среза.
Например, если бы пересечение плоскости и конуса было вертикальным, поперечное сечение образовало бы треугольник.
Практические вопросы
Вопрос 1:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше треугольное.
Вопрос 2:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.
Вопрос 3:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой параллелограмм.
Вопрос 4:
Опишите поперечное сечение правой прямоугольной призмы, приведенное ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.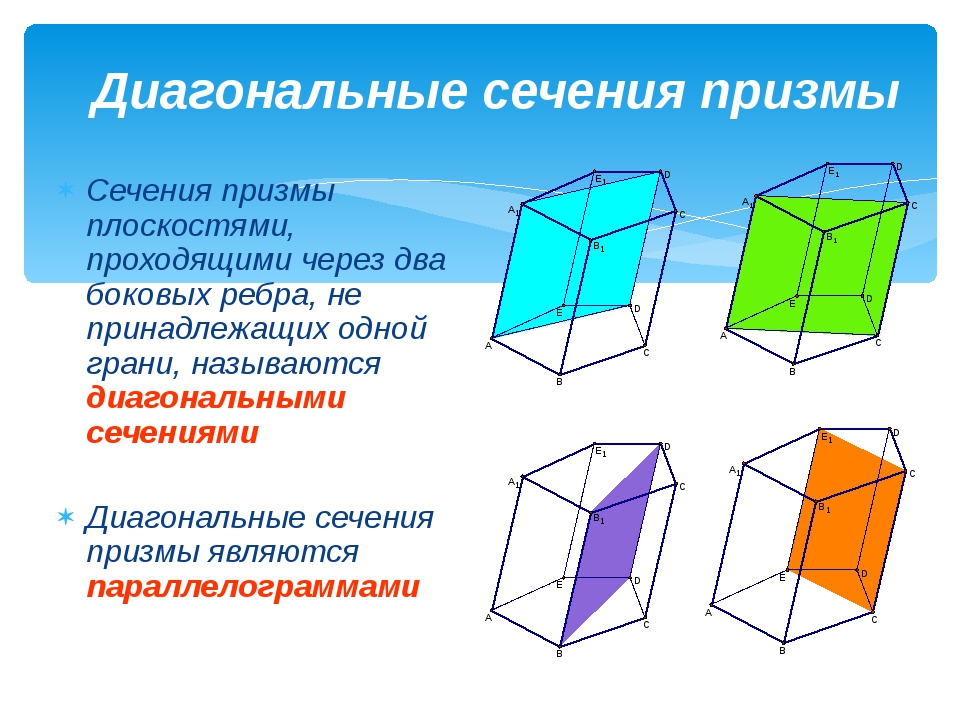
Вопрос 5:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение указанной выше правой прямоугольной призмы представляет собой треугольник или равносторонний треугольник.
Вопрос 6:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше представляет собой прямоугольник.
Вопрос 7:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы выше треугольное.
Вопрос 8:
Опишите поперечное сечение правой прямоугольной призмы, приведенной ниже, с названием ее формы.
Ответ:
Поперечное сечение правой прямоугольной призмы вверху представляет собой кривую в форме радуги.
Вопрос 9:
Возможно ли круглое сечение в правой прямоугольной призме?
Ответ:
Нет, в правой прямоугольной призме нет кривых.
Вопрос 10:
Показана правая прямоугольная пирамида с неквадратным основанием.
(В правой пирамиде точка, где встречаются треугольные стороны, центрирована над основанием.)
Какова форма основания и каждой стороны пирамиды?
Ответ:
Форма основания — прямоугольник, а форма каждой стороны — треугольник.
Помимо вышеперечисленного, если вам нужны еще какие-либо сведения по математике, воспользуйтесь нашим пользовательским поиском Google здесь.
Если у вас есть какие-либо отзывы о наших математических материалах, напишите нам:
Мы всегда ценим ваши отзывы.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебраные задачи на 4 слова
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариации
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование общепринятых единиц в текстовые задачи
Преобразование в метрические единицы в словесных задачах
Проблемы со словами по простым процентам
Проблемы со словами по сложным процентам
Проблемы со словами по типам ngles
Проблемы со словами с дополнительными и дополнительными углами
Проблемы со словами с двойными фактами
Проблемы со словами тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Разметка и разметка задачи
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами о линейных неравенствах
Слово соотношения и пропорции Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами по теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами при сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Поиск квадратного корня с использованием long di видение
Л.
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток при делении 2 в степени 256 на 17
Остаток при делении 17 в степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
Призмы с примерами
Перейти к площади или объему поверхности.
Призма — это твердый объект с:
- одинаковые концы
- плоские грани
- и тот же сечение по всей длине!
Поперечное сечение — это форма, полученная прямым разрезом по объекту.
Поперечное сечение этого объекта — треугольник …
.. имеет одинаковое поперечное сечение по всей длине…
… значит, это треугольная призма .
Затем представьте, что он выходит из листа бумаги … |
Без кривых!
Призма — это многогранник, а это значит, что все грани плоские!
Например, цилиндр не является призмой , потому что у него изогнутые стороны.
Базы
Концы призмы параллельны
и каждый называется базой.
Стороны
Боковые грани призмы — параллелограммы
(4-х сторонние формы с параллельными противоположными сторонами)
Это все призмы:
и более!
Пример: гексагональный кристалл льда.
Похоже на шестиугольник, но из-за некоторой толщины на самом деле это шестиугольная призма!
Фотография НАСА / Алексей Клятов.
Обычная и неправильная призмы
Все предыдущие примеры — это призмы Regular , потому что поперечное сечение является правильным (другими словами, это форма с равными длинами кромок и равными углами).
Вот пример неправильной призмы :
| Неправильная пятиугольная призма: | ||
| | ||
| Поперечное сечение | ||
| Это «нерегулярно», потому что
Поперечное сечение не «правильной» формы. | ||
Правая и наклонная призма
Когда два конца идеально выровнены, это правая призма, в противном случае — наклонная призма:
Площадь призмы
Площадь поверхности = 2 × площадь основания
+ периметр основания × длина
Пример: какова площадь поверхности призмы, у которой площадь основания 25 м
2 , периметр основания 24 м, а длина 12 м:Площадь поверхности = 2 × Площадь основания + Периметр основания × Длина
= 2 × 25 м 2 + 24 м × 12 м
= 50 м 2 + 288 м 2
= 338 м 2
(Примечание: у нас есть инструмент для расчета площади)
Объем призмы
Объем призмы — это площадь одного конца, умноженная на длину призмы.
Объем = Базовая площадь × длина
Пример: каков объем призмы с площадью основания 25 м
2 и длиной 12 м:Объем = Площадь × Длина
= 25 м 2 × 12 м
= 300 м 3
Поиграй с этим здесь.
Формула также работает, когда он «наклоняется» ( наклон ), но помните, что высота находится под прямым углом к основанию:
И вот почему:
Стек может наклоняться, но имеет тот же объем
Подробнее о боковых гранях
Боковые грани призмы — параллелограммы (четырехсторонняя форма с параллельными противоположными сторонами)
Призма может наклоняться в одну сторону, что делает ее наклонной призмой , но два конца по-прежнему параллельны, а боковые грани по-прежнему параллелограммы!
Но если два конца не параллельны , это не призма .
Что такое призма? — Определение, факты и пример
Prism Games
Объем твердых телНайдите объем твердых тел, умножив площадь основания на высоту твердого тела. Помните, что эта объемная область может быть добавлена.
охватывает Common Core Curriculum 5.MD.5.cИграть сейчасСмотреть все игры по геометрии >>Учитесь с полной программой обучения математике K-5
Что такое Prism
Призма — это трехмерная форма с двумя одинаковыми формами, обращенными друг к другу.Эти идентичные формы называются «основаниями».
Основание может быть треугольником, квадратом, прямоугольником или любым другим многоугольником.
Остальные грани призмы — параллелограммы или прямоугольники.
Поперечное сечение призм
Поперечное сечение геометрической формы или объекта — это форма, полученная прямым разрезом. Это также называется пересечением плоскости с трехмерным объектом.Поперечное сечение призмы, параллельное основанию призмы, такое же, как и ее основание.
Обычная и неправильная призма
Основание призмы может быть правильным или неправильным многоугольником. В зависимости от формы основания призмы бывают правильными или неправильными.
Площадь поверхности и объем призмы
Площадь поверхности призмы — это сумма площадей всех ее граней.
Объем призмы — это объем пространства внутри призмы.
Давайте посмотрим, как найти площадь поверхности и объем треугольной призмы.
Площадь поверхности = Площадь базовых треугольников + Площадь боковых параллелограммов
= 2 × (1 2 x шир x в) + 2 × (l x s) + (l x b)
= bh + 2ls + фунт
Объем = Площадь базового треугольника × длина
= (1 2 ш x в) × l
= 1 2 бхл
Пример: Рассчитайте площадь поверхности и объем следующей призмы.
Длина (l) = 12 см, высота (h) = 4 см, основание (b) = 6 см, стороны = 5 см
Площадь поверхности = bh + 2ls + lb = 6 × 4 + 2 × 12 × 5 + 12 × 6 = 24 + 120 + 72 = 216 см 2 | Объем = 1 2 мл = 1 2 × 6 × 4 × 12 = 144 см 3 |
Правая призма и наклонная призма
Когда два основания призмы идеально выровнены и ее грани являются прямоугольниками (перпендикулярными основанию), это прямая призма, иначе это наклон.Они характеризуются следующим образом:
Правая призма | Косая призма | |
| Высота | Высота по боковой кромке. | Высота — это высота за пределами призмы. |
Боковые поверхности | Боковые грани — прямоугольники. | Боковые грани — параллелограммы. |
Площадь | bh + 2ls + lb | bh + 2ls + lb |
| Объем | 1 2 бхл | 1 2 бхл |
Интересные факты |
Поперечные сечения — Easy Peasy All-in-One Homeschool
В этом уроке мы узнаем, как определять и описывать двумерные фигуры, известные как поперечные сечения, полученные в результате разрезания трехмерных фигур.
Другими словами, вы можете разрезать трехмерную фигуру (прямоугольную призму, пирамиду, конус, цилиндр и сферу), чтобы показать двумерное изображение (прямоугольник, квадрат, треугольник, круг, трапеция…). Двумерный вид называется поперечным сечением.
Давайте начнем с формы, которую многие из вас уже видели раньше — торта! Думаю об этом. Знаете ли вы, что многие торты имеют форму цилиндра? Посмотрите на торт ниже. Сверху он кажется круглым, но что произойдет, если вы разрежете себе кусок?
Вы видите прямоугольник внутри? Когда вы нарезаете торт, он такой же, как поперечное сечение.Поперечное сечение — это просто вид изнутри трехмерной фигуры после того, как она была разрезана. В математике мы пытаемся визуализировать плоскости, пересекающие трехмерные фигуры. Есть несколько способов вырезать трехмерную фигуру, опирающуюся на основу:
Пример 1Рассмотрим прямоугольную призму.
Поскольку он опирается на свое прямоугольное основание, мы разрезаем его плоскостью Параллельно этому основанию. Поперечное сечение имеет форму прямоугольника.Он имеет ту же форму и размер, что и основание.
Теперь мы разрежем его плоскостью, перпендикулярной основанию. Помните, что перпендикулярные линии пересекают основание под углом девяноста градусов. И снова поперечное сечение имеет форму прямоугольника. Однако на этот раз он имеет ту же форму и размер, что и другая грань призмы.
Подумайте о разрезании призмы плоскостью, отклоненной от ее основания. На этот раз поперечное сечение будет иметь форму параллелограмма.
Пример 2 Другим примером поперечного сечения может быть такое поперечное сечение, которое образуется, когда мы разрезаем конус через его вершину.Конечно, конус стоит на круглом основании. Если разрезать его перпендикулярно основанию и через вершину, поперечное сечение будет иметь форму равнобедренного треугольника.
Основание треугольника будет основанием конуса.
Конус образовал бы форму круга, если бы плоскость разрезала его параллельно его основанию
Пример 3Затем давайте изобразим трехмерную фигуру, у которой одно основание имеет форму многоугольника (плоская фигура, по крайней мере, с тремя прямыми сторонами и углами), а другие грани имеют форму треугольников, имеющих общую вершину.Вы можете догадаться, что это?
Пирамида названа в честь формы ее основания. Давайте посмотрим на квадратную пирамиду (имеет квадратное основание). Представьте себе вертикальную плоскость, пересекающую пирамиду перпендикулярно ее основанию. Поперечное сечение будет иметь форму треугольника. Если вы разрежете пирамиду параллельно основанию, поперечное сечение будет иметь форму квадрата (основания). Теперь вырежьте пирамиду перпендикулярно основанию, но НЕ по вершине. Это даст вам трапецию!
Помните! Когда вы разрезаете любую форму параллельно ее основанию, ВСЕГДА получите фигуру, которая является формой основы.
Посмотрите видео, чтобы увидеть интерактивные примеры различных типов поперечных сечений, которые можно создать из кубов и пирамид.
Сопоставьте срез и форму
Совместите описание с формой.
- Разрежьте прямоугольную призму параллельно ее основанию.
- Нарежьте куб перпендикулярно его основанию.
- Разрежьте шестиугольную пирамиду на вершину перпендикулярно основанию.
- Разрежьте квадратную пирамиду перпендикулярно основанию, а не вершине.
- Разрежьте цилиндр параллельно его основанию.
- Нарежьте кубик, не наклоняя его ни горизонтально, ни вертикально по отношению к граням.
(источник)
Interactivate: сечения
Наставник: Если вы разрежете кубик, какая форма будет вырезана?
Студент: Квадрат!
Наставник: Это всегда правда? Что, если разрезать куб под углом?
Студент: Ну, тогда две стороны будут длиннее двух других, поэтому я предполагаю, что форма будет
прямоугольник.
Наставник: Верно. Что бы произошло, если бы вы разрезали куб под другим углом — скажем, если бы вы просто отрезать самый кончик кубика?
Студент: Тогда … я думаю, это будет треугольник, например:
Наставник: Совершенно верно! Какие еще формы, по вашему мнению, можно было бы создать, разрезав поперечное сечение квадрат?
Студент: Хм, я уверен, что если вы можете создать треугольник, отрезав только угол куба, тогда вы можете создать пятиугольник, отрезав кусок побольше, например:
Наставник: Это хорошо, так что вы видите, что вы можете создать поперечное сечение с большим количеством сторон, чем у оригинала. форма.Что произойдет, если вы наклоните поперечное сечение еще больше, чтобы верхний угол поперечное сечение тоже было отрезано?
Студент: Тогда у вас будет … шестиугольник!
Наставник: Совершенно верно! Как вы думаете, можно ли построить фигуру с большим количеством сторон, например, семиугольник?
Студент: Я не могу понять, как это сделать, так как я не могу отрезать больше двух из четырех углы.
Наставник: Не волнуйтесь, то, что я просил сделать, на самом деле невозможно! На кубе всего шесть граней, так что максимальное количество сторон — шесть.
Студент: В этом есть смысл. Бьюсь об заклад, вы можете сделать это с любой призмой — просто нужно наклонить сечение правильно, чтобы пересечь все грани.
Наставник: Вы совершенно правы, любую призму можно разрезать так, чтобы в поперечном сечении было как можно больше сторон. поскольку у призмы есть грани. Однако не все формы обладают этим же свойством. Вы можете придумать 3-х мерная фигура, стороны которой не может ли все быть рассечено одной и той же плоскостью?
Ученик: Возможно, это икосаэдр, потому что нет плоскости, которая могла бы пересечь все двадцать его сторон:
Наставник: Хорошо, Икосаэдр — это пример многогранника, который не является призмой.
Если рассматривать призмы
только то, что будет с поперечными сечениями призмы, если количество боковых граней
приблизилась к бесконечности?
Студент: Я никогда не слышал о призме с бесконечной гранью …
Наставник: Ну, когда вы пытаетесь визуализировать то, чего раньше не видели, попробуйте построить то, что вы уже знаете. Представьте себе правильный квадрат, затем правильный пятиугольник, затем правильный квадрат. шестиугольник и так далее. По мере увеличения количества сторон, какая еще форма делает фигуру? подход?
Студент: Хм, он начинает больше походить на круг, потому что вы не видите никого из людей. стороны.
Наставник: Совершенно верно. Фактически, математики формально определяют круг как правильный многоугольник с бесконечной количество сторон. Итак, что произойдет, если вы разрежете круговую призму, также известную как цилиндр?
Ученик: Ну, очевидно, вы могли бы сделать круг, если бы разрезать фигуру по горизонтали, и вы могли бы сделать прямоугольник, если вырезать фигуру вертикально. Однако более интересным является тот факт, что вы можете сделайте овал, если разрезать цилиндр под углом:
Наставник: Существует бесконечное количество трехмерных фигур, каждая из которых имеет собственное поперечное сечение.Фактически, любую двумерную форму можно определить как поперечное сечение трехмерного объекта. форма. Это пригодится при обсуждении конических сечений, но также будет полезно, если вы решили пройти обучение по многомерному исчислению и другие математические классы высокого уровня.
Студент: Зачем определять двумерные формы как поперечные сечения? Почему бы просто не оставить их в двух измерениях?
Наставник: Когда мы имеем дело с двумерными фигурами, обычно — это , проще оставить их в двух измерениях.Тем не менее, поперечные сечения широко используются для
рассчитать объем неправильных фигур.
Изучив исчисление, вы научитесь
вычислить площадь практически любой двумерной формы. Поскольку трехмерный объект может быть
разделенные на большое количество поперечных сечений, площади этих поперечных сечений можно использовать для
рассчитать объем трехмерного объекта.
Геометрия: призмы
Призмы
Предположим, у вас есть многоугольник, например, треугольник или прямоугольник, и вы его клонируете.Теперь у вас есть два конгруэнтных многоугольника, лежащих бок о бок. Если ваши многоугольники не ладят друг с другом, и плоскость недостаточно велика для них обоих, одному из них придется переместиться. Идите вперед и переместите один из ваших многоугольников на новую плоскость. Не скручивайте, не поворачивайте и не поворачивайте каким-либо образом. Просто поднимите его (или опустите, если хотите) на новую плоскость, параллельную старой. Он не обязательно должен быть прямо над другим многоугольником (или под ним, если вы решили его опустить); вы можете сдвинуть его в сторону, если дух движет вами.Цель состоит в том, чтобы два многоугольника располагались в параллельных плоскостях с одинаковой ориентацией.
Как известно, отсутствие заставляет сердце полнеть. Теперь, когда ваши полигоны разделены, они могут пропустить друг друга. Это не значит, что они хотят снова жить в одной плоскости. Они могут просто захотеть установить какую-то связь. В конце концов, это конгруэнтные многоугольники, и соответствующие вершины могут захотеть сохранить свое соединение. Нарисуем отрезки линий, соединяющие каждую пару соответствующих вершин.Результат? Твердый? фигура известна как призма . Две призмы (одна основана на треугольнике, другая — на прямоугольнике) показаны на рисунке 21.1. Обратите внимание, что два многоугольника лежат в параллельных плоскостях.
Рисунок 21.1 Два примера призм.
Чтобы поговорить об этой новой форме, мне нужно познакомить вас с некоторыми терминами для частей призмы.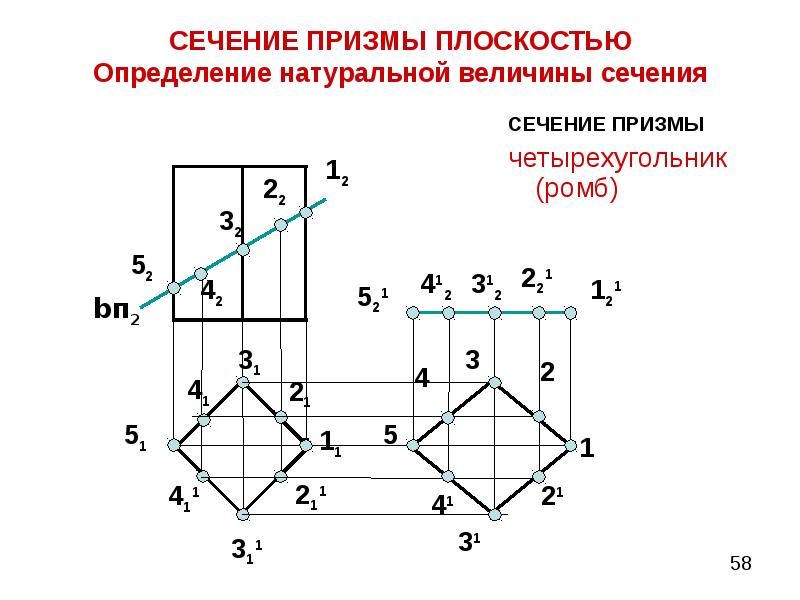
Конгруэнтные многоугольники, лежащие в параллельных плоскостях, представляют собой оснований призмы, а стороны этих многоугольников называются базовыми ребрами .Сегменты линии, соединяющие соответствующие вершины конгруэнтных многоугольников, называются боковыми краями призмы. Многоугольники, образованные боковыми гранями, называются боковыми гранями призмы. Вершины конгруэнтных многоугольников — это вершин призмы. У призмы всегда будет вдвое больше вершин, чем у базового многоугольника.
Эврика!
Призма — это область, образованная двумя параллельными конгруэнтными многоугольниками, имеющими соответствующие вершины, соединенные линейными сегментами.
Основания призмы — это конгруэнтные многоугольники, лежащие в параллельных плоскостях.
Края основания призмы — это края основания призмы.
Вершина призмы — это точка пересечения двух базовых ребер.
боковые кромки призмы — это отрезки прямых, соединяющие соответствующие вершины оснований призмы.
Боковая грань призмы — это четырехугольник, образованный парой соответствующих базовых ребер и боковых ребер, которые соединяют соответствующие вершины.
В треугольной призме один из двух равных треугольников находится прямо над другим. В этом случае боковые края перпендикулярны краям основания, и призма называется правой призмой . Если основания правой призмы — правильные многоугольники (напомним, что правильный многоугольник — это равносторонний и равноугольный многоугольник), то призма называется правильной призмой .
В прямоугольной призме (призма, созданная из совпадающих прямоугольников), показанной на рисунке 21.1 боковые кромки не перпендикулярны основным кромкам. Это пример наклонной призмы .
К настоящему времени вы могли заметить, что название призмы связано с формой ее основания.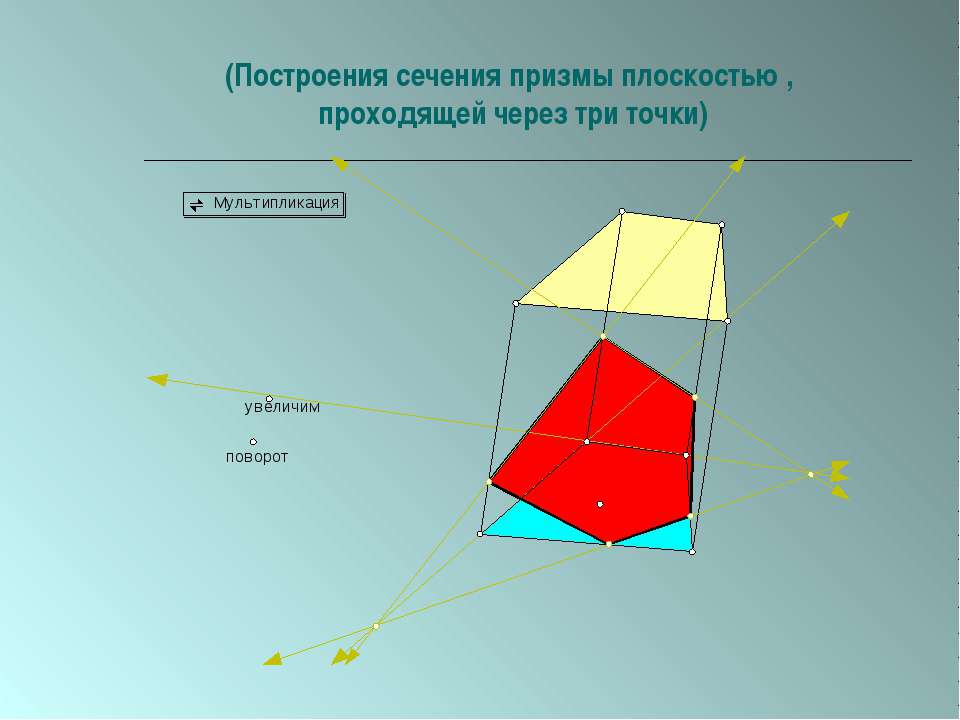
Треугольная призма имеет треугольное основание; прямоугольная призма имеет прямоугольное основание и т. д. Этот шаблон будет соблюдаться до конца времени (или, по крайней мере, до тех пор, пока не истечет ваша способность давать имена полигонам).
Solid Facts
Правая призма — это призма, в которой боковые края перпендикулярны основным краям в вершинах.
Наклонная призма — это призма, в которой угол, образованный между боковым краем и краем основания, не является прямым.
Правильная призма — это правая призма, основание которой представляет собой правильный многоугольник.
Самая знакомая призма — это куб. Куб — это призма с квадратным основанием. Но это только начало! Боковые грани куба перпендикулярны основным ребрам, поэтому куб — это прямая призма. Но ждать! Есть еще кое-что! Основания куба — это квадраты, которые представляют собой правильные многоугольники.Итак, куб — это правая призма, основание которой — правильный многоугольник. Другими словами, куб — это правильная призма. Но куб — это еще не все. У куба есть боковые ребра, длина которых равна длине основных ребер. Этого достаточно, чтобы отнести куб к очень элитной категории. Это в таком элитном классе, что есть только пять форм, достойных входа. Вы узнаете больше об этом классе в конце этого раздела.
Эврика!
Чтобы назвать призму, начните с имени многоугольника, образующего ее основу.Затем определите, является ли основание призмы правильным многоугольником. Если да, то у вас обычная призма. Если нет, то у вас просто обычная призма. Наконец, определите, перпендикулярны ли боковые кромки основным кромкам. Если да, значит, призма правая; в противном случае у вас будет наклонная призма. Соедините все части вместе, и вы назвали эту призму.
Призмы называют и классифицируют по основанию и соотношению между их боковыми краями и краями основания.
Давайте практиковаться.
- Пример 1 : Назовите и классифицируйте каждый тип призмы, показанный на рисунке 21.2.
Рисунок 21.2 Три призмы, которые нужно назвать и классифицировать.
- Решение : Первая призма имеет шестиугольное основание (не равностороннее) и боковые края, перпендикулярные краям основания. Это делает его правильной шестиугольной призмой. Вторая призма имеет пятиугольное основание (не равностороннее), а боковые края не перпендикулярны основанию, поэтому это наклонная пятиугольная призма.Третья призма имеет треугольное основание, и она равносторонняя. По теореме 14.3 он также равноугольный, что делает его регулярным. Поскольку боковые края перпендикулярны краям основания, это правая призма. Таким образом, это правильная правильная треугольная призма.
Выдержка из The Complete Idiot’s Guide to Geometry 2004 Дениз Сечей, доктор философии. Все права защищены, включая право на полное или частичное воспроизведение в любой форме. Используется по договоренности с Alpha Books , членом Penguin Group (USA) Inc.
Чтобы заказать эту книгу непосредственно у издателя, посетите веб-сайт Penguin USA или позвоните по телефону 1-800-253-6476. Вы также можете приобрести эту книгу на Amazon.com и Barnes & Noble.
Усик призмы | eMathZone
Фрустум
Если взять плоский разрез правой призмы, параллельный ее концу (т. Е. Перпендикулярно ее оси), это сечение называется поперечным сечением призмы, и два положения призмы по-прежнему являются призмами.Однако, если взятое плоское сечение не параллельно концам, часть призмы между плоским сечением и основанием называется усеченной.
Объем ствола призмы
Рисунок $$ ABCEFGHI $$ представляет собой усеченную грань призмы, секущая плоскость которой $$ EFGH $$ наклонена под углом $$ \ theta $$ к горизонтали.