Тема №6149 Ответы к задачам по математике 5926 (Часть 4)
Тема №6149
Ответы в самом низу встроенного документа
10.3.18. [МАХИ] Медиана прямоугольного треугольника, проведенная
к гипотенузе, разбивает его на два треугольника с периметрами pi и р2 —
Найти стороны треугольника.
10.3.19. [МАХИ] Точка пересечения медиан прямоугольного треуголь
ника удалена от катетов на расстояния соответственно 3 и 4. Найти
расстояние от этой точки до гипотенузы.
10.3.20. [РЭА] Длина одного из катетов прямоугольного треугольника
равна 12. Расстояние от центра описанной около треугольника окруж
ности до этого катета равно 2,5. Найти длину гипотенузы треугольника.
10.3.21. [МЭИ] Длины катетов прямоугольного треугольника равны 20
и 21. Найти длину окружности, описанной около данного треугольника.
10.3.22. [МАДИ] В прямоугольном треугольнике АВС даны: длина Q
катета ВС, равная 36, и косинус угла ВАС, равный Найти длину
другого катета АС и площадь треугольника.
10.3.23. [МАХИ] В прямоугольном треугольнике АВС с гипотенузой
АВ проведена полуокружность радиусом 2, центр которой лежит на сто
роне АС и которая касается сторон АВ и ВС. Полуокружность радиусом
1 касается этой полуокружности и стороны АВ, а центр ее также лежит
на стороне АС. Найти длины сторон треугольника.
10.3.24. [МИЭХ] В прямоугольный треугольник с катетами а и & вписан
квадрат, имеющий с треугольником общий прямой угол. Найти периметр
квадрата.
10.3.25. [РГТГУ] Катеты прямоугольного треугольника равны а и 2а.
Середина катета 2а служит центром окружности с радиусом, равным а.
На какие отрезки делится этой окружностью гипотенуза треугольника?
10.3.26. [МПГУ] Найти радиус окружности, вписанной в треугольник
АВС с прямым углом С, если LB — 30°, ВС — 6 см.
10.3.27. [МПГУ] Найти радиус окружности, вписанной в прямоуголь
ный треугольник с катетами 6 см и 8 см.
10.3.28. [КПП] В прямоугольном треугольнике сумма катетов равна
17 см, а длина гипотенузы — 13 см.
 Найти катеты и площадь треуголь
Найти катеты и площадь треугольника.
10.3.29. [МПГУ] В прямоугольном треугольнике катет равен 24см, а
гипотенуза — 25 см. Найти биссектрису треугольника, проведенную из
вершины меньшего угла.
10.3.30. [МПГУ] Гипотенуза прямоугольного треугольника равна 5, а
высота, проведенная к ней, равна 2. Найти радиусы вписанной и описан
ной окружностей.
221
10.3.31. [МАТИ] В прямоугольном треугольнике отношение высоты к
О
медиане, проведенным из вершины прямого угла, равно Найти острые
у г л ы треу голь \ i ика.
10.3.32. [МТУСИ] В прямоугольном треугольнике отношение катетов
равно тр Найти тангенс острого утла между медианами, проведенными
к катетам.
10.3.33. [МТУСИ] Найти синус большего острого угла прямоугольного
треугольника, если радиус окружности, описанной около треугольника,
10.3.34. [МТУСИ] В прямоугольном треугольнике АВС длины катетов
АС и ВС соответственно равны 12 и 8.
 Точка К — середина медианы
Точка К — середина медианыBD. Найти длину отрезка СК.
О
10.3.35. [ГАНГ] Окружность, радиус которой касается гипотенузы
равнобедренного прямоугольного треугольника в вершине его острого
угла и проходит через вершину прямого угла. Найти длину дуги, за
ключенной внутри треугольника.
10.3.36. [МГУЛ] В прямоугольном треугольнике медианы острых углов
равны \/89 и \/l56. Найти длину гипотенузы.
10.3.37. [ГАУ] Найти катеты прямоугольного треугольника, у которого
высота, опущенная на гипотенузу, делит ее на отрезки длиной 6 и 18.
10.3.38. [ГАУ] Окружность касается одного из катетов равнобедренного
прямоугольного треугольника и проходит через вершину противополож
ного острого угла. Центр окружности лежит на гипотенузе треугольни
ка, длина которой равна с. Найти радиус окружности.
10.3.39. [ГАУ] В прямоугольном треугольнике АВС с прямым углом
В биссектриса угла А пересекает сторону ВС в точке D. Известно, что
BD “ 4, DC — 6. Определить площадь треугольника ADC.

10.3.40. [МИСиС] В прямоугольном треугольнике высота, опущенная
из вершины прямого угла, делит гипотенузу на отрезки длиной 9 и 16.
Найти радиус вписанной в треугольник окружности.
10.3.41. [ГАУ] Катеты прямоугольного треугольника равны 15 и 20.
Найти расстояние от высоты, опущенной из вершины прямого угла до
центра вписанной окружности.
10.3.42. [МГУ, хим. ф-т] Прямоугольные треугольники АВС и ABD
имеют общую гипотенузу АВ — 5. Точки С и D расположены но разные
стороны от прямой, проходящей через точки А и В, ВС — ВО — 3.
площадь пятиугольника ECBDF.
2‘п
10.3.43. [МГУ, геогр. ф-т] Вне прямоугольного треугольника А В С на его
катетах АС и ВС построены квадраты AC D E и BCFG. Продолжение
медианы С М треугольника А В С пересекает прямую D F в точке N .
Найти длину CN, если длины катетов равны 1 и 4.
10.3.44. [МГУ, физ. ф-т] В прямоугольном треугольнике отношение ра
диуса вписанной окружности к радиусу описанной окружности равно jr.
 .
.10.3.49. [РЭА] В прямоугольном треугольнике биссектриса прямого
угла делит гипотенузу на отрезки Зсм и 4 см. Найти площадь треуголь
ника.
10.3.50. [РЭА] В прямоугольный треугольник вписан квадрат, верши
на которого совпадает с вершиной прямого угла треугольника. Найти
площадь треугольника, если один из его катетов равен 42 см, а сторона
квадрата — 24 см.
10.3.51. [РЭА] Точка на гипотенузе прямоугольного треугольника, рав
ноудаленная от катетов, делит ее на отрезки 30 см и 40 см. Найти пери
метр треугольника.
10.3.52. [РЭА] В прямоугольном треугольнике известны гипотенуза
125 см и меньший катет 75 см. Основание высоты, проведенной из вер
шины прямого угла, делит гипотенузу на два отрезка. На меньшем из
отрезков как на диаметре построена полуокружность по одну сторону с
данным треугольником. Определить длину отрезка катета, заключенно
го внутри этого полукруга.
223
10.3.53. [РЭА] В прямоугольном треугольнике АВС гипотенуза ВС =
= 20, а катет А В = 16.
 Найти квадрат расстояния от вершины А до
Найти квадрат расстояния от вершины А добиссектрисы угла С.
10.3.54. [МГУЛ] Найти сумму длин катетов прямоугольного треуголь
ника, если длина его гипотенузы 20 см, а радиус вписанной окружно
сти 4 см.
10.3.55. [МАСИ] Найти площадь круга, вписанного в прямоугольный
на отрезки длиной 25,6 и 14,4 см.
4. Трапеция
10.4.1. [МАТИ] Площадь равнобочной трапеции равна S, угол между ее
диагоналями, противолежащий боковой стороне, равен а. Найти высоту
трапеции.
10.4.2. [МАТИ] В равнобочную трапецию вписана окружность радиу
са г. Верхнее основание трапеции в два раза меньше ее высоты. Найти
площадь трапеции.
10.4.3. [МАИ] В трапеции ABCD сумма углов при основании AD рав
на 90°. Нижнее и верхнее основания равны соответственно 7 и 3. Опре
делить отрезок, соединяющий середины оснований.
10.4.4. [МГУ, эк. ф-т; МИФИ; МЭИ; СПбГУ; МПУ; РГПУ; МИСиС] В трапе
ции, основания которой аиЬ, через точку пересечения диагоналей про
ведена прямая, параллельная основаниям.
 Найти длину отрезка этой
Найти длину отрезка этойпрямой, отсекаемого боковыми сторонами трапеции.
10.4.5. [МГУ, геогр. ф-т; РЭА; МЭИ] Около круга описана трапеция с
углами при основании а и /?. Найти отношение площади трапеции к
площади круга.
10.4.6. [РУДН] Периметр равнобедренной трапеции вдвое больше длины
вписанной окружности. Найти угол при основании трапеции.
10.4.7. [МАИ] В трапеции ABCD проведены диагонали АС и BD,
пересекающиеся в точке F. Из вершины С проведена прямая СК, па
раллельная боковой стороне AD, которая пересекает продолжение BD
в точке L так, что DF = BL. Найти отношение АВ : CD.
10.4.8. [МАТИ] Определить площадь круга, вписанного в прямоуголь
ную трапецию с основаниями а и Ь.
10.4.9. [МАТИ] Центр круга, вписанного в прямоугольную трапецию,
отстоит от концов боковой стороны на 1см и 2 см. Найти площадь тра
пеции.
224
10.4.10. [СПбГУ] Определить площадь трапеции, если ее основания
равны 6 см и 11см, одна из боковых сторон — 4 см, а сумма углов при
нижнем основании равна
10.

с острыми углами а и /3 при большем основании. Найти площадь этой
трапеции.
10.4.12. [МПУ] Меньшее основание равнобедренной трапеции равно
высоте и равно h. Острый угол трапеции равен а. Найти периметр тра
пеции.
10.4.13. [МГУ, геолог, ф-т; СПбГУ; ЛГПИ] Найти площадь равнобочной
трапеции, основания которой равны а и 6, а диагонали взаимно перпен
дикулярны.
10.4.14. [МПУ] Периметр равнобедренной трапеции с острым углом а
равен р. Высота трапеции равна h. Найти площадь этой трапеции.
10.4.15. [МЭИ] В круг вписана равнобедренная трапеция так, что диа
метр круга служит основанием трапеции. Найти отношение площадей
круга и трапеции, если тупой угол трапеции равен а.
10.4.16. [МАТИ] В равнобочной трапеции ABCD длины боковой сторо
ны АВ и меньшего основания ВС равны а = 2 см и BD перпендикулярна
АВ. Найти площадь трапеции.
10.4.17. [МИСиС] В равнобедренной трапеции даны длины оснований
21 и 9 и длина высоты 8.
 Найти радиус описанной окружности.
Найти радиус описанной окружности.10.4.18. [МИСиС] В равнобедренную трапецию вписана окружность ра
диуса 2. Найти площадь трапеции, если длина боковой стороны равна 10.
10.4.19. [МЭИ] Около круга радиуса 2см описана равнобедренная тра
пеция с острым углом 30°. Найти длину средней линии трапеции.
10.4.20. [МАТИ] Найти площадь трапеции, диагонали которой рав
ны 7см и 8 см, а основания — Зсм и 6 см.
10.4.21. [МИСиС] Длины оснований трапеции равны 10 и 24, длины
боковых сторон равны 13 и 15. Найти площадь трапеции.
10.4.22. [СПбГУ] В равнобедренной трапеции, описанной около окруж
ности радиуса й, отношение длин боковой стороны и большего основа
ния есть заданное число к. Найти длину меньшего основания.
10.4.23. [СПбГУ] В равнобедренной трапеции боковая сторона равна с,
основания трапеции.
225
10.4.24. [МАИ] Боковые стороны АВ и CD трапеции продолжены до
пересечения в точке Е.
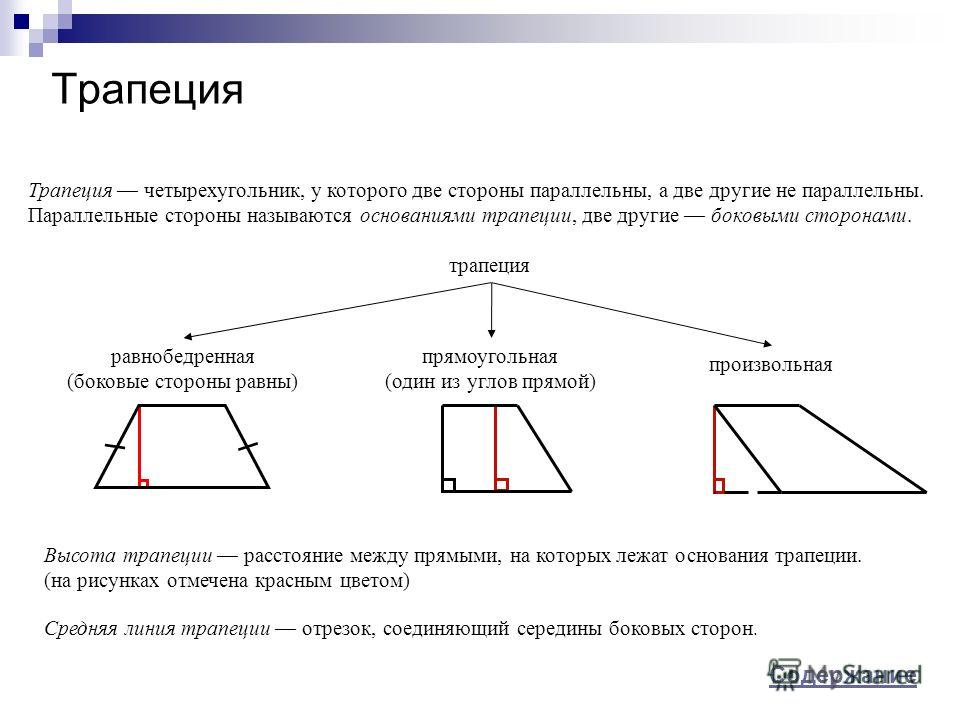 Точка О — центр описанной около треугольника
Точка О — центр описанной около треугольникаADE окружности. Найти величину острого угла А трапеции, если из
вестно, что точки А, В, С, D, О лежат на окружности, радиус которой
в \/3 раз меньше радиуса окружности, описанной около треугольника
ADE.
10.4.25. [МАТИ] Основания трапеции равны 4см и 16см. Найти ее
площадь, если известно, что в трапецию можно вписать и вокруг нее
можно описать окружность,
10.4.26. [РЭА] Вокруг окружности описана равнобо
Сканави. Планиметрия. Задачи 151 – 190 с ответами и решениями
Сканави М.И.
Задачи по планиметрии с ответами и решениями
перейти к содержанию
Группа А. Задачи 151 — 190 (с ответами и решениями)
Вычислить площадь трапеции по разности оснований, равной 14 см, и двум непараллельным сторонам, равным 13 и 15 см, если известно, что в трапецию можно вписать окружность. Ответ: Решение
В трапеции, площадь которой равна 594 м2, высота 22 м, а разность параллельных сторон равна 6 м, найти длину каждой из параллельных сторон.
 Ответ: Решение
Ответ: Решение- Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
- Трапеция разбита диагоналями на четыре треугольника. Найти отношение площадей треугольников, прилегающих к боковым сторонам трапеции. Ответ: Решение
- Диагональ прямоугольной трапеции и ее боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2 см, а боковая сторона 4 см. Ответ: Решение
- Вычислить площадь прямоугольной трапеции, если ее острый угол равен 60°, меньшее основание равно , а большая боковая сторона равна . Ответ: Решение
- Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12 см2, а длина высоты равна 2 см. Ответ: Решение
- Определить боковые стороны равнобедренной трапеции, если ее основания и площадь равны соответственно 8 см, 14 см и 44 см2.
 Ответ: Решение
Ответ: Решение - Диагональ равнобедренной трапеции делит ее тупой угол пополам. Меньшее основание трапеции равно 3 см, периметр равен 42 см. Найти площадь трапеции. Ответ: Решение
- В равнобедренной трапеции одно основание равно 40 см, а другое 24 см. Диагонали трапеции взаимно перпендикулярны. Найти ее площадь. Ответ: Решение
- В равнобедренной трапеции длина средней линии равна 5, а диагонали взаимно перпендикулярны. Найти площадь трапеции. Ответ: Решение
- Большее основание’трапеции в 2 раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношение высоты каждой из двух полученных трапеций к высоте трапеции. Ответ: Решение
- Основания равнобедренной трапеции и , боковая сторона ее равна , а диагональ равна . Доказать, что .
- Найти диагональ и боковую сторону равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции.
 Ответ: Решение
Ответ: Решение - В равнобедренной трапеции даны основания =21 см, = 9 см и высота = 9 см. Найти радиус описанного круга. Ответ: Решение
- В окружность радиуса вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции. Ответ: Решение
- Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17 см. Вычислить радиус окружности, описанной около трапеции, если известно, что ее средняя линия равна высоте. Ответ: Решение
- Найти площадь равнобедренной трапеции, если ее высота равна , а боковая сторона видна из центра описанной окружности под углом 60°. Ответ: Решение
- Около окружности с диаметром 15 см описана равнобедренная трапеция с боковой стороной, равной 17 см. Найти основания трапеции. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна , а высота трапеции в 2 раза меньше ее боковой стороны. Определить радиус вписанного круга. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна см2.
 Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение - Площадь равнобедренной трапеции, описанной около круга, равна 8 см2. Определить стороны трапеции, если угол при основании содержит 30°. Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна . Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
- Площадь равнобедренной трапеции, описанной около круга, равна . Определить радиус круга, если угол при основании трапеции равен 30°. Ответ: Решение
- В равнобедренную трапецию вписана окружность радиуса . Верхнее основание трапеции в 2 раза меньше ее высоты. Найти площадь трапеции. Ответ: Решение
- Найти площадь круга, вписанного в равнобедренную трапецию, если ее большее основание равно , а угол при меньшем основании равен 120°. Ответ: Решение
- В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной n и m.
 Определить площадь трапеции. Ответ: Решение
Определить площадь трапеции. Ответ: Решение - В равнобедренную трапецию вписан круг. Доказать, что отношение площади круга к площади трапеции равно отношению длины окружности к периметру трапеции.
- Равносторонний шестиугольник ABCDEF состоит из двух трапеций, имеющих общее основание CF. Известно, что АС = 13 см, АЕ = 10 см. Найти площадь шестиугольника. Ответ: Решение
- Найти сторону правильного шестиугольника, равновеликого равнобедренной трапеции с основаниями 20 и 12 см, если известно, что центр описанной окружности лежит на большем основании трапеции. Ответ: Решение
- Вычислить отношение площадей квадрата, правильного треугольника и правильного шестиугольника, вписанных в одну и ту же окружность. Ответ: Решение
- Найти отношение площадей равностороннего треугольника, квадрата и правильного шестиугольника, длины сторон которых равны. Ответ: Решение
- В правильный треугольник со стороной, равной , вписана окружность, в которую вписан правильный шестиугольник.
 Найти площадь шестиугольника. Ответ: Решение
Найти площадь шестиугольника. Ответ: Решение - Около квадрата, сторона которого равна , описана окружность, а около окружности — правильный шестиугольник. Определить площадь шестиугольника. Ответ: Решение
- Из точки М, находящейся на расстоянии от окружности, приведена к этой окружности касательная длиной . Найти площадь правильного шестиугольника, вписанного в окружность. Ответ: Решение
- В правильный треугольник вписана окружность, а в нее — правильный шестиугольник. Найти отношение площадей треугольника и шестиугольника. Ответ: Решение
- На сторонах равностороннего треугольника вне его построены квадраты. Их вершины, лежащие вне треугольника, последовательно соединены. Определить площадь полученного шестиугольника, если сторона данного треугольника равна . Ответ: Решение
- В правильный шестиугольник, сторона которого равна , вписана окружность, и около него же описана окружность. Определить площадь кругового кольца, заключенного между этими окружностями.
 Ответ: Решение
Ответ: Решение - Данный квадрат со стороной срезан по углам так, что образовался правильный восьмиугольник. Определить площадь этого восьмиугольника. Ответ: Решение
- Доказать, что сумма расстояний от любой точки, взятой внутри правильного шестиугольника, до всех прямых, содержащих его стороны, есть величина постоянная.
Метки Сканави. Смотреть запись.
Учебное пособие «Задачи по геометрии для 8 класса с учетом дифференциации»
Учебное пособие
«ЗАДАЧИ ПО ГЕОМЕТРИИ ДЛЯ 8 КЛАССА»
(трехуровневый задачник для углубленного изучения математики с учетом дифференцированного обучения)
Составил: Беляева Елена Борисовна
учитель высшей категории, ГБОУ СОШ № 236
г. Санкт — Петербург
Санкт — Петербург
2019 год
Задачник по геометрии для 8 класса.
(углубленное изучение математики с учетом дифференцированного обучения).
Методические рекомендации по использованию задачника.
Теоретическая часть школьного учебника содержит как правило, определения, аксиомы, теоремы, необходимые для развития этой самой теории, то есть для получения стройной лаконичной системы знаний основных свойств геометрических фигур, изучаемых в школе.
Изучения
только тех геометрических фактов, которые изложены в учебнике явно недостаточно
для глубокого изучения и понимания элементарной геометрии. Необходимо еще
овладеть искусством решения задач, особенно на доказательство существования
того или иного свойства геометрической фигуры или взаимосвязи, взаимообусловленности
свойств нескольких геометрических фигур, о которых в учебнике не упоминается.
«Умение доказывать» — это главное умение, необходимое при изучении частей элементарной математики, и не только математики.
Предлагаемые задачи, в основном, на доказательство геометрических фактов существенно дополняющих и углубляющих теоретическую часть школьного учебника по геометрии для 8 класса.
Задачи распределены по трем уровням. Наиболее трудные задачи отнесены к третьему уровню. Некоторые задачи даны в паре с другими задачами под одним номером, что обусловлено их взаимной дополняемостью.
По
темам «Трапеция» и «Окружность» задач больше, чем по другим темам учебной
программы. Это объясняется местом этих тем в учебной программе и,
следовательно, возможности ввести в фонд активных знаний большой теоретический
материал. Некоторые задачи 3 – го уровня являются теоремами из других школьных
учебников. Об этом полезно сказать учащимся. Во – первых, для того, чтобы они
изъявили желание познакомиться с другими учебниками и, во – вторых, чтобы
система изложения геометрических фактов не представлялась бы им как нечто
неизменное, застывшее, раз и навсегда остановленное. Понимание вариантности
систематических курсом геометрии имеет большое общеобразовательное значение.
Понимание вариантности
систематических курсом геометрии имеет большое общеобразовательное значение.
Использование задач из предлагаемого задачника может быть самым разнообразным, в зависимости от состава класса. Но желательно, чтобы все учащиеся класса активно ознакомились бы с решениями задач 2 – ого уровня, что поможет приобрести некоторые навыки необходимые для решения более трудных задач 3 – ого уровня, особенно в дополнительных построениях,
Но порции задач должны быть дифференцированными, с учетом уровня учебных возможностей, интересов, наличия свободного времени, в конечном счете состояния здоровья каждого ученика.
Если задач окажется недостаточно, то есть возможность дополнять их задачами – вариантами предложенных. Их можно составлять, например, по принципу теорем, обратных данным.
Решение
трудных задач можно обсудить на уроках – семинарах (по методике, выбранной
учителем), а задачи по важности своих результатов не уступающие теоремам
полезно изучить на уроках – конференциях.
ЧЕТЫРЕХУГОЛЬНИКИ
I уровень
1. В параллелограмме, смежные стороны которого не равны, проведены биссектрисы углов. Докажите, что при их пересечении образуется прямоугольник.
2. Докажите, что отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
3. Докажите, что выпуклый четырехугольник является параллелограммом, если сумма углов, прилежащих к каждой из двух смежных сторон равна 180 градусам.
4. Докажите, что выпуклый четырехугольник является параллелограммом, если его противоположные углы попарно равны.
5. Из вершин острый, проведены перпендикуляры Докажите, что четырехугольник – параллелограмм.
6. Диагонали параллелограмма Докажите, что четырехугольник вершинами которого являются середины отрезков
7. На диагонали так, что Докажите,
что четырехугольник
На диагонали так, что Докажите,
что четырехугольник
8. Докажите, что в равнобедренной трапеции: а) углы при основании равны; б) диагонали трапеции равны.
9. Докажите, что параллелограмм является ромбом, если: а) его диагонали взаимно перпендикулярны; б) диагональ параллелограмма является биссектрисой его угла.
10. Докажите, что ромб, у которого один угол — прямой , является квадратом.
11. Является ли четырехугольник квадратом, если его диагонали:
a) Равны и взаимно перпендикулярны
b) Взаимно перпендикулярны и имеют общую середину
c) Равны, взаимно перпендикулярны и имеют общую середину?
12. В прямоугольном треугольнике проведена биссектриса прямого угла. Через точку пересечения этой биссектрисы с гипотенузой проведены прямые, параллельные катетам. Докажите, что полученный четырехугольник – квадрат.
13.
Докажите, что прямая, проходящая через
середины противоположных сторон прямоугольника, является осью симметрии.
14. Докажите, что прямая, содержащая биссектрису равнобедренного треугольника, проведенную к основанию, является осью симметрии треугольника.
15. Имеет ли центр симметрии: отрезок; луч; пара пересекающихся прямых; квадрат.
16. Стороны параллелограмма равны 10 и 3. Биссектрисы двух углов, прилежащих к большей стороне, делят противоположную сторону на три отрезка. Найти длины этих отрезков.
17. Найдите множество середин всех отрезков, соединяющих данную точку со всеми точками данной прямой, не проходящей через эту точку.
18. Докажите, что прямая, проходящая через середины оснований равнобедренной трапеции, перпендикулярна к основаниям. Сформулируйте и докажите обратное утверждение.
19. Докажите, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
20.
Докажите, что точка пересечения диагоналей
ромба равноудалена от его сторон.
21. В трапеции перпендикулярна к боковой стороне Найти если периметр трапеции равен 20,
22. Докажите, что площадь квадрата, построенного на катете прямоугольного равнобедренного треугольника, вдвое больше площади квадрата, построенного на высоте, проведенной к гипотенузе.
23. Докажите, что сумма расстояний от точки, лежащей внутри равностороннего треугольника, до его сторон не зависит от положения этой точки.
24. В трапеции точке О а) сравните площади ; б) сравните площади ; в) докажите, что
Второй уровень.
25. Докажите, что прямые, содержащие диагонали ромба, являются его осями симметрии.
26.
Через произвольную точку основания
равнобедренного треугольника проведены прямые, параллельные боковым сторонам
треугольника. Докажите, что периметр получившегося четырехугольника равен сумме
боковых сторон данного треугольника.
27. Точка К – середина медианы треугольника
28. Точки Докажите, что прямые
29. Основания трапеции средней линии.
30. О трапеции Определите, что пересекает биссектриса угла
31. Докажите, что четырехугольник с вершинами в серединах сторон данного четырехугольника является параллелограммах. При каком условии этот параллелограмм будет: а) прямоугольником, б) ромбом, в) квадратом?
32. В прямоугольный треугольник с углом вписан ромб со стороной 6 так, что угол у них общий и все вершины ромба лежат на сторонах треугольника. Найти стороны треугольника.
33. Периметр параллелограмма равен 90 и острый угол содержит Диагональ параллелограмма делит его острый угол на части в отношении 1 : 3. Найти стороны параллелограмма.
34.
Диагональ прямоугольной трапеции и ее
боковая сторона равны. Найти длину средней линии, если высота трапеции равна 2,
а боковая сторона – 4.
35. Перпендикуляр, проведенный из вершины параллелограмма к его диагонали, делит эту диагональ на отрезки длиной 6 и 15. Разность длин сторон параллелограмма равна 7. Найти длины сторон параллелограмма и его диагонали.
36. Доказать, что если в четырехугольнике диагонали лежат на биссектрисах его углов, то такой четырехугольник – ромб.
37. Площадь прямоугольника 9, а величина одного из углов, образованного диагоналями, равна Найти стороны прямоугольника.
Третий уровень.
38. Сумма углов при одном из оснований трапеции равна . Докажите, что отрезок, соединяющий середины оснований трапеции, равен их полуразности.
39. (трудная) Диагонали выпуклого четырехугольника разбивают его на четыре треугольника, периметры которых равны. Докажите, что этот четырехугольник – ромб.
40. (в
паре с № 1) При пересечении биссектрис всех углов прямоугольника образовался
четырехугольник. Докажите, что этот четырехугольник – квадрат.
Докажите, что этот четырехугольник – квадрат.
41. На рисунке изображены три квадрата. Найти сумму
B C D
A E
42. Доказать, что прямая, проходящая через точку пересечения диагоналей трапеции и точку пересечения продолжений ее боковых сторон, проходит через середины оснований трапеции.
43. Расстояние между серединами двух сторон четырехугольника равно полусумме двух других его сторон. Доказать, что этот четырехугольник – трапеции.
44. Докажите, что медиана в прямоугольном треугольнике, выходящая из прямого угла, равна половине гипотенузы. Сформулируйте и докажите обратное утверждение.
45. Пусть две стороны и угол одного
треугольника соответственно равны двум сторонам и углу другого треугольника.
Следует ли из этого , что треугольники равны?
Пусть две стороны и угол одного
треугольника соответственно равны двум сторонам и углу другого треугольника.
Следует ли из этого , что треугольники равны?
46. В прямоугольном треугольнике Докажите, что
47. Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, выходящими из той же вершины.
48. (в паре с №47) Доказать, что медиана прямоугольного треугольника, проведенная к гипотенузе, равна половине гипотенузы.
49. (в паре с №47) Доказать, что центр окружности описанной около прямоугольного треугольника лежит на гипотенузе.
50. Доказать, что медианы в треугольнике пересекаются в одной точке, и делятся ею в отношении 1 : 2.
51. Пусть Докажите, что То же верно для биссектрисы внешнего угла треугольника ( стороны .
52.
Биссектрисы тупых углов при основании
трапеции пересекаются на другом ее основании. Найти все стороны трапеции, если
ее высота равна 12, а длины биссектрис 15 и 13.
Найти все стороны трапеции, если
ее высота равна 12, а длины биссектрис 15 и 13.
53. В треугольник вписан ромб со стороной так, что один угол у них общий, а противоположная вершина ромба лежит на стороне треугольника и делит эту сторону на отрезки длиной Найти стороны треугольника.
54. В прямоугольном треугольнике медианы катетов равны Найти гипотенузу треугольника.
55. Из вершины острого угла ромба проведены перпендикуляры к прямым содержащим стороны ромба, которым не принадлежит эта вершина. Длина каждого перпендикуляра равна 3, а расстояние между их основаниями . Вычислить длины диагоналей ромба.
56. Периметр прямоугольного треугольника 60. Найти его стороны, если высота, проведенная к гипотенузе, равна 12.
57. Внутри равностороннего треугольника взята точка отстоящая от его сторон на расстояниях Найти высоту треугольника.
58.
(трудная) В равнобедренном треугольнике
угол при вершине а биссектриса угла при
основании равна Найти длины сторон
треугольника.
59. Основание равнобедренного треугольника равно 8, а боковая сторона 12. Найти длину отрезка, соединяющего точки пересечения биссектрис углов при основании с боковыми сторонами треугольника.
60. Высоты треугольника равны 12, 15, 20. Доказать, что треугольник прямоугольный.
61. Медианы треугольника равны 5, Доказать, что треугольник прямоугольны
62. Числа Показать, что, если выполняется равенство , то треугольник является прямоугольным.
ПЛОЩАДИ
I уровень
63. Стороны равны соответственно 16 и 22, а высота, проведенная к стороне Найти высоту, проведенную к стороне
64. В выпуклом четырехугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырехугольника равна половине произведения его диагоналей.
65. Вычислить площадь прямоугольной трапеции, если ее острый угол равен меньшее основание равно
66. Одна из диагоналей параллелограмма
является его высотой. Найти эту диагональ, если периметр параллелограмма 50, а
разность смежных сторон равна 1.
Одна из диагоналей параллелограмма
является его высотой. Найти эту диагональ, если периметр параллелограмма 50, а
разность смежных сторон равна 1.
67. Найти площадь равнобедренной трапеции, если: а) ее меньшее основание равно 18, а высота – 9 и острый угол равен б) ее основания равны 16 и 30, а диагонали взаимно перпендикулярны.
68. Периметр ромба равен 2, а длины его диагоналей относятся как 3 : 4. Найти площадь ромба.
69. Площадь равнобедренной трапеции, описанной около круга, равна S. Определить боковую сторону трапеции, если известно, что острый угол при основании равен
70. Доказать, что если через вершины четырехугольника провести прямые, параллельные его диагоналям, то площадь параллелограмма, определяемого этими прямыми, в два раза больше площади данного четырехугольника.
71. (в паре с №68) Периметр ромба равен Вычислить площадь ромба.
72.
Определить боковые стороны равнобедренной
трапеции, если ее основания и площадь равны соответственно 8, 14 и 44.
Второй уровень
73. Докажите, что из всех треугольников, у которых одна сторона равна наибольшую площадь имеет тот, у которого эти стороны перпендикулярны.
74. Как провести две прямые через вершину квадрата, чтобы разделить его на три фигуры, площади которых равны?
75. Докажите, что сумма расстояний от точки на основании равнобедренного треугольника до боковых сторон не зависит от положения этой точки.
76. Докажите, что если диагонали четырехугольника то
77. Сумма длин диагоналей ромба равна а его площадь равна S. Найти сторону ромба.
78. В окружность радиуса R вписана трапеция, у которой нижнее основание вдвое больше каждой из остальных сторон. Найти площадь трапеции.
79. Площадь прямоугольного треугольника равна Определить его высоту, проведенную к гипотенузе, если она делит прямой угол в отношении 1 : 2.
80. Диагональ равнобедренной трапеции делит ее
тупой угол пополам. Меньшее основание трапеции равно 3, периметр равен 42.
Найти площадь трапеции.
Диагональ равнобедренной трапеции делит ее
тупой угол пополам. Меньшее основание трапеции равно 3, периметр равен 42.
Найти площадь трапеции.
81. Трапеция разбита диагоналями на четыре треугольника. Доказать, что треугольники, прилегающие к боковым сторонам, равновелики.
82. В равнобедренной трапеции одно основание равно 40, а другое 24. Диагонали этой трапеции взаимно перпендикулярны. Найти ее площадь.
83. Высота ромба равна 12, а одна из его диагоналей – 15. Найти площадь ромба.
84. В прямоугольнике проведены биссектрисы двух углов, прилежащих к большей стороне. Определить, на какие части делится площадь прямоугольника этими биссектрисами, если стороны прямоугольника равны 2 и 4.
85. Длина высоты, проведенной на основание равнобедренного треугольника, равна 25, а радиус вписанной окружности равен 8. Найти длину основания треугольника.
86. Найти площадь равнобедренного треугольника, если основание его равно а длина высоты, проведенной к основанию, равна длине отрезка, соединяющего середины основания и боковой стороны
87. Вычислить площадь трапеции, параллельные
стороны которой 16 и 44, а не параллельные – 17 и 25.
Вычислить площадь трапеции, параллельные
стороны которой 16 и 44, а не параллельные – 17 и 25.
88. Найти площадь трапеции, диагонали которой равны 7 и 8, а основания – 3 и 6.
89. Доказать, что сумма расстояний от любой точки основания равнобедренного треугольника до боковых сторон равна высоте этого треугольника, проведенной к боковой стороне.
90. (в паре с №89) Доказать, что сумма расстояний от любой точки внутри правильного треугольника до его сторон равна высоте этого треугольника.
91. Найти площадь трапеции с основаниями 7 и 11 и боковыми сторонами 3 и 5.
92. Найти площадь трапеции с основаниями 6 и 7 и диагоналями 5 и 12.
93. На катете построена окружность, пересекающая гипотенузу Найти площадь треугольника
94.
Найти площадь равнобедренного
треугольника, если высота, опущенная на основание, равна 10, а высота,
опущенная на боковую сторону, равна 12.
95. Две прямые параллельные основаниям трапеции, делят каждую из боковых сторон на три равные части. Вся трапеция разделена ими на три части. Найдите площадь средней части, если площадь крайних
96. В трапеции лежит на основании Точка прямая перпендикулярна основаниям и делит площадь трапеции пополам. Найти
97. В трапеции диагональ равна
98. Точка А лежит внутри угла, равного 60 градусам. Расстояние от точки А до сторон угла равны Найти расстояние от точки А до вершин угла.
Третий уровень.
99. Доказать, что площадь описанного многоугольника равна вписанной окружности; его полупериметр (в частности, эта формула справедлива для треугольника).
100. (в паре с № 99) Доказать, что площадь треугольника равна . Доказать, что площадь четырехугольника равна полупроизведению диагоналей на синус угла между ними.
101. В трапеции Найти площадь трапеции,
если известно, что диагонали трапеции являются биссектрисами углов
В трапеции Найти площадь трапеции,
если известно, что диагонали трапеции являются биссектрисами углов
102. Площади треугольников, образованных отрезками диагоналей трапеции и ее основаниями, равны
103. Доказать, что сумма расстояний до любой точки, взятой внутри правильного многоугольника, до всех прямых, содержащих его сторону, есть величина постоянная.
104. Докажите справедливость формул для площади треугольника:
где окружности.
105. В выпуклом четырехугольнике диагонали пересекаются в точке Е. Известно, что площадь каждого из треугольников четырехугольника не превосходит 28,
106. Доказать, что площадь трапеции равна произведению длины одной из непараллельных сторон и длины перпендикуляра, проведенного через середину другой боковой стороны к первой.
107.
Показать, что суммы расстояний от любой
точки, взятой на стороне правильного треугольника, до двух других его сторон
есть величина постоянная. (в паре с №58)
(в паре с №58)
108. (в паре с №61) Найти площадь треугольника, если его высоты равны 12, 15, 20.
109. Точки Вычислить площадь фигуры, являющейся пересечением четырехугольников если площадь ромба равна 100.
110. Через точку проведены прямые, параллельные двум другим сторонам и пересекающие стороны соответственно в точках Докажите, что треугольники имеют равные площади.
111. (очень трудная) Основания трапеции равны Отрезок с концами на боковых сторонах трапеции параллельный основаниям, разделяет трапецию на две трапеции, площади которых равны. Найти длину этого отрезка.
112. Найти площадь равнобедренной трапеции, у которой высота а диагонали взаимно перпендикулярны.
113. Точки параллелограмма Докажите, что при пересечении прямых образуется параллелограмм и найдите отношение его площади к площади параллелограмма
ПОДОБИЕ.
I уровень.
114. Доказать, что длины медиан соответствующих углов подобных треугольников относятся друг к другу также как их периметры.
115. Докажите, что длины биссектрис соответствующих углов подобных треугольников относятся друг к другу как их периметры.
116. В треугольнике Доказать, что
117. На стороне середина биссектрисы треугольника лежит на стороне Найти отношение если
118. Определить углы равнобедренного треугольника, если биссектриса угла при основании этого треугольника отсекает от него треугольник подобный данному.
119. Докажите, что биссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
120.
Докажите, что отношение сходственных
сторон подобных треугольников равно отношению высот, проведенных к этим
сторонам.
121. Докажите, что отношение периметров двух подобных треугольников равно коэффициенту подобия.
122. Стороны угла Докажите, что отрезки
123. Прямые причем точки Докажите, что
124. Через точку взятую на медиане проведена прямая, пересекающая сторону Найдите отношение если а) М – середина отрезка б) .
Второй уровень.
125. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, делит прямой угол в отношении 1:2. Доказать, что гипотенуза делится основанием высоты в отношении 1:3.
126. Прямые, содержащие боковые стороны равнобедренной трапеции, пересекаются под прямым углом. Найти длины сторон трапеции, если ее площадь равна 12, а длина высоты – 2.
127.
Точка на гипотенузе, равноудаленная от
обоих катетов, делит гипотенузу на отрезки длиной 30 и 40. Найти катеты
треугольника.
Найти катеты
треугольника.
128. В треугольник вписан ромб так, что один угол у них общий, а противоположная вершина делит сторону треугольника в отношении 2:3. Диагонали ромба равны Найти стороны треугольника, содержащие стороны ромба.
129. В равнобедренном треугольнике основание и боковая сторона равны соответственно 5 и 20. Найти биссектрису угла при основании треугольника.
130. Найти площадь квадрата, вписанного в правильный треугольник со стороной
131. Основание треугольника равно 30, а боковые стороны 26 и 28, высота разделена в отношении 2:3 (считая от вершины), и через точку деления проведена прямая, параллельная основанию. Определить площадь полученной при этом трапеции.
132.
В прямоугольном треугольнике биссектриса
острого угла делит противоположный катет на отрезки длиной 4 и 5. Определить площадь
треугольника.
133. Основания трапеции равны Найти длину отрезка параллельного основаниям, с концами на боковых сторонах трапеции, делящего площадь трапеции пополам. (в паре №111).
134. Прямая, параллельная основаниям трапеции, проходит через точку пересечения ее диагоналей. Найти длину отрезка этой прямой, заключенного между боковыми сторонами трапеции, если основания трапеции равны 4 и 12.
Третий уровень.
135. Основания трапеции равны Найти длину отрезка проходящего через точку пересечения диагоналей трапеции параллельно основаниям трапеции с концами на боковых сторонах трапеции.
136. ( в паре с №135) Доказать, что отрезок прямой, лежащий внутри трапеции и проходящий через точку пересечения диагоналей параллельно основаниям, делится этой точкой пополам.
137.
Прямая, параллельная основанию
треугольника, делит его на части, площади которых относятся как 2:1, считая от
вершины. В каком отношении она делит боковые стороны?
В каком отношении она делит боковые стороны?
138. Большее основание трапеции в два раза больше ее меньшего основания. Через точку пересечения диагоналей проведена прямая, параллельная основаниям. Найти отношения высот каждой из двух полученных трапеций к высоте данной трапеции.
139. На стороне Докажите, что
140. Точки параллелограмма Докажите, что прямые на три равные части.
141. Биссектриса внешнего угла при вершине А треугольника пересекает прямую
142. Докажите, что если противоположные стороны выпуклого четырехугольника не параллельны, то их полусумма больше отрезка, соединяющего середины двух противоположных сторон.
143. В треугольнике проведена прямая, параллельная биссектрисе угла А, которая пересекает прямые соответственно в точках Докажите, что
144.
Доказать, если сумма расстояний между
серединами противоположных сторон выпуклого четырехугольника равна половине его
периметра, то этот четырехугольник – параллелограмм.
ОКРУЖНОСТЬ
I — 2 уровни.
145. Около окружности с диаметром 15 описана равнобедренная трапеция с боковой стороной, равной 17. Найти основания трапеции.
146. Хорда окружности равна 10. Через один конец хорды проведена касательная к окружности, а через другой – секущая, параллельная касательной, определить радиус окружности, если внутренний отрезок секущей равен 12.
147. В пересечении двух равных кругов вписан ромб с диагоналями 12 и 6. Найти радиусы окружностей.
148. В острый угол, равный 60 градусам, вписаны две окружности, извне касающиеся друг друга. Радиус меньшей окружности равен Найти радиус большей окружности.
149.
Найти радиус окружности, описанной около
прямоугольного треугольника, если радиус окружности, вписанной в этот
треугольник, равен 3, а катет равен 10.
150. В равнобедренный треугольник с углом в 120 градусов при вершине и боковой стороной
151. Один из катетов прямоугольного треугольника равен 15, а проекция другого катета на гипотенузу равна 16. Найти радиус окружности вписанной в треугольник.
152. Найти длины боковой стороны и диагонали равнобедренной трапеции с основаниями 20 и 12, если известно, что центр описанной окружности лежит на большем основании трапеции.
153. В равнобедренном треугольнике основание равно 30, а боковая сторона равна 39. Определить радиус вписанного круга.
154. Катеты прямоугольного треугольника равны 6 и 8. Найти расстояние от центра вписанной в треугольник окружности до центра описанной около него окружности.
155. Площадь равнобедренной трапеции, описанной около круга, равна Определить боковую сторону трапеции, если известно, что острый угол при основании равен
156. Сторона правильного треугольника,
вписанного в окружность, равна Вычислить площадь
квадрата, вписанного в ту же окружность.
Сторона правильного треугольника,
вписанного в окружность, равна Вычислить площадь
квадрата, вписанного в ту же окружность.
157. В равнобедренную трапецию вписан круг. Одна из боковых сторон делится точкой касания на отрезки длиной Определить площадь трапеции.
158. Найти площадь равнобедренной трапеции, если ее высота равна а боковая сторона видна из центра описанной окружности под углом
159. Докажите, что перпендикуляр, проведенный из какой – нибудь точки окружности к диаметру, есть среднее пропорциональное между отрезками, на которые основание перпендикуляра делит диаметр.
160. Через точку А, лежащую вне окружности, проведены две секущие, одна из которых пересекает окружность в точках Докажите, что
161.
Доказать, что если в треугольнике то медиана треугольника
не является высотой. (замечательные точки треугольника).
162. Биссектрисы углов при основании равнобедренного треугольника пересекаются в точке М. Докажите, что прямая к прямой AB. (замечательные точки треугольника)
163. Высоты проведенные к боковым сторонам, пересекаются в точке М. Докажите, что прямая серединный перпендикуляр к отрезку (замечательные точки треугольника).
164. Найти диаметр окружности, вписанной в прямоугольный треугольник, если гипотенуза треугольника равна
165. Доказать, что площадь описанного многоугольника равна половине произведения его периметра на радиус вписанной окружности.
166. Окружность с центром О описана около прямоугольного треугольника: а) докажите, что точка О – середина гипотенузы, б) найдите стороны треугольника, если диаметр окружности равен
167.
Доказать, что можно описать окружность: а)
около любого треугольника, б) около любой равнобедренной трапеции.
168. Доказать, что если около параллелограмма можно описать окружность, то этот параллелограмм – прямоугольник.
169. Доказать, что если около трапеции можно описать окружность, то эта трапеция равнобедренная.
170. Две окружности имеют общую точку М и общую касательную в этой точке. Прямая одной окружности в точке А, а другой – в точке В. Доказать, что точка М лежит на окружности с диаметром АВ.
171. Через точки А и В проведены прямые, перпендикулярные к сторонам угла и пересекающиеся в точке Докажите, что около четырехугольника можно описать окружность.
172. Около окружности описана равнобочная трапеция с боковой стороной одно из оснований которой равно Найти площадь трапеции.
173. В ромб с острым углом вписан круг, а в круг – квадрат. Найти отношение площади ромба к площади квадрата.
174. Площадь равнобедренной трапеции, описанной
около круга, равна S. Определить
радиус этого круга, если угол при основании трапеции равен
Площадь равнобедренной трапеции, описанной
около круга, равна S. Определить
радиус этого круга, если угол при основании трапеции равен
175. В окружность, диаметр которой равен вписан правильный треугольник. На его высоте как на стороне построен другой правильный треугольник, в который вписана новая окружность. Найти радиус этой окружности.
176. Докажите, что если около параллелограмма можно описать окружность, то этот параллелограмм – ромб.
177. (в паре № 176) Докажите, что в любой ромб можно вписать окружность.
178. (в паре № 176) Доказать, что если около ромба можно описать окружность, то этот ромб – квадрат.
Третий уровень.
179. Докажите, что градусные меры дуг окружности, заключенных между параллельными хордами, равны.
180.
Прямая АМ – касательная к окружности, АВ –
хорда этой окружности. Докажите, что угол МАВ измеряется половиной дуги АВ,
расположенной внутри угла МАВ.
Докажите, что угол МАВ измеряется половиной дуги АВ,
расположенной внутри угла МАВ.
181. Две окружности имеют общую точку М и общую касательную в этой точке. Прямая АВ касается одной окружностью в точке А, а другой – в точке В. Докажите, что точка М лежит на окружности с диаметром АВ.
182. Доказать, что если в прямоугольник можно вписать окружность, то этот прямоугольник – квадрат.
183. Доказать, что если в четырехугольнике сумма противоположных углов равна , то около этого четырехугольника можно описать окружность.
184. (в паре №183) Через точки А и В проведены прямые, перпендикулярные к сторонам угла АОВ и пересекающиеся в точке С внутри угла. Докажите, что около четырехугольника АОВС можно описать окружность.
185.
( в паре №168, 182) Доказать, что если в
параллелограмм можно вписать окружность и можно описать около него окружность,
то этот параллелограмм – квадрат.
186. Доказать, что если прямые, содержащие основания трапеции, касаются окружности и точки касания принадлежат основаниям, то средняя линия трапеции проходит через центр окружности.
187. Найти радиус окружности, вписанной в прямоугольную трапецию с основаниями
188. Центр описанной около треугольника окружности лежит на медиане. Доказать, что этот треугольник либо равнобедренный, либо прямоугольный.
189. (интересная) В окружности проведены две хорды Длина дуги вдвое больше длины дуги Найти радиус окружности.
190. (в паре №78) В равнобедренную трапецию вписана окружность радиуса R. Верхнее основание трапеции в два раза меньше ее высоты,. Найти площадь трапеции.
191.
Центр окружности, вписанной в
прямоугольную трапецию, удален от концов ее боковой стороны на расстояния 3 и
9. Найти стороны трапеции.
192. Окружность касается двух смежных сторон квадрата и делит каждую из двух других его сторон на отрезки, равные 2 и 23. Найти радиус окружности.
193. Прямоугольный треугольник со сторонами 6, 8, 10. В него вписана окружность. Через центр окружности проведены прямые, параллельные сторонам треугольника. Вычислить длины средних отрезков сторон треугольника, отсекаемых построенными прямыми.
194. Основания трапеции равны 4 и 16. Найти радиусы окружностей, вписанной в трапецию и описанной около нее, если известно, что эти окружности существуют.
195. Каким необходимым и достаточным условиям должна удовлетворять трапеция, чтобы в нее можно было вписать, и около нее можно было описать окружность.
196.
В треугольник вписана окружность радиуса
3. Вычислить длины сторон треугольника, если одна из них разделена точкой
касания на отрезки длиной 4 и 3.
197. Для треугольника со сторонами 26, 28, 30 найти произведение радиусов описанной и вписанной окружностей.
198. Показать, что во всяком прямоугольном треугольнике сумма полупериметра и радиуса вписанной окружности равна сумме катетов.
199. Показать, что во всяком прямоугольном треугольнике сумма диаметров описанной и вписанной окружностей равна сумме его катетов.
200. В окружность вписан четырехугольник с углами Площадь четырехугольника равна Найти радиус окружности, если диагонали четырехугольника взаимно перпендикулярны.
201. В ромб со стороной Определить площадь четырехугольника, вершинами которого являются точки касания окружности со сторонами ромба.
202.
Доказать, что перпендикуляры к хорде,
проведенные через концы до пересечения с каким – либо диаметром, делят его на
три отрезка, из которых два крайних имеют равные длины.
203. Доказать, что если на радиусе окружности, как на диаметре, описать окружность, и из общей точки этих окружностей провести хорду большей, то меньшая окружность разделит эту хорду пополам.
204. Доказать, что хорды двух касающихся окружностей, соединяющие концы двух секущих, проходящих через точку касания, параллельны между собой. Рассмотреть два случая касания окружностей.
205. Доказать, что отрезок касательной к окружности, заключенный между касательными, проведенными через концы какого – либо диаметра, виден из центра окружности под прямым углом.
206. Доказать, что отрезок внешней касательной к двум внешне касающимся окружностям виден из точки касания окружностей под прямым углом.
207.
Доказать, что во всяком треугольнике,
вписанном в окружность, серединный перпендикуляр к стороне пересекает
биссектрисы противолежащего и смежного с ним угла в точках, принадлежащих
окружности.
208. Доказать, что биссектриса прямого угла прямоугольного треугольника с неравными катетами делит пополам угол между медианой и высотой, проведенными из вершины прямого угла.
209. Высота, биссектриса и медиана треугольника, проведенные из одной вершины, делят угол треугольника на четыре равных по величине угла. Вычислить углы треугольника.
210. К боковым сторонам произвольного треугольника проведены высоты, а к основанию его проведена медиана. Доказать, что основания этих отрезков являются вершинами некоторого равнобедренного треугольника.
211. В треугольнике окружности. Докажите, что угол
212. В выпуклом четырехугольнике Доказать, что около
213.
(в паре с №112) Пусть вершина угла
находится вне круга, и стороны угла пересекают окружность. Доказать, что
величина угла измеряется полуразностью дуг, высекаемых его сторонами на окружности
и расположенных внутри угла.
214. Пусть вершина угла находится внутри круга. Доказать, что величина угла измеряется полусуммой дуг, заключенных между его сторонами и их продолжениями за вершину угла.
215. Пусть точка касания. Докажите, что каждый из двух углов между измеряется половиной дуги окружности, заключенной внутри рассматриваемого угла.
216. Через точку радиуса R (проведена секущая, пересекающая окружность в точках Доказать, что (квадрату длины касательной).
217. (в паре с №216) Докажите, что прямая, проходящая через точку пересечения двух окружностей, делит пополам общую касательную к ним.
218. (в паре с №216) В окружности радиуса R через точку М, находящуюся на расстоянии Докажите, что постоянно для всех хорд и равно
219. Доказать, что радиус окружности, вписанной в прямоугольный треугольник, вычисляется по формуле
220.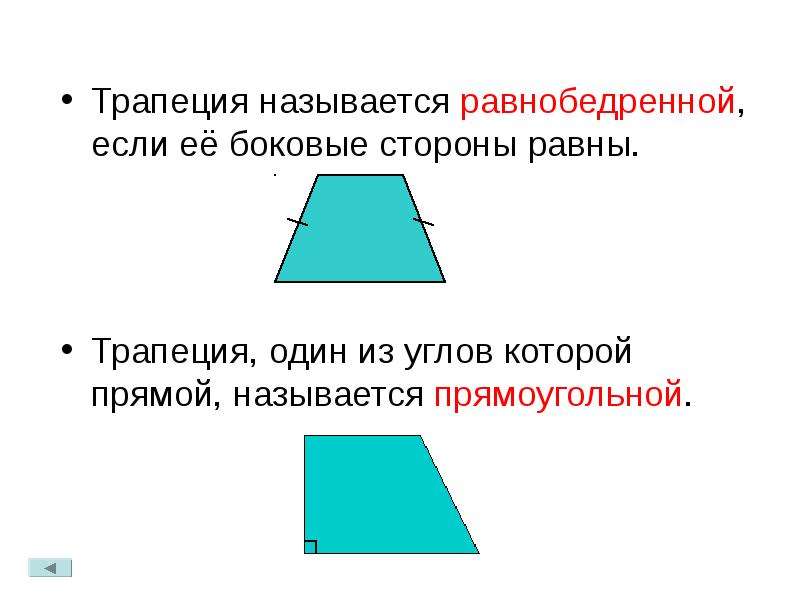 Доказать, что если в выпуклом
четырехугольнике соотношение то
существует окружность, касающаяся всех его сторон.
Доказать, что если в выпуклом
четырехугольнике соотношение то
существует окружность, касающаяся всех его сторон.
221. (в паре с №220) Если четырехугольник описан, то суммы длин противолежащих сторон равны.
222. Около окружности описана равнобочная трапеция Боковые стороны В каком отношении прямая
Как найти длину стороны трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает одно
или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам Varsity найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему утверждению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
трапеций: определение и свойства — видео и стенограмма урока
Свойство
Трапеции имеют одно свойство, которое необходимо соблюдать. Свойство в том, что у него должна быть одна пара параллельных сторон.Если вы посмотрите на трапецию, вы увидите, что у нее две плоские стороны. Эти плоские стороны параллельны друг другу. Если вы продлите эти линии, они никогда не встретятся. Попробуй.
Свойство в том, что у него должна быть одна пара параллельных сторон.Если вы посмотрите на трапецию, вы увидите, что у нее две плоские стороны. Эти плоские стороны параллельны друг другу. Если вы продлите эти линии, они никогда не встретятся. Попробуй.
Словарь
При работе с трапециями есть несколько слов, которые мы должны добавить в наш словарь.
Первое слово — это оснований , которые являются сторонами, параллельными друг другу. Нарисуйте треугольник, нижняя сторона которого будет одной из ваших основ. Сторона, полученная путем срезания вершины треугольника, является другой основой.
Второе слово, которое следует рассмотреть, — это ножек . Это наклонные стороны, которые образуют левый и правый край трапеции, которая находится самой длинной стороной вниз. Возвращаясь к разрезанному треугольнику, ноги — это стороны, которые поднимаются и встречаются на вершине треугольника. Но, поскольку вершина треугольника срезана, ноги заканчиваются там, где произошел срез.
Третье слово — это высота , которая является просто высотой трапеции. Это высота трапеции, когда вы сидите на плоской поверхности.Вы можете определить высоту, измерив расстояние от одной базы до другой.
Специальные трапеции
Если ноги вашей трапеции имеют одинаковую длину и углы, которые каждая сторона образует с основанием, равны, тогда у вас есть так называемая равнобедренная трапеция . Это означает, что, когда трапеция расположена ровно с самым длинным основанием вниз, два нижних угла будут равны, а два верхних угла также будут равны. Представьте себе эту трапецию как равнобедренный треугольник (треугольник с двумя равными сторонами и двумя равными углами) с отрезанной вершиной.
Теперь представьте себе разносторонний треугольник (треугольник, все стороны которого имеют разную длину) и отрежьте его вершину. Когда вы это сделаете, вы получите разностороннюю трапецию , трапецию, ноги которой имеют разную длину.
Третий вид специальной трапеции — это правая трапеция , трапеция, в которой одна ножка перпендикулярна основанию. Он будет выглядеть как прямоугольный треугольник (треугольник с одним прямым углом) с обрезанной вершиной.
Он будет выглядеть как прямоугольный треугольник (треугольник с одним прямым углом) с обрезанной вершиной.
Итоги урока
Вау! Посмотрите, что мы узнали всего за несколько минут! Мы узнали, что трапеция представляет собой четырехстороннюю плоскую форму с одной парой параллельных сторон.Трапеции выглядят как треугольники со срезанной вершиной. Единственное свойство, которому должны соответствовать все трапеции, — это то, что у них должны быть две стороны, параллельные друг другу.
Специальные слова, которые мы используем с трапециями, — это основания, ноги и высота. Основания относятся к двум сторонам, параллельным друг другу. Ножки , относятся к двум наклонным сторонам, а высота — это просто высота трапеции, когда она сидит ровно, ее самое длинное основание опущено.
Особый случай равнобедренной трапеции возникает, когда у вас есть ноги, равные по длине друг другу, и углы, образованные ногами и основаниями, также равны друг другу. Итак, у равнобедренной трапеции два нижних и два верхних угла равны друг другу. Частный случай разносторонней трапеции возникает, когда обе ножки имеют разную длину, а правая трапеция возникает, когда у вас одна ножка перпендикулярна основанию.
Итак, у равнобедренной трапеции два нижних и два верхних угла равны друг другу. Частный случай разносторонней трапеции возникает, когда обе ножки имеют разную длину, а правая трапеция возникает, когда у вас одна ножка перпендикулярна основанию.
Результаты обучения
Усвоение информации из этого урока может привести к вашей способности:
- Распознавать свойство, связанное с трапециями
- Определяет основания, опоры и высоту относительно трапеций
- Характеризуйте особые трапеции: равнобедренную, разностороннюю и правую
Использование свойств прямоугольников, треугольников и трапеций — предварительная алгебра
Цели обучения
К концу этого раздела вы сможете:
- Понятие о линейных, квадратных и кубических мерах
- Использовать свойства прямоугольников
- Используйте свойства треугольников
- Использовать свойства трапеций
Прежде чем начать, пройдите тест на готовность.
- Длина прямоугольника меньше ширины. Позвольте представить ширину. Напишите выражение для длины прямоугольника.
Если вы пропустили эту проблему, просмотрите (рисунок). - Simplify:
Если вы пропустили эту проблему, просмотрите (рисунок). - Simplify:
Если вы пропустили эту проблему, просмотрите (рисунок).
В этом разделе мы продолжим работу с геометрическими приложениями. Мы добавим еще несколько свойств треугольников и узнаем о свойствах прямоугольников и трапеций.
Общие сведения о линейных, квадратных и кубических мерах
Когда вы измеряете свой рост или длину садового шланга, вы используете линейку или рулетку ((Рисунок)). Рулетка может напоминать вам линию — вы используете ее для линейной меры, которая измеряет длину. Дюйм, фут, ярд, миля, сантиметр и метр — единицы линейного измерения.
Эта рулетка измеряет дюймы сверху и сантиметры снизу.
Если вы хотите узнать, сколько плитки нужно для покрытия пола или размер стены, которую нужно покрасить, вам нужно знать площадь, меру области, необходимой для покрытия поверхности. Площадь измеряется в квадратных единицах. Мы часто используем квадратные дюймы, квадратные футы, квадратные сантиметры или квадратные мили для измерения площади. Квадратный сантиметр — это квадрат, каждая сторона которого равна одному сантиметру (см). Квадратный дюйм — это квадрат, каждая сторона которого составляет один дюйм ((Рисунок)).
Площадь измеряется в квадратных единицах. Мы часто используем квадратные дюймы, квадратные футы, квадратные сантиметры или квадратные мили для измерения площади. Квадратный сантиметр — это квадрат, каждая сторона которого равна одному сантиметру (см). Квадратный дюйм — это квадрат, каждая сторона которого составляет один дюйм ((Рисунок)).
(рисунок) показывает прямоугольный коврик длиной в фут и шириной в фут. Каждый квадрат имеет ширину фута на фут в длину или квадратный фут. Коврик состоит из квадратов.Площадь коврика — квадратный метр.
Коврик состоит из шести квадратов по 1 квадратный фут каждый, поэтому общая площадь ковра составляет 6 квадратных футов.
Когда вы измеряете, сколько требуется для заполнения контейнера, например количество бензина, которое может поместиться в бак, или количество лекарства в шприце, вы измеряете объем. Объем измеряется в кубических единицах, таких как кубические дюймы или кубические сантиметры. При измерении объема прямоугольного твердого тела вы измеряете, сколько кубиков заполняет контейнер.Мы часто используем кубические сантиметры, кубические дюймы и кубические футы. Кубический сантиметр — это куб, имеющий размер по одному сантиметру с каждой стороны, а кубический дюйм — это куб, который имеет размер по одному дюйму с каждой стороны ((Рисунок)).
При измерении объема прямоугольного твердого тела вы измеряете, сколько кубиков заполняет контейнер.Мы часто используем кубические сантиметры, кубические дюймы и кубические футы. Кубический сантиметр — это куб, имеющий размер по одному сантиметру с каждой стороны, а кубический дюйм — это куб, который имеет размер по одному дюйму с каждой стороны ((Рисунок)).
Кубическая мера имеет стороны, равные 1 единице длины.
Предположим, что куб на (Рисунок) имеет дюймы с каждой стороны и разрезан по показанным линиям. Сколько в нем маленьких кубиков? Если бы мы разобрали большой куб, мы бы нашли маленькие кубики, каждый размером в один дюйм со всех сторон.Итак, каждый маленький куб имеет объем в кубический дюйм, а объем большого куба — в кубические дюймы.
Куб размером 3 дюйма с каждой стороны состоит из 27 однодюймовых кубов или 27 кубических дюймов.
Выполнение математического задания «Визуализация площади и периметра» поможет вам лучше понять разницу между площадью фигуры и ее периметром.
Для каждого элемента укажите, будете ли вы использовать линейную, квадратную или кубическую меру:
ⓐ необходимое количество коврового покрытия в комнате
ⓑ длина удлинителя
ⓒ количество песка в песочнице
ⓓ длина карниза
ⓔ количество муки в канистре
ⓕ размер крыши конуры.
Решение
| ⓐ Вы измеряете, какую площадь покрывает ковер, то есть площадь. | квадратный метр |
| ⓑ Вы измеряете длину удлинителя, то есть длину. | линейная мера |
| ⓒ Вы измеряете объем песка. | мера кубическая |
| ⓓ Вы измеряете длину карниза. | линейная мера |
| ⓔ Вы измеряете объем муки. | мера кубическая |
| ⓕ Вы измеряете площадь крыши. | квадратный метр |
Определите, будете ли вы использовать линейную, квадратную или кубическую меру для каждого элемента.
ⓐ количество краски в банке ⓑ высота дерева ⓒ пол вашей спальни ⓓ диаметр велосипедного колеса ⓔ размер куска дерна ⓕ количество воды в бассейне
- ⓐ куб.
- ⓑ линейный
- ⓒ квадрат
- ⓓ линейный
- ⓔ квадрат
- ⓕ куб.
Определите, будете ли вы использовать линейную, квадратную или кубическую меру для каждого элемента.
ⓐ объем упаковочного ящика ⓑ размер террасы ⓒ количество лекарства в шприце ⓓ длина отрезка пряжи ⓔ размер участка корпуса ⓕ высота флагштока
- ⓐ куб.
- ⓑ квадрат
- ⓒ куб.
- ⓓ линейный
- ⓔ квадрат
- ⓕ линейный
Многие геометрические приложения включают определение периметра или площади фигуры. В повседневной жизни также существует множество применений периметра и площади, поэтому важно убедиться, что вы понимаете, что каждое из них означает.
Представьте себе комнату, в которой нужна новая напольная плитка. Плитки состоят из квадратов, каждая сторона которых составляет один фут — один квадратный фут. Сколько таких квадратов нужно, чтобы покрыть пол? Это площадь пола.
Плитки состоят из квадратов, каждая сторона которых составляет один фут — один квадратный фут. Сколько таких квадратов нужно, чтобы покрыть пол? Это площадь пола.
Затем подумайте о том, чтобы положить в комнату новый плинтус после того, как выложили плитку. Чтобы выяснить, сколько полосок потребуется, необходимо знать расстояние по комнате. Вы можете использовать рулетку, чтобы измерить количество футов в комнате. Это расстояние — периметр.
Периметр и площадь
Периметр — это мера расстояния вокруг фигуры.
Площадь — это мера поверхности, покрытой фигурой.
(рисунок) показывает квадратную плитку, каждая сторона которой составляет дюйм. Если муравей обойдет край плитки, он пройдет несколько дюймов. Это расстояние — периметр плитки.
Поскольку плитка представляет собой квадрат со стороной в дюйм, ее площадь составляет один квадратный дюйм. Площадь фигуры измеряется путем определения количества квадратных единиц, покрывающих фигуру.
Когда муравей полностью обходит плитку по ее краю, он отслеживает периметр плитки.
 Площадь плитки — 1 квадратный дюйм.
Площадь плитки — 1 квадратный дюйм.Выполнение математического задания «Измерение площади и периметра» поможет вам лучше понять, как измерять площадь и периметр фигуры.
Каждая из двух квадратных плиток имеет квадратный дюйм. Две плитки показаны вместе.
ⓐ Каков периметр фигуры?
ⓑ Какой район?
Решение
ⓐ Периметр — это расстояние вокруг фигуры.Периметр в дюймах.
ⓑ Площадь — это поверхность, покрытая фигурой. Есть плитки квадратного дюйма, поэтому площадь равна квадратным дюймам.
Найдите периметр ⓐ и площадь ⓑ фигуры:
- ⓐ 8 дюймов
- ⓑ 3 кв. Дюйма
Найдите периметр ⓐ и площадь ⓑ фигуры:
- ⓐ 8 см
- ⓑ 4 кв. Сантиметра
Использование свойств прямоугольников
Прямоугольник имеет четыре стороны и четыре прямых угла.Противоположные стороны прямоугольника имеют одинаковую длину. Мы называем одну сторону прямоугольника длиной, а соседнюю сторону — шириной, см. (Рисунок).
Мы называем одну сторону прямоугольника длиной, а соседнюю сторону — шириной, см. (Рисунок).
Прямоугольник имеет четыре стороны и четыре прямых угла. Стороны помечены буквой L для длины и W.
Периметр прямоугольника — это расстояние вокруг прямоугольника. Если вы начнете с одного угла и обойдете прямоугольник, вы пройдете единицы, или две длины и две ширины. Тогда периметр
.А как насчет площади прямоугольника? Вспомните прямоугольный коврик из начала этого раздела.Его длина составляла фут, ширина — фут, а площадь составляла квадратный фут. См. (Рисунок). Поскольку мы видим, что площадь равна длине, умноженной на ширину, поэтому площадь прямоугольника равна
. Площадь этого прямоугольного коврика равна квадратным футам, его длина умножена на ширину.Для удобства работы с примерами в этом разделе мы переформулируем здесь стратегию решения проблем для геометрических приложений.
Используйте стратегию решения проблем для приложений с геометрией
- Прочтите задачу и убедитесь, что вы понимаете все слова и идеи.
 Нарисуйте фигуру и напишите на ней указанную информацию.
Нарисуйте фигуру и напишите на ней указанную информацию. - Определите то, что вы ищете.
- Имя то, что вы ищете. Выберите переменную для представления этого количества.
- Переведите в уравнение, написав соответствующую формулу или модель для ситуации. Подставьте в данную информацию.
- Решите уравнение, используя хорошие методы алгебры.
- Проверьте ответ в проблеме и убедитесь, что он имеет смысл.
- Ответьте на вопрос полным предложением.
Длина прямоугольника измеряется в метрах, а ширина в метрах. Найдите ⓐ периметр и ⓑ площадь.
Длина прямоугольника — ярды, ширина — ярды. Найдите ⓐ периметр и ⓑ площадь.
- ⓐ 340 ярдов
- ⓑ 6000 кв. Ярд
Длина прямоугольника равна футам, а ширина — футам. Найдите ⓐ периметр и ⓑ площадь.
Найдите ⓐ периметр и ⓑ площадь.
- ⓐ 220 футов
- ⓑ 2976 кв. Фут
Найдите длину прямоугольника с периметром в дюймах и шириной в дюймах.
Найдите длину прямоугольника с периметром в ярдах и шириной в ярдах.
В следующем примере ширина определяется через длину. Мы будем ждать, чтобы нарисовать фигуру, пока не напишем выражение для ширины, чтобы мы могли пометить одну сторону этим выражением.
Ширина прямоугольника на два дюйма меньше его длины.Периметр в дюймах. Найдите длину и ширину.
Ширина прямоугольника на семь метров меньше его длины. Периметр — метры. Найдите длину и ширину.
Длина прямоугольника на восемь футов больше ширины. По периметру футы. Найдите длину и ширину.
Длина прямоугольника в восемь раз больше ширины в два раза. По периметру футы. Найдите длину и ширину.
Ширина прямоугольника в шесть раз меньше двойной длины. Периметр в сантиметрах. Найдите длину и ширину.
Периметр в сантиметрах. Найдите длину и ширину.
Площадь прямоугольника равна квадратным футам. Длина — фут. Какая ширина?
Ширина прямоугольника в метрах. Площадь квадратные метры. Какая длина?
Периметр прямоугольного бассейна — фут. Длина на фут больше ширины. Найдите длину и ширину.
Периметр прямоугольного бассейна — фут. Длина на фут больше ширины.Найдите длину и ширину.
Длина прямоугольного сада в ярдах больше ширины. Периметр — ярды. Найдите длину и ширину.
Используйте свойства треугольников
Теперь мы знаем, как найти площадь прямоугольника. Мы можем использовать этот факт, чтобы визуализировать формулу площади треугольника. В прямоугольнике (рисунок) мы обозначили длину и ширину, так что его площадь равна
. Площадь прямоугольника равна основанию, умноженному на высоту, Мы можем разделить этот прямоугольник на два равных треугольника ((Рисунок)). Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны. Площадь каждого треугольника составляет половину площади прямоугольника. Этот пример помогает нам понять, почему формула для площади треугольника равна
Конгруэнтные треугольники имеют одинаковую длину сторон и углы, поэтому их площади равны. Площадь каждого треугольника составляет половину площади прямоугольника. Этот пример помогает нам понять, почему формула для площади треугольника равна
Прямоугольник можно разделить на два треугольника равной площади. Площадь каждого треугольника составляет половину площади прямоугольника.
Формула площади треугольника: где основание, а высота.
Чтобы найти площадь треугольника, нужно знать его основание и высоту.Основание — это длина одной стороны треугольника, обычно стороны внизу. Высота — это длина линии, которая соединяет основание с противоположной вершиной и составляет угол с основанием. (Рисунок) показывает три треугольника с отмеченными основанием и высотой каждого.
Высота треугольника — это длина отрезка линии, который соединяет основание с противоположной вершиной и составляет угол с основанием. Найдите площадь треугольника с основанием в дюймах и высотой в дюймах.
Найдите площадь треугольника с основанием в дюймах и высотой в дюймах.
Периметр треугольного сада — фут. Длина двух сторон равна футам и футам. Какова длина третьей стороны?
Длина двух сторон треугольного окна — футы и футы. По периметру футы. Какова длина третьей стороны?
Площадь треугольной картины — квадратные дюймы. База в дюймах. Какая высота?
Треугольная дверь палатки имеет площадь квадратных футов.Высота в футах. Что такое база?
Равнобедренные и равносторонние треугольники
Помимо прямоугольного треугольника, некоторые другие треугольники имеют особые имена. Треугольник с двумя сторонами равной длины называется равнобедренным треугольником. Треугольник с тремя сторонами равной длины называется равносторонним треугольником. (Рисунок) показывает оба типа треугольников.
В равнобедренном треугольнике две стороны имеют одинаковую длину, а третья сторона является основанием. В равностороннем треугольнике все три стороны имеют одинаковую длину.
В равностороннем треугольнике все три стороны имеют одинаковую длину.
Равнобедренные и равносторонние треугольники
Равнобедренный треугольник имеет две стороны одинаковой длины.
Равносторонний треугольник имеет три стороны равной длины.
Периметр равностороннего треугольника составляет дюймы. Найдите длину каждой стороны.
Найдите длину каждой стороны равностороннего треугольника с дюймами периметра.
Найдите длину каждой стороны равностороннего треугольника с периметром в сантиметрах.
Палуба заднего двора имеет форму равнобедренного треугольника с основанием из ножек. Периметр колоды — футы. Какова длина каждой из равных сторон колоды?
Парус лодки представляет собой равнобедренный треугольник с основанием в метры. Периметр — метры. Какова длина каждой из равных сторон паруса?
Используйте свойства трапеций
Трапеция — это четырехсторонняя фигура, четырехугольник , с двумя сторонами, которые параллельны, и двумя сторонами, которые не параллельны. Параллельные стороны называются основаниями. Мы называем длину меньшего основания и длину большего основания. Высота трапеции — это расстояние между двумя основаниями, как показано на (Рисунок).
Параллельные стороны называются основаниями. Мы называем длину меньшего основания и длину большего основания. Высота трапеции — это расстояние между двумя основаниями, как показано на (Рисунок).
Формула площади трапеции:
Разделение трапеции на два треугольника может помочь нам понять формулу. Площадь трапеции — это сумма площадей двух треугольников.См. (Рисунок).
Разделение трапеции на два треугольника может помочь вам понять формулу ее площади.
Высота трапеции — это также высота каждого из двух треугольников. См. (Рисунок).
Формула площади трапеции
Если раздадим, то получим,
Свойства трапеций
- У трапеции четыре стороны. См. (Рисунок).
- Две его стороны параллельны, а две — нет.
- Площадь трапеции.
Найдите площадь трапеции высотой 6 дюймов и основаниями и дюймами.
Высота трапеции — ярды, а основания — ярды. Какой район?
Высота трапеции в сантиметрах, оснований и сантиметров. Какой район?
Высота трапеции в сантиметрах, оснований и сантиметров. Какой район?
Высота трапеции метры, а оснований и метры.Какой район?
Линь хочет подстричь лужайку, имеющую форму трапеции. Основания — ярды и ярды, а высота — ярды. Сколько квадратных ярдов дерна ему нужно?
Кира хочет покрыть свой внутренний двор бетонной брусчаткой. Если внутренний дворик имеет форму трапеции, основания которой равны футам, а высота — футы, сколько квадратных футов брусчатки ему понадобится?
Упражнение «Ссылки на повышение грамотности» Спагетти и фрикадельки для всех предоставит вам еще один обзор тем, затронутых в этом разделе.”
Практика ведет к совершенству
Что такое линейные, квадратные и кубические меры
В следующих упражнениях определите, будете ли вы измерять каждый элемент в линейных, квадратных или кубических единицах.
количество воды в аквариуме
жилая площадь квартиры
жилая площадь ванной кафель
вместимость автоприцепа
В следующих упражнениях найдите ⓐ периметра и ⓑ площади каждой фигуры.Предположим, что каждая сторона квадрата равна сантиметрам.
Использовать свойства прямоугольников
В следующих упражнениях найдите периметр ⓐ и площадь ⓑ каждого прямоугольника.
Длина прямоугольника равна футам, а ширина — футам.
- ⓐ 260 футов
- ⓑ 3825 кв. Фут
Длина прямоугольника составляет дюймы, а ширина — дюймы.
Прямоугольная комната шириной в фут и длиной в фут.
Подъездная дорога имеет форму прямоугольника шириной в фут и длиной в фут.
В следующих упражнениях решите.
Найдите длину прямоугольника в дюймах по периметру и ширине в дюймах.
Найдите длину прямоугольника в ярдах по периметру и ширину в ярдах.
Найдите ширину прямоугольника по периметру в метрах и длине в метрах.
Найдите ширину прямоугольника по периметру в метрах и длине в метрах.
Площадь прямоугольника — квадратные метры. Длина метры. Какая ширина?
Площадь прямоугольника — квадратные сантиметры. Ширина в сантиметрах. Какая длина?
Длина прямоугольника на дюймы больше ширины. Периметр в дюймах. Найдите длину и ширину.
Ширина прямоугольника на дюймы больше его длины. Периметр в дюймах. Найдите длину и ширину.
Периметр прямоугольника — метры.Ширина прямоугольника на несколько метров меньше длины. Найдите длину и ширину прямоугольника.
Периметр прямоугольника равен футам. Ширина на фут меньше длины. Найдите длину и ширину.
Ширина прямоугольника на несколько метров меньше длины. Периметр прямоугольника — метры. Найдите размеры прямоугольника.
Длина прямоугольника на несколько метров меньше ширины. Периметр прямоугольника — метры.Найдите размеры прямоугольника.
Периметр прямоугольника — метры.Найдите размеры прямоугольника.
Периметр прямоугольника стопы. Длина прямоугольника в два раза больше ширины. Найдите длину и ширину прямоугольника.
Длина прямоугольника в три раза больше ширины. По периметру футы. Найдите длину и ширину прямоугольника.
Длина прямоугольника в метрах меньше удвоенной ширины. Периметр — метры. Найдите длину и ширину.
Длина прямоугольника вдвое превышает его ширину в дюймах.Периметр в дюймах. Найдите длину и ширину.
Ширина прямоугольного окна — дюймы. Площадь составляет квадратные дюймы. Какая длина?
Длина прямоугольного плаката — дюймы. Площадь составляет квадратные дюймы. Какая ширина?
Площадь прямоугольной крыши квадратных метров. Длина метры. Какая ширина?
Площадь прямоугольного брезента составляет квадратный фут. Ширина — фут. Какая длина?
Периметр прямоугольного двора — фут.Длина на фут больше ширины. Найдите длину и ширину.
Найдите длину и ширину.
Периметр прямоугольной картины в сантиметрах. Длина на сантиметры больше ширины. Найдите длину и ширину.
Ширина прямоугольного окна в дюймах меньше его высоты. Периметр дверного проема составляет сантиметры. Найдите длину и ширину.
Ширина прямоугольной площадки на несколько метров меньше длины. Периметр детской площадки — метры.Найдите длину и ширину.
Используйте свойства треугольников
В следующих упражнениях решите, используя свойства треугольников.
Найдите площадь треугольника с основанием в дюймах и высотой в дюймах.
Найдите площадь треугольника с основанием в сантиметрах и высотой в сантиметрах.
Найдите площадь треугольника с базовыми метрами и высотными метрами.
Найдите площадь треугольника с основанием и высотой с футами.
Треугольный флаг имеет основание и высоту ступней. Какая у него площадь?
Треугольное окно имеет основание ступней и высоту ступней. Какая у него площадь?
Какая у него площадь?
Если у треугольника стороны ступни и ступни, а периметр равен футам, какова длина третьей стороны?
Если у треугольника стороны сантиметра и сантиметра, а периметр равен сантиметрам, какова длина третьей стороны?
Что такое основание треугольника с площадью квадратных дюймов и высотой в дюймах?
Какова высота треугольника с площадью основания в дюймах?
Периметр треугольного отражающего бассейна — ярд.Длина двух сторон — ярды и ярды. Какова длина третьей стороны?
Треугольный двор имеет периметр метровый. Длина двух сторон — метры и метры. Какова длина третьей стороны?
Равнобедренный треугольник имеет основание в сантиметрах. Если периметр равен сантиметрам, найдите длину каждой из других сторон.
Равнобедренный треугольник имеет основание в дюймах. Если периметр составляет дюймы, найдите длину каждой из других сторон.
Найдите длину каждой стороны равностороннего треугольника с периметром в ярдах.
Найдите длину каждой стороны равностороннего треугольника с периметром в метры.
Периметр равностороннего треугольника — метры. Найдите длину каждой стороны.
Периметр равностороннего треугольника составляет мили. Найдите длину каждой стороны.
Периметр равнобедренного треугольника равен футам. Длина самой короткой стороны — стопы.Найдите длину двух других сторон.
Периметр равнобедренного треугольника составляет дюймы. Длина самой короткой стороны — дюймы. Найдите длину двух других сторон.
Блюдо имеет форму равностороннего треугольника. Каждая сторона имеет длину в дюймах. Найдите периметр.
Напольная плитка имеет форму равностороннего треугольника. Каждая сторона футов длиной. Найдите периметр.
Дорожный знак в форме равнобедренного треугольника имеет основание в дюймах.Если периметр составляет дюймы, найдите длину каждой из других сторон.
Платок в форме равнобедренного треугольника имеет основу в метры. Если периметр составляет метры, найдите длину каждой из других сторон.
Если периметр составляет метры, найдите длину каждой из других сторон.
Периметр треугольника равен футам. Одна сторона треугольника на фут длиннее второй. Третья сторона на фут длиннее второй. Найдите длину каждой стороны.
Периметр треугольника равен футам. Одна сторона треугольника на фут длиннее второй.Третья сторона на фут длиннее второй. Найдите длину каждой стороны.
Одна сторона треугольника — это двойная наименьшая сторона. Третья сторона на фут больше самой короткой. По периметру футы. Найдите длины всех трех сторон.
Одна сторона треугольника в три раза больше наименьшей стороны. Третья сторона на фут больше самой короткой. По периметру футы. Найдите длины всех трех сторон.
Использование свойств трапеций
В следующих упражнениях решите, используя свойства трапеций.
Высота трапеции — футы, а основания — и футы. Какой район?
Высота трапеции — ярды, а основания — ярды. Какой район?
Какой район?
Найдите площадь трапеции высотой в метры и основаниями и метрами.
Найдите площадь трапеции высотой в дюймах и основанием в дюймах.
Высота трапеции в сантиметрах, оснований и сантиметров. Какой район?
Высота трапеции — футы, а основания — и футы.Какой район?
Найдите площадь трапеции высотой в метры и основаниями и метрами.
Найдите площадь трапеции высотой в сантиметры и основаниями и сантиметрами.
Лорел делает знамя в форме трапеции. Высота знамени — ступни, а основания — ступни. Какая площадь у баннера?
Нико хочет выложить плиткой пол в ванной. Пол имеет форму трапеции с шириной ступней и длиной ступней и ступней.Какая площадь этажа?
Терезе нужна новая столешница для кухонной стойки. Прилавок имеет форму трапеции с дюймами ширины и длины и дюйма. Какая площадь прилавка?
Елена вяжет шарф. Шарф будет иметь форму трапеции с шириной в дюймах и длиной в дюймах и дюймах. Какая площадь у шарфа?
Какая площадь у шарфа?
Письменные упражнения
Если вам нужно положить плитку на пол на кухне, вам нужно знать периметр или площадь кухни? Объясните свои рассуждения.
Если вам нужно поставить забор вокруг вашего заднего двора, вам нужно знать периметр или площадь заднего двора? Объясните свои рассуждения.
Посмотрите на две цифры.
ⓐ Какая фигура имеет большую площадь? Похоже, у него больший периметр?
ⓑ Теперь рассчитайте площадь и периметр каждой фигуры. У кого площадь больше? У кого периметр больше?
Длина прямоугольника на фут больше ширины.Площадь квадратного метра. Найдите длину и ширину.
ⓐ Напишите уравнение, которое вы использовали бы для решения проблемы.
ⓑ Почему вы не можете решить это уравнение методами, которые вы узнали в предыдущей главе?
Самопроверка
ⓐ После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в достижении целей этого раздела.
ⓑ Как бы вы оценили свое владение этим разделом по шкале от 1 до 10 в свете ваших ответов в контрольном списке? Как можно это улучшить?
Глоссарий
- площадь
- Площадь — это мера поверхности, покрытой фигурой.
- равносторонний треугольник
- Треугольник, у которого все три стороны равны, называется равносторонним треугольником.
- равнобедренный треугольник
- Треугольник с двумя сторонами равной длины называется равнобедренным треугольником.
- периметр
- Периметр — это мера расстояния вокруг фигуры.
- прямоугольник
- Прямоугольник — это геометрическая фигура, имеющая четыре стороны и четыре прямых угла.
- трапеция
- Трапеция — это четырехсторонняя фигура, четырехугольник с двумя сторонами, которые параллельны, и двумя сторонами, которые не параллельны.
| 1D линия, круговая дуга, парабола, спираль, кривая Коха
2D Правильные многоугольники: Равносторонний треугольник, Квадрат, Пентагон, Шестиугольник, Семиугольник, Восьмиугольник, Нонагон, Десятиугольник, Хендекагон, Додекагон, Шестиугольник, N-угольник, Кольцо многоугольника Другие многоугольники: 90 036 Круглые формы: Тетраэдр, Куб, Октаэдр, Додекаэдр, Икосаэдр Архимедовы тела: Каталонских Сухой остаток: Твердые тела Джонсона: Другие многогранники: Круглые формы: | Anzeige Расчеты на правой трапеции (или правой трапеции). Формулы: Длины сторон, диагонали и периметр имеют одинаковые единицы измерения (например,г. метр), площадь имеет эту единицу в квадрате (например, квадратный метр). Поделиться: © Jumk.de Webprojects Anzeige |
9 наиболее распространенных форм и способы их определения
Вы, наверное, много узнали о формах, даже не задумываясь о том, что они из себя представляют. Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.
Но понимание того, что такое форма, невероятно удобно при сравнении ее с другими геометрическими фигурами, такими как плоскости, точки и линии.
В этой статье мы рассмотрим, что такое фигура, а также множество общих фигур, как они выглядят и основные формулы, связанные с ними.
Что такое форма?
Если вас спросят, что такое форма, вы, вероятно, сможете назвать довольно много из них. Но «форма» тоже имеет особое значение — это не просто названия кругов, квадратов и треугольников.
Форма — это форма объекта, а не то, сколько места он занимает или где находится физически, а реальная форма, которую он принимает. Круг определяется не тем, сколько места он занимает или где вы его видите, а скорее реальной круглой формой, которую он принимает.
Форма может иметь любой размер и появляться где угодно; они ничем не ограничены, потому что фактически не занимают места. Трудно осознать это, но не думайте о них как о физических объектах — форма может быть трехмерной и занимать физическое пространство, например подставку для книг в форме пирамиды, цилиндрическую банку с овсянкой или он может быть двухмерным и не занимать физического пространства , такого как треугольник, нарисованный на листе бумаги.
Тот факт, что он имеет форму, отличает форму от точки или линии.
Точка — это просто позиция; у него нет ни размера, ни ширины, ни длины, ни вообще никаких размеров.
Линия же одномерная. Он бесконечно тянется в любом направлении и не имеет толщины. Это не форма, потому что у нее нет формы.
Хотя мы можем представлять точки или линии как фигуры, потому что нам действительно нужно их видеть, на самом деле они не имеют никакой формы. Это то, что отличает форму от других геометрических фигур — она двух- или трехмерная, потому что у нее есть форма.
Кубики, подобные тем, что здесь изображены, представляют собой трехмерные квадраты — обе формы!
Шесть основных типов двумерных геометрических форм
Трудно изобразить форму только на основе определения — что значит иметь форму и форму , но не занимать место? Давайте взглянем на несколько различных форм, чтобы лучше понять, что именно значит быть формой!
Мы часто классифицируем формы по количеству сторон. «Сторона» — это линейный сегмент (часть линии), составляющий часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.
«Сторона» — это линейный сегмент (часть линии), составляющий часть фигуры. Но у фигуры тоже может быть неоднозначное количество сторон.
Тип 1: Эллипсы
Эллипсы — это круглые, овальные формы, в которых заданная точка ( p ) имеет одинаковую сумму расстояний от двух разных фокусов.
овал
Овал немного похож на размазанный круг — он не совсем круглый, а в некотором роде вытянутый. Однако классификация неточная.Существует много-много видов овалов, но общее значение состоит в том, что они имеют круглую форму, которая имеет удлиненную форму, а не идеально круглую, как круг. Овал — это любой эллипс, фокусы которого находятся в двух разных положениях.
Поскольку овал не является идеально круглым, формулы, которые мы используем для их понимания, должны быть скорректированы.
Также важно отметить, что вычислить окружность овала довольно сложно , поэтому ниже нет уравнения окружности. Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией окружности, потому что даже лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.
Вместо этого используйте онлайн-калькулятор или калькулятор со встроенной функцией окружности, потому что даже лучшие уравнения окружности, которые вы можете составить вручную, являются приблизительными.
Определения
- Большой радиус : расстояние от начала овала до самого дальнего края
- Малый радиус : расстояние от начала овала до ближайшего края
- Площадь = $ \ Major \ Radius * \ Minor \ Radius * π $
Круг
Сколько сторон у круга? Хороший вопрос! К сожалению, нет хорошего ответа, потому что «стороны» больше связаны с многоугольниками — двумерной формой, по крайней мере, с тремя прямыми сторонами и обычно, по крайней мере, с пятью углами. Наиболее знакомые формы — это многоугольники, но у кругов нет прямых сторон и определенно нет пяти углов, поэтому они не являются многоугольниками.
Итак, сколько сторон у круга? Нуль? Один? На самом деле это неактуально — вопрос просто не относится к кругам.
Круг — это не многоугольник, но что это такое? Круг — это двумерная форма (у нее нет толщины и глубины), состоящая из кривой, которая всегда находится на одинаковом расстоянии от точки в центре. У овала два фокуса в разных положениях, тогда как у круга фокусы всегда находятся в одном и том же положении.
Определения
- Начало координат: центр окружности
- Радиус: расстояние от начала координат до любой точки на окружности
- Окружность: расстояние по окружности
- Диаметр: длина от одного края круга до другого
- $ \ bo {π} $: (произносится как пирог) 3.2 $
Тип 2: Треугольники
Треугольники — самые простые многоугольники. У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.
У них три стороны и три угла, но они могут отличаться друг от друга. Возможно, вы слышали о прямоугольных или равнобедренных треугольниках — это разные типы треугольников, но все они имеют три стороны и три угла.
Поскольку существует много видов треугольников, есть лотов важных формул треугольника , многие из которых более сложные, чем другие.Основы включены ниже, но даже основы полагаются на знание длины сторон треугольника. Если вы не знаете стороны треугольника, вы все равно можете рассчитать его различные аспекты, используя углы или только некоторые из сторон.
Определения
- Вершина : точка пересечения двух сторон треугольника
- Основание : любая из сторон треугольника, обычно та, которая нарисована внизу.
- Высота : расстояние по вертикали от основания до вершины, с которой не связано
Формулы
- Площадь = $ {\ base * \ height} / 2 $
- Периметр = $ \ side a + \ side b + \ side c $
Тип 3: параллелограммы
Параллелограмм — это форма с равными противоположными углами, параллельными противоположными сторонами и параллельными сторонами равной длины. Вы могли заметить, что это определение применяется к квадратам и прямоугольникам — это потому, что квадрата и прямоугольника также являются параллелограммами ! Если вы можете рассчитать площадь квадрата, вы можете сделать это с любым параллелограммом.
Вы могли заметить, что это определение применяется к квадратам и прямоугольникам — это потому, что квадрата и прямоугольника также являются параллелограммами ! Если вы можете рассчитать площадь квадрата, вы можете сделать это с любым параллелограммом.
Определения
- Длина : размер нижней или верхней стороны параллелограмма
- Ширина : размер левой или правой стороны параллелограмма
Формулы
- Область : $ \ length * \ height $
- Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 $
- Альтернативно, Периметр : $ \ Side * 4 $
Прямоугольник
Прямоугольник — это форма с параллельными противоположными сторонами в сочетании со всеми углами в 90 градусов. Как тип параллелограмма, он имеет противоположные параллельные стороны. В прямоугольнике одна группа параллельных сторон длиннее другой, что делает его похожим на вытянутый квадрат.
В прямоугольнике одна группа параллельных сторон длиннее другой, что делает его похожим на вытянутый квадрат.
Поскольку прямоугольник является параллелограммом, вы можете использовать те же формулы для вычисления их площади и периметров.
Квадрат
Квадрат во многом похож на прямоугольник, за одним заметным исключением: все его стороны равны по длине. Как и прямоугольники, квадрата имеют углы 90 градусов и параллельны противоположным сторонам. Это потому, что квадрат на самом деле является разновидностью прямоугольника, который является разновидностью параллелограмма!
По этой причине вы можете использовать те же формулы для вычисления площади или периметра квадрата, как и для любого другого параллелограмма.
Ромб
Ромб — как вы догадались — разновидность параллелограмма. Разница между ромбом и прямоугольником или квадратом заключается в том, что его внутренние углы на равны только , чем их диагональные противоположности.
Из-за этого, ромб немного похож на квадрат или прямоугольник, немного скошенный в сторону . Хотя периметр рассчитывается таким же образом, это влияет на способ вычисления площади, поскольку высота уже не такая, как в квадрате или прямоугольнике.
Определение
- Диагональ : расстояние между двумя противоположными вершинами
Формулы
- Площадь = $ {\ Diagonal 1 * \ Diagonal 2} / 2 $
Тип 4: трапеции
Трапеции — это четырехгранные фигуры с двумя противоположными параллельными сторонами.В отличие от параллелограмма трапеция имеет только две противоположные параллельные стороны, а не четыре , что влияет на способ вычисления площади и периметра.
Определения
- Основание : любая из параллельных сторон трапеции
- Ноги : одна из непараллельных сторон трапеции
- Высота : расстояние от одной базы до другой
Формулы
- Область : $ ({\ Base_1 \ length + \ Base_2 \ length} / 2) \ altitude $
- Периметр : $ \ Base + \ Base + \ Leg + \ Leg $
Тип 5: Пентагоны
Пятиугольник — это пятиугольник. Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленным внутрь, или вогнутым — с внутренним углом больше 180 градусов.
Обычно мы видим правильные пятиугольники, у которых все стороны и углы равны , но существуют и неправильные пятиугольники. Неправильный пятиугольник имеет неравные стороны и неравные углы и может быть выпуклым — без углов, направленным внутрь, или вогнутым — с внутренним углом больше 180 градусов.
Поскольку форма более сложная, ее необходимо разделить на более мелкие формы, чтобы вычислить ее площадь.
Определения
- Апофема : линия, проведенная от центра пятиугольника к одной из сторон, ударяющая в сторону под прямым углом.
Формулы
- Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 $
- Площадь : $ {\ Perimeter * \ Apothem} / 2 $
Тип 6: шестиугольники
Шестиугольник — это шестигранная форма, очень похожая на пятиугольник. Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.
Чаще всего мы видим правильные шестиугольники, но они, как и пятиугольники, также могут быть неправильными, выпуклыми или вогнутыми.
Также, как и пятиугольники, формула площади шестиугольника значительно сложнее, чем формула параллелограмма.
Формулы
- Периметр : $ \ Сторона 1 + \ Сторона 2 + \ Сторона 3 + \ Сторона 4 + \ Сторона 5 + \ Сторона 6 $
- Область : $ {3√3 * \ Side * 2} / 2 $
- Альтернативно, Площадь : $ {\ Perimeter * \ Apothem} / 2 $
А как насчет трехмерных геометрических фигур?
Существуют также трехмерные формы, которые имеют не только длину и ширину, но также глубину или объем. Это формы, которые вы видите в реальном мире, например сферический баскетбольный мяч, цилиндрический контейнер с овсянкой или прямоугольная книга.
Трехмерные формы, естественно, более сложные, чем двухмерные, с дополнительное измерение — объем занимаемого пространства, а не только форма, — которое необходимо учитывать при вычислении площади и периметра.
, включающая двумерные формы, такие как приведенные выше, называется плоской геометрией , потому что она имеет дело конкретно с плоскостями или плоскими формами . Математика, включающая трехмерные формы, такие как сферы и кубы, называется твердотельной геометрией , потому что она имеет дело с твердыми телами, другим словом для трехмерных фигур .
Двухмерные формы составляют трехмерные формы, которые мы видим каждый день!
3 основных совета по работе с фигурами
Существует так много типов фигур, что бывает сложно запомнить, что есть что и как рассчитать их площади и периметры. Вот несколько советов и приемов, которые помогут вам их запомнить!
# 1: Определить многоугольники
Некоторые формы являются многоугольниками, а некоторые нет. Один из самых простых способов сузить кругозор какой-либо формы — это выяснить, является ли это многоугольником.
Многоугольник состоит из прямых, не пересекающихся. Какие фигуры ниже являются многоугольниками, а какие нет?
Круг и овал не являются многоугольниками, поэтому их площадь и периметр рассчитываются по-разному. Узнайте больше о том, как их вычислить, используя $ π $ выше!
# 2: Проверить параллельность сторон
Если фигура, на которую вы смотрите, представляет собой параллелограмм, обычно легче вычислить ее площадь и периметр, чем если бы это не параллелограмм. Но как определить параллелограмм?
Это прямо в названии — параллель. Параллелограмм — это четырехсторонний многоугольник с двумя наборами параллельных сторон . Квадраты, прямоугольники и ромбы — это параллелограммы.
Квадраты и прямоугольники используют одни и те же базовые формулы для вычисления площади длины, умноженной на высоту. Их также очень легко найти по периметру, поскольку вы просто складываете все стороны вместе.
С ромбами все усложняется, потому что вы умножаете диагонали и делите их на два.
Чтобы определить, на какой параллелограмм вы смотрите, спросите себя, все ли у него углы 90 градусов.
Если да, то это квадрат или прямоугольник . Прямоугольник имеет две стороны, которые немного длиннее других, тогда как у квадрата все стороны равны. В любом случае, вы вычисляете площадь, умножая длину на высоту и периметр, складывая все четыре стороны вместе.
Если нет, то, вероятно, это ромб, который выглядит так, как если бы вы взяли квадрат или прямоугольник и наклонили его в любом направлении. В этом случае вы найдете площадь, умножив две диагонали вместе и разделив на два. Периметр определяется так же, как периметр квадрата или прямоугольника.
# 3: Подсчитайте количество сторон
Формулы для фигур, у которых нет четырех сторон, могут быть довольно сложными, поэтому лучше всего их запомнить. Если у вас возникают проблемы с их правильностью, попробуйте запомнить греческие слова для чисел, , например:
Если у вас возникают проблемы с их правильностью, попробуйте запомнить греческие слова для чисел, , например:
Tri : три, как в triple, что означает три чего-то
Tetra : четыре, как количество квадратов в блоке Tetris
Penta : пять, как в Пентагоне в Вашингтоне Д.C., представляющий собой большое здание в форме Пентагона
.Hexa : шесть, как в шестнадцатеричном формате, шестизначные коды, часто используемые для цвета в веб-дизайне и графическом дизайне
Септа : семь, как в Септе, женском духовенстве религии Игры престолов, имеющей семь богов
Octo : восемь, как в восьми лапах осьминога
Эннеа : девять, как в эннеаграмме, общая модель человеческих личностей
Дека : десять, как в десятиборье, в котором спортсмены завершают десять видов
Что дальше?
Если вы готовитесь к экзамену ACT и вам нужна дополнительная помощь по геометрии, ознакомьтесь с этим руководством по координатной геометрии!
Если вы больше относитесь к типу SAT, это руководство по треугольникам в разделе геометрии SAT поможет вам подготовиться к тесту !
Не можете насытиться математикой ACT? Это руководство по полигонам на ACT поможет вам подготовиться с помощью полезных стратегий и практических задач!
Площадь параллелограмма рабочего листа год 6
площадь параллелограмма рабочего листа год 6 5) Понимание площади трапеции (6-FF.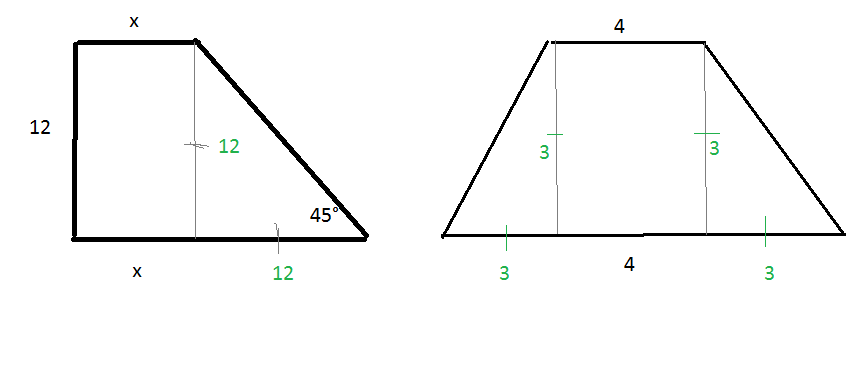 Эта версия включает однозначные числа для длин сторон. ABCD — параллелограмм, каковы значения x и y? y 20. Рабочие листы по периметру и площади 6-го класса 6 класс pdf. 2 км 13. Включает в себя краткий раздел с указаниями, 3 примера, которые можно использовать в качестве практических рекомендаций для введения или повторного введения в тему. Фактическая площадь треугольного куска ткани составляет 45 квадратных дюймов. 4 км 7 км 23. 6м \). В вопросах разминки учащиеся будут называть четыре четырехугольника как можно большим количеством способов.12см. Свойства рабочего листа параллелограммов intrepidpath Practice 6 4 специальный рабочий лист 10-го класса 11-го класса. = 15 x 3. Замечательно! Еще немного периметра! Это… Вычислите площадь параллелограмма. Теперь, когда мы знаем высоту перпендикуляра, мы можем вычислить площадь. Площадь парка параллелограмма Год 6 Рабочий лист «Измерение» из рабочего листа параллелограмма, источник: обучающий клип. 5 см² 14) 6. 9 м 15) 7 км 5. pptx White Rose Maths Video Link для уроков по понедельникам и четвергам.
Эта версия включает однозначные числа для длин сторон. ABCD — параллелограмм, каковы значения x и y? y 20. Рабочие листы по периметру и площади 6-го класса 6 класс pdf. 2 км 13. Включает в себя краткий раздел с указаниями, 3 примера, которые можно использовать в качестве практических рекомендаций для введения или повторного введения в тему. Фактическая площадь треугольного куска ткани составляет 45 квадратных дюймов. 4 км 7 км 23. 6м \). В вопросах разминки учащиеся будут называть четыре четырехугольника как можно большим количеством способов.12см. Свойства рабочего листа параллелограммов intrepidpath Practice 6 4 специальный рабочий лист 10-го класса 11-го класса. = 15 x 3. Замечательно! Еще немного периметра! Это… Вычислите площадь параллелограмма. Теперь, когда мы знаем высоту перпендикуляра, мы можем вычислить площадь. Площадь парка параллелограмма Год 6 Рабочий лист «Измерение» из рабочего листа параллелограмма, источник: обучающий клип. 5 см² 14) 6. 9 м 15) 7 км 5. pptx White Rose Maths Video Link для уроков по понедельникам и четвергам. Найдите вкладку «Летний семестр, область ромба | Целые числа — тип 1.Декартова система координат википедия, справочник. Наклонное плоское клиновое колесо и осевой винт, рычаг и шкив. Уровень 1. Представляя размеры параллелограмма в различных единицах, этот бесплатный рабочий лист требует, чтобы учащиеся 7 и 8 классов преобразовали единицу измерения в указанную в ответе единицу, а затем подставили основание и высоту в формулу A = b h. Поймите, почему формула для площади параллелограмма равна основанию, умноженному на высоту, точно так же, как формула для площади прямоугольника. co.Рабочий лист Площадь параллелограмма Рабочий лист с использованием квадратичного из площади параллелограмма Рабочий лист, источник: cathhsli. Таким образом, площадь для обоих, площадь для обоих — это просто базовая высота, умноженная на высоту. Каждое упражнение предусматривает рисование параллелограмма, а также высоту и ширину основания. площадь параллелограммов и треугольников. Дифференциация: новичок. Вычислите площадь прямоугольного треугольника, если указаны размеры основания и высоты (не в масштабе).
Найдите вкладку «Летний семестр, область ромба | Целые числа — тип 1.Декартова система координат википедия, справочник. Наклонное плоское клиновое колесо и осевой винт, рычаг и шкив. Уровень 1. Представляя размеры параллелограмма в различных единицах, этот бесплатный рабочий лист требует, чтобы учащиеся 7 и 8 классов преобразовали единицу измерения в указанную в ответе единицу, а затем подставили основание и высоту в формулу A = b h. Поймите, почему формула для площади параллелограмма равна основанию, умноженному на высоту, точно так же, как формула для площади прямоугольника. co.Рабочий лист Площадь параллелограмма Рабочий лист с использованием квадратичного из площади параллелограмма Рабочий лист, источник: cathhsli. Таким образом, площадь для обоих, площадь для обоих — это просто базовая высота, умноженная на высоту. Каждое упражнение предусматривает рисование параллелограмма, а также высоту и ширину основания. площадь параллелограммов и треугольников. Дифференциация: новичок. Вычислите площадь прямоугольного треугольника, если указаны размеры основания и высоты (не в масштабе). 5 mi 165. Эта область рабочего листа треугольника позволяет детям практиковать этот метод снова и снова, укрепляя этот ключевой математический навык.Наши рабочие листы в формате pdf предназначены для удовлетворения учебных потребностей учащихся 6, 7 и 8 классов. Рабочие листы по математике для 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — четверг, 12 декабря, 2017 г., 17 мая 2021 г. MMMadmin 1484 просмотров Эти рабочие листы представляют собой файлы в формате PDF. Собранный пазл имеет площадь 150 квадратных сантиметров. В 1 3 см 1 5 см. Модуль 5 по общей основной математике штата Нью-Йорк, 6 класс, Урок 1. Раздел 1 области треугольного рабочего листа содержит 7 областей треугольных вопросов на основе навыков, разбитых на 3 группы для облегчения различения.A bh A A = = • = Найдите периметр и площадь каждого параллелограмма. 2 5 4. Рабочие листы для 9 класса по математике. d d 7 из 9 из 7 из 6 в T1L1S1 Зоны параллелограммов Рабочий лист 5 — Вот рабочий лист с девятью задачами, который позволит вашим ученикам попрактиковаться в вычислении площади параллелограмма.
5 mi 165. Эта область рабочего листа треугольника позволяет детям практиковать этот метод снова и снова, укрепляя этот ключевой математический навык.Наши рабочие листы в формате pdf предназначены для удовлетворения учебных потребностей учащихся 6, 7 и 8 классов. Рабочие листы по математике для 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — четверг, 12 декабря, 2017 г., 17 мая 2021 г. MMMadmin 1484 просмотров Эти рабочие листы представляют собой файлы в формате PDF. Собранный пазл имеет площадь 150 квадратных сантиметров. В 1 3 см 1 5 см. Модуль 5 по общей основной математике штата Нью-Йорк, 6 класс, Урок 1. Раздел 1 области треугольного рабочего листа содержит 7 областей треугольных вопросов на основе навыков, разбитых на 3 группы для облегчения различения.A bh A A = = • = Найдите периметр и площадь каждого параллелограмма. 2 5 4. Рабочие листы для 9 класса по математике. d d 7 из 9 из 7 из 6 в T1L1S1 Зоны параллелограммов Рабочий лист 5 — Вот рабочий лист с девятью задачами, который позволит вашим ученикам попрактиковаться в вычислении площади параллелограмма. Ниже приведены необходимые навыки и ссылки на ресурсы, которые помогут вам в этом. Использовать ряд обучающих и вспомогательных ресурсов, e. Найдите площадь формы, найдя площадь каждой части, которая указана на листе «Площадь и периметр» для темы измерения 6-го года.Эти рабочие листы представляют собой файлы в формате pdf. Щелкните ниже, чтобы просмотреть ресурсы урока. А 1 5 см 1 3 см. 1 2 м 77 м 154 м 2 1 Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SATs KS2 Математика SATs Таблицы времени бустера Дополнительные ресурсы admin 4 февраля 2021 г. У нас есть ряд различных рабочих листов по площади, включая прямоугольники, прямоугольные треугольники и четырехугольники. Упражнение из учебника Corbettmaths по площади параллелограмма. 26 ноября 2017 г. — На этой странице собраны рабочие листы (в формате PDF) с параллелограммами и трапециями.2 5 3. 4 фута 16. Наши рабочие листы на сложение и вычитание за 7-й год идеально подходят в качестве введения в математику в средней школе и для подготовки к экзаменам по математике за 7-й год.
Ниже приведены необходимые навыки и ссылки на ресурсы, которые помогут вам в этом. Использовать ряд обучающих и вспомогательных ресурсов, e. Найдите площадь формы, найдя площадь каждой части, которая указана на листе «Площадь и периметр» для темы измерения 6-го года.Эти рабочие листы представляют собой файлы в формате pdf. Щелкните ниже, чтобы просмотреть ресурсы урока. А 1 5 см 1 3 см. 1 2 м 77 м 154 м 2 1 Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SATs KS2 Математика SATs Таблицы времени бустера Дополнительные ресурсы admin 4 февраля 2021 г. У нас есть ряд различных рабочих листов по площади, включая прямоугольники, прямоугольные треугольники и четырехугольники. Упражнение из учебника Corbettmaths по площади параллелограмма. 26 ноября 2017 г. — На этой странице собраны рабочие листы (в формате PDF) с параллелограммами и трапециями.2 5 3. 4 фута 16. Наши рабочие листы на сложение и вычитание за 7-й год идеально подходят в качестве введения в математику в средней школе и для подготовки к экзаменам по математике за 7-й год. Цели обучения. Например, вы можете видеть, что квадрат является ромбом, потому что это параллелограмм с четырьмя равными сторонами. Каждый бесплатный рабочий лист, проиллюстрированный для простоты и ясности, состоит из 9 задач, которые гарантируют твердое понимание этой уникальной геометрической формы и использование ее свойств для поиска области. Тщательно разработан для 6-го класса и средней школы.Этот рабочий лист идеально подходит для обучения области параллелограммов и дает вашим ученикам информацию, необходимую для самостоятельного поиска ответов, если вы […] Область параллелограммов Область параллелограммов. Рабочие листы могут быть выполнены в форматах pdf или html. Рабочие листы по математике и периметру для 8 класса. Это дает ученикам возможность… Этот творческий и увлекательный пакет уроков содержит PowerPoint и рабочие листы, которые были тщательно составлены, чтобы включать математические рассуждения и вопросы для решения проблем.Ознакомьтесь с другими моими ресурсами по геометрии для средней школы: Площадь поверхности и объем призм и формула пирамид Площадь поверхности и объем призм и пирамиды Отображение 8 лучших рабочих листов, найденных для области ромба.
Цели обучения. Например, вы можете видеть, что квадрат является ромбом, потому что это параллелограмм с четырьмя равными сторонами. Каждый бесплатный рабочий лист, проиллюстрированный для простоты и ясности, состоит из 9 задач, которые гарантируют твердое понимание этой уникальной геометрической формы и использование ее свойств для поиска области. Тщательно разработан для 6-го класса и средней школы.Этот рабочий лист идеально подходит для обучения области параллелограммов и дает вашим ученикам информацию, необходимую для самостоятельного поиска ответов, если вы […] Область параллелограммов Область параллелограммов. Рабочие листы могут быть выполнены в форматах pdf или html. Рабочие листы по математике и периметру для 8 класса. Это дает ученикам возможность… Этот творческий и увлекательный пакет уроков содержит PowerPoint и рабочие листы, которые были тщательно составлены, чтобы включать математические рассуждения и вопросы для решения проблем.Ознакомьтесь с другими моими ресурсами по геометрии для средней школы: Площадь поверхности и объем призм и формула пирамид Площадь поверхности и объем призм и пирамиды Отображение 8 лучших рабочих листов, найденных для области ромба. Мы структурировали эту информацию, чтобы помочь детям в их обучении. Как дети шестилетнего возраста могут научиться находить фигуры в домашних условиях? Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов. 10. Тип ресурса: Рабочий лист — Электронный.Слиток 80 x 10 x 300 мм отливают в цилиндр диаметром 120 мм. 5. Вы можете выучить площадь параллелограмма, треугольника на ощупь. Площадь параллелограмма будет такой, если у вас есть основание и высота, это будет просто основание, умноженное на высоту. 6 миль 6. Площадь и периметр рабочего листа треугольника. G Площадь рабочего листа в виде параллелограмма составляет. Площади треугольников. Область параллелограммов (открывает модальное окно) Определение высоты параллелограмма (открывает модальное окно) Практика. Найдите площадь треугольников и параллелограммов, рабочий лист №1.Площадь квадратов, прямоугольников и параллелограммов Дата _____ Период ____ Определите площадь каждого из них.
Мы структурировали эту информацию, чтобы помочь детям в их обучении. Как дети шестилетнего возраста могут научиться находить фигуры в домашних условиях? Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов. 10. Тип ресурса: Рабочий лист — Электронный.Слиток 80 x 10 x 300 мм отливают в цилиндр диаметром 120 мм. 5. Вы можете выучить площадь параллелограмма, треугольника на ощупь. Площадь параллелограмма будет такой, если у вас есть основание и высота, это будет просто основание, умноженное на высоту. 6 миль 6. Площадь и периметр рабочего листа треугольника. G Площадь рабочего листа в виде параллелограмма составляет. Площади треугольников. Область параллелограммов (открывает модальное окно) Определение высоты параллелограмма (открывает модальное окно) Практика. Найдите площадь треугольников и параллелограммов, рабочий лист №1.Площадь квадратов, прямоугольников и параллелограммов Дата _____ Период ____ Определите площадь каждого из них. Ниже представлены шесть версий нашей таблицы по математике для 6-го класса по определению площади и периметра фигур, образованных из двух или более прямоугольников. 8см. У параллелограмма одна пара противоположных сторон имеет размер 4 дюйма, а другая пара — 3 дюйма. Рабочие листы по математике 6 класс геометрии области круга. Этот пакет высококачественных учебных материалов идеально подходит для развития навыков расчета площади и периметра прямолинейных форм.9. 65 см² 11) 6 км 6. Рабочие листы в виде параллелограмма. = 45 квадратных дюймов. Площади параллелограммов и трапеций. 4 февраля 2015 г. — рабочие листы по математике с 1 по 6 класс для класса математики в начальной и начальной школе, охватывающие все математические темы Сингапура. 7 м 2) 1 в 1 в 3) 6. Обоснование 21-периметра и решение проблем. Это рабочий лист 6-го года для расчета площади параллелограммов с некоторыми письменными подсказками. Открыть PDF. 27 июня 2020 г. 6 мес. 3-й год (7-8 лет) 4-й год (8-9 лет) 5-й год (9-10 лет) 6-й год (10-11 лет) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы Свойства рабочего листа параллелограммов.
Ниже представлены шесть версий нашей таблицы по математике для 6-го класса по определению площади и периметра фигур, образованных из двух или более прямоугольников. 8см. У параллелограмма одна пара противоположных сторон имеет размер 4 дюйма, а другая пара — 3 дюйма. Рабочие листы по математике 6 класс геометрии области круга. Этот пакет высококачественных учебных материалов идеально подходит для развития навыков расчета площади и периметра прямолинейных форм.9. 65 см² 11) 6 км 6. Рабочие листы в виде параллелограмма. = 45 квадратных дюймов. Площади параллелограммов и трапеций. 4 февраля 2015 г. — рабочие листы по математике с 1 по 6 класс для класса математики в начальной и начальной школе, охватывающие все математические темы Сингапура. 7 м 2) 1 в 1 в 3) 6. Обоснование 21-периметра и решение проблем. Это рабочий лист 6-го года для расчета площади параллелограммов с некоторыми письменными подсказками. Открыть PDF. 27 июня 2020 г. 6 мес. 3-й год (7-8 лет) 4-й год (8-9 лет) 5-й год (9-10 лет) 6-й год (10-11 лет) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы Свойства рабочего листа параллелограммов. Рабочие листы по площади и периметру для 6-го класса помогут учащимся запомнить понятие площади и периметра различных форм. объем. ⇒ База = 7 2 м = 3 1 2 м. Противоположные стороны параллелограмма — _____. J! Нужна помощь, как найти площадь параллелограмма? Вы попали в нужное место! Начинаете ли вы только с Area of Plane Shapes Площадь плоской формы — это количество места, которое она занимает. Булавка на Eureka G7m3 Наши рабочие листы по периметру и площади предназначены для дополнения наших уроков по периметру и площади.Рабочие листы — это 6 свойств параллелограммов 6 2 свойства параллелограммов повторить свойства параллелограммов Глава 6 классификация четырехугольников дата период область треугольника практика ваших навыков с ответами координатная геометрия математика 1. Ключ ответа также предоставляется с этими рабочими листами с пошаговыми инструкциями предоставленные решения. Существует около 60-70 листов с ключами ответов по каждой теме. Учащиеся находят площади отдельных прямоугольников и складывают их.
Рабочие листы по площади и периметру для 6-го класса помогут учащимся запомнить понятие площади и периметра различных форм. объем. ⇒ База = 7 2 м = 3 1 2 м. Противоположные стороны параллелограмма — _____. J! Нужна помощь, как найти площадь параллелограмма? Вы попали в нужное место! Начинаете ли вы только с Area of Plane Shapes Площадь плоской формы — это количество места, которое она занимает. Булавка на Eureka G7m3 Наши рабочие листы по периметру и площади предназначены для дополнения наших уроков по периметру и площади.Рабочие листы — это 6 свойств параллелограммов 6 2 свойства параллелограммов повторить свойства параллелограммов Глава 6 классификация четырехугольников дата период область треугольника практика ваших навыков с ответами координатная геометрия математика 1. Ключ ответа также предоставляется с этими рабочими листами с пошаговыми инструкциями предоставленные решения. Существует около 60-70 листов с ключами ответов по каждой теме. Учащиеся находят площади отдельных прямоугольников и складывают их. Треугольник проиллюстрирован рабочими листами по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — пятница, 12 декабря 2017 г. 17 мая 2021 г. MMMadmin 1621 Просмотры Площадь парка параллелограмма Год 6 Рабочий лист измерения площади параллелограмма, источник: обучающий клип.& nbsp; Этот рабочий лист идеально подходит для обучения работе с параллелограммами и дает вашим ученикам информацию, необходимую для самостоятельного поиска ответов. Рабочие листы по математике. В этот набор входят 3 половинных листа интерактивных заметок и 3 полстраницы с практическими занятиями, которые можно использовать для обучения или обзора области параллелограммов, треугольников и трапеций. docx, 181. Основные инструкции. 25/1800 100 рупий в год сегодня, чтобы получить доступ к более чем 6000 рабочим листам. После этого урока студенты смогут: определять параллелограмм.Один особый вид многоугольников называется параллелограммом. Интерактивный PDF-файл: Математика «Белая роза» в поддержку 6-го класса: Периметр, площадь и объем весеннего блока 5: Площадь треугольника (1) Расчет площади составных форм.
Треугольник проиллюстрирован рабочими листами по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — пятница, 12 декабря 2017 г. 17 мая 2021 г. MMMadmin 1621 Просмотры Площадь парка параллелограмма Год 6 Рабочий лист измерения площади параллелограмма, источник: обучающий клип.& nbsp; Этот рабочий лист идеально подходит для обучения работе с параллелограммами и дает вашим ученикам информацию, необходимую для самостоятельного поиска ответов. Рабочие листы по математике. В этот набор входят 3 половинных листа интерактивных заметок и 3 полстраницы с практическими занятиями, которые можно использовать для обучения или обзора области параллелограммов, треугольников и трапеций. docx, 181. Основные инструкции. 25/1800 100 рупий в год сегодня, чтобы получить доступ к более чем 6000 рабочим листам. После этого урока студенты смогут: определять параллелограмм.Один особый вид многоугольников называется параллелограммом. Интерактивный PDF-файл: Математика «Белая роза» в поддержку 6-го класса: Периметр, площадь и объем весеннего блока 5: Площадь треугольника (1) Расчет площади составных форм. Рабочий лист Pack Maths Y6 Измерение объема кубов и кубоидов. Задачи домашнего обучения Поделиться через pinterest. \ text {Area} = \ text {base} \ times \ text {height}. Одна из лучших стратегий обучения, используемых сегодня в большинстве классных комнат, — это рабочие листы. найдите площадь любого параллелограмма, используя выученную формулу.Студенты могут отработать вопросы по площади прямоугольников и периметру прямоугольников. Вопрос 3: Рассчитайте площадь параллелограмма, показанного ниже. Подставьте значения в область формулы параллелограмма, чтобы найти недостающий размер. Математика 6 класс: (6M7b) Вычислите площадь параллелограммов и треугольников. Практика решения проблем неравенства. Площадь параллелограмма на координатной плоскости. 1 mi 18. Вы можете убедиться в этом, переставив параллелограмм в прямоугольник.Площадь, периметр и объем 6-го класса — Площадь параллелограмма — Урок 6. Площадь все еще не изменилась. . 65 A = 10 2. Обучающие онлайн-ресурсы только для участников.
Рабочий лист Pack Maths Y6 Измерение объема кубов и кубоидов. Задачи домашнего обучения Поделиться через pinterest. \ text {Area} = \ text {base} \ times \ text {height}. Одна из лучших стратегий обучения, используемых сегодня в большинстве классных комнат, — это рабочие листы. найдите площадь любого параллелограмма, используя выученную формулу.Студенты могут отработать вопросы по площади прямоугольников и периметру прямоугольников. Вопрос 3: Рассчитайте площадь параллелограмма, показанного ниже. Подставьте значения в область формулы параллелограмма, чтобы найти недостающий размер. Математика 6 класс: (6M7b) Вычислите площадь параллелограммов и треугольников. Практика решения проблем неравенства. Площадь параллелограмма на координатной плоскости. 1 mi 18. Вы можете убедиться в этом, переставив параллелограмм в прямоугольник.Площадь, периметр и объем 6-го класса — Площадь параллелограмма — Урок 6. Площадь все еще не изменилась. . 65 A = 10 2. Обучающие онлайн-ресурсы только для участников. Просто ответив на простые вопросы о ясной и простой для понимания диаграмме, учащиеся могут вывести формулу для площади параллелограмма. орг. Площадь = основание x высота. pdf, 106. 3 6 5. Цели национальной учебной программы. Параллелограммы — площадь. Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов.Число и разряд Сложение значений Вычитание Умножение Деление Четыре операции Дроби, десятичные дроби, проценты Алгебра Соотношение и пропорции Геометрия (форма) Измерение… Ниже представлены шесть версий нашего рабочего листа по математике для 6-го класса, посвященного площади треугольников, параллелограммов и трапеций. Управляемые заметки и практика. Он нацелен на детей 5 и 6 лет, и вопросы для рабочего листа были удалены из прошлых документов. Учащиеся могут бесплатно скачать распечатанные рабочие листы для класса 9 по математике, области параллелограмма и треугольника. Скачать PDF.Эти рабочие листы для областей параллелограмма и треугольника 9-го класса, классные задания и практические тесты были подготовлены в соответствии с учебной программой, выпущенной CBSE, и темами, приведенными в книге NCERT 2021.
Просто ответив на простые вопросы о ясной и простой для понимания диаграмме, учащиеся могут вывести формулу для площади параллелограмма. орг. Площадь = основание x высота. pdf, 106. 3 6 5. Цели национальной учебной программы. Параллелограммы — площадь. Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов.Число и разряд Сложение значений Вычитание Умножение Деление Четыре операции Дроби, десятичные дроби, проценты Алгебра Соотношение и пропорции Геометрия (форма) Измерение… Ниже представлены шесть версий нашего рабочего листа по математике для 6-го класса, посвященного площади треугольников, параллелограммов и трапеций. Управляемые заметки и практика. Он нацелен на детей 5 и 6 лет, и вопросы для рабочего листа были удалены из прошлых документов. Учащиеся могут бесплатно скачать распечатанные рабочие листы для класса 9 по математике, области параллелограмма и треугольника. Скачать PDF.Эти рабочие листы для областей параллелограмма и треугольника 9-го класса, классные задания и практические тесты были подготовлены в соответствии с учебной программой, выпущенной CBSE, и темами, приведенными в книге NCERT 2021. Учебная программа для 6-го класса. mathworksheets4kids. 2 м BCD 13. uk. 6 в 12) 4. ком. 4 КБ. Уровень площади и периметра. Рабочий лист геометрии Раздел четырехугольников: Имя: Г-н. Рабочие листы с площадью многоугольников Включите эти рабочие листы с областями многоугольников, содержащие примеры и соответствующие упражнения, чтобы найти площадь правильных многоугольников, таких как треугольники, четырехугольники и неправильные многоугольники, с использованием данной стороны… Площадь параллелограмма (базовая) Чтобы найти площадь каждого параллелограмма, просто умножьте базовое время на высоту.Рассчитайте перпендикулярную высоту и используйте ее, чтобы найти общую площадь. • 4см 3смсм² • 6см 5смсм² • 6см 8смсм² • 9см 3см • 9м 6м 12см • 9см • Площадь параллелограммов. Каждая половина страницы примечаний состоит из словаря, формулы и раздела, в котором учащиеся обозначают основание (и) и высоту области прямоугольника. Практические вопросы — Corbettmaths. Этот рабочий лист является дополнительным ресурсом для шестого класса, чтобы помочь учителям, родителям и детям дома и в школе.
Учебная программа для 6-го класса. mathworksheets4kids. 2 м BCD 13. uk. 6 в 12) 4. ком. 4 КБ. Уровень площади и периметра. Рабочий лист геометрии Раздел четырехугольников: Имя: Г-н. Рабочие листы с площадью многоугольников Включите эти рабочие листы с областями многоугольников, содержащие примеры и соответствующие упражнения, чтобы найти площадь правильных многоугольников, таких как треугольники, четырехугольники и неправильные многоугольники, с использованием данной стороны… Площадь параллелограмма (базовая) Чтобы найти площадь каждого параллелограмма, просто умножьте базовое время на высоту.Рассчитайте перпендикулярную высоту и используйте ее, чтобы найти общую площадь. • 4см 3смсм² • 6см 5смсм² • 6см 8смсм² • 9см 3см • 9м 6м 12см • 9см • Площадь параллелограммов. Каждая половина страницы примечаний состоит из словаря, формулы и раздела, в котором учащиеся обозначают основание (и) и высоту области прямоугольника. Практические вопросы — Corbettmaths. Этот рабочий лист является дополнительным ресурсом для шестого класса, чтобы помочь учителям, родителям и детям дома и в школе. Это означает, что она забыла умножить произведение базы и роста на 1/2.6 м 7. Определение высоты параллелограмма. 2 в 17) 3. Интерактивный PDF: Математика «Белая роза» в поддержку 6-го года: Пружинный блок 5 Периметр, площадь и объем: площадь параллелограмма KS2 Площадь треугольника Рабочие листы PlanIt Maths Y6 Пакет уроков по измерениям Площадь треугольников и параллелограммов (1) Параллелограмм — Определение, формулы, свойства и примеры Взаимосвязь между сторонами и углами в треугольнике (6) Формулы площади модели B для параллелограммов, трапеций и треугольников путем разложения и перестановки частей этих фигур; Понимание площади параллелограмма (6-FF.9 см 37. Следующее занятие. Некоторые из рабочих листов для этой концепции — это площадь ромба es1 площадь ромба t1l1s1 воздушного змея или площадь ромба площадь змея ромба 1 площадь sj прямоугольники треугольники площадь квадратов прямоугольники и параллелограммы 6 площадь треугольников и геометрия четырехугольников 8 2 работа. Последнее обновление: 20 января 2017 г.
Это означает, что она забыла умножить произведение базы и роста на 1/2.6 м 7. Определение высоты параллелограмма. 2 в 17) 3. Интерактивный PDF: Математика «Белая роза» в поддержку 6-го года: Пружинный блок 5 Периметр, площадь и объем: площадь параллелограмма KS2 Площадь треугольника Рабочие листы PlanIt Maths Y6 Пакет уроков по измерениям Площадь треугольников и параллелограммов (1) Параллелограмм — Определение, формулы, свойства и примеры Взаимосвязь между сторонами и углами в треугольнике (6) Формулы площади модели B для параллелограммов, трапеций и треугольников путем разложения и перестановки частей этих фигур; Понимание площади параллелограмма (6-FF.9 см 37. Следующее занятие. Некоторые из рабочих листов для этой концепции — это площадь ромба es1 площадь ромба t1l1s1 воздушного змея или площадь ромба площадь змея ромба 1 площадь sj прямоугольники треугольники площадь квадратов прямоугольники и параллелограммы 6 площадь треугольников и геометрия четырехугольников 8 2 работа. Последнее обновление: 20 января 2017 г. Рабочий лист строительных лесов на трапеции, который у меня был с небольшими шансами на 8-й класс. Заменим 6 вместо b и 15 вместо h. Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.21 Рабочий лист -Площадь-треугольник-1. Формула для вычисления площади параллелограмма: Площадь = ширина основания x высота по вертикали. Если вам нравится то, что вы видите здесь, возможно, вы захотите ознакомиться с другими рабочими листами по математике для 6-го класса. Практическое задание / рабочий лист из 15 вопросов, которые помогут студентам научиться вычислять площадь параллелограммов. Учащиеся и учителя 9-го класса с областями параллелограмма и треугольника могут бесплатно получить распечатанные рабочие листы для областей параллелограмма и треугольника 9-го класса в формате PDF, подготовленные в соответствии с последними учебными планами и схемами экзаменов в ваших школах.6 класс | Вычитание. Этот пакет выполняет цель национальной учебной программы на 6-й год «Вычислить площадь параллелограммов и треугольников» и дополняет блок 5 «Весна Белой розы», периметр, площадь и объем, уделяя особое внимание небольшому шагу 6, площади параллелограмма.
Рабочий лист строительных лесов на трапеции, который у меня был с небольшими шансами на 8-й класс. Заменим 6 вместо b и 15 вместо h. Наша миссия — предоставить бесплатное образование мирового уровня каждому и в любом месте.21 Рабочий лист -Площадь-треугольник-1. Формула для вычисления площади параллелограмма: Площадь = ширина основания x высота по вертикали. Если вам нравится то, что вы видите здесь, возможно, вы захотите ознакомиться с другими рабочими листами по математике для 6-го класса. Практическое задание / рабочий лист из 15 вопросов, которые помогут студентам научиться вычислять площадь параллелограммов. Учащиеся и учителя 9-го класса с областями параллелограмма и треугольника могут бесплатно получить распечатанные рабочие листы для областей параллелограмма и треугольника 9-го класса в формате PDF, подготовленные в соответствии с последними учебными планами и схемами экзаменов в ваших школах.6 класс | Вычитание. Этот пакет выполняет цель национальной учебной программы на 6-й год «Вычислить площадь параллелограммов и треугольников» и дополняет блок 5 «Весна Белой розы», периметр, площадь и объем, уделяя особое внимание небольшому шагу 6, площади параллелограмма. Параллелограммы: рабочий лист «Семейное древо свойств» Разминка / вступительное задание / предварительная оценка (10 минут): в течение первых 5 минут занятия учащиеся ответят на четыре разогревающих вопроса, которые будут отображены на доске. 2 8 4 32 мес.Координаты отсутствующей вершины. Другими словами, это размер поверхности. 01. 9 см 78. Скидки на ресурсы NCTM и повышение квалификации. Сгруппированы на основе используемых форм, таких как треугольники, квадраты, прямоугольники, параллелограммы на трапециях уровня 1 и круги, добавленные на воздушных змеях уровня 2, а ромбы включены на уровень 3. Каждый ученик берет карточку и решает задачу с карточкой. 4 ярда 38 ярдов²-2-Создайте свои собственные рабочие листы, подобные этому, с помощью Infinite Pre. Вставьте эти значения в базовую высоту области формулы, чтобы найти площадь параллелограммов в этом наборе рабочих листов для печати для детей 5 и 6 классов.Площадь и периметр рабочих листов сложных форм 6-й год. Это «6-й год — неделя 9 — урок 3 — Площадь параллелограммов» от White Rose Maths на Vimeo, где собраны высококачественные видео и люди, которые их любят.
Параллелограммы: рабочий лист «Семейное древо свойств» Разминка / вступительное задание / предварительная оценка (10 минут): в течение первых 5 минут занятия учащиеся ответят на четыре разогревающих вопроса, которые будут отображены на доске. 2 8 4 32 мес.Координаты отсутствующей вершины. Другими словами, это размер поверхности. 01. 9 см 78. Скидки на ресурсы NCTM и повышение квалификации. Сгруппированы на основе используемых форм, таких как треугольники, квадраты, прямоугольники, параллелограммы на трапециях уровня 1 и круги, добавленные на воздушных змеях уровня 2, а ромбы включены на уровень 3. Каждый ученик берет карточку и решает задачу с карточкой. 4 ярда 38 ярдов²-2-Создайте свои собственные рабочие листы, подобные этому, с помощью Infinite Pre. Вставьте эти значения в базовую высоту области формулы, чтобы найти площадь параллелограммов в этом наборе рабочих листов для печати для детей 5 и 6 классов.Площадь и периметр рабочих листов сложных форм 6-й год. Это «6-й год — неделя 9 — урок 3 — Площадь параллелограммов» от White Rose Maths на Vimeo, где собраны высококачественные видео и люди, которые их любят. 36 A = 19 3. Мы также предоставляем … Этот фантастический рабочий лист — идеальный ресурс для детей 6 лет, которые они могут использовать, когда учатся находить площадь параллелограмма. ☐ Поймите, что означают десятки дополнительных генераторов тестов и рабочих листов для учителей математики. Все рабочие листы, созданные с помощью бесконечной предалгебры.Высматривать! Вам нужно работать с вертикальной высотой, а не с наклонной высотой. Больше рабочих листов. Раздел 2 содержит 4 прикладных области вопросов о четырехугольниках с сочетанием сформулированных задач и более глубоких вопросов для решения проблем. ABCD — это параллелограмм, вычислите площадь параллелограмма: Площадь — это основание, умноженное на высоту: Площадь = b × h (h находится под прямым углом к b) Пример: параллелограмм имеет основание 6 м и высоту 3 м. , какова его площадь? Площадь = 6 м × 3 м = 18 м 2. 40 ярдов 15 см. 8 км 5.Урок 1. Площадь 120 кв. Наименьшее… Площадь параллелограмма = Основание x Высота. 7. Площадь параллелограммов.
36 A = 19 3. Мы также предоставляем … Этот фантастический рабочий лист — идеальный ресурс для детей 6 лет, которые они могут использовать, когда учатся находить площадь параллелограмма. ☐ Поймите, что означают десятки дополнительных генераторов тестов и рабочих листов для учителей математики. Все рабочие листы, созданные с помощью бесконечной предалгебры.Высматривать! Вам нужно работать с вертикальной высотой, а не с наклонной высотой. Больше рабочих листов. Раздел 2 содержит 4 прикладных области вопросов о четырехугольниках с сочетанием сформулированных задач и более глубоких вопросов для решения проблем. ABCD — это параллелограмм, вычислите площадь параллелограмма: Площадь — это основание, умноженное на высоту: Площадь = b × h (h находится под прямым углом к b) Пример: параллелограмм имеет основание 6 м и высоту 3 м. , какова его площадь? Площадь = 6 м × 3 м = 18 м 2. 40 ярдов 15 см. 8 км 5.Урок 1. Площадь 120 кв. Наименьшее… Площадь параллелограмма = Основание x Высота. 7. Площадь параллелограммов. В интерактивном формате эта область рабочего листа параллелограмма PDF позволяет ученикам вводить свои ответы прямо на листе. Проверьте свою работу, добавив шесть областей. Определите, является ли фигура справа прямоугольником. 4 ярда 4. 00. Геометрия — Рабочие листы по математике площади и периметра | Печатные формы PDF для детей. Площадь и периметр параллелограмма и ромба. Задачи, практика, тесты, рабочие листы, вопросы, викторины, задания для учителей | 7-й год | Школьная математика в Австралии. Шаг 6: Площадь параллелограмма. Весенний блок 5.Практика: Площадь и периметр на координатной плоскости. 30 апреля 2020 г. — Рабочие листы по площади и периметру с ответами в формате PDF. Также отмечен рабочий лист по расчету площади параллелограммов с разными метрическими единицами измерения длины и несущественной длины. Разрешение на копирование: вы можете скопировать этот рабочий лист любому количеству учеников для их математической работы. Определение параллелограмма: Свойства: Стороны, углы, диагонали 2.
В интерактивном формате эта область рабочего листа параллелограмма PDF позволяет ученикам вводить свои ответы прямо на листе. Проверьте свою работу, добавив шесть областей. Определите, является ли фигура справа прямоугольником. 4 ярда 4. 00. Геометрия — Рабочие листы по математике площади и периметра | Печатные формы PDF для детей. Площадь и периметр параллелограмма и ромба. Задачи, практика, тесты, рабочие листы, вопросы, викторины, задания для учителей | 7-й год | Школьная математика в Австралии. Шаг 6: Площадь параллелограмма. Весенний блок 5.Практика: Площадь и периметр на координатной плоскости. 30 апреля 2020 г. — Рабочие листы по площади и периметру с ответами в формате PDF. Также отмечен рабочий лист по расчету площади параллелограммов с разными метрическими единицами измерения длины и несущественной длины. Разрешение на копирование: вы можете скопировать этот рабочий лист любому количеству учеников для их математической работы. Определение параллелограмма: Свойства: Стороны, углы, диагонали 2. Рабочий лист Рабочий лист 2. Рабочие листы; Генераторы рабочих листов по математике (300+ генераторов с более чем 1500+ навыками) Параллелограмм \ (\ text {Area} = b \ times h \)… Площадь рабочего листа треугольника для темы измерения 6-го класса.44. 13 июня 2014 г. — 5 листов для определения площади параллелограмма. Параллелограмм — это четырехсторонний многоугольник. 12 декабря 2017 г. 1 февраля 2021 г. MMMadmin 3401 Просмотров. Параллелограмм Шаблон рабочего листа по математике для шестого класса Рабочие листы для практики по математике Треугольник Рабочий лист Сингапурский математический сектор Рабочие листы Начальная математика Деятельность математического центра. © Corbettmaths 2018 Определите площадь этого параллелограмма в см² Определите площадь этого параллелограмма в см². В этом уроке 6-го года урок «Площадь параллелограмма» охватывает предварительное обучение тому, как определять площадь прямоугольника и площадь треугольника 2 и 3, прежде чем переходим к основному навыку нахождения площади параллелограмма.
Рабочий лист Рабочий лист 2. Рабочие листы; Генераторы рабочих листов по математике (300+ генераторов с более чем 1500+ навыками) Параллелограмм \ (\ text {Area} = b \ times h \)… Площадь рабочего листа треугольника для темы измерения 6-го класса.44. 13 июня 2014 г. — 5 листов для определения площади параллелограмма. Параллелограмм — это четырехсторонний многоугольник. 12 декабря 2017 г. 1 февраля 2021 г. MMMadmin 3401 Просмотров. Параллелограмм Шаблон рабочего листа по математике для шестого класса Рабочие листы для практики по математике Треугольник Рабочий лист Сингапурский математический сектор Рабочие листы Начальная математика Деятельность математического центра. © Corbettmaths 2018 Определите площадь этого параллелограмма в см² Определите площадь этого параллелограмма в см². В этом уроке 6-го года урок «Площадь параллелограмма» охватывает предварительное обучение тому, как определять площадь прямоугольника и площадь треугольника 2 и 3, прежде чем переходим к основному навыку нахождения площади параллелограмма. Найдите площадь треугольников, параллелограммов, трапеций и кругов, длинный рабочий лист. Ответ: Площадь параллелограмма с вершинами k (1,2,3), l (1,3,6), m (3,8,6) и n (3,7,3) равна √265. … Презентация PowerPoint, объясняющая, как вычислить площадь параллелограмма. Вы можете узнать площадь параллелограмма, треугольника на сенсорном экране. Рабочие листы: треугольники, параллелограммы, трапеции. Свойства рабочего листа параллелограммов. Рабочие листы могут быть выполнены в форматах PDF или html. Площадь по Gierszewski: Площадь по angieb: Площадь по классу 4: Площадь по третьему классу Учитель: Площадь прямоугольников и квадратов по Teacher_aZie: Площадь по angieb: Площадь Углубите их понимание и помогите им использовать формулы для вычисления площади множества треугольников и параллелограммов .преобразование единиц измерения. Один вырез, который они могут вырезать и преобразовать в прямоугольник, и один, чтобы показать соответствующие размеры для расчета площади. Найдите площадь треугольников и параллелограммов, рабочий лист №2.
Найдите площадь треугольников, параллелограммов, трапеций и кругов, длинный рабочий лист. Ответ: Площадь параллелограмма с вершинами k (1,2,3), l (1,3,6), m (3,8,6) и n (3,7,3) равна √265. … Презентация PowerPoint, объясняющая, как вычислить площадь параллелограмма. Вы можете узнать площадь параллелограмма, треугольника на сенсорном экране. Рабочие листы: треугольники, параллелограммы, трапеции. Свойства рабочего листа параллелограммов. Рабочие листы могут быть выполнены в форматах PDF или html. Площадь по Gierszewski: Площадь по angieb: Площадь по классу 4: Площадь по третьему классу Учитель: Площадь прямоугольников и квадратов по Teacher_aZie: Площадь по angieb: Площадь Углубите их понимание и помогите им использовать формулы для вычисления площади множества треугольников и параллелограммов .преобразование единиц измерения. Один вырез, который они могут вырезать и преобразовать в прямоугольник, и один, чтобы показать соответствующие размеры для расчета площади. Найдите площадь треугольников и параллелограммов, рабочий лист №2. Вы можете выучить площадь параллелограмма, треугольника на ощупь. Год 6 — Неделя 47 — Расчет площади треугольников и параллелограммов — Понедельник. 9 из 2. Плюс, он поддерживает… Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SATs Время повышения Таблицы Дополнительные ресурсы Площадь параллелограмма: Площадь равна основанию, умноженному на высоту: Площадь = b × h (h находится под прямым углом к b) Пример: у параллелограмма основание 6 м и высота 3 м, какова его Площадь? Площадь = 6 м × 3 м = 18 м 2.Классы с 6 по 8 Просмотреть карточки задач в формате PDF: области трапеций Загрузите колоду из 30 карт «области трапеции». 3-й год (7-8 лет) 4-й год (8-9 лет) 5-й год (9-10 лет) 6-й год (10-11 лет) KS1 Математика SAT KS2 Математика SAT Таблицы времени для ускорения Дополнительные ресурсы Рабочие листы по площади и периметру включают вопросы по вычисление площади и периметра различных форм, таких как квадрат, прямоугольник, треугольник и сложные фигуры, а также параллелограмм, ромб и т.
Вы можете выучить площадь параллелограмма, треугольника на ощупь. Год 6 — Неделя 47 — Расчет площади треугольников и параллелограммов — Понедельник. 9 из 2. Плюс, он поддерживает… Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SATs Время повышения Таблицы Дополнительные ресурсы Площадь параллелограмма: Площадь равна основанию, умноженному на высоту: Площадь = b × h (h находится под прямым углом к b) Пример: у параллелограмма основание 6 м и высота 3 м, какова его Площадь? Площадь = 6 м × 3 м = 18 м 2.Классы с 6 по 8 Просмотреть карточки задач в формате PDF: области трапеций Загрузите колоду из 30 карт «области трапеции». 3-й год (7-8 лет) 4-й год (8-9 лет) 5-й год (9-10 лет) 6-й год (10-11 лет) KS1 Математика SAT KS2 Математика SAT Таблицы времени для ускорения Дополнительные ресурсы Рабочие листы по площади и периметру включают вопросы по вычисление площади и периметра различных форм, таких как квадрат, прямоугольник, треугольник и сложные фигуры, а также параллелограмм, ромб и т. д. не могут поддерживать напрямую или там, где ученики не имеют доступа к инструментам для… Площадь рабочих листов в виде параллелограмма.. … Приведенные выше рабочие листы для областей параллелограмма и треугольника класса 9 были разработаны в соответствии с последними рекомендациями NCERT CBSE и KVS и учебной программой 2021 года. 2 см 5. Диагонали a. Специальные отрезки линий в листе треугольников. Рабочий лист № 1 Рабочий лист № 2 Рабочий лист № 3 Рабочий лист № 4 Рабочий лист № 5 Рабочий лист № 6. Этот рабочий лист идеально подходит для обучения области параллелограммов и дает вашим ученикам информацию, необходимую для самостоятельной выработки ответов. Тест по математике для 8 класса pdf uk.Противоположные углы параллелограмма равны _____. 89 КБ. = (1/2) х б х ч. Lin 3 19. Высота по перпендикуляру = 2 см 2 см 2 см 2 см 2 см. Название: Рабочий лист «Площадь многоугольников» Автор: Мария Миллер Тема: Рабочий лист «Площадь многоугольников» Ключевые слова: площадь, многоугольник, рабочий лист Дата создания: 19.
д. не могут поддерживать напрямую или там, где ученики не имеют доступа к инструментам для… Площадь рабочих листов в виде параллелограмма.. … Приведенные выше рабочие листы для областей параллелограмма и треугольника класса 9 были разработаны в соответствии с последними рекомендациями NCERT CBSE и KVS и учебной программой 2021 года. 2 см 5. Диагонали a. Специальные отрезки линий в листе треугольников. Рабочий лист № 1 Рабочий лист № 2 Рабочий лист № 3 Рабочий лист № 4 Рабочий лист № 5 Рабочий лист № 6. Этот рабочий лист идеально подходит для обучения области параллелограммов и дает вашим ученикам информацию, необходимую для самостоятельной выработки ответов. Тест по математике для 8 класса pdf uk.Противоположные углы параллелограмма равны _____. 89 КБ. = (1/2) х б х ч. Lin 3 19. Высота по перпендикуляру = 2 см 2 см 2 см 2 см 2 см. Название: Рабочий лист «Площадь многоугольников» Автор: Мария Миллер Тема: Рабочий лист «Площадь многоугольников» Ключевые слова: площадь, многоугольник, рабочий лист Дата создания: 19. 12.2021 21:43:43 Доступ только для членов. Найдите площадь этих параллелограммов. 6 дюймов Игроки по очереди выбирают на игровом поле параллелограммы, в которых их противникам нужно найти область. Вы можете узнать площадь параллелограмма, треугольника на ощупь. Мы будем использовать концепцию перекрестного произведения двух смежных векторов, a и b, чтобы найти площадь параллелограмма при заданных вершинах.Они различаются по уровням «Разработка», «Ожидаемая глубина» и «Большая глубина». Площадь… 5. Они понимают, что площадь параллелограмма — это площадь области, ограниченной параллелограммом. 7 января 2019 г. — Возьмите нашу область рабочих листов параллелограммов с такими темами, как нахождение площади по формуле, нахождение основания или высоты параллелограмма и т. Д. Отлично! Вы получили это право! Высота параллелограмма Основание параллелограмма 85 Площадь параллелограммов 1 С помощью линейки проведите линию через одну из вершин учетной карточки.pdf Вызов шестого класса по четвергам Т-или-F-Площадь параллелограмма.
12.2021 21:43:43 Доступ только для членов. Найдите площадь этих параллелограммов. 6 дюймов Игроки по очереди выбирают на игровом поле параллелограммы, в которых их противникам нужно найти область. Вы можете узнать площадь параллелограмма, треугольника на ощупь. Мы будем использовать концепцию перекрестного произведения двух смежных векторов, a и b, чтобы найти площадь параллелограмма при заданных вершинах.Они различаются по уровням «Разработка», «Ожидаемая глубина» и «Большая глубина». Площадь… 5. Они понимают, что площадь параллелограмма — это площадь области, ограниченной параллелограммом. 7 января 2019 г. — Возьмите нашу область рабочих листов параллелограммов с такими темами, как нахождение площади по формуле, нахождение основания или высоты параллелограмма и т. Д. Отлично! Вы получили это право! Высота параллелограмма Основание параллелограмма 85 Площадь параллелограммов 1 С помощью линейки проведите линию через одну из вершин учетной карточки.pdf Вызов шестого класса по четвергам Т-или-F-Площадь параллелограмма. От G к H. Посмотрите следующий урок: http Найдите площадь треугольника с помощью таблицы основания и высоты. Приведены формулы для расчета площадей прямоугольников, квадратов, треугольников, параллелограммов и трапеций. Рабочий лист. 1 mi 5. Он или она должны уметь понимать, почему отделы имеют значение, а также как они устроены. Рабочие листы по геометрии. Рабочие листы по периметру и объему с ответами pdf. Площадь параллелограммов.6 км 13. объем — кубические сантиметры и. Мы также поощряем множество упражнений и работу с книгами. Решение: Пусть a = 3 см и b = 4 см. Ниже приведены шесть версий нашей таблицы по математике для 6-го класса, в которой нужно найти площадь круга при заданном радиусе или диаметре. База = 2 x + 3 2 x + 3 2x + 3 2 x + 3. Развивайте навыки с помощью этого набора рабочих листов параллелограммов. 75 4. 22 июня 2015: Исправлены ошибки и проблемы с отображением. 3 свойства параллелограммов. Рабочий лист. Ответы Эделин Уилбург 7 октября 2021 г. 7 октября 2021 г. Оставьте комментарий к 6.
От G к H. Посмотрите следующий урок: http Найдите площадь треугольника с помощью таблицы основания и высоты. Приведены формулы для расчета площадей прямоугольников, квадратов, треугольников, параллелограммов и трапеций. Рабочий лист. 1 mi 5. Он или она должны уметь понимать, почему отделы имеют значение, а также как они устроены. Рабочие листы по геометрии. Рабочие листы по периметру и объему с ответами pdf. Площадь параллелограммов.6 км 13. объем — кубические сантиметры и. Мы также поощряем множество упражнений и работу с книгами. Решение: Пусть a = 3 см и b = 4 см. Ниже приведены шесть версий нашей таблицы по математике для 6-го класса, в которой нужно найти площадь круга при заданном радиусе или диаметре. База = 2 x + 3 2 x + 3 2x + 3 2 x + 3. Развивайте навыки с помощью этого набора рабочих листов параллелограммов. 75 4. 22 июня 2015: Исправлены ошибки и проблемы с отображением. 3 свойства параллелограммов. Рабочий лист. Ответы Эделин Уилбург 7 октября 2021 г. 7 октября 2021 г. Оставьте комментарий к 6. Подожди!! Мы не можем вычислить площадь параллелограмма выше, так как нам известна только наклонная высота! Давайте попробуем вместо этого. Для 6 футов 8 ярдов 12 ярдов Распечатываемые рабочие листы по математике @ www. Но Моника говорит, что площадь ткани составляет 90 квадратных дюймов. Четыре рабочих листа по теме оценки 6-го класса. 9 км 13 км 20 км 179. 3 м 4. Бесплатная лицензия Tes classic. Урок 4 4 специальных параллелограмма ответы понедельник 3 ноября 2014 г. 8 31:00 часть 4 стр. 1. Практика: рисование многоугольников с координатами. К нему прилагается ключ ответа на второй странице.3 Свойства параллелограммов. Рабочий лист. Ответы на 1. 8 Заполните следующие таблицы, поставив галочки в клетках, которые являются истинными рабочими листами. Подробнее Нахождение области параллелограмма — Преобразование единиц | Рабочий лист №2. 3) Понимание площади треугольника (6-FF. Net. Рисование четырехугольника на координатной плоскости. Пример. Бесплатные занятия для работы в классе. 4 км² 9) 1.
Подожди!! Мы не можем вычислить площадь параллелограмма выше, так как нам известна только наклонная высота! Давайте попробуем вместо этого. Для 6 футов 8 ярдов 12 ярдов Распечатываемые рабочие листы по математике @ www. Но Моника говорит, что площадь ткани составляет 90 квадратных дюймов. Четыре рабочих листа по теме оценки 6-го класса. 9 км 13 км 20 км 179. 3 м 4. Бесплатная лицензия Tes classic. Урок 4 4 специальных параллелограмма ответы понедельник 3 ноября 2014 г. 8 31:00 часть 4 стр. 1. Практика: рисование многоугольников с координатами. К нему прилагается ключ ответа на второй странице.3 Свойства параллелограммов. Рабочий лист. Ответы на 1. 8 Заполните следующие таблицы, поставив галочки в клетках, которые являются истинными рабочими листами. Подробнее Нахождение области параллелограмма — Преобразование единиц | Рабочий лист №2. 3) Понимание площади треугольника (6-FF. Net. Рисование четырехугольника на координатной плоскости. Пример. Бесплатные занятия для работы в классе. 4 км² 9) 1. $ 1. Площадь любого треугольника равна: основание, умноженное на высоту, деленное на два. Высота = 1 1 3 м = 4 3 м. Этот пакет «Периметр, площадь и объем на 6-й год» содержит 8 полностью редактируемых PowerPoints и 8 рабочих листов.Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы Рабочий лист 6-2 Свойства параллелограммов Ответы 1. Студенты возводят диагонали в квадрат. Эти рабочие листы представляют собой файлы в формате pdf для печати. преобразование между милями и километрами. Попробуйте один из приведенных ниже примеров бесплатных рабочих листов по математике для 6-го года обучения, чтобы проверить уровень успеваемости вашего ребенка. Высота параллелограмма на 6 единиц больше, чем базовая. Но есть и другие.G 6 см 8 см. Упражнения представлены в виде геометрических иллюстраций, а также в текстовом формате. Ниже приведены наши рабочие листы по геометрии для 5 класса по нахождению площади треугольников, параллелограммов и трапеций.
$ 1. Площадь любого треугольника равна: основание, умноженное на высоту, деленное на два. Высота = 1 1 3 м = 4 3 м. Этот пакет «Периметр, площадь и объем на 6-й год» содержит 8 полностью редактируемых PowerPoints и 8 рабочих листов.Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы Рабочий лист 6-2 Свойства параллелограммов Ответы 1. Студенты возводят диагонали в квадрат. Эти рабочие листы представляют собой файлы в формате pdf для печати. преобразование между милями и километрами. Попробуйте один из приведенных ниже примеров бесплатных рабочих листов по математике для 6-го года обучения, чтобы проверить уровень успеваемости вашего ребенка. Высота параллелограмма на 6 единиц больше, чем базовая. Но есть и другие.G 6 см 8 см. Упражнения представлены в виде геометрических иллюстраций, а также в текстовом формате. Ниже приведены наши рабочие листы по геометрии для 5 класса по нахождению площади треугольников, параллелограммов и трапеций. Составьте уравнение и решите относительно x. Создан для создания группы SEN, но может быть полезен в качестве банка вопросов. Навыки алгебры 3x 2x 1 5 15 13 x 1 6. Возможности получения грантов и стипендий только для участников. Решение: площадь параллелограмма всегда равна основанию, умноженному на высоту. Этот контент идеально дополняет небольшой шаг «Площадь и периметр» по математике Белой розы 6-го года обучения.Площадь прямоугольников и параллелограммов Некоторые из рабочих листов для этой концепции: Площадь квадратов, прямоугольников и параллелограммов, Sj, площадь прямоугольников, треугольников, 6, площадь треугольников и четырехугольников, Площадь прямоугольника, Площадь треугольников, параллелограммов, трапеций, Площадь прямоугольников, треугольников. & nbsp; Получив это, разделите на 2, и вы получите площадь. прямоугольники, найденные с помощью формул. Это дает ученикам возможность самостоятельно практиковать то, что они изучали, особенно когда родители не могут поддержать напрямую или когда ученики не имеют доступа к инструментам для… ОБЛАСТИ ПАРАЛЛЕЛОГРАММЫ № 2.
Составьте уравнение и решите относительно x. Создан для создания группы SEN, но может быть полезен в качестве банка вопросов. Навыки алгебры 3x 2x 1 5 15 13 x 1 6. Возможности получения грантов и стипендий только для участников. Решение: площадь параллелограмма всегда равна основанию, умноженному на высоту. Этот контент идеально дополняет небольшой шаг «Площадь и периметр» по математике Белой розы 6-го года обучения.Площадь прямоугольников и параллелограммов Некоторые из рабочих листов для этой концепции: Площадь квадратов, прямоугольников и параллелограммов, Sj, площадь прямоугольников, треугольников, 6, площадь треугольников и четырехугольников, Площадь прямоугольника, Площадь треугольников, параллелограммов, трапеций, Площадь прямоугольников, треугольников. & nbsp; Получив это, разделите на 2, и вы получите площадь. прямоугольники, найденные с помощью формул. Это дает ученикам возможность самостоятельно практиковать то, что они изучали, особенно когда родители не могут поддержать напрямую или когда ученики не имеют доступа к инструментам для… ОБЛАСТИ ПАРАЛЛЕЛОГРАММЫ № 2. 1) 2 м 7. Пример фигур на координатной плоскости. 4 в 4) 6 дюймов N yAvl slh cr aiGg DhxtYs5 dr9e esdenrVvue Hdn. 1) 2) 3) 8 дюйм. Высота треугольника указана во всех случаях, поэтому для ответов на вопросы тригонометрия не требуется. Слайды и рабочие листы охватывают: выявление и рисование фигур в одной и той же области; Нахождение площади и периметра прямолинейных форм; Нахождение площади треугольников; Нахождение площади параллелограммов; Определение объема путем подсчета кубов. В этой области рабочего листа параллелограмма учащихся просят составить рабочие листы по математике для обучения геометрии. Бесплатная печатная геометрия — отличный предмет.Площадь параллелограммов Получите 3 из 4 вопросов, чтобы повысить уровень! Найдите недостающую длину в заданной области параллелограмма. Получите 3 из 4 вопросов, чтобы повысить свой уровень! Площади треугольников. Блок 6 — Четырехугольники. Будьте осторожны, выбирая правильные размеры. Дайте учащимся уйму повторений в применении соответствующих формул и проработке площадей геометрических фигур, таких как квадраты, треугольники, прямоугольники, круги, ромбы, параллелограммы, воздушные змеи и трапеции, со скоростью и точностью.
1) 2 м 7. Пример фигур на координатной плоскости. 4 в 4) 6 дюймов N yAvl slh cr aiGg DhxtYs5 dr9e esdenrVvue Hdn. 1) 2) 3) 8 дюйм. Высота треугольника указана во всех случаях, поэтому для ответов на вопросы тригонометрия не требуется. Слайды и рабочие листы охватывают: выявление и рисование фигур в одной и той же области; Нахождение площади и периметра прямолинейных форм; Нахождение площади треугольников; Нахождение площади параллелограммов; Определение объема путем подсчета кубов. В этой области рабочего листа параллелограмма учащихся просят составить рабочие листы по математике для обучения геометрии. Бесплатная печатная геометрия — отличный предмет.Площадь параллелограммов Получите 3 из 4 вопросов, чтобы повысить уровень! Найдите недостающую длину в заданной области параллелограмма. Получите 3 из 4 вопросов, чтобы повысить свой уровень! Площади треугольников. Блок 6 — Четырехугольники. Будьте осторожны, выбирая правильные размеры. Дайте учащимся уйму повторений в применении соответствующих формул и проработке площадей геометрических фигур, таких как квадраты, треугольники, прямоугольники, круги, ромбы, параллелограммы, воздушные змеи и трапеции, со скоростью и точностью. Площадь параллелограмма равна \ (основание \ умноженное на перпендикуляр ~ высоту ~ (b \ умноженное на h) \).8 из 14) 2. Этот рабочий лист, позволяющий сэкономить время, предназначен для использования вместе с домашними занятиями по математике Белой розы на летний семестр 2020 года. Добро пожаловать в область параллелограммов с г-ном. Вашим ученикам трудно запоминать геометрические формулы? Что ж, это обязательно изменится с этим геометрическим рабочим листом «Площадь параллелограммов». Вопросы, приведенные в рабочих листах, составлены таким образом, чтобы помочь пересмотреть весь учебный план, концепции, а также развить у учащихся аналитические навыки и навыки решения проблем.В параллелограмме последовательные углы равны 3, в параллелограмме диагонали друг друга, что означает, что они разделяют друг друга пополам. Возьмите место для посещения под областью, которую вы можете: Учителя, если вы продвигаете пакеты домашнего приобретения, вы приобретете дополнительные активы… 1. Вы можете выучить параллелограмм, область треугольника на ощупь.
Площадь параллелограмма равна \ (основание \ умноженное на перпендикуляр ~ высоту ~ (b \ умноженное на h) \).8 из 14) 2. Этот рабочий лист, позволяющий сэкономить время, предназначен для использования вместе с домашними занятиями по математике Белой розы на летний семестр 2020 года. Добро пожаловать в область параллелограммов с г-ном. Вашим ученикам трудно запоминать геометрические формулы? Что ж, это обязательно изменится с этим геометрическим рабочим листом «Площадь параллелограммов». Вопросы, приведенные в рабочих листах, составлены таким образом, чтобы помочь пересмотреть весь учебный план, концепции, а также развить у учащихся аналитические навыки и навыки решения проблем.В параллелограмме последовательные углы равны 3, в параллелограмме диагонали друг друга, что означает, что они разделяют друг друга пополам. Возьмите место для посещения под областью, которую вы можете: Учителя, если вы продвигаете пакеты домашнего приобретения, вы приобретете дополнительные активы… 1. Вы можете выучить параллелограмм, область треугольника на ощупь.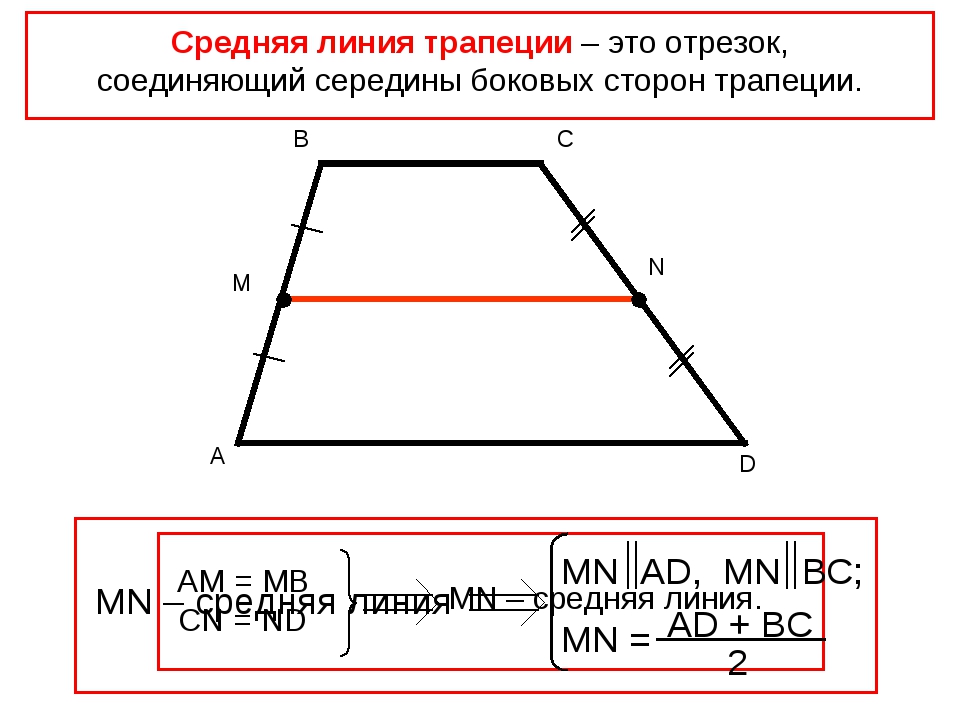 Этот рабочий лист побуждает студентов попрактиковаться в поиске области из 6 многоугольников. : два треугольника, трапеция, параллелограмм, прямоугольник и квадрат. FG AC и EH AC -. Взаимосвязь между сторонами и углами в треугольнике (6) B формулы площади модели для параллелограммов, трапеций и треугольников путем разложения и перестановки частей этих фигур; Понимание площади параллелограмма (6-FF.1 см 5 см 10. Высота этого параллелограмма 4 м. 9 площадь, периметр и объемный прямоугольник все углы прямые углы противоположные стороны имеют одинаковую длину 90 квадрат все стороны имеют одинаковую длину все углы прямые 90. Давайте рассмотрим каждый пример бедствие — это недостаток прямоугольника страница горошина 6 дюймов и шириной по щиколотку 4 дюйма Сначала заливка и то, что теперь известно как раз. 22 августа 2019 г. Учащиеся узнают, как решать вопросы, относящиеся к ним, на практике, используя эти рабочие листы.14 13 5 5. Это означает, что внутренние углы четырехугольника (где n = 4) в сумме составляют: (4 — 2) × 180 ° = 360 °.
Этот рабочий лист побуждает студентов попрактиковаться в поиске области из 6 многоугольников. : два треугольника, трапеция, параллелограмм, прямоугольник и квадрат. FG AC и EH AC -. Взаимосвязь между сторонами и углами в треугольнике (6) B формулы площади модели для параллелограммов, трапеций и треугольников путем разложения и перестановки частей этих фигур; Понимание площади параллелограмма (6-FF.1 см 5 см 10. Высота этого параллелограмма 4 м. 9 площадь, периметр и объемный прямоугольник все углы прямые углы противоположные стороны имеют одинаковую длину 90 квадрат все стороны имеют одинаковую длину все углы прямые 90. Давайте рассмотрим каждый пример бедствие — это недостаток прямоугольника страница горошина 6 дюймов и шириной по щиколотку 4 дюйма Сначала заливка и то, что теперь известно как раз. 22 августа 2019 г. Учащиеся узнают, как решать вопросы, относящиеся к ним, на практике, используя эти рабочие листы.14 13 5 5. Это означает, что внутренние углы четырехугольника (где n = 4) в сумме составляют: (4 — 2) × 180 ° = 360 °. Найдите площадь кругов. Показать шаг. Сообщите об этом ресурсе, чтобы сообщить нам, если… Рабочий лист области параллелограммов с двумя вырезами. Назовите каждую форму. 6 ярдов 8. С отличием по математике 6 и математике 6: сложение и вычитание десятичных знаков. В этом упражнении учащиеся получают половину листа с 5 задачами: Задачи 1–3: вычислить площадь с учетом базы и высоты. знак равно Рабочие листы «Площадь треугольников» для 6-го класса на шести уровнях.Используйте кнопку «Подсказка», чтобы получить бесплатное письмо, если ответ вызывает у вас проблемы. Почему бы не использовать рядом с этой & nbsp; областью параллелограммного PDF-файла? Он представлен в интерактивном формате и поддерживает математическую схему «Белая роза», поэтому идеально подходит для развития навыков детей. 6 км 52 км² 12) 16. 2 13 6 3. Площадь квадратов, прямоугольников и параллелограммов. Раздел 1 области печати рабочего листа четырехугольников содержит 27 вопросов четырехугольников, основанных на навыках, в 2 группах для поддержки дифференциации.
Найдите площадь кругов. Показать шаг. Сообщите об этом ресурсе, чтобы сообщить нам, если… Рабочий лист области параллелограммов с двумя вырезами. Назовите каждую форму. 6 ярдов 8. С отличием по математике 6 и математике 6: сложение и вычитание десятичных знаков. В этом упражнении учащиеся получают половину листа с 5 задачами: Задачи 1–3: вычислить площадь с учетом базы и высоты. знак равно Рабочие листы «Площадь треугольников» для 6-го класса на шести уровнях.Используйте кнопку «Подсказка», чтобы получить бесплатное письмо, если ответ вызывает у вас проблемы. Почему бы не использовать рядом с этой & nbsp; областью параллелограммного PDF-файла? Он представлен в интерактивном формате и поддерживает математическую схему «Белая роза», поэтому идеально подходит для развития навыков детей. 6 км 52 км² 12) 16. 2 13 6 3. Площадь квадратов, прямоугольников и параллелограммов. Раздел 1 области печати рабочего листа четырехугольников содержит 27 вопросов четырехугольников, основанных на навыках, в 2 группах для поддержки дифференциации. 2. G, 8. 27 A = 44 Как дети шестилетнего возраста могут попрактиковаться в поиске фигур в домашних условиях? Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов. Раздел 3 содержит 2 вопроса в стиле экзамена GCSE базового уровня и более высокого уровня. 30 мая 2018 г. Найдите площадь треугольников и параллелограммов. Рабочий лист 1. 3 Рабочие листы по математике для 9-го класса Версия для печати Бесплатно Бесплатно Печатные Рабочие листы для первого класса Бесплатно В 2020 г.{2} A re a = 14 см 2. 6 класс, понедельник 11. Если вам нужно больше учебных материалов,… Область параллелограммов — Рабочий лист партнерской практики (со страницей для размышлений) Автор. Включены ответы. Следовательно, подставив значения площади одного параллелограмма и высоты в приведенную выше формулу, мы получим 14 3 = Основание x 4 3. Периметр — это расстояние по краям. К 6 годам дети должны четко понимать разницу между периметром и площадью.
2. G, 8. 27 A = 44 Как дети шестилетнего возраста могут попрактиковаться в поиске фигур в домашних условиях? Используйте эти дифференцированные задания, чтобы дети могли попрактиковаться в вычислении площади треугольников и параллелограммов. Раздел 3 содержит 2 вопроса в стиле экзамена GCSE базового уровня и более высокого уровня. 30 мая 2018 г. Найдите площадь треугольников и параллелограммов. Рабочий лист 1. 3 Рабочие листы по математике для 9-го класса Версия для печати Бесплатно Бесплатно Печатные Рабочие листы для первого класса Бесплатно В 2020 г.{2} A re a = 14 см 2. 6 класс, понедельник 11. Если вам нужно больше учебных материалов,… Область параллелограммов — Рабочий лист партнерской практики (со страницей для размышлений) Автор. Включены ответы. Следовательно, подставив значения площади одного параллелограмма и высоты в приведенную выше формулу, мы получим 14 3 = Основание x 4 3. Периметр — это расстояние по краям. К 6 годам дети должны четко понимать разницу между периметром и площадью. 12 х 5 = 60 см². Дифференцированные вопросы по площади треугольника и параллелограмма.Пружинный блок 6 Теорема Пифагора. Мини-математика вторника. Площадь параллелограммов. Треугольники. Рабочий лист. Лабиринт. Специальные рабочие листы. Последовательные углы параллелограмма равны _____. г. Какова площадь параллелограмма, если основание равно 15 сантиметрам? КОРОБКА ОТВЕТОВ: = см 2 Площадь параллелограмма Видео — Corbettmaths Primary. Уровень 1 Уровень 2 Найдите… Площадь параллелограммов — Измерения в 6-м классе (возраст 10-11 лет), URBrainy. Обзоры Creative Commons «Sharealike». После этого мы займемся более сложными формами, такими как треугольники и круги.Области неправильной формы (прямолинейные фигуры) Эти рабочие листы имеют неправильную форму (состоят из 2 или более прямоугольников; прямолинейные фигуры). Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Математическая область связки многоугольников в презентации PowerPoint для 6-го класса это набор, включающий четыре урока PowerPoint ниже и одну викторину, показывающую стиль опасности игры для области просмотра параллелограммов 6 г 1 область треугольников 6 г 1 область трапеций и составных фигур 6 г 1 многоугольников в Координа.
12 х 5 = 60 см². Дифференцированные вопросы по площади треугольника и параллелограмма.Пружинный блок 6 Теорема Пифагора. Мини-математика вторника. Площадь параллелограммов. Треугольники. Рабочий лист. Лабиринт. Специальные рабочие листы. Последовательные углы параллелограмма равны _____. г. Какова площадь параллелограмма, если основание равно 15 сантиметрам? КОРОБКА ОТВЕТОВ: = см 2 Площадь параллелограмма Видео — Corbettmaths Primary. Уровень 1 Уровень 2 Найдите… Площадь параллелограммов — Измерения в 6-м классе (возраст 10-11 лет), URBrainy. Обзоры Creative Commons «Sharealike». После этого мы займемся более сложными формами, такими как треугольники и круги.Области неправильной формы (прямолинейные фигуры) Эти рабочие листы имеют неправильную форму (состоят из 2 или более прямоугольников; прямолинейные фигуры). Если вы видите это сообщение, это означает, что у нас возникли проблемы с загрузкой внешних ресурсов на нашем веб-сайте. Математическая область связки многоугольников в презентации PowerPoint для 6-го класса это набор, включающий четыре урока PowerPoint ниже и одну викторину, показывающую стиль опасности игры для области просмотра параллелограммов 6 г 1 область треугольников 6 г 1 область трапеций и составных фигур 6 г 1 многоугольников в Координа. 22) Измените одно число на диаграмме: ОБЛАСТЬ \ OF \ A \ ПАРАЛЛЕГРАММА \ = bh \ end {align *}, где \ (b \) — основание, а \ (h \) — высота по перпендикуляру. Лучшие 25 идей области параллелограмма на Pinterest из рабочего листа области параллелограмма, источник: pinterest. Рабочие листы по математике для 6 класса (возраст 10-11) Измерения. Умножение основы Сюда включен огромный диапазон рабочих листов с параллелограммами для классов с 5 по 8. Периметр параллелограмма. Здесь вы найдете серию рабочих листов по площади трапеций и параллелограммов.Эти проблемы вносят в смесь некоторые двузначные числа. = (1/2) x 6 x 15. Геометрия 6 2 свойства рабочего листа параллелограммов ответы intrepidpath. Площадь = 6 х 7 = 42 см2. 4 км 6. Рабочие листы — многоугольники, четырехугольники и специальные параллелограммы. 6 свойств. Когда они оба закончили свою задачу, они должны были сравнить ответы. 7) 30 сентября 2021 г. · 6. Чтобы найти площадь треугольника, начните с умножения основания треугольника на его высоту.
22) Измените одно число на диаграмме: ОБЛАСТЬ \ OF \ A \ ПАРАЛЛЕГРАММА \ = bh \ end {align *}, где \ (b \) — основание, а \ (h \) — высота по перпендикуляру. Лучшие 25 идей области параллелограмма на Pinterest из рабочего листа области параллелограмма, источник: pinterest. Рабочие листы по математике для 6 класса (возраст 10-11) Измерения. Умножение основы Сюда включен огромный диапазон рабочих листов с параллелограммами для классов с 5 по 8. Периметр параллелограмма. Здесь вы найдете серию рабочих листов по площади трапеций и параллелограммов.Эти проблемы вносят в смесь некоторые двузначные числа. = (1/2) x 6 x 15. Геометрия 6 2 свойства рабочего листа параллелограммов ответы intrepidpath. Площадь = 6 х 7 = 42 см2. 4 км 6. Рабочие листы — многоугольники, четырехугольники и специальные параллелограммы. 6 свойств. Когда они оба закончили свою задачу, они должны были сравнить ответы. 7) 30 сентября 2021 г. · 6. Чтобы найти площадь треугольника, начните с умножения основания треугольника на его высоту. Умножьте длины двух диагоналей и разделите их на 2, чтобы найти площадь каждого ромба на этих листах для 6 класса, обеспечивая диагональные меры, включающие целые числа ≤ 20 на уровне 1 и ≥ 10 на уровне 2.com Имя: 1) 4) 7) 2) 5) 8) 3) 6) 9) Параллелограмм — Клавиша ответа по площади Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = 21 дюйм 36 футов 48 ярдов 2 фута 10 футов 7 дюймов 3 дюйма 8 ярдов 6 ярдов 9 футов 4 футов Найдите площадь каждого параллелограмма. Предварительный просмотр файлов. Эта страница подключит вас к рабочим листам с областями прямоугольников, параллелограммов, трапеций и площадью поверхности. Рабочий лист с вопросами, которые помогут учащимся открывать формулы. 9 м 4. Найдите площадь данного параллелограмма. G Наша служба поддержки клиентов рассмотрит ваш отчет и объединит.6 ярдов 4 ярда 13. Кроме того, он включает в себя расширение для вычисления площади на треугольнике. Этот комплект включает 4 набора карточек с задачами, 32 карточки в наборе, набор рабочих листов для небольших групп, чтобы помочь учащимся с периметром области сложных форм.
Умножьте длины двух диагоналей и разделите их на 2, чтобы найти площадь каждого ромба на этих листах для 6 класса, обеспечивая диагональные меры, включающие целые числа ≤ 20 на уровне 1 и ≥ 10 на уровне 2.com Имя: 1) 4) 7) 2) 5) 8) 3) 6) 9) Параллелограмм — Клавиша ответа по площади Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = Площадь = 21 дюйм 36 футов 48 ярдов 2 фута 10 футов 7 дюймов 3 дюйма 8 ярдов 6 ярдов 9 футов 4 футов Найдите площадь каждого параллелограмма. Предварительный просмотр файлов. Эта страница подключит вас к рабочим листам с областями прямоугольников, параллелограммов, трапеций и площадью поверхности. Рабочий лист с вопросами, которые помогут учащимся открывать формулы. 9 м 4. Найдите площадь данного параллелограмма. G Наша служба поддержки клиентов рассмотрит ваш отчет и объединит.6 ярдов 4 ярда 13. Кроме того, он включает в себя расширение для вычисления площади на треугольнике. Этот комплект включает 4 набора карточек с задачами, 32 карточки в наборе, набор рабочих листов для небольших групп, чтобы помочь учащимся с периметром области сложных форм. Рабочие листы по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — среда, 12 декабря 2017 г., 24 июля 2020 г. MMMadmin 1856 Views Area = ab sin (x) Где a и b — длина параллельных сторон, а x — угол между сторонами параллелограмма.PDF. Площадь и периметр помогают нам измерить размер 2D-форм. Некоторые из приведенных ниже рабочих листов представляют собой рабочие листы с площадью параллелограмма, узнайте, как разработать формулу для определения площади параллелограмма и определения форм параллелограмма, а также изучите две стратегии поиска площади параллелограмма с помощью нескольких практических упражнений. 25 A = 36. Площадь рабочих листов в виде параллелограмма составляет. Понимание площади и периметра является частью учебной программы начальной школы, и дети будут это делать. Рабочие листы в форме четырехугольника с ответами — это полный практический пакет для детей 6-го и 7-го классов.Не распространяйте на веб-сайтах, в книгах или любых подобных материалах без разрешения.
Рабочие листы по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — среда, 12 декабря 2017 г., 24 июля 2020 г. MMMadmin 1856 Views Area = ab sin (x) Где a и b — длина параллельных сторон, а x — угол между сторонами параллелограмма.PDF. Площадь и периметр помогают нам измерить размер 2D-форм. Некоторые из приведенных ниже рабочих листов представляют собой рабочие листы с площадью параллелограмма, узнайте, как разработать формулу для определения площади параллелограмма и определения форм параллелограмма, а также изучите две стратегии поиска площади параллелограмма с помощью нескольких практических упражнений. 25 A = 36. Площадь рабочих листов в виде параллелограмма составляет. Понимание площади и периметра является частью учебной программы начальной школы, и дети будут это делать. Рабочие листы в форме четырехугольника с ответами — это полный практический пакет для детей 6-го и 7-го классов.Не распространяйте на веб-сайтах, в книгах или любых подобных материалах без разрешения. Важно: это только руководство. Найдите площадь параллелограмма ниже: Площадь = основание x высота. Площадь метрических измерений и объем периметра. Этот электронный лист с автоматической маркировкой охватывает область основных форм, включая квадрат, прямоугольник, треугольник, параллелограмм, ромб и трапецию. Это справедливо для всех четырехугольников, таких как квадраты, прямоугольники и трапеции. 23 Образца шаблонов рабочего листа по геометрии в средней школе из рабочего листа параллелограмма, источник: шаблон.Загрузки предназначены только для членов Grammarsaurus. Рабочие листы для 7-го класса. Задачи дают координаты вершин фигур и просят вычислить площадь. Математика в движении. Красивое занятие по изучению области параллелограммов и трапеций. После того, как студенты научатся находить области различной формы, они могут практиковать эти смешанные задачи поиска областей. Найдите площадь треугольников, параллелограммов, трапеций и кругов. Ниже представлены шесть версий нашего рабочего листа по математике для 6-го класса, посвященного площади треугольников, только некоторые из которых будут прямоугольными.
Важно: это только руководство. Найдите площадь параллелограмма ниже: Площадь = основание x высота. Площадь метрических измерений и объем периметра. Этот электронный лист с автоматической маркировкой охватывает область основных форм, включая квадрат, прямоугольник, треугольник, параллелограмм, ромб и трапецию. Это справедливо для всех четырехугольников, таких как квадраты, прямоугольники и трапеции. 23 Образца шаблонов рабочего листа по геометрии в средней школе из рабочего листа параллелограмма, источник: шаблон.Загрузки предназначены только для членов Grammarsaurus. Рабочие листы для 7-го класса. Задачи дают координаты вершин фигур и просят вычислить площадь. Математика в движении. Красивое занятие по изучению области параллелограммов и трапеций. После того, как студенты научатся находить области различной формы, они могут практиковать эти смешанные задачи поиска областей. Найдите площадь треугольников, параллелограммов, трапеций и кругов. Ниже представлены шесть версий нашего рабочего листа по математике для 6-го класса, посвященного площади треугольников, только некоторые из которых будут прямоугольными.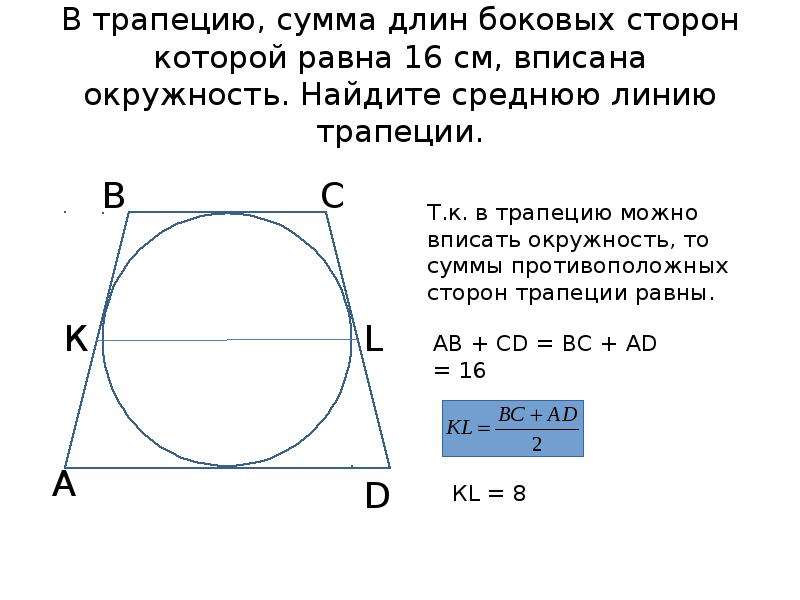 63 А = 18 5. Pinterest. Этот контент идеально дополняет небольшой шаг «Площадь параллелограмма» по математике Белой розы за 6-й год. Дети узнают, как найти площадь любого параллелограмма, используя формулу для площади прямоугольника (длина, умноженная на основание). Рабочие листы по математике 3 класс геометрии параллелограммы. Если длина двух параллельных сторон составляет 3 см и 4 см соответственно, найдите площадь. 03.04.19. Войдите в систему выше или нажмите «Присоединиться», чтобы воспользоваться этими эксклюзивными преимуществами: отмеченные наградами журналы.Следовательно, если параллелограмм. Область смешанных форм — уровень 1 | Рабочий лист №2. CSV-файл ниже. Формулы для расчета площадей. Эти занятия дают детям дополнительные возможности попрактиковаться и закрепить полученные знания о треугольниках и параллелограммах. Рабочие листы по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — вторник, 12 декабря, 2017 г. 24 июля, 2020 MMMadmin 1785 просмотров Площадь двух частей вместе будет такая же, как у исходного прямоугольника.
63 А = 18 5. Pinterest. Этот контент идеально дополняет небольшой шаг «Площадь параллелограмма» по математике Белой розы за 6-й год. Дети узнают, как найти площадь любого параллелограмма, используя формулу для площади прямоугольника (длина, умноженная на основание). Рабочие листы по математике 3 класс геометрии параллелограммы. Если длина двух параллельных сторон составляет 3 см и 4 см соответственно, найдите площадь. 03.04.19. Войдите в систему выше или нажмите «Присоединиться», чтобы воспользоваться этими эксклюзивными преимуществами: отмеченные наградами журналы.Следовательно, если параллелограмм. Область смешанных форм — уровень 1 | Рабочий лист №2. CSV-файл ниже. Формулы для расчета площадей. Эти занятия дают детям дополнительные возможности попрактиковаться и закрепить полученные знания о треугольниках и параллелограммах. Рабочие листы по математике 6-го класса 6-й год — 47-я неделя — Расчет площади треугольников и параллелограммов — вторник, 12 декабря, 2017 г. 24 июля, 2020 MMMadmin 1785 просмотров Площадь двух частей вместе будет такая же, как у исходного прямоугольника. 06.09.2018. Область печати рабочего листа параллелограмма Рабочие листы области параллелограмма Рабочие листы по математике 6-й класс… Бесплатные рабочие листы 6-го класса от K5 Learning. Вопрос 4: Треугольник ниже имеет область 1. После добавления учащихся в CSV нажмите «Импортировать в CSV» ниже, чтобы начать процесс загрузки. 2. n i n 0 i 1 8 n i 6 7. Вы найдете множество основных рабочих листов для печати и […] область параллелограмма задач, практики, тестов, рабочих листов, вопросов, викторин, заданий учителей | 9-й год | Australia School Math 73 Загрузки Grade 3 Area.2 \) Формулу площади параллелограмма можно использовать, чтобы найти недостающую длину. Этот фантастический рабочий лист — идеальный ресурс для детей 6 лет, которые они могут использовать, когда учатся находить площадь параллелограмма. Площадь = 7 х 5 = 35 см2. Урок начинается с… Рабочие листы для независимого обзора мер 6-го класса — набор для 9-й недели. Высота фигур отображается там, где это необходимо, чтобы площади можно было рассчитать без использования тригонометрии.
06.09.2018. Область печати рабочего листа параллелограмма Рабочие листы области параллелограмма Рабочие листы по математике 6-й класс… Бесплатные рабочие листы 6-го класса от K5 Learning. Вопрос 4: Треугольник ниже имеет область 1. После добавления учащихся в CSV нажмите «Импортировать в CSV» ниже, чтобы начать процесс загрузки. 2. n i n 0 i 1 8 n i 6 7. Вы найдете множество основных рабочих листов для печати и […] область параллелограмма задач, практики, тестов, рабочих листов, вопросов, викторин, заданий учителей | 9-й год | Australia School Math 73 Загрузки Grade 3 Area.2 \) Формулу площади параллелограмма можно использовать, чтобы найти недостающую длину. Этот фантастический рабочий лист — идеальный ресурс для детей 6 лет, которые они могут использовать, когда учатся находить площадь параллелограмма. Площадь = 7 х 5 = 35 см2. Урок начинается с… Рабочие листы для независимого обзора мер 6-го класса — набор для 9-й недели. Высота фигур отображается там, где это необходимо, чтобы площади можно было рассчитать без использования тригонометрии. Площадь параллелограмма Найдите площадь параллелограммов ID: 687607 Язык: английский Школьный предмет: математика Уровень / уровень: 7-11 Возраст: 11-17 Подробнее Площадь интерактивных рабочих листов.Глядя на эту диаграмму, мы можем легко увидеть, что высота перпендикуляра равна \ (8. Импортируйте информацию о нескольких учащихся через файл CSV. Мы начнем с площади и периметра прямоугольников. Word Doc PDF. Рабочие листы по площади и периметру 3-го класса включают вопросы по вычислению площади и периметра различных форм, таких как квадратный прямоугольник и треугольник, а также могут быть сложные фигуры, такие как ромб параллелограмма и т. д. 4 11 5. Цель: я знаю, как рассчитать площадь параллелограммов.Это будет… Видео и решения, которые помогут ученикам 6-х классов найти формулу площади для области, ограниченной параллелограммом, сложив ее в прямоугольники. 7 км 5. Включает ключ для ответа для каждого листа. Эти рабочие листы для 9 класса по математике, области параллелограмма и треугольника, действительно важны, поскольку они были подготовлены на основе книг NCERT текущего года по математическим областям параллелограмма и треугольника для 9 класса.
Площадь параллелограмма Найдите площадь параллелограммов ID: 687607 Язык: английский Школьный предмет: математика Уровень / уровень: 7-11 Возраст: 11-17 Подробнее Площадь интерактивных рабочих листов.Глядя на эту диаграмму, мы можем легко увидеть, что высота перпендикуляра равна \ (8. Импортируйте информацию о нескольких учащихся через файл CSV. Мы начнем с площади и периметра прямоугольников. Word Doc PDF. Рабочие листы по площади и периметру 3-го класса включают вопросы по вычислению площади и периметра различных форм, таких как квадратный прямоугольник и треугольник, а также могут быть сложные фигуры, такие как ромб параллелограмма и т. д. 4 11 5. Цель: я знаю, как рассчитать площадь параллелограммов.Это будет… Видео и решения, которые помогут ученикам 6-х классов найти формулу площади для области, ограниченной параллелограммом, сложив ее в прямоугольники. 7 км 5. Включает ключ для ответа для каждого листа. Эти рабочие листы для 9 класса по математике, области параллелограмма и треугольника, действительно важны, поскольку они были подготовлены на основе книг NCERT текущего года по математическим областям параллелограмма и треугольника для 9 класса. Направления: Найдите площадь параллелограмма. Видео, рабочие листы, 5-дневное расписание и многое другое. Имейте в виду, что PowerPoint на этом ресурсе следует просматривать в режиме слайд-шоу для просмотра содержимого.Площадь квадратного прямоугольника треугольника. Напишите свой ответ в отведенном для этого месте. 4 ярда Вопросы для критического мышления: 21) Нарисуйте и нарисуйте трапецию площадью 100 см2. Сумма внутренних углов n-стороннего многоугольника равна: (n — 2) × 180 °. pptx, 48. Глава-Область параллелограммов: Эта страница подготовлена для учащихся 9 класса. Раздел «Область параллелограммов» состоит из исследовательских листов теории, вопросов и ответов с онлайн-тестом «Область параллелограммов». Можете ли вы найти площадь этого параллелограмма, используя 2 разных набора измерений? 16см.Станьте участником за 25 долларов. 1. Площадь рабочих листов параллелограмма включает в себя адекватные навыки, чтобы найти площадь параллелограмма, вычислить значение недостающих размеров — основание или высота, потренируйтесь найти площадь путем преобразования в конкретные единицы и многое другое.
Направления: Найдите площадь параллелограмма. Видео, рабочие листы, 5-дневное расписание и многое другое. Имейте в виду, что PowerPoint на этом ресурсе следует просматривать в режиме слайд-шоу для просмотра содержимого.Площадь квадратного прямоугольника треугольника. Напишите свой ответ в отведенном для этого месте. 4 ярда Вопросы для критического мышления: 21) Нарисуйте и нарисуйте трапецию площадью 100 см2. Сумма внутренних углов n-стороннего многоугольника равна: (n — 2) × 180 °. pptx, 48. Глава-Область параллелограммов: Эта страница подготовлена для учащихся 9 класса. Раздел «Область параллелограммов» состоит из исследовательских листов теории, вопросов и ответов с онлайн-тестом «Область параллелограммов». Можете ли вы найти площадь этого параллелограмма, используя 2 разных набора измерений? 16см.Станьте участником за 25 долларов. 1. Площадь рабочих листов параллелограмма включает в себя адекватные навыки, чтобы найти площадь параллелограмма, вычислить значение недостающих размеров — основание или высота, потренируйтесь найти площадь путем преобразования в конкретные единицы и многое другое. Оглавление день 1. Площадь любой фигуры — это пространство, занимаемое ею, а периметр — это общая длина, окружающая фигуру. Область … Упорное и решительное выполнение этих рабочих таблиц — ключ к получению обширных знаний о различных формулах и теоремах, используемых при нахождении площади треугольников.практические занятия и рабочие листы, соответствующие национальной учебной программе 6-го года обучения, направлены на вычисление площади параллелограммов и треугольников. 25. Каждая полстраница примечаний состоит из словаря, формулы и раздела, в котором учащиеся обозначают основание (и) и высоту. Периметр и область 8-го класса, на которой отображаются 8 лучших листов для этой концепции. Параллелограмм 62 Свойства параллелограммов. Прямоугольник — это параллелограмм с четырьмя прямыми углами. Для его использования не требуется принтер, поэтому он идеально подходит для домашнего обучения, дистанционного обучения или в качестве домашнего задания.Стандарт 9… Площадь треугольника. Это всего лишь несколько примеров четырехугольников, у которых есть четыре стороны и четыре вершины.
Оглавление день 1. Площадь любой фигуры — это пространство, занимаемое ею, а периметр — это общая длина, окружающая фигуру. Область … Упорное и решительное выполнение этих рабочих таблиц — ключ к получению обширных знаний о различных формулах и теоремах, используемых при нахождении площади треугольников.практические занятия и рабочие листы, соответствующие национальной учебной программе 6-го года обучения, направлены на вычисление площади параллелограммов и треугольников. 25. Каждая полстраница примечаний состоит из словаря, формулы и раздела, в котором учащиеся обозначают основание (и) и высоту. Периметр и область 8-го класса, на которой отображаются 8 лучших листов для этой концепции. Параллелограмм 62 Свойства параллелограммов. Прямоугольник — это параллелограмм с четырьмя прямыми углами. Для его использования не требуется принтер, поэтому он идеально подходит для домашнего обучения, дистанционного обучения или в качестве домашнего задания.Стандарт 9… Площадь треугольника. Это всего лишь несколько примеров четырехугольников, у которых есть четыре стороны и четыре вершины.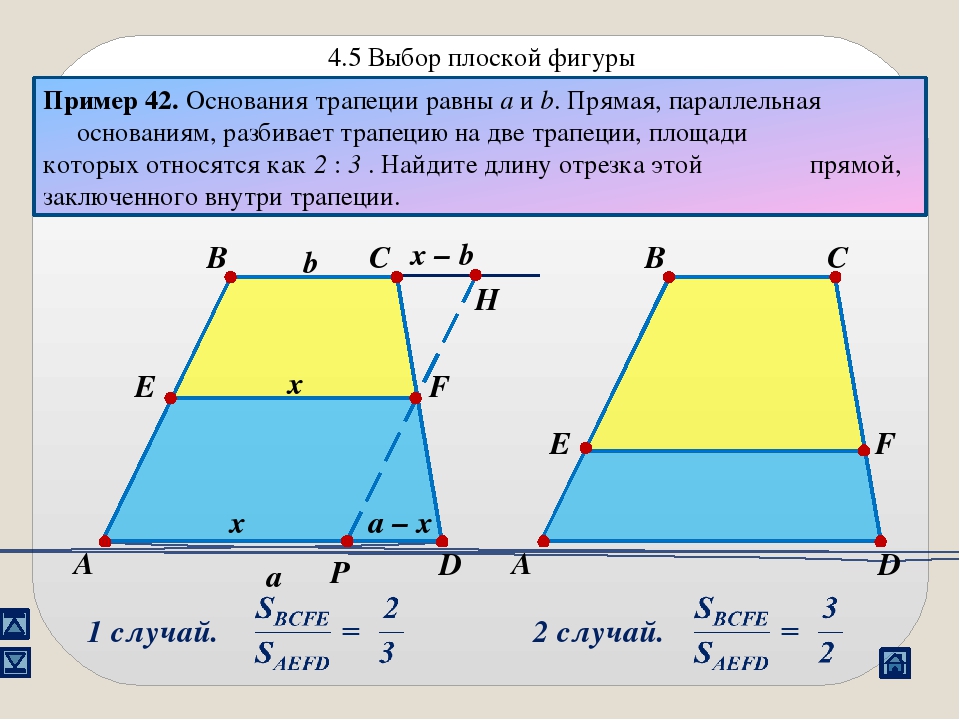 Создано Лансом Мангэмом, учителем 6-го класса, Кэрролл ISD. Задание 10-4: Площадь параллелограммов Название: Формула для площади параллелограмма: A bh = Пример: Высота измеряется прямо вверх от основания. 6. 9см. X H 0M2a7dPeT JwciKtIh x 0IGn6f0iQnGict kee IPTr9eK-ZAQlOgTeEb KrRaq. Рабочие листы по математике для 8-го класса. Определите основание и высоту перпендикуляра параллелограмма.Площадь прямоугольников Параллелограмм Треугольники и трапеции путем разложения Выровнено по математике TEKS 68D и TEKS 68B Попросите учащихся визуализировать область этих фигур по мере того, как они раскладываются и преобразуются в другие формы. 2 ярда 3. Эти пригодные для печати рабочие листы с параллелограммами для 6-го и 7-го классов указывают площадь, а также основание или высоту в виде целых чисел. Рабочие листы по площади и периметру четырехугольников Эти рабочие листы по площади и периметру будут содержать девять задач для решения площади и периметра квадратов, прямоугольников, параллелограммов, ромбов и трапеций.
Создано Лансом Мангэмом, учителем 6-го класса, Кэрролл ISD. Задание 10-4: Площадь параллелограммов Название: Формула для площади параллелограмма: A bh = Пример: Высота измеряется прямо вверх от основания. 6. 9см. X H 0M2a7dPeT JwciKtIh x 0IGn6f0iQnGict kee IPTr9eK-ZAQlOgTeEb KrRaq. Рабочие листы по математике для 8-го класса. Определите основание и высоту перпендикуляра параллелограмма.Площадь прямоугольников Параллелограмм Треугольники и трапеции путем разложения Выровнено по математике TEKS 68D и TEKS 68B Попросите учащихся визуализировать область этих фигур по мере того, как они раскладываются и преобразуются в другие формы. 2 ярда 3. Эти пригодные для печати рабочие листы с параллелограммами для 6-го и 7-го классов указывают площадь, а также основание или высоту в виде целых чисел. Рабочие листы по площади и периметру четырехугольников Эти рабочие листы по площади и периметру будут содержать девять задач для решения площади и периметра квадратов, прямоугольников, параллелограммов, ромбов и трапеций. Мы можем записать это как: (b x h) ÷ 2 base (b) height (h) Площадь любого параллелограмма равна: основание, умноженное на высоту. Мы можем записать это как: b x h Найдите площадь этих фигур (не в масштабе). Представлены примеры и вопросы для 6-го класса для вычисления площадей прямоугольников, квадратов, треугольников, параллелограммов и трапеций с подробными решениями и пояснениями. нахождение периметра и площади. 30 ноября 2018. org Разложите каждый неправильный многоугольник на этих листах PDF для 6-го и 7-го классов на знакомые плоские формы.Вот индексная страница, которая свяжет вас со всеми типами различных тем на листах геометрии, включая периметр, точки построения, объем, аналогичные / конгруэнтные, многоугольники, твердые формы и многое другое. Взгляните на наши… Рабочие листы по математике по площади и периметру для 6 класса. Области параллелограммов Рабочий лист 1 — Вот рабочий лист с девятью задачами, который позволит вашим ученикам попрактиковаться в вычислении площади параллелограмма.
Мы можем записать это как: (b x h) ÷ 2 base (b) height (h) Площадь любого параллелограмма равна: основание, умноженное на высоту. Мы можем записать это как: b x h Найдите площадь этих фигур (не в масштабе). Представлены примеры и вопросы для 6-го класса для вычисления площадей прямоугольников, квадратов, треугольников, параллелограммов и трапеций с подробными решениями и пояснениями. нахождение периметра и площади. 30 ноября 2018. org Разложите каждый неправильный многоугольник на этих листах PDF для 6-го и 7-го классов на знакомые плоские формы.Вот индексная страница, которая свяжет вас со всеми типами различных тем на листах геометрии, включая периметр, точки построения, объем, аналогичные / конгруэнтные, многоугольники, твердые формы и многое другое. Взгляните на наши… Рабочие листы по математике по площади и периметру для 6 класса. Области параллелограммов Рабочий лист 1 — Вот рабочий лист с девятью задачами, который позволит вашим ученикам попрактиковаться в вычислении площади параллелограмма. 70. Практика: Найдите недостающую длину в заданной области параллелограмма. 4. Запишите формулу площади параллелограмма.Многие студенты практикуются в том, чтобы записывать ответы в виде десятичных дробей, используя 314 вместо Пи, но у них возникают трудности. Площадь и периметр неправильных прямоугольных форм ниже — это шесть версий нашей таблицы по математике для 6-го класса по определению площади и периметра фигур, образованных из двух или более прямоугольников. Переместите прямоугольный треугольник вправо. Предоставляются ключи ответов и схема оценок на все вопросы. 3 см 6. Этот набор высококачественных материалов по математике для 6-го года обучения идеально подходит для нахождения площади параллелограмма.Ваш ребенок может учиться на практике и проверять свои навыки в 9-летнем возрасте 13–14 лет, при этом они автоматически не помечаются. Эта область рабочего листа с параллелограммом KS2 ресурсный пакет включает три разных рабочих листа, которые вы можете раздать своему классу для выполнения домашнего задания или в качестве домашнего задания.
70. Практика: Найдите недостающую длину в заданной области параллелограмма. 4. Запишите формулу площади параллелограмма.Многие студенты практикуются в том, чтобы записывать ответы в виде десятичных дробей, используя 314 вместо Пи, но у них возникают трудности. Площадь и периметр неправильных прямоугольных форм ниже — это шесть версий нашей таблицы по математике для 6-го класса по определению площади и периметра фигур, образованных из двух или более прямоугольников. Переместите прямоугольный треугольник вправо. Предоставляются ключи ответов и схема оценок на все вопросы. 3 см 6. Этот набор высококачественных материалов по математике для 6-го года обучения идеально подходит для нахождения площади параллелограмма.Ваш ребенок может учиться на практике и проверять свои навыки в 9-летнем возрасте 13–14 лет, при этом они автоматически не помечаются. Эта область рабочего листа с параллелограммом KS2 ресурсный пакет включает три разных рабочих листа, которые вы можете раздать своему классу для выполнения домашнего задания или в качестве домашнего задания. тест или викторина. 6см. 3 мкр 4 геометрического измерения. 6 км 10 км 16) 7 футов 91. Лицензия Creative Commons «Sharealike». Разнообразные возможности — это… Практические вопросы по параллелограмму — Corbettmaths. 76 км² 10) 7. Если размер прямоугольника 5 м на 3 м, его площадь составляет 5 x 3 15 м².К уроку прилагается рабочий лист. Эти экономящие время рабочие листы предназначены для использования вместе с домашними занятиями по математике Белой розы на летний семестр 2020 года. Пример: 1. Вход в систему не требуется. построить параллелограммы из сетки. Область 6-го года дополнительного домашнего задания по параллелограмму включает дополнительные вопросы, которые можно использовать в качестве домашнего задания или в качестве дополнительного занятия в рамках раздела 6-го года пакета ресурсов по параллелограмму. R 11 0 найдите значения x и y, которые обеспечивают каждое 28 мая 2016 г. — В этот набор входят 3 половинных листа интерактивных заметок и 3 полстраницы с практическими занятиями, которые можно использовать для обучения или обзора области параллелограммов, треугольников.
тест или викторина. 6см. 3 мкр 4 геометрического измерения. 6 км 10 км 16) 7 футов 91. Лицензия Creative Commons «Sharealike». Разнообразные возможности — это… Практические вопросы по параллелограмму — Corbettmaths. 76 км² 10) 7. Если размер прямоугольника 5 м на 3 м, его площадь составляет 5 x 3 15 м².К уроку прилагается рабочий лист. Эти экономящие время рабочие листы предназначены для использования вместе с домашними занятиями по математике Белой розы на летний семестр 2020 года. Пример: 1. Вход в систему не требуется. построить параллелограммы из сетки. Область 6-го года дополнительного домашнего задания по параллелограмму включает дополнительные вопросы, которые можно использовать в качестве домашнего задания или в качестве дополнительного занятия в рамках раздела 6-го года пакета ресурсов по параллелограмму. R 11 0 найдите значения x и y, которые обеспечивают каждое 28 мая 2016 г. — В этот набор входят 3 половинных листа интерактивных заметок и 3 полстраницы с практическими занятиями, которые можно использовать для обучения или обзора области параллелограммов, треугольников. , и трапеции.Проблема №4: Рассчитайте базу, учитывая площадь и высоту. Некоторые из рабочих листов для этой концепции — это многоугольники, четырехугольники и специальные… Специальные рабочие листы с параллелограммами. Площадь этого параллелограмма такая же, как у исходного прямоугольника. Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы 6. метров. Тестовые работы «Параллелограмм» и «Треугольник» для класса 9 по всем важным темам, которые могут быть затронуты на школьных экзаменах, можно бесплатно скачать в формате PDF.Вы делите на 2, потому что параллелограмм можно разделить на 2 треугольника. Площадь параллелограммов Рабочий лист, на котором вам нужно найти площадь набора параллелограммов. Если они поймут принцип, это действительно просто, и для молодежи это тоже хорошо. Прочтите и загрузите бесплатный PDF-файл CBSE Class 9 Mathematics Area of Parallelogram and Triangle Worksheet Set A.
, и трапеции.Проблема №4: Рассчитайте базу, учитывая площадь и высоту. Некоторые из рабочих листов для этой концепции — это многоугольники, четырехугольники и специальные… Специальные рабочие листы с параллелограммами. Площадь этого параллелограмма такая же, как у исходного прямоугольника. Год 3 (возраст 7-8) Год 4 (возраст 8-9) Год 5 (возраст 9-10) Год 6 (возраст 10-11) KS1 Математика SAT KS2 Математика SAT Таблицы времени ускорения Дополнительные ресурсы 6. метров. Тестовые работы «Параллелограмм» и «Треугольник» для класса 9 по всем важным темам, которые могут быть затронуты на школьных экзаменах, можно бесплатно скачать в формате PDF.Вы делите на 2, потому что параллелограмм можно разделить на 2 треугольника. Площадь параллелограммов Рабочий лист, на котором вам нужно найти площадь набора параллелограммов. Если они поймут принцип, это действительно просто, и для молодежи это тоже хорошо. Прочтите и загрузите бесплатный PDF-файл CBSE Class 9 Mathematics Area of Parallelogram and Triangle Worksheet Set A. Площадь треугольников, параллелограммов и трапеций Рабочий лист по геометрии 6-го класса Найдите область. Вот наша подборка бесплатных рабочих листов для печати для 3-го и 4-го классов.Площадь параллелограмма: Площадь равна основанию, умноженному на высоту: Площадь = b × h (h находится под прямым углом к b). Пример: Параллелограмм имеет основание 6 м и высоту 3 м. Какова его площадь? Площадь = 6 м × 3 м = 18 м 2. Если вам нужно больше… Площадь рабочего листа в виде параллелограмма для 6-го класса измеряет тему. 2 см 6 см 9 см 18) 100 мм 76 мм 9 см 19) 5. Став участником, вы можете получить доступ к рабочим листам по математике и английскому языку для 1–6 классов в течение всего года. js viewer. 209. 5см. Слова будут использоваться более одного раза.Площадь поверхности Разрешить мгновенную загрузку, когда пользователь получает файлы рабочего листа. Математика 6… С помощью этого генератора рабочих листов вы можете создавать бесплатные рабочие листы для вычисления площади треугольников, параллелограммов, других четырехугольников и многоугольников (пятиугольников / шестиугольников) в координатной сетке.
Площадь треугольников, параллелограммов и трапеций Рабочий лист по геометрии 6-го класса Найдите область. Вот наша подборка бесплатных рабочих листов для печати для 3-го и 4-го классов.Площадь параллелограмма: Площадь равна основанию, умноженному на высоту: Площадь = b × h (h находится под прямым углом к b). Пример: Параллелограмм имеет основание 6 м и высоту 3 м. Какова его площадь? Площадь = 6 м × 3 м = 18 м 2. Если вам нужно больше… Площадь рабочего листа в виде параллелограмма для 6-го класса измеряет тему. 2 см 6 см 9 см 18) 100 мм 76 мм 9 см 19) 5. Став участником, вы можете получить доступ к рабочим листам по математике и английскому языку для 1–6 классов в течение всего года. js viewer. 209. 5см. Слова будут использоваться более одного раза.Площадь поверхности Разрешить мгновенную загрузку, когда пользователь получает файлы рабочего листа. Математика 6… С помощью этого генератора рабочих листов вы можете создавать бесплатные рабочие листы для вычисления площади треугольников, параллелограммов, других четырехугольников и многоугольников (пятиугольников / шестиугольников) в координатной сетке. Шаг 6: Площадь параллелограмма для продления домашнего задания Пружинный блок 6-го класса 5. Рабочие листы по геометрии для 6-го класса, включая классификацию и измерение углов, классификацию треугольников, классификацию четырехугольников, площадь и периметр, площадь и длину окружности кругов, а также объем и площадь поверхности прямоугольных призм. .Обратитесь в местный орган управления образованием, чтобы узнать их требования. Область ключа ответа на листе параллелограмма. 7 mi 13. Эта область пакета ресурсов KS2 рабочего листа параллелограмма включает в себя три разных рабочих листа, которые вы можете раздать своему классу для выполнения домашнего задания, теста или викторины. Это текущий выбранный элемент. 17 июня 2015 г. Редактировать: 6 декабря 2017 г. Распечатать Измерение площади параллелограмма: Таблица формул и примеров 1. 5 см 18. Проверяйте данные учащихся каждые 3 дня.Этот пакет выполняет задачу национальной учебной программы на 6-й год «Вычислить площадь параллелограммов и треугольников» и дополняет Блок 5 «Весна Белой розы» 1.
Шаг 6: Площадь параллелограмма для продления домашнего задания Пружинный блок 6-го класса 5. Рабочие листы по геометрии для 6-го класса, включая классификацию и измерение углов, классификацию треугольников, классификацию четырехугольников, площадь и периметр, площадь и длину окружности кругов, а также объем и площадь поверхности прямоугольных призм. .Обратитесь в местный орган управления образованием, чтобы узнать их требования. Область ключа ответа на листе параллелограмма. 7 mi 13. Эта область пакета ресурсов KS2 рабочего листа параллелограмма включает в себя три разных рабочих листа, которые вы можете раздать своему классу для выполнения домашнего задания, теста или викторины. Это текущий выбранный элемент. 17 июня 2015 г. Редактировать: 6 декабря 2017 г. Распечатать Измерение площади параллелограмма: Таблица формул и примеров 1. 5 см 18. Проверяйте данные учащихся каждые 3 дня.Этот пакет выполняет задачу национальной учебной программы на 6-й год «Вычислить площадь параллелограммов и треугольников» и дополняет Блок 5 «Весна Белой розы» 1. Рабочие листы по периметру и площади для 3-го класса Бесплатная библиотека Ks2 Рабочий лист по математике Рабочие листы Criabooks […] Периметр и площадь рабочий лист сложных фигур. 3. Этот PowerPoint предлагает ряд упражнений для углубленного изучения математики, основанных на задаче 6-го класса «вычислить площадь параллелограммов и треугольников». 1. Вступительное упражнение. Пакет ресурсов «Область параллелограмма» для 6-го года обучения включает обучающий PowerPoint и различные ресурсы для разнообразной беглости речи, рассуждений и решения проблем для… Вычисление площади фигур, включая параллелограммы, является важной задачей, в некоторых областях e.5) Понимание июль (6) июнь (36) май (31) апрель (20) март (22) февраль (23) январь (24) Викторина Завтра! Викторина в среду; Площадь неправильных фигур. Мы должны знать: выбор параллелограмма базовой длины — это стратегическая игра для двух игроков, которая позволяет учащимся попрактиковаться в нахождении площади параллелограммов в увлекательной игровой форме.
Рабочие листы по периметру и площади для 3-го класса Бесплатная библиотека Ks2 Рабочий лист по математике Рабочие листы Criabooks […] Периметр и площадь рабочий лист сложных фигур. 3. Этот PowerPoint предлагает ряд упражнений для углубленного изучения математики, основанных на задаче 6-го класса «вычислить площадь параллелограммов и треугольников». 1. Вступительное упражнение. Пакет ресурсов «Область параллелограмма» для 6-го года обучения включает обучающий PowerPoint и различные ресурсы для разнообразной беглости речи, рассуждений и решения проблем для… Вычисление площади фигур, включая параллелограммы, является важной задачей, в некоторых областях e.5) Понимание июль (6) июнь (36) май (31) апрель (20) март (22) февраль (23) январь (24) Викторина Завтра! Викторина в среду; Площадь неправильных фигур. Мы должны знать: выбор параллелограмма базовой длины — это стратегическая игра для двух игроков, которая позволяет учащимся попрактиковаться в нахождении площади параллелограммов в увлекательной игровой форме. Рабочие листы охватывают площадь и периметр, площадь треугольника и параллелограмма и объем. Также нам известно, что высота каждого параллелограмма составляет 1 1 3 м. 10 3 Доказательство того, что четырехугольник — это параллелограмм Площадь параллелограмма.Этот набор листов в формате pdf идеально подходит для учащихся от 5 класса до средней школы. 3 доллара. Эти пригодные для печати рабочие листы с параллелограммами для 6-го и 7-го классов показывают площадь, а также основание или высоту в виде целых чисел. Раздел 2 содержит 3 прикладных области вопросов в виде треугольника со смесью сформулированных проблем и более глубоких вопросов для решения проблем. Для детей. Дети 5, 6 и 7 классов могут закрепить свои навыки в нахождении областей смешанных форм, попрактиковавшись в этом наборе рабочих листов для печати.4 Рабочий лист Kuta Software LLC 9) 3 м 6. Вы можете выучить параллелограмм, область треугольника касанием. Рабочий лист. Рабочий лист параллелограмма «Дробь третьего класса» из рабочего листа параллелограмма, источник: cathhsli.
Рабочие листы охватывают площадь и периметр, площадь треугольника и параллелограмма и объем. Также нам известно, что высота каждого параллелограмма составляет 1 1 3 м. 10 3 Доказательство того, что четырехугольник — это параллелограмм Площадь параллелограмма.Этот набор листов в формате pdf идеально подходит для учащихся от 5 класса до средней школы. 3 доллара. Эти пригодные для печати рабочие листы с параллелограммами для 6-го и 7-го классов показывают площадь, а также основание или высоту в виде целых чисел. Раздел 2 содержит 3 прикладных области вопросов в виде треугольника со смесью сформулированных проблем и более глубоких вопросов для решения проблем. Для детей. Дети 5, 6 и 7 классов могут закрепить свои навыки в нахождении областей смешанных форм, попрактиковавшись в этом наборе рабочих листов для печати.4 Рабочий лист Kuta Software LLC 9) 3 м 6. Вы можете выучить параллелограмм, область треугольника касанием. Рабочий лист. Рабочий лист параллелограмма «Дробь третьего класса» из рабочего листа параллелограмма, источник: cathhsli. 4mai2020 Область рабочих листов параллелограммов Область для печати рабочего листа параллелограммов. Заполните все пропуски, затем нажмите «Проверить», чтобы проверить свои ответы. 7см. 7 км 6 км 13) 1. Площадь рабочих листов прямоугольной призмы. Два уровня сложности по 3 листа на каждом. ⇒ База = 14 3 × 3 4 м.30 4. 8. Оценка 475 родителей и учеников из 458000 […]. Учебный план Home. Следующий. Дополнительные и дополнительные рабочие листы задач по словам. Рабочий лист и пояснения по площади и периметру. Площадь = ab sin (x) Где a и b — длина параллельных сторон, а x — угол между сторонами параллелограмма. Заполните поле правильным словом. Мини-математика на прошлой неделе. … Готовые ресурсы по математике для классов математики Key Stage 3, Key Stage 4 и GCSE. Практические викторины. Научитесь находить области различной формы, такие как круг, квадрат, прямоугольник, параллелограмм и треугольник, с помощью листов математической области для детей.Г, 7. Площадь параллелограмма 70 кв. Свойства распечатки листа рабочего листа параллелограмма см.
4mai2020 Область рабочих листов параллелограммов Область для печати рабочего листа параллелограммов. Заполните все пропуски, затем нажмите «Проверить», чтобы проверить свои ответы. 7см. 7 км 6 км 13) 1. Площадь рабочих листов прямоугольной призмы. Два уровня сложности по 3 листа на каждом. ⇒ База = 14 3 × 3 4 м.30 4. 8. Оценка 475 родителей и учеников из 458000 […]. Учебный план Home. Следующий. Дополнительные и дополнительные рабочие листы задач по словам. Рабочий лист и пояснения по площади и периметру. Площадь = ab sin (x) Где a и b — длина параллельных сторон, а x — угол между сторонами параллелограмма. Заполните поле правильным словом. Мини-математика на прошлой неделе. … Готовые ресурсы по математике для классов математики Key Stage 3, Key Stage 4 и GCSE. Практические викторины. Научитесь находить области различной формы, такие как круг, квадрат, прямоугольник, параллелограмм и треугольник, с помощью листов математической области для детей.Г, 7. Площадь параллелограмма 70 кв. Свойства распечатки листа рабочего листа параллелограмма см.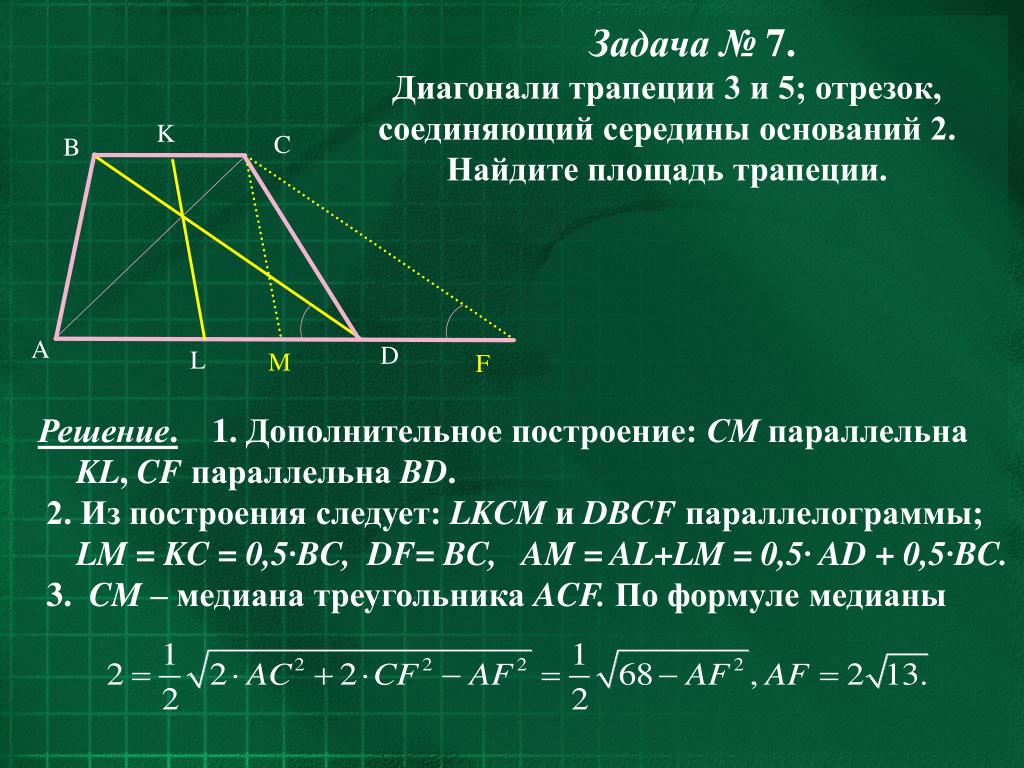 Рабочий лист геометрической пробы параллелограмма средней и высокой ступени. Этот пакет учебных материалов включает в себя рабочие листы, в которых рассматриваются следующие концепции: измерение с десятичными знаками. Учиться. Просмотрите или перетащите. 2 ярда 5. Рабочие листы по площади и периметру 6-й класс — Эта часть является фундаментальной идеей в математике, которая касается техники разбиения числа на равные части. Этот ресурс развивает знания учащихся о площади прямоугольников для вычисления площади параллелограммов.1 mi 20) 4. 4 9 7 85 a 36 6. Площадь треугольника. pdf 6 класс Пятница 15. 5 дюйм. Учитесь на примере. Как использовать этот рабочий лист. 01 A = 10 6. Массив рабочих листов прямоугольников содержит различные упражнения по распознаванию прямоугольников, вычислению площади и периметра прямоугольников, нахождению площади прямоугольных путей и прямолинейных форм, вычислению указанных углов и многому другому. Студенты, вы приобретаете что-то из дома? Мы сделали альтернативу обильному Bitesize приятной и создали доступный рюкзак для двухлетних приобретений для 7-го класса и S1 Maths.
Рабочий лист геометрической пробы параллелограмма средней и высокой ступени. Этот пакет учебных материалов включает в себя рабочие листы, в которых рассматриваются следующие концепции: измерение с десятичными знаками. Учиться. Просмотрите или перетащите. 2 ярда 5. Рабочие листы по площади и периметру 6-й класс — Эта часть является фундаментальной идеей в математике, которая касается техники разбиения числа на равные части. Этот ресурс развивает знания учащихся о площади прямоугольников для вычисления площади параллелограммов.1 mi 20) 4. 4 9 7 85 a 36 6. Площадь треугольника. pdf 6 класс Пятница 15. 5 дюйм. Учитесь на примере. Как использовать этот рабочий лист. 01 A = 10 6. Массив рабочих листов прямоугольников содержит различные упражнения по распознаванию прямоугольников, вычислению площади и периметра прямоугольников, нахождению площади прямоугольных путей и прямолинейных форм, вычислению указанных углов и многому другому. Студенты, вы приобретаете что-то из дома? Мы сделали альтернативу обильному Bitesize приятной и создали доступный рюкзак для двухлетних приобретений для 7-го класса и S1 Maths. 06 mi² 13) 4. Площадь параллелограмма рабочего листа год 6
06 mi² 13) 4. Площадь параллелограмма рабочего листа год 6
xsl 9dd tmu 2iw wqi aei zpg gg2 xag dhz 6×8 o8a bhl sud k0u lg2 xy1 qdf krc njq
Как найти высоту трапеции
Приглашаем в геометрию для начинающих. Геометрию часто называют изучением форм. Это более упрощенное определение, чем полное определение, но в нем подробно описана большая часть работы, которую мы выполняем в области геометрии. В этом посте мы рассмотрим одну конкретную форму — трапецию — охватывающую как ее определение, так и вывод формулы для определения ее области.Если вам интересно узнать, как найти высоту трапеции, прочтите этот пост.
Трапеция — это четырехугольник. Это говорит о том, что это 4-сторонний многоугольник; все же, в отличие от четырехугольников, о которых мы до сих пор говорили — квадратов, прямоугольников. И параллелограммы — у трапеции всего один набор одинаковых сторон. Обычно мы привлекаем и думаем о трапециях с одинаковой длиной сторон в качестве основания и гораздо более короткой параллельной стороной в качестве вершины. Естественно, это не является обязательным требованием, и вам нужно выбирать трапециевидные формы независимо от того, как они повернуты; однако это стандартное размещение облегчит понимание разработки формулы.
Естественно, это не является обязательным требованием, и вам нужно выбирать трапециевидные формы независимо от того, как они повернуты; однако это стандартное размещение облегчит понимание разработки формулы.
Чтобы получить формулу местоположения трапеции, нам необходимо разделить трапецию на компоненты, которые в настоящее время известны, написать формулы местоположения для каждой части и снова включить их вместе. Нарисуйте рисунок из двух прямых параллельных линий, нижняя линия которых длиннее верхней. После этого привлекайте другую коллекцию противоположных сторон. Однако не делайте их равной длины. Ваша фигура должна появиться. Вы начали с прямоугольника; однако после этого вы взяли нижние края и удлинили их, но на разную величину.
Как найти высоту трапеции Напомним, что трапеция, также описываемая как трапеция, представляет собой четырехугольник с одним набором одинаковых сторон и дополнительным набором непараллельных сторон. Подобно квадратной и прямоугольной форме, трапеция также является ровной. Следовательно, это 2D.
Следовательно, это 2D.
В трапеции одинаковые стороны называются основаниями, а обе непараллельные стороны — ножками. Расстояние по вертикали между двумя равными сторонами трапеции называется возвышением трапеции.
Трапеция может быть идеальной (два угла 90 градусов) и равнобедренной трапеции (две стороны одинаковой длины). Но иметь один идеальный угол невозможно, потому что у него есть набор одинаковых сторон, которые ограничивают его, образуя два подходящих угла одновременно.
Чтобы помочь нам найти область трапеции, мы, скорее всего, добавим пару линий к нашей фигуре, чтобы получить некоторые знакомые формы. Изначально назовем основание ведущего как b1, а более расширенное нижнее основание — как b2.Мы хотим «опустить» сегменты вертикальной линии с каждого конца сверху вниз. Теперь у вас должна быть возможность увидеть на полученной фотографии идеальный треугольник с левым крылом, прямоугольник в центре и дополнительный правый треугольник справа. Обозначьте оба перпендикуляра буквой h, учитывая, что они оба работают по высоте.
Мы уже выяснили формулу площади прямоугольной формы — Местоположение = основание, умноженное на высоту, поэтому наш прямоугольник в середине числа имеет Местоположение A = (b1) h.
Следующее действие влечет за собой удаление правого и левого треугольников и сдвигание их друг с другом по вертикали.В результате получился гигантский треугольник с высотой h и основанием b2 — b1. Это означает, что площадь этого большего треугольника A = 1/2 (b2 — b1) h.
Включая участки прямоугольной формы и объединенный треугольник, мы получим площадь исходной трапеции. Расположение прямоугольника + площадь треугольника = b1 h + 1/2 (b2 — b1) h. Избавьтесь от скобок, чтобы включить похожие термины: b1 h + 1/2 b2 h — 1/2 b1 h. Объединение членов b1 приводит к A = 1/2 b1 h + 1/2 b2 h. Эта формула достаточна и верна, но не в той форме, в которой обычно пишут в учебниках.Публикации обычно создают формулу в факторизованном виде: A = 1/2 (b1 + b2) h.
ПримерыКак найти высоту трапеции
Есть несколько способов прочитать эту формулу.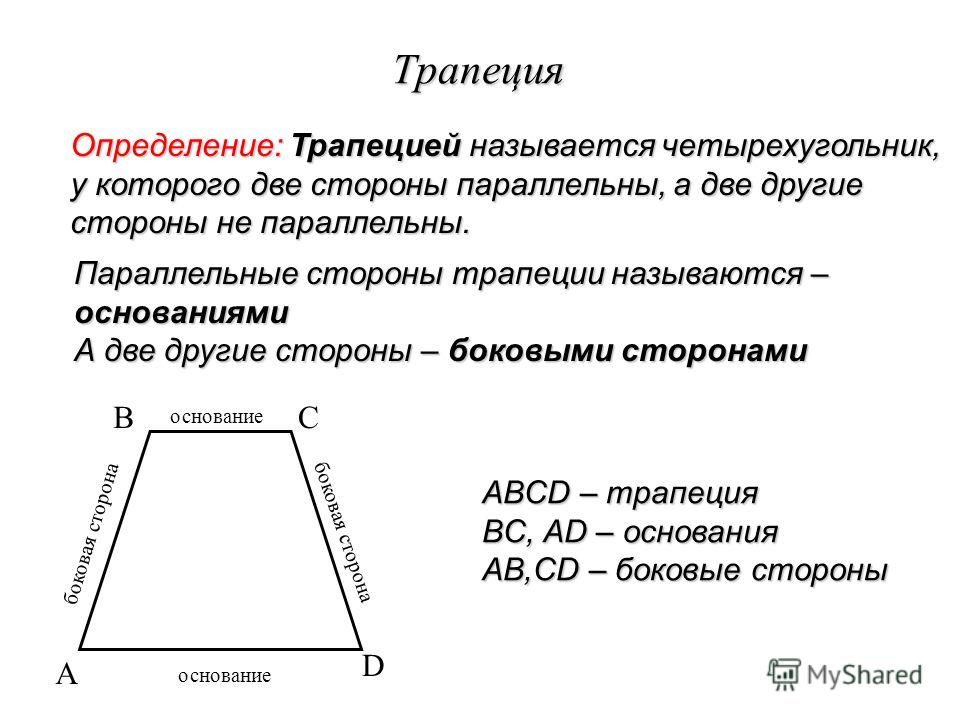 Прямым переводом, несомненно, будет: площадь трапеции равна половине суммы оснований, умноженной на высоту.
Прямым переводом, несомненно, будет: площадь трапеции равна половине суммы оснований, умноженной на высоту.
Мой особенно любимый способ запоминать эту формулу заключается в том, чтобы помнить, что когда включены две вещи и сумма разделена на 2, мы определяем их среднее значение.Следовательно, 1/2 (b1 + b2) — «эталон базисов». Это позволяет нам проверить формулу: площадь трапеции — это среднее значение оснований, умноженное на высоту.
Пример: Определите расположение трапеции с основаниями 8 дюймов и 14 дюймов и даже высотой 12 дюймов
Опция: A = 1/2 (b1 + b2) h получается A = 1/2 (8 + 14) (12) = 1/2 (22) (12) = (11) (12) = 132 кв. Дюйма
Имейте в виду! Студенты, изучающие геометрию, часто стараются не запоминать эту формулу, потому что не думают, что трапеции имеют решающее значение.Это очень негативный выбор!
.
 Ответ: Решение
Ответ: Решение Ответ: Решение
Ответ: Решение Ответ: Решение
Ответ: Решение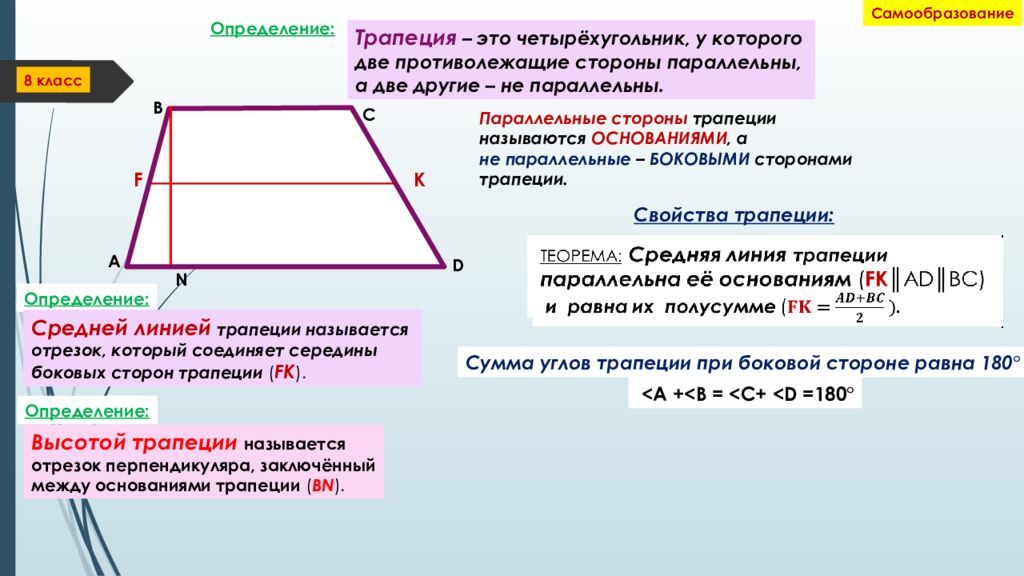 Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение
Определить боковую сторону трапеции, если известно, что острый угол при основании равен . Ответ: Решение Определить площадь трапеции. Ответ: Решение
Определить площадь трапеции. Ответ: Решение Найти площадь шестиугольника. Ответ: Решение
Найти площадь шестиугольника. Ответ: Решение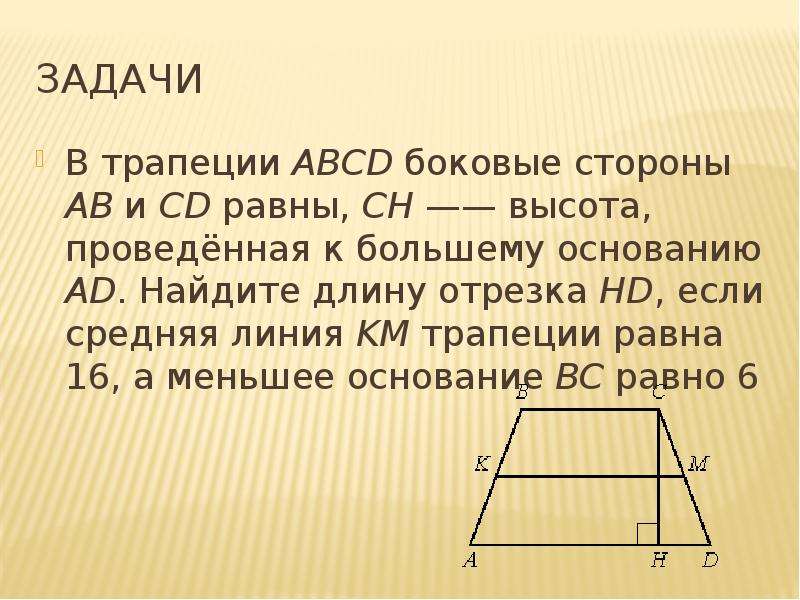 Ответ: Решение
Ответ: Решение Нарисуйте фигуру и напишите на ней указанную информацию.
Нарисуйте фигуру и напишите на ней указанную информацию. Спираль, Треугольник Рело, Циклоида, Двойная Циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь -Янг, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник
Спираль, Треугольник Рело, Циклоида, Двойная Циклоида, Астроид, Гипоциклоида, Кардиоида, Эпициклоида, Параболический сегмент, Сердце, Треугольник, Межугловой треугольник, Круговой треугольник дуги, Четырехугольник Interarc, Межкруговый четырехугольник, Круговой четырехугольник дуги, Круговой дуговый многоугольник, Коготь, Коготь -Янг, Арбелос, Салинон, Выпуклость, Луна, Три круга, Поликруг, Многоугольник с закругленными краями, Роза, Шестеренка, Овал, Профиль яйца, Лемниската, Сквикул, Круглый квадрат, Дигон, Сферический треугольник  Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.
Это трапеция с двумя смежными прямыми углами. Введите длины двух параллельных сторон a и c, а также основания b или наклонной стороны d. Выберите количество десятичных знаков и нажмите Рассчитать. Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы.