Центр шара определение. Чем шар отличается от сферы

Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.

Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Сфера и шар: в чем разница и в чем сходство?

Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера — это бесконечно тонкий слой, шар же — это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера — это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.

Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:

• обе они обладают одинаковой симметрией;
• для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
• обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.

Сфера и шар равного радиуса приведены на рисунке ниже.

Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).

Элементы сферы

Так называются геометрические величины,

medicroslavl.ru

Сфера геометрическая фигура. Чем шар отличается от сферы

Сфера и шар

Слово «сфера» произошло от греческого слова «сфайра», которое переводится на русский язык как «мяч».

ШАР-символ будущего.

Символ шара-глобальность шара Земли. Символ будущего, он отличается от креста тем, что последний олицетворяет собой страдание и человеческую смерть. В Древнем Египте впервые пришли к заключению, что земля шарообразна. Это предположение послужило основой для многочисленных размышлений о бессмертии земли и возможности бессмертия населяющих ее живых организмах.

Человек, держащий шар в руках, символизирует субъекта, несущего тяготы мира Не случайно подобными скульптурами украшены некоторые вокзалы Западной Европы, например в Хельсинки: здесь запечатлены тяготы, выпадающие на плечи путешественника.

Таким образом, шар и глобус — это знаки промысла, проведения, вечности, власти и могущество коронованных особ

Каменное полушарие сферы воплощается в религиозных храмах — куполах православных церквей в России; ступах, связанных с местом пребывания бодхисаттв в Индии. В Индонезии ступы приобрели форму колокола с каменным шпилем наверху и называются дагобы.

В греко-римской мифологии шар символизировал удачу, судьбу, ассоциируясь с Тихэ (Фортуной), стоящей на шаре. Знаменитая картина Пикассо «Девочка на шаре» — танцующая Фортуна.

Форма шара в природе Многие ягоды имеют форму шара.

Планеты имеют форму шара.

Некоторые деревья имеют сферическую форму.

Определение сферы Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки

Сфера –это поверхность, полученная вращением полуокружности вокруг диаметра

Данная точка (О) называется центром сферы. Любой отрезок, соединяющий центр и какую-нибудь точку сферы, называется радиусом сферы (R-радиус сферы). Отрезок, соединяющий две точки сферы и проходящий через её центр, называется диаметром сферы. Очевидно, что диаметр сферы равен 2R.

Определение шара Шар – это тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки (или фигура, ограниченная сферой). Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

Шаровой сегмент Шаровым сегментом называется часть шара, отсекаемая от него какой — нибудь плоскостью.

Шаровой слой Шаровым слоем называется часть шара, заключенная между двумя параллельными секущими плоскостями.

Шаровой сектор Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 900, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.

Плоскость,проходящая через центр шара,называется диаметральной плоскостью. Сечение шара диаметральной плоскостью называется большим кругом,а сечение сферы — большой окружностью. Сечение шара

Закрепляем Решите задачу № 573, №574 (а)

Уравнение сферы в прямоугольной системе координат M(x;y;z)-произвольная точка, принадлежащая сфере. /MC/= v(x-x0)2+(y-y0)2+(z-z0)2 т.к. MC=R, то (x-x0)2+(y-y0)2+(z-z0)2=R2

Задание 1.Найдите координаты центра и радиуса сферы, заданной уравнением: x?+y?+z?=49 (X-3)?+(y+2)?+z?=2 2. Напишите уравнение сферы радиуса R с центром А, если A(2;-4;7) R=3 A(0;0;0) R=v2 A(2;0;0) R=4 3. Решите задачу №577(а)

Взаимное расположение сферы и плоскости Обозначим радиус сферы буквой R, а расстояние от ее центра до плоскости?-буквой d. Введем систему координат так, чтобы плоскость Oxy совпадала с плоскостью?, а центр С сферы лежал на положительной полуоси Oz.

В этой системе координат точка C (о;о;d), поэтому сфера имеет уравнение x2+y2+(z-d)2=R? Плоскость совпадает с координатной плоскостью Oxy, и поэтому ее уравнение имеет вид z=0

Таким образом вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений. Подставив z=0 во второе уравнение, получим x?+y?=R?-d? Возможны 3 случая:

x?+y?=R?-

uformat.ru

Сфера и шар самое основное. Чем шар отличается от сферы

Шар и сфера — это прежде всего геометрические фигуры, и если шар — это геометрическое тело, то сфера — это поверхность шара. Этими фигурами интересовались еще многие тысячи лет назад до н.э.

Впоследствии когда было открыто, что Земля — это шар, а небо — небесная сфера, получило развитие новое увлекательное направление в геометрии — геометрия на сфере или сферическая геометрия. Для того, чтобы рассуждать о размере и объеме шара, нужно сначала дать ему определение.

Шар

Шаром радиуса R с центром в точке О в геометрии называют тело, которое создано всеми точками пространство, имеющими общее свойство. Эти точки находятся на расстоянии, не превышающем радиуса шара, то есть заполняют все пространство меньше радиуса шара во все стороны от его центра. Если мы рассмотрим только те точки, которые равноудалены от центра шара — мы будем рассматривать его поверхность или оболочку шара.

Как можно получить шар? Мы можем вырезать из бумаги круг и начать его вращать вокруг его же диаметра. То есть диаметр круга будет осью вращения. Образованная фигура — будет шар. Поэтому шар называют также телом вращения. Потому что он может быть образован путем вращения плоской фигуры — круга.

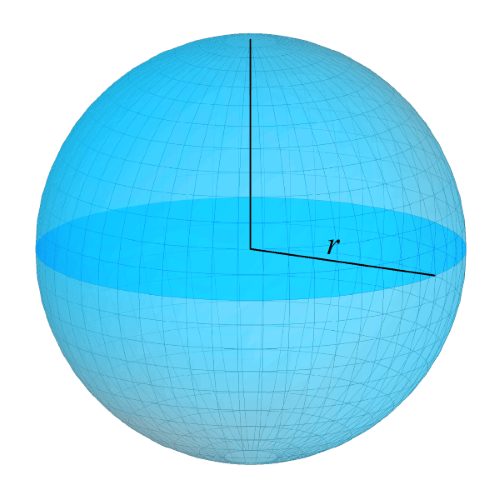Возьмем какую-нибудь плоскость и разрежем ею наш шар. Подобно тому как мы режем ножом апельсин. Кусок, который мы отсечем от шара, называется шаровым сегментом.

В Древней Греции умели не только работать с шаром и сферой, как с геометрическими фигурами, например, использовать их при строительстве, а также умели расчитывать площадь поверхности шара и объем шара.

Сферой иначе называется поверхность шара. Сфера — это не тело — это поверхность тела вращения. Однако так как и Земля и многие тела имеют сферическую форму, например капля воды, то изучение геометрических соотношений внутри сферы получило большое распространение.

Например, если мы соединим две точки сферы между собой прямой линией, то эта прямая линия назовется хордой, а если эта хорда пройдет через центр сферы, который совпадает с центром шара, то хорда назовется диаметром сферы.

Если мы проведем прямую линию, которая коснется сферы всего в одной точке, то эта линия будет называться касательной. Кроме того, эта касательная к сфере в этой точке будет перпендикулярна к радиусу сферы, проведенному в точку касания.

Если мы продолжим хорду до прямой в одну и другую сторону от сферы, то эта хорда станет называться секущей. Или можно сказать иначе — секущая к сфере содержит в себе ее хорду.

Объем шара

Формула для вычисления объема шара имеет вид:

где R — радиус шара.

Если нужно найти объем шарового сегмента — воспользуйтесь формулой:

V сег =πh 2 (R-h/3), h — высота шарового сегмента.

Площадь поверхности шара или сферы

Чтобы вычислить площадь сферы или площадь поверхности шара (это одно и то же):

где R — радиус сферы.

Архимед очень любил шар и сферу, он даже попросил оставить на его гробницу рисунок, на котором в цилин

www.vera-autoservice.ru

Шар и сфера, объем шара, площадь сферы, формулы. Чем шар отличается от сферы

Сфера — это одно из первых тел, обладающих высокой симметрией, свойства которого изучают в школьном курсе геометрии. В данной статье рассматривается формула сферы, ее отличие от шара, а также приводится расчет площади поверхности нашей планеты.

Сфера: понятие в геометрии

Чтобы лучше понять формулу поверхности, которая будет дана ниже, необходимо познакомиться с понятием сферы. В геометрии она представляет собой трехмерное тело, которое заключает в себе некоторый объем пространства. Математическое определение сферы следующее: это совокупность точек, которые лежат на определенном одинаковом расстоянии от одной фиксированной точки, называемой центром. Отмеченное расстояние — это радиус сферы, который обозначается r или R и измеряется в метрах (километрах, сантиметрах и других единицах длины).

На рисунке ниже приведена описанная фигура. Линии показывают контуры ее поверхности. Черная точка — центр сферы.

Получить эту фигуру можно, если взять окружность и начать ее вращать вокруг любой из осей, проходящей через диаметр.

Сфера и шар: в чем разница и в чем сходство?

Часто школьники путают эти две фигуры, которые внешне похожи друг на друга, но обладают совершенно разными физическими свойствами. Сфера и шар в первую очередь отличаются своей массой: сфера — это бесконечно тонкий слой, шар же — это объемное тело конечной плотности, которая одинакова во всех его точках, ограниченных сферической поверхностью. То есть шар обладает конечной массой и является вполне реальным объектом. Сфера — это фигура идеальная, не имеющая массы, которая в действительности не существует, но она является удачной идеализацией в геометрии при изучении ее свойств.

Примерами реальных объектов, форма которых практически соответствует сфере, являются новогодняя игрушка в виде шарика для украшения елки или мыльный пузырь.

Что касается сходства между рассматриваемыми фигурами, то можно назвать следующие их признаки:

• обе они обладают одинаковой симметрией;
• для обеих формула площади поверхности является одинаковой, более того, они обладают равной площадью поверхности, если их радиусы равны;
• обе фигуры при равных радиусах занимают одинаковый объем в пространстве, только шар его заполняет полностью, а сфера лишь ограничивает своей поверхностью.

Сфера и шар равного радиуса приведены на рисунке ниже.

Заметим, что шар, так же как и сфера, является телом вращения, поэтому его можно получить, если вращать вокруг диаметра круг (не окружность!).

Элементы сферы

Так называются геометрические величины, знание которых позволяет описать либо всю фигуру, либо отдельные ее части. Основными ее элементами являются следующие:

• Радиус r, который уже был упомянут ранее. Он является расстоянием от центра фигуры до сферической поверхности. По сути, это единственная величина, которая описывает все свойства сферы.
• Диаметр d, или D. Это отрезок, концы которого лежат на сферической поверхности, а середина проходит через центральную точку фигуры. Диаметр сферы можно провести бесконечным числом способов, но все полученные отрезки будут иметь одинаковую длину, которая равна удвоенному радиусу, то есть D = 2*R.
• Площадь поверхности S — двумерная характеристика, формула для которой будет приведена ниже.
• Связанные со сферой трехмерные углы измеряются в стерадианах. Один стерадиан — это угол, вершина которого лежит в центре сферы, и который опирается на часть сферической поверхности, имеющей площадь R 2 .

Геометрические свойства сферы

Из приведенного описания этой фигуры можно самостоятельно догадаться об этих свойствах. Они следующие:

• Любая прямая, которая пересекает сферу и проходит через ее центр, является осью симметрии фигуры. Поворот сферы вокруг этой оси на любой угол переводит ее в саму себя.
• Плоскость, которая пересекает рассматриваемую фигуру через ее центр, делит сферу на две равные части, то есть является плоскостью отражения.

Площадь поверхности фигуры

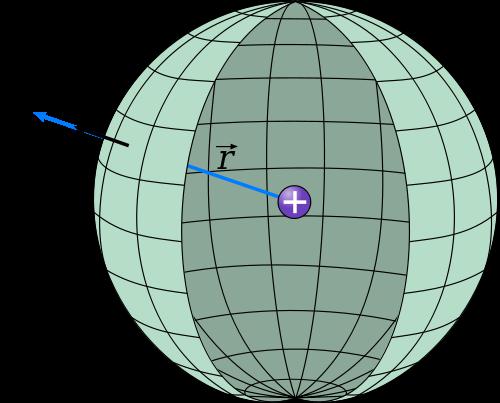
Эта величина обозначается латинской буквой S. Формула вычисления площади сферы имеет следующий вид:

S = 4*pi*R 2 , где pi ≈ 3,1416.

Формула демонстрирует, что площадь S может быть вычислена при условии знания радиуса фигуры. Если же известен ее диаметр D, тогда формулу сферы можно записать так:

Иррациональное число pi, для которого приведены четыре знака после запятой, в ряде математических расчетов можно использовать с точностью до сотых, то есть 3,14.

Любопытно также рассмотреть вопрос, скольким стерадианам соответствует вся поверхность рассматриваемой фигуры. Исходя из определения этой величины, получаем:

Ω = S/R 2 = 4*pi*R 2 /R 2 = 4*pi стерадиан.

Для вычисления любого объемного угла следует в выражение выше подставить соответствующее значение площади S.

Поверхность планеты Земля

Формулу сферы можно применить для определения на которой мы живем. Перед тем как приступать к вычислениям, следует сделать пару оговорок:

• Во-первых, Земля не обладает идеальной сферической поверхностью. Ее экваториальный и полярный радиусы равны 6378 км и 6357 км соответственно.

bestzagar.ru

Шарообразный шар. Разница между шаром и сферой

Когда людям задают вопрос, чем отличается сфер от шара, многие попросту пожимают плечами, думая, что фактически это одно и то же (аналогия с кругом и окружностью). Действительно, все ли из нас хорошо знают из школьной программы геометрию и могут сходу ответить на данный вопрос? Сфера имеет некоторые отличия от шара, которые нужно знать не только школьникам, чтобы получить хорошую оценку за свои продемонстрированные знания, но и многим другим людям, например, чья работа непосредственно связана с чертежами.

Определение

Шар – совокупность всех точек пространства. Все эти точки находятся от центра геометрического тела на расстоянии, которое не больше заданного. Само данное расстояние называется радиусом. Шар, как геометрическое тело, образуется следующим образом: происходит вращение полукруга возле его диаметра. Что касается сферы, то это и есть поверхность шара (например, замкнутый шар включает ее, открытый – нет). Вычисление площади или объема шара – это целые геометрические формулы, которые очень сложны, несмотря на кажущуюся простоту самой геометрической фигуры.

Сфера , как было отмечено выше, представляет собой поверхность шара, его оболочку. От центра сферы все точки в пространстве равноудалены. Что касается радиуса геометрического тела, то им называют любой отрезок, одна точка которого – непосредственно центр сферы, а другая может находиться в любой точке на поверхности. Можно сказать, что сфера является оболочкой шара без какого-либо содержимого (более конкретные примеры будут приведены ниже). Также как и шар, сфера является телом вращения. Кстати, многие также задаются вопросом, чем же отличаются круг и окружность от сферы и шара. Здесь все просто: в первом случае это фигуры на плоскости, во втором – в пространстве.

Сравнение

Уже было сказано о том, что сфера является поверхностью шара, что уже дает возможность говорить об одном весомом признаке отличия. Разница между двумя геометрическими телами наблюдается и в некоторых других аспектах:

• Все точки шара находятся на одинаковом расстоянии от центра, при этом тело ограничено поверхностью (сферой, которая является пустой внутри). Иными словами, сфера полая. Обычно для простоты понимания приводят простой пример с воздушным и бильярдным шаром. Оба этих предмета называют шарами, однако в первом случае мы имеем дело со сферой, а во втором с полноценным шаром со своим содержимым внутри.
• Сфера имеет свою площадь, но при этом у нее нет объема. Шар же наоборот: его объем можно вычислить, в то время как у него нет площади. Кто-то может сказать, что это главный признак отличия, но он проявляется только в том случае, если необходимо производить какие-то расчеты (сложные геометрические формулы). Поэтому главным отличием является то, что сфера полая, а шар – тело с содержимым внутри.
• Еще одно отличие кроется в радиусе. Например, радиусом сферы называется не только расстояние точек до центра. Радиусом может называться любой отрезок, соединяющий точку на сфере с ее центром. Все эти отрезки равны между собой. Что касается шара, то лежащие внутри него точки удалены от центра меньше, чем на радиус (как раз из-за ограничивающей его сферы).

Выводы сайт

1. Сфера полая, в то время как шар является заполненным внутри телом. Например, воздушный шар – это сфера, бильярдный шар – это полноценный шар.
2. Сфера имеет площадь и не имеет объем, шар же наоборот.
3. Третье отличие – это измерение радиуса двух геометрических тел.

В главе 2 мы продолжим “строительную геометрию» и расскажем о строении и свойствах важнейших пространственных фигур — шара и сферы, цилиндров и конусов, призм и пирамид. Большинство предметов, созданных руками человека, — здания, машины, мебель, посуда и т.д., и т.п., состоит из частей, имеющих форму этих фигур.

§ 4. СФЕРА И ШАР

После прямых и плоскостей сфера и шар — самые простые, но очень важные и богатые разнообразными свойствами пространственные фигуры. О геометрических свойствах шара и его поверхности — сферы — написаны целые книги. Некоторые из этих свойств были известны еще древнегреческим геометрам, а некоторые найдены совсем недавно, в последние годы. Эти свойства (вместе с законами естествознания) объясняют, почему, например, форму шара имеют небесные тела и икринки рыб, почему в форме шара делают батискафы и футбольные мячи, почему так распространены в технике шарикоподшипники и т.д. Мы можем доказать лишь самые простые свойства шара. Доказательства других, хотя и очень важных свойств, часто требуют применения совсем не элементарных методов, хотя формулировки таких свойств могут быть очень простыми: например, среди всех тел, имеющих данную площадь поверхности, наибольший объем у шара.

4.1. Определения сферы и шара.

Определяются сфера и шар в пространстве совершенно так же, как окружность и круг на плоскости. Сферой называется фигура, состоящая из всех точек пространства, удаленных от данной

ной точки на одно и то же (положительное) расстояние.

Эта точка называется центром сферы, а расстояние — ее радиусом (рис. 4.1).

Итак, сфера с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Шаром называется фигура, образованная всеми точками пространства, находящимися на расстоянии не большем данного (положительного) расстояния от данной точки. Эта точка называется центром шара, а данное расстояние — его радиусом.

Итак, шар с центром О и радиусом R — это фигура, образованная всеми точками X пространства, для которых

Те точки X шара с центром О и радиусом R, для которых образуют сферу. Говорят, что эта сфера ограничивает данный шар или что она является его поверхностью.

Шар – это тело, состоящее из всех точек пространства, которые находятся на расстоянии, не большем данного от данной точки. Эта точка называется центром шара, а данное расстояние – радиусом шара. Граница шара называется шаровой поверхностью или сферой. Точками сферы являются все точки шара, которые удалены от центра на расстояние, равное радиусу. Любой отрезок, который соединяет центр шара с точкой шаровой поверхности, тоже называется радиусом. Проходящий через центр шара отрезок, который соединяет две точки шаровой поверхности, называется диаметром. Концы любого диаметра называются диаметрально противоположными точками шара.

Шар является телом вращения, так же как конус и цилиндр. Шар получается при вращении полукруга вокруг его диаметра как оси.

Площадь поверхности шара можно найти по формулам:

где r – радиус шара, d – диаметр шара.

Объём шара находится по формуле:

V = 4 / 3 πr 3 ,

где r – радиус шара.

Теорема. Всякое сечение шара плоскостью есть круг. Центр этого круга есть основание перпендикуляра, опущенного из центра шара на секущую плоскость.

Исходя из данной теоремы, если шар с центром O и радиусом R пересечён плоскостью α, то в сечении получается круг радиуса r с центром K. Радиус сечения шара плоскостью можно найти по формуле

Из формулы видно, что плоскости, равноудалённые от центра, пересекают шар по равным кругам. Радиус сечения тем больше, чем ближе секущая плоскости к центру шара, то есть чем меньше расстояние ОК. Наибольший радиус имеет сечение плоскостью, проходящей через центр шара. Радиус этого круга равен радиусу шара.

Плоскость, проходящая через центр шара, называется диаметральной плоскостью. Сечение шар

hentaixxx.ru

Сфера, шар, сегмент и сектор. Формулы и свойства

Определение.

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Сферу можно описать, как объёмную фигуру, которая образуется вращением окружности вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

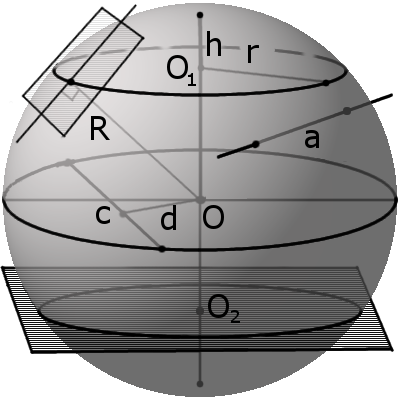
Определение.

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

Шар можно описать как объёмную фигуру, которая образуется вращением круга вокруг своего диаметра на 180° или полуокружности вокруг своего диаметра на 360°.

Определение. Радиус сферы (шара) (R) — это расстояние от центра сферы (шара) O к любой точке сферы (поверхности шара).

Определение. Диаметр сферы (шара) (D) — это отрезок, соединяющий две точки сферы (поверхности шара) и проходящий через ее центр.

Формула. Объём шара: Формула. Площадь поверхности сферы через радиус или диаметр:

S = 4πR² = πD²

Уравнение сферы

1. Уравнение сферы с радиусом R и центром в начале декартовой системе координат:

x² + y² + z² = R²

2. Уравнение сферы с радиусом R и центром в точке с координатами (x₀, y₀, z₀) в декартовой системе координат:

(x — x₀)² + (y — y₀)² + (z — z₀)² = R²

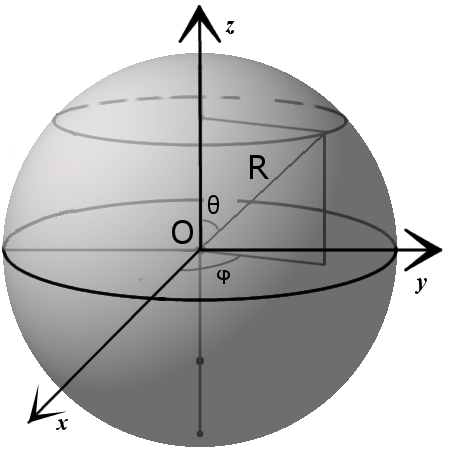3. Параметрическое уравнение сферы с центром в точке (x₀, y₀, z₀):
x = x₀ + R · sin θ · cos φy = y₀ + R · sin θ · sin φz = z₀ + R · cos θ
где θ ϵ [0,π], φ ϵ [0,2π].

Определение. Диаметрально противоположными точками называются любые две точки на поверхности шара (сфере), которые соединены диаметром.

Основные свойства сферы и шара

1. Все точки сферы одинаково удалены от центра.

2. Любое сечение сферы плоскостью является окружностью.

3. Любое сечение шара плоскостью есть кругом.

4. Сфера имеет наибольший объём среди всех пространственных фигур с одинаковой площадью поверхности.

5. Через любые две диаметрально противоположные точки можно провести множество больших окружностей для сферы или кругов для шара.

6. Через любые две точки, кроме диаметрально противоположных точек, можно провести только одну большую окружность для сферы или большой круг для шара.

7. Любые два больших круга одного шара пересекаются по прямой, проходящей через центр шара, а окружности пересекаются в двух диаметрально противоположных точках.

8. Если расстояние между центрами любых двух шаров меньше суммы их радиусов и больше модуля разности их радиусов, то такие шары пересекаются, а в плоскости пересечения образуется круг.

Секущая, хорда, секущая плоскость сферы и их свойства

Определение. Секущая сферы — это прямая, которая пересекает сферу в двух точках. Точки пересечения называются точками протыкания поверхности или точками входа и выхода на поверхности.

Определение. Хорда сферы (шара) — это отрезок, соединяющий две точки сферы (поверхности шара).

Определение. Секущая плоскость — это плоскость, которая пересекает сферу.

Определение. Диаметральная плоскость — это секущая плоскость, проходящая через центр сферы или шара, сеченме образует соответственно большую окружность и большой круг. Большая окружность и большой круг имеют центр, который совпадают с центром сферы (шара).

Любая хорда, проходящая через центр сферы (шара) является диаметром.

Хорда является отрезком секущей прямой.

Расстояние d от центра сферы до секущей всегда меньше чем радиус сферы:

d < R

Расстояние m между секущей плоскостью и центром сферы всегда меньше радиуса R:

m < R

Местом сечения секущей плоскости на сфере всегда будет малая окружность, а на шаре местом сечения будет малый круг. Малая окружность и малый круг имеют свои центры, не совпадающих с центром сферы (шара). Радиус r такого круга можно найти по формуле:

r = √R² — m²,

где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.

Определение. Полусфера (полушар) — это половина сферы (шара), которая образуется при ее сечении диаметральной плоскостью.

Касательная, касательная плоскость к сфере и их свойства

Определение.Касательная к сфере — это прямая, которая касается сферы только в одной точке.

Определение.Касательная плоскость к сфере — это плоскость, которая соприкасается со сферой только в одной точке.

Касательная пряма (плоскость) всегда перпендикулярна радиусу сферы проведенному к точке соприкосновения

Расстояние от центра сферы до касательной прямой (плоскости) равно радиусу сферы.

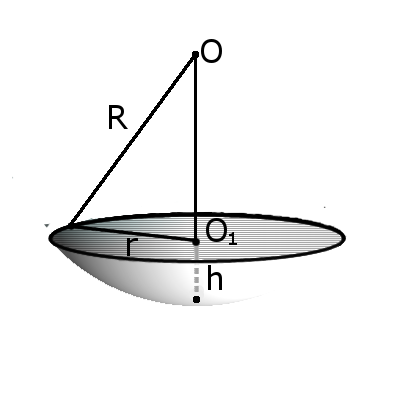Определение. Сегмент шара — это часть шара, которая отсекается от шара секущей плоскостью. Основой сегмента называют круг, который образовался в месте сечения. Высотой сегмента h называют длину перпендикуляра проведенного с середины основы сегмента к поверхности сегмента. Формула. Площадь внешней поверхности сегмента сферы с высотой h через радиус сферы R:

S = 2πRh

Формула. Объём сегмента сферы с высотой h через радиус сферы R: Определение. Срез шара — это часть шара, которая образуется в результате его сечения двумя параллельными плоскостями и находится между ними. 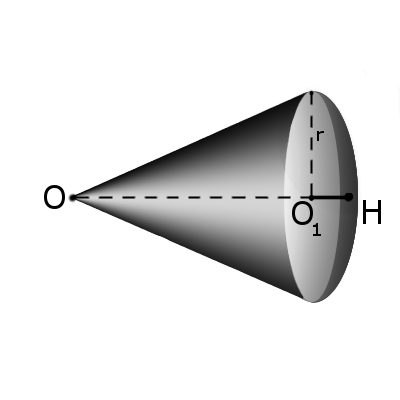Определение. Сектором называется часть шара, ограниченная совокупностью всех лучей, исходящих из центра шара О и образующих круг на его поверхности с радиусом r. Формула. Площадь поверхности сектора S с высотой O₁H (h) через радиус шара OH (R):

S = πR(2h + √2hR — h²)

Формула. Объём сектора V с высотой O₁H (h) через радиус шара OH (R):

Определение. Касательными сферами (шарами) называются любые две сферы (шара), которые имеют одну общую точку соприкосновения. Если расстояние между центрами больше суммы радиусов, то фигуры не касаются и не пересекаются.

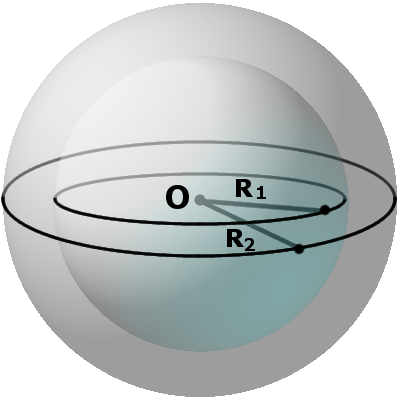Определение. Концентрическими сферами называются любые две сферы, которые имеют общий центр и радиусы различной длины.

ru.onlinemschool.com

Круг и сфера 2019

Земля, на которой мы живем, может напоминать нам о круге, хотя и не совсем идеальном, и его «область, на которой находится человеческая популяция, в этом случае может быть отождествлена ​​с сферой. Поэтому геометрия кругов и сфер имеет широкое применение во всех областях науки, начиная, например, в географии, геологии и геодезии. Сферические формы действительно можно найти в разных местах природы, и из-за человеческого любопытства необходимо их описание.

Что такое Круг?

Круговая линия представляет собой набор точек в плоскости с тем свойством, что все точки этой линии находятся на равном расстоянии r неподвижной точки этой плоскости, называемой центром круговой линии. Каждая линия, соединяющая центр с некоторой точкой круговой линии, называется радиусом, а число г — длиной радиуса этой круговой линии. В литературе термин круг, вероятно, чаще всего используется. Круг является частным случаем эллипса. Эллипс можно определить как геометрическую фигуру точек в плоскости с постоянной суммой расстояний между двумя неподвижными точками. В случае круга эти две точки (центр и фокус) одинаковы. Известно, что каждый круг имеет уникальный набор из трех точек, которые не лежат в одном направлении. Эти точки определяют ребра треугольника, а центр описанной окружности этого треугольника находится в поперечном сечении линий биссекции. Расстояние от центра до любой из трех заданных точек — это радиус круга. Другой способ определить круг через три точки состоит в том, чтобы написать уравнение общей формы круга в канонической (стандартной) форме или в виде точки, чтобы включить координаты данных точек и решить систему. Площадь данного круга с радиусом r равна πr².

Что такое Сфера?

Пространство можно рассматривать как множество точек, называемых элементами пространства. Шарик — это геометрическое тело, которое является подмножеством пространства. Это множество точек плоскости, которые находятся на определенном расстоянии (длине) от неподвижной точки О. Точка O является центром сферы, а длина, соединяющая центр с самой дальней точкой сферы, называется радиус. Диаметр — это линия, соединяющая две самые отдаленные граничные точки (самую длинную прямую линию) сферы и проходящую через ее центр. Круг, образованный пересечением сферы и плоскости, проходящей через центр сферы, называется большим кругом сферы. Все остальные окружности, образованные пересечением плоскости и сферы, называются малыми кругами сферы. Через каждый набор из трех точек сферы есть только один круг, который принадлежит ей.

• Площадь сферы равна 4πr²;
• Объем сферы составляет 4 / 3πr³;

Разница между кругом и сферой

Круг — замкнутая изогнутая линия. Каждая точка на этой криволинейной линии находится на том же расстоянии от фокальной точки (в центре) круга. Локус точки, которая находится на фиксированной длине от другой точки, называется кругом. Фиксированная точка — это центр круга, а длина между этими двумя точками — его радиус. Аналогично

ru.esdifferent.com