Конспект урока по физике на тему :»ПРИМЕНЕНИЕ ЗАКОНА АРХИМЕДА»
Данная разработка может быть использована при проведении итогового урока по теме «Закон Архимеда».
Урок физики в 7 классе по теме: «Применение закона Архимеда»
Учитель: Кудрявцева Наталья Анатольевна
МБОУ «ООШ № 26»
Цели урока:
-образовательные: повторение и закрепление закона Архимеда, формулы для архимедовой силы, условия плавания тел; знакомство с применением закона Архимеда для создания надводных и подводных средств передвижения и при расчете грузоподъемности плавсредств, значения закона Архимеда и возможности использования его в повседневной жизни;
-развивающие: развитие умения увидеть в явлениях окружающего мира действие законов природы; развитие способности на основе полученных знаний делать предсказания и объяснять происходящие явления; развитие способности анализировать, делать выводы, логично рассуждать; развитие воображения, умения делать необходимые расчеты; развитие экспериментальных навыков;
-воспитательные: убеждение учащихся в познаваемости окружающего мира; формирование интереса к познанию законов природы и их применению; создание позитивного отношения учащихся к изучаемому разделу.
Оборудование: стальной гвоздь, пластиковая бутылка с водой и плавающей внутри пробиркой, стеклянный стакан объемом 250 мл, прозрачный сосуд (обрезанная пластиковая бутылка) объемом 1000 мл, широкая стеклянная чаша с водой, плакат «Устройство подъемной лодки»; пластилин пластиковая бутылка с водой и плавающей внутри пробкой, пенал от фотопленки с крышкой, измерительный цилиндр (мензурка), разновесы, весы.
Дополнительные материалы: презентация Power Point.
Тип урока: урок систематизации и обобщения знаний.
Ι. Вступление.
Если внимательно присмотреться, можно заметить великое множество событий, происходящих вокруг нас. С некоторыми из них мы сталкиваемся крайне редко. Мало кому удается в жизни видеть такое величественное зрелище, как айсберг, или наблюдать солнечное затмение. С другими явлениями мы встречаемся ежедневно, и в силу их привычности и обыденности едва обращаем на них внимание. Вот зашумел на кухне закипающий чайник, упало с ветки в саду созревшее яблоко.
Люди, познавшие эти законы, могут, конечно, не перехитрить природу, но по-доброму с ней договориться и избежать многих неприятностей. Об одном из таких законов сегодня пойдет речь. Закон этот всем известен, но у него так много проявлений, что, надеюсь, мы сегодня не только повторим известный факты и формулы, но и получим полезную информацию. Речь пойдет о практическом применении закона Архимеда.
Архимед был греком, хотя и жил на острове Сицилия. А греки, как известно, любили море и морские путешествия. Поэтому предлагаю совершить путешествие в мир явлений, связанных с законом Архимеда, с которым можно встретиться в открытом море. Программа нашего путешествия такова. Вначале мы обсудим, как учитывают и применяют закон Архимеда при создании современных средств передвижения по воде, затем проведем небольшое исследование для одного не совсем обычного плавательного средства. В заключение попробуем выявить лучших знатоков закона Архимеда в нашем классе. Давайте считать, что в нашем распоряжении имеется этот корабль, на котором мы отправляемся в плавание. Будем внимательно следить за всем, что встретится на нашем пути.
В заключение попробуем выявить лучших знатоков закона Архимеда в нашем классе. Давайте считать, что в нашем распоряжении имеется этот корабль, на котором мы отправляемся в плавание. Будем внимательно следить за всем, что встретится на нашем пути.
Перенесемся в Сиракузы, ΙΙΙ век до н.э.
Сценка
Закон Архимеда
Жил в Сиракузах мудрец Архимед,
Был другом царя Гиерона.
Какой для царя самый
Важный предмет?
Вы все догадались – корона!
Захотелось Гиерону
Сделать новую корону.
Золота отмерил строго.
Взял не мало и не много,
Сколько нужно, в самый раз.
Ювелиру дал заказ.
Через месяц Гиерону
Ювелир принес корону.
Взял корону Гиерон,
Оглядел со всех сторон.
Чистым золотом сверкает…
Но ведь всякое бывает,
И добавить серебро
Можно к золоту хитро,
А того и хуже – медь
(Если совесть не иметь)…
И царю узнать охота:
Честно ль сделана работа?
Не желал терпеть урон Гиерон.
И позвал он Архимеда…
Началась у них беседа.
Гиерон. Вот корона, Архимед
Золотая или нет?
Архимед. Чистым золотом сверкает…
Гиерон. Но, ты знаешь, все бывает!
И добавить серебро
Можно к золоту хитро.
А того и хуже – медь,
Если совесть не иметь.
Сомневаться стал я что-то.
Честно ль сделана работа?
Можно ль это, ты скажи, определить?
Но корону не царапать, не пилить…
И задумался ученый:
— Что известно? ВЕС короны.
Ну, а как найти ОБЪЕМ?
Думал ночью, думал днем.
И однажды, в ванне моясь,
Погрузился он по пояс.
На пол вылилась вода –
Догадался он тогда,
Как найти ОБЪЕМ короны,
И помчался к Гиерону,
Не обут и не одет…
А народ кричал вослед:
-Что случилось, Архимед?
— Может быть, землетрясенье
Или в городе пожар?
Всполошился весь базар!
Закрывали лавки даже.
Шум и крики, и смятенье!
Он помчался мимо стражи.
— Эврика! Нашел решенье! –
Во дворец примчался он.
— Я придумал, Гиерон!
( Во дворце)
Архимед. Эврика! Раскрыл секрет!
Гиерон. Ты оденься, Аримед!
Вот сандалии, хитон.
А расскажешь все потом!
Архимед. Пусть весы сюда несут
И с водой большой сосуд…
Все доставить Гиерону!..
(Слуги все приносят)
На весы кладем корону,
И теперь такой же ровно
Ищем слиток золотой…
(Находят кусок золота, по весу равный короне.)
Гиерон. Все понятно!
Архимед. Нет, постой!
Мы теперь корону нашу
Опускаем в эту чашу.
Гиерон! Смотри сюда –
В чаше поднялась вода!
Ставлю черточку по краю.
Гиерон. А корону?
Архимед. Вынимаю
В воду золото опустим.
Гиерон. В воду – золото? Допустим…
Архимед. Поднялась опять вода,
Метку ставлю я.
Гиерон. Куда?
Архимед. Ну, конечно же, по краю.
Гиерон. Ничего не понимаю…
Лишь две черточки я вижу.
Эта – выше, это – ниже.
Но какой же вывод главный?
Архимед. Равный вес.
Объем не равный!
Понимаешь, Гиерон,
Я сейчас открыл закон.
Тот закон совсем простой.
Тело вытеснит…
Гиерон. Постой!
Говоришь, объем не равный?
Мастер мой – мошенник явный!
За фальшивую корону
Он ответит по закону!
А ты за разгадку
Получишь дары!
На этом прервалась беседа…
Немало воды утекло с той поры,
Но помнят закон Архимеда!
Два обстоятельства важны в этой легенде.
- Архимед нашел способ измерить объем твердого тела сложной формы.
- Он сопоставил веса различных веществ друг с другом, а не с весом воды, т.е. впервые обратил внимание на свойство физических тел, которое мы называем плотностью, открыл гидростатический способ взвешивания.

ΙΙ. Актуализация знаний обучающихся.
1. Дайте формулировку силы Архимеда.
2. Сформулируйте закон Архимеда.
3. Какая сила, кроме архимедовой, действует на тело, погруженное в жидкость или газ?
4. Каково направление этихсил?
5. Каким может быть соотношение между этими силами и к какому результату это приводит?
6. Сформулируйте условие плавания судов.
7. Что называют ватерлинией и осадкой судна? Водоизмещением судна?
8. Грузоподъемность судна. Как ее вычислить?
ΙΙΙ. Применение закона Архимеда и наблюдение его в быту, технике, природе.
1. При плавании военных надводных судов:
Решение задачи. (Ученик комментирует решение у доски).
Каково водоизмещение торпедного катера Г- 5, сражавшегося с немцами на «голубых дорогах» Великой Отечественной войны, если его длина 20 метров, ширина 3,5 м, осадка 0,6 м?
2. При плавании подводных судов:
Демонстрационный опыт с картезианским водолазом (поплавком Декарта). Выяснения вопроса, касающегося его всплытия и погружения. Учащиеся пытаются установить аналогию между движением подводной лодки и картезианского водолаза.
Выяснения вопроса, касающегося его всплытия и погружения. Учащиеся пытаются установить аналогию между движением подводной лодки и картезианского водолаза.
Демонстрация видеофрагмента о способе движения подводного судна.
3. В воздухоплавании:
Плавание в воздухе не менее увлекательно и хранит в себе много секретов.
Сообщения трех учащихся ополет первого аэростата ( 5 июня 1783 г.) , заполненного горячим воздухом;
о первом пилотируемом воздушном шаре ( 1 декабря 1783 г.), заполненном водородом;
о полете Д. И. Менделеева на воздушном шаре «Русский» (7 августа 1887 г.).
ΙV. Практическая часть. Работа обучающихся с тестами
Проверь себя
А. На каком известном вам законе основано плавание судов?
1. На законе Паскаля. 2. На законе Архимеда.
Б. С увеличением количества груза на судне архимедова сила на судно…
1. увеличивается. 2. уменьшается. 3. не изменяется.
В. Почему стальной лист тонет в воде, а судно, корпус которого сделан из стальных листов, плавает? 1. Средняя плотность судна меньше плотности воды.
Средняя плотность судна меньше плотности воды.
2.На судне имеется установка, удерживающая его на воде.
Г. Изменится ли водоизмещение судна при переходе из реки в море?
1. Уменьшится. 2. Не изменится. 3. Увеличится.
Д. Какая из названных ниже лодок погрузится до дна, если наполнится водой:
1. деревянная. 2. металлическая.
Е. Как изменится осадка корабля, если… 1. его загружают? 2. его разгружают? 3. Понижается температура до 40С, в которой плавает корабль? 4. увеличивается уровень воды из-за прилива?
Ж. Осадка увеличится. З. Уменьшится. К. Останется неизменной.
Одновременно происходит работа в 4 группах:
1 группа выясняет вопрос о независимости архимедовой силы от формы тела.
Приборы и материалы: три кусочка пластилина равного объема, динамометр, емкость с водой.
2 группа выясняет вопрос о том, зависит ли архимедова сила от плотности вещества, из которого изготовлено тело.
Приборы и материалы: два одинаковые по объему цилиндра, изготовленные из чугуна и алюминия, динамометр, емкость с водой.
3 группа выясняет зависимость архимедовой силы от глубины погружения.
Приборы и материалы: динамометр, твердое тело, емкость с водой.
4 группа: имея в распоряжении два кусочка пластилина, изменяют и придают одному форму лодочки, демонстрируя тем самым зависимость архимедовой силы от объема тела.
Вывод по экспериментальной части формулируется и выводится на слайде13 презентации в виде таблицы:
Результаты эксперимента
Архимедова сила
зависит
не зависит
от плотности жидкости
от глубины погружения
от объема погруженного в жидкость тела (или его части)
от формы тела
от плотности тела
V. Учитель подводит итог урока.
Глядя на мир, нельзя не удивляться.
К. Прутков
Не привыкайте к чудесам,
Дивитесь им, дивитесь.
Приглядывайтесь к небесам,
Прислушивайтесь к птицам,
Прикладывайтесь к родникам,
Ничто не повторится.
VΙ. Домашнее задание (интегрированное):
1. В Лондоне есть музей восковых фигур, в котором представлены скульптуры выдающихся личностей, выполненные из воска в натуральную величину.
Определите массу воска, необходимую для изготовления вашей фигуры. Линейная усадка воска равна 1,2 раза, что приводит к уменьшению объема в
1,2 3 раза.Плотность воска 900 кг/м3.
2. Используя дополнительные сайты, попробуй найти интересную информацию для сообщения на уроке:
http://class-fizika.narod.ru/
http://physica-vsem.narod.ru/
http://physics03.narod.ru/
http://elkin52.narod.ru/
3. На данном сайте найти и выполнить соответствующее задание: http://school-collection. edu.ru/
edu.ru/
Ресурс:
Действие жидкости и газа на погруженное в них тело (N 205951)
Вид ЦОР:
Интерактивное задание,Мультимедиа
Поставщик ЦОР:
ФГУП «Издательство «Просвещение»
Аннотация:
Вводится понятие выталкивающей силы. Объясняются причины возникновения выталкивающей силы. Выводится формула для расчета выталкивающей силы.
Рубрикаторы:
Класс
7 класс
Предмет
Физика
Тематический рубрикатор
(рубрикатор хранилища)
Закон Архимеда
«Физика. 7-9 классы»
(инновационный учебный материал)
Открытый урок «Выталкивающая сила в жидкостях и газах. Закон Архимеда»
Урок __ Выталкивающая сила в жидкостях и газах. Закон Архимеда
Цель урока: Учебная. Выяснить причины возникновения выталкивающей силы в жидкостях и газах и объяснить природу ее происхождения. Развивающая. Развивать творческие способности и логическое мышление учащихся; показать ученикам практическую значимость полученных знаний. Воспитательная. Воспитывать культуру оформления задач.
Развивающая. Развивать творческие способности и логическое мышление учащихся; показать ученикам практическую значимость полученных знаний. Воспитательная. Воспитывать культуру оформления задач.
Тип урока: урок изучения нового материала.
Оборудование: учебная презентация, компьютер, раздаточный материал, сборник задач.
План урока:
І. организационный этап
ІІ. Проверка домашнего задания
III. Актуализация опорных знаний И УМЕНИЙ
IV. Изучение нового материала
V. ЗАКРЕПЛЕНИЕ НОВЫХ ЗНАНИЙ И УМЕНИЙ
VІ. Подведение итогов урока
VІІ. ДОМАШНЕЕ ЗАДАНИЕ
ход урока
І. организационный этап
Сообщение темы и целей урока. (СЛ. 1)
Вступительное слово:
«Жидкости на тело давят,
Вверх его все поднимают,
При этом силу создают,
Что Архимедовой зовут!
Ее считать умеем мы:
Надо знать лишь вес воды,
Что-то тело вытесняет
Все закон нам объясняет
Открыл его великий грек,
Ему имя – Архимед.
Сегодня тема нашего урока Выталкивающая сила в жидкостях и газах. закон Архимеда. На этом уроке, мы узнаем, как был открыт закон Архимеда, выясним причины возникновения выталкивающей силы в жидкостях и газах и объясним природу ее происхождения. Поработаем над формулами, решим несколько задач.
II. Проверка домашнего задания (сл.2-3)
1. Что называют давлением?
Давление р — это физическая величина, характеризующая результат действия силы и равна отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
2. Как определяют давление? ()
3. Как можно определить силу давления? ()
4. Сформулируйте закон Паскаля.
Давление, создаваемое на поверхность неподвижной жидкости, передается жидкостью одинаково во всех направлениях.
5. Какое давление называют гидростатическим?
Давление неподвижной жидкости называют гидростатическим давлением.
6. По какой формуле исчисляется гидростатическое давление? (р = ρgh)
III. Актуализация опорных знаний И УМЕНИЙ (сл.4-6)
Проблемные вопросы:
Почему мяч, который погрузили в воду и отпустили, выскакивает над поверхностью воды?
Почему тяжелый камень, который на суше нельзя сдвинуть с места, легко поднять под водой?
Правда ли, что человек в воде находится в состоянии невесомости?
( СЛ 7) Рассмотрим стеклянный поплавок, который плавает вблизи поверхности. Если слегка погрузить в воду и отпустить его будем наблюдать, как он возвращается в предыдущее состояние. Создается впечатление, что вода выталкивает его на поверхность.
Попробуем разобраться!
IV. Изучение нового материала
1. Выталкивающая сила
(СЛ 8) Подвесим к коромыслу весов шар и уравновесим весы (рис. А). Подставим под шар пустой сосуд (рис. Б). Нальем в сосуд воду и увидим, что равновесие весов нарушится (рис. В) — какая-то сила пытается вытолкнуть шар из воды.
Б). Нальем в сосуд воду и увидим, что равновесие весов нарушится (рис. В) — какая-то сила пытается вытолкнуть шар из воды.
Откуда берется эта сила?
(СЛ 9) Рассмотрим погружен в жидкость кубик.
Силы гидростатического давления и противоположны по направлению и равные по значению (площади боковых граней одинаковы, и грани расположены на одинаковой глубине).
Такие силы уравновешивают друг друга. Они не выталкивают брусок вверх, а только сжимают его по бокам.
(СЛ. 10) Силы F1 и F2 НЕ уравновешивают друг друга.
S — площадь грани
(СЛ.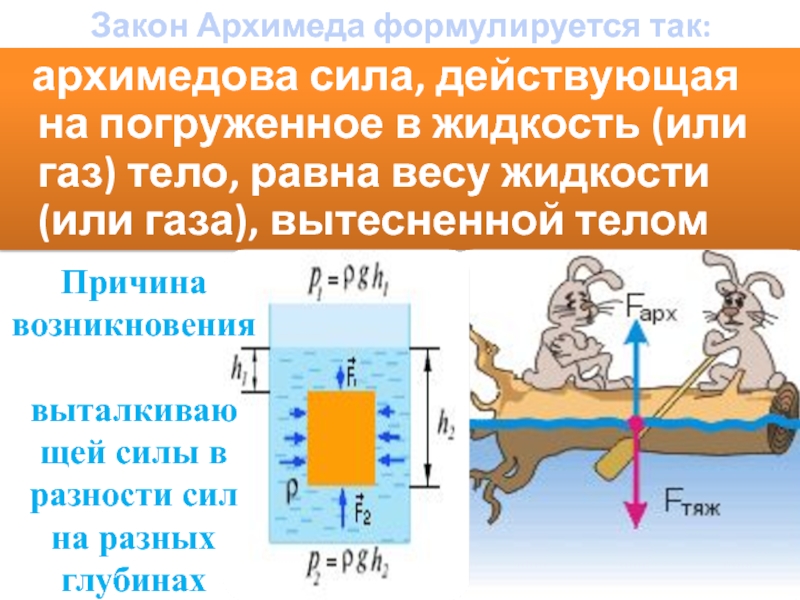 11) На тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх. Ее существование обусловлено разницей давлений на нижнюю и верхнюю грани тела.
11) На тело, погруженное в жидкость, действует выталкивающая сила, направленная вертикально вверх. Ее существование обусловлено разницей давлений на нижнюю и верхнюю грани тела.
(СЛ. 12). В случае с плавающим поплавком в существовании разницы давлений можно убедится с помощью жидкостного манометра, измеряя давление воды вблизи его нижней и верхней части. На тело, погруженное в газе также действует выталкивающая сила, но она значительно меньше. Это связано с тем, что плотность газа намного меньше плотности жидкости.
( СЛ. 13)2. Архимедова сила
Выталкивающую силу, действующую на тело в жидкости или в газе, называют также архимедовой силой.
( СЛ. 14)
(висота кубика)
( СЛ. 15)
(масса жидкости в объеме кубика)
( СЛ. 16) Убедимся в справедливости данного утверждения на опыте. Для проведения эксперимента используем электрический регистратор силы, соединенный с измерительным комплексом. Также нам понадобится: сливная посудина, заполненная водой, дополнительный стаканчик для собирания воды со сливной посудины, штатив и поднимающийся столик. Подвесим резиновый шар к датчику силы и поместим ее над поверхностью воды в сливной посудине, включим регистратор силы. С помощью поднимающегося столика полностью погрузим шар в воду. Часть воды, равная объему шара, вытечет в дополнительный стаканчик. Дождемся окончания записи данных. Измерительный комплекс построил график изменения силы, с которой шар действует на подвес. Установив на график курсоры, определим разницу в показаниях до и после погружения шара. Это и будет значение выталкивающей силы, что действует на полностью погруженный шар. В нашем эксперименте значение составило 0,43 Н.
16) Убедимся в справедливости данного утверждения на опыте. Для проведения эксперимента используем электрический регистратор силы, соединенный с измерительным комплексом. Также нам понадобится: сливная посудина, заполненная водой, дополнительный стаканчик для собирания воды со сливной посудины, штатив и поднимающийся столик. Подвесим резиновый шар к датчику силы и поместим ее над поверхностью воды в сливной посудине, включим регистратор силы. С помощью поднимающегося столика полностью погрузим шар в воду. Часть воды, равная объему шара, вытечет в дополнительный стаканчик. Дождемся окончания записи данных. Измерительный комплекс построил график изменения силы, с которой шар действует на подвес. Установив на график курсоры, определим разницу в показаниях до и после погружения шара. Это и будет значение выталкивающей силы, что действует на полностью погруженный шар. В нашем эксперименте значение составило 0,43 Н.
Продолжим эксперимент, и определим вес воды, которая вылилась со сливного стакана. Для этого установим стакан, с водой что вылилась на подвес, соединенный с датчиком силы, и запустим регистратор. Снимим стаканчик, выльем с него воду, и повторно поставим на подвес. Дождемся окончания записи данных. Установим курсоры на полученный график на участки с полным и пустым стаканчиком. Разница показаний соответствует весу воды, что была в стакане. И в этом эксперименте значение составило 0,43 Н. т.е. Мы получили доказательство того, что сила Архимеда равна весу вытесненной жидкости.
Для этого установим стакан, с водой что вылилась на подвес, соединенный с датчиком силы, и запустим регистратор. Снимим стаканчик, выльем с него воду, и повторно поставим на подвес. Дождемся окончания записи данных. Установим курсоры на полученный график на участки с полным и пустым стаканчиком. Разница показаний соответствует весу воды, что была в стакане. И в этом эксперименте значение составило 0,43 Н. т.е. Мы получили доказательство того, что сила Архимеда равна весу вытесненной жидкости.
Мы рассматривали случай, когда тело полностью погружено в жидкость, но полученный результат оправдывается и в случаях, когда тело погружено в жидкость не полностью. Тогда для расчетов принимают объем, погруженной в жидкость части тела
(СЛ. 17) А как же Архимед закон открыл? — Существует легенда о том, как Архимед пришел к открытию, что выталкивающая сила равна весу жидкости в объеме тела.
Архимедова сила равна весу жидкости в объеме кубика:
(СЛ 18) Закон Архимеда:
На тело, погруженное в жидкость или газ, действует выталкивающая сила, равная весу жидкости или газа в объеме погруженной части тела.
Архимедова сила приложена к центру погруженной части тела и направлена вертикально вверх.
V. ЗАКРЕПЛЕНИЕ НОВЫХ ЗНАНИЙ И УМЕНИЙ
Решение задач
№ 20.5 (с. 107) На полностью погруженное в воду тело действует сила Архимеда 12 Н. Какой объем имеет тело?
Дано:
| Решение
Ответ: |
№ 20.14. На тело, которое полностью погруженное в керосин, действует архимедова сила 4 Н. Какую плотность имеет тело, если его масса составляет 900 г?
Дано:
| Решение
Ответ:
|
№ 20. 16. Какая выталкивающая сила действует на стальную деталь массой 156 кг, полностью погруженную в воду?
16. Какая выталкивающая сила действует на стальную деталь массой 156 кг, полностью погруженную в воду?
Дано:
| Решение
Відповідь: Fарх =200 Н.
|
№ 20.19. Что покажет динамометр, если подвешенное к нему тело полностью погрузить в воду? Масса тела 200 г, объем — 50 cм3
Дано: | Решение
Ответ: |
VI. Подведение итогов урока
Подведение итогов урока
Беседа по вопросам
- Куда направлена сила, действующая со стороны жидкости или газа на тело, в них погружено?
- Что является причиной возникновения выталкивающей силы?
- Как еще называют выталкивающей силы?
- Сформулируйте закон Архимеда.
- Теряет вес тело, погруженное в жидкость или газ? Почему?
- В каких случаях на тело, погруженное в жидкость, не действует выталкивающая сила?
VII. ДОМАШНЕЕ ЗАДАНИЕ
Изучить § 31 Упражнение № 20.6, 20.15, 20.20
Контрольная работа №4 «закон архимеда» вариант 1
Контрольная работа №4
«Закон Архимеда»
Вариант 1
Какая глубина в море соответствует давлению воды равному 412 кПа?
В мензурку налили керосин, а затем долили воду.
 Как расположатся в ней жидкости?
Почему?
Как расположатся в ней жидкости?
Почему?Стержень плавает в воде таким образом, что под водой находится ¾ его объема. Определите плотность материала, из которого изготовлен стержень.
Длина прямоугольной баржи 4 м, ширина 2 м. Определите вес помешенного на баржу груза, если после нагрузки она осела на 0,5 м.
Вариант 2
С какой силой давит атмосфера на поверхность страницы тетради, размер которой 16 × 20 см при атмосферном давлении 0,1 МПа?
Каково должно быть соотношение сил, действующих на опущенное в жидкость тело, чтобы оно стало всплывать? Приведите примеры.
Железный шар плавает в ртути. Какая часть его объема погружена в ртуть?
После разгрузки баржи ее осадка в реке уменьшилась на 60 см.
 Определите
массу снятого с нее груза, если площадь
сечения баржи на уровне воды 240 м2?
Определите
массу снятого с нее груза, если площадь
сечения баржи на уровне воды 240 м2?
Вариант 3
Вычислите архимедову силу, действующую на брусок размером 2×10×4см, если он наполовину погружен в спирт.
Определите силу, действующую на поверхность площадью 4 м2, если произведенное ей давление равно 2 Н/см2.
Высота столба воды в сосуде 8 см. какой должна быть высота столба керосина, налитого в сосуд вместо воды, чтобы давление на дно осталось прежним?
Какова масса трактора, если опорная площадь его гусениц равна 1,3 м2, а давление на почву составляет 40 кПа?
Цинковый шар весит 3,6 Н, а при погружении в воду – 2,8 Н. Сплошной ли это шар или имеет полость? Если шар полый, то чему равен объем полости?
Вариант 4
При погружении в жидкость на тело объемом 2 дм3 действует архимедова сила 14,2 Н.
 Какая это жидкость.
Какая это жидкость.Определите давление, оказываемое двухосным прицепом на дорогу, если его масса вместе с грузом 2,5 т, а площадь соприкосновения каждого колеса с дорогой равна 125 см2.
Какова сила давления на каждый квадратный сантиметр поверхности тела водолаза, находящегося на глубине 50 м?
Высота столба ртути в ртутном барометре равна 760 мм. Во сколько раз высота столба керосина, уравновешивающего это же давление, будет больше?
При полном погружении полого латунного кубика массой 170 г в керосин на кубик действует архимедова сила 4 Н. Каков объем полости?
Методическая разработка урока по теме « Закон Архимеда .Решениезадач по теме давление, сила Архимеда»
|
Деятельность учителя |
Деятельность учащихся |
Планируемые результаты |
Формы и методы диагностики |
|||
|
Метапредметные |
||||||
|
1. |
Организует актуализацию изученных способов действий. Создает условия для возникновения у ученика внутренней потребности включения в учебную деятельность. |
Выполняют самостоятельно задания на изученные способы действий. Осознают свою область «знания», сами определяют, что необходимо повторить, чтобы освоить новые способы действий. |
Умение приводить эксперимент составлять таблицу. Используя табличные данные формулироватьновые задачирешать и оформлять их по алгоритму. |
Регулятивные (Р): самостоятельное оценивание правильности выполнения задания, внесение необходимых корректив. Познавательные (П):умение ориентироваться в своей системе знаний. Коммуникативные (К):умение оформлять свои мысли в устной и письменной речи. |
Формирование смыслов учебной деятельности на основе развития познавательных интересов, учебных мотивов. |
Прием «Знаю» — «Повторить» — «Хочу узнать» |
|
2. Целеполагание |
Предлагает проблемную ситуацию. Задает наводящие вопросы. Подводит учащихся к определению цели и темы урока. |
Пробуют разгадать «загадку». Осознают проблемную ситуацию. Формулируют цель и тему урока. |
(Р) определение цели учебной деятельности (П) анализ условия,поиск способа решения задачи (К) выражение своих мыслей с достаточной полнотой и точностью; учет разных мнений |
Формирование познавательного интереса к изучению нового |
||
|
3. Открытие нового знания |
Организует работу по «открытию» алгоритма составления и оформления задач по результатам полученным при работе с приборами. |
Отвечают на вопросы. Составляют и проговаривают план действий. Формулируют алгоритм. |
Знание алгоритма составления и оформления задач по результатам полученным при работе с приборами. |
(Р) прогнозирование результата и определение средств решения проблемы (П) структурирование знаний (К) выражение своих мыслей с достаточной полнотой и точностью; учет разных мнений |
Формирование смыслов учебной деятельности на основе развития познавательных интересов, учебных мотивов. |
|
|
4. Первичное закрепление |
Организует усвоение учащимися нового способа действия. |
Учащиеся решают типовые задания с проговариванием алгоритма у доски и в парах. |
Умениесоставлять и оформлять задачи по результатам полученным при работе с приборами. |
(Р) умение проговаривать последовательность действий (П) выполнение действий по алгоритму (К) умение оформлять свои мысли в устной и письменной речи, организовывать взаимодействие в паре |
Формирование смыслов учебной деятельности на основе развития познавательных интересов, учебных мотивов. |
Взаимоконтроль при выполнении заданий в парах |
|
5. Самостоятельная работа с самопроверкой по образцу |
Организует проверку знаний. При необходимости осуществляет коррекцию. Подводит итоги самостоятельной работы |
Самостоятельно выполняют задания по вариантам. Осуществляют самопроверку по образцу. Следуют своему маршруту при решении задач. |
Умение составлять и оформлять задачи по результатам полученным при работе с приборами. |
(Р) умение находить и исправлять свои ошибки; определение степени успешности выполненной работы (П) выполнение действий по алгоритму |
Формирование смыслов учебной деятельности на основе развития познавательных интересов, учебных мотивов. |
Самостоятельная работа с самопроверкой, самооценка |
|
6. Включение в систему знаний |
Предлагает задание, содержащее изученный ранее материал. |
Самостоятельно выполняют задание, используя подсказки. Обсуждают решение в парах. Делают выводы о возможных способах решения задачи. |
Знание о других способах проведения эксперимента |
(Р) прогнозирование результата (П) построение логической цепи рассуждений (К) умение оформлять свои мысли в устной и письменной речи, организовывать взаимодействие в паре |
Формирование познавательного интереса к изучению нового |
Взаимоконтроль при выполнении заданий в парах |
|
Организует рефлексию, самооценку учебной деятельности. |
Отвечают на вопросы. Осуществляют самооценку. Записывают домашнее задание. |
(К) выражение своих мыслей с достаточной полнотой и точностью |
Умение осуществлять самооценку на основе критерия успешной деятельности |
Вопросы для рефлексии |
||
определение и формула. Возникновение Силы Архимеда
1 / 5
Закон Архимеда формулируется следующим образом : на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела . Сила называется силой Архимеда :
F A = ρ g V , {\displaystyle {F}_{A}=\rho {g}V,}где
ρ
{\displaystyle \rho } — плотность жидкости (газа),
g
{\displaystyle {g}} — ускорение свободного падения , а
V
{\displaystyle V} — объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности). Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Если тело плавает на поверхности (равномерно движется вверх или вниз), то выталкивающая сила (называемая также архимедовой силой) равна по модулю (и противоположна по направлению) силе тяжести, действовавшей на вытесненный телом объём жидкости (газа), и приложена к центру тяжести этого объёма.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
Что касается тела, которое находится в газе, например в воздухе, то для нахождения подъёмной силы нужно заменить плотность жидкости на плотность газа. Например, шарик с гелием летит вверх из-за того, что плотность гелия меньше, чем плотность воздуха.
Закон Архимеда можно объяснить при помощи разности гидростатических давлений на примере прямоугольного тела.
P B − P A = ρ g h {\displaystyle P_{B}-P_{A}=\rho gh} F B − F A = ρ g h S = ρ g V , {\displaystyle F_{B}-F_{A}=\rho ghS=\rho gV,}где P A , P B — давления в точках A и B , ρ — плотность жидкости, h — разница уровней между точками A и B , S — площадь горизонтального поперечного сечения тела, V — объём погружённой части тела.
В теоретической физике также применяют закон Архимеда в интегральной форме:
F A = ∬ S p d S {\displaystyle {F}_{A}=\iint \limits _{S}{p{dS}}} ,где S {\displaystyle S} — площадь поверхности, p {\displaystyle p} — давление в произвольной точке, интегрирование производится по всей поверхности тела.
В отсутствие гравитационного поля, то есть в состоянии невесомости , закон Архимеда не работает. Космонавты с этим явлением знакомы достаточно хорошо. В частности, в невесомости отсутствует явление (естественной) конвекции , поэтому, например, воздушное охлаждение и вентиляция жилых отсеков космических аппаратов производятся принудительно, вентиляторами .
Обобщения
Некий аналог закона Архимеда справедлив также в любом поле сил, которое по-разному действуют на тело и на жидкость (газ), либо в неоднородном поле. Например, это относится к полю сил инерции (например, центробежной силы) — на этом основано центрифугирование . Пример для поля немеханической природы: диамагнетик в вакууме вытесняется из области магнитного поля большей интенсивности в область с меньшей.
Вывод закона Архимеда для тела произвольной формы
Гидростатическое давление жидкости на глубине h {\displaystyle h} есть p = ρ g h {\displaystyle p=\rho gh} . При этом считаем ρ {\displaystyle \rho } жидкости и напряжённость гравитационного поля постоянными величинами, а h {\displaystyle h} — параметром. Возьмём тело произвольной формы, имеющее ненулевой объём. Введём правую ортонормированную систему координат O x y z {\displaystyle Oxyz} , причём выберем направление оси z совпадающим с направлением вектора g → {\displaystyle {\vec {g}}} . Ноль по оси z установим на поверхности жидкости. Выделим на поверхности тела элементарную площадку d S {\displaystyle dS} . На неё будет действовать сила давления жидкости направленная внутрь тела, d F → A = − p d S → {\displaystyle d{\vec {F}}_{A}=-pd{\vec {S}}} . Чтобы получить силу, которая будет действовать на тело, возьмём интеграл по поверхности:
F → A = − ∫ S p d S → = − ∫ S ρ g h d S → = − ρ g ∫ S h d S → = ∗ − ρ g ∫ V g r a d (h) d V = ∗ ∗ − ρ g ∫ V e → z d V = − ρ g e → z ∫ V d V = (ρ g V) (− e → z) {\displaystyle {\vec {F}}_{A}=-\int \limits _{S}{p\,d{\vec {S}}}=-\int \limits _{S}{\rho gh\,d{\vec {S}}}=-\rho g\int \limits _{S}{h\,d{\vec {S}}}=^{*}-\rho g\int \limits _{V}{grad(h)\,dV}=^{**}-\rho g\int \limits _{V}{{\vec {e}}_{z}dV}=-\rho g{\vec {e}}_{z}\int \limits _{V}{dV}=(\rho gV)(-{\vec {e}}_{z})}
При переходе от интеграла по поверхности к интегралу по объёму пользуемся обобщённой теоремой Остроградского-Гаусса . {**}grad(h)=\nabla h={\vec {e}}_{z}}
{**}grad(h)=\nabla h={\vec {e}}_{z}}
Получаем, что модуль силы Архимеда равен ρ g V {\displaystyle \rho gV} , а направлена она в сторону, противоположную направлению вектора напряжённости гравитационного поля.
Другая формулировка (где ρ t {\displaystyle \rho _{t}} — плотность тела, ρ s {\displaystyle \rho _{s}} — плотность среды, в которую оно погружено).
Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF
Введение
Актуальность: Если внимательно присмотреться к окружающему миру, то можно открыть для себя множество событий, происходящих вокруг. Издревле человека окружает вода. Когда мы плаваем в ней, то наше тело выталкивает на поверхность какие-то силы. Я давно задаю себе вопрос: «Почему тела плавают или тонут? Вода выталкивает предметы?»
Моя исследовательская работа направлена на то, чтобы углубить полученные на уроке знания об архимедовой силе. Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук — это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Ответы на интересующие меня вопросы, используя жизненный опыт, наблюдения за окружающей действительностью, провести собственные эксперименты и объяснить их результаты, которые позволят расширить знания по данной теме. Все науки связаны между собой. А общий объект изучения всех наук — это человек «плюс» природа. Я уверен, что исследование действия архимедовой силы сегодня является актуальным.
Гипотеза: Я предполагаю, что в домашних условиях можно рассчитать величину выталкивающей силы действующей на погруженное в жидкость тело и определить зависит ли она от свойств жидкости, объема и формы тела.
Объект исследования: Выталкивающая сила в жидкостях.
Задачи:
Изучить историю открытия архимедовой силы;
Изучить учебную литературу по вопросу действия архимедовой силы;
Выработать навыки проведения самостоятельного эксперимента;
Доказать, что значение выталкивающей силы зависит от плотности жидкости.
Методы исследования:
Исследовательские;
Расчетные;
Информационного поиска;
Наблюдений
1. Открытие силы Архимеда
Открытие силы Архимеда
Существует знаменитая легенда о том, как Архимед бежал по улице и кричал «Эврика!» Это как раз повествует об открытии им того, что выталкивающая сила воды равна по модулю весу вытесненной им воды, объем которой равен объему погруженного в нее тела. Это открытие названо законом Архимеда.
В III веке до нашей эры жил Гиерон — царь древнегреческого города Сиракузы и захотел он сделать себе новую корону из чистого золота. Отмерил его строго сколько нужно, и дал ювелиру заказ. Через месяц мастер вернул золото в виде короны и весила она столько, сколько и масса данного золота. Но ведь всякое бывает и мастер мог схитрить, добавив серебро или того хуже — медь, ведь на глаз не отличишь, а масса такая, какая и должна быть. А царю узнать охота: честно ль сделана работа? И тогда, попросил он ученого Архимеда, проверить из чистого ли золота сделал мастер ему корону. Как известно, масса тела равна произведению плотности вещества, из которого сделано тело, на его объем: . Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Если у разных тел одинаковая масса, но они сделаны из разных веществ, то значит, у них будет разный объем. Если бы мастер вернул царю не ювелирно сделанную корону, объем которой определить невозможно из-за ее сложности, а такой же по форме кусок металла, который дал ему царь, то сразу было бы ясно, подмешал он туда другого металла или нет. И вот принимая ванну, Архимед обратил внимание, что вода из нее выливается. Он заподозрил, что выливается она именно в том объеме, какой объем занимают его части тела, погруженные в воду. И Архимеда осенило, что объем короны можно определить по объему вытесненной ей воды. Ну а коли можно измерить объем короны, то его можно сравнить с объемом куска золота, равного по массе. Архимед погрузил в воду корону и измерил, как увеличился объем воды. Также он погрузил в воду кусок золота, у которого масса была такая же, как у короны. И тут он измерил, как увеличился объем воды. Объемы вытесненной в двух случаях воды оказались разными. Тем самым мастер был изобличен в обмане, а наука обогатилась замечательным открытием.
Из истории известно, что задача о золотой короне побудила Архимеда заняться вопросом о плавании тел. Опыты, проведенные Архимедом, были описаны в сочинении «О плавающих телах», которое дошло до нас. Седьмое предложение (теорема) этого сочинения сформулировано Архимедом следующим образом: тела более тяжелые, чем жидкость, опущенные в эту жидкость, будут опускаться пока не дойдут до самого низа, и в жидкости станут легче на величину веса жидкости в объеме, равном объему погруженного тела.
Интересно, что сила Архимеда равна нулю, когда погруженное в жидкость тело плотно, всем основанием прижато ко дну.
Открытие основного закона гидростатики — крупнейшее завоевание античной науки.
2. Формулировка и пояснения закона Архимеда
Закон Архимеда описывает действие жидкостей и газов на погруженное в них тело, и является одним из главных законов гидростатики и статики газов.
Закон Архимеда формулируется следующим образом: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу жидкости (или газа) в объёме погруженной части тела — эта сила называется силой Архимеда :
,
где — плотность жидкости (газа), — ускорение свободного падения, — объём погружённой части тела (или часть объёма тела, находящаяся ниже поверхности).
Следовательно, архимедова сила зависит только от плотности жидкости, в которую погружено тело, и от объема этого тела. Но она не зависит, например, от плотности вещества тела, погруженного в жидкость, так как эта величина не входит в полученную формулу.
Следует заметить, что тело должно быть полностью окружено жидкостью (либо пересекаться с поверхностью жидкости). Так, например, закон Архимеда нельзя применить к кубику, который лежит на дне резервуара, герметично касаясь дна.
3. Определение силы Архимеда
Силу, с которой тело, находящееся в жидкости, выталкивается ею, можно определить на опыте используя данный прибор:
Небольшое ведерко и тело цилиндрической формы подвешиваем на пружине, закрепленной в штативе. Растяжение пружины отмечаем стрелкой на штативе, показывая вес тела в воздухе. Приподняв тело, под него подставляем стакан с отливной трубкой, наполненный жидкостью до уровня отливной трубки. После чего тело погружают целиком в жидкость. При этом часть жидкости, объём которой равен объёму тела, выливается из отливного сосуда в стакан. Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
Указатель пружины поднимается вверх, пружина сокращается, показывая уменьшение веса тела в жидкости. В данном случае на тело, наряду с силой тяжести, действует еще и сила, выталкивающая его из жидкости. Если в ведёрко налить жидкость из стакана (т.е. ту, которую вытеснило тело), то указатель пружины возвратится к своему начальному положению.
На основании этого опыта можно заключить, что сила, выталкивающая тело, целиком погруженное в жидкость, равна весу жидкости в объёме этого тела. Зависимость давления в жидкости (газе) от глубины погружения тела приводит к появлению выталкивающей силы (силы Архимеда), действующей на любое тело, погруженное в жидкость или газ. Тело при погружении двигается вниз под действием силы тяжести. Архимедова сила направлена всегда противоположно силе тяжести, поэтому вес тела в жидкости или газе всегда меньше веса этого тела в вакууме.
Данный опыт подтверждает, что архимедова сила равна весу жидкости в объёме тела.
4. Условие плавания тел
На тело, находящееся внутри жидкости, действуют две силы: сила тяжести, направленная вертикально вниз, и архимедова сила, направленная вертикально вверх. Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
Рассмотрим, что будет происходить с телом под действием этих сил, если вначале оно было неподвижно.
При этом возможны три случая:
1) Если сила тяжести больше архимедовой силы, то тело опускается вниз, то есть тонет:
, то тело тонет;
2) Если модуль силы тяжести равен модулю архимедовой силы, то тело может находиться в равновесии внутри жидкости на любой глубине:
, то тело плавает;
3) Если архимедова сила больше силы тяжести, то тело будет поднимается из жидкости — всплывать:
, то тело плавает.
Если всплывающее тело частично выступает над поверхностью жидкости, то объем погруженной части плавающего тела такой, что вес вытесненной жидкости равен весу плавающего тела.
Архимедова сила больше силы тяжести, если плотность жидкости больше плотности погруженного в жидкость тела, если
1) =— тело плавает в жидкости или газе,2) >— тело тонет,3)
Именно эти принципы соотношения силы тяжести и силы Архимеда применяются в судоходостронии. Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Однако на воде держатся громадные речные и морские суда, изготовленные из стали, плотность которой почти в 8 раз больше плотности воды. Объясняется это тем, что из стали делают лишь сравнительно тонкий корпус судна, а большая часть его объема занята воздухом. Среднее значение плотности судна при этом оказывается значительно меньше плотности воды; поэтому оно не только не тонет, но и может принимать для перевозки большое количество грузов. Суда, плавающие по рекам, озерам, морям и океанам, построены из разных материалов с различной плотностью. Корпус судов обычно делают из стальных листов. Все внутренние крепления, придающие судам прочность, также изготавливают из металлов. Для постройки судов используют разные материалы, имеющие по сравнению с водой как большую, так и меньшую плотность. Вес воды, вытесненной подводной частью судна, равен весу судна с грузом в воздухе или силе тяжести, действующей на судно с грузом.
Для воздухоплавания вначале использовали воздушные шары, которые раньше наполняли нагретым воздухом, сейчас — водородом или гелием. Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
Для того чтобы шар поднялся в воздух, необходимо, чтобы архимедова сила (выталкивающая), действующая на шар, была больше силы тяжести.
5. Проведение эксперимента
Исследовать поведение сырого яйца в жидкостях разного рода.
Задача: доказать, что значение выталкивающей силы зависит от плотности жидкости.
Я взял одно сырое яйцо и жидкости разного рода (приложение 1):
Вода чистая;
Вода, насыщенная солью;
Подсолнечное масло.
Сначала я опустил сырое яйцо в чистую воду — яйцо утонуло — «пошло ко дну» (приложение 2). Потом в стакан с чистой водой я добавил столовую ложку поваренной соли, в результате яйцо плавает (приложение 3). И наконец, я опустил яйцо в стакан с подсолнечным маслом — яйцо опустилось на дно (приложение 4).
Вывод: в первом случае плотность яйца больше плотности воды и поэтому яйцо утонуло. Во втором случае плотность солёной воды больше плотности яйца, поэтому яйцо плавает в жидкости. В третьем случае плотность яйца также больше плотности подсолнечного масла, поэтому яйцо утонуло.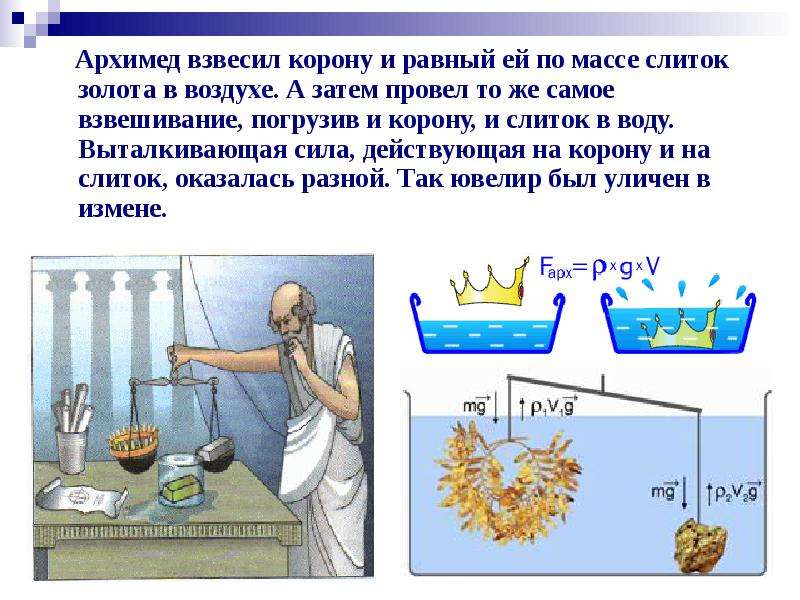 Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
Следовательно, чем больше плотность жидкости, тем сила тяжести меньше.
2. Действие Архимедовой силы на тело человека в воде.
Определить на опыте плотность тела человека, сравнить ее с плотностью пресной и морской воды и сделать вывод о принципиальной возможности человека плавать;
Вычислить вес человека в воздухе, архимедову силу, действующую на человека в воде.
Для начала с помощью весов я измерил массу своего тела. Затем измерил объем тела (без объема головы). Для этого я налил в ванну воды столько, чтобы при погружении в воду я был полностью в воде (за исключением головы). Далее с помощью сантиметровой ленты отметил от верхнего края ванны расстояние до уровня воды ℓ 1 , а затем — при погружении в воду ℓ 2 . После этого с помощью предварительно проградуированной трехлитровой банки стал наливать в ванну воду от уровня ℓ 1 до уровня ℓ 2 — так я измерил объем вытесненной мной воды (приложение 5). Плотность я рассчитал с помощью формулы:
Сила тяжести, действующая на тело в воздухе, была рассчитана по формуле: , где — ускорение свободного падения ≈ 10 . Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Значение выталкивающей силы было рассчитано с помощью формулы описанной в пункте 2.
Вывод:Тело человекаплотнее пресной воды, а, значит, оно в ней тонет. Человеку легче плавать в море, чем в реке, так как плотность морской воды больше, а следовательно больше значение выталкивающей силы.
Заключение
В процессе работы над этой темой мы узнали для себя много нового и интересного. Круг наших познаний увеличился не только в области действия силы Архимеда, но и применении ее в жизни. Перед началом работы мы имели о ней далеко неподробное представление. При проведении опытов мы подтвердили экспериментально справедливость закона Архимеда и выяснили, что выталкивающая силазависит от объема тела и плотности жидкости, чем больше плотность жидкости, тем архимедова сила больше. Результирующая сила, которая определяет поведение тела в жидкости, зависит от массы, объёма тела и плотности жидкости.
Помимо проделанных экспериментов, была изучена дополнительная литература об открытии силы Архимеда, о плавании тел, воздухоплавании.
Каждый из Вас может сделать удивительные открытия, и для этого не нужно обладать ни особенными знаниями, ни мощным оборудованием. Нужно лишь немного внимательней посмотреть на окружающий нас мир, быть чуть более независимым в своих суждениях, и открытия не заставят себя ждать. Нежелание большинства людей познавать окружающий мир оставляет большой простор любознательным в самых неожиданных местах.
Список литературы
1.Большая книга экспериментов для школьников — М.: Росмэн, 2009. — 264 с.
2. Википедия: https://ru.wikipedia.org/wiki/Закон_Архимеда.
3. Перельман Я.И. Занимательная физика. — книга 1. — Екатеринбург.: Тезис, 1994.
4. Перельман Я.И. Занимательная физика. — книга 2.- Екатеринбург.: Тезис, 1994.
5. Перышкин А.В. Физика: 7 класс: учебник для общеобразовательных учреждений / А.В. Перышкин. — 16-е изд., стереотип. — М.: Дрофа, 2013. — 192 с.: ил.
Приложение 1
Приложение 2
Приложение 3
Приложение 4
Класс: 7
УЧЕБНЫЕ ЦЕЛИ:
- Продолжить формирование знаний обучающихся о
выталкивающей силе, выяснить, от каких величин
зависит (не зависит) значение Архимедовой силы.

- Формировать умение проводить физический эксперимент, по его результатам делать выводы, обобщения.
РАЗВИВАЮЩИЕ ЦЕЛИ:
- Развивать мотивационные качества суворовцев, познавательный интерес к предмету.
- Развивать творческие способности.
- Развивать умения применять приобретенные знания в новой учебной ситуации, анализировать изученный материал.
- Развивать учебно-организационные, учебно-интеллектуальные, учебно-информационные, учебно-коммуникативные компетентности.
ВОСПИТАТЕЛЬНЫЕ ЦЕЛИ:
- Содействовать формированию научного мировоззрения.
- Показать практическую значимость изученной темы.
- Воспитывать умение работать в группах для решения совместной задачи.
ТИП УРОКА: урок формирования новых знаний и умений.
ВИД УРОКА: эвристическая беседа с элементами исследования.
МАТЕРИАЛЬНОЕ ОБЕСПЕЧЕНИЕ:
Приборы и оборудование: наборы тел,
динамометры, различные виды жидкостей,
равноплечий рычаг, емкости для жидкости, ведерко
Архимеда, пластилин.
Интерактивная доска, презентация урока, раздаточный материал (тесты, рабочие листы для оформления результатов исследования, таблицы достижений).
УЧЕБНЫЕ ВОПРОСЫ:
- Архимедова сила.
- Проявление Архимедовой силы в природе, быту и технике.
Ход урока
Организационный момент
Создание положительной мотивации.
Прежде чем мы начнем наш урок, посмотрите на листы, которые лежат перед вами. Найдите “Рабочий лист”, на нем вы будете вести все записи на уроке, потом его вклеите в рабочую тетрадь. В “Лист достижений” вы будете заносить набранные баллы за работу на уроке, в конце урока все баллы суммируете и выставите себе оценку. От вашей работы зависит и ваш результат. Разноцветные сигнальные карточки отложите в сторону, они вам понадобятся только в конце урока.
Актуализация опорных знаний
Сегодня на уроке мы продолжим изучение темы
“Действие жидкости и газа на погруженные в них
тела”. Вспомните, какая сила действует на тело,
погруженное в жидкость или газ? (Выталкивающая).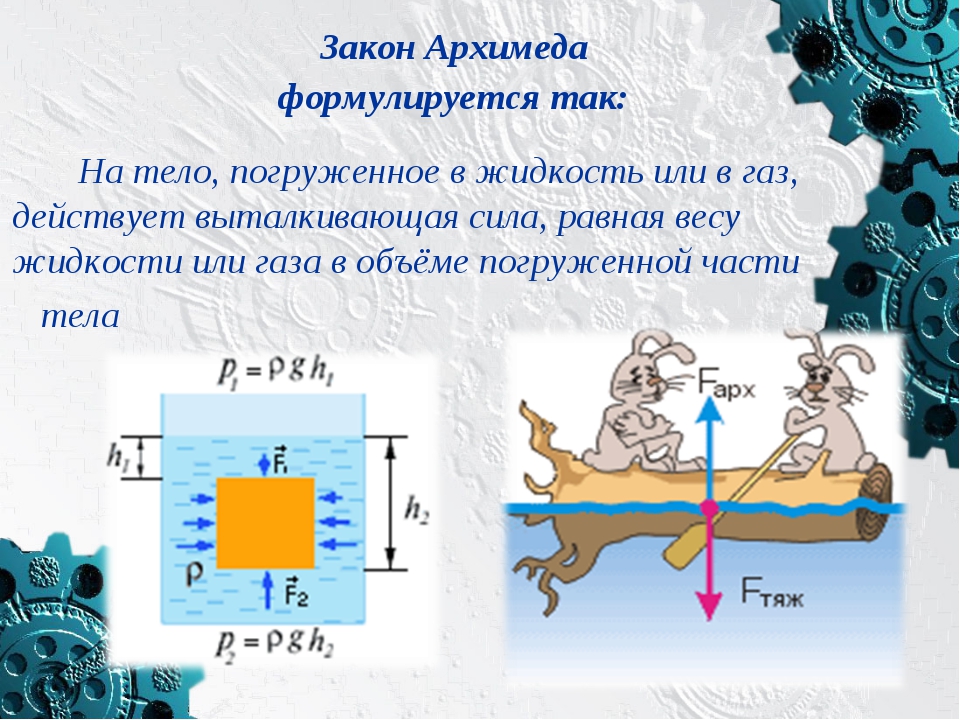
Как она направлена? (Вертикально вверх).
Какой простой опыт может подтвердить сказанное? (Опыт с теннисным шариком). Опыт демонстрирует суворовец.
Чему равна выталкивающая сила? (Сила, выталкивающая тело из жидкости или газа, равна весу жидкости, или газа в объеме погруженного тела или части его тела.)
Как на опыте можно определить значение выталкивающей силы? (Необходимо измерить вес тела в воздухе, затем вес тела в жидкости и из веса тела в воздухе вычесть вес тела в жидкости).
На каждое тело, погруженное в жидкость или газ, действует выталкивающая сила? (Да.)
Демонстрация опыта. (Постановка проблемного
вопроса) На равноплечем рычаге уравновешивают
2 груза по 1н. Затем грузы опускают в сосуды, один с
простой водой, другой соленой водой и наблюдают
нарушение равновесия. Почему нарушилось
равновесие уравновешенного в воздухе рычага с
грузами одинакового веса при помещении их в
жидкость? Суворовцы делают предположения, но
ответить правильно на вопрос не могут. Сегодня на
уроке вам предстоит ответить на этот вопрос.
Первым изучил выталкивающую силу древний
греческий ученый Архимед, поэтому эта сила так и
называется Архимедова сила. Возьмите “Рабочий
лист” и запишите тему урока: “Архимедова сила”.
Сегодня на
уроке вам предстоит ответить на этот вопрос.
Первым изучил выталкивающую силу древний
греческий ученый Архимед, поэтому эта сила так и
называется Архимедова сила. Возьмите “Рабочий
лист” и запишите тему урока: “Архимедова сила”.
Цель нашего урока: изучить Архимедову силу, т.е. выяснить, от каких величин зависит, а от каких не зависит данная сила, научиться определять ее и узнать, где эта сила нашла свое применение.
Кто же такой Архимед?
Формирование новых знаний
Архимед – выдающийся ученый Древний Греции,
родился в 3-ем веке до нашей эры в городе Сиракузы
на острове Сицилия. Архимед получил блестящее
образование у своего отца, астронома и
математика Фидия, родственника сиракузского
тирана Гиерона. В юности он провел несколько лет
в крупнейшем культурном центре Александрии, где
он дружил с астрономом Кононом и математиком
Эратосфеном. Это послужило толчком к развитию
его выдающихся способностей. Он прославился
многочисленными научными трудами, в области
физики и геометрии. Его изобретением была машина
для поливки полей “винт-улитка”, он разработал
теорию рычага. Он был подлинным патриотом своего
города. В то время шла 2-ая Пуническая война. Город
осадило римское войско, обладавшее превосходным
флотом. Архимед организовал инженерную оборону.
Он построил множество удивительных машин,
которые топили вражеские корабли. После Архимеда
осталось много трудов. Одним из важнейших
открытий стал закон, впоследствии названный
законом Архимеда.
Его изобретением была машина
для поливки полей “винт-улитка”, он разработал
теорию рычага. Он был подлинным патриотом своего
города. В то время шла 2-ая Пуническая война. Город
осадило римское войско, обладавшее превосходным
флотом. Архимед организовал инженерную оборону.
Он построил множество удивительных машин,
которые топили вражеские корабли. После Архимеда
осталось много трудов. Одним из важнейших
открытий стал закон, впоследствии названный
законом Архимеда.
Сейчас вам как юным Архимедам предстоит исследовать выталкивающую силу. Сформулируйте цели исследования
- Обнаружить выталкивающее действие жидкости.
- Выяснить, от каких факторов зависит Архимедова сила.
- Выяснить, от каких факторов не зависит Архимедова сила.
Проблемный вопрос. Предложите, какие факторы будут влиять на значение выталкивающей силы.
Возможные предположения: (гипотезы)
- объем тела
- плотность тела
- форма тела
- плотность жидкости
- глубина погружения
Как мы можем проверить наши предположения? На
опытах и с помощью теоретических выводов.
Давайте проверим ваши предположения. Сейчас вы разделитесь на 5 групп, получите оборудование и соответствующее задание. Оформите результат своей работы на рабочих листах, сделаете вывод и занесете свой результат в сводную таблицу на доске.
Задание 1 группе
Оборудование: сосуд с водой, динамометр, алюминиевый и стальной бруски на нити одинакового объема.
- Сделайте вывод о зависимости (независимости) Архимедовой силы от плотности тела.
F а 1 = F а2 =
Задание 2 группе
Оборудование: сосуд с водой, динамометр, металлическое тело на нити.
- Определите Архимедову силу, действующую на 1/2 объема тела, погруженного в воду.
- Определить Архимедову силу, действующую на целиком погруженное тело в жидкость.
- Сравните эти силы.
- Сделайте вывод о зависимости (независимости) Архимедовой силы от объема погруженной части тела.
Р в возд = Р в воде = F а1 =
F а 1 = F а2 =
Задание 3 группе
Оборудование: динамометр, сосуды с чистой и
соленой водой, стальной брусок на нити.
Задание 4 группе
Оборудование: тела из пластилина одинакового объема, но разной формы, сосуд с водой, динамометр.
- Определите Архимедову силу, действующую на тело шарообразной формы
- Определите Архимедову силу, действующую на тело прямоугольной формы
- Сравните эти силы
- Сделайте вывод о зависимости (независимости) Архимедовой силы от формы тела.
Р в возд = Р в воде = F а1 =
Р в возд = Р в воде = F а 2 =
F а 1 = F а2 =
Задание 5 группе
Оборудование: сосуд с водой, динамометр, металлический цилиндр, измерительная линейка.
- Определите Архимедову силу, действующую на тело при погружении на глубину 5 см
- Определите Архимедову силу, действующую на тело при погружении на глубину 10 см
- Сравните Архимедову силу, действующую на тело при погружении на глубину на 5 см и на 10 см
- Сделайте вывод о зависимости (независимости)
Архимедовой силы от глубины погружения тела.

Р в возд = Р в воде = F а1 =
Р в возд = Р в воде = F а 2 =
F а 1 = F а2 =
В это время теоретик работает у доски по плану, данному преподавателем, он находит архимедову силу как вес вытесненной жидкости. Fa= ж g V
После получения результатов делается общий вывод. Вывод записывается суворовцами в тетрадь.
Сравнивая результат теоретического вывода и выводы экспериментаторов, видим, что они совпали.
Подытожим наши знания за два урока.
Способы нахождения Архимедовой силы
Сила, выталкивающая целиком, погруженное в жидкость тело, равна весу жидкости в объеме этого тела. Этот закон справедлив и для газов.
Существует легенда, что эта мысль посетила Архимеда, когда он принимал ванну. Давайте послушаем и посмотрим эту легенду. Сценка из поэмы Е.С. Ефимовского “История жизни, открытий, борьбы и гибель великого ученого древности Архимеда”.
Опыт с ведерком Архимеда. Демонстрирует
суворовец, игравший Архимеда. К пружине
подвешено ведерко и цилиндр. Объем цилиндра
равен внутреннему объему ведерка. Растяжение
пружины отмечено указателем. При погружении
целиком цилиндра в отливной стакан с водой видим,
что пружина сократилась, а вода вылилась в
стакан. Объем вылившейся воды равен объему
погруженного в воду тела. Выльем в ведерко воду
из стакана и увидим, что указатель пружины
возвратился к начальному положению. Значит, сила,
которая вытолкнула воду, равна весу воды,
вытесненной телом.
При погружении
целиком цилиндра в отливной стакан с водой видим,
что пружина сократилась, а вода вылилась в
стакан. Объем вылившейся воды равен объему
погруженного в воду тела. Выльем в ведерко воду
из стакана и увидим, что указатель пружины
возвратился к начальному положению. Значит, сила,
которая вытолкнула воду, равна весу воды,
вытесненной телом.
Где вы в жизни встречаетесь с Архимедовой силой? Демонстрация фотозадач
Фото №1. (Мертвое море) На территории Палестины и Израиля есть странное, на первый взгляд море. В море нельзя утонуть. Почему?
Фото №2. (Рыбы) Рыбы могут легко регулировать глубину своего погружения, меняя объем своего тела благодаря плавательному пузырю. Погружаться или всплывать будет рыба, при уменьшении объема плавательного пузыря? (Погружаться, т.к. при уменьшении объема тела, уменьшается и Архимедова сила).
Фото №3. (Кит) Кит, хотя и живет в воде, но дышит
легкими. Однако, имея легкие, кит не проживет и
часа, если окажется на суше. Почему? (Громадная
сила тяжести прижмет животное к земле. Скелет
кита не приспособлен к тому, чтобы выдержать эту
тяжесть, даже дышать кит не сможет, т.к. для вдоха
он должен расширить легкие, т.е. приподнять мышцы,
окружающие грудную клетку, а в воздухе эти мышцы
весят несколько десятков тысяч ньютонов).
Скелет
кита не приспособлен к тому, чтобы выдержать эту
тяжесть, даже дышать кит не сможет, т.к. для вдоха
он должен расширить легкие, т.е. приподнять мышцы,
окружающие грудную клетку, а в воздухе эти мышцы
весят несколько десятков тысяч ньютонов).
Фото №4. (Корабли, подводные лодки, воздушные шары) Примеры применения Архимедовой силы.
Первичное закрепление
Подумай и ответь:
№1. Одинакового объема тела (стальное и стеклянное) опущены в воду. Одинаковые ли выталкивающие силы действуют на них?
№2. Первоклассник и семиклассник нырнули в воду. Кого вода выталкивает сильнее?
№3. Один раз мальчик нырнул на глубину 2м, а в другой – на 3м. В каком случае его вода выталкивает сильнее?
Резерв* Вариант№1. Определите выталкивающую силу, действующую на полностью погруженную в море батисферу объемом 4м 3 ? Плотность морской воды 1030кг/м 3 .(41200н)
Вариант№2. Железобетонная плита объемом 0,3м 3
наполовину погружена в воду. Какова архимедова
сила, действующая на нее? Плотность воды 1000кг/м 3 . (1500н)
(1500н)
Закрепление изученного материала
Определяется задача по работе с тестами. Суворовцы слушают преподавателя, письменно и (на компьютерах) отвечают на вопросы теста и осуществляют самопроверку.
Проверь себя. Хорошо ли изучили силу Архимеда? Тест (см. приложение)
Подведение итогов урока и задание на самоподготовку
Наш урок подошел к концу пора подводить итоги. Сосчитайте все набранные вами баллы.
Рефлексия. Поднимите желтый треугольник, кто за урок получил оценку 3, зеленый квадрат кто получил – 4 и красную звездочку – 5 .
Задание на самоподготовку: Перышкин А.В. “Физика-7” § 49, упр.24 № 3,4
Творческое задание: написать сочинение на тему: “Если бы Архимедова сила исчезла…”.
| № | Вопрос | Варианты ответов | Ответ | |
| 1 | А) На первое Б) На второе В) На оба тела одинаковая | |||
| 2 | На какое тело действует меньшая выталкивающая сила? | А) На третье Б) На второе В) На первое | ||
| 3 | На какое тело действует большая архимедова сила? | А) На первое Б) На второе В) На третье | ||
| 4 | К коромыслу весов подвешены два
алюминиевых цилиндра одинакового объема. Нарушится ли равновесие весов, если один цилиндр
поместить в воду, а другой – в спирт? Нарушится ли равновесие весов, если один цилиндр
поместить в воду, а другой – в спирт? | А)Перевесит цилиндр в спирте Б)Перевесит цилиндр в воде В) Не нарушится | ||
| 5 | Определите выталкивающую силу, действующую на погруженное в воду тело объемом 0,001м3 | А) 10Н Б) 100Н В) 1000Н | ||
РАБОЧИЙ ЛИСТ
| АРХИМЕДОВА СИЛА | |
| ЗАВИСИТ ОТ: 1. 2. | НЕ ЗАВИСИТ ОТ: 1. 2. 3. |
СПОСОБЫ НАХОЖДЕНИЯ АРХИМЕДОВОЙ СИЛЫ
1.
2.
3.
Примеры проявления Архимедовой силы в быту, природе, технике
ЛИСТ ДОСТИЖЕНИЙ
ЗАДАНИЕ ДЛЯ “ТЕОРЕТИКА”
- Запишите формулу для выталкивающей силы,
действующей на тело, погруженное в жидкость.

- Как найти вес жидкости?
- Как найти массу жидкости?
- Чему равен объем вытесненной жидкости
- Как найти выталкивающую (Архимедову силу)?
- Проанализируйте формулу. Сделайте вывод: от каких факторов зависит значение Архимедовой силы?
1. Давление. Законы Паскаля и Архимеда
1) Давление твердых тел — действие силы на поверхность тела.
Давление — величина, равная отношению силы, действующей перпендикулярно поверхности, к площади этой поверхности.
2) Формула
p — давление, Па; F — приложенная сила, Н; S — площадь поверхности, М23) Единицы измерения — Па (Паскаль)
4) Способы уменьшения и увеличения давления:
Для того, чтобы увеличить давление, необходимо увеличить приложенную силу и/или уменьшить площадь ее приложения;
И наоборот, для уменьшения давления, необходимо уменьшить приложенную силу и/или увеличить площадь ее приложения.
5) Атмосферная оболочка Земли и ее значение:
Атмосфера — газовая оболочка небесного тела, удерживаемая гравитацией. Ее значение очень велико как для людей, так и для всей живой природы в целом. Она защищает нас от жесткого солнечного излучения, сохраняет тепло, дает необходимый для жизни кислород, и т. д.
Ее значение очень велико как для людей, так и для всей живой природы в целом. Она защищает нас от жесткого солнечного излучения, сохраняет тепло, дает необходимый для жизни кислород, и т. д.
6) Вес воздуха можно вычислить следующим образом: берут колбу, заполненную воздухом при обычном давлении и измеряют ее массу. Затем откачивают из нее воздух и снова измеряют ее массу, которая стала меньше. Из массы колбы с воздухом вычитают массу колбы без воздуха и данное значение как раз и является массой воздуха, который заполняет колбу. Значение напрямую зависит от объема колбы.
7) Атмосферное давление равняется примерно 760 мм ртутного столба (при 0⁰С)
8) Для измерения атмосферного давления используются специальные приборы — барометры.
9) Единицы измерения атмосферного давления — мм рт ст (миллиметр ртутного столба), бар, и др.
10) Опыт Торричелли состоит в следующем: в стеклянную колбу метровой длины, запаянную с одной стороны, налита ртуть. Горшок, набранный ртутью установлен в нормальном положении. Колба установлена в горшке так, что открытый конец находится ниже уровня поверхности ртути. При этом ртутный столб внутри колбы опускается до уровня 760 мм. Оставшаяся часть, кажущаяся пустой, по настоящему состоит из паров ртути. Воздуха там не может быть. Чем выше атмосферное давление, тем выше уровень ртутного столба и наоборот.
Горшок, набранный ртутью установлен в нормальном положении. Колба установлена в горшке так, что открытый конец находится ниже уровня поверхности ртути. При этом ртутный столб внутри колбы опускается до уровня 760 мм. Оставшаяся часть, кажущаяся пустой, по настоящему состоит из паров ртути. Воздуха там не может быть. Чем выше атмосферное давление, тем выше уровень ртутного столба и наоборот.
11) Передача давления жидкостями и газами. Жидкости и газы передают давление по разному. Давление жидкости прямо зависит от высоты ее столба. Давление газов зависит от концентрации молекул, а еще и от их температуры.
12) Закон Паскаля: Давление, производимое на жидкость или газ, передается в любую точку жидкости или газа одинаково по всем направлениям.
13) Давление жидкости и газа на стенки и дно сосуда. Внутри жидкости на любой ее высоте существует давление, которое на одном и том же уровне одинаково по всем направлениям, в том числе и вверх. С глубиной давление возрастает. Так что на глбине дна, давление на дно равно давлению на стенки при дне. Сверху давление меньше, чем у дна.
Так что на глбине дна, давление на дно равно давлению на стенки при дне. Сверху давление меньше, чем у дна.14) Формула
15) Закон Архимеда — зависимость давления в жидкости или газе от глубины погружения тела приводит к появлению выталкивающей силы, действующей на любое тело, погруженное в жидкость или газ.
16) Условия плавания тел — любой предмет может плыть, если его плотность меньше, чем плотность той жидкости, в которой он плывет. Это относится как к кораблям, так и к некоторым воздушным средствам передвижения — аэростатам, дирижаблям, воздушным шарам.
Выталкивающая сила. Закон Архимеда
Урок по теме «Выталкивающая сила. Закон Архимеда. »
с элементами исследования.
Тип урока: урок изучения нового учебного материала.
Вид урока: урок теоретических и практических работ исследовательского типа.
Методы и приемы обучения: эвристический и исследовательский метод.
Структура урока: 1.Организационный момент. Домашнее задание.
2. Актуализация прежних знаний.
3.Формирование новых понятий.
4.Формирование умений и навыков.
Цель урока: продолжить формирование умений применять приобретенные знания в новой учебной ситуации, анализировать учебный материал, добывать знания путем эксперимента по намеченному плану, по результатам экспериментов делать выводы и обобщения, имея свое собственное мнение и прислушиваясь к мнению других, давать оценку своей деятельности и деятельности одноклассников; сформировать понятие архимедовой силы, вывести формулу для ее определения на основе закона Паскаля; осветить роль Архимеда в физике.
Обеспечение урока.
УМК: Генденштейн Л.Э.
Приборы и оборудование: на демонстрационном столе: емкость с пресной водой, с соленой водой, мяч, металлический цилиндр, динамометр, яйцо.
на ученических партах: (в зависимости от типа предложенных экспериментов) динамометры, мензурки, алюминиевый и медный цилиндры, стаканы с пресной водой, с маслом, пластилин, тела разного объема из пластилина.)
Интерактивные доска, раздаточный материал (рабочие листы для фронтального опроса и для оформления исследовательской работы с таблицами-заготовками).
Ход урока.
1.Организационный момент и запись домашнего задания: параграф учебника, номера задач из задачника (из предложенных номеров выбрать
задания с учетом индивидуальных возможностей.)
2.Актуализация опорных знаний.
Для того чтобы перейти к изучению следующей темы предлагаю ученикам вспомнить уже изученный материал, прибегая к фронтальному опросу (тип проверки: взаимопроверка после выведения учителем слайда с ответами на доску; ответы записываются на листе отчета, на этом же листе будет вся дальнейшая работа, листы после урока сдаются учителю для выставления оценок в журнал. )
)
Перечень вопросов: (нечетные — первому варианту, четные второму)
1.Формула для определения массы тела.
2.Формула для определения объема бруска.
3 Формула для определения давления твердого тела.
4. Формула для определения силы давления.
5.Формула для определения гидростатического давления.
6.Что происходит с давлением жидкости на тело при увеличении глубины его погружения.
7.Как называется прибор для измерения силы.
8.Перечислите все известные вам силы.
9.Как измерить вес тела в воздухе.
10.Сформулируйте закон Паскаля.
Открываю первый слайд с ответами, ребята обмениваются листочками и проверяют друг друга (каждый правильный ответ-1 балл, неправильный — минус 1балл), выставляя количество баллов.
3. Формирование новых понятий. Внимание на доску.
Формирование новых понятий. Внимание на доску.
Предлагаю ребятам второй слайд с отрывком из рассказа А.П.Чехова «Степь».
«Егорушка разбежался и полетел с полутора саженой высоты, описав в воздухе
дугу, он упал в воду, но дна не достал. Какая-то сила, холодная и приятная на
ощупь, подхватила его и понесла обратно наверх.»
Прочитав текст, предлагаю ребятам выдвинуть гипотезу об услышанной силе и приглашаю желающего провести эксперимент для всех у доски, имея мяч и емкость с водой, показав действие такой же силы на мяч при погружении его в воду. Как правило, после эксперимента данную силу называют выталкивающей.
Открываем рабочую тетрадь и записываем тему урока: «Выталкивающая сила».
Затем предлагаю опустить в воду гирю, обнаруживаем, что гиря утонула; опускаем яйцо в воду пресную, в воду соленую; видим разный результат.
Выявили проблему: на все ли тела действует выталкивающая сила?
Как можно проблему решить: либо теоретически, либо практически. Пробуем оба способа.
Раз сила есть измерим ее с помощью динамометра.
Р1 (вес тела в воздухе)
Опускаем гирю на динамометре в воду, измеряем вес тела в жидкости Р2. Видим, что силы не равны, ребята делают вывод, что разница этих сил и есть выталкивающая сила.
Открываю третий слайд, на котором демонстрируется первый способ определения выталкивающей силы.
F=РВ ВОЗДУХЕ –РВ ЖИДКОСТИ
Записываем формулу в тетрадь.
Пробуем определить выталкивающую силу теоретически , используя понятие равнодействующей силы, сил давления со стороны жидкости на тело и повторенные ранее формулы.
К доске вызывается ученик для вывода формулы. Ему предлагается рисунок на интерактивной доске (брусок внутри жидкости в сосуде). Ученик расставляет все силы, действующие на все грани бруска, показывает, какие силы равны и почему, какие не равны и как найти их равнодействующую, которая и является выталкивающей. Затем записывает формулу силы давления, гидростатического давления, формулу объема бруска и получает расчетную формулу для выталкивающей силы. Если вышедший к доске ученик испытывает, какие-либо затруднения пользуемся, помощью класса за дополнительные баллы, либо помогает учитель, наводящими вопросами. На местах в тетрадях проводится такая же работа.
Ему предлагается рисунок на интерактивной доске (брусок внутри жидкости в сосуде). Ученик расставляет все силы, действующие на все грани бруска, показывает, какие силы равны и почему, какие не равны и как найти их равнодействующую, которая и является выталкивающей. Затем записывает формулу силы давления, гидростатического давления, формулу объема бруска и получает расчетную формулу для выталкивающей силы. Если вышедший к доске ученик испытывает, какие-либо затруднения пользуемся, помощью класса за дополнительные баллы, либо помогает учитель, наводящими вопросами. На местах в тетрадях проводится такая же работа.
Полученную формулу записываем в тетрадь с расписыванием всех входящих величин и их единиц измерения. FF
F=Ps=pghs=pgv
Р-плотность жидкости (кг/м3)
g=10Н/кг-постоянная величина
V-объем тела (м3), или части тела, погруженной в жидкость.
Далее сообщаю учащимся, что впервые эту силу измерил древнегреческий ученый Архимед, сформулировавший закон , названный законом Архимеда, ищем формулировку закона в учебнике и записываем ее в тетрадь, и предлагаю для просмотра слайд с краткой исторической справкой об Архимеде и видеофрагмент из мультфильма: «Коля, Оля и Архимед». (Во время просмотра ребята, сменив деятельность, немного расслабятся и отдохнут).
(Во время просмотра ребята, сменив деятельность, немного расслабятся и отдохнут).
После просмотренного ставим следующую проблему,: от каких факторов зависит и не зависит выталкивающая сила, которую называют архимедовой силой.
И предлагаю решить эту проблему опытным путем.
4.Формирование умений и навыков. Практическая часть (работа в парах).
Предлагаю ребятам, посмотрев на оборудование, стоящее перед ними, подумать, от каких факторов можно определить зависимость или независимость архимедовой силы. Как правило, выдвигаются предположения, или помогаю наводящими вопросами:
От объема тела
От плотности тела
От формы тела
От плотности жидкости
От глубины погружения.
В зависимости от стоящего на столах оборудования и предложенных отчетных листов на столах ребята проводят эксперимент и сами делают выводы, которые потом озвучат для класса.
Отчетные листы по группам и набор оборудования на столах.
1.Сосуд с водой, динамометр, алюминиевый и медный цилиндры, нить.
№ | Вещество цилиндр | Плотность | Вес тела в воздухе, Р1,Н | Вес тела в жидкости, Р2, Н | Выталкивающая сила, FА=Р1-Р2,Н |
1 | Алюминий | ||||
2 | Медь |
Вывод: в результате опыта мы выяснили, что архимедова сила______________________________
2. Сосуд с водой, тела разного объема из пластилина, динамометр, нить.
Сосуд с водой, тела разного объема из пластилина, динамометр, нить.
№ | Объём тела, см3 | Вес тела в воздухе | Вес тела в жидкости | Выталкивающая сила |
1 | ||||
2 |
Вывод: в результате опыта мы выяснили, что архимедова сила___________________________
3.Динамометр, нить, сосуд с пресной водой, сосуд с маслом, алюминиевый цилиндр.
№ | Вес тела в воздухе | Жидкость | Вес тела в жидкости | Выталкивающая сила |
1 | Вода | |||
2 | Масло |
Вывод: в результате опыта мы выяснили, что архимедова сила___________________________
4. Мензурка с водой, алюминиевый цилиндр, нить, динамометр.
Мензурка с водой, алюминиевый цилиндр, нить, динамометр.
Высота столба жидкости | Вес тела в воздухе | Вес тела в жидкости | Выталкивающая сила |
5см | |||
15см |
Вывод: в результате опыта мы выяснили, что архимедова сила___________________________
Кусок пластилина, сосуд с водой, динамометр.
Форма тела | Вес тела в воздухе | Вес тела в жидкости | Архимедова сила |
Шар | |||
Куб |
Вывод: в результате опыта мы выяснили, что архимедова сила___________________________
После отведенного времени ребята озвучивают свои выводы, затем работа с учебником: ищем подтверждение или опровержение их в параграфе, закрепляя материал, и записываем выводы в форме таблицы по предложенному на доске варианту. При этом выставляет каждый себе по баллу за верное утверждения, но не снимают баллы за неверное.
При этом выставляет каждый себе по баллу за верное утверждения, но не снимают баллы за неверное.
Архимедова сила | |
Зависит от | Не зависит от |
Объема погруженной части тела | Плотности тела |
Плотности жидкости | Формы тела |
Глубины погружения | |
Итог урока. (Рефлексия).
Каждый ученик считает свои собственные баллы и записывает их количество на лист после вывода. Если баллов 5 и больше можно в дневник поставить оценку « отлично»; меньшее количество баллов переходит в накопитель баллов (переносятся в рабочую тетрадь).
Все рабочие листы передаются учителю для подтверждения баллов.
Урок закончен.
Используемые источники.
1.Рисунок. http://images.yandex.ru/yandsearch?text=рисунки%20к%20архимедовой%20силы&stype=image&lr=10871&noreask=1&source=wiz.
2.Материалы http://images.yandex.ru/yandsearch?text=рисунки%20к%20архимедовой%20силы&stype=image&lr=10871&noreask=1&source=wiz
3.Отрывок из мультфильма. http://ratkino.ru/video/obzori-i-uroki/16-olja-iz-cheljabinskoj-oblasti.html
Закон Архимеда
Принцип Архимеда гласит, что:
«Если твердое тело плавает или погружено в жидкость, жидкость оказывает направленную вверх силу тяги — a выталкивающая сила — на тело, равную к силе тяжести, действующей на жидкость, вытесняемую телом».
Буяющая сила может быть выражена как
F B = W
= V γ = V γ
= V ρ G (1)
где
F B = Buyant Force, действующие на погруженное или плавающее тело (N, LB F )
W = Вес (сила тяжести) смещенной жидкости (N, LB F )
V = объем тела под поверхностью жидкости (м 3 , футы 3 )
γ = ρ г = удельный вес жидкости (вес на единицу объема) (Н/м 3 , LB F / FT 3 )
)
ρ = плотность жидкости (кг / м 3 , слизни / футы 3 )
г = ускорение гравитации у (9.81 м/с 2 , 32,174 фут/с 2 )
м
3 . Для плавучего тела выталкивающая сила равна весу воды, вытесненной телом.
F B = W
или
или
V B ρ B G = V W ρ W G
Где
= Кузов объема (M 3 )
ρ b = плотность тела ( кг / м 3 )
= Объем воды (M 3 )
ρ W = плотность воды ( кг/м 3 )
Уравнение можно преобразовать в
90 002 ρ B = V W ρ W / W / V Bс 95% кузова погружены на
0. 95 V B = V W
95 V B = V W
9
и плотность тела можно рассчитать как
ρ b = 0,95 v b (1000 кг / м 3 ) / V b
= 950 кг/м 3
/4 x 8 (дюймов)
погружен в воду с плотностью 1.940 слагов/фут 3 . Объем кирпича можно рассчитатьV кирпич = (3 5/8 дюйма) (2 1/4 дюйма) (8 дюймов)
= 65,25 дюйма 3
действующая на кирпич, равна весу воды, вытесненной кирпичом, и может быть рассчитана как
F B = (( 65,25 in 3 ) / (1728 дюйм/фут 3 )) ( 1,940 проб/фут 3 ) ( 32.174 FT / S 2 ) )
= 2.36 LB F
Вес или сила тяжести, действующие на кирпича — общий красный кирпич имеет удельную гравитацию 1. 75 — можно рассчитать до
75 — можно рассчитать до
B = (2.36 LB F ) 1.75
= 4.12 LB F
Полученная сила, действующая на кирпиче, может быть рассчитана как
W (WB — FB) = (4 .12 фунтов F ) — (2.36 LB F )
= 1.76 LB F
Archimedes Принцип: Формула, вывод, приложения
Принцип Archimedes, впервые заявленный Archimedes, рассказывает нам связь между кажущийся вес объекта, погруженного в воду, и вес вытесненной им воды. Он включает в себя такие факторы, как Выталкивающая сила , с помощью которых устанавливается эта взаимосвязь. Принцип Архимеда также находит свое применение в некоторых случаях реальной жизни.
Принцип Архимеда: Определение
Принцип Архимеда гласит, что когда объект полностью или частично погружен в воду, он испытывает восходящую выталкивающую силу, равную весу воды, вытесненной погруженным объектом.
Выталкивающая сила – это, по существу, направленная вверх сила, которая вызывает видимое уменьшение веса погруженного объекта. Также уменьшение веса объекта равно вытесненной им воде.
Принцип Архимеда: Важные примечания
Принцип Архимеда: Формула и деривация
Формула для принципов Archimedes может быть дана как
FB = ρ XGX V
FB = Buyant Force,
г = ускорение к силе тяжести,
p = плотность
V = объем.
Вывод
Мы знаем, что
Вес = масса × сила тяжести (м × г)
Следовательно, масса = плотность × объем (p × V)
Таким образом, вес вытесненной жидкости =
W = плотность × объем × сила тяжести
W = p × V × g
Из принципа Архимеда:
Вес вытесненной жидкости = кажущийся вес объекта = выталкивающая сила
Итак,
F b = p × V × V g,
, где
F b = выталкивающая сила,
p = плотность жидкости,
V = объем жидкости
g = ускорение свободного падения.
Кажущийся вес: Пояснение
Фактический вес объекта, помещенного на любую твердую поверхность, направлен вниз через центр тяжести. Когда этот объект погружается в воду, он испытывает восходящую силу, которая является выталкивающей силой.
Эта выталкивающая сила в некоторой степени уменьшает падающую силу объекта, и объект кажется легче, что соответствует кажущемуся весу объекта.
Чтобы рассчитать кажущийся вес, можно вычесть выталкивающую силу из фактического веса объекта.
Эффекты закона Архимеда: плавание и опускание
Когда объект погружен в воду, он либо всплывает, либо тонет в зависимости от плотности объекта и жидкости. Примем W 1 за действительный вес объекта и W 2 за выталкивающую силу.
- Когда W 1 > W 2 , плотность объекта больше плотности жидкости, из-за которой он тонет.
- Когда W 1 = W 2 , плотности объекта и жидкости равны, и объект будет плавать в воде на любой глубине и оставаться полностью погруженным в жидкость.

- Когда W 1 < W 2 , плотность объекта меньше плотности жидкости, из-за чего он плавает (частично погружен).
Принцип Архимеда: Приложения
Принцип Архимеда имеет несколько реальных применений.
- Принцип Архимеда помогает вычислять объем и плотность объектов. Соотношение составляющих металлов в сплаве можно определить с помощью закона Архимеда.
- Корабли плывут по воде благодаря Теории Архимеда.Корабли сделаны полыми, чтобы их плотность была меньше воды и поэтому они оставались погруженными в воду лишь частично.
- Глубина плавания подводных лодок определяется по закону Архимеда. Подводные лодки имеют балластную цистерну, в которую заливается вода. Вес подводной лодки может быть увеличен или уменьшен путем изменения количества воды в балластной цистерне, которая затем используется для определения глубины, на которой она плавает.
- Ареометры, используемые для расчета плотности жидкости, работают по закону Архимеда.

Интересные факты, основанные на законе Архимеда
- Плавающие объекты не имеют видимого веса.
- В 250 г. до н.э. Теория Архимеда сыграла ключевую роль в изучении гидростатики.
Что нужно помнить на основе закона Архимеда
- Закон Архимеда, открытый Архимедом, объясняет взаимосвязь между кажущимся весом объекта, погруженного в воду, и весом вытесненной им воды.
- Выталкивающая сила — это направленная вверх сила, ответственная за кажущееся уменьшение веса погруженного объекта.
- Формула для принципа Archimedes может быть предоставлена как
- F B = ρ xgx V = ρ xgx v = ρ xgx v
5
F B = Buyant Force,
G = ускорение из-за гравитации,
p = плотность
V = объем.
- Когда объект погружен в воду, он либо всплывает, либо тонет в зависимости от плотности объекта и жидкости.
- Принцип Архимеда имеет несколько применений в реальной жизни.
 Корабли и подводные лодки плавают/погружаются по этому принципу.Через него также можно рассчитать объем и плотность объектов.
Корабли и подводные лодки плавают/погружаются по этому принципу.Через него также можно рассчитать объем и плотность объектов.
Примеры вопросов, основанные на законе Архимеда
Вопросы 1. Деревянный брусок имеет следующие размеры: 0,12 на 0,34 на 0,43 кубических метра. Он плывет по реке самой широкой стороной вниз. Древесина погружена на высоту 0,053 метра. Какова масса куска дерева? [3 балла]
Отв. Согласно закону Архимеда, вес вытесненной воды равен выталкивающей силе:
W 1 = F b
Чтобы удерживать дерево на плаву, выталкивающая сила должна иметь ту же величину, что и сила
F b = масса дерева × г
Объем вытесненной воды равен
Таким образом, масса вытесненной воды равна
Вопрос 2.
 Сферический шар плотностью ρ=0,70 кгL имеет радиус r=10см. Если мяч положить на поверхность воды и отпустить, какая часть мяча погрузится в воду? g=10 мс 2 [3 балла]
Сферический шар плотностью ρ=0,70 кгL имеет радиус r=10см. Если мяч положить на поверхность воды и отпустить, какая часть мяча погрузится в воду? g=10 мс 2 [3 балла] Ответ. Мы знаем, что,
Если объект плавает, выталкивающая сила равна весу объекта.
Объем сферы:- 4/3πr³
V = 4/3π(10 см) ³
V = 4000π/3 см³
V= 4π/3 л
Теперь, умножая это на плотность, получаем:
М = 4π/3 Д × 0.70 кг/л
= 2,93 кг.
Масса вытесненной воды. Теперь
V= m/p = 2,93 л
Вопрос 3. Вы погружаете баскетбольный мяч в воду до тех пор, пока половина его объема не окажется под водой. Если радиус баскетбольного мяча равен 12 см, какова выталкивающая сила мяча из-за воды? [4 балла]
Ответ. Выталкивающая сила равна массе вытесненной воды, умноженной на ускорение свободного падения:
Объем вытесненной воды равен половине объема баскетбольного мяча:
V вытесненной воды = ½ V баскетбольного мяча
= 2/3πr³
Здесь r = 12 см.
 В метрах радиус равен
В метрах радиус равенИспользуя уравнение плотности, масса вытесненной воды равна
Выталкивающая сила равна
M (вытесненная вода) = P воды × V вытесненной воды
Выталкивающая сила равна
F= M (вытесненная вода)
=P воды × V вытесненной воды
= 35 N
Ques 4. Металлический шар радиусом 2 см полностью погружен в воду. Найдите силу плавучести при плотности воды 1000 кг на метр кубический.[2 балла]
Ответ. Радиус сферы = 2 см = 0,02 м
Объем сплошной сферы =
Выталкивающая сила = плотность воды x объем под водой x ускорение свободного падения
Вопрос 5. Что тяжелее: хлопок или железо ? Ответ на основе закона Архимеда. [1 балл]
Ответ. Кажущийся вес обоих материалов одинаков, но выталкивающая сила, которую испытывает хлопок, велика, поскольку объем хлопка больше, чем объем железа.Следовательно, истинный вес хлопка больше.

Вопросы 6. В каком из следующих случаев корабль будет плавать выше: в пресной или морской воде? Объяснять. [1 балл]
Ответ. Выталкивающая сила равна весу вытесненной жидкости. Плотность соленой воды больше, чем пресной. Таким образом, требуется вытеснить меньше воды из-за высокой плотности, чтобы поддерживать плавучесть объекта. Таким образом, корабль будет плавать выше в соленой воде из-за ее высокой плотности.
Принцип Архимеда. Узнайте о его формулах с выводом
Вы когда-нибудь задумывались, почему монета тонет в воде, а корабль нет?
Ответить на этот вопрос можно с помощью закона Архимеда.Архимед предположил, что
«Когда тело частично или полностью погружено в покоящуюся жидкость, оно испытывает направленную вверх силу, равную весу вытесненной жидкости».
В этой статье давайте разберемся с принципом Архимеда. Перед этим давайте узнаем о жидкости.
Жидкость : Вещества, обладающие способностью течь, определяются как жидкости.
 Пример: нефть, вода, газы и т. д.
Пример: нефть, вода, газы и т. д.Для простоты предположим, что жидкостью является вода.Теперь рассмотрим стакан, наполненный водой (жидкостью). Когда тело погружается в воду, оно должно создавать пространство между молекулами воды. Это пространство равно объему погруженного тела. Следовательно, такой же объем воды вытесняется (выпадает из стакана).
Согласно закону Архимеда, на тело действует направленная вверх сила, равная весу вытесненной воды. Эта сила известна как «плавучесть» или «выброс», которая направлена нормально к земле в направлении вверх. Поскольку эта сила действует в направлении, противоположном гравитационному притяжению, вес тела, погруженного в воду, оказывается меньше его веса в воздухе.Вес объекта при погружении в воду, также называемый кажущимся весом, рассчитывается как:
вес объекта в воде = вес объекта в воздухе (вакуум) – вес вытесненной воды
Принцип Архимеда ФормулаРассмотрим твердый куб со стороной l , погруженный в жидкость на глубину d от поверхности жидкости, как показано на рисунке ниже-
Поскольку твердое тело погружено в жидкости на каждую сторону куба действует сила из-за давления внутри жидкости.
 Пусть P t и P b давлением сверху и снизу куба соответственно. Пусть F t и F b — силы, действующие на верхнюю и нижнюю части куба соответственно.
Пусть P t и P b давлением сверху и снизу куба соответственно. Пусть F t и F b — силы, действующие на верхнюю и нижнюю части куба соответственно.Мы знаем, что
F T = P T L 2 (Force = давление • площадь поверхности)F B = P B L 2
действующие на остальные стороны куба, уравновешиваются, так как они равны, противоположны и направлены.
Пусть F N Будьте сети, действующие на куб, то
F N = F B -F T
= P B L 2 -P T L 2
= (P B -PR T ) L 2 — (1)
Now
P T = ⍴ DG ( Давление = плотность•глубина•ускорение свободного падения)
Где ⍴ — плотность жидкости
Аналогично
P b =⍴( d+l)g
=⍴ 7 90 007 dg1 + 90 LG
Подставление в (1)
F N = (⍴ DG + ⍴ LG — ⍴ DG ) L 2
F N = ⍴ GL 3
Где л 3 — объем куба, который также равен объему вытесненной воды
Следовательно,
F n = M w г (Масса = 9 0002 Плотность) Где M w – масса вытесненной воды.

Следовательно, результирующая сила, действующая на куб из-за давления жидкости, также известная как плавучесть, рассчитывается как
F b = ⍴ гВ
Где F b : выталкивающая сила
жидкость
В: Объем вытесненной жидкости
г: Ускорение свободного падения
Эта формула чрезвычайно важна, если помнить об основной программе JEE. Убедитесь, что вы хорошо понимаете концепцию.
Расчет кажущегося веса с использованием формулы принципа Архимеда Кажущийся вес = вес объекта в воздухе (вакууме) – вес вытесненной жидкости вытесненное равно объему погруженного тела. - Кажущееся уменьшение веса погруженного объекта равно весу вытесненной жидкости.
- Выталкивающая сила (или выталкивающая сила) пропорциональна плотности жидкости и не зависит от плотности объекта.
Итак, все дело в законе Архимеда. Попрактикуйтесь в том же в нашем бесплатном приложении Testbook. Скачать сейчас!
Скачать сейчас!
Q.1 Как был открыт принцип Архимеда?
Ответ.1 С открытием закона Архимеда связана интересная история. Архимед провел большую часть своей жизни в Сиракузах. Легенды гласят, что царь Сиракуз, царь Гиерон II, подозревал, что заказанная им золотая корона подделана каким-то другим металлом того же цвета, что и золото. Он поручил Архимеду определить, сделана корона из чистого золота или нет. В то время было трудно определить чистоту золота, однако было известно, что золото является самым плотным материалом, известным в то время.Легенды также гласят, что, когда Архимед вошел в ванну, он увидел, что из воды выпало равное количество воды. Это вдохновило его связать это с плотностью, и с дальнейшими подтверждающими экспериментами он пришел к тому, что мы знаем как принцип Архимеда. После открытия принципа и того, как его можно применять для определения плотности, он выбежал на улицу с криком «Эврика!» «Эврика!» (в переводе с греческого означает «Я нашел!»).
Q.2 Почему важен принцип Архимеда?
Ответ.2Поскольку принцип Архимеда помогает понять, почему объект тонет или плавает, он помогает в проектировании кораблей и создании конструкций современных машин и транспортных средств, которые передвигаются по воде или под водой.
Q.3 Почему некоторые объекты плавают, а некоторые нет, даже если они сделаны из одного и того же материала?
Ответ 3Теперь вернемся к вопросу, поднятому в начале статьи. Если объект тонет в воде, это означает, что гравитационное притяжение больше, чем выталкивающая сила i.E,
M O G > M W G
или Mили M O > M W
или V O > V⍴ W (Mass = Volume • плотность)
или ⍴ o > ⍴ w
Следовательно, если объект тонет, если его плотность больше плотности жидкости.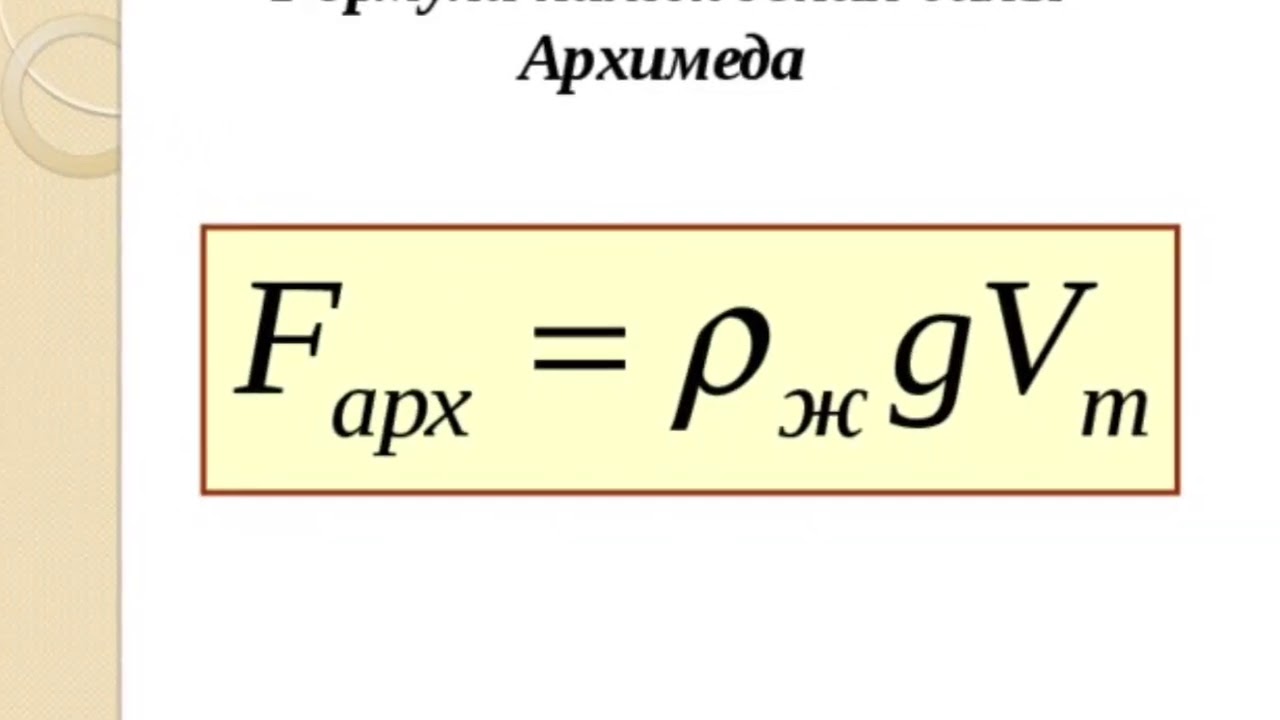
Теперь, даже если монета и корабль сделаны из одного и того же материала, форма и дизайн будут влиять на плотность объекта. Следовательно, следует учитывать плотность объектов, а не плотность используемого материала.
Q.4 Выполняется ли принцип Архимеда в случае газов?
Ответ 4Да, принцип Архимеда применим ко всем жидкостям, и газы также относятся к категории жидкостей. Газы также обладают выталкивающей силой, но она мала по величине.
В.5 В каких случаях принцип Архимеда не работает?
Ответ 5 Эксперименты показали исключение из принципа Архимеда, известное как нижний (или боковой) случай. Когда сторона объекта касается дна (или стороны) контейнера с жидкостью, он погружается в него. Кроме того, жидкость не просачивается вдоль этой стороны. В этом случае полная сила, действующая на объект, оказывается отличной от рассчитанной по закону Архимеда.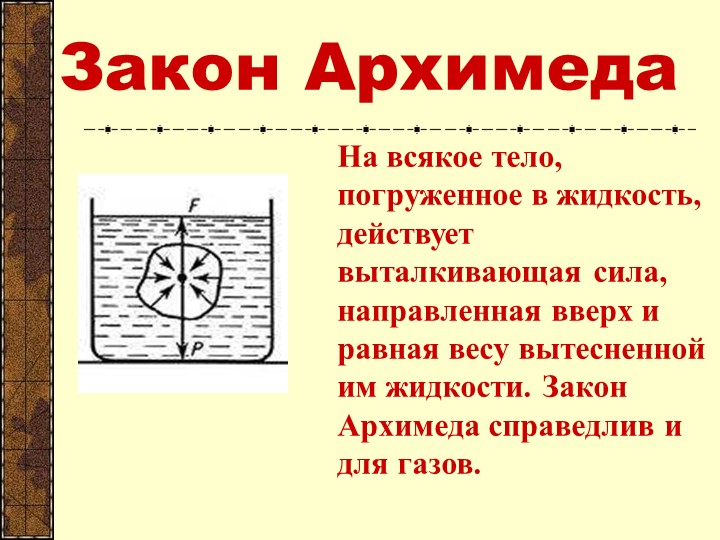
Создайте бесплатную учетную запись, чтобы продолжить чтение
Получайте мгновенные оповещения о вакансиях бесплатно!
Получите ежедневные капсулы GK и текущих событий и PDF-файлы
Получите более 100 бесплатных пробных тестов и викторин
Подпишитесь бесплатно У вас уже есть аккаунт? Войти
Следующий пост
Принцип Архимеда — Колледж физики
Цели обучения
- Определение выталкивающей силы.
- Государственный закон Архимеда.
- Поймите, почему объекты плавают или тонут.
- Понять взаимосвязь между плотностью и законом Архимеда.
Когда вы встаете после принятия теплой ванны, ваши руки кажутся странно тяжелыми. Это потому, что у вас больше нет плавучей поддержки воды. Откуда берется эта выталкивающая сила? Почему одни вещи плавают, а другие нет? Получают ли объекты, которые тонут, какую-либо поддержку от жидкости? Ваше тело поддерживается атмосферой или это касается только гелиевых шаров? (См.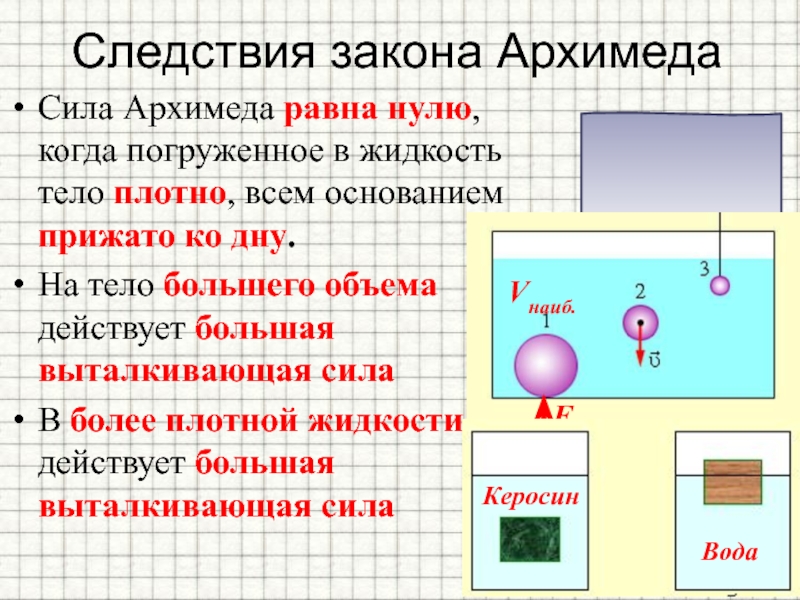 (Рисунок).)
(Рисунок).)
(а) Даже объекты, которые тонут, как этот якорь, частично поддерживаются водой при погружении. (b) Подводные лодки имеют регулируемую плотность (балластные цистерны), так что они могут плавать или тонуть по желанию. (Фото: Allied Navy) (c) Наполненные гелием воздушные шары тянут вверх свои нити, демонстрируя плавучесть воздуха. (кредит: Кристалл)
Ответы на все эти и многие другие вопросы основаны на том факте, что давление в жидкости увеличивается с глубиной. Это означает, что восходящая сила на нижней части объекта в жидкости больше, чем направленная вниз сила на верхней части объекта.На любой объект в любой жидкости действует направленная вверх или выталкивающая сила. (См. (Рисунок).) Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Выталкивающая сила
Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости.
Давление из-за веса жидкости увеличивается с глубиной, так как . Это давление и связанная с ним восходящая сила на дне цилиндра больше, чем направленная вниз сила на верхней части цилиндра. Их отличие заключается в выталкивающей силе. (Горизонтальные силы компенсируются.)Насколько велика эта выталкивающая сила? Чтобы ответить на этот вопрос, подумайте о том, что происходит, когда погруженный объект вынимают из жидкости, как показано на рисунке.
Пространство, которое он занимает, заполнено жидкостью, имеющей вес .Этот вес поддерживается окружающей жидкостью, поэтому выталкивающая сила должна равняться весу жидкости, вытесненной объектом. Это дань уважения гению греческого математика и изобретателя Архимеда (ок. 287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
287–212 до н. э.), который сформулировал этот принцип задолго до того, как понятия силы были прочно установлены. Говоря словами, принцип Архимеда выглядит следующим образом: выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
где — выталкивающая сила, а — вес жидкости, вытесненной телом.Принцип Архимеда действителен в целом для любого объекта в любой жидкости, полностью или частично погруженного в воду.
Закон Архимеда
В соответствии с этим принципом выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости. В форме уравнения принцип Архимеда равен
.где — выталкивающая сила, а — вес жидкости, вытесненной телом.
Humm … Высокотехнологичные купальники для тела были представлены в 2008 году в рамках подготовки к Олимпийским играм в Пекине.Одна проблема (и международное правило) заключалась в том, что эти костюмы не должны давать никакого преимущества в плавучести. Как вы думаете, можно ли проверить это правило?
Как вы думаете, можно ли проверить это правило?
Установление связей: домашнее расследование
Плотность алюминиевой фольги в 2,7 раза больше плотности воды. Возьмите кусок фольги, скатайте его в шар и бросьте в воду. Он тонет? Почему или почему нет? Можете ли вы заставить его утонуть?
Плавающие и тонущие
Бросьте кусок глины в воду. Он утонет.Затем слепите кусок глины в форме лодки, и она будет плавать. Из-за своей формы лодка вытесняет больше воды, чем глыба, и испытывает большую выталкивающую силу. То же самое и со стальными кораблями.
Расчет выталкивающей силы: зависимость от формы
(a) Рассчитайте выталкивающую силу на 10 000 метрических тонн твердой стали, полностью погруженной в воду, и сравните ее с весом стали. б) Какова максимальная выталкивающая сила, которую вода могла бы воздействовать на ту же сталь, если бы из нее сделали лодку, способную вытеснять воду?
Стратегия для (а)
Чтобы найти выталкивающую силу, мы должны найти вес вытесненной воды. Мы можем сделать это, используя плотности воды и стали, указанные на (рис.). Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Мы можем сделать это, используя плотности воды и стали, указанные на (рис.). Заметим, что, поскольку сталь полностью погружена в воду, ее объем и объем воды одинаковы. Зная объем воды, мы можем найти ее массу и вес.
Раствор для (а)
Сначала мы используем определение плотности, чтобы найти объем стали, а затем подставляем значения массы и плотности. Это дает
Поскольку сталь полностью погружена в воду, это также объем вытесненной воды, .Теперь мы можем найти массу вытесненной воды из соотношения между ее объемом и плотностью, оба из которых известны. Это дает
По закону Архимеда вес вытесненной воды равен , поэтому выталкивающая сила равна
Вес стали , что намного больше, чем выталкивающая сила, поэтому сталь останется погруженной. Обратите внимание, что выталкивающая сила округляется до двух цифр, потому что плотность стали выражается только двумя цифрами.
Стратегия для (б)
Здесь нам дан максимальный объем воды, который может вытеснить стальная лодка. Выталкивающая сила равна весу этого объема воды.
Выталкивающая сила равна весу этого объема воды.
Раствор для (б)
Масса вытесненной воды определяется по ее отношению к плотности и объему, оба из которых известны. То есть
Максимальная выталкивающая сила равна весу такого количества воды, или
Обсуждение
Максимальная выталкивающая сила в десять раз превышает вес стали, а это означает, что корабль может нести груз, в девять раз превышающий его собственный вес, и не утонуть.
Установление связей: домашнее расследование
Кусок бытовой алюминиевой фольги равен 0.Толщина 016 мм. Возьмите кусок фольги размером 10 на 15 см. а) Какова масса этого куска фольги? (b) Если фольгу сложить так, чтобы получились четыре стороны, и добавить к этой «лодке» скрепки или шайбы, то какая форма лодки позволит вместить больше всего «груза» при погружении в воду? Проверьте свой прогноз.
Плотность и закон Архимеда
Плотность играет решающую роль в законе Архимеда. Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он.Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Средняя плотность объекта — это то, что в конечном итоге определяет, плавает ли он.Если его средняя плотность меньше плотности окружающей жидкости, он будет плавать. Это связано с тем, что жидкость, имеющая более высокую плотность, содержит большую массу и, следовательно, больший вес в том же объеме. Таким образом, выталкивающая сила, равная весу вытесненной жидкости, больше веса объекта. Точно так же объект, более плотный, чем жидкость, утонет.
Степень погружения плавучего объекта зависит от того, как плотность объекта связана с плотностью жидкости. Например, на (Рисунке) незагруженный корабль имеет меньшую плотность и меньшая часть его погружена по сравнению с тем же загруженным кораблем.Мы можем получить количественное выражение для фракции, погруженной в воду, учитывая плотность. Погруженная доля представляет собой отношение погруженного объема к объему объекта, или
. Погруженный объем равен объему вытесненной жидкости, который мы называем . Теперь мы можем получить связь между плотностями, подставив в выражение.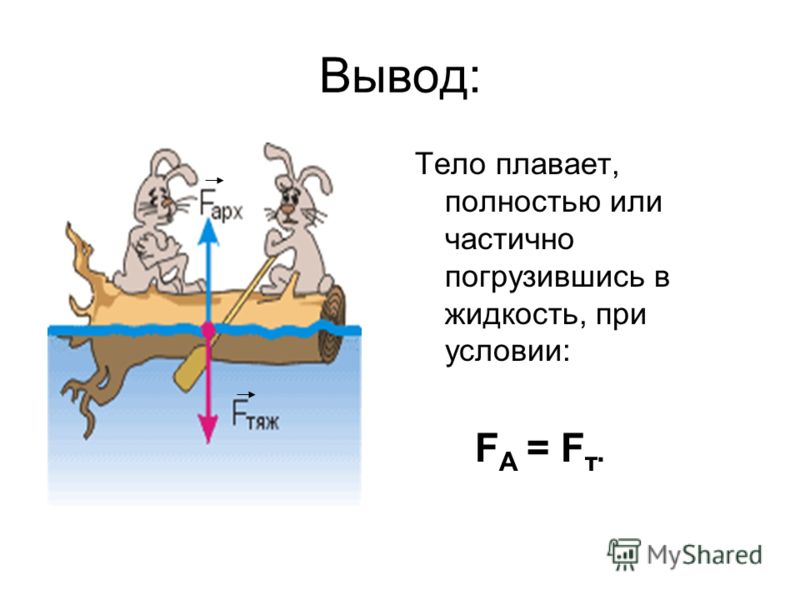 Это дает
Это дает
где — средняя плотность объекта, а — плотность жидкости. Поскольку объект плавает, его масса и масса вытесненной жидкости равны, поэтому они исключаются из уравнения, в результате чего остается
Незагруженный корабль (а) плавает выше в воде, чем загруженный корабль (б).
Мы используем это последнее соотношение для измерения плотности. Это делается путем измерения доли погруженного плавучего объекта, например, с помощью ареометра. Полезно определить отношение плотности объекта к жидкости (обычно воде) как удельный вес:
где — средняя плотность объекта или вещества, а — плотность воды при 4,00°C. Удельный вес безразмерен и не зависит от того, какие единицы измерения используются для . Если объект плавает, его удельный вес меньше единицы.Если он тонет, его удельный вес больше единицы. Более того, доля плавучего объекта, находящегося под водой, равна его удельному весу. Если удельный вес объекта точно равен 1, то он останется в жидкости во взвешенном состоянии, не тонет и не плавает. Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Один прибор для измерения удельного веса показан на (рис.).
Аквалангисты пытаются получить это состояние, чтобы они могли парить в воде. Мы измеряем удельный вес жидкостей, таких как аккумуляторная кислота, радиаторная жидкость и моча, как показатель их состояния. Один прибор для измерения удельного веса показан на (рис.).
Удельный вес
Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Этот ареометр плавает в жидкости с удельным весом 0,87. Стеклянный ареометр наполнен воздухом и утяжелен свинцом на дне. Он лучше всего всплывает в самых плотных жидкостях и был откалиброван и промаркирован таким образом, чтобы по нему можно было напрямую считывать удельный вес.
Расчет средней плотности: плавающая женщина
Предположим, 60.Женщина массой 0 кг плавает в пресной воде, часть ее объема находится под водой, когда ее легкие наполнены воздухом. Какая у нее средняя плотность?
Стратегия
Мы можем найти плотность женщины, решив уравнение
для плотности объекта. Это дает
Это дает
Нам известна и доля погруженного в воду, и плотность воды, поэтому мы можем рассчитать плотность женщины.
Раствор
Подставляя известные значения в выражение для ее плотности, получаем
Обсуждение
Ее плотность меньше плотности жидкости.Мы ожидаем этого, потому что она плавает. Плотность тела — один из показателей процентного содержания жира в организме человека, представляющий интерес для медицинской диагностики и спортивных тренировок. (См. (Рисунок).)
Субъект находится в «жировом резервуаре», где его взвешивают, пока он полностью погружен в воду, в рамках определения плотности тела. Субъект должен полностью опорожнить легкие и удерживать металлический груз, чтобы утонуть. Делаются поправки на остаточный воздух в его легких (измеряемый отдельно) и вес металла. Его скорректированный вес в погруженном состоянии, его вес в воздухе и щипковые тесты стратегических жировых областей используются для расчета его процентного содержания жира в организме.
Существует много очевидных примеров объектов или веществ с более низкой плотностью, плавающих в жидкостях с более высокой плотностью: масло на воде, воздушный шар, кусочек пробки в вине, айсберг и горячий воск в «лавовой лампе». назвать несколько. Менее очевидные примеры включают лаву, поднимающуюся из вулкана, и горные хребты, плавающие на более плотной коре и мантии под ними. Даже кажущаяся твердой Земля обладает жидкими характеристиками.
Больше измерений плотности
Один из наиболее распространенных методов определения плотности показан на (Рисунок).
(а) Монета взвешивается в воздухе. (b) Определяется кажущийся вес монеты, когда она полностью погружена в жидкость известной плотности. Эти два измерения используются для расчета плотности монеты.
Предмет, в данном случае монета, взвешивается в воздухе, а затем снова взвешивается при погружении в жидкость. Плотность монеты, показатель ее подлинности, можно рассчитать, если известна плотность жидкости. Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты.Все эти расчеты основаны на законе Архимеда.
Этот же метод можно использовать и для определения плотности жидкости, если известна плотность монеты.Все эти расчеты основаны на законе Архимеда.
Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесненной жидкости. Это, в свою очередь, означает, что объект кажется весящим меньше в погруженном состоянии; мы называем это измерение кажущимся весом объекта . Объект испытывает кажущуюся потерю веса , равную весу вытесненной жидкости. В качестве альтернативы, на весах, измеряющих массу, объект испытывает кажущуюся потерю массы , равную массе вытесненной жидкости.Это
или
Следующий пример иллюстрирует использование этой техники.
Это возвращает нас к принципу Архимеда и тому, как он возник. Как гласит история, царь Сиракуз поручил Архимеду определить, поставляет ли королевский коронщик корону из чистого золота. Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы.Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Чистоту золота трудно определить по цвету (оно может быть разбавлено другими металлами и все равно выглядеть таким же желтым, как чистое золото), а другие аналитические методы еще не были придуманы.Однако даже древние люди понимали, что плотность золота больше, чем у любого другого известного тогда вещества. Архимед якобы мучился над своей задачей и однажды получил вдохновение в общественных банях, размышляя о поддержке, которую вода оказала его телу. Он придумал свой ныне знаменитый принцип, увидел, как применять его для определения плотности, и голышом побежал по улицам Сиракуз с криком «Эврика!» (по-гречески «я нашел»). Подобное поведение время от времени можно наблюдать и у современных физиков!
Исследования PhET: Плавучесть
Когда объекты всплывут и когда они утонут? Узнайте, как плавучесть работает с блоками.Стрелки показывают приложенные силы, и вы можете изменять свойства блоков и жидкости.
Резюме раздела
- Выталкивающая сила — это чистая направленная вверх сила, действующая на любой объект в любой жидкости.
 Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости. - Принцип Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости.
- Удельный вес — это отношение плотности объекта к жидкости (обычно воде).
Концептуальные вопросы
Чтобы вытащить пробку в полной ванне, требуется большее усилие, чем когда она пуста. Противоречит ли это принципу Архимеда? Поясните свой ответ.
Оказывают ли жидкости выталкивающую силу в «невесомой» среде, например, в космическом челноке? Поясните свой ответ.
Будет ли один и тот же корабль плавать выше в соленой воде, чем в пресной? Поясните свой ответ.
Мрамор упал в частично заполненную раковину ванны до дна. Часть их веса приходится на выталкивающую силу, но сила, действующая на дно ванны, увеличивается точно на вес шариков. Объяснить, почему.
Проблемные упражнения
Какая часть льда находится под водой, когда он плавает в пресной воде, если плотность воды при 0°C очень близка к ?
Бревна иногда плавают вертикально в озере, потому что один конец стал заболоченным и более плотным, чем другой.Какова средняя плотность бревна одинакового диаметра, которое плавает над водой на протяжении всей его длины?
Найдите плотность жидкости, в которой плавает ареометр, имеющий плотность с
*** QuickLaTeX не может скомпилировать формулу:
\текст{92,0%}
*** Сообщение об ошибке:
Файл завершился при сканировании с использованием \text@.
Экстренная остановка.
его объема погружено под воду.
Если ваше тело имеет плотность , какая часть вашего тела будет погружена при плавном плавании в: (а) пресной воде? б) соленая вода плотностью ?
В костях птиц есть воздушные карманы, чтобы уменьшить их вес — это также дает им среднюю плотность, значительно меньшую, чем у костей других животных. Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и находит, что ее масса равна и ее кажущаяся масса в погруженном состоянии равна (кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
Предположим, орнитолог взвешивает птичью кость в воздухе и в воде и находит, что ее масса равна и ее кажущаяся масса в погруженном состоянии равна (кость водонепроницаема). а) Какая масса воды вытесняется? б) Каков объем кости? в) Какова его средняя плотность?
(а) 41,4 г
(б)
(в)
Установлено, что камень массой 540 г в воздухе имеет кажущуюся массу 342 г при погружении в воду. а) Какая масса воды вытесняется? б) Каков объем камня? в) Какова его средняя плотность? Соответствует ли это стоимости гранита?
Принцип Архимеда можно использовать для расчета плотности жидкости и твердого тела.Предположим, что кусок железа массой 390,0 г в воздухе имеет кажущуюся массу 350,5 г, когда он полностью погружен в неизвестную жидкость. а) Какую массу жидкости вытесняет железо? (b) Каков объем железа, используя его плотность, как показано на (рисунок) (c) Рассчитайте плотность жидкости и определите ее.
(а) 39,5 г
(б)
(в)
Это этиловый спирт.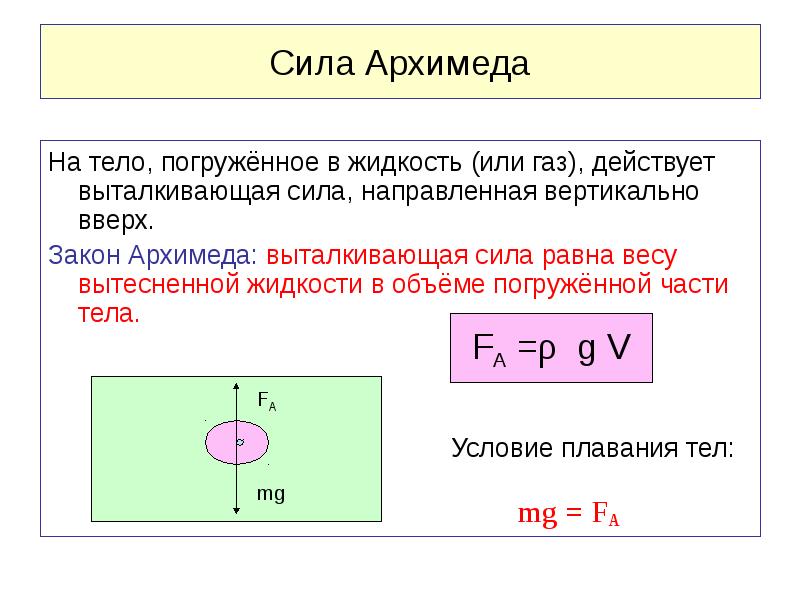
При иммерсионном измерении плотности женщины установлено, что ее масса равна 62.0 кг в воздухе и кажущаяся масса 0,0850 кг при полном погружении с пустыми легкими. а) Какую массу воды она вытесняет? б) Каков ее объем? (c) Рассчитайте ее плотность. (d) Если объем ее легких составляет 1,75 л, может ли она плавать, не топчась на месте, с легкими, наполненными воздухом?
Плотность некоторых рыб немного меньше плотности воды, и они должны прилагать усилия (плавать), чтобы оставаться под водой. Какую силу должен приложить морской окунь массой 85,0 кг, чтобы оставаться погруженным в соленую воду, если плотность его тела равна ?
(а) Рассчитайте выталкивающую силу на 2.00-литровый гелиевый баллон. (b) Учитывая, что масса резины в воздушном шаре составляет 1,50 г, какова результирующая вертикальная сила, действующая на воздушный шар, если его отпустить? Можно пренебречь объемом резины.
(a) Какова плотность женщины, которая плавает в пресной воде, если часть ее объема находится над поверхностью? Это можно измерить, поместив ее в резервуар с отметками на боку, чтобы измерить, сколько воды она вытесняет, когда плавает и удерживается под водой (кратковременно). б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде?
б) Сколько процентов ее объема находится над поверхностью, когда она плавает в морской воде?
(а)
(б)
Она действительно больше плавает в морской воде.
Некий человек имеет массу 80 кг и плотность (без учета воздуха в легких). а) Вычислите его объем. б) Найдите выталкивающую силу воздуха, действующую на него. в) Каково отношение выталкивающей силы к его весу?
Простой компас можно сделать, поместив небольшой стержневой магнит на пробку, плавающую в воде. а) Какая часть простой пробки окажется под водой, когда она будет плавать в воде? б) Если пробка массой 10,0 г поместить на нее магнит массой 20,0 г, какая часть пробки окажется под водой? в) Будут ли стержневой магнит и пробка плавать в этиловом спирте?
(а)
(б)
(c) Да, пробка всплывет, потому что
Какая часть веса железного якоря будет поддерживаться выталкивающей силой при погружении в соленую воду?
Известны случаи, когда подлые мошенники выдавали позолоченные вольфрамовые слитки за чистое золото и продавали их жадным по ценам намного ниже стоимости золота, но заслуженно намного выше стоимости вольфрама.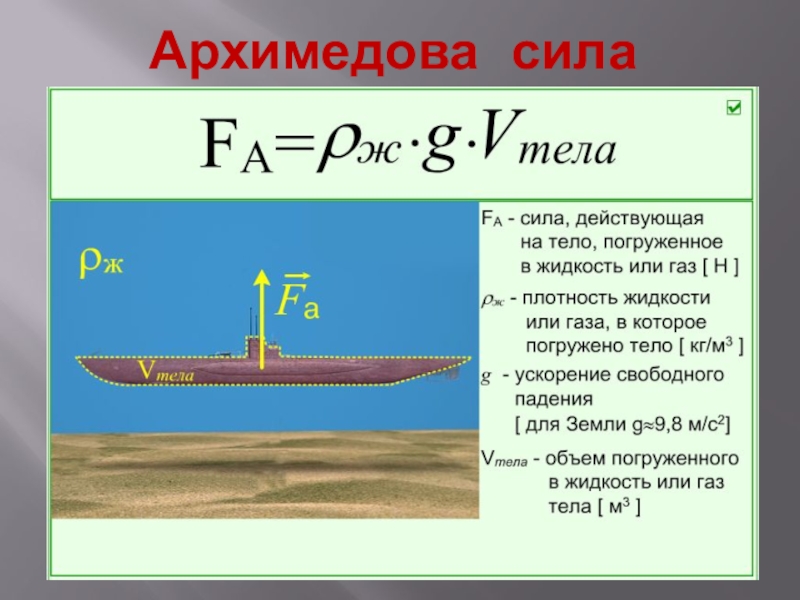 С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
С какой точностью вы должны быть в состоянии измерить массу такого слитка в воде и вне воды, чтобы сказать, что это почти чистый вольфрам, а не чистое золото?
Разница
Двуспальный надувной матрас, используемый для кемпинга, имеет размеры 100 см на 200 см на 15 см в надутом состоянии. Вес матраса 2 кг. Насколько тяжелый человек может выдержать надувной матрас, если его поместить в пресную воду?
(a) Человек массой 75,0 кг плавает в пресной воде, при этом его объем над водой составляет, когда его легкие пусты, и его объем над водой, когда его легкие полны.Вычислите объем вдыхаемого им воздуха, который называется емкостью легких, в литрах. (b) Кажется ли этот объем легких приемлемым?
Глоссарий
- Закон Архимеда
- выталкивающая сила, действующая на объект, равна весу вытесняемой им жидкости
- выталкивающая сила
- результирующая восходящая сила, действующая на любой объект в любой жидкости
- удельный вес
- отношение плотности объекта к жидкости (обычно воде)
Понимание закона Архимеда — студенческий урок
Архимед открыл принцип плавучести, который используется в различных приложениях, включая корабли. Это позволяет им плавать, когда вес вытесненной воды равен весу корабля. Все, что имеет форму, позволяющую вытеснять воду под собственным весом до того, как оно достигнет точки, в которой оно погрузится, несомненно, будет плавать.
Это позволяет им плавать, когда вес вытесненной воды равен весу корабля. Все, что имеет форму, позволяющую вытеснять воду под собственным весом до того, как оно достигнет точки, в которой оно погрузится, несомненно, будет плавать.
Сегодня вы познакомитесь с определением, приложениями, формулой, выводом, экспериментами, примером и расчетом закона Архимеда.
Подробнее: Электрическая сила
Что такое закон Архимеда?
Принцип Архимеда касается сил, действующих на объект со стороны окружающих его жидкостей.Эта приложенная сила уменьшает чистый вес объекта, погруженного в жидкость. Этот принцип также можно рассматривать как физический закон плавучести, который помогает нам понять, как корабли плавают в воде. Другими словами, любой предмет, полностью или частично погруженный в жидкость или жидкость, выталкивается вверх силой, равной весу жидкости, вытесненной этим предметом. В данном случае принцип Архимеда позволяет рассчитать плавучесть любого плавучего объекта, частично или полностью погруженного в жидкость.
Сила, действующая на объект, направленная вниз, — это то, что мы называем весом. Восходящая или выталкивающая сила, действующая на объект, — это то, о чем гласил принцип Архимеда. Итак, результирующая сила, действующая на объект, есть разница между величинами выталкивающей силы и его веса. Если эта результирующая сила отрицательна, объект обязательно опустится, а если положительна, объект поднимется. Если объект равен нулю, объект имеет нейтральную плавучесть, то есть он остается на месте, не тонет и не поднимается.
Подробнее: Как Force изменяет состояние движения
Посмотрите видео ниже, чтобы узнать больше о законе Архимеда:
Проще говоря, принцип Архимеда гласит, что когда тело полностью или частично погружено в жидкость, оно явно теряет в весе. Этот вес равен весу жидкости, вытесненной погруженной частью тела. Этот принцип можно сформулировать так: направленная вверх выталкивающая сила, действующая на тело, погруженное в жидкость, частично или полностью погруженное, равна весу жидкости, вытесняемой телом, и действует в направлении вверх в центре масс тела. вытесненная жидкость.
Этот вес равен весу жидкости, вытесненной погруженной частью тела. Этот принцип можно сформулировать так: направленная вверх выталкивающая сила, действующая на тело, погруженное в жидкость, частично или полностью погруженное, равна весу жидкости, вытесняемой телом, и действует в направлении вверх в центре масс тела. вытесненная жидкость.
Подробнее: Связь между силой и движением
Принцип Архимеда — это закон физики, лежащий в основе гидромеханики.
Применение закона Архимеда
Ниже показано применение принципа Архимеда в различных областях:
Подводная лодка:
Применение Архимеда на подводных лодках так распространено из-за их связи с морем. Они могли оставаться под водой благодаря компоненту, называемому балластной цистерной, которая позволяет воде течь в него. Это заставляет подводную лодку находиться в подводном положении, поскольку вес больше, чем выталкивающая сила.
Ареометр:
Для измерения относительной плотности жидкостей используется ареометр. Он сделан из свинцовой дроби, которая заставляет их плавать вертикально в жидкости. Когда ареометр опустится ниже, плотность жидкости будет меньше.
Он сделан из свинцовой дроби, которая заставляет их плавать вертикально в жидкости. Когда ареометр опустится ниже, плотность жидкости будет меньше.
Подробнее: Понимание гидромеханики
Воздушный шар:
Воздушные шары могут парить в воздухе из-за того, что выталкивающая сила воздушного шара меньше, чем у окружающего воздуха. Таким образом, шар опустится, когда выталкивающая сила больше. Это достигается изменением количества горячего воздуха в воздушном шаре.
Формула закона Архимеда
Как уже говорилось ранее, закон Архимеда гласит, что выталкивающая сила, действующая на объект, равна весу жидкости, вытесненной объектом. Это записывается математически как:
F b = ρ x g x V где:
F b выталкивающая сила
P — плотность жидкости
В — погружной объем
g — ускорение свободного падения.
Подробнее: Понимание различных типов потока жидкости
Вывод закона Архимеда
Масса вытесненной жидкости.
Масса = Плотность × Объем = ρ × V
Это потому, что плотность (ρ) определяется как
Плотность, ρ = MassVolume = MV
Таким образом, вес этой вытесненной жидкости:
Вес = Масса × Ускорение под действием гравитации
W = M × g = ρ × V × g
Таким образом, из принципа Архимеда мы можем написать:
Кажущаяся потеря веса = вес вытесненной воды = ρ×V×g
Таким образом, Сила тяги равна,
Тяга = ρ × V × g
Где:
- ρ — плотность жидкости
- В — объем жидкости, вытесненной
Подробнее: Что нужно знать о насосе
Сила тяги также известна как выталкивающая сила, потому что она отвечает за плавание объектов.Таким образом, это уравнение также называют законом плавучести.
Решенные примеры закона Архимеда
Q1. Вычислите результирующую силу, если стальной шарик радиусом 6 см погрузить в воду.Ответ: Дано,
Радиус стального шарика = 6 см = 0,06 м
Объем стального шара, V = 43πr3
В = 43π0,063
∴V = 9,05 × 10 -4 м 3
Плотность воды, ρ = 1000 кг. м -3
м -3
Ускорение свободного падения, g = 9,8 м.с -2
Формула из принципа Архимеда
F b = ρ × g × V
F b = (1000 кг.м -3 ) (9,8 м.с -2 ) (9,05 × 10 -4 м 3 )
∴F б = 8,87 Н
Подробнее: Понятие о поршневом насосе
Q2. Вычислите выталкивающую силу, если плавучее тело на 95 % погружено в воду.Плотность воды 1000 кг.м -3 . Ответ: Дано,
Плотность воды, p = 1000 кг.м -3
формула из принципа Архимеда
F b = ρ × g × V
или
В б × ρ б × г = ρ × г × В
Где:
ρ,g и V — плотность, ускорение свободного падения и объем воды
V b , ρ b , g — объем, плотность и ускорение под действием силы тяжести погруженного тела
.
Изменение уравнения,
ρb=VρVb
Так как 95% корпуса погружено,
0.95 × В б = В
∴ρ б = 950 кг.м -3
Заключение
Принцип Архимеда касается сил, действующих на объект со стороны окружающих его жидкостей. Эта приложенная сила уменьшает чистый вес объекта, погруженного в жидкость. Этот принцип также можно рассматривать как физический закон плавучести, который помогает нам понять, как корабли плавают в воде. Это все, что касается этого поста, где обсуждались определение, приложения, формула, вывод, эксперименты, примеры и расчеты принципа Архимеда.Обязательно посмотрите встроенное видео, чтобы узнать больше о том, как работает принцип Архимеда
.Я надеюсь, что вы многому научились из этого поста, если да, поделитесь с другими учениками. Спасибо за чтение, увидимся в следующий раз!
Плавучесть | Encyclopedia.com
КОНЦЕПЦИЯ
Принцип плавучести гласит, что выталкивающая или подъемная сила объекта, погруженного в жидкость, равна весу вытесненной им жидкости.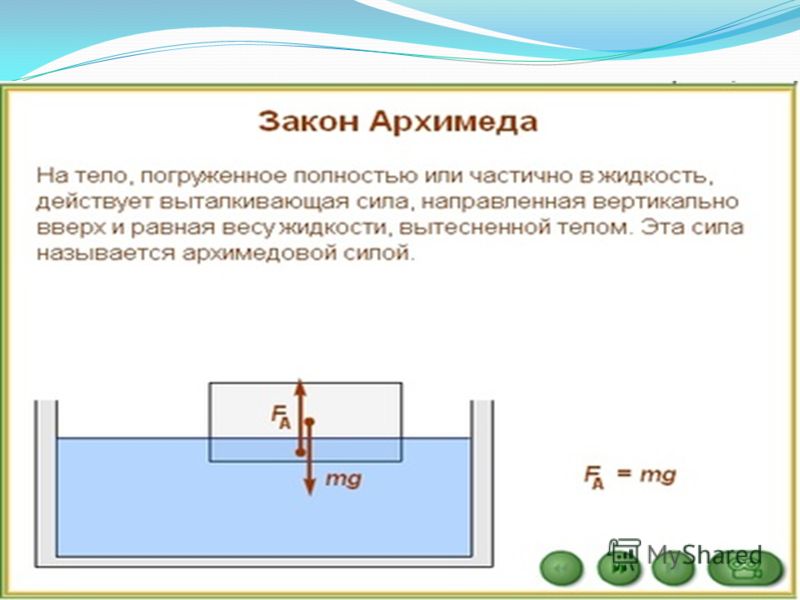 Эта концепция также известна как принцип Архимеда в честь греческого математика, физика и изобретателя Архимеда (ок.287-212 до н.э.), которые открыли его. Применение принципа Архимеда можно увидеть в широком вертикальном спектре: от объектов глубоко под океаном до тех, что плавают на его поверхности, и от поверхности до верхних пределов стратосферы и за ее пределами.
Эта концепция также известна как принцип Архимеда в честь греческого математика, физика и изобретателя Архимеда (ок.287-212 до н.э.), которые открыли его. Применение принципа Архимеда можно увидеть в широком вертикальном спектре: от объектов глубоко под океаном до тех, что плавают на его поверхности, и от поверхности до верхних пределов стратосферы и за ее пределами.
КАК ЭТО РАБОТАЕТ
Архимед открывает плавучесть
Существует известная история о том, что сэр Исаак Ньютон (1642-1727) открыл принцип гравитации, когда ему на голову упало яблоко. Сказка, преувеличенная версия реальных событий, настолько стала частью массовой культуры, что ее стали пародировать в телевизионных рекламных роликах.Почти столь же известна легенда о том, как Архимед открыл понятие плавучести.
Уроженец Сиракуз, греческой колонии на Сицилии, Архимед состоял в родстве с одним из царей этого города, Гиероном II (308?–216 до н. э.). После учебы в Александрии, Египет, он вернулся в свой родной город, где провел остаток своей жизни. В какой-то момент королевский двор нанял (или вынудил) его приступить к определению веса золота в королевской короне. Архимед находился в своей ванне, размышляя над этой задачей, когда ему вдруг пришло в голову, что выталкивающая сила подводного объекта равна весу вытесненной им жидкости.
В какой-то момент королевский двор нанял (или вынудил) его приступить к определению веса золота в королевской короне. Архимед находился в своей ванне, размышляя над этой задачей, когда ему вдруг пришло в голову, что выталкивающая сила подводного объекта равна весу вытесненной им жидкости.
Легенда гласит, что он был так взволнован, что выпрыгнул из ванны и голышом побежал по улицам Сиракуз с криком «Эврика!» (Я нашел это). Архимед признал принцип огромной ценности — как будет показано — для судостроителей своего времени, да и для кораблестроителей настоящего.
Что касается истории науки, то это было особенно важное открытие; немногие полезные и устойчивые принципы физики относятся к периоду до Галилео Галилея (1564-1642 гг.).) Даже среди тех немногих древних физиков и изобретателей, которые внесли непреходящий вклад в работу, — Архимеда, Героя Александрийского (ок. 65–125 гг. н. э.) и некоторых других, — существовала тенденция упускать более важные последствия их работы. Например, Герой, открывший силу пара, считал ее полезной лишь в качестве игрушки, и в результате это колоссально важное открытие игнорировалось на протяжении семнадцати столетий.
Например, Герой, открывший силу пара, считал ее полезной лишь в качестве игрушки, и в результате это колоссально важное открытие игнорировалось на протяжении семнадцати столетий.
Однако в случае с Архимедом и плавучестью практическое значение открытия было более очевидным.В то время как паровая энергия действительно должна была казаться древним причудливой идеей, в океанских судах не было ничего неправдоподобного. Судостроители уже давно столкнулись с проблемой, как удержать судно на плаву, контролируя, с одной стороны, размер его груза, а с другой стороны, его склонность к раскачиванию над водой. Здесь Архимед предложил ответ.
Плавучесть и вес
Почему кажется, что объект под водой весит меньше, чем над поверхностью? Как это корабль
из стали, которая явно тяжелее воды, может плавать? Как мы можем определить, будет ли воздушный шар подниматься в воздухе или подводная лодка будет опускаться в воду? На эти и другие вопросы отвечает принцип плавучести, который можно объяснить с точки зрения свойств, прежде всего силы тяжести, неизвестных Архимеду.
Чтобы понять действующие факторы, полезно начать с мысленного эксперимента. Представьте себе определенное количество жидкости, погруженной в большее тело из той же жидкости. Обратите внимание, что термины «жидкость» или «вода» не использовались: не только «жидкость» является гораздо более общим термином, но и в общих физических терминах и для целей настоящего обсуждения нет существенной разницы между газы и жидкости. Оба соответствуют форме сосуда, в который они помещены, и, таким образом, оба являются жидкостями.
Возвращаясь к мысленному эксперименту, то, что было постулировано, на самом деле представляет собой «мешок» с жидкостью, то есть «мешок», сделанный из жидкости и содержащий жидкость, ничем не отличающуюся от вещества вне «мешка». На этот «мешок» действует ряд сил. Во-первых, это его вес, который стремится утянуть его на дно контейнера. Существует также давление жидкости вокруг него, которое зависит от глубины: чем глубже контейнер, тем больше давление.
Давление — это просто приложение силы к двумерной области.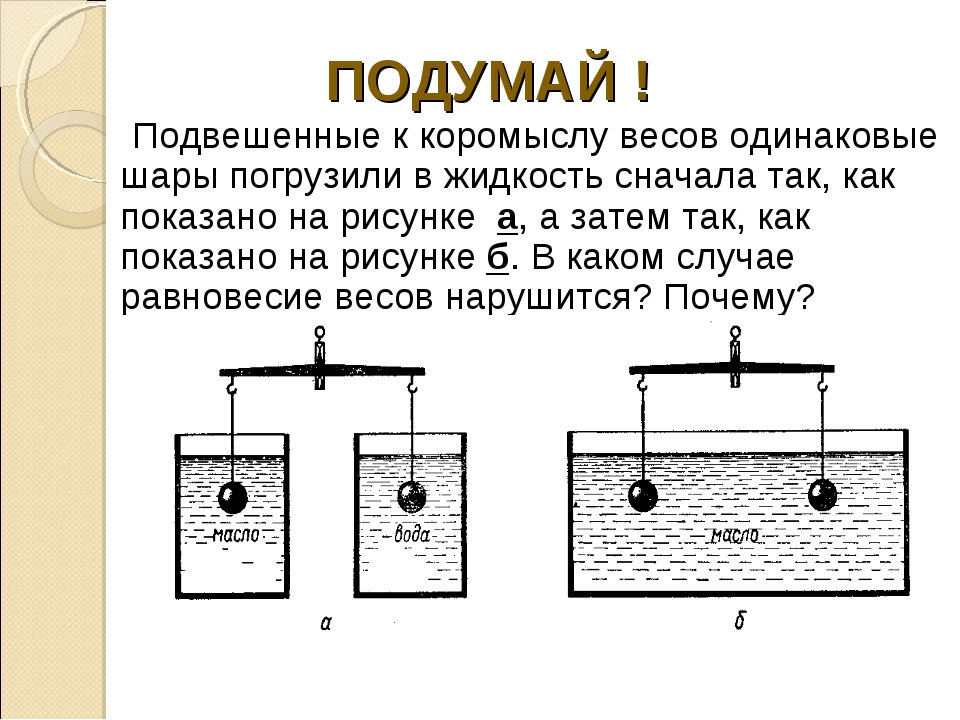 Таким образом, жидкость как бы состоит из огромного количества двумерных «слоев» жидкости, расположенных один над другим, как страницы в газете. Чем глубже проникаешь в больший объем жидкости, тем больше давление; однако именно эта повышенная сила на дне жидкости стремится подтолкнуть «мешок» вверх против силы тяжести.
Таким образом, жидкость как бы состоит из огромного количества двумерных «слоев» жидкости, расположенных один над другим, как страницы в газете. Чем глубже проникаешь в больший объем жидкости, тем больше давление; однако именно эта повышенная сила на дне жидкости стремится подтолкнуть «мешок» вверх против силы тяжести.
Теперь посчитаем вес этой «сумки». Вес — это сила — произведение массы на ускорение, то есть нисходящее ускорение из-за гравитационного притяжения Земли.Для объекта, взвешенного в жидкости, полезно заменить массу другим термином. Масса равна объему или количеству трехмерного пространства, занимаемого объектом, умноженному на плотность. Поскольку плотность равна массе, деленной на объем, это означает, что объем, умноженный на плотность, равен массе.
Мы установили, что вес жидкого «мешка» равен Vdg, , где V — объем, d — плотность, g — ускорение свободного падения.Теперь представьте, что «мешок» заменен твердым предметом точно такого же размера. Твердый объект будет испытывать точно такое же давление, как и воображаемый «мешок», и, следовательно, он также будет испытывать ту же выталкивающую силу, толкающую его снизу вверх. Это означает, что выталкивающая сила равна весу — Vdg — вытесненной жидкости.
Твердый объект будет испытывать точно такое же давление, как и воображаемый «мешок», и, следовательно, он также будет испытывать ту же выталкивающую силу, толкающую его снизу вверх. Это означает, что выталкивающая сила равна весу — Vdg — вытесненной жидкости.
Плавучесть всегда обоюдоострая вещь. Если выталкивающая сила, действующая на объект, больше, чем вес этого объекта — другими словами, если объект весит меньше, чем количество вытесненной им воды, — он будет плавать.Но если выталкивающая сила меньше веса объекта, он утонет. Выталкивающая сила — это не то же самое, что результирующая сила: если объект весит больше, чем вытесняемая им вода, сила его веса уравновешивается и фактически «отменяет» силу выталкивающей силы.
В основе проблемы лежит плотность. Часто плотность объекта по отношению к воде называют его удельным весом: говорят, что большинство металлов, которые тяжелее воды, имеют высокий удельный вес. И наоборот, продукты на основе нефти обычно плавают на поверхности воды, потому что их удельный вес низкий. Обратите внимание на тесную связь между плотностью и весом, когда речь идет о плавучести: на самом деле, самые плавучие объекты имеют относительно большой объем и относительно низкую плотность.
Обратите внимание на тесную связь между плотностью и весом, когда речь идет о плавучести: на самом деле, самые плавучие объекты имеют относительно большой объем и относительно низкую плотность.
Это можно показать математически с помощью формулы, отмеченной ранее, согласно которой плотность равна массе, деленной на объем. Если Vd = V(m/V), увеличение плотности может означать только увеличение массы. Поскольку вес — это произведение массы на г (которое считается постоянным числом), то увеличение плотности означает увеличение массы и, следовательно, увеличение веса, а это нехорошо, если кто-то хочет получить объект. держаться на плаву.
ПРИМЕНЕНИЕ В РЕАЛЬНОЙ ЖИЗНИ
Оставаться на плаву
В начале 1800-х годов молодой оператор плоских лодок на реке Миссисипи подал заявку на патент, описывающую устройство для «поддерживания судов на мелководье». Изобретение предлагало предотвратить проблему, с которой он часто сталкивался на реке — лодки садились на мель на песчаных отмелях, — путем оснащения лодок регулируемыми плавучими воздушными камерами. Молодой человек даже вырезал модель своего изобретения,
но ему не суждено было прославиться как изобретателю; вместо этого Авраам Линкольн (1809-1865) был известен гораздо другим.На самом деле у Линкольна была здравая идея с его предложением использовать выталкивающую силу для защиты лодок от посадки на мель.
Молодой человек даже вырезал модель своего изобретения,
но ему не суждено было прославиться как изобретателю; вместо этого Авраам Линкольн (1809-1865) был известен гораздо другим.На самом деле у Линкольна была здравая идея с его предложением использовать выталкивающую силу для защиты лодок от посадки на мель.
Плавучесть на поверхности воды имеет ряд легко заметных эффектов в реальном мире. (Установив определение жидкости, с этого момента в дальнейшем будем обсуждать в первую очередь те жидкости, которые наиболее часто встречаются: воду и воздух.) Именно благодаря плавучести рыбы, люди-пловцы, айсберги и корабли остаются на плаву. Рыбы предлагают интересное применение изменения объема как средства изменения плавучести: у рыб есть внутренний плавательный пузырь, наполненный газом.Когда ему нужно подняться или опуститься, он меняет объем своего плавательного пузыря, который затем меняет свою плотность. Примеры пловцов и айсбергов непосредственно иллюстрируют принцип плотности — со стороны воды в первом случае, а со стороны самого объекта — во втором.
Для пловца разница между плаванием в пресной и соленой воде показывает, что выталкивающая сила зависит как от плотности жидкости, так и от вытесненного объема. Пресная вода имеет плотность 62.4 фунта/фут 3 (9 925 Н/м 3 ), тогда как для соленой воды 64 фунта/фут 3 (10 167 Н/м 3 ). По этой причине соленая вода обеспечивает большую выталкивающую силу, чем пресная; в израильском Мертвом море, самом соленом водоеме на Земле, купающиеся испытывают огромную выталкивающую силу.
Вода — необычное вещество во многих отношениях, не в последнюю очередь из-за своего поведения при замерзании. Ближе к точке замерзания вода сгущается, но когда она превращается в лед, она становится менее плотной.Вот почему плавают кубики льда и айсберги. Однако их низкая плотность по сравнению с окружающей их водой означает, что только часть айсберга остается на поверхности. Процент погружения айсберга равен отношению плотности льда к плотности воды: 89%.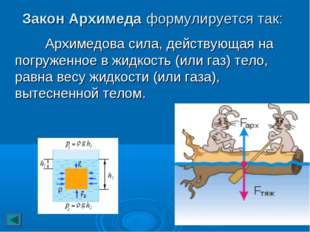
Корабли в море
Поскольку вода сама по себе относительно плотная, объект большого объема с низкой плотностью, вероятно, вытеснит воду более плотную и тяжелую, чем сам объект. Напротив, стальной шар, брошенный в воду, опустится прямо на дно, потому что это объект небольшого объема и высокой плотности, который перевешивает вытесненную им воду.
Это возвращает к предыдущему вопросу: как может корабль, сделанный из стали, с плотностью 487 фунтов/фут 3 (77 363 Н/м 3 ), плавать в соленой воде океана со средней плотностью только около одной восьмой этой суммы? Ответ кроется в конструкции корпуса корабля. Если бы корабль был плоским, как плот, или если бы вся сталь в нем была сжата в шар, он бы действительно затонул. Однако вместо этого полый корпус вытесняет объем воды, превышающий собственный вес корабля: снова объем был максимальным, а плотность — минимальной.
Чтобы корабль был мореходным, он должен поддерживать тонкий баланс между плавучестью и остойчивостью. Слишком легкий сосуд, то есть слишком большой объем и слишком маленькая плотность, будет качаться на поверхности воды. Следовательно, ему необходимо нести определенное количество груза, а если не груза, то воды или какого-либо другого балласта. Балласт — тяжелое вещество, увеличивающее вес объекта, испытывающего плавучесть, и тем самым улучшающее его устойчивость.
Слишком легкий сосуд, то есть слишком большой объем и слишком маленькая плотность, будет качаться на поверхности воды. Следовательно, ему необходимо нести определенное количество груза, а если не груза, то воды или какого-либо другого балласта. Балласт — тяжелое вещество, увеличивающее вес объекта, испытывающего плавучесть, и тем самым улучшающее его устойчивость.
В идеале центр тяжести корабля должен быть выровнен по вертикали с его центром плавучести.Центр тяжести — это геометрический центр веса корабля — точка, в которой вес наверху равен весу внизу, вес на носу равен весу на корме, а вес на правом борту (правом борту) равен весу на левом борту (слева). ) боковая сторона. Центр плавучести — это геометрический центр его подводного объема, а в устойчивом корабле он находится на некотором расстоянии прямо под центром тяжести.
Водоизмещение или вес жидкости, смещаемой с места при погружении объекта, дает некоторое представление об остойчивости корабля.Если корабль, посаженный в океан, вызывает вытеснение 1000 тонн (8,896 · 10 6 северной широты) воды, говорят, что он имеет водоизмещение 1000 тонн.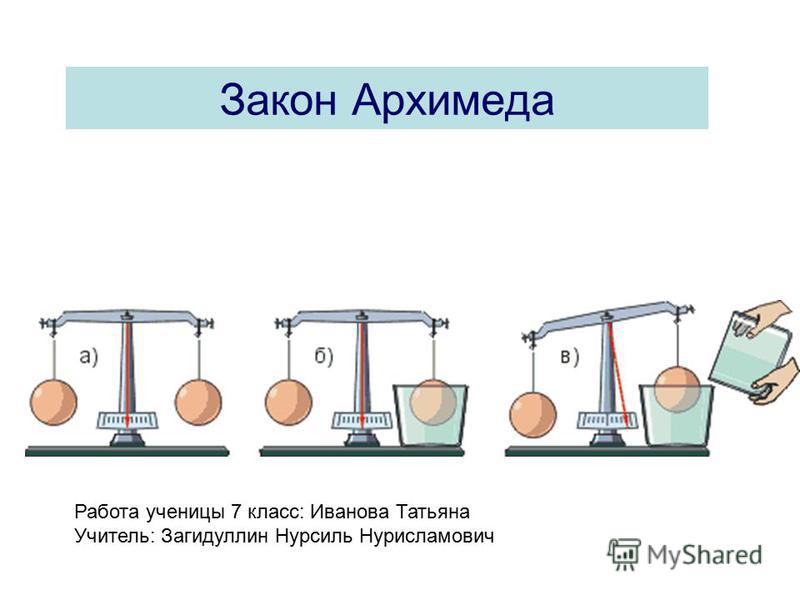 Очевидно, что желательна высокая степень смещения. Принцип водоизмещения помогает объяснить, как авианосец может оставаться на плаву, даже если он весит многие тысячи тонн.
Очевидно, что желательна высокая степень смещения. Принцип водоизмещения помогает объяснить, как авианосец может оставаться на плаву, даже если он весит многие тысячи тонн.
На глубину
Подводная лодка использует балласт для спуска и всплытия под водой: когда капитан подводной лодки приказывает экипажу спустить судно на дно, судну разрешается набирать воду в балластные цистерны.Если, с другой стороны, будет дана команда подняться к поверхности, откроется клапан для выпуска сжатого воздуха в баки. Воздух выталкивает воду и заставляет корабль подниматься.
Подводная лодка — подводный корабль; его обтекаемая форма предназначена для облегчения движения. С другой стороны, есть определенные виды подводных судов, известных как подводные аппараты, которые предназначены для погружения — для наблюдения или сбора данных со дна океана. Первоначально идея подводного аппарата была тесно связана с самим дайвингом.Одним из первых подводных аппаратов был водолазный колокол, устройство, созданное известным английским астрономом Эдмундом Галлеем (1656–1742). позволяют дайверам выходить за пределы относительно небольших глубин. Во-первых, водолазный колокол получал воздух с поверхности: во времена Галлея не существовало технологии забора запаса кислорода снизу. Он также не обеспечивал существенной защиты от воздействия повышенного давления на больших глубинах.
позволяют дайверам выходить за пределы относительно небольших глубин. Во-первых, водолазный колокол получал воздух с поверхности: во времена Галлея не существовало технологии забора запаса кислорода снизу. Он также не обеспечивал существенной защиты от воздействия повышенного давления на больших глубинах.
ОПАСНОСТИ ГЛУБИН.
Самым непосредственным из этих эффектов является, конечно, тенденция объекта, испытывающего такое давление, просто взрываться, как консервная банка в тисках. Кроме того, человеческое тело испытывает несколько серьезных реакций на большую глубину: под водой газообразный азот накапливается в тканях тела дайвера, вызывая два разных, но одинаково пугающих эффекта.
Азот в нормальных условиях инертный газ, однако при высоком давлении океанских глубин он превращается в сильный наркотик, вызывая азотный наркоз, часто известный под поэтически звучащим названием «восторг глубин».» Под влиянием этой смертельной эйфории дайверы начинают считать себя непобедимыми, а их измененные суждения могут поставить их в потенциально смертельные ситуации.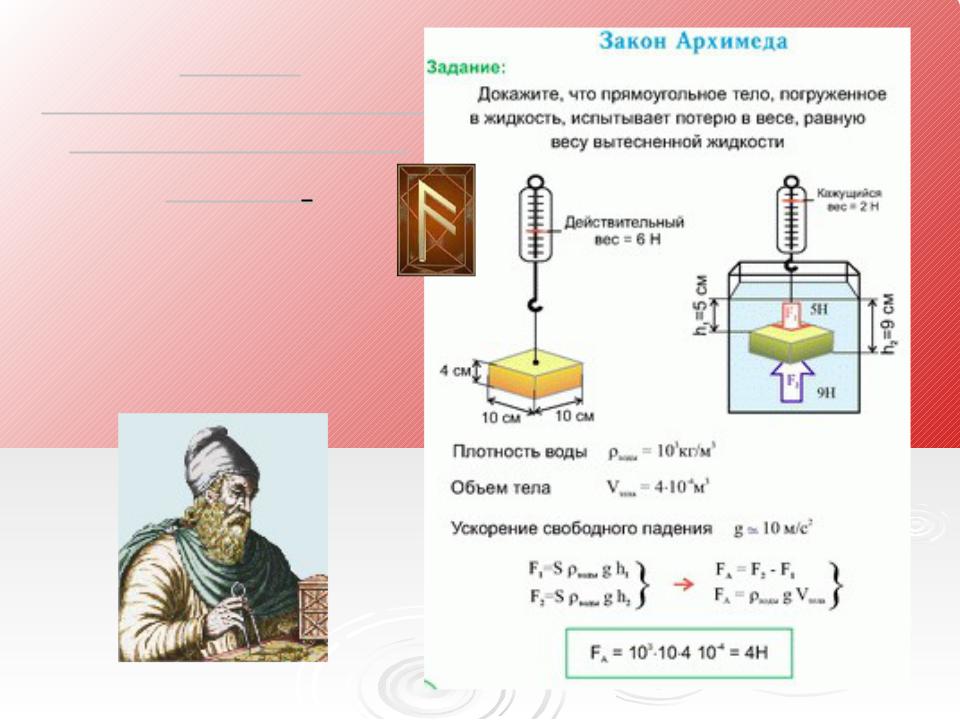 преодолевается простым возвращением на поверхность.Однако не следует возвращаться на поверхность слишком быстро, особенно после погружения на значительную глубину в течение значительного периода времени.В таком случае при возвращении на поверхность газообразный азот будет пузыриться внутри тела, вызывая декомпрессионную болезнь, известную в просторечии как «изгибы».Это состояние может проявляться зудом и другими кожными проблемами, болями в суставах, удушьем, слепотой, судорогами, потерей сознания и даже постоянными неврологическими дефектами, такими как параплегия. а в 1907 году Джон Скотт Холдейн (1860-1936) разработал метод противодействия декомпрессионной болезни.Он рассчитал набор декомпрессионных таблиц, которые рекомендовали ограничения на количество времени на заданных глубинах.Он рекомендовал то, что он назвал поэтапной декомпрессией, что означает, что всплывающий дайвер останавливается каждые несколько футов во время всплытия и ждет несколько минут на каждом уровне, давая тканям тела время приспособиться к новому давлению.
преодолевается простым возвращением на поверхность.Однако не следует возвращаться на поверхность слишком быстро, особенно после погружения на значительную глубину в течение значительного периода времени.В таком случае при возвращении на поверхность газообразный азот будет пузыриться внутри тела, вызывая декомпрессионную болезнь, известную в просторечии как «изгибы».Это состояние может проявляться зудом и другими кожными проблемами, болями в суставах, удушьем, слепотой, судорогами, потерей сознания и даже постоянными неврологическими дефектами, такими как параплегия. а в 1907 году Джон Скотт Холдейн (1860-1936) разработал метод противодействия декомпрессионной болезни.Он рассчитал набор декомпрессионных таблиц, которые рекомендовали ограничения на количество времени на заданных глубинах.Он рекомендовал то, что он назвал поэтапной декомпрессией, что означает, что всплывающий дайвер останавливается каждые несколько футов во время всплытия и ждет несколько минут на каждом уровне, давая тканям тела время приспособиться к новому давлению. Современные дайверы используют декомпрессионную камеру, герметичный контейнер, имитирующий этапы декомпрессии.
Современные дайверы используют декомпрессионную камеру, герметичный контейнер, имитирующий этапы декомпрессии.
БАТИСФЕРА, АКВАЛАНГ И БАТИСКАФ.
В 1930 году американский натуралист Уильям Биб (1877-1962) и американский инженер Отис Бартон создали батисферу. Это был первый подводный аппарат, который обеспечил дайверам, находящимся внутри, достаточную защиту от внешнего давления. Изготовленная из стали и имеющая сферическую форму, батисфера имела толстые кварцевые окна и была способна поддерживать обычное атмосферное давление даже при опускании с помощью троса на относительно большие глубины.В 1934 году батисфера опустилась на чрезвычайно впечатляющую тогда глубину: 3028 футов (923 м). Однако батисфера была сложной в эксплуатации и маневрировании, и со временем ее заменили более работоспособным судном — батискафом.
Однако до появления батискафа, в 1943 году, два француза создали средство для погружения дайверов без какой-либо внешней камеры. Конечно, ныряльщик с этим новым аппаратом не мог бы погрузиться даже близко к тем глубинам, к которым приближается батисфера; тем не менее, новый акваланг позволял проводить длительное время под поверхностью без необходимости в воздухе. Теперь дайверу теоретически было возможно спуститься вниз без какой-либо помощи или припасов сверху, потому что он носил весь свой запас кислорода на спине. Имя одного из изобретателей, Эмиля Ганьяна, едва ли можно назвать нарицательным; но у другого — Жака Кусто (1910–1997) — определенно есть. Так же и название их изобретения: s elf- c ontained u nderwater b reathing a аппарат, более известный как акваланг.
Теперь дайверу теоретически было возможно спуститься вниз без какой-либо помощи или припасов сверху, потому что он носил весь свой запас кислорода на спине. Имя одного из изобретателей, Эмиля Ганьяна, едва ли можно назвать нарицательным; но у другого — Жака Кусто (1910–1997) — определенно есть. Так же и название их изобретения: s elf- c ontained u nderwater b reathing a аппарат, более известный как акваланг.
Наиболее важной особенностью акваланга был регулятор нагрузки, который позволял дайверам дышать воздухом под тем же давлением, что и под водой.Это, в свою очередь, способствовало более нормальному и удобному дыханию. Еще одной важной особенностью снаряжения современного водолаза является устройство компенсации плавучести. Подобно кораблю на поверхности воды, ныряльщик хочет иметь только такую большую плавучесть — не настолько большую, чтобы заставить его всплыть на поверхность.
Что касается батискафа — термина, два греческих корня которого означают «глубокий» и «лодка», — он дебютировал через пять лет после акваланга. Построенный швейцарским физиком и авантюристом Огюстом Пикаром (1884-1962), батискаф состоял из двух отсеков: тяжелой стальной кабины экипажа, устойчивой к морскому давлению, и над ней более крупного и легкого контейнера, называемого поплавком.Поплавок был заполнен бензином, который в данном случае использовался не в качестве топлива, а для обеспечения дополнительной плавучести из-за низкого удельного веса бензина.
Построенный швейцарским физиком и авантюристом Огюстом Пикаром (1884-1962), батискаф состоял из двух отсеков: тяжелой стальной кабины экипажа, устойчивой к морскому давлению, и над ней более крупного и легкого контейнера, называемого поплавком.Поплавок был заполнен бензином, который в данном случае использовался не в качестве топлива, а для обеспечения дополнительной плавучести из-за низкого удельного веса бензина.
При спуске пассажиры батискафа — их могло быть только двое, поскольку герметичная камера была всего 79 дюймов (2,01 м) в диаметре — выпустили часть бензина, чтобы уменьшить плавучесть. Они также несли на борту железные балластные гранулы, которые выпускали при подготовке к всплытию. Благодаря гребным винтам с батарейным приводом батискаф был намного маневреннее, чем когда-либо была батисфера; кроме того, он был разработан для достижения таких глубин, которые Биби и Бартон вряд ли могли себе представить.
ДОСТИГАЯ НОВЫХ ГЛУБИН.
Потребовалось несколько лет безуспешных погружений, но в 1953 году батискаф установил первый из многих рекордов глубины. Этим первым кораблем был Trieste, , пилотируемый Пикаром и его сыном Жаком, который спустился на 10 335 футов (3150 м) ниже Средиземного моря у Капри, Италия. Год спустя в Атлантическом океане у Дакара, Французская Западная Африка (ныне Сенегал), французские дайверы Жорж Уо и Пьер-Анри Вильм достигли 13 287 футов (4063 м) на FNRS 3.
Этим первым кораблем был Trieste, , пилотируемый Пикаром и его сыном Жаком, который спустился на 10 335 футов (3150 м) ниже Средиземного моря у Капри, Италия. Год спустя в Атлантическом океане у Дакара, Французская Западная Африка (ныне Сенегал), французские дайверы Жорж Уо и Пьер-Анри Вильм достигли 13 287 футов (4063 м) на FNRS 3.
Затем, в 1960 году, Жак Пикар и лейтенант ВМС США Дон Уолш установили рекорд, который стоит до сих пор: 35 797 футов (10 911 м) — на 23% больше, чем высота горы Эверест, самой высокой вершины в мире. Это они сделали в Триесте примерно в 250 милях (402 км) к юго-востоку от Гуама в Марианской впадине, самом глубоком месте Тихого океана и действительно самом глубоком месте на Земле. Пикар и Уолш прошли весь путь до дна, спуск, который занял у них 4 часа 48 минут. Подъем занял 3 часа 17 минут.
Тридцать пять лет спустя, в 1995 году, японское судно Kaiko также совершило спуск на Марианские острова и
подтвердил измерения Пиккара и Уолша. Но достижения Kaiko были далеко не такими впечатляющими, как у Trieste с экипажем из двух человек: Kaiko, , фактически не имел экипажа. К 1990-м годам сложные технологии дистанционного зондирования позволили отправлять беспилотные океанские экспедиции, и стало меньше необходимости подвергать людей невероятным рискам, с которыми столкнулись Пикарды, Уолши и другие.
Но достижения Kaiko были далеко не такими впечатляющими, как у Trieste с экипажем из двух человек: Kaiko, , фактически не имел экипажа. К 1990-м годам сложные технологии дистанционного зондирования позволили отправлять беспилотные океанские экспедиции, и стало меньше необходимости подвергать людей невероятным рискам, с которыми столкнулись Пикарды, Уолши и другие.
СЪЕМКИ ТИТАНИК.
Примером такого беспилотного судна является судно, показанное в первых минутах оскароносного фильма «Титаник » (1997). Само судно, затопление которого в 1912 году унесло более 1000 жизней, покоится на такой большой глубине в Северной Атлантике, что нецелесообразно ни поднимать его, ни отправлять пилотируемые экспедиции для исследования недр затонувшего корабля. Таким образом, лучшим решением является дистанционно управляемое судно, которое также используется для таких целей, как картографирование дна океана, разведка месторождений нефти и других месторождений и сбор данных о технологии подводных плит.
Судно, использованное в фильме, имеющее «руки» для захвата объектов, специально разработано для подъема предметов с кораблекрушений. Для сцен, показывающих то, что должно было быть Титаником в качестве действующего судна, режиссер Джеймс Кэмерон использовал модель в масштабе 90%, которая изображала правый борт корабля — сторону, пораженную айсбергом. Поэтому при показе его левого борта, как, например, когда он покидал док Саутгемптона, Англия, 15 апреля 1912 года, все кадры пришлось перевернуть: фактические знаки на доке были написаны наоборот, чтобы казаться правильными при взгляде на них. окончательная версия.А вот для сцены с разбитым судном, лежащим на дне океана, Кэмерон использовал настоящий Титаник .
Для этого ему пришлось использовать подводный аппарат; но он не хотел снимать только изнутри подводного аппарата, как это было сделано в фильме IMAX 1992 года « Титаника». Поэтому его брат Майк Кэмерон в сотрудничестве с Panavision построил специальную камеру, которая могла выдержать 400 атм (3,923 · 10 7 Па), то есть в 400 раз больше атмосферного давления на уровне моря. Камера была прикреплена к внешней стороне подводного аппарата, который для этих внешних снимков обслуживали операторы российских подводных лодок.
Поскольку специальная камера вмещала только двенадцать минут пленки, необходимо было совершить в общей сложности двенадцать погружений. На двух последних в затонувший корабль вошёл дистанционно управляемый подводный аппарат, который было бы слишком опасно для людей в пилотируемом корабле. Кэмерон задумал дистанционно управляемую подводную лодку как простую опору, но, в конце концов, его вид внутри разрушенного Титаника добавил один из самых острых штрихов во весь фильм. Позже к ним он добавил сцены с участием объектов, характерных для сюжета фильма, таких как сейф.Их он снимал в контролируемой подводной среде, которая выглядела как интерьер Титаника .
В небо
В более раннем описании конструкции батискафа Пиккара было отмечено, что корабль состоит из двух отсеков: тяжелой стальной кабины экипажа, устойчивой к морскому давлению, и над ним более крупного и легкого контейнера, называемого поплавком. Если это больше похоже на конструкцию воздушного шара, то в этом нет ничего случайного.
В 1931 году, почти за два десятилетия до дебюта батискафа, Пикар и еще один швейцарский ученый Пауль Кипфер установили рекорд другого рода с помощью воздушного шара.Вместо того, чтобы идти ниже чем кто-либо когда-либо, как Пикар и его сын Жак сделали в 1953 году — и как Жак и Уолш сделали еще больше в 1960 году — Пиккар и Кипфер поднялись выше, чем когда-либо, поднявшись на 55 563 фута (16 940 м). Это сделало их первыми двумя людьми, проникшими в стратосферу, которая является следующим атмосферным слоем над тропосферой, слоем высотой примерно 10 миль (16,1 км), покрывающим поверхность Земли.
Пикар, без сомнения, испытал самый большой наземный диапазон высот среди всех людей за всю жизнь: почти 12.5 миль (20,1 км) от его самого высокого максимума до самого низкого минимума, 84% из них над уровнем моря, а остальные ниже. Таким образом, его карьера была данью силе выталкивающей силы и способности преодолевать выталкивающую силу для спуска в океанские глубины. Действительно, то же самое можно сказать и о семье Пикар в целом: не только Жак установил мировой рекорд глубины, но годы спустя сын Жака Бертран поднялся в небо для еще одного рекордного полета на воздушном шаре.
В 1999 году Бертран Пикар и британский инструктор по воздухоплаванию Брайан Уилсон стали первыми людьми, совершившими кругосветное путешествие на воздушном шаре Breitling Orbiter 3 . Корабль простирался на 180 футов (54,86 м) от верхней части оболочки — части воздушного шара, содержащей плавучие газы — до нижней части гондолы, части, удерживающей всадников. В герметичной кабине была одна койка, на которой один пилот мог спать, пока другой летал, а впереди находилась компьютеризированная панель управления, которая позволяла пилоту управлять горелками, переключать баллоны с пропаном и освобождать пустые. Пикарду и Уилсону потребовалось всего 20 дней, чтобы облететь Землю, что далеко от первых дней полета на воздушном шаре двумя веками ранее.
ПЕРВЫЕ ШАРЫ.
Семья Пикар хоть и швейцарская, но франкоязычная; то есть они происходят из франкоязычной части Швейцарии. Это интересно, потому что в истории человеческих встреч с плавучестью — под океаном и, тем более, в воздухе — преобладали французские имена. На самом деле именно братья-французы Жозеф-Мишель (1740-1810) и Жак-Этьен (1745-1799) Монгольфье запустили первый воздушный шар в 1783 году. и Уилбур Райт, в связи с изобретением, которое двенадцать десятилетий спустя заменило воздушный шар: самолет.
В тот первый полет Монгольфьеры отправили в воздух модель диаметром 30 футов (9,15 м), сделанную из бумаги с льняной подкладкой. Он достиг высоты 6000 футов (1828 м) и оставался в воздухе в течение 10 минут, прежде чем снова спуститься. Позднее в том же году Монгольфьеры запустили первый полет на воздушном шаре с живыми существами — овцой, петухом и уткой, а еще позже, в 1783 году, Жан-Франсуа Пилатр де Розье (1756–1785) стал первым человеком, поднявшимся наверх. на воздушном шаре.
Розье поднялся только на 84 фута (26 м), что равнялось длине веревки, которая привязывала его к земле.Однако по мере того, как производители и пользователи воздушных шаров научились правильно использовать балласт, время полета увеличилось, и полеты на воздушном шаре стали еще более практичными. На самом деле первое в мире военное использование полетов относится не к двадцатому веку, а к восемнадцатому, а именно к 1794 году, когда Франция создала корпус воздухоплавателей.
КАК ПЛАВАЕТ ВОЗДУШНЫЙ ШАР.
Для подъема воздушного шара подходят только три газа: водород, гелий и горячий воздух. Каждый из них намного менее плотный, чем обычный воздух, и это придает им плавучесть.На самом деле водород — самый легкий из известных газов, и поскольку его производство дешево, он был бы идеальным, за исключением того факта, что он чрезвычайно легко воспламеняется. После крушения дирижабля Hindenburg, в 1937 году эра использования водорода для транспорта легче воздуха фактически закончилась.
Гелий, с другой стороны, совершенно безопасен и лишь немного менее плавучий, чем водород. Это делает его идеальным для воздушных шаров, которыми дети наслаждаются на вечеринках; но гелий дорог и поэтому нецелесообразен для больших воздушных шаров.Следовательно, горячий воздух, особенно воздух, нагретый до температуры около 570 ° F (299 ° C), является единственным действительно жизнеспособным вариантом.
Закон Шарля, один из законов поведения газов, гласит, что нагревание газа увеличивает его объем. Молекулы газа, в отличие от своих жидких или твердых собратьев, крайне непривлекательны, то есть имеют тенденцию распространяться на относительно большие расстояния друг от друга. Между молекулами газа уже много пустого пространства, и увеличение объема только увеличивает количество пустого пространства.Следовательно, плотность снижается, и воздушный шар всплывает.
ДИРИЖАБЛЕРЫ.
Примерно в то же время, когда братья Монгольфье запустили свои первые воздушные шары, другой французский дизайнер, Жан-Батист-Мари Менье, начал экспериментировать с более обтекаемая, маневренная модель. В конце концов, ранние воздушные шары могли маневрировать только вдоль одной оси, вверх и вниз: когда дело доходило до движения вбок или вперед и назад, они в значительной степени зависели от стихии.
Прошло более века, прежде чем идея Менье — прототип воздушного корабля — стала реальностью.В 1898 году Альберто Сантос-Дюмон из Бразилии объединил воздушный шар с пропеллером, приводимым в действие прибором внутреннего сгорания, создав машину, которая улучшила воздушный шар, так же как батискаф позже улучшил батисферу. Дирижабль Сантос-Дюмона был нежестким, как воздушный шар. Он также использовал водород, который имеет тенденцию сжиматься во время спуска и разрушать оболочку. Чтобы решить эту проблему, Сантос-Дюмон создал баллонет, внутреннюю подушку безопасности, предназначенную для обеспечения плавучести и стабилизации полета.
Одной из величайших фигур в истории полетов легче воздуха, человеком, чье имя, наряду с дирижаблем и дирижаблем, стало синонимом дирижабля, был граф Фердинанд фон Цеппелин (1838–1917). Именно он создал легкую конструкцию из алюминиевых балок и колец, которая позволяла дирижаблю сохранять жесткость в различных атмосферных условиях. Тем не менее, первые запуски Zeppelin в десятилетие, последовавшее за 1898 годом, были сопряжены с рядом проблем, не последней из которых были катастрофы, вызванные воспламеняемостью водорода.
В 1911 году Zeppelin, наконец, удалось запустить дирижабли для общественного транспорта, и последующие четверть века стали золотым веком путешествий на дирижаблях. Не то чтобы все было «золотым» в этом возрасте: во время Первой мировой войны Германия использовала дирижабли в качестве бомбардировщиков, запустив первый лондонский налет в мае 1915 года. зенитные технологии быстро расправились бы с любым цеппелином; но к тому времени самолеты уже давно заменили дирижабли.
Однако в течение 1920-х дирижабли, такие как Graf Zeppelin , конкурировали с самолетами в качестве гражданского транспорта. Это признак предполагаемой безопасности дирижаблей над самолетами в то время, когда в 1928 году Graf Zeppelin совершил свой первый трансатлантический полет с грузом пассажиров. Всего за год до этого Чарльз Линдберг совершил первый в истории самостоятельный беспосадочный трансатлантический перелет на самолете. Сегодня это было бы равносильно полету человека на Луну или даже на Марс, и не было бы и речи о перевозке пассажиров.Кроме того, Линдберг прославлялся как герой до конца своей жизни, в то время как пассажиры на борту Graf Zeppelin заслужили за храбрость не больше, чем искатели удовольствий на борту круиза.
ОГРАНИЧЕНИЯ ПЕРЕВОЗКИ ЛЕГЧЕ ВОЗДУХА.
В течение нескольких лет дирижабли представляли собой роскошные лайнеры в небе; но крушение Hindenburg ознаменовало конец относительно широко распространенного транспорта дирижаблей. В любом случае, к моменту крушения Hindenburg в 1937 году транспорт легче воздуха уже не был ведущим соперником в области летных технологий.
По иронии судьбы, к 1937 году самолет уже давно доказал свою жизнеспособность, хотя на самом деле он был тяжелее воздуха. Принципы, которые заставляют самолет летать, имеют мало общего с плавучестью как таковой и связаны с разницей в давлении, а не в плотности. Тем не менее замена летательных аппаратов легче воздуха на передний край полета не означала, что воздушные шары и дирижабли были отправлены в музей; вместо этого их цели изменились.
Возрождение интереса к дирижаблю произошло во время Второй мировой войны, хотя и исключительно в качестве разведывательного корабля для вооруженных сил Соединенных Штатов.В послевоенный период ВМС США наняли Goodyear Tire and Rubber Company для производства дирижаблей, и в результате этих отношений Goodyear создала самый заметный дирижабль со времен Graf Zeppelin и Hindenburg: Goodyear Blimp.
ДВИГАТЕЛИ И ВОЗДУШНЫЕ ШАРЫ: НА САМОМ ДЕЛЕ?.
Дирижабль, известный зрителям по бесчисленным спортивным мероприятиям, гораздо лучше, чем самолет или вертолет, подходит для телекамер с видом на стадион с высоты птичьего полета, а для рекламодателей — с заметным рекламным щитом.Военные силы и научные круги также сочли дирижабли полезными для неожиданных целей. Их виртуальная невидимость для радаров возродила интерес к дирижаблям со стороны Министерства обороны США, которое обсуждало планы использования дирижаблей в качестве радиолокационных платформ в более крупной Стратегической воздушной инициативе. Кроме того, французские ученые использовали дирижабли для изучения верхушек деревьев или крон деревьев в тропических лесах.
Воздушные шары сыграли важную роль в освоении космоса, что является символом взаимосвязи между транспортом легче воздуха и более совершенными средствами полета.В 1961 году Малкольм Д. Росс и Виктор А. Протер из ВМС США установили рекорд высоты на воздушном шаре, поднявшись на высоту 113 740 футов (34 668 м). Технология, которая позволила им выжить на высоте более 21 мили (33,8 км) в воздухе. позже был использован при создании систем жизнеобеспечения космонавтов.
Астрономия на воздушном шаре дает одни из самых четких изображений космоса: телескопы, установленные на огромных беспилотных воздушных шарах на высоте до 120 000 футов (35 000 м) — намного выше пыли и дыма Земли — предлагают изображения с высоким разрешением.Воздушные шары использовались даже на других планетах: в 1985 году два аэростата, запущенные советской беспилотной экспедицией на Венеру, собирали данные из атмосферы этой планеты в течение 46 часов.
Американские ученые также рассмотрели возможность использования комбинации большого воздушного шара и меньшего шара, наполненного гелием, для сбора данных о поверхности и атмосфере Марса во время экспедиций на эту планету. Поскольку воздушный шар днем нагревается солнечным теплом, он будет подниматься для сбора информации об атмосфере.(На самом деле «воздух» нагревается из атмосферы Марса, состоящей в основном из углекислого газа.) Затем ночью, когда Марс остывает, воздушный шар теряет плавучесть и опускается, а гелиевый шар удерживает его в вертикальном положении. в то время как он собирал данные с земли.
ГДЕ УЗНАТЬ БОЛЬШЕ
«Плавучесть» (веб-сайт).
«Плавучесть» (веб-сайт).
«Основы плавучести» Nova/PBS (веб-сайт).
Чаллонер, Джек. Плавающий и тонущий. Остин, Техас: Рейнтри Стек-Вон, 1997.
Кобб, Аллан Б. Супер научные проекты об океанах. Нью-Йорк: Розен, 2000.
Гибсон, Гэри. Заставить вещи плавать и тонуть. Иллюстрировано Тони Кеньоном.Брукфилд, Коннектикут: Коппер Бек Брукс, 1995.
Тейлор, Барбара. Жидкость и плавучесть. New York: Warwick Press, 1990.
КЛЮЧЕВЫЕ ТЕРМИНЫ
ПРИНЦИП АРХИМЕДА:
Закон физики, согласно которому выталкивающая сила объекта, погруженного в жидкость, равна весу жидкости, вытесненной этим объектом. Он назван в честь греческого математика, физика и изобретателя Архимеда (ок. 287–212 до н. э.), который первым его определил.
БАЛЛАСТ:
Тяжелое вещество, которое за счет увеличения веса плавучего объекта улучшает его устойчивость.
ПЛАВУЧЕСТЬ:
Склонность объекта, погруженного в жидкость, плавать. Это можно объяснить принципом Архимеда.
ПЛОТНОСТЬ:
Масса, деленная на объем.
ПЕРЕМЕЩЕНИЕ:
Мера веса жидкости, которая должна быть перемещена с места, чтобы предмет можно было погрузить. Если корабль, посаженный в океан, вызывает вытеснение 1000 тонн воды, говорят, что он обладает водоизмещением 1000 тонн.
ЖИДКОСТЬ:
Любое вещество, будь то газ или жидкость, которое соответствует форме своего сосуда.
СИЛА:
Произведение массы на ускорение.
МАССА:
Мера инерции, показывающая сопротивление объекта изменению его движения. Для объекта, погруженного в жидкость, масса равна объему, умноженному на плотность.
ДАВЛЕНИЕ:
Действие силы на двумерную площадь; следовательно, формула давления — это сила, деленная на площадь. Британская система мер обычно измеряет давление в фунтах на квадратный дюйм.В метрических терминах это измеряется в ньютонах (Н) на квадратный метр, число, известное как паскаль (Па).
УДЕЛЬНЫЙ ВЕС:
Плотность объекта или вещества по отношению к плотности воды; или, в более общем смысле, соотношение между плотностями двух объектов или веществ.
ОБЪЕМ:
Объем трехмерного пространства, занимаемого объектом. Объем обычно измеряется в кубических единицах.
ВЕС:
Сила, равная массе, умноженной на ускорение свободного падения (32 фута/9.8 м/с 2 ). Для объекта, погруженного в жидкость, вес равен объему, умноженному на плотность, умноженному на ускорение свободного падения.
Принцип Архимеда: уравнение с решаемыми примерами
Вы когда-нибудь задумывались, почему большие и массивные стальные корабли не тонут, а маленькая монета тонет?
Ответ кроется в законе Архимеда, тесно связанном с выталкивающими силами.
К объектам, находящимся в жидкости (например, в воде или даже в воздухе!), приложены две основные силы: восходящая выталкивающая сила и нисходящая гравитационная сила.Конкуренция между этими двумя силами определяет, тонет ли объект в жидкости или плавает.
Здесь мы собираемся изучить эту тему с некоторыми основными и важными решенными примерами.
Этот фундаментальный принцип, открытый греческим математиком в шестом веке до нашей эры. состояния и определения, как показано ниже:
Любой объект, полностью или частично погруженный в жидкость, поднимается вверх под действием силы, равной весу жидкости, вытесненной этим объектом.
Когда вы поднимаете тяжелый предмет в бассейне, фактически вы испытываете действие принципа Архимеда, поскольку вода частично поддерживает вас, чтобы преодолеть вес помещенного в нее предмета.
Или, используя принцип Архимеда, мы можем объяснить, почему воздушные шары поднимаются в воздух.
Когда тело помещается в жидкость, на него всегда действует восходящая сила со стороны окружающей жидкости, которая частично или полностью уменьшает воздействие направленной вниз силы веса. Эта направленная вверх сила, называемая выталкивающей силой, была объяснена на решенных примерах в другом руководстве.
Вывод закона Архимеда:
Метод 1: простой аргумент
Предположим, два тела одинакового размера и формы помещены в жидкость на некоторой глубине.
Один заполнен неизвестным веществом массой $m$, а другой заполнен окружающей его жидкостью с массой $m’$.
Поскольку оба объекта находятся на одной глубине, выталкивающие силы, действующие на них, одинаковы.
Эти выталкивающие силы должны быть уравновешены весом объектов, чтобы объекты оставались на одной глубине (или сохраняли равновесие).
Для объекта массой $m$ согласно второму закону движения Ньютона $F_B=mg$, и аналогично для объекта массы $m’$ имеем $F_B=m’g$. Следовательно, \[mg=F_B=m’f\] Как видите, это проще, вместо того, чтобы уравновешивать выталкивающую силу неизвестным весом $mg$, мы можем сделать это известным весом $m’g$, который равен вес тела жидкости, объем которого равен объему исходного объекта.
Это закон Архимеда.
Метод 2: Физической причиной направленной вверх силы, действующей на объекты в нем, является разница давлений между верхней и нижней сторонами объекта из-за того, что они находятся на разных глубинах жидкости.
На поверхности на глубине $h$ ниже уровня жидкости давление равно $P=P_0+\rho$, где $P_0$ — давление на поверхности жидкости, а $\rho$ — плотность жидкости.
Как видите, нижняя сторона объекта находится на большей глубине, поэтому по определению давления $P=\frac FA$ на него действует большая сила.
Обратите внимание, что на объект в жидкости также действуют горизонтальные силы, но, поскольку они расположены на одной глубине, их результирующая величина равна нулю.
На самом деле можно показать, что все горизонтальные силы, воздействующие на объект произвольной формы, компенсируют друг друга.
Остаются только вертикальные силы, приложенные к верхней и нижней сторонам погруженного тела, которые, суммируя вектора, дают выталкивающую силу $F_b$.
Применяя теперь второй закон Ньютона и уравновешивая все силы в вертикальном направлении, мы получаем следующую формулу принципа Архимеда
выталкивающая сила = вес тела
или \[F_b=W\] Где выталкивающая сила определяется как произведение плотности жидкости, объема жидкости, вытесненного в нее объектом, и гравитационной постоянной $g=10\,{\rm м/с^2}$ или \[F_b=\rho_{жидкость}\times V_{dis}\times g\]
Теперь пришло время решить несколько примеров, чтобы понять закон Архимеда.
Пример: деревянный брусок плавает в пресной воде с погруженным на две пятых объема V и в масле с погруженным на 0,75V. Найдите плотность: а) дерева, б) масла.
Решение : поскольку древесина плавает в воде, ее вес должен быть уравновешен выталкивающей силой.
а) Каков объем предмета?
(b) Сколько он весит в воздухе?
Решение : Поскольку тело стало легче в воде, на объект должна действовать направленная вверх сила, которая компенсирует часть силы веса, направленной вниз. В жидкостях эта сила называется плавучей силой или силой плавучести.
(a) Согласно закону Архимеда, $200\,{\rm N}$ — это сила плавучести, действующая на тело, которая получается по следующей формуле \begin{align*} F_b &= \rho_{water} \times V_{объект} \times g \\ \\ 200&=100\times V_{объект}\times 10 \\ \\ \Rightarrow V_{объект}&=\frac{2}{100}\quad {\rm m^ 3}\конец{выравнивание*}
(b) Вес тела, $W=\rho V g$ в воздухе, рассчитывается как \[W=(7800)\left(\frac{2}{100}\right)(10)=1560\,{\ rm N}\] Где $V$ — фактический объем тела.3}$ медленно помещается в пресную воду. На какую глубину $h$ погружена плита?
Решение : согласно закону Архимеда, вода будет воздействовать на плиту выталкивающей силой, величина которой равна весу воды, вытесненной плитой.
Таким образом, выталкивающая сила, действующая на плиту, равна $F_b=m_{water}g=\rho_{water}V_{dis}g$, где $V_{dis}$ — вытесненный объем воды или объем плиты который находится под водой. Пусть $h$ — высота плиты с нижней стороны.Таким образом, $V_{dis}=Ah$, где $A$ — площадь основания плиты.
Вес плиты также определяется как $W=\rho_{slab}V_{slab}g$.
Далее, используя основное уравнение Архимеда в виде $F_b=W$, получаем \begin{align*}\rho_{water}\times (Ah) \times g&=\rho_{slab}\times V_{slab}\ раз г \\ \\ \Rightarrow h&=\frac{\rho_{slab}V_{slab}}{\rho_{water}A}\\ \\ &=\frac{600\times 0,6}{1000\times 5,7 } \\ \\&=0,0632\quad {\rm m}\end{align*}
Критерии всплытия или затопления:
Принцип Архимеда просто дает нам эмпирическое правило, позволяющее определить, тонет ли объект, помещенный в жидкость, или плавает.Согласно этому принципу, если записать все силы, приложенные неподвижной жидкостью к погруженному в нее телу, в виде выталкивающей вверх силы $F_b$ и направленной вниз силы веса $W$, то в зависимости от знака результирующей силы возможны три ситуации $F_{net}=F_b \стрелка вверх-W\стрелка вниз$:
(1) Тонет : когда происходит $F_{net}<0$, в этом случае выталкивающая сила вверх меньше силы его веса вниз, тогда объект тонет. \[\underbrace{\rho_{fluid}V_{fluid}g}_{плавучесть}<\underbrace{\rho_{obj}V_{obj}g}_{вес}\] Например, камень плотнее воды, поэтому, когда его помещают в воду, он тонет.
(2) Плавающий : когда происходит $F_{net}>0$, следовательно, положительная восходящая выталкивающая сила уравновешивается отрицательной направленной вниз силой тяжести (весом), тогда объект плавает на поверхности жидкости. \[\underbrace{\rho_{fluid}V_{fluid}g}_{плавучесть}=\underbrace{\rho_{obj}V_{obj}g}_{вес}\] Древесина менее плотна, чем вода, поэтому она поплавки.
(3) Нейтральная плавучесть: есть третий случай, когда $F_{net}=0$. В этих ситуациях объект остается в точке выброса в жидкость неподвижным.Это происходит, когда плотности объекта и жидкости равны. Примером нейтральной плавучести являются плавающие в воде рыбы. Рыбы имеют плавательный пузырь, который может наполняться воздухом вместе с их плотью, образуя составной объект со средней отрегулированной таким образом, что уравновешивает плотность воды и, следовательно, он не тонет и не плавает в воде.
Вопрос: Какая часть объема айсберга находится ниже уровня моря.
Решение : согласно закону Архимеда, поскольку айсберг плавает на воде, выталкивающая сила, направленная вверх, равна его весу.Величина выталкивающей силы является произведением объема айсберга под водой, плотности воды и ускорения свободного падения.
С другой стороны, вес определяется как произведение фактического объема айсберга, плотности айсберга и ускорения свободного падения.
Применение условия плавучести для определения доли объема айсберга ниже уровня моря. \begin{align*}F_b&=W\\ \rho_{SW}V_{в воде}g&=\rho_{IB}Vg\\ \\ \Rightarrow \frac{V_{в воде}}{V}& =\frac{\rho_{IB}}{\rho_{SW}}\\ \\ &=\frac{0.3} \\ \\ &=0.9\end{align*} Где выше $\rho_{IB}$ и $\rho_{SW}$ — плотности айсберга и морской воды соответственно. Как видите, около 90% объема айсберга находится под водой.
Автор: Али Немати
Страница создана: 31.01.2021
(a) В частично погруженном теле выталкивающая сила $F_b$ определяется как произведение плотности жидкости $\rho_f$ на вытесненный объем жидкости $V_{dis}$, умноженный на ускорение свободного падения $g$.3}$ оказывается на 200 Н легче в воде, чем на воздухе.

 Как расположатся в ней жидкости?
Почему?
Как расположатся в ней жидкости?
Почему? Определите
массу снятого с нее груза, если площадь
сечения баржи на уровне воды 240 м2?
Определите
массу снятого с нее груза, если площадь
сечения баржи на уровне воды 240 м2? Какая это жидкость.
Какая это жидкость. Актуализация знаний
Актуализация знаний 



 Организует обсуждение и запись домашнего задания
Организует обсуждение и запись домашнего задания 
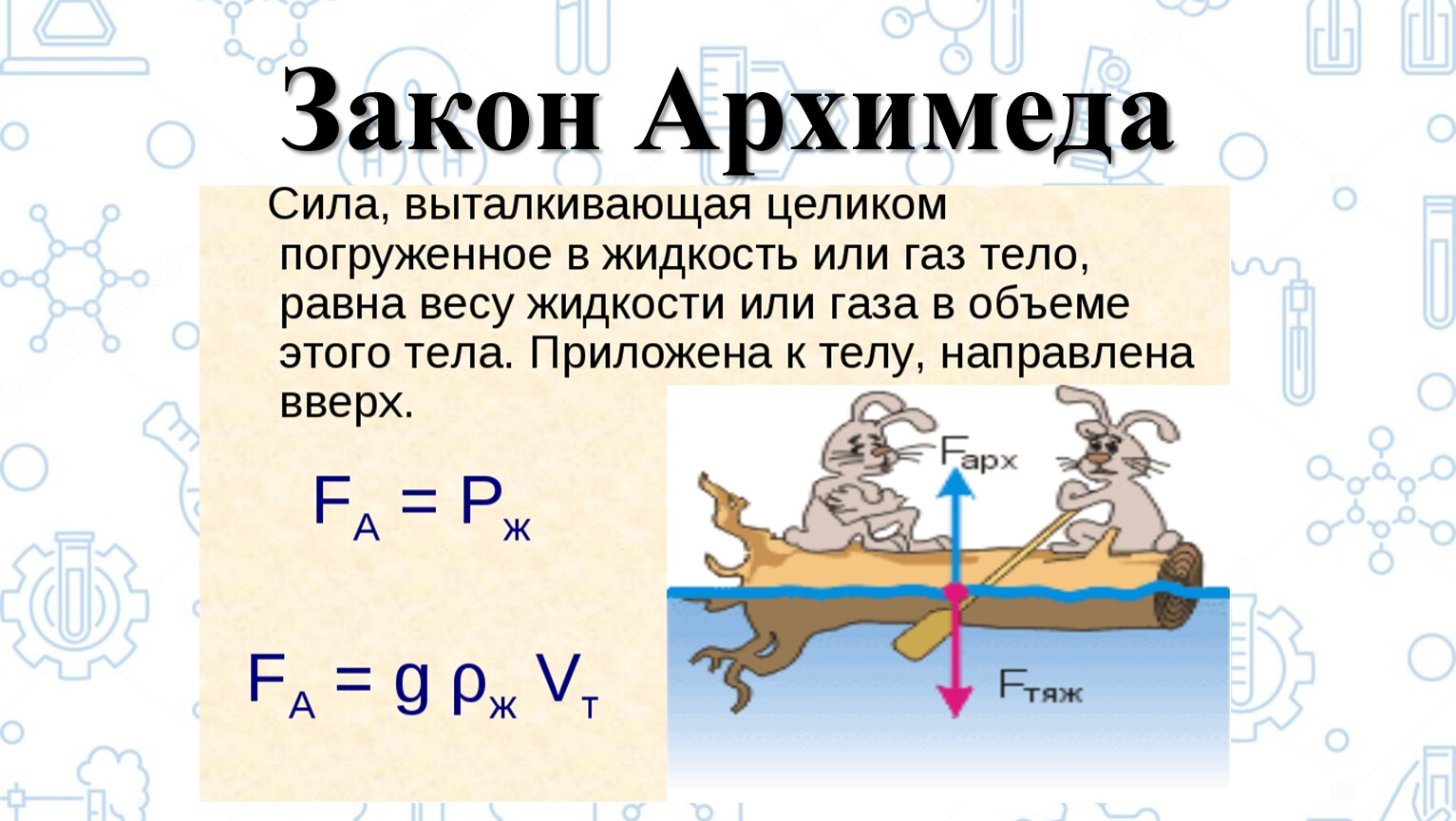



 Корабли и подводные лодки плавают/погружаются по этому принципу.Через него также можно рассчитать объем и плотность объектов.
Корабли и подводные лодки плавают/погружаются по этому принципу.Через него также можно рассчитать объем и плотность объектов. Сферический шар плотностью ρ=0,70 кгL имеет радиус r=10см. Если мяч положить на поверхность воды и отпустить, какая часть мяча погрузится в воду? g=10 мс 2 [3 балла]
Сферический шар плотностью ρ=0,70 кгL имеет радиус r=10см. Если мяч положить на поверхность воды и отпустить, какая часть мяча погрузится в воду? g=10 мс 2 [3 балла]  В метрах радиус равен
В метрах радиус равен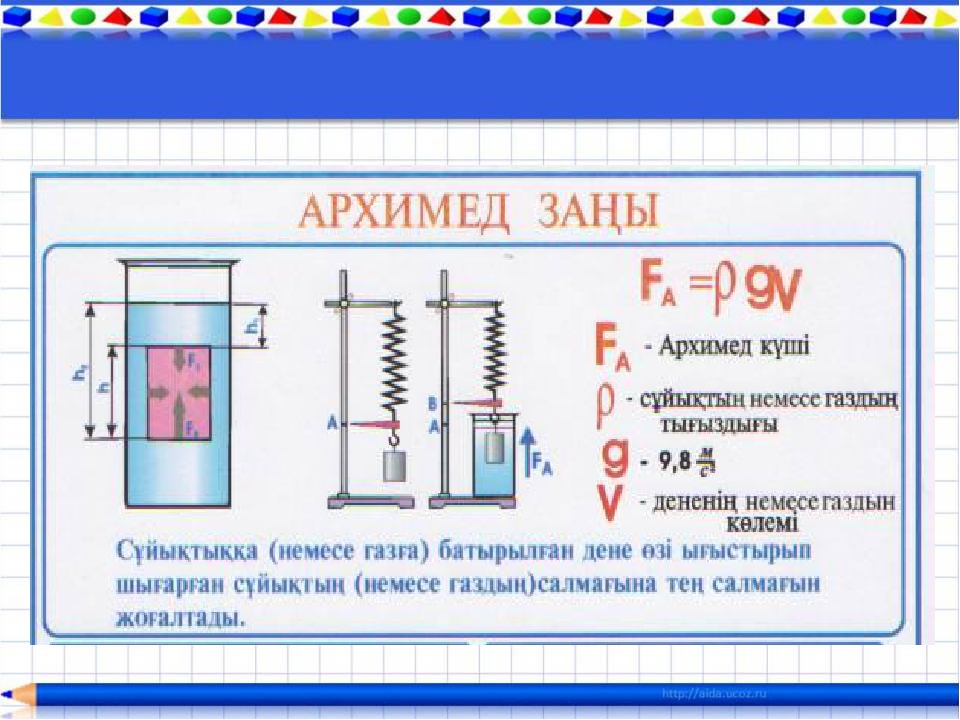
 Пример: нефть, вода, газы и т. д.
Пример: нефть, вода, газы и т. д. Пусть P t и P b давлением сверху и снизу куба соответственно. Пусть F t и F b — силы, действующие на верхнюю и нижнюю части куба соответственно.
Пусть P t и P b давлением сверху и снизу куба соответственно. Пусть F t и F b — силы, действующие на верхнюю и нижнюю части куба соответственно.
 Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.
Если выталкивающая сила больше веса объекта, объект поднимется на поверхность и всплывет. Если выталкивающая сила меньше веса тела, то оно утонет. Если выталкивающая сила равна весу объекта, объект останется подвешенным на этой глубине. Выталкивающая сила всегда присутствует независимо от того, плавает ли объект, тонет или находится в жидкости.