сходимость интегралов от z n a к o n E R m e n-й функции/(x), а знак предыдущего числа является некорректным интегралом 119 с n o l o f и T E Людмила Фирмаль
бесконечными пределами. Эта функция интегрируема, функция/(x) также интегрируема, и далее b C o l y t n o. ООО Например, Интеграл\предлагается следующим образом Дядя ах 1 Тогда Интеграл функции справа сходится, и[n°285, теорема 1] сходится Интеграл функции слева, сходится он (абсолютно) и предлагает Интеграл. Как видно, z n A K o p e R e m e n o-я функция для рассмотрения, описанного здесь, может установить сходимость только в благоприятных случаях. Если интегралы данной функции расходятся или сходятся, но не являются абсолютными, то эти случаи невозможно отличить по признакам, установленным для положительных функций.
Смотрите также:
Решение задач по математическому анализу
Несобственный интеграл онлайн
Определённый интеграл называется несобственным, если выполняется хотя бы одно из двух условий:
Один (или оба) из пределов интегрирования равен или . В этом случае, интеграл называется несобственным интегралом первого рода, например: .
В любой точке на отрезке интегрирования, подинтегральная функция терпит бесконечный разрыв. В этом случае, интеграл называется несобственным интегралом второго рода, например: в точке .
Рассмотрим в качестве примера несобственный интеграл первого рода . График подинтегральной функции на отрезке интегрирования имеет вид:
Геометрически, данный несобственный интеграл равен площади под графиком функции
на отрезке
.
Рассматриваемый интеграл является сходящимся, потому что указанная площадь равна
— конечному числу. Однако, несобственные интегралы бывают и расходящимися, например:
Алгоритм вычисления несобственного интеграла первого рода выглядит следующим образом:
Сначала мы заменяем бесконечный предел на некоторый параметр, например и получаем определенный интеграл. Этот интеграл мы вычисляем обычным образом: берем неопределенный интеграл и далее используем формулу Ньютона-Лейбница. На завершающем этапе, мы вычисляем предел при и, если, данный предел существует и конечен, тогда исходный несобственный интеграл является сходящимся, а в противном случае — расходящимся.
Алгоритм вычисления несобственного интеграла второго рода заключается в разбивке интервала интегрирования на отрезки в каждом из которых подинтегральная функция является непрерывной (разрывы допускаются только на концах отрезка).
Далее, вычисляются полученные
определенные интегралы, а при подстановке значений в формулу Ньютона-Лейбница вычисляются соответствующие пределы. И если все эти пределы существуют и конечны, тогда, как и раньше, интеграл является сходящимся, а в противном случае — расходящимся. Приведем пример:
Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен вычислить очень многие типы несобственных интегралов. При этом, если интеграл расходится, калькулятор выдает сообщение: integral does not converge.
Определение сходимости интеграла онлайн. Несобственные интегралы
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков.
На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте.
Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн.
Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения.
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы. Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади .
При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно .
Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела. У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет .
Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах). Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения.
В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе.
Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой .
Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала. У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования.
Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования . В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: .
Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу. В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
3+1}.
\]
Несобственные интегралы первого рода: распространение понятия определённого интеграла на случаи интегралов с бесконечным верхним или нижними пределами интегрирования, или оба предела интегрирования бесконечны.
Несобственные интегралы второго рода: распространение понятия определённого интеграла на случаи интегралов от неограниченных функций, подынтегральная функция в конечном числе точек конечного отрезка интегрирования не существует, обращаясь в бесконечность.
Для сравнения. При введении понятия определённого интеграла предполагалось, что функция f (x ) непрерывна на отрезке [a , b ], а отрезок интегрирования является конечным, то есть ограничен числами, а не бесконечностью. Некоторые задачи приводят к необходимости отказаться от этих ограничений. Так появляются несобственные интегралы.
Геометрический смысл несобственного интеграла выясняется довольно просто.
В случае, когда график функции y = f (x ) находится выше оси Ox , определённый интеграл
выражает площадь криволинейной трапеции, ограниченной кривой y = f (x )
,
осью абсцисс и ординатами x = a , x = b .
В свою очередь несобственный интеграл
выражает площадь неограниченной (бесконечной) криволинейной трапеции, заключённой между линиями y = f (x )
(на рисунке ниже — красного цвета), x = a и осью абсцисс.
Аналогичным образом определяются несобственные интегралы и для других бесконечных интервалов:
Площадь бесконечной криволинейной трапеции может быть конечным числом и в этом случае несобственный интеграл называется сходящимся. Площадь может быть и бесконечностью и в этом случае несобственный интеграл называется расходящимся.
Использование предела интеграла вместо самого несобственного
интеграла. Для того, чтобы вычислить несобственный интеграл, нужно использовать предел
определённого интеграла. Если этот предел существует и конечен (не равен бесконечности), то
несобственный интеграл называется сходящимся, а в противном случае — расходящимся. К чему стремится
переменная под знаком предела, зависит от того, имеем мы дело с несобственным интегралом первого рода
или второго рода.
Узнаем об этом сейчас же.
Несобственные интегралы первого рода — с бесконечными пределами и их сходимость
Несобственные интегралы с бесконечным верхним пределом
Итак, запись несобственного интеграла как отличается от обычного определённого интеграла тем, что верхний предел интегрирования бесконечен.
Определение. Несобственным интегралом с бесконечным верхним пределом интегрирования от непрерывной функции f (x ) на промежутке от a до ∞ называется предел интеграла этой функции с верхним пределом интегрирования b и нижним пределом интегрирования a при условии, что верхний предел интегрирования неограниченно растёт , т.е.
.
Если этот предел существует и равен некоторому числу, а не бесконечности, то несобственный интеграл называется сходящимся , а число, которому равен предел, принимается за его значение. В противном случае несобственный интеграл называется расходящимся и ему не приписывается никакого значения.
Пример 1. Вычислить несобственный интеграл (если он сходится).
Решение. На основании определения несобственного интеграла находим
Так как предел существует и равен 1, то и данный несобственный интеграл сходится и равен 1.
В следующем примере подынтегральная функция почти как в примере 1, только степень икса — не двойка, а буква альфа, а задача состоит в исследовании несобственного интеграла на сходимость. То есть предстоит ответить на вопрос: при каких значениях альфы данный несобственный интеграл сходится, а при каких расходится?
Пример 2. Исследовать на сходимость несобственный интеграл (нижний предел интегрирования больше нуля).
Решение. Предположим сначала, что , тогда
В полученном выражении перейдём к пределу при :
Нетрудно видеть, что предел в правой части существует и равен нулю, когда , то есть , и не существует, когда , то есть .
В первом случае, то есть при
имеет место .
Если , то
и
не существует.
Вывод нашего исследования следующий: данный несобственный интеграл сходится при и расходится при .
Применяя к изучаемому виду несобственного интеграла формулу Ньютона-Лейбница , можно вывести следующую очень похожую на неё формулу:
.
Это обобщённая формула Ньютона-Лейбница.
Пример 3. Вычислить несобственный интеграл (если он сходится).
Предел этого интеграла существует:
Второй интеграл, составляющий сумму, выражающую исходный интеграл:
Предел этого интеграла также существует:
.
Находим сумму двух интегралов, являющуюся и значением исходного несобственного интеграла с двумя бесконечными пределами:
Несобственные интегралы второго рода — от неограниченных функций и их сходимость
Пусть функция f (x ) задана на
отрезке от a до b и неограниченна на нём. Предположим, что функция обращается в бесконечность в точке b ,
в то время как во всех остальных точках отрезка она непрерывна.
Определение. Несобственным интегралом функции f (x ) на отрезке от a до b называется предел интеграла этой функции с верхним пределом интегрирования c , если при стремлении c к b функция неограниченно возрастает, а в точке x = b функция не определена , т.е.
.
Если этот предел существует, то несобственный интеграл второго рода называется сходящимся, в противном случае — расходящимся.
Используя формулу Ньютона-Лейбница, выводим.
Несобственные интегралы
Сегодня я подготовил для вас подробную статью о несобственных интегралах.
Определенные интегралы , для которых отрезок [a; b] конечен, а функция f(x) – непрерывна на этом отрезке, называют собственными.
С целью обобщения понятия интеграла рассмотрим:
1) определенные интегралы от непрерывных функций, но с бесконечными пределами интегрирования;
2) определенные интегралы с конечными пределами интегрирования, но от функций, имеющих бесконечный разрыв на промежутке интегрирования.
Такие определенные интегралы называют несобственными.
1. Интегралы с бесконечными пределами.
Пусть функция f(x) определена на промежутке [a; +∞) и пусть f(x) интегрирована на любом отрезке [a; b] (b> a– произвольные действительные числа).
Определение 1.1. Предел интеграла при b→+∞ называется несобственными интегралом функции f(x) от а до +∞ и обозначается символом:
Если предел (1.1) есть конечное число, то несобственный интеграл называют сходящимся. Если предел (1.1) не существует или равен бесконечности, то несобственный интеграл называют расходящимся.
Пример 1.1. Исследовать на сходимость интеграл
Решение. Вычислим определенный интеграл
Имеем
Следовательно, заданный интеграл сходится и он равен
Из рассмотренного следует, что вопрос о сходимости (расходимости) несобственных интегралов решается с помощью первоначальной функции для подынтегральной функции.
Это обстоятельство сильно сужает круг практического использования понятия несобственного интеграла. В отдельных случаях вопрос о сходимости (расхождении) несобственного интеграла можно решить, не находя первообразной для подынтегральной функции. При этом пользуются так называемыми признаками сходимости несобственных интегралов. Простейшим признаком сходимости является признак сравнения.
Теорема 1.1. Пусть для всех x ≥ a функции f(x) и g(x) определены и выполняются неравенства 0 ≤ f(x) ≤ g(x). Тогда:
Для функции f(x), непрерывной на бесконечном промежутке -∞ < x ≤ b, определяется несобственный интеграл
Для функции f(x), непрерывной на всей числовой оси, несобственный интеграл определяется равенством:
где с – произвольное действительное число.
2. Интегралы от неограниченных функций.
Пусть функция f(x) такая, что для произвольного малого ɛ>0 она определена, ограничена и интегрирована на отрезке [a+ɛ; b] и неограниченна на (a; b].
Определение 1.2. Предел определенного интеграла при ɛ→0 называется несобственным интегралом функции f(x) на отрезке [a; b] и обозначается символом
Аналогично для функции f(x), определенной, непрерывной и интегрированной на отрезке [a; b- ɛ] и неограниченной на [a; b) обозначается несобственный интеграл:
Если пределы (1.4), (1.5) есть конечные числа, то несобственные интегралы называются сходящимися, а если эти пределы не существуют, то несобственные интегралы называются расходящимися.
В конце отметим, что для функции f(x), которая имеет на промежутке (a; b) точку с, в окрестности которой f(x) неограниченная, но является ограниченной и интегрированной на каждом из отрезков [a; c- ɛ] и [ñ + ɛ; b], интеграл определяется равенством.
Аналогично обозначается несобственный интеграл на отрезке [a; b] от функции, которая непрерывна на нем всюду, кроме конечного числа точек, и неограниченной вблизи этих точек.
Пример 1.2.Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение:
Решение.
а) функция
ограничена и непрерывна, а потому и интегрируемая. Предельное значение
существует; таким образом,
ограничена и непрерывна, но
расходится.
Пример 1.3.
Исследовать сходимость интегралов. Для сходящихся интегралов найти их значение
Решение.
если α > 0, интеграл сходится; если α ≤ 0, то интеграл расходится;
если α > 1; если 0 < α ≤ 1, интеграл расходится как и при α = 1:
так и при 0 < α < 1:
Пример 1.4. Найти несобственный интеграл
Решение. Функция непрерывна при 0 ≤ x < 2 и имеет бесконечный разрыв в точке x=2, поэтому имеем
Поэтому данный интеграл сходится и равен 2√2.
Пример 1.5. Исследовать сходимость интегралы. Для сходящихся интегралов найти их значение:
Решение.
то есть, несобственный интеграл расходится
то есть, несобственный интеграл I2 сходится и равен .
Пример 1.
5. Исследовать на сходимость интегралы:
Решение.
Если у Вас есть ко мне вопросы, или нужна помощь, консультация по решению несобственных интегралов, записывайтесь на мои занятия. Буду рад Вам помочь.
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Исследовать на сходимость несобственный интеграл онлайн с решением. Определенный интеграл онлайн
Вы еще здесь? =) Нет, я никого не пытался запугать, просто тема несобственных интегралов – очень хорошая иллюстрация тому, как важно не запускать высшую математику и другие точные науки. Для освоения урока на сайте всё есть – в подробной и доступной форме, было бы желание….
Итак, начнем-с. Образно говоря, несобственный интеграл – это «продвинутый» определенный интеграл, и на самом деле сложностей с ними не так уж и много, к тому же у несобственного интеграла есть очень хороший геометрический смысл.
Что значит вычислить несобственный интеграл?
Вычислить несобственный интеграл – это значит, найти ЧИСЛО (точно так же, как в определенном интеграле), или доказать, что он расходится (то есть, получить в итоге бесконечность вместо числа).
Несобственные интегралы бывают двух видов.
Несобственный интеграл с бесконечным пределом (ами) интегрированияИногда такой несобственный интеграл называют несобственным интегралом первого рода . В общем виде несобственный интеграл с бесконечным пределом чаще всего выглядит так: . В чем его отличие от определенного интеграла? В верхнем пределе. Он бесконечный: .
Реже встречаются интегралы с бесконечным нижним пределом или с двумя бесконечными пределами: , и их мы рассмотрим позже – когда войдёте во вкус:)
Ну а сейчас разберём самый популярный случай . В подавляющем большинстве примеров подынтегральная функция непрерывна на промежутке , и этот важный факт следует проверять в первую очередь! Ибо если есть разрывы, то есть дополнительные нюансы.
Для определённости предположим, что и тогда типичная криволинейная трапеция будет выглядеть так:
Обратите внимание, что она бесконечна (не ограничена справа), и несобственный интеграл численно равен её площади . При этом возможны следующие варианты:
1) Первая мысль, которая приходит в голову: «раз фигура бесконечная, то », иными словами, площадь тоже бесконечна. Так быть может. В этом случае говорят, что несобственный интеграл расходится .
2) Но . Как это ни парадоксально прозвучит, площадь бесконечной фигуры может равняться… конечному числу! Например: . Может ли так быть? Запросто. Во втором случае несобственный интеграл сходится .
3) О третьем варианте чуть позже.
В каких случаях несобственный интеграл расходится, а в каком сходится? Это зависит от подынтегральной функции , и конкретные примеры мы очень скоро рассмотрим.
А что будет, если бесконечная криволинейная трапеция расположена ниже оси? В этом случае, несобственный интеграл (расходится) либо равен конечному отрицательному числу.
Таким образом, несобственный интеграл может быть отрицательным .
Важно! Когда Вам для решения предложен ЛЮБОЙ несобственный интеграл, то, вообще говоря, ни о какой площади речи не идет и чертежа строить не нужно . Геометрический смысл несобственного интеграла я рассказал только для того, чтобы легче было понять материал.
Коль скоро, несобственный интеграл очень похож на определенный интеграл, то вспомним формулу Ньютона- Лейбница: . На самом деле формула применима и к несобственным интегралам, только ее нужно немного модифицировать. В чем отличие? В бесконечном верхнем пределе интегрирования: . Наверное, многие догадались, что это уже попахивает применением теории пределов, и формула запишется так: .
В чем отличие от определенного интеграла? Да ни в чем особенном! Как и в определенном интеграле, нужно уметь находить первообразную функцию (неопределенный интеграл), уметь применять формулу Ньютона-Лейбница. Единственное, что добавилось – это вычисление предела.
У кого с ними плохо, изучите урок Пределы функций. Примеры решений , ибо лучше поздно, чем в армии.
Рассмотрим два классических примера:
Пример 1
Для наглядности я построю чертеж, хотя, еще раз подчеркиваю, на практике строить чертежи в данном задании не нужно .
Подынтегральная функция непрерывна на полуинтервале , значит, всё нормально и несобственный интеграл можно вычислить «штатным» методом.
Применение нашей формулы и решение задачи выглядит так:
То есть, несобственный интеграл расходится, и площадь заштрихованной криволинейной трапеции равна бесконечности.
В рассмотренном примере у нас простейший табличный интеграл и такая же техника применения формулы Ньютона-Лейбница, как в определенном интеграле. Но применятся эта формула под знаком предела. Вместо привычной буквы «динамической» переменной выступает буква «бэ». Это не должно смущать или ставить в тупик, потому что любая буква ничем не хуже стандартного «икса».
Если Вам не понятно почему при , то это очень плохо, либо Вы не понимаете простейшие пределы (и вообще не понимаете, что такое предел), либо не знаете, как выглядит график логарифмической функции. Во втором случае посетите урок Графики и свойства элементарных функций .
При решении несобственных интегралов очень важно знать, как выглядят графики основных элементарных функций!
Чистовое оформление задания должно выглядеть примерно так:
“
! При оформлении примера всегда прерываем решение, и указываем, что происходит с подынтегральной функцией – непрерывна она на промежутке интегрирования или нет . Этим мы идентифицируем тип несобственного интеграла и обосновываем дальнейшие действия.
Пример 2
Вычислить несобственный интеграл или установить его расходимость.
Выполним чертеж:
Во-первых, замечаем следующее: подынтегральная функция непрерывна на полуинтервале . Гуд. Решаем с помощью формулы :
(1) Берем простейший интеграл от степенной функции (этот частный случай есть во многих таблицах).
Минус лучше сразу вынести за знак предела, чтобы он не путался под ногами в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы по формуле Ньютона-Лейбница.
(3) Указываем, что при (Господа, это уже давно нужно понимать) и упрощаем ответ.
Вот здесь площадь бесконечной криволинейной трапеции равна конечному числу! Невероятно, но факт.
Чистовое оформление примера должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на
“
Что делать, если вам встретится интеграл наподобие – с точкой разрыва на интервале интегрирования? Это говорит о том, что в примере опечатка (вероятнее всего) , либо о продвинутом уровне обучения. В последнем случае, в силу свойства аддитивности , следует рассмотреть два несобственных интеграла на промежутках и и затем разобраться с суммой.
Иногда вследствие опечатки либо умысла несобственного интеграла может вовсе не существовать , так, например, если в знаменатель вышеуказанного интеграла поставить квадратный корень из «икс», то часть промежутка интегрирования вообще не войдёт в область определения подынтегральной функции.
Более того, несобственного интеграла может не существовать даже при всём «видимом благополучии». Классический пример: . Несмотря на определённость и непрерывность косинуса, такого несобственного интеграла не существует! Почему? Всё очень просто, потому что:
– не существует соответствующего предела .
И такие примеры пусть редко, но встречаются на практике! Таким образом, помимо сходимости и расходимости, есть ещё и третий исход решения с полноправным ответом: «несобственного интеграла не существует».
Следует также отметить, что строгое определение несобственного интеграла даётся именно через предел, и желающие могут ознакомиться с ним в учебной литературе. Ну а мы продолжаем практическое занятие и переходим к более содержательным задачам:
Пример 3
Вычислить несобственный интеграл или установить его расходимость.
Сначала попытаемся найти первообразную функцию (неопределенный интеграл). Если нам не удастся этого сделать, то несобственный интеграл мы, естественно, тоже не решим.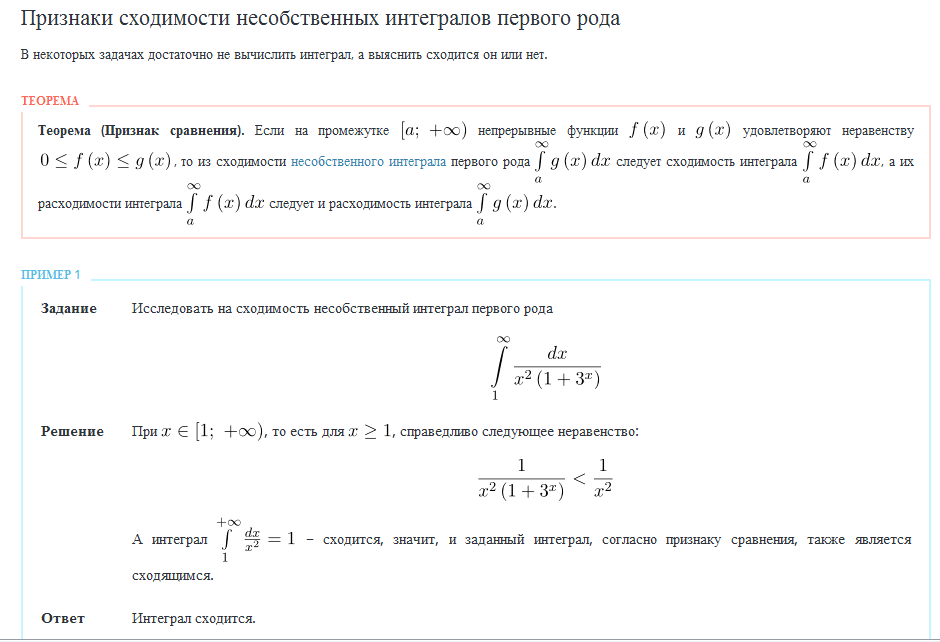
На какой из табличных интегралов похожа подынтегральная функция? Напоминает она арктангенс: . Из этих соображений напрашивается мысль, что неплохо бы в знаменателе получить квадрат. Делается это путем замены.
Проведем замену:
Неопределенный интеграл найден, константу в данном случае добавлять не имеет смысла.
На черновике всегда полезно выполнить проверку, то есть продифференцировать полученный результат:
Получена исходная подынтегральная функция, значит, неопределенный интеграл найден правильно.
Теперь находим несобственный интеграл:
(1) Записываем решение в соответствии с формулой . Константу лучше сразу вынести за знак предела, чтобы она не мешалась в дальнейших вычислениях.
(2) Подставляем верхний и нижний пределы в соответствии с формулой Ньютона-Лейбница. Почему при ? Смотрите график арктангенса в уже неоднократно рекомендованной статье.
(3) Получаем окончательный ответ. Тот факт, что полезно знать наизусть.
Продвинутые студенты могут не находить отдельно неопределенный интеграл, и не использовать метод замены, а использовать метод подведения функции под знак дифференциала и решать несобственный интеграл «сразу». В этом случае решение должно выглядеть примерно так:
“
Подынтегральная функция непрерывна на .
“
Пример 4
Вычислить несобственный интеграл или установить его расходимость.
! Это типовой пример, и похожие интегралы встречаются очень часто. Хорошо его проработайте! Первообразная функция здесь находится методом выделения полного квадрата, более подробно с методом можно ознакомиться на уроке Интегрирование некоторых дробей .
Пример 5
Вычислить несобственный интеграл или установить его расходимость.
Этот интеграл можно решить подробно, то есть сначала найти неопределенный интеграл, проведя замену переменной. А можно решить «сразу» – подведением функции под знак дифференциала.
У кого какая математическая подготовка.
Полные решения и ответы в конце урока.
Примеры решений несобственных интегралов с бесконечным нижним пределом интегрирования можно посмотреть на странице Эффективные методы решения несобственных интегралов . Там же разобран случай, когда оба предела интегрирования бесконечны.
Несобственные интегралы от неограниченных функцийИли несобственные интегралами второго рода . Несобственные интегралы второго рода коварно «шифруются» под обычный определенный интеграл и выглядят точно так же: Но, в отличие от определенного интеграла, подынтегральная функция терпит бесконечный разрыв (не существует): 1) в точке , 2) или в точке , 3) или в обеих точках сразу, 4) или даже на отрезке интегрирования. Мы рассмотрим первые два случая, для случаев 3-4 в конце статьи есть ссылка на дополнительный урок.
Сразу пример, чтобы было понятно: . Вроде бы это определенный интеграл. Но на самом деле – это несобственный интеграл второго рода, если мы подставим в подынтегральную функцию значение нижнего предела , то знаменатель у нас обращается в ноль, то есть подынтегральной функции просто не существует в этой точке!
Вообще при анализе несобственного интеграла всегда нужно подставлять в подынтегральную функцию оба предела интегрирования .
В этой связи проверим и верхний предел: . Здесь всё хорошо.
Криволинейная трапеция для рассматриваемой разновидности несобственного интеграла принципиально выглядит так:
Здесь почти всё так же, как в интеграле первого рода.
Наш интеграл численно равен площади заштрихованной криволинейной трапеции, которая не ограничена сверху. При этом могут быть два варианта*: несобственный интеграл расходится (площадь бесконечна) либо несобственный интеграл равен конечному числу (то есть, площадь бесконечной фигуры – конечна!).
* по умолчанию привычно полагаем, что несобственный интеграл существует
Осталось только модифицировать формулу Ньютона-Лейбница. Она тоже модифицируется с помощью предела, но предел стремится уже не к бесконечности, а к значению справа. Легко проследить по чертежу: по оси мы должны бесконечно близко приблизиться к точке разрыва справа .
Посмотрим, как это реализуется на практике.
Пример 6
Вычислить несобственный интеграл или установить его расходимость.
Подынтегральная функция терпит бесконечный разрыв в точке (не забываем устно или на черновике проверить, всё ли нормально с верхним пределом!)
Сначала вычислим неопределенный интеграл:
Замена:
У кого возникли трудности с заменой, обратитесь к уроку Метод замены в неопределенном интеграле .
Вычислим несобственный интеграл:
(1) Что здесь нового? По технике решения практически ничего. Единственное, что поменялось, это запись под значком предела: . Добавка обозначает, что мы стремимся к значению справа (что логично – см. график). Такой предел в теории пределов называют односторонним пределом . В данном случае у нас правосторонний предел .
(2) Подставляем верхний и нижний предел по формуле Ньютона Лейбница.
(3) Разбираемся с при . Как определить, куда стремится выражение? Грубо говоря, в него нужно просто подставить значение , подставляем три четверти и указываем, что . Причесываем ответ.
В данном случае несобственный интеграл равен отрицательному числу.
В этом никакого криминала нет, просто соответствующая криволинейная трапеция расположена под осью .
А сейчас два примера для самостоятельного решения.
Пример 7
Вычислить несобственный интеграл или установить его расходимость.
Пример 8
Вычислить несобственный интеграл или установить его расходимость.
Если подынтегральной функции не существует в точке
Бесконечная криволинейная трапеция для такого несобственного интеграла принципиально выглядит следующим образом.
Определенные интегралы онлайн на сайт для закрепления студентами и школьниками пройденного материала. И тренировки своих практических навыков. Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Определенные интегралы онлайн на сайт для полноценного закрепления студентами и школьниками пройденного материала и тренировки своих практических навыков.
Полноценное решение определенных интегралов онлайн для вас в считанные мгновения поможет определить все этапы процесса.. Интегралы онлайн — определенный интеграл онлайн. Для нас определенный интеграл онлайн взять не представляется чем-то сверх естественным, изучив данную тему по книге выдающихся авторов. Огромное им спасибо и выражаем респект этим личностям. Поможет определить определенный интеграл онлайн сервис по вычислению таких задач в два счета. Только укажите правильные данные и все будет Good! Всякий определенный интеграл как решение задачи повысит грамотность студентов. Об этом мечтает каждый ленивец, и мы не исключение, признаем это честно. Если все-таки получится вычислить определенный интеграл онлайн с решением бесплатно, то, пожалуйста, напишите адрес сайт всем желающим им воспользоваться. Как говорится, поделишься полезной ссылкой — и тебя отблагодарят добрые люди за даром. Очень интересным будет вопрос разбора задачки, в которой определенный интеграл будет калькулятор решать самостоятельно, а не за счет траты вашего драгоценного времени.
На то они и машины, чтобы пахать на людей. Однако решение определенных интегралов онлайн не всякому сайту по зубам, и это легко проверить, а именно, достаточно взять сложный пример и попытаться решить его с помощью каждого такого сервиса. Вы почувствуете разницу на собственной шкуре. Зачастую найти определенный интеграл онлайн без прилагаемых усилий станет достаточно сложно и нелепо будет выглядеть ваш ответ на фоне общей картины представления результата. Лучше бы сначала пройти курс молодого бойца. Всякое решение несобственных интегралов онлайн сводится сначала к вычислению неопределенного, а затем через теорию пределов вычислить как правило односторонние пределы от полученных выражений с подставленными границами A и B. Рассмотрев указанный вами определенный интеграл онлайн с подробным решением, мы сделали заключение, что вы ошиблись на пятом шаге, а именно при использовании формулы замены переменной Чебышева. Будьте очень внимательны в дальнейшем решении. Если ваш определенный интеграл онлайн калькулятор не смог взять с первого раза, то в первую очередь стоит перепроверить написанные данные в соответствующие формы на сайте.
Убедитесь, что все в порядке и вперёд, Go-Go! Для каждого студента препятствием является вычисление несобственных интегралов онлайн при самом преподе, так как это либо экзамен, либо коллоквиум, или просто контрольная работа на паре.. Как только заданный несобственный интеграл онлайн калькулятор будет в вашем распоряжении, то сразу вбивайте заданную функцию, подставляйте заданные пределы интегрирования и нажимайте на кнопку Решение, после этого вам будет доступен полноценный развернутый ответ. И все-таки хорошо, когда есть такой замечательный сайт как сайт, потому что он и бесплатный, и простой в пользовании, также содержит очень много разделов. которыми студенты пользуются повседневно, один из них как раз есть определенный интеграл онлайн с решением в полном виде. В этом же разделе можно вычислить несобственный интеграл онлайн с подробным решением для дальнейших применений ответа как в институте, так и в инженерных работах. Казалось бы, всем определить определенный интеграл онлайн дело нехитрое, если заранее решить такой пример без верхней и нижней границы, то есть не интеграл Лейбница, а неопределенный интеграл.
Но тут мы с вами не согласны категорически, так как на первый взгляд это может показаться именно так, однако есть существенная разница, давайте разберем все по полочкам. Такой определенный интеграл решение дает не в явном виде, а в следствие преобразования выражения в предельное значение. Другими словами, нужно сначала решить интеграл с подстановкой символьных значений границ, а затем вычислить предел либо на бесконечности, либо в определенной точке. Отсюда вычислить определенный интеграл онлайн с решением бесплатно означает ни что иное как представление точного решения по формуле Ньютона-Лейбница. Если же рассматривать наш определенный интеграл калькулятор поможет его подсчитать за несколько секунд прямо на ваших глазах. Такая спешка нужна всем желающим как можно быстрее справиться с заданием и освободиться для личных дел. Не стоит искать в интернете сайты, на которых попросят вас регистрироваться, затем пополнить деньги на баланс и все ради того, чтобы какой-нибудь умник подготавливал решение определенных интегралов якобы онлайн.
Запомните адрес Math34 — это бесплатный сервис для решения множества математических задач, в том же числе мы поможем найти определенный интеграл онлайн, и чтобы в этом убедиться, просим проверить наше утверждение на конкретных примерах. Введите подынтегральную функцию в соответствующее поле, затем укажите либо бесконечные предельные значения (в это случае будет вычислен и получено решение несобственных интегралов онлайн), либо задайте свои числовые или символьные границы и определенный интеграл онлайн с подробным решением выведется на странице после нажатия на кнопку «Решение». Неправда ли — это очень просто, не требует от вас лишних действий, бесплатно, что самое главное, и в то же время результативно. Вы можете самостоятельно воспользоваться сервисом, чтобы определенный интеграл онлайн калькулятор принес вам максимум пользы, и вы бы получили комфортное состояние, не напрягаясь на сложность всех вычислительных процессов, позвольте нам сделать все за вас и продемонстрировать всю мощь компьютерных технологий современного мира.
Если погружаться в дебри сложнейших формул и вычисление несобственных интегралов онлайн изучить самостоятельно, то это похвально, и вы можете претендовать на возможность написания кандидатской работы, однако вернемся к реалиям студенческой жизни. А кто такой студент? В первую очередь — это молодой человек, энергичный и жизнерадостный, желающий успеть отдохнуть и сделать домашку! Поэтому мы позаботились об учениках, которые стараются отыскать на просторах глобальной сети несобственный интеграл онлайн калькулятор, и вот он к вашему вниманию — сайт — самая полезная для молодежи решалка в режиме онлайн. Кстати наш сервис хоть и преподносится как помощник студентам и школьникам, но он в полной мере подойдет любому инженеру, потому что нам под силу любые типы задач и их решение представляется в профессиональном формате. Например, определенный интеграл онлайн с решением в полном виде мы предлагаем по этапам, то есть каждому логическому блоку (подзадачи) отводится отдельная запись со всеми выкладками по ходу процесса общего решения.
Это конечно же упрощает восприятие многоэтапных последовательных раскладок, и тем самым является преимуществом проекта сайт перед аналогичными сервисами по нахождению несобственный интеграл онлайн с подробным решением.
Определенный интеграл как предел интегральной суммы
может существовать (т.е. иметь определенное конечное значение) лишь при выполнении условий
Если
хотя бы одно из этих условий нарушено,
то определение теряет смысл. Действительно,
в случае бесконечного отрезка, например
[a ;
)
его нельзя разбить на п частей конечной длины
,
которая к тому же с увеличением количества
отрезков стремилась бы к нулю. В случае
же неограниченной в некоторой точкес [a ; b ]
нарушается требование произвольного
выбора точки
на частичных отрезках – нельзя выбрать=с ,
поскольку значение функции в этой точке
не определено. Однако и для этих случаев
можно обобщить понятие определенного
интеграла, введя еще один предельный
переход.
Интегралы по бесконечным
промежуткам и от разрывных (неограниченных)
функций называют несобственными .
Определение.
Пусть
функция
определена на промежутке [a ;
)
и интегрируема на любом конечном отрезке
[a ; b ],
т.е. существует
для любого b > a .
Предел вида
называютнесобственным
интегралом первого
рода (или
несобственным интегралом по бесконечному
промежутку) и обозначают
.
Таким
образом, по определению,
=
.
Если
предел справа существует и конечен, то
несобственный интеграл
называютсходящимся .
Если этот предел бесконечен, или не
существует вообще, то говорят, что
несобственный интеграл расходится .
Аналогично
можно ввести понятие несобственного
интеграла от функции
по промежутку (–; b ]:
=
.
А
несобственный интеграл от функции
по промежутку (–;
+)
определяется как сумма введенных выше
интегралов:
=
+
,
где а – произвольная точка.
Этот интеграл
сходится, если сходятся оба слагаемых,
и расходится, если расходится хотя бы
одно из слагаемых.
С
геометрической точки зрения, интеграл
,
,
определяет численное значение площади
бесконечной криволинейной трапеции,
ограниченной сверху графиком функции
,
слева – прямой
,
снизу – осью ОХ. Сходимость интеграла
означает существование конечной площади
такой трапеции и равенство ее пределу
площади криволинейной трапеции с
подвижной правой стенкой
.
На случай интеграла с бесконечным пределом можно обобщить и формулу Ньютона-Лейбница :
=
=F(+ )
– F(a ),
где
F(+ )
=
.
Если этот предел существует, то интеграл
сходится, в противном случае – расходится.
Мы рассмотрели обобщение понятия определенного интеграла на случай бесконечного промежутка.
Рассмотрим теперь обобщение для случая неограниченной функции.
Определение
Пусть
функция
определена на промежутке [a ; b ),
неограниченна в некоторой окрестности
точки b ,
и непрерывна на любом отрезке
,
где>0
(и, следовательно, интегрируема на этом
отрезке, т.
е.
существует). Предел вида
называетсянесобственным
интегралом второго рода (или несобственным интегралом от
неограниченной функции) и обозначается
.
Таким образом, несобственный интеграл от неограниченной в точке b функции есть по определению
=
.
Если предел справа существует и конечен, то интеграл называется сходящимся . Если конечного предела не существует, то несобственный интеграл называется расходящимся.
Аналогично
можно определить несобственный интеграл
от функции
имеющей бесконечный разрыв в точкеа :
=
.
Если
функция
имеет бесконечный разрыв во внутренней
точкес
,
то несобственный интеграл определяется
следующим образом
=
+
=
+
.
Этот интеграл сходится, если сходятся оба слагаемых, и расходится, если расходится хотя бы одно слагаемое.
С геометрической точки зрения, несобственный интеграл от неограниченной функции также характеризует площадь неограниченной криволинейной трапеции:
Поскольку
несобственный интеграл выводится путем
предельного перехода из определенного
интеграла, то все свойства определенного
интеграла могут быть перенесены (с
соответствующими уточнениями) на
несобственные интеграла первого и
второго рода.
Во многих задачах, приводящих к несобственным интегралам, не обязательно знать, чему равен этот интеграл, достаточно лишь убедиться в его сходимости или расходимости. Для этого используют признаки сходимости . Признаки сходимости несобственных интегралов:
1) Признак сравнения .
Пусть
для всех х
.
Тогда, если
сходится, то сходится и
,
причем
.
Если
расходится, то расходится и
.
2)
Если сходится
,
то сходится и
(последний интеграл в этом случае
называетсяабсолютно
сходящимся ).
Признаки сходимости и расходимости несобственных интегралов от неограниченных функций аналогичны сформулированным выше.
Примеры решения задач.
Пример 1.
а)
;
б)
;
в)
г)
; д)
.
Решение.
а) По определению имеем:
.
б) Аналогично
Следовательно, данный интеграл сходится и равен .
в)
По определению
=
+
,
причем,а – произвольное число.
Положим в нашем
случае
,
тогда получим:
Данный интеграл сходится.
Значит, данный интеграл расходится.
д)
Рассмотрим
.
Чтобы найти первообразную подынтегральной
функции, необходимо применить метод
интегрирования по частям. Тогда получим:
Поскольку
ни
,
ни
не существуют, то не существует и
Следовательно, данный интеграл расходится.
Пример 2.
Исследовать сходимость интеграла в зависимости от п .
Решение.
При
имеем:
Если
,
то
и.
Следовательно, интеграл расходится.
Если
,
то
,
а
,
тогда
=,
Следовательно, интеграл сходится.
Если
,
то
следовательно, интеграл расходится.
Таким
образом,
Пример 3.
Вычислить несобственный интеграл или установить его расходимость:
а)
;
б)
;
в)
.
Решение.
а)
Интеграл
является несобственным интегралом
второго рода, поскольку подынтегральная
функция
не ограничена в точке
.
3+1}.
\]
Решение высшей математики онлайн
‹— Назад
Напомним, что мы выяснили выше, что достаточно рассматривать только свойства интегралов вида , а свойства интегралов вида их будут повторять с очевидными исправлениями.
Доказательство. Докажем, что из сходимости следует сходимость при . Из аддитивности интеграла следует, что при любом имеет место равенство
Переходя в этом равенстве к пределу при , получаем:
причём несобственный интеграл в правой части сходится по условию теоремы, а интеграл вовсе не зависит от , то есть при вычислении предела при служит постоянным слагаемым.
Значит, предел, задающий интеграл , существует (и равен ), что доказывает сходимость интеграла .Доказано на самом деле даже больше: кроме самомго факта сходимости интеграла , мы доказали формулу (4.3).
Из той же формулы (4.2) следует и второе утверждение теоремы. Действительно, по условию теоремы интеграл по конечному отрезку существует, поскольку функция интегрируема, так что при любом из формулы (4.2) получаем:
Отсюда переходом к пределу при получаем, что
причём существование предела, задающего интеграл в левой части, следует из предположенной сходимости несобственного интеграла в правой части.
Замечание 4.2 Доказанное свойство говорит о том, что свойство несобственного интеграла быть сходящимся — это свойство, связанное с поведением функции «на бесконечности»: изменение значений функции на любом конечном отрезке никак не сказывается на сходимости (или расходимости) интеграла , а следовательно, и на факте сходимости (или, соответственно, расходимости) интеграла , хотя такое изменение может, конечно, привести к изменению значения этого интеграла.
Доказательство. Поскольку , то функция не убывает (геометрически значение функции равно площади криволинейной трапеции, лежащей над отрезком , а эта площадь, очевидно, не убывает, если увеличивать ). Точно так же не убывает и функция , причём по теореме об интегрировании неравенства получаем: из следует, что
Так как не убывает, то сходимость интеграла означает, что предел при существует и при всех .
Поэтому при всех , то есть функция ограничена сверху постоянной . Но мы знаем, что неубывающая ограниченная сверху функция непременно имеет предел при , не больший ограничивающей постоянной: существует предел По определению, этот предел равен значению несобственного интеграла: так что сходимость интеграла от меньшей функции доказана, а полученное неравенство означает, что доказано неравенство (4.4).Геометрически доказанное утверждение почти очевидно: оно означает, что если площадь под верхним графиком на следующем рисунке (она заштрихована), конечна, то конечна и имеет меньшее значение площадь под нижним графиком (она имеет двойную штриховку).
Рис.4.6.
Доказательство второго утверждения теоремы сразу следует из первого утверждения по принципу «от противного»: предположим, что интеграл от меньшей функции расходится. Если бы утверждение было неверно и интеграл от большей функции оказался бы сходящимся, то вместе с ним сходился бы и интеграл от меньшей функции, вопреки предположению.
Значит, второе утверждение теоремы верно.
Геометрически оно означает, что если площадь, обозначенная на рисунке двойной штриховкой, бесконечна, то, тем более, бесконечна и вся заштрихованная площадь.
Доказанная теорема означает, что сходимость несобственного интеграла — это такое свойство, которое выполняется «тем лучше», чем меньше значения подынтегральной функции (однако, заметим, эти значения должны быть неотрицательными)!
Если условие неотрицательности функций и не предполагается, то оба утверждения теоремы могут оказаться не верны: так, если взять и при всех , то интеграл от большей функции,
оказывается сходящимся (его значение, очевидно, равно 0), а интеграл от меньшей функции, — расходится (докажите расходимость, вычислив интеграл и рассмотрев его поведение при ).Тот же пример показывает, что если функции не неотрицательны, то из расходимости интеграла от меньшей функции может не следовать расходимость интеграла от большей.
При помощи теоремы 4.2 мы можем в некоторых случаях исследовать сходимость интеграла, не вычисляя его значения. Для доказательства сходимости интеграла от функции достаточно найти более простую функцию , для которой интеграл легко вычисляется и сходится. Согласно теореме, тогда исходный интеграл тоже сходится, причём мы получаем оценку его величины: . Если же нам нужно доказать расходимость интеграла , то достаточно найти такую (более просто устроенную) функцию , что и интеграл расходится.
Приведём примеры, показывающие этот приём в действии и разъясняющие, как определять, что же для данного интеграла нужно доказывать: сходимость или расходимость10.
Пример 4.3 Покажем, что интеграл Эйлера — Пуассона сходится. (Заметим сразу, что соответствующий неопределённый интеграл — неберущийся, то есть не выражается через элементарные функции.
Так что надежды вычислить этот интеграл «в лоб», применив формулу Ньютона — Лейбница, нет.)Для сравнения выберем функцию , неопределённый интеграл от которой легко считается:
Очевидно, что обе функции, и , положительны. Покажем, что при достаточно больших имеет место неравенство . Поскольку — возрастающая функция переменного , неравенство эквивалентно неравенству между показателями степени: которое, как легко видеть, выполняется при всех . Значит, при . Однако интеграл от большей функции сходится: Согласно замечанию 4.3 и теореме 4.2, отсюда следует сходимость интегралаДля многих примеров при доказательстве сходимости или расходимости интеграла естественно сравнивать подынтегральную функцию с функцией вида . Определим, при каких значениях показателя интеграл
cходится.Рассмотрим случай .
Тогда
Рассмотрим случай . Тогда
поскольку (то есть предела не существует) и . Значит, при интеграл расходится.Рассмотрим случай . Тогда
поскольку при Значит, при интеграл расходится.Итак, интеграл сходится (и функция определена и равна ) только при ; при интеграл расходится.
Пример 4.4 Исследуем сходимость несобственного интеграла При больших значениях (которые, вследствие замечания 4.3, только и имеют значение для сходимости интеграла) дробь имеет почти такие же значения, как дробь . Действительно, поделив числитель и знаменатель дроби на , получим Дроби и при больших принимают пренебрежимо малые значения, так что ведущую роль будет играть функция , получающаяся при отбрасывании этих малых слагаемых в числителе и знаменателе.
Интеграл от функции сходится: поскольку , то получаем сходящийся интеграл
Теперь аккуратно проверим выполнение условий теоремы 4.2. При достаточно больших (больших большего корня уравнения ) обе функции, и , принимают положительные значения и Поэтому из сходимости интеграла от , которую мы уже проверили, следует сходимость интеграла от по промежутку .На основании теоремы 4.1 сходится и исходный интеграл.
Пример 4.5 Исследуем сходимость несобственного интеграла Наводящие соображения насчёт того, с какой функцией сравнивать подынтегральную функцию таковы: при больших значениях ведущую роль в знаменателе играет , поскольку при больших ; значит, если откинуть 1, получим функцию Поскольку её показатель больше 1, то интеграл сходится. В то же время имеет место неравенство поскольку, очевидно,Итак, интеграл от большей функции сходится, откуда следует сходимость исходного интеграла
Пример 4.
6 Исследуем сходимость несобственного интеграла При больших в числителе ведущую роль играет , поскольку и , а в знаменателе ведущая роль принадлежит , поскольку . Поэтому при больших подынтегральная функция принимает почти такие же значения, что и функция Интеграл от расходится, поскольку показатель меньше 1. (Для интеграла по промежутку мы это проверяли выше, а расходимость интеграла по промежутку следует из теоремы 4.1.) Значит, для исходного интеграла от функции нужно доказывать расходимость. Проверим выполнение соответствующих условий теоремы 4.2: во-первых, функция , очевидно, определена на и принимает только положительные значения; во-вторых, имеет место неравенство Действительно, у дроби в левой части числитель больше, а знаменатель меньше, чем у первой дроби в правой части.Итак, условия теоремы 4.2 проверены. На основании этой теоремы (точнее, её второго утверждения) мы можем заключить, что данный нам интеграл расходится.
Докажем ещё одно важное свойство несобственного интеграла первого рода.
Теорема 4.3 Если интеграл сходится, то сходится также интеграл причём имеет место неравенствоДоказательство. Представим в виде разности двух неотрицательных функций и :
Для этого достаточно положить и (Проверьте, что тогда действительно получается .) Согласно определению функций и , получаем также равенство Поскольку и , отсюда сразу получаем, что имеют место неравенства и Поэтому, по теореме 4.2, несобственные интегралы от функций и сходятся, поскольку по предположению сходится интеграл от . Вычислим теперь несобственный интеграл от :Мы доказали тем самым, что интеграл сходится. Поскольку , то
Но поскольку , это же неравенство можно написать и для функции , получив тем самым, одновременно и Взятые вместе, эти два неравенства означают, что и доказательство закончено.
Заметим, что доказанная только что теорема означает в точности, что любой абсолютно сходящийся интеграл сходится.
Доказательство. Поскольку и интеграл сходится, то по теореме 4.2 интеграл также сходится. Это означает, что интеграл сходится абсолютно, откуда следует сходимость самого интеграла , причём
что и завершает доказательство.Таким образом, чтобы установить сходимость несобственного интеграла , достаточно найти для на такую мажоранту , что интеграл сходится.
Математика, вышка, высшая математика, математика онлайн, вышка онлайн, онлайн математика, онлайн решение математики, ход решения, процес решения, решение, задачи, задачи по математике, математические задачи, решение математики онлайн, решение математики online, online решение математики, решение высшей математики, решение высшей математики онлайн, матрицы, решение матриц онлайн, векторная алгебра онлайн, решение векторов онлайн, система линейных уравнений, метод Крамера, метод Гаусса, метод обратной матрицы, уравнения, системы уравнений, производные, пределы, интегралы, функция, неопределенный интеграл, определенный интеграл, решение интегралов, вычисление интегралов, решение производных, интегралы онлайн, производные онлайн, пределы онлайн, предел функции, предел последовательности, высшие производные, производная неявной функции
11.
3 Тесты на сходимость неправильных интеграловИсчисление одной действительной переменной Пхенг Ким ВингГлава 11: Методы интеграции Раздел 11.3: Тесты на сходимость неправильных интегралов |
11,3 |
Возврат
К содержанию
Перейти к проблемам и решениям
Существуют несобственные интегралы, которые нельзя вычислить
фундаментальная теорема исчисления, поскольку первообразные
их подынтегральных выражений не могут быть найдены.В этой ситуации мы все еще можем
определить сходятся они или нет по
проверка их сходимости, которая выполняется путем сравнения их с более простыми несобственными
интегралы, поведение которых (сходимость
или расхождение) известно.
Перейти к проблемам и решениям Вернуться к Начало страницы
Проверку сходимости несобственных интегралов проводит
сравнивая эти интегралы с известными более простыми несобственными
интегралы.Теперь мы рассмотрим некоторые из таких интегралов. Они известны как p — интегралы.
Фиг.2,3
|
p — Интегралы
Все 4 интеграла выше с показателем p в знаменателях называются p -интегралами .
Различить их
мы уточняем, в чем их неправильная точка. Обобщена их основная терминология.
в таблице ниже.
Обратите внимание, что at в имени интеграла используется для указания неправильного
точка интеграла. Обратите внимание, что
p -интегралы являются несобственными интегралами базового типа — .
Теорема 2.1 p — Интегралы
Каждый приведенный выше интеграл называется p -интеграл .Обратите внимание, что часть ii является частным случаем 1-го интеграла части iii, где a = 0. |
Проба
Следовательно, аналогично части ii :
Пример 2.
1Для каждого из следующих интегралов определите, сходится или расходится, не вычисляя его.
Решение
EOS
Перейти к проблемам и решениям Вернуться к Начало страницы
3. Стандартный сравнительный тест (SCT) |
Допустим, у нас есть функция f и мы хотим знать, сходится или расходится его интеграл.Если f ( x ) может быть
по сравнению с
подынтегральное выражение p -интеграла, то мы можем нарисовать
вывод об интеграле f .
|
Доказательство теоремы 3.
1 ниже использует следующие
свойство действительных чисел.
Фундаментальный Недвижимость за вещественными номерами
Теорема 3.1 г. Стандартный сравнительный тест (SCT)
Этот тест на сходимость несобственного базового типа
интеграл называется стандартным сравнительным тестом , сокращенно |
Проба
EOP
Примечания 3.
1
Пример 3.1
Установить совпадение или расхождение следующих интеграл без его фактического вычисления.
Решение
сходится.
EOS
Перейти к проблемам и решениям Вернуться к Начало страницы
4.Тест сравнения пределов (LCT) |
SCT не всегда применяется
Отношение интегралов
Теорема 4.1 Тест сравнения пределов (LCT)
Предположим: где L — некоторое
конечное положительное число. Поскольку этот тест на сходимость несобственного базового типа интеграл использует предел, это называется тестом сравнения пределов , сокращенно LCT . |
Тогда несобственные интегралы от f и г с теми же пределами
интегрирование ведет себя одинаково, т.е. либо оба сходятся, либо оба расходятся.Проба
EOP
Когда мы не можем найти неправильный интеграл для применения преобразуя SCT в данный несобственный интеграл, мы попробуем LCT.
Пример 4.1
Определите, сходится ли следующий интеграл или расходится без расчета:
Решение 1
Таким образом, по LCT данный интеграл сходится.
EOS
Решение 2
EOS
Пример 4.
2Установить сходимость или расхождение этого интеграла. без фактического расчета:
Решение
EOS
Перейти к проблемам и решениям Вернуться к Начало страницы
Сравнения Между собственными интегралами
Сравнение собственных интегралов происходит из
свойства определенных интегралов, и мы уже знаем о них.
См. Раздел 9.3 Теорема 6.1 Часть 6 . Напомним, что все собственные интегралы конечны.
числа, поэтому все они сходятся.
Однако мы можем захотеть сравнить правильный интеграл функции f с другим правильным интегралом, если первообразная
из ф
не может быть найден. Для примера см. Проблема
& Решение 4 .
Сравнения с Не p -Интегральные
p -интегралы
не единственные интегралы, используемые в сравнительных тестах.
Есть другие функции
что иногда должно быть
использовал. Для примера иллюстрации см. Проблема
& Решение 4 .
Вернуться к началу страницы
1. Для каждого из следующих интегралов определите сходится ли он или расходится, не вычисляя его.
Решение
а. Единственный неправильный балл — 0. Взлом:
Вернуться к началу страницы
2. Установить схождение или расхождение каждого из следующие интегралы, не вычисляя его.
Решение
Вернуться к началу страницы
3. Для каждого из следующих интегралов решите
сходится ли он или расходится, без фактического вычисления его значения.
Решение
расходится.
Вернуться к началу страницы
Решение
г. У нас:
Примечание
В части b первое сравнение проводится между надлежащими
интегралов, а второй — до интеграла, который не является интегралом p .
См. Часть 5 .
Вернуться к началу страницы
5. Докажите, что:
сходится, не пытаясь вычислить его значение.
Решение
Вернуться к началу страницы Вернуться К содержанию
3.
7 Неправильные интегралы — том 2 исчисленияЦели обучения
- 3.7.1 Вычислите интеграл на бесконечном интервале.
- 3.7.2 Вычислить интеграл по замкнутому интервалу с бесконечным разрывом внутри интервала.
- 3.7.3 Используйте теорему сравнения, чтобы определить, сходится ли определенный интеграл.
Является ли область между графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) конечной или бесконечной? Если эта же область вращается вокруг оси x , будет ли объем конечным или бесконечным? Удивительно, но площадь описываемой области бесконечна, но объем твердого тела, полученный путем поворота этой области вокруг оси x , конечен.
В этом разделе мы определяем интегралы по бесконечному интервалу, а также интегралы от функций, содержащих разрыв на интервале. Интегралы этих типов называются несобственными интегралами.
Мы исследуем несколько методов вычисления несобственных интегралов, все из которых связаны с определением пределов.
Интегрирование в бесконечном интервале
Как нам подойти к определению интеграла типа ∫a + ∞f (x) dx? ∫a + ∞f (x) dx? Мы можем интегрировать ∫atf (x) dx∫atf (x) dx для любого значения t, t, поэтому разумно посмотреть на поведение этого интеграла, когда мы подставляем большие значения t.т. Рисунок 3.17 показывает, что ∫atf (x) dx∫atf (x) dx можно интерпретировать как площадь для различных значений t.t. Другими словами, мы можем определить несобственный интеграл как предел, взятый, когда один из пределов интегрирования неограниченно увеличивается или уменьшается.
Фигура 3,17 Чтобы интегрировать функцию на бесконечном интервале, мы рассматриваем предел интеграла, когда верхний предел неограниченно возрастает.
Определение
- Пусть f (x) f (x) непрерывна на интервале вида [a, + ∞).
[а, + ∞). Тогда
A + ∞f (x) dx = limt → + ∞∫atf (x) dx, ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx,(3,16)
при условии, что этот предел существует. - Пусть f (x) f (x) непрерывна на интервале вида (−∞, b]. (- ∞, b]. Тогда
∫ − ∞bf (x) dx = limt → −∞∫tbf (x) dx, ∫ − ∞bf (x) dx = limt → −∞∫tbf (x) dx,(3,17)
при условии, что этот предел существует.
В любом случае, если предел существует, то говорят, что несобственный интеграл сходится. Если предел не существует, то говорят, что несобственный интеграл расходится. - Пусть f (x) f (x) непрерывна на (−∞, + ∞). (- ∞, + ∞). Тогда
∫ − ∞ + ∞f (x) dx = ∫ − ∞0f (x) dx + ∫0 + ∞f (x) dx, ∫ − ∞ + ∞f (x) dx = ∫ − ∞0f (x) dx + ∫0 + ∞f (x) dx,(3,18)
при условии, что ∫ − ∞0f (x) dx∫ − ∞0f (x) dx и ∫0 + ∞f (x) dx∫0 + ∞f (x) dx сходятся. Если один или оба этих интеграла расходятся, то ∫ − ∞ + ∞f (x) dx∫ − ∞ + ∞f (x) dx расходится. (Можно показать, что на самом деле ∫ − ∞ + ∞f (x) dx = ∫ − ∞af (x) dx + ∫a + ∞f (x) dx∫ − ∞ + ∞f (x) dx = ∫− ∞af (x) dx + ∫a + ∞f (x) dx для любого значения a. ) A.)
[а, + ∞). Тогда 
) A.)В нашем первом примере мы возвращаемся к вопросу, который мы поставили в начале этого раздела: является ли область между графиком f (x) = 1xf (x) = 1x и осью xx на интервале [1, + ∞) [1, + ∞) конечное или бесконечное?
Пример 3.47
Поиск места
Определите, является ли область между графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) конечной или бесконечной.
Решение
Сначала мы делаем быстрый набросок рассматриваемой области, как показано на следующем графике.
Фигура 3,18 Мы можем найти площадь между кривой f (x) = 1 / xf (x) = 1 / x и осью x на бесконечном интервале.Мы видим, что площадь этой области равна A = ∫1∞1xdx.А = ∫1∞1xdx. Тогда у нас есть
A = ∫1∞1xdx = limt → + ∞∫1t1xdx Перепишите несобственный интеграл как предел.
= Limt → + ∞ln | x || 1t Найдите первообразную. = Limt → + ∞ (ln | t | −ln1) Вычислите первообразную . = + ∞. Вычислить предел. A = ∫1∞1xdx = limt → + ∞∫1t1xdx Перепишите несобственный интеграл как предел. = Limt → + ∞ln | x || 1t. Найдите первообразную. = Limt → + ∞ (ln | t | −ln1) Вычислить первообразную. = + ∞. Вычислить предел.Поскольку несобственный интеграл расходится до + ∞, + ∞, площадь области бесконечна.
Пример 3.48
В поисках тома
Найдите объем твердого тела, полученный вращением области, ограниченной графиком f (x) = 1xf (x) = 1x и осью x на интервале [1, + ∞) [1, + ∞) относительно оси xx.
Решение
Твердое тело показано на Рисунке 3.19. Дисковым методом видим, что объем V равен
V = π∫1 + ∞1x2dx. V = π∫1 + ∞1x2dx. Фигура
3,19
Тело вращения можно создать, вращая бесконечную область вокруг оси x .
Тогда у нас есть
V = π∫1 + ∞1x2dx = πlimt → + ∞∫1t1x2dx Перепишите как предел. = Πlimt → + ∞ − 1x | 1t Найдите первообразную. = Πlimt → + ∞ (−1t + 1) Вычислите первообразную. = Π.V = π∫1 + ∞1x2dx = πlimt → + ∞∫1t1x2dx Перепишите как предел. = πlimt → + ∞ − 1x | 1t Найдите первообразную. = πlimt → + ∞ (−1t + 1) Вычислите первообразную. = π.Несобственный интеграл сходится к π.π. Следовательно, объем тела вращения равен π.π.
В заключение, хотя площадь области между осью x и графиком f (x) = 1 / xf (x) = 1 / x на интервале [1, + ∞) [1, + ∞ ) бесконечен, объем твердого тела, образованного вращением этой области вокруг оси x , конечен.Произведенное твердое тело известно как Рожок Габриэля .
Пример 3,49
Начало главы: Дорожные происшествия в городе
Фигура 3.20 (кредит: модификация работы Дэвида МакКелви, Flickr)
В начале главы мы сформулировали следующую проблему: предположим, что на оживленном перекрестке дорожно-транспортные происшествия происходят в среднем один раз в три месяца.
После того, как жители пожаловались, светофор на перекрестке был изменен.Прошло восемь месяцев с момента внесения изменений, и несчастных случаев не было. Были ли изменения эффективны или 8-месячный перерыв в отсутствии несчастных случаев — это случайность?
Теория вероятностей говорит нам, что если среднее время между событиями равно k, k, вероятность того, что X, X, время между событиями, находится между aa и bb, равна
. P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <0ke − kxifx≥0.P (a≤x≤b) = ∫abf (x) dxwheref (x) = {0ifx < 0ke − kxifx≥0.Таким образом, если несчастные случаи происходят с частотой один раз в 3 месяца, то вероятность того, что X, X, время между несчастными случаями, находится между aa и bb, равна
. P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <03e − 3xifx≥0.P (a≤x≤b) = ∫abf (x) dx, где f (x) = {0ifx <03e − 3xifx≥0. Чтобы ответить на вопрос, мы должны вычислить P (X≥8) = ∫8 + ∞3e − 3xdxP (X≥8) = ∫8 + ∞3e − 3xdx и решить, вероятно ли, что 8 месяцев могли бы пройти без ДТП, если не было улучшения дорожной ситуации.
Решение
Нам нужно вычислить вероятность как неправильный интеграл:
P (X≥8) = ∫8 + ∞3e − 3xdx = limt → + ∞∫8t3e − 3xdx = limt → + ∞ − e − 3x | 8t = limt → + ∞ (−e − 3t + e − 24) ≈ 3.8 × 10−11.P (X≥8) = ∫8 + ∞3e − 3xdx = limt → + ∞∫8t3e − 3xdx = limt → + ∞ − e − 3x | 8t = limt → + ∞ (−e − 3t + e − 24) ≈3.8 × 10-11.Значение 3,8 × 10–113,8 × 10–11 представляет вероятность отсутствия аварий в течение 8 месяцев при начальных условиях. Поскольку это значение очень и очень мало, можно сделать вывод, что изменения вступили в силу.
Пример 3,50
Вычисление неправильного интеграла за бесконечный интервал
Вычислить ∫ − ∞01×2 + 4dx.∫ − ∞01×2 + 4dx. Укажите, сходится или расходится несобственный интеграл.
Решение
Начните с переписывания ∫ − ∞01×2 + 4dx∫ − ∞01×2 + 4dx в качестве предела, используя уравнение 3.
17 из определения. Таким образом,
Несобственный интеграл сходится к π4.π4.
Пример 3,51
Вычисление несобственного интеграла на (−∞, + ∞) (- ∞, + ∞)
Вычислить ∫ − ∞ + ∞xexdx.− ∞ + ∞xexdx. Укажите, сходится или расходится несобственный интеграл.
Решение
Начнем с разделения интеграла:
− ∞ + ∞xexdx = ∫ − ∞0xexdx + ∫0 + ∞xexdx.∫ − ∞ + ∞xexdx = ∫ − ∞0xexdx + ∫0 + ∞xexdx. Если либо ∫ − ∞0xexdx∫ − ∞0xexdx, либо ∫0 + ∞xexdx∫0 + ∞xexdx расходится, то ∫ − ∞ + ∞xexdx∫ − ∞ + ∞xexdx расходится.
Вычислите каждый интеграл отдельно. Для первого интеграла
Первый несобственный интеграл сходится. Для второго интеграла
∫0 + ∞xexdx = limt → + ∞∫0txexdx Перепишите как предел.
= Limt → + ∞ (xex − ex) | 0t Найдите первообразную. = Limt → + ∞ (tet − et + 1) Вычислите первообразную. = Limt → + ∞ ((t − 1) et + 1) Перепишите. (Tet − etis неопределенно.) = + ∞. Вычислите предел. 0 + ∞xexdx = limt → + ∞∫0txexdx Перепишите как предел. = Limt → + ∞ (xex − ex) | 0t Найти первообразную. = limt → + ∞ (tet − et + 1) Вычислить первообразную. = limt → + ∞ ((t − 1) et + 1) Перепишите. (tet − etis неопределенный.) = + ∞. Вычислить предел.Таким образом, ∫0 + ∞xexdx∫0 + ∞xexdx расходится.Поскольку этот интеграл расходится, − ∞ + ∞xexdx∫ − ∞ + ∞xexdx также расходится.
Контрольно-пропускной пункт 3,27
Вычислить ∫ − 3 + ∞e − xdx.∫ − 3 + ∞e − xdx. Укажите, сходится или расходится несобственный интеграл.
Интегрирование разрывного интеграла
Теперь рассмотрим интегралы от функций, содержащих бесконечный разрыв в интервале, на котором происходит интегрирование. Рассмотрим интеграл вида ∫abf (x) dx, ∫abf (x) dx, где f (x) f (x) непрерывна над [a, b) [a, b) и разрывна в b. Фигура
3,21
Поскольку t приближается к b слева, значение области от a до t приближается к области от a до b . Мы используем аналогичный подход для определения ∫abf (x) dx, ∫abf (x) dx, где f (x) f (x) непрерывно над (a, b] (a, b] и разрывно в aa. (3,19) (3.20) (3.21) Следующие примеры демонстрируют применение этого определения. Оцените ∫0414 − xdx, ∫0414 − xdx, если возможно. Укажите, сходится ли интеграл или расходится. Функция f (x) = 14 − xf (x) = 14 − x непрерывна на [0,4) [0,4) и разрывна на 4.Используя уравнение 3.19 из определения, перепишите ∫0414 − xdx∫0414 − xdx как предел: Несобственный интеграл сходится. Оценить ∫02xlnxdx.∫02xlnxdx. Поскольку f (x) = xlnxf (x) = xlnx непрерывно на (0,2] (0,2] и разрывно в нуле, мы можем переписать интеграл в предельной форме, используя уравнение 3.20: Несобственный интеграл сходится. Вычислить ∫ − 111x3dx.∫ − 111x3dx. Укажите, сходится или расходится несобственный интеграл. Поскольку f (x) = 1 / x3f (x) = 1 / x3 имеет разрыв в нуле, используя уравнение 3.21, мы можем записать Если один из двух интегралов расходится, то исходный интеграл расходится. Начнем с ∫ − 101x3dx: ∫ − 101x3dx: Следовательно, ∫ − 101x3dx∫ − 101x3dx расходится. Оценить ∫021xdx.∫021xdx. Укажите, сходится ли интеграл или расходится. Непосредственное вычисление неправильного интеграла не всегда просто или даже возможно; однако, сравнивая его с другим тщательно подобранным интегралом, можно определить его сходимость или расхождение.Чтобы убедиться в этом, рассмотрим две непрерывные функции f (x) f (x) и g (x) g (x), удовлетворяющие 0≤f (x) ≤g (x) 0≤f (x) ≤g (x) для x ≥ax≥a (рисунок 3.22). В этом случае мы можем рассматривать интегралы этих функций по интервалам вида [a, t] [a, t] как области, поэтому мы имеем соотношение Таким образом, если , затем ∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = + ∞. С другой стороны, если ∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L∫a + ∞g (x) dx = limt → + ∞∫atg (x) dx = L для некоторого действительного числа L, L , затем ∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx∫a + ∞f (x) dx = limt → + ∞∫atf (x) dx должен сходиться к некоторому значению, меньшему или равному L , L, поскольку ∫atf (x) dx∫atf (x) dx увеличивается с увеличением tt и ∫atf (x) dx≤L∫atf (x) dx≤L для всех t≥a.t≥a. Если площадь области между графиком g (x) g (x) и осью x над [a, + ∞) [a, + ∞) конечна, то площадь области между график f (x) f (x) и оси x над [a, + ∞) [a, + ∞) также конечен. Эти выводы резюмируются в следующей теореме. Пусть f (x) f (x) и g (x) g (x) непрерывны над [a, + ∞). [A, + ∞). Предположим, что 0≤f (x) ≤g (x) 0≤f (x) ≤g (x) для x≥a.x≥a. Используйте сравнение, чтобы показать, что ∫1 + ∞1xexdx∫1 + ∞1xexdx сходится. Мы видим, что , поэтому если ∫1 + ∞e − xdx∫1 + ∞e − xdx сходится, то сходится и ∫1 + ∞1xexdx. Поскольку 1 + ∞e − xdx∫1 + ∞e − xdx сходится, то же самое происходит и с ∫1 + ∞1xexdx.∫1 + ∞1xexdx. Используйте теорему сравнения, чтобы показать, что ∫1 + ∞1xpdx∫1 + ∞1xpdx расходится для всех p <1.p <1. Для p <1, p <1, 1 / x≤1 / (xp) 1 / x≤1 / (xp) over [1, + ∞). [1, + ∞). В примере 3.47 мы показали, что ∫1 + ∞1xdx = + ∞.∫1 + ∞1xdx = + ∞. Следовательно, ∫1 + ∞1xpdx∫1 + ∞1xpdx расходится при всех p <1.p <1. Используйте сравнение, чтобы показать, что ∫e + ∞lnxxdx∫e + ∞lnxxdx расходится. В последних нескольких главах мы рассмотрели несколько способов использования интеграции для решения реальных проблем. В этом следующем проекте мы собираемся изучить более сложное приложение интеграции: интегральные преобразования. В частности, мы описываем преобразование Лапласа и некоторые его свойства. Преобразование Лапласа используется в технике и физике для упрощения вычислений, необходимых для решения некоторых проблем.Он принимает функции, выраженные в терминах времени, и преобразует их в функции, выраженные в терминах частоты. Оказывается, что во многих случаях вычисления, необходимые для решения задач в частотной области, намного проще, чем вычисления, необходимые для временной области. Преобразование Лапласа определяется интегралом как Обратите внимание, что входные данные для преобразования Лапласа являются функцией времени, f (t), f (t), а выходные данные — функцией частоты, F (s).F (s). Хотя многие примеры из реального мира требуют использования комплексных чисел (включая мнимое число i = −1), i = −1), в этом проекте мы ограничиваемся функциями действительных чисел. Начнем с простого примера. Здесь мы вычисляем преобразование Лапласа f (t) = tf (t) = t. Имеем Это неправильный интеграл, поэтому мы выражаем его через предел, что дает Теперь мы используем интегрирование по частям для вычисления интеграла.Обратите внимание, что мы интегрируем относительно t , поэтому мы рассматриваем переменную s как константу. У нас Тогда получаем Вычислите следующие интегралы. Если интеграл не сходится, ответьте «расходится». ∫24dx (x − 3) 2∫24dx (x − 3) 2 ∫0∞14 + x2dx∫0∞14 + x2dx ∫0214 − x2dx∫0214 − x2dx ∫1∞1xlnxdx∫1∞1xlnxdx ∫1∞xe − xdx∫1∞xe − xdx ∫ − ∞∞xx2 + 1dx∫ − ∞∞xx2 + 1dx Без интегрирования определите, сходится или расходится интеграл ∫1∞1×3 + 1dx∫1∞1×3 + 1dx, сравнив функцию f (x) = 1×3 + 1f (x) = 1×3 + 1 с g (x) = 1×3. г (х) = 1×3. Без интегрирования определить, сходится или расходится интеграл ∫1∞1x + 1dx∫1∞1x + 1dx. Определите, сходятся или расходятся несобственные интегралы.Если возможно, определите значение сходящихся интегралов. ∫0∞e − xcosxdx∫0∞e − xcosxdx ∫1∞lnxxdx∫1∞lnxxdx ∫ − ∞∞1×2 + 1dx∫ − ∞∞1×2 + 1dx ∫ − 22dx (1 + x) 2∫ − 22dx (1 + x) 2. ∫0∞e − xdx∫0∞e − xdx ∫0∞sinxdx∫0∞sinxdx ∫ − ∞∞ex1 + e2xdx∫ − ∞∞ex1 + e2xdx ∫01dx1 − x2∫01dx1 − x2 ∫031x − 1dx∫031x − 1dx ∫355 (x − 4) 2dx∫355 (x − 4) 2dx Определите сходимость каждого из следующих интегралов путем сравнения с заданным интегралом. Если интеграл сходится, найдите число, к которому он сходится. ∫1∞dxx2 + 4x; ∫1∞dxx2 + 4x; сравните с ∫1∞dxx2.∫1∞dxx2. ∫1∞dxx + 1; ∫1∞dxx + 1; сравните с ∫1∞dx2x.∫1∞dx2x. Вычислите интегралы. Если интеграл расходится, ответьте «расходится». ∫ − ∞0dxx2 + 1∫ − ∞0dxx2 + 1 ∫ − 11dx1 − x2∫ − 11dx1 − x2 ∫0∞xe − xdx∫0∞xe − xdx ∫ − ∞∞x (x2 + 1) 2dx∫ − ∞∞x (x2 + 1) 2dx ∫0∞e − xdx∫0∞e − xdx Вычислите несобственные интегралы. Каждый из этих интегралов имеет бесконечный разрыв либо в конце, либо во внутренней точке интервала. ∫ − 271dxx2 / 3∫ − 271dxx2 / 3 ∫03dx9 − x2∫03dx9 − x2 ∫624dttt2−36∫624dttt2−36 ∫04xln (4x) dx∫04xln (4x) dx ∫03×9 − x2dx∫03×9 − x2dx Вычислить ∫.51dx1 − x2.∫.51dx1 − x2. (Будьте осторожны!) (Выразите свой ответ, используя три десятичных знака.) Вычислить ∫14dxx2−1.∫14dxx2−1. (Выразите ответ в точной форме.) Вычислить ∫2∞dx (x2−1) 3 / 2.2∞dx (x2−1) 3/2. Найдите площадь области в первом квадранте между кривой y = e − 6xy = e − 6x и осью x . Найдите площадь области, ограниченной кривой y = 7×2, y = 7×2, осью x и слева x = 1.x = 1. Найдите площадь под кривой y = 1 (x + 1) 3/2, y = 1 (x + 1) 3/2, ограниченной слева x = 3.x = 3. Найдите площадь под y = 51 + x2y = 51 + x2 в первом квадранте. Найдите объем твердого тела, образованного вращением вокруг оси x области под кривой y = 3xy = 3x от x = 1x = 1 до x = ∞.х = ∞. Найдите объем твердого тела, образованного вращением вокруг оси y области под кривой y = 6e − 2xy = 6e − 2x в первом квадранте. Найдите объем твердого тела, образованного вращением вокруг оси x области под кривой y = 3e − xy = 3e − x в первом квадранте. Преобразование Лапласа непрерывной функции на интервале [0, ∞) [0, ∞) определяется как F (s) = ∫0∞e − sxf (x) dxF (s) = ∫0∞e − sxf ( x) dx (см. Студенческий проект).Это определение используется для решения некоторых важных начальных задач в дифференциальных уравнениях, о которых будет сказано ниже. Область F — это набор всех действительных чисел s , так что неправильный интеграл сходится. Найдите преобразование Лапласа F для каждой из следующих функций и задайте домен F . Используйте формулу для длины дуги, чтобы показать, что длина окружности x2 + y2 = 1×2 + y2 = 1 равна 2π.2π. Неотрицательная функция является функцией плотности вероятности, если она удовлетворяет следующему определению: ∫ − ∞∞f (t) dt = 1.∫ − ∞∞f (t) dt = 1. Вероятность того, что случайная величина x находится между a и b , определяется как P (a≤x≤b) = ∫abf (t) dt.P (a≤x≤b) = ∫abf (t ) dt. Покажите, что f (x) = {0ifx <07e − 7xifx≥0f (x) = {0ifx <07e − 7xifx≥0 - функция плотности вероятности. Найдите вероятность того, что x находится в диапазоне от 0 до 0,3. (Используйте функцию, определенную в предыдущей задаче.) Используйте точность до четырех знаков после запятой. Неправильные интегралы с плохо ведущимися пределами — это интегралы, у которых один или оба предела бесконечны. Эти интегралы выглядят как Если только один предел интегрирования бесконечен, то другой предел интегрирования, c , будет конечной константой. Помните, что запись ± ∞ для пределов интегрирования — это сокращение. Эти несоответствующие целостные существа действительно ограничены. Интеграл на самом деле означает Точно так же Чтобы оценить этот тип неправильного интеграла, мы должны вычислить интеграл внутри предела, а затем оценить предел. Когда только один из пределов интеграции бесконечен, мы можем работать напрямую. Когда оба предела интегрирования бесконечны, мы должны сначала разбить интеграл на две части. Здесь происходят некоторые странные вещи. Если мы возьмем значение p > 1, интеграл сходится. Но если мы возьмем значение p <1, тот же самый интеграл расходится.И графики даже не выглядят по-другому! Возьмем, например, p = 2 и: Один из способов объяснить это: график может ограничивать конечную область над осью x на [1, ∞), потому что он приближается к нулю быстрее, чем график. Здесь происходит еще одна вещь, на которую мы должны обратить внимание. Пусть Тогда функция f ( x ) сходится к 0, когда x приближается к ∞.В символах Однако интеграл расходится. Функция может сходиться к 0 на ∞, но для несобственного интеграла функции с верхним пределом ∞ расходиться. Однако, если функция f ( x ) расходится на ∞, то нет никакой надежды на схождение интеграла . Независимо от того, что такое c , если f уменьшается до ± ∞ или не может решить, что равняться x приближается к ∞, тогда будет расходиться. Фактически, если равно чему-либо, кроме 0, даже если предел сходится, тогда будут расходиться. Если тогда функция и ось x будут охватывать бесконечную область на интервале [ c , ∞). При использовании другого типа несобственного интеграла функция может расходиться, а несобственный интеграл сходится. Будьте осторожны: Когда вы говорите о схождении или расхождении чего-либо, убедитесь, что вы говорите, что делает сближение или расхождение.Сказать, что функция сходится, и сказать, что интеграл сходится — это не одно и то же. Эти идеи конвергенции и расхождения снова возникнут, когда мы будем говорить о последовательностях и рядах. До сих пор мы рассматривали интегралы только с одним бесконечным пределом. Если оба предела бесконечны, нам нужно разбить интеграл где-то посередине. В символах , где c — любое действительное число, которое вам нравится (обычно мы выбираем что-нибудь простое, например 0 или 1, в зависимости от функции).Поскольку каждый из интегралов в правой части на самом деле является замаскированным пределом, это уравнение говорит: Сумма пределов существует только в том случае, если существуют оба указанных предела. Это и хорошие новости, и плохие новости. Хорошая новость заключается в том, что если вы пойдете на тренировку и обнаружите, что либо расходится, либо , либо расходится, тогда все готово. Расходит и интеграл . Плохая новость заключается в том, что если действительно существует, вы должны определить оба предела и , а затем сложить их. Однако здесь есть и хорошие новости. Вы уже нашли первообразную для f ( x ) после первого предела, поэтому второе ограничение не будет таким большим трудом. Один из типов несобственного интеграла — это интеграл, в котором одна из конечных точек находится (приближается) к бесконечности.2}} \, dx ∫02 3 (x − 1) 2 1 dx = b → 1 − lim ∫0b 3 (x − 1) 2 1 dx + a → 1 + lim ∫a2 3 (х − 1) 2 1 дх , чтобы присвоить значение для определения его значения, при условии, что каждый из интегралов сходится. {t} f (x) dx∫ab f (x) dx = t → b − lim ∫at f (x) dx.{2} \ frac {1} {\ sqrt {2-x}} dx = 2 \ sqrt {2} ⇒∫02 2 − x 1 dx = 22 Отсюда ясно, что данный интеграл равен сходится в точке 222 \ sqrt {2} 22. Давайте начнем с рассмотрения вопроса о том, сходится ли гармонический ряд. Теперь посмотрим на неправильный интеграл. Поскольку интеграл расходится, значит расходится гармонический ряд.Вы уже знаете это, потому что это серия p , p = 1. Это просто еще один метод, который доказывает, что гармонический ряд расходится. Вот пример использования интегрального теста . Давайте определим, сходится или расходится ряд, показанный ниже. Первый шаг — установить неправильный интеграл. Это выглядит так. Затем вы вычисляете интеграл. Поскольку интеграл расходится, значит расходится ряд. Вот еще один пример использования интегрального теста. Вы хотите определить, сходится ли ряд или расходится. Помните, что первый шаг — это установка неправильного интеграла, а затем вы вычисляете этот интеграл. Поскольку этот интеграл сходится к определенному значению, это означает, что ряд сходится.Помните, что значение интеграла НЕ равно сумме ряда. Ранее мы рассмотрели, как интегральный тест доказывает, что гармонический ряд расходится. Теперь давайте посмотрим на серию p в целом и посмотрим, как интегральный тест подтверждает их правила сходимости. Сначала давайте посмотрим на серию p , когда p > 1. Сначала зададим несобственный интеграл. Затем вы вычисляете интеграл. Помните, что p > 1. Поскольку интеграл имеет конечное значение, это означает, что ряд сходится. Итак, мы только что с помощью интегрального теста доказали, что все серии p с p > 1 сходятся. Для серии p , где 0 < p <1, интегральный тест выглядит так. Поскольку интеграл расходится, то расходятся все серии p , где 0 < p <1. Итак, мы только что показали, как интегральный тест доказывает правила сходимости для серии p ! Интегральный тест — еще один способ проверить, сходится или расходится ряд.
б. Поскольку функция f (x) f (x) непрерывна по [a, t] [a, t] для всех значений tt, удовлетворяющих a
приступить к формальному определению. Определение
Abf (x) dx = limt → b − ∫atf (x) dx.abf (x) dx = limt → b − ∫atf (x) dx.
Abf (x) dx = limt → a + ∫tbf (x) dx.abf (x) dx = limt → a + ∫tbf (x) dx.
В любом случае, если предел существует, то говорят, что несобственный интеграл сходится. Если предел не существует, то говорят, что несобственный интеграл расходится.
Abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx, ∫abf (x) dx = ∫acf (x) dx + ∫cbf (x) dx,
при условии, что ∫acf (x) dx∫acf (x) dx и ∫cbf (x) dx∫cbf (x) dx сходятся. Если любой из этих интегралов расходится, то расходится ∫abf (x) dx∫abf (x) dx.
Пример
3,52
Интегрирование прерывного интеграла
Решение
Пример
3,53
Интегрирование прерывного интеграла
Укажите, сходится ли интеграл или расходится. Решение
Пример
3,54
Интегрирование прерывного интеграла
Решение
Поскольку ∫ − 101x3dx∫ − 101x3dx расходится, − 111x3dx∫ − 111x3dx расходится. Контрольно-пропускной пункт
3,28
Теорема сравнения
То есть, если площадь области между графиком f (x) f (x) и осью x над [a, + ∞) [a, + ∞) бесконечна, то площадь области между графиком g (x) g (x) и осью x над [a, + ∞) [a, + ∞) также бесконечно.
Теорема
3,7
Теорема сравнения
Пример
3,55
Применение теоремы сравнения
Решение
∫1 + ∞1xexdx. Чтобы вычислить ∫1 + ∞e − xdx, ∫1 + ∞e − xdx, сначала перепишите его как предел: Пример
3.56
Применение теоремы сравнения
Решение
Контрольно-пропускной пункт
3,29
Студенческий проект
Преобразования Лапласа
Преобразования Лапласа часто используются для решения дифференциальных уравнений. Дифференциальные уравнения подробно не рассматриваются до конца этой книги; а пока давайте посмотрим на взаимосвязь между преобразованием Лапласа функции и преобразованием Лапласа ее производной.
Начнем с определения преобразования Лапласа. У нас
L {f (t)} = ∫0∞e − stf (t) dt = limz → ∞∫0ze − stf (t) dt.L {f (t)} = ∫0∞e − stf (t) dt = limz → ∞∫0ze − stf (t) dt.
После интеграции по частям и оценки лимита вы должны увидеть, что
L {f (t)} = f (0) s + 1s [L {f ′ (t)}]. L {f (t)} = f (0) s + 1s [L {f ′ (t)}. ].
Затем
L {f ′ (t)} = sL {f (t)} — f (0). L {f ′ (t)} = sL {f (t)} — f (0).
Таким образом, дифференцирование во временной области упрощается до умножения на с в частотной области.
Последнее, что мы рассмотрим в этом проекте, — это то, как связаны преобразования Лапласа функции f (t) f (t) и ее первообразной. Пусть g (t) = ∫0tf (u) du.g (t) = ∫0tf (u) du. Затем
L {g (t)} = ∫0∞e − stg (t) dt = limz → ∞∫0ze − stg (t) dt.L {g (t)} = ∫0∞e − stg (t) dt = limz → ∞∫0ze − stg (t) dt.
Как и следовало ожидать, вы должны увидеть, что
L {g (t)} = 1s · L {f (t)}. L {g (t)} = 1s · L {f (t)}.
Интеграция во временной области упрощается до деления на с в частотной области. Раздел 3.7 Упражнения
Неопределенные интегралы — неправильные интегралы
Один неверный предел за раз
Конвергенция и расхождение
Два плохо используемых предела
Неправильные интегралы | Блестящая вики по математике и науке
Использование интегрального теста на сходимость серий
Использование интегрального теста на сходимость
Интегральный тест и
стр. — серия Резюме урока