Силы в механике — формулы и определение с примерами
Содержание:
Закон всемирного тяготения:
Каждый из нас на личном опыте ощущает силу притяжения к Земле, благодаря которой мы можем ходить и бегать. Но, споткнувшись, именно под действием этой силы мы падаем на землю. В 7-м классе вы узнали, что эта сила называется силой тяжести и определяется произведением массы тела на ускорение свободного падения:
Почему Земля притягивает все тела? Чем определяется модуль ускорения падающего на Землю тела и, следовательно, сила притяжения к Земле?
Какие причины вызывают движение Луны вокруг Земли практически по круговой орбите?
Почему планеты Солнечной системы и в том числе наша Земля движутся вокруг Солнца?
Ньютон был первым ученым, который сначала высказал гипотезу, объясняющую все эти явления, а потом строго ее доказал. Он предположил, что между любыми телами существуют силы тяготения, и, например, падение камня и движение Луны по своей орбите определяется силой притяжения Земли.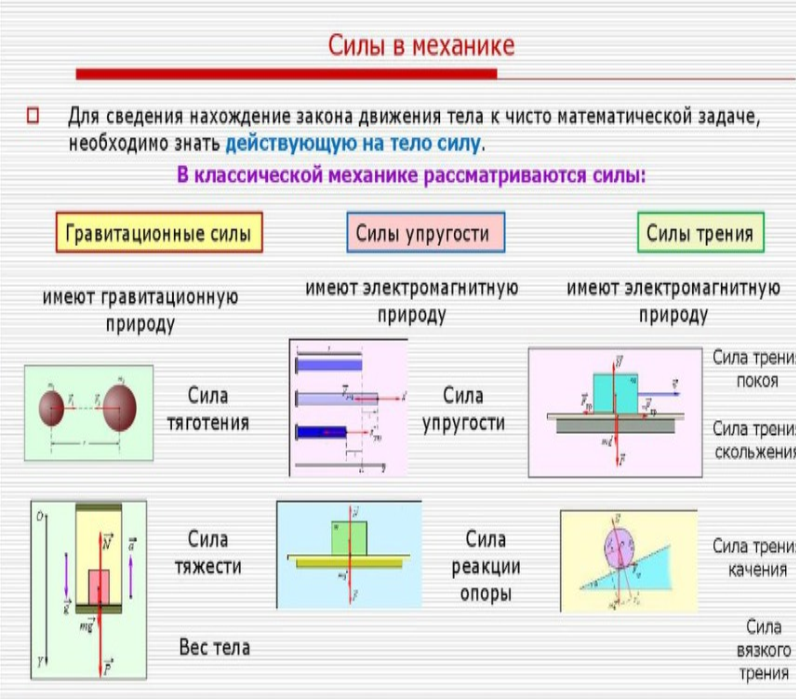
Камень, брошенный горизонтально с некоторой начальной скоростью, двинется к Земле по криволинейной траектории (рис. 54). Если увеличивать начальную скорость бросания, то дальность полета тела также возрастает. Из-за кривизны поверхности Земли при определенной начальной скорости камень вообще может не достигнуть Земли и начнет двигаться вокруг нее подобно Луне (рис. 55).
Рис. 55 |
Из этого мысленного эксперимента Ньютон сделал вывод, что движение камня и движение Луны обусловлены одной и той же причиной — притяжением Земли.
В то же время, по известным астрономическим данным (расстоянию до Луны и периоду ее обращения вокруг Земли), можно было определить ускорение Луны. Вычисленное таким образом центростремительное ускорение Луны оказалось равным 0,0027 , что примерно в 3600 раз меньше ускорения свободного падения (9,8) камня, движущегося у поверхности Земли.
Так как Луна приблизительно в 60 раз дальше от центра Земли, чем камень, то Ньютон предположил, что ускорение, которое сообщает телам сила тяготения Земли, обратно пропорционально квадрату расстояния до центра Земли. Поскольку ускорение прямо пропорционально действующей на тело силе, то сила тяготения Земли также по величине обратно пропорциональна квадрату расстояния до центра Земли.
Зависит ли сила тяготения от массы тел? Опыты Галилея доказали, что ускорение свободного падения не зависит от массы тела. Это возможно только в том случае, если сила тяготения пропорциональна массе тела: F ~ m. Действительно, тогда увеличение или уменьшение массы, например, в два раза вызовет соответствующее изменение силы тяготения в два раза, но ускорение по второму закону Ньютона останется прежним:
C другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы. Следовательно, сила тяготения должна быть пропорциональна массе обоих тел. Так Ньютон пришел к выводу, что сила тяготения между телом и Землей прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами:
Так Ньютон пришел к выводу, что сила тяготения между телом и Землей прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами:
Выполняется этот закон только для Земли или является всеобщим?
Чтобы ответить на этот вопрос, Ньютон рассмотрел кинематические законы движения планет Солнечной системы, сформулированные немецким ученым Иоганном Кеплером на основании многолетних астрономических наблюдений датского ученого Тихо Браге.
Орбиты, по которым движутся планеты под действием силы тяготения Солнца, очень близки к круговым. Тогда один из законов Кеплера может быть записан в форме:
где T1 и T2, R1 и R2— периоды обращения и средние радиусы орбит при вращении вокруг Солнца двух каких-либо планет Солнечной системы.
Используя формулу , Ньютон рассчитал центростремительные ускорения планет. Он обнаружил, что сила тяготения Солнца сообщает всем планетам ускорения, не зависящие от их массы и убывающие обратно пропорционально квадрату расстояния от Солнца.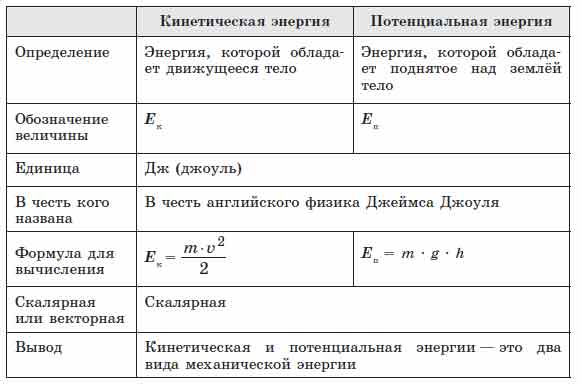
Ньютон доказал, что силы тяготения между планетами и Солнцем также подчиняются установленной им закономерности, и в 1667 г. сформулировал закон всемирного тяготения.
Так как размеры планет много меньше их расстояний до Солнца, то планеты можно рассматривать как материальные точки. В этом случае формулировка закона всемирного тяготения наиболее точна:
Если размерами взаимодействующих тел нельзя пренебречь, то, чтобы определить силу тяготения между ними, необходимо разбить тела на такие малые обьемы, которые можно было бы считать материальными точками. Для нахождения силы тяготения между телами необходимо будет найти все силы притяжения между этими «материальными точками» и векторно их сложить.
Если тела представляют собой однородные шары массами m1 и m2, то расчеты показывают, что формула для силы тяготения между ними будет такая же, как и для материальных точек, но в этом случае r — расстояние межlу центрами шаров (рис.
Рис. 56
Коэффициент пропорциональности G называется гравитационной постоянной (лат. gravitas — тяжесть). Определить величину гравитационной постоянной на основании астрономических данных Ньютон не мог, так как массы планет и Солнца в то время были не известны.
Впервые эта величина была определена в 1798 г. английским физиком Кавендишем с помощью прибора, называемого крутильными весами (рис. 57). Основной частью этого прибора было легкое коромысло с двумя шарами на концах, подвешенное на упругой проволоке. Рядом с ними неподвижно закрепляли два тяжелых шара. Под действием сил тяготения между этими шарами и подвешенными шарами коромысло поворачивалось на некоторый угол.
Зная величину этого угла, массы взаимодействующих тел, расстояния между их центрами и упругие свойства проволоки, Кавендиш рассчитал величину гравитационной постоянной:
Н* м2
Силы всемирного тяготения самые универсальные из сил природы, так как действуют между любыми телами. Но из-за такой малой величины гравитационной постоянной силы тяготения являются значительными только для тел с очень большой массой, например для планет и других космических тел.
Если известен кинематический закон движения спутника какого-либо космического тела (планеты, звезды, кометы), то, используя закон всемирного тяготения и второй закон Ньютона, можно рассчитать массу этого тела. Так и были определены массы различных космических тел (рис. 58): Солнца, Луны, Земли, других планет и их спутников.
Рис. 58
При изучении физики в 8-м и 9-м классах вы узнали, что электрические и магнитные взаимодействия тел определяются существующими вокруг них электрическими и магнитными полями.
Аналогично вокруг любого тела существует особая форма материи — гравитационное поле, характеристики которого зависят от массы тела. Если масса одного тела много больше массы другого, то его гравитационным полем можно пренебречь по сравнению с полем первого тела. Поэтому говорят, например, что самолет движется в гравитационном поле Земли или планеты Солнечной системы движутся в гравитационном поле Солнца.
Поэтому говорят, например, что самолет движется в гравитационном поле Земли или планеты Солнечной системы движутся в гравитационном поле Солнца.
Закон всемирного тяготения стал важнейшей ступенью в развитии всей физики, так как выявил новое свойство массы тела.
Сила гравитационного взаимодействия пропорциональна массам тел, т. е. масса является мерой тяготения, и, следовательно, ее можно назвать гравитационной.
Во втором законе Ньютона масса определяет инертные свойства тела, т. е. его способность приобретать большее или меньшее ускорение, и ее естественно назвать
Одинаковы ли эти массы? Многочисленные опыты показывают, что эти массы равны друг другу.
Опытный факт равенства гравитационной и инертной масс, называемый принципом эквивалентности, Альберт Эйнштейн положил в основу общей теории относительности, обобщающей и уточняющей более простую теорию тяготения Исаака Ньютона.
Главные выводы
- Силы гравитационного взаимодействия (тяготения) универсальны, действуют между любыми телами и пропорциональны произведению масс взаимодействующих тел.

- Силы гравитационного взаимодействия двух материальных точек обратно пропорциональны квадрату расстояния между ними, для однородных шаров — обратно пропорциональны квадрату расстояния между их центрами.
- Используя закон всемирного тяготения, известный кинематический закон движения спутника какого-либо космического тела и второй закон Ньютона, можно рассчитать массу этого космического тела.
Как мы уже обсуждали, исторически сложилось, что силой тяжести называется сила, с которой Земля притягивает тело. Масса данного тела — величина постоянная, и, следовательно, силу тяжести определяет ускорение свободного падения. А почему ускорение свободного падения принимают равным 9,8 ? От чего оно зависит?
Измерения, проведенные в различных точках поверхности Земли, показывают, что ускорение свободного падения может иметь различные значения, а 9,8 — это среднее значение данной величины. Как это объяснить?
Теперь вы знаете, что силу, с которой на тело действует Земля, можно рассчитать по закону всемирного тяготения. Будем считать Землю однородным шаром массой M и радиусом R. Любое тело по сравнению с нашей планетой можно считать материальной точкой. Если тело находится на небольшой высоте
Будем считать Землю однородным шаром массой M и радиусом R. Любое тело по сравнению с нашей планетой можно считать материальной точкой. Если тело находится на небольшой высоте
Сравнивая модули силы тяжести и гравитационного взаимодействия, можно найти модуль ускорения свободного падения:
Полученная формула показывает, что ускорение свободного падения зависит только от массы Земли и ее радиуса, и поэтому его модуль одинаков для всех тел.
Если высотой тела над поверхностью Земли нельзя пренебречь, то расстояние между телом и центром земного шара равно r = R + h, и модуль ускорения свободного падения будет тем меньше, чем дальше тело от поверхности.
Поэтому часто для ускорения свободного паления вблизи поверхности вводят индекс «0», а для ускорения свободного падения на некоторой высоте от поверхности Земли — индекс «h»:
Следовательно, и модуль силы тяжести будет отличаться при различном расположении тела относительно поверхности Земли: mg0 или mgh.
Какую удивительную возможность дает нам полученная формула для g0?
Эта формула позволяет определить массу нашей планеты (рис. 59), ведь среднее значение модуля ускорения свободного падения и средний радиус Земли уже давно определены опытным путем:
Именно потому, что с помощью закона всемирного тяготения возможны подобные расчеты, его иногда в шутку называют «всемирными весами».
Аналогично можно получить формулы для ускорения свободного падения и силы тяжести вблизи любого космического тела: Луны, Марса, Солнца, только в них соответственно будут входить масса и радиус этого космического тела.
Так как мы получили формулы для ускорения свободного падения, рассматривая самую простую модель гравитационного взаимодействия, то иногда говорят, что это формулы для расчета ускорения свободного падения в «первом приближении».
Какие еще факторы влияют на модуль ускорения свободного падения, например, вблизи данной точки земной поверхности?
- Земля не является шаром.
 Форма нашей планеты в честь ее греческого имени Гея носит название «геоид», так как радиус кривизны ее поверхности у полюсов больше, чем на экваторе.
Форма нашей планеты в честь ее греческого имени Гея носит название «геоид», так как радиус кривизны ее поверхности у полюсов больше, чем на экваторе. - Наша планета не однородна по строению, состоит из различных слоев, в которых есть области различной плотности, например залежи нефти и газа или залежи тяжелых металлов.
- В рассмотренной модели не учтено суточное вращение Земли.
- При расчетах не учитывалось гравитационное взаимодействие тела с другими космическими телами: Луной, Солнцем и т. п.
Именно поэтому модуль ускорения свободного падения отличается для различных точек на поверхности Земли. Например, на полюсах , a на экваторе — .
При решении задач, если в условии ничего не сказано о форме планеты, ее строении, параметрах вращательного движения, используется рассмотренная нами простейшая модель гравитационного взаимодействия и полученные формулы.
Главные выводы:
- Причиной существования силы тяжести является гравитационное взаимодействие между телом и Землей.

- Если не учитывать особенности строения и формы Земли и участие ее во вращательном движении, то модуль ускорения свободного падения определяется только ее массой и радиусом.
- При удалении от поверхности Земли модули ускорения свободного падения и силы тяжести уменьшаются.
Каждый человек в своей жизни наблюдал движение различных тел под действием силы притяжения к Земле (рис. 60). Падает вниз с парты ручка или резинка, плавно опускается лист дерева, движется по сложной траектории после удара мяч и т. п. Причем каждый наблюдал, что если с одной ветки одновременно начали падать лист и яблоко, то яблоко движется быстрее.
Рис. 60
На основании таких наблюдений до опытов известного итальянского ученого Галилео Галилея считалось, что более тяжелые тела с одной и той же высоты падают быстрее, чем легкие. По преданию, Галилей изучал падение различных тел со знаменитой Пизанской башни (рис. 61) и установил, что все тела, независимо от их массы, падают с одинаковым ускорением, если их движению ничто не мешает.
61) и установил, что все тела, независимо от их массы, падают с одинаковым ускорением, если их движению ничто не мешает.
Рис. 61
Проведем такой опыт. В стеклянную трубку, один конец которой запаян, а другой закрыт пробкой с краном, поместим птичье перо, кусок пенопласта и свинцовую дробинку. Перевернув трубку, мы обнаружим, что эти тела упадут на дно не одновременно (рис. 62, а): первой на дне окажется свинцовая дробинка, а позже всех упадет птичье перо. Так, может, не прав Галилей?
Чтобы ответить на этот вопрос, проведем опыт при других условиях. Откачаем насосом воздух из трубки, закроем кран и вновь быстро перевернем трубку. Теперь все три предмета упадут на дно трубки одновременно (рис. 62, б), потому что их движению не мешает воздух, и, следовательно, вывод Галилея подтверждается.
Рис. 62
Свободным падением называется движение тела только под действием силы тяжести с любой начальной скоростью.
Свободное падение — модель реального движения тела вблизи поверхности Земли под действием ее силы притяжения, при котором не учитываются суточное вращение Земли, размеры тела и сопротивление воздуха его движению. В физических задачах эта модель применяется при рассмотрении движения, например, падающего с горы камня, мяча после подачи игрока, пули, выпущенной из ружья, и т. п.
В физических задачах эта модель применяется при рассмотрении движения, например, падающего с горы камня, мяча после подачи игрока, пули, выпущенной из ружья, и т. п.
При этих условиях сила тяжести считается постоянной и рассчитывается по формуле , где . Если тело движется только под действием силы тяжести, то по второму закону Ньютона ускорение свободно падающего тела и не зависит от массы тела.
Поэтому разные тела движутся с одинаковыми ускорениями, как показано на рисунке 63. Этот рисунок сделан с фотографии, которую получили, открывая объектив и чередуя вспышки света каждые с (такая фотография называется стробоскопической).
Рис. 63
Следовательно, свободное падение — частный случай равноускоренного движения, и если, то можно записать выражения для радиус-вектора и мгновенной скорости тела:
Рассмотрим наиболее часто встречающиеся случаи свободного падения тела.
1) Пусть тело свободно падает без начальной скорости с высоты h над поверхностью Земли. Для описания механического движения необходимо выбрать систему отсчета, и в данном случае полезно рассмотреть движение тела в двух системах координат.
Для описания механического движения необходимо выбрать систему отсчета, и в данном случае полезно рассмотреть движение тела в двух системах координат.
а) Выберем начало первой системы координат под точкой начала падения тела, а ось Oy направим вверх (рис. 64). Ось Ox не нужна, так как все векторы расположены вдоль оси Оу. Найдем проекции векторов и запишем уравнения для координаты и проекции мгновенной скорости:
Рис. 64
Найдем время падения тела tk, используя то, что в последний момент движения тело попадает в начало выбранной оси Оу, т. е. его конечная координата равна:
Тогда
Зная все время падения тела, можно найти проекцию его скорости в последний момент движения:
Проекция скорости тела отрицательна, так как скорость направлена противоположно выбранному направлению оси Оу.
б) Можно выбрать и другую систему координат (рис. 65). Тогда проекции векторов:
65). Тогда проекции векторов:
Рис. 65
и уравнения для координаты тела и для проекции мгновенной скорости в любой момент времени будут иметь вид:
В последний момент движения в этой системе отсчета конечная координата тела равна:
Отсюда все время движения:
а проекция конечной скорости тела:
Мы получили для расчета времени падения ту же формулу, а формула для проекции скорости отличается только знаком, указывающим направление скорости по отношению к выбранной системе координат.
Как и следовало ожидать, полученные результаты не зависят от выбора системы координат.
2) Рассмотрим другой случай свободного падения: тело брошено с начальной скоростью υ0, направленной вертикально вверх (рис. 66), и вернулось в точку бросания. Например, вы бросили вверх мяч и поймали его при возвращении.
Рис. 66
Выберем начало оси Oyв точке начала движения тела (рис. 67). Тогда проекции векторов:
67). Тогда проекции векторов:
Рис. 67
Уравнения для координаты тела и для проекции мгновенной скорости в любой момент времени:
Найдем все время движения тела, или время возвращения тела в точку бросания tk, учитывая, что в последний момент движения тело попадает в начало оси Оу, т. е. его конечная координата:
Это квадратное уравнение имеет два корня:
которые соответствуют начальному моменту движения и моменту возвращения тела в исходную точку.
Найдем скорость тела в последний момент движения, подставив все время движения в уравнение для проекции скорости:
Отсюда следует: с какой скоростью мяч брошен вертикально вверх, с такой же скоростью по модулю, но противоположной по направлению, вернется в точку бросания (и ударит по бросившим его рукам!).
Найдем время подъема тела на максимальную высоту и значение этой высоты.
При движении тела вверх проекция мгновенной скорости уменьшается.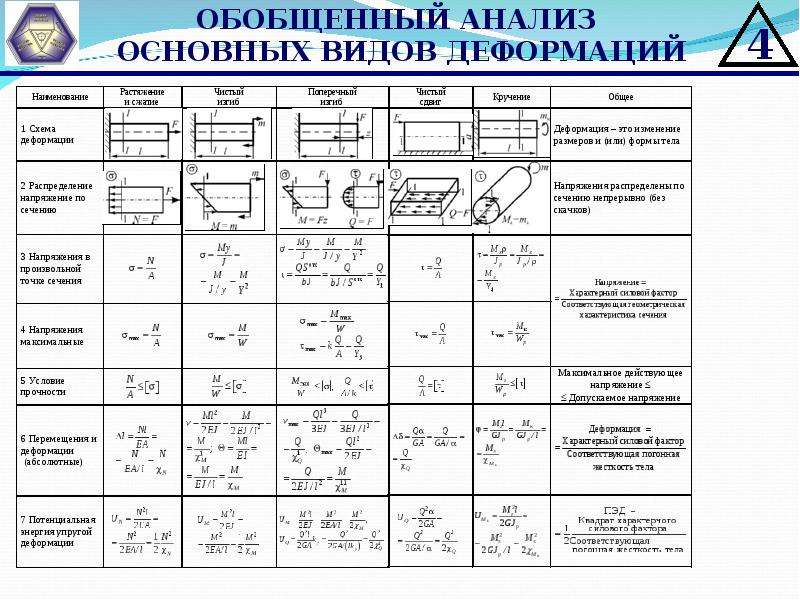 В момент максимального подъема тело на мгновение останавливается (а затем начинает падать вниз), т. е. υty = 0 = υo-gtn. Тогда время подъема тела на максимальную высоту:
В момент максимального подъема тело на мгновение останавливается (а затем начинает падать вниз), т. е. υty = 0 = υo-gtn. Тогда время подъема тела на максимальную высоту:
,
т. е. равно половине всего времени движения:
,
а максимальное значение координаты или высоты подъема:
или
.
Следовательно, сколько времени тело поднималось до максимальной высоты, столько же времени с этой высоты возвращалось в исходную точку.
Можно показать, что для брошенного вертикально вверх тела: 1) скорость, с которой оно проходит при подъеме любую точку на некоторой высоте, равна по модулю и противоположна по направлению скорости, с которой оно проходит эту же точку на спуске; 2) время подъема тела между любыми двумя точками по вертикали равно времени падения между этими же точками.
Знание этих соотношений позволяет более просто решить некоторые задачи.
Если сопротивлением воздуха пренебречь нельзя, то время подъема вертикально брошенного тела до максимальной высоты всегда меньше времени возвращения с этой высоты, а конечная скорость при возвращении в исходную точку всегда меньше начальной.
Аналогично можно рассмотреть движение тела, брошенного вертикально вниз с некоторой высоты с начальной скоростью.
Главные выводы:
- Свободное падение — это движение тела только под действием силы тяжести.
- Если начальная скорость тела равна нулю или коллинеарна вектору ускорения свободного падения, то свободное падение представляет собой частный случай равноускоренного прямолинейного движения с ускорением: .
- Для тела, брошенного вертикально вверх: а) скорость прохождения точки на некоторой высоте при подъеме равна по модулю и противоположна по направлению скорости при прохождении этой же точки на спуске; б) время подъема между двумя точками по вертикали равно времени падения между этими же точками.
Рассмотрим свободное падение тел в случаях, когда вектор начальной скорости направлен не вертикально. Для наглядного представления такой траектории удобно рассматривать полет струи воды, вытекающей под напором из шланга (рис. 68).
Для наглядного представления такой траектории удобно рассматривать полет струи воды, вытекающей под напором из шланга (рис. 68).
Рис. 68
Например, мяч в результате броска (рис. 69, а) начинает двигаться под углом к горизонту или во время игры человек бросает мяч в горизонтальном направлении (рис. 69,6). Из личного опыта каждый знает, что в обоих случаях мяч движется по криволинейной траектории.
Рис. 69
1) При броске в горизонтальном направлении тело начинает движение со скоростью , направленной горизонтально, т. е. перпендикулярно вектору ускорения свободного падения:
Выберем начало системы отсчета па вертикальной линии под точкой бросания (рис. 70). В этом случае векторы расположены в одной вертикальной плоскости. Следовательно, вектор будет в любой момент времени расположен в этой плоскости. Значит, тело будет двигаться по траектории, лежащей в этой же плоскости, а для описания движения тела можно использовать только две оси декартовой системы координат Ox и Оу.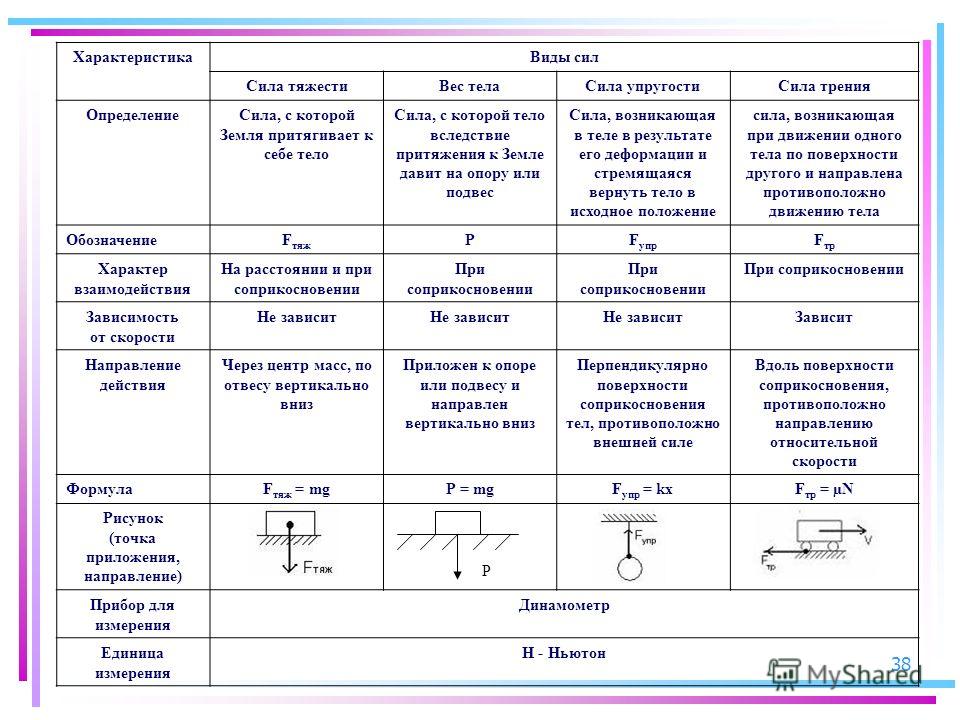
Тогда
и можно записать кинематические уравнения для координат тела и проекций его скорости:
Первые две формулы показывают, что координата х1 прямо пропорциональна времени, а проекция скорости на ось Oxне зависит от времени, т. е. эти уравнения соответствуют уравнению равномерного прямолинейного движения.
Две последние формулы описывают равноускоренное движение. Следовательно, рассматриваемое сложное движение в плоскости можно представлять в виде двух движений: одно — свободное падение без начальной скорости, а второе — равномерное движение в горизонтальном направлении.
Записанные кинематические уравнения позволяют решить основную задачу механики: найти координаты тела в любой момент времени, получить уравнение траектории движения тела, а также формулы для расчета времени движения, дальности полета, величины и направления скорости тела в последний момент движения.
Как известно, уравнение траектории представляет собой функциональную зависимость координат точки друг от друга. Получим уравнение траектории, х.
Получим уравнение траектории, х.
выражая время и подставляя его в уравнение для координаты:
Следовательно, траектория движения тела представляет собой ветвь параболы.
Например, если при стрельбе по мишени спортсмен держит винтовку горизонтально, то пуля движется по параболе и за время полета до мишени опустится тем ниже начального уровня, чем дальше мишень. Это обязательно учитывают спортсмены, для того чтобы показать лучшие результаты.
Найдем полное время движения тела, используя то, что в выбранной системе отсчета конечная его координата равна нулю:
Полученная формула показывает, что полное время движения тела, начальная скорость которого направлена горизонтально, не зависит от ее значения. Следовательно, если два тела одновременно начали движение с одной и той же высоты, одно — горизонтально с начальной скоростью, а второе — вниз без начальной скорости, то они упадут одновременно (конечно, если не учитывать сопротивление воздуха).
Получим формулу для дальности полета тела, которую рассчитывают как расстояние, пройденное телом в горизонтальном направлении, т. е. в выбранной системе отсчета:
Из этой формулы следует, что, чем больше начальная скорость тела и высота, с которой оно брошено, тем больше дальность его полета.
Скорость тела направлена по касательной к параболической траектории (рис. 71), а ее модуль в любой момент времени можно найти по теореме Пифагора: В последний момент движения конечная скорость тела:
Угол между направлением скорости тела в любой момент движения и горизонталью можно определить из прямоугольного треугольника, образованного вектором скорости и его проекциями на оси координат (см. рис. 71):
Рис. 71
Например, в последний момент движения:
Для описания движения тела, брошенного горизонтально, можно выбрать и другую систему отсчета. Попробуйте сделать это самостоятельно и описать движение тела в этой системе отсчета.
2) Движение тела, брошенного с начальной скоростью , направленной под углом , к горизонту, происходит по криволинейной траектории аналогично струе воды на рисунке 68.
Пусть в конце движения тело возвращается на тот же уровень относительно Земли, с которого начало движение.
Выберем начало отсчета в точке бросания тела (рис. 72). Векторы , расположены в одной вертикальной плоскости, и, следовательно, тело будет двигаться по траектории, лежащей в этой же плоскости. Для описания его движения можно использовать только две оси декартовой системы координат Ox и Оу.
Тогда
и можно записать кинематические уравнения для координат точки и проекций ее скорости:
Из первых двух уравнений следует, что проекция скорости на ось Ox не зависит от времени, а координата x1 прямо пропорциональна времени, т. е. это кинематические уравнения равномерного движения.
Два последних выражения представляют собой кинематические уравнения равноускоренного движения.
Таким образом, сложное движение тела в плоскости можно представить как наложение двух простых, одномерных: равномерного вдоль оси Ox и равноускоренного вдоль оси Оу.
Рис. 72
Эти уравнения позволяют решить основную задачу механики: определить координаты тела в любой момент времени, а также рассчитать, например, время подъема на максимальную высоту и ее величину, все время движения и дальность полета тела, найти модуль скорости тела и ее направление в любой момент времени.
Получим уравнение траектории тела, выразив время из уравнения для координаты х1 и подставив в уравнение для координаты y1:
Так как , то траектория тела — парабола (рис. 73), по касательной к которой направлена мгновенная скорость.
Найдем время подъема тела на максимальную высоту, используя уравнение для проекции скорости , которая с начала движения убывает и в высшей точке подъема тела равна нулю: . Отсюда . Следовательно, максимальная координата тела по оси Оу, или высота подъема:
Отсюда . Следовательно, максимальная координата тела по оси Оу, или высота подъема:
Найдем все время движения, используя уравнение для координаты y1, которая в выбранной системе отсчета в последний момент движения равна нулю:
Это квадратное уравнение имеет два корня, первый из которых соответствует начальному моменту времени t0 = 0, а второй — всему времени движения тела:
Следовательно, все время движения вдвое больше времени подъема, или сколько времени тело поднимается на максимальную высоту, столько же и спускается с нее.
Можно показать, что это же будет справедливо при полете тела по параболе между двумя любыми уровнями по высоте вверх и при полете по параболической траектории между этими же двумя уровнями вниз.
В выбранной системе отсчета дальность полета тела — его конечная координата по оси Ох:
Модуль скорости тела в любой момент времени можно найти по теореме Пифагора:, а направление — из треугольника, образованного вектором скорости и его проекциями на оси координат (как показано на рисунке 71):
Например, в конечный момент времени:
Эти выражения показывают, что конечная скорость тела равна по модулю начальной и направлена к горизонту под углом, равным по модулю первоначальному.
Можно показать, что при движении по параболической траектории модуль скорости и модуль угла, который вектор скорости образует с горизонтом. на любом одном и том же уровне относительно Земли одинаковы.
Используя понятия нормального и тангенциального ускорений, можно рассчитать радиус кривизны параболической траектории в любой момент времени. Как уже обсуждалось, вектор полного ускорения можно разложить на сумму тангенциального и нормального ускорений.
Разложим вектор ускорения свободного падения на векторы тангенциального и нормального ускорений (рис. 74): . Модули этих ускорений можно выразить через ускорение свободного падения и угол между направлением мгновенной скорости и горизонталью :
Так как , то можно определить радиус траектории тела в любой момент времени:
Если тело брошено под углом к горизонту с некоторой высоты над Землей, то необходимо вновь выбрать одну из систем отсчета и записать кинематические уравнения для координат и проекций скоростей, которые позволяют найти искомые величины.
Главные выводы:
- Если вектор начальной скорости тела лежит в вертикальной плоскости, но не коллинеарен вектору ускорения свободного падения, то тело движется по параболической траектории, расположенной в этой вертикальной плоскости.
- Сложное движение тела по параболической траектории можно представить в виде двух более простых движений: равноускоренного с вдоль вертикального направления и равномерного вдоль горизонтального направления.
- Во многих случаях при описании движения тела по параболической траектории выбор оптимальной системы отсчета позволяет более рационально математически найти искомые физические величины.
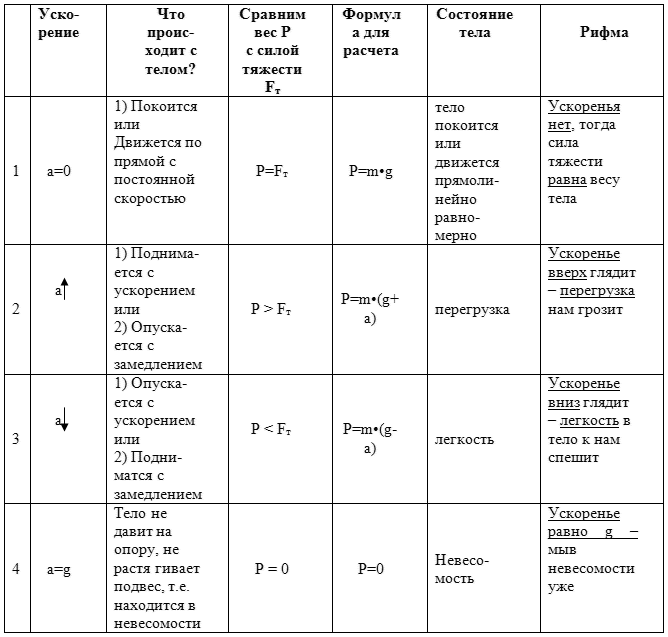
Силой веса (весом) называется сила, с которой тело вследствие земного притяжения действует на опору или подвес, неподвижные относительно его.
Под действием силы тяготения тело двигалось бы к Земле, но опора или подвес противодействуют силе притяжения. В результате этого в теле и опоре начинается процесс деформации, т. е. изменение формы и размеров. Этому процессу противодействуют силы взаимодействия между молекулами внутри вещества.
В результате этого в теле и опоре начинается процесс деформации, т. е. изменение формы и размеров. Этому процессу противодействуют силы взаимодействия между молекулами внутри вещества.
В механике для того, чтобы не рассматривать эти сложные межмолекулярные взаимодействия, вводят силу реакции опоры (или подвеса ). Согласно третьему закону Ньютона вес и сила реакции опоры связаны соотношением = — и являются силами одной физической природы.
Следовательно, сила веса отличается от силы тяжести тем, что ее возникновение обусловлено силой тяготения и межмолекулярными силами в веществе, а сила тяжести — гравитационная сила. Кроме того, сила тяжести приложена к телу, а сила веса — к опоре или подвесу.
Рассмотрим, от чего зависит сила веса, ведь опора или подвес могут и покоиться относительно Земли, и двигаться с какой-либо скоростью или ускорением.
Пусть, например, тело массой m подвешено на динамометре, прикрепленном к потолку лифта (рис. 75). По второму закону Ньютона:, где — сила, действующая на тело со стороны динамометра (подвеса), а ее модуль — это показание динамометра. По третьему закону Ньютона: или P = F.
75). По второму закону Ньютона:, где — сила, действующая на тело со стороны динамометра (подвеса), а ее модуль — это показание динамометра. По третьему закону Ньютона: или P = F.
Рис. 75
Рассмотрим различные случаи движения лифта относительно инерциальной системы отсчета, связанной с Землей.
1) Пусть лифт покоится, и тогда ускорение лифта, подвеса и тела α = 0 (см. рис. 75). Спроецируем на ось Oy и выразим силу веса тела P1в этом случае:
Тогда
т. е. динамометр показывает вес, равный по модулю силе тяжести.
Если лифт поднимается вертикально вверх или спускается вертикально вниз равномерно, то ускорение его и тела также равно нулю, и мы получим тот же результат.
Следовательно, при равномерном вертикальном движении подвеса с телом или когда вся система покоится, сила веса равна силе тяжести, направлена в ту же сторону, но приложена к подвесу (или опоре).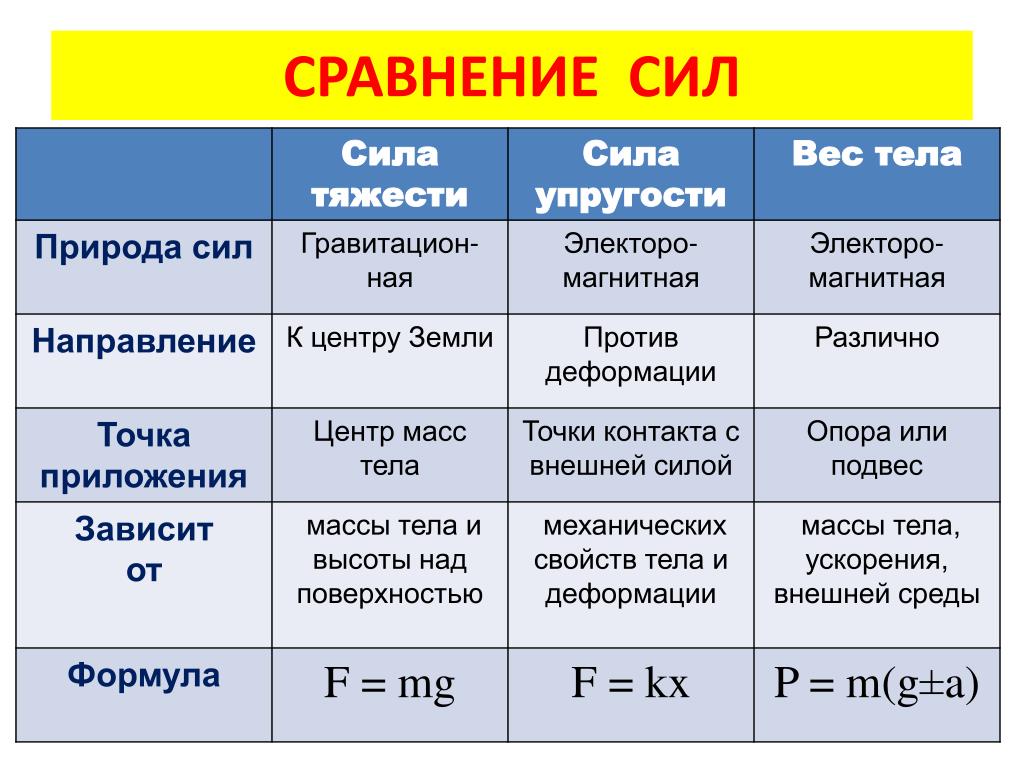
2) Пусть лифт поднимается с постоянным ускорением, направленным противоположно вектору ускорения свободного падения: Так как тело с подвесом поднимается вместе с лифтом, то его ускорение такое же, и чтобы вектор был направлен вверх, по второму закону Ньютона сила упругости должна быть больше силы тяжести (рис. 76).
Для проекции на ось Оу:
Тогда
и
Динамометр в этом случае показывает силу веса большую, чем сила тяжести тела, и чтобы характеризовать это явление, вводят термин перегрузка.
Чаще всего количественно перегрузку определяют как отношение силы веса к силе тяжести тела:
Перегрузки — одна из особенностей работы летчиков при выполнении фигур высшего пилотажа, космонавтов при старте космического корабля, гонщиков, участвующих в соревнованиях скоростных автомобилей. Тренированный человек может без серьезных последствий кратковременно выдержать примерно шестикратную перегрузку. Например, при взлете космического корабля стартовое ускорение не должно превышать 5g.
Например, при взлете космического корабля стартовое ускорение не должно превышать 5g.
3) Пусть лифт движется с ускорением, направленным так же, как и ускорение свободного падения Тело движется с таким же ускорением , и чтобы вектор та был направлен вниз, по второму закону Ньютона сила упругости должна быть меньше силы тяжести (рис. 77).
Для проекции на ось Оу.
Тогда
т. е. в данном случае динамометр покажет вес меньше, чем сила тяжести тела. Но если ускорение по модулю a > 2g, то вес вновь будет больше силы тяжести.
Рис. 77
Важно отметить, что при движении подвеса с ускорением, равным по модулю и направлению ускорению свободного падения , вес тела будет равен нулю:
Чтобы охарактеризовать это явление, вводят понятие состояние невесомости, или невесомость, которое подразумевает отсутствие веса, так как тело с опорой или тело с подвесом движутся с ускорением свободного падения в пространстве вместе, но практически не взаимодействуют друг с другом (рис.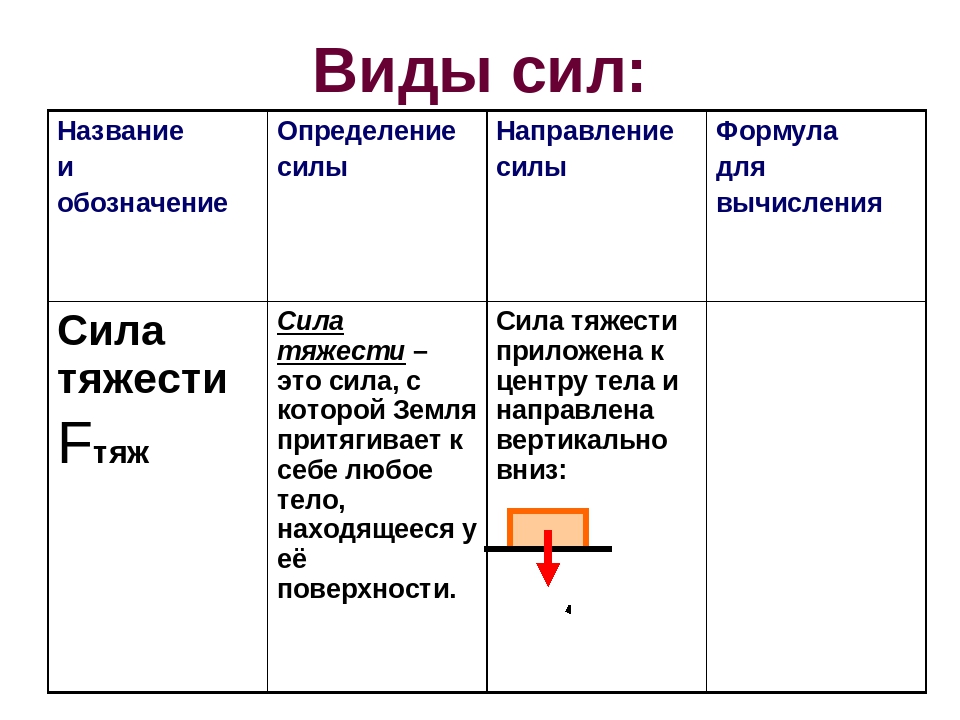 78).
78).
Рис. 78
Так как тело не взаимодействует с опорой, то нет и деформации обоих тел.
Например, человек в условиях невесомости на космическом корабле испытывает особые ощущения, в его организме в определенной степени изменяются физиологические процессы. Это происходит потому, что человек на Земле всегда взаимодействует с какой-либо опорой, и, следовательно, все процессы в организме осуществляются при наличии деформации.
Например, деформация позвоночного столба при вертикальном положении человека приводит к тому, что в конце дня его рост меньше, чем утром.
Состояние невесомости при определенных условиях можно испытать в самолете. Если пренебречь сопротивлением воздуха, то можно считать, что на самолет, набравший скорость и движущийся с выключенными двигателями, действует только сила тяжести. При этих условиях для тел в самолете наблюдается состояние невесомости.
В некотором интервале можно подобрать такой угол между скоростью самолета и горизонтом в начальный момент движения, чтобы время безопасного полета с отключенными двигателями было достаточно для тренировки космонавтов или съемок эпизодов для кинофильмов.
Рассмотренные случаи отличия модуля веса от модуля силы тяжести возникают и при участии тела во вращательном движении. Например, вес тела, измеренный одним и тем же динамометром на полюсе Земли больше, чем вес этого тела на экваторе. Это связано с тем, что на экваторе тело вместе с динамометром и поверхностью Земли участвует во вращательном движении (рис. 79).
Рис. 79
Пусть — сила тяготения. По третьему закону Ньютона , где — показание динамометра. Так как тело покоится, то
Следовательно, на полюсе вес тела равен по модулю силе тяжести.
На экваторе тело вместе с подвешенным к опоре динамометром движется с ускорением a = ω2R. где ω— угловая скорость вращения Земли, R — радиус Земли. Тело движется с этим ускорением под действием силы притяжения и силы со стороны динамометра: По третьему закону Ньютона: . Запишем второй закон Ньютона для проекций: Следовательно, на экваторе вес тела меньше:
Из полученной формулы видно, что если бы угловая скорость вращения Земли вдруг начала возрастать, то при определенном ее значении вес тел на экваторе стал бы равным нулю.
Рассмотренные примеры иллюстрируют, что при решении различных задач вес тела должен определяться в каждом конкретном случае на основании второго и третьего законов Ньютона.
Главные выводы:
- Модуль веса тела в общем случае не равен модулю силы тяжести.
- Модуль веса тела зависит от характера движения тела и опоры (подвеса) и их взаимного расположения.
- При совместном движении тела и опоры или подвеса с ускорением свободного падения наблюдается состояние невесомости.
До сих пор мы рассматривали простейшую модель, в которой приняли, что сила тяжести тела — это и есть сила его гравитационного взаимодействия с Землей. Но если сила тяжести совпадает с силой гравитационного тяготения, то она должна быть направлена вдоль радиуса Земли к ее центру.
На опыте направление силы тяжести можно определить по «отвесу» — направлению нити, на которой подвешен тяжелый груз. Например, каменщик, укладывая кирпичную стену, проверяет, вертикальна ли грань стены, именно таким способом (рис. 81).
Например, каменщик, укладывая кирпичную стену, проверяет, вертикальна ли грань стены, именно таким способом (рис. 81).
Точные измерения показывают, что в каждой местности «отвесная линия» не совпадает с направлением на центр земного шара, т. е. направление силы тяжести не совпадает с направлением силы тяготения. Только на полюсах и экваторе земного шара сила тяжести направлена к его центру.
Как это можно объяснить?
Рис. 81
Все точки поверхности Земли, за исключением полюсов, участвуют во вращательном движении вокруг земной оси.
Рассмотрим тело, лежащее в какой-то точке на поверхности Земли с широтой φ и участвующее вместе с ней в суточном вращении. Широтой данной точки местности, как известно, называется угол φ между радиусом Земли, проведенным в эту точку, и плоскостью экватора (рис. 82).
Рис. 82
Выберем начало инерциальной системы отсчета в центре земного шара, а оси координат направим на неподвижные звезды. Запишем закон всемирного тяготения, считая тело материальной точкой по сравнению с Землей:
где М — масса Земли, R — ее радиус, g0— ускорение свободного падения на поверхности Земли без учета ее суточного вращения.
Тело движется по окружности радиуса r со скоростью данной точки поверхности и центростремительным ускорением:
где ω — угловая скорость вращения Земли.
Для Беларуси, например, средние величины скорости вращения и центростремительного ускорения точек поверхности:
На покоящееся тело действуют сила тяготения со стороны Земли, направленная по радиусу к ее центру, и сила реакции опоры. По второму закону Ньютона: . Следовательно, вектор равнодействующей силы тяготения и реакции опоры должен быть направлен, как и ускорение, к центру окружности, по которой движется тело. Это возможно только в случае, когда сила реакции опоры направлена под некоторым углом к радиальному направлению (рис. 83).
Рис. 83
В Солнечной системе вокруг многих планет вращаются космические тела, которые называют естественными спутниками.
По аналогии с этим любой объект, созданный руками человека и движущийся вокруг данного небесного тела, называют искусственным спутником. Для вывода спутника на орбиту необходима работа мощных двигателей, но при движении спутника по постоянной орбите двигатели на спутнике выключены. Почему же он движется по орбите?
Для вывода спутника на орбиту необходима работа мощных двигателей, но при движении спутника по постоянной орбите двигатели на спутнике выключены. Почему же он движется по орбите?
Чтобы ответить на данный вопрос, давайте рассмотрим упрощенную модель движения
искусственного спутника. Будем считать, что он движется с постоянной по модулю скоростью по круговой орбите вокруг данной планеты в безвоздушном пространстве и только под действием ее сил тяготения (рис. 85). Силами тяготения со стороны других космических тел можно пренебречь.
Рис. 85
Если нет сопротивления воздуха, а сила тяготения в любой момент перпендикулярна скорости движения, то создаваемое ею ускорение также перпендикулярно скорости и не может изменять ее модуль. Вот почему такой идеальный спутник должен бесконечно долго вращаться по своей орбите с выключенными двигателями. Реальные искусственные спутники Земли постепенно приближаются к ее поверхности, и в конце концов попадая в атмосферу, сгорают в ней.
Какова должна быть скорость спутника, чтобы он двигался по круговой орбите?
Определим эту скорость, считая, что спутник движется на высоте H над поверхностью однородной шарообразной планеты массы M и радиуса R. Так как движение происходит по окружности, то спутник имеет центростремительное ускорение:
которое ему сообщает сила тяготения:
и, следовательно.
Отсюда скорость движения спутника по орбите на высоте H над поверхностью:
Если использовать формулу для ускорения свободного падения вблизи поверхности планеты, то скорость спутника на высоте H от поверхности планеты равна:
Первой космической скоростью для планеты называется скорость, которую нужно сообщить спутнику, чтобы он двигался по круговой орбите вблизи поверхности планеты, т. е. .
Тогда величина первой космической скорости определяется по формуле:
При движении спутников на высоте 200—300 км от поверхности Земли первая космическая скорость равна 7,9.
Из приведенных формул следует, что, чем выше над поверхностью планеты расположена орбита спутника, тем меньше его скорость и тем больше его период обращения. Спутники с космонавтами летают на высоте 200—300 км и облетают нашу планету меньше чем за полтора часа. Спутники связи расположены на большом удалении от поверхности, летят с меньшей скоростью, чем первая космическая скорость.
Вы, наверное, часто слышали, что в открытом космосе и на спутнике космонавты находятся в состоянии невесомости, а по телевизору наблюдали их как бы плавающие движения в космическом корабле (рис. 86). Космонавты и все предметы движутся вместе со спутником по орбите под действием только силы тяготения Земли, т. е. находятся в свободном падении.
Рис. 86
Возможно ли это: спутник свободно падает и в то же время остается на постоянной орбите? Примем для простоты расчетов, что ускорение свободного падения равно 10 и скорость спутника 8000 . Тогда за 1 с свободного падения спутник должен пройти по направлению к Земле расстояние h = 5 м и одновременно переместиться перпендикулярно этому направлению на 8000 м. В результате этих двух движений спутник движется по своей орбите (рис. 87).
В результате этих двух движений спутник движется по своей орбите (рис. 87).
Рис. 87
Главные выводы:
- Движение искусственных спутников по орбите происходит только под действием силы тяготения.
- Скорость спутника на круговой орбите зависит от массы планеты, ее радиуса и высоты спутника над поверхностью планеты. Первая космическая скорость определяется только массой и радиусом планеты.
- Невесомость на спутнике объясняется тем, что в любой момент времени он движется с ускорением свободного падения для данной точки пространства.
Как вы уже знаете, одно из проявлений взаимодействия тел — их деформация, т. е. изменение формы и размеров, происходящее из-за неодинакового смещения различных частей одного тела в результате воздействия другого тела.
Почему деформации неодинаковы у различных тел? Какую роль они играют во взаимодействии тел и в механическом движении?
Чтобы ответить на первый вопрос, вспомним, что вы узнали о строении вещества при изучении физики в 8-м классе.
Все вещества состоят из частиц (молекул, атомов, ионов), между которыми существуют силы взаимодействия. Это силы электромагнитной природы, которые в зависимости от расстояния между частицами проявляются то как силы притяжения, то как силы отталкивания.
Если воздействие на тело вызывает увеличение расстояния между молекулами, то силы межмолекулярного притяжения препятствуют этому. Уменьшению расстояния между молекулами противодействуют силы отталкивания. Чтобы не рассматривать сложные электромагнитные взаимодействия, в механике для характеристики этих явлении вводят силу упругости .
Силой упругости называется сила, возникающая при деформации любых твердых тел, а также при сжатии жидкостей и газов.
Какую роль играет эта сила при взаимодействии тел?
Проделаем следующий опыт. Возьмем толстый кусок поролона, нарисуем по его торцу горизонтальные линии на одинаковом расстоянии друг от друга, а затем, медленно опуская, поставим на него груз (рис. 88, а).
88, а).
Если смотреть во время опускания груза на торец поролона, то хорошо видно, как при сжатии поролона под действием груза сближаются между собой линии, но лишь до определенного расстояния (рис. 88, б). Движение груза прекращается при некоторой деформации поролона, т. е. сила упругости уравновешивает силу тяжести.
Рис. 88
Также же наблюдения можно провести, подвешивая груз на резиновой ленте с нанесенными на ней линиями. При подвешенном грузе расстояние между линиями на ленте больше.
Мы взяли для опытов поролон и резиновую ленту, потому что для этих тел под действием даже небольших сил наблюдается значительная деформация и ее легко наблюдать.
Аналогичные явления происходят при любых взаимодействиях тел, но часто деформации так малы, что их можно зафиксировать только с помощью очень чувствительных приборов.
Проведем еще один опыт (рис. 89, а). Прикрепим к бруску, лежащему на столе, резиновый шнур (с метками на одинаковом расстоянии друг от друга) и медленно начнем тянуть его в горизонтальном направлении.
Под действием силы шнур растягивается, и только когда весь шнур растянется на некоторую величину, брусок придет в движение. Как это объяснить?
При растяжении шнура происходит смещение одних его частей относительно других, в результате чего в шнуре возникает сила упругости, равная но величине деформирующей силе. C этого момента шнур играет роль «передающего звена» (рис. 89. б).
Такие же явления всегда происходят, когда движение от одного тела к другому передается при помощи «связей», т. е. нитей, шнуров, пружин, тросов, различных сцепок и т. п.
Рис. 89
По характеру смещения частей тела (а вернее, молекулярных слоев внутри его) друг относительно друга различают деформации: растяжения, сжатия, изгиба, кручения, сдвига.
При деформации растяжения расстояние между молекулярными слоями увеличивается (рис. 90, а), а при деформации сжатия — уменьшается (рис. 90, б). Деформацию растяжения испытывают тросы подъемных кранов, канатных дорог, буксирные тросы, струны музыкальных инструментов. Сжатию подвергаются стены и фундаменты зданий.
Сжатию подвергаются стены и фундаменты зданий.
Если в результате воздействия одни молекулярные слои растягиваются, а другие сжимаются, то наблюдается деформация изгиба (рис. 90, в). Деформацию изгиба испытывают балки перекрытий в зданиях и мостах.
При деформации кручения происходит поворот одних молекулярных слоев относительно других (рис. 90, г).
Если одни слои молекул смещаются относительно других, то происходит деформация сдвига (рис. 90, б).
Рис. 90
Деформации также разделяют на упругие и неупругие, или пластичные.
Деформация называется упругой, если после прекращения воздействия тело полностью восстанавливает первоначальные форму и размеры, а если этого не происходит, то деформация называется неупругой или пластичной.
Конечно, деформация конкретного тела может быть как упругой, так и неупругой, так как ее характер зависит не только от свойств тела, но и от величины воздействия на него. Например, при больших воздействующих силах и стальная линейка потеряет форму, а при очень малых — и пластилин восстановит свою форму.
Главные выводы:
- Сила упругости возникает при изменении формы и размеров твердых тел, а также при сжатии жидкостей и газов.
- Силы упругости, возникающие в нитях, подвесах, опорах и других «связях>, обеспечивают передачу воздействия или движения от одного тела к другому.
- По характеру смещения молекулярных слоев друг относительно друга выделяют деформации: растяжения, сжатия, изгиба, кручения и сдвига.
- Деформации разделяют на упругие и пластичные по степени восстановления формы и размеров тела после прекращения действия деформирующей силы.
Различные виды деформаций возникают в любых сооружениях и механизмax, и необходимо установить законы, которые позволят рассчитать величину тих деформаций.
Наиболее часто встречаются и достаточно просто математически описываются упругие деформации растяжения или сжатия.
Проведем опыт, прикрепив один конец резинового шнура с метками к вертикальной стенке, а другой — к динамометру (рис. 91, а), на который будем действовать силой. Расположим под шнуром линейку. Определяя силу, действующую на конец шнура, по динамометру, будем фиксировать смещение конца JHypa вдоль линейки и изменение расстояний между метками.
Мы заметим, что общее удлинение шнура, определяемое по смещению его конца, является суммой удлинений всех его частей. Аналогично общее укоронение, например при сжатии пружины, является суммой уменьшений расстояний между всеми ее витками (рис. 91,6).
Рис. 91
Если обозначить начальную длину шнура L0, а конечную длину — L, то для характеристики деформаций растяжения или сжатия можно ввести абсолютное удлинение △L = |L — L0|.
Если шнур под действием деформирующей силы больше не удлиняется, то ее действие уравновешивает упругая сила , т. е. .
Роберт Гук установил экспериментально. что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе. На практике часто необходимо определить силу упругости, возникающую в теле при его деформации, и закон Гука формулируется следующим образом:
что при малых деформациях растяжения или сжатия абсолютное удлинение тела прямо пропорционально деформирующей силе. На практике часто необходимо определить силу упругости, возникающую в теле при его деформации, и закон Гука формулируется следующим образом:
модуль силы упругости, возникающей при малых деформациях сжатия или растяжения тела, прямо пропорционален величине абсолютного удлинения:
где k — коэффициент пропорциональности, называемый жесткостью тела.
Жесткость является характеристикой данного тела (пружины, шнура, стержня и т. п.) и зависит от его поперечных и продольных размеров, химического состава и строения вещества, из которого тело изготовлено. Так как , то жесткость измеряется в ньютонах на метр .
При расчетах движения тел под действием силы упругости необходимо учитывать ее направление. Если выбрать начало отсчета под крайней точкой недеформированного тела (рис. 92), то абсолютное удлинение можно характеризовать координатой х конца деформированного тела. При растяжении (см. рис. 92, а) и при сжатии (см. рис. 92, б) образца сила упругости направлена противоположно смещению его конца. Тогда можно записать закон Гука для проекции силы упругости на выбранную ось:
При растяжении (см. рис. 92, а) и при сжатии (см. рис. 92, б) образца сила упругости направлена противоположно смещению его конца. Тогда можно записать закон Гука для проекции силы упругости на выбранную ось:
Ту или иную форму записи закона Гука используют в зависимости от условия задачи и величины, которую нужно определить. Сила упругости, как и любая из сил, рассматриваемых в механике, подчиняется законам Ньютона, а по закону Гука можно рассчитать деформации, возникающие при взаимодействиях тел. Однако необходимо отметить, что закон Гука хорошо выполняется только при малых деформациях тел.
Главные выводы:
- При упругих деформациях растяжения и сжатия абсолютное удлинение прямо пропорционально деформирующей силе.
- При упругих деформациях сила упругости прямо пропорциональна абсолютному удлинению.
- Жесткость тела зависит от его поперечных и продольных размеров, химического состава и строения вещества, из которого изготовлено тело.

Для строительства зданий, мостов, самолетов, автомобилей необходимо знать механические свойства используемых материалов: дерева, бетона, стали, алюминия и т. п. Нужно также учитывать поведение этих веществ при больших деформациях, способных привести к разрушениям.
При деформации по всему объему тела возникают упругие силы, т. е. тело находится в напряженном состоянии. Для характеристики этого состояния вводят механическое напряжение — физическую величину, равную отношению модуля силы упругости к площади поперечного сечения тела:
Эта величина численно равна силе упругости, возникающей в единичном сечении тела, и измеряется в ньютонах на квадратный метр или в паскалях (Па), как давление.
На практике вы сталкивались с тем, что абсолютное удлинение зависит от начальных размеров тела, например, под действием одной и той же силы длинный резиновый шнур растягивается больше, чем короткий (рис. 93).
93).
Поэтому вводят относительное удлинение:
которое показывает, на какую долю первоначальной длины тела изменяется каждая ее единица. В некоторых случаях относительное удлинение выражают в процентах.
Рис. 93
При исследовании растяжений различных тел было обнаружено, что наблюдается сложная зависимость напряжения от относительного удлинения тела, называемая диаграммой растяжения (рис. 94). Обсудим, какие процессы в деформируемом теле отражают различные участки этой диаграммы.
Рис. 94
На участке OA напряжение прямо пропорционально относительному удлинению, и если воздействие прекратилось, то тело восстанавливает свою форму и размеры, т. е. происходит упругая деформация. На практике такая зависимость наблюдается при небольших относительных деформациях и только до определенного напряжения σn, которое называется пределом пропорциональности.
На участке AB такая зависимость нарушается, но до некоторого напряжения, называемого пределом упругости σynp: после прекращения воздействия размеры и форма тела полностью восстанавливаются.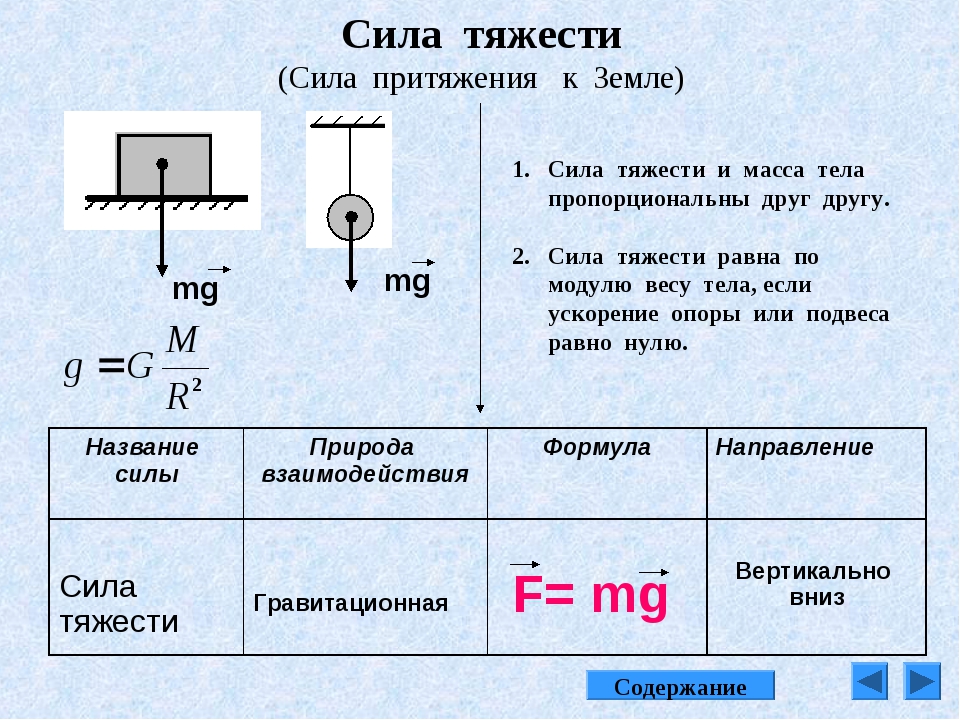
При напряжениях, превышающих предел упругости, наблюдается пластичная деформация (участок BD). На участке CD деформация происходит почти без увеличения напряжения. Это явление называется текучестью материала, а образцы, для которых область текучести велика, могут без разрушения выдерживать большие деформации.
Материалы, у которых область текучести почти отсутствует, являются хрупкими. Они разрушаются даже при небольших деформациях. Хрупкость характерна для стекла, кирпича, бетона, чугуна.
Точка диаграммы E соответствует напряжению, называемому пределом прочности σпp, при дальнейшей деформации образец разрушается.
Зависимость, отраженная на диаграмме участком OA. соответствует закону Гука в другой форме:
механическое напряжение в упруго деформированном теле прямо пропорционально относительной деформации:
где E — модуль продольной упругости, который в честь ученого Томаса Юнга называется модулем Юнга и является характеристикой вещества, из которого сделано тело. Так, модуль продольной упругости живого дерева (рис. 95) больше, чем сухого дерева (рис. 96). Так как относительная деформация безразмерная величина, то модуль Юнга измеряется, как и механическое напряжение, в паскалях (Па).
Так, модуль продольной упругости живого дерева (рис. 95) больше, чем сухого дерева (рис. 96). Так как относительная деформация безразмерная величина, то модуль Юнга измеряется, как и механическое напряжение, в паскалях (Па).
Рис. 95 | Рис. 96 |
Как видно из формулы, модуль Юнга численно равен напряжению, возникающему в теле при относительной деформации, равной единице, т. е. при увеличении длины образца вдвое, так как при , L-L0=L0 и L=2L0 .
Если использовать соответствующие формулы для напряжения и относительного удлинения, то установленную зависимость для модуля силы упругости можно записать следующим образом:
Сравнив с записью закона Гука, получим выражение для жесткости:
которое поясняет зависимость жесткости тела от его начальных размеров и свойств вещества.
Для некоторых тел, например стержней, нитей, тросов, при небольших деформациях площадь поперечного сечения практически остается постоянной, и закон Гука для модуля силы упругости можно использовать в форме:
Модуль упругости и предел прочности различных веществ можно узнать в справочниках.
Главные выводы:
- Механическое напряжение вводится для характеристики сил упругости, возникающих в теле.
- Для различных тел на опыте установлена сложная зависимость механического напряжения от относительной деформации, называемая диаграммой напряжения.
- Модуль упругости вещества определяется его химическим составом и строением.
Как вы уже знаете, взаимодействие различных тел может либо вызывать движение конкретного тела, либо препятствовать ему. Например, если мы дуем в сторону легкого листа бумаги на столе, то заставляем двигаться воздух, а тот, в свою очередь, приводит в движение бумагу. Если мы поднимем тот же лист и отпустим, то он начнет двигаться под действием силы тяжести, а воздух будет препятствовать этому движению (рис. 97).
Если мы поднимем тот же лист и отпустим, то он начнет двигаться под действием силы тяжести, а воздух будет препятствовать этому движению (рис. 97).
Рис. 97
На практике все силы сопротивления движению разделяют на силы сухого (внешнего) трения (покоя, скольжения и качения), которые возникают при взаимодействии соприкасающихся твердых тел друг с другом, а также силы вязкого трения, проявляющиеся при движении тела в жидкости или газе.
Рассмотрим на опыте, как проявляется и от чего зависит сила трения покоя. К бруску, лежащему на горизонтальной поверхности, прикрепим динамометр, на который будем действовать в горизонтальном направлении (рис. 98).
Рис. 98
Потянем слегка за динамометр, но так, чтобы брусок оставался в покое. Отметим показание прибора и проанализируем результаты нашего действия.
Так как брусок покоится, то по второму закону Ньютона векторная сумма всех сил, действующих на него, равна нулю.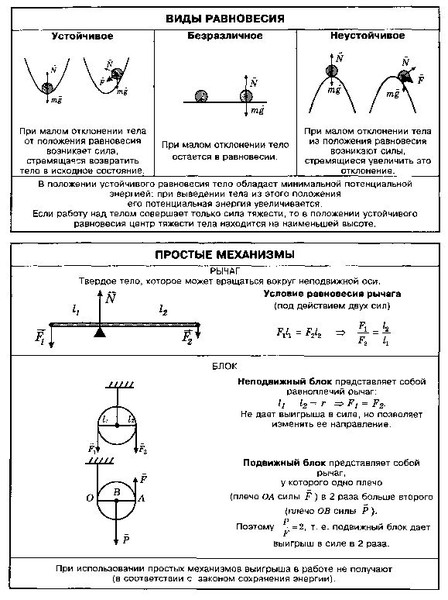 Сила тяжести уравновешивается силой упругости стола в вертикальном направлении.
Сила тяжести уравновешивается силой упругости стола в вертикальном направлении.
Следовательно, и в горизонтальном направлении воздействие динамометра на брусок должно быть компенсировано какой-то силой. При изучении физики в 7-м классе вы узнали, что так проявляется сила трения покоя . Почему она возникает?
Под микроскопом на поверхности любого твердого тела хорошо видны разнообразные выступы и впадины (рис. 99).
рис. 99
Многочисленные неровности соприкасающихся поверхностей цепляются друг за друга, деформируются и препятствуют относительному перемещению тел. Кроме того, расстояние между молекулами, расположенными на выступах соприкасающихся поверхностей, мало, и поэтому возможно электромагнитное взаимодействие молекул.
Все эти сложные взаимодействия в механике характеризуются силой трения покоя, или силой трения сцепления.
Уменьшится ли сила трения покоя, если отшлифовать поверхность тел? Да, уменьшится, но только до определенной степени шлифовки, а при дальнейшей обработке сила трения покоя возрастает. Это происходит потому, что по мере сглаживания неровностей соприкасающихся поверхностей в значительной мере увеличивается число межмолекулярных взаимодействий.
Это происходит потому, что по мере сглаживания неровностей соприкасающихся поверхностей в значительной мере увеличивается число межмолекулярных взаимодействий.
Продолжим опыт, постепенно увеличивая силу воздействия. Показания динамометра увеличиваются, а тело еще покоится, следовательно, и сила трения покоя тоже возрастает. В этом основная особенность силы трения покоя.
Сила трения покоя равна по модулю и направлена противоположно силе, приложенной к покоящемуся телу параллельно поверхности соприкосновения его с другим телом:
Если еще увеличивать действующую силу, то при определенном показании динамометра тело начнет двигаться. Это значит, что существует определенная максимальная сила трения покоя, и действующая сила должна ее превысить, чтобы тело приобрело ускорение.
Вы знаете, что наиболее трудно на практике сдвинуть с места тяжелые предметы. Давайте выясним, почему это так.
Поставим на брусок добавочный груз и измерим максимальную силу трения покоя (рис. 100). Ее численное значение увеличивается. При добавлении еще одного груза сила трения покоя вновь возрастает.
100). Ее численное значение увеличивается. При добавлении еще одного груза сила трения покоя вновь возрастает.
Рис. 100
Снимем с бруска грузы и подействуем на него добавочной силой вертикально вниз (рис. 101). Сила трения покоя также увеличивается. Как объяснить эти опыты?
Рис. 101
При добавлении грузов, как и при воздействии вертикальной силой, увеличивается сила давления бруска на опору. Опыт показывает, что модуль максимальной силы трения покоя прямо пропорционален силе давления тела на опору:
,
Где μ0 — коэффициент трения покоя, F1 — сила давления тела на опору.
Коэффициент трения покоя зависит от веществ, из которых изготовлены соприкасающиеся тела, и степени обработки их поверхностей.
Сила трения покоя удерживает тело, лежащее на наклонной плоскости (рис. 102), а также брусок, прижимаемый к вертикальной стене (рис. 103). Чем тяжелее брусок, тем больше должна быть сила трения покоя, чтобы уравновешивать силу тяжести.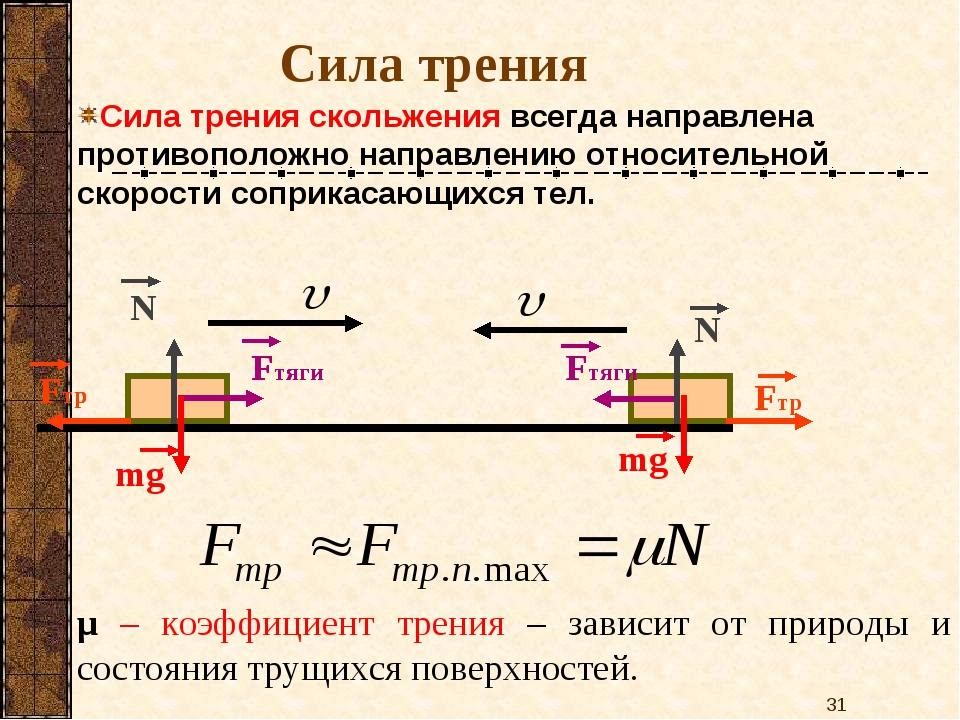 Поэтому тяжелый брусок приходится прижимать к стене со значительной по модулю силой.
Поэтому тяжелый брусок приходится прижимать к стене со значительной по модулю силой.
Рис. 102 | Рис. 103 |
По третьему закону Ньютона , где — сила нормальной реакции опоры, действующая на тело. Так как , то часто используют формулу:
Возникает вопрос: всегда ли сила трения покоя препятствует движению? Нет, не всегда. Во многих случаях сила трения покоя способствует движению.
Например, кирпич, неподвижно лежащий на ленте транспортера, движется вместе с ней, потому что на него со стороны ленты действует сила трения покоя (рис. 104).
Рис. 104
Ведущее колесо автомобиля, если не пробуксовывает, действует на опору против направления движения с силой . По третьему закону Ньютона со стороны опоры на него действует сила трения покоя , вызывающая движение (рис. 105):
Рис. 105
При ходьбе сила трения покоя дает возможность человеку толкнуть опору с некоторой силой.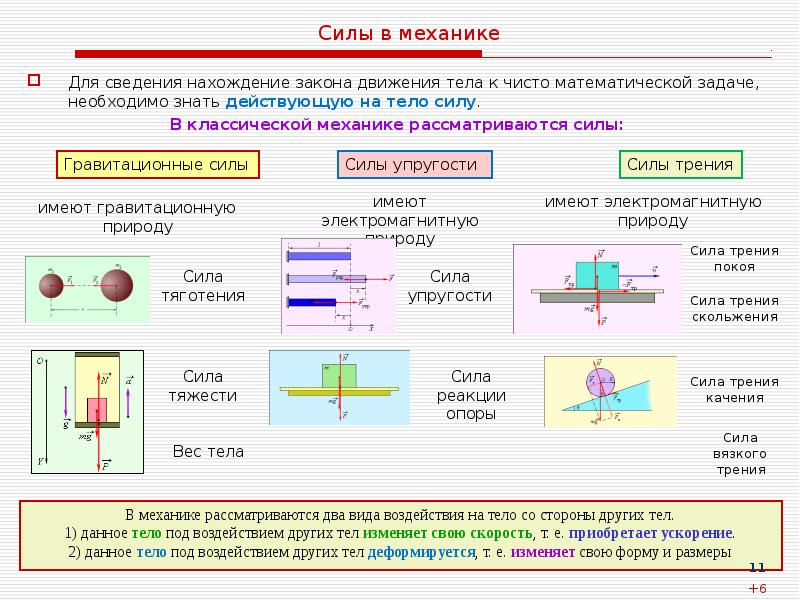 По третьему закону Ньютона на человека действует такая же по величине и противоположная по направлению сила.
По третьему закону Ньютона на человека действует такая же по величине и противоположная по направлению сила.
Трение покоя позволяет человеку брать руками различные тела, например топор, лопату, руль велосипеда или автомобиля, а также управлять движением этих тел, использовать их для совершения работы.
Главные выводы:
- Сила трения покоя (сцепления) всегда направлена параллельно поверхности соприкосновения двух тел и противоположно силе, стремящейся вывести это тело из состояния покоя.
- Модуль силы трения покоя может быть различен и в данный момент равен модулю силы, стремящейся вывести тело из состояния покоя.
- Максимальная сила трения покоя, действующая на тело со стороны опоры, прямо пропорциональна силе нормального давления тела на данную опору.
Термин «скольжение» в физике используется для описания движения одного тела по поверхности другого тела.
Рассмотрим равномерное движение бруска по горизонтальной поверхности доски (рис. 106), т. е. его скольжение по опоре. Мы действуем с определенной горизонтальной силой на динамометр, а он передает наше воздействие бруску и показывает модуль действующей на брусок силы. Если скорость бруска постоянна, то силу, вызывающую движение, должна компенсировать сила взаимодействия бруска с опорой.
Рис. 106
При изучении физики в 7-м классе вы узнали, что эта сила называется силой трения скольжения. Она возникает из-за электромагнитного взаимодействия молекул на неровностях соприкасающихся поверхностей, зацепления неровностей и их пластичной деформации при относительном движении тел.
Из эксперимента следует, что сила трения скольжения, действующая на тело, направлена противоположно направлению его движения. По третьему закону Ньютона на опору при движении тела действует сила трения скольжения Eτp, направленная в сторону движения тела.
Поместим на брусок груз такой же массы и будем тянуть горизонтально динамометр так, чтобы брусок с грузом двигался равномерно (рис. 107). Динамометр при этом покажет вдвое большую силу. Если еще увеличить массу бруска, то сила трения скольжения также возрастет.
107). Динамометр при этом покажет вдвое большую силу. Если еще увеличить массу бруска, то сила трения скольжения также возрастет.
Рис. 107
Опыты показывают, что модуль силы трения скольжения прямо пропорционален модулю силы нормального давления:
где μ — коэффициент трения скольжения. Так как по третьему закону Ньютона Fд = N, то можно записать
Рассмотрим равномерное движение бруска с грузом по другой стороне доски, более шероховатой (рис. 108). При постоянной скорости движения динамометр показывает большую силу, хотя сила нормального давления не изменилась. Значит, изменился коэффициент трения скольжения, и именно он зависит от качества обработки соприкасающихся поверхностей.
Если заменить доску листом стекла или другого материала, то показания динамометра снова изменятся, т. е. коэффициент трения зависит от свойств обоих веществ соприкасающихся поверхностей.
Рис. 108
Однако опыт показывает, что коэффициент трения не зависит от относительного положения тел. Например, коэффициент трения льда по железу такой же, как и железа при скольжении по льду.
Например, коэффициент трения льда по железу такой же, как и железа при скольжении по льду.
Зависит ли коэффициент трения от площади соприкосновения тел? Если сравнить показания динамометра при равномерном движении бруска в различных положениях (рис. 109), то оказывается, что показания во всех трех случаях совпадают, т. е. коэффициент трения не зависит от площади соприкосновения тел.
Рис. 109
Вы знаете из личного опыта, что сдвинуть тело с места труднее, чем перемещать его с постоянной скоростью. Многочисленные эксперименты показывают, что действительно при движении с малыми скоростями величина силы трения скольжения немного меньше величины максимальной силы трения покоя и практически не зависит от скорости тела.
Это объясняется тем, что коэффициент трения скольжения в большинстве случаев немного меньше коэффициента трения покоя. Так как различия невелики, то при решении задач коэффициенты трения принимают равными по величине и обозначают одной буквой μ. Поэтому силу трения скольжения в большинстве задач считают постоянной и приближенно равной максимальной силе трения покоя.
Поэтому силу трения скольжения в большинстве задач считают постоянной и приближенно равной максимальной силе трения покоя.
Одним из достижений в истории человечества считается изобретение несколько тысяч лет назад такого привычного для нас колеса. Если вращающиеся колесо или шар участвуют и в поступательном движении по какой-то поверхности, то возникает сила сопротивления движению, которую называют силой трения качения. Чтобы объяснить причины ее возникновения, рассмотрим качение тяжелого цилиндра по куску поролона, деформация которого при этом хорошо наблюдается (рис. 110).
Цилиндр соприкасается с поролоном на очень малой площади, а значит, оказывает на него достаточно большое давление. Поролон при этом деформируется.
Рис. 110
Вследствие этой деформации перед катящимся цилиндром возникает как бы горка. Для характеристики этого явления в механике вводят силу трения качения.
Чем более пластична возникающая деформация, тем больше сила трения качения. Если цилиндр катится по такой поверхности, что ее деформация упруга и незначительна, то сила трения качения невелика. Она во много раз меньше силы трения скольжения, которая возникала бы только при поступательном движении этого же тела.
Если цилиндр катится по такой поверхности, что ее деформация упруга и незначительна, то сила трения качения невелика. Она во много раз меньше силы трения скольжения, которая возникала бы только при поступательном движении этого же тела.
В таких случаях при относительном движении тел выгоднее скольжение заменить качением, и поэтому используют колеса для транспорта и подшипники в различных механизмах.
Если при движении происходит значительная деформация тела и опоры или только опоры, то сила трения качения велика, и поэтому, например, зимой у телеги заменяют колеса на полозья.
Главные выводы:
- Сила трения скольжения препятствует движению, всегда направлена противоположно относительной скорости тела.
- Модуль силы трения скольжения прямо пропорционален модулю силы нормального давления тела на опору.
- Коэффициент трения скольжения зависит от свойств веществ соприкасающихся поверхностей, степени их обработки и не зависит от взаимного расположения поверхностей и площади их соприкосновения.

- Сила трения качения намного меньше силы трения скольжения, если деформации взаимодействующих при движении тел очень малы.
При движении твердого тела в жидкости или газе также возникает сила сопротивления движению, которую в этих случаях называют силой жидкого или вязкого трения.
Экспериментально установлено, что сила, действующая на движущееся тело в жидкости или газе, также направлена в сторону, противоположную движению, но численно она во много раз меньше силы трения скольжения при небольших скоростях движения.
В отличие от сухого трения для тела в жидкости или газе отсутствует сила трения покоя и даже самая маленькая сила, приложенная к телу, вызывает его движение, если этому не препятствуют другие силы. Следовательно, сила вязкого трения не противодействует возникновению движения, и поэтому в механизмы вводят разнообразные смазки для движущихся друг относительно друга частей.
Проведем опыт. Возьмем два одинаковых тетрадных листа и отпустим в горизонтальном положении с одной высоты (рис. 111, а). Листы плавно и почти одновременно упадут на пол. Сделаем из одного листа плотный и маленький комок, а другой лист просто сомнем и повторим опыт. Первым упадет маленький комок (рис. 111, б). Как вы думаете, почему, ведь массы листов одинаковы?
Рис. 111
Да, вы правы, сопротивление воздуха движению тел зависит от их формы и размеров. На рисунке 112 показаны тела различной формы: диск, шар и каплеобразное тело, у которых площади одного из поперечных сечений одинаковы.
При движении этих тел в жидкости или газе в направлении, перпендикулярном этому сечению, наибольшая сила вязкого трения действует на плоскую шайбу, а наименьшая — на тело каплеобразной формы.
Рис. 112
Форму тела, при которой сила вязкого трения (сопротивления) мала, называют обтекаемой и ее стараются придать телам, движущимся в жидкости или газе. Обтекаемую форму имеют ракеты и самолеты, подводные лодки и скоростные автомобили.
Обтекаемую форму имеют ракеты и самолеты, подводные лодки и скоростные автомобили.
Установлено, что сила вязкого трения зависит от скорости движения тела. При малых скоростях ее модуль прямо пропорционален скорости движения тела относительно среды:
Fc=k1υ,
Где k1 — коэффициент сопротивления, зависящий от формы, размеров тела, состояния его поверхности и свойств среды.
При больших скоростях движения модуль силы сопротивления пропорционален квадрату скорости:
Fc=k2υ2,
Это объясняется тем, что при большой скорости тела возникают сложные движения слоев среды. и поэтому появляется добавочное сопротивление.
Качественный график зависимости проекции силы сопротивления на направление скорости от модуля скорости представлен на рисунке 113. Сила сопротивления всегда направлена противоположно скорости. Если скорость невелика, то сила сопротивления линейно зависит от скорости, а при больших скоростях график имеет вид параболы.
Рис. 113
Следовательно, при ускоренном движении тела в жидкости или газе, на пример под действием силы тяжести, вместе с ростом скорости растет и сила вязкого трения. При некотором значении скорости тела сила вязкого трения становится равной его силе тяжести, и затем тело движется с установившейся скоростью, тем большей, чем больше сила тяжести тела.
Например, размеры и форма парашюта подбираются с таким расчетом, чтобы скорость установившегося движения была безопасной для человека при его приземлении — около 6 ∙. При нераскрытом парашюте сила вязкого трения станет равной силе тяжести только при весьма большой скорости падения — около 50-60 .
Учет всех сил сопротивления на практике достаточно сложен, поэтому при решении задач нужно внимательно прочесть условие и оценить, какой вид трения необходимо учесть и каким в данных условиях можно пренебречь.
Главные выводы
- Сила вязкого трения при малых скоростях пропорциональна модулю скорости, а при больших — квадрату модуля скорости тела.

- Сила вязкого трения зависит от формы тела. Форму тела, при которой сила сопротивления движению (вязкого трения) минимальна, называют обтекаемой.
- Сила вязкого трения, как правило, много меньше силы трения скольжения, и поэтому в различных механизмах используют смазку.
| Формирование проблемной ситуации | 1. Какие вы можете назвать силы
проявляющиеся в этом примере? 2. А кто пересчитает мне все силы проявляющиеся при этих взаимодействиях? Сколько их? 3. Назовите все виды сил которые существуют в механике! Учитель тем самым подводит учащихся к тому, что взаимодействия бывают разными, но их объединяет одна и та же природа проявления. |
Заслушиваются разные варианты ответа:
выделяется взаимосвязь между телами и
проявлением того или иного вида сил: т. е. силы
упругости, силы сопротивления движению (силы
трения), силы тяжести и веса тела. Учащиеся
приходят к выводу что трудно просчитать все силы,
проявляющиеся при этих взаимодействиях.
Учащиеся делают вывод, что сколько тел столько и
сил, так какколичественной характеристикой
взаимодействия тел является сила. При этом
понимая, что легче выделить ту или иную группу
сил, имеющих общую природу. е. силы
упругости, силы сопротивления движению (силы
трения), силы тяжести и веса тела. Учащиеся
приходят к выводу что трудно просчитать все силы,
проявляющиеся при этих взаимодействиях.
Учащиеся делают вывод, что сколько тел столько и
сил, так какколичественной характеристикой
взаимодействия тел является сила. При этом
понимая, что легче выделить ту или иную группу
сил, имеющих общую природу. |
Этап систематизации знаний по теме (15 мин) |
Вводная беседа учителя о
проявлении сил в природе: гравитационных,
электромагнитных, ядерных(сильных) и слабых
взаимодействий. Учитель демонстрирует примеры взаимодействия тел каждого вида , кратко рассказывает и обосновывает их природу. Гравитационные силы действуют между всеми
телами – все тела притягиваются друг к другу. Электромагнитные силы действуют между заряженными частицами. В атомах, молекулах, живых организмах именно они являются главными Область ядерных сил очень ограничена. Они заметны только внутри атомных ядер(т.е. на расстоянии 10 -12 см.) Слабые взаимодействия проявляются на ещё меньших расстояниях. Они вызывают превращение элементарных частиц друг в друга Ставится цель урока: Представить характеристику F(силы):1.Силы тяжести. 2. Веса тела. 3. Силы упругости. 4. Силы трения. Для достижения поставленной цели урока
использую один из эффективных приемов
систематизации знаний — это планы обобщенного
характера, использование которых в обучении
приводит к сформированности системных и
метапредметных знаний. Учащиеся на уроке самостоятельно прорабатывают параграф учебника и УМК, выделяют элементы знаний для характеристики данного физического понятия, пользуясь обобщенными планами изучения. Учитель организует беседу с коллективным обсуждением характеристики с учетом дополнений, а также корректирует и дополняет ответы учащихся Что надо знать о величинах 1.Какое явление или свойство тел (веществ), процесс характеризует данная величина. 2. Определение физической величины. 3. Обозначение. 4. Определительная формула (для производной величины – формула, выражающая связь данной величины с другими). 5. Какая эта величина – скалярная или векторная. 6. Единица измерения величины в СИ. 7. Способы измерения величины. 8. Разновидности величин (например, сила тяжести, сила упругости, сила электростатического
взаимодействия и т. Главный вывод: Разумная постановка образовательных целей предоставляет ученику возможность самому выбирать ту глубину изучения темы, которая его устраивает, обеспечивая индивидуализацию обучения и гарантированный минимум знаний по теме у всех и более глубокие у тех, кто в этом заинтересован |
Ученики записывают в тетрадях
информацию о классификации всех сил проявления в
природе на 4 группы: а) гравитационной, б) электромагнитной, в) сильного взаимодействия, г) слабого взаимодействия. Проанализировав полученные разные варианты делают вывод: Все силы в механике делятся на два вида:(гравитационной иэлектромагнитной природы) Весь класс разбивается на 4 группы по 6 человек. У всех на столах раскрыты УМК “Основы механики” на опорном конспекте:
Задание всем учащимся: Применяя план изучения Физической величины дать характеристику
(5 мин) План изучения физической величины: 1. Определение физической величины. 2 . Математическая запись формулы нахождения физической величины с пояснением величин , входящих в нее. 3. Введение основной единицы измерения физической величины. 4. Прибор для измерения физической величины. Учащиеся используют дополнительно текст учебника “Физика 10 класс” под редакцией Г. Я. Мякишева, Б.
и составляют характеристику соответствующей силы. Затем по желанию учащиеся презентируют свои записи на доске и озвучивают их. |
Обобщение знаний материала (15 мин) |
Задача: обобщить полученные
учащимися знания, умения и навыки. В качестве
обобщения материала предлагается заполнить
таблицу. Смотреть приложение
В итоге изучения темы учащиеся должны уметь
выделять конкретные взаимодействия тел,
определять их природу, характеризовать их
физическими величинами и законами. |
Учащиеся, заранее подготовившие
презентацию по теме урока о любой из сил
дополняют ответ представляя свою презентацию на
обсуждение. Предлагается вместе с учителем заполнить таблицу |
Этап информирования обучающихся о
домашнем задании (2 мин) |
Дается домашнее задание, учитель
комментирует его. Д/З: 1 уровень: п.33-37, стр.102-103 знать краткие итоги; 2 уровень: задача № 2, из упр.№7. 3 уровень: заполнить таблицу (смотреть №2 из приложений к уроку). Всему классу подготовиться к решению задач по теме “Силы в механике”, и выучить все формулы(смотреть №4из приложений к уроку “Основные формулы по теме”). |
Домашнее задание записывается в
дневник. 3 уровень: заполнить таблицу Силы в механике
|
Урок 9.
 закон гука — Физика — 10 класс
закон гука — Физика — 10 классФизика, 10 класс
Урок 9. Закон Гука
Перечень вопросов, рассматриваемых на этом уроке
1.Закона Гука.
2.Модели видов деформаций.
3. Вычисление и измерение силы упругости, жёсткости и удлинение пружины.
Глоссарий по теме
Сила упругости – это сила, возникающая в теле в результате его деформации и стремящаяся вернуть тело в исходное положение.
Деформация – изменение формы или размеров тела, происходящее из-за неодинакового смещения различных частей одного и того же тела в результате воздействия другого тела. Виды деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
Закон Гука – сила упругости, возникающая при деформации тела (растяжение или сжатие пружины), пропорциональна удлинению тела (пружины), и направлена в сторону противоположную направлению перемещений частиц тела
Основная и дополнительная литература по теме:
Г. Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Я. Мякишев., Б.Б.Буховцев., Н.Н.Сотский. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017стр. 107-112
Рымкевич А.П. Сборник задач по физике. 10-11класс.- М.:Дрофа,2009. Стр 28-29
ЕГЭ 2017. Физика. 1000 задач с ответами и решениями. Демидова М.Ю., Грибов В.А., Гиголо А.И. М.: Экзамен, 2017.
Основное содержание урока
В окружающем нас мире мы наблюдаем, как различные силы заставляют тела двигаться, делать прыжки, перемещаться, взаимодействовать.
Однако можно также наблюдать как происходят разрушения, так называемые деформации, различных сооружений: мостов, домов, разнообразных машин.
Что необходимо знать инженеру конструктору, строителю, чтобы строить надёжные сооружения: дома, мосты, машины?
Почему деформации различны, какие виды деформации могут быть у конкретных тел? Почему одни тела после деформации могут восстановиться, а другие нет? От чего зависит и можно ли рассчитать величину этих деформаций?
Деформация — это изменение формы или размеров тела, в результате воздействия на него другого тела.
Почему деформации не одинаковы у различных тел, если мы их, к примеру, сжимаем? Давайте вспомним что мы знаем о строении вещества.
Все вещества состоят из частиц. Между этими частицами существуют силы взаимодействия- эти силы электромагнитной природы. Эти силы в зависимости от расстояний между частицами проявляются, то как силы притяжения, то как силы отталкивания.
Сила упругости – сила, возникающая при деформации любых тел, а также при сжатии жидкостей и газов. Она противодействует изменению формы тел.
Мы можем наблюдать несколько видов деформаций: сжатие, растяжение, изгиб, сдвиг, кручение.
При деформации растяжения межмолекулярные расстояния увеличиваются. Такую деформацию испытывают струны в музыкальных инструментах, различные нити, тросы, буксирные тросы.
При деформации сжатия межмолекулярные расстояния уменьшаются. Под такой деформацией находятся стены, фундаменты сооружений и зданий.
При деформации изгиба происходят неординарные изменения, одни межмолекулярные слои увеличиваются, а другие уменьшаются. Такие деформации испытывают перекрытия в зданиях и мостах.
Такие деформации испытывают перекрытия в зданиях и мостах.
При кручении – происходят повороты одних молекулярных слоёв относительно других. Эту деформацию испытывают: валы, витки цилиндрических пружин, столярный бур, свёрла по металлу, валы при бурении нефтяных скважин. Деформация среза тоже является разновидностью деформации сдвига.
Первое научное исследование упругого растяжения и сжатия вещества провёл английский учёный Роберт Гук.
Роберт Гук установил, что при малых деформациях растяжения или сжатия тела абсолютное удлинение тела прямо пропорционально деформирующей силе.
F упр = k ·Δℓ = k · Iℓ−ℓ0I закон Гука.
k− коэффициент пропорциональности, жёсткость тела.
ℓ0 — начальная длина.
ℓ — конечная длина после деформации.
Δℓ = I ℓ−ℓ₀ I- абсолютное удлинение пружины.
— единица измерения жёсткости в системе СИ.
При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе, а слишком большие деформации разрушают тело.
Для расчёта движения тел под действием силы упругости, нужно учитывать направление этой силы. Если принять за начало отсчёта крайнюю точку недеформированного тела, то абсолютное удлинение тела можно характеризовать конечной координатой деформированного тела. При растяжении и сжатии сила упругости направлена противоположно смещению его конца.
Закон Гука можно записать для проекции силы упругости на выбранную координатную ось в виде:
F упр x = − kx — закона Гука.
k – коэффициент пропорциональности, жёсткость тела.
x = Δℓ = ℓ−ℓ0 удлинение тела (пружины, резины, шнура, нити….)
Fупр x = − kx
Закон Гука:
Fупр = k·Δℓ = k · Iℓ−ℓ0I
Графиком зависимости модуля силы упругости от абсолютного удлинения тела является прямая, угол наклона которой к оси абсцисс зависит от коэффициента жёсткости k. Если прямая идёт круче к оси силы упругости, то коэффициент жёсткости этого тела больше, если же уклон прямой идёт ближе к оси абсолютного удлинения, следует понимать, что жёсткость тела меньше.
График, зависимости проекции силы упругости на ось ОХ, того же тела от значения х.
Необходимо помнить, что закон Гука хорошо выполняется при только при малых деформациях. При больших деформациях изменение длины перестаёт быть прямо пропорциональным приложенной силе.
Разбор тренировочных заданий
1. По результатам исследования построен график зависимости модуля силы упругости пружины от её деформации. Чему равна жёсткость пружины? Каким будет удлинение этой пружины при подвешивании груза массой 2кг?
Решение: По графику идёт линейная зависимость модуля силы упругости и удлинение пружины. Зависимость физических величин по Закону Гука:
F упр x = − kx (1)
Fупр =k·Δℓ = k · Iℓ−ℓ0I (2)
Из формулы (1) выражаем:
Зная что Fт = mg = 20 Н, Fт = Fупр= k·Δℓ следовательно
Ответ: жёсткость пружины равна 200 Н/м, удлинение пружины равно 0,1м.
2. К системе из кубика массой 1 кг и двух пружин приложена постоянная горизонтальная сила. Система покоится. Между кубиком и опорой трения нет. Левый край первой пружины прикреплён к стенке. Удлинение первой пружины 0,05 м. Жёсткость первой пружины равна 200 Н/м. Удлинение второй пружины 0,25 м.
- Чему равна приложенная к системе сила?
- Чему равна жёсткость второй пружины?
- Во сколько раз жёсткость второй пружины меньше чем первой?
Решение:
1. По условию задачи система находится в покое. Зная жёсткость и удлинение пружины найдём силу, которая уравновешивает приложенную постоянную горизонтальную силу.
F = F упр =k1·Δℓ1= 200 Н/м·0,05 м = 10 Н
2. Жёсткость второй пружины:
3. k1/ k2 = 200/40 = 5
Ответ: F=10 Н; k2 = 40 Н/м; k1/k2 = 5.
Формула силы тяги в физике
Содержание:
В том случае, если тело при перемещении имеет ускорение, то на него кроме всех прочих обязательно действует некоторая сила, которая является
силой тяги в рассматриваемый момент времени. В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также
действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя
равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
В действительности, если тело движется прямолинейно и с постоянной скоростью, то сила тяги также
действует, так как тело должно преодолевать силы сопротивления. Обычно силу тяги находят, рассматривая силы, действующие на тело, находя
равнодействующую и применяя второй закон Ньютона. Жестко определенной формулы для силы тяги не существует.
Не следует считать, что сила тяги, например, транспортного средства действует со стороны двигателя, так как внутренние силы не могут менять
скорость системы как единого целого, что входило бы в противоречие с законом сохранения импульса. Однако следует отметить, что для получения у
силы трения покоя необходимого направления, мотор вращает колеса, колеса «цепляются за дорогу» и порождается сила тяги. Теоретически было бы
возможно не использовать понятие «сила тяги», а говорить о силе трения покоя или силе реакции воздуха. Но удобнее внешние силы, которые действуют
на транспорт делить на две части, при этом одни силы называть силами тяги
$(/bar{F}_T)$, а другие — силами сопротивления
$\bar{F}_S$ . Это делается для того,
чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
Это делается для того,
чтобы уравнения движения не потеряли свой универсальный вид и полезная механическая мощность (P) имела простое выражение:
Определение и формула силы тяги
Определение
Исходя из формулы (1) силу тяги можно определить через полезную мощность, и скорость транспортного средства (v):
$$F_{T}=\frac{P}{v}(2)$$Для автомобиля, поднимающегося в горку, которая имеет уклон , масса автомобиля m сила тяги (FT) войдет в уравнение:
$$F_{T}-F_{s}-m g \sin \alpha=m a(3)$$где a – ускорение, с которым движется автомобиль.
Единицы измерения силы тяги
Основной единицей измерения силы в системе СИ является: [FT]=Н
В СГС: [FT]=дин
Примеры решения задач
Пример
Задание. На автомобиль имеющий массу 1 т при его движении по горизонтальной поверхности, действует сила трения,
которая равна $\mu$=0,1 от силы тяжести. {3}(H)$$
{3}(H)$$
Ответ. FT=2,98 кН
Мы помогли уже 4 372 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. На гладкой горизонтальной поверхности лежит доска массой M. На доске находится тело массы m. Коэффициент трения тела о доску равен $\mu$ . К доске приложена сила горизонтальная сила тяги, которая зависит от времени как: F=At (где A=const). В какой момент времени доска начнет выскальзывать из-под тела?
Решение. Сделаем рисунок.
Для решения задачи нам потребуются проекции сил на осиX и Y, которые отличны от нуля. Для тела массы m:
$$ \begin{array}{c} X: m a_{1}=F_{t r}(2.1) \\ Y: m g=N(2.2) \\ F_{t r}=\mu N=\mu m g \rightarrow m a_{1}=\mu m g \rightarrow a_{1}=\mu g(2.3) \end{array} $$Для тела массы M:
$$M a_{2}=F-F_{t r} \rightarrow M a_{2}=A t-F_{t r} \rightarrow a_{2}=\frac{A t-F_{t r}}{M}(2. 2)$$
2)$$Обозначим момент времени, в который доска начнет выскальзывать из-под тела t0, тогда
$$\mu g=\frac{A t_{0}-\mu m g}{M} \rightarrow t_{0}=\frac{m+M}{A} \mu g$$Ответ. $t_{0}=\frac{m+M}{A} \mu g$
Читать дальше: Формула силы упругости.
Таблицы DPVA.ru — Инженерный Справочник | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Такой страницы нет Поделиться:
| |||||
| Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. Вложите в письмо ссылку на страницу с ошибкой, пожалуйста. | ||||||
| Коды баннеров проекта DPVA.ru Начинка: KJR Publisiers Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса.
Free xml sitemap generator | |||||
Пёрышкин. Решебник с подробными пояснениями
Структура решебника
§ 1. Что изучает физика
Вопросы
Задание
§ 2. Некоторые физические термины
Вопросы
§ 3. Наблюдения и опыты
Вопросы
§ 4. Физические величины. Измерение физических величин
Вопросы
Упражнение 1
Задание
§ 5. Точность и погрешность измерений
Вопросы
Задание
§ 6. Физика и техника
Вопросы
Задание
§ 7. Строение вещества
Вопросы
§ 8. Молекулы
Вопросы
§ 9. Броуновское движение
Вопросы
Задание
§ 10. Диффузия в газах, жидкостях и твёрдых телах
Вопросы
Задание
§ 11.
 Взаимное притяжение и отталкивание молекул
Взаимное притяжение и отталкивание молекулВопросы
Задание
§ 12. Агрегатные состояния вещества
Вопросы
§ 13. Различие в молекулярном строении твёрдых тел, жидкостей
Вопросы
Задание
Проверь себя
§ 14. Механическое движение
Вопросы
Упражнение 2
Задание
§ 15. Равномерное и неравномерное движение
Вопросы
Задание
§ 16. Скорость. Единицы скорости
Вопросы
Упражнение 3
Задание
§ 17. Расчёт пути и времени движения
Вопросы
Упражнение 4
Задание
§ 18. Инерция
Вопросы
Упражнение 5
Задание
§ 19. Взаимодействие тел
Вопросы
§ 20. Масса тела. Единицы массы
Вопросы
Упражнение 6
§ 21. Измерение массы тела на весах
Вопросы
Задание
§ 22. Плотность вещества
Вопросы
Упражнение 7
Задание
§ 23.
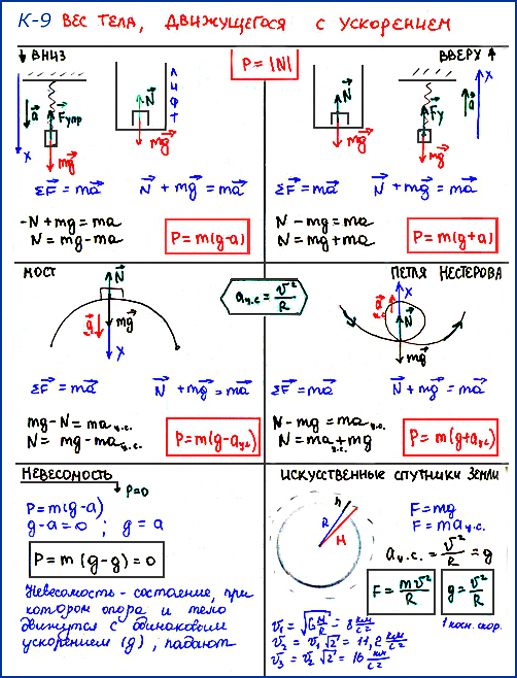 Расчёт массы и объёма тела по его плотности
Расчёт массы и объёма тела по его плотностиВопросы
Упражнение 8
Задание
§ 24. Сила
Вопросы
Упражнение 9
§ 25. Явление тяготения. Сила тяжести
Вопросы
§ 26. Сила упругости. Закон Гука
Вопросы
§ 27. Вес тела
Вопросы
§ 28. Единицы силы. Связь между силой тяжести и массой тела
Вопросы
Упражнение 10
§ 29. Сила тяжести на других планетах. Физические характеристики планет
Вопросы
Задание
§ 30. Динамометр
Вопросы
Упражнение 11
§ 31. Сложение двух сил, направленных по одной прямой. Равнодействующая сил
Вопросы
Упражнение 12
§ 32. Сила трения
Вопросы
Упражнение 13
§ 33. Трение покоя
Вопросы
§ 34. Трение в природе и технике
Вопросы
Проверь себя
§ 35. Давление.
 Единицы давления
Единицы давленияВопросы
Упражнение 14
Задание
§ 36. Способы уменьшения и увеличения давления
Вопросы
Упражнение 15
Задание
§ 37. Давление газа
Вопросы
Задание
§ 38. Передача давления жидкостями и газами. Закон Паскаля
Вопросы
Упражнение 16
Задание
§ 39. Давление в жидкости и газе
Вопросы
§ 40. Расчёт давления жидкости на дно и стенки сосуда
Вопросы
Упражнение 17
Задание
§ 41. Сообщающиеся сосуды
Вопросы
Упрожнение 18
Задание
§ 42. Вес воздуха. Атмосферное давление
Вопросы
Упрожнение 19
Задание
§ 43. Почему существует воздушная оболочка Земли
Вопросы
Упражнение 20
§ 44. Измерение атмосферного давления. Опыт Торричелли
Вопросы
Упражнение 21
Задание
§ 45.
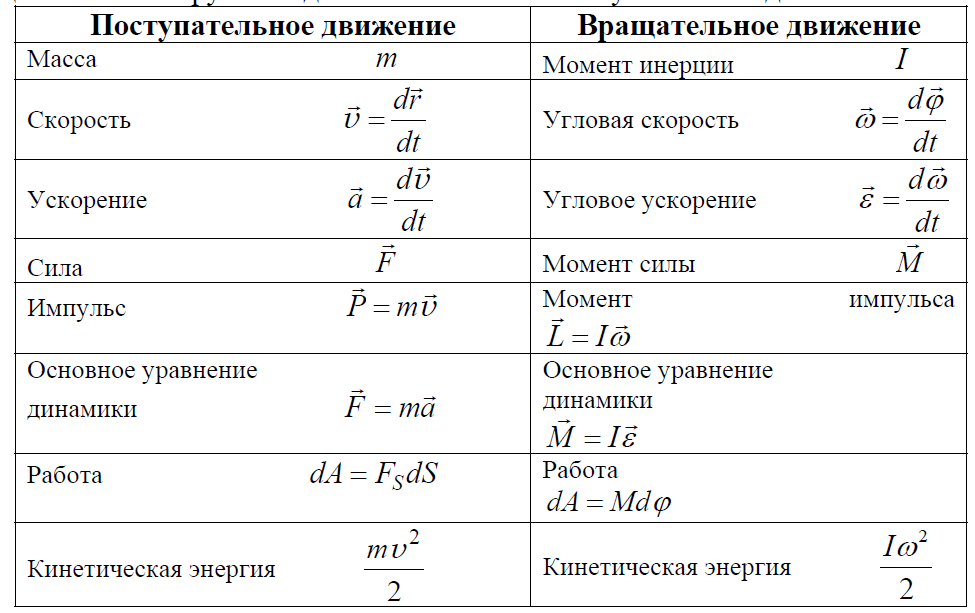 Барометр-анероид
Барометр-анероидВопросы
Упражнение 22
§ 46. Атмосферное давление на различных высотах
Вопросы
Упражнение 23
Задание
§ 47. Манометры
Вопросы
§ 48. Поршневой жидкостный насос
Вопросы
Упражнение 24
§ 49. Гидравлический пресс
Вопросы
Упражнение 25
Задание
§ 50. Действие жидкости и газа на погружённое в них тело
Вопросы
§ 51. Архимедова сила
Вопросы
Упражнение 26
§ 52. Плавание тел
Вопросы
Упражнение 27
Задание
§ 53. Плавание судов
Вопросы
Упражнение 28
Задание
§ 54. Воздухоплавание
Вопросы
Упражнение 29
Проверь себя
§ 55. Механическая работа. Единицы работы
Вопросы
Упражнение 30
Задание
§ 56. Мощность. Единицы мощности
Вопросы
Упражнение 31
Задание
§ 57.
 Простые механизмы
Простые механизмыВопросы
§ 58. Рычаг. Равновесие сил на рычаге
Вопросы
§ 59. Момент силы
Вопросы
§ 60. Рычаги в технике, быту и природе
Вопросы
Упражнения
Задание
§ 61. Применение закона равновесия рычага к блоку
Вопросы
§ 62. Равенство работ при использовании простых механизмов. «Золотое правило» механики
Вопросы
Упражнение 33
Задание
§ 63. Центр тяжести тела
Вопросы
§ 64. Условия равновесия тел
Вопросы
§ 65. Коэффициент полезного действия механизма
Вопросы
§ 66. Энергия
Вопросы
§ 67. Потенциальная и кинетическая энергия
Вопросы
Упражнение 34
§ 68. Превращение одного вида механической энергии в другой
Вопросы
Упражнение 35
Проверь себя
Лабораторные работы
Что такое Формула Силы? — Определение и объяснение — Видео и стенограмма урока
Формула силы
Формула силы утверждает, что сила равна массе, умноженной на ускорение. Итак, если вы знаете массу и ускорение, просто перемножьте их вместе, и теперь вы знаете силу! Единицами ускорения являются метры в секунду в квадрате ( м/с2), а единицами измерения массы являются килограммы (кг).
Итак, если вы знаете массу и ускорение, просто перемножьте их вместе, и теперь вы знаете силу! Единицами ускорения являются метры в секунду в квадрате ( м/с2), а единицами измерения массы являются килограммы (кг).
Давайте рассмотрим пример:
Мэри пытается поднять коробку с пола на полку.Она разгоняет ящик массой 2 кг со скоростью 2 м/с2. С какой силой Мэри действует на ящик?
Чтобы решить эту задачу, просто умножьте массу (2 кг) на ускорение (2 м/с2), чтобы получить окончательный ответ: на ящик была приложена сила 4 Н. Помните, что в физике всегда включайте все единицы, как в вашей задаче, когда вы показываете свою математику, так и когда вы пишете свой окончательный ответ.
Решение для других переменных
Вы также можете вычислить любую другую переменную в уравнении, если у вас есть две из трех.Например, если у вас есть масса и сила, вы можете рассчитать ускорение.
Если вы немного не в ладах с алгебраическими уравнениями, вот вам короткий путь!
Используя круг, проведите горизонтальную линию через середину. Затем разделите нижнюю половину круга на две части. Вверху напишите F для силы, а внизу введите м для массы в одном сечении и a для ускорения в другом.Горизонтальная линия будет использоваться для деления, а вертикальные линии обозначают умножение. Затем закройте пальцем любую переменную, которую вы хотите найти. Например, предположим, что мы хотим найти ускорение. Накройте и на круге. Теперь у вас осталось F разделить на м. Это будет математический расчет силы! Довольно легко, да?
Затем разделите нижнюю половину круга на две части. Вверху напишите F для силы, а внизу введите м для массы в одном сечении и a для ускорения в другом.Горизонтальная линия будет использоваться для деления, а вертикальные линии обозначают умножение. Затем закройте пальцем любую переменную, которую вы хотите найти. Например, предположим, что мы хотим найти ускорение. Накройте и на круге. Теперь у вас осталось F разделить на м. Это будет математический расчет силы! Довольно легко, да?
Давайте рассмотрим пример:
Джордан пытается передвинуть через комнату большой стул для своей тети.Она хочет, чтобы это было на солнце, чтобы она могла читать днем. Джордан прикладывает силу 300 Н к стулу весом 300 кг. С какой скоростью должен разогнаться Джордан, чтобы сдвинуть стул?
Давайте снова воспользуемся кругом. Закройте переменную, которую вы хотите найти, a. Теперь у нас осталось F разделить на м. Теперь мы можем подставить наши числа. Сила (300 Н), деленная на массу (300 кг), равна 1 м/с2 — ускорению, которое Джордан должен использовать, чтобы сдвинуть стул.
Теперь мы можем подставить наши числа. Сила (300 Н), деленная на массу (300 кг), равна 1 м/с2 — ускорению, которое Джордан должен использовать, чтобы сдвинуть стул.
Net Force
Обычно на объекты одновременно действует множество сил, а не одна, как мы видели до сих пор.Чтобы рассчитать другие переменные, нам нужно сложить силы, чтобы увидеть, что такое результирующая сила или сумма сил, действующих на объект. Сила считается вектором , что означает, что она имеет величину и направление. Обычно мы обозначаем силы, направленные вниз, как отрицательные, а силы, направленные вверх, как положительные. Точно так же силы, направленные влево, отрицательны, а силы, направленные вправо, положительны.
Ученые придумали отличный способ систематизировать суммарные силы, действующие на объект, который называется диаграммой свободного тела. Диаграммы свободного тела — это изображения, которые включают все силы, действующие на объект. Вы начинаете с точки, представляющей объект. Затем вы рисуете силы, действующие на объект, выходящий из точки со стрелками на конце. Так, например, если я толкну коробку вправо с силой 10 Н, я нарисую линию на диаграмме свободного тела справа, помеченную 10 Н. После того, как вы записали все свои силы, пришло время их сложить! Мы добавляем силы только в одном направлении за раз.
Затем вы рисуете силы, действующие на объект, выходящий из точки со стрелками на конце. Так, например, если я толкну коробку вправо с силой 10 Н, я нарисую линию на диаграмме свободного тела справа, помеченную 10 Н. После того, как вы записали все свои силы, пришло время их сложить! Мы добавляем силы только в одном направлении за раз.
Если в задаче задействовано более одной силы, вам придется сначала нарисовать диаграмму свободного тела, рассчитать результирующую силу, а затем использовать круг или алгебру для решения.
Давайте рассмотрим пример:
Керри хочет повесить новую модную лампу весом 150 кг, которую она нашла в комиссионном магазине. Она знает, что Fg для лампы, или ее вес, составляет 200 Н. Натяжение троса, на котором она должна ее подвесить, составляет всего 150 Н. Каково ускорение лампы?
Сначала рисуем диаграмму свободного тела, где F g идет вниз, так как это связано с гравитацией, а F T идет вверх, так как веревка тянет лампу к потолку.
Далее, поскольку F g опускается, эта сила будет отрицательной, а поскольку F T возрастает, это число будет положительным. Когда мы добавляем -200 Н плюс положительные 150 Н, мы получаем -50 Н. Это означает, что результирующая сила, действующая на нашу лампу, уменьшается, то есть лампа тоже падает. Не похоже, что этот кабель подойдет Керри! Однако давайте продолжим решать проблему, потому что нам нужно было найти ускорение.
Теперь, когда у нас есть чистая сила, мы можем использовать круг или алгебру.Когда мы подставляем числа, мы получаем -50 Н (сила), разделенная на 150 кг (масса), что дает нам ускорение -0,33 м/с2.
Резюме урока
Формула для силы говорит, что сила равна массе ( м ), умноженной на ускорение ( ). Если у вас есть любые две из трех переменных, вы можете найти третью. Сила измеряется в ньютонах (Н), масса – в килограммах (кг), а ускорение – в метрах в секунду в квадрате (м/с2). Если у вас есть более одной силы в задаче, сначала нарисуйте диаграмму свободного тела, затем добавьте свои силы, чтобы получить результирующую силу, и, наконец, решите свою проблему.
Что нужно помнить
- Сила равна произведению массы на ускорение.
- Сила измеряется в Ньютонах.
- Вы также можете использовать уравнение силы, чтобы найти массу или ускорение объекта.
- Чтобы рассчитать результирующую силу, действующую на объект, полезно нарисовать диаграмму свободного тела.
Результаты обучения
Просмотрите, а затем просмотрите этот видеоурок о формуле силы, чтобы с легкостью решить следующие задачи:
- Напишите определение силы и поймите, как ее измеряют
- Распознать формулу расчета силы
- Создать свободную диаграмму тела
- Найдите другие переменные и рассчитайте чистую силу
Нормальная сила и вес — AP Physics 1
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно
или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному агенту, указанному ниже. Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Если университетские наставники примут меры в ответ на
ан
Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент
средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
8.1 Линейный импульс, сила и импульс — физика
Раздел Цели обучения
К концу этого раздела вы сможете делать следующее:
- Описать импульс, что может изменить импульс, импульс и теорему об импульсе-импульсе
- Опишите второй закон Ньютона в терминах импульса
- Решение задач с использованием теоремы об импульсе-импульсе
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:
- (6) Научные концепции.
 Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:- (C) рассчитать механическую энергию, мощность, генерируемую внутри, приложенный к ней импульс и импульс физической системы.
Основные термины раздела
| изменение импульса | импульс | теорема об импульсе-импульсе | линейный импульс |
Служба поддержки учителей
Служба поддержки учителей
[BL][OL] Изучите законы инерции и законы движения Ньютона.
[AL] Начать обсуждение движения и столкновения. На примере футболистов укажите, что и масса, и скорость объекта являются важными факторами при определении последствий столкновений. Направление, а также величина скорости очень важны.
Импульс, импульс и теорема об импульсе-импульсе
Линейный импульс — это произведение массы системы на ее скорость. В форме уравнения линейный импульс p равен
Из уравнения видно, что импульс прямо пропорционален массе объекта ( m ) и скорости ( v ).Следовательно, чем больше масса объекта или больше его скорость, тем больше его импульс. Большой, быстро движущийся объект имеет больший импульс, чем меньший, более медленный объект.
Импульс является вектором и имеет то же направление, что и скорость v . Поскольку масса является скаляром, когда скорость имеет отрицательное направление (т. е. противоположное направлению движения), импульс также будет иметь отрицательное направление; и когда скорость имеет положительное направление, импульс также будет иметь положительное направление.Единицей импульса в системе СИ является кг м/с.
Импульс настолько важен для понимания движения, что такие физики, как Ньютон, назвали его количеством движения . Сила влияет на импульс, и мы можем изменить второй закон Ньютона, чтобы показать взаимосвязь между силой и импульсом.
Сила влияет на импульс, и мы можем изменить второй закон Ньютона, чтобы показать взаимосвязь между силой и импульсом.
Вспомним наше исследование второго закона движения Ньютона ( F нетто = м a ). Ньютон фактически сформулировал свой второй закон движения в терминах количества движения: чистая внешняя сила равна изменению количества движения системы, деленному на время, в течение которого оно изменяется.Изменение импульса есть разница между конечным и начальным значениями импульса.
В форме уравнения этот закон равен
., где F net — чистая внешняя сила, ΔpΔp — изменение количества движения, а ΔtΔt — изменение во времени.
Мы можем найти ΔpΔp, переформулировав уравнение
будет
FnetΔtFnetΔt
называется импульсом, а это уравнение известно как теорема об импульсе-импульсе. Из уравнения мы видим, что импульс равен средней чистой внешней силе, умноженной на время действия этой силы. Он равен изменению импульса. Воздействие силы на объект зависит от того, как долго она действует, а также от силы силы. Импульс — полезная концепция, поскольку она количественно определяет действие силы. Очень большая сила, действующая в течение короткого времени, может сильно повлиять на импульс объекта, например, сила удара ракетки по теннисному мячу. Небольшая сила могла бы вызвать такое же изменение количества движения, но она должна была бы действовать в течение гораздо более длительного времени.
Он равен изменению импульса. Воздействие силы на объект зависит от того, как долго она действует, а также от силы силы. Импульс — полезная концепция, поскольку она количественно определяет действие силы. Очень большая сила, действующая в течение короткого времени, может сильно повлиять на импульс объекта, например, сила удара ракетки по теннисному мячу. Небольшая сила могла бы вызвать такое же изменение количества движения, но она должна была бы действовать в течение гораздо более длительного времени.
Служба поддержки учителей
Служба поддержки учителей
[OL][AL] Объясните, что большой, быстро движущийся объект имеет больший импульс, чем меньший, но более медленный объект.Это качество называется импульсом.
[BL][OL] Повторите уравнение второго закона Ньютона. Укажите два различных уравнения закона.
Второй закон Ньютона в терминах импульса
Когда второй закон Ньютона выражается в терминах импульса, его можно использовать для решения задач, связанных с изменением массы, поскольку Δp=Δ(mv)Δp=Δ(mv) . В более традиционной форме закона, с которой вы привыкли работать, предполагается, что масса постоянна. Фактически эта традиционная форма является частным случаем закона, когда масса постоянна.Fnet=maFnet=ma на самом деле получается из уравнения:
В более традиционной форме закона, с которой вы привыкли работать, предполагается, что масса постоянна. Фактически эта традиционная форма является частным случаем закона, когда масса постоянна.Fnet=maFnet=ma на самом деле получается из уравнения:
Чтобы понять взаимосвязь между вторым законом Ньютона в двух его формах, давайте воссоздадим вывод Fnet=maFnet=ma из
., подставив определения ускорения и импульса.
Изменение импульса ΔpΔp определяется выражением
Если масса системы постоянна, то
Подставив mΔvmΔv вместо ΔpΔp, второй закон Ньютона примет вид
Fnet=ΔpΔt=mΔvΔtFnet=ΔpΔt=mΔvΔtдля постоянной массы.
Потому что
мы можем подставить, чтобы получить знакомое уравнение
, когда масса системы постоянна.
Служба поддержки учителей
Служба поддержки учителей
[BL][OL][AL] Покажите две разные формы второго закона Ньютона и то, как одна из них может быть получена из другой.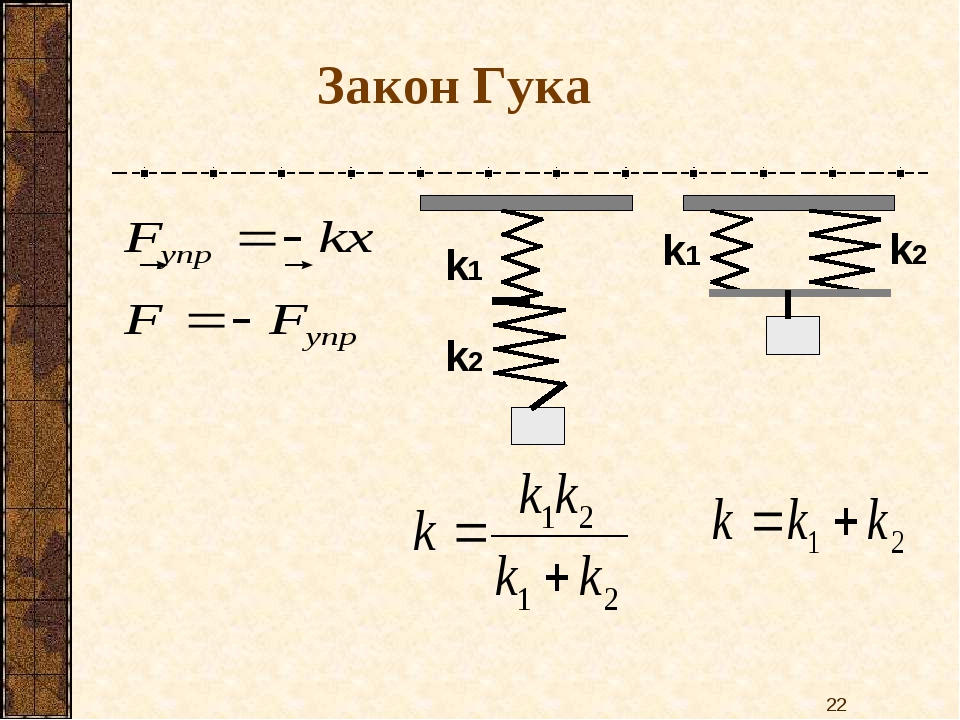
Советы для достижения успеха
Мы только что показали, что Fnet=maFnet=ma применяется только тогда, когда масса системы постоянна. Примером того, когда эта формула неприменима, может быть движущаяся ракета, которая сжигает достаточно топлива, чтобы значительно изменить массу ракеты.В этом случае вам нужно будет использовать второй закон Ньютона, выраженный в терминах импульса, чтобы учесть изменение массы.
Snap Lab
Движение рук и импульс
В этом упражнении вы будете экспериментировать с различными типами движений рук, чтобы интуитивно понять взаимосвязь между силой, временем и импульсом.
- один шарик
- одна ванна с водой
Процедура:
- Попробуйте поймать мяч, пока отдает с мячом, подтягивая руки к телу.
- Затем попробуйте поймать мяч, не двигая руками.
- Ударьте по воде в ванне полной ладонью.
 Ваша полная ладонь представляет собой пловца, который делает прыжок на животе.
Ваша полная ладонь представляет собой пловца, который делает прыжок на животе. - После того, как вода успокоится, снова коснитесь воды, погрузив руку пальцами в воду. Ваша ныряющая рука представляет пловца, ныряющего.
- Объясните, что происходит в каждом случае и почему.
Проверка захвата
Назовите еще примеры движений, на которые влияет импульс?
- столкновение футболиста с другим игроком или автомобиля, движущегося с постоянной скоростью
- автомобиль, движущийся с постоянной скоростью, или объект, движущийся по траектории
- автомобиль, движущийся с постоянной скоростью, или ракетка, ударяющая по мячу
- столкновение футболиста с другим игроком или удар ракеткой по мячу
Служба поддержки учителей
Служба поддержки учителей
[OL][AL] Обсудите удар, который человек ощущает, когда падает или прыгает. Перечислите факторы, влияющие на это влияние.
Перечислите факторы, влияющие на это влияние.
Ссылки на физику
Инженерное дело: спасение жизней с помощью концепции импульса
За последние несколько десятилетий автомобили стали намного безопаснее. Ремни безопасности играют важную роль в обеспечении безопасности автомобиля, предотвращая попадание людей в лобовое стекло в случае аварии. Другие средства безопасности, такие как подушки безопасности, менее заметны или очевидны, но также эффективны в снижении смертельного исхода при автомобильных авариях (см. рис. 8.2). Многие из этих функций безопасности используют концепцию импульса из физики.Напомним, что импульс – это чистая сила, умноженная на продолжительность удара. Это было выражено математически как Δp=FnetΔtΔp=FnetΔt.
Рисунок 8.2 В автомобилях установлены такие средства безопасности, как подушки безопасности и ремни безопасности.
Подушки безопасности позволяют силе, действующей на пассажиров в автомобиле, действовать в течение гораздо более длительного времени при внезапной остановке. Изменение импульса одинаково для пассажира независимо от того, развернута подушка безопасности или нет. Но сила, останавливающая пассажира, будет намного меньше, если она будет действовать в течение большего времени.Преобразовав уравнение для импульса, чтобы найти силу Fnet=ΔpΔt, Fnet=ΔpΔt, можно увидеть, как увеличение ΔtΔt при неизменном ΔpΔp уменьшит F net . Это еще один пример обратной зависимости. Точно так же мягкая приборная панель увеличивает время, в течение которого действует сила удара, тем самым уменьшая силу удара.
Изменение импульса одинаково для пассажира независимо от того, развернута подушка безопасности или нет. Но сила, останавливающая пассажира, будет намного меньше, если она будет действовать в течение большего времени.Преобразовав уравнение для импульса, чтобы найти силу Fnet=ΔpΔt, Fnet=ΔpΔt, можно увидеть, как увеличение ΔtΔt при неизменном ΔpΔp уменьшит F net . Это еще один пример обратной зависимости. Точно так же мягкая приборная панель увеличивает время, в течение которого действует сила удара, тем самым уменьшая силу удара.
Современные автомобили имеют много пластиковых компонентов. Одним из преимуществ пластмасс является их меньший вес, что приводит к лучшему расходу топлива.Еще одним преимуществом является то, что автомобиль сминается при столкновении, особенно при лобовом столкновении. Более длительное время столкновения означает, что сила, действующая на пассажиров автомобиля, будет меньше. Смертность во время автомобильных гонок резко сократилась, когда жесткие рамы гоночных автомобилей были заменены деталями, которые могли смяться или разрушиться в случае аварии.
Проверка захвата
Возможно, вы слышали совет сгибать колени при прыжках. В этом примере друг предлагает вам спрыгнуть со скамейки в парке на землю, не сгибая колени.Вы, конечно, отказываетесь. Объясните своему другу, почему это было бы глупо. Покажите это, используя теорему об импульсе-импульсе.
- Сгибание коленей увеличивает время удара, тем самым уменьшая силу.
- Сгибание коленей сокращает время удара, тем самым уменьшая силу.
- Сгибание коленей увеличивает время удара, тем самым увеличивая силу.
- Сгибание коленей сокращает время удара, тем самым увеличивая силу.
Решение задач с использованием теоремы об импульсе-импульсе
Поддержка учителей
Поддержка учителей
Расскажите о различных стратегиях, которые можно использовать при решении задач. Убедитесь, что учащиеся знают предположения, сделанные в каждом уравнении относительно того, что определенные величины являются постоянными или некоторыми величинами можно пренебречь.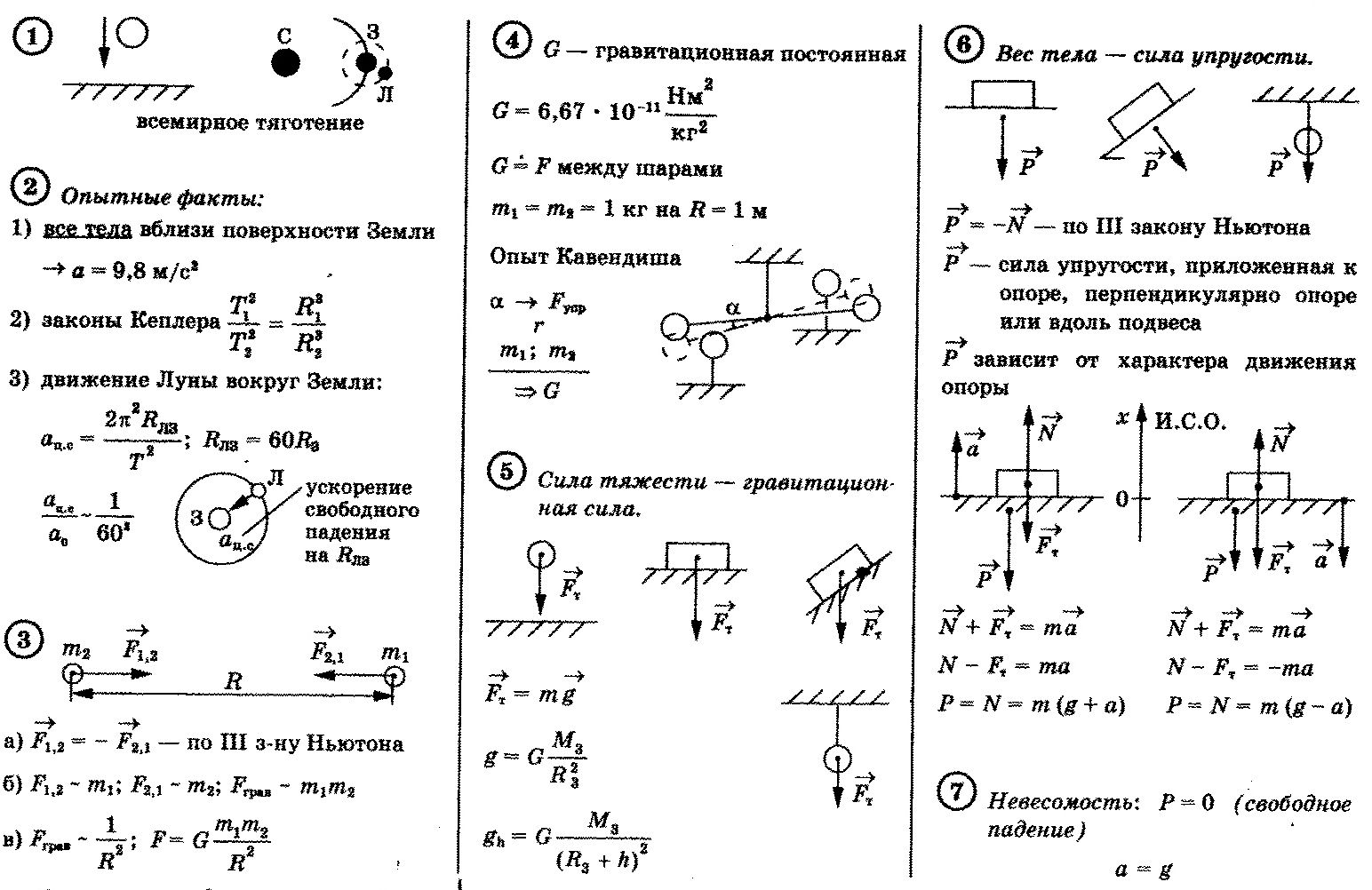
Рабочий пример
Расчет импульса: футболист и футбольный мяч
(a) Рассчитайте импульс футболиста массой 110 кг, бегущего со скоростью 8 м/с.(b) Сравните импульс игрока с импульсом футбольного мяча массой 0,410 кг, брошенного со скоростью 25 м/с.
Стратегия
Нет информации о направлении футболиста или футбольного мяча, поэтому мы можем вычислить только величину импульса, p . (Символ, выделенный курсивом, обозначает величину.) В обеих частях этого примера величина импульса может быть рассчитана непосредственно из определения импульса:
.Раствор для (а)
Чтобы найти импульс игрока, подставьте в уравнение известные значения массы и скорости игрока.
pplayer=(110 кг)(8 м/с)=880кг⋅м/spplayer=(110 кг)(8 м/с)=880кг⋅м/сРешение для (б)
Чтобы найти импульс мяча, подставьте известные значения массы и скорости мяча в уравнение.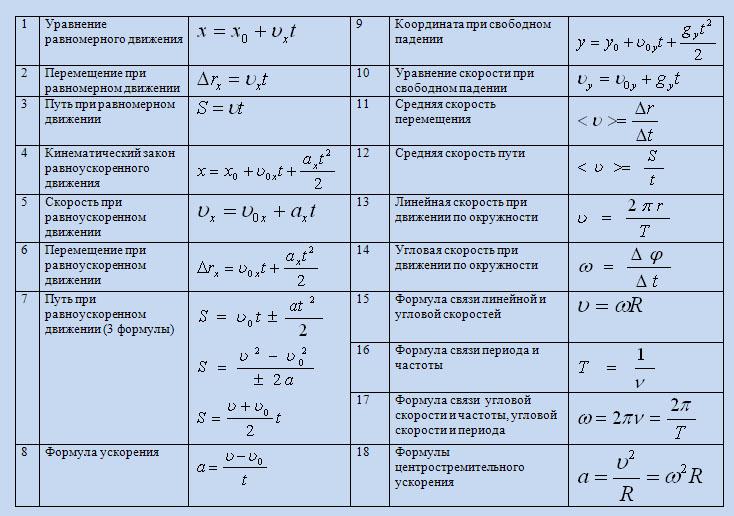
Отношение импульса игрока к импульсу мяча равно
pplayerpball=88010,3=85,9.pplayerpball=88010,3=85,9.Обсуждение
Хотя у мяча большая скорость, масса игрока гораздо больше.Следовательно, импульс игрока примерно в 86 раз больше, чем импульс футбольного мяча.
Рабочий пример
Расчет силы: ракетка Venus Williams
Во время Открытого чемпионата Франции 2007 года Винус Уильямс (рис. 8.3) выполнила самую быструю зарегистрированную подачу в главном женском матче, достигнув скорости 58 м/с (209 км/ч). С какой средней силой ракетка Вильямса действовала на теннисный мяч массой 0,057 кг? Предположим, что скорость мяча сразу после удара составляла 58 м/с, горизонтальной скоростью до удара можно пренебречь и что мяч оставался в контакте с ракеткой в течение 5 мс (миллисекунд).
Рисунок 8.3 Винус Уильямс, играющая на US Open 2013 (Эдвин Мартинес, Flickr)
Стратегия
Напомним, что второй закон Ньютона, выраженный через импульс, равен
.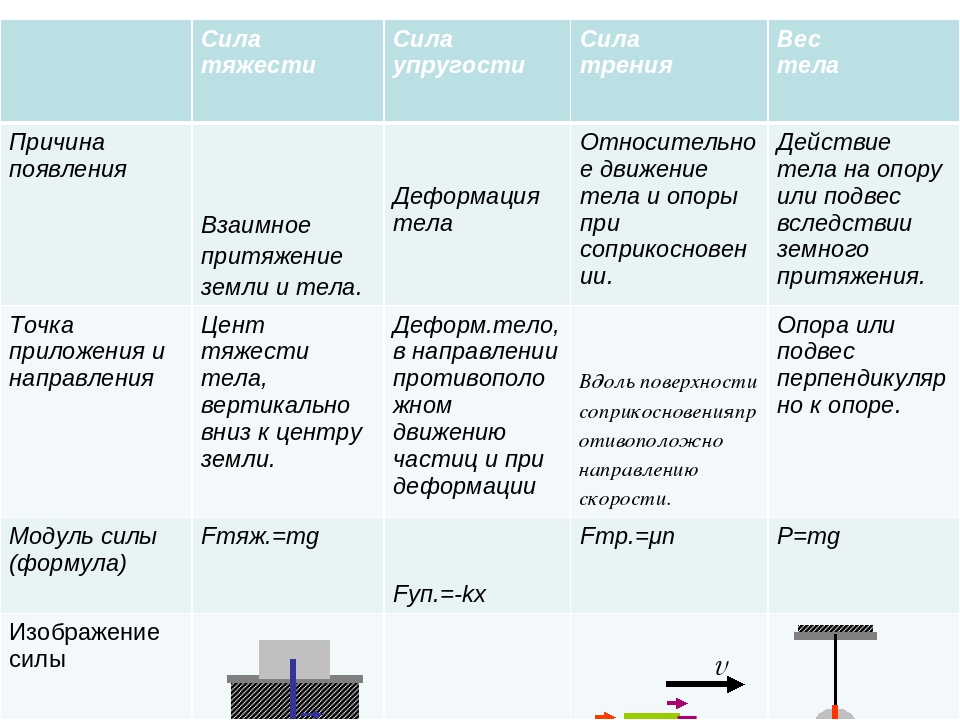
Как отмечалось выше, когда масса постоянна, изменение импульса равно
Δp=mΔv=m(vf−vi), Δp=mΔv=m(vf−vi),, где v f — конечная скорость, а v i — начальная скорость. В этом примере даны скорость сразу после удара и изменение во времени, поэтому после того, как мы найдем ΔpΔp, мы можем использовать Fnet=ΔpΔtFnet=ΔpΔt, чтобы найти силу.
Решение
Чтобы определить изменение количества движения, подставьте значения массы, а также начальную и конечную скорости в приведенное выше уравнение.
Δp=m(vf−vi)=(0,057 кг)(58 м/с – 0 м/с)=3,306 кг·м/с ≈ 3,3 кг·м/с Δp=m(vf−vi)=(0,057 кг) (58 м/с – 0 м/с)=3,306 кг·м/с ≈ 3,3 кг·м/с8,1
Теперь мы можем найти величину чистой внешней силы, используя Fnet=ΔpΔtFnet=ΔpΔt
Fnet=ΔpΔt=3,3065×10−3=661 N≈660 N. Fnet=ΔpΔt=3,3065×10-3=661 N≈660 N.8,2
Обсуждение
Эта величина представляла собой среднюю силу, с которой ракетка Винус Уильямс действовала на теннисный мяч во время его кратковременного удара. Эту задачу также можно решить, сначала найдя ускорение, а затем используя F net = m a , но нам пришлось бы сделать еще один шаг. В этом случае использование импульса было кратчайшим путем.
Эту задачу также можно решить, сначала найдя ускорение, а затем используя F net = m a , но нам пришлось бы сделать еще один шаг. В этом случае использование импульса было кратчайшим путем.
Практические задачи
1.Чему равен импульс шара для боулинга массой 5\,\text{кг} и скоростью 10\,\text{м/с}?
- 0.5\,\text{кг} \cdot \text{м/с}
- 2\,\text{кг} \cdot \text{м/с}
- 15\,\text{кг} \cdot \text{м/с}
- 50\,\text{кг} \cdot \text{м/с}
Как изменится импульс, вызванный суммарной силой 120\,\text{N}, действующей на объект в течение 2 секунд?
- 60\,\text{кг} \cdot \text{м/с}
- 118\,\text{кг} \cdot \text{м/с}
- 122\,\text{кг} \cdot \text{м/с}
- 240\,\text{кг} \cdot \text{м/с}
Проверьте свое понимание
3.
Что такое линейный импульс?
- сумма массы системы и ее скорости
- отношение массы системы к ее скорости
- произведение массы системы на ее скорость
- произведение момента инерции системы на ее скорость
Если масса объекта постоянна, чему пропорционален его импульс?
- Его скорость
- Его вес
- Его водоизмещение
- Его момент инерции
Какое уравнение для второго закона движения Ньютона в терминах массы, скорости и времени, когда масса системы постоянна?
- Fnet=ΔvΔmΔtFnet=ΔvΔmΔt
- Fnet=mΔtΔvFnet=mΔtΔv
- Fnet=mΔvΔtFnet=mΔvΔt
- Fnet=ΔmΔvΔtFnet=ΔmΔvΔt
Приведите пример системы, масса которой непостоянна.
- Волчок
- Бейсбольный мяч летит по воздуху
- Ракета запущена с Земли
- Блок, скользящий по наклонной плоскости без трения
Служба поддержки учителей
Служба поддержки учителей
Используйте вопросы «Проверьте свое понимание», чтобы оценить, справляются ли учащиеся с целями обучения в этом разделе. {2}$$
{2}$$
Сопротивление материалов | Механика материалов
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения.Пожалуйста, включите JavaScript.
Эта страница использует JavaScript для форматирования уравнений для правильного отображения.Пожалуйста, включите JavaScript.
Сопротивление материалов , также известный как механика материалов , ориентирован на анализ напряжений и прогибов в материалах под нагрузкой. Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки.
Стресс и напряжение
Когда сила приложена к элементу конструкции, этот элемент будет испытывать как напряжение, так и деформацию в результате действия силы.Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила/дюйм 2 (psi) для обычных единиц США и Н/м 2 (Па) для единиц СИ:
где F — приложенная сила, а A — площадь поперечного сечения, на которое действует сила. Приложенная сила заставит элемент конструкции деформироваться на некоторую длину пропорционально его жесткости. Деформация – это отношение деформации к исходной длине детали:
Деформация – это отношение деформации к исходной длине детали:
где L — деформированная длина, L 0 — исходная недеформированная длина, а δ — деформация (разница между ними).
Существуют различные типы нагрузки, которые приводят к различным типам напряжения, как указано в таблице ниже:
| Тип загрузки | Тип напряжения | Иллюстрация |
|---|---|---|
| Осевая сила |
| |
| Сила сдвига | Напряжение поперечного сдвига | |
| Изгибающий момент | Напряжение при изгибе | |
| Торсион | Напряжение кручения |
Осевое напряжение и напряжение изгиба являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно площади, противодействующей силе. Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.
Напряжение поперечного сдвига и напряжение кручения являются формами напряжения сдвига , τ, поскольку направление силы параллельно площади, противодействующей силе.
| Нормальное напряжение | |
|---|---|
| Осевое напряжение: | |
| Напряжение при изгибе: | |
| Напряжение сдвига | |
|---|---|
| Поперечное напряжение: | |
| Напряжение кручения: | |
В уравнениях для осевого напряжения и поперечного напряжения сдвига F — сила, а A — площадь поперечного сечения элемента.В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I c — центральный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения кручения T — это кручение, r — радиус, а J — полярный момент инерции поперечного сечения.
В случае осевого напряжения на прямолинейном участке напряжение распределяется равномерно по всей площади.В случае касательного напряжения распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F/A, и это среднее напряжение сдвига обычно используется при расчете напряжения. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и напряжения кручения максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.
Так же, как первичными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига .В случае нормальной деформации деформация нормальна к области, воспринимающей силу:
В случае деформации поперечного сдвига деформация параллельна площади, несущей силу:
где γ – деформация сдвига (безразмерная), а ϕ — деформированный угол в радианах.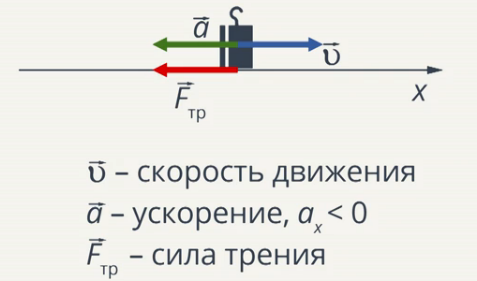
В случае деформации кручения элемент скручивается на угол ϕ вокруг своей оси.Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется по формуле:
где ϕ — угол закручивания, r — радиус стержня, а L — длина.
Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:
где ρ — радиальное расстояние от оси стержня.
Закон Гука
Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, где кривая является линейной).
Нормальный стресс и деформация связаны:
σ = E ϵ
где E — модуль упругости материала, σ — нормальное напряжение, ϵ это нормальное напряжение.
Касательное напряжение и деформация связаны соотношением:
т = G γ
где G — модуль сдвига материала, τ — касательное напряжение, γ — сдвиговая деформация. Модуль упругости и модуль сдвига связаны соотношением:
Модуль упругости и модуль сдвига связаны соотношением:
где ν — коэффициент Пуассона.
Закон Гука аналогичен уравнению силы пружины, F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно изменить, чтобы получить деформацию (удлинение) материала:
| Осевое удлинение (от нормального напряжения) | ||
| Угол закручивания (от напряжения сдвига/кручения) |
Энергия деформации
Когда к элементу конструкции прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина.Энергия деформации (т. е. количество потенциальной энергии, накопленной в результате деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и выражается в дюймо-фунтах в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах предела упругости, то вся энергия деформации может быть восстановлена.
Энергия деформации рассчитывается как:
| Общая форма: | U = Работа = ∫ F дл | (площадь под кривой нагрузки-прогиба) |
| В пределах эластичности: | (площадь под кривой нагрузки-прогиба) | |
| (потенциальная энергия пружины) |
Обратите внимание, что есть два уравнения для энергии деформации в пределе упругости.Первое уравнение основано на площади под кривой отклонения нагрузки. Второе уравнение основано на уравнении потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.
Более подробную информацию об энергии деформации можно найти здесь.
Жесткость
Жесткость, обычно называемая жесткостью пружины, представляет собой усилие, необходимое для деформации элемента конструкции на единицу длины.Все конструкции можно рассматривать как наборы пружин, а силы и деформации в конструкции связаны уравнением пружины:
F = k δ макс.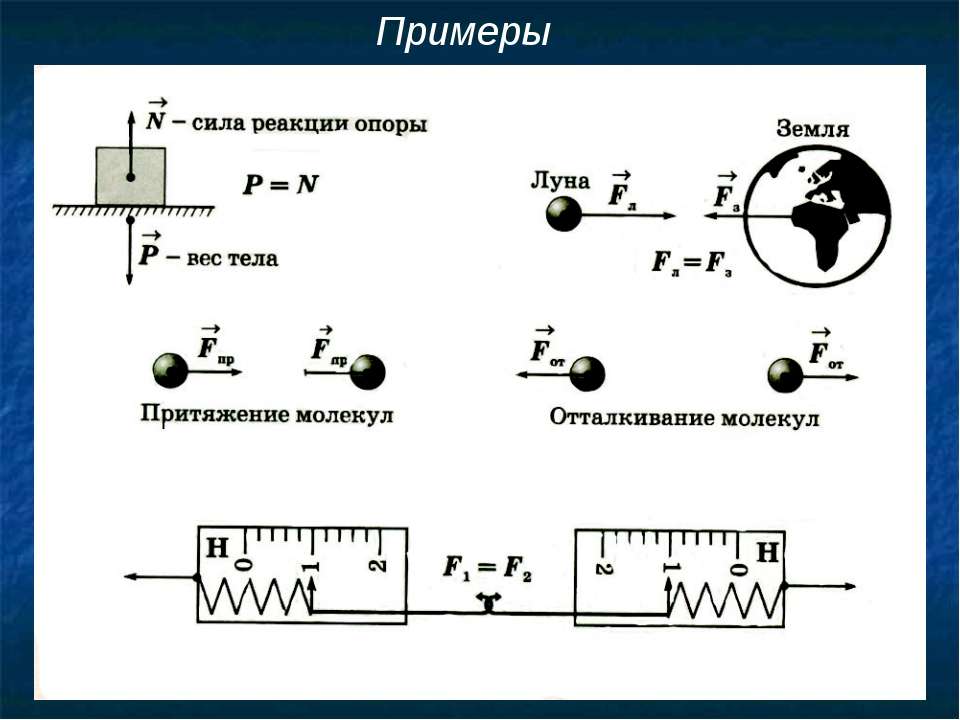
где k — жесткость, F — приложенная сила, а δ max — максимальный прогиб элемента.
Если прогиб известен, то жесткость элемента можно найти, решив k = F/δ max . Однако максимальное отклонение обычно неизвестно, поэтому жесткость необходимо рассчитывать другими способами.Таблицы прогиба балки можно использовать для общих случаев. Два наиболее полезных уравнения жесткости, которые нужно знать, — это уравнения жесткости для балки с осевой нагрузкой и для консольной балки с торцевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.
Крутильный эквивалент уравнения пружины:
Т = к ϕ
Особый интерес представляет жесткость вала при нагрузке на кручение:
| Жесткость [дюйм*фунт-сила/рад] | Макс. отклонение [рад] | Иллюстрация | |
|---|---|---|---|
| Вал с торсионной нагрузкой: |
Конструкция с несколькими путями нагрузки
Если в конструкции несколько путей нагрузки (т. е. если в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.
е. если в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы найти нагрузку, которую несет какой-либо отдельный элемент, сначала рассчитайте эквивалентную жесткость элементов на пути нагрузки, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация последовательно соединенных и параллельных пружин.
Если элементы на пути нагрузки нельзя рассматривать просто как пружины, соединенные последовательно или как пружины, соединенные параллельно, а скорее они представляют собой комбинацию пружин, соединенных последовательно и параллельно, то проблему необходимо будет решать итеративно.Найдите подгруппу стержней, которые расположены последовательно или параллельно, и используйте предоставленные уравнения для расчета эквивалентной жесткости, силы и прогиба в подгруппе. Затем подгруппу можно рассматривать как одну пружину с рассчитанными жесткостью, силой и прогибом, и эту пружину можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.
Концентрация стресса
Можно представить, что силы и напряжения протекают через материал, как показано на рисунке ниже.Когда геометрия материала изменяется, линии потока перемещаются ближе или дальше друг от друга, чтобы приспособиться. Если в материале есть разрыв, такой как отверстие или выемка, напряжение должно течь вокруг разрыва, и линии потока будут собираться вблизи этого разрыва. Эта внезапная упаковка линий потока приводит к скачку напряжения — это пиковое напряжение называется концентрацией напряжения . Элемент, который вызывает концентрацию напряжения, называется концентратор напряжения .
Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в непосредственной близости от несплошности, рассчитайте номинальное напряжение в этой области, а затем масштабируйте его с помощью соответствующего коэффициента концентрации напряжения:
σ макс. = K σ ном.
= K σ ном.
где σ max — фактическое (масштабированное) напряжение, σ nom — номинальное напряжение, а K — коэффициент концентрации напряжения.При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше следует использовать наименьшую площадь в основании скругления.
Многие справочники содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрий. Двумя наиболее полными наборами факторов концентрации стресса являются факторы концентрации стресса Петерсона и формулы Рорка для стресса и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации напряжений.
Концентрация напряжения будет рассеиваться по мере удаления от источника напряжения. Принцип Сен-Венана — это общее практическое правило, согласно которому расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.
Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах локальная текучесть позволит перераспределить напряжения и уменьшит напряжение вокруг райзера.По этой причине коэффициенты концентрации напряжений обычно не применяются к конструктивным элементам, изготовленным из пластичных материалов. Коэффициенты концентрации напряжения также обычно не применяются при наличии избыточного пути нагрузки, и в этом случае текучесть одного элемента позволит перераспределить силы на элементы на других путях нагрузки. Примером этого является шаблон болтов. Если один болт начнет прогибаться, то другие болты в схеме примут на себя большую нагрузку.
Комбинированные напряжения
В любой точке нагруженного материала общее напряженное состояние можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью касательными напряжениями (по два в каждом направлении):
Нижние индексы нормальных напряжений σ указывают направление нормальных напряжений. Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Нижние индексы касательных напряжений τ состоят из двух компонентов. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.
Обычно напряжения в одном направлении равны нулю, так что полное напряженное состояние возникает в одной плоскости, как показано на рисунке ниже. Это называется плоскостное напряжение . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Поверхностные напряжения обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и напряжение кручения максимальны на поверхности.
На рисунке выше σ x и σ y — нормальные напряжения, а τ — напряжение сдвига. Напряжения уравновешиваются так, что точка находится в статическом равновесии. Поскольку все напряжения сдвига равны по величине, индексы для простоты опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани y . )
)
Надлежащие соглашения о знаках показаны на рисунке.При нормальном напряжении растягивающее напряжение положительно, а сжимающее отрицательно. Для касательного напряжения направление по часовой стрелке является положительным, а против часовой стрелки — отрицательным.
Если напряжения на рисунке выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ по отношению к горизонтали, как показано на рисунке ниже. Приведенные ниже уравнения преобразования дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.
| Нормальное напряжение: | |
| Напряжение сдвига: |
Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.
В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимальны и минимальны. Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное напряжения сдвига называются экстремальными напряжениями сдвига . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальное и минимальное напряжения сдвига называются экстремальными напряжениями сдвига . Углы главных напряжений и экстремальных касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.
| Углы главных напряжений: | |
| Углы предельного напряжения сдвига: |
Приведенные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и предельных касательных напряжений:
| Главные напряжения: | |
| Экстремальные напряжения сдвига: |
Углы, под которыми возникают главные напряжения, составляют 90 ° друг от друга.Главные напряжения всегда сопровождаются нулевым касательным напряжением. Углы, под которыми возникают предельные касательные напряжения, составляют 45 ° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ x + σ y )/2.
Углы, под которыми возникают предельные касательные напряжения, составляют 45 ° от углов главных напряжений. Экстремальные касательные напряжения сопровождаются двумя равными нормальными напряжениями (σ x + σ y )/2.
Пара полезных отношений:
| σ 1 +плюс; σ 2 = σ x +плюс; о г | Сумма нормальных напряжений постоянна. |
| Максимальное касательное напряжение равно половине разности главных напряжений. |
Круг Мора
Круг Мора — это способ визуализации напряженного состояния в точке нагруженного материала. Это дает интуитивное представление об уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы главные напряжения, экстремальные касательные напряжения и углы, под которыми эти напряжения возникают.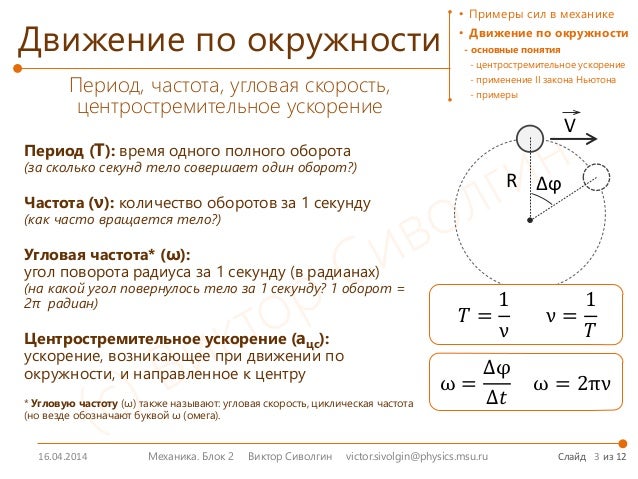 Пример круга Мора показан на рисунке ниже:
Пример круга Мора показан на рисунке ниже:
Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:
Поместите точки на круге, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты ( σ x , −τ ), а напряжения на грани y будут иметь координаты ( σ y , τ ).Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты ( σ 1 , 0 ), а минимальное главное напряжение будет иметь координаты ( σ 2 , 0 ). Поместите точки на окружность для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 1 ), а минимальное экстремальное напряжение сдвига будет иметь координаты ( σ c , τ 2 ).
Все точки будут лежать на периметре окружности. Окружность имеет радиус, равный величине предельных касательных напряжений:
Окружность имеет радиус, равный величине предельных касательных напряжений:
Напряженное состояние на x и y гранях напрягаемого элемента представлено черной линией в круге Мора, соединяющей точки ( σ x , −τ ) и ( σ y , τ ). Эта линия в круге Мора соответствует невращенному элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек в конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента.Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, точки грани x и грани y разнесены на 180 градусов на круге Мора, но только на 90 градусов на элементе напряжения.
Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в нагруженном элементе и как меняется напряженное состояние в зависимости от угла поворота, см. прилагаемый калькулятор круга Мора.
Приложения
Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:
Подробности анализа этих компонентов приведены в других разделах:
Расчетное допустимое напряжение
Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предусмотренные для них нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции.Предел текучести материала обычно выбирают в качестве предела прочности, с которым сравнивают расчетные напряжения.
Коэффициент безопасности , FS, рассчитывается как:
где σ фактическое — расчетное напряжение в конструкции, а σ предел — максимальный предел напряжения, обычно прочность материала, такая как предел текучести (S ty ). Коэффициент безопасности показывает, насколько фактическое напряжение ниже предельного напряжения.Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию.Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10.
Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т.е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько предсказуемы нагрузки и т. д.). Высокий FS приведет к созданию очень безопасной конструкции, но если значение FS слишком велико, то конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою предназначенную функцию.Поэтому существует множество компромиссов при выборе подходящего фактора безопасности. Типичные значения FS варьируются от 1,15 до 10.
Запас прочности рассчитывается как:
В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы безопасности обычно представляются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции равно 1.В 5 раз выше, чем фактическое напряжение, имеется запас 50% (MS = 0,5).
При сообщении коэффициентов безопасности и пределов безопасности иногда требуемый коэффициент безопасности будет «запекаться» в сообщаемых факторах. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, так что FS req = 2. Чтобы обеспечить требуемый коэффициент безопасности, сообщаемые FS и MS рассчитываются как:
Обратите внимание, что при включении требуемого коэффициента запаса прочности, FS req , сообщаемые FS и MS фактически являются запасами по отношению к FS req , а не по отношению к напряжению.
PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице прочности материалов. Этот курс можно использовать для выполнения кредитных требований PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, заработайте за это признание!
Каталожные номера
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е издание.
- Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е издание.
- Гир, Джеймс М., «Механика материалов», 6-е издание.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е издание.
- Пилки, Уолтер Д. и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
- «Формулы Рорка для стресса и напряжения», 8-е издание.
Электромагнитная сила – Гиперучебник по физике
Обсуждение
введение
Магнетизм — это сила, с которой движущиеся заряды действуют друг на друга.Это формальное определение основано на этом простом уравнении.
F B = q v × B
Вспомним, что электричество — это (по сути) сила, с которой заряды действуют друг на друга. Поскольку эта сила существует независимо от того, движутся заряды или нет, ее иногда называют электростатической силой. Можно сказать, что магнетизм является электродинамической силой, но так бывает редко. Сочетание электрических и магнитных сил, действующих на заряженный объект, известно как сила Лоренца .
F = q ( E + v × B )
Для больших объемов заряда…
| F B = q | v × B | ||||
| F B = q | д х | × Б = | дк | ℓ × Б | |
| дт | дт | ||||
| F B = I | ℓ × B | ||||
Эта формула для магнитной силы на проводе с током является основой для эксперимента, который использовался для определения ампера с 1948 по 2019 год.
Ампер — это такой постоянный ток, который, если его поддерживать в двух прямых параллельных проводниках бесконечной длины с ничтожно малым круглым поперечным сечением, расположенных на расстоянии одного метра друг от друга в вакууме, создавал бы между этими проводниками силу, равную 2 × 10 −7 ньютонов на метр длины
МБМВ, 1948
Используя закон Ампера, мы вывели формулу для силы магнитного поля, окружающего длинную прямолинейную проволоку с током…
Подставьте это выражение в формулу магнитной силы.(Поскольку два провода параллельны, поле одного из них падает на другой под прямым углом, и перекрестное произведение сводится к прямому умножению.) Решите силу на единицу длины, как описано в эксперименте…
| Ф Б | = | I ℓ × B | ||
| Ф Б | = | л | мк 0 I | |
| 2π р | ||||
| Ф Б | = | мк 0 I 2 | ||
| ℓ | 2π р | |||
Это устанавливает необычно точное значение проницаемости свободного пространства (необычно точное для физической константы).Подставьте значения для измерений, описанных в эксперименте BIPM, в последнее полученное уравнение…
| = | ||
| (2 × 10 −7 N) | = | мк 0 (1 А) 2 |
| (1 м) | 2π(1 м) |
и решить для проницаемости свободного пространства…
| мк 0 = | 2π(1 м)(2 × 10 −7 Н) | |
| (1 м)(1 А) 2 | ||
| мк 0 = | 4π × 10 −7 Н/Д 2 | |
Возвращение к формуле для магнитной силы, действующей на провод с током, приводит к следующему определению напряженности магнитного поля и ее единицы, тесла.
| d F B = I d ℓ 0 5 × 9 B 9000 | ⇒ | Б = | Ф Б | ⇒ | ⎡ ⎢ ⎣ | Т = | Н | ⎤ ⎥ ⎦ |
| л | Ам |
Третье правило правой/левой руки
Электронно-лучевая трубка: цветной телевизор (цветной монитор), осциллограф,
масс-спектрометр
циклотрон
космическая погода, полярное сияние, радиационные пояса Ван Аллена
электродвигатель
электромагнитный рельсовый пистолет
ядерный магнитный резонанс?
Воздействие струи — Лабораторное руководство по прикладной гидромеханике
Движущаяся жидкость в естественных или искусственных системах может воздействовать на объекты, соприкасающиеся с ней.Для анализа движения жидкости обычно выбирается конечная область жидкости (контрольный объем), а валовые воздействия потока, такие как его сила или крутящий момент на объект, определяются путем расчета чистой массовой скорости, втекающей и вытекающей. контрольного объема. Эти силы можно определить, как и в механике твердого тела, с помощью второго закона Ньютона или уравнения количества движения. Силу, действующую струей жидкости на плоскую или изогнутую поверхность, можно решить, применив уравнение количества движения. Изучение этих сил имеет важное значение для изучения гидромеханики и гидравлических машин.
Инженеры и конструкторы используют уравнение импульса для точного расчета силы, с которой движущаяся жидкость может воздействовать на твердое тело. Например, на гидроэлектростанциях турбины используются для выработки электроэнергии. Турбины вращаются за счет силы, создаваемой одной или несколькими струями воды, направленными по касательной к лопаткам или лопаткам турбины. Воздействие воды на лопасти создает крутящий момент на колесе, заставляя его вращаться и вырабатывать электричество.
Целью этого эксперимента является исследование сил реакции, вызванных изменением количества движения потока жидкости, когда струя воды ударяется о плоскую пластину или изогнутую поверхность, и сравнение результатов этого эксперимента с расчетными силами путем применения уравнение импульса.
Сила импульса определяется путем измерения сил, создаваемых струей воды, падающей на твердые плоские и криволинейные поверхности, которые отклоняют струю под разными углами.
Для проведения эксперимента со столкновением со струей требуется следующее оборудование:
- Стол гидравлики F1-10,
- Ф1-16 удары струйного аппарата с тремя дефлекторами потока с углами отклонения 90, 120 и 180 градусов и
- Секундомер для измерения времени измерения расхода.
Струйный аппарат представляет собой прозрачный акриловый цилиндр, сопло и дефлектор потока (рис. 5.1). Вода поступает вертикально сверху цилиндра через сопло, поражающее цель, закрепленное на штоке, и выходит через выпускные отверстия в основании цилиндра. Вентиляционное отверстие в верхней части цилиндра поддерживает атмосферное давление внутри цилиндра. В верхней части штока установлен утяжеляющий поддон, позволяющий уравновешивать силу ударной воды приложенными массами [5].
Рисунок 5.1: F1-16 Воздействие струйного аппаратаСкорость воды ( v ), выходящей из сопла с площадью поперечного сечения (A), можно рассчитать по формуле:
, где Q — скорость потока.
Применение уравнения энергии между точкой выхода сопла и поверхностью дефлектора показывает, что величина скорости потока не меняется при обтекании дефлектора водой; меняется только направление потока.
Применение уравнения импульса к контрольному объему, охватывающему отклоненный поток, дает:
где:
F y : сила, с которой дефлектор действует на жидкость
: плотность жидкости
: 180-, , где — угол отклонения потока (рис. 5.2).
Рисунок 5.2: Примеры углов отклонения потока для плоских и полусферических дефлекторов
Из равновесия сил в вертикальном направлении F y уравновешивается приложенным весом на чаше весов, W ( W = мг , где m — приложенная масса), т. е. Fy = В . Следовательно:
Так как Q = vA , это уравнение можно записать как:
Проведите эксперимент, выполнив следующие действия:
- Снимите верхнюю пластину (ослабив гайки с накаткой) и прозрачный цилиндр с оборудования, проверьте и запишите выходной диаметр сопла.
- Замените цилиндр и навинтите 90-градусный отражатель на конец вала.
- Подсоедините впускную трубку к быстроразъемному разъему на столе.
- Замените верхнюю пластину прозрачного цилиндра, но не затягивайте три гайки с накаткой.
- С помощью спиртового уровня, прикрепленного к верхней пластине, выровняйте цилиндр, отрегулировав ножки.
- Замените три гайки с накаткой, затем последовательно затягивайте, пока встроенный круглый спиртовой уровень не покажет, что верхняя пластина находится в горизонтальном положении.Не затягивайте гайки с накаткой слишком сильно, так как это повредит верхнюю пластину. Гайки должны быть затянуты только настолько, чтобы выровнять пластину.
- Убедитесь, что вертикальный вал может свободно двигаться и поддерживается пружиной под чашей весов.
- При отсутствии грузов на чаше весов отрегулируйте высоту указателя уровня, пока он не совместится с базовой линией на чаше весов. Проверьте правильность положения, осторожно покачивая чашу.
- Поместите груз массой 50 грамм на чашу весов и включите насос.
- Медленно откройте клапан скамьи и дайте воде попадать на цель, пока исходная линия на чаше весов не окажется на уровне манометра. Оставьте поток постоянным. Наблюдайте и отмечайте поведение потока во время теста.
- Измерьте расход с помощью мерного резервуара. Это достигается путем закрытия шарового крана и измерения времени, необходимого для накопления известного объема жидкости в баке, измеренного по смотровому стеклу. Вы должны собирать воду не менее одной минуты , чтобы свести к минимуму ошибки синхронизации.
- Повторяйте эту процедуру, постепенно добавляя дополнительные 50 граммов, пока не будет применена максимальная масса 500 граммов.
- Повторите все испытания для каждого из двух других дефлекторов потока.
Используйте эту ссылку для доступа к рабочей книге Excel для этого эксперимента.
9.1. РезультатыИспользуйте следующие таблицы для записи ваших измерений.
Таблица исходных данных| Тест № | Углы отклонения (градусы) | ||||||||
| 90 | 120 | 180 | |||||||
| Объем (литр) | Время (с) | Применяемая масса (кг) | Объем (литр) | Время (с) | Применяемая масса (кг) | Объем (литр) | Время (с) | Применяемая масса (кг) | |
| 1 | |||||||||
| 2 | |||||||||
| 3 | |||||||||
| 4 | |||||||||
| 5 | |||||||||
| 6 | |||||||||
| 7 | |||||||||
| 8 | |||||||||
| 9 | |||||||||
| 10 | |||||||||
Форсунка должна иметь следующие размеры.
- Диаметр патрубка: d= 0,008 м
- Площадь поперечного сечения сопла: A= 5,0265×10 -5 м 2
Эти значения могут быть измерены как часть экспериментальной процедуры и заменены указанными выше размерами.
Для каждого набора измерений вычислите прилагаемый вес ( W ), расход ( Q ), квадрат скорости ( v 2 ), силу ( F y ), а также теоретические и экспериментальные данные. наклон ( S ) отношения между W и v 2 .Теоретический наклон определяется из уравнения 5 следующим образом:
Экспериментальное значение S получено из графика W от v 2 .
| Диаметр сопла (м)= | Площадь потока (м 2 ) = | Угол дефлектора (градусы) = | |||||
| Тест № | Прилагаемый вес (Н) | Расход (м 3 /с) | Скорость (м/с) | Скорость 2 (м/с) 2 | Сила (Н) | Теоретическая Наклонная | Экспериментальный склон |
| 1 | |||||||
| 2 | |||||||
| 3 | |||||||
| 4 | |||||||
| 5 | |||||||
| 6 | |||||||
| 7 | |||||||
| 8 | |||||||
| 9 | |||||||
| 10 | |||||||
Используйте предоставленный шаблон для подготовки лабораторного отчета для этого эксперимента.Ваш отчет должен включать следующее:
- Таблица(и) исходных данных
- Таблицы результатов
- График(и)
- Постройте график квадрата скорости, v 2 , (ось x) в зависимости от приложенного веса, W , (ось y). Подготовьте один график, представляющий результаты для всех трех дефлекторов, и используйте линейную линию тренда, установив точку пересечения на ноль, чтобы показать эту взаимосвязь. Найдите наклоны этих прямых. Запишите наклоны в таблицу результатов в качестве экспериментальных наклонов.
- Сравните наклоны этого графика с наклонами, рассчитанными по теоретическому соотношению из уравнения 5.
- Постройте график измеренной силы от грузов ( W ) в зависимости от силы воды на дефлекторе ( F y ), рассчитанной с использованием уравнения количества движения, т. е. уравнения 2.
- Обсудите свои результаты, сосредоточив внимание на следующем:
- Предоставляет ли этот эксперимент осуществимые средства проверки сохранения уравнения импульса? Постарайтесь быть количественным в сравнении между экспериментальными и расчетными результатами.

 Форма нашей планеты в честь ее греческого имени Гея носит название «геоид», так как радиус кривизны ее поверхности у полюсов больше, чем на экваторе.
Форма нашей планеты в честь ее греческого имени Гея носит название «геоид», так как радиус кривизны ее поверхности у полюсов больше, чем на экваторе.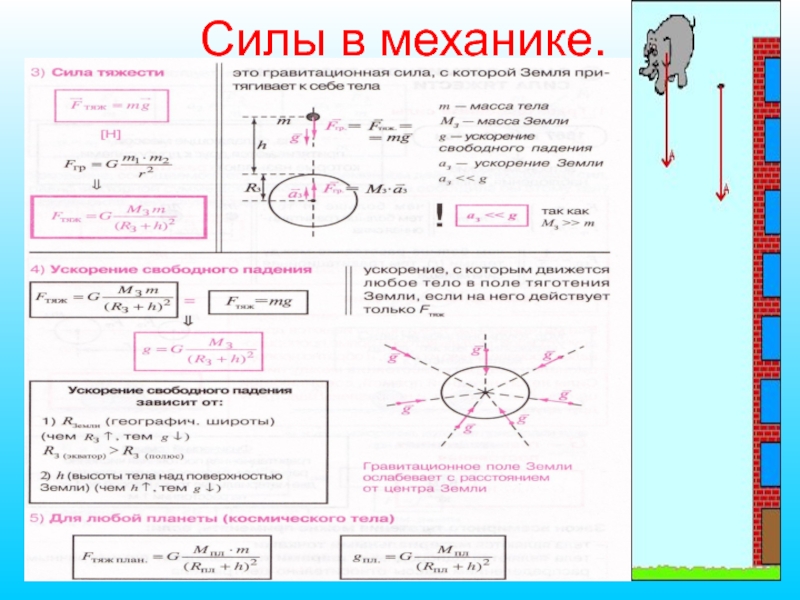
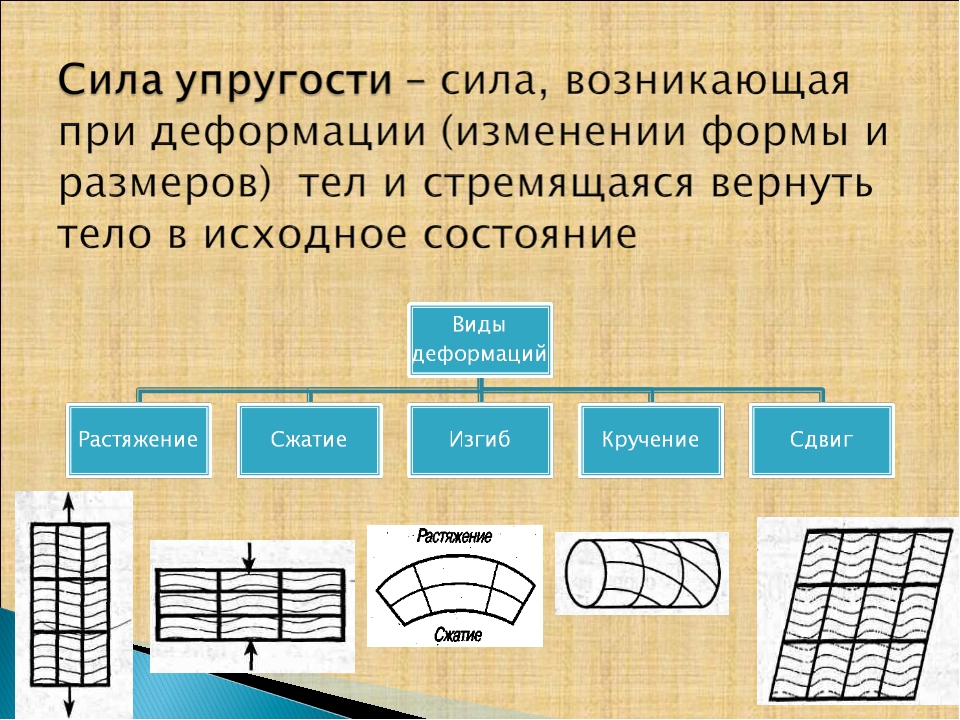
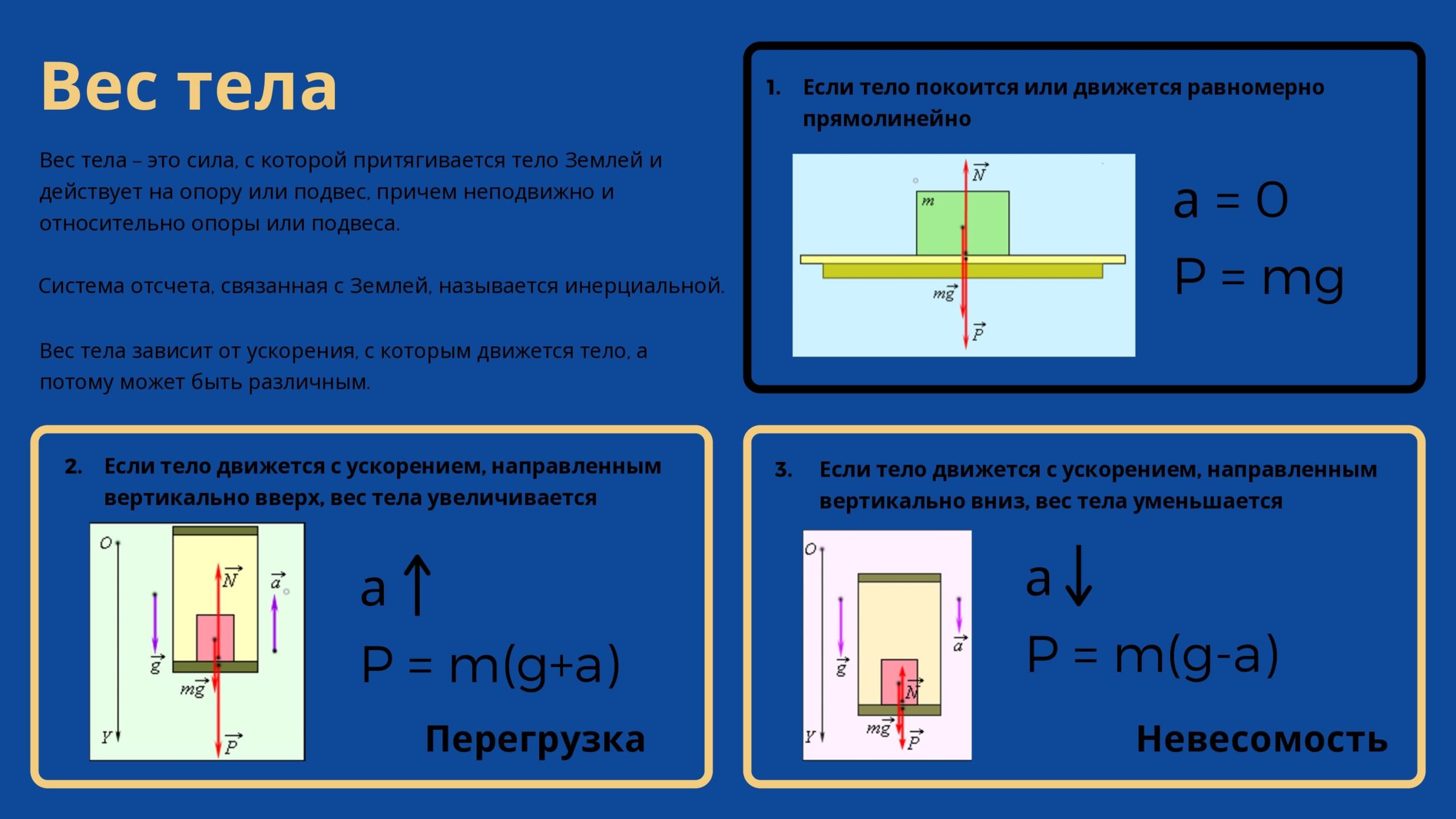

 Но
это притяжение существенно лишь тогда, когда
хотя бы одно из взаимодействующих сил так же
велико, как Земля или луна.
Но
это притяжение существенно лишь тогда, когда
хотя бы одно из взаимодействующих сил так же
велико, как Земля или луна. п.).
п.).
 Б. Буховцева, Н. Н. Сотского.
Б. Буховцева, Н. Н. Сотского. Приводить
примеры явлений, обусловленных изучаемыми
взаимодействиями
Приводить
примеры явлений, обусловленных изучаемыми
взаимодействиями
 Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент:
Учащийся знает, что изменения происходят в физической системе, и применяет законы сохранения энергии и импульса. Ожидается, что студент: Ваша полная ладонь представляет собой пловца, который делает прыжок на животе.
Ваша полная ладонь представляет собой пловца, который делает прыжок на животе.