Формула Эйлера — Википедия
Геометрический смысл формулы ЭйлераФормула Эйлера связывает комплексную экспоненту с тригонометрическими функциями. Названа в честь Леонарда Эйлера, который её ввёл.
Формула Эйлера утверждает, что для любого вещественного числа x{\displaystyle x} выполнено следующее равенство:
- eix=cosx+isinx{\displaystyle e^{ix}=\cos x+i\sin x},
где e{\displaystyle e} — одна из важнейших математических констант, определяющаяся следующей формулой: e=limx→∞(1+1x)x{\displaystyle e=\lim _{x\to \infty }\left(1+{\frac {1}{x}}\right)^{x}},
- i{\displaystyle i} — мнимая единица.
Формула Эйлера впервые была приведена в статье английского математика Роджера Котса (помощника Ньютона) «Логометрия» (лат. Logometria), опубликованной в журнале «Философские труды Королевского общества» в 1714 году[1] и перепечатана в книге «Гармония мер» (лат. Harmonia mensurarum), которая была издана в 1722 году, уже после смерти автора[2]. Котс привёл её как небольшое предложение среди множества геометрических построений, которое после перевода на современный математический язык и исправления ошибки в знаке, имеет вид[3]:
- ln(cosx+isinx)=ix{\displaystyle \ln(\cos x+i\sin x)=ix}.
Эйлер опубликовал формулу в её привычном виде в статье 1740 года и в книге «Введение в анализ бесконечно малых» (лат. Introductio in analysin infinitorum) (1748)[4], построив доказательство на равенстве бесконечных разложений в степенные ряды правой и левой частей. Ни Эйлер, ни Котс не представляли себе геометрической интерпретации формулы: представление о комплексных числах как точках на комплексной плоскости появилось примерно 50 лет спустя у К. Весселя.
При помощи формулы Эйлера можно определить функции sin{\displaystyle \sin } и cos{\displaystyle \cos } следующим образом:
- sinx=eix−e−ix2i{\displaystyle \sin x={\frac {e^{ix}-e^{-ix}}{2i}}},
- cosx=eix+e−ix2{\displaystyle \cos x={\frac {e^{ix}+e^{-ix}}{2}}}.
Далее можно ввести понятие тригонометрических функций комплексной переменной. Пусть x=iy{\displaystyle x=iy}, тогда:
- siniy=e−y−ey2i=ishy{\displaystyle \sin iy={\frac {e^{-y}-e^{y}}{2i}}=i\mathop {\mathrm {sh} } \,y},
- cosiy=e−y+ey2=chy{\displaystyle \cos iy={\frac {e^{-y}+e^{y}}{2}}=\mathop {\mathrm {ch} } \,y}.
Известное тождество Эйлера, связывающее пять фундаментальных математических констант:
- eiπ+1=0{\displaystyle e^{i\pi }+1=0}
является частным случаем формулы Эйлера при x=π{\displaystyle x=\pi }.
В аналитической теории чисел часто рассматриваются специальные суммы вида ∑x∈Xe2πif(x){\displaystyle \sum \limits _{x\in X}{e^{2\pi if(x)}}}, где X{\displaystyle X} — некоторое множество рассматриваемых объектов, а f: X→R{\displaystyle f:\ X\to {\mathbb {R} }} — функция, отражающая изучаемые свойства объектов.
Для теории чисел, изучающей целые числа, имеют значение прежде всего выводимые из формулы Эйлера индикаторные тождества, касающиеся произвольного целого числа n{\displaystyle n}.
- ∑k=1pe2πnkpi=p[p|n]={p,n≡0(modp)0,n≢0(modp){\displaystyle \sum \limits _{k=1}^{p}{e^{2\pi {\frac {nk}{p}}i}}=p[p|n]=\left\{{\begin{matrix}p,&n\equiv 0{\pmod {p}}\\0,&n\not \equiv 0{\pmod {p}}\end{matrix}}\right.}
- ∫01e2πnαi=[n=0]={1,n=00,n≠0{\displaystyle \int \limits _{0}^{1}{e^{2\pi n\alpha i}}=[n=0]=\left\{{\begin{matrix}1,&n=0\\0,&n\not =0\end{matrix}}\right.}
Благодаря формуле Эйлера появилась так называемая тригонометрическая и показательная запись комплексного числа: x=a+ib=|x|(cosφ+isinφ)=|x|eiφ{\displaystyle x=a+ib=|x|(\cos \varphi +i\sin \varphi )=|x|e^{i\varphi }}.
Также значительным следствием можно считать формулы возведения комплексного числа в произвольную степень: x=|x|eiφ{\displaystyle x=|x|e^{i\varphi }}, xn=|x|neniφ{\displaystyle x^{n}=|x|^{n}e^{ni\varphi }}. Геометрический смысл данной формулы следующий: при возведении числа x{\displaystyle x} в степень n{\displaystyle n} его расстояние до центра возводится в степень n{\displaystyle n}, а угол поворота относительно оси OX{\displaystyle OX} увеличивается в n{\displaystyle n} раз.
Формула возведения в степень верна не только для целых n{\displaystyle n}, но и для вещественных. В частности, показательная запись числа позволяет находить корни любой степени из любого комплексного числа.
Формула Эйлера предоставляет связь между математическим анализом и тригонометрией, а также позволяет интерпретировать функции синуса и косинуса как взвешенные суммы экспоненциальной функции:
- cosx=Re(eix)=eix+e−ix2{\displaystyle \cos x=\mathrm {Re} \left(e^{ix}\right)={e^{ix}+e^{-ix} \over 2}}
- sinx=Im(eix)=eix−e−ix2i.{\displaystyle \sin x=\mathrm {Im} \left(e^{ix}\right)={e^{ix}-e^{-ix} \over 2i}.}
Вышеуказанные уравнения могут быть получены путём сложения или вычитания формул Эйлера:
- eix=cosx+isinx{\displaystyle e^{ix}=\cos x+i\sin x\;}
- e−ix=cos(−x)+isin(−x)=cosx−isinx{\displaystyle e^{-ix}=\cos(-x)+i\sin(-x)=\cos x-i\sin x\;}
с последующим решением относительно синуса или косинуса.
Также эти формулы могут служить определением тригонометрических функций комплексной переменной. Например, выполняя подстановку x = iy, получаем:
- cos(iy)=e−y+ey2=cosh(y){\displaystyle \cos(iy)={e^{-y}+e^{y} \over 2}=\cosh(y)}
- sin(iy)=e−y−ey2i=−1iey−e−y2=isinh(y).{\displaystyle \sin(iy)={e^{-y}-e^{y} \over 2i}=-{1 \over i}{e^{y}-e^{-y} \over 2}=i\sinh(y).}
Комплексные экспоненты позволяют упростить тригонометрические расчеты, поскольку ими проще манипулировать, нежели синусоидальными компонентами. Один из подходов предусматривает преобразование синусоид в соответствующие экспоненциальные выражения. После упрощения результат выражения остается вещественным. Например:
- cosx⋅cosy=(eix+e−ix)2⋅(eiy+e−iy)2=12⋅ei(x+y)+ei(x−y)+ei(−x+y)+ei(−x−y)2=12[ei(x+y)+e−i(x+y)2⏟cos(x+y)+ei(x−y)+e−i(x−y)2⏟cos(x−y)].{\displaystyle {\begin{aligned}\cos x\cdot \cos y&={\frac {(e^{ix}+e^{-ix})}{2}}\cdot {\frac {(e^{iy}+e^{-iy})}{2}}\\&={\frac {1}{2}}\cdot {\frac {e^{i(x+y)}+e^{i(x-y)}+e^{i(-x+y)}+e^{i(-x-y)}}{2}}\\&={\frac {1}{2}}\left[\underbrace {\frac {e^{i(x+y)}+e^{-i(x+y)}}{2}} _{\cos(x+y)}+\underbrace {\frac {e^{i(x-y)}+e^{-i(x-y)}}{2}} _{\cos(x-y)}\right].\end{aligned}}}
Суть другого подхода в представлении синусоид в качестве вещественных частей комплексного выражения и проведения манипуляций непосредственно с комплексным выражением. Например:
- cos(nx)=Re{ einx }=Re{ ei(n−1)x⋅eix }=Re{ ei(n−1)x⋅(eix+e−ix−e−ix) }=Re{ ei(n−1)x⋅(eix+e−ix)⏟2cos(x)−ei(n−2)x }=cos[(n−1)x]⋅2cos(x)−cos[(n−2)x].{\displaystyle {\begin{aligned}\cos(nx)&=\mathrm {Re} \{\ e^{inx}\ \}=\mathrm {Re} \{\ e^{i(n-1)x}\cdot e^{ix}\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot (e^{ix}+e^{-ix}-e^{-ix})\ \}\\&=\mathrm {Re} \{\ e^{i(n-1)x}\cdot \underbrace {(e^{ix}+e^{-ix})} _{2\cos(x)}-e^{i(n-2)x}\ \}\\&=\cos[(n-1)x]\cdot 2\cos(x)-\cos[(n-2)x].\end{aligned}}}
Данная формула используется для рекурсивного вычисления значений cos(nx) для целых значений n и произвольных значений x (в радианах).
Доказательство формулы Эйлера можно провести с использованием ряда Маклорена. Разложим функцию eix{\displaystyle e^{ix}} в ряд Тейлора в окрестности точки a = 0 (в ряд Маклорена) по степеням x{\displaystyle x}. Получим:
eix=1+ix1!+(ix)22!+(ix)33!+…=(1−x22!+x44!−x66!+…)+i(x1!−x33!+x55!−x77!+…){\displaystyle e^{ix}=1+{\frac {ix}{1!}}+{\frac {(ix)^{2}}{2!}}+{\frac {(ix)^{3}}{3!}}+\ldots =\left(1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots \right)+i\left({\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots \right)}
Но
1−x22!+x44!−x66!+…=cosx{\displaystyle 1-{\frac {x^{2}}{2!}}+{\frac {x^{4}}{4!}}-{\frac {x^{6}}{6!}}+\ldots =\cos x}
x1!−x33!+x55!−x77!+…=sinx{\displaystyle {\frac {x}{1!}}-{\frac {x^{3}}{3!}}+{\frac {x^{5}}{5!}}-{\frac {x^{7}}{7!}}+\ldots =\sin x}
Поэтому eix=cosx+isinx{\displaystyle e^{ix}=\cos x+i\sin x}, что и требовалось доказать.
Наглядная демонстрация[править | править код]
Известно, что ex=limn→∞(1+xn)n{\displaystyle e^{x}=\lim _{n\to \infty }\left(1+{\frac {x}{n}}\right)^{n}}. Нижеследующие изображения иллюстрируют, что предел eiφ=limn→∞(1+iφn)n{\displaystyle e^{i\varphi }=\lim _{n\to \infty }\left(1+{\frac {i\varphi }{n}}\right)^{n}} стремится к точке, находящейся на единичной окружности, и длина дуги от этой точки до точки 1 равняется φ{\displaystyle \varphi }. Это, в частности, связано с тем, что limx→0sinxx=1{\displaystyle \lim \limits _{x\to 0}{\frac {\sin x}{x}}=1}.
Процесс изменения eφi{\displaystyle e^{\varphi i}} при изменении φ{\displaystyle \varphi } можно также наглядно продемонстрировать через производную. Общеизвестно, что (ex)′=ex{\displaystyle \left({e^{x}}\right)’=e^{x}} и (ef(x))′=f′(x)ef(x){\displaystyle \left({e^{f(x)}}\right)’=f'(x)e^{f(x)}}. Этот же факт остаётся верным и для комплексного значения функции. Рассматривая функцию f(φ)=eφi{\displaystyle f(\varphi )=e^{\varphi i}}, получим f′(φ)=if(φ){\displaystyle f'(\varphi )=if(\varphi )}. Поскольку в геометрическом представлении комплексных чисел умножение на i{\displaystyle i} аналогично повороту на 90 градусов, то графическое изображение функции f(φ)=eφi{\displaystyle f(\varphi )=e^{\varphi i}} и её производной будет аналогично чертежу действия центростремительной силы, для которого известен физический смысл.
Показательная и тригонометрические формы комплексных чисел связаны между собой формулой Эйлера.
Пусть комплексное число z{\displaystyle z} в тригонометрической форме имеет вид z=r(cosφ+isinφ){\displaystyle z=r(\cos \varphi +i\sin \varphi )} . На основании формулы Эйлера выражение в скобках можно заменить на показательное выражение. В результате получим:
- z=reiφ{\displaystyle z=re^{i\varphi }}
Эта запись называется показательной формой комплексного числа. Так же, как и в тригонометрической форме, здесь r=|z|{\displaystyle r=|z|} , φ=argz{\displaystyle \varphi =\arg z}.
Формулы приведения в тригонометрии: примеры, таблицы, доказательства
Формулы приведения — это соотношения, которые позволяют перейти от тригонометрических функций синус, косинус, тангенс и котангенс с углами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha` к этим же функциям угла `\alpha`, который находится в первой четверти единичной окружности. Таким образом, формулы приведения «приводят» нас к работе с углами в пределе от 0 до 90 градусов, что очень удобно.
Содержание статьи:
Формулы приведения: список и таблицы
Всех вместе формул приведения есть 32 штуки. Они несомненно пригодятся на ЕГЭ, экзаменах, зачетах. Но сразу предупредим, что заучивать наизусть их нет необходимости! Нужно потратить немного времени и понять алгоритм их применения, тогда для вас не составит труда в нужный момент вывести необходимое равенство.
Сначала запишем все формулы приведения:
Для угла (`\frac {\pi}2 \pm \alpha`) или (`90^\circ \pm \alpha`):
`sin(\frac {\pi}2 — \alpha)=cos \ \alpha;` ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha`
`cos(\frac {\pi}2 — \alpha)=sin \ \alpha;` ` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`
`tg(\frac {\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`\pi \pm \alpha`) или (`180^\circ \pm \alpha`):
`sin(\pi — \alpha)=sin \ \alpha;` ` sin(\pi + \alpha)=-sin \ \alpha`
`cos(\pi — \alpha)=-cos \ \alpha;` ` cos(\pi + \alpha)=-cos \ \alpha`
`tg(\pi — \alpha)=-tg \ \alpha;` ` tg(\pi + \alpha)=tg \ \alpha`
`ctg(\pi — \alpha)=-ctg \ \alpha;` ` ctg(\pi + \alpha)=ctg \ \alpha`
Для угла (`\frac {3\pi}2 \pm \alpha`) или (`270^\circ \pm \alpha`):
`sin(\frac {3\pi}2 — \alpha)=-cos \ \alpha;` ` sin(\frac {3\pi}2 + \alpha)=-cos \ \alpha`
`cos(\frac {3\pi}2 — \alpha)=-sin \ \alpha;` ` cos(\frac {3\pi}2 + \alpha)=sin \ \alpha`
`tg(\frac {3\pi}2 — \alpha)=ctg \ \alpha;` ` tg(\frac {3\pi}2 + \alpha)=-ctg \ \alpha`
`ctg(\frac {3\pi}2 — \alpha)=tg \ \alpha;` ` ctg(\frac {3\pi}2 + \alpha)=-tg \ \alpha`
Для угла (`2\pi \pm \alpha`) или (`360^\circ \pm \alpha`):
`sin(2\pi — \alpha)=-sin \ \alpha;` ` sin(2\pi + \alpha)=sin \ \alpha`
`cos(2\pi — \alpha)=cos \ \alpha;` ` cos(2\pi + \alpha)=cos \ \alpha`
`tg(2\pi — \alpha)=-tg \ \alpha;` ` tg(2\pi + \alpha)=tg \ \alpha`
`ctg(2\pi — \alpha)=-ctg \ \alpha;` ` ctg(2\pi + \alpha)=ctg \ \alpha`
Часто можно встретить формулы приведения в виде таблицы, где углы записаны в радианах:
Чтобы воспользоваться ею, нужно выбрать строку с нужной нам функцией, и столбец с нужным аргументом. Например, чтобы узнать с помощью таблицы, чему будет равно ` sin(\pi + \alpha)`, достаточно найти ответ на пересечении строки ` sin \beta` и столбца ` \pi + \alpha`. Получим ` sin(\pi + \alpha)=-sin \ \alpha`.
И вторая, аналогичная таблица, где углы записаны в градусах:
Мнемоническое правило формул приведения или как их запомнить
Как мы уже упоминали, заучивать все вышеприведенные соотношения не нужно. Если вы внимательно на них посмотрели, то наверняка заметили некоторые закономерности. Они позволяют нам сформулировать мнемоническое правило (мнемоника — запоминать), с помощью которого легко можно получить любую с формул приведения.
Сразу отметим, что для применения этого правила нужно хорошо уметь определять (или запомнить) знаки тригонометрических функций в разных четвертях единичной окружности.
Само привило содержит 3 этапа:
- Аргумент функции должен быть представлен в виде `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, причем `\alpha` — обязательно острый угол (от 0 до 90 градусов).
- Для аргументов `\frac {\pi}2 \pm \alpha`, `\frac {3\pi}2 \pm \alpha` тригонометрическая функция преобразуемого выражения меняется на кофункцию, то есть противоположную (синус на косинус, тангенс на котангенс и наоборот). Для аргументов `\pi \pm \alpha`, `2\pi \pm \alpha` функция не меняется.
- Определяется знак исходной функции. Полученная функция в правой части будет иметь такой же знак.
Чтобы посмотреть, как на практике можно применить это правило, преобразим несколько выражений:
1. ` cos(\pi + \alpha)`.
Функция на противоположную не меняется. Угол ` \pi + \alpha` находится в III четверти, косинус в этой четверти имеет знак «-» , поэтому преобразованная функция будет также со знаком «-» .
Ответ: ` cos(\pi + \alpha)= — cos \alpha`
2. `sin(\frac {3\pi}2 — \alpha)`.
Согласно мнемоническому правилу функция изменится на противоположную. Угол `\frac {3\pi}2 — \alpha` находится в III четверти, синус здесь имеет знак «-» , поэтому результат также будет со знаком «-» .
Ответ: `sin(\frac {3\pi}2 — \alpha)= — cos \alpha`
3. `cos(\frac {7\pi}2 — \alpha)`.
`cos(\frac {7\pi}2 — \alpha)=cos(\frac {6\pi}2+\frac {\pi}2-\alpha)=cos (3\pi+(\frac{\pi}2-\alpha))`. Представим `3\pi` как `2\pi+\pi`. `2\pi` — период функции.
Важно: Функции `cos \alpha` и `sin \alpha` имеют период `2\pi` или `360^\circ`, их значения не изменятся, если на эти величины увеличить или уменьшить аргумент.
Исходя из этого, наше выражение можно записать следующим образом: `cos (\pi+(\frac{\pi}2-\alpha)`. Применив два раза мнемоническое правило, получим: `cos (\pi+(\frac{\pi}2-\alpha)= — cos (\frac{\pi}2-\alpha)= — sin \alpha`.
Ответ: `cos(\frac {7\pi}2 — \alpha)=- sin \alpha`.
Лошадиное правило
Второй пункт вышеописанного мнемонического правила еще называют лошадиным правилом формул приведения. Интересно, почему лошадиным?
Итак, мы имеем функции с аргументами `\frac {\pi}2 \pm \alpha`, `\pi \pm \alpha`, `\frac {3\pi}2 \pm \alpha`, `2\pi \pm \alpha`, точки `\frac {\pi}2`, `\pi`, `\frac {3\pi}2`, `2\pi` — ключевые, они располагаются на осях координат. `\pi` и `2\pi` на горизонтальной оси абсцисс, а `\frac {\pi}2` и `\frac {3\pi}2` на вертикальной оси ординат.
Задаем себе вопрос: «Меняется ли функция на кофункцию?». Чтобы ответить на этот вопрос, нужно подвигать головой вдоль оси, на которой расположена ключевая точка.
То есть для аргументов с ключевыми точками, расположенными на горизонтальной оси, мы отвечаем «нет», мотая головой в стороны. А для углов с ключевыми точками, расположенными на вертикальной оси, мы отвечаем «да», кивая головой сверху вниз, как лошадь 🙂
Рекомендуем посмотреть видеоурок, в котором автор подробно объясняет, как запомнить формулы приведения без заучивания их наизусть.
Практические примеры использования формул приведения
Применение формул приведения начинается еще в 9, 10 классе. Немало задач с их использованием вынесено на ЕГЭ. Вот некоторые из задач, где придется применять эти формулы:
- задачи на решение прямоугольного треугольника;
- преобразования числовых и буквенных тригонометрических выражений, вычисление их значений;
- стереометрические задачи.
Пример 1. Вычислите при помощи формул приведения а) `sin 600^\circ`, б) `tg 480^\circ`, в) `cos 330^\circ`, г) `sin 240^\circ`.
Решение: а) `sin 600^\circ=sin (2 \cdot 270^\circ+60^\circ)=-cos 60^\circ=-\frac 1 2`;
б) `tg 480^\circ=tg (2 \cdot 270^\circ-60^\circ)=ctg 60^\circ=\frac{\sqrt 3}3`;
в) `cos 330^\circ=cos (360^\circ-30^\circ)=cos 30^\circ=\frac{\sqrt 3}2`;
г) `sin 240^\circ=sin (270^\circ-30^\circ)=-cos 30^\circ=-\frac{\sqrt 3}2`.
Пример 2. Выразив косинус через синус по формулам приведения, сравнить числа: 1) `sin \frac {9\pi}8` и `cos \frac {9\pi}8`; 2) `sin \frac {\pi}8` и `cos \frac {3\pi}10`.
Решение: 1)`sin \frac {9\pi}8=sin (\pi+\frac {\pi}8)=-sin \frac {\pi}8`
`cos \frac {9\pi}8=cos (\pi+\frac {\pi}8)=-cos \frac {\pi}8=-sin \frac {3\pi}8`
`-sin \frac {\pi}8> -sin \frac {3\pi}8`
`sin \frac {9\pi}8>cos \frac {9\pi}8`.
2) `cos \frac {3\pi}10=cos (\frac {\pi}2-\frac {\pi}5)=sin \frac {\pi}5`
`sin \frac {\pi}8<sin \frac {\pi}5`
`sin \frac {\pi}8<cos \frac {3\pi}10`.
Доказательство формул приведения
Докажем сначала две формулы для синуса и косинуса аргумента `\frac {\pi}2 + \alpha`: ` sin(\frac {\pi}2 + \alpha)=cos \ \alpha` и` cos(\frac {\pi}2 + \alpha)=-sin \ \alpha`. Остальные выводятся из них.
Возьмем единичную окружность и на ней точку А с координатами (1,0). Пусть после поворота на 
угол `\alpha` она перейдет в точку `А_1(х, у)`, а после поворота на угол `\frac {\pi}2 + \alpha` в точку `А_2(-у,х)`. Опустив перпендикуляры с этих точек на прямую ОХ, увидим, что треугольники `OA_1H_1` и `OA_2H_2` равны, поскольку равны их гипотенузы и прилежащие углы. Тогда исходя из определений синуса и косинуса можно записать `sin \alpha=у`, `cos \alpha=х`, ` sin(\frac {\pi}2 + \alpha)=x`, ` cos(\frac {\pi}2 + \alpha)=-y`. Откуда можно записать, что ` sin(\frac {\pi}2 + \alpha)=cos \alpha` и ` cos(\frac {\pi}2 + \alpha)=-sin \alpha`, что доказывает формулы приведения для синуса и косинуса угла `\frac {\pi}2 + \alpha`.
Выходя из определения тангенса и котангенса, получим ` tg(\frac {\pi}2 + \alpha)=\frac {sin(\frac {\pi}2 + \alpha)}{cos(\frac {\pi}2 + \alpha)}=\frac {cos \alpha}{-sin \alpha}=-ctg \alpha` и ` сtg(\frac {\pi}2 + \alpha)=\frac {cos(\frac {\pi}2 + \alpha)}{sin(\frac {\pi}2 + \alpha)}=\frac {-sin \alpha}{cos \alpha}=-tg \alpha`, что доказывает формулы приведения для тангенса и котангенса угла `\frac {\pi}2 + \alpha`.
Чтобы доказать формулы с аргументом `\frac {\pi}2 — \alpha`, достаточно представить его, как `\frac {\pi}2 + (-\alpha)` и проделать тот же путь, что и выше. Например, `cos(\frac {\pi}2 — \alpha)=cos(\frac {\pi}2 + (-\alpha))=-sin(-\alpha)=sin(\alpha)`.
Углы `\pi + \alpha` и `\pi — \alpha` можно представить, как `\frac {\pi}2 +(\frac {\pi}2+\alpha)` и `\frac {\pi}2 +(\frac {\pi}2-\alpha)` соответственно.
А `\frac {3\pi}2 + \alpha` и `\frac {3\pi}2 — \alpha` как `\pi +(\frac {\pi}2+\alpha)` и `\pi +(\frac {\pi}2-\alpha)`.
Материалы по теме:
Поделиться с друзьями:
Загрузка…sin x = 2 решение
Добрый вечер!
Вы задали очень интересный вопрос: sin x = 2. Это самое обычное задание. И да, всегда в первую очередь, учитывая всё, что вы знаете, Вы можете сразу приняться решать. И да, даже то, что arcsin 2 вы не найдёте в таблице, то это тоже не препятствие.
Итак, открою Вам страшную тайну. Такие функции как sin и cos не могут равняться какому-либо число, которое равняется больше единицы.
То есть логично предположить, что решения у данного уравнения нет. Это нужно запомнить, чтоб не совершать глупых ошибок в дальнейшем.
Давайте попробуем решить что-то похожее, но то, что имеет решение. А не как это задание. Например:
Теперь приступим к решению.
Для этого есть определённое правило решения подобных уравнений, которое всегда надо использовать и примет такой общий вид:
Как только мы разобрались с общим решением, то теперь можем преступить к решению именно Вашего уравнения:
Значение мы найдём при помощи таблицы. И исходя из этого получаем, что
Ответ:
Таблица синусов углов (градусы, значения)
В данной таблице представлены значения синусов от 0° до 360°. Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.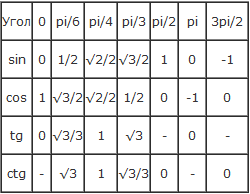
https://uchim.org/matematika/tablica-sinusov — uchim.org
Таблица синусов для 0°-180°
|
|
|
|
Таблица синусов для 181°-360°
|
|
|
|
Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Как легко запомнить таблицу синусов (видео)
Таблицу важно всегда помнить на алгебре, чтобы найти синус.
Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)
Чтобы добавить страницу в закладки, нажмите Ctrl+D.
Если страница помогла, сохраните её и поделитесь ссылкой с друзьями:
Ссылка: https://uchim.org/matematika/tablica-sinusov
Группа с кучей полезной информации (подпишитесь, если предстоит ЕГЭ или ОГЭ):