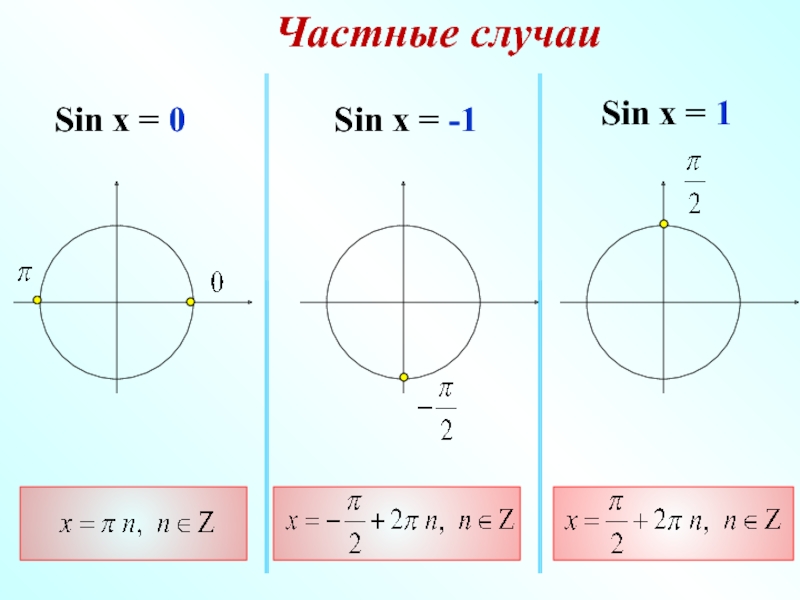
Тригонометрические уравнения. Простейшие тригонометрические уравнения Решить тригонометрическое уравнение sinx 1 2
Основными методами решения тригонометрических уравнений являются: сведение уравнений к простейшим (с использованием тригонометрических формул), введение новых переменных, разложение на множители. Рассмотрим их применение на примерах. Обратите внимание на оформление записи решений тригонометрических уравнений.
Необходимым условием успешного решения тригонометрических уравнений является знание тригонометрических формул (тема 13 работы 6).
Примеры.
1. Уравнения, сводящиеся к простейшим.
1) Решить уравнение
Решение:
Ответ:
2) Найти корни уравнения
(sinx + cosx) 2 = 1 – sinxcosx, принадлежащие отрезку .
Решение:
Ответ:
2. Уравнения, сводящиеся к квадратным.
1) Решить уравнение 2 sin 2 x – cosx –1 = 0.
Решение: Используя формулу sin 2 x = 1 – cos 2 x, получаем
Ответ:
2) Решить уравнение cos 2x = 1 + 4 cosx.
Решение: Используя формулу cos 2x = 2 cos 2 x – 1, получаем
Ответ:
3) Решить уравнение tgx – 2ctgx + 1 = 0
Решение:
Ответ:
3. Однородные уравнения
1) Решить уравнение 2sinx – 3cosx = 0
Решение: Пусть cosx = 0, тогда 2sinx = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1. Значит cosx ≠ 0 и можно поделить уравнение на cosx. Получим
Ответ:
2) Решить уравнение 1 + 7 cos 2 x = 3 sin 2x
Решение:
Используем формулы 1 = sin 2 x + cos 2 x и sin 2x = 2 sinxcosx, получим
sin 2 x + cos 2 x + 7cos 2 x = 6sinxcosx
sin 2 x – 6sinxcosx+ 8cos 2 x = 0
Пусть cosx = 0, тогда sin 2 x = 0 и sinx = 0 – противоречие с тем, что sin 2 x + cos 2 x = 1.
Значит cosx ≠ 0 и можно поделить уравнение на cos 2 x .
Получим
tg 2 x – 6 tgx + 8 = 0
Обозначим tgx = y
y 2 – 6 y + 8 = 0
y 1 = 4; y 2 = 2
а) tgx = 4, x= arctg4 + 2 k , k
б) tgx = 2, x= arctg2 + 2 k , k .
Ответ: arctg4 + 2 k , arctg2 + 2 k, k
4. Уравнения вида a sinx + b cosx = с, с ≠ 0.
1) Решить уравнение .
Решение:
Ответ:
5. Уравнения, решаемые разложением на множители.
1) Решить уравнение sin2x – sinx = 0.
Корнем уравнения f ( х ) = φ ( х ) может служить только число 0. Проверим это:
cos 0 = 0 + 1 – равенство верно.
Число 0 единственный корень данного уравнения.
Ответ: 0.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Простейшие тригонометрические уравнения решаются, как правило, по формулам. Напомню, что простейшими называются вот такие тригонометрические уравнения:
sinx = а
cosx = а
tgx = а
ctgx = а
х — угол, который нужно найти,
а — любое число.
А вот и формулы, с помощью которых можно сразу записать решения этих простейших уравнений.
Для синуса:
Для косинуса:
х = ± arccos a + 2π n, n ∈ Z
Для тангенса:
х = arctg a + π n, n ∈ Z
Для котангенса:
х = arcctg a + π n, n ∈ Z
Собственно, это и есть теоретическая часть решения простейших тригонометрических уравнений. Причём, вся!) Совсем ничего. Однако, количество ошибок по этой теме просто зашкаливает. Особенно, при незначительном отклонении примера от шаблона. Почему?
Да потому, что масса народу записывает эти буковки, не понимая их смысла совершенно! С опаской записывает, как бы чего не вышло…) С этим надо разобраться. Тригонометрия для людей, или люди для тригонометрии, в конце концов!?)
Разберёмся?
Один угол у нас будет равен arccos a, второй: -arccos a.
И так будет получаться всегда.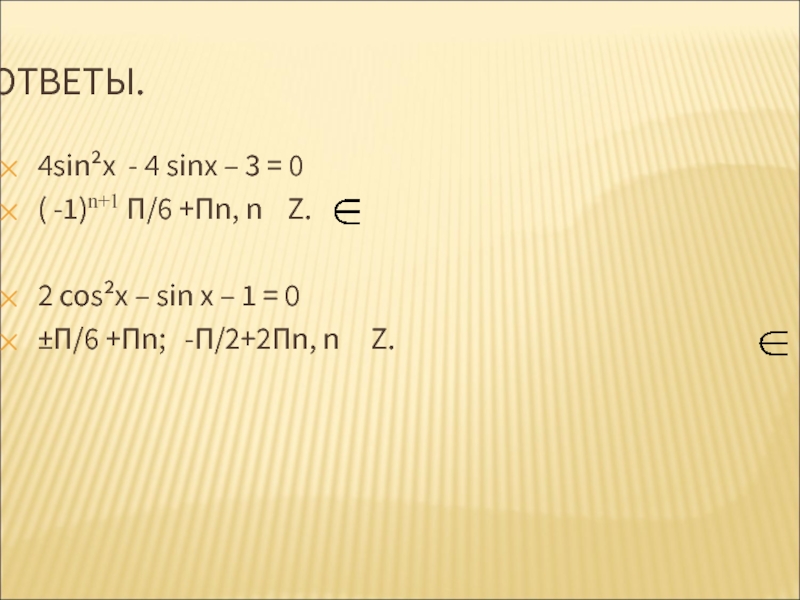
При любом а.
Если не верите, наведите курсор мышки на картинку, или коснитесь рисунка на планшете.) Я изменил число а на какое-то отрицательное. Всё равно, один угол у нас получился arccos a, второй: -arccos a.
Следовательно, ответ можно всегда записать в виде двух серий корней:
х 1 = arccos a + 2π n, n ∈ Z
х 2 = — arccos a + 2π n, n ∈ Z
Объединяем эти две серии в одну:
х= ± arccos а + 2π n, n ∈ Z
И все дела. Получили общую формулу для решения простейшего тригонометрического уравнения с косинусом.
Если вы понимаете, что это не какая-то сверхнаучная мудрость, а просто сокращённая запись двух серий ответов, вам и задания «С» будут по плечу. С неравенствами, с отбором корней из заданного интервала… Там ответ с плюсом/минусом не катит. А если отнестись к ответу делово, да разбить его на два отдельных ответа, всё и решается.
) Собственно, для этого и разбираемся. Что, как и откуда.
В простейшем тригонометрическом уравнении
sinx = а
тоже получается две серии корней. Всегда. И эти две серии тоже можно записать одной строчкой. Только эта строчка похитрее будет:
х = (-1) n arcsin a + π n, n ∈ Z
Но суть остаётся прежней. Математики просто сконструировали формулу, чтобы вместо двух записей серий корней, сделать одну. И всё!
Проверим математиков? А то мало ли…)
В предыдущем уроке подробно разобрано решение (безо всяких формул) тригонометрического уравнения с синусом:
В ответе получились две серии корней:
х 1 = π /6 + 2π n, n ∈ Z
х 2 = 5π /6 + 2π n, n ∈ Z
Если мы будем решать это же уравнение по формуле, получим ответ:
х = (-1) n arcsin 0,5 + π n, n ∈ Z
Вообще-то, это недоделанный ответ.) Ученик обязан знать, что arcsin 0,5 = π
/6.
Полноценный ответ будет:
х = (-1) n π /6 + π n, n ∈ Z
Тут возникает интересный вопрос. Ответ через х 1 ; х 2 (это правильный ответ!) и через одинокий х (и это правильный ответ!) — одно и то же, или нет? Сейчас узнаем.)
Подставляем в ответ с х 1 значения n =0; 1; 2; и т.д., считаем, получаем серию корней:
х 1 = π/6; 13π/6; 25π/6 и так далее.
При такой же подстановке в ответ с х 2 , получаем:
х 2 = 5π/6; 17π/6; 29π/6 и так далее.
А теперь подставляем значения n (0; 1; 2; 3; 4…) в общую формулу для одинокого х . Т.е возводим минус один в нулевую степень, затем в первую, вторую, и т.д. Ну и, разумеется, во второе слагаемое подставляем 0; 1; 2 3; 4 и т.д. И считаем. Получаем серию:
х = π/6; 5π/6; 13π/6; 17π/6; 25π/6 и так далее.
Вот всё и видно.
) Общая формула выдаёт нам точно такие же результаты, что и два ответа по отдельности. Только все сразу, по порядочку. Не обманули математики.)
Формулы для решения тригонометрических уравнений с тангенсом и котангенсом тоже можно проверить. Но не будем.) Они и так простенькие.
Я расписал всю эту подстановку и проверку специально. Здесь важно понять одну простую вещь: формулы для решения элементарных тригонометрических уравнений есть, всего лишь, краткая запись ответов. Для этой краткости пришлось вставить плюс/минус в решение для косинуса и (-1) n в решение для синуса.
Эти вставки никак не мешают в заданиях, где нужно просто записать ответ элементарного уравнения. Но если надо решать неравенство, или далее нужно что-то делать с ответом: отбирать корни на интервале, проверять на ОДЗ и т.п, эти вставочки могут запросто выбить человека из колеи.
И что делать? Да либо расписать ответ через две серии, либо решать уравнение/неравенство по тригонометрическому кругу.
Тогда исчезают эти вставочки и жизнь становится легче.)
Можно подвести итоги.
Для решения простейших тригонометрических уравнений существуют готовые формулы ответов. Четыре штуки. Они хороши для мгновенной записи решения уравнения. Например, надо решить уравнения:
sinx = 0,3
Легко: х = (-1) n arcsin 0,3 + π n, n ∈ Z
cosx = 0,2
Без проблем: х = ± arccos 0,2 + 2π n, n ∈ Z
tgx = 1,2
Запросто: х = arctg 1,2 + π n, n ∈ Z
ctgx = 3,7
Одной левой: x= arcctg3,7 + π n, n ∈ Z
cos x = 1,8
Если вы, блистая знаниями, мгновенно пишете ответ:
х= ± arccos 1,8 + 2π n, n ∈ Z
то блистаете вы уже, это… того… из лужи.) Правильный ответ: решений нет. Не понимаете, почему? Прочитайте, что такое арккосинус. Кроме того, если в правой части исходного уравнения стоят табличные значения синуса, косинуса, тангенса, котангенса, — 1; 0; √3; 1/2; √3/2 и т.
п. — ответ через арки будет недоделанным. Арки нужно обязательно перевести в радианы.
А если уж вам попалось неравенство, типа
то ответ в виде:
х πn, n ∈ Z
есть редкая ахинея, да…) Тут надо по тригонометрическому кругу решать. Чем мы и займёмся в соответствующей теме.
Для тех, кто героически дочитал до этих строк. Я просто не могу не оценить ваши титанические усилия. Вам бонус.)
Бонус:
При записи формул в тревожной боевой обстановке, даже закалённые учёбой ботаны частенько путаются, где πn, а где 2π n. Вот вам простой приёмчик. Во всех формулах стоит πn. Кроме единственной формулы с арккосинусом. Там стоит 2πn. Два пиэн. Ключевое слово — два. В этой же единственной формуле стоят два знака в начале. Плюс и минус. И там, и там — два.
Так что, если вы написали два знака перед арккосинусом, легче вспомнить, что в конце будет два пиэн.
А ещё наоборот бывает. Пропустит человек знак ± , доберётся до конца, напишет правильно два пиэн, да и спохватится. Впереди-то два знака! Вернётся человек к началу, да ошибку-то и исправит! Вот так.)
Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Когда-то я стал свидетелем разговора двух абитуриентов:
– Когда надо прибавить 2πn, а когда – πn? Никак не могу запомнить!
– И у меня такая же проблема.
Так и хотелось им сказать: «Не запоминать надо, а понимать!»
Данная статья адресована прежде всего старшеклассникам и, надеюсь, поможет им с «пониманием» решать простейшие тригонометрические уравнения:
Числовая окружность
Наряду с понятием числовой прямой есть еще и понятие числовой окружности.
Как мы знаем, в прямоугольной системе координат окружность,с центром в точке (0;0) и радиусом 1, называется единичной. Вообразим числовую прямую тонкой нитью и намотаем ее на эту окружность: начало отсчета (точку 0), приставим к «правой» точке единичной окружности, положительную полуось обмотаем против движения часовой стрелки, а отрицательную – по направлению (рис. 1). Такую единичную окружность называют числовой.
Свойства числовой окружности
- Каждое действительное число находится на одной точке числовой окружности.
- На каждой точке числовой окружности находятся бесконечно много действительных чисел. Так как длина единичной окружности равна 2π, то разность между любыми двумя числами на одной точке окружности равна одному из чисел ±2π ; ±4π ; ±6π ; …
Сделаем вывод: зная одно из чисел точки A, мы можем найти все числа точки A .
Проведем диаметр АС (рис. 2). Так как x_0 – одно из чисел точки А, то числа x_0±π ; x_0±3π; x_0±5π; … и только они будут числами точки C.
Выберем одно из этих чисел, скажем, x_0+π, и запишем с его помощью все числа точки C: x_C=x_0+π+2πk ,k∈Z. Отметим, что числа на точках A и C можно объединить в одну формулу: x_(A ; C)=x_0+πk ,k∈Z (при k = 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки C).
Сделаем вывод: зная одно из чисел на одной из точек A или C диаметра АС, мы можем найти все числа на этих точках.
- Два противоположных числа находятся на симметричных относительно оси абсцисс точках окружности.
Проведем вертикальную хорду АВ (рис. 2). Так как точки A и B симметричны относительно оси Ox, то число -x_0 находится на точке B и, значит, все числа точки B задаются формулой: x_B=-x_0+2πk ,k∈Z. Числа на точках A и B запишем одной формулой: x_(A ; B)=±x_0+2πk ,k∈Z. Сделаем вывод: зная одно из чисел на одной из точек A или B вертикальной хорды АВ, мы можем найти все числа на этих точках. Рассмотрим горизонтальную хорду AD и найдем числа точки D (рис. 2). Так как BD – диаметр и число -x_0 принадлежит точке В, то -x_0 + π одно из чисел точки D и, значит, все числа этой точки задаются формулой x_D=-x_0+π+2πk ,k∈Z.
k∙x_0+πk ,k∈Z . (при k= 0; ±2; ±4; … получим числа точки A, а при k = ±1; ±3; ±5; … – числа точки D).
Сделаем вывод: зная одно из чисел на одной из точек A или D горизонтальной хорды AD, мы можем найти все числа на этих точках.
Шестнадцать основных точек числовой окружности
На практике решение большинства простейших тригонометрических уравнений связано с шестнадцатью точками окружности (рис. 3). Что это за точки? Красные, синие и зеленые точки делят окружность на 12 равных частей. Так как длина полуокружности равна π, то длина дуги A1A2 равна π/2, длина дуги A1B1 равна π/6, а длина дуги A1C1 равна π/3.
Теперь можем указать по одному числу на точках:
π/3 на С1 и
Вершины оранжевого квадрата – середины дуг каждой четверти, следовательно, длина дуги A1D1 равна π/4 и, значит, π/4 – одно из чисел точки D1. Воспользовавшись свойствами числовой окружности, мы можем записать с помощью формул все числа на всех отмеченных точках нашей окружности.
На рисунке отмечены также и координаты этих точек (опустим описание их получения).
Усвоив выше сказанное, мы имеем теперь достаточную подготовку для решения частных случаев (для девяти значений числа a) простейших уравнений.
Решить уравнения
1) sinx=1⁄(2) .
– Что от нас требуется?
– Найти все те числа x, синус которых равен 1/2 .
Вспомним определение синуса: sinx – ордината точки числовой окружности, на которой находится число x . На окружности имеем две точки, ордината которых равна 1/2 . Это концы горизонтальной хорды B1B2 . Значит, требование «решить уравнение sinx=1⁄2 » равнозначно требованию «найти все числа на точке B1 и все числа на точке B2».
2) sinx=-√3⁄2 .
Нам надо найти все числа на точках C4 и C3.
3) sinx=1 . На окружности имеем только одну точку с ординатой 1 – точка A2 и, значит, нам надо найти только все числа этой точки.
Ответ: x=π/2+2πk , k∈Z .
4) sinx=-1 .
Только точка A_4 имеет ординату -1. Все числа этой точки и будут конями уравнения.
Ответ: x=-π/2+2πk , k∈Z .
5) sinx=0 .
На окружности имеем две точки с ординатой 0 – точки A1 и A3 . Можно указать числа на каждой из точек по отдельности, но, учитывая, что эти точки диаметрально противоположные, лучше объединить их в одну формулу: x=πk ,k∈Z .
Ответ: x=πk ,k∈Z .
6) cosx=√2⁄2 .
Вспомним определение косинуса: cosx — абсцисса точки числовой окружности на которой находится число x. На окружности имеем две точки с абсциссой √2⁄2 – концы горизонтальной хорды D1D4 . Нам нужно найти все числа на этих точках. Запишем их, объединив в одну формулу.
Ответ: x=±π/4+2πk , k∈Z .
7) cosx=-1⁄2 .
Надо найти числа на точках C_2 и C_3 .
Ответ: x=±2π/3+2πk , k∈Z .
10) cosx=0 .
Только точки A2 и A4 имеют абсциссу 0, значит, все числа на каждой из этих точках и будут решениями уравнения.
.
Решениями уравнения системы являются числа на точках B_3 и B_4 .Неравенству cosxОтвет: x=-5π/6+2πk , k∈Z .
Заметим,что при любом допустимом значении x второй множитель положителен и, следовательно,уравнение равносильно системе
Решениями уравнения системы являются чила точек D_2 и D_3 . Числа точки D_2 не удовлетворяют неравенству sinx≤0,5 ,а числа точки D_3-удовлетворяют.
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Сходимость ряда — @дневники: асоциальная сеть
понедельник, 02 апреля 2018
Добрый день! Могли бы проверить мое решение для следующей задачи:`a_1 = 1, a_(n+1) = sin(a_n)`.
Сходится ли ряд `a_n`?Док-во:
1) При `n >= 1` выполнено: `sin(1/n) > 1/(n+1)`, в силу эквивалнтости `sin(1/n) `
2) Теперь докажем по индукции, что `sin(sin(..(sin(1)))` (так n раз) `> 1/n` — для всех `n>1`. а) База верна б) Пусть верно `sin(sin(….(sin(1))) > 1/n`. Тогда возьмем синус от обеих частей. Так как это монотонное преобразование для величин, лежащих в отрезке `[0;1]`, то неравенство останется верным. Тогда Получаем `sin(sin(sin(…(sin(1)))) > sin(1/n)`. Исходя из пункта 1) `sin(1/n) > 1/(n+1)`, шаг индукции доказан.
3) Ограничили снизу гармоническим рядом, значит и исходный расходится
Мне моё решение не нравится. Оно выглядит довольно громоздким. Я понимаю логически что будет происходить: когда мы будем больше и больше раз применять синус, то он будет идти к нулю. Но в с каждым разом это стремление будет всё медленнее и медленнее. Например, `sin(0.1) = 0.099`. И получаем очень сильную расходимость, сумма будет очень быстро расти. Я не могу перевести в данном случае «очень медленно стремится к нулю».
@темы: Ряды
- ← Предыдущая запись
- Следующая запись →
Этот пост будет безвозвратно удален:
Вы уверены в том, что действительно хотите это сделать?
Да Нет
Russian — Доказательство: lim (sin x)/x=1
И снова здравствуйте!
Теперь, когда мы хорошо понимаем, в чем состоит теорема сжатия
(или ее еще называют теоремой о 2-ух милиционерах),
мы будем использовать ее, чтобы доказать, что предел…
(напишу желтым цветом)…
предел при х, стремящемся к 0-лю, [(sin x)/x]=1.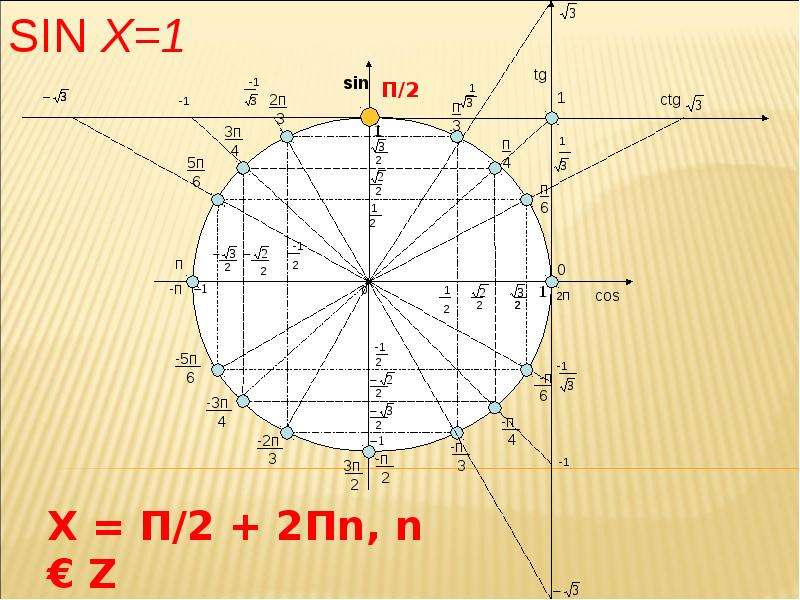
Итак, докажем эту теорему.
Мы должны сопровождать доказательство графическим подтверждением.
Поэтому я нарисую, хотя бы, 1-ую и 4-ую четверти единичной окружности.
Нарисую лиловым. Итак, посмотрим…
Нужно нарисовать побольше.
Так… Нужно нарисовать их очень большими. Поэтому я вот так рисую.
Ну, пусть будет так. И нарисую оси. Это ось Y, а это ось Х. Вот так.
Это наша единичная окружность.
Теперь нарисую радиус,
только я нарисую его выходящим за пределы окружности.
Нарисую еще кое-что, чтобы решить нашу задачу.
Нет, это не то, что я хотела сделать.
Я хотела начать вот с этой точки.
А из этой точки я хотела провести линию…и еще одну линию из той же точки. Вот так.
Теперь мы готовы приступить к решению.
Итак, это единичная окружность, правильно?
Что значит «единичная окружность»?
Это значит, что радиус этой окружности равен единице.
Т.е. расстояние от этой точки до этой равно единице.
И если это угол х (в радианах), то чему равна длина вот этого отрезка?
По определению, sin х является Y-координатой
любой точки на единичной окружности.
Потому это – sin x (мне не хватает здесь места чтобы написать, поэтому нарисую стрелочку… так, вот это – sin х).
А теперь задам вопрос посложнее. Чему равна длина вот этого отрезка?
Давайте подумаем. Что такое тангенс (tg)?
Вернемся к нашему SOH-CAH-TOA-определению тангенса. Вспомните еще такое?
Тангенс, т.е. отношению противолежащего катета (от англ. «opposite»)
к прилежащему (от англ. «adjacent») — это тангенс. Тогда чему равен tg x?
Если это прямоугольный треугольник, то тангенс –
это отношение длины противолежащего катета к длине прилежащего, правильно?
Назовем длину этого катета о (от англ.
«opposite»).
А чему равна длина прилежащего катета?
Чему равно основание вот этого, большего, треугольника?
Это ведь единичная окружность, правильно?
Значит, расстояние от этой точки до этой будет равно единице.
Потому что это – тоже радиус окружности. И равен он единице.
Итак, отношение противолежащего катета к прилежащему равно tg x.
Но если подставить в это соотношение единицу вместо прилежащего катета,
то получится, что противолежащий катет (вот этот) будет равен tg x.
Иначе говоря, tg x равен длине вот этого катета, деленной на единицу;
или tg x равен длине вот этого катета. Запишу это.
Этот катет равен tg x.
А теперь давайте подумаем о площадях других частей нарисованной здесь фигуры.
Может, стоило нарисовать ее побольше, но, думаю, у нас и так получится.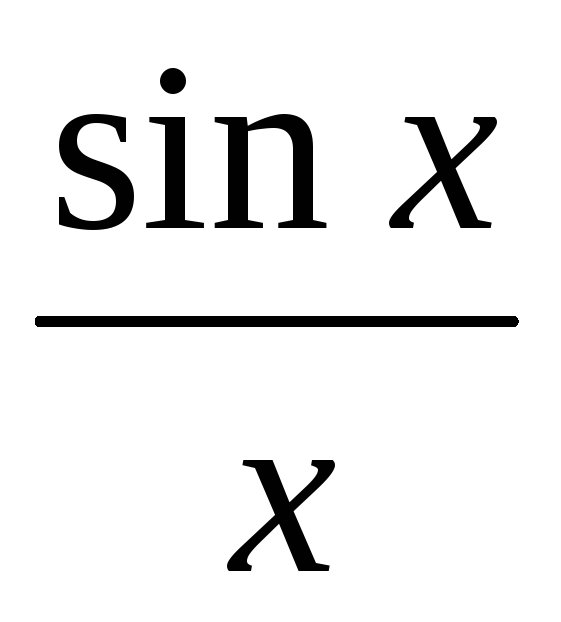
Итак, первым делом выберу относительно небольшой треугольник.
Возьму вот этот треугольник. Обведу его зеленым.
Итак, чему равна площадь вот этого зеленого треугольника?
Она будет равна 1/2, умножить на основание и умножить на высоту.
Т.е. 1/2 умножить на основание, которое равно единице, правильно?
А чему равна высота? Мы только что выяснили, что вот эта высота равна sin x.
Значит, умножить на sin x. Это площадь вот этого зеленого треугольника.
А чему равна площадь… не этого, не зеленого…
Обведу другим цветом. Например, красным.
Чему равна площадь вот этого сектора? Вот этого сектора.…
Надеюсь, вы видите. Нет, все-таки этот цвет не сильно отличается.
Итак, вот этот сектор. Сначала вот этот радиус, а затем дуга…
Т.е. эта площадь будет больше площади треугольника, которую мы только что вычислили.
Она будет немного больше потому,
что включает в себя площадь между треугольником и дугой, правильно?
Чему же она равна?
Если этот угол равен х радиан,
то какую долю он составляет от целой единичной окружности?
В целой единичной окружности 2π радиан, так?
Тогда чему будет равна вот эта площадь?
Она будет равна доле угла х от целой единичной окружности, так?
Т.е. х радиан разделить на 2π радиан
(это доля, которую составляет вот этот угол от 360 градусов, если перейти к градусам)
и умножить еще на площадь всего круга, правильно?
Вот это показывает, какую долю от окружности занимает наша фигура,
и нам нужно умножить это еще на площадь всего круга.
А чему равна площадь всего этого круга?
Она равна πR², а радиус равен единице, правильно?
Значит, площадь всего круга равна просто п.
(πR², где R=1).
Тогда площадь всего вот этого сектора будет равна…
π сокращаются, значит, получится х/2.
Итак, площадь вот этого, первого, небольшого зеленого треугольника равна 1/2*sin x.
Это площадь вот этого, зеленого, треугольника.
Площадь вот этого сектора (мы только что нашли) равна х/2.
А теперь давайте найдем площадь вот этого, большого треугольника.
Она равна 1/2 умножить на основание, и умножить на высоту.
Итак, основание опять равно единице, умножить на высоту, т.е. tg x.
Значит, площадь равна 1/2*tg x.
При взгляде на эту схему сразу должно быть ясно
(и неважно, где нарисована вот эта линия),
что площадь вот этого, зеленого, треугольника меньше площади вот этого сектора,
а площадь сектора меньше площади вот этого, большого, треугольника.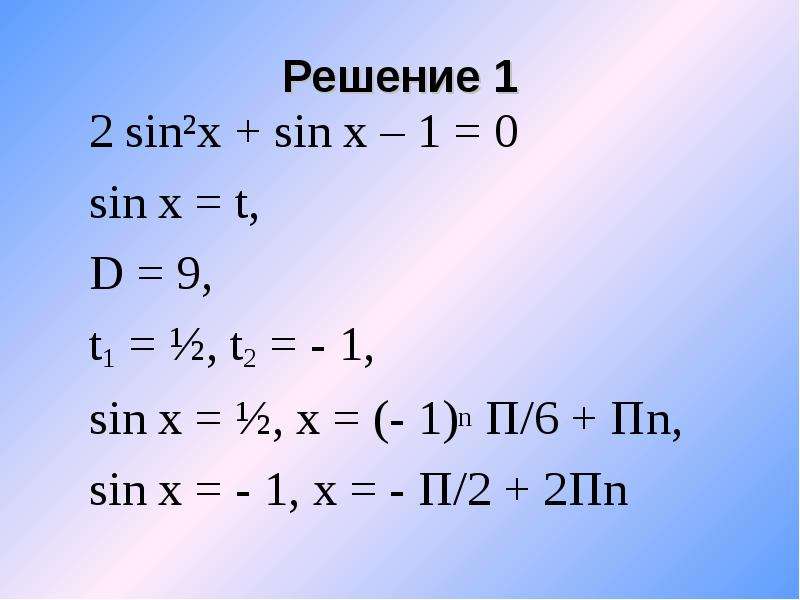
Правильно?
Запишем это в виде неравенства.
Площадь зеленого треугольника, т.е. 1/2*sin x,
меньше площади вот этого сектора, которая равна х/2.
И обе эти площади меньше площади вот этого,
большого, треугольника, которая равна 1/2*tg x.
Когда это неравенство справедливо?
Оно справедливо, пока мы находимся в 1-ой четверти, правильно?
Пока мы находимся в 1-ой четверти.
Также оно почти справедливо, если мы переходим в 4-ую четверть,
за исключением того, что тогда синус и тангенс становятся отрицательными,
и х также становится отрицательным.
Но если мы возьмем абсолютные значения, т.е. модуль,
то неравенство все еще будет справедливым и в 4-ой четверти.
Потому что, если пойти в отрицательном направлении,
и при этом брать абсолютные значения, то расстояние будет сохраняться,
значит, и значения площадей будут положительными.
Итак, моя цель – найти предел при х, стремящемся к 0-лю.
И чтобы этот предел был вообще определен, неравенство должно быть справедливым
как с положительной, так и с отрицательной стороны.
Давайте возьмем абсолютные значения в неравенстве.
Надеюсь, вам это понятно.
Если провести линию вниз, то это будет синусом х, это – тангенсом.…
И если вы берете абсолютные значения, то делаете то же самое, что и в первой четверти.
Итак, давайте возьмем абсолютные значения.
От этого ничего не должно измениться, особенно, если вы находитесь в 1-ой четверти.
Итак, у нас есть это неравенство. Посмотрим, можно ли его как-то преобразовать.
Прежде всего, давайте избавимся от 1/2-ой, умножив все на 2.
Итак, модуль sin x меньше модуля х,
который в свою очередь меньше модуля tg x.
Надеюсь, я не запутала вас этими модулями.
Начальное неравенство, которое я записала, полностью соблюдалось в 1-й четверти.
Но т.к. я хотела, чтобы это неравенство соблюдалось и в 1-ой, и в 4-ой четверти,
потому что ищу предел при х, стремящемся к 0-лю с обеих сторон,
то беру здесь абсолютные значения.
Т.е. можно было бы провести линию вниз
и то же самое, что мы делали здесь, сделать и для 4-ой четверти,
но при этом брать абсолютные значения, и неравенство снова должно сработать.
Вернемся к задаче. Итак, у нас есть это неравенство.
Возьмем это выражение и разделим все его части…
Можно сказать, что у него 3 части – левая, средняя и правая.
Разделим их все на модуль sin x.
И поскольку мы знаем, что модуль sin x – это положительное число,
Давайте разделим.
Итак, модуль sin x, деленный на модуль sin x – это просто единица.
Единица меньше модуля х, деленного на модуль sin x, а это в свою очередь меньше.…
Повторю, что я делю вот это неравенство на модуль sin x.
Чему равен модуль tg x, деленный на модуль sin x?
Тангенс – это отношение синуса к косинусу.
Итак, это равно… Просто преобразуем правую часть.
Это равно отношению синуса к косинусу, деленному еще на синус.
И можно сказать, что это то же самое, что модуль, и модуль, деленные на модуль.
Что останется? Останется только единица разделить на….
синусы сокращаются, значит, останется единица разделить на модуль cos x.
Мы уже близки к разгадке. Вот это выглядит как наша функция, только перевернутая.
И чтобы в средней части получить нашу функцию, давайте перевернем неравенство.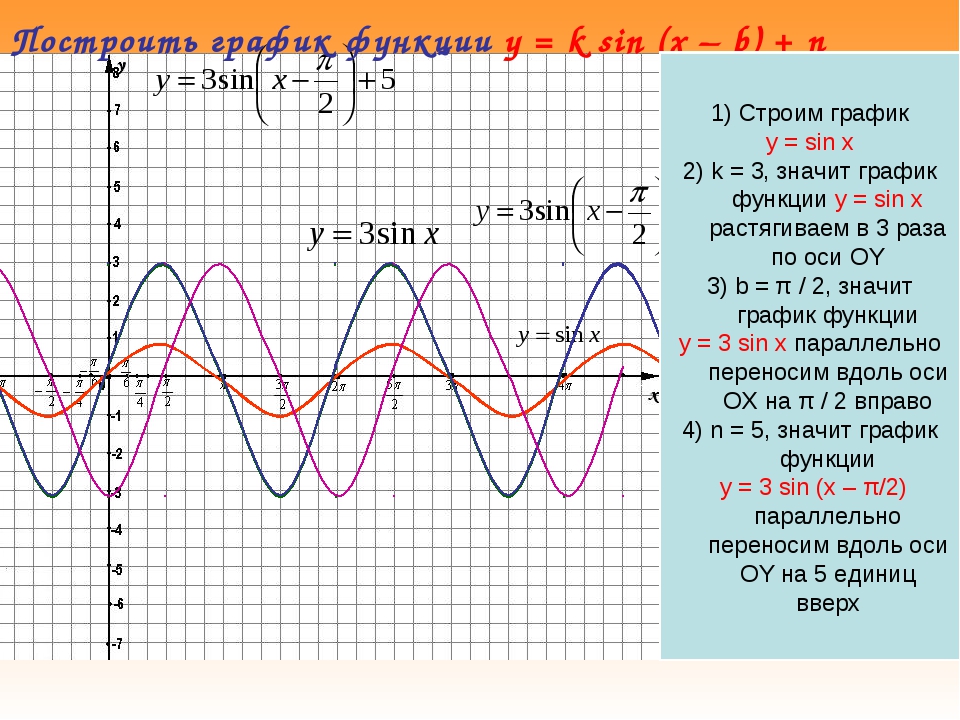
Что тогда произойдет?
Прежде всего, что будет, если перевернуть единицу?
1/1 – это просто единица.
Но если вы перевернете все части неравенства,
то и знак неравенства поменяется, правильно?
Если вам это непонятно, рассуждайте так:
то получу 2>1/2. Надеюсь, что так вам более понятно.
Т.е. если я переворачиваю все части этого неравенства,
то знаки неравенства я должна изменить.
Итак, единица больше модуля sin x, деленного на модуль х,
что в свою очередь больше модуля cos x.
Теперь я задам вам вопрос.
Модуль sin x… прежде всего, sin x/x.
Будет ли такой случай, когда выражение sin x/x
в 1-ой или 4-ой четверти будет иметь знак «минус»?
В 1-ой четверти значения sin x будут положительными, значения х тоже.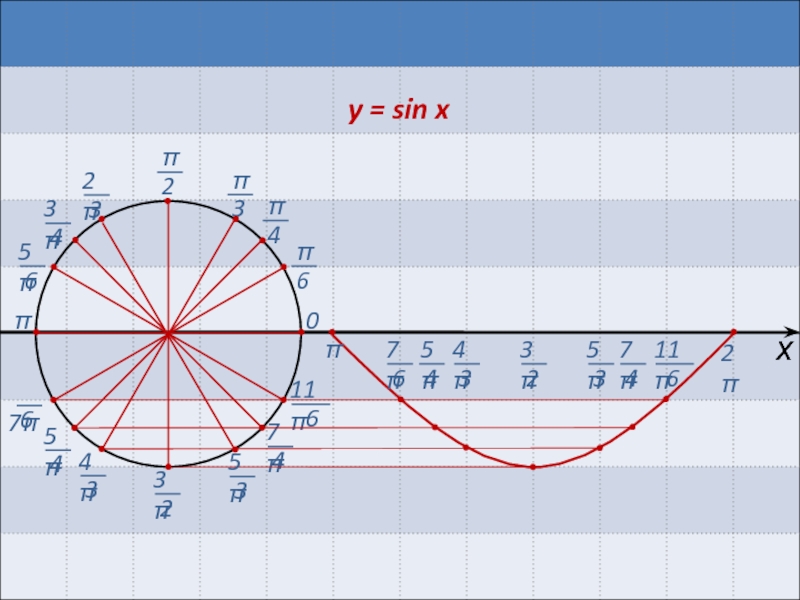
Положительное значение, деленное на положительное,
в результате также даст положительное значение.
А в 4-ой четверти синус принимает отрицательные значения
(т.к. y отрицательный и угол отрицательный),
значит, значения х также будут отрицательными.
В этом случае sin x/x – принимает отрицательное значение, деленное на отрицательное значение,
что в результате даст положительное значение.
Значит, sin x/x –всегда будет положительным. Поэтому знаки модуля тут не нужны.
Тогда можно записать так: единица больше sin x/x…
И по той же логике: в 1-ой и 4-ой четвертях,
т.е. если имеем дело, например, с (-π/2), которое меньше x,
а х в свою очередь меньше π/2.
Т.е. мы идем от (-π/2) до π/2, в 1-ой и 4-ой четвертях.
Будет ли cos x отрицательным?
По определению, значения косинуса в 1-ой и 4-ой четвертях всегда положительные.
Значит, и в правой части неравенства
можно убрать знаки абсолютного значения и оставить только cos x.
Теперь мы готовы использовать теорему о двух милиционерах.
Итак, чему равен предел при х, стремящемся к 0-лю, функции единицы?
Функция единицы всегда равна единице.
Т.е. я могу искать ее предел при х, стремящемся к бесконечности, при х, стремящемся к π.
И он всегда будет равен единице.
Т.е. при х, стремящемся к 0-лю, этот предел равен единице.
А чему равен предел при х, стремящемся к 0-лю, функции cos x?
Это тоже легко. При х, стремящемся к 0-лю, косинус нуля равен просто единице.
Как вы знаете, косинус – это непрерывная функция, значит, предел равен единице.
Итак, мы готовы использовать теорему сжатия.
При х, стремящемся к 0-лю, вот эта функция стремится к единице,
и вот эта функция тоже стремится к единице.
А вот эта – она здесь находится между двумя другими функциями.
И если она находится между двумя…
Т.е. если эта функция стремится к единице при х, стремящемся к 0-лю,
и эта функция также стремится к единице при х, стремящемся к 0-лю,
а эта находится между ними, то она тоже должна стремиться к единице
при х, стремящемся к 0-лю.
Используем теорему о двух милиционерах, основанную на этом и на этом.
И можно было бы сказать, что вследствие этой теоремы
(потому что вот это соблюдается, вот это соблюдается и это тоже)
предел sin x/x при х, стремящемся к 0-лю, равен единице.
Надеюсь, что это понятно. Можно пойти и другим путем:
если вот эта линия все ниже и ниже опускается к нулю,
если х стремится к 0-лю, то эта площадь и эта площадь сходятся в одну,
значит, и площадь, которая между ними, сводится к ним обеим.
Если вы хотите увидеть графическое отображение, то оно вот здесь.
Посмотрю, получится ли показать вам график… Тогда вы мне поверите.
Итак, мы говорили, что единица всегда больше sin x/х,
что в свою очередь больше cos x в промежутке от (-π/2) до π/2.
И, конечно, sin x/х не определен при х=0.
Но мы можем найти предел. Здесь можно его увидеть.
Синяя линия – это график функции единицы, т.е. y=1.
Светло-голубая линия – это график косинуса х.
А красная – это график sin x/х. Это обозначено вот здесь.
Итак, график sin x/х в промежутке (-π/2, π/2) или в 1-ой и 4-ой четвертях,
т.е. красная линия, всегда находится между синей и светло-голубой линиями.
Я это говорю, чтоб вы поняли, что происходит в теореме о двух милиционерах.
Мы знаем, что для этой светло-голубой лини
предел равен единице, при х, стремящемся к 0.
И знаем также, что для этой верхней, синей, линии
предел равен единице, при х, стремящемся к 0.
А эта красная линия находится всегда между ними,
значит, предел этой функции тоже будет равен единице.
Что и требовалось доказать.
Мы использовали теорему сжатия и немного тригонометрии, чтобы доказать,
что предел при х, стремящемся к 0-лю, функции sin x/х равен единице.
Еще этот предел называют замечательным пределом.
Почему его так называют, вы узнаете позже.
Надеюсь, вы все поняли, и я вас не запутала.
На сегодня все! До встречи на следующем уроке!
- Title:
- Доказательство: lim (sin x)/x=1
- Description:
-
В этом видео с использованием теоремы сжатия приводится подробное доказательство того, что предел функции [sin x/x] при х, стремящемся к 0, равен 1.
Этот предел еще называют замечательным пределом.Это видео — русская версия видео «Proof: lim (sin x)/x» Академии Хана (http://www.khanacademy.org/video?v=Ve99biD1KtA). Перевод и дублирование выполнены командой проектов «Edukit» (http://www.edukit.org.ua) и «Study Planner» (http://www.studyplanner.org).
This video is a Russian dubbed version of the Khan Academy video «Proof: lim (sin x)/x» (http://www.khanacademy.org/video?v=Ve99biD1KtA). The translation and sampling are made by the «Edukit» (http://www.edukit.org.ua) and «Study Planner» team (http://www.studyplanner.org).
Наша страница на Facebook — http://www.facebook.com/KhanAcademyRussian
more » « less - Video Language:
- Russian
- Duration:
- 18:06
Этот предел еще называют замечательным пределом.Таблица синусов углов (градусы, значения)
В данной таблице представлены значения синусов от 0° до 360°.
Таблица синусов нужна, когда у вас под рукой нет калькулятора. Чтобы узнать, чему равен синус угла, просто найдите нужный градус в таблице. Для начала короткая версия таблицы.
https://uchim.org/matematika/tablica-sinusov — uchim.org
Таблица синусов для 0°-180°
|
|
|
|
2924
6561
8988
9994
9397
7314
4226
0349Таблица синусов для 181°-360°
|
|
|
|
309
6561
891
9976
9511
7547
454
0698Существуют также следующие таблицы тригонометрических функций: таблица косинусов, таблица тангенсов и таблица котангенсов.
Как легко запомнить таблицу синусов (видео)
Таблицу важно всегда помнить на алгебре, чтобы найти синус.
Всё для учебы » Математика в школе » Таблица синусов углов (градусы, значения)
| 1 | Найдите производную — d / dx | натуральное журнал x | |
| 2 | Оцените интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найдите производную — d / dx | е ^ х | |
| 4 | Оцените интеграл | интеграл от e ^ (2x) относительно x | |
| 5 | Найдите производную — d / dx | 1 / х | |
| 6 | Найдите производную — d / dx | х ^ 2 | |
| 7 | Найдите производную — d / dx | 1 / (х ^ 2) | |
| 8 | Найдите производную — d / dx | грех (х) ^ 2 | |
| 9 | Найдите производную — d / dx | сек (x) | |
| 10 | Оцените интеграл | интеграл e ^ x относительно x | |
| 11 | Оцените интеграл | интеграл x ^ 2 относительно x | |
| 12 | Оцените интеграл | интеграл квадратного корня x относительно x | |
| 13 | Найдите производную — d / dx | соз (х) ^ 2 | |
| 14 | Оцените интеграл | интеграл от 1 / x по отношению к x | |
| 15 | Оцените интеграл | интеграл sin (x) ^ 2 относительно x | |
| 16 | Найдите производную — d / dx | х ^ 3 | |
| 17 | Найдите производную — d / dx | сек (x) ^ 2 | |
| 18 | Оцените интеграл | интеграл cos (x) ^ 2 относительно x | |
| 19 | Оцените интеграл | интеграл от sec (x) ^ 2 относительно x | |
| 20 | Найдите производную — d / dx | е ^ (х ^ 2) | |
| 21 | Оцените интеграл | интеграл от 0 до 1 кубического корня из 1 + 7x относительно x | |
| 22 | Найдите производную — d / dx | грех (2x) | |
| 23 | Найдите производную — d / dx | загар (x) ^ 2 | |
| 24 | Оцените интеграл | интеграл 1 / (x ^ 2) относительно x | |
| 25 | Найдите производную — d / dx | 2 ^ х | |
| 26 | График | натуральное бревно из | |
| 27 | Найдите производную — d / dx | cos (2x) | |
| 28 | Найдите производную — d / dx | хе ^ х | |
| 29 | Оцените интеграл | интеграл от 2x относительно x | |
| 30 | Найдите производную — d / dx | (натуральный логарифм x) ^ 2 | |
| 31 | Найдите производную — d / dx | натуральный логарифм (x) ^ 2 | |
| 32 | Найдите производную — d / dx | 3x ^ 2 | |
| 33 | Оцените интеграл | интеграл xe ^ (2x) относительно x | |
| 34 | Найдите производную — d / dx | 2e ^ x | |
| 35 | Найдите производную — d / dx | натуральное бревно 2x | |
| 36 | Найдите производную — d / dx | -син (х) | |
| 37 | Найдите производную — d / dx | 4x ^ 2-x + 5 | |
| 38 | Найдите производную — d / dx | y = 16 корень четвертой степени из 4x ^ 4 + 4 | |
| 39 | Найдите производную — d / dx | 2x ^ 2 | |
| 40 | Оцените интеграл | интеграл e ^ (3x) относительно x | |
| 41 | Оцените интеграл | интеграл cos (2x) относительно x | |
| 42 | Найдите производную — d / dx | 1 / (квадратный корень из x) | |
| 43 | Оцените интеграл | интеграл e ^ (x ^ 2) относительно x | |
| 44 | Оценить | e ^ бесконечность | |
| 45 | Найдите производную — d / dx | х / 2 | |
| 46 | Найдите производную — d / dx | -cos (x) | |
| 47 | Найдите производную — d / dx | грех (3x) | |
| 48 | Найдите производную — d / dx | 1 / (х ^ 3) | |
| 49 | Оцените интеграл | интеграл tan (x) ^ 2 относительно x | |
| 50 | Оцените интеграл | интеграл 1 по x | |
| 51 | Найдите производную — d / dx | х ^ х | |
| 52 | Найдите производную — d / dx | x натуральное бревно x | |
| 53 | Найдите производную — d / dx | х ^ 4 | |
| 54 | Оценить предел | предел, когда x приближается к 3 из (3x-5) / (x-3) | |
| 55 | Оцените интеграл | интеграл x ^ 2 натуральный логарифм x относительно x | |
| 56 | Найдите производную — d / dx | f (x) = квадратный корень из x | |
| 57 | Найдите производную — d / dx | х ^ 2sin (х) | |
| 58 | Оцените интеграл | интеграл sin (2x) относительно x | |
| 59 | Найдите производную — d / dx | 3e ^ x | |
| 60 | Оцените интеграл | интеграл xe ^ x относительно x | |
| 61 | Найдите производную — d / dx | у = х ^ 2 | |
| 62 | Найдите производную — d / dx | квадратный корень из x ^ 2 + 1 | |
| 63 | Найдите производную — d / dx | грех (x ^ 2) | |
| 64 | Оцените интеграл | интеграл от e ^ (- 2x) относительно x | |
| 65 | Оцените интеграл | интеграл натурального логарифма квадратного корня x относительно x | |
| 66 | Найдите производную — d / dx | е ^ 2 | |
| 67 | Найдите производную — d / dx | х ^ 2 + 1 | |
| 68 | Оцените интеграл | интеграл sin (x) относительно x | |
| 69 | Найдите производную — d / dx | арксин (х) | |
| 70 | Оценить предел | предел, когда x приближается к 0 of (sin (x)) / x | |
| 71 | Оцените интеграл | интеграл e ^ (- x) относительно x | |
| 72 | Найдите производную — d / dx | х ^ 5 | |
| 73 | Найдите производную — d / dx | 2 / х | |
| 74 | Найдите производную — d / dx | натуральное бревно из 3х | |
| 75 | Найдите производную — d / dx | х ^ (1/2) | |
| 76 | Найдите производную — d / d @ VAR | f (x) = квадратный корень из x | |
| 77 | Найдите производную — d / dx | соз (х ^ 2) | |
| 78 | Найдите производную — d / dx | 1 / (х ^ 5) | |
| 79 | Найдите производную — d / dx | кубический корень из x ^ 2 | |
| 80 | Оцените интеграл | интеграл cos (x) относительно x | |
| 81 | Оцените интеграл | интеграл e ^ (- x ^ 2) относительно x | |
| 82 | Найдите производную — d / d @ VAR | е (х) = х ^ 3 | |
| 83 | Оцените интеграл | интеграл от 0 до 10 из 4x ^ 2 + 7 по x | |
| 84 | Оцените интеграл | интеграл (натуральный логарифм x) ^ 2 относительно x | |
| 85 | Найдите производную — d / dx | журнал x | |
| 86 | Найдите производную — d / dx | арктан (x) | |
| 87 | Найдите производную — d / dx | натуральное бревно 5x | |
| 88 | Найдите производную — d / dx | 5e ^ x | |
| 89 | Найдите производную — d / dx | cos (3x) | |
| 90 | Оцените интеграл | интеграл x ^ 3 относительно x | |
| 91 | Оцените интеграл | интеграл x ^ 2e ^ x относительно x | |
| 92 | Найдите производную — d / dx | Корень четвертой степени из 4x ^ 4 + 4 (16) | |
| 93 | Найдите производную — d / dx | х / (е ^ х) | |
| 94 | Оценить предел | предел, когда x приближается к 3 от arctan (e ^ x) | |
| 95 | Оцените интеграл | интеграл от (e ^ x-e ^ (- x)) / (e ^ x + e ^ (- x)) относительно x | |
| 96 | Найдите производную — d / dx | 3 ^ х | |
| 97 | Оцените интеграл | интеграл xe ^ (x ^ 2) относительно x | |
| 98 | Найдите производную — d / dx | 2sin (х) | |
| 99 | Оценить | сек (0) ^ 2 | |
| 100 | Найдите производную — d / dx | натуральный логарифм x ^ 2 |
Мощность Икс.
экспоненциальный / Логарифмический
Тригонометрический Тригонометрический Результат Обратный Тригонометрический Обратный Тригонометрический результат
Гиперболический Нажмите на доказательство для доказательства / обсуждения теоремы.  |
Математическая сцена — Производные, урок 5
Математическая сцена — Производные, урок 5 — Правило цепочки2009 Rasmus ehf & Jhann sak | Производные |
Урок 5
Цепное правило
Пример 1
Дифференцировать f (x) = (x 3 +1) 2 .
Только так у нас есть пока это делается путем умножения скобок, а затем дифференцируя. Если мы сделаем это, мы получим
f (x) = x 6 + 2x 3 +1 и, следовательно, f (x) = 6x 5 + 6x 2 .
Это не проблема с
простой пример, такой как приведенный выше, но что произойдет, если, например, у нас есть
е (х) = (х 3 +1) 6 ?
В этом случае требуется слишком много усилий, чтобы перемножить скобки перед
дифференцируя.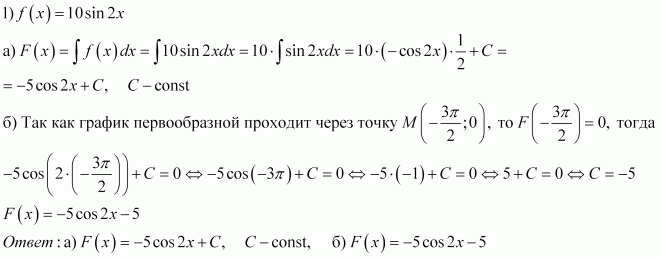
Чтобы различать такие составные функции, мы используем так называемое правило цепочки.
Сделаем пример 1
еще раз, чтобы увидеть, как это работает.
f (x) является примером
составная функция, как было введено в функциях 2.
Его можно записать как f (u) = u 2 , где u = x 3 +1, u равно
функция от x, то есть u (x) = x 3 +1.
Правило цепочки гласит, что мы
сначала дифференцируйте f (u), рассматривая u как переменную, и получите f (u) = 2u (так же, как (x 2 ) = 2x)
Далее дифференцируем u и получаем
u (x) = 3x 2 .Наконец, мы умножаем два результата
вместе и получаем
f (x) =
2u3x 2 . Возвращая значение u, получаем f (x)
= 2 (x 3 +1) 3x 2 = 6x 5 + 6x 2
Это дает нам правило называется цепным правилом, которое гласит, что
(е (и (х)) = е (и (х)) и (х) |
Мы только указали
здесь правило, но его легко доказать для всех непрерывных дифференцируемых
функции.
Пример 2
Дифференцируйте композицию функция f (x) = sin 2 x.
Обозначение грех 2 х это другой способ записи (sin x) 2 так что квадрат является внешней функцией, а sin x — внутренней функцией. Начать мы разделим это на две части, но с практикой это не будет нужно.
f (x) = (грех х) 2 можно записать как f (u) = u 2 где u = sin x.
f (u) = 2u и u = cos x, так что умножая вместе получаем
f (x) = 2ucos x = 2 sin x cos x
Цепное правило гласит, что дифференцируем составную функцию, мы дифференцируем внешнюю функцию и умножить на производную внутренней функции.
Пример 2 +
Продифференцируем f (x) = sin x 2 . Это можно записать как f (u) = sin u, где u = х 2
Итак, в этом случае синус — это внешняя функция, а квадрат внутренний функция
f (x) = cos x 2 2x
Пример 3
Мы можем использовать правила cos x = sin (/ 2 x)
и sin x = cos (/ 2 x), чтобы найти производную cos x.
cos x = f (x) = sin (/ 2 x)
Производная синуса, внешняя функция — cos и производная от (/ 2 x), внутренняя функция равна 1, поэтому мы получаем
f (x) = cos (/ 2 x) (1)
= грех х (1)
= грех х
Пример 4
Найдите производную f (x) = sin 2 x 2 .
Это можно записать как f (x) = (грех x 2 ) 2 так что у нас есть тройная составная функция. Самая внешняя функция является квадратичной, затем синус и, наконец, еще один квадратичный.
Мы можем написать f = u 2 , где u = sinv и v = х 2 . Различение каждой функции и умножение дает 2 u cos v 2x, и, возвращая значения u и v, получаем результат:
f (x) = 2 sin x 2 cos x 2 2x | Первый
дифференцируем квадрат, оставляя sin x 2 без изменений. |
Затем мы дифференцируем синусоидальную функцию, чтобы получить cos и оставить
the x 2 без изменений, наконец, мы дифференцируем
х 2 и получите 2х. Пример 5
a) f (x) = e 2x | Дифференцирование экспоненциальной функции не меняет ее. производная 2x равна 2. |
Дифференцирование экспоненциальной функции не меняет ее, производная x 2 + 1 равна 2x. |
c) f (x) = e sin
x | Дифференцирование экспоненциальной функции не меняет ее,
производная sin x равна cos x. |
Теперь мы хотим найти правило для различения f (x) = ln x.
Мы используем метод под названием неявное дифференцирование , что означает различение обеих сторон уравнение.
Если f (x) = ln x, то e f (x) = х. Если мы продифференцируем обе части уравнения, мы получим следующее:
e f (x) = х
e f (x) f (x) = 1 Использование правила цепочки.
Решая для f (x), получаем
f (x) = 1 / e f (x)
= 1 / х Помните, что x = e f (x) .
Теперь мы можем найти производную от других логарифмические функции.
Найдите производную f (x) = log x.
Прежде всего мы должны напомнить себе о правила логарифмирования и отношения между бревнами с разными основаниями. Этот это правило нам нужно:
Таким образом мы можем переписать
любой логарифм
как натуральный логарифм ln x.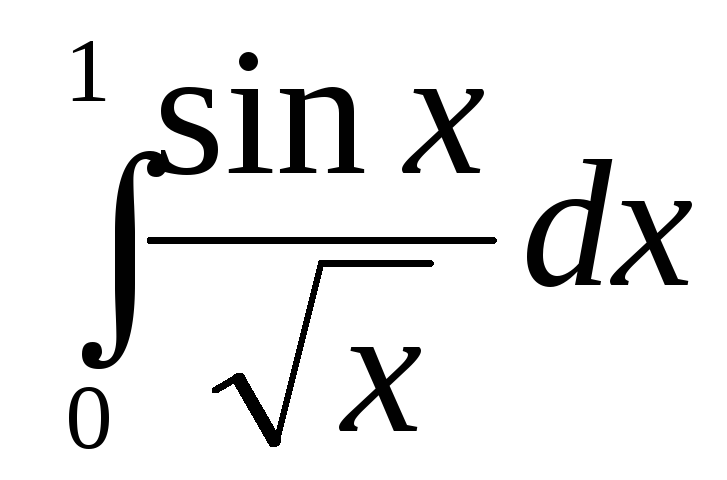
Логарифм ln 10 — константа, не влияющая на производная, остальное несложно.
Аналогичные расчеты работают для любой функции журнала, поэтому мы можем резюмировать следующие три правила:
Пример 6
Продифференцируем f (x) = ln (x 2 + 1).
Пример 7
Продифференцируем f (x) = xln х х + 5.
f (x) = 1lnx + x1 / x 1 = ln x
Обобщение деривативов
Производная:
к = 0 k = константа Икс = 1
(x n ) = nx n1 n может быть любым действительным числом.
(e x ) = e x
( x ) = x ln
(грех х) = cos x
(соз х) = грех х
Правила:
(УФ) = УФ + УФ
(е (г (х)) = е (г (х)) г (х)
Попрактикуйтесь в этих методах, а затем
пройдите тест 5 по производным.
л.с. Запомните свой контрольный список.
Примеры пределовsin (1 / x) и x sin (1 / x)
примеров пределов sin (1 / x) и x sin (1 / x)Поведение функций sin (1 / x) и x sin (1 / x), когда x близок к нулю стоит отметить.
Ниже приведены графики sin (1 / x) для небольшого положительного x.
Мы видим, что по мере приближения x к нулю функция сохраняет колебание (или колебание ) назад и вперед между -1 и 1.
Фактически, sin (1 / x) колеблется между -1 и 1 бесконечное количество раз. от 0 до любого положительного значения x , независимо от того, насколько оно мало.
Чтобы убедиться в этом, предположим, что sin (x) равен нулю при каждом кратном пи,
и колеблется между 0 и 1 или -1 между каждым кратным.
Следовательно, sin (1 / x) будет равен нулю при каждом x = 1 / (pi k ), где k — это
положительное число.
Между каждой последовательной парой этих значений sin (1 / x)
колеблется от 0 до -1, до 1 и обратно до 0.
Таких пар бесконечно много, и все они находятся в диапазоне от 0 до 1 / пи.
Более того, между любым положительным значением x и
1 / pi, поэтому между x и 0 должно быть бесконечно много.
Мы можем заключить, что поскольку x приближается к 0 справа, функция sin (1 / x) не устанавливается ни на какое значение L , поэтому предел как x подходов 0 справа не существует.
А вот функция x sin (1 / x) — это несколько другая история. Поскольку x приближается к нулю, а x приближается к нулю, умножение sin (1 / x) на него приведет к другой величине, которая приближается к нулю. Ниже приведены некоторые наглядные доказательства. Желтые линии — это y = x и y = -x, в то время как синяя кривая — это x sin (1 / x):
Это пример так называемой теоремы о сэндвиче.
Теорема о сэндвиче гласит, что
, если g (x) ≤ f (x) ≤ h (x), и
g (x) и h (x) оба приближаются к L, когда x приближается к a ,
, тогда f (x) должен также приближайтесь к L, когда x приближается к a .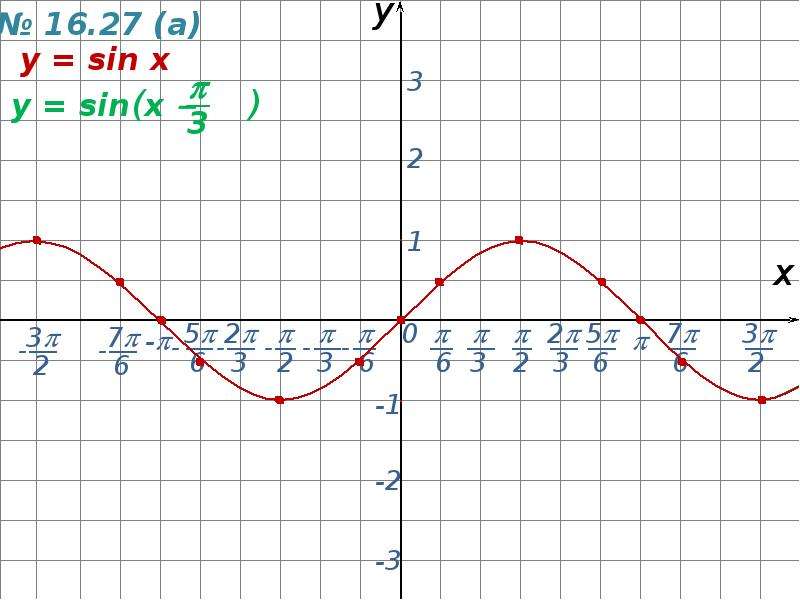
В этом случае мы знаем, что, поскольку -1 ≤ sin (1 / x) ≤ 1, мы можем сделать вывод, что -x ≤ x sin (1 / x) ≤ x для положительных значений x. Затем, поскольку x и -x оба приближаются к 0, когда x приближается к 0 справа, так должен x sin (1 / x).
Вы можете привести аналогичный аргумент слева и заключить, что предел, когда x приближается к 0, из x sin (1/ x ) равен 0. Вот изображение, которое показывает движение слева от нуля.
назад на страницу доктора Конроя в UW
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
РЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙРЕШЕНИЕ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
Примечание: Если вы хотите получить обзор тригонометрии, щелкните тригонометрия.
Пример 1: Решите относительно x в следующем уравнении.
Есть бесконечное множество решений этой проблемы.
Выделите синусоидальный член. Для этого перепишем левую часть уравнения в
эквивалентная факторизованная форма.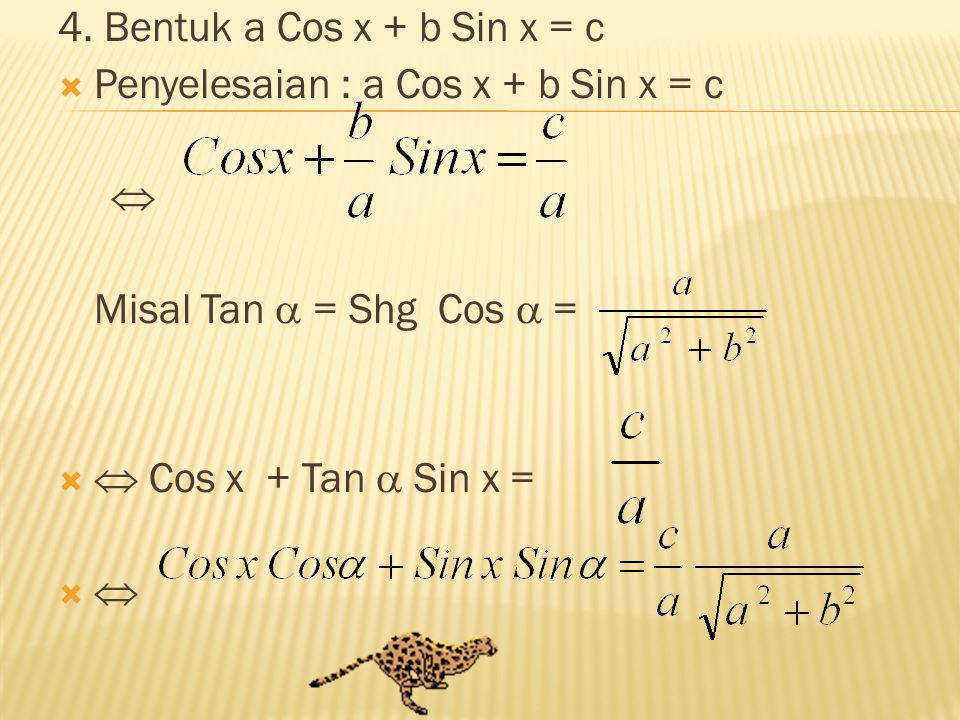
Произведение двух множителей равно нулю, если хотя бы один из множителей равен нули. Это значит, что если или же
Мы просто превратили сложную проблему в две более простые.Найти решения исходного уравнения, , находим решения уравнений а также
а также
Как нам изолировать x? Мы могли взять арксинус обеих сторон. Однако синусоидальная функция не является взаимно однозначной.
Давайте ограничим область, чтобы функция была однозначной на ограниченном домен с сохранением исходного диапазона. График синусоидальной функции взаимно однозначно на интервале Если мы ограничим область определения синусоидальной функции этим интервалом, мы можем взять арксинус обеих частей каждого уравнения.
Мы знаем это Следовательно, если , тогда
Завершаем задачу, решая второй фактор.
С периода
равно,
эти решения будут повторяться
каждый
единицы измерения. Точные решения
где n — целое число.
Приблизительные значения этих решений:
где n — целое число.
Каждое решение можно проверить алгебраически, подставив каждое решение в исходное уравнение.Если после подстановки левая часть исходное уравнение равно правой части исходного уравнения, решение действительно.
Можно также проверить решения графически, построив график функции, образованной левой частью исходного уравнения, и построив график функции, образованной правой частью исходного уравнения. Х-координаты точек пересечения являются решениями. Правая часть уравнения равна 0, а f ( x ) = 0 — ось абсцисс.Итак, на самом деле вы ищете x-пересекает функцию, образованную левой частью уравнения.
Алгебраическая проверка:
Проверить решение
Левая сторона:
Правая сторона: 0
Поскольку левая часть исходного уравнения равна правой части
исходное уравнение при замене -0,52359878 для x, тогда -0,52359878 — решение.
Проверить решение
Левая сторона:
Правая сторона: 0
Поскольку левая часть исходного уравнения равна правой части исходное уравнение при замене 3.665191 для x, тогда 3,665191 — решение.
Проверить решение
Левая сторона:
Правая сторона: 0
Поскольку левая часть исходного уравнения равна правой части исходное уравнение, когда вы подставляете 1,5707963 вместо x, тогда 1,5707963 является решением.
Мы только что проверили, что точные решения , а также являются решениями, и эти решения повторяются каждый единицы измерения. Приблизительные значения этих решений: и 1.5707963 и эти решения повторяются каждые единицы измерения.
Графическая проверка:
Изобразите уравнение Обратите внимание, что график пересекает ось x много раз, указывая на множество решения.
График пересекает ось абсцисс в точке -0,52359878. Поскольку период ,
вы можете убедиться, что график также пересекает ось x
снова в -0,52359878 + 6,2831853 = 5,7595865 и при ,
и т.
п.
График пересекает ось абсцисс в точке . Поскольку период , график также снова пересекает ось x при tex2 html c omment m ark > 3.665191 + 6,2831853 = 9,9483763 и при , так далее..
График пересекает ось абсцисс в точке . Поскольку период , график также снова пересекает ось x при tex2 html c omment m ark > 1,5707963 + 6,2831853 = 7,8539816 и при , и т.п.
Примечание: если проблема заключалась в том, чтобы найти решение в интервале , затем вы выбираете эти решения из множества бесконечных решения, принадлежащие множеству , а также 5.7595865.
Если вы хотите проработать другой пример, нажмите «Пример».
Если вы хотите проверить себя, решив некоторые задачи, подобные этой Например, щелкните «Проблема».
Если вы хотите перейти к следующему разделу, нажмите далее.
Если вы хотите вернуться к предыдущему разделу, нажмите предыдущее .
Если вы хотите вернуться к оглавлению уравнения, щелкните Содержание.
[Алгебра] [Тригонометрия] [Геометрия] [Дифференциальные уравнения] [Исчисление] [Комплексные переменные] [Матричная алгебра]
S.O.S MATHematics — домашняя страница
Автор: Нэнси МаркусАвторские права 1999-2021 MathMedics, LLC. Все права защищены.
Свяжитесь с нами
Math Medics, LLC. — П.О. Box 12395 — El Paso TX 79913 — США
пользователя онлайн за последний час
Использование теоремы о сжатии для определения пределов математических функций
Примеры с решениями
Пример 1
Найти предел lim x → 0 x 2 cos (1 / x) Решение примера 1:
Когда x приближается к 0, 1 / x становится очень большим по абсолютной величине, а cos (1 / x) становится сильно колеблющимся.
Однако cos (1 / x) принимает значения в интервале [-1,1], который является диапазоном cos x, поэтому
-1 ≤ cos (1 / x) ≤ 1
Умножьте все члены приведенного выше неравенства на x 2 (x не равно 0)
— x 2 ≤ x 2 cos (1 / x) ≤ x 2
Приведенное выше неравенство справедливо для любого значения x, кроме 0, где x 2 cos (1 / x) не определено. Когда x приближается к 0, оба — x 2 и x 2 приближаются к 0, и согласно теореме сжатия мы получаем
lim x → 0 x 2 cos (1 / x) = 0
Пример 2
Найти предел lim x → 0 sin x / x Решение примера 2:
Предположим, что 0 
A — точка на единичной окружности, а AB касается окружности в A.
Точка C — это точка на единичной окружности (радиус = 1), имеющая координаты (cos x, sin x). Найдем площади треугольника OAC, сектора OAC и треугольника
площадь треугольника OAC = (1/2) * (основание) * (высота)
= (1/2) * (1) * (координата y точки C) = (1/2) (sin x)
Примечание: мы использовали base = radius = 1
площадь сектора OAC = (1/2) * (x) * (радиус) 2
= (1/2) (1) 2 x = (1/2) x
площадь треугольника OAB = (1/2) * (основание) * (высота)
= (1/2) * (1) * (tan x) = (1/2) tan x
Сравнивая три области, можно записать неравенство
площадь треугольника OAC <площадь сектора OAC <площадь треугольника OAB
Замените площади в приведенном выше неравенстве их выражениями, полученными выше.
(1/2) (sin x) <(1/2) x <(1/2) tan x
Умножение всех членов на 2 / sin x дает
1
1> sin x / x> cos x
Что то же самое, что
cos x
и
lim x → 0 1 = 1,
мы можем применить теорему сжатия, чтобы получить
lim x → 0 sin x / x = 1
Этот результат очень важен и будет использован для нахождения других пределов тригонометрических функций и производных.
Подробнее о лимитах Учебники и задачи по исчислению
Производная sin x — подход к исчислению
12
Производная sin x
Производная от cos x
Производная от tan x
Производная от детской кроватки x
Производная sec x
Производная от csc x
ПРОИЗВОДНАЯ sin x — это cos x .Для доказательства воспользуемся следующим тождеством:
sin A — sin B = 2 cos ½ ( A + B ) sin ½ ( A — B ).
(Тема 20 тригонометрии.)
Проблема 1. Используйте это удостоверение, чтобы показать:
| sin ( x + h ) — sin x | = |
Чтобы увидеть доказательство, наведите указатель мыши на цветную область.
Чтобы закрыть ответ еще раз, нажмите «Обновить» («Reload»).
Сначала решите проблему сами!
| sin ( x + h ) — sin x | = | 2 cos ½ ( x + h + x ) sin ½ ( x + h — x ) |
| = | 2 cos ½ (2 x + h ) sin ½ h | |
| = | ||
Однако, прежде чем перейти к производной sin x , мы должны доказать лемму; что является предварительной вспомогательной теоремой, необходимой для доказательства основной теоремы.Эта лемма требует следующего тождества:
Задача 2. Докажите, что tan θ, разделенный на sin θ, равен.
| tan θ sin θ | = | 1 cos θ | . |
(См. Раздел 20 Тригонометрии.)
| tan θ sin θ | = | тангенс угла θ · | 1 sin θ | = | sin θ cos θ | · | 1 sin θ | = | 1 cos θ |
Лемма, которую мы должны доказать, обсуждается в теме 14 Тригонометрии.
(Взгляните на это.) Вот он:
ЛЕММА. Когда θ измеряется в радианах, тогда
Доказательство. Это невозможно доказать, применяя обычные теоремы о пределах (Урок 2). Мы должны перейти к геометрии и к значениям sin θ и радианной меры.
Пусть O будет центром единичной окружности, то есть окружности радиуса 1;
и пусть θ будет центральным углом первого квадранта BOA , измеренным в радианах.
Тогда, поскольку длина дуги с = r θ и r = 1, дуга BA равна θ. (Тема 14 Тригонометрии.)
Угол вытяжки B’OA равен углу θ, в результате дуга AB ‘ равна дуге BA ;
начертите прямую BB ‘, разрезая AO на P ;
и нарисуйте прямые BC, B’C , касательные к окружности.
Затем
BB ‘ BAB’ BC + CB ‘.
Теперь, в этом единичном круге, BP = PB ‘ = sin θ, (Тема 17 Тригонометрии),
, так что BB ‘ = 2 sin θ;
и BC = CB ‘ = tan θ. (Для tg θ = | BC OB | = | BC 1 | = до н.э. .) |
Таким образом, продолжающееся неравенство, приведенное выше, становится:
2 грех θ θ θ.
При делении каждого члена на 2 sin θ:
| 1 | θ sin θ | 1 cos θ | . |
(Задача 2.) И принимая обратные, меняя таким образом смысл:
| 1> | грех θ θ | > cos θ. |
(Урок 11 по алгебре, теорема 5.)
При смене знаков снова меняется смысл:
| -1 | sin θ θ | −cos θ, |
(Урок 11 алгебры, теорема 4),
и если мы добавим 1 к каждому члену:
| 0 | 1– | грех θ θ | 1 — cos θ. |
Теперь, когда θ становится очень близким к 0 (θ 0), cos θ становится очень близким к 1; следовательно, 1 — cos θ становится очень близким к 0. Выражение в середине, будучи меньше , чем 1 — cos θ, становится еще ближе к 0 (а слева ограничено 0), поэтому выражение в середине точно приблизится к нулю. Это означает:
Что мы и хотели доказать.
Учащийся должен помнить, что для «приближения» переменной к нулю или любому пределу (Определение 2.1), не означает, что переменная когда-либо равна этому пределу.
Производная sin x
| d dx | грех x | = cos x |
Чтобы доказать это, мы применим определение производной (Урок 5). Сначала мы рассчитаем коэффициент разницы.
| = | , проблема 1, | ||
| = | , при делении числителя и знаменателя на 2, | ||
| = | |||
Теперь возьмем предел как h 0.
Но предел продукта равен произведению пределов. (Урок 2.) Множитель справа имеет вид sin θ / θ. Следовательно, согласно лемме при h 0 его предел равен 1. Следовательно,
| d dx | грех x | = cos x . |
Мы разработали формулу.
Производная от cos x
| d dx | cos x | = −sin x |
Чтобы установить это, мы будем использовать следующий идентификатор:
| cos x = sin ( | π 2 | — х ). |
Функция любого угла равна совместной функции его дополнения.
(Тема 3 тригонометрии).
Следовательно, при применении цепного правила:
Мы установили формулу.
Производная от tan x
| Теперь загар x = | sin x cos x | . | (Тема 20 тригонометрии.) |
Следовательно, согласно правилу частного:
| d dx | желто-коричневый x | = | d dx | sin x cos x | = | cos x · cos x — sin x (−sin x ) cos 2 x | ||
| = | cos 2 x + sin 2 x cos 2 x | |||||||
| = | 1 cos 2 x | |||||||
| = | сек 2 x . | |||||||
Мы разработали формулу.
Задача 3. Производная от детской кроватки х . Доказательство:
| d dx | детская кроватка x = −csc 2 x |
| d dx | детская кроватка x | = | d dx | cos x sin x | ||||
| = | sin x (−sin x ) — cos x · cos x sin 2 x | |||||||
| = | — (sin 2 x + cos 2 x ) sin 2 x | |||||||
| = | – | 1 sin 2 x | ||||||
| = | −csc 2 x . | |||||||
Производная sec x
| d dx | сек x | = сек x желто-коричневый x |
| Так как сек x = | 1 cos x | = | (cos x ) -1 | , |
, затем об использовании цепного правила и общего правила мощности:
Мы установили формулу.
Проблема 4. Производная от csc x . Доказательство:
| d dx | csc x | = | −csc x детская кроватка x |
Пример. Вычислить производную sin ax 2 .
Решение . О применении цепного правила,
| d dx | грех топор 2 | = | cos ax 2 · | d dx | топор 2 | = | cos ax 2 · | 2 топор | = | 2 ax cos ax 2 . |
Задача 5. Вычислить эти производные.
| а) | d dx | грех 5 x | = | 5 cos 5 x |
| б) | d dx | ½ sin 2 x | = | sin x cos x |
| в) | d dx | 2 cos 3 x | = | −6 грех 3 x |
| г) | d dx | x cos x | = | cos x — x sin x |
| e) | d dx | sin 2 x cos x | = | 2 cos 2 x cos x — sin 2 x sin x |
| е) | d dx | желто-коричневый (3 x ) 2 | = | 18 x сек 2 (3 x ) 2 |
| г) | d dx | 2 детская кроватка | x 2 | = | — csc 2 | x 2 |
| ч) | d dx | сек 4 x | = | 4 секунды 4 x желто-коричневый 4 x |
| i) | d dx | a csc bx | = | — ab csc bx детская кроватка bx |
| к) | = |
Проблема 6.