Синус sin x косинус cos x

Справочные данные по тригонометрическим функциям синус (sin x) и косинус (cos x). Геометрическое определение, свойства, графики, формулы. Таблица синусов и косинусов, производные, интегралы, разложения в ряды, секанс, косеканс. Выражения через комплексные переменные. Связь с гиперболическими функциями.

Геометрическое определение синуса и косинуса

|BD| —  длина дуги окружности с центром в точке A.
α — угол, выраженный в радианах.

Синус (sin α)

– это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.

Косинус (cos α)

– это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.

Принятые обозначения

;
;
.

;
;
.

График функции синус, y = sin x

График функции косинус, y = cos x

Свойства синуса и косинуса

Периодичность

Функции   y = sin x   и   y = cos x   периодичны с периодом   2π.

Четность

Функция синус – нечетная. Функция косинус – четная.

Область определения и значений, экстремумы, возрастание, убывание

Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).

	y = sin x	y = cos x
Область определения и непрерывность	– ∞ < x < + ∞	– ∞ < x < + ∞
Область значений	–1 ≤ y ≤ 1	–1 ≤ y ≤ 1
Возрастание
Убывание
Максимумы, y = 1
Минимумы, y = –1
Нули, y = 0
Точки пересечения с осью ординат, x = 0	y = 0	y = 1

Основные формулы

Сумма квадратов синуса и косинуса

Формулы синуса и косинуса от суммы и разности

Формулы произведения синусов и косинусов

Формулы суммы и разности

Выражение синуса через косинус

Далее мы полагаем, что – целое число.

;
;
    ;
    .

Выражение косинуса через синус

;
;
    ;
    .

Выражение через тангенс

;     .

При   , имеем:
;     .

При   :
;     .

Таблица синусов и косинусов, тангенсов и котангенсов

В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.

Выражения через комплексные переменные

;    

Формула Эйлера

Выражения через гиперболические функции

;    
;    

Производные

;     .     Вывод формул > > >

Производные n-го порядка:
;     .

Интегралы

;    
См. также раздел Таблица неопределенных интегралов >>>

Разложения в ряды

    { –∞ < x < +∞ }
    { –∞ < x < +∞ }

Секанс, косеканс

   

Обратные функции

Обратными функциями к синусу и косинусу являются арксинус и арккосинус, соответственно.

Арксинус, arcsin

   
   
   

Арккосинус, arccos

   
   
   

Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.

Автор: Олег Одинцов.     Опубликовано: 15-02-2014   Изменено: 23-12-2018

1cov-edu.ru

Уравнение sin x = a

Значения синуса заключены в промежутке [-1; 1], т.е. -1 ≤ sin α ≤ 1. Поэтому если |а| > 1, то уравнение sin x = a не имеет корней. Например, уравнение sin x = 2 корней не имеет.

Обратимся к некоторым задачам.

Задача 1.

Решить уравнение sin x = 1/2.

Решение.

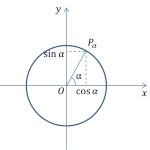
Отметим, что sin x – это ордината точки единичной окружности, которая получена в результате поворота точки Р (1; 0) на угол х вокруг начала координат.

Ордината, равная ½, присутствует у двух точек окружности М₁ и М₂.

Так как 1/2 = sin π/6, то точка М₁ получается из точки Р (1; 0) посредством поворота на угол х₁ = π/6, а также на углы х = π/6 + 2πk, где k = +/-1, +/-2, …

Точка М₂ получается из точки Р (1; 0) в результате поворота на угол х₂ = 5π/6, а также на углы х = 5π/6 + 2πk, где k = +/-1, +/-2, …, т.е. на углы х = π – π/6 + 2πk, где k = +/-1, +/-2, ….

Итак, все корни уравнения sin х = 1/2 можно найти по формулам х = π/6 + 2πk, х = π – π/6 + 2πk, где k € Z.

Эти формулы могут объединиться в одну: х = (-1)ⁿ π/6 + πn, где n € Z     (1).

Действительно, если n – четное число, т.е. n = 2k, то из формулы (1) получаем х = π/6 + 2πk, а если n – нечетное число, т.е. n = 2k + 1, то из формулы (1) получаем х = π – π/6 + 2πk.

Ответ. х = (-1)ⁿ π/6 + πn, где n € Z.

Задача 2.

Решить уравнение sin x = -1/2.

Решение.

Ординату -1/2 имеют две точки единичной окружности М₁ и М₂, где х₁ = -π/6, х₂ = -5π/6. Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -π/6 + 2πk, х = -5π/6 + 2πk, k € Z.

Эти формулы мы можем объединить в одну: х = (-1)ⁿ (-π/6) + πn, n € Z    (2).

Действительно, если n = 2k, то по формуле (2) получаем х = -π/6 + 2πk, а если n = 2k – 1, то по формуле (2) находим х = -5π/6 + 2πk.

Ответ. х = (-1)ⁿ (-π/6) + πn, n € Z.

Таким образом, каждое из уравнений sin x = 1/2 и sin x = -1/2 имеет бесконечное множество корней.

На отрезке -π/2 ≤ х ≤ π/2 каждое из этих уравнений имеет только один корень:
х₁ = π/6 – корень уравнения sin x = 1/2 и х₁ = -π/6 – корень уравнения sin x = -1/2.

Число π/6 называют арксинусом числа 1/2 и записывают: arcsin 1/2 = π/6; число -π/6 называют арксинусом числа -1/2 и пишут: arcsin (-1/2) = -π/6.

Вообще уравнение sin x = а, где -1 ≤ а ≤ 1, на отрезке -π/2 ≤ х ≤ π/2 имеет лишь один корень. Если а ≥ 0, то корень заключен в промежутке [0; π/2]; если а < 0, то в промежутке [-π/2; 0). Этот корень называют арксинусом числа а и обозначают arcsin а.

Таким образом, арксинусом числа а € [–1; 1] называется такое число а € [–π/2; π/2], синус которого равен а.

аrcsin а = α, если sin α = а и -π/2 ≤ х ≤ π/2        (3).

Например, аrcsin √2/2 = π/4, так как sin π/4 = √2/2 и – π/2 ≤ π/4 ≤ π/2;
аrcsin (-√3/2) = -π/3, так как sin (-π/3) = -√3/2 и – π/2 ≤ – π/3 ≤ π/2.

Аналогично тому, как это сделано при решении задач 1 и 2, можно показать, что корни уравнения sin х = а, где |а| ≤ 1, выражаются формулой

х = (-1)ⁿ аrcsin а + πn, n € Z          (4).

Также мы можем доказать, что для любого а € [-1; 1] справедлива формула аrcsin (-а) = -аrcsin а.

Из формулы (4) следует, что корни уравнения
sin х = а при а = 0, а = 1, а = -1 можно находить по более простым формулам:

sin х = 0           х = πn, n € Z                        (5)

sin х = 1           х = π/2 + 2πn, n € Z          (6)

sin х = -1        х = -π/2 + 2πn, n € Z          (7)

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

www.mathway.com

Все формулы по тригонометрии

Все формулы по тригонометрии

Подождите пару секунд пока подгрузятся формулы

Основные тригонометрические тождества

$$sin^2x+cos^2x=1$$

---

$$tgx= \frac{sinx}{cosx}$$

---

$$ctgx= \frac{cosx}{sinx}$$

---

$$tgxctgx=1$$

---

$$tg^2x+1= \frac{1}{cos^2x}$$

---

$$ctg^2x+1= \frac{1}{sin^2x}$$

Формулы двойного аргумента (угла)

$$sin2x=2cosxsinx$$

---

\begin{align} sin2x &=\frac{2tgx}{1+tg^2x}\\ &= \frac{2ctgx}{1+ctg^2x}\\ &= \frac{2}{tgx+ctgx} \end{align}

---

\begin{align} cos2x & = \cos^2x-sin^2x\\ &= 2cos^2x-1\\ &= 1-2sin^2x \end{align}

---

\begin{align} cos2x & = \frac{1-tg^2x}{1+tg^2x}\\ &= \frac{ctg^2x-1}{ctg^2x+1}\\ &= \frac{ctgx-tgx}{ctgx+tgx} \end{align}

---

\begin{align} tg2x & = \frac{2tgx}{1-tg^2x}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{2}{ctgx-tgx} \end{align}

---

\begin{align} ctg2x & = \frac{ctg^2x-1}{2ctgx}\\ &= \frac{2ctgx}{ctg^2x-1}\\ &= \frac{ctgx-tgx}{2} \end{align}

Формулы тройного аргумента (угла)

$$sin3x=3sinx-4sin^3x$$

---

$$cos3x=4cos^3x-3cosx$$

---

$$tg3x= \frac{3tgx-tg^3x}{1-3tg^2x}$$

---

$$ctg3x= \frac{ctg^3x-3ctgx}{3ctg^2x-1}$$

Формулы половинного аргумента (угла)

$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$

---

$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$

---

$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$

---

$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$

---

\begin{align} tg \frac{x}{2} & = \frac{1-cosx}{sinx}\\ &= \frac{sinx}{1+cosx} \end{align}

---

\begin{align} ctg \frac{x}{2} & = \frac{1+cosx}{sinx}\\ &= \frac{sinx}{1-cosx} \end{align}

Формулы квадратов тригонометрических функций

$$sin^2x= \frac{1-cos2x}{2}$$

---

$$cos^2x= \frac{1+cos2x}{2}$$

---

$$tg^2x= \frac{1-cos2x}{1+cos2x}$$

---

$$ctg^2x= \frac{1+cos2x}{1-cos2x}$$

---

$$sin^2 \frac{x}{2}= \frac{1-cosx}{2}$$

---

$$cos^2 \frac{x}{2}= \frac{1+cosx}{2}$$

---

$$tg^2 \frac{x}{2}= \frac{1-cosx}{1+cosx}$$

---

$$ctg^2 \frac{x}{2}= \frac{1+cosx}{1-cosx}$$

Формулы кубов тригонометрических функций

$$sin^3x= \frac{3sinx-sin3x}{4}$$

---

$$cos^3x= \frac{3cosx+cos3x}{4}$$

---

$$tg^3x= \frac{3sinx-sin3x}{3cosx+cos3x}$$

---

$$ctg^3x= \frac{3cosx+cos3x}{3sinx-sin3x}$$

Формулы тригонометрических функций в четвертой степени

$$sin^4x= \frac{3-4cos2x+cos4x}{8}$$

---

$$cos^4x= \frac{3+4cos2x+cos4x}{8}$$

Формулы сложения аргументов

$$sin(\alpha + \beta) = sin \alpha cos \beta + cos \alpha sin \beta$$

---

$$cos(\alpha + \beta) = cos \alpha cos \beta — sin \alpha sin \beta$$

---

$$tg(\alpha + \beta)= \frac{tg \alpha + tg \beta}{1 — tg \alpha tg \beta}$$

---

$$ctg(\alpha + \beta)= \frac{ctg \alpha ctg \beta -1}{ctg \alpha + ctg \beta}$$

---

$$sin(\alpha — \beta) = sin \alpha cos \beta — cos \alpha sin \beta$$

---

$$cos(\alpha — \beta) = cos \alpha cos \beta + sin \alpha sin \beta$$

---

$$tg(\alpha — \beta)= \frac{tg \alpha — tg \beta}{1 + tg \alpha tg \beta}$$

---

$$ctg(\alpha — \beta)= \frac{ctg \alpha ctg \beta +1}{ctg \alpha — ctg \beta}$$

Формулы суммы тригонометрических функций

$$sin\alpha + sin\beta = 2sin \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

---

$$cos\alpha + cos\beta = 2cos \frac{\alpha + \beta }{2} \cdot cos \frac{\alpha — \beta }{2}$$

---

$$tg\alpha + tg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

---

$$ctg\alpha + ctg\beta = \frac{sin(\alpha + \beta) }{cos \alpha cos \beta}$$

---

$$(sin\alpha + cos\alpha)^2= 1+sin2\alpha$$

Формулы разности тригонометрических функций

$$sin\alpha — sin\beta = 2sin \frac{\alpha — \beta }{2} \cdot cos \frac{\alpha + \beta }{2}$$

---

$$cos\alpha — cos\beta = -2sin \frac{\alpha + \beta }{2} \cdot sin \frac{\alpha — \beta }{2}$$

---

$$tg\alpha — tg\beta = \frac{sin(\alpha — \beta) }{cos \alpha cos \beta}$$

---

$$ctg\alpha — ctg\beta = — \frac{sin(\alpha — \beta) }{sin \alpha sin \beta}$$

---

$$(sin\alpha + cos\alpha)^2= 1-sin2\alpha$$

Формулы произведения тригонометрических функций

$$sin\alpha \cdot sin\beta = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{2}$$

---

$$sin\alpha \cdot cos\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{2}$$

---

$$cos\alpha \cdot cos\beta = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{2}$$

---

\begin{align} tg\alpha \cdot tg\beta & = \frac{cos(\alpha — \beta)-cos(\alpha + \beta)}{cos(\alpha — \beta)+cos(\alpha + \beta)}\\ &= \frac{tg\alpha + tg\beta}{ctg\alpha + ctg\beta} \end{align}

---

\begin{align} ctg\alpha \cdot ctg\beta & = \frac{cos(\alpha — \beta)+cos(\alpha + \beta)}{cos(\alpha — \beta)-cos(\alpha + \beta)}\\ &= \frac{ctg\alpha + ctg\beta}{tg\alpha + tg\beta} \end{align}

---

$$tg\alpha \cdot ctg\beta = \frac{sin(\alpha — \beta)+sin(\alpha + \beta)}{sin(\alpha + \beta)-sin(\alpha — \beta)}$$

www.100formul.ru

Все формулы (уравнения) тригонометрии : sin(x) cos(x) tg(x) ctg(x)

Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

 

 

 

 

 

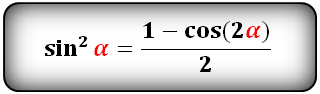
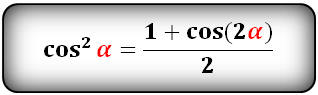
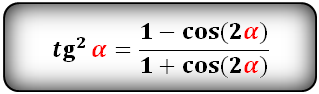
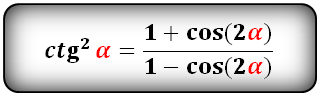
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

 

sin(2α)- через sin и cos:

 

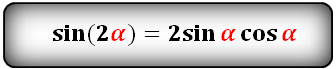
sin(2α)- через tg и ctg:

 

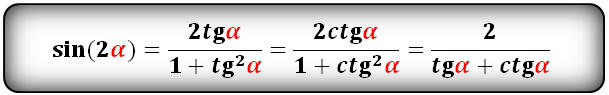
cos(2α)- через sin и cos:

 

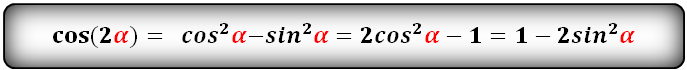
cos(2α)- через tg и ctg:

 

 

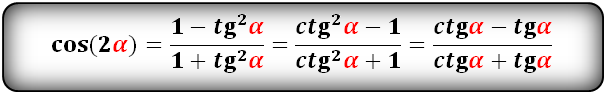
tg(2α) и сtg(2α):

 

 

---

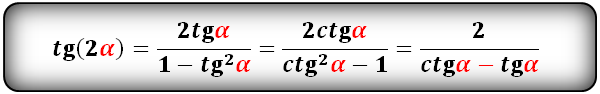
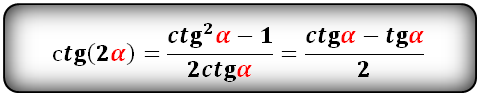
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

 

 

 

 

---

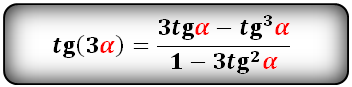
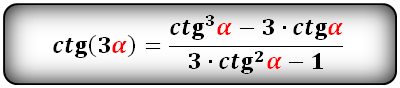
Тригонометрические формулы преобразования разности аргументов

 

 

 

 

 

 

---

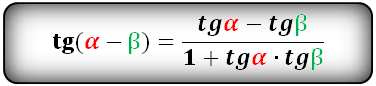
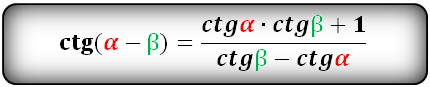
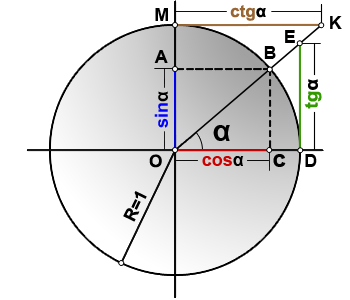
sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

 

Значения функций для некоторых углов, α

 

---

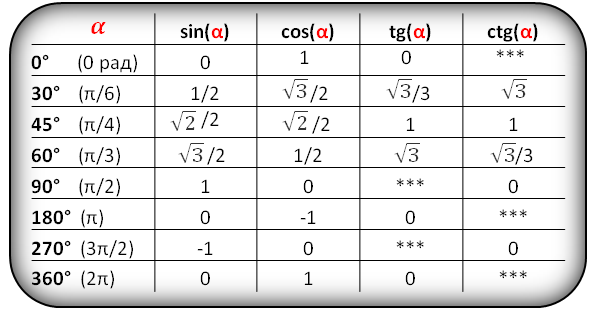
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

 

 

www-formula.ru

Основные формулы тригонометрии | umath.ru

1. Определения синуса, косинуса, тангенса и котангенса угла.

Синус угла 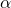 (обозначается 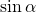) – ордината точки 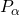, полученной поворотом точки 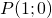вокруг начала координат на угол .

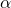Косинус угла 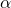(обозначается 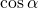) – абсцисса точки 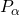, полученной поворотом точки 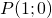вокруг начала координат на угол .

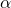Тангенс угла 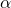(обозначается 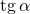) – отношение синуса угла 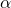к его косинусу, т.е.

Котангенс угла 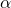(обозначается 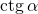) – отношение косинуса угла 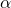к его синусу, т.е.
2. Основное тригонометрическое тождество:
3. Зависимость между синусом, косинусом, тангенсом и котангенсом:
4. Чётность, нечётность и периодичность тригонометрических функций.

Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :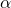

Синус и косинус – периодические с периодом 2\pi функции, а тангенс и котангенс – периодические с периодом 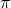функции: Число 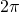является наименьшим положительным периодом синуса и косинуса, а число 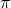– наименьшим положительным периодом тангенса и котангенса.
Для любого целого 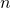справедливы равенства
5. Формулы сложения:
6. Формулы двойного и тройного аргумента:
7. Формулы понижения степени:
8. Формулы приведения:
9. Формулы суммы и разности синусов:
10. Формулы суммы и разности косинусов:
11. Формулы суммы и разности тангенсов:
12. Преобразование произведения синусов и косинусов в сумму (разность):
13. Выражение синуса и косинуса через тангенс половинного аргумента:

umath.ru

sin x = 1 / 2 чему равен х

Задание.
Найти значение х при .

Решение.
Найти значение аргумента функции синус, при котором он равен какому-либо значению, означает определить, при каких аргументах значение синуса будет именно таким, как указано в условии.
В данном случае нам нужно выяснить, при каких значениях значение синуса будет равным 1/2. Это можно сделать несколькими способами.

Например, использовать график функции синус, по которому определить при каких значениях х функция синус будет равна 1/2.
Другим способом является использование тригонометрического круга. Напомню, что значения синусов лежат на оси Оу.
Самым распространенным способом является обращение к таблице значений синуса, особенно если речь идет о таких стандартных для этой функции значениях, как 1/2.
Во всех случаях не стоит забывать об одном из важнейших свойств синуса — о его периоде.
Найдем в таблице значение 1/2 для синуса и посмотрим какие аргументы ему соответствуют. Интересующие нас аргументы равны Пи / 6 и 5Пи / 6.
Запишем все корни, которые удовлетворяют заданное уравнение. Для этого записываем интересующий нас неизвестный аргумент х и одно из значений аргумента, полученное из таблицы, то есть Пи / 6. Запишем для него, учитывая период синуса, все значения аргумента:

   

Возьмем второе значение, и проделаем те же шаги, что и в предыдущем случае:

   

Полным решением исходного уравнения будет:
и
q может принимать значение любого целого числа.

Ответ. и , q — целое.

ru.solverbook.com