Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
Если график квадратичной функции был симметричен оси Оу, то график кубической параболы симметричен относительно начала координат, то есть точки (0;0).
Свойства кубической функции
Перечислим основные свойства кубической функции
- При х =0, у=0. у>0 при х>0 и y
- У кубической функции не существует не максимального ни минимального значения.
- Кубическая функция возрастает на всей числовой оси (-∞;+∞).
- Противоположным значениям х, соответствуют противоположные значения y.
Нужна помощь в учебе?
Предыдущая тема: Умножение одночленов и возведение одночлена в степень + примеры
Следующая тема:   Абсолютная погрешность: понятие, как вычислить + примеры
Построение графиков содержащих знак модуля построение графика функции содержащей переменную или функцию под знаком модуля согласно определению модуля
Построение графиков, содержащих знак модуля
Построение графика функции, содержащей переменную
или функцию под знаком модуля согласно определению модуля:
x, если х>=0 f(x), если f(x)>=0
|x| = ; |f(x) | =
-x, если x
Пример:
Построить график функции у=|2x-3|-х.
Рассмотрим два случая.
2х-3>=0 2х-3
y=2x-3-x или y=-2x+3-x
x>= xSUB>
y=x-3 y= -3x+3
Таким образом, чтобы построить график функции у=|2x-3|-x, надо построить графики функций, заданными различными выражениями на различных промежутках.
х-3, х>=
у=
— 3х+3, хSUB>
График изображен ниже:
y=|2x-3|-x
Построить график:
Y=|X|+X
Y=|X| · (X-2)
Y=|X+4| · X
Y=
Y=
Y=2–1)
Y=2+4X+3)
Y=
Y=
Y=X — 1 — |X-1|
Y=|3X-4|-X
Y=
13. Y=
Y=
Y=
Y=
Y=X2 — 2|X+1|-1
Y=X+
Y=|X2-4X+3|+2X
Y=
Y=|X2-4|+4X
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеют вид |y| = f(x):
Надо построить график у = f(x)
Часть графика, расположенную выше оси Ох (и на самой оси) оставить без изменения
Часть графика расположенную ниже оси Ох стереть
Для оставленной части построить симметричную относительно оси Ох
Пример:
Построить график |y| = 2х-1
Построить график:
Y|=5X-4
|Y|=9-X2
|Y|=
|Y|=(X+4)2-5
|Y|=
|Y|=X+2
|Y|=X2-6X+8
|Y|=X2-4X
X|Y|=2
|Y|=
|Y| · (X+1)=1
|Y|=1-
|Y|=|2X-X2|
Y2=-2X
|Y|=8+2X-X2
Y2=0,5X
Элементарные преобразования графика функции у=f(x)
Если формула зависимости у = f(|x|):
Надо построить график функции у = f(x), часть графика расположенную правее оси Оу(и на самой оси) оставить без изменения
Часть графика расположенную левее оси Оу стереть
Построить для оставленной части симметричную относительно оси Оу
Пример:
Построить график у=2|x|-1
Построить график:
Y=5|X|-5
Y=9-|X|2
Y=
Y=
Y=
Y=(|X|+4)2-5
Y=
Y=
Y=|X|-1
Y=
Y=X2-|X|-6
Y=-X2+6|X|-8
Постройте график.
 С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
2-, если |X|
у= , если |X|>4
Y=X2-|X|-2
Решите уравнение X2+3|X|-18=0 графически.
Y=|X|-X2
Y=
Элементарные преобразования графика функции у=f(x)
Если формула зависимости имеет вид у = |f(x)|,
График функции у = f(x) выше оси Ох (и на самой оси Ох) оставить без изменения
Для части графика расположенной ниже оси Ох строят симметричную относительно
оси Ох
Часть графика расположенная ниже оси Ох стирается.
Пример:
Построить график функции у=|2x-1|
Построить график:
Y=|5X-4|
Y=|9 -X2|
Y=
Y=|(X-4)2-5)|
Y=|X+2|
Y=|X-1|
Y=|X2+2X|
Y=
Y=|
Y=||X2-3|-1|
Y=|X2-1|
Y=|X+1|-2
Y=4+|X-3|
Y=3 ∙ |X-2|
Найдите наибольшее и наименьшее значение функции Y=:
а)на отрезке [-2;2]
б)на луче [0;+ )
в)на луче (- ;3]
г)на отрезке [-5;0]
16. Найдите наименьшее и наибольшее значение функции Y=:
Найдите наименьшее и наибольшее значение функции Y=:
а)на луче (- ;5]
б)на отрезке [4;7]
в)на луче [2;+ )
г)на полуинтервале [-1;6]
17.Решите уравнение графически:
а)|X2-9|=5 б)|X-2|=X2 в)|X+1|= -2X2
г)|X2-1|=|X2-X+1| д)|X-3|=X2+1 е)|X+5|=-X-1
ё) -2(X+2)2 ж) з)(X+3)2
и)-X
Построение графиков уравнений, содержащих несколько модулей
Пример: построить график функции
1). Найти те значения переменной, при которых выражение, стоящее под знаком модуля, равно нулю. ; ; .
2). Числовую прямую разбивают на промежутки точками, соответствующими найденным значениям переменной
0 1
3). На каждом промежутке определяют знак выражения, стоящего под знаком модуля (берут числа из промежутка и ставят в под модульное выражение). Определяют знак выражения стоящего под знаком модуля
Определяют знак выражения стоящего под знаком модуля
− 0 − 1 +
− + +
4). Берут промежуток, раскрывают модуль (пользуясь определением модуля) на данном промежутке и упрощают
Составляют формулу кусочной функции
y
Строят график кусочной функции
1
x
0 1
1). Найдите промежутки убывания функции и ее наибольшее значение на отрезке . Ответ: , .
2). Найдите множество значений функции и ее наименьшее значение на отрезке . Ответ: , .
3). Найдите множество значений функции и значения, которые функция принимает ровно три раза. Ответ: ; ; .
4). Найдите все значения , при которых значения функции положительны и значения, принимаемые функцией ровно 2 раза. Ответ: ; , .
Ответ: ; , .
5). Постройте график функции и для каждого укажите количество общих точек этого графика и прямой .
а). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При , бесконечное множество точек.
б). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При ,, три точки;
При , четыре точки.
6). Найдите наибольшее и наименьшее значения функции на отрезке . Ответ: ; .
7). Найдите наименьшее значение функции
а). .Ответ: при .
б). .Ответ: при .
9). Докажите, что если , то наименьшее значение функции равно .
10). Исследуйте функцию на промежутки монотонности
а). . Ответ: На промежутках
б). . Ответ: На промежутках ; функция убывает. На промежутках и возрастает. На промежутках и функция постоянна.
11). Постройте графики функций
1). 2).
3). 4).
Решение неравенств, содержащих знак модуля
Неравенства вида
> , где > 0
Если выражение, стоящее под знаком модуля , обозначить через t (f(x) = t), то данное неравенство примет вид > . Используя геометрический смысл модуля (модуль на числовой прямой представляет собой расстояние от точки, которая изображает данное число, до точки ноль). Изображаем на числовой прямой все точки, расстояние от которых до ноля больше .
———∙——————∙—————∙————►t
—0
t или t >
Решаем совокупность неравенств
Пример:
Решите неравенство > 11
Решение: > 11
Пусть , >11
———∙——————∙—————∙————►t
-11 0 11
; ;
Ответ: ; ;
Неравенство вида > , гдеB>0 верно при всех из области допустимых значений неравенства.
Решите неравенства
1). > 11. Ответ:
2). . Ответ:
3). . Ответ: : .
4). . Ответ: . .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). >2. Ответ: .
Неравенства вида
>
Учитывая свойство модуля =
и свойство неравенства: если обе части неравенства неотрицательны, то при возведении в квадрат получаем неравенство равносильное данному .
Неравенство > можно заменить равносильным неравенством > это — >0 (—) ∙ (+) >0
Далее решать методом интервалов или заменить совокупностью систем
Аналогично решаются неравенства вида .
Решите неравенства
1). . Ответ: .
2). Найти целочисленные решения неравенства .
Ответ: -8; -7; -6; … -1;0.
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: .
13). . Ответ: .
14). . Ответ: .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: .
21). . Ответ: .
Ответ: .
22). . Ответ: .
23). . Ответ: .
Решение неравенств вида
;
Неравенство
Доказательство:
.
Неравенство
Доказательство:
.
.
Решите неравенства
1). . Ответ: .
2). . Ответ: .
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: или .
7). . Ответ: .
8). . Ответ: ; .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: или .
. Ответ: или .
13). . Ответ: ; .
14). . Ответ: или .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: ; .
Решение неравенств, содержащих несколько модулей методом интервалов
Суть метода состоит в следующем:
Пример:
1). Находят те значения переменной при которых выражения, стоящие под знаком модуля равно нулю.
2). Числовую ось разбивают на промежутки точками, соответствующими значениям переменной
1
3). На каждом промежутке, определяют знак выражения, стоящего под знаком модуля (берут число из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)
— 0 + 1 +
-1 — — +
4). Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство
Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство
5). Проверяют, принадлежат ли найденные решения неравенства рассматриваемому промежутку; если принадлежат, то их включают в ответ
0
2
Если нет – отбрасывают. Так поступают с каждым промежутком.
6). Объединяют все решения исходного неравенства, найденные на всех промежутках, и учитывая область допустимых значений первоначального неравенства, выписывают ответ.
Ответ: -2SUB>
Решите неравенство
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5).Укажите целочисленные решения неравенства Ответ: 3;4
6). Ответ:
7). Ответ:
8). Ответ:
Ответ:
9). Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
14). Ответ:
15). Ответ:
16). Ответ:
Решение неравенств, содержащих знак модуля, методом введения новой переменной.
1). Найти область значений переменной, входящей в неравенство.
2). Если в уравнении неоднократно встречается фиксированное выражение, зависящее от неизвестной величины, то имеет смысл обозначить это выражение, какой либо буквой. Когда вводится обозначение желательно сразу отбросить все или некоторые значения при которых уравнение = не имеет решений , т.е. полезно сразу указать область значений функции = .
3). Решить неравенство относительно введенной неизвестной.
4). Решить неравенство относительно исходной переменной.
5). Учитывая область допустимых значений исходного неравенства записать ответ.
Пример:
Учитывая свойство модулей имеем Пусть = , , тогда неравенство примет вид =1; =-3. f
Учитывая, что имеем
Учитывая область допустимых значений исходного неравенства Ответ:
Решите неравенства
1). Ответ:
2). Ответ:
3). Ответ:
4). Ответ:
5). Ответ:
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
Изображение на координатной плоскости множества точек, координаты которых удовлетворяют данному неравенству
Чтобы на координатной плоскости изобразить множество точек, координаты которых удовлетворяют неравенству надо:
1). Построить множество точек, координаты которых удовлетворяют уравнению (если неравенство строгое, то линия изображается пунктирной, если не строгое, то сплошной).
Построить множество точек, координаты которых удовлетворяют уравнению (если неравенство строгое, то линия изображается пунктирной, если не строгое, то сплошной).
2). График или графики уравнений разбивают координатную плоскость на части.
3). Взять координаты точки, принадлежащей каждой части по очереди и поставить в неравенство. Если координаты точки удовлетворяют неравенству, то эту часть координатной плоскости заштриховать.
Пример: Изобразить на координатной плоскости множество точек, координаты которых удовлетворяют неравенству .
1). Построим график уравнения .
или
III II I
-1 0 1
Прямые и изображаем сплошными линиями, так как неравенство не строгое. Прямые разбивают координатную плоскость на три области. Неравенству удовлетворяют координаты точек, принадлежащих II части, поэтому заштриховываем II часть.
Изобразите на координатной плоскости множество точек, координаты которых удовлетворяют неравенству.
1). .
2). .
3). .
4). .
5). .
6). .
7). .
8). .
9). .
10). .
11). .
12). .
13). .
14). .
15). .
16). .
17). .
18). .
19).
20). .
21). .
22). .
23. .
24). .
Изобразите на координатной плоскости множество точек, удовлетворяющих условию
а) . б).
в) г)
д) е) .
Системы неравенств с параметрами, содержащие знак модуля
1). Найдите все значения параметра , при которых система неравенств имеет единственное решение.
а). Ответ: При .
б). Ответ: При .
2). При каких значениях параметра система неравенств имеет ровно одно решение?. Для всех таких найдите это решение.
а). Ответ: При , ;
При , .
б). Ответ: При , ;
При , .
3). При каких значениях параметра система не имеет решения.
а). Ответ: При .
б). Ответ: При .
4). Для каждого значения параметра решите систему неравенств.
а). Ответ: При , ;
При , ;
При , ;
При , .
б). Ответ: При и , ;
При , ;
При , ;
При , ;
При , .
Нестандартные уравнения и неравенства, содержащие знак модуля
К нестандартным ,обычно относятся такие уравнения и неравенства, где традиционные алгоритмы решения не проходят. Во многих случаях, решение таких уравнений и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых свойств функций, содержащихся в левой и правой частях уравнения или неравенства.
Если, например, наименьшее значение одной из функций совпадает с наибольшим значением функции , то уравнение = заменяют равносильной системой , где — наименьшее значение или наибольшее значение .
Решение системы является решением уравнения = .
1). Решите уравнение
Уравнение необходимо решить графически. Ответ:
2). Решите неравенство
. Применить метод оценки. Ответ:
Ответ:
3). Решите уравнение
. Решить уравнение графически. Ответ:
4). Решите уравнение
. Применить свойство: сумма неотрицательных функций равна нулю тогда и только тогда, когда все функции одновременно равны нулю. Ответ:
5). Решите уравнение
.Область допустимых значений (ОДЗ) уравнения состоит из конечного числа значений. Для решения достаточно проверить все эти значения. Ответ:
Применение свойства = для любого
при нахождении значения выражения
Вычислите:
1). Ответ: -6
2). , если t = -10; t = 127. Ответ: -8; 127
3). ∙ . Ответ: 0,125
4). −. Ответ: -6
5). − . Ответ: 2
6). − . Ответ: 8
7). + . Ответ: 2
8). + . Ответ: 6
+ . Ответ: 6
9). + . Ответ: 2
10). + . Ответ: 10
11). − . Ответ: -3
12). − . Ответ: -6
13). − − 0,5. Ответ: 0
14). + . Ответ:1
15). + Ответ: 1
16). . Ответ: 8
17). Найти и , если = — . Ответ: 28; -2
18). Найти и , если = — . Ответ: 40; -2
19). Сравните значение выражения
с числом . Ответ:
20). Сравните значение выражения
с числом . Ответ:
Ответ:
21). Докажите, что выражение ∙ является корнем уравнения = 1.
22). Докажите, что выражение является корнем уравнения = 1.
23). Удовлетворяет ли число − неравенству 7+58+13>0 .
Ответ: нет
24). Удовлетворяет ли число − неравенству 11+26-730 .
Ответ: да
Л и т е р а т у р а
1). Алгебра: 8; 9; 10 – 11 класс.
Авторы: А.Г.Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.
2). Задания по математике для подготовки к письменному экзамену в 9 классе.
Авторы: Л.И. Звавич, Д.И.Аверьянов, Б.П. Пигарёв, Т.Н. Грушанина.
3). Сборник задач по алгебре 8 – 9 класс.
Авторы: М.Л. Галицкий,А.М. Гольдман, Л.И. Звавич.
4). Сборник для проведения письменного экзамена за курс средней школы 11 класс. 3+ 1$.
3+ 1$.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. рис. 3).
Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4. Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три.Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U; график f(х) = х + 2 – это прямая, параллельная прямой f(х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции – это значения переменной «х», при которых у = 0, то есть это точки пересечения графика с осью Х. {2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
{2}}}}
), приравняйте знаменатель к нулю и найдите «х». В полученных значения переменной «х» функция не определена (в нашем примере проведите пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты существуют не только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3. 9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n – заданное натуральное число. Х. Показатель – четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а > 0 при а
«Квадратичная функция и её график» — Решение. у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
у=4x А(0,5:1) 1=1 А-принадлежит. При а=1 формула у=аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. x. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x=-1. y.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём с построения графика квадратичной функции вида y=x²+bx+c и y= -x²+bx+c.
Пример.
Построить график функции y=x²+2x-3.
Решение:
y=x²+2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1;-4) строим график параболы y=x²(как от начала координат. Вместо (0;0) — вершина (-1;-4). От (-1;-4) идём вправо на 1 единицу и вверх на 1 единицу, затем влево на 1 и вверх на 1; далее: 2 — вправо, 4 — вверх, 2- влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек недостаточно, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y= -x²+bx+c — парабола, ветви которой направлены вниз. Для построения графика ищем координаты вершины и от неё строим параболу y= -x².
Пример.
Построить график функции y= -x²+2x+8.
Решение:
y= -x²+2x+8 — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
От вершины строим параболу y= -x² (1 — вправо, 1- вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить графики функций y=x² и y= -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать точные значения точек пересечения графика с осью Ох, придется дополнительно решить уравнение x²+bx+c=0 (или —x²+bx+c=0), даже если эти точки непосредственно можно определить по рисунку.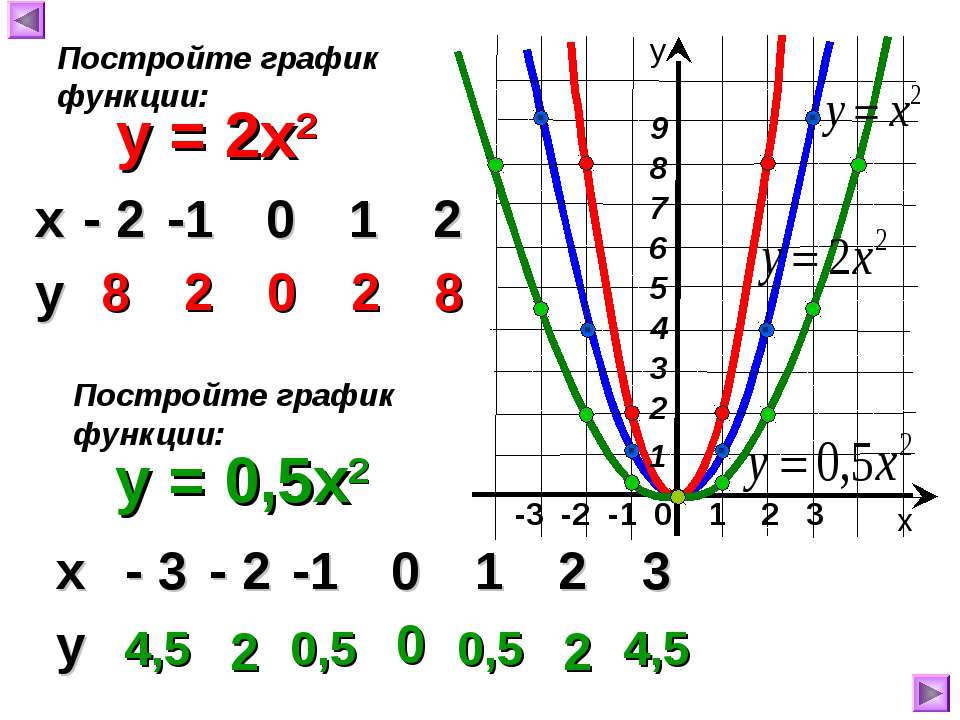
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x=хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y=x²+5x+4.
Решение:
y=x²+5x+4 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем . В точке пересечения с осью Ох y=0: x²+5x+4=0. Корни квадратного уравнения х1=-1, х2=-4, то есть получили две точки графике (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х=0: y=0²+5∙0+4=4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х=1, тогда y=1²+5∙1+4=10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямой, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y= -x²-3x.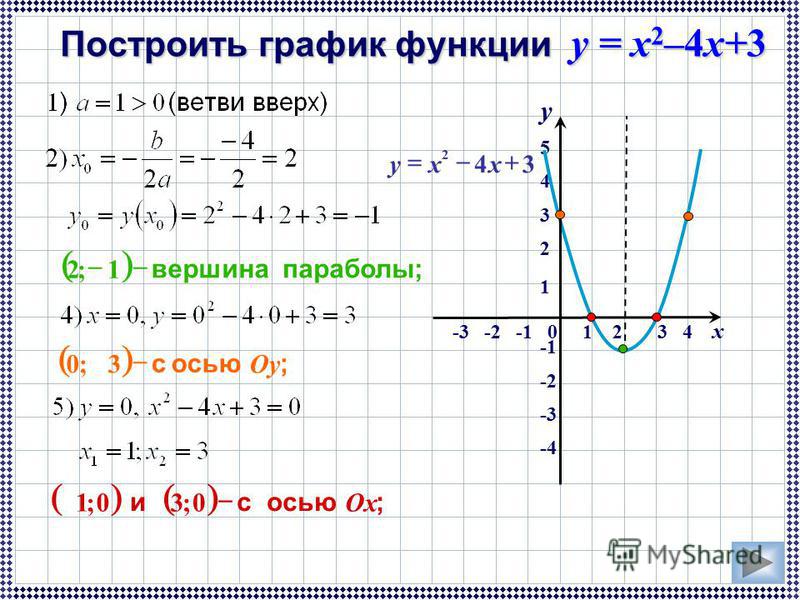
Решение:
y= -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y=0, то есть решаем уравнение -x²-3x=0. Его корни — х=0 и х=-3, то есть (0;0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х=1 y=-1²-3∙1=-4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по сравнению с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.
Прежде чем продолжить построение графиков квадратичных функций вида y=ax²+bx+c, рассмотрим построение графиков функций с помощью геометрических преобразований. Графики функций вида y=x²+c также удобнее всего строить, используя одно из таких преобразований — параллельный перенос.
Рубрика: |Функция y=x^2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке ниже.
Квадратичная функция
Рис 1. Общий вид параболы
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную оси Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы которая лежит на оси симметрии называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0;0).
Основные свойства квадратичной функции
1. При х =0, у=0, и у>0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x=0; Следует также заметить, что максимального значения у функции не существует.
3. Функция убывает на промежутке (-∞;0] и возрастает на промежутке }
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y=f(x) – соответствие, при котором каждому числу x из множества D сопоставляется единственное число y из множества E.
x– аргумент функции, y – значение функции; D или D(f) – область определения функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E(f) – область значений функции; это совокупность всех значений, которые может принимать выражение f(x).
График функции y=f(x) – множество точек (x,y) на координатной плоскости, где x принимает все возможные значения из D(f), а y=f(x).
Четная функция: f(-x)=f(x) для всех ; Нечетная функция: f(-x)=-f(x) для всех ;График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T>0: f(x+T)=f(x) для всех .
Нули функции – значения x такие, что f(x)=0. Интервалы знакопостоянства – множества значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x=b, x=c, x=d; интервалы знакопостоянства: y>0 при ; y. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых , если x12, то f(x1)2). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых , если x12, то f(x1)>f(x2).3. Некоторые алгебраические функции
а) линейная . График функции – прямая линия, проходящая через точки (0, b) и .Функция возрастает при a>0, убывает при a<0.
Частные случаи: y=b – прямая, параллельная оси OX;
y=ax – прямая, проходящая через начало координат.
Точки пересечения с осями координат:
с осью OX – (x1, 0) и (x2, 0),
где , D=b2-4ac – корни квадратного трехчлена;с осью OY – (0, c).
Пример 1. График какой функции является возрастающим:
а) ; б) у = х3 – 27; в) y=2-x?Решение:
Рассмотрим каждую из функций в отдельности:
а) – степенная функция. Область определения этой функции: . На всей области определения функция монотонна.Возьмём два значения х1 = 1 и х2 = 4. Им соответствует у1 = – 1, у2 = – 2. Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
б) у = х3 – 27 – алгебраическая функция. Область определения – множество всех действительных чисел. На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
На всей области определения функция монотонна. Возьмём два значения х1 = 3, х2 = 4. Им соответствует у1 = 0, у2 = 37.
Видим, что если х1 < x2 , то и у1 < у2. Функция возрастающая.
в) y=2-x – показательная функция. Областью определения является множество всех действительных чисел. На всей области определения функция монотонна. Пусть х1 = 0, х2 = 1. Им соответствуют у1 = 1, у2 = 0,5.
Видим, что если х1 < x2 , то у1 > у2. Функция убывающая.
Ответ: б) у = х3 – 27.
Пример 2. Парабола у = 2х2 – (а – 3)х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а. Т.к. парабола проходит через начало системы координат, то координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 02 – (а – 3) ∙ 0 + а + 3; а = – 3.
Уравнение параболы примет вид: у = 2х2 + 6х.
Абсцисса вершины параболы находится по формуле: . Получаем .Ответ: – 1, 5.
Пример 3. В каких точках график функции f(x) = x2 – 3 пересекает прямую у(х) = х – 1?
Решение:
Ответом на данный вопрос является решение системых2 – 3 = х – 1; х2 – х – 2 = 0; х1= – 1, или х2 = 2.
Соответственно, у1 = – 2, у2 = 1.
Ответ: (– 1; – 2), (2; 1).
Пример 4. При каких значениях k прямые – kх + 7у = – 13 и 14у – 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k1х + b1 и у = k2х + b2 параллельны, если k1 = k2, но при этом b1 ≠ b2.
В обоих уравнениях выразим у через х.
. Следовательно, . При этом .
При этом .Ответ: при k = – 1,5.
Пример 5. Найти точки пересечения прямой у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = – 5.
Когда график функции пересекает ось OY, значение х = 0, т.е. у = 5.
Ответ: (– 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1)∙(х – 2).
Решение:
Решаем уравнение (х + 1)∙(х – 2) = 0.
х + 1 = 0 или х – 2 = 0; х1 = – 1, х2 = 2.
Ответ: (– 1; 0), (2; 0).
Пример 7. Найти область значений функции .Решение:
Оцениваем последовательно:
. Ответ: .Пример 8. Найдите сумму целых значений функции у = 3 – 2 sin x.
Решение:
Оценим значение 3 – 2 sin x.
. Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.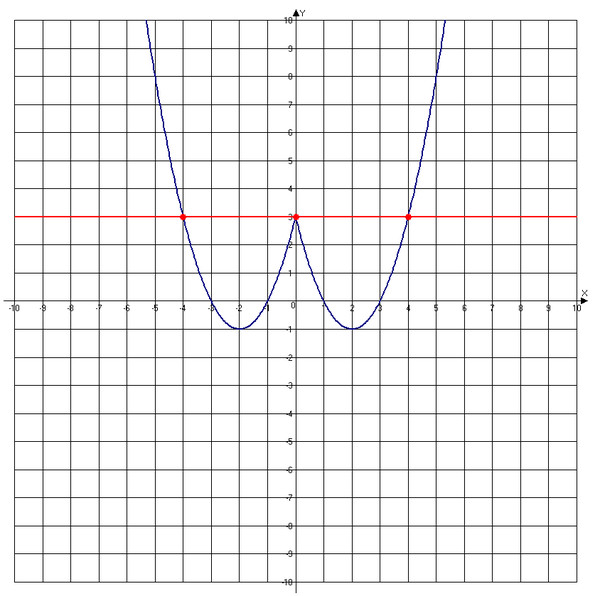
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А(0; 2), проходящая через точку В(2; – 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах2 + bх + с.
1) точка А является вершиной параболы, следовательно .Уравнение примет вид: у = ах2 + с.
2) точка А принадлежит графику, следовательно её координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: – 6 = а ∙ 22 + 2, – 8 = 4 ∙ а, а = – 2.
Получили уравнение у = – 2х2 + 2.
Ответ: у = – 2х2 + 2.
Пример 13. Найдите g (x) , если f (x) = 2x – 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x – 3 = 1, х = 2.
Следовательно, g (f (x)) = 2, т.е. g (1) = 2.
Ответ: g (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y=52x, y=53x-1 и через точку параболы y=(2x-1)2, в которой производная функции, задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4). Согласно уравнению прямой, проходящей через две точки, имеем:– 21х + 21 = 0,5у – 12,5; – 42х + 42 = у – 25; у = – 42х + 47.
Ответ: у = – 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции в точке х0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f(-1)-f(1). 4) Найдите g(f(x)), если Вычислите g(f(2)).
Укажите длину интервала области определения для функций:
24) .25) y=log4(5x+6-x2)
26) y=log6(x2+3).
Укажите области значения функций:
27) y=-3sinx.
28) y=0,7cos3x.
29) .Решите задачи:
30) Сколько натуральных значений может принять функция y=log2(4-x2) на всей области определения?
31) Найдите сумму целых значений функции y=3cosx-5.
32) Укажите функцию, областью значений которой является множество . .33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y=-x0,5; 2) y=1-e-x; 3) y=ctg2x; 4) y=|-x|.
35) Найдите нули функции . 36) Найдите нули функции37) Найдите наименьшее значение функции f(x)=32x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = – 2х2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямой у = 5 – 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = – 2х.
41) В каких точках график функции f (x) = 3x2 + 6x пересекает прямую у = 6 – х?
42) Укажите промежутки возрастания функции y=sin3x на интервале . 43) Укажите промежутки убывания функции y=-2cosx на интервале .Ответы
1) 0; 2) -3/14; 3) – 1; 4) 3; 5) ; 6) ; 7) ;График показательной функции, область определения и область значений функции — Алгебра 11 класс — Osvita.name
1. Функция y=3x−1 образована от показательной функции y=3x (показательной функцией называется функция, которая записана в виде y=ax, где (a>0, a≠1). Чтобы построить график этой функции, необходимо составить следующую таблицу с произвольно выбранными значениями аргумента x:
| x | −2 | −1 | 0 | 1 | 2 |
| y |
2. Чтобы вычислить соответствующие значения функции, необходимо подставить соответствующие значения аргумента x в формулу функции y=3x:
Чтобы вычислить соответствующие значения функции, необходимо подставить соответствующие значения аргумента x в формулу функции y=3x:
a) y=3−2=132=19
б) y=3−1=131=13
в) y=30=1
г) y=31=3
д) y=32=9
3. Вычисленные значения функции записываем в таблицу:
x | -2 | -1 | 0 | 1 | 2 |
y | 19 | 13 | 1 | 3 | 9 |
4. Используя таблицу, строим график функции y=3x:
Используя таблицу, строим график функции y=3x:
5. Функцию y=3x−1 можно записать в виде y=f(x)+a, где a≠0.
* Если a>0, то график функции y=f(x) переместится вдоль оси Oy на a единиц вверх.
* Если a<0, то график функции y=f(x) переместится вдоль оси Oy
Как строить функцию в Excel — Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МS Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека. Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках.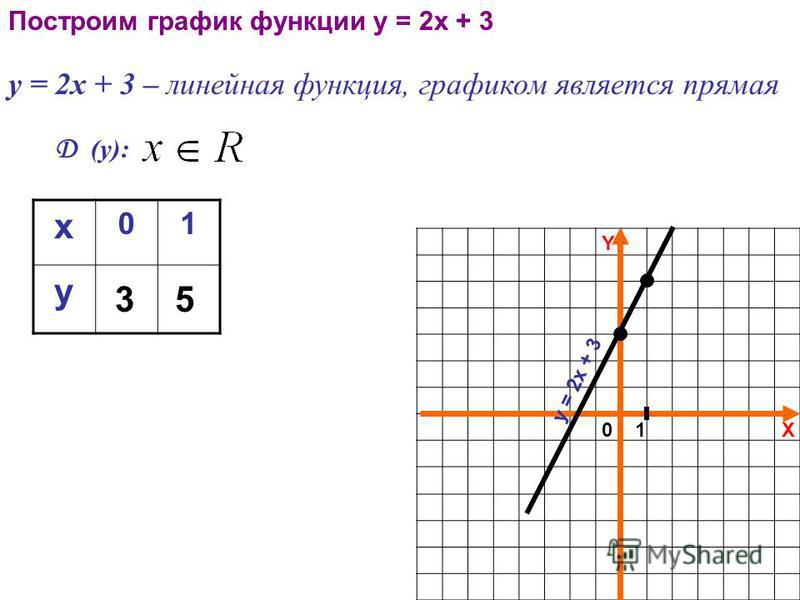 Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графический. Графиком функции y=f(x) называется множество всех точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания обладает очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
- y=kx+b;
- y=;
- y=|x|;
- y=kx2 (y=ax2+bx+c);
- y= ,
а также способы построения графиков функций y=f(x+l), y=f(x)+m, если известен график функции y=f(x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и той системе координат для каждой группы, чтобы наглядно продемонстрировать их отличия. На уроке графики тех же функций дети построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1-я группа
- y=3x+5;
- y=x+5;
- y=3x+5;
- y=3x-1;
- y=-3x+5;
- y=-x+5;
2-я группа
3-я группа
- y=x2;
- y=x2-1;
- y=(x-1)2;
- y=x2-5x+4;
- y=-x2-1;
- y=-(x-1)2;
4-я группа
5-я группа
Работу учащихся опишем на примере построения графика функции y=:
- Определим промежуток построения графика функции.
 Пусть х1=-2, х2=2.
Пусть х1=-2, х2=2. - В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежуток на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этого в ячейке А4 введем формулу =A3+0,1 и скопируем эту формулу в ячейки с А5 по А43.
Рис. 1. В ячейке А4 вводим формулу =A3+0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2). Для этого в ячейку В3 введем формулу: =(A3+1)/(F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1)в ячейки В4 — В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 — В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми». График функции y=построен. При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно продемонстрировать отличительные характеристики каждой из функций в отдельно взятой группе.
Новинка! согласно определению модуля:x, если х> = 0 f (x), если f (x)> = 0
| x | знак равно | f (x) | =
-x, if x
Пример:
Построить график функции у = | 2x-3 | -х.
Рассмотрим два случая.
2х-3> = 0 2х-3
y = 2x-3-x или y = -2x + 3-x
x> = xSUB>
y = x-3 y = -3x + 3
Таким образом, чтобы построить график функции у = | 2x-3 | -x, надо построить графики функций, заданными различными выражениями на различных промежутках.
х-3, х> =
у =
— 3х + 3, хSUB>
График изображен ниже:
y = | 2x-3 | -x
Построить график:
Y = | X | + X
Y = | X | · (X-2)
Y = | X + 4 | · X
Y =
Y =
Y = 2 –1)
Y = 2 + 4X + 3)
Y =
Y =
Y = X — 1 — | X-1 |
Y = | 3X-4 | -X
Y =
13.Y =
Y =
Y =
Y =
Y = X 2 — 2 | X + 1 | -1
Y = X +
Y = | X 2 -4X + 3 | + 2X
Y =
Y = | X 2 -4 | + 4X
Y =
Элементарные преобразования графика функции у = f (x)
формула зависимости имеют вид | y | = f (x):
Надо построить график у = f (x)
Часть графика расположенную выше оси Ох (и на самой оси) оставить без изменений
Часть графика расположенную ниже оси Ох стереть
Для оставленной части построить симметричную относительно оси Ох
Пример:
Построить график | y | = 2х-1
Построить график :
Y | = 5X-4
| Y | = 9-X 2
| Y | =
| Y | = (X + 4) 2 -5
| Y | =
| Y | = X + 2
| Y | = X 2 -6X + 8
| Y | = X 2 -4X
X | Y | = 2
| Y | =
| Y | · (X + 1) = 1
| Y | = 1-
| Y | = | 2X-X 2 |
Y 2 = -2X
| Y | = 8 + 2X-X 2
Y 2 = 0,5X
Элементарные преобразования графика функции у = f (x)
Если формула зависимости у = f (| x |):
Надо построить график функции у = f (x), часть графика расположенную правее оси Оу (и на самой оси) оставить без изменений
Построить для оставленной части симметричной относительно оси Оу
Построить для оставленной части симметричной оси Оу
Пример:
Построить график у = 2 | x | -1
Построить график:
Y = 5 | X | -5
Y = 9- | X | 2
Y =
Y =
Y =
Y = (| X | +4) 2 -5
Y =
Y =
Y = | X | -1
Y =
Y = X 2 — | X | -6
Y = -X 2 +6 | X | -8
Постройте график.
 С его помощью укажите пути функций, интервалы знаковопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функций, интервалы знаковопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
2- , если | X |
у = , если | X |> 4
Y = X 2 — | X | -2
Решите уравнение X 2 +3 | X | -18 = 0 графически.
Y = | X | -X 2
Y =
Элементарные преобразования графика функции у = f (x)
Если формула в зависимости имеет вид = | f ( x) |,
График функции у = f (x) выше оси Ох (и на самой оси Ох) оставить без изменений
Для части расположенной ниже оси Ох строят симметричную относительно
оси Ох
Часть графика расположенная ниже оси Ох стирается.
Пример:
Построить график функции у = | 2x-1 |
Построить график:
Y = | 5X-4 |
Y = | 9 -X 2 |
Y =
Y = | (X-4) 2 -5) |
Y = | X + 2 |
Y = | X-1 |
Y = | X 2 + 2X |
Y =
Y = | |
Y = || X 2 -3 | -1 |
Y = | X 2 -1 |
Y = | X + 1 | -2
Y = 4 + | X-3 |
Y = 3 ∙ | X-2 |
Найдите наибольшее и наименьшее значение функции Y = :
а) на отрезке [-2; 2]
б) на луче [0; +)
в) на луче (-; 3 ]
г) на отрезке [-5; 0]
16. Найдите наименьшее и наибольшее значение функции Y = :
Найдите наименьшее и наибольшее значение функции Y = :
а) на луче (-; 5]
б) на отрезке [4; 7]
в) на луче [2; +)
г) на полуинтервале [-1; 6]
17.Решите уравнение графически:
а) | X 2 -9 | = 5 б) | X-2 | = X 2 в) | X + 1 | = -2X 2
г) | X 2 -1 | = | X 2 -X + 1 | д) | X-3 | = X 2 +1 е) | X + 5 | = -X-1
ё) -2 (X + 2) 2 ж) з) (X + 3) 2
и) -X
Построение графиков используются, несколько модулей
Пример: построить график функции
1).Найти те значения, стоящее под знаком модуля, равно нулю. ; ; .
2). Числовую прямую разбивают на точки точками, соответствует найденным значениям
0 1
3). На каждом промежутке определяют знак выражения, стоящего под знаком модуля (берут числа из промежутка и ставят в под модульное выражение). Определяют знак стоящего под знаком модуля
Определяют знак стоящего под знаком модуля
— 0 — 1 +
— + +
4).Используется форму промежутка, раскрывают модуль (пользуясь определением модуля) на данном промежутке и упрощают
Составляют структурную функцию
y
графиккусочной функции
1
x
0 1
1). Найдите промежутки убывания функции и ее наибольшее значение на отрезке .Ответ: , .
2). Найдите множество значений функции и ее наименьшее значение на отрезке . Ответ: , .
3). Найдите множество значений функции и значения, которые функция принимает ровно три раза. Ответ: ; ; .
4). Найдите все значения , при которых значения функции положительные и принимаемые функции ровно 2 раза. Ответ: ; , .
Ответ: ; , .
5). Постройте график функций , и для каждого укажите количество общих точек этого прямого графика и .
а). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При , бесконечное множество точек.
б). . Ответ: Общих точек нет при ;
При , одна точка;
При и , две точки;
При , , три точки;
При , четыре точки.
6). Найдите наибольшее и наименьшее значение функции на отрезке . Ответ: ; .
7). Найдите наименьшее значение функции
а). .Ответ: при .
б). .Ответ: при .
9). Докажите, что если , то наименьшее значение функции равно .
10). Исследуйте функцию на промежутки монотонности
а). . Ответ: На промежутках ; функция убывает. На промежутках возрастает.
б). . Ответ: На промежутках ; функция убывает. На промежутках и возрастает. На промежутках и функция постоянна.
11). Постройте графики функций
1). 2).
3). 4).
Решение неравенств, показ модуля знака
Неравенства вида
> , где > 0
Если выражение, стоящее под знаком модуля, обозначить через t (f (x ) = t), то данное неравенство примет вид > .Используя геометрический смысл модуля (модуль на числовой прямой представляет собой расстояние от точки, которое представляет данное число, до точки ноль). Изображаем на числовой прямой все точки, расстояние от которых до ноля больше .
Изображаем на числовой прямой все точки, расстояние от которых до ноля больше .
——— ∙ —————— ∙ ————— ∙ ———— ►t
— 0
t или t>
Решаем совокупность неравенств
Пример:
Решите неравенство > 11
Решение: > 11
Пусть , > 11
——— ∙ ——————— ∙ ————— ∙ ———— ►т
-11 0 11
; ;
Ответ: ; ;
Неравенство вида > , где B> 0 верно при всех в области допустимых значений неравенства.
Решите неравенства
1). > 11. Ответ:
2). . Ответ:
3). . Ответ: : .
4). . Ответ: . .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). > 2. Ответ: .
Неравенства вида
>
Учитывая свойство модуля =
и свойство неравенства: если обе части неравенства неотрицательны, то при возведении в квадрат получается неравенство равносильного данного.
Неравенство > можно равносильным неравенством > это — > 0 ( — ) ∙ ( + )> 0
Далее методом интервалов или заменить совокупностью систем
Аналогично решаются неравенства вида .
Решите неравенства
1). . Ответ: .
2). Найти целочисленные решения неравенства .
Ответ: -8; -7; -6; … -1; 0.
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). . Ответ: .
7). . Ответ: .
8). . Ответ: .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: .
13). . Ответ: .
14). . Ответ: .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
Ответ: .
20). . Ответ: .
21). . Ответ: .
22). . Ответ: .
23). . Ответ: .
Решение неравенств вида
;
Неравенство
Доказательство:
.
Неравенство
Доказательство:
.
.
Решите неравенства
1). . Ответ: .
2). . Ответ: .
3). . Ответ: .
4). . Ответ: .
5). . Ответ: .
6). .Ответ: или .
7). . Ответ: .
8). . Ответ: ; .
. Ответ: ; .
9). . Ответ: .
10). . Ответ: .
11). . Ответ: .
12). . Ответ: или .
13). . Ответ: ; .
14). . Ответ: или .
15). . Ответ: .
16). . Ответ: .
17). . Ответ: .
18). . Ответ: .
19). . Ответ: .
20). . Ответ: ; .
Решение неравенств, несколько модулей методом интервалов
Суть метода в следующем:
Пример:
1).Находят значения стоящие под знаком модуля равно нулю.
2). Числовую ось разбивают на промежутки точками, значениям заменители
1
3). На каждом промежутке числа определяют знак выражения, стоящего под знаком модуля (берут из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)
На каждом промежутке числа определяют знак выражения, стоящего под знаком модуля (берут из промежутка, ставят в подмодульное выражение, определяют знак выражения, стоящего под знаком модуля)
— 0 + 1 +
-1 — — +
4).Берут промежуток, раскрывают каждый модуль, пользуясь определением модуля на данном промежутке, и решают неравенство
5). Проверяют, принадлежат ли найденные решения неравенства рассматриваемому промежутку; если принадлежат, то их включают в ответ
0
2
Если нет — отбрасывают. Так поступают с каждым промежутком.
6). Объединяют все решения исходного неравенства, найденные на всех промежутках.
Ответ: -2SUB>
Решите неравенство
1). Ответ:
2). Ответ:
Ответ:
3). Ответ:
4). Ответ:
5) .Укажите целочисленные решения неравенства Ответ: 3; 4
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
11). Ответ:
12). Ответ:
13). Ответ:
14). Ответ:
15). Ответ:
16). Ответ:
Решение неравенств, новый знак модуля, метода новой новой модели.
1). Найти область переменных, входящую в неравенство.
2). В уравнении часто встречается фиксированное выражение, зависящее от неизвестной величины, то имеет значение обозначить это выражение, какой либо буквой. Когда вводится обозначение желательно сразу отбросить все или некоторые значения при уравнении = не имеет решений, т.е. указывает сразу указать область значений функции = .
Когда вводится обозначение желательно сразу отбросить все или некоторые значения при уравнении = не имеет решений, т.е. указывает сразу указать область значений функции = .
3). Решить неравенство относительно введенной неизвестной.
4). Решить неравенство относительно исходной переменной.
5). Учитывая область допустимых значений исходного неравенства записать ответ.
Пример:
Характеристики модулей имеют Пусть = , , тогда неравенство примет вид = 1; = -3.f
Учитывая, что имеем
Учитывая область допустимых значений неравенства Ответ:
Решите неравенства
1). Ответ:
2). Ответ:
Ответ:
3). Ответ:
4). Ответ:
5). Ответ:
6). Ответ:
7). Ответ:
8). Ответ:
9). Ответ:
10). Ответ:
Изображение на координатной плоскости точек, координаты которых соответствуют данному неравенству
Чтобы на координатной плоскости изобразить множество точек, координаты задают неравенству надо:
1).Построить множество точек, координаты которых: удовлетворяют уравнение (если линия изображается пунктирной, если не строго, то сплошной).
2). График или графики разбивают координатную плоскость на части.
3). Взять координаты точки, принадлежащей каждой части по очереди и поставить в неравенство. Если координаты точки удовлетворяют неравенству, то часть координатной плоскости заштриховать.
Если координаты точки удовлетворяют неравенству, то часть координатной плоскости заштриховать.
Пример: Изобразить на координатной системе множество точек, координаты которых удовлетворенству .
1). Построим график уравнения .
или
III II I
-1 0 1
Прямые и изображаем сплошными линиями, так как неравенство не строгое. Прямые разбивают координатную плоскость на три области. Неравенству удовлетворяют координаты точек, принадлежащих II части, поэтому заштриховываем II часть.
Изобразите координатную систему множества точек, координаты которых удовлетворяют.
1). .
2). .
3). .
4). .
5). .
6). .
7). .
8). .
9). .
.
10). .
11). .
12). .
13). .
14). .
15). .
16). .
17). .
18). .
19).
20). .
21). .
22). .
23. .
24). .
Изобразите на координатной плоскости множество точек, удовлетворяющих условию
а) . б) .
в) г)
д) е) .
006 Системы неравенств с Совета, Системный план модуля 1). Найдите все значения , при которых система неравенств имеет единственное решение.
а). Ответ: При .
б). Ответ: При .
2). При каких значениях программы система неравенств имеет ровно одно решение ?. Для всех таких найдите это решение.
Для всех таких найдите это решение.
а). Ответ: При , ;
При , .
б). Ответ: При , ;
При , .
3). При каких значениях параметров система не имеет решения.
а). Ответ: При .
б). Ответ: При .
4). Для каждого значения параметра решите систему неравенств.
а). Ответ: При , ;
При , ;
При , ;
При , .
б). Ответ: При и , ;
При , ;
При , ;
При , ;
При , .
Нестандартные уравнения и неравенства, стандартные решения не проходят. Во многих случаях решение таких функций и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых функций, выполняются уравнения в левой и правой частях уравнения или неравенства.
Во многих случаях решение таких функций и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых функций, выполняются уравнения в левой и правой частях уравнения или неравенства.
Если, например, наименьшее значение одной из функций совпадает с наибольшим значением функции , то уравнение = заменяют равносильную систему , где — наименьшее значение илиее .
Решение системы является решением уравнений = .
1). Решите уравнение
Уравнение необходимо решить графически. Ответ:
2). Решите неравенство
. Применить метод оценки. Ответ:
3). Решите уравнение
. Решить уравнение графически. Ответ:
4). Решите уравнение
.Пририцательное свойство: сумма неотрицательных функций равна нулю тогда и только тогда, когда все функции равны равны нулю. Ответ:
Ответ:
5). Решите уравнение
.Область допустимых значений (ОДЗ) уравнения из конечного числа значений. Для решения достаточно проверить все эти значения. Ответ:
Применение свойств = для любого
при нахождении значений выражения
Вычислите:
1). Ответ: -6
2). , если t = -10; t = 127. Ответ: -8; 127
3). ∙ . Ответ: 0,125
4). — . Ответ: -6
5). — . Ответ: 2
6). — . Ответ: 8
7). + . Ответ: 2
8). + . Ответ: 6
9). + .Ответ: 2
10). + . Ответ: 10
11). — . Ответ: -3
12). — . Ответ: -6
— . Ответ: -6
13). — — 0,5 . Ответ: 0
14). + . Ответ: 1
15). + Ответ: 1
16). . Ответ: 8
17). Найти и , если = — .Ответ: 28; -2
18). Найти и , если = — . Ответ: 40; -2
19). Другое значение выражения
с числом . Ответ:
20). Другое значение выражения
с числом . Ответ:
21). Докажите, что выражение ∙ является корнем уравнения = 1.
22). Док, что выражение является корнем уравнения = 1.
Док, что выражение является корнем уравнения = 1.
23). Удовлетворяет ли число — неравенству 7 +58 +13> 0.
Ответ: нет
24). Удовлетворяет ли число — неравенству 11 +26 -73 0.
Ответ: да
Л и т е р а т у р а
1). Алгебра: 8; 9; 10 — 11 класс.
Авторы: А.Г.Мордкович, Т.Н. Мишустина, Е.Е. Тульчинская.
2). Задания по математике для подготовки к письменному экзамену в 9 классе.
Авторы: Л.И. Звавич, Д.И.Аверьянов, Б.П. Пигарёв, Т.Н. Грушанина.
3). Сборник задач по алгебре 8 — 9 класс.
Авторы: М.Л. Галицкий, А.М. Гольдман, Л.И. Звавич.
4). Сборник для письменного экзамена за курс средней школы 11 класс.
Авторы: Г.В. Дорофеев, Г.К.Муравин, Е.А.Седова.
5). Алгебраический тренажер.
Алгебраический тренажер.
Авторы: А.Г. Мерзляк, В.Б.Полонский, М.С.Якир
6). Материалы ЦТ и ЭГЭ за 2002 — 2005 годы.
7). Математика. Самостоятельные и контрольные работы 8; 9; 10 — 11 классы.
Авторы: А.П. Ершова, В.В. Голобородько.
8). Различные сборники для поступающих в В У З Ы.
Постройте график функции y x2 4x 3. Квадратичная и кубическая функции. Основные свойства квадратичной функции
Разберем как строить график с модулем.
Найдены точки при переходе между модулями меняются.
Каждое выражение, которое под модулем приравниваем к 0. У нас их два x-3 и x + 3.
х-3 = 0 и х + 3 = 0
х = 3 и х = -3
У нас числовая прямая разделится на три интервала (-∞; -3) U (-3; 3) U (3; + ∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞; -3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х = -4
х-3 = -4-3 = -7 и х + 3 = -4 + 3 = -1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞; -3).
г = — (х-3) — ( — (х + 3)) = — х + 3 + х + 3 = 6
На интервале (-∞; -3) получился график линейной функции (прямой) у = 6
2. Рассмотрим второй интервал (-3; 3). Найдем как будет выглядеть уравнение графика на этом отрезке.Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х = 0
x-3 = 0-3 = -3 и x + 3 = 0 + 3 = 3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x + 3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
г = — (х-3) — ( + (x + 3)) = — х + 3-х-3 = -2x
На интервале (-3; 3) получился график линейной функции (прямой) у = -2х
3. Рассмотрим третий интервал (3; + ∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
Рассмотрим третий интервал (3; + ∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х = 5
х-3 = 5-3 = 2 и х + 3 = 5 + 3 = 8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3; + ∞).
г = + (х-3) — ( + (х + 3)) = х-3-х-3 = -6
На интервале (3; + ∞) получился график линейной функции (прямая) у = -6
4.Теперь подведем итог.Постоим график y = | x-3 | — | x + 3 |.
На интервале (-∞; -3) строим график линейной функции (прямая) у = 6.
На интервале (-3; 3) строим график линейной функции () у = -2х.
Чтобы построить график у = -2х подберем несколько точек.
x = -3 y = -2 * (- 3) = 6 получилась точка (-3; 6)
x = 0 y = -2 * 0 = 0 получилась точка (0; 0)
x = 3 y = — 2 * (3) = — 6 получилась точка (3; -6)
На интервале (3; + ∞) строим график линейной функции (прямой) у = -6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при котором прямая y = kx имеет график y = | x-3 | — | x + 3 | данной функции ровно одну общую точку.
Прямая y = kx при любом значении k всегда будет проходить через точку (0; 0). Поэтому мы можем изменить угол наклона данной прямой y = kx, а за наклон у нас коэффициент k.
Если k будет любое положительное число, то будет одно пересечение, прямой y = kx с графиком y = | x-3 | — | x + 3 |.Этот вариант нам подходит.
Если k будет принимать значение (-2; 0), то пересечений прямой y = kx с графиком y = | x-3 | — | x + 3 | будет три.Этот вариант нам не подходит.
Если k = -2, решений будет множество [-2; 2], потому что прямая y = kx будет совпадать с графиком y = | x-3 | — | x + 3 | на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y = kx с графиком y = | x-3 | — | x + 3 | Будет иметь одно пересечение.
Если k = 0, то пересечений прямого y = kx с графиком y = | x-3 | — | x + 3 | также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞; -2) U; график f (х) = х + 2 — это прямая, параллельная прямая f (х) = х, но сдвинутая на две единицы вверх и поэтому проходящая через точку с координатами (0,2) (потому что постоянная равна 2).
Построение графика сложной функции
Найдите нули функции. Нули функции — это значения «х», при которых у = 0, то есть это точки пересечения графика с осью Х.Имейте в виду, что нули не все функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
Найдите и отметьте горизонтальные асимптоты. Асимптота — это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0). Асимптоту отметьте пунктирной линией. Если переменная «х» находится в знаменателе дроби (например, y = 1 4 — x 2 {\ displaystyle y = {\ frac {1} {4-x ^ {2}}}}
), приравняйте знаменатель к нулю и найдите «х». В представленном примере «х» функция определена (в примере представлены пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты не существуют только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
В представленном примере «х» функция определена (в примере представлены пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты не существуют только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
«Натуральный логарифм» — 0,1. Натуральные логарифмы. 4. «Логарифмический дартс». 0,04. 7. 121.
«Степенная функция 9 класс» — У. Кубическая парабола. У = х3.9 класс учитель Ладошкина И.А. У = х2. Гипербола. 0. У = хn, у = х-n где n — заданное натуральное число. Х. Показатель — четное натуральное число (2n).
«Квадратичная функция» — 1 Определение квадратичной функции 2 Свойства функции 3 Графики функции 4 Квадратичные неравенства 5 Вывод. Свойства: Неравенства: Подготовил ученик 8А класса Герлиц Андрей. План: График: -Промежутки монотонности при а> 0 при а
«Квадратичная функция и её график» — Решение.у = 4x А (0,5: 1) 1 = 1 А-принадлежит.При а = 1 формула у = аx принимает вид.
«8 класс квадратичная функция» — 1) Построить вершину параболы. Построение графика квадратичной функции. Икс. -7. Построить график функции. Алгебра 8 класс Учитель 496 школы Бовина Т. В. -1. План построения. 2) Построить ось симметрии x = -1. у.
Как построить параболу? Существует несколько способов построения графика квадратичной функции. Каждый из них имеет свои плюсы и минусы. Рассмотрим два способа.
Начнём построения графика квадратичной функции вида y = x² + bx + c и y = -x² + bx + c.
Пример.
Построить график функции y = x² + 2x-3.
Решение:
y = x² + 2x-3 — квадратичная функция. График — парабола ветвями вверх. Координаты вершины параболы
От вершины (-1; -4) строим график параболы y = x² (как от начала координат. Вместо (0; 0) — вершина (-1; -4). От (-1; -4) идём вправо на 1 затем: 2 — вправо, 4 — вверх, 2 — влево, 4 — вверх; 3 — вправо, 9 — вверх, 3 — влево, 9 — вверх. Если этих 7 точек, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек, далее — 4 вправо, 16 — вверх и т. д.).
График квадратичной функции y = -x² + bx + c — парабола, приводящей вниз. Для построения графика ищем координаты вершины и от нее строим параболу y = -x².
Пример.
Построить график функции y = -x² + 2x + 8.
Решение:
y = -x² + 2x + 8 — квадратичная функция. График — парабола ветвями вниз.Координаты вершины параболы
От вершины строим параболу y = -x² (1 — вправо, 1 — вниз; 1 — влево, 1 — вниз; 2 — вправо, 4 — вниз; 2 — влево, 4 — вниз и т. Д.):
Этот способ позволяет построить параболу быстро и не вызывает затруднений, если вы умеете строить тесты функций y = x² и y = -x². Недостаток: если координаты вершины — дробные числа, строить график не очень удобно. Если требуется знать значения точек пересечения графика с осью Ох, необходимо также решить уравнение x² + bx + c = 0 (или —x² + bx + c = 0), если эти точки непосредственно можно определить по рисунку.
Другой способ построения параболы — по точкам, то есть можно найти несколько точек графика и через них провести параболу (с учетом того, что прямая x = хₒ является её осью симметрии). Обычно для этого берут вершину параболы, точки пересечения графика с осями координат и 1-2 дополнительные точки.
Построить график функции y = x² + 5x + 4.
Решение:
y = x² + 5x + 4 — квадратичная функция. График — парабола ветвями вверх.Координаты вершины параболы
то есть вершина параболы — точка (-2,5; -2,25).
Ищем. В точке пересечения с осью Ох y = 0: x² + 5x + 4 = 0. Корни квадратного уравнения х1 = -1, х2 = -4, то есть получили две точки графика (-1; 0) и (-4; 0).
В точке пересечения графика с осью Оy х = 0: y = 0² + 5 ∙ 0 + 4 = 4. Получили точку (0; 4).
Для уточнения графика можно найти дополнительную точку. Возьмем х = 1, тогда y = 1² + 5 ∙ 1 + 4 = 10, то есть еще одна точка графика — (1; 10). Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямого, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямого, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Построить график функции y = -x²-3x.
Решение:
y = -x²-3x — квадратичная функция. График — парабола ветвями вниз. Координаты вершины параболы
Вершина (-1,5; 2,25) — первая точка параболы.
В точках пересечения графика с осью абсцисс y = 0, то есть решаем уравнение -x²-3x = 0. Его корни — х = 0 и х = -3, то есть (0; 0) и (-3; 0) — еще две точки графика. Точка (о; 0) является также точкой пересечения параболы с осью ординат.
При х = 1 y = -1²-3 ∙ 1 = -4, то есть (1; -4) — дополнительная точка для построения графика.
Построение параболы по точкам — более трудоёмкий, по с первым, способ. Если парабола не пересекает ось Oх, дополнительных точек потребуется больше.2 называется квадратичной функцией. Графиком квадратичной функции является парабола. Общий вид параболы представлен на рисунке.
Квадратичная функция
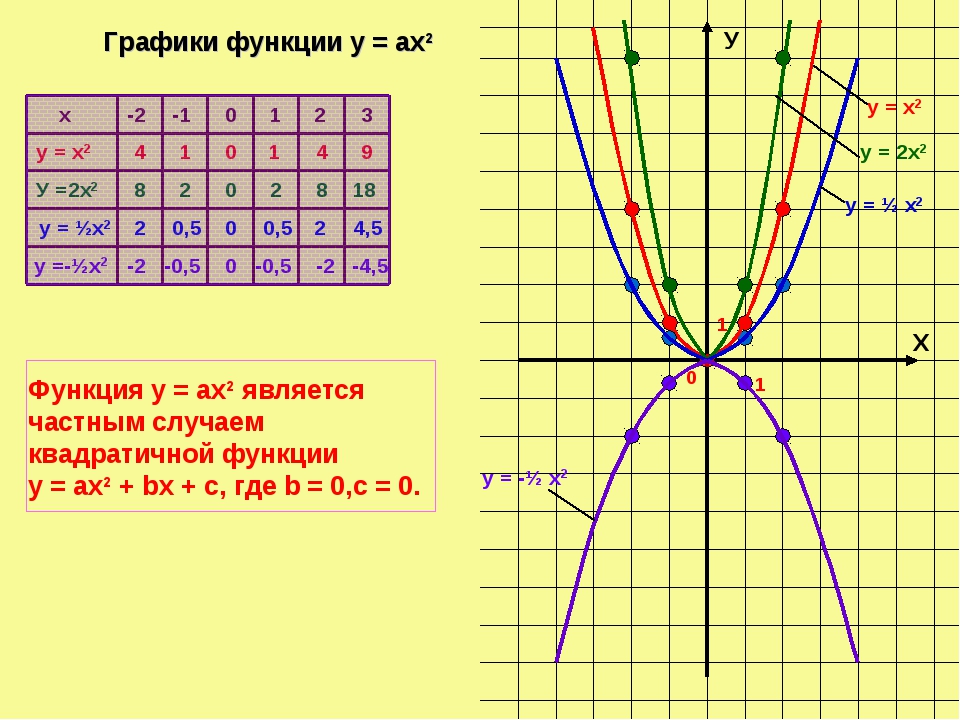
Рис 1. Общий вид параболы.
Как видно из графика, он симметричен относительно оси Оу. Ось Оу называется осью симметрии параболы. Это значит, что если провести на графике прямую параллельную ось Ох выше это оси. То она пересечет параболу в двух точках. Расстояние от этих точек до оси Оу будет одинаковым.
Ось симметрии разделяет график параболы как бы на две части. Эти части называются ветвями параболы. А точка параболы, которая лежит на оси симметрии, называется вершиной параболы. То есть ось симметрии проходит через вершину параболы. Координаты этой точки (0; 0).
Основные свойства квадратичной функции
1. При х = 0, у = 0, и у> 0 при х0
2. Минимальное значение квадратичная функция достигает в своей вершине. Ymin при x = 0; Следует также заметить, что размеры значения у функции не существует.3 долл. 3 $
1.3 $ имеет противоположные значения, то график функции симметричен относительно начала координат.
Теперь отметим точки на координатной плоскости и построим график (см. Рис. 1).
Эта кривая называется кубической параболой.
Примеры
I. На небольшом корабле полностью закончилась пресная вода. Необходимо привезтиное количество воды из города. Вода заказывается заранее и оплачивается за полный куб, даже если залить её чуть меньше.3+ 1 $.
1. Составим таблицу значений:
2. Построим точки. Мы видим, что эти точки симметричны относительно точки с координатами (0,1). В итоге получаем кубическую параболу, смещенную вверх по оси OY (см. Рис. 3).
Решения | Контр. 6. Квадратная функция — Математика, 8 класс
1. 2 — 1: $ Ответ: а) $ (- 3; -1).2 — 1:
$ Ответ: б) $ (4; 3).
$ 3. Укажите график функции, заданной формулой
Вариант 1
$ y = x2 — 5 $
Ответ: а) $ (- 3; -1).2 $
Ответ: б) $ (4; 3).
$ 4. 2} {3} $ является квадратной;
в) Любая парабола пересекает ось ординат;
г) множеством действительных значений квадратной функции множество всех возможных чисел. Ответ: г).
Вариант 2
а) областью определения квадратной функции является множество всех действительных чисел;
б) графиком квадратной функции является гипербола;
в) ось симметрии параболы параллельна оси абсцисс;
г) график квадратной функции пересекает ось ординат в двух точках.
Ответ: а).
5.2-6x + 5 $ 6. С помощью графика функции из задания №5 найдите:
- значения аргумента, при которых значения функции отрицательны [2 в.: положительны];
- промежуток возрастания функции [2 в.: Убывание];
- уравнение оси симметрии параболы [2 в: множество параметров функции].
7.2 $] смещением его на три [2в .: пять] единичных отрезков вправо [2в .: влево] вдоль оси абсцисс и на восемь [2в .: три] единичных отрезков вдоль оси ординат.
Вариант 1
Смещенный график на три единицы права и восемь единиц вниз: $ y = 2 (x-3) ^ 2 — 8.2 — 2x + 1 = 0. $
Находим дискриминант:
$ D = 4-3 = 1, $
$ x = \ dfrac {2 ± 1} {\ dfrac {3} {2}},
$ $ x = 2, x = \ dfrac {2} {3}, $
$ y = 1-2 ⋅ \ dfrac {2} {3} = — \ dfrac {1} {3}, $
Ответ: $ (\ dfrac {2} {3}; — \ dfrac {1} {3}).
долларов США. 9.2-100 ≥ -100 $ при $ x є R. $ Наименьшее значение при $ x = 10, $ при $ y = -10. $
10. Постройте график функции:
Вариант 1
$ y = \ sqrt {x ^ 2 + 8x ^ 2 + 16x ^ 2}; $
$ y = \ sqrt {(x ^ 2 + 4x) ^ 2}; $
$ y = | х ^ 2 + 4х |.2-3x |. $
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y = f (x) — соответствие, при котором данному x из множества D сопоставляется единственное число y из числа E.
x– аргумент функции, y — значение функции; D или D (f) — определения области функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E (f) — область значений функции; это совокупность всех значений, которые могут принимать выражение f (x).
График функции y = f (x) — множество точек (x, y) на координатной плоскости, где x принимает все возможные значения из D (f), а y = f (x).
Четкая функция: f (-x) = f (x) для всех; Нечетная функция: f (-x) = — f (x) для всех; График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T> 0: f (x + T) = f (x) для всех. Нули функции — значения x такие, что f (x) = 0. Интервалы знакопостоянства — множество значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x = b, x = c, x = d; интервалы знакопостоянства: y> 0 при; у. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых, если x 1 2 , то f (x 1 ) 2 ). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых, если x 1 2 , то f (x 1 )> f (x 2 ). 3. Некоторые алгебраические функции
а) линейная . График функции — прямая линия, проходящая через точки (0, b) и. Функция возрастает при a> 0, убывает при a <0.
Частные случаи: y = b — прямая, параллельная оси OX;
y = ax — прямая, проходящая через начало координат.
б) квадратичная . График функции — парабола. Ветви параболы движется вверх при a> 0, вниз при a. Точки пересечения с осями координат:
с осью OX — (x 1 , 0) и (x 2 , 0),
где, D = b 2 -4ac — корни квадратного трехчлена; с осью OY — (0, c).
Пример 1. График какой функции является возрастающим:
а); б) у = х 3 — 27; в) y = 2 -x ? Решение:
Рассмотрим каждую из функций в отдельной:
а) — степенная функция.Область определения этой функции:. На всей области определения функция монотонна. Возьмём два значения х 1 = 1 и х 2 = 4. Им соответствует у 1 = — 1, у 2 = — 2. Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
б) у = х 3 — 27 — алгебраическая функция. Область определения — множество всех действительных чисел. На всей области определения функция монотонна.Возьмём два значения х 1 = 3, х 2 = 4. Им соответствует у 1 = 0, у 2 = 37.
Видим, что если х 1 2 , то и у 1 <у 2 . Функция возрастающая.
в) y = 2 -x — показательная функция. Областью создания множества всех действительных чисел. На всей области определения функция монотонна. Пусть х 1 = 0, х 2 = 1.Им соответствуют у 1 = 1, у 2 = 0,5.
Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
Ответ: б) у = х 3 — 27.
Пример 2. Парабола у = 2х 2 — (а — 3) х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а.Т.к. парабола проходит через начало системы координат, в координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 0 2 — (а — 3) ∙ 0 + а + 3; а = — 3.
Уравнение параболы примет вид: у = 2х 2 + 6х.
Абсцисса вершины параболы находится по формуле:. Получаем. Ответ: — 1, 5.
Пример 3. В каких точках график функции f (x) = x 2 — 3 пересекает прямую у (х) = х — 1?
Решение:
Ответом на данный вопрос является решение системы х 2 — 3 = х — 1; х 2 — х — 2 = 0; х 1 = — 1, или х 2 = 2.
Соответственно у 1 = — 2, у 2 = 1.
Ответ: (- 1; — 2), (2; 1).
Пример 4. При каких значениях k прямые — kх + 7у = — 13 и 14у — 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k 1 х + b 1 и у = k 2 х + b 2 параллельны, если k 1 = k 2 , но при этом b 1 ≠ b 2 .
В обоих уравнениях выразим у через х.
. Следовательно,. При этом. Ответ: при k = — 1,5.
Пример 5. Найти точки пересечения прямого у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = — 5.
Когда график функции пересекает ось OY, значение х = 0, т .е. у = 5.
Ответ: (- 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1) ∙ (х — 2).
Решение:
Решаем уравнение (х + 1) ∙ (х — 2) = 0.
х + 1 = 0 или х — 2 = 0; х 1 = — 1, х 2 = 2.
Ответ: (- 1; 0), (2; 0).
Пример 7. Найти область значений функции. Решение:
Оцениваем последовательно:
. Ответ: . Пример 8. Найдите сумму целых значений функции у = 3 — 2 sin x.
Решение:
Оценим значение 3 — 2 sin x.
. Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А (0; 2), проходящая через точка В (2; — 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах 2 + bх + с.
1) точка А является вершиной параболы, следовательно. Уравнение примет вид: у = ах 2 + с.
2) точка А принадлежит графику, следовательно ее координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах 2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: — 6 = а ∙ 2 2 + 2, — 8 = 4 ∙ а, а = — 2.
Получили уравнение у = — 2х 2 + 2.
Ответ: у = — 2х 2 + 2.
Пример 13. Найдите g (x), если f (x) = 2x — 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x — 3 = 1, х = 2.
Следовательно , g (f (x)) = 2, т.е. г (1) = 2.
Ответ: г (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y = 5 2x , y = 5 3x-1 и через точку параболы y = (2x-1) 2 , в которой производная функция , задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4).Согласно уравнению прямого, проходящей через две точки, имеем: — 21х + 21 = 0,5у — 12,5; — 42х + 42 = у — 25; у = — 42х + 47.
Ответ: у = — 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции в точке х 0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f (-1) -f (1). 4) Найдите g (f (x)), если Вычислите g (f (2)). Укажите длину интервала определения функций:
24). 25) y = log 4 (5x + 6-x 2 )
26) y = log 6 (x 2 +3).
Укажите области значений функций:
27) y = -3sinx.
28) y = 0,7cos3x.
29). Решите задачи:
30) Сколько натуральных значений может принять функцию y = log 2 (4-x 2 ) на всей области определения?
31) Найдите сумму целых значений функции y = 3cosx-5.
32) Укажите функцию, областью значений которой является множество. . 33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y = -x 0,5 ; 2) y = 1-e -x ; 3) y = ctg2x; 4) у = | -х |.
35) Найдите нули функции. 36) Найдите нули функции 37) Найдите наименьшее значение функции f (x) = 3 2x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = — 2х 2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямого у = 5 — 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = — 2х.
41) В каких точках график функции f (x) = 3x 2 + 6x пересекает прямую у = 6 — х?
42) Укажите промежутки возрастания функции y = sin3x на интервале. 43) Укажите промежутки убывания функции y = -2cosx на интервале.2 — 2x — 3 ‘)
plt.ylabel (‘Ось y’)
plt.xlabel (‘Ось x’)
plt.grid ()
plt.axis ([- 10, 16, -10, 10])
plt.scatter (x1, y1, s = 1, c = ‘b’)
plt.scatter (x1, -y1, s = 1, c = ‘b’)
plt.plot (x2, y2, ‘r—‘)
plt.plot (x2, -y2, ‘r—‘)
plt.show () Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
| у | может быть только больше нуля, нам нужно указать функции, которые> = 0 и нарисовать в основной части графика только их.Для этого мы делаем булевую маску для всех значений f (x) (в моём коде это значение обозначено как y , но мой y это не y из вашей формулы).
инд = у> = 0
Более понятно можно записать так:
инд = (у> = 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y> = 0 и False , где y <0 .
Далее, мы отбираем по этой маске значения из наших массивов x и y :
x1 = x [инд.]
y1 = y [инд]
А также отбираем остальные значения x и y , для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x [~ ind]
y2 = y [~ ind]
После этого мы рисуем основной график, причём два раза - один раз используя f (x) , другой раз -f (x) (по формуле | y | = f (x) получается, что у нас есть два графика: y = f (x) и y = -f (x) ).
И рисуем псевдо-график там, где функция f (x) могла бы продолжаться, но из-за условий равенства модулю | y | она в этом месте прерывается.
Как строить функцию в Excel - Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МС Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека.Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках. Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графическим.Графиком функции y = f (x) называется множество точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
- y = kx + b ;
- y = ;
- y = | x | ;
- y = kx 2 (y = ax 2 + bx + c) ;
- y = ,
также способы построения графиков функций y = f ( x + l ), y = f 934 (934 934 ) + 934 x m , если известен график функции y = f (x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и системе координат для каждой группы, чтобы наглядно представить их отличия. На уроке графики тех же функций построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1- я группа
- y = 3 x +5 ;
- у = х + 5;
- у = 3х + 5;
- y = 3x-1 ;
- у = -3х + 5;
- у = - х + 5;
2- я группа
3- я группа
- y = x 2 ;
- y = x 2 -1;
- y = (x-1) 2 ;
- y = x 2 -5x + 4;
- y = -x 2 -1;
- y = - (x-1) 2 ;
4- я группа
5-я группа
Работу учащихся опишем на рисунках графика функции y = :
- Определим промежуток построения графика функции.Пусть х 1 = -2, х 2 = 2.
- В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежутка на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этой ячейки А4 введем формулу = A3 + 0,1 и скопируем эту формулу в ячейки А5 по А43.
Рис. 1. В ячейке А4 вводим формулу = A 3 + 0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2).Для этой ячейки В3 введем формулу: = (A3 + 1) / (F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1) в ячейки В4 - В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 - В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми».График функции y = построен. При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно показали отличительные характеристики каждой из функций в взятой группе.
.
 Для всех таких найдите это решение.
Для всех таких найдите это решение.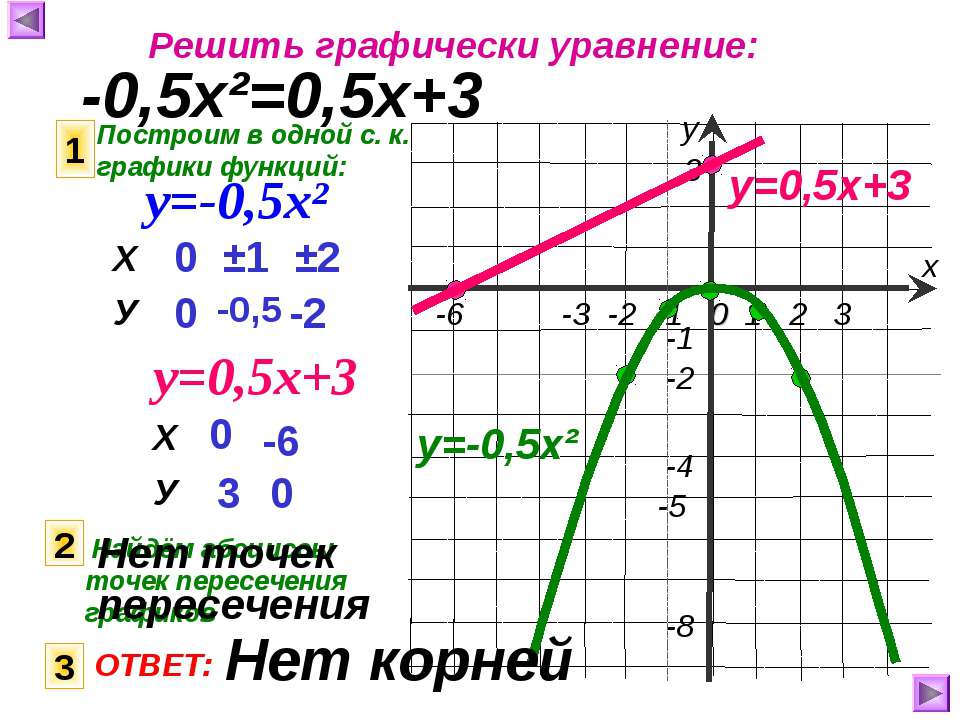 Во многих случаях решение таких функций и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых функций, выполняются уравнения в левой и правой частях уравнения или неравенства.
Во многих случаях решение таких функций и неравенств осуществляется на функциональном уровне, т.е с помощью графиков, или за счет сопоставления некоторых функций, выполняются уравнения в левой и правой частях уравнения или неравенства.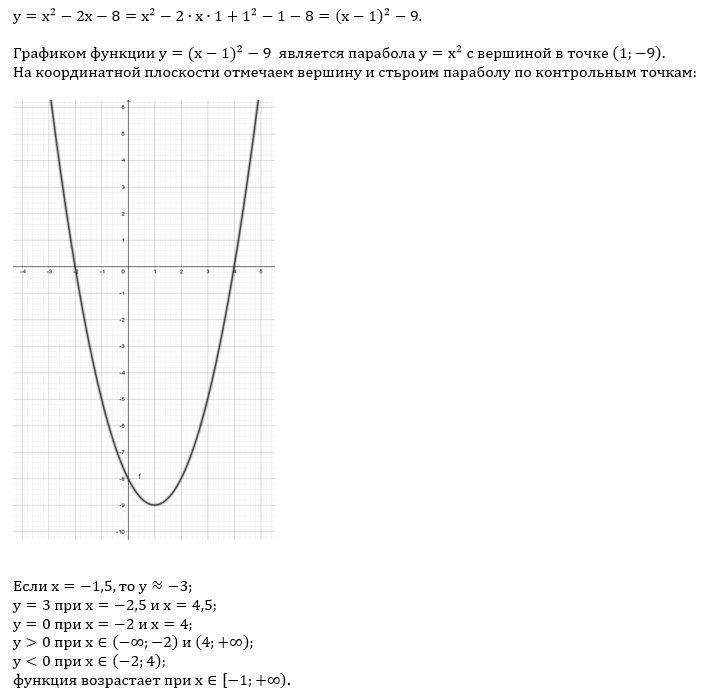 Ответ:
Ответ:  — . Ответ: -6
— . Ответ: -6 Док, что выражение является корнем уравнения = 1.
Док, что выражение является корнем уравнения = 1.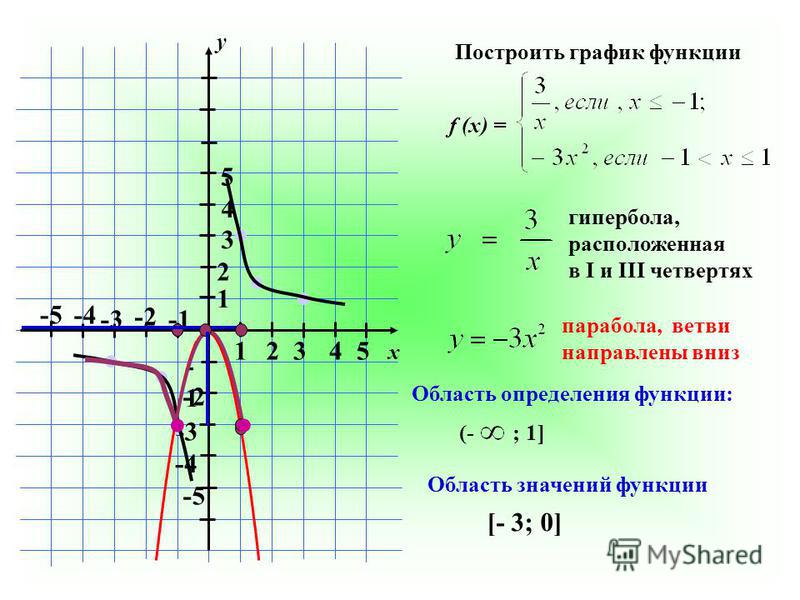 Алгебраический тренажер.
Алгебраический тренажер.Каждое выражение, которое под модулем приравниваем к 0. У нас их два x-3 и x + 3.
х-3 = 0 и х + 3 = 0
х = 3 и х = -3

х = -4
х-3 = -4-3 = -7 и х + 3 = -4 + 3 = -1
х = 0
x-3 = 0-3 = -3 и x + 3 = 0 + 3 = 3
 Рассмотрим третий интервал (3; + ∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
Рассмотрим третий интервал (3; + ∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.х-3 = 5-3 = 2 и х + 3 = 5 + 3 = 8
На интервале (-∞; -3) строим график линейной функции (прямая) у = 6.
На интервале (-3; 3) строим график линейной функции () у = -2х.
Чтобы построить график у = -2х подберем несколько точек.
x = -3 y = -2 * (- 3) = 6 получилась точка (-3; 6)
x = 0 y = -2 * 0 = 0 получилась точка (0; 0)
x = 3 y = — 2 * (3) = — 6 получилась точка (3; -6)
На интервале (3; + ∞) строим график линейной функции (прямой) у = -6.


Найдите нули функции. Нули функции — это значения «х», при которых у = 0, то есть это точки пересечения графика с осью Х.Имейте в виду, что нули не все функции. Чтобы найти нули функции, приравняйте ее к нулю. Например:
Найдите и отметьте горизонтальные асимптоты. Асимптота — это прямая, к которой график функции приближается, но никогда не пересекает ее (то есть в этой области функция не определена, например, при делении на 0). Асимптоту отметьте пунктирной линией. Если переменная «х» находится в знаменателе дроби (например, y = 1 4 — x 2 {\ displaystyle y = {\ frac {1} {4-x ^ {2}}}}
), приравняйте знаменатель к нулю и найдите «х». В представленном примере «х» функция определена (в примере представлены пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты не существуют только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
В представленном примере «х» функция определена (в примере представлены пунктирные линии через х = 2 и х = -2), потому что на 0 делить нельзя. Но асимптоты не существуют только в случаях, когда функция содержит дробное выражение. Поэтому рекомендуется пользоваться здравым смыслом:
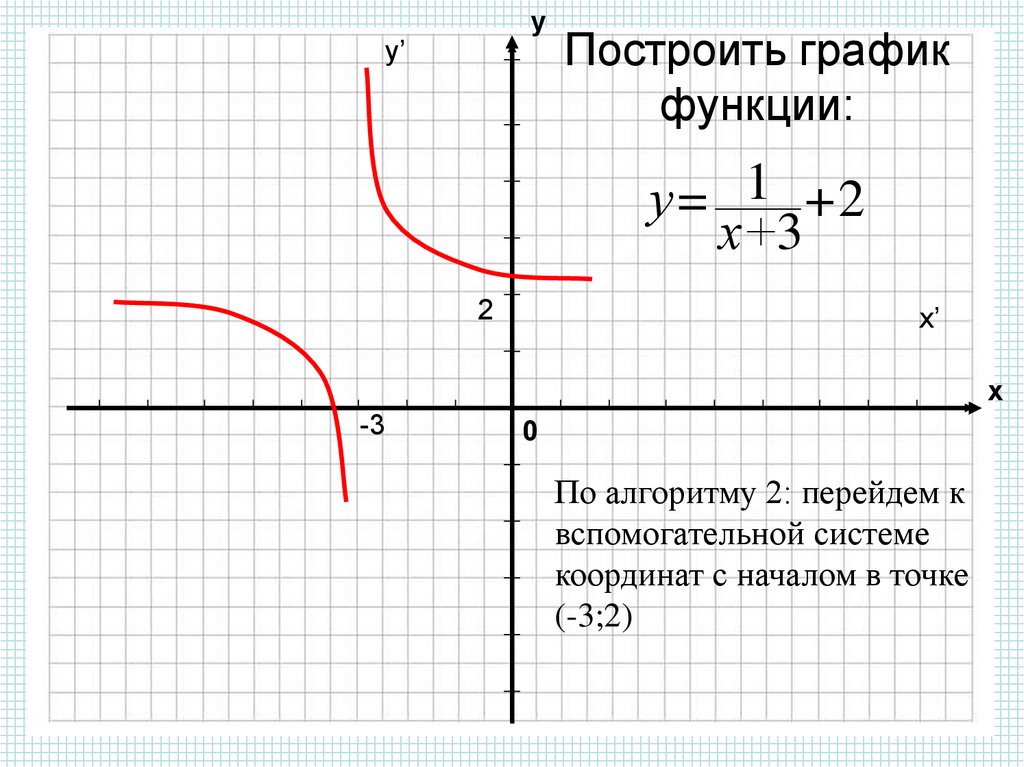
 Если этих 7 точек, далее — 4 вправо, 16 — вверх и т. д.).
Если этих 7 точек, далее — 4 вправо, 16 — вверх и т. д.).
 Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямого, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:
Отмечаем эти точки на координатной плоскости. С учетом симметрии параболы относительно прямого, проходящей через её вершину, отметим еще две точки: (-5; 6) и (-6; 10) и проведем через них параболу:Ответ: а) $ (- 3; -1).2 — 1:
$Ответ: б) $ (4; 3).
$3. Укажите график функции, заданной формулой
Вариант 1
$ y = x2 — 5 $
Ответ: а) $ (- 3; -1).2 $
Ответ: б) $ (4; 3).
$ 4. 2} {3} $ является квадратной;
в) Любая парабола пересекает ось ординат;
г) множеством действительных значений квадратной функции множество всех возможных чисел. Ответ: г).
Вариант 2
а) областью определения квадратной функции является множество всех действительных чисел;
б) графиком квадратной функции является гипербола;
в) ось симметрии параболы параллельна оси абсцисс;
г) график квадратной функции пересекает ось ординат в двух точках.
Ответ: а).
5.2-6x + 5 $ 6. С помощью графика функции из задания №5 найдите:
- значения аргумента, при которых значения функции отрицательны [2 в.: положительны];
- промежуток возрастания функции [2 в.: Убывание];
- уравнение оси симметрии параболы [2 в: множество параметров функции].
7.2 $] смещением его на три [2в .: пять] единичных отрезков вправо [2в .: влево] вдоль оси абсцисс и на восемь [2в .: три] единичных отрезков вдоль оси ординат.
Вариант 1
Смещенный график на три единицы права и восемь единиц вниз: $ y = 2 (x-3) ^ 2 — 8.2 — 2x + 1 = 0. $
Находим дискриминант:
$ D = 4-3 = 1, $
$ x = \ dfrac {2 ± 1} {\ dfrac {3} {2}},
$ $ x = 2, x = \ dfrac {2} {3}, $
$ y = 1-2 ⋅ \ dfrac {2} {3} = — \ dfrac {1} {3}, $
Ответ: $ (\ dfrac {2} {3}; — \ dfrac {1} {3}).
долларов США. 9.2-100 ≥ -100 $ при $ x є R. $ Наименьшее значение при $ x = 10, $ при $ y = -10. $
10. Постройте график функции:
Вариант 1
$ y = \ sqrt {x ^ 2 + 8x ^ 2 + 16x ^ 2}; $
$ y = \ sqrt {(x ^ 2 + 4x) ^ 2}; $
$ y = | х ^ 2 + 4х |.2-3x |. $
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y = f (x) — соответствие, при котором данному x из множества D сопоставляется единственное число y из числа E.
x– аргумент функции, y — значение функции; D или D (f) — определения области функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E (f) — область значений функции; это совокупность всех значений, которые могут принимать выражение f (x).
График функции y = f (x) — множество точек (x, y) на координатной плоскости, где x принимает все возможные значения из D (f), а y = f (x).
Четкая функция: f (-x) = f (x) для всех; Нечетная функция: f (-x) = — f (x) для всех; График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T> 0: f (x + T) = f (x) для всех. Нули функции — значения x такие, что f (x) = 0. Интервалы знакопостоянства — множество значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x = b, x = c, x = d; интервалы знакопостоянства: y> 0 при; у. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых, если x 1 2 , то f (x 1 ) 2 ). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых, если x 1 2 , то f (x 1 )> f (x 2 ). 3. Некоторые алгебраические функции
а) линейная . График функции — прямая линия, проходящая через точки (0, b) и. Функция возрастает при a> 0, убывает при a <0.
Частные случаи: y = b — прямая, параллельная оси OX;
y = ax — прямая, проходящая через начало координат.
б) квадратичная . График функции — парабола. Ветви параболы движется вверх при a> 0, вниз при a. Точки пересечения с осями координат:
с осью OX — (x 1 , 0) и (x 2 , 0),
где, D = b 2 -4ac — корни квадратного трехчлена; с осью OY — (0, c).
Пример 1. График какой функции является возрастающим:
а); б) у = х 3 — 27; в) y = 2 -x ? Решение:
Рассмотрим каждую из функций в отдельной:
а) — степенная функция.Область определения этой функции:. На всей области определения функция монотонна. Возьмём два значения х 1 = 1 и х 2 = 4. Им соответствует у 1 = — 1, у 2 = — 2. Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
б) у = х 3 — 27 — алгебраическая функция. Область определения — множество всех действительных чисел. На всей области определения функция монотонна.Возьмём два значения х 1 = 3, х 2 = 4. Им соответствует у 1 = 0, у 2 = 37.
Видим, что если х 1 2 , то и у 1 <у 2 . Функция возрастающая.
в) y = 2 -x — показательная функция. Областью создания множества всех действительных чисел. На всей области определения функция монотонна. Пусть х 1 = 0, х 2 = 1.Им соответствуют у 1 = 1, у 2 = 0,5.
Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
Ответ: б) у = х 3 — 27.
Пример 2. Парабола у = 2х 2 — (а — 3) х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а.Т.к. парабола проходит через начало системы координат, в координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 0 2 — (а — 3) ∙ 0 + а + 3; а = — 3.
Уравнение параболы примет вид: у = 2х 2 + 6х.
Абсцисса вершины параболы находится по формуле:. Получаем. Ответ: — 1, 5.
Пример 3. В каких точках график функции f (x) = x 2 — 3 пересекает прямую у (х) = х — 1?
Решение:
Ответом на данный вопрос является решение системы х 2 — 3 = х — 1; х 2 — х — 2 = 0; х 1 = — 1, или х 2 = 2.
Соответственно у 1 = — 2, у 2 = 1.
Ответ: (- 1; — 2), (2; 1).
Пример 4. При каких значениях k прямые — kх + 7у = — 13 и 14у — 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k 1 х + b 1 и у = k 2 х + b 2 параллельны, если k 1 = k 2 , но при этом b 1 ≠ b 2 .
В обоих уравнениях выразим у через х.
. Следовательно,. При этом. Ответ: при k = — 1,5.
Пример 5. Найти точки пересечения прямого у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = — 5.
Когда график функции пересекает ось OY, значение х = 0, т .е. у = 5.
Ответ: (- 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1) ∙ (х — 2).
Решение:
Решаем уравнение (х + 1) ∙ (х — 2) = 0.
х + 1 = 0 или х — 2 = 0; х 1 = — 1, х 2 = 2.
Ответ: (- 1; 0), (2; 0).
Пример 7. Найти область значений функции. Решение:
Оцениваем последовательно:
. Ответ: . Пример 8. Найдите сумму целых значений функции у = 3 — 2 sin x.
Решение:
Оценим значение 3 — 2 sin x.
. Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А (0; 2), проходящая через точка В (2; — 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах 2 + bх + с.
1) точка А является вершиной параболы, следовательно. Уравнение примет вид: у = ах 2 + с.
2) точка А принадлежит графику, следовательно ее координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах 2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: — 6 = а ∙ 2 2 + 2, — 8 = 4 ∙ а, а = — 2.
Получили уравнение у = — 2х 2 + 2.
Ответ: у = — 2х 2 + 2.
Пример 13. Найдите g (x), если f (x) = 2x — 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x — 3 = 1, х = 2.
Следовательно , g (f (x)) = 2, т.е. г (1) = 2.
Ответ: г (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y = 5 2x , y = 5 3x-1 и через точку параболы y = (2x-1) 2 , в которой производная функция , задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4).Согласно уравнению прямого, проходящей через две точки, имеем: — 21х + 21 = 0,5у — 12,5; — 42х + 42 = у — 25; у = — 42х + 47.
Ответ: у = — 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции в точке х 0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f (-1) -f (1). 4) Найдите g (f (x)), если Вычислите g (f (2)). Укажите длину интервала определения функций:
24). 25) y = log 4 (5x + 6-x 2 )
26) y = log 6 (x 2 +3).
Укажите области значений функций:
27) y = -3sinx.
28) y = 0,7cos3x.
29). Решите задачи:
30) Сколько натуральных значений может принять функцию y = log 2 (4-x 2 ) на всей области определения?
31) Найдите сумму целых значений функции y = 3cosx-5.
32) Укажите функцию, областью значений которой является множество. . 33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y = -x 0,5 ; 2) y = 1-e -x ; 3) y = ctg2x; 4) у = | -х |.
35) Найдите нули функции. 36) Найдите нули функции 37) Найдите наименьшее значение функции f (x) = 3 2x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = — 2х 2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямого у = 5 — 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = — 2х.
41) В каких точках график функции f (x) = 3x 2 + 6x пересекает прямую у = 6 — х?
42) Укажите промежутки возрастания функции y = sin3x на интервале. 43) Укажите промежутки убывания функции y = -2cosx на интервале.2 — 2x — 3 ‘)
plt.ylabel (‘Ось y’)
plt.xlabel (‘Ось x’)
plt.grid ()
plt.axis ([- 10, 16, -10, 10])
plt.scatter (x1, y1, s = 1, c = ‘b’)
plt.scatter (x1, -y1, s = 1, c = ‘b’)
plt.plot (x2, y2, ‘r—‘)
plt.plot (x2, -y2, ‘r—‘)
plt.show () Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
| у | может быть только больше нуля, нам нужно указать функции, которые> = 0 и нарисовать в основной части графика только их.Для этого мы делаем булевую маску для всех значений f (x) (в моём коде это значение обозначено как y , но мой y это не y из вашей формулы).
инд = у> = 0
Более понятно можно записать так:
инд = (у> = 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y> = 0 и False , где y <0 .
Далее, мы отбираем по этой маске значения из наших массивов x и y :
x1 = x [инд.]
y1 = y [инд]
А также отбираем остальные значения x и y , для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x [~ ind]
y2 = y [~ ind]
После этого мы рисуем основной график, причём два раза - один раз используя f (x) , другой раз -f (x) (по формуле | y | = f (x) получается, что у нас есть два графика: y = f (x) и y = -f (x) ).
И рисуем псевдо-график там, где функция f (x) могла бы продолжаться, но из-за условий равенства модулю | y | она в этом месте прерывается.
Как строить функцию в Excel - Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МС Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека.Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках. Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графическим.Графиком функции y = f (x) называется множество точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
- y = kx + b ;
- y = ;
- y = | x | ;
- y = kx 2 (y = ax 2 + bx + c) ;
- y = ,
также способы построения графиков функций y = f ( x + l ), y = f 934 (934 934 ) + 934 x m , если известен график функции y = f (x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и системе координат для каждой группы, чтобы наглядно представить их отличия. На уроке графики тех же функций построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1- я группа
- y = 3 x +5 ;
- у = х + 5;
- у = 3х + 5;
- y = 3x-1 ;
- у = -3х + 5;
- у = - х + 5;
2- я группа
3- я группа
- y = x 2 ;
- y = x 2 -1;
- y = (x-1) 2 ;
- y = x 2 -5x + 4;
- y = -x 2 -1;
- y = - (x-1) 2 ;
4- я группа
5-я группа
Работу учащихся опишем на рисунках графика функции y = :
- Определим промежуток построения графика функции.Пусть х 1 = -2, х 2 = 2.
- В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежутка на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этой ячейки А4 введем формулу = A3 + 0,1 и скопируем эту формулу в ячейки А5 по А43.
Рис. 1. В ячейке А4 вводим формулу = A 3 + 0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2).Для этой ячейки В3 введем формулу: = (A3 + 1) / (F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1) в ячейки В4 - В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 - В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми».График функции y = построен. При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно показали отличительные характеристики каждой из функций в взятой группе.
.
б) графиком квадратной функции является гипербола;
в) ось симметрии параболы параллельна оси абсцисс;
г) график квадратной функции пересекает ось ординат в двух точках.
6. С помощью графика функции из задания №5 найдите:
- значения аргумента, при которых значения функции отрицательны [2 в.: положительны];
- промежуток возрастания функции [2 в.: Убывание];
- уравнение оси симметрии параболы [2 в: множество параметров функции].
7.2 $] смещением его на три [2в .: пять] единичных отрезков вправо [2в .: влево] вдоль оси абсцисс и на восемь [2в .: три] единичных отрезков вдоль оси ординат.
Вариант 1
Смещенный график на три единицы права и восемь единиц вниз: $ y = 2 (x-3) ^ 2 — 8.2 — 2x + 1 = 0. $
Находим дискриминант:
$ D = 4-3 = 1, $
$ x = \ dfrac {2 ± 1} {\ dfrac {3} {2}},
$ $ x = 2, x = \ dfrac {2} {3}, $
$ y = 1-2 ⋅ \ dfrac {2} {3} = — \ dfrac {1} {3}, $
Ответ: $ (\ dfrac {2} {3}; — \ dfrac {1} {3}).
долларов США. 9.2-100 ≥ -100 $ при $ x є R. $ Наименьшее значение при $ x = 10, $ при $ y = -10. $
10. Постройте график функции:
Вариант 1
$ y = \ sqrt {x ^ 2 + 8x ^ 2 + 16x ^ 2}; $
$ y = \ sqrt {(x ^ 2 + 4x) ^ 2}; $
$ y = | х ^ 2 + 4х |.2-3x |. $
Тема 7. Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Тема 7. Функции
1. Понятие функции
Функция y = f (x) — соответствие, при котором данному x из множества D сопоставляется единственное число y из числа E.
x– аргумент функции, y — значение функции; D или D (f) — определения области функции; это совокупность всех значений x, для которых можно вычислить значение функции. E или E (f) — область значений функции; это совокупность всех значений, которые могут принимать выражение f (x).
График функции y = f (x) — множество точек (x, y) на координатной плоскости, где x принимает все возможные значения из D (f), а y = f (x).
Четкая функция: f (-x) = f (x) для всех; Нечетная функция: f (-x) = — f (x) для всех; График четной функции симметричен относительно оси OY. График нечетной функции симметричен относительно начала координат.
Периодическая функция с периодом T> 0: f (x + T) = f (x) для всех. Нули функции — значения x такие, что f (x) = 0. Интервалы знакопостоянства — множество значений аргумента, при которых значения функции только положительны или только отрицательны.
На рисунке изображена функция с областью определения [a, e]. Нули функции: x = b, x = c, x = d; интервалы знакопостоянства: y> 0 при; у. Функция возрастает на множестве X, если большему значению аргумента соответствует большее значение функции. То есть для любых, если x 1 2 , то f (x 1 ) 2 ). Функция убывает на множестве X, если большему значению аргумента соответствует меньшее значение функции. Т.е. для любых, если x 1 2 , то f (x 1 )> f (x 2 ). 3. Некоторые алгебраические функции
а) линейная . График функции — прямая линия, проходящая через точки (0, b) и. Функция возрастает при a> 0, убывает при a <0.
Частные случаи: y = b — прямая, параллельная оси OX;
y = ax — прямая, проходящая через начало координат.
б) квадратичная . График функции — парабола. Ветви параболы движется вверх при a> 0, вниз при a. Точки пересечения с осями координат:
с осью OX — (x 1 , 0) и (x 2 , 0),
где, D = b 2 -4ac — корни квадратного трехчлена; с осью OY — (0, c).
Пример 1. График какой функции является возрастающим:
а); б) у = х 3 — 27; в) y = 2 -x ? Решение:
Рассмотрим каждую из функций в отдельной:
а) — степенная функция.Область определения этой функции:. На всей области определения функция монотонна. Возьмём два значения х 1 = 1 и х 2 = 4. Им соответствует у 1 = — 1, у 2 = — 2. Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
б) у = х 3 — 27 — алгебраическая функция. Область определения — множество всех действительных чисел. На всей области определения функция монотонна.Возьмём два значения х 1 = 3, х 2 = 4. Им соответствует у 1 = 0, у 2 = 37.
Видим, что если х 1 2 , то и у 1 <у 2 . Функция возрастающая.
в) y = 2 -x — показательная функция. Областью создания множества всех действительных чисел. На всей области определения функция монотонна. Пусть х 1 = 0, х 2 = 1.Им соответствуют у 1 = 1, у 2 = 0,5.
Видим, что если х 1 2 , то у 1 > у 2 . Функция убывающая.
Ответ: б) у = х 3 — 27.
Пример 2. Парабола у = 2х 2 — (а — 3) х + а + 3 проходит через начало координат. Найдите абсциссу вершины параболы.
Решение:
Найдём значение параметра а.Т.к. парабола проходит через начало системы координат, в координаты точки (0; 0) являются корнями уравнения параболы: 0 = 2 ∙ 0 2 — (а — 3) ∙ 0 + а + 3; а = — 3.
Уравнение параболы примет вид: у = 2х 2 + 6х.
Абсцисса вершины параболы находится по формуле:. Получаем. Ответ: — 1, 5.
Пример 3. В каких точках график функции f (x) = x 2 — 3 пересекает прямую у (х) = х — 1?
Решение:
Ответом на данный вопрос является решение системы х 2 — 3 = х — 1; х 2 — х — 2 = 0; х 1 = — 1, или х 2 = 2.
Соответственно у 1 = — 2, у 2 = 1.
Ответ: (- 1; — 2), (2; 1).
Пример 4. При каких значениях k прямые — kх + 7у = — 13 и 14у — 3х + 5 = 0 параллельны?
Решение:
Две различные прямые у = k 1 х + b 1 и у = k 2 х + b 2 параллельны, если k 1 = k 2 , но при этом b 1 ≠ b 2 .
В обоих уравнениях выразим у через х.
. Следовательно,. При этом. Ответ: при k = — 1,5.
Пример 5. Найти точки пересечения прямого у = 5 + х с осями координат.
Решение:
Когда график функции пресекает ось ОХ, значение у = 0.
Получаем уравнение 5 + х = 0, х = — 5.
Когда график функции пересекает ось OY, значение х = 0, т .е. у = 5.
Ответ: (- 5; 0), (0; 5).
Пример 6. Найти нули функции у = (х + 1) ∙ (х — 2).
Решение:
Решаем уравнение (х + 1) ∙ (х — 2) = 0.
х + 1 = 0 или х — 2 = 0; х 1 = — 1, х 2 = 2.
Ответ: (- 1; 0), (2; 0).
Пример 7. Найти область значений функции. Решение:
Оцениваем последовательно:
. Ответ: . Пример 8. Найдите сумму целых значений функции у = 3 — 2 sin x.
Решение:
Оценим значение 3 — 2 sin x.
. Сумма целых чисел: 1 + 2 + 3 + 4 + 5 = 15.
Ответ: 15.
Пример 12. Графиком квадратичной функции является парабола с вершиной в точке А (0; 2), проходящая через точка В (2; — 6). Задайте эту функцию формулой.
Решение:
Уравнение квадратичной функции у = ах 2 + bх + с.
1) точка А является вершиной параболы, следовательно. Уравнение примет вид: у = ах 2 + с.
2) точка А принадлежит графику, следовательно ее координаты удовлетворяют уравнению, т.е. 2 = а ∙ 0 + с; с = 2.
Уравнение примет вид: у = ах 2 + 2.
3) график проходит через точку В. Её координаты также удовлетворяют уравнению: — 6 = а ∙ 2 2 + 2, — 8 = 4 ∙ а, а = — 2.
Получили уравнение у = — 2х 2 + 2.
Ответ: у = — 2х 2 + 2.
Пример 13. Найдите g (x), если f (x) = 2x — 3, g (f (x)) = x. Вычислите g (1).
Решение:
Так как нужно вычислить g (1), то это значит, что нужно найти x такое, что f (x) = 1.
2x — 3 = 1, х = 2.
Следовательно , g (f (x)) = 2, т.е. г (1) = 2.
Ответ: г (1) = 2.
Пример 14. Написать уравнение прямой, проходящей через точку пересечения кривых y = 5 2x , y = 5 3x-1 и через точку параболы y = (2x-1) 2 , в которой производная функция , задающей параболу, равна 8.
Решение:
1) найдём точку пересечения кривых:
2) найдём точку пересечения кривых:
2) найдём точку параболы, в которой производная равна 8:
3) прямая проходит через две точки (1; 25) и (1,5; 4).Согласно уравнению прямого, проходящей через две точки, имеем: — 21х + 21 = 0,5у — 12,5; — 42х + 42 = у — 25; у = — 42х + 47.
Ответ: у = — 42х + 47.
Задания для самостоятельного решения
Базовый уровень
1) Вычислите значение функции в точке х 0 = 1. 2) Найдите значение функции при х = 4. 3) Для функции вычислите f (-1) -f (1). 4) Найдите g (f (x)), если Вычислите g (f (2)). Укажите длину интервала определения функций:
24). 25) y = log 4 (5x + 6-x 2 )
26) y = log 6 (x 2 +3).
Укажите области значений функций:
27) y = -3sinx.
28) y = 0,7cos3x.
29). Решите задачи:
30) Сколько натуральных значений может принять функцию y = log 2 (4-x 2 ) на всей области определения?
31) Найдите сумму целых значений функции y = 3cosx-5.
32) Укажите функцию, областью значений которой является множество. . 33) Укажите график функции, возрастающей на отрезке [-3; 2].
34) Укажите функцию, которая возрастает на всей области определения.
1) y = -x 0,5 ; 2) y = 1-e -x ; 3) y = ctg2x; 4) у = | -х |.
35) Найдите нули функции. 36) Найдите нули функции 37) Найдите наименьшее значение функции f (x) = 3 2x-1 на промежутке [-3; 1].
38) Вычислите координаты точек пересечения графика функции у = — 2х 2 + 4х + 6 с осью OY.
39) Вычислите ординату точки пересечения прямого у = 5 — 2х с осью ОY.
40) Укажите точки пересечения графиков функций у = 2х + 4 и у = — 2х.
41) В каких точках график функции f (x) = 3x 2 + 6x пересекает прямую у = 6 — х?
42) Укажите промежутки возрастания функции y = sin3x на интервале. 43) Укажите промежутки убывания функции y = -2cosx на интервале.2 — 2x — 3 ‘)
plt.ylabel (‘Ось y’)
plt.xlabel (‘Ось x’)
plt.grid ()
plt.axis ([- 10, 16, -10, 10])
plt.scatter (x1, y1, s = 1, c = ‘b’)
plt.scatter (x1, -y1, s = 1, c = ‘b’)
plt.plot (x2, y2, ‘r—‘)
plt.plot (x2, -y2, ‘r—‘)
plt.show () Вывод:
Надеюсь, из кода всё понятно, но немного поясню.
| у | может быть только больше нуля, нам нужно указать функции, которые> = 0 и нарисовать в основной части графика только их.Для этого мы делаем булевую маску для всех значений f (x) (в моём коде это значение обозначено как y , но мой y это не y из вашей формулы).
инд = у> = 0
Более понятно можно записать так:
инд = (у> = 0)
В ind у нас теперь булева маска, содержащая True на тех позициях, где y> = 0 и False , где y <0 .
Далее, мы отбираем по этой маске значения из наших массивов x и y :
x1 = x [инд.]
y1 = y [инд]
А также отбираем остальные значения x и y , для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот:
x2 = x [~ ind]
y2 = y [~ ind]
После этого мы рисуем основной график, причём два раза - один раз используя f (x) , другой раз -f (x) (по формуле | y | = f (x) получается, что у нас есть два графика: y = f (x) и y = -f (x) ).
И рисуем псевдо-график там, где функция f (x) могла бы продолжаться, но из-за условий равенства модулю | y | она в этом месте прерывается.
Как строить функцию в Excel - Построение в Excel графиков математических и тригонометрических функций
Графика функций. Построение графиков функций в среде МС Excel
- Войнова Татьяна Олеговна, учитель математики
- Гусев Александр Николаевич, учитель информатики и ИКТ
Разделы: Математика
В настоящее время компьютеры используются во всех сферах деятельности человека.Внедрение информационных технологий в учебный процесс сегодня актуально. С целью повышения эффективности обучения учитель-предметник должен уметь использовать компьютерные технологии на своих уроках. Одним из популярных программных средств, используемых на уроках математики, является MS Excel. Excel позволяет выполнять сложные вычислительные процедуры, автоматизировать рутинные вычисления, строить диаграммы, гистограммы и графики различной сложности.
Известно, что одним из способов задания функции является графическим.Графиком функции y = f (x) называется множество точек плоскости, координаты которых удовлетворяют данному уравнению. Графический способ задания очень важным преимуществом: он самый наглядный из всех. Графики часто используются в физике и технике, так как иногда они являются единственно возможными.
Учащимся 8-го класса известны следующие виды функций:
- y = kx + b ;
- y = ;
- y = | x | ;
- y = kx 2 (y = ax 2 + bx + c) ;
- y = ,
также способы построения графиков функций y = f ( x + l ), y = f 934 (934 934 ) + 934 x m , если известен график функции y = f (x) и элементарные методы исследования.
По каждому из указанных видов функций учащимся в качестве домашнего задания было предложено построить несколько графиков в одной и системе координат для каждой группы, чтобы наглядно представить их отличия. На уроке графики тех же функций построили в среде MS Excel и провели их исследование. В качестве групп функций были предложены следующие:
1- я группа
- y = 3 x +5 ;
- у = х + 5;
- у = 3х + 5;
- y = 3x-1 ;
- у = -3х + 5;
- у = - х + 5;
2- я группа
3- я группа
- y = x 2 ;
- y = x 2 -1;
- y = (x-1) 2 ;
- y = x 2 -5x + 4;
- y = -x 2 -1;
- y = - (x-1) 2 ;
4- я группа
5-я группа
Работу учащихся опишем на рисунках графика функции y = :
- Определим промежуток построения графика функции.Пусть х 1 = -2, х 2 = 2.
- В ячейке А3 электронной таблицы введем начальное значение промежутка (-2).
- Разобьем промежутка на равные отрезки с учетом желаемой точности. Допустим, шаг разбиения равен 0,1. Для этой ячейки А4 введем формулу = A3 + 0,1 и скопируем эту формулу в ячейки А5 по А43.
Рис. 1. В ячейке А4 вводим формулу = A 3 + 0,1
- Вычислим значение функции в начальной точке отрезка (в точке −2).Для этой ячейки В3 введем формулу: = (A3 + 1) / (F3-1) (1).
Рис. 2. Вычислим значение функции в начальной точке отрезка
- Вычислим значения функции в каждой точке промежутка разбиения. Для этого скопируем формулу (1) в ячейки В4 - В43.
- Построим график функции. Для этого выделим числовой блок
Рис. 3. Построим график функции
ячейки А3 - В43, откроем вкладку «Вставка», выберем тип графика «Точечная» и вид «С гладкими кривыми».График функции y = построен. При желании на график можно наложить цвет, вертикальную сетку, сделать пояснительные записи. Для этого используется инструментарий вкладки «Макет».
Рис. 4. Построим график функции
Таким образом, учащиеся не только смогли получить навыки построения графиков функций в среде MS Excel, но и наглядно показали отличительные характеристики каждой из функций в взятой группе.
.
$ y = \ sqrt {(x ^ 2 + 4x) ^ 2}; $
$ y = | х ^ 2 + 4х |.2-3x |. $
| у | может быть только больше нуля, нам нужно указать функции, которые> = 0 и нарисовать в основной части графика только их.Для этого мы делаем булевую маску для всех значений f (x) (в моём коде это значение обозначено как y , но мой y это не y из вашей формулы). инд = у> = 0
инд = (у> = 0)
ind у нас теперь булева маска, содержащая True на тех позициях, где y> = 0 и False , где y <0 . x и y : x1 = x [инд.]
y1 = y [инд]
x и y , для чего инвертируем маску с помощью булевой операции инверсии ~ (где было True станет False и наоборот: x2 = x [~ ind]
y2 = y [~ ind]
f (x) , другой раз -f (x) (по формуле | y | = f (x) получается, что у нас есть два графика: y = f (x) и y = -f (x) ). f (x) могла бы продолжаться, но из-за условий равенства модулю | y | она в этом месте прерывается.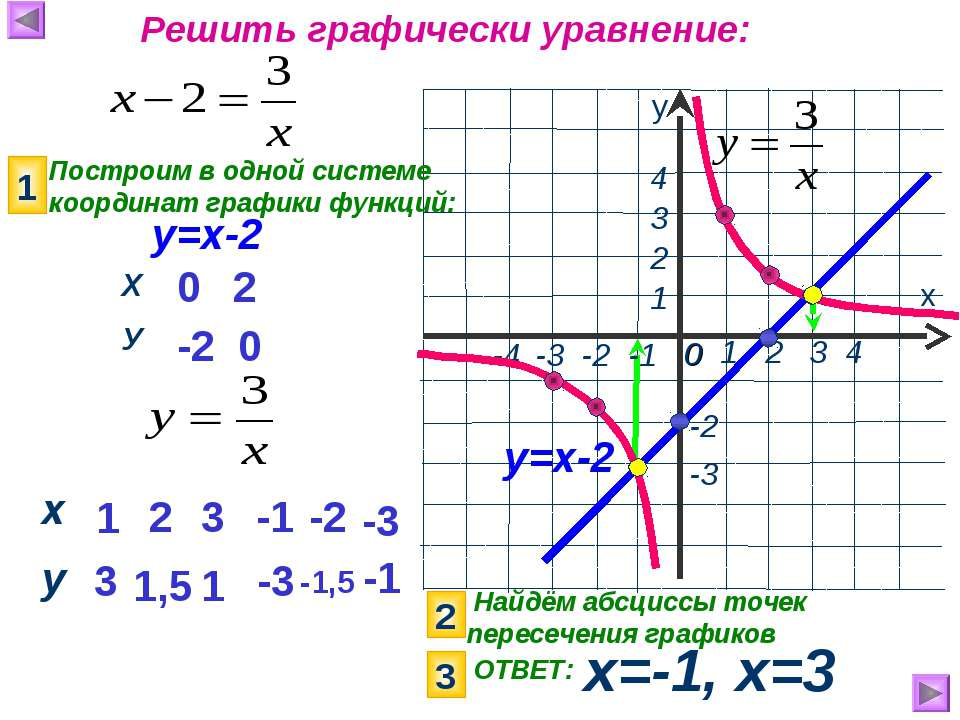 С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функции, интервалы знакопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции: Функции — Материалы для подготовки к вступительным экзаменам в СГГА
Функции — Материалы для подготовки к вступительным экзаменам в СГГА Пусть х1=-2, х2=2.
Пусть х1=-2, х2=2. С его помощью укажите пути функций, интервалы знаковопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции:
С его помощью укажите пути функций, интервалы знаковопостоянства, промежутки монотонности, наибольшее и наименьшее значения функции, область значений функции: