это отношение каких сторон треугольника?» – Яндекс.Кью
Число е появилось относительно поздно, в довольно сложных уже моделях, изучали его продвинутыми методами анализа — оно родилось в математике, а не в физике. А математика к тому времени уже оторвалась от физики. При этом могло, в принципе, случиться так, что знаменитым стало бы не число е, а скажем, корень из е. Но для многих математических моделей удобнее использовать именно е. Скорее всего, этим объясняется, что именно оно закрепилось в традиции. Исторически сложилось, что число е имеет математический смысл, а не физический.
Выбор постоянных подвержен все-таки некоторому произволу. То, что мы пользуемся числом ПИ — тоже результат традиции. Математика могла сложиться так, что специальное обозначение получило бы не отношение длины окружности к диаметру, а отношение длины окружности к радиусу. На развитие математики это не сильно бы повлияло, но некоторые формулы выглядели бы иначе, а число 3,1415… не было бы таким знаменитым и никто бы не считал кучу его знаков после запятой.
Тем не менее, число е может встречаться в законах реального мира. Например, центральная предельная теорема описывает очень многие явления. (Она говорит, что сумма многих независимых случайных одинаково распределенных величин имеет нормальное распределение.) Казалось бы, для описания нормального распределения требуется число е; но корень из е тоже бы подошел, может быть, даже еще лучше. Нельзя сказать, что здесь можно получить физический смысл числа е из ЦПТ. Скорее, наоборот — нормальное распределение стали выражать через е, потому что уже привыкли к этому числу.
Интегральный синус — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 апреля 2019; проверки требуют 2 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 апреля 2019; проверки требуют 2 правки.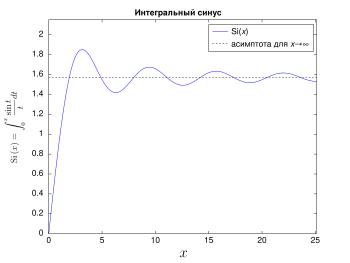 График интегрального синуса для 0 ≤ x ≤ 8π.
График интегрального синуса для 0 ≤ x ≤ 8π.Интегра́льный си́нус — специальная функция, определяемая интегралом[1]:
Six=∫0xsinttdt.{\displaystyle \operatorname {Si} \,x=\int \limits _{0}^{x}{\frac {\sin t}{t}}\,dt.}
Иногда также пользуются обозначением six:{\displaystyle \operatorname {si} \,x:}
six=−∫x∞sinttdt=Six−π2.{\displaystyle \operatorname {si} \,x=-\int \limits _{x}^{\infty }{\frac {\sin t}{t}}\,dt=\operatorname {Si} \,x-{\frac {\pi }{2}}.}
Интегральный синус может быть определён через интегральную показательную функцию по аналогии с синусом[2]:
six=12i(Ei(ix)−Ei(−ix)).{\displaystyle \operatorname {si} \,x={\frac {1}{2i}}\left(\operatorname {Ei} \,(ix)-\operatorname {Ei} \,(-ix)\right).}
Интегральный синус был введён Лоренцо Маскерони в 1790 году.
- Si(−x)=−Six.{\displaystyle \operatorname {Si} \,(-x)=-\,\operatorname {Si} \,x.}
- limx→+∞Six=π2,{\displaystyle \lim _{x\to +\infty }\operatorname {Si} \,x={\frac {\pi }{2}},}
- limx→+∞six=0,{\displaystyle \lim _{x\to +\infty }\operatorname {si} \,x=0,}
- limx→−∞Six=−π2,{\displaystyle \lim _{x\to -\infty }\operatorname {Si} \,x=-{\frac {\pi }{2}},}
- limx→−∞six=−π.{\displaystyle \lim _{x\to -\infty }\operatorname {si} \,x=-\pi .}
- Интегральный синус имеет локальные экстремумы в точках x=±π,±2π,±3π,⋯{\displaystyle x=\pm \pi ,\,\pm 2\pi ,\,\pm 3\pi ,\,\cdots }
- Six=x−x33⋅3!+x55⋅5!−x77⋅7!+⋯=∑n=0∞(−1)n(2n+1)!(2n+1)x2n+1.{\displaystyle \operatorname {Si} \,x=x-{\frac {x^{3}}{3\cdot 3!}}+{\frac {x^{5}}{5\cdot 5!}}-{\frac {x^{7}}{7\cdot 7!}}+\cdots =\sum _{n=0}^{\infty }{\frac {(-1)^{n}}{(2n+1)!(2n+1)}}x^{2n+1}.}
Этот ряд применяется для практического вычисления интегрального синуса, причём в соответствии c теоремой Лейбница погрешность будет меньше модуля последнего взятого члена этого ряда.
- ↑ Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. // М.: Наука, 1968. — С. 625.
- ↑ Бейтмен Г., Эрдейи А. Высшие трансцендентные функции, т. 2 // М.: Наука, 1974. — С. 149.
- Математический энциклопедический словарь. — М., 1995. — С. 238.
Синус-верзус — Википедия
Материал из Википедии — свободной энциклопедии
 Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус.
Определение тригонометрических функций на единичной окружности. Отрезок CD описывает версинус.Синус-верзус (sinus versus — обращённый синус; другие написания: версинус, синус версус, называется также «стрелка дуги») — одна из редко используемых тригонометрических функций. Синус-верзус угла ϑ{\displaystyle \vartheta } обозначается символом versinϑ;{\displaystyle \operatorname {versin} \,\vartheta ;} иногда используются обозначения versϑ,sinversϑ.{\displaystyle \operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .}
Синус-верзус определяется с помощью синуса и косинуса как
- versinϑ=1−cosϑ=2sin2(ϑ2).{\displaystyle \operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}\left({\frac {\vartheta }{2}}\right).}
Синус-верзус вместе с косинусом составляет радиус окружности.

График функции синус-верзус.
Версинус — периодическая функция с периодом 2π. Определена, непрерывна и бесконечно дифференцируема для всех действительных чисел.
versin{\displaystyle {\rm {versin}}} можно использовать в плоскости комплексных чисел.
Производная версинуса — синус:
- ddzversinz=sinz.{\displaystyle {\frac {d}{dz}}\operatorname {versin} \,z=\sin z.}
Первообразная:
- ∫versinzdz=z−sinz+C.{\displaystyle \int \operatorname {versin} \,z\,dz=z-\sin z+C.}
Синус-верзус играл важную роль в навигации по звёздам[1].
- ↑ Schenk, Bobby. Astronavigation – ohne Formeln – praxisnah (неопр.). — Bielefeld: Verlag Delius Klasing & Co, 1978.
- Weisstein, Eric W. Versine (англ.) на сайте Wolfram MathWorld.
- M. Abramowitz, I. A. Stegun: Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, (9)1972, New York: Dover, стр. 78
Редко используемые тригонометрические функции — Википедия
Материал из Википедии — свободной энциклопедии
Редко используемые тригонометрические функции — функции угла, которые в настоящее время используются редко по сравнению с шестью основными тригонометрическими функциями (синусом, косинусом, тангенсом, котангенсом, секансом и косекансом). К ним относятся:
 Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.
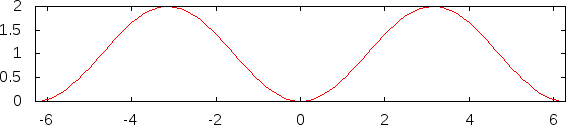
Графики версинуса, коверсинуса и гаверсинуса
Определение тригонометрических функций через окружность. Отрезки CD и DE описывают соответственно версинус и эксеканс.
Графики версинуса, коверсинуса и гаверсинуса- Синус-верзус (другие написания: версинус, синус версус, называется также «стрелка дуги»). Определяется как versinϑ=1−cosϑ=2sin2ϑ2.{\displaystyle \operatorname {versin} \,\vartheta =1-\cos \vartheta =2\sin ^{2}{\frac {\vartheta }{2}}.} Представляет собой расстояние от центральной точки дуги, измеряемой удвоенным данным углом, до центральной точки хорды, стягивающей дугу. Иногда используются обозначения versϑ,sinversϑ.{\displaystyle \operatorname {vers} \,\vartheta ,\quad \sin \,\operatorname {vers} \,\vartheta .}
- Косинус-верзус (другие написания: коверсинус, косинус версус). Определяется как vercosϑ=versin(π2−ϑ)=1−sinϑ.{\displaystyle \operatorname {vercos} \,\vartheta =\operatorname {versin} \,\left({\frac {\pi }{2}}-\vartheta \right)=1-\sin \vartheta .} Иногда используются обозначения cvsϑ,cosversϑ.{\displaystyle \operatorname {cvs} \,\vartheta ,\quad \cos \,\operatorname {vers} \,\vartheta .}
- Гаверсинус (лат. haversinus, сокращение от half the versed sine). Определяется как haversinϑ=versinϑ2=sin2ϑ2.{\displaystyle \operatorname {haversin} \,\vartheta ={\frac {\operatorname {versin} \,\vartheta }{2}}=\sin ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение havϑ.{\displaystyle \operatorname {hav} \,\vartheta .}
- Гаверкосинус (лат. havercosinus, сокращение от half the versed cosine). Определяется как havercosϑ=vercosϑ2=cos2ϑ2.{\displaystyle \operatorname {havercos} \,\vartheta ={\frac {\operatorname {vercos} \,\vartheta }{2}}=\cos ^{2}{\frac {\vartheta }{2}}.} Используется также обозначение hacϑ.{\displaystyle \operatorname {hac} \,\vartheta .}
- Эксеканс (лат. exsecant) или экссеканс. Определяется как exsecϑ=secϑ−1.{\displaystyle \operatorname {exsec} \,\vartheta =\sec \vartheta -1.}
- Экскосеканс — дополнительная функция к эксекансу: excscϑ=exsec(π2−ϑ)=cosecϑ−1.{\displaystyle \operatorname {excsc} \,\vartheta =\operatorname {exsec} \,\left({\frac {\pi }{2}}-\vartheta \right)=\operatorname {cosec} \,\vartheta -1.}
Версинус, коверсинус и гаверсинус были удобны для ручных расчётов с использованием логарифмов, поскольку они всюду неотрицательны, однако в связи с развитием вычислительных средств эта область применения неактуальна. В настоящее время эти функции используются для описания соответствующих сигналов в электронике (например, в функциональных генераторах). Гаверсинус также используется в навигационных расчётах для избежания ошибок округления в вычислительных системах с ограниченной разрядностью.