Решение простейших тригонометрических уравнений

Решение простейших тригонометрических уравнений.

Решение тригонометрических уравнений любого уровня сложности в конечном итоге сводится к решению простейших тригонометрических уравнений. И в этом наилучшим помощником снова оказывается тригонометрический круг.

Вспомним определения косинуса и синуса.

Косинусом  угла  называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствующей повороту на данный угол

.

Синусом угла называется ордината (то есть координата по оси  ) точки на единичной окружности, соответствующей повороту на данный угол .

Положительным направлением движения по тригонометрическому кругу считается движение против часовой стрелки. Повороту на 0 градусов ( или 0 радиан) соответствует точка с координатами (1;0)

Используем  эти определения для решения простейших тригонометрических уравнений.

1. Решим уравнение

Этому уравнению удовлетворяют все такие значения угла поворота , которые соответствуют точкам окружности, ордината которых равна .

Отметим на оси ординат точку с ординатой

:

 Проведем горизонтальную линию параллельно оси абсцисс до пересечения с окружностью. Мы получим две точки, лежащие на окружности и имеющие  ординату. Эти точки соответствуют углам поворота на и радиан:

 Если мы, выйдя из точки, соответствующей углу поворота на радиан, обойдем полный круг, то мы придем в точку, соответствующую углу поворота на радиан и имеющую ту же ординату. То есть этот угол поворота также удовлетворяет нашему уравнению. Мы можем делать сколько угодно «холостых» оборотов, возвращаясь в ту же точку, и все эти значения углов будут удовлетворять нашему уравнению. Число «холостых» оборотов обозначим буквой

(или ). Так как мы можем совершать эти обороты как в положительном, так и в отрицательном направлении, (или ) могут принимать любые целые значения.

То есть первая серия решений исходного уравнения имеет вид:

,  , — множество целых чисел (1)

Аналогично, вторая серия решений имеет вид:

, где ,  

. (2)

Как вы догадались, в основе этой серии решений лежит точка окружности, соответствующая углу поворота на .

Эти две серии решений можно  объединить в одну запись:

   

Если мы в этой записи возьмем ( то есть четное

), то мы получим первую серию решений.

Если мы в этой записи возьмем ( то есть нечетное ), то мы получим вторую  серию решений.

2. Теперь давайте решим уравнение

Так как — это абсцисса точки единичной окружности, полученной поворотом на угол

, отметим на оси точку с абсциссой :

  Проведем вертикальную линию параллельно оси до пересечения с окружностью. Мы получим две точки, лежащие на окружности  и имеющие  абсциссу

. Эти точки соответствуют углам поворота на и радиан. Вспомним, что при движении по часовой стрелки мы получаем отрицательный угол поворота:

 

Запишем две серии решений:

,  

,  

(Мы попадаем в нужную точку, пройдя из основной полный круг, то есть .

Объедим эти две серии в одну запись:

   

 

3. Решим уравнение

Линия тангенсов проходит через точку с координатами (1,0) единичной окружности параллельно оси OY

Отметим на ней точку, с ординатой равной 1 (мы ищем, тангенс каких углов равен 1):

Соединим эту точку с началом координат прямой линией и отметим точки пересечения прямой с единичной окружностью. Точки пересечения прямой и окружности соответствуют углам поворота на и :

 

Так как точки, соответствующие углам поворота, которые удовлетворяют нашему уравнению, лежат на расстоянии  радиан друг от друга, то мы можем записать решение таким образом:

,

4. Решим уравнение

Линия котангенсов проходит через точку с координатами единичной окружности параллельно оси .

Отметим на линии котангенсов точку с абсциссой -1:

 Соединим эту точку с началом координат прямой  и продолжим ее до пересечения с окружностью. Эта прямая пересечет окружность в точках, соответствующих углам поворота на и радиан:

Поскольку эти точки отстоят друг от  друга на расстояние, равное , то общее решение этого уравнения мы можем записать так:

   

 В приведенных примерах, иллюстрирующих решение простейших тригонометрических уравнений были использованы табличные значения тригонометрических функций.

Однако, если в правой части уравнения стоит не табличное значение, то мы в общее решение уравнения подставляем значение обратной тригонометрической функции:

 

 

ОСОБЫЕ РЕШЕНИЯ:

1

Отметим на окружности точки, ордината которых равна 0:

 

2.

Отметим на окружности единственную точку, ордината которой равна 1:

 

 

3.

Отметим на окружности единственную точку, ордината которой равна -1:

Так как принято указывать значения, наиболее близкие у нулю, решение запишем так:

4.

Отметим на окружности точки, абсцисса которых равна 0:

 

5.
Отметим на окружности единственную точку, абсцисса которой равна 1:

 

 

6.

Отметим на окружности единственную точку, абсцисса которой равна -1:

 

И чуть более сложные примеры:

1. 

Синус равен единице, если аргумент равен  

Аргумент у нашего синуса равен , поэтому получим:

. Разделим обе части равенства на 3:

Ответ:

2. 

Косинус равен нулю, если аргумент косинуса равен

Аргумент у нашего косинуса равен , поэтому получим:

Выразим , для этого сначала перенесем  вправо с противоположным знаком:

Упростим правую часть:

Разделим обе части на -2:

Заметим, что перед слагаемым  знак не меняется, поскольку   k может принимать любые целые значения.

Ответ:

И в заключение посмотрите видеоурок «Отбор корней в тригонометрическом уравнении с помощью тригонометрической окружности»

На этом разговор о решении простейших тригонометрических уравнений мы закончим. Следующий раз мы с вами поговорим о том, как решать простейшие тригонометрические неравенства.

И.В. Фельдман, репетитор по математике.

Купить видеокурс «ВСЯ ТРИГОНОМЕТРИЯ. Часть В и Задание 13»

ege-ok.ru

Mathway | Популярные задачи

1	Найти точное значение	sin(30)
2	Найти точное значение	sin(45)
3	Найти точное значение	sin(60)
4	Найти точное значение	sin(30 град. )
5	Найти точное значение	sin(60 град. )
6	Найти точное значение	tan(30 град. )
7	Найти точное значение	arcsin(-1)
8	Найти точное значение	sin(pi/6)
9	Найти точное значение	cos(pi/4)
10	Найти точное значение	sin(45 град. )
11	Найти точное значение	sin(pi/3)
12	Найти точное значение	arctan(-1)
13	Найти точное значение	cos(45 град. )
14	Найти точное значение	cos(30 град. )
15	Найти точное значение	tan(60)
16	Найти точное значение	csc(45 град. )
17	Найти точное значение	tan(60 град. )
18	Найти точное значение	sec(30 град. )
19	Преобразовать из радианов в градусы	(3pi)/4
20	График	y=sin(x)
21	Преобразовать из радианов в градусы	pi/6
22	Найти точное значение	cos(60 град. )
23	Найти точное значение	cos(150)
24	Найти точное значение	tan(45)
25	Найти точное значение	sin(30)
26	Найти точное значение	sin(60)
27	Найти точное значение	cos(pi/2)
28	Найти точное значение	tan(45 град. )
29	График	y=sin(x)
30	Найти точное значение	arctan(- квадратный корень 3)
31	Найти точное значение	csc(60 град. )
32	Найти точное значение	sec(45 град. )
33	Найти точное значение	csc(30 град. )
34	Найти точное значение	sin(0)
35	Найти точное значение	sin(120)
36	Найти точное значение	cos(90)
37	Преобразовать из радианов в градусы	pi/3
38	Найти точное значение	sin(45)
39	Найти точное значение	tan(30)
40	Преобразовать из градусов в радианы	45
41	Найти точное значение	tan(60)
42	Упростить	квадратный корень x^2
43	Найти точное значение	cos(45)
44	Упростить	sin(theta)^2+cos(theta)^2
45	Преобразовать из радианов в градусы	pi/6
46	Найти точное значение	cot(30 град. )
47	Найти точное значение	arccos(-1)
48	Найти точное значение	arctan(0)
49	График	y=cos(x)
50	Найти точное значение	cot(60 град. )
51	Преобразовать из градусов в радианы	30
52	Упростить	( квадратный корень x+ квадратный корень 2)^2
53	Преобразовать из радианов в градусы	(2pi)/3
54	Найти точное значение	sin((5pi)/3)
55	Упростить	1/( кубический корень от x^4)
56	Найти точное значение	sin((3pi)/4)
57	Найти точное значение	tan(pi/2)
58	Найти угол А	tri{}{90}{}{}{}{}	
59	Найти точное значение	sin(300)
60	Найти точное значение	cos(30)
61	Найти точное значение	cos(60)
62	Найти точное значение	cos(0)
63	Найти точное значение	arctan( квадратный корень 3)
64	Найти точное значение	cos(135)
65	Найти точное значение	cos((5pi)/3)
66	Найти точное значение	cos(210)
67	Найти точное значение	sec(60 град. )
68	Найти точное значение	sin(300 град. )
69	Преобразовать из градусов в радианы	135
70	Преобразовать из градусов в радианы	150
71	Преобразовать из радианов в градусы	(5pi)/6
72	Преобразовать из радианов в градусы	(5pi)/3
73	Преобразовать из градусов в радианы	89 град.
74	Преобразовать из градусов в радианы	60
75	Найти точное значение	sin(135 град. )
76	Найти точное значение	sin(150)
77	Найти точное значение	sin(240 град. )
78	Найти точное значение	cot(45 град. )
79	Преобразовать из радианов в градусы	(5pi)/4
80	Упростить	1/( кубический корень от x^8)
81	Найти точное значение	sin(225)
82	Найти точное значение	sin(240)
83	Найти точное значение	cos(150 град. )
84	Найти точное значение	tan(45)
85	Вычислить	sin(30 град. )
86	Найти точное значение	sec(0)
87	Упростить	arcsin(-( квадратный корень 2)/2)
88	Найти точное значение	cos((5pi)/6)
89	Найти точное значение	csc(30)
90	Найти точное значение	arcsin(( квадратный корень 2)/2)
91	Найти точное значение	tan((5pi)/3)
92	Найти точное значение	tan(0)
93	Вычислить	sin(60 град. )
94	Найти точное значение	arctan(-( квадратный корень 3)/3)
95	Преобразовать из радианов в градусы	(3pi)/4
96	Вычислить	arcsin(-1)
97	Найти точное значение	sin((7pi)/4)
98	Найти точное значение	arcsin(-1/2)
99	Найти точное значение	sin((4pi)/3)
100	Найти точное значение	csc(45)

www.mathway.com

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

---

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах.

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

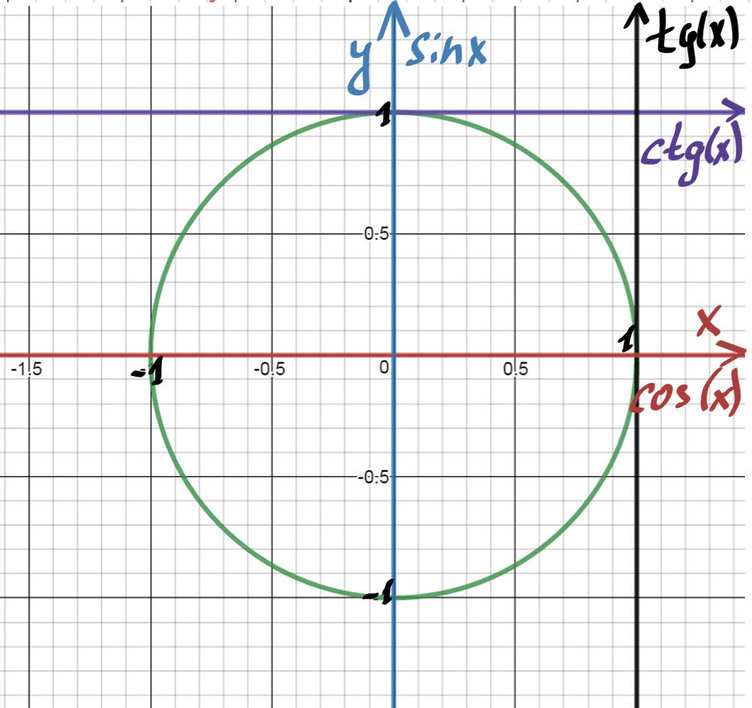
Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

А теперь отметим основные значения градусов и радиан на окружности. 

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

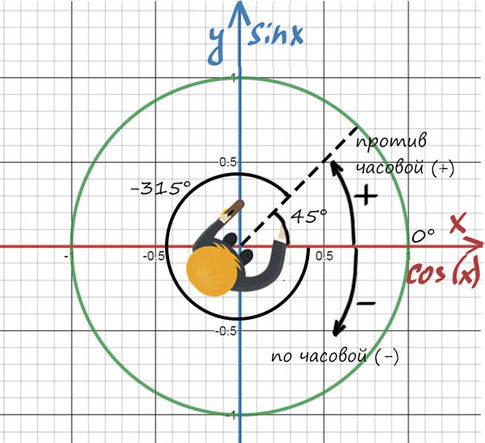
От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

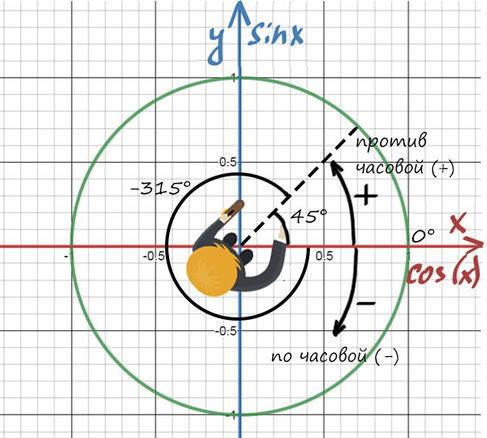
Главное — направление, куда мы будем смотреть, а не угол! 

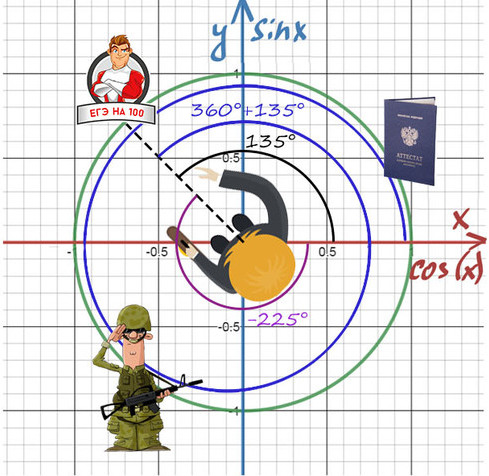
Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°…

А теперь у тебя есть два пути: 

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

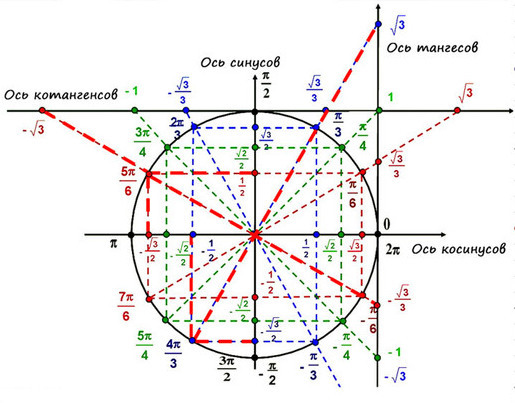
А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

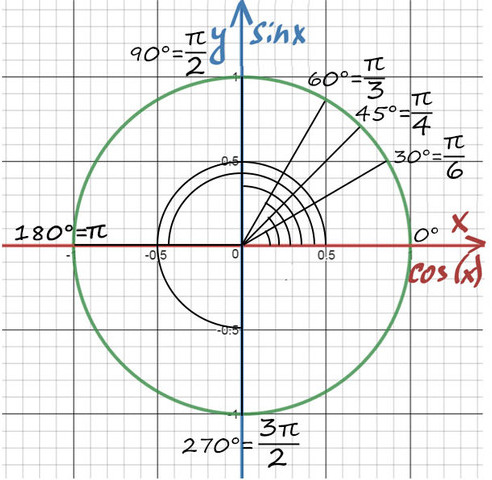
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений. 

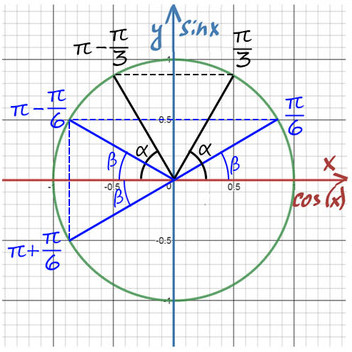
Сразу попробуем разобрать на примере: 

Пример №1. cos(x) = ½

1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

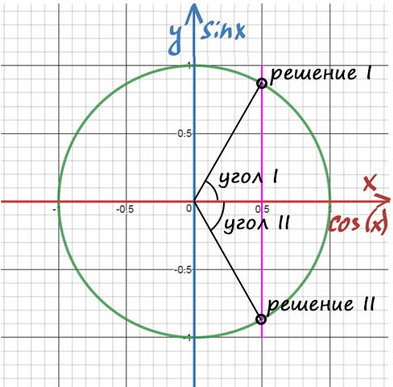
2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения. 

Дело за малым — найти эти углы. 

Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°. 

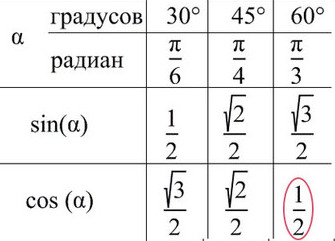
Или запомнить такой прием: 

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2): π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

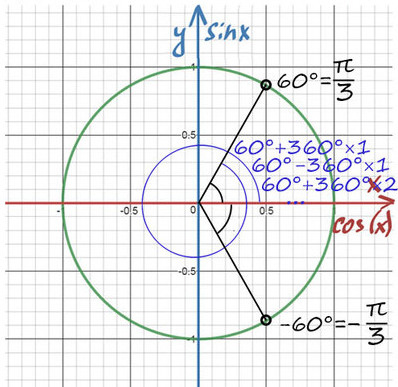
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на …=-225°=135°=495°=…

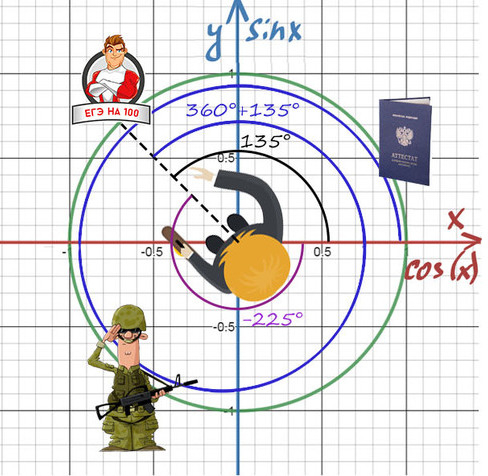
То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: …,60°-360°, 60°, 60°+360°,…

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= −π/3 + 2πk, (n, k)∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

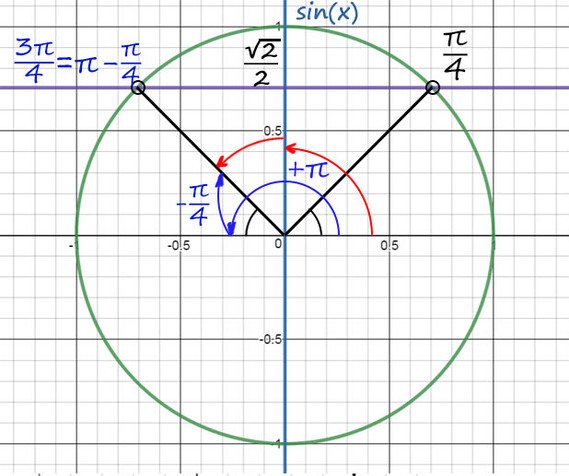
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

 Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки. 

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

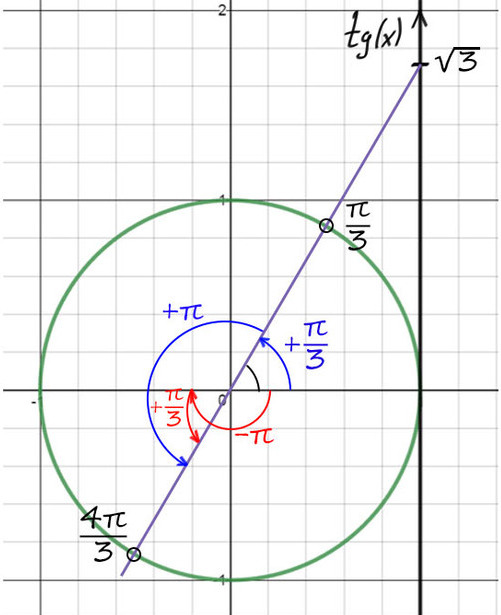
4) Но мы нашли только y, вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

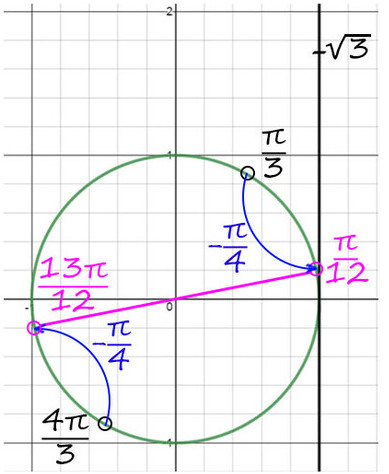
Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

 Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

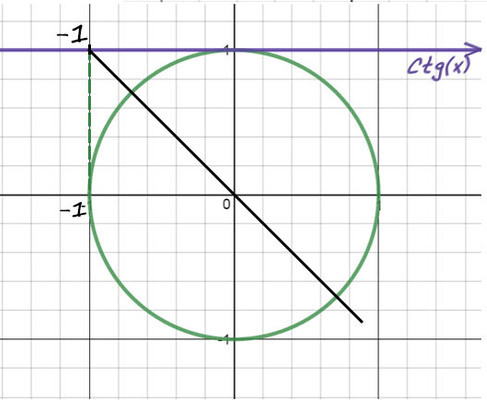
2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π…) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = −√3/2):

1. Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
2. Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
3. Точки пересечения с окружностью и будут являться корнями уравнения.
4. Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания. 

Будь в курсе новых статеек, видео и легкого математического юмора.

ik-study.ru

Примеры решения простейших тригонометрических неравенств

Часть 2.

Начало здесь.

Если вы беретесь за изучение темы «Простейшие тригонометрические неравенства», то должны прежде знать, где находятся оси тангенса и котангенса и уметь решать простейшие тригонометрические уравнения (часть III).

Кстати, для сдающих ЕГЭ по математике, –   умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Примеры решения простейших тригонометрических  неравенств

Пример 1. 

Решить неравенство:

Решение: 

Отмечаем на оси тангенсов 1. Указываем все значения тангенса, меньшие 1 – ниже 1.

Далее, отмечаем все точки тригонометрического круга, значение тангенса в которых будет меньше 1.  Для этого мы мысленно соединяем каждую точку оси тангенсов ниже 1 с началом координат; тогда каждая проведенная прямая пересечет дважды тригонометрический круг. Вот эти-то точки круга нас и интересуют! Они выстраиваются в две дуги (точнее в две серии дуг). Значения тангенса в них – меньше 1.

Заметим, кстати, что дуга повторяет дугу равно через пол круга, то есть через (период функции – это ).

Все подходящие значения можно записать в виде следующего двойного неравенства:

или так

Пример 2. 

Решить неравенство:

Решение: 

Отмечаем на оси тангенсов . Указываем все значения тангенса, большие или равные  – выше   (включая саму точку).

«Транслируем» отмеченные точки оси тангенсов  на тригонометрический круг.

 

Все подходящие значения можно записать в виде следующего двойного неравенства:

или такого (разницы – никакой):

 

Пример 3.

Решить неравенство:

Решение: 

Отмечаем на оси котангенсов . Указываем все значения котангенса, большие или равные  – правее  (включая саму точку).

«Транслируем» отмеченные точки оси котангенсов  на тригонометрический круг:

Все подходящие значения можно записать в виде следующего двойного неравенства:

Вы обратили внимание, решая тригонометрическое неравенство с тангенсом,  – мы не включаем в ответ точки (значение тангенса в этих точках не определено)?

А, решая тригонометрическое неравенство с котангенсом,  – мы не включаем в ответ точки  (значение котангенса в этих точках не определено).

Пример 4.

Решить неравенство:

Решение: 

Проверьте себя

Помните,  решения (ответы)  к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. (См., например,  задание 2).

 1. Решить неравенство:

Ответ: + показать

2. Решить неравенство:

Ответ: + показать

3. Решить неравенство:

Ответ: + показать

Если у вас  есть  вопросы, – пожалуйста, – пишите в комментариях!

egemaximum.ru

Решение простейших тригонометрических неравенств | Подготовка к ЕГЭ по математике

Часть 1. 

(Часть 2 см. здесь)

Примеры решения простейших тригонометрических неравенств

Простейшими тригонометрическими неравенствами называются неравенства вида

,

 ,

 ,

,

где – один из знаков , .

Вы должны прежде, конечно, хорошо ориентироваться в тригонометрическом круге и уметь решать простейшие тригонометрические уравнения (часть I,  часть II).

Кстати, умение решать тригонометрические неравенства может пригодиться, например, в заданиях №11 ЕГЭ по математике.

Сначала мы рассмотрим простейшие тригонометрические неравенства с синусом и косинусом. Во второй части статьи – с тангенсом, котангенсом.

Пример 1.

Решить неравенство:

Решение: 

Отмечаем на оси  косинусов

Все значения , меньшие – левее точки на оси косинусов.

Отмечаем все точки (дугу, точнее – серию дуг) тригонометрического круга, косинус которых будет меньше

Полученную дугу мы проходим против часовой стрелки (!), то есть от точки до .

Обратите внимание, многие, назвав первую точку вместо второй точки    указывают точку , что неверно!

Становится видно, что неравенству удовлетворяют следующие значения

Следите за тем, чтобы «правая/вторая точка» была бы больше «левой/первой».

Не забываем «накидывать» счетчик 

Вот так выглядит графическое решение неравенства не на тригонометрическом круге, а в прямоугольной системе координат:

Пример 2.

Решить неравенство:

Решение:

Отмечаем на оси  косинусов

Все значения , большие или равные – правее точки , включая саму точку.

Тогда выделенные красной дугой аргументы отвечают тому условию, что  .

Пример 3.

Решить неравенство:

Решение:

Отмечаем на оси синусов

Все значения , большие или равные – выше точки , включая саму точку.

«Транслируем» выделенные точки на тригонометрический круг:

 

Пример 4.

Решить неравенство:

Решение:

Кратко:

или все , кроме

Пример 5.

Решить неравенство:

Решение:

Неравенство равносильно уравнению , так как область значений функции –

Пример 6.

Решить неравенство:

Решение:

Действия  – аналогичны применяемым в примерах выше. Но дело мы имеем не с табличным значением синуса.

Здесь, конечно, нужно знать определение арксинуса.

Если не очень понятно, загляните сюда –>+ показать

Согласны с таким вариантом (одним из) названия углов, соответствующих тому, что синус в них равен

А теперь мы должны позаботиться о том, чтобы правый конец промежутка, являющего собой решение неравенства, был бы больше левого конца.

Поэтому

Тренируемся в решении простейших тригонометрических неравенств

Имейте ввиду, решения (ответы) к одному и тому же неравенству могут выглядеть по-разному, неся один и тот же смысл собою. Например, в задании 2 ответ можно было записать и так:

 

1. Решить неравенство:

Ответ: + показать

2. Решить неравенство:

Ответ: + показать

3. Решить неравенство:

Ответ: + показать

4. Решить неравенство:

Ответ: + показать

5. Решить неравенство:

Ответ: + показать

Часть 2
Если у вас  есть  вопросы, – пожалуйста, – спрашивайте!

egemaximum.ru

Ответы@Mail.Ru: 2sinx=1

Решение: 1) cosx=sinx tgx=1 x=π/4+πn 2) sin2x+2sinx=cosx+1 2sinx*cosx+2sinx-(cosx+1)=0 2sinx(cosx+1)-(cosx+1)=0 (cosx+1)(2sinx-1) a) cosx+1=0 cosx=-1 x1=π+2πn б) 2sinx-1=0 sinx=1/2 x2=(-1)^nπ/6+πn 3) sinx+sin3x=0 2sin2x*cos(-x)=0 a) sin2x=0 2x=πn x1=πn/2 б) сosx=0 x2=π/2+πn 4) 2sin2x+3cos2x+2sinx=0 4sinx*cosx+2sinx+3(2cos²x-1)=0 2sinx(2cosx+1)+3(2cosx+1)(2cosx-1)=0 (2cosx+1)(2sinx+6cosx-3)=0 a) 2cosx+1=0 cosx=-1/2 x1=±2π/3+2πn б) 2sinx+6cosx-3=0 4sin(x/2)*cos(x/2)+6cos²(x/2)-6sin²(x/2)-3cos²(x/2)-3sin²(x/2)=0 4sin(x/2)*cos(x/2)+3cos²(x/2)-9sin²(x/2)=0 9tg²(x/2)-4tg(x/2)-3=0 пусть tg(x/2)=t 9t²-4t-3=0 t1=2+√31 t2=2-√31 a) tg(x/2)=2+√31 x/2=arctg(2+√31)+πn x3=2arctg(2+√31)+2πn б) tg(x/2)=2-√31 x/2=arctg(2-√31)+πn x4=2arctg(2-√31)+2πn 5) 2sin2x+cos2x=3sinxcosx Решается как предыдущее через тангенс х

sinx=1/2 x=30 градусов ой я ошибся смотри решение Marius =)

2sinx=1 sinx=1\2 на числовой окружности отметьте где синус равен 1\2 он равен в точках пи\6+2пиN и 5пи\6+2пиN, где N принадлежит Z, множеству целых чисел <img src=»//content.foto.my.mail.ru/mail/ssa-93/_answers/i-162.jpg» >

О­ль­г­а, с­па­си­б­о, чт­о по­с­ов­ет­овал­а <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&amp;st.cmd=logExternal&amp;st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&amp;https://mail.ru &amp;st.name=externalLinkRedirect&amp;st» target=»_blank»>fond2019.ru</a> Вы­п­лати­ли 28 тыс­я­ч за 20 м­инут ка­к т­ы и н­апи­сала. Ж­а­ль ч­то р­а­ньш­е не зна­ла пр­о таки­е ф­о­н­д­ы, на рабо­ту бы х­оди­ть не пр­ишлось:)

touch.otvet.mail.ru

Помогите пожалуйста) ) sin x= (-1/2) Синус икс = (минус одна вторая).

Решить уравнение sin x = -1/2. Решение. Ординату -1/2 имеют две точки единичной окружности М1 и М2, где х1 = -&#960;/6, х2 = -5&#960;/6. Следовательно, все корни уравнения sin x = -1/2 можно найти по формулам х = -&#960;/6 + 2&#960;k, х = -5&#960;/6 + 2&#960;k, k € Z. Эти формулы мы можем объединить в одну: х = (-1)n (-&#960;/6) + &#960;n, n € Z (2). Действительно, если n = 2k, то по формуле (2) получаем х = -&#960;/6 + 2&#960;k, а если n = 2k – 1, то по формуле (2) находим х = -5&#960;/6 + 2&#960;k. Ответ. х = (-1)n (-&#960;/6) + &#960;n, n € Z.

и в чем помогать?

формулу смотри

sin x = -1/2. х = (-1)^n+1 *π/6 + πn, n € Z

touch.otvet.mail.ru