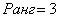Матрицы, определители, системы линейных уравнений (Лекция №12)
ОПРЕДЕЛЕНИЕ МАТРИЦЫ. ВИДЫ МАТРИЦ
Матрицей размером m×n называется совокупность m·n чисел, расположенных в виде прямоугольной таблицы из m строк и n столбцов. Эту таблицу обычно заключают в круглые скобки. Например, матрица может иметь вид:
Для краткости матрицу можно обозначать одной заглавной буквой, например, А или В.
В общем виде матрицу размером m×n записывают так
.
Числа, составляющие матрицу, называются элементами матрицы. Элементы матрицы удобно снабжать двумя индексами aij: первый указывает номер строки, а второй – номер столбца. Например, a23 – элемент стоит во 2-ой строке, 3-м столбце.
Если в матрице число строк равно числу столбцов, то матрица называется квадратной, причём число ее строк или столбцов называется порядком матрицы. В приведённых выше примерах квадратными являются вторая матрица – её порядок равен 3, и четвёртая матрица – её порядок 1.
Матрица, в которой число строк не равно числу столбцов, называется прямоугольной. В примерах это первая матрица и третья.
Различаются также матрицы, имеющие только одну строку или один столбец.
Матрица, у которой всего одна строка , называется матрицей – строкой (или строковой), а матрица, у которой всего один столбец, матрицей – столбцом.
Матрица, все элементы которой равны нулю, называется нулевой и обозначается (0), или просто 0. Например,
.
Главной диагональю квадратной матрицы назовём диагональ, идущую из левого верхнего в правый нижний угол.
Квадратная матрица, у которой все элементы, лежащие ниже главной диагонали, равны нулю, называется треугольной матрицей.
.Квадратная матрица, у которой все элементы, кроме, быть может, стоящих на главной диагонали, равны нулю, называется диагональной матрицей. Например, или .
Диагональная матрица, у которой все диагональные элементы равны единице, называется единичной матрицей и обозначается буквой E. Например, единичная матрица 3-го порядка имеет вид .
ДЕЙСТВИЯ НАД МАТРИЦАМИ
Равенство матриц. Две матрицы A и B называются равными, если они имеют одинаковое число строк и столбцов и их соответствующие элементы равны aij = bij. Так если и , то A=B, если a11 = b11, a12 = b12, a21 = b21 и a22 = b22.
Транспонирование. Рассмотрим произвольную матрицу A из m строк и n столбцов. Ей можно сопоставить такую матрицу
Эту матрицу B называют транспонированной матрицей A, а переход от A к B транспонированием.
Таким образом, транспонирование – это перемена ролями строк и столбцов матрицы. Матрицу, транспонированную к матрице A, обычно обозначают AT.
Связь между матрицей A и её транспонированной можно записать в виде .
Например. Найти матрицу транспонированную данной.
Сложение матриц. Пусть матрицы A и B состоят из одинакового числа строк и одинакового числа столбцов, т.е. имеют одинаковые размеры. Тогда для того, чтобы сложить матрицы A и B нужно к элементам матрицы A прибавить элементы матрицы B, стоящие на тех же местах. Таким образом, суммой двух матриц A и B называется матрица C, которая определяется по правилу, например,
или
Примеры. Найти сумму матриц:
- .
- — нельзя, т.к. размеры матриц различны.
- .
Легко проверить, что сложение матриц подчиняется следующим законам: коммутативному A+B=B+A и ассоциативному (A+B)+C=A+(B+C).
Умножение матрицы на число. Для того чтобы умножить матрицу A на число k нужно каждый элемент матрицы A умножить на это число. Таким образом, произведение матрицы A на число k есть новая матрица, которая определяется по правилу или .
Для любых чисел a и b и матриц A и B выполняются равенства:
- .
Примеры.
- .
- Найти 2A-B, если , .
.
- Найти C=–3A+4B.
Матрицу C найти нельзя, т.к. матрицы A и B имеют разные размеры.
Умножение матриц. Эта операция осуществляется по своеобразному закону. Прежде всего, заметим, что размеры матриц–сомножителей должны быть согласованы. Перемножать можно только те матрицы, у которых число столбцов первой матрицы совпадает с числом строк второй матрицы (т.е. длина строки первой равна высоте столбца второй). Произведением матрицы A не матрицу B называется новая матрица C=AB, элементы которой составляются следующим образом:
.
Таким образом, например, чтобы получить у произведения (т.е. в матрице C) элемент, стоящий в 1-ой строке и 3-м столбце c13
, нужно в 1-ой матрице взять 1-ую строку, во 2-ой – 3-й столбец, и затем элементы строки умножить на соответствующие элементы столбца и полученные произведения сложить. И другие элементы матрицы-произведения получаются с помощью аналогичного произведения строк первой матрицы на столбцы второй матрицы.В общем случае, если мы умножаем матрицу A = (aij) размера m×n на матрицу B = (bij) размера n×p, то получим матрицу C размера m×p, элементы которой вычисляются следующим образом: элемент cij получается в результате произведения элементов i-ой строки матрицы A на соответствующие элементы j-го столбца матрицы B и их сложения.
Из этого правила следует, что всегда можно перемножать две квадратные матрицы одного порядка, в результате получим квадратную матрицу того же порядка. В частности, квадратную матрицу всегда можно умножить саму на себя, т.е. возвести в квадрат.
Другим важным случаем является умножение матрицы–строки на матрицу–столбец, причём ширина первой должна быть равна высоте второй, в результате получим матрицу первого порядка (т.е. один элемент). Действительно,
.
Примеры.
- Пусть
Найти элементы c12, c23 и c21 матрицы C.
- Найти произведение матриц.
.
- .
- — нельзя, т.к. ширина первой матрицы равна 2-м элементам, а высота второй – 3-м.
- Пусть
Найти АВ и ВА.
Найти АВ и ВА.
, B·A – не имеет смысла.
Таким образом, эти простые примеры показывают, что матрицы, вообще говоря, не перестановочны друг с другом, т.е. A∙B ≠ B∙A
. Поэтому при умножении матриц нужно тщательно следить за порядком множителей.Можно проверить, что умножение матриц подчиняется ассоциативному и дистрибутивному законам, т.е. (AB)C=A(BC) и (A+B)C=AC+BC.
Легко также проверить, что при умножении квадратной матрицы A на единичную матрицу E того же порядка вновь получим матрицу A, причём AE=EA=A.
Можно отметить следующий любопытный факт. Как известно произведение 2-х отличных от нуля чисел не равно 0. Для матриц это может не иметь места, т.е. произведение 2-х не нулевых матриц может оказаться равным нулевой матрице.
Например, если , то
.
ПОНЯТИЕ ОПРЕДЕЛИТЕЛЕЙ
Пусть дана матрица второго порядка – квадратная матрица, состоящая из двух строк и двух столбцов .
Определителем второго порядка, соответствующим данной матрице, называется число, получаемое следующим образом:
Определитель обозначается символом .
Итак, для того чтобы найти определитель второго порядка нужно из произведения элементов главной диагонали вычесть произведение элементов по второй диагонали.
Примеры. Вычислить определители второго порядка.
- .
- Вычислить определитель матрицы D, если D= -А+2В и
Аналогично можно рассмотреть матрицу третьего порядка и соответствующий ей определитель.
Определителем третьего порядка, соответствующим данной квадратной матрице третьего порядка, называется число, обозначаемое и получаемое следующим образом:
.
Таким образом, эта формула даёт разложение определителя третьего порядка по элементам первой строки a11, a12, a13 и сводит вычисление определителя третьего порядка к вычислению определителей второго порядка.
Примеры. Вычислить определитель третьего порядка.
- .
- .
- Решите уравнение..
.
(x+3)(4x-4-3x)+4(3x-4x+4)=0.
(x+3)(x-4)+4(-x+4)=0.
(x-4)(x-1)=0.
x1 = 4, x2 = 1.
Аналогично можно ввести понятия определителей четвёртого, пятого и т.д. порядков, понижая их порядок разложением по элементам 1-ой строки, при этом знаки «+» и «–» у слагаемых чередуются.
Итак, в отличие от матрицы, которая представляют собой таблицу чисел, определитель это число, которое определённым образом ставится в соответствие матрице.
1. Системы линейных уравнений с квадратной невырожденной матрицей
Пусть число уравнений системы равно числу переменных, т.е.
(1) 
Тогда
матрица системы является квадратной,
а ее определитель
= |A|
называется
определителем
системы. Запишем систему вида (1) в
матричном виде, обозначив матрицу
коэффициентов при неизвестных  ,
матрицу столбец свободных членов
,
матрицу столбец свободных членов ,
матрицу столбец неизвестных
,
матрицу столбец неизвестных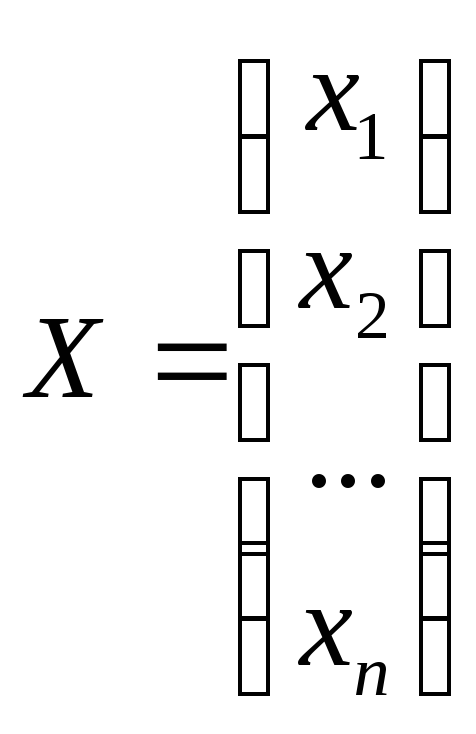 .
Умножая матрицы АХ, получаем новую
матрицу, элементами которой являются
левые части уравнений системы (1). На
основании равенства матриц систему (1)
можно записать систему (1) в виде АХ=В.
.
Умножая матрицы АХ, получаем новую
матрицу, элементами которой являются
левые части уравнений системы (1). На
основании равенства матриц систему (1)
можно записать систему (1) в виде АХ=В.
Предположим, что матрица системы А невырожденная, т.е. ее определитель отличен от нуля. Тогда существует обратная матрица А-1. Следовательно решение системы (1) имеет вид Х = А-1 В. Т.е., чтобы найти решение системы, нужно обратную матрицу умножить на столбец свободных членов справа.
Пример 1. Дана система линейных уравнений
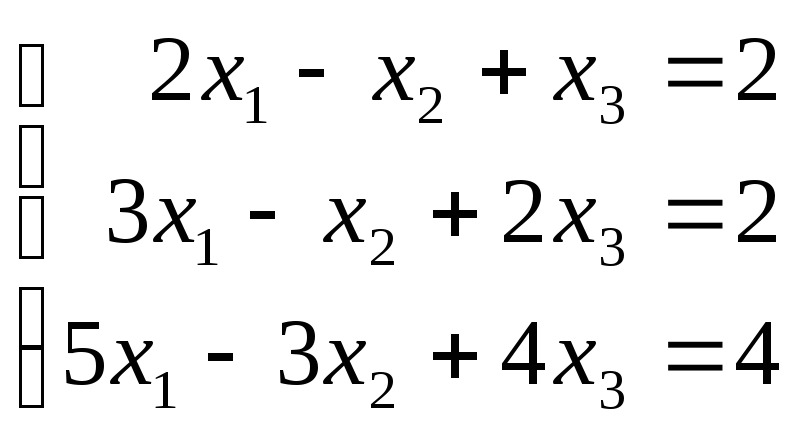 .
.
Доказать ее совместность и решить средствами матричного исчисления.
РЕШЕНИЕ
Докажем совместность. Запишем расширенную матрицу системы

и
найдем ее ранг. Элемент матрицы  ,
стоящий в левом верхнем углу,отличен
от нуля, следовательно
,
стоящий в левом верхнем углу,отличен
от нуля, следовательно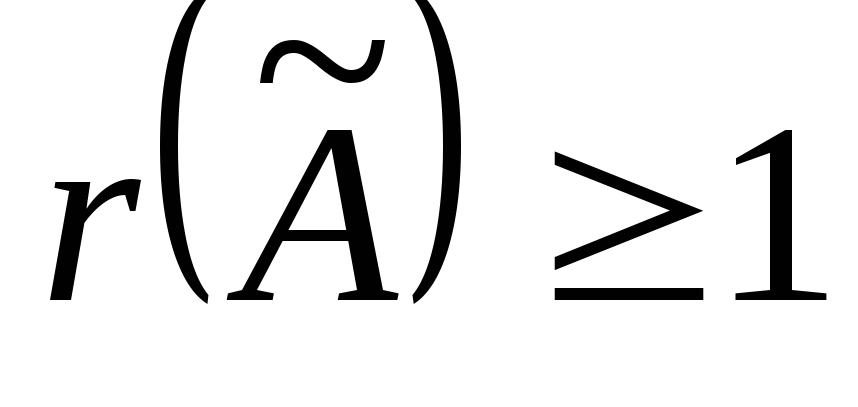 среди миноров второго порядка, окаймляющих
(включающих в себя) этот элемент, также
есть отличные от нуля, например,
среди миноров второго порядка, окаймляющих
(включающих в себя) этот элемент, также
есть отличные от нуля, например,
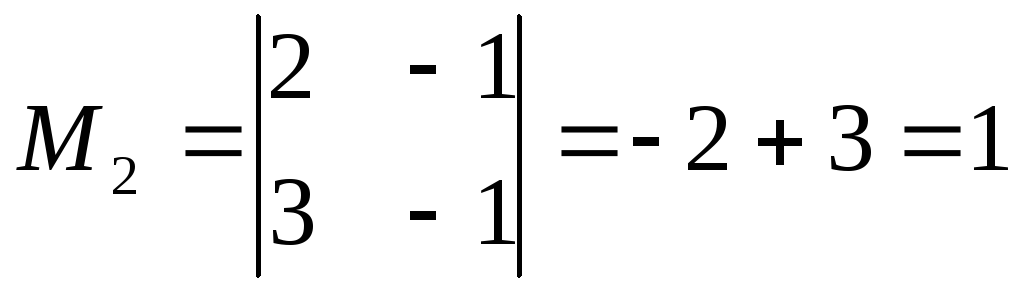 ,
т.е.
,
т.е. 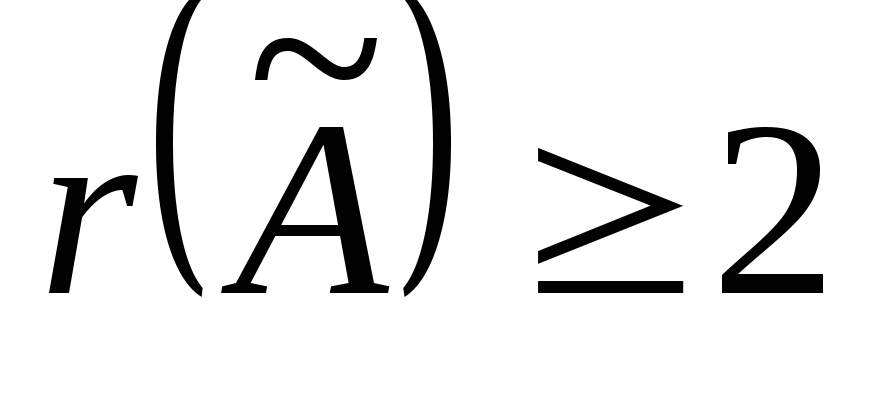 .
.
Из
миноров третьего порядка, окаймляющих  , возьмем минор
, возьмем минор
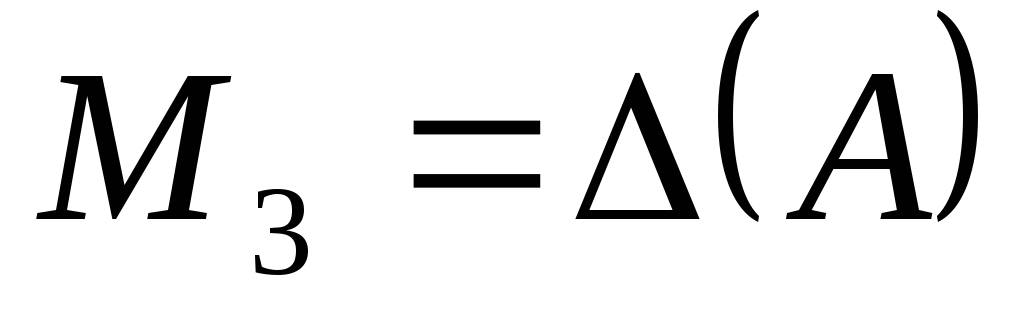 :
:
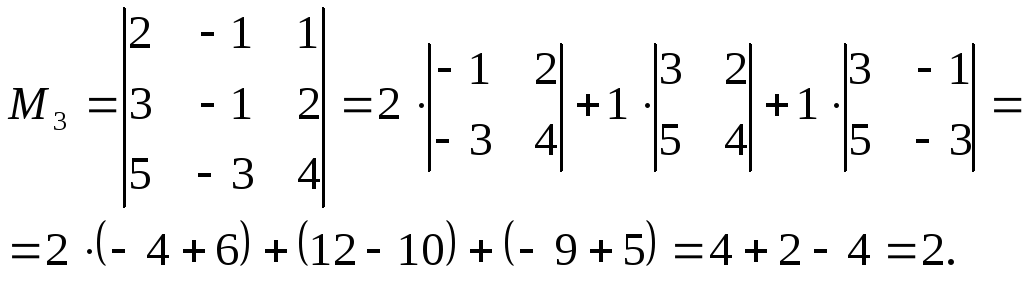
Т.к.  то
то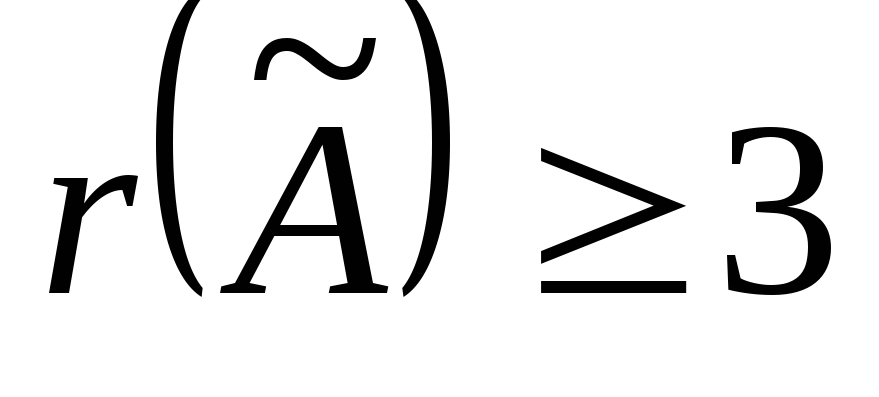 ,
а т.к. у матрицы
,
а т.к. у матрицы миноров 4-го порядка не существует, то
миноров 4-го порядка не существует, то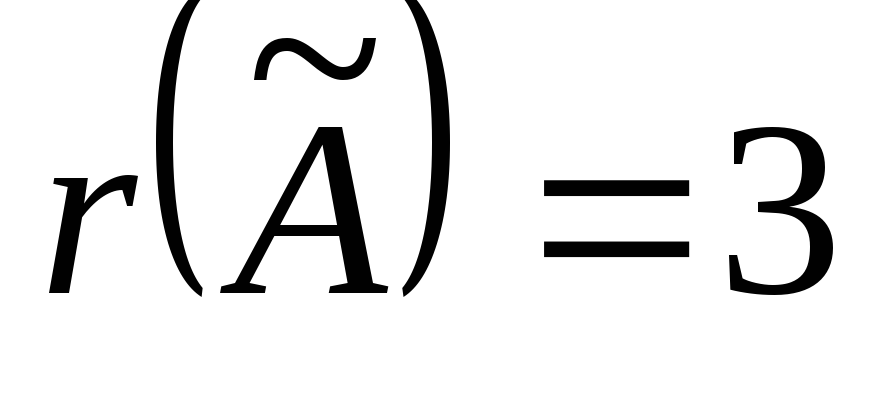 .
Так как
.
Так как 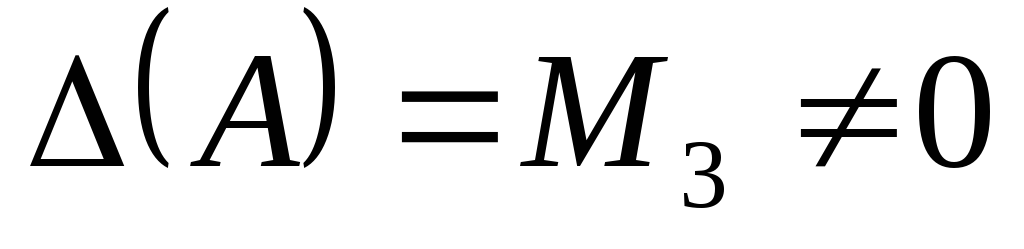 ,
то и
,
то и  .
Таким образом,
.
Таким образом, 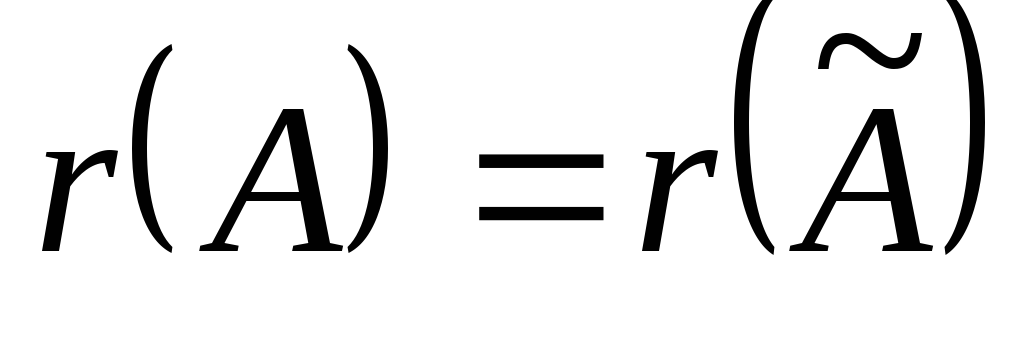 ,
и совместность доказана.
,
и совместность доказана.
Применяем матричный метод к решению системы. Формируем матрицы, состоящие из элементов системы:
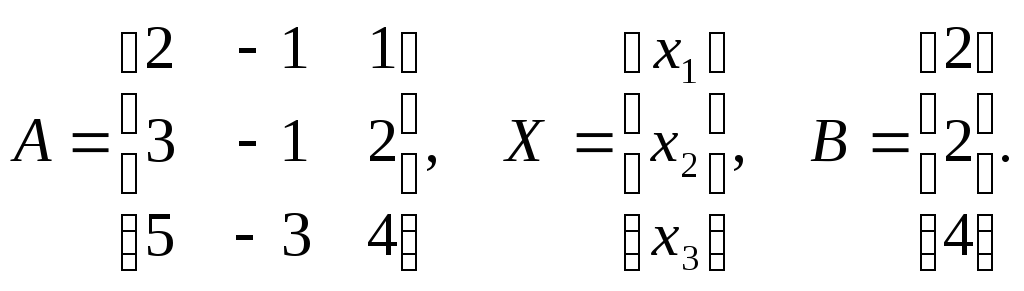
а)
Определитель системы 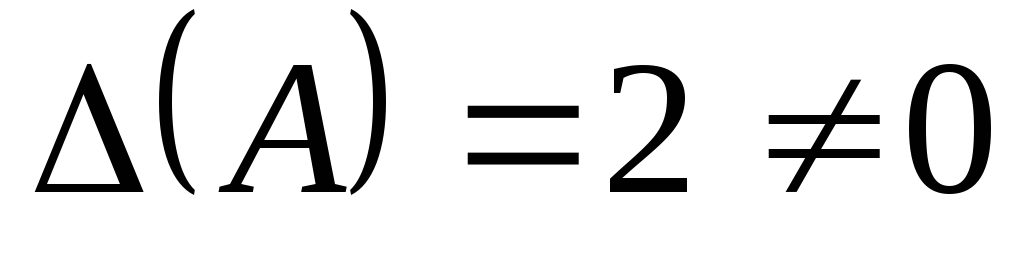 ,
значит, матричный метод применим.
,
значит, матричный метод применим.
б)
Запишем систему в матричном виде 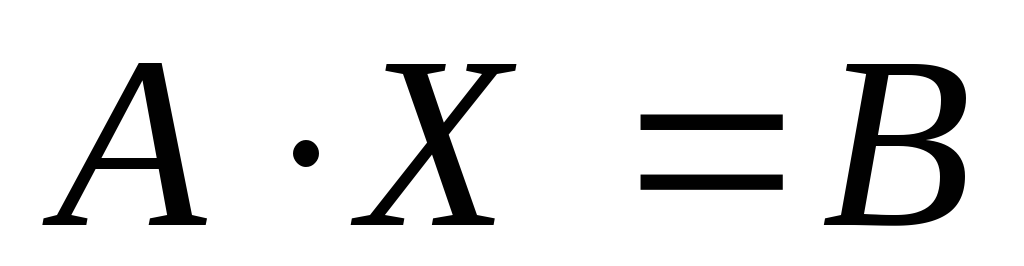 :
:

в)
Вычисляем алгебраические дополнения  .
.
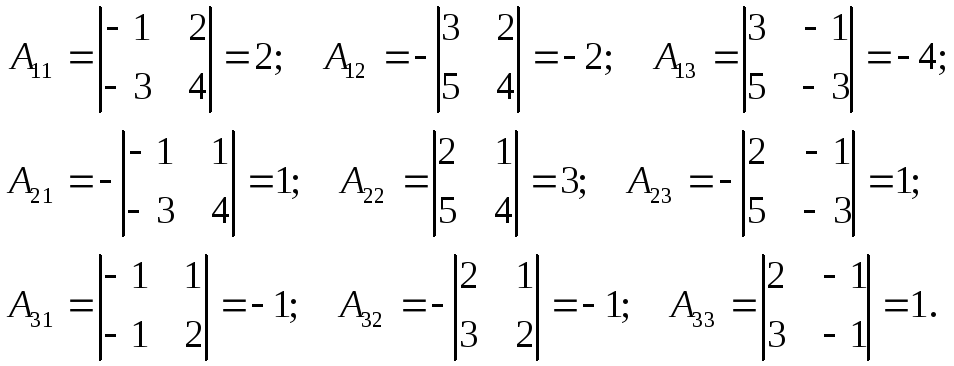
Подставляя
найденные значения  в формулу (6.3), получим:
в формулу (6.3), получим:
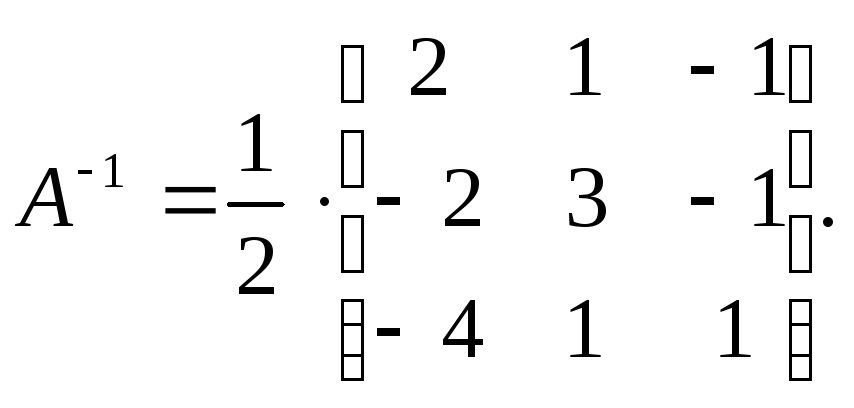
г) воспользуемся формулой (6.4).
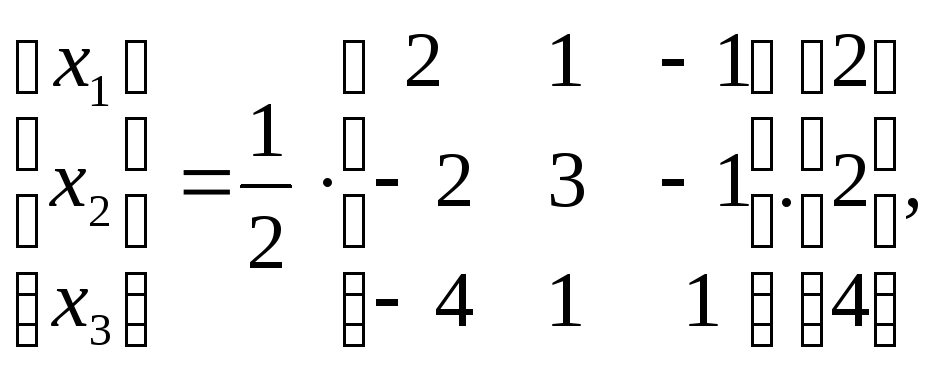
получим:
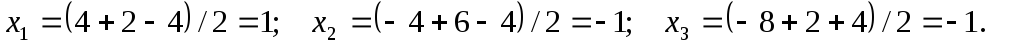
Итак,
решение системы: 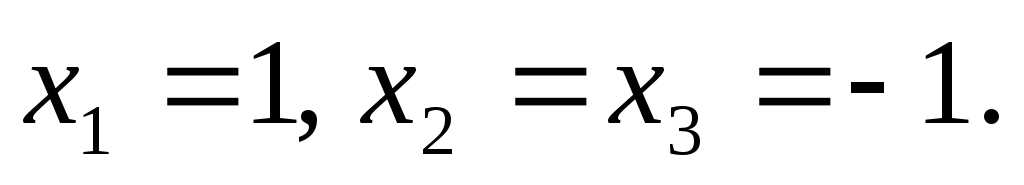
Пример 2. Решить систему уравнений матричным методом.
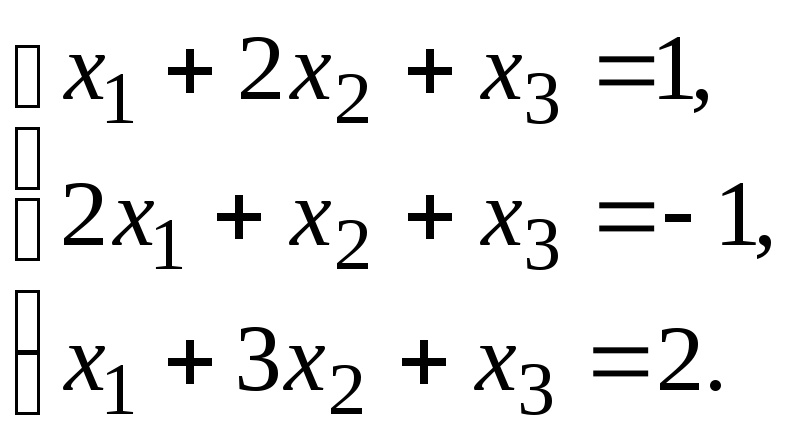
Решение: 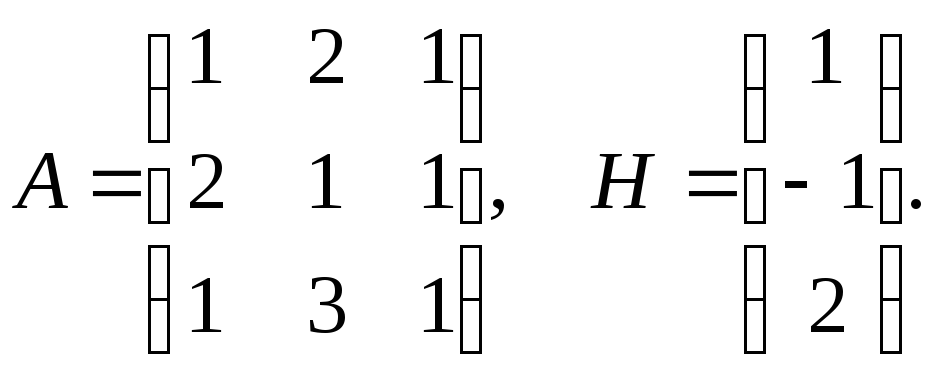
Находим обратную матрицу (самостоятельно)
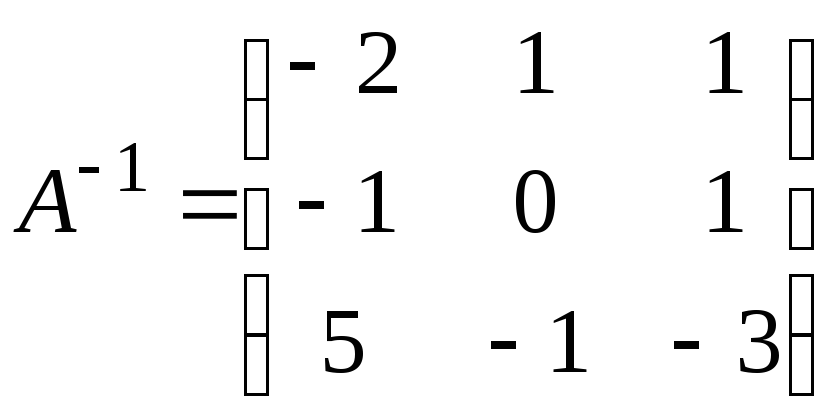 .
Следовательно, по формуле Х
= А-1Н,
получаем
.
Следовательно, по формуле Х
= А-1Н,
получаем 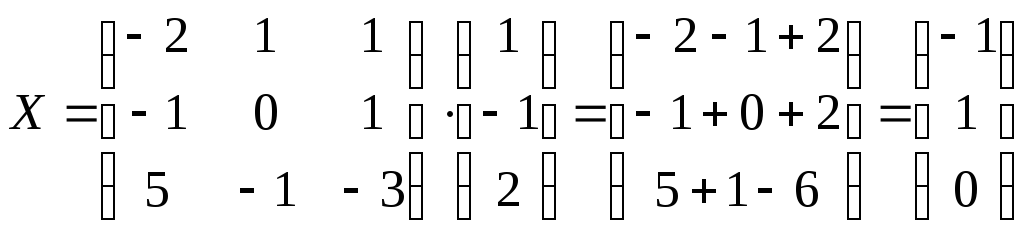 ,
,
т.е. 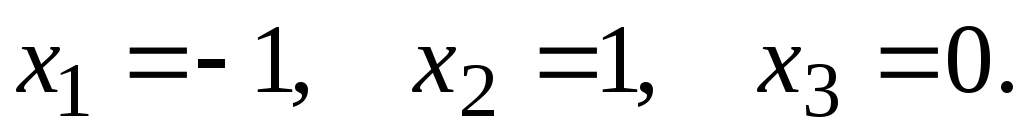
Ответ: 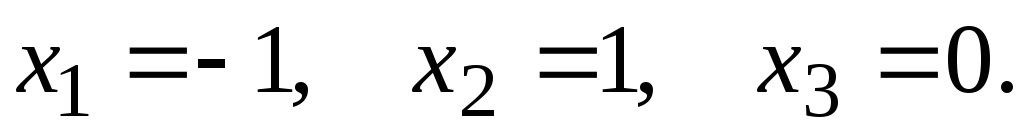
Лекция 7. Решение систем линейных уравнений по формулам Крамера.
Решение систем по формулам Крамера.
Рассмотрим решение системы двух уравнений с двумя переменными:
(3) 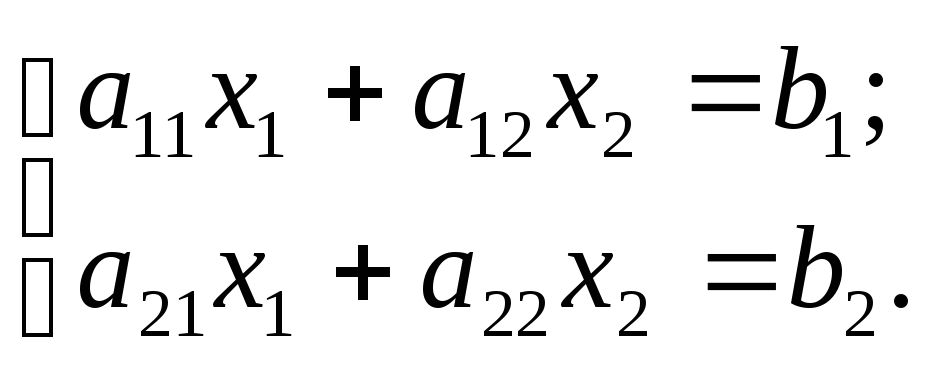 в
которой хотя бы один из коэффициентов
при переменных отличен
от нуля.
в
которой хотя бы один из коэффициентов
при переменных отличен
от нуля.
Для решения этой системы исключим переменную х2, умножив первое уравнение на a22, второе — на (-a12) и сложив их. Затем исключим переменную х1, умножив первое уравнение на (-a21 ), второе — на a11 и также сложив их. В результате получим систему:
 Выражение
в скобках есть определитель системы
Выражение
в скобках есть определитель системы 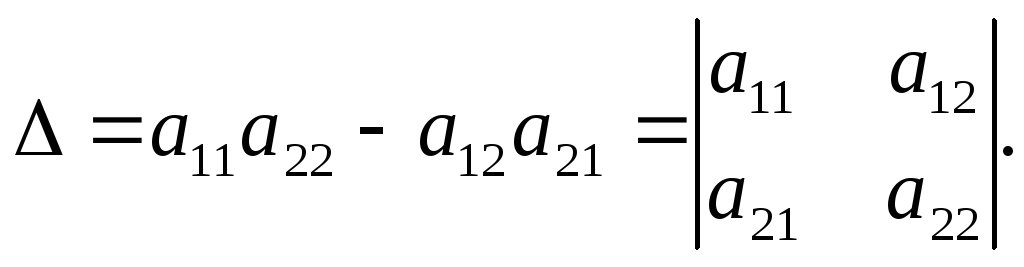
Обозначив 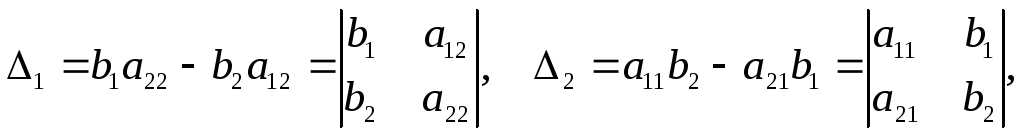 система
примет вид:
система
примет вид: Из
полученной системы следует, что если
определитель системы
= 0, то система имеет единственное
решение, определяемое
по формулам:
Из
полученной системы следует, что если
определитель системы
= 0, то система имеет единственное
решение, определяемое
по формулам: 
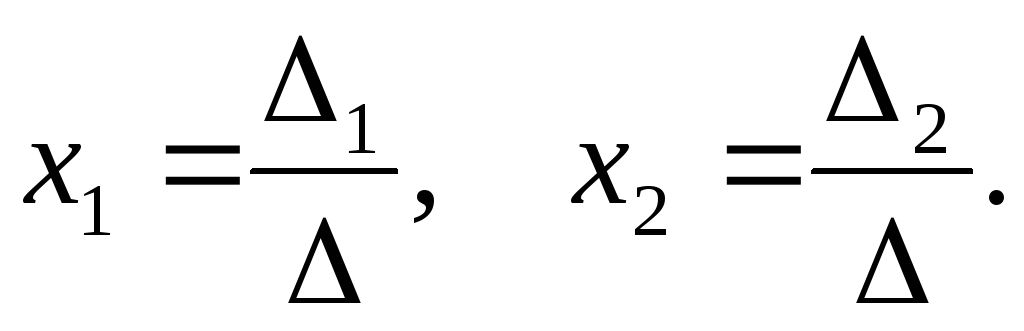
Если
= 0, a
1
0
(или 2
0),
то система (3) несовместная,
так как в этом случае приводится к виду: 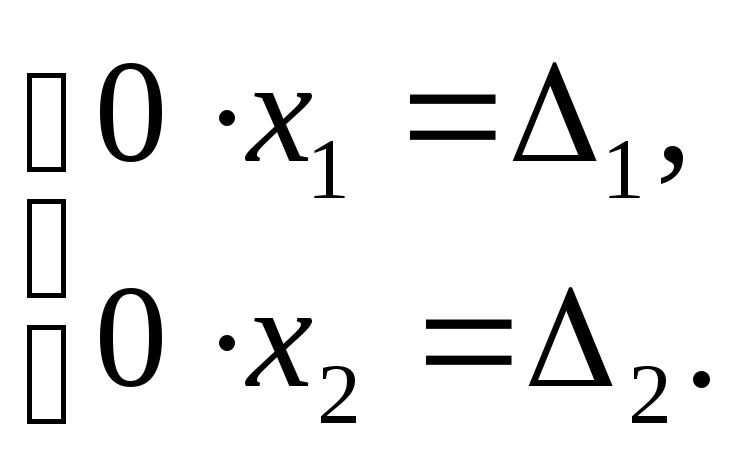
Если
= 1=
2 = 0 , то система (2) неопределенная и имеет
бесконечное
множество решений, так как в этом случае
приводится к виду: 
Для получения решения системы (2) в общем виде предположим, что квадратная матрица системы Аnn невырожденная, т.е. ее определитель |A| 0. В этом случае существует обратная матрица А-1.
Умножая слева обе части матричного равенства на матрицу А-1, получим A-1(AX)=A-1 В. Так как A-1(AX)=(A-1A)B= ЕХ = X , то
Теорема Крамера. Пусть — определитель матрицы системы A, a j — определитель матрицы, получаемой из матрицы А заменой j-го столбца столбцом свободных членов. Тогда, если 0, то система имеет единственное решение, определяемое по формулам:

Эти формулы получили название формул Крамера.
Доказательство:
решением системы методом обратной
матрицы будет
матрица-столбец X=A-1B.
Обратная матрица A-1=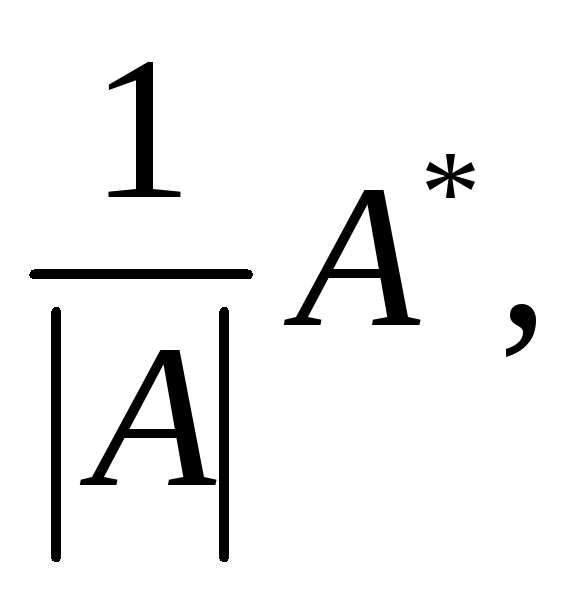 , где
A* — матрица,
присоединенная к матрице А.
Так
как элементы матрицы
А* есть
алгебраические дополнения элементов
матрицы АT , транспонированной
к А,
то
запишем данное равенство в развернутой
форме:
, где
A* — матрица,
присоединенная к матрице А.
Так
как элементы матрицы
А* есть
алгебраические дополнения элементов
матрицы АT , транспонированной
к А,
то
запишем данное равенство в развернутой
форме:
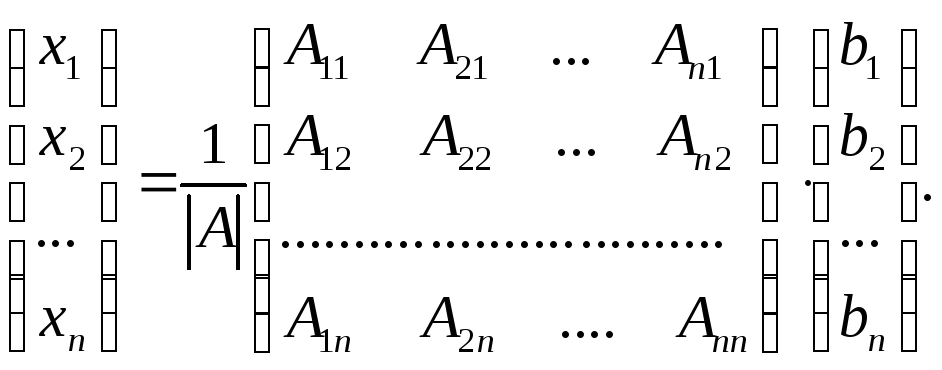 Учитывая,
что
Учитывая,
что 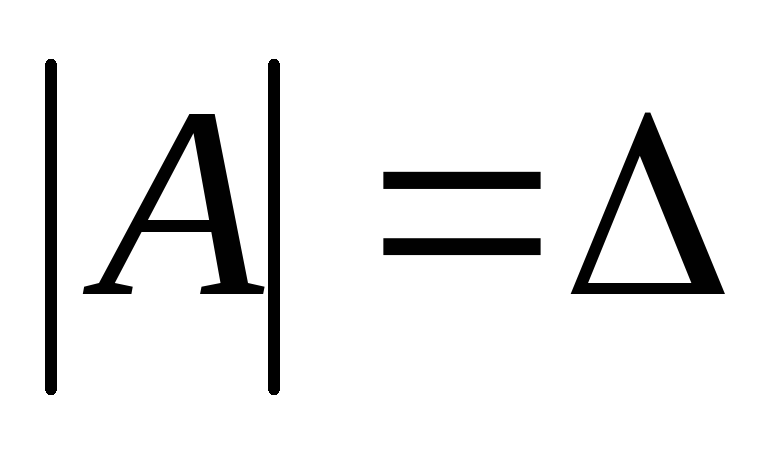 ,
получим после умножения матриц
,
получим после умножения матриц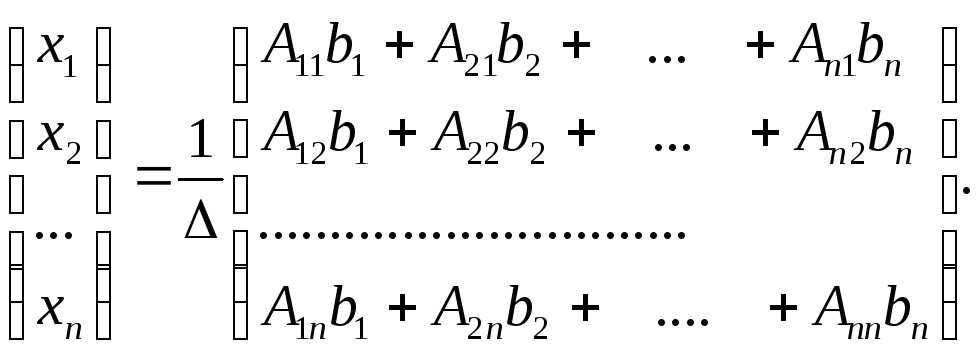 Откуда следует, что для любогоj
(j
= 1,2,3,4,…,n)
Откуда следует, что для любогоj
(j
= 1,2,3,4,…,n) 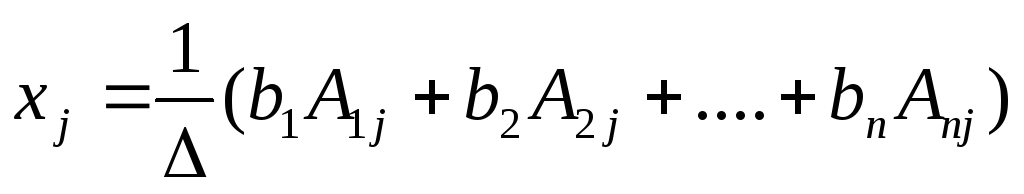 .
.
На
основании свойств определителей  ,
гдеj – определитель матрицы, полученной из
матрицы А заменой j-го
столбца столбцом свободных членов.
Следовательно,
,
гдеj – определитель матрицы, полученной из
матрицы А заменой j-го
столбца столбцом свободных членов.
Следовательно, 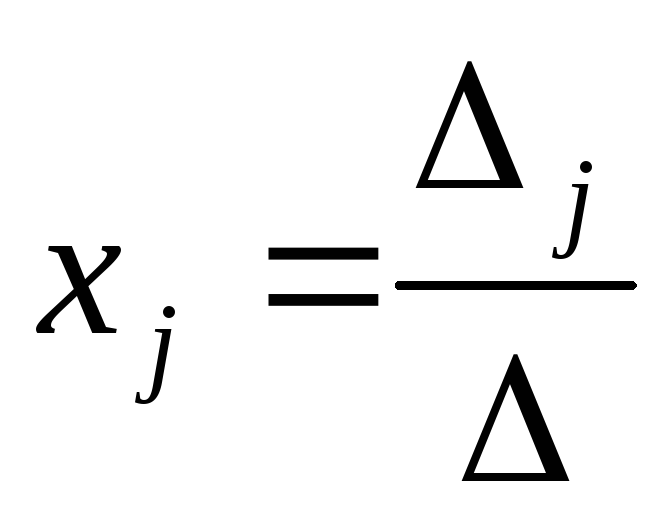 .(j
= 1,2,3,4,….n)
, т.е.
.(j
= 1,2,3,4,….n)
, т.е.
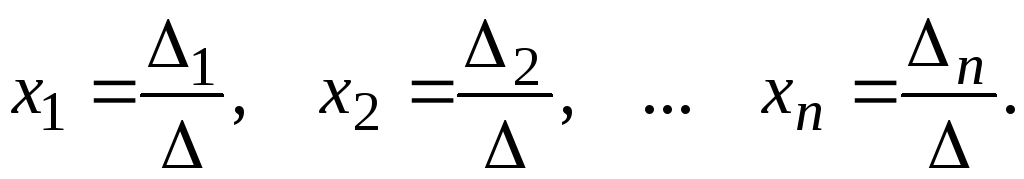
Пример
1.
Решить систему уравнений 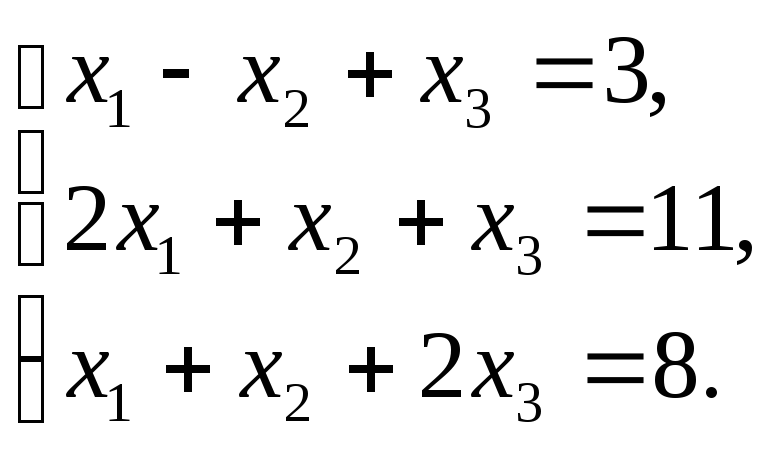 по формулам Крамера.
по формулам Крамера.
Решение. Найдем определитель системы = |А| = 5 . Так как 0, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц 1, 2, 3, полученных из матрицы А, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
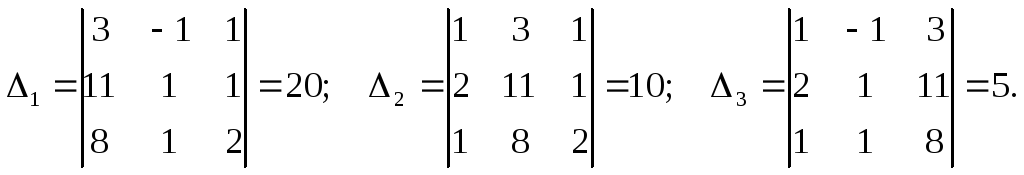
Теперь
по формулам Крамера получаем 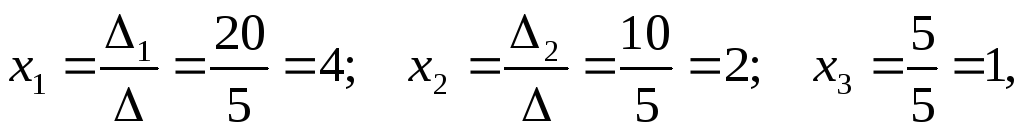 т.е.
решение системы (4; 2; 1).
т.е.
решение системы (4; 2; 1).
В конце решения системы (любым способом) рекомендуем сделать проверку, подставив найденные значения в уравнения системы, и убедиться в том, что они обращаются в верные равенства.
Пример 2. Решить систему по формулам Крамера.
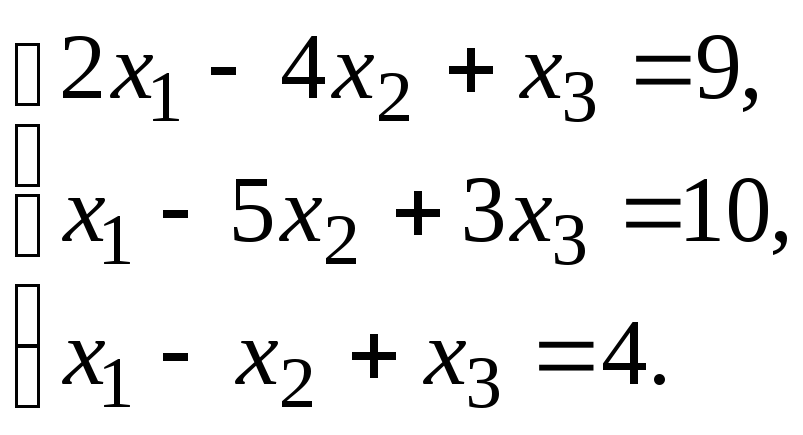
Решение.
Составим 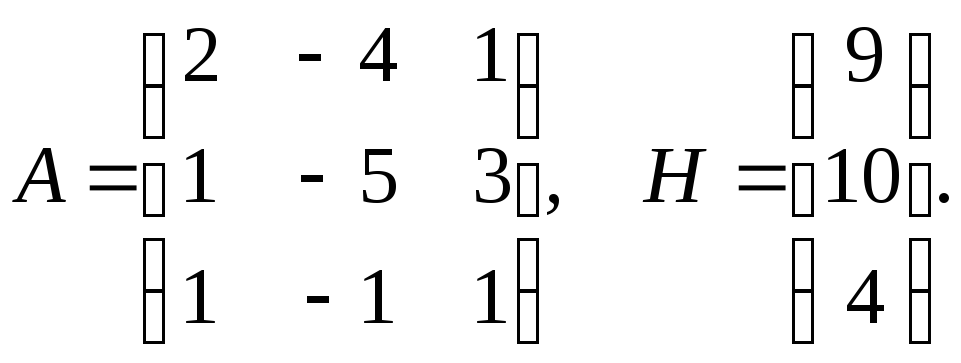
Вычислим определитель этой системы:
 .
.
Последовательно заменяя в определителе ∆ первый, второй и третий столбцы столбцом свободных членов, получим:
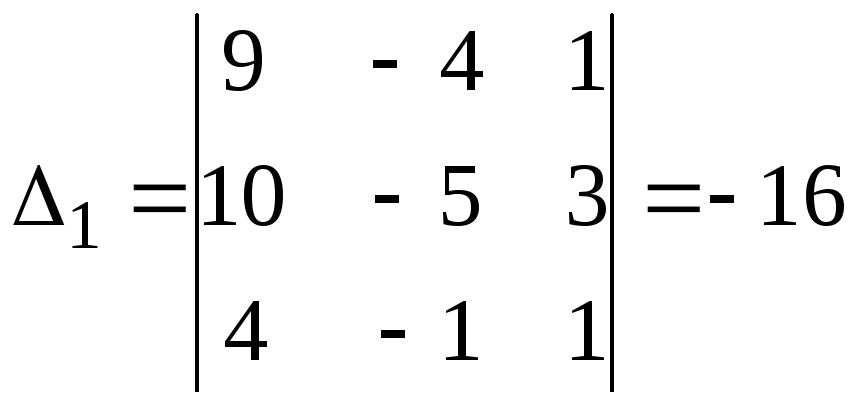 ,
,  ,
,  .
.
Подставим значения определителей в формулы Крамера.

Ответ: 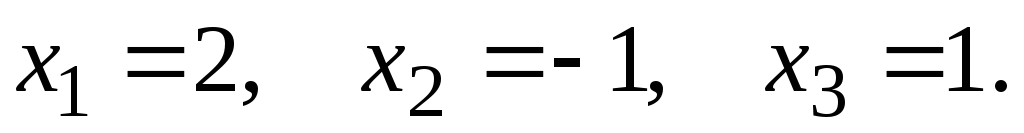
Существенным недостатком решения систем n линейных уравнений с n переменными по формулам Крамера и методом обратной матрицы является их большая трудоемкость, связанная с вычислением определителей и нахождением обратной матрицы. Поэтому эти методы представляют скорее теоретический интерес и на практике не могут быть использованы для решения реальных экономических задач, сводящихся часто к системам с большим числом уравнений и переменных.
Лекция 8. Общее решение систем линейных уравнений.
Расширенная матрица, формула и примеры
Пусть задана СЛАУ
Матрица , составленная из коэффициентов при неизвестных , называется основной матрицей системы или матрицей системы:
Матрица , полученная из основной матрицы, дописыванием справа столбца свободных членов, называется расширенной матрицей СЛАУ:
Примеры решения задач с расширенными матрицами
| Понравился сайт? Расскажи друзьям! | |||
3. Как исследовать систему линейных уравнений на совместность?
Нередко помимо решения системы линейных уравнений по условию предварительно требуется исследовать её на совместность, то есть доказать, что какое-либо решение вообще существует. Ключевую роль в такой проверке играет теорема Кронекера-Капелли, которую я сформулирую в необходимом виде:
Если ранг матрицы системы равен рангу расширенной матрицы системы, то система совместна, причём, если данное число совпадает с количеством неизвестных, то решение единственно.
Таким образом, для исследования системы
на совместность нужно проверить равенство 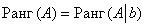 ,
где
,
где  – матрица системы (вспоминаем
терминологию из урока Метод Гаусса),
а
– матрица системы (вспоминаем
терминологию из урока Метод Гаусса),
а 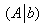 – расширенная матрица системы (т.е.
матрица с коэффициентами при переменных
+ столбец свободных членов).
– расширенная матрица системы (т.е.
матрица с коэффициентами при переменных
+ столбец свободных членов).
Всё просто: обратный матрица алгебраический уравнение
Пример 7
Исследовать систему на совместность и найти её решение, если система совместна
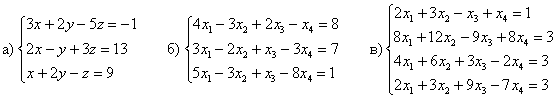
А когда системы уже прорешаны – просто вдвойне… нет – втройне =)
Решение: тем не менее, обратим внимание на строгую верхнюю строчку – по условию,
в первую очередь, требуется проверить систему на совместность. Как начать решение?
В любом случае записываем расширенную матрицу системы и с помощью элементарных преобразований приводим её к ступенчатому виду:
а) Пример №1 статьи о методе исключения неизвестных:
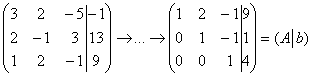
Элементарные преобразования не меняют ранга матриц, поэтому в результате выполненных действий получены эквивалентные исходным матрица системы

и расширенная матрица системы
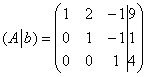 .
.
Максимальный порядок ненулевого минора матрицы системы равен трём. Здесь таковой минор в единственном экземпляре и совпадает он, понятно, с определителем самой матрицы:

(см. урок о методах вычисления определителя)
Следовательно,  .
.
Максимальный порядок ненулевого минора расширенной матрицы системы также равен трём:
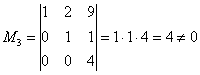
(взяты первые два столбца + столбец свободных членов).
Таким образом, 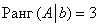 .
.
Вывод: 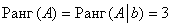 ,
значит, по теореме Кронекера-Капелли
система совместна; и поскольку количество
переменных (
,
значит, по теореме Кронекера-Капелли
система совместна; и поскольку количество
переменных ( – 3 шт.) совпадает с рангом, то система
имеет единственное решение.
– 3 шт.) совпадает с рангом, то система
имеет единственное решение.
Что дальше? Дальше следует непосредственно решить систему. Если по условию не предложен способ, то, конечно же, раскручиваем обратный ход метода Гаусса. Если требуется решить систему методом Крамера или с помощью обратной матрицы, ну что поделать….
б) Пример №1 статьи о несовместных системах и системах с общим решением:

В результате элементарных преобразований получена эквивалентная матрица системы
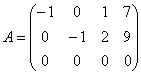
и расширенная матрица системы
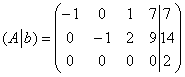 .
.
Максимальный порядок ненулевого минора матрицы системы равен двум, например:
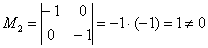 ,
,
поэтому 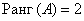
Заметьте, что здесь есть возможность выбрать и другой минор 2-го порядка, но проще всего в качестве примера взять ступенчатый определитель.
Максимальный порядок ненулевого минора расширенной матрицы системы равен трём, например:
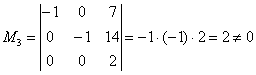
(первые два столбца + столбец свободных членов).
Таким образом,
 .
.
Вывод:
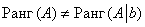 ,
,
значит, по теореме Кронекера-Капелли система несовместна.
Однако помните – если по условию не требуется исследовать систему на совместность, то вполне достаточно ограничиться стандартным ответом (см. решение вышеуказанного урока).
в) Пример №3 той же статьи:
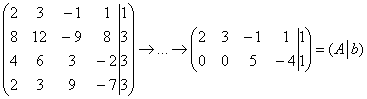
В результате элементарных преобразований
получена эквивалентная матрица системы 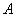 и расширенная матрица системы
и расширенная матрица системы  .
.
Максимальный порядок ненулевого минора матрицы системы равен двум, например:
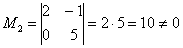 ,
,
следовательно, 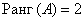 .
.
Максимальный порядок ненулевого минора расширенной матрицы системы также равен двум, например:
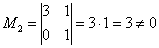 ,
,
Поэтому
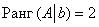
Второй абзац можно полностью заменить хитрой лаконичной фразой: «по этой же причине
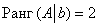 «.
«.
Вывод:
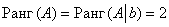 ,
,
значит, по теореме Кронекера-Капелли
система совместна. Поскольку ранг меньше
количества переменных ( – 4 шт.), то система имеет бесконечно
много решений.
– 4 шт.), то система имеет бесконечно
много решений.
Далее находим общее решение по стандартной схеме.
Готово.
Образец исследования системы на совместность также можно посмотреть в начале
Примера №1 урока о нахождении различных базисных решений системы.
…Всё-таки иногда удивительно обманываются ожидания – порой думаешь, что статья получится огромной, а она оказывается весьма компактной, а иногда, как сейчас – наоборот. Посмотрел статистику и жутко удивился добрым 20-ти тысячам символов. Поэтому всем высокого ранга и до скорых встреч!
Решения и ответы:
Пример 2: Решение: поскольку в матрице есть ненулевые элементы, то её ранг не меньше единицы.
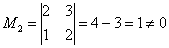 ,
,
значит, ранг матрицы не менее двух.
Рассмотрим миноры 3-го порядка, при этом в них обязательно должен содержаться ненулевой минор

. Таких миноров два:
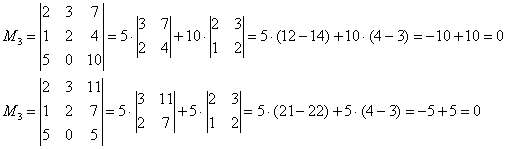
Максимальный порядок ненулевого минора равен двум.
Ответ: 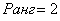
Пример 4: Решение: с помощью элементарных преобразований приведем матрицу к ступенчатому виду:
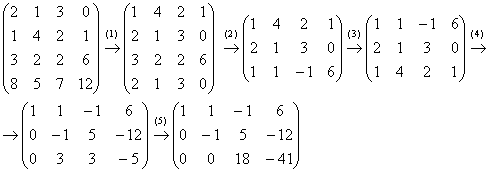
(1) Первую и вторую строки поменяли местами. К 4-й строке прибавили 3-ю строку, умноженную на –2.
(2) Вторая и 4-я строки одинаковы, 4-ю строку удалили. К третьей строке прибавили вторую строку, умноженную на –1.
(3) Первую и третью строки поменяли местами.
(4) Ко второй строке прибавили первую строку, умноженную на –2. К 3-й строке прибавили первую строку, умноженную на –1.
(5) К третьей строке прибавили вторую строку, умноженную на 3.
В результате получены 3 строки, значит, ранг матрицы равен 3.
Ответ: 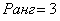
Пример 6: Решение: ранг матрицы не превосходит минимальной размерности, то есть, трёх.
В матрице есть ненулевые элементы, значит, ранг не менее единицы.

Максимальный порядок ненулевого минора равен трём
Ответ: