Раздел 5. Системы линейных уравнений.
55
5.1. Матричная запись линейной системы.
Определение. Системой линейных алгебраических уравнений,содержащейmуравнений и пнеизвестных , называется выражение следующего вида:
(1)
где 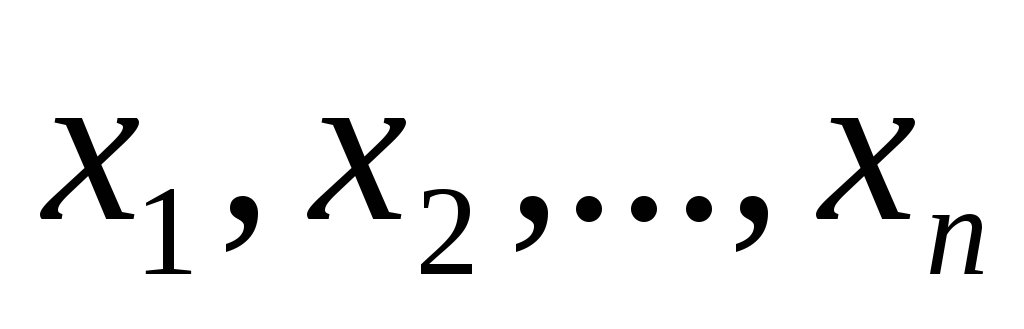 — неизвестные,
— неизвестные, — коэффициент изi-го
уравнения при неизвестном
— коэффициент изi-го
уравнения при неизвестном ,
, ‑
свободный членi-го
уравнения.
‑
свободный членi-го
уравнения.
Введем обозначения:

 — столбец неизвестных,
— столбец неизвестных,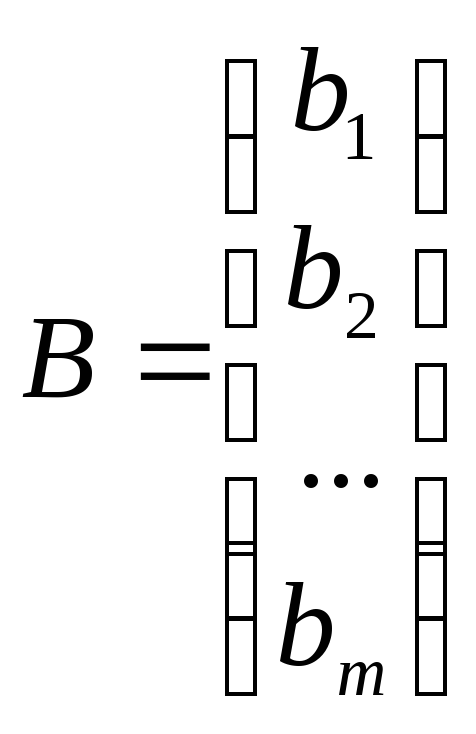 — столбец свободных членов.
— столбец свободных членов.
Используя введенные обозначения и правила действия над матрицами, систему (1) можно записать в матричной форме
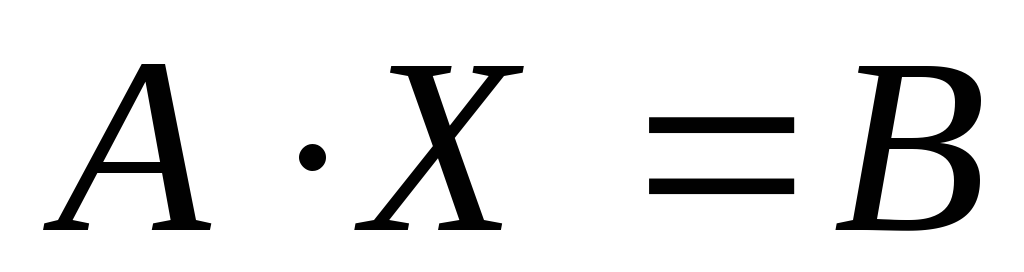 .
(2)
.
(2)
Определение.Совокупность чисел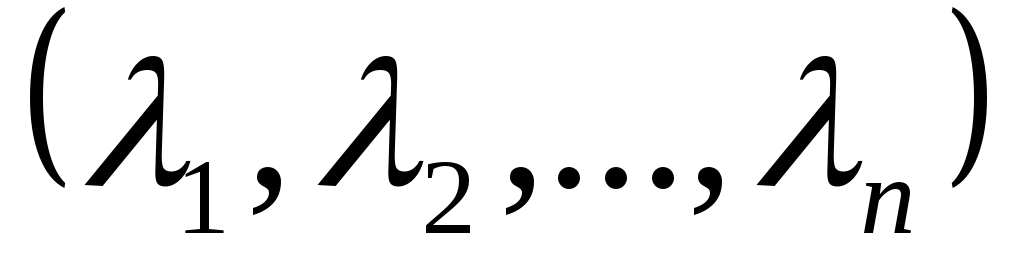 называетсярешением системы(1), если
после подстановки в каждое из уравнений
(1) вместо неизвестных
называетсярешением системы(1), если
после подстановки в каждое из уравнений
(1) вместо неизвестных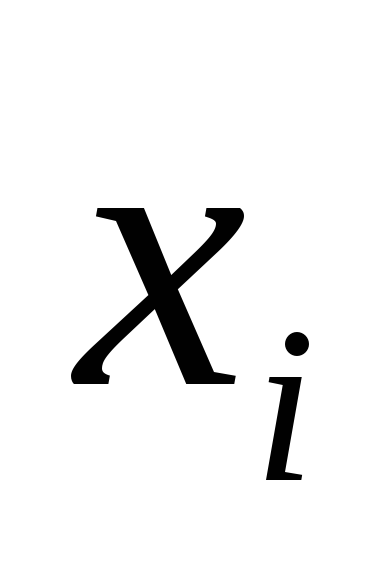

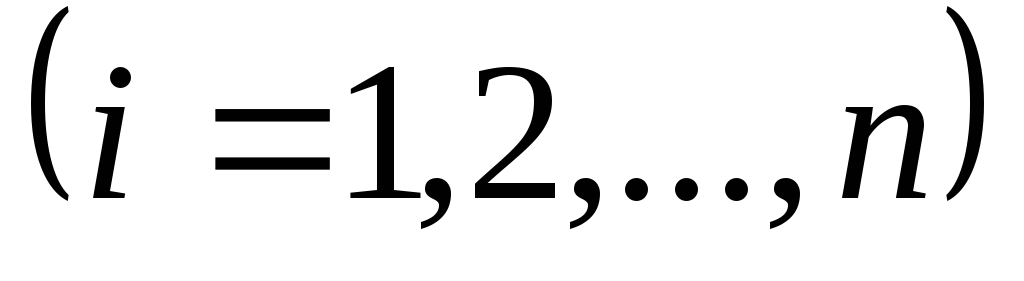 ,
это уравнение превращается в верное
равенство.
,
это уравнение превращается в верное
равенство.Определение.Система(1) называетсясовместной,если она имеет хотя бы одно решение, инесовместнойв противном случае.
Мы начнем с исследования частного случая
системы (1), когда 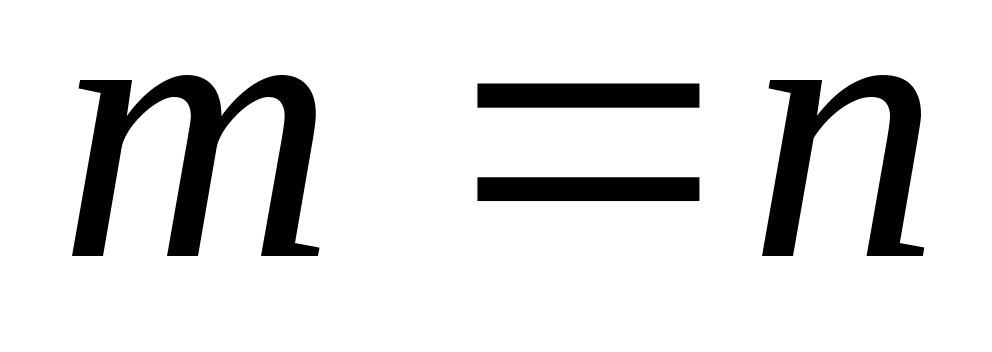 ,
т.е. число уравнений равно числу
неизвестных, и при этом матрицаАсистемы невырожденная.
,
т.е. число уравнений равно числу
неизвестных, и при этом матрицаАсистемы невырожденная.
5.2. Решение линейной системы с помощью обратной матрицы.
Рассмотрим частный случай, когда число уравнений совпадает с числом неизвестных.
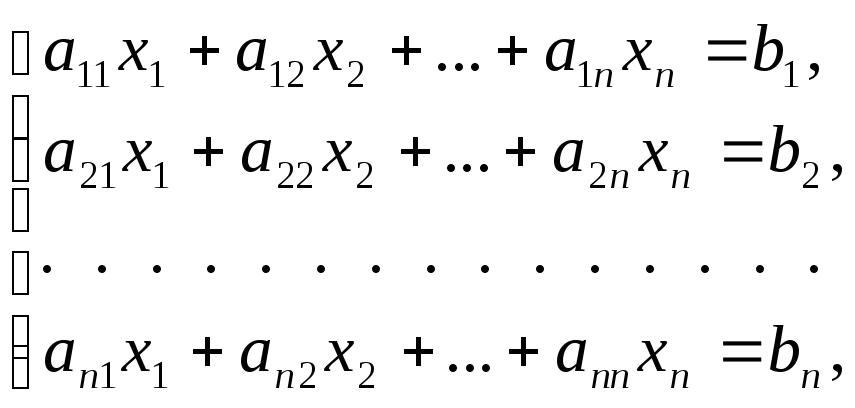 (1)
(1)
или
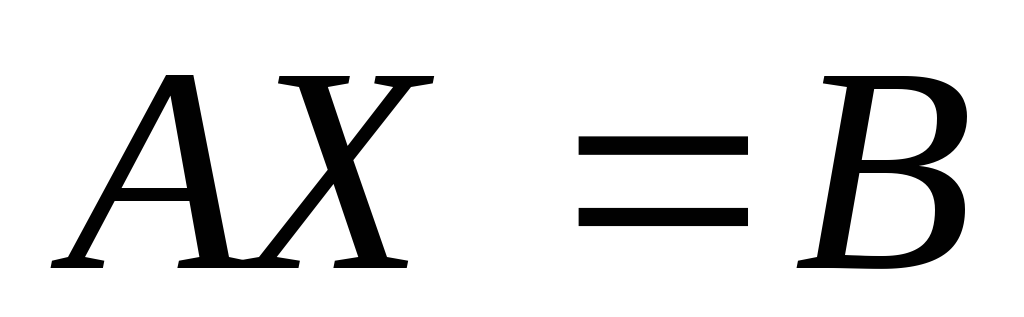
В этом случае 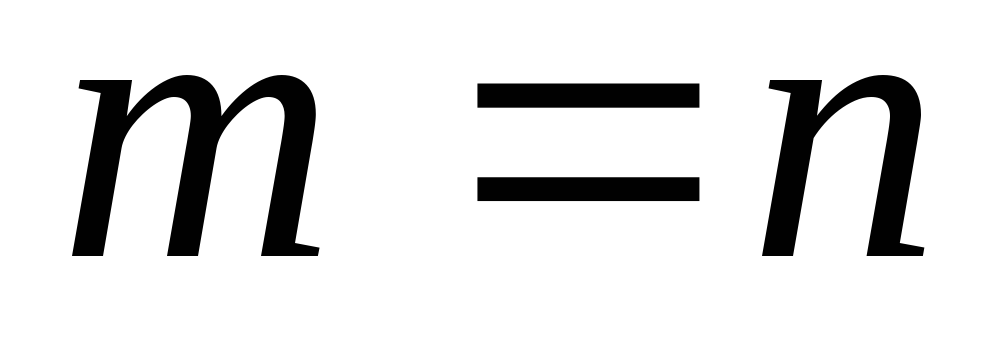 и матрица системы
и матрица системы
 — квадратная.
— квадратная.
Покажем, что решение системы (1) сводится к решению матричного уравнения (2).
Действительно, связь между системой
(1) и уравнением (2) заключается в том, что
совокупность чисел 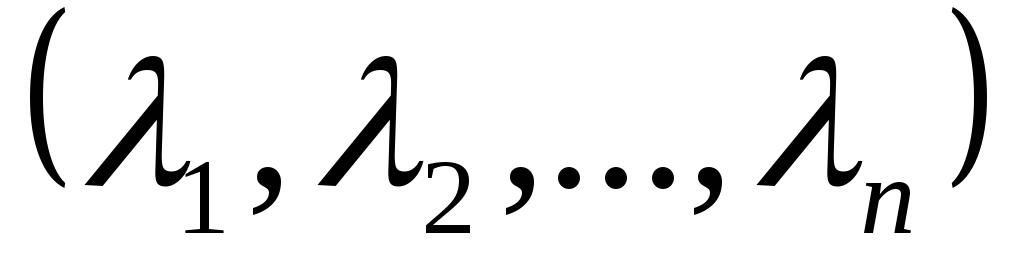 является решением данной системы тогда
и только тогда, когда
является решением данной системы тогда
и только тогда, когда
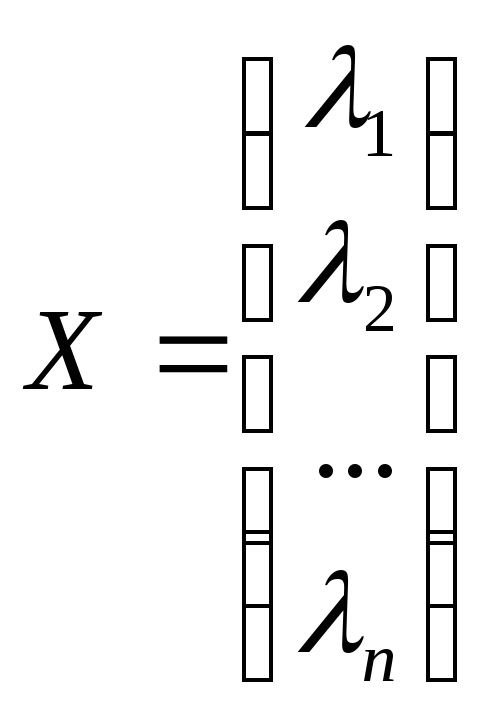
есть решение уравнения (2). Это утверждение означает выполнение равенства
или
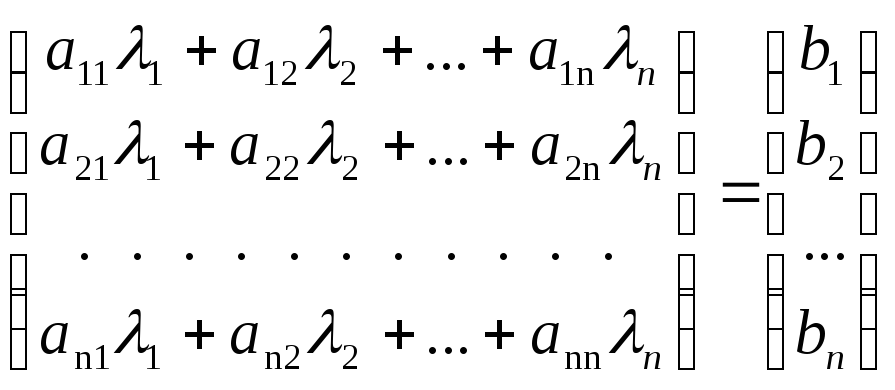 .
.
Последнее равенство, как равенство матриц, равносильно системе равенств
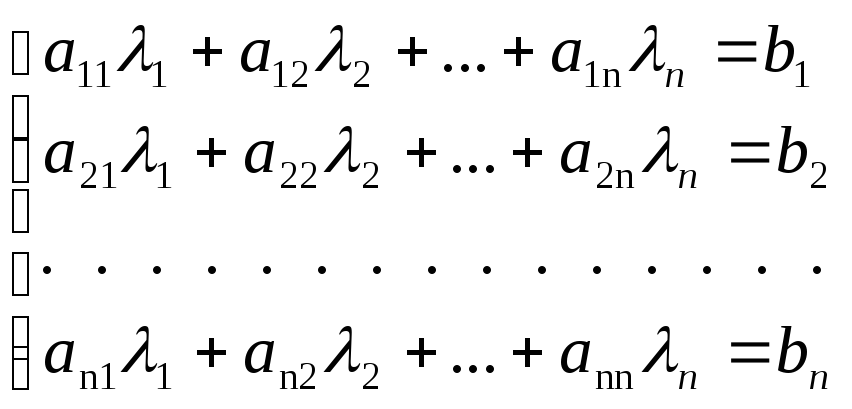
которая означает, что  — решение системы (1).
— решение системы (1).
Итак, решение системы (1) сводится к решению уравнения (2).
Так как 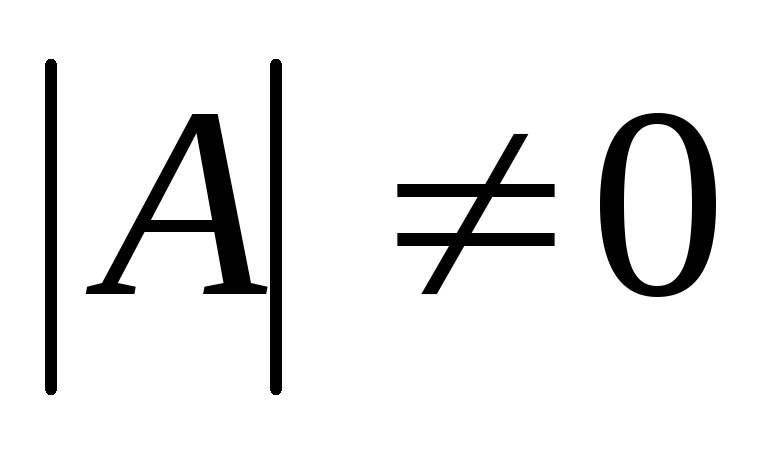 ,
то существует обратная матрица
,
то существует обратная матрица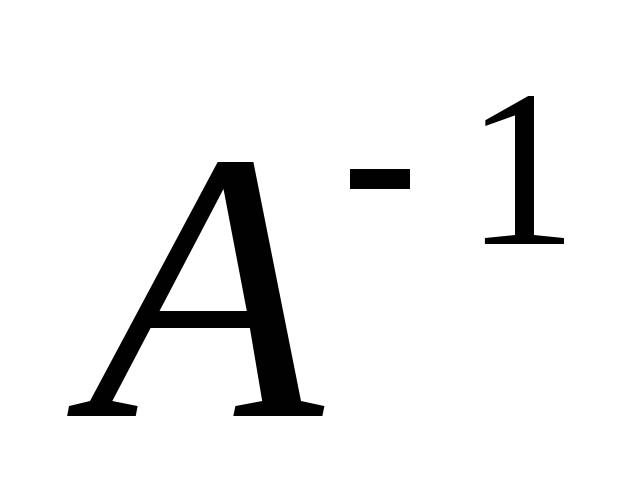 .
Умножим обе части матричного уравнения
(2) на
.
Умножим обе части матричного уравнения
(2) на
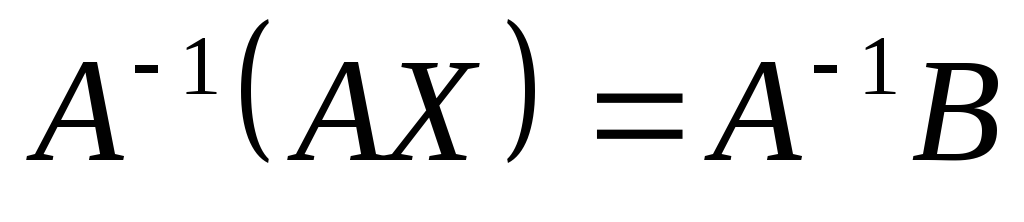 .
Отсюда, так как
.
Отсюда, так как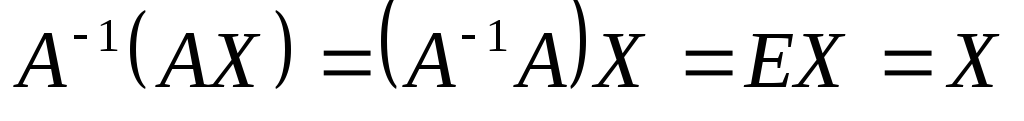 ,
находим
,
находим  .
(3)
.
(3)
Следовательно, если уравнение (2) имеет
решение, то оно задается формулой (3). С
другой стороны, подставив 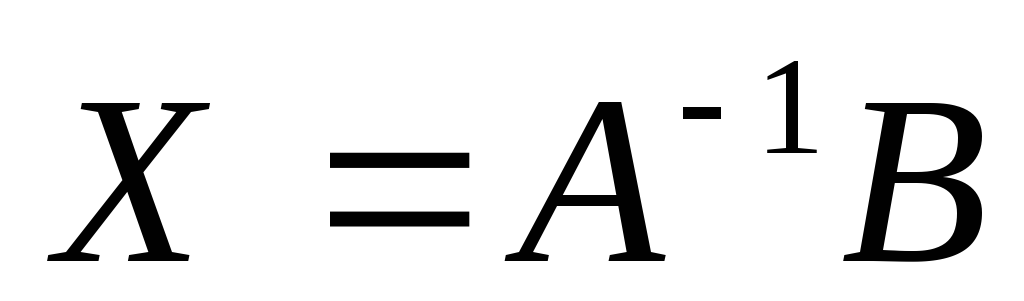 в (2) получим
в (2) получим
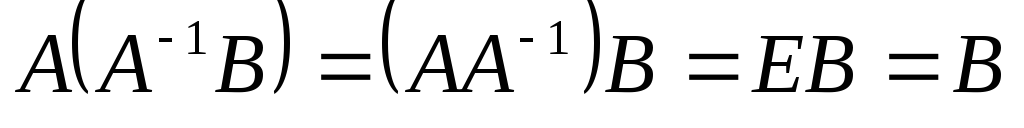 ,
,
поэтому (3) является единственным решением уравнения (2).
Пример.Записать в матричной форме и решить систему при помощи обратной матрицы
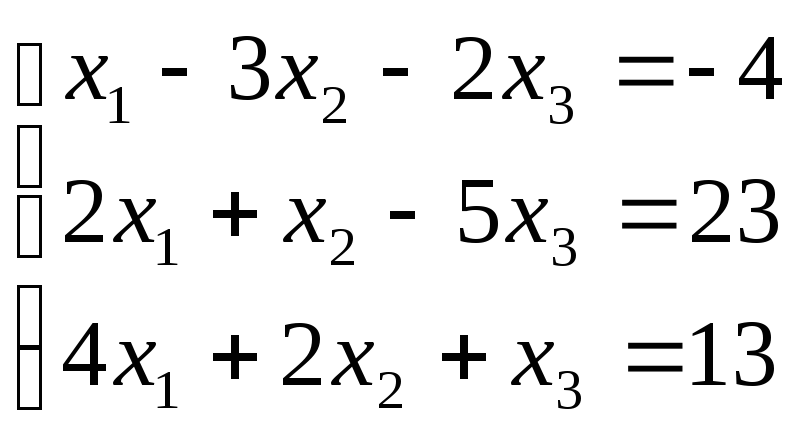
Решение.Запишем систему в матричной
форме: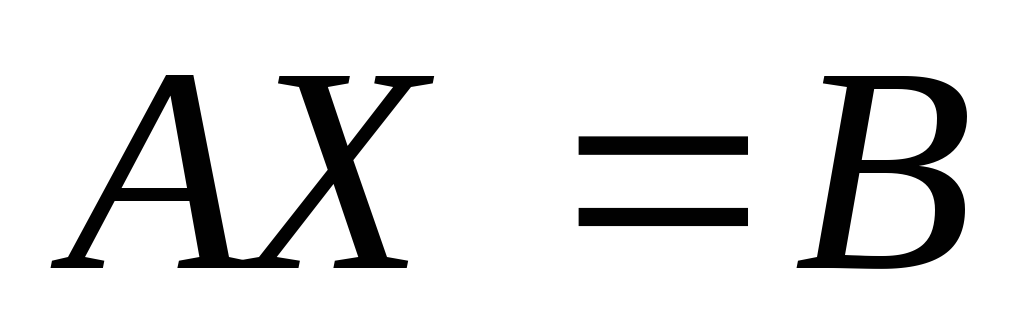 .
Здесь
.
Здесь
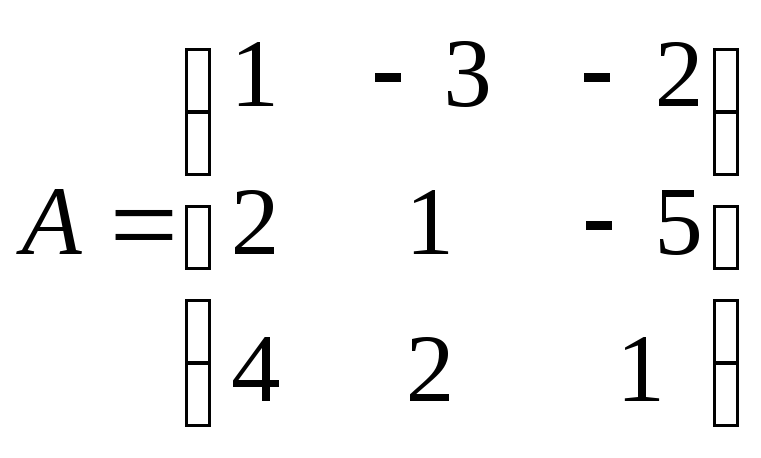 ,
,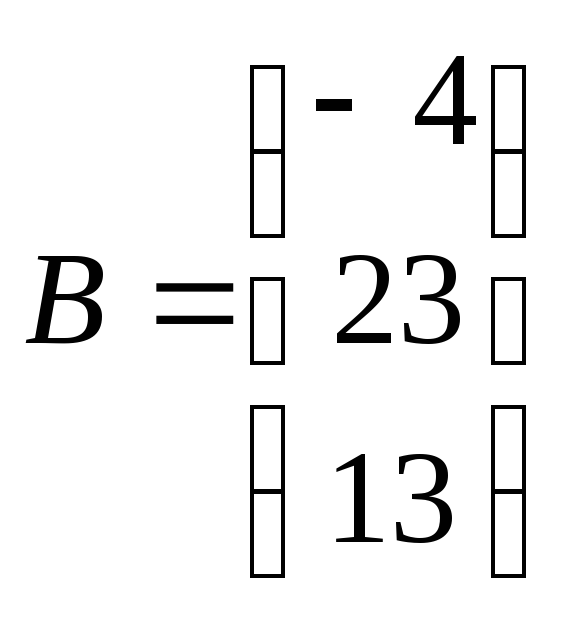 ,
,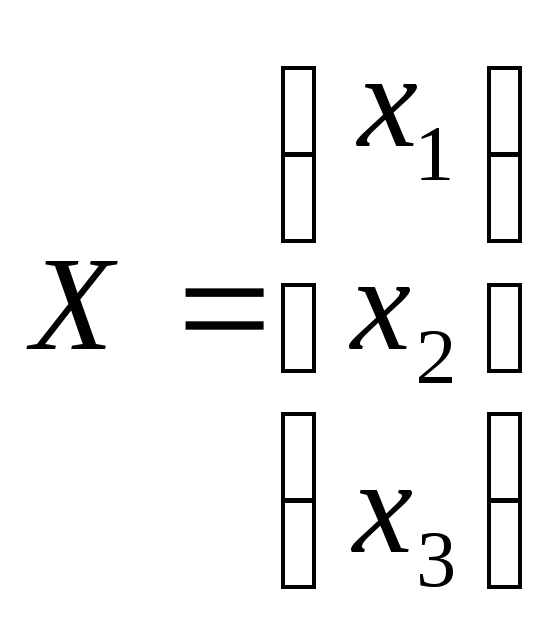 .
.
Имеем:
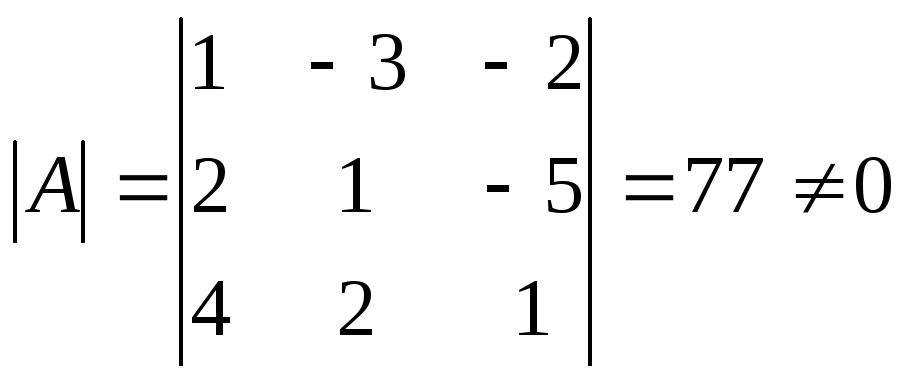 .
.
Следовательно, существует обратная
матрица 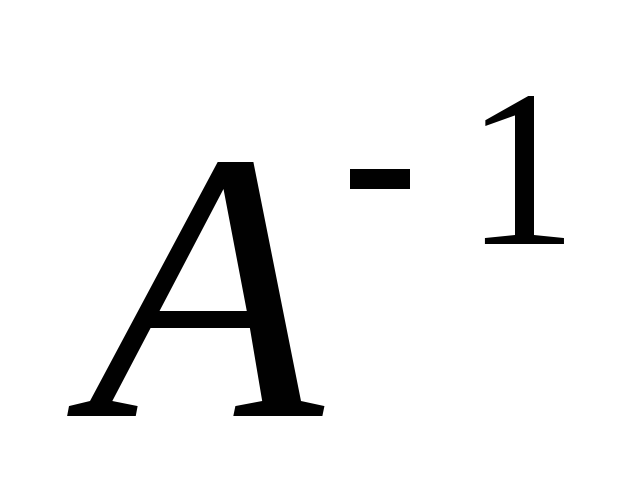 .
Найдем ее:
.
Найдем ее:

 ,
,
откуда  .
.
5.3. Правило Крамера.
Пусть дана система плинейных уравнений спнеизвестными
 (1)
(1)
или
 (2)
(2)
с действительными или комплексными коэффициентами.
Введем обозначения:
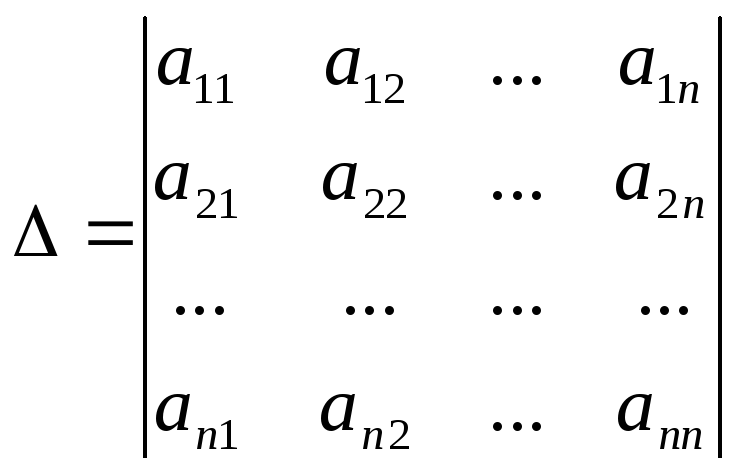
 ,
,
где - определитель
системы, а
 .
. Теорема (правило Крамера).Если
определитель линейной системы (1) отличен
от нуля ,
то система имеет и притом единственное
решение, которое определяется по
формулам:
,
то система имеет и притом единственное
решение, которое определяется по
формулам:
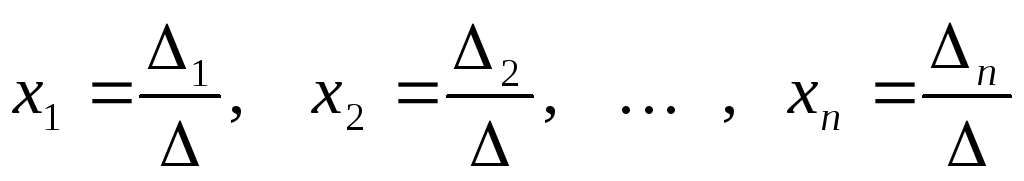 .
(3)
.
(3)
Доказательство.
Было доказано, что решение системы (1)
сводится к решению матричного уравнения
(2) и так как 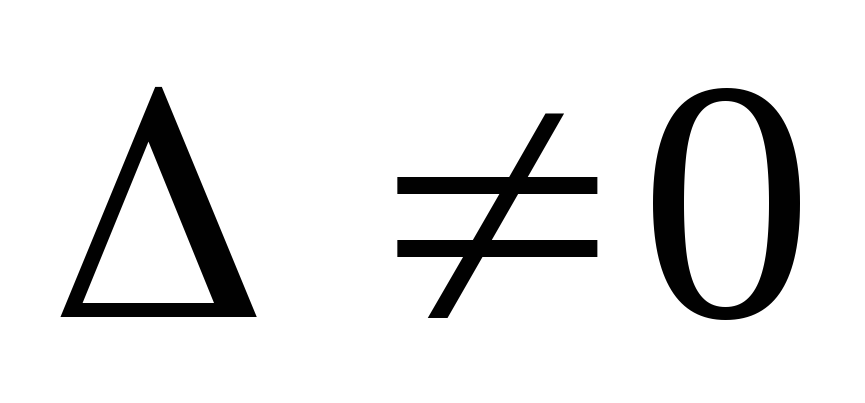 ,
то существует единственное решение
уравнения (2), которое определяется
формулой
,
то существует единственное решение
уравнения (2), которое определяется
формулой
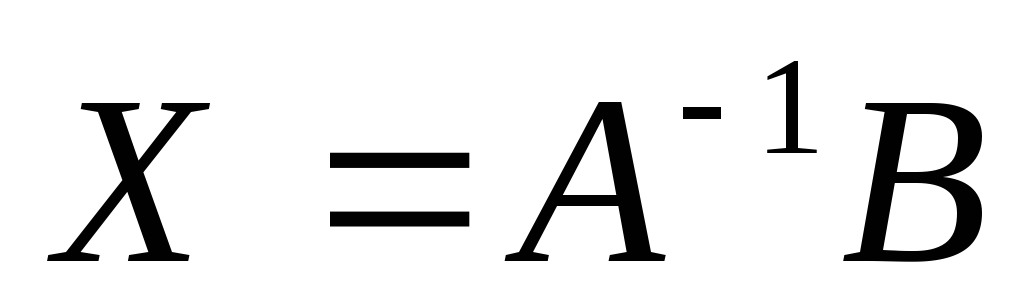 .
(4)
.
(4)
Напомним, что
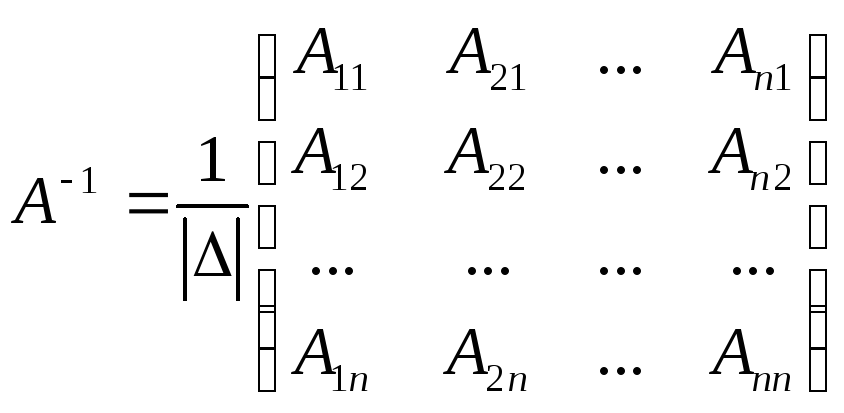 ,
,
где  — алгебраическое дополнение элемента
— алгебраическое дополнение элемента матрицыА, тогда
матрицыА, тогда
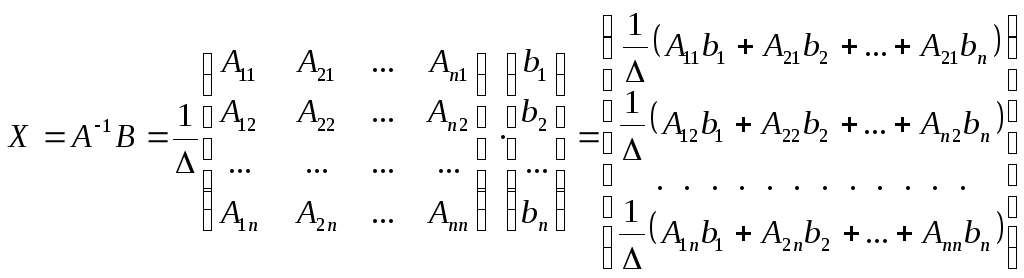 .
.
Раскрывая определитель  поi—му столбцу,
получим,
поi—му столбцу,
получим,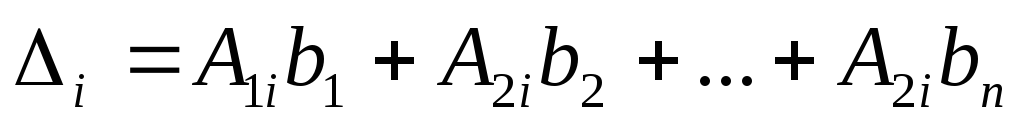

откуда 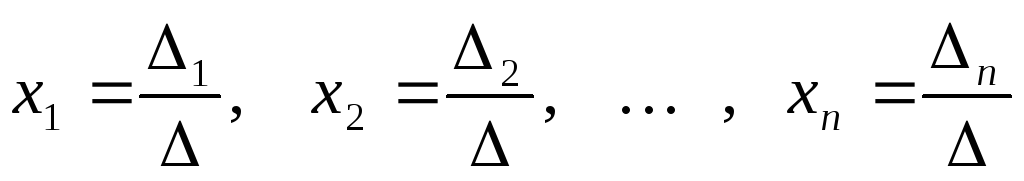 .
.
Пример.Записать в матричной форме и решить систему при помощи правила Крамера
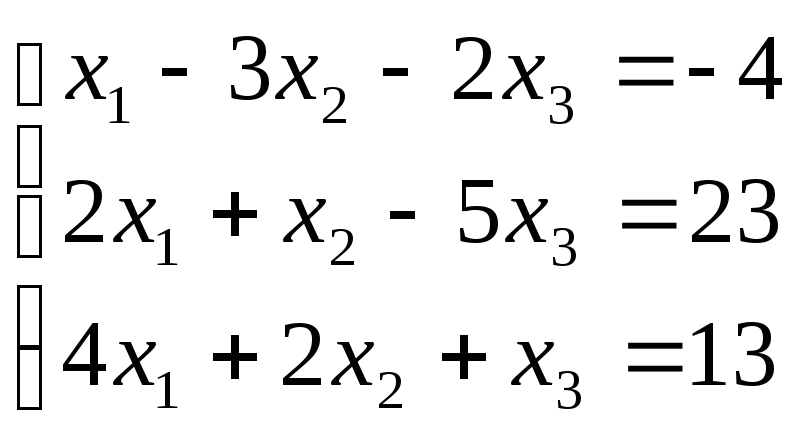 .
.
Решение.Запишем систему в матричной
форме: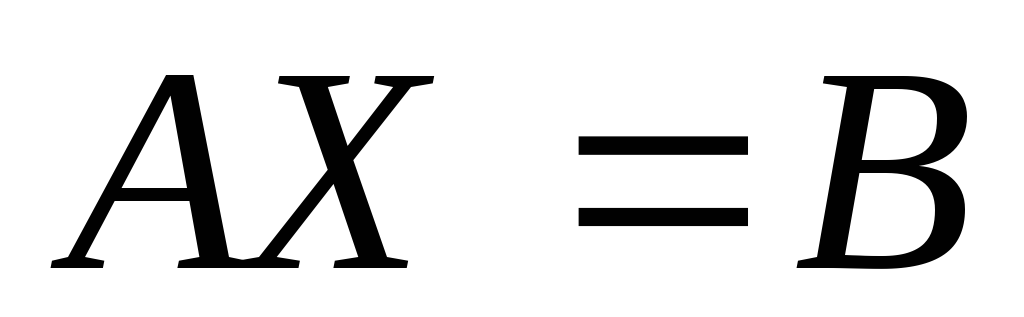 .
Здесь
.
Здесь
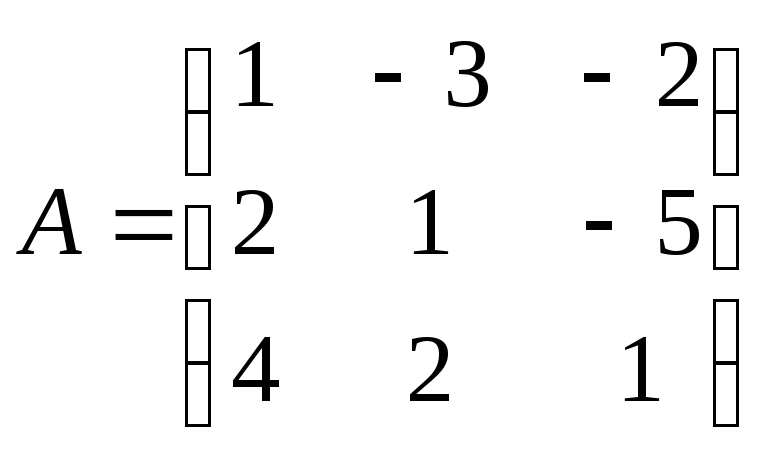 ,
,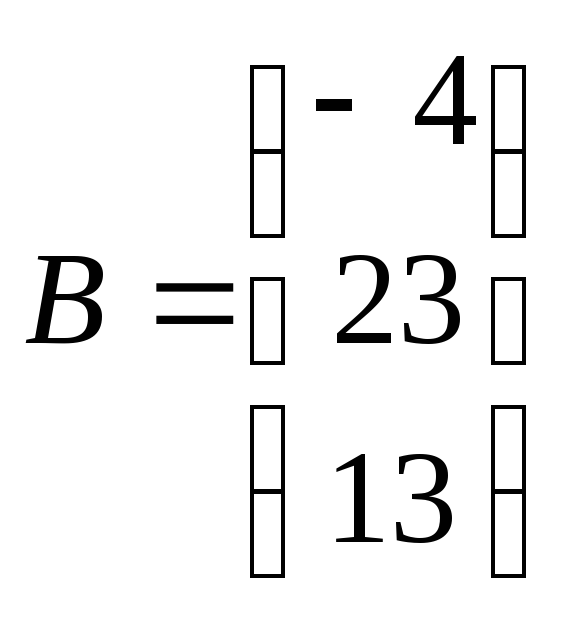 ,
,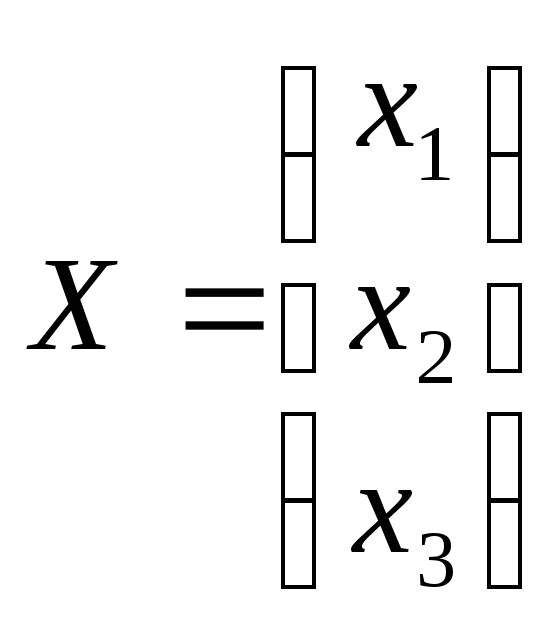
Имеем:
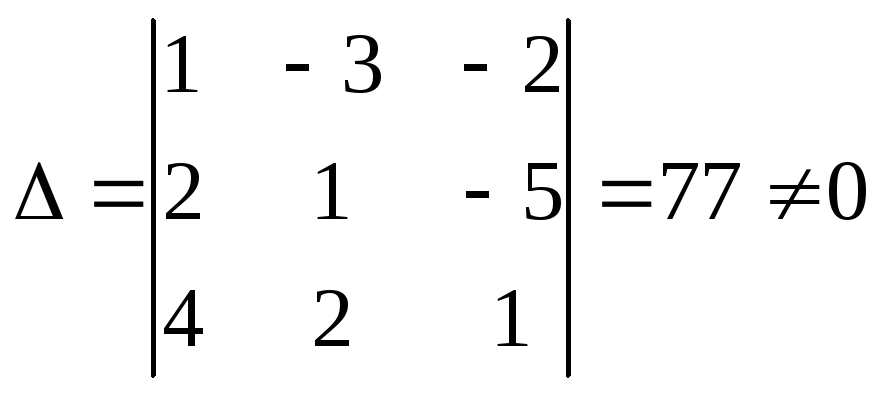 .
.
Найдем
 ,
,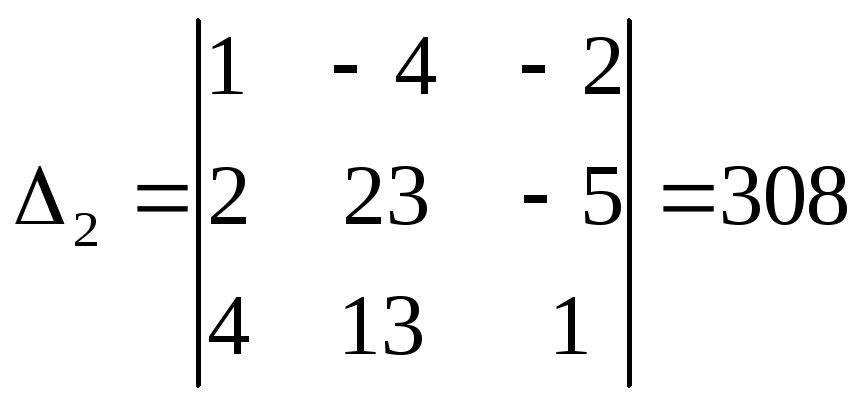 ,
,
Наконец,
 ,
, ,
,
откуда 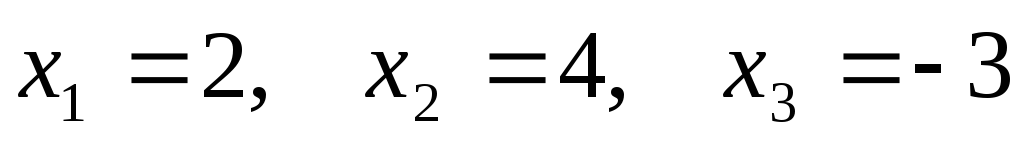 .
.
7.Матричная форма записи и матричный метод решения системы линейных уравнений.
Ответ Пусть имеется квадратная матрица n-го порядка
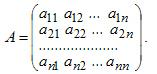
Матрица А-1 называется обратной матрицей по отношению к матрице А, если А*А-1 = Е, где Е — единичная матрица n-го порядка.
Единичная матрица — такая квадратная матрица, у которой все элементы по главной диагонали, проходящей от левого верхнего угла к правому нижнему углу, — единицы, а остальные — нули, например:

Обратная матрица может существовать только для квадратных матриц т.е. для тех матриц, у которых число строк и столбцов совпадают.
Теорема условия существования обратной матрицы
Для того чтобы матрица имела обратную матрицу необходимо и достаточно, чтобы она была невырожденной.
Матрица
А = (А1, А2,…Аn)
называется невырожденной,
если векторы-столбцы являются линейно
независимыми. Число линейно независимых
векторов-столбцов матрицы называется
рангом матрицы 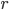 .
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
.
Поэтому можно сказать, что для того,
чтобы существовала обратная матрица,
необходимо и достаточно, чтобы ранг
матрицы равнялся ее размерности, т.е. r
= n.
Алгоритм нахождения обратной матрицы
Записать в таблицу для решения систем уравнений методом Гаусса матрицу А и справа (на место правых частей уравнений) приписать к ней матрицу Е.
Используя преобразования Жордана, привести матрицу А к матрице, состоящей из единичных столбцов; при этом необходимо одновременно преобразовать матрицу Е.
Если необходимо, то переставить строки (уравнения) последней таблицы так, чтобы под матрицей А исходной таблицы получилась единичная матрица Е.
Записать обратную матрицу А-1, которая находится в последней таблице под матрицей Е исходной таблицы.
Пример 1
Для матрицы А найти обратную матрицу А-1
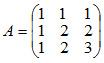
Решение: Записываем матрицу А и справа приписываем единичную матрицу Е. Используя преобразования Жордана, приводим матрицу А к единичной матрице Е. Вычисления приведены в таблице 31.1.
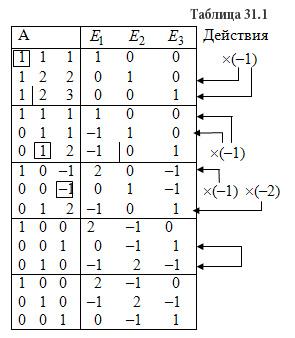
Проверим правильность вычислений умножением исходной матрицы А и обратной матрицы А-1.
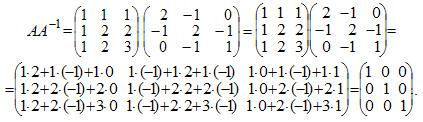
В результате умножения матриц получилась единичная матрица. Следовательно, вычисления произведены правильно.
Ответ: 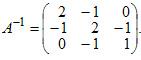
Решение матричных уравнений
Матричные уравнения могут иметь вид:
АХ = В, ХА = В, АХВ = С,
где А,В,С — задаваемые матрицы, Х- искомая матрица.
Матричные уравнения решаются с помощью умножения уравнения на обратные матрицы.
Например,
чтобы найти матрицу  из
уравнения
из
уравнения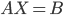 ,
необходимо умножить это уравнение
на
,
необходимо умножить это уравнение
на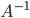 слева.
слева.
Тогда: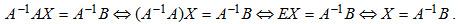
Следовательно,
чтобы найти решение 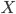 уравнения
уравнения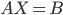 ,
нужно найти обратную матрицу
,
нужно найти обратную матрицу и
умножить ее на матрицу
и
умножить ее на матрицу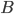 ,
стоящие в правой части уравнения.
,
стоящие в правой части уравнения.
Аналогично решаются другие уравнения.

Пример 2
Решить
уравнение АХ = В, если 
Решение: Так как обратная матрица равняется (см. пример 1)
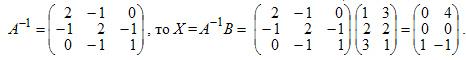
8.Главный определитель системы и определители неизвестных. Теорема Крамера
Ответ:.Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.
Определение.
Определитель, составленный из коэффициентов
при неизвестных, называется определителем
системы и обозначается  (дельта).
(дельта).
Определители 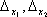
получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:
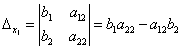 ;
;
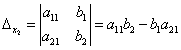 .
.
Формулы Крамера для нахождения неизвестных:
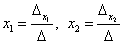 .
.
Найти
значения 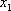 и
и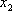 возможно
только при условии, если
возможно
только при условии, если
 .
.
Этот вывод следует из следующей теоремы.
Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.
Пример 1. Решить систему линейных уравнений:
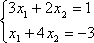 .
(2)
.
(2)
Согласно теореме Крамера имеем:
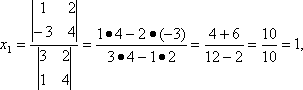

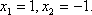
Итак, решение системы (2): 9.операции над множествами . диаграммы Вьена.
Ответ:
Диаграммы Эйлера-Венна – геометрические представления множеств. Построение диаграммы заключается в изображении большого прямоугольника, представляющего универсальное множество U, а внутри его – кругов (или каких-нибудь других замкнутых фигур), представляющих множества. Фигуры должны пересекаться в наиболее общем случае, требуемом в задаче, и должны быть соответствующим образом обозначены. Точки, лежащие внутри различных областей диаграммы, могут рассматриваться как элементы соответствующих множеств. Имея построенную диаграмму, можно заштриховать определенные области для обозначения вновь образованных множеств.
Операции над множествами рассматриваются для получения новых множеств из уже существующих.
Определение. Объединением множеств
А и В называется множество, состоящее
из всех тех элементов, которые принадлежат
хотя бы одному из множеств А, В (рис. 1):

Определение. Пересечением множеств
А и В называется множество, состоящее
из всех тех и только тех элементов,
которые принадлежат одновременно как
множеству А, так и множеству В (рис. 2):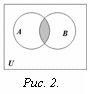

Ответ: —
Определение. Разностью множеств
А и В называется множество всех тех и
только тех элементов А, которые не
содержатся в В (рис. 3):

Определение. Симметрической
разностью множеств
А и В называется множество элементов
этих множеств, которые принадлежат либо
только множеству А, либо только множеству
В (рис. 4):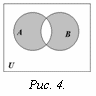
Вопрос 9. Матричная форма записи системы линейных уравнений.
7-Применение определителей к системе линейных уравнений.
Рассмотрим кв.систему линейных ур-ний:
а 11х1+а12х2+…+а1nxn=b1 (1)
11х1+а12х2+…+а1nxn=b1 (1)
an1x1+an2x2+…+annxn=bn
d
 et
A=а11 а12 а1n
et
A=а11 а12 а1n
an1 an2 ann
Теорема 1 (Крамера)
пусть кв. система лин. ур-ний (1) имеет отличный от нуля определитель D (D≠0), тогда сист.(1) является определенной – имеет единственное решение (k1, k2, …, kn) и решение находится по формуле kj=Dj/D . Dj– определитель, получаемый из определителя D заменой его j-столбца на столбец свободных членов сист.(1).
Теорема 2.
Если система n-линейных однородных уравнений с n неизвестными имеет ненулевые решения, то определитель системы D=0.
Доказательство:
Тк столбец свободных членов нулевой, то D1=D2=…=Dn=0, тк каждый такой определитель создает нулевой столбец kj=Dj/D. Если D≠0, то тогда решение (k1, k2, …, kn)=(0,0,…,0), по т.1(Крамера) решение единственное. Если D=0, система неопределенная и кроме тривиальных решений сущ. ненулевые решения. Система дает необх.условие существования ненулевых решений. D=0 кв.система однород.ур-ний имеет ненулевые решения.
18. Доказать теорему: базис системы векторов есть максимальная линейно независимая часть этой системы.
Пусть ai1, ai2, …, air – базис сист.векторов a1, a2,…,an.
Добавим любой aj из данной системы. Получим ai1, ai2, …, air, aj. По определению базиса, любой вектор данной сист.векторов разлагается по базису: aj=k1ai1+k2ai2+…+krair. По теореме 2 (сист.векторов явл.л.з. óесли хотя бы 1 из них явл.лин.комбинацией остальных векторов)=> ai1, ai2, …, air, aj – лин.з.=> ai1, ai2, …, air – max л.н.часть.
Билет 10.
Пусть квадр.матрица
порядка n-
это А.Квадратн.матрица
назыв.неособенной(невырожденной),если
ее определитель не равен нулю.Если ее
определитель равен нулю,то она
особенная(вырожденная).Если существует
матрица В,такая что АВ=ВА=Е,то В
назыв.обратной матр.А(В=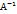 ).
).
Теорема:Если матрица невырожденная,то она имеет обратную матрицу и при том единственную.
Д-во: Пусть А= – квадратная. DetA≠0-невырожденный,составим
à =
– квадратная. DetA≠0-невырожденный,составим
à = 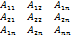 ,где
,где 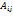 -алгебраическое
дополнение элементов
-алгебраическое
дополнение элементов  в определителе А. det
в определителе А. det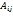 =1,n.Подчеркнём,что
в i-ой строке матрицы Ã стоят
алгебраич.дополнения к элементам i-ого
столбца DetA.Матрицу
à наз.присоединенной матрицей А.Умножим
все элементы Ã на число
=1,n.Подчеркнём,что
в i-ой строке матрицы Ã стоят
алгебраич.дополнения к элементам i-ого
столбца DetA.Матрицу
à наз.присоединенной матрицей А.Умножим
все элементы Ã на число 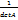 =
=
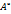 =
=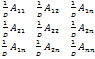
Докажем,что матрица 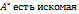 обратная матрица.Составим произв-е
обратная матрица.Составим произв-е 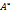 *
А
*
А
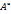 =
=  *
*  =
= 
По свойству 3
определителя суммы расположен на главной
диагонали 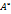 *
А есть DetA=D
по св-ву 5 определителя,все остальные
суммы равны нулю.
*
А есть DetA=D
по св-ву 5 определителя,все остальные
суммы равны нулю.
А* =
= 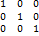 = Е. Докажем сущ-е
= Е. Докажем сущ-е 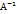 :Докажем
единственность
:Докажем
единственность 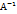 .Предположим
сущ-е еще матр.ЕС,такая что АС=СА=Е.
.Предположим
сущ-е еще матр.ЕС,такая что АС=СА=Е.
 *
АС=
*
АС=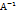 *А*С=ЕС=С
;
*А*С=ЕС=С
; 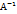 *
АС=
*
АС= след. С=
след. С=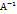
Билет 26.
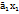 +
+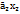 +…+
+…+ — однородная система ур-й (1). АХ=
— однородная система ур-й (1). АХ= ,(2)
,(2)  -матрица
коэф-ов системы ; Х-столбец неизвестности
-матрица
коэф-ов системы ; Х-столбец неизвестности
Свойства:1. Если 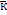 -решение
(2), то λ
-решение
(2), то λ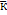 ,
где λ-число,тоже решение однородн.сис-мы.
2.Если
,
где λ-число,тоже решение однородн.сис-мы.
2.Если  -решение(2),то
(
-решение(2),то
(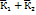 )-решение(2).
3.Если
)-решение(2).
3.Если  …
…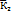 -решение(2),то
их линейная комбинация
-решение(2),то
их линейная комбинация  +…+
+…+ -решение(2).
-решение(2).
Применяя теорему(совместная система будет неопределенной,если ранг сис-мы ур-й меньше,чем число неизвестных)к однородн.системе ур-й.Сделаем след.выводы: если r(A)=n,то (2) имеет единств.тривиальное решение. 2)если r(A)<n,то (2) явл. Неопредел.,т.е иметт нетривиал.реш-я.Мы знаем,что всякая сис-ма n-мерных векторов,включ. Более n-векторов будет л.-з. Решениями(2)явл. n-мерные векторы.Поэтому из них можно выбрать конечную максим. Л-н.систему,т.е. такую,что любое решение(2) будет л.комбинацией этих выбран.векторов. Всякая максим.лин-незав.система решений однор.сис-мы ур-ий назыв.её ФСР.Условие сущ-я ФСР устанавливает след.теорема: Если r(A)<n, то ФСР однор.сис-мы(2) суш-ет и состоит из n решений.
№29. Собственные вектора и собственные значения лин-го преобр-я, их отыскание
Ненулевой вектор х(с чертой наверху, далее просто черта) назыв-ся собственным вектором л.п. α (альфа), если оно переводит х(ч) в коллинеарный ему λх(черта):
α (х(черта))= λх(черта) (1)
Число λ в (1) наз-ся собственным значением преобразования α (альфа), соответствующим собственному вектору х(черта). Найдем все собственные векторы:
Пусть:
е1(четра), е2(четра),…, еn(четра) – базис Rn
Система (фигурные скобки): (2)
λх1=a11x1+a12x2+…+a1nxn,
λх2= a21x1+a22x2+…+a2nxn,
…
λхn= an1x1+an2x2+…+annxn .
Система (3):
(a11-λ)x1+a12x2+…+a1nxn=0,
a21x1+(a22-λ)x2+…+a2nxn=0,
…
an1x1+an2x2+…+(ann-λ)xn=0.
Однородная система (3) имеет ненулевые решения тогда и только тогда, когда ее определитель = 0.
Определитель (прямые скобки): (4)
a11-λ a12 … a1n
a21 a22-λ … a2n = 0
…
an1 … ann-λ
Многочлен n-ой степени относительно λ в левой части уравнения (4) – характеристический многочлен преобразования α (альфа).
Уравнение (4) – характеристическое уравнение преобразования α (альфа).
Всякому действительному корню λ 0 ур-я (4) отвечает собственный вектор, который находится путем реш-я совместной системы (3) относительно x1,x2,…,xn после подстановки λ 0 вместо λв эту систему.
Замечание:
В матричной форме система (3):
(A- λE)X=θ , где
A — матрица лин. преобр-я α (альфа),
Е – единичная матрица того же порядка, что и А,
Х – вектор-столбец из координат вектора х(черта).
Отыскание:
1)множество собственных значений лин. преобр-я α (х(черта)):
det(A- λE)=0 – характеристическое уравнение
2)Собственные векторы:
(A- λiE)X=θ
Пусть дана система m линейных уравнений с n неизвестными:
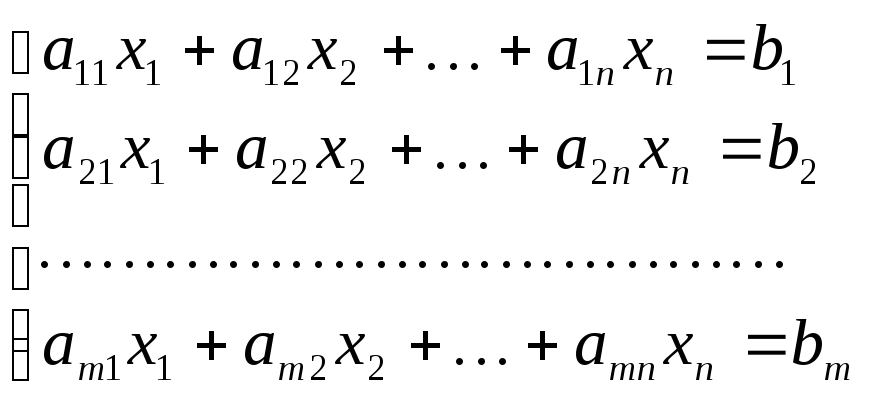 (1)
(1)
Выпишем матрицу, составленную из коэффициентов при неизвестных в системе (1)
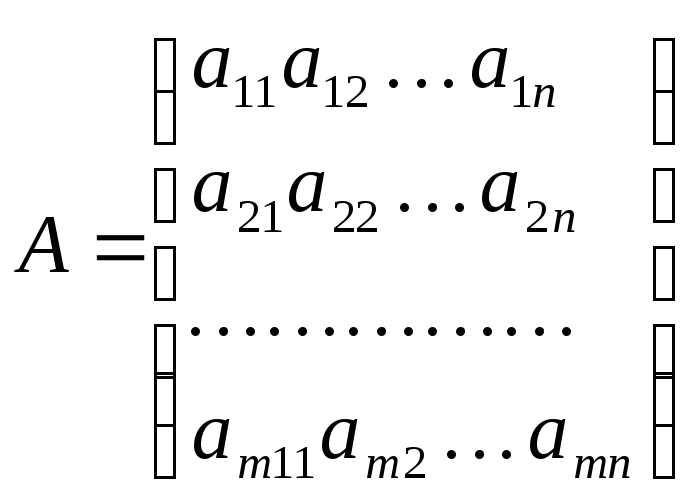 —
матрица системы (1)
—
матрица системы (1)
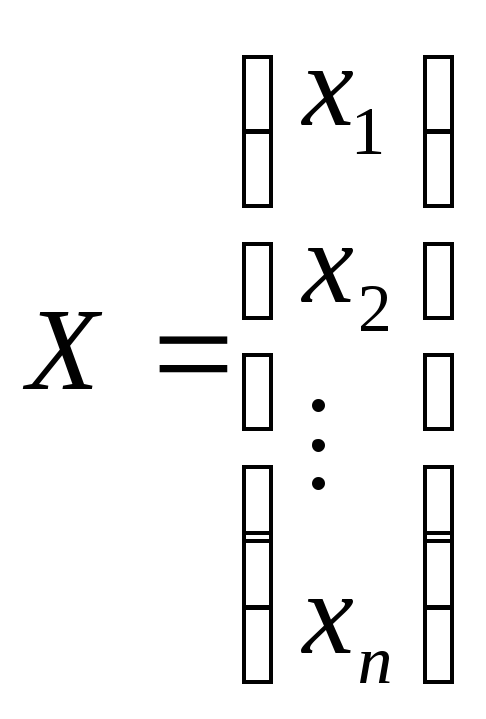 —
матрица-столбец из неизвестных системы
(1)
—
матрица-столбец из неизвестных системы
(1)
 —
матрица-столбец из свободных членов
системы (1)
—
матрица-столбец из свободных членов
системы (1)
AX – существует
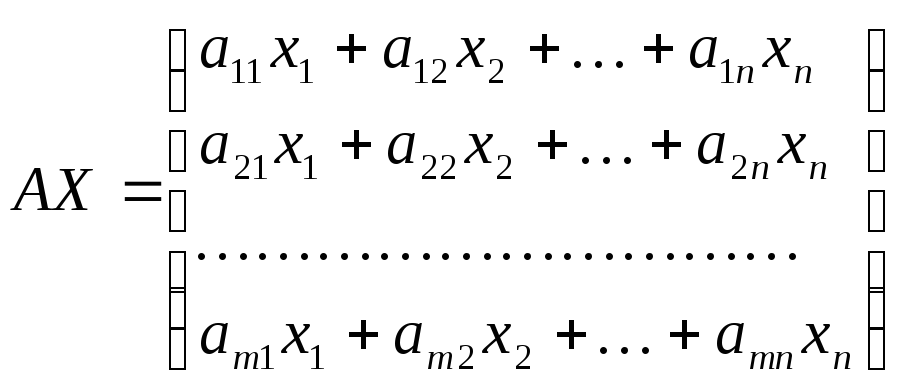
АХ имеет m строк и 1 столбец, — это матрица-столбец, элементы которого являются левые части уравнения (1)
АХ=В – матричная форма записи системы линейных уравнений
19 билет. Доказать теорему: каждую линейно независимую часть системы векторов а1, а2…аs можно дополнить до базиса этой системы.
Если данные лин-независимые части не явл-ся базисом данной системы векторов, то она не максимальна, и к ней можно добавить 1 вектор из сис-мы а1, а2, … anтак, что полученная новая часть ai1, ai2, … ais, ais+1 – Лин. Нез.
Если эта новая часть все еще не максимальна, то к ней можно добавить еще один вектор и т.д.
Процесс расширения Лин. Нез. части после добавления очередного вектора должен закончиться, т.к. к ЛН части а1…аsсис-мы векторов а1,а2…аnможно добавлять не более (n-s) векторов.
Следствие. Если в сис-ме векторов есть ненулевой вектор, то она меняет базис.
Док-во. Сис-ма, состоящая из 1 ненулевого вектора, — ЛН: а1 ≠ Ө, k1а1=Ө k1=0 => сис-ма из одного ненулевого вектора ЛН => тогда, по осн. теореме 3, ЛН часть системы, состоящую из одного ненулевого вектора можно дополнить до базиса этой сис-мы.
№3 Исследование и решение систем линейных уравнений методом Ж- Гаусса.
Сущность метода Ж- Гаусса заключается в том, что при нахождении конечного числа элементарных преобразований система линейных уравнений преобразуется в эквивалентную- т.е разрешённую систему уравнений или эквивалентную ей несовместную систему. Процесс решений состоит из ряда последовательных этапов расчетов. После выполнения каждого этапа, система линейных уравнений становится разрешаемой относительно какого-либо неизвестного.
Процесс преобразований закончится в след. 2-х случаях:
1)мы придём к системе уравнений, содержащих уравнение вида 0=b, b≠0,тем самым установим несовместность исходной системы(1.2)
2)получим разрешённую систему уравнений ,эквивалентную системе (1.2) , очевидно число уравнений (r) в разрешенной системе ≤m-числа уравнений в системе (1.2) т.к в процессе преобразования мы отбросили уравнение 0=0…..r<n
r-число уравнений в разрешённой системе…. n-число неизвестных
*r=n т.е. система
совместная и определённая,
система уравнений имеет вид 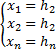 (1.13)
(1.13)
Система
(1.13) и равносильная ей (1.2) имеют единственное
решение(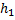 ,
,  ,
,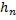 )-
совместная; определённая
)-
совместная; определённая
*r<n разрешённая система имеет вид 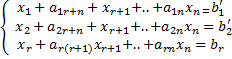 (1.14)
(1.14)
В
системе (1,14) неизвестные ( ,
,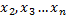 )
составляют набор разрешённых
неизвестных,
а остальные неизвестные- называются свободными
неизвестными.
)
составляют набор разрешённых
неизвестных,
а остальные неизвестные- называются свободными
неизвестными.
Возьмём
для свободных неизвестных произвольные
числовые значения  подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных —
подставим их в систему (1.14) вместо
соответствующих неизвестных, найдём
значение для разрешённых (базисных)
неизвестных —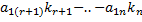
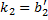 —
—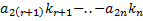
 —
—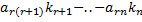
Легко
проверить, что набор чисел (
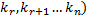 является решением системы (1.14) →равносильной
ей системы (1,2) т к свободным неизвестным
можно передавать произвольное числовое
значение, то таким образом можно найти
бесконечное множество решений системы
(1,2), в случае r<n
система (1.2) является совместной,
но неопределённой.
является решением системы (1.14) →равносильной
ей системы (1,2) т к свободным неизвестным
можно передавать произвольное числовое
значение, то таким образом можно найти
бесконечное множество решений системы
(1,2), в случае r<n
система (1.2) является совместной,
но неопределённой.
Каждое
решение такой системы называется её
частным решением, выраженным в базисных
и неизвестных через свободные т.е. 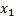 =
=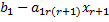 -..-
-..-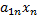
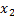 =
= -…-
-…-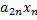 (1.15)
(1.15)
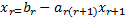 -..-
-..-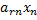
Называется общим решением системы (1,2) и (1,14) среди частных решений. Выделим базисные, которые получаются при нулевых значениях всех свободных неизвестных.
Базисное
решение 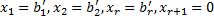
Из всего сказанного можно сделать выводы: система линейных уравнений будет несовместной, если при выполнении этапов преобразования по методу Ж- Гаусса мы получим противоречивое уравнение, если же такого уравнения нет, то система будет совместной.
Совместная система будет определённой, если она приводится к разрешённой системе в которой число уравнений равно числу неизвестных. И неопределённой, если в разрешённой системе число уравнений меньше числа неизвестных.
Следствие1! Если m<n, то система уравнений либо несовместная, либо неопределённая
Доказательство: Если система уравнений (1,2) является совместной, то она является определённой или неопределённой, это зависит от числа разрешённых в уравнении.
r≤ m ≤n, то система (1,2)- неопределённая .
Замечание1.Рассмотрим
систему линейных уравнений, в которой
свободные члены всех уравнений=0 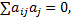 i=1,m
(1.16)
i=1,m
(1.16)
J=1
Такая система (1.16) называется системой линейных однородных уравнений. Эта система всегда совместна т к имеет тривиальное (нулевое) решение.
Для системы (1,16) вопрос стоит в том, определённая она или не определённая. Система (1,16) является определённой, если она имеет только тривиальное решение и неопределённая, если кроме тривиального есть не нулевые.
Следствие2! Если m<n то система помимо нулевого имеет и ненулевое решение.
Замечание2 чтобы
записать систему (1,2) нужно знать
коэффициенты уравнений и свободные
члены. Выписываем их в виде таблицы. 
Получим таблицу из чисел, которая содержит m строк и n+1 столбцы. Всякая прямоугольная таблица из чисел называется МАТРИЦЕЙ. Числа, составляющие матрицу,- её Элементы.
Элементы
одного n
столбца имеют 2 индекса. 
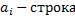
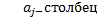
Матрица  является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
является расширенной матрицей системы
(1,2) она получается путём присоединения
к матрице из коэффициентов сист (1,2)
столбца свободных членов.
Билет 25. Теорема: любая совокупность значений свободных неизвестных определяет однозначно решение системы линейных уравнений
Пусть дана сис-ма
ур-й  1x1+
1x1+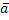 2x2+…+
2x2+…+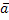 nxn =
nxn = 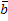 (1)
(1)
Док-во.
Пусть  1, 2…
1, 2…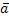 r образуют базис системы векторов –
коэффициентов. Ранг сис-мы равен n,
остальные неизвестные будут свободными.
r образуют базис системы векторов –
коэффициентов. Ранг сис-мы равен n,
остальные неизвестные будут свободными.
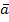 1х1+…+
1х1+…+ rхr=
rхr= 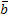 —
— 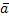 r+1xr+1 — … —
r+1xr+1 — … — 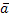 nxn(2)
nxn(2)
Зададим свободным
неизвестным любые значения: xr+1=kr+1,
xr+2=kr+2,
… , xn=kn. Подставим
эти значения в правую часть (2) вместо
неизвестных:  =
=  –
– 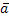 r+1kr+1 — … —
r+1kr+1 — … — 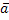 nkn
nkn
Перепишем рав-во
(2) в виде:  1x1+…+
1x1+…+ 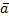 rxr =
rxr =  (3)
(3)
Рав-во (3) можно
рассматривать как разложение вектора 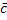 по векторам базиса, коэффициенты кот.
x1=k1,
… , xr=kr есть значения
базисных неизвестных. Числа k1,
k2…
kr – значения базисных неизвестных,
определяются однозначно => однозначно
определяется решение системы уравнений
(1):
по векторам базиса, коэффициенты кот.
x1=k1,
… , xr=kr есть значения
базисных неизвестных. Числа k1,
k2…
kr – значения базисных неизвестных,
определяются однозначно => однозначно
определяется решение системы уравнений
(1):  = (k1,
k2,
… , kr+1,
… kn)
= (k1,
k2,
… , kr+1,
… kn)
Решение, кот.
появляется при нулевых значениях  =(
=( 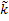 1,
1, 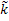 2,
… ,
2,
… ,  r,
0 … 0) называется базисным решением.
r,
0 … 0) называется базисным решением.
19 билет. Доказать
теорему:
каждую линейно независимую часть системы
векторов 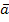 1,
1, 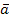 2…
2…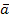 s можно дополнить до базиса этой системы.
s можно дополнить до базиса этой системы.
Если данные
лин-независимые части не явл-ся базисом
данной системы векторов, то она не
максимальна, и к ней можно добавить 1
вектор из сис-мы 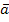 1,
1, 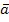 2,
…
2,
…  nтак, что
полученная новая часть
nтак, что
полученная новая часть  i1,
i1, 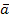 i2,
…
i2,
… 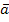 is,
is, 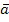 is+1 – Лин. Нез.
is+1 – Лин. Нез.
Если эта новая часть все еще не максимальна, то к ней можно добавить еще один вектор и т.д.
Процесс расширения
Лин. Нез. части после добавления очередного
вектора должен закончиться, т.к. к ЛН
части  1…
1… sсис-мы
векторов
sсис-мы
векторов 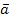 1,
1,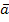 2…
2… nможно
добавлять не более (n-s)
векторов.
nможно
добавлять не более (n-s)
векторов.
Следствие. Если в сис-ме векторов есть ненулевой вектор, то она меняет базис.
Док-во.
Сис-ма, состоящая из 1 ненулевого вектора,
— ЛН: 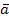 1 ≠ Ө,
k1
1 ≠ Ө,
k1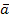 1=Ө
k1=0
=> сис-ма из одного ненулевого вектора
ЛН => тогда, по осн. теореме 3, ЛН часть
системы, состоящую из одного ненулевого
вектора можно дополнить до базиса этой
сис-мы.
1=Ө
k1=0
=> сис-ма из одного ненулевого вектора
ЛН => тогда, по осн. теореме 3, ЛН часть
системы, состоящую из одного ненулевого
вектора можно дополнить до базиса этой
сис-мы.
Билет №1
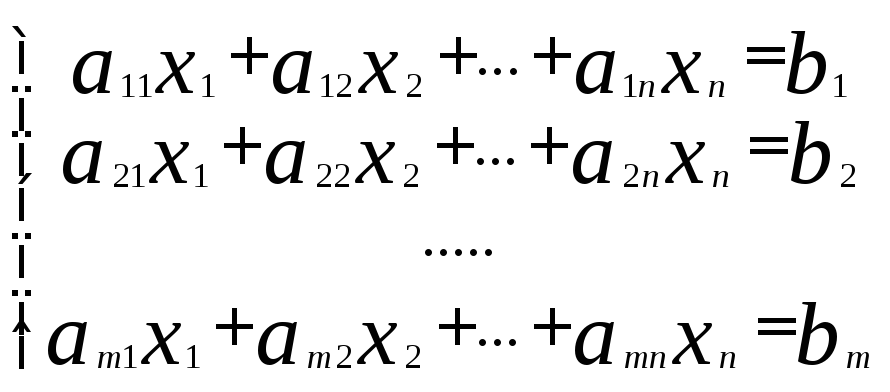 (1)
(1)
(а) 2 уравнения системы (1) меняются местами
(б) одно уравнение
системы (1) умножается на число 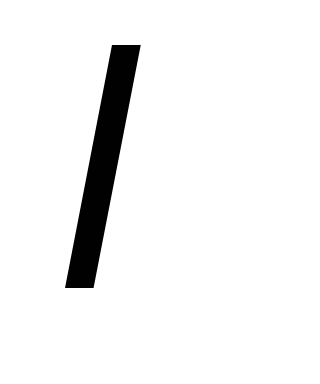 ,
отличное от нуля
,
отличное от нуля
(в) к уравнению
системы (1) прибавляется другое уравнение,
умноженное на на число 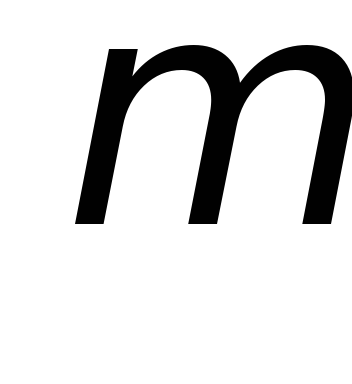
Теорема об элементарных преобразованиях системы линейных уравнений
При любом элементарном преобразовании системы лин. уравнений получается система уравнений, эквивалентная данной
Доказательство:
очевидно, что при преобразовании (а) получается система, эквивалентная данной
выполним преобразование
(б). i-тое
уравнение системы (1) умножить на число 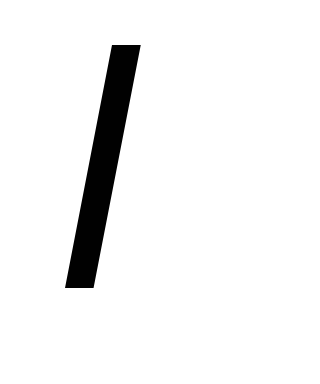 ,
отличное от нуля.
,
отличное от нуля.
 — i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
— i-тое
уравнение системы(2), все остальные
уравнения, как в (1)
Пусть  ,
,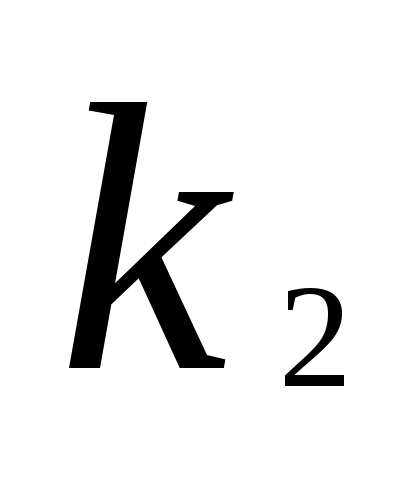 ,…,
,…,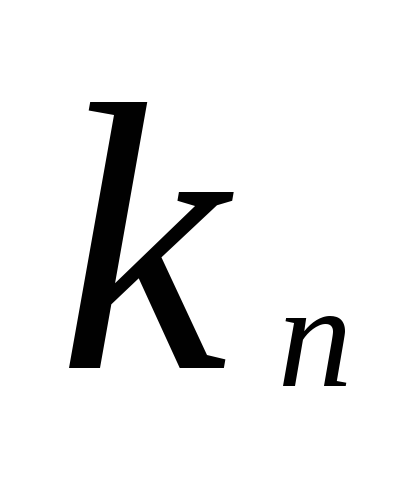 —
решения системы (1), в том числеi-того
уравнения системы (1)
—
решения системы (1), в том числеi-того
уравнения системы (1)
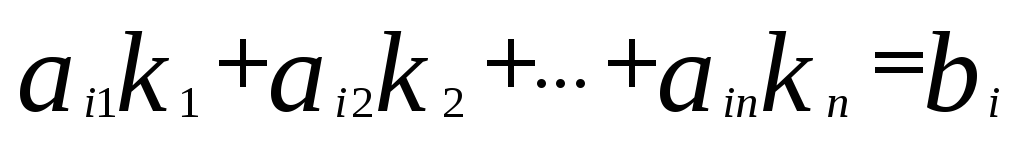
подставим
эти же числа 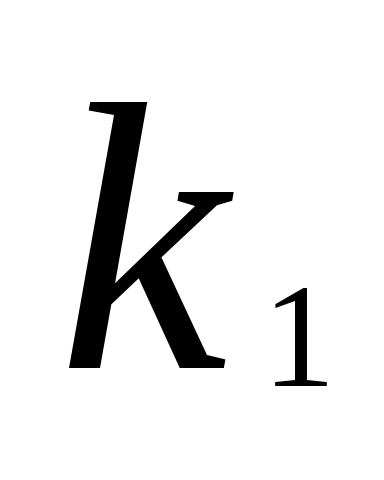 ,
,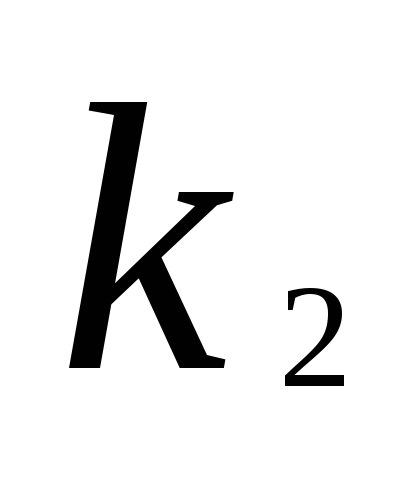 ,…,
,…, в левую частьi-того
уравнения системы (2)
в левую частьi-того
уравнения системы (2)
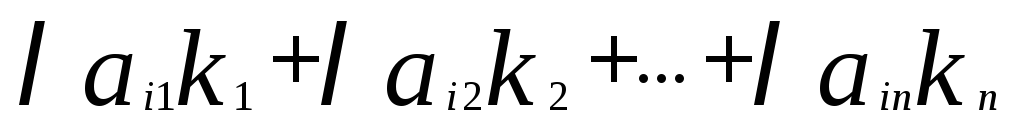 =
= 
Набор 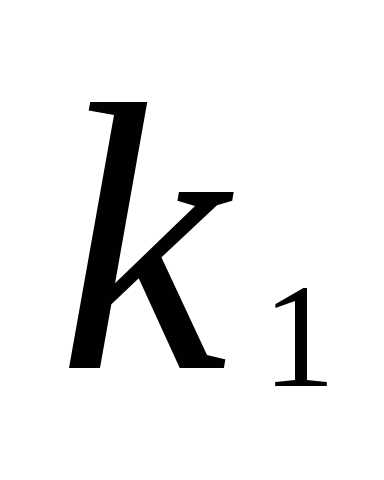 ,
,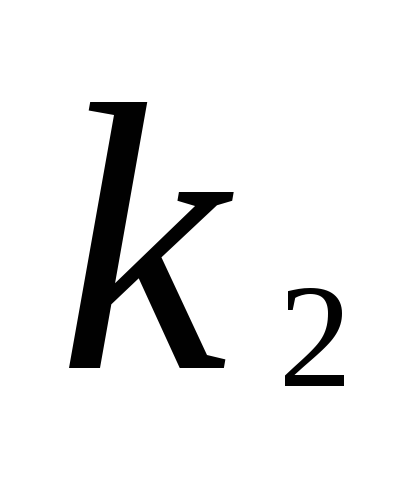 ,…,
,…,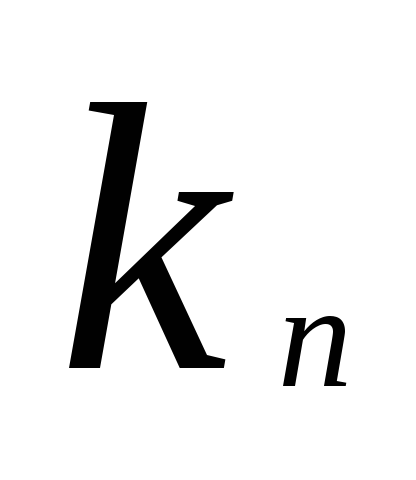 является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как
является решениемi-того
уравнения системы (2), а значит и решением
системы (2), поскольку все остальные
уравнения в (2) такие же как в системе
(1). Так как  ,
, ,…,
,…,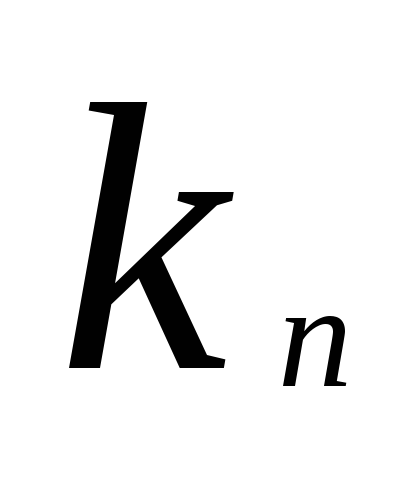 -произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
-произвольные
решения системы (1), то всякое решение
системы (1) является решением системы
(2)
Заметим, что
систему (1) можно получить из системы
(2) также при помощи преобразования (б).
для этого нужно i-тое
уравнение системы (1) умножить на число 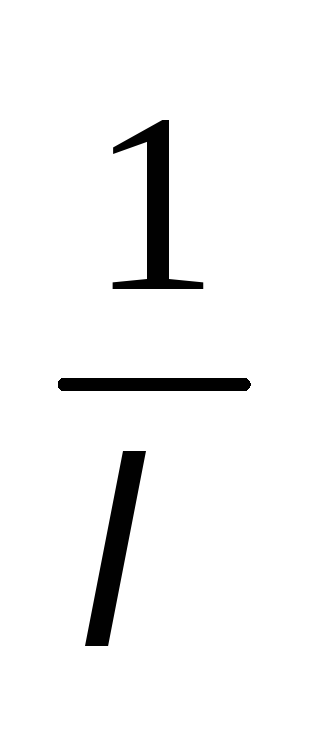 .
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
.
В соответствии с доказанным всякое
решение системы (2) будет решением (1)
выполним преобразование
(в). К i-тому
уравнению системы (1) прибавим j-тое
уравнение 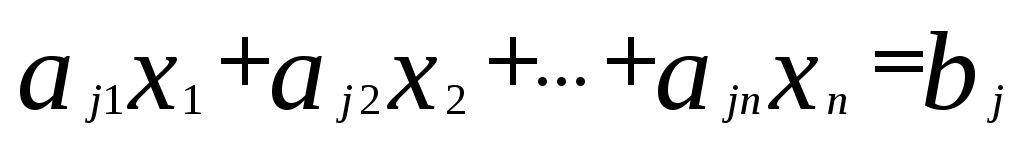 (3) , умноженное на число
(3) , умноженное на число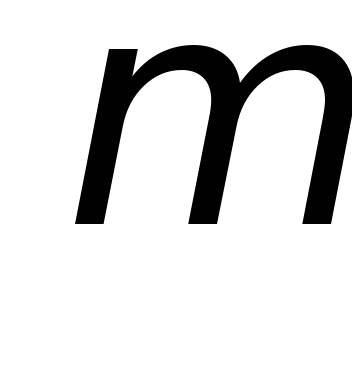 .
Преобразованное в системе (3)j-тое
уравнение будет таким
.
Преобразованное в системе (3)j-тое
уравнение будет таким 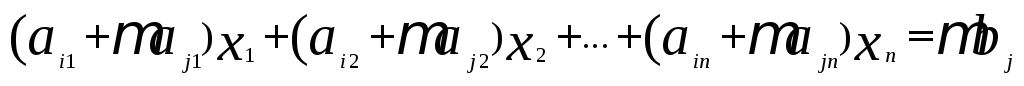
Пусть  ,
,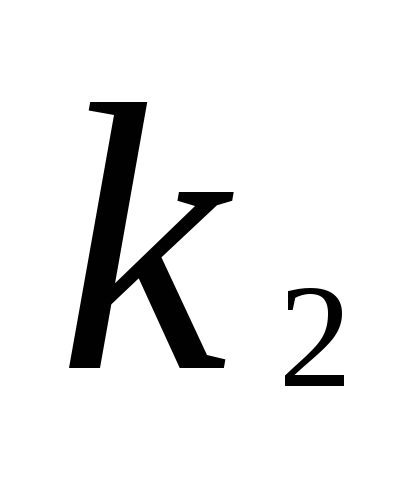 ,…,
,…, -произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
-произвольные
решения системы (1), в том числеi-того
и j-того
уравнения
 ,
, 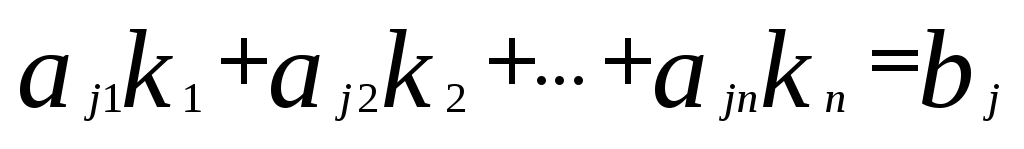
Подставим этот же набор чисел вместо неизвестных в левую часть j-того уравнения (3)
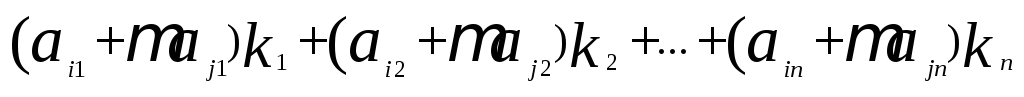 =
=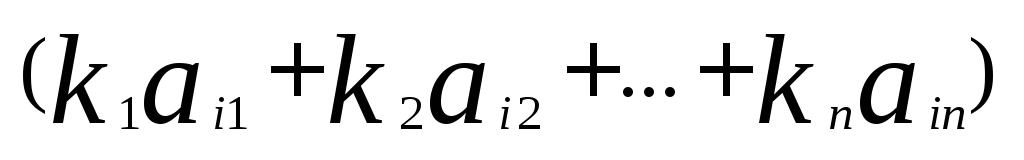 +
+ =
= Это означает, что
Это означает, что ,
,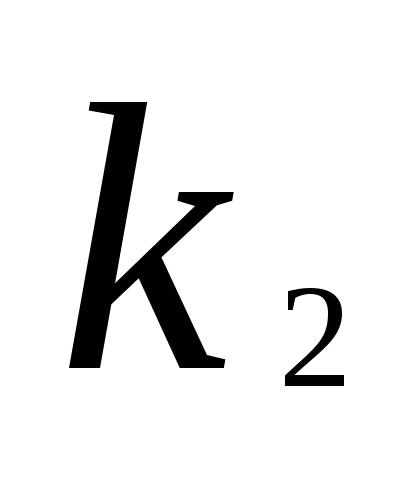 ,…,
,…, —
есть решениеi-того
уравнения системы (3) и всех остальных
решений, так как они такие же как как в
системе (1).
—
есть решениеi-того
уравнения системы (3) и всех остальных
решений, так как они такие же как как в
системе (1).
Билет №11. Решение матричного уравнения AX=B (существование и единственность).
Пусть А — квадр.,
невырожденная, n-порядка,
тогда АХ=В имеет единственное решение,
которое находится по формуле 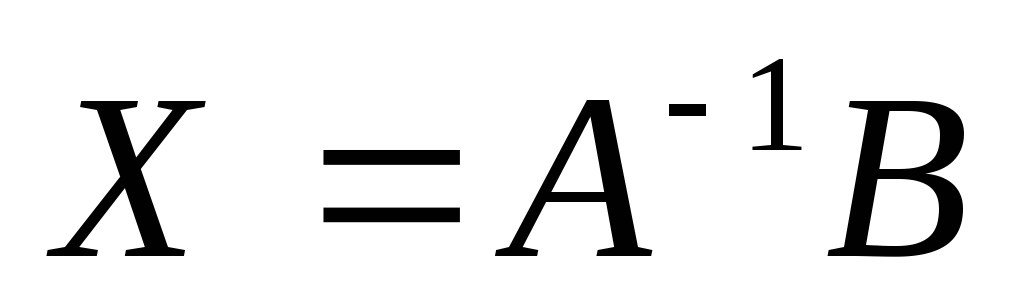 (1)
(1)
Док-во.
Пусть 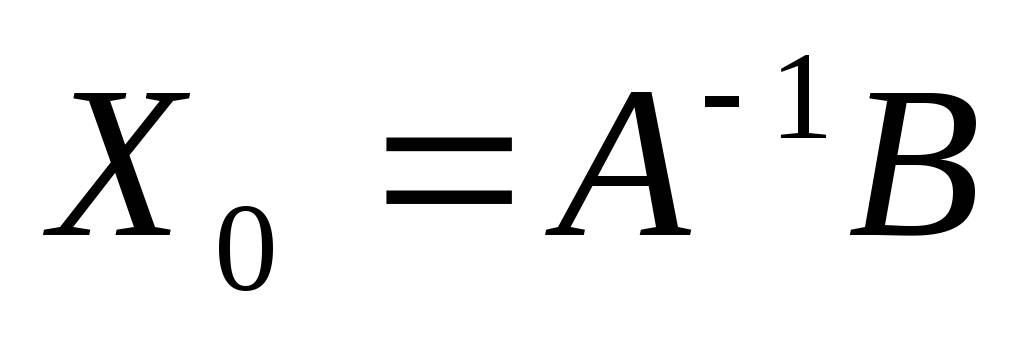 —
решение. Подставим
—
решение. Подставим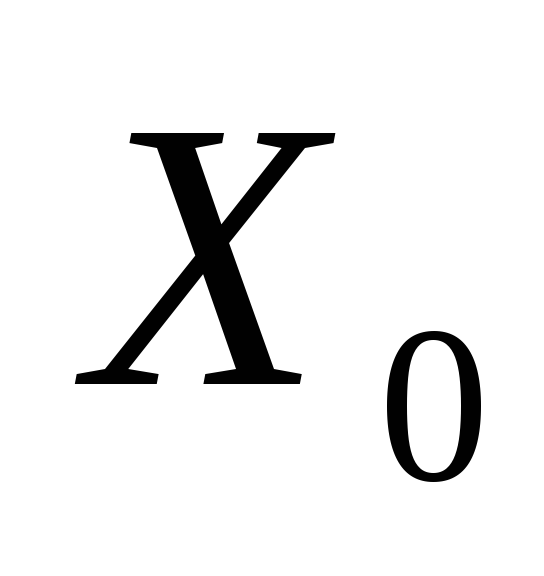 в (1) :.
Умножим обе части на
в (1) :.
Умножим обе части на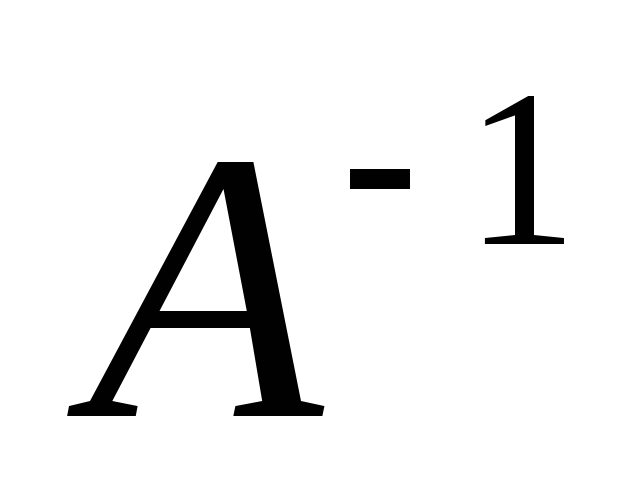 :
: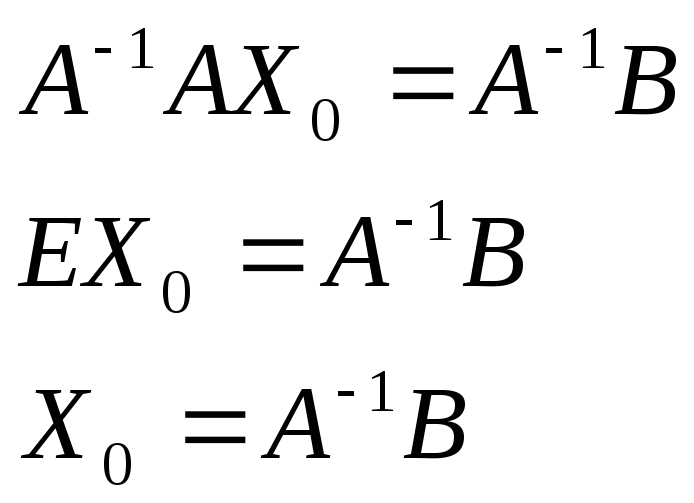
Следовательно, решение существует и оно единственное.
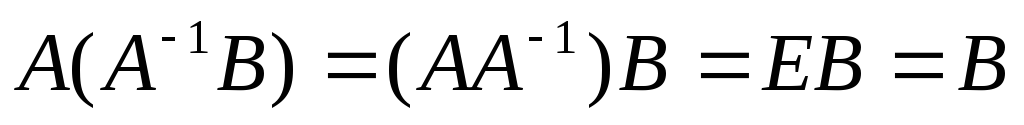
1.2. Решение систем линейных уравнений.(слу)
Вопросы:
1.2.1.Определение СЛУ;
1.2.2.Матричная форма записи системы;
1.2.3. Решение СЛУ с помощью формул Крамера;
1.2.4.Решение СЛУ методом Гаусса;
1.2.1. Системы линейных уравнений
Определение 1.Система вида
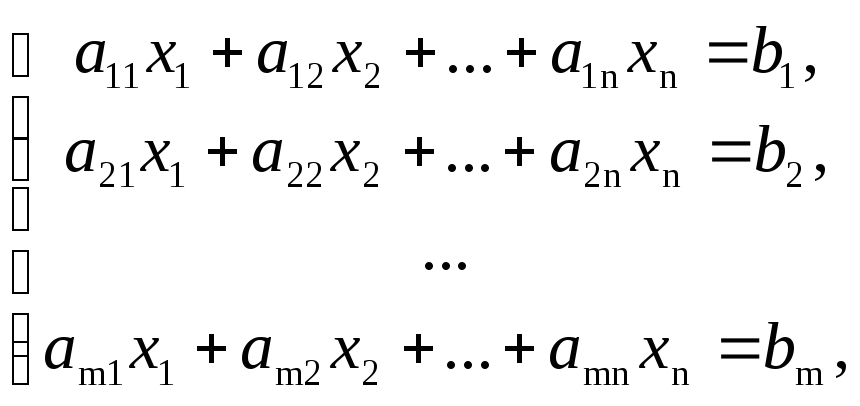
называется
системой m линейных уравнений с n неизвестными, где x1,x2, …,xn— неизвестные,aij, i=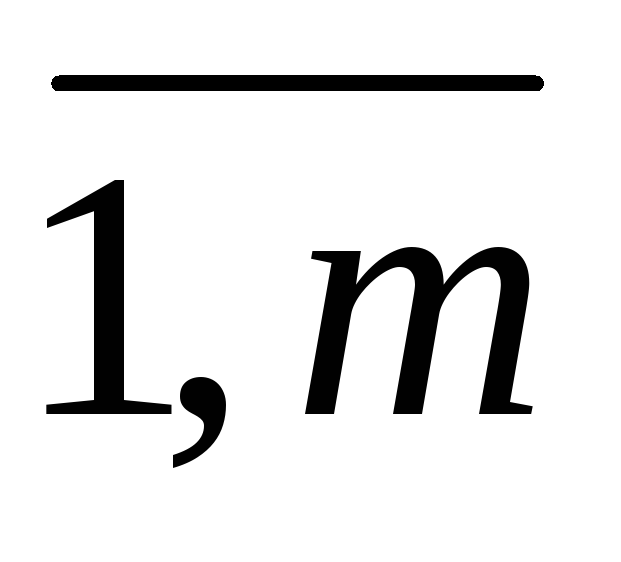 , j=
, j=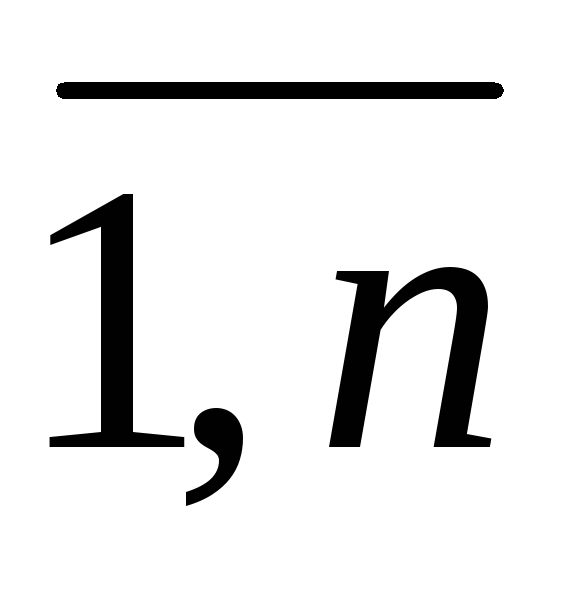 —
коэффициенты при неизвестных,b1,b2, …,bm— свободные члены.
—
коэффициенты при неизвестных,b1,b2, …,bm— свободные члены.
Определение 2.Если все свободные члены равны нулю, то система называется однородной, и неоднородной — в противном случае.
Определение 3.Решением системы называется совокупность изnчиселс1,с2, …,сn, при подстановке которой в систему вместо неизвестных будет полученоmчисловых тождеств.
Определение 4. Система называется совместной, если она имеет хотя бы одно решение, и несовместной в противном случае.
Определение 5. Совместная система называется определенной, если она имеет единственное решение, и неопределенной — в противном случае.
При изучении систем исследуют три вопроса:
совместна система или нет;
если система совместна, то является ли она определенной или неопределенной;
нахождение единственного решения в случае определенной системы и всех решений в случае неопределенной.
1.2.2. Матричная форма записи системы
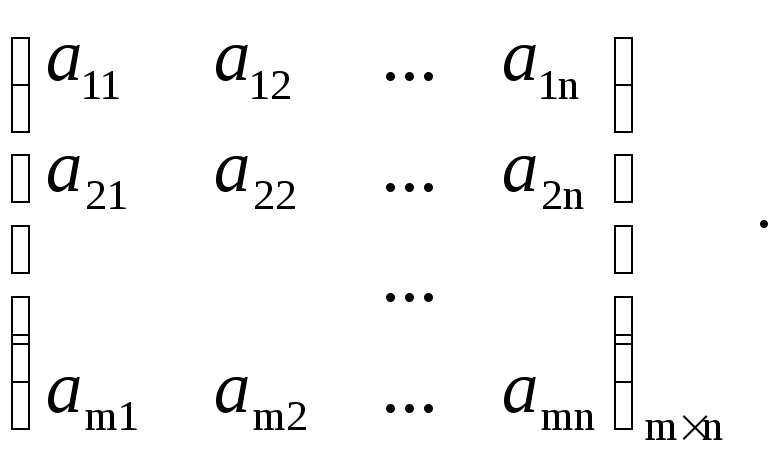
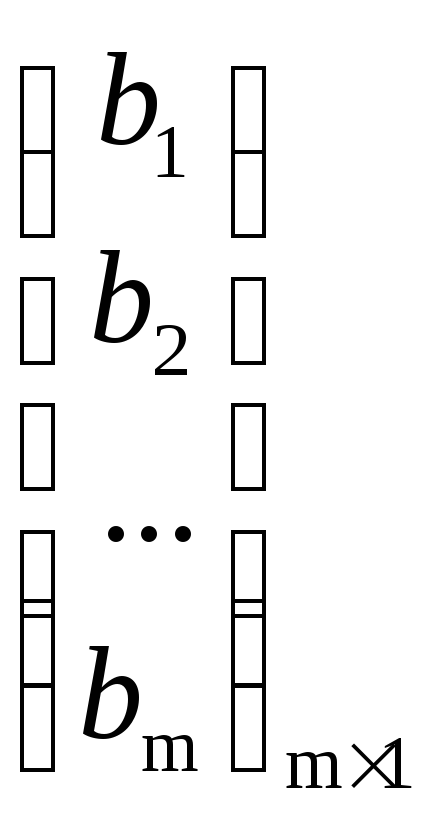
Пусть дана система
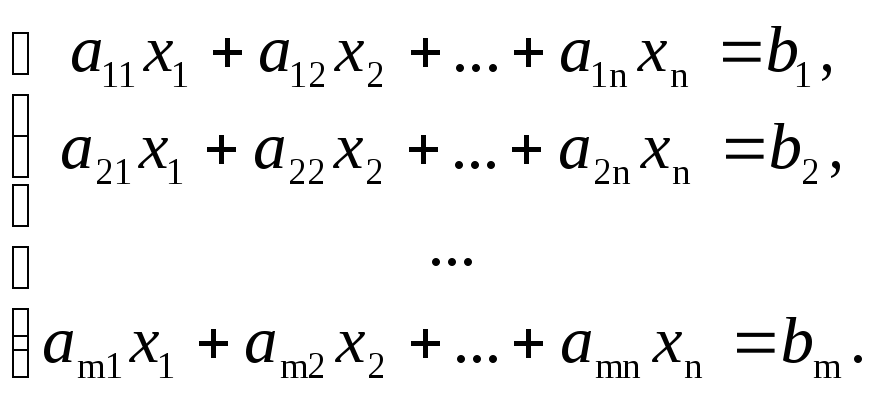
Рассмотрим матрицы
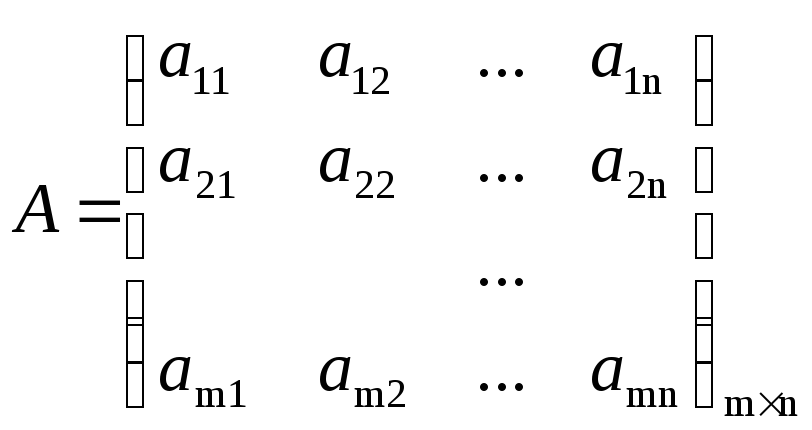 ,
,  ,
, 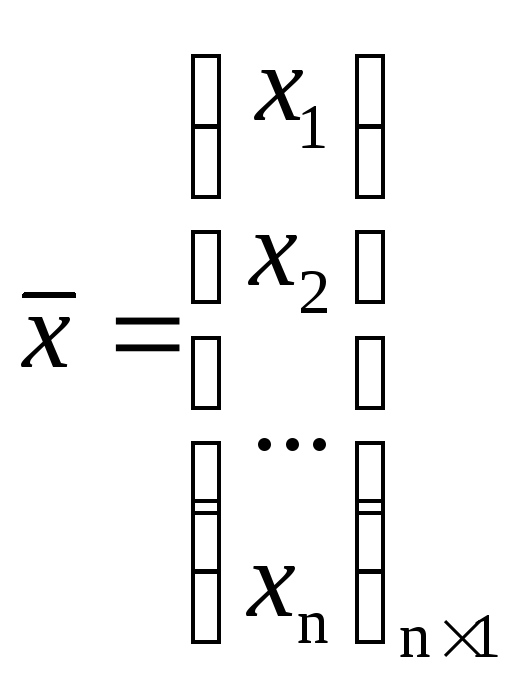 .
.
С помощью этих
матриц систему можно записать в виде  .
.
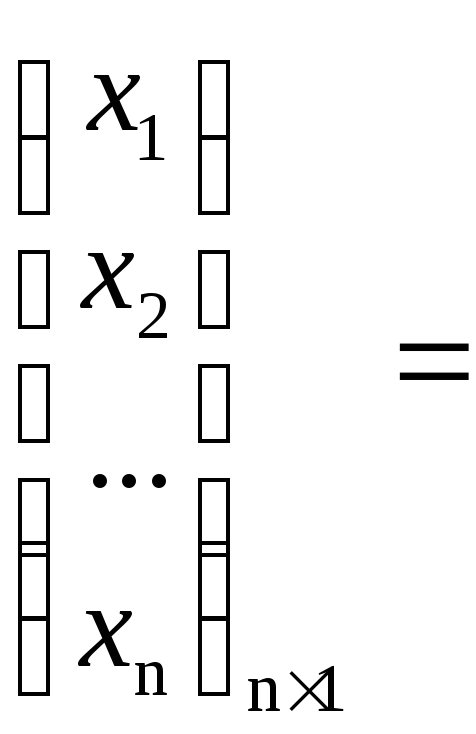
 ,
,
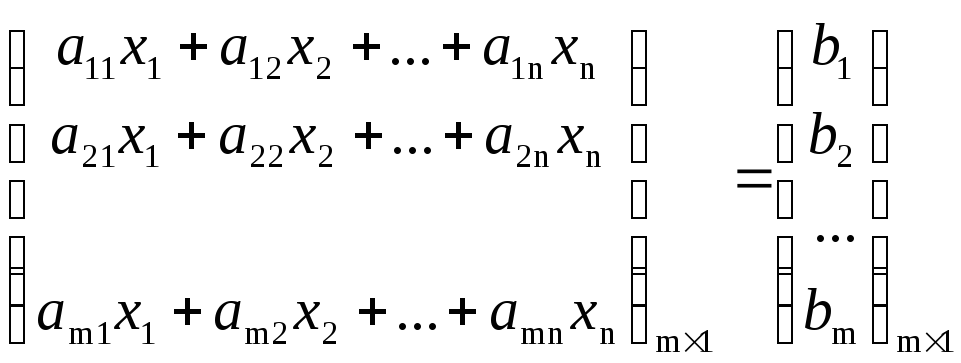 .
.
1.2.3. Решение системы с помощью формул Крамера
Рассмотрим неоднородную системуnлинейных уравнений сnнеизвестными:
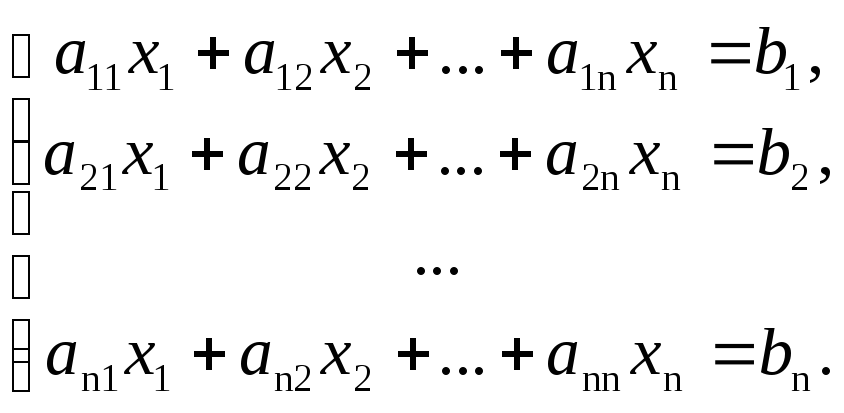
Теорема
(теорема Крамера).Еслиопределитель
матрицы, составленной из
коэффициентов при неизвестных, отличен
от нуля ( ),
то системаимеет
единственное решение,
которое можно найти по формулам Крамера:
),
то системаимеет
единственное решение,
которое можно найти по формулам Крамера:
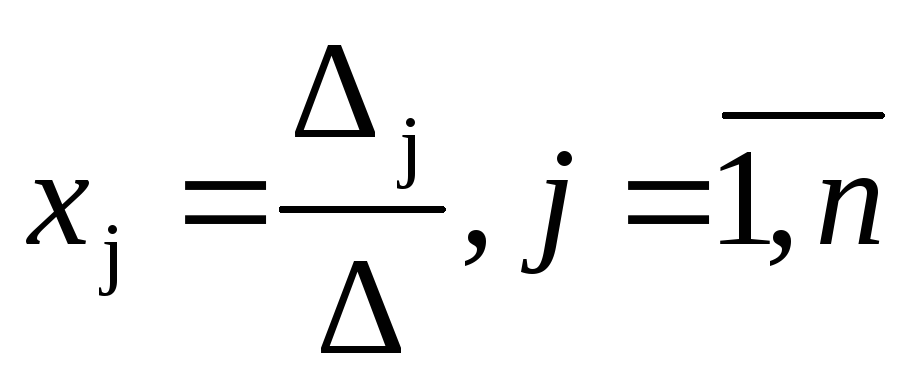 ,
где
,
где 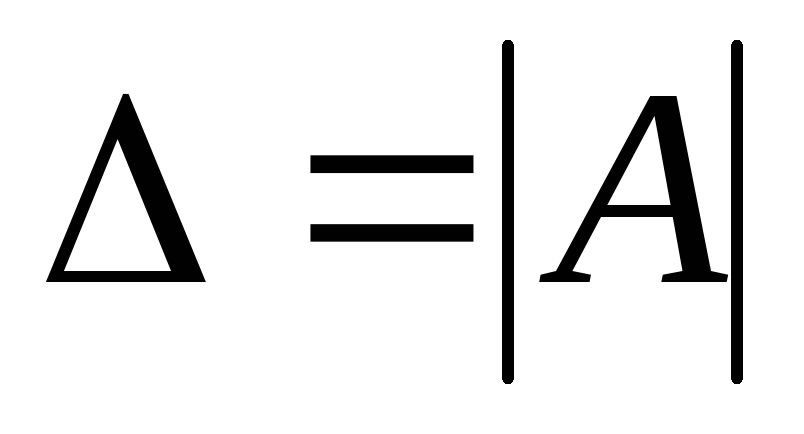 — главный определитель,
— главный определитель, — j-йвспомогательный
определитель, который получен из
определителя
— j-йвспомогательный
определитель, который получен из
определителя  заменой j-гостолбца столбцом свободных членов.
заменой j-гостолбца столбцом свободных членов.
Если главный определитель равен нулю и хотя бы один их вспомогательных определителей отличен от нуля, то система решений не имеет.
Если главный определитель и все вспомогательные определители равны нулю, то система имеет бесконечно много решений.
1.2.4. Решение слу методом Гаусса.
Определение 1. Элементарными преобразованиями системы называются:
умножение уравнения на число, отличное от нуля;
прибавление к одному уравнению другого уравнения, умноженного на некоторое число, отличное от нуля.
перестановка двух уравнений;
отбрасывание уравнения 0=0.
Если получено уравнение 0=k, то система несовместна.
Метод Гаусса состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных. Количество исключенных неизвестных равно числу линейно независимых уравнений. Переменная считается исключенной, если она содержится только в одном уравнении с коэффициентом 1.
Пример.
 .
.
Метод Гаусса удобно применять к расширенной матрице системы, левую часть которой с помощью элементарных преобразований матрицы нужно привести к единичной матрице. Составим расширенную матрицу:
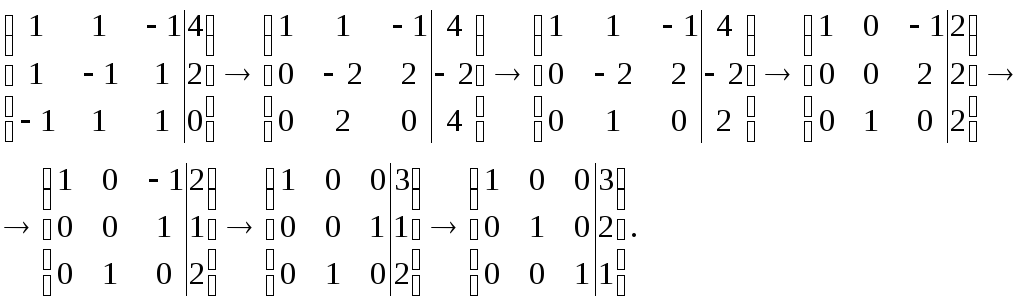
Получено решение системы х (3;2;1).
Вопросы для самопроверки.
1.Что представляет собой система линейных уравнений с п неизвестными?
2. Перечислите способы решения СЛУ.
3. Какие прикладные задачи можно решать матричным способом?
4. Назовите формулы Крамера.
Перечислите этапы метода Гаусса.
Резюме к разделу 1.
Изучение раздела 1формирует у обучающихся умения по работе с матрицами и определителями, используемые для решения систем линейных уравнений. Основной целью изучения дисциплины является приобретение студентами теоретических знаний и прак
Перечень терминов, определений.
Матрицы, операции над ними. Определите матриц, их вычисления. Обратная матрица. Определители матриц, их свойства. Алгебраическое дополнение. Минор матрицы. Ранг матрицы. Обратная матрица, способы ее нахождения. Системы п-линейных уравнений с п переменными. Матричный метод решения СЛУ, с помощью формул Крамера, методом Гаусса.
Вопрос 43. Система линейных уравнений, однородная и неоднородная система, решение системы, совместная и несовместная система, эквивалентные системы
Системой 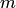 линейных
алгебраических уравнений
с
линейных
алгебраических уравнений
с 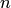 неизвестными называется
система уравнений вида
неизвестными называется
система уравнений вида
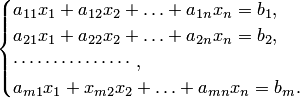
Числа 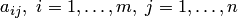 называются коэффициентами
системы;
называются коэффициентами
системы; 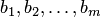 — свободными
членами,
— свободными
членами, 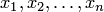 — неизвестными.
Количество
— неизвестными.
Количество 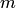 уравнений
в системе может быть меньше, больше или
равно числу
уравнений
в системе может быть меньше, больше или
равно числу 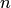 неизвестных.
неизвестных.
Система называется однородной, если все свободные члены равны нулю; в противном случае она называется неоднородной.
Решением
системы называется
упорядоченная совокупность  чисел
чисел 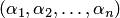 такая,
что после замены неизвестных
такая,
что после замены неизвестных 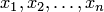 соответственно
числами
соответственно
числами 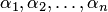 каждое
уравнение системы превращается в верное
числовое равенство.
каждое
уравнение системы превращается в верное
числовое равенство.
Система называется совместной, если она имеет хотя бы одно решение. Если система не имеет ни одного решения, то она называется несовместной.
Две системы уравнений называются эквивалентными, если множество их решений совпадают
Вопрос 44. Матрица системы линейных уравнений, матричная форма записи системы
И сходную Системой
линейных алгебраических уравнений можно записать в матричном виде:
сходную Системой
линейных алгебраических уравнений можно записать в матричном виде:
,
где матрица 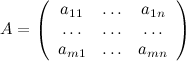 называется матрицей
системы, это матрица,
составленная из коэффициентов при
неизвестных;
называется матрицей
системы, это матрица,
составленная из коэффициентов при
неизвестных; 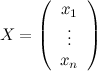 — вектором-столбцом
неизвестных,
— вектором-столбцом
неизвестных, 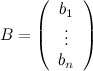 — вектором-столбцом
правых частей или свободных
коэффициентов.
— вектором-столбцом
правых частей или свободных
коэффициентов.
Вопрос 45. Правило Крамера
Системой однородных линейных уравнений называется система вида
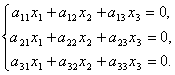
Ясно, что в этой случае 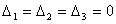 ,
т.к. все элементы одного из столбцов в
этих определителях равны нулю.
,
т.к. все элементы одного из столбцов в
этих определителях равны нулю.
Так как неизвестные находятся
по формулам 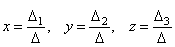 ,
то в случае, когда Δ ≠ 0, система имеет
единственное нулевое решение x = y = z =
0. Однако, во многих задачах интересен
вопрос о том, имеет ли однородная система
решения отличные от нулевого.
,
то в случае, когда Δ ≠ 0, система имеет
единственное нулевое решение x = y = z =
0. Однако, во многих задачах интересен
вопрос о том, имеет ли однородная система
решения отличные от нулевого.
Вопрос 46. Минор к-ого порядка, ранг матрицы, базисный минор
Определитель, который образован элементами матрицы, стоящими на пересечении произвольно выбранных k строк и k столбцов, называется минором k-го порядкаэтой матрицы ( при этом минор 1-го порядка – это произвольный элемент данной матрицы).
Рангом матрицыназывается наивысший порядок ее миноров, отличных от нуля (ранг нулевой матрицы полагается равным нулю). Ранг матрицы А обозначается символомr(А).
Всякий неравный нулю минор, порядок которого равен рангу матрицы, называется ее базисным минором.
Вопрос 47. Элементарные преобразования над матрицами
Элементарными преобразованиями матрицы называются следующие 4 операции:
перестановка двух строк (столбцов)
умножение строки (столбца) на число, неравное нулю
прибавление к строке (столбцу) другой строки ( другого столбца), умноженной (умноженного) на любое число
отбрасывание нулевой строки (нулевого столбца)
Вопрос 48. Теорема об элементарных преобразованиях
Ранг матрицы не меняется при ее элементарных преобразованиях.
Вопрос 49. Теорема Кронекера-Капелли
Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы.
Система имеет единственное решение, если ранг равен числу неизвестных, и бесконечное множество решений, если ранг меньше числа неизвестных.
Решить систему — это значит выяснить, совместна она или несовместна. Если система совместна, найти ее общее решение.
Вопрос 50. Условия существования ненулевого решения у однородной системы mхn и системы nхn
Условия существования ненулевого решения у однородной системы mхn:однородная система mхn имеет ненулевое решение тогда и только тогда, когда ранг матрицы системы меньше числа неизвестных.
Условия существования ненулевого решения у однородной системы nхn:однородная система nхn имеет ненулевое решение тогда и только тогда, когда определитель системы равен нулю.
Вопрос 51. Изображение на числовой оси множеств действительных чисел, заданных равенством и неравенством
52. Модуль действительного числа и его свойства
Модулем неотрицательного действительного числа х называют само это число: | х | = х; модулем отрицательного действительного числа х называют противоположное число: I х | = — х.
INCLUDEPICTURE «http://school.xvatit.com/images/f/f3/14-06-125.jpg»
\* MERGEFORMATINET 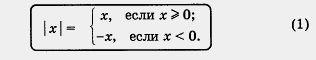
1. |а| 0.
2.|аb| =|a| |b|.
INCLUDEPICTURE «http://school.xvatit.com/images/b/b2/14-06-127.jpg»
\* MERGEFORMATINET 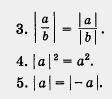
53. Геометрический смысл модуля числа и модуля разности двух чисел
Геометрический смысл – расстояние от точки с координатой Х на числовой прямой до начала координат.
Модуль разности – расстояние между соответствующими точками на числовой прямой.
54. Определение функции, определение графика функции
Функция (отображение, оператор, преобразование) — математическое понятие, отражающее связь между элементами множеств. Можно сказать, что функция — это «закон», по которому каждому элементу одного множества (называемого областью определения) ставится в соответствие некоторый элемент другого множества (называемого областью значений).
График функции — понятие в математике, которое даёт представление о геометрическом образе функции.
В этом случае, график функции — это
геометрическое место точек плоскости,
абсциссы (x) и ординаты (y) которых связаны
указанной функцией: точка располагается
(или находится) на графике функции тогда
и только тогда, когда INCLUDEPICTURE
«http://upload.wikimedia.org/math/7/c/1/7c1c9491ba7c6e8d6d2cfa82e39b22ca.png»
\* MERGEFORMATINET 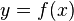
Матричная запись систем линейных алгебраических уравнений
Умножение матриц удобно применять для записи систем линейных алгебраических уравнений.
Пример 2.7. Записать с помощью матричных равенств систему уравнений:
3x + 7 y = 25x + 2 y =13
Обозначим А квадратную матрицу:
3 | 7 | ||
A = |
|
|
|
| 5 | 2 |
|
|
| ||
В этой матрице первая строчка совпадает с коэффициентами при неизвестных х и у в первом уравнении заданной системы, а вторая строка – с коэффициентами при неизвестных во втором уравнении системы. Поэтому матрица А называется матрицей коэффициентов при неизвестных системы уравнений.
Пусть Х=(х у)т и В=(2 13)т матрицы-столбцы. Говорят, что Х является
столбцом неизвестных, а В – столбцом правых частей исходной системы.
Тогда после умножения А на Х имеем: АХ=(3х+7у 5х+2у)т. Поэтому заданная система уравнений означает систему поэлементных равенств матриц АХ и В, а исходная система уравнений может быть записана в виде одного мат-
ричного уравнения АХ=В. Говорят, что исходная система эквивалентна одному матричному уравнению АХ=В.
Задача 2.6. Используя умножение матриц, записать в матричном виде системы уравнений:
5x − 2 y = 7 | 7x − y = 8 | x − y + 2z = 2 | ||
1) | 3x + y = 4 | 2) | + 2 y = 5 | 3) |
| x | 2x + y − z = 2 | ||
Таким образом, для того чтобы найти решение исходной системы уравнений, остается решить только одно это матричное уравнение АХ=В
Пример 2.8. Рассмотрим систему двух уравнений 3х+5у=2 и 4х+7у=3 с двумя неизвестными. Для того, чтобы решить эту систему уравнений, надо исключить одно из неизвестных. Например, чтобы исключить неизвестное х, можно умножить первое уравнение на 4, а второе на 3. Тогда коэффициенты при неизвестном х в обоих уравнениях станут одинаковыми. После указанных умножений получим:
12х+20у=8 12х+21у=9.
Теперь, после вычитания первого уравнения из второго, остается: у=1. Подставляя в первое уравнение у=1, имеем: 3х+5=2, откуда 3х=2-5=-3 и, следовательно, х= -1. Таким образом, х= -1, у=1 – решение заданной системы. В матричном виде это решение есть: (х у)=(-1 1), и его можно записать в виде матрицы-строки или матрицы-столбца.
А как можно решать матричное уравнение АХ=В? Для того, чтобы научиться это делать, можно использовать разные приемы, которые сводятся к различным вариантам действий с матрицами.
Матричная запись системы линейных уравнений. — КиберПедия
Рассмотрим систему (I) ( см. §1).
Обозначим:
— матрица коэффициентов при неизвестных
,
— матрица – столбец свободных членов
— матрица – столбец неизвестных
.
Определение 1. Матрица называется основной матрицей системы (I), а матрица — расширенной матрицей системы (I).
По определению равенства матриц системе (I) соответствует матричное равенство:
.
Правую часть этого равенства по определению произведения матриц (см. определение 3 § 5 главы 1) можно разложить на множители:
, т.е.
. (2)
Равенство (2) называется матричной записью системы (I).
Решение системы линейных уравнений методом Крамера.
Пусть в системе (I) ( см. §1) m=n , т.е. число уравнений равно числу неизвестных, и основная матрица системы невырожденная, т.е. . Тогда система (I) из §1 имеет единственное решение
, (3)
где Δ = det A называется главным определителем системы (I), Δi получается из определителя Δ заменой i-го столбца на столбец из свободных членов системы (I).
Пример.
Решить систему методом Крамера :
.
По формулам (3) .
Вычисляем определители системы:
,
,
,
.
Чтобы получить определитель , мы заменили в определителе первый столбец на столбец из свободных членов; заменяя в определителе 2-ой столбец на столбец из свободных членов, получаем ; аналогичным образом, заменяя в определителе 3-ий столбец на столбец из свободных членов, получаем . Решение системы :
.
Решение систем линейных уравнений с помощью обратной матрицы.
Пусть в системе(I) (см. §1) m=n и основная матрица системы невырожденная . Запишем систему (I) в матричном виде (см. §2):
, (2)
т.к. матрица A невырожденная, то она имеет обратную матрицу (см. теорему 1 §6 главы 1). Умножим обе части равенства (2) на матрицу , тогда
. (3)
По определению обратной матрицы . Из равенства (3) имеем
,
отсюда
. (4)
Пример 1.
Решить систему с помощью обратной матрицы
.
Обозначим
; ; .
В примере (§ 3)мы вычислили определитель , следовательно, матрица A имеет обратную матрицу . Тогда в силу (4)
, т.е.
. (5)
Найдем матрицу (см. §6 главы 1)
, , ,
, , ,
, , ,
,
.
Ответ:
Метод Гаусса.
Пусть задана система линейных уравнений:
. (I)
Требуется найти все решения системы (I) или убедиться в том, что система несовместна.
Определение 1. Назовем элементарным преобразованием системы (I) любое из трёх действий :
1) вычёркивание нулевого уравнения;
2) прибавление к обеим частям уравнения соответствующих частей другого уравнения, умноженных на число l;
3) перемена местами слагаемых в уравнениях системы так, чтобы неизвестные с одинаковыми номерами во всех уравнениях занимали одинаковые места, т.е. если, например, в 1-ом уравнении мы поменяли 2-ое и 3-е слагаемые, тогда то же самое необходимо сделать во всех уравнениях системы.
Метод Гаусса состоит в том, что система (I) с помощью элементарных преобразований приводится к равносильной системе, решение которой находится непосредственно или устанавливается её неразрешимость.
Как было описано в §2 система (I) однозначно определяется своей расширенной матрицей и любое элементарное преобразование системы (I) соответствует элементарному преобразованию расширенной матрицы :
.
Преобразование 1) соответствует вычёркиванию нулевой строки в матрице , преобразование 2) равносильно прибавлению к соответствующей строке матрицы другой её строки, умноженной на число l, преобразование 3) эквивалентно перестановке столбцов в матрице .
Легко видеть, что, наоборот, каждому элементарному преобразованию матрицы соответствует элементарное преобразование системы (I). В силу сказанного, вместо операций с системой (I) мы будем работать с расширенной матрицей этой системы.
В матрице 1-ый столбец состоит из коэффициентов при х1, 2-ой столбец — из коэффициентов при х2и т.д. В случае перестановки столбцов следует учитывать, что это условие нарушается. Например, если мы поменяем 1-ый и 2-ой столбцы местами, то теперь в 1-ом столбце будут коэффициенты при х2, а во 2-ом столбце — коэффициенты при х1.
Будем решать систему (I) методом Гаусса.
1. Вычеркнем в матрице все нулевые строки, если такие имеются (т.е. вычеркнем в системе (I) все нулевые уравнения).
2. Проверим, есть ли среди строк матрицы строка, в которой все элементы, кроме последнего, равны нулю (назовём такую строку несовместной). Очевидно, что такой строке соответствует несовместное уравнение в системе (I) , следовательно, система (I) решений не имеет и на этом процесс заканчивается.
3. Пусть матрица не содержит несовместных строк (система (I) не содержит несовместных уравнений). Если a11=0, то находим в 1-ой строке какой-нибудь элемент (кроме последнего) отличный от нуля и переставляем столбцы так, чтобы в 1-ой строке на 1-ом месте не было нуля. Будем теперь считать, что (т.е. поменяем местами соответствующие слагаемые в уравнениях системы (I)).
4. Умножим 1-ую строку на и сложим результат со 2-ой строкой, затем умножим 1-ую строку на и сложим результат с 3-ей строкой и т.д. Очевидно, что этот процесс эквивалентен исключению неизвестного x1 из всех уравнений системы (I), кроме 1-ого. В новой матрице получаем нули в 1-ом столбце под элементом a11 :
.
5. Вычеркнем в матрице все нулевые строки, если они есть, проверим, нет ли несовместной строки (если она имеется, то система несовместна и на этом решение заканчивается). Проверим, будет ли a22 /=0, если да, то находим во 2-ой строке элемент, отличный от нуля и переставляем столбцы так, чтобы . Далее умножаем элементы 2-ой строки на и складываем с соответствующими элементами 3-ей строки, затем — элементы 2-ой строки на и складываем с соответствующими элементами 4-ой строки и т.д., пока не получим нули под a22 /
.
Произведенные действия эквивалентны исключению неизвестного х2 из всех уравнений системы (I), кроме 1-ого и 2-ого. Так как число строк конечно, поэтому через конечное число шагов мы получим, что либо система несовместна, либо мы придём к ступенчатой матрице (см. определение 2 §7 главы 1) :
,
где
.
Выпишем систему уравнений, соответствующую матрице . Эта система равносильна системе (I)
.
Из последнего уравнения выражаем ; подставляем в предыдущее уравнение, находим и т.д., пока не получим .
Замечание 1. Таким образом, при решении системы (I) методом Гаусса мы приходим к одному из следующих случаев.
1. Система (I) несовместна.
2. Система (I) имеет единственное решение, если в матрице число строк равно числу неизвестных ( ).
3. Система (I) имеет бесчисленное множество решений, если число строк в матрице меньше числа неизвестных ( ).
Отсюда имеет место следующая теорема.
Теорема. Система линейных уравнений либо несовместна, либо имеет единственное решение, либо – бесконечное множество решений.
Примеры. Решить систему уравнений методом Гаусса или доказать ее несовместность:
а) ;
б) ;
в) .
Решение.
а) Перепишем заданную систему в виде:
.
Мы поменяли местами 1-ое и 2-ое уравнение исходной системы, чтобы упростить вычисления (вместо дробей мы с помощью такой перестановки будем оперировать только целыми числами).
Составляем расширенную матрицу:
.
Нулевых строк нет; несовместных строк нет, ; исключим 1-ое неизвестное из всех уравнений системы, кроме 1-го. Для этого умножим элементы 1-ой строки матрицы на «-2» и сложим с соответствующими элементами 2-ой строки, что равносильно умножению 1-го уравнения на «-2» и сложению со 2-ым уравнением. Затем умножим элементы 1-ой строки на «-3» и сложим с соответствующими элементами третьей строки, т.е. умножим 2-ое уравнение заданной системы на «-3» и сложим с 3-им уравнением. Получим
.
Матрице соответствует система уравнений
.
В матрице нулевых строк нет, несовместных строк также нет, исключим неизвестное из 3-го уравнения системы, для этого умножим элементы 2-ой строки матрицы на «-1» и сложим с элементами 3-ей строки :
.
Матрица содержит несовместную строку (в 3-ей строке все элементы равны нулю, кроме последнего). Этой строке соответствует несовместное уравнение . Следовательно, система решений не имеет ( ), система несовместна.
б) Составляем расширенную матрицу:
.
Нулевых строк нет, несовместных строк нет, , исключаем неизвестное из 2-го и 3-го уравнения заданной системы, для этого умножим элементы 1-ой строки матрицы на «-2», затем на «-3» и сложим соответственно с элементами 2-ой и 3-ей строк, получим
.
Рекомендуем читателю проанализировать, какие операции при этом совершаются с заданной системой уравнений. Умножаем элементы 2-ой строки матрицы на «-1» и складываем с элементами 3-ей строки, получаем:
,
где — матрица ступенчатого вида.
Записываем систему уравнений, соответствующую этой матрице
.
Теперь двигаемся снизу вверх. Из последнего уравнения находим .
Подставляя это равенство в предпоследнее уравнение, находим .
Подставляя и в первое уравнение, получаем : .
Ответ: — система имеет единственное решение.
в) Составляем расширенную матрицу:
1. Переставим местами 1-ую и 2-ую строку для упрощения вычислений (меняем местами уравнения в заданной системе).
2. Умножим элементы 2-ой строки матрицы последовательно на «-2», «-1» и «-5» и сложим соответственно с элементами 2-ой, 3-ей и 4-ой строк (для получения нулей под элементом ).
3. Аналогичным образом, получаем нули под элементом .
4. Вычеркиваем нулевые строки.
Последняя матрица – ступенчатая. Переходим от нее к системе уравнений:
;
из последнего уравнения получаем:
,
подставляя это равенство в 1-ое уравнение системы, находим
.
Ответ: — система имеет бесчисленное множество решений. Давая произвольные значения переменным и , мы каждый раз будем получать частные решения заданной системы уравнений.
Замечание . Количество уравнений в окончательной системе при решении методом Гаусса всегда равно рангу матрицы — (см. определение 3§7 главы 1).