Тригонометрические функции примеры – Сборник индивидуальных заданий по математике. Раздел: Тригонометрические функции. — Детская игровая комната «Волшебный лес»

Posted on 03.10.202016.01.2020 by alexxlab

Содержание

Тригонометрия. Видеоурок. Идеи и смыслы

На этом уроке мы поговорим, как возникает необходимость во введении тригонометрических функций и почему их изучают, что нужно понимать в этой теме, а где просто необходимо набить руку (что является техникой). Заметим, что техника и понимание – это разные вещи. Согласитесь, есть разница: научиться кататься на велосипеде, то есть понимать, как это делать, или стать профессиональным велогонщиком. Мы будем говорить именно о понимании, о том, зачем нужны тригонометрические функции.

Существует четыре тригонометрические функции, но их все можно выразить через одну используя тождества (равенства, которые их связывают).

Формальные определения тригонометрических функций для острых углов в прямоугольных треугольниках (Рис. 1).

Синусом острого угла прямоугольного треугольника называют отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называют отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называют отношение противоположного катета к прилежащему катету.

Котангенсом острого угла прямоугольного треугольника называют отношение прилежащего катета к противолежащему катету.

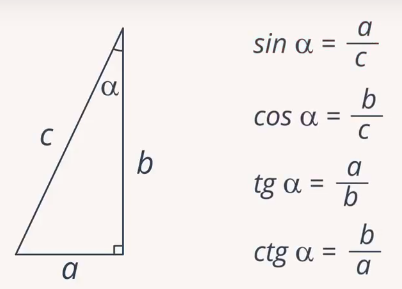
Рис. 1. Определение тригонометрических функций острого угла прямоугольного треугольника

Эти определения являются формальными. Правильнее сказать, что существует только одна функция, например, синус. Если бы они не были так нужны (не так часто использовались) в технике, не вводили бы и столько разных тригонометрических функций.

Например, косинус угла равен синусу этого же угла с добавлением (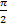

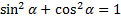). Кроме того, косинус угла всегда можно выразить через синус этого же угла с точностью до знака, используя основное тригонометрическое тождество (

). Тангенс угла – это отношение синуса к косинусу или перевёрнутый котангенс (Рис. 2). Некоторые не используют котангенс вообще, заменяя его на

. Поэтому важно понимать и уметь работать с одной тригонометрической функцией.

Рис. 2. Связь различных тригонометрических функций

Но зачем вообще понадобились такие функции? Для решения каких практических задач их используют? Давайте рассмотрим несколько примеров.

Два человека (А и В) выталкивают машину из лужи (Рис. 3). Человек В может толкать машину вбок, при этом он вряд ли поможет А. С другой стороны, направление его усилий может постепенно сдвигаться (Рис. 4).

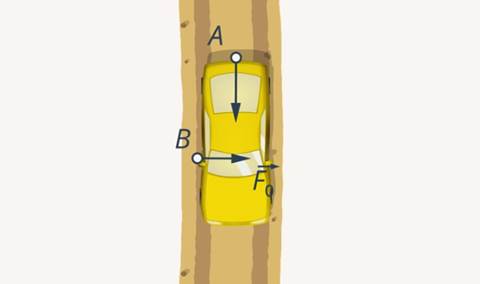
Рис. 3. В толкает машину вбок

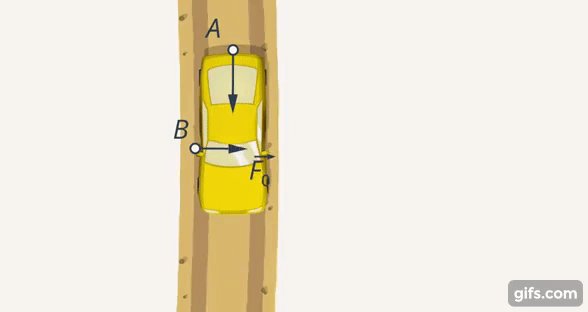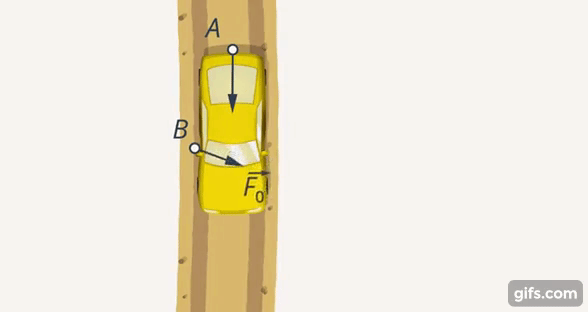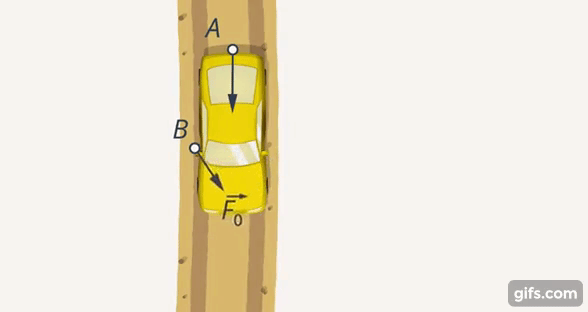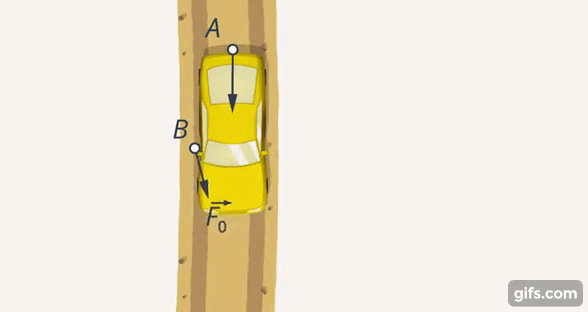
Рис. 4. В начинает менять направление своих усилий

Ясно, что наиболее эффективно их усилия сложатся тогда, когда они будут толкать машину в одну сторону (Рис. 5).

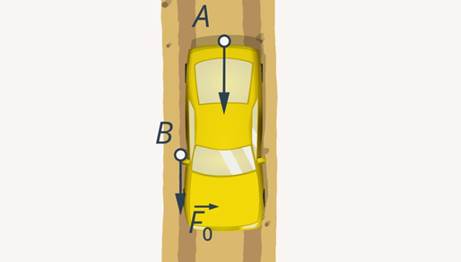
Рис. 5. Наиболее эффективное совместное направление усилий

То, насколько В помогает выталкиванию машины, насколько направление его силы близко к направлению силы, с которой действует А, является функцией угла и выражается через его косинус (Рис. 6).

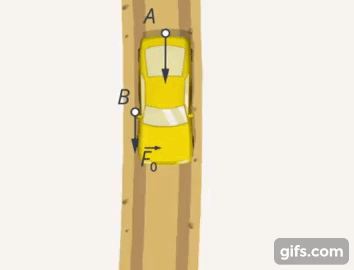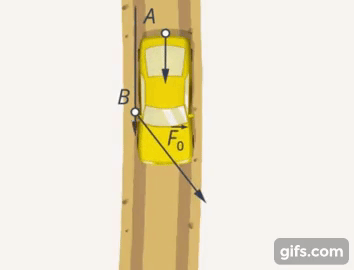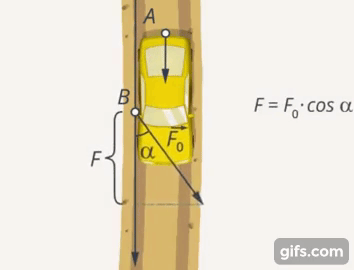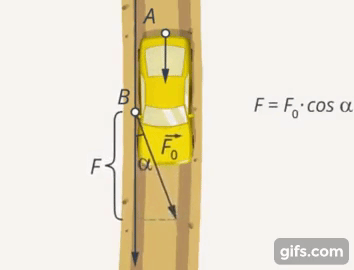
Рис. 6. Косинус, как характеристика эффективности усилий В

Если умножить величину силы, с которой действует В, на косинус угла, получим проекцию его силы на направление силы, с которой действует А. Чем ближе угол между направлениями сил к , тем эффективнее будет результат совместных действий А и В (Рис. 7). Если они будут толкать машину с одинаковой силой в противоположных направлениях, то машина останется на месте (Рис. 8).

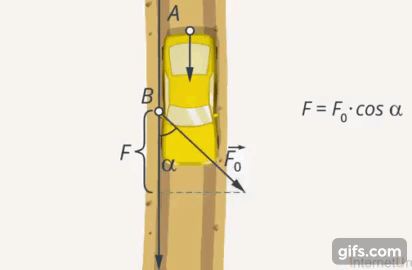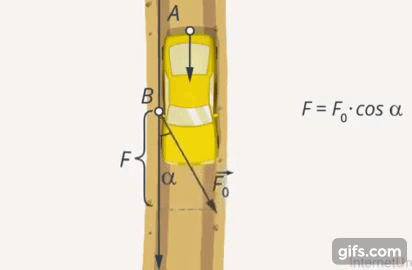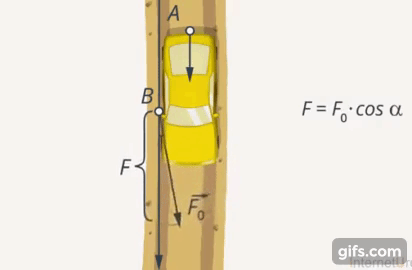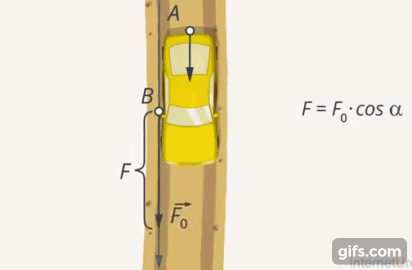
Рис. 7. Эффективность совместных усилий А и В

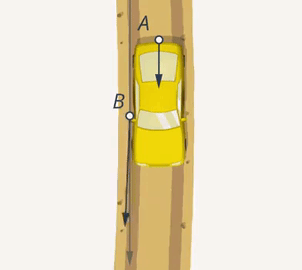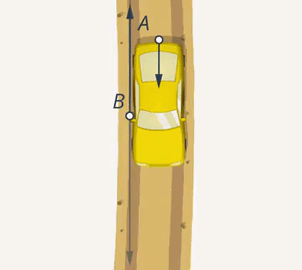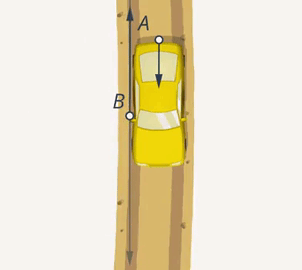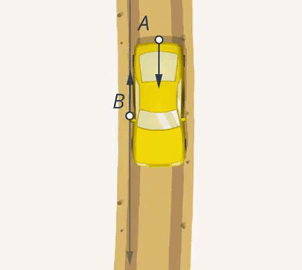
Рис. 8. Противоположное направление действия сил А и В

Важно понимать, почему мы можем заменить угол (его вклад в конечный результат) на косинус (или другую тригонометрическую функцию угла). На самом деле это следует из такого свойства подобных треугольников. Так как фактически мы говорим следующее: угол можно заменить на отношение двух чисел (катет-гипотенуза или катет-катет). Это было бы невозможно, если бы, например, для одного и того же угла разных прямоугольных треугольников эти отношения были бы разные (Рис. 9).

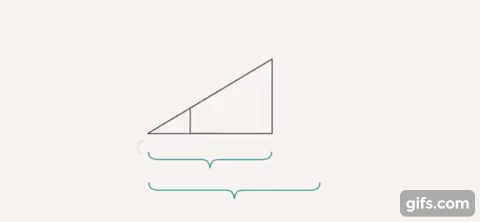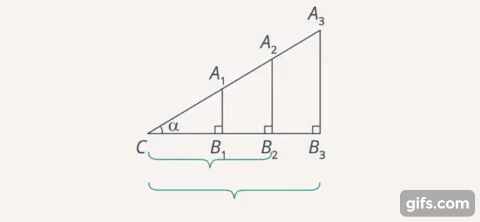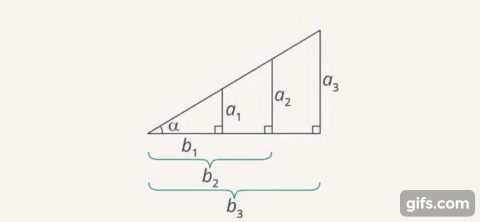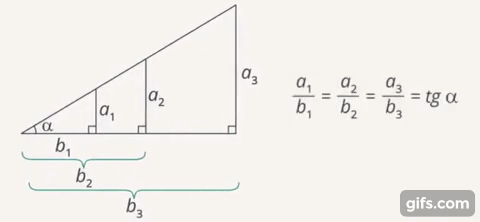
Рис. 9. Равные отношения сторон в подобных треугольниках

Например, если бы отношение 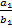и отношение 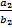было бы разным, то мы бы не смогли ввести функцию тангенса, так как для одного и того же угла в разных прямоугольных треугольниках тангенс оказался бы разным. Но благодаря тому, что отношения длин катетов подобных прямоугольных треугольников одинаковы, значение функции не будет зависеть от треугольника, а значит, острый угол и значения его тригонометрических функций взаимно однозначны.

Предположим, мы знаем высоту некоего дерева (Рис. 10). Как измерить высоту здания, расположенного рядом?

Рис. 10. Иллюстрация условия примера 2

Находим точку 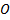, такую, что линия, проведённая через эту точку и вершину дома, пройдёт через вершину дерева (Рис. 11).

Рис. 11. Иллюстрация решения задачи примера 2

Мы можем измерить расстояние от этой точки до дерева, расстояние от неё до дома и знаем высоту дерева. Из пропорции можно найти высоту дома: .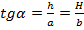

Пропорция – это равенство отношения двух чисел. В данном случае равенство отношения длин катетов подобных прямоугольных треугольников. Причём эти отношения равны некоторой мере угла, которая выражается через тригонометрическую функцию (по определению, это тангенс). Получаем, что для каждого острого угла значение его тригонометрической функции однозначно. То есть синус, косинус, тангенс, котангенс – это действительно функции, так как каждому острому углу соответствует ровно одно значение каждой из них. Следовательно, их можно дальше исследовать и пользоваться их свойствами. Значения тригонометрических функций для всех углов уже вычислены, ими можно пользоваться (их можно узнать из таблиц Брадиса или с помощью любого инженерного калькулятора). А вот решить обратную задачу (например, по значению синуса восстановить меру угла, который ему соответствует) мы можем не всегда.

Пусть синус некоторого угла равен 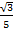или приблизительно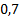

(Рис. 12). Какой угол будет соответствовать данному значению синуса? Конечно, мы может опять воспользоваться таблицей Брадиса и найти какое-то значение, но оказывается, что оно не будет единственным (Рис. 13).

Рис. 12. Нахождение угла по значению его синуса

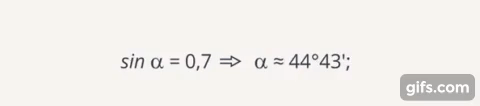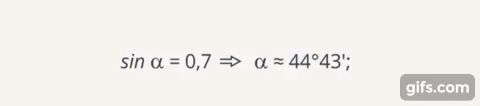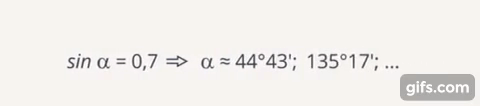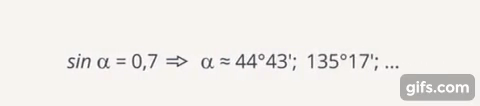
Рис. 13. Многозначность обратных тригонометрических функций

Следовательно, при восстановлении по значению тригонометрической функции угла, возникает многозначность обратных тригонометрических функций. Это может показаться сложным, но на самом деле мы сталкиваемся с похожими ситуациями каждый день.

Если зашторить окна и не знать, светло или темно на улице, или же оказаться в пещере, то, проснувшись, трудно сказать, сейчас час дня, ночи или же следующего дня (Рис. 14). На самом деле, если спросить у нас «Который час?», мы должны честно ответить: «Час плюс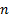

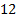умножить на

, где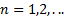

Рис. 14. Иллюстрация многозначности на примере с часами

Можно сделать вывод, что 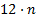– это период (промежуток, через который часы будут показывать то же время, что и сейчас). Периоды есть и у тригонометрических функций: синуса, косинуса и т.д. То есть их значения через некоторое изменение аргумента повторяются.

Если бы на планете не было смены дня и ночи или смены сезонов, то мы не могли бы пользоваться периодическим временем. Ведь у нас только нумерация лет идёт по возрастающей, а в сутках 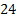часа, и каждые новые сутки счёт начинается заново. С месяцами та же ситуация: если сейчас январь, то через 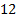месяцев опять наступит январь и т.д. Использовать периодический счёт времени ( часа, 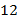месяцев) нам помогают внешние ориентиры – например, вращение Земли вокруг своей оси и изменение положения Солнца и Луны на небе. Если бы Солнце всегда висело в одном и том же положении, то для подсчёта времени нам бы считать количество секунд (минут) с момента возникновения этого самого подсчёта. Дата и время могли бы тогда звучать так: миллиард секунд.

Вывод: никаких сложностей в плане многозначности обратных функций нет. Действительно могут быть варианты, когда для одного и того же синуса существуют разные значения угла (Рис. 15).

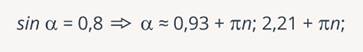
Рис. 15. Восстановление угла по значению его синуса

Обычно при решении практических задач мы всегда работаем в стандартном диапазоне от до 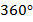. В этом диапазоне для каждого значения тригонометрической функции есть всего два соответствующих значения меры угла.

Рассмотрим движущуюся ленту и маятник в виде ведра с отверстием, из которого высыпается песок. Маятник качается, лента движется (Рис. 16). В результате песок оставит след в виде графика функции синус (или косинус), который называют синусоида.

На самом деле графики синуса и косинуса отличаются друг от друга только точкой отсчёта (если нарисовать один из них, а затем стереть оси координат, то определить, какой именно график был нарисован, не получится). Поэтому называть график косинусоида нет смысла (зачем придумывать отдельное название для того же самого графика)?

Рис. 16. Иллюстрация постановки задачи в примере 4

По графику функции также можно понять, почему обратные функции будут иметь много значений. Если значение синуса зафиксировать, т.е. провести прямую параллельно оси абсцисс, то на пересечении получим все точки, в которых синус угла равен данному. Понятно, что таких точек будет бесконечно много. Как в примере с часами, где было значение времени отличалось на , только здесь значение угла будет отличаться на величину (Рис. 17).

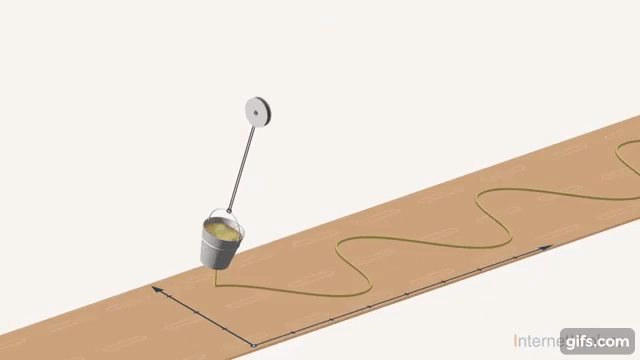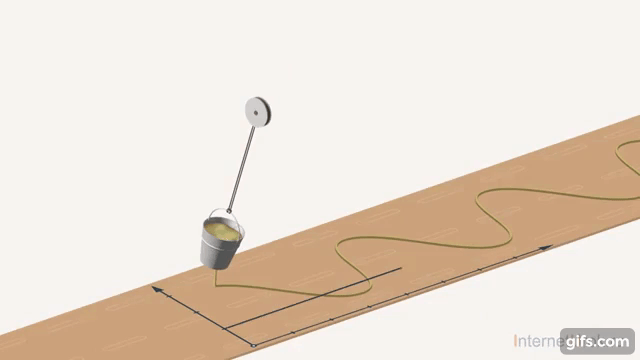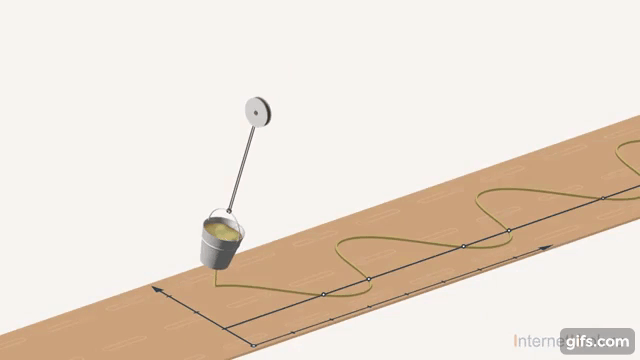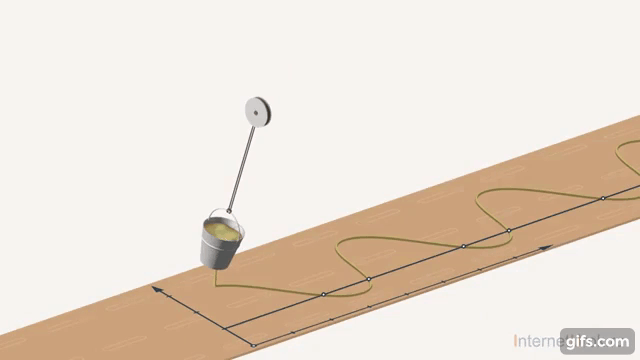
Рис. 17. Иллюстрация многозначности для синуса

Если рассмотреть пример с часами, то точка (конец часовой стрелки) двигается по окружности. Точно так же можно определить и тригонометрические функции – рассматривать не углы в прямоугольном треугольнике, а угол между радиусом окружности и положительным направлением оси 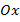. Количество кругов, который пройдёт точка (договорились считать движение по часовой стрелке со знаком минус, а против – со знаком плюс), это период (Рис. 18).

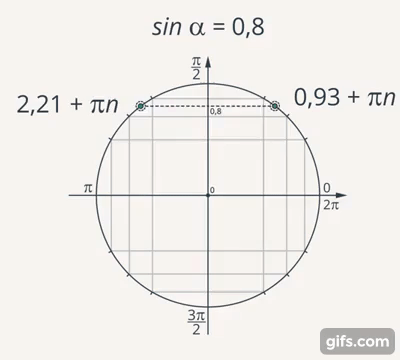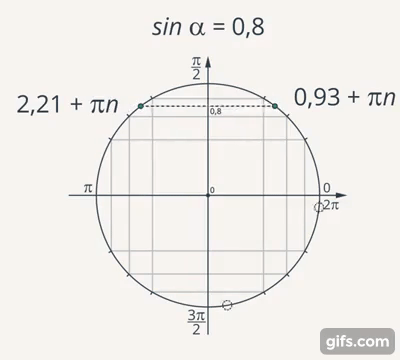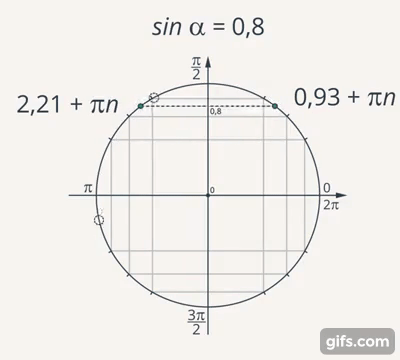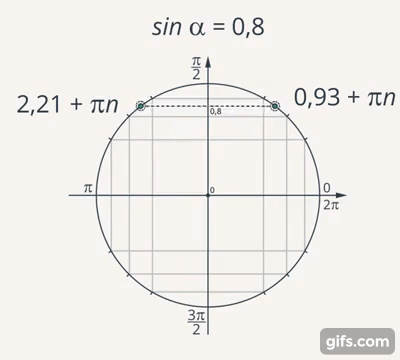
Рис. 18. Значение синуса на окружности

Итак, обратная функция однозначно определена на некотором интервале. Для этого интервала мы можем посчитать её значения, а все остальные получить из найденных значений, добавляя и вычитая период функции.

Рассмотрим ещё один пример периода. Машина движется по дороге. Представим, что её колесо въехало в краску или в лужу. Можно увидеть периодические отметины от краски или лужи на дороге (Рис. 19).

Рис. 19. Иллюстрация периода

Тригонометрических формул в школьном курсе достаточно много, но по большому счёту достаточно помнить всего одну (Рис. 20).

Рис. 20. Тригонометрические формулы

Дальше, если помнить свойства чётности/нечётности, легко вывести такую же формулу для разности .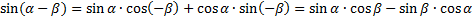

Формулу двойного угла так же легко вывести из синуса суммы, подставив (аналогично для косинуса). Также можно вывести формулы произведения.

На самом деле помнить нужно очень мало, так как с решением задач эти формулы сами запомнятся. Конечно, кто-то много решать поленится, но ему тогда эта техника, а значит, и сами формулы, нужны и не будут.

А раз формулы не понадобятся, то не нужно их и запоминать. Нужно просто понимать идею, что тригонометрические функции – это функции, при помощи которых рассчитываются, например, мосты. Без их использования и расчёта не обходится практически ни один механизм.

1. Часто возникает вопрос, могут ли провода быть абсолютно параллельны земле. Ответ: нет, не могут, так как одна сила действует вниз, а другие параллельно – они никогда не уравновесятся (Рис. 21).

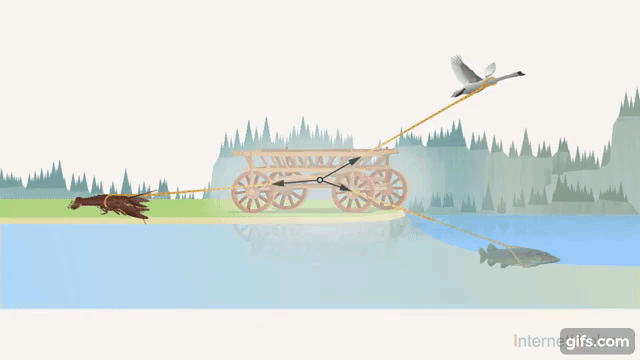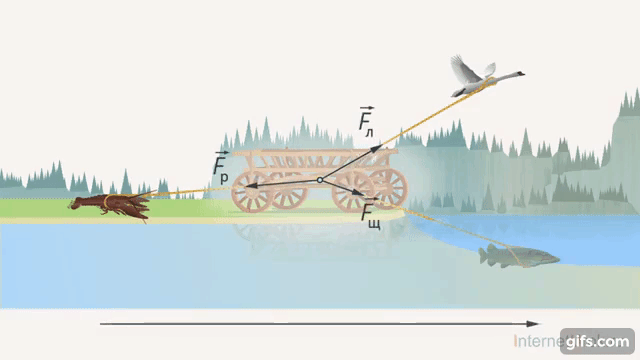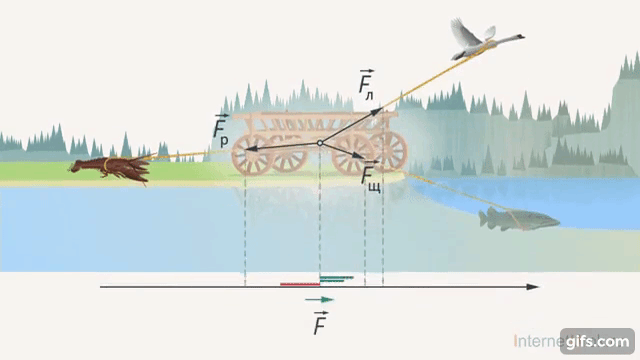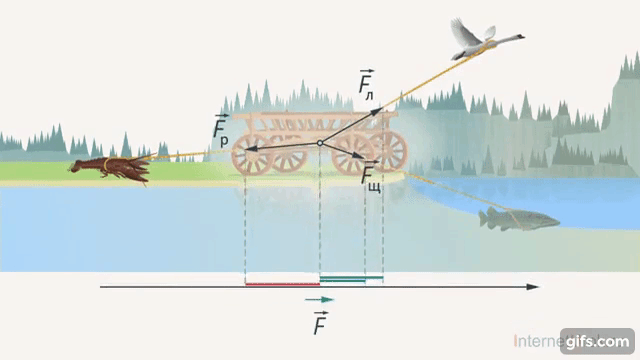
2. Лебедь, рак и щука тянут воз в одной плоскости. Лебедь летит в одну сторону, рак тянет в другую, а щука – в третью (Рис. 22). Их силы могут уравновешиваться. Посчитать это уравновешивание можно как раз с помощью тригонометрических функций.

3. Вантовый мост (Рис. 23). Тригонометрические функции помогают посчитать количество вантов, как они должны быть направлены и натянуты.

Рис. 23. Вантовый мост

Рис. 24. «Струнный мост»

Рис. 25. Большой Обуховский мост

Ссылки на материалы сайта InternetUrok

Математика 6 класс:

Отношения

Геометрия 8 класс:

Синус, косинус и тангенс острого угла прямоугольного треугольника
Значения синуса, косинуса и тангенса для углов 30, 45 и 60 градусов

Геометрия 9 класс:

Синус, косинус и тангенс угла. Основное тригонометрическое тождество

Алгебра 10 класс:

Введение. Длина дуги окружности
Числовая окружность
Числовая окружность на координатной плоскости
Решение задач по теме «Числовая окружность на координатной плоскости»
Синус и косинус
Тангенс и котангенс
Тригонометрические функции числового аргумента
Тригонометрические функции числового аргумента (типовые задачи)
Тригонометрические функции углового аргумента
Тригонометрические функции углового аргумента и типовые задачи
Формулы приведения
Формулы приведения и решение типовых задач
Функция y=sinx, ее основные свойства и график
Функция y=sinx, её свойства, график и типовые задачи
Функция y=cos t, её основные свойства и график
Функция y=cos t, её свойства, график и типовые задачи
Периодичность функций y=sin t, y=cos t
График гармонического колебания
Функция y=tgx, ее свойства и график
Функция y=сtgx, ее свойства и график
Синус и косинус суммы аргументов
Синус и косинус разности аргументов
Решение задач на косинус и синус разности аргументов
Тангенс суммы и разности аргументов
Фо

Математика. Тригонометрические функции. Примеры + решения.

Тригонометрические функции – это математические функции, зависящие от угла. Определяют тригонометрические функции обычно как отношения сторон прямоугольного треугольника или длины определённых отрезков в единичной окружности.

Определения и формулы всех тригонометрических функций

Рассмотрим произвольный прямоугольный треугольник , углы и – острые. (рис. 1). Тогда – гипотенуза (это сторона противолежащая прямому углу), самая длинная сторона в прямоугольном треугольнике. Катет – это катет, являющийся противолежащим по отношению к углу . Катет – это катет, прилежащий к углу .

Рис. 1

ОПРЕДЕЛЕНИЕСинусом угла называется отношение противолежащего катета к гипотенузе или

Это отношение не зависит от выбора , содержащего угол , так как все такие треугольники подобны.

ОПРЕДЕЛЕНИЕ

Косинусом угла называется отношение прилежащего катета к гипотенузе или

Замечание 1. Катет AC, прилежащий к углу , является противолежащим по отношению к углу . Аналогично с катетом , он противолежащий для угла и прилежащий к углу . Таким образом, синус одного острого угла в треугольнике равен косинусу второго его острого угла, и наоборот:

ОПРЕДЕЛЕНИЕТангенсом угла называется отношение противолежащего катета к прилежащему катету AC или

Также тангенс выражается через косинус и синус следующим образом:

ОПРЕДЕЛЕНИЕКотангенсом угла называется отношение прилежащего катета AC к противолежащему катету или

Котангенс выражается через косину и синус следующим образом:

Замечание 2. Котангенс одного острого угла в прямоугольном треугольнике равен тангенсу второго его острого угла, и наоборот:

Секансом угла называется отношение гипотенузы к прилежащему катету или

ОПРЕДЕЛЕНИЕСеканс выражается через косинус следующим образом:

Косекансом угла называется отношение гипотенузы к противолежащему катету или

Косеканс можно выразить через синус:

Обратные тригонометрические функции

Основные обратные тригонометрические функции:

1. – арксинус;

2. – арккосинус;

3. – арктангенс;

4. – арккотангенс.

ОПРЕДЕЛЕНИЕ

Арксинусом числа x, где , называется такое число из промежутка , синус которого равен x.

Арксинус является нечетной функцией, то есть: .

ПРИМЕР 1

Задание

Найти значения обратных тригонометрических функций:

Решение

1) Вычислим значение , для этого нам нужно найти такой угол из промежутка , чтобы . Воспользуемся таблицей значений синуса:

Выбираем в строке значений синуса значение, равное и определяем, что этому значению соответствует угол . Так как , то получаем: .

2) Вычислим значение

Рис. 1

Первый способ. Найдем угол из промежутка , такой что . Воспользуемся тригонометрическим кругом (рис. 1). Значениям синуса соответствуют точки на оси . Отметим на ней значение . Этому значению соответствует и , но промежутку принадлежит только . Таким образом, .

Второй способ. Используем то, что функция арксинус нечетная, тогда . А найдем, используя таблицу значений синуса: при . Тогда окончательно имеем .

Ответ

ОПРЕДЕЛЕНИЕ

Арккосинус числа x, где , называется такое число из промежутка , косинус которого равен x.

Для арккосинуса справедливо следующее равенство

ПРИМЕР 2

Задание

Найти значения обратных тригонометрических функций:

Решение

Для вычисления значение , необходимо найти такой угол из промежутка , чтобы . Воспользуемся таблицей значений косинуса:

Выбираем в строке значений косинуса значение, равное и определяем, что ему соответствует угол . Так как , то получаем: .

Вычислим значение .

Рис. 2

Первый способ. Найдем угол из промежутка , такой что . Воспользуемся тригонометрическим кругом (рис. 2). Значениям косинуса соответствуют точки на оси . Отметим на ней значение . Значению соответствует два угла и . Промежутку принадлежит только , тогда, .

Второй способ. Воспользуемся равенством . Тогда . Найдем , используя таблицу значений клсинуса. Получим, что значению соответствует . Тогда используя последнее равенство

Ответ:

Таблица синусов и косинусов

Таблица 1

С помощью этой таблицы можно найти стандартные значение синуса или косинуса. Искомое значение будет лежать на пересечении столбца соответствующего заданному аргументу (в радианах или в градусах) и строки соответствующей заданной функции.

Свойства тригонометрических функций

Свойства синуса

Область определения – множество всех действительных чисел.
Область изменения (множество значений) – отрезок .
Функция – нечетная, то есть .
Функция периодическая, с периодом .
Нули функции: при .
Промежутки знакопостоянства
Функция непрерывная и имеет производную при любом значении аргумента:
Функция возрастает при , и убывает при .
Функция имеет минимальные значения, равные , при , и максимальные значение равные 1, при .

Подробнее про синус угла читайте по ссылке.

Свойства косинуса

Область определения – множество всех действительных чисел.
Область изменения (множество значений) – отрезок .
Функция – четная, то есть .
Функция периодическая, с периодом .
Нули функции: при .
Промежутки знакопостоянства
Функция непрерывная и имеет производную в любом значении аргумента
Функция возрастает при , и убывает при .
Минимальные значения функции равные принимает при , а максимальные значение равные 1, при .

Подробнее про косинус угла читайте по ссылке.

Свойства тангенса

Область определения – множество всех действительных чисел, кроме чисел
Область изменения (множество значений) – множество всех действительных чисел.
Функция – нечетная, то есть .
Функция периодическая, её период равен .
Нули функции: при .
Промежутки знакопостоянства
Функция непрерывная и дифференцируема при любом значении аргумента из области определения функции:
Функция возрастает в каждом из промежутков .

Свойства котангенса

Область определения – множество всех действительных чисел, кроме чисел
Область изменения (множество значений) – множество всех действительных чисел.
Функция – нечетная, то есть .
Функция периодическая, её период равен .
Нули функции: при .
Промежутки знакопостоянства
Функция непрерывная и дифференцируема при любом значении аргумента из области определения функции:
Функция убывает в каждом из промежутков .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Тригонометрические функции углового аргумента — урок. Алгебра, 10 класс.

С терминами «синус», «косинус», «тангенс», «котангенс» мы встречались и ранее в геометрии, когда рассматривали синус, косинус, тангенс и котангенс угла, а не числа, как было в предыдущих темах.

На самом деле, эти два подхода к данным определениям тесно взаимосвязаны.

Возьмём угол с градусной мерой α° и расположим его в числовой окружности на координатной плоскости так, чтобы вершина угла совместилась с центром окружности (началом системы координат), одна сторона угла совместилась с положительным лучом оси абсцисс, а вторая сторона пересекала бы окружность в точке \(M\) (см. рис.).

Ордината точки \(M\) называется синусом угла α°, а

абсцисса точки \(M\) называется косинусом угла α°.

Каждый раз выполнять такие построения необязательно, достаточно заметить, что дуга \(AM\) составляет такую же часть единичной окружности, которую угол α° составляет от угла 360°.

Обозначив длину дуги \(AM\) буквой \(t\), получим равенство:

α°360°=t2π;t=πα180.

Говорят, что α° — это градусная мера угла, а πα180 — это радианная мера того же угла.

Т. е. α° \(=\) πα180 рад.

Следовательно,

1°=π180 рад. или

\(1\) рад \(=\) 180°π.

Пример:

35°=π180⋅35=35π180=7π36 рад;

2π3 рад \(=\) 180°π⋅2π3=120°.

Обозначение рад обычно не пишут, т. е. вполне допустима запись

2π3 \(=\) 180°π⋅2π3=120°.

Угол в 1° — это центральный угол, опирающийся на дугу, составляющую 1360 часть окружности.

Угол в \(1\) радиан — это центральный угол, опирающийся в единичной окружности на дугу длиной \(1\).

Из формулы

\(1\) рад \(=\) 180°π получаем, что \(1\) рад ≈57,3°.

Рассматривая ту или иную тригонометрическую функцию, можно считать её функцией как числового, так и углового аргумента.

Пример:

sin30°=sinπ⋅30180=sinπ6=12;cos90°=cosπ⋅90180=cosπ2=0.

Формулы тригонометрии — YouClever.org

Важное замечание!
Если вместо формул ты видишь абракадабру, почисти кэш. Как это сделать в твоем браузере написано здесь: «Как почистить кэш браузера».

Сегодня мы с тобой разберем ряд полезных формул тригонометрии, которые без труда позволят тебе решать большинство задачек на тригонометрию в части B в ЕГЭ.

Мы решим 22 примера!!! И ты точно будешь знать формулы тригонометрии и сможешь решить любую задачу на ЕГЭ!

Эти задачки будут в основном связаны с упрощением некоторых изначально “страшных” выражений до милого и приятного вида, для того, чтобы потом ты мог вычислить значение выражения в некоторой заданной точке.

Конечно, ты можешь возразить мне, что можно и без всякого упрощения все посчитать. Ну что мне сказать, можно!

Я бы с удовольствием посмотрел на тебя, как ты посчитаешь значение, скажем выражения:

при . Не думаю, что у тебя выйдет что-то путное за вменяемое время, ты уж меня извини.

Тут тебя может спасти только знание формул тригонометрии. Так что к их изучению мы и приступим.

Как ты уже понял, тригонометрические выражения – это выражения, в котором переменная содержится под знаком тригонометрических функций. Стоп! Вот прямо здесь мы и остановимся! Я задам тебе вопрос: какие тригонометрические функции ты знаешь? Верно! Их всего четыре!

Хотя, положа руку на сердце, я скажу тебе, что знание последней не так уж и обязательно (хотя желательно!), поскольку она легко выражается через тангенс.

Да и сам тангенс, по сути – тоже лишь тригонометрическое выражение, зависящее от синуса и косинуса.

Таким образом, у нас есть две основные тригонометрические функции – синус и косинус и две «второстепенные» — тангенс и котангенс.

Я не буду сейчас определять, что такое синус и косинус, ты и так это уже знаешь из предыдущих разделов. Я лишь скажу пару слов про важность этих понятий.

Итак, пара слов: первые зачатки тригонометрии возникли более 3 тысяч лет назад. Я думаю, что тебе очевидно, что тогда люди не занимались «формулами ради формул».

Так что тригонометрические функции имеют полезные практические свойства. Я не буду их перечислять. Если тебе интересно, ты всегда можешь найти море информации в интернете. Сейчас я приведу тебе некоторые основные соотношения между тригонометрическими величинами, которые оказываются полезными при решении задач.

Уже получилось 7 формул! К сожалению, это еще далеко не предел. Совсем не предел.

Тем не менее последние 4 формулы есть ни что иное, как простое следствие первой.

Формула 4 получается делением обеих частей формулы 1 на и применением формулы 2.

Формула 5 получается аналогично: разделим обе части формулы 1 на и вместо выражения запишем , исходя из определения 3. Формулы 1 – 5 мы трактуем вполне однозначно. Чего нельзя сказать про формулы 6 и 7.

В чем «фишка» формул 6 и 7? Их особенность заключается в знаке , который стоит перед корнем.

А понимать надо так: в некоторых случаях мы ставим плюс, а в некоторых – минус.

Теперь у тебя должен возникнуть вопрос: в каких-таких «некоторых случаях»? Туманность этой формулировки снимается следующим правилом:

Есть опять некий «запутанный» момент в правиле, не так ли? В чем осталось разобраться?

Осталось понять, как связан угол со знаком тригонометрической функции. Ответом на этот вопрос (если ты, конечно, забыл) служат следующие картинки:

Они подскажут тебе, какой нужно выбирать знак для той или иной функции, так что ты не допустишь досадной ошибки.

К тому же это избавит тебя от мучительных размышлений по поводу того «а зачем в этом примере нужен этот угол?!».

Тебе не кажется, что пришла пора мне уже перейти от теории к некоторой практике? Давай начнем!

1. Так как , то подставим сюда значение , тогда

Теперь дело за малым: разобраться со знаком. Что нам для этого нужно? Знать, в какой четверти находится наш угол.

По условию задачи: . Смотри на картинку. Какая это четверть? Четвертая.

Каков знак косинуса в четвертой четверти? На картинке стоит знак «плюс», значит косинус в четвертой четверти положительный.

Тогда нам остается выбрать знак «плюс» перед . , тогда .

Ответ: .

Ну вот видишь, ничего сложного. Абсолютно ничего. Нужно лишь запомнить знаки синуса, косинуса и тангенса (котангенса) по четвертям. Ну а как это делать автоматически описано в статье, посвященной тригонометрической окружности.

Давай разберем оставшиеся примеры.

2. Так как , то все, что нам нужно – это подставить в нашу формулу. Что мы с тобой и сделаем:

Опять нужно определиться со знаком. Смотрим на рисунок. Четверть – снова четвертая. Знак синуса четвертой четверти – отрицательный. Ставим знак «минус». , тогда .

Ответ: .

3. Ничего нового. Скорее для закрепления. Снова подставляем в формулу значение :

Смотрим на знак косинуса при . Какая это четверть? Вторая. Косинус второй четверти отрицательный. Тогда выбираем знак «минус».

Ответ: .

4. Здесь перед нами стоит задачка чуть сложнее. Однако, не стоит огорчаться. Давай вспомним, что такое тангенс. Это ведь отношение синуса к косинусу. Синус нам уже дан.

Давай вначале найдем косинус. Как это сделать, ты уже знаешь. .

Так как (это угол в третьей четверти, а косинус в третьей четверти имеет знак «минус»), то .

Теперь все, что нам осталось, это воспользоваться определением тангенса:

Ответ: .

Уф, выдохнули! Ну вот мы с тобой решили некоторые (довольно типичные и распространенные) примеры.

Ты спросишь: «и что, это все?». Я отвечу, увы нет. Это далеко не все.

Далее нам потребуются более сложные формулы тригонометрии.

Как распознать, что тебе требуются именно эти, а не какие-нибудь другие формулы?

Очень просто: если ты видишь косинус, синус, тангенс от суммы двух углов или двойных углов, то это должно служить тебе индикатором – мне нужно применить одну из формул для суммы/разности или для двойного угла.

Звучит несколько путано? Давай посмотрим на примеры. Заодно я дам еще ряд важных комментариев.

4. Найдите , если

5. Найдите , если

6. Найдите , если и .

7. Найдите , если .

8. Найдите , если

9. Найдите , если .

Список этих заданий можно продолжать бесконечно… Но я выбрал здесь а) не самые сложные формулы б) не самые «страшные» углы.

Страшные углы я припас нам напоследок. А пока что давай разберем 9 примеров.

Кстати, здесь тебе понадобится знание также тех формул, которые я привел в самом начале. Поехали!

Ни ты, ни я не знаем, чему в точности равен синус или косинус градусов, и чему равен синус градусов.

Тогда применим формулу синуса двойного угла:

Подставим это значение в знаменатель нашей дроби и сократим!

Ответ: .

Пример решился в одну строчку с применением одной единственной формулы. Другое дело, иногда не совсем очевидно, какую из формул применять. Тут тебе нужен опыт. Нужно, как говорится, «набить руку» на таких примерах.

Опять-таки, сразу можно заметить, что . градуса стоит в косинусе.

Это говорит о том, что в примере спрятан косинус двойного угла. Вспомним его определение:

А там все наоборот: синус в квадрате вычитается из косинуса в квадрате. Тогда в числителе у нас написана формула чего?

Да все того же косинуса двойного угла, только «наоборот», со знаком «минус»!

Ответ: .

Пример №3

Здесь нет ничего сложного, абсолютно ничего! Но есть одно «но!».

Это «но» заключается в том, что тебе нужно помнить таблицу значений тригонометрических функций для углов хотя бы первой четверти!

Я сейчас нарисую здесь эту таблицу, а потом объясню тебе, как сделать ее запоминание проще:

Или ее расширенный вариант для всех «основных углов»:

Я ни в коей мере не настаиваю (и даже не надеюсь), что ты выучишь вторую таблицу. Сказать по-правде, я и сам ее не знаю.

Но первую таблицу знать совершенно необходимо.

Не всегда на экзамене у тебя будет время, чтобы вывести самостоятельно, скажем, синус градусов.

Для того, чтобы запомнить первую таблицу можно поступить так:

Запомнить всего 5 значений для, скажем, синуса. Затем тебе не составит труда заметить, что для косинуса все значения идут «наоборот»:

Например, синус градусов равен нулю значит, косинус градусов — наоборот единица.
Синус градусов равен единице, значит косинус градусов равен нулю.
Синус градусов равен , значит косинус градусов равен и т. д.

Тангенс можно получить, разделив синус угла на косинус. Как же всегда вывести большую таблицу, зная малую, я тебе непременно расскажу чуть позднее.

Но давай вернемся к нашему примеру и посмотрим в таблицу:

, . Подставим эти значения в нашу формулу:

Ответ:

Вот видишь, знание первой таблицы совершенно необходимо! Без нее – вообще нет никакой тригонометрии. Так что, пожалуйста, будь добр, выучи.

Это не потребует от тебя значительных усилий и избавит от массы глупых ошибок в будущем.

Еще раз специально скажу: большую таблицу учить не надо!!!

Пример №4

По условию

Нам же надо найти:

Что тогда нужно сделать?

Верно, наша цель – выразить косинус двойного угла через угол «одинарный». Есть ли такая формула? Конечно, есть! Вот она:

Тогда

Ответ:

Пример №5

Дано:

Надо вычислить:

Ну что же, надо отталкиваться от того, что есть. Вроде бы этого должно быть достаточно. Здесь все опять несложно!6.

Нужно лишь заметить, что . Давай это и подставим в числитель исходной дроби. Что же мы имеем?

О чудо: косинусы сократились, а чему равен мы знаем из условия!

Ответ: .

Пример №6

Дано:

Нужно вычислить:

На самом деле здесь можно поступать двояко. Но о втором способе я скажу тебе чуть позже. А пока давай подумаем, что нужно найти.

А найти нужно по сути косинус от суммы двух углов. Причем один из них известен. Давай не будем долго думать и разложим косинус суммы на произведение:

Вспомни единичную окружность (ну или на худой конец посмотри в расширенную таблицу). Косинус углов: равен нулю! Тогда , а синусы: равны при этом и соответственно. Тогда . Окончательно получим:

Но вот незадача: синус-то нам не дан! Вместо него мы знаем, что и . Как по этим данным найти неизвестный синус – ты уже знаешь! Мы в самом начале решали такие задачки. Так что результат будет таков:

Снова нужно определиться со знаком: . Это значит, что четверть четвертая, а синус в четвертой четверти имеет знак «минус». Тогда , что значит, что .

Ответ:

Пример №7

Дано:

Нужно найти:

Тут все можно сделать только зная, что такое тангенс и основное тригонометрическое тождество. По-порядку:

Тогда решить задачу можно вот как: найти по-отдельности значения синуса в квадрате и косинуса в квадрате, а затем при помощи полученных значений найти тангенс. Так мы с тобой и сделаем:

Вначале найдем синус в квадрате.

Так как , то

Тогда из , получим, что

Наконец, найдем тангенс:

Ответ:

Пример №8

Дано:

Надо найти:

На какую мысль тебя это должно было натолкнуть?

А на ту, что если нам дан тангенс, то и наше выражение нужно привести к такому виду, чтобы оно зависело от тангенсов, которые мы потом в него и подставим.

Напомню тебе, что:

У меня же в выражении есть просто косинусы и синусы. Что нам нужно сделать?

Давай возьмем и «насильно» разделим числитель и знаменатель дроби на . Это поможет мне «выделить» тангенс в чистом виде:

Конечно, есть одна неприятность: у нас появились дроби с косинусами. Но есть надежда, что мы с ними справимся! А пока что давай подставим вместо его числовое значение . Тогда получим:

Ну вот! Косинусы сократятся и мы получим ответ: .

Ответ: .

Пример №9

Дано:

Найти:

Давай опять проанализируем, что нам нужно вычислить: искомая формула состоит из разности косинуса от суммы двух углов и синуса от суммы двух углов.

Давай упрощать: раскроем каждую из сумм (опять-таки повторюсь, что далее я опишу способ, который позволит обходиться без раскрытия такого рода сумм):

Опять-таки, тебе должно быть известно, что .

Если тебе это неизвестно, то настоятельно рекомендую тебе повторить тему тригонометрическая окружность.

Тогда моя формула примет вид:

Теперь с синусом:

Снова, грамотные люди, такие как ты, вспоминают окружность (или, на худой конец, таблицу): , тогда

Нам осталось подставить найденные значения в исходную формулу:

Ответ: .

Формулы приведения

Теперь мы знаем уже почти что все. Осталось совсем немного.

Последнее, на что я хочу обратить внимание, это обещанный мною метод «легкого» перехода от большой таблицы значений углов к маленькой.

Этот переход обеспечивают так называемые формулы приведения.

Еще раз поясню, зачем они используются: ты будешь их применять в том случае, когда тебе нужно найти синус, косинус или тангенс угла, большего чем градусов.

Например, найти синус угла градусов.

Здесь мы поступаем следующим образом. Во-первых, нам понадобятся следующие знания:

Синус и косинус имеют период   ( градусов), то есть

Тангенс (котангенс) имеют период   ( градусов)

  – любое целое число
Синус и тангенс – функции нечетные, а косинус – четная:

Теперь непосредственно сам алгоритм:

Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул (2). Например:
Отбрасываем для синуса и косинуса его периоды: (по градусов), а для тангенса – «половинки» ( градусов). Например:
Если оставшийся «уголок» меньше градусов, то задача решена: ищем его в «малой таблице»
Иначе ищем, в какой четверти лежит наш угол : это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!
Представляем угол в одной из следующих форм
  (если во второй четверти)
  (если во второй четверти)
  (если в третьей четверти)
  (если в третьей четверти)
  (если в четвертой четверти)
  (если в четвертой четверти)

так, чтобы оставшийся угол   был больше нуля и меньше   градусов. Например:

…

В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.
Теперь смотрим, что у нас получилось: если ты выбрал запись через или градусов плюс минус что-либо, то знак функции меняться не будет: ты просто убираешь или и записываешь синус, косинус или тангенс оставшегося угла. Если же ты выбрал запись через или градусов, то синус меняем на косинус, косинус на синус, тангенс на котангенс, котангенс – на тангенс.
Ставим перед получившимся выражением знак из пункта 4.

Давай продемонстрируем все вышесказанное на 3-х примерах:

Вычислить
Вычислить
Найдите значение выражения:

Решение примера №1. Действуем согласно нашему алгоритму. Выделяем целое число кругов.

1. Действуем согласно нашему алгоритму. Выделяем целое число кругов для :

В общем, делаем вывод, что в угол помещается целиком 5 раз по , а сколько осталось? Осталось . Тогда

Ну вот, лишнее мы отбросили. Теперь разбираемся со знаком.

лежит в 4 четверти. Синус четвертой четверти имеет знак «минус», его я и не должен забыть поставить в ответе. Далее, представляем согласно одной из двух формул пункта 5 правил приведения. Я выберу:

Теперь смотрим, что получилось: у нас случай с градусами, тогда отбрасываем и синус меняем на косинус. И ставим перед ним знак «минус»!

градусов – угол в первой четверти. Мы знаем (ты мне обещал выучить малую таблицу!!) его значение:

Тогда получим окончательный ответ:

Ответ:

Решение премера №2. Все то же самое, но вместо градусов – радианы.

Все то же самое, но вместо градусов – радианы. Ничего страшного. Главное помнить, что

Но можно и не заменять радианы на градусы. Это вопрос твоего вкуса. Я не буду ничего менять. Начну опять-таки с отбрасывания целых кругов:

Отбрасываем — это два целых круга. Осталось вычислить . Данный угол находится в третьей четверти. Косинус третьей четверти отрицательный. Не забудем поставить знак «минус» в ответе. можно представить как . Снова вспоминаем правило: у нас случай «целого» числа ( или ), тогда функция не меняется:

Тогда .

Ответ: .

Решение примера №3. Нужно проделать все то же самое, но уже с двумя функциями.

Нужно проделать все то же самое, но уже с двумя функциями.

Я буду несколько более краток: и градусов – углы второй четверти.

Косинус второй четверти имеет знак «минус», а синус – «плюс». можно представить как: , а как , тогда

Оба случая – «половинки от целого ». Тогда синус меняется на косинус, а косинус – на синус. Причем перед косинусом стоит знак «минус»:

Ответ: .

Тренировка. Реши эти 10 заданий и ты научишься пользоваться формулами тригонометрии!

Ну вот, теперь на мой взгляд, ты готов к решению всех оставшихся «за бортом» задач. Страшные углы теперь тебе более не помеха.

Попробуй прорешать примеры самостоятельно, а потом мы с тобой сравним результаты.

9. Найдите значение выражения , если .

10. Найдите , если и .

Начнем проверять вместе

Пример №1

Ключ к успеху – заметить, что:

!!! Тогда, например :

– угол первой четверти. Косинус первой четверти – положительный. Поскольку мы вычитаем из градусов, то косинус меняется на синус:

Ответ: .

Пример №2

Опять задача целиком на формулы приведения. Вначале….

… избавимся от минуса, вынеся его перед синусом (поскольку синус – функция нечетная!!!). Затем рассмотрим углы

Отбрасываем целое количество кругов – то есть три круга . Остается вычислить:
Также поступаем и со вторым углом:

Удаляем целое число кругов –3 круга ( ) тогда:

Теперь думаем: в какой четверти лежит оставшийся угол? Он «не дотягивает» до всего . Тогда какая это четверть? Четвертая. Каков знак косинуса четвертой четверти? Положительный. Теперь представим . Так как вычитаем мы из целого количества , то знак косинуса не меняем:

Подставляем все полученные данные в формулу:

Ответ: .