Методы решения систем уравнений — урок. Алгебра, 11 класс.
При постановке задачи — найти такие пары значений \((x;y)\), которые одновременно удовлетворяют уравнению \(p(x;y)=0\) и уравнению \(q(x;y)=0\), то говорят, что данные уравнения образуют систему уравнений:p(x;y)=0,q(x;y)=0.
Пару значений \((x;y)\), которая одновременно является решением и первого, и второго уравнений системы, называют решением системы уравнений.
Решить систему уравнений — означает найти все её решения или показать, что решений нет.
Встречаются системы из трёх уравнений с тремя переменными:p(x;y;z)=0,q(x;y;z)=0,r(x;y;z)=0.
Две системы уравнений называют равносильными, если они имеют одинаковые решения или обе системы не имеют решений.
Чтобы решить систему уравнений, можно использовать способы:1. подстановки,
2. алгебраического сложения,
3. введения новых переменных,
4. графический.
Пример:
реши систему уравнений:
3x=y+1;7y−2x+2=7⋅7y−4x+6.y=3x−1;73x−1−2x+2=7⋅73x−1−4x+6.y=3x−1;7x+1=7⋅7−x−1+6.
В ходе решения подставили вместо \(y\) выражение \(3x-1\), полученное из первого уравнения.
Введём во втором уравнении новую переменную
t=7x+1;7−x−1=7−x+1=t−1=1t.
Решая второе уравнение с переменной \(t\), получим:
t=7t+6;t2−6t−7=0,t≠0;t1=−1,t2=7.
Возвращаясь к введённому обозначению \(t\), решаем полученные уравнения и находим \(x\):
7x+1=t↙↘7x+1=−1;7x+1=7=71;x∈∅.x+1=1;x=0.
Найдём \(y\), подставляя вместо \(x=0\).
Получим, что \(y=-1\).
Решение системы — пара чисел \((0;-1)\).
В ходе решения были использованы два метода: подстановки и введения новой переменной
.Пример:
реши систему уравнений:
3x+2y=1x−y=−3|⋅2+3x+2y=12x−2y=−63x+2x+2y−2y=1+(−6);5x=−5;x=−1. 2 -xy-2x+1 = 0\\x-y=1\end{cases} $$
2 -xy-2x+1 = 0\\x-y=1\end{cases} $$Поскольку второе уравнение этой системы линейно относительно каждой из переменных х и у, то одна из этих переменных,; например у, легко выражается через другую:
у = х — 1.
Подставляя это выражение для у в первое уравнение системы, получаем:
x2 + 3 (х — 1)2 — х (х — 1) — 2х + 1 = 0,
откуда
3x2 — 7x +4 = 0; x1 = 4
Этим значениям х согласно второму уравнению системы соответствуют следующие значения у: y1 = 1/3; y2 = 0.
Таким образом, данная система уравнений имеет два решения:
x1 = 4/3; y1 = 1/3; и x2 = 1; y2 = 0. 2 =8\end{cases} \;\;\; (1) $$
2 =8\end{cases} \;\;\; (1) $$
Характерная особенность этой системы уравнений состоит в том, что она содержит лишь выражения x2, y2 и ху, суммарная степень х и у в которых постоянна и равна 2.
Для решения данной системы выполним следующие преобрaзования. Из первого уравнения системы (1) вычтем второе, умноженное на 2. В результате получим уравнение
2x2 — 3ху + y2 = 0, (2)
правая часть которого равна 0.
Заметим, что х \(\neq\) 0. В противном случае из (2) вытекало бы, что у = 0, а это явно противоречит уравнениям системы (1). Но если х \(\neq\) 0, то уравнение (2) можно почленно разделить на x2, что дает
2- 3 y/x + ( y/x )2 = 0.
Мы получили квадратное уравнение относительно y/x. Из него следует, что либо y/x = 1, либо y/x = 2.
Рассмотрим эти два случая отдельно.
1) Если y/x = 1, то у = х. Замена у в первом уравнении данной системы на х приводит к следующему результату:
4x2 + 5x2 + 3x2 = 16,
или
12x2 = 16.
Следовательно,
$$ x=\pm\sqrt{\frac{16}{12}} = \pm\sqrt{\frac{4}{3}} = \pm\frac{2}{\sqrt3} $$Отсюда получаем следующие два решения данной системы:
x1 = 2/√3 , y1=2/√3 ; x2= — 2/√3 , y2= — 2/√3
2) Если y/x
= 2, то у = 2х. Заменяя у в первом уравнении данной системы на 2х, получаем:
Заменяя у в первом уравнении данной системы на 2х, получаем:14x2 — 10x2 + 12x2 = 16,
или
16x2 = 16.
Следовательно, х = ±1. Отсюда, учитывая, что у = 2х, получаем еще два решения данной системы:
x1 = 1, y1=2; x2= — 1 , y2= — 2
Проверка показывает, что ни одно из полученных четырех решений системы (1) не является «посторонним».
Ответ. Данная система уравнений имеет 4 решения:
1) x1 = 2/√3 , y
3) x1 = 1, y1=2; 4) x2= — 1 , y2= — 2
Пример 3. Решить систему уравнений
Решить систему уравнений
Если только данная система уравнений имеет решение, то по теореме, обратной теореме Виета, это решение должно состоять из корней квадратного уравнения (см. § 52):
x2 — 6x — 7 = 0.
Это уравнение имеет корни x1= -1, x2 = +7. Следовательно, в роли решений данной системы уравнений могут выступать только следующие две пары чисел:
x1 = — 1, y1 = 7 и x2 = 7, y2 = — 1.
Элементарная проверка показывает, что каждая из этих пар чисел является решением нашей системы.
Ответ. Данная система уравнений имеет два решения:
x1 = — 1, y1 = 7 и x2 = 7, y2 = — 1. 2 = 5 \\ xy= -2 \end{cases} $$
2 = 5 \\ xy= -2 \end{cases} $$
Из второго уравнения получаем x2y2 = 4. Но в таком случае по теореме, обратной теореме Виета, x2 и y2 можно рассматривать как корни квадратного уравнения
z2 — 5z + 4 = 0,
откуда z1 = 4, z2 = 1. Поэтому возможны два случая: 1)
Случай 1. Если х = + 2, то у = -1 (согласно второму уравнению исходной системы ху = — 2 ). Если х =- 2, то у = 1.
Случай 2. Если x = 1, то у = — 2, если же x = — 1, то у = 2.
Мы получили 4 решения данной системы уравнений:
x1 = 2, y1 = — 1 ; x2 = — 2, y2 = 1;
x3 = 1, y3 = — 2 ; x4 = — 1, y4 = 2. 2 + y = 4\\x + y = 2 \end{cases} $$
2 + y = 4\\x + y = 2 \end{cases} $$
На одном и том же рисунке начертим две кривые, первая из которых имеет уравнение x2 + у = 4, или у = 4 — x2, а вторая — уравнение х + у = 2, или у = 2 — х. Очевидно, что искомыми решениями данной системы уравнений будут координаты точек пересечения этих двух кривых.
Как видно из рисунка, рассматриваемые кривые пересекаются в двух точках: А с координатами (- 1,3) и В с координатами (2, 0). Поэтому данная система уравнений имеет два решения: x = — 1, у = 3 и x = 2, у = 0.
« назад
Страница не найдена — Саянский медицинский колледж
Я, субъект персональных данных, в соответствии с Федеральным законом от 27 июля 2006 года № 152 «О персональных данных» предоставляю ОГБПОУ «Саянский медицинский колледж» (далее — Оператор), расположенному по адресу Иркутская обл.
- Состав предоставляемых мной персональных данных является следующим: Имя, адрес электронной почты.
- Целями обработки моих персональных данных являются: обеспечение обмена короткими текстовыми сообщениями в режиме онлайн-диалога или обмена текстовыми сообщениями через электронную почту.
- Согласие предоставляется на совершение следующих действий (операций) с указанными в настоящем согласии персональными данными: сбор, систематизацию, накопление, хранение, уточнение (обновление, изменение), использование, передачу (предоставление, доступ), блокирование, удаление, уничтожение, осуществляемых как с использованием средств автоматизации (автоматизированная обработка), так и без использования таких средств (неавтоматизированная обработка).
- Я понимаю и соглашаюсь с тем, что предоставление Оператору какой-либо информации о себе, не являющейся контактной и не относящейся к целям настоящего согласия, а равно предоставление информации, относящейся к государственной, банковской и/или коммерческой тайне, информации о расовой и/или национальной принадлежности, политических взглядах, религиозных или философских убеждениях, состоянии здоровья, интимной жизни запрещено.

- В случае принятия мной решения о предоставлении Оператору какой-либо информации (каких-либо данных), я обязуюсь предоставлять исключительно достоверную и актуальную информацию и не вправе вводить Оператора в заблуждение в отношении своей личности, сообщать ложную или недостоверную информацию о себе.
- Я понимаю и соглашаюсь с тем, что Оператор не проверяет достоверность персональных данных, предоставляемых мной, и не имеет возможности оценивать мою дееспособность и исходит из того, что я предоставляю достоверные персональные данные и поддерживаю такие данные в актуальном состоянии.
- Согласие действует по достижении целей обработки или в случае утраты необходимости в достижении этих целей, если иное не предусмотрено федеральным законом.
- Согласие может быть отозвано мною в любое время на основании моего письменного заявления.
Метод Крамера
Метод Крамера предназначен для решения тех систем линейных алгебраических уравнений (СЛАУ), у которых определитель матрицы системы отличен от нуля. Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
Естественно, при этом подразумевается, что матрица системы квадратна (понятие определителя существует только для квадратных матриц). Решение системы уравнений методом Крамера проходит за три шага простого алгоритма:
- Составить определитель матрицы системы (его называют также определителем системы), и убедиться, что он не равен нулю, т.е. $\Delta\neq 0$.
- Для каждой переменной $x_i$($i=\overline{1,n}$) необходимо составить определитель $\Delta_{x_i}$, полученный из определителя $\Delta$ заменой i-го столбца столбцом свободных членов заданной СЛАУ.
- Найти значения неизвестных по формуле $x_i=\frac{\Delta_{x_{i}}}{\Delta}$ ($i=\overline{1,n}$).
Перед переходом к чтению примеров рекомендую ознакомиться с правилами вычисления определителей второго и третьего порядка, изложенными здесь.
Пример №1
Решить СЛАУ $\left\{\begin{aligned}
& 3x_1+2x_2=-11;\\
& -x_1+5x_2=15.
\end{aligned}\right. $ методом Крамера.
$ методом Крамера.
Решение
Матрица системы такова: $ A=\left( \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array} \right)$. Определитель этой матрицы:
$$\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|=3\cdot 5-2\cdot(-1)=17.$$Как вычисляется определитель второго порядка можете глянуть здесь.
Так как определитель системы не равен нулю, то продолжаем решение методом Крамера. Вычислим значения двух определителей: $\Delta_{x_1}$ и $\Delta_{x_2}$. Определитель $\Delta_{x_1}$ получаем из определителя $\Delta=\left| \begin{array} {cc} 3 & 2\\ -1 & 5 \end{array}\right|$ заменой первого столбца (именно этот столбец содержит коэффициенты при $x_1$) столбцом свободных членов $\left(\begin{array} {c} -11\\ 15\end{array}\right)$:
$$ \Delta_{x_1}=\left|\begin{array}{cc}-11&2\\15&5\end{array}\right|=-55-30=-85. $$Аналогично, заменяя второй столбец в $\Delta=\left|\begin{array}{cc}3&2\\-1&5\end{array}\right|$ столбцом свободных членов, получим:
$$ \Delta_{x_2}=\left|\begin{array} {cc} 3 & -11\\ -1 & 15\end{array}\right|=45-11=34. $$
$$
Теперь можно найти значения неизвестных $x_1$ и $x_2$.
$$x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{-85}{17}=-5;\;x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{34}{17}=2.$$В принципе, можно ещё проверить, правильно ли решена система методом Крамера. Подставим в заданную СЛАУ $x_1=-5$, $x_2=2$:
$$\left\{\begin{aligned} & 3x_1+2x_2=3\cdot(-5)+2\cdot{2}=-11;\\ & -x_1+5x_2=-(-5)+5\cdot{2}=15. \end{aligned}\right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно. Осталось лишь записать ответ.
Ответ: $x_1=-5$, $x_2=2$.
Пример №2
Решить СЛАУ $ \left\{\begin{aligned} & 2x_1+x_2-x_3=3;\\ & 3x_1+2x_2+2x_3=-7;\\ & x_1+x_3=-2. \end{aligned} \right.$, используя метод Крамера.
Решение
Определитель системы:
$$\Delta=\left| \begin{array} {ccc} 2 & 1 & -1\\ 3 & 2 & 2 \\ 1 & 0 & 1 \end{array}\right|=4+2+2-3=5. $$
$$
Как вычисляется определитель третьего порядка можете глянуть здесь.
Заменяя первый столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_1}$:
$$ \Delta_{x_1}=\left| \begin{array} {ccc} 3 & 1 & -1\\ -7 & 2 & 2 \\ -2 & 0 & 1 \end{array}\right|=6-4-4+7=5. $$Заменяя второй столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_2}$:
$$ \Delta_{x_2}=\left| \begin{array} {ccc} 2 & 3 & -1\\ 3 & -7 & 2 \\ 1 & -2 & 1 \end{array}\right|=-14+6+6-7-9+8=-10. $$Заменяя третий столбец в $\Delta$ столбцом свободных членов, получим $\Delta_{x_3}$:
$$ \Delta_{x_3}=\left| \begin{array} {ccc} 2 & 1 & 3\\ 3 & 2 & -7 \\ 1 & 0 & -2 \end{array}\right|=-8-7-6+6=-15. $$Учитывая все вышеизложенное, имеем:
$$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{5}{5}=1;\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-10}{5}=-2; \; x_3=\frac{\Delta_{x_3}}{\Delta}=\frac{-15}{5}=-3. $$
$$Метод Крамера завершён. Можно проверить, верно ли решена система уравнений методом Крамера, подставив значения $x_1=1$, $x_2=-2$ и $x_3=-3$ в заданную СЛАУ:
$$\left\{\begin{aligned} & 2x_1+x_2-x_3=2\cdot{1}+(-2)-(-3)=3;\\ & 3x_1+2x_2+2x_3=3\cdot{1}+2\cdot(-2)+2\cdot(-3)=-7;\\ & x_1+x_3=1+(-3)=-2. \end{aligned} \right.$$Проверка пройдена, решение системы уравнений методом Крамера найдено верно.
Ответ: $x_1=1$, $x_2=-2$, $x_3=-3$.
Пример №3
Решить СЛАУ $\left\{\begin{aligned} & 2x_1+3x_2-x_3=15;\\ & -9x_1-2x_2+5x_3=-7. \end{aligned}\right.$ используя метод Крамера.
Решение
Матрица системы $ \left( \begin{array} {ccc} 2 & 3 & -1\\ -9 & -2 & 5 \end{array} \right) $ не является квадратной. Однако это вовсе не означает, что решение системы уравнений методом Крамера невозможно. Преобразуем заданную СЛАУ, перенеся переменную $x_3$ в правые части уравнений:
$$ \left \{ \begin{aligned} & 2x_1+3x_2=x_3+15;\\ & -9x_1-2x_2=-5x_3-7. \end{aligned} \right.
$$
\end{aligned} \right.
$$
Теперь матрица системы $ \left( \begin{array} {cc} 2 & 3 \\ -9 & -2 \end{array} \right) $ стала квадратной, и определитель её $\Delta=\left| \begin{array} {cc} 2 & 3\\ -9 & -2 \end{array}\right|=-4+27=23$ не равен нулю. Применим метод Крамера аналогично предыдущим примерам:
$$ \begin{aligned} & \Delta_{x_1} =\left| \begin{array} {cc} x_3+15 & 3\\ -5x_3-7 & -2 \end{array}\right| =-2x_3-30-\left(-15x_3-21\right) =13x_3-9;\\ \\ & \Delta_{x_2} =\left| \begin{array} {cc} 2 & x_3+15\\ -9 & -5x_3-7 \end{array}\right| =-10x_3-14-\left(-9x_3-135\right) =-x_3+121. \end{aligned} $$ $$ x_1=\frac{\Delta_{x_1}}{\Delta}=\frac{13x_3-9}{23};\; x_2=\frac{\Delta_{x_2}}{\Delta}=\frac{-x_3+121}{23}. $$
Ответ можно записать в таком виде: $\left\{\begin{aligned}
& x_1=\frac{13x_3-9}{23};\\
& x_2=\frac{-x_3+121}{23};\\
& x_3\in R. \end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
\end{aligned}\right.$ Переменные $x_1$, $x_2$ – базисные (в иной терминологии – основные), а переменная $x_3$ – свободная (в иной терминологии – неосновная). Проверка, при необходимости, проводится так же, как и в предыдущих примерах.
Примечание
В подобных примерах возможна ситуация, когда после переноса переменной (или переменных) в правые части уравнений, определитель системы равняется нулю. В этом случае можно перенести в правую часть иную переменную (или переменные). Например, рассмотрим СЛАУ
$\left\{\begin{aligned}
& 2x_1-5x_2+10x_3=14;\\
& -4x_1+10x_2-7x_3=5.
\end{aligned}\right.$. Если перенести в правые части уравнений $x_3$, получим: $
\left\{\begin{aligned}
&2x_1-5x_2=-10x_3+14;\\
&-4x_1+10x_2=7x_3+5.
\end{aligned}\right.$. Определитель данной системы $\Delta=\left| \begin{array} {cc} 2 & -5\\ -4 & 10 \end{array}\right|=20-20=0$. Однако если перенести в правые части уравнений переменную $x_2$, то получим систему $
\left\{\begin{aligned}
&2x_1+10x_3=5x_2+14;\\
&-4x_1-7x_3=-10x_2+5. \end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
\end{aligned}\right.$, определитель которой $\Delta=\left| \begin{array} {cc} 2 & 10\\ -4 & -7 \end{array}\right|=-14+40=26$ не равен нулю. Дальнейшее решение аналогично рассмотренному в примере №3.
Пример №4
Решить СЛАУ
$$\left\{\begin{aligned} &x_1-5x_2-x_3-2x_4+3x_5=0;\\ &2x_1-6x_2+x_3-4x_4-2x_5=0; \\ &-x_1+4x_2+5x_3-3x_4=0. \end{aligned}\right.$$методом Крамера.
Решение
Матрица системы $\left(\begin{array} {ccccc} 1 & -5 & -1 & -2 & 3 \\ 2 & -6 & 1 & -4 & -2 \\ -1 & 4 & 5 & -3 & 0 \end{array}\right)$ не является квадратной. Преобразуем заданную СЛАУ, перенеся переменные $x_4$, $x_5$ в правые части уравнений, и применим метод Крамера:
$$ \left\{\begin{aligned} & x_1-5x_2-x_3=2x_4-3x_5;\\ & 2x_1-6x_2+x_3=4x_4+2x_5; \\ & -x_1+4x_2+5x_3=3x_4. \end{aligned}\right. $$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5.
\end{aligned}
$$
$$
$$
\begin{aligned}
& \Delta
=\left| \begin{array} {ccc} 1 & -5 & -1\\ 2 & -6 & 1\\-1 & 4 & 5 \end{array}\right|
=19;\\
\\
& \Delta_{x_1}
=\left| \begin{array} {ccc} 2x_4-3x_5 & -5 & -1\\ 4x_4+2x_5 & -6 & 1\\3x_4 & 4 & 5 \end{array}\right|
=-17x_4+144x_5;\\
\\
& \Delta_{x_2}
=\left| \begin{array} {ccc} 1 & 2x_4-3x_5 & -1\\ 2 & 4x_4+2x_5 & 1\\-1 & 3x_4 & 5 \end{array}\right|
=-15x_4+41x_5;\\
\\
& \Delta_{x_3}
=\left| \begin{array} {ccc} 1 & -5 & 2x_4-3x_5\\ 2 & -6 & 4x_4+2x_5\\-1 & 4 & 3x_4 \end{array}\right|
=20x_4-4x_5.
\end{aligned}
$$
Ответ таков: $\left\{\begin{aligned}
& x_1=\frac{-17x_4+144x_5}{19};\\
& x_2=\frac{-15x_4+41x_5}{19};\\
& x_3=\frac{20x_4-4x_5}{19}; \\
& x_4\in R; \; x_5\in R.
\end{aligned}\right. $ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
$ Переменные $x_1$, $x_2$, $x_3$ – базисные, переменные $x_4$, $x_5$ – свободные.
Естественно, что применение метода Крамера в случаях вроде того, что рассмотрен в примере №4, не всегда оправдано с точки зрения временных затрат. Мы ведь не можем гарантировать, что после переноса каких-либо переменных в правые части уравнений, определитель системы не будет равен нулю. А перебирать различные варианты – слишком долгий процесс. Гораздо удобнее в таком случае применить метод Гаусса. Я привёл пример №4 лишь с одной целью – показать, что метод Крамера применим вне зависимости от содержимого правых частей уравнений заданной СЛАУ (числа, переменные, функции – не имеет значения). Главное, чтобы определитель матрицы системы был отличен от нуля.
Решение систем линейных уравнений с двумя переменными — алгебра среднего уровня
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Решить систему уравнений подстановкой
- Решить систему уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Прежде чем начать, пройдите этот тест на готовность.
- Для уравнения
ⓐ Есть решение? ⓑ Есть решение?
Если вы пропустили эту проблему, просмотрите (рисунок).
- Найти наклон и y -пересечение линии
Если вы пропустили эту проблему, просмотрите (рисунок).
- Найдите точки пересечения x и y линии
Если вы пропустили эту проблему, просмотрите (рисунок).
Определить, является ли упорядоченная пара решением системы уравнений
В разделе «Решение линейных уравнений» мы научились решать линейные уравнения с одной переменной.Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений.
Система линейных уравнений
Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений .
В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Мы будем решать более крупные системы уравнений позже в этой главе.
Ниже показан пример системы двух линейных уравнений.Мы используем фигурную скобку, чтобы показать, что два уравнения сгруппированы вместе, чтобы сформировать систему уравнений.
Линейное уравнение с двумя переменными, например имеющее бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на прямой — это решение уравнения, а каждое решение уравнения — это точка на прямой.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары, которые делают оба уравнения верными.Они называются решениями системы уравнений.
Решения системы уравнений
решений системы уравнений являются значениями переменных, которые делают все уравнений верными. Решение системы двух линейных уравнений представлено упорядоченной парой
Решение системы двух линейных уравнений представлено упорядоченной парой
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения верными, это решение системы.
Определить, является ли заказанная пара решением системы
ⓐⓑ
ⓐ
ⓑ
Определить, является ли заказанная пара решением системы
ⓐⓑ
Определить, является ли заказанная пара решением системы
ⓐⓑ
Решение системы линейных уравнений с помощью графика
В этом разделе мы будем использовать три метода для решения системы линейных уравнений.Первый метод, который мы будем использовать, — это построение графика.
График линейного уравнения представляет собой линию. Каждая точка на прямой является решением уравнения. Для системы двух уравнений мы начертим две линии. Тогда мы сможем увидеть все точки, являющиеся решениями каждого уравнения. И, найдя, что общего у линий, мы найдем решение системы.
Тогда мы сможем увидеть все точки, являющиеся решениями каждого уравнения. И, найдя, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, решениями являются все числа.
Аналогичным образом, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий на одной плоскости, возможны три случая, как показано.
Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его на одной и той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.
Как решить систему уравнений с помощью графика
Решите систему, построив график
Решите систему с помощью графика:
Решите систему с помощью графика:
Здесь показаны шаги, необходимые для решения системы линейных уравнений с помощью графика.
Решите систему линейных уравнений с помощью графика.
- Нарисуйте первое уравнение.
- Постройте график второго уравнения в той же прямоугольной системе координат.
- Определите, пересекаются ли линии, параллельны или являются одной и той же линией.
- Определите решение системы.
- Если линии пересекаются, определите точку пересечения. Это решение системы.
- Если прямые параллельны, система не имеет решения.
- Если линии одинаковые, система имеет бесконечное число решений.
- Проверьте решение обоих уравнений.
В следующем примере мы сначала перепишем уравнения в форме наклона и точки пересечения, так как это облегчит нам быстрое построение линий.
Решите систему с помощью графика:
Мы решим оба этих уравнения, чтобы мы могли легко построить их график, используя их наклоны и точки пересечения и .
Решите систему с помощью графика:
Решите систему с помощью графика:
Во всех системах линейных уравнений линии пересекались, а решением была одна точка. В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, имеющую бесконечное число решений.
В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, имеющую бесконечное число решений.
Решите систему с помощью графика:
| Для построения графика первого уравнения воспользуемся его наклон и у -пересечение. | |
| Чтобы построить график второго уравнения, мы будем использовать перехвата. | |
| Нарисуйте линии. | |
| Определите точки пересечения. | Линии параллельны. Поскольку на обеих линиях нет точек, упорядоченная пара, которая составляет оба уравнения правда. У этой системы нет решения. |
Решите систему с помощью графика:
Решите систему с помощью графика:
Иногда уравнения в системе представляют одну и ту же прямую. Поскольку каждая точка на прямой делает оба уравнения верными, существует бесконечно много упорядоченных пар, которые делают оба уравнения верными. Система имеет бесконечно много решений.
Решите систему с помощью графика:

Так как каждая точка на прямой составляет
уравнений верны, их бесконечно много
упорядоченных пары, которые делают оба уравнения верными.
У этой системы бесконечно много решений.
Если вы запишете второе уравнение в форме наклона и пересечения, вы поймете, что уравнения имеют один и тот же наклон и одинаковые и пересечения.
Решите систему с помощью графика:
бесконечно много решений
Решите систему с помощью графика:
бесконечно много решений
Когда мы рисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две прямые совпадают. Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
Совпадающие линии
Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
Системы уравнений на (Рисунок) и (Рисунок) имеют по две пересекающиеся прямые. Каждая система имела одно решение.
На (рис.) уравнения дали совпадающие линии, поэтому система имела бесконечно много решений.
Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая хотя бы одно решение, называется -непротиворечивой -системой.
Система с параллельными прямыми, подобная (рисунок), не имеет решения. Мы называем такую систему уравнений несовместимой. Не имеет решения.
Непротиворечивые и противоречивые системы
Непротиворечивая система уравнений — это система уравнений, имеющая хотя бы одно решение.
Несовместная система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, то каждое из них имеет собственный набор решений. Пересекающиеся прямые и параллельные прямые независимы.
Если два уравнения независимы, то каждое из них имеет собственный набор решений. Пересекающиеся прямые и параллельные прямые независимы.
Если два уравнения являются зависимыми, то все решения одного уравнения также являются решениями другого уравнения. Когда мы рисуем два зависимых уравнения, мы получаем совпадающие линии.
Подведем итоги, взглянув на графики трех типов систем. См. ниже и (рисунок).
| Линии | Пересечение | Параллельный | Совпадение |
|---|---|---|---|
| Количество растворов | 1 балл | Нет решения | Бесконечно много |
| Последовательный/непоследовательный | Последовательный | Несоответствие | Последовательный |
| Зависимый/ независимый | Независимый | Независимый | Зависимый |
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐⓑ
ⓐ Сравним наклоны и точки пересечения двух линий.
Система уравнений, графики которой представляют собой параллельные прямые, не имеет решения, является противоречивой и независимой.
ⓑ Сравним наклон и точки пересечения двух линий.
Система уравнений, графики которой пересекаются, имеет 1 решение, непротиворечива и независима.
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐⓑ
ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐⓑ
ⓐ нет решения, противоречивое, независимое ⓑ одно решение, последовательное, независимое
Решение систем линейных уравнений с помощью графика — хороший способ визуализировать возможные решения. Однако во многих случаях решение системы с помощью графика неудобно или неточно. Если графики выходят за пределы небольшой сетки с размерами x и y между числами и 10, графическое изображение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
Если графики выходят за пределы небольшой сетки с размерами x и y между числами и 10, графическое изображение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
Решение системы уравнений путем замены
Теперь будем решать системы линейных уравнений методом подстановки.
Мы будем использовать ту же систему, что и для построения графиков.
Сначала мы решим одно из уравнений либо для x , либо для y .Мы можем выбрать любое уравнение и найти решение для любой переменной, но мы постараемся сделать такой выбор, который облегчит нам работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение только с одной переменной, и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и найдем другую переменную. Наконец, мы проверяем наше решение и убеждаемся, что оба уравнения верны.
Наконец, мы проверяем наше решение и убеждаемся, что оба уравнения верны.
Как решить систему уравнений путем замены
Решите систему подстановкой:
Решите систему подстановкой:
Решите систему подстановкой:
Решите систему уравнений подстановкой.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Будьте очень осторожны со знаками в следующем примере.
Решите систему подстановкой:
Нам нужно решить одно уравнение для одной переменной. Мы решим первое уравнение для y .
Решите систему подстановкой:
Решите систему подстановкой:
Решить систему уравнений методом исключения
Мы решили системы линейных уравнений с помощью графиков и подстановок. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения. Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.
Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Для любых выражений a, b, c, и d .
Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
и прибавляются к нулю, и у нас есть одно уравнение с одной переменной.
Давайте попробуем еще:
На этот раз мы не видим переменную, которую можно сразу исключить, если добавить уравнения.
Но если мы умножим первое уравнение на, мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на
Мы должны умножить каждый член в обеих частях уравнения на
Тогда перепишите систему уравнений.
Теперь мы видим, что коэффициенты членов x являются противоположными, поэтому x будут исключены, когда мы добавим эти два уравнения.
Как только мы получим уравнение с одной переменной, мы решим его. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.
Как решить систему уравнений методом исключения
Решить систему методом исключения:
Решить систему методом исключения:
Решить систему методом исключения:
Шаги перечислены здесь для удобства.
Решите систему уравнений методом исключения.
- Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Теперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Решить систему методом исключения:
В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты. Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположные значения.
Чтобы получить противоположные коэффициенты и , мы будем
умножьте первое уравнение на 2 и
второе уравнение на 3.

оба исходных уравнений.
Решить систему методом исключения:
Решите каждую систему методом исключения:
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.
Решить систему методом исключения:
В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
| Чтобы убрать дроби, умножьте каждую Уравнение на ЖК-дисплее. | |
| Упрощение. | |
| Теперь мы готовы устранить один переменных. . | |
| Мы можем исключить, умножив первое уравнение на | |
| Упростить и добавить. Подставить в одно из исходных уравнений. | |
| Решите для . | |
| Запишите решение в виде упорядоченной пары. | Заказанная пара |
| Убедитесь, что заказанная пара является решением оба исходных уравнения. | |
| Решение |
Решите каждую систему методом исключения:
Решите каждую систему методом исключения:
Когда мы решили систему с помощью графика, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой.Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой.Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
То же самое верно для замены или исключения. Если уравнение в конце подстановки или исключения является верным утверждением, мы имеем непротиворечивую, но зависимую систему, а система уравнений имеет бесконечно много решений. Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.
Решить систему методом исключения:
Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, вы заметили, что два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.
Решить систему методом исключения:
бесконечно много решений
Решить систему методом исключения:
бесконечно много решений
Выберите наиболее удобный метод решения системы линейных уравнений
Когда вы решаете систему линейных уравнений в приложении, вам не сообщают, какой метод использовать.Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Для каждой системы линейных уравнений решите, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐⓑ
ⓐ
Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
ⓑ
Так как одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением. Поясните свой ответ.
Поясните свой ответ.
ⓐⓑ
ⓐ Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения. ⓑ Так как одно уравнение уже решено для x , наиболее удобным будет использование подстановки.
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением.Поясните свой ответ.
ⓐⓑ
ⓐ Поскольку одно уравнение уже решено для y , наиболее удобным будет использование подстановки. ⓑ Так как оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
Ключевые понятия
- Как решить систему линейных уравнений с помощью графика.
- Нарисуйте первое уравнение.
- Постройте график второго уравнения в той же прямоугольной системе координат.
- Определите, пересекаются ли линии, параллельны или являются одной и той же линией.

- Определите решение системы.
Если линии пересекаются, укажите точку пересечения. Это решение системы.
Если прямые параллельны, система не имеет решения.
Если линии одинаковые, система имеет бесконечное число решений.
- Проверьте решение обоих уравнений.
- Как решить систему уравнений подстановкой.
- Решите одно из уравнений для любой переменной.
- Подставьте выражение из шага 1 в другое уравнение.
- Решите полученное уравнение.
- Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
- Как решить систему уравнений методом исключения.
- Запишите оба уравнения в стандартной форме.
 Если какие-либо коэффициенты являются дробями, очистите их.
Если какие-либо коэффициенты являются дробями, очистите их. - Сделайте коэффициенты одной переменной противоположными.
Решите, какую переменную вы удалите.
Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
- Добавьте уравнения, полученные на шаге 2, чтобы исключить одну переменную.
- Найдите оставшуюся переменную.
- Подставьте решение шага 4 в одно из исходных уравнений. Затем найдите другую переменную.
- Запишите решение в виде упорядоченной пары.
- Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
- Запишите оба уравнения в стандартной форме.
Практика делает совершенным
Определить, является ли упорядоченная пара решением системы уравнений
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
Решение системы линейных уравнений с помощью графика
В следующих упражнениях решите следующие системы уравнений, построив график.
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
1 балл, непротиворечивый и независимый
1 балл, непротиворечивый и независимый
бесконечные решения, непротиворечивые, зависимые
Решение системы уравнений подстановкой
В следующих упражнениях решите системы уравнений путем замены.
Решение системы уравнений методом исключения
В следующих упражнениях решите системы уравнений методом исключения.
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения.
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ замена ⓑ устранение
ⓐ
ⓑ
ⓐ
ⓑ
ⓐ исключение ⓑ замена
Письменные упражнения
В системе линейных уравнений два уравнения имеют одинаковые точки пересечения. Опишите возможные решения системы.
Решите систему уравнений подстановкой и объясните все свои действия словами:
Решите систему уравнений методом исключения и объясните все свои действия словами:
Решить систему уравнений
ⓐ по графику ⓑ по подстановке
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
Если большинство ваших чеков:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретными.
Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретными.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого можно попросить о помощи? Ваши одноклассники и преподаватель являются хорошими ресурсами. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
…нет – не понимаю! Это предупреждающий знак, и вы не должны его игнорировать. Вы должны немедленно обратиться за помощью, иначе вы быстро будете поражены. Как можно скорее обратитесь к инструктору, чтобы обсудить вашу ситуацию. Вместе вы можете придумать план, как получить необходимую вам помощь.
Глоссарий
- совпадающие строки
- Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
- согласованные и несогласованные системы
- Непротиворечивая система уравнений — это система уравнений, имеющая хотя бы одно решение; несовместная система уравнений – это система уравнений, не имеющая решения.
- решения системы уравнений
- Решениями системы уравнений являются значения переменных, которые делают все уравнения истинными; решение представлено упорядоченной парой
- система линейных уравнений
- Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений.
Независимая система уравнений Примеры
Дополнительная практика — независимые системы уравнений
В следующих примерах учащиеся определят, является ли система независимой или зависимой, изучая графики или уравнения, и найдут решения для независимых систем.
Практические задачи
1. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
2. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
3. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
4. Определить, является ли система уравнений независимой. Если она независима и прямые не параллельны, решите систему.
Решения
1. Преобразуем второе уравнение в форму пересечения наклона. Решив y во втором уравнении, мы получим
 Эта система независима, и линии не параллельны. Используя замену, мы можем заменить y во втором уравнении на 3 x + 1, чтобы получить
Эта система независима, и линии не параллельны. Используя замену, мы можем заменить y во втором уравнении на 3 x + 1, чтобы получить2. Преобразование первого уравнения в форму пересечения наклона,
3. Система независима, поскольку на графике видно, что две линии различны.Решение системы находится там, где пересекаются линии, поэтому решение (4, 0).
4. Преобразовав второе уравнение в форму пересечения наклона, мы получим

Системы уравнений — Задачи и ответы
Системы 2-х линейных уравнений — задачи с решениями
Тест
Задача 1 Две из следующих систем уравнений имеют решение (1;3).Узнайте их, проверив.
а) $\begin{array}{|l} x + y = 5 \\ 2x — y = 7; \end{array}$
б) $\begin{array}{|l} 2x + y = 5 \\ x — y = 2 \end{array}$
c) $\begin{array}{|l } 3х+у=6\4х-3у=-5; \end{array}$d) $\begin{array}{|l} \frac{1}{x — 1} = y-3 \\ x — y = -2; \end{array}$
e) $\begin{array}{|l} \frac{9x + 4y}{3}-\frac{5x-11}{2} = 13-y \\ 13x — 7y = -8; \end{array}$
Ответ: c и e имеют решение (1; 3)
Задача 2 Эквивалентны ли системы (проверьте, совпадают ли решения обеих систем):
$\begin{array}{|l} 4x + 5y = 11 \\ x — y = 5 \end{array}$
и
$\begin{array}{|l} 4x — 5y = 11 \\ 2x + y = 9? \end{array}$
Ответ: Нет.
(3-32) Решите систему уравнений:
Проблема 3
$\begin{array}{|l} 2x — y = -5 \\ y = 1-3x \end{array}$
Ответ: x = 1, y = -2.
Проблема 4
$\begin{array}{|l} 3x — y = 13 \\ 3y — 2x = -4 \end{array}$
Ответ: x = 5, y = 2.
Проблема 5
$\begin{array}{|l} 6x — y = 11 \\ 12x — 2y — 22 = 0 \end{array}$
Ответ: Решением является любая пара чисел, являющаяся решением уравнения $6x — у = 11$.
Проблема 6
$\begin{array}{|l} 5u — 6v = -2 \\ 7u + 18v = 2 \end{array}$
Ответ: $x = -1, y = \frac{1}{2}$ .
Проблема 7
$\begin{array}{|l} 8x — 5y + 16 = 0 \\ 1x + 3y — 17 = 0 \end{array}$
Ответ: $x = \frac{1}{2}, y = 4$.
Проблема 8
$\begin{array}{|l} 4(x + 2) — 7(x — y) = 7 \\ 7(x + y) + 10(x — 2) = 79 \end{array}$
Ответ: $x = 5, y = 2.$
Проблема 9
$\begin{array}{|l} 3x + 4(x — 3) = 3(2y — 3) — 3y \\ 3y + 2(x — 4) = 5(y + 2) — 28\end{ массив}$
Ответ: (-4; 1).2 — y(4y — 3) + 12x — 15 = 0\end{array}$
Ответ: Решением является любая пара, являющаяся решением уравнения 4x — 3y — 2 = 0.
Проблема 13
$\begin{array}{|l} \frac{y + 2}{6} — \frac{y-4}{2} = \frac{x}{3} \\ \frac{4}{3 }(y — 1) — 2x = -2\end{массив}$
Ответ: x = 3, y = 4.
Проблема 14
$\begin{array}{|l} 0,25x — 0,04y = 1 \\ 0,4x + 1,5y = 40,7\end{array}$
Ответ: x = 8, y = 25.
Проблема 15
$\begin{array}{|l} \frac{5x-3y}{4} = \frac{x-5y}{3} \\ 7x + y = 12\end{array}$
Ответ: x = 2, у = -2
Проблема 16
$\begin{array}{|l} \frac{3x+1}{5}+2y-3 = 0 \\ \frac{4y-5}{6}+3y-9 = -\frac{1} {2}\end{array}$
Ответ: $x = -\frac{42}{11}, y = \frac{28}{11}$
Проблема 17
$\begin{array}{|l} \frac{3x-1}{5}+3y-4 = 15 \\ \frac{3y-5}{6}+2x-8 = \frac{23}{ 3}\end{array}$
Ответ: $x = 7, y = 5$
Проблема 18
$\begin{array}{|l} \frac{2x-z}{6}+\frac{2x-z}{9} = 3 \\ \frac{x+z}{3}-\frac{ xz}{4} = 4\end{массив}$
Ответ: x = y = 6
Проблема 19
$\begin{array}{|l} \frac{x-1}{3} + \frac{5y+1}{2} = \frac{x+10y-8}{6} \\ \frac{ (x+2)(5y-2)}{2} = 5+\frac{5xy}{2}-2(x+1)\end{массив}$
Ответ: Решения нет.
Проблема 20
$\begin{array}{|l} \frac{5x-1}{6} + \frac{3y-1}{10} = 3 \\ \frac{11-x}{6} + \frac{ 11+y}{4} = 3\end{array}$
Ответ: x = 5, y = -3.
Проблема 21
$\begin{array}{|l}y-0.2(x — 2) = 1.4\\ \frac{5}{2} — \frac{2y — 3}{4} = \frac{4x — y} {8}\end{массив}$
Ответ: $x = 5, y = 2.$
Проблема 22
$\begin{array}{|l}\frac{x}{5} + 0,03(10y — 20) = 0,8\\ \frac{2x + 4,5}{20} — 0,75 = \frac{y — 3} {8}\end{массив}$
Ответ: $x = 4, y = 2.$
Проблема 23
$\begin{array}{|l}yx-\frac{5x-4}{2}=3-\frac{11y+17}{4}\\ x+\frac{9y+11}{4}- \frac{3y+4}{7}=6\end{массив}$
Ответ: $x = 2, y = 1.$
Проблема 24
$\begin{массив}{|l}\frac{5x-3y}{3}-\frac{2y-3x}{5}=x+1\\ \frac{2x-3y}{3}-\ frac{3y-4x}{2}=y+1\end{массив}$
Ответ: $x = 3, y = 2.$
Проблема 25
$\begin{array}{|l}\frac{x-1}{4}\frac{1+y}{2}=\frac{1}{6}-\frac{x+2y}{6 }\\ \frac{x-2}{3}+\frac{x}{15}=\frac{y+4}{5}-\frac{4x-y}{15}\end{array}$
Ответ: Решением является любая пара, которая является решением уравнения $5x — 2y = 11. $
$
Проблема 26
$\begin{array}{|l}\frac{x+2y}{4}-\frac{x-2y}{2}=1-\left[x-\frac{7-2y}{3} \right]\\ 3x-2y=8\end{массив}$
Ответ: $x = 3, y = \frac{1}{2}.$
Проблема 27
$\begin{array}{|l}\frac{7+x}{5}-\frac{2x-y}{4}-3y=-5\end{array}$
$\begin{array} {|l}\frac{5y-7}{2}+\frac{4x-3}{6}-18=-5x\end{массив}$
Ответ: x = 3, y = 2.
Проблема 28
$\begin{array}{|l}\frac{11y}{20}-0,8\left(\frac{x}{4}+2.5\right)=\frac{5}{2}\end{array}$
$\begin{array}{|l}\frac{6x-0.3y}{2}-\frac{3}{2} =2(1+x)\end{массив}$
Ответ: x = 5, y = 10.
Проблема 29
$\begin{array}{|l}0,5x-\frac{y-4}{5}=0,3x-\frac{y-4}{2}\end{array}$
$\begin{array }{|l}0,5y-\frac{x-4}{6}=\frac{7y}{12}-\frac{x-3}{3}\end{array}$
Ответ: x = 3 , у = 2.
Проблема 30
$\begin{array}{|l}\frac{2(xy)}{3}+1.6=\frac{8x}{15}-\frac{3y-10}{5}\end{array}$
$\begin{массив}{|l}\frac{3x+4}{4}+\frac{y}{8}=\frac{5x}{6}-\frac{y-17}{12} \end{array}$
Ответ: x = 5, y = 4. 2=2(1+2y)(x-1)\end{array}$
2=2(1+2y)(x-1)\end{array}$
Ответ: Решением является любая пара, являющаяся решением уравнения x + 5y = 5
Системы 2-х линейных уравнений — задачи с решениями
Тест
Системы линейных уравнений
В первой половине этого учебника мы будем в основном заниматься пониманием решений систем линейных уравнений.
Определение
Уравнение с неизвестными x,y,z,… называется линейным , если обе части уравнения представляют собой сумму (постоянных) кратных x,y,z,…, плюс необязательная константа.
Например,
3x+4y=2z-x-z=100
— это линейные уравнения, а
3x+yz=3sin(x)−cos(y)=2
нет.
Обычно мы переносим неизвестные в левую часть уравнения, а константы — в правую.
Система линейных уравнений представляет собой набор нескольких линейных уравнений, таких как
Ax+2y+3z=62x−3y+2z=143x+y−z=−2.(1.1.1)
Определение (наборы решений)
- Решение системы уравнений представляет собой список чисел x,y,z,.
 .. которые делают все уравнения истинными одновременно.
.. которые делают все уравнения истинными одновременно. - Набор решений системы уравнений представляет собой совокупность всех решений.
- Решить систему означает найти все решения с формулами, включающими некоторое количество параметров.
Система линейных уравнений может не иметь решения. Например, не существует чисел x и y, для которых одновременно верны следующие два уравнения:
Сх+2у=3х+2у=-3.
В этом случае набор решений пуст .Поскольку это довольно важное свойство системы уравнений, оно имеет собственное название.
Определение
Система уравнений называется несовместимой , если она не имеет решений. Он называется последовательным иначе.
Решением системы уравнений с n переменными является список из n чисел. Например, (x,y,z)=(1,−2,3) является решением (1.1.1). Поскольку в этом тексте мы будем изучать решения систем уравнений, самое время закрепить наши представления о списках чисел.
Мы используем R для обозначения множества всех действительных чисел, т. е. числовой прямой. Он содержит такие числа, как 0,32,−π,104,…
.Определение
Пусть n — целое положительное число. Определяем
Rn=все упорядоченные n-наборы вещественных чисел(x1,x2,x3,…,xn).
Набор из n действительных чисел называется точкой Rn.
Другими словами, Rn — это просто набор всех (упорядоченных) списков n действительных чисел. Через мгновение мы нарисуем Rn, но имейте в виду, что — это определение .Например, (0,32,−π) и (1,−2,3) являются точками R3.
Пример (числовая строка)
Когда n=1, мы просто возвращаем R обратно: R1=R. Геометрически это числовая линия.
Пример (евклидова плоскость)
Когда n=2, мы можем думать о R2 как о плоскости xy. Мы можем это сделать, потому что каждая точка на плоскости может быть представлена упорядоченной парой действительных чисел, а именно ее координатами x и y.
Пример (3-пробел)
Когда n=3, мы можем думать о R3 как о пространстве , в котором мы (кажется) живем.Мы можем сделать это, потому что каждая точка в пространстве может быть представлена упорядоченной тройкой действительных чисел, а именно ее координатами x, y и z.
Так что же такое R4? или Р5? или Рн? Их труднее визуализировать, поэтому вам придется вернуться к определению: Rn — это множество всех упорядоченных n-кортежей действительных чисел (x1,x2,x3,…,xn).
Они по-прежнему являются «геометрическими» пространствами в том смысле, что наша интуиция относительно R2 и R3 часто распространяется на Rn.
Мы дадим определения и сформулируем теоремы, которые применимы к любому Rn, но мы будем рисовать только для R2 и R3.
Сила использования этих пространств заключается в возможности маркировать различных объектов интереса, таких как геометрические объекты и решения систем уравнений, точками Rn.
В приведенных выше примерах было полезно с психологической точки зрения заменить список из четырех чисел (представляющих транспортный поток) или 841 числа (представляющих QR-код) одним фрагментом данных: точкой в некотором Rn. Это мощная концепция; начиная с раздела 2.2, мы почти исключительно будем записывать решения систем линейных уравнений таким образом.
Это мощная концепция; начиная с раздела 2.2, мы почти исключительно будем записывать решения систем линейных уравнений таким образом.
Перед обсуждением того, как решить приведенную ниже систему линейных уравнений, полезно посмотреть на некоторые изображения того, как эти наборы решений выглядят геометрически.
Одно уравнение с двумя переменными
Рассмотрим линейное уравнение x+y=1. Мы можем переписать это как y=1−x, что определяет линию на плоскости: наклон равен −1, а точка пересечения с осью x равна 1.
Определение (линии)
Для наших целей линия — это луч, который прямой и бесконечный в обоих направлениях.
Одно уравнение с тремя переменными
Рассмотрим линейное уравнение x+y+z=1. Это неявное уравнение для плоскости в пространстве.
Определение (плоскости)
Плоскость представляет собой плоский лист, бесконечный во всех направлениях.
Уравнение x+y+z+w=1 определяет «3-плоскость» в 4-пространстве, и, в более общем смысле, одно линейное уравнение с n переменными определяет «(n−1)-плоскость» в n-пространстве. . Мы уточним эти утверждения в разделе 2.7.
. Мы уточним эти утверждения в разделе 2.7.
Два уравнения с двумя переменными
Теперь рассмотрим систему двух линейных уравнений
Сх-3у=-32х+у=8.
Каждое уравнение индивидуально определяет линию на плоскости, показанную ниже.
Решением системы обоих уравнений является пара чисел (x,y), которая делает оба уравнения истинными одновременно. Другими словами, это как точка, лежащая одновременно на обеих прямых. На картинке выше видно, что есть только одна точка пересечения прямых: следовательно, эта система имеет ровно одно решение.(Это решение (3,2), как может убедиться читатель.)
Обычно две линии на плоскости пересекаются в одной точке, но, конечно, это не всегда так. Рассмотрим теперь систему уравнений
Сх-3у=-3х-3у=3.
Они определяют параллельных линий на плоскости.
Тот факт, что линии не пересекаются, означает, что система уравнений не имеет решения. Конечно, это легко увидеть алгебраически: если x−3y=−3, то не может быть и так, что x−3y=3.
Есть еще одна возможность. Рассмотрим систему уравнений
Cx-3y=-32x-6y=-6.
Второе уравнение кратно первому, поэтому эти уравнения определяют ту же прямую на плоскости.
В этом случае существует бесконечно много решений системы уравнений.
Два уравнения с тремя переменными
Рассмотрим систему двух линейных уравнений
Бх+у+г=1х-г=0.
Каждое уравнение индивидуально определяет плоскость в пространстве.Решениями системы обоих уравнений являются точки, лежащие на обеих плоскостях. На картинке ниже мы видим, что плоскости пересекаются по прямой. В частности, эта система имеет бесконечно много решений.
Рисунок 21. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по красной линии, которая является набором решений системы обоих уравнений. В общем случае решения системы уравнений с n переменными есть пересечение «(n−1)-плоскостей» в n-пространстве. Это всегда какое-то линейное пространство, как мы обсудим в разделе 2. 4.
4.
Согласно этому определению, решение системы уравнений означает запись всех решений в терминах некоторого количества параметров. Мы дадим систематический способ сделать это в разделе 1.3; пока мы даем параметрические описания в примерах предыдущего пункта.
строки
Рассмотрим линейное уравнение x+y=1 из этого примера. В этом контексте мы называем x+y=1 неявным уравнением прямой. Мы можем записать ту же строку в параметрической форме следующим образом:
(x,y)=(t,1−t)для любого t∈R.
Это означает, что каждая точка на прямой имеет вид (t,1−t) для некоторого действительного числа t. В этом случае мы называем t параметром , так как он параметризует точек на линии.
Теперь рассмотрим систему двух линейных уравнений
Вх+у+г=1х-г=0
этого примера. В совокупности они образуют неявных уравнений для линии в R3. (Для определения линии в пространстве необходимо как минимум два уравнения. ) Эта линия также имеет параметрическую форму с одним параметром t:
) Эта линия также имеет параметрическую форму с одним параметром t:
(х, у, г) = (т, 1-2т, т).
Рисунок 24. Плоскости, определяемые уравнениями x+y+z=1 и x−z=0, пересекаются по желтой линии, которая параметризуется выражением (x,y,z)=(t,1−2t,t). Переместите ползунок, чтобы изменить параметризованную точку.Обратите внимание, что в каждом случае параметр t позволяет нам использовать R для меток точек на линии. Однако ни одна из прямых не совпадает с числовой прямой R: действительно, каждая точка первой строки имеет две координаты, например точка (0,1), а каждая точка второй строки имеет три координаты, например (0,1 ,0).
Самолеты
Рассмотрим линейное уравнение x+y+z=1 из этого примера. Это неявное уравнение плоскости в пространстве. Эта плоскость имеет уравнение в параметрической форме : мы можем записать каждую точку на плоскости как
.(x,y,z)=(1−t−w,t,w)для любого t,w∈R.
В данном случае нам нужны два параметра t и w для описания всех точек на плоскости.
Обратите внимание, что параметры t,w позволяют нам использовать R2 для меток точек на плоскости. Однако эта плоскость , а не , как и плоскость R2: действительно, каждая точка на этой плоскости имеет три координаты, как и точка (0,0,1).
При наличии единственного решения, как в этом примере, нет необходимости использовать параметры для описания набора решений.
Система уравнений
Системы уравнений — это наборы уравнений, решением которых является точка (точки) пересечения между уравнениями.Большинство систем уравнений, которые вы видите в алгебре, представляют собой наборы двух линейных уравнений в стандартной форме Ax + By = C.
Для решения систем линейных уравнений обычно используются три метода: построение графика, метод подстановки и метод исключения. Эти методы можно применять и к более сложным системам нелинейных уравнений.
Графический метод
Решение систем уравнений с помощью графика выполняется путем построения графика каждого уравнения в системе и определения точки (точек) пересечения.Может быть проще изобразить уравнения в виде графиков, преобразовав стандартную форму каждого уравнения в форму пересечения наклона.
Пример
|
Метод замещения
Решение систем уравнений методом подстановки включает замену переменной в одном уравнении эквивалентом этой переменной, рассчитанным с использованием другого уравнения.См. пример ниже.
Первым шагом метода подстановки является нахождение переменной в одном уравнении.
Вы можете решить, какую переменную решать, изучив каждый коэффициент. Переменные с коэффициентами, равными 1, найти проще всего, потому что вам не придется ни на что делить. Переменные с коэффициентами, которые плохо делятся на другие коэффициенты, создают беспорядочные дроби.
Переменные с коэффициентами, равными 1, найти проще всего, потому что вам не придется ни на что делить. Переменные с коэффициентами, которые плохо делятся на другие коэффициенты, создают беспорядочные дроби.
Пример
| 3x + у = 31 | → | у = -3х + 31 |
| 2x — 5y = 15 | → | -5г = 15 — 2х |
Затем подставьте эквивалент только что найденной переменной в соответствующую переменную в другом уравнении.
г = -3x + 31
2х — 5у = 15
2x — 5(-3x + 31) = 15
Теперь, поскольку в уравнении осталась только одна переменная, вы можете решить для этой переменной!
2x — 5 (-3x + 31) = 15
2х + 15х — 155 = 15
17х = 170
х = 10
Чтобы найти оставшуюся переменную, вы можете подставить значение переменной, для которой вы только что нашли, в любое из исходных уравнений.
х = 10
2(10) — 5 лет = 15
-5 лет = -5
г = 1
Теперь у вас есть значения обеих координат! Решением системы уравнений является (10, 1).
Вы можете проверить свои ответы, подставив значения x и y в исходные уравнения и упростив их. Если оба уравнения возвращают верные утверждения, как показано ниже, то вы успешно использовали метод подстановки!
| х = 10 | г = 1 |
| 3x + у = 31 | 2х — 5у = 15 |
| 3(10) + (1) = 31 | 2(10) — 5(1) = 15 |
| 31 = 31 | 15 = 15 |
Метод исключения
Для решения систем уравнений методом исключения необходимо исключить одну переменную.Прежде чем начать, очень важно, чтобы оба уравнения были в стандартной форме Ax + By = C. Это организует системы уравнений, выравнивая каждый член в одном уравнении с соответствующим членом в другом.
При использовании метода исключения постарайтесь представить систему уравнений как один большой столбец сложения, за исключением того, что здесь нет переноса, и вы можете только складывать и вычитать соответствующие переменные и константы.
Пример
| 6x + 2y | = 18 | |
| + | 5x + 4y | = 22 |
| ? |
Цель исключения — исключить переменную.Это означает, что когда у вас есть уравнения, выстроенные в ряд по столбцу и переменной, как в приведенном выше примере, вы хотите, чтобы сумма столбца переменной равнялась 0. Для этого вам нужно умножить один, а иногда и оба, из уравнения в системе на константу, которая создаст коэффициент, который имеет такое же значение, но противоположный знак от соответствующей переменной в другом уравнении.
Чтобы решить, какое уравнение использовать и на какую константу его умножить, мы можем проверить каждую пару переменных.Спросите себя: «На что я могу умножить эту переменную, чтобы исключить переменную в другом уравнении?»
В этом примере 6x и 5x труднее манипулировать для компенсации, чем 2y и 4y. Вы можете умножить верхнее уравнение на (или нижнее на, но это затруднит работу с остальной частью любого уравнения. Вы также можете умножить верхнее уравнение на 5, а нижнее на -6, но это также даст числа с которыми сложнее работать, чем с вариантом, представленным ниже.
Вы также можете умножить верхнее уравнение на 5, а нижнее на -6, но это также даст числа с которыми сложнее работать, чем с вариантом, представленным ниже.
Использование 2y и 4y приводит к относительно простому уравнению, поскольку вы можете умножить первое уравнение на -2, чтобы сократить 4y во втором уравнении, как показано ниже.
| -2(6х + 2у | = | 18) | |
| + | 5x + 4y | = | 22 |
| ? |
| -12x — 4г | = | -36 | |
| + | 5x + 4y | = | 22 |
| ? |
Примечание. Не забудьте умножить все уравнение на константу, включая правую часть знака равенства.Если вы не умножите все уравнение, оно уже не будет одним и тем же уравнением!
Теперь вы можете добавить каждый столбец:
| -12x — 4г | = | -36 | |
| + | 5x + 4y | = | 22 |
Тогда найди х!
Затем подставьте значение x в одно из исходных уравнений, чтобы найти значение y.
Теперь у вас есть значения обеих координат. Таким образом, решением системы уравнений является (2, 3).
Затем вы можете проверить правильность своего решения, подставив значения x и y в исходные уравнения.
| х = 2 | г = 3 |
| 6х + 2у = 18 | 5х + 4у = 22 |
| 6(2) + 2(3) = 18 | 5(2) + 4(3) = 22 |
| 12 + 6 = 18 | 10 + 12 = 22 |
| 18 = 18 | 22 = 22 |
Системы линейных уравнений не имеют решения (параллельные прямые), одно решение (пересекающиеся прямые) или бесконечные решения (одинаковые прямые).
Во всех приведенных выше примерах было одно решение. Давайте рассмотрим другие случаи.
Когда система линейных уравнений не имеет решения, прямые параллельны друг другу и поэтому никогда не пересекаются.
Каждый метод, который вы попробуете, приведет к устранению обеих переменных, а его упрощение оставит вас с утверждением, которое не соответствует действительности.
Пример
| -15x + 3 года | = 9 |
| -5х + у | = 2 |
Первое использование метода подстановки:
| -15х + 3(5х + 2) | = 9 |
| -15x + 15x + 6 | = 9 |
Результат, полученный с помощью метода подстановки, дает ложное утверждение, поскольку 6 ≠ 9.
Метод исключения:
| -15x + 3 года | = 9 | |
| + | (-3)(-5х + у | = 2) |
| ? |
| -15x + 3 года | = 9 | |
| + | 15x — 3 года | = 6 |
Результат, полученный методом исключения, также дает ложное утверждение, поскольку 0 ≠ 3
Использование графического метода:
Поскольку линии параллельны, они имеют одинаковый наклон и никогда не пересекутся. Следовательно, система уравнений не имеет решения.
Следовательно, система уравнений не имеет решения.
Используя эти знания, можно распознавать системы линейных уравнений, в которых нет решения, поскольку коэффициенты каждого набора переменных будут кратны друг другу, и обе пары будут иметь одинаковый множитель (число, которое вы умножаете, чтобы получить кратность). Если константы не кратны или не имеют того же множителя, что и коэффициенты, то система не будет иметь решения.
С другой стороны, если вы можете умножить одно из уравнений системы на константу, чтобы получить в точности другое уравнение, это означает, что уравнения описывают одну и ту же прямую и что система будет иметь бесконечные решения.Системы линейных уравнений с бесконечными решениями сокращают обе переменные, что дает верное утверждение. Это связано с тем, что одинаковые линии имеют одинаковый наклон и точку пересечения по оси Y и будут пересекаться в каждой точке.
Пример
| -15x + 3 года | = 9 |
| -5х + у | = 3 |
Метод замены:
| -15х + 3(5х + 3) | = 9 |
| -15x + 15x + 9 | = 9 |
Поскольку результатом использования метода подстановки является истинное утверждение, 9 = 9, система уравнений имеет бесконечные решения.
Метод устранения:
| -15x + 3 года | = 9 | |
| + | (-3)(-5х + у | = 3) |
| ? |
| -15x + 3 года | = 9 | |
| + | 15x — 3 года | = -9 |
Как и в случае с методом подстановки, поскольку результатом метода исключения является другое истинное утверждение, 0 = 0, система уравнений имеет бесконечное число решений.
Графический метод:
График двух уравнений позволяет нам увидеть, что выглядит только одна линия. Это потому, что система уравнений определяет одну и ту же линию, подтверждая, что существует бесконечное количество решений.
Системы нелинейных уравнений — ChiliMath
« система уравнений » – это набор двух или более уравнений , которые решаются одновременно. Ранее я рассмотрел несколько примеров, показывающих, как решать систему линейных уравнений с помощью методов замены и исключения.Это считается линейной системой, потому что все уравнения в наборе являются линиями.
Ранее я рассмотрел несколько примеров, показывающих, как решать систему линейных уравнений с помощью методов замены и исключения.Это считается линейной системой, потому что все уравнения в наборе являются линиями.
Что такое нелинейная система уравнений?
С другой стороны, нелинейная система представляет собой набор уравнений, которые могут содержать некоторые уравнения линии, но не все из них. В этом уроке мы будем иметь дело только с системой нелинейных уравнений с двумя уравнениями с двумя неизвестными, x и y.
В этом уроке семь (7) примеров.
Примеры решения систем нелинейных уравнений
Пример 1: Решите приведенную ниже систему нелинейных уравнений.
Эта система имеет по два уравнения каждого вида: линейное и нелинейное. Начните с первого уравнения, так как оно линейное. Вы можете решить для x или y. Для этого давайте найдем у через х.
Подставьте значение y во второе уравнение, а затем найдите x. В этой задаче переместите все в одну часть уравнения, оставив противоположную сторону равной нулю. После этого вынесите простой трехчлен на множители, а затем установите каждый множитель равным нулю, чтобы найти x.
В этой задаче переместите все в одну часть уравнения, оставив противоположную сторону равной нулю. После этого вынесите простой трехчлен на множители, а затем установите каждый множитель равным нулю, чтобы найти x.
Решив уравнение, мы получили два значения x. Подставьте эти числовые значения в любое из двух исходных уравнений. Однако выберите «более простое» уравнение, чтобы упростить вычисления. Очевидно, что линейное уравнение x + y = 1 — лучший выбор!
Ответ: (– 3, 4)
Ответ: (2, –1)
Таким образом, множество решений данной системы нелинейных уравнений состоит из двух точек: (– 3, 4) и (2, –1) .2}.
Я заменю выражение y, которое равно \color{blue}x+3, из нижнего уравнения на y из верхнего уравнения. Тогда мы должны быть в состоянии найти x.
Используйте эти значения x, чтобы найти соответствующие значения y. Я бы выбрал более простое уравнение (нижнее уравнение) y=x+3 для решения для y.
Ответ: (0, 3)
Ответ: (– 3, 0)
Конечными ответами являются точки (0, 3) и (– 3, 0) .Это точки пересечения заданной прямой и окружности с центром в начале координат.
Пример 3: Решите приведенную ниже систему уравнений.
Эта проблема очень похожа на проблему №2. У нас есть прямая (верхнее уравнение), которая пересекает окружность (нижнее уравнение) в двух точках.
Шаг 1 : Решите первое уравнение для y.
Шаг 2 : Подставьте значение y в нижнее уравнение. Вам нужно будет возвести в квадрат двучлен, объединить одинаковые члены и вынести трехчлен, чтобы получить значения x.Вот решение:
Следовательно, значения x равны
Шаг 3 : Обратно подставьте эти x{\rm{ — значения}} в верхнее уравнение x + y = — 1, чтобы получить соответствующие y{\rm{ — значения}}.
Ответ: (– 3, 2)
Ответ: (2, – 3)
Шаг 4 : Вот график линии, пересекающей окружность в точках (– 3, 2) и (2, – 3) .
Пример 4: Решение системы нелинейных уравнений
Замените выражение y из верхнего уравнения на y из нижнего уравнения.Примените распределительное свойство, затем переместите все влево. Вынесите трехчлен на множители, затем установите каждый множитель равным нулю, чтобы найти x.
Итак, у нас есть
Поскольку теперь у нас есть значения x, выберите любое из исходных уравнений для решения относительно y. Очевидным выбором является y=x+3, потому что он намного проще, чем другой.
Ответ: (–1, 2)
Ответ: (– 2, 1)
На графике показано пересечение косой гиперболы и прямой в точках (–1, 2) и (– 2, 1) .
Пример 5: Решение системы нелинейных уравнений
Обратите внимание, что первое уравнение представляет собой окружность с центром в точке (-2, 2) и радиусом 1. Второе уравнение представляет собой параболу стандартной формы с вершиной в точке (-2, 3). Мы ожидаем, что решениями этой системы нелинейных уравнений являются точки, в которых парабола (квадратичная функция) пересекает заданную окружность.
Мы решим это двумя способами. Сначала методом замещения, затем методом исключения.2} второго уравнения и подставьте его в первое уравнение.
Затем подставьте это во второе уравнение, которое дает нам уравнение с одной переменной только в y.
Приравняв каждый множитель к нулю и найдя у, мы получим
Теперь мы хотим найти соответствующие значения x, когда y=2 и y=3. Я буду использовать уравнение окружности, чтобы сделать именно это.
Ответ: (–1, 2) и (– 3, 2)
Ответ: (– 2, 3)
Следовательно, полными решениями являются точки пересечения квадратичной функции и окружности (–1, 2) , (– 3, 2) и (– 2, 3) . 2} терм исчез, у нас осталось простое квадратное уравнение с переменной y, и только тогда его можно решить с помощью факторизации.
2} терм исчез, у нас осталось простое квадратное уравнение с переменной y, и только тогда его можно решить с помощью факторизации.
Начните с расширения биномиального члена, объедините одинаковые члены, переместите все влево, разложите полученный трехчлен на множители и приравняйте каждый множитель к нулю, чтобы найти y.
Приравняв каждый множитель к нулю и найдя у, мы получим
Обратите внимание, что мы получили те же значения y, используя метод подстановки, как показано выше. С этого момента решение теперь такое же, как показано выше, поэтому я не буду показывать остальную часть.2, а затем применяя квадратный корень с обеих сторон, чтобы получить значения x. Не забывайте прикреплять знак плюс или минус всякий раз, когда вы получаете квадратный корень из чего-либо.
Выберите любое из двух исходных уравнений и найдите значения y, когда \color{blue}x = \pm\, 3. Я буду использовать первое уравнение, потому что оно намного проще!
Ответ: (3, 1) и (3, –1)
Ответ: (– 3, 1) и (– 3, –1)
Решения этой системы нелинейных уравнений состоят из четырех точек пересечения:
(3, 1), (3, –1), (– 3, 1) и (– 3, –1)
Фактически это точки пересечения заданного эллипса (первое уравнение) и гиперболы (второе уравнение). 2, а затем извлекаем квадратный корень из обеих частей уравнения.
2, а затем извлекаем квадратный корень из обеих частей уравнения.
Обратно подставьте значения x в любое из исходных уравнений, чтобы найти y. Используем первое уравнение.
Ответ: (3, 2) и (3, – 2)
Ответ: (– 3, 2) и (– 3, – 2)
Решениями этой нелинейной системы являются точки пересечения заданного эллипса и гиперболы.
4.1 Решение систем линейных уравнений с двумя переменными — Алгебра среднего уровня 2e
Цели обучения
К концу этого раздела вы сможете:
- Определить, является ли упорядоченная пара решением системы уравнений
- Решите систему линейных уравнений, построив график
- Решить систему уравнений подстановкой
- Решить систему уравнений методом исключения
- Выберите наиболее удобный способ решения системы линейных уравнений
Будьте готовы 4.1
Прежде чем начать, пройдите этот тест на готовность.
Для уравнения y=23x−4,y=23x−4,
ⓐ Является ли (6,0)(6,0) решением? ⓑ Является ли (−3,−2)(−3,−2) решением?
Если вы пропустили эту проблему, просмотрите пример 3.2.
Будьте готовы 4.2
Найдите наклон и y -пересечение линии 3x−y=12.3x−y=12.
Если вы пропустили эту проблему, просмотрите пример 3.16.
Будьте готовы 4.3
Найдите точки пересечения x- и y прямой 2x−3y=12.2x−3y=12.
Если вы пропустили эту проблему, просмотрите пример 3.8.
Определить, является ли упорядоченная пара решением системы уравнений
В разделе «Решение линейных уравнений» мы научились решать линейные уравнения с одной переменной. Теперь мы будем работать с двумя или более линейными уравнениями, сгруппированными вместе, что известно как система линейных уравнений.
Система линейных уравнений
Когда два или более линейных уравнения группируются вместе, они образуют систему линейных уравнений .
В этом разделе мы сосредоточим нашу работу на системах двух линейных уравнений с двумя неизвестными. Мы будем решать более крупные системы уравнений позже в этой главе.
Ниже показан пример системы двух линейных уравнений. Мы используем фигурную скобку, чтобы показать, что два уравнения сгруппированы вместе, чтобы сформировать систему уравнений.
{2x+y=7x−2y=6{2x+y=7x−2y=6Линейное уравнение с двумя переменными, например 2x+y=7,2x+y=7, имеет бесконечное число решений. Его график представляет собой линию. Помните, что каждая точка на прямой — это решение уравнения, а каждое решение уравнения — это точка на прямой.
Чтобы решить систему двух линейных уравнений, мы хотим найти значения переменных, которые являются решениями обоих уравнений. Другими словами, мы ищем упорядоченные пары (x,y)(x,y), которые делают оба уравнения верными. Они называются решениями системы уравнений.
Решения системы уравнений
решений системы уравнений являются значениями переменных, которые делают все уравнений верными. Решение системы двух линейных уравнений представлено упорядоченной парой (x,y).(x,y).
Решение системы двух линейных уравнений представлено упорядоченной парой (x,y).(x,y).
Чтобы определить, является ли упорядоченная пара решением системы двух уравнений, мы подставляем значения переменных в каждое уравнение. Если упорядоченная пара делает оба уравнения верными, это решение системы.
Пример 4.1
Определить, является ли упорядоченная пара решением системы {x−y=−12x−y=−5.{x−y=−12x−y=−5.
ⓐ (−2,−1)(−2,−1) ⓑ (−4,−3)(−4,−3)
Решение
ⓐ
ⓑ
Попробуйте 4.1
Определите, является ли упорядоченная пара решением системы {3x+y=0x+2y=-5.{3x+y=0x+2y=-5.
ⓐ (1,−3)(1,−3) ⓑ (0,0)(0,0)
Попробуйте 4.2
Определить, является ли упорядоченная пара решением системы {x−3y=−8−3x−y=4.{x−3y=−8−3x−y=4.
ⓐ (2,−2)(2,−2) ⓑ (−2,2)(−2,2)
Решение системы линейных уравнений с помощью графика
В этом разделе мы будем использовать три метода для решения системы линейных уравнений. Первый метод, который мы будем использовать, — это построение графика.
Первый метод, который мы будем использовать, — это построение графика.
График линейного уравнения представляет собой линию. Каждая точка на прямой является решением уравнения. Для системы двух уравнений мы начертим две линии. Тогда мы сможем увидеть все точки, являющиеся решениями каждого уравнения. И, найдя, что общего у линий, мы найдем решение системы.
Большинство линейных уравнений с одной переменной имеют одно решение, но мы видели, что некоторые уравнения, называемые противоречиями, не имеют решений, а для других уравнений, называемых тождествами, решениями являются все числа.
Аналогичным образом, когда мы решаем систему двух линейных уравнений, представленную графиком из двух линий на одной плоскости, возможны три случая, как показано.
Рисунок 4.2
Каждый раз, когда мы демонстрируем новый метод, мы будем использовать его на одной и той же системе линейных уравнений. В конце раздела вы решите, какой метод был наиболее удобным для решения этой системы.
Пример 4.2
Как решить систему уравнений с помощью графика
Решите систему, построив график {2x+y=7x−2y=6.{2x+y=7x−2y=6.
Попробуйте 4.3
Решите систему с помощью графика: {x−3y=−3x+y=5.{x−3y=−3x+y=5.
Попробуйте 4.4
Решите систему с помощью графика: {−x+y=13x+2y=12.{−x+y=13x+2y=12.
Здесь показаны шаги, необходимые для решения системы линейных уравнений с помощью графика.
How To
Решите систему линейных уравнений с помощью графика.
- Шаг 1. Нарисуйте график первого уравнения.
- Шаг 2. Постройте график второго уравнения в той же прямоугольной системе координат.
- Шаг 3. Определите, пересекаются ли прямые, параллельны ли они или являются одной и той же линией.
- Шаг 4. Определите решение системы.
- Если линии пересекаются, определите точку пересечения. Это решение системы.

- Если прямые параллельны, система не имеет решения.
- Если линии одинаковые, система имеет бесконечное число решений.
- Если линии пересекаются, определите точку пересечения. Это решение системы.
- Шаг 5. Проверьте решение обоих уравнений.
В следующем примере мы сначала перепишем уравнения в форме наклона и точки пересечения, так как это облегчит нам быстрое построение линий.
Пример 4.3
Решите систему с помощью графика: {3x+y=−12x+y=0.{3x+y=−12x+y=0.
Решение
Мы решим оба этих уравнения относительно yy, чтобы мы могли легко построить их график, используя их наклоны и y -перехваты.
Попробуйте 4.5
Решите систему, построив график: {−x+y=12x+y=10.{−x+y=12x+y=10.
Попробуйте 4.6
Решите систему с помощью графика: {2x+y=6x+y=1.{2x+y=6x+y=1.
Во всех системах линейных уравнений линии пересекались, а решением была одна точка.В следующих двух примерах мы рассмотрим систему уравнений, не имеющую решения, и систему уравнений, имеющую бесконечное число решений.
Пример 4.4
Решите систему графически: {y=12x−3x−2y=4.{y=12x−3x−2y=4.
Попробуйте 4.7
Решите систему с помощью графика: {y=-14x+2x+4y=-8.{y=-14x+2x+4y=-8.
Попробуйте 4.8
Решите систему графически: {y=3x−16x−2y=6.{y=3x−16x−2y=6.
Иногда уравнения в системе представляют одну и ту же прямую.Поскольку каждая точка на прямой делает оба уравнения верными, существует бесконечно много упорядоченных пар, которые делают оба уравнения верными. Система имеет бесконечно много решений.
Пример 4.5
Решите систему графически: {y=2x−3−6x+3y=−9.{y=2x−3−6x+3y=−9.
Решение
Если вы запишете второе уравнение в форме наклон-пересечение, вы можете заметить, что уравнения имеют одинаковый наклон и одинаковые и -пересечение.
Попробуйте 4.9
Решите систему с помощью графика: {y=−3x−66x+2y=−12. {y=−3x−66x+2y=−12.
{y=−3x−66x+2y=−12.
Попробуйте 4.10
Решите систему графически: {y=12x−42x−4y=16.{y=12x−42x−4y=16.
Когда мы рисовали вторую линию в последнем примере, мы нарисовали ее прямо над первой линией. Мы говорим, что две прямые совпадают. Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
Совпадающие линии
Совпадающие линии имеют одинаковый наклон и одинаковую точку пересечения и .
Каждая из систем уравнений в примере 4.2 и примере 4.3 имеет по две пересекающиеся прямые. Каждая система имела одно решение.
В примере 4.5 уравнения давали совпадающие прямые, поэтому система имела бесконечно много решений.
Системы в этих трех примерах имели по крайней мере одно решение. Система уравнений, имеющая хотя бы одно решение, называется -непротиворечивой -системой.
Система с параллельными прямыми, как в примере 4.4, не имеет решения.Мы называем такую систему уравнений несовместимой. Не имеет решения.
Непротиворечивые и противоречивые системы
Непротиворечивая система уравнений — это система уравнений, имеющая хотя бы одно решение.
Несовместная система уравнений — это система уравнений, не имеющая решения.
Мы также классифицируем уравнения в системе уравнений, называя уравнения независимыми или зависимыми . Если два уравнения независимы, то каждое из них имеет собственный набор решений.Пересекающиеся прямые и параллельные прямые независимы.
Если два уравнения являются зависимыми, то все решения одного уравнения также являются решениями другого уравнения. Когда мы рисуем два зависимых уравнения, мы получаем совпадающие линии.
Подведем итоги, взглянув на графики трех типов систем. См. ниже и Таблицу 4.1.
См. ниже и Таблицу 4.1.
| Линии | Пересечение | Параллельный | Совпадение |
|---|---|---|---|
| Количество растворов | 1 балл | Нет решения | Бесконечно много |
| Последовательный/непоследовательный | Последовательный | Несоответствие | Последовательный |
| Зависимый/ независимый | Независимый | Независимый | Зависимый |
Таблица 4. 1
1
Пример 4.6
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y=3x−16x−2y=12{y=3x−16x−2y=12 ⓑ {2x+y=−3x−5y=5{2x+y=−3x−5y=5
Решение
ⓐ Сравним наклоны и точки пересечения двух линий.
| Первое уравнение уже находится в форме пересечения наклона. | {y=3x−16x−2y=12y=3x−1{y=3x−16x−2y=12y=3x−1 |
| Запишите второе уравнение в форме пересечения наклона. | 6x−2y=12−2y=−6x+12−2y−2=−6x+12−2y=3x−66x−2y=12−2y=−6x+12−2y−2=−6x+12−2y =3x−6 |
| Найдите наклон и точку пересечения каждой прямой. | y=3x-1y=3x-6m=3m=3b=-1b=-6y=3x-1y=3x-6m=3m=3b=-1b=-6 |
Поскольку наклоны одинаковые, а точки пересечения и разные, линии параллельны. |
Система уравнений, графики которой представляют собой параллельные прямые, не имеет решения, является противоречивой и независимой.
ⓑ Сравним наклон и точки пересечения двух линий.
| {2x+y=-3x-5y=5{2x+y=-3x-5y=5 | |
| Запишите оба уравнения в форме наклона и пересечения. | 2x+y=-3x-5y=5y=-2x-3-5y=-x+5-5y-5=-x+5-5y=15x-12x+y=-3x-5y=5y=-2x −3−5y=−x+5−5y−5=−x+5−5y=15x−1 |
| Найдите наклон и точку пересечения каждой прямой. | y=-2x-3y=15x-1m=-2m=15b=-3b=-1y=-2x-3y=15x-1m=-2m=15b=-3b=-1 |
| Поскольку наклоны разные, линии пересекаются. |
Система уравнений, графики которой пересекаются, имеет 1 решение, непротиворечива и независима.
Попробуйте 4.11
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y=−2x−44x+2y=9{y=−2x−44x+2y=9 ⓑ {3x+2y=22x+y=1{3x+2y=22x+y=1
Попробуйте 4.12
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
ⓐ {y=13x−5x−3y=6{y=13x−5x−3y=6 ⓑ {x+4y=12−x+y=3{x+4y=12−x+y=3
Решение систем линейных уравнений с помощью графика — хороший способ визуализировать возможные решения.Однако во многих случаях решение системы с помощью графика неудобно или неточно. Если графики выходят за пределы небольшой сетки с размерами x и y в диапазоне от −10−10 до 10, графическое отображение линий может быть громоздким. И если решения системы не являются целыми числами, может быть трудно точно прочитать их значения по графику.
Решение системы уравнений путем замены
Теперь будем решать системы линейных уравнений методом подстановки.
Мы будем использовать ту же систему, что и для построения графиков.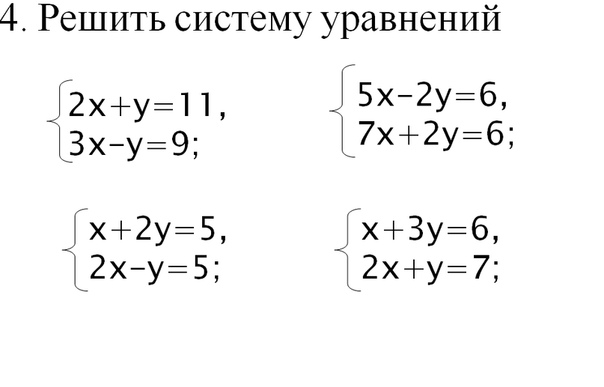
Сначала мы решим одно из уравнений либо для x , либо для y . Мы можем выбрать любое уравнение и найти решение для любой переменной, но мы постараемся сделать такой выбор, который облегчит нам работу.
Затем мы подставляем это выражение в другое уравнение. В результате получается уравнение только с одной переменной, и мы знаем, как его решить!
После того, как мы найдем значение одной переменной, мы подставим это значение в одно из исходных уравнений и найдем другую переменную.Наконец, мы проверяем наше решение и убеждаемся, что оба уравнения верны.
Пример 4.7
Как решить систему уравнений путем замены
Решите систему подстановкой: {2x+y=7x−2y=6.{2x+y=7x−2y=6.
Попробуйте 4.13
Решите систему подстановкой: {−2x+y=−11x+3y=9.{−2x+y=−11x+3y=9.
Попробуйте 4.14
Решите систему подстановкой: {2x+y=−14x+3y=3. {2x+y=−14x+3y=3.
{2x+y=−14x+3y=3.
How To
Решите систему уравнений путем замены.
- Шаг 1. Решите одно из уравнений для любой переменной.
- Шаг 2. Подставьте выражение из шага 1 в другое уравнение.
- Шаг 3. Решить полученное уравнение.
- Шаг 4. Подставьте решение шага 3 в любое из исходных уравнений, чтобы найти другую переменную.
- Шаг 5. Запишите решение в виде упорядоченной пары.
- Шаг 6. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Будьте очень осторожны со знаками в следующем примере.
Пример 4.8
Решите систему подстановкой: {4x+2y=46x−y=8.{4x+2y=46x−y=8.
Решение
Нам нужно решить одно уравнение для одной переменной. Мы решим первое уравнение для y .
Попробуйте 4. 15
15
Решите систему подстановкой: {x−4y=−4−3x+4y=0.{x−4y=−4−3x+4y=0.
Попробуйте 4.16
Решите систему подстановкой: {4x−y=02x−3y=5.{4x−y=02x−3y=5.
Решить систему уравнений методом исключения
Мы решили системы линейных уравнений с помощью графиков и подстановок. Графики хорошо работают, когда переменные коэффициенты малы, а решение имеет целые значения. Подстановка работает хорошо, когда мы можем легко решить одно уравнение для одной из переменных и не иметь слишком много дробей в результирующем выражении.
Третий метод решения систем линейных уравнений называется методом исключения.Когда мы решали систему подстановкой, мы начинали с двух уравнений и двух переменных и сводили ее к одному уравнению с одной переменной. То же самое мы сделаем и с методом исключения, но у нас будет другой способ добраться туда.
Метод исключения основан на свойстве сложения равенства. Свойство сложения равенства говорит о том, что, когда вы добавляете одно и то же количество к обеим частям уравнения, вы все равно получаете равенство. Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Мы расширим свойство равенства сложения, чтобы сказать, что когда вы добавляете равные количества к обеим частям уравнения, результаты равны.
Для любых выражений a, b, c, и d .
ifa=bandc=dthena+c=b+d.ifa=bandc=dthena+c=b+d.Чтобы решить систему уравнений методом исключения, мы начинаем с обоих уравнений в стандартной форме. Затем мы решаем, какую переменную будет проще всего исключить. Как мы решаем? Мы хотим, чтобы коэффициенты одной переменной были противоположными, чтобы мы могли сложить уравнения и исключить эту переменную.
Обратите внимание, как это работает, когда мы складываем эти два уравнения вместе:
{3x+y=52x−y=0—————5x=5{3x+y=52x−y=0—————5x=5y прибавляются к нулю, и мы получаем единицу уравнение с одной переменной.
Давайте попробуем еще:
{х+4у=22х+5у=-2{х+4у=22х+5у=-2 На этот раз мы не видим переменную, которую можно сразу исключить, если добавить уравнения.
Но если мы умножим первое уравнение на −2,−2, мы сделаем коэффициенты x противоположными. Мы должны умножить каждый член в обеих частях уравнения на −2,−2.
Тогда перепишите систему уравнений.
Теперь мы видим, что коэффициенты членов x являются противоположными, поэтому x будут исключены, когда мы добавим эти два уравнения.
Как только мы получим уравнение с одной переменной, мы решим его. Затем мы подставляем это значение в одно из исходных уравнений, чтобы найти оставшуюся переменную. И, как всегда, мы проверяем наш ответ, чтобы убедиться, что он является решением обоих исходных уравнений.
Теперь мы посмотрим, как использовать исключение для решения той же системы уравнений, которую мы решали с помощью графика и подстановки.
Пример 4.9
Как решить систему уравнений методом исключения
Решите систему методом исключения: {2x+y=7x−2y=6. {2x+y=7x−2y=6.
{2x+y=7x−2y=6.
Попробуйте 4.17
Решите систему методом исключения: {3x+y=52x−3y=7.{3x+y=52x−3y=7.
Попробуйте 4.18
Решите систему методом исключения: {4x+y=−5−2x−2y=−2.{4x+y=−5−2x−2y=−2.
Шаги перечислены здесь для удобства.
How To
Решите систему уравнений методом исключения.
- Шаг 1. Запишите оба уравнения в стандартной форме. Если какие-либо коэффициенты являются дробями, очистите их.
- Шаг 2.Сделайте коэффициенты одной переменной противоположными.
- Решите, какую переменную вы удалите.
- Умножьте одно или оба уравнения так, чтобы коэффициенты этой переменной были противоположны.
- Шаг 3. Добавьте уравнения, полученные в результате шага 2, чтобы исключить одну переменную.
- Шаг 4. Найдите оставшуюся переменную.
- Шаг 5. Подставим решение шага 4 в одно из исходных уравнений.
 Затем найдите другую переменную.
Затем найдите другую переменную. - Шаг 6.Запишите решение в виде упорядоченной пары.
- Шаг 7. Убедитесь, что упорядоченная пара является решением обоих исходных уравнений.
Теперь сделаем пример, где нам нужно умножить оба уравнения на константы, чтобы сделать коэффициенты одной переменной противоположными.
Пример 4.10
Решите систему методом исключения: {4x−3y=97x+2y=−6.{4x−3y=97x+2y=−6.
Решение
В этом примере мы не можем умножить только одно уравнение на любую константу, чтобы получить противоположные коэффициенты.Поэтому мы стратегически умножим оба уравнения на разные константы, чтобы получить противоположные значения.
Попробуйте 4.19
Решите систему методом исключения: {3x−4y=−95x+3y=14.{3x−4y=−95x+3y=14.
Попробуйте 4.20
Решите каждую систему методом исключения: {7x+8y=43x−5y=27. {7x+8y=43x−5y=27.
{7x+8y=43x−5y=27.
Когда система уравнений содержит дроби, мы сначала очистим дроби, умножив каждое уравнение на ЖК-дисплей всех дробей в уравнении.
Пример 4.11
Решите систему методом исключения: {x+12y=632x+23y=172.{x+12y=632x+23y=172.
Решение
В этом примере оба уравнения содержат дроби. Нашим первым шагом будет умножение каждого уравнения на ЖК-дисплей всех дробей в уравнении, чтобы очистить дроби.
Попробуйте 4.21
Решите каждую систему методом исключения: {13x−12y=134x−y=52.{13x−12y=134x−y=52.
Попробуйте 4.22
Решите каждую систему методом исключения: {x+35y=−15−12x−23y=56.{х+35у=-15-12х-23у=56.
Когда мы решили систему с помощью графика, мы увидели, что не все системы линейных уравнений имеют в качестве решения одну упорядоченную пару. Когда два уравнения действительно представляли собой одну прямую, решений было бесконечно много. Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
Мы назвали это последовательной системой. Когда два уравнения описывали параллельные прямые, решения не было. Мы назвали это непоследовательной системой.
То же самое верно для замены или исключения. Если уравнение в конце подстановки или исключения является верным утверждением, мы имеем непротиворечивую, но зависимую систему, а система уравнений имеет бесконечно много решений.Если уравнение в конце подстановки или исключения является ложным утверждением, мы имеем противоречивую систему, и система уравнений не имеет решения.
Пример 4.12
Решите систему методом исключения: {3x+4y=12y=3−34x.{3x+4y=12y=3−34x.
Решение
| {3x+4y=12y=3−34x{3x+4y=12y=3−34x | |
| Запишите второе уравнение в стандартной форме. | {3x+4y=1234x+y=3{3x+4y=1234x+y=3 |
Очистите дроби, умножив второе уравнение на 4. | {3x+4y=124(34x+y)=4(3){3x+4y=124(34x+y)=4(3) |
| Упрощение. | {3x+4y=123x+4y=12{3x+4y=123x+4y=12 |
| Чтобы исключить переменную, мы умножаем второе уравнение на −1. Упростить и добавить. | {3x+4y=12−3x−4y=−12______________0=0{3x+4y=12−3x−4y=−12______________0=0 |
Это верное утверждение. Уравнения непротиворечивы, но зависимы. Их графики были бы одной линией. Система имеет бесконечно много решений.
После того, как мы очистили дроби во втором уравнении, вы заметили, что два уравнения были одинаковыми? Это означает, что у нас есть совпадающие линии.
Попробуйте 4.23
Решите систему методом исключения: {5x−3y=15y=−5+53x.{5x−3y=15y=−5+53x.
Попробуйте 4.24
Решите систему методом исключения: {x+2y=6y=−12x+3.{x+2y=6y=−12x+3.
Выберите наиболее удобный метод решения системы линейных уравнений
Когда вы решаете систему линейных уравнений в приложении, вам не сообщают, какой метод использовать. Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Вам нужно будет принять это решение самостоятельно. Таким образом, вы захотите выбрать метод, который проще всего сделать и сводит к минимуму вероятность ошибок.
Пример 4.13
Для каждой системы линейных уравнений решите, будет ли удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐ {3x+8y=407x−4y=−32{3x+8y=407x−4y=−32 ⓑ {5x+6y=12y=23x−1{5x+6y=12y=23x−1
Решение
ⓐ
{3x+8y=407x−4y=−32{3x+8y=407x−4y=−32 Поскольку оба уравнения имеют стандартную форму, наиболее удобным будет использование метода исключения.
ⓑ
{5x+6y=12y=23x−1{5x+6y=12y=23x−1Так как одно уравнение уже решено для y , наиболее удобным будет использование подстановки.
Попробуйте 4.25
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением. Поясните свой ответ.
ⓐ {4x−5y=−323x+2y=−1{4x−5y=−323x+2y=−1 ⓑ {x=2y−13x−5y=−7{x=2y−13x−5y=−7
Попробуйте 4.26
Для каждой системы линейных уравнений решите, как удобнее решать ее подстановкой или исключением.Поясните свой ответ.
ⓐ {y=2x−13x−4y=−6{y=2x−13x−4y=−6 ⓑ {6x−2y=123x+7y=−13{6x−2y=123x+7y=−13
Раздел 4.1 Упражнения
Практика ведет к совершенству
Определить, является ли упорядоченная пара решением системы уравнений
В следующих упражнениях определите, являются ли следующие точки решениями данной системы уравнений.
{2x−6y=03x−4y=5{2x−6y=03x−4y=5
ⓐ (3,1)(3,1) ⓑ (−3,4)(−3,4)
2.{−3x+y=8−x+2y=−9{−3x+y=8−x+2y=−9
ⓐ (−5,−7)(−5,−7) ⓑ (−5,7)(−5,7)
3.{х+у=2у=34х{х+у=2у=34х
ⓐ (87,67)(87,67) ⓑ (1,34)(1,34)
4. {2x+3y=6y=23x+2{2x+3y=6y=23x+2
ⓐ (−6,2)(−6,2) ⓑ (−3,4)(−3,4)
Решение системы линейных уравнений с помощью графика
В следующих упражнениях решите следующие системы уравнений, построив график.
5.{3x+y=-32x+3y=5{3x+y=-32x+3y=5
6.{−x+y=22x+y=−4{−x+y=22x+y=−4
7.{у=х+2у=-2х+2{у=х+2у=-2х+2
8.{у=х-2у=-3х+2{у=х-2у=-3х+2
9.{у=32х+1у=-12х+5{у=32х+1у=-12х+5
10.{у=23х-2у=-13х-5{у=23х-2у=-13х-5
11.{х+у=-4-х+2у=-2{х+у=-4-х+2у=-2
12.{−x+3y=3x+3y=3{−x+3y=3x+3y=3
13.{−2x+3y=3x+3y=12{−2x+3y=3x+3y=12
14.{2x−y=42x+3y=12{2x−y=42x+3y=12
15.{х+3у=-6у=-43х+4{х+3у=-6у=-43х+4
16.
{-x+2y=-6y=-12x-1{-x+2y=-6y=-12x-1
17.{−2x+4y=4y=12x{−2x+4y=4y=12x
18.{3x+5y=10y=-35x+1{3x+5y=10y=-35x+1
19.{4x−3y=88x−6y=14{4x−3y=88x−6y=14
20.{х+3у=4-2х-6у=3{х+3у=4-2х-6у=3
21.{х=-3у+42х+6у=8{х=-3у+42х+6у=8
22.{4x=3y+78x−6y=14{4x=3y+78x−6y=14
23.{2x+y=6-8x-4y=-24{2x+y=6-8x-4y=-24
24.{5x+2y=7-10x-4y=-14{5x+2y=7-10x-4y=-14
Без построения графика определите количество решений, а затем классифицируйте систему уравнений.
25.{у=23х+1-2х+3у=5{у=23х+1-2х+3у=5
26.{у=32х+12х-3у=7{у=32х+12х-3у=7
27.{5x+3y=42x−3y=5{5x+3y=42x−3y=5
28.{у=-12х+5х+2у=10{у=-12х+5х+2у=10
29.{5x−2y=10y=52x−5{5x−2y=10y=52x−5
Решение системы уравнений подстановкой
В следующих упражнениях решите системы уравнений путем замены.
30.{2x+y=-43x-2y=-6{2x+y=-43x-2y=-6
31.
{2x+y=-23x-y=7{2x+y=-23x-y=7
32.{х-2у=-52х-3у=-4{х-2у=-52х-3у=-4
33.{х-3у=-92х+5у=4{х-3у=-92х+5у=4
34.{5x−2y=−6y=3x+3{5x−2y=−6y=3x+3
35.{−2x+2y=6y=−3x+1{−2x+2y=6y=−3x+1
36.{2x+5y=1y=13x−2{2x+5y=1y=13x−2
37.{3x+4y=1y=-25x+2{3x+4y=1y=-25x+2
38.{2x+y=5x−2y=−15{2x+y=5x−2y=−15
39.{4x+y=10x−2y=−20{4x+y=10x−2y=−20
40.{у=-2х-1у=-13х+4{у=-2х-1у=-13х+4
41.{у=х-6у=-32х+4{у=х-6у=-32х+4
42.{х=2у4х-8у=0{х=2у4х-8у=0
43.{2x−16y=8−x−8y=−4{2x−16y=8−x−8y=−4
44.{у=78х+4-7х+8у=6{у=78х+4-7х+8у=6
45.{у=-23х+52х+3у=11{у=-23х+52х+3у=11
Решение системы уравнений методом исключения
В следующих упражнениях решите системы уравнений методом исключения.
46.{5x+2y=2-3x-y=0{5x+2y=2-3x-y=0
47.{6x−5y=−12x+y=13{6x−5y=−12x+y=13
48.{2x−5y=73x−y=17{2x−5y=73x−y=17
49.
{5x−3y=−12x−y=2{5x−3y=−12x−y=2
50.{3x−5y=−95x+2y=16{3x−5y=−95x+2y=16
51.{4x−3y=32x+5y=−31{4x−3y=32x+5y=−31
52.{3x+8y=-32x+5y=-3{3x+8y=-32x+5y=-3
53.{11x+9y=-57x+5y=-1{11x+9y=-57x+5y=-1
54.{3x+8y=675x+3y=60{3x+8y=675x+3y=60
55.{2x+9y=-43x+13y=-7{2x+9y=-43x+13y=-7
56.{13x−y=−3x+52y=2{13x−y=−3x+52y=2
57.{х+12у=3215х-15у=3{х+12у=3215х-15у=3
58.{х+13у=-113х+12у=1{х+13у=-113х+12у=1
59.{13x−y=−323x+52y=3{13x−y=−323x+52y=3
60.{2x+y=36x+3y=9{2x+y=36x+3y=9
61.{х-4у=-1-3х+12у=3{х-4у=-1-3х+12у=3
62.{−3x−y=86x+2y=−16{−3x−y=86x+2y=−16
63.{4x+3y=220x+15y=10{4x+3y=220x+15y=10
Выберите наиболее удобный метод решения системы линейных уравнений
В следующих упражнениях решите, будет ли удобнее решать систему уравнений путем замены или исключения.
64.
ⓐ {8x−15y=−326x+3y=−5{8x−15y=−326x+3y=−5
ⓑ {x=4y−34x−2y=−6{x=4y−34x−2y=− 6

ⓐ {y=7x−53x−2y=16{y=7x−53x−2y=16
ⓑ {12x−5y=−423x+7y=−15{12x−5y=−423x+7y=−15
ⓐ {y=4x+95x−2y=−21{y=4x+95x−2y=−21
ⓑ {9x−4y=243x+5y=−14{9x−4y=243x+5y=−14
ⓐ {14x−15y=−307x+2y=10{14x−15y=−307x+2y=10
ⓑ {x=9y−112x−7y=−27{x=9y−112x−7y=−27
Письменные упражнения
68.В системе линейных уравнений два уравнения имеют одинаковые точки пересечения.Опишите возможные решения системы.
69.Решите систему уравнений подстановкой и объясните все свои шаги словами: {3x+y=12x=y−8.{3x+y=12x=y−8.
70.Решите систему уравнений методом исключения и объясните все свои шаги словами: {5x+4y=102x=3y+27.{5x+4y=102x=3y+27.
71.Решить систему уравнений {x+y=10x−y=6{x+y=10x−y=6
ⓐ графически ⓑ подстановкой
ⓒ Какой метод вы предпочитаете? Почему?
Самопроверка
После выполнения упражнений используйте этот контрольный список, чтобы оценить свое мастерство в выполнении целей этого раздела.
Если большинство ваших чеков:
…уверенно. Поздравляем! Вы достигли целей в этом разделе. Подумайте об учебных навыках, которые вы использовали, чтобы вы могли продолжать их использовать. Что вы сделали, чтобы обрести уверенность в своих способностях делать эти вещи? Быть конкретными.
…с некоторой помощью. Это нужно решать быстро, потому что темы, которые вы не осваиваете, становятся выбоинами на вашем пути к успеху. В математике каждая тема основывается на предыдущей работе.Прежде чем двигаться дальше, важно убедиться, что у вас есть прочная основа. Кого вы можете попросить о помощи? Ваши одноклассники и преподаватель являются хорошими источниками информации. Есть ли в кампусе место, где есть репетиторы по математике? Можно ли улучшить свои учебные навыки?
… нет — не понимаю! Это предупреждающий знак, и вы не должны его игнорировать.


 Обратите внимание, что оба уравнения находятся в
Обратите внимание, что оба уравнения находятся в
 Если какие-либо коэффициенты являются дробями, очистите их.
Если какие-либо коэффициенты являются дробями, очистите их. .. которые делают все уравнения истинными одновременно.
.. которые делают все уравнения истинными одновременно.
 Затем найдите другую переменную.
Затем найдите другую переменную.