Основные методы решения систем двух линейных уравнений с двумя переменными

Основные Методы решения систем линейных уравнений
с двумя переменными
7 класс
Ростов-на-Дону 2018 Г.

Цели урока:
- Обобщение знаний о методах решения систем линейных уравнений с двумя переменными
- Повторение и закрепление алгоритмов решения систем методом сложения и графическим методом
- Развитие навыков решения систем
Задачи урока:
- Образовательная: выработать прочные навыки решения систем двух уравнений с двумя неизвестными;
- Развивающая: развитие внимания и логического мышления, памяти, активизация самостоятельной деятельности;
- Воспитательная: способствовать развитию творческой деятельности учащихся, любознательности.

Разминка
- Актуализация опорных знаний. “ Без теории — нет практики”
А) Что такое система уравнений?
Б)Что называется решением системы уравнений?
В)Что значит решить систему уравнений?
Г)Назовите методы решения систем уравнения.
Д)Как решить систему уравнений графически?
Е)Как решить систему уравнений методом алгебраического сложения?
2. Решите уравнения
А) х — 8,1= 9,9 Б) 5х = -3,5 В) 3х – 7 = 2 Г) 3(х-7) = 2х + 4
3. Выразите у через х
А) 5х + у = 11 Б) 3х — у = 5 В) 10х + 5у = 5

Проверим результаты
1. Актуализация опорных знаний
А) Система уравнений -это уравнения, которые имеют одинаковые решения (х;y) и объединены фигурной скобкой.
Б) Решение системы — пара чисел (х;y) которая одновременно является решением и первого и второго уравнения системы.
В) Решить систему — это значит найти все ее решения или установить, что их нет.
Г) Графический метод, метод алгебраического сложения, метод подстановки.
Д) Нужно построить графики каждого уравнения на одной координатной плоскости и найти координаты точки пересечения этих графиков.
Е) Метод заключается в сложении двух уравнений системы почленно, с целью исключения одной переменной и сведению системы уравнений к одному линейному уравнению с одной переменной.

2. Решите уравнения
А) х = 18 Б) х = — 0,7 В) х = 3 Г) х = 25
3. Выразите у через х

«Оторви лишний лепесток, который является решением системы уравнений »
«Оторви
(4;1)
(4;1)
(4;(1)
( )
(3;2)
(5;0)
3;2)
3;2)
2х – у = 7,
х + у = 5
(5;3)
(2;3)
3;2)
3;2)
(4;0)
(1;4)
3;2)
(6;5)
3;2)

Системы линейных уравнений
Метод
сложения
Метод
подстановки
Графический
метод

Решение системы графическим методом
х + у =5,
y = -x + 5,
— x + y =1;
y = х +1;
(2; 3)
Построим графики двух линейных уравнений в одной системе координат
y = х +1
y = -x + 5
х
х
y
y
1
1
2
4
2
2
3
3
Ответ: (2; 3).

Решение системы методом сложения
Сложим почленно
левые и правые части
уравнения
Найдем значение х
х + у=5,
— x + y =1;
х+3=5
х = 2;
2у = 6
Найдем значение у
у = 3
х = 2
y = 3;
Ответ: (2; 3).


Историческая справка :
ЕГИПЕТ. Первые задачи на составление и решение систем уравнений с
несколькими переменными встречаются в египетских и вавилонских текстах второго тысячелетия до нашей эры, а также в трудах древнегреческих и индийских ученых. Решались они различными искусственными способами, единого алгоритма не было.
КИТАЙ. Алгоритм решения систем линейных уравнений был напечатан в Китае в труде “Математика в девяти книгах” (206 г. до н.э.), где рассматривались системы и давились правила их решения. При этом все изложение словесно. Коэффициенты системы располагались на счетной доске в виде таблицы. При повторных действиях было замечено, что следует поступать по одному и тому же правилу систематически.
Первым появился способ сложения, а затем — способ подстановки. В книге
“ Всеобщая арифметика” (1707 г.) Ньютон излагает уже все способы решения систем, изучаемые ныне в школе.

Самостоятельная работа
1. Решить систему уравнений графическим методом
2х + у = 1
3х + у = 2
2. Решить систему уравнений методом алгебраического сложения
2х-3y=11
4х+5y=-11
3*. Решить систему одним из изученных методов
2(3х+2y)+9=4х+21
2х+10=3-(6х+5y)

Ответы:
1)(1;-1)
2) (1;-3)
3)(-4;5)

Решение задач с помощью систем уравнений
Расстояние между двумя пунктами по реке равно 80 км. Это расстояние
лодка проплывает по течению реки за 4 ч, а против течения – за 5 ч.
Найдите собственную скорость лодки и скорость течения реки?
Решение:
1 этап. Составление математической модели.
Пусть х ( км/ч ) – собственная скорость лодки, y ( км/ч ) – скорость течения реки. Заполним таблицу:
Составим систему уравнений:
(х + y)4=80
(х — y)5=80
S =vt
S, км
по течению
v, км/ч
против течения
80
t, ч
х+y
80
4
х-y
5

2 этап. Работа с математической моделью. Решение системы уравнений.
(х + y)4=80 : 4
(х — y)5=80 : 5
х + y=20 18+y=20
х — y=16 y=20-18
2х=36 : 2 y=2
х=18
х=18
y=2 — решение системы.
3 этап. Ответ на вопрос задачи.
18 км/ч- собственная скорость лодки
2 км/ч – скорость течения реки.

Игровой момент
Задумайте два числа. Найдите их сумму и их разность. Результаты сообщите мне, и я назову задуманные числа.
Решение:
Пусть задуманы числа х и у, тогда
х + y = a
х — y = в

Продолжи предложение:
- Сегодня на занятии я научился ………………………………..
- Мне понравилось …………………………………………….
- Я повторил ………………………………………………………….
- Я закрепил …………………………………………………………..
- Я оцениваю свою работу на занятии на (хор., отл., уд.)
- Какие виды работ вызвали затруднения и требуют повторения ……………………………………………………
- В каких знаниях уверен………………………………………

СПАСИБО ЗА ВНИМАНИЕ !
videouroki.net
План-конспект урока по алгебре (9 класс) на тему: Урок по теме: «Методы решения систем уравнений с двумя переменными»
МБОУ «Будницкая ОШ» Велижского района Смоленской области
Конспект урока в 9 классе по теме:
«Методы решения систем уравнений с двумя переменными»
Учитель математики
Двоянова Т. В.
Будница, 2016
Цели урока:
Общие:
- Образовательная: формирование теоретических знаний, специальных умений и навыков.
- Воспитательная: формирование мировоззрения, убеждений, нравственных привычек, определенных качеств личности (внимание, аккуратность, настойчивость).
- Развивающая: развитие интеллектуальных умений и способностей (формирование приемов умственной деятельности, сравнение, обобщение, анализ, синтез, умение самостоятельно решать проблемы).
Цели урока по данной теме:
- обобщить и закрепить изученный материал по теме «Методы решения систем уравнений с двумя переменными», подготовиться к контрольной работе. Познакомиться с заданиями второй части, предлагаемыми на выпускных экзаменах в 9 классе.
- Воспитание интереса к предмету путем использования разных форм работы.
ПЛАН УРОКА
- Постановка цели урока.
- Актуализация опорных знаний: опрос и устный тест.
- Групповая работа (решение системы уравнений тремя способами).
- Самостоятельное решение системы уравнений с последующей проверкой.
- Фронтальная работа (система уравнений с параметром).
- Самостоятельная работа.
- Итог урока и домашнее задание.
ХОД УРОКА
Французский писатель Анатоль Франс заметил: «Чтобы переваривать знания, надо поглощать их с аппетитом». Последуем совету писателя, будем на уроке активны, внимательны, будем поглощать знания с большим желанием, ведь они вам скоро пригодятся. Умение решать системы уравнений позволяет существенно расширить класс текстовых задач и перед нами стоит следующая задача: повторить способы решения систем уравнений, проверить свое умение самостоятельно применять полученные знания.
Цель нашего сегодняшнего урока обобщить и закрепить изученный материал. Познакомиться с заданиями, предлагаемыми на выпускных экзаменах в 9 классе. Наша задача не только проверить себя, но и ответить на те вопросы, которые, может, у вас есть по этой теме.
Сегодня у нас повторительно – обобщающий урок по теме «Методы решения систем уравнений». На первом этапе нашего урока мы поработаем устно.
- Устная работа.
Опрос:
- Что называется системой уравнений с двумя переменными? (Если поставлена задача найти такие пары значений (x; y), которые одновременно удовлетворяют уравнению и , то говорят, что указанные уравнения образуют систему уравнений: ).
- Что называется решением системы уравнений? (Пару значений (x; y), которая одновременно является решением и первого и второго уравнений системы, называют решением системы уравнений).
- Что значит решить систему? (Решить систему уравнений – это значит найти все ее решения или установить, что решений нет).
- Какие методы решения систему двух уравнений с двумя переменными вам известны? (графический метод, метод сложения, метод подстановки, метод введения новой переменной).
ТЕСТ
1. Решите систему уравнений методом алгебраического сложения:
А. , Б. (1;-1), В. (1;1), Г. нет решений.
2. Выберите пару чисел, являющейся решением системы уравнений:
А. (1;6), Б. (6;1), В. (-12;-0,5), Г. нет такой пары.
3. На рисунке изображены парабола и три прямые. Укажите систему уравнений, которая имеет два решения.
А. Б.
Г. В. Все три указанные системы.
4. Пользуясь рисунком, найдите решение системы уравнений
Ответ: (-3;0), (-1;2).
- Сколько решений имеет система уравнений:
А. одно Б. два В. три Г. ни одного.
II. Групповая работа.
Решить систему уравнений
1 группа – графически.
— окружность с центром в начале координат и радиусом 5.
— обратная пропорциональность, графиком является гипербола, ветви которой расположены в 1 и 3 координатной четверти.
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
2 группа – метод сложения.
или
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
3 группа – метод подстановки.
Вернемся к y:
Ответ: (-4;-3), (-3;-4), (3;4), (4;3).
III. Самостоятельное решение системы уравнений с последующей проверкой.
Данная система уравнений была предложена во второй части экзаменационной работы в прошлом году.
или
Ответ:
IV. Фронтальная работа.
1) При каких значениях m имеет решение система уравнений
Все три уравнения системы – это уравнения прямых. Чтобы система имела решение, нужно, чтобы все три прямые пересекались в одной точке. Сначала найдем координаты точки пересечения первых двух прямых, то есть решим систему уравнений:
Ответ: при m = 4.
2) При каком значении параметра а система уравнений имеет единственное решение. Найдите это решение.
Если корни этого уравнения различны, то существует два решения системы уравнений. То есть необходимо, чтобы данное уравнение имело один корень, то есть дискриминант должен равняться нулю. Тогда
Ответ: при .
V. Самостоятельная работа.
На «3»
I ВАРИАНТ | II ВАРИАНТ |
Решите систему уравнений 1) 2) | Решите систему уравнений 1) 2) |
На «4» и «5». Выберите 2 понравившиеся вам системы.
I ВАРИАНТ | II ВАРИАНТ |
1) Решите систему уравнений а) б) 2) При каких значениях b система имеет одно решение? | 1) Решите систему уравнений а) б) 2) При каких значениях b система имеет одно решение? |
VI. Итог урока и домашнее задание.
Ребята, скажите, чем сегодня мы занимались на уроке, выполнили ли мы с вами его цель?
Каким из методов решения систем уравнений вы будите пользоваться?
Как по 5 бальной системе вы оцените свои знания по данной теме?
Уровень А | Уровень Б | ||
I вариант | II вариант | I вариант | II вариант |
а) | а) | а) | а) |
б) | б) | б) | б) |
в) | в) | в) | в) |
Дополнительное задание:
Задача – шутка:
В теплом хлеве у бабуси
Жили кролики и гуси.
Бабка странною была
Счет животным так вела:
Выйдет утром за порог
Сосчитает – 300 ног
А потом без лишних слов
Насчитает 100 голов.
И со спокойною душой
Идет снова на покой
Кто ответит поскорей
Сколько было там гусей?
Кто узнает из ребят
Сколько было там крольчат?
nsportal.ru
Урок по алгебре «Методы решения системы уравнения с двумя переменными» ( 9 класс)
Тема: Методы решения систем уравнений с двумя переменными.
Цели урока:
Обучающие:
— совершенствовать навыки решения систем уравнений второй степени;
— уметь применять свои знания при решении практических задач
Развивающие:
— развивать у обучающихся познавательный интерес к предмету;
— формировать умение преодолевать трудности при решении задач;
— формировать аналитическую деятельность
Воспитательные:
— продолжить формировать у обучающихся потребность к приобретению знаний;
— воспитывать умение контролировать внимание на всех этапах урока;
— воспитывать качества взаимопомощи, поддержки
Тип урока: урок применения знаний, умений и навыков
Оборудование: мультимедийное оборудование; компьютерная презентация.
Ход урока.
1.Организационный момент (определение и разъяснение целей занятия).
2.Актуализация опорных знаний.
1)В форме фронтального опроса повторяются основные понятия, определения, связанные с системами уравнений с двумя переменными
Определения
Системой уравнений называется некоторое количество уравнений, объединенных фигурной скобкой. Фигурная скобка означает, что все уравнения должны выполняться одновременно
Решением системы уравнений с двумя переменными называется пара значений переменных, обращающая каждое уравнение системы в верное равенство
Решить систему уравнений — это значит найти все её решения или установить, что их нет
Способы решения систем уравнений
Способ подстановки:
— Из какого-либо уравнения выразить одну переменную через другую
— Подставить полученное выражение для переменной в другое уравнение и решить его
— Сделать подстановку найденного значения переменной и вычислить значение второй переменной
— Записать ответ: х=…; у=…
Способ алгебраического сложения:
— Уравнять модули коэффициентов при какой-нибудь переменной
— Сложить почленно уравнения системы
— Составитьновую систему: одно уравнение новое, другое — одно из старых
— Решить новое уравнение и найти значение одной переменной
— Подставить значение найденной переменной в старое уравнение и найти значение другой переменной
— Записать ответ: х=…; у=… .
Графический способ
— Выразить у через х в каждом уравнении
— Построить в одной системе координат график каждого уравнения
— Определить координаты точки пересечения
— Записать ответ: х=…; у=… ,или (х; у)
3)Проверка домашнего задания через тетради.
4)Индивидуальная работа по карточкам
1.Установить соответствие между графиками
2.Решить уравнение
3.Решить неравенство
4.Найти значение выражения
5.Решите системы уравнений
Вариант I1.
В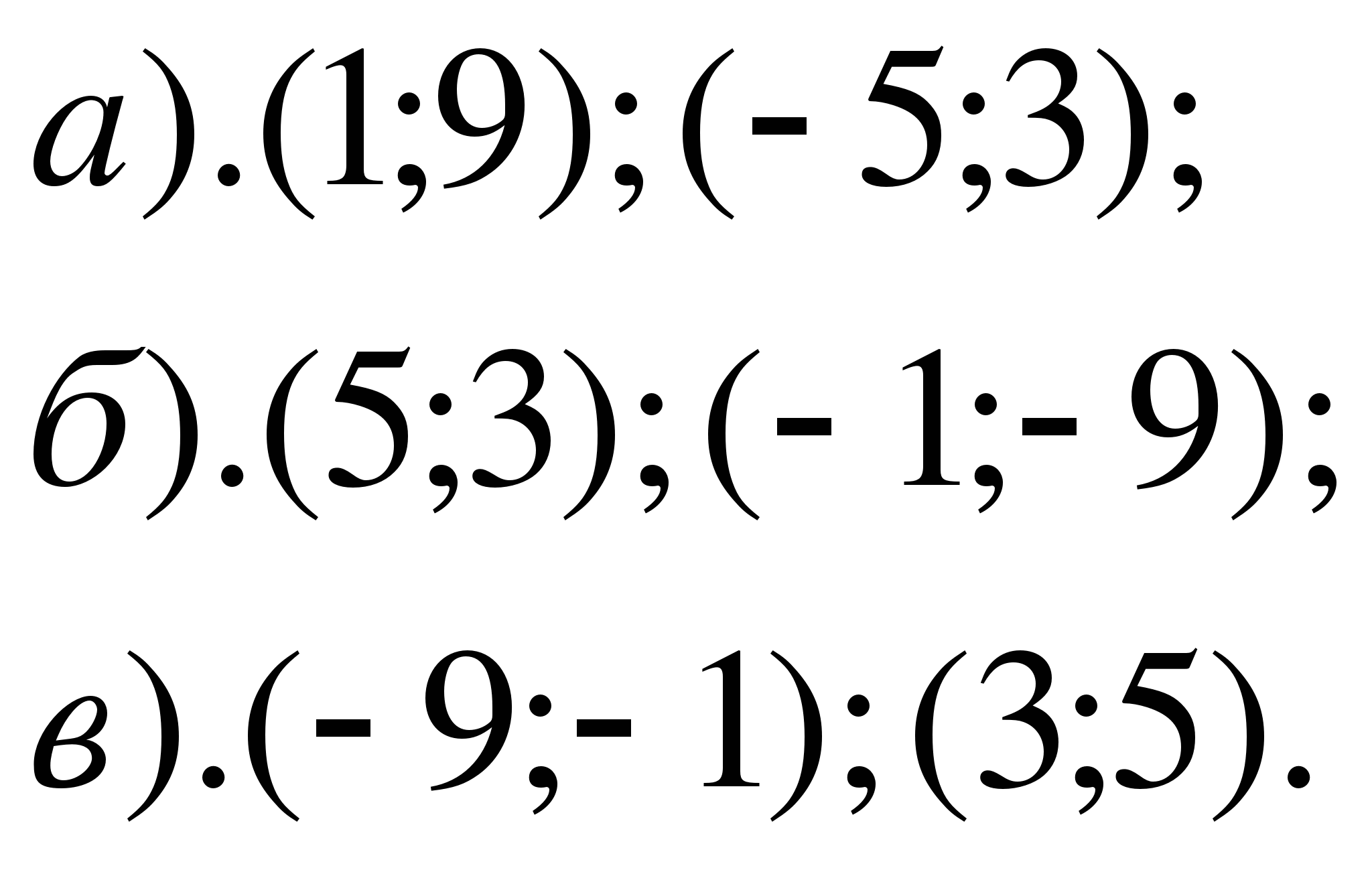 арианты ответов:
арианты ответов:
Вариант II
1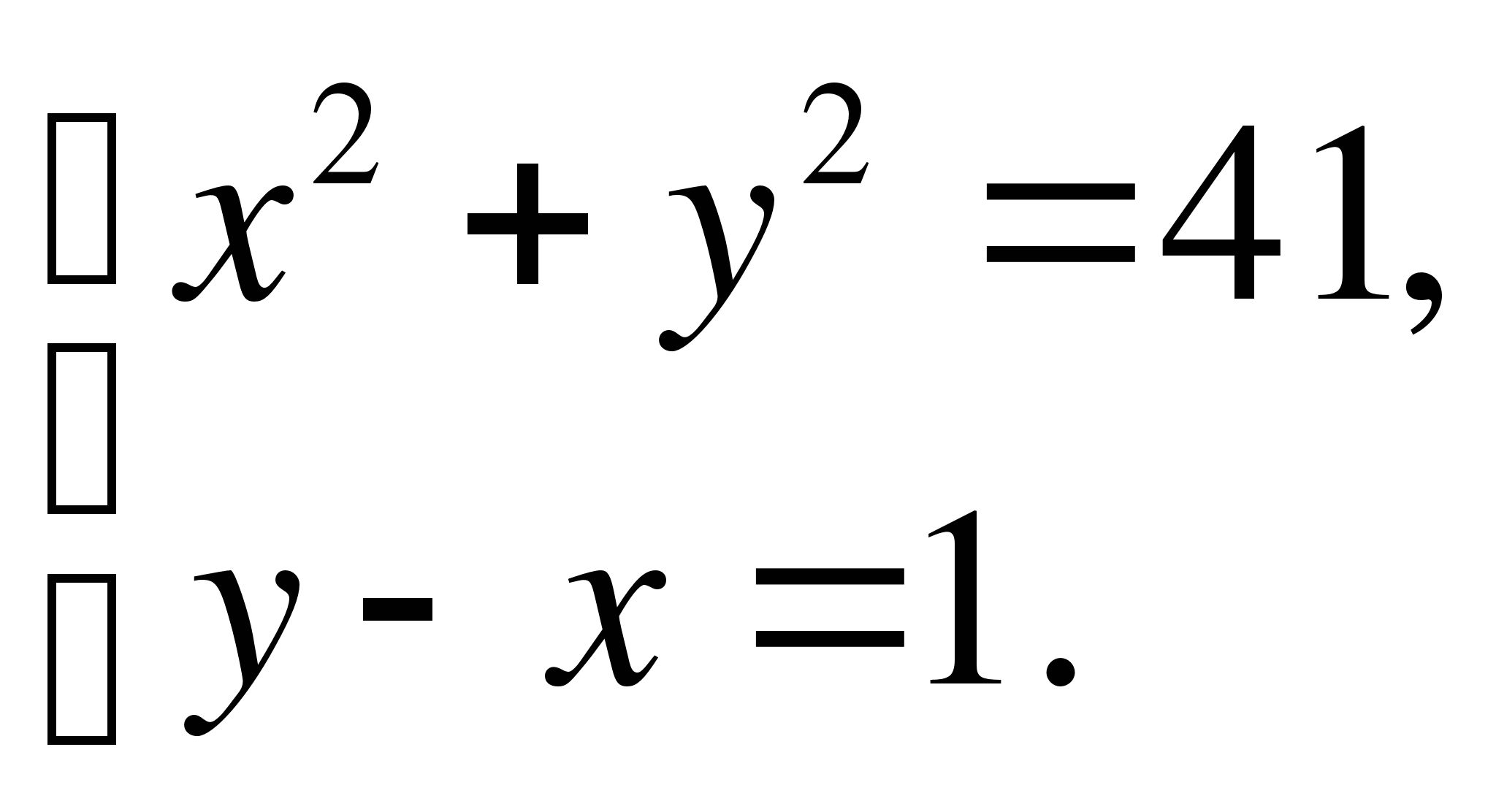 .
.
Варианты ответов:
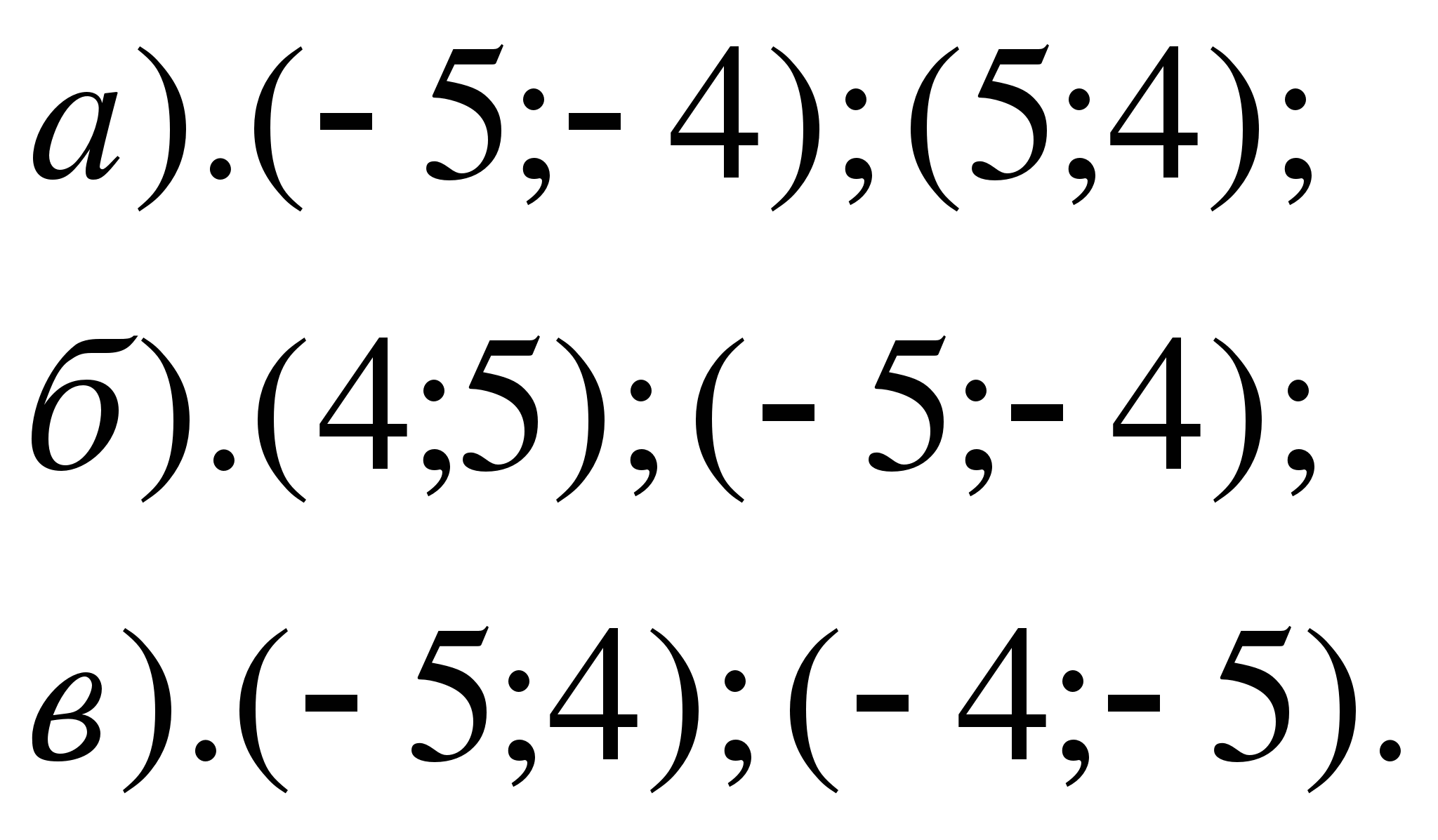
6.Отработка вычислительных навыков
2 уровень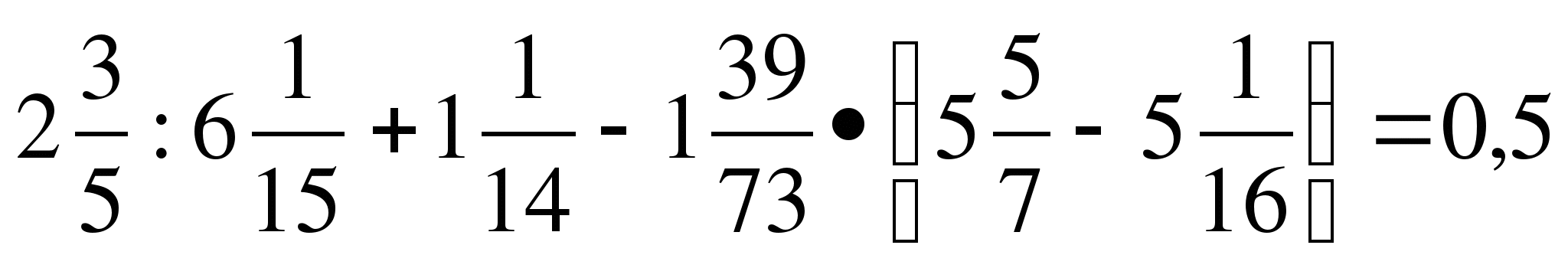
1)
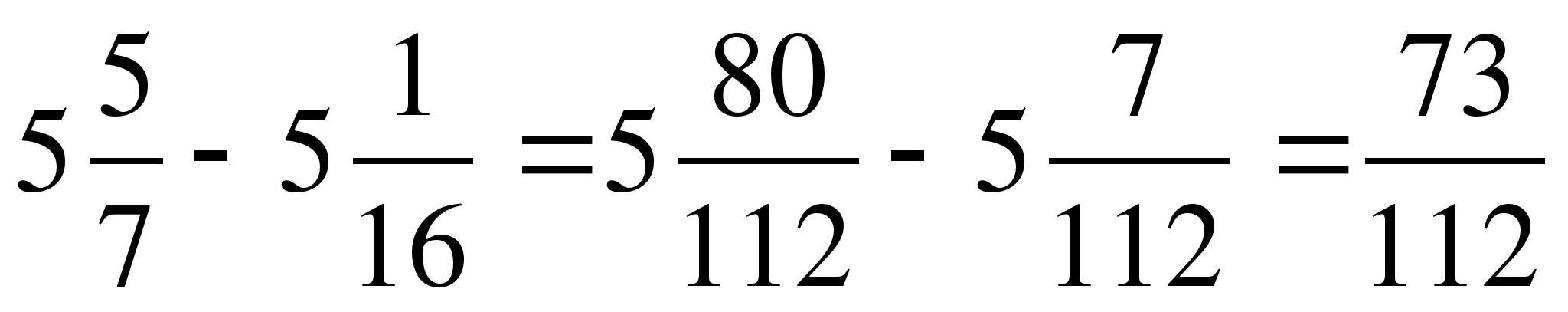
2)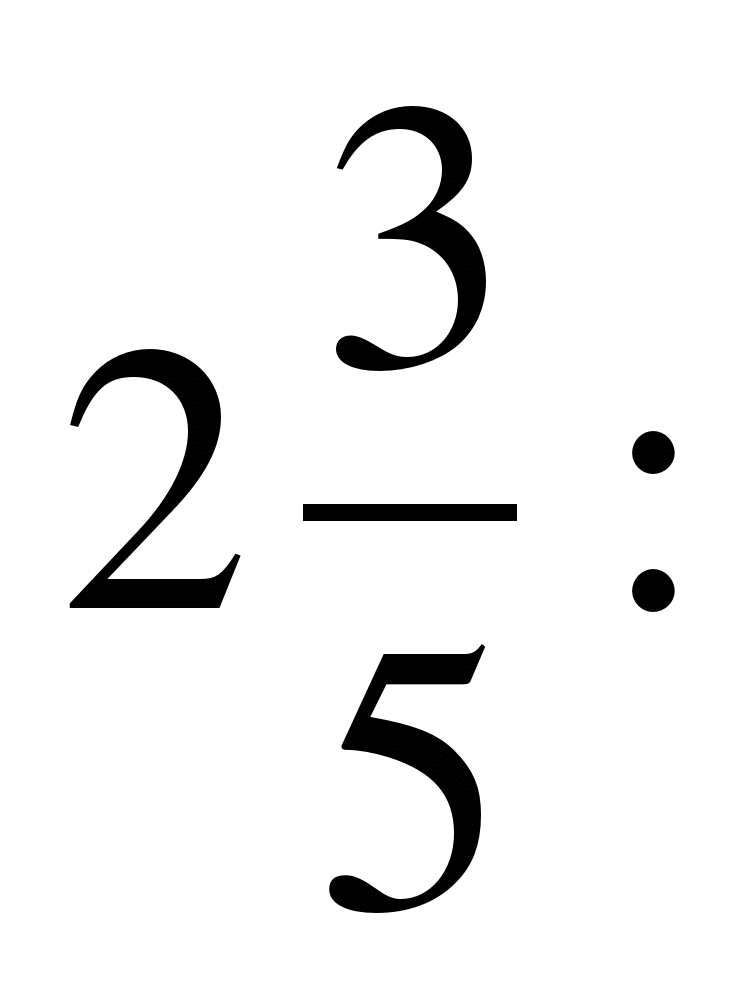
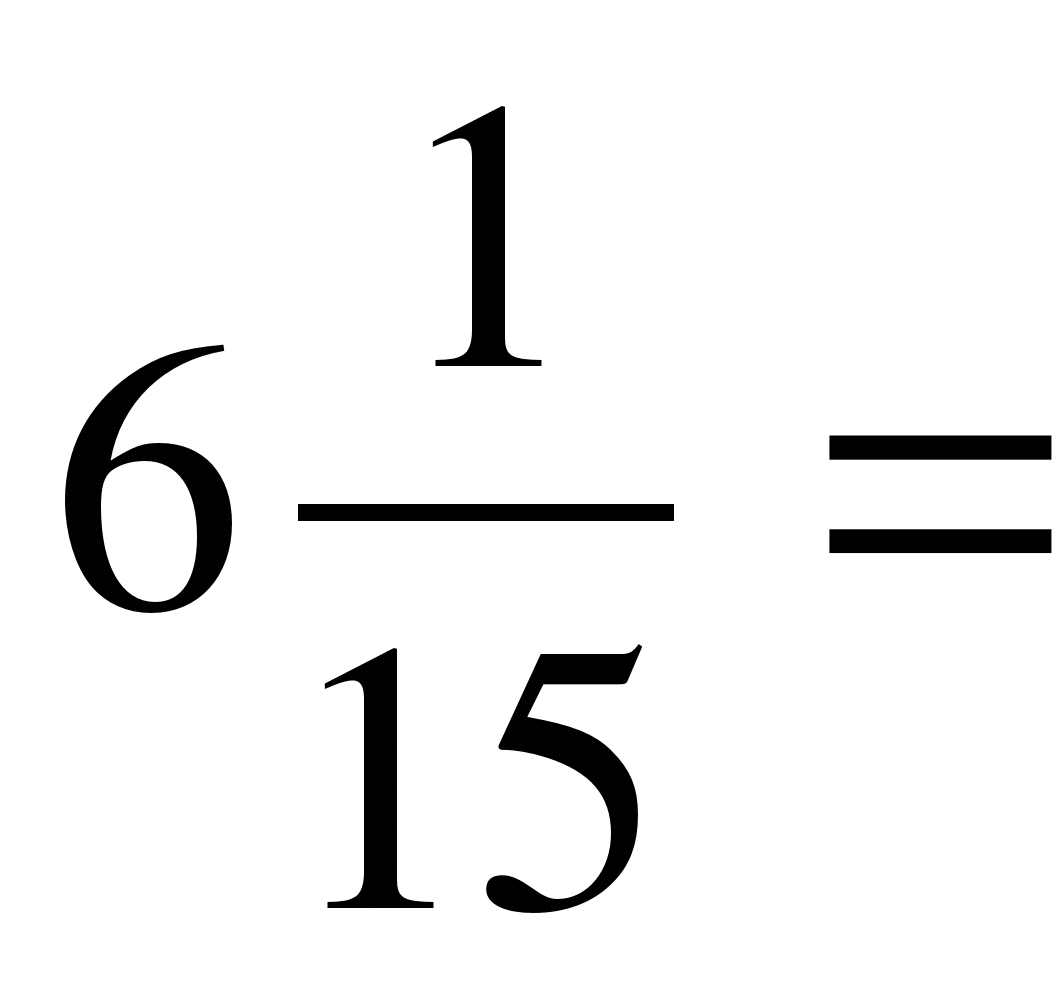
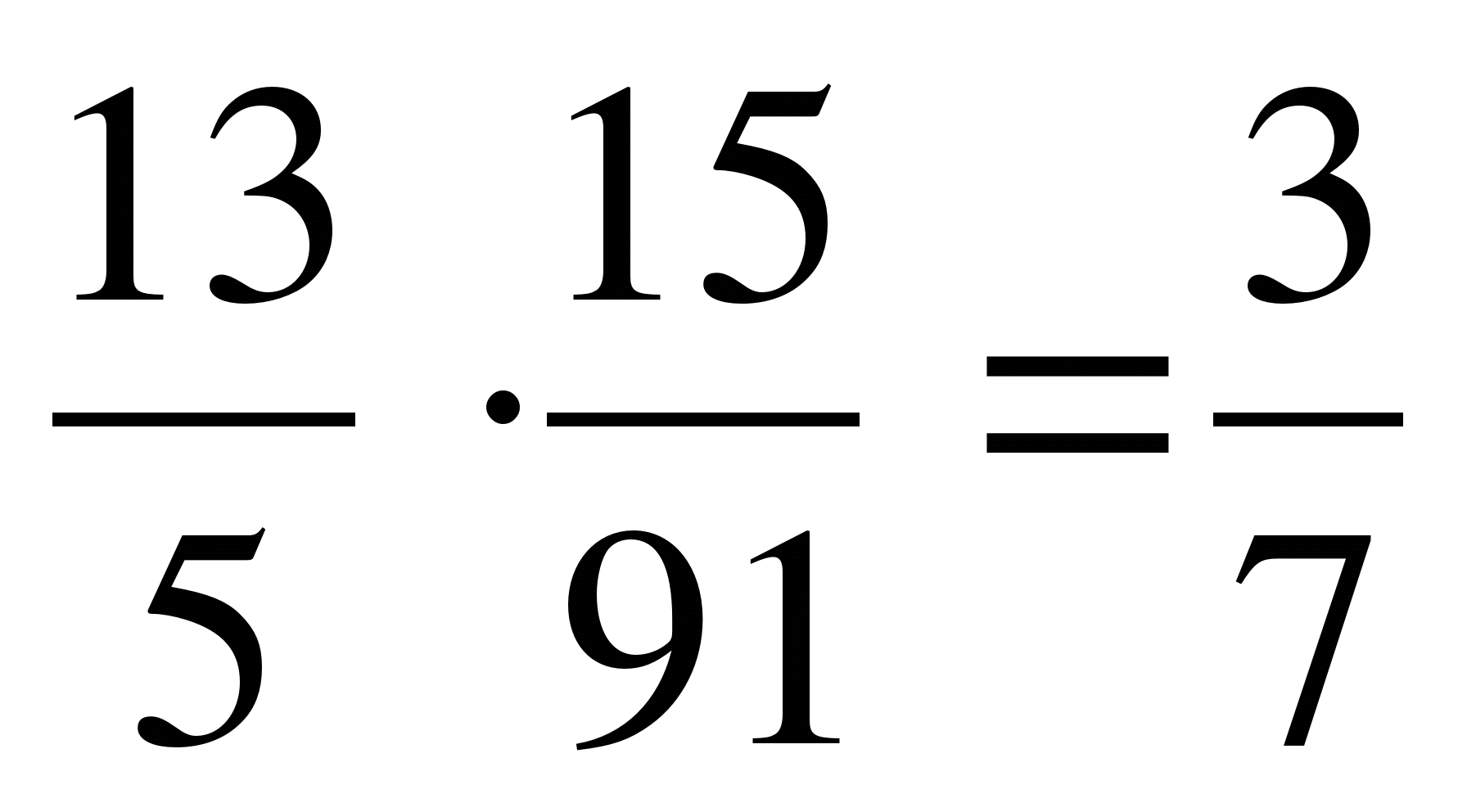
3)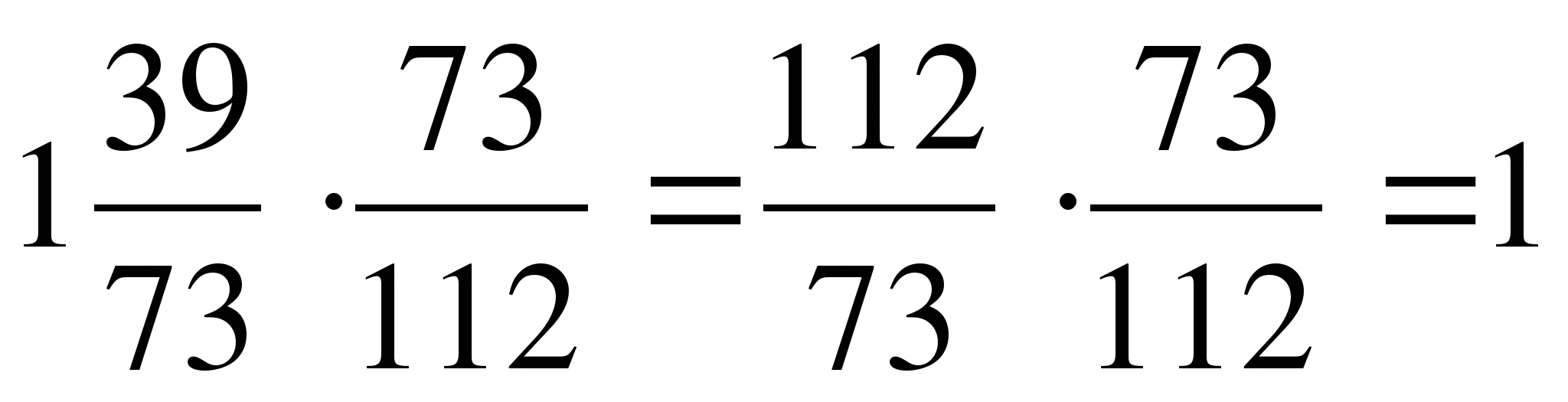
4)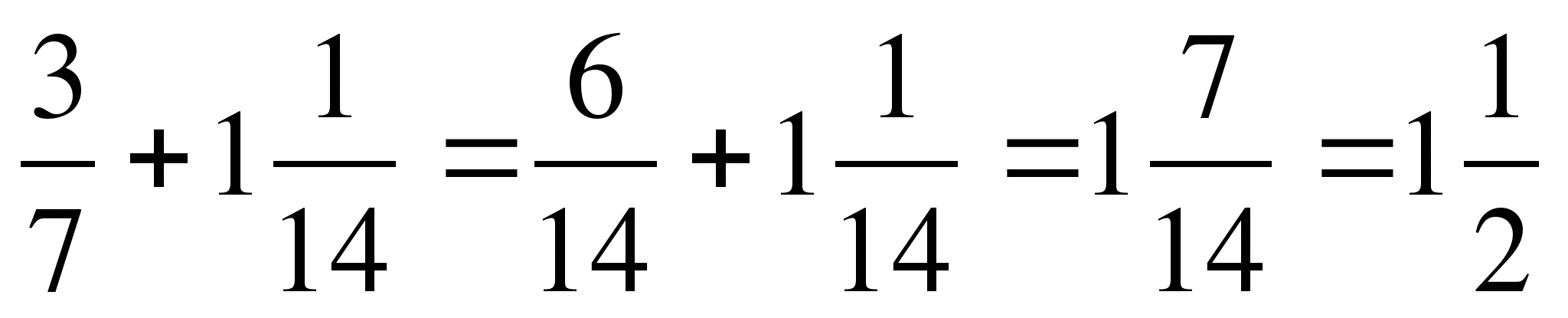
5)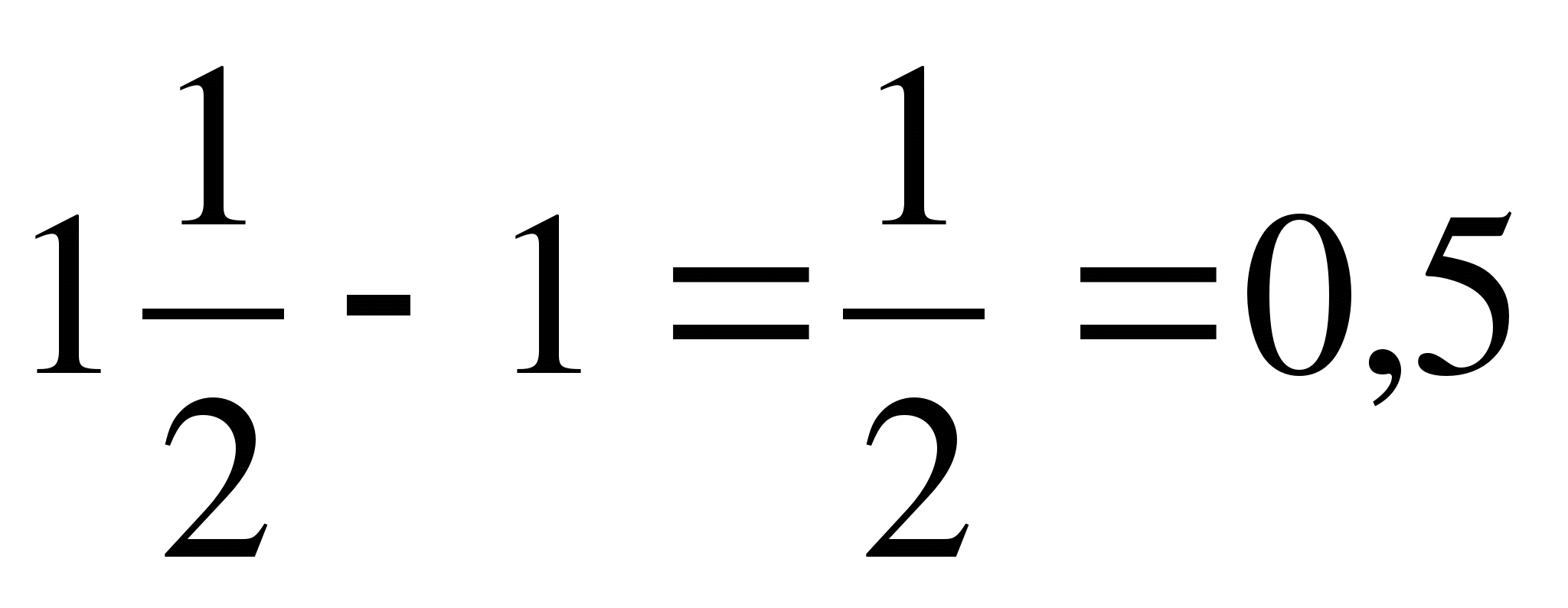
Найти наименьшее значение выражения 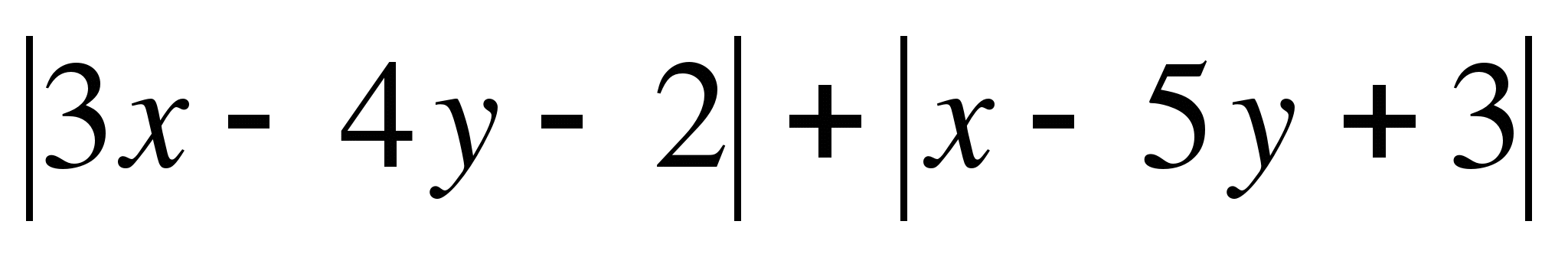 и определить при каких хи у оно достигается
и определить при каких хи у оно достигается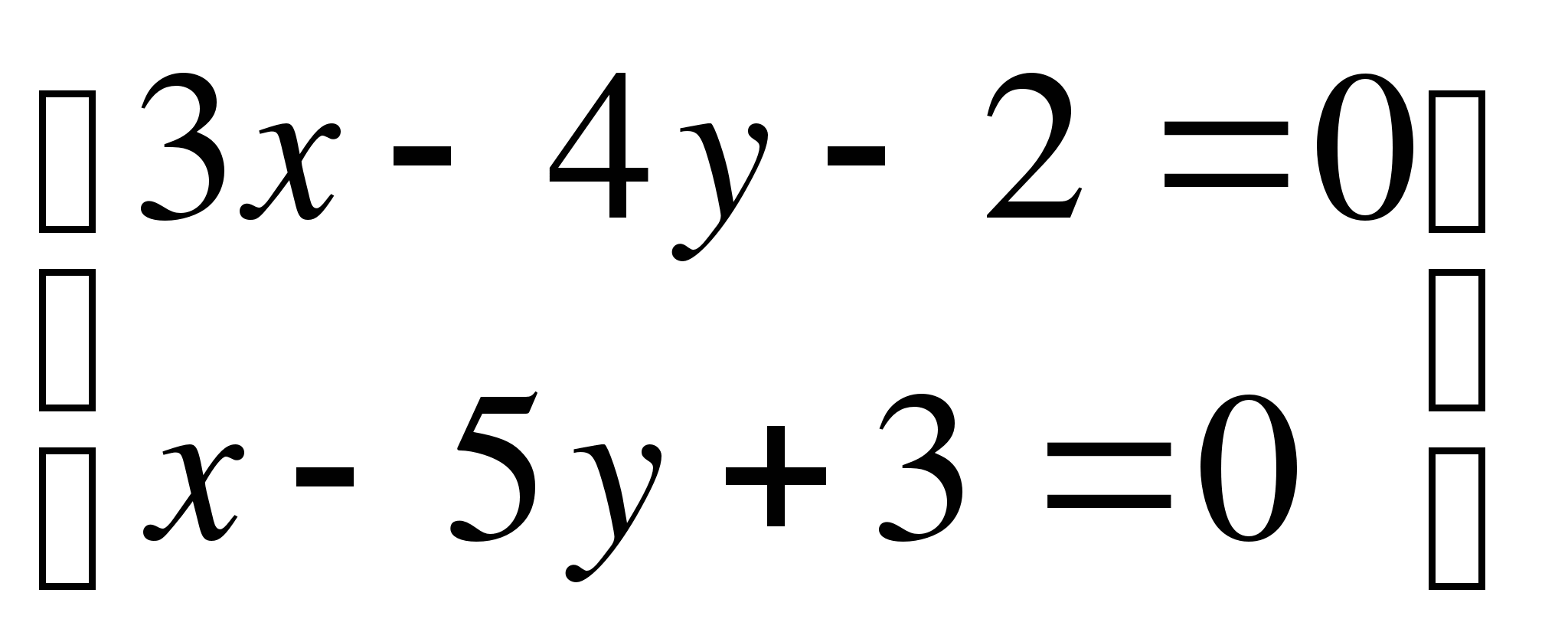
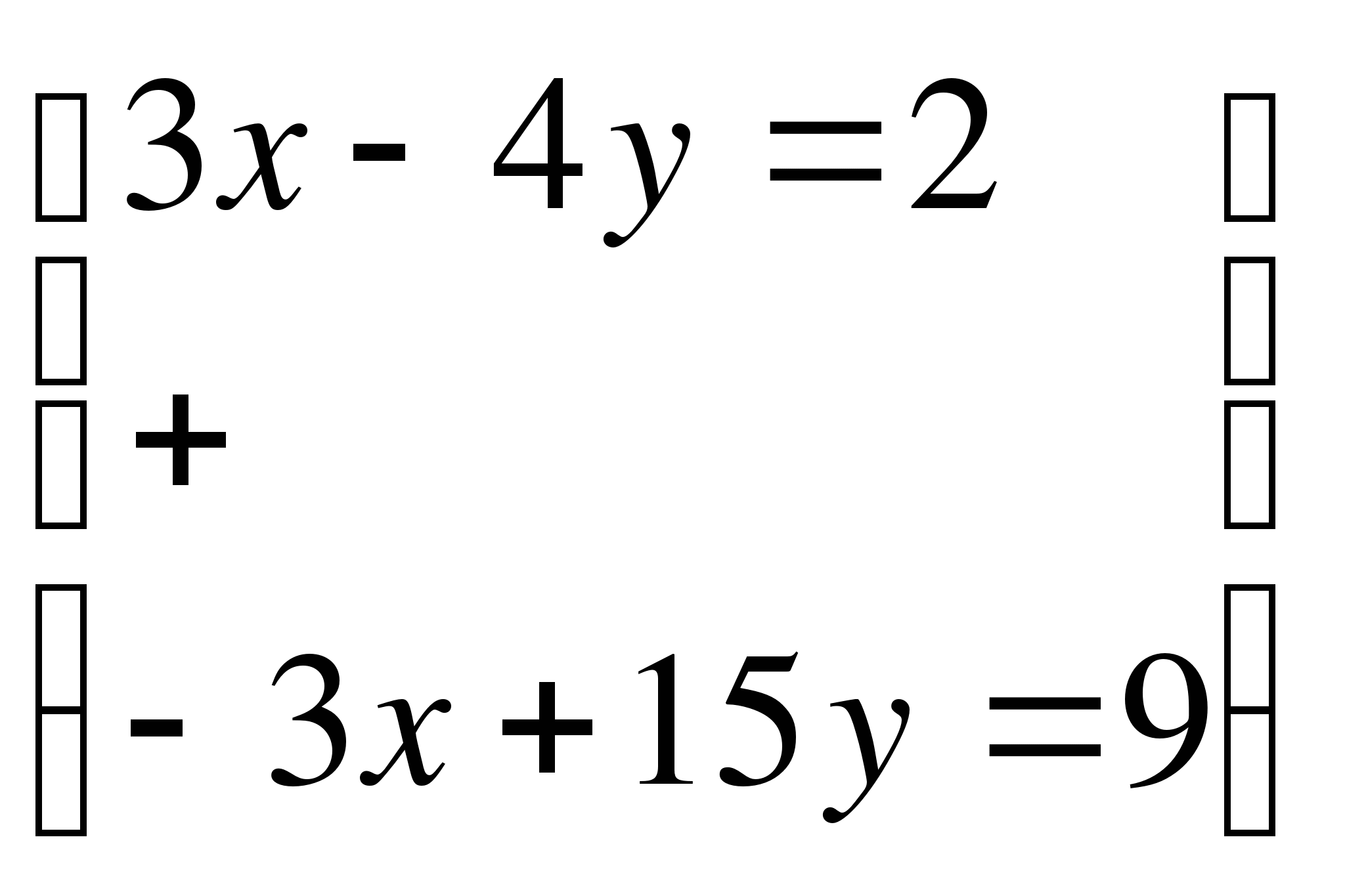
11у=11
У=1
Х-5=-3
Х=2
Ответ 0,(2;1)
7.Решите системы уравнений
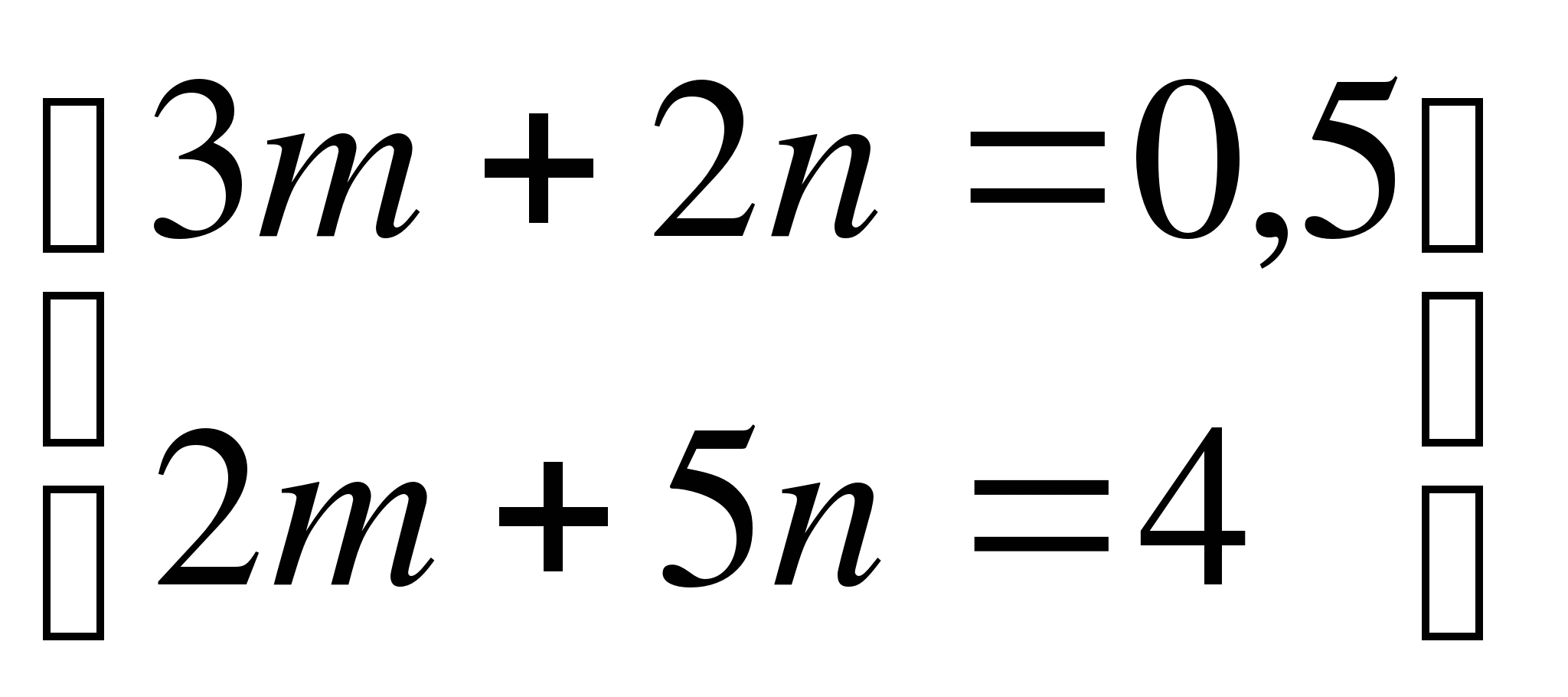
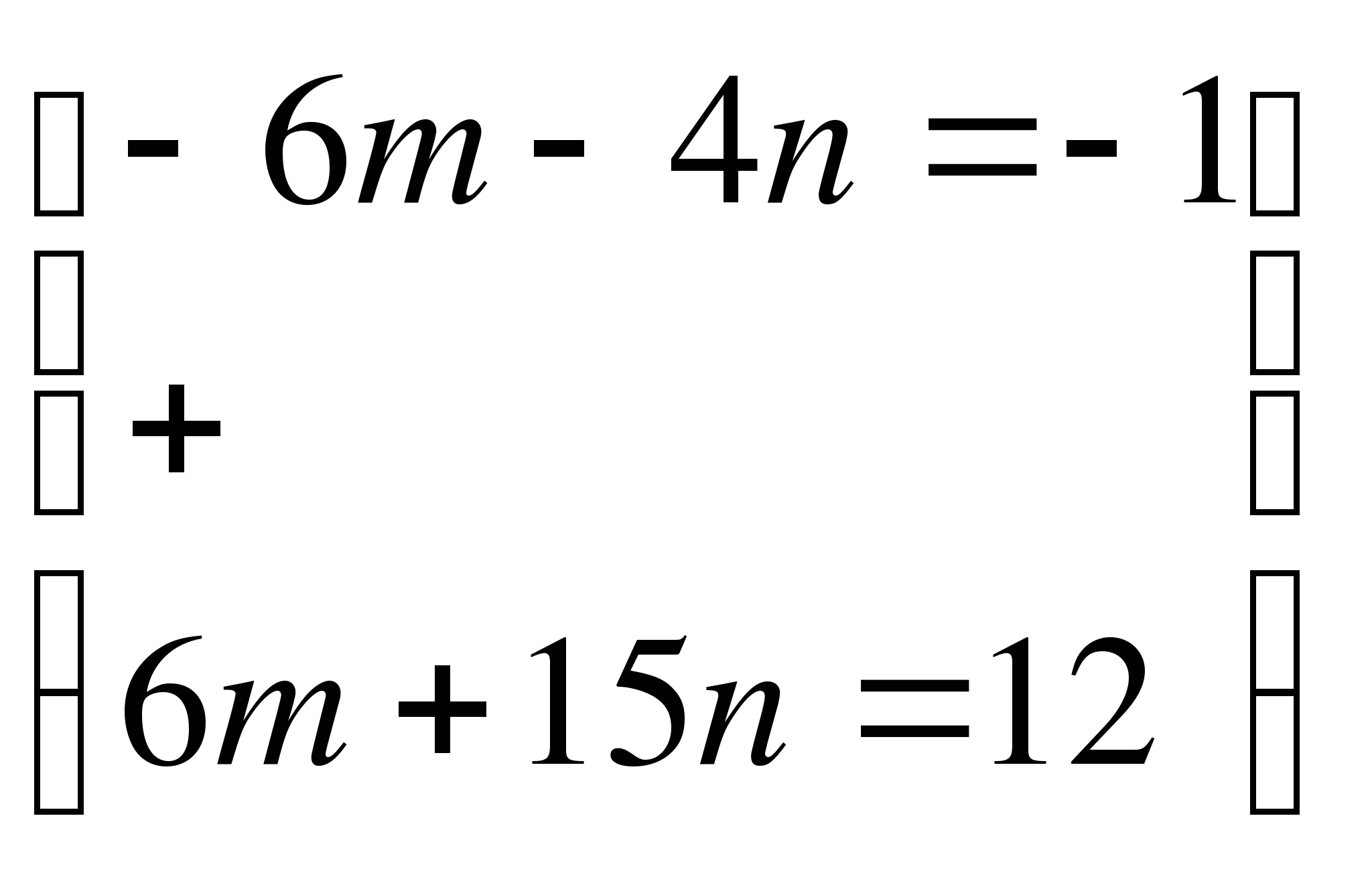
11п=11
п=1
2т+5=4
т=-0,5 Ответ(-0,5;1)
6.10(б)
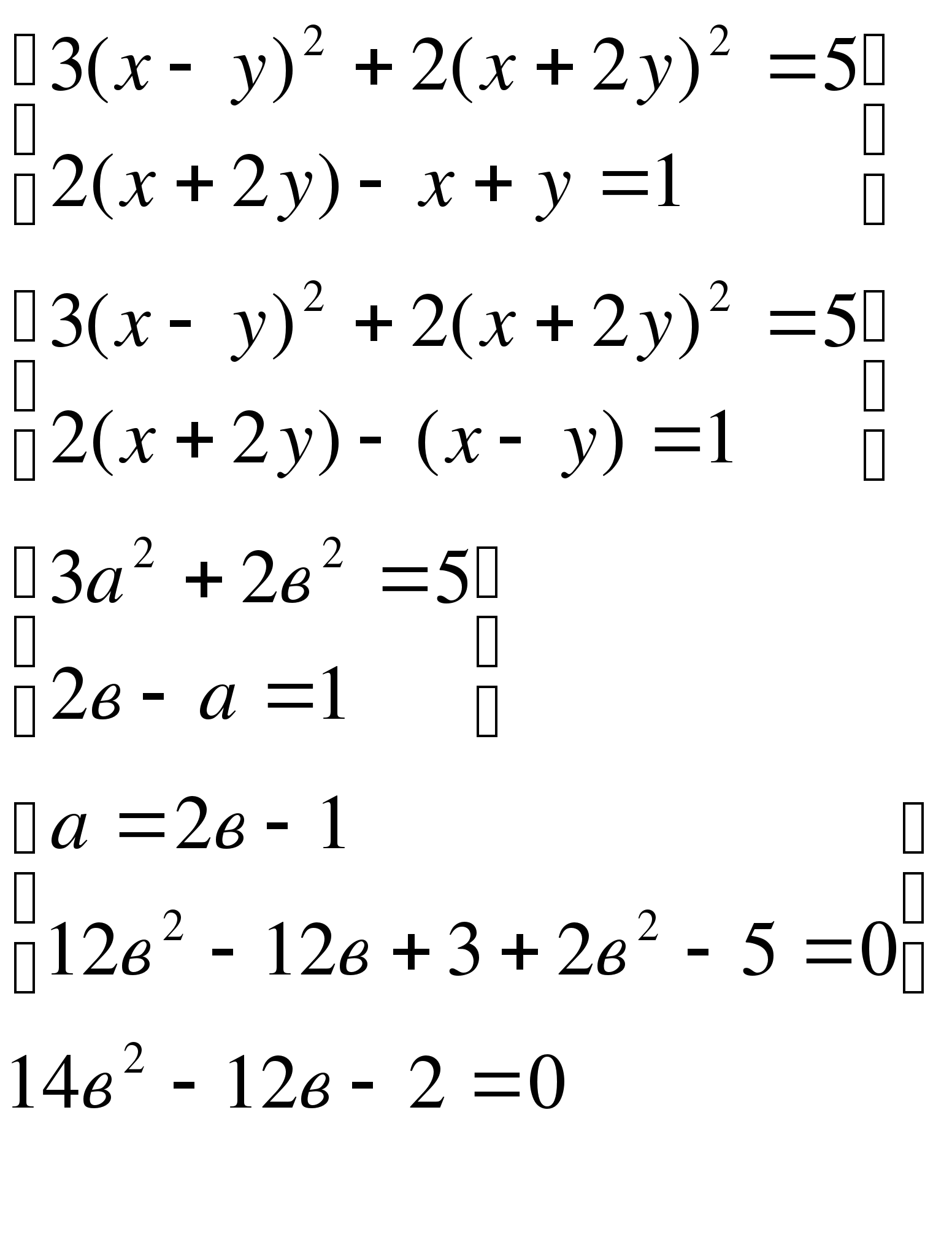
7в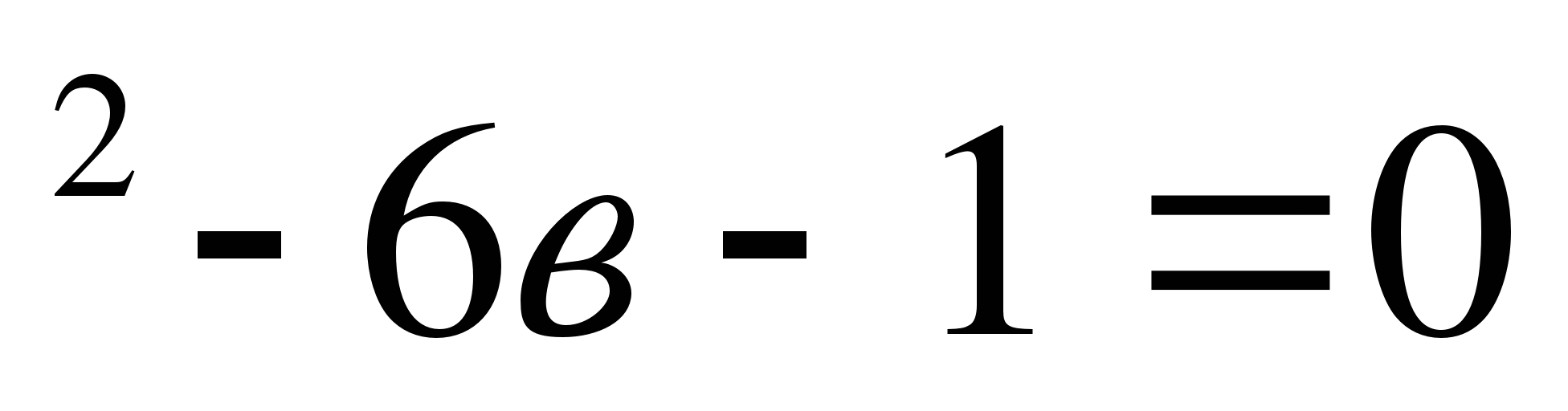 Д=64, в
Д=64, в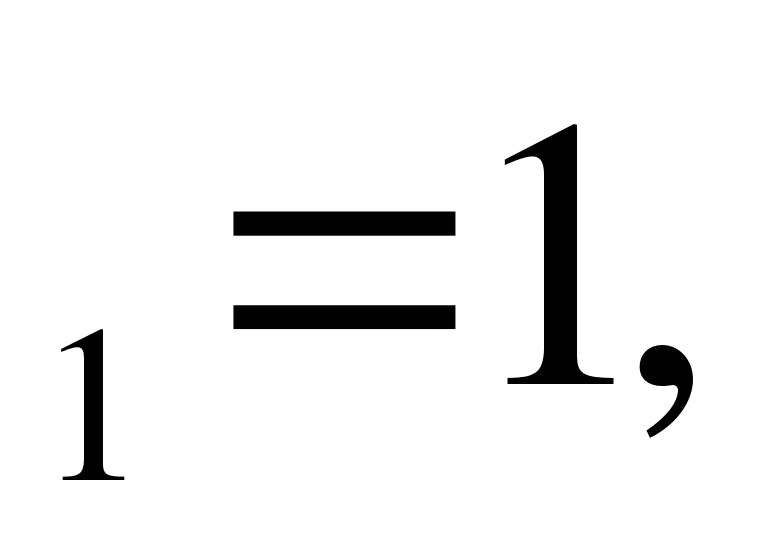 в
в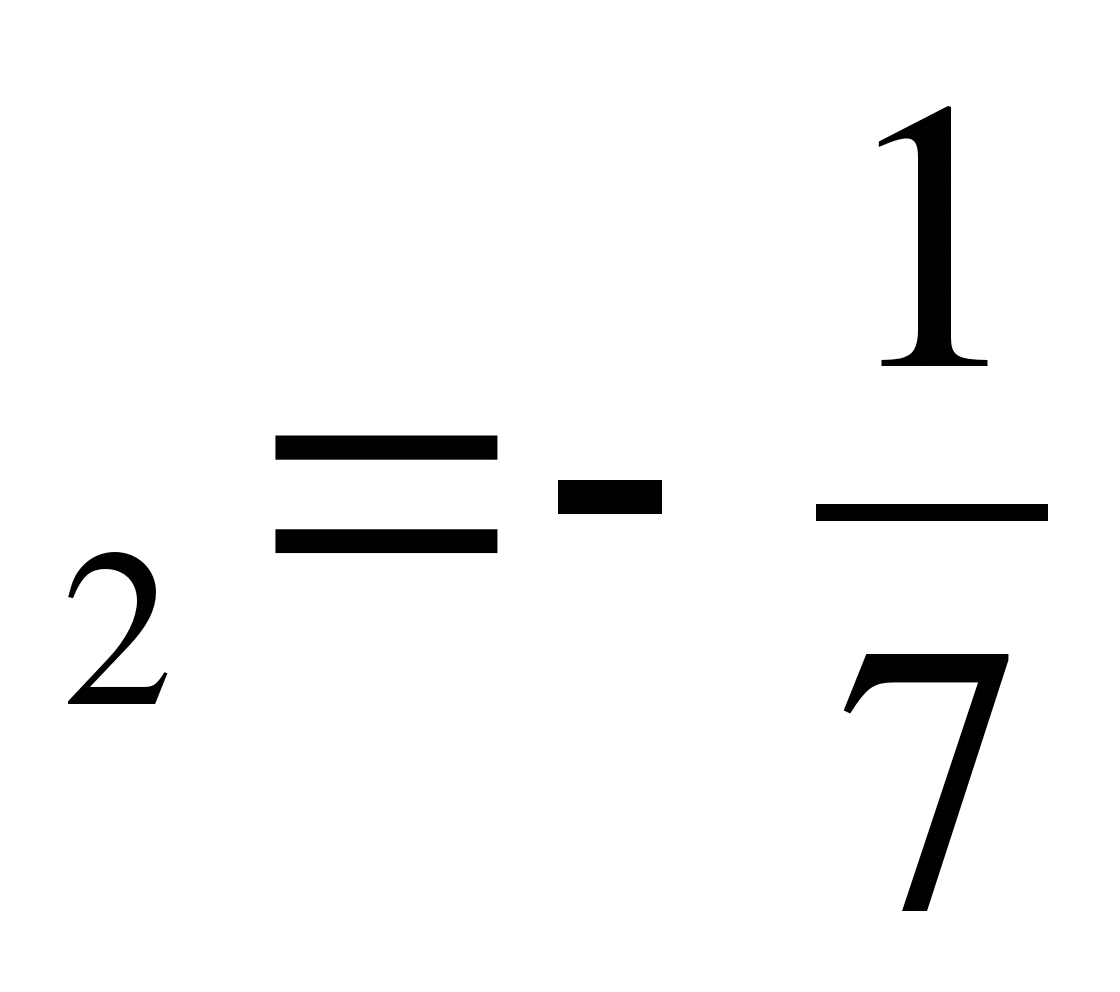
8.Самостоятельная работа выполняется по карточкам, дифференцированно, с учётом индивидуальных способностей обучающихся и их подготовленностью
Критерии оценивания:
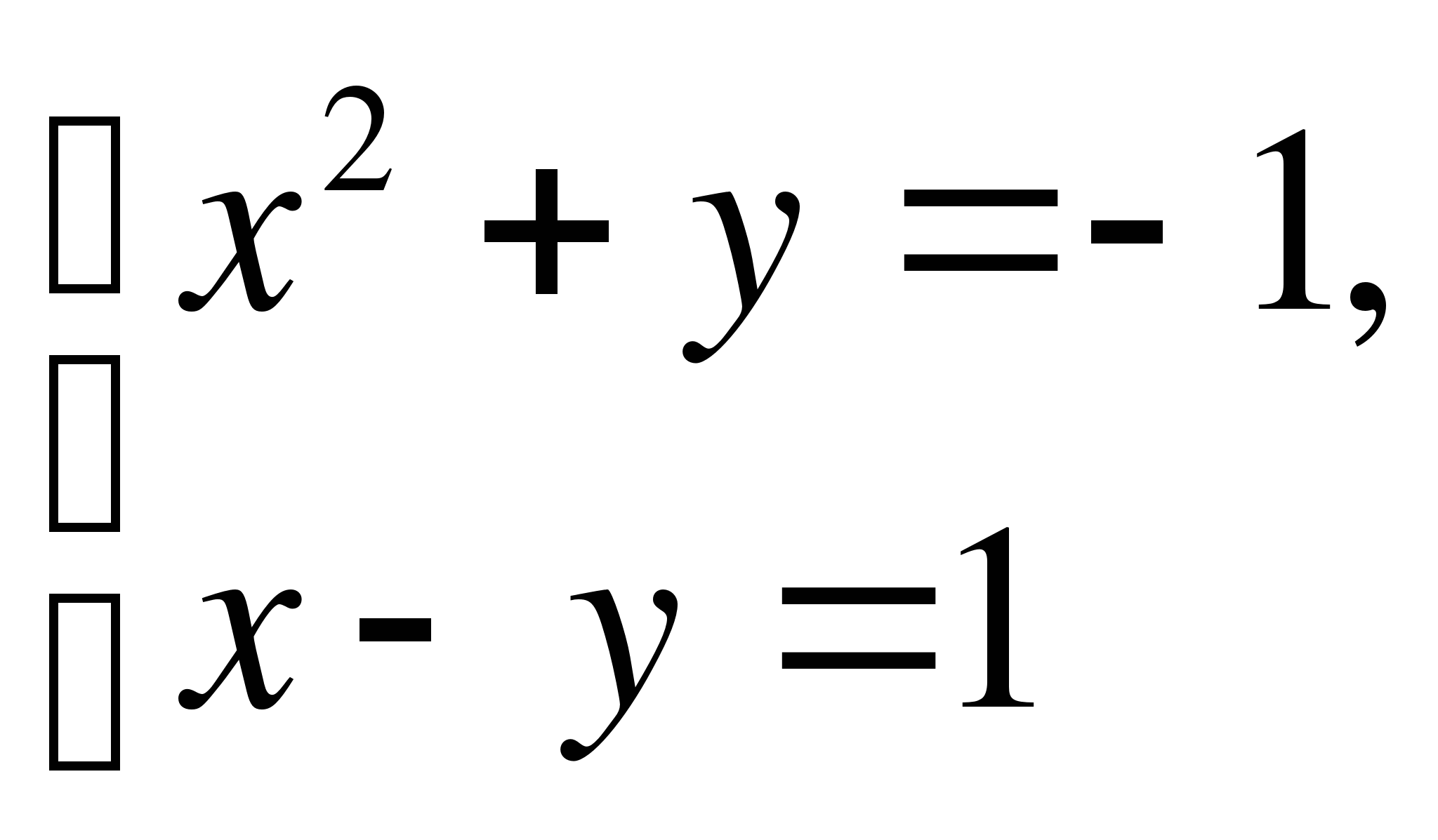
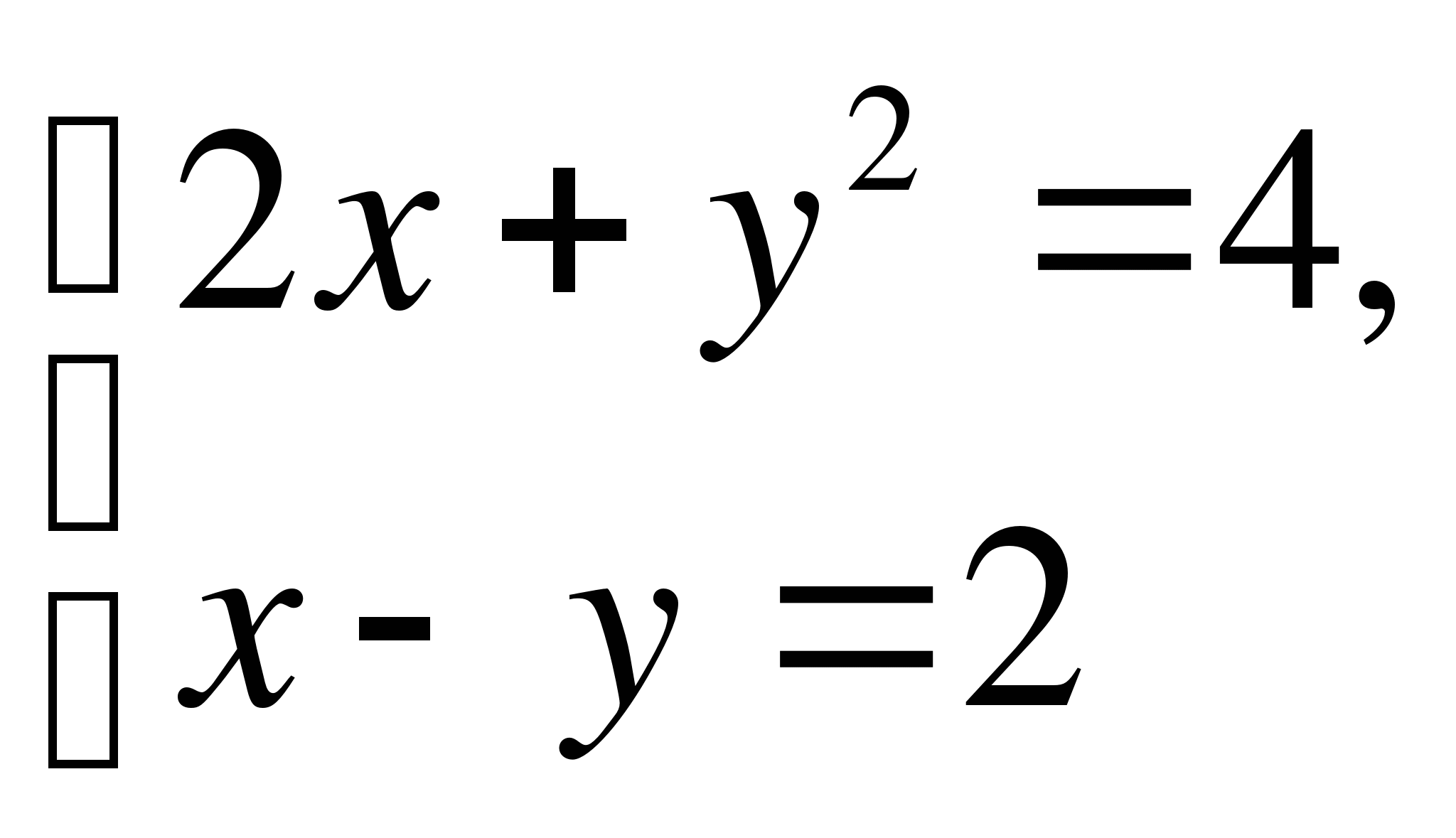
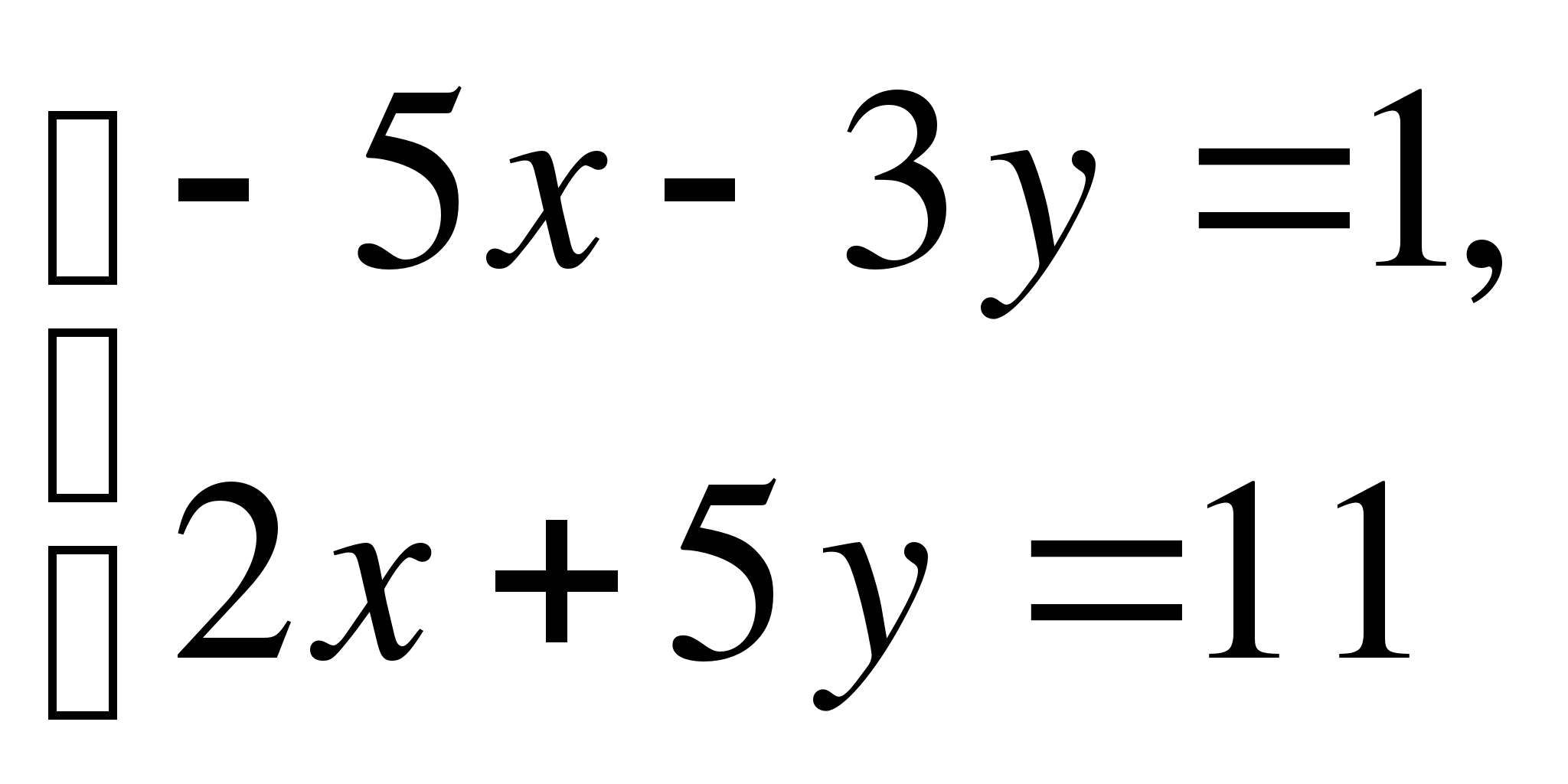
Вариант 2
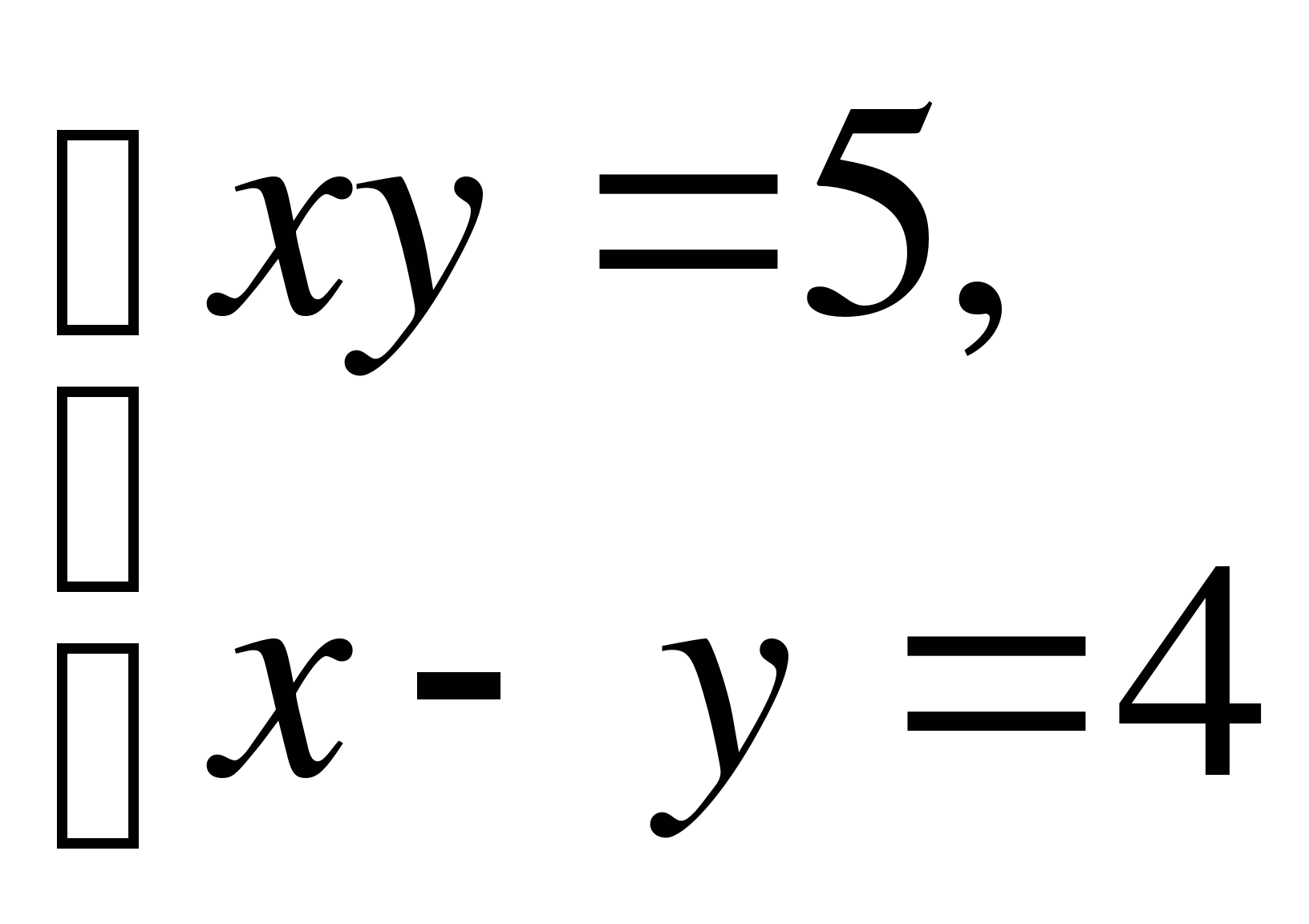
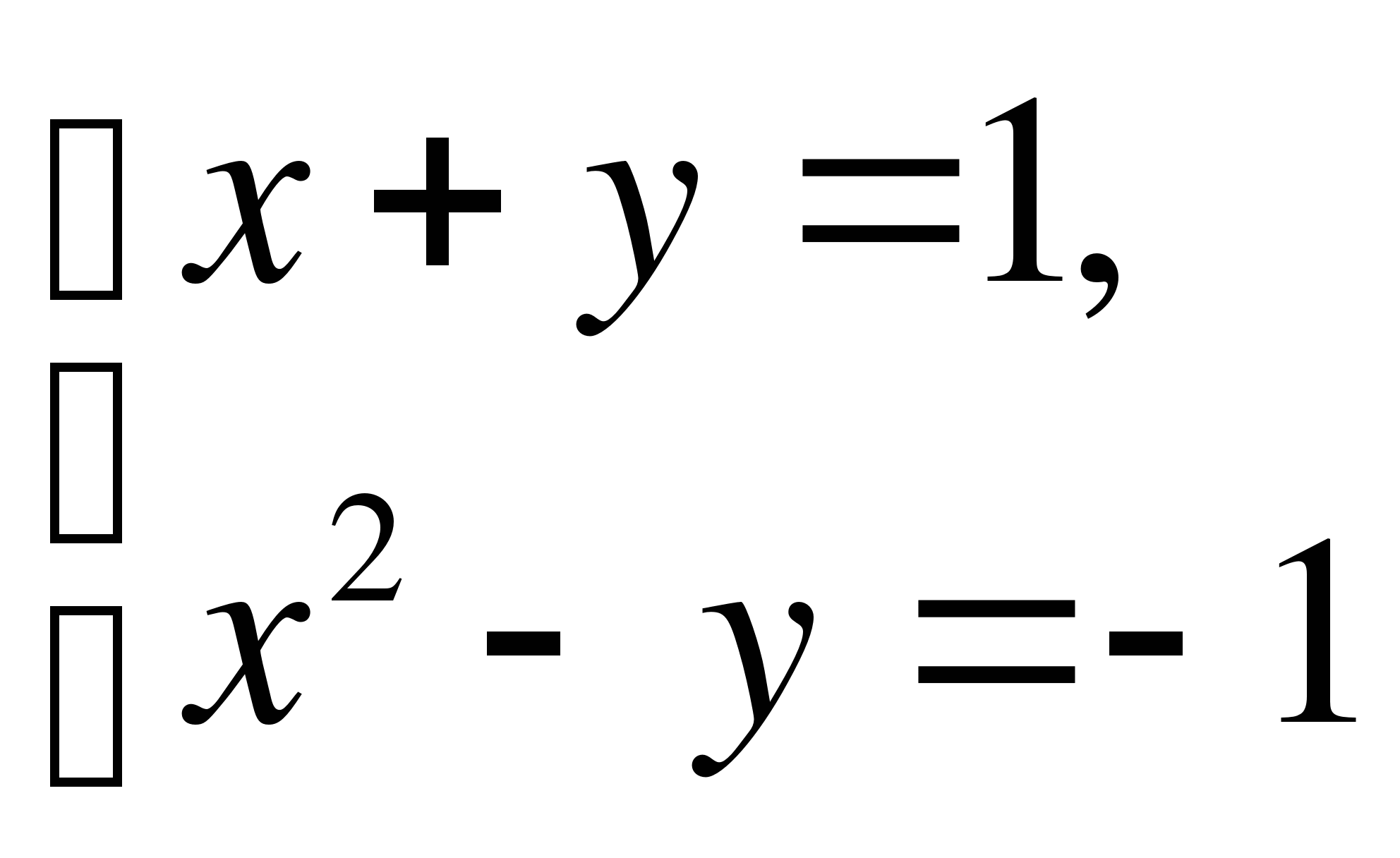
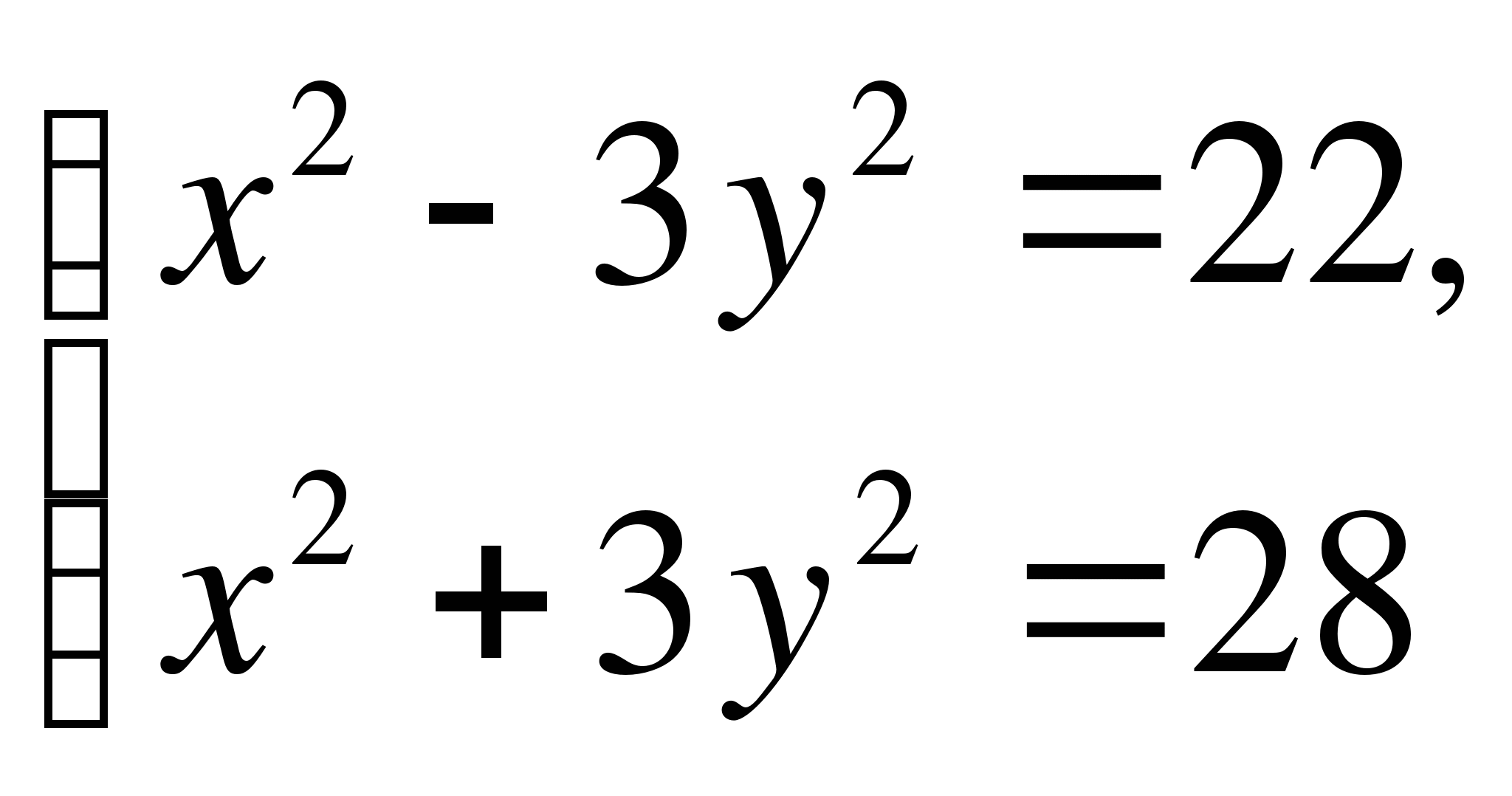
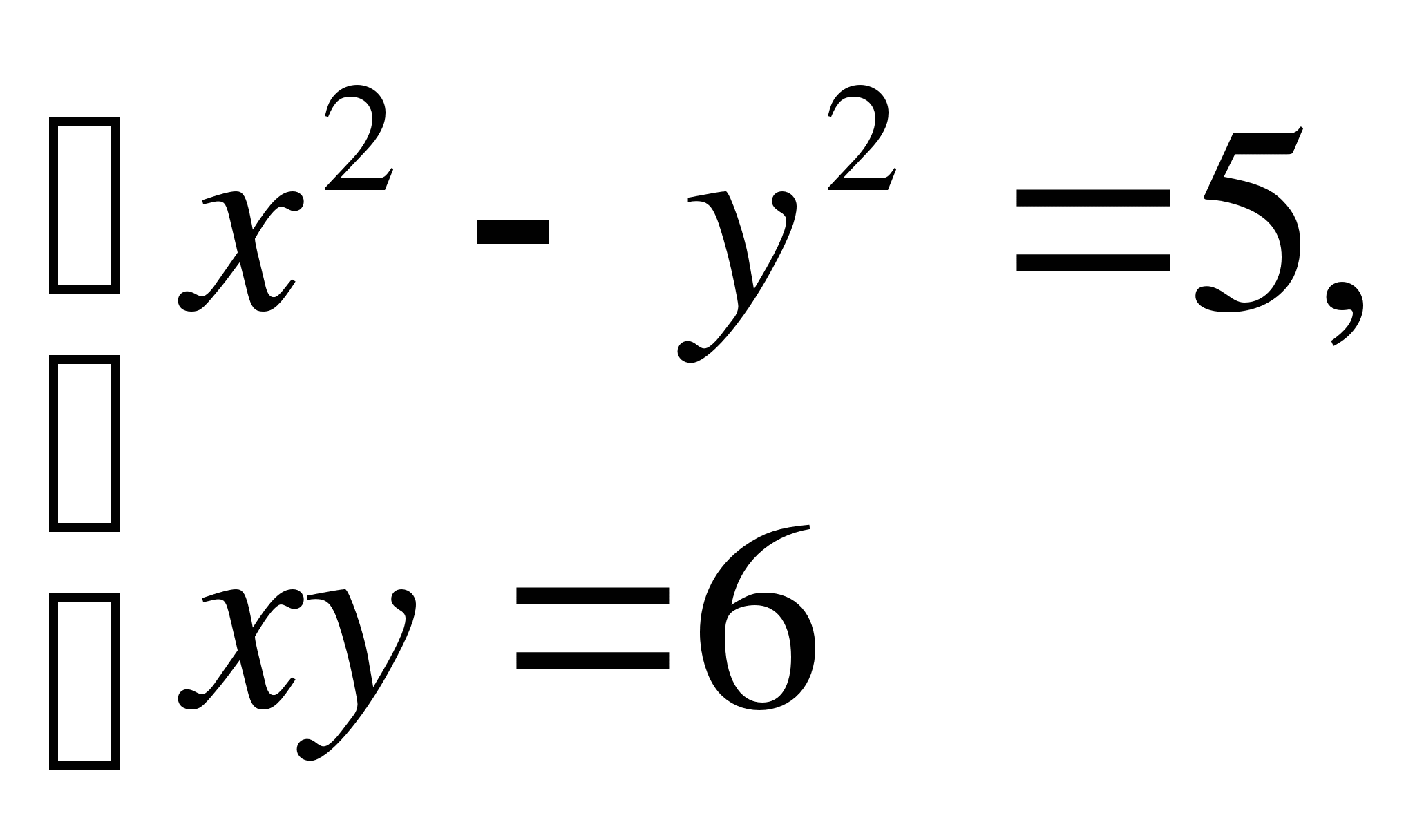
Вариант 3
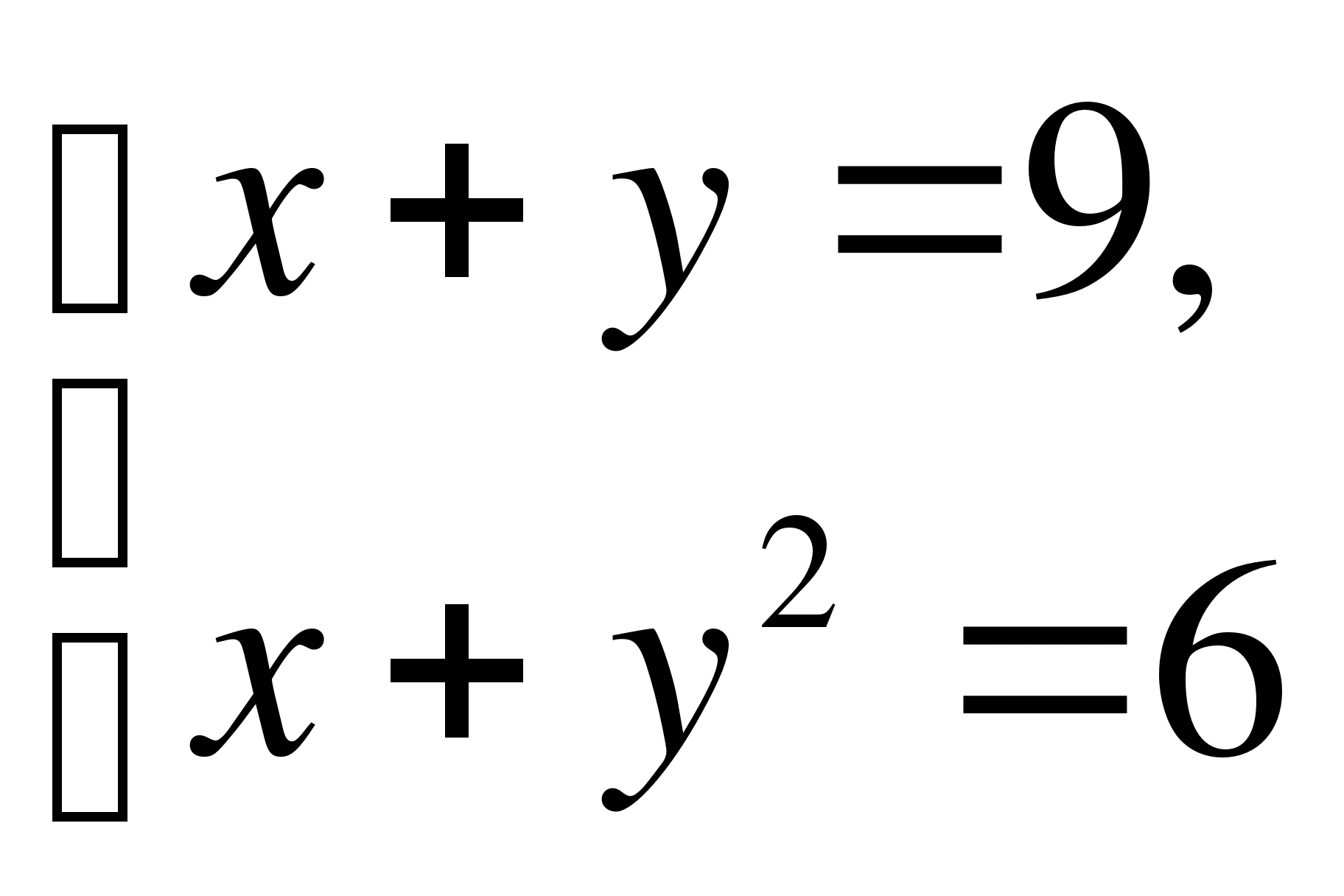
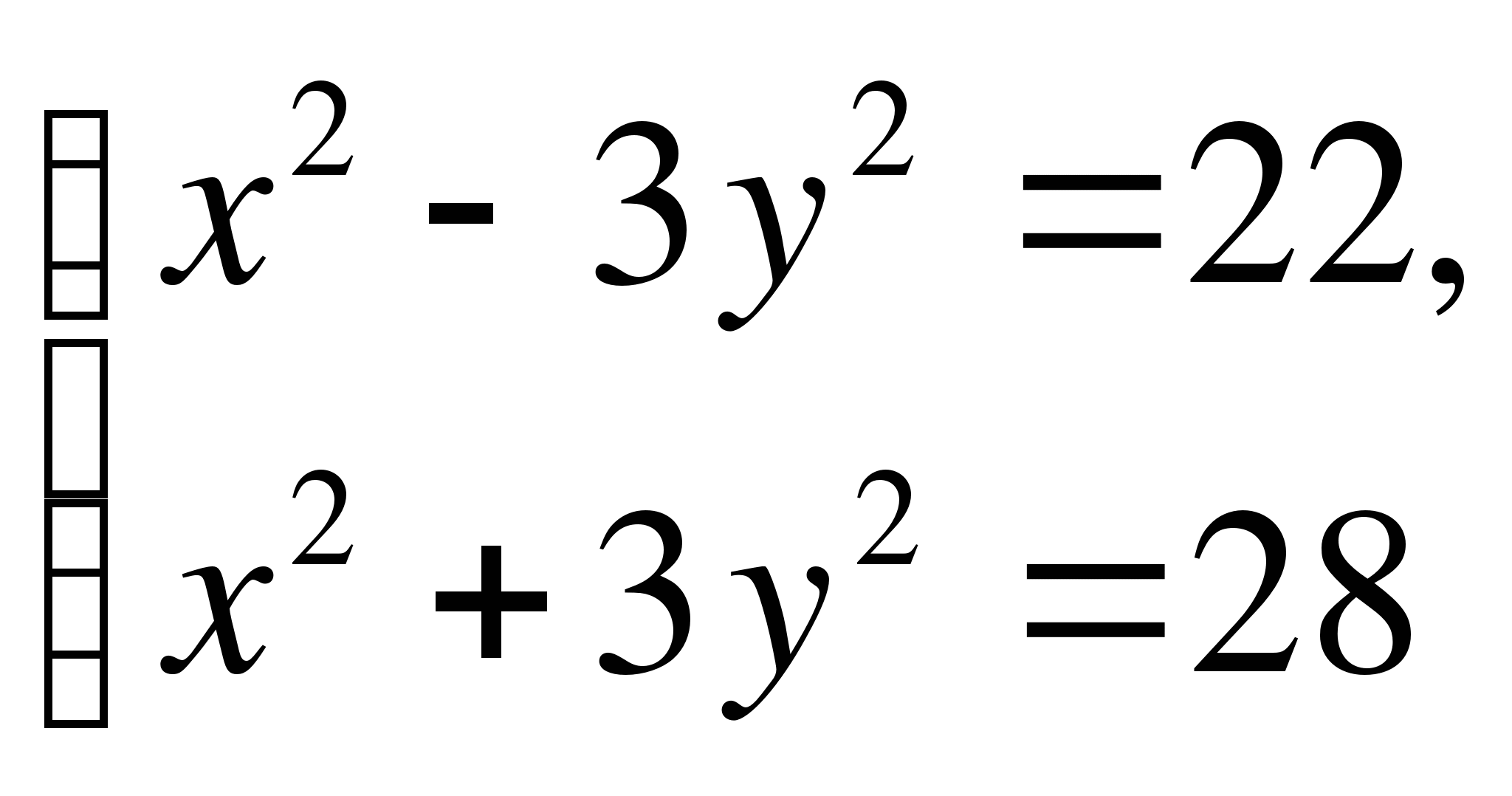
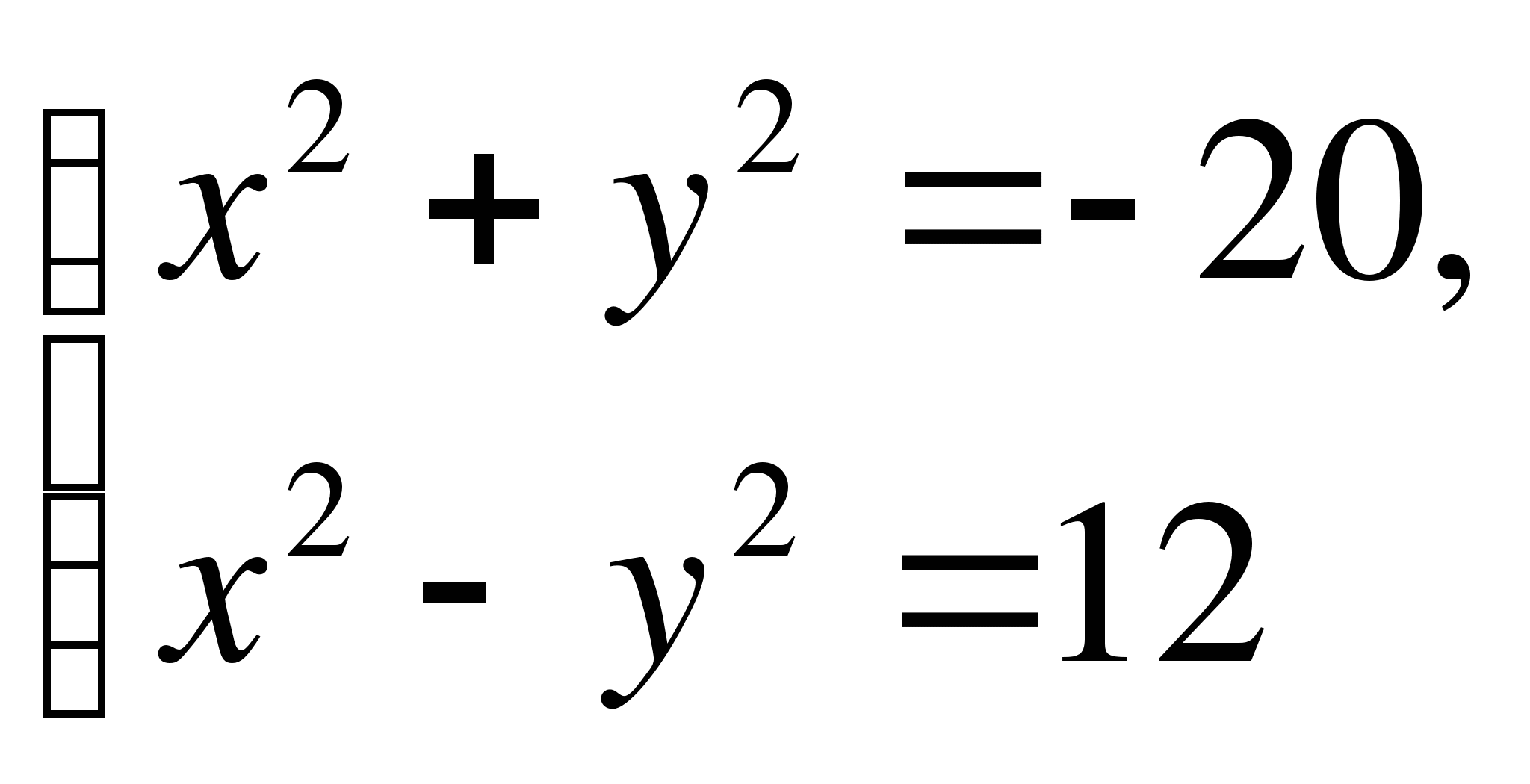
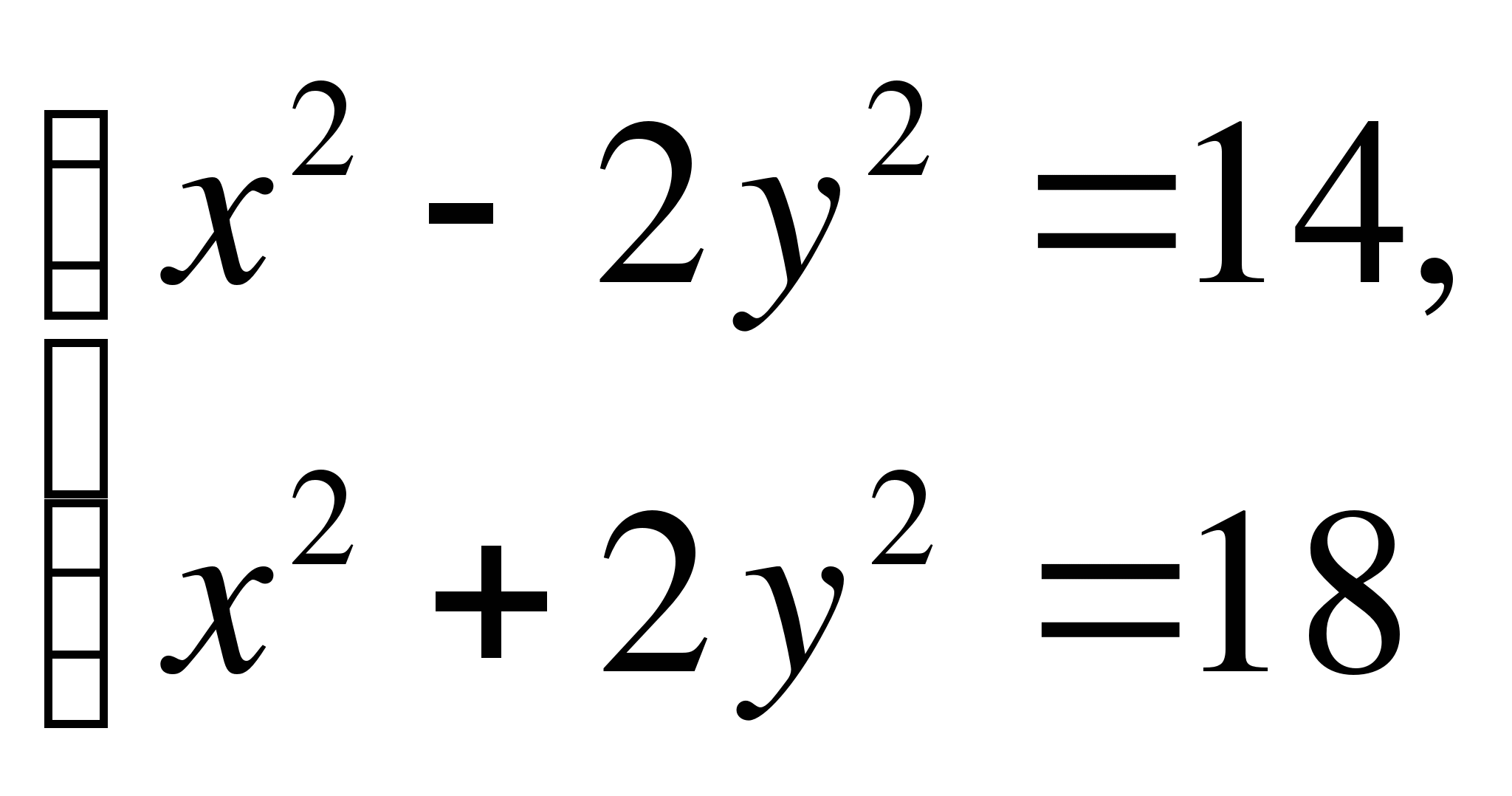
Вариант 4
Постройте график функции 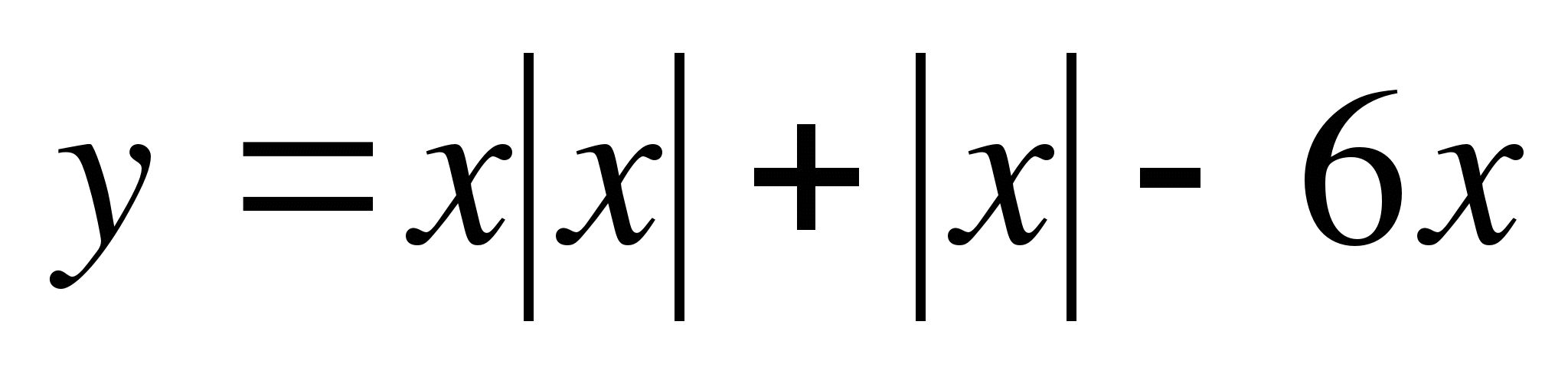 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку
9.Итог урока. Рефлексия
Учащимся предлагаются две картины с изображением пейзажа. Одна картина проникнута грустным, печальным настроением, другая — радостным, веселым. Ученики выбирают ту картину, которая соответствует их настроению.
10.Инструктаж по выполнению домашнего задания
infourok.ru
Системы уравнений с двумя переменными (конспект+презентация)
Тема: «Системы уравнений с двумя переменными».
Цели урока:
Обучающие: систематизировать знания по данной теме, выработать умение решать системы уравнений, содержащие уравнения второй степени графическим способом, способами подстановки и сложения.
Развивающие: развивать вычислительную технику, мыслительную активность, логическое мышление, интерес к предмету; способствовать формированию ключевых понятий; выполнение заданий различного уровня сложности.
Воспитывающие: воспитывать внимательность, аккуратность, умения четко организовывать самостоятельную и индивидуальную работу.
Мотивация обучающихся к учебной деятельности. (Слайд 2)
Девизом нашего урока будут слова: «Дорогу осилит идущий, а математику – мыслящий»
Как вы понимаете эти слова?
Актуализация знаний (Слайд 3)
Что является решением системы уравнений с двумя переменными? (пара чисел, которые при постановке в эту систему превращают каждое ее уравнение в верное равенство)
Что значит решить систему уравнений с двумя переменными? ( найти все ее решения или установит , что их нет)
Какие существуют способы решения систем уравнений с двумя переменными?
(Слайд 4)Определите, какая из этих систем имеет одно решение, не имеет решений, имеет бесконечное множество решений.
а) 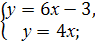
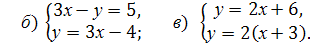
5. (Слайд 5) Определите, решением каких систем является пара чисел (3;5).
а) 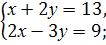
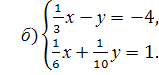
III. Сообщение темы и целей урока.
IV. Работа в группах.(Слайд 6)
Класс разделён на 3 группы. Задания для групп:
1 группа: Алгоритм решения систем уравнений способом подстановки. Примеры.
Способ подстановки.
1) Выразить из одного уравнения системы одну переменную через другую.
2) Полученное выражение подставить во второе уравнение системы.
3) Решить полученное уравнение с одной переменной.
4) Найти соответствующие значения второй переменной.
1) 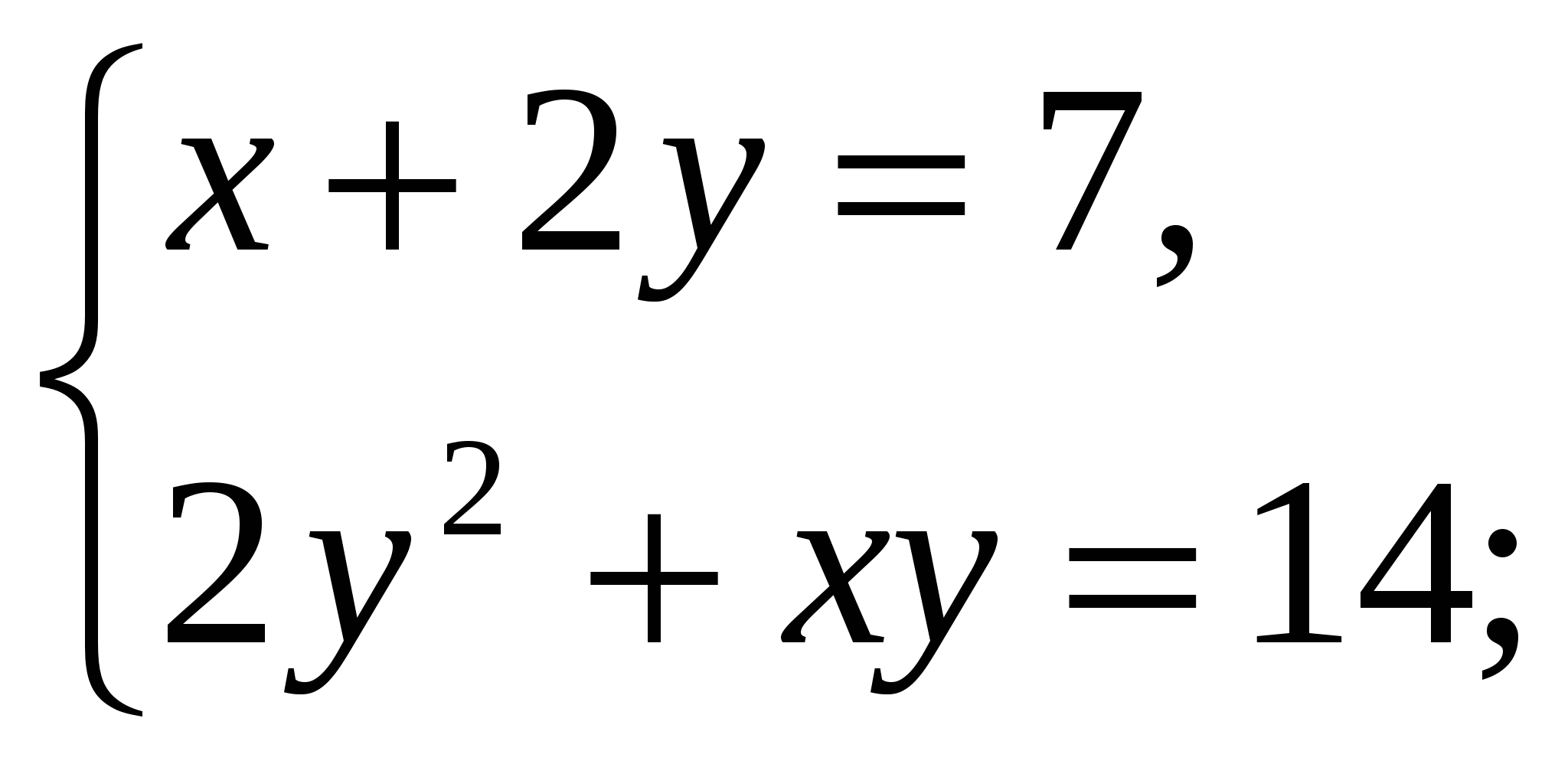 3)
3) 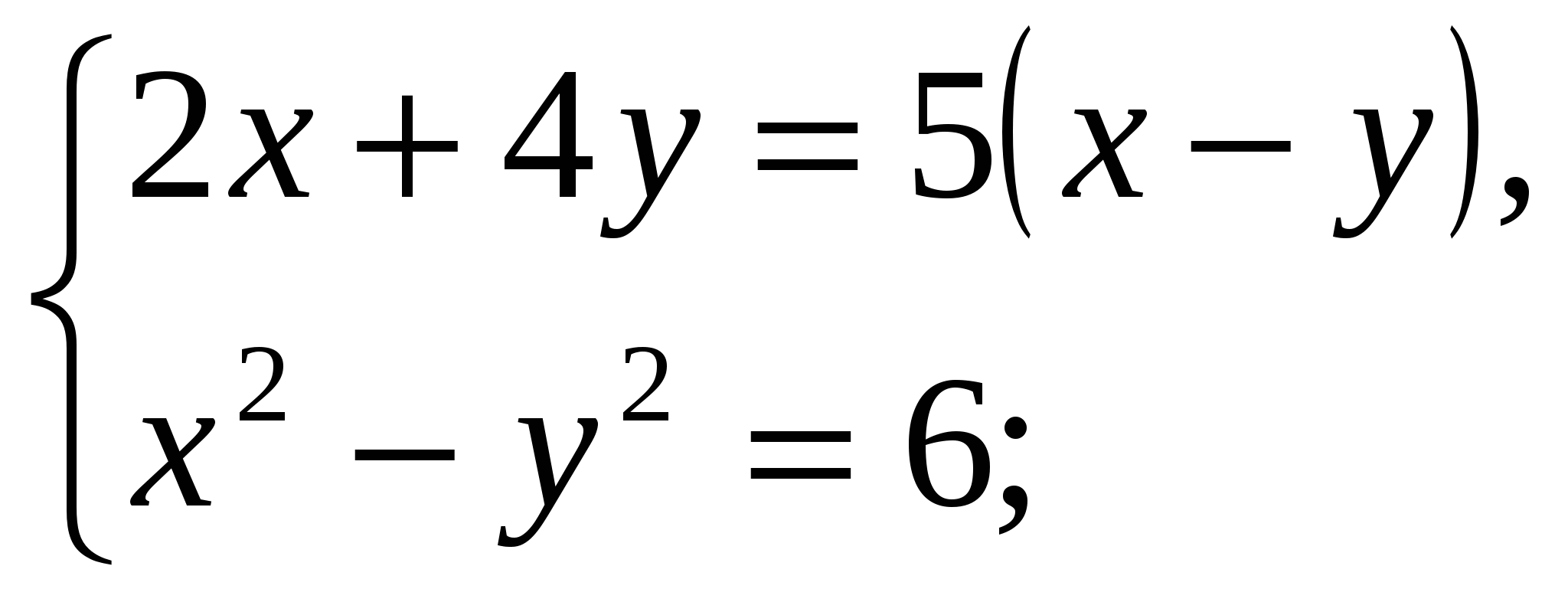
2) 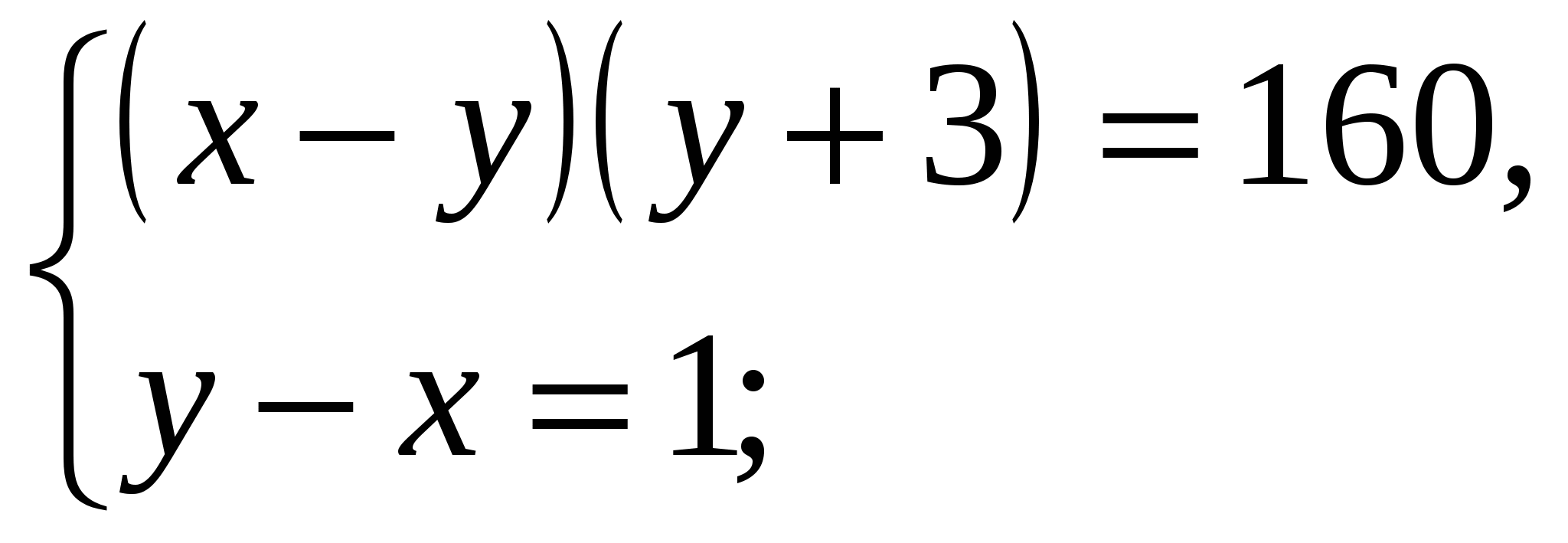 4)
4) 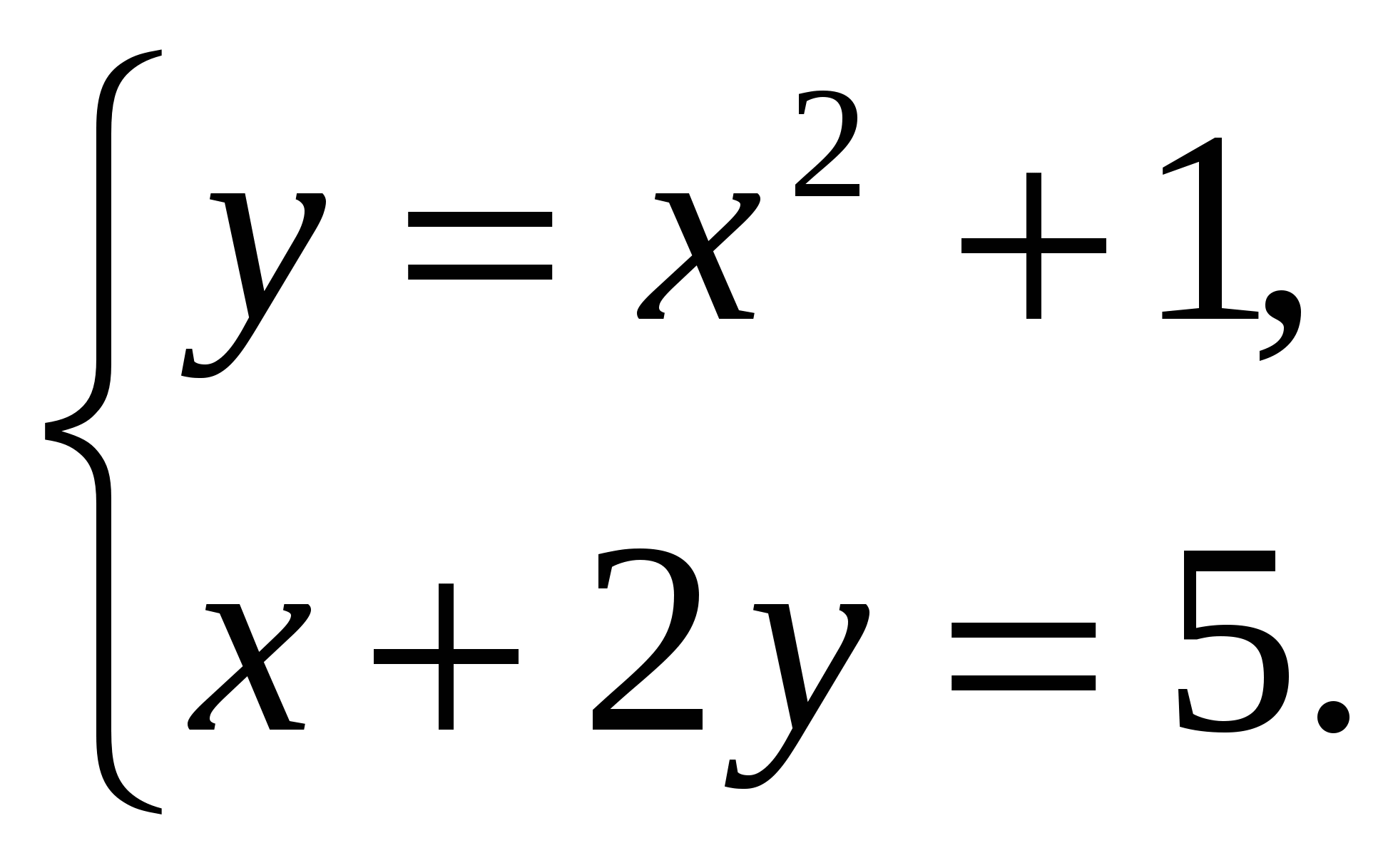
2 группа: Алгоритм решения систем уравнений способом сложения. Примеры.
Способ сложения.
1) Домножить уравнения системы на такие числа, чтобы при сложении уравнений системы коэффициент перед одной из переменных стал равен нулю.
2) Сложить получившиеся уравнения.
3) Решить полученное в результате сложения уравнение с одной переменной.
4) Найти соответствующие значения второй переменной.
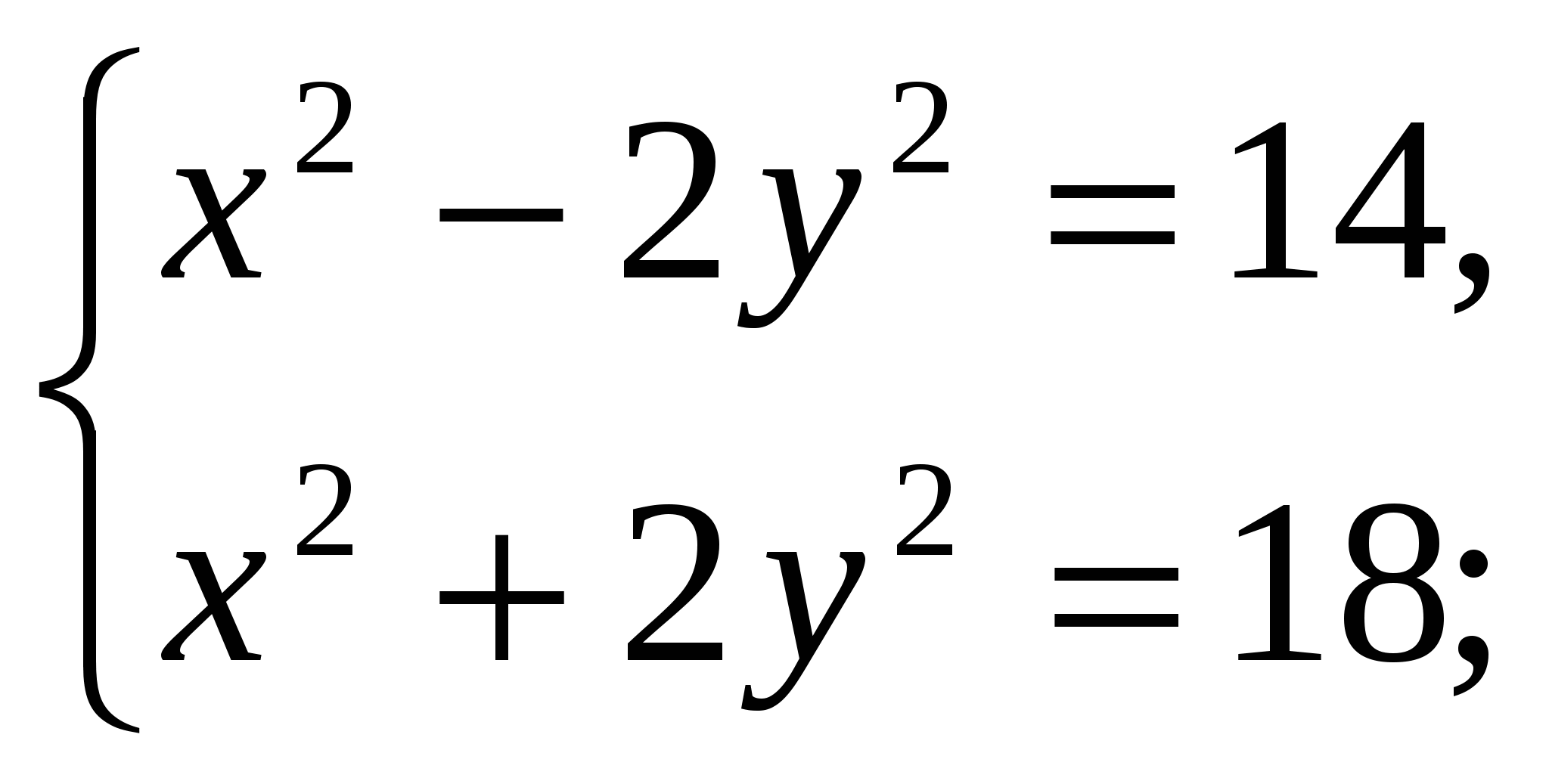 3)
3) 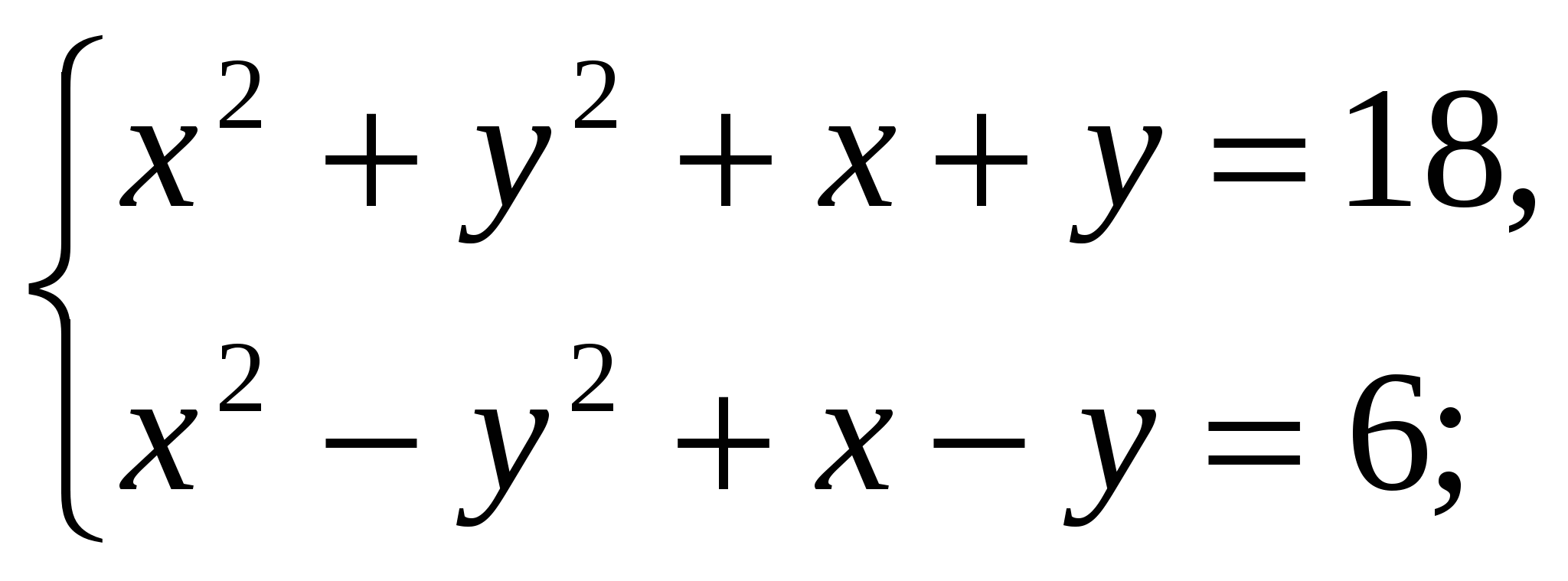
2) 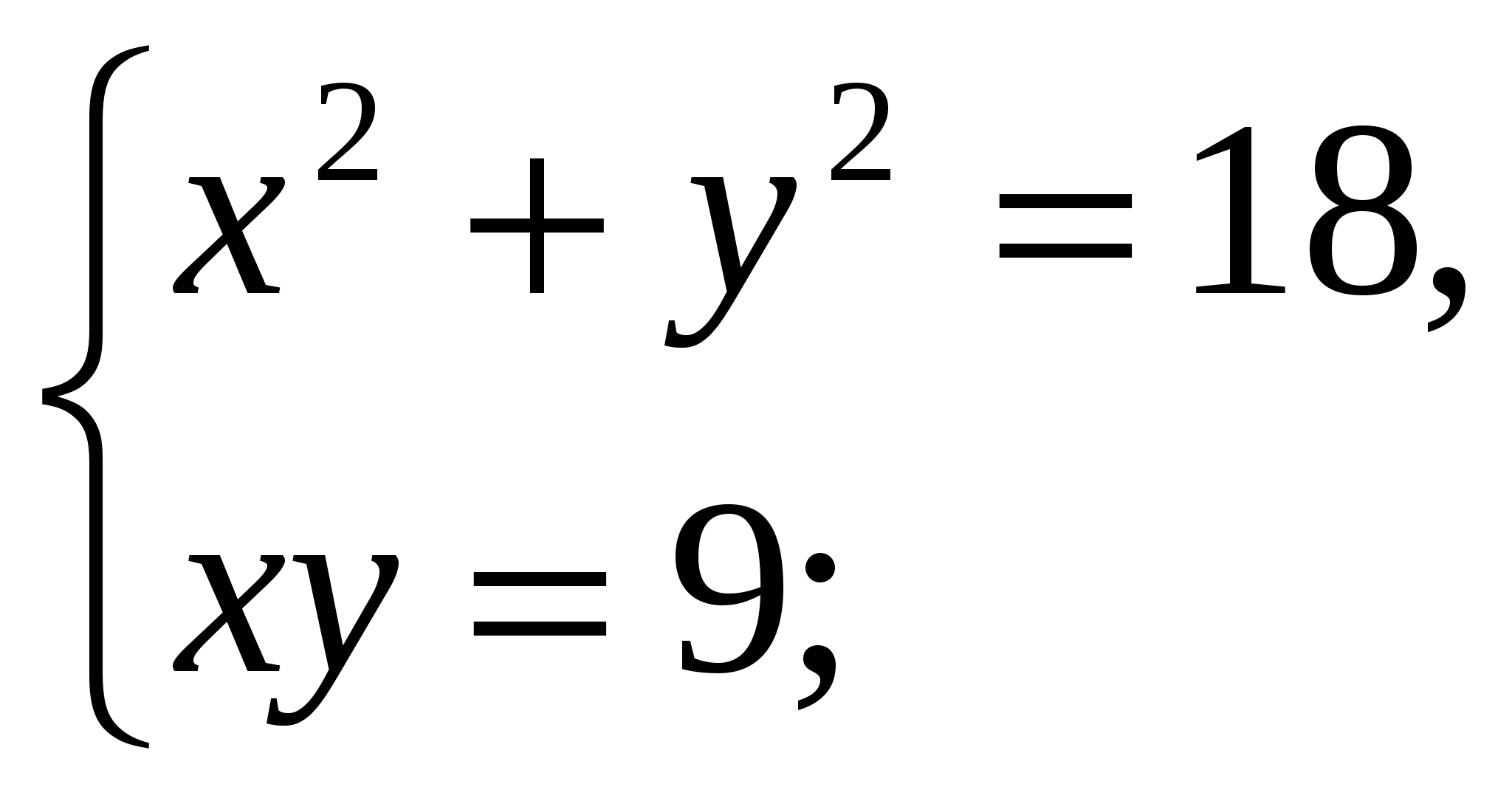 4)
4) 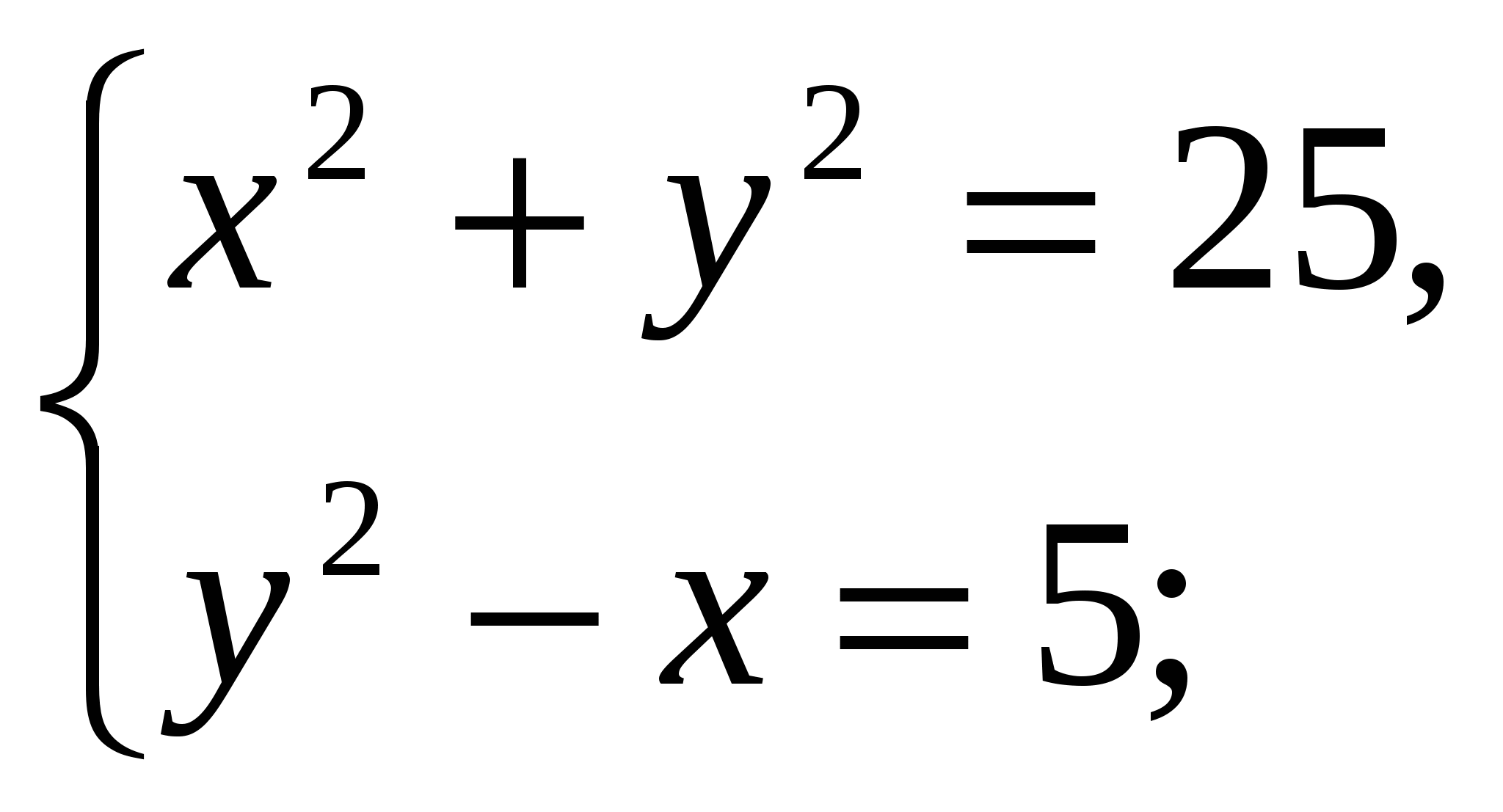
3 группа: Алгоритм решения систем уравнений графическим способом. Примеры.
Графический способ.
1) Построить график каждого уравнения системы (в одной системе координат).
2) Найти значения координат точек пересечения построенных графиков.
3) Записать ответ: координаты точек пересечения графиков.
1) 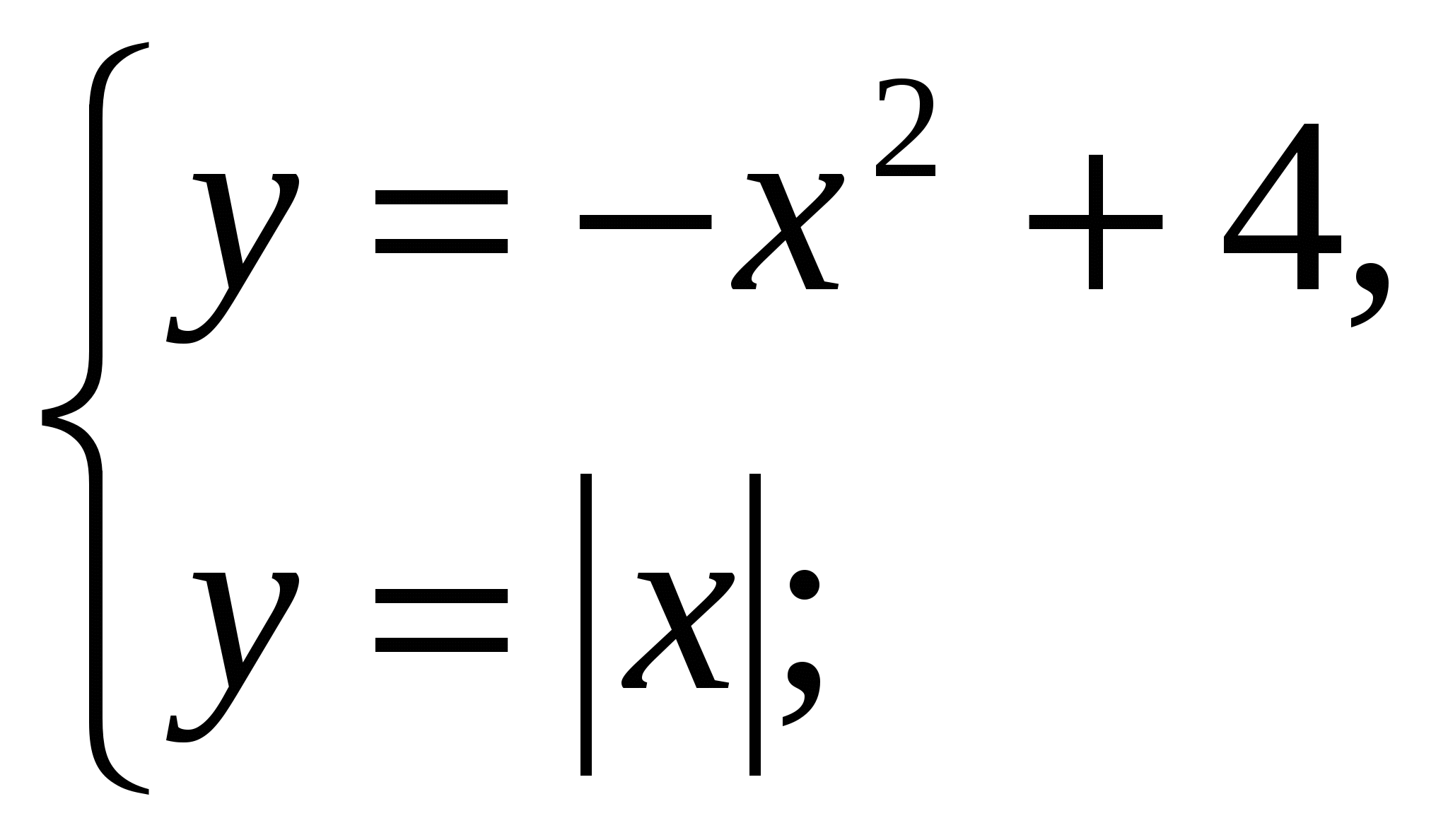 3)
3) 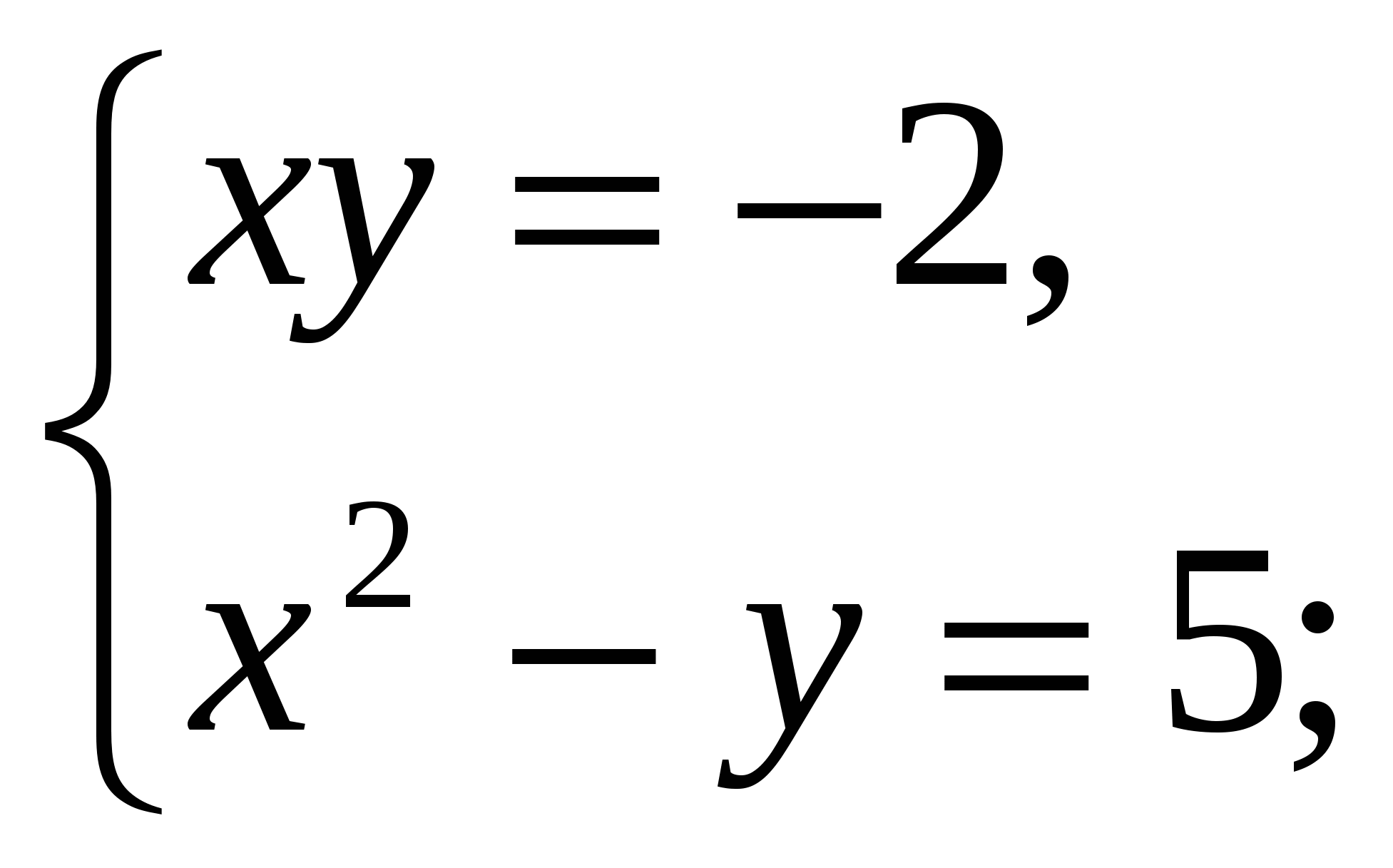
2) 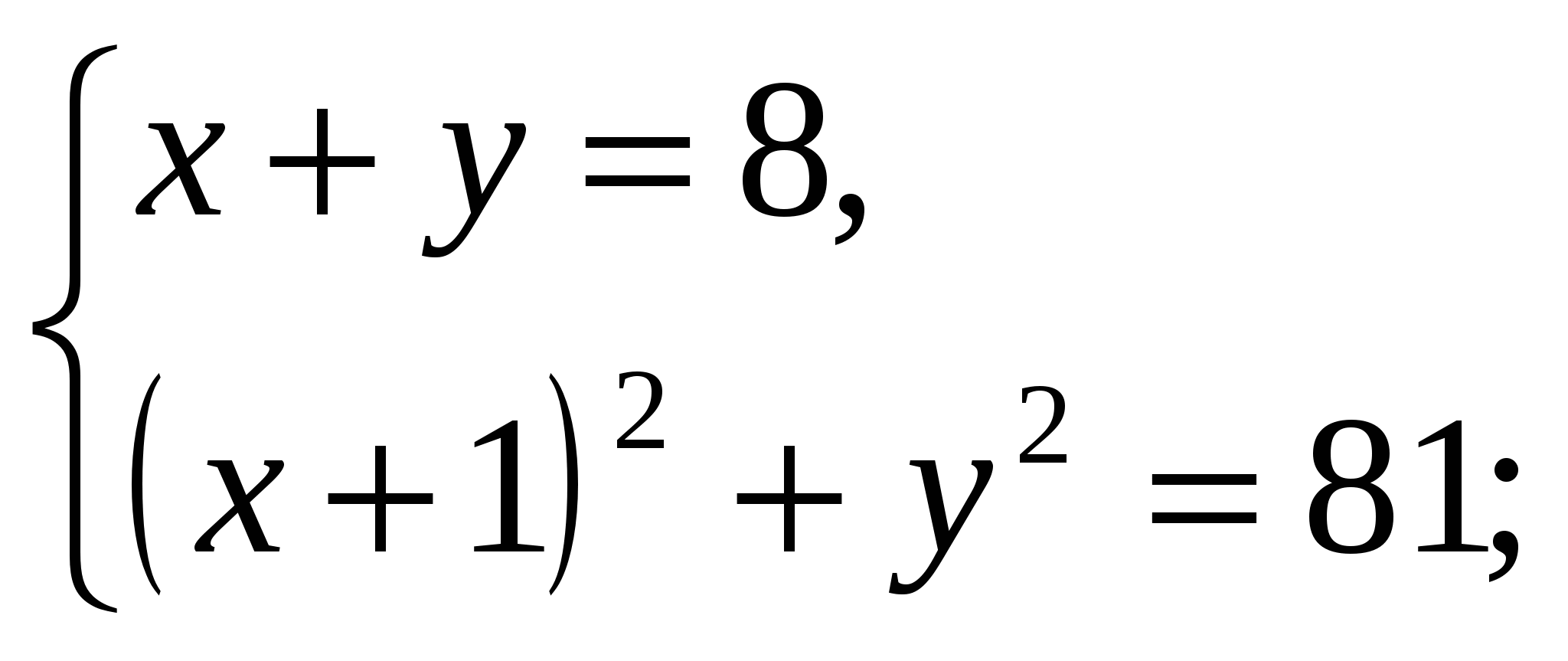 4)
4) 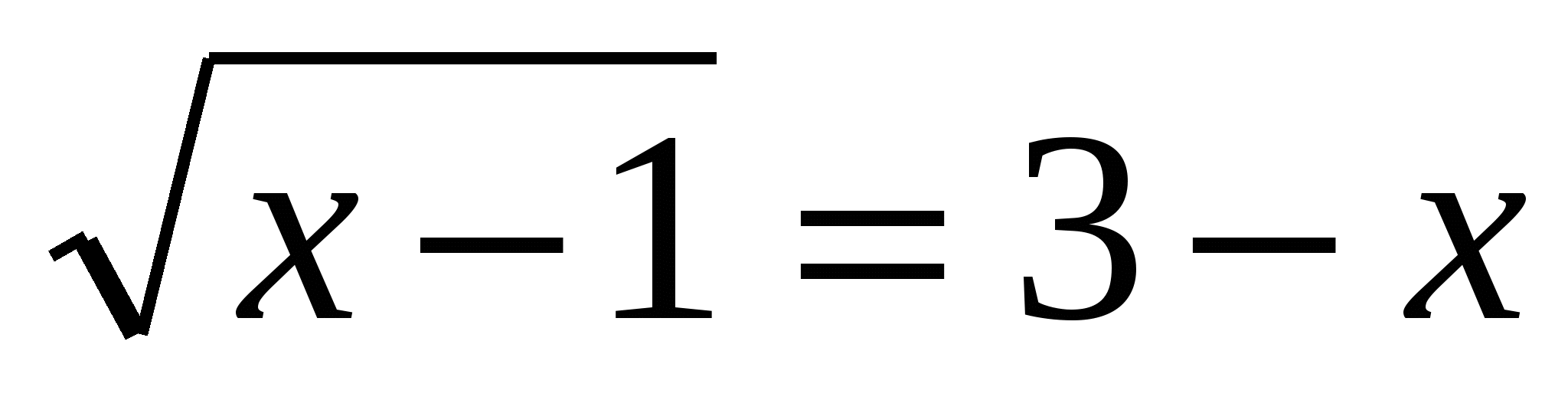 ;
;
Ученики задают вопросы выступающим ученикам и учителю. Обсуждаются достоинства и недостатки каждого метода.
V. (Слайд 7) Работа в парах с консультантом (класс разбивается на пары “сильный-слабый”). Решить любым удобным способом.
Образец (составить при работе с консультантом)
Выполнить самостоятельно
Решите систему уравнений:
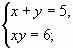
Решите систему уравнений:
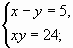
VI. Самостоятельная работа. (Слайд 8)
Решить систему уравнений:
Уровень А
Уровень Б
I вариант
II вариант
I вариант
II вариант
а)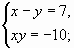
а)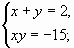
а) 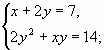
а)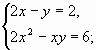
б)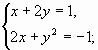
б)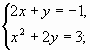
б)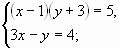
б)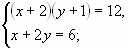
в)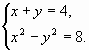
в)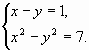
в) 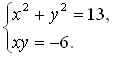
в)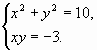
Подводятся итоги работы:
а) Повторить, какие способы применялись при решении систем?
б) Может ли применяться несколько способов при решении одной системы?
(привести пример из решенных систем).
в) В чем суть решения систем уравнений второй степени?
VII. (Слайд 9) Рефлексия.
Рефлексия деятельности на уроке
«Лестница успеха».
Спасибо за активное участие, за хорошее настроение и знание!
infourok.ru
Решение системы линейных уравнений с двумя переменными методом сложения
Г.Уральск, СОШ №31
Калиев А.А.-учитель математики.
Урок математики в 6 классе
Тема урока: Решение систем линейных уравнений с двумя переменными способом сложения.
Цель урока: Сформировать умение решать системы двух линейных уравнений с двумя переменными методом сложения.
Задачи:
Образовательные:
Развивающие:
развитие математической речи учащихся;
умения анализировать, сравнивать, сопоставлять;
развитие внимания, наблюдательности, памяти;
развитие познавательного интереса учащихся через введение исторического материала;
Воспитательные:
воспитывать интерес к предмету через использование ИКТ;
воспитывать математическую культуру.
выработать умение анализировать проделанную работу и её оценивать.
Тип урока: комбинированный.
Методы обучения: словесный, наглядный, практический.
Формы обучения: коллективная, индивидуальная.
Оборудование: интерактивная доска, учебник по математике, раздаточный материал.
План урока:
1 Организационный момент
2 Устный счет
3. Проверка домашнего задания
4 Актуализация знаний
5 Изучение новой темы
6 Физминутка
7 Закрепление –работа с учебником
8 Обучающая самостоятельная работа
9 Подведение итогов урока
10 Задание на дом.
11 Рефлексия
(все этапы урока продемонстрированы на интерактивной доске).
Ход урока
1.Организационный момент
… Математика — это цепь понятий: выпадет одно звенышко — и не понятно будет дальнейшее.
Надежда Крупская
2.Устная работа
Вычислите: 52, (-3а)2, (-1)4, (-1)7.
Упростите: 8в+2в, -8а+(-4а), 7х-8х, -у+у.
Согласны ли вы с решением следующего уравнения
3х- 5=7х-3,
3х-7х=-3- 5,
-4х=-8,
х =2. Ответ: х =2. ?
3. Проверка домашнего задания
Проверка домашнего задания осуществляется взаимопроверкой, заранее решенный пример проецируется на экран.
4.Актуализация знаний
Какие из пар (3;0), (4;-2), (5;-2), (-1;8) являются решениями уравнения 2х+у=6?
Что называется решением системы уравнений с двумя переменными?
Что значит решить систему уравнений?
5. Изучение новой темы
Мы умеем решать системы уравнений графически и способом подстановки. Давайте вспомним эти способы.
Двое учеников решают систему, один способом подстановки, другой графически
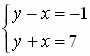
Итак, одна и та же система решена двумя способами.
Какой из них вам показался более удобным?
В чем недостаток графического метода?
Сегодня на уроке мы рассмотрим еще один способ решения систем линейных уравнений – это способ сложения.
Рассмотрим три случая решение системы линейных уравнений с двумя переменными способом сложения.
Случай 1. В уравнениях, входящих в систему, коэффициенты одной переменной — противоположные числа.
Например: решим систему уравнений способом сложения
Сложив почленно левую и правую части уравнений, получим:
9х=36, х=4.
Подставив значение х в любое из уравнений системы, найдем соответствующее значение у.
6х+2у=30,
6·4+2у=30,
у=3.
Ответ: (4;3)
Случай 2: Коэффициенты при одной переменной в обоих уравнениях системы равны.
Чтобы решить эту систему уравнений способом сложения, надо обе части одного из уравнений умножить на (-1) и почленно сложить (1случай), или из одного уравнения системы вычесть другое.
Ответ: (-1;8).
Например.
3х+2у=5,|*(-1) -3х-2у=-5, х=-5, х=-5,
-5х+2у=45; -5х+2у=45 3*(-5)+2у=5, у=10.
-8х=40, -15+2у=5,
х=-5; 2у=5+15,
2у=20,
у=10, Ответ: (-5;10)
Случай 3:Коэффициенты при переменных в обоих уравнениях не равны между собой и не являются противоположными числами.
В данном случае нужно первое и второе уравнение системы умножить на такое число, чтобы коэффициенты при одной из переменных в обоих уравнениях оказались противоположными числами. Затем, умножив каждое уравнение системы на соответствующие множители, надо заменить данную систему на равносильную. В данном случае первое уравнение умножим на 7, а второе – на (-2):
тогда
Подставим найденное значение у в уравнение , получим:
проверка:
Ответ: (5;2)
Во всех трех системах при решении был применен способ сложения. Чем отличалось решение в каждом случае?
Алгоритм решения системы двух линейных уравнений с двумя переменными способом сложения (раздается ребятам).
1. Умножают почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными.
2. Складывают почленно левые и правые части уравнений системы.
3. Решают получившееся уравнение с одной переменной.
4. Находят соответствующее значение второй переменной.
6. Физминутка
БЫСТРО все ребята встали
Руки БЫСТРО вверх подняли.
БЫСТРО хлопнули 5 раз.
А теперь морганье глаз:
БЫСТРО-БЫСТРО поморгали
И… ногами постучали.
БЫСТРО влево наклонились
И сейчас же распрямились!
Вправо-влево 10 раз –
Отдохнул уставший класс…
Как пингвины полетели
И за парты тихо сели!
Давайте закрепим все, что мы изучили сегодня на уроке.
7. Закрепление Работа с учебником № 1534, 1536, 1547, 1549.
8. Самостоятельная работа с помощью онлайн приложения Kahoot
9. Подведение итогов
Ребята, что вы нового узнали?
Что для себя отметили -важным?
10.Задание на дом П 9.5 стр 199-201 № 1535, №1538.
11.Рефлексия
Урок понравился — синяя карточка
Не очень понравился – желтая карточка
Не понравился — зеленая карточка.
infourok.ru
Урок по теме»Решение систем линейных уравнений с двумя переменными способом сложения «
Открытый урок по алгебре на тему
«Решение систем линейных уравнений с двумя переменными способом сложения».
Учитель Попкова Людмила Григорьевна
Цели образовательная: освоить еще один способ решения систем уравнений – способ сложения, закрепление, систематизация и обобщение знаний о методах решения и исследования системы уравнений, контроль за усвоением ЗУН;
воспитательная: привитие интереса к изучаемому предмету;
развивающая: формирование навыков самостоятельной деятельности, выработка внимания, наблюдательности и сообразительности.
выработать критерии оценки своей работы, умение анализировать проделанную работу и адекватно её оценивать.
Ход урока.
1. Организационный момент.
Представим себе, что сегодня наш класс – научно-исследовательский институт. А вы, ученики, — сотрудники этого института. А именно, сотрудники различных лабораторий по проблемам математики. Вас всех пригласили принять участие в заседании учёного совета этого НИИ, чтобы обсудить с вами тему «Решение систем линейных уравнений с двумя переменными». В процессе работы в НИИ вы должны: закрепить изученный материал, показать уровень усвоения темы, рассмотреть еще один способ решения систем линейных уравнений, проконтролировать и оценить свои знания. Девизом нашего заседания является лозунг: «Дорогу осилит идущий, а математику мыслящий». Но прежде, чем войти в лаборатории НИИ, вам необходимо пройти испытание, которое будет пропуском в эти лаборатории.
Устный счет “ одним взглядом ”
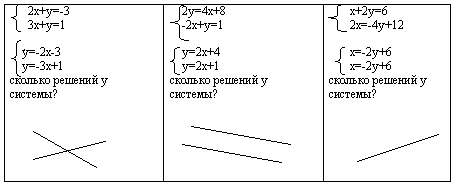
Вывод: система линейных уравнений может иметь одно решение, не иметь решений, иметь множество решений.
Итак, мы получили пропуск в лаборатории. Перед нами лаборатория теоретиков.
2. Повторение и проверка домашнего задания
Лаборатория теоретиков и исследований.
Давайте примем участие в работе этих лабораторий.
Сейчас два наших сотрудника пройдут в лабораторию исследований и выполнят задания
У доски 2 ученика решают домашние системы 2-мя способами 3х – у = 2,
х – 3у =6, х + 2у = 10 (графически),
2у — 5х = -4( способом подстановки),
А с остальными мы пройдем в лабораторию теоретиков
В лаборатории теоретиков много правил, по которым мы работаем.
проводится фронтальный опрос по теме урока:
Какие уравнения с двумя переменными называются линейными?
Что является графиком линейного уравнения с двумя переменными?
Из уравнения 3х-5у=7 выразить каждую переменную через другую.
Что называется решением системы линейных уравнений с двумя переменными?
Что значит решить уравнение с двумя переменными?
Перечислить известные способы решения систем линейных уравнений с двумя неизвестными.
В чем достоинство и недостаток графического способа решения систем линейных уравнений с двумя неизвестными?
Сформулировать алгоритм решения систем линейных уравнений с двумя неизвестными графическим способом и способом подстановки.
Какой из них вам показался более удобным?
Владение математикой – это умение решать задачи, причём не только стандартные, но и требующие оригинальности, изобретательности, смекалки, находчивости.
Лаборатория исследований.
3. Изучение нового материала. 2х -7у = 3,
3х + 7у = 7
Поступило задание: Решить систему уравнений:
Каким способом удобно решить? Заметим, что в уравнениях системы коэффициенты при переменной у являются противоположными числами. Сложим почленно уравнения системы:2х+3х-7у+7у=3+7. Получим линейное уравнение с одной переменной у, а именно 5х=10. Заменим одно из уравнений системы полученным уравнением, получим равносильную систему:
5х=10,
3х +7у=7. (2)
Из первого уравнения находим: х=2
Подставим это значение во второе уравнение системы и получим линейное уравнение с переменной х: 3*2+7у=7, откуда: у=1/7. Пара чисел(2;1/7) является решением системы(2),а, следовательно, и равносильной системы(1). В равносильности этих систем можно убедиться графически.
Из разобранного примера видно, что при сложении уравнений системы получилось уравнение только с одной переменной. В качестве второго уравнения системы можно выбрать любое уравнение данной системы. В результате таких преобразований была получена система, равносильная данной. В этом и состоит суть метода сложения.
Поступило еще одно задание:
Пример 2. Решить систему уравнений способом сложения:
3а — 5b = 9,
2a — 7b = 17.
В отличие от предыдущего примера в это случае коэффициенты при a, а также и при b не являются противоположными числами. Поэтому сложение уравнений не позволит получить уравнение с одной переменной. Следовательно, необходимо добиться того, чтобы в уравнениях коэффициенты при любой переменной, например, при b стали противоположными числами.
Коэффициенты при b являются простыми числами 5 и 7. Поэтому умножим все члены первого уравнения на число 7, а второе уравнение на -5. При этом уравнения будут равносильными и система также равносильна данной 21a – 35b = 63,
-10a + 35b = -85
В данной системе коэффициенты при b – противоположные числа. Поэтому сложим уравнения системы и получим линейное уравнение с одной переменной: 21a-35b-10a+35b=63-85 или 11a = -22.
Запишем систему, равносильную данной. В качестве первого уравнения выберем полученное уравнение, в качестве второго уравнения – например, первое уравнение данной системы. Имеем, 11a = -22,
3a – 5b = 9.
Из первого уравнения найдем a=-2 и подставим это значение во второе уравнение. Получаем линейное уравнение с одной переменной: 3(-2)-5b=9,
-6-5b=9,
-5b=9+6,
-5b=15,
b=-3.
Итак, данная система уравнений имеет единственное решение a=-2, b=-3.
Уважаемые сотрудники, уточните тему нашего урока. Какое название можно дать рассмотренному способу решения систем уравнений с 2-мя переменными?
Давайте сформулируем алгоритм решения систем уравнений способом сложения:
Итак, при решении систем линейных уравнений методом сложения:
1.умножают уравнения системы подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами
2.складывают почленно левые и правые части уравнений системы
3.решают полученное уравнение с одной переменной
4.находят соответствующее значение второй переменной.
Отметим, что если в уравнениях системы коэффициенты при одной из переменных являются противоположными числами, то при решении пункт 1 пропускают и начинают сразу с пункта 2.
Производственная гимнастика
Наступило время производственной гимнастики (кулачками, кошачьи лапки, вращение плеч, глазами и поморгали).
4. Закрепление полученных знаний.
Лаборатория систем линейных уравнений.
Перед нами лаборатория систем линейных уравнений. Давайте примем участие в исследованиях этой лаборатории.
Выдающийся физик Альберт Эйнштейн – основоположник теории относительности — говорил так: «Мне приходится делить время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Вот и займёмся решением систем линейных уравнений. Попробуем применить известный алгоритм к решению систем уравнений.
Задания из учебника №№1082(а, в), 1083(а, в), 1085(б, г).
2х+11у=15, 4х-7у=30, х-6у=17, 3х+2у=-5, 7х+2у=1, 4х+7у=90,
10х-11у=9 4х-5у=90 5х+6у=13(с/п) -5х+2у=45 17х+6у=-9 5х-6у=20.
5. Обучающая самостоятельная работа.
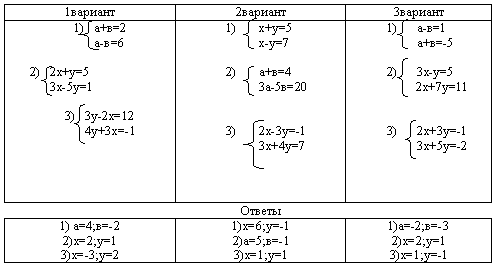
6. Подведение итогов.
Итак, уважаемые сотрудники, мы заканчиваем наше исследование. Вы сегодня хорошо потрудились. Вспомним алгоритм решения систем уравнений с двумя переменными способом сложения.
Запишите домашнее задание: п.44,№№1082(б, г), 1083(б, г).
7.Притча:
Шёл мудрец, а навстречу ему 3 человека, которые везли под горячим солнцем тележки с камнями для строительства. Мудрец остановился и задал каждому по вопросу. У первого спросил «Что ты делал целый день? И тот с ухмылкой ответил, что целый день возил камни. У второго мудрец спросил «А что ты делал целый день?» и тот ответил «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием «А я принимал участие в строительстве храма»
Ребята, давайте мы попробуем с вами оценить каждый свою работу за урок.
Кто возил камни? (приклейте жёлтый жетон)
Кто добросовестно работал? (приклейте синий жетон)
Кто строил храм? (приклейте красный жетон)
8. В конце урока выставляются оценки.
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
Вариант 1 Вариант 2 Вариант 3
a + b = 2, х + у = 5, a – b = 1,
a – b = 6. х – у = 7 a + b = -5
Вариант 4 Вариант 5 Вариант 6
2х + у = 5, a + b = 4, 3х – у = 5,
3х — 5у = 1 3a — 5b = 20 2х + 7у = 11
Вариант 7 Вариант 8 Вариант 9
3у — 2х = 12, 2х — 3у= -1, 2х + 3у= -1,
4у + 3х = -1 3х + 4у = 7 3х + 5у = -2
infourok.ru
Конспект урока по алгебре «Графический метод решения систем уравнений с двумя переменными» (9 класс)
Конспект урока. 9 класс. Графический способ решения систем уравнений с двумя переменными.
Предмет: алгебра
Класс: 9
Авторы УМК: Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б.
Тема урока: Графический способ решения систем уравнений с двумя переменными
Тип урока: Урок усвоения новых знаний, применения знаний и умений. (сдвоенный урок)
Цель урока: Научить находить корни уравнения с помощью графиков.
Задачи урока:
Личностные: Воспитывать чувство ответственности за результат своего труда. Учить сопереживать успехам и неудачам одноклассников.
Метапредметные: Формировать у учащихся умение выделять основные признаки, устанавливать сходства и различия. Обогащать словарный запас. Развивать речь, усложняя её смысловую функцию. Развивать логическое мышление, познавательный интерес, культуру графического построения, память, любознательность.
Предметные: Выработать умение самостоятельно применять знания в комплексе, переносить их в новые условия, строить графики и находить количество корней в заданных уравнениях.
2.Мотивация учебной деятельности
1.Вспомнить известные функции и их графики
2.Организовать деятельность учащихся по установке тематических рамок: решение систем уравнений графическим способом.
3.Создать условия для возникновения у ученика внутренней потребности включения в учебную деятельность
-Сначала вы напишите маленькую самостоятельную работу, чтобы вспомнить все известные нам функции и их графики. Все это мы уже проходили. Готовим листочки. На самостоятельную 10-15 минут.
Учитель раздает карточки с заданиями.
Через 10-15 минут учитель собрал работы.
— Теперь приступим к новой теме – графический способ решения систем уравнений.
-Напомню, что пара значений переменных, обращающая каждое уравнение системы уравнений с двумя переменными в верное равенство, называется решением системы. То есть решить систему – значит найти все ее решения или доказать, что решений нет.
Пусть требуется решить систему:
Для этого необходимо построить в одной системе координат графики уравнений:
Учитель задает вопросы:
-Какие функции у нас представлены и чем являются их графики?
-Точки пересечения этих двух графиков и будут являться решением системы, потому что координаты любой точки пересечения окружности и параболы удовлетворяют как первому уравнению системы, так и второму, то есть являются решением рассмотренной системы.
Нашли приближенные значения точек пересечения и записали ответ.
А(-2,2;-4,5). В(0;5). С(2,2;4,5). D(4;-3)
-Что не понятно? Задайте вопросы.
Ученики получают карточки. И решают задания с карточки в соответствии с требованиями.
Вариант 1
№1 построить график функции
№2 Построить график функции
№3 построить график функции
Вариант 2
№1 построить график функции
№2 построить график функции
№3 построить график функции
Ученики записывают тему в тетради.
Ученики все записывают
Ученики отвечают:
— Графиком является окружность у первой функции, а вторая функции квадратичная, и графиком является парабола
Ученики задают вопросы, если они есть
3. Актуализация знаний и фиксация затруднения в пробном учебном действии.
1. организовать актуализацию изученных способов действий, достаточных для построения нового знания: определять графики функций, строить их на координатной плоскости, находить точки пересечения, определять координаты точек пересечения.
2. Зафиксировать актуализированные способы действий в речи
3. Организовать актуализацию мыслительных операций, достаточных для построения нового знания: анализ, синтез, обобщение.
4) Организовать самостоятельное выполнение пробного учебного действия
5) Организовать фиксацию индивидуальных затруднений в выполнении учащимися пробного учебного действия.
-Итак, посмотрим номер 415. Надо выяснить, является ли решением системы уравнений пара чисел (-2;1) и (1;-2). Что для этого надо сделать?
-Молодцы. Теперь вторую точку проверьте самостоятельно в тетради и скажите, что у вас получилось
— Совершенно верно. Теперь решим систему графически.
Учитель вызывает ученика к доске. №426
-Сначала в обоих уравнениях выразим функцию (у)
— Первый урок закончился, продолжим на втором. Отдыхайте.
Ученики отвечают.
-Подставить координаты в первое уравнение системы и во второе, и посмотреть, выполняется ли равенство в обоих случаях.
Подставим (-2;1).
Равенство выполняется
2)
-12+5≠-4
Равенство не выполняется, значит точка с координатами (-2;1) не является решением системы.
Подставляют точку с координатами(1;-2) в систему.
-Точка является решением системы
Построим в одной системе координат графики обоих уравнений.
— квадратичная функция, график – парабола
– линейная функция, график – прямая
Получили две точки пересечения: А(-1;1) и В(2,5;8)
4. Составление плана действий и его реализация.
Первичное закрепление во внешней речи
1. Организовать фиксацию преодоления затруднения
2.Организовать реализацию построенного проекта в соответствии с планом.
3.Организовать фиксацию преодоления затруднения
4. Организовать уточнение общего характера нового знания (возможность применения нового способа действий для решения всех заданий данного типа).
— Итак, какой алгоритм решения системы графическим способом?
-Составьте план действий
Учитель вызывает ученика к доске, чтобы он проделал этот алгоритм на пробном задании.
Следит за тем, чтобы ученик проговаривал свои действия
— Теперь сделаем номер 417. Там просто надо с помощью графика показать, что система имеет 4 решения.
Учитель вызывает ученика к доске
-Так как нам надо только показать, что система имеет 4 решения, а не находить эти решения, то достаточно определить направление ветвей параболы и координаты вершины.
— Совершенно верно. Давайте дальше решать системы, но теперь у нас будут другие графики.
Учитель вызывает ученика к доске.
Учитель вызывает двух учеников к доске.
— Надо изобразить схематически графики уравнений и узнать, сколько решений имеет система.
— Итак, теперь немного отвлечемся. Мы повторим еще раз графики некоторых функций, но не обычным образом. Я вам читаю пословицу, а вы должны догадаться, какой график описывается.
Например:
«Как аукнется, так и откликнется»
-Отклик=ауканью, а значит х=у. Это график чего?
«Чем быстрее едешь, тем быстрее приедешь»
«Светит, да не греет»
«Ни кола, ни двора»
— сначала приводим оба уравнения системы к стандартному виду, то есть выражаем у (функцию)
— Затем определяем вид функции и ее график
— Строим в одной системе координат графики обеих функций
— Определяем количество точек пересечения
— Находим по графику координаты точек пересечения (приближенно)
— Записываем ответ
№418
– графиком является окружность. R=10, O(0;0)- центр окружности
– квадратичная функция, график – парабола
Три точки пересечения: А(0;-10) В(6;8) и С(-6;8)
Ответ (0;-10) (6;8)
(-6;8)
– график – окружность. О(0;0) – центр окружности, R=5.
– квадратичная функция, график – парабола
-Ветви направлены вверх, (0;-6) – вершина.
4 точки пересечения, а значит 4 решения.
№420 б
Выразим функции в обоих уравнениях
– обратная пропорциональная зависимость, график – гипербола
линейная функция, график – прямая.Точек пересечения нет, значит решений нет.
№421 в г
– квадратичная функция, график – парабола
Вершина (0;1), ветви направленны вверх
— обратная пропорциональная зависимость, график – гипербола
Одна точка пересечения, значит одно решение.
Г)
Уравнения окружностей.
Окружности не пересекаются, решений нет.
Ученики думают и выдвигают свои версии
— График прямой
Ученики вместе думают и отвечают. Это гипербола, то только в первой четверти
— Парабола, потому что напоминает лампочку
Совещаются
-Точка.
5. Включение в систему знаний и повторение
Тренировать навыки использования нового содержания совместно с ранее изученным материалом: самостоятельное решение систем уравнений графическим способом
-Теперь самостоятельно в тетрадях решите графически две системы. Первые три ученика, кто решит правильно, получат 5. Системы записаны на доске.
Следит за правильностью выполнения, задает вопросы
Решают у себя в тетрадях
– квадратичная функция, график парабола
– линейная функция, график прямая.
Решений нет
— обратная пропорциональная зависимость, график – гипербола
– окружность
О(о;о) – центр, R=1
Решений нет
6. Рефлексия деятельности на уроке.
1.Организовать рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся
2. Организовать оценивание
Учитель задает вопросы
-что нового вы узнали на уроке?
— Какую цель вы ставили сегодня на уроке?
_Вы достигли цели урока?
-Что вам помогло достичь цели урока?
_ На чем основан графический метод решения систем уравнений?
Предлагает продолжить предложение:
«Сегодня на уроке
Я повторил….
Я закрепил…
Я научился….
Я узнал….»
Отвечают с места
Ответы фиксируются в тетради
7. Информация о домашнем задании
Обеспечение понимания детьми цели, содержания и способов выполнения домашнего задания
Учитель записывает на доске номера:
№419а №420а
№421а б
№422
Раздает листочки с дополнительным домашним заданием для желающих, по просьбе учеников (лист с дополнительным домашним заданием представлен ниже)
Записывают домашнее задание
Дополнительное домашнее задание (ученики сами просили найти что-нибудь интересное, что можно было бы построить)
ЗАДАНИЕ: Постройте точки по координатам и соедините их последовательно:
(1;-6)
(0;11)
(8,5;0)
(2;-3)
В итоге получается дельфин! Фотография прилагается. 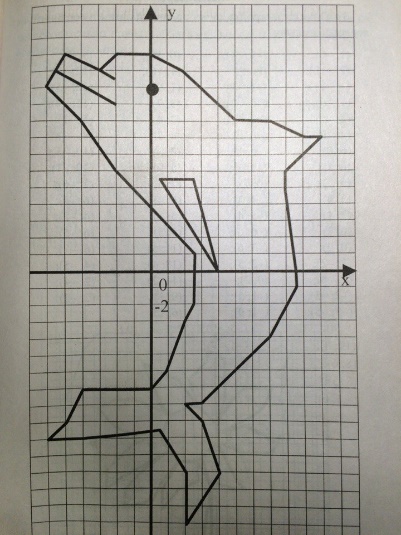
infourok.ru