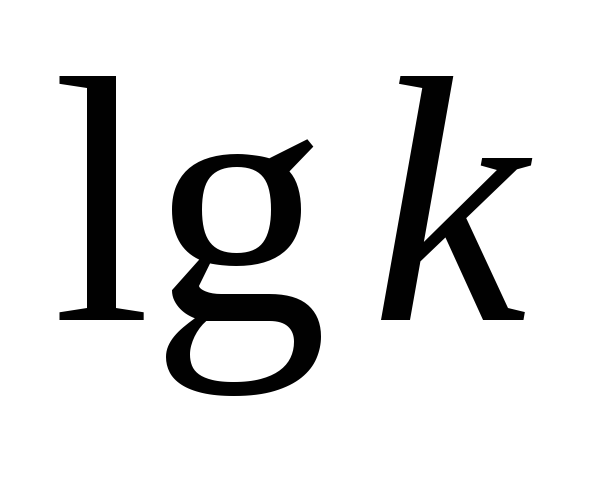2.3. Зависимость скорости реакции от температуры
Зависимость
скорости химической реакции от температуры
определяется эмпирическим правилом
Вант-Гоффа, согласно которому при
повышении температуры на  скорость реакции возрастает примерно
в 2-4 раза.
скорость реакции возрастает примерно
в 2-4 раза.
Число, показывающее
во сколько раз увеличивается скорость
химической реакции, а следовательно и
константа скорости её при повышении
температуры на 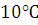 ,
называется температурным коэффициентом
скорости реакции
,
называется температурным коэффициентом
скорости реакции 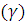 .
.
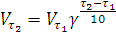
где 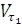 —
скорость реакции при температуре
—
скорость реакции при температуре 
 —
скорость реакции при температуре
—
скорость реакции при температуре 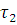
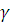 — температура коэффициент скорости
равный 2
— температура коэффициент скорости
равный 2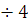
Пример. Срок хранения автомобильных покрышек при температуре 20˚С – 5 лет, а при температуре 10˚С – 13 лет. Сколько лет можно хранить покрышки при 5˚С?
Решение. Средняя скорость старения резины обратно пропорциональна сроку хранения. Следовательно, при охлаждении с 20˚С до 10˚С скорость старения уменьшится в 13/5 = 2,6 раза. Это означает, что температурный коэффициент γ = 2,6. При охлаждении еще на 5˚С скорость реакции уменьшится в γ1/2 = 1,6 раза:

В такое же число раз возрастет срок хранения покрышек, который в этом случае составит уже 13 ∙ 1,6 = 21 год.
Увеличение скорости реакции с повышением температуры объясняется тем, что для химической реакции необходимо соударение активных молекул. При повышении температуры число активных молекул возрастает, поэтому скорость химической реакции резко возрастает.
Избыточная энергия, которой должны обладать молекулы для того, что бы их столкновение могло привести к образованию нового вещества, называется
Молекулы, обладающие такой энергией, называются активными молекулами.
Если энергия активации мала (< 40 кДж/моль), то скорость химической реакции велика, если энергия активации велика ( >120 кДж/моль) то скорость реакции очень мала.
В 1889 году шведский
ученый Аррениус вывел уравнение, которое
носит его имя: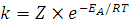 —
уравнение Аррениуса, где k
– константа скорости реакции,
—
уравнение Аррениуса, где k
– константа скорости реакции,  —
энергия активации, R
– газовая постоянная, T
– абсолютная температура, Z
– число столкновений.
—
энергия активации, R
– газовая постоянная, T
– абсолютная температура, Z
– число столкновений.
Множитель  характеризует
долю активных столкновений от их общего
числа. Мы видим, что константа скорости
тем больше, чем меньше энергия активации
и чем выше температура.
характеризует
долю активных столкновений от их общего
числа. Мы видим, что константа скорости
тем больше, чем меньше энергия активации
и чем выше температура.
Реакции, требующие для своего протекания заметной энергии активации, начинаются с ослабления связи между атомами в молекулах исходных веществ.
При этом вещества переходят в неустойчивое промежуточное состояние с большим запасом энергии, это состояние называется активированным комплексом. Для его образования и необходима энергия активации (рис. 2.1.).
Рис. 2.1. Энергетическая диаграмма для реакции образования продукта АВ из исходных веществ А и В. | В активированном комплексе старые связи еще не разорваны, но уже ослаблены, новые связи наметились, но еще не образовались. Для образования переходного комплекса и необходима энергия активации. Если энергия столкновения молекул А и В больше или равна энергии активации Еа, то энергетический барьер преодолевается, и происходит перемещение вдоль координаты реакции r от исходных веществ к продукту. Вершина энергетического барьера соответствует переходному состоянию (активированному комплексу), в котором связь А–В образовалась частично. |
Вопрос 3. Зависимость скорости реакции от температуры. Правило
Вант-Гоффа. Уравнение Аррениуса.
При фиксированной температуре реакция возможна, если взаимодействующие молекулы обладают определенным запасом – энергией активации, а сами молекулы являются активированными. По Аррениусу константа скорости реакции k и энергия активации связаны соотношением, получившим название уравнение Аррениуса:

Здесь
k0 – предэкспоненциальный множитель,
характеризующий общее число соударений.
k0=Z0.P;
Z0—
число всех соударений; Р- доля соударений,
благоприятных в пространственном
отношении для перераспределения связей;  —
доля активных столкновений, т.е.
благоприятных в энергетическом отношении
соударений; R-
универсальная газовая постоянная, Т-
температура.
—
доля активных столкновений, т.е.
благоприятных в энергетическом отношении
соударений; R-
универсальная газовая постоянная, Т-
температура.
Таким
образом, при постоянной температуре
скорость реакции определяется энергией
активации. Чем больше энергия активации,
тем меньше число активных молекул и тем
медленнее протекает реакция. При
уменьшении Е
Уравнение Аррениуса часто представляют в логарифмической форме:
lnk = lnk0 – Ea/RT.
Если известны константы скорости при двух температурах, то энергию активации можно оценить:
lnk1 = lnk0 – Ea/RT1.
lnk2 = lnk0 – Ea/RT2.
Вычитая из второго уравнения первое, получаем:


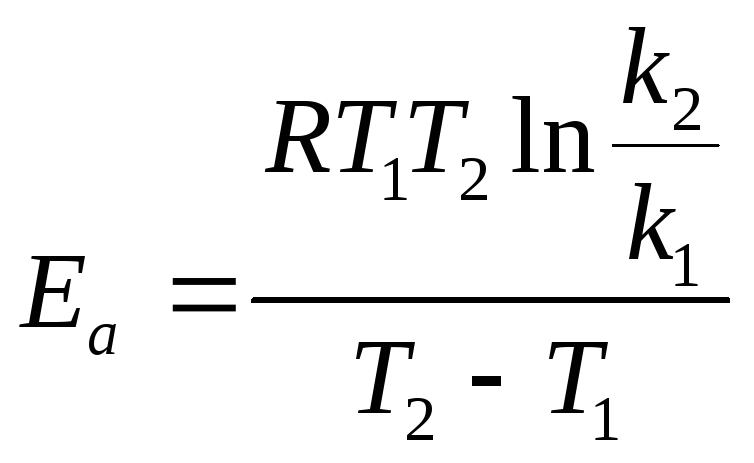
Если Еа= 50-100 кДж/моль, то при изменении температуры на каждые 10 градусов, ее скорость возрастает в 2-4 раза.
Это правило было установлено Вант-Гоффом, согласно которому повышение температуры на каждые 10 градусов увеличивают скорость реакции примерно в 2-4 раза:

где  —
скорость реакции при температуре Т2;
—
скорость реакции при температуре Т2;  —
скорость реакции при температуре Т1;
—
скорость реакции при температуре Т1;  —
температурный коэффициент скорости
реакции, который находится в пределах
от 2 до 4.
—
температурный коэффициент скорости
реакции, который находится в пределах
от 2 до 4.
Правило
Вант-Гоффа имеет ограниченное применение,
поскольку величина 
Анализируя еще уравнение Аррениуса, приходим к выводу, что существует две возможности ускорения реакции: 1) увеличение температуры; 2) снижение энергии активации.
Вопрос 4. Зависимость скорости реакции от катализатора
Одним из важнейших способов воздействия на скорость химической реакции является использование катализаторов. Катализатор – это вещество, изменяющее скорость химической реакции и не расходующееся в процессе взаимодействия. Влияние катализатора на скорость химической реакции называют катализом.
В зависимости от фазового состояния реагирующих веществ и катализатора различают два вида катализа – гомогенный и гетерогенный. Если реагенты и катализатор находятся в одинаковом агрегатном состоянии, и между ними нет поверхности раздела, то катализ гомогенный. При гетерогенном катализе реакция протекает на поверхности раздела двух фаз, одна из которых является катализатором.
Примеры некоторых каталитических реакций:
Реакция | Катализатор | |
гомогенный | гетерогенный | |
SO2(г)+ ½ O2(г) = SO3(г) | NO(г) | V2O5(тв) |
Н2О2(ж) = Н2О(ж) + ½ О2(г) | K2Cr2O7 | MnO2(тв) |
С2Н4(г) + Н2(г) = С2Н6(г) | _________ | Ni(тв) |
Детальный механизм действия катализатора очень сложен. Однако можно сказать, что в случае гомогенного катализа катализатор, взаимодействуя с реагентами, образует с ними промежуточные соединения (интермедианты). В итоге величина энергии активации реакции с участием катализатора оказывается ниже энергии активации такой же реакции при его отсутствии. Практически реакция идет по другому пути, через другое переходное состояние (рис.4)
Еа, К < Еа.
В некоторых случаях каталитические реакции протекают с образованием не одногo, а двух и более переходных состояний (например, окисление оксида серы (IV) в присутствии катализатора NO: сначала происходит взаимодействие катализатора с кислородом: NO+ ½ O2 = NO2(Ea2), затем промежуточное соединение NO2 Взаимодействует с оксидом серы (IV): NO2 + SO2 = SO3 + NO (Ea3). Суммарная энергия активации каталитического процесса все равно ниже, чем процесса без катализатора:
Еа2 + Еа3 < Еа1
Уменьшение энергии активации соответствует значительному увеличению частиц, обладающих энергией, превышающей энергию активации, и приводит к возрастанию скорости реакции.
При гетерогенном катализе снижение Еакт., достигается в результате адсорбции реагентов на поверхности катализатора, следствием чего является ослабление химических связей в адсорбированных молекулах. Например, при дожигании оксида углерода (II) выхлопных газов кислородом происходит адсорбция газов на поверхности платинового катализатора. Реакция адсорбированных молекул газов с ослабленными внутримолекулярными связями протекает с меньшей энергией активации, чем аналогичная реакция в газовой среде. Затем происходит десорбция образовавшихся молекул с поверхности катализатора.
Катализ играет важную роль и в биохимических процессах. В роли катализаторов выступают ферменты – сложные белки.
Для
количественной оценки воздействия
катализатора на химический процесс
используют уравнение Аррениуса, которое
до введения катализатора имеет вид  ,
после введения катализатора —
,
после введения катализатора —  .
Температура величина постоянная. Поделим
второе уравнение на первое и
прологарифмируем:
.
Температура величина постоянная. Поделим
второе уравнение на первое и
прологарифмируем:
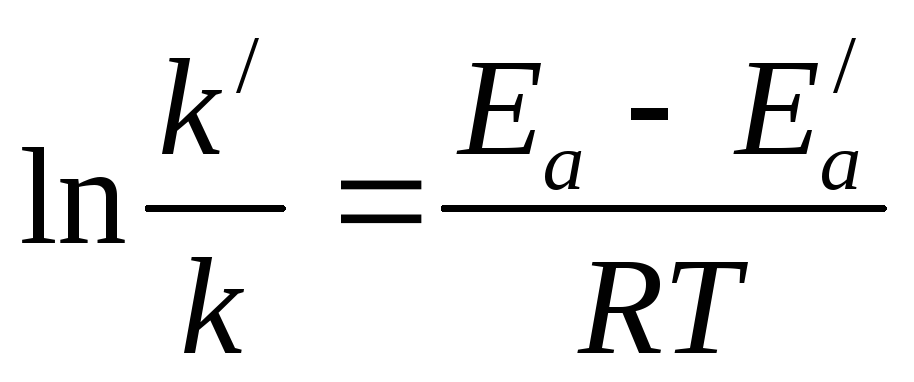
Существуют вещества, которые, напротив, уменьшают скорость реакции, их называют ингибиторами. Они изменяют путь реакции, переводя исходные вещества в интермедиант (эта реакция имеет небольшую энергию активации Еа2 << Ea1). Энергия активации процесса перехода промежуточного состояния в конечный продукт оказывается чрезвычайно большой (Еa3>>Ea1), и такой процесс становится маловероятным. В результате интермедиант снова распадается с образованием исходных веществ.
Примером ингибитора для перекиси водорода может служить фосфорная кислота.
Таким образом, подведем итог:
Отличительные черты катализаторов:
Имеет очень высокую эффективность. Например, одна частица мелкодисперсной платины (платиновая чернь) в одну секунду разлагает 105молекул Н2О2.
По окончании реакции катализатор остается в химически неизменном состоянии и не расходуется, т.е. его участие в реакции не отражается общим стехиометрическим уравнением. Однако физически катализатор изменяется. Например, кристаллический MnO2в процессе каталитического разложения хлората калияKClO3превращается в мелкодисперсный порошок. Эти изменения свидетельствуют о том, что в ходе реакции на определенных стадиях катализатор вступает во взаимодействие с реагентами, а по окончании ее вновь выделяется.
Катализатор одинаково ускоряет как прямую, так и обратную реакцию, т.е. не смещает равновесие и не влияет на его константу, а лишь уменьшает время достижения равновесного состояния.
Действие катализатора сводится к понижению Еа при образовании промежуточных нестойких соединений, которые в дальнейшем распадаются на продукты реакции с выделением катализатора в химически неизменном виде. Следует отметить одну важную особенность катализаторов. Они не влияют на термодинамику реакций, т.е. не изменяют энтальпию и энергию Гиббса реакции. Если G>0, то в присутствии катализаторов она не станет самопроизвольной.
6.4. Зависимость скорости химической реакции от температуры
Зависимость скорости химической реакции от температуры определяется правилом Вант-Гоффа и уравнением Аррениуса.
Правило Вант-Гоффа: при увеличении температуры на каждые 100 скорость химической реакции возрастает в 2-4 раза.
Математически это запишется следующим образом:
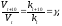 (7)
(7)
где: Vtиkt– скорость и константа скорости химической реакции при температуреt;Vt+10иkt+10– скорость и константа скорости химической реакции при температуреt+10; – температурный коэффициент скорости химической реакции, показывающий во сколько раз увеличивается скоростьреакции при увеличении температуры на 10 градусов; для большинства реакций значения= 2 ÷ 4.
В общем случае, когда температура процесса изменилась на t, уравнение (7) можно преобразовать к виду
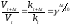 .
(8)
.
(8)
Уравнение Аррениуса. Уравнения (7) и (8) лишь приближенно оценивают зависимости V = f(t) и k = f(t). Функциональная зависимость константы скорости химической реакции (скорости химической реакции) от температуры была установлена шведским ученым Св. Аррениусом (1889 г.). Она выражается уравнением, названным в его честь уравнением Аррениуса:
k = A e—Ea/RT, (9)
где: А – предэкспоненциальный множитель; ЕА – энергия активации химической реакции.
А и ЕА являются важными характеристиками каждой химической реакции. Выясним физический смысл этих величин.
Предэкспоненциальный множитель
А = р·z, (10)
где z – число соударений молекул реагирующих веществ в единице объема за единицу времени; р – стерический (вероятностный) фактор, учитывает влияние пространственной ориентации молекул на скорость реакции (или константу скорости). Значения р = 10-9 ÷1. Малые значения р отвечают реакциям между сложными по своей структуре органическими соединениями.
Энергия активации химической реакции. Не все сталкивающиеся молекулы взаимодействуют с образованием продуктов реакции, а только те активные молекулы, которые обладают достаточной энергией, чтобы разорвать или ослабить связи в исходных молекулах, создав возможность образования новых молекул.
Например, при химическом взаимодействии: H2 + I2 = 2HI должны разорваться связи НН и II и образоваться связи Н I. В некоторый момент времени возникает переходное состояние, когда одни связи не полностью разорвались, а другие уже начали формироваться. Такой нестабильный ассоциат называется активным (активированным) комплексом. Его образование можно представить следующей схемой:
Н I Н · · · I НI
| + | → ∶ ∶ →
Н I H · · · I НI
Исходные вещества Активный комплекс Продукты реакции
Для образования активного комплекса нужно преодолеть некоторый энергетический барьер, затратив энергию ЕА. Эта энергия и есть энергия активации – некоторая избыточная энергия, по сравнению со средней при данной температуре энергией, которой должны обладать молекулы для того, чтобы их столкновения были эффективными.
В общем случае для химической реакции А + В = С +Д переход от исходных веществ А и В к продуктам реакции С и Д через состояние активного комплекса А + В = АВ = С + D схематически можно представить в виде энергетических диаграмм (рис. 6.2).
Энергия
активации ЕА – один из основных параметров, который
характеризует скорость химического
взаимодействия. Она
зависит от природы реагирующих веществ.
Чем больше ЕА,
тем меньше (при прочих равных условиях)
скорость реакции. При повышении
температуры число активных частиц
сильно возрастает, благодаря чему резко
увеличивается скорость реакции. 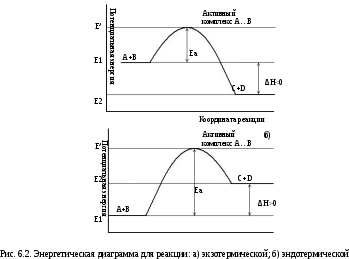
Обычно реакции между веществами с прочными ковалентными связями характеризуются большими значениями ЕА и идут медленно, например:
а) взаимодействия между органическими веществами | Скорость этих процессов при стандартных условиях близка к нулю |
б) H2 + 1/2О2 = H2О | |
в) N2 + 3H2 = 2NH3 |
Низкими значениями ЕА и очень большими скоростями характеризуются ионные взаимодействия в растворах электролитов. Например:
Ca+2 + SO = CaSO4.
= CaSO4.
Объясняется это тем, что разноименно заряженные ионы притягиваются друг к другу и не требуется затрат энергии на преодоление сил отталкивания взаимодействующих частиц.
2.6. Зависимость скорости химической реакции от температуры
2.6.1. Уравнение Аррениуса
В большинстве случаев скорость химической реакции увеличивается при повышении температуры.
Зависимость константы скорости реакции от температуры выражается уравнением Аррениуса
| (2.14) |
где k — константа скорости реакции;
A — константа, называемая предэкспоненциальным
множителем;
 —
основание натурального логарифма;
—
основание натурального логарифма;
Еa— энергия активации, Дж/моль;
Т — температура, К;
R — газовая постоянная, 8,31 Дж/мольК.
2.6.2. Энергия активации
Для того чтобы произошла реакция, необходимо преодолеть отталкивание электронных оболочек молекул и разорвать или ослабить связи между атомами. На это надо затратить определенную энергию.
Энергия активации в элементарных реакциях – минимальная энергия реагентов (атомов, молекул и др. частиц), достаточная для того, чтобы они вступили в химическую реакцию, т. е. для преодоления барьера на поверхности потенциальной энергии, отделяющего реагенты от продуктов реакции.
Потенциальный барьер – максимум потенциальной энергии, через который должна пройти система в ходе элементарного акта химического превращения.
В ходе реакции вещества переходят в неустойчивое промежуточное состояние, характеризующееся большим запасом энергии. Это состояние называется активированным комплексом или переходным состоянием. Именно для его образования необходима энергия активации (рис. 4, 5).
Число частиц, входящих в активированный комплекс, определяет молекулярность данной стадии реакции.
Неустойчивый
активированный комплекс существует
очень короткое время ( ).
Он распадается с образованием исходных
веществ или продуктов реакции.
).
Он распадается с образованием исходных
веществ или продуктов реакции.
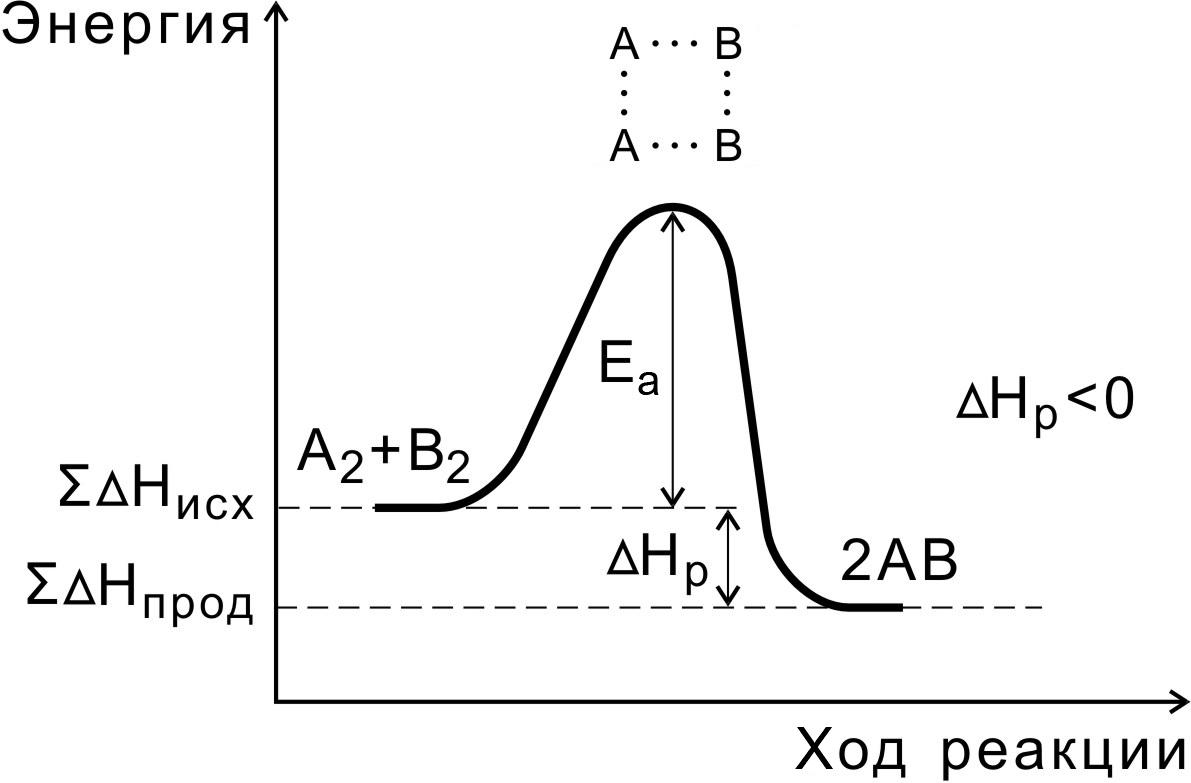
Рис. 4. Энергетическая диаграмма экзотермической реакции
Переходное состояние возникает в ходе как прямой, так и обратной реакций (рис. 6). Разность энергий активации прямой и обратной реакций равна изменению внутренней энергии (тепловому эффекту) реакции
Нр = Еа(пр) — Еа (обр).
В макроскопической химической кинетике энергия активации – параметр Еa, входящий в уравнение Аррениуса (2.14). В общем случае сложных реакций параметр Еaявляется функцией энергий активации отдельных стадий, и определяемая энергия активации называется эффективной (эмпирической, кажущейся).
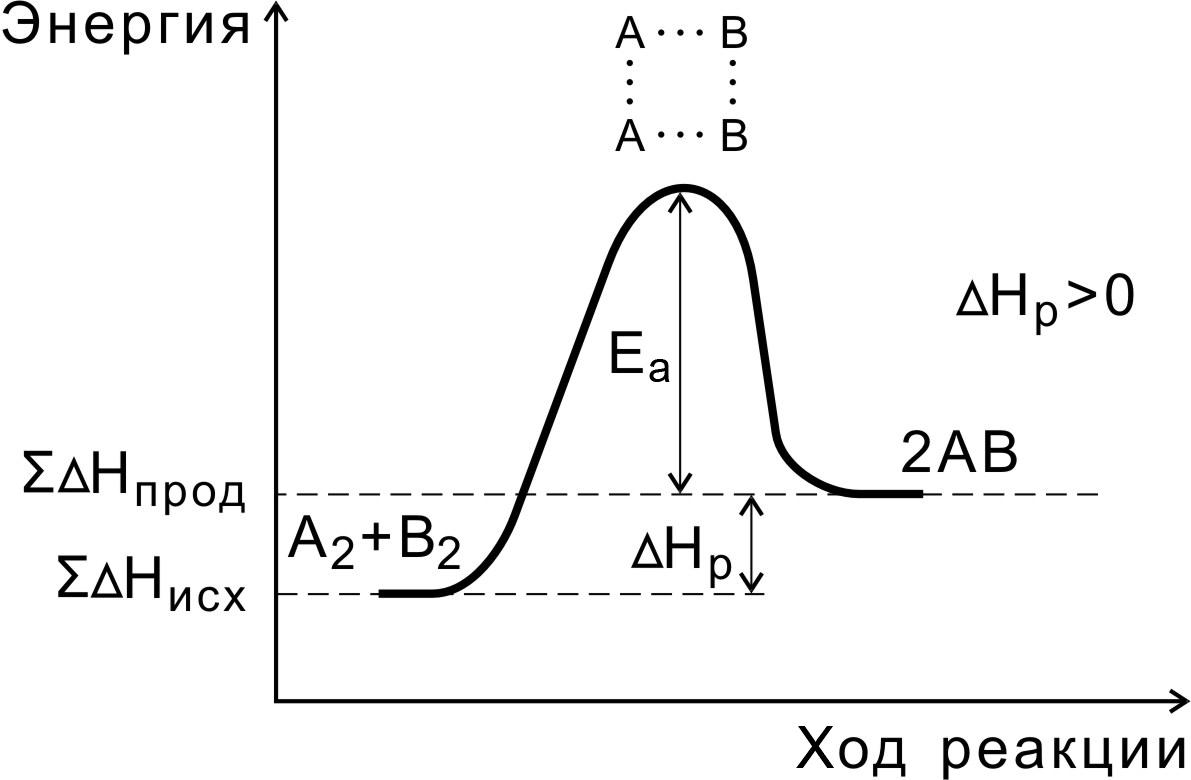
Рис. 5. Энергетическая диаграмма эндотермической реакции
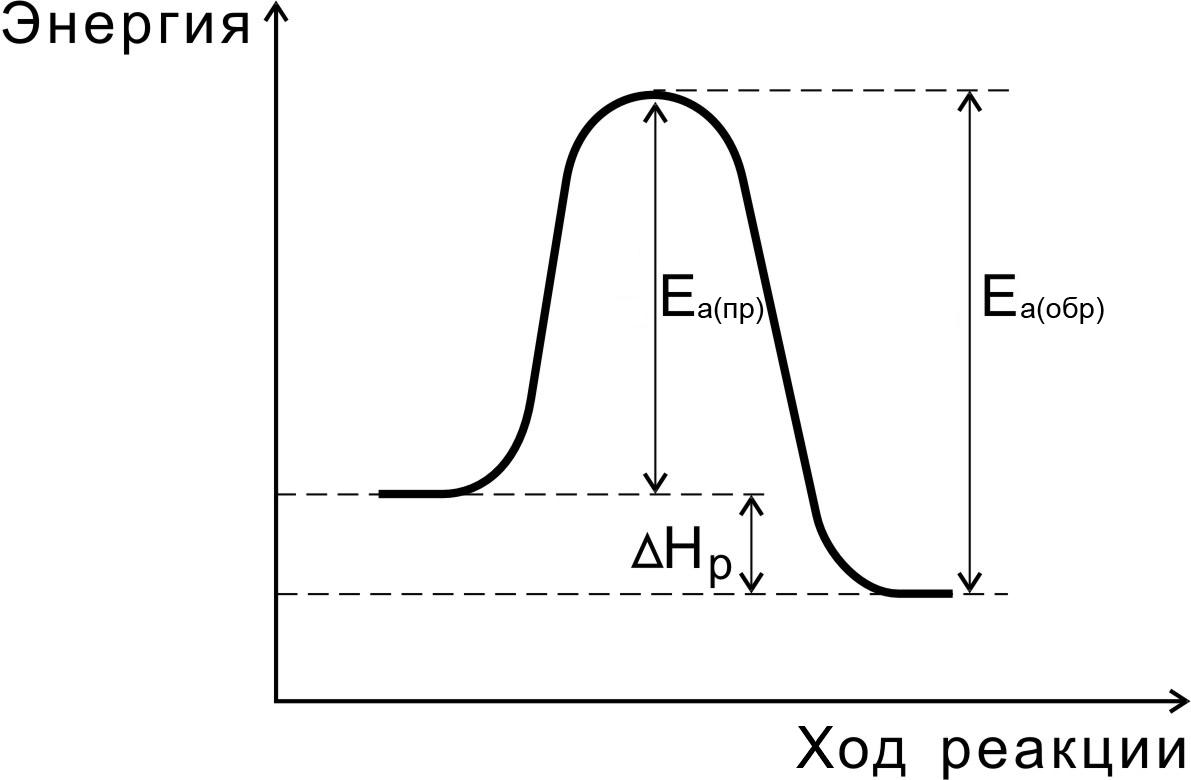
Рис.6. Соотношение между энергиями активации прямой
и обратной реакций и теплового эффекта
Зависимость скорости реакции от температуры
Правило Вант-Гоффа
С повышением температуры скорость реакции увеличивается. Зависимость скорости реакции от температуры приближенно описывается эмпирическим правилом Вант-Гоффа: при повышении температуры на каждые 10° скорость реакции увеличивается в 2-4 раза.
Математическое выражение правила Вант-Гоффа:
 (16),
(16),
а при условии, что концентрации всех реагирующих веществ равны 1 моль/л:
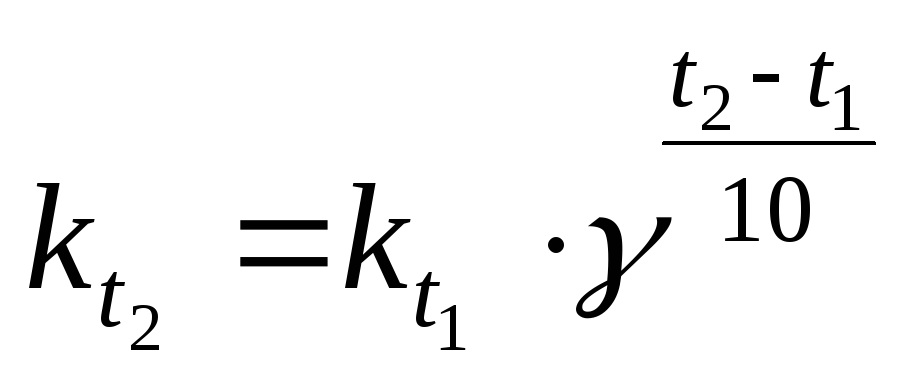 (17),
(17),
где 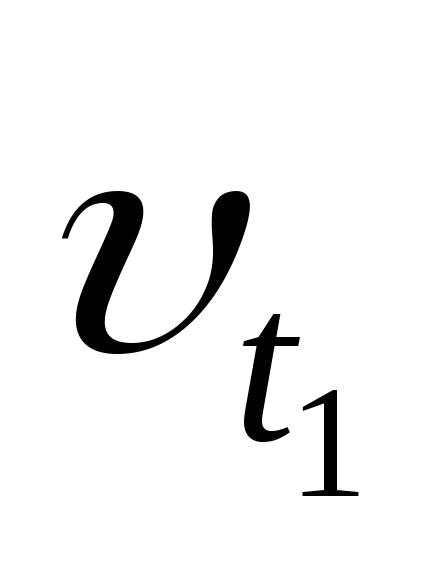 ,
, 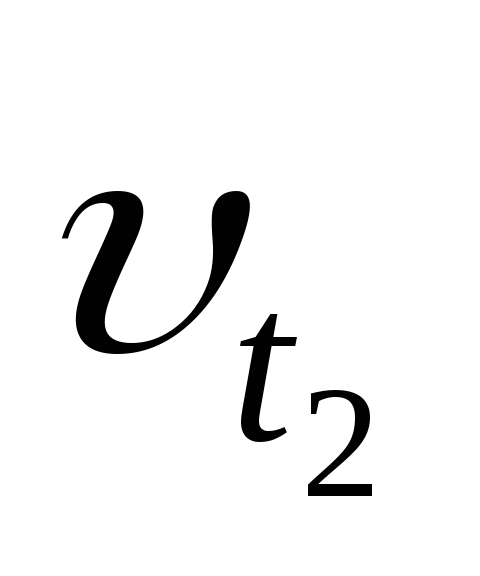 и
и  ,
, 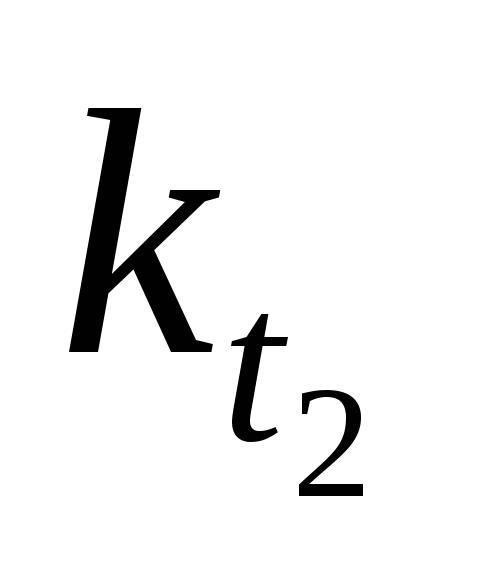 — соответственно скорости и константы
скоростей реакции при температурах
— соответственно скорости и константы
скоростей реакции при температурах  и
и  .
.
Температура
может быть выражена как в °С, так и в К,
так как изменение температуры не зависит
от единиц измерения ( ).
).
 — температурный
коэффициент скорости реакции,
который показывает, во сколько раз
возрастает скорость реакции при повышении
температуры на 10 градусов:
— температурный
коэффициент скорости реакции,
который показывает, во сколько раз
возрастает скорость реакции при повышении
температуры на 10 градусов:
 (18)
(18)
Поскольку
при концентрациях реагирующих веществ
1 моль/л скорость химической реакции
численно равна константе скорости  ,
то
,
то
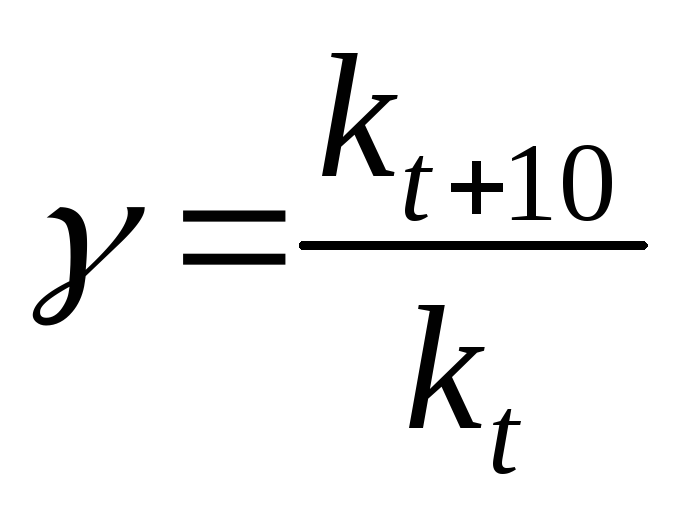 (19)
(19)
Учитывая
тот факт, что скорость реакции обратно
пропорциональна времени ее протекания
из уравнения (18), при 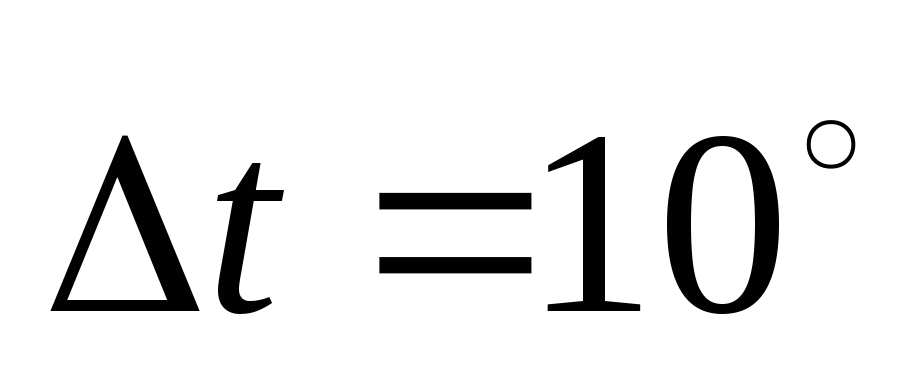 получаем
получаем
 (20)
(20)
Используя уравнения (16 – 20), можно рассчитать:
константу скорости (или скорость) реакции при заданной температуре, если известны значения этих величин при двух других температурах;
на сколько градусов надо повысить (или понизить) температуру реакции, чтобы скорость ее увеличилась (или уменьшилась) в N раз;
при какой температуре следует проводить реакцию, чтобы она закончилась за определенное время, если известны температурный коэффициент реакции и скорость ее при любой температуре;
температурный коэффициент реакции и т. д.
Пример
7. Рассчитайте
константу скорости химической реакции
при  °С,
если константа скорости этой реакции
при температурах 400 °С и 500 °С равна
соответственно 0,03 и 50,3.
°С,
если константа скорости этой реакции
при температурах 400 °С и 500 °С равна
соответственно 0,03 и 50,3.
Решение
а).
Для определения  запишем уравнение Вант-Гоффа (17), используя
запишем уравнение Вант-Гоффа (17), используя 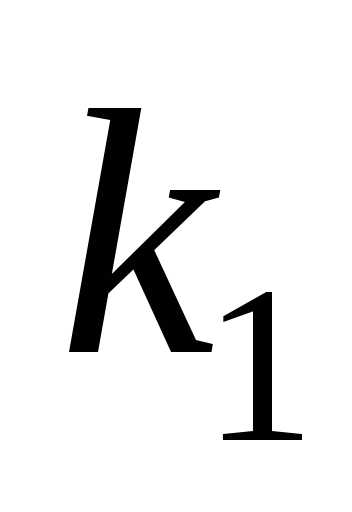 или
или  :
:
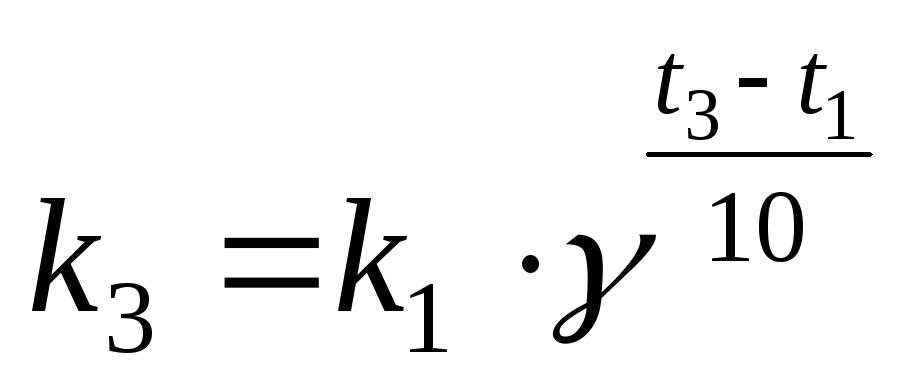 или
или 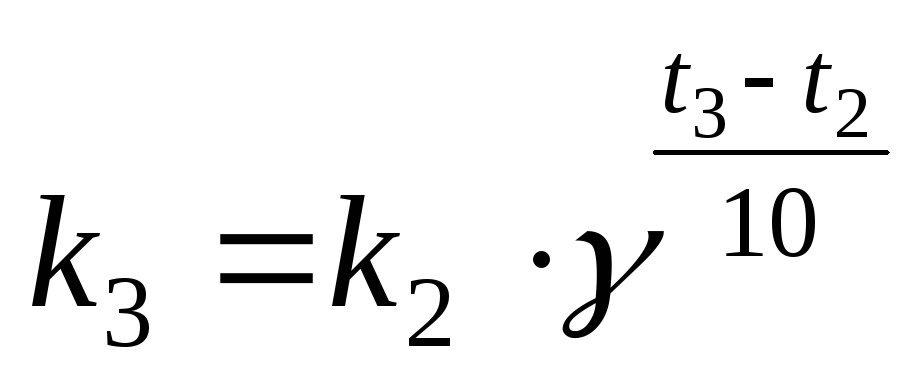
Учитывая:
 ,
,  ,
получаем:
,
получаем:
 или
или  (21)
(21)
б).
Температурный коэффициент  рассчитываем из отношения
рассчитываем из отношения 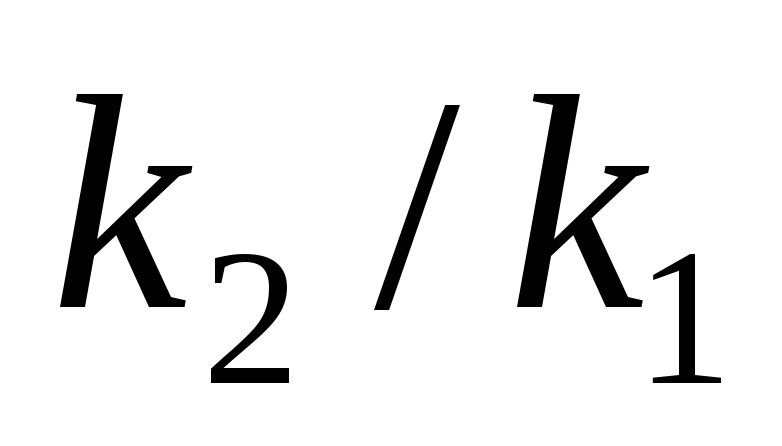 ,
полученного из уравнения (17):
,
полученного из уравнения (17):
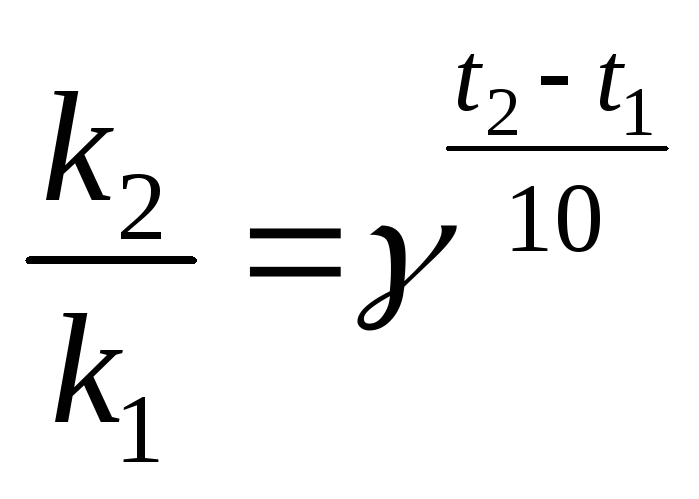

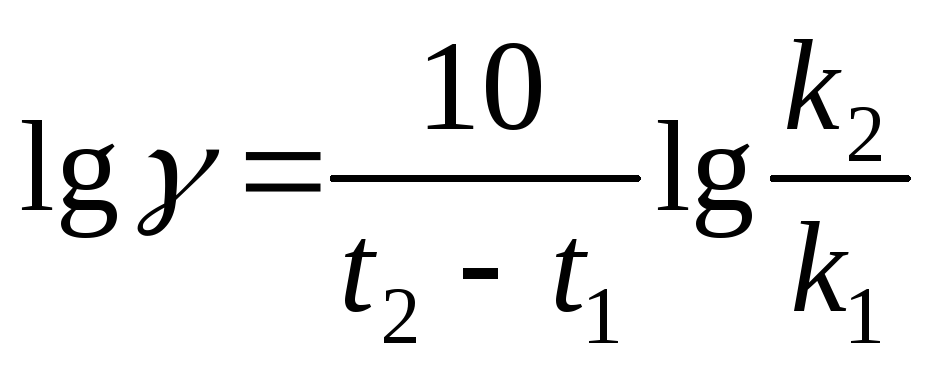

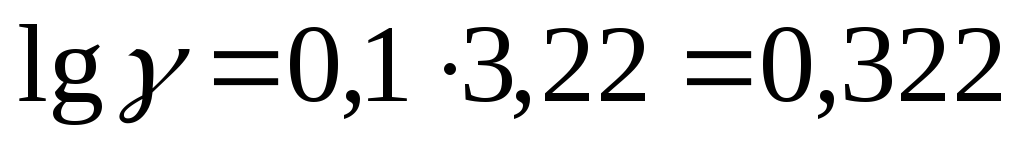
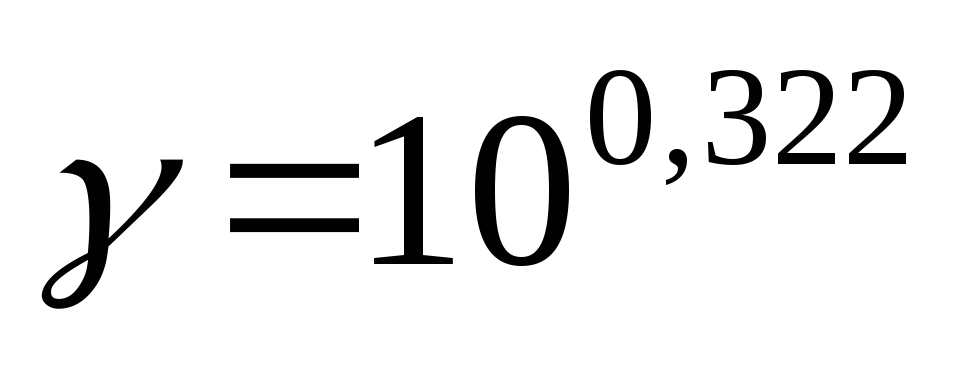
 .
.
в) рассчитываем, подставляя полученное
значение
рассчитываем, подставляя полученное
значение  в уравнения (21):
в уравнения (21):


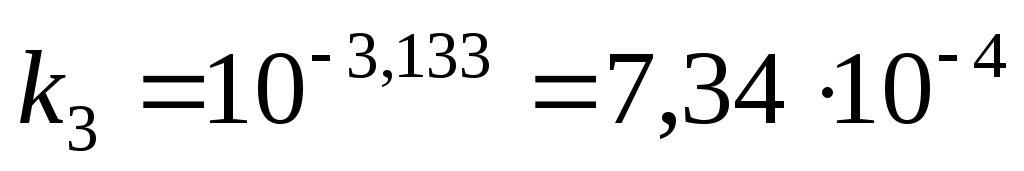
или
Ответ: 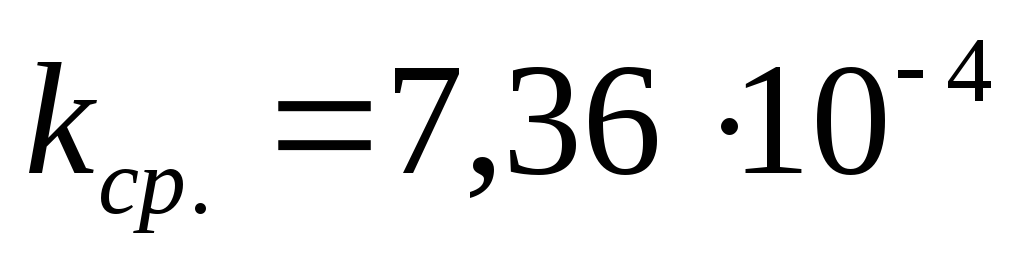 при
при 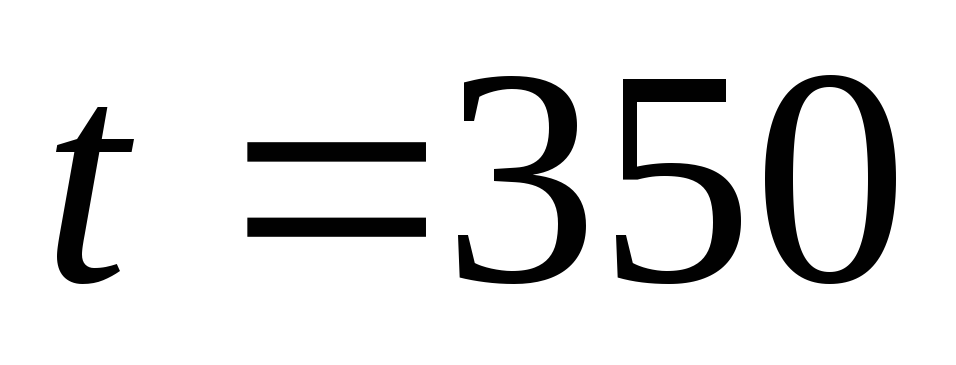 °С.
°С.
Пример
8. На сколько
градусов надо повысить температуру
реакции, чтобы скорость ее увеличилась
в 15 раз, если 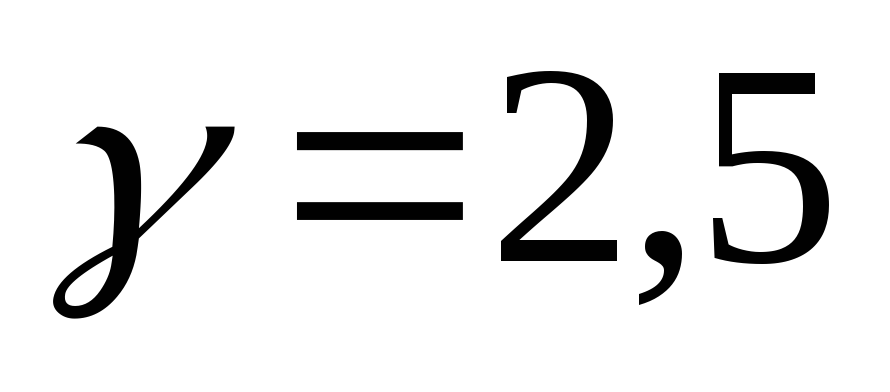 .
.
Решение. Из математического выражения правила Вант-Гоффа (16) и условия задачи получаем:
 ,
откуда
,
откуда
 (22)
(22)
Логарифмируя
уравнение (22), получаем формулу для
определения  :
:

 (23)
(23)
Подставляя в (23) условия задачи, получаем:
 °
°
Ответ: Температуру реакции надо повысить на 7,78 °.
Примечание:
Если известна температура ( ),
при которой проводилась реакция ранее,
то используя полученные данные, можно
рассчитать температуру (
),
при которой проводилась реакция ранее,
то используя полученные данные, можно
рассчитать температуру ( ),
при которой следует проводить реакцию,
чтобы скорость ее увеличилась в N раз:
),
при которой следует проводить реакцию,
чтобы скорость ее увеличилась в N раз:
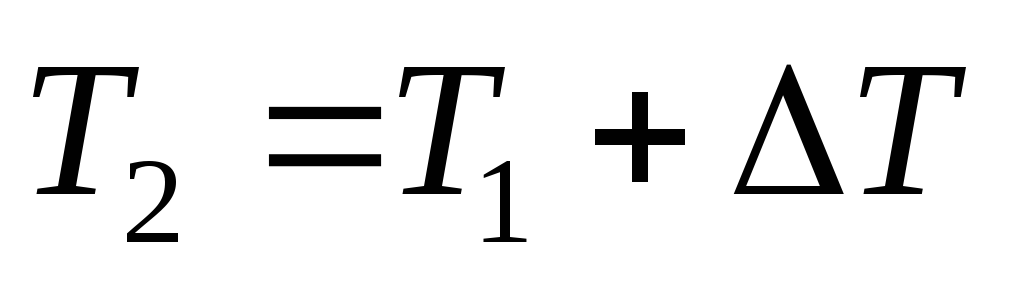 .
.
Пример 9.
Сколько времени потребуется для
проведения реакции при температуре 348
°К, если при температуре 298 °К она
заканчивается за 30 минут;  .
.
Решение
Из правила Вант-Гоффа (16) следует:
 (24)
(24)
Поскольку скорость реакции обратно пропорциональна времени (1, 4), то
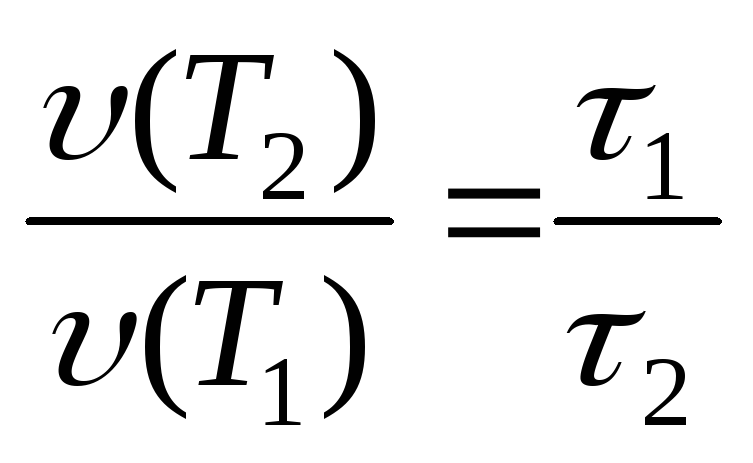 (25)
(25)
Из (24), (25) получаем:
 ,
, 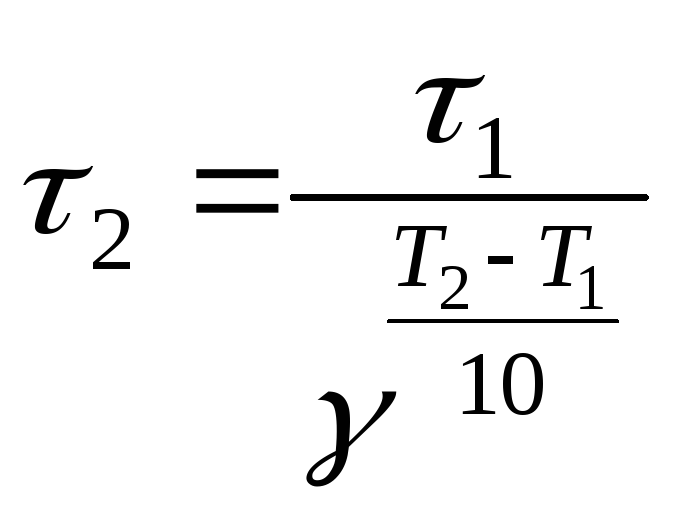

Таким
образом, при  К реакция закончится за 0,94мин.
К реакция закончится за 0,94мин.
Уравнение Аррениуса
Более точно зависимость константы скорости реакции от температуры описывается уравнением Аррениуса:
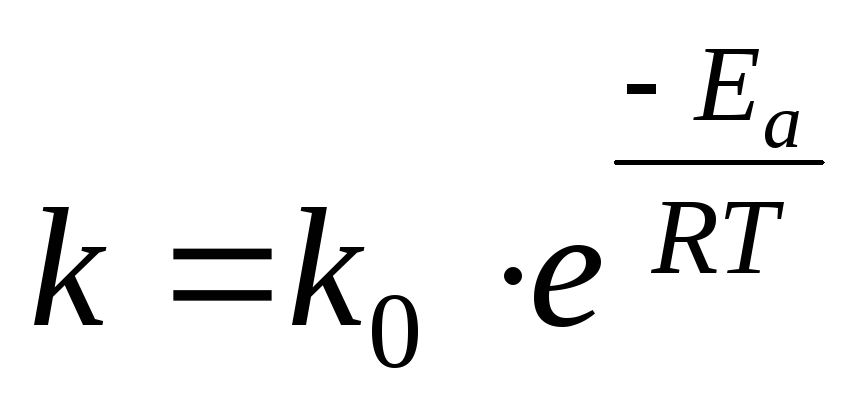 , (26)
, (26)
Если при изменении температуры концентрация реагентов остается постоянной, то зависимость скорости реакции от температуры описывается уравнением:
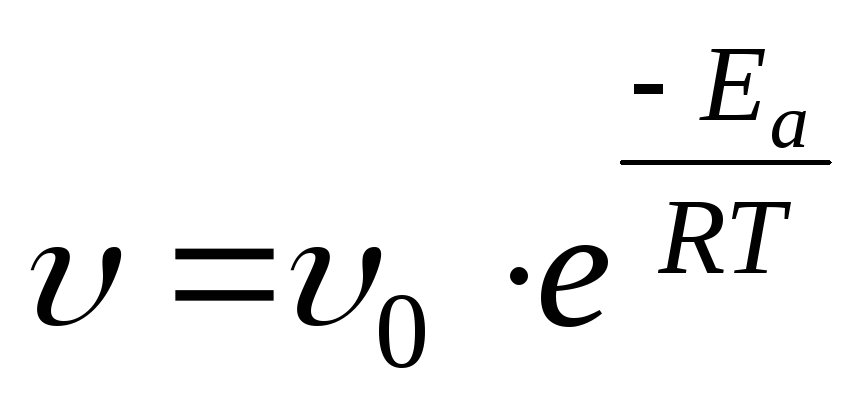 ,
где (27)
,
где (27)
 —
основание натурального логарифма;
—
основание натурального логарифма;
 —
энергия активации реакции, Дж/моль;
—
энергия активации реакции, Дж/моль;
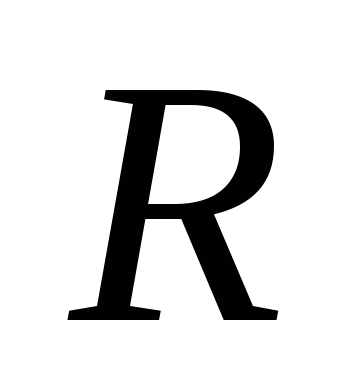 —
универсальная газовая постоянная,
—
универсальная газовая постоянная,  Дж/моль·К;
Дж/моль·К;
 —
температура, К;
—
температура, К;
 —
предэкспоненциальный множитель;
—
предэкспоненциальный множитель;
 при
при 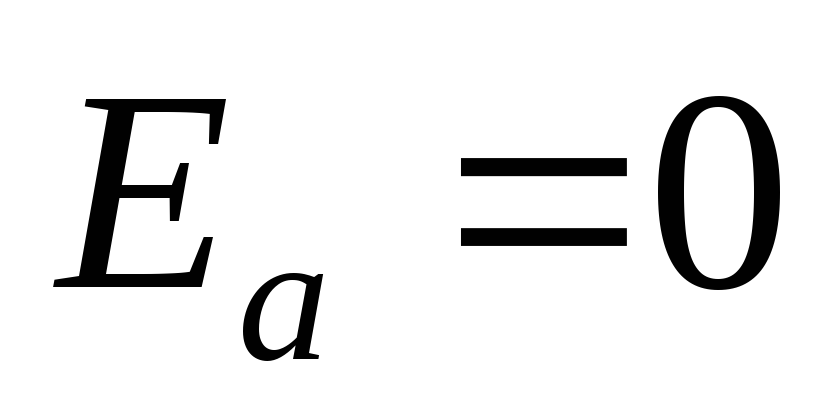 .
.
Энергия
активации – это минимальная дополнительная
или избыточная энергия по сравнению со
средней энергией реагирующих частиц,
которой должны обладать соударяющиеся
частицы, чтобы вступить в реакцию. Частицы, обладающие такой энергией,
называются активными. Энергия активации
процесса зависит от природы реагирующих
веществ. Значения энергии активации
для химических реакций могут составлять
от 40 до 200 кДж/моль. По
гипотезе Аррениуса химическое
взаимодействие осуществляется только
при соударении активных частиц, доля
которых в системе пропорциональна
величине 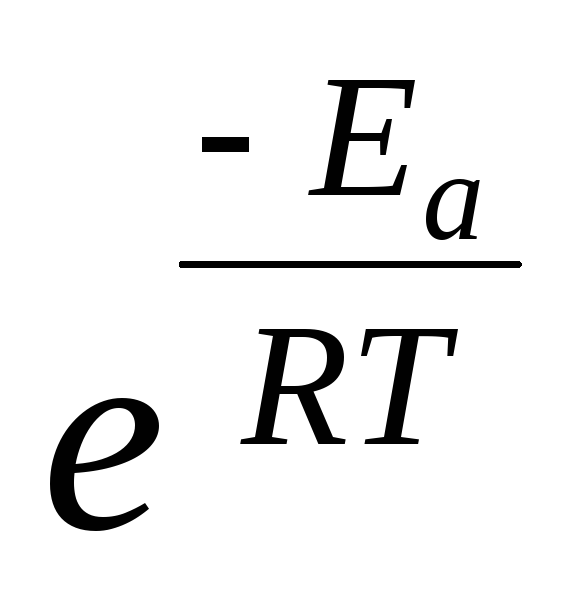 .
С увеличением температуры доля этих
частиц в системе растет и соответственно
растет скорость реакции.
.
С увеличением температуры доля этих
частиц в системе растет и соответственно
растет скорость реакции.
Используя уравнение Аррениуса можно рассчитать:
 и
и  реакции, если известны константы
скорости реакции при двух температурах;
реакции, если известны константы
скорости реакции при двух температурах;константу скорости реакции при заданной температуре, если известны энергия активации реакции и константа скорости при какой-либо температуре.
Скорости при нескольких температурах можно рассчитать двумя способами.
Пример 10. Рассчитайте энергию активации процесса, если известно:
| 726 | 746 | 766 |
| 0,0103 | 0,02447 | 0,05803 |
Решение. 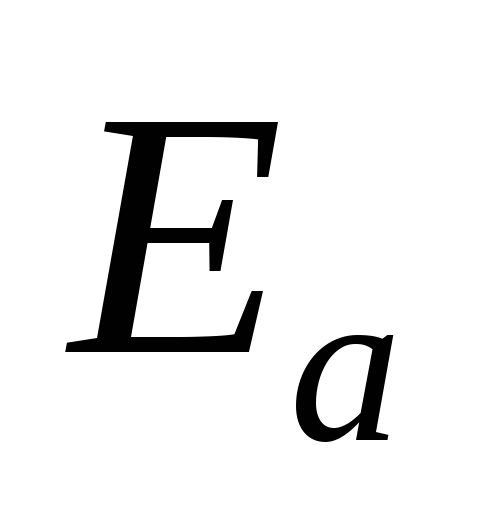 рассчитываем, используя уравнение
Аррениуса (26) для двух температур:
рассчитываем, используя уравнение
Аррениуса (26) для двух температур:
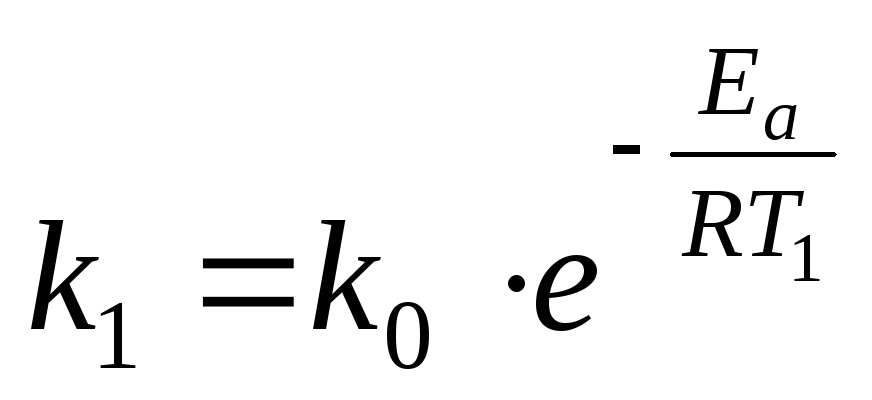 и
и 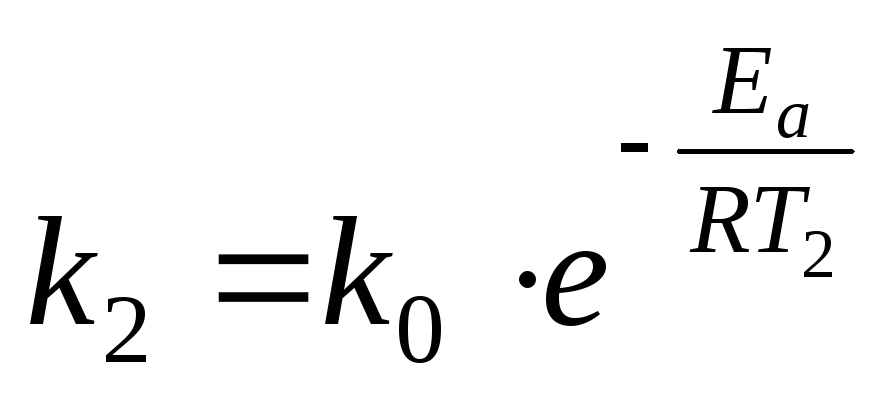
Откуда:
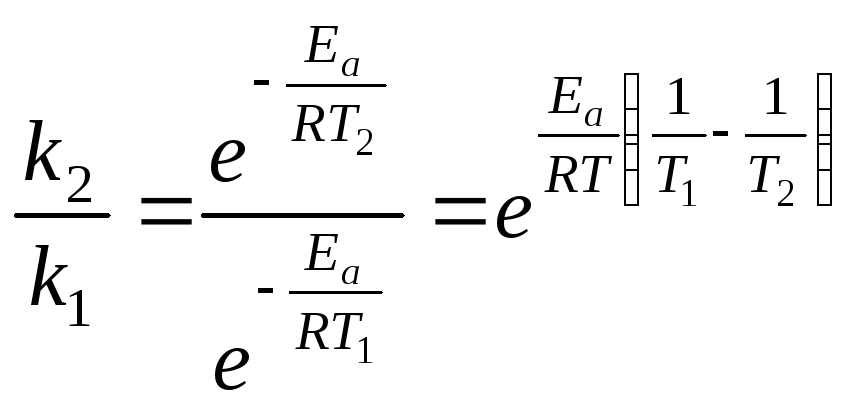
Прологарифмировав
последнее уравнение, с учетом того, что 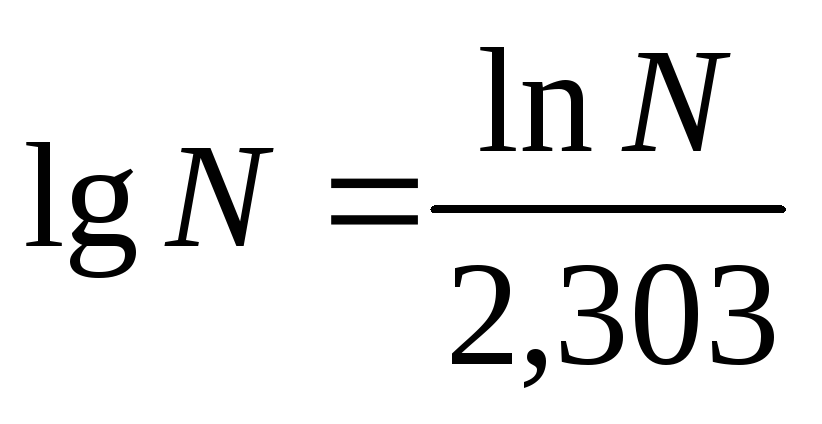 получаем:
получаем:

и, соответственно:
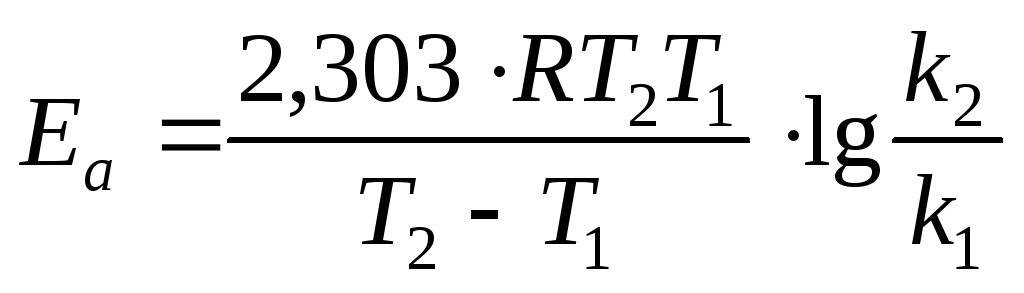
Для 726 К и 746 К:
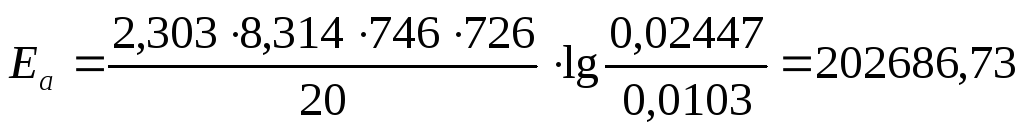 Дж/моль.
Дж/моль.
Для 726 К и 766 К:
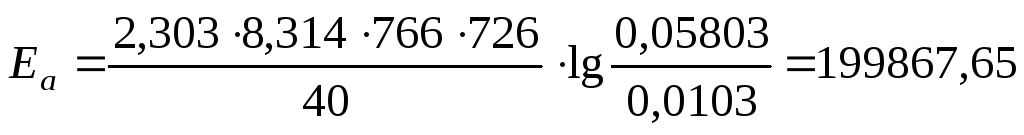 Дж/моль.
Дж/моль.
Для 746 К и 766 К:
 Дж/моль.
Дж/моль.
Средняя
энергия активации равна
 кДж/моль.
кДж/моль.
Пример
11. Рассчитайте  и
и  процесса, если известны константы
скоростей реакции при различных
температурах.
процесса, если известны константы
скоростей реакции при различных
температурах.
| 283 | 303 | 313 |
| 2,43 | 10,53 | 21,9 |
Решение.  ,
, 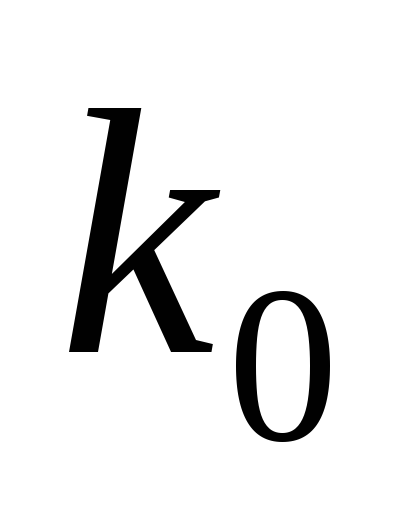 определяем графическим методом, используя
логарифмическую форму уравнения
Аррениуса (26):
определяем графическим методом, используя
логарифмическую форму уравнения
Аррениуса (26):
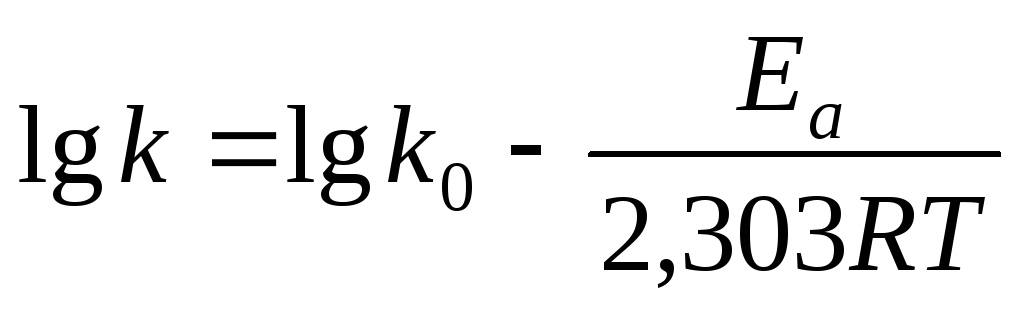 (28)
(28)
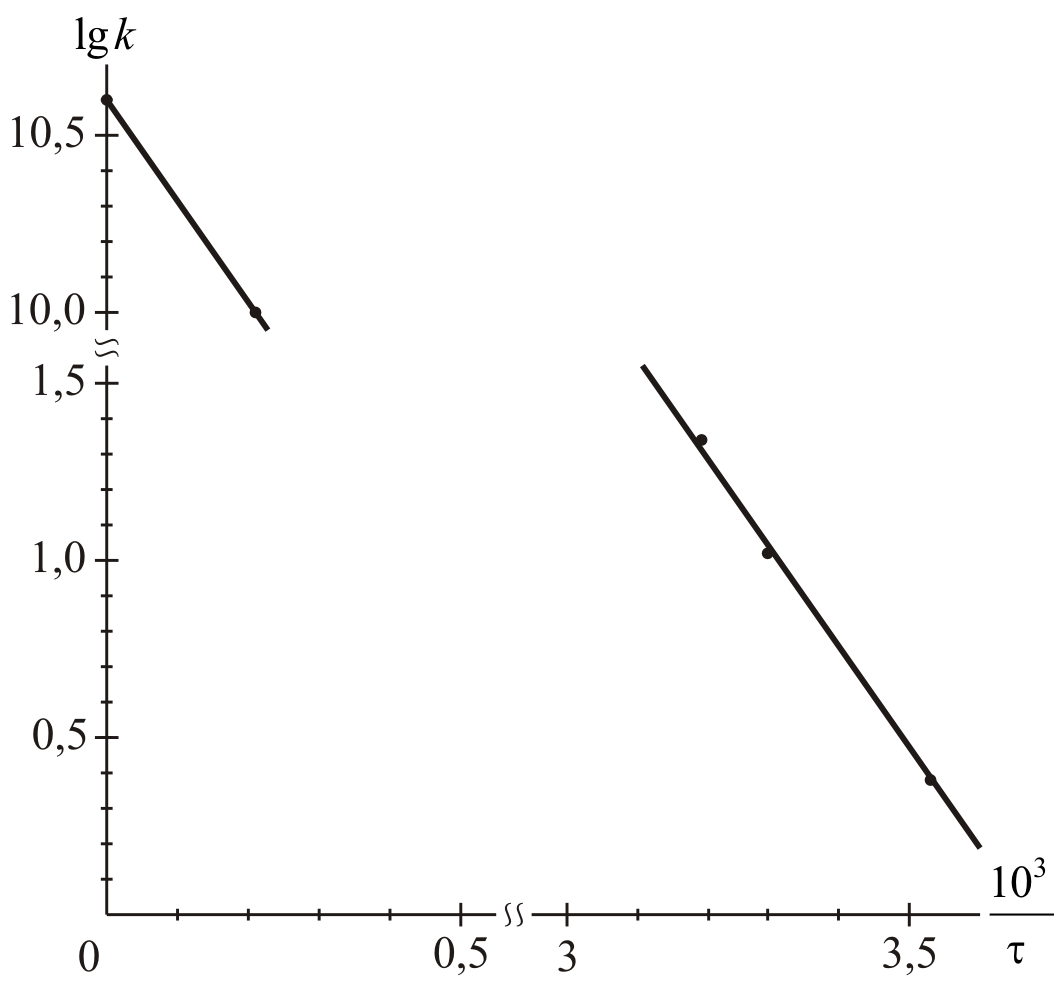
Для этого представим экспериментальные данные в следующем виде:
| 3,53 | 3,30 | 3,19 |
| 0,38 | 1,02 | 1,34 |
На
их основе строим график зависимости 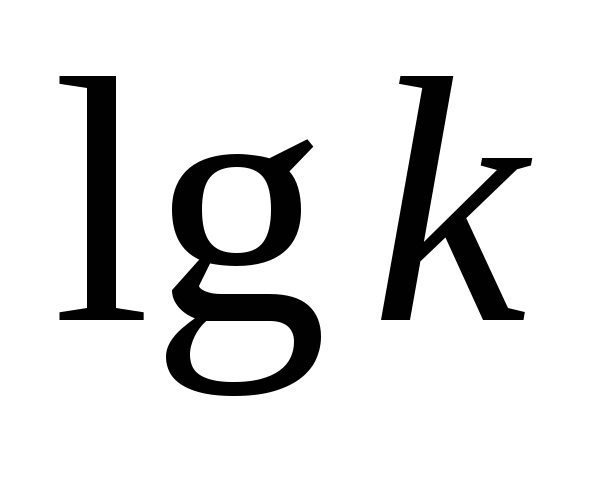 от
от  (см. рис. 1).
(см. рис. 1).
Из рис.1, согласно уравнению (26)
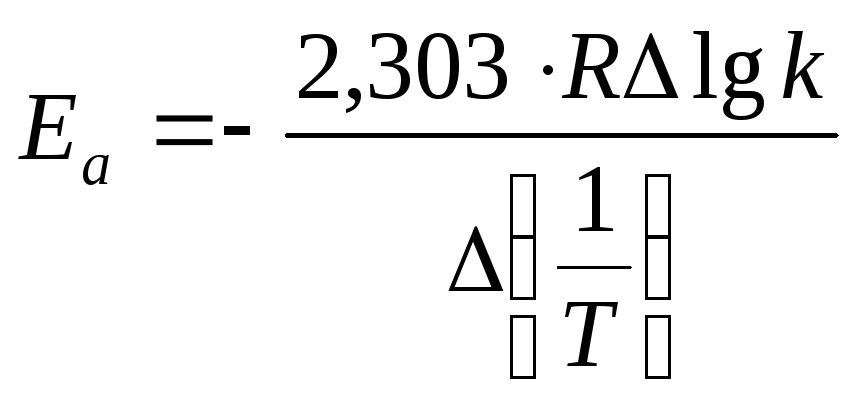
 находим
из графика:
находим
из графика:

 Дж/моль.
Дж/моль.
Из уравнения (24) следует:
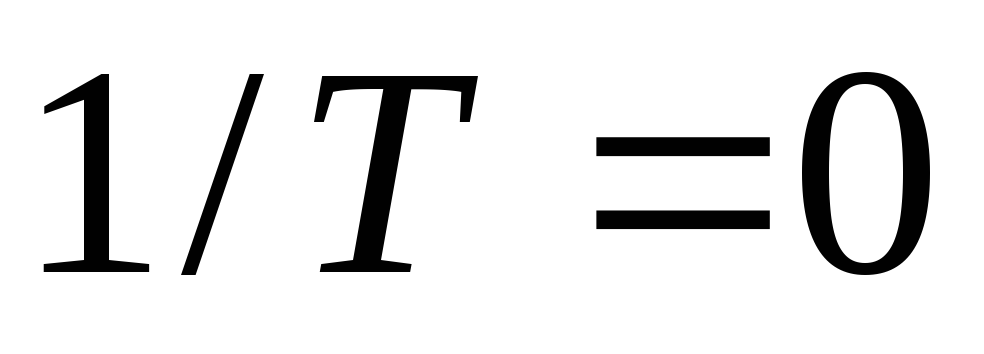 .
. 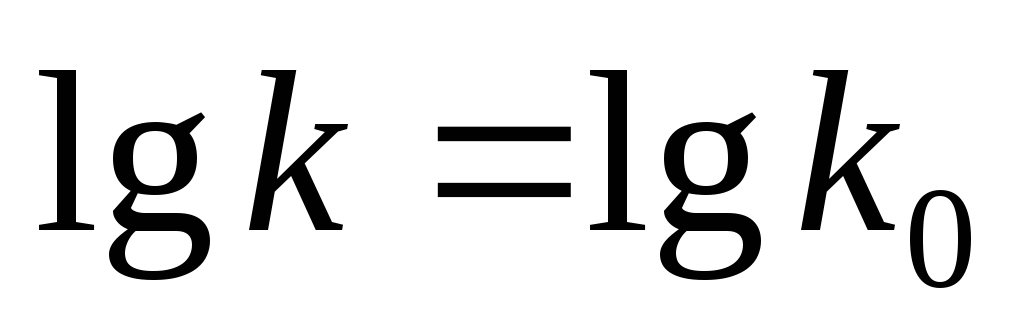 .
.
Продлив
график до пересечения с осью  ,
получаем
,
получаем
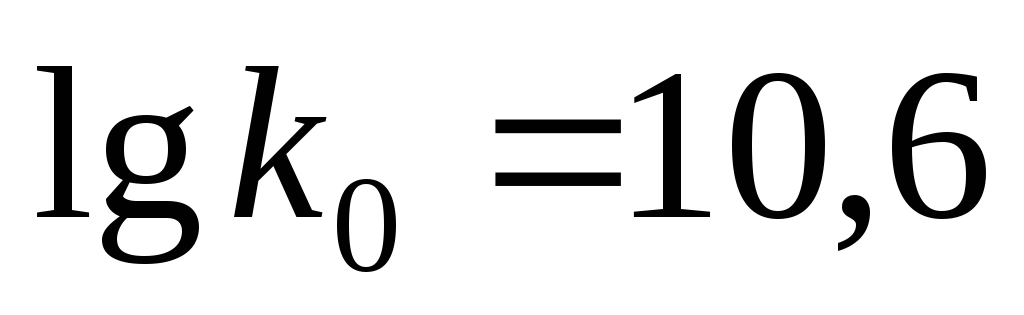
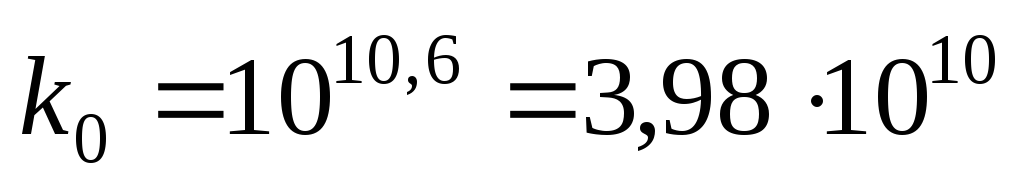 .
.
Таким
образом: 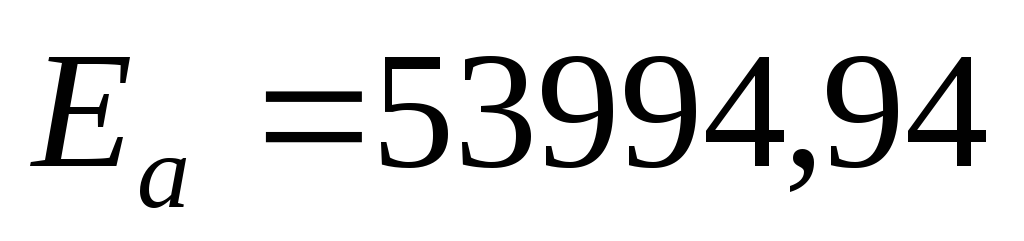 Дж/моль,
Дж/моль,  .
.
Приложение 1
Федеральное агентство по образованию Новосибирский государственный архитектурно-строительный университет Кафедра химии Индивидуальное задание по химии Работу выполнил студент: ______________________ группа_____ «___»____________2009 г. Работу проверил преподаватель: ________________________ «___»____________2009 г. Новосибирск 2009 |
27
40.Зависимость скорости реакции от температуры и от природы реагирующих веществ.
Правило Вант – Гоффа. Повышение температуры ускоряет большинство химических реакций. Согласно эмпирическому правилу Вант- Гоффа при повышении температуры на 10 К скорость многих реакций увеличивается в 2 – 4 раза
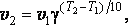
где v2 и v1 — скорости реакции при температурах Т2 и Т1, γ — коэффициент, значение которого для эндотермической реакции выше, чем для экзотермической. Для многих реакцийγ лежит в пределах 2 – 4.
При концентрациях реагирующих веществ 1 моль/л скорость реакции численно равна константе скорости k. Правило Вант – Гоффа запишется так:

Уравнение показывает, что константа скорости зависит от температуры так же, как и скорость процесса.
Эти два уравнения можно использовать лишь для ориентировочных расчетов, так как точность их не очень высока.
41. Необратимые и обратимые реакции.
Химическое равновесие. Многие химические реакции протекают в одном направлении до полного исчерпания реагирующих веществ. Такие реакции называются химически необратимыми. Другие реакции протекают вначале в прямом направлении, а затем в прямом и обратном благодаря взаимодействию продуктов реакции. В результате образуется смесь, содержащая одновременно исходные вещества и продукты реакции. Такие реакции называют химически обратимыми. В результате химически обратимого процесса наступает истинное (устойчивое) химическое равновесие, признаками которого являются:
1) в отсутствии внешних воздействий состояние системы остается неизменным неограниченно долго;
2) любое изменение внешних условий приводит к изменению состояния системы;
3) состояние равновесия не зависит от того, с какой стороны оно достигнуто.
Кроме истинных равновесий очень часто встречаются кажущиеся (ложные, заторможенные) равновесия, когда состояние системы сохраняется во времени очень долго, но небольшое воздействие на систему может привести к сильному изменению ее состояния.
ХИМИЧЕСКОЕ РАВНОВЕСИЕ – состояние химической системы, при котором возможны реакции, идущие с равными скоростями в противоположных направлениях. При химическом равновесии концентрации реагентов, температура и другие параметры системы не изменяются со временем.
42.Факторы, определяющие направление протекания химических реакций.
Скорость химической реакции зависит от природы реагирующих веществ и условий протекания реакции: концентрации с, температуры t , присутствия катализаторов, а также от некоторых других факторов (например, от давления — для газовых реакций, от измельчения — для твердых веществ, от радиоактивного облучения).Влияние концентраций реагирующих веществ. Чтобы осуществлялось химическое взаимодействие веществ А и В, их молекулы (частицы) должны столкнуться. Чем больше столкновений, тем быстрее протекает реакция. Число же столкновений тем больше, чем выше концентрация реагирующих веществ. Отсюда на основе обширного экспериментального материала сформулирован основной закон химической кинетики, устанавливающий зависимость скорости реакции от концентрации реагирующих веществ:Cкорость химической реакции пропорциональна произведению концентраций реагирующих веществ.Для реакции ( I ) этот закон выразится уравнением v = kcA cB , (1)
где сА и сВ — концентрации веществ А и В, моль/л; k — коэффициент пропорциональности, называемый константой скорости реакции. Основной закон химической кинетики часто называют законом действующих масс.Из уравнения (1) нетрудно установить физический смысл константы скорости k : она численно равна скорости реакции, когда концентрации каждого из реагирующих веществ составляют 1 моль/л или когда их произведение равно единице.Константа скорости реакции k зависит от природы реагирующих веществ и от температуры, но не зависит от их концентраций.Уравнение (1), связывающее скорость реакции с концентрацией реагирующих веществ, называется кинетическим уравнением реакции. Если опытным путем определено кинетическое уравнение реакции, то с его помощью можно вычислять скорости при других концентрациях тех же реагирующих веществ
2.3 Влияние температуры на скорость химических реакций.
Температура оказывает на скорость более сильное влияние, чем концентрации реагирующих веществ. В подавляющем большенстве случав при повышении температуры скорость реакции возрастает. Так, осуществить синтез воды (2Н2 + О2 – 2Н2О) при 200С даже на 15 % практически невозможно. На это потребуется 54 миллиона лет; при 5000С на это потребуется всего 50 минут, а уже при 7000С реакция протекает мгновенно.
Исследование выражения V = К * Сn показывает, что изменение скорость реакции с температурой может быть сопряжено с измене7нием 3-х величин: константы, концентрации и порядка реакции.
Обычно концентрация (особенно для реакций в жидкой фазе) изменяется с температурой мало. Изменение порядка реакции под влиянием температуры – довольно редкое явление.
Вследствие этого в химической кинетике изменение скорости реакции под влиянием температуры в первую очередь связывает с изменением константы скорости реакции. Исторически известны два вида зависимости константы скорости от температуры: эмпирическое правило Вант-Гоффа и более строгое уравнение Аррениуса.
В области умеренных температур для гомогенных и многих гетерогенных реакций справедливо правило Вант-Гоффа: при постоянных концентрациях реагирующих веществ увеличение температуры на 100С (или 10 К) приводит к возрастанию скорости реакции в 2 ÷ 4 раза.
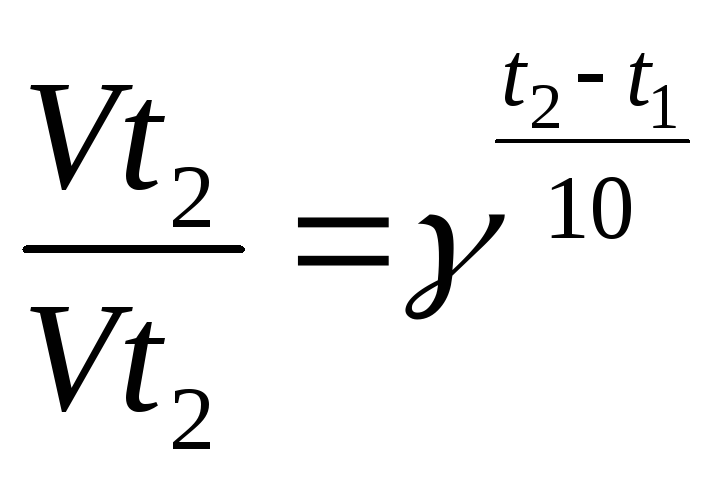 или
или (2.11)
(2.11)
Величина γ = 2 – 4, постоянная для данного процесса, называется коэффициентом Вант-Гоффа или температурным коэффициентом. Из выражения (2.11) следует, что скорость возрастает тем сильнее, чем больше для нее коэффициент Вант-Гоффа.
При γ = 2 увеличение температуры на 100 К ведет к росту скорости реакции в 210=1024 раза, а при γ = 3 – в 310 ≈ 60000 раз.
Более строгая зависимость константы скорости от температуры выражается уравнением Аррениуса (1889):
ln K = — 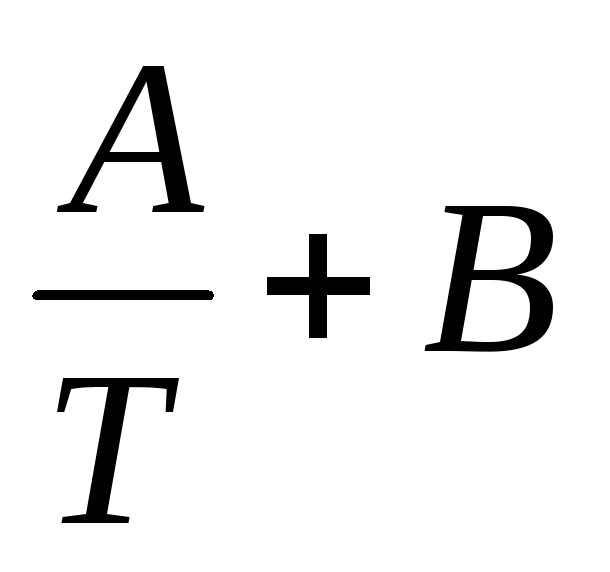 (2.12)
(2.12)
которое показывает, что логарифм (натуральный и десятичный) константы скорости линейно зависит от обратной абсолютной температуры.
В уравнении (2.12) А и В –
эмпирические константы для данной
реакции, которые можно определить
графическим способом. Для этого в
координатах 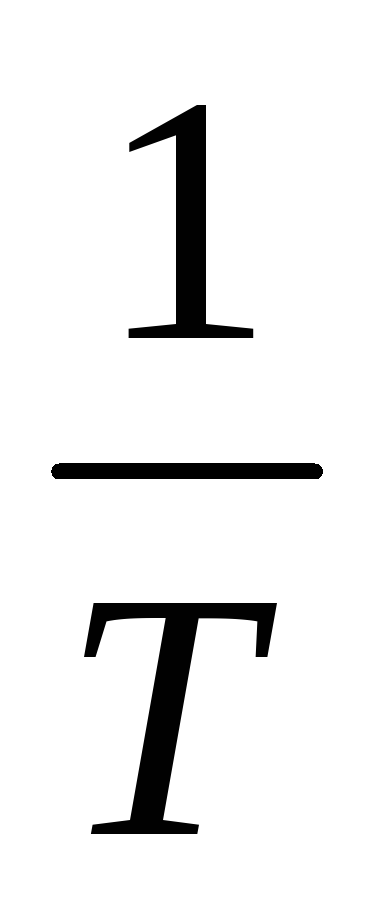 —
ln К строят график по экспериментальным
значениям константы скорости изучаемой
реакции при различных температурах.
Опытные точки в пределах статистического
разброса данных находятся на прямой
линии
—
ln К строят график по экспериментальным
значениям константы скорости изучаемой
реакции при различных температурах.
Опытные точки в пределах статистического
разброса данных находятся на прямой
линии
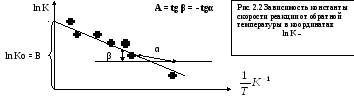
Константа А вычисляется
как тангенс угла наклона прямой к оси
абсцисс, а постоянная В численно равна
отрезку, отсекаемому прямой на оси
ординат при  =
0
=
0
Для объяснения предложенного уравнения Аррениус использовал некоторые теоретические представления о механизме реакций. Как уже было сказано, необходимым условием того, что бы между частицами (атомами, молекулами, ионами) исходных веществ произошло химическое взаимодействие, является их соударение. Но если бы каждое соударение оканчивалось взаимодействием, то все реакции протекали бы со скоростью взрыва; ведь молекулы содержащиеся в 1 см3 газа, испытывают ежесекундно такое колоссальное число соударений, что ему должна отвечать скорость превышающая экспериментальную в сотни и миллиарды раз.
Так, при р = 101,3 кПа и 5000С ежесекундное число столкновений в 1 см3 газа составляет ≈ 1028. Но, этот факт не противоречит закону действующих масс, так как число столкновений приводящих к реакции, пропорционально общему числу. Аррениус высказал гипотезу о том, что в реакцию вступают только молекулы, которые в момент столкновения находятся в активном состоянии, т.е. достигли энергетического уровня, характерного для данной реакции, ее энергетического барьера. Чем больше активных молекул при данных условиях, тем больше скорость реакции.
Активность молекул неразрывно связана с процессом, в котором они участвуют. Вне процесса понятие активности не имеет смысла. Например, одни и те же молекулы водорода при одних и тех же условиях по отношению к реакции Н2 + F2 = 2НF могут быть активными, а по отношению к реакции Н2 + I2 = 2НI неактивными.
Какие же молекулы следует считать активными?
Всякая молекула, обладающая избытком энергии по сравнению со средней энергией и вступающая в реакцию данного типа, называется активной по отношению к этой реакции.
А та избыточная энергия, которой должна обладать молекула, чтобы быть активной по отношению к данному процессу, называется энергией активации этого процесса – Еа. Она измеряется в Дж/моль или кДж/ моль.
Чем больше энергия активации данного процесса, тем меньше будет активных молекул среди общего числа их по отношению к данному процессу, тем меньше будет скорость.
Таким образом, первое необходимое условие химического взаимодействия двух частиц – их столкновение – должно быть дополнено вторым необходимым условием – активным состоянием частиц в момент столкновения. Величина энергии активации есть тот фактор по средством, которого сказывается влияние природы реагирующих веществ на скорость реакции. Другими словами, что бы прореагировать в данной реакции, молекула должна иметь внутреннюю энергию, превышающую некоторую пороговую величину. При этом надо помнить, что ни какой особой формой энергией активации – не существует. Это некоторое избыточное количество внутренней энергии и оно может представлять собой:
а. повышенную кинетическую энергию поступательного движения;
б. повышенную кинетическую энергию вращательного движения;
в. Повышенную энергию колебательного движения атома или атомных групп в молекуле;
г. повышенную энергию электронов в молекуле, атоме или радикале.
С. Аррениус установил, что энергия активации связана с константой А (уравнение 2.12) простым соотношением
Еа = А * R, А = Еа / R (2.13)
Где R – универсальная газовая постоянная.
R = 
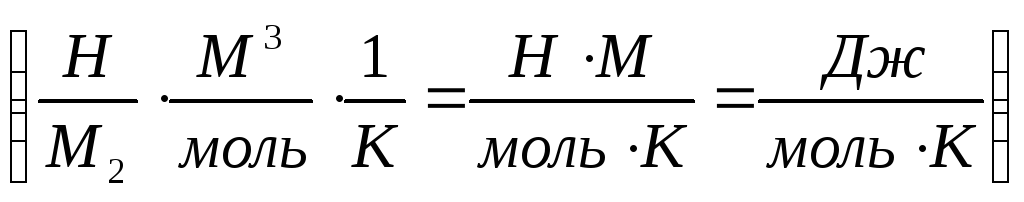
Подставив в уравнение (2.12) величину А из уравнения (2.13), получим
1nK= — 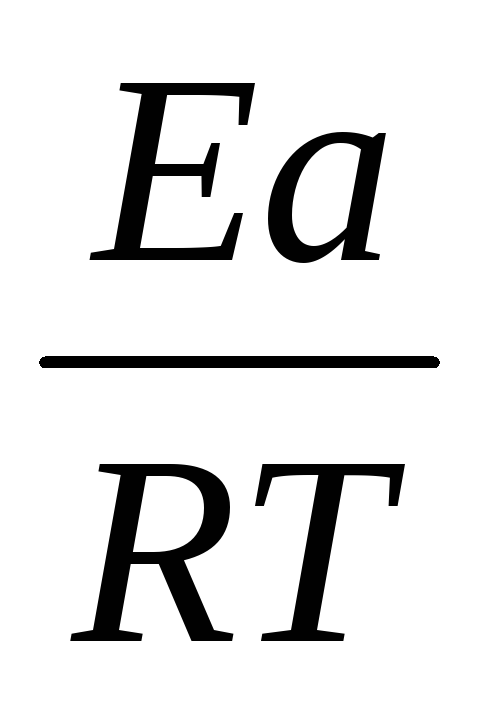 +
В (2.14)
+
В (2.14)
Дифференцируя (2.14) по температуре при Еа = const прейдем к уравнению:
 (2.15)
(2.15)
которое называется уравнением Аррениуса в дифференциальном виде.
Из него путем интегрирования можно получить уравнение (2.14), где В постоянное интегрирование. Обозначив В = 1nK0 из уравнения (2.14) получим:
1nK = 1nK0 – Еа/RТ (2.16)
Или
К = К0 * е-Еа/RТ (2.17)
Глее К0 – предэкспоненциальный множитель константы скорости реакции (т.е. множитель стоящий перед показательной функцией).
Уравнение (2.17) называется уравнение Аррениуса в интегральной форме. Величины Еа и К0 определяются природой реакции и практически не зависят от температуры.
Энергию активации можно рассчитать по экспериментальным данным графическим или аналитическим способом.
Графический способ заключается в нахождении величины А = — tg α по графику зависимости 1nK = f ( )
для данной реакции с последующим расчетом
Еа по уравнению Еа = А *R.
)
для данной реакции с последующим расчетом
Еа по уравнению Еа = А *R.
Аналитический способ представляет применение уравнения (2.16) для двух различных температур (Т2 > Т1; К(т2) = К2; К(т1) = К1):
1nK2 = 1nK0 – Еа/RТ2
1nK1 = 1nK0 – Еа/RТ1
В результате вычитания второго уравнения из первого получим
1n 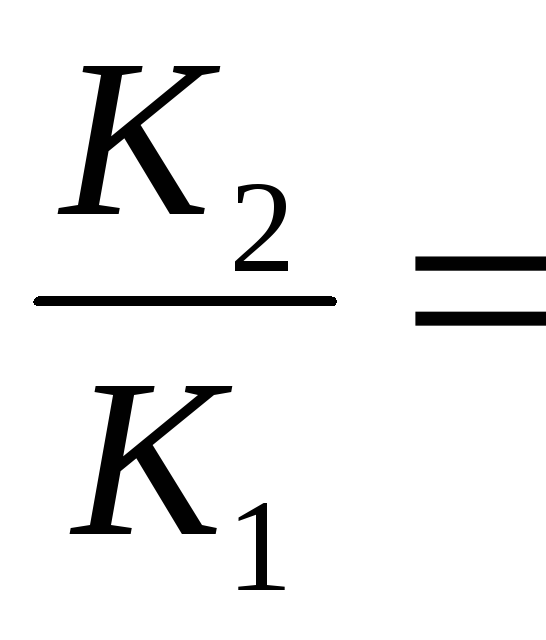
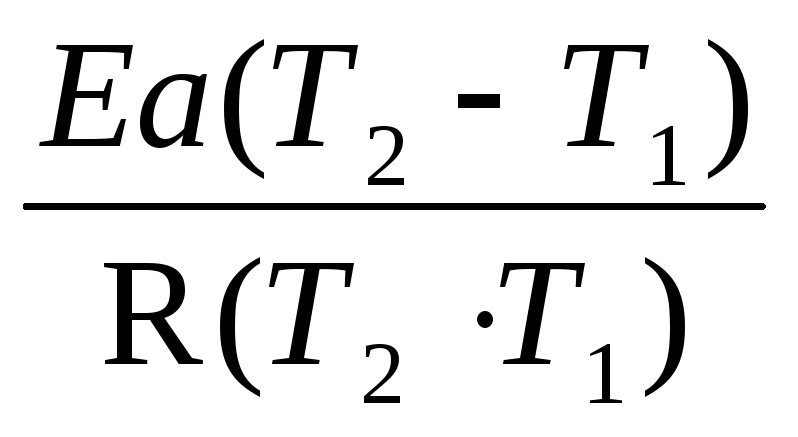 (2.14)
(2.14)
По уравнению (2.14) можно рассчитать энергию активации данной реакции, используя два экспериментальных значения константы скорости при двух различных температурах, или произвести пересчет константы скорости с одной температуры на другую, если известна энергия активации.
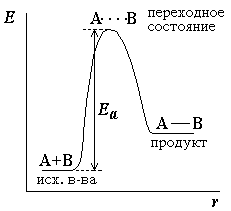
 ,
,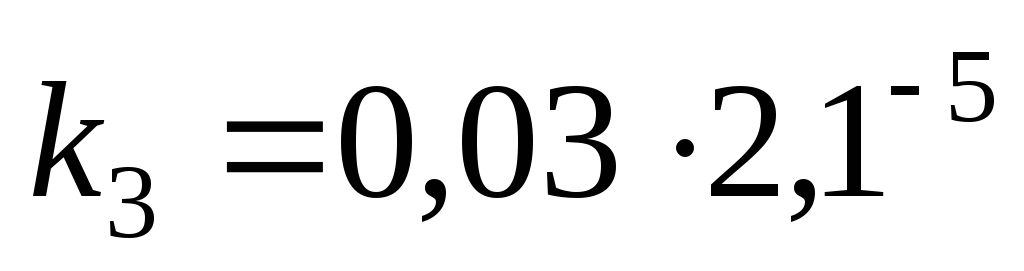

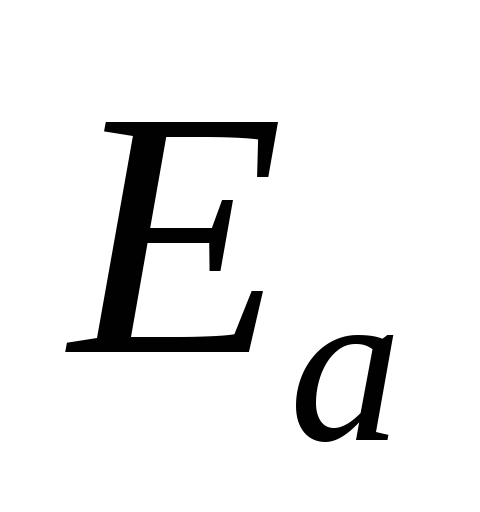 и
и  реакции, если известны константы
скорости реакции при двух температурах;
реакции, если известны константы
скорости реакции при двух температурах;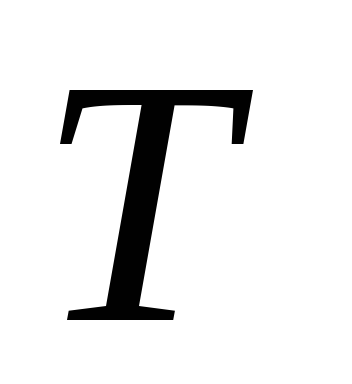 ,
К
,
К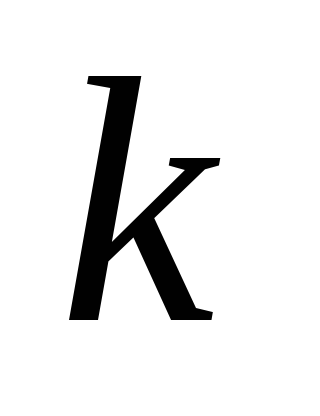 ,
с-1
,
с-1 ,
К
,
К ,
л·моль-1·мин-1
,
л·моль-1·мин-1