Сложение скоростей — Википедия

Материал из Википедии — свободной энциклопедии

При рассмотрении сложного движения (когда точка или тело движется в одной системе отсчёта, а эта система отсчёта в свою очередь движется относительно другой системы) возникает вопрос о связи скоростей в двух системах отсчёта.

В классической механике абсолютная скорость точки равна векторной сумме её относительной и переносной скоростей:

v→a=v→r+v→e.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{r}+{\vec {v}}_{e}.}

Данное равенство представляет собой содержание утверждения теоремы о сложении скоростей^[1].

Простым языком: Скорость движения тела относительно неподвижной системы отсчёта равна векторной сумме скорости этого тела относительно подвижной системы отсчета и скорости (относительно неподвижной системы) той точки подвижной системы отсчёта, в которой в данный момент времени находится тело.

Примеры[править | править код]

1. Абсолютная скорость мухи, ползущей по радиусу вращающейся граммофонной пластинки, равна сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно земли (то есть с которой её переносит пластинка за счёт своего вращения).
2. Если человек идёт по коридору вагона со скоростью 5 километров в час относительно вагона, а вагон движется со скоростью 50 километров в час относительно Земли, то человек движется относительно Земли со скоростью 50 + 5 = 55 километров в час, когда идёт по направлению движения поезда, и со скоростью 50 — 5 = 45 километров в час, когда он идёт в обратном направлении. Если человек в коридоре вагона движется относительно Земли со скоростью 55 километров в час, а поезд со скоростью 50 километров в час, то скорость человека относительно поезда 55 — 50 = 5 километров в час.
3. Если волны движутся относительно берега со скоростью 30 километров в час, и корабль также со скоростью 30 километров в час, то волны движутся относительно корабля со скоростью 30 — 30 = 0 километров в час, то есть относительно корабля они становятся неподвижными.

В XIX веке физика столкнулась с проблемой распространения этого правила сложения скоростей на оптические (электромагнитные) процессы. По существу произошёл конфликт между двумя идеями классической механики (первая — Пространство-время теории Ньютона, вторая — принцип относительности), перенесёнными в новую область — теорию электромагнитных процессов.

Например, если рассмотреть пример с волнами на поверхности воды из предыдущего раздела и попробовать обобщить на электромагнитные волны, то получится противоречие с наблюдениями (см., например, опыт Майкельсона).

Классическое правило сложения скоростей соответствует преобразованию координат от одной системы осей к другой системе, движущиеся относительно первой без ускорения. Если при таком преобразовании мы сохраняем понятие одновременности, то есть сможем считать одновременными два события не только при их регистрации в одной системе координат, но и во всякой другой инерциальной системе, то преобразования называются

галилеевыми. Кроме того, при галилеевых преобразованиях пространственное расстояние между двумя точками — разница между их координатами в одной инерциальной системе отсчёта — всегда равно их расстоянию в другой инерциальной системе.

Вторая идея — принцип относительности. Находясь на корабле, движущемся равномерно и прямолинейно, нельзя обнаружить его движение какими-то внутренними механическими эффектами. Распространяется ли этот принцип на оптические эффекты? Нельзя ли обнаружить абсолютное движение системы по вызванным этим движением оптическим или, что то же самое, электродинамическим эффектам? Интуиция (довольно явным образом связанная с классическим принципом относительности) говорит, что абсолютное движение нельзя обнаружить какими бы то ни было наблюдениями. Но если свет распространяется с определённой скоростью относительно каждой из движущихся инерциальных систем, то эта скорость изменится при переходе от одной системы к другой. Это вытекает из классического правила сложения скоростей. Говоря математическим языком, величина скорости света не будет инвариантна относительно галлилеевых преобразований. Это нарушает принцип относительности, вернее, не позволяет распространить принцип относительности на оптические процессы. Таким образом электродинамика разрушила связь двух, казалось бы, очевидных положений классической физики — правила сложения скоростей и принципа относительности. Более того, эти два положения применительно к электродинамике оказались несовместимыми.

Специальная теория относительности даёт ответ на этот вопрос. Она расширяет понятие принципа относительности, распространяя его и на оптические процессы. Одновременно специальная теория относительности кардинально изменяет представления о пространстве и времени. Правило сложения скоростей при этом не отменяется совсем, а лишь уточняется для больших скоростей с помощью преобразования Лоренца:

vrel=v1+v21+v1v2c2.{\displaystyle v_{rel}={\frac {{v}_{1}+{v}_{2}}{1+{\dfrac {{v}_{1}{v}_{2}}{c^{2}}}}}.}

Можно заметить, что в случае, когда v/c→0{\displaystyle v/c\rightarrow 0}, преобразования Лоренца переходят в преобразования Галилея. Это говорит о том, что механика в специальной теории относительности сводится к механике Ньютона при скоростях, малых по сравнению со скоростью света. Это объясняет, каким образом соотносятся специальная теория относительности и классическая механика — первая является обобщением второй.

Б. Г. Кузнецов Эйнштейн. Жизнь, смерть, бессмертие. — М.: Наука, 1972.
Четаев Н. Г. Теоретическая механика. — М.: Наука, 1987.
Теорема о сложении скоростей — Википедия
Теоре́ма о сложе́нии скоросте́й — одна из теорем кинематики, связывает между собой скорости материальной точки в различных системах отсчёта. Утверждает, что при сложном движении материальной точки её абсолютная скорость равна сумме относительной и переносной скоростей[1][2].
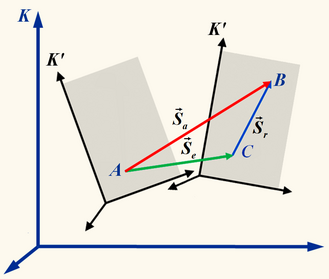  Сложное движение.
Движение в механике всегда рассматривается по отношению к какой-либо системе отсчёта. Однако в некоторых случаях бывает целесообразно или даже необходимо изучать движение материальной точки (МТ) относительно двух различных систем отсчёта одновременно. Одну из этих систем отсчёта условно считают неподвижной, базовой, а другую полагают движущейся относительно первой. Тогда движение точки можно рассматривать, как состоящее из двух движений: первое — движение относительно движущейся системы отсчёта, второе — движение вместе с движущейся системой относительно неподвижной. Такое движение точки называют сложным или составным.
Условно неподвижную систему отсчёта принято называть абсолютной. Соответственно, абсолютными называют движение, перемещение, скорость и ускорение точки относительно этой СО. На рисунке система отсчёта K выбрана в качестве абсолютной.
Условно подвижную систему отсчёта принято называть относительной. Движение, перемещение, скорость и ускорение точки относительно этой системы также именуют относительными. Система K’ на рисунке является относительной.
Движение, совершаемое подвижной системой K’ и всеми жёстко связанными с нею точками пространства[3] относительно системы К, называют перено́сным. Если некоторая МТ движется относительно подвижной системы K’, то в общем случае та точка системы K’, в которой в данный момент находится МТ, также движется относительно неподвижной системы К. Мгновенную скорость этой точки системы K’ называют переносной скоростью МТ.
Пусть МТ в некоторый момент времени находилась в точке А, а через промежуток времени Δt{\displaystyle \Delta t} оказалась в точке В (см. рис.). Тогда её перемещение относительно системы К (абсолютное перемещение) будет равно S→a{\displaystyle {\vec {S}}_{a}}. Точка А подвижной системы K’ за время  переместилась вместе с K’ и оказалась в точке С, совершив перемещение относительно системы К (переносное перемещение), изображённое на рисунке вектором S→e{\displaystyle {\vec {S}}_{e}}.
С точки зрения наблюдателя, связанного с системой K’, точка С является той точкой, в которой МТ находилась первоначально, поэтому вектор S→r{\displaystyle {\vec {S}}_{r}} представляет собой перемещение МТ относительно подвижной системы K’, то есть относительное перемещение.
Из сказанного и векторной диаграммы на рисунке следует
S→a=S→e+S→r.{\displaystyle {\vec {S}}_{a}={\vec {S}}_{e}+{\vec {S}}_{r}.}
Деля данное равенство на промежуток времени Δt{\displaystyle \Delta t}, а затем устремляя его к нулю, в пределе получаем
v→a=v→e+v→r,{\displaystyle {\vec {v}}_{a}={\vec {v}}_{e}+{\vec {v}}_{r},}
где v→a{\displaystyle {\vec {v}}_{a}} — абсолютная, v→e{\displaystyle {\vec {v}}_{e}} — переносная, а
v→r{\displaystyle {\vec {v}}_{r}} — относительная скорость движения МТ.
Полученное равенство является математическим выражением теоремы о сложении скоростей, которая формулируется так:
 При сложном движении абсолютная скорость материальной точки равна геометрической сумме переносной и относительной скоростей.
Теорему о сложении скоростей называют также правилом параллелограмма скоростей[4].
В общем случае движение системы K’ можно представить как сумму двух движений: поступательного движения со скоростью, равной скорости начала координат  системы K’, и вращательного движения вокруг мгновенной оси, проходящей через это начало. Можно показать, что переносная скорость v→e{\displaystyle {\vec {v}}_{e}}, скорость начала координат  v→0{\displaystyle {\vec {v}}_{0}} и угловая скорость вращательного движения системы ω→{\displaystyle {\vec {\omega }}} связаны соотношением[5]
v→e=v→0+[ω→×r′→].{\displaystyle {\vec {v}}_{e}={\vec {v}}_{0}+[{\vec {\omega }}\times {\vec {r’}}].}
С учётом этого равенства математическое выражение теоремы приобретает вид
v→a=v→0+[ω→×r′→]+v→r.{\displaystyle {\vec {v}}_{a}={\vec {v}}_{0}+[{\vec {\omega }}\times {\vec {r’}}]+{\vec {v}}_{r}.}
Утверждение теоремы, доказанное для двух систем отсчёта нетрудно обобщить на случай произвольного их количества. Действительно, предположим, что считавшаяся нами до сих пор неподвижной система К движется относительно некоторой третьей системы. Тогда для абсолютной скорости va′→{\displaystyle {\vec {v’_{a}}}} МТ в этой системе в силу доказанной теоремы будет выполняться
va′→=ve′→+v→e+v→r,{\displaystyle {\vec {v’_{a}}}={\vec {v’_{e}}}+{\vec {v}}_{e}+{\vec {v}}_{r},}
где ve′→{\displaystyle {\vec {v’_{e}}}} — переносная скорость точки системы К, в которой в данный момент времени находится МТ, движение которой мы изучаем. Очевидно, что рассуждая аналогичным образом, можно получить формулу сложения скоростей, пригодную для любого количества систем отсчёта.
 
Утверждение теоремы о сложении скоростей справедливо только до тех пор, пока скорости, о которых идёт речь в теореме, много меньше скорости света. В противном случае следует использовать релятивистскую  формулу сложения скоростей.
Замечание.
Радиус-вектор r(t){\displaystyle r(t)} МТ в системе отсчёта К всегда можно представить в виде суммы двух векторов:
r→(t)=R→(t)+r′→(t),{\displaystyle {\vec {r}}(t)={\vec {R}}(t)+{\vec {r’}}(t),}
где R→(t){\displaystyle {\vec {R}}(t)} — радиус-вектор начала подвижной системы координат, а r′→(t){\displaystyle {\vec {r’}}(t)} — радиус-вектор МТ в подвижной системе K’. После дифференцирования из равенства следует
v→a=dR→(t)dt+dr′→(t)dt.{\displaystyle {\vec {v}}_{a}={\frac {d{\vec {R}}(t)}{dt}}+{\frac {d{\vec {r’}}(t)}{dt}}.}
Полученное соотношение справедливо для любой МТ и для любого момента времени. Следует, однако, иметь в виду, что в общем случае первый член суммы не равен переносной скорости, а второй — не равен относительной скорости. Действительно, dR→(t)dt{\displaystyle {\frac {d{\vec {R}}(t)}{dt}}} — это скорость 
 
 начала системы координат K’ v→0{\displaystyle {\vec {v}}_{0}} и при наличии вращения системы K’ не совпадает со скоростью той точки системы, в которой в данный момент находится МТ. В свою очередь dr′→(t)dt{\displaystyle {\frac {d{\vec {r’}}(t)}{dt}}} представляет собой скорость МТ относительно начала координат, то есть, определяется иначе, чем относительная скорость v→r{\displaystyle {\vec {v}}_{r}}. Равенства dR→(t)dt=v→e{\displaystyle {\frac {d{\vec {R}}(t)}{dt}}={\vec {v}}_{e}} и  dr′→(t)dt=v→r{\displaystyle {\frac {d{\vec {r’}}(t)}{dt}}={\vec {v}}_{r}} выполняются только в тех случаях, когда система K’ движется поступательно, то есть когда она не совершает поворотов (ω→=0{\displaystyle {\vec {\omega }}=0}) и все её точки движутся одинаково
 [6].
В системе отсчёта, связанной с Землёй, скорость пассажира[7], идущего по коридору вагона, можно рассматривать, как складывающуюся из двух скоростей. Первая из них — скорость, с которой движется точка вагона, в которой в данный момент находится пассажир, — переносная скорость, то есть скорость, с которой вагон «переносит» пассажира. Второе слагаемое — скорость движения пассажира относительно вагона. Если вагон движется по закруглению пути, то направление абсолютной скорости пассажира изменяется за счёт изменения переносной скорости.
Абсолютная скорость мухи[8], ползущей по вращающейся граммофонной пластинке, равна геометрической сумме скорости её движения относительно пластинки и той скорости, которую имеет точка пластинки под мухой относительно Земли — переносной скорости.
Движение точки колеса (окружности), катящегося по горизонтальной поверхности без проскальзывания, можно рассматривать как сложное движение, состоящее из движения колеса в целом со скоростью v{\displaystyle v} и вращения точек колеса вокруг его оси с угловой скоростью ω{\displaystyle \omega }. Тогда в соответствии с теоремой о сложении скоростей проекции абсолютной скорости точки колеса на горизонтальную и вертикальную оси можно записать в виде
 
vx=v−vcos⁡ωt{\displaystyle v_{x}=v-v\cos \omega t}
vy=vsin⁡ωt,{\displaystyle v_{y}=v\sin \omega t,}
где R{\displaystyle R} — радиус колеса. После интегрирования и с учётом v=ωR{\displaystyle v=\omega R} из этих уравнений следует:
x=ωRt−Rsin⁡ωt{\displaystyle x=\omega Rt-R\sin \omega t}
y=R−Rcos⁡ωt.{\displaystyle y=R-R\cos \omega t.}
Полученные уравнения представляют собой параметрические уравнения циклоиды, соответственно траекторией движения точки колеса является циклоида.
↑ Тарг С. М. Краткий курс теоретической механики. — М.
 : Высшая школа, 1995. — С. 156-158. — 416 с. — ISBN 5-06-003117-9.
↑ Бухгольц Н. Н. Основной курс теоретической механики / Издание шестое, переработанное и дополненное С. М. Таргом. — М.: «Наука», 1965. — Т. 1. — С. 88-90.
↑ То есть точками, неподвижными относительно системы K’.
↑ Кильчевский Н. А. Курс теоретической механики. — М.: «Наука», 1977. — Т. I. — С. 144.
↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит, 2005. — Т. I. Механика. — С. 362. — 560 с. — ISBN 5-9221-0225-7.
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 119. — 720 с. — ISBN 5-211-04244-1.
↑ В данном случае это абсолютная скорость.
↑ Скорость относительно Земли.
Релятивистский закон сложения скоростей: определение, особенности и формула
Классическая механика, законы которой были сформулированы Ньютонов в конце XVII века, около двухсот лет считалась все объясняющей и непогрешимой. Вплоть до XIX столетия ее принципы казались всемогущими и составляли основу физики. Однако к указанному периоду начали появляться новые факты, которые невозможно было втиснуть в привычные рамки известных законов. Со временем они получили иное объяснение. Случилось это с появлением теории относительности и загадочной науки – квантовой механики. В данных дисциплинах радикальному пересмотру подверглись все ранее принятые представления о свойствах времени и пространства. В частности, релятивистский закон сложения скоростей красноречиво доказал ограниченность классических догм.
Простое сложение скоростей: когда это возможно?
Классика Ньютона в физике и поныне считается верной, а законы ее применяются для решения многих задач. Только следует учитывать, что действуют они в привычном для нас мире, где скорости самых разных объектов, как правило, не бывают значительными.
Представим ситуацию, что поезд едет из Москвы. Скорость его перемещения составляет 70 км/час. А в это время по ходу движения из одного вагона в другой путешествует пассажир, пробегая 2 метра за одну секунду. Чтобы узнать быстроту его перемещения относительно домов и деревьев, мелькающих за окном поезда, указанные скорости следует просто сложить. Поскольку 2 м/с соответствуют 7,2 км/час, то искомая скорость окажется 77,2 км/час.
Мир высоких скоростей
Другое дело фотоны и нейтрино, они подчиняются совершенно другим правилам. Для них-то и действует релятивистский закон сложения скоростей, а показанный выше принцип считается для них совершенно неприменимым. Почему?
Согласно специальной теории относительности (СТО), любой объект не может перемещаться со скоростью быстрее света. Она в крайнем случае только способна приблизительно быть сравнимой с этим параметром. Но если на секунду представить (хотя на практике это невозможно), что в предыдущем примере поезд и пассажир двигаются примерно таким образом, то скорость их относительно покоящихся на земле предметов, мимо которых проезжает состав, оказалась бы равной практически двум световым. А этого быть не должно. Как же производят расчеты в этом случае?
Известный из курса физики 11 класса релятивистский закон сложения скоростей представляется формулой, приведенной ниже.
Что это значит?
Если имеются две системы отсчета, скорость некоего объекта относительно которых V1и V2, то для расчетов можно пользоваться указанным соотношением, независимо от значения определенных величин. В случае когда обе они значительно меньше скорости света, знаменатель в правой части равенства практически равен 1. Это значит, что формула релятивистского закона сложения скоростей превращается в самую обычную, то есть V2= V1+ V.
Следует также обратить внимание, что когда V1= C (то есть скорости света), при любом значении V, V2 не превысит эту величину, то есть тоже окажется равной С.
Из области фантастики
С – это фундаментальная константа, величина ее равна 299 792 458 м/с. Со времен Эйнштейна считается, что ни один объект во Вселенной не может превзойти движение света в вакууме. Именно так можно определить кратко релятивистский закон сложения скоростей.
Однако писатели-фантасты не захотели с этим смириться. Они придумывали и продолжают сочинять множество потрясающих историй, герои которых опровергают подобное ограничение. В мгновение ока их космические корабли перемещаются в далекие галактики, находящиеся за много тысяч световых лет от старушки Земли, сводя на нет при этом все установленные законы мироздания.
Но почему Эйнштейн и его последователи уверены, что на практике подобного не может случиться? Следует поговорить о том, по какой причине так незыблем световой предел и неприкосновенен релятивистский закон сложения скоростей.
Связь причин и следствий
Свет – носитель информации. Он является отражением реальности Вселенной. А световые сигналы, достигающие наблюдателя, воссоздают в его сознании картины действительности. Так бывает в привычном для нас мире, где все идет своим чередом и подчиняется обычным правилам. И мы с рождения приучены к тому, что не может быть иначе. Но если представить, что все вокруг изменилось, и некто отправился в космос, путешествуя на сверхсветовой скорости? Поскольку он опережает фотоны света, мир начинает видеться ему как в кинопленке, прокрученной назад. Вместо завтра для него наступает вчера, потом позавчера и так далее. А завтрашний день он никогда не увидит, пока не остановится, конечно.
Кстати, подобную идею тоже активно взяли на вооружение писатели-фантасты, создавая по таким принципам аналог машины времени. Их герои попадали в прошлое и путешествовали там. Однако рушились причинно-следственные связи. И оказывалось очевидно, что на практике такое вряд ли возможно.
Другие парадоксы
Причина не может опережать следствие. Это противоречит нормальной человеческой логике, ведь во Вселенной должен быть порядок. Однако СТО предполагает и другие парадоксы. Она вещает, что, если даже поведение объектов подчиняется строгому определению релятивистского закона сложения скоростей, в точности сравняться в быстроте перемещения с фотонами света ему тоже невозможно. Почему? Да потому что начинают происходить в полном смысле волшебные превращения. Масса бесконечно увеличивается. Размеры материального объекта в направлении движения неограниченно приближаются к нулю. И опять же пертурбаций со временем избежать полностью не удается. Оно хоть и не движется назад, но при достижении скорости света полностью останавливается.
Затмение Ио
СТО утверждает, что фотоны света являются самыми быстрыми объектами во Вселенной. В таком случае, как же удалось измерить их скорость? Просто человеческая мысль оказалась проворней. Она смогла решить подобную дилемму, а следствием ее и стал релятивистский закон сложения скоростей.
Подобные вопросы решались еще во времена Ньютона, в частности, в 1676 году датским астроном О. Ремером. Он сообразил, что скорость сверхбыстрого света возможно определить лишь только в том случае, когда он проходит огромные расстояния. Подобное, как он подумал, бывает возможным только на небе. А случай воплотить указанную идею в жизнь вскоре представился, когда Ремер наблюдал в телескоп затмение одного из спутников Юпитера под названием Ио. Промежуток времени между входом в затемнение и появлением в поле зрения этой планеты в первый раз составил около 42,5 часа. И на этот раз все примерно соответствовало предварительным расчетам, проведенным согласно известному периоду обращения Ио.
Через несколько месяцев Ремер вновь произвел свой эксперимент. В этот период Земля значительно удалилась от Юпитера. И оказалось, что Ио опоздал показать свой лик на 22 минуты в сравнении со сделанными ранее предположениями. Что это значило? Объяснение было в том, что спутник совсем не задержался, а вот световым сигналам от него понадобилось некоторое время, чтобы преодолеть значительное расстояние до Земли. Произведя на основе этих данных расчеты, астроном подсчитал, что скорость света очень значительна и составляет около 300 000 км/с.
Опыт Физо
Предвестник релятивистского закона сложения скоростей – опыт Физо, произведенный почти двумя веками позже, подтвердил правильно догадок Ремера. Только известный французский физик в 1849 году провел уже лабораторные опыты. А для реализации их был придуман и сконструирован целый оптический механизм, аналог которого можно увидеть на рисунке ниже.
Свет, исходил от источника (это был этап 1). Потом он отражался от пластины (этап 2), проходил между зубцами вращающегося колеса (этап 3). Далее лучи попадали на зеркало, расположенное на значительном расстоянии, измеряемом в значении 8,6 километра (этап 4). В заключении свет отражался обратно и проходил через зубцы колеса (этап 5), попадал в глаза наблюдателя и фиксировался им (этап 6).
Вращение колеса осуществлялось с разной скоростью. При медленном передвижении, свет был виден. При увеличении скорости, лучи начинали исчезать, не достигая зрителя. Причина в том, что на перемещение лучам требовалось некоторое время, а за данный период, зубья колеса немного сдвигались. Когда же скорость вращения снова возрастала, свет опять достигал глаза наблюдателя, ведь теперь зубья, перемещаясь быстрее, вновь позволяли лучам проникать сквозь зазоры.
Принципы СТО
Релятивистская теория впервые была представлена миру Эйнштейном в 1905 году. Посвящена данная работа описанию событий, происходящих в самых разных системах отсчета, поведению магнитных и электромагнитных полей, частиц и объектов при движении их, максимально сравнимом со скоростями света. Великий физик описал свойства времени и пространства, а также рассмотрел поведение других параметров, размеров физических тел и их масс в указанных условиях. Среди основных принципов Эйнштейн назвал равноправие любых инерциальных систем отсчета, то есть он имел в виду сходство процессов, протекающих в них. Другой постулат релятивистской механики – закон сложения скоростей в новом, неклассическом варианте.
Пространство, согласно данной теории, представляется, как пустота, где функционирует все остальное. Время определяется как некая хронология происходящих процессов и событий. Оно же впервые называется в качестве четвертого измерения самого пространства, получающего теперь наименование «пространство-время».
Преобразования Лоренца
Подтверждают релятивистской закон сложения скоростей преобразования Лоренца. Так принято называть математические формулы, которые в окончательном своем варианте представлены ниже.
Эти математические соотношения занимают центральное место в теории относительности и служат для преобразования координат и времени, будучи написаны для четырехместного пространства-времени. Указанное наименование представленные формулы получили по предложению Анри Пуанкаре, которые разрабатывая математический аппарат для теории относительности, заимствовал у Лоренца некоторые идеи.
Подобные формулы доказывают не только невозможность преодоления сверхзвукового барьера, но и незыблемость принципа причинности. Согласно им, появилась возможность математически обосновать замедление времени, сокращение длин объектов и прочие чудеса, происходящие в мире сверхвысоких скоростей.
Физические основы механики
Мы говорили, что скорость света — максимально возможная скорость распространения сигнала. Но что будет, если свет испускается движущимся источником в направлении его скорости 
 V ? Согласно закону сложения скоростей, следующему из преобразований Галилея, скорость света должна быть равна c + V. Но в теории относительности это невозможно. Посмотрим, какой закон сложения скоростей следует из преобразований Лоренца. Для этого запишем их для бесконечно малых величин:
По определению скорости ее компоненты в системе отсчета K находятся как отношения соответствующих перемещений к временным интервалам:
Аналогично определяется скорость объекта в движущейся системе отсчета K’, только пространственные расстояния и временные интервалы надо взять относительно этой системы:
Следовательно, разделив выражение dx на выражение dt, получим:
Разделив числитель и знаменатель на dt’, находим связь x-компонент скоростей в разных системах отсчета, которая отличается от галилеевского правила сложения скоростей:
Кроме того, в отличие от классической физики, меняются и компоненты скоростей, ортогональные направлению движения. Аналогичные вычисления для других компонент скоростей дают:
Таким образом, получены формулы для преобразования скоростей в релятивистской механике. Формулы обратного преобразования получаются при замене штрихованных величин на нештрихованные и обратно и заменой V на –V.
Теперь мы можем ответить на вопрос, поставленный в начале данного раздела. Пусть в точке 0′ движущейся системы отсчета K’ установлен лазер, посылающий импульс света в положительном направлении оси 0’х’. Какой будет скорость импульса для неподвижного наблюдателя в системе отсчета К? В этом случае скорость светового импульса в системе отсчета К’ имеет компоненты
Применяя закон релятивистского сложения скоростей, находим для компонент скорости импульса относительно неподвижной системы К :
 Мы получаем, что скорость светового импульса и в неподвижной системе отсчета, относительно которой источник света движется, равна
Тот же результат получится при любом направлении распространения импульса. Это естественно, так как независимость скорости света от движения источника и наблюдателя заложена в одном из постулатов теории относительности. Релятивистский закон сложения скоростей — следствие этого постулата.
Действительно, когда скорость движения подвижной системы отсчета V << c, преобразования Лоренца переходят в преобразования Галилея, мы получаем обычный закон сложения скоростей
При этом ход течения времени и длина линейки будут одинаковы в обеих системах отсчета. Таким образом, законы классической механики применимы, если скорости объектов много меньше скорости света. Теория относительности не зачеркнула достижения классической физики, она установила рамки их справедливости.
Пример. Тело со скоростью v0 налетает перпендикулярно на стенку, двигающуюся ему навстречу со скоростью v. Пользуясь формулами для релятивистского сложения скоростей, найдем скорость v1 тела после отскока. Удар абсолютно упругий, масса стенки намного больше массы тела.
Воспользуемся формулами, выражающими релятивистский закон сложения скоростей.
Направим ось х вдоль начальной скорости тела v0 и свяжем систему отсчета K’ со стенкой. Тогда vx = v0 и V = –v. В системе отсчета, связанной со стенкой, начальная скорость v’0 тела равна
Поскольку стенку можно считать бесконечно массивной, по закону сохранения энергии после упругого удара тело отскочит в обратном направлении с тем же (относительно стенки) абсолютным значением скорости:
Вернемся теперь назад в лабораторную систему отсчета К. Подставляя в релятивистский закон сложения скоростей v’1 вместо v’x и учитывая опять же V = –v, находим после преобразований:
Проанализируем теперь предельные случаи.
Если скорости тела и стенки малы (v0 << с, v << с), то можно пренебречь всеми членами, где эти скорости и их произведение делятся на скорость света. Получаем тогда из найденной формулы результат классической механики

Скорость шара после отскока увеличивается на удвоенную скорость стенки; направлена она, естественно, противоположно начальной. Ясно, что в релятивистском случае этот результат не годится. В частности, при v0 =  v = с/3 из него следует, что скорость тела после отскока будет равна v1 = –с, чего не может быть.

Пусть теперь на стенку налетает тело, двигающееся со скоростью света (например, лазерный луч отражается от двигающегося зеркала). Подставляя v0 = с в найденное соотношение, получаем

Иными словами, скорость лазерного луча изменила направление, но не свою абсолютную величину, как и должно быть.
Рассмотрим теперь случай, когда стенка движется с релятивистской скоростью. В этом случае найденное соотношение дает нам

Тело после отскока также будет двигаться со скоростью, близкой к скорости света.
Наконец, подставим в найденное соотношение значения v0 = v = с/3 :

В отличие от классической механики, теория относительности дает для скорости после отскока значение, меньшее скорости света.
Напоследок посмотрим, что случится, если стенка удаляется от тела с той же скоростью (v = –v0). Имеем в этом случае:

Как и в классической механике, тело стенку не догонит, и его скорость не изменится.
Сложное движение точки Теорема Кориолиса
 Здесь мы покажем, что при сложном движении, абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
 .
Абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
 ,
где      – кориолисово ускорение.
 Пример применения изложенной ниже теории приводится на странице “Сложное движение точки. Пример решения задачи”.
Сложное (составное) движение точки
 Часто встречаются случаи, когда точка совершает известное движение относительно некоторого твердого тела. А это тело, в свою очередь, движется относительно неподвижной системы координат. Причем движение точки относительно тела и закон движения тела относительно неподвижной системы координат известны или заданы. Требуется найти кинематические величины (скорость и ускорение) точки относительно неподвижной системы координат.
 Такое движение точки называется сложным или составным.
Сложное или составное движение точки
– это движение в подвижной системе координат. То есть движение точки описывается в системе координат, которая сама совершает движение относительно неподвижной системы координат.
 Далее, для ясности изложения, будем считать, что подвижная система координат жестко связана с некоторым твердым телом. Мы будем рассматривать движение точки относительно тела (относительное движение) и движение тела относительно неподвижной системы координат (переносное движение).
Относительное движение точки при сложном движении
– это движение точки относительно тела (подвижной системы координат) считая, что тело покоится.
Переносное движение точки при сложном движении
– это движение точки, жестко связанной телом, вызванное движением тела.
Абсолютное движение точки при сложном движении
– это движение точки относительно неподвижной системы координат, вызванное движением тела и движением точки относительно тела.
Сложное движение. Точка M движется относительно движущегося тела.
 Пусть Oxyz – неподвижная система координат, On xo yo zo  – подвижная система координат, жестко связанная с телом. Пусть    – единичные векторы (орты), направленные вдоль осей  xo , yo , zo    подвижной системы координат. Тогда радиус-вектор      точки M  в неподвижной системе определяется по формуле:
(1)    ,
где      – радиус-вектор точки On    – начала подвижной системы координат, связанной с телом.
Относительная скорость и ускорение
 При относительном движении изменяются координаты   xo , yo , zo    точки относительно тела. А векторы      являются постоянными, не зависящими от времени. Дифференцируя (1) по времени, считая      постоянными, получаем формулы для относительной скорости и ускорения:
(2)    ;
(3)    .
Относительная скорость точки при сложном движении
– это скорость точки при неподвижном положении тела (подвижной системы координат), вызванная движением точки относительно тела.
Относительное ускорение точки при сложном движении
– это ускорение точки при неподвижном положении тела, вызванное движением точки относительно тела.
Переносная скорость и ускорение
 При переносном движении изменяются векторы    , определяющие положение тела. Относительные координаты точки xo , yo , zo    являются постоянными. Дифференцируя (1) по времени, считая xo , yo , zo  постоянными, получаем формулы для переносной скорости и ускорения:
(4)    ;
(5)    .
Переносная скорость точки при сложном движении
– это скорость точки, жестко связанной с телом, вызванная движением тела.
Переносное ускорение точки при сложном движении
– это ускорение точки, жестко связанной с телом, вызванное движением тела.
 Производные по времени от      – это скорость и ускорение начала подвижной системы координат On  :    ;    .
 Найдем формулы для производных по времени от векторов    . Для этого возьмем две произвольные точки твердого тела A и B. Их скорости связаны соотношением:

(см. страницу “Скорость и ускорение точек твердого тела”). Рассмотрим вектор    , проведенный из точки A в точку B. Тогда
 .
Дифференцируем по времени и применяем предыдущую формулу:
 .
Итак, мы нашли формулу для производной по времени от вектора, соединяющего две точки тела:
 .
Поскольку векторы      жестко связаны с телом, то их производные по времени определяются по этой формуле:
(6)    ,    ,    .
 Подставляем в (4):

 .
Таким образом, выражение (4) приводит к формуле для скорости точек твердого тела.
 Выполняя подобные преобразования над формулой (5), получим формулу для ускорения точек твердого тела:
 ,
где      – угловое ускорение тела.
Абсолютная скорость и ускорение
 При абсолютном движении изменяются как векторы    , определяющие положение тела, так и относительные координаты точки   xo , yo , zo  .
Абсолютная скорость точки при сложном движении
– это скорость точки в неподвижной системе координат.
Абсолютное ускорение точки при сложном движении
– это ускорение точки в неподвижной системе координат.
Теорема о сложении скоростей
 При составном движении абсолютная скорость точки равна векторной сумме относительной и переносной скоростей:
 .
Доказательство
 Дифференцируем (1) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (2) и (4).
(1)    ;
(7)   
 .
Теорема Кориолиса о сложении ускорений
 При составном движении абсолютное ускорение точки равно векторной сумме относительного, переносного и кориолисова (поворотного) ускорений:
 ,
где
   – кориолисово ускорение.
Доказательство
 Дифференцируем (7) по времени, применяя правила дифференцирования суммы и произведения. Затем подставляем (3) и (5).
(7)    .


 .
 В последнем члене применим (6) и (2).

 .
Тогда
 .
Автор: Олег Одинцов.     Опубликовано: 23-10-2015
Сложное движение — Википедия
В физике, при рассмотрении нескольких систем отсчёта (СО), возникает понятие сложного движения — когда материальная точка движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой системы отсчёта. При этом возникает вопрос о связи движений точки в этих двух системах отсчета (далее СО).
 Материальная точка в двух СО[1].
Обычно принимают одну из СО за базовую («абсолютную», «лабораторную», «неподвижную», «СО неподвижного наблюдателя», «первую», «нештрихованную» и т. п.), другую называют «подвижной» («СО подвижного наблюдателя», «штрихованной», «второй» и т. п.) и вводят следующие термины:
Переносная скорость V→e(t){\displaystyle {\vec {V}}_{e}(t)} — это скорость в базовой системе отсчёта произвольной точки, зафиксированной относительно подвижной СО, обусловленная движением этой подвижной СО относительно базовой. Например, это скорость той точки подвижной системы отсчёта, в которой в данный момент времени находится материальная точка. Переносная скорость V→e(t){\displaystyle {\vec {V}}_{e}(t)} равна V→R(t)=dR→dt{\displaystyle {\vec {V}}_{R}(t)={\frac {d{\vec {R}}}{dt}}} только в тех случаях, когда подвижная СО движется поступательно.
Вводятся также понятия соответствующих ускорений a→r(t){\displaystyle {\vec {a}}_{r}(t)}, a→r′(t){\displaystyle {\vec {a}}_{r’}(t)}, a→R(t){\displaystyle {\vec {a}}_{R}(t)}, ε→R(t).{\displaystyle {\vec {\varepsilon }}_{R}(t).} и a→e(t){\displaystyle {\vec {a}}_{e}(t)}.
С точки зрения только чистой кинематики (задачи пересчёта кинематических величин — координат, скоростей, ускорений — от одной системы отсчета к другой) не имеет значения, является ли какая-то из систем отсчета инерциальной или нет; это никак не сказывается на формулах преобразования кинематических величин при переходе от одной системы отсчета к другой (то есть эти формулы можно применять и для перехода от одной произвольной неинерциальной вращающейся системы отсчета к другой).
Однако для динамики инерциальные системы отсчета имеют особое значение: в них механические явления описываются наиболее простым образом и, соответственно, уравнения динамики формулируются изначально именно для инерциальных систем отсчета[3]. Поэтому особенно важны случаи перехода от инерциальной системы отсчета к другой инерциальной, а также от инерциальной к неинерциальной и обратно.
В дальнейшем изложении по умолчанию базовая СО предполагается инерциальной, а на подвижную никаких ограничений не накладывается.
Классическая механика опирается на представления о Евклидовом пространстве и принцип относительности Галилея, что позволяет использовать преобразования Галилея.
Кинематика сложного движения точки[править | править код]
  Траектории одного и того же движения в разных системах отсчёта.
Вверху (в инерциальной системе): дырявое ведро с краской двигают на колосниках по прямой над поворачивающейся театральной сценой. Траектория прямая.
Внизу (в неинерциальной системе): то же самое, но при взгляде с точки зрения наблюдателя, стоящего на вращающейся сцене. Траектория кривая, и соответствует следу от краски на сцене.
Кинематика движения, основанная на анализе траектории движущегося тела, в общем случае не даёт полной информации для классификации этих движений. Так, движение по прямой в неинерциальной системе отсчёта может быть криволинейным (и, следовательно, обусловленным действующими на тело силами) в инерциальной СО. И, наоборот, прямолинейное в инерциальной СО может быть криволинейным в неинерциальной, и, следовательно, провоцировать представление о якобы действующих на тело силах.
Путь[править | править код]
Абсолютное движение и его путь представлены изменением радиуса вектора r→{\displaystyle {\vec {r}}}, рассматриваемого в виде суммы векторов переносного и относительного движений:
r→=R→+r′→.{\displaystyle {\vec {r}}={\vec {R}}+{\vec {r’}}.}
Скорость[править | править код]
Основные задачи кинематики сложного движения заключаются в установлении зависимостей между кинематическими характеристиками абсолютного и относительного движений точки (или тела) и характеристиками движения подвижной системы отсчета, то есть переносного движения. Связь скоростей определяется дифференцированием связи для положений. Для точки эти зависимости являются следующими: абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей, то есть:
V→r=V→r′+V→e.{\displaystyle {\vec {V}}_{r}={\vec {V}}_{r’}+{\vec {V}}_{e}.}
Данное равенство представляет собой содержание теоремы о сложении скоростей[4].
Следует отметить, что вместе с приведённым равенством всегда справедливо и соотношение
dr→dt=d(R→+r′→)dt=dR→dt+dr′→dt.{\displaystyle {\frac {d{\vec {r}}}{dt}}={\frac {d({\vec {R}}+{\vec {r’}})}{dt}}={\frac {d{\vec {R}}}{dt}}+{\frac {d{\vec {r’}}}{dt}}.}
Однако в общем случае в этом соотношении dR→dt{\displaystyle {\frac {d{\vec {R}}}{dt}}} не является переносной скоростью, а dr′→dt{\displaystyle {\frac {d{\vec {r’}}}{dt}}} не относительная скорость. Таковыми они становятся только в тех случаях, когда подвижная СО движется поступательно, то есть, не вращаясь[5].
Ускорение[править | править код]
Связь ускорений можно найти путём дифференцирования связи для скоростей, не забывая, что относительное перемещение также может зависеть от времени.
Абсолютное ускорение a→r(t){\displaystyle {\vec {a}}_{r}(t)} будет равно сумме:
a→r  =  d2r→dt2  =  d2R→dt2  +  dω→dt×r′→  +  ω→×[ω→×r′→]  +  2 ω→×V→r′  +  a→r′.{\displaystyle {\vec {a}}_{r}\ \ =\ \ {\frac {d^{2}{\vec {r}}}{dt^{2}}}\ \ =\ \ {\frac {d^{2}{\vec {R}}}{dt^{2}}}\ \ +\ \ {\frac {d{\vec {\omega }}}{dt}}\times {\vec {r’}}\ \ +\ \ {\vec {\omega }}\times \left[{\vec {\omega }}\times {\vec {r’}}\right]\ \ +\ \ {2\ {\vec {\omega }}\times {\vec {V}}_{r’}}\ \ +\ \ {\vec {a}}_{r’}.}

Здесь:
сумма первых трех членов называется переносным ускорением a→e{\displaystyle {\vec {a}}_{e}}.
первый член — переносное поступательное ускорение второй системы относительно первой,
второй член — переносное вращательное ускорение второй системы, возникающее из-за неравномерности её вращения.
третий член представляет собой вектор, противоположно направленный осестремительной составляющей r′→n{\displaystyle {\vec {r’}}_{n}} вектора r→{\displaystyle {\vec {r}}}, перпендикулярной ω→{\displaystyle {\vec {\omega }}} (что можно получить, рассматривая это двойное векторное произведение — оно равно −r′→nω2{\displaystyle -{\vec {r’}}_{n}\omega ^{2}}) и потому представляет собой осестремительное ускорение. Оно совпадает с нормальным переносным ускорением той точки вращающейся системы, с которой в данный момент совпадает движущаяся точка (не путать с нормальным ускорением движущейся точки, направленным по нормали к её траектории).
четвертый член есть Кориолисово ускорение, порождаемое взаимным влиянием переносного вращательного движения второй системы отсчета и относительного поступательного движения точки относительно её.
последний член a→r′=dV→r′dt{\displaystyle {\vec {a}}_{r’}={\frac {d{\vec {V}}_{r’}}{dt}}} — ускорение точки относительно подвижной системы отсчета.
Кинематика сложного движения тела[править | править код]
Согласно Первому закону Ньютона, все виды движений при их рассмотрении в инерциальной системе координат могут быть отнесены к одной из двух категорий. А именно — к категории прямолинейных и равномерных (то есть имеющих постоянную скорость) движений, возможных исключительно при отсутствии нескомпенсированных сил, действующих на тело.
Нередко встречающееся, даже в справочной литературе[6] , отнесение этого вида движений к категории поступательных движений противоречит определению понятия «Поступательное движение», поскольку движение, имеющее классификационный признак поступательного, в инерциальной системе может происходить по любой траектории, но не обязательно исключительно по прямой.
К другой категории относятся все остальные виды движений.
Для твёрдого тела, когда все составные (то есть относительные и переносные) движения являются поступательными, абсолютное движение также является поступательным со скоростью, равной геометрической сумме скоростей составных движений. Если составные движения тела являются вращательными вокруг осей, пересекающихся в одной точке (как, например, у гироскопа), то результирующее движение также является вращательным вокруг этой точки с мгновенной угловой скоростью, равной геометрической сумме угловых скоростей составных движений. В общем случае движение будет слагаться из серии мгновенных винтовых движений.
Рассчитать взаимосвязь скоростей разных точек твёрдого тела в разных системах отсчёта можно с помощью комбинирования формулы сложения скоростей и формулы Эйлера для связи скоростей точек твёрдого тела. Связь ускорений находится простым дифференцированием полученного векторного равенства по времени.
Динамика сложного движения точки[править | править код]
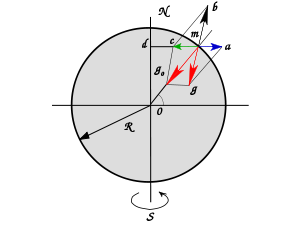  Силы, действующие на тело, находящееся на поверхности Земли. Чертёж относится к рассмотрению сил, действующих на тело, в двух различных системах отсчёта. Первая — инерциальная система отсчёта, вторая — неинерциальная система отсчёта, связанная с вращающейся Землёй. В первом случае на тело действуют сила гравитационного притяжения и реакция опоры. Их сумма (зелёный вектор) играет роль центростремительной силы и заставляет тело вращаться вместе с Землёй. Во втором случае действует дополнительная сила — переносная сила инерции (синий вектор), в результате действие всех сил уравновешивается, и тело в этой системе отсчёта ускорения не испытывает.
Концепция Ньютона о пропорциональности получаемого телом ускорения под действием любой силы в инерциальных системах отсчёта выполняется всегда. Под силой при этом понимается мера механического действия на данное материальное тело других тел[7], обязательно являющаяся результатом взаимодействия тел[8]. Альтернатив этой концепции в классическом разделе материалистической физики нет.
Однако при рассмотрении движений в неинерциальной системе отсчёта, наряду с силами, происхождение которых можно проследить, как результат взаимодействия с другими телами и полями, возможно ввести в рассмотрение и физические величины другой природы — силы инерции. Их введение и использование позволяет придать уравнению движения тел в неинерциальных системах отсчёта форму, совпадающую с формой уравнения второго закона Ньютона в инерциальных системах отсчёта.
Для того, чтобы различать силы двух упомянутых видов, термин силы инерции часто сопровождают дополнительным определением, таким, как, например фиктивные[9] или кажущиеся[10].
Привлечение представлений о силах инерции для описания движения тел в неинерциальных системах отсчёта может быть полезным и эффективным. Например, действием силы инерции в системе отсчёта, связанной с вращающейся вокруг своей оси Землёй, может быть объяснён эффект замедления хода маятниковых часов, наблюдающийся по мере их приближения к экватору. Другой пример — действие силы Кориолиса на воду в реках, текущих в меридиональном направлении. Следствием такого действия является неодинаковость размыва правых и левых (по направлению течения) берегов рек. Ещё более значительным является действие силы Кориолиса на морские течения и воздушные потоки в атмосфере[9].
Релятивистская механика опирается на неевклидово пространство Минковского и принцип относительности Эйнштейна, что вынуждает прибегать к более сложному преобразованию Лоренца. При скоростях, существенно меньших скорости света, релятивистская механика может быть сведена к классической.
Скорость[править | править код]
При скоростях, близких к скорости света, преобразования Галилея не являются точно инвариантными и классическая формула сложения скоростей перестаёт выполняться. Вместо этого, инвариантными являются преобразования Лоренца, а связь скоростей в двух инерциальных СО получается следующей:
vx′=vx−u1−(vxu)/c2,vy′=vy1−u2c21−(vxu)/c2,vz′=vz1−u2c21−(vxu)/c2,{\displaystyle v_{x}’={\frac {v_{x}-u}{1-(v_{x}u)/c^{2}}},v_{y}’={\frac {v_{y}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},v_{z}’={\frac {v_{z}{\sqrt {1-{\frac {u^{2}}{c^{2}}}}}}{1-(v_{x}u)/c^{2}}},}
в предположении, что скорость u→{\displaystyle {\vec {u}}} направлена вдоль оси х системы S. Легко убедиться, что в пределе нерелятивистских скоростей преобразования Лоренца сводятся к преобразованиям Галилея.
Однако вводится величина — быстрота — которая аддитивна при переходе от одной СО к другой.
Неинерциальные СО[править | править код]
Связь скоростей и ускорений в системах отсчёта, движущихся друг относительно друга ускоренно, является значительно более сложной и определяется локальными свойствами пространства в рассматриваемых точках (зависит от производной тензора Римана).
Четаев Н. Г. Теоретическая механика. М.: Наука.— 1987.— 368 с.
Гернет М. М. Курс теоретической механики. М.: Высшая школа.— 1973.— 464 с.
Тарг С. М. Относительное движение // Физическая энциклопедия / Прохоров А. М. (гл. ред.). — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 493. — 672 с. — ISBN 5-85270-019-3.
Тарг С. М. Относительное движение // Физический энциклопедический словарь / Введенский Б. А. (гл. ред.). — М.: Советская энциклопедия, 1963. — Т. 3. — С. 553. — 624 с.
↑ Бронштейн И. Н., Семендяев К. А.. Справочник по математике. М.: Издательство «Наука». Редакция справочной физико-математической литературы, 1964 г., 608 стр. с ил., С.216 и далее.
↑ То есть точек, неподвижных относительно движущейся системы.
↑ Ландау Л. Д., Лифшиц Е. М. Механика. — М.: Наука, 1988. — Т. «Теоретическая физика», том I. — С. 13-15. — 215 с. — ISBN 5-02-013850-9.
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 156. — 416 с. — ISBN 5-06-003117-9.
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 119. — 720 с. — ISBN 5-211-04244-1.
↑ Физический энциклопедический словарь/ Гл. ред. А. М. Прохоров. Ред.кол. Д. М. Алексеев, А. М. Бонч-Бруевич,А. С. Боровик-Романов и др. -М.: Сов.энциклопедия, 1983.-323 с.,ил, 2 л.цв.ил. страница 282
↑ Тарг С. М. Сила // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1994. — Т. 4. Пойнтинга—Робертсона эффект — Стримеры. — С. 494. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 59-60. — 546 p. — ISBN 0-07-035048-5.
↑ 1 2 Зоммерфельд А. Механика. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — 368 с. — ISBN 5-93972-051-X.
↑ Борн М. Эйнштейновская теория относительности. — М.: «Мир», 1972. — С. 81. — 368 с.
Обсуждение:Сложение скоростей — Википедия
Материал из Википедии — свободной энциклопедии
Формула сложения скоростей из теории относительности[править код]
Нужно срочно написать формулу, заменив шаблон внимание. К сожалению, я забыл её точный вид. Alexsmail 20:15, 9 сентября 2007 (UTC)
Подумать как по другому разделить эти статьи в плане их конфликта в электродинамике. Alexsmail 20:15, 9 сентября 2007 (UTC)
В мире сверх скоростей[править код]
«Можно заметить, что в случае, когда c→∞{\displaystyle c\rightarrow \infty }, преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда v/c→0{\displaystyle v/c\rightarrow 0}. Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последнее объясняет, каким образом сочетаются эти две теории — первая является уточнением второй.»
Что за псевдонаука? В каком это мире с бесконечной скоростью света? Я в таком не жил, Эйнштейн с Лорецем то-же. Кто решил что формулы сложения скоростей подходят в фантастике? Может в мире с бесконечной скоростью света вообще нет формул? Формула сложение скоростей предназначена для нашей вселенной а не для фантастов.  79.181.203.139 07:53, 20 апреля 2011 (UTC)
Есть сомнения? Можно вставить запрос источника утверждения. Например, вставить код {{подст:АИ}} возле подозрительного места —Fractaler 08:46, 20 апреля 2011 (UTC)
Уже вставил. Просто источником может служить только житель другой вселенной. Вообще написать «в случае, когда π→10{\displaystyle \pi \rightarrow 10}, либо «в случае, когда заряд электрона стремится в нолю» не имеет ни какого физического смысла. Все равно что написать «если 5→∞{\displaystyle 5\rightarrow \infty } то у коровы будет восемь ног». —79.181.203.139 13:27, 20 апреля 2011 (UTC)