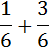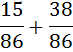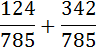Сложение и вычитание дробей с одинаковыми знаменателями
Что можно складывать? Все, что угодно. Числа: 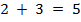 . Яблоки:
. Яблоки: 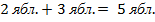 Сантиметры:
Сантиметры: 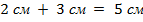 . Даже что-то, про что мы вообще ничего не знаем:
. Даже что-то, про что мы вообще ничего не знаем: 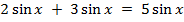 .
.
Самое важное при сложении, чтобы объекты для сложения были одинаковые. Так как сложно сложить 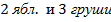 , или
, или 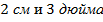
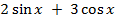 .
.Итак, одинаковое можно складывать. Это относится и к дробям.
Вспомним, что мы уже знаем про дроби: знаменатель (нижняя часть дроби) указывает, на сколько частей мы делили, какие доли мы получили. Числитель (верхняя часть) указывает, сколько таких долей взяли, сколько их содержит дробь (см. рис. 1).
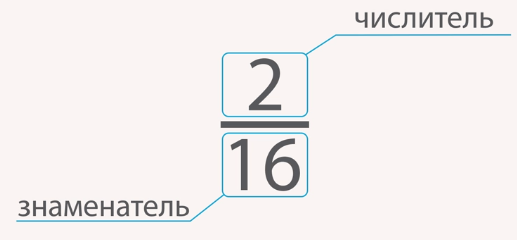
Рис. 1. Дробь
Сколько долей  в дроби
в дроби  ? Пять, так как
? Пять, так как 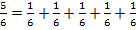
Во сколько раз 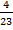 больше, чем
больше, чем 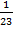 ? В 4 раза. Так как дробь
? В 4 раза. Так как дробь 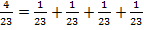 .
.
Чему равна сумма 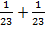 ?
?
Два одинаковых объекта можно сложить: 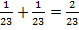 .
.
Чему равна сумма 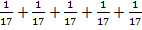
Получаем: 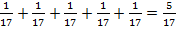 .
.
Сложим 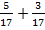 . Сколько всего семнадцатых? Пять и три. Пять и три семнадцатых.
. Сколько всего семнадцатых? Пять и три. Пять и три семнадцатых. 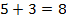 , всего восемь семнадцатых:
, всего восемь семнадцатых: 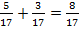 .
.
Сложим 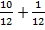 . Сколько всего двенадцатых?
. Сколько всего двенадцатых? 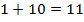
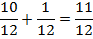
Итак, чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители.
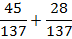
У дробей одинаковые знаменатели, значит, чтобы сложить эти дроби, нужно сложить их числители: 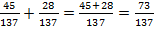 .
.
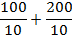
Знаменатели одинаковые, значит, можно складывать числители:
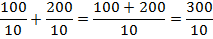
Вычитать дроби с одинаковыми знаменателями так же просто, как и складывать.
Выполнить вычитание: 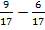 .
.
Вычтем из числителя первой дроби числитель второй дроби: 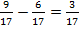 .
.
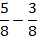
Выполним вычитание числителей: 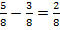 .
.
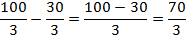
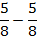
Вычитаем числители 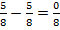 . Но обычно такую запись редко используют. Пишут просто ноль:
. Но обычно такую запись редко используют. Пишут просто ноль: 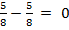 .
.
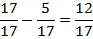
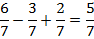
Итак, чтобы сложить или вычесть дроби с одинаковым знаменателем, нужно сложить или вычесть их числители соответственно. Открытым остался вопрос: А что делать, если знаменатели разные? Если нужно сложить, например, 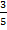 и
и 
Список рекомендованной литературы
- Математика. 5 класс. Зубарева И.И., Мордкович А.Г. 14-е изд., испр. и доп. — М.: 2013. – 270
- Математика. 5 класс. Мерзляк А.Г., Полонский В.Б., Якир М.С. М.: 2014. — 304 с.
- Математика. 5 класс. Виленкин Н.Я., Жохов В.И. и др. 24-е изд., испр. — М: 2008. — 280с.
Домашнее задание
Вычислите:
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал Urokimatematiki.ru (Источник).
- Интернет-портал Festival.1september.ru (Источник).
- Интернет-портал Onlinegdz.net (Источник).
interneturok.ru
Сложение десятичных дробей: правила и примеры
Сложение десятичных дробей можно выполнить двумя способами:
- Представить десятичные дроби в виде обыкновенных дробей и выполнить их сложение.
- Выполнить сложение десятичных дробей столбиком.
Сложение путём перевода в обыкновенные дроби
При сложении десятичных дробей путём их перевода в обыкновенные дроби следует руководствоваться следующим правилом:
- Нужно сравнить количество десятичных знаков у десятичных дробей.
- Если количество десятичных знаков одинаково, то переводим десятичные дроби в обыкновенные и складываем их.
- Если количество десятичных знаков различно, то сначала нужно уравнять их количество, приписав справа к десятичной дроби с меньшим количеством знаков необходимое число нулей.
Пример 1. Выполнить сложение чисел 3,1 и 4,7.
Решение. Так как количество десятичных знаков одинаково, то просто переводим десятичные дроби в обыкновенные и складываем. Десятичной дроби 3,1 соответствует обыкновенная дробь  , а десятичной дроби 4,7 – обыкновенная дробь
, а десятичной дроби 4,7 – обыкновенная дробь  , значит:
, значит:

Пример 2. Сложить числа 3,45 и 7,368.
Решение. Так как количество десятичных знаков различно, то сначала уравняем их количество, приписав справа к дроби 3,45 цифру 0. Десятичной дроби 3,450 соответствует обыкновенная дробь  , а десятичной дроби 7,368 – обыкновенная дробь
, а десятичной дроби 7,368 – обыкновенная дробь  , значит:
, значит:

Сложение десятичных дробей столбиком
Десятичные дроби можно складывать столбиком.
При сложении десятичных дробей столбиком следует руководствоваться следующим правилом:
- Записать десятичные дроби в столбик так, чтобы цифры одинаковых разрядов стояли друг под другом. Запятые десятичных дробей так же должны стоять друг под другом.
- Если количество десятичных знаков у дробей различно, для удобства можно уравнять их число, приписав справа к десятичной дроби с меньшим количеством десятичных знаков необходимое число нулей.
- Не обращая внимание на запятые, выполнить сложение так, как выполняется сложение столбиком натуральных чисел.
- В полученной сумме поставить запятую так, чтобы она стояла под запятыми слагаемых.
Пример 1. Сложить числа 3,1 и 4,7.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел, не обращая внимание на запятые:

Пример 2. Сложить 3,45 и 7,368.
Решение. Выполняем сложение так, как выполняется сложение столбиком натуральных чисел. Для удобства, можно уравнять количество десятичных знаков в складываемых дробях:

Сложение десятичной дроби с натуральным числом
Правило сложения десятичных дробей с натуральными числами:
Чтобы сложить десятичную дробь и натуральное число, нужно данное натуральное число прибавить к целой части десятичной дроби, а дробную часть оставить без изменений.
Пример. Вычислить сумму 14,3 и 29.
Решение. Для удобства сложения, любое натуральное число можно представить в виде десятичной дроби. Для этого нужно поставить запятую после разряда единиц и приписать после запятой нужное количество нулей. Сложение выполняется по правилу сложения десятичных дробей столбиком:

Сложение десятичной дроби с обыкновенной дробью
Правило сложения десятичных дробей с обыкновенной дробью:
Сложение десятичной дроби с обыкновенной дробью сводится к сложению обыкновенных дробей. Для этого десятичная дробь переводится в обыкновенную дробь.
Пример. Выполнить сложение десятичной дроби 0,28 и обыкновенной дроби  .
.
Решение. Переводим десятичную дробь 0,28 в обыкновенную:  . И далее выполняем уже сложение обыкновенных дробей
. И далее выполняем уже сложение обыкновенных дробей  и
и  :
:

| О сайте: | конспекты по математике, русскому языку и химии |
| Связь: | [email protected] |
| Новое на сайте | © 2018 – 2019 | |
izamorfix.ru
5.4.7. Примеры на сложение и вычитание обыкновенных дробей математика-повторение
I. Чтобы сложить дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тот же.
Примеры.
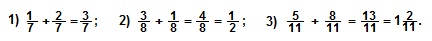
II. Если нужно сложить дроби с разными знаменателями, то сначала дроби приводят к наименьшему общему знаменателю, а затем складывают дроби с одинаковыми знаменателями.
Примеры.

III. Чтобы выполнить вычитание дробей с одинаковыми знаменателями, из числителя первой дроби вычитают числитель второй дроби, а знаменатель оставляют тот же.
Примеры.
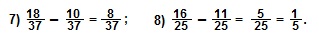
IV. Если нужно выполнить вычитание дробей с разными знаменателями, то их сначала приводят к общему знаменателю, а затем выполняют вычитание дробей с одинаковыми знаменателями.
Примеры.
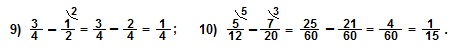
V. При выполнении действий сложения или вычитания смешанных чисел эти действия выполняют отдельно для целых частей и для дробных частей, а затем результат записывают в виде смешанного числа.
Примеры.
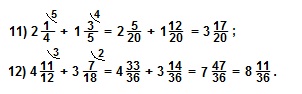 Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.
Да, складывать нужно отдельно целые части и отдельно дробные части смешанного числа.
Нет, не нужно расписывать целые и дробные части смешанных чисел по отдельности.
Важно: не начинайте выполнять сложение, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ).
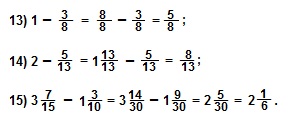 Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.
Помним, что единицу можно представить в виде обыкновенной дроби, числитель и знаменатель которой, являются любыми равными друг другу числами.
Важно: не начинайте выполнять вычитание, пока не приведете дробные части данных смешанных чисел к наименьшему общему знаменателю (НОЗ) и не убедитесь, что из числителя первой дроби можно вычесть числитель второй дроби. А если нельзя вычесть?
Тогда «занимаете» у целой части уменьшаемого одну целую единицу, представляете ее в виде неправильной дроби с таким же знаменателем (НОЗ), и добавляете эту неправильную дробь (раздробленную единицу) к дробной части уменьшаемого.
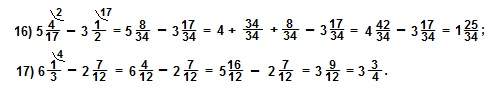
Запись имеет метки: сложение и вычитание обыкновенных дробей, сложение и вычитание смешанных чисел
www.mathematics-repetition.com
8 класс. Алгебра. Алгебраические дроби. — Сложение и вычитание алгебраических дробей.
Комментарии преподавателя
В данном уроке будет рассмотрено сложение и вычитание алгебраических дробей с одинаковыми знаменателями. Мы уже знаем, как складывать и вычитать обыкновенные дроби с одинаковыми знаменателями. Оказывается, что алгебраические дроби подчиняются тем же самым правилам. Умение работать с дробями с одинаковыми знаменателями является одним из краеугольных камней в изучении правил работы с алгебраическими дробями. В частности, понимание данной темы позволит легко освоить более сложную тему – сложение и вычитание дробей с разными знаменателями. В рамках урока мы изучим правила сложения и вычитания алгебраических дробей с одинаковыми знаменателями, а также разберём целый ряд типовых примеров
Сформулируем правило сложения (вычитания) алгебраических дробей с одинаковыми знаменателями (оно совпадает с аналогичным правилом для обыкновенных дробей):  То есть для сложения или вычитания алгебраических дробей с одинаковыми знаменателями необходимо составить соответствующую алгебраическую сумму числителей, а знаменатель оставить без изменений.
То есть для сложения или вычитания алгебраических дробей с одинаковыми знаменателями необходимо составить соответствующую алгебраическую сумму числителей, а знаменатель оставить без изменений.
Это правило мы разберём и на примере обыкновенных дробей, и на примере алгебраических дробей.
Пример 1. Сложить дроби:  .
.
Решение
Сложим числители дробей, а знаменатель оставим таким же. После этого разложим числитель и знаменатель на простые множители и сократим. Получим:  .
.
Примечание: стандартная ошибка, которую допускают при решении подобного рода примеров, заключается в следующем способе решения:  . Это грубейшая ошибка, поскольку знаменатель остаётся таким же, каким был в исходных дробях.
. Это грубейшая ошибка, поскольку знаменатель остаётся таким же, каким был в исходных дробях.
Ответ:  .
.
Пример 2. Сложить дроби:  .
.
Решение
Данная задача ни
www.kursoteka.ru
Как складывать дроби с разными знаменателями
Чтобы понять, как складывать дроби с разными знаменателями, сначала изучим правило, а затем рассмотрим конкретные примеры.
Чтобы сложить или вычесть дроби с разными знаменателями, надо:
1) Найти наименьший общий знаменатель (НОЗ) данных дробей.
2) Найти дополнительный множитель к каждой дроби. Для этого новый знаменатель нужно разделить на старый.
3) Умножить числитель и знаменатель каждой дроби на дополнительный множитель и сложить или вычесть дроби с одинаковыми знаменателями.
4) Проверить, является ли полученная в результате дробь правильной и несократимой.
В следующих примерах надо сложить или вычесть дроби с разными знаменателями:
Решение:
1) Чтобы вычесть дроби с разными знаменателями, сначала ищем наименьший общий знаменатель данных дробей. Выбираем большее из чисел и проверяем, делится ли оно на меньшее. 25 на 20 не делится. Умножаем 25 на 2. 50 на 20 не делится. Умножаем 25 на 3. 75 на 20 не делится. Умножаем 25 на 4. 100 на 20 делится. Значит, наименьший общий знаменатель равен 100.
2) Чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель разделить на старый. 100:25=4, 100:20=5. Соответственно, к первой дроби дополнительный множитель 4, ко второй — 5.
3) Умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем дроби по правилу вычитания дробей с одинаковыми знаменателями.
4) Полученная дробь — правильная и несократимая. Значит, это — ответ.
1) Чтобы сложить дроби с разными знаменателями, сначала ищем наименьший общий знаменатель. 16 на 12 не делится. 16∙2=32 на 12 не делится. 16∙3=48 на 12 делится. Значит, 48 — НОЗ.
2) 48:16=3, 48:12=4. Это — дополнительные множители к каждой дроби.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и складываем новые дроби.
4)Полученная в результате дробь — правильная и несократимая.
1) 30 на 20 не делится. 30∙2=60 на 20 делится. Значит, 60 — наименьший общий знаменатель этих дробей.
2) чтобы найти дополнительный множитель к каждой дроби, надо новый знаменатель поделить на старый: 60:20=3, 60:30=2.
3) умножаем числитель и знаменатель каждой дроби на дополнительный множитель и вычитаем новые дроби.
4) полученную дробь надо сократить на 5.
1) 8 на 6 не делится. 8∙2=16 на 6 не делится. 8∙3=24 делится и на 4, и на 6. Значит, 24 — это и есть НОЗ.
2) чтобы найти дополнительный множитель к каждой дроби, нужно новый знаменатель разделить на старый. 24:8=3, 24:4=6, 24:6=4. Значит, 3, 6 и 4 — дополнительные множители к первой, второй и третьей дроби.
3) умножаем числитель и знаменатель каждой долби на дополнительный множитель. Складываем и вычитаем. Полученная дробь — неправильная, поэтому необходимо выделить целую часть.
www.for6cl.uznateshe.ru
Дидактический материал по математике «Сложение и вычитание дробей с разными знаменателями» (6 класс)
Тема урока
«Сложение дробей
с разными знаменателями».
Работа в парах.
Сложите дроби:
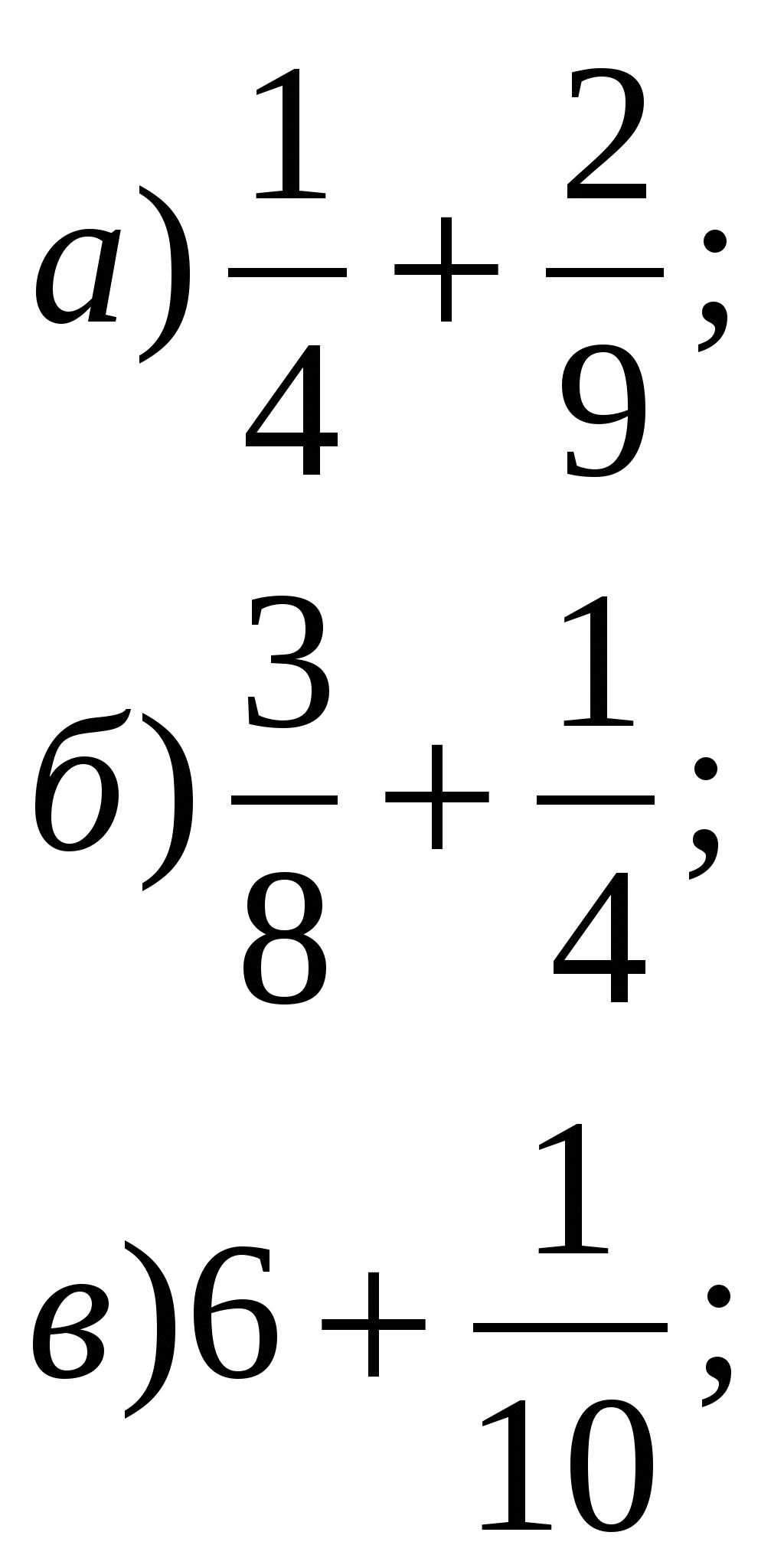
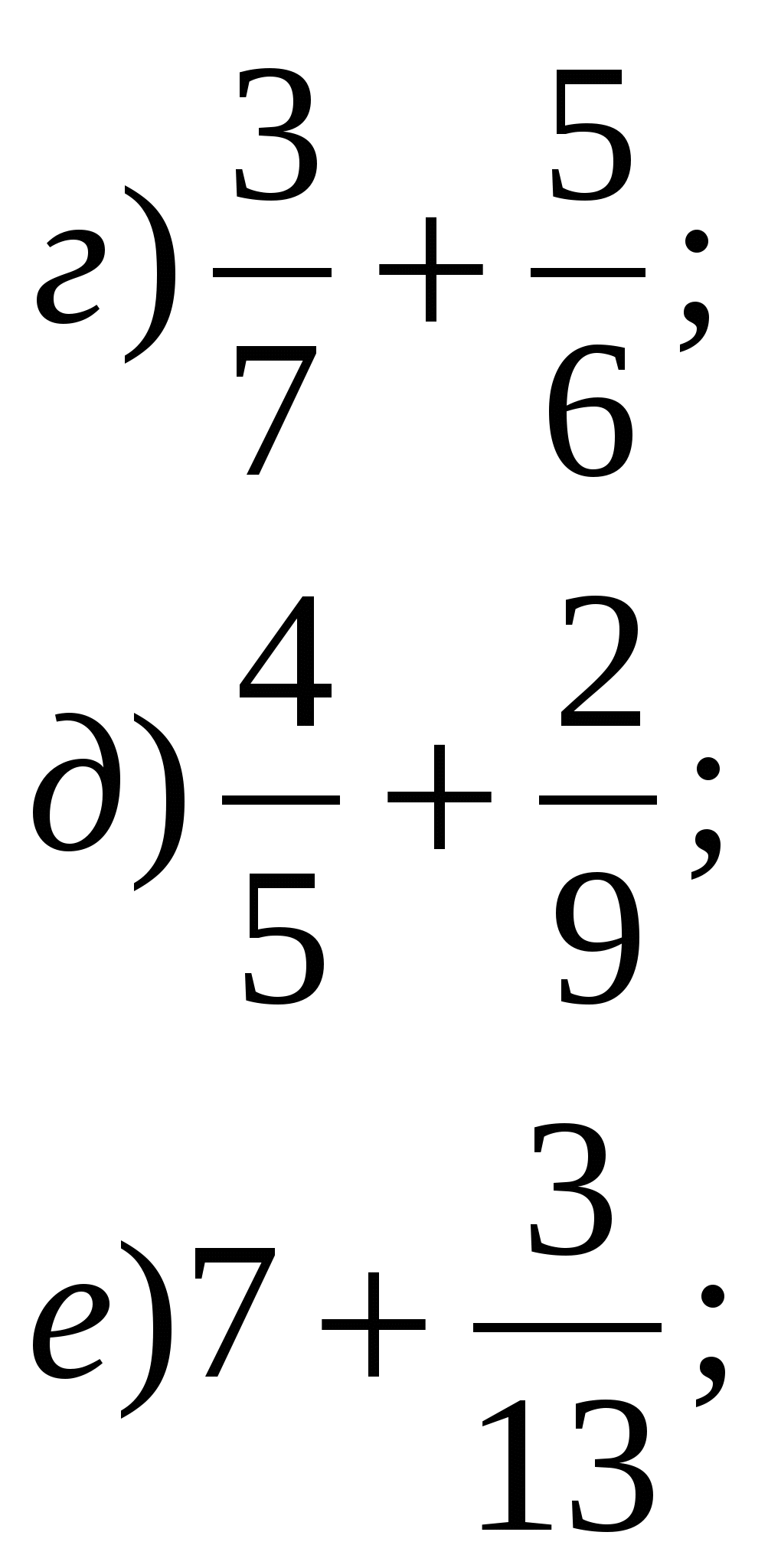
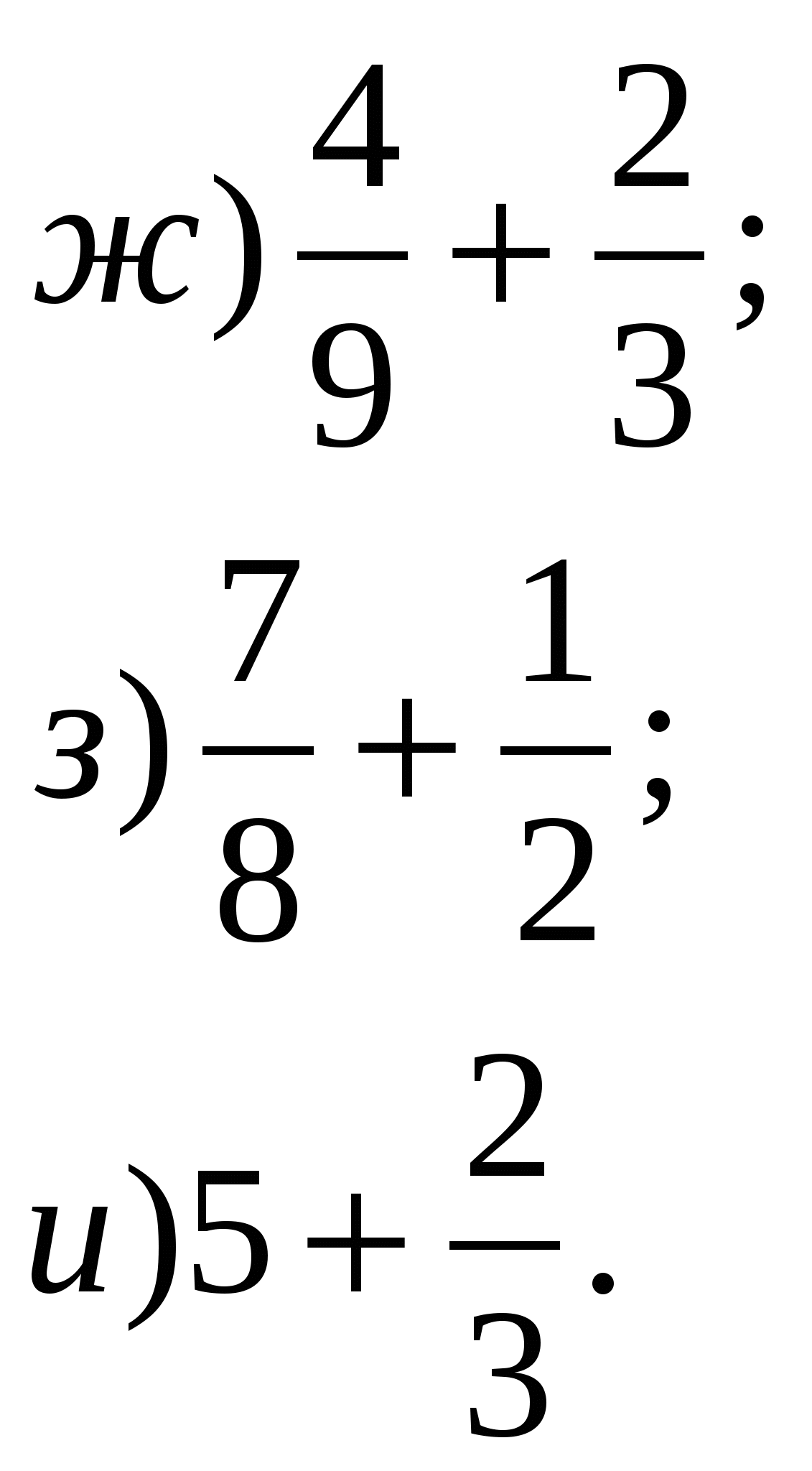
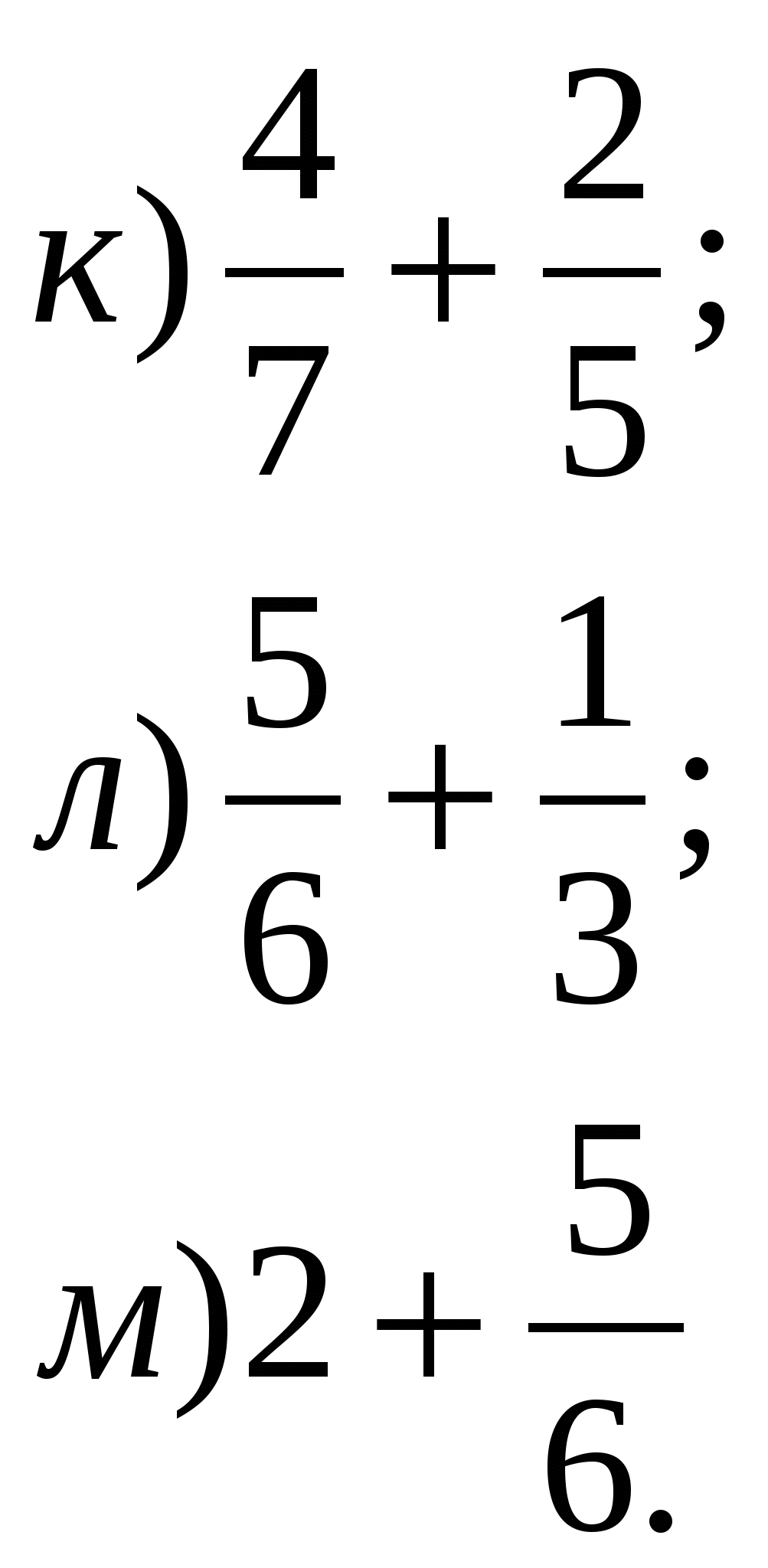
2. Приведите дроби к наименьшему общему знаменателю:
а)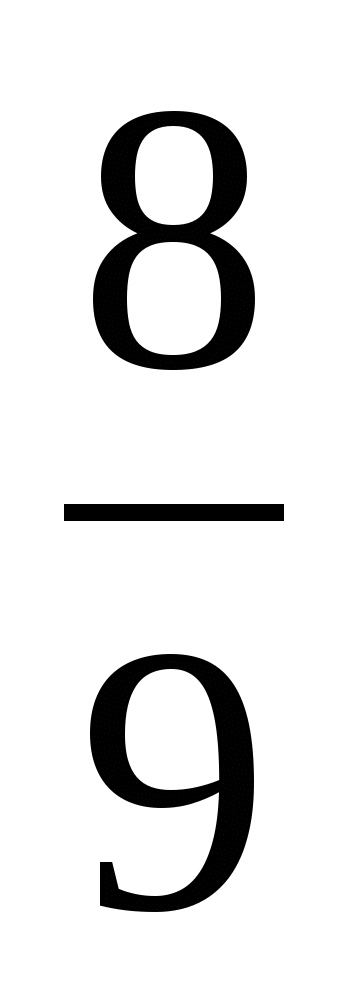 и
и 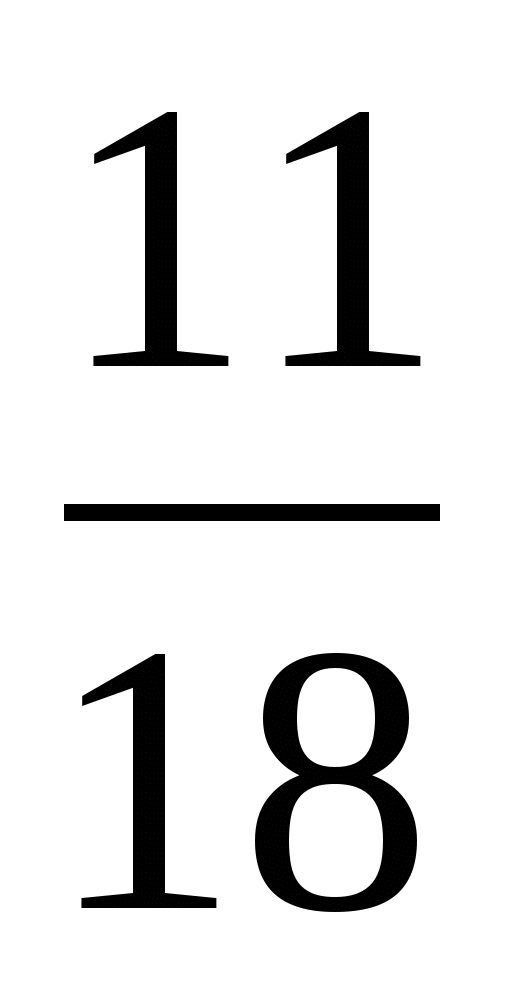 ; б)
; б)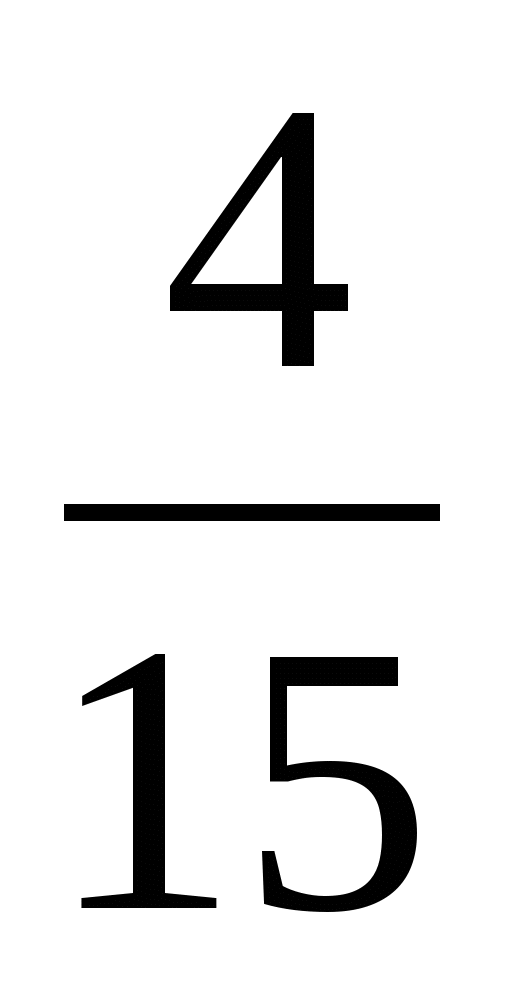 и
и 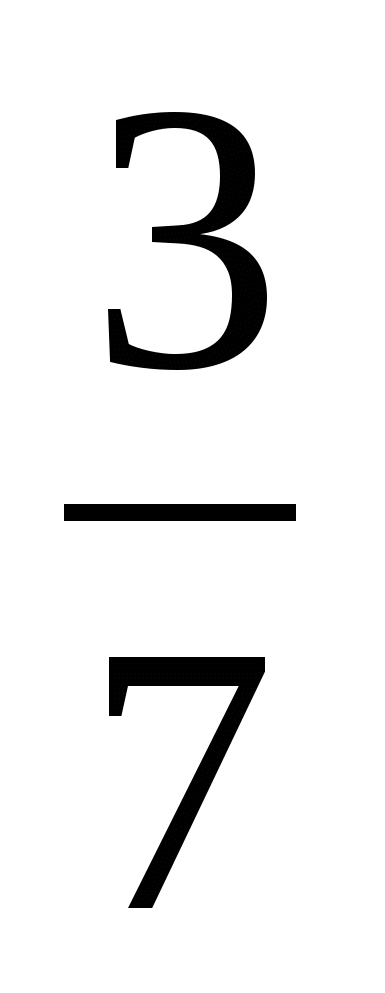 ; в)
; в)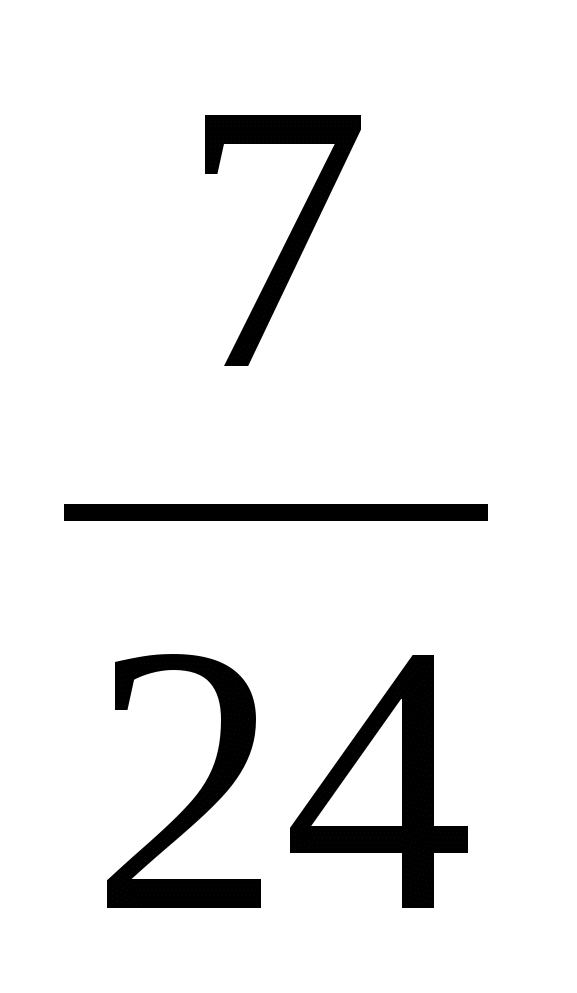 и
и 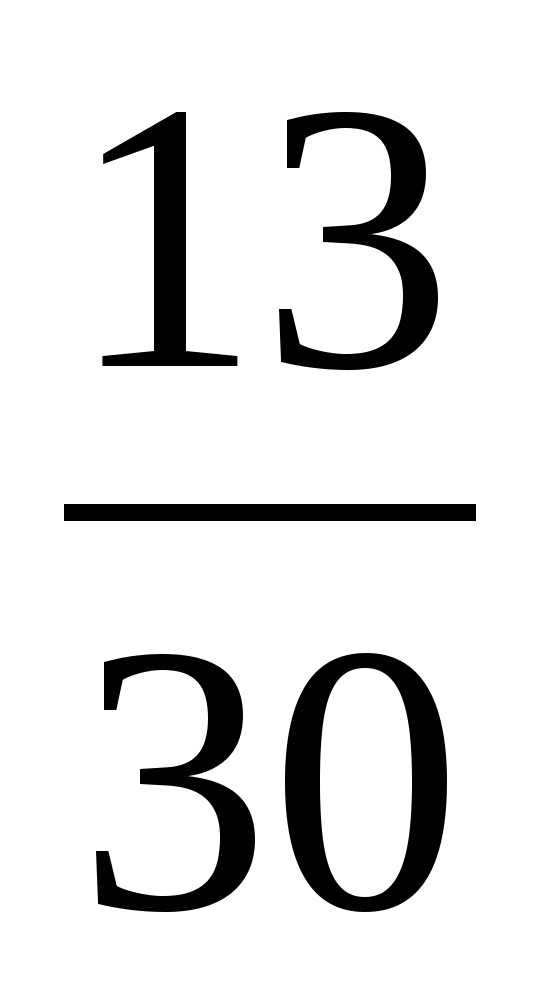 .
.
3. Сравните дроби:
а) 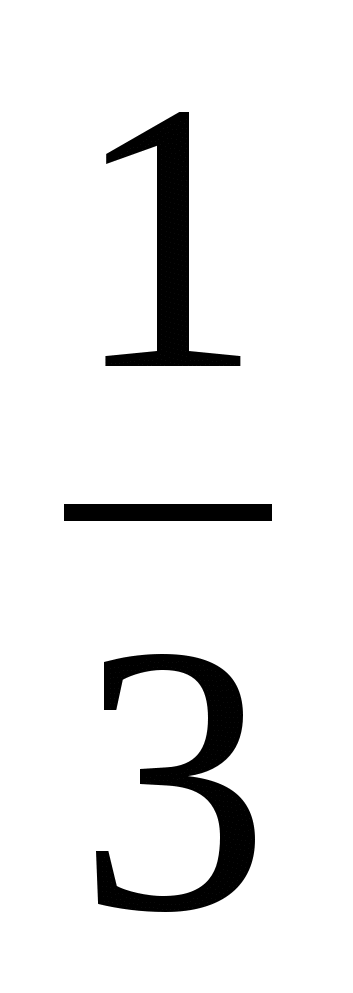 и
и 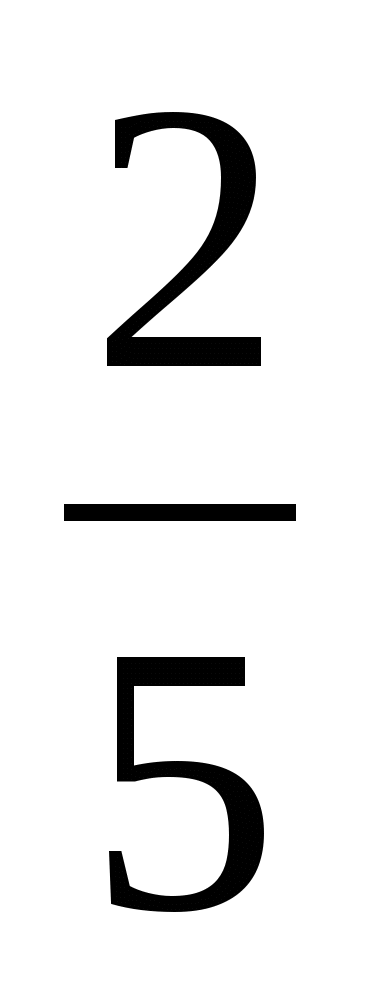 ; б)
; б) 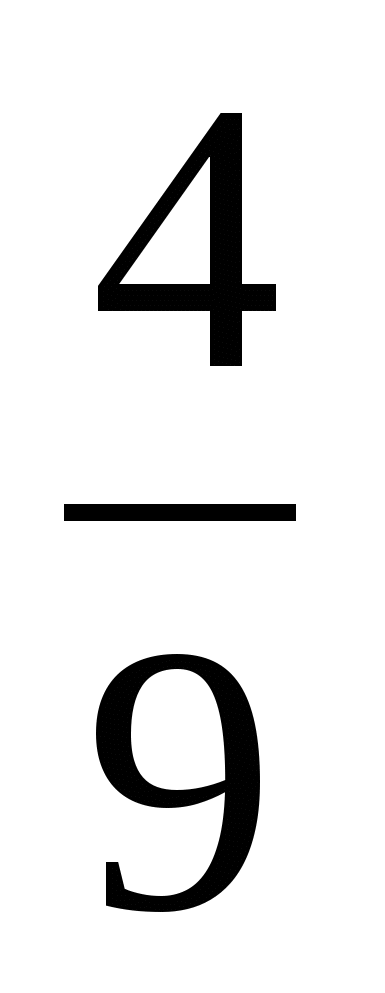 и
и 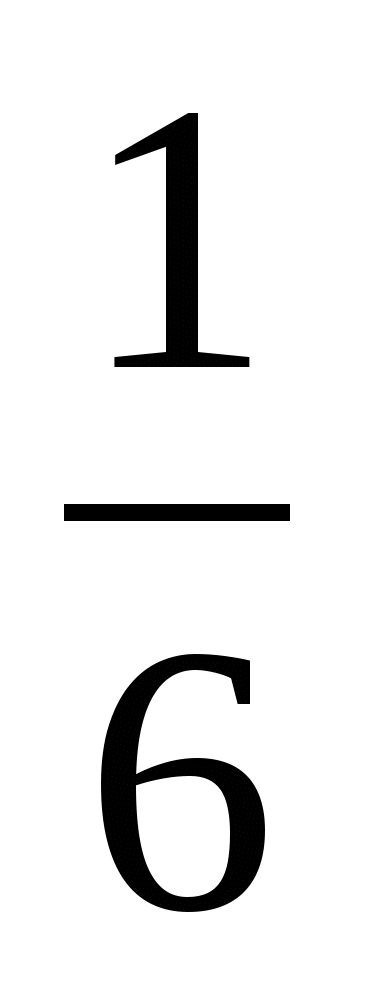 ; в)
; в)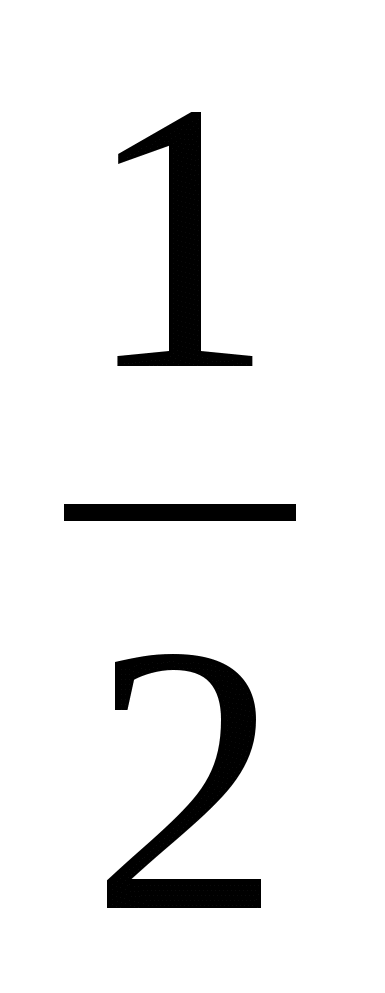 и
и 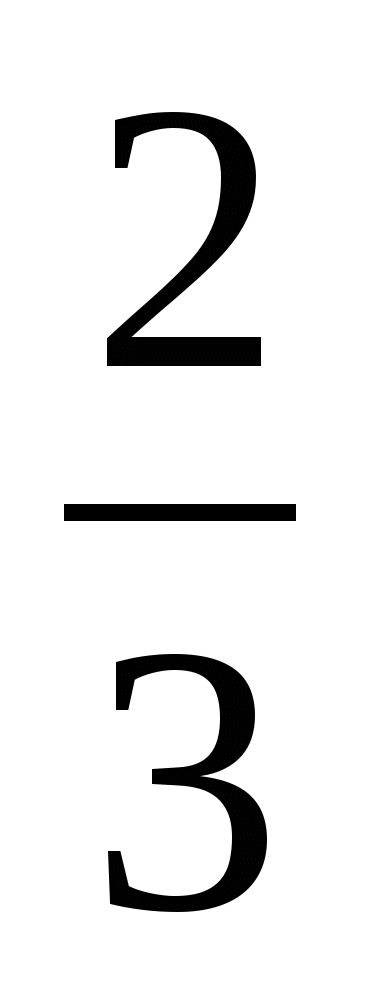 .
.
4. Сложите дроби:
а) 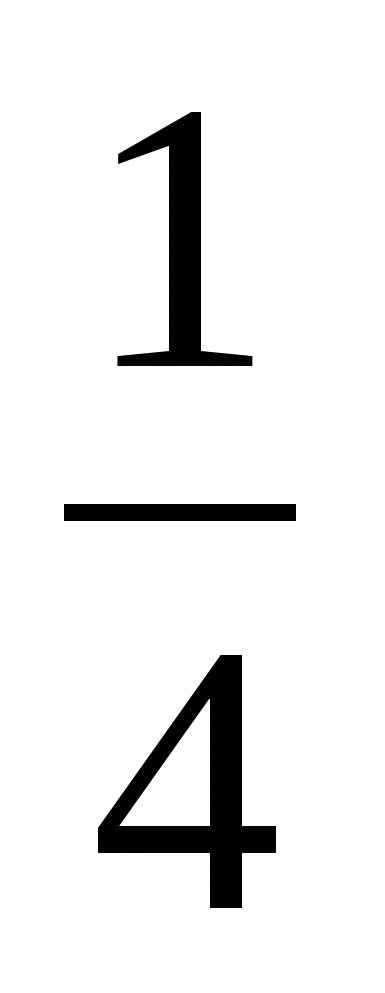 +
+ 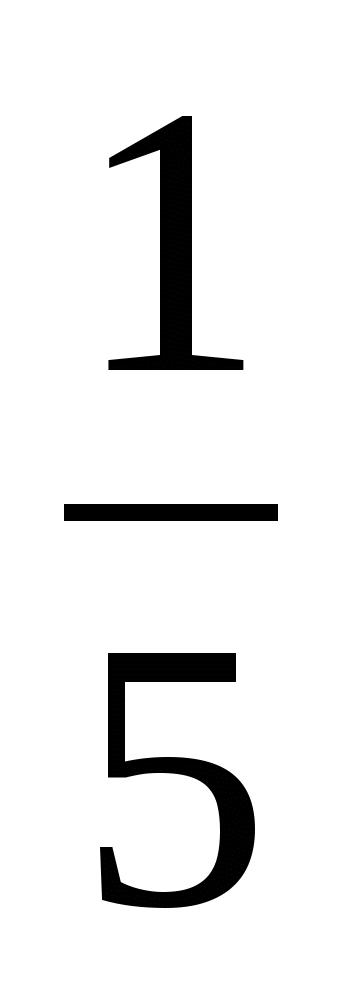 ; б )
; б )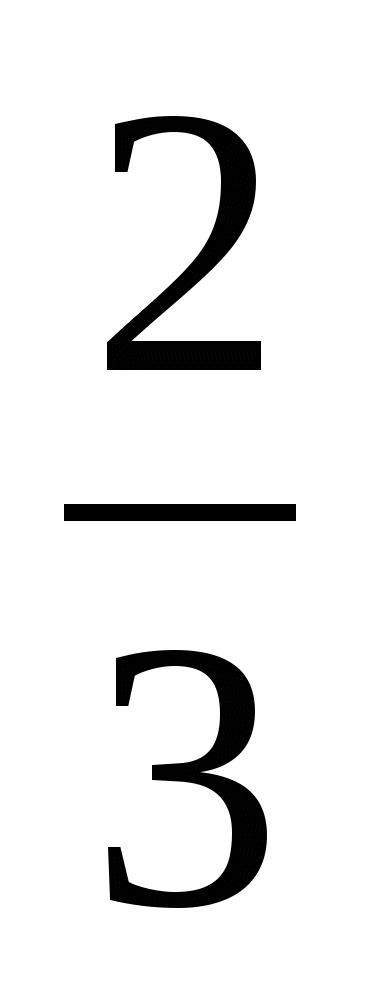 +
+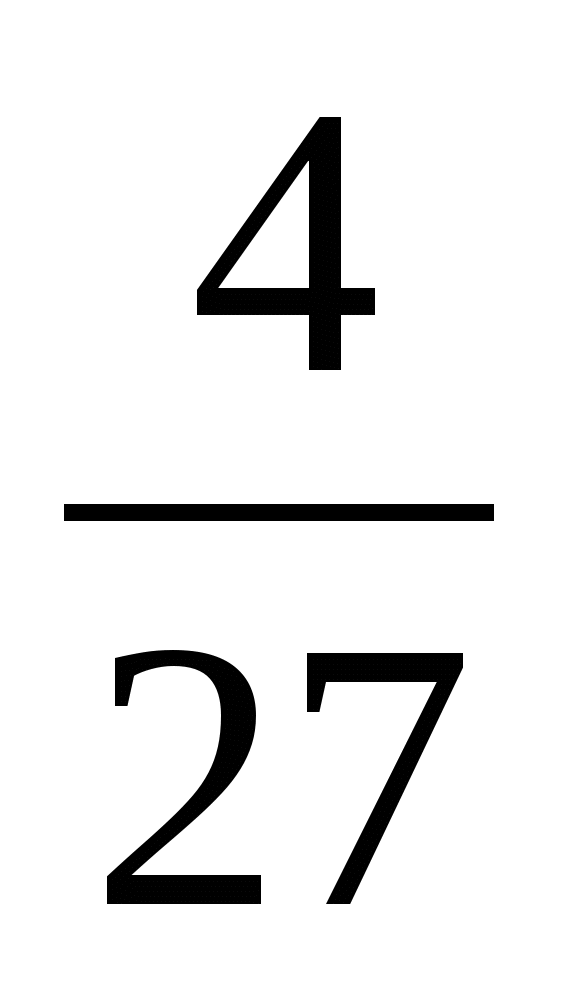 ; в)
; в) 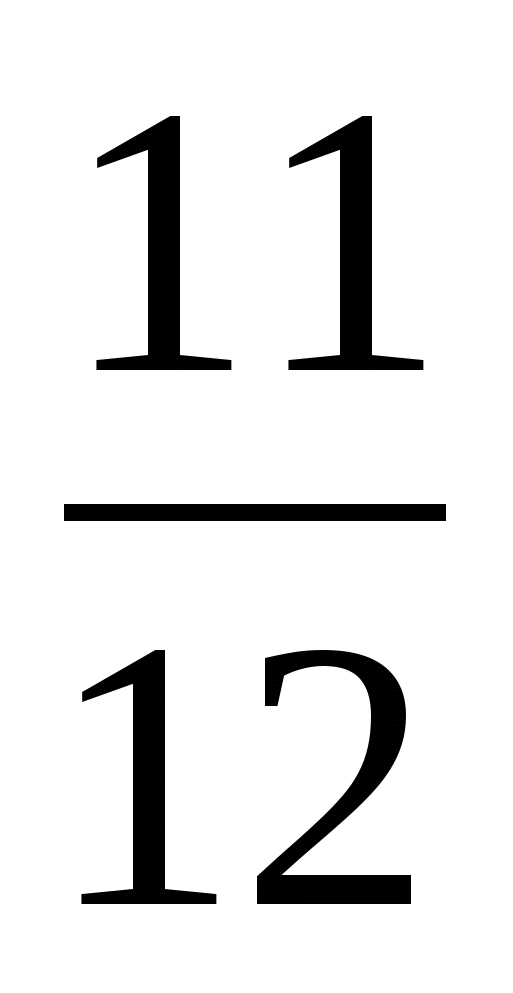 +
+ 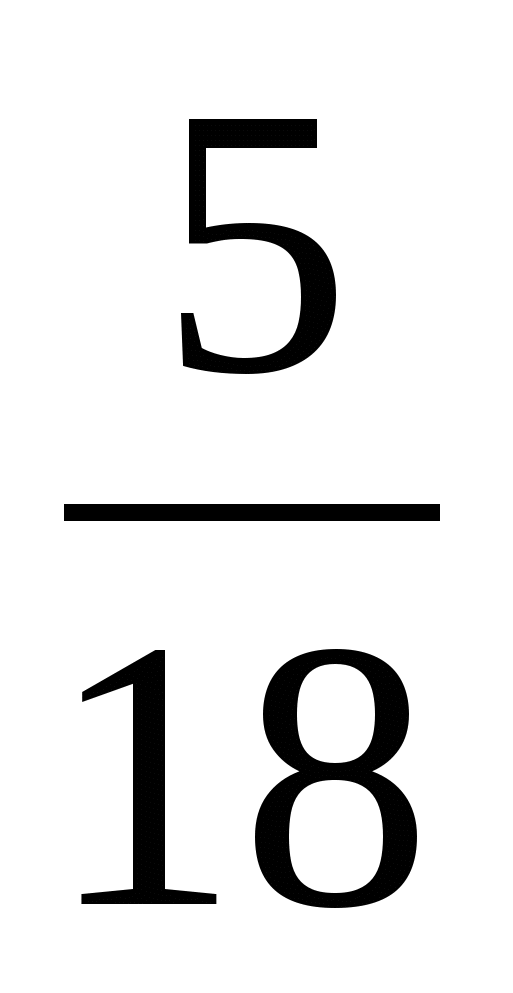 .
.
5. Чему равен х?
а)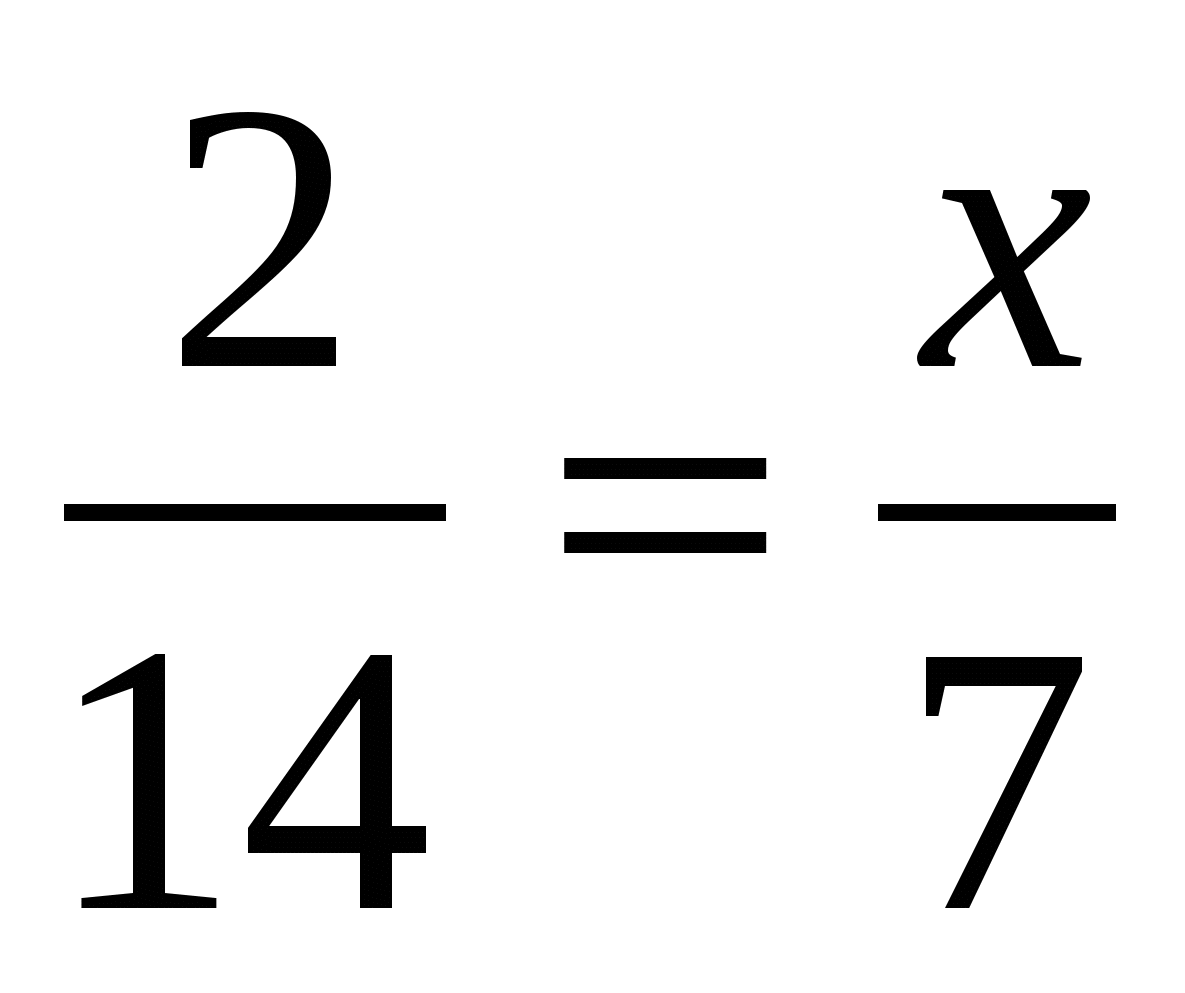 ; б)
; б)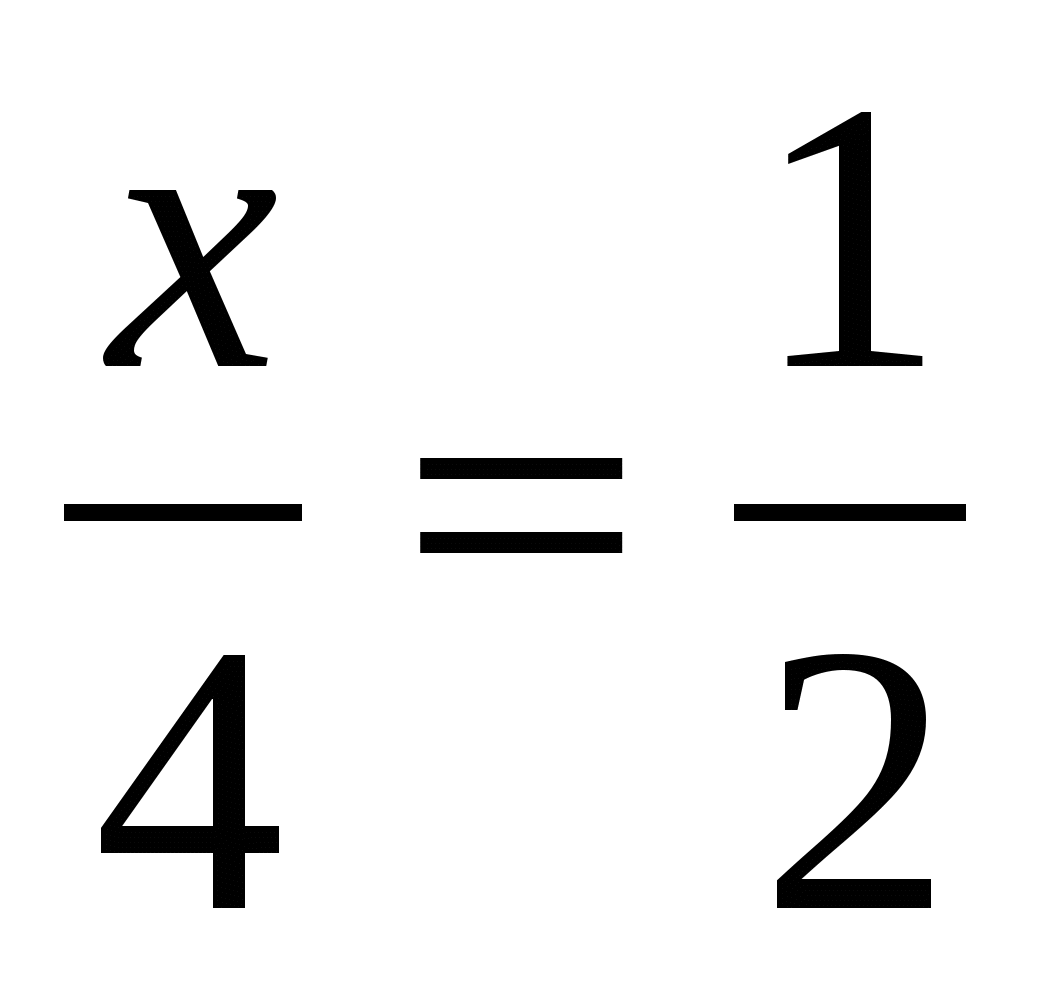 ; в)
; в)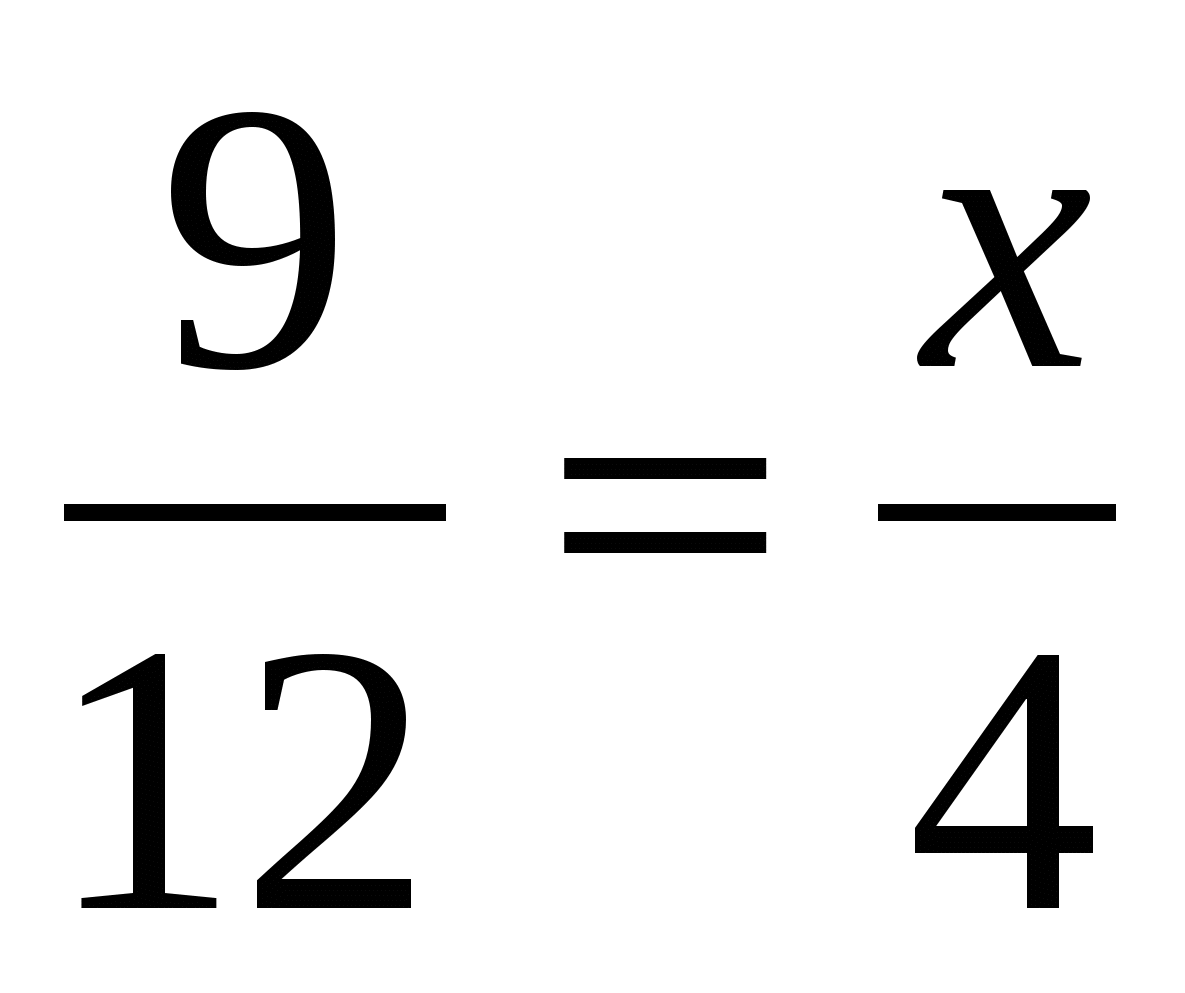 ; г)
; г)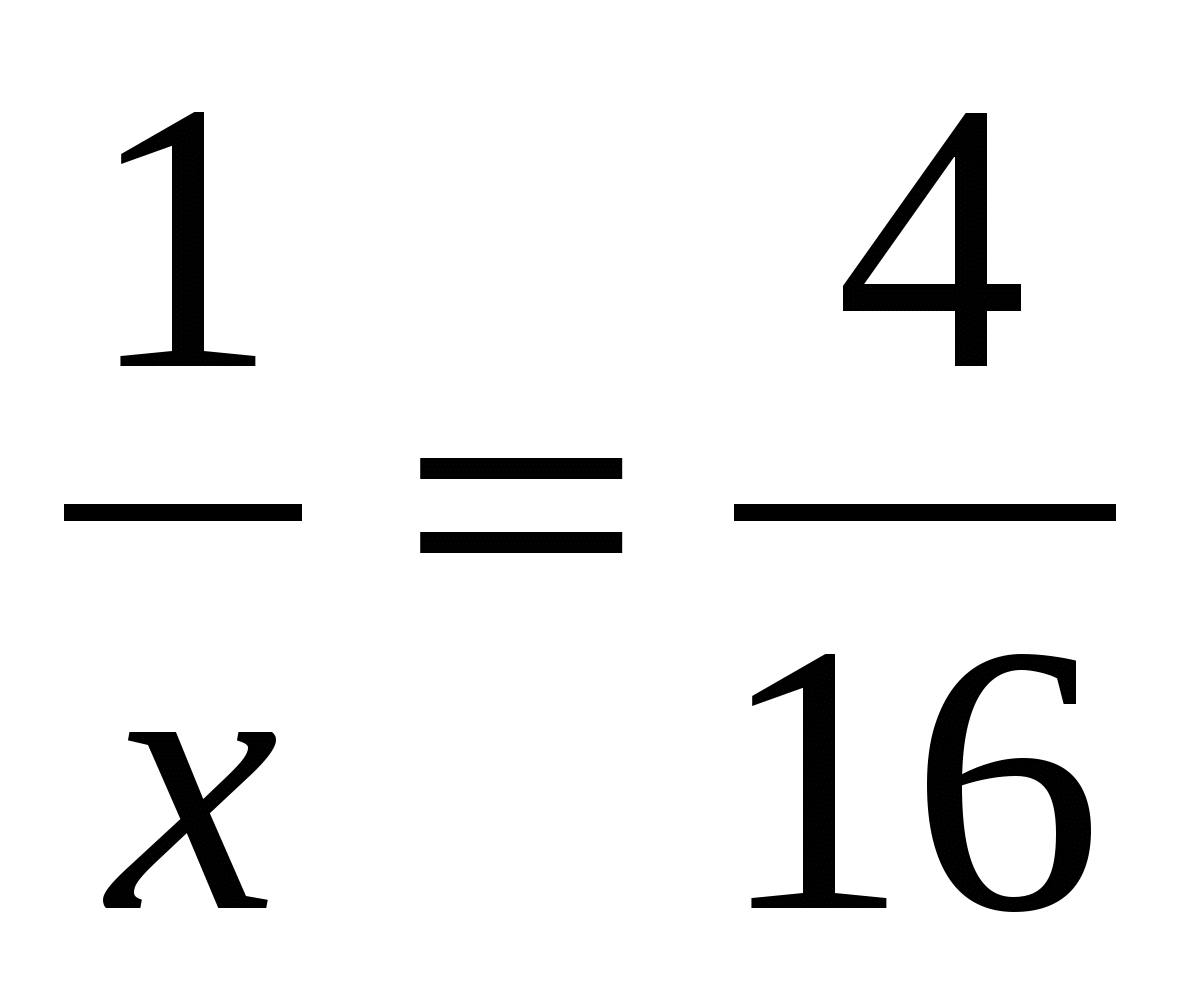 ;
;
д)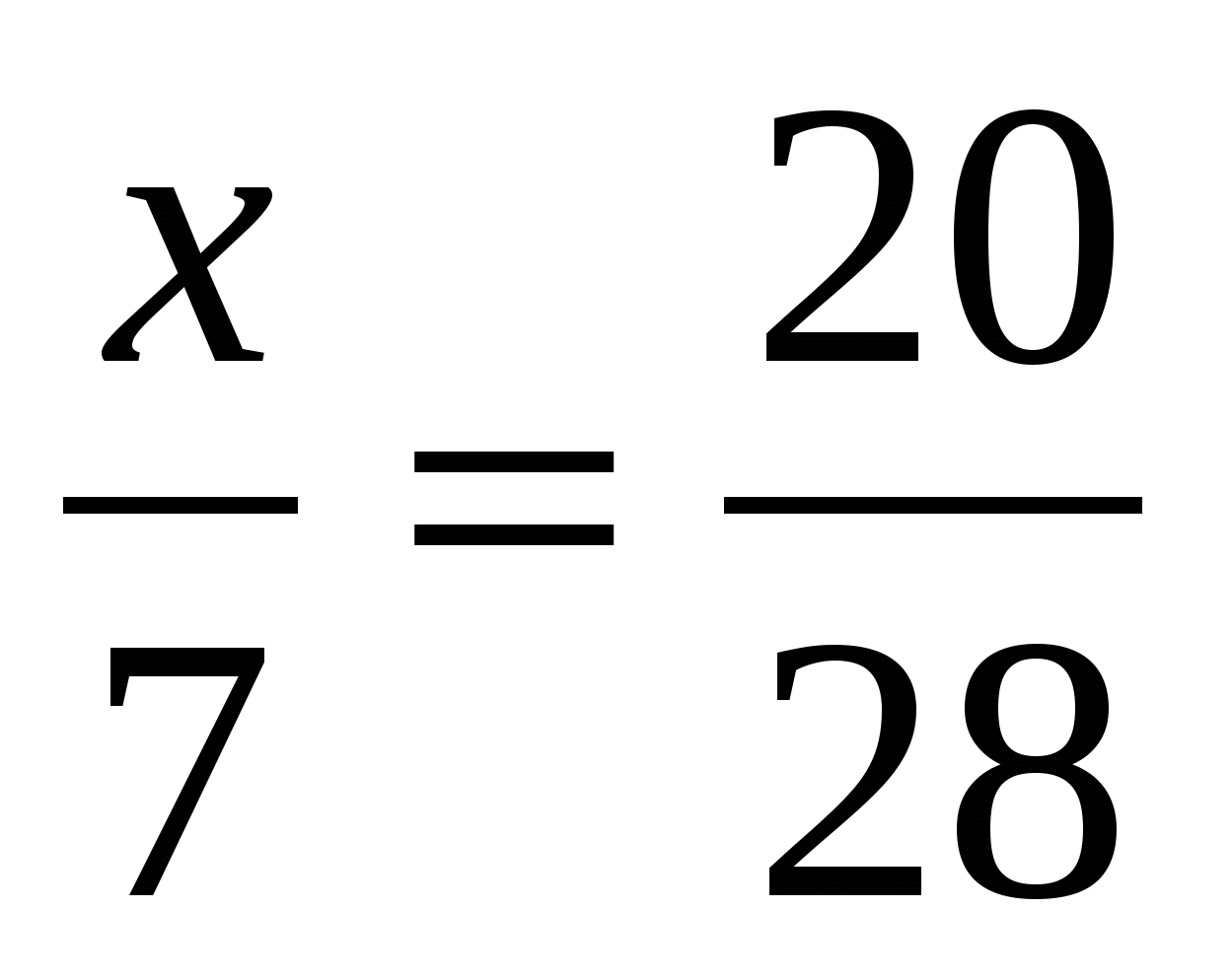 ; е)
; е)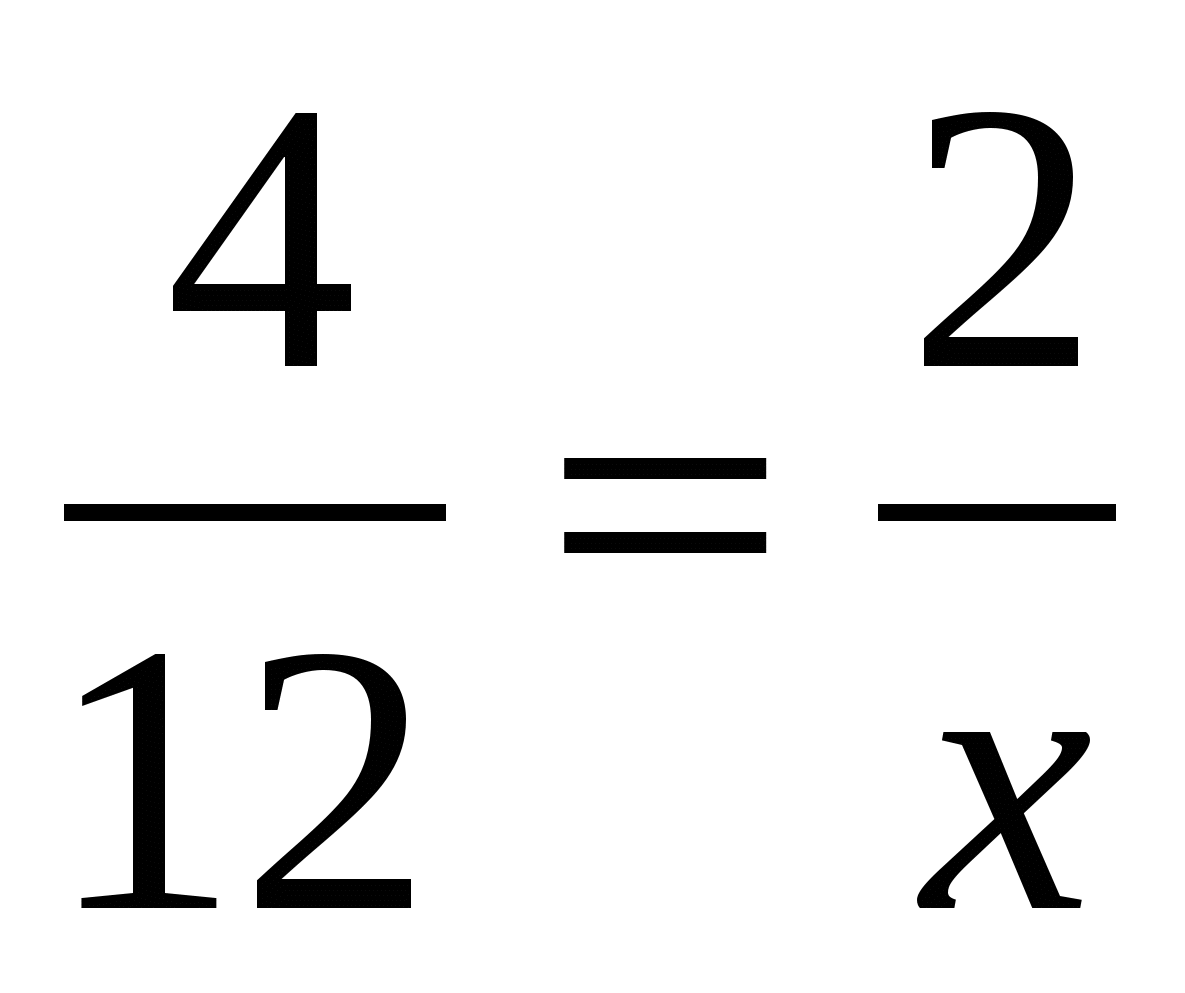 ; ж)
; ж)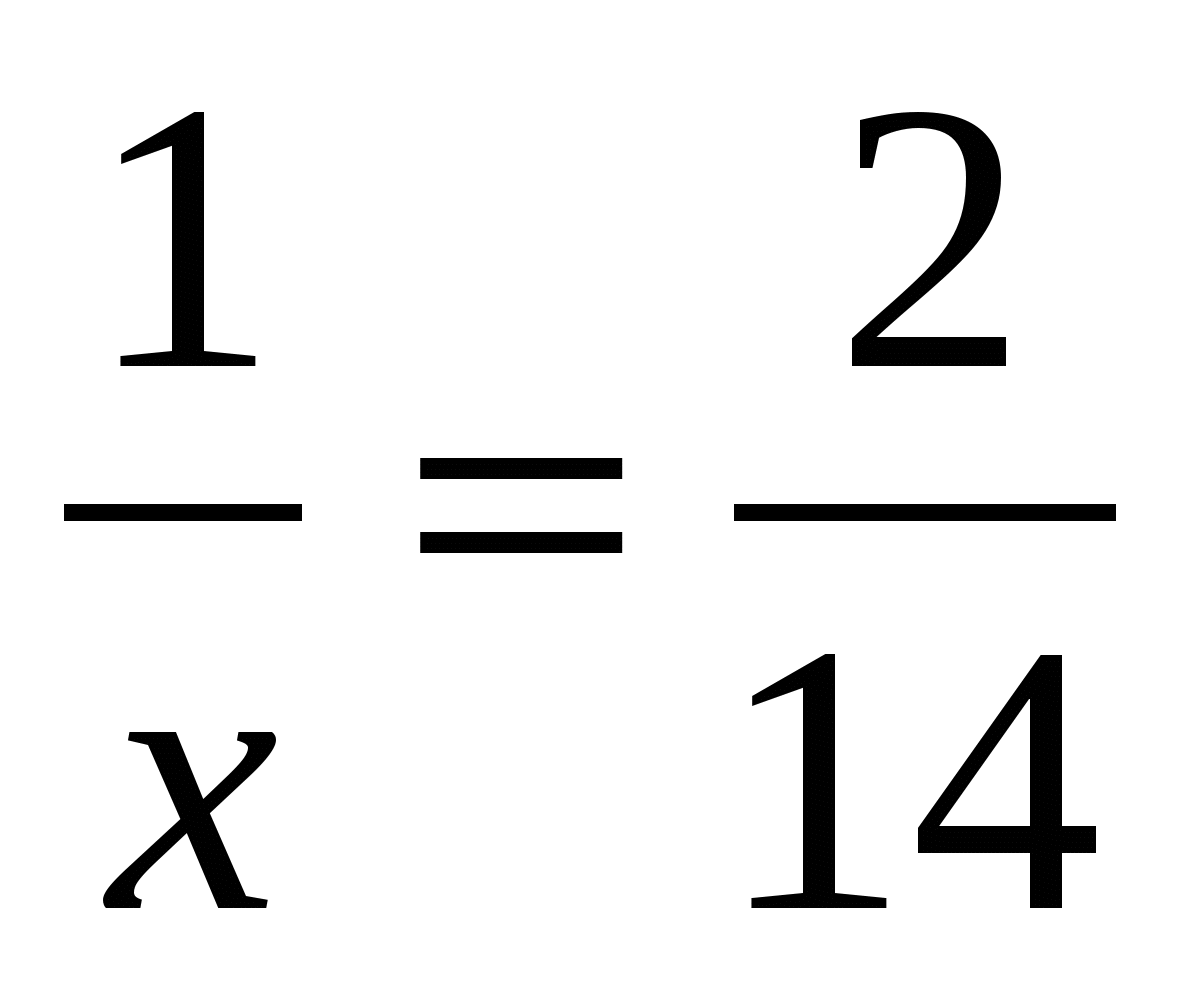 .
.
6. Верно ли утверждение?
а) 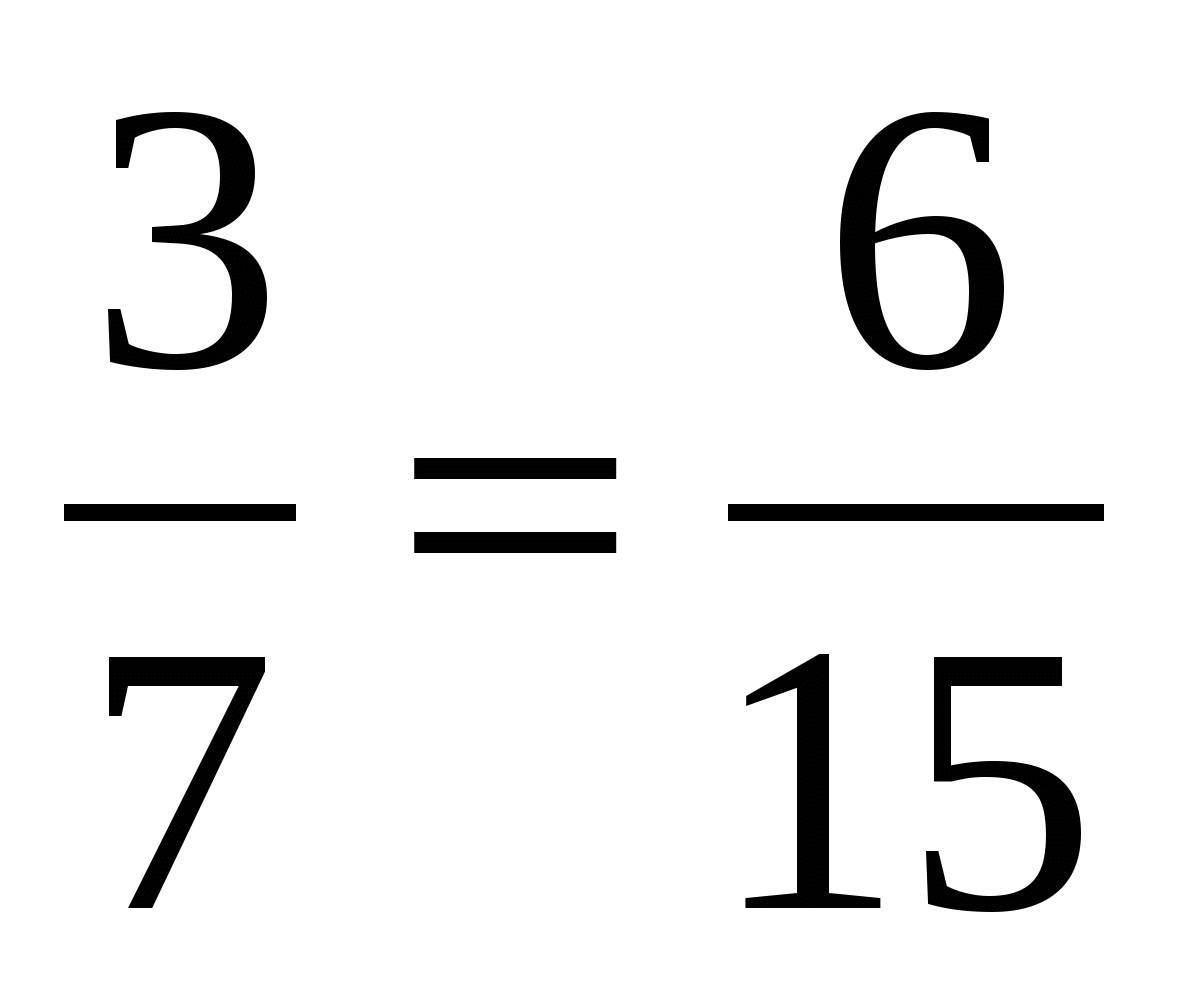 ; б)
; б)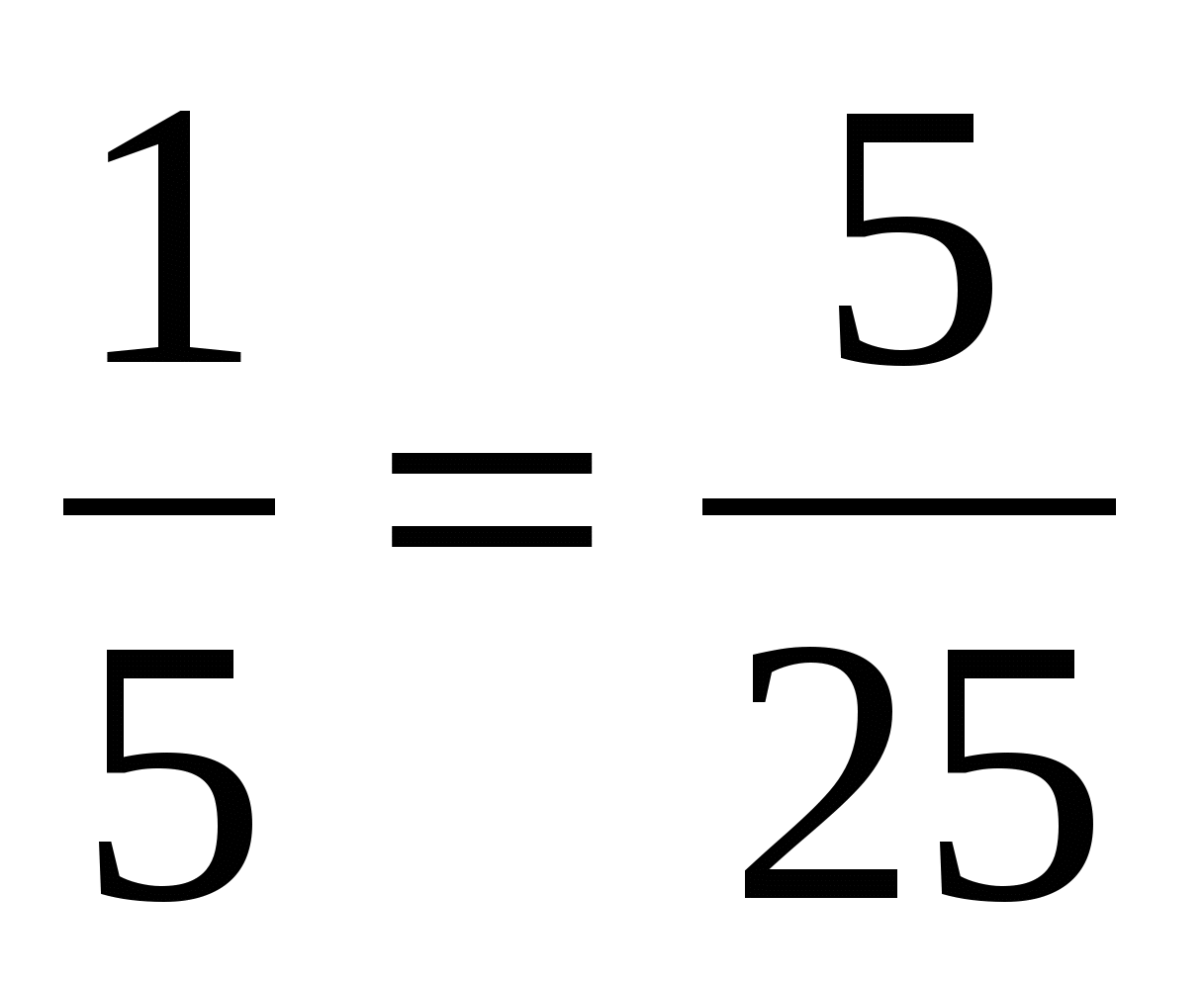 ; в)
; в)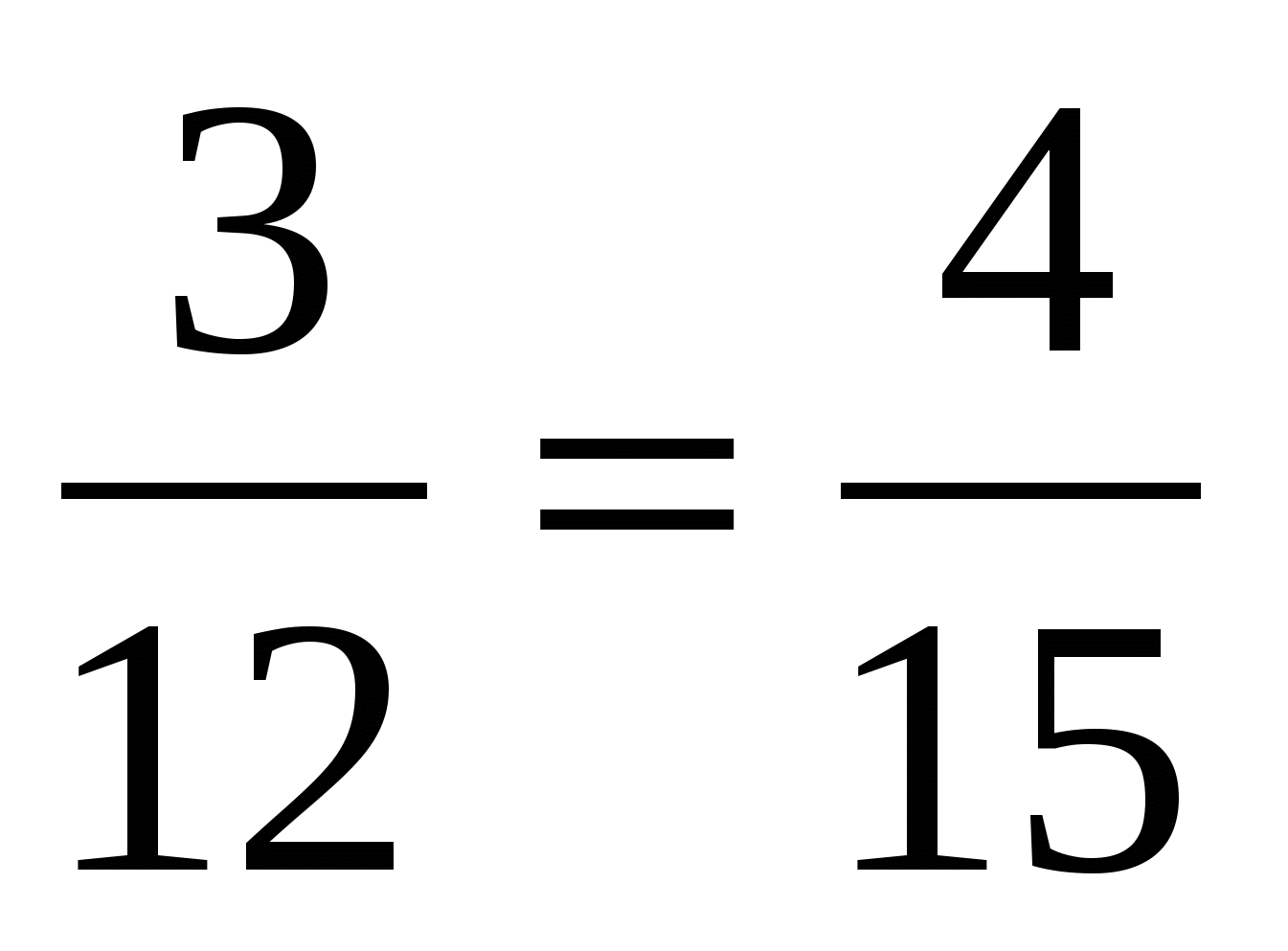 ; г)
; г)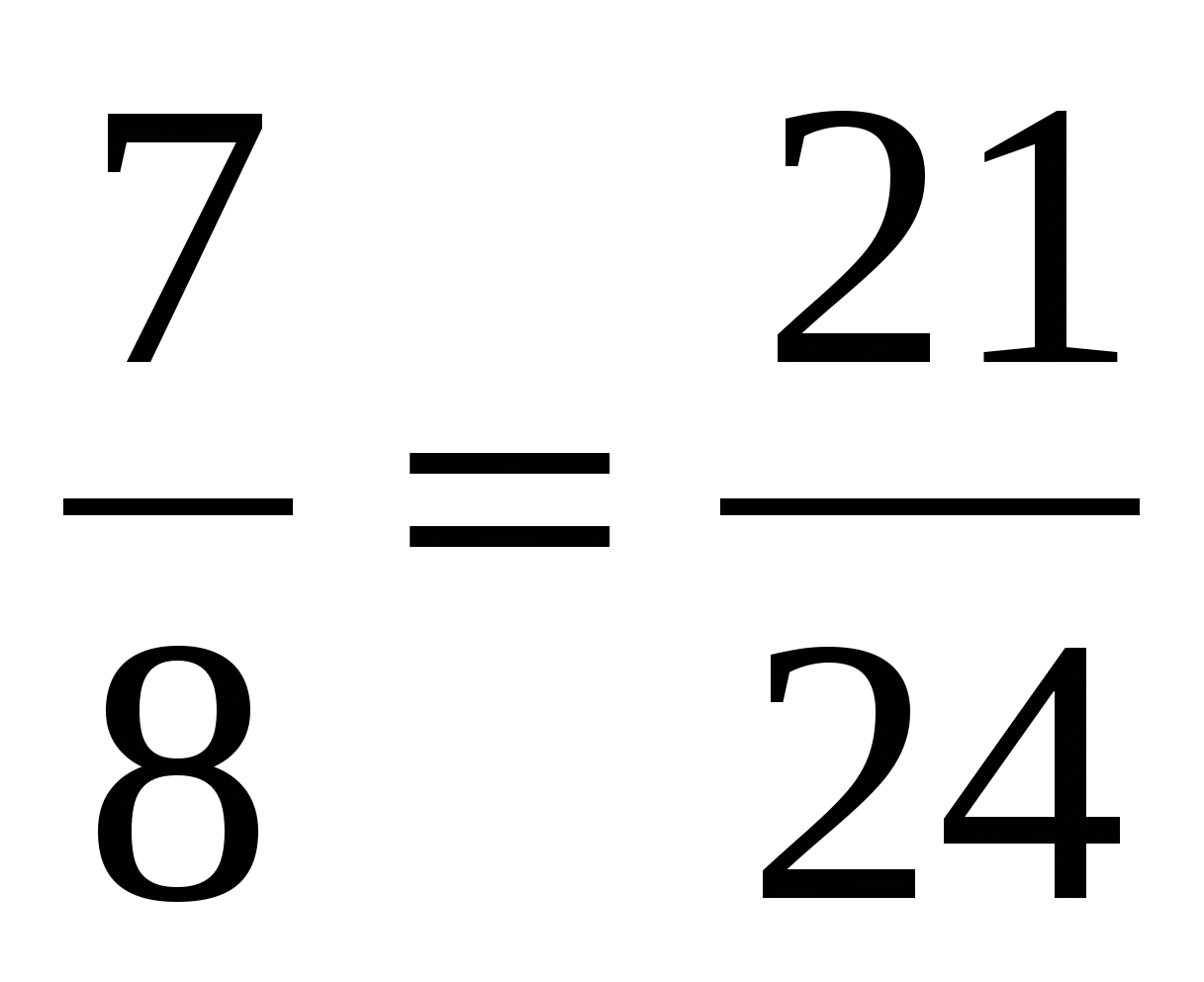 ;
;
д)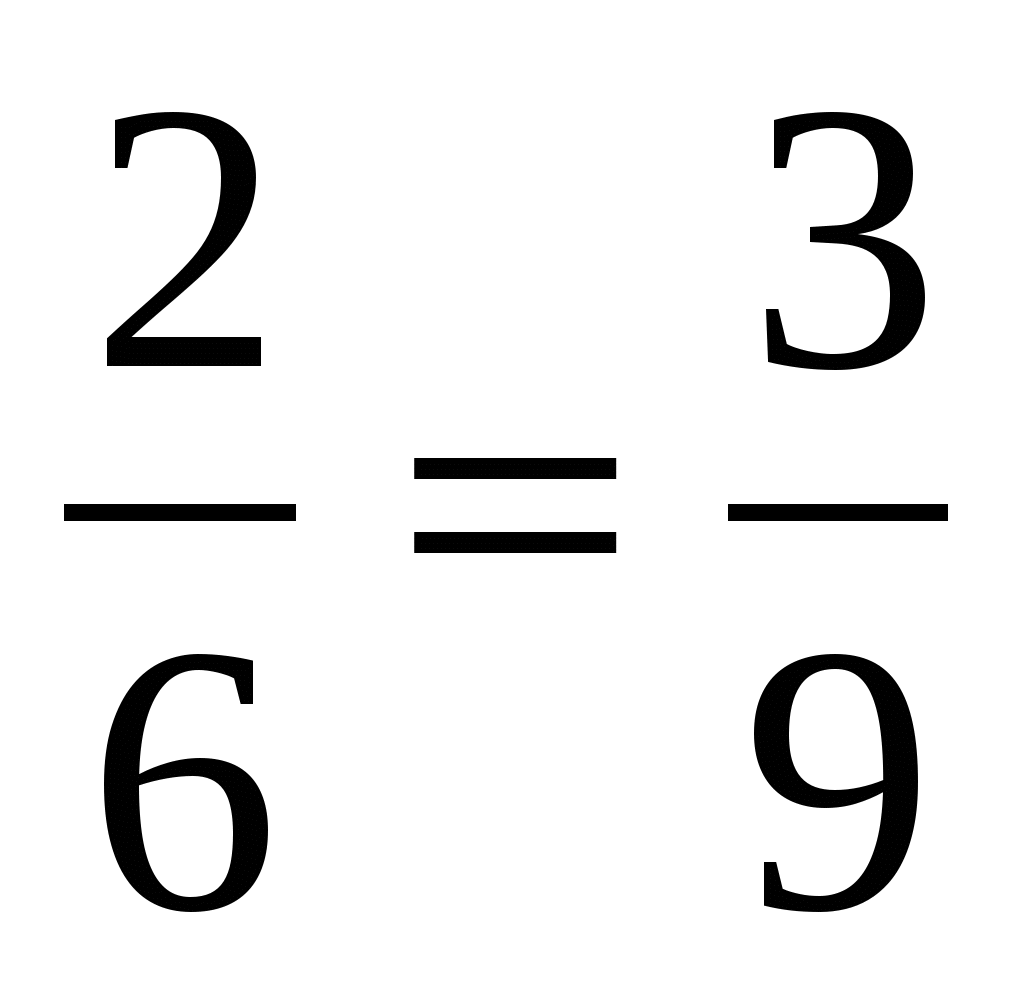 ; е)
; е)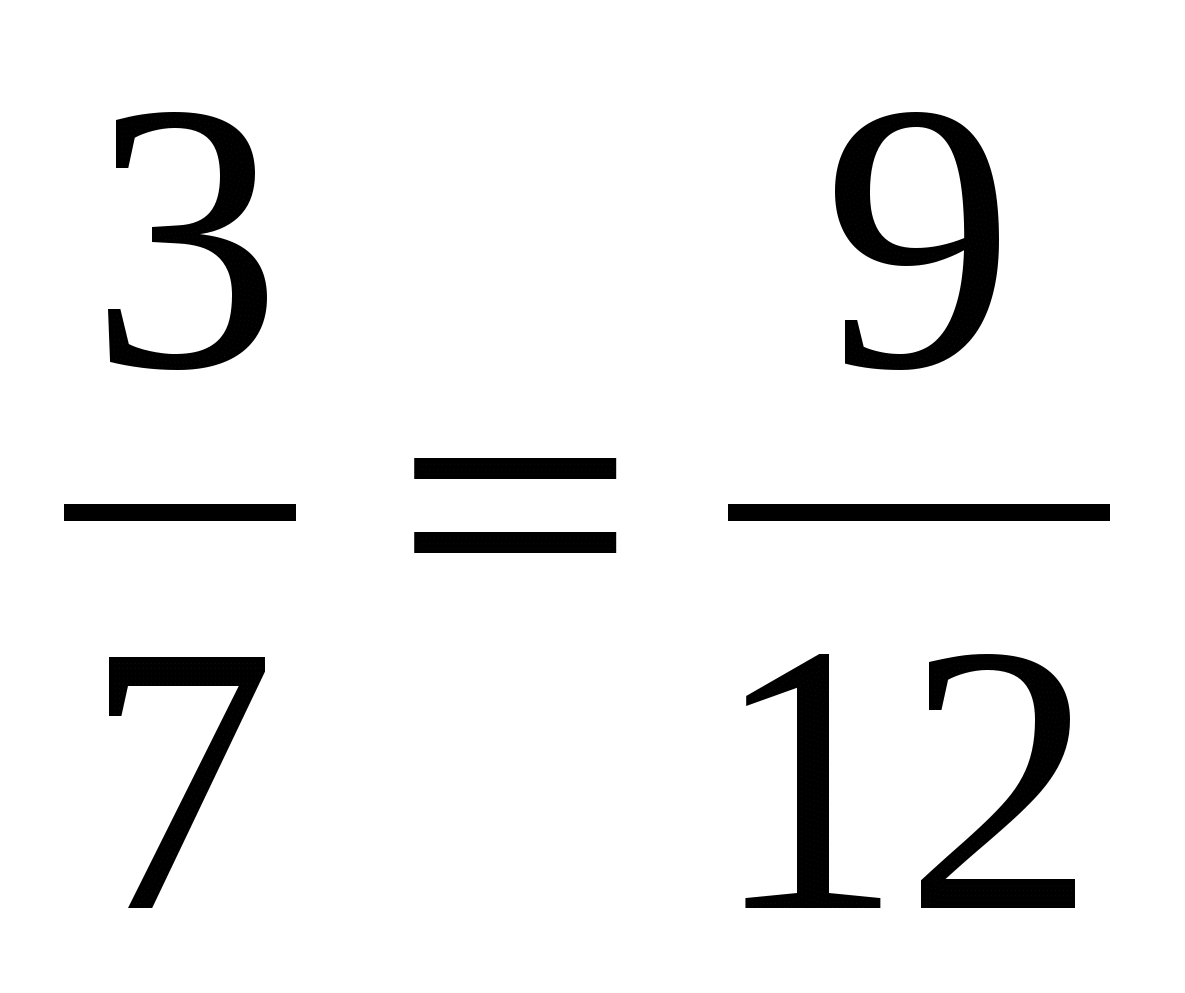 ; ж)
; ж)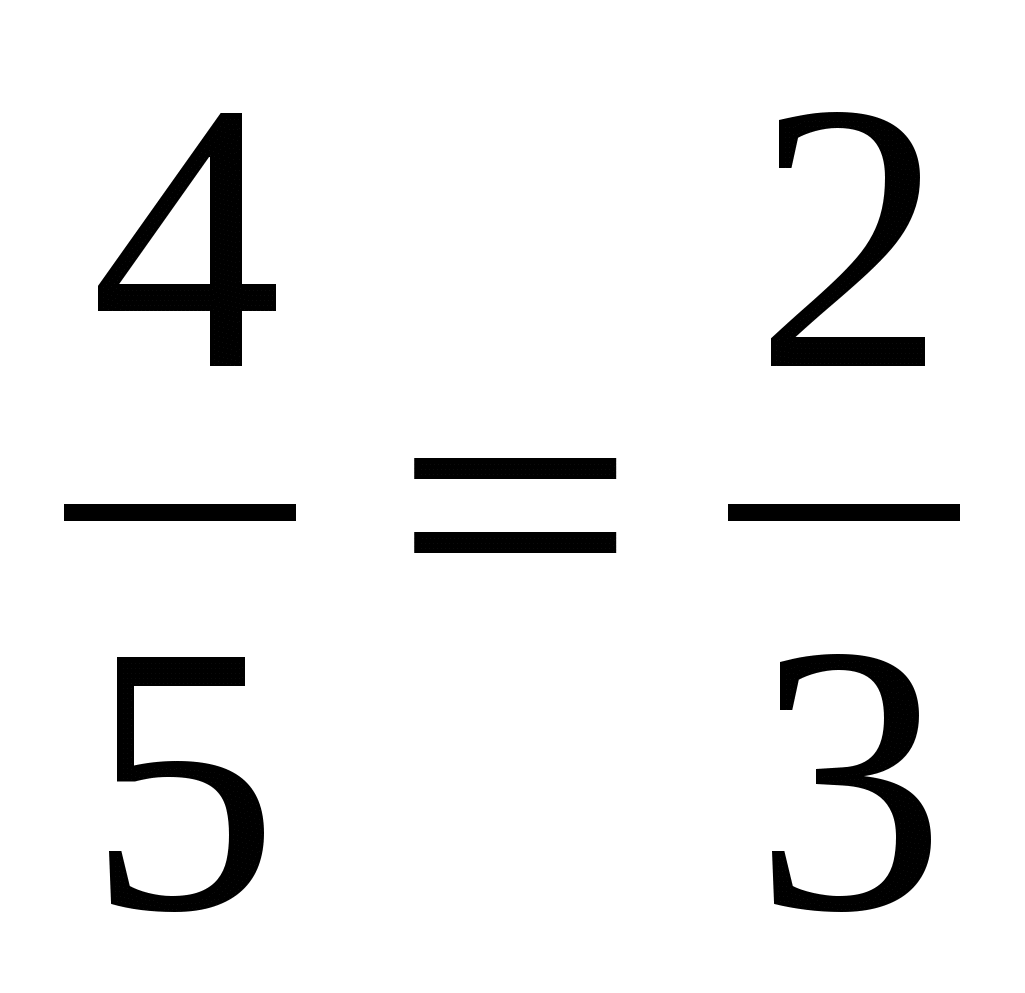 .
.
7. Определите, какая из дробей наибольшая, а какая наименьшая?
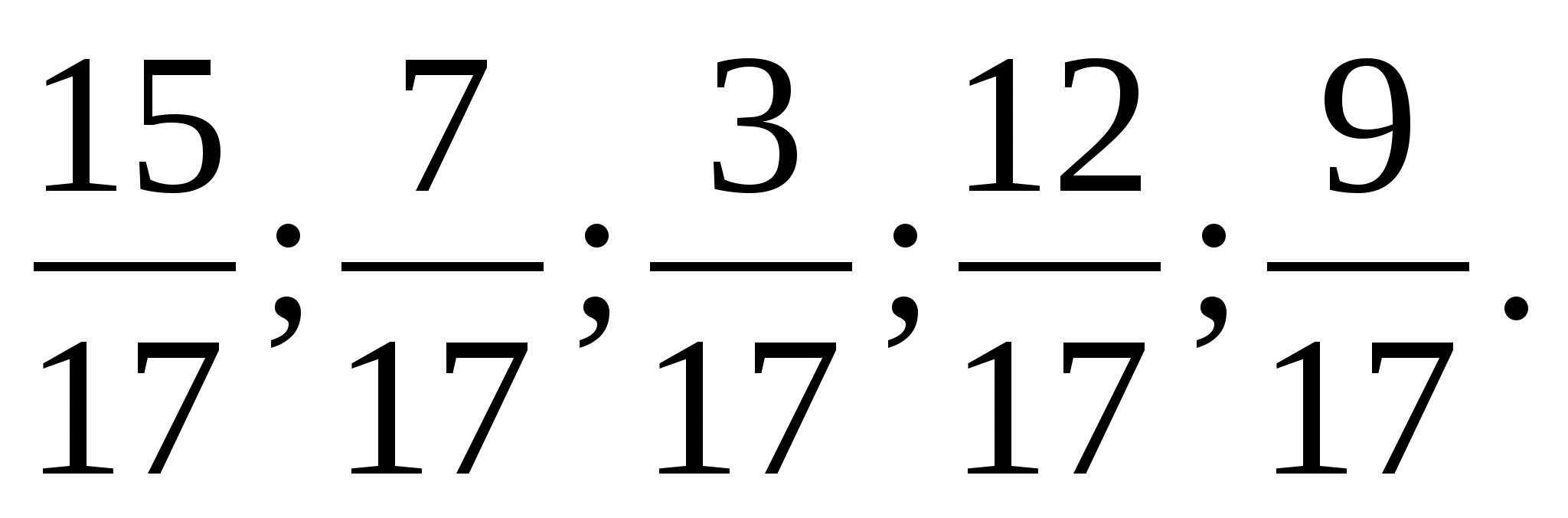
Домашнее задание:
прочитать с 79-80;
№9, №10, №11 с 77-78.
Тема урока
«Сложение дробей
с разными знаменателями».
Работа в парах.
Сложите дроби:
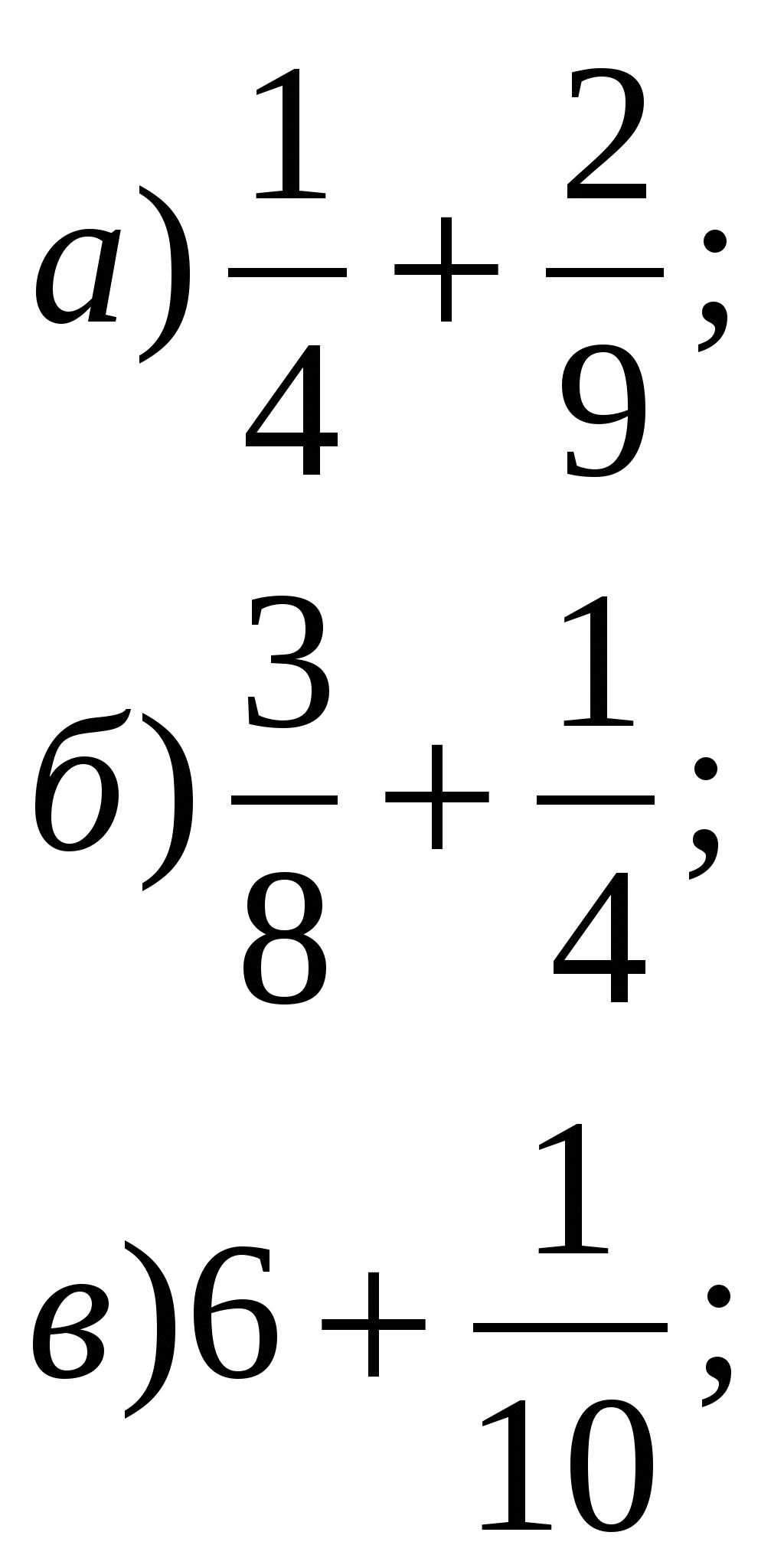
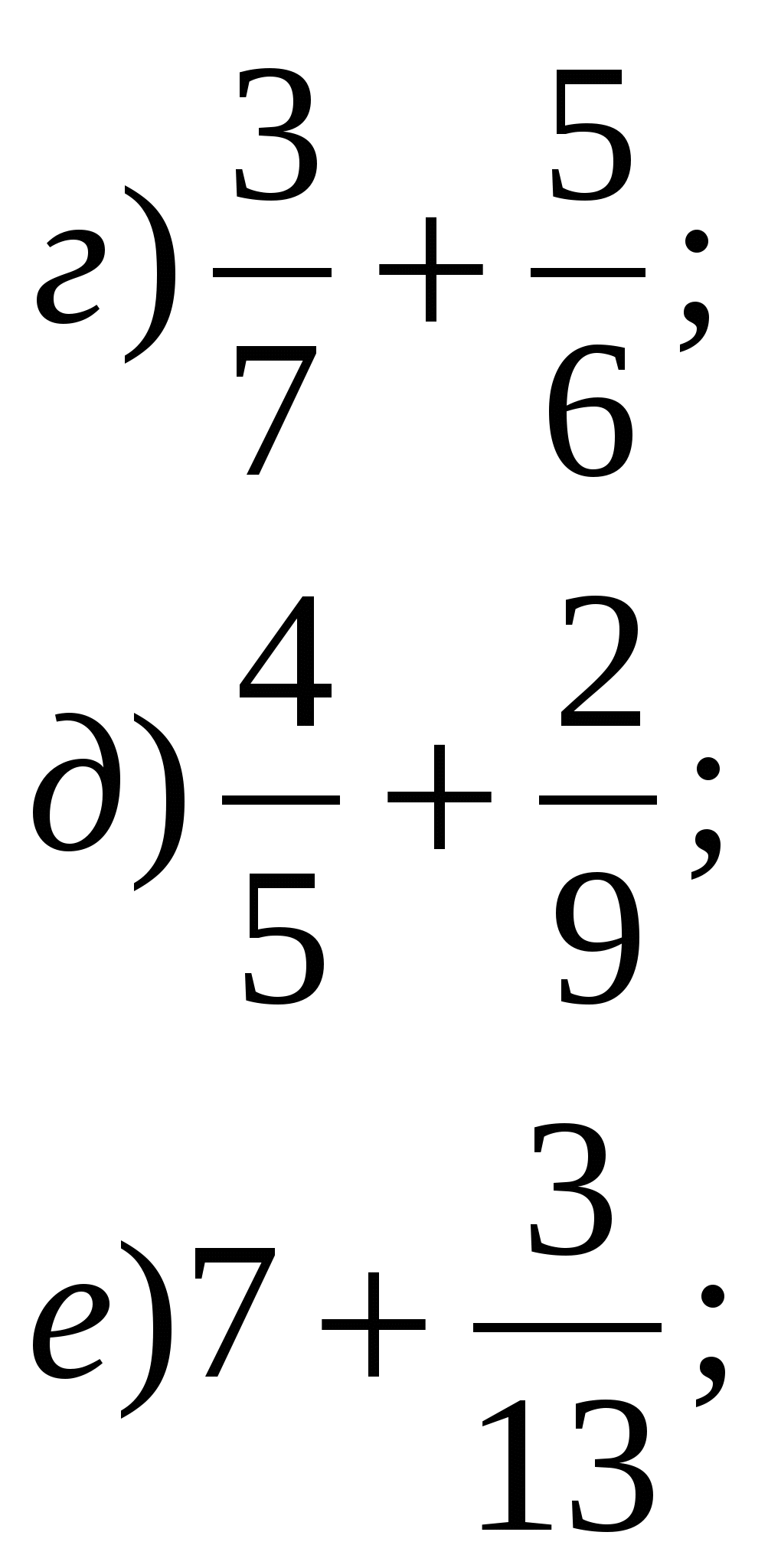
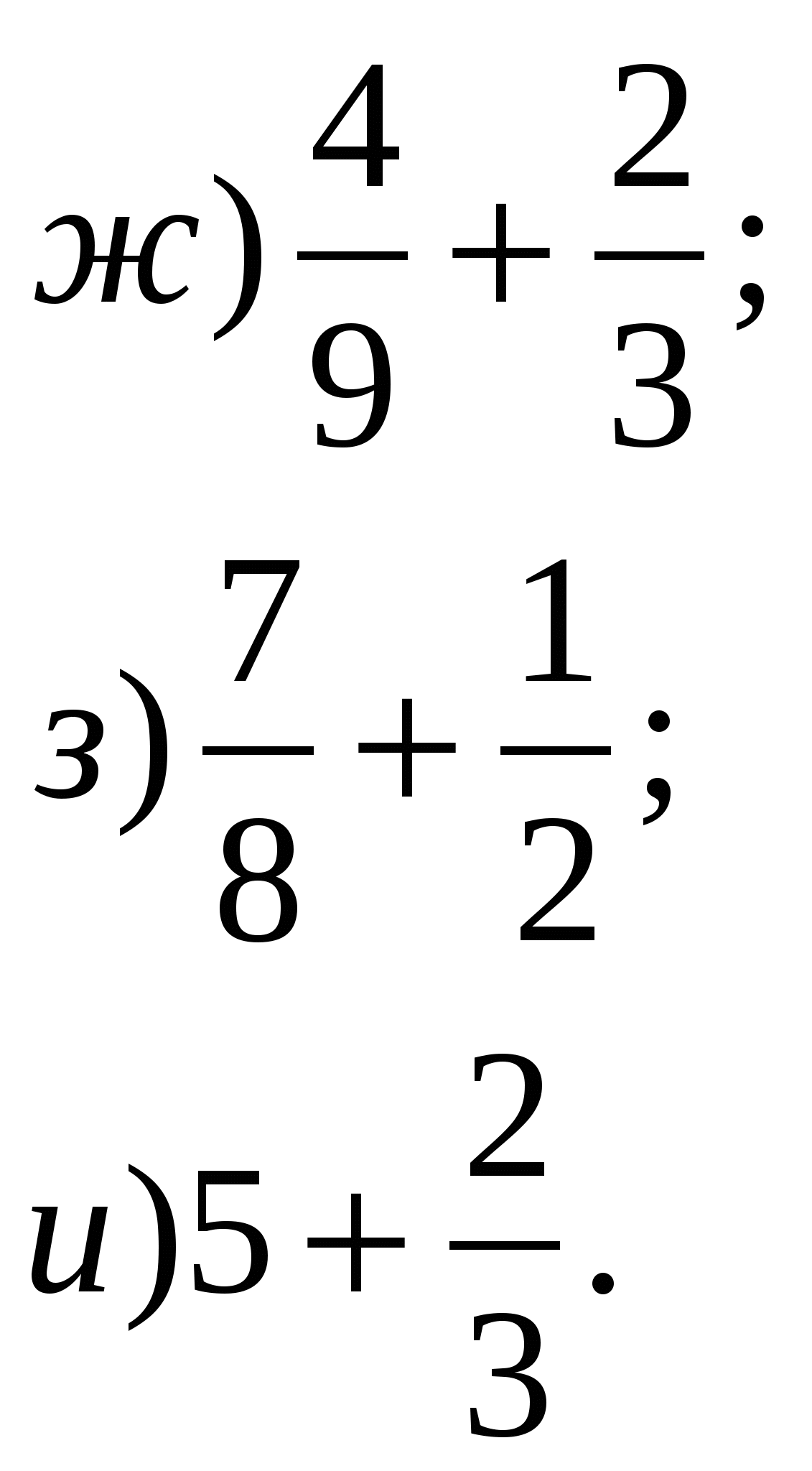
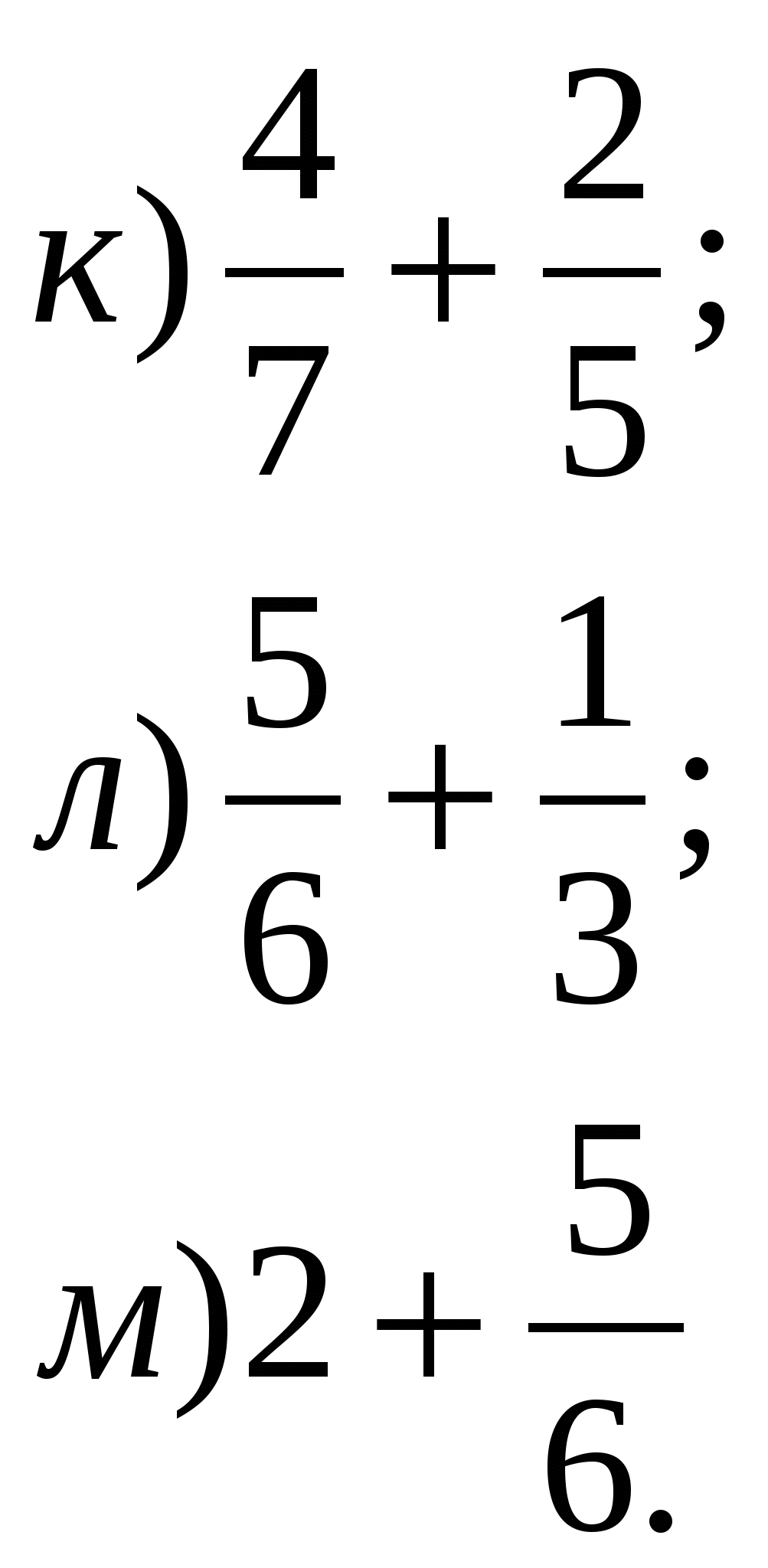
2. Приведите дроби к наименьшему общему знаменателю:
а)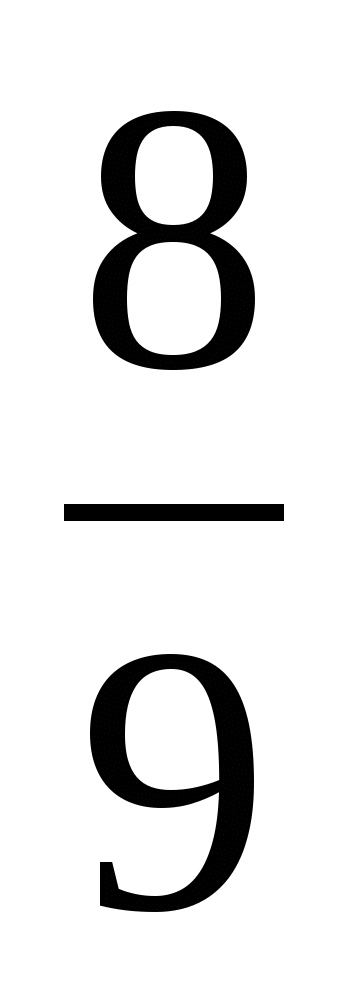 и
и 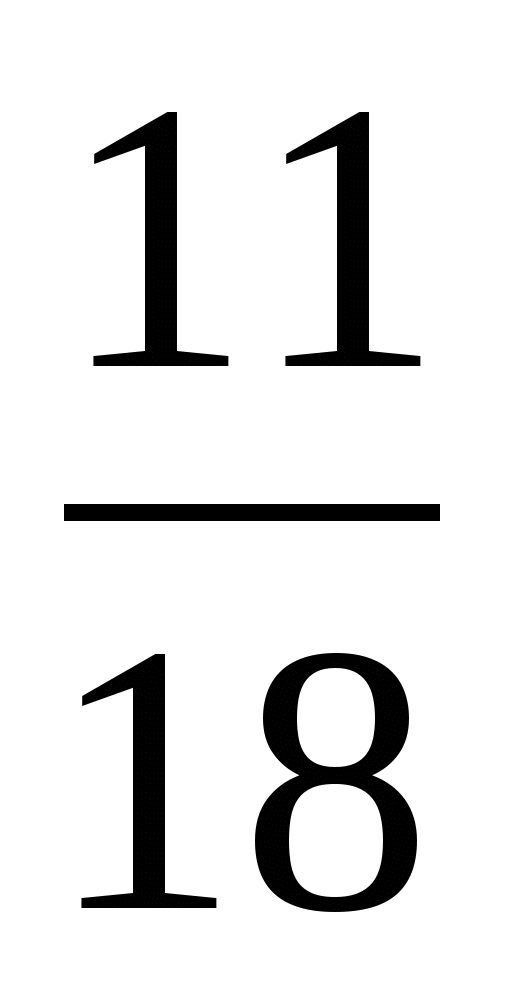 ; б)
; б)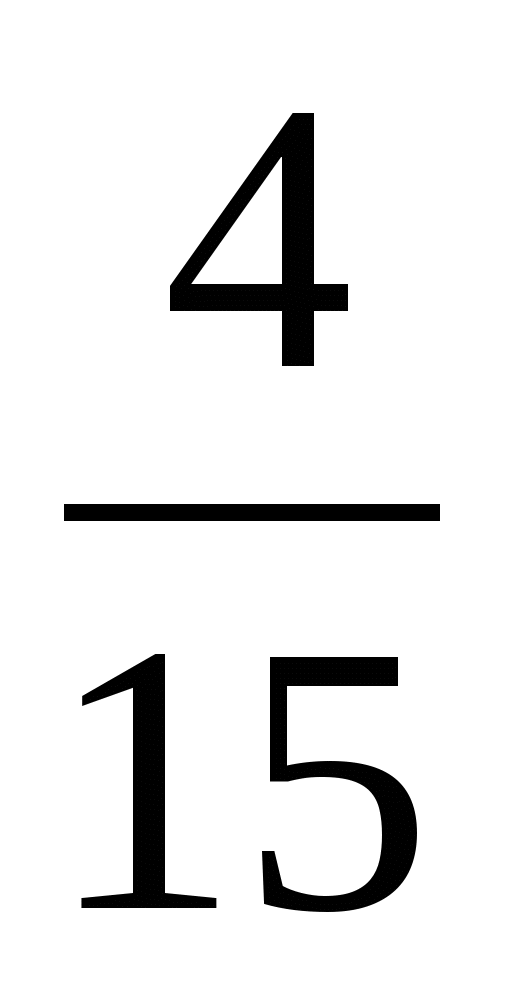 и
и 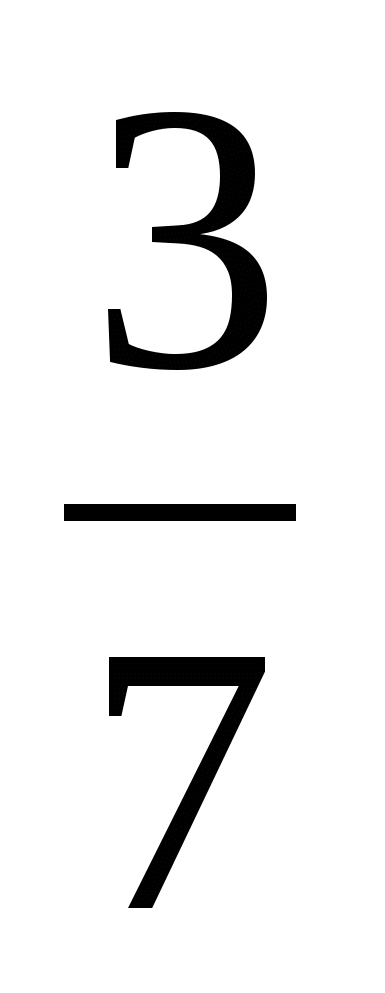 ; в)
; в)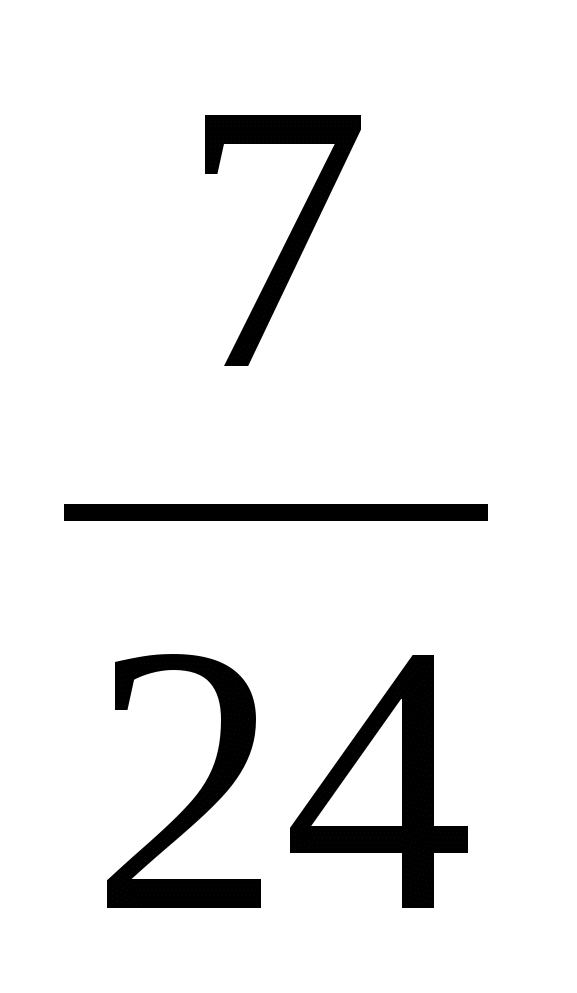 и
и 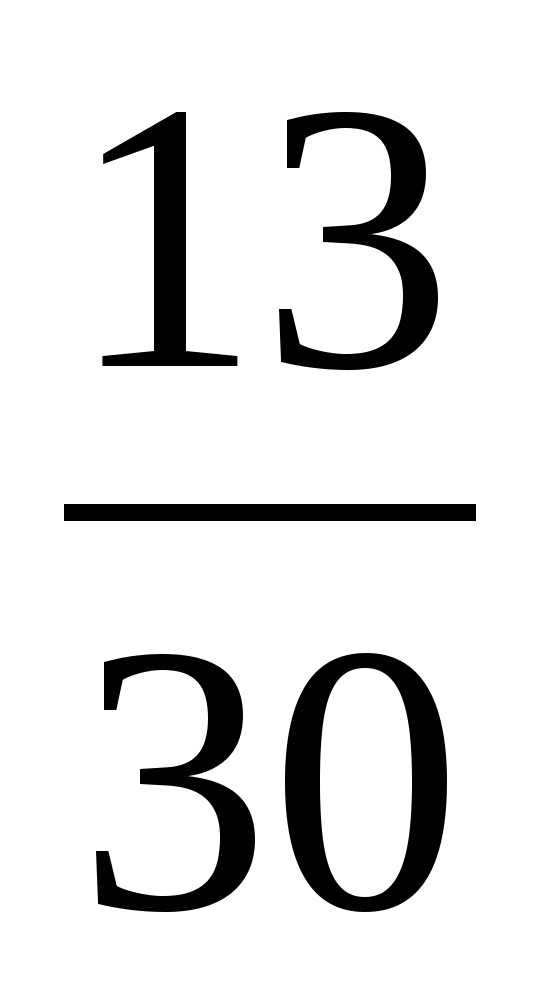 .
.
3. Сравните дроби:
а) 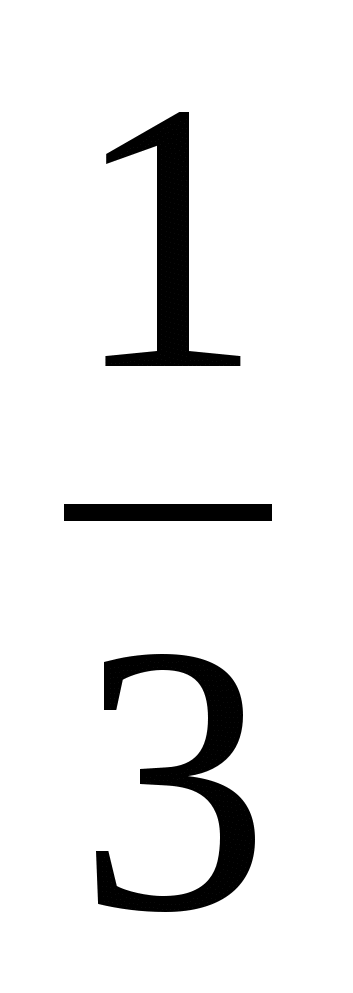 и
и 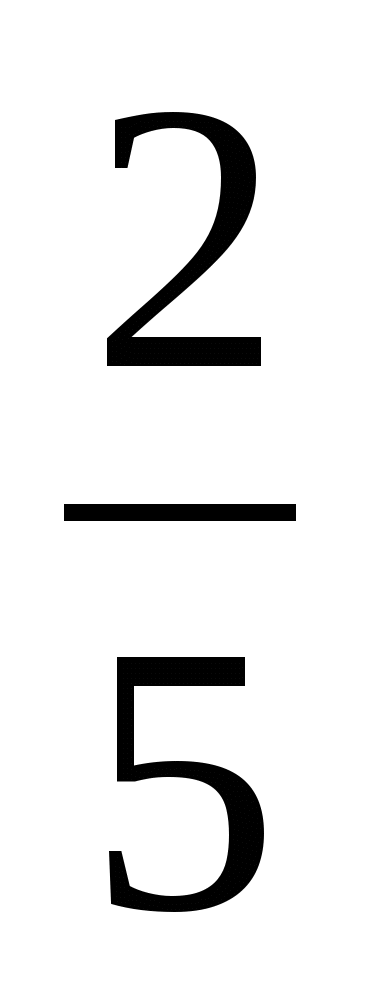 ; б)
; б) 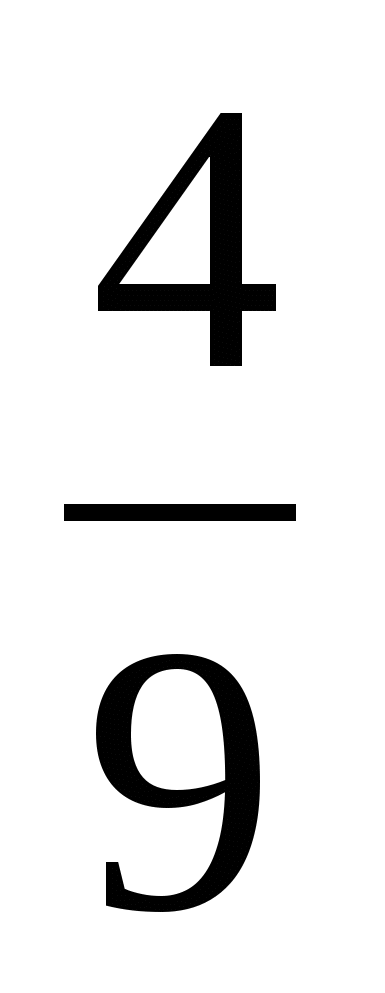 и
и 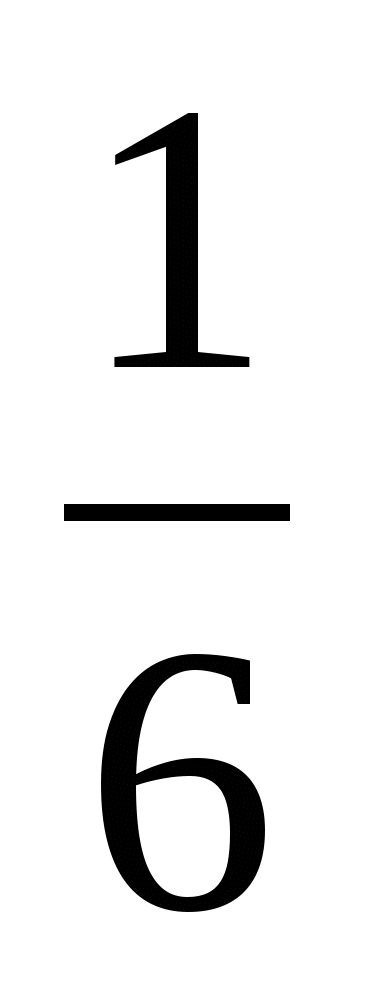 ; в)
; в)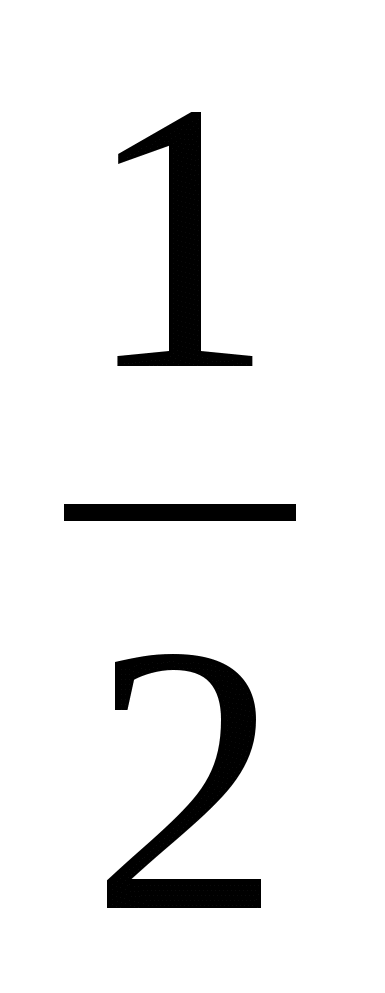 и
и 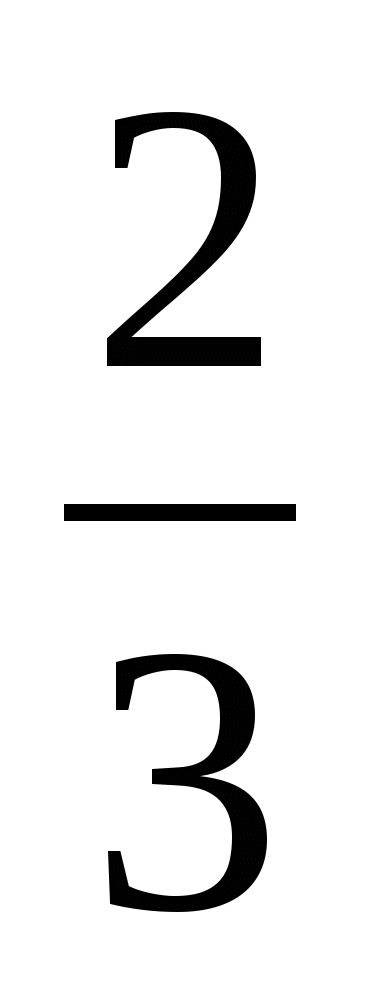 .
.
4. Сложите дроби:
а) 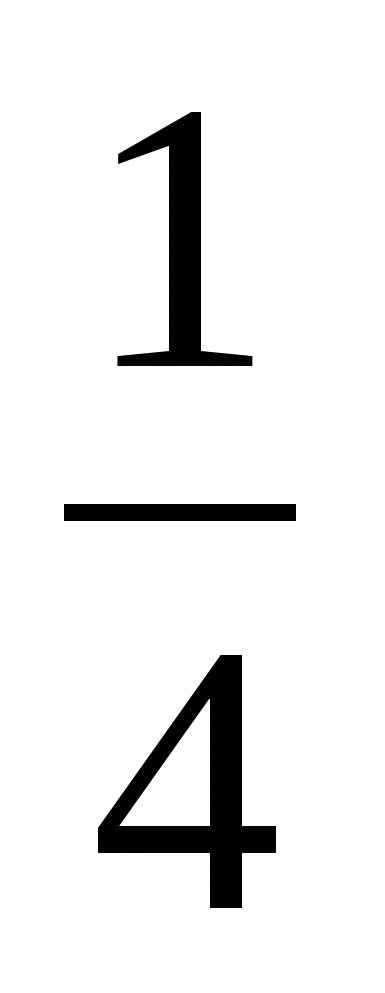 +
+ 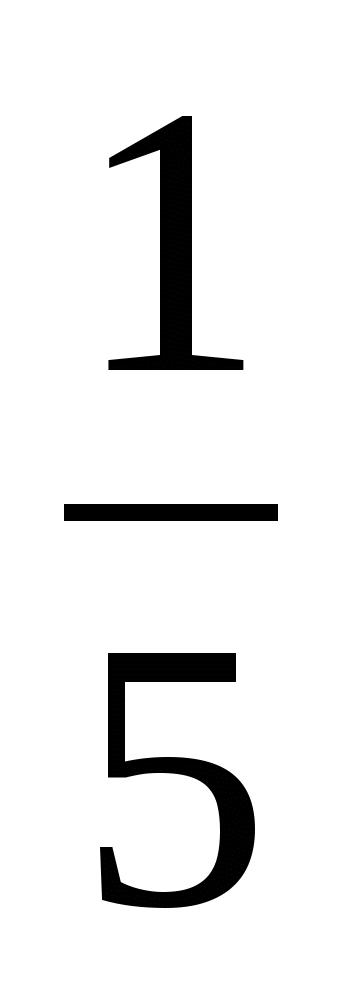 ; б )
; б )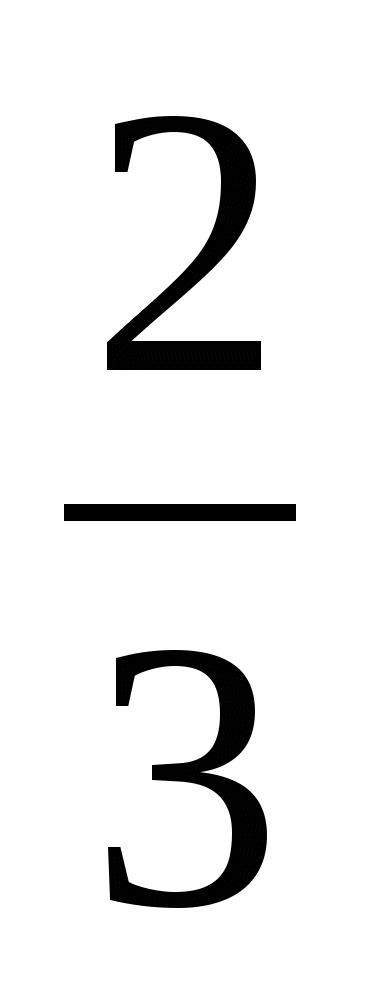 +
+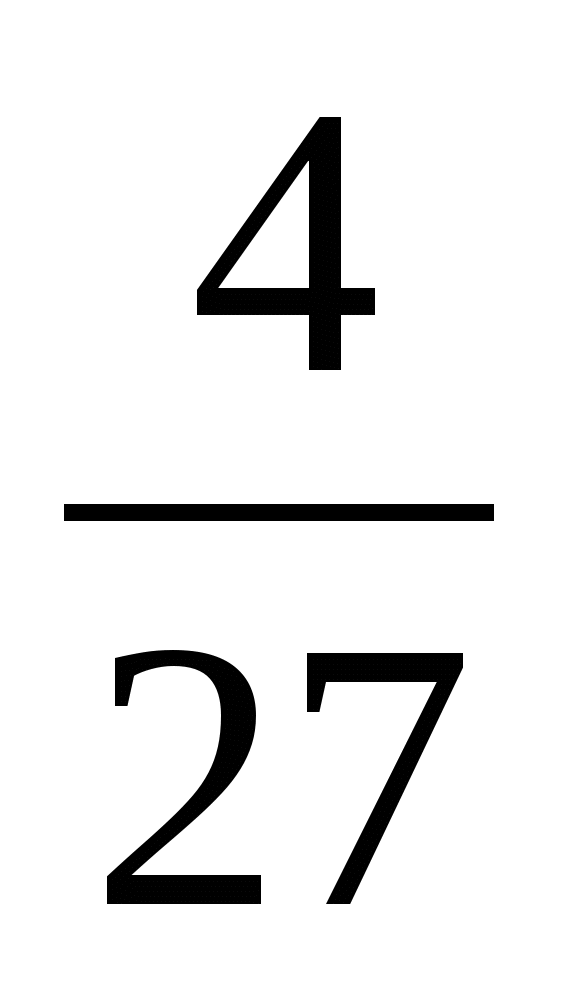 ; в)
; в) 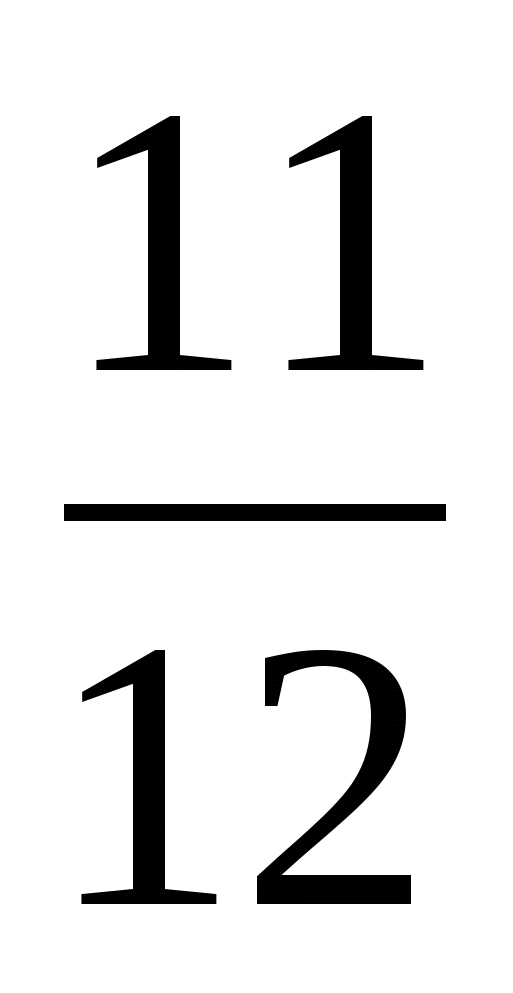 +
+ 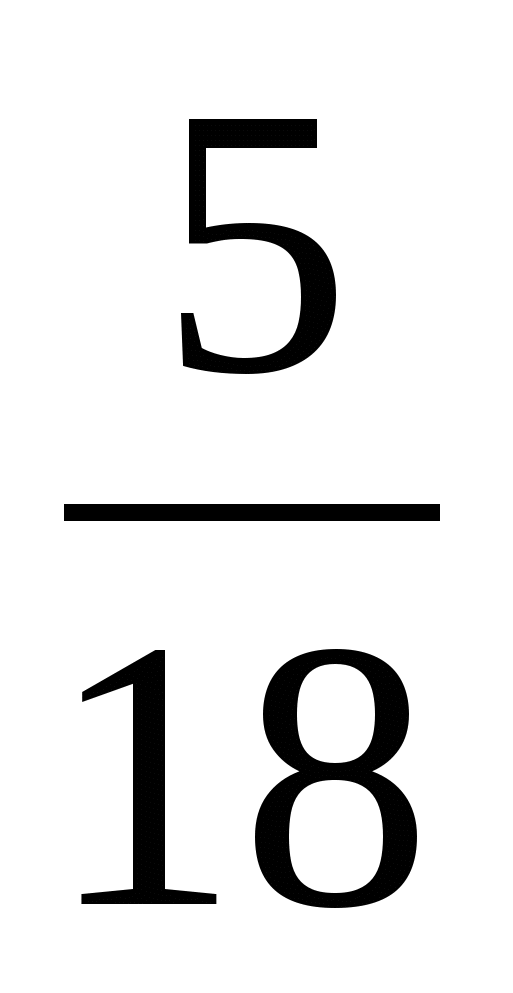 .
.
5. Чему равен х?
а)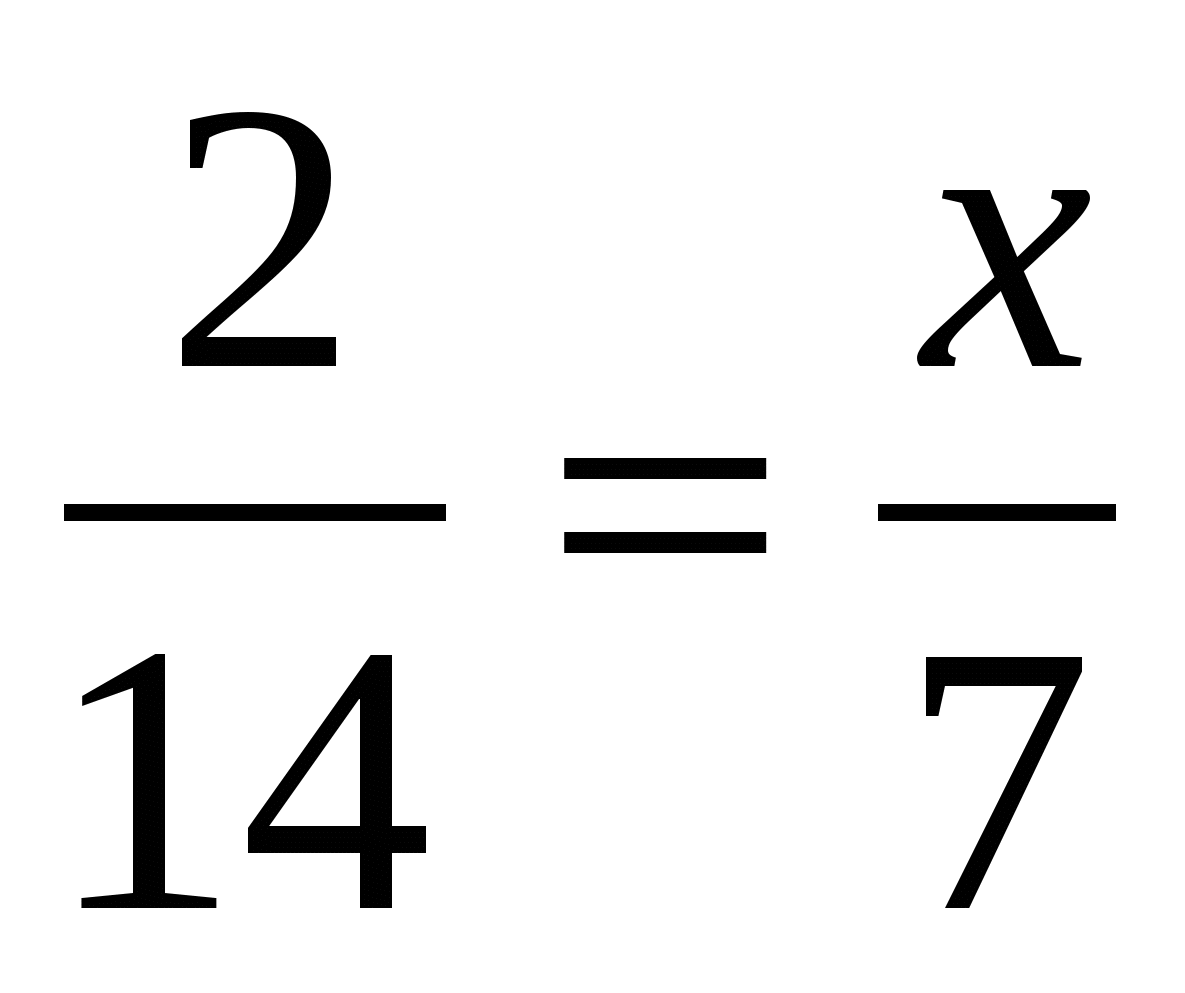 ; б)
; б)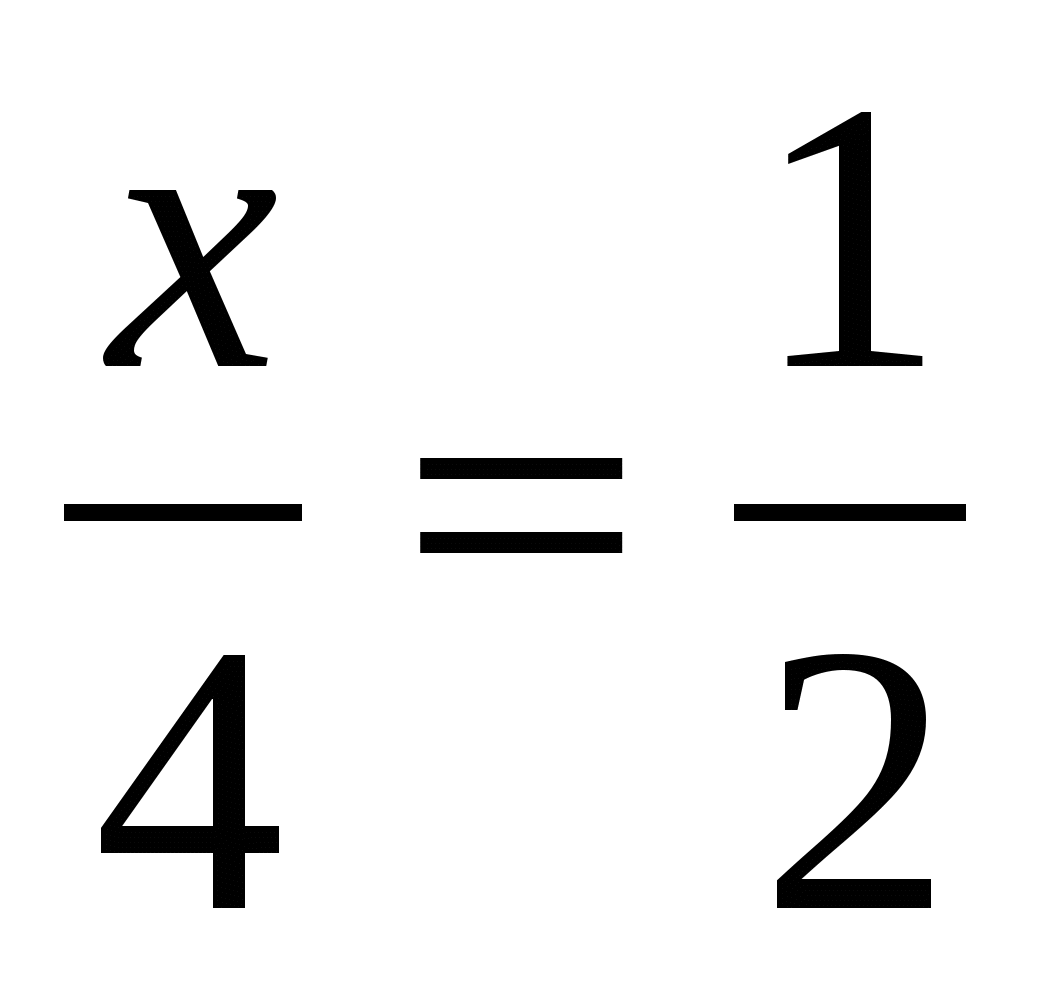 ; в)
; в)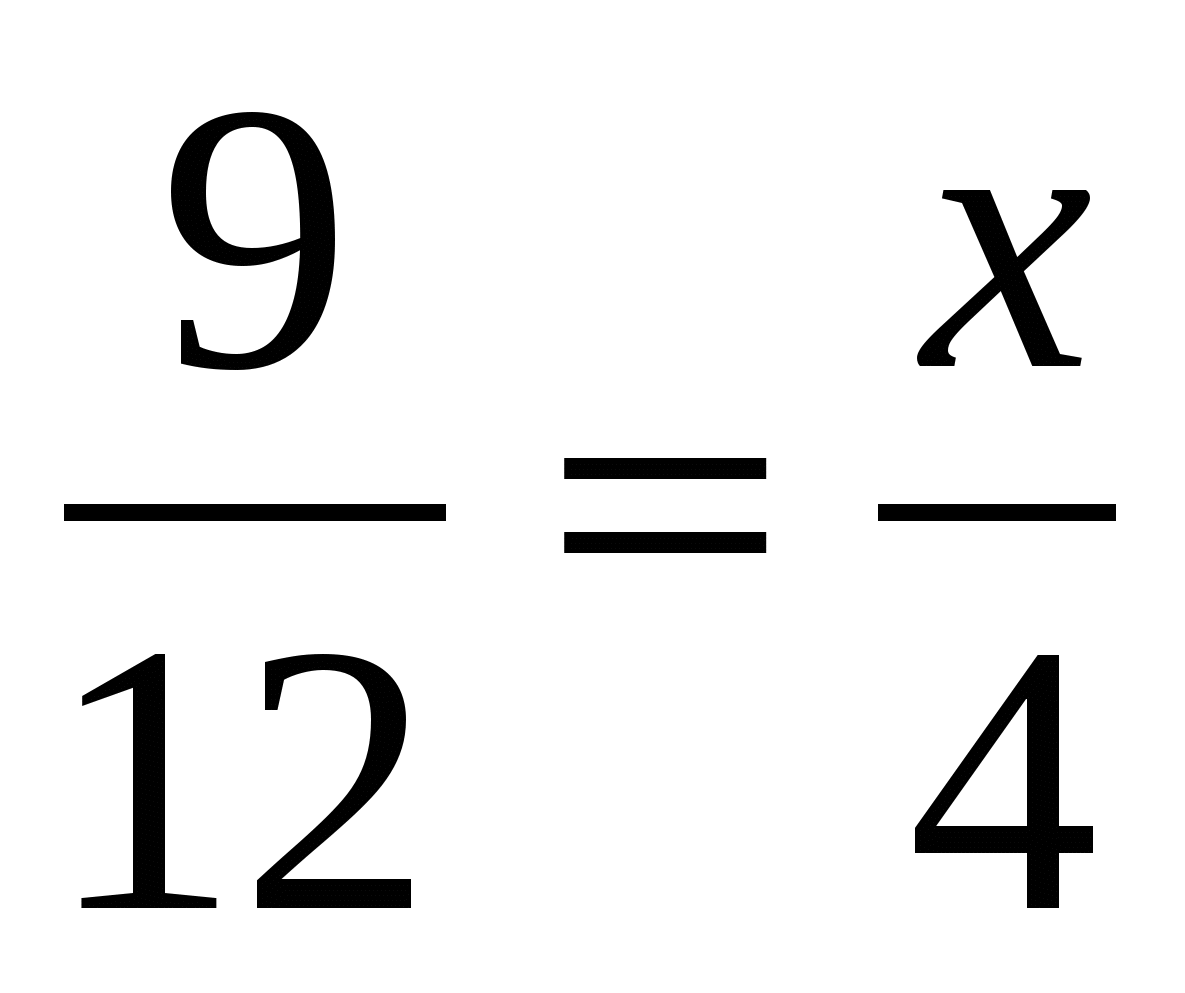 ; г)
; г)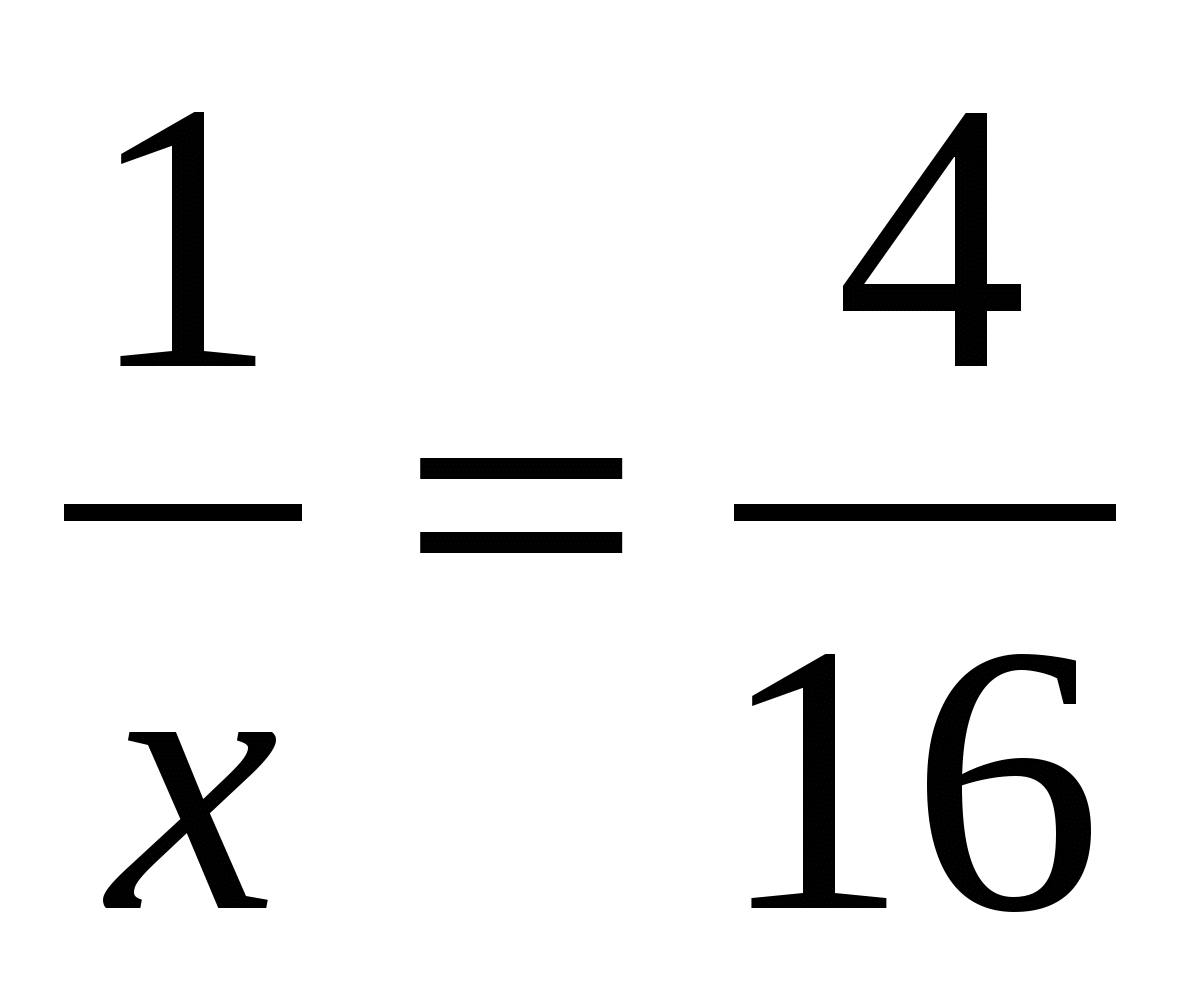 ;
;
д)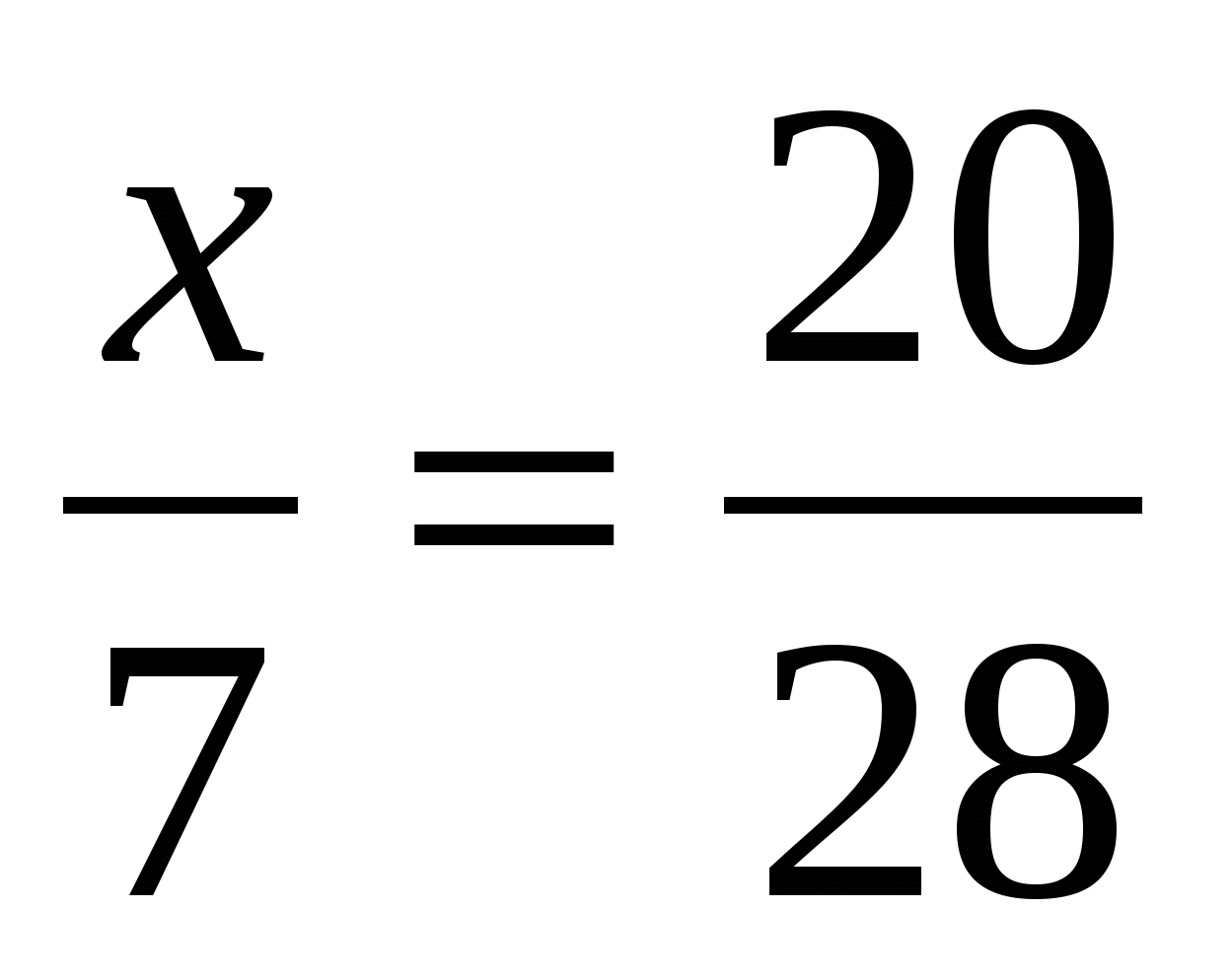 ; е)
; е)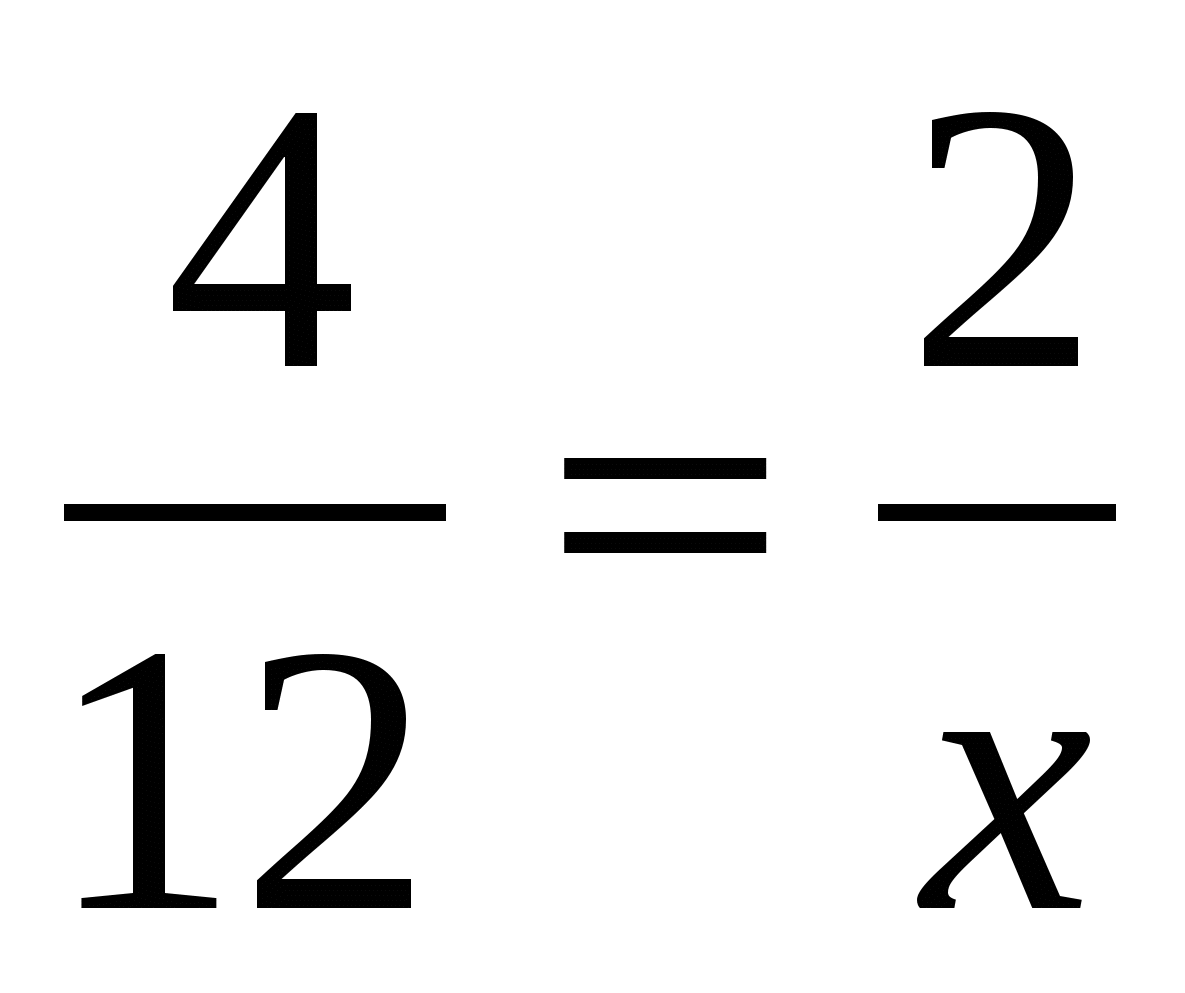 ; ж)
; ж)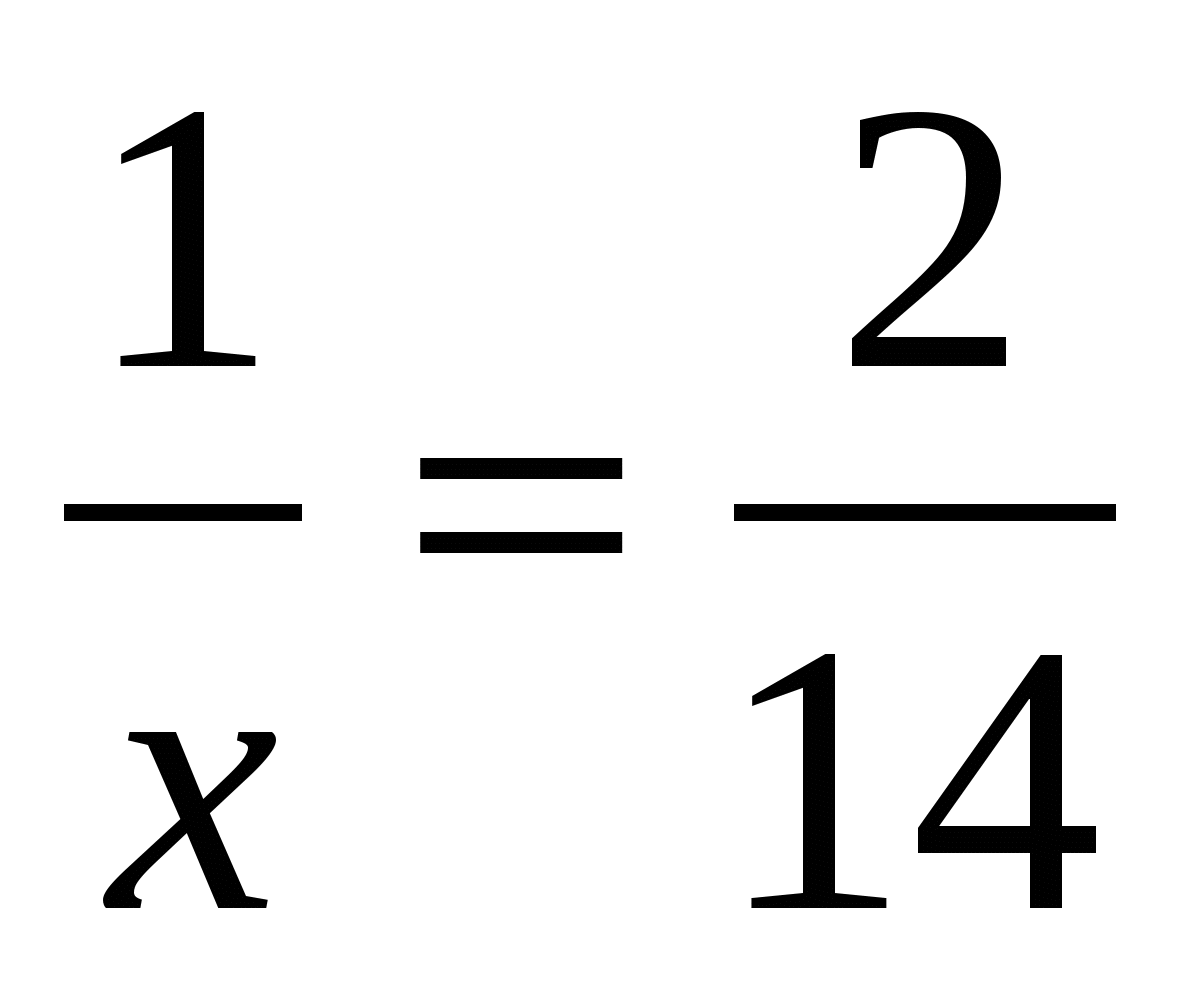 .
.
6. Верно ли утверждение?
а) 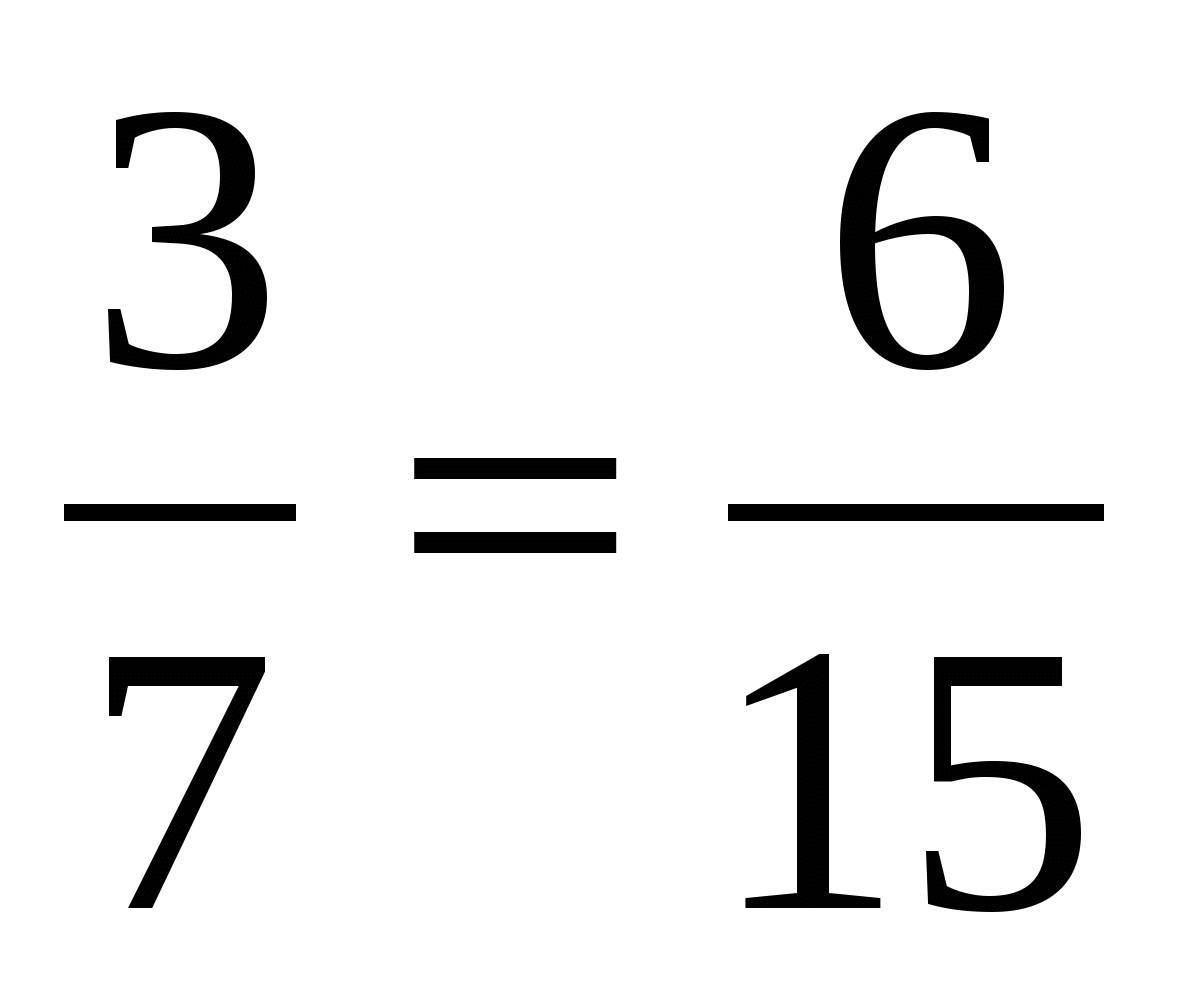 ; б)
; б)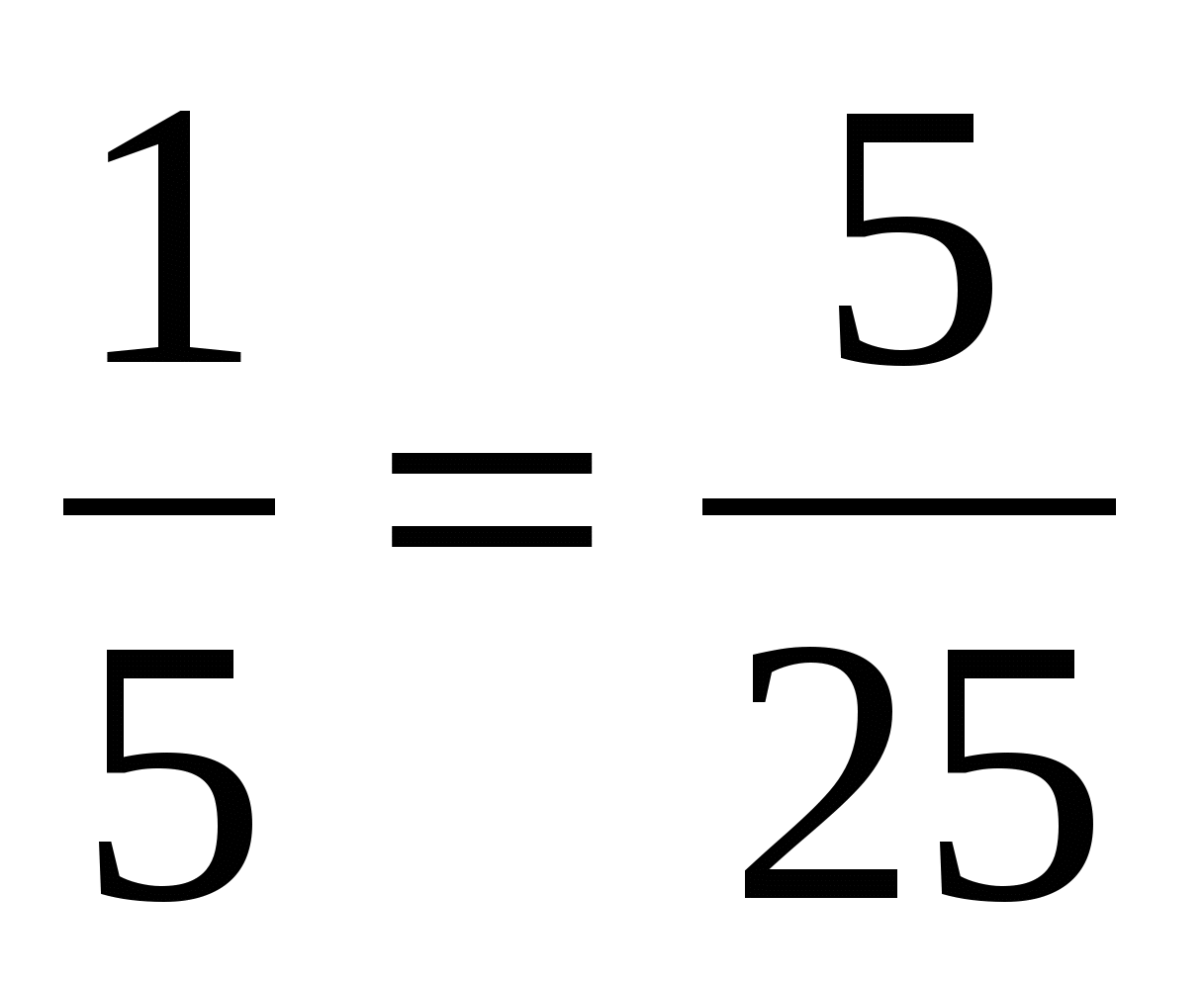 ; в)
; в)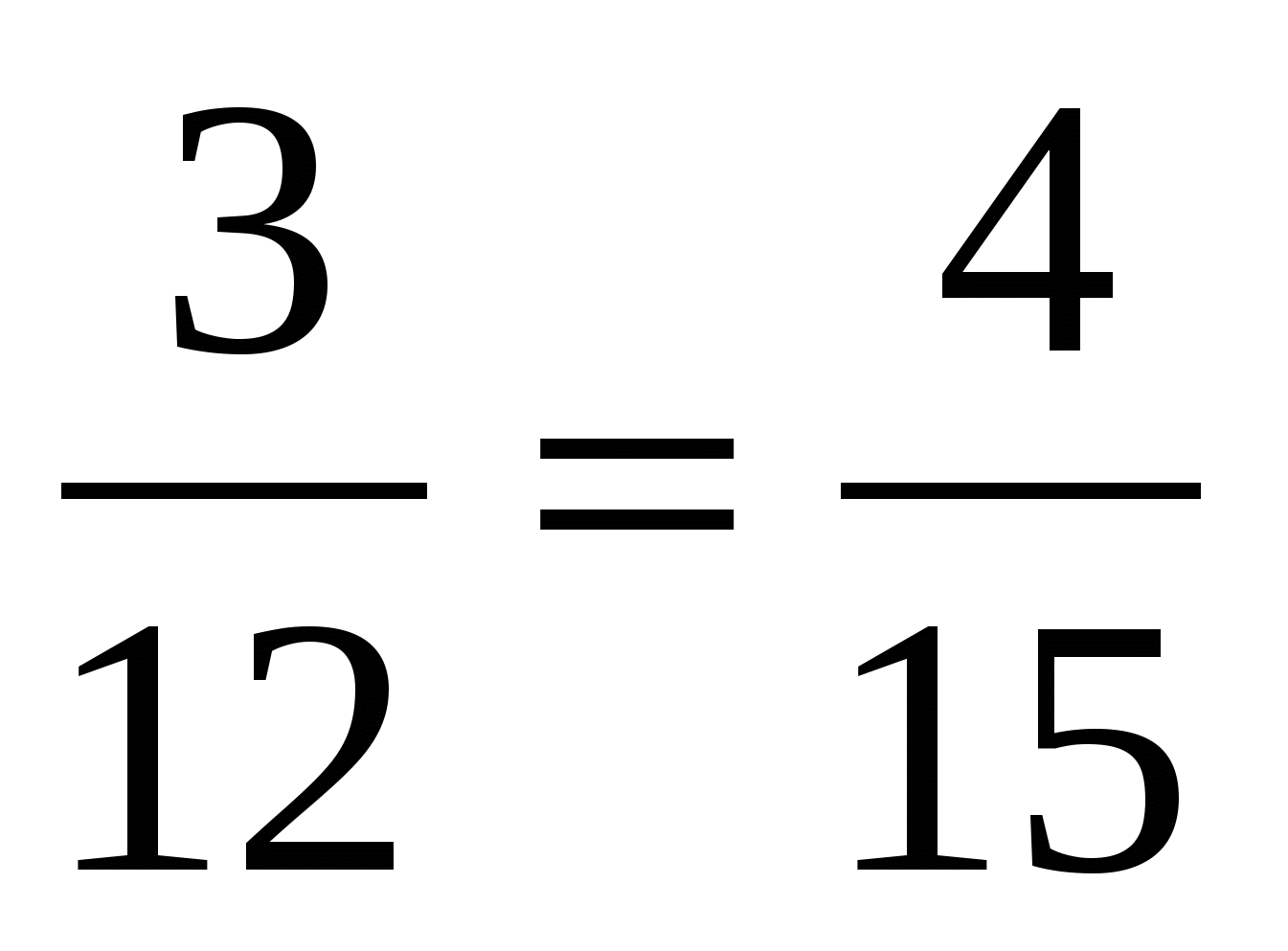 ; г)
; г)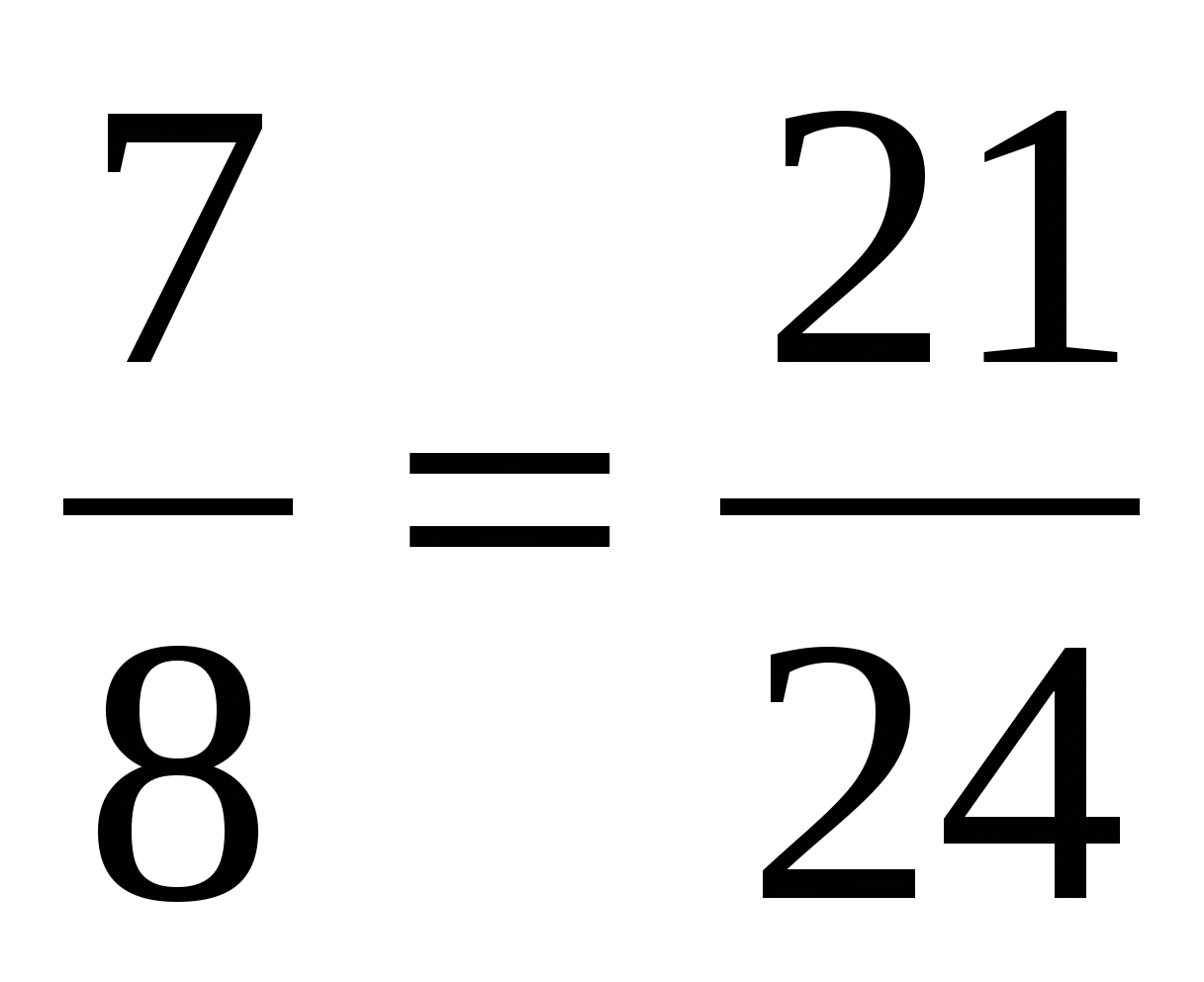 ;
;
д)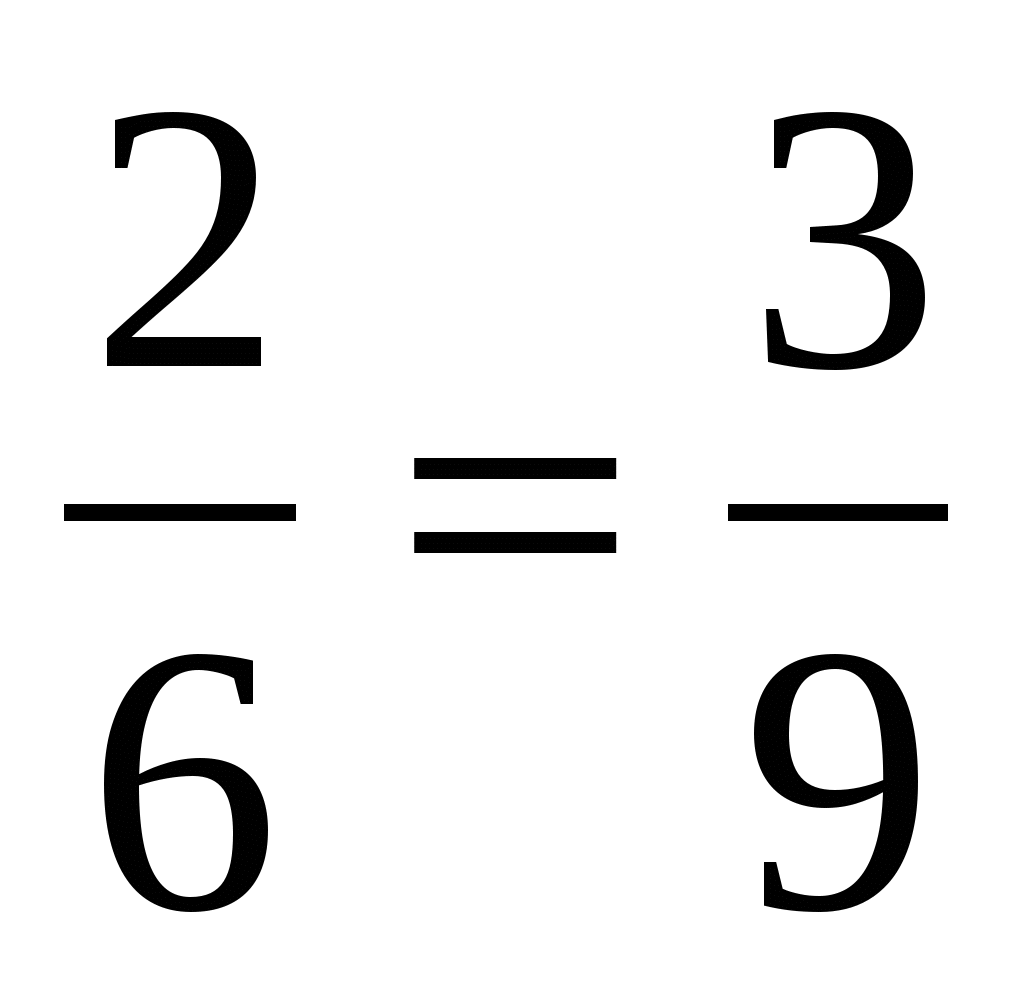 ; е)
; е)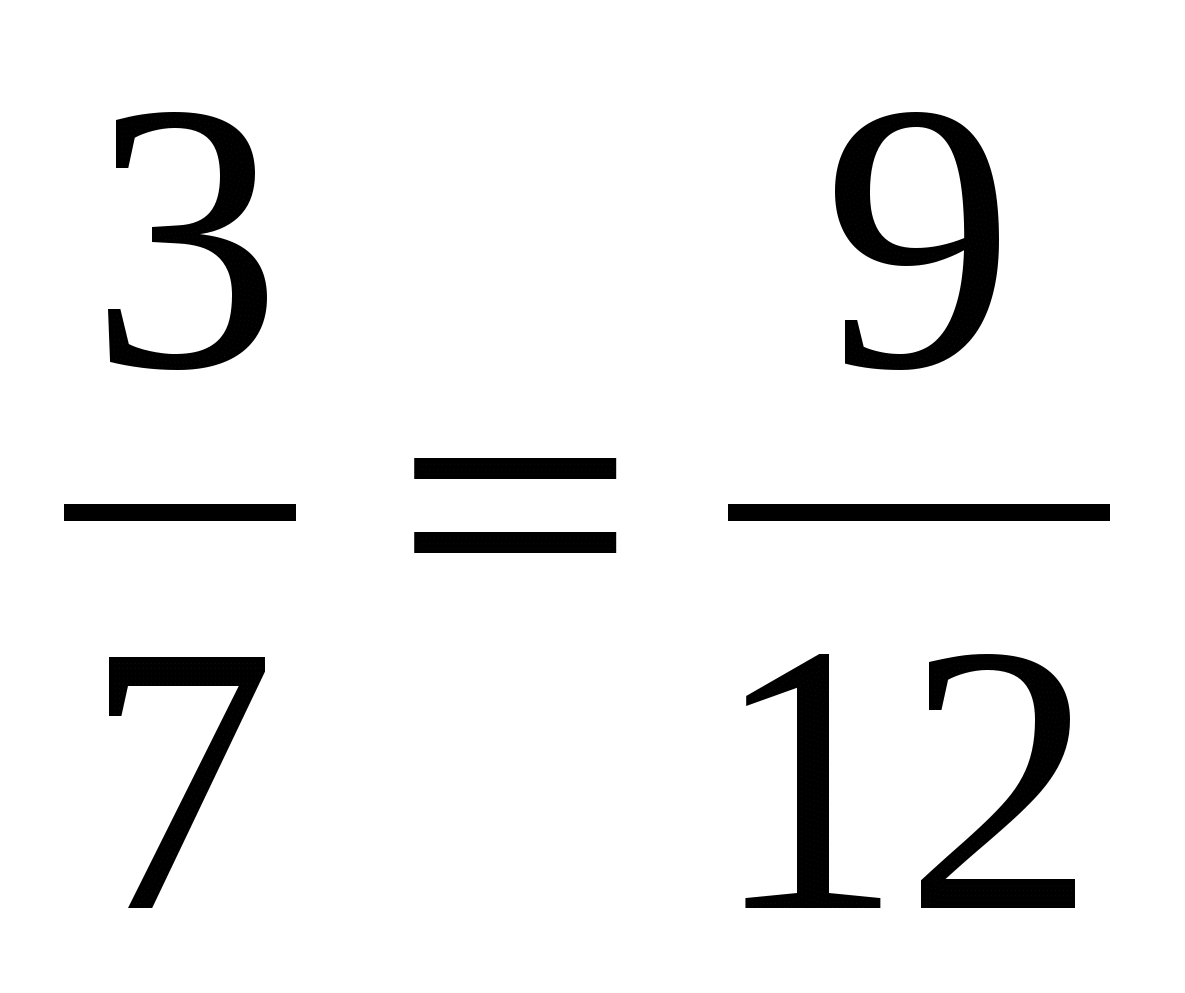 ; ж)
; ж)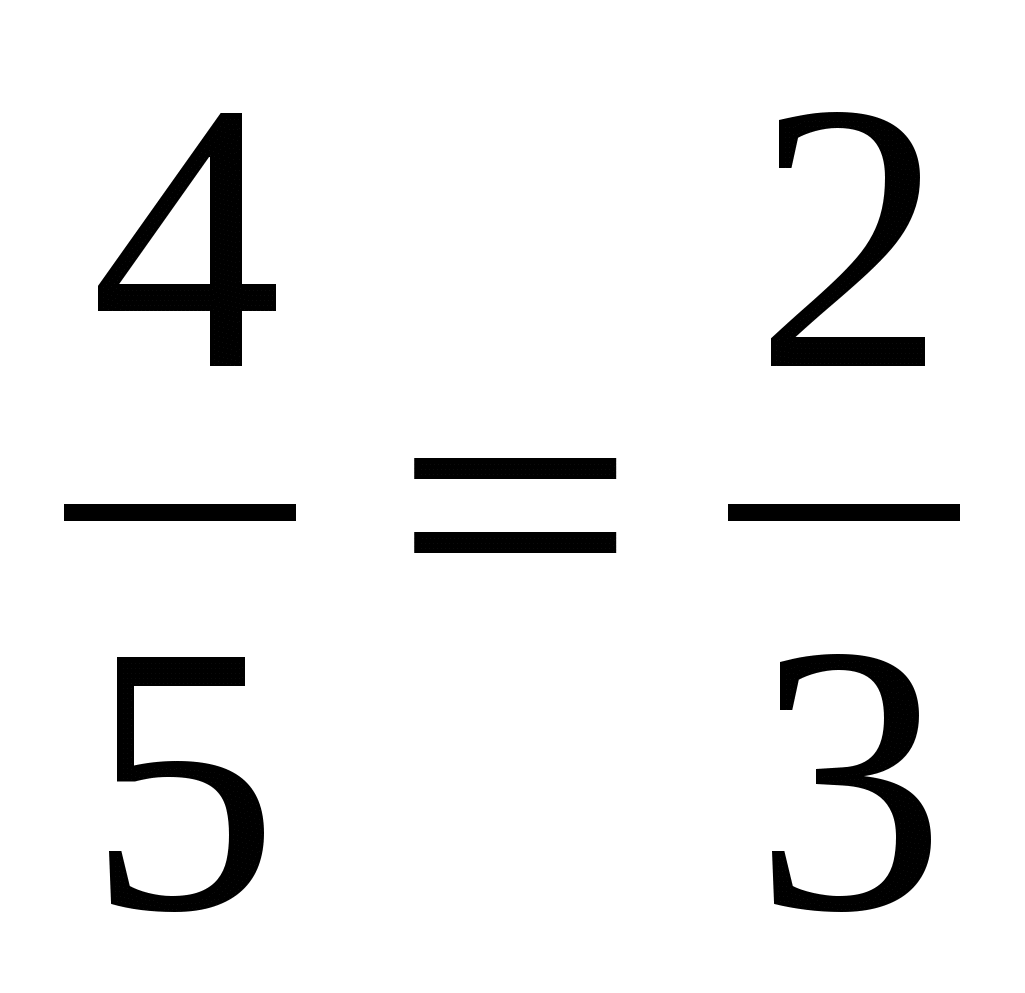 .
.
7. Определите, какая из дробей наибольшая, а какая наименьшая?
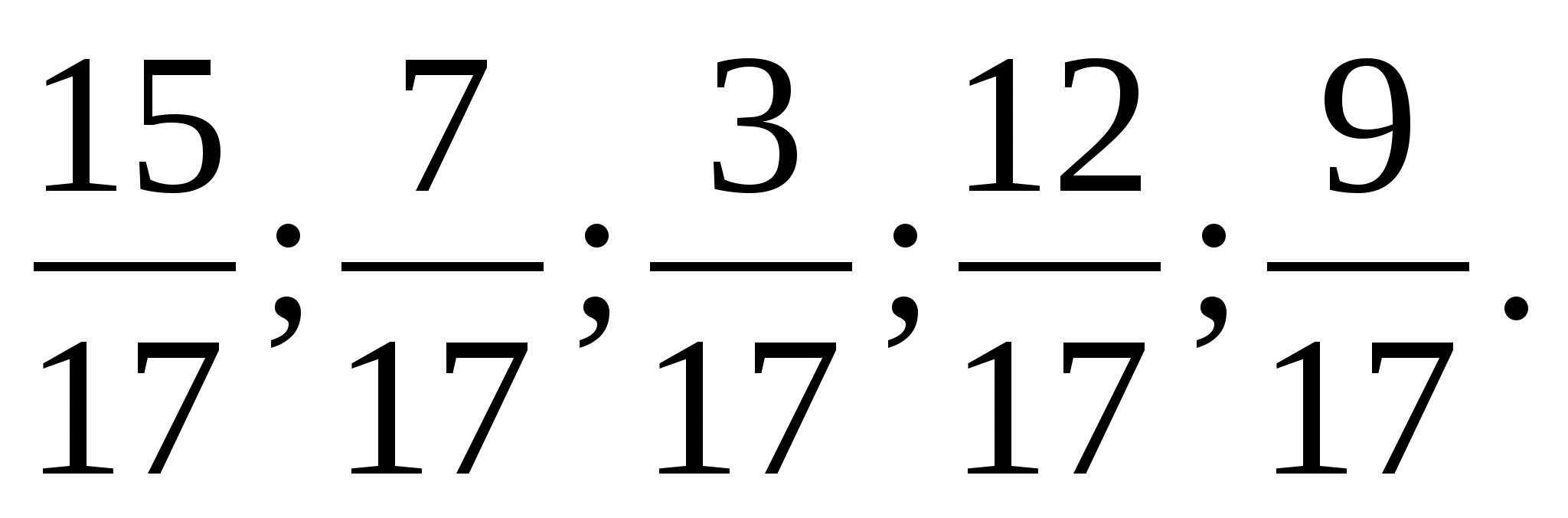
Домашнее задание:
прочитать с 79-80;
№9, №10, №11 с 77-78.
infourok.ru