Способы словообразования | Стать грамотным

Это задание связано с определением способа образования слова. 

Все способы словообразования можно разделить на две группы: морфологические и неморфологические.

Морфологические способы словообразования

При морфологических способах (их ещё называют морфемными)  слово изменяет свой внешний облик:

• к производящей основе добавляется приставка, суффикс или обе эти морфемы одновременно;
• от производящей основы отсекается суффикс.

К морфологическим относятся следующие способы образования слов: приставочный, суффиксальный, приставочно-суффиксальный, бессуффиксный, сложение. 

Приставочный способ словообразования

Приставочный способ заключается в добавлении к производящей основе приставки:

Суффиксальный способ словообразования

При суффиксальном способе к производящей основе добавляется суффикс:

Приставочно-суффиксальный способ словообразования

Приставочно-суффиксальный способ – образование нового слова посредством одновременного добавления к производящей основе приставки и суффикса:

Бессуффиксный способ словообразования

Бессуффиксный способ — образование слова в результате усечения суффикса:

Это единственный в русском языке способ словообразования, при котором морфема усекается, а не прибавляется. Иногда для образования слова усекается окончание, но способ по аналогии называется бессуффиксным:

Запомните: бессуффиксным способом образуются только имена существительные, которые имеют добавочное значение действия или признака. Образуются они, как правило, от глаголов или прилагательных.

Сложение как способ словообразования

Сложение — образование нового слова путём сложения двух или нескольких основ (или целых слов) с соединительной гласной или без неё.

В результате сложения образуется сложное слово, то есть слово не с одним корнем, а с двумя или несколькими:

Разновидностью сложения считается аббревиация — образование

сложносокращённого слова, которое по-другому называется аббревиатурой:

Иногда об аббревиации говорят как о самостоятельном способе словообразования.

Неморфологические способы словообразования

Неморфологические способы словообразования характеризуются тем, что в образовании слова не участвуют морфемы. Внешний облик слова остаётся неизменным, однако оно приобретает новое значение, изменяются морфологические признаки слова, другой становится его синтаксическая роль.

Принято различать следующие неморфологические способы.

Переход слова из одной части речи в другую:

Сращение

— два или несколько слов сливаются в одно, не изменяясь при этом внешне:

Образование омонимов,

т.е. слов, пишущихся и звучащих одинаково, но имеющих абсолютно разные лексические значения:

Итак, это самое главное, что нужно знать о способах словообразования, идя на ЕГЭ по русскому языку. Чтобы оценить свои знания по этой теме, выполни тест.

Сложение — Википедия

В учебниках часто объясняют сложение с помощью яблок и равенства 3 + 2 = 5^[1]

Сложе́ние (прибавле́ние^[2]) — одна из основных бинарных математических операций (арифметических действий) двух аргументов (слагаемых), результатом которой является новое число (сумма), получаемое увеличением значения первого аргумента на значение второго аргумента. То есть каждой паре элементов (a,b){\displaystyle (a,b)} из множества A{\displaystyle A} ставится в соответствие элемент c=a+b{\displaystyle c=a+b}, называемый суммой a{\displaystyle a} и b{\displaystyle b}. Это одна из четырёх элементарных^[en] математических операций арифметики. Приоритет её в обычном порядке операций равен приоритету вычитания, но ниже, чем у возведения в степень, извлечения корня, умножения и деления^[3]. На письме сложение обычно обозначается с помощью знака «плюс»: a+b=c{\displaystyle a+b=c}.

Сложение возможно, только если оба аргумента принадлежат одному множеству элементов (имеют одинаковый тип). Так, на картинке справа запись 3+2{\displaystyle 3+2} обозначает три яблока и два яблока вместе, что в сумме дает пять яблок. Но нельзя сложить, например, 3 яблока и 2 груши.

Используя систематические обобщения, сложение можно определить для абстрактных величин, таких как целые числа, рациональные числа, вещественные числа и комплексные числа и для других абстрактных объектов, таких как векторы и матрицы.

У сложения есть несколько важных свойств (например, для A={\displaystyle A=}R{\displaystyle \mathbb {R} }) (см. Сумма):

Коммутативность: a+b=b+a,∀a,b∈ A{\displaystyle a+b=b+a,\quad \forall a,b\in \ A}^{[см. «Коммутативность»]}

Ассоциативность: (a+b)+c=a+(b+c),∀a,b,c∈ A{\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A}^{[см. «Ассоциативность»]}

Дистрибутивность: x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A.{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.}

Прибавление 0{\displaystyle 0} (нулевого элемента) даёт число, равное исходному: x+0=0+x=x,∀x∈A,∃0∈A.{\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}

Сложение очень маленьких чисел понятно даже детям; простейшая задача, 1+1{\displaystyle 1+1}, может быть решена пятимесячным ребёнком и даже некоторыми животными^{[уточнить]}. В начальной школе учат считать в десятичной системе счисления и постепенно переходят к более сложным задачам.

Известны различные устройства для сложения: от древних абаков до современных компьютеров.

Сложение записывается с использованием символа плюса «+» между слагаемыми; такая форма записи называется инфиксной нотацией. Результат записывается с использованием знака равенства. Например,

a+b=c{\displaystyle a+b=c} («а плюс бэ равно цэ»)

1+1=2{\displaystyle 1+1=2} («один плюс один равно двум»)

2+2=4{\displaystyle 2+2=4} («два плюс два равно четырём»)

5+4+2=11{\displaystyle 5+4+2=11} (см. «ассоциативность» ниже)

3+3+3+3=12{\displaystyle 3+3+3+3=12} (см. «умножение» ниже)

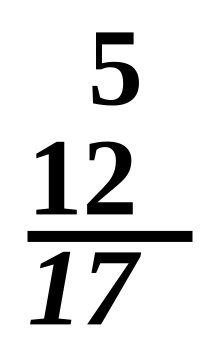Сложение в столбик:
5 + 12 = 17

В ряде ситуаций подразумевается сложение, но при этом символы сложения не используются:

• В записи чисел в позиционных системах счисления: запись числа an−1an−2…a1a0,{\displaystyle a_{n-1}\;a_{n-2}\ldots \;a_{1}\;a_{0},} подразумевает суммирование ряда an−1⋅Pn−1+an−2⋅Pn−2+…+a1⋅P1+a0⋅P0{\displaystyle a_{n-1}\cdot P^{n-1}+a_{n-2}\cdot P^{n-2}+\ldots +a_{1}\cdot P^{1}+a_{0}\cdot P^{0}}^[4].
• Если имеется столбец чисел, последнее (нижнее) число в котором подчёркнуто, то обычно подразумевается, что все числа в этом столбце складываются, а полученная сумма записывается ниже подчеркнутого числа.
• Если имеется запись, когда перед дробью стоит целое число, то эта запись означает сумму двух слагаемых — целого числа и дроби, которую называют смешанным числом^[5]. Например,
  3½ = 3 + ½ = 3.5.
  Такая запись может вызвать путаницу, поскольку в большинстве других случаев подобная запись означает умножение, а не сложение^[6].

Сумма ряда связанных чисел может быть записана с использованием символа Σ, который позволяет компактно записать итерацию. Например,

∑k=15k2=12+22+32+42+52=55.{\displaystyle \sum _{k=1}^{5}k^{2}=1^{2}+2^{2}+3^{2}+4^{2}+5^{2}=55.}

Слагаемые — это числа или объекты, складываемые друг с другом^[7].

Символ плюса «+» (Юникод:U+002B; ASCII: +) — упрощение латинского слова «et», означающего «и»^[8]. Впервые этот символ встречается в книгах, начиная с 1489 г.^[9]

Сложение используется для моделирования бесчисленного множества физических процессов. Даже для простого сложения натуральных чисел существует много различных интерпретаций и ещё больше способов визуального представления.

Комбинирование наборов[править | править код]

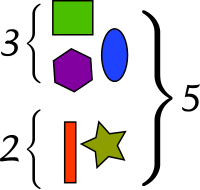
Возможно, самая фундаментальная интерпретация сложения — комбинирование наборов:

• Если два или более не пересекающихся наборов объектов объединены в один набор, то число объектов в полученном наборе равно сумме числа объектов в исходных наборах.

Эту интерпретацию легко визуализировать, при этом опасность двусмысленности будет минимальной. Однако непонятно, как с помощью этой интерпретации сложения объяснить сложение дробных или отрицательных чисел^[10].

Одним из возможных решений будет обращение к набору объектов, которые могут быть легко разделены, например, пироги или стержни с сегментами^[11]. Вместо комбинирования наборов сегментов стержни могут быть присоединены друг к другу концами, что иллюстрирует другую концепцию сложения: складываются не стержни, складываются их длины.

Расширение длины[править | править код]

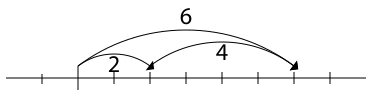
Визуализация суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 2 и затем сдвиг на 4 — это то же самое, что и сдвиг на 6.

Еще один вариант визуализации суммы 2 + 4 = 6 на числовой прямой. Сдвиг на 4 — это то же самое, что и четыре сдвига по 1.

Вторая интерпретация сложения заключается в расширении начальной длины на величину добавляемой длины:

• Когда начальная длина расширяется добавляемой длиной, то полученная длина равна сумме начальной длины и длины, которую к ней добавили^[12].

Сумму a + b можно интерпретировать как бинарную операцию объединения a и b в алгебраическом смысле, также её можно интерпретировать как добавление b единиц к числу a. В последней интерпретации части суммы a + b играют асимметричные роли, и операция a + b рассматривается как применение к числу a унарной операции +b^[13]. Унарный подход позволяет перейти к вычитанию, ведь каждая унарная операция сложения имеет обратную унарную операцию вычитания и наоборот.

Операция сложения на числовых множествах N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } имеет следующие основные свойства:

Коммутативность[править | править код]

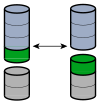
Визуализация 4 + 2 = 2 + 4 при помощи блоков

Сложение коммутативно — от перемены мест слагаемых сумма не меняется (это свойство также известно как переместительный закон сложения): a+b=b+a,∀a,b∈ A.{\displaystyle a+b=b+a,\quad \forall a,b\in \ A.} Есть и другие законы коммутативности: например, существует коммутативный закон умножения. Тем не менее многие бинарные операции, например, вычитание и деление, не коммутативны.

Ассоциативность[править | править код]

Визуализация 2+(1+3) = (2+1)+3 при помощи стержней с сегментами

Сложение ассоциативно — при последовательном выполнении сложения трёх или более чисел последовательность выполнения операций не имеет значения (сочетательный закон сложения): (a+b)+c=a+(b+c),∀a,b,c∈ A.{\displaystyle (a+b)+c=a+(b+c),\quad \forall a,b,c\in \ A.}

Дистрибутивность[править | править код]

Сложение дистрибутивно, это — свойство согласованности двух бинарных операций, определённых на одном и том же множестве (распределительный закон)^[14] : x⋅(a+b)=(x⋅a)+(x⋅b),∀a,b∈ A.{\displaystyle x\cdot (a+b)=(x\cdot a)+(x\cdot b),\quad \forall a,b\in \ A.}

Нейтральный элемент[править | править код]

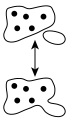Визуализация 5 + 0 = 5 при помощи сумок с точками

Относительно сложения в множестве A{\displaystyle A} существует единственный нейтральный элемент, сложение числа с 0{\displaystyle 0} (нулевым или нейтральным элементом) даёт число, равное исходному: x+0=0+x=x,∀x∈A,∃0∈A.{\displaystyle x+0=0+x=x,\quad \forall x\in A,\quad \exists 0\in A.}

Этот закон был впервые описан в Исправленном трактате Брахмы^[en], который был написан Брахмагуптой в 628 г. Он написал этот закон в виде трёх отдельных законов: для отрицательного, положительного и нулевого числа a, и для описания этих законов он использовал слова, а не алгебраические символы. Позже индийские математики уточнили понятия; около 840 г., Махавира^[en] написал, что «ноль становится таким же, как то, что добавляется к нему», что соответствовало записи 0 + a = a. В XII веке Бхаскара II написал: «Если добавить ничего или вычесть ничего, то количество, положительное или отрицательное, остаётся таким же, как и было», что соответствует записи a + 0 = a^[15].

Обратный элемент[править | править код]

Сложение с противоположным элементом даёт 0{\displaystyle 0}: a+(−a)=0,∀a∈A,∃−a∈A.{\displaystyle a+(-a)=0,\quad \forall a\in A,\quad \exists -a\in A.}^[16]

Кроме того, сложение не выводит результат за пределы данного множества чисел, следовательно, N,Z,Q,R,C{\displaystyle \mathbb {N} ,\mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } замкнуты относительно операции сложения. Эти множества с операциями +{\displaystyle +} и ⋅{\displaystyle \cdot } образуют кольца (коммутативные кольца с единицей)^[17]. На языке общей алгебры вышеперечисленные свойства сложения говорят о том, что Z,Q,R,C{\displaystyle \mathbb {Z} ,\mathbb {Q} ,\mathbb {R} ,\mathbb {C} } — абелевы группы относительно операции сложения.

Операцию сложения можно представить как некий «черный ящик» с двумя слагаемыми на входе и одним выходом — суммой:^[18][19]

При практическом решении задачи сложения двух чисел необходимо свести её к последовательности более простых операций: «простое сложение»

[источник не указан 1234 дня], перенос, сравнение и др. Для этого разработаны различные методы сложения, например для чисел, дробей, векторов и др. На числовых множествах используется алгоритм поразрядного сложения^[20]. При этом следует рассматривать сложение как процедуру (в отличие от операции).

Примерный алгоритм процедуры поразрядного сложения двух чисел^[21]

Как видим, процедура достаточно сложная, состоит из относительно большого числа шагов и при сложении больших чисел может занять продолжительное время.

«Простое сложение» — в данном контексте обозначает операцию сложения одноразрядных чисел, которая может быть легко сведена к инкрементированию.^{[источник не указан 1234 дня]} Является гипероператором инкрементирования:

Пример пошагового сложения чисел 2 и 4 на числовой прямой.

a+b=hyper1⁡(a,b)=hyper⁡(a,1,b)=a(1)b.{\displaystyle a+b=\operatorname {hyper1} (a,b)=\operatorname {hyper} (a,1,b)=a^{(1)}b.}

a(1)b=a+b=1+1+⋯+1⏟a+1+1+⋯+1⏟b.{\displaystyle a{^{(1)}}b=a+b=\underbrace {1+1+\dots +1} _{a}+\underbrace {1+1+\dots +1} _{b}.}

где 1+1+⋯+1{\displaystyle 1+1+\dots +1} — последовательность операций инкрементирования, выполненная a{\displaystyle a} и b{\displaystyle b} раз.

Врождённая способность[править | править код]

Исследования развития математических способностей, которые начались в 1980-х годах, рассматривали феномен привыкания: младенцы смотрят дольше на ситуации, которые являются для них неожиданными^[22]. В эксперименте Карен Винн^[en] 1992 года использовались куклы Микки Мауса, с которыми проводились различные манипуляции за ширмой. Этот эксперимент показал, что пятимесячные младенцы ожидают, что 1 + 1 — это 2, и удивляются тому, когда оказывается, что 1 + 1 — это 1 или 3. Позже этот результат был подтверждён в других лабораториях с использованием разных методов^[23]. В другом эксперименте в 1992 году с малышами постарше, в возрасте от 18 до 35 месяцев, использовалось развитие моторных функций детей, позволявшее им доставать шарики для пинг-понга из коробки; младшие ребята хорошо справлялись с небольшим числом шариков, более старшие научились считать сумму до 5^[24].

Даже некоторые животные проявляют способность складывать, в особенности приматы. Эксперимент 1995 года был аналогичен эксперименту Винн 1992 года, но вместо кукол использовались баклажаны. Выяснилось, что макаки-резусы и эдиповы тамарины показывают схожие человеческим младенцам способности. Более того, один шимпанзе, после того, как его научили различать и понимать смысл арабских цифр от 0 до 4, смог считать сумму двух чисел без какой-либо подготовки^[25]. Позже было выяснено, что азиатские слоны способны овладеть базовыми арифметическими операциями^[26].

Овладение сложением детьми[править | править код]

Как правило, сначала дети учатся подсчёту^[en]. Когда даётся задача, в которой требуется объединить два предмета и три предмета, маленькие дети обращаются к помощи конкретных предметов, например, счёт на пальцах или помощь рисунка. По мере приобретения опыта, они учат или открывают для себя стратегию «подсчета»: когда требуется найти, сколько будет два плюс три, дети перечисляют два числа, идущие после числа три, проговаривая: «три, четыре, пять» (обычно загибая пальцы), и, в итоге, получая пять. Эта стратегия кажется почти универсальной; дети могут легко перенять её у сверстников или учителей^[27]. Многие дети сами доходят до этого. Накопив какой-то опыт, дети учатся складывать быстрее, используя коммутативность сложения, начиная перечислять числа от самого большого числа в сумме, как в описанном выше случае, начиная с трёх и перечисляя: «четыре, пять». В конце концов, дети начинают использовать какие-либо факты о сложении («примеры сложения наизусть^[en]»), получая их либо опытным путём, либо запоминая их. Когда одни факты осядут в памяти, дети начинают выводить неизвестные факты из известных. Например, ребёнок, складывающий шесть и семь, может знать, что 6 + 6 = 12, и что поэтому 6 + 7 на один больше, то есть 13^[28]. К такому способу вывода приходят довольно быстро и большинство учеников начальной школы полагаются на смесь всего того, что они запомнили и того, что они могут вывести, что в итоге позволяет им бегло складывать^[29].

В разных странах к изучению целых чисел и арифметики приступают в разных возрастах, в основном сложению учат в учреждениях дошкольного образования^[30]. При этом по всему миру к концу первого года начальной школы школьники обучаются сложению^[31].

Таблица сложения[править | править код]

Детям часто показывают таблицу сложения пар чисел от 1 до 10 для лучшего запоминания^{[обтекаемое выражение]}. Зная эту таблицу, можно выполнить любое сложение.

таблица для сложения в десятичной системе счисления

+	0	1	2	3	4	5	6	7	8	9
0	0	1	2	3	4	5	6	7	8	9
1	1	2	3	4	5	6	7	8	9	10
2	2	3	4	5	6	7	8	9	10	11
3	3	4	5	6	7	8	9	10	11	12
4	4	5	6	7	8	9	10	11	12	13
5	5	6	7	8	9	10	11	12	13	14
6	6	7	8	9	10	11	12	13	14	15
7	7	8	9	10	11	12	13	14	15	16
8	8	9	10	11	12	13	14	15	16	17
9	9	10	11	12	13	14	15	16	17	18

Десятичная система[править | править код]

Для успешного сложения в десятичной системе нужно помнить или уметь быстро выводить 100 «фактов (примеров) сложения» для одноразрядных чисел. Кто-то может запомнить все эти факты, заучивая их, но стратегии изучения сложения путём использования шаблонов более информативны и для большинства людей более эффективны:^[32]

• Коммутативное свойство: использование шаблона a+b=b+a{\displaystyle a+b=b+a} снижает количество «фактов о сложении», которых нужно запомнить, со 100 до 55.
• На один или на два больше: прибавление 1 или 2 — это базовая задача, и решить её можно перечислением (подсчетом) или, в конце концов, полагаясь на интуицию^[32].
• Ноль: поскольку ноль является нейтральным элементом для операции сложения (аддитивной единицей), постольку прибавить ноль просто. Тем не менее, во время изучения арифметики некоторым ученикам сложение представляется как процесс, во время которого слагаемые всегда увеличиваются; акцент на словесной формулировке^[en] задачи может помочь понять «исключительность» нуля^[32].
• Удваивание: складывание числа с самим собой связано с задачей удвоенного (повторного) подсчёта и умножением. Факты об удваивании являются основой для многих связанных с ними фактов, и ученикам легко их относительно легко понять^[32].
• Почти-удваивание (Суммы, близкие к операции удваивания): сумма 6 + 7 = 13 может быть быстро выведена из факта об удваивании 6 + 6 = 12 и прибавления единицы, или из факта 7 + 7 = 14 и вычитания единицы^[32].
• Пять и десять: суммы вида 5 + x и 10 + x обычно запоминаются рано и могут быть использованы для выведения других фактов. Например, результат суммы 6 + 7 = 13 может быть выведен с использованием факта 5 + 7 = 12 добавлением к последнему единицы^[32].
• Получение десятки (достраивание до десяти): существует такая стратегия, в которой 10 используется в качестве промежуточного результата при наличии слагаемых 8 или 9; например, 8 + 6 = 8 + 2 + 4 = 10 + 4 = 14^[32].

По мере взросления ученики запоминают всё больше фактов, и учатся быстро выводить из них другие факты. Многие ученики не запоминают все факты, но могут быстро вывести требуемый^[29].

Перенос[править | править код]

В стандартном алгоритме сложения многоразрядных чисел^{[обтекаемое выражение]} цифры, из которых состоят записи складываемых чисел, располагаются одна под другой. Выполняют сложение цифр отдельно в каждом столбце, начиная с правого. Если сумма цифр в столбце превышает 10, лишняя цифра «переносится» в следующий столбец (левее). Например, в сумме 27 + 59

  ¹
  27
+ 59
————
  86

7 + 9 = 16 и цифра 1 переносится в следующий столбец. В альтернативном способе начинают сложение с наиболее значимой цифры слева; в этой стратегии перенос выполняется несколько грубее, но быстрее получается приблизительная сумма. Существует много других методов переноса.

Сложение десятичных дробей[править | править код]

Способ сложения десятичных дробей является простой модификацией сложения многоразрядных чисел, описанного выше^[33]. При сложении столбиком дроби располагают таким образом, чтобы запятые^[стиль] находились точно друг под другом. При необходимости можно добавлять нули справа и слева к более короткой дроби (см. замыкающий ноль^[en] и ведущие нули), чтобы сделать её равной по длине более длинной дроби. Итак, сложение производится таким же образом, как и в описанном выше способе сложения многоразрядных чисел, только запятая располагается в ответе точно там же, где она располагалась у слагаемых.

Например, сумму 45,1 + 4,34 можно вычислить следующим образом:

   4 5 , 1 0
+  0 4 , 3 4
————————————
   4 9 , 4 4

Экспоненциальная запись[править | править код]

В экспоненциальной записи числа записываются в виде a=±x⋅P±n{\displaystyle a=\pm x\cdot P^{\pm n}}, где x{\displaystyle x} — мантисса, Pn{\displaystyle P^{n}} — характеристика числа, P{\displaystyle P} — основание системы счисления. Для сложения двух чисел, которые записаны в экспоненциальной форме, требуется, чтобы у них были одинаковые характеристики: a⋅Pn+b⋅Pn=(a+b)⋅Pn,{\displaystyle a\cdot P^{n}+b\cdot P^{n}=(a+b)\cdot P^{n},} согласно свойству дистрибутивности.

Например:

2.3⋅10−5+5.67⋅10−6=2.34⋅10−5+0.567⋅10−5=(2.34+0.567)⋅10−5=2.907⋅10−5{\displaystyle 2.3\cdot 10^{-5}+5.67\cdot 10^{-6}=2.34\cdot 10^{-5}+0.567\cdot 10^{-5}=(2.34+0.567)\cdot 10^{-5}=2.907\cdot 10^{-5}}

Особый случай — сложение чисел, различающихся на неско

сложение части слова с целым словом Примеры этих слов пожалуйста

Слова, образованные путём сложения двух и более основ или слов, называются сложными . Слова, образованные путём сложения сокращённых частей слов, называются сложносокращёнными. Способы словообразования 1. Суффиксальный Суффикс присоединяется к основе производящего слова (новый — новость) 2. Приставочный Приставка присоединяется к целому производящему слову (гулять — погулять) 3. Постфиксальный Постфикс присоединяется к целому производящему слову (мыть — мыться) 4. Приставочно-суффиксальный Приставка и суффикс одновременно присоединяются к основе производящего слова (берег — прибрежный) 5. Приставочно-постфиксальный Приставка и постфикс одновременно присоединяются к целому слову (бежать — разбежаться) 6. Суффиксально-постфиксальный Суффикс и постфикс одновременно присоединяются к основе слова (ссора — ссориться) 7. Переход из одной части речи в другую Перейдя из одной части речи в другую, слово меняет свои морфологические и синтаксические свойства: становится другой частью речи и другим членом предложения (учительская (прил. ) — учительская (сущ. ) 8. Слияние нескольких слов Слово образуется путём слияния целых слов, составляющих словосочетание (выше указанный — вышеуказанный) 9. Сложение Соединительная морфема объединяет основу слова и целое слово (светлый, розовый — светло-розовый) 10. Сложение в сочетании с суффиксальным способом Слово образуется путём сложения нескольких основ с одновременным присоединением суффикса (четыре этажа — четырёхэтажный) 11. Сложение сокращённых слов Слово образуется путём сложения части основы и целого слова, частей основ нескольких слов, начальных букв слов (заведующий складом — завскладом)

Физкультура, драмкружок, госдума, спецодежда, редколлегия, спортзал

Детсад, универмаг, сельхоз, универсам.

правсоюз, педсовет

физкультура, драмкружок

ето была в учбнике ятк пнимаю

Педсовет (педагогический совет)

Физкультура, драмкружок, госдума, спецодежда, редколлегия, спортзал правсоюз, педсовет

Помогаем дружно)

Слова, образованные путём сложения двух и более основ или слов, называются сложными . Слова, образованные путём сложения сокращённых частей слов, называются сложносокращёнными. Способы словообразования 1. Суффиксальный Суффикс присоединяется к основе производящего слова (новый — новость) 2. Приставочный Приставка присоединяется к целому производящему слову (гулять — погулять) 3. Постфиксальный Постфикс присоединяется к целому производящему слову (мыть — мыться) 4. Приставочно-суффиксальный Приставка и суффикс одновременно присоединяются к основе производящего слова (берег — прибрежный) 5. Приставочно-постфиксальный Приставка и постфикс одновременно присоединяются к целому слову (бежать — разбежаться) 6. Суффиксально-постфиксальный Суффикс и постфикс одновременно присоединяются к основе слова (ссора — ссориться) 7. Переход из одной части речи в другую Перейдя из одной части речи в другую, слово меняет свои морфологические и синтаксические свойства: становится другой частью речи и другим членом предложения (учительская (прил. ) — учительская (сущ. ) 8. Слияние нескольких слов Слово образуется путём слияния целых слов, составляющих словосочетание (выше указанный — вышеуказанный) 9. Сложение Соединительная морфема объединяет основу слова и целое слово (светлый, розовый — светло-розовый) 10. Сложение в сочетании с суффиксальным способом Слово образуется путём сложения нескольких основ с одновременным присоединением суффикса (четыре этажа — четырёхэтажный) 11. Сложение сокращённых слов Слово образуется путём сложения части основы и целого слова, частей основ нескольких слов, начальных букв слов (заведующий складом — завскладом)

примеры образования слов (сложение) то есть там должно быть 2 слова соеденённые без соеденительной гласной!

плащ-палатка, диван-кровать — это составные слова, которые образуются при сложении) ) Сложение — это способ образования новых слов соединением двух и более основ или СЛОВ. В зависимости от того, что объединяется при образовании новой лексической единицы, различаются способы сложения СЛОВ и сложения основ. При сложении СЛОВ образуются составные слова, которые пишутся через дефис: выставка-продажа, диван-кровать, плащ-палатка. При сложении ОСНОВ образуются сложные слитные слова. Основы могут соединяться при помощи соединительных гласных -о-, -е- (чернозём, сталевар) или без помощи соединительных гласных (завуч, спецкор) . При соединении основ без соединительных гласных образуется сложносокращённое слово — аббревиатура .

Теракт, туроператор

Двадцатидвухмиллиметровый.

Дурдом, психбольница, вендиспансер.

Например: Стенгазета, универсам.

спецназ или дурдом

например УЗКоПЛЕЧий, ПЯТиЭТАЖный, ВАГОНоРЕМОНТный, СНЕГоПАД, ЛЕСоСТЕПЬ, САМоЛЕТ, ТЕПЛоХОД.

Классный вопрос::::::::: _____))))))))))))))))

Приведите примеры, 10 слов образованных путем сложения целых слов.

1)Диван-кровать, плащ-палатка, платье-халат, школа-интернат, кресло-кровать, автомобиль-цистерна склоняются обе части слов. ( обе части слов изменяемые) Р. л. дивана-кровати, плаща-палатки и т. д. 2) кафе-клуб, альфа-излучение, бета-частица, гамма-излучатель ( первая часть неизменяемая) склоняется вторая часть. Р. п. кафе-клуба, альфа-излучения Д. п. кафе-клубу, альфа-излучению и т. д.

летчик-испытатель, школа-интернат, кафе-мороженое, кресло-качалка, кафе-бар, суп-пюре, телефон-автомат, шкаф-купе, плащ-палатка, дом-музей, вагон-ресторан, школа-студия, город-герой, платье-костюм, кресло-качалка, пила-рыба, премьер-министр, генерал-лейтенант, роман-газета. «При сложении целых слов первая часть слова не изменяется: в плащ-палатке, нет диван- сновным по смыслу в таких словах часто является вторая часть-слово, а первое слово-часть несколько дифференцирует понятие через определенный признак: основное назначение предмета для спанья (кровать) в слове диван-кровать, но этот предмет в виде дивана (диван) ; в слове телефон-автомат, пожалуй, отношения обратные: основное для “потребителя” — телефон, представленный в виде автоматической связи вне дома — в части автомат; слово роман-газета предполагает тесное переплетение обеих частей слова, при исходной более главной роли, видимо, в первой части. При изменении таких слов нет строгих правил. Первая частьможет тоже изменяться или чаще остается неизменной: У меня нет роман-газеты. У телефона-автомата появилась очередь». См <a rel=»nofollow» href=»http://window.edu.ru/library/pdf2txt/153/22153/5380/page9″ target=»_blank»>http://window.edu.ru/library/pdf2txt/153/22153/5380/page9</a>

1)Диван-кровать, плащ-палатка, платье-халат, школа-интернат, кресло-кровать, автомобиль-цистерна склоняются обе части слов. ( обе части слов изменяемые) Р. л. дивана-кровати, плаща-палатки и т. д. 2) кафе-клуб, альфа-излучение, бета-частица, гамма-излучатель ( первая часть неизменяемая) склоняется вторая часть. Р. п. кафе-клуба, альфа-излучения Д. п. кафе-клубу, альфа-излучению и т. д.

1)Диван-кровать, плащ-палатка, платье-халат, школа-интернат, кресло-кровать, автомобиль-цистерна склоняются обе части слов. ( обе части слов изменяемые) Р. л. дивана-кровати, плаща-палатки и т. д. 2) кафе-клуб, альфа-излучение, бета-частица, гамма-излучатель ( первая часть неизменяемая) склоняется вторая часть. Р. п. кафе-клуба, альфа-излучения Д. п. кафе-клубу, альфа-излучению и т. д.

ветлечебница спецодежда медсестра спортзал универмаг

вай ответы есть лублу