Линейное уравнение с одной переменной. Часть 2. Тожественные преобразования уравнений

При переписывании в эквивалентном виде условия задачи может получиться любое уравнение, необязательно вида 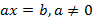. Но есть много уравнений, которые можно свести к такому виду с помощью эквивалентных преобразований, например, 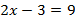. В этом нам помогут тождественные преобразования уравнений.

---

 

Тождественные преобразования

Тождественные преобразования – это такие преобразования, которые меняют только внешний вид уравнения, но не меняют информацию, которая в нем содержится.

Например, 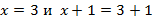. Понятно, что в обоих уравнениях неизвестное будет равняться 3.

Чтобы сформулировать более строгое определение, сначала познакомимся с понятием равносильных (эквивалентных) уравнений.

Определение 1. Два уравнения называются равносильными, если они имеют одинаковые корни или оба не имеют корней.

Например,

 

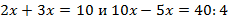
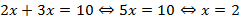
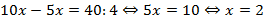
Определение 2. Тождественным, или равносильным, называют такое преобразование уравнения, при котором полученное уравнение равносильно исходному.

Например, если прибавить к обеим частям уравнения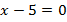

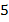 число , то получится равносильное уравнение .

---

 

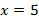Представим, что у нас есть две чаши весов, которые уравновешены (Рис. 3).

Рис. 3. Уравновешенные чаши весов

Нарушится ли равенство, если мы добавим на каждую из чаш гирю одинаковой массы? Конечно, нет (Рис. 4).

Рис. 4. Равенство весов не нарушается при добавлении гирь одинаковой массы на каждую из чаш

Вернемся к уравнению: .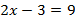

Левую и правую части уравнения можно считать чашами таких весов. То есть мы можем прибавить к обеим частям уравнения одинаковые выражения – от этого равенство не нарушится, мы получим эквивалентное уравнение.

---

 

Почему это преобразование будет тождественным

Уравнение – это равенство, которое содержит переменную.

Равенство может быть верным, если в качестве переменной подставить корень уравнения, а может быть неверным, если подставить любое другое число, которое не является корнем уравнения.

Если равенство было верным, то, прибавляя к обеим частям одно и то же число (или выражение), мы снова получим верное равенство.

Если же равенство было неверным, то и после прибавления одного и того же выражения к обеим частям оно останется неверным.

Проводя аналогию с весами: если весы были уравновешены и мы поставили на каждую чашу гирю одинаковой массы, то равновесие сохранится. А если весы не уравновешены, то и после того, как мы поставим на каждую чашу гири одинаковой массы, они уравновешенными не станут.

---

 

Эквивалентные (тождественные) преобразования позволяют использовать стандартный математический приём – свести задачу к предыдущей.

В нашем примере: привести линейное уравнение к стандартному виду, в котором мы уже умеем его решать. Например, если в уравнении 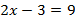 к обеим частям прибавить 3, то получим: .

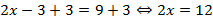А такое уравнение записано в стандартном виде и мы можем его решить:

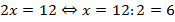
Аналогично мы могли бы убирать с чаш весов одинаковые гири, равновесие при этом не нарушится. Значит, если вычитать одинаковые выражения из обеих частей уравнения, то мы получим уравнение, равносильное исходному, то есть не изменим информацию, которая в нем содержалась.

Внимательно посмотрим на уравнения :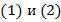

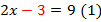
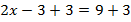
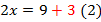
Уравнения 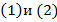 отличаются тем, что  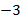перешло из левой части в правую и при этом сменило свой знак – стало .

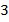Первое тождественное преобразование уравнений можно сформулировать по-другому: если слагаемое перенести из одной части уравнения в другую, при этом изменив его знак на противоположный, то мы получим новое уравнение, равносильное исходному.

Снова вернемся к аналогии с весами: пусть сначала они были уравновешены (Рис. 5), а потом мы положили на каждую чашу еще ровно столько, сколько там было, т.е. увеличили массу в 2 раза. При этом равновесие не нарушится (Рис. 6).

Рис. 5. Уравновешенные весы

Рис. 6. Уравновешенные чаши весов после увеличения массы в 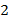 раза

Если увеличить массу на каждой чаше весов в 3 раза или в 100 раз, то равновесие все равно сохранится. Так, если обе части уравнения умножить на одно и то же ненулевое число, то полученное уравнение будет эквивалентно предыдущему.

Аналогично, можно забрать с каждой чаши половину, треть или какую-то другую одинаковую часть (уменьшить в несколько раз) – равновесие не нарушится. Если обе части уравнения разделить на одно и то же ненулевое число, то при этом получится уравнение, эквивалентное исходному.

 

Обратите внимание, что ни умножать, ни делить обе части уравнения на 0 не имеет смысла. С делением на 0 понятно – оно не определено, а вот почему умножение на 0 не имеет смысла, читайте ниже.

---

 

Почему не имеет смысла умножать на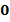

Пусть есть два уравнения: 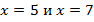. Они несут разную информацию. Когда мы умножаем на 0, то всегда получаем 0.

Поэтому, если умножить обе части обоих уравнений на 0, мы получим два уравнения:

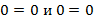
Во-первых, эти равенства достигаются при любых значениях переменных, а во-вторых, они несут в себе одну и ту же информацию. То есть, умножая на 0, мы стираем всю информацию, которая заключалась в равенствах.

Если провести аналогию с весами, то при умножении на 0 мы убираем содержимое с обеих чаш весов. То есть независимо от того, что было на весах, были они уравновешены или нет, после умножения на 0 мы всегда получим равновесие.

---

 

interneturok.ru

V Международный конкурс научно-исследовательских и творческих работ учащихся Старт в науке

Приемы решения линейных уравнений с одной переменной от Древнего Египта до наших дней

Николаева М.В. 1

---

1МБОУ СОШ №8

Петрунина Е.В. 1

---

1МБОУ СОШ № 8

Текст работы размещён без изображений и формул.

Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

Введение.

Уравнения для меня важнее, потому что

политика — для настоящего,

а уравнения — для вечности

Альберт Эйнштейн

Алгебра, как искусство решать уравнения, зародилась очень давно в связи с потребностью практики, в результате поиска общих приёмов решения однотипных задач. Самые ранние, дошедшие до нас рукописи свидетельствуют о том, что в Древнем Вавилоне и Древнем Египте были известны приёмы решения линейных уравнений. Теория уравнений интересовала и интересует математиков всех времён и народов, потому что уравнения играют важную роль для человека в повседневной жизни. Я тоже заинтересовалась вопросом: «Как можно легче и быстрее решить уравнение? Какие существуют методы и алгоритмы их решения? Что значит решить уравнение? Что значит исследовать уравнение?» Я думаю, что если найти новые приемы решения уравнений, то можно повысить интерес к математике и успеваемость моих одноклассников.

Класс линейных уравнений — первый в курсе алгебры, поэтому от характера его изучения в значительной мере зависит успешное освоение всей темы «Уравнения».

Можно все линейные уравнения решать, опираясь на два известных тождественных преобразований. Но это путь маленькими шажочками по длинной дороге, что часто приводит к большому количеству вычислительных ошибок. В этом я убедилась на собственном опыте. Я решила помочь себе и своим одноклассникам и найти новые методы для более качественного освоения такой важной темы, как линейные уравнения.

Гипотеза исследования: существуют другие приемы решения линейных уравнений с одной переменной.

Цель работы: систематизировать линейные уравнения по их решениям, познакомиться с новыми приемами решения.

Задачи:

Проанализировать, что мне известно о линейных уравнениях из школьного курса математики;

Найти и изучить новые приемы решения линейных уравнений;

Познакомить одноклассников с новыми приемами решения линейных уравнений;

Провести сравнительный анализ достижений в решении уравнений

Объект исследования: линейные уравнения

Предмет исследования: приёмы решения линейных уравнений с одной переменной.

Методы исследования: опрос (анкетирование) учащихся 6-7 классов МБОУ СОШ №8 г. Калуги, анализ литературы, диагностика.

Актуальность

По моему мнению, математика — предмет, без которого не может быть изучено ни одно явление, ни один процесс в окружающем мире. Применение математических исчислений, в том числе линейных уравнений, является составной частью в новых научных исследованиях и вносит большой вклад в развитие современной науки и технического прогресса в целом.

Уравнения в математике занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.) А также изучение математики развивает у человека логическое мышление, память, гибкость ума, приучает его к точности, к умению видеть главное, сообщает необходимые сведения для понимания сложных задач, возникающих в различных областях деятельности современного человека.

В своей работе я хочу показать разные способы решения уравнений, возможно, некоторые из них будут легче, некоторые интереснее для учеников, и решение уравнений уже не станет для них бесполезным и непонятным делом.

Для подтверждения гипотезы и выполнения поставленных нами задач было проведено анкетирование учащихся на базе МБОУ СОШ №8 г. Калуги. Результаты моей исследовательской деятельности отражены во второй главе.

Новизна

Существуют разные способы решения уравнений, но многими из них мы не пользуемся, а некоторые даже и не знают об их существовании. Новизна моей работы заключается в изучении данной проблемы на примере успеваемости учащихся 6-7 классов моей школы и в анализе различных способов решения уравнений.

Основная часть

Глава 1. Основные понятия. Линейные уравнения: исследование, способы решений, уравнения, приводимые к линейным.

1.1. Исторический экскурс.

Кто придумал уравнения? Ответить на этот вопрос невозможно! Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла. Еще 3–4 тысячи лет до нашей эры египтяне и вавилоняне умели решать простейшие уравнения, вид которых не был похож на современные. Греки унаследовали знания египтян и пошли дальше. Наибольших успехов в развитии учения об уравнениях достиг греческий ученый Диофант¹.

“Он уйму всяких разрешил проблем.

И засухи предсказывал и ливни.

Поистине его познанья дивны”

В одном из древних рукописных сборников задач в стихах жизнь Диофанта описывается в виде следующей алгебраической загадки, представляющей надгробную надпись на его могиле:

«Прах Диофанта гробница покоит; дивись ей—и камень

Мудрым искусством его скажет усопшего век.

Волей богов шестую часть жизни он прожил ребенком.

И половину шестой встретил с пушком на щеках.

Только минула седьмая, с подругою он обручился.

С нею пять лет проведя, сына дождался мудрец;

Только полжизни отцовской возлюбленный сын его прожил.

Отнят он был у отца ранней могилой своей.

Дважды два года родитель оплакивал тяжкое горе,

Тут и увидел предел жизни печальной своей»

Задача-загадка сводится к составлению и решению уравнения:

Решение этого уравнения я рассмотрю позднее.

Большой вклад в преобразование линейных уравнений внес среднеазиатский ученый математик, астроном, историк, географ — один из крупнейших ученых средневековья Мухаммед аль Хорезми (IX век). Его труды по арифметике, изложенные в «Книге об индийском счете», привели к грандиозным последствиям в науке вообще и древней математики в частности.

Аль — Хорезми написал сочинение «Китаб аль — джебр валь — мукабала». На русский переводится как: «Книга о восстановлении и противопоставлении». О каком восстановлении и противопоставлении идет речь?

Рассмотрим решение уравнения: 5x – 9 = 12 — 2x

Вот так рассуждал в своём сочинении аль Хорезми: «-9 перенесём вправо с противоположным знаком и -2x влево, тоже с противоположным знаком: 5x + 2x = 12 + 9

Минусов нет, приведём подобные члены: 7x = 21. Выполняем деление: х = 3

Число 9 было слева от знака равенства, мы его не стали писать с этой стороны, а восстановили (аль — джебр) справа.

Выражение -2х было справа от знака равенства, мы его уничтожили там, но восстановили (аль — джебр) слева. Потом сложили 5х и 2х, сопоставив их рядом (валь – мукабала), а потом поступили так же с 12 и 9»

1.2. Основные понятия.

Уравнение — это равенство, которое выполняется лишь при некоторых значениях входящих в него переменных. Решить уравнение — это значитнайти все значения неизвестных, при которых оно обращается в верное числовое равенство, или установить, что таких значений нет. Такие значения называются корнем уравнения. Корень уравнения — это такое значение переменной, при подстановке которого уравнениеобращается в верное числовое равенство².

Можно провести исследование уравнения. Что это значит? Это значит рассмотреть все особые случаи, которые могут представиться при решении его, и уяснить значение этих случаев для той задачи, из условий которой уравнение составлено. При исследовании уравнения мы подходим более основательно, рассматриваем все особые случаи, которые могут встретиться при его решении. При самом решении уравнении, нашей основной задачей является найти значения переменной

Объектом исследования в работе я выбрала линейные уравнения. Проанализировав теоретический материал учебника, я заметила, что он ограничен только общей теорией и алгоритмом решения простейшего линейного уравнения. Но этого недостаточно для решения задач разного уровня сложности. Поэтому на первом этапе работы я классифицировала методы решения линейных уравнений, опираясь на целесообразность применения тех или иных преобразований. В классификацию были включены также уравнения, решения которых сводится к линейным.

тип – преобразование уравнений;

тип – нахождение общего знаменателя;

тип – пропорция;

тип — уравнение с модулем

тип – уравнение с параметром

1.3. Линейные уравнения

Линейное уравнение с одной переменной — это уравнение, приводимое к виду ax = b, где x – переменная , a и b – некоторые числа.

Разберёмся, сколько корней может иметь линейное уравнение? Количество корней зависит от значений a и b:

Когда a = b = 0, т.е. уравнение принимает вид 0х = 0, решением данного уравнения является х — любое число, т.е у него есть неограниченное количество решений.

Когда a = 0, b ≠ 0, т.е. уравнение принимает вид 0х = b, данное уравнение не имеет корней. А еще говорят, что его решение – пустое множество.

Когда a ≠ 0, b≠ 0 у уравнения есть только один корень x =

1.4 .Способы решения линейных уравнений

Фальшивое правило.³ Способ решения, примененный Ахмесом, называется методом одного ложного положения, использовался метод в Древнем Египте и Вавилоне.

Уравнение первой степени с одним неизвестным мо­жно привести всегда к виду ах + b = с, в котором а, b, с — целые числа. По правилам арифметических действий ах = с — b,

Если b > с, то с — b число отрицательное. (Отрицательные числа были египтянам и многим другим, более поздним народам неизвестны, равноправно с положительными числами их стали употреблять в математике только в семнадцатом веке).

В папирусе Ахмеса 15 задач решается этим методом. Египтяне имели особый знак для обозначения неизвестного числа, который до недавнего прошлого читали “хау” и переводили словом “куча” (“куча” или “неизвестное количество” единиц). Теперь читают неточно: “ага”.

Познакомиться с рассуждениями автора можно в приложении⁴.

Метод «Пристального взгляда» Иногда корень уравнения можно легко увидеть, например, в уравнении 2х + 1 = 3 корень х = 1.

Но чаще всего, чтобы решить уравнение, его надо преобразовать. Для этого используются свойства, которые можно найти в приложении 2.⁵

3. Школьный способ — алгоритмический ⁶

На просторах Internet я нашла видео, в котором рассказывают, как учат американских школьников решать линейные уравнения. Они предлагают два способа: для ленивых и для талантливых учеников.

4.1. Американский способ для «ленивых» учеников⁷

25х + 5 = 105

Первое, что нужно сделать – вычесть с обеих сторон 5, т.е. надо выполнить действие обратное данному. Учитель заставляет ленивых школьников писать все шаги (steps).

Получится: 25х + 5 = 105

+ -5 -5

Подводим черту и выполняем действие, получаем уравнение

25х = 100

Дальше обе стороны уравнения делим на 25:

= ; х = 4

4.2. Американский способ для талантливых детей. Основная идея его состоит в том, что все наши действия идут от обратного:

25х + 5= 105

В уме берём 105 и переходим в обратную сторону и делаем обратное действие:

105 — 5 = 100,

Получаем 25х = 100, но этот результат не записываем, а держим его в уме.

Еще раз идём в обратную сторону и делаем обратное действие

100: 25 = 4

х = 4

Запись в тетради выглядит так,

5. Метод полных форм⁸. Если нам удалось преобразовать уравнение к виду ax + b = cx +d – полная форма линейного уравнения

ax – cx = d – b

x(a — c) = d – b

x =

Если d = b, a = c, то уравнение имеет бесконечно много решений.

Если d ≠ b, a = c, то уравнение не имеет решений.

Далее я хочу рассмотреть несколько типов уравнений, которые сводятся к линейным уравнениям

1.5. Уравнения, приводимые к линейным

I. Нахождение общего знаменателя.

Рассмотрим решение уравнения Диофанта⁹.

Вот сколько лет жил Диофант.

II. Уравнение — пропорции¹⁰:

Пропорцией называется равенство двух отношений:

= или a : b = с : d.

При решении таких уравнений разумно пользоваться основным свойством пропорции: произведение крайних членов пропорции равно произведению средних ее членов: ad = bc

Используя это свойство, решим уравнение:

=

7(5х — 4) = 2(16х + 1)

35х – 28 = 32х + 2

35х – 32х = 2 + 28

3х = 30

х = 30: 3

х = 6

Ответ: 6

Уравнения с модулями

Модуль числа – это абсолютная величина этого числа, т.е.

Модуль числа не может быть равен отрицательному числу.

∣x — 4∣ = 5

х – 4 = 5 или х – 4 = -5

х = 9 х = -1

Ответ: -1; 9.

Уравнение с параметром¹¹.

Уравнение с параметром – это уравнение, в котором некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами (параметрами). Такие уравнения называют еще параметрическими.

Решить такое уравнение – это значит, для всех значений параметра найти все решения. Если хотя бы один случай остался неисследованным, признать такое решение удовлетворительным нельзя. Требуется указать возможные значения параметра, при которых уравнение обладает определенными свойствами. Например, имеет одно решение, не имеет решений, имеет решения, принадлежащие промежутку и т. д. В таких заданиях необходимо четко указать, при каком значении параметра требуемое условие выполняется.

а) Рассмотрим уравнение: х (а – 2) = 4;

При а = 2, (а – 2) = 0, получим уравнение 0х = 4, которое не имеет корней.

Если а – 2 ≠ 0, а ≠ 2, то х =

б) Найдите все целые значения а, при которых корень уравнения ах = 8 является целым числом.

Решение. Найдем значение х при а ≠ 0, х = . Чтобы корень уравнения был целым числом, необходимо, чтобы а являлось делителем числа 8. Следовательно, а = {-8; -4; -2; -1; 1; 2; 4; 8}

Глава 2. Экспериментальная часть

Эксперимент №1. Изучение потребностей учеников 6 — 7 классов в изучении данной темы.

Для того чтобы выяснить актуальность исследуемой темы, мы решили провести опрос среди учащихся 6-7 классов нашей школы. Опрос проводился посредством анкетирования. Респондентам были заданы вопросы¹²: Математику назвали интересным предметом — 76% опрошенных, 83 % — оценили свои знания как хорошие и удовлетворительные.

Многие учащиеся испытывают трудности при изучении предмета.

Эксперимент №2. Диагностика умения решать уравнения

Практическая часть включает в себя изучение динамики развития навыков решения линейных уравнений с одной переменной. Была выдвинута следующая гипотеза: владение новыми способами решения уравнений повышает интерес учащихся к предмету и дает возможность сократить время вычислений. Объекты исследования: учащиеся 7а и 7б классов.

Этапы исследования:

Проверка имеющихся навыков решения уравнений;

Знакомство учащихся с новыми способами решения уравнений;

Проведение повторной диагностики;

Подведение результатов исследования.

В данном исследовании приняло участие 54 семиклассника моей школы.

Для проверки имеющихся навыков мы провели диагностическую работу, в которую включили четыре уравнения. На первом этапе (октябрь 2017 года) работы учащиеся показали, что существуют определённые сложности при решении уравнений. Основные ошибки: перенос слагаемых из одной части уравнения в другую, смена знака при переносе слагаемых и нахождение значения переменной. Следующим этапом нашей работы (ноябрь — декабрь) был поиск, изучение и отработка новых способов решения уравнений. После этого (январь 2018 года) был проведен повторный срез, который показал, что учащиеся в 1,5 раза быстрее справились со своими заданиями, допустив гораздо меньше ошибок. Результаты работы приведены в приложении 6 ¹³.

В работах учащихся уверенно прослеживается динамика развития навыков решения уравнений и повышения интереса к ним. Исследование показало, что после того как одноклассники узнали больше по решению линейных уравнений, у них повысился интерес к изучаемой теме, а вместе с ним повысились их результаты.

Заключение

Изучив математическую литературу в данной научной исследовательской работе, были проанализированы различные приёмы решения линейных уравнений с одной переменной, в том числе фальшивое правило и американская методика решения уравнений, что повысило интерес учащихся к данной теме. Также были решены поставленные задачи исследования: проанализирован материал школьного курса математики о линейных уравнениях; найдены и изучены новые приемы решения линейных уравнений; одноклассники узнали новые приемы решения линейных уравнений; проведен сравнительный анализ достижений в решении уравнений.

На основе поставленных задач и проведенных методов была достигнута поставленная цель по систематизации линейных уравнений, по их решениям, знакомству с новыми приемами решения.

Доказана гипотеза, что существуют другие приемы решения линейных уравнений, подтвердилась.

Список использованных источников и литературы

Алимов, Ш. А. Алгебра: Учебник для 7 класса средней школы / Ш. А. Алимов, Ю. М. Колягин, Ю. В. Сидоров и др. – М.: Просвещение, 1991. – 191 с.: ил.

Мерзляк, А. Г. Алгебра: 7 класс: учебник для учащихся общеобразовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. – 2-е изд., дораб. – М.: Вентана-Граф, 2017. – 272 с.: ил.

Мордкович, А. Г. Алгебра 7 кл. В двух частях. Ч. 1: Учебник для образовательных учреждений. / А. Г. Мордкович, – 5-е изд. – М.: Мнемозина, 2002 . – 160с.: ил.

Парканова, С. И., Линейные уравнения// С. И. Парканова, С. И. Ревтова, Т. М. Катлерова. Школьная педагогика. – 2016. – №2. – С. 19-22.

Пичурин, Л. Ф. За страницами учебника алгебры: Кн. для учащихся 7-9 классов средней школы/ Л. Ф. Пичурин – М.: Просвещение, 1990. – 224с.: ил.

www.uic.unn.ru/~zny/miscellanea/Miscellanea/Magnitski.ps

Приложение

Приложение 1.

“Куча. Ее седьмая часть (подразумевается: “дают в сумме”) 19. Найти кучу”.

Запишем задачу нашими знаками:

Решение Ахмеса может быть представлено в наших символах в следующих четырех столбцах:

Опишем это решение

1) Делается предположение, что куча есть 7; тогда ее часть есть 1. (Это записано в первом столбце)

2) Во втором столбце записано, что при предположении х = 7 куча и ее часть дали бы 8 вместо 19.

3) Удвоение предположения дает 16

4) Автор, (в уме), прикидывает, что дальше удваивать предположение нельзя, так как тогда получится больше 19.

5) Он записывает 16, ставит перед числом две точки для обозначения удвоения первоначального предположения и отмечает значком (у нас — звездочкой) результат;

6) для получения в сумме 19 первоначальное предположение надо умножить — на 2 с некоторым добавлением, так как для получения точного результата, 19, не хватает еще 19—16=3.

7) Ахмес находит от 8, получает 4. Так как это больше нехватки 3, то на предположение умножить нельзя.

8) Но от 8 есть 2, 9) от восьми 1.

9) Ахмес видит, что и первоначального результата дают точно те 3 единицы, которых не хватало.

10) Отметив и значками, Ахмес убедился, что первоначальное предположение для кучи (7) надо помножить на

11) Умножение числа 7 на смешанное число Ахмес заменяет умножением смешанного числа на 7. В третьем столбце выписаны: часть искомой кучи есть , удвоенное это число: и учетверенное: . Сумма этих трех чисел, равная числу , есть произведение первоначального предположения 7 на .

12) Итак, куча равна .

В последнем столбце Ахмес делает проверку, складывая полученное значение для кучи и его части . В сумме получается 19, и решение заканчивается обычным для автора заключением: “Будет хорошо”.

Приложение 2.

Словесная формулировка	Запись в общем виде	Пример
1.Если к обеим частям верного равенства прибавить одно и то же число или из обеих частей верного равенства вычесть одно и то же число, то получится верное равенство.	Если а = b и l – любое число, то a+ l = b + l, a – l = b — l	7 = 7 7+ 2=7+2 7 – 2 = 7 — 2
2.Если обе части верного равенства умножить или разделить на одно и то же не равное 0 число, то получится верное равенство.	Если a = b и m≠0, то a × m = b × m a : m = b : m	27= 27 27×3 = 27 × 3 27 : 3 = 27 : 3

Приложение 3.

Алгоритм решения линейных уравнений с одной переменной.

Решить уравнение	4х – (60 — 3х) = 10х + (22 +2х)
Раскрыть все скобки	4х – 60 + 3х = 10х + 22 +2х
Соберите слагаемые с переменной в левой части уравнения, а свободные слагаемые в правой части. Внимание: При переносе слагаемых из одной части уравнения в другую, необходимо менять их знак на противоположный	4х + 3х – 10х – 2х = 22 + 60
Упростите левую и правую части уравнений Внимание: Вы должны получить уравнение вида ах = в	— 5х = 82
Найдите значение переменной, разделив число стоящее в правой части уравнения на число стоящее в левой части, т.е х = в: а	х= 82 : (-5)
Запишите х = …	х = 16,4
Запишите ответ	Ответ: 16,4

Приложение 4.

Приложение 5.

Эксперимент №1. Изучение потребностей учеников 6 — 7 классов в изучении данной темы.

Да	55
Нет	15
Не знаю	2

Хорошие	24
Удовлетворительные	36
Неудовлетворительные	15

несерьезное отношение к учебе;	16
трудности при изучении учебного материала;	40
отсутствие интереса к предмету	8
увлеченность другим делом	19
слабая математическая подготовка	15
другие причины	4

Приложение 6.

Эксперимент №2. Диагностика умения решать уравнения

Диагностическая работа

Решите уравнения:

25х + 5 = 105

1.  
2.  

4х – (60 — 3х) = 10х + (22 +2х)

Результаты исследования

	1 этап	2 этап
1 уравнение	52	54
2 уравнение	26	41
3 уравнение	16	34
4 уравнение	38	48

1 ^{www.uic.unn.ru/~zny/miscellanea/Miscellanea/Magnitski.ps}

2 ^{Алгебра: 7 класс: учебник для учащихся общеобразовательных организаций. А.Г. Мерзляк, В.Б. Полонский, М.С. Якир.}

3 ^{www.uic.unn.ru/~zny/miscellanea/Miscellanea/Magnitski.ps}

4 ^{Приложение 1}

5 ^{Приложение 2}

6 ^{Приложение 3}

7 ^{https://www.youtube.com/watch?v=ZRPlh6sFHbk}

8 ^{www.uic.unn.ru/~zny/miscellanea/Miscellanea/Magnitski.ps}

9 ^{Приложение 4}

10 ^{.Алгебра: Учебник для 7 класса средней школы. Ш. А. Алимов,}

11 ^{Алгебра 7 класс. В двух частях. Ч. 1: Учебник для образовательных учреждений. А. Г. Мордкович}

12 ^{Приложение 5}

13 ^{Приложение 6}

Просмотров работы: 700

school-science.ru

Линейное уравнение с одной переменной.

Тема: Линейное уравнение с одной переменной.

Цели: формировать умение решать линейные уравнения с одной переменной, развивать память, интеллект, логическое мышление, воспитывать самостоятельность, ответственность, целеустремлённость.

Основные понятия: линейное уравнение с одной переменной.

Тип урока: комбинированный.

Ход урока:

1.Организационный момент.

Приветствие. Проверка готовности учащихся к уроку.

2. Проверка домашнего задания.

3. Актуализация опорных знаний.

Приём «Верно-неверно».

Учащимся предлагается ряд утверждений среди которых они должны выбрать верные и неверные.

-Коэффициент это числовой множитель в произведении.

-При переносе слагаемых из одной части уравнения в другую их знак не меняется.

-Подобные слагаемые имеют одинаковую буквенную часть.

-Корнем уравнения называется значение переменной, при котором уравнение обращается в верное неравенство.

-Равносильные уравнения имеют одни и те же корни.

4. Сообщение темы урока. Постановка цели и задач.

Учитель предлагает учащимся поработать с текстом учебника и подготовить ответ на вопрос: «Какому понятию посвящен текст?»

Формулировка и запись темы в тетрадь.(Линейное уравнение с одной переменной)

Задачи урока:

Прием «Корзина идей».

Учитель: «Чему мы хотим научиться?»

На доске: Линейное уравнение с одной переменной:

-определение

-вид

-элементы линейного уравнения

-алгоритм решения

5.Изучение нового материала.

Прием «Чтение вслух с остановками».

Учитель предлагает учащимся читать по очереди, в конце каждого абзаца делаем остановку, для того чтобы ответить на вопрос: «Что узнали из этого абзаца?»

Прием «Незаконченное предложение».

Учитель предлагает закрыть учебник и при помощи вопросов учителя попытаться сформулировать определение линейного уравнения.

-линейное уравнение с одной переменной это (что?)… уравнение

-вида (какого?)… ах=b

-где (элементы?)… х-переменная, а и b некоторые числа

Затем учащиеся открывают учебник и сравнивают с определением автора, делают запись в тетрадь.

После этого учитель предлагает вернуться к задачам урока и проанализировать, что уже узнали. (Один из учеников делает вывод, что они сформулировали определение, научились записывать линейное уравнение в общем виде, запомнили, из каких элементов оно состоит, осталось записать алгоритм его решения.)

Прием «Инсерт».

При прочтении следующего абзаца, учащимся предлагается делать на полях пометки:

+ информация знакома

— новая информация

? хотелось бы узнать

После прочтения идет анализ текста, затем рассматриваются примеры и с помощью наводящих вопросов учителя составляется алгоритм решения линейного уравнения.

Вопросы:

-Сколько корней может иметь линейное уравнение?

-Если коэффициент а не равен нулю, сколько корней имеет уравнение? Приведите пример.

-Если коэффициент а и b равен нулю, сколько корней имеет уравнение? Пример.

-Если коэффициент а равен нулю, а b не равен нулю, уравнение имеет сколько корней? Привести пример.

В тетрадях у учащихся следующая запись. (слайд 4)

Линейное уравнение с одной переменной

Уравнение вида ах=b, где х-переменная, а и b некоторые числа, называется линейным уравнением с одной переменной.

Алгоритм решения:

1.Привести уравнение к виду ах=b.

2.Решить уравнение ах=b.

Если:

а) а≠0, то уравнение имеет один корень

б) а=0, b=0 уравнение имеет бесконечно много корней

в) а=0, b≠0 уравнение не имеет корней

6. Решение заданий.

1. а) Заполните таблицу:

2. Решите уравнение:

а) -2х-4,3=-0,5 г)3,8х-5,6=3,8х-8,4

б) 3-х=2(2х-5) д)2,8(х+3)-1,5(х-1)=1,3х

в) 7,2х-5,4=-3,6х-5,4 е) 4,5х+4,6-2,3(х+2)=2,1

3. Для уравнения 20 – (4-3х)=5(х-2)-2х+а найдите значение а, при котором:

а) любое значение х является корнем этого уравнения;

б) уравнение не имеет корней.

7. Подведение итогов. Рефлексия.

Учащиеся отвечают на вопросы учителя:

—Доволен ли я результатом своей работы на уроке?

-Чему я научился на уроке?

-С какими трудностями я столкнулся при изучении нового материала?

-Смогу ли я понятно объяснить, как решить линейное уравнение?

8. Домашнее задание.

Выучить определение и алгоритм решения линейного уравнения.

Решить №127(а,в), №130 (а,з), №132(а,б), №137.

videouroki.net