Разложение на простые множители 2
Разложение на простые множители — урок 2 — ДЕЛИМОСТЬ ЧИСЕЛ — ОБЫКНОВЕННЫЕ ДРОБИ 23.9.21
Цели: отрабатывать умения и навыки разложения чисел на простые множители, решения комбинаторных задач; повторить степень числа; проверить знания и умения учащихся по изученному материалу.
Информация для учителя
Обратить внимание учащихся на особенность разложения разрядных единиц на простые множители и чисел, оканчивающихся 0.
Ход урока
I. Организационный момент
II. Устный счет
1. Разложите числа на простые множители: а) 4; б) 6; в) 8; г) 9; д) 10; е) 12; ё) 14; ж) 22.
2. Найдите значение выражений
3. № 126 стр. 22.
(Ответ: при а = 1, так как произведение 23а делится только на 1 и само на себя, то есть на 23.)
—
Почему не подходят другие значения а? (Если взять любое другое значение а, то
тогда произведение будет делится на 23 и на а, следовательно, по определению
простых чисел произведение 23а не будет являться простым числом.
— Составьте аналогичное задание. (При каких значениях с произведение 37с является простым числом?)
4. № 129 стр. 22.
(Ответ: 19, 23, 29, 31, 37, 41, 43.)
— Как изменить запись неравенства, чтобы простых чисел в решении стало на одно больше? (17? р <44; 16 < р < 44; 17 < р < 48.)
5. На огороде посадили 54 куста малины в 9 рядов и 90 кустов клубники в 5 рядов. Какой из рядов короче? Во сколько раз? (54 : 9 = 6 (к) — малины в 1 ряду, 90 : 5 = 18 (к.) — клубники в 1 ряду, 18 : 6 = 3 (раза).)
III. Индивидуальная работа
1 карточка
Какие из чисел 2781, 6300, 52 125, 63 309, 530 240, 21 195, 123 278 делятся:
а) на 2; (6300, 530 240, 123 278)
б) на 5; (6300, 52 125, 530 240, 21 195)
в) на 10; (6300, 530 240)е) на 3; (2781, 6300, 52 125, 63 309, 21 195)
ж) на 9; (2781, 6300, 21 195)
2 карточка
Какие из чисел 7776, 7290, 31 125, 33 507, 200 640, 11 165, 211 214 делятся:
а) на 2; (7776, 7290, 200 640, 211 214)
б) на 5; (7290, 31 125, 200 640, 11 165)
в) на 10; (7290, 200 640)
е) на 3; (7776, 7290, 31 125, 33 507, 200 640)
ж) на 9; (7776, 7290, 33 507)
IV. Сообщение темы урока
Сообщение темы урока
Сегодня мы с вами продолжим раскладывать числа на простые множители.
V. Изучение нового материала
1. Подготовительная работа.
— Разложите на простые множители:
10, 100, 1000, 10 000, 100 000, 1000 000.
Решение:
и т. д.
— Какие простые числа являются делителями этих чисел? (2, 5.)
— Сколько раз они встречаются в разложении каждого из чисел? (Если в числе 5 нулей, то множители 2 и 5 встречаются 5 раз, то есть 100 000 = 10 · 10 · 10 · 10 · 10 = 25 · 55.)
2. Работа над новой темой.
а) Разложите на простые множители числа 80, 600, 25 000. Но записывать мы будем по-другому.
(Учитель показывает образец записи.)
Можно сразу писать так:
80 = 24 · 5 600 = 23 · 3 · 52 2000 = 24 · 53.
б) № 121 (б) стр. 21 (у доски с комментированием и в тетрадях).
— Какие простые множители обязательно будут иметь эти числа? (2, 5.)
—
Сколько раз они обязательно будут повторяться? (Все зависит от количества нулей
в записи числа. )
)
VI. Физкультминутка
VII. Работа над задачей
1. № 137 стр. 23 (Самостоятельно, к доске пригласить тех учащихся, которые не знают, как решать данную задачу. С ними подробно разобрать решение).
— Какая цифра может стоять на первом месте в записи числа? (2, 3, 4, 5.)
— Какие цифры будут стоять на втором и третьем месте в записи числа? (Любая из пяти.)
— А на последнем? (Только четные: 2, 4, 0.)
По правилу умножения получаем:
4 · 5 · 5 · 3 = 300 (чисел).
2. № 134 (а) стр. 22.
— Прочитайте задачу.
— Что известно?
— Что надо узнать?
— Что примем за х? (Стоимость альбома.)
— Что значит книга на 100% дороже альбома? (Это два раза нужно взять стоимость альбома, то есть х + х = 2х.)
— Как узнать, на сколько процентов альбом дешевле книги? (Нужно найти разность стоимости книги и альбома, а затем найти процентное отношение.)
Решение:
Пусть х — стоимость альбома.
2х
— стоимость книги.
2х — х = х
х — это 1/2 от 2х или 50%
(Ответ: альбом дешевле книги на 50%.)
VIII. Закрепление изученного материала
(Ответ: 512 = 29; 675 = 33 · 52; 1024 = 210.)
2. № 122 стр. 21 (самостоятельно с последующей проверкой). (Ответ: а) 25 = 5 · 5, 49 = 7 · 7; б) 27 = 3 · 3 · 3.)
3. — Назовите все простые числа от 2 до 10. (2, 3, 5, 7.)
4. № 123 стр. 21 (у доски и в тетрадях с объяснением).
— Как удобнее найти эти двузначные числа? (Умножить каждое число на 2, 3, 5, 7, проверить является ли двузначным получившееся число, например, 47 надо умножать только на 2, а 11 · 2 = 22, 11 · 3 = 33, 11 · 5 = 55, 11 · 7 = 77.)
IX. Самостоятельная работа (10 мин)
Разложите числа на простые множители.
Вариант I. 630, 2175, 1998.
Вариант II. 720, 1845, 2520.
Ответы:
Вариант
I. 630 = 2 · 32 · 5 · 7, 2175 = 3 · 52 · 29, 1998 = 2 · 33 · 37.
Вариант II. 720 = 24 · 32 · 5, 1845 = 32 · 5 · 41, 25 20 = 23 · 32 · 5 · 7.
X. Подведение итогов урока
— Существуют ли составные числа, которые нельзя разложить на простые множители?
— Чем могут отличаться два разложения одного и того же числа на простые множители?
— Если число оканчивается цифрой 0, то какие простые делители оно обязательно имеет?
Домашнее задание
№ 143, 139 (3, 4), № 141 (в) стр. 23.
Выучить математические термины:
1. Делимое.
2. Делитель.
3. Комбинаторика.
4. Кратное.
5. Множитель.
6. Признак делимости.
7. Произведение.
8. Простое число.
9. Разложение.
10. Составное число.
11. Частное.
Задачи по математике на тему Разложение на простые множители
121 Разложите на простые множители числа 216; 162; 144; 512; 675; 1024; 60; 180; 220; 350; 400; 1200; 8000; 11; 1001; 1225; 21780; 45 630.РЕШЕНИЕ
122 Напишите все двузначные числа, разложение которых на простые множители состоит: а) из двух; б) из трех одинаковых множителей.
РЕШЕНИЕ
123 Запишите все двузначные числа, которые раскладываются на два различных простых множителя, один из которых равен: 11; 13; 23; 47.
РЕШЕНИЕ
124 Выясните, делится ли число a на b без остатка, если a = 2·2·2·3·5·7 и b = 2·3·7; a = 3·3·5·5·11 и b = 3· 3 5;…в случае, когда а делится на b найдите частное.
РЕШЕНИЕ
125 Вычислите устно: 3,99 + 2,01; 2,3 + 0,007; 3,62 + 1,08; 3,06 + 1,94; 12,77 + 0,13; 0,7-0,06; 1- 0,48; 2-1,02; 0,65 — 0,5; 0,8-0,25; 1,6:100; 5:10; 12:1000; 2,3:0,1; 4:0,01; 0,4 0,31-25; 3,8-1,7-2,8-1,7; 4,7-12,5-0,8; 3,1 · 3,7 + 3,1 — 6,3; 49,3 + 0 49,3.
РЕШЕНИЕ
126 При каких натуральных значениях a произведение 23a является простым числом?
РЕШЕНИЕ
127 Существует ли прямоугольник, стороны которого выражаются натуральными числами, а периметр простым числом?
РЕШЕНИЕ
128 Найдите по два простых делителя каждого из чисел: 64; 62; 148; 182; 3333; 5005.
РЕШЕНИЕ
129 Какие простые числа являются решениями неравенства 17<p<44?
РЕШЕНИЕ
130 Могут ли быть простыми числами координаты точек A, B, C и D, если p простое число?
РЕШЕНИЕ
131 Представьте число 3 в виде дроби со знаменателем 5; число 1 — со знаменателем 12.
РЕШЕНИЕ
132 Выполните действия
РЕШЕНИЕ
133 Из 35 учащихся пятого класса 22 выписывают журнал Юный натуралист , 27 газету Пионерская правда , а 3 ученика не выписывают ни газету, ни журнал. Сколько учащихся выписывают газету и журнал?
РЕШЕНИЕ
134 Книга на 100% дороже альбома. На сколько процентов альбом дешевле книги? Масса гуся на 25% больше массы утки. На сколько процентов масса утки меньше чем гуся?
РЕШЕНИЕ
135 Для какого числового выражения составлена программа вычислений на микрокалькуляторе
РЕШЕНИЕ
136 Стороны треугольника 12 см, 17 см и x см. Составьте выражение для вычисления периметра этого треугольника. Каким может и не может быть значение x.
РЕШЕНИЕ
137 Сколько четных четырехзначных чисел можно составить из цифра 0,2,3,4,5?
РЕШЕНИЕ
138 1) Две бригады хлопкоробов собрали вместе 20,4 ц хлопка за день. При атом первая бригада собрала на 1,52 ц больше второй. Сколько центнеров хлопка собрала каждая бригада? 2) Два комбайнера убрали пшеницу с 64,2 га. Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?
Сколько гектаров убрал каждый комбайнер, если первый убрал на 2,8 га меньше, чем второй?
РЕШЕНИЕ
139 Найдите значение выражения (13-9,5:3,8)· 0,3; (16,1:4,6-3,07)· 0,2; (1,3·2,8 + 1): 0,8; (3,7·2,3-5):0,3
РЕШЕНИЕ
140 На поверхности куба найдите кратчайший путь из точки А в точку C через точку B; из А в C, который пересекал бы все боковые ребра куба, кроме AC.
РЕШЕНИЕ
141 Разложите на простые множители числа 54; 65; 99; 162; 10 000; 1500; 7000; 3240; 4608.
РЕШЕНИЕ
142 Выполните действия
РЕШЕНИЕ
143 Два тракториста вспахали 12,32 га земли, причем один из них вспахал в 1,2 раза меньше другого. Сколько гектаров земли вспахал каждый тракторист?
РЕШЕНИЕ
144 Подставьте в таблицу подходящие натуральные значения x и y и сделайте выводы о четности или нечетности результата каждого действия.
РЕШЕНИЕ
145 Выполните действия (424,2 — 98,4): 3,6 · 0,9 + 9,1; (96,6+98,6): 6,4 · 1,2 — 0,2.
РЕШЕНИЕ
Урок 26. Простые числа. Разложение числа на простые множители
н. 879
879
Условие:
Решение:
Советы:
Внимательно читайте условие задания.
н.880
Условие:
Решение:
Советы:
Соседи числа — это число, которое предшествует этому числу при счете (предыдущее число), и число, которое при счёте следует за ним.
н.881
Условие:
Решение:
Советы:
Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".
н.882
Условие:
Решение:
Советы:
Внимательно читайте условие задания.
н.883
Условие:
Решение:
Советы:
Внимательно читайте условие задания.
н.884
Условие:
Решение:
Советы:
Трех последовательных натуральных чисел не существует.
н.885
Условие:
Решение:
Советы:
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми.
н. 886
886
Условие:
Решение:
Советы:
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго чисел плюс квадрат второго числа.
н.887
Условие:
Решение:
Советы:
Непростые натуральные числа, больше 1, называют составными числами.
н.888
Условие:
Решение:
Советы:
Вычитание — обратное сложению арифметическое действие, посредством которого от одной величины отнимается другая величина.
н.889
Условие:
Решение:
Советы:
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа и второго плюс утроенное произведение первого числа и квадрата второго плюс куб второго числа.
н.890
Условие:
Решение:
Советы:
Чтобы определить, делиться ли одно натуральное число на другое, можно это делимое число разложить на множители.
н.891
Условие:
Решение:
Советы:
Запомните: натуральные числа - те, которые используем при счете (когда нам необходимо посчитать людей или предметы). 
н.892
Условие:
Решение:
Советы:
Задача на нахождение суммы всегда решается действием сложения. Задача на нахождение остатка решается действием вычитания. знак "-"
н.893
Условие:
Решение:
Советы:
Разность квадратов двух чисел равно произведению суммы этих чисел и их разности.
н.894
Условие:
Решение:
Советы:
Решение а Случайное, так как выбранное число может быть и составным. Решение б Достоверное, так как все числа в множестве кратны 5. Решение в Случайное, так как выбранное число может и не делится на 10. Решение г Случайное, так как выбранное число может быть и простым.
н.895
Условие:
Решение:
Советы:
Не попал ни в простаки, ни в составники ученик, который родился 1−го числа.
н.896
Условие:
Решение:
Советы:
Любое число можно разложить на простые множители единственным способом.
н.897
Условие:
Решение:
Советы:
Натуральные числа не могут быть отрицательными.Поэтому натуральное число получаем, если мы из большего отнимаем меньшее, но не наоборот.
н.898
Условие:
Решение:
Советы:
Сантиметр (см) – единица измерения длины. Дециметр (дм) – более крупная единица измерения длины.1 дм = 10 см.
н.899
Условие:
Решение:
Советы:
10 единиц какого−либо разряда, дает 1 единицу более высокого разряда.
н.900
Условие:
Решение:
Советы:
Два действительных числа равны между собой, если они имеют одинаковые знаки и их абсолютные величины имеют одинаковые целые части и одинаковые цифры соответствующих разрядов.
н.901
Условие:
Решение:
Советы:
Умножение обратно делению и наоборот деление обратное умножению. Так как в примерах первое число сначала делится(умножается) на одно число и умножается(делится) на это же число, то решением уравнения будет первое число из выражения.
н.902
Условие:
Решение:
Советы:
Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности.
н.903
Условие:
Решение:
Советы:
Высота треугольника h при увеличении числа сторон многоугольника все меньше и меньше отличается от радиуса соответствующей окружности.
н.904
Условие:
Решение:
Советы:
Правила: от перемены местами множителей произведение не меняется; чтобы найти неизвестный множитель, нужно произведение разделить на известный множитель; чтобы найти неизвестное делимое, нужно частное умножить на делитель; чтобы найти неизвестный делитель, нужно делимое разделить на частное
н.905
Условие:
Решение:
Советы:
Рациональные числа − это числа, которые можно записать в виде десятичной периодической дроби.
н.906
Условие:
Решение:
Советы:
Иррациональные числа − это числа, которые можно записать в виде бесконечной десятичной непериодической дроби.
н.907
Условие:
Решение:
Советы:
Действительные числа − это все рациональные и иррациональные числа.
н.908
Условие:
Решение:
Советы:
Свойства многочленов: 1) Члены многочлена можно менять местами. 2) Прибавление к многочлену нуля или нулевого многочлена не изменят его. 3) В многочлене можно приводить подобные члены.
н.909
Условие:
Решение:
Советы:
Чтобы раскрыть скобки, перед которыми стоит знак "+", скобки можно опустить, не меняя знаки слагаемых в скобках.
н.910
Условие:
Решение:
Советы:
Чтобы раскрыть скобки, перед которыми стоит знак "−", скобки можно опустить, изменив знак каждого слагаемого в скобках, не противоположный. Чтобы заключить многочлен в скобки со знаком "+" перед ними, нужно записать в скобках все его члены с теми же знаками. Чтобы заключить многочлен в скобки со знаком "−" перед ними, нужно записать в скобках все его члены с противоположными знаками.
н.913
Условие:
Решение:
Советы:
Внимательно читайте условие задания.
н. 915
915
Условие:
Решение:
Советы:
Увеличить число на несколько единиц - использовать действие сложение, знак"+" Уменьшить на несколько единиц- использовать действие вычитание, знак "-".
н.916
Условие:
Решение:
Советы:
Внимательно читайте условие задания.
н.917
Условие:
Решение:
Советы:
Сумма, разность, произведение рациональных чисел является рациональным числом (без деления на нуль).
н.918
Условие:
Решение:
Советы:
Сложение — это математическое действие. Числа, которые складываются, называются слагаемыми.
н.919
Условие:
Решение:
Советы:
Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого и второго чисел плюс квадрат второго числа.
н.920
Условие:
Решение:
Советы:
Непростые натуральные числа, больше 1, называют составными числами.
н.921
Условие:
Решение:
Советы:
Вычитание — обратное сложению арифметическое действие, посредством которого от одной величины отнимается другая величина.
н.922
Условие:
Решение:
Советы:
Точно так же, выписав все простые числа в пределах от 1000 до 2000, можно доказать, что есть простые числа, выходящие за пределы второй тысячи, и т.д. Вывод: простых чисел бесконечно много
н.923
Условие:
Решение:
Советы:
Куб суммы двух чисел равен кубу первого числа плюс утроенное произведение квадрата первого числа и второго плюс утроенное произведение первого числа и квадрата второго плюс куб второго числа.
н.924
Условие:
Решение:
Советы:
Чтобы определить, делиться ли одно натуральное число на другое, можно это делимое число разложить на множители.
н.925
Условие:
Решение:
Советы:
Запомните: натуральные числа - те, которые используем при счете (когда нам необходимо посчитать людей или предметы).
н.926
Условие:
Решение:
Советы:
Задача на нахождение суммы всегда решается действием сложения.Задача на нахождение остатка решается действием вычитания. знак "-"
н.927
Условие:
Решение:
Советы:
Разность квадратов двух чисел равно произведению суммы этих чисел и их разности.
Алгоритм нахождения простых чисел / Хабр
Оптимизация алгоритма нахождения простых чисел
2 3 5 7 11 13 17 19 23 29 31… $250.000…
Дело было давно, в университете, когда мы начали изучать язык программирования Pascal и домашним заданием стало создание алгоритма нахождения простых чисел.
Алгоритм был придуман и тутже реализован на изучаемом языке. Программа запрашивала у пользователя число N и искала все простые числа до N включительно. После первого успешного теста сразу же возникло непреодолимое желание ввести N = «много». Программа работала, но не так быстро как хотелось бы. Естественно, дело было в многочисленных проверках (порядка N*N/2), поэтому пришлось избавиться от лишних. В итоге получилось 5 похожих алгоритмов каждый из которых работал быстре предыдущего. Недавно захотелось их вспомнить и реализовать, но на этот раз на Python.
Недавно захотелось их вспомнить и реализовать, но на этот раз на Python.
Итак, поехали. Первый алгоритм, ударивший в студенческую голову, продемонстрирован в Листинге 1.
# Листинг 1
# вводим N
n = input("n=")
# создаем пустой список для хранения простых чисел
lst = []
# в k будем хранить количество делителей
k = 0
# пробегаем все числа от 2 до N
for i in xrange(2, n+1):
# пробегаем все числа от 2 до текущего
for j in xrange(2, i):
# ищем количество делителей
if i % j == 0:
k = k + 1
# если делителей нет, добавляем число в список
if k == 0:
lst.append(i)
else:
k = 0
# выводим на экран список
print lst
Очень быстро понимаешь, что в подсчете делителей каждого числа нет никакой надобности и поэтому переменную k можно освободить от своих обязанностей. Действительно, если хотябы один делитель имеется, то число уже не простое. Смотрим Листинг 2.
# Листинг 2
n = input("n=")
lst = []
for i in xrange(2, n+1):
for j in xrange(2, i):
if i % j == 0:
# если делитель найден, число не простое. break
else:
lst.append(i)
print lst
break
else:
lst.append(i)
print lst
Конструкция break позволяет нам завершить выполнение внутреннего цикла и перейти к следующей итерации внешнего.
Далее возникает вопрос: «а зачем делить на 4, если на 2 число не делится?». Приходим к выводу, что искать делители нужно только среди простых чисел не превышающих делимое. Наш алгоритм превращается в… см. Листинг 3.
# Листинг 3
n = input("n=")
lst=[]
for i in xrange(2, n+1):
# пробегаем по списку (lst) простых чисел
for j in lst:
if i % j == 0:
break
else:
lst.append(i)
print lst
А потом вспоминаем теорию чисел и понимаем, что переберать надо только числа, не превосходящие корня из искомого. К примеру, если число M имеет делитель pi, то имеется делитель qi, такой, что pi * qi = M. То есть, чтобы найти пару, достаточно найти меньшее. Среди всех пар, предполагаемая пара с максимальным наименьшим — это пара с равными pi и qi, то есть pi * pi = M => pi = sqrt(M). Смотрим Листинг 4.
Смотрим Листинг 4.
# Листинг 4
from math import sqrt
n = input("n=")
lst=[]
for i in xrange(2, n+1):
for j in lst:
if j > int((sqrt(i)) + 1):
lst.append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
Код из Листинга 4 при N=10000 выполняется примерно в 1000 раз быстрее, чем самый первый вариант. Есть еще один «ускоритель», проверять только те числа, которые заканчиваются на 1, 3, 7 или 9 (так как остальные очевидно делятся на 2 или 5). Наблюдаем Листинг 5.
# Листинг 5
from math import sqrt
n = input("n=")
lst=[]
for i in xrange(2, n+1):
if (i > 10):
if (i%2==0) or (i%10==5):
continue
for j in lst:
if j > int((sqrt(i)) + 1):
lst.append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
В следствии незначительного изменения Листинга 5 получаем небольшую прибавку в скорости:
# Листинг 6
from math import sqrt
n = input("n=")
lst=[2]
for i in xrange(3, n+1, 2):
if (i > 10) and (i%10==5):
continue
for j in lst:
if j > int((sqrt(i)) + 1):
lst. append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
Итого: Программа из последнего листинга выполняется, примерно, в 1300 раз быстрее первоначального варианта.
Я не ставил перед собой задачи написать программу максимально быстро решающую данную задачу, это скорее демонстрация начинающим программистам того, что правильно составленный алгоритм играет далеко не последнюю роль в оптимизации Ваших программ.
P.S.
Благодаря замечаниям получаем Листинг 7:
# Листинг 7
n = input("n=")
lst=[2]
for i in xrange(3, n+1, 2):
if (i > 10) and (i%10==5):
continue
for j in lst:
if j*j-1 > i:
lst.append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
при N=10000, поучаем время:
time 1 = 26.24
time 2 = 3.113
time 3 = 0.413
time 4 = 0.096
time 5 = 0.087
time 6 = 0.083
time 7 = 0. 053
053
Решето Эратосфена:
# Листинг 8
n = input("n=")
a = range(n+1)
a[1] = 0
lst = []
i = 2
while i <= n:
if a[i] != 0:
lst.append(a[i])
for j in xrange(i, n+1, i):
a[j] = 0
i += 1
print lst
Результаты при n = 1 000 000:
time 7 = 7.088
time 8 = 1.143
С++. Задачи с решениями. Числа и циклы.
С++. Задачи с решениями. Числа и циклы.
- Составьте программу, выводящую на экран квадраты чисел от 10 до 20 включительно. Решение
- Даны натуральные числа от 35 до 87. Вывести на консоль те из них, которые при делении на 7 дают остаток 1, 2 или 5. Решение
- Найдите сумму , где число вводится пользователем с клавиатуры. Решение
- Найдите произведение цифр трехзначного числа. Решение
- Найдите количество четных цифр данного натурального числа. Решение
- Найдите наибольшую цифру данного натурального числа. Решение
- Найдите все четырехзначные числа, сумма цифр каждого из которых равна 15.
 Решение
Решение - Определите, является ли натуральное число простым. Таблица простых чисел Что такое простое число Решение
- Найдите все делители данного натурального числа. Решение
- Даны и . Вычислите без использования логарифма и экспоненты. Решение
- В последовательности целых чисел найдите минимальное число и количество его повторений. Решение
- На плоскости задан круг с центром в начале координат и набор точек. Его радиус, количество точек и их координаты вводятся с клавиатуры. Найдите точку вне круга, ближайшую к нему. Решение
- Вдоль координатной прямой размещены отрезков. Каждый отрезок задается координатами начала и конца и . Нужно найти какую-либо точку, принадлежащую всем отрезкам, или сообщить, что таких точек нет. Решение
- Отрезок последовательности целых чисел образует числа, идущие в ней подряд. Найдите номера чисел, которыми начинается и заканчивается отрезок с максимальной суммой, а также эту сумму. Решение
- Вам нужно разбить бронированные плиты на оборонной башне противника, которая в плане имеет вид -угольника.
 Для каждой стороны известно количество прикрывающих ее плит. Стрельба ведется из специальной двуствольной пушки — она ездит по рельсам вокруг башни и за один выстрел разбивает (по вашему желанию) или две плиты на одной стороне башни, или по одной плите на двух соседних сторонах. Найдите наименьшее число выстрелов, необходимых для разрушения всех плит.
Для каждой стороны известно количество прикрывающих ее плит. Стрельба ведется из специальной двуствольной пушки — она ездит по рельсам вокруг башни и за один выстрел разбивает (по вашему желанию) или две плиты на одной стороне башни, или по одной плите на двух соседних сторонах. Найдите наименьшее число выстрелов, необходимых для разрушения всех плит.
Вход. В первой строке текста — количество тестов , в каждой из следующих строк — тест. Тест задает число сторон и целых неотрицательных чисел — количества плит на сторонах. Решение - Стрелки часов движутся с постоянными угловыми скоростями и показывают часов минут. Найдите число полных минут до ближайшего момента, в который стрелки совпадут. Решение
- Строка состоит из клеток, пронумерованных от 1 до . Состояние клетки можно изменить — если она пуста, поставить в нее шашку (занять ее), иначе убрать из нее шашку (освободить ее). Вначале строка пуста. Нужно занять все клетки, соблюдая следующее правило.
 Изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Решение
Изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Решение - Разбить последовательность чисел от 1 до на подпоследовательностей так, чтобы все они состояли из чисел и имели равные суммы. Если решений несколько, то вывести любое из них. Решение
- Составить программу поиска всех решений ребуса VOLVO + FIAT = MOTOR. Разным буквам соответствуют разные цифры, одинаковым — одинаковые. Старшая цифра каждого числа отличается от нуля. Решение
- Каждое натуральное число , однозначно раскладывается в произведение простых сомножителей, например, , , . Разложите натуральное число на простые множители (факторизация числа). Решение
к списку задач
Метки задачи, циклы. Смотреть запись.
Нахождение простой факторизации с показателями — видео и расшифровка урока
Факторы
Когда мы объединяем два простых числа и перемножаем их, чтобы получить другое число, простые числа также называются факторами , числами, которые перемножаются вместе, чтобы получить другое число. Собственно, любые числа, которые умножаются на другие числа, называются множителями. Например, числа 2 и 3 в 2 * 3 называются множителями, потому что они перемножаются. В этом примере 2 и 3 также являются простыми числами.
Собственно, любые числа, которые умножаются на другие числа, называются множителями. Например, числа 2 и 3 в 2 * 3 называются множителями, потому что они перемножаются. В этом примере 2 и 3 также являются простыми числами.
Факторизация простых чисел
Что такое 2 * 3? Это 6. Итак, мы можем сказать, что 6 можно разбить на 2 * 3. Мы называем этот процесс простой факторизацией , разложением числа на простые числа, которые умножаются на исходное число. Например, простая факторизация числа 6 — это 2 * 3. Как только мы достигнем 2 * 3, мы не сможем двигаться дальше, потому что оба числа являются простыми числами.
Давайте рассмотрим пример. Каковы простые делители числа 12?
Используя разложение на простые множители, мы начнем с деления нашего числа на наименьший из возможных простых множителей.В данном случае это 2. Итак, делим 12 на 2; получаем 6. Можно ли еще разбить 6? Да, оно может. Мы также можем разделить 6 на 2; мы получаем 3. Итак, наши 12 теперь выглядят так: 12 = 2 * 2 * 3. Все эти числа теперь простые, так что мы закончили. Мы можем сказать, что простая факторизация числа 12 равна 2 * 2 * 3.
Все эти числа теперь простые, так что мы закончили. Мы можем сказать, что простая факторизация числа 12 равна 2 * 2 * 3.
Этот процесс похож на разборку чего-то вроде часов на все его мелкие компоненты. Как только мы доберемся до шестерёнок часов, мы закончим, так как мы больше не можем разбирать шестерёнки.
Попробуем еще. Каковы простые делители числа 15?
Начнем с деления наименьшего простого числа, которое сможем. В данном случае это 3. Мы можем разделить 15 на 3 и 5. Теперь у нас есть 15 = 3 * 5. Можем ли мы разбить любое из этих чисел, 3 или 5, дальше? Нет, потому что они оба простые. Это означает, что мы закончили. Таким образом, простая факторизация числа 15 равна 3 * 5.
Добавление показателей степени
Если наша простая факторизация приводит к тому, что одно и то же простое число появляется более одного раза, мы можем добавить показатели степени.Помните, что показатели степени говорят нам, сколько раз нужно умножить определенное число. Например, 23 означает, что мы умножаем 2 три раза (23 = 2 * 2 * 2). Для простой факторизации 12 мы можем добавить показатели и переписать нашу простую факторизацию с показателями следующим образом: 12 = 2 * 2 * 3 = 22 * 3.
Для простой факторизации 12 мы можем добавить показатели и переписать нашу простую факторизацию с показателями следующим образом: 12 = 2 * 2 * 3 = 22 * 3.
Итоги урока
Давайте повторим, что мы узнали. Простое число — это число, которое делится без остатка только на 1 или само на себя. Коэффициент — это число, которое умножается на другие числа, чтобы получить другое число. Разложение на простые множители — это разложение числа на простые числа, которые умножаются на исходное число. Например, разложение числа 12 на простые множители равно 2 * 2 * 3. Мы можем складывать показатели степени, когда одно и то же простое число встречается более одного раза. Таким образом, простую факторизацию числа 12 также можно записать как 22 * 3.
Результаты обучения
После того, как вы закончите этот урок, вы сможете:
- Вспомнить, что такое простые числа
- Разложить число на простые числа
- Использование показателей степени для выражения нескольких экземпляров фактора
Уникальная простая факторизация
То Фундаментальный
Теорема арифметики утверждает, что каждое натуральное число больше
1
можно записать как произведение
простые числа
, и это вверх
перестановке множителей это произведение уникальный . Это
называется основной
факторизация числа.
Это
называется основной
факторизация числа.
Пример:
36 можно записать как 6 × 6 , или 4 × 9 , или 3 × 12 , или 2 × 18 . Но есть только один способ записать его в виде произведения, где все множители простые:
36 знак равно 2 × 2 × 3 × 3
Это первичная факторизация 36 , часто записывается с показателями:
36 знак равно 2 2 × 3 2
Для простого числа, такого как
13
или
11
, первичная факторизация — это просто она сама. Любой составной число (то есть целое число с более чем двумя делителями) имеет нетривиальную простую факторизацию.
Любой составной число (то есть целое число с более чем двумя делителями) имеет нетривиальную простую факторизацию.
Первичную факторизацию числа можно найти с помощью дерево факторов . Начните с поиска двух множителей, которые при перемножении дают число. Продолжайте разбивать каждую ветвь дерева на пару множителей, пока все ветви не оканчиваются простыми числами.
Вот дерево факторов для 1386 .Мы начинаем с того, что замечаем, что 1386 четно, поэтому 2 является фактором. Деление на 2 , мы получили 1386 знак равно 2 × 693 , и мы исходим оттуда.
Это показывает, что первичная факторизация
1386
является
2
×
3
×
3
×
7
×
11
.
Вы можете использовать простые факторизации, чтобы выяснить ЗКФ s (наибольшие общие факторы), ЛКМ s (наименьшие общие кратные) и количество (и сумма) делители н .
| Метод 1: Дерево множителей Этот метод хорош тем, что вы можете начать с любого множителя, а не только с простых множителей. Затем вы продолжаете разветвляться до тех пор, пока у вас не останутся только простые множители. Вот пример: Мы можем начать с 45 х 10, потому что 45 х 10 = 450. Каждое число разветвляется на пару множителей. В конце ветвей у нас остаются простые множители 450. 450 = 2 x 3 2 x 5 2 Наиболее распространенная ошибка при использовании дерева множителей состоит в том, что некоторые люди выбирают числа, которые складываются для получения значения. Таким образом, простая факторизация числа 280 равна 2 3 х 5 х 7. Метод 2: Перевернутое деление Мы также можем поместить число в перевернутую черту деления, чтобы получить разложение на простые множители. Число находится внутри, а простые множители написаны снаружи. Мы разделим данное число на простое, чтобы получить другое новое число для деления. Этот шаг будет повторяться до тех пор, пока у вас не останется простое число. Вот пример. Из перевернутого деления у нас есть все простые множители. Итак, теперь мы можем написать простую факторизацию. 960 = 2 6 х 3 х 5 Если вам интересно, верна ли ваша простая факторизация, вы просто проверяете ее.Проверить свой ответ несложно. Все, что вам нужно сделать, это перемножить все простые числа и посмотреть, вернетесь ли вы к исходному числу. Здесь мы закончили там, где начали. Следовательно, наша простая факторизация числа 150 верна. Давайте посмотрим: Факторизация простых чисел — это произведение простых чисел, которые можно перемножить, чтобы получить исходное число. Два возможных способа получения списка простых чисел включают факторное дерево и перевернутое деление. Вы можете проверить правильность своего ответа, решив произведение простых чисел. |
Разложение числа на простые множители
Этот калькулятор найдет все простые множители заданного числа. Простая факторизация или целочисленная факторизация числа — это вычисление набора простых чисел, которые умножаются вместе, чтобы получить исходное целое число. Он также известен как первичное разложение.
Число 1 (один) называется единицей. У него нет простых множителей. Когда число является простым числом (т.е., 2,3,5,7, 11), простая факторизация — это просто простое число. Другие числа называются составными числами и имеют как минимум два простых делителя. Повторяю, простое число — это натуральное число, которое делится без остатка само на себя и на единицу, а не на другие натуральные числа.
Проблемы практики:
Проблемы практики:
27 = 3 × 3 × 3198 = 2 × 3 2 × 11
1024 = 2 10
19823 = 43 × 461
30258037 = 30258037
Слово Проблемы и примеры с участием простых номеров
- Сколько
Сколько различных прямоугольников с целыми длинами страниц имеют площадь S = 60 см²? - Земельный участок
Земельный участок, который имеет размеры 220 м и 308 м, собственник хочет разделить на равные квадратные участки максимально возможной площади.Какой длины будет одна сторона сюжета? - Простые множители
Запишем 98 как произведение простых множителей - Напоминание и частное
Даны числа A = 135, B = 315. Найдите наименьшее натуральное число R, большее 1, чтобы отношения R:A, R: Б с остатком 1. - Снеговик 2
На медальке, имеющей форму круга диаметром 18 см, нарисован снеговик таким образом, чтобы выполнялись следующие требования: 1. Снеговик состоит из трех кругов, 2. пространство над снеговиком такое же, как и под ним, 3. диаметры всех кругов выражают
пространство над снеговиком такое же, как и под ним, 3. диаметры всех кругов выражают - пример
пример шутливо для 6 класса по математике и я не знаю как объяснить дочке, когда не хочу использовать калькулятор для вычисления кубического корня. Таким образом: Из бруска моделина размером 16х18х48 мм был сделан прямоугольный параллелепипед. Каким будет край t - Квадратная комната
Каков размер самой маленькой квадратной комнаты, которую можно вымостить плиткой размером 55 см и 45 см? Сколько таких плиток нужно? - Напоминание и частное
Даны числа C = 281, D = 201.Найдите наибольшее натуральное число S так, чтобы C:S, D:S были с остатком 1, - Шаги
Петя делает шаги длиной 70 см, Джон 45 см. Через сколько метров их шаги встречаются? - Плитка
Задана площадь 5м х 4м. Размер одной плитки 40 х 40 см. Сколько плиток нужно на площади 5 м х 4 м? И сколько плиток нужно отрезать (если плитки не могут упасть ровно)? - Джон Смит
Джон Смит читает 435-страничный роман. Если он прочитает такое же количество страниц в день, и это число будет простым числом больше 10, сколько страниц в день он прочитает?
Если он прочитает такое же количество страниц в день, и это число будет простым числом больше 10, сколько страниц в день он прочитает? - Колышки
Из двух палочек длиной 240 см и 210 см необходимо вырезать максимально длинные колышки для цветов, чтобы не осталось остатков.Сколько будет колышков? - Апельсины
Мать разделила апельсины трех своих детей в соотношении 6:5:4. Двое детей дали 45 апельсинов. Сколько было апельсинов? - Группы
В 6 классе 60 девочек и 72 мальчика. Мы хотим разделить их на группы так, чтобы количество девочек и мальчиков было одинаковым. Сколько групп вы можете создать? Сколько девушек будет в группе? - Трамвайная остановка
На трамвайной остановке встречались трамваи №4 и №4. 5 в 10 утра. Трамвай №.4 ходит каждые 5 минут, трамвай №5 с интервалом 7 минут. Сколько раз встретимся до 12 часов? - Веревка
Веревку можно разрезать на куски одинаковой длины без остатка веревки. Длина может быть 15 см, 18 см или 25 см. Какова наименьшая возможная длина веревки?
Какова наименьшая возможная длина веревки?
другие математические задачи »
Калькулятор факторизации простых чисел
Введите целое число, чтобы найти его простые множители, а также дерево множителей.
Калькулятор связанных коэффициентов | Калькулятор общего множителя
Что такое простое число?
Простые числа — это натуральные числа (положительные целые числа, которые иногда включают 0 в некоторых определениях), которые больше 1 и не могут быть образованы путем умножения двух меньших чисел.Примером простого числа является 7, так как его можно получить только путем умножения чисел 1 и 7. Другие примеры включают 2, 3, 5, 11 и т. д.
Числа, которые можно составить из двух других натуральных чисел, больших 1, называются составными числами. Примеры этого включают такие числа, как 4, 6, 9 и т. д.
. Простые числа широко используются в теории чисел благодаря основной теореме арифметики. Эта теорема утверждает, что натуральные числа больше 1 либо простые, либо могут быть разложены на множители как произведение простых чисел. Например, число 60 можно разложить на произведение простых чисел следующим образом:
Например, число 60 можно разложить на произведение простых чисел следующим образом:
60 = 5 х 3 х 2 х 2
Как видно из примера выше, в факторизации нет составных чисел.
Что такое первичная факторизация?
Факторизация простых чисел — это разложение составного числа на произведение простых чисел. Существует множество алгоритмов факторинга, некоторые сложнее других.
Испытательный отдел:
Одним из методов нахождения простых множителей составного числа является пробное деление.Пробное деление — один из самых простых алгоритмов, хотя и очень утомительный. Он включает в себя проверку каждого целого числа путем деления рассматриваемого составного числа на целое число и определение того, может ли целое число делиться на целое число и сколько раз. В качестве простого примера ниже приведена простая факторизация числа 820 с использованием пробного деления:
.820 ÷ 2 = 410
410 ÷ 2 = 205
Поскольку 205 больше не делится на 2, проверьте следующие целые числа. 205 нельзя разделить на 3 без остатка.4 не простое число. Однако его можно разделить на 5:
205 нельзя разделить на 3 без остатка.4 не простое число. Однако его можно разделить на 5:
205 ÷ 5 = 41
Поскольку 41 — простое число, на этом пробное деление заканчивается. Таким образом:
820 = 41 × 5 × 2 × 2
Продукты также могут быть записаны как:
820 = 41 × 5 × 2 2
По сути, это метод «грубой силы» для определения простых множителей числа, и хотя 820 является простым примером, он может очень быстро стать гораздо более утомительным.
Первичное разложение:
Другой распространенный способ проведения простой факторизации называется простой декомпозицией и может включать использование факторного дерева.Создание дерева множителей включает в себя разбиение составного числа на множители составного числа, пока все числа не станут простыми. В приведенном ниже примере простые множители находятся путем деления 820 на простой множитель 2 с последующим делением результата до тех пор, пока все множители не станут простыми. Пример ниже демонстрирует два способа создания дерева факторов с использованием числа 820:
Пример ниже демонстрирует два способа создания дерева факторов с использованием числа 820:
Таким образом, можно видеть, что простая факторизация числа 820 в любом случае снова равна:
820 = 41 × 5 × 2 × 2
Хотя эти методы работают для меньших чисел (и существует много других алгоритмов), не существует известного алгоритма для гораздо больших чисел, и даже машинам может потребоваться много времени, чтобы вычислить простые факторизации больших чисел; В 2009 году ученые завершили проект с использованием сотен машин для факторизации 232-значного числа RSA-768, и на это ушло два года.
Разложение простых чисел на простые множители
Ниже приведены простые факторизации некоторых обычных чисел.
Простая факторизация 2: простое число
Разложение числа 3 на простые множители: простое число
Разложение числа 4 на простые множители: 2 2
Разложение 5 на простые множители: простое число
Разложение числа 6 на простые множители: 2 × 3
Простая факторизация 7: простое число
Разложение числа 8 на простые множители: 2 3
Разложение числа 9 на простые множители: 3 2
Разложение числа 10 на простые множители: 2 × 5
Разложение 11 на простые множители: простое число
Разложение числа 12 на простые множители: 2 2 × 3
Разложение числа 13 на простые множители: простое число
Разложение числа 14 на простые множители: 2 × 7
Разложение числа 15 на простые множители: 3 × 5
Разложение числа 16 на простые множители: 2 4
Разложение числа 17 на простые множители: простое число
Разложение числа 18 на простые множители: 2 × 3 2
Разложение числа 19 на простые множители: простое число
Разложение числа 20 на простые множители: 2 2 × 5
Разложение числа 21 на простые множители: 3 × 7
Разложение числа 22 на простые множители: 2 × 11
Разложение числа 23 на простые множители: простое число
Разложение числа 24 на простые множители: 2 3 × 3
Разложение числа 25 на простые множители: 5 2
Разложение числа 26 на простые множители: 2 × 13
Разложение числа 27 на простые множители: 3 3
Разложение числа 28 на простые множители: 2 2 × 7
Разложение числа 29 на простые множители: простое число
Разложение числа 30 на простые множители: 2 × 3 × 5
Разложение числа 31 на простые множители: простое число
Разложение числа 32 на простые множители: 2 5
Разложение числа 33 на простые множители: 3 × 11
Разложение числа 34 на простые множители: 2 × 17
Разложение числа 35 на простые множители: 5 × 7
Разложение числа 36 на простые множители: 2 2 × 3 2
Разложение числа 37 на простые множители: простое число
Разложение числа 38 на простые множители: 2 × 19
Разложение числа 39 на простые множители: 3 × 13
Разложение числа 40 на простые множители: 2 3 × 5
Разложение числа 41 на простые множители: простое число
Разложение числа 42 на простые множители: 2 × 3 × 7
Разложение числа 43 на простые множители: простое число
Разложение числа 44 на простые множители: 2 2 × 11
Разложение числа 45 на простые множители: 3 2 × 5
Разложение числа 46 на простые множители: 2 × 23
Разложение числа 47 на простые множители: простое число
Разложение числа 48 на простые множители: 2 4 × 3
Разложение числа 49 на простые множители: 7 2
Разложение числа 50 на простые множители: 2 × 5 2
Разложение числа 51 на простые множители: 3 × 17
Разложение числа 52 на простые множители: 2 2 × 13
Разложение числа 53 на простые множители: простое число
Разложение числа 54 на простые множители: 2 × 3 3
Разложение числа 55 на простые множители: 5 × 11
Разложение числа 56 на простые множители: 2 3 × 7
Разложение числа 57 на простые множители: 3 × 19
Разложение числа 58 на простые множители: 2 × 29
Разложение числа 59 на простые множители: простое число
Разложение числа 60 на простые множители: 2 2 × 3 × 5
Разложение числа 61 на простые множители: простое число
Разложение числа 62 на простые множители: 2 × 31
Разложение числа 63 на простые множители: 3 2 × 7
Разложение числа 64 на простые множители: 2 6
Разложение числа 65 на простые множители: 5 × 13
Разложение числа 66 на простые множители: 2 × 3 × 11
Разложение числа 67 на простые множители: простое число
Разложение числа 68 на простые множители: 2 2 × 17
Разложение числа 69 на простые множители: 3 × 23
Разложение числа 70 на простые множители: 2 × 5 × 7
Разложение числа 71 на простые множители: простое число
Разложение числа 72 на простые множители: 2 3 × 3 2
Разложение числа 73 на простые множители: простое число
Разложение числа 74 на простые множители: 2 × 37
Разложение числа 75 на простые множители: 3 × 5 2
Разложение числа 76 на простые множители: 2 2 × 19
Разложение числа 77 на простые множители: 7 × 11
Разложение числа 78 на простые множители: 2 × 3 × 13
Разложение числа 79 на простые множители: простое число
Разложение числа 80 на простые множители: 2 4 × 5
Разложение числа 81 на простые множители: 3 4
Разложение числа 82 на простые множители: 2 × 41
Разложение числа 83 на простые множители: простое число
Разложение числа 84 на простые множители: 2 2 × 3 × 7
Разложение числа 85 на простые множители: 5 × 17
Разложение числа 86 на простые множители: 2 × 43
Разложение числа 87 на простые множители: 3 × 29
Разложение числа 88 на простые множители: 2 3 × 11
Разложение числа 89 на простые множители: простое число
Разложение числа 90 на простые множители: 2 × 3 2 × 5
Разложение числа 91 на простые множители: 7 × 13
Разложение числа 92 на простые множители: 2 2 × 23
Разложение числа 93 на простые множители: 3 × 31
Разложение числа 94 на простые множители: 2 × 47
Разложение числа 95 на простые множители: 5 × 19
Разложение числа 96 на простые множители: 2 5 × 3
Разложение числа 97 на простые множители: простое число
Разложение числа 98 на простые множители: 2 × 7 2
Разложение числа 99 на простые множители: 3 2 × 11
Разложение числа 100 на простые множители: 2 2 × 5 2
Разложение числа 101 на простые множители: простое число
Разложение числа 102 на простые множители: 2 × 3 × 17
Разложение числа 103 на простые множители: простое число
Разложение числа 104 на простые множители: 2 3 × 13
Разложение числа 105 на простые множители: 3 × 5 × 7
Разложение числа 106 на простые множители: 2 × 53
Разложение числа 107 на простые множители: простое число
Разложение числа 108 на простые множители: 2 2 × 3 3
Разложение числа 109 на простые множители: простое число
Разложение числа 110 на простые множители: 2 × 5 × 11
Разложение числа 111 на простые множители: 3 × 37
Разложение числа 112 на простые множители: 2 4 × 7
Разложение числа 113 на простые множители: простое число
Разложение числа 114 на простые множители: 2 × 3 × 19
Разложение числа 115 на простые множители: 5 × 23
Разложение числа 116 на простые множители: 2 2 × 29
Разложение числа 117 на простые множители: 3 2 × 13
Разложение числа 118 на простые множители: 2 × 59
Разложение числа 119 на простые множители: 7 × 17
Разложение числа 120 на простые множители: 2 3 × 3 × 5
Разложение числа 121 на простые множители: 11 2
Разложение числа 122 на простые множители: 2 × 61
Разложение числа 123 на простые множители: 3 × 41
Разложение числа 124 на простые множители: 2 2 × 31
Разложение числа 125 на простые множители: 5 3
Разложение числа 126 на простые множители: 2 × 3 2 × 7
Разложение числа 127 на простые множители: простое число
Разложение числа 128 на простые множители: 2 7
Разложение числа 129 на простые множители: 3 × 43
Разложение числа 130 на простые множители: 2 × 5 × 13
Разложение числа 131 на простые множители: простое число
Разложение числа 132 на простые множители: 2 2 × 3 × 11
Разложение числа 133 на простые множители: 7 × 19
Разложение числа 134 на простые множители: 2 × 67
Разложение числа 135 на простые множители: 3 3 × 5
Разложение числа 136 на простые множители: 2 3 × 17
Разложение числа 137 на простые множители: простое число
Разложение числа 138 на простые множители: 2 × 3 × 23
Разложение числа 139 на простые множители: простое число
Разложение числа 140 на простые множители: 2 2 × 5 × 7
Разложение числа 141 на простые множители: 3 × 47
Разложение числа 142 на простые множители: 2 × 71
Разложение числа 143 на простые множители: 11 × 13
Разложение числа 144 на простые множители: 2 4 × 3 2
Разложение числа 145 на простые множители: 5 × 29
Разложение числа 146 на простые множители: 2 × 73
Разложение числа 147 на простые множители: 3 × 7 2
Разложение числа 148 на простые множители: 2 2 × 37
Разложение числа 149 на простые множители: простое число
Разложение числа 150 на простые множители: 2 × 3 × 5 2
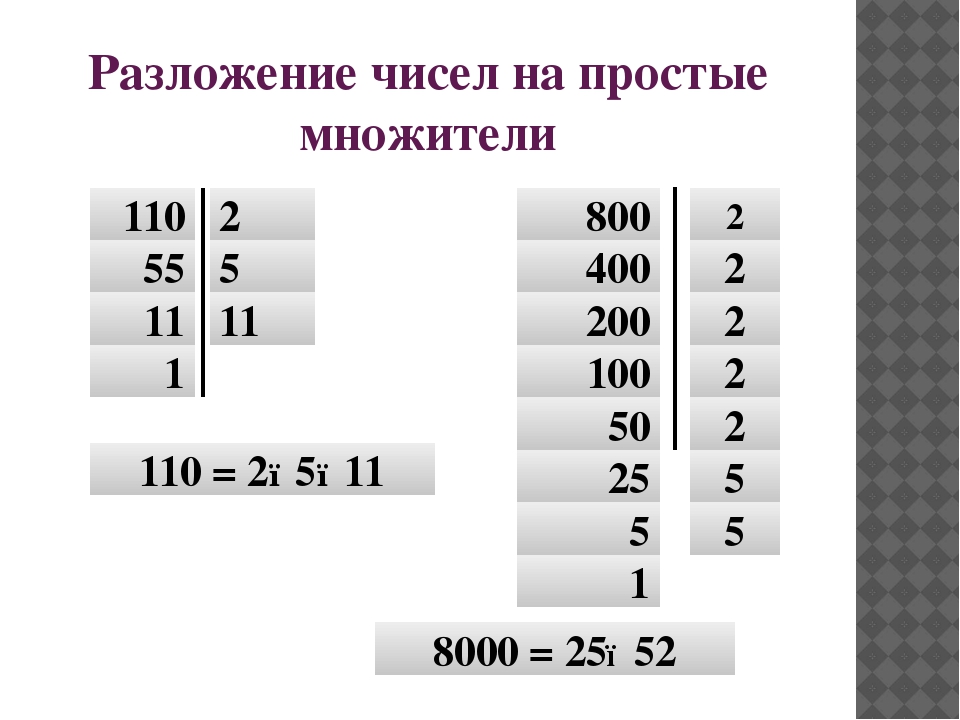
Разложение числа 200 на простые множители: 2 3 × 5 2
Разложение числа 300 на простые множители: 2 2 × 3 × 5 2
Разложение числа 400 на простые множители: 2 4 × 5 2
Разложение числа 500 на простые множители: 2 2 × 5 3
Разложение числа 600 на простые множители: 2 3 × 3 × 5 2
Разложение числа 700 на простые множители: 2 2 × 5 2 × 7
Разложение числа 800 на простые множители: 2 5 × 5 2
Разложение числа 900 на простые множители: 2 2 × 3 2 × 5 2
Разложение числа 1000 на простые множители: 2 3 × 5 3
Что значит записать простую факторизацию числа? – Кухня
Разложение на простые множители — это способ выражения числа в виде произведения его простых множителей . Простое число — это число, которое имеет ровно два делителя: 1 и само число. Число 6 выражается как 2 × 3, так как 3 и 2 — простые числа. Таким образом, простая факторизация числа 30 равна 2 × 3 × 5,
Простое число — это число, которое имеет ровно два делителя: 1 и само число. Число 6 выражается как 2 × 3, так как 3 и 2 — простые числа. Таким образом, простая факторизация числа 30 равна 2 × 3 × 5,
Как записать простую факторизацию числа?
Как записать простую факторизацию составных чисел
- Поместите простой множитель снаружи слева, а результат или частное (количество раз, когда оно делится без остатка) под ним.
- Разделите частное (число внизу) на другое простое число и продолжайте делать это до тех пор, пока нижнее число не станет простым.
Как записать простую факторизацию числа 50?
Коэффициенты 50
- Коэффициенты 50: 1, 2, 5, 10, 25, 50.
- Простая факторизация числа 50: 2 × 5 × 5.
Какова простая факторизация числа 72?
Например, мы можем записать число 72 как произведение простых множителей: 72 = 2 3 ⋅ 3 2. Говорят, что выражение 2 3 ⋅ 3 2 представляет собой простую факторизацию числа 72.
Какова простая факторизация числа 123456789?
Разложение числа 123 456 789 на простые множители равно 3 2 × 3607 × 3803.Поскольку у него всего 4 простых делителя, 123 456 789 — составное число.
Какова простая факторизация числа 3825?
, поэтому 3, 5, 17 — простые множители.
Какова простая факторизация числа 84?
Делители числа 84 — это целые числа, которые можно без остатка разделить на 84. Всего 12 делителей, из которых 84 — самый большой делитель, а простые делители числа 84 — 2, 3 и 7. Простые делители числа 84 равны 2 2 × 3 × 7,
Какова простая факторизация числа 50 с использованием показателей степени?
10×5 =50.
Каковы все простые числа для числа 50?
Простые числа от 1 до 50 равны 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43 и 47.
Какова простая факторизация чисел 50 и 60?
Разложение чисел 50 и 60 на простые множители равно (2 × 5 × 5) и (2 × 2 × 3 × 5) соответственно. Как видно, числа 50 и 60 имеют общие простые делители. Следовательно, GCF 50 и 60 равен 2 × 5 = 10,
.Сколько простых делителей у числа 72?
Делители 72 — это список целых чисел, которые можно без остатка разделить на 72.Всего есть 12 множителей из 72, среди которых 72 — самый большой множитель, а 2 и 3 — его простые множители. Сумма всех множителей числа 72 равна 195.
Какова простая факторизация числа 72 в экспоненциальной форме?
Разложение числа 72 на простые множители в экспоненциальной форме равно 23 × 32.
Как написать 123456789?
Примечания
- ( BrE ) сто двадцать три миллиона четыреста пятьдесят шесть тысяч семьсот восемьдесят девятый.
- ( AmE ) сто двадцать три миллиона четыреста пятьдесят шесть тысяч семьсот восемьдесят девятый.

Сколько простых чисел меньше 100?
Итак, всего существует 25 простых чисел до 100. Следовательно, простые числа от 1 до 100 могут быть перечислены как 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.
Что такое HCF 21 и 35?
GCF 21 и 35 путем перечисления общих множителей. Существует 2 общих множителя 21 и 35, то есть 1 и 7.Следовательно, наибольший общий делитель 21 и 35 равен 7,
.2.10: Факторизация простых чисел и наименьшее общее кратное (часть 2)
Одной из причин, по которой мы рассматриваем кратные и простые числа, является использование этих методов для нахождения наименьшего общего кратного двух чисел. Это будет полезно, когда мы будем складывать и вычитать дроби с разными знаменателями.
Метод кратных листингов
Общее кратное двух чисел — это число, кратное обоим числам.Предположим, мы хотим найти общие кратные 10 и 25. Мы можем перечислить первые несколько кратных каждого числа. Затем мы ищем кратные, общие для обоих списков — это общие кратные.
Затем мы ищем кратные, общие для обоих списков — это общие кратные.
\[\begin{split} 10 & \двоеточие \; 10, 20, 30, 40, \textbf{50}, 60, 70, 80, 90, \textbf{100}, 110, \ldots \\ 25 & \двоеточие \; 25, \textbf{50}, 75, \textbf{100}, 125, \ldots \end{split} \nonumber \]
Мы видим, что \(50\) и \(100\) есть в обоих списках. Они являются общими кратными \(10\) и \(25\).Мы бы нашли больше общих кратных, если бы продолжили список кратных для каждого.
Наименьшее число, кратное двум числам, называется наименьшим общим кратным (НОК). Таким образом, наименьший НОК из \(10\) и \(25\) равен \(50\).
КАК: НАЙТИ НАИМЕНЬШУЮ ОБЩУЮ КРАСТНУЮ (НОК) ДВУХ ЧИСЕЛ ПО ПЕРЕЧИСЛЕНИЮ КРАСТНЫХ
Шаг 1. Перечислите первые несколько кратных каждого числа.
Шаг 2. Найдите кратные, общие для обоих списков. Если в списках нет общих кратных, выпишите дополнительные кратные для каждого числа.
Шаг 3. Найдите наименьшее число, общее для обоих списков.
Шаг 4. Этот номер является LCM.
Пример \(\PageIndex{5}\): lcm
Найдите НОК чисел \(15\) и \(20\), перечислив кратные.
Раствор
Выведите несколько первых кратных \(15\) и \(20\). Найдите первое общее кратное.
\[\begin{split}15 & \двоеточие\; 15, 30, 45, \textbf{60}, 75, 90, 105, 120 \\ 20 & \двоеточие\; 20, 40, \textbf{60}, 80, 100, 120, 140, 160 \end{split} \nonumber\]
Наименьшее число, встречающееся в обоих списках, равно \(60\), поэтому \(60\) является наименьшим общим кратным чисел \(15\) и \(20\).Обратите внимание, что \(120\) также присутствует в обоих списках. Это общее кратное, но не наименьшее общее кратное.
Упражнение \(\PageIndex{9}\)
Найдите наименьшее общее кратное (НОК) данных чисел: \(9\) и \(12\)
- Ответить
\(36\)
Упражнение \(\PageIndex{10}\)
Найдите наименьшее общее кратное (НОК) данных чисел: \(18\) и \(24\)
- Ответить
\(72\)
Метод простых факторов
Другой способ найти наименьшее общее кратное двух чисел — использовать их простые делители. Мы будем использовать этот метод, чтобы найти LCM \(12\) и \(18\).
Мы будем использовать этот метод, чтобы найти LCM \(12\) и \(18\).
Начнем с нахождения простой факторизации каждого числа.
\[12 = 2 \cdot 2 \cdot 3 \qquad \qquad 18 = 2 \cdot 3 \cdot 3 \nonnumber\]
Затем мы записываем каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.
\[\begin{split} 12 & = 2 \cdot 2 \cdot 3 \\ 18 & = 2 \cdot \quad \; 3 \cdot 3 \end{split} \nonumber \]
Теперь выведем простые числа в каждом столбце.LCM является продуктом этих факторов.
Обратите внимание, что простые множители \(12\) и простые множители \(18\) включены в LCM. При сопоставлении общих простых чисел каждый общий простой множитель используется только один раз. Это гарантирует, что \(36\) является наименьшим общим кратным.
КАК: НАЙТИ LCM, ИСПОЛЬЗУЯ МЕТОД ПРАЙМ-ФАКТОРОВ
Шаг 1. Найдите простую факторизацию каждого числа.
Шаг 2. Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали.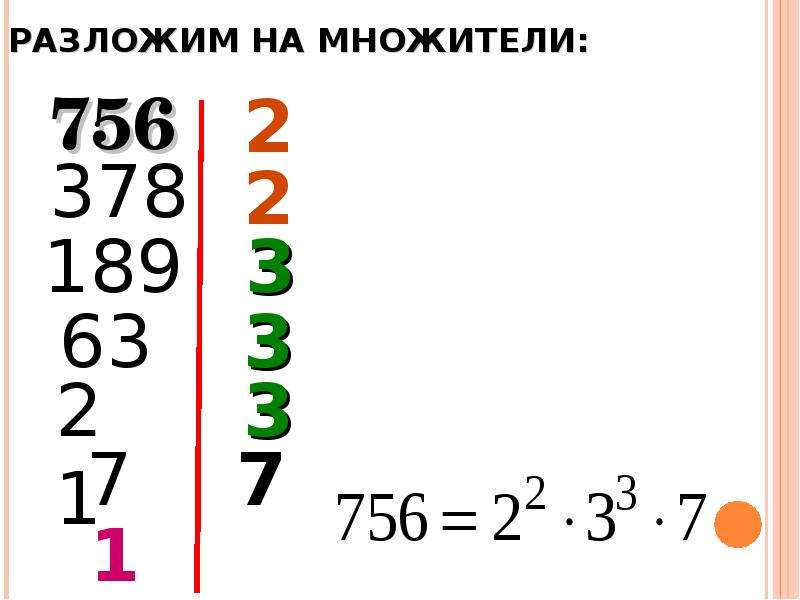
Шаг 3. Опустите простые числа в каждом столбце.
Шаг 4. Перемножьте коэффициенты, чтобы получить LCM.
Пример \(\PageIndex{6}\): lcm
Найдите НОК чисел \(15\) и \(18\), используя метод простых множителей.
Раствор
| Запишите каждое число как произведение простых чисел. | \(15 = 3 \cdot 5 \qquad \qquad 18 = 2 \cdot 3 \cdot 3\) |
| Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали. | \(\begin{split} 15 & = \quad \; 3 \cdot \qquad 5 \\ 18 & = 2 \cdot 3 \cdot 3 \end{split}\) |
| Сократите простые числа в каждом столбце. | |
| Умножьте множители, чтобы получить LCM. | НОК = 2 • 3 • 3 • 5 LCM 15 и 18 равен 90. |
Упражнение \(\PageIndex{11}\)
Найдите LCM методом простых множителей: \(15\) и \(20\)
- Ответить
\(60\)
Упражнение \(\PageIndex{12}\)
Найдите LCM методом простых множителей: \(15\) и \(35\)
- Ответить
\(105\)
Пример \(\PageIndex{7}\): lcm
Найдите НОК для \(50\) и \(100\), используя метод простых множителей.
Раствор
| Напишите простую факторизацию каждого числа. | \(50 = 2 \cdot 5 \cdot 5 \qquad 100 = 2 \cdot 2 \cdot 5 \cdot 5\) |
| Запишите каждое число как произведение простых чисел, по возможности сопоставляя простые числа по вертикали. | \(\begin{split} 50 & = \quad \; 2 \cdot 5 \cdot 5 \\ 100 & = 2 \cdot 2 \cdot 5 \cdot 5 \end{split}\) |
| Сократите простые числа в каждом столбце. | |
| Умножьте множители, чтобы получить LCM. | НОКМ = 2 • 2 • 5 • 5 НОК 50 и 100 равен 100. |
Упражнение \(\PageIndex{13}\)
Найдите LCM методом простых множителей: \(55, 88\)
- Ответить
\(440\)
Упражнение \(\PageIndex{14}\)
Найдите НОК методом простых множителей: \(60, 72\)
- Ответить
\(360\)

 Поэтому натуральное число получаем, если мы из большего отнимаем меньшее, но не наоборот.
Поэтому натуральное число получаем, если мы из большего отнимаем меньшее, но не наоборот.



 Задача на нахождение остатка решается действием вычитания. знак "-"
Задача на нахождение остатка решается действием вычитания. знак "-"
 break
else:
lst.append(i)
print lst
break
else:
lst.append(i)
print lst
 append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
append(i)
break
if (i % j == 0):
break
else:
lst.append(i)
print lst
 Решение
Решение Для каждой стороны известно количество прикрывающих ее плит. Стрельба ведется из специальной двуствольной пушки — она ездит по рельсам вокруг башни и за один выстрел разбивает (по вашему желанию) или две плиты на одной стороне башни, или по одной плите на двух соседних сторонах. Найдите наименьшее число выстрелов, необходимых для разрушения всех плит.
Для каждой стороны известно количество прикрывающих ее плит. Стрельба ведется из специальной двуствольной пушки — она ездит по рельсам вокруг башни и за один выстрел разбивает (по вашему желанию) или две плиты на одной стороне башни, или по одной плите на двух соседних сторонах. Найдите наименьшее число выстрелов, необходимых для разрушения всех плит. Изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Решение
Изменение клетки допустимо, если она имеет номер 1 или расположена непосредственно после занятой клетки, имеющей минимальный номер среди занятых клеток. Решение 2) 27 = 3 x 3 x 3 = 3 3 (Мы не хотим писать 3 x 9, потому что 9 не простое число.)
2) 27 = 3 x 3 x 3 = 3 3 (Мы не хотим писать 3 x 9, потому что 9 не простое число.)

 пространство над снеговиком такое же, как и под ним, 3. диаметры всех кругов выражают
пространство над снеговиком такое же, как и под ним, 3. диаметры всех кругов выражают Если он прочитает такое же количество страниц в день, и это число будет простым числом больше 10, сколько страниц в день он прочитает?
Если он прочитает такое же количество страниц в день, и это число будет простым числом больше 10, сколько страниц в день он прочитает? Какова наименьшая возможная длина веревки?
Какова наименьшая возможная длина веревки?