Решение систем уравнений способом подстановки.
1. Ф.И.О. учителя: ____Ткачук Наталья Петровна _________________________________________________________________________________________________
2. Класс: _8 Дата: .11.03________Предмет_-математика , №71 урока по расписанию:
3. Тема урока Решение систем способом подстановки 4. Место и роль урока в изучаемой теме:. Урок закрепления знаний. Цель урока:
Образовательная: развить знания решения систем уравнений способом подстановки. Знать/понимать: если графики имеют общие точки, то система имеет решения; если у графиков нет общих точек, то система решений не имеет; алгоритм решения систем уравнений. Уметь решать системы способом подстановки Содействовать развитию умений применять полученные знания в нестандартных (типовых) условиях Развивающая: Способствовать развитию умений учащихся обобщать полученные знания, проводить анализ, синтез, сравнения, делать необходимые выводы. Содействовать развитию умений применять полученные знания в нестандартных и типовых условиях.
Характеристика этапов урока
Деятельностьучеников
Самоопределение.
3
Активизировать познавательную активность
Решить систему
словесный
Фронтальная
Приветствие учащихся. проведение. Создание ситуации готовности к уроку, успеха на предстоящем уроке.
Проверяют готовность к уроку.
2.Актуализация знаний .
7
Выявить качество и уровень овладения знаниями и умениями, полученными на предыдущих уроках по теме
Выяснить, является ли пара чисел решением системы. х=5 у=9
Какие операции можно производить с уравнениями?
( умножать обе части уравнения на одно и тоже число, делить на число не равное нулю ….)
Работа в группе
Фронтальная. Гупповая-разбор алгоритмов решения задач;
При необходимости задает наводящие вопросы.
Отвечают на поставленные вопросы.
3.Постановка учебной задачи, целей урока.
1
Формирование
и развитие умения
определять и формулировать
проблему, цель и тему
для изучения линий
Как решается система уравнений способом сложения, способом подстановки.
Какой способ целесообразно применить при решении. данной системы?
,,
Работа в группе.
Индивидуальная.
Фронтальная.
Какие действия мы проделали, чтобы узнать стоимость покупки?
Какую тему мы будем изучать?
Побуждает к высказыванию своего мнения.
Высказываются.
4. Этап актуализации знаний по теме
20
Содействовать развитию умений различать и сопоставлять линии. Обеспечить условия для развития умений грамотно, чётко и точно выражать свои мысли.
№ 621
Выяснить взаимное расположение прямых
2х+0.5у= 1,2 и х- 4у=0
Можно ли определить пересекаются прямые или нет по их коэффициентам?
2. составь уравнения прямых которые параллельны между собой.
Работа с учнбником
Работа в парах с самопроверкой
Фронтальная, индивидуальная. практикум по решению задач
При необходимости задает наводящие вопросы . Проводит параллель с ранее изученным материалом.
Обеспечивает мотивацию выполнения предложенных задач.
Подводит обучающихся к выводу о существованию формул.
Решают задачи , отвечают на вопросы учителя при необходимости Выполняют упражнение в тетради.
По очереди комментируют, анализируют, определяют причины и способы решения.
5.Работа по самостоятельному
применению полученных знаний. Актуализация знаний и умений в решении задач.
7
Формирование и развитие умений чтения чисел.Планирование своей деятельности для решения поставленной задачи, контроль полученного результата, коррекция полученного результата, само регуляция
1 вар –
2 вар
Самостоятельная работа. Проверка соседа.
«мозговой штурм»,
Контролирует выполнение работы.
Осуществляет: индивидуальный контроль; выборочный контроль.
Побуждает к высказыванию своего мнения.
Решают задачи. Осуществляют: самооценку;взаимопроверку; выставляют предварительную оценку.
6.Оценка урока, самооценка.
3
Формирование и развитие умения анализировать и осмысливать свои достижения.
Умение определять уровень овладения учебным материалом .
Оценка промежуточных результатов и само регуляция для повышения мотивации учебной деятельности
Оценка на каждом этапе
1. умеешь ли ты строить графики линейных уравнений?
2.Умеешь ли ты определять, пересекаются они или нет.
3.знаешь ли ты алгоритм решения систем уравнений?
4. какие способы ты знаешь решения систем уравнений?
Работа в группе.
Групповая и индивидуальная..
Побуждает к высказыванию своего мнения.
Осуществляют: самооценку и оценку товарища.
7.Итоги урока. Домашнее задание.
4
Умение соотносить цели и результаты собственной дея-тельности. Под-держание здоро-вого духа сопер-ничества для под-держания мотива-ции учебной дея-тельности; участие в коллективном обсуждении проблем.
п п. 4.4 №623
Работа в группе.
Фронтальная-Выделение и формулиров-ание поз-навательной цели рефлексия способов и условий действия
Анализ и синтез объектов
Побуждает к высказыванию своего мнения.
Дает комментарий к домашнему заданию; задание на поиск в тексте особенностей…
Дети участвуют в дискуссии, анализируют, проговаривают. Осмысливают и фиксируют свои достижения.
-Сегодня на уроке я узнал…
-сегодня на уроке я научился…
«Решение систем уравнений способом подстановки» (7 класс)
Урок №Тема: «Решение систем линейных уравнений способом подстановки».
Цель урока:
— обучающие: ввести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки;
Этапы урока:
№
Этап урока
Время
Задачи этапа
1.
Организационный момент
1 мин.
2.
Проверка домашнего задания
3 мин.
Проверка правильности выполнения домашнего задания.
3.
Актуализация опорных знаний учащихся
5 мин.
Повторить основные определения; активизировать осознанность применения знаний при решении задач.
4.
Изучение нового материала
15 мин.
Знакомство учащихся с алгоритмом решения системы двух уравнений с двумя переменными методом подстановки (обратить внимание на оформление решений)
6.
Закрепления изученного материала
15 мин.
Сформировать умение решать системы уравнений методом подстановки
7.
Подведение итогов
4 мин.
Повторить изученное на уроке
8.
Домашнее задание
2 мин.
Инструктаж по домашнему заданию
Ход урока.
Этап №1
Слайд №1.
Приготовились к уроку, встали у своих мест.
-Здравствуйте, ребята. Сегодня у нас на уроке присутствуют гости, поздоровайтесь, пожалуйста, садитесь.
Слайд №2
Мы с вами начинаем очередной рабочий урок и эпиграфом к нему я подобрала следующее высказывание И. Гёте: «Настоящий ученик умеет выводить известное из неизвестного и этим приближается к учителю». Так вот мы с вами сегодня будем пытаться стать настоящими учениками, чтобы хоть чуть-чуть почувствовать себя учителем.
Цель нашего урока – это вывести алгоритм решения системы двух линейных уравнений с двумя переменными способом подстановки, сформировать умение решать системы двух линейных уравнений с двумя переменными способом подстановки.
Этап№2
На прошлом уроке мы с вами познакомились с новой математической моделью.
Эта математическая модель представляет собой систему двух линейных уравнений с двумя переменными. Перед нами стояла задача найти такие пары значений (х; у), которые одновременно удовлетворяют и первому, и второму уравнению.
-Кто может мне сказать:
Что называется решением системы двух линейных уравнений с двумя переменными?
Слайд№3. (открыть после ответа уч-ся).
—Хорошо.
-А что значит решить систему двух линейных уравнений с двумя переменными?
Слайд №4. (открыть после ответа уч-ся).
-Ребята! Скажите мне, пожалуйста, а как назывался метод решения системы, которым мы пользовались на прошлых уроках и в домашнем задании? (Ответ: графический метод).
Проверим домашнее задание.

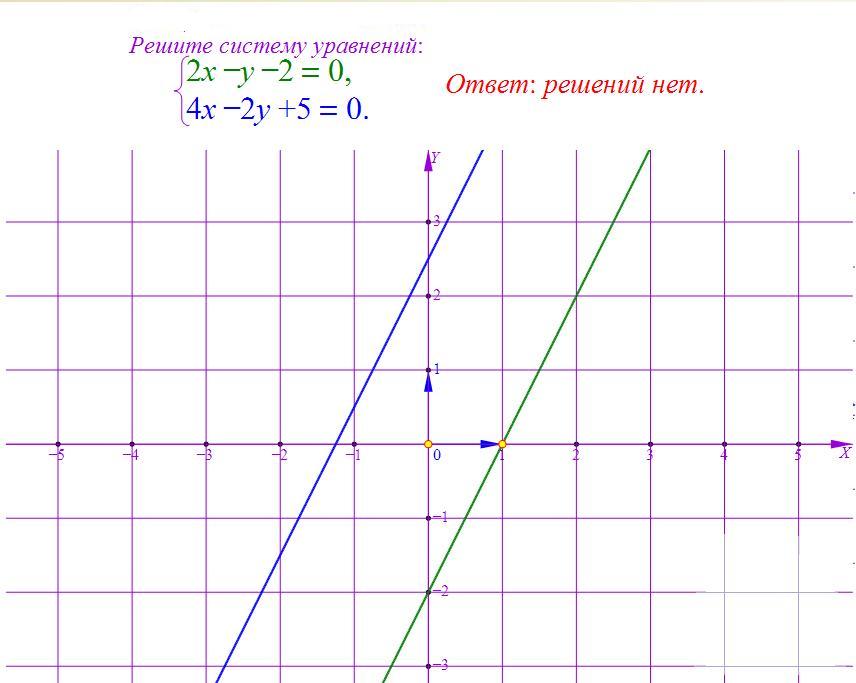
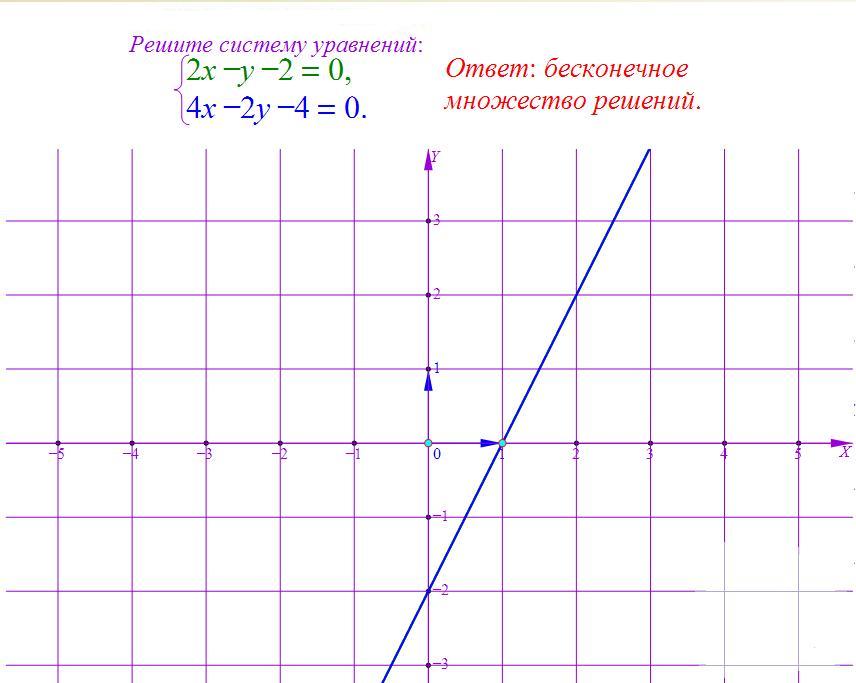
—Пока мы будем проверять домашнее задание, у доски нам решит систему графическим методом…(вызвать ученика к доске, задание на карточке).
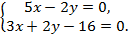
Открыли тетради, взяли зеленую пасту, проверяем:
Слайды №5, №6, №7, №8, №9, №10.
-У кого не было ошибок, может поставить себе «5», у кого были помарки, исправления, неточности – зеленой пастой пишут: Домашнее задание проверено.
-Дома, я также просила поработать вас с текстом параграфа №27, и найти ответ на вопрос: «Какие важные выводы можно сделать с помощью графического способа решения систем уравнений?». Кто нашел ответ на этот вопрос? (стр.63 учебника).
Слайд №11. (строки «выпускать» по мере ответа уч-ся).
—ученик закончил решение системы. Сейчас он прокомментирует нам ее решение.
-Спасибо, садись.
Этап№3
-А сейчас, внимание на экран, я хочу показать вам решение графическим методом еще одной системы:
Слайд№12.
— На чертеже: построен синим цветом график первого линейного уравнения и зеленым цветом график второго уравнения. Как видите, графики пересекаются.
Координаты точки пересечения графиков и будут являться решением данной системы. Координаты данной точки являются решением и первого и второго линейных уравнений, т.к. точка принадлежит и первому и второму графикам функций. Однако, чему конкретно равны абсцисса и ордината точки, определить очень сложно. Точка «висит» внутри определенной клеточки.
Из этого примера видно, что графический метод решения выручает нас не всегда. Значит, нам нужно располагать надежным алгебраическим методом, который нас не подведет в случае с дробными значениями координат точки.
Этим мы и займемся сегодня на уроке.
Этап№4
-В тетрадях запишите, пожалуйста, число 17 апреля. Классная работа.
Тема урока: «Решение систем уравнений способом подстановки».
Слайд№13-14.
Для удачного использования этого метода, нам необходимо повторить, как можно из линейного уравнения выразить одну переменную через другую. Мы это уже делали с вами на прошлых уроках. И так:
№1.
Устный счет
Выразить у через х и х через у:
1. х + 3у = 10 3x-y = 3
2. х + у = 2 5x + 2y = 4
3. 2х + 7у = 8 4x + 2y = 6
4. 6х — 5у = 4 6x – 3y = 9
№2. Попробуем решить систему, которая была вам задана домой, другим способом: (учитель начинает рассуждение, затем продолжают ученики). Слайд №15
 Выразим из 2 уравнения x через y:
Выразим из 2 уравнения x через y: 

Подставим в первое уравнение вместо x выражение, которое мы получили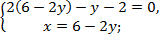
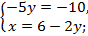
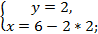
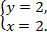 Решаем первое уравнение с одной переменной
Решаем первое уравнение с одной переменной 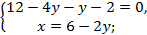

Ответ(2;2)
-Чем эти рассуждения отличались от тех, которые вы применяли дома при решении этой системы графическим методом?
-Откройте, пожалуйста, учебник на странице 236 и, прочитав текст, ответьте мне на этот вопрос.
-Как же мы рассуждали? Еще раз по учебнику прочитает нам………..
-Подобный метод рассуждений назвали методом подстановки, кто заметил из рассуждений — почему?
Итак: — выразили
— подставили
— решили
-нашли
-записали ответ
В учебнике найдите алгоритм решения и внимательно прочитайте его.
Слайд№17. («выпускать» строки по мере озвучения уч-ся)
-Метод подстановки широко используется и в более сложных системах уравнений, не обязательно линейных, о таких системах речь впереди – в старших классах.
Рассмотрев алгоритм может возникнуть вопрос, а почему мы выражаем переменную У из первого уравнения и подставляем во второе? Никакой причины нет, выражайте ту переменную, какую хотите, но ищите наиболее простые способы.
Слайд №18.
-Давайте вернемся к системе, которая осталась без ответа и решим ее способом подстановки (вызвать к доске….)
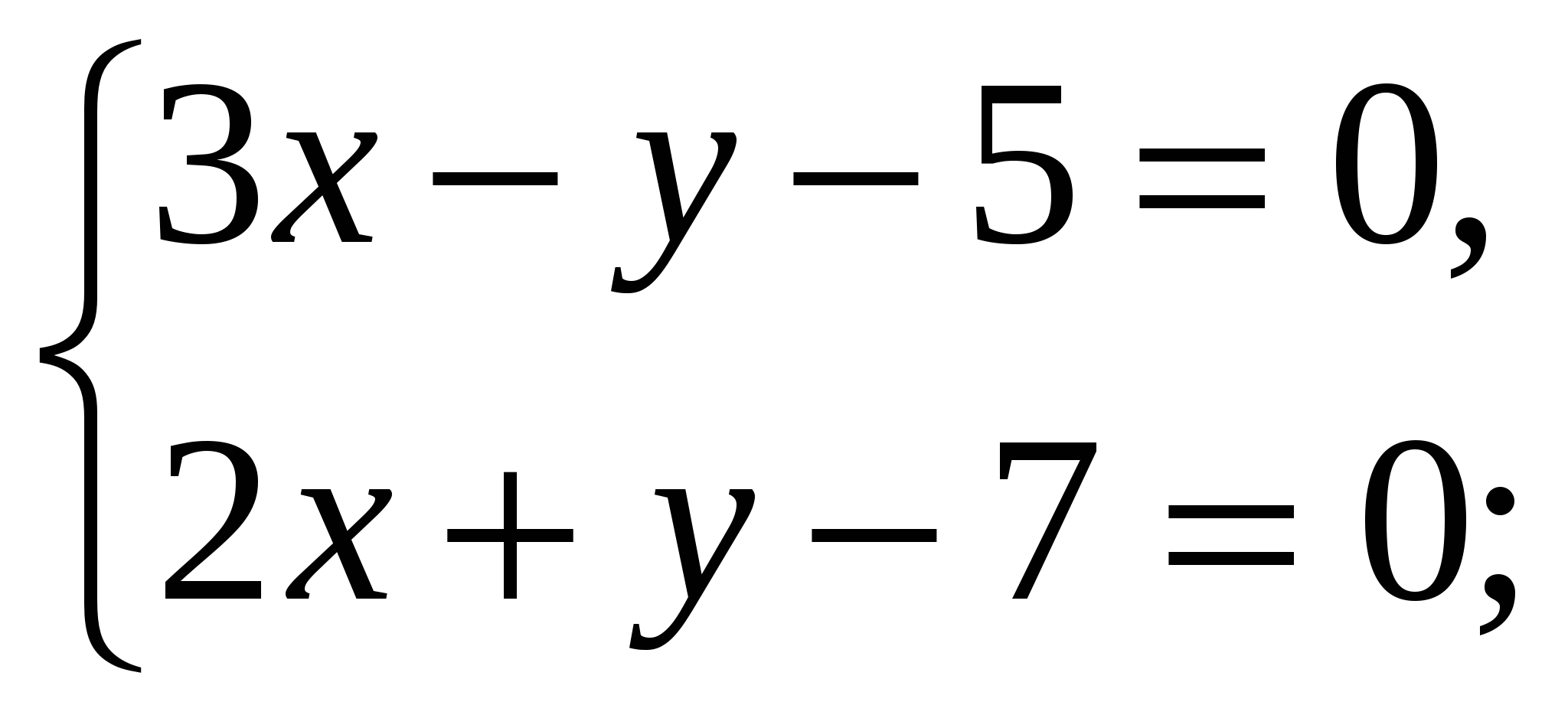
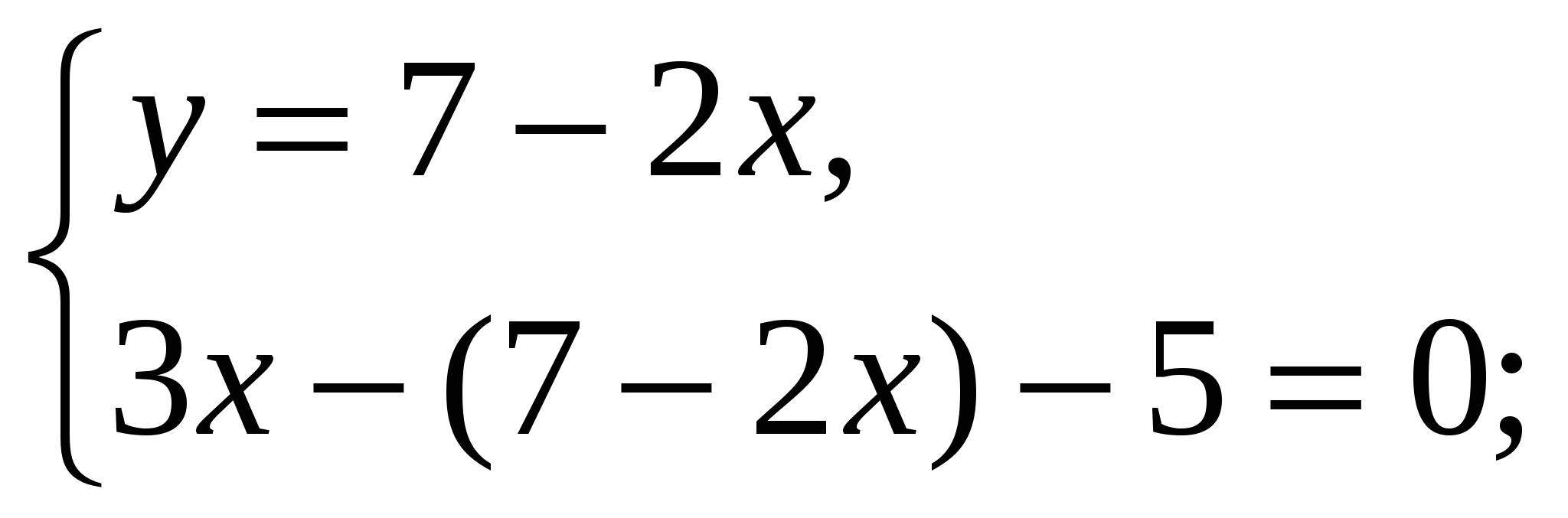
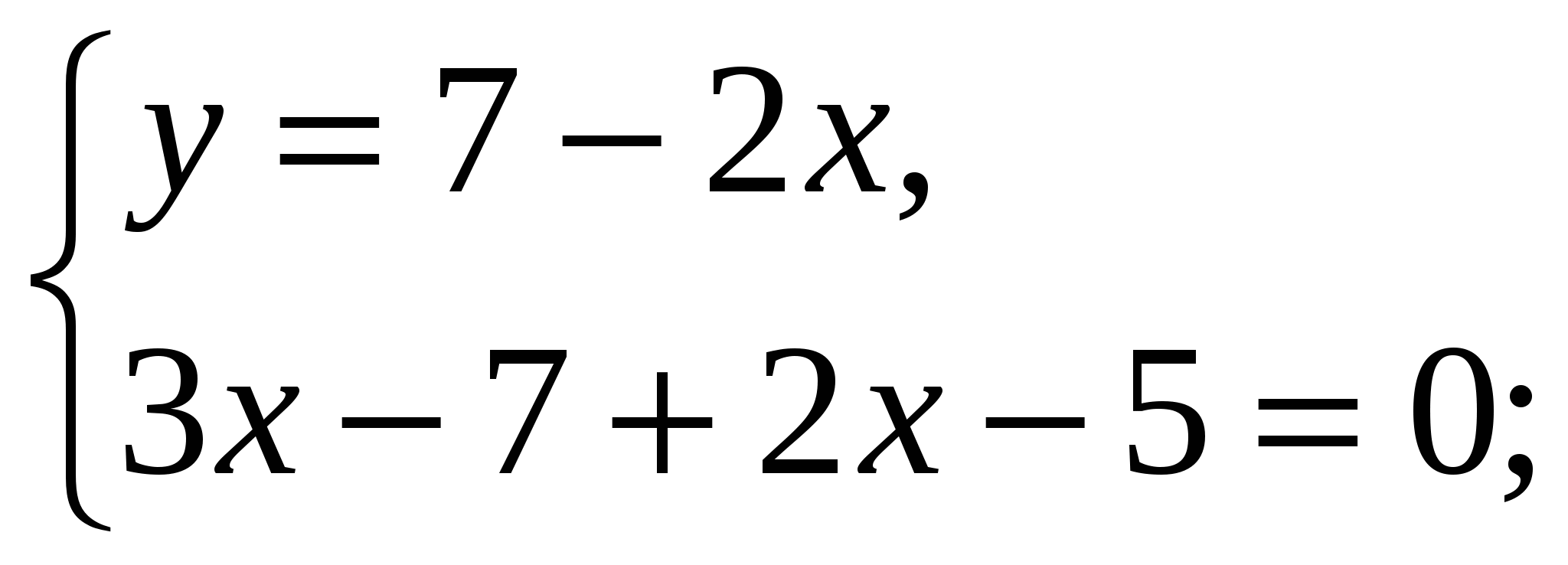
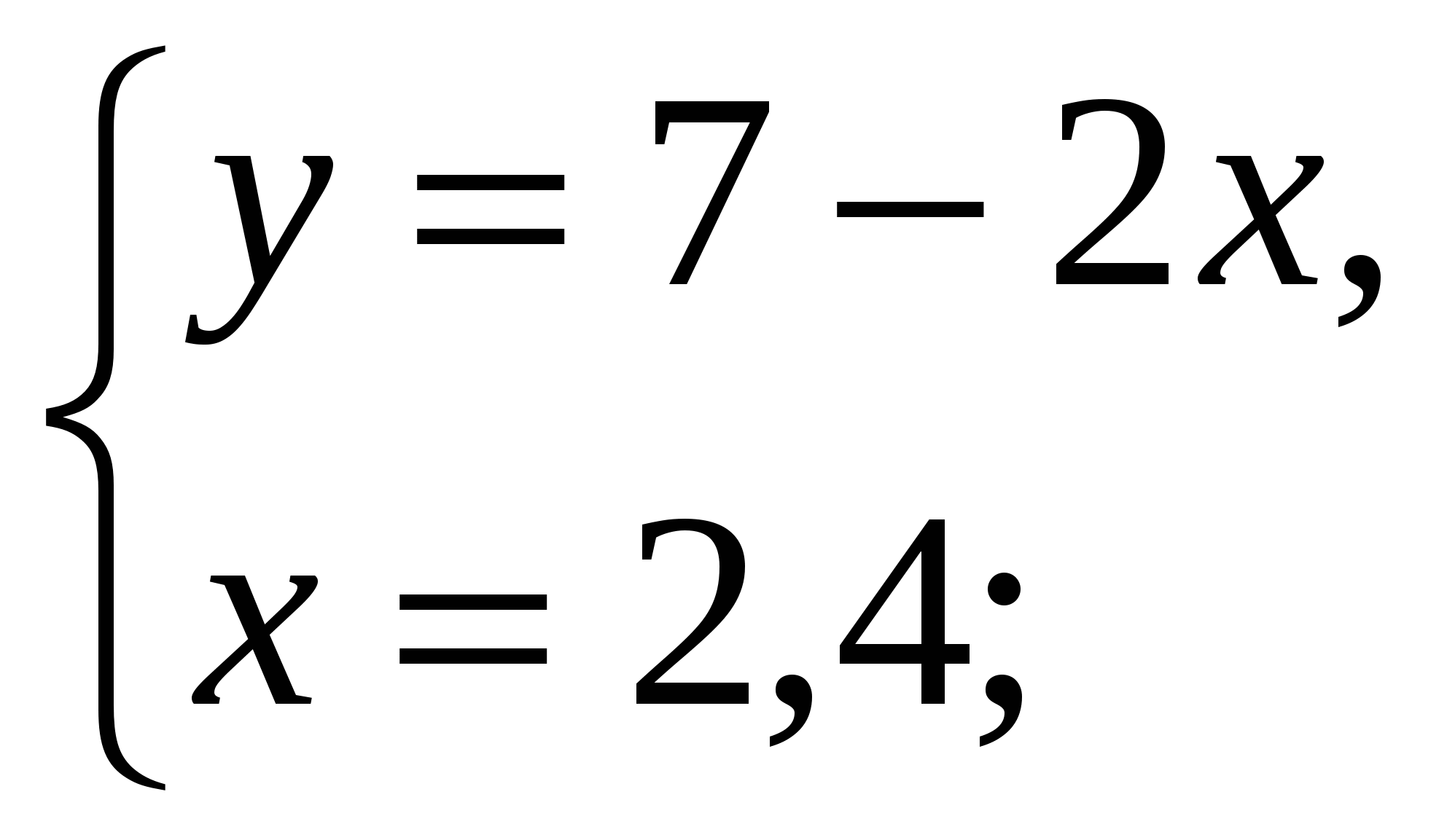
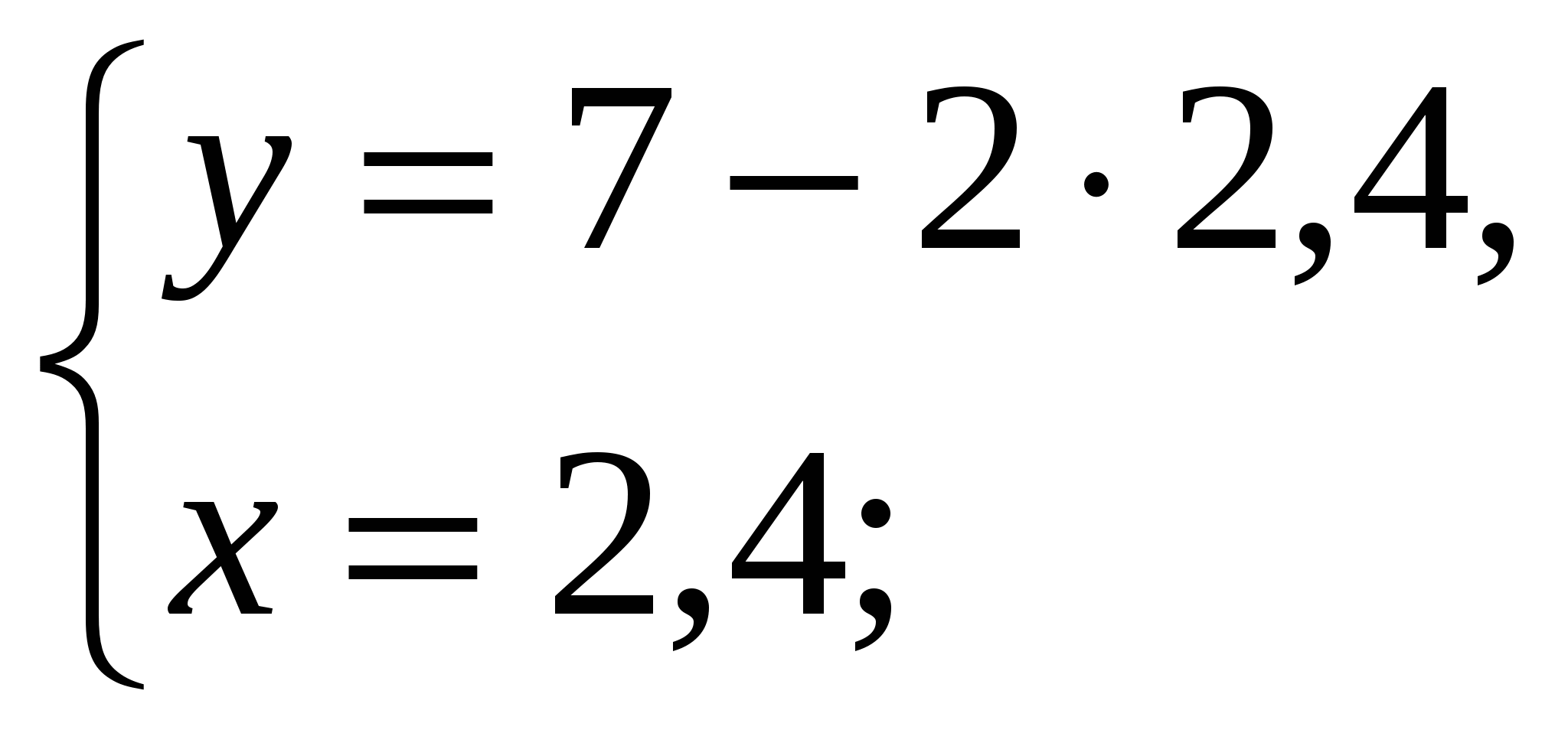
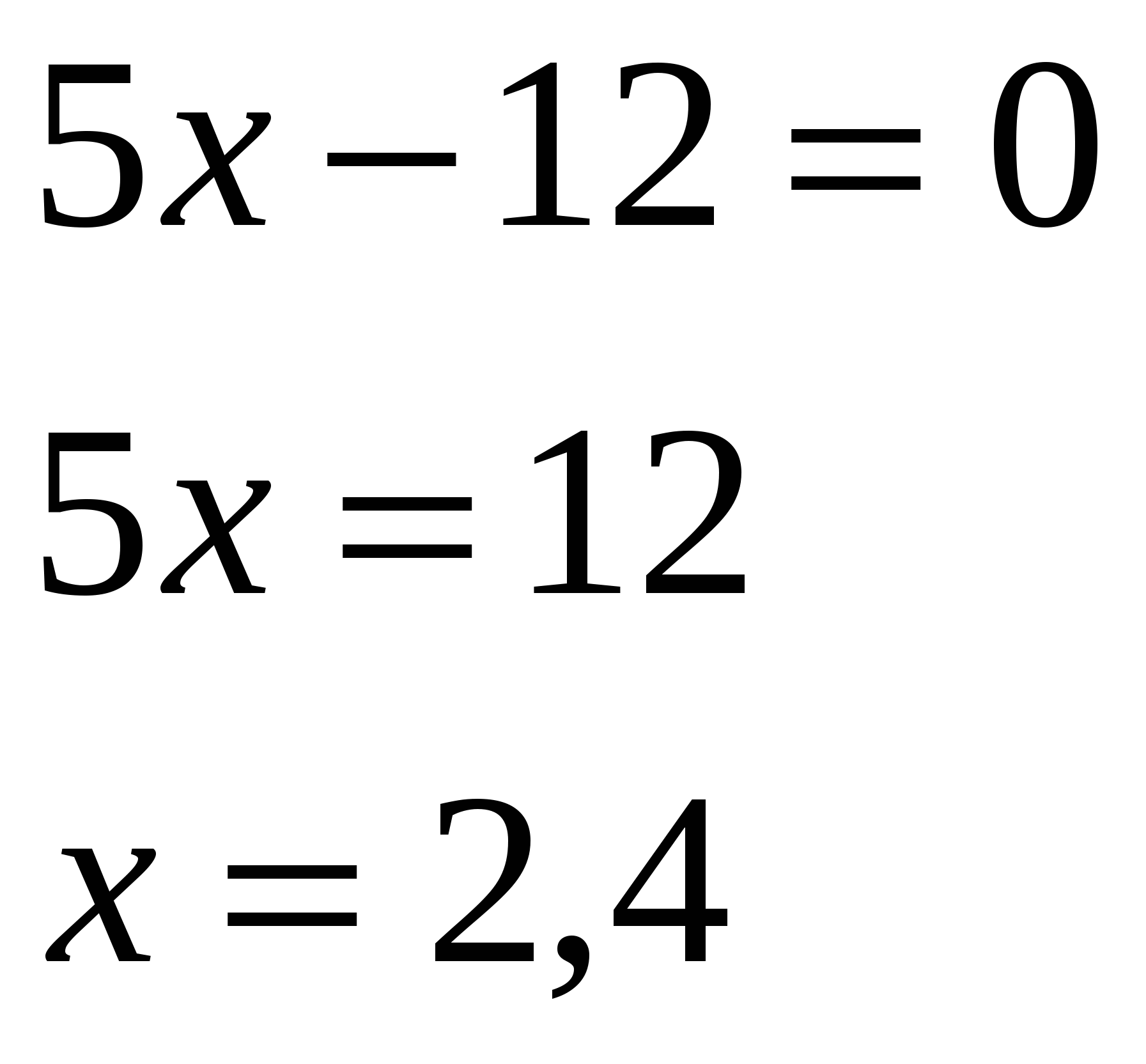
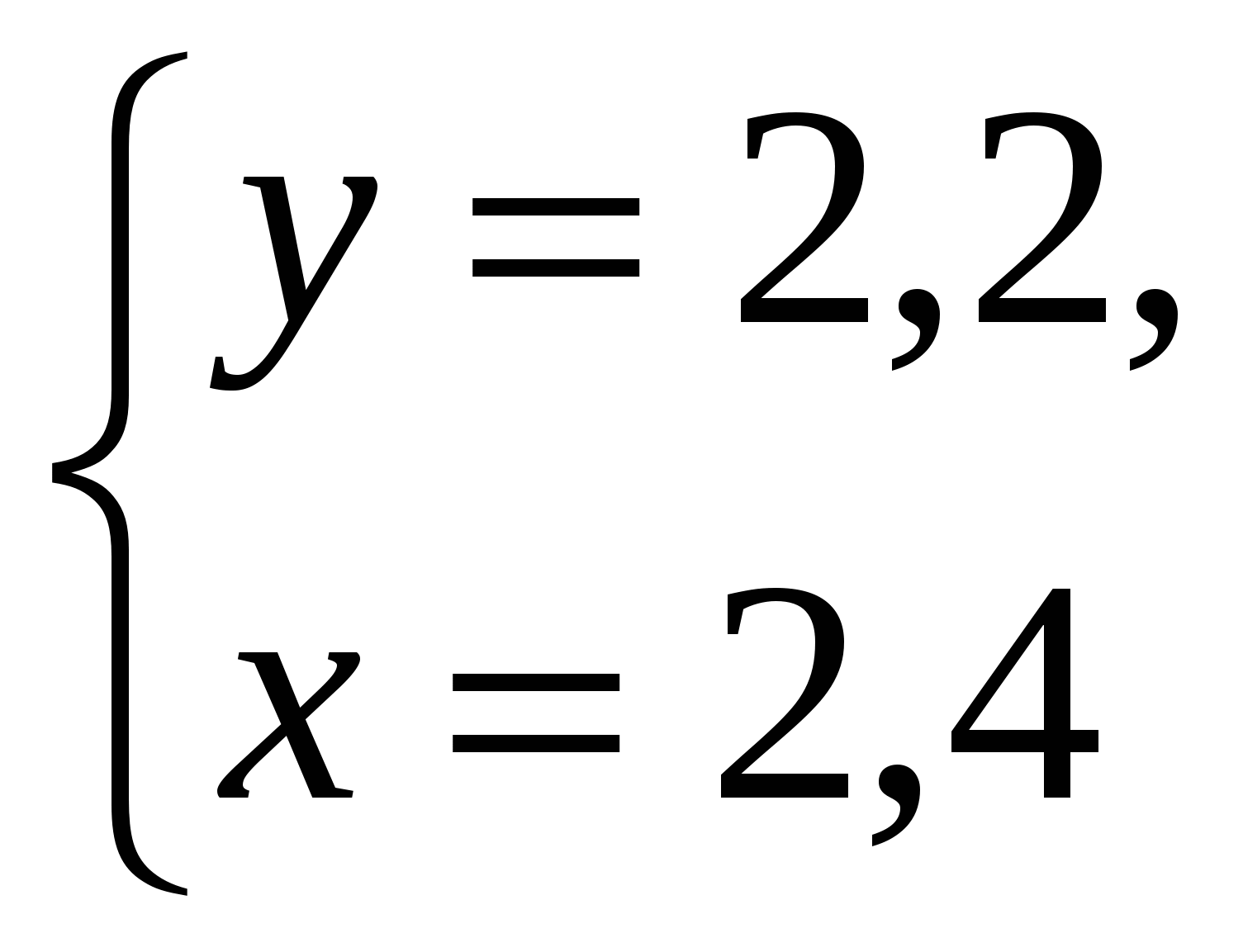 Ответ: ( 2,4 ;2,2)
Ответ: ( 2,4 ;2,2)
Слайд №19.
Еще раз проговорим этапы алгоритма: (проговорить этапы, слайд мультимедиа)
Теперь будем работать по учебнику стр. 238, № 1086 (а), 1088 (б), 1091 (б).
-Сегодня мы познакомились с вами с еще одним способом решения систем двух линейных уравнений с двумя переменными. Сформулировали алгоритм этого метода. На следующих уроках мы отработаем этот алгоритм на более сложных системах и познакомимся с еще одним очень интересным способом решения.
Домашнее задание: параграф 27 знать алгоритм № 1087, 1090, 1092*.
Оценки сегодня получили:……….
Спасибо за урок. До свидания.
«Решение систем линейных уравнений методом подстановки»
План – конспект урока по алгебре в 7-м классе на тему:
«Решение систем линейных уравнений методом подстановки»
Цели урока:
Образовательные: – разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки.
Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Развивающие: — развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Задачи:
1.Предметные: разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки продолжить формирование мотивации обучающихся к изучению предмета.
2.Метапредметные: развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе, активизировать их творческое мышление; продолжить формирование определенных компетенций обучающихся, которые будут способствовать их эффективной социализации, навыков самообразования и самовоспитания
3.Личностные: воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, жизни; воспитывать инициативу и самостоятельность в деятельности; подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.
Тип урока: урок изучения новой темы.
Вид урока: комбинированный.
Оборудование: мультимедийный проектор, компьютер.
Ход урока.
Актуализация знаний
Запись даты и темы урока.
Напомнить учащимся, что на предыдущих уроках мы учились решать системы линейных уравнений.
Предложить вспомнить:
Что такое система двух линейных уравнений с двумя переменными? (Математическая модель, состоящая из двух линейных уравнений с двумя переменными)
Что мы называем решением системы уравнений? (Пара чисел (х;у), которая одновременно является решением первого и второго уравнений системы)
Какими способами мы умеем решать системы уравнений? (Метод подбора и графический метод)
Проверка домашнего задания (работа в парах)
Для повторения предлагаю вам выполнить следующие задания:
1. Раскрыть скобки (устно с повторением правил раскрытия скобок)
2(3x – y)
– 3(2a – 3)
2x – 3(x + y)
a – (a – b)
2. Выразить из уравнения одну переменную через другую. (задание выполняется на доске с комментариями)
3a + b = 12
c – 8d = 15
18m + n = 3
– p – 9q = 4
7x – y = 17
2n – 4k = – 6
Вопрос: Какую переменную легче выразить через другую в каждом из уравнений и почему?
3. Является ли пара чисел (2;3) решением системы уравнений:
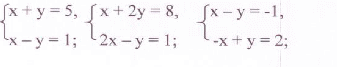
4.Сколько решений имеет система уравнений:
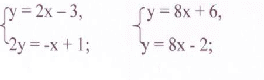
Изучение нового материала.
Системы уравнений с двумя переменными, которые имеют одни и те же решения или не имеют решений, называются равносильными.

Эти системы равносильны, т. к. имеют одно и то же решение (2;1). (проверить устно, подставив в каждую из систем)
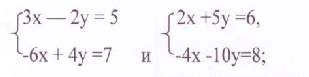
Эти системы равносильны, т. к. каждая из них не имеет решений. (проверить устно)
При решении системы уравнений с помощью преобразований ее заменяют более простой равносильной системой. Одним из способов решения системы является способ методом подстановки. Давайте решим систему уравнений, составляя таблицу.
Решим методом подстановки
1. Выражаем. Из любого уравнения выражаем одну переменную.
1. Выражаем
Видно, что во втором уравнении имеется переменная x с коэффициентом 1, отсюда получается, что легче всего выразить переменную x из второго уравнения.
x=3+10y
2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.
2.После того как выразили х через у, подставляем в первое уравнение «3+10y» вместо переменной « x».
2(3+10y) +5y=1
3. Решаем полученное уравнение с одной переменной.
4. Находим вторую переменную.
3.Решаем полученное уравнение.
2(3+10y) +5y=1 (раскрываем скобки)
6+20y+5y=1
25y= 1-6
25y= -5
y= -5:25
y= — 0,2
Подставить найденное значение у в выражение х через у.
x=3+10y
x=3+10*(-0,2)=1
4. Записываем ответ: х=…; у=…
Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.
Ответ: (1; -0,2) или х=1 и у=-0,2
Необходимо обратить внимание учащихся, что выражать следует ту переменную, при которой стоит более «удобный» коэффициент (в частности +— 1).
Мы составили алгоритм решения системы методом подстановки.
Формирование умений и навыков.
Желательно, чтобы в течение урока учащиеся запомнили алгоритм решения систем уравнений методом подстановки и могли его применять, не обращаясь к записям в тетрадях и разобранным примерам.
Задание на уроке: №12.5(аб), №12.2(а), №12.8(аб)
Для решения каждой системы следует вызывать к доске по одному учащемуся. Необходимо требовать, чтобы они вслух комментировали все свои шаги.
Контрольные вопросы:
– Какие вы знаете способы решения систем уравнений?
– Сформулируйте алгоритм решения систем уравнений способом подстановки
– Из какого уравнения системы лучше выражать переменную?
Задание на дом:
№12.4(аб), №12.6(аб), 12.9(аб)
Открытый урок «Решение систем линейных уравнений методом подстановки»
Открытый урок алгебры в 7 классе
Тема урока:
«Решение систем линейных уравнений методом подстановки»
Вид урока:
«Урок — мастерская»
Ведущая идея урока:
«Ученик учится САМ, учитель только помогает»
Цели урока:
а) повторить предыдущие темы курса математики 7 класса;
б) показать алгоритм решения системы линейных уравнений
методом подстановки;
в) отработать навыки решения систем линейных уравнений
методом подстановки;
г) научить аккуратно и четко оформлять решение
систем линейных уравнений.
д) воспитание трудолюбия, самостоятельности, инициативности учащихся на уроке;
е) воспитание чувства дружбы, взаимовыручки, умения работать в
команде и ответственности за результаты совместной работы.
Оборудование урока:
1. Компьютер.
2.Переносные доски с алгоритмом решения систем линейных уравнений методом подстановки.
3. Игровой материал по теме «Формулы сокращенного умножения».
4. Индивидуальные магнитные доски.
5. Оформление классной доски.
6. Раздаточный материал в виде «пакета заданий».
7. Маршрутные карты мини-соревнования «Алгебраическая пробежка».
Реализация урока
Первый этап урока. Подготовительный.
1. Приветствие. Представление гостей. Дата дня.
2.Объявление темы, цели, вида урока.
3.Урок нацелен на подготовку к итоговой контрольной работе, на выделение ключевых моментов основных тем программы 7 класса, на изучение небольшого фрагмента нового материала.
Работа в группах способствует развитию дружбы, коллективизма, умению слушать одноклассников, принимать общее решение. Элементы соревнования развивают стремление быть лучшими, первыми.
4. Класс делится на две группы:
«РИТМ» (Решать. Искать. Творить. Мечтать.)
«ХУZ» (Хотеть. Уметь. Zнать.)
Второй этап урока. Повторение.
Задание 1. Сложить «домино» по теме «Формулы сокращенного умножения» (ФСУ). От каждой группы по 1 человеку.
(х2- 4ху +4) \ х3 +27 = (х — 3)(х2 +3х +9)\х2 — 25 =
(х — 5) ( х + 5 )\ ( у +6 )2 = у2 +12у + 36 \ 4 — 16а2 =
(2 — 4а)(2 +4а)\ (х2 — 9в2) = (х- 3в)(х + 3в) и т. д.
Задание 2. Компьютерное тестирование по теме «Многочлены». По одному 1человеку от группы.
Задание 3. Решить на доске уравнение:
2х — (х-2)/2 = х/3 — 6
1+ (х+1)/3 = х — (3х+1)/8
Фронтальная работа в группах по повторению.
1.Правила на ФСУ (устно)
2.Письменная работа на индивидуальных магнитных досочках
а) раскрыть скобки:(2х — 3у)2 =… (3х -5у)2 =… (4а+в)2 =…
(6х + 2у)2=… (- а — в)2 =… (-х -2у)2=…
(5 — 6р)2 =… (1 — у )2=… (7х+4)2=…
(-у — х)2 =… (-2у — 2х)2=… (-3 +а)2=…
(а — 0,5в)2=… (а — 0,5в)2=… (-0,3у — х)2=…
б) выразить одну переменную через другую: у+4х =8; 2х — у +3 =7;
к — 7у =0; х +5у = 11;
12 -х =5у; 2р — 3к = 0
5х — 6 =3у; х +3у +5 = 2.
Работа в группах с «пакетом заданий»
1) повторение теоретического материала (лист №1)
2) устные упражнения «упростить выражение» (лист №2)
3) преобразовать выражение с помощью ФСУ (лист №3)
4) записать многочлен в стандартном виде (лист№4)
5) выполнить действия с многочленами (лист№5)
Третий этап урока. Домашнее задание.
На отрывных листах составлена домашняя контрольная работа в 8 вариантах. Ученики подходят и отрывают для себя лист с заданиями.
Домашнее задание решается на этих же листах и сдается учителю на проверку на следующем уроке.
Четвертый этап урока. Изучение нового материала.
Объяснить новую тему урока «Решение систем уравнений способом подстановки» учитель предлагает по одному ученику от каждой группы. Заранее классу было дано задание познакомиться с соответствующим пунктом учебника.
Дает обобщение материала на доске и заостряет внимание на более рациональное решение и компактное оформление.
{ 8х-4у = 4; -х =4 — 8у; х = 8у — 4
2х-21у =2.
2(8у -4) -21у = 2;
16у — 8 — 21у = 2;
-5у = 10;
у = -2.
x = 8*(-2) — 4
х = -20.
Ответ: ( -20; -2).
Пятый этап урока. Закрепление изученного материала.
Два ученика решают системы уравнений на задней доске, остальные в тетрадях. Учитель консультирует и помогает ученикам по мере необходимости и по их желанию.
{ У- 2х = 1; { х — 2у = 5;
6х — у =7. 7х — 3у = 13.
Ответ: (2; 5) Ответ: (1; 2)
Шестой этап урока. Проверка изученного материала.
Заканчивается урок игровым моментом — «алгебраической пробежкой», которая проводится в коридорах школы по типу соревнования. Группы, получают маршрутные листы и задание: решить системы уравнений методом подстановки и найти сумму корней.
{ х = 2 — у; { у — х = 20;
3х — 2у =11. 2х — 15у = -1
Ответ: ( 3; -1). Ответ: ( -23; -3).
{ х + у = 6; { 2у — 5х = 3;
3х -5у = 2. у + 3х = 7.
Ответ: (4; 2). Ответ: (1; 4).
Сумма корней равна ( -13).
Седьмой этап урока. Подведение итогов урока.
Группа — победитель фотографируется на память. Самым активным учащимся вручаются бэйджики «Молодец». Выставляются и комментируются оценки.
Самоанализ открытого урока алгебры в 7 классе по теме:
«Решение систем линейных уравнений методом подстановки»
При подготовке и проведении открытого урока кроме общеучебных и воспитательных ставились и другие цели:
1) саморазвитие и самоусовершенствование;
2) оценка и экспертиза коллегами моей методики препо-давания и наличия элементов новизны в ней:
3) желание поделиться своими находками и наработками с коллегами.
Перед проведением урока я познакомила присутствующих с темой и типом урока, его ведущей идеей. Были указаны цели и оборудование урока, а также дана харак-теристика класса, в котором будет проводиться открытый урок. Кроме того, коллеги имели перед собой проект урока и план его реализации, позволяющие отслеживать соответствие фактического хода урока запланированному и судить, насколько удачны методы и формы работы учителя, как взаимосвязаны этапы урока.
Основные формы работы на уроке — фронтальная и групповая, а также учебные диалоги «ученик — ученик» и «ученик — учитель». Порадовала меня и монологическая речь учащихся при объяснении ими нового материала.
Учитывая фактор соревновательности, класс был поделён на равносильные группы, при этом преследовалась цель взаимовыручки и сотрудничества в группах. Предварительного распределения обязанностей в группах не было, предусматривалось, что дети должны самоорганизоваться (как классный руководитель я заинтересована в развитии самоуправления в классе).
Учащиеся активно работали в группах с пакетом заданий: обсуждали предложенные теоретические вопросы и давали на них ответы, выполняли устные задания и решали самостоятельно.
Думаю, что методической находкой является изготовление отрывного математического календаря, с перечислением изученных тем и индивидуализированным домашним заданием. Отрывать лист с домашним заданием, несмотря на то, что предстоит серьезная работа, детям было интересно, это напоминало одновременно и лотерею, и игру «Кто вперёд!».
По возможности я включаю в свою работу новые информационные технологии. На уроках регулярно используется индивидуальная и групповая работа учащихся за компьютером (тестирование, практикум по решению задач).
Закрепление изученной темы будет продолжено на следующем уроке. Кроме того, последний этап урока, «алгебраическая пробежка», нацелен не столько на проверку знаний, сколько на закрепление изученного.
Временные рамки каждого из этапов урока, намеченные в плане, были более или менее соблюдены. Домашнее задание дано в середине урока и прокомментировано. Заключительный игровой момент немного захватил перемены, но это я предвидела и заранее оговорила с учащимися.
На основании сказанного можно сделать вывод о том, что выбор дидактической структуры урока представляется близким к оптимальному. Дети были активны, проявили сплоченность и заинтересованность на всех этапах урока.
Урок прошел по намеченном плану, в течение всего отведенного на урок времени отрабатывались общеучебные навыки. Продуктивным оказалось сочетание фронтальной, групповой и индивидуальной форм обучения. Считаю, что урок получился и поставленные задачи решались успешно.
Долговременными целями остаются: индивидуализация обучения и сохранение уровня качества знаний.
Анализ урока математики в 7 классе
Тема: Решение систем линейных уравнений методом подстановки
Урок проводился в классе, в котором 7 учащихся.
Уровень сформированности познавательных интересов высокий у Олентич В., средний – Кашумовой К., Машауовой А., Габдуллина С., Пилипец А., низкий – у Казова Р, и Шевчук А.
Урок проводился в компьютерном классе. Олентич Влада была помощником учителя.
Урок включал в себя 7 этапов.
Ведущая идея педагога: «Ученик учится Сам, учитель только помогает.»
Цели урока:
а) повторить предыдущие темы курса математики 7 класса;
б) показать алгоритм решения системы линейных уравнений
методом подстановки;
в) отработать навыки решения систем линейных уравнений
методом подстановки;
г) научить аккуратно и четко оформлять решение
систем линейных уравнений.
д) воспитание трудолюбия, самостоятельности, инициативности учащихся на уроке;
е) воспитание чувства дружбы, взаимовыручки, умения работать в
команде и ответственности за результаты совместной работы.
Урок целей достиг.
Команды сфотографировались на память. Все получили оценки «4». Олентич Влада – «5».
Анализ урока составила: Николаева Л.И., учитель математики 1 категории Писаревской СШ
Урок «Решение систем линейных уравнений способом подстановки»
Тема | Решение систем линейных уравнений способом подстановки | |
Класс | 9-ый | |
Автор | Лось Татьяна Николаевна | |
Учреждение образования | ГУО «Гимназия г. Иваново» | |
Тип урока | Изучение нового материала в рамках системы «Перевернутый урок» | |
Дидактическая цель урока | Предполагается, что к концу урока учащиеся:
| |
Задачи личностного развития |
| |
Подготовительная работа учителя | Слово учителя в конце предыдущего урока: Способ сложения – не единственный способ решения систем линейных уравнений. Существует ещё способ подстановки, с которым вам предстоит познакомиться дома, изучив материалы, которые вы найдете по ссылке http://school — assistant.ru/?predmet=algebra&theme=reshenie_sistem_2_lin_uravnenij_2_perem_podstanovki Вы можете использовать и другие источники, которые найдёте сами. Так как тема новая, у вас могут возникнуть вопросы, ответы на которые мы найдём на следующем уроке. После разбора задания вам предстоит выполнить несколько заданий и составить алгоритм решения систем линейных уравнений способом подстановки. Кроме этого постарайтесь определить, что было самым сложным в восприятии материала. Надеюсь, эта тема вызовет у вас истинный интерес. | |
Используемые педагогические технологии, методы, приемы | Образовательная стратегия «Перевернутый урок» | |
Оборудование | компьютеры | |
Дидактическое обеспечение урока | Раздаточный материал: задания для самостоятельного выполнения | |
Список учебной и дополнительной литературы; |
| |
Ход урока
Организационный момент
Как вам кажется, есть ли польза от стойки на голове? Если да, то в чем?
(улучшается кровоснабжение головы и обогащение питательными веществами и кислородом – улучшается цвет лица, состояние волос; обращение потока крови дает сердцу возможность отдохнуть; улучшается пищеварение; укрепляются мышцы спины и плеч)
Легко ли выполнить эту стойку? Конечно, нет!
Вот и мы сегодня работаем с новым материалом, используя непростой подход в обучении – «превернутый урок».
Формулировка темы урока, принятие дидактической цели урока
С новым материалом вы познакомились дома. А, значит, сами можете назвать тему урока: «Решение систем линейных уравнений способом подстановки»
Число, классная работа
Как вам кажется, какие цели мы поставим перед этим уроком? (Систематизируем информацию, полученную дома самостоятельно, научимся ее применять)
Активизация мыслительной деятельности
1. Из предложенных уравнений выберите те, которые являются линейными уравнениями с двумя переменными:
а) 3х + 3у – 1 = 0 г) 1/х +1/у = 3
б) 3х2 + у = 5 д) х + у = 3
в) 5х + 5 = 6х е) 1/2х + у – 5/6 = 0
Что такое система линейных уравнений с двумя переменными?
Что значит решить систему линейных уравнений?
Что называется решением системы линейных уравнений?
Выразите х из уравнения: 5х-10у=20; 12х + 3у= 1,2
Выразите у из уравнения: у+5х=0; 4х- 3у=5
Назовите алгоритм, который вы составили.
Проверка понимания изученного
№ 3.21 (1, 3) на доске с комментарием
Работа в парах по вариантах
1 вариант
Решите систему уравнений методом подстановки:
а)
б)
в)
2 вариант
Решите систему уравнений методом подстановки:
а)
б)
в)
5. Психологическая пауза
Проверим реакцию. Предлагается притча: однажды индийский раджа устроил для своих подданных соревнование: кто пробежит по стене, неся на голове кувшин с водой, не разлив ни капли. Под стеной стояла масса народу, каждый из которых кричал, дудел в трубы, бил в барабаны. Лишь одному человеку удалось донести кувшин, не разлив воду. Когда раджа спросил, как ему это удалось, он ответил, что ничего не слышал, т.к. нес воду. Учитель называет слова (каникулы, экзамен, решение, рождество, система, Астана, подстановка, метель, Минск, уравнение, праздник, Москва. стол, Киев, Париж), учащиеся должны расслышать: 1) математические термины, 2) столицы государств.
6.Проверка усвоения материала
Займите свои места за компьютером. Выполните тест.
7.Рефлексия и подведение итогов
Какую цель мы ставили на урок? Достигли ли её? Продолжите фразу
На уроке я научился….
Мне было трудно…
Самым интересным было…
Самым трудным было…
Домашнее задание
Дома вам предстоит решить из учебника № 3.22 (неч.)
«Решение систем линейных уравнений методом подстановки».
План – конспект урока по алгебре в 7-м классе на тему:
«Решение систем линейных уравнений способом подстановки»
Цели урока:
Образовательные: – разобрать, в чем состоит способ подстановки решения систем линейных уравнений; вывести алгоритм применения этого способа; сформировать умение решать системы уравнений способом подстановки.
Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Развивающие: — развитие математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Задачи:
разобрать, в чем состоит способ подстановки решения систем линейных уравнений;
вывести алгоритм применения этого способа;
сформировать умение решать системы уравнений способом подстановки продолжить формирование мотивации обучающихся к изучению предмета,
развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе,
воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, учёбе;
воспитывать инициативу и самостоятельность в деятельности;
подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.
Тип урока: урок изучения новой темы.
Вид урока: комбинированный.
Оборудование: мультимедийный проектор, компьютер, презентация в программе Microsoft Office Power Point, учебник и задачник по алгебре.
Литература:
1. Алгебра. 7 класс. В 2 ч., А. Г. Мордкович. Учебник и задачник для общеобразовательных учреждений – М. Мнемозина,2011 г
2. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 7 класс./ С.А. Пушкин, И.Л. Гусева. – М.: «Интеллект», 2013.
3. Т.Ю.Дюмина, А.А.Махонина, «Алгебра. Поурочные планы» — Волгоград: «Учитель», 2013 г.
План урока:
Организационный момент.Нацелить учащихся на урок
1 мин.
2
Актуализация опорных знаний.
Игра «Лови ошибку» (устная работа по повторению пройденного материала)
3 мин.
3
Проверка домашнего задания.
Разбор домашнего задания, выход на проблемный вопрос и мотивация к деятельности.
4 мин.
4
Изучение нового материала.
Ответ на проблемный вопрос, разбор нового метода решения систем с выведением алгоритма.
10 мин.
5
Физминутка
Разминка
2 мин.
6
Закрепление изученного материала.
Отработка алгоритма решения системы линейных уравнений. Групповая работа. Фронтальная работа. Самостоятельная работа.
15мин
7
Подведение итогов урока.
Рефлексия. Оценивание.
3 мин.
8
Домашнее задание
Разъяснить содержание домашнего задания.
2 мин.
Ход урока.
1. Организационный момент.
— Здравствуйте, ребята. Все готовы к уроку?
— Я хочу пожелать вам, чтобы сегодня у нас на уроке было хорошее рабочее настроение.
(Садитесь).
2. Актуализация опорных знаний. — Новые знания нам будет очень трудно осваивать без умения быстро и верно решать простейшие уравнения с одной переменной и умения выражать одну переменную через другую. Я предлагаю вам проверить, верно ли выполнены задания на слайдах (Лови ошибку!)
у — х = 7 у = x+7
2х+4у = 0 4у = -2x у = 0,5x
у – 16х = 13 у =16х – 13
9х- 2у = 5 -2у = -9х+5 у =-4,5х +2,5
- 5x-6=2x+12
5x -2x = 6
3x =6
x=2
3(x+2) = 11
3х+2 =11
3x = 9
x =3
— Молодцы! Вы нашли все ошибки, и заодно повторили правила переноса слагаемых из одной части уравнения в другую.
2. Проверка домашнего задания.
— Переходим к проверке домашнего задания. Какую работу вы выполняли дома? (решали системы графическим методом)
— Давайте проверим ваши результаты. Посмотрите на слайды и сравните их со своим решением. (Слайды 1 и 2)
Слайд 1.
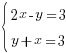
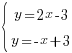
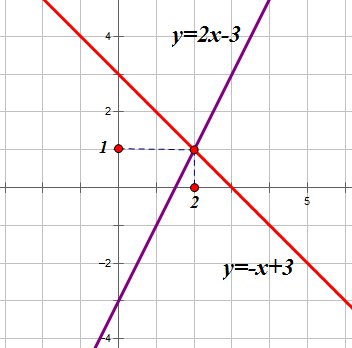
Ответ: (2;1)
Слайд 2.
— В чём отличие первой системы от второй? (в первой координаты точки точно определились, а во второй нет)
— Как вы думаете, почему во второй системе у вас получились разные ответы? (были погрешности при построении, например плохо заточен карандаш, или неровно приложили линейку)
— Тогда логично будет задать вопрос: Всегда ли применим графический метод решения систем линейных уравнений? (Проблемный вопрос) (нет).
— Но систему решить нужно, поэтому возникает потребность в другом методе решения систем. С таким методом мы познакомимся сегодня на уроке. Его название – Метод подстановки. Запишите в тетрадях число и тему урока: «Способ подстановки».
— Итак, на сегодняшнем уроке мы с вами познакомимся с методом подстановки для решения систем линейных уравнений, выведем алгоритм применения этого способа и научимся решать системы этим новым способом. Для этого на уроке вы должны быть собранными, внимательными, открытыми и доброжелательными.
4. Изучение нового материала.
Рассмотрим систему уравнений, которая вызвала у вас затруднения дома.
Давайте её решим. Для этого мы должны изучить алгоритм решения и пошагово следовать по каждому пункту алгоритма.
В чём же заключается этот метод? (Слайд)
Алгоритм решения системы уравнения методом подстановки.
Выразить одну переменную через другую в одном из уравнений системы.
Подставить полученное выражение в другое уравнение системы.
Решить полученное уравнение с одной переменной.
Найти значение другой переменной. (подставив, найденной значение)
Записать ответ в виде пары значений (х;у).
Учитель на доске показывает решение этой системы. Ученики записывают решение.
— Этим методом часто пользуются при решении систем на экзаменах!
5.Физкультминутка.
—А сейчас давайте сделаем паузу. Встанем и разомнёмся.(выполняем несколько упражнений + гимнастика для глаз)
Закрепление изученного материала.
Решение системы из учебника.№12.8 (в) – один человек у доски с подробным комментированием каждого шага алгоритма, остальные в тетрадях.
Групповая работа. Класс разбивается на 5 групп по 4 человека. Каждая группа должна решить систему. При этом разрешается членам группы помогать друг другу, объяснять задание. Учитель оказывает также помощь по необходимости, наблюдает за ребятами. Далее учитель на слайде демонстрирует решение задания. Ребята проверяют свои данные с решениями на слайде.
Самостоятельная работа. В тетрадях ребята решают систему. Далее меняются тетрадями и проверяют друг друга.
 (резерв)
(резерв)
Итоги урока:
— О чём вы узнали на сегодняшнем уроке?
-В чём преимущества этого метода решения в отличие от графического метода?
Напомните алгоритм решения систем методом подстановки.
Учитель выставляет оценки за урок
Домашнее задание: Выучить алгоритм в пункте 12, №12.5, 12.3 (а), 12.8(а).
Рефлексия. Ребята, посмотрите на слайд и ответьте на представленные вопросы:
Доволен ли ты тем, как прошел урок?
Возникали ли проблемы при решении заданий?
Сможете ли вы самостоятельно выполнить домашнее задание?
И по результатам поднимите карточки, которые лежат на ваших столах.
— Я рада, что для вас урок прошёл с пользой. Мы обязательно будем разбирать этот метод на следующих уроках и на консультациях. И я надеюсь, что на региональном экзамене с этими заданиями справятся все. Урок окончен. Спасибо за внимание!
Конспект «Решение систем уравнений методом подстановки 7 класс»
Тема урок: «Решение систем уравнений методом подстановки»
Тип урока: Урок обобщения и систематизации
Цель урока: отработать навыки решения систем уравнений методом подстановки с помощью составленных уравнений с двумя переменными
Задачи:
— Образовательные: актуализация знаний о решении систем уравнений методом подстановки, повторение алгоритма метода, показ важности метода при решении систем уравнений;
— Развивающие: создание условий для развития интереса к предмету, развитие математического мышления, умение анализировать, сравнивать, оценивать свою деятельность, умение быстро мыслить и быть внимательными;
— Воспитательные: формировать навыки аккуратной записи и оформления решения систем уравнений, воспитывать дружеские взаимоотношения в классе, воспитывать у учащихся грамотную математическую речь.
Прогнозируемы результаты:
1. Предметные:
— закрепить знания учеников о решении систем уравнений методом подстановки;
— научить применять данный метод на практике.
2. Метапредметные:
— способность принимать и сохранять цели и задачи учебной деятельности, находить способы её осуществления;
— умение планировать, контролировать и оценивать учебные действия в соответствии с поставленной задачей и условиями её выполнения;
— умение включаться в диалог с учителем и сверстниками, в коллективное обсуждение проблем;
— умение оценивать себя и результаты своей работы.
Технологии, методы и приемы:
Прием создания проблемной ситуации
Частично-поисковый метод
Оборудование урока:
Учебник (справочный материал)
Задачник
Карточки (2 варианта самостоятельной работы)
Список используемой литературы:
Мордкович, А.Г. Алгебра 7 класс, в двух частях, часть 1 учебник / А.Г. Мордкович. – М.: Мнемозина, 2012. – 160 с.
Мордкович, А.Г. Алгебра 7 класс, в двух частях, часть 2 задачник / А.Г. Мордкович. – М.: Мнемозина, 2012. – 270 с.
Ход урока
I. Подготовка учащихся к воспроизведению изученного материала
1.Организационный момент
Приветствие учеников, проверка отсутствующих, проверка готовности помещения к уроку.
2.Проверка домашнего задания
№12.16 (А и Б). (Ученик работает у доски с объяснением решения, класс контролирует правильность решения)
А)4x-7y=33
2x+5y=25
2x=25-5y
2(25-5y)-7y=33
2x=25-5y
50-10y-7y=33
-17y=-17
2x=25-5y
x=10
y=1
Ответ: (10;1)
Б)
5y-6x=2
8x-3y=1
x=
1=
3
x=
y=1
x=0,5
Ответ: (0,5;1)
Подставить полученные ответы вместо переменных в уравнениях и проверить правильно найденного решения.
№12.18 (Ученик работает у доски с объяснением решения, класс контролирует правильность решения)
4(x-y)=-23x-7y=-2,5-2(x+y)
4x-4y=-2
3x-7y+2x+2y=-2,5
4x-4y=-2
5x-5y=-2,5
x=y-0,5
5y-5(y-0,5)=-2,5
x=y-0,5
0=0
Получили верное равенство => система имеет бесконечно много решений
Ответ: Б.м.р.
№12.19 (А и Б) (Ученик работает у доски с объяснением решения, класс контролирует правильность решения)
А)2-3x=2(1-y)
4(x+y)=x-1,5
3x-2y=0
3x+4y=-1,5
y=1,5x
3x+6x=-1,5
x=
y=
Ответ: (;)
Б)
6x+3=8x-3(2y-4)
2(2x-3y)-4x=2y-8
2x-6y=-9
-8y=-8
y=1
2x=-3
y=1
x=-1,5
Ответ: (-1,5;1)
Подставить полученные ответы вместо переменных в уравнениях и проверить правильно найденного решения.
3.Мотивация к учебной деятельности
Сегодня, наш урок будет посвящен закреплению изученного материала. Мы уже знаем два способа решения систем уравнений с двумя переменными. Какие это способы? (Это графический способ и способ подстановки.)
Верно! Каким недостатком обладает графический способ решения систем уравнений? (Это неточность.)
Правильно, именно поэтому мы познакомились с таким решением систем уравнений как метод подстановки.
4.Целеполагание
Так как на прошлом уроке мы изучили тему «Метод подставки», как вы думаете, какие цели и какая тема нашего урока? (Закрепить наши знания на эту тему с помощью решения систем уравнений данным методом и повторения алгоритма решения, а тема, решение систем уравнений методом подстановки)
II. Процесс повторения изученных знаний
1.Актуализация опорных знаний
Перед тем как начать закрепление изученного материала, давайте сначала повторим алгоритм решения систем уравнений с помощью метода подстановки. Кто может его проговорить? (Фронтальный опрос)
Алгоритм:
Выразить y через x из первого уравнения системы.
Подставить полученное на первом шаге выражение вместо y во второе уравнение системы.
Решить полученное на втором шаге уравнение относительно x.
Подставить найденное на третьем шаге значение x в выражение y через x, полученное на первом шаге.
Записать ответ в виде пары значений (x;y), которые были найдены соответственно на третьем и четвертом шагах.
Подставить полученное решение вместо переменных и проверить правильность найденного решения.
Верно! Но не будем забывать дети, что если в нашем алгоритме поменять x и y местами, он останется правильным. То есть:
Выразить x через y из первого уравнения системы.
Подставить полученное на первом шаге выражение вместо x во второе уравнение системы.
Решить полученное на втором шаге уравнение относительно y.
Подставить найденное на третьем шаге значение y в выражение x через y, полученное на первом шаге.
Записать ответ в виде пары значений (x;y), которые были найдены соответственно на третьем и четвертом шагах.
Подставить полученное решение вместо переменных и проверить правильность найденного решения.
2.Закрепление изученного материала
Теперь применим наш алгоритм на практике, для закрепления изученного алгебраического метода решения систем уравнений, а именно, метода подстановки. (Ученик работает у доски с объяснением решения, класс контролирует правильность решения)
-2x-y=37x+2y=0
y=-2x-3
7x-4x-6=0
y=-2x-3
3x=6
x=2
y=-7
Ответ: (2;-7)
(Ученик работает у доски с объяснением решения, класс контролирует правильность решения)
2x+y=74x+2y=11
y=7-2x
4x+14-4x=11
y=7-2x
14=11 !!!
Получили не верное равенство => система не имеет решений.
Ответ: нет решения.
3.Самостоятельная работа
Для окончательного закрепления материала, выполните самостоятельную работу по вариантам.
I ВариантII Вариант
1)
x=2y+5
2x+3y=-4
Ответ: (1;-2)
1)
y=2-3x
5x+4y=-6
Ответ: (2;-4)
2)
6(x+y)=5-(2x+y)
3x-2y=-3y-3
Ответ: (-2;3)
2)
2+3(x+5y)=-(2x+3y)
3x+4y=-8
Ответ: (-4;1)
III. Итоговая часть урока
1.Подведение итогов
На этом уроке мы закрепили наши знания о методе решения систем уравнений, а именно методе подстановки. Так же мы повторили и алгоритм решения систем уравнений методом подстановки. Кто может его озвучить?
Алгоритм:
Выразить y через x из (или x через y) первого уравнения системы.
Подставить полученное на первом шаге выражение вместо y во второе уравнение системы.
Решить полученное на втором шаге уравнение относительно x.
Подставить найденное на третьем шаге значение x в выражение y через x, полученное на первом шаге.
Записать ответ в виде пары значений (x;y), которые были найдены соответственно на третьем и четвертом шагах.
Подставить полученное решение вместо переменных и проверить правильность найденного решения.
2.Информация о выполнение домашнего задания
Решить систему уравнений методом подстановки №12.17, №12.19 (В и Г), №12.20, сделать проверку полученного решения.
3.Рефлексия
Ребята, какие замечания вы можете сделать по этому уроку?
Что вам понравилось (не понравилось)?
Что бы вы добавили на этом уроке?
Может быть, у вас есть предложения по улучшению урока?
Какие ваши общие впечатления от урока?
(Выслушать и учесть ответы детей на эти вопросы)
4.Оценка содержательного аспекта деятельности учащихся
Оценки будут выставлены в соответствии с самостоятельной работой, которую вы выполнили на уроке.
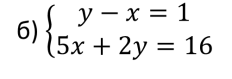 (резерв)
(резерв)