Сравнение отрицательных десятичных дробей: Сравнение отрицательных десятичных дробей — задание. Математика, 6 класс. — Детская игровая комната «Волшебный лес»

Posted on 07.05.197206.01.2022 by alexxlab

Содержание

Сравнение рациональных чисел

Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.

Из предыдущих уроков мы узнали, что чем правее число располагается на координатной прямой, тем оно больше. И соответственно, чем левее располагается число на координатной прямой, тем оно меньше.

Например, если сравнивать числа 4 и 1, то можно сразу ответить, что 4 больше чем 1. Это вполне логичное утверждение и каждый с этим согласится.

В качестве доказательства можно привести координатную прямую. На ней видно, что четвёрка лежит правее единицы

4 > 1

Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:

Из двух положительных чисел больше то число, модуль которого больше.

Чтобы ответить на вопрос какое число больше, а какое меньше, сначала нужно найти модули этих чисел, сравнить эти модули, а потом уже ответить на вопрос.

Например, сравним те же числа 4 и 1, применяя вышеприведенное правило

Находим модули чисел:

|4| = 4

|1| = 1

Сравниваем найденные модули:

4 > 1

Отвечаем на вопрос:

4 > 1

Для отрицательных чисел существует другое правило, выглядит оно следующим образом:

Из двух отрицательных чисел больше то число, модуль которого меньше.

Например, сравним числа −3 и −1

Находим модули чисел

|−3| = 3

|−1| = 1

Сравниваем найденные модули:

3 > 1

Отвечаем на вопрос:

−3 < −1

Нельзя путать модуль числа с самим числом. Частая ошибка многих новичков. К примеру, если модуль числа −3 больше, чем модуль числа −1, это не означает, что число −3 больше, чем число −1.

Число −3 меньше, чем число −1. Это можно понять, если воспользоваться координатной прямой

Видно, что число −3 лежит левее, чем −1. А мы знаем, что чем левее, тем меньше.

Если сравнивать отрицательное число с положительным, то ответ будет напрашиваться сам. Любое отрицательное число будет меньше любого положительного числа. Например, −4 меньше, чем 2

−4 < 2

Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».

Здесь в первую очередь нужно смотреть на знаки чисел. Минус перед числом будет говорить о том, что число отрицательное. Если знак числа отсутствует, то число положительное, но вы можете записать его для наглядности. Напомним, что это знак плюса

−4 < +2

Мы рассмотрели в качестве примера целые числа, вида −4, −3 −1, 2. Сравнить такие числа, а также изобразить на координатной прямой не составляет особого труда.

Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет видоизменять, чтобы сделать его более простым для сравнения и восприятия.

Пример 1. Сравнить рациональные числа

Итак, требуется сравнить отрицательное число с положительным. Любое отрицательное число меньше любого положительного числа. Поэтому не теряя времени отвечаем, что меньше, чем

Пример 2. Сравнить рациональные числа и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное больше, чем , потому что модуль числа меньше, чем модуль числа

Пример 3. Сравнить числа 2,35 и

Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем что 2,35 больше, чем

2,35 >

Пример 4. Сравнить рациональные числа и

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём в неправильные дроби и приведём к общему знаменателю

Пример 5. Сравнить рациональные числа 0 и

Требуется сравнить ноль с отрицательным числом. Ноль больше любого отрицательного числа, поэтому не теряя времени отвечаем, что 0 больше, чем

Пример 6. Сравнить рациональные числа 0 и

Требуется сравнить ноль с положительным числом. Ноль меньше любого положительного числа, поэтому не теряя времени отвечаем, что 0 меньше, чем

Пример 7. Сравнить рациональные числа 4,53 и 4,403

Требуется сравнить два положительных числа. Из двух положительных чисел больше то число, модуль которого больше.

Сделаем в обеих дробях количество цифр после запятой одинаковым. Для этого в дроби 4,53 припишем в конце один ноль

4,530

Далее применим правило сравнения положительных чисел.

Находим модули чисел

|4,530| = 4,530

|4,403| = 4,403

Сравниваем найденные модули:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше.

Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403

4,53 > 4,403

Пример 8. Сравнить рациональные числа и

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно переведём смешанное число в неправильную дробь, затем приведём обе дроби к общему знаменателю:

Сравнивать десятичные дроби намного проще, чем обыкновенные дроби и смешанные числа. В некоторых случаях, посмотрев на целую часть такой дроби, можно сразу ответить на вопрос какая дробь больше, а какая меньше.

Чтобы сделать это, нужно сравнить модули целых частей. Это позволит быстро ответить на вопрос в задаче. Ведь как известно, целые части в десятичных дробях имеют вес больший, чем дробные.

Пример 9. Сравнить рациональные числа 15,4 и 2,1256

Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256

|15| = 15

|2| = 2

15 > 2

поэтому и дробь 15,4 больше, чем дробь 2,1256

15,4 > 2,1256

Другими словами, нам не пришлось тратить время на дописывание нулей дроби 15,4 и сравнивать получившиеся дроби, как обычные числа

15,4000 2,1256

154000 > 21256

Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.

Пример 10. Сравнить рациональные числа −15,2 и −0,152

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей

|−15| = 15

|−0| = 0

15 > 0

Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.

А значит рациональное −0,152 больше, чем −15,2 потому что модуль целой части числа −0,152 меньше, чем модуль целой части числа −15,2

−0,152 > −15,2

Пример 11. Сравнить рациональные числа −3,4 и −3,7

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то число, модуль которого меньше. Но мы сравним только модули целых частей. Но проблема в том, что модули целых чисел равны:

|−3| = 3

3 = 3

В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули

|−3,4| = 3,4

|−3,7| = 3,7

Сравниваем найденные модули:

Согласно правилу, из двух отрицательных чисел больше то число, модуль которого меньше. Значит рациональное −3,4 больше, чем −3,7 потому что модуль числа −3,4 меньше, чем модуль числа −3,7

−3,4 > −3,7

Пример 12. Сравнить рациональные числа 0,(3) и

Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.

Переведём периодическую дробь 0,(3) в обыкновенную дробь и сравним её с дробью . После перевода периодической дроби 0,(3) в обыкновенную, она обращается в дробь

Находим модули чисел:

Сравниваем найденные модули. Но сначала приведём их к понятному виду, чтобы проще было сравнить, а именно приведём к общему знаменателю:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число больше, чем 0,(3) потому что модуль числа больше, чем модуль числа 0,(3)

0,(3) <

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Сравнение десятичных дробей — как правильно? правила и примеры

Понятие десятичной дроби

Прежде чем мы расскажем, как сравнивать десятичные дроби, вспомним основные определения, виды дробей и разницу между ними.

Дробь — это число в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:

обыкновенный вид — 1/2 или a/b,
десятичный вид — 0,5.

В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.

В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Ее записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:

Конечная десятичная дробь — это когда количество цифр после запятой точно определено.

Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.

Свойства десятичных дробей

Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:

0,600 = 0,6
21,10200000 = 21,102

Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:

Целая часть десятичной дроби равна целой части смешанной дроби. Если числитель меньше знаменателя, то целая часть равна нулю.
Дробная часть десятичной дроби содержит те же цифры, что и числитель этой же дроби в обыкновенном виде, если знаменатель обыкновенной дроби равен 10, 100,1000 и т. д.
Количество цифр после запятой зависит от количества нулей в знаменателе обыкновенной дроби, если знаменатель обыкновенной дроби равен 10, 100,1000 и т. д. То есть 1 цифра — делитель 10, 4 цифры — делитель 10000.

Курсы по математике в онлайн-школе Skysmart помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Правило сравнения десятичных дробей

Чтобы сравнить две десятичные дроби, сначала нужно сравнить их целые части. Если целые части равны, продолжаем искать первый несовпадающий разряд. Большей будет та дробь, у которой соответствующий разряд больше.

Вот так с первой строчки раскрыли тему сравнения десятичных дробей 😜 Но это еще не все — едем дальше.

Алгоритм сравнения десятичных дробей

Убедиться, что у обеих десятичных дробей одинаковое количество знаков (цифр) справа от запятой. Если нет, то дописать (убрать) нужное количество нулей в одной из десятичных дробей.
Сравнить десятичные дроби слева направо. Целую часть с целой, десятые с десятыми, сотые с сотыми и т. д.
Когда одна из частей десятичной дроби окажется больше, чем другая, эту дробь можно назвать большей.

Применим правило на практике. Сравним десятичные дроби: 15,7 и 15,719.

Как решаем:

Допишем в первой десятичной дроби нужное количество нулей, чтобы уравнять количество знаков справа от запятой: 15,700 и 15,719.
Сравним десятичные дроби слева направо.

Целую часть с целой частью: 15 = 15. Целые части равны.

Десятые с десятыми: 7 = 7. Десятые также равны.

Сотые с сотыми: 0 < 1. Так как сотые второй десятичной дроби больше, значит и сама дробь больше: 15,700 < 15,719.

Ответ: 15,7 < 15,719.

Еще один способ сравнения десятичных дробей:

Чтобы сравнить две десятичные дроби, нужно уравнять количество знаков после запятой (приписать к одной из них справа нули), затем отбросить запятую, и сравнить два натуральных числа.

Сравним 3,656 и 3,48.

Как решаем:

Уравниваем количество знаков справа после запятой: 3,656 и 3,480.
Отбросим запятые: 3656 и 3480.
Сравним полученные числа: 3656 > 3480.

Ответ: 3,656 > 3,48.

Запоминаем!

Меньшая десятичная дробь лежит на координатном луче левее большей, а большая — правее меньшей.

Например, 0,3 < 0,4 < 0,5, поэтому точка A (0,3) лежит левее точки B (0,4), а точка C (0,5) лежит правее точки B (0,4).

Как сравнить разные дроби. Персонажи, используемые для записи в калькуляторе

Существуют определённые правила сравнения чисел. Рассмотрим следующий пример.

Вчера термометр показывал 15˚ C, а сегодня показывает 20˚ C. Сегодня теплее, чем вчера. Число 15 меньше числа 20, можем записать так: 15

А сейчас рассмотрим отрицательные температуры. Вчера на улице было -12˚ C, а сегодня -8˚ C. Сегодня теплее, чем вчера. Поэтому считают, что число -12 меньше числа -8. На горизонтальной координатной прямой точка со значением -12 расположена левее точки со значением -8. Можем записать так: -12

Итак, если сравнивать числа с помощью горизонтальной координатной прямой, из двух чисел меньшим считается то, изображение которого на координатной прямой расположено левее, а большим то, изображение которого расположено правее. Например, у нас на рисунке А > B и C, но B > C.

На координатной прямой положительные числа располагаются справа от нуля, а отрицательные – слева от нуля, всякое положительное число больше нуля, а всякое отрицательное меньше нуля, и поэтому всякое отрицательное число меньше всякого положительного числа.

Значит, первое на что необходимо обратить внимание при сравнении чисел, – это знаки сравниваемых чисел. Число с минусом (отрицательное) всегда меньше положительного.

Если же мы сравниваем два отрицательных числа, то нужно сравнить их модули: большим будет то число, модуль которого меньше, а меньшим то число, модуль которого меньше. Например, -7 и -5. Сравниваемые числа – отрицательные. Сравниваем их модули 5 и 7. 7 больше чем 5, значит -7 меньше чем -5. Если отметить на координатной прямой два отрицательных числа, то левее окажется меньшее число, а большее будет расположено правее. -7 расположено левее -5, значит -7

Сравнение обыкновенных дробей

Из двух дробей с одинаковыми знаменателями меньше та, у которой меньше числитель, и больше та, у которой больше числитель.

Можно сравнивать дроби только с одинаковыми знаменателями.

Алгоритм сравнения обыкновенных дробей

1) Если у дроби есть целая часть, сравнение начинаем именно с неё. Большей будет та дробь, у которой целая часть больше. Если целой части у дробей нет или они равны, переходим к следующему пункту.

2) Если дроби с разными знаменателями необходимо привести их к общему знаменателю.

3) Сравниваем числители дробей. Большей будет та дробь, у которой числитель больше.

Обратите внимание, дробь с целой частью всегда будет больше дроби без целой части.

Сравнение десятичных дробей

Десятичные дроби можно сравнивать только с одинаковым количеством цифр (знаков) справа от запятой.

Алгоритм сравнения десятичных дробей

1) Обращаем внимание на количество знаков справа от запятой. Если количество цифр одинаковое, можем приступать к сравнению. Если – нет, дописываем нужное количество нулей в одной из десятичных дробей.

2) Сравниваем десятичные дроби слева направо: целые с целыми, десятые с десятыми, сотые с сотыми и т.д.

3) Большей будет та дробь, в которой одна из частей окажется больше, чем в другой дроби (сравнение начинаем с целых чисел: если целая часть одной дроби больше, значит, и вся дробь больше).

Например, сравним десятичные дроби:

1) Допишем в первой дроби необходимое количество нулей, чтобы уравнять количество знаков после запятой

57,300 и 57,321

2) Сравнивать начинаем слева направо:

целые с целыми: 57 = 57;

десятые с десятыми: 3 = 3;

сотые с сотыми: 0

Так как сотые первой десятичной дроби оказались меньше, вся дробь и будет меньше:

57,300

сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.

Сравнить две дроби – значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми числителями

При сравнении двух дробей, у которых одинаковые числители, больше будет та дробь, у которой знаменатель меньше.

Например, больше , так как количество взятых долей в обеих дробях одинаковое, но первая дробь содержит более крупные доли, чем вторая:

Сравнение дробей с одинаковыми знаменателями

При сравнении двух дробей, у которых одинаковые знаменатели, больше будет та дробь, у которой числитель больше.

Например, меньше , так как первая дробь содержит меньше взятых долей, чем вторая:

Сравнение дробей с разными знаменателями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Например, сравним две дроби: и . Приводим их к общему знаменателю:

Теперь сравниваем их:

так как , значит

Равенство дробей

Две обыкновенные дроби считаются равными, если равны их числители и знаменатели или, если они выражают одну и ту же часть единицы.

Сравнение дроби с натуральным числом

Правильная дробь меньше любого натурального числа.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби, затем привести дроби к общему знаменателю. После приведения дробей к общему знаменателю, их сравнивают по правилу сравнения дробей с одинаковыми знаменателями.

Пример. Сравним неправильную дробь с числом 5.

1. Переводим натуральное число в неправильную дробь:

2. Приводим дроби к общему знаменателю:

3. Сравниваем:

так как , значит

Онлайн калькулятор сравнения дробей

Данный калькулятор поможет вам сравнить обыкновенные дроби. Просто введите две дроби и нажмите кнопку.

описание

Вам не нужно иметь навыки программирования для написания сложных сценариев или тратить время на классифицирование классифицированных программ — Excel или Word.

Как сравнить фракции

Теперь вы можете использовать готовые решения в повседневной работе.

Алгоритм поможет сразу отсортировать значения в алфавитном и обратном порядке, чтобы строить данные по количеству символов в слове или любому значению символа.

инструкции

Инструмент отлично справляется с добавленной стоимостью в столбце и отдельными словами, заданными запятой или пробелом.

Скопируйте данные, необходимые для сортировки в левом окне, укажите одну из четырех функций и нажмите кнопку Сортировать по .

По умолчанию он доступен Алфавитный порядок (A — R / 0 — 9) .

По выбору Обратный порядок (H — A / 9 — 0) , алгоритм сразу отображает матрицу в обратном направлении.

черты Значения на длину (от малого до большого) и Значения по длине (от более высокой до нижней) работайте по аналогичному принципу, но сортировка основана на количестве символов в строке.

Написать комментарий

Для меня важно знать, как работает служба и как ее можно улучшить. Написать комментарий по почте [email protected] или в нижней форме.

Как работать с калькулятором регулярных фракций?

Калькулятор предназначен для спасения простые фракции и фракции с целыми числами (смешанный ). Функция десятичных дробей запланирована в будущем, но в настоящее время она недоступна.

Чтобы начать работу с частичным калькулятором, вам нужно понять очень простой принцип ввод данных.

Все целые числа вводятся с помощью больших кнопок слева. Все счетчики вводятся с маленькими белыми кнопками, расположенными в верхней правой части цифр. Все символы вводятся нажатием кнопки в правом нижнем углу. Метод ввода данных является своего рода инновационным, поскольку он четко описывает весь числитель и знаменатель, который позволяет проводить расчеты, экономит время и позволяет более эффективно взаимодействовать с использованием. », а затем на номер шесть на главной клавиатуре.

В результате мы получаем готовый пример:

в настоящее время Нажмите эквивалентную кнопку и перейдите стоимость результата .

В приведенном выше примере показан почти весь арсенал дробных калькуляторов. Вы можете сделать то же самое так же размножение, деление и вычитание фракций , так же просто, как алгебраические, с одинаковыми и разными знаменателями, целыми числами и т. д.

Калькулятор также может рассчитывать фракции из фракций, что не часто требуется, но тем не менее очень важно решить ряд неотложных проблем.

Чтобы получить положительное отрицательное число, сначала введите номер и нажмите кнопку «+/-».

После этого число или часть автоматически завертываются в скобки с отрицательным значением или наоборот (в зависимости от начального состояния номера). Чтобы удалить число, счетчик или знаменатель, используйте соответствующую стрелку возврат на одну позицию , который находится в блоке как числителя, так и знаменателя.

Стрелки работают одинаково, а затем удаляют номера или символы на экране компьютера.

Управляйте частичным калькулятором с клавиатуры.

Используйте его Калькулятор веб-фракций не только с компьютерной мышью, но и с клавиатурой.

Логика очень проста:

Все вводится как обычно, нажимая цифровые клавиши.
Все счетчики вводятся путем добавления клавиши CTRL (например, CTRL + 1).
Все знаменатели вводятся путем добавления клавиши ALT (например, ALT + 2).

Меры умножения, деления, добавления и вычитания, а также запуска соответствующих клавиш на клавиатуре, если они есть (обычно расположены с правой стороны, так называемая область Numpad).

Удаление выполняется нажатием клавиши Backspace. Очистка (красная кнопка «C») запускается нажатием клавиши «C». Квадратный корень — нажатием соседней клавиши «V».

Удаление выполняется нажатием клавиши Backspace.

Зачем вам нужен онлайн-калькулятор?

Дробный калькулятор онлайн предназначен для обработки гладкий и смешанный дробей (с целым числом).

Решение фракций часто необходимо для студентов и студентов, а также для инженеров и выпускников. Наш калькулятор позволяет создавать следующие действия с частицами: расщепление фракций, умножение фракций, добавление фракций и вычитание фракций . Калькулятор также может работать с корнями и ставками, а также с отрицательными числами, что делает его несколько раз превышает аналогичные веб-приложения.

Простой калькулятор фракционной дроби онлайн поможет вам решить дела с фракциями, поэтому вам не нужно беспокоиться о том, как противодействовать фракции.

Он становится здесь автоматически , поскольку само приложение вычисляет общий знаменатель и, наконец, показывает конечный результат.

Каковы преимущества этого метода для решения фракций?

калькулятор поддерживает работу с скобками , что позволяет решать фракции, даже в сложных математических случаях. Кампании часто необходимы для скобок алгебраические дроби или отрицательные фракции , над которыми мы должны постоянно избегать всех учащихся средних школ.

Калькулятор для сравнения фракций

Кроме того, вы можете использовать этот калькулятор сокращение фракций или дробные растворы с разными знаменателями . Кроме того, этот калькулятор, в отличие от многих других бесплатных сервисов, может работать с двумя, тремя, четырьмя и вообще с любым количеством дробей и чисел.

Калькулятор регулярных фракций абсолютно бесплатно и не требует регистрации.

Вы можете использовать его в любое время дня и ночи. Вы можете сделать это с помощью мыши или непосредственно с клавиатуры (это относится к числу и действиям). Мы попытались реализовать максимум удобный интерфейс частичные вычисления, которые делают сложные математические расчеты меняющимися в одно удовольствие!

Сравнение обыкновенных дробей

Удобный и простой онлайн-калькулятор фракций с точным решением вы можете:

Складывайте, вычитайте, размножайте и размещайте фрагменты в Интернете,
Получите частичное решение изображения и просто загрузите его.

Результат фракций будет здесь …

Наш калькулятор онлайн-калькуляторов имеет быстрый ввод .

Например, если вы хотите получить частичное решение , просто введите 1/2 + 2/7 в калькулятор и нажмите кнопку «Rescue Faction».

Калькулятор напишет вам детальное решение фракций и вопросы легко скопировать изображение .

Персонажи, используемые для записи в калькуляторе

Вы можете ввести пример решения с клавиатуры или с помощью кнопки.

Характеристики калькулятора веб-фракций

Калькулятор фракций может выполнять операции только с двумя простыми фракциями.

Они могут быть правильными (счетчик меньше знаменателя) или неверны (счетчик больше знаменателя). Числа в числителе и знаменателе не должны быть отрицательными и больше 999.
Наш онлайн-калькулятор принимает решения по фракциям и направляет ответ на правильный формат — уменьшает долю и, при необходимости, назначает всю часть.

Просто используйте свойства минус, чтобы сохранить отрицательные части. При умножении и делении отрицательных дробей знак плюс добавляет плюс. Это означает, что продукт и распределение отрицательных дробей идентичны произведению и распределению того же положительного. Если фракция отрицательная, если вы ее умножаете или делите, удалите минус и добавьте ее в ответ. При добавлении отрицательных фракций результат будет таким же, как добавление одинаковых положительных пропорций.

Если вы добавите одну отрицательную долю, то это то же самое, что и вычесть тот же самый положительный результат.
При вычитании отрицательных дробей результат будет таким же, как если бы они были изменены в местах и стали положительными.

Сравнение фракций

Это означает, что минус минус в этом случае дает плюс, и сумма не изменяется от суммы. Те же правила, которые мы используем при подсчете фракций, один из которых отрицателен.

Чтобы решить смешанные фракции (фракции, в которых размещена вся часть), просто заполните всю фракцию во фракцию.

Чтобы сделать это, умножьте всю часть на знаменатель и добавьте его в счетчик.

Если вы хотите сохранить 3 или более акций в Интернете, они должны быть приняты. Во-первых, подсчитайте первые две фракции, затем с полученным ответом определите следующую долю и так далее. Выполните операции на линии 2 фракций, и в конце вы получите правильный ответ.

Зачем принимать решения в калькуляторе

Решения в калькуляторе должны узнать, как сохранить дроби.
Калькулятор не имеет намерения решать фракции для вас.

Это не универсальный резак, это инструмент обучения. Это поможет вам понять решение, так что вы можете легко решить фракции самостоятельно. В дополнение к учебному калькулятору мы также рекомендуем изучить наши материалы: «Как разрешить фракции». Решение фракций. «

Если вы заметили какие-либо ошибки или неудобства при использовании калькулятора, пожалуйста, свяжитесь с нами в комментариях. Насколько это возможно, мы закончим калькулятор!

Онлайн калькулятор. Сравнение фракций.

Студент видит на экране несколько номеров с интересной цветовой схемой.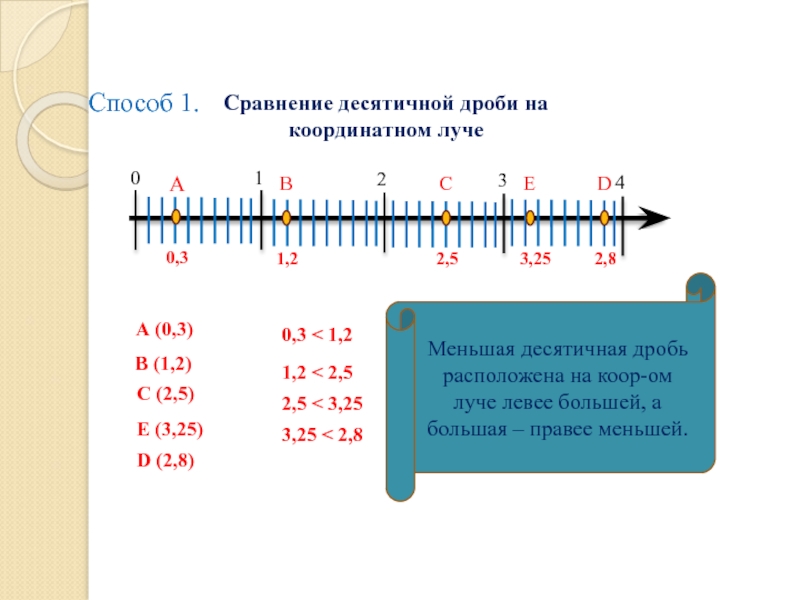 Эти числа расположены в случайном порядке. Ребенок, который знает правильный порядок учетной записи, должен отредактировать от малого до большого. Проблема с упражнением заключается в том, что цифры, показанные на рисунке, не обязательно идут один за другим.

Фактически, промежутки между ними могут быть важными. Но студент, который выполняет эту задачу, должен помнить, какой из чисел больше и меньше. Когда ребенок создает последовательность, он немедленно переходит на следующий уровень (если ответ правильный) или после просмотра правильной опции — если он совершает ошибку.

Это упражнение не только развивает логическое мышление, оно учит вас анализировать и готовить последовательные выводы из образа, но также помнить о правильной последовательности чисел при подсчете.

Порядок увеличения является естественным для многих партий, поэтому ребенок может легко обнаружить его.

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Yandex.RTB R-A-339285-1

Сравнение дробей с одинаковыми знаменателями

Когда производится сравнение дробей с одинаковыми знаменателями, мы работаем только с числителем, а значит, сравниваем доли числа. Если имеется дробь 3 7 , то она имеет 3 доли 1 7 , тогда дробь 8 7 имеет 8 таких долей. Иначе говоря, если знаменатель одинаковый, производится сравнение числителей этих дробей, то есть 3 7 и 8 7 сравниваются числа 3 и 8 .

Отсюда следует правило сравнения дробей с одинаковыми знаменателями:из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Пример 1

Произвести сравнение заданных дробей 65 126 и 87 126 .

Решение

Так как знаменатели дробей одинаковые, переходим к числителям. Из чисел 87 и 65 очевидно, что 65 меньше. Исходя из правила сравнения дробей с одинаковыми знаменателями имеем, что 87 126 больше 65 126 .

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

найти общий знаменатель;
сравнить дроби.

Рассмотрим данные действия на примере.

Пример 2

Произвести сравнение дробей 5 12 и 9 16 .

Решение

В первую очередь необходимо привести дроби к общему знаменателю. Это делается таким образом: находится НОК, то есть наименьший общий делитель, 12 и 16 . Это число 48 . Необходимо надписать дополнительные множители к первой дроби 5 12 , это число находится из частного 48: 12 = 4 , для второй дроби 9 16 – 48: 16 = 3 . Запишем получившееся таким образом: 5 12 = 5 · 4 12 · 4 = 20 48 и 9 16 = 9 · 3 16 · 3 = 27 48 .

После сравнения дробей получаем, что 20 48

Ответ: 5 12

Имеется еще один способ сравнения дробей с разными знаменателями. Он выполняется без приведения к общему знаменателю. Рассмотрим на примере. Чтобы сравнить дроби a b и c d , приводим к общему знаменателю, тогда b · d , то есть произведение этих знаменателей. Тогда дополнительные множители для дробей будут являться знаменатели соседней дроби. Это запишется так a · d b · d и c · b d · b . Используя правило с одинаковыми знаменателями, имеем, что сравнение дробей свелось к сравнениям произведений a · d и c · b . Отсюда получаем правило сравнения дробей с разными знаменателями:если a · d > b · c , тогда a b > c d , но если a · d

Пример 3

Произвести сравнение дробей 5 18 и 23 86 .

Решение

Данный пример имеет a = 5 , b = 18 , c = 23 и d = 86 . Тогда необходимо вычислить a · d и b · c . Отсюда следует, что a · d = 5 · 86 = 430 и b · c = 18 · 23 = 414 . Но 430 > 414 , тогда заданная дробь 5 18 больше, чем 23 86 .

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Пример 4

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Имеем, что числители одинаковые, значит, что дробь, имеющая знаменатель 19 больше дроби, которая имеет знаменатель 31 . Это понятно, исходя из правила.

Ответ: 54 19 > 54 31 .

Иначе можно рассмотреть на примере. Имеется две тарелки, на которых 1 2 пирога, анна другой 1 16 . Если съесть 1 2 пирога, то насытишься быстрей, нежели только 1 16 . Отсюда вывод, что наибольший знаменатель при одинаковых числителях является наименьшим при сравнении дробей.

Сравнение дроби с натуральным числом

Сравнение обыкновенной дроби с натуральным числом идет как и сравнение двух дробей с записью знаменателей в виде 1 . Для детального рассмотрения ниже приведем пример.

Пример 4

Необходимо выполнить сравнение 63 8 и 9 .

Решение

Необходимо представить число 9 в виде дроби 9 1 . Тогда имеем необходимость сравнения дробей 63 8 и 9 1 . Далее следует приведение к общему знаменателю путем нахождения дополнительных множителей. После этого видим, что нужно сравнить дроби с одинаковыми знаменателями 63 8 и 72 8 . Исходя из правила сравнения, 63

Ответ: 63 8

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (

Ученые-математики уже позаботились о готовых правилах, позволяющие сразу ответить на вопрос какая дробь больше, а какая меньше. Эти правила можно смело применять.

Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.

Содержание урока

Сравнение дробей с одинаковыми знаменателями

Дроби, которые нужно сравнить, попадаются разные. Самый удачный случай это когда у дробей одинаковые знаменатели, но разные числители. В этом случае применяют следующее правило:

Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше. И соответственно меньше будет та дробь, у которой числитель меньше.

Например, сравним дроби и и ответим, какая из этих дробей больше. Здесь одинаковые знаменатели, но разные числители. У дроби числитель больше, чем у дроби . Значит дробь больше, чем . Так и отвечаем. Отвечать нужно с помощью значка больше (>)

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Следующий случай, в который мы можем попасть, это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласиться с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.

Например, сравнить дроби и . Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби и к одинаковому (общему) знаменателю. Найдём (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Теперь найдём второй дополнительный множитель. Разделим НОК на знаменатель второй дроби . НОК это число 6, а знаменатель второй дроби это число 3. Делим 6 на 3, получаем дополнительный множитель 2. Записываем его над второй дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому, что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби , получим следующее выражение:

Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа, иногда можно обнаружить, что всё идёт не так гладко, как хотелось бы. Часто случается так, что при решении какого-нибудь примера ответ получается не таким, каким он должен быть.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Например, 10−8=2

10 — уменьшаемое

8 — вычитаемое

2 — разность

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2

5 — уменьшаемое

7 — вычитаемое

−2 — разность

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать, как это сделать. Если испытываете затруднения, обязательно повторите .

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю.

Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.

Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:

Из двух положительных чисел больше то число, модуль которого больше.

Например, сравним те же числа 4 и 1, применяя вышеприведенное правило

Находим модули чисел:

|4| = 4

|1| = 1

Сравниваем найденные модули:

4 > 1

Отвечаем на вопрос:

4 > 1

Для отрицательных чисел существует другое правило, выглядит оно следующим образом:

Из двух отрицательных чисел больше то число, модуль которого меньше.

Например, сравним числа −3 и −1

Находим модули чисел

|−3| = 3

|−1| = 1

Сравниваем найденные модули:

3 > 1

Отвечаем на вопрос:

−3

Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой

Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.

Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».

Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия.

Пример 1. Сравнить рациональные числа

Пример 2.

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули:

Пример 3. Сравнить числа 2,34 и

Требуется сравнить положительное число с отрицательным. Любое положительное число больше любого отрицательного числа. Поэтому не теряя времени отвечаем, что 2,34 больше, чем

Пример 4. Сравнить рациональные числа и

Находим модули чисел:

Пример 5.

Пример 6. Сравнить рациональные числа 0 и

Пример 7 . Сравнить рациональные числа 4,53 и 4,403

Находим модули чисел

Сравниваем найденные модули:

Согласно правилу, из двух положительных чисел больше то число, модуль которого больше. Значит рациональное число 4,53 больше, чем 4,403 потому что модуль числа 4,53 больше, чем модуль числа 4,403

Пример 8. Сравнить рациональные числа и

Находим модули чисел:

Пример 9. Сравнить рациональные числа 15,4 и 2,1256

Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256

поэтому и дробь 15,4 больше, чем дробь 2,1256

15,4 > 2,1256

154000 > 21256

Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.

Пример 10. Сравнить рациональные числа −15,2 и −0,152

Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.

−0,152 > −15,2

Пример 11. Сравнить рациональные числа −3,4 и −3,7

В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули

Сравниваем найденные модули:

−3,4 > −3,7

Пример 12. Сравнить рациональные числа 0,(3) и

Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.

Находим модули чисел:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Сравнение чисел

Существуют определённые правила сравнения чисел. Рассмотрим следующий пример.

Вчера термометр показывал 15˚ C, а сегодня показывает 20˚ C. Сегодня теплее, чем вчера.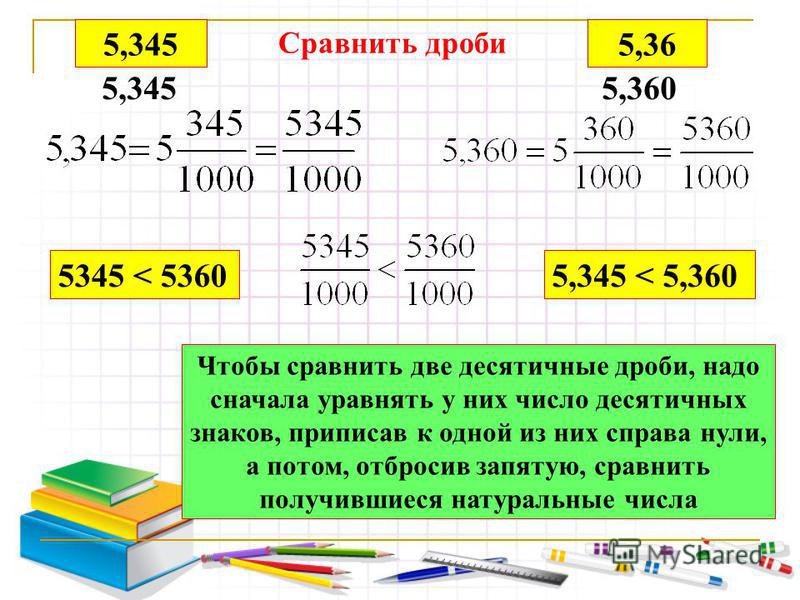 Число 15 меньше числа 20, можем записать так: 15 < 20. А, если мы представим эти числа на координатной прямой, то точка со значением 15 будет расположена левее точки со значением 20.

Сравнение обыкновенных дробей

Можно сравнивать дроби только с одинаковыми знаменателями.

Алгоритм сравнения обыкновенных дробей

2) Если дроби с разными знаменателями необходимо привести их к общему знаменателю.

3) Сравниваем числители дробей. Большей будет та дробь, у которой числитель больше.

Обратите внимание, дробь с целой частью всегда будет больше дроби без целой части.

Сравнение десятичных дробей

Десятичные дроби можно сравнивать только с одинаковым количеством цифр (знаков) справа от запятой.

Алгоритм сравнения десятичных дробей

2) Сравниваем десятичные дроби слева направо: целые с целыми, десятые с десятыми, сотые с сотыми и т.д.

Например, сравним десятичные дроби:

57,3 и 57,321

1) Допишем в первой дроби необходимое количество нулей, чтобы уравнять количество знаков после запятой

57,300 и 57,321

2) Сравнивать начинаем слева направо:

целые с целыми: 57 = 57;

десятые с десятыми: 3 = 3;

сотые с сотыми: 0 < 2.

Так как сотые первой десятичной дроби оказались меньше, вся дробь и будет меньше:

57,300 < 57,321

Сравнение чисел: положительных, отрицательных

Сравнение чисел — одна из самых легких и приятных тем из курса математики. Впрочем, нужно сказать, что она не так уж и проста. Например, мало кто испытывает трудности со сравнением однозначных или двузначных положительных чисел.

Но числа с большим количеством знаков уже вызывают проблемы, часто люди теряются при сравнении отрицательных чисел и не помнят, как сравнить два числа с разными знаками. На все эти вопросы мы и постараемся ответить.

Правила относительно сравнения положительных чисел

Начнем с самого простого — с чисел, перед которыми не стоит никакого знака, то есть с положительных.

Прежде всего, стоит запомнить, что все положительные числа по определению больше нуля, даже если речь идет о дробном числе без целого. Например, десятичная дробь 0,2 будет больше, чем нуль, поскольку на координатной прямой соответствующая ей точка все-таки отстоит от нуля на два небольших деления.
Если речь идет о сравнении двух положительных чисел с большим количеством знаков, то нужно сравнивать каждый из разрядов. Например — 32 и 33. Разряд десятков у этих чисел одинаков, но число 33 больше, поскольку в разряде единиц «3» больше, чем «2».
Как сравнить между собой две десятичные дроби? Здесь нужно смотреть прежде всего на целую часть — например, дробь 3,5 будет меньше, чем 4,6. А если целая часть одинакова, но различаются знаки после запятой? В этом случае действует правило для целых чисел — нужно сравнивать знаки по разрядам до тех пор, пока не обнаружатся большие и меньшие десятые, сотые, тысячные доли. Например — 4,86 больше 4,75, поскольку восемь десятых больше, чем семь.

Сравнение отрицательных чисел

Если у нас в задаче есть некие числа –а и –с, и нам нужно определить, какое из них больше, то применяется универсальное правило. Сначала выписываются модули этих чисел — |a| и |с| — и сравниваются между собой. То число, модуль которого больше, окажется меньшим в сравнении отрицательных чисел, и наоборот — большим числом будет то, модуль которого меньше.

Что делать, если сравнить нужно отрицательное и положительное число?

Здесь работает всего одно правило, и оно элементарно. Положительные числа всегда больше чисел со знаком «минус» — какими бы они ни были. Например, число «1» всегда будет больше числа «-1458» просто потому, что единица стоит справа от нуля на координатной прямой.

Также нужно помнить, что любое отрицательное число всегда меньше нуля.

Сравнение десятичных чисел онлайн калькулятор больше меньше. Сравнение чисел

Продолжаем изучать рациональные числа. В данном уроке мы научимся сравнивать их.

Для этого случая есть и правило, которое при желании можно использовать. Выглядит оно следующим образом:

Из двух положительных чисел больше то число, модуль которого больше.

Например, сравним те же числа 4 и 1, применяя вышеприведенное правило

Находим модули чисел:

|4| = 4

|1| = 1

Сравниваем найденные модули:

4 > 1

Отвечаем на вопрос:

4 > 1

Для отрицательных чисел существует другое правило, выглядит оно следующим образом:

Из двух отрицательных чисел больше то число, модуль которого меньше.

Например, сравним числа −3 и −1

Находим модули чисел

|−3| = 3

|−1| = 1

Сравниваем найденные модули:

3 > 1

Отвечаем на вопрос:

−3

Число −3 меньше, чем число −1 . Это можно понять, если воспользоваться координатной прямой

Видно, что число −3 лежит левее, чем −1 . А мы знаем, что чем левее, тем меньше.

Видно, что −4 лежит левее, чем 2. А мы знаем, что «чем левее, тем меньше».

Намного сложнее сравнивать другие виды чисел, такие как обыкновенные дроби, смешанные числа и десятичные дроби, некоторые из которых являются отрицательными. Здесь уже в основном придётся применять правила, потому что точно изобразить такие числа на координатной прямой не всегда возможно. В некоторых случаях, число надо будет , чтобы сделать его более простым для сравнения и восприятия.

Пример 1. Сравнить рациональные числа

Пример 2.

Требуется сравнить два отрицательных числа. Из двух отрицательных чисел больше то, модуль которого меньше.

Находим модули чисел:

Сравниваем найденные модули:

Пример 3. Сравнить числа 2,34 и

Пример 4. Сравнить рациональные числа и

Находим модули чисел:

Пример 5.

Пример 6. Сравнить рациональные числа 0 и

Пример 7 . Сравнить рациональные числа 4,53 и 4,403

Находим модули чисел

Сравниваем найденные модули:

Пример 8. Сравнить рациональные числа и

Находим модули чисел:

Пример 9. Сравнить рациональные числа 15,4 и 2,1256

Модуль целой части дроби 15,4 больше, чем модуль целой части дроби 2,1256

поэтому и дробь 15,4 больше, чем дробь 2,1256

15,4 > 2,1256

154000 > 21256

Правила сравнения остаются всё теми же. В нашем случае мы сравнивали положительные числа.

Пример 10. Сравнить рациональные числа −15,2 и −0,152

Видим, что модуль целой части дроби −15,2 больше, чем модуль целой части дроби −0,152.

−0,152 > −15,2

Пример 11. Сравнить рациональные числа −3,4 и −3,7

В этом случае придётся пользоваться старым методом: найти модули рациональных чисел и сравнить эти модули

Сравниваем найденные модули:

−3,4 > −3,7

Пример 12. Сравнить рациональные числа 0,(3) и

Требуется сравнить два положительных числа. Причем сравнить периодическую дробь с простой дробью.

Находим модули чисел:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Рассмотрим пример:

Сравните дроби \(\frac{7}{26}\) и \(\frac{13}{26}\).

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

\(\frac{7}{26}

Сравнение дробей с равными числителями.

Если у дроби одинаковые числители, то больше та дробь, у которой знаменатель меньше.

Понять это правило можно, если привести пример из жизни. У нас есть торт. К нам в гости могут прийти 5 или 11 гостей. Если придут 5 гостей, то мы разрежем торт на 5 равных кусков, а если придут 11 гостей, то разделим на 11 равных кусков. А теперь подумайте в каком случаем на одного гостя придется кусок торта большего размера? Конечно, когда придут 5 гостей, кусок торта будет больше.

Или еще пример. У нас есть 20 конфет. Мы можем поровну раздать конфеты 4 друзьям или поровну поделить конфеты между 10 друзьями. В каком случае у каждого друга будет конфет больше? Конечно, когда мы разделим только на 4 друзей, количество конфет у каждого друга будет больше. Проверим эту задачу математически.

\(\frac{20}{4} > \frac{20}{10}\)

Если мы до решаем эти дроби, то получим числа \(\frac{20}{4} = 5\) и \(\frac{20}{10} = 2\). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Сравните дроби с одинаковым числителем \(\frac{1}{17}\) и \(\frac{1}{15}\) .

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

\(\frac{1}{17}

Сравнение дробей с разными знаменателями и числителями.

Чтобы сравнить дроби с разными знаменателями, необходимо дроби привести к , а потом сравнить числители.

Сравните дроби \(\frac{2}{3}\) и \(\frac{5}{7}\).

Сначала найдем общий знаменатель дробей. Он будет равен числу 21.

\(\begin{align}&\frac{2}{3} = \frac{2 \times 7}{3 \times 7} = \frac{14}{21}\\\\&\frac{5}{7} = \frac{5 \times 3}{7 \times 3} = \frac{15}{21}\\\\ \end{align}\)

Потом переходим к сравнению числителей. Правило сравнения дробей с одинаковыми знаменателями.

\(\begin{align}&\frac{14}{21}

Сравнение .

Неправильная дробь всегда больше правильной. Потому что неправильная дробь больше 1, а правильная дробь меньше 1.

Пример:
Сравните дроби \(\frac{11}{13}\) и \(\frac{8}{7}\).

Дробь \(\frac{8}{7}\) неправильная и она больше 1.

\(1

Дробь \(\frac{11}{13}\) правильная и она меньше 1. Сравниваем:

\(1 > \frac{11}{13}\)

Получаем, \(\frac{11}{13}

Вопросы по теме:
Как сравнить дроби с разными знаменателями?
Ответ: надо привести к общему знаменателю дроби и потом сравнить их числители.

Как сравнивать дроби?
Ответ: сначала нужно определиться к какой категории относятся дроби: у них есть общий знаменатель, у них есть общий числитель, у них нет общего знаменателя и числителя или у вас правильная и неправильная дробь. После классификации дробей применить соответствующее правило сравнения.

Что такое сравнение дробей с одинаковыми числителями?
Ответ: если у дробей одинаковые числители, та дробь больше у которой знаменатель меньше.

Пример №1:
Сравните дроби \(\frac{11}{12}\) и \(\frac{13}{16}\).

Решение:
Так как нет одинаковых числителей или знаменателей, применяем правило сравнения с разными знаменателями. Нужно найти общий знаменатель. Общий знаменатель будет равен 96. Приведем дроби к общему знаменателю. Первую дробь \(\frac{11}{12}\) умножим на дополнительный множитель 8, а вторую дробь \(\frac{13}{16}\) умножим на 6.

\(\begin{align}&\frac{11}{12} = \frac{11 \times 8}{12 \times 8} = \frac{88}{96}\\\\&\frac{13}{16} = \frac{13 \times 6}{16 \times 6} = \frac{78}{96}\\\\ \end{align}\)

Сравниваем дроби числителями, та дробь больше у которой числитель больше.

\(\begin{align}&\frac{88}{96} > \frac{78}{96}\\\\&\frac{11}{12} > \frac{13}{16}\\\\ \end{align}\)

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac{5}{10} \).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac{3}{5} \).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

\(\begin{align}&\frac{3}{5} = \frac{3 \times 2}{5 \times 2} = \frac{6}{10}\\\\&\frac{5}{10}

Ответ: у папы результат лучше.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются , такими как больше (>) или меньше (

Мы рассмотрим все эти правила и попробуем разобраться, почему происходит именно так.

Содержание урока

Сравнение дробей с одинаковыми знаменателями

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Каждый согласиться с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Нередко случается так, что приходиться сравнивать дроби с разными числителями и разными знаменателями.

Умножим дроби на свои дополнительные множители:

После выделения целой части в дроби , получим следующее выражение:

Теперь можно легко понять, почему больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Например, 10−8=2

10 — уменьшаемое

8 — вычитаемое

2 — разность

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5−7=−2

5 — уменьшаемое

7 — вычитаемое

−2 — разность

Например, решим пример .

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Из двух дробей с одинаковыми знаменателями больше та, у которой числитель больше, и меньше та, у которой числитель меньше . На самом деле, ведь знаменатель показывает, на сколько частей разделили одну целую величину, а числитель показывает, сколько таких частей взяли.

Получается, что делили каждый целый круг на одно и то же число 5 , а брали разное количество частей: больше взяли — большая дробь и получилась.

Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше. Ну и, в самом деле, если мы один круг разделим на 8 частей, а другой на 5 частей и возьмем по одной части от каждого из кругов. Какая часть будет больше?

Конечно, от круга, поделенного на 5 частей! А теперь представьте, что делили не круги, а торты. Вы бы какой кусочек предпочли, точнее, какую долю: пятую или восьмую?

Чтобы сравнить дроби с разными числителями и разными знаменателями, надо привести дроби к наименьшему общему знаменателю, а затем сравнивать дроби с одинаковыми знаменателями.

Примеры. Сравнить обыкновенные дроби:

Приведем эти дроби к наименьшему общему знаменателю. НОЗ(4; 6)=12. Находим дополнительные множители для каждой из дробей. Для 1-й дроби дополнительный множитель 3 (12: 4=3 ). Для 2-й дроби дополнительный множитель 2 (12: 6=2 ). Теперь сравниваем числители двух получившихся дробей с одинаковыми знаменателями. Так как числитель первой дроби меньше числителя второй дроби (9, то и сама первая дробь меньше второй дроби.

Yandex.RTB R-A-339285-1

Сравнение дробей с одинаковыми знаменателями

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Пример 1

Произвести сравнение заданных дробей 65 126 и 87 126 .

Решение

Ответ: 87 126 > 65 126 .

Сравнение дробей с разными знаменателями

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

найти общий знаменатель;
сравнить дроби.

Рассмотрим данные действия на примере.

Пример 2

Произвести сравнение дробей 5 12 и 9 16 .

Решение

После сравнения дробей получаем, что 20 48

Ответ: 5 12

Пример 3

Произвести сравнение дробей 5 18 и 23 86 .

Решение

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Рассмотрим на примере.

Пример 4

Произвести сравнение дробей 54 19 и 54 31 .

Решение

Ответ: 54 19 > 54 31 .

Сравнение дроби с натуральным числом

Пример 4

Необходимо выполнить сравнение 63 8 и 9 .

Решение

Ответ: 63 8

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter

Калькулятор сравнения дробей онлайн

Вам могут также быть полезны следующие сервисы

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор со скобками

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление.

Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона.

Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора.

Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Калькулятор сравнения дробей

Использование калькулятора

Сравните дроби, чтобы определить, какая дробь больше, а какая меньше. Вы также можете использовать этот калькулятор для сравнения смешанных чисел, сравнения десятичных чисел, сравнения целых чисел и сравнения неправильных дробей.

Как сравнивать дроби

Чтобы сравнить дроби с разными знаменателями, преобразуйте их в эквивалентные дроби с одинаковым знаменателем.

Если у вас смешанные числа, преобразуйте их в неправильные дроби
Найдите наименьший общий знаменатель (ЖКД) дробей.
Преобразуйте каждую дробь в ее эквивалент с ЖК-дисплеем в знаменателе
Сравните дроби: Если знаменатели совпадают, вы можете сравнить числители. Дробь с большим числителем — это большая дробь.

Пример:

Сравните 5/6 и 3/8.

Найдите ЖК-дисплей: кратные 6 равны 6, 12, 18, 24, 30 и т. Д. Кратные 8 равны 8, 16, 24, 32 и т. Д. Наименьшее общее кратное — 24, поэтому мы используем его как наименьшее. общий знаменатель.

Преобразуйте каждую дробь в ее эквивалентную дробь с помощью ЖК-дисплея.
Для 5/6 умножьте числитель и знаменатель на 4, чтобы получить LCD = 24 в знаменателе.

\ (\ dfrac {5} {6} \ times \ dfrac {4} {4} = \ dfrac {20} {24} \)

Для 3/8 умножьте числитель и знаменатель на 3, чтобы получить LCD = 24 в знаменателе.

\ (\ dfrac {3} {8} \ times \ dfrac {3} {3} = \ dfrac {9} {24} \)

Сравните дроби. Поскольку знаменатели похожи, вы можете сравнивать числители. 20 больше 9, поэтому:

\ (\ dfrac {20} {24}> \ dfrac {9} {24} \)

заключаем

\ (\ dfrac {5} {6}> \ dfrac {3} {8} \)

Для получения дополнительной информации о дробях см. Наш Калькулятор дробей, Упростите калькулятор дробей и Калькулятор смешанных чисел.

Ссылки: Справка по дробям Нахождение наименьшего общего знаменателя.

Использование числовой строки для сравнения десятичных, дробных и целых чисел — Видео и стенограмма урока

Целые числа на числовой строке

Сначала мы возьмем целые числа на числовой строке. Вспомните, что целых чисел — это ваши счетные числа, например 1, 2, 3 и так далее.

Найти целые числа в числовой прямой довольно просто. Почему это? Что ж, если вы посмотрите на свою числовую линию или даже на линейку, что вы увидите?

Целые числа в числовой строке

Да ведь вы видите свои целые числа. Вы видите 0 в середине числовой строки. Справа вы видите свои положительные числа. Идя вправо от 0, мы получаем 1, 2, 3, 4 и так далее. Вы продолжаете движение вправо, и ваши числа становятся все больше.

Идя налево от 0, у нас есть отрицательные числа, и они становятся все более и более отрицательными. У нас есть -1, -2, -3 и так далее. Итак, если бы мы хотели найти, например, число 5, что, по вашему мнению, нам нужно было бы сделать? Да, мы перешли бы вправо на 5 пробелов от 0, чтобы найти нашу 5.

Для построения целых чисел мы используем аналогичную процедуру. Если бы мы хотели построить 3, мы бы начали с 0, а затем прошли бы три деления вправо, чтобы найти, где находится наша 3. В этот момент мы размещаем нашу точку.

Десятичные и дроби в числовой строке

А как насчет десятичных знаков (числа с десятичной точкой) и дробей (чисел, представляющих часть целого)? Как найти и нанести эти числа на график? Для этих типов чисел сначала мы должны понять, что они говорят вам, что ваше число больше, чем целое число. Эти числа включают часть целого числа. Например, десятичная дробь 3,5 говорит вам, что у вас есть три целых, а затем половина.Если бы мы подумали о пирогах, у нас было бы три целых пирога, а затем половина пирога. Итак, числа после десятичной точки говорят вам, сколько у вас другого целого — сколько у вас другого пирога.

Дроби связаны с десятичными знаками, так как вы можете перемещаться между дробями и большинством десятичных знаков. Например, дробь 3 1/2 может быть преобразована в нашу десятичную дробь 3,5. Мы сделали преобразование, разделив 1 и 2, а затем добавив их к 3. Это тот вид преобразования, который мы сделали бы для смешанных дробей.С другой стороны, если бы у нас была дробь 7/2, мы бы сделали прямое деление, чтобы найти нашу десятичную дробь. 7 разделить на 2 также будет 3,5. Все эти числа совпадают.

При поиске дробей в числовой строке для меня наиболее разумно сначала преобразовать их в десятичные числа, а затем искать их. И это то, что я хочу, чтобы вы сделали. Преобразуйте дроби в десятичные, прежде чем работать с ними на числовой строке.

Чтобы найти десятичную дробь или дробь, преобразованную в десятичную в числовой строке, мы сначала находим целую часть числа, а затем выясняем, сколько еще нам нужно сделать для части после десятичной дроби, части целого.Например, чтобы найти число 3,5, мы сначала находим нашу 3. Мы находим это, перемещая 3 пробела справа от 0. Теперь нам нужно выяснить, сколько нам нужно потратить, чтобы учесть 0,5 после трех. Для этого мы можем поставить маленькие косые черты между нашими 3 и 4, чтобы разделить этот раздел на 10 пробелов.

Поместите косую черту в числовую строку, чтобы найти десятичные дроби.

В итоге мы поставим 9 отметок, расположенных на одинаковом расстоянии друг от друга, чтобы разделить эту область на 10 равных промежутков.Теперь мы можем посчитать и найти пятую отметку, чтобы найти наш 0,5. Если бы наша десятичная дробь была 3,53, мы бы сделали то же самое, чтобы найти 3,5, а затем разделили бы следующее пространство на 10 пробелов, как мы делали, чтобы найти 0,5, чтобы мы могли найти наш .53. Сделайте эти отметки небольшими, чтобы было видно, что они даже меньше, чем другие нанесенные вами отметки. Тогда наш .53 будет третьей маленькой отметкой после нашей .5

. Чтобы нанести эти числа, вы сначала находите их на числовой прямой, а затем рисуете точку в этом месте.Итак, чтобы нарисовать число 3,5, вы сначала его находите, а затем помещаете в это место красивую большую точку.

Сравнение чисел в числовой строке

Теперь, когда вы знаете, как находить числа и наносить их на график, давайте поговорим о сравнении этих чисел. Допустим, вы хотите сравнить числа 5 и 6.5. Вы должны сначала построить оба этих числа, найдя их и затем поставив на них точку. Обозначьте эти точки, чтобы знать, какой номер какой.

Теперь ваша задача — посмотреть, какой из них больше. Поскольку наша числовая линия становится больше, когда вы идете вправо, точка справа от другой точки будет больше. Итак, сравнивая наши числа 5 и 6.5, мы видим, что 6.5 больше, чем 5. 5, значит, меньше 6.5. И вот оно. Вот как вы используете числовую линию для сравнения чисел.

Резюме урока

Итак, теперь давайте рассмотрим то, что мы узнали. Мы узнали, как построить целых чисел (или подсчет чисел), десятичных чисел (числа с десятичной точкой) и дробей (числа, представляющие часть целого) на числовой строке , строке с числами размещены в порядке через равные промежутки времени.Мы узнали, что на числовой строке цифра 0 находится посередине. Цифры становятся все выше и выше по направлению вправо. Цифры становятся все меньше и меньше влево. Слева от 0 мои отрицательные числа, а справа от 0 мои положительные числа.

Чтобы нанести числа на числовую прямую, мы сначала находим наше число на числовой прямой, а затем ставим на него точку. Мы можем обозначить нашу точку только что нанесенным числом. Чтобы сравнить два или более чисел друг с другом, мы наносим их на числовую линию, а затем сравниваем их положение по отношению друг к другу.Если одна точка находится справа от других точек, она больше остальных. Если точка слева, она меньше остальных. Просто помните, что переход вправо в числовой строке приводит к большим числам, а переход влево — к меньшим.

Результаты обучения

После этого урока вы сможете:

Определить числовую строку
Опишите, как нанести на числовую строку целые числа, десятичные дроби и дроби.
Объясните, как сравнивать числа с помощью числовой строки

Подавление систематической ошибки целых чисел при сравнении десятичных чисел: исследование отрицательного прайминга, связанного с развитием

https: // doi.org / 10.1016 / j.jecp.2018.08.010Получить права и контент

Основные моменты

•: Смещение целых чисел является корнем ошибок в задачах сравнения десятичных величин.
•: Смещение целого числа должно быть запрещено для сравнения величины десятичных чисел.
•: К возрасту 12 лет подавление смещения целых чисел в значительной степени автоматизируется.

Реферат

Основным источником ошибок в задачах сравнения десятичных величин является неправильное применение правил целых чисел.В частности, при сравнении величины десятичных чисел и наименьшего числа имеет наибольшее количество цифр после десятичной точки (например, 0,9 против 0,476), используя свойство целых чисел, такое как «чем больше количество цифр, тем больше его величина »может привести к ошибочным ответам. Используя парадигму отрицательного прайминга, текущее исследование было направлено на то, чтобы определить, была ли способность семиклассников и взрослых сравнивать десятичные дроби, в которых наименьшее число имеет наибольшее количество цифр после десятичной точки, частично связана со способностью подавлять «большее». количество цифр, тем больше его величина »заблуждение.Мы обнаружили, что после того, как участникам нужно было сравнить десятичные числа, в которых наименьшее число имеет наибольшее количество цифр после десятичной точки (например, 0,9 против 0,476), они были менее эффективны при сравнении десятичных чисел, в которых наибольшее число имеет наибольшее число. количество цифр после десятичной точки (например, 0,826 против 0,3), чем после сравнения десятичных чисел с таким же количеством цифр после десятичной точки (например, 0,981 против 0,444). Отрицательные эффекты прайминга, отмеченные у семиклассников и взрослых, предполагают, что тормозящий контроль необходим в любом возрасте, чтобы избежать ошибок при сравнении десятичных дробей, когда наименьшее число имеет наибольшее количество цифр после десятичной точки.

Ключевые слова

Числовое познание

Рациональные числа

Десятичные числа

Смещение целых чисел

Ингибирующий контроль

Отрицательное прайминг

Рекомендуемые статьи Цитирующие статьи (0)

Просмотреть полный текст

Ссылки на статьи

Порядок десятичных знаков

«Можно мне 3,65 и 0,8, пожалуйста…? «
НЕТ, не ТОГО типа заказа. Я имею в виду наведение порядка …

Упорядочить десятичные дроби бывает непросто. Потому что часто мы смотрим на 0,42 и 0,402 и говорим, что 0,402 должно быть больше, потому что цифр больше. Но нет!

Мы можем использовать этот метод, чтобы увидеть, какие десятичные дроби больше:

Создайте таблицу с десятичной точкой в том же месте для каждого числа.
Введите каждое число.
Заполните пустые квадраты нулями .
Сравните, используя первый столбец слева
Если цифры равны, переходите к следующему столбцу вправо, пока не выиграет одно число.

Если вам нужен порядок по возрастанию , вы всегда выбираете наименьший из первых
Если вы хотите упорядочить по убыванию , вы всегда выбираете самый большой первый

Пример: поместите следующие десятичные знаки в порядке возрастания:

1. 506, г. 1,56, 0,8

В таблице они выглядят так:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
1	.	5	0	6
1	.	5	6
0	.	8

Заполните пустые квадраты нулями:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
1	.	5	0	6
1	.	5	6	0
0	.	8	0	0

Сравнить по первому столбцу (Единицы)

Два из них — «1», а другой — «0». В порядке возрастания сначала нужны наименьшие, поэтому победителем будет «0»:

Ответить на данный момент: 0.8

Теперь мы можем удалить 0.8 из списка:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
1	.	5	0	6
1	.	5	6	0
–	.	–	–	–

Сравните десятые

Теперь есть два числа с одинаковым значением «десятых», равным 5, так что переходите к «сотым» для решения проблемы

Сравните сотые

У одного из них 6 сотых, а у другого 0, поэтому 0 выигрывает (помните, что мы ищем наименьшее значение каждый раз).Другими словами, 1,506 меньше 1,56:

На данный момент ответ: 0,8, 1,506

Удалить 1,506 из списка:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
–	.	–	–	–
1	.	5	6	0
–	.	–	–	–

Осталось только одно число, оно должно быть самым большим:

Ответ: 0,8, 1,506, 1,56

Готово!

Пример. Поместите следующие десятичные дроби в УНИВЕРСАЛЬНОМ порядке:

0,402, 0,42, 0,375, 1,2, 0,85

В таблице они выглядят так:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
0	.	4	0	2
0	.	4	2
0	.	3	7	5
1	.	2
0	.	8	5

И мы хотим перейти от к самому низкому (по убыванию).

Заполните пустые квадраты нулями:

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
0	.	4	0	2
0	.	4	2	0
0	.	3	7	5
1	.	2	0	0
0	.	8	5	0

Сравните, используя первый столбец (Единицы):

Здесь 1, все остальные 0. В порядке убывания сначала нужно наибольшее, поэтому 1,2 должно быть наивысшим. (Запишите это в своем ответе и вычеркните из таблицы).

Ответ на данный момент: 1,2

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
0	.	4	0	2
0	.	4	2	0
0	.	3	7	5
–	–	–	–	–
0	.	8	5	0

Сравните десятые.

8 является самым высоким значением, поэтому следующим по значению будет 0,85.

Ответ на данный момент: 1,2, 0,85

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
0	.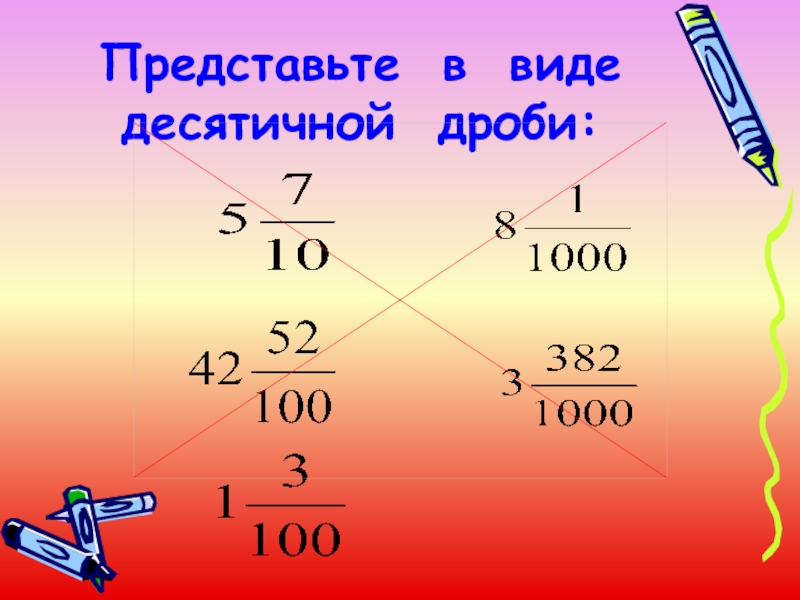	4	0	2
0	.	4	2	0
0	.	3	7	5
–	–	–	–	–
–	–	–	–	–

Теперь есть два числа с одинаковым значением «десятых», равным 4, поэтому переходите к «сотым» для определения тай-брейка

У одного числа 2 в сотых, а у другого 0, поэтому выигрывает 2.Таким образом, 0,42 больше, чем 0,402:

Ответ на данный момент: 1,2, 0,85, 0,42, 0,402

Единицы	Десятичный Путевая точка	Десятые	сотых	тысячных
–	–	–	–	–
–	–	–	–	–
0	.	3	7	5
–	–	–	–	–
–	–	–	–	–

Осталось всего 0,375, поэтому ответ:

Ответ: 1,2, 0,85, 0,42, 0,402, 0,375

Больше и меньше

Может быть сложно запомнить, какой знак или символ неравенства использовать при сравнении чисел, но у нас есть простой трюк с памятью, который может помочь!

Видите, как у символа неравенства широкий конец и узкий конец?

Широкий конец открывается для большего значения, а узкий конец указывает на меньшее значение.Если мы опишем изображение ниже слева направо, это будет выглядеть так, как будто все люди-пауки больше (или больше), чем просто один паук-ветчина.

Если мы перевернем все вокруг, мы все равно сможем читать слева направо, но теперь он читается так, как будто один Паучок меньше (или меньше), чем все люди-пауки.

Мы можем применить ту же концепцию к сравнению чисел. Широкий конец знака всегда должен открываться на большее число.

Как найти большее число? 🕵🏿‍♀️

Когда мы сравниваем числа, мы сравниваем разряды слева направо.Число, которое имеет первое значение с большей цифрой, находится дальше от 0 в числовой строке.

Крайнее правое число в числовой строке — большее число.

Помните, что цифры, расположенные дальше вправо, больше, если представить себе сигнальные полосы телефона — полосы становятся все больше и больше по мере продвижения вправо.

Это также означает, что любое положительное число больше любого отрицательного числа.

Почему большее отрицательное число меньше меньшего отрицательного числа? 🤔
Помните, числа увеличиваются по мере того, как мы перемещаемся вправо по числовой строке.
Для отрицательных чисел, вы можете думать, что «больше чем» означает «какое число является менее отрицательным (или более положительным)».
−2> −7
Поскольку −2 правее −7, −2 больше −7.
Ознакомьтесь с нашими или изучите наши разделы и, чтобы узнать больше о том, как сравнивать числа, дроби и десятичные дроби, и проверить свое понимание.
CalculatorExplore
Вы также можете использовать меню быстрых ссылок слева, чтобы перейти к нужному разделу.
Вы также можете использовать раскрывающееся меню «Быстрые ссылки» выше, чтобы перейти к нужному разделу.
Объяснитель урока: сравнение и упорядочение целых чисел
В этом пояснительном механизме мы узнаем, как сравнивать и упорядочивать положительные и отрицательные целые числа, представленные либо в математической модели, либо в реальной ситуации.
Определение: целые числа
Целые числа — это все целые числа, 0,1,2,3,4,5,6« и вскоре, а также их аддитивные обратные числа (или противоположности), которые являются отрицательными числами, −1, −2, −3, −4, −5, −6, .andsoon
Вы уже знаете, как найти целые числа в числовой строке. Помните, что целые числа — это числа, которые можно писать без десятичных знаков. Каждое положительное целое число находится справа нуля, и мы можем думать о них как о находящихся на расстоянии от нуля. Например, 3 — это расстояние 3 от нуля в положительном направлении. Отрицательные числа появляются слева от нуль. Противоположность 3, которая является отрицательной 3 или −3, является расстоянием 3 от ноль в отрицательном направлении.
Вам также должно быть удобно сравнивать целые числа (положительные целые числа вместе с нуль).На числовой строке, показывающей целые числа, числа уменьшаются по мере продвижения вправо. влево и больше при движении слева направо.
Это также верно, когда мы расширяем числовую строку, чтобы включить отрицательные целые числа. Числа по-прежнему становится меньше при движении влево и больше при движении вправо.
Итак, если мы хотим сравнить числа −8, −3, 3 и 8, мы могли бы нарисовать их все на числовой прямой. Мы знаем, как найти 3 и 8, чтобы найти их противоположностей (или аддитивных обратных), мы должны найти числа, которые находятся на расстоянии 3 и 8 от нуля в обратном направлении.
Тогда мы знаем, что наименьшие числа находятся слева, а наибольшие числа — на правильно. Итак, −8 — наименьшее из четырех чисел, 8 — наибольшее из чисел, и мы можем написать следующие операторы сравнения между каждой парой чисел. −8−3−33388> 33> −3−3> −8−83−388> −33−8−888> −8
Теперь давайте посмотрим на пример сравнения двух отрицательных чисел.
Пример 1. Сравнение отрицательных целых чисел в числовой строке
В таблице показана средняя температура в двух городах зимой.Сравните два температуры с использованием.
Город Температура (∘F)
A −5
B −2
Ответ
Чтобы сравнить −5 и −2, мы можем построить числа на числовая строка.
Оба числа отрицательны, поэтому они будут слева от нуля. Номер −2 будет таким же расстоянием от нуля, что и 2, но с противоположным направление.Аналогично, −5 будет на 5 единиц слева от нуля.
Теперь, поскольку мы знаем, что числа увеличиваются по мере того, как мы перемещаемся слева направо по числу линии, мы знаем, что −5 меньше −2. Следовательно, −5−2.
Далее мы увидим, как сравнить положительное и отрицательное число.
Пример 2: Сравнение положительных и отрицательных целых чисел
Что из следующего верно?
−13697
−136 = 97
−136> 97
Ответ
Здесь мы должны сравнить −136 и 97.
Для этого подумайте, где бы числа располагались на числовой прямой.
Мы знаем, что 97 меньше 136 и что эти положительные числа расположены справа. нуля на числовой строке. Чтобы найти −136, мы должны посмотреть на отрицательный числа, стоящие слева от нуля. Число −136 находится в то же расстояние от нуля, что и 136, но в отрицательном направлении (слева от нуль).
Поскольку мы знаем, что числа увеличиваются при перемещении слева направо по числовой строке, мы знайте, что −136 меньше 97.Следовательно, −13697.
Наконец, мы будем использовать то, что мы знаем, чтобы упорядочить набор целых чисел по возрастанию (от наименьшего к наибольшему). или по убыванию (от наибольшего к наименьшему).
Пример 3: Порядок целых чисел с помощью числовой строки
В таблице показаны игроки в карточной игре и их соответствующие результаты. Заказать оценки по убыванию.
Игрок Оценка
1 +16
2 −11
3 +2
4 −8
5 −2
6 −19
7 +6
8 +18
Ответ
Нам нужно расположить оценки от наибольшего к наименьшему. Мы можем сделать это, построив оценки на числовой строке.
Чтобы построить результаты, учитывайте их расстояние от нуля и помните, что положительные числа находятся справа от нуля, а отрицательные числа — слева. Итак, −2 и +2 будет таким же расстоянием от нуля, но в противоположных направлениях.
После того, как вы нашли все числа в числовой строке, вы можете использовать уменьшение числа при движении справа налево. Следовательно, в порядке убывания баллы 18,16,8,6,2, −2, −11, −19.
Пример 4: Сравнение сумм путем представления их в виде целых чисел
На прошлой неделе Самех положил 385 долларов в свой банк. счет, потратил 95 долларов на обед и одолжил 70 долларов другу. Выразите каждую транзакцию как целое число и затем расположите их в порядке возрастания.
Ответ
Во-первых, нам нужно представить каждую ситуацию целым числом. Помните, что положительный целые числа представляют собой прибыль или депозиты, а отрицательные целые числа представляют собой убытки или снятие средств.
Итак, депозит в размере 385 долларов США представляет собой увеличение количество денег на его счету. Мы можем представить это усиление положительным числом: депозита или всего 136⟶ + 136136 долларов.
Расходы 95 долларов США представляют собой уменьшение суммы денег в его аккаунте. Мы можем представить эту потерю отрицательным числом: расходы 95⟶ − 95 долларов.
Одолжение 70 долларов другу также представляет собой убыток от его счет, поэтому представим его отрицательным числом: ссуду 70⟶ − 70 долларов.
Далее мы должны расположить 136, −95 и −70 по возрастанию. приказ.
Нанесите числа на числовую строку, помня, что отрицательные числа появляются слева. равны нулю и находятся на том же расстоянии от нуля, что и их аддитивная обратная (или противоположная). Итак, −95 и 95 — это одинаковое расстояние от нуля в противоположных направлениях. Это означает, что −70 ближе всего к нулю, а +136 — к нулю. дальше всего от нуля.
Поскольку мы знаем, что числа увеличиваются при перемещении слева направо по числовой строке, мы знайте, что −95 — наименьшее из трех чисел, а 136 — самый большой.Следовательно, порядок равен −95, −70,136.
Мы можем резюмировать шаги, необходимые для сравнения целых чисел, следующим образом.
Как: сравнение и упорядочение целых чисел с числовой линией
Чтобы сравнить целые числа, нанесите их на числовую линию, запомнив следующие моменты:
Положительные числа отображаются справа от нуля, и отрицательные числа появляются слева.
Положительное число (например, 2) то же самое расстояние от нуля как его аддитивная обратная или противоположная (например,г., −2).
При просмотре числовой строки числа увеличиваются при перемещении слева направо.
Тормозной контроль и сравнение десятичных чисел у детей школьного возраста
Abstract
Дети школьного возраста ошибочно полагают, что 1,45 больше 1,5, потому что 45 больше, чем 5. Используя парадигму отрицательного прайминга, мы исследовали, можно ли сравнивать величину десятичных чисел в контексте, в котором наименьшее число имеет наибольшее значение. наибольшее количество цифр после десятичной точки (1.45 vs. 1.5) частично коренится в способности подавлять заблуждение «чем больше количество цифр, тем больше его величина», вытекающее из свойства целых чисел. В эксперименте 1 мы обнаружили типичный отрицательный эффект прайминга у 7 ^-го классников, которым требовалось больше времени для сравнения десятичных чисел, в которых наибольшее число имеет наибольшее количество цифр после десятичной точки (1,65 против 1,5) после сравнения десятичных чисел в в котором наименьшее число имеет наибольшее количество цифр после десятичной точки (1.45 против 1,5), чем после сравнения десятичных чисел с таким же количеством цифр после десятичной точки (1,5 против 1,6). В эксперименте 2 мы обнаружили отрицательный эффект прайминга, когда десятичным числам предшествовали элементы, в которых 7 ^– учащихся должны были сравнить длину двух строк. Взятые вместе, наши результаты показывают, что способность сравнивать десятичные числа, в которых наименьшее число имеет наибольшее количество цифр, частично основана на способности подавлять заблуждение «чем больше число цифр, тем больше его величина», а частично — на возможность запретить длину десятичного числа как такового.
Образец цитирования: Roell M, Viarouge A, Houdé O, Borst G (2017) Контроль подавления и сравнение десятичных чисел у детей школьного возраста. PLoS ONE 12 (11): e0188276. https://doi.org/10.1371/journal.pone.0188276
Редактор: Берт Де Смедт, Katholieke Universiteit Leuven, БЕЛЬГИЯ
Поступила: 5 мая 2017 г .; Одобрена: 3 ноября 2017 г .; Опубликован: 20 ноября 2017 г.
Авторские права: © 2017 Roell et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Все соответствующие данные находятся в документе и его файлах с вспомогательной информацией.
Финансирование: Авторы не получали специального финансирования на эту работу.
Конкурирующие интересы: Авторы заявили об отсутствии конкурирующих интересов.
Введение
Понимание десятичных чисел имеет решающее значение для последующего академического и профессионального успеха [1]. Однако, согласно национально репрезентативной выборке из 1000 учителей математики в США, плохое знание «рациональных чисел и операций с дробями и десятичными знаками» является одним из двух самых серьезных препятствий, мешающих их ученикам изучать алгебру [2]. Действительно, хотя учащиеся изучают десятичные дроби в начальных школах, учащиеся средних школ используют десятичные дроби без адекватного знания соответствующих понятий [3,4,5].Понимание десятичных чисел остается слабым даже у студентов из стран, которые являются лучшими в международном сравнении математических достижений, таких как Китай [6]. Примечательно, что учащимся не хватает понимания сравнительного размера десятичных чисел [7]. Сложность десятичного сравнения была документально подтверждена не только у детей в школе [8,9,10], но и у взрослых [11,12].
Десятичное сравнение оказывается особенно трудным, когда сравниваемые десятичные числа не имеют одинакового количества десятичных знаков [13].В этом контексте дети, как правило, ошибочно думают, что 1,45 больше 1,5, потому что 45 больше, чем 5. Эти ошибки, вероятно, являются результатом смещения «целого числа» в данном конкретном случае, используя свойство целых чисел, такое как « чем больше количество цифр, тем больше его величина »для сравнения десятичных чисел, в которых наименьшее из них имеет наибольшее количество цифр после десятичной точки [12,14,15, 16].
Действительно, хотя компетентное понимание целых чисел имеет решающее значение для развития математического понимания, оно также может мешать математическим рассуждениям, когда задействованы рациональные числа [15]. Учащиеся могут неявно или явно предполагать, что особенности целых чисел продолжают применяться к рациональным числам, вызывая систематические ошибки, когда рациональные числа ведут себя иначе, чем целые числа [4,16,17]. По мнению Восняду и его коллег [16,18,19], в дошкольном возрасте у детей формируется исходное представление о числах. Эта концепция, основанная на целых числах, включает в себя предположения, убеждения и ожидания относительно того, что считается числом и как оно должно себя вести. Поскольку информация о рациональных числах нарушает основной принцип концепции целых чисел, дети должны реструктурировать концепцию целых чисел и построить новое представление рациональных чисел.Это новое представление, однако, не заменяет исходное представление целых чисел, а скорее сосуществует с ним [20]. Например, люди совершают больше ошибок и требуют больше времени для сравнения десятичных чисел в элементах, в которых свойства целого числа мешают свойствам десятичного числа (т. Е. Неконгруэнтные элементы, такие как 1,45 против 1,5), чем в элементах, в которых свойства целого числа совпадают со свойствами десятичных чисел (т. е. совпадающими элементами, такими как 1,45 против 1.4) [21].
Ван Хоф и его коллеги [22,23] также представили доказательства систематической ошибки целых чисел у учащихся средних школ, обрабатывающих алгебраические выражения («умножение и сложение всегда приводят к большим результатам» и «деление и вычитание всегда приводят к меньшим результатам») и при сравнении дробей. (учитывая, что дроби — это два (натуральных) числа, а не одно число), как предполагает более высокий уровень точности конгруэнтного (например, x * 5
Наконец, Дуркин и Риттл-Джонсон [24] в продольном исследовании, оценивающем знания и диагностирующем неправильные представления о десятичных дробях у учеников 4-х и 5-х классов, обнаружили, что заблуждение «чем больше количество цифр, тем больше его величина») является одним из наиболее распространенных. заблуждения при сравнении десятичных чисел, и что это заблуждение со временем уменьшилось. До сих пор исследования были сосредоточены на определении контекста, в котором возникают ошибки десятичного сравнения, и неправильных представлений, которые могут быть причиной этих ошибок.Однако механизмы, позволяющие детям преодолевать такие ошибки, остаются в значительной степени неизвестными.
В свете того факта, что управляющие функции и, в частности, тормозящий контроль (т. Е. Способность сопротивляться привычкам, автоматизму и заблуждениям [25]) являются одним из основных механизмов когнитивного развития [26,27,28,29,30, 31] и математического развития, в частности [21,32,33,34,35,36,37,38], мы предположили, что тормозящий контроль может быть одним из механизмов, позволяющих детям преодолевать систематические ошибки при сравнении десятичных чисел, таких как 1.45 и 1.5. В самом деле, Булл и Ли [39] в своем повествовательном обзоре подчеркивают различные способы, которыми запрет может влиять на математические достижения: запрет может подавлять использование информации из словесной задачи, которая не имеет отношения к решению (например, «прибавить, если больше, или вычесть, если меньше »[40]), это может подавить несоответствующие стратегии (например, сложение, когда требуется вычитание) или представление числа сторонников (например, смещение целых чисел).
Это предположение согласуется с теорией двойственного процесса человеческого рассуждения, согласно которой систематические ошибки рассуждения (или смещения рассуждений, такие как смещение целых чисел) в различных областях могут быть частично связаны с нашей склонностью полагаться на эвристику (т.е. быстрые автоматические и целостные стратегии, такие как стратегия «чем больше число цифр, тем больше его величина») в контекстах, в которых мы должны полагаться на алгоритмические стратегии (т.е. медленные, требующие когнитивных способностей и аналитические стратегии) [41,42]. Чтобы правильно реагировать на ситуации, когда алгоритмические стратегии противоречат эвристическим стратегиям, исследования предоставили конвергентные доказательства того, что тормозящий контроль необходим, чтобы избежать использования вводящей в заблуждение эвристической стратегии [43,44,45].
Таким образом, в настоящем исследовании мы исследовали в Эксперименте 1, является ли способность детей сравнивать величину пары десятичных чисел, при которой самое маленькое из них имеет наибольшее количество цифр после десятичной точки (например, 1,45 против 1,5), имеет корень. в способности подавлять заблуждение «чем больше число цифр, тем больше его величина». В эксперименте 2 мы стремились определить, нужно ли в этом контексте также ограничивать длину десятичного числа (то есть пространственную протяженность числа в смысле непрерывной пространственной величины) как таковую.
В обоих экспериментах мы использовали парадигму отрицательного прайминга, чтобы определить, может ли потребоваться ингибирование. Парадигма негативного прайминга основывается на логике, согласно которой, если стратегия (или заблуждение) запрещена в отношении данного элемента, то активация этой стратегии (или заблуждения) в отношении следующего элемента должна быть более сложной, о чем свидетельствует более низкая производительность [46, 47]. Используя подход негативного прайминга, исследования предоставили доказательства роли тормозящего контроля в преодолении систематических ошибок при решении арифметических словесных проблем у детей, взрослых и экспертов [37,40], в количественных рассуждениях в геометрии [26], в логике. рассуждения о включении классов [48,49] и сохранении числа [50], а также в понимании физического принципа, управляющего плаванием объектов [51].Обратите внимание, что подход с отрицательной праймингом требует, чтобы участники могли выполнять задачи выше вероятности для основных предметов. Поскольку предварительные тесты показали, что дети до 7 класса имели случайный уровень успеваемости при сравнении величины десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр после десятичной точки (например, 4,5 против 4,233), мы включили 7 В нашем исследовании приняли участие ^-й классников.
Эксперимент 1
Мы использовали парадигму отрицательного прайминга, чтобы определить, нужно ли подавлять заблуждение «чем больше число цифр, тем больше его величина», чтобы сравнить величину десятичных чисел, в которых наименьшее число имеет наибольшее количество цифр после десятичная точка.Мы разработали парадигму отрицательного прайминга, в которой как для простых, так и для проверочных элементов дети должны были сравнивать десятичные числа и определять наибольшее. В условиях тестирования совпадающие элементы проверки, в которых наибольшее число имело наибольшее количество цифр после десятичной точки (например, 7,899 по сравнению с 7,4, контекст, который автоматически запускает заблуждение «чем больше количество цифр, тем больше его величина») , таким образом помогая определить наибольшее десятичное число) предшествовали неконгруэнтные простые элементы (т.е., простое число), в котором наименьшее десятичное число имело наибольшее количество цифр после десятичной точки (например, 4,5 по сравнению с 4,233, контекст, который предположительно требует подавления заблуждения «чем больше количество цифр, тем больше его величина»). ). В контрольных условиях одним и тем же конгруэнтным элементам пробы предшествовали нейтральные простые элементы, для которых стратегия «чем больше количество цифр, тем больше его величина» не имела значения, поскольку оба десятичных числа имели одинаковое количество десятичных разрядов (например.г., 8.1 против 8.5).
Мы рассудили, что если неправильное представление «чем больше число цифр, тем больше его величина» должно быть запрещено для сравнения неконгруэнтных элементов, десятичных чисел, в которых наименьшее число имеет наибольшее количество цифр после десятичной точки, то должен быть отрицательный эффект прайминга. Обратите внимание: дети должны быть менее эффективны, чтобы определить, какое из двух десятичных чисел является наибольшим в конгруэнтных элементах (например, 7,899 против 7,4) после сравнения величины десятичных чисел в несовпадающем элементе (например, 7,899 против 7,4).g., 4,5 против 4,233), чем после сравнения двух десятичных чисел в нейтральном элементе (например, 8,1 против 8,5).
Метод
участников.
Мы набрали 26 детей со средним возрастом 12,4 ± 0,52 года с нормальным или исправленным зрением из государственной средней школы, обслуживающей разнообразное население (Париж, Франция). Мы исключили двух детей, набравших наивысший балл, в результате получилась группа из 24 детей (9 мальчиков) со средним возрастом 12,35 ± 0,51 года. Мы получили информированное письменное согласие родителей, а также устное согласие всех детей.Дети были протестированы в соответствии с национальными и международными нормами, регулирующими использование участников исследования на людях. Факультет психологии (Парижский университет Декарта) предоставил этическое разрешение на проведение этого исследования.
Материалы.
Стимулы были представлены на портативном компьютере (разрешение 1366 × 768 пикселей и частота обновления 60 Гц) с использованием E-Prime 2.0. Основные элементы состояли из пар десятичных знаков, написанных 24-пунктирным шрифтом Courier New, каждая из которых располагалась в левой или правой части экрана под знаком 0.Угол обзора 5 ° от центра. В условиях теста простые элементы представляли собой пары десятичных чисел, в которых наименьшее десятичное число имело наибольшее количество цифр после десятичной точки (например, 3,453 против 3,6). В условиях контроля простые элементы состояли из пар десятичных чисел с одинаковым количеством цифр после десятичной точки (например, 7,3 против 7,6). В обоих условиях элементы проверки состояли из пар десятичных чисел, в которых наибольшее десятичное число имело наибольшее количество цифр после десятичной точки (например,g. , 5.644 против 5.4). Десятичные числа имеют одну, две или три цифры после десятичной точки. У десятичных знаков в парах либо одинаковое количество десятичных знаков, либо разное количество знаков после десятичной точки. Сложность сравнения систематически варьировалась, манипулируя числовым расстоянием между первыми цифрами после десятичной точки каждого десятичного числа в паре (расстояние варьировалось от 1 до 6).
Порядок действий.
Детей тестировали индивидуально, сидя на расстоянии примерно 75 см от портативного компьютера.Для каждой пары представленных десятичных чисел детям было предложено определить, какое из двух десятичных чисел было наибольшим. Дети нажимали левую кнопку мыши, чтобы указать, что десятичное число в левой части экрана было наибольшим, и правую кнопку, чтобы указать, что десятичное число справа было наибольшим. Как показано на рис. 1, каждое испытание начиналось с представления креста фиксации (500 мс), затем отображалась пара десятичных чисел (до тех пор, пока дети не ответили с ограничением по времени 2500 мс).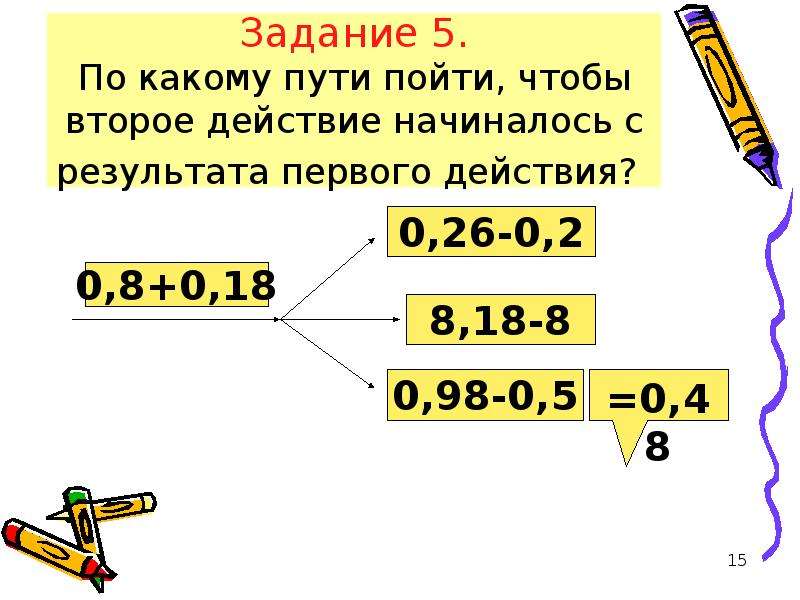 Как только дети давали ответ, снова появлялась точка фиксации (500 мс), за которой следовала другая пара десятичных чисел, которая сохранялась до тех пор, пока дети не предоставили ответ (с ограничением по времени 2500 мс). Визуальная маска была представлена между каждым испытанием, чтобы избежать передачи процессов от зонда одного испытания к начальному значению следующего испытания (1000 мс). Сначала дети выполнили блок из 6 практических испытаний, в котором им сначала были представлены 2 совпадающих предмета, затем 2 нейтральных предмета и, наконец, 2 несовместимых предмета с парами десятичных чисел, отличными от тех, которые использовались в экспериментальных испытаниях.Дети получили простые отзывы (правильные / неправильные) об их точности во время практических испытаний. Затем они выполнили блоки из 48 испытаний (24 в тестовых и 24 в контрольных). Все последовательности моторных ответов между праймом и зондом появлялись одинаково часто. Порядок испытаний был рандомизирован, за исключением того, что подряд могло проводиться не более трех испытаний или контрольных испытаний.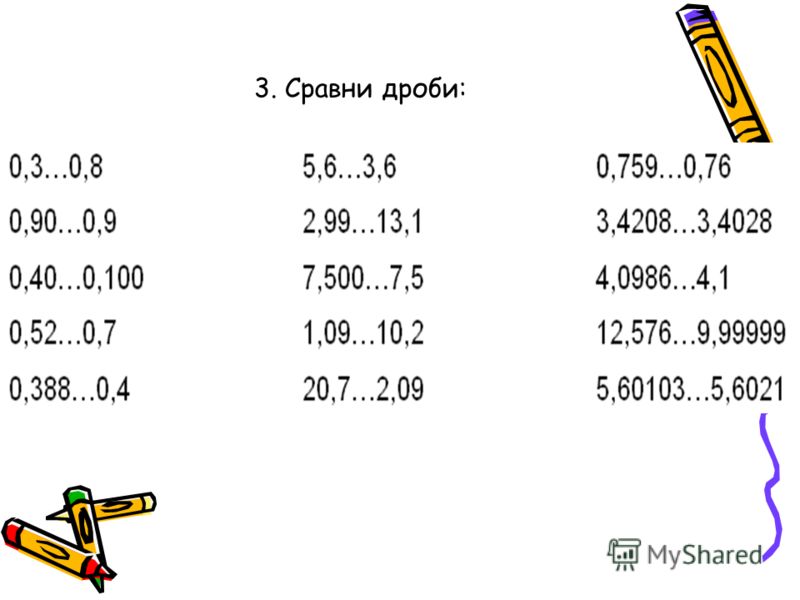
Рис. 1. Пример элементов заправки и зонда, представленных в тесте и условиях контроля.
Прайм-предметы (т.е., неконгруэнтные и нейтральные элементы) различались между двумя условиями, но тестовые элементы (т. е. конгруэнтные элементы) были похожи.
https://doi.org/10.1371/journal.pone.0188276.g001
Результаты
Прайм или время отклика зонда (RT) меньше или больше 2 SD от индивидуального среднего для данного условия были удалены (M = 7 ± 5%). Для каждого ребенка мы усредняли RT и точности отдельно для контрольных и тестовых праймов и зондов. Обратите внимание, что в соответствии с логикой парадигмы NP, мы только проанализировали точность, RT и IES для элементов зонда, которым предшествовали основные элементы, выполненные правильно.Затем мы вычислили для каждого ребенка обратную оценку эффективности (т. Е. RT, разделенные на долю правильных ответов [52,53]) для простых чисел и тестов контроля и условий теста. Обратите внимание, что наши данные соответствовали рекомендациям Bruyer и Brysbaert [52] по использованию показателя обратной эффективности (IES): точность была высокой (т. е. более 85%), точности и RT шли в том же направлении, и мы не наблюдали никаких изменений. компромисс скорость-точность ( r с <0,26, p с > .21). IES позволяет нам упростить наш анализ, объединяя оценки точности и RT в одну переменную и соответствующим образом взвешивая влияние скорости и точности. Для каждого анализа мы указываем величину эффекта в виде разницы средних значений (d Коэна). Двусторонний байесовский парный t-критерий (с априорной шириной Коши по умолчанию r = 0,707) использовался для количественной оценки доказательств в пользу (BF ₀₁) или против (BF ₁₀) нулевой гипотезы. Байесовский анализ проводился с использованием программного обеспечения JASP (версия 0.8.3.1).
Парный двусторонний t-тест на простые значения точности, RT и IES показал, что дети менее эффективно сравнивали величину двух десятичных чисел в неконгруэнтных заданиях (например, 1,45 против 1,5), чем в нейтральных заданиях (например, 7,45). против 7,55), t (23) = 4,47, p <0,001, d = 0,91, BF ₁₀ = 165 для точности, t (23) = 6,34, p <0,001, d = 1,29, BF ₁₀ = 10575 для RT и t (23) = 5,30, p <. 001, d = 1.08, BF ₁₀ = 1050 для IES (см. Таблицу 1 и Таблицу S1).
Таблица 1. Точности, RT и IES в двух типах основных элементов (неконгруэнтные и нейтральные) и двух типов конгруэнтных тестовых элементов (которым предшествуют неконгруэнтные или нейтральные простые элементы) в эксперименте 1.
Стандартные отклонения указаны в скобках . Отрицательное заполнение отражает разницу в производительности между двумя типами конгруэнтных зондов.
https: // doi.org / 10.1371 / journal.pone.0188276.t001
Парный двусторонний t-тест на пробных RT и IES выявил отрицательный эффект прайминга: дети менее эффективно сравнивали величину двух десятичных чисел в конгруэнтных заданиях (5,456 против 5,4 ) после сравнения пары десятичных чисел в неконгруэнтных элементах (например, 1,45 против 1,5), чем после сравнения пары десятичных чисел в нейтральных элементах (например, 7,45 против 7,55), t (23) = 3,74, p < 0,001, d = 0,79, BF ₁₀ = 33 для RT и t (23) = 3. 18, p = 0,004, d = 0,64, BF ₁₀ = 10 для IES. Парный двусторонний t-тест на точность зонда не выявил разницы в точности между конгруэнтными элементами, которым предшествуют неконгруэнтные элементы, и конгруэнтными элементами, которым предшествуют нейтральные элементы, t <1, BF ₀₁ = 4, вероятно, из-за эффекта потолка (точность выше 98%) (см. Таблицу 1).
Обсуждение
В соответствии с предыдущими исследованиями [3,12,14,15,16,24] мы обнаружили, что дети менее эффективно сравнивают величину двух десятичных чисел в неконгруэнтных заданиях, когда у самого маленького из них было наибольшее количество цифр после десятичной дроби. точка (1.5 против 1,45), чем в нейтральных элементах, когда два десятичных числа имеют одинаковое количество десятичных знаков (1,5 против 1,4). Важно отметить, что дети менее эффективно определяли, какое из двух десятичных чисел было наибольшим в конгруэнтных заданиях, когда у самого большого из них было наибольшее количество цифр после десятичной точки (1,545 против 1,4, т. Е. В контексте, в котором «большее число количество цифр, тем больше его величина »(заблуждение приводит к правильному ответу), когда ему предшествует неконгруэнтный элемент, чем когда ему предшествует нейтральный элемент.Взятые вместе, наши результаты показывают, что способность детей сравнивать величину десятичных чисел в контексте, в котором наименьшее число имеет наибольшее количество цифр после десятичной точки, частично коренится в способности подавлять «большее количество цифр». тем больше его величина »представление. Наше открытие согласуется и дополняет результаты предыдущих исследований, показывающих, что управляющие функции и тормозящий контроль, в частности, играют важную роль в развитии математических способностей [21,32,33,34,35,36,37,38].
Ограничением эксперимента 1 является ограниченное количество участников, которые могли повлиять на способность обнаруживать значительный эффект между интересующими условиями. Обратите внимание, однако, что мы наблюдали значительную разницу между этими условиями (а) с большим размером эффекта, ds> . 64 и (b) байесовские факторы в пользу гипотезы, альтернативной нулевой гипотезе, все BF ₁₀> 10.
Заблуждение «чем больше число цифр, тем больше его величина», как правило, считается следствием чрезмерного обобщения знаний детей целых чисел до десятичных [4,20].В частности, дети склонны рассматривать все числа как дискретные величины, и что числа с большим количеством цифр больше [54]. Предположительно, дети порождают заблуждение «чем больше число цифр, тем больше его величина», когда они интегрируют рациональные числа в свою концепцию чисел, изначально основанную на целых числах. В эксперименте 2 мы исследовали, может ли сложность сравнения десятичных чисел, у которых наименьшее число имеет большее количество цифр после десятичного разряда (1,45 против 1,5), также может быть связана с тем, что наименьшее число (1.45) длиннее самого большого (1,5).
Эксперимент 2
Исследования развития математического познания предоставили доказательства существования довербальных числовых способностей до получения математического образования [55]. Например, новорожденные уже обладают способностью приблизительно оценить количество предметов в коллекции (то есть их численность [56,57]). Представление о численности связано с активацией популяции нейронов внутри теменной борозды (IPS) у людей [58] независимо от их культуры происхождения [59,60] и у приматов [59].
Однако нейроны в IPS активируются не только в ответ на обработку численности, но также и в ответ на несимвольные измерения величины, такие как длина, плотность и размер [61]. Важно отметить, что из-за перекрытия между кодированием численности нейронной популяции и кодом, кодирующим несимвольные измерения величины, эти несимволические измерения величины имеют тенденцию мешать числовому суждению [62,63]. Яркий пример такого рода помех можно наблюдать в задаче Пиаже по сохранению числа, в которой дети до 7 лет совершают систематические ошибки при оценке относительной численности двух рядов жетонов, когда они различаются по длине, но не по количеству [50 , 64,65].Поскольку символьная числовая обработка активирует те же области IPS, что и те, которые активированы в ответ на обработку числовых значений [66], несимвольные измерения величины, такие как длина, также потенциально могут мешать символьной числовой обработке. В случае обработки десятичных чисел сложность сравнения десятичных чисел, у которых наименьшее число имеет больше цифр после десятичного разряда (1,45 против 1,5), может быть частично связана с тем, что наименьшее число (1,45) длиннее, чем самый большой (1.5).
В эксперименте 2 мы разработали парадигму отрицательного прайминга для проверки следующей гипотезы: седьмых классов попросили сравнить на простом значении пары десятичных чисел, а затем, на датчике, длину пары строк. . В условии теста — неконгруэнтный элемент, пара десятичных чисел, в которых наименьшее число имеет наибольшее количество цифр (например, 7,299 против 7,4, контекст, который предположительно требует запретить длину десятичных чисел для обработки их величины) , предшествует паре строк (контекст, в котором сравнение величины основано на длине стимулов).В контрольном условии паре строк предшествовали нейтральные элементы, пара десятичных чисел с одинаковым количеством десятичных знаков (например, 8.1 и 8.5, контекст, в котором два числа имеют одинаковую длину).
Мы рассудили, что если сравнение десятичных чисел, у которых наименьшее число имеет наибольшее количество цифр, требует запретить длину чисел (т. Е. Пространственную протяженность чисел в смысле непрерывной пространственной величины) для обработки их величины, то потомки должно быть менее эффективным для сравнения длины двух строк, когда им предшествует пара десятичных чисел, в которых наименьшее число имеет наибольшее количество цифр, чем пара десятичных чисел с таким же количеством десятичных знаков.
Метод
участников.
Мы набрали 37 детей (M = 12,82 ± 0,92 года, 21 мальчик) с нормальным или исправленным зрением из той же государственной средней школы, что и дети, набранные в эксперименте 1. Ни один из детей не участвовал в эксперименте 1. Мы получили информированное письменное согласие всех учреждений и родителей, а также устное согласие всех детей. Дети были протестированы в соответствии с национальными и международными нормами, регулирующими использование участников исследования на людях. Факультет психологии (Парижский университет Декарта) предоставил этическое разрешение на проведение этого исследования.
Материалы и порядок действий.
Материалы и процедура были идентичны тем, которые использовались в эксперименте 1, за исключением того, что зонды состояли из пар линий: одна линия появляется справа, а другая — слева в центре экрана в случайном месте. Соотношение длин между двумя линиями в паре было выбрано таким образом, чтобы разница в длине была легко заметна.Были использованы четыре различных соотношения длин (1,10, 1,2, 1,25 и 1,37) с тремя уровнями длины (10, 12 и 15 см), в результате чего получилось 12 различных пар. Длина варьировалась от 7,29 до 18,75 для всех 12 пар. В каждом испытании дети выполняли две задачи сравнения: сначала по паре десятичных знаков (т. Е. Простое число), а затем по паре строк (т. Е. Зонд), см. Рис. 2. По первому знаку дети решали, какой из двух десятичные дроби были самыми большими, а на датчике — какая из двух строк была самой длинной при нажатии левой или правой кнопки мыши, чтобы указать, что стимул, представленный в левой или правой части экрана, был самым большим (для десятичных числа) или самый длинный (для строк). Неконгруэнтные элементы, пары десятичных чисел, в которых наименьшее десятичное число имело наибольшее количество цифр после десятичной точки (например, 3,453 против 3,6), служило простыми числами в условиях теста, а нейтральные элементы, пары десятичных чисел с одинаковым числом цифр после десятичной точки (например, 7,3 против 7,6) служило штрихом в условии контроля. И в тестовых, и в контрольных условиях зонд представлял собой пару линий разной длины. Мы также включили простые числа-заполнители, состоящие из конгруэнтных элементов, десятичных пар, в которых наибольшее десятичное число имело наибольшее количество цифр после десятичной точки (например,g., 5.644 vs. 5.4), чтобы дети не могли систематически выбирать наименьшее десятичное число, когда длина двух десятичных чисел различается.
Рис. 2. Пример элементов заправки и зонда, представленных в тесте и условиях контроля.
Прайм-предметы (т. Е. Неконгруэнтные и нейтральные) различались между двумя условиями, но предметы для проверки были похожи.
https://doi.org/10.1371/journal.pone.0188276.g002
Дети сначала выполнили блок из 5 практических упражнений с парами десятичных чисел (1 конгруэнтный предмет, затем 2 нейтральных предмета и, наконец, 2 несовместимых предмета) и 5 пары линий, отличные от использованных в экспериментальных испытаниях.Дети получали простые отзывы (правильные / неправильные) о правильности своих ответов. Затем дети выполнили блок из 60 испытаний: 24 контрольных, 24 тестовых и 12 фильтрующих. Все последовательности моторных ответов между праймом и зондом появлялись одинаково часто. Порядок испытаний был рандомизирован, за исключением того, что подряд могло проводиться не более трех испытаний или контрольных испытаний.
результатов.
После удаления выбросов, определенных как в эксперименте 1 (M = 10 ± 9%), мы усреднили RT и точности отдельно для контрольных и тестовых простых чисел и зондов.Как и в эксперименте 1, мы затем вычислили для каждого ребенка их IES для простых чисел и зондов контроля и условий тестирования. Обратите внимание, что в соответствии с логикой парадигмы NP, мы только проанализировали точность, RT и IES для элементов зонда, которым предшествовали основные элементы, выполненные правильно. Как и в эксперименте 1, наши данные соответствовали рекомендациям Bruyer и Brysbaert [52] по использованию IES: уровень точности был высоким (т.е. более 95%), точность и RT шли в одном направлении, и мы не наблюдали скорости — компромисс точности ( r s>.12, p s> .45) IES позволяет нам упростить наш анализ, объединяя оценки точности и RT в одной переменной и соответствующим образом взвешивая влияние скорости и точности. Для каждого из анализов мы сообщаем величину эффекта либо в ANOVA (частичный квадрат этажа), либо в терминах разницы средних (d Коэна). Байесовский дисперсионный анализ с повторными измерениями и двусторонний байесовский парный t-критерий (с априорной шириной Коши по умолчанию r = 0,707) использовались для количественной оценки доказательств для (BF ₀₁) или против (BF ₁₀) нулевого значения. гипотеза.Байесовский анализ проводился с использованием программного обеспечения JASP (версия 0.8.3.1).
Дисперсионный анализ с повторными измерениями (ANOVA) для простых значений RT, IES и точности выявил значительный основной эффект типа простого числа (конгруэнтные, нейтральные и неконгруэнтные элементы) для RT, F (2, 72) = 12,81 , p <0,001, η _p ² = 0,26, BF ₁₀ = 1082 и для IES, F (2, 72) = 13,20, p <0,001, η _п. ² =.26, BF ₁₀ = 1418, но не для точности, вероятно, из-за эффекта потолка, F <1, BF ₀₁ = 9 (см. Таблицу 2). Апостериорный парный двусторонний t-тест с использованием поправки Бонферрони для простых RT и IES показал, что дети менее эффективно сравнивали величину двух десятичных чисел в неконгруэнтных заданиях (например, 1,45 против 1,5), чем в нейтральных заданиях ( например, 7,45 против 7,55), t (36) = 3,94, p <0,001, d = 0,64, BF ₁₀ = 78 для RT и t (36) = 4.01, p <.001, d = 0,66, BF ₁₀ = 94 для IES. Дети также были менее эффективны при сравнении величины двух десятичных чисел в неконгруэнтных заданиях (например, 1,45 против 1,5), чем в конгруэнтных испытаниях (например, 5,644 против 5,4), t (36) = 3,57, p = 0,003, d = 0,58, BF ₁₀ = 30 для RT и t (36) = 3,60, p <0,001, d = 0,59, BF ₁₀ = 33 для IES. Однако мы не обнаружили разницы в RT и IES между конгруэнтными (например,g., 5,644 против 5,4) и нейтральные (например, 7,45 против 7,55) элементы, соответственно, t (36) = 1,28, p = 0,62, BF ₀₁ = 2, для RTs и t (36) = 1,31, p = 0,59, BF ₀₁ = 2 для IES (см. Таблицу 2 и таблицу S2).
Таблица 2. Точности (%), RT (мс) и IES в трех типах первичных элементов (неконгруэнтные, нейтральные и конгруэнтные элементы) и трех типов тестовых элементов (которым предшествует неконгруэнтный, нейтральный или конгруэнтный элементарный элемент) в Эксперимент 2.
Стандартные отклонения указаны в скобках.Отрицательная заливка отражает разницу в производительности между неконгруэнтными и нейтральными зондами.
https://doi.org/10.1371/journal.pone.0188276.t002
ANOVA с повторными измерениями на точность датчиков, RT и IES выявил основное влияние типа датчиков (т. е. зонды, которым предшествуют конгруэнтные и нейтральные против инконгруэнтных простых элементов), F (2, 72) = 10,16, p <0,001, η _p ² = 0,22, BF ₁₀ = 467 для точности, F (2, 72 ) = 10.24, p <0,001, η _p ² = 0,22, BF ₁₀ = 186 для RT и F (2, 72) = 15,13, p <0,001, η _p ² = 0,22, BF ₁₀ = 4825 для IES. Апостериорный парный двусторонний t-тест с использованием поправки Бонферрони на точность датчиков, RT и IES показал, что дети были менее эффективны при сравнении длины двух строк после того, как правильно сравнили величину двух десятичных чисел в неконгруэнтных заданиях (например,g., 1,45 против 1,5), чем в нейтральных элементах (например, 7,45 против 7,55), t (36) = 3,92, p <0,001, d = 0,64, BF ₁₀ = 74 для точности, t (36) = 4,70, p <0,001, d = 0,77, BF ₁₀ = 615 для RT и t (36) = 5,28, p <0,001, d = .86, BF ₁₀ = 3106 для IES (см. Таблицу 2). Точно так же дети были менее эффективны при сравнении длины двух строк после того, как правильно сравнили величину двух десятичных чисел в несовместимых элементах (например,g., 1,45 против 1,5), чем в совпадающих элементах (например, 5,644 против 5,4), t (36) = 2,93, p = 0,018, d = 0,33, BF ₁₀ = 6 для IES и t (36) = 2,85, p = 0,02 d = 0,47, BF ₁₀ = 5 для точности. Однако не было обнаружено значительных различий для RT, t (36) = 2,04, p = 0,14, BF ₀₁ = 0,8 (см. Таблицу 2). Наконец, мы не обнаружили различий в успеваемости детей между тестами, которым предшествовали совпадающие элементы (например, 5,644 vs.5.4) и зонды, которым предшествуют нейтральные элементы (например, 7,45 против 7,55), t (36) = 1,24, p = 0,66, BF ₀₁ = 2, для точности и t (36) = 2,39, p = 0,39, BF ₀₁ = 0,4, для RT, кроме IES, t (36) = 2,64, p = 0,03, d = 0,43, BF ₁₀ = 3 (см. Таблицу 2) .
Обсуждение
Как и в эксперименте 1 и в соответствии с предыдущими исследованиями [3,12,14,15,16,24], мы обнаружили, что дети менее эффективно сравнивают величину двух десятичных чисел в неконгруэнтных заданиях, когда наименьшее десятичное число имеет наибольшее значение. количество цифр после десятичной точки (например,g., 1,45 против 1,5), чем в нейтральных элементах, когда два десятичных числа с одним и тем же десятичным знаком (например, 7,45 против 7,55). Кроме того, было обнаружено, что дети менее эффективны для сравнения двух десятичных чисел в неконгруэнтных элементах (например, 1,45 против 1,5), чем в конгруэнтных элементах, десятичных парах, где у самого большого десятичного числа было наибольшее количество цифр после десятичной точки (например, 5,644 vs. 5.4). Важно отметить, что дети были менее эффективны при сравнении длины двух строк после сравнения величины двух десятичных чисел в неконгруэнтных заданиях (например,g., 1,45 против 1,5, контекст, который требует запретить длину чисел для сравнения их величины), чем после сравнения величины двух десятичных знаков в нейтральных элементах (например, 7,45 против 7,55, контекст, в котором длина не мешает и не облегчает сравнение величин). Более того, дети были менее эффективны при сравнении длины двух строк после сравнения величины двух десятичных чисел в неконгруэнтных заданиях (например, 1,45 против 1,5), чем после сравнения величины двух десятичных чисел в конгруэнтных заданиях (например.g., 5.644 против 5.4). Взятые вместе результаты эксперимента 2 предполагают, что сложность сравнения величины десятичных чисел может быть частично связана с трудностью запретить длину числа, когда оно мешает его величине, например, в контексте, в котором наименьшее десятичное число имеет наибольшее количество цифр (например, 1,45 против 1,5). Мы подозреваем, что перекрытие сети нейронов в IPS, участвующих в обработке символьных чисел и численности, и нейронов, кодирующих несимволическую непрерывную величину, такую как размер и длина [61,62,63,67], может быть в основе трудность сравнивать величину десятичных чисел, когда их длина противоречит их величине.
Обратите внимание, что мы не обнаружили разницы в реакции детей на конгруэнтные и нейтральные предметы или на вопросы, которым предшествовали конгруэнтные и нейтральные простые предметы. Отсутствие различий между нейтральными и конгруэнтными элементами — чего можно было бы ожидать, если люди спонтанно сосредотачивались на длине числа как таковом для сравнения величины десятичных чисел — может быть связано с тем, что конгруэнтные элементы использовались в качестве заполнителей и, таким образом, представлялись реже, чем другие предметы (совпадающие предметы представлялись вдвое реже, чем нейтральные и неконгруэнтные: 12 раз vs.24 раза), что приводит к потенциальному эффекту чудаков [68].
Общее обсуждение
Настоящее исследование направлено на определение: (а) должны ли 7 ^{-го ученика}-го класса запрещать стратегию «чем больше число цифр, тем больше его величина», чтобы правильно сравнивать величину десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1,45 против 1,5) и (b) может ли сложность сравнения десятичных чисел в этом контексте быть также связана с тем, что наименьшее число (1.45) длиннее (по длине в пространственно-непрерывном смысле), чем самая большая (1,5).
В соответствии с предыдущими исследованиями [3,12,14,15,16,24], в экспериментах 1 и 2 мы обнаружили, что 7 ^{учащихся} классов были менее эффективны при сравнении величины двух десятичных чисел, когда наименьшее из них имеет наибольшее значение. количество цифр (1,45 против 1,5), чем когда два десятичных числа имеют одинаковое количество десятичных разрядов (1,8 против 1,9).
В эксперименте 1 дети были менее эффективны при сравнении величины двух десятичных чисел, у самого большого из которых было наибольшее количество цифр (например,g., 1,345 против 1,2) после сравнения величины двух цифр, в которых наименьшая из них имела наибольшее количество цифр (1,45 против 1,5), чем после сравнения двух десятичных чисел с одинаковым числом десятичных разрядов (1,8 против 1,9). ). Этот типичный эффект отрицательного прайминга предполагает, что дети должны подавлять заблуждение «чем больше число цифр, тем больше его величина» при сравнении величины десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1.45 vs. 1.5). Это заблуждение, вероятно, является следствием чрезмерного обобщения знаний детей о целых числах до десятичных [4,20,69] и, в частности, знания детей о том, что числа с большим количеством цифр больше [54]. Наш вывод хорошо согласуется с теориями концептуальных изменений, утверждающими, что правильное понимание рациональных десятичных чисел может сосуществовать с более ранним интуитивным пониманием целых чисел [15]. Предыдущие исследования на самом деле продемонстрировали, что образованные взрослые и математические эксперты все еще демонстрируют признаки систематической ошибки целых чисел в различных задачах с рациональными числами [12, 70,71].
В эксперименте 2 мы обнаружили, что 7 ^-го классников были менее эффективны при сравнении длины двух строк после сравнения величины десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1,45 против 1,5), чем после сравнение величины двух десятичных чисел с одинаковым числом десятичных разрядов (1,8 против 1,9). Отрицательный эффект прайминга, описанный в эксперименте 2, предполагает, что сравнение величины десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1.45 vs. 1.5) может потребовать запретить длину десятичного числа как такового в дополнение к подавлению заблуждения «чем больше число цифр, тем больше его величина».
Мы подозреваем, что запрет на длину десятичного числа для обработки его величины в этом контексте может быть необходим, потому что нейроны в IPS, участвующие в обработке символьных чисел и численности, перекрываются с нейронами, кодирующими несимвольную непрерывную величину, такую как длина [ 61,62,63].
Перекрытие функциональных сетей, задействованных в символическом измерении величины и несимволическом измерении величины, таком как длина, могло быть следствием повторного цикла нейронов, вызванного изучением математики.Согласно теории рециклинга нейронов, культурные инструменты, такие как чтение и математика, появились слишком недавно, чтобы повлиять на геном человека, и, таким образом, эти культурные инструменты полагаются на процесс рециклинга нейронов, в соответствии с которым существующие схемы мозга рециркулируются, чтобы нести -из этих новых функций [72]. Математическое обучение, в частности, будет стимулировать переработку нейронов IPS, первоначально предназначенных для обработки непрерывных несимволических измерений величины для обработки символьных и несимволических дискретных измерений величины [59].Ранее существующие свойства рециклируемых нейронов могут вызывать ошибки, подобные тем, которые наблюдаются при десятичном сравнении, а тормозящий контроль может быть основным механизмом, позволяющим исправлять ошибки, вызванные процессом рециклинга нейронов. Это предположение согласуется с выводами о том, что преодоление систематических ошибок при чтении и, в частности, ошибок зеркального отражения (путаница «b» с «d») зависело от способности подавлять исходную функцию (здесь процесс зеркального обобщения) повторно используемых нейронов [41, 73].
Обратите внимание, что хотя оба эксперимента демонстрируют, что необходимо подавить смещение целых чисел, чтобы сравнить величину десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (т. Е. Неконгруэнтные элементы), они позволили нам определить природу когнитивные конструкции, которые были заторможены. Таким образом, два эксперимента предоставляют доказательства того, что смещение целых чисел частично связано с количеством цифр после десятичных знаков (т. Е. «Чем больше число цифр, тем больше его величина», см. Эксперимент 1), а частично — с длина самого десятичного числа (т.е.д., см. эксперимент 2).
Можно утверждать, что отрицательный эффект прайминга, наблюдаемый на конгруэнтных элементах зонда между контрольными и тестовыми условиями, может быть, по существу, обусловлен разницей в сложности между неконгруэнтными элементами и нейтральными элементами, представленными на простых числах соответственно в тестовых и контрольных условиях. . Тем не менее, предыдущие исследования предоставили доказательства того, что отрицательный эффект прайминга не является побочным продуктом выполнения простых и более сложных заданий на прайм-листе [74,75,76].Например, об отрицательных эффектах прайминга обычно сообщается в задаче Струпа, в которой неконгруэнтные элементы представлены в первую очередь как в тестовых, так и в контрольных условиях. В этих парадигмах наблюдается отрицательный эффект прайминга, когда участникам требуется больше времени для определения цвета чернил (т. Е. Релевантной для задачи информации) в неконгруэнтном элементе Струпа (например, СИНИЙ, напечатанный красным), когда цвет чернил соответствует обозначенному цвету. словом (то есть информация, не относящаяся к задаче, которую нужно запретить) в предыдущем неконгруэнтном элементе Струпа (например,g., КРАСНЫЙ, напечатанный зеленым), чем когда цвет чернил не является цветом, обозначенным словом в предыдущем неконгруэнтном элементе Stroop (например, ЖЕЛТЫЙ, напечатанный зеленым).
Более того, можно утверждать, что парадигма адаптации к конфликту могла бы предоставить лучшее свидетельство того, что тормозящий контроль необходим для сравнения величины десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр после десятичной точки. Однако конфликтная адаптация сама по себе не дает доказательств того, что тормозящий контроль требуется для данной задачи, она позволяет исследовать, что когнитивный контроль может поддерживаться от одного элемента к другому [77,78].Кроме того, задачи адаптации к конфликту зависят от способности задействовать проактивный контроль, который все еще развивается в возрасте от 8 до 10 лет [79] и может взаимодействовать с эффектами адаптации к конфликту [80]. Наконец, в отличие от парадигмы адаптации к конфликту, парадигма негативного прайминга позволяет определить природу стратегии, предвзятости или заблуждения, которые необходимо предотвратить, что является одной из целей настоящего исследования [37,41,46,64, 73].
Несмотря на то, что наши результаты были получены в лабораторных экспериментах, они имеют важное образовательное значение.Во-первых, в свете недостаточной осведомленности учителей о роли, которую играет тормозной контроль в фундаментальном академическом обучении [81], кажется важным повысить их осведомленность о важности торможения при сравнении десятичных величин. Следствием этой неосведомленности в контексте сравнения десятичных величин является то, что учителя могут интерпретировать ошибки учеников как показывающие непонимание математических принципов, регулирующих сравнение десятичных чисел, в то время как эти ошибки могут фактически выявить трудности, препятствующие «большему» количество цифр тем больше его величина »заблуждение, как предполагает настоящее исследование.
Во-вторых, учитывая, что неспособность запретить «чем больше число цифр, тем больше его величина», заблуждение может быть причиной систематических ошибок при сравнении десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1,45 против 1,5 ), педагогических вмешательств, основанных исключительно на изучении математических принципов, управляющих сравнением десятичных чисел, может быть недостаточно для преодоления этих систематических ошибок. Таким образом, педагогические вмешательства, основанные на метакогнитивном исполнительном (тормозящем) обучении, могут предоставить более эффективный способ помочь детям преодолеть систематические трудности при сравнении десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1.45 vs. 1.5). Вмешательство по метакогнитивному тормозящему контролю обычно заключается в подчеркивании как логико-математических принципов, которые необходимо использовать, так и неправильного представления о запрете, чтобы избежать систематических ошибок при решении проблемы. Несколько исследований предоставили сходные доказательства того, что этот тип вмешательства более эффективен в преодолении систематических логико-математических ошибок рассуждений, чем более классические вмешательства, подчеркивающие использование только логико-математических принципов [28,82,83]. В контексте обучения сравнению десятичных чисел вмешательство по метакогнитивному тормозящему контролю обычно подчеркивает необходимость подавления заблуждения «чем больше число цифр, тем выше его величина») и необходимость активировать математические принципы, управляющие сравнением десятичных чисел ( я.е., сравнение десятичных чисел путем сравнения величины различных значений разряда, начиная с первого после десятичной точки).
Хотя ни одно исследование на сегодняшний день не тестировало эффективность такого метакогнитивного ингибирующего контрольного вмешательства в контексте сравнения десятичных чисел, результаты одного предыдущего исследования показывают, что повышение осведомленности детей о заблуждении «чем больше число цифр, тем больше его величина» (автор: представление правильных и неправильных примеров) уже может улучшить их понимание математических принципов, управляющих величиной десятичного числа [24], см. также [84] для аналогичных свидетельств в других областях.Таким образом, вероятно, что повышение осведомленности детей об этом заблуждении и явное обучение их предотвращению этого заблуждения при сравнении десятичных чисел, в которых наименьшее десятичное число имеет наибольшее количество цифр (1,45 против 1,5), может быть эффективным для преодоления систематических ошибок в этот контекст.
В заключение, наши результаты предполагают, что тормозящий контроль является одним из основных механизмов, лежащих в основе математического развития [21,32,33,34,35,36,37,38,85] и, в более общем плане, когнитивного развития [26 , 27,28,29,30,31].
Ссылки
1. Lortie-Forgues H, Tian J, Siegler RS. Почему так сложно выучить дробную и десятичную арифметику? Обзор развития. 2015; 38: стр. 201–221.
2. Hoffer TB, Venkataraman L, Hedberg EC, Shagle S. Заключительный отчет о национальном опросе учителей алгебры для Национальной группы по математике. Чикаго; 2007.
3. Нешер П., Пелед И. Сдвиги в рассуждениях. Педагогические исследования по математике. 1986; 17: стр.67–79.
4. Резник Л. Б., Нешер П., Леонард Ф, Магоне М., Омансон С., Пелед И. Концептуальные основы арифметических ошибок: случай десятичных дробей. Журнал исследований в области математического образования. 1989; п. 8–27.
5. Гроссман А.С. Десятичная система счисления: важный результат исследования. Учитель арифметики. 1983; 30: стр. 32–33.
6. Лю Р.Д., Дин И, Цзун М., Чжан Д. Разработка концепции десятичных знаков у китайских учащихся начальной школы: концептуальный подход к изменению.Школьные науки и математика. 2014; 114: стр. 326–338.
7. Молони К., Стейси К. Изменения с возрастом в представлениях студентов о десятичной системе счисления. Журнал исследований математического образования. 1997; 9: стр. 25–38.
8. Стейнл В., Стейси К. Распространенность неправильных представлений о десятичной системе счисления среди учащихся 5-10 классов. 1998; Сидней.MERGA; 1998. с. 548–555.
9. Уирн Д., Хиберт Дж. Когнитивный подход к осмысленному обучению математике: проверка локальной теории с использованием десятичных чисел. Журнал исследований в области математического образования. 1988; 19: стр. 371–384.
10. Белл А.В., Костелло Дж.К.Д. Обзор исследований в области математического образования: Часть A, Исследования в области обучения и преподавания. Британский журнал образовательных исследований. 1984; 32: с. 280–282.
11. Putt IJ. Преподаватели Preservice Порядок десятичных чисел: когда больше меньше, а меньше больше! Сосредоточьтесь на учебных задачах по математике.1995; 17: стр. 1–15.
12. Вамвакусси X, Ван Дурен В., Вершаффель Л. Естественно предвзято? В поисках доказательства времени реакции для систематической ошибки натуральных чисел у взрослых. Журнал математического поведения. 2012; 31: стр. 344–355.
13. Рош А. Дольше значит больше — или это так? Австралийский класс начальной математики. 2005; 10: стр. 11–16.
14. Sackur-Grisvard C, Леонар Ф. Промежуточные когнитивные организации в процессе изучения математической концепции: порядок положительных десятичных чисел.Познание и обучение. 1985; 2: стр. 157–174.
15. Ван Дурен В., Лехтинен Э., Вершаффель Л. Устранение разрыва между натуральными и рациональными числами. Обучение и обучение. 2015; 37: стр. 1–4.
16. Вамвакусси X, Восниаду С. Сколько десятичных знаков между двумя дробями? Аспекты понимания учащимися средних школ рациональных чисел и их обозначений. Познание и обучение. 2010; 28: с. 181–209.
17. Смит CL, Соломон GEA, Кэри С.Никогда до нуля: понимание учениками начальной школы бесконечной делимости числа и материи. Когнитивная психология. 2005; 51: стр. 101–140. pmid: 16081058
18. Восниаду С., Вамвакусси Х, Скопелити И. Подход теории рамок к проблеме концептуального изменения. В: Восниаду С. Международный справочник исследований концептуальных изменений. Нью-Йорк: Рутледж; 2008. с. 3–34.
19. Восниаду С., Скопелити И. Концептуальные изменения со стороны теории рамок.Научное образование. 2014; 23: стр. 1427–1445.
20. ДеВольф М., Восниаду С. Пересмотр представления величины дробной части и целого числа. Обучение и обучение. 2015; 37: стр. 39–49.
21. Ван Хоф Дж., Янссен Р., Вершаффель Л., Ван Дорен В. Запрещение естественных знаний в четвероклассниках: к всеобъемлющему инструменту дегустации. ZDM: Международный журнал математического образования. 2014; 47: 849–857.
22. Ван Хоф Дж., Вандевалле Дж., Вершаффель Л., Ван Дурен В.В поисках систематической ошибки натуральных чисел в интерпретации учащимися средних школ эффекта арифметических операций. Обучение и обучение. 2015; 37: стр. 30–38.
23. Ван Хоф Дж., Лайнен Т., Вершаффель Л., Ван Дурен В. Учащиеся средних школ все еще страдают от смещения натуральных чисел? Исследование времени реакции на задачи сравнения фракций. Исследования в области математического образования. 2013; 15: стр. 154–164.
24. Дуркин К., Риттл-Джонсон Б. Диагностика заблуждений: выявление меняющихся знаний о десятичной дроби.Обучение и обучение. 2015; 37: стр. 21–29.
25. Даймонд А. Исполнительные функции. Ежегодный обзор психологии. 2013; 64: с. 135–168. pmid: 23020641
26. Бабай Р., Эйдельман Р. Р., Стави Р. Предварительная активация тормозных механизмов управления препятствует интуитивному мышлению. Международный журнал естественно-математического образования. 2012; 10: стр. 763–775.
27. Демпстер Ф.Н., Брейнерд С.Дж. Вмешательство и торможение познания. Сан-Диего: Academic Press; 1995 г.
28. Houdé O. Торможение и когнитивное развитие: объект, число, категоризация и рассуждение. Когнитивное развитие. 2000; 15: стр. 63–73.
29. Houdé O, Borst G. Измерение тормозящего контроля у детей и взрослых: визуализация мозга и ментальная хронометрия. Границы психологии. 2014; 5: стр. 616. pmid: 24994993
30. Рейна В.Ф., Ллойд Ф.Дж., Брейнерд CJ. Память, развитие и рациональность: интегративная теория суждений и принятия решений.В: Шнайдер С.Л., Шанто Дж. Кембридж, серия статей о суждениях и принятии решений: новые перспективы в исследованиях суждений и решений. Махва: Эрлбаум; 2003. с. 201–245.
31. Симоно М., Марковиц Х. Рассуждения с посылками, которые не являются эмпирически верными: доказательства роли торможения и извлечения. Психология развития. 2003; 39: стр. 964. pmid: 14584978
32. Аттридж Н., Инглис М. Увеличение когнитивного торможения с трудной предыдущей задачей: последствия для математического мышления.ZDM: Международный журнал математического образования. 2015; 47: с. 723–734.
33. Клейтон С., Гилмор С. Ингибирование в задачах сравнения точек. ZDM: Международный журнал математического образования. 2015; 47: с. 759–770.
34. Гиллард Э., Ван Дурен В., Шекен В., Вершаффель Л. Пропорциональные рассуждения как эвристический процесс: временные ограничения и рассмотрение двойной задачи. Экспериментальная психология. 2009; 56: с. 92–99. pmid: 19261584
35.Гилмор С., Кибл С., Ричардсон С., Крэгг Л. Роль когнитивного торможения в различных компонентах арифметики. ZDM: Международный журнал математического образования. 2015; 47: с. 771–782.
36. Гилмор С., Аттридж Н., Клейтон С., Крэгг Л., Джонсон С., Марлоу Н. и др. Индивидуальные различия в тормозящем контроле, а не в остроте невербальных чисел, коррелируют с успеваемостью по математике. ПлоС один. 2013; 8: с. e67374. pmid: 23785521
37. Любин А., Видаль Дж., Ланоэ С., Худе О, Борст Г.Тормозной контроль необходим для решения арифметических словесных проблем: исследование отрицательного прайминга в процессе развития. Журнал педагогической психологии. 2013; 105: стр. 701.
38. Szucs D, Devine A, Soltesz F, Nobes A, Gabriel F. Дискалькулия развития связана с зрительно-пространственной памятью и нарушением торможения. Cortex. 2013; 49: стр. 2674–2688. pmid: 238
39. Бык Р., Ли К. Исполнительное функционирование и математические достижения. Перспективы развития ребенка.2014; 8: с. 36–41.
40. Любин А., Росси С., Ланоэ С., Видаль Дж., Худе О., Борст Г. Экспертиза, тормозящий контроль и арифметические задачи со словами: исследование с отрицательным праймингом среди экспертов по математике. Обучение и обучение. 2016; 45: стр. 40–48.
41. Ар Э, Худе О, Борст Г. Торможение процесса зеркального обобщения при чтении у детей школьного возраста. Журнал экспериментальной детской психологии. 2016; 145: с. 157–165. pmid: 26827098
42. Гилович Т., Гриффин Д., Канеман Д.Эвристика и предубеждения: психология интуитивного суждения. Кембридж: Издательство Кембриджского университета; 2002.
43. Бьорклунд Д.Ф., Харнишфегер К.К. Роль тормозных механизмов в эволюции познания и поведения человека. В: Dempster FN, Brainerd CJ. Новые взгляды на вмешательство и торможение познания. Нью-Йорк: Academic Press; 1995. стр. 141–173.
44. Borst G, Aïte A, Houdé O. Запрещение вводящей в заблуждение эвристики как основной механизм типичного когнитивного развития: данные поведенческих исследований и исследований с использованием изображений мозга.Медицина развития и детская неврология. 2015; 57: стр. 21–25.
45. Даймонд А. Исполнительные функции. Ежегодный обзор психологии. 2013; 64: с. 135–168. pmid: 23020641
46. Самосвал SP. Отрицательный эффект затравки: ингибирующая затравка игнорируемыми объектами. Ежеквартальный журнал экспериментальной психологии. 1985; 37: стр. 571–590. pmid: 4081101
47. Борст Г., Мутье С., Худе О. Отрицательное прайминг в логико-математических рассуждениях. Новые подходы в исследовании рассуждений.В: Де Нейс В., Осман М. Новые подходы в исследовании рассуждений. New Yrok: Psychology Press; 2013. с. 34–50.
48. Borst G, Poirel N, Pineau A, Cassotti M, Houdé O. Эффективность ингибирующего контроля в задаче включения класса, подобной Piaget, у детей школьного возраста и взрослых: исследование негативного прайминга в развитии. Психология развития. 2013; 49: стр. 1366–1374. pmid: 22889392
49. Перрет П., Паур Дж. Л., Блей А. Соответствующие вклады уровней торможения и знаний в развитие включения в класс: исследование отрицательного прайминга.Наука о развитии. 2003; 6: стр. 283–8.
50. Houdé O, Guichart E. Отрицательный эффект прайминга после подавления интерференции числа / длины в задаче типа Пиаже. Наука о развитии. 2001; 4: стр. 119–123.
51. Potvin P, Masson S, Lafortune S, Cyr G. Устойчивость интуитивной концепции, что более тяжелые предметы тонут больше: исследование времени реакции с различными уровнями помех. Международный журнал естественно-математического образования. 2015; 13: стр.21–43.
52. Bruyer R, Brysbaert M. Сочетание скорости и точности в когнитивной психологии: является ли показатель обратной эффективности (IES) более зависимой переменной, чем среднее время реакции (RT) и процент ошибок (PE)? Psychologica Belgica. 2011; 51: стр. 5–13.
53. Таунсенд Дж. Т. и Эшби Ф. Г. (1983). Стохастическое моделирование элементарных психологических процессов . Кембридж: Издательство Кембриджского университета.
54. Стафилиду С., Восниаду С.Развитие у студентов понимания числового значения дробей. Обучение и обучение. 2004; 14: с. 503e518.
55. Фейгенсон Л., Дехаен С., Спелке Э. Основные системы чисел. Тенденции в когнитивных науках. 2004; 8: с. 307–314. pmid: 15242690
56. Пьяцца М., Изард В. Как люди считают: численность и теменная кора. Невролог. 2009; 15: стр. 261–273. pmid: 19436075
57. Изард В., Санн К., Спелке Е.С., Стрири А.Новорожденные младенцы воспринимают абстрактные числа. Труды Национальной академии наук. 2009; 106: с. 10382–10385.
58. Culham JC, Cavina-Pratesi C, Singhal A. Роль теменной коры в зрительно-моторном контроле: что мы узнали из нейровизуализации? Нейропсихология. 2006; 44: с. 2668–2684. pmid: 16337974
59. Dehaene S, Cohen L. Культурная переработка кортикальных карт. Нейрон. 2007; 56: с. 384–398. pmid: 17964253
60. Тан И, Чжан В., Чен К., Фенг С., Джи И, Шен Дж и др.Арифметическая обработка в мозге, сформированном культурами. Труды Национальной академии наук. 2006; 103: стр. 10775–10780.
61. Dormal V, Pesenti M. Общие и специфические вклады интрапариетальных борозд в обработку численности и длины. Картирование человеческого мозга. 2009; 30: стр. 2466–2476. pmid: 19294652
62. Гебуис Т., Рейнвоет Б. Роль визуальной информации в оценке численности. ПлоС один. 2012; 7: стр. e37426. pmid: 22616007
63.Чиккини GM, Anobile G, Burr DC. Сжатое отображение числа в пространство отражает механизмы динамического кодирования, а не статическое логарифмическое преобразование. Труды Национальной академии наук. 2014; 111: стр. 7867–7872.
64. Houdé O, Pineau A, Leroux G, Poirel N, Perchey G, Lanoë C и др. Исследование задачи сохранения числа Пиаже с помощью функциональной магнитно-резонансной томографии у детей дошкольного и школьного возраста: неопиажеский подход. Журнал экспериментальной детской психологии.2011; 110: с. 332–46. pmid: 21636095
65. Пиаже Дж. Истоки интеллекта у детей. Нью-Йорк: издательство международных университетов; 1952.
66. Шуман М., Канвишер Н. Числовая величина в теменной доле человека: тесты репрезентативной общности и специфичности предметной области. Нейрон. 2004; 44: с. 557–569. pmid: 15504334
67. Пинель П., Пьяцца М., Ле Бихан Д., Дехен С. Распределенные и перекрывающиеся церебральные представления числа, размера и яркости во время сравнительных суждений.Нейрон. 2004; 41: с. 983–993. pmid: 15046729
68. Бирнгрубер Т., Шрётер Х., Ульрих Р. Восприятие длительности визуальных и слуховых необычных стимулов: модулирует ли задача суждения временный эффект необычного? Внимание, восприятие и психофизика. 2014; 76: с. 814–828.
69. Kc Irwin. Использование повседневных знаний о десятичных дробях для улучшения понимания. Журнал исследований в области математического образования. 2001; 32: с. 399–420.
70. Оберштайнер А., Ван Дурен В., Ван Хоф Дж., Вершаффель Л.Смещение натурального числа и представление величины в сравнении дробных чисел опытными математиками. Обучение и обучение. 2013; 28: с. 64–72.
71. Вамвакусси X, Ван Дурен В., Вершаффель Л. Краткий отчет. Образованные взрослые все еще находятся под влиянием интуиции о влиянии арифметических операций: данные исследования времени реакции. Образовательные исследования по математике. 2013; 82: стр. 323–330.
72. Дехайн С. Эволюция корковых цепей человека для чтения и арифметики: гипотеза «рециклинга нейронов».В: Dehaene S, Duhamel JR, Hauser M, Rizolatti G. От мозга обезьяны к мозгу человека. Кембридж, Массачусетс: MIT Press; 2005. с. 133–57.
73. Borst G, Ahr E, Roell M, Houdé O. Стоимость блокировки процесса зеркального обобщения при чтении: доказательства роли тормозящего контроля в различении букв с боковыми зеркальными копиями. Психономический бюллетень и обзор. 2015; 22: стр. 228–234.
74. Dalrymple-Alford EC, Budayr B. Изучение некоторых аспектов теста Струпа по цветному слову.Вечные моторные навыки. 1966; 23: стр. 1211–1214.
75. Притчард В.Е., Нойман Э. Отрицательные эффекты прайминга у детей, занятых непространственными задачами: свидетельства раннего развития интактного тормозного механизма. Психология развития. 2004; 40: с. 191–203. pmid: 14979760
76. Притчард В.Э., Нойман Э. Избегание потенциальных ловушек использования отрицательных задач прайминга в исследованиях развития: оценка тормозящего контроля у детей, подростков и взрослых.Психология развития. 2009; 45: стр. 272–283. pmid: 19210008
77. Ботвиник М.М., Бравер Т.С., Барч Д.М., Картер С.С., Коэн Д.Д. Мониторинг конфликтов и когнитивный контроль. Психологическое обозрение. 2001; 108: стр. 624–652. pmid: 11488380
78. Кунде В., Ройсс Х., Кизель А. Сознание и когнитивный контроль. Успехи в когнитивной психологии. 2012; 8: с. 9–18. pmid: 22419962
79. Деметриу А., Спанудис Г. О структуре и развитии исполнительных функций в среднем и позднем детстве: ремоделирование и комментарии к Бриджесу, Фоксу, Риду и Андерсону.Интеллект. 2015; 50: с. 131–134.
80. Эгнер Т. Множественные механизмы управления конфликтом в человеческом мозге. Тенденции в когнитивных науках. 2008; 12: стр. 374–380. pmid: 18760657
81. Гилмор Ч., Крэгг Л. Понимание учителями роли управляющих функций в обучении математике. Разум, мозг и образование. 2014; 8: с. 132–136.
82. Moutier S, Houdé O. Суждение при обучении запрету на ошибку неопределенности и конъюнкции.Мышление и рассуждение. 2003; 9: стр. 185–201.
83. Moutier S, Angeard N, Houde O. Дедуктивное мышление и обучение ингибированию смещения сопоставления: данные из парадигмы устранения смещения. Мышление и рассуждение. 2002; 8: с. 205–224.
84. Große CS, Renkl A. Обнаружение и исправление ошибок в рабочих примерах: может ли это способствовать результатам обучения? Обучение и обучение. 2007; 17: стр. 612–634.
85. Гилмор CK, Маккарти SE, Spelke ES. Несимволические арифметические способности и достижения по математике в первый год формального обучения.Познание. 2010; 115: стр. 394–406. pmid: 20347435
.