Средняя скорость
При решении этих задач обязательно помним, что средняя скорость может быть найдена только делением всего пути на все время движения, даже если какое-то время объект не двигался (делал остановку). Если путь не задан, то необходимо ввести буквенное обозначение длины пути.
Задача 1. Поезд прошел путь 200 км. В течение времени  ч он двигался со скоростью
ч он двигался со скоростью  км/ч, затем сделал остановку на время
км/ч, затем сделал остановку на время  мин. Оставшуюся часть пути он шел со скоростью
мин. Оставшуюся часть пути он шел со скоростью 
Путь в этой задаче известен. Значит, осталось определить время движения поезда. Кроме того, известно и время его движения на первом участке, значит, нам осталось определить время движения поезда на последнем кусочке, где он двигался со скоростью  км/ч. Нетрудно понять, что длина этого отрезка пути равна 100 км, так как поезд уже преодолел 100 км за первый час. Поэтому
км/ч. Нетрудно понять, что длина этого отрезка пути равна 100 км, так как поезд уже преодолел 100 км за первый час. Поэтому
![Rendered by QuickLaTeX.com \[S_3=200-\upsilon_1 \cdot t_1=200-100\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b3803b43137502ff87165489bfd2d0dc_l3.png)
![Rendered by QuickLaTeX.com \[t_3=\frac{S_3}{\upsilon_3}=\frac{100}{40}=2,5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-878c0d4a09d70dbba34d650ed70e0753_l3.png)
Таким образом,
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{S}{t_1+t_2+t_3}=\frac{200}{1+0,5+2,5}=50\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4407f8afa79d093dee01ce61133997c2_l3.png)
Ответ: 50 км/ч
Задача 2. Определить среднюю скорость поезда, если первую половину пути он шел со скоростью  км/ч, а вторую половину пути – со скоростью
км/ч, а вторую половину пути – со скоростью  км/ч.
км/ч.
В этой задаче путь неизвестен. Обозначим его  . Тогда время движения поезда на первой половине пути
. Тогда время движения поезда на первой половине пути
![Rendered by QuickLaTeX.com \[t_1=\frac{\frac{S}{2}}{\upsilon_1}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-483864771d6cbbb5bf092cfb98eb512b_l3.png)
Время движения на второй половине –
![Rendered by QuickLaTeX.com \[t_1=\frac{\frac{S}{2}}{\upsilon_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c5563c1b427be26165976367fb4b3a11_l3.png)
Средняя скорость – результат деления всего пути, пройденного поездом, на все время:
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{S}{t_1+t_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b5e5cdedfd353b1778f3718e4ecbd00e_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-589a38375d9f050716b1af93bd7ce6c1_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-23ef6f0b8b3466a12b347d1b487b9418_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-47028a0a4227b9fc5dede96913b97c71_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{2 \cdot50\cdot100}{150}=\frac{10000}{150}=66,7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-42fe518faae3ece1d266e484a9e7a415_l3.png)
Ответ:  км/ч
км/ч
Задача 3. Два автомобиля одновременно выехали из Москвы в Петербург. Один автомобиль первую половину пути ехал со скоростью  км/ч, а вторую половину – со скоростью
км/ч, а вторую половину – со скоростью  км/ч. Другой автомобиль первую половину времени ехал со скоростью
км/ч. Другой автомобиль первую половину времени ехал со скоростью  км/ч, а вторую – со скоростью
км/ч, а вторую – со скоростью 
Если окажется, что средняя скорость одного из автомобилей больше, чем у другого, то он и должен прибыть раньше. Определим среднюю скорость каждого автомобиля. Первый:
![Rendered by QuickLaTeX.com \[\upsilon_{sr1}=\frac{S}{t_1+t_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9fd2e08b687eb7160e7a26944bfbde87_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr1}=\frac{S}{\frac{S}{2\upsilon_1}+\frac{S}{2\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-97cccdc98f5da5a0b037fb138c5917cb_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr1}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-35e746f7085689d225f27815135751fa_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr1}=\frac{2 \upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f2dd1d124eac6ef91a5aed2bff32cf72_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr1}=\frac{2 \cdot120\cdot80}{200}=\frac{19200}{200}=96\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0945d696edab0f69e8b6354154f6bc6_l3.png)
Второй за первую половину времени прошел:
![Rendered by QuickLaTeX.com \[S_1=\frac{t}{2}\cdot \upsilon_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bd3e54439d71348783859451978b3ffa_l3.png)
За вторую половину времени:
![Rendered by QuickLaTeX.com \[S_2=\frac{t}{2}\cdot \upsilon_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c9cf3e7c6bc86308288c2a604e2d0177_l3.png)
Тогда его средняя скорость:
![Rendered by QuickLaTeX.com \[\upsilon_{sr2}=\frac{S}{t}=\frac{S_1+S_2}{t}=\frac{t\cdot \upsilon_1+t\cdot\upsilon_2}{2t}=\frac{\upsilon_1+\upsilon_2}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-816541f0a7f3c41c2ab2ccd6a62fe7b3_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr2}=\frac{120+80}{2}=100\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bd7418c04e0484ec3388c4838a0aefbc_l3.png)
Таким образом, второй автомобиль прибудет раньше.
Задача 4. Найти среднюю скорость самолета, если известно, что первую треть пути он летел со скоростью 
 км/ч, а последнюю часть пути – со скоростью, вдвое большей средней скорости на первых двух участках пути.
км/ч, а последнюю часть пути – со скоростью, вдвое большей средней скорости на первых двух участках пути.Найдем среднюю скорость самолета на двух первых участках пути.
![Rendered by QuickLaTeX.com \[\upsilon_{sr12}=\frac{\frac{2S}{3}}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2fff2f31db69819476e56753e83c319c_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr12}=\frac{2}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3762e798d58d1529b4bc35520ba1b50e_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr12}=\frac{2\upsilon_1 \upsilon_2}{\upsilon_1+\upsilon_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a5672fff4ae97fdf075f0a02d3f53317_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr12}=\frac{2\cdot700 \cdot500}{700+500}=583\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9a623624c3788bcfae42924722bd9d9d_l3.png)
Тогда  .
.
Определяем среднюю скорость на всем участке пути:
![Rendered by QuickLaTeX.com \[\upsilon_{sr123}=\frac{S}{\frac{S}{3\upsilon_1}+\frac{S}{3\upsilon_2}+\frac{S}{3\upsilon_3}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a06c2c793d3cbd06aa2bd93c695a3400_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr123}=\frac{3}{\frac{1}{\upsilon_1}+\frac{1}{\upsilon_2}+\frac{1}{\upsilon_3}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a2b5b6fcd1fc6b1013c83f2302794b33_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr123}=\frac{3\upsilon_1 \upsilon_2 \upsilon_3}{\upsilon_1\upsilon_2+\upsilon_2\upsilon_3+\upsilon_1\upsilon_3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-71fde005823380cf149d1d0a0799c4a3_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr123}=\frac{500\cdot700 \cdot1166}{500\cdot700+700\cdot1166+500\cdot1166}=700\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-86a2fae51ea2201e9bad2229aef9b1c4_l3.png)
Ответ: 700 км/ч
Задача 5. Найти среднюю скорость поезда, если известно, что на прохождение отдельных участков дистанции, длины которых относятся как  , потребовались промежутки времени, находящиеся в отношении
, потребовались промежутки времени, находящиеся в отношении  , и на последнем участке скорость поезда
, и на последнем участке скорость поезда  км/ч. Считать, что на каждом из участков поезд двигался равномерно.
км/ч. Считать, что на каждом из участков поезд двигался равномерно.
Определим весь путь по его частям:
![Rendered by QuickLaTeX.com \[S_1:S_2:S_3:S_4=1: 3: 4: 2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9e0ce653deba6b4f826257b31356463d_l3.png)
Если  , то
, то  ,
,  ,
,  , а весь путь
, а весь путь
![Rendered by QuickLaTeX.com \[S_1+S_2+S_3+S_4=l+3l+4l+2l=10l\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6b1f233f49aee7a18676addce76d9320_l3.png)
Определим время движения поезда на последнем участке, зная его скорость:
![Rendered by QuickLaTeX.com \[t_4=\frac{2l}{\upsilon }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dc4d3f6d25d23bc8ca2780c0d3730e74_l3.png)
Тогда, так как
![Rendered by QuickLaTeX.com \[t_1:t_2:t_3:t_4=2:4:3:1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e86a8c631107ef363781ba8a8db79ce7_l3.png)
Отсюда найдем  :
:
![Rendered by QuickLaTeX.com \[t_3=3t_4=\frac{6l}{\upsilon }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c6f9675d108db7b7cf324f02eaef5fef_l3.png)
![Rendered by QuickLaTeX.com \[t_2=\frac{4}{3}t_3=\frac{8l}{\upsilon }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f8653a7dc82ca095812305659d03e381_l3.png)
![Rendered by QuickLaTeX.com \[t_1=\frac{1}{2}t_3=\frac{4l}{\upsilon }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-23de253e714124eacdba2c31777067fa_l3.png)
Общее время движения:
![Rendered by QuickLaTeX.com \[t_1+t_2+t_3+t_4=\frac{4l}{\upsilon }+\frac{8l}{\upsilon }+\frac{6l}{\upsilon }+\frac{2l}{\upsilon }=\frac{20l}{\upsilon }\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e3e464610cd376c307c1208ae511d052_l3.png)
Наконец, находим среднюю скорость:
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{S}{t}=\frac{10l}{\frac{20l}{\upsilon }}=\frac{\upsilon }{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b9138a6d409f3335974f64b66880eebb_l3.png)
![Rendered by QuickLaTeX.com \[\upsilon_{sr}=\frac{80}{2}=40\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1ac5d642cd7ffb6f6400daac1401de68_l3.png)
Ответ: средняя скорость поезда – 40 км/ч.
easy-physic.ru
Конспект «Неравномерное движение. Средняя скорость»
Неравномерное движение.
Средняя скорость
Неравномерное движение — это движение, при котором за равные промежутки времени тело проходит разные пути.

 Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя путевая скорость — это физическая величина, равная отношению пути, пройденного телом за рассматриваемый промежуток времени, к длительности этого промежутка.
Средняя путевая скорость — скалярная неотрицательная величина.
Средняя скорость тела за промежуток времени t — это физическая величина, равная отношению перемещения 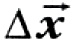 , совершённого телом, к длительности этого промежутка времени.
, совершённого телом, к длительности этого промежутка времени.
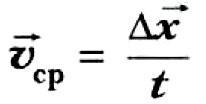
Средняя скорость — вектор. Она направлена туда, куда направлено перемещение тела за рассматриваемый промежуток времени.
Если тело всё время движется в одном направлении, то модуль средней скорости равен средней путевой скорости. Если же в процессе своего движения тело меняет направление движения, то модуль средней скорости меньше средней путевой скорости.

Пример решения задач на среднюю скорость при неравномерном движении
Автомобиль проехал за первый час 50 км, а за следующие два часа он проехал 160 км. Какова его средняя скорость за все время движения?

Ответ: 70 км/ч
Еще больше задач на движение (с решениями и ответами) в конспекте «Задачи на движение»

Это конспект по физике за 7 класс по теме «Неравномерное движение. Средняя скорость». Выберите дальнейшие действия:
uchitel.pro
Как найти среднюю скорость

В данной статье рассказано о том, как найти среднюю скорость. Дано определение этого понятия, а также рассмотрено два важных частных случая нахождения средней скорости. Представлен подробный разбор задач на нахождение средней скорости тела от репетитора по математике и физике.
Определение средней скорости
Средней скоростью движения 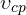 тела называется отношение пути
тела называется отношение пути  , пройденного телом, ко времени
, пройденного телом, ко времени 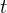 , в течение которого двигалось тело:
, в течение которого двигалось тело:
![Rendered by QuickLaTeX.com \[ \upsilon_{cp} = \frac{s}{t}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-3ef4719c781f9011e08fb55b5c271fd0_l3.png)
Научимся ее находить на примере следующей задачи:
| Тело двигалось 3 мин. со скоростью 5 м/с, после чего 7 мин. двигалось со скоростью 3 м/с. Найти среднюю скорость движения тела. |
Обратите внимание, что в данном случае это значение не совпало со средним арифметическим скоростей 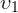 и
и 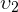 , которое равно:
, которое равно: м/с.
м/с.
Частные случаи нахождения средней скорости
1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью 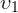 , а вторую половину пути — со скоростью
, а вторую половину пути — со скоростью 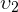 . Требуется найти среднюю скорость движения тела.
. Требуется найти среднюю скорость движения тела.
- Пусть
 — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени
— общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени  . Аналогично, на втором участке пути тело двигалось в течение интервала времени
. Аналогично, на втором участке пути тело двигалось в течение интервала времени  .
. - Тогда средняя скорость движения равна:
![Rendered by QuickLaTeX.com \[ \upsilon_{cp} = \frac{s}{t_1+t_2} = \frac{s}{\frac{s}{2\upsilon_1}+\frac{s}{2\upsilon_2}} = \frac{2\upsilon_1\upsilon_2}{\upsilon_1+\upsilon_2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-7360def65faa837f59240afaf124708c_l3.png)
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью 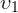 в течение некоторого промежутка времени, а затем стало двигаться со скоростью
в течение некоторого промежутка времени, а затем стало двигаться со скоростью 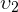 в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.
- Пусть
 — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен:
— общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен:  . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен:
. Аналогично, путь, пройденный телом в течение второй половины времени движения, равен:  .
. - Тогда средняя скорость движения равна:
![Rendered by QuickLaTeX.com \[ \upsilon_{cp} = \frac{s_1+s_2}{t} = \frac{\upsilon_1\frac{t}{2}+\upsilon_2\frac{t}{2}}{t} = \frac{\upsilon_1+\upsilon_2}{2}. \]](/800/600/https/yourtutor.info/wp-content/ql-cache/quicklatex.com-98e13b71ea8c002dffee60fcb598f94f_l3.png)
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей 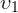 и
и 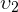 на двух участках пути.
на двух участках пути.
Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.
Пройденный телом путь составляет: 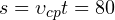 м. Можно найти также путь, который прошло тело за последние
м. Можно найти также путь, который прошло тело за последние 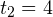 с своего движения:
с своего движения: 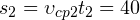 м. Тогда за первые
м. Тогда за первые 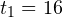 с своего движения тело преодолело путь в
с своего движения тело преодолело путь в 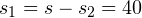 м. Следовательно, средняя скорость на этом участке пути составила:
м. Следовательно, средняя скорость на этом участке пути составила: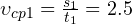 м/с.
м/с.
Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!
Репетитор по физике на Юго-Западной
Сергей Валерьевич
yourtutor.info
Средняя скорость. Решение задач по физике
Средняя скорость. Решение задач по физике
Задачи по физике — это просто!
Среднюю скорость движения иначе называют путевой скоростью.
где
Sобщ — общий путь, т.е. сумма всех отрезков пути
t общ — общее время, т.е. время, за которое был пройден весь путь
При решении задач очень помогает простенький чертеж, на котором надо показать все отрезки пути.
Около каждого отрезка для наглядности укажите буквенные обозначения скорости, времени, пути (с нужным индексом) и формулы для их расчета (если это необходимо).
Переходим к решению задач.
От простых к сложным!
Элементарные задачи из курса школьной физики
Задача 1
Автомобиль проехал 100 метров за 25 секунд, а следующие 300 метров за 1 минуту.
Определить среднюю скорость движения автомобиля.
Задача 2
Автомобиль ехал 2 минуты со скоростью 10 м/с, а затем проехал еще 500 метров за 30 секунд.
Определить среднюю скорость движения.
Задача 3
Автомобиль проехал 10 секунд со скоростью 10 м/с, а затем ехал еще 2 минуты со скоростью 20 м/c.
Определить среднюю скорость автомобиля.
Задача 4
Автомобиль проехал первую половину пути со скоростью 10 м/с, а вторую половину пути со скоростью 20 м/с. Определить среднюю скорость автомобиля на всем пути.
Пусть S — общий пройденный путь.
Задача 5
Автомобиль одну треть времени движения ехал со скоростью 10 м/с, а остальное время со скоростью 20 м/с. Определить среднюю скорость за все время движения.
Пусть t — общее время движения.
class-fizika.ru
Формула средней скорости
ОПРЕДЕЛЕНИЕСредняя скорость тела – это отношение пути ко времени прохождения этого пути. Скорость движения при этом не обязана быть постоянной.
Здесь – средняя скорость, – весь путь, пройденный телом, – время прохождения пути.
Единица измерения скорости – м/с (метр в секунду).
Средняя скорость – скалярная величина. Если тело двигалось с разными скоростями равные промежутки времени, то средняя скорость равна среднему арифметическому всех скоростей, в противном случае
Где – отрезок пути, – время прохождения этого отрезка.
Примеры решения задач по теме «Средняя скорость»
| Понравился сайт? Расскажи друзьям! | |||
ru.solverbook.com
Физика 7 класс → Неравномерное движение. Средняя скорость – eSchool.by
Равномерное движение – большая редкость. Обычно движущиеся тела меняют свою скорость.
Автомобиль замедляется на светофоре, а пешеход, спеша на автобус, ускоряет шаг. Часто
пройденный путь состоит из отрезков, которые тело проходит с разной скоростью. Это движение
называется неравномерным.
| Неравномерное движение – движение, при котором тело проходит разные отрезки пути за равные промежутки времени (то есть движется с разной скоростью). |
Пример:
Туристы прошли 12 километров за 3 часа и сделали привал на 1 час. Оставшиеся 9,6 километра туристы прошли за 2 часа. Надо найти их скорость на отдельных участках дороги и среднюю скорость на всём пути.
Весь путь туристов состоит из 3 частей: первая часть пути длилась 3 часа, вторая часть пути (отдых) длилась 1 час и последняя часть пути (переход) длилась 2 часа. Попробуем найти скорость туристов на каждом отрезке пути.
Мы нашли мгновенные скорости (υ1, υ2, υ3) туристов на отдельных участках.
| Мгновенная скорость – скорость тела в данный момент времени. |
Но, чтобы узнать скорость на всём пути, надо использовать понятие средней скорости. Средняя скорость показывает, какой скоростью обладало бы тело, если бы двигалось равномерно и преодолело бы такой же путь за это же время.
Чтобы её найти, нужно весь путь разделить на всё затраченное время.
Обратите внимание: средняя скорость обозначается 〈υ〉 (в скобках-ромбиках) и измеряется в м/с
(метры в секунду). Среднюю скорость тела нельзя найти как среднее арифметическое его мгновенных скоростей! Если это сделать: (1,11 + 0 +1,33)/3 = 0,813 – мы получим неверный ответ.
Формула средней скорости для трёх участков пути с различной скоростью:
Важно! Средняя скорость на всём пути не равна среднему арифметическому скоростей на отдельных участках пути:
(то есть нельзя складывать разные скорости тела на разных участках и делить на их количество, чтобы найти среднюю скорость).
| График неравномерного движения серьёзно отличается от графика равномерного: он строится из отдельных отрезков, на которых тело имело постоянную скорость. Чтобы найти среднюю скорость движения тела из графика υ(t), надо вычислить площади фигур, ограниченных графиками и их перпендикулярами, и сложить их. |
| Вопросы: 1. Какое движение называют неравномерным? |
eschool.by
Мгновенная и средняя скорости — Класс!ная физика
Мгновенная и средняя скорости
«Физика — 10 класс»
Какую скорость показывает спидометр?
Может ли городской транспорт двигаться равномерно и прямолинейно?
Реальные тела (человек, автомобиль, ракета, теплоход и т. д.), как правило, не движутся с постоянной скоростью. Они начинают двигаться из состояния покоя, и их скорость увеличивается постепенно, при остановке скорость уменьшается также постепенно, таким образом, реальные тела движутся неравномерно.
Неравномерное движение может быть как прямолинейным, так и криволинейным.
Чтобы полностью описать неравномерное движение точки, надо знать её положение и скорость в каждый момент времени.
Скорость точки в данный момент времени называется мгновенной скоростью.
Что же понимают под мгновенной скоростью?
Пусть точка, двигаясь неравномерно и по кривой линии, в некоторый момент времени t занимает положение М (рис. 1.24). По прошествии времени Δt1 от этого момента точка займёт положение М1, совершив перемещение Δ1. Поделив вектор Δ1 на промежуток времени Δt1 найдём такую скорость равномерного прямолинейного движения, с которой должна была бы двигаться точка, чтобы за время Δt попасть из положения М в положение М1. Эту скорость называют средней скоростью перемещения точки за время Δt1.
Обозначив её через ср1, запишем: Средняя скорость направлена вдоль секущей ММ1. По той же формуле мы находим скорость точки при равномерном прямолинейном движении.
Скорость, с которой должна равномерно и прямолинейно двигаться точка, чтобы попасть из начального положения в конечное за определённый промежуток времени, называется средней скоростью перемещения.
Для того чтобы определить скорость в данный момент времени, когда точка занимает положение М, найдём средние скорости за всё меньшие и меньшие промежутки времени:
Интересно, верно ли следующее определение мгновенной скорости: «Скорость тела в данной точке траектории называется мгновенной скоростью»?
При уменьшении промежутка времени Δt перемещения точки уменьшаются по модулю и меняются по направлению. Соответственно этому средние скорости также меняются как по модулю, так и по направлению. Но по мере приближения промежутка времени Δt к нулю средние скорости всё меньше и меньше будут отличаться друг от друга. А это означает, что при стремлении промежутка времени Δt к нулю отношение стремится к определённому вектору как к своему предельному значению. В механике такую величину называют скоростью точки в данный момент времени или просто мгновенной скоростью и обозначают
Мгновенная скорость точки есть величина, равная пределу отношения перемещения Δ к промежутку времени Δt, в течение которого это перемещение произошло, при стремлении промежутка Δt к нулю.
Выясним теперь, как направлен вектор мгновенной скорости. В любой точке траектории вектор мгновенной скорости направлен так, как в пределе, при стремлении промежутка времени Δt к нулю, направлена средняя скорость перемещения. Эта средняя скорость в течение промежутка времени Δt направлена так, как направлен вектор перемещения Δ Из рисунка 1.24 видно, что при уменьшении промежутка времени Δt вектор Δ уменьшая свою длину, одновременно поворачивается. Чем короче становится вектор Δ, тем ближе он к касательной, проведённой к траектории в данной точке М, т. е. секущая переходит в касательную. Следовательно,
мгновенная скорость направлена по касательной к траектории (см. рис. 1.24).
В частности, скорость точки, движущейся по окружности, направлена по касательной к этой окружности. В этом нетрудно убедиться. Если маленькие частички отделяются от вращающегося диска, то они летят по касательной, так как имеют в момент отрыва скорость, равную скорости точек на окружности диска. Вот почему грязь из-под колёс буксующей автомашины летит по касательной к окружности колёс (рис. 1.25).
Понятие мгновенной скорости — одно из основных понятий кинематики. Это понятие относится к точке. Поэтому в дальнейшем, говоря о скорости движения тела, которое нельзя считать точкой, мы можем говорить о скорости какой-нибудь его точки.
Помимо средней скорости перемещения, для описания движения чаще пользуются средней путевой скоростью cps.
Средняя путевая скорость определяется отношением пути к промежутку времени, за который этот путь пройден:
Когда мы говорим, что путь от Москвы до Санкт-Петербурга поезд прошёл со скоростью 80 км/ч, мы имеем в виду именно среднюю путевую скорость движения поезда между этими городами. Модуль средней скорости перемещения при этом будет меньше средней путевой скорости, так как s > |Δ|.
Для неравномерного движения также справедлив закон сложения скоростей. В этом случае складываются мгновенные скорости.
Источник: «Физика — 10 класс», 2014, учебник Мякишев, Буховцев, Сотский
Кинематика — Физика, учебник для 10 класса — Класс!ная физика
Физика и познание мира — Что такое механика — Механическое движение. Система отсчёта — Способы описания движения — Траектория. Путь. Перемещение — Равномерное прямолинейное движение. Скорость. Уравнение движения — Примеры решения задач по теме «Равномерное прямолинейное движение» — Сложение скоростей — Примеры решения задач по теме «Сложение скоростей» — Мгновенная и средняя скорости — Ускорение — Движение с постоянным ускорением — Определение кинематических характеристик движения с помощью графиков — Примеры решения задач по теме «Движение с постоянным ускорением» — Движение с постоянным ускорением свободного падения — Примеры решения задач по теме «Движение с постоянным ускорением свободного падения» — Равномерное движение точки по окружности — Кинематика абсолютно твёрдого тела. Поступательное и вращательное движение — Кинематика абсолютно твёрдого тела. Угловая скорость. Связь между линейной и угловой скоростями — Примеры решения задач по теме «Кинематика твёрдого тела»
class-fizika.ru
 . Аналогично, на втором участке пути тело двигалось в течение интервала времени
. Аналогично, на втором участке пути тело двигалось в течение интервала времени 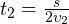 .
.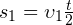 . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен:
. Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: 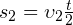 .
.