Степень числа. Квадрат и куб числа
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Натуральные числа и действия над ними
- Степень числа. Квадрат и куб числа
Определение.
Выражение «» читают так: » в степени » или » — ая степень числа «, и называют степенью. При этом в этой записи число «» называют основанием степени, а число «», которое показывает число множителей в произведении, — показателем степени.
Например, найдем значение следующих степеней:
24 = 2222 = 422 = 82 = 16;
36 = 333333 = 93333 = 27333 = 8133 =2433 = 729.
Квадрат числа — это вторая степень числа. Квадрат числа записывают так: . Читают: » в квадрате» или » во второй степени».
Например, найдем квадрат чисел 4 и 8:
42 = 44 = 16;
82 = 88 = 64.
Куб числа — это третья степень числа. Куб числа записывают так: . Читают: » в кубе» или » в третей степени».
Например, найдем куб чисел 5 и 7:
53 = 555 = 255 = 125;
73 = 777 = 495 = 343;
Степенью числа «» с показателем = 1 является само это число, то есть .
Ноль в любой степени — это ноль, единица — это единица.
0n = 0;
1n = 1.
Действительно, т.к. степень можно расписать как произведение, то, если в основании находится ноль, то мы получим произведение n нолей, если единица — произведение n единиц.
Возведение числа в степень — это пятое арифметическое действие, поэтому стоит учитывать, что:
Если в числовое выражение входит степень, то сначала выполняют возведение в степень, а потом — остальные действия, в соответствии с порядком их выполнения.
Например, найдем значение выражения 642 — (3 + 2):
Сначала выполним возведение во 2 степень числа 4, затем находим значение выражения, находящегося в скобках, после чего выполняем умножение, и последним действием выполняем вычитание:
642 — (3 + 2) = 616 — (3 + 2) = 616 — 5 = 96 — 5 = 91.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Понятие о натуральном числе
Сложение натуральных чисел
Вычитание натуральных чисел
Умножение натуральных чисел
Деление натуральных чисел
Порядок выполнения действий
Меньше или больше
Меньше или больше на сколько? во сколько раз?
Формулы
Уравнения
Натуральные числа и действия над ними
Правило встречается в следующих упражнениях:
5 класс
Задание 653, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 660, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 668, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 775, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1050, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1442, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1799, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Номер 632, Мерзляк, Полонский, Якир, Учебник
Номер 634, Мерзляк, Полонский, Якир, Учебник
Номер 1222, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 106, Мерзляк, Полонский, Якир, Учебник
Номер 126, Мерзляк, Полонский, Якир, Учебник
Номер 6, Мерзляк, Полонский, Якир, Учебник
Номер 350, Мерзляк, Полонский, Якир, Учебник
Номер 352, Мерзляк, Полонский, Якир, Учебник
Номер 751, Мерзляк, Полонский, Якир, Учебник
Номер 1167, Мерзляк, Полонский, Якир, Учебник
Номер 1345, Мерзляк, Полонский, Якир, Учебник
Задание 433, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1143, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 классНомер 3, Мерзляк, Полонский, Якир, Учебник
Номер 64, Мерзляк, Полонский, Якир, Учебник
Номер 129, Мерзляк, Полонский, Якир, Учебник
Номер 135, Мерзляк, Полонский, Якир, Учебник
Номер 140, Мерзляк, Полонский, Якир, Учебник
Номер 144, Мерзляк, Полонский, Якир, Учебник
Номер 145, Мерзляк, Полонский, Якир, Учебник
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 349, Мерзляк, Полонский, Якир, Учебник
Номер 564, Мерзляк, Полонский, Якир, Учебник
© budu5.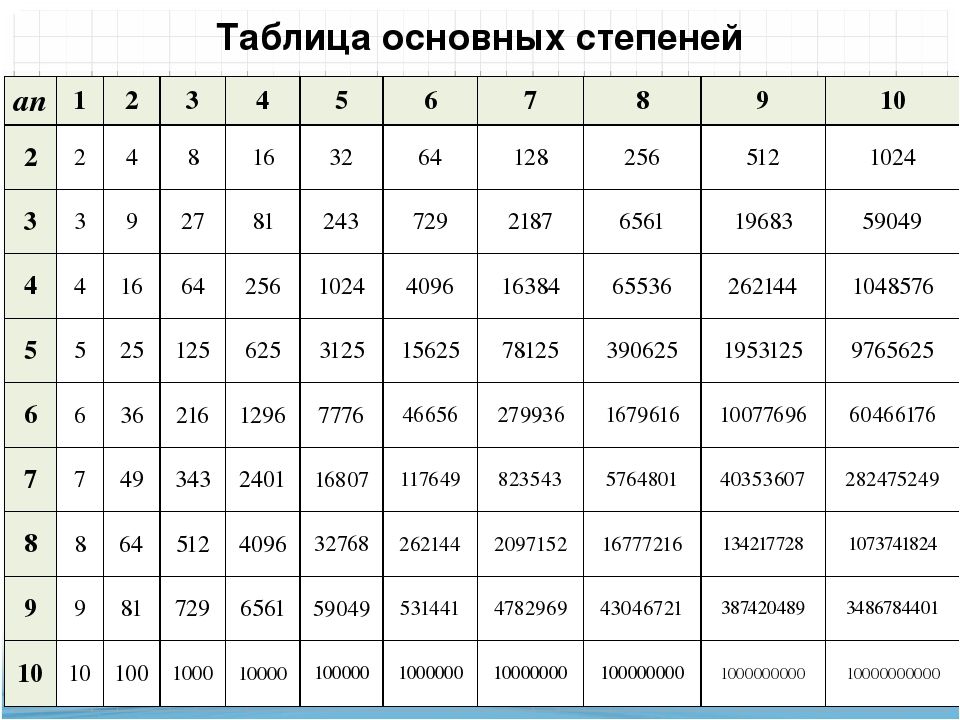 com, 2022
com, 2022
Пользовательское соглашение
Copyright
Открытая Математика. Алгебра. Степень с целым показателем
В § 1.1.2 было определено понятие степени натурального числа с натуральным показателем. Обобщим это определение на случай произвольного действительного числа.
Пусть a − любое действительное число; n − натуральное число, большее единицы. Назовем n-ной степенью числа a называется произведение n множителей, каждый из которых равен a. Если n = 1, то по определению считают, что a1 = a. Число a называется основанием степени, число n − показателем степени.
Справедливы следующие свойства степени:
- an ċ ak = an + k.
- an : ak = an – k, если n > k.

- (an)k = ank.
- an ċ bn = (ab)n.
- anbn=(ab)n, b≠0.
Например, 33ċ32=33+2=35, (32)4=32ċ4=38, (32)2=3222=94.
По определению полагают, что a0 = 1 для любого a ≠ 0. Нулевая степень числа нуль не определена.
По определению полагают, что если a≠0, n − натуральное число, то a-n=1an.
Справедливо равенство (ab)-n=(ba)n. Например, (-2)-2=1(-2)2=14, (32)-1=23.
Совершенно аналогично вводится понятие степени рациональных выражений. Чтобы возвести рациональную дробь в натуральную степень, нужно отдельно возвести в эту степень числитель, и отдельно − знаменатель: (PQ)n=PnQn.
Преобразовать в дробь степень (2x2x-1)2.
(2x2x-1)2=4×4(x-1)2=4x4x2-2x+1.
Ответ. 4x4x2-2x+1.
Возведение рациональной дроби в отрицательную степень происходит по следующей формуле:
(PQ)-n=(QP)n.
Преобразовать в дробь степень ((x+1)2(x-1)5(x+2)3)-2.
((x+1)2(x-1)5(x+2)3)-2=((x+2)3(x+1)2(x-1)5)2=(x+2)6(x+1)4(x-1)10.
Ответ. (x+2)6(x+1)4(x-1)10.
3. Степень числа. Арифметический корень
МАТЕРИАЛ ДЛЯ ПОВТОРЕНИЯСтепень числаСтепенью числа а с показателем k, где k принадлежит множеству натуральных чисел, называется произведение k множителей, каждый из которых равен а:
Число а называется основанием степени, а число k — показателем степени.
Свойства1. Четная степень отрицательного числа есть число положительное.
2. Нечетная степень отрицательного числа есть число отрицательное.
3. Любая степень положительного числа — положительное число.
4. При возведении нуля в любую натуральную степень получим нуль. Нуль в нулевой степени не определен.
5. При возведении единицы в любую натуральную степень получим единицу.
6. При возведении числа в отрицательную степень заменяем его на частное 1 и этого числа в положительной степени:
8. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остается прежним:
9. При возведении степени в степень показатели степеней перемножаются, а основание остается прежним:
10. Степень произведения равна произведению степеней множителей:
11. Степень частного равна частному степеней делимого и делителя:
Арифметический корень
Арифметическим корнем n-ой степени из положительного действительного числа а называется неотрицательное число b, n-ая степень которого равна а.
Корень 2-ой степени из числа а обозначается:
Свойства 1. Корень степени n из числа в степени n равен самому числу, если n нечетно, или модулю числа, если n четно.
Решение:
Не подходят:
2. Сравните с единицей числа:
Решение:
3. Вычислите:
Решение:
4. а) Запишите числовое выражение (83· 85)2 в виде степени с основанием 2.
б) Запишите числовое выражение (94· 96)3 в виде степени с основанием 3.
Решение:
5. Найдите значения выражения:
Решение:
6. Определите знак выражения:
Решение:
Ответ: выражение положительно.7. Упростите выражение:
Решение:
а)
Ответ: -9
8.
 Упростите выражение:
Упростите выражение:Решение:
9. Вычислите:
Решение:
а)
Ответ: 0,01.
10. Упростите выражение:
Решение:
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Укажите два последовательных целых числа, между которыми заключено число:
2. Имеет ли смысл выражение:
3. Найдите значение выражения:
4. Найдите значения выражения: а) 411 · 4-9; б) 6-5 : 6-3.
5. Выполните действия:
6. Вычислите:
7. Вычислите:
8. Выполните действия:
9. Найдите значение выражения:
10. Упростите выражение:
ПРОВЕРЬТЕ СЕБЯ
5.
 4. Свойства корней степени n
4. Свойства корней степени n304
Условие:
Решение:
Советы:
Изучить теорию параграфа
305
Условие:
Решение:
Советы:
Вспомните определение натуральных и действительных чисел
306
Условие:
Решение:
Советы:
Использовать свойства степеней
307
Условие:
Решение:
Советы:
Сократить степени
308
Условие:
Решение:
Советы:
Представить число в виде степени.
309
Условие:
Решение:
Советы:
Разложить число под корнем на множители
310
Условие:
Решение:
Советы:
Представить произведение корней как корень произведения.
311
Условие:
Решение:
Советы:
Записать всё под один корень
312
Условие:
Решение:
Советы:
Чтобы внести число под знак корня ,нужно возвести это число в степень корня
313
Условие:
Решение:
Советы:
Если под корнем есть дробь с произведением ,можно сократить
314
Условие:
Решение:
Советы:
Внести под один корень и сократить
315
Условие:
Решение:
Советы:
Внести степень под корень
316
Условие:
Решение:
Советы:
Повторить свойства степеней
317
Условие:
Решение:
Советы:
Поставить число в виде степени
318
Условие:
Решение:
Советы:
Умножаем до нужной степени
319
Условие:
Решение:
Советы:
Квадратный корень - это корень второй степени
320
Условие:
Решение:
Советы:
При возведении степени в степень, степени перемножаются
321
Условие:
Решение:
Советы:
Пример а возвести в 6 степень, пример б в 8 степень
322
Условие:
Решение:
Советы:
Представить корни в одной степени
323
Условие:
Решение:
Советы:
Представить в виде одной степени и внести под один корень
324
Условие:
Решение:
Советы:
Степени перемножить
325
Условие:
Решение:
Советы:
Сначала преобразовывать внутренние корни
326
Условие:
Решение:
Советы:
Разложить на множители
327
Условие:
Решение:
Советы:
Вспомните определение целых чисел.
328
Условие:
Решение:
Советы:
Использовать формулы сокращённого умножения
Сколько будет (1+1/n) в степени n ? | Математика не для всех
Продолжение. Первая часть про замечательный тригонометрический предел — здесь.
Итак, второй замечательный предел представляет из себя предел показательной функции:
Если бы кто-то проводил голосование, какой предел более замечательный, я без раздумий проголосовал бы за второй, ведь его пределом является не менее замечательное число e, которое входит в самую красивую формулу математики всех времен и народов:
Кстати, на рисунке выше показало Число Эйлера, а вот кто сталкивался с постоянной Эйлера? Пишите в комментариях.Кстати, на рисунке выше показало Число Эйлера, а вот кто сталкивался с постоянной Эйлера? Пишите в комментариях.
Кстати, если перевернуть формулу и устремить х к 0, ничего не изменитсяКстати, если перевернуть формулу и устремить х к 0, ничего не изменится
Получается тот-самый натуральный логарифм с основанием eПолучается тот-самый натуральный логарифм с основанием e
Поиграемся с n, которое входит в запись предела.
Здесь я умышленно во славу педагогики нарушаю законы математики и пищу «0». Я просто хочу подчеркнуть, что 1+»0″ — это хоть и бесконечно малая величина, но она всё же не равна нулю. Поэтому и возникает так называемая «неопределенность». Например,
Заметьте, что эта формула не записывает второго замечательного предела. так как 100000 не равно 1/0,0001. Уберите один ноль из степени и получите, то что нужно.Заметьте, что эта формула не записывает второго замечательного предела. так как 100000 не равно 1/0,0001. Уберите один ноль из степени и получите, то что нужно.
Таким образом неясно, как ведет себя эта неопределенность: возрастает ли бесконечно с ростом степени или ограничена каким-либо пределом?
В математике неопределенность записывают в квадратных скобках. Кстати, первый замечательный предел раскрывает неопределенности типа [0/0].
Попробуем решить парочку примеров со вторым замечательным пределом. c
c
В целом самым распространенным подходом к решению является сложение/вычитание единицы, а затем домножение/деление степени.
************************************************************************
Спасибо! Надеюсь, было очень интересно и познавательно! Буду рад, если Вы поддержите меня ПОДПИСКОЙ, ЛАЙКОМ или даже критическим комментарием.
**************************************************************************
О чем я еще пишу:
Теорема неслучайности: неравенство Чебышева
Про факториал
Как запомнить синус и косинус основных углов?
Правда интересные числа, «мамой клянусь»
Экзотические тригонометрические формулы, которые не дают в школе
Онлайн урок: Степень числа.
 Квадрат и куб числа по предмету Математика 5 класс
Квадрат и куб числа по предмету Математика 5 классВторую степень числа называют квадратом числа.
Так, квадрат любого натурального числа а будет представлять собой произведение двух одинаковых множителей: а ∙ а = а2(говорят и читают «а в квадрате»).
Например,
22 (два во второй степени) иначе говорят и читают «два в квадрате».
102 (десять во второй степени) иначе говорят и читают «десять в квадрате».
272 (двадцать семь во второй степени) иначе говорят и читают «двадцать семь в квадрате».
Давайте сосчитаем квадраты первого десятка натуральных чисел (возведем во вторую степень первые десять натуральных чисел), используя таблицу умножения.
Один в квадрате равняется одному: 12 = 1 ∙ 1 = 1.
Два в квадрате равняется четырем: 22 = 2 ∙ 2 = 4.
Три в квадрате равняется девяти: 32 = 3 ∙ 3 = 9.
Четыре в квадрате равняется шестнадцати: 42 = 4 ∙ 4 = 16.
Пять в квадрате равняется двадцати пяти: 52 = 5 ∙ 5 = 25.
Шесть в квадрате равняется тридцати шести: 62 = 6 ∙ 6 = 36.
Семь в квадрате равняется сорока девяти: 72 = 7 ∙ 7 = 49.
Восемь в квадрате равняется шестидесяти четырем: 82 = 8 ∙ 8 = 64.
Девять в квадрате равняется восьмидесяти одному: 92 = 9 ∙ 9 = 81.
Десять в квадрате равняется сотне: 102 = 10 ∙ 10 = 100.
Оформим полученные данные квадратов натуральных чисел от 1 до 10 в виде таблицы.
Таблица квадратов первых десяти натуральных чисел | ||||||||||
а | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
а2 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
Пример.
Учитывая данные таблицы квадратов, решим уравнение.
Решим уравнение х2 = 49.
Решить уравнение- это значит найти корень уравнения (в нашем случае установить значение х).
По таблице квадратов видно, что 49 = 72.
Следовательно, корень уравнения (х) равен семи.
х2 = 49
х = 7
Проверка: подставим найденное значение неизвестной (х = 7) в исходное уравнение х2 = 49, получим:
72 = 49
7 ∙ 7 = 49
49 = 49
Ответ: х = 7.
У меня есть дополнительная информация к этой части урока!
ЗакрытьЧтобы возвести в любую степень число 10, необходимо дописать после единицы нули, количество которых показывает показатель степени.
Разберем пример первый.
Найдите четвертую степень десяти (десять в четвертой степени 104).
10— это основание.
4— это показатель степени.
Так как по вышеизложенному правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
104 = 10000
На самом деле, если перемножить (по определению степени) четыре десятки, то получим:
104 = 10 ∙ 10 ∙ 10 ∙ 10 = 10000
Пример второй: найдите третью степень десяти (десять в третьей степени 103).
10— это основание.
3— это показатель степени.
Так как по правилу количество нулей после единицы должно быть равно показателю степени, то результат запишем следующим образом:
103 = 1000
Соответственно, если перемножить (по определению степени) три десятки, то получим:
103 = 10 ∙ 10 ∙ 10 = 1000
Рассмотрим обратную ситуацию:
Представим число 100 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (100).
Число 100 содержит два нуля, следовательно, это число в виде степени с основанием 10 представим следующим образом:
100 = 102
10— это основание.
2— это показатель степени.
Рассмотрим еще один подобный пример.
Представим число 10000 в виде степени с основанием 10.
Запишем основание 10, а показателем будет число, равное количеству нулей исходного числа (10000).
Данное число содержит четыре нуля, следовательно, 10000 в виде степени с основанием 10 представим следующим образом:
10000 = 104
10— это основание.
4— это показатель степени
Третья степень числа тоже имеет свое название.
Число в третьей степени называют кубом числа.
Так, куб любого натурального числа а будет представлять собой произведение трех одинаковых множителей: а ∙ а ∙ а = а3 (говорят и читают «а в кубе»).
Например,
23 (два в третьей степени) иначе говорят и читают «два в кубе».
103 (десять в третьей степени) иначе говорят и читают «десять в кубе».
273 (двадцать семь в третьей степени) иначе говорят и читают «двадцать семь в кубе».
Давайте определим кубы первого десятка натуральных чисел (возведем в третью степень первые десять натуральных чисел), используя таблицу умножения.
Один в кубе: 13 = 1 ∙ 1 ∙ 1 = 1.
Два в кубе: 23 = 2 ∙ 2 ∙ 2 = 8.
Три в кубе: 33 = 3 ∙ 3 ∙ 3 = 27.
Четыре в кубе: 43 = 4 ∙ 4 ∙ 4 = 64.
Пять в кубе: 53 = 5 ∙ 5 ∙ 5 = 125.
Шесть в кубе: 63 = 6 ∙ 6 ∙ 6 = 216.
Семь в кубе: 73 = 7 ∙ 7 ∙ 7 = 343.
Восемь в кубе: 83 = 8 ∙ 8 ∙ 8 = 512.
Девять в кубе: 93 = 9 ∙ 9 ∙ 9 = 729.
Десять в кубе: 103 = 10 ∙ 10 ∙ 10 = 1000.
Оформим полученные данные кубов натуральных чисел от 1 до 10 в виде таблицы.
Таблица кубов первых десяти натуральных чисел | ||||||||||
а | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
а3 | 1 | 8 | 27 | 64 | 125 | 216 | 343 | 512 | 729 | 1000 |
С помощью таблицы кубов можно легко и просто решать примеры и задачи, в которых необходимо высчитывать третью степень числа.
Пример.
Представим в виде куба число 343.
По таблице кубов видим, что 343 = 73
Проверим: найдем произведение трех семерок:
73 = 7 ∙ 7 ∙ 7 = 49 ∙ 7 = 343
Ответ: 343 = 73.
На прошлом уроке мы подробно разобрали порядок выполнения арифметических действий в выражениях.
Выяснили, что в первую очередь выполняются арифметические действия в скобках, затем-действия второй ступени (умножение и деление) по порядку их следования слева направо, и только потом выполняются действия первой ступени (сложение и вычитание) по порядку слева направо.
Однако, в математических выражениях, в которых отсутствуют скобки, но есть действия первой, второй ступени и степень, возведение в степень выполняется раньше других действий, только потом умножают, делят, складывают и вычитают в установленном правилами порядке.
Если в скобках содержится степенное выражение, то действия в скобках выполняются по порядку слева направо, начиная с действий высшей ступени- возведение в степень, и далее по известным нам правилам.
За скобками действия выполняют, соблюдая порядок выполнения действий без скобок, рассмотренный выше.
Рассмотрим поясняющие примеры.
При решении различных задач и примеров будем пользоваться составленными таблицами степеней.
Пример 1.
Найдите значение выражения 82 ÷ 4 — 10.
Определим порядок действий в выражении и найдем его значение.
Так как исходное выражение не содержит скобки, а возведение в степень- это действие более высокой ступени, чем умножение, деление, сложение и вычитание, следовательно, в первую очередь необходимо выполнить вычисление степени, затем слева направо в порядке следования сначала действия второй ступени (деление), затем- действия первой ступени (вычитание).
82 ÷ 4 — 10 = 6
1) 82 = 8 ∙ 8 = 64 (по определению степени или по таблице квадратов).
2) 64 ÷ 4 = 16
3) 16 — 10 = 6
Пример 2.
Найдите значение выражения (21 — 11)2 ∙ 23.
Найдем значение данного выражения, определив порядок действий в нем.
(21 — 11)2 ∙ 23 = 800
Согласно порядка выполнения действий сначала выполняются действия в скобках.
Найдем разность 21 и 11.
1) 21 — 11 = 10
Далее выполняется действие высшей ступени (возведение в степень), т.е. разность, полученную в скобках, возведем в квадрат.
Найдем, чему равно 102по определению степени или по таблице квадратов.
2) 102 = 10 ∙ 10 = 100
Затем выполним действия, которые находятся в исходном выражении за скобками.
Определим третью степень двойки по таблице кубов или по определению степеней.
3) 23 = 2 ∙ 2 ∙ 2 = 8
Далее перемножим результаты, полученные в во втором и в третьем действии соответственно, т.е. найдем произведение 100 и 8.
4) 100 ∙ 8 = 800
У меня есть дополнительная информация к этой части урока!
ЗакрытьС давних пор основными арифметическими операциями являются операции сложения, вычитания, умножения и деления.
Представление о степени, как об отдельной операции возникло не сразу.
Однако степени применялись при вычислении площадей и объемов уже у древних народов: степень числа высчитывали при решении различных задач в Древнем Египте, Древней Греции, в Вавилоне.
Диофант Александрийский древнегреческий математик, философ (III век н.э.) в своем знаменитом труде «Арифметика» описал первые натуральные степени чисел.
Диофант первым из античных ученых предложил специальные обозначения для шести степеней неизвестного (квадрат, куб, квадрато-квадраты, квадрато-кубы и т.д.)
Древнегреческий ученый Пифагор и его последователи (пифагорейцы) проявляли большой интерес к числам, искали в них скрытый смысл, закономерности и приписывали им различные свойства.
Пифагорейцы предполагали, что каждое число можно представить в виде фигуры.
Так, например, числа 4, 9, 16, 25 они представляли в виде квадратов.
В Древнем Вавилоне для вычисления и расчетов был создан целый ряд вычислительных таблиц: таблицы умножения, таблицы квадратов и кубов и многие другие.
В Древней Индии успешно развивалась наука.
Высоких результатов индийцы добились в астрономии, медицине, математике.
Индийские ученые часто оперировали большими числами.
В Древней Индии существовало понятие степени числа, математики того времени умели вычислять площади и объемы фигур, разработали алгоритмы вычисления всех арифметических операций, в том числе определение степени числа.
Важнейшим открытием индийских ученых в математике стало изобретение позиционной системы счисления, а также запись (чтение) чисел, для каждой цифры был придуман свой знак.
Математические труды их были изложены в основном в словесной форме на древнеиндийском языке в священных писаниях, книгах, сказаниях.
Потребность в решении более сложных математических задач со степенями заставляла ученых разных стран расширять понятие о степени, систематизировать и обобщать известные уже данные о ней.
В начале XV века самаркандский математик Гияс ад-Дин Джемшид Аль-Каши рассматривал нулевой показатель степени, в это же время французский ученый Никола Шюке применял в своих трудах нулевой и отрицательный показатель степени.
В 1544 г. немецкий математик Михаэль Штифель в своей книге «Полная арифметика» впервые ввел понятие «Показатель степени».
Постепенно понятие степени становится все шире, оно применяется не только к числу, но и к переменной.
Математики средневековья пытались установить единое обозначение степени и сделать ее компактней.
Французский ученый математик Франсуа Виет ввел буквенное обозначение (N, Q, C) для первой, второй и третьей степени.
Нидерландский математик Симон Стевин предложил называть степень по их показателям, отвергая тем самым словесные обозначения степеней, составленные Диофантом.
Современное обозначение степеней (аn), где а-основание степени, n-показатель степени, ввел французский математик Рене Декарт.
Показатель степени в математике с примерами решения и образцами выполнения
При введении понятия о степени подразумевалось, что показатель степени — целое положительное число. Все правила действий над степенями были выведены в этом предположении.
Все правила действий над степенями были выведены в этом предположении.
В математике наряду со степенями с целыми положительными показателями рассматриваются также и степени с нулевым, отрицательным и дробным показателями. Более того, исследование некоторых вопросов, имеющих очень большое значение, требует рассмотрения степеней с иррациональными показателями.
В этой главе будет введено понятие о степени с любым вещественным показателем и будет показано, что все правила действий над степенями, выведенные для целых положительных показателей, сохраняются и для любых вещественных показателей.
Понятие о степени с нулевым и отрицательным показателемОпределение. Если а ≠ 0, то а⁰ = 1. Нулевая степень числа, отличного от нуля, равна единице.
Например, 2°= 1; (0,75)°= 1; (—√3)° = 1. Выражение 0° смысла не имеет.
Определение:
Если а ≠ 0 и q — целое положительное число, то
Целая отрицательная степень числа, отличного от нуля, равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,
Например,
Теорема:
При любых целых положительных m и n справедливо правило деления степеней
Доказательство:
Если m > n, утверждение в доказательстве не нуждается.
Если m = n, справедливость утверждения вытекает из определения нулевого показателя.
Если m < n, справедливость утверждения вытекает из определения целого отрицательного показателя.
Теорема доказана.
Определение нулевого и отрицательного показателей возникло в связи с желанием обобщить установленное ранее правило деления степеней одной и той же величины. Это правило
было выведено в предположении, что m и n— целые положительные числа и что m > n.
Допустим, что правило деления степеней можно применять и.тогда, когда показатель степени делимого равен показателю степени делителя и когда» показатель степени делимого меньше показателя степени делителя.
Пусть m = n, тогда
С другой стороны,
Сравнение результатов (1) и (2) показывает, что a° = 1
Пусть m < n , т. е. n = m + q, где q — положительное число.
е. n = m + q, где q — положительное число.
Тогда имеем
С другой стороны, посредством сокращения получаем
Сравнение результатов (3) и (4) показывает, что целесообразно считать
где q — целое положительное число.
Рассуждения, которые приведены выше, не являются, конечно,
доказательствами того, что Эти рассуждения проведены только для того, чтобы показать, что принимаемые нами определения нулевого и отрицательного показателя подсказаны нам опытом деления степеней с одним и тем же основанием и единственно возможны, если мы желаем сохранить правило деления степеней для случая, когда показатель степени делимого не превосходит показателя степени-делителя.
Замечание:
Не следует думать, что введением отрицательного показателя дробное выражение превращается в целое . Выражение является лишь другой формой записи выражения
Понятие о степени с дробным показателемОпределение:
Если a > 0 и числа m и n натуральные, то
Пример:
Определение дробного показателя возникло в связи с желанием обобщить правило извлечения корня на случай, когда показатель подкоренного количества не делится на показатель корня. Правило
Правило
было выведено в предположении, что m и n натуральные и m делится на n. Теперь, это правило можно применять и тогда, когда m и n— любые натуральные числа.
Известно, что рациональная дробь может быть представлена в различных видах. Например, может быть представлена как и т. п. Выражение с дробным показателем не зависит oт того, в каком виде представлен показатель. Пусть
Тогда
В силу (1) правые части равенств (2) и (3) тождественны. Поэтому
Определение дробного показателя не распространяется на степени с отрицательными основаниями, так как тогда выражения с дробными показателями не обладали бы столь простым и важным свойством, которое указано.
Пример:
Допустим, что определение дробного показателя распространено на степени с отрицательным основанием. Тогда
В то же время
Замечание:
Не следует думать, что введением дробного показателя иррациональное выражение превращается в рациональное . Если выражение иррациональное, то и выражение тоже иррациональное. Выражение является лишь другой формой записи выражения
Если выражение иррациональное, то и выражение тоже иррациональное. Выражение является лишь другой формой записи выражения
Определение:
Если а — положительное число, то
где m и n— любые натуральные числа.
То есть дробная отрицательная степень положительного числа равна единице, деленной на степень того же числа с показателем, равным абсолютной величине отрицательного показателя. Например,
Теорема:
При любом целом х
Доказательство:
Если x > 0 справедливость утверждения вытекает из определения дробного показателя.
Если х = 0, то
С другой стороны,
Пусть x < 0. Положим х = — m,m > 0. Имеем :
Действия над степенями с рациональными показателямиВ этом параграфе буквы m, n, р, q обозначают целые положительные числа, буква r, а также r₁— любые рациональные числа.
Теорема:
Произведение степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным сумме показателей.
Короче: при умножении степеней с одинаковыми основаниями показатели степеней складываются, т. е.
Доказательство:
Переместительный закон умножения справедлив для любых действительных чисел. При любых рациональных r и r₁ степени —действительные числа, поэтому
Для доказательства теоремы достаточно рассмотреть следующие случат
Случай 1. r = 0; r₁ — любое рациональное число. Имеем
Случай 2.Имеем
Случай 3. Имеем
Случай 4. имеем
На основании доказанного в случае 2
Значит,
Методом математической индукции можно показать, что теорема верна для любого количества множителей.
Пример:
Пример:
Теорема:
Частное от деления степеней с одинаковыми основаниями равно степени с тем же основанием и с показателем, равным разности показателей делимого и делителя.
Короче; при делении степеней с одинаковыми основаниями показатели степеней вычитаются, т. е.
Доказательство:
На основании правила умножения степеней
Отсюда по определению деления
Пример:
Пример:
Теорема:
Степень произведения двух чисел равна произведению степеней сомножителей, т. е.
Доказательство:
Возможны три случая:
Случай 1. r = 0. Имеем
Следовательно,
Случай 2. . Имеем
Случай 3. Имеем
На основании доказанного в случае 2
Значит,
Методом математической индукции можно показать, что теорема верна для любого количества множителей.
Теорема:
Степень дроби равна частному от деления степени числителя с показателем, равным показателю дроби на степень знаменателя с показателем, равным показателю дроби.
Короче: степень дроби равна частному от деления степени числителя на степень знаменателя, т. е.
Доказательство:
Возможны три случая:
Случай 1. r = 0. Имеем
Следовательно,
Случай 2. Имеем
Случай 3. Имеем
На основании доказанного в случае 2
Значит,
Пример:
Теорема:
Результат возведения степени в степень равен степени с тем же основанием и с показателем, равным произведению показателей, участвующих в действии.
Короче: при возведении степени в степень показатели перемножаются, т. е.
Доказательство:
Возможны шесть случаев:
Случай 1. r = 0. Имеем
Случай 2. r₁=0. Имеем
Случай 3. r > 0; r₁ > 0. Положим Тогда
Случай 4, r < 0, r₁ > 0. Положим r = — r₂r₂, > 0. Тогда
На основании теоремы 4 и доказанного в случае 3
Значит,
Случай 5. r > 0; r₁ < 0. Положим r₁ = — r₃, r₃, > 0. Тогда
r > 0; r₁ < 0. Положим r₁ = — r₃, r₃, > 0. Тогда
На основании доказанного в случае 3
Значит,
Случай 6. r < 0; r₁ < 0. Положим r = -r₂, r₁ = — r₃, r₂ > 0, r₃ >0. Тогда
На oсновании доказанного в случае 4
Значит,
Следствие.
Пример:
Из доказанных теорем вытекает, что для степеней с любыми рациональными показателями справедливы следующие правила, которые были ранее установлены для степеней с натуральными показателями:
1) правило умножения степеней;
2) правило деления степеней;
3) правило возведения произведения в степень;
4) правило возведения дроби в степень;
5) правило возведения степени в степень.
Пример:
Вычислить при а = 2,5 и b= 20
Решение:
При а = 2,5; b = 20 имеем
Ответ. А = 4
Степень с рациональным показателемТеорема:
Пусть r рационально, тогда
1) если а > 1 и r > 0, то > 1; .
2) если 0 < a < 1 и r > 0 , то < 1
3) если а > 1 и r < 0, то < 1;
4) если 0 < a < 1 и r < 0, то > 1
Доказательство:
1) Пусть а > 1 и , где m и n— натуральные числа. Тогда
Так как
2) Пусть а< 1 и . Положим тогда a₁ > 1. Имеем
так как по доказанному в п. 1)
3) Пусть а > 1 и , тогда
так как по доказанному в п. 1)
4) Пусть а < 1 и , тогда
так как < 1 (по доказанному в п; 2).
Теорема:
Если а > 1 и рациональное r больше рационального r₁, то если же 0 < а < 1, то , т. е. если а > 1 то при возрастании r возрастает и степень , а если 0 < a < 1, то при возрастании r степень убывает.
Доказательство:
Пусть a > 1 и r > r₁ Рассмотрим разность
Так как и, следовательно, , т. е.
е.
Пусть а < 1 и r > r₁. Рассмотрим разность
Так как
Теорема:
Если c > 0, то последовательность имеет пределом единицу, т. е.
Доказательство:
Имеем последовательность
При с = 1 утверждение проверяется легко. Остается рассмотреть два случая: c > 1 и c < 1.
Предположим сначала, что с > 1. Тогда каждый член последовательности (3) больше единицы. Обозначим
Тогда последовательность (3) может быть переписана так:
где при любом n.
Пусть теперь n >1 тогда (см. теорему 1 § 9 гл. V)
Но значит,
Последнее неравенство показывает, что по любому заданному положительному e можно указать столь большой номер N, что при всех n >N число будет меньше e. Действительно, чтобы было меньше е, достаточно, чтобы Таким образом, за N можно принять любое целое число, бoльшее Отсюда вытекает, что а тогда
Пусть теперь подкоренное выражение c₁ меньше единицы. Положим Тогда последовательность
Положим Тогда последовательность
примет такой вид:
или, что все равно,
Последовательность (4), составленная из знаменателей последовательности (7), как показано, стремится к единице, значит, и последовательность (7) стремится к единице, т. е. опять
Понятие о степени с иррациональным показателемПусть а — какое-нибудь положительное число и а — иррациональное. Какой смысл следует придать выражению ?
Чтобы сделать изложение более наглядным, проведем его на частном примере. Именно, положим а = 2 и а = 1,624121121112…. Здесь, а — бесконечная десятичная дробь, составленная по такому закону: начиная с четвертого десятичного знака, для изображения а употребляются только цифры 1 и 2, и при этом количество цифр 1, записываемых подряд перед цифрой 2, все время увеличивается на одну. Дробь а непериодическая, так как иначе количество цифр 1, записываемых подряд в его изображении, было бы ограниченным. Следовательно, а — иррациональное число.
Итак, какой же смысл следует придать выражению
Чтобы ответить на этот вопрос, составим последовательности значений а с недостатком и избытком с точностью до . Получим
1,6; 1,62; 1,624; 1,6241; …, (1)
1,7; 1,63; 1,625; 1,6242; … (2)
Составим соответствующие последовательности степеней числа 2:
Последовательность (3) возрастает, так как возрастает последовательность (1) (теорема 2 § 6).
Последовательность (4) убывает, так как убывает последовательность (2).
Каждый член последовательности (3) меньше каждого члена последовательности (4), и, таким образом, последовательность (3) ограничена сверху, а последовательность (4) ограничена снизу.
На основании теоремы о монотонной ограниченной последовательности каждая из последовательностей (3) и (4) имеет предел. Если теперь окажется, что разность последовательностей (4) и (3) сходится к нулю, то из этого будет вытекать, что обе эти последовательности, имеют общий предел.
Разность первых членов последовательностей (3) и (4)
Разность вторых членов
Разность n-х членов
На основании теоремы 3 § 6
Итак, последовательности (3) и (4) имеют общий предел. Этот предел является единственным вещественным числом, которое больше всех членов последовательности (3) и меньше всех членов последовательности (4), его и целесообразно считать точным значением .
Из сказанного вытекает, что и вообще целесообразно принять следующее определение:
Определение:
Если a > 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых есть рациональные приближения а с недостатком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с избытком.
Если a < 1 то степенью числа а с иррациональным показателем а называется такое действительное число, которое больше всех степеней этого числа, показатели которых — рациональные приближения а с избытком, и меньше всех степеней этого числа, показатели которых — рациональные приближения а с недостатком.
.Если а= 1, то степенью его с иррациональным показателем а является 1.
Пользуясь понятием предела, это определение можно сформулировать так:
Степенью положительного числа с иррациональным показателем а называется предел, к которому стремится последовательность рациональных степеней этого числа при условии, что последовательность показателей этих степеней стремится к а, т. е.
Пример:
Вычислить с точностью до 0,1 число , если а= 1,624121121112 … (а то же, что и выше).
Решение:
Для приближенного вычисления заметим, что
Далее,
Таким образом, < 3,09.
Испытанием уходим, что (3,03)⁵ = 255,3954324543 < 256. Поэтому . Выходит, что
Число вычислено с точностью до: 0,06.
Свойства степени с любым вещественным показателемТеорема:
1) Если а > 1 и а > 0, то
2) если 0 < а < 1 и а>0, то
3) если а > 1 и а < 0, то
4) если 0 < а < 1 и а<0, то
Доказательство:
1) Это утверждение доказано для случая, когда о рационально (теорема 1 § 6).
Пусть о иррациональное. Рассмотрим последовательность {} десятичных приближений а с недостатком с точностью до . Среди членов этой последовательности должны находиться, и положительные числа, так как если бы при всех n, то и
Пусть (теорема 1 §6). Но Значит,
2) Положим , тогда a₁ >. 1. По доказанному , значит,
3) Пусть а > 1; а < 0. Положим . Рассмотрим
По доказанному в п. (1) Значит,
4) Пусть а<1; а<0. Положим. Тогда
так как (по доказанному в п. 2).
Теорема:
Если а > 1 и число а больше , то т. е. при а > 1 функция возрастает.
Если 0 < a < 1 и a > то , т. е. при 0 < a < 1 функция убывает.
Доказательство:
Пусть . Рассмотрим разность
Так как , то и, следовательно, . Пусть Рассмотрим
Так как
Решение заданий и задач по предметам:
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
Что такое показатель?
МАТЕМАТИКА ОБЗОР: ПОЛЕЗНАЯ МАТЕМАТИКА ДЛЯ КАЖДОГО СЕКЦИЯ
3. 2. Что такое ЭКСПОНЕНТ?
2. Что такое ЭКСПОНЕНТ?
вернуться к Экспоненты, Страница 1
Сначала давайте посмотрим, как работать с переменными в заданной степени, например, 3 .
Есть пять правил работы с экспонентами:
1.a m * a n = a (m+n)
2. (а * б) н = а н * б н
3. (а м ) н = а (м * п)
4. а м / а н = а (м-н)
5. (а/б) н = а н / б н
Давайте подробно рассмотрим каждый из них.
1. a m * a n = a (m+n) говорит, что когда вы берете
число а, умноженное само на себя m раз и умноженное на
одно и то же число a, умноженное само на себя n раз, это то же самое, что взять
это число а и возведение его в степень, равную сумме m + n.
Вот пример, где
а = 3
м = 4
n = 5а м * a n = a (m+n)
3 4 * 3 5 = 3 (4+5) = 3 9 = 19 683
2. (а * б) п = a n * b n говорит, что при умножении два числа, а затем умножить это произведение само на себя n раз, это то же самое, что умножить первое число само на себя n раз и умножить что на второе число, умноженное само на себя n раз.
Давайте разработаем пример, где
а = 3
б = 6
н = 5(а * б) н = а н * б н
(3 * 6) 5 = 3 5 * 6 5
18 5 = 3 5 * 6 5 = 243 * 7 776 = 1 889 568
3. ( м ) n =
a (m*n) говорит, что когда вы берете
число, a , и умножьте его само на себя m раз, затем умножьте это
произведение само по себе n раз, это то же самое, что умножить число
a сам по себе m * n раз.
( м ) n =
a (m*n) говорит, что когда вы берете
число, a , и умножьте его само на себя m раз, затем умножьте это
произведение само по себе n раз, это то же самое, что умножить число
a сам по себе m * n раз.
Давайте разработаем пример где
а = 3
м = 4
н = 5( м ) n = а (м * п)
(3 4 ) 5 = 3 (4 * 5) = 3 20 = 3 486 784 401
4. а м / н =
a (m-n) говорит, что когда вы
возьми число а и умножь его само на себя m раз, затем раздели
это произведение на а, умноженное само на себя в n раз, это то же самое
как умноженное само на себя m-n раз.
Вот пример, где
а = 3
м = 4
п = 5а м / а н = а (м-н)
3 4 / 3 5 = 3 (4-5) = 3 -1 (Запомните, как поднять числа в отрицательную степень.)
3 4 / 3 5 = 1/3 1 = 1/3
5. (а/б) п =
a n / b n говорит
что при делении числа а на другое число b, а затем
умножь это частное
само по себе n раз, это то же самое, что умножить число само на себя
n раз, а затем разделив это произведение на число b, умноженное на
сам по себе n раз.
Давайте разработаем пример, где
а = 3
б = 6
п = 5(а/б) н = а н / б н
(3/6) 5 = 3 5 / 6 5
Помните, что 3/6 можно уменьшить до 1/2. Итак имеем:
(1/2) 5 = 243/7776 = 0.03125
Понимание показателей степени подготовит вас к использованию логарифмов.
в Логарифмы
Для больше информации об этом сайте свяжитесь с Дистанцией Координатор по образованию.
Авторские права © 2004 регентами Миннесотского университета, равные возможности работодатель и педагог.
экспонентов
показатель степени числа говорит сколько раз использовать число при умножении.
В 8 2 «2» говорит о том, что при умножении дважды используется 8,
, поэтому 8 2 = 8 × 8 = 64
Прописью: 8 2 можно было бы назвать «8 в степени 2» или «8 во второй степени», или просто «8 в квадрате»
Экспоненты также называются степенями или индексами.
Еще несколько примеров:
Пример:
5 3 = 5 × 5 × 5 = 125- Прописью: 5 3 можно назвать «5 в третьей степени», «5 в степени 3» или просто «5 в кубе»
Пример:
2 4 = 2 × 2 × 2 × 2 = 16- Прописью: 2 4 можно было бы назвать «2 в четвертой степени» или «2 в степени 4» или просто «2 к 4-му»
Экспоненты упрощают запись и использование многих операций умножения
Пример: 9 6 легче писать и читать, чем 9 × 9 × 9 × 9 × 9 × 9
Вы можете умножать любое число само по себе столько раз , сколько хотите, используя показатели степени. 4 = 2 × 2 × 2 × 2 = 16
4 = 2 × 2 × 2 × 2 = 16
Отрицательные показатели
Отрицательный? Что может быть противоположным умножению? Разделение!
Итак, мы каждый раз делим на число, что равносильно умножению на 1 число
Пример: 8 -1 = 1 8 = 0,125
Мы можем продолжить так:
Пример: 5 -3 = 1 5 × 1 5 × 1 5 = 0.008
Но часто проще сделать так:
5 -3 также можно рассчитать как:
1 5 × 5 × 5 = 1 5 3 = 1 125 = 0,008
Отрицательный? Переверни позитив!
В последнем примере показан более простой способ обработки отрицательных показателей:
|
Другие примеры:
| Отрицательная экспонента | Обратная величина Положительная экспонента | Ответить | ||
|---|---|---|---|---|
| 4 -2 | = | 1 / 4 2 | = | 1/16 = 0.0625 |
| 10 -3 | = | 1 / 10 3 | = | 1/1000 = 0,001 |
| (-2) -3 | = | 1 / (-2) 3 | = | 1/(-8) = -0,125 |
Что делать, если показатель степени равен 1 или 0?
| 1 | Если показатель степени равен 1, то у вас есть только само число (пример 9 1 = 9 ) | |
| 0 | Если показатель степени равен 0, то вы получаете 1 (пример 9 0 = 1 ) | |
А как насчет 0 0 ? Это может быть либо 1, либо 0, поэтому люди говорят, что это «неопределенное» . |
Все имеет смысл
Если вы посмотрите на эту таблицу, вы увидите, что положительный, нулевой или отрицательные показатели на самом деле являются частью одного и того же (довольно простого) шаблона:
| Пример: Степени числа 5 | |||
|---|---|---|---|
| .. и т.д.. | |||
| 5 2 | 5 × 5 | 25 | |
| 5 1 | 5 | 5 | |
| 5 0 | 1 | 1 | |
| 5 -1 | 1 5 | 0.2 | |
| 5 -2 | 1 5 × 1 5 | 0,04 | |
. . и т.д.. . и т.д.. | |||
Будьте осторожны с группировкой
Во избежание путаницы используйте круглые скобки () в таких случаях:
| С () : | (−2) 2 = (−2) × (−2) = 4 |
| Без () : | −2 2 = −(2 2 ) = −(2 × 2) = −4 |
| С () : | (ab) 2 = ab × ab |
| Без () : | ab 2 = a × (b) 2 = a × b × b |
305, 1679, 306, 1680, 1077, 1681, 1078, 1079, 3863, 3864
Что такое «Сила N»?
За последние несколько месяцев многие спрашивали меня, что означает «сила N». Эта фраза очень проста, но в ней много разных смысловых слоев и смыслов.
Эта фраза очень проста, но в ней много разных смысловых слоев и смыслов.
В математических терминах это представляет собой постоянно растущее число возможностей. Это метафора того, чем мы, нанотехнологи, занимаемся.
Традиционная наука редуктивна: она сужает известные возможности до тех пор, пока мы не придем к заключению. Мы движемся в противоположном направлении к неизвестному. Мы стремимся открывать процессы в природе, которые человечеству еще предстоит понять или представить.
Это путешествие, полное открытий. Конечно, мы идем дальше в рамках науки или, точнее, в рамках многих различных научных дисциплин (таких как инженерия, химия, биология, геология, информатика, сельское хозяйство, медицинские науки и т. д.), но они служат нашим пункт отправления, а не конечный пункт назначения.
Концепция объекта или сущности, находящегося «в степени N», представляет собой экспоненциальный потенциал для роста, обучения, лидерства и процветания, причем процветание является нашей конечной целью.
N также является начальной буквой трех наших областей концентрации:
Нанотехнологии относится к нашей способности манипулировать материей на молекулярном уровне. Работа на этом наноуровне привела к многим прорывам в нашем понимании того, как функционирует материя. Еще более захватывающим является то, что он открывает нам глаза на потенциал использования этого понимания для разработки технологий, которые позволяют найти новые решения проблем в областях, которые ранее были неразрешимыми.
Природа представляет дисциплину биомимикрии, которая включает в себя наблюдение за естественными свойствами материи, объектов, систем и существ.Основываясь на этом фундаментальном понимании, мы затем пытаемся воспроизвести эти процессы и манипулировать ими, чтобы узнать, что возможно, когда они используются с другими процессами или материалами.
Сети — настоящий рубеж научных открытий. Как только мы понимаем основы материи и процессов, нам остается понять, как эти явления взаимодействуют друг с другом. Как обрабатывается информация, которая принимает форму молекулярных взаимодействий? Это приводит к более широкому потенциалу использования этого обмена молекулярной информацией для использования нанотехнологий для создания возникающей функциональности как неотъемлемого свойства при решении сложных проблем.
Как обрабатывается информация, которая принимает форму молекулярных взаимодействий? Это приводит к более широкому потенциалу использования этого обмена молекулярной информацией для использования нанотехнологий для создания возникающей функциональности как неотъемлемого свойства при решении сложных проблем.
Благодаря этой системе открытий мы собрали динамичную команду ученых, которые работают совместно (в разных дисциплинах) для изучения потенциала материалов следующего поколения, которые могут, например, ощущать окружающую среду, усиливать информацию, генерировать энергию и изменение физических характеристик.
Это новый рубеж науки, который функционирует на молекулярном уровне и имеет гораздо более широкое применение в отношении добычи ресурсов, рационального использования окружающей среды, здравоохранения, обработки информации и производства ценных продуктов и услуг, которые определят будущее Альберты. , Канада и остальной мир.
Это Power of N, и он подводит итог тому, чем мы занимаемся в Ingenuity Lab.
Экспоненциальные правила | Законы показателей
Правила экспоненты, законы экспоненты и примеры.
Что такое показатель степени
Основание a, возведенное в степень n, равно произведению a, n раз:
а п = × × … ×
n раз
а — основание, а n — показатель степени.
Примеры
3 1 = 3
3 2 = 3 × 3 = 9
3 3 = 3 × 3 × 3 = 27
3 4 = 3 × 3 × 3 × 3 = 81
3 5 = 3 × 3 × 3 × 3 × 3 = 243
Экспоненты правила и свойства
| Имя правила | Правило | Пример |
|---|---|---|
| Правила продукта | а н ⋅ а м = а н+м | 2 3 ⋅ 2 4 = 2 3+4 = 128 |
| а н ⋅ б н = ( а ⋅ б ) 7 н | 3 2 ⋅ 4 2 = (3⋅4) 2 = 144 | |
| Частные правила | a n / a m = a n — m | 2 5 / 2 3 = 2 5-3 = 4 |
| а н / б н = ( а / б ) н 7 7 | 4 3 / 2 3 = (4/2) 3 = 8 | |
| Силовые правила | ( б н ) м = б н⋅м | (2 3 ) 2 = 2 3⋅2 = 64 |
| б н м = б ( н м ) | 2 3 2 = 2 (3 2 ) = 512 | |
| м √( б н ) = б н / м | 2 √(2 6 ) = 2 6/2 = 8 | |
| б 1/ н = н √ б | 8 1/3 = 3 √8 = 2 | |
| Отрицательные показатели степени | б -н = 1 / б п | 2 -3 = 1/2 3 = 0. 125 125 |
| Нулевые правила | б 0 = 1 | 5 0 = 1 |
| 0 n = 0 , для n >0 | 0 5 = 0 | |
| Единые правила | б 1 = б | 5 1 = 5 |
| 1 п = 1 | 1 5 = 1 | |
| Минус одно правило | (-1) 5 = -1 | |
| Производное правило | ( x n ) ‘ = n ⋅ x n -1 | ( х 3 ) ‘ = 3⋅ х 3-1 |
| Интегральное правило | ∫ x n dx = x n +1 /( n +1)+ C | ∫ x 2 dx = x 2+1 /(2+1)+ C |
Экспоненты правил продукта
Правило продукта с той же базой
a n ⋅ a m = a n+m
Пример:
2 3 ⋅ 2 4 = 2 3+4 = 2 7 = 2⋅2⋅2⋅2⋅2⋅2⋅2 = 128
Правило произведения с одинаковым показателем
а н ⋅ б н = ( а ⋅ б ) н
Пример:
3 2 ⋅ 4 2 = (3⋅4) 2 = 12 2 = 12⋅12 = 144
См. : Умножение показателей степени
: Умножение показателей степени
Частные правила степени
Частное правило с тем же основанием
a n / a m = a n — m
Пример:
2 5 / 2 3 = 2 5-3 = 2 2 = 2⋅2 = 4
Частное правило с одинаковым показателем
a n / b n = ( a / b ) n
Пример:
4 3 / 2 3 = (4/2) 3 = 2 3 = 2⋅2⋅2 = 8
См.: Показатель степени деления
Экспоненты степенных правил
Силовое правило I
( а н ) м = а н⋅м
Пример:
(2 3 ) 2 = 2 3⋅2 = 2 6 = 2⋅2⋅2⋅2⋅2⋅2 = 64
Силовое правило II
N N M = A ( N M )
Пример:
2 3 2 = 2 (3 2 ) = 2 (3⋅3) = 2 9 = 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512
Силовое правило с радикалами
м √( a n ) = a n / м
Пример:
2 √(2 6 ) = 2 6/2 = 2 3 = 2⋅2⋅2 = 8
Правило отрицательных показателей степени
б -н = 1 / б п
Пример:
2 -3 = 1/2 3 = 1/(2⋅2⋅2) = 1/8 = 0.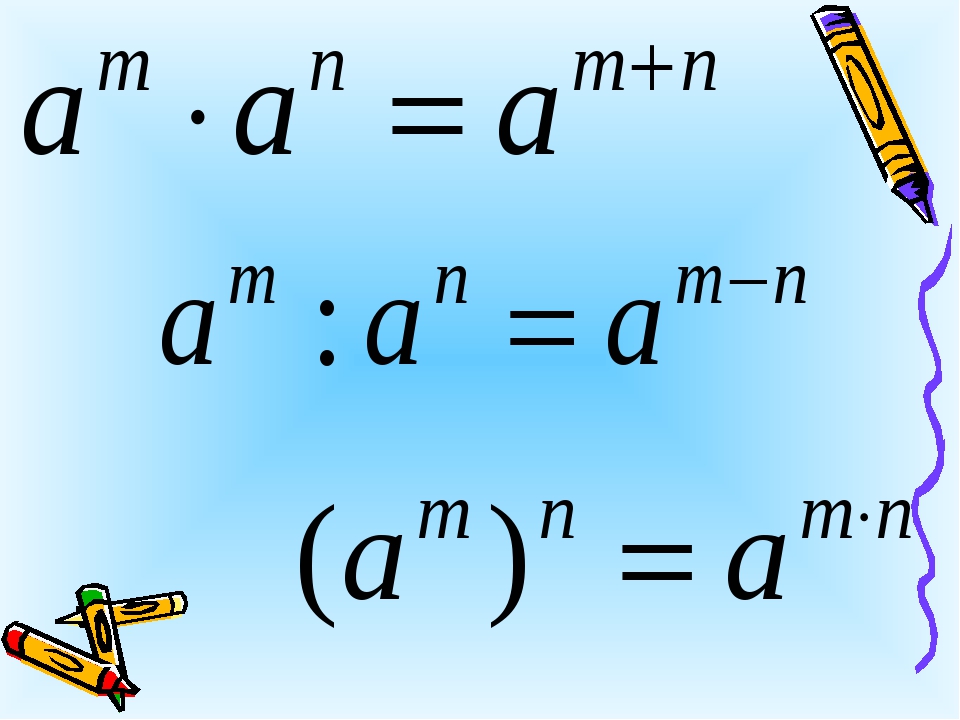 125
125
См.: Отрицательные показатели степени
Калькулятор экспоненты ►
См. также
Степени и степени
Степень есть произведение числа , умножающего число само на себя.
Обычно степень представлена основанием, и показателем степени. Базовое число сообщает , какое число умножается. Показатель степени , небольшое число, написанное выше и справа от основного числа, сообщает , сколько раз умножается основное число.
Например, ?6 в 5-й степени? можно записать как ?6 5 .? Здесь базовое число равно 6, а показатель степени равен 5. Это означает, что 6 умножается само на себя 5 раз: 6 х 6 х 6 х 6 х 6
6 х 6 х 6 х 6 х 6 = 7,776 или 6 5 = 7 776
| 2-й мощности | 3-й мощности | 4-й мощности | 5-й мощности | 5-й мощности | 1 | 1 | 1 | 1 | 1 | |||||||
| 2 | 4 | 8 | 16 | 32 | 3 | 9 | 27 | 916 | 0243 | 9 | 9 | 4 | 16 | 64 | 256 | 1 024 |
| 5 | 25 | 125 | 625 | 625 | 3 125 | 6 | 36 | 0216 | 1 296 | 7 776 | 7 | 49 9 | 49 | 343 | 2401 | 16807 |
| 8 | 64 | 512 | 4096 | 32768 | ||||||||||||
| 9 | 81 | 729 | 6561 | 59049 | ||||||||||||
| 10 | 100 | 1000 | 10000 | 100000 | ||||||||||||
| 11 | 121 | 1331 | 14641 | 161051 | ||||||||||||
| 12 | 144 | 1728 | 20,736 | 248832 |
факториалов чисел и формул Таблица умножения
Полномочия и экспонент (предварительная алгебра, открытие дробей и множителей) – Mathplanet
Мы знаем, как вычислить выражение 5 х 5.


 е. 1/а п )
е. 1/а п )