Степень натуральных показателей: Понятие степени с натуральным показателем — урок. Алгебра, 7 класс. — Детская игровая комната «Волшебный лес»

Posted on 24.04.201914.04.2021 by alexxlab

Содержание

формулировки, доказательства, примеры, формулы степеней

Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.

Свойства степени с натуральным показателем

Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:

Определение 1

1. Главное свойство степени: am·an=am+n

Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.

2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n

3. Свойство степени произведения: (a·b)n=an·bn

Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn

4. Свойство частного в натуральной степени: (a:b)n=an:bn

5. Возводим степень в степень: (am)n=am·n,

Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk

6. Сравниваем степень с нулем:

если a>0, то при любом натуральном n, an будет больше нуля;
при a, равном 0, an также будет равна нулю;
при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.

7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.

8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.

В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными.

Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: am·an=am+n — то же самое, что и am+n=am·an. В таком виде оно часто используется при упрощении выражений.

Далее мы разберем каждое свойство подробно и попробуем привести доказательства.

1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?

Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:

Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.

Разберем конкретный пример, подтверждающий это.

Пример 1

Итак, у нас есть две степени с основанием 2. Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.

Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32

В итоге у нас вышло: 22·23=25. Свойство доказано.

В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:

an1·an2·…·ank=an1+n2+…+nk.

Пример 2

Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.

2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.

Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.

Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:

am−n·an=a(m−n)+n=am

Из него можно вывести: am−n·an=am

Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.

Пример 3

Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3

3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.

Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:

Вспомнив свойства умножения, запишем: . Это значит то же самое, что и an·bn.

Пример 4

Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:

(a1·a2·…·ak)n=a1n·a2n·…·akn

Пример 5

С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a

4. После этого мы попробуем доказать свойство частного: (a:b)n=an:bn при любых действительных a и b, если b не равно 0, а n – натуральное число.

Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.

Пример 6

Подсчитаем пример: 312:-0.53=3123:(-0,5)3

5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.

Пример 7

Начнем сразу с примера: (52)3=52·3=56

А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:

Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:

apqys=ap·q·y·s

Пример 8

Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30

6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.

Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?

Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.

Пример 9

35>0, (0,00201)2>0 и 3491351>0

Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.

Пример 10

Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.

Тогда:

Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a2·m также положительны.

Пример 11

Например, (−6)4>0, (−2,2)12>0 и -296>0

А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.

Тогда

Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.

Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0

7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).

Как это доказать?

an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.

Нужна помощь преподавателя?

Опиши задание — и наши эксперты тебе помогут!

Описать задание Пример 12

Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124

8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.

Докажем эти утверждения.

Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an

Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.

У нас вышло, что am−an<0 и am<an. Свойство доказано.

Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.

Пример 13

Пример с конкретными числами: 37>32

Основные свойства степеней с целыми показателями

Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).

Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:

Определение 2

1. am·an=am+n

2. am:an=am−n

3. (a·b)n=an·bn

4. (a:b)n=an:bn

5. (am)n=am·n

6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b

7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1 am>an.

Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.

Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.

Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)

Условия: p=0 или натуральное число; q– аналогично.

Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:

(a0)q=1q=1 a0·q=a0=1

Следовательно, (a0)q=a0·q

Для q=0 все точно так же:

(ap)0=1 ap·0=a0=1

Итог: (ap)0=ap·0.

Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.

Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.

Вспомним доказанное выше свойство частного в степени и запишем:

1apq=1qapq

Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q

Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.

Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).

И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)

Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.

Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.

Тогда неравенство можно преобразовать следующим образом:

1an>1bn

Запишем правую и левую части в виде разности и выполним необходимые преобразования:

1an-1bn=bn-anan·bn

Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: — an<bn, в итоге: bn−an>0.

an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.

Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.

Основные свойства степеней с рациональными показателями

В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:

Определение 3

1. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).

2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).

3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).

4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).

5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).

6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 — ap>bp (свойство сравнения степеней с равными рациональными показателями).

7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq

Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.

Согласно тому, что из себя представляет степень с дробным показателем, получим:

am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2

Свойства корня позволят нам вывести равенства:

am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2

Из этого получаем: am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2

Преобразуем:

am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2

Показатель степени можно записать в виде:

m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2

Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:

am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2

Доказательства остальных равенств:

a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2

Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 — ap>bp

Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.

Используем свойство корней и выведем: amn<bmn

Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.

Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.

Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.

Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n

Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.

Их можно переписать в следующем виде:

am1n<am2nam1n>am2n

Тогда можно сделать преобразования и получить в итоге:

am1n<am2nam1n>am2n

Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.

Основные свойства степеней с иррациональными показателями

На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):

Определение 4

1. ap·aq=ap+q

2. ap:aq=ap−q

3. (a·b)p=ap·bp

4. (a:b)p=ap:bp

5. (ap)q=ap·q

6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp

7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.

Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.

Степень с натуральными показателями. Математика, 5 класс: уроки, тесты, задания.

1.	Произведение в виде степени (положительные числа) Сложность: лёгкое	3,5
2.	Основание и показатель степени (числа) Сложность: лёгкое	3
3.	Степень бинома Сложность: лёгкое	1,5
4.	Основание и показатель степени (бином) Сложность: лёгкое	2
5.	Произведение одинаковых множителей (одночлен) Сложность: лёгкое	1
6.	Произведение одинаковых множителей (бином) Сложность: лёгкое	1
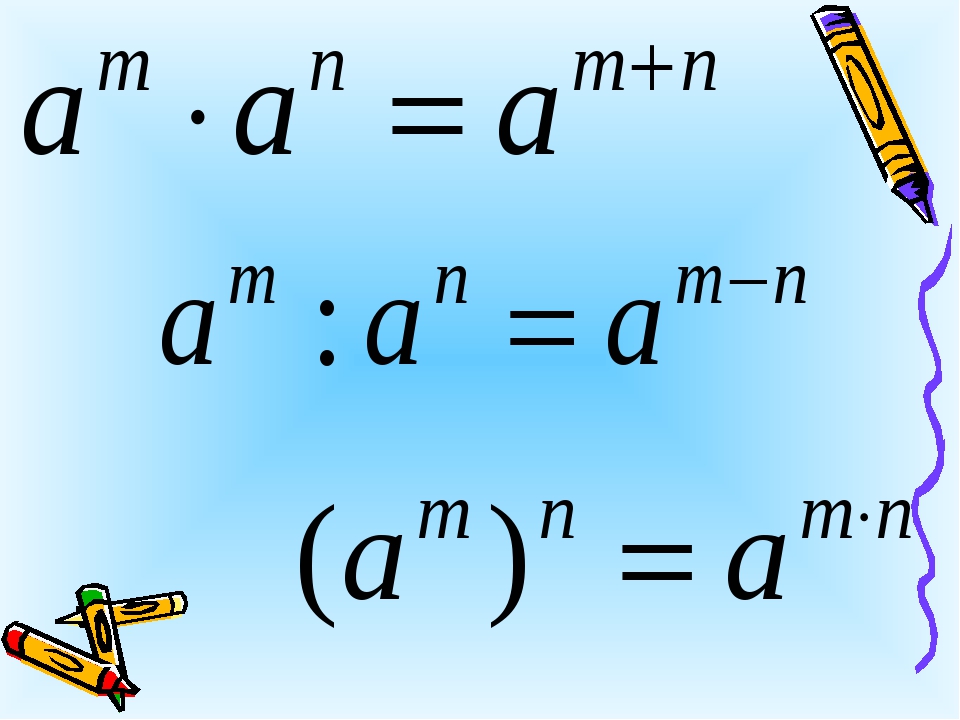
7.	Степень числа (показатель степени — n) Сложность: лёгкое	2
8.	Степень числа (основание) Сложность: лёгкое	2
9.	Значение степени (обыкновенная дробь) Сложность: лёгкое	2
10.	Площадь квадрата Сложность: лёгкое	2
11.	Квадрат числа (минус перед числом) Сложность: лёгкое	2
12.	Числовые неравенства, сравнение Сложность: лёгкое	1
13.	Возведение в степень десятичных дробей Сложность: лёгкое	1
14.	Возведение в степень целых чисел Сложность: лёгкое	1
15.	Возведение в степень дробей (смешанных чисел) Сложность: среднее	2
16.	Произведение степеней и простых чисел Сложность: среднее	3
17.	Произведение (целые числа) Сложность: среднее	3
18.	Частное (чётная степень) Сложность: среднее	3
19.	Дробь Сложность: среднее	3
20.	Разность произведений Сложность: среднее	4
21.	Сумма произведений Сложность: среднее	5
22.	Уравнение Сложность: среднее	5
23.	Убывание (возрастание) степеней Сложность: среднее	4

7.1. Степень с натуральным показателем.

Автор Татьяна Андрющенко На чтение 3 мин. Просмотров 73 Опубликовано 29 ноября 2012

I. Произведение n сомножителей, каждый из которых равен а называется n-й степенью числа а и обозначается аⁿ.

Примеры. Записать произведение в виде степени.

1) mmmm; 2) aaabb; 3) 5·5·5·5·ccc; 4) ppkk+pppk-ppkkk.

Решение.

1) mmmm=m⁴, так как, по определению степени, произведение четырех сомножителей, каждый из которых равен m, будет четвертой степенью числа m.

2) aaabb=a³b²; 3) 5·5·5·5·ccc=5⁴c³; 4) ppkk+pppk-ppkkk=p²k²+p³k-p²k³.

II. Действие, посредством которого находится произведение нескольких равных сомножителей, называется возведением в степень. Число, которое возводится в степень, называется основанием степени. Число, которое показывает, в какую степень возводится основание, называется показателем степени. Так, аⁿ – степень, а – основание степени, n – показатель степени. Например:

2³ — это степень. Число 2 — основание степени, показатель степени равен 3. Значение степени 2³равно 8, так как 2³=2·2·2=8.

Примеры. Написать следующие выражения без показателя степени.

5) 4³; 6) a³b²c³; 7) a³-b³; 8 ) 2a⁴+3b².

Решение.

5) 4³=4·4·4; 6) a³b²c³=aaabbccc; 7) a³-b³=aaa-bbb; 8) 2a⁴+3b²=2aaaa+3bb.

III. а⁰=1 Любое число (кроме нуля) в нулевой степени равно единице. Например, 25⁰=1.
IV. а¹=а Любое число в первой степени равно самому себе.

V. a^m∙aⁿ=a^m⁺ⁿ При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.

Примеры. Упростить:

9) a·a³·a⁷; 10) b⁰+b²·b³; 11) c²·c⁰·c·c⁴.

Решение.

9) a·a³·a⁷=a¹⁺³⁺⁷=a¹¹; 10) b⁰+b²·b³=1+b²⁺³=1+b⁵;

11) c²·c⁰·c·c⁴=1·c²·c·c⁴=c²⁺¹⁺⁴=c⁷.

VI. a^m:aⁿ=a^m^—ⁿ При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.

Примеры. Упростить:

12) a⁸:a³; 13) m¹¹:m⁴; 14) 5⁶:5⁴.

12) a⁸:a³=a^8-3=a⁵; 13) m¹¹:m⁴=m^11-4=m⁷; 14) 5⁶:5⁴=5²=5·5=25.

VII. (a^m)ⁿ=a^mn При возведении степени в степень основание оставляют прежним, а показатели перемножают.

Примеры. Упростить:

15) (a³)⁴; 16) (c⁵)².

15) (a³)⁴=a^3·4=a¹²; 16) (c⁵)²=c^5·2=c¹⁰.

Обратите внимание, что, так как от перестановки множителей произведение не меняется, то:

15) (a³)⁴=(a⁴)³; 16) (c⁵)²=(c²)⁵.

VIII. (a∙b)ⁿ=aⁿ∙bⁿ При возведении произведения в степень возводят в эту степень каждый из множителей.

Примеры. Упростить:

17) (2a²)⁵; 18) 0,2⁶·5⁶; 19) 0,25²·40².

Решение.

17) (2a²)⁵=2⁵·a^2·5=32a¹⁰; 18) 0,2⁶·5⁶=(0,2·5)⁶=1⁶=1;

19) 0,25²·40²=(0,25·40)²=10²=100.

IX. При возведении в степень дроби возводят в эту степень и числитель и знаменатель дроби.

Примеры. Упростить:

Решение.

Свойства степени с натуральными показателями. 7 класс

1. Свойства степени с натуральными показателями Алгебра 7 класс

СВОЙСТВА СТЕПЕНИ
С НАТУРАЛЬНЫМИ
ПОКАЗАТЕЛЯМИ
АЛГЕБРА 7 КЛАСС
Учитель математики Краузе Т.В.
2. Эпиграф урока
«Пусть кто-нибудь
попробует
вычеркнуть
из математики
степени,
и он увидит,
что без них
далеко не уедешь».
М.В. Ломоносов
3. Михаил Васильевич Ломоносов (1711-1765)
первый русский учёныйестествоиспытатель мирового
значения, энциклопедист,
химик и физик, астроном,
приборостроитель, географ,
металлург, геолог, поэт,
художник, историк,
действительный член
Академии наук и художеств,
профессор химии.
4. Примеры использования степени в реальной действительности
5. Примеры использования степени в реальной действительности
6. Примеры использования степени в реальной действительности
Продолжительность
обращения планет вокруг
Солнца (и спутников
вокруг планет)
связана с расстояниями
от центра обращения
степенной зависимостью:
отношение R3/T2
одинаково для всех
планетарных орбит.
7. Примеры использования степени в реальной действительности
Электростатическое
и магнитное
взаимодействия,
свет, звук ослабевают
пропорционально
второй степени
расстояния
8. Примеры использования степени в реальной действительности
Инженер, производя расчёты
на прочность, имеет дело
с четвёртыми степенями,
а при других вычислениях
(например, диаметра паропровода) –
–даже с шестой степенью.
9. Примеры использования степени в реальной действительности
Исследуя силу,
с которой текучая
вода увлекает камни,
гидротехник
наталкивается
на зависимость
также шестой
степени.
10. Примеры использования степени в реальной действительности
Яркость нити
накаливания
в электрической
лампочке растёт
при белом калении
с двенадцатой
степенью
температуры
11. Примеры использования степени в реальной действительности
а при красном –
– с тридцатой
степенью
температуры
12. Ответы к заданиям блиц-опроса
I вариант
1) 1
2) -1
8
3) 10
4) 15
5) 7
II вариант
1) 1
2) 1
10
3) 10
4) 23
5) 6
13.
Критерии оценивания Количество
верно выполненных
заданий
Отметка
5
5
4
4
3
3
Меньше 3
Будь внимательнее!
Необходимо ещё поработать
над данной темой.
14. Составь формулу:
am ∙an
2. am : an
3. (am) n
1.
Ответ: 1→ … , 2 → … , 3→…
а) a m • n
б) m + n
в) a m : n
г) m ̶ n
д) m • n
е) a m ̶ n
ж) a m + n
15. Заполни пропуски
Правило 1. При умножении степеней
с одинаковыми основаниями основание оставляют
прежним, а показатели складывают.
Правило 2. При делении степеней
с одинаковыми основаниями основание оставляют
прежним, а из показателя делимого вычитают
показатель делителя .
Правило 3. При возведении степени
в степень основание оставляют прежним,
а показатели перемножают.
16. Представьте выражение в виде степени:
a9∙ a15=
b30∙ b=
c12∙ c ∙ c50=
d5 ∙ d19∙ d ∙ d45=
(a+b)6 ∙ (a+b)29 =
(cd) ∙(cd)37 ∙ (cd)12 =
17. Представьте выражение в виде степени:
m25: m5=
n63: n9 : n18=
(p-q)72 :(p-q)8 :(p-q)=
(rs)45 :(rs) :(rs)11=
18. Представьте выражение в виде степени:
(x7)8=
((x+y)15)6=
((uv)24)5=
((z2)3)5=
19. История развития понятия «степень»
У математиков не сразу сложилось
представление о возведении
в степень как о самостоятельной
операции, хотя в самых древних
математических текстах Древнего
Египта и Междуречья встречаются
задачи на вычисление степеней.
20. В III веке вышла книга греческого ученого Диофанта «Арифметика»
В своей знаменитой «Арифметике» Диофант
Александрийский описывает первые натуральные степени
чисел так:
«Все числа… состоят из некоторого количества единиц;
ясно, что они продолжаются, увеличиваясь
до бесконечности. …среди них находятся: квадраты,
получающиеся от умножения некоторого числа самого
на себя; это же число называется стороной квадрата, затем
кубы, получающиеся от умножения квадратов на их
сторону, далее квадрато-квадраты —
от умножения квадратов самих на себя,
далее квадрато-кубы, получающиеся от умножения
квадрата на куб его стороны,
далее кубо-кубы — от умножения кубов самих на себя».
22. Символы, которые использовал Диофант для обозначения первых шести степеней неизвестного
М
к
S
К
Из практики решения более сложных
алгебраических задач и оперирования
со степенями возникла необходимость
обобщения понятия степени и расширения
его посредством введения в качестве
показателя нуля, отрицательных
и дробных чисел.
24. Николай Орем (1323–1382 гг.)
Дробные показатели степени
и наиболее простые правила
действий над степенями
с дробными показателями
встречаются
у французского математика
Николая Орема
в его труде
“Алгоризм пропорций”.
25. Никола Шюке (ХV век)
Французский математик и врач, бакалавр медицины,
автор трактата по арифметике и алгебре
«Наука о числе» (1484)
(опубликованном только в 1848 г. в Лионе),
смело ввёл не только нулевой,
но и отрицательный показатель степени.
Он писал его мелким шрифтом сверху и справа
от коэффициента.
Алгебраическая символика Шюке приближалась
к современной, кроме того, у него впервые встречаются
термины «биллион», «триллион», «квадриллион».
26. Немецкие математики Средневековья
стремились ввести единое обозначение
и сократить число символов.
Книга Михаэля Штифеля
«Полная арифметика» (1544 г.)
сыграла в этом значительную роль.
27. Михаэль Штифель (1487-1567)
немецкий математик, один
из изобретателей логарифмов,
дал определение a0=1
и ввел название «показатель»
(это буквенный перевод
немецкого Exponent),
причём подробно
анализировал и целые,
и дробные показатели.
28. Франсуа Виет (1540-1603)
французский математик,
основоположник
символической алгебры,
юрист по образованию
и основной профессии,
ввел буквы для обозначения
не только переменных,
но и их коэффициентов.
Он применял сокращения:
N, Q, C – для первой, второй
и третьей степеней.
29. Симон Стевин (1548—1620)
нидерландский математик,
механик и инженер, обозначал
неизвестную величину кружком,
внутри которого указывал
показатели степени.
Стевин предложил называть
степени по их показателям четвёртой, пятой и т.д. и отверг
диофантовы составные
выражения «квадрато-квадрат»,
«квадрато-куб»…
30. Альберт Жирар (1595-1632)
французский математик,
живший и работавший
в Нидерландах,
в своей книге
«Новое изобретение
в алгебре» (1629)
использует
такую форму записи:
(2)17 вместо 172
31. Рене Декарт (1596-1650)
(французский философ,
математик, физик и физиолог)
ввел в XVII веке современные
обозначения степеней (a4, a5,…).
Любопытно, что Декарт считал,
что a∙a не занимает больше
места, чем a2 и не пользовался
этим обозначением при записи
произведения двух одинаковых
множителей.
32. Готфрид Вильгельм Лейбниц (1646-1716)
немецкий математик
(физик, юрист, философ),
применял знак a2, считая,
что упор должен быть
сделан на необходимость
применения символики
для всех записей
произведений
одинаковых множителей.
Современные определения
и обозначения степени с нулевым,
отрицательным и дробным
показателем берут начало
от работ английских математиков
Джона Валлиса
и Исаака Ньютона.
34. Джон Валлис, (Уоллис) (1616-1703)
английский математик,
сын священника, феноменальный
счётчик, не получивший однако
никакого математического
образования, занимаясь
самостоятельно.
Он впервые (в 1665 г.) подробно
писал о целесообразности введения
нулевого, отрицательных
и дробных показателей
и современных символов.
35. Исаак Ньютон (1643-1727)
английский физик,
математик, механик
и астроном,
завершивший дело
Джона Валлиса.
Стал систематически
применять новые
символы, после чего
они вошли в общий
обиход.
36. Литература
Глейзер Г.И. История математики в школе VII-VIII кл.
Пособие для учителей. – М.: Просвещение, 1982. –
240 с.
Дидактические материалы по алгебре для 7 класса
/ Б.Г.Зив, В.А. Гольдич. – 2003. – 136 с.: ил.
Ершова А.П., Голобородько В.В., Ершова А.С.
Самостоятельные и контрольные работы по
алгебре и геометрии для 7 класса. – М.: Илекса,
Харьков: Гимназия, 2001. – 96 с.
Перельман Я.И. Занимательная алгебра. – Д.: ВАП,
1994. – 200 с.
формулировки, доказательства, примеры Степени с натуральным показателем и их свойства
алгебра 7 класс
учитель математики
филиала МБОУТСОШ№1
в с.Полетаево Зуева И.П.
Полетаево 2016
Тема: « Свойства степени с натуральным показателем »
ЦЕЛЬ
Повторение, обобщение и систематизирование изученного материала по теме «Свойства степени с натуральным показателем».
Проверка знаний учащихся по данной теме.
Применение полученных знаний при выполнении различных заданий.
ЗАДАЧИ
предметные :
повторить, обобщить и систематизировать знания по теме; создать условия контроля (взаимоконтроля) усвоения знаний и умений; продолжить формирование мотивации обучающихся к изучению предмета;
метапредметные:
развивать операционный стиль мышления; способствовать приобретению учащимися навыков общения при совместной работе; активизировать их творческое мышление; п родолжить формирование определенных компетенций обучающихся, которые будут способствовать их эффективной социализации; навыков самообразования и самовоспитания.
личностные:
воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение друг к другу, людям, жизни; воспитывать инициативу и самостоятельность в деятельности; подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.
ТИП УРОКА
урок обобщения и систематизации ЗУН.
Оборудование: компьютер, проектор, экран для проецирования, доска, раздаточный материал.
Программное обеспечение: ОС Windows 7: MS Office 2007 (обязательно приложение — PowerPoint ).
Подготовительный этап:
презентация «Свойства степени с натуральным показателем»;
раздаточный материал;
зачетный лист.
Структура
Организационный момент. Постановка целей и задач урока — 3 минуты.
Актуализация, систематизация опорных знаний — 8 минут.
Практическая часть -28 минут.
Обобщение, вывод -3 минута.
Домашнее задание — 1 минута.
Рефлексия — 2 минуты .
Идея урока
Проверка в интересной и эффективной форме ЗУН обучающихся по данной теме.
Организация урока Урок проводится в 7 классе. Ребята работают в парах, самостоятельно, учитель выступает в роли консультанта-наблюдателя.
Ход урока
Организационный момент:
Здравствуйте, ребята! Сегодня у нас необычный урок-игра. Каждому из вас предоставляется прекрасная возможность проявить себя, показать свои знания. Возможно, во время урока вы раскроете в себе скрытые способности, которые вам пригодятся в дальнейшем.
У вас у каждого на столе лежат зачетный лист и карточки для выполнения в них заданий. Возьмите в руки зачетный лист, он нужен вам для того, чтобы вы сами оценили свои знания в течение урока. Подпишите его.
Итак, приглашаю вас на урок!
Ребята, посмотрите на экран и послушайте стихотворение.
Слайд №1
Умножать и делить
Степень в степень возводить…
Свойства эти нам знакомы
И давно уже не новы.
Пять несложных правил этих
Каждый в классе уж ответил
Но если свойства позабыл,
Считай, пример ты не решил!
А чтобы в школе жить без бед
Дам дельный я тебе совет:
Не хочешь правило забыть?
Попробуй просто заучить!
Ответьте на вопрос:
1) Какие действия в нем упоминаются?
2) Как вы думаете, о чем мы сегодня будем говорить на уроке?
Таким образом, тема нашего урока:
«Свойства степени с натуральным показателем» (Слайд3).
Постановка целей и задач урока
На уроке мы повторим, обобщим и приведем в систему изученный материал по теме «Свойства степени с натуральным показателем»
Посмотрим, как вы научились умножать и делить степени с одинаковыми основаниями, а также возводить степень в степень
Актуализация опорных знаний. Систематизация теоретического материала.
1) Устная работа
Поработаем устно
1)Сформулируйте свойства степени с натуральным показателем.
2)Заполните пробелы: (Слайд 4)
1)5 12 : 5 5 =5 7 2) 5 7 ∙ 5 17 = 5 24 3) 5 24 : 125= 5 21 4)(5 0 ) 2 ∙5 24 =5 24
5)5 12 ∙ 5 12 = (5 8 ) 3 6)(3 12 ) 2 = 3 24 7) 13 0 ∙ 13 64 = 13 64
3)Чему равно значение выражения: (Слайд5-9)
а m ∙ а n; (а m+n ) а m : a n (а m-n ) ; (a m ) n ; а 1; а 0 .
2) Проверка теоретической части (Карточка№1)
А сейчас возьмите в руки карточку №1 и заполните пропуски
1)Если показатель четное число, то значение степени всегда_______________
2)Если показатель нечетное число, то значение степени совпадает со знаком ____.
3)Произведение степеней a n · a k = a n + k
При умножении степеней с одинаковыми основаниями, надо основание ____________, а показатели степеней________.
4)Частное степеней a n : a k = a n — k
При делении степеней с одинаковыми основаниями, надо основание _____, а из показателя делимого ____________________________.
5)Возведение степени в степень (a n ) к = a nk
При возведении степени в степень надо основание _______, а показатели степеней______.
Проверка ответов. (Слайды 10-13)
Основная часть
3) А сейчас открываем тетради, записываем число 28.01 14г, классная работа
Игра «Хлопушка » (Слайд 14)
Выполните задания в тетрадях самостоятельно
Выполните действия: а) х 11 ∙х∙х 2 б) х 14 : х 5 в) (а 4 ) 3 г) (-За) 2 .
Сравнить значение выражения с нулем: а)(- 5) 7 , б)(-6) 18 ,
в)(- 4) 11 . ( -4) 8 г)( — 5) 18 ∙ (- 5) 6 , д)-(- 4) 8 .
Вычислить значение выражения:
а)-1∙ 3 2 , б)(-1 ∙ 3) 2 в)1∙(-3) 2 , г) — (2 ∙ 3) 2 , д)1 2 ∙ (-3) 2
Проверяем, если ответ не правильный делаем один хлопок в ладоши.
Подсчитайте количество баллов и занесите их в зачетный лист.
4) А сейчас проведем гимнастику для глаз, снимем напряжение, и будем работать дальше. Внимательно следим за перемещением предметов
Начинаем! (Слайд 15,16,17,18).
5) А теперь приступим к следующему виду нашей работы. (Карточка2)
Запишите ответ в виде степени с основанием С и вы узнаете фамилию и имя великого французского математика, который первым ввел понятие степени числа.
Угадай фамилию ученого математика.
1.
С 5 ∙С 3
6.
С 7 : С 5
2.
С 8 : С 6
7.
(С 4 ) 3 ∙С
3,
(С 4 ) 3
8.
С 4 ∙ С 5 ∙ С 0
4.
С 5 ∙С 3 : С 6
9.
С 16 : С 8
5.
С 14 ∙ С 8
10.
(С 3 ) 5
О твет: РЕНЕ ДЕКАРТ
Р
Ш
М
Ю
К
Н
А
Т
Е
Д
С 8
С 5
С 1
С 40
С 13
С 12
С 9
С 15
С 2
С 22
А сейчас послушаем сообщение ученика о «Рене Декарт»
Рене Декарт родился 21 марта 1596 года в маленьком городке Ла — Гэ в Турени. Род Декартов принадлежал к незнатному чиновному дворянству. Детство Рене провел в Турени. В 1612 году Декарт закончил школу. Он провел в ней восемь с половиной лет. Декарт далеко не сразу нашел свое место в жизни. Дворянин по происхождению, окончив коллеж в Ла — Флеше, он с головой окунается в светскую жизнь Парижа, затем бросает все ради занятий наукой. Декарт отводил математике особое место в своей системе, он считал ее принципы установления истины образцом для других наук. Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв х, у, z для неизвестных; а, в, с — для коэффициентов, для степеней. Интересы Декарта не ограничиваются математикой, а включают механику, оптику, биологию. В 1649 г. Декарт после долгих колебаний переезжает в Швецию. Это решение оказалось для его здоровья роковым. Через полгода Декарт умер от пневмонии.
6) Работа у доски:
1. Решите уравнение
А) х 4 ∙ (х 5 ) 2 / х 20 : х 8 =49
Б) (t 7 ∙ t 17 ) : (t 0 ∙ t 21 )= -125
2. Вычислите значение выражения:
(5-x) 2 -2x 3 +3x 2 -4x+x-x 0
а) при x=-1
б) при x=2 Самостоятельно
7) Возьмите в руки карточку №3 выполните тест
Вариант 1
Вариант 2.
1. Выполни деление степеней 2 17 : 2 5
2 12
2 45
2. Запиши в виде степени (х+у)(х+у)=
х 2 +у 2
(х+у) 2
2(х+у)
3. Замени * степенью, чтобы выполнялось равенство а 5 · * =а 15
a 10
а 3
(а 7 ) 5 ?
a ) а 12
b ) а 5
c ) а 35
3 = 8 15
8 12
6.Найди значение дроби
1. Выполни деление степеней 9 9 : 9 7
9 16
9 63
2. Запиши в виде степени (х-у)(х-у)=…
х 2 -у 2
(х-у) 2
2(х-у)
3. Замени * степенью, чтобы выполнялось равенство b 9 · * = b 18
b 17
b 1 1
4. Чему равно значение выражения (с 6 ) 4 ?
a) с 10
b ) с 6
c ) с 24
5. Из предложенных вариантов выбери тот, которым можно заменить * в равенстве (*) 3 = 5 24
5 21
6.Найди значение дроби
Проверьте друг у друга работу и поставьте оценку своим товарищам в зачетный лист.
1 вариант
а
б
б
с
б
3
2 вариант
а
б
с
с
а
4
Дополнительные задания для сильных обучающихся
Каждое задание оценивается отдельно.
Найти значение выражения:
8) А сейчас посмотрим результативность нашего урока ( Слайд 19 )
Для этого, выполняя задание вычеркните буквы, соответствующие ответам.
АОВСТЛКРИЧГНМО
Упростите выражение:
1.
С 4 ∙С 3
5.
(С 2 ) 3 ∙ С 5
2.
(С 5 ) 3
6.
С 6 ∙ С 5 : С 10
3.
С 11 : С 6
7.
(С 4 ) 3 ∙С 2
4.
С 5 ∙С 5 : С
Шифр: А — С 7 В- С 15 Г — С И — С 30 К — С 9 М — С 14 Н — С 13 О — С 12 Р — С 11 С — С 5 Т — С 8 Ч — С 3
Какое слово у вас получилось? ОТВЕТ: ОТЛИЧНО! (Слайд 20)
Подведение итогов, оценивание, выставление отметок (Слайд 21)
Подведем итог нашего урока, на сколько успешно мы повторили, обобщили и систематизировали знания по теме « Свойства степени с натуральным показателем»
Берем зачетные листы и подсчитываем общее количество баллов и записываем их в строку итоговой оценки
Встаньте кто набрал 29-32 баллов: оценка -отлично
25-28 баллов: оценка -хорошо
20-24 баллов: оценка — удовлетворительно
Я еще раз проверю правильность выполнения заданий по карточкам, сверю ваши результаты с выставленными баллами в зачетном листе. Оценки поставлю в журнал
А за активную работу на уроке оценки:
Ребята прошу вас оценить свою деятельность на уроке. Отметка в листе настроения.
Зачетный лист
Фамилия Имя
Оценка
1.Теоретическая часть
2.Игра «Хлопушка»
3. Тест
4. «Шифр»
Дополнительная часть
Итоговая оценка:
Эмоциональная оценка
О себе
Об уроке
Удовлетворен
Неудовлетворен
Домашнее задание (Слайд 22)
Составьте кроссворд с ключевым словом СТЕПЕНЬ. На следующем уроке мы рассмотрим самые интересные работы.
№ 567
Список использованных источников
Учебник «Алгебра 7 класс».
Стихотворение. http://yandex.ru/yandsearch
Н.Е. Щуркова. Культура современного урока. М.: Российское педагогическое агентство, 1997.
А.В. Петров. Методологические и методические основы личностно-развивающего компьютерного образования. Волгоград. «Перемена», 2001.
А.С. Белкин. Ситуация успеха. Как ее создать. М.: «Просвещение»,1991.
Информатика и образование №3. Операционный стиль мышления, 2003
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n -ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 1
1. Главное свойство степени: a m · a n = a m + n
Можно обобщить до: a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
2. Свойство частного для степеней, имеющих одинаковые основания: a m: a n = a m − n
3. Свойство степени произведения: (a · b) n = a n · b n
Равенство можно расширить до: (a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
4. Свойство частного в натуральной степени: (a: b) n = a n: b n
5. Возводим степень в степень: (a m) n = a m · n ,
Можно обобщить до: (((a n 1) n 2) …) n k = a n 1 · n 2 · … · n k
6. Сравниваем степень с нулем:
если a > 0 , то при любом натуральном n, a n будет больше нуля;
при a , равном 0 , a n также будет равна нулю;
при a
при a
7. Равенство a n
8. Неравенство a m > a n будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: a m · a n = a m + n — то же самое, что и a m + n = a m · a n . В таком виде оно часто используется при упрощении выражений.
1. Начнем с основного свойства степени: равенство a m · a n = a m + n будет верным при любых натуральных m и n и действительном a . Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
Это можно сократить до (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m + n . Таким образом, a m + n , значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1
Итак, у нас есть две степени с основанием 2 . Их натуральные показатели — 2 и 3 соответственно. У нас получилось равенство: 2 2 · 2 3 = 2 2 + 3 = 2 5 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 2 2 · 2 3 = (2 · 2) · (2 · 2 · 2) = 4 · 8 = 32 и 2 5 = 2 · 2 · 2 · 2 · 2 = 32
В итоге у нас вышло: 2 2 · 2 3 = 2 5 . Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n 1 , n 2 и др. буквой k , мы получим верное равенство:
a n 1 · a n 2 · … · a n k = a n 1 + n 2 + … + n k .
Пример 2
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство a m: a n = a m − n , которое справедливо при любых натуральным m и n (причем m больше n)) и любом отличном от нуля действительном a .
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0 n = 0). Условие, чтобы число m обязательно было больше n , нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m , мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
a m − n · a n = a (m − n) + n = a m
Из него можно вывести: a m − n · a n = a m
Вспомним про связь деления и умножения. Из него следует, что a m − n – частное степеней a m и a n . Это и есть доказательство второго свойства степени.
Пример 3
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π : π 5: π 2 = π 5 − 3 = π 3
3. Следующим мы разберем свойство степени произведения: (a · b) n = a n · b n при любых действительных a и b и натуральном n .
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
Вспомнив свойства умножения, запишем: . Это значит то же самое, что и a n · b n .
Пример 4
2 3 · — 4 2 5 4 = 2 3 4 · — 4 2 5 4
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a 1 · a 2 · … · a k) n = a 1 n · a 2 n · … · a k n
Пример 5
С конкретными числами получим следующее верное равенство: (2 · (- 2 , 3) · a) 7 = 2 7 · (- 2 , 3) 7 · a
4. После этого мы попробуем доказать свойство частного: (a: b) n = a n: b n при любых действительных a и b , если b не равно 0 , а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a: b) n · b n = ((a: b) · b) n = a n , а (a: b) n · b n = a n , то из этого выходит, что (a: b) n есть частное от деления a n на b n .
Пример 6
Подсчитаем пример: 3 1 2: — 0 . 5 3 = 3 1 2 3: (- 0 , 5) 3
Пример 7
Начнем сразу с примера: (5 2) 3 = 5 2 · 3 = 5 6
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства:
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p , q , r , s , то верно будет:
a p q y s = a p · q · y · s
Пример 8
Добавим конкретики: (((5 , 2) 3) 2) 5 = (5 , 2) 3 · 2 · 5 = (5 , 2) 30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему a n > 0 при условии, что а больше 0 ?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени a n с положительным основанием и натуральным показателем это будет верно.
Пример 9
3 5 > 0 , (0 , 00201) 2 > 0 и 34 9 13 51 > 0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10
0 3 = 0 и 0 762 = 0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2 · m , где m – натуральное число.
Вспомним, как правильно умножать отрицательные числа: произведение a · a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда и степень a 2 · m также положительны.
Пример 11
Например, (− 6) 4 > 0 , (− 2 , 2) 12 > 0 и — 2 9 6 > 0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2 · m − 1 .
Тогда
Все произведения a · a , согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a , то конечный результат будет отрицателен.
Тогда получим: (− 5) 3
Как это доказать?
a n
Пример 12
Например, верны неравенства: 3 7 (0 , 75) 124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что a m
Вынесем a n за скобки, после чего наша разность примет вид a n · (a m − n − 1) . Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m − n > 0 , тогда a m − n − 1 –отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что a m − a n
Осталось привести доказательство второй части утверждения, сформулированного выше: a m > a справедливо при m > n и a > 1 . Укажем разность и вынесем a n за скобки: (a m − n − 1) .Степень a n при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a > 1 степень a m − n больше единицы. Выходит, a m − a n > 0 и a m > a n , что нам и требовалось доказать.
Пример 13
Пример с конкретными числами: 3 7 > 3 2
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 2
1. a m · a n = a m + n
2. a m: a n = a m − n
3. (a · b) n = a n · b n
4. (a: b) n = a n: b n
5. (a m) n = a m · n
6. a n b − n при условии целого положительного n , положительных a и b , a
7. a m n и 0 1 a m > a n .
Если основание степени равно нулю, то записи a m и a n имеют смысл только лишь в случае натуральных и положительных m и n . В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (a p) q = a p · q , (a − p) q = a (− p) · q , (a p) − q = a p · (− q) и (a − p) − q = a (− p) · (− q)
Условия: p = 0 или натуральное число; q – аналогично.
Если значения p и q больше 0 , то у нас получится (a p) q = a p · q . Схожее равенство мы уже доказывали раньше. Если p = 0 , то:
(a 0) q = 1 q = 1 a 0 · q = a 0 = 1
Следовательно, (a 0) q = a 0 · q
Для q = 0 все точно так же:
(a p) 0 = 1 a p · 0 = a 0 = 1
Итог: (a p) 0 = a p · 0 .
Если же оба показателя нулевые, то (a 0) 0 = 1 0 = 1 и a 0 · 0 = a 0 = 1 , значит, (a 0) 0 = a 0 · 0 .
Вспомним доказанное выше свойство частного в степени и запишем:
1 a p q = 1 q a p q
Если 1 p = 1 · 1 · … · 1 = 1 и a p q = a p · q , то 1 q a p q = 1 a p · q
Эту запись мы можем преобразовать в силу основных правил умножения в a (− p) · q .
Так же: a p — q = 1 (a p) q = 1 a p · q = a — (p · q) = a p · (- q) .
И (a — p) — q = 1 a p — q = (a p) q = a p · q = a (- p) · (- q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a − n > b − n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b .
Тогда неравенство можно преобразовать следующим образом:
1 a n > 1 b n
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1 a n — 1 b n = b n — a n a n · b n
Вспомним, что в условии a меньше b , тогда, согласно определению степени с натуральным показателем: — a n 0 .
a n · b n в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь b n — a n a n · b n , которая в итоге также дает положительный результат. Отсюда 1 a n > 1 b n откуда a − n > b − n , что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 3
1. a m 1 n 1 · a m 2 n 2 = a m 1 n 1 + m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство произведения степеней с одинаковыми основаниями).
2. a m 1 n 1: b m 2 n 2 = a m 1 n 1 — m 2 n 2 , если a > 0 (свойство частного).
3. a · b m n = a m n · b m n при a > 0 и b > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 и (или) b ≥ 0 (свойство произведения в дробной степени).
4. a: b m n = a m n: b m n при a > 0 и b > 0 , а если m n > 0 , то при a ≥ 0 и b > 0 (свойство частного в дробной степени).
5. a m 1 n 1 m 2 n 2 = a m 1 n 1 · m 2 n 2 при a > 0 , а если m 1 n 1 > 0 и m 2 n 2 > 0 , то при a ≥ 0 (свойство степени в степени).
6. a p 0 ; если p b p (свойство сравнения степеней с равными рациональными показателями).
7. a p q при 0 0 – a p > a q
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n -ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
a m 1 n 1 = a m 1 n 1 и a m 2 n 2 = a m 2 n 2 , следовательно, a m 1 n 1 · a m 2 n 2 = a m 1 n 1 · a m 2 n 2
Свойства корня позволят нам вывести равенства:
a m 1 · m 2 n 1 · n 2 · a m 2 · m 1 n 2 · n 1 = a m 1 · n 2 · a m 2 · n 1 n 1 · n 2
Из этого получаем: a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Преобразуем:
a m 1 · n 2 · a m 2 · n 1 n 1 · n 2 = a m 1 · n 2 + m 2 · n 1 n 1 · n 2
Показатель степени можно записать в виде:
m 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 · n 2 n 1 · n 2 + m 2 · n 1 n 1 · n 2 = m 1 n 1 + m 2 n 2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
a m 1 n 1: a m 2 n 2 = a m 1 n 1: a m 2 n 2 = a m 1 · n 2: a m 2 · n 1 n 1 · n 2 = = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 · n 2 n 1 · n 2 — m 2 · n 1 n 1 · n 2 = a m 1 n 1 — m 2 n 2
Доказательства остальных равенств:
a · b m n = (a · b) m n = a m · b m n = a m n · b m n = a m n · b m n ; (a: b) m n = (a: b) m n = a m: b m n = = a m n: b m n = a m n: b m n ; a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = a m 1 n 1 m 2 n 2 = = a m 1 m 2 n 1 n 2 = a m 1 · m 2 n 1 n 2 = = a m 1 · m 2 n 2 · n 1 = a m 1 · m 2 n 2 · n 1 = a m 1 n 1 · m 2 n 2
Следующее свойство: докажем, что для любых значений a и b больше 0 , если а меньше b , будет выполняться a p b p
Представим рациональное число p как m n . При этом m –целое число, n –натуральное. Тогда условия p 0 будут распространяться на m 0 . При m > 0 и a
Используем свойство корней и выведем: a m n
Учитывая положительность значений a и b , перепишем неравенство как a m n
Таким же образом при m b m , получаем a m n > b m n значит, a m n > b m n и a p > b p .
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q , p > q при 0 0 будет верно a p > a q .
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m 1 n и m 2 n
Здесь m 1 и m 2 – целые числа, а n – натуральное. Если p > q , то m 1 > m 2 (учитывая правило сравнения дробей). Тогда при 0 1 – неравенство a 1 m > a 2 m .
Их можно переписать в следующем виде:
a m 1 n a m 2 n
Тогда можно сделать преобразования и получить в итоге:
a m 1 n a m 2 n
Подводим итог: при p > q и 0 0 – a p > a q .
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a > 0 , b > 0 , показатели p и q – иррациональные числа):
Определение 4
1. a p · a q = a p + q
2. a p: a q = a p − q
3. (a · b) p = a p · b p
4. (a: b) p = a p: b p
5. (a p) q = a p · q
6. a p b p
7. a p 0 , то a p > a q .
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a > 0 обладают теми же свойствами.
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
После того как определена степень числа , логично поговорить про свойства степени . В этой статье мы дадим основные свойства степени числа, при этом затронем все возможные показатели степени. Здесь же мы приведем доказательства всех свойств степени, а также покажем, как применяются эти свойства при решении примеров.
Навигация по странице.
Свойства степеней с натуральными показателями
По определению степени с натуральным показателем степень a n представляет собой произведение n множителей, каждый из которых равен a . Отталкиваясь от этого определения, а также используя свойства умножения действительных чисел , можно получить и обосновать следующие свойства степени с натуральным показателем :
основное свойство степени a m ·a n =a m+n , его обобщение ;
свойство частного степеней с одинаковыми основаниями a m:a n =a m−n ;
свойство степени произведения (a·b) n =a n ·b n , его расширение ;
свойство частного в натуральной степени (a:b) n =a n:b n ;
возведение степени в степень (a m) n =a m·n , его обобщение (((a n 1) n 2) …) n k =a n 1 ·n 2 ·…·n k ;
сравнение степени с нулем:
если a>0 , то a n >0 для любого натурального n ;
если a=0 , то a n =0 ;
если a0 , если a
если a и b – положительные числа и a
если m и n такие натуральные числа, что m>n , то при 00 справедливо неравенство a m >a n .

Сразу заметим, что все записанные равенства являются тождественными при соблюдении указанных условий, и их правые и левые части можно поменять местами. Например, основное свойство дроби a m ·a n =a m+n при упрощении выражений часто применяется в виде a m+n =a m ·a n .
Теперь рассмотрим каждое из них подробно.
Начнем со свойства произведения двух степеней с одинаковыми основаниями, которое называют основным свойством степени : для любого действительного числа a и любых натуральных чисел m и n справедливо равенство a m ·a n =a m+n .
Докажем основное свойство степени. По определению степени с натуральным показателем произведение степеней с одинаковыми основаниями вида a m ·a n можно записать как произведение . В силу свойств умножения полученное выражение можно записать как , а это произведение есть степень числа a с натуральным показателем m+n , то есть, a m+n . На этом доказательство завершено.
Приведем пример, подтверждающий основное свойство степени. Возьмем степени с одинаковыми основаниями 2 и натуральными степенями 2 и 3 , по основному свойству степени можно записать равенство 2 2 ·2 3 =2 2+3 =2 5 . Проверим его справедливость, для чего вычислим значения выражений 2 2 ·2 3 и 2 5 . Выполняя возведение в степень , имеем 2 2 ·2 3 =(2·2)·(2·2·2)=4·8=32 и 2 5 =2·2·2·2·2=32 , так как получаются равные значения, то равенство 2 2 ·2 3 =2 5 — верное, и оно подтверждает основное свойство степени.
Основное свойство степени на базе свойств умножения можно обобщить на произведение трех и большего числа степеней с одинаковыми основаниями и натуральными показателями. Так для любого количества k натуральных чисел n 1 , n 2 , …, n k справедливо равенство a n 1 ·a n 2 ·…·a n k =a n 1 +n 2 +…+n k .
Например, (2,1) 3 ·(2,1) 3 ·(2,1) 4 ·(2,1) 7 = (2,1) 3+3+4+7 =(2,1) 17 .
Можно переходить к следующему свойству степеней с натуральным показателем – свойству частного степеней с одинаковыми основаниями : для любого отличного от нуля действительного числа a и произвольных натуральных чисел m и n , удовлетворяющих условию m>n , справедливо равенство a m:a n =a m−n .
Прежде чем привести доказательство этого свойства, обговорим смысл дополнительных условий в формулировке. Условие a≠0 необходимо для того, чтобы избежать деления на нуль, так как 0 n =0 , а при знакомстве с делением мы условились, что на нуль делить нельзя. Условие m>n вводится для того, чтобы мы не выходили за рамки натуральных показателей степени. Действительно, при m>n показатель степени a m−n является натуральным числом, в противном случае он будет либо нулем (что происходит при m−n ), либо отрицательным числом (что происходит при m
Доказательство. Основное свойство дроби позволяет записать равенство a m−n ·a n =a (m−n)+n =a m . Из полученного равенства a m−n ·a n =a m и из следует, что a m−n является частным степеней a m и a n . Этим доказано свойство частного степеней с одинаковыми основаниями.
Приведем пример. Возьмем две степени с одинаковыми основаниями π и натуральными показателями 5 и 2 , рассмотренному свойству степени отвечает равенство π 5:π 2 =π 5−3 =π 3 .
Теперь рассмотрим свойство степени произведения : натуральная степень n произведения двух любых действительных чисел a и b равна произведению степеней a n и b n , то есть, (a·b) n =a n ·b n .
Действительно, по определению степени с натуральным показателем имеем . Последнее произведение на основании свойств умножения можно переписать как , что равно a n ·b n .
Приведем пример: .
Данное свойство распространяется на степень произведения трех и большего количества множителей. То есть, свойство натуральной степени n произведения k множителей записывается как (a 1 ·a 2 ·…·a k) n =a 1 n ·a 2 n ·…·a k n .
Для наглядности покажем это свойство на примере. Для произведения трех множителей в степени 7 имеем .
Следующее свойство представляет собой свойство частного в натуральной степени : частное действительных чисел a и b , b≠0 в натуральной степени n равно частному степеней a n и b n , то есть, (a:b) n =a n:b n .
Доказательство можно провести, используя предыдущее свойство. Так (a:b) n ·b n =((a:b)·b) n =a n , а из равенства (a:b) n ·b n =a n следует, что (a:b) n является частным от деления a n на b n .
Запишем это свойство на примере конкретных чисел: .
Теперь озвучим свойство возведения степени в степень : для любого действительного числа a и любых натуральных чисел m и n степень a m в степени n равна степени числа a с показателем m·n , то есть, (a m) n =a m·n .
Например, (5 2) 3 =5 2·3 =5 6 .
Доказательством свойства степени в степени является следующая цепочка равенств: .
Рассмотренное свойство можно распространить на степень в степени в степени и т.д. Например, для любых натуральных чисел p , q , r и s справедливо равенство . Для большей ясности приведем пример с конкретными числами: (((5,2) 3) 2) 5 =(5,2) 3+2+5 =(5,2) 10 .
Осталось остановиться на свойствах сравнения степеней с натуральным показателем.
Начнем с доказательства свойства сравнения нуля и степени с натуральным показателем.
Для начала обоснуем, что a n >0 при любом a>0 .
Произведение двух положительных чисел является положительным числом, что следует из определения умножения. Этот факт и свойства умножения позволяют утверждать, что результат умножения любого числа положительных чисел также будет положительным числом. А степень числа a с натуральным показателем n по определению является произведением n множителей, каждый из которых равен a . Эти рассуждения позволяют утверждать, что для любого положительного основания a степень a n есть положительное число. В силу доказанного свойства 3 5 >0 , (0,00201) 2 >0 и .
Достаточно очевидно, что для любого натурального n при a=0 степень a n есть нуль. Действительно, 0 n =0·0·…·0=0 . К примеру, 0 3 =0 и 0 762 =0 .
Переходим к отрицательным основаниям степени.
Начнем со случая, когда показатель степени является четным числом, обозначим его как 2·m , где m — натуральное. Тогда . По каждое из произведений вида a·a равно произведению модулей чисел a и a , значит, является положительным числом. Следовательно, положительным будет и произведение и степень a 2·m . Приведем примеры: (−6) 4 >0 , (−2,2) 12 >0 и .
Наконец, когда основание степени a является отрицательным числом, а показатель степени есть нечетное число 2·m−1 , то . Все произведения a·a являются положительными числами, произведение этих положительных чисел также положительно, а его умножение на оставшееся отрицательное число a дает в итоге отрицательное число. В силу этого свойства (−5) 3 .
Переходим к свойству сравнения степеней с одинаковыми натуральными показателями, которое имеет следующую формулировку: из двух степеней с одинаковыми натуральными показателями n меньше та, основание которой меньше, а больше та, основание которой больше. Докажем его.
Неравенство a n свойств неравенств справедливо и доказываемое неравенство вида a n (2,2) 7 и .
Осталось доказать последнее из перечисленных свойств степеней с натуральными показателями. Сформулируем его. Из двух степеней с натуральными показателями и одинаковыми положительными основаниями, меньшими единицы, больше та степень, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше. Переходим к доказательству этого свойства.
Докажем, что при m>n и 00 в силу исходного условия m>n , откуда следует, что при 0
Осталось доказать вторую часть свойства. Докажем, что при m>n и a>1 справедливо a m >a n . Разность a m −a n после вынесения a n за скобки принимает вид a n ·(a m−n −1) . Это произведение положительно, так как при a>1 степень a n есть положительное число, и разность a m−n −1 есть положительное число, так как m−n>0 в силу начального условия, и при a>1 степень a m−n больше единицы. Следовательно, a m −a n >0 и a m >a n , что и требовалось доказать. Иллюстрацией этого свойства служит неравенство 3 7 >3 2 .
Свойства степеней с целыми показателями
Так как целые положительные числа есть натуральные числа, то все свойства степеней с целыми положительными показателями в точности совпадают со свойствами степеней с натуральными показателями, перечисленными и доказанными в предыдущем пункте.
Степень с целым отрицательным показателем , а также степень с нулевым показателем мы определяли так, чтобы оставались справедливыми все свойства степеней с натуральными показателями, выражаемые равенствами. Поэтому, все эти свойства справедливы и для нулевых показателей степени, и для отрицательных показателей, при этом, конечно, основания степеней отличны от нуля.
Итак, для любых действительных и отличных от нуля чисел a и b , а также любых целых чисел m и n справедливы следующие свойства степеней с целыми показателями :
a m ·a n =a m+n ;
a m:a n =a m−n ;
(a·b) n =a n ·b n ;
(a:b) n =a n:b n ;
(a m) n =a m·n ;
если n – целое положительное число, a и b – положительные числа, причем ab −n ;
если m и n – целые числа, причем m>n , то при 01 выполняется неравенство a m >a n .
При a=0 степени a m и a n имеют смысл лишь когда и m , и n положительные целые числа, то есть, натуральные числа. Таким образом, только что записанные свойства также справедливы для случаев, когда a=0 , а числа m и n – целые положительные.
Доказать каждое из этих свойств не составляет труда, для этого достаточно использовать определения степени с натуральным и целым показателем, а также свойства действий с действительными числами. Для примера докажем, что свойство степени в степени выполняется как для целых положительных чисел, так и для целых неположительных чисел. Для этого нужно показать, что если p есть нуль или натуральное число и q есть нуль или натуральное число, то справедливы равенства (a p) q =a p·q , (a −p) q =a (−p)·q , (a p) −q =a p·(−q) и (a −p) −q =a (−p)·(−q) . Сделаем это.
Для положительных p и q равенство (a p) q =a p·q доказано в предыдущем пункте. Если p=0 , то имеем (a 0) q =1 q =1 и a 0·q =a 0 =1 , откуда (a 0) q =a 0·q . Аналогично, если q=0 , то (a p) 0 =1 и a p·0 =a 0 =1 , откуда (a p) 0 =a p·0 . Если же и p=0 и q=0 , то (a 0) 0 =1 0 =1 и a 0·0 =a 0 =1 , откуда (a 0) 0 =a 0·0 .
Теперь докажем, что (a −p) q =a (−p)·q . По определению степени с целым отрицательным показателем , тогда . По свойству частного в степени имеем . Так как 1 p =1·1·…·1=1 и , то . Последнее выражение по определению является степенью вида a −(p·q) , которую в силу правил умножения можно записать как a (−p)·q .
Аналогично .
И .
По такому же принципу можно доказать все остальные свойства степени с целым показателем, записанные в виде равенств.
В предпоследнем из записанных свойств стоит остановиться на доказательстве неравенства a −n >b −n , которое справедливо для любого целого отрицательного −n и любых положительных a и b , для которых выполняется условие a. Так как по условию a0 . Произведение a n ·b n тоже положительно как произведение положительных чисел a n и b n . Тогда полученная дробь положительна как частное положительных чисел b n −a n и a n ·b n . Следовательно, откуда a −n >b −n , что и требовалось доказать.
Последнее свойство степеней с целыми показателями доказывается так же, как аналогичное свойство степеней с натуральными показателями.
Свойства степеней с рациональными показателями
Степень с дробным показателем мы определяли, распространяя на нее свойства степени с целым показателем. Иными словами, степени с дробными показателями обладают теми же свойствами, что и степени с целыми показателями. А именно:
Доказательство свойств степеней с дробными показателями базируется на определении степени с дробным показателем, на и на свойствах степени с целым показателем. Приведем доказательства.
По определению степени с дробным показателем и , тогда . Свойства арифметического корня позволяют нам записать следующие равенства . Дальше, используя свойство степени с целым показателем, получаем , откуда по определению степени с дробным показателем имеем , а показатель полученной степени можно преобразовать так: . На этом доказательство завершено.
Абсолютно аналогично доказывается второе свойство степеней с дробными показателями:
По схожим принципам доказываются и остальные равенства:
Переходим к доказательству следующего свойства. Докажем, что для любых положительных a и b , a b p . Запишем рациональное число p как m/n , где m – целое число, а n – натуральное. Условиям p0 в этом случае будут эквивалентны условия m0 соответственно. При m>0 и a
Аналогично, при mb m , откуда , то есть, и a p >b p .
Осталось доказать последнее из перечисленных свойств. Докажем, что для рациональных чисел p и q , p>q при 00 – неравенство a p >a q . Мы всегда можем привести к общему знаменателю рациональные числа p и q , пусть при этом мы получим обыкновенные дроби и , где m 1 и m 2 – целые числа, а n — натуральное. При этом условию p>q будет соответствовать условие m 1 >m 2 , что следует из . Тогда по свойству сравнения степеней с одинаковыми основаниями и натуральными показателями при 01 – неравенство a m 1 >a m 2 . Эти неравенства по свойствам корней можно переписать соответственно как и . А определение степени с рациональным показателем позволяет перейти к неравенствам и соответственно. Отсюда делаем окончательный вывод: при p>q и 00 – неравенство a p >a q .
Свойства степеней с иррациональными показателями
Из того, как определяется степень с иррациональным показателем , можно заключить, что она обладает всеми свойствами степеней с рациональными показателями. Так для любых a>0 , b>0 и иррациональных чисел p и q справедливы следующие свойства степеней с иррациональными показателями :
a p ·a q =a p+q ;
a p:a q =a p−q ;
(a·b) p =a p ·b p ;
(a:b) p =a p:b p ;
(a p) q =a p·q ;
для любых положительных чисел a и b , a0 справедливо неравенство a p b p ;
для иррациональных чисел p и q , p>q при 00 – неравенство a p >a q .
Отсюда можно сделать вывод, что степени с любыми действительными показателями p и q при a>0 обладают этими же свойствами.
Список литературы.
Виленкин Н.Я., Жохов В.И., Чесноков А.С., Шварцбурд С.И. МатематикаЖ учебник для 5 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 7 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 9 кл. общеобразовательных учреждений.
Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Предварительный просмотр:
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 11
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ ГОРОД – КУРОРТ АНАПА
Номинация «Физико-математические науки (математика)»
План – конспект урока по теме:
7 класс
Разработала: Быкова Е.А., учитель математики высшей квалификационной категории
Анапа, 2013
Открытый урок по алгебре в 7-м классе на тему:
«Свойства степени с натуральным показателем»
Цели урока:
Образовательные: – отработка умений систематизировать, обобщать знания о степени с натуральным показателем, закрепить и усовершенствовать навыки простейших преобразований выражений, содержащих степени с натуральным показателем.
Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.
Развивающие: — развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.
Задачи:
1. Предметные: повторить, обобщить и систематизировать знания по теме, создать условия контроля (взаимоконтроля) усвоения знаний и умений; продолжить формирование мотивации обучающихся к изучению предмета.
2. Метапредметные: развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе,активизировать их творческое мышление; продолжить формирование определенных компетенций обучающихся, которые будут способствовать их эффективной социализации, навыков самообразования и самовоспитания
3. Личностные: воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, жизни; воспитывать инициативу и самостоятельность в деятельности; подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.
Тип урока: обобщающий урок по теме.
Вид урока: комбинированный.
Структура урока:
1. Организационный момент.
2. Сообщение темы, целей и задач урока.
3. Воспроизведение изученного и его применение в стандартных ситуациях.
4. Перенос приобретенных знаний, их первичное применение в новых или изменённых условиях, с целью формирования умений.
5.Элементы здорорвьесберегающих технологий.
6.Самостоятельное выполнение учащимися заданий под контролем учителя.
7.Подведение итогов урока и постановка домашнего задания.
Оборудование: мультимедийный проектор, компьютер.
Презентация в программе Microsoft Office Power Point 2007 (Приложение 1)
План урока:
Этап урока
Время
Организационный момент.
Нацелить учащихся на урок
1 мин.
Проверка домашнего задания
Коррекция ошибок
3 мин.
Сообщение темы, целей и задач урока.
Постановка целей урока
1 мин.
Устная работа. Повторение свойств степени с натуральным показателем.
Актуализировать опорные знания
7 мин.
Тренировочные упражнения.
Сформировать навык преобразования степеней с натуральным показателем.
10 мин.
Физкультурная пауза.
Применение здоровья сберегающих технологий
2 мин.
Индивидуальная проверочная работа по карточкам.
Коррекция ошибок
12 мин
Итоги урока.
Обобщить теоретические сведения, полученные на уроке
2 мин
Постановка домашнего задания.
Разъяснить содержание домашнего задания
2 мин
Литература:
1. Алгебра: учебн. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев, Н.Г.Миндюк и др.; под редакцией С.А. Теляковского. – М.: Просвещение, 2008.
2. Звавич Л.И., Кузнецова Л.В., Суворова С.Б. Дидактические материалы по алгебре для 7 класса. – М.: Просвещение, 2009.
3. Сборник тестовых заданий для тематического и итогового контроля. Алгебра 7 класс./ С.А. Пушкин, И.Л. Гусева. – М.: «Интеллект», 2013.
4. Т.Ю.Дюмина, А.А.Махонина, «Алгебра. Поурочные планы.», — Волгоград: «Учитель», 2013 г.
Ход урока
1.Организационный момент.
2. Проверка домашнего задания
3. Тема урока. Цели и задачи урока.
Математика, друзья,
Абсолютно всем нужна.
На уроке работай старательно,
И успех тебя ждет обязательно!
4.Устная работа.
а) Повторение свойств степени с натуральным показателем. Дана таблица. В левом столбце заполнить пропущенные места, в правом – выполнить задания.
Степенью числа а с натуральным показателем п называется ____________ п ____________,
каждый из которых равен а.
1. Представьте в виде степени произведение:
а). (-8) * (-8) * (-8) * (-8) * (-8) * ;
б). (x-y) * (x-y) * (x-y) * (x-y) * ;
2. Возведите в степень:
3 4 ; (-0,2) 3 ; (2/3) 2
Назовите основание и показатель записанных степеней.
При умножении степеней с одинаковыми основаниями ___________ оставляют прежним, а ___________ складывают.
Выполните действия:
а 4 * а 12 ;
а 6 * а 9 * а ;
3 2 * 3 3
При делении степеней с одинаковыми основаниями ___________ оставляют прежним, а из __________ числителя _________ __________ знаменателя.
Выполните действия:
а 12 : а 4 ;
п 9 : п 3 : п ;
3 5 : 3 2
При возведении степени в степень _______________ оставляют прежним, а __________ перемножают.
Выполните действия:
;
(m 3 ) 7 ; (k 4 ) 5 ; (4 2 ) 3
При возведении в степень произведения возводят в эту степень _____________ ____________ и результаты перемножают.
Выполнить возведение в степень:
(-2 a 3 b 2 ) 5 ; (1/3p 2 q 3 ) 3
Степень числа a , не равного нулю, с нулевым показателем равна
Вычислите:
3x 0 при x= 2,6
б) Выполняя задания на преобразования выражений, содержащих степени, ученик допустил следующие ошибки: (запись на доске)
1) а) ; б) ;
в) ; г) ;
2) а) ; б) ;
в) ; г) ;
3) а) ; б) ;
в) .
Какие определения, свойства, правила не знает ученик?
5. Тренировочные упражнения.
№ 447 – на доске и в тетрадях с подробным комментированием, используя свойства степеней;
№ 450 (а,в) – на доске и в тетрадях;
№ 445 – устно.
6. Физминутка
Быстро встали, улыбнулись,
Выше-выше подтянулись.
Ну-ка плечи распрямите,
Поднимите, опустите.
Вправо, влево повернитесь,
Рук коленями коснитесь.
Сели, встали, сели, встали,
И на месте побежали.
Учится с тобою молодёжь
Развивать и волю, и смекалку.
7. Индивидуальная проверочная работа.
Каждый учащийся выполняет задания, к ним прилагается ключ, в котором использован весь алфавит, чтобы исключить угадывание ответов по буквам. В случае правильного решения – правильное слово.
Задания для каждого ряда индивидуальные.
№ п/п
Задание 1 ряд
№ п/п
Задание 2 ряд
№ п/п
Задание 3 ряд
m 3 * m 2 * m 8
a 4 * a 3 * a 2
a 4 * a * a 3 * a
p 20 : p 17
(2 4 ) 5 : (2 7 ) 2
(7x) 2
c 5 : c 0
3 * 3 2 * 3 0
p * p 2 * p 0
(3a) 3
(2y) 5
c * c 3 * c
m * m 5 * m 3 * m 0
(m 2 ) 4 * m
m * m 4 * (m 2 ) 2 * m 0
2 14 : 2 8
(2 3 ) 2
(2 3 ) 7 : (2 5 ) 3
(-x) 3 * x 4
(-x 3 ) *(- x) 4
X 3 * (-x) 4
(p * p 3 ) : p 5
(p 2 * p 5 ) : p 4 * p 0
(p 2 ) 4 : p 5
3 7 * (3 2 ) 3 : 3 10
(3 5 ) 2 * 3 7 : 3 14
(3 4 ) 2 * (3 2 ) 3 : 3 11
Ключ
32y 5
49x 2
27a 3
m 13
81a 3
16a 4
10y 5
9y 7
32x 5
49y 3
Результаты работы высвечиваются на слайде для самопроверки:
Математика
8. Итоги урока:
Подведение итогов урока, выставление оценок.
– Перечислите свойства степени с натуральным показателем.
Оценки за урок поставим после проверки работы с тестами, учитывая, ответы тех учащихся, которые отвечали в течение урока.
Отгадайте кроссворд
По вертикали:
Он делит делимое
Элементарная фигура на плоскости
Верное равенство
Единица с девятью нулями
Его складывают с подобным
Два в степени три
По горизонтали:
2. Число сторон в треугольнике
4. Сумма одночленов
5. Суммировать
7. Отрезок, соединяющий точку окружности с её центром
8. Имеет числитель и знаменатель
9. Задание на дом:
Степенью числа а с натуральным показателем п называется ____________ п ____________, каждый из которых равен а. 1. Представьте в виде степени произведение: а). (-8) * (-8) * (-8) * (-8) * (-8) * ; б). (x-y)* (x-y) * (x-y) * (x-y) * ; 2. Возведите в степень: 3 4 ; (-0,2) 3 ; (2 /3) 2 Назовите основание и показатель записанных степеней. При умножении степеней с одинаковыми основаниями ___________ оставляют прежним, а ___________ складывают. Выполните действия: а 4 * а 12 ; а 6 * а 9 * а; 3 2 * 3 3 При делении степеней с одинаковыми основаниями ___________ оставляют прежним, а из __________ числителя _________ __________ знаменателя. Выполните действия: а 12: а 4 ; п 9: п 3: п; 3 5: 3 2 При возведении степени в степень _______________ оставляют прежним, а __________ перемножают. Выполните действия: ; (m 3) 7 ; (k 4) 5 ; (4 2) 3 При возведении в степень произведения возводят в эту степень _____________ ____________ и результаты перемножают. Выполнить возведение в степень: (-2 a 3 b 2) 5 ; (1 /3p 2 q 3) 3 Степень числа a , не равного нулю, с нулевым показателем равна Вычислите: 3 x 0 при x = 2,6 Повторим!
Мозговой штурм
Быстро встали, улыбнулись, Выше-выше подтянулись. Ну-ка плечи распрямите, Поднимите, опустите. Вправо, влево повернитесь, Рук коленями коснитесь. Сели, встали, сели, встали, И на месте побежали. Учится с тобою молодёжь Развивать и волю, и смекалку.
Индивидуальная проверочная работа № п / п Задание 1 ряд № п/п Задание 2 ряд № п/п Задание 3 ряд 1 m 3 * m 2 * m 8 1 a 4 * a 3 * a 2 1 a 4 * a * a 3 * a 2 p 20: p 17 2 (2 4) 5: (2 7) 2 2 (7x) 2 3 c 5: c 0 3 3 * 3 2 * 3 0 3 p * p 2 * p 0 4 (3a) 3 4 (2y) 5 4 c * c 3 * c 5 m * m 5 * m 3 * m 0 5 (m 2) 4 * m 5 m * m 4 * (m 2) 2 * m 0 6 2 14: 2 8 6 (2 3) 2 6 (2 3) 7: (2 5) 3 7 (-x) 3 * x 4 7 (-x 3) *(- x) 4 7 -x 3 * (-x) 4 8 (p * p 3) : p 5 8 (p 2 * p 5) : p 4 * p 0 8 (p 2) 4: p 5 9 3 7 * (3 2) 3: 3 10 9 (3 5) 2 * 3 7: 3 14 9 (3 4) 2 * (3 2) 3: 3 11
Проверь себя! Ключ! А Б В Г Д Е Ж З И К m 9 32y 5 81 a 9 x 3 49x 2 m 5 p 4 c 5 27a 3 Л М Н О П Р С Т У Ф 64 3 4 p 3 27 2 5 x 7 p 6 m 3 m 13 a 8 Х Ц Ч Ш Щ Ъ Ь Ы Э Ю 81a 3 c 7 16a 4 25 10y 5 9y 7 -x 7 a 2 32x 5 49y 3 Я x 5
математика
ОТГАДАЙТЕ КРОССВОРД По вертикали: 1. Он делит делимое 2. Элементарная фигура на плоскости 3. Верное равенство 4. Единица с девятью нулями 5. Его складывают с подобным 6. Два в степени три По горизонтали: 2. Число сторон в треугольнике 4. Сумма одночленов 5. Суммировать 7. Отрезок, соединяющий точку окружности с её центром 8. Имеет числитель и знаменатель
Итог урока Выставление оценок Задание на дом Ответить на вопросы стр. 101, № 450(б,г) , № 534, № 453.
основание и показатель степени. Онлайн калькулятор
Степень числа — это выражение, обозначающее краткую запись произведения одинаковых сомножителей.
Рассмотрим умножение одинаковых чисел, например:
5 · 5 · 5 = 125.
Произведение 5 · 5 · 5 можно записать так: 5³ (пять в третьей степени). Выражение 5³ — это степень. Следовательно,
5 · 5 · 5 = 5³ = 125.
Рассмотрим выражение 5³ . В этом выражении число 5 — основание степени, а число 3 — показатель степени.
Основание степени — это повторяющийся множитель. Показатель степени — это число, указывающее количество повторений, то есть показатель степени показывает сколько одинаковых множителей содержится в произведении.
Читаются степени так:
7² — семь во второй степени.
Вторую степень числа также называют квадратом этого числа. Следовательно, выражение 7² можно прочесть так: семь в квадрате или квадрат числа семь.

2³ — два в третьей степени.
Третью степень числа также называют кубом этого числа. Следовательно, выражение 2³ можно прочесть так: два в кубе или два куб.

6⁴ — шесть в четвёртой степени.

10¹⁵ — десять в пятнадцатой степени.

aⁿ — a в энной степени или a в степени эн.

Пример. Записать в виде степени:
a) 5 · 5;
б) 10 · 10 · 10 · 10;
в) 8 · 8 · 8.
Решение:
a) 5 · 5 = 5²;
б) 10 · 10 · 10 · 10 = 10⁴;
в) 8 · 8 · 8 = 8³.
Возведение в степень
Возведение числа в степень — это вычисление произведения одинаковых множителей. Например, возвести число 2 в третью степень (2³) — это значит найти произведение 2 · 2 · 2 , то есть
2³ = 2 · 2 · 2 = 8.
Результат возведения в степень называется степенью (также как и само выражение, значение которого вычисляется). В выражении:
2³ = 8,
2 — это основание степени, ³ — показатель степени, 8 — степень.
Пример. Вычислите:
a) 11²;
б) 2⁵;
в) 10⁴.
Решение:
a) 11² = 11 · 11 = 121;
б) 2⁵ = 2 · 2 · 2 · 2 · 2 = 32;
в) 10⁴ = 10 · 10 · 10 · 10 = 10000.
Выражения со степенями. Порядок действий
Если выражение не содержит скобки и содержит степени, то сначала выполняется возведение в степень в порядке следования степеней (слева направо), а затем все остальные арифметические действия. Если выражение содержит скобки, то сначала выполняются действия в скобках, с учётом всех правил порядка выполнения действий.
Рассмотрим два выражения:
5² + 2²
и
(5 + 2)²
В соответствии с порядком выполнения действий в первом случае сначала выполняется возведение в степень, а затем вычисляется сумма. Во втором случае сначала вычисляется сумма, а затем результат возводится в квадрат.
5² + 2² = 25 + 4 = 29,
(5 + 2)² = 7² = 49.
Пример 1. Найти значение выражения:
5 · (10 — 8)³.
Решение: Сначала выполняется действие, заключённое в скобки:
1) 10 — 8 = 2.
Затем, по правилам порядка действий, выполняется возведение в степень:
2) 2³ = 2 · 2 · 2 = 8.
И последним действием вычисляется произведение:
3) 5 · 8 = 40.
Ответ: 5 · (10 — 8)³ = 40.
Пример 2. Вычислить:
a) (4 + 2) · 3²;
б) 3 · 5² — 50;
в) 3 · 4 + 6².
Решение:
a) (4 + 2) · 3² = 54
4 + 2 = 6

3² = 9

6 · 9 = 54

б) 3 · 5² — 50 = 25
5² = 25

3 · 25 = 75

75 — 50 = 25

в) 3 · 4 + 6² = 48
6² = 36

3 · 4 = 12

12 + 36 = 48

Калькулятор возведения в степень
Данный калькулятор поможет вам выполнить возведение в степень. Просто введите основание с показателем степени и нажмите кнопку Вычислить.
Свойства степени с натуральными показателями

Однажды к учителю подошел ученик поймавший бабочку и спросил: «Учитель, какая у меня в руках бабочка: живая или мертвая?». Учитель, даже не взглянув на ученика, ответил: «Все в твоих руках».
Вот и наш сегодняшний урок в наших руках.

В Древней Индии была такая легенда. Стоит камень размером в кубический километр, в миллион раз тверже алмаза. Один раз в миллион лет к нему прилетает птичка и трется клювом о камень. В конце концов в результате этого камень износится. Как вы думаете, сколько лет понадобится для того, чтобы камень износился до основания?
Вычисления математиков показывают, что для этого понадобится 10 35 лет.

Свойства степени с натуральным показателем
урок по алгебре, 7 класс

Цель:
1. вывести свойства степени с натуральными показателями;
2. изучить свойства степени с натуральным показателем, их формулировки и символическую запись;
3. выработать практические умения и навыки по применению изученных свойств.

Большая часть математических утверждений проходит в своем становлении три этапа.
На первом этапе человек в ряде конкретных случаев подмечает одну и ту же закономерность.
На втором этапе он пытается сформулировать подмеченную закономерность в общем виде, т.е. предполагает, что эта закономерность действует не только в рассмотренных случаях, но и во всех других аналогичных случаях.
На третьем этапе он пытается доказать, что закономерность, сформулированная в общем виде, на самом деле верна.

Открытие первое

Открытие второе

Открытие третье

Запомните:
Правило 1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остается неизменным.
Правило 2. При делении степеней с одинаковыми основаниями показатели вычитаются, а основание остается неизменным.
Правило 3. При возведении степени в степень
показатели перемножаются, а основание остается неизменным.

Свойства степеней

Ответы

Найдите ошибки
2 10
5 4
2 20
7
8х 3
1
а 6
2 10

Подумайте, чем можно заменить ?

Ответы
n 10
x 12
a 0
b 14
k 55
m 15
d 30
c 45
t 10
5 4
2 4
7 7
4
4
0

Высказывания Козьмы Пруткова
Выполните преобразования. Используя найденные ответы, запишите в таблицах два высказывания Козьмы Пруткова:
будь
быть
что
не
им
хочешь
плачем
имеем
потерявши
храним
счастливым

Самопроверка
что имеем не храним потерявши плачем
Что имеем не храним, потерявши плачем.
хочешь быть счастливым будь им
Хочешь быть счастливым — будь им.

Домашнее задание:
На «3 » : § 17, №17.3, 17.18, 17.31
На «4» : § 17, №17.3, 17.18, 17.31, 17. 35
На «5» : § 17, №17.3, 17.18, 17.31, 17. 35, доказательство свойств степеней

Магический квадрат. Задание на скорость
Заполните свободные клетки квадрата так, чтобы произведение выражений каждого столбца, каждой строки и диагонали равнялось х 12

Список использованной литературы:
1. Лебединцева Е.А., Беленкова Е.Ю. Алгебра 7 класс. Задание для обучения и развития учащихся. – М.: Интеллект-центр, 2005.
2. Мордкович А.Г. и др. Алгебра 7 класс, Учебник, М.: Мнемозина, 2007;
3. Мордкович А.Г. и др. Алгебра 7 класс, Задачник, М.: Мнемозина, 2007;
4. Мордкович А.Г., Тульчинская Е.Е. Алгебра: Тесты для 7-9 класса общеобразовательных учреждений. – М.: Мнемозина, 2002.
Индикаторы природных кислот и щелочей
Есть много обычных товаров для дома и садовых растений, которые можно использовать в качестве индикаторов pH. Большинство растений содержат антоцианы, чувствительные к pH, что делает их идеальными для определения кислотного и щелочного уровней. Многие из этих естественных индикаторов pH имеют широкий диапазон цветов.
Растения, которые можно использовать для проверки уровня pH
Мир природы дал нам множество растений, от свеклы до винограда и лука, которые можно использовать для проверки уровня pH раствора.Эти естественные индикаторы pH включают:
Свекла: Очень щелочной раствор (с высоким pH) изменит цвет свеклы или свекольного сока с красного на фиолетовый.
Ежевика: Ежевика, черная смородина и черная малина меняют цвет с красного в кислой среде на синий или фиолетовый в основной среде.
Черника: Черника голубая при pH 2,8–3,2, но становится красной по мере того, как раствор становится еще более кислым.
Вишни: Вишни и их сок красны в кислом растворе, но они становятся синими или пурпурными в основном растворе.
Порошок карри: Карри содержит пигмент куркумин, цвет которого изменяется от желтого при pH 7,4 до красного при pH 8,6.
Лепестки дельфиниума: Антоциановый дельфинидин изменяется от голубовато-красного в кислом растворе до фиолетово-синего в основном растворе.
Лепестки герани: Герань содержит антоцианин пеларгонидин, цвет которого изменяется от оранжево-красного в кислом растворе до синего в основном растворе.
Виноград: Красный и фиолетовый виноград содержат множество антоцианов.Синий виноград содержит моноглюкозид мальвидина, цвет которого изменяется от темно-красного в кислом растворе до фиолетового в основном растворе.
Листья конского каштана: Замочите листья конского каштана в спирте для экстракции флуоресцентного красителя эскулина. Эскулин бесцветен при pH 1,5, но становится флуоресцентно-синим при pH 2. Для наилучшего эффекта светите черным светом на индикаторе.
Утренняя слава: Утренняя слава содержит пигмент, известный как «небесно-синий антоциан», который меняется с пурпурно-красного на пурпурный при pH 6.От 6 до синего при pH 7,7.
Лук: Лук является обонятельным индикатором. Вы не чувствуете запаха лука в сильно щелочных растворах. Красный лук также меняет цвет с бледно-красного в кислом растворе на зеленый в основном растворе.
Petunia Petals: Антоциановый петунин изменяется от красновато-пурпурного в кислом растворе до фиолетового в основном растворе.
Ядовитая примула: Primula sinensis имеет оранжевые или синие цветы. Цветки апельсина содержат смесь пеларгонинов.В синих цветках содержится мальвин, цвет которого меняется от красного к пурпурному по мере того, как раствор переходит от кислого к щелочному.
Пурпурные пионы: Пеонин меняется от красновато-пурпурного или пурпурного в кислом растворе до темно-фиолетового в основном растворе.
Красная (пурпурная) капуста: Краснокочанная капуста содержит смесь пигментов, используемых для обозначения широкого диапазона pH.
Лепестки роз: Оксониевая соль цианина меняет цвет с красного на синий в щелочном растворе.
Куркума: Эта специя содержит желтый пигмент куркумин, который меняет свой цвет с желтого на pH 7.4 становится красным при pH 8,6.
Бытовые химические вещества, являющиеся индикаторами pH
Если у вас нет под рукой какого-либо из вышеперечисленных материалов, вы также можете использовать некоторые обычные бытовые химикаты для проверки уровня pH. Это включает:
Пищевая сода: Пищевая сода будет шипеть при добавлении ее в кислый раствор, например уксус, но не будет шипеть в щелочном растворе. Реакция не всегда полностью меняется, поэтому, хотя пищевую соду можно использовать для проверки раствора, ее нельзя использовать повторно.
Помада, меняющая цвет: Вам нужно будет протестировать свою изменяющую цвет помаду, чтобы определить ее диапазон pH, но большинство косметических средств, которые меняют цвет, реагируют на изменения pH (они отличаются от косметики, которая меняет цвет в зависимости от угла свет).
ExLax Tablets: Эти таблетки содержат фенолфталеин, который является индикатором pH, который бесцветен в растворах с более кислотным, чем pH 8,3, и от розового до темно-красного цвета в растворах с более щелочным, чем pH 9.
Экстракт ванили: Экстракт ванили является обонятельным индикатором.Вы не можете почувствовать характерный запах при высоких значениях pH, потому что молекула находится в ионной форме.
Сода для стирки: Как и пищевая сода, сода шипит в кислотном растворе, но не в щелочном растворе.
индикаторов — Chemistry LibreTexts
Цели обучения
Объясните изменение цвета индикаторов.
Определите константы кислотной диссоциации K _a или K _ai индикаторов.
Индикаторы — это вещества, растворы которых меняют цвет из-за изменения pH. Это так называемые кислотно-основные индикаторы. Обычно это слабые кислоты или основания, но их сопряженные основания или кислотные формы имеют разный цвет из-за различий в их спектрах поглощения. Знаете ли вы, что цвет цветков гортензии зависит от pH почвы, в которой они выращены?
Рисунок \ (\ PageIndex {1} \): На этом рисунке показаны различные цвета цветов гортензии. (CC BY-SA 4.-} \) преобладает цвет, тогда как цвет из-за \ (\ mathrm {\ color {Blue} HIn} \) доминирует, если \ (\ ce {[H +]} <\ dfrac {K _ {\ large \ textrm {ai}} } {10} \). Вышеприведенное уравнение показывает, что изменение цвета является наиболее чувствительным, когда \ (\ ce {[H +]} = K _ {\ large \ textrm {ai}} \) в числовом значении.
Мы определяем p K _ai = — log ( K _ai), а значение p K _ai также является значением pH, при котором цвет индикатора наиболее чувствителен к изменениям pH. .-}] = [\ mathrm {\ color {Blue} HIn}] \). Другими словами, когда pH такой же, как p K _ai, существуют равные количества кислотной и основной форм. Когда две формы имеют одинаковую концентрацию, изменение цвета наиболее заметно.
Цвета субстанций делают мир прекрасным местом. Благодаря цветам и структуре цветы, растения, животные и минералы проявляют свой уникальный характер. Многие индикаторы извлекаются из растений. Например, краснокочанный сок и чайные пигменты имеют разные цвета при разном pH.Цвет чая темнеет в базовом растворе, но цвет становится светлее при добавлении лимонного сока. Сок краснокочанной капусты становится синим в щелочном растворе, но имеет отчетливый красный цвет в кислом растворе.
Общие индикаторы: некоторые общие индикаторы и их значения pK _ai (также называемые pK _a) представлены в виде таблицы.
Имя Кислотный цвет Диапазон изменения цвета pH Базовый цвет
метиловый фиолетовый желтый 0.0 — 1,6 Синий
Тимоловый синий Красный 1,2 — 2,8 желтый
Метиловый оранжевый Красный 3,2 — 4,4 желтый
Бромкрезоловый зеленый желтый 3,8 — 5,4 Синий
Метил красный Красный 4.8 — 6,0 желтый
Лакмус Красный 5,0 — 8,0 Синий
Бромтимоловый синий желтый 6,0 — 7,6 Синий
Тимоловый синий желтый 8,0 — 9,6 Синий
Фенолфталеин Бесцветный 8. 2} {0.{-6} \\
& = 5,05 \\ \\
\ ce {pH} & = 14 — 5,05 \\
& = 8,95
\ end {align *} \]
Фенолфталеин в приведенной выше таблице имеет значение p K _ai, равное 9,7, что является наиболее близким к значению pH точки эквивалентности при этом титровании. Этот индикатор бесцветен в кислом растворе, но светлый РОЗОВЫЙ появляется, когда pH> 8. Цвет становится более ИНТЕНСИВНЫМ РОЗОВЫМ по мере повышения pH. Парад интенсивностей цвета показан ниже:
Точка эквивалентности — это когда цвет меняется наиболее быстро, а не когда раствор изменил цвет.Неправильное использование индикаторов приведет к неточности результатов титрования.
Цвета индикаторного раствора
Индикаторы постепенно меняют цвет при различных значениях pH. Предположим, что кислотная форма имеет синий цвет, а основная форма — красный цвет. Ниже показано изменение цвета при разном pH. Цвет фона влияет на их внешний вид и наше восприятие.
RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB
RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB RnB
_______
Длинный растянутый цвет в середине последней строки имеет одинаковую интенсивность СИНИЙ и КРАСНЫЙ.Если цвет раствора соответствует этому, pH будет таким же, как p K _ai индикатора, при условии, что сопряженные формы индикатора имеют СИНИЙ и КРАСНЫЙ цвета.
вопросов
Растения содержат множество природных индикаторов. Краситель краснокочанной капусты, фиолетовый цвет винограда и даже цвет некоторых цветов — вот некоторые примеры. Почему некоторые фрукты меняют цвет при созревании?
Выберите верное утверждение:
Все слабые кислоты являются индикаторами.
Все слабые базы являются индикаторами.
Слабые кислоты и основания являются индикаторами.
Все индикаторы — слабые кислоты.
Пара кислотно-основных конъюгатов имеет разные цвета.
Любой индикатор меняет цвет при pH его раствора 7.
Все индикаторы меняют цвет при pH 7 (да / нет)?
Решения
Ответ \ (\ ce {[H +]} \) сока меняется.
Подсказка …
Изменения pH или \ (\ ce {[H +]} \) вызывают изменение цвета красителя, если их сопряженные пары кислота-основание имеют разные цвета. Могут быть и другие причины. Указывают ли цвета, насколько они хороши или плохи на вкус?
Ответ д.
Подсказка …
Изменение цвета является обязательным условием для индикаторов.
Ответ Нет!
Совет …
Фенолфталеин меняет цвет при pH ~ 9. Бромтимоловый синий имеет значение p K _n , равное 7.1. При pH 7 его цвет меняется с желтого на синий. Некоторые индикаторы меняют цвет при pH, отличном от 7.
Авторы и ссылки
Натуральных экстрактов растений как кислотно-основных индикаторов и определение их значения pKa
Обычно используемые индикаторы для кислотно-основного титрования являются синтетическими, и эта работа была направлена на выявление экологически чистых природных индикаторов и определение их значений pKa. Аналитический потенциал экстрактов цветов очень многообещающий, что видно из их применения в кислотно-щелочной титриметрии.Было обнаружено, что эти отобранные цветочные экстракты лучше подходят для титрования сильного кислотно-сильного основания, чем слабого кислотно-сильного основания. Мы получили резкое и четкое изменение цвета от красного до коричневато-желтого для экстракта Bougainvillea glabra , от красного до желтого для экстракта Bauhinia purpurea и от красного до коричневато-желтого для экстракта Impatiens balsamina . Все три экстракта цветов дали отчетливое изменение цвета с помощью кислот и оснований, и изменение цвета поддерживалось с помощью различных кислот и оснований.Резкий контраст между их цветами в кислоте и основе сделал пигмент подходящим для использования в качестве кислотно-основных индикаторов. Поскольку эти цветочные экстракты имеют очень простую, экономичную, экологически безопасную процедуру экстракции и отличные характеристики с резким изменением цвета в конечных точках титрования, можно было бы заменить стандартные индикаторы, используемые в обычных лабораториях, индикаторами естественных цветов.
1. Введение
Титрование — это наиболее распространенный лабораторный метод количественного химического анализа, который используется для определения концентрации анализируемого вещества.Большинство современных лабораторий оснащены цифровыми автоматическими титраторами, которые оснащены датчиками (датчик pH / электрод напряжения), некоторые из них не требуют индикаторов, точность высока, а количество ошибок, связанных с человеческим фактором, также меньше, чем при использовании традиционных методов титрования. Однако кинетические факторы, касающиеся химической реакции и реакции индикаторной системы, имеют первостепенное значение. Конфигурация ячейки, перемешивание и расположение детектора конечной точки и ввода титранта должны быть рассмотрены для обеспечения высокой точности.Поршневые бюретки и перистальтические насосы обычно используются в качестве устройств для автоматической перекачки титранта в автоматические титраторы. Поршневые бюретки очень надежны, но дороги, в то время как перистальтические насосы очень универсальны, но требуют частой калибровки из-за постоянных изменений физических свойств используемых гибких трубок и имеют относительно короткий срок службы [1]. Стоимость автоматических титраторов вместе с недостатками, рассматриваемыми как основные препятствия для использования автоматических титраторов во многих развивающихся странах мира, и, следовательно, традиционные титриметрические методы все еще широко используются в аналитических и исследовательских лабораториях этих стран.
С тех пор, как мир стал осведомлен об экологических проблемах, различные части растений, такие как цветы и листья, являются символическими и считаются символом любовных желаний. Таким образом, цветы — это чудо природы. Синтетические соединения сильно загрязняют окружающую среду, вредны, опасны и намного дороже как для исследовательской, так и для аналитической работы. Поэтому многие ученые всего мира активно проводят различные исследования в этой области натуральных продуктов, поскольку они менее опасны, дешевы, легкодоступны и экологичны [2].
Химические вещества обладают очевидным изменением цвета анализируемого вещества и реакционной смеси титранта, очень близко к точке текущего титрования, известной как индикатор, который помогает исследовать и определять точку эквивалентности при кислотно-основном титровании [3, 4] . Природные красители и пигменты растений — это сильно окрашенные вещества, которые могут менять цвет при изменении pH [5]. Цвета частей растений выражают их неповторимый характер. Некоторые органические и неорганические соединения ответственны за свойство окраски частей растения, такие как флавоноиды, флавонолы, ацилированные флавоноиды, антоцианы, глюкозилированный ацилированный антоцианин, хинины, имины, полиметины, нафтахиноны, антрахметиноноиды, индигидропиригоиды, дигидропиригоиды.[6]. Некоторые из этих соединений показывают разные цвета при разном pH, и, таким образом, это свойство можно использовать в качестве естественного индикатора. Индикатор pH — это просто слабое кислотно-слабое основание с разноокрашенными кислотными и сопряженными формами основания. Синие и красные пигменты цветов были выделены и всесторонне изучены Вильштеттером в 1913 году. Были разработаны природные индикаторы, такие как лакмусовая бумажка, для обозначения определенных уровней pH. Вещества в растительных продуктах, таких как чай, краснокочанная капуста или виноград, вступают в реакцию с кислотами или основаниями, что приводит к изменениям на молекулярном уровне, что приводит к различию их цвета при разных значениях pH.Сок краснокочанной капусты использовался как естественный индикатор pH [7]. Этот индикатор содержит антоцианин, пигмент которого по-разному реагирует на кислоты и основания [7].
Каждое соединение, которое может действовать как индикатор, имеет специфическое значение p K _и, и это важный физический параметр, указывающий на кислотность молекул. Для большинства индикаторов диапазон pH находится в пределах ± 1 от значения p K _до. Целью данной работы было выявление экологически чистых природных индикаторов и определение их значений pKa.Для этого исследования использовали водные экстракты трех растений Bougainvillea glabra, Impatiens balsamina, и Bauhinia purpurea .
Бугенвиллея глабра — вечнозеленый плетистый кустарник с колючими стеблями. Крошечные белые цветы обычно появляются группами, окруженными разноцветными бумажными прицветниками. Эти прицветники содержат одиннадцать типов пигментов бугенвиллей-v (бетацианин) [8].
Impatiens balsamina (садовый бальзам) произрастает в таких местах Южной Азии, как Индия, Шри-Ланка, Бангладеш и Мьянма.Это однолетнее растение высотой 20–75 см с толстым, но мягким стеблем. Листья расположены по спирали. Цветки розовые, красные, лиловые, лиловые или белые. Лепестки содержат антоцианидин и пеларгонидин в качестве красящих пигментов [9].
Bauhinia purpurea , пурпурная орхидея, — экзотическое тропическое дерево, которое цветет в течение длительного периода времени. Красивые и похожие на орхидеи цветы Bauhinia purpurea произрастают в Индии. Лепестки Bauhinia содержат в качестве красящих пигментов халкон и бутеин [10].
2. Материалы и методы
2.1. Приготовление экстрактов
Цветки зеленых растений Bougainvillea glabra и Impatiens balsamina были получены из сада Восточного университета, Ченкалади, Баттикалоа, Шри-Ланка, а цветок Bauhinia purpurea был получен из Thambiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri, Ampiluvilri. . Лепестки каждого цветка собирали, промывали дистиллированной водой и зажимали между подушечками впитывающей бумаги для удаления воды с поверхности.Свежие лепестки (5 г) каждого цветка переносили в химические стаканы (100 мл), содержащие 50 мл дистиллированной воды отдельно. Его нагревали до 50–60 ° С в течение 10 минут. Экстракты трех цветков разделяли фильтрованием через чистую фильтровальную бумагу Whatman® № 1 (размер пор 11 мкм мкм). Экстракты хранили в сухом и темном месте.
2.2. Кислотно-основное титрование
Три типа титрования, такие как сильное кислотно-сильное основание, сильное кислотно-слабое основание и слабое кислотно-сильное основание, были выполнены с использованием экстрактов цветов в качестве индикаторов, и их точность сравнивалась с коммерчески доступными синтетическими индикаторами, такими как как метиловый оранжевый, метиловый красный и фенолфталеин.Каждое титрование проводили в трех экземплярах.
2.3. Приготовление растворов с различным pH
Мерные колбы (50 мл) были помечены номерами от 1 до 10. В каждую колбу добавляли экстракт цветов (2,0 мл). Растворы 0,1 M Na ₂ HPO ₄ и 0,1 M KH ₂ PO ₄ также добавляли в каждую колбу, как указано в таблице 1. Каждый раствор разбавляли до метки дистиллированной водой. Эту процедуру повторили для всех трех экстрактов цветов [11].
902 902 902 902 902 902 902 902
Колба No. KH ₂ PO ₄ (мл) Na ₂ HPO ₄ (мл)
1 10,0 0,0 0,0 0,0 902 1,0
3 10,0 2,0
4 20,0 10,0
5 10.0 10,0
6 10,0 20,0
7 2,0 10,0
8 2,0 20,0 902 902 902 902
10 0,0 10,0
2,4. Измерение pH растворов
pH каждого раствора измеряли с помощью зондов pH (PHC301), подключенных к откалиброванному многопараметрическому датчику Hach hq40d.
Калибровка прибора: (I) зонд pH был подсоединен к прибору, и контргайка была установлена правильно. Измеритель был включен. (II) После нажатия кнопки «калибровка» зонд был промыт деионизированной водой, и его осторожно, без пузырьков воздуха, поместили в стандартный буферный раствор pH при легком перемешивании. (III) Затем значок « чтение ». (IV) Та же процедура (III) была проделана для каждого стандартного раствора pH. (V) Наконец, была нажата кнопка« Готово », и калиброванные данные были сохранены.
2,5. Спектрофотометрическое определение значений pKa индикаторов
Цветочный экстракт (2,0 мл), дистиллированная вода (10,0 мл) и 8 капель кон. HCl переносили в 50 мл мерную колбу, обозначенную как A , и раствор разбавляли до метки дистиллированной водой. Во вторую мерную колбу, обозначенную как B , переносили экстракт цветков (2,0 мл), дистиллированную воду (10,0 мл) и 24 капли 4 М NaOH, и раствор доводили до метки дистиллированной водой.Это повторили для всех трех цветочных экстрактов.
Для этого исследования использовался спектрофотометр Biobase BK-D580. УФ-видимые спектры были получены между 300 и 800 нм для A и B каждого раствора экстракта цветов и для метилового красного. Была выбрана одна длина волны ( λ, ₁), при которой раствор A поглощает сильно, а раствор B — слабо, и вторая длина волны ( λ ₂), при которой раствор A поглощает слабо, а раствор B — сильно.Наконец, абсорбция каждого набора из 10 растворов была сведена в таблицу относительно холостого раствора при выбранных длинах волн λ ₁ и λ ₂ (Таблица 2). Здесь холостой раствор включает все химические вещества и дистиллированную воду, кроме экстракта цветков [11–14].
6 λ 2 3612 905 905 9067
Индикатор Параметр Поглощение 10 растворов при pH от 7,29 до 8,52
7.29 7,32 7,36 7,39 7,53 7,59 7,95 7,99 8,14 8,52
0,028 0,026 0,021 0,020 0,018 0,018 0,017 0,017 0,015 0,015
0,362 0,366 0,370 0,373 0,375 0,376 0,379 0,382 0,416
Кислотный макс. 0,325 0,325 0,325 0,325 0,325
Макс.баз 0,577 0,577 0,577 0.577 0,577 0,577 0,577 0,577 0,577 0,577
Bauhinia purpurea 0,044 0,033 0,026 0,020 0,022 0,017 0,013
λ ₂ 0.581 0,604 0,614 0,646 0,642 0,641 0,659 0,663 0,674 0,712
Кислота макс. 0,132 0,132 0,132 0,132 0,132
Макс.баз 0,752 0,752 0,752 0.752 0,752 0,752 0,752 0,752 0,752 0,752
Бугенвиль1 902 902 905 902 902 902 902 905 905 905 905 905 902 905 905 906 0,05 0,05 0,05 0,04 0,05 0,05 0,04
λ ₂ 0.04 0,04 0,04 0,04 0,06 0,06 0,07 0,08 0,09 0,13
Макс. 0,11 0,11 0,11 0,11 0,11
Макс.баз 0,04 0,04 0,04 0,04 0.04 0,04 0,04 0,04 0,04 0,04
Метил красный λ _{1 _{7 0,302 902 902 902}} 0,261 0,258 0,262 0,258 0,227
λ ₂ 2,326 2,363 2.392 2,314 2,357 2,368 2,379 2,398 2,452 2,760
Кислота макс. 2,796 2,796 2,796
Макс.баз 2,42 2,42 2,42 2,42 2,42 2.42 2,42 2,42 2,42 2,42
Вышеупомянутая процедура была проделана для всех трех экстрактов цветов, и результаты их экспериментов сравнивались с показателем метилового апельсина.
Индикаторы представляют собой слабое основание или слабую кислоту, которые имеют разные цвета при разном pH. Равновесная реакция индикатора показана в следующем уравнении [12]:
Большинство индикаторов представлены в виде HIn в растворе сильной кислоты и имеют соответствующий цвет HIn, тогда как в растворе сильного основания большинство индикаторов представлены в виде In ^— и имеют соответствующий цвет In ^—.
Равновесное выражение уравнения (1) можно записать следующим образом: где K _a известно как константа диссоциации или константа равновесия индикатора, а [In ^—] и [HIn] известны как концентрация основных и кислотных форм индикатора, соответственно:
Уравнение можно записать как
Значения отношения были определены из спектрофотометрических измерений, выполненных на двух длинах волн ( λ ₁ и λ ₂) чтобы построить график зависимости pH от.
Согласно закону Бера абсорбция при λ ₁ и λ ₂ was где абсорбция, молярная абсорбционная способность и длина пути клетки.
При любом pH общая концентрация () как In ^—, так и HIn была постоянной, и сумма индивидуальных концентраций обеих форм:
В растворе с низким pH все индикаторы находятся в форме. В результате в сильнокислом растворе и
В растворе с высоким pH все индикаторы имеют вид [In ^—].В результате в высокоосновном решении
и
Наконец, соотношение может быть определено путем деления отношения уравнений (5) — (8) на соотношение уравнений (6) — (9) [11, 12]:
3. Результаты и обсуждение
Все экстракты цветов имели разную окраску в кислых и основных растворах и имели разные самые высокие пики (макс. Лямбда) в сильнокислой и сильнощелочной среде (таблица 2). Было обнаружено, что конечные точки, определенные для кислотно-основного титрования с использованием экстрактов цветов в качестве индикаторов, очень похожи на таковые для стандартных индикаторов, используемых в лабораториях (таблица 3).
90OH215 Цвет фторсодержащего водорода 8,87 ± 0,057767 От желтого до желтого 6797 ± 0,05775 от коричневато-желтого до красного.17 ± 0,0577 NaOH до красного цвета
Индикатор Титрант / титрант Изменение цвета Требуемый объем титранта
NH ₄ OH / HCl От розового до бесцветного 14,57 ± 0,0577
CH ₃ COOH / NaOH От бесцветного до розового .07 ± 0,0577
s Метиловый оранжевый NaOH / HCl От желтого до красного 9,17 ± 0,0577
NH ₄ OH / HCl 905 от желтого до красного
CH ₃ COOH / NaOH От красного до желтого 5,27 ± 0,0577
Метиловый красный NaOH / HCl
NH ₄ OH / HCl От желтого к красному 16,13 ± 0,0577
CH ₃ COOH / NaOH От красного к желтому 902,13 ± 0,0577
Bougainvillea glabra NaOH / HCl От коричневато-желтого до красного 8,97 ± 0,0577
NH ₄ OH / HCl
CH ₃ COOH / NaOH От красного до коричневато-желтого 12,23 ± 0,0577
Impatiens balsamina
9,07 ± 0,0577
NH ₄ OH / HCl От коричневато-желтого до красного 15,3 ± 0,1
CH ₃ COOH / NaOH От красного до коричневато-желтого 12220 .13 ± 0,0577
Bauhinia purpurea NaOH / HCl От желтого к красному 8,93 ± 0,0577
NH 16 4 желтый к красному ± 0,0577
CH ₃ COOH / NaOH От красного к желтому 12,3 ± 0,1
P K извлекает значения 9011 и _{для всех значений цветов метиловый оранжевый (для сравнения) рассчитывались непосредственно из пересечения графиков, как показано на рисунке 1.Значения R ² этих трех цветочных экстрактов, которые были выше (0,9551, 0,9569 и 0,9649), чем у индикатора метилового красного (0,9260), указывают на лучшую линейную взаимосвязь для трех индикаторов цветов по сравнению с синтетическим индикатором, используемым для сравнение. Рассчитанные значения p K _a и диапазон pH для соответствующих индикаторов приведены в таблице 4.}
905
Индикатор pKa Диапазон pH
Bougainvillea glabra 6.9966 ≈ 7,0 6,0–8,0
Impatiens balsamina 4,3766 ≈ 4,4 3,4–5,4
Bauhinia purpurea 7,0325 3,4003 ≈ 3,4 2,4–4,4
Изменение требуемых объемов титранта при использовании цветочных индикаторов для титрования сильной кислотой и сильным основанием составляет от 0.04–0,1, тогда как вариация синтетических индикаторов находится в диапазоне от 0,1 до 0,3. Для титрования сильной кислотой и слабым основанием изменение требуемого объема титранта составляло от 0,03 до 0,13, в то время как синтетические индикаторы показывают изменение от 0,46 до 1,56. В случае соединения слабая кислота-сильное основание вариации для синтетических индикаторов были очень высокими, так как индикатор метиловый оранжевый не подходит для титрования слабая кислота-сильное основание. Однако показатели метилового красного, Bauhinia purpurea и Impatiens balsamina показывают значение, очень близкое к стандартному показателю — фенолфталеину.Диапазон pH Bougainvillea glabra и Bauhinia purpurea очень близок к диапазону pH фенолфталеина (8,2–10,0). Метиловый апельсин не смог обнаружить острые конечные точки для слабого кислотно-сильного основания, в то время как экстракты цветов Bougainvillea glabra и Bauhinia purpurea обнаруживают конечные точки более точно, чем синтетические индикаторы.
Эти индикаторы натуральных цветов очень важны в современных лабораториях, когда автоматические титраторы не могут титровать некоторые химически активные жидкости.Углеводород может реагировать с пластиковыми материалами, используемыми в цифровых титраторах, поэтому использовать эти современные цифровые измерители нельзя. Методы, предложенные Американским обществом испытаний и материалов, ASTM D974 и ASTM D5984, используют титрование с помощью цветного индикатора для определения основных компонентов в нефтепродуктах и смазочных материалах. Колориметрическое титрование использует визуальные изменения химического соединения, когда его среда меняется с кислой на щелочную. Другими словами, цвет этого индикатора изменится при pH, соответствующем точке перегиба.Метиловый красный используется в качестве индикатора, меняя свой цвет с пурпурного на желтый при pH, соответствующем точке перегиба. В ASTM D974, как и в D4739, в качестве титранта используется соляная кислота; смесь толуола и изопропилового спирта, содержащая небольшое количество воды, используется в качестве системы растворителей, а p -нафтолбензеин используется в качестве цветного индикатора, который имеет оранжевый цвет по кислоте и зелено-коричневый цвет по основанию [15]. Эти синтетические индикаторы могут быть заменены индикаторами из натуральных цветов даже в современных лабораториях.
4. Выводы
Результаты, полученные в результате настоящего исследования, показывают, что аналитический потенциал экстрактов цветков очень многообещающий, что подтверждается их применением в кислотно-щелочной титриметрии. Было обнаружено, что эти экстракты лучше всего подходят для титрования сильной кислотой и сильным основанием по сравнению со слабым кислотно-сильным основанием с резким и четким изменением цвета от красного до коричневато-желтого для экстракта Bougainvillea glabra , от красного до желтого для Bauhinia. purpurea и от красного до коричневато-желтого для экстракта Impatiens balsamina .Все три экстракта цветов дали отчетливое изменение цвета с помощью кислот и оснований, и изменение цвета поддерживалось с помощью различных кислот и оснований. Резкий контраст между их цветами в кислоте и основе сделал пигмент подходящим для использования в качестве кислотно-основных индикаторов.
Доступность и простая процедура экстракции с отличными характеристиками и точными результатами сделали бы эти индикаторы для натуральных цветов подходящими заменителями синтетических индикаторов, используемых во многих лабораториях и исследовательских институтах.Короче говоря, отрасли, исследовательские лаборатории, школы и химические компании, использующие индикаторы для определения кислотности, щелочности, влажности, степени реакций и т. Д., Сочтут предварительные результаты этого исследования ценными для получения эффективных индикаторов из цветы как заменители или возможная замена стандартных индикаторов. Американское общество испытаний и материалов (ASTM) использует колориметрическое титрование с синтетическими индикаторами в качестве стандартного метода для количественной оценки устойчивости смазки к разрушающему воздействию кислотных компонентов.Эти синтетические индикаторы могут быть заменены индикаторами из натуральных цветов в современных лабораториях. Однако недостатком цветочного экстракта является то, что их нужно готовить в свежем виде, поскольку они подвержены грибковому росту через три дня.
Доступность данных
Данные, использованные для подтверждения результатов этого исследования, включены в статью.
Раскрытие информации
Эта работа была проведена в лаборатории кафедры химии факультета естественных наук Восточного университета, Шри-Ланка.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Общие индикаторы кислотной основы | Наука
Обновлено 1 марта 2020 г.
Розанн Козловски
Рецензент: Лана Бандойм, Б.С.
Кислотные и щелочные индикаторы используются в химии для определения pH вещества. Они меняют свой цвет в зависимости от того, добавлены ли они к кислоте, основанию или нейтральному веществу. Большинство индикаторов являются слабыми кислотами и реагируют на изменение концентрации ионов водорода.
Шкала pH и индикаторы кислоты и щелочи
Диапазон pH составляет от 0 до 14, где 7 является нейтральным. PH выше 7 указывает на основание, а значение ниже 7 указывает на кислоту. Шкала pH является логарифмической, и при изменении каждого отдельного числа на шкале происходит десятикратное изменение кислотности или щелочности (основности).
Кислотные и щелочные индикаторы чувствительны к изменению pH или, точнее, к изменению концентрации ионов водорода , H ⁺ в растворе.
Большинство кислотных и основных индикаторов представляют собой большие органические молекулы, которые содержат чередующиеся двойные и одинарные углерод-углеродные связи. В основных растворах кислотные и основные индикаторы становятся ионами, теряя ионы водорода из своего химического состава, обычно из группы ОН. Это изменяет структуру молекулы, заставляя индикаторы поглощать свет с разной длиной волны и менять цвет.
Типы индикаторов
Многие типы индикаторов работают со всей шкалой pH.Важно выбрать тот, который соответствует рассматриваемому диапазону pH. Ниже приведены несколько общих индикаторов.
Лакмусовая бумага
Одним из распространенных индикаторов кислот и оснований является лакмусовая бумага, созданная обработкой фильтровальной бумаги красителем, полученным из лишайников. Раствор, нанесенный на лакмусовую бумагу, либо сохранит цвет лакмусовой бумаги, либо изменит его.
Красная лакмусовая кислота — слабая дипротонная кислота; он может отдавать два атома водорода. При pH ниже 4,5 красная лакмусовая бумажка остается красной, но становится синей в основе.При pH выше 8,3 синяя лакмусовая бумажка остается синей, но становится красной в кислоте.
Лакмусовая бумажка не способна определять значение pH, только различает кислоты и основания . Нейтральная лакмусовая бумага пурпурного цвета.
Индикатор фенолфталеина
Индикатор фенолфталеина представляет собой слабую кислоту, имеющую две разные структуры в зависимости от того, находится ли она в щелочном (розовом) или кислотном (бесцветном) растворе. Раствор щелочи поглощает свет в видимом спектре света, и человеческий глаз воспринимает изменение цвета на розовый при уровне pH 8.2, продолжая становиться ярко-пурпурным при pH 10 и выше.
Фенолфталеин обычно используется в качестве индикатора в экспериментах по кислотно-щелочному титрованию в химической лаборатории. Раствор известной концентрации осторожно добавляют к раствору неизвестной концентрации и индикатора фенолфталеина. Когда раствор превращается из бесцветного в розовый (или наоборот), это означает, что титрование , или точка нейтрализации достигнуты, и можно рассчитать неизвестную концентрацию.
Индикатор бромтимолового синего
Бромтимоловый синий, слабая кислота, чаще всего используется в качестве индикатора для относительно нейтральных растворов — слабых кислот и оснований.Диапазон pH составляет от 6 до 7,6. Раствор выглядит желтым до pH 6, в нейтральном растворе он становится зеленым, а в щелочных растворах с pH 7,6 он становится синим.
В лаборатории бромтимоловый синий часто используется в качестве красителя для биологических препаратов , для тестирования фотосинтеза и может использоваться для определения pH в плавательных бассейнах.
Индикатор метилового красного
В качестве индикатора кислоты и основания метиловый красный становится красным в кислых растворах при pH 4,4 и ниже и желтым при pH 6.2 достигается. Между этими конечными значениями цвета, в диапазоне pH от 4,4 до 6,2, цвет оранжевый.
Метиловый красный может использоваться как индикатор кислоты и основания в лаборатории и как азокраситель, самая большая группа синтетических красителей , , обычно используемых для обработки текстильных изделий.
Универсальный индикатор
Универсальный индикатор — это раствор, содержащий смесь индикаторов, часто фенолфталеина, метилового красного и бромтимолового синего. Определение приблизительного pH достигается добавлением в раствор нескольких капель универсального индикатора.
Красный означает сильную кислоту в диапазоне pH от 1 до 4, тогда как слабая кислота имеет оранжевый оттенок. В нейтральном растворе цвет становится желто-зеленым. Пурпурный указывает на сильное основание, pH выше 11, тогда как слабые основания имеют голубоватый оттенок.
Влияние условий в системе на естественные индикаторы
D. A. ABUGRI ET AL. 121
Таблица 5. Т-тест теоретического мольного отношения.
Тестовое значение = 1 (теоретическое молярное отношение)
95% достоверности
Интервал разницы
Показатели *
df Sig.(Двусторонний) Среднее значение
Разница Нижнее Верхнее
NI1 4 0 –0,72 –0,73 –0,72
MR1 4 0 –0,88 –0,88 –0,88
MO1 4 0 –0,40 –0,41 –0,40
NI2 4 0 — 0,89 –0,89 –0,89
MR2 4 0 –0,21 –0,21 –0,21
MO2 4 0 –0,84 –0,84 –0,84
Ph3 4 0 –0,81 –0,81 –0,81
NI3 4 0 2,57 2,57 2,57
0 1,53 1,50 1,55
MO3 4 0 –0,88 –0,88 –0,88
NI4 4 0 10.54 10,54 10,54
MR4 4 0 9,22 9,04 9,40
MO4 4 0 14,48 14,43 14,54
NB: * NI = Натуральный показатель; МО = метиловый оранжевый; MR = метиловый красный; PH =
Фенолфталеин. Цифры 1, 2, 3 и 4 обозначают различные системы кислота /
оснований, HCl / NaOH, Ch4COOH / NaHCO3 и HCl / NaHCO3 соответственно
. Статистические данные были получены с доверительным интервалом 95%.
Индикаторы и процесс нейтрализации: следующие —
химических уравнений; Уравнения (1) — (4) рассматривались как реакции, протекающие в процессе нейтрализации neu-
в присутствии визуальных индикаторов при 25 ° C.Мольные отношения стехиометрического уравнения
были приняты в качестве истинного мольного отношения (со значением
1,0). Это сравнивалось с экспериментально определенными мольными отношениями
, полученными путем вычетов из значений титра.
Органический индикатор, 25 ° C
HCl + NaOH NaCl + h3O (1)
Органический индикатор, 25 ° C
HCl + NaHCO3 NaCl + CO2 + h3O (2)
Органический индикатор, 25 ° C
Ch4COOH + NaOH Ch4COONa + h3O (3)
Органический индикатор, 25 ° C
Ch4COOH + NaHCO3 Ch4COONa + CO2 + h3O
(4)
4.Заключение
В данной статье предлагается использовать природные индикаторы
для предотвращения токсичности
среди пользователей и загрязнения окружающей среды. Также очевидно, что листья
, подготовленные в качестве коммерческих индикаторов, будут служить источником
экономических выгод для фермеров и стран, производящих
урожая. Также в заключение, исследование показывает
, что стандартные индикаторы могут быть успешно заменены
экстрактом листьев ваакье (натуральный индикатор) для простого кислотно-основного титрования
.
СПРАВОЧНАЯ ИНФОРМАЦИЯ
[1] Ф. О. Нвосу, Ф. А. Адекола и К. К. Иедиоха, «Простые титриметрические индикаторы цвета
из некоторых природных цветов
лепестков», Centrepoint (Science Edition), Vol. 12, No. 1, 2004,
pp. 74-89.
[2] K .S. Патад, С. Б. Патил, М. С. Конда-вар, Н. С. Найк-
Уэйд и К. С. Магдум, «Morus Alba Fruit-Herbal Al-
, альтернативный индикатор синтетической кислотной основы», Internatio-
nal Journal of ChemTech Research, Vol.1, № 3, 2009,
, с. 549-551.
[3] С. Б. Патил, М. С. Кондавар, Д. С. Год-ке, Н. С. Найк-
Уэйд и К. С. Магдум, «Использование экстрактов цветов в качестве индикатора
при кислотно-щелочном титровании», Research Journal of.
Фармация и технологии, Vol. 2, No. 2, 2009, pp. 421-
422.
[4] IS Udachan, AK Sahoo and GM Hend, «Экстракция
и характеристика крахмала сорго (Sorghum bicolor L.
Moench)», Международный журнал исследований пищевых продуктов,
Vol.19, No. 1, 2012, pp. 15-319.
[5] Д.А. Абугри, Б.Дж. Тиймоб, В.А. Апалангья, Г. Притчетт
и У.Х. Макэлхенни, «Биоактивное и питательное соединение —
фунтов в красных листьях сорго двухцветного (гвинейская кукуруза)
и их влияние на здоровье», «Journal of Food Chemis —
try, 2012.
[6] Н. Туркмен, Ф. Сари и Ю.С. Велиоглу,« Влияние тяговых растворителей Ex-
на концентрацию и антиоксидантную активность —
черных и черных ». Полифенолы чая мате Детер-
, добытые с помощью методов тартрата железа и фолина-Чокальтеу »,
Food Chemistry, Vol.99, No. 4, 2006, pp. 835-841.
DOI: 10.1016 / j.foodchem.2005.08.034.
[7] Б. Дж. Сюй и С. К. К. Чанг, «Сравнительное исследование фенольных профилей
и антиоксидантной активности легимов
под действием экстракционных растворителей», Journal of Food Sci-
ence, Vol. 72, № 2, 2007 г., стр. S159-S166.
doi: 10.1111 / j.1750-3841.2006.00260.xPMid: 17995858
[8] HS Yim, FY Chye, SK Ho и CW Ho, «Фенольные
Профили избранных съедобных диких грибов подвергаются воздействию
при экстракции. Растворитель, время и температура », Asia Jour-
nal of Food Argo-Industry, Vol.2, No. 3, 2009, pp. 392-
401.
[9] ML Price, S. Vanscoyoc and LG Butler, «A Critical
Evaluation of the Vanillin Reaction as a Assay for Tan-
nin в зерне сорго », Journal of Agriculture and Food
Chemistry, Vol. 26, No. 5, 1978, pp. 1214-1218.
DOI: 10.1021 / jf60219a031.
[10] У. Д. Чаван, Ф. Шахиди и М. Нацк, «Извлечение
конденсированных танинов из пляжного гороха (Lathyrus maritimus
L.) под воздействием различных растворителей », Food Chemistry,
Vol. 75, No. 4, 2001, pp. 509-512.
DOI: 10.1016 / S0308-8146 (01) 00234-5.
Авторские права © 2012 SciRes. GSC
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно.Ниже приведены наиболее частые причины:
В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
Дата на вашем компьютере в прошлом.Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу.Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта.Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Химия капусты — поиск кислот и оснований
Ключевые концепции
Химия
Кислоты
Базы
Свет
Введение
Возможно, вы проводили эксперименты с хорошо обозначенными кислотами и основаниями в школе, но задавались ли вы когда-нибудь вопросом, является ли определенный продукт питания или химическое вещество в доме кислотой или основанием? Вы можете узнать это, используя краснокочанную капусту для приготовления индикаторного раствора.
Когда два или более ингредиента полностью растворяются друг в друге, у вас есть решение. Например, при смешивании соли с водой получается прозрачный раствор, даже если соль есть и раствор имеет соленый вкус. При смешивании с водой химическое вещество «жертвует» заряженную частицу (называемую ионом) раствору — в данном случае ион водорода — или «принимает» один из них, определяет, будет ли это раствор кислотным или основным. Индикатор меняет цвет при воздействии такой смеси в зависимости от того, является ли раствор кислотным или основным.
Фон
Кислоты — это растворы, которые теряют ионы водорода и обычно имеют кислый вкус. Кислоты, такие как соки цитрусовых и домашний уксус, являются очень распространенными бытовыми растворами. Основания — это растворы, которые вытягивают ионы водорода из раствора на себя, «принимают» их и обычно кажутся скользкими. Основания имеют множество практических применений. Например, «антациды», такие как TUMS, используются для снижения кислотности в желудке. Другие основы делают полезные бытовые чистящие средства.
Чтобы определить, является ли что-то кислотой или щелочью, вы можете использовать химическое вещество, называемое индикатором. Индикатор меняет цвет, когда сталкивается с кислотой или щелочью. Есть много различных типов индикаторов, одни из которых являются жидкостями, а другие сконцентрированы на маленьких полосках лакмусовой бумаги. Индикаторы могут быть извлечены из множества различных источников, включая пигмент многих растений. Например, краснокочанная капуста содержит молекулу индикаторного пигмента, называемого флавином, который представляет собой тип молекулы, называемый антоцианом.Очень кислые растворы сделают антоцианово-красным, тогда как нейтральные растворы сделают его багровым, а щелочные растворы — зеленовато-желтым. Следовательно, цвет, который меняет раствор антоциана, можно использовать для определения pH раствора — показателя того, насколько щелочной или кислый раствор является.
Материалы
• Маленькая краснокочанная капуста
• Кастрюля с кипятком
• Фильтр
• Две большие миски или горшки
• Терка
• Дозатор столовой
• Большая ложка (необязательно)
• Три или более маленьких белых бумажных стаканчика (также подойдут маленькие белые бумажные стаканы или посуда)
• Очки или другие защитные очки
• Лимонный или лаймовый сок
• Уксус
• Чистящее средство на основе отбеливателя
• Другие продукты для тестирования, такие как газированная вода, раствор пищевой соды, яичные белки, помидоры, творог (по желанию)
Подготовка
• Натереть на терке небольшую красную капусту.Если вы не хотите тереть всю капусту на терке, достаточно натереть половину кочанной капусты. Переложите мелко натертую на терке капусту в большую миску или кастрюлю.
• Вскипятите кастрюлю с водой. Будьте осторожны при обращении с кипящей водой. Влейте кипяток в миску с капустной мякотью, пока вода не покроет капусту.
• Оставьте капустную смесь настаиваться, периодически помешивая, пока жидкость не станет комнатной температуры. Это должно занять не менее получаса. Жидкость станет красной или пурпурно-красной.
• Поместите ситечко на другую большую миску или кастрюлю и вылейте капустную смесь через ситечко, чтобы удалить мякоть. Нажмите на мякоть в сетчатом фильтре, например, большой ложкой, чтобы выжать из мякоти больше жидкости.
• Теперь в миске должна быть только жидкость фиолетового или синего цвета. Это будет ваш индикаторный раствор, который вы будете использовать для проверки pH различных жидкостей.
• Дети должны носить защитные очки или другие защитные очки, а взрослые должны соблюдать осторожность и соблюдать осторожность при обращении с отбеливателем и уксусом, поскольку они могут вызвать раздражение глаз и кожи.
Процедура
• Наполните небольшой белый бумажный стаканчик, стакан или белую посуду одной столовой ложкой раствора индикатора капусты. Какого цвета ваш индикаторный раствор?
• Добавляйте в индикаторный раствор капли сока лимона или лайма до тех пор, пока раствор не изменится в цвете. Аккуратно перемешайте раствор и убедитесь, что цвет не изменился. Какого цвета стал раствор?
• Цвет раствора будет меняться в зависимости от его pH: красный цвет означает, что pH равен 2; Фиолетовый означает pH 4; Фиолетовый означает pH 6; Синий означает pH 8; Сине-зеленый означает pH 10; Зеленовато-желтый означает pH 12.
• Каков pH раствора сока лимона или лайма в зависимости от его цвета?
• В другой маленький белый бумажный стаканчик добавьте одну столовую ложку исходного раствора индикатора капусты. Добавляйте капли уксуса, пока не увидите, как раствор меняет цвет. Какого цвета стал раствор уксуса? Каков pH раствора?
• В третий маленький белый бумажный стаканчик добавьте одну столовую ложку исходного раствора индикатора капусты. Обращаясь с ним осторожно, добавляйте капли отбеливающего чистящего средства до тех пор, пока раствор не изменит цвет. Какого цвета стал отбеливающий раствор и что это говорит о его pH?
• Если вы хотите проверить pH других продуктов, снова добавьте одну столовую ложку исходного раствора индикатора капусты в небольшой белый бумажный стаканчик и добавляйте капли пищи, пока не увидите, как раствор меняет цвет. Если пища не в жидкой форме, раздавите ее или растворите в небольшом количестве воды перед добавлением в индикаторный раствор. Какого цвета стал раствор и что это говорит о его pH?
• Extra: Есть и другие овощи и фрукты, которые также можно использовать для создания индикаторов pH: красный лук, кожура яблок, черника, кожица винограда и сливы. Какие различные источники пигмента дают наилучшие показатели?
• Extra: Вы можете использовать индикаторное решение для написания секретных сообщений. Просто используйте крепкий лимонный сок, чтобы написать невидимое сообщение на бумаге, и дайте ему высохнуть. Чтобы раскрыть сообщение, нарисуйте индикатор капусты по бумаге кистью.
Наблюдения и результаты
Изменился ли цвет индикаторного раствора, когда вы добавили сок лайма или лимона, уксус и отбеливатель? Указывает ли цвет раствора на то, что сок лайма или лимона и уксус были кислыми (имели более низкий pH) и что отбеливатель был щелочным (с более высоким pH)?
Раствор с pH от 5 до 7 является нейтральным, 8 или выше — это основание, а 4 или ниже — кислота.Сок лайма, лимонный сок и уксус являются кислотами, поэтому они должны были сделать индикаторный раствор красным или пурпурным. Отбеливатель — сильная основа, поэтому он должен был придать раствору индикатора зеленовато-желтый цвет.
Posted in Разное
Навигация по записям
Теории химического строения – —
Что называют явлениями – Attention Required! | Cloudflare
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Воспитание
Детям
Идеи
Полезно
Родителям
Советы
Разное
2015-2019 © Игровая комната «Волшебный лес», Челябинск
тел.:+7 351 724-05-51, +7 351 777-22-55 игровая комната челябинск, праздник детям челябинск