Практическая работа по математике: «Степень с рациональным показателем»
Практическая работа № 10
Тема: «Степень с рациональным показателем»
Цель: систематизировать знания о степени с рациональным показателем, решение примеров с рациональным показателем.
Ход работы.
Теоретическая часть.
Определение. Степенью числа а0 с рациональным показателем r, где m – целое рациональное число, а n – натуральное (n1), называется число .
Для любых рациональных чисел r и s и любых положительных a и b справедливы равенства:
Для любых рациональных чисел r и s из неравенства rs следует, что
Решение типового варианта.
Разложите на множители.
а)
б) a-
в) 3+
г)
Найдите значения выражения:
а) –
б)
в)
г)
Представьте выражение в виде степени с рациональным показателем:
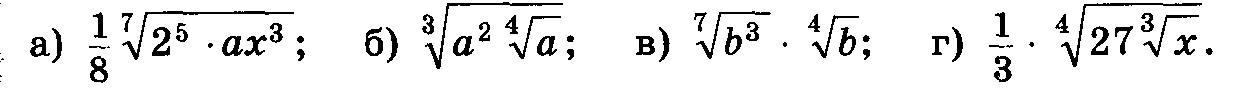
Упростите выражение:
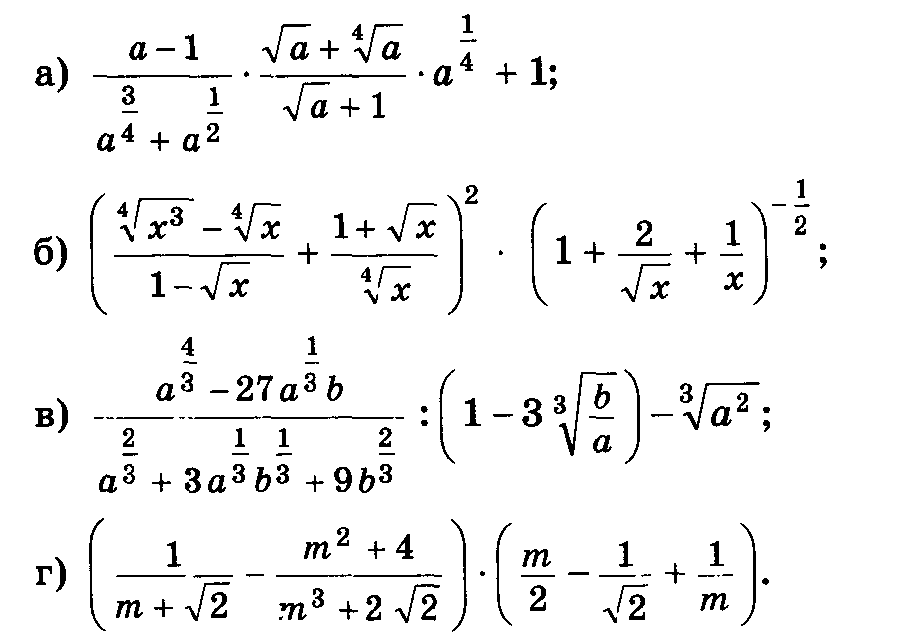
Проверочная работа.
Найдите значение числового выражения:

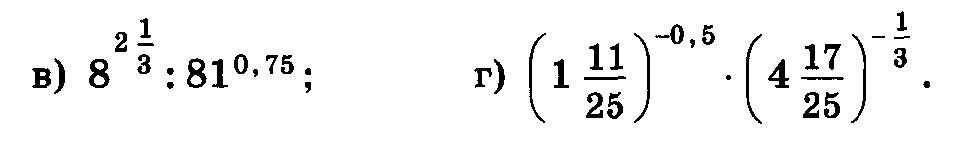
Упростите выражение:
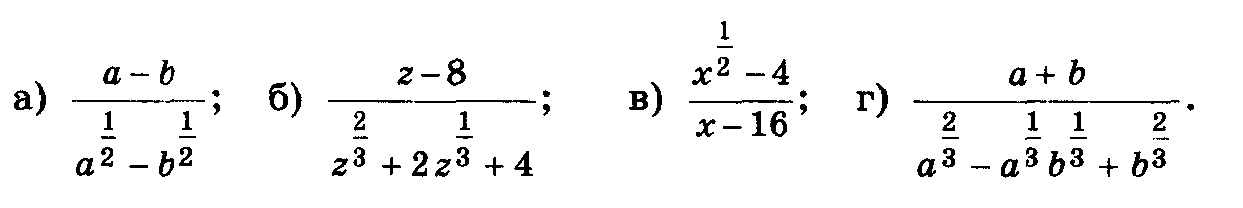
Найдите значение числового выражения:

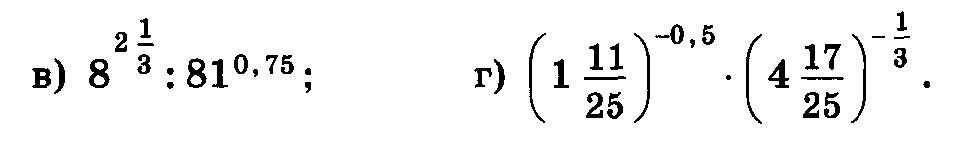
Упростите выражение:
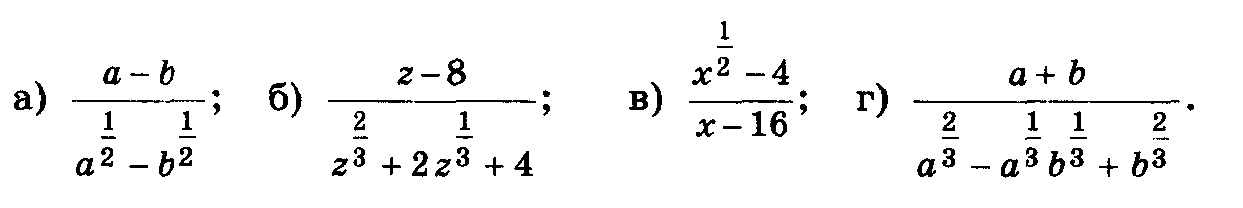
Проверочная работа.
Найдите значение числового выражения:

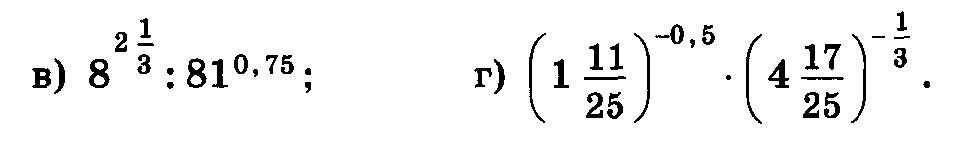
Упростите выражение:
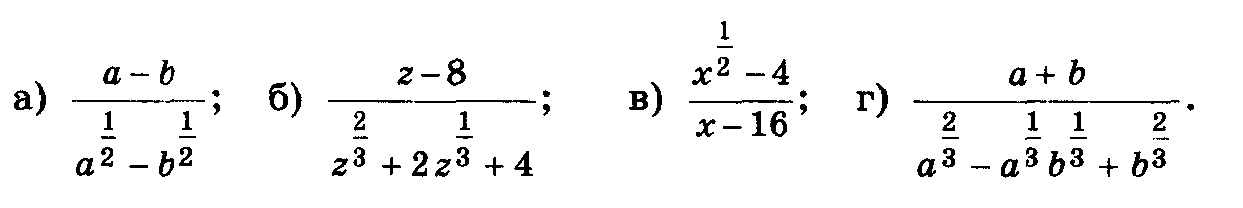
Степень с рациональным показателем
Просмотр содержимого документа
«Степень с рациональным показателем»

Устный счет
10/7/18 10:00:08 PM
- Вычислите: ,
- Представить в виде обыкновенной дроби:
0,5; 1,2; 0,75; 1,5; 0,4; 0,1; 0,25.

Обозначения числовых множеств
- Множество натуральных чисел. Используются при счете.
- Множество целых чисел (натуральные + натуральные со знаком “-”+ нуль).
- Множество рациональных чисел (дроби)
- Множество иррациональных чисел (корни)
- Действительные числа (рациональные+иррациональные)
N
Z
Q
I
R
10/7/18 10:00:08 PM

Степень с натуральным показателем
a — основание степени, n – показатель степени
Степень с целым показателем
10/7/18 10:00:08 PM

10/7/18 10:00:08 PM
Степень с рациональным показателем
Урок алгебры в 9 классе

Определение
10/7/18 10:00:08 PM
Если n – натуральное число,
И обратно:

Задание № 1. Записать в виде степени с рациональным показателем
10/7/18 10:00:08 PM

10/7/18 10:00:08 PM
Задание № 2. Записать в виде корня из степени с целым показателем
1)
2)
3)
4)
5)
6)

Задание № 3. Вычислите:
10/7/18 10:00:08 PM

Задание № 3. Вычислите:
10/7/18 10:00:08 PM
 0, b0) Примеры «
0, b0) Примеры «
Свойства степени с рациональным показателем
10/7/18 10:00:08 PM
Все свойства степени с натуральным показателем верны и для степени с любым рациональным показателем и положительным основанием. (p и q – рациональные числа, a0, b0)
 0, b0) Примеры «
0, b0) Примеры «
10/7/18 10:00:08 PM
Свойства степени с рациональным показателем (2)
Верно и обратное (p и q – рациональные числа, a0, b0)

Задание 4. Вычислите:
10/7/18 10:00:08 PM

Задание 4. Вычислите:
10/7/18 10:00:08 PM

Задание № 5. Записать в виде степени с рациональным показателем
10/7/18 10:00:08 PM

Задание № 5. Записать в виде степени с рациональным показателем
10/7/18 10:00:08 PM

Домашнее задание
Вычислите:
1)
3)
4)
№ 64, 65
10/7/18 10:00:08 PM

10/7/18 10:00:09 PM

10/7/18 10:00:09 PM

10/7/18 10:00:09 PM

Свойства степеней. Примеры.
10/7/18 10:00:09 PM
1)
2)
3)
4)
5)
Назад

Свойства степеней (2). Примеры.
Далее
10/7/18 10:00:09 PM
Презентация «Степень с рациональным показателем»
Описание презентации по отдельным слайдам:
1 слайд
Степень с рациональным показателем
2 слайд Описание слайда:
Описание слайда:Степень с натуральным показателем
3 слайд Описание слайда:
Описание слайда:Свойства степеней
4 слайд Описание слайда:
Описание слайда:Степень с отрицательным показателем
5 слайд Описание слайда:
Описание слайда:Свойства степеней
6 слайд Описание слайда:
Описание слайда:Примеры:
7 слайд Описание слайда: 8 слайд
Описание слайда: 8 слайд  Описание слайда:
Описание слайда:Найти значение выражения:
9 слайд Описание слайда: 10 слайд
Описание слайда: 10 слайд  Описание слайда:
Описание слайда:Запишите число в стандартном виде:
11 слайд Описание слайда:
Описание слайда:Определение степени с дробным показателем Дайте определение степени с дробным показателем. Для какого дробного показателя определена степень с основанием равным нулю? Определяется ли степень с дробным показателем для отрицательного основания?
12 слайд Описание слайда:
Описание слайда:Степень с дробным показателем не определена для отрицательного основания
13 слайд Описание слайда:
Описание слайда:При положительном дробном показателе, основание степени может быть неотрицательным. При отрицательном дробном показателе, основание только — положительное.
14 слайд Описание слайда:
Описание слайда:Представьте степень с дробным показателем в виде корня: 1. 2. 3. не имеет смысла 4. 5.
15 слайд Описание слайда:
Описание слайда:Представьте в виде степени с дробным показателем: 1. 2. 3. 4. 5.
16 слайд Описание слайда:
Описание слайда:1. Какое из чисел является рациональным числом 2. Найти значение выражения: 3. Вычислить:
17 слайд Описание слайда:
Описание слайда:4. Сократить дробь:
18 слайд Описание слайда:
Описание слайда:5. Упростить выражение:
19 слайд Описание слайда: 20 слайд
Описание слайда: 20 слайд  Описание слайда: 21 слайд
Описание слайда: 21 слайд  Описание слайда:
Описание слайда:Представить степень в виде арифметического корня:
22 слайд Описание слайда:
Описание слайда:Представить в виде степени:
23 слайд Описание слайда:
Описание слайда:Вычислить:
24 слайд Описание слайда:
Описание слайда:Упростить:
25 слайд Описание слайда:
Описание слайда:Упростить:
26 слайд Описание слайда:
Описание слайда:Решить уравнения:
27 слайд Описание слайда:
Описание слайда:Решить уравнения: НЕТ корней посторонний корень

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДВ-462230
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийПрезентация по математике» Степень с рациональным показателем и ее свойства».
Инфоурок › Алгебра ›Презентации›Презентация по математике» Степень с рациональным показателем и ее свойства».Описание презентации по отдельным слайдам:
1 слайд Описание слайда:
Описание слайда:Степень с рациональным показателем и ее свойства. Урок математики в10 классе Учитель математики Судеркина М.В.
2 слайд Описание слайда:
Описание слайда:Степень с рациональным показателем и ее свойства.
3 слайд Описание слайда:
Описание слайда:“Пусть кто-нибудь попробует вычеркнуть из математики степени, и он увидит, что без них далеко не уедешь”. (М.В. Ломоносов)
4 слайд Описание слайда:
Описание слайда:Цели урока: обобщить и систематизировать знания учащихся по теме “Степень”; проконтролировать уровень усвоения материала; формировать навыки самоконтроля учащихся; создать атмосферу заинтересованности каждого ученика в работе, развивать познавательную активность учащихся; воспитывать интерес к предмету, к истории математики .
5 слайд Описание слайда:
Описание слайда:Блиц-опрос Дайте определение степени с дробным показателем.
6 слайд Описание слайда:
Описание слайда:Блиц-опрос Степенью числа а>0 с рациональным показателем r = , где p— целое число, а q -натуральное (q ≥2), называется число т.е.
7 слайд Описание слайда:
Описание слайда:Блиц-опрос Для какого дробного показателя определена степень с основанием равным нулю?
8 слайд Описание слайда:
Описание слайда:Блиц-опрос Степень числа 0 определена только для положительных показателей; по определению = 0 для любого r >0.
9 слайд Описание слайда:
Описание слайда:Блиц-опрос Может ли быть отрицательным числом степень с рациональным показателем положительного числа?
10 слайд Описание слайда:
Описание слайда:Блиц-опрос Положительное число в степени с любым рациональным показателем положительно.
11 слайд Описание слайда:
Описание слайда:Блиц-опрос Свойства степеней с рациональным показателем.
12 слайд Описание слайда:
Описание слайда:Свойства степени с рациональным показателем.
13 слайд Описание слайда:
Описание слайда:Решаем устно
14 слайд Описание слайда:
Описание слайда:Представьте степень с дробным показателем в виде корня: 1. 2. 3. не имеет смысла 4. 5.
15 слайд Описание слайда:
Описание слайда:Представьте в виде степени с дробным показателем: 1. 2. 3. 4. 5.
16 слайд Описание слайда:
Описание слайда:Вычислите: а) б) в) г) д) е) ж)
17 слайд Описание слайда:
Описание слайда:Слово: 1) 2) 3) 4) 5) 6) 7) 64 5/3 4/9 1 5 9 Д И О Ф А Н Т Х1\3=4 2) у-1=3\5 3) а1\2= 2\3 4) х-0,5 х1,5 = 1 5) у1\3 =2 6) а2\7а12\7 = 25 7) а1\2 : а = 1\3 8 Л Т Н Р Ш О Ь И Е Ф К А Д Ю 9\4 9 5 11 -2 4\9 20 5\3 1\3 1 3 8 64 2
18 слайд Описание слайда:
Описание слайда:-81\3 2) 811\2 3) (3\5)-1 4) (5\7)0 5) 27-1\3 6) (2\3)-2 7) 161\2 * 1251\3 Слово: 1) 2) 3) 4) 5) 6) 7) -2 9 5/3 1 1/3 9/4 20 Ш Т И Ф Е Л Ь Л Т Н Р Ш О Ь И Е Ф К А Д Ю 9\4 9 5 11 -2 4\9 20 5\3 1\3 1 3 8 64 2
19 слайд Описание слайда:
Описание слайда:Слово: 1) 2) 3) 4) 5) 6) 64 1/3 3 8 11 9 Д Е К А Р Т Х1\3=4 2) у-1= 3 3) ( х+6)1\2 = 3 4) у1\3 =2 5) (у-3)1\3=2 6) а1\2 : а = 1\3 Л Т Н Р Ш О Ь И Е Ф К А Д Ю 9\4 9 5 11 -2 4\9 20 5\3 1\3 1 3 8 64 2
20 слайд Описание слайда:
Описание слайда:Исследовательская работа Выполнила: ученица 10 класса Рязанова Олеся
21 слайд Описание слайда:
Описание слайда:Цель работы: Узнать, какие ученые внесли свой вклад в развитие понятия “степень”и «корня n-степени». Представить сведения из их автобиографии.
22 слайд Описание слайда:
Описание слайда:В III веке вышла книга греческого ученого Диофанта “Арифметика”, в которой было положено начало введению буквенной символики. Диофант вводит символы для первых шести степеней неизвестного и обратных им величин. В этой книге квадрат обозначается знаком Δ с индексом r; куб – знаком k c индексом r и т.д.
23 слайд Описание слайда:
Описание слайда:Дробные показатели степени и наиболее простые правила действии над степенями с дробными показателями встречаются у французского математика Николая Орема (1323–1382 гг.) в его труде “Алгоризм пропорций”. Николай Оре́м или Николай Орезмский (Nicolas Oresme, 1323 — 1382) — католический богослов, епископ, один из наиболее известных французских философов и учёных XIV в.
24 слайд Описание слайда:
Описание слайда:Позже дробные и отрицательные, показатели встречаются в “Полной арифметике” (1544 г.) немецкого математика М.Штифеля и у Симона Стевина. Симон Стевин предположил подразумевать под а в степени 1/n корень n-ой степени из а. Си́мон Сте́вин (лат. Simon Stevin, 1548—1620) — фламандский математик-универсал, инженер.
25 слайд Описание слайда:
Описание слайда:Немецкий математик М.Штифель (1487–1567 гг.) дал определение а0=1 при а≠0 и ввел название показатель (это буквенный перевод с немецкого Exponent). Немецкое potenzieren означает возведение в степень. Немецкий математик 15-16 века Один из изобретателей логарифмов
26 слайд Описание слайда:
Описание слайда:В конце ХVI века Франсуа Виет ввел буквы для обозначения не только переменных, но и их коэффициентов. Он применял сокращения: N, Q, C – для первой, второй и третьей степеней. Но современные обозначения (типа ) в XVII в ввел Рене Декарт
27 слайд Описание слайда:
Описание слайда:Упростите выражения и вычислите их значения, применяя свойства степени: 1 группа №2.004 2 группа №2.018 3 группа №2.019
28 слайд Описание слайда:
Описание слайда:Упростите выражения и вычислите их значения, применяя свойства степени: №2.004 №2.018 0,04 №2.019 16
29 слайд Описание слайда:
Описание слайда:Найдите способы решения уравнений и решите их: 1. 2.
30 слайд Описание слайда:
Описание слайда:Решение уравнения 1:
31 слайд Описание слайда:
Описание слайда:Решение уравнения 2
32 слайд Описание слайда:
Описание слайда:Решение уравнения 2
33 слайд Описание слайда:
Описание слайда:Ваше настроение Я доволен уроком, он полезен для меня, Я понимал все, о чем говорилось на нем Я не очень доволен уроком, он полезен для меня, но Я понимал не все, о чем говорилось на нем, у меня были ошибки Я не доволен уроком, он не интересен для меня, Я не понимал, о чем говорилось на нем. К ответам был не готов.
34 слайд Описание слайда:
Описание слайда:Домашнее задание:

Курс профессиональной переподготовки
Учитель математики

Курс повышения квалификации
Курс повышения квалификации
Найдите материал к любому уроку,
указав свой предмет (категорию), класс, учебник и тему:
Выберите категорию: Все категорииАлгебраАнглийский языкАстрономияБиологияВсеобщая историяГеографияГеометрияДиректору, завучуДоп. образованиеДошкольное образованиеЕстествознаниеИЗО, МХКИностранные языкиИнформатикаИстория РоссииКлассному руководителюКоррекционное обучениеЛитератураЛитературное чтениеЛогопедия, ДефектологияМатематикаМузыкаНачальные классыНемецкий языкОБЖОбществознаниеОкружающий мирПриродоведениеРелигиоведениеРодная литератураРодной языкРусский языкСоциальному педагогуТехнологияУкраинский языкФизикаФизическая культураФилософияФранцузский языкХимияЧерчениеШкольному психологуЭкологияДругое
Выберите класс: Все классыДошкольники1 класс2 класс3 класс4 класс5 класс6 класс7 класс8 класс9 класс10 класс11 класс
Выберите учебник: Все учебники
Выберите тему: Все темы
также Вы можете выбрать тип материала:

Общая информация
Номер материала: ДБ-271689
Похожие материалы
Вам будут интересны эти курсы:
Оставьте свой комментарийУрок математики 11 класс по теме «Степень с рациональным показателем»
Тема: «Степень с рациональным показателем»
Математика-это музыка разума.
Музыка-это математика чувств.
(Джеймс Джозеф Сильвестр)
Урок повторения и обобщения материала.
Цели урока:
Обобщение и систематизация знаний, умений, навыков.
Актуализация опорных знаний в условиях сдачи ЕГЭ.
Контроль и самоконтроль знаний, умений, навыков с помощью тестов.
Развитие умения сравнивать, обобщать.
План урока.
Формулировка цели урока.
Устная работа: «Дополни предложение», «Найди ошибку».
Математический диктант.
Решение серии примеров на основе демонстрационного варианта ЕГЭ.
Работа по учебнику.
Физминутка.
Самостоятельная работа на основе демонстрационного варианта ЕГЭ.
Задание на дом.
Подведение итогов урока.
Оборудование: проектор.
1. Друзья! Перед вашими глазами часть высказывания английского математика Джеймса Джозефа Сильвестра (1814–1897) о математике “Математика – это музыка разума”. Не правда ли, как романтично?
Вопрос. А как вы думаете, как определил он музыку?
“Музыка – это математика чувств”.
К чувствам мы можем отнести различного рода переживания. В этом году одной из причин ваших и моих переживаний является успешная сдача ЕГЭ и, как следствие, поступление в ВУЗ. Очень хочется, чтобы преобладали положительные эмоции. Должна быть уверенность, а это наши знания и навыки. Сегодня на уроке мы продолжим подготовку к ЕГЭ, повторяя и обобщая понятие степени.
Итак, тема сегодняшнего урока – «Степень с рациональным показателем».
2. Устная работа
Дополните предложения:
При умножении степеней с одинаковыми основаниями: показатели складываются
При делении степеней с одинаковыми основаниями : показатели вычитаются
Степень степени равна: произведению показателей
Степень числа а, не равного нулю с нулевым показателем равна :1
Степень произведения равна :произведению степеней
Степень дроби равна :дроби степеней
Степень с дробным показателем m/n есть:

2. «Найди ошибку»:
1. Имеют смысл выражения:
а)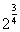 б)
б)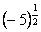 в)
в) 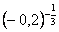 с)
с) 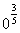 д)
д) 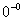
3. Уравнение имеет три корня
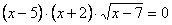 (нет, корень один: 7, т.к.
(нет, корень один: 7, т.к. )
)
3. Математический диктант
Вариант 1
1. представьте выражение в виде степени с рациональным показателем
а) 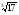 ; б)
; б) 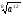 .
.
2. представьте выражение в виде корня из числа или выражения
а) 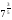 ; б)
; б) 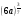 .
.
3. вычислите:
а) 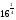 ; б)
; б) 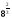 в)
в) 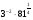 .
.
Вариант 2
1. представьте выражение в виде степени с рациональным показателем
а) 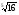 ; б)
; б) 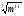 ;
;
2. представьте выражение в виде корня из числа или выражения
а) 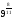 ; б)
; б) 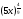 .
.
3. вычислите:
а) 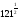 ; б)
; б) 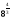 в)
в) 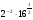 .
.
Матрица ответов:
Задание 1
Задание 2
Задание 3
Вариант 1

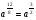

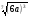
2
4

Вариант 2

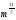
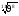
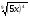
11
16
1
Решение серии примеров на основе демонстрационного варианта ЕГЭ
Задания выполняются на доске, с последующей проверкой ответов. (три человека по три примера, одновременно)
Найдите значение выражения
27∙253:502=
98∙411:367=
34∙58:154=
79∙1110:779=
 при x=3
при x=3
 при x=9
при x=9
 при x=5
при x=5
5. Работа по учебнику: №436(а,б), №441(а,б)
6. Физминутка.
6.Самостоятельная работа на основе демонстрационного варианта ЕГЭ с последующей проверкой на доске.
А теперь самое время потренироваться: перед вами примеры из демонстрационного варианта ЕГЭ.
Вы их видите как на доске, так и на листочках. Ваша задача – быстро решить и заполнить таблицы с ответами. Соответствие букв и чисел перед вами. Правильно вычислив или упростив выражения в таблице, вы прочтёте то, что необходимо вам при сдаче ЕГЭ.
1 вариант – удача;
2 вариант — знания;
3 вариант – уверенность.
7.Задание на дом п.34, №436(в,г), №441(в,г).
8.Подведение итогов урока.
Итак, сегодня на уроке мы увидели насколько широко понятие степени используется при сдаче ЕГЭ. Закрепить полученные навыки вы сможете, выполнив домашнюю работу
Методическая разработка плана-конспекта урока в 10 классе по теме » Степень с рациональным показтелем»


 МЕТОДИЧЕСКАЯ РАЗРАБОТКА
МЕТОДИЧЕСКАЯ РАЗРАБОТКА
План-конспект урока математики в 10-м классе по теме:
«Степень с рациональным показателем и ее свойства»
Урок изучения нового материала
Цель урока: обобщить и систематизировать знания по теме; закрепить навыки действий со степенями.
Задачи:
образовательные:
обобщить теоретический материал по теме урока;
проверить знания основных понятий на определение степени с рациональным показателем.
воспитательные:
воспитать умения и навыки групповой и самостоятельной работы;
расширить кругозор обучающихся в историческом аспекте; прививать трудолюбие, аккуратность в математических вычислениях и записях.
развивающие:
развивать умения анализировать учебный материал;
развивать любознательность, внимание, наблюдательность;
развивать интерес учащихся к математике, при анализе жизненных
ситуаций;
Формы организации познавательной деятельности учащихся:
фронтальная, самостоятельная работа, работа в группах.
Оборудование урока: компьютер, колонки, интерактивная доска.
Этапы урока:
I. Организационный момент (2 мин).
II. Подготовка к основному этапу занятия (2 мин).
III.Закрепление и систематизация раннее изученного материала. (12 мин.)
IV. Самостоятельная работа (7 мин).
V. Физкультминутка (3 мин).
VI. Работа в группах (8 мин).
VII. Итоги урока (2 мин).
VIII. Информация о домашнем задании (2 мин).
IX. Выставление оценок и их комментирование (1 мин).
X. Рефлексия (1 мин).
Девиз урока: «Математику нельзя изучать, наблюдая, как это делает сосед!»
А. Нивен
Ход урока:
Организационный момент.
Приветствие, проверка присутствующих. Объявление целей и задач урока.
На уроке закрепляем и систематизируем ранее изученный материал по теме «Степень с рациональным показателем и ее свойства». Учащиеся задают вопросы по домашней работе. Обсуждение наиболее проблемных заданий. Учитель озвучивает оценки по самостоятельной работе, проведенной на предыдущем уроке. Заранее на доске записана тема урока и домашнее задание.
Подготовка к основному этапу занятия.
Повторим!
Определение. Арифметическим корнем n-й степени (n
 N, n
N, n  2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а. Имеют место формулы:
2) из неотрицательного числа a называется такое неотрицательное число, n – я степень которого равна а. Имеют место формулы:
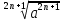 =
= 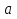 , n
, n  N
N
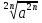 =
= 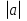 , n
, n  N
N
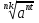 =
= 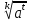 , при
, при 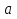
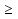 0.
0.
2) Определение. Степень с рациональным показателем
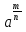 =
= 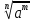 , где m
, где m  Z, n
Z, n  N,
N, 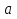
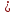 0;
0;
Если 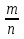
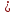 0, то
0, то 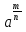 =
= 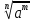 , при
, при 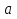
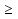 0.
0.
3) Свойства степени с рациональным показателем:
При a > 0, b > 0; p,q  Q :
Q :
а) 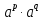 =
= 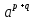 , г)
, г) 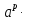
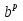 =
= 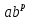 ,
,
б ) 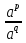 =
= 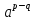 , д)
, д) 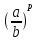 =
= 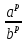 ,
,
в) 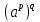 =
= 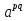 , е)
, е) 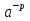 =
= 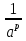 .
.
Закрепление и систематизация раннее изученного материала.
Представьте выражение в виде степени числа m:
а) 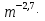
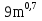 ,
, 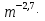
 ,
, 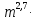
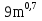
б) 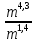 ,
,  ,
, 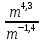 ,
, 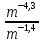 .
.
2. Вычислите:
1) 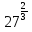 6)
6) 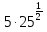
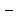
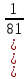
2) 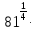
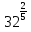 7)
7) 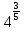

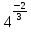 :
: 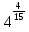
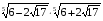 3)
3) 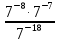 8)
8)
4) 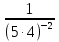

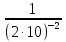 9)
9) 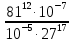
5) 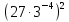 . 10)
. 10) 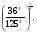
3. Найдите значение выражения:
а)  , в)
, в) 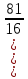 +
+ 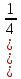 ,
,
б) 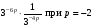 , г)
, г) 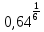

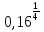 .
.
4. Имеет ли смысл выражение:
а)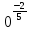 , в)
, в) 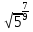 ,
,
б) 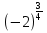 , г)
, г) 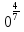 ?
?
5. Решите уравнение:
а) 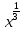 = 2, в)
= 2, в)  =
= 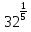 ,
,
б) 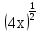 = 8, г)
= 8, г) 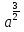 =
= 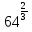 .
.
Самостоятельная работа (разноуровневая).
1 вариант
2 вариант
1. Вычислите:
а)
 ,
,б)

в)

2. Сократите дробь:
а)
 , б)
, б) .
.3.Решите уравнение:
а)
 = 2
= 2 ,
,б)
 = 1,
= 1,1. Вычислите:
а)
 ,
,б)

в)
 ,
,2. Сократите дробь:
а)
 , б)
, б) .
.3. Решите уравнение:
а)
 =
=  ,
,б)
 = 3.
= 3.
Для сильных учащихся:
3 вариант
1. Вычислите:
а)
 , б)
, б)  ,
,2. Упростите выражение:
а)
 б)
б) 
3. Решите уравнение:
а)
 2 = 0, б)
2 = 0, б)  2 = 0.
2 = 0.
Самостоятельную работу могут проверить 2-3 сильных учащихся по заранее заготовленным учителем критериям и ответам. Оценки озвучиваются и выставляются в дневник.
Физкультминутка.
На интерактивной доске открыт слайд с кроссвордом. Учитель предлагает учащимся отдохнуть, разгадывая кроссворд.
По горизонтали:
Показатель степени.
Геометрическая фигура, у которой все стороны равны и углы равны между собой. Выпуклый четырехугольник, у которого только две противолежащие стоны параллельны между собой, а две другие – нет.
Параллелограмм, у которого все углы прямые.
Восполнение (от араб. اَلْجَبْرْ, «аль-джабр» ).
По вертикали:
Раздел математики, изучающий соотношения между сторонами и углами треугольника.
Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю.
Произведение, состоящее из одинаковых множителей.
Геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.


Работа в группах.
Учитель делит класс на группы по 2 человека. (1учащийся с высокой мотивацией к учебе и 1 2 учащихся со средним (или низким) уровнем знаний).
2 учащихся со средним (или низким) уровнем знаний).
1.Вычислите:
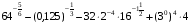
а)
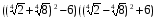
б)
2. Упростите:
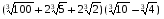
а)

б)
в) 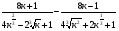

г) .
После коллективного обсуждения и решения в парах, вызывается слабый ученик к доске. На выбор учащийся комментирует решение любых одного-двух примеров. После чего можно всем сверить ответы с ответами на интерактивной доске.
Итоги урока.
Учащиеся из сильной группы опрашивают учащихся со средней и слабой мотивацией к учебе.
а) Что такое степень с рациональным показателем?
б) Какие формулы применяются при решении заданий по данной теме?
2. Учитель дает задание решить уравнение:
а)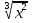 = 1, б)
= 1, б) 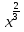 = 1.
= 1.
По желанию 1 ученик решает у доски с комментариями.
Решение:
а) Возведя обе части уравнения в куб, получим:
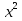 = 1;
= 1;
 =
= 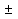 1.
1.
б) Это практически то же самое уравнение, что и в пункте а), но с одной существенной оговоркой: поскольку переменная  возводится в дробную степень, она по определению должна принимать только положительные значения. Значит, из найденных выше двух значений
возводится в дробную степень, она по определению должна принимать только положительные значения. Значит, из найденных выше двух значений  в качестве корня уравнения мы имеем право взять лишь значение
в качестве корня уравнения мы имеем право взять лишь значение  = 1.
= 1.
Ответ: а) 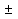 1 ; б) 1.
1 ; б) 1.
Информация о домашнем задании.
1.Решите уравнения:
1) 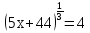
2) 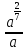 =
= 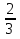
2. Вычислите: 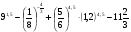
3. Из КИМов по математике ЕГЭ выписать и решить 10 заданий по теме «Степень с рациональным показателем и ее свойства»
Для сильных учащихся.
4. Упрстите:
1) 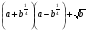 , 2)
, 2) 
Выставление оценок и их комментирование.
Разбираются ошибки в самостоятельной работе. Затем учитель дает свои комментарии по поводу оценок, в том числе оценивая работу сильных учащихся.
Рефлексия .
Учитель предлагает учащимся выбрать смайлик из предложенных трех вариантов которые лежат на парте.
Рис. №1 – тема несложная. Я легко справлюсь с домашним заданием.
Рис. №2 – тема сложная, но мне достаточно ещё раз самому сесть и прочитать параграф учебника. Почитать конспекты. Выполнить вдумчиво домашнее задание.
Рис. №3 – тема очень сложная, и мне нужна дополнительная работа с учителем по этой теме.
Поднимите тот, который ближе всего отражает ваше настроение в конце урока.
Рис. №1. Рис. №2. Рис. №3.
Урок окончен. Спасибо за хорошую работу!
Практическая работа по теме «Степень с рациональным показателем, корень n-ой степени»
Практическая работа по темам
«Степень с рациональным показателем, корень n-ой степени»
Вариант 1
Вариант 2
Задание 1. Вычислить:
а) 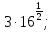 б)
б) 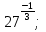 в)
в) 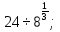
г) 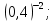 д)
д) 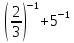 .
.
Задание 2. Вычислить:
а) 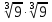 ; б)
; б) 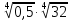 ; в)
; в) 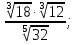
г) 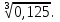
Задание 3. Найдите значение выражения 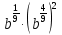 при
при 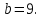
Задание 4. Найдите значение выражения 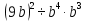 при
при 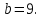
Задание 5. Найдите значение выражения 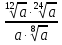 при
при 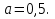
Задание 6. Вычислить: 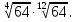
Задание 1. Вычислить:
а) 5 б)
б) 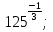 в) 81
в) 81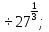
г) 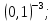 д)
д) 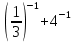 .
.
Задание 2. Вычислить:
а) 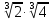 ; б)
; б)  ;
;
в) 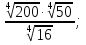 г)
г) 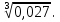
Задание 3. Найдите значение выражения  при
при 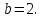
Задание 4. Найдите значение выражения 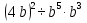 при
при 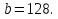
Задание 5. Найдите значение выражения 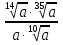 при
при 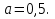
Задание 6. Вычислить: 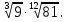
Вариант 3
Вариант 4
Задание 1. Вычислить:
а) 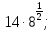 б)
б) 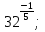 в)
в) 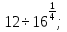
г) 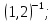 д)
д) 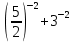 .
.
Задание 2. Вычислить:
а)  ; б)
; б) 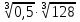 ;
;
в) 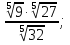 г)
г) 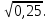
Задание 3. Найдите значение выражения 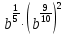 при
при 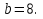
Задание 4. Найдите значение выражения  при
при 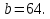
Задание 5. Найдите значение выражения 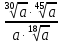 при
при 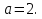
Задание 6. Вычислить: 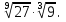
Задание 1. Вычислить:
а) 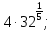 б)
б) 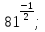 в) 3
в) 3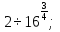
г) 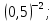 д)
д)  .
.
Задание 2. Вычислить:
а) 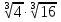 ; б)
; б) 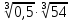 ;
;
в) 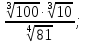 г)
г) 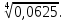
Задание 3. Найдите значение выражения  при
при 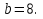
Задание 4. Найдите значение выражения 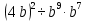 при
при 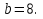
Задание 5. Найдите значение выражения 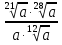 при
при 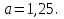
Задание 6. Вычислить: 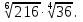
Время выполнения – 45 минут
Практическая работа по темам
«Степень с рациональным показателем, корень n-ой степени»
Вариант 5
Вариант 6
Задание 1. Вычислить:
а) 7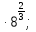 б)
б) 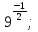 в)
в) 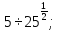
г) 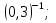 д)
д) 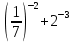 .
.
Задание 2. Вычислить:
а) 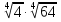 ; б)
; б) 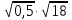 ; в)
; в) 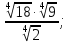
г) 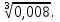
Задание 3. Найдите значение выражения 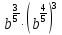 при
при 
Задание 4. Найдите значение выражения 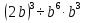 при
при 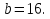
Задание 5. Найдите значение выражения 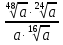 при
при 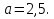
Задание 6. Вычислить: 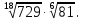
Задание 1. Вычислить:
а) 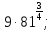 б)
б) 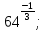 в)
в) 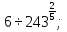
г)  д)
д)  .
.
Задание 2. Вычислить:
а)  ; б)
; б)  ;
;
в) 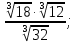 г)
г) 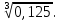
Задание 3. Найдите значение выражения 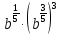 при
при 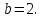
Задание 4. Найдите значение выражения 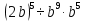 при
при 
Задание 5. Найдите значение выражения  при
при 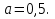
Задание 6. Вычислить: 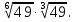
Вариант 7
Вариант 8
Задание 1. Вычислить:
а) 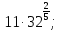 б)
б) 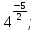 в)
в) 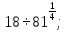
г) 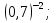 д)
д) 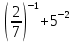 .
.
Задание 2. Вычислить:
а) 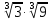 ; б)
; б) 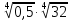 ; в)
; в) 
г) 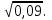
Задание 3. Найдите значение выражения 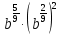 при
при 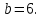
Задание 4. Найдите значение выражения 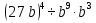 при
при 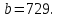
Задание 5. Найдите значение выражения  при
при 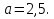
Задание 6. Вычислить: 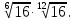
Задание 1. Вычислить:
а) 10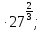 б)
б) 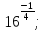 в)
в) 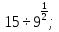
г)  д)
д) 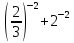 .
.
Задание 2. Вычислить:
а) 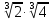 ; б)
; б) 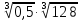 ;
;
в) 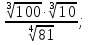 г)
г) 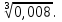
Задание 3. Найдите значение выражения 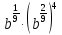 при
при 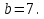
Задание 4. Найдите значение выражения 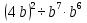 при
при 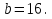
Задание 5. Найдите значение выражения 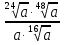 при
при 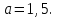
Задание 6. Вычислить: 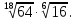
Время выполнения – 45 минут
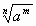
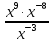 при x=3
при x=3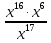 при x=9
при x=9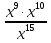 при x=5
при x=5
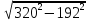

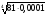 ,
,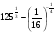
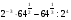
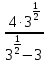 , б)
, б)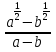 .
. ,
,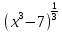 = 1,
= 1,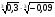 ,
,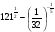
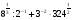 ,
,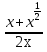 , б)
, б)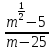 .
.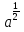 =
= 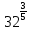 ,
,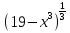 = 3.
= 3.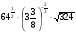 , б)
, б) 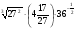 ,
,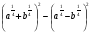 б)
б) 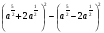
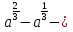 2 = 0, б)
2 = 0, б) 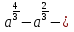 2 = 0.
2 = 0.