, ,

: V = Sh S — .	— , ­ . — , ­ ­, — ­. — ; h —
	— , ­ ­. ­
: V = a•b•c : S = 2(ab + bc + ca) d 2 = a 2 + b 2 + c 2	— ­, ­ . и: — , b — , — ; d — ( )
S = 6a 2 d 2 =3a 2	— ­, . = b =, V = 3 (­ — «»), d —
:	— , ­, ­, . S — ; h —
	– . – .
	– .
1. 2. 3. 4. 5.	– . . •  – 4, – , – 6, – 4. •  – 6, – , – 12, – 8. •  – 8, – , – 12, – 6. •  – 12, – , – 30, – 20. – 20, – , – 30, – 12.
1. 2.	. •  . •  S – . V – .
	–
	. R — ; — ; h —
	. R — ; — ; h —
	. R — , a , b — , h —

www.calc.ru

Предмет стереометрии. Аксиомы стереометрии. Видеоурок. Геометрия 10 Класс

Напомним: геометрия – это наука, которая изучает свойства геометрических фигур.

Геометрическая фигура – это любая совокупность точек. Геометрия подразделяется на планиметрию и на стереометрию, которую мы начинаем изучать.

Мы начнем изучение стереометрии с основных понятий, основных фигур, аксиом, точно также как это делалось в планиметрии. 

Основными фигурами стереометрии являются точка, прямая, плоскость. Примеры стереометрических фигур: шар, сфера, конус, цилиндр, параллелепипед и т.д.

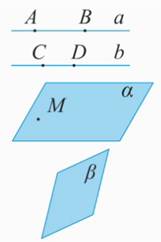
Рис. 1.

А, В, С, D – точки. Точки обозначаются прописными латинскими буквами.

АВ = 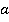, CD = b – прямые. Прямые обозначаются строчными латинскими буквами.

 – плоскости. Плоскости обозначаются греческими буквами. (Рис. 1).

Рассмотрим прямую 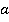. На ней лежат точки А и В. Прямая 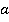может быть также обозначена как АВ.

Рассмотрим прямую b, на ней лежат точки С и D. Прямая b может быть также обозначена как СD.

Специфика всей стереометрии заключается в том, что пространственные фигуры мы будем изображать на плоскости.

Так же, как и в планиметрии, важен знак принадлежности,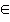

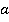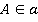. Например, точка А принадлежит прямой : .

Рассмотрим плоскость 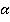 (Рис. 1). Точка М принадлежит плоскости 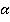: 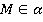. А вот прямая  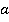не принадлежит плоскости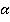

: . 

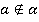Аксиомы стереометрии.

Аксиома 1 (А1)

Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна. 

Пояснение к аксиоме А1.

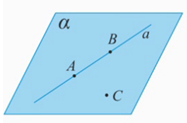
Рис. 2.

Рассмотрим три точки: А, В, С, причем точка С не принадлежит прямой АВ: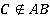 (Рис. 2). Тогда через три точки А, В, С, не лежащие на одной прямой, проходит плоскость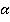

, и притом только одна.

Плоскость 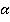можно также обозначить через три точки АВС. 

Аксиома 2 (А2)

Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости. 

По-иному говорят, что прямая лежит в плоскости или что плоскость проходит через прямую. 

Пояснение к аксиоме А2.

Рассмотрим плоскость 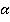, точки А, В прямой 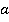принадлежат плоскости 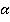(Рис. 3).

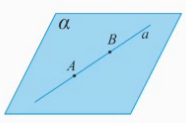
Рис. 3.

Аксиома утверждает – все точки прямой 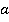(прямой АВ) принадлежат плоскости 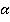, т.е. вся прямая лежит в плоскости 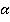или плоскость 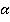проходит через прямую 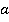. Смысл заключается в следующем: из того, что только две точки принадлежат плоскости, вытекает, что бесчисленное множество точек прямой лежат в этой плоскости.

Эту аксиому можно записать следующим образом:

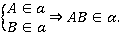
Следствие: Может ли быть только три общие точки у прямой и плоскости? Нет, не может быть. Может быть две точки, и тогда вся прямая лежит в плоскости.

Если у прямой и плоскости одна общая точка М, то тогда говорят, что прямая 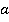и плоскость 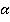пересекаются в точке М (Рис. 4). Этот факт записывается следующим образом: .

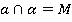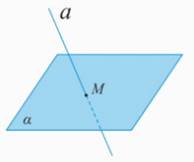
Рис. 4. 

Аксиома 3 (А3)

Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей. Говорят, что плоскости пересекаются по прямой. 

Пояснение к аксиоме А3.

Имеем разные плоскости: плоскость 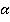, плоскость . Известно, что они имеют общую точку М, точка М принадлежит плоскости и плоскости

. (Рис. 5)

Рис. 5.

Отсюда вытекает, что существует прямая 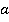, которая проходит через точку М, которая одновременно принадлежит и плоскости a, и плоскости b. Вот в этом случае и говорят, что плоскости 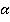и пересекаются по прямой .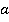

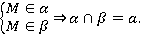
Смысл аксиом разъясняется в многочисленных вопросах и задачах. Вот некоторые из них. 

Решение задач

Дан тетраэдр АВСD (Рис. 6). Даны следующие точки: точка Е – внутренняя точка ребра АВ, точка Р – внутренняя точка отрезка ЕD, точки М и К, соответственно, на ребрах ВD и DС.

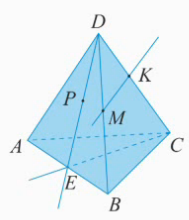
Рис. 6. 

Задача 1

а) В какой плоскости лежит прямая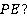

Ответ: . Прямая РЕ лежит в плоскости АВD, так как в этой плоскости лежат две точки этой прямой. Точка Е лежит в плоскости АВD и точка Р лежит в этой же плоскости. Значит, по второй аксиоме все точки прямой РЕ лежат в плоскости АВD.

 б) В какой плоскости лежит прямая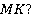

Ответ: 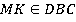. Прямая MK лежит в плоскости DBC, так как в этой плоскости лежат две точки этой прямой. Точка M лежит в плоскости DBC и точка K лежит в плоскости DBC. По второй аксиоме все точки прямой MK лежат в плоскости DBC.

 в) В каких плоскостях лежит прямая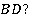

Ответ: Прямая BD лежит в плоскостиBDА и в плоскости BDС. Значит, прямая BD одновременно лежит в двух плоскостях. Прямая BD есть линия пересечения двух плоскостей. Говорят, что грани АBD, BDС пересекаются по прямой BD. Это можно записать так:

г) В каких гранях лежит прямая ?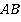

Ответ: Прямая АB лежит в грани АВС и в грани АBD. Значит, прямая АВ есть линия пересечения двух этих граней.

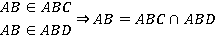
д) В каких гранях лежит прямая ?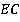

Ответ: Прямая EC лежит в плоскости АВС и в плоскости ECD, так как точки Е и С лежат одновременно в плоскости АВС и в плоскости ECD. Значит, прямая ЕС есть линия пересечения этих плоскостей. 

 

Задача 2.

а) Найдите точку пересечения прямой DК с плоскостью АВС.

Решение:

Прямая DК содержит точку С. Плоскость АВС содержит точку С. Значит, прямая DК и плоскость АВС пересекаются в точке С.

б) Найдите точку пересечения прямой СЕ с плоскостью АDВ.

Решение: 

Точка Е принадлежит и прямой СЕ, и плоскости АDВ. Значит, Прямая СЕ пересекается с плоскостью АDВ в точке Е. 

Задача 3.

а) Найдите точки, лежащие одновременно в плоскостях АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, 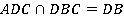. Все точки прямой DВ являются ответом. 

б) Найдите прямые, по которым пересекаются плоскость АDВ и DВС.

Решение:

Точка В и точка D одновременно лежат и в АDВ, и в DВС. Значит, прямая DВ есть прямая, по которой пересекаются заданные плоскости. 

в) Назовите прямые, по которым пересекаются плоскости АDВ и СDА.

Решение:

Точки А, D лежат в плоскости АDВ, а также точки А, D лежат в другой плоскости СDА. Значит, АD – линия их пересечения: .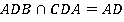 

г) Назовите прямые, по которым пересекаются плоскости РDС и АВС.

Решение: 

Плоскость РDС совпадает с плоскостью ЕDС. Точка Е и точка С одновременно лежат в двух плоскостях: РDС и АВС. Значит, СЕ – это линия пересечения двух плоскостей.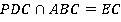  

Итак, мы рассмотрели предмет стереометрии, три основные аксиомы, их применение. На этих аксиомах строится все грандиозное здание стереометрии.

 

Список рекомендованной литературы

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

2. Геометрия. 10-11 класс: Учебник для общеобразовательных учебных заведений / Шарыгин И. Ф. – М.: Дрофа, 1999. – 208 с.: ил.

3. Геометрия. 10 класс: Учебник для общеобразовательных учреждений с углубленным и профильным изучением математики /Е. В. Потоскуев, Л. И. Звалич. – 6-е издание, стереотип. – М. : Дрофа, 008. – 233 с. :ил.

 

Рекомендованные ссылки на ресурсы интернет

1. Математика  (Источник).

2. Физ-мат класс (Источник).

3. ЯКласс (Источник).

 

Рекомендованное домашнее задание

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с. : ил.

Задания 2, 4 на стр. 9.

Перечислите известные вам аксиомы стереометрии.

Рис 7. 

2. Дан куб .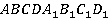

В каких плоскостях лежат прямые:

а) AB

б) AC₁

в) DC

3. Назовите прямые, по которым пересекаются плоскости

а) ABC  и ABB₁

б) DCC₁ и  BB₁C. 

interneturok.ru

Стереометрия

Стереометрия – раздел геометрии, в котором изучаются свойства пространственных фигур, то есть фигур, не принадлежащих одной плоскости. В стереометрии рассматриваются различные случаи взаимного расположения прямых и плоскостей в пространстве, такие пространственные фигуры, как призма, пирамида, тела вращения, правильные многогранники и др. При изучении стереометрии обобщаются некоторые планиметрические понятия: вектор, геометрическое преобразование, прямоугольная система координат и др. Важными вопросами в стереометрии являются вопросы измерения площадей и объёмов рассматриваемых пространственных фигур.

Большинство пространственных фигур представляют собой абстракцию различных предметов. Изучение стереометрии включает не только усвоение некоторых фактов и понятий, но владение математическими методами, которые применяются для обоснования этих фактов. Обратим внимание на структуру стереометрии, как учебного курса. Стереометрия строится следующим образом:

• перечисляются исходные понятия, которые принимаются без определения;
• приводится список аксиом;
• при помощи исходных понятий даются определения другим геометрическим понятиям;
• на основании аксиом и определений доказываются теоремы.

Исходными понятиями стереометрии являются следующих три понятия: «точка», «расстояние между точками»,  «плоскость». С их помощью определяются и другие понятия стереометрии. Определить понятие (дать ему определение) – это значит указать его существенные, характерные особенности, указать признаки. Некоторые из  этих признаков являются признаками сходства и устанавливают связь данного понятия с другими, уже известными понятиями; иные – признаки различия, указывающие на особенные свойства данных понятий.

Исходным геометрическим понятием непосредственно определение не даётся. Их нельзя свести и каким-либо другим понятиям в принятой системе изложения. Но это не значит, что они остаются совершенно неопределёнными. Они обозначаются косвенно, через перечисление некоторых признаков и свойств в аксиомах. С помощью аксиом логическим путём выводятся другие свойства геометрических понятий. Утверждения такого рода называются теоремами, а рассуждения, в ходе которых они устанавливаются – доказательствами.

Приведём некоторые обозначения, применяемые в стереометрии:

α, β, γ, … – обозначения плоскостейα, β,  γ…;

А, В, С,… – точки;

а, b, с,… – прямые;

А = В, а = b, α = β – точки А и В совпадают, прямые а и b совпадают, плоскости α и β совпадают;

А ≠ В, а ≠ b, α ≠ β – точки А и В не совпадают, прямые а и b не совпадают, плоскости α и β не совпадают;

А Є а, А Є α – точка А принадлежит прямой а, точка А принадлежит плоскости α;

А Ȼ а, А Ȼ α – точка А не принадлежит прямой а, точка А  не принадлежит плоскости α.

© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.

blog.tutoronline.ru

Основные понятия стереометрии ℹ️ определения, теоремы с доказательствами, аксиомы и следствия из них, названия фигур и их свойства

Основные понятия стереометрии

Стереометрия — это раздел геометрии, в котором изучаются свойства фигур в пространстве. Слово «стереометрия» происходит от греческих слов «στερεοσ» — объемный, пространственный и «μετρεο» — измерять.

Многогранник представляет собой геометрическое тело, ограниченное конечным числом плоских многоугольников, любые два из которых, имеющие общую сторону, не лежат в одной плоскости. При этом сами многоугольники называются гранями, их стороны – ребрами многогранника, а их вершины – вершинами многогранника.

Фигура, образованная всеми гранями многогранника, называется его поверхностью (полной поверхностью), а сумма площадей всех его граней – площадью (полной) поверхности.

Куб – это многогранник, имеющий шесть граней, которые являются равными квадратами. Стороны квадратов называются ребрами куба, а вершины – вершинами куба.

Параллелепипед – это многогранник, у которого шесть граней и каждая из них – параллелограмм. Стороны параллелограммов называются ребрами параллелепипеда, а их вершины – вершинами параллелепипеда. Две грани параллелепипеда называются противолежащими, если они не имеют общего ребра, а имеющие общее ребро называются смежными. Иногда какие-нибудь две противолежащие грани параллелепипеда выделяются и называются основаниями, тогда остальные грани – боковыми гранями, а их стороны, соединяющие вершины оснований параллелепипеда, – его боковыми ребрами.

Прямой параллелепипед – это такой параллелепипед, у которого боковые грани – прямоугольники.

Прямоугольный параллелепипед – это параллелепипед, у которого все грани – прямоугольники. Заметим, что всякий прямоугольный параллелепипед является прямым параллелепипедом, но не любой прямой параллелепипед есть прямоугольный.

Две вершины параллелепипеда, не принадлежащие одной грани, называются противолежащими. Отрезок, соединяющий противолежащие вершины параллелепипеда, называется диагональю параллелепипеда. У параллелепипеда всего четыре диагонали.

Призма (n-угольная) – это многогранник, у которого две грани – равные n-угольники, а остальные n граней – параллелограммы. Равные n-угольники называются основаниями, а параллелограммы – боковыми гранями призмы.

Прямая призма – это такая призма, у которой боковые грани – прямоугольники. Правильная n-угольная призма – это призма, у которой все боковые грани – прямоугольники, а ее основания – правильные n-угольники.

Сумма площадей боковых граней призмы называется площадью ее боковой поверхности (обозначается Sбок). Сумма площадей всех граней призмы называется площадью поверхности призмы (обозначается Sполн).

Пирамида (n-угольная) – это многогранник, у которого одна грань – какой-нибудь n-угольник, а остальные n граней – треугольники с общей вершиной; n-угольник называется основанием; треугольники, имеющие общую вершину, называются боковыми гранями, а их общая вершина называется вершиной пирамиды. Стороны граней пирамиды называются ее ребрами, а ребра, сходящиеся в вершине, называются боковыми.

Сумма площадей боковых граней пирамиды называется площадью боковой поверхности пирамиды (обозначается Sбок). Сумма площадей всех граней пирамиды называется площадью поверхности пирамиды (площадь поверхности обозначается Sполн).

Правильная n-угольная пирамида – это такая пирамида, основание которой – правильный n-угольник, а все боковые ребра равны между собой. У правильной пирамиды боковые грани – равные друг другу равнобедренные треугольники.

Треугольная пирамида называется тетраэдром, если все ее грани – равные правильные треугольники. Тетраэдр является частным случаем правильной треугольной пирамиды (т.е. не каждая правильная треугольная пирамида будет тетраэдром).

Аксиомы стереометрии

Аксиома 1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.

Аксиома 2. Если две точки прямой лежат в плоскости, то все точки данной прямой лежат в этой плоскости. В этом случае говорят, что прямая лежит в плоскости или что плоскость проходит через прямую.

Аксиома 3. Если две плоскости имеют общую точку, то они имеют общую прямую, которой принадлежат все общие точки этих плоскостей. В этом случае говорят, что плоскости пересекаются по прямой.

Аксиома 4. В любой плоскости пространства выполняются все аксиомы планиметрии. Таким образом, в любой плоскости пространства можно использовать все доказанные теоремы и формулы из планиметрии.

Следствия из аксиом

Следствие 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.

Следствие 2. Через две пересекающиеся прямые проходит плоскость и притом только одна.

Следствие 3. Через две параллельные прямые проходит плоскость и притом только одна. 

Следствие 4. Из аксиомы 2 следует, что прямая, не лежащая в плоскости, не может иметь с плоскостью более одной общей точки. Если прямая и плоскость имеют только одну общую точку, то говорят, что прямая пересекает плоскость.

Основные теоремы стереометрии

Теоремы о параллельности прямых и плоскостей

Определение: Прямая и плоскость называются параллельными, если они не имеют общих точек. Если прямая а параллельна плоскости β, то пишут: a // β

Теорема 1: Если прямая AB параллельна какой-нибудь прямой CD, расположенной в плоскости P, то она параллельна самой плоскости.

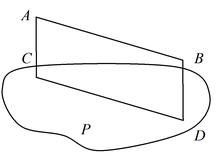
Теорема 2: Если плоскость R проходит через прямую AB, параллельную другой плоскости P, и пересекает эту плоскость, то линия пересечения CD параллельна первой прямой AB.

Теорема 3: Если две параллельные плоскости P и Q пересекаются третьей плоскостью R, то линии пересечения AB и CD параллельны.

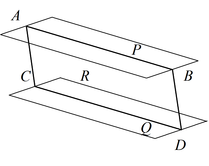
Теорема 4: Если две пересекающиеся прямые AB и DC одной плоскости соответственно параллельны двум прямым A₁ B₁ и C₁ D₁  другой плоскости, то эти плоскости параллельны.

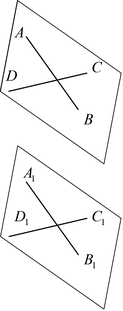
Теоремы о перпендикулярности прямых и плоскостей

Теорема 1: Для того что бы прямая AB была перпендикулярна плоскости P, необходимо и достаточно, чтобы она была перпендикулярна двум произвольным непараллельным прямым CD и EF, лежащим в этой плоскости.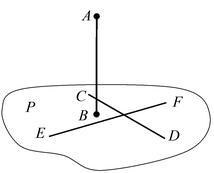

Теорема 2: Для того, чтобы прямая DE проведенная на плоскости P через основание наклонной AC была ей перпендикулярна, необходимо и достаточно, чтобы эта прямая была перпендикулярна к проекции BC, наклонной на плоскость P (Достаточное условие этой теоремы называется «Теоремой о трех перпендикулярах»: AC, BC, DE).

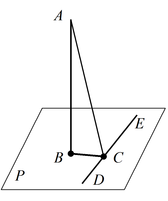
Теорема 3: Если две прямые AB и CD перпендикулярны одной плоскости P, то они параллельны между собой.

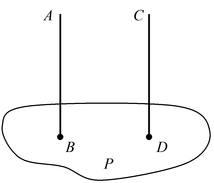
Теорема 4: Если две плоскости P и Q перпендикулярны одной прямой AB, то они параллельны друг другу.

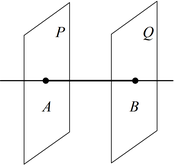
Теоремы о перпендикулярности плоскостей

Двугранный угол называется прямым, если его линейный угол прямой. Прямой двугранный угол равен смежному с ним двугранному углу.

Определение: Две плоскости называются взаимно перпендикулярными, если они образуют прямые двугранные углы.

Теорема 1:Перпендикулярность прямых в пространстве. Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они то же перпендикулярны.

Теорема 2: Признак перпендикулярности прямой и плоскости. Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна данной плоскости.

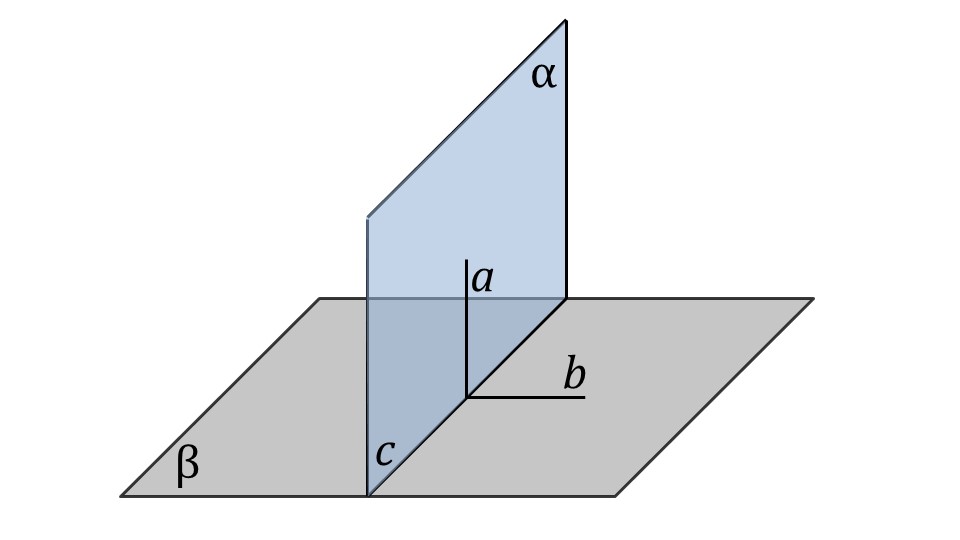
Следствие 1: Если из точки одной из двух взаимно перпендикулярных плоскостей проведен перпендикуляр к другой плоскости, то он принадлежит первой плоскости.

Следствие 2: Если две плоскости, перпендикулярные к третьей плоскости, пересекаются, то их линия пересечения есть перпендикуляр к этой плоскости.

Теорема о скрещивающихся прямых

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема 1: Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на этой прямой, то эти прямые скрещивающиеся.

Доказательство

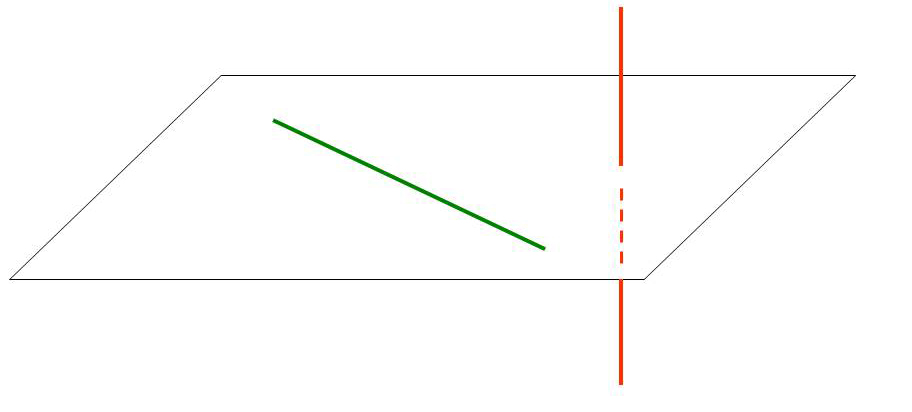
Пусть нам дана плоскость α. Прямая АВ лежит в плоскости α, а прямая DC пересекается с плоскостью α в точке С, которая не лежит на прямой АВ (Рис. 1.). Докажем, что прямые АВ и DC являются скрещивающимися.

Используем метод от противного. Предположим, что существует плоскость β, в которой лежит, и прямая АВ и прямая DC. Тогда в плоскости β лежит прямая АВ и точка С. Через прямую и точку, не лежащую на ней проходит единственная плоскость — α. Значит, такой плоскости β, в которой лежит, и прямая АВ и прямая DC, не существует. То есть, прямые АВ и DC – скрещивающиеся. Теорема доказана.

Теорема 2: Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Доказательство.

Пусть нам даны две скрещивающиеся прямые АВ и CD. Докажем, что через прямую АВ проходит плоскость, параллельная прямой CD, и притом только одна.

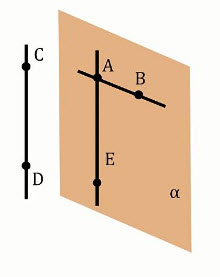
Проведем через точку А прямую АЕ, параллельную прямой DC (Рис. 6.). По теореме о параллельных прямых, такая прямая существует и единственная. Тогда через две пересекающиеся прямые АВ и АЕ можно провести единственную плоскость α. Так как прямая DC, которая не лежит в плоскости α, параллельна прямой АЕ, лежащей в плоскости α,  значит, что прямая DC параллельна плоскости α, по признаку параллельности прямой и плоскости. Существование доказано.

Докажем единственность такой плоскости. Пусть существует другая плоскость β, которая проходит через прямую АВ и параллельна прямой DC. Тогда прямая АЕ пересекает плоскость β, а значит и параллельная ей прямая DC пересекает плоскость β, по лемме. То есть, прямая DC не параллельна плоскости β. Получили противоречие. Следовательно, плоскость α – единственная. Теорема доказана.

Теорема о трех перпендикулярах

Теорема 1: Теорема о трех перпендикулярах. Прямая, проведенная в плоскости и перпендикулярная проекции наклонной на эту плоскость, перпендикулярна и самой наклонной. Верно и обратное утверждение:

Теорема 2: (о трех перпендикулярах). Прямая, проведенная в плоскости и перпендикулярная наклонной, перпендикулярна и ее проекции на эту плоскость.

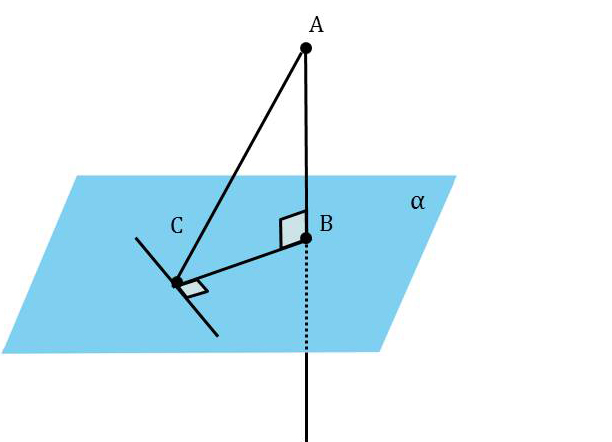
Доказательство.

Пусть AB — перпендикуляр к плоскости a, AC — наклонная и c — прямая в плоскости 

, проходящая через точку C и перпендикулярная проекции BC. Проведём прямую CK параллельно прямой AB. Прямая CK перпендикулярна плоскости a (так как она параллельна AB), а значит, и любой прямой этой плоскости, следовательно, CK перпендикулярна прямой c. Проведём через параллельные прямые AB и CK плоскость b (параллельные прямые определяют плоскость, причём только одну). Прямая c перпендикулярна двум пересекающимся прямым, лежащим в плоскости b, это BC по условию и CK по построению, значит, она перпендикулярна и любой прямой, принадлежащей этой плоскости, значит, перпендикулярна и прямой AC.

Взаимное расположение прямых в пространстве

Прямые в пространстве могут лежать в одной плоскости или в разных плоскостях.

1. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не имеют общих точек.
2. Две прямые в пространстве называются пересекающимися, если они лежат в одной плоскости и имеют общую точку.
3. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости

Основные фигуры в стереометрии

Симметрия фигур

1. Точки M и M1 называются симметричными относительно точки O, если O является серединой отрезка MM1.
2. Точки M и M1 называются симметричными относительно прямой l, если прямая l проходит через середину отрезка MM1 и перпендикулярна ему.
3. Точки M и M1 называются симметричными относительно плоскости α, если плоскость α проходит через середину отрезка MM1 и перпендикулярна этому отрезку.
4. Точка O (прямая l, плоскость α) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно точки O (прямой l, плоскости α) некоторой точке этой же фигуры.
5. Выпуклый многогранник называется правильным, если все его грани – равные между собой правильные многоугольники и в каждой вершине сходится одно и то же число ребер.

Двугранный угол

Двугранным углом называется фигура, образованная двумя полуплоскостями с общей граничной прямой и частью пространства, для которой эти полуплоскости служат границей.
Линейным углом двугранного угла называется угол, сторонами которого являются лучи с общим началом на ребре двугранного угла, которые проведены в его гранях перпендикулярно ребру.

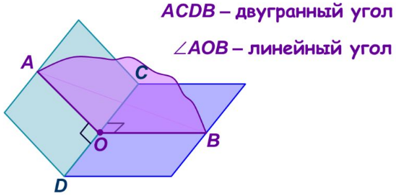
Таким образом, линейный угол двугранного угла – это угол, образованный пересечением двугранного угла плоскостью, перпендикулярной его ребру. Все линейные углы двугранного угла равны между собой. Градусной мерой двугранного угла называется градусная мера его линейного угла.

Двугранный угол называется прямым (острым, тупым), если его градусная мера равна 90° (меньше 90°, больше 90°). 

Двугранным углом при ребре многогранника называется двугранный угол, ребро которого содержит ребро многогранника, а грани двугранного угла содержат грани многогранника, которые пересекаются по данному ребру многогранника.

Углом между пересекающимися плоскостями называется угол между прямыми, проведенными соответственно в данных плоскостях перпендикулярно их линии пересечения через некоторую ее точку.

Две плоскости называются перпендикулярными, если угол между ними равен 90°.

Теоремы:

Теорема 1: (признак перпендикулярности плоскостей). Если одна из двух плоскостей проходит через прямую, перпендикулярную другой плоскости, то эти плоскости перпендикулярны.

Теорема 2: Прямая, лежащая в одной из двух перпендикулярных плоскостей и перпендикулярная прямой, по которой они пересекаются, перпендикулярна другой плоскости.

Призма

Призма – многогранник, две грани которого являются равными многоугольниками, лежащими в параллельных плоскостях, а остальные грани – параллелограммами, имеющими общие стороны с этими многоугольниками.

Основания – это две грани, являющиеся равными многоугольниками, лежащими в параллельных плоскостях. На чертеже это: ABCDE и KLMNP.

Боковые грани – все грани, кроме оснований. Каждая боковая грань обязательно является параллелограммом. На чертеже это: ABLK, BCML, CDNM, DEPN и EAKP.

Боковая поверхность – объединение боковых граней.

Полная поверхность – объединение оснований и боковой поверхности.

Боковые ребра – общие стороны боковых граней. На чертеже это: AK, BL, CM, DN и EP.

Высота – отрезок, соединяющий основания призмы и перпендикулярный им. На чертеже это, например, KR.

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани. На чертеже это, например, BP.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания. Другое определение: диагональная плоскость – плоскость, проходящая через два боковых ребра призмы, не принадлежащих одной грани.

Диагональное сечение – пересечение призмы и диагональной плоскости. В сечении образуется параллелограмм, в том числе, иногда, его частные случаи – ромб, прямоугольник, квадрат. На чертеже это, например, EBLP.

Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру. Площадь поверхности и объём призмы.

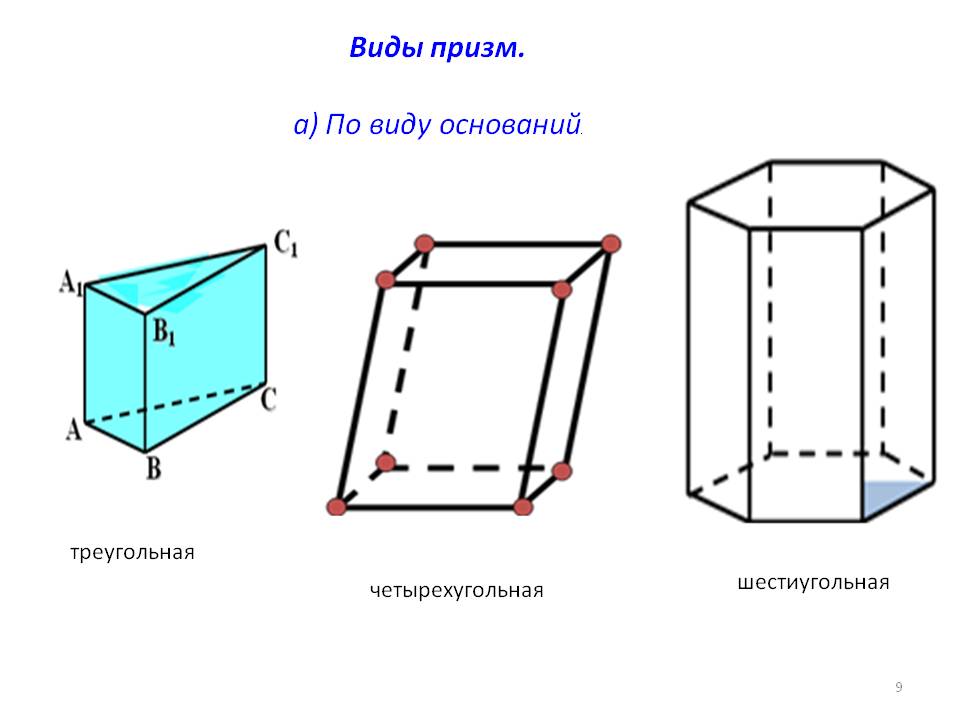
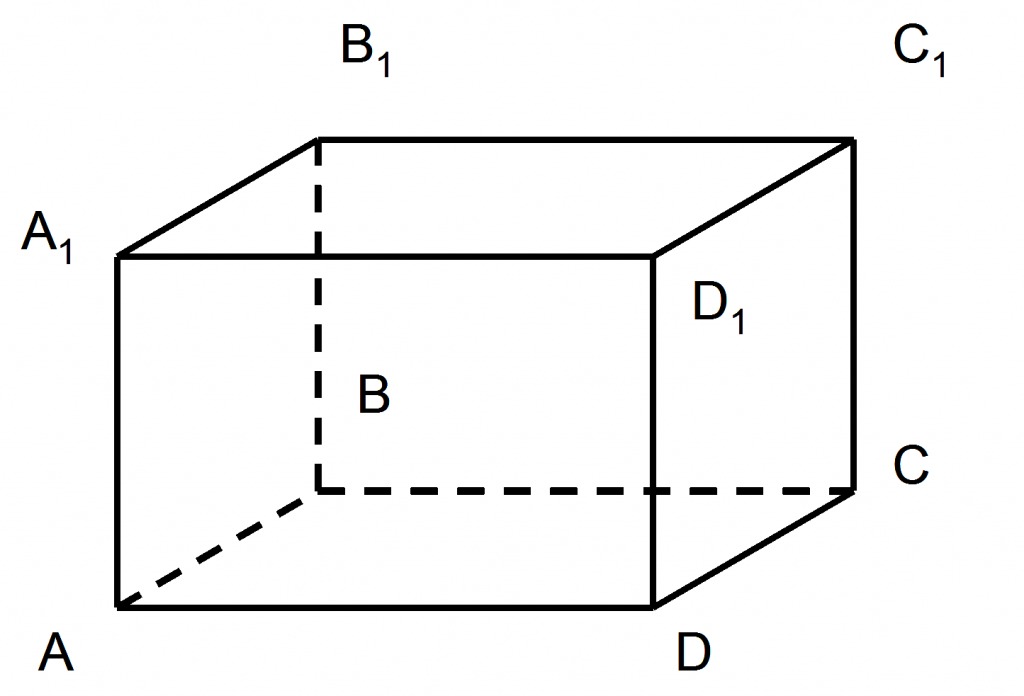
Площадь поверхности и объём призмы

Пусть H — высота призмы, A₁ B₁ — боковое ребро призмы, Pосн — периметр основания призмы, осн S площадь основания призмы, бок S — площадь боковой поверхности призмы, полн S — площадь полной поверхности призмы, V — объем призмы, P — периметр перпендикулярного сечения призмы, S — площадь перпендикулярного сечения призмы. Тогда имеют место следующие соотношения:

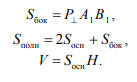
Свойства призмы:

• Основания призмы являются равными многоугольниками.
• Боковые грани призмы являются параллелограммами.
• Боковые ребра призмы параллельны и равны.
• Объём призмы равен произведению её высоты на площадь основания

Параллелепипед

Параллелепипедом называется призма, основанием которой служит параллелограмм.

Параллелограммы, из которых составлен параллелепипед, называются его гранями, их стороны – ребрами, а вершины параллелограммов – вершинами параллелепипеда.

У параллелепипеда все грани — параллелограммы.

Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные.

Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани ― боковыми гранями параллелепипеда.

Ребра параллелепипеда, не принадлежащие основаниям, называют боковыми ребрами.

Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих ребер — противоположными.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда. A1 H h2 A2 An A3 B1 B2 n B3 B A B C D A1 B1 C1 D1 7

Прямой параллелепипед, у которого основанием является прямоугольник, называется прямоугольным параллелепипедом. У прямоугольного параллелепипеда все грани — прямоугольники.

Длины непараллельных ребер прямоугольного параллелепипеда называются его линейными размерами (измерениями).

Свойства параллелепипеда:

1. Противоположные грани параллелепипеда равны и параллельны.
2. Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Боковые грани прямого параллелепипеда — прямоугольники.
4. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений. Диагонали прямоугольного параллелепипеда равны.

Пирамида

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину. По числу углов основания различают пирамиды треугольные, четырёхугольные и так далее. 

Основание – многоугольник, которому не принадлежит вершина пирамиды. На чертеже основание это BCDE.

Грани, отличные от основания, называются боковыми. 

Общая вершина боковых граней называется вершиной пирамиды (именно вершиной всей пирамиды, а не просто вершиной, как все остальные вершины). 

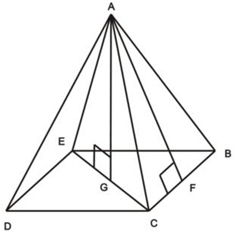
Высотой пирамиды называется перпендикуляр, проведенный из вершины пирамиды на ее основание. Длина этого перпендикуляра обозначается буквой H.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. 

Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину пирамиды и диагональ основания.

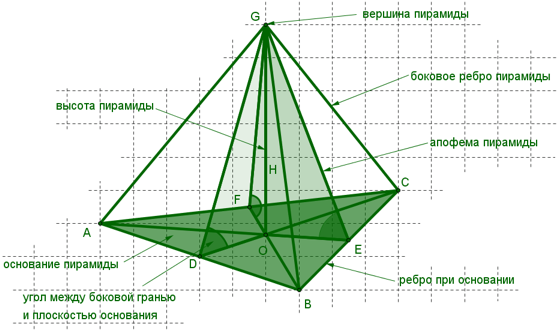
Свойства пирамиды:

1. Боковые ребра пирамиды равны.
2. Боковые ребра пирамиды одинаково наклонены к основанию пирамиды.
3. Вершина пирамиды проектируется в центр окружности, описанной около основания пирамиды.
4. Высоты всех боковых граней пирамиды, проведенные из вершины пирамиды, равны, а высота пирамиды лежит внутри пирамиды.
5. Все двугранные углы при основании пирамиды равны.
6. Вершина пирамиды проектируется в центр окружности, вписанной в основание.
7. Высоты всех боковых граней пирамиды, проведённые из вершины пирамиды, равны, а высота пирамиды лежит вне пирамиды.
8. Двугранные углы между боковыми гранями и плоскостью основания пирамиды равны.
9. Вершина пирамиды проектируется в центр окружности, вневписанной в основание пирамиды.

Правильная пирамида

Пирамида называется правильной, если её основанием является правильный многоугольник, а вершина проецируется в центр основания.

Свойства правильной пирамиды:

1. В правильной треугольной пирамиде противоположные ребра попарно перпендикулярны.
2. Боковые ребра правильной пирамиды равны между собой.
3. Двугранные углы при основании правильной пирамиды равны между собой.
4. Двугранные углы при боковых рёбрах правильной пирамиды равны.

Тетраэдр

Тетраэдр – простейший многогранник, гранями которого являются четыре треугольника, иными словами, треугольная пирамида. Для тетраэдра любая из его граней может служить основанием. Всего у тетраэдра 4 грани, 4 вершины и 6 рёбер.

Тетраэдр называется правильным, если все его грани – равносторонние треугольники.

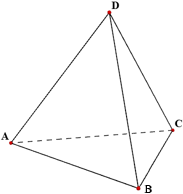
Свойства тетраэдра:

1. Все ребра правильного тетраэдра равны между собой.
2. Все грани правильного тетраэдра равны между собой.
3. Периметры, площади, высоты и все остальные элементы всех граней соответственно равны между собой.

Прямоугольная пирамида

При решении задач по стереометрии, пирамида называется прямоугольной, если одно из боковых рёбер пирамиды перпендикулярно основанию. В таком случае, это ребро и является высотой пирамиды. Ниже примеры треугольной и пятиугольной прямоугольных пирамид.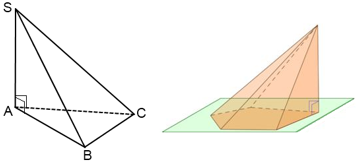 

Усечённая пирамида

Усеченной пирамидой называется многогранник, у которого вершинами служат вершины основания и вершины ее сечения плоскостью, параллельной основанию.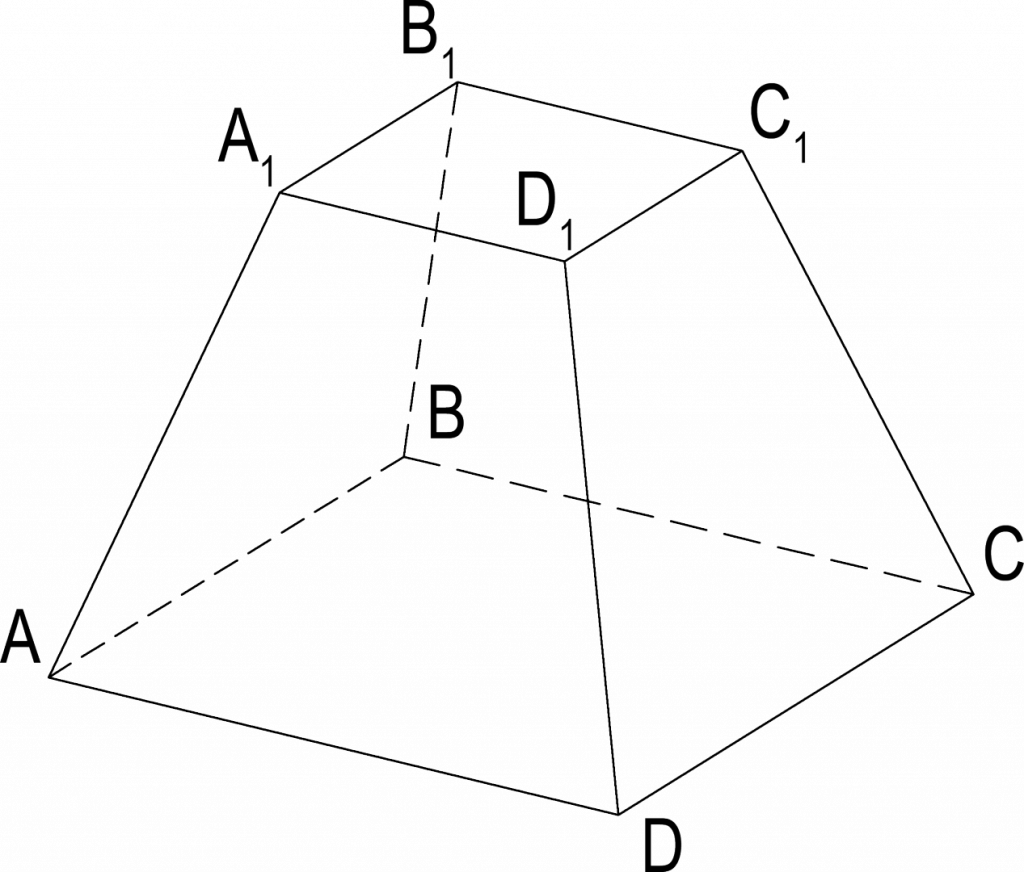

Свойства усечённой пирамиды:

1. Основания усечённой пирамиды — подобные многоугольники.
2. Боковые грани усечённой пирамиды — трапеции.
3. Боковые ребра правильной усеченной пирамиды равны и одинаково наклонены к основанию пирамиды.
4. Боковые грани правильной усечённой пирамиды — равные между собой равнобедренные трапеции и одинаково наклонены к основанию пирамиды.
5. Двугранные углы при боковых рёбрах правильной усечённой пирамиды равны.

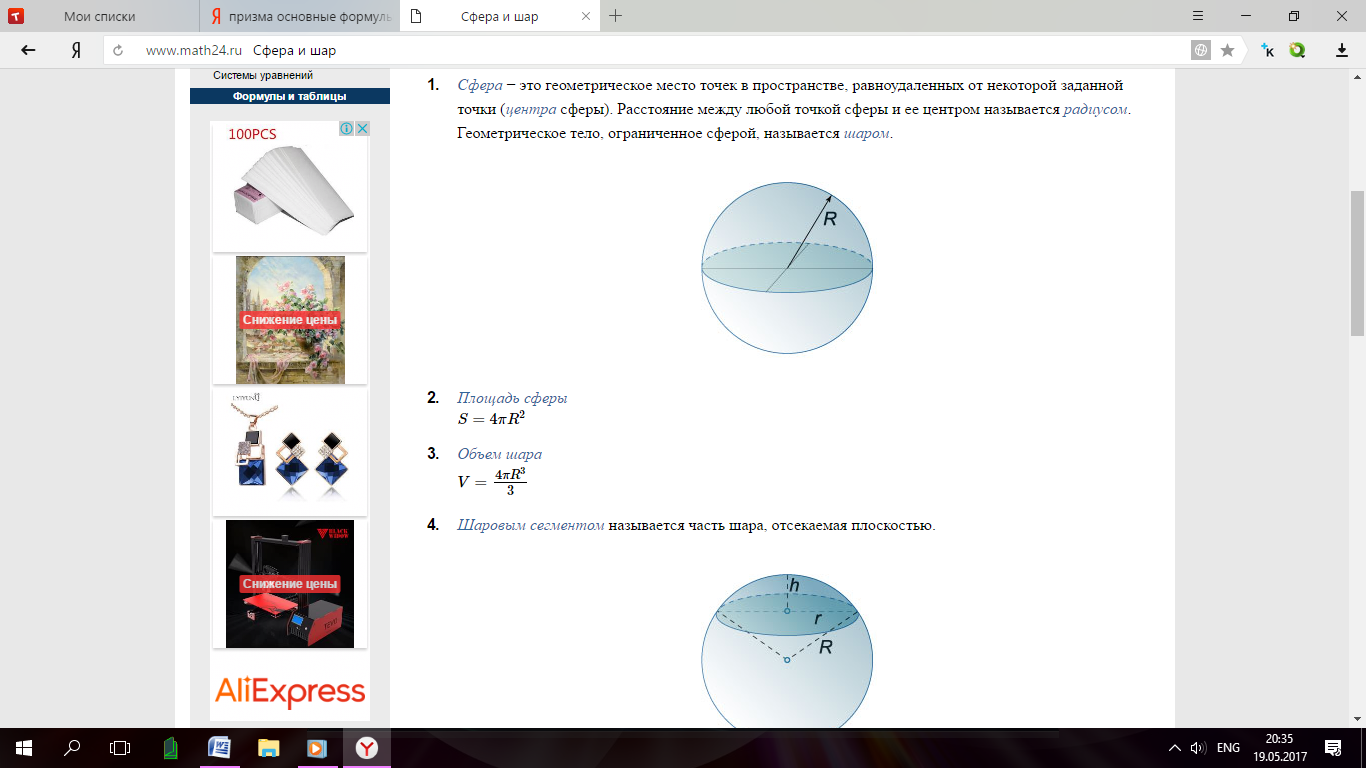
Сфера и шар

Сфера – замкнутая поверхность, геометрическое место точек в пространстве, равноудалённых от данной точки, называемой центром сферы. Сфера также является телом вращения, образованным при вращении полуокружности вокруг своего диаметра. Радиусом сферы называется отрезок, соединяющий центр сферы с какой-либо точкой сферы.

Хордой сферы называется отрезок, соединяющий две точки сферы.

Диаметром сферы называется хорда, проходящая через ее центр. Центр сферы делит любой его диаметр на два равных отрезка. Любой диаметр сферы радиусом R равен 2R.

Шар – геометрическое тело; совокупность всех точек пространства, которые находятся на расстоянии не большем заданного от некоторого центра. Это расстояние называется радиусом шара. Шар образуется вращением полукруга около его неподвижного диаметра.

Обратите внимание: поверхность (или граница) шара называется сферой. Можно дать и такое определение шара: шаром называется геометрическое тело, состоящее из сферы и части пространства, ограниченного этой сферой.

Радиусом, хордой и диаметром шара называются радиус, хорда и диаметр сферы, которая является границей данного шара.

Теорема 1: (о сечении сферы плоскостью). Сечение сферы плоскостью есть окружность. Заметим, что утверждение теоремы остается верным и в случае, если плоскость проходит через центр сферы.
Теорема 2: (о сечении шара плоскостью). Сечение шара плоскостью есть круг, а основание перпендикуляра, проведенного из центра шара к плоскости сечения, есть центр круга, полученного в сечении.

Доказательство

Наибольший круг, из числа тех, которые можно получить в сечении данного шара плоскостью, лежит в сечении, проходящем через центр шара О. Он то и называется большим кругом. Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара AB. Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра (на рис. A и B), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.

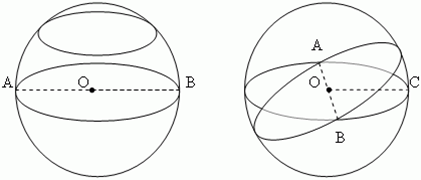
Касательной плоскостью к сфере называется плоскость, имеющая со сферой только одну общую точку, а их общая точка называется точкой касания плоскости и сферы.

Касательной плоскостью к шару называется касательная плоскость к сфере, которая является границей этого шара.

Любая прямая, лежащая в касательной плоскости сферы (шара) и проходящая через точку касания, называется касательной прямой к сфере (шару). По определению касательная плоскость имеет со сферой только одну общую точку, следовательно, касательная прямая также имеет со сферой только одну общую точку – точку касания.

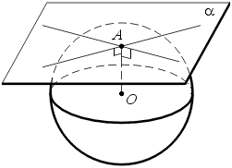
Теорема 1: (признак касательной плоскости к сфере). Плоскость, перпендикулярная радиусу сферы и проходящая через его конец, лежащий на сфере, касается сферы.
Теорема 2: (о свойстве касательной плоскости к сфере). Касательная плоскость к сфере перпендикулярна радиусу, проведенному в точку касания.

Многогранники

Геометрическим телом (или просто телом) называется ограниченная связная фигура в пространстве, которая содержит все свои граничные точки, причем сколь угодно близко от любой граничной точки находятся внутренние точки фигуры. Границу геометрического тела называют также его поверхностью и говорят, что поверхность ограничивает тело.

Плоскость, по обе стороны которой имеются точки данного тела, называется секущей плоскостью.

Фигура, которая образуется при пересечении тела плоскостью, называется сечением тела.

Многогранником или многогранной поверхностью называется поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело. Тело, ограниченное многогранником, часто также называют многогранником.

Многоугольники, из которых составлен многогранник, называют его гранями. Стороны граней называются ребрами, а концы ребер — вершинами многогранника.

Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю многогранника.

Многогранники бывают выпуклые и невыпуклые.

Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани. Все грани выпуклого многогранника являются выпуклыми многоугольниками.

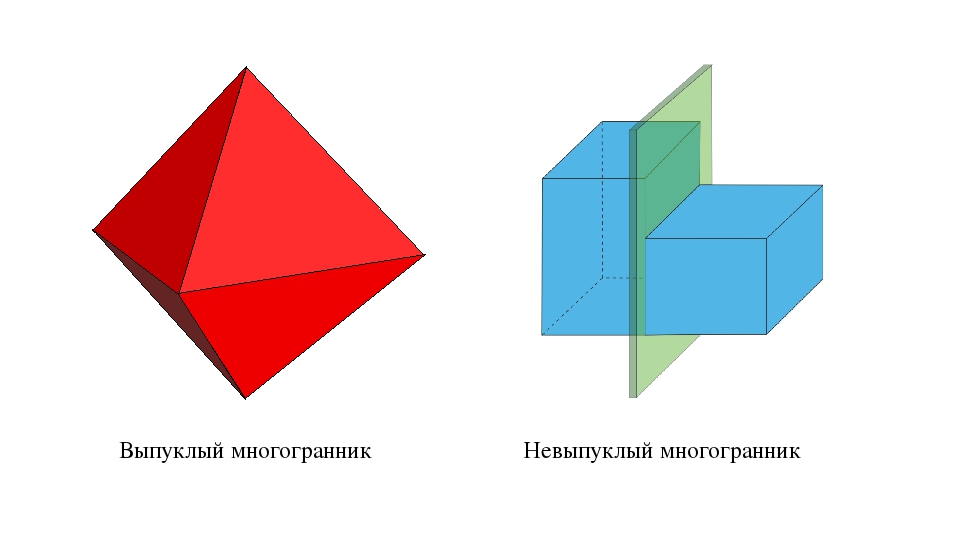
Свойства многогранников:

1. В выпуклом многограннике все грани являются выпуклыми многоугольниками.
2. Выпуклый многогранник может быть составлен из пирамид с общей вершиной, основания которых образуют поверхность многогранника.
3. Выпуклый многогранник лежит по одну сторону от плоскости каждой своей грани.
4. В любом выпуклом многограннике найдется грань с числом ребер меньшим или равным пяти.

Правильные многогранники

Выпуклый многогранник называется правильным, если все его грани — равные правильные многоугольники, и в каждой его вершине сходится одно и то же число ребер.

Все ребра правильного многогранника равны, все двугранные углы правильного многогранника равны, все многогранные углы правильного многогранника равны.

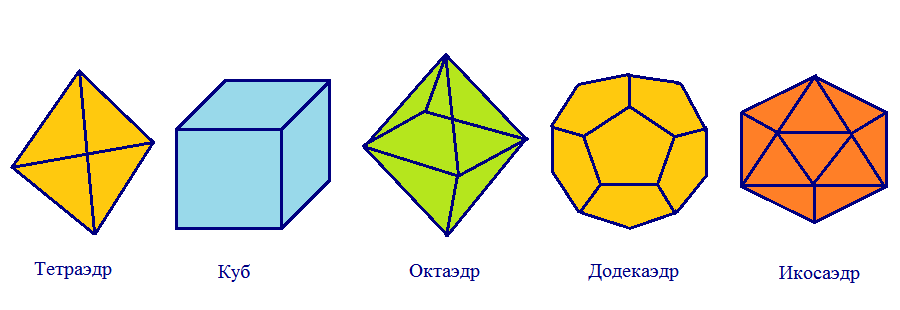
Существует ровно пять выпуклых правильных многогранников:

Выпуклый многогранник называется правильным, если его грани являются правильными многоугольниками с одним и тем же числом сторон, и в каждой вершине многогранника сходится одно и то же число ребер. Все ребра правильного многогранника равны друг другу. Равны также все его двугранные углы, содержащие две грани с общим ребром.

1.Правильный тетраэдр (четырехгранник) ― многогранник, составленный из четырех правильных треугольников. 

2. Правильный гексаэдр (шестигранник) или куб ― многогранник, составленный из шести правильных четырехугольников (квадратов) .

3. Правильный октаэдр (восьмигранник) ― многогранник, составленный из восьми правильных треугольников.

4. Правильный додекаэдр (двенадцатигранник) ― многогранник, составленный из двенадцати правильных пятиугольников.

5. Правильный икосаэдр (двадцатигранник) ― многогранник, составленный из двадцати правильных треугольников.

Цилиндр

В некоторой плоскости рассмотрим окружность с центром O и радиусом R. Через каждую точку окружности проведем прямую, перпендикулярную плоскости окружности. 

Цилиндрической поверхностью называется фигура, образованная этими прямыми, а сами прямые называются образующими цилиндрической поверхности. Все образующие цилиндрической поверхности параллельны друг другу, так как они перпендикулярны плоскости окружности.

Прямым круговым цилиндром или просто цилиндром называется геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, которые перпендикулярны образующим цилиндрической поверхности. Неформально, можно воспринимать цилиндр как прямую призму, у которой в основании круг. Это поможет легко понять, а при необходимости и вывести формулы для объема и площади боковой поверхности цилиндра.

Боковой поверхностью цилиндра называется часть цилиндрической поверхности, расположенная между секущими плоскостями, которые перпендикулярны ее образующим, а части (круги), отсекаемые цилиндрической поверхностью на параллельных плоскостях, называются основаниями цилиндра. Основания цилиндра – это два равных круга.

Образующей цилиндра называется отрезок (или длина этого отрезка) образующей цилиндрической поверхности, расположенный между параллельными плоскостями, в которых лежат основания цилиндра. Все образующие цилиндра параллельны и равны между собой, а также перпендикулярны основаниям.

Осью цилиндра называется отрезок, соединяющий центры кругов, являющихся основаниями цилиндра.

Высотой цилиндра называется перпендикуляр (или длина этого перпендикуляра), проведенный из какой-нибудь точки плоскости одного основания цилиндра к плоскости другого основания. В цилиндре высота равна образующей.

Радиусом цилиндра называется радиус его оснований.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Цилиндр можно получить поворотом прямоугольника вокруг одной из его сторон на 360°.

Если секущая плоскость параллельна оси цилиндра, то сечением цилиндра служит прямоугольник, две стороны которого – образующие, а две другие – хорды оснований цилиндра.
Осевым сечением цилиндра называется сечение цилиндра плоскостью, проходящей через его ось. Осевое сечение цилиндра – прямоугольник, две стороны которого есть образующие цилиндра, а две другие – диаметры его оснований.

Если секущая плоскость, перпендикулярна оси цилиндра, то в сечении образуется круг равный основаниям. На чертеже ниже: слева – осевое сечение; в центре – сечение параллельное оси цилиндра; справа – сечение параллельное основанию цилиндра.   

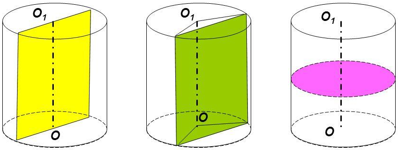
Свойства цилиндра:

1. Основания цилиндра равны
2. Основания лежат в параллельных плоскостях
3. Образующие цилиндра параллельны и равны

nauka.club

Справочник стереометрия

Теоретический материал по теме «Стереометрия на ЕГЭ по математике, часть 2».

1. Плоскость в пространстве. Взаимное расположение плоскостей
Плоскость, прямая, точка — основные понятия геометрии.

Две плоскости в пространстве либо параллельны, либо пересекаются. Примеры в окружающем пространстве найти легко.

Мы не рассматриваем отдельно случай «плоскости совпадают». Раз совпадают — значит, это одна плоскость, а не две.

2. Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые

На плоскости две прямые или пересекаются, или параллельны друг другу. А в пространстве возможны три случая взаимного расположения прямых.

Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.

Если две прямые параллельны третьей, то они параллельны друг другу.

Скрещивающиеся прямые не пересекаются и не параллельны друг другу. Через них невозможно провести плоскость. Скрещивающиеся прямые лежат в параллельных плоскостях.

3. Параллельность прямой и плоскости

Прямая и плоскость могут пересекаться или быть параллельными друг другу. Еще один случай — прямая лежит в плоскости.

Определение: Прямая параллельна плоскости, если она не имеет с плоскостью общих точек.

Но как на практике проверить, что бесконечная прямая нигде не пересечет бесконечную плоскость? Для практического применения используется признак параллельности прямой и плоскости:

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости.

 

Этот признак часто используется в решении задач по стереометрии. Например, в правильной четырехугольной пирамиде SABCD прямая АВ параллельна прямой СD — значит, АВ параллельна всей плоскости SCD.

 

4. Угол между прямой и плоскостью. Перпендикулярность прямой и плоскости

Если две прямые лежат в одной плоскости, угол между ними легко измерить — например, с помощью транспортира. А как измерить угол между прямой и плоскостью?

Пусть прямая пересекает плоскость, причем не под прямым, а под каким-то другим углом. Такая прямая называется наклонной.

Опустим перпендикуляр из какой-либо точки наклонной на нашу плоскость. Соединим основание перпендикуляра с точкой пересечения наклонной и плоскости. Мы получили проекцию наклонной на плоскость.

 

Определение. Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Обратите внимание — в качестве угла между прямой и плоскостью мы выбираем острый угол.

Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.

Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.

Определение. Прямая перпендикулярна плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.

На практике применяется признак перпендикулярности прямой и плоскости:

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.

 

 

5. Параллельность плоскостей

Определение. Две плоскости параллельны, если они не имеют общих точек.

В практических целях чаще используется признак параллельности плоскостей:

Плоскости параллельны друг другу, если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости.

 

Свойства параллельных плоскостей:

1) Если две плоскости параллельны третьей, то они параллельны друг другу.

 

2) Линии пересечения двух параллельных плоскостей третьей плоскостью параллельны.

3) Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны.

 

 

6. Угол между плоскостями. Перпендикулярность плоскостей

Пусть плоскости α и β пересекаются по прямой с.

Определение. Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.

Другими словами, в плоскости α мы провели прямую а, перпендикулярную с. В плоскости β — прямую b, также перпендикулярную с. Угол между плоскостями α и β равен углу между прямыми а и b.

Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. В качестве угла между плоскостями мы берем острый угол.

Определение. Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны.

Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость α проходит через перпендикуляр к плоскости β, то плоскости α и β перпендикулярны.

 

7. Угол между скрещивающимися прямыми и расстояние между ними.

Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.

Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?

Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.

Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях α и β. Проведем в плоскости β прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.

 

 

Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.

8. Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.

 

 

Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.

Расстояние между скрещивающимися прямыми можно найти также как расстояние от одной из них до параллельной ей плоскости, в которой лежит вторая прямая.

Все три способа используются при решении задач.

Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.

Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.

Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.

9. Теорема о трех перпендикулярах

Рассмотрим чертеж. На нем изображены плоскость α и лежащая в ней прямая m. Наклонная a пересекает плоскость α в точке М. Прямая а₁ — проекция наклонной а на плоскость α.

Сформулируем теорему о трех перпендикулярах:

Прямая, лежащая в плоскости, перпендикулярна наклонной тогда и только тогда, когда она перпендикулярна проекции этой наклонной на данную плоскость.

 

 

На рисунке показаны все три перпендикуляра.
Если прямая m, лежащая в плоскости, перпендикулярна проекции наклонной, то она перпендикулярна и самой наклонной.

Слова «тогда и только тогда» в формулировке теоремы означают, что прямая m перпендикулярна одновременно и наклонной, и ее проекции. Если m перпендикулярна наклонной, значит, перпендикулярна и ее проекции, и наоборот.

На нашем чертеже прямая m проведена через основание наклонной. Этого требует формулировка теоремы о трех перпендикулярах в большинстве учебников. Но прямая m, лежащая в плоскости, вовсе не обязана проходить через основание наклонной. Главное — чтобы она была перпендикулярна проекции наклонной. Тогда она будет перпендикулярна и самой наклонной:

Теорема о трех перпендикулярах — полезный инструмент для решения задач.

Например, с ее помощью можно доказать, что диагональ куба АС₁ перпендикулярна прямой BD:

 

 

Или — что скрещивающиеся ребра тетраэдра взаимно перпендикулярны:

 

Или — что в правильной треугольной призме прямая А₁М (где М — середина ВС) перпендикулярна ребру ВС.

 

10. Параллельное проецирование. Площадь проекции фигуры

В задачах по геометрии успех зависит не только от знания теории, но от качественного чертежа.
С плоскими чертежами все более-менее понятно. А в стереометрии дело обстоит сложнее. Ведь изобразить надо трехмерное тело на плоском чертеже, причем так, чтобы и вы сами, и тот, кто смотрит на ваш чертеж, увидели бы то же самое объемное тело.

Как это сделать?
Конечно, любое изображение объемного тела на плоскости будет условным. Однако существует определенный набор правил. Существует общепринятый способ построения чертежей — параллельное проецирование.

Возьмем объемное тело.
Выберем плоскость проекции.
Через каждую точку объемного тела проведем прямые, параллельные друг другу и пересекающие плоскость проекции под каким-либо углом. Каждая из этих прямых пересекает плоскость проекции в какой-либо точке. А все вместе эти точки образуют проекцию объемного тела на плоскость, то есть его плоское изображение.

 

Как строить проекции объемных тел?
Представьте, что у вас есть каркас объемного тела — призмы, пирамиды или цилиндра. Освещая его параллельным пучком света, получаем изображение — тень на стене или на экране. Заметим, что в разных ракурсах получаются разные изображения, но некоторые закономерности все же присутствуют:

Проекцией отрезка будет отрезок.

 

Конечно, если отрезок перпендикулярен плоскости проекции — он отобразится в одну точку.
Проекцией круга в общем случае окажется эллипс.

 

 

Проекцией прямоугольника — параллелограмм.

 

Вот как выглядит проекция куба на плоскость:

Здесь передняя и задняя грани параллельны плоскости проекции

Можно сделать по-другому:

Какой бы ракурс мы ни выбрали, проекциями параллельных отрезков на чертеже тоже будут параллельные отрезки. Это один из принципов параллельного проецирования.

Рисуем проекции пирамиды,

цилиндра:

и шара:

Еще раз повторим основной принцип параллельного проецирования. Выбираем плоскость проекции и через каждую точку объемного тела проводим параллельные друг другу прямые. Эти прямые пересекают плоскость проекции под каким-либо углом. Если этот угол равен 90° — речь идет о прямоугольном проецировании. С помощью прямоугольного проецирования строятся чертежи объемных деталей в технике. В этом случае мы говорим о виде сверху, виде спереди и виде сбоку.

 

Иногда в задачах требуется найти площадь прямоугольной проекции фигуры.

Пусть S — площадь фигуры. Тогда площадь ее прямоугольной проекции равна S cosφ, где φ — угол между плоскостью фигуры и плоскостью проекции.

 

11. Как строить чертежи в задачах по стереометрии

Часто бывает так, что вы построили чертеж — и непонятно, что делать дальше. На чертеже ничего хорошего не видно. Почему?

Не спешите обвинять себя в отсутствии пространственного мышления. Может быть, просто ракурс выбран неудачно.

Очень важно, чтобы объемное тело на вашем чертеже выглядело действительно объемным, а не складывалось, как зонтик. Следите, чтобы одна грань не накладывалась на другую, а непараллельные отрезки (например, ребро куба и его диагональ) не совпадали.

Приведем примеры удачных и неудачных чертежей.

Мы рисуем чертеж крупным, чтобы на нем всё было хорошо видно.

Видимые линии изображаем сплошными, невидимые — штриховыми. Если решаете задачу векторно-координатным методом, ставьте рядом с точками их координаты. Это удобно.

Общий принцип: не понравился чертеж – не возитесь с ним, сделайте другой. Посмотрите на задачу с другого ракурса.

Иногда одного чертежа недостаточно. Чаще всего для решения задач по стереометрии, кроме «объемного» чертежа, нужен один или несколько плоских.

Чем же все-таки признак отличается от определения? Есть, например, определение перпендикулярности прямой и плоскости — и признак перпендикулярности прямой и плоскости. В чем разница между ними?

Предположим, в конкретной задаче нам надо доказать, что прямая l перпендикулярна плоскости α.

Если применять определение – придется перебрать все прямые, лежащие в плоскости α. Сделать это невозможно, да и не нужно. Достаточно, чтобы прямая l была перпендикулярна двум пересекающимся прямым в плоскости α

12. Еще две полезные теоремы для решения задач по стереометрии:

1) Теорема о прямой и параллельной ей плоскости.

Пусть прямая а параллельна плоскости α,
плоскость β проходит через прямую а.
Тогда линия пересечения плоскостей α и β параллельна прямой а.

 

2) Теорема о трех плоскостях, пересекающихся по параллельным прямым.
Пусть пересекающиеся плоскости α и β проходят через параллельные прямые а и b. Тогда линия пересечения плоскостей α и β параллельна прямым а и b.

Легко запомнить – на рисунке эта конструкция похожа на домик : -)

13. Правила решения задач по стереометрии:

1. Начинаем с построения чертежа.

Строим чертеж ручкой,( не карандашом!), с помощью линейки. Невидимые элементы объемного тела изображаем штриховыми линиями.

2. Записываем каждый шаг решения. Помним, что в задаче по стереометрии необходимы подробные объяснения. Не просто «Прямая АВ перпендикулярна плоскости  », а «Прямая АВ перпендикулярна плоскости , потому что она перпендикулярна пересекающимся прямым  и , лежащим в плоскости ». Конечно, все это лучше записать не словами, а символами.

3. От объемной задачи переходим к плоской, планиметрической. Все необходимые плоские чертежи рисуем отдельно.

Звоните нам: 8 (800) 775-06-82 (бесплатный звонок по России)                        +7 (495) 984-09-27 (бесплатный звонок по Москве)

Или нажмите на кнопку «Узнать больше», чтобы заполнить контактную форму. Мы обязательно Вам перезвоним.

ege-study.ru

Материал на тему «Стереометрические тела»

Содержание

Введение 3

Стереометрические тела, виды 4

Многогранники 5

Тела вращения 11

Заключение 15

Список литературы 16

Введение

Первые стереометрические понятия возникли в доисторические времена. Разные формы материальных тел наблюдал человек в природе: формы растений и животных, гор и извилин рек, круга и серпа Луны и т. п. Однако человек не только пассивно наблюдал природу, но практически осваивал и использовал ее богатства. Практическая деятельность человека служила основой открытия простейших геометрических зависимостей и соотношений.

В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения.

Часть геометрии, в которой изучаются свойства куба, призмы, параллелепипеда и других геометрических тел и пространственных фигур, издавна называется стереометрией (от греческого «стереос»- объемный, пространственный). Слово это греческого происхождения и встречается еще у знаменитого древнегреческого философа Аристотеля. Стереометрия возникла позже, чем планиметрия.

В своей деятельности человеку повсюду приходится сталкиваться с необходимостью изучать форму, размеры, взаимное расположение пространственных фигур. Подобные задачи решают и астрономы, имеющие дело с самыми большими масштабами, и физики, исследующие структуру атомов и молекул.

Может показаться парадоксальным, но фактически понятие «плоскость» в планиметрии — геометрии на плоскости — не нужно. Ведь если мы, например, говорим, что в плоскости многоугольника дана точка, мы тем самым подразумеваем, что такие точки существуют и вне этой плоскости. В планиметрии такое предположение излишние: все происходит в одной и той же единственной плоскости. В стереометрии нам приходится иметь дело уже с несколькими плоскостями. В каждой из них сохраняют свою силу все известные из планиметрии определения и теоремы, относящиеся к точкам, прямым, расстояниям и т. д., но свойства самих плоскостей необходимо описывать отдельно.

Стереометрические тела, виды

Стереометрическое тело — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.

Стереометрическое тело возможно выделить замкнутой поверхностью, т.е. его границей.

Еще стереометрическим телом можно назвать компактное множество точек, и 2 точки из множества возможно соединить отрезком, этот отрезок целиком проходит внутри границы тела, это указывает на то, что стереометрическое тело состоит из множества внутренних точек.

Наружная граница стереометрического тела является его гранью, у тела может быть одна либо несколько граней. Множество плоских граней определяет множество вершин и ребер геометрического тела.

Все геометрические тела делятся на 2 вида:

Многогранник или полиэдр — зачастую замкнутая поверхность, состоящая из многоугольников. Ее, бывает, зовут тело, которое ограничено этой поверхностью.

Многогранник – тело, у которого граница, это объединение ограниченного количества многоугольников.

Существует несколько видов многогранников: правильные многогранники, полуправильные многогранники, правильные звездчатые многогранники.

Правильным многогранником является многогранник, с гранями из правильных равных многоугольников, также, каждый двугранный угол имеет одинаковое значение.

Есть 5 видов правильных многогранников:

• Тетраэдр;

• Гексаэдр;

• Октаэдр;

• Додекаэдр;

• Икосаэдр.

Однако существуют другие многогранники – все многогранные углы равны, а грани – правильные, при этом разноименные правильные многоугольники. Такие многогранники являются равноугольно-полуправильными многогранниками.

Это: усеченный тетраэдр, усеченный оксаэдр, усеченный икосаэдр, усеченный куб, усеченный додекаэдр, кубооктаэдр, икосододекаэдр, усеченный кубооктаэдр, усеченный икосододекаэдр, ромбокубооктаэдр, ромбоикосододекаэдр, «плосконосый» (курносый) куб, «плосконосый» (курносый) додекаэдр.

Кроме полуправильных многогранников из правильных многогранников — Платоновых тел, возможно получить правильные звездчатые многогранники.

Таких многогранников существует только 4, еще их зовут телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, и назвал его «колючий» либо «еж», и большой додекаэдр. Пуансо открыл другие 2 правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

Тела вращения — это объёмные тела, которые возникают следствием вращения плоской геометрической фигуры, которая ограничена кривой, вокруг оси. Эта ось лежит в той же плоскости.

Если вращать контуры фигур, образуется поверхность вращения (к примеру, сфера, которая образовывается из окружности), а если вращать заполненные контуры – возникают тела (шар, который образован из круга).

К телам вращения можно отнести следующие тела:

• Шар;

• Сфера;

• Цилиндр;

• Конус;

• Тор (тороид).

Многогранники

Поверхность составленную из многоугольников и ограничивающую некоторое геометрическое тело, будет называть многогранной поверхностью или многогранником.

Рассмотрим основные характеристики многогранников.

Призма

Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и параллелограммов, называется призмой. Многоугольники называются основаниями, а параллелограммы – боковыми гранями призмы. Отрезки называются боковыми ребрами призмы.

Если боковые ребра перпендикулярны к основаниям, то призма называется прямой.

Если в основании прямой призмы лежат правильные многоугольники, то призма называется правильной. (Рис. 1)

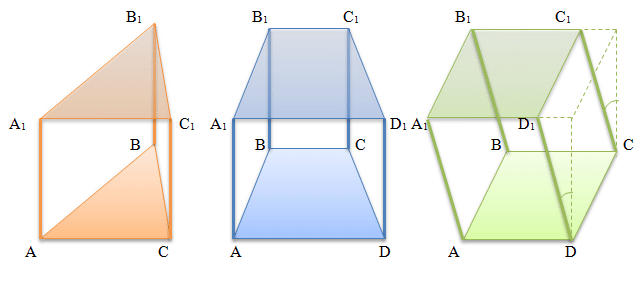
Рис.1 Виды призм.

Свойства призмы

• Основания призмы равны

• Каждая из боковых граней обязательно является параллелограммом

• Боковые ребра призмы параллельны и равны между собой

• Боковые грани правильной призмы представляют собой равные прямоугольники

• При пересечении призмы и диагональной плоскости сечение представляет собой параллелограмм

• Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы

• Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах

• Перпендикулярное сечение перпендикулярно ко всем боковым граням

• Площадь боковой поверхности правильной призмы S_бок=P_оснℓ=(a₁+a₂+…+a_n)ℓ, где P_осн − периметр основания призмы, a₁,a₂,…,a_n − стороны основания, ℓ − длина бокового ребра в прямой призме боковое ребро совпадает с высотой h.

• Площадь боковой поверхности наклонной призмы S_бок=pℓ,

• где p − полупериметр перпендикулярного сечения призмы, ℓ − боковое ребро.

• Объем призмы V=S_оснh=S_сечℓ, где S_осн − площадь основания, h − высота призмы, S_сеч − площадь перпендикулярного сечения, ℓ − боковое ребро призмы.

Параллелепипед

Если в основании призмы лежит параллелограмм, то призма называется параллелепипедом. Параллелепипеды бывают наклонные, прямые и прямоугольные.

Прямоугольный параллелепипед имеет три измерения: длину, высоту и ширину. У параллелепипеда 8 вершин, 12 ребер, 6 граней. Каждая грань параллелепипеда – прямоугольник. Противоположенные грани параллелепипеда равны. Среди всех параллелепипедов особую роль играет куб.

Существует несколько видов параллелепипедов:

Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.

Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником. (Рис. 2)

Рис. 2. Прямой параллелепипед.

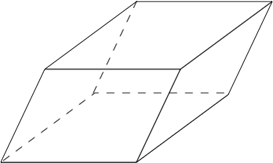
Рис. 3. Наклонный параллелепипед.

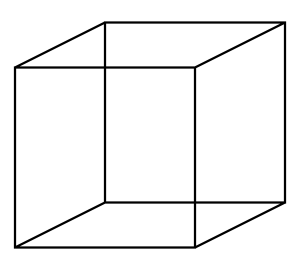
Рис. 4. Куб

Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов. (Рис. 3)

Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты. (Рис. 4)

Свойства параллелепипеда.

• Параллелепипед симметричен относительно середины его диагонали.

• Всякий отрезок с концами, которые принадлежат поверхности параллелепипеда и который проходит через середину его диагонали, делится ею на две равные части. Все диагонали параллелепипеда пересекаются в 1-ой точке и делятся ею на две равные части.

• Противоположные грани параллелепипеда параллельны и имеют равные размеры.

• Диагональ прямоугольного параллелепипеда

d=

S=2(ab+ac+bc) 

V=abc

• Диагональ куба d=a

• Радиус шара, вписанного в куб r=

• Радиус описанного шара R=

• Площадь полной поверхности куба S=6a²

• Объем куба V=a³

Пирамида

Важным и интересным семейством многогранников является пирамида. У пирамиды различают основание и боковые грани. Боковые грани – треугольники, сходящиеся в одной вершине, а основание – многоугольник, противолежащий этой вершине. В основании может лежать многоугольник с любым количеством сторон. Пирамиду называют по числу сторон ее основания: треугольная пирамида, четырехугольная пирамида, шестиугольная пирамида… Простейшей пирамидой и даже простейшем многогранником является треугольная пирамида. Все ее грани – треугольники, и каждая из них может считаться основанием.

Пирамида называется правильной, если ее основание – правильный многоугольник, и вершина пирамиды проектируется в центр этого многоугольника. Все боковые ребра правильной пирамиды равны, а боковые грани являются равными равнобедренными треугольниками. (Рис. 5)

Многогранник, гранями которого является многоугольники, расположенные в параллельных плоскостях, и четырехугольников — боковые грани называют усеченной пирамидой.

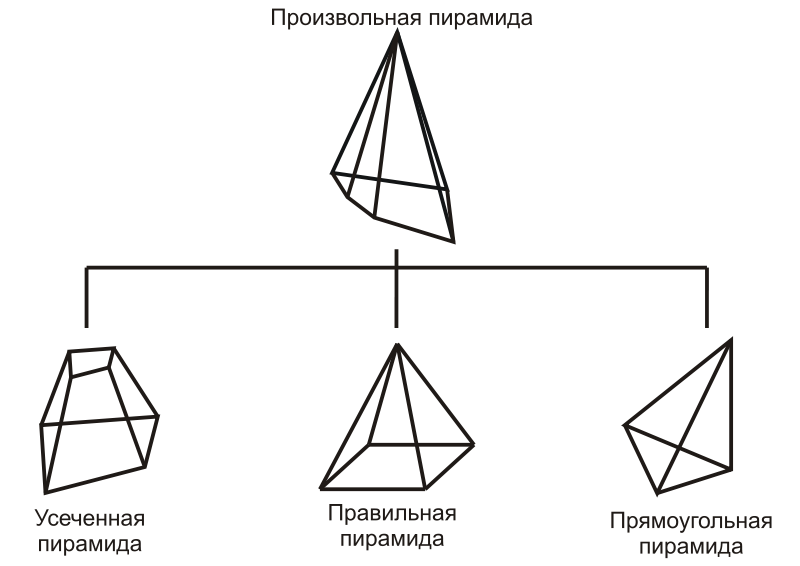
Рис. 5. Виды пирамид

, где b − боковое ребро, a − сторона основания, n − число сторон многоугольника в основании.

• Высота боковой грани называется апофемой. В правильной пирамиде длина апофемы выражается формулой

• Площадь боковой поверхности правильной пирамиды

S_бок=man=an =pm

• Площадь основания правильной пирамиды S_осн=pr, где p − полупериметр многоугольника в основании, r − радиус вписанной окружности.

• Площадь полной поверхности S=S_осн+S_бок

• Объем произвольной пирамиды V=S_оснh

• Объем правильной пирамиды V=prh

Правильные многогранники

Ни одни геометрические тела не обладают таким совершенством и красотой, как правильные многогранники. «Правильных многогранников вызывающе мало, — написал когда-то Л. Кэролл, — но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук».

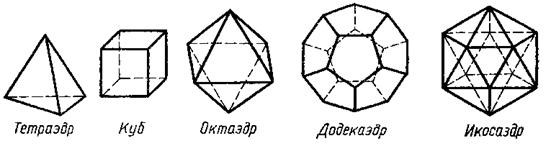
Рис. 6. Виды правильных многогранников

Названия правильных многогранников пришли из Греции. В дословном переводе с греческого «тетраэдр», «октаэдр», «гексаэдр», «додекаэдр», «икосаэдр» означают: «четырехгранник», «восьмигранник», «шестигранник». «двенадцатигранник», «двадцатигранник». Этим красивым телам посвящена 13-я книга «Начал» Евклида. Их еще называют телами Платона, т. к. они занимали важное место в философской концепции Платона об устройстве мироздания. Четыре многогранника олицетворяли в ней четыре сущности или «стихии». Тетраэдр символизировал огонь, т. к. его вершина устремлена вверх; икосаэдр — воду, т. к. он самый «обтекаемый»; куб — землю, как самый «устойчивый»; октаэдр — воздух, как самый «воздушный». Пятый многогранник, додекаэдр, воплощал в себе «все сущее», символизировал все мироздание, считался главным.

Основные свойства платоновых тел 

Тело

Число вершин

Число ребер

Число граней

Тетраэдр

4

6

4

Куб

8

12

6

Октаэдр

6

12

8

Икосаэдр

12

30

20

Додекаэдр

20

30

12

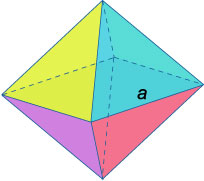
Октаэдр − правильный многогранник с 8 гранями в форме треугольников. 

Икосаэдр − правильный многогранник с 20 гранями, имеющих форму треугольника. 

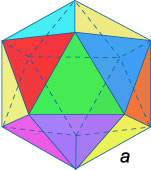
Додекаэдр − правильный многогранник с 12 гранями, каждая из которых имеет форму правильного пятиугольника. 

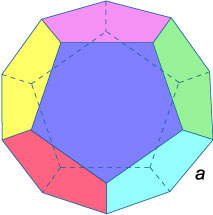
Тела вращения

Тела вращения — объёмные тела, возникающие при вращении плоской геометрической фигуры, ограниченной кривой, вокруг оси, лежащей в той же плоскости.

Шар и сфера

Сферой называют поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки. Данная точка называется центром сферы, а донное расстояние радиусом сферы.

Тело, ограниченное сферой называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара.

Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.

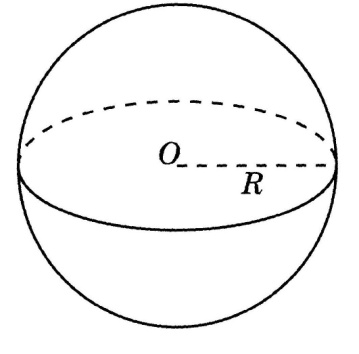
Рис. 7. Сфера.

Цилиндр

Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами, называют цилиндром. Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги основаниями цилиндра. Образующие цилиндрической поверхностью называются образующими цилиндра, прямая — осью цилиндра. Все образующие цилиндра параллельны и равны друг другу как отрезки параллельных прямых, заключенные между параллельными плоскостями.

Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основаниями цилиндра.

Образующие цилиндрической поверхности называются образующими цилиндра.

Прямая, проходящая через центры оснований, называется осью цилиндра.

Длина образующей называется высотой, а радиус основания – радиусом цилиндра.

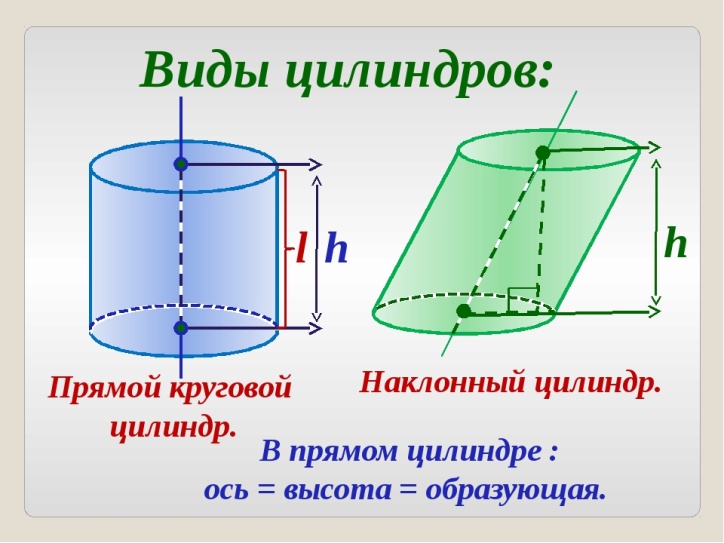
Рис. 8. Виды цилиндров

Конус

Тело, ограниченное конической поверхностью и кругом с границей, называется конусом. Коническая поверхность называется боковой поверхностью конуса, а круг – основанием конуса. Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов.

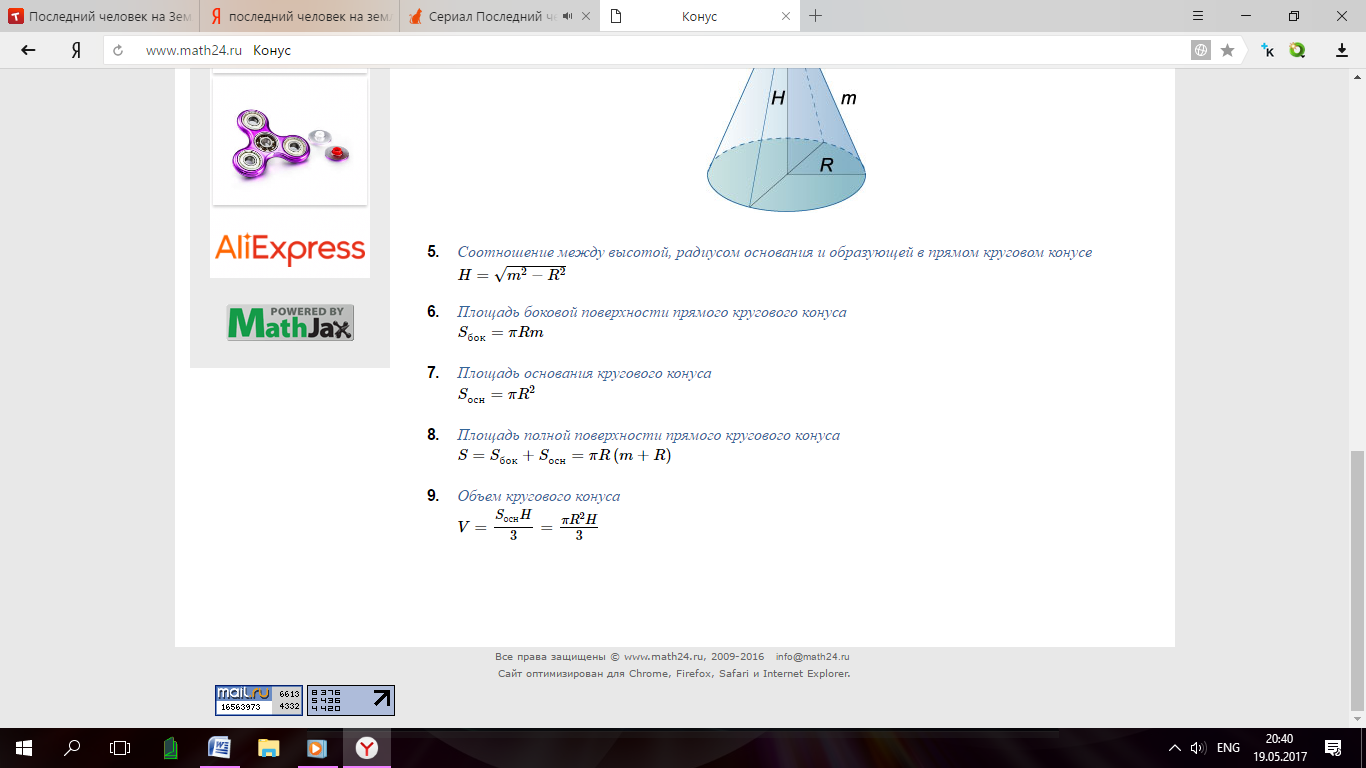
Объем кругового конуса

Усеченный конус

Если взять секущую плоскость, и провести ей по конусу, перпендикулярно к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей представляет из себя конус, а другая называется усеченным конусом. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок соединяющие их центры, — высотой усеченного конуса.

Часть конической поверхности, ограничивающая конус, называется ее боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называется образующими усеченного конуса. Все образующие усеченного конуса равны друг другу.

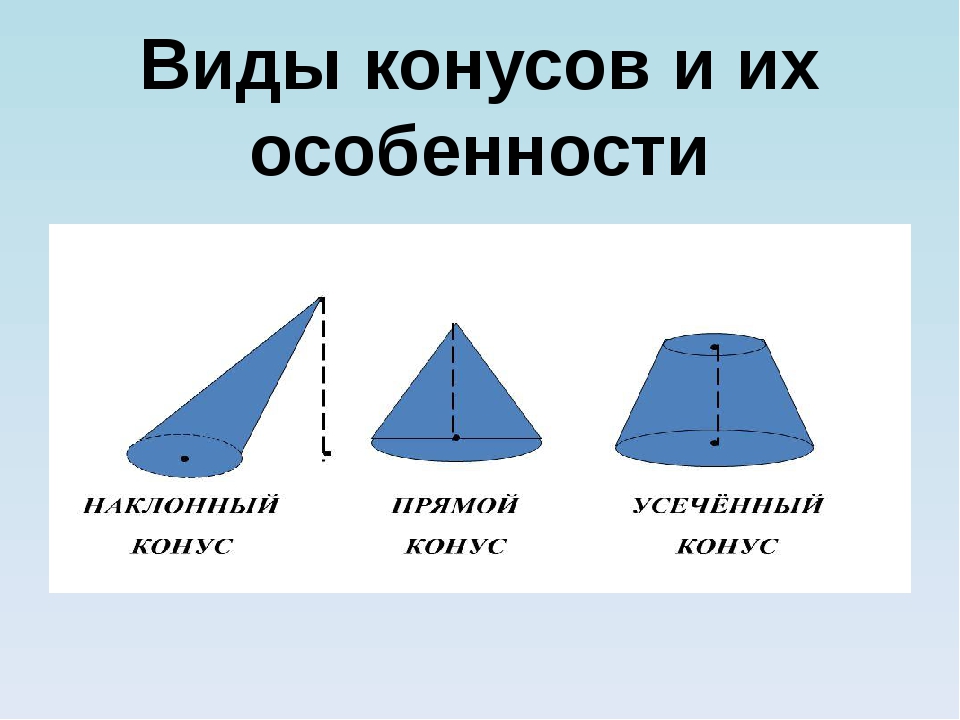
Рис. 8. Виды конусов

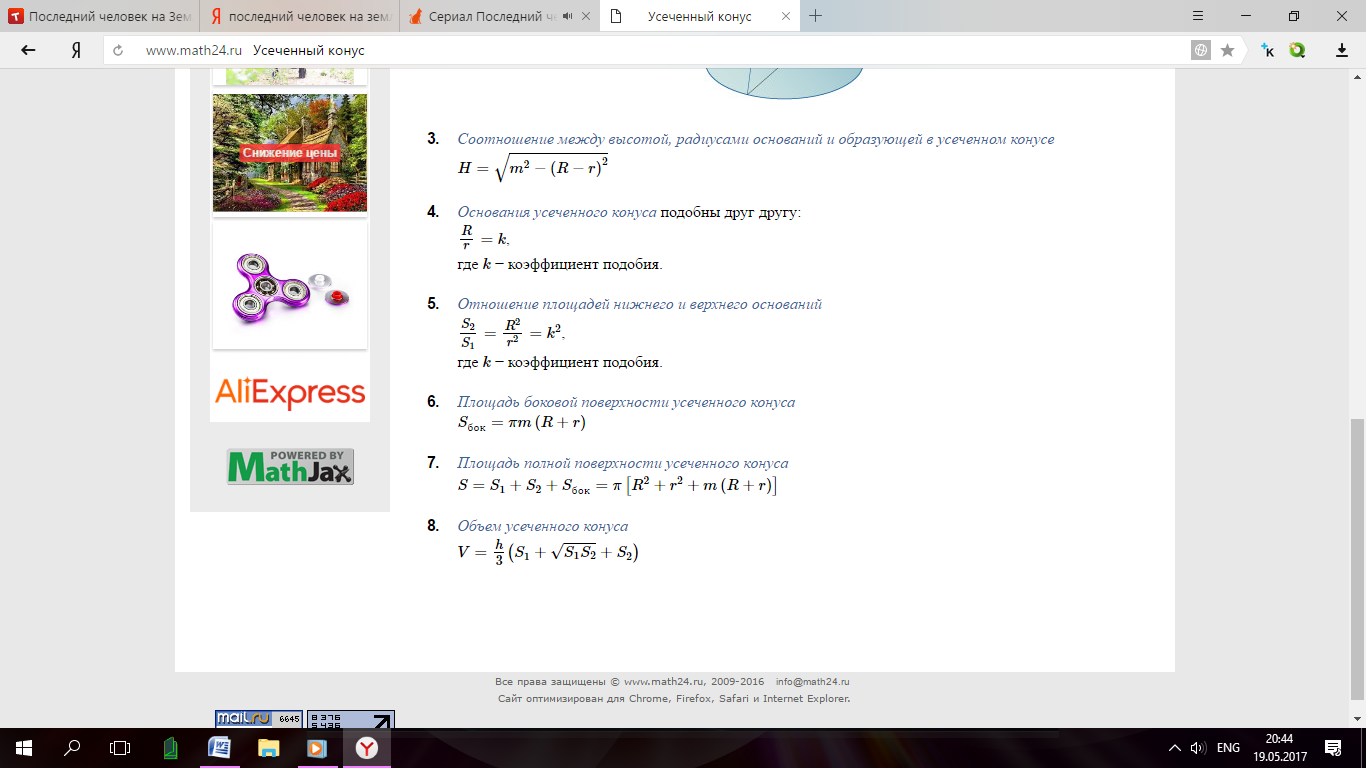
Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её.

Рис. 9. Тор.

• Площадь поверхности тора: .

• Объём тела, который ограничивается тором: .

Заключение

Итак, стереометрические тела изучает раздел геометрии под названием стереометрия. Все геометрические тела делятся на 2 вида: многогранники и тела вращения.

Многогранники бывают разных видов (пирамида, призма и т.д.) и имеют разные свойства.

Телами вращения называют шар, сферу, цилиндр и конус.

Также, следует отметить, что стереометрические тела в отличие от плоских фигур имеют объем и располагаются в пространстве.

Большинство окружающих нас предметов находятся в пространстве, и изучение многогранников и тел вращения помогает нам составить представление об окружающей нас реальности с точки зрения геометрии.

Список литературы

1. Геометрия. Стереометрия. Пособие для подготовки к ЕГЭ/ Смирнов В.А. – МЦНМО, 2009 – 260 с.

2. Геометрия, 10-11 классы: учебник для общеобразоват. учреждений: базовый и профильный уровни/ Атанасян Л.Н., Бутузов В.Ф., Кадомцев С.Б. – М. Просвещение, 2009. – 255 с.

3. Наглядная стереометрия в теории, задачах, чертежах/Бобровская А.В. — Ростов н/Д.: Феникс, 2013. — 167 с.

5. Стереометрия. 10-11 класс/Погорелов А.В. Геометрия: — Учебник. — 4-е изд. — К.: Школяр, 2004. — 142 с.

Интернет-ресурсы

6. https://www.calc.ru/Geometricheskiye-Tela.html

7. http://www.math34.ru/содержание-формулы-и-таблицы.html

infourok.ru

Лекция по математике на тему «Предмет стереометрии»

Лекция по теме «Предмет стереометрии»

Предмет стереометрии

Геометрия – это наука, которая изучает свойства геометрических фигур.

Школьный курс геометрии подразделяется на два раздела: планиметрию и стереометрию.

Планиметрия – раздел геометрии, который изучает свойства геометрических фигур на плоскости.

Планиметрию мы изучали в 7-9 классах.

В этом году мы начинаем изучать второй раздел геометрии — стереометрию

Стереометрия – это раздел геометрии, в котором изучаются свойства геометрических фигур в пространстве.

Слово «стереометрия» происходит от греческих слов «стереос» объемный, пространственный и «метрио» измерять.

В стереометрии рассматриваются математические модели тех материальных объектов, с которыми имеют дело архитекторы, конструкторы, строители и другие специалисты.

Кроме того, школьный курс стереометрии служит основой для черчения и начертательной геометрии – важнейших дисциплин любого технического вуза.

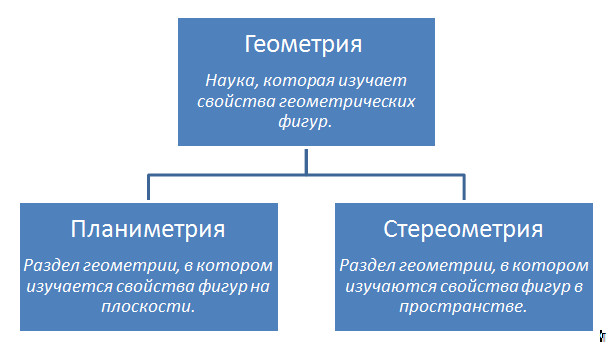
Основные фигуры стереометрии

Итак, стереометрия изучает свойства геометрических фигур в пространстве.

Геометрических фигур в пространстве.

называют телами.

В стереометрии мы будем изучать свойства геометрических тел, вычислять их площади и объемы.

При изучении пространственных фигур используются их изображение на чертеже.

Изображением пространственной фигуры служит ее проекция на ту или иную плоскость. Одна и та же фигура допускает различные изображения.

Обычно выбирают то из них, которое наиболее удобно для исследования ее свойств.

На экране вы видите многогранники – куб, параллелепипед и пирамида, тела вращения – шар, конус и цилиндр.

При изображении пространственных фигур невидимые части этих фигур изображены штриховыми линиями.

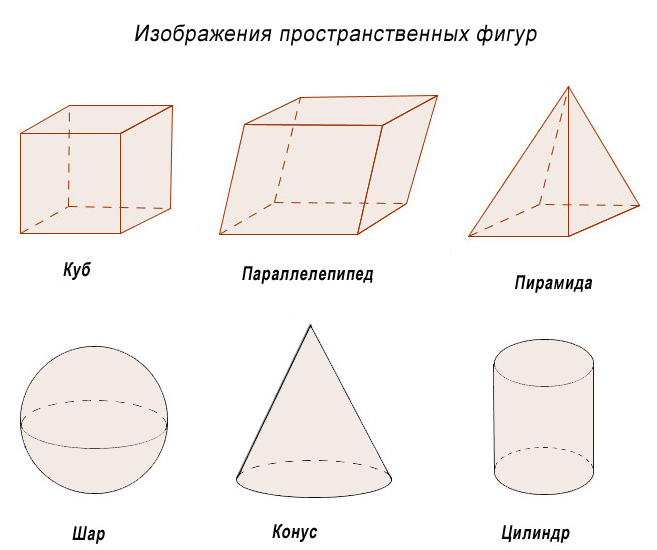
С чего начинается стереометрия?

Также как планиметрия.

Планиметрию мы начинали изучать с основных понятий, фигур и аксиом.

Основные понятия стереометрии

Во-первых, это точка и прямая, как в планиметрии. И еще добавляется плоскость.

Итак, основными понятиями стереометрии являются: тоска, прямая, плоскость. Они принимаются без определений.

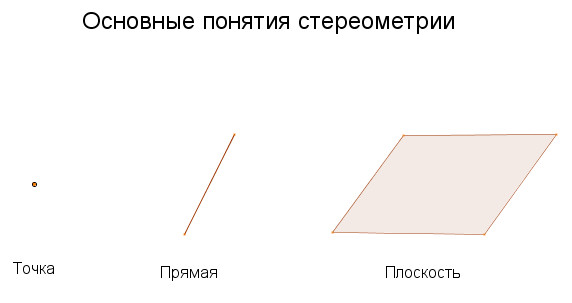
Новым для нас понятием является плоскость.

Плоскость, как и прямая в планиметрии, бесконечна. Она простирается во все стороны на неограниченное расстояние.

Геометрическими моделями части плоскости являются, например, поверхность стола, доски и т. д.

Изображают плоскости в виде параллелограмма, либо в виде произвольной области.

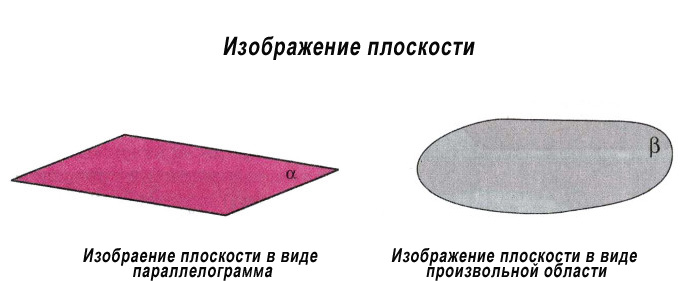
Обозначение, которые мы будем применять.

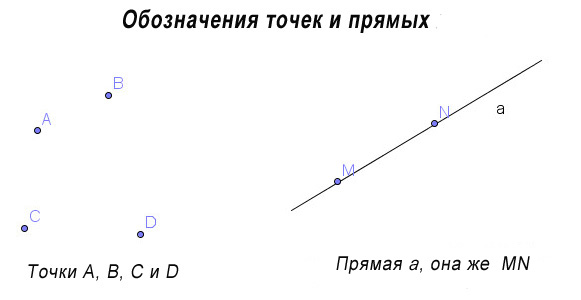
Точки. Как и ранее, точки будем обозначать прописными латинскими буквами A, B, C ….

На экране изображены 4 точки. Они обозначены буквами A, B, C и D

Прямые. Прямые обозначают строчными латинскими буквами a, b, c …, или двумя прописными латинскими буквами AB, CD, …

Во втором случае используются обозначения

двух точек, через которые прямая проходит.

На экране вы видите прямую a. На ней лежат точки M и N.

Прямая a может быть также обозначена как MN.

Плоскости. Плоскости обычно обозначают строчными греческими буквами 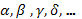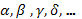(альфа, бета, гамма, дельта, …)

Плоскости также можно называть по трем точкам, через которые плоскости проходят.

Например, на экране плоскость синего цвета обозначена как α, она же может называться ABC.

Плоскость бежевого цвета обозначена β, она же может быть обозначена как KLN или KLM. Берутся любые три точки, через которые плоскость проходит.

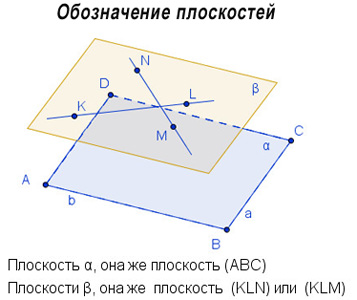
Так же, как и в планиметрии, в стереометрии мы будем применять для точек знак: 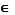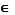(принадлежит плоскости), а для прямых знак: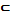 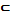(лежит в плоскости).

Перечеркнутые знаки означают отрицание – не принадлежит плоскости, не лежит в плоскости.

На рисунке вы видите, что две точки A и B принадлежат плоскости α (плоскость проходит через эти точки), а точки M, N, K не принадлежат этой плоскости (плоскость не проходит через эти точки).

Коротко это записывается так:

Точка А принадлежит плоскости α, точка B принадлежит плоскости α.

Точка M не принадлежит плоскости α, точка N не принадлежит плоскости α, точка K не принадлежит плоскости α.

.

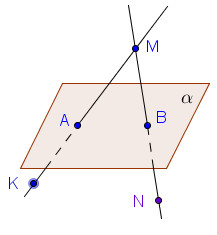
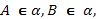
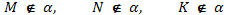
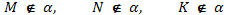На этом уроке мы познакомились с новым разделом геометрии – стереометрией.

Узнали, что основными понятиями стереометрии являются точка, прямая, плоскость. Вспомнили, как изображаются точки и прямые. Узнали как изображается и обозначается плоскость.

Переходим к решению задач.

Задача 1.

Дано:

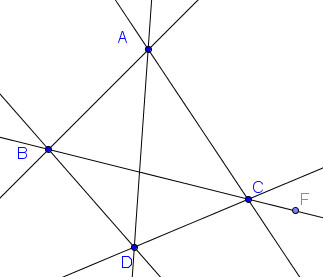
Точки A, B, C и D не лежащие в одной плоскости.

Указать плоскости, которым принадлежит:

а) прямая AB;

б) точка F;

в) точка C.

Решение.

а) Прямая AB лежит в двух плоскостях: ABC и ABD;

б) Точка F принадлежит плоскостям: ABC и BCD;

в) Точка C принадлежит трем плоскостям: ABC, BCD, ACD.

Дано:

Точки A, B, C и D не лежащие в одной плоскости.

Указать плоскости, которым принадлежит:

а) прямая AB;

б) точка F;

в) точка C.

Решение.

а)

б)

в)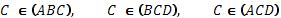

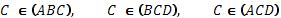
Задача 2 (№6, Атанасян 10-11 класс)

Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.

Доказательство.

Пусть данные точки это А, В, С. Проведем через них плоскость (мы знаем что через любые три точки можно провести плоскость и при том только одну).

Тогда прямая АВ лежит в плоскости (АВС), следовательно отрезок АВ тоже лежит в плоскости (АВС). Аналогично Отрезки АС и ВС лежат в плоскости (АВС).

Дано: точки А, В, С лежат в одной плоскости

Доказать что отрезки АВ, АС, ВС лежат в одной плоскости.

Доказательство:

Проведем через точки А, В, С плоскость (АВС)

Тогда прямая АВ 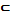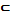(АВС), отрезок АВ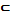 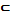(АВС). Аналогично Отрезки АС и ВС лежат в плоскости (АВС).

infourok.ru
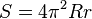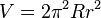