| Параллелограмм — четырёхугольник, у которого противолежащие стороны попарно параллельны, то есть лежат на параллельных прямых.  Частными случаями параллелограмма являются прямоугольник, квадрат и ромб. Как выглядит параллелограммНа приведенном рисунке параллелограмм обозначен синими линиями. Элементы параллелограмма, указанные на рисунке: Свойства параллелограмма
Признаки параллелограммаЧетырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий:
Как найти площадь параллелограммаФормулы нахождения площади параллелограмма приведены ниже:
Как найти стороны параллелограммаСтороны параллелограмма можно найти через:
Как найти диагонали параллелограмма
Как найти периметр параллелограммаПериметр параллелограмма может быть найден:
Трапеция, описанная вокруг окружности | Описание курса | Параллелограмм.  Задачи про площадь и стороны Задачи про площадь и стороны
|
Как найти площадь параллелограмма? Ответ на webmath.ru
Остались вопросы?
Здесь вы найдете ответы.
Каким образом можно доказать утверждение о том, что площадь параллелограмма есть число, получаемое в результате умножения длин двух его сторон, являющихся смежными, и синуса угла, который образуется между ними?
Параллелограмм следует расположить по горизонтали. Обозначим его верхнее основание как АВ, а противоположное ему основание – как CD. Из точек ВЕ и AF проведем перпендикулярные прямые на нижнее основание фигуры. В результате получится прямоугольник ABEF. Площадь образовавшейся прямоугольной фигуры равна площади параллелограмма по той причине, что параллелограмм ABCD и фигура с прямыми углами ABEF являются равносоставленными, о чем свидетельствует равенство треугольников ВEC и DAF.
Площадь (S) прямоугольника представляет собой произведение длин сторон EF и FA, которое, в свою очередь, равно:
CD*AD*sin(CDA)
Именно это и требовалось доказать.
Параллелограмм имеет смежные стороны длиной 26 см и 32 см. Один из углов данной фигуры равен 150 градусам. Каким способом можно вычислить площадь параллелограмма?
Обозначим имеющийся параллелограмм как АВСD. Тогда одна его сторона АВ равна 26 см, а другая АD – 32 см. Угол АВС параллелограмма составляет 150 градусов.
Принимая во внимание тот факт, что сумма внутренних односторонних углов параллелограмма равна 180 градусов, можно говорить о том, что его угол ВАD составляет 30 градусов. Проведем высоту ВК, и в итоге получим треугольник АВК с прямым углом. Длина опущенной высоты как катета, расположенного противоположно углу в 30 градусов, равна 13 см. Площадь (S) параллелограмма есть число, полученное в результате умножения длины высоты на длину стороны. Это значит, что:
S (АВСD) = 13 *32 = 416 см кв.
Ответ: Площадь параллелограмма равна 416 см кв.
Прямая АС проведена через середины двух сторон параллелограмма, которые являются смежными. Данная прямая отсекает от параллелограмма два треугольника – FMD и АDС. Площадь одного из отсеченных треугольников составляет 32 см кв. Как высчитать площадь параллелограмма?
Прямая АС представляет собой диагональ биссектрисы. В этом случае образовавшиеся посредством ее проведения треугольники FMD и АDС являются подобными по причине наличия общего угла А и равенства сторон. На основании этого можно говорить о том, что:
SADC=1/2*ab*sin a
SFDM=1/2 *2a*2b sin a
SADC / SFDM= 32/x
1/4=32/x
x=128
Теперь можно рассчитать площадь параллелограмма (S), которая будет равна 2*х:
S = 128*2 = 256 см кв.
Ответ: Площадь параллелограмма равна 256 см кв.
Параллелограмм имеет стороны, длины которых составляют 10 см и 6 см.
Обозначим угол в 150 градусов буквой В. Зная о том, что внутренние односторонние углы параллелограмма в сумме дают 180 градусов, можно вычислить второй угол А. Он будет равен:
∠А = 180-150 = 30 градусов.
Теперь следует провести высоту ВВ1, которая образует треугольник АВВ1, являющийся прямоугольным. Длина ВВ1 будет равна половине длины стороны, равной 6 см:
ВВ1 = 6/2 = 3 см.
Тогда площадь (S) параллелограмма можно рассчитать, умножив длину ВВ1 на 10 см (длина смежной стороны):
S = 3*10 = 30 см кв.
Ответ: Площадь параллелограмма равна 30 см кв.
Проведенные диагонали делят параллелограмм на четыре треугольных фигуры. Площадь одной из них равна 7 м кв. Каким образом можно найти площадь параллелограмма?
Обозначим имеющийся параллелограмм как ABCD. Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов. Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Точкой пересечения его
диагоналей является точка О. Образованные диагоналями треугольные фигуры
ABO, BCO, CDO, DAO являются одинаковыми по площади. Об этом
свидетельствует тот факт, что диагонали параллелограмма делятся ровно
пополам в точке их пересечения. Свидетельством того, что все четыре
треугольника имеют одинаковые площади, выступает равенство синусов смежных
углов. Площадь является ½ числа, которое получено в результате умножения
длин сторон треугольника и синуса угла, образованного между ними.
Параметры, которые отвечают вычислению площадей треугольников, равны, а
это означает равенство и самих площадей.
Если площади всех четырех треугольных фигур равны, то площадь самого параллелограмма будет в четыре раза превышать площадь любого из них. Это значит, что площадь (S) параллелограмма может быть вычислена следующим образом:
S = 4*7 = 28 м кв.
Ответ: Площадь параллелограмма равна 28 м кв.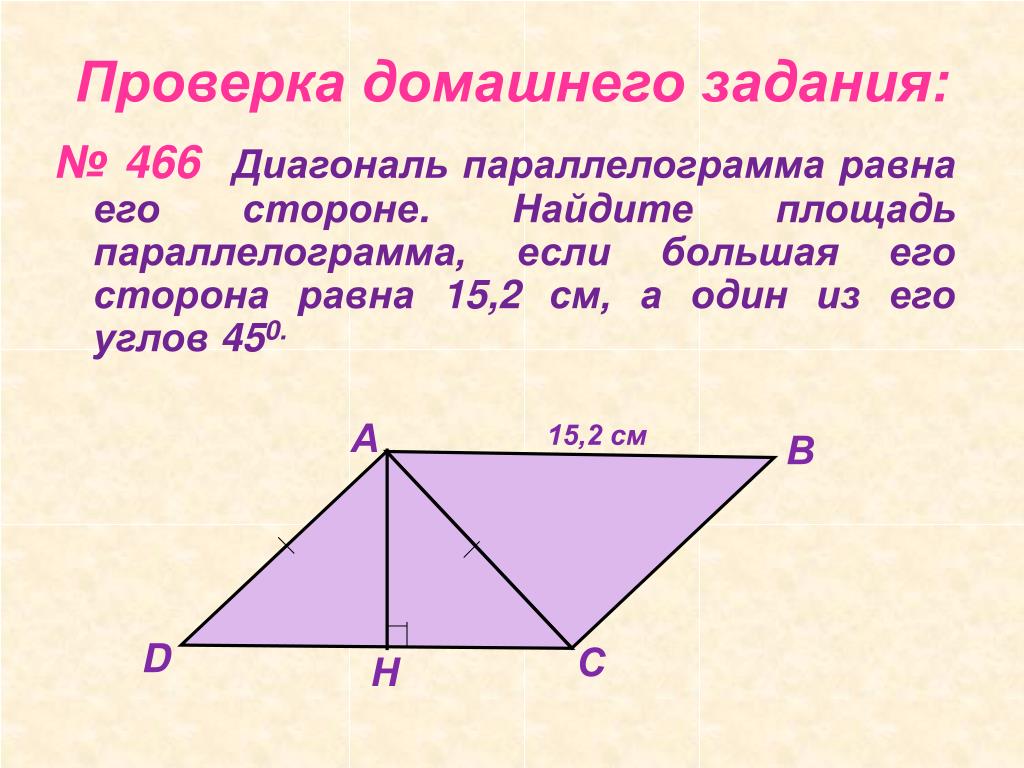
Дан параллелограмм ABCD, на одной из сторон которого АВ поставлена точка М. Известно, что площадь треугольника MCD составляет 38 см кв. Как найти площадь параллелограмма?
Площадь (S) параллелограмма рассчитывается путем умножения длины его основания на длину его высоты.
Прямые МС и МD, проведенные из точки М, делят параллелограмм на треугольники. Площадь первого из них вычисляется как:
S₁ = 1/2 * a * h = 38 см кв.
Формула для расчета площади второго треугольника выглядит так:
S₂ = 1/2 * a₁* h
Площадь третьего треугольника можно найти следующим образом:
S₃ = 1/2 *a₃* h,
где а =а₁ + а₂
Теперь через площади образованных треугольников можно вычислить площадь параллелограмма:
S = S₁ + S₂ + S₃ = 1/2 *(a * h +a₁ * h +a₂ * h) = 1/2 * (a * h + h(a₁ +
a₂)) = 1/2 * (a * h + a * h) = 2 * 38 = 76 см. кв.
кв.
Ответ: Площадь параллелограмма равна 76 см кв.
Длина основания параллелограмма составляет 5 см, а его высота равна 3 см. Как найти площадь параллелограмма?
Формула расчета площади параллелограмма (S) включает длину его высоты и длину его основания. Данные элементы нужно перемножить, для того чтобы вычислить площадь фигуры:
S = a*h= 5*6=30 см кв.
Ответ: Параллелограмм имеет площадь 30 см кв.
Имеется параллелограмм ABCD. Посередине его стороны АВ поставлена точка Е, из которой проведена прямая, образующая треугольник CDE площадью 36 см кв. Каким образом можно найти площадь параллелограмма?
На продолжение стороны CD опустим перпендикуляр ЕН из точки Е. Он представляет собой высоту для параллелограмма ABCD и треугольника CDE.
Известно, что площадь (S) параллелограмма является произведением длины его
стороны и высоты, которая на нее опущена. Площадь треугольника
представляет собой ½ от числа, которое получилось в результате умножения
длины стороны на высоту, опущенную на нее. На основании этого можно
сделать вывод о том, что:
Площадь треугольника
представляет собой ½ от числа, которое получилось в результате умножения
длины стороны на высоту, опущенную на нее. На основании этого можно
сделать вывод о том, что:
S(ABCD) = EH*CD
S(∆CDE) = ½*EH*CD => 2*S(∆CDE) = EH*CD.
Из этого следует, что:
2*S(∆CDE) = S(ABCD) = 2*36 ед² = 72 ед. кв.
Ответ: Площадь параллелограмма составляет 72 кв. ед.
В каком виде представлена формула, которая предназначена для вычисления площади параллелограмма?
Для получения возможности рассчитать, чему равна площадь (S) параллелограмма, нужно располагать сведениями о длине его основания (а) и высоты (h). В этом случае площадь можно высчитать при помощи следующей формулы:
S = а* h.
Как найти площадь параллелограмма через синус, если известно, что длины его сторон равны 8 см и 10 см, а синус одного из его углов составляет 0,05?
Формула, которая предназначена для вычисления площади параллелограмма (S) через синус, выглядит следующим образом:
S = a × b × sin A
В данной формуле буквами a и b обозначены стороны параллелограмма,
являющиеся смежными, а А означает угол, который образован между этими
сторонами.
Доказано, что синусы смежных углов являются равными. Это значит, что синус тупого угла равен синусу острого угла.
Площадь параллелограмма вычисляем следующим образом:
S = 8 × 10 × 0,05 = 4 см кв.
Ответ: Параллелограмм имеет площадь, равную 4 см кв.
Имеется параллелограмм ABCD, в котором опущена высота на его сторону АВ. Ее длина равна 12 см. При этом длина AD составляет 24 см. Каким образом можно высчитать значение синуса угла А?
Высота, опущенная на сторону АВ параллелограмма, обозначена как СК. Полученный в результате треугольник КВС имеет прямой угол.
Sin B=АВ/ВС.
В этом случае ВС=AD=24 см. Так, синус угла В равен:
sinВ=12/24=1/2, что соответствует углу 30 градусов.
В параллелограмме проведены диагонали, длины которых равны 5 см и 28 см. Между ними образован угол, составляющий 30 градусов. Как можно найти площадь параллелограмма через синус в данном случае?
Площадь любой из четырехугольных фигур может быть вычислена, если известны
длины ее диагоналей и синус угла, образованного между ними. Для этого
нужно произвести умножение упомянутых величин, а затем разделить
полученное число на 2. В случае с параллелограммом, обозначенным как ABCD,
площадь рассчитывается по этой же формуле:
Для этого
нужно произвести умножение упомянутых величин, а затем разделить
полученное число на 2. В случае с параллелограммом, обозначенным как ABCD,
площадь рассчитывается по этой же формуле:
S = 1/2 AC*BD*sin∠AOB = ½*28*5*sin30° = 14*5*1/2 = 7*5 = 35 кв. см.
Ответ: Площадь параллелограмма равна 35 см кв.
Представляется ли возможным высчитать площадь параллелограмма при условии, что длины двух его диагоналей и образованный в месте их пересечения угол являются известными величинами?
Площадь параллелограмма (S) представляет собой половину числа, полученного после умножения друг на друга длин проведенных в нем диагоналей, которое умножено на синус образовавшегося в итоге их пересечения угла:
S = ½*d 1*d 2*sin α
Возможно ли рассчитать площадь параллелограмма по диагоналям, длины которых
равны 6 см и 4 см? При этом известно, что образованный ими угол является
прямым.
Для определения площади параллелограмма через известные длины проведенных в нем диагоналей применяется приведенная ниже формула:
S = ½*d 1*d 2*sin α,
где диагонали фигуры обозначены как d 1 и d 2, а синус образованного в результате их пересечения угла — sin α.
Подставим в указанное равенство величины, приведенные в задании:
S = 1/2 * 4 см * 6 см * sin 90° = 12 см кв.
Ответ: Площадь параллелограмма, вычисленная через диагонали, равна 12 см кв.
На одной из сторон параллелограмма ABCD, обозначенной как ВС, отмечена точка М. Чему будет равна площадь параллелограмма при условии, что площадь треугольника МАD составляет 21 см кв.?
Под площадью параллелограмма (S) понимается величина, полученная в результате умножения длины его стороны (b) на высоту (h), которая опущена к ней. В виде формулы это выглядит следующим образом:
S =b*h
Площадь треугольной фигуры представляет собой ½ числа, полученного произведением длины стороны на высоту, которая к ней проведена:
S=1/2*b*h,
Отсюда получаем, что:
b*h=2Sт=2*21=42 см кв.
Если говорить о треугольнике МАD, то в нем сторона АD представлена в качестве стороны b, как и в случае с параллелограммом. Высота указанного треугольника будет также представлять собой высоту параллелограмма. Это обусловлено тем, что точка М расположена на стороне, которая противоположна стороне ВС. Из этого следует, что площадь параллелограмма равна 42 см кв.
Ответ: Площадь параллелограмма равна 42 см кв.
Параллелограмм ABCD имеет стороны длиной 10 см и 14 см, а также острый угол в 60 градусов. Каким образом можно вычислить площадь параллелограмма?
В параллелограмме ABCD нужно провести высоту ВН на сторону AD. После этого получается треугольник АВН с углом в 90 градусов. Можно рассчитать, чему равен еще один угол данного треугольника:
АВН = 90-60 = 30
ВН = АВ*sin60 = 10*корень3/2 = 5*корень3
Таким образом, можно узнать, чему будет равна площадь параллелограмма:
S = AD*ВН = 14*5*√3 = 70*√3 см кв.
Ответ: Площадь параллелограмма составляет 70*√3 см кв.
Дан параллелограмм, через середины пары смежных сторон которого проведена прямая. Она отсекает треугольную фигуру площадью 32 см кв. Чему в данном случае равна площадь параллелограмма?
АС представляет собой диагональ биссектрисы. В этом случае оба треугольника FMD и ADC являются подобными по той причине, что они имеют общий угол А и их стороны равны. Из этого следует, что:
S ADC = 1/2*ab*sina
S FDM=1/2 *2a*2bsina
Отношение площадей двух треугольников выглядит как:
S ADC / S FDM= 32/x
1/4=32/x
x=128
Теперь можно высчитать площадь параллелограмма:
S = 128*2 = 256 см кв.
Верно ли утверждение что площадь параллелограмма. Площадь параллелограмма
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).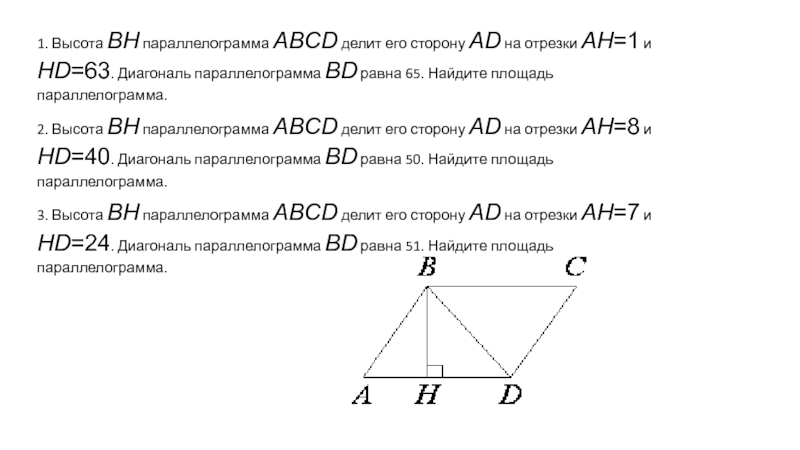
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – .
Первый урок – бесплатно!
blog.сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры.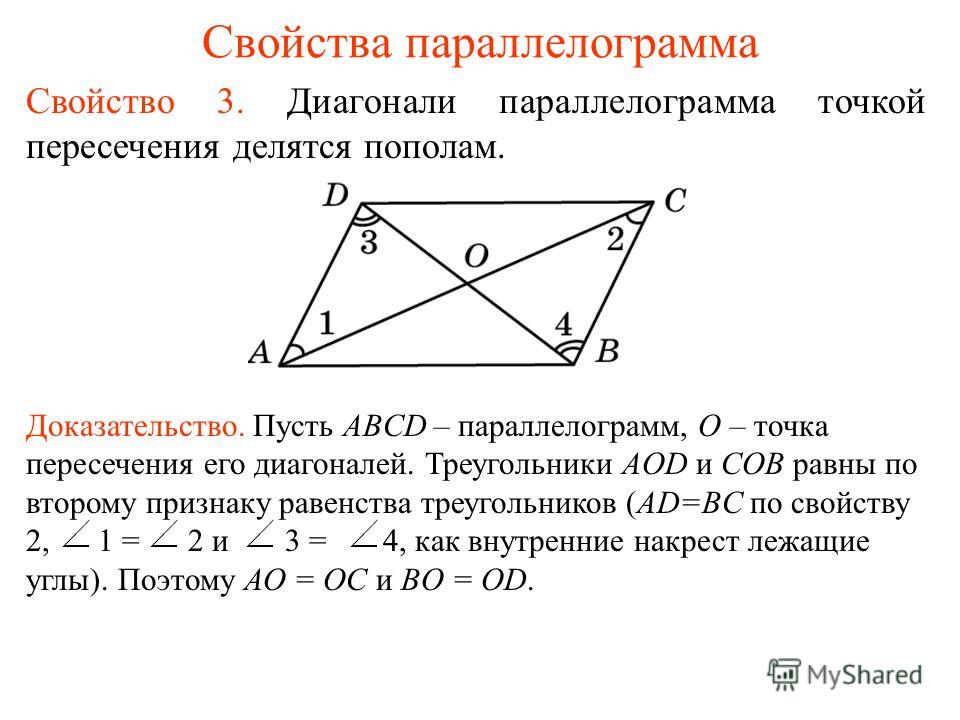 Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник.
 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. - Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinα
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Условимся одну из сторон параллелограмма называть основанием , а перпендикуляр, проведённый из любой точки противоположной стороны к прямой, содержащей основание, — высотой параллелограмма .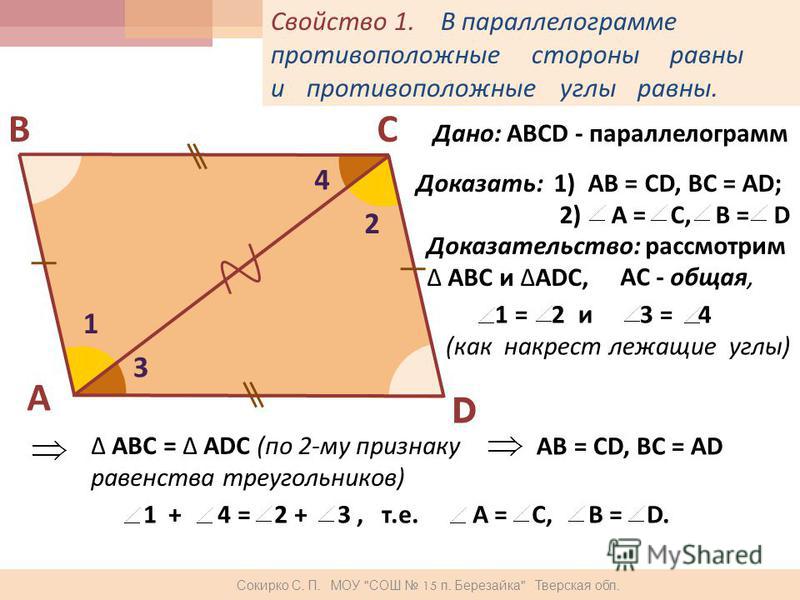
Теорема
Доказательство
Рассмотрим параллелограмм ABCD с площадью S. Примем сторону AD за основание и проведём высоты ВН и СК (рис. 182). Докажем, что S = AD ВН.
Рис. 182
Докажем сначала, что площадь прямоугольника НВСК также равна S. Трапеция АВСК составлена из параллелограмма ABCD и треугольника DCK. С другой стороны, она составлена из прямоугольника НВСК и треугольника АВН. Но прямоугольные треугольники DCK и АВН равны по гипотенузе и острому углу (их гипотенузы АВ и CD равны как противоположные стороны параллелограмма, а углы 1 и 2 равны как соответственные углы при пересечении параллельных прямых АВ и CD секущей AD), поэтому их площади равны.
Следовательно, площади параллелограмма ABCD и прямоугольника НВСК также равны, т. е. площадь прямоугольника НВСК равна S. По теореме о площади прямоугольника S = ВС ВН, а так как ВС = AD, то S = AD ВН. Теорема доказана.
Площадь треугольника
Одну из сторон треугольника часто называют его основанием .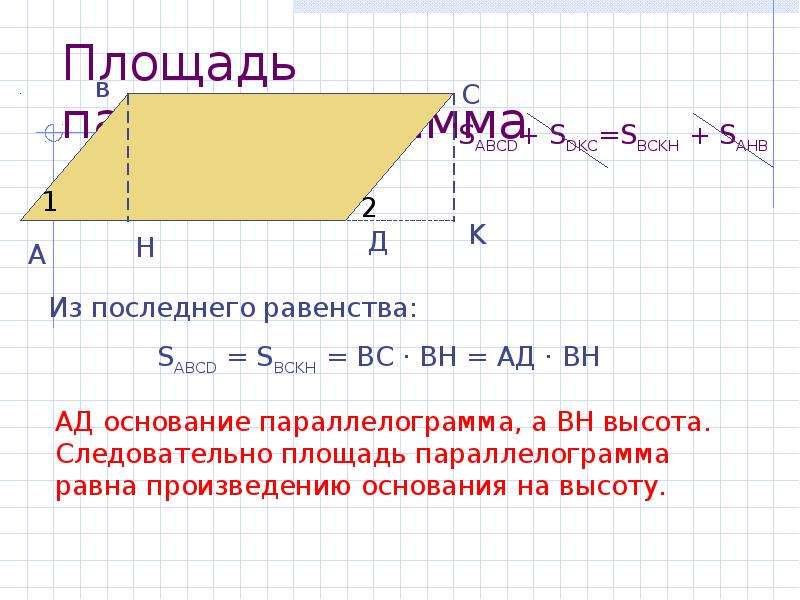 Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведённую к основанию. Теорема
Если основание выбрано, то под словом «высота» подразумевают высоту треугольника, проведённую к основанию. Теорема
Доказательство
Пусть S — площадь треугольника АВС (рис. 183). Примем сторону АВ за основание треугольника и проведём высоту СН. Докажем, что .
Рис. 183
Достроим треугольник АВС до параллелограмма ABDC так, как показано на рисунке 183. Треугольники АВС и DCB равны по трём сторонам (ВС — их общая сторона, АВ = CD и АС = BD как противоположные стороны параллелограмма ABDC), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма ABDC, т. е. . Теорема доказана.
Следствие 1
Следствие 2
Воспользуемся следствием 2 для доказательства теоремы об отношении площадей треугольников, имеющих по равному углу.
Теорема
Доказательство
Пусть S и S 1 — площади треугольников АВС и A 1 B 1 C 1 , у которых ∠A = ∠A 1 (рис. 184, а). Докажем, что .
184, а). Докажем, что .
Рис. 184
Наложим треугольник A 1 B 1 C 1 на треугольник ABC так, чтобы вершина А 1 совместилась с вершиной А, а стороны А 1 В 1 и A 1 С 1 наложились соответственно на лучи АВ и АС (рис. 184, б). Треугольники АВС и АВ 1 С имеют общую высоту — CН, поэтому .
Треугольники АВ 1 С и АВ 1 С 1 также имеют общую высоту — В 1 Н 1 , поэтому . Перемножая полученные равенства, находим:
Теорема доказана.
Для вычисления площади произвольного многоугольника обычно поступают так: разбивают многоугольник на треугольники и находят площадь каждого треугольника. Сумма площадей этих треугольников равна площади данного многоугольника (рис. 185, а). Используя этот приём, выведем формулу для вычисления площади трапеции. Условимся называть высотой трапеции перпендикуляр, проведённый из любой точки одного из оснований к прямой, содержащей другое основание. На рисунке 185, б отрезок ВН (а также отрезок DH 1) — высота трапеции ABCD.
Рис. 185
Теорема
Доказательство
Рассмотрим трапецию ABCD с основаниями AD и ВС, высотой ВН и площадью S (см. рис. 185, б).
Докажем, что
Диагональ BD разделяет трапецию на два треугольника ABD и BCD, поэтому S = S ABD + S BCD .
Примем отрезки AD и ВН за основание и высоту треугольника ABD, а отрезки ВС и DH 1 за основание и высоту треугольника BCD. Тогда
.
Теорема доказана.
Задачи
459. Пусть а — основание, h — высота, a S — площадь параллелограмма. Найдите: a) S, если а = 15 см, h = 12 см; б) а, если S = 34 cм 2 , h = 8,5 см; в) а, если S = 162 cм 2 , h = 1/2a; г) h, если h = 3а, S = 27.
460. Диагональ параллелограмма, равная 13 см, перпендикулярна к стороне параллелограмма, равной 12 см. Найдите площадь параллелограмма.
461. Смежные стороны параллелограмма равны 12 см и 14 см, а его острый угол равен 30°. Найдите площадь параллелограмма.
462. Сторона ромба равна 6 см, а один из углов равен 150°. Найдите площадь ромба.
Найдите площадь ромба.
463. Сторона параллелограмма равна 8,1 см, а диагональ, равная 14 см, образует с ней угол в 30°. Найдите площадь параллелограмма.
464. Пусть а и b — смежные стороны параллелограмма, S — площадь, a h 1 и h 2 — его высоты. Найдите: a) h 2 , если а = 18 см, b = 30 см, h 1 = 6 см, h 2 > h 1 ; б) h 1 , если а =10 см, 6 =15 см, h 2 = 6 см, h 2 > h 1 в) h 1 и h 2 , если S = 54 см 2 , а = 4,5 см, b = 6 см.
465. Острый угол параллелограмма равен 30°, а высоты, проведённые из вершины тупого угла, равны 2 см и 3 см. Найдите площадь параллелограмма.
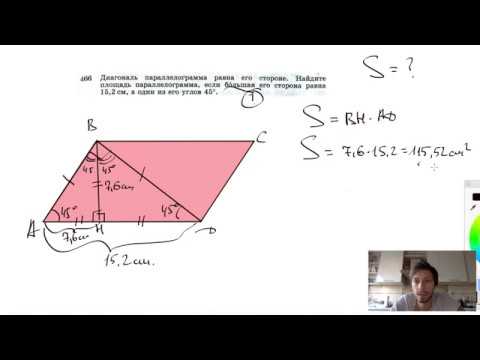
466. Диагональ параллелограмма равна его стороне. Найдите площадь параллелограмма, если большая его сторона равна 15,2 см, а один из его углов 45°.
467. Квадрат и ромб, не являющийся квадратом, имеют одинаковые периметры. Сравните площади этих фигур.
468. Пусть а — основание, h — высота, a S — площадь треугольника. Найдите: a) S, если а = 7 см, h = 11 см; б) S, если а = 2√3 см, h = 5 см; в) h, если S = 37,8 см 2 , а — 14 см; г) а, если S = 12 см 2 , h = 3√2 см.
469. Стороны АВ и ВС треугольника АВС равны соответственно 16 см и 22 см, а высота, проведённая к стороне АВ, равна 11 см. Найдите высоту, проведённую к стороне ВС.
470. Две стороны треугольника равны 7,5 см и 3,2 см. Высота, проведённая к большей стороне, равна 2,4 см. Найдите высоту, проведённую к меньшей из данных сторон.
471. Д Найдите площадь прямоугольного треугольника, если его катеты равны: а) 4 см и 11 см; б) 1,2 дм и 3 дм.
472. Площадь прямоугольного треугольника равна 168 см 2 . Найдите его катеты, если отношение их длин равно 7/12.
473. Через вершину С треугольника АВС проведена прямая m, параллельная стороне АВ. Докажите, что все треугольники с вершинами на прямой m и основанием АВ имеют равные площади.
474. Сравните площади двух треугольников, на которые разделяется данный треугольник его медианой.
475. Начертите треугольник АВС. Через вершину А проведите две прямые так, чтобы они разделили этот треугольник на три треугольника, имеющие равные площади.
476. Докажите, что площадь ромба равна половине произведения его диагоналей. Вычислите площадь ромба, если его диагонали равны: а) 3,2 дм и 14 см; б) 4,6 дм и 2 дм.
477. Найдите диагонали ромба, если одна из них в 1,5 раза больше другой, а площадь ромба равна 27 см 2 .
478. В выпуклом четырёхугольнике диагонали взаимно перпендикулярны. Докажите, что площадь четырёхугольника равна половине произведения его диагоналей.
479. Точки D и Е лежат на сторонах АВ и АС треугольника АВС. Найдите: a) S ADE , если АВ = 5 см, АС = 6 см, AD = Зсм, АЕ = 2 см, S ABC = 10 cм 2 ; б) AD, если АВ = 8 см, АС = 3 см, АЕ = 2 см, S ABC = 10 см 2 , S ADE = 2 см 2 .
480. Найдите площадь трапеции ABCD с основаниями АВ и CD, если:
а) АВ = 21 см, CD= 17 см, высота ВН равна 7 см;
б) ∠D = 30°, АВ = 2 см, CD = 10 см, DA = 8 см;
в) ВС ⊥ АВ, АВ = 5 см, ВС = 8 см, CD = 13 см.
481. Найдите площадь прямоугольной трапеции, у которой две меньшие стороны равны 6 см, а больший угол равен 135°.
482. Тупой угол равнобедренной трапеции равен 135°, а высота, проведённая из вершины этого угла, делит большее основание на отрезки 1,4 см и 3,4 см. Найдите площадь трапеции.
Ответы к задачам
459. а) 180 см 2 ; б) 4 см; в) 18 см; г) 9.
460. 156 см 2 .
461. 84 см 2 .
462. 18 см 2 .
463. 56,7 см 2 .
464. а) 10 см; б) 4 см; в) 12 см и 9 см.
465. 12 см 2 .
466. 115,52 см 2 .
467. Площадь квадрата больше.
468. а) 38,5 см 2 ; б) 5√3 см 2 ; в) г) 4√2 см.
470. 5,625 см.
471. а) 22 см 2 ; б) 1,8 дм 2 .
472. 14 см и 24 см.
473. Указание. Воспользоваться теоремой п. 38.
474. Площади треугольников равны.
475. Указание. Сначала разделить сторону ВС на три равные части.
476. а) 224 см 2 ; б) 4,6 дм 2 . Указание. Учесть, что диагонали ромба взаимно перпендикулярны.
477. 6 см и 9 см.
479. а) 2 см 2 ; б) 2,4 см. Указание. Воспользоваться второй теоремой п. 53.
480. а) 133 см 2 ; б) 24 см 2 ; в) 72 см 2 .
481. 54 см 2 .
482. 4,76 см 2 .
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.
 Найти площадь параллелограмма.
Найти площадь параллелограмма.Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
Как вычислить площадь параллелограмма. Параллелограмм и его свойства
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .
В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания. По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.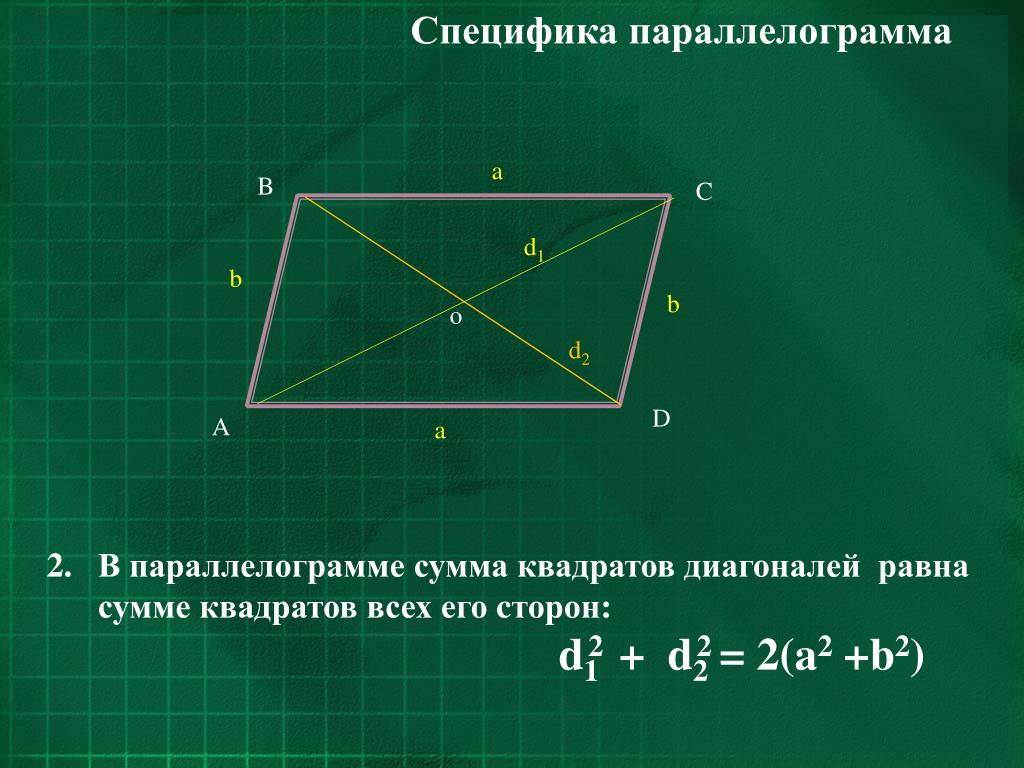
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.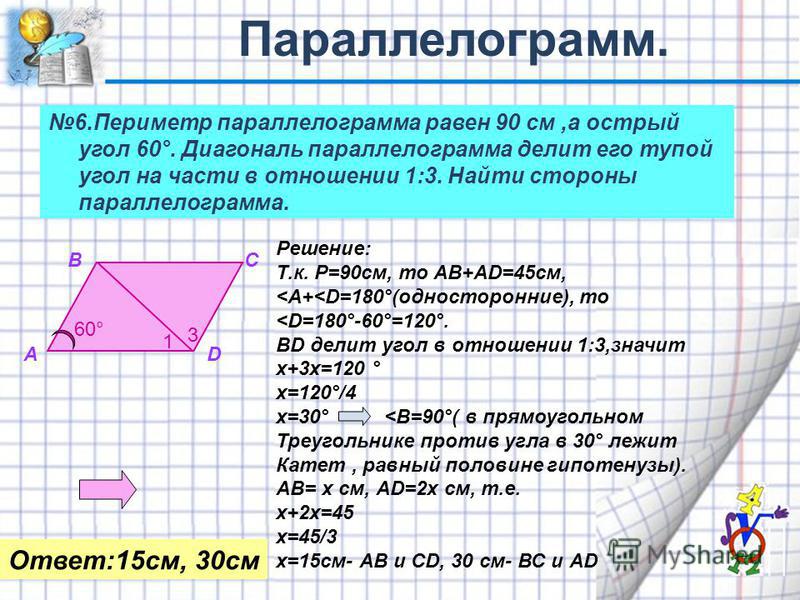
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограмм представляет собой четырехугольную фигуру, у которой противолежащие стороны попарно параллельны и попарно равны. Равны у него также и противоположные углы, а точка пересечения диагоналей параллелограмма делит их пополам, являясь при этом центром симметрии фигуры. Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Частными случаями параллелограмма являются такие геометрические фигуры как квадрат, прямоугольник и ромб. Площадь параллелограмма может быть найдена различными способами, в зависимости от того, какими исходными данными сопровождается постановка задачи.
Ключевой характеристикой параллелограмма, очень часто используемой при нахождении его площади, является высота. Высотой параллелограмма принято называть перпендикуляр, опущенный из произвольной точки противоположной стороны к отрезку прямой, образующей данную сторону.
- В самом простом случае площадь параллелограмма определяется как произведение его основания на высоту.
S = DC ∙ h
где S — площадь параллелограмма;
a — основание;
h — высота, проведенная к данному основанию.Данную формулу очень легко понять и запомнить, если взглянуть на следующий рисунок.
Как видно из данного изображения, если слева от параллелограмма отрезать воображаемый треугольник и присоединить его справа, то в результате мы получим прямоугольник.
 А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. - Площадь параллелограмма может быть также найдена в результате перемножения длин двух смежных оснований и синуса угла между ними:
S = AD∙AB∙sinα
где AD, AB — смежные основания, образующие точку пересечения и угол а между собой;
α — угол между основаниями AD и AB. - Также площадь параллелограмма можно найти разделив пополам произведение длин диагоналей параллелограмма на синус угла между ними.
S = ½∙AC∙BD∙sinβ
где AC, BD — диагонали параллелограмма;
β — угол между диагоналями. - Существует также формула для нахождения площади параллелограмма через радиус вписанной в него окружности. Она записывается следующий образом:
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. 2)
.
2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.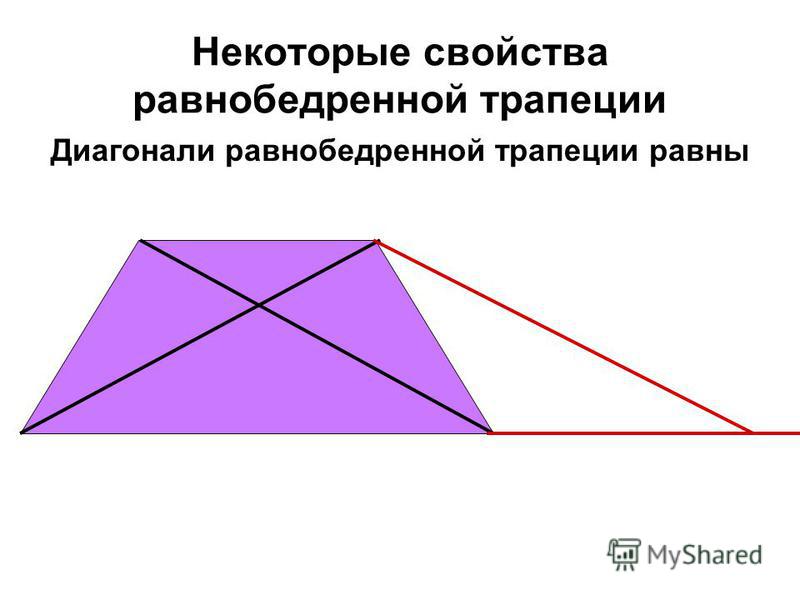
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Рекомендуем также
Площадь параллелограмма если известны стороны. Периметр и площадь параллелограмма
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.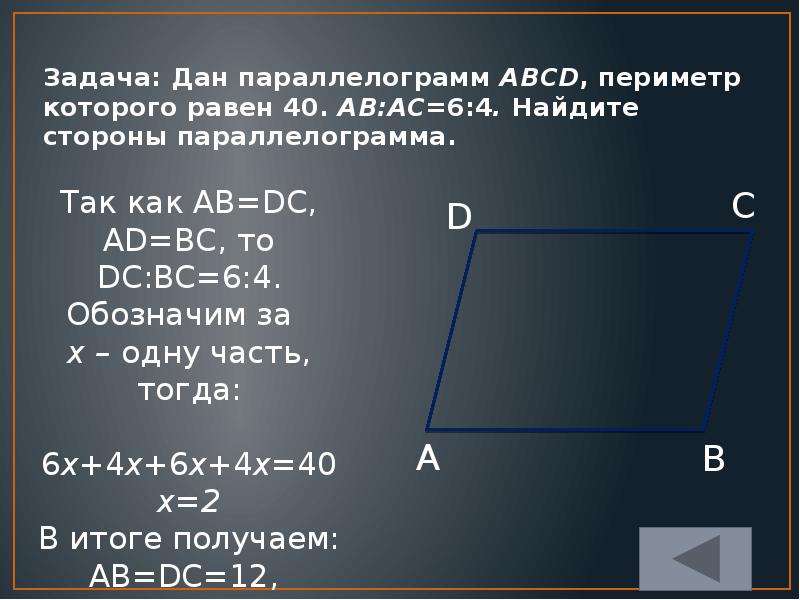
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Параллелограммом называют четырехугольник у которого противоположные стороны параллельны между собой. Основные задачи в школе по данной теме заключаются в вычислении площади параллелограмма, его периметра, высоты, диагоналей. Указанные величины и формулы для их вычисления будут приведены ниже. 2)
.
2)
.
Основные признаки параллелограммов:
1. Четырехугольник у которого противоположные стороны попарно параллельны является параллелограммом.
2. Четырехугольник с равными противоположными сторонами является параллелограммом.
3. Четырехугольник с равными и параллельными противоположными сторонами является параллелограммом.
4. Если диагонали четырехугольника в точке пересечения делятся пополам то это параллелограмм.
5. Четырехугольник у которого противоположные углы попарно равны является параллелограммом
Биссектрисы параллелограмма
Биссектрисы противоположных углов в параллелограмме могут быть параллельными или совпадать.
Биссектрисы соседних углов (прилегающие к одной стороне) пересекаются под прямым углом (перпендикулярные).
Высота параллелограмма
Высота параллелограмма
— это отрезок который проведен с угла перпендикулярно к основанию. Из этого следует что из каждого угла можно провести две высоты.
Формула площади параллелограмма
Площадь параллелограмма
равна произведению стороны на высоту проведенную к ней. Формула площади следующая
Вторая формула не менее популярная при вычислениях и определяется так: площадь параллелограмма равна произведению соседних сторон на синус угла между ними
На основе приведенных формул Вы будете знать как вычислить площадь параллелограмма.
Периметр параллелограмма
Формула для вычисления периметру параллелограмма имеет вид
то есть периметр равен удвоенному значению суммы сторон. Задачи на параллелограмм будут рассмотрены в соседних материалах, а пока изучайте формулы. Большинство задач по вычислению сторон, диагоналей параллелограмма достаточно просты и сводятся к знанию теоремы синусов и теоремы Пифагора.
Примечание . Это часть урока с задачами по геометрии (раздел параллелограмм). Если Вам необходимо решить задачу по геометрии, которой здесь нет — пишите об этом в форуме. Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Для обозначения действия извлечения квадратного корня в решениях задач используется символ √ или sqrt(), при чем в скобках указано подкоренное выражение.
Теоретический материал
Пояснения к формулам нахождения площади параллелограмма:
- Площадь параллелограмма равна произведению длины одной из его сторон на высоту, опущенную на эту сторону
- Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними
- Площадь параллелограмма равна половине произведения его диагоналей на синус угла между ними
Задачи на нахождение площади параллелограмма
Задача .В параллелограмме меньшая высота и меньшая сторона равны 9 см и корню из 82 соответственно.Большая диагональ 15 см.Найти площадь параллелограмма.
Решение .
Обозначим меньшую высоту параллелограмма ABCD, опущенную из точки B на большее основание AD как BK.
Найдем значение катета прямоугольного треугольника ABK, образованного меньшей высотой, меньшей стороной и частью большего основания.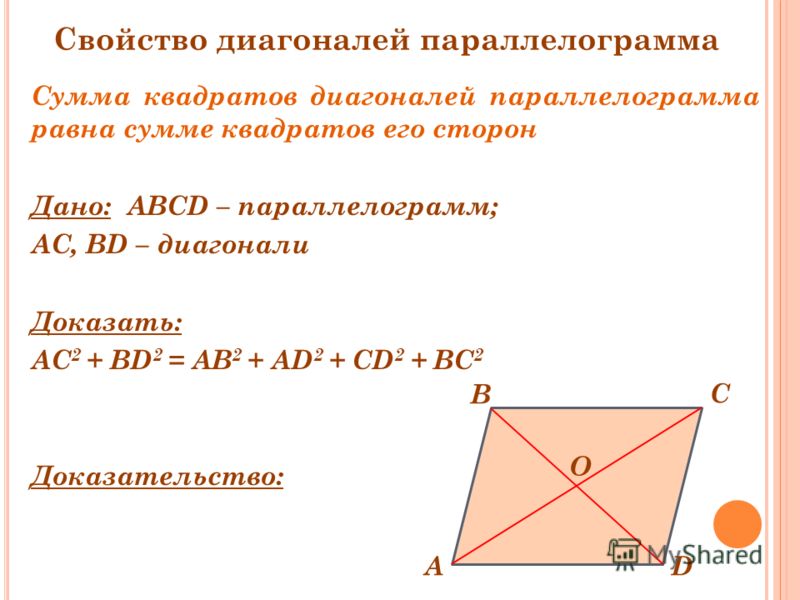 По теореме Пифагора:
По теореме Пифагора:
AB 2 = BK 2 + AK 2
82 = 9 2 + AK 2
AK 2 = 82 — 81
AK = 1
Продлим верхнее основание параллелограмма BC и опустим на него высоту AN из его нижнего основания. AN = BK как стороны прямоугольника ANBK. У получившегося прямоугольного треугольника ANC найдем катет NC.
AN 2 + NC 2 = AC 2
9 2 + NC 2 = 15 2
NC 2 = 225 — 81
NC 2 = √144
NC = 12
Теперь найдем большее основание BC параллелограмма ABCD.
BC = NC — NB
Учтем, что NB = AK как стороны прямоугольника, тогда
BC = 12 — 1 = 11
Площадь параллелограмма равна произведению основания на высоту к этому основанию.
S = ah
S = BC * BK
S = 11 * 9 = 99
Ответ : 99 см 2 .
Задача
В параллелограмме АВСД на диагональ АС опущен перпендикуляр ВО. Найдите площадь параллелограмма, если АО=8, ОС=6 и ВО=4.Решение .
Опустим на диагональ АС дополнительно еще один перпендикуляр DK.
Соответственно, треугольники AOB иDKC, COB и AKD попарно равны. Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Одна из сторон является противолежащей стороной параллелограмма, один из углов — прямой, так как является перпендикуляром к диагонали, а один из оставшихся углов является внутренним накрест лежащим для параллельных сторон параллелограмма и секущей диагонали.
Таким образом, площадь параллелограмма равна площади указанных треугольников. То есть
Sпаралл = 2S AOB +2S BOC
Площадь прямоугольного треугольника равна половине произведения катетов. Откуда
S = 2 (1/2 8 * 4) + 2 (1/2 6 * 4) = 56 см 2
Ответ : 56 см 2 .
Видеокурс «Получи пятерку» включает все темы, необходимые для успешной сдачи ЕГЭ по математике на 60-65 баллов. Полностью все задачи 1-13 Профильного ЕГЭ по математике. Подходит также для сдачи Базового ЕГЭ по математике. Если вы хотите сдать ЕГЭ на 90-100 баллов, вам надо решать часть 1 за 30 минут и без ошибок!
Курс подготовки к ЕГЭ для 10-11 класса, а также для преподавателей. Все необходимое, чтобы решить часть 1 ЕГЭ по математике (первые 12 задач) и задачу 13 (тригонометрия). А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
А это более 70 баллов на ЕГЭ, и без них не обойтись ни стобалльнику, ни гуманитарию.
Вся необходимая теория. Быстрые способы решения, ловушки и секреты ЕГЭ. Разобраны все актуальные задания части 1 из Банка заданий ФИПИ. Курс полностью соответствует требованиям ЕГЭ-2018.
Курс содержит 5 больших тем, по 2,5 часа каждая. Каждая тема дается с нуля, просто и понятно.
Сотни заданий ЕГЭ. Текстовые задачи и теория вероятностей. Простые и легко запоминаемые алгоритмы решения задач. Геометрия. Теория, справочный материал, разбор всех типов заданий ЕГЭ. Стереометрия. Хитрые приемы решения, полезные шпаргалки, развитие пространственного воображения. Тригонометрия с нуля — до задачи 13. Понимание вместо зубрежки. Наглядное объяснение сложных понятий. Алгебра. Корни, степени и логарифмы, функция и производная. База для решения сложных задач 2 части ЕГЭ.
Как в евклидовой геометрии точка и прямая — главные элементы теории плоскостей, так и параллелограмм является одной из ключевых фигур выпуклых четырехугольников. Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Из него, как нитки из клубка, втекают понятия «прямоугольника», «квадрата», «ромба» и других геометрических величин.
Вконтакте
Определение параллелограмма
Выпуклый четырехугольник, состоящий из отрезков, каждая пара из которых параллельна, известен в геометрии как параллелограмм.
Как выглядит классический параллелограмм изображает четырехугольник ABCD. Стороны называются основаниями (AB, BC, CD и AD), перпендикуляр, проведенный из любой вершины на противоположную этой вершине сторону, — высотой (BE и BF), линии AC и BD — диагоналями.
Внимание! Квадрат, ромб и прямоугольник — это частные случаи параллелограмма.
Стороны и углы: особенности соотношения
Ключевые свойства, по большому счету, предопределены самим обозначением , их доказывает теорема. Эти характеристики следующие:
- Стороны, которые являются противоположными, — попарно одинаковые.
- Углы, расположенные противоположно друг другу — попарно равны.

Доказательство: рассмотрим ∆ABC и ∆ADC, которые получаются вследствие разделения четырехугольника ABCD прямой AC. ∠BCA=∠CAD и ∠BAC=∠ACD, поскольку AC для них общая (вертикальные углы для BC||AD и AB||CD, соответственно). Из этого следует: ∆ABC = ∆ADC (второй признак равенства треугольников).
Отрезки AB и BC в ∆ABC попарно соответствуют линиям CD и AD в ∆ADC, что означает их тождество: AB = CD, BC = AD. Таким образом, ∠B соответствует ∠D и они равны. Так как ∠A=∠BAC+∠CAD, ∠C=∠BCA+∠ACD, которые так же попарно одинаковые, то ∠A = ∠C. Свойство доказано.
Характеристики диагоналей фигуры
Основной признак этих линий параллелограмма: точка пересечения разделяет их пополам.
Доказательство: пусть т. Е — это точка пересечения диагоналей AC и BD фигуры ABCD. Они образуют два соизмеримых треугольника — ∆ABE и ∆CDE.
AB=CD, так как они противоположные. Согласно прямых и секущей, ∠ABE = ∠CDE и ∠BAE = ∠DCE.
По второму признаку равенства ∆ABE = ∆CDE. Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Это означает, что элементы ∆ABE и ∆CDE: AE = CE, BE = DE и при этом они соразмерные части AC и BD. Свойство доказано.
Особенности смежных углов
У смежных сторон сумма углов равна 180° , поскольку они лежат по одну сторону параллельных линий и секущей. Для четырехугольника ABCD:
∠A+∠B=∠C+∠D=∠A+∠D=∠B+∠C=180º
Свойства биссектрисы:
- , опущенные на одну сторону, являются перпендикулярными;
- противолежащие вершины имеют параллельные биссектрисы;
- треугольник, полученный проведением биссектрисы, будет равнобедренным.
Определение характерных черт параллелограмма по теореме
Признаки этой фигуры вытекают из ее основной теоремы, которая гласит следующее: четырехугольник считается параллелограммом в том случае, если его диагонали пересекаются, а эта точка разделяет их на равные отрезки.
Доказательство: пусть в т. Е прямые AC и BD четырехугольника ABCD пересекаются. Так как ∠AED = ∠BEC, а AE+CE=AC BE+DE=BD, то ∆AED = ∆BEC (по первому признаку равенства треугольников). То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
То есть ∠EAD = ∠ECB. Они также являются внутренними перекрестными углами секущей AC для прямых AD и BC. Таким образом, по определению параллельности — AD || BC. Аналогичное свойство линий BC и CD выводится также. Теорема доказана.
Вычисление площади фигуры
Площадь этой фигуры находится несколькими методами, одним из самых простых: умножения высоты и основания, к которому она проведена.
Доказательство: проведем перпендикуляры BE и CF из вершин B и C. ∆ABE и ∆DCF — равные, поскольку AB = CD и BE = CF. ABCD — равновеликий с прямоугольником EBCF, так как они состоят и соразмерных фигур: S ABE и S EBCD , а также S DCF и S EBCD . Из этого следует, что площадь этой геометрической фигуры находится так же как и прямоугольника:
S ABCD = S EBCF = BE×BC=BE×AD.
Для определения общей формулы площади параллелограмма обозначим высоту как hb , а сторону — b . Соответственно:
Другие способы нахождения площади
Вычисления площади через стороны параллелограмма и угол , который они образуют, — второй известный метод.
,
Sпр-ма — площадь;
a и b — его стороны
α — угол между отрезками a и b.
Этот способ практически основывается на первом, но в случае, если неизвестна. всегда отрезает прямоугольный треугольник, параметры которого находятся тригонометрическими тождествами, то есть . Преобразуя соотношение, получаем . В уравнении первого способа заменяем высоту этим произведением и получаем доказательство справедливости этой формулы.
Через диагонали параллелограмма и угол, который они создают при пересечении, также можно найти площадь.
Доказательство: AC и BD пересекаясь, образуют четыре треугольника: ABE, BEC, CDE и AED. Их сумма равна площади этого четырехугольника.
Площадь каждого из этих ∆ можно найти за выражением , где a=BE, b=AE, ∠γ =∠AEB. Поскольку , то в расчетах используется единое значение синуса. То есть . Поскольку AE+CE=AC= d 1 и BE+DE=BD= d 2 , формула площади сводится до:
.
Применение в векторной алгебре
Особенности составляющих частей этого четырехугольника нашли применение в векторной алгебре, а именно: сложении двух векторов. Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Правило параллелограмма утверждает, что если заданные векторы и не коллинеарны, то их сумма будет равна диагонали этой фигуры, основания которой соответствуют этим векторам.
Доказательство: из произвольно выбранного начала — т. о. — строим векторы и . Далее строим параллелограмм ОАСВ, где отрезки OA и OB — стороны. Таким образом, ОС лежит на векторе или сумме .
Формулы для вычисления параметров параллелограмма
Тождества приведены при следующих условиях:
- a и b, α — стороны и угол между ними;
- d 1 и d 2 , γ — диагонали и в точке их пересечения;
- h a и h b — высоты, опущенные на стороны a и b;
| Параметр | Формула |
| Нахождение сторон | |
| по диагоналям и косинусу угла между ними | |
| по диагоналям и стороне | |
| через высоту и противоположную вершину | |
| Нахождение длины диагоналей | |
| по сторонам и величине вершины между ними | |
Параллелограмм — это четырёхугольник — Документ
Параллелограмм — это четырёхугольник,
у которого противолежащие стороны
попарно параллельны, т. е. лежат на
параллельных прямых (от греч. parallelos — параллельный и gramme — линия).
е. лежат на
параллельных прямых (от греч. parallelos — параллельный и gramme — линия).
Свойства параллелограмма
Противоположные стороны параллелограмма равны
Противоположные углы параллелограмма равны
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам
Сумма углов, прилежащих к одной стороне, равна 180°.
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырёх сторон
Признаки параллелограмма
Четырёхугольник является параллелограммом, если выполняется одно из следующих условий:
Противоположные стороны попарно равны
Противоположные углы попарно равны
Две противоположные стороны равны и параллельны
Частные случаи параллелограммов
Параллелограммы можно найти
среди четырехугольников. Из всех
возможных параллелограммов часто
рассматриваются такие, у которых все
углы прямые. Их называют прямоугольниками.
Из всех
возможных параллелограммов часто
рассматриваются такие, у которых все
углы прямые. Их называют прямоугольниками.
Бывают такие параллелограммы, у которых все стороны равны. Их называют ромбами. Термин образован от греческого romboz — “бубен”.
Кроме того, среди прямоугольников есть такие, у которых все стороны равны. То есть некоторые прямоугольники в то же время являются ромбами. А у некоторых ромбов все углы прямые и потому они — прямоугольники.
Параллелограммы, у которых все углы прямые и все стороны равны, называют квадратами.
Свойства и признаки прямоугольников, ромбов, квадратов
Поскольку прямоугольники, ромбы, квадраты являются параллелограммами, то они обладают всеми свойствами параллелограммов.
Но, частные случаи параллелограммов обладают особыми свойствами, не присущими другим параллелограммам.
Особые свойства прямоугольника
1. Если параллелограмм является прямоугольником, то его диагонали равны.
2. Если параллелограмм является прямоугольником, то около него можно
описать окружность.Особые свойства ромба
1. Если параллелограмм является ромбом, то его диагонали перпендикулярны и делят углы ромба пополам.
2. Если параллелограмм является ромбом, то в него можно
вписать окружность.Квадрат
Так как квадрат является прямоугольником, то обладает всеми свойствами прямоугольников. Квадрат является ромбом, потому обладает всеми свойствами ромбов.
Своих собственных особых свойств у квадрата нет.
Признаки, позволяющие установить, является ли параллелограмм прямоугольником, ромбом или квадратом
1.
 Если диагонали параллелограмма
равны, то он прямоугольник.
Если диагонали параллелограмма
равны, то он прямоугольник.2. Если диагонали параллелограмма перпендикулярны, то он ромб.
3. Если обе диагонали параллелограмма делят его противоположные углы пополам, то он ромб.
Площадь параллелограмма
Если четырехугольник параллелограмм, то его площадь S равна произведению стороны на высоту параллелограмма, проведенную к этой стороне.
Например, высота МА и МВ. Тогда S = MA LN
S = MB KL
Задачи
1. Сторона параллелограмма равна 21 см, а высота, проведённая к ней, 15 см. Найдите площадь параллелограмма.
2. В параллелограмме КМРТ диагональ МТ перпендикулярна стороне МК, КМ=13 см, МТ=5см. Найдите площадь параллелограмма и его высоту, если МР= 14.
3. Площадь параллелограмма равна 48 см
2, а его периметр 40 см. Найдите стороны
параллелограмма, если высота, проведённая
к одной из них, в 3 раза меньше этой
стороны.
Найдите стороны
параллелограмма, если высота, проведённая
к одной из них, в 3 раза меньше этой
стороны.Площадь параллелограмма по стороне и высоте. Как найти площадь параллелограмма? Особенности смежных углов
Площадь геометрической фигуры — численная характеристика геометрической фигуры показывающая размер этой фигуры (части поверхности, ограниченной замкнутым контуром данной фигуры). Величина площади выражается числом заключающихся в нее квадратных единиц.
Формулы площади треугольника
- Формула площади треугольника по стороне и высоте
Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты - Формула площади треугольника по трем сторонам и радиусу описанной окружности
- Формула площади треугольника по трем сторонам и радиусу вписанной окружности
Площадь треугольника равна произведения полупериметра треугольника на радиус вписанной окружности. где S — площадь треугольника,
где S — площадь треугольника,
— длины сторон треугольника,
— высота треугольника,
— угол между сторонами и,
— радиус вписанной окружности,
R — радиус описанной окружности,
Формулы площади квадрата
- Формула площади квадрата по длине стороны
Площадь квадрата равна квадрату длины его стороны. - Формула площади квадрата по длине диагонали
Площадь квадрата равна половине квадрата длины его диагонали. где S — Площадь квадрата,
— длина стороны квадрата,
— длина диагонали квадрата.
Формула площади прямоугольника
- Площадь прямоугольника равна произведению длин двух его смежных сторон
где S — Площадь прямоугольника,
— длины сторон прямоугольника.
Формулы площади параллелограмма
- Формула площади параллелограмма по длине стороны и высоте
Площадь параллелограмма - Формула площади параллелограмма по двум сторонам и углу между ними
Площадь параллелограмма равна произведению длин его сторон умноженному на синус угла между ними.
a · b · sin α
где S — Площадь параллелограмма,
— длины сторон параллелограмма,
— длина высоты параллелограмма,
— угол между сторонами параллелограмма.
Формулы площади ромба
- Формула площади ромба по длине стороны и высоте
Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты. - Формула площади ромба по длине стороны и углу
Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба. - Формула площади ромба по длинам его диагоналей
Площадь ромба равна половине произведению длин его диагоналей. где S — Площадь ромба,
— длина стороны ромба,
— длина высоты ромба,
— угол между сторонами ромба,
1 , 2 — длины диагоналей.
Формулы площади трапеции
- Формула Герона для трапеции
Где S — Площадь трапеции,
— длины основ трапеции,
— длины боковых сторон трапеции,
Прежде чем узнать, как найти площадь параллелограмма, нам необходимо вспомнить, что такое параллелограмм и что называется его высотой. Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Параллелограмм – четырехугольник, противолежащие стороны которого попарно параллельны (лежат на параллельных прямых). Перпендикуляр, проведенный из произвольной точки противоположной стороны к прямой, содержащей эту сторону называется высотой параллелограмма.
Квадрат, прямоугольник и ромб – это частные случаи параллелограмма.
Площадь параллелограмма обозначается как (S).
Формулы нахождения площади параллелограмма
S=a*h , где а – это основание, h – это высота, которая проведена к основанию.
S=a*b*sinα , где a и b – это основания, а α — угол между основаниями а и b.
S =p*r , где р – это полупериметр, r – это радиус окружности, которая вписана в параллелограмм.
Площадь параллелограмма, который образован векторами a и b равна модулю произведения заданных векторов, а именно:
Рассмотрим пример №1: Дан параллелограмм, сторона которого равна 7 см, а высота 3 см. Как найти площадь параллелограмма, формула для решения нам необходима.
Таким образом, S= 7×3. S=21. Ответ: 21 см 2 .
S=21. Ответ: 21 см 2 .
Рассмотрим пример №2: Даны основания 6 и 7 см, а также дан угол между основаниями 60 градусов. Как найти площадь параллелограмма? Формула, используемая для решения:
Таким образом, сначала найдем синус угла. Синус 60 = 0,5, соответственно S = 6*7*0,5=21 Ответ: 21 см 2 .
Надеюсь, что эти примеры Вам помогут при решении задач. И помните, главное – это знание формул и внимательность
Определение параллелограмма
Параллелограмм — это четырехугольник, в котором противоположные стороны равны и параллельны.
Онлайн-калькулятор
Параллелограмм обладает некоторыми полезными свойствами, которые упрощают решение задач, связанных с этой фигурой. Например, одно из свойств заключается в том, что противоположные углы параллелограмма равны.
Рассмотрим несколько способов и формул с последующим решением простых примеров.
Формула площади параллелограмма по основанию и высоте
Данный способ нахождения площади является, наверно, одним из основных и простых, так как он практически идентичен формуле по нахождению площади треугольника за небольшим исключением. Для начала разберем обобщенный случай без использования чисел.
Для начала разберем обобщенный случай без использования чисел.
Пусть дан произвольный параллелограмм с основанием a a a , боковой стороной b b b и высотой h h h , проведенной к нашему основанию. Тогда формула для площади этого параллелограмма:
S = a ⋅ h S=a\cdot h S = a ⋅ h
A a
a — основание;
h h
h — высота.
Разберем одну легкую задачу, чтобы потренироваться в решении типовых задач.
ПримерНайти площадь параллелограмма, в котором известно основание, равное 10 (см.) и высота, равная 5 (см.).
Решение
A = 10 a=10
a
= 1
0
h = 5 h=5
h
= 5
Подставляем в нашу формулу. Получаем:
S = 10 ⋅ 5 = 50 S=10\cdot 5=50
S
= 1
0
⋅ 5
= 5
0 (см. кв.)
Ответ: 50 (см. кв)
Формула площади параллелограмма по двум сторонам и углу между ними
В этом случае искомая величина находится так:
S = a ⋅ b ⋅ sin (α) S=a\cdot b\cdot\sin(\alpha) S = a ⋅ b ⋅ sin (α )
A , b a, b
a
,
b — стороны параллелограмма;
α \alpha
α — угол между сторонами a a
a и b b
b . {\circ})=12.5
S
= 2 1 ⋅ 1
0
⋅ 5
⋅ sin
(3
0
∘ )
= 1
2
.
5 (см. кв.)
{\circ})=12.5
S
= 2 1 ⋅ 1
0
⋅ 5
⋅ sin
(3
0
∘ )
= 1
2
.
5 (см. кв.)
При решении задач по данной теме кроме основных свойств параллелограмма и соответственных формул можно запомнить и применять следующее:
- Биссектриса внутреннего угла параллелограмма отсекает от него равнобедренный треугольник
- Биссектрисы внутренних углов прилежащие к одной из сторон параллелограмма взаимно перпендикулярные
- Биссектрисы, выходящие из противоположных внутренних углов параллелограмма, параллельные между собой либо лежат на одной прямой
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон
- Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними
Рассмотрим задачи, при решении которых используются данные свойства.
Задача 1.
Биссектриса угла С параллелограмма АВСD пересекает сторону АD в точке М и продолжение стороны АВ за точку А в точке Е. Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Найдите периметр параллелограмма, если АЕ = 4, DМ = 3.
Решение.
1. Треугольник СМD равнобедренный. (Свойство 1). Следовательно, СD = МD = 3 см.
2. Треугольник ЕАМ равнобедренный.
Следовательно, АЕ = АМ = 4 см.
3. АD = АМ + МD = 7 см.
4. Периметр АВСD = 20 см.
Ответ. 20 см.
Задача 2.
В выпуклом четырёхугольнике АВСD проведены диагонали. Известно, что площади треугольников АВD, АСD, ВСD равны. Докажите, что данный четырёхугольник является параллелограммом.
Решение.
1. Пусть ВЕ – высота треугольника АВD, СF – высота треугольника АCD. Так как по условию задачи площади треугольников равны и у них общее основание АD, то высоты этих треугольников равны. ВЕ = СF.
2. ВЕ, СF перпендикулярны АD. Точки В и С расположены по одну сторону относительно прямой АD. ВЕ = СF. Следовательно, прямая ВС || AD. (*)
3. Пусть АL – высота треугольника АСD, BK – высота треугольника BCD. Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
Так как по условию задачи площади треугольников равны и у них общее основание СD, то высоты этих треугольников равны. АL = BK.
4. АL и BK перпендикулярны СD. Точки В и А расположены по одну сторону относительно прямой СD. АL = BK. Следовательно, прямая АВ || СD (**)
5. Из условий (*), (**) вытекает – АВСD параллелограмм.
Ответ. Доказано. АВСD – параллелограмм.
Задача 3.
На сторонах ВС и СD параллелограмма АВСD отмечены точки М и Н соответственно так, что отрезки ВМ и НD пересекаются в точке О;
Решение.
1. В треугольнике DОМ
2. В прямоугольном треугольнике DНС
(
Тогда (Так как в прямоугольном треугольнике катет, который лежит против угла в 30 о, равен половине гипотенузы).
Но СD = АВ. Тогда АВ: НD = 2: 1.
3.
4.
Ответ: АВ: НD = 2: 1,
Задача 4.
Одна из диагоналей параллелограмма длиною 4√6, составляет с основанием угол 60 о, а вторая диагональ составляет с тем же основанием угол 45 о. Найти вторую диагональ.
Найти вторую диагональ.
Решение.
1. АО = 2√6.
2. К треугольнику АОD применим теорему синусов.
АО/sin D = OD/sin А.
2√6/sin 45 о = OD/sin 60 о.
ОD = (2√6sin 60 о) / sin 45 о = (2√6 · √3/2) / (√2/2) = 2√18/√2 = 6.
Ответ: 12.
Задача 5.
У параллелограмма со сторонами 5√2 и 7√2 меньший угол между диагоналями равен меньшему углу параллелограмма. Найдите сумму длин диагоналей.
Решение.
Пусть d 1 , d 2 – диагонали параллелограмма, а угол между диагоналями и меньший угол параллелограмма равен ф.
1. Посчитаем двумя разными
способами его площадь.
S ABCD = AB · AD · sin A = 5√2 · 7√2 · sin ф,
S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin ф.
Получим равенство 5√2 · 7√2 · sin ф = 1/2d 1 d 2 sin ф или
2 · 5√2 · 7√2 = d 1 d 2 ;
2. Используя соотношение между сторонами и диагоналями параллелограмма запишем равенство
(АВ 2 + АD 2) · 2 = АС 2 + ВD 2 .
((5√2) 2 + (7√2) 2) · 2 = d 1 2 + d 2 2 .
d 1 2 + d 2 2 = 296.
3. Составим систему:
{d 1 2 + d 2 2 = 296,
{d 1 + d 2 = 140.
Умножим второе уравнение системы на 2 и сложим с первым.
Получим (d 1 + d 2) 2 = 576. Отсюда Id 1 + d 2 I = 24.
Так как d 1 , d 2 – длины диагоналей параллелограмма, то d 1 + d 2 = 24.
Ответ: 24.
Задача 6.
Стороны параллелограмма 4 и 6. Острый угол между диагоналями равен 45 о. Найдите площадь параллелограмма.
Решение.
1. Из треугольника АОВ, используя теорему косинусов, запишем соотношение между стороной параллелограмма и диагоналями.
АВ 2 = АО 2 + ВО 2 2 · АО · ВО · cos АОВ.
4 2 = (d 1 /2) 2 + (d 2 /2) 2 – 2 · (d 1 /2) · (d 2 /2)cos 45 о;
d 1 2 /4 + d 2 2 /4 – 2 · (d 1 /2) · (d 2 /2)√2/2 = 16.
d 1 2 + d 2 2 – d 1 · d 2 √2 = 64.
2. Аналогично запишем соотношение для треугольника АОD.
Учтем, что
Получим уравнение d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
3. Имеем систему
{d 1 2 + d 2 2 – d 1 · d 2 √2 = 64,
{d 1 2 + d 2 2 + d 1 · d 2 √2 = 144.
Вычитая из второго уравнения первое, получим 2d 1 · d 2 √2 = 80 или
d 1 · d 2 = 80/(2√2) = 20√2
4. S ABCD = 1/2 AС · ВD · sin AОВ = 1/2 · d 1 d 2 sin α = 1/2 · 20√2 · √2/2 = 10.
Примечание: В этой и в предыдущей задаче нет надобности, решать полностью систему, предвидя то, что в данной задаче для вычисления площади нам нужно произведение диагоналей.
Ответ: 10.
Задача 7.
Площадь параллелограмма равна 96, а его стороны равны 8 и 15. Найдите квадрат меньшей диагонали.
Решение.
1. S ABCD = AВ · АD · sin ВAD. Сделаем подстановку в формулу.
Получим 96 = 8 · 15 · sin ВAD. Отсюда sin ВAD = 4 / 5 .
2. Найдём cos ВАD. sin 2 ВAD + cos 2 ВАD = 1.
(4 / 5) 2 + cos 2 ВАD = 1. cos 2 ВАD = 9 / 25 .
По условию задачи мы находим длину меньшей диагонали. Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
Диагональ ВD будет меньшей, если угол ВАD острый. Тогда cos ВАD = 3 / 5.
3. Из треугольника АВD по теореме косинусов найдём квадрат диагонали ВD.
ВD 2 = АВ 2 + АD 2 – 2 · АВ · ВD · cos ВАD.
ВD 2 = 8 2 + 15 2 – 2 · 8 · 15 · 3 / 5 = 145.
Ответ: 145.
Остались вопросы? Не знаете, как решить геометрическую задачу?
Чтобы получить помощь репетитора – зарегистрируйтесь .
Первый урок – бесплатно!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Что такое параллелограмм? Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
1. Площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot h_{a}\]
где:
a – сторона параллелограмма,
h a – высота, проведенная к этой стороне.
2. Если известны длины двух смежных сторон параллелограмма и угол между ними, то площадь параллелограмма вычисляется по формуле:
\[ \LARGE S = a \cdot b \cdot sin(\alpha) \]
3. {2} \)
{2} \)
В параллелограмме угол между высотами равен его острому углу: \(\angle K B H =\angle A \) .
Биссектрисы углов, прилежащих к одной стороне параллелограмма, взаимно перпендикулярны.
Биссектрисы двух противоположных углов параллелограмма параллельны.
Признаки параллелограмма
Четырехугольник будет параллелограммом, если:
\(AB = CD \) и \(AB || CD \)
\(AB = CD \) и \(BC = AD \)
\(AO = OC \) и \(BO = OD \)
\(\angle A = \angle C \) и \(\angle B = \angle D \)
В вашем браузере отключен Javascript.Чтобы произвести расчеты, необходимо разрешить элементы ActiveX!
Свойства параллелограмма — теоремы, доказательства, примеры
Свойства параллелограмма помогают нам легко и быстро идентифицировать параллелограмм из заданного набора фигур. Прежде чем мы узнаем о свойствах, давайте сначала узнаем о параллелограммах. Это четырехсторонняя замкнутая фигура с равными и параллельными противоположными сторонами и равными противоположными углами. Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
Давайте узнаем больше о свойствах параллелограмма подробно в этой статье.
Каковы свойства параллелограмма?
Параллелограмм — это тип четырехугольника, в котором противоположные стороны параллельны и равны.В параллелограмме при вершинах четыре угла. Понимание свойств параллелограмма помогает легко связать его углы и стороны. Кроме того, свойства полезны для вычислений в задачах, касающихся сторон и углов параллелограмма.
Четыре важных свойства углов и сторон параллелограмма заключаются в следующем:
- Противоположные стороны параллелограмма равны и параллельны друг другу.
- Противоположные углы равны, т.е.e ∠A = ∠C и ∠B = ∠D.
- Все углы параллелограмма в сумме дают 360°, то есть ∠A + ∠B + ∠C + ∠D = 360°.
- Последовательные углы параллелограмма являются дополнительными, т. е.
∠А + ∠В = 180°
∠В + ∠С = 180°
∠С + ∠D = 180°
∠D + ∠А = 180°
Все вышеперечисленные свойства справедливы для всех типов параллелограммов, но теперь давайте также узнаем об отдельных свойствах некоторых специальных параллелограммов. Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Три разных параллелограмма — квадрат, прямоугольник и ромб, которые отличаются друг от друга из-за своих свойств, но все они подпадают под категорию параллелограммов.
Свойства квадрата:
- Все четыре стороны квадрата равны.
- Все четыре угла равны и по 90 градусов каждый.
- Диагонали квадрата делят его углы пополам.
- Обе диагонали имеют одинаковую длину.
- Противоположные стороны равны и параллельны друг другу.
Свойства прямоугольника:
- Противоположные стороны прямоугольника равны и параллельны.
- Все четыре угла равны и равны 90 градусов каждый.
- Обе диагонали имеют одинаковую длину.
Свойства ромба:
- Все стороны имеют одинаковую длину.
- Диагонали делят друг друга пополам под углом 90 градусов.
- Сумма любых двух смежных внутренних углов равна 180 градусов.
- Противоположные стороны равны и параллельны друг другу.

Теперь давайте расширим наши знания, изучив свойства диагоналей параллелограммов в разделе ниже.
Свойства диагоналей параллелограмма
Сначала напомним значение диагонали. Диагонали – это отрезки, соединяющие противоположные вершины. В параллелограмме ABCD (см. рисунок выше) диагонали AC и BD.Предположим, что O — точка пересечения диагоналей AC и BD. Свойства диагоналей параллелограмма следующие:
- Диагонали параллелограмма делят друг друга пополам, т. е. OB = OD и OA = OC.
- Каждая диагональ делит параллелограмм на два конгруэнтных треугольника, т. е. ΔCDA ≅ ΔABC и ΔBAD ≅ ΔDCB.
- Закон параллелограмма: Сумма квадратов сторон равна сумме квадратов диагоналей, т. е. AB 2 + BC 2 + CD 2 + DA 2 = AC 2 + БД 2 .
Теоремы о свойствах параллелограмма
Теоремы о свойствах параллелограмма помогают определить правила решения задач на параллелограммы. Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
Свойства, относящиеся к сторонам и углам параллелограмма, легко понять и применить для решения различных задач. Кроме того, эти теоремы также поддерживают понимание концепций других четырехугольников. Ниже приведены четыре важные теоремы, относящиеся к свойствам параллелограмма:
- Противоположные стороны параллелограмма равны
- Противоположные углы параллелограмма равны
- Диагонали параллелограмма делят друг друга пополам
- Если одна пара противоположных сторон равна и параллельна в четырехугольнике, то это параллелограмм
Теорема 1. В параллелограмме противоположные стороны равны.
Доказательство:
Дано: ABCD — параллелограмм.
Доказать: Противоположные стороны равны, AB = CD и BC = AD.
В параллелограмме ABCD сравните треугольники ABC и CDA. В этих треугольниках:
Следовательно, по критерию ASA оба треугольника конгруэнтны и соответствующие стороны равны. Следовательно, мы имеем AB = CD и BC = AD.
Следовательно, мы имеем AB = CD и BC = AD.
Обратное к теореме 1: если в четырехугольнике противоположные стороны равны, то это параллелограмм.
Доказательство:
Дано: В четырехугольнике ABCD противоположные стороны равны, AB = CD, BC = AD.
Доказать: ABCD — параллелограмм.
В четырехугольнике ABCD дано, что AB = CD и AD = BC. Теперь сравните два треугольника ABC и CDA. Здесь у нас есть
- AC = AC (общие стороны)
- AB = CD (поскольку внутренние углы равны)
- г. н.э. = до н.э. (дано).
Таким образом, по критерию SSS оба треугольника равны и соответствующие углы равны. Отсюда можно сделать вывод, что ∠BAC = ∠DCA, а ∠BCA = ∠DAC.
Поэтому AB || CD, Британская Колумбия || AD, ABCD — параллелограмм.
Теорема 2. В параллелограмме противоположные углы равны.
Доказательство:
Дано: ABCD — параллелограмм, ∠A, ∠B, ∠C, ∠D — четыре угла.
Доказать: ∠A = ∠C и ∠B = ∠D
Предположим, что ABCD — параллелограмм.Теперь сравните треугольники ABC и CDA. Здесь у нас есть,
- AC = CA (общая сторона)
- ∠1 = ∠4 (чередующиеся внутренние углы)
- ∠2 = ∠3 (чередующиеся внутренние углы)
Таким образом, согласно ASA, два треугольника конгруэнтны, а это означает, что ∠B = ∠D. Точно так же мы можем показать, что ∠A = ∠C. Это доказывает, что противоположные углы в любом параллелограмме равны.
Обратное к теореме 2: Если в четырехугольнике противоположные углы равны, то это параллелограмм.
Доказательство:
Дано: ∠A = ∠C и ∠B = ∠D в четырехугольнике ABCD.
Доказать: ABCD — параллелограмм.
Предположим, что ∠A = ∠C и ∠B = ∠D в приведенном выше параллелограмме ABCD. Нам нужно доказать, что ABCD — параллелограмм. У нас есть:
∠А + ∠В + ∠С + ∠D = 360º
2(∠А + ∠В) =360º
∠А + ∠В = 180º.
Это должно означать, что AD || ДО НАШЕЙ ЭРЫ. Аналогично можно показать, что AB || КОМПАКТ ДИСК.Следовательно, АД || до н.э. и АВ || КОМПАКТ ДИСК. Следовательно, ABCD — параллелограмм.
Теорема 3. Диагонали параллелограмма делят друг друга пополам.
Доказательство:
Дано: PQTR — параллелограмм. PT и QR — диагонали параллелограмма.
Доказать: Диагонали PT и RQ делят друг друга пополам, т. е. PE = ET и ER = EQ.
Сначала предположим, что PQTR — параллелограмм. Сравните треугольники TER и треугольник PEQ.У нас есть,
- PQ = RT (противоположные стороны параллелограмма PQTR)
- ∠QRT = ∠PQR (альтернативные внутренние углы)
- ∠PTR = ∠QPT (альтернативные внутренние углы).
По критерию ASA два треугольника конгруэнтны, что означает по CPCTC, PE = ET и RE = EQ. Таким образом, две диагонали PT и RQ делят друг друга пополам, а PE = ET и ER = EQ.
Обратное к теореме 3: Если диагонали в четырехугольнике делят друг друга пополам, то это параллелограмм.В четырехугольнике PQTR, если PE=ET и ER=EQ, то это параллелограмм.
Дано: Диагонали PT и QR делят друг друга пополам.
Доказать: PQRT — параллелограмм.
Доказательство: Предположим, что диагонали PT и QR делят друг друга пополам. Еще раз сравните треугольник RET и треугольник PEQ. У нас есть:
- РЭ = эквалайзер
- ET = PE (диагонали делят друг друга пополам)
- ∠RET =∠PEQ (вертикально противоположные углы).
Следовательно, по критерию SAS два треугольника конгруэнтны. Это означает, что ∠QRT = ∠PQR и ∠PRT = ∠QPT. Следовательно, PQ || РТ и РТ || КТ. Таким образом, PQRT является параллелограммом.
Теорема 4. Если в четырехугольнике одна пара противоположных сторон равна и параллельна, то это параллелограмм.
Доказательство:
Дано: Дано, что AB = CD и AB || КОМПАКТ ДИСК.
Доказать: ABCD — параллелограмм.
Сравним треугольник AEB и треугольник CED. У нас есть,
- AB = CD (дан)
- ∠1 = ∠3 (чередующиеся внутренние углы)
- ∠2 = ∠4 (чередующиеся внутренние углы)
Таким образом, по критерию ASA два треугольника конгруэнтны. Отсюда можно сделать вывод, что по CPCTC AE = EC, а BE = ED. Следовательно, диагонали AC и BD делят друг друга пополам, а это в дальнейшем означает, что ABCD — параллелограмм.
Важные примечания:
Четырехугольник является параллелограммом, когда:
- Противоположные стороны четырехугольника равны и параллельны.
- противоположные углы четырехугольника равны.
- диагонали делят друг друга пополам.
- одна пара противоположных сторон равна и параллельна.

Вы знаете?
- Почему воздушный змей не является параллелограммом?
- Является ли равнобедренная трапеция параллелограммом?
Также проверьте:
Часто задаваемые вопросы о свойствах параллелограмма
Каковы 7 свойств параллелограмма?
Семь свойств параллелограмма таковы:
- Противоположные стороны равны.
- Противоположные углы параллелограмма равны.
- Последовательные углы являются дополнительными.
- Если один угол параллелограмма прямой, то все углы прямые.
- Диагонали параллелограмма делятся пополам.
- Каждая диагональ параллелограмма делит его пополам на два равных треугольника.
- Если одна пара противоположных сторон четырехугольника равна и параллельна, то четырехугольник является параллелограммом.
Каковы свойства параллелограмма относительно диагоналей?
Диагонали параллелограмма обладают двумя важными свойствами. Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Диагональ параллелограмма делит параллелограмм на два равных треугольника. А диагонали параллелограмма делят друг друга пополам.
Равны ли диагонали параллелограмма?
Диагонали параллелограмма НЕ равны. Противоположные стороны и противоположные углы параллелограмма равны.Диагонали квадрата и прямоугольника равны, что является особым видом параллелограмма.
Каковы четыре важных свойства параллелограмма?
Параллелограмм – это четырехугольник, у которого противоположные стороны равны и параллельны. Противоположные углы параллелограмма также равны. Короче говоря, параллелограмм можно рассматривать как скрученный прямоугольник. Это скорее прямоугольник, но углы при вершинах не обязательно должны быть прямыми. Четыре важных свойства параллелограмма таковы:
- Противоположные стороны равны
- Противоположные углы равны
- Смежные углы дополнительные
- Диагонали параллелограмма делят друг друга пополам
Можно ли прямоугольник назвать параллелограммом?
Противоположные стороны прямоугольника равны и параллельны.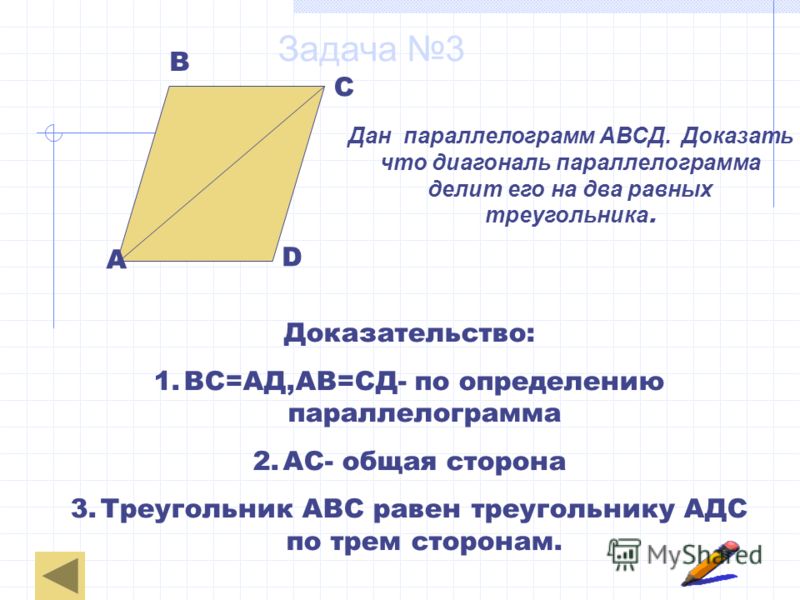 Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Таким образом, прямоугольник удовлетворяет всем свойствам параллелограмма, поэтому его можно назвать параллелограммом.
Каковы уникальные свойства параллелограммов?
Уникальные свойства параллелограмма, отличающие его от других четырехугольников, приведены ниже:
- Противоположные стороны каждого параллелограмма равны и параллельны.
- Противоположные углы всегда равны.
- Сумма смежных углов всегда равна 180°.
Каковы различные свойства каждого специального параллелограмма?
Существует три особых типа параллелограммов — квадрат, прямоугольник и ромб. Квадрат – это четырехугольник, у которого все стороны и углы равны. У прямоугольника противоположные стороны равны и параллельны. Все углы квадратов и прямоугольников равны и равны 90 градусов каждый. Ромб — это параллелограмм с четырьмя равными сторонами, но его углы не обязательно должны быть прямыми.
Как отличить параллелограмм от четырехугольника по свойствам параллелограмма?
Каждый параллелограмм можно назвать четырехугольником, но не каждый четырехугольник можно назвать параллелограммом. Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом.
Трапецию и воздушного змея можно назвать четырехугольниками, но они не полностью удовлетворяют свойствам параллелограмма и, следовательно, не могут быть названы параллелограммом.
Как найти длину диагонали параллелограмма
Если вы считаете, что контент, доступный с помощью Веб-сайта (как это определено в наших Условиях обслуживания), нарушает одно или более ваших авторских прав, пожалуйста, сообщите нам, предоставив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному агенту, указанному ниже.Если университетские наставники примут меры в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, предоставившей такой контент средства самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении может быть направлено стороне, предоставившей контент, или третьим лицам, таким как
в виде
ChillingEffects. org.
org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или деятельность нарушают ваши авторские права.Таким образом, если вы не уверены, что содержимое находится на Веб-сайте или на который ссылается Веб-сайт, нарушает ваши авторские права, вам следует сначала обратиться к адвокату.
Чтобы подать уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись владельца авторских прав или лица, уполномоченного действовать от его имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, как вы утверждаете, нарушает ваши авторские права, в \
достаточно подробно, чтобы преподаватели университета могли найти и точно идентифицировать этот контент; например, мы требуем
а
ссылку на конкретный вопрос (а не только название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; и
Заявление от вас: (а) что вы добросовестно полагаете, что использование контента, который, как вы утверждаете, нарушает
ваши авторские права не разрешены законом или владельцем авторских прав или его агентом; б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство вы
либо владельцем авторских прав, либо лицом, уполномоченным действовать от их имени.
Отправьте жалобу нашему назначенному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
Сент-Луис, Миссури 63105
Или заполните форму ниже:
Параллелограмм
(Переход к области параллелограмма или периметру параллелограмма)
Параллелограмм – это плоская фигура, у которой противоположные стороны параллельны и равны по длине.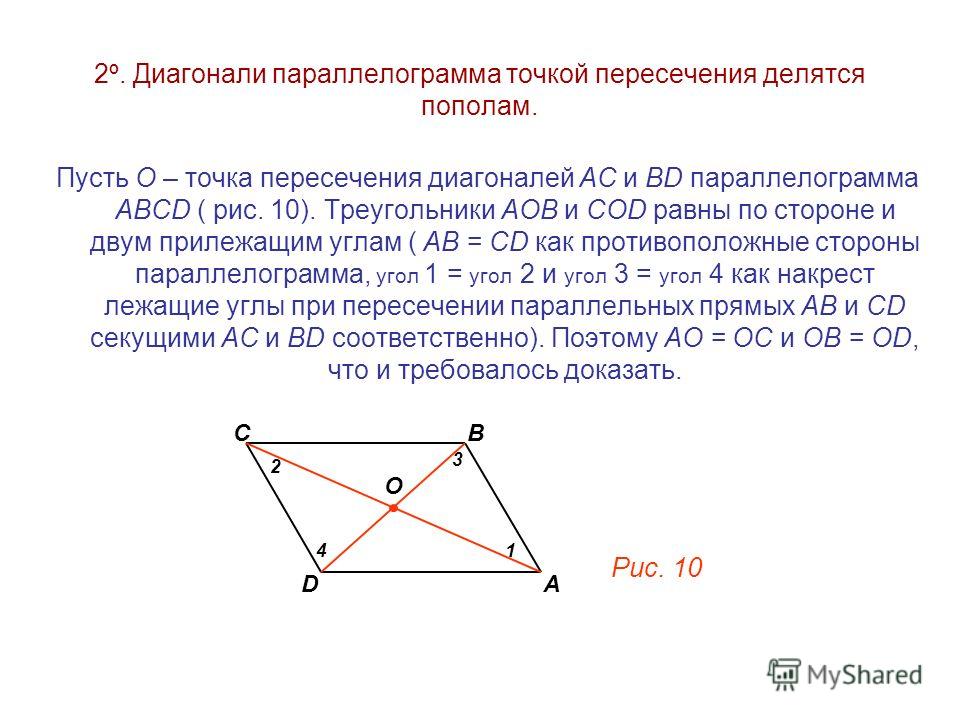
| Противоположные стороны параллельны | |
Противоположные стороны равны по длине | |
| Противоположные углы равны (углы А одинаковы, а углы В одинаковы) | |
| Угол A и угол B в сумме дают 180°, поэтому они являются дополнительными углами. |
Игра с параллелограммом:
изображения/geom-quad.js?mode=параллелограмм
ПРИМЕЧАНИЕ. Квадраты, прямоугольники и ромбы Параллелограммы!
Пример:
Параллелограмм , в котором все углы прямые, является прямоугольником !
Район параллелограмма
Площадь равна основанию , умноженному на высоту : .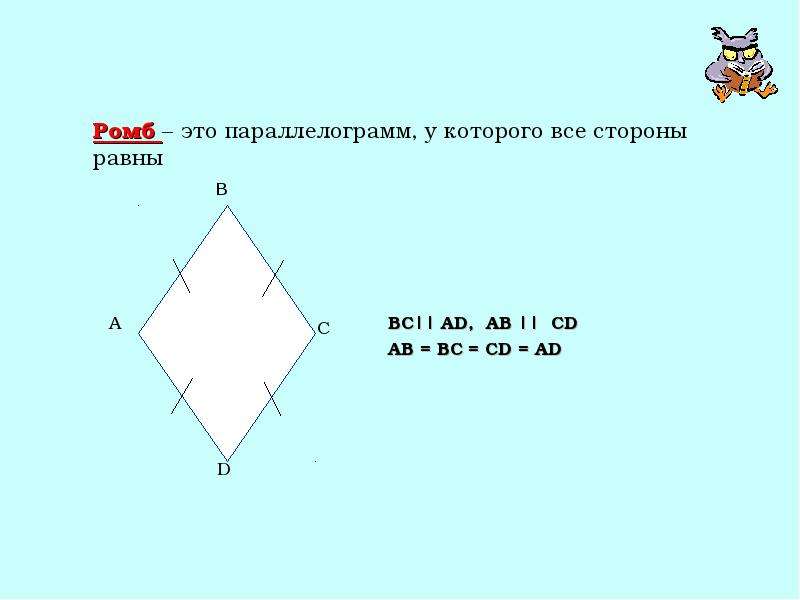 Площадь = b × h ( h находится под прямым углом к b ) |
Пример: параллелограмм имеет основание 6 м и высоту 3 м, какова его площадь?
Площадь = 6 м × 3 м = 18 м 2
Периметр параллелограмма
Периметр — это расстояние по краям.
Периметр равен 2 раза (длина основания + сторона) : Периметр = 2(b+s) |
Пример: Основание параллелограмма 12 см, а длина стороны 6 см. Каков его периметр?
Периметр = 2 × (12 см + 6 см) = 2 × 18 см = 36 см
Диагонали параллелограмма
Диагонали параллелограмма делятся пополам.
Другими словами, диагонали пересекаются на полпути.
Внутри любого четырехугольника
И в любом четырехугольнике есть параллелограмм.
9121, 9122, 9123, 9124, 9125, 9126, 9127, 9128, 9129, 9130
Что такое параллелограмм? [Определение, факты и примеры]
Что такое параллелограмм?
Параллелограмм – это особый вид четырехугольника, у которого противоположные стороны равны и параллельны.
На данном рисунке изображен параллелограмм ABCD, у которого AB параллелен CD, а AD параллелен BC.
Кроме того, AD = BC и AB = CD.
Мы также видим много параллелограммных форм и объектов вокруг нас.
Свойства параллелограмма
Противоположные стороны параллелограмма параллельны друг другу. Здесь, AB ∥ CD и AD ∥ BC
| |
Противоположные стороны параллелограмма равны по длине. Здесь AB = CD и AD = BC
| |
Противоположные углы параллелограмма равны по величине. Здесь угол A = угол C и угол B = угол D. | |
Смежные углы параллелограмма в сумме дают 180° Здесь угол A + угол B = 180° Угол B + угол C = 180° Угол C + угол D = 180° + угол D + угол А = 180° | |
Диагонали параллелограмма делят друг друга пополам. Здесь AC и BD делят друг друга пополам. |
Типы параллелограмма
Существует три специальных типа параллелограмма.
1. Ромб : Параллелограмм, у которого все стороны равны.
Здесь АВ = ВС = CD = DA. ABCD — ромб.
2. Прямоугольник : Параллелограмм, в котором все углы прямые, а диагонали равны.
Здесь все углы прямые. Диагонали PN и OM равны.
3. Квадрат : Параллелограмм со всеми равными сторонами и всеми углами, равными 90 градусам. Диагонали квадрата также равны.
Диагонали квадрата также равны.
Здесь все стороны равны и все углы прямые.
Диагонали AC и BD равны.
Интересные факты
|
карточек по геометрии | Quizlet
Четырехсторонний правильный многоугольник со всеми равными сторонами и всеми внутренними углами 90° Свойства и советы
• Если диагонали ромба равны, то этот ромб должен быть квадратом. Диагонали квадрата (примерно в 1,414 раза) больше длины стороны квадрата.
• Квадрат также может быть определен как прямоугольник со всеми равными сторонами, или ромб со всеми равными углами, или параллелограмм с равными диагоналями, делящими углы пополам.
• Если фигура является и прямоугольником (прямые углы), и ромбом (равные длины ребер), то она является квадратом. (Прямоугольник (четыре равных угла) + Ромб (четыре равные стороны) = Квадрат)
(Прямоугольник (четыре равных угла) + Ромб (четыре равные стороны) = Квадрат)
• Если круг описан вокруг квадрата, площадь круга в π/2 (около 1,57) умножается на площадь квадрата.
• Если в квадрат вписан круг, площадь круга в π/4 (около 0,79) умножается на площадь квадрата.
• Квадрат имеет большую площадь, чем любой другой четырехугольник с таким же периметром.2/2, где dd — длина любой из диагоналей
• Каждая диагональ квадрата является серединным перпендикуляром к другой. То есть каждый разрезает другой на две равные части, и они пересекаются и образуют прямой угол (90°).
• Длина каждой диагонали равна s квадратному корню из 2, где s — длина любой стороны.
Квадрат является одновременно ромбом (стороны равны) и прямоугольником (углы равны) и поэтому обладает всеми свойствами обеих этих фигур, а именно:
Диагонали квадрата делят друг друга пополам.
• Диагонали квадрата делят его углы пополам.
• Диагонали квадрата перпендикулярны.
• Противоположные стороны квадрата параллельны и равны.
• Все четыре угла квадрата равны. (Каждый равен 360/4 = 90 градусов, поэтому каждый угол квадрата прямой.)
• Диагонали квадрата равны.
Квадрат можно рассматривать как частный случай других четырехугольников, например
• прямоугольник, но с равными смежными сторонами
• параллелограмм, но с равными смежными сторонами и углами по 90°
• ромб, но со всеми углами 90°
Диагонали делят параллелограмм на четыре равные части
В сегодняшнем уроке мы докажем, что взаимодействующие диагонали параллелограмма делят его на четыре треугольника, все из которых имеют равные площади.
Каждая из диагоналей параллелограмма делит его на два конгруэнтных треугольника, как мы видели, когда доказывали такие свойства, как равенство противоположных сторон или конгруэнтность двух пар противоположных углов. Поскольку эти два треугольника равны, их площади равны.
Мы также видели, что диагонали параллелограмма делят друг друга пополам, образуя две дополнительные пары конгруэнтных треугольников.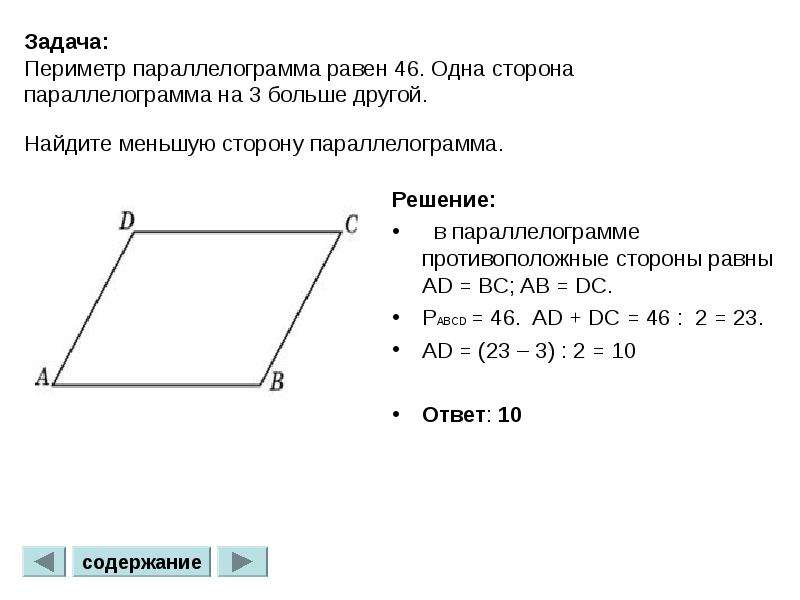
Теперь сделаем еще один шаг и, опираясь на то, что треугольники с одинаковым основанием и одинаковой высотой имеют равные площади, мы увидим, что все четыре треугольника, образованные пересекающимися диагоналями параллелограмма, имеют равные площади.
Задача
ABCD — параллелограмм с диагоналями AC и BD, пересекающимися в точке O. Докажите, что все четыре треугольника, образованные этими диагоналями — ΔAOD, ΔCOD, ΔAOB и ΔCOB — имеют равные площади.
Стратегия
Мы уже знаем, что противоположные пары треугольников (ΔAOD≅ ΔCOB; ΔAOB≅ ΔCOD) конгруэнтны и, следовательно, имеют равные площади. Поэтому, если мы сможем показать, что одна из других пар также имеет одинаковую площадь, все четыре будут равны.
Сравнивая отношения площадей треугольников, мы часто ищем равное основание или равную высоту — в этом случае мы имеем и то, и другое: высота — БЭ.
Значит, их площади равны, значит, все четыре площади равны.
Доказательство
Сначала повторим доказательство конгруэнтности двух противоположных пар треугольников:
(1) ABCD — параллелограмм //Дано
(2) AD || BC // Из определения параллелограммы
(3) AD = BC // противоположные стороны параллелограммы равны размеру
(4) ∠oBC ≅ ∠ODA // Альтернативные углы внутренней стороны теорема
(5) ∠OCB ≅ ∠ OAD // Альтернативные углы внутренних углов
(6) Δobc ≅ Δoda // (3), (4), (5), угол угловой боковы
(7) bo = od // Соответствующие стороны в конгруэнтных треугольниках (CPCTC)
(8) AO=OC // Соответственные стороны в равных треугольниках (CPCTC)
(9) AB=DC // Противоположные стороны параллелограмма равны по размеру
(10) ΔAOB ≅ ΔCOD // ), (9), Сторона-Сторона-Сторона
Теперь посмотрим на площади этих треугольников:
(11) Площадь ΔOBC = Площадь ΔODA //(6), площади конгруэнтных треугольников равны
(12 ) Площадь ΔAOB = Площадь ΔCOD //(10), конгруэнтно треугольники имеют равные площади
(13) Площадь ΔAOB =BE·AO/2 //Площадь треугольника
(14) Площадь ΔOBC =BE·OC/2 //Площадь треугольника
(15) Площадь ΔOBC = Площадь ΔAOB //(13), (14), (8) , треугольники с равными основаниями и высотами.
(16) Площадь ΔOBC = Площадь ΔAOB = Площадь ΔODA = Площадь ΔCOD
Итак, мы доказали, что диагонали параллелограмма делят его на четыре треугольника, все из которых имеют равные площади.
Площадь параллелограмма – объяснение и примеры
Как следует из названия, параллелограмм представляет собой четырехугольник, образованный двумя парами параллельных прямых . Он отличается от прямоугольника мерой углов при углах.У параллелограмма противоположные стороны равны по длине и противоположные углы равны по размеру, а у прямоугольника все углы равны 90 градусов.
В этой статье вы узнаете, как вычислить площадь параллелограмма, используя формулу площади параллелограмма.
Чтобы узнать, чем его площадь отличается от площади других четырехугольников и многоугольников, посетите предыдущие статьи.
Как найти площадь параллелограмма?
Площадь параллелограмма – это пространство, ограниченное двумя парами параллельных прямых. Прямоугольник и параллелограмм имеют схожие свойства, поэтому площадь параллелограмма равна площади прямоугольника.
Прямоугольник и параллелограмм имеют схожие свойства, поэтому площадь параллелограмма равна площади прямоугольника.
Площадь параллелограмма Формула
Рассмотрим параллелограмм ABCD , показанный ниже. Площадь параллелограмма – это пространство, ограниченное сторонами AD, DC, CB, и AB.
Площадь состояний формулы параллелограмма;
Площадь параллелограмма = основание х высота
A = (b * h) кв.единицы
Где b = основание параллелограмма и,
h = высота или высота параллелограмма.
Высота или высота – это перпендикулярная линия (обычно пунктирная) от вершины параллелограмма к любому из оснований.
Пример 1
Вычислите площадь параллелограмма, основание которого равно 10 сантиметрам, а высота 8 сантиметрам.
Раствор
A = (b * h) кв.единицы.
A = (10 * 8)
A = 80 см 2
Пример 2
А = (b * h) кв. единицы.
единицы.
= (24 * 13) квадратных дюймов.
= 312 квадратных дюймов.
Пример 3
Если основание параллелограмма в 4 раза больше высоты, а площадь равна 676 см², найдите основание и высоту параллелограмма.
Решение
Пусть высота параллелограмма = x
и основание = 4x
Но площадь параллелограмма = b * h
676 см² = (4x * x) кв.
676 = 4x 2
Разделив обе части на 4, получим
169 = x 2
. .
Основание = 4 * 13 = 52 см
Высота = 13 см.
Следовательно, основание и высота параллелограмма равны 52 см и 13 см соответственно.
Помимо формулы площади параллелограмма, существуют и другие формулы для вычисления площади параллелограмма.
Давайте посмотрим.
Как найти площадь параллелограмма без высоты?
Если высота параллелограмма нам неизвестна, мы можем использовать понятие тригонометрии, чтобы найти его площадь.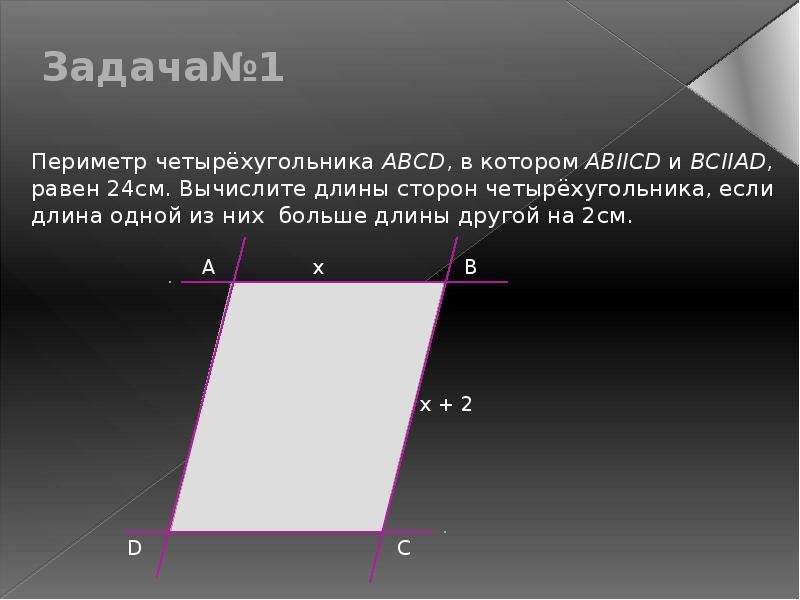
Площадь = абсинус (α) = абсинус (β)
Где a и b — длины параллельных сторон, а β или α — угол между сторонами параллелограмма.
Пример 4
Найдите площадь параллелограмма, если две его параллельные стороны равны 80 см и 40 см, а угол между ними равен 56 градусов.
Решение
Пусть a = 80 см и b = 40 см.
Угол между a и b = 56 градусов.
Площадь = абсинус (α)
Замена.
A = 80 × 40 синусов (56)
A = 3200 синусов 56
A = 2652,9 кв.см.
Пример 5
Вычислите углы между двумя сторонами параллелограмма, если его стороны равны 5 м и 9 м, а площадь параллелограмма равна 42.8 м 2 .
Раствор
площадь параллелограммы = ab синус (α)
42,8 м 2 = 9 * 5 синус (α)
42,8 = 45 синус (α)
Разделите обе стороны к 45.
0,95111 = SIN (α)
α = Sine -1 0,95111
α = 72 °
, но β + α = 180 °
β = 180 ° С 72 °
= 108 °
Следовательно, углы между двумя параллельными сторонами параллелограмма равны; 108° и 72°.
Пример 6
Вычислите высоту параллелограмма, параллельные стороны которого равны 30 см и 40 см, а угол между этими двумя сторонами равен 36 градусам. Примите основание параллелограмма равным 40 см.
Решение
Площадь = ab синус (α) = bh
30 * 40 синус (36) = 40 * h
1200 синус (36) = 40 * h.
Разделите обе стороны на 40.
h = (1200/40) синус 36
= 30 синус 36
h = 17.63 см
Итак, высота параллелограмма 17,63 см.
Как найти площадь параллелограмма по диагоналям?
Предположим, что d 1 и d 2 являются диагоналями параллелограмма ABCD, тогда площадь параллелограмма определяется как β) = ½ × d 1 × d 2 синус (α)
Где β или α — угол пересечения диагоналей d 1 и d 2 .
Пример 7
Вычислите площадь параллелограмма, диагонали которого равны 18 см и 15 см, а угол пересечения диагоналей равен 43°.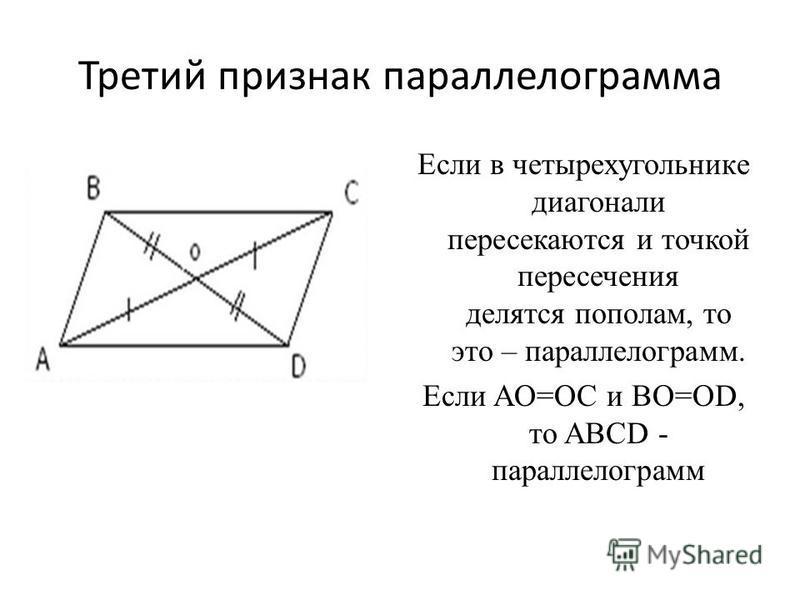

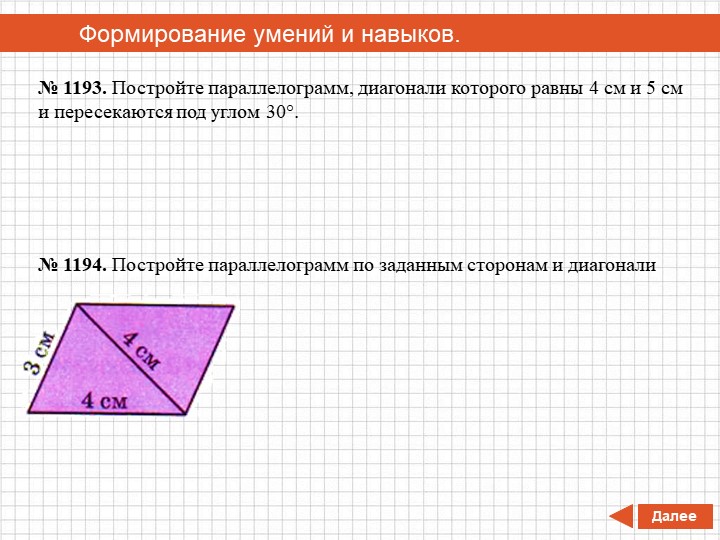 Как видно из чертежа, произведение b sin α равно высоте, опущенной на другую сторону, что в итоге дает нам предыдущую формулу
Как видно из чертежа, произведение b sin α равно высоте, опущенной на другую сторону, что в итоге дает нам предыдущую формулу А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону. А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.
А как известно, площадь прямоугольника находится перемножением его длины на высоту. Только в случае параллелограмма длина будет являться основанием, а высота прямоугольника — высотой параллелограмма, опущенной на данную сторону.