Конспект «Параллелограмм: свойства и признаки»

«Параллелограмм: свойства и признаки»

---

---

Параллелограмм — четырехугольник, у которого противолежащие стороны попарно параллельны. AB ∥ CD,  BC ∥ AD.

Высота параллелограмма — перпендикуляр, проведенный из любой точки одной стороны на противолежащую сторону (расстояние между противолежащими сторонами).

Свойства параллелограмма:
1. Противолежащие стороны равны.
2. Противолежащие стороны параллельны.
3. Противолежащие углы равны.
4. Сумма соседних углов равна 180.
5. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
6. Диагональ делит параллелограмм на два равных треугольника.
7. Сумма квадратов диагоналей равна сумме квадратов его четырех сторон.

8. Диагонали параллелограмма делят его на четыре равновеликих треугольника.

Признаки параллелограмма:
— две противолежащие стороны равны и параллельны,
— противолежащие стороны попарно равны,
— диагонали пересекаются и точкой пересечения делятся пополам,
— каждая диагональ делит четырехугольник на два равных треугольника.

---

Это конспект по теме «Свойства и признаки параллелограмма». Выберите дальнейшие действия:

 

uchitel.pro

Параллелограмм

Определение

Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.

 

Теорема (первый признак параллелограмма)

Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.

 

Доказательство

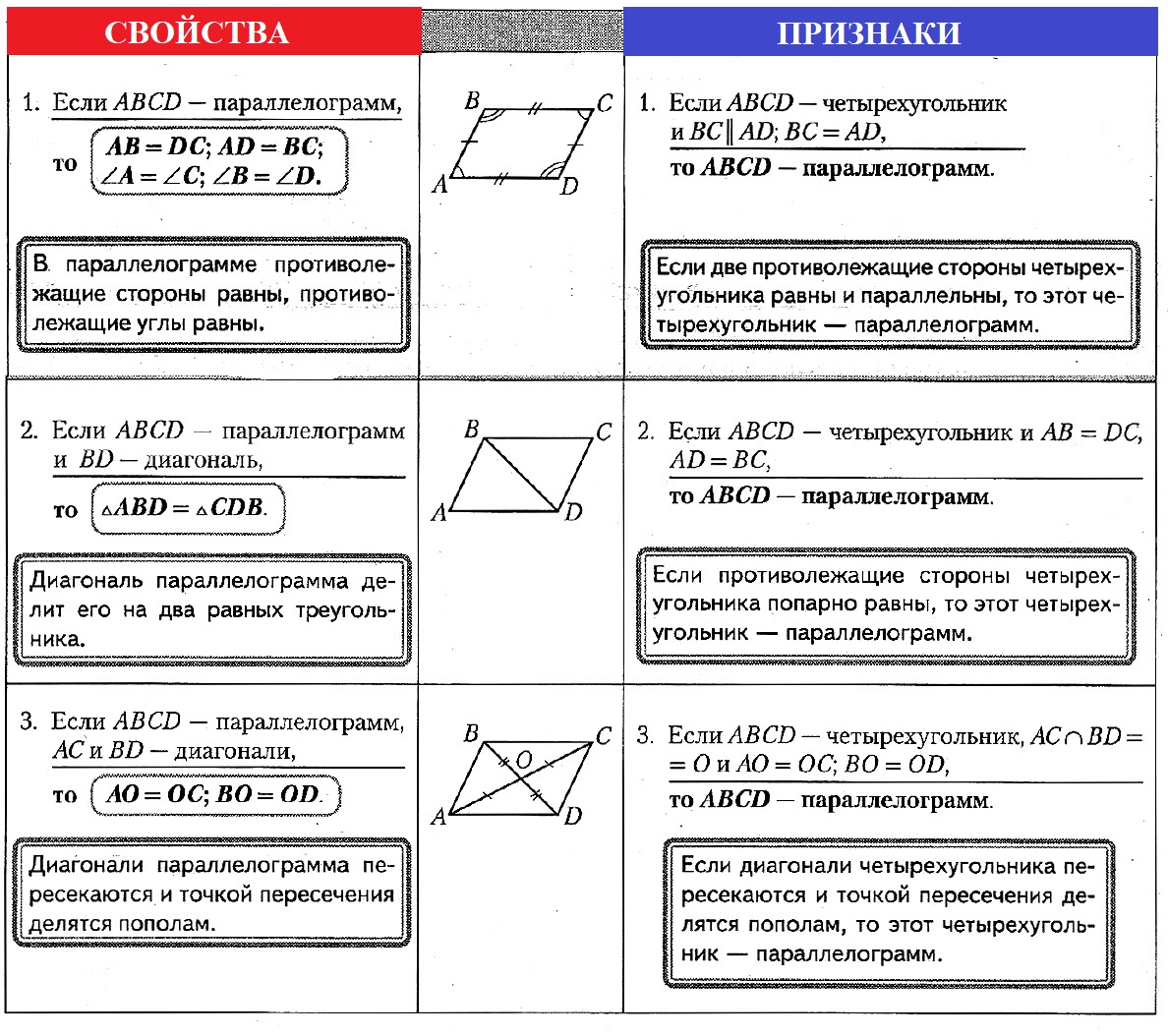
Пусть в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) параллельны и \(AB = CD\).

 

Проведём диагональ \(AC\), разделяющую данный четырехугольник на два равных треугольника: \(ABC\) и \(CDA\). Эти треугольники равны по двум сторонам и углу между ними (\(AC\) – общая сторона, \(AB = CD\) по условию, \(\angle 1 = \angle 2\) как накрест лежащие углы при пересечении параллельных прямых \(AB\) и \(CD\) секущей \(AC\)), поэтому \(\angle 3 = \angle 4\). Но углы \(3\) и \(4\) накрест лежащие при пересечении прямых \(AD\) и \(BC\) секущей \(AC\), следовательно, \(AD\parallel BC\). Таким образом, в четырехугольнике \(ABCD\) противоположные стороны попарно параллельны, и, значит, четырехугольник \(ABCD\) – параллелограмм.

 

Теорема (второй признак параллелограмма)

Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.

 

Доказательство

Проведём диагональ \(AC\) данного четырехугольника \(ABCD\), разделяющую его на треугольники \(ABC\) и \(CDA\).

 

Эти треугольники равны по трем сторонам (\(AC\) – общая, \(AB = CD\) и \(BC = DA\) по условию), поэтому \(\angle 1 = \angle 2\) – накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\). Отсюда следует, что \(AB\parallel CD\). Так как \(AB = CD\) и \(AB\parallel CD\), то по первому признаку параллелограмма четырёхугольник \(ABCD\) – параллелограмм.

 

Теорема (третий признак параллелограмма)

Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.

 

Доказательство

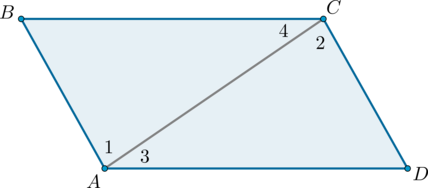
Рассмотрим четырехугольник \(ABCD\), в котором диагонали \(AC\) и \(BD\) пересекаются в точке \(O\) и делятся этой точкой пополам.

 

Треугольники \(AOB\) и \(COD\) равны по первому признаку равенства треугольников (\(AO = OC\), \(BO = OD\) по условию, \(\angle AOB = \angle COD\) как вертикальные углы), поэтому \(AB = CD\) и \(\angle 1 = \angle 2\). Из равенства углов \(1\) и \(2\) (накрест лежащие при \(AB\) и \(CD\) и секущей \(AC\)) следует, что \(AB\parallel CD\).

Итак, в четырехугольнике \(ABCD\) стороны \(AB\) и \(CD\) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник \(ABCD\) – параллелограмм.

 

Свойства параллелограмма:

1. В параллелограмме противоположные стороны равны и противоположные углы равны.

 

2. Диагонали параллелограмма точкой пересечения делятся пополам.

 

Свойства биссектрисы параллелограмма:

1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.

 

2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.

 

3. Отрезки биссектрис противоположных углов равны и параллельны.

 

Доказательство

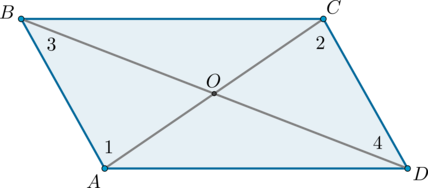
1) Пусть \(ABCD\) – параллелограмм, \(AE\) – биссектриса угла \(BAD\).

 

Углы \(1\) и \(2\) равны как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(AE\). Углы \(1\) и \(3\) равны, так как \(AE\) – биссектриса. В итоге \(\angle 3 = \angle 1 = \angle 2\), откуда следует, что треугольник \(ABE\) – равнобедренный.

 

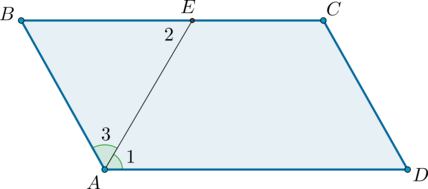
2) Пусть \(ABCD\) – параллелограмм, \(AN\) и \(BM\)– биссектрисы углов \(BAD\) и \(ABC\) соответственно.

 

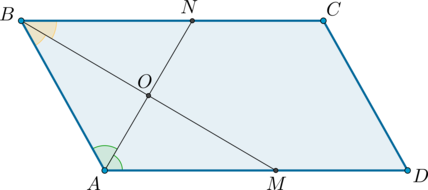
Так как сумма односторонних углов при параллельных прямых и секущей равна \(180^{\circ}\), тогда \(\angle DAB + \angle ABC = 180^{\circ}\).

 

Так как \(AN\) и \(BM\) – биссектрисы, то \(\angle BAN + \angle ABM = 0,5(\angle DAB + \angle ABC) = 0,5\cdot 180^\circ = 90^{\circ}\), откуда \(\angle AOB = 180^\circ — (\angle BAN + \angle ABM) = 90^\circ\).

 

3. Пусть \(AN\) и \(CM\) – биссектрисы углов параллелограмма \(ABCD\).

 

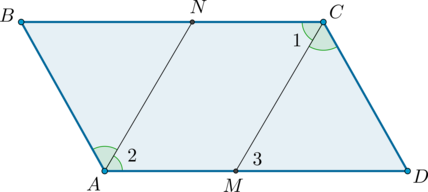
Так как в параллелограмме противоположные углы равны, то \(\angle 2 = 0,5\cdot\angle BAD = 0,5\cdot\angle BCD = \angle 1\). Кроме того, углы \(1\) и \(3\) равны как накрест лежащие при параллельных прямых \(AD\) и \(BC\) и секущей \(CM\), тогда \(\angle 2 = \angle 3\), откуда следует, что \(AN\parallel CM\). Кроме того, \(AM\parallel CN\), тогда \(ANCM\) – параллелограмм, следовательно, \(AN = CM\).

shkolkovo.net

Параллелограмм — Википедия

Материал из Википедии — свободной энциклопедии

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  |AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

  d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Видео по теме

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

1. У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
2. Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
3. У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
4. Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
5. Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
6. Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
7. Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
8. Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

Также площадь параллелограмма может быть выражена через стороны a, b{\displaystyle a,\ b} и длину любой из диагоналей d{\displaystyle d} по формуле Герона как сумма площадей двух равных примыкающих треугольников:

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)/2.{\displaystyle p=(a+b+d)/2.}

См. также

Примечания

wiki2.red

Параллелограмм — Википедия

Материал из Википедии — свободной энциклопедии

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  |AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d2{\displaystyle d_{2}} — длины диагоналей; тогда

  d12+d22=2(a2+b2).{\displaystyle d_{1}^{2}+d_{2}^{2}=2(a^{2}+b^{2}).}

Тождество параллелограмма есть простое следствие формулы Эйлера для произвольного четырехугольника: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумма квадратов его диагоналей. У параллелограмма противоположные стороны равны, а расстояние между серединами диагоналей равно нулю.

• Аффинное преобразование всегда переводит параллелограмм в параллелограмм. Для любого параллелограмма существует аффинное преобразование, которое отображает его в квадрат.

Признаки параллелограмма

Четырёхугольник ABCD является параллелограммом, если выполняется одно из следующих условий (в этом случае выполняются и все остальные):

1. У четырёхугольника без самопересечений две противоположные стороны одновременно равны и параллельны: AB=CD,AB∥CD{\displaystyle AB=CD,AB\parallel CD}.
2. Все противоположные углы попарно равны: ∠A=∠C,∠B=∠D{\displaystyle \angle A=\angle C,\angle B=\angle D}.
3. У четырёхугольника без самопересечений все противоположные стороны попарно равны: AB=CD,BC=DA{\displaystyle AB=CD,BC=DA}.
4. Все противоположные стороны попарно параллельны: AB∥CD,BC∥DA{\displaystyle AB\parallel CD,BC\parallel DA}.
5. Диагонали делятся в точке их пересечения пополам: AO=OC,BO=OD{\displaystyle AO=OC,BO=OD}.
6. Сумма соседних углов равна 180 градусов: ∠A+∠B=180∘,∠B+∠C=180∘,∠C+∠D=180∘,∠D+∠A=180∘{\displaystyle \angle A+\angle B=180^{\circ },\angle B+\angle C=180^{\circ },\angle C+\angle D=180^{\circ },\angle D+\angle A=180^{\circ }}.
7. Сумма расстояний между серединами противоположных сторон выпуклого четырехугольника равна его полупериметру.
8. Сумма квадратов диагоналей равна сумме квадратов сторон выпуклого четырёхугольника: AC2+BD2=AB2+BC2+CD2+DA2{\displaystyle AC^{2}+BD^{2}=AB^{2}+BC^{2}+CD^{2}+DA^{2}}.

Площадь параллелограмма

Здесь приведены формулы, свойственные именно параллелограмму. См. также формулы для площади произвольных четырёхугольников.

Площадь параллелограмма равна произведению его основания на высоту:

S=ah{\displaystyle S=ah} , где a{\displaystyle a} — сторона, h{\displaystyle h} — высота, проведенная к этой стороне.

Площадь параллелограмма равна произведению его сторон на синус угла между ними:

S=absin⁡α,{\displaystyle S=ab\sin \alpha ,}

где a{\displaystyle a} и b{\displaystyle b} — стороны, а α{\displaystyle \alpha } — угол между сторонами a{\displaystyle a} и b{\displaystyle b}.

Также площадь параллелограмма может быть выражена через стороны a, b{\displaystyle a,\ b} и длину любой из диагоналей d{\displaystyle d} по формуле Герона как сумма площадей двух равных примыкающих треугольников:

S=2p(p−a)(p−b)(p−d){\displaystyle S=2{\sqrt {p(p-a)(p-b)(p-d)}}}

где p=(a+b+d)/2.{\displaystyle p=(a+b+d)/2.}

См. также

Примечания

wikipedia.green

Параллелограмм. Определение, свойства и признаки

Свойства параллелограмма

1. Противоположные стороны тождественны.

Доказательство

Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.

Так как ABCD — параллелограмм, то справедливо следующее:

AD || BC \Rightarrow \angle 1 = \angle 2 как лежащие накрест.

AB || CD \Rightarrow \angle3 = \angle 4 как лежащие накрест.

Следовательно, \triangle ABC = \triangle ADC (по второму признаку: \angle 1 = \angle 2, \angle 3 = \angle 4 и AC — общая).

И, значит, \triangle ABC = \triangle ADC, то AB = CD и AD = BC.

Доказано!

2. Противоположные углы тождественны.

Доказательство

Согласно доказательству свойства 1 мы знаем, что \angle 1 = \angle 2, \angle 3 = \angle 4. Таким образом сумма противоположных углов равна: \angle 1 + \angle 3 = \angle 2 + \angle 4. Учитывая, что \triangle ABC = \triangle ADC получаем \angle A = \angle C, \angle B = \angle D.

Доказано!

3. Диагонали разделены пополам точкой пересечения.

Доказательство

Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.

Таким образом видно, что \triangle AOB = \triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов \angle 2 и \angle 1) и AO = OC (напротив углов \angle 3 и \angle 4 соответственно).

Доказано!

Признаки параллелограмма

Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.

Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.

1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD; AB || CD \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим подробнее. Почему AD || BC?

\triangle ABC = \triangle ADC по свойству 1: AB = CD, AC — общая и \angle 1 = \angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.

Но если \triangle ABC = \triangle ADC, то \angle 3 = \angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (\angle 3 и \angle 4 — накрест лежащие тоже равны).

Первый признак верен.

2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD, AD = BC \Rightarrow ABCD — параллелограмм.

Доказательство

Рассмотрим данный признак. Еще раз проведем диагональ AC.

По свойству 1 \triangle ABC = \triangle ACD.

Из этого следует, что: \angle 1 = \angle 2 \Rightarrow AD || BC и \angle 3 = \angle 4 \Rightarrow AB || CD, то есть ABCD — параллелограмм.

Второй признак верен.

3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

\angle A = \angle C, \angle B = \angle D \Rightarrow ABCD — параллелограмм.

Доказательство

2 \alpha + 2 \beta = 360^{\circ} (поскольку ABCD — четырехугольник, а \angle A = \angle C, \angle B = \angle D по условию).

Получается, \alpha + \beta = 180^{\circ}. Но \alpha и \beta являются внутренними односторонними при секущей AB.

И то, что \alpha + \beta = 180^{\circ} говорит и о том, что AD || BC.

При этом \alpha и \beta — внутренние односторонние при секущей AD. И это значит AB || CD.

Третий признак верен.

4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC; BO = OD \Rightarrow параллелограмм.

Доказательство

BO = OD; AO = OC, \angle 1 = \angle 2 как вертикальные \Rightarrow \triangle AOB = \triangle COD, \Rightarrow \angle 3 = \angle 4, и \Rightarrow AB || CD.

Аналогично BO = OD; AO = OC, \angle 5 = \angle 6 \Rightarrow \triangle AOD = \triangle BOC \Rightarrow \angle 7 = \angle 8, и \Rightarrow AD || BC.

Четвертый признак верен.

academyege.ru

Параллелограмм — СПИШИ У АНТОШКИ

Параллелограммом называется четырехугольник, у которого противолежащие стороны попарно параллельны.

На рисунке изображен параллелограмм АВCD

AB||CD и BC||AD противоположные стороны

∠DAB = ∠BCD, ∠ABC = ∠CDA

Признаки параллелограмма

Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:

1. Если в четырехугольнике две стороны равны и параллельны (AB||CD, AB = CD (или BC||AD, BC = AD), то этот четырехугольник — параллелограмм.

2. Если в четырехугольнике противоположные стороны попарно равны (AB = CD, BC = AD), то этот четырехугольник – параллелограмм.

3. Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам (AO = OC, BO = OD), то этот четырехугольник – параллелограмм.

4. Если  четырехугольнике противоположные углы попарно равны (∠DAB = ∠BCD, ∠ABC = ∠CDA), то этот четырехугольник – параллелограмм.

5. Если сумма углов четырехугольника прилегающих к любой стороне равна 180°:

∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°, то этот четырехугольник – параллелограмм.

6. Если в четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:

AC² + BD² = AB² + BC² + CD² + AD², то этот четырехугольник – параллелограмм.

Свойства параллелограмма

Квадрат, прямоугольник и ромб — есть параллелограммом. Поэтому паралллелограмм обладает свойствами этих геометрических фигур.
1. Противоположные стороны параллелограмма имеют одинаковую длину:

AB = CD = а, BC = AD = b

2. Противоположные стороны параллелограмма параллельны:

AB||CD, BC||AD

3. Противоположные углы параллелограмма одинаковые:

∠ABC = ∠CDA, ∠BCD = ∠DAB

4. Cумма углов, прилежащих к одной стороне, равна 180°;

5. Сумма углов параллелограмма равна 360°:

∠1+ ∠2+ ∠3 + ∠4= 360°

6. Сумма квадратов диагоналей равна сумме квадратов всех сторон:

d1² + d2² = 2a² + 2b² 

7. Каждая диагональ делит параллелограмма на два равных треугольника

7. Две диагональ делят параллелограмм на две пары равных треугольников

8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам

9. Точка пересечения диагоналей называется центром симметрии параллелограмма

10. Биссектрисы противоположных углов параллелограмма всегда параллельны

11. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)

Диагонали параллелограмма

 

Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.

Параллелограмм имеет две диагонали — длинную d₁, и короткую — d₂

Если параллелограмм имеет равные стороны, то диагонали параллелограмма будут равны.

Формулы определения длины диагонали параллелограмма:

1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)

d₁ = √(a² + b² — 2ab·cosβ)

d₂ = √(a² + b² + 2ab·cosβ)

2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)

d₁ = √(a² + b² + 2ab·cosα)

d₂ = √(a² + b² — 2ab·cosα)

3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:

d₁ = √(2a² + 2b² — d₂²)

Периметр параллелограмма

 Периметром параллелограмма называется сумма длин всех сторон параллелограмма.

Формулы определения длины периметра параллелограмма:

1. Формула периметра параллелограмма через стороны параллелограмма:

P = 2a + 2b = 2(a + b)

2. Формула периметра параллелограмма через одну сторону и две диагонали:

P = 2a + √(2d₁² + 2d₂² — 4a²)

P = 2b + √(2d₁² + 2d₂² — 4b²)

Площадь параллелограмма

Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.

Формулы определения площади параллелограмма:

1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:

S = a · ha

S = b · hb

2. Формула площади параллелограмма через две стороны и синус угла между ними:

S = ab sinα

S = ab sinβ

3. Формула площади параллелограмма через две диагонали и синус угла между ними:

S =  0.5 d₂²  d₂² sinα

spishy-u-antoshki.ru

Параллелограмм Википедия

Параллелограмм

Параллелогра́мм (др.-греч. παραλληλόγραμμον от παράλληλος — параллельный и γραμμή — линия) — это четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых. Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.

Свойства[ | ]

Противоположные стороны параллелограмма равны, а диагонали в точке пересечения делятся пополам. Противоположные углы параллелограмма равны, а сумма соседних равна 180°.

• Противолежащие стороны параллелограмма равны.
• Противолежащие углы параллелограмма равны.
• Сумма углов, прилежащих к одной стороне, равна 180° (по свойству параллельных прямых).
• Диагонали параллелограмма пересекаются, и точка пересечения делит их пополам:

  |AO|=|OC|,|BO|=|OD|{\displaystyle \left|AO\right|=\left|OC\right|,\left|BO\right|=\left|OD\right|}.

• Точка пересечения диагоналей является центром симметрии параллелограмма.
• Параллелограмм диагональю делится на два равных треугольника.
• Средние линии параллелограмма пересекаются в точке пересечения его диагоналей. В этой точке две его диагонали и две его средние линии делятся пополам.
• Тождество параллелограмма: сумма квадратов диагоналей параллелограмма равна удвоенной сумме квадратов его двух смежных сторон: пусть а — длина стороны AB, b — длина стороны BC, d1{\displaystyle d_{1}} и d

ru-wiki.ru