Наука геометрия — Люди Роста

Человек сталкивается с геометрией повсюду и постоянно. Без неё невозможно было бы построить дом, смастерить стол и стул, повесить люстру.

Геометрию как науку начинают изучать в 7 классе общеобразовательной школы. Именно тогда, на первых же уроках, детям рассказывают, что геометрия — это раздел математики, который изучает фигуры на плоскости и в пространстве. С древнегреческого геометрия — есть «измерение земли».

Помните: точка, прямая, отрезок, угол, аксиома, теорема, доказательство? Да-да, это всё оттуда.

Кто придумал геометрию?

Достоверно известно, что наука геометрия появилась примерно в 300 году до нашей эры. И спасибо за это стоит сказать великому ученому, философу Евклиду. Именно он собрал все познания в единую науку, составив так называемые «Элементы» Евклида. Ими на протяжении двух тысяч лет пользовались все учёные мира.

На основы геометрии опирались и в Древнем Вавилоне, и в Древнем Египте. Чудо света — пирамиды невозможно было бы возвести без геометрии. А без знаний о числе «Пи» — вычислить параметры круга.

Зачем нужна геометрия современным детям?

Главная задача при изучении геометрии состоит в том, чтобы:

• Научить детей мыслить логически.
• Развить абстрактное воображение.
• Представлять предметы в пространстве.
• Знать геометрические фигуры.

Многие актуальные сегодня профессии просто немыслимы без знаний геометрии. Это и дизайнер, и конструктор, и модельер, и инженер, и простой строитель. А как мужчина построит дом, если не сможет вычислить необходимые параметры? Сделать элементарный ремонт в квартире, и то нужно просчитать площадь и закупить материалы.

Да и никто не поспорит, что геометрия очень хорошо тренирует мозг. Лишних и ненужных знаний не бывает. Сегодня кажется, что геометрия нам ни к чему, а завтра жизнь приподнесет сюрприз, и без нее мы не сможем мыслить свои будни. Кто знает, что будет завтра? Поэтому учиться никогда не поздно! Учитесь, господа!

Надо признаться, что попытка трактовать естественные проблемы без геометрии есть попытка сделать невозможное (Галилео Галилей)

Существует ли самое большое число, читайте здесь.

Геометрия в жизни человека

Геометрия в жизни человека

Енюкова Ю.С. 1

---

1ГБОУ гимназия им.С.В.Байменова города Похвистнево

Антонова Г.В. 1

---

1ГБОУ гимназия имени С.В. Байменова города Похвистнево Самарской области

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке «Файлы работы» в формате PDF

1.Введение

«Если бы геометрия так же противоречила

нашим страстям и интересам, как нравственность,

то мы бы так же спорили против нее 

и нарушали ее вопреки всем доказательствам»

Готфрид Вильгельм Лейбниц

Актуальность:  В прошлом учебном году я начала изучать предмет геометрию и, по мнению многих учащихся (провела опрос учащихся седьмых классов), он является одним из сложных школьных предметов. Многие, 81% из опрошенных учащихся, не совсем понимают, а зачастую и не знают практического значения геометрии в жизни. Я также не совсем понимала необходимость изучения предмета геометрия.

Проблема: Для чего мы изучаем геометрию, где можно применить полученные знания, как часто приходится сталкиваться с геометрическими фигурами? Встречается ли где-нибудь информация, связанная с геометрией, кроме уроков математики?

Гипотеза: Если человечество на протяжении многих веков приобретало всё новые и новые знания по геометрии, то где эти знания применяются и используются.

Объект: геометрия.

Предмет: использование геометрии вне школы.

Цель: найти доказательство практической значимости геометрии в жизни человека.

Задачи:

Изучить историю возникновения геометрии.

Познакомиться с профессиями, которые напрямую связаны с геометрией.

Узнать, чем может помочь геометрия на практике.

Провести анализ полученных результатов.

Теоретическая значимость

Геометрия — раздел математики, изучающий пространственные отношения и формы, а также другие отношения и формы, сходные с пространственными по своей структуре. Слово геометрия — греческое, в переводе на русский язык означает землемерие. Такое название связано с применением геометрии для измерений на местности. Геометрия в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура, как она рассматривается в геометрии, и есть пространственная форма. Поэтому в геометрии говорят, например, шар, а не тело шарообразной формы. Расположение и размеры определяются пространственными отношениями. Наконец, преобразование, как его понимают в геометрии, также есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.

1.1. Историческая справка

Геометрия возникла давно, это одна из самых древних наук. Геометрия (от греч. ge — земля и metrein — измерять)— наука о пространстве, точнее — наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения. Развитие геометрии принесло с собой глубоко идущую эволюцию понятия о пространстве. В том значении, в котором пространство как математический термин широко употребляется современными геометрами, оно уже не может служить первичным понятием, на котором покоится определение геометрии, а, напротив, само находит себе определение в ходе развития геометрических идей. Важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем. Но они не были еще систематизированы и передавались от поколения к поколению в виде правил и рецептов, например, правил нахождения площадей фигур, объемов тел, построение прямых углов и т.д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории. Геометрия дает общее понятие о геометрической фигуре, под которой понимают не только тело, поверхность, линию или точку, но и любую их совокупность. Геометрия в первоначальном значении есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура и есть пространственная форма; поэтому в геометрии, например, говорят, «шар», а не «тело шарообразной формы». Расположение и размеры определяются пространственными отношениями; наконец, преобразование, как его понимают в геометрии, так же есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.

1.2. Геометрия в 21 веке

Посмотрите вокруг — всюду геометрия! Современные здания и космические станции, подводные лодки, интерьеры квартир — всё имеет геометрическую форму. Геометрические знания являются сегодня профессионально значимыми для многих современных специальностей: для дизайнеров и конструкторов, для рабочих и учёных. И уже этого достаточно, чтобы ответить на вопрос: «Нужно ли нам геометрия?»

Недостаток жизненного опыта позволяет некоторым школьникам и даже студентам думать, что больше половины изучаемых предметов абсолютно бесполезны и никогда не пригодятся в жизни. На самом деле, знания могут прийти на помощь в неожиданный момент, и доставать учебники уже не будет времени. Одна из полезнейших наук — геометрия, некоторые виды деятельности без нее немыслимы.

Без знания геометрии невозможно построить дом или отремонтировать квартиру. Например, при установке стропил на крышу понадобится формула расчета высоты треугольника, особенно, если крыша несимметричная. Без этого нельзя будет рассчитать длину перекладин, а также узнать количество кровельного материала. Чтобы посчитать количество блоков или кирпичей для стены, плиток для ремонта ванной комнаты, досок для пола — необходимы знания формул площади поверхности, а для объемных покрытий, например, утеплителей — формул объема. Для разработки системы вентиляции, обогрева, канализации или водоснабжения в доме или квартире потребуется расчет внутреннего объема труб, а это невозможно сделать без формулы площади круга. Конечно, можно доверить это профессионалам — но без знания геометрии будет невозможно даже разобраться в чертежах и проверить качество работы. Вообще, чертежи встречаются даже далекому от них человеку на протяжении всей жизни. Это чертеж дома или план ремонта, чертежи деталей на заводе, знать которые нужно не только конструктору и технологу, но и токарю, сварщику, контролеру, менеджерам отделов закупок и продаж. С чертежами непременно столкнется автолюбитель, который захочет провести ремонт своей машины.

Геометрия присутствует практически во всех сферах нашей жизни: нас окружают круглые, квадратные, прямоугольные, треугольные, сферические, кубические, цилиндрические, конические и другие объекты.

Обычно мы не задумываемся о том, почему объекты имеют ту или иную форму, а ее выбор далеко не случаен.

Одна из самых распространенных форм – это окружность и то, что ею ограничено, то есть круг. Вы, наверное, не задумывались, почему трубы – круглые в сечении? Одна из причин в том, что окружность – это замкнутая дуга с постоянной шириной. По этой причине, например, люки не проваливаются вниз, что приводило бы к несчастным случаям, а будь они квадратной или прямоугольной формы, это стало бы неизбежным.

Еще одно свойство окружности: из всех замкнутых кривых заданной длины круг покрывает наибольшую площадь. Это объясняет тот факт, что природа часто использует круг и его объемный эквивалент – сферу.  Природа всегда останавливает выбор на самых стабильных формах, минимально расходующих энергию.

2.Основная часть

2.1. Профессии, связанные с геометрией

Конечно, математика нужна нам везде: в автобусе, в магазине, дома и в школе. Однако профессии, где нужна только геометрия, не встречаются.

Архитектор

 Архитектура – это музыка, застывшая в камне. На мой взгляд, самая “геометрическая профессия” – архитектор.  Архитектура — одна из наиболее всеобъемлющих областей человеческой деятельности, занимающаяся организацией пространства и времени и решающая любые пространственные и временные задачи, от разработки стратегий развития агломераций до дизайна дверных ручек. Перед тем как построить жилое здание, проектируют будущую постройку на чертежах в уменьшенном масштабе. Архитектор придумывает основную концепцию здания, его облик, увязывает воедино все нюансы. Задача архитектора — спроектировать сооружение, максимально отвечающее потребностям заказчика.

Инженер

Еще одна немаловажная профессия — инженер. Инженер-строитель — это производитель работ, т.е. прораб, он руководит общестроительными работами, монтажом конструкций, осуществляет контроль над качеством.

В проектных организациях инженеры выполняют работы по комплексному проектированию: архитектурной, конструктивной части (электроснабжение, отопление и вентиляция, водопровод и канализация, слаботочные системы — телефон, пожарная сигнализация, теленаблюдение и др.). Кроме того, разрабатывают генеральные планы проектируемых комплексов, куда входят дороги, земляные работы, организация строительства. Направление деятельности строителей очень широкое —  кроме возведения зданий, производственных комплексов, фабрик, они проектируют мосты, гидротехнические сооружения, плотины, дамбы и т. д.

Дизайнер

     Дизайн — это творческая деятельность, целью которой является определение формальных качеств изделий промышленности. Эти качества включают и внешние черты изделия, но главным образом те структурные взаимосвязи, которые превращают изделие в единое целое, как с точки зрения потребителя, так и с точки зрения изготовителя. Быть дизайнером это означает быть творческой личностью. Для этого те, кто решил выбрать эту профессию, отправляются на специальные курсы подготовки, куда обязательно будут входить изучение черчения, геометрии и других специальных программ, которые пригодятся будущему специалисту.

Конструктор

      Конструктор осуществляет конструкторское и технологическое проектирование, разрабатывает и внедряет инновационные технологические процессы производства, разрабатывает технологические конструкции различного назначения, отдельные их элементы и части, цехи. Проводит исследования в области конструирования с использованием новых разработок, достижений различных областей науки. Для того чтобы стать конструктором, необходимо изучать технику, механику, физику, алгебру, геометрию, химию… И обладать такими качествами как: высокая концентрация и устойчивость внимания, логика, технический склад ума.

Модельер

 Модельер — специалист по изготовлению моделей одежды, создатель экспериментальных образцов, определяющий образ и стиль, общее конструктивное решение, изобретающий новые технологические решения и разрабатывающий декор, выбирающий цвет и материалы, продумывающий аксессуары и дополнения. Благодаря работе модельера наши вещи становятся более удобными, стильными и качественными.

Психолог

Наш характер определяется многими признаками, но оказывается, не  остается в стороне и геометрия. Когда мы смотрим на какие-либо предметы, то на подсознательном уровне, сопоставляем их с какими-то геометрическими фигурами и стараемся окружить себя такими же.

Существует даже такая наука — психогеометрия. Суть её состоит в исследовании личности. В её основе лежит учение Карла Юнга о психических типах личностей. Однако автором психогеометрии является Сьюзен Деллингер — специалист по социально-психологической подготовке управленческих кадров. Работа С. Деллингер «Психогеометрия: как использовать психогеометрию для воздействия на людей» очень популярна в США. В нашей стране труд С. Деллингер был переработан нашими соотечественниками Анатолием Алексеевым и Ларисой Громовой.

Психогеометрия — это уникальная практическая система анализа личности. Она позволяет:

Мгновенно определить тип личности интересующего вас человека и вашу собственную форму.

Дать подробную характеристику личностных качеств и особенностей поведения любого человека.

Составить сценарий поведения для каждой формы личности в типичных ситуациях.

Чтобы определиться в мире психогеометрии, которая как оказалось, влияет на все наши поступки, Деллингер выявила пять психологических типов, каждому из которых соответствует своя геометрическая фигура: квадрат, круг, треугольник, зигзаг, прямоугольник. Каждая фигура имеет свои психологические особенности и по-разному взаимодействует с остальными. Что ж, заманчиво, не правда ли? Да и не поспоришь ведь, что «круглые» глаза  иногда смотрят на мир иначе, чем «квадратные»!

Исследование личности с помощью психогеометрии позволяет быстро и точно нарисовать психологический портрет испытуемого, узнать какие черты его характера являются главными, а какие – второстепенными, а также понять, с кем человеку сложнее всего взаимодействовать.

2.2. Применение геометрии на практике

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Завариваем чай

Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 1). В каком чайнике заваренный чай останется тёплым дольше?

Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере ( ).

Рис. 1

И справление ошибки кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? 

Решение. Для исправления ошибки вы можете разрезать один из треугольников, например, так, как показано на рисунке 2, а затем сложить из него нужный треугольник.

Рис. 2

Строим прямой угол на земле

Известен старинный способ построения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ?

Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 3. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.

Рис. 3

Выдерживание прямых углов

Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? 

Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строительный угольник (см. рис.4), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны, и диагонали? Геометрия утверждает, что да! Например, на рис. 5 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.

Рис. 5

Рис. 4

Укрепляем калитку

Прямоугольная калитка (рис. 6, слева) со временем расшатывается и становится похожей на параллелограмм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать.

Решение.

В

Рис. 6

ыбор такого положения планки, как показано на рис. 6, (справа) основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

3.Заключение

Метод решения хорош, если с самого начала мы можем предвидеть — и далее подтвердить это, — что, следуя этому методу, мы достигнем цели. Так говорил великий немецкий философ, логик, математик Готфрид Вильгельм Лейбниц. Значение геометрии огромно. Геометрия встречается во многих профессиях, без которых человечество не смогло обойтись. Например, перед тем как построить жилое здание, люди проектируют будущую постройку на чертежах в уменьшенном масштабе. Этим занимается архитектор. Тот, кто руководит общестроительными работами и осуществляет контроль над качеством, называется инженером-строителем. Конструктор разрабатывает элементы, части технологических конструкций. Для того чтобы стать конструктором, необходимо сначала выучить множество наук, среди которых присутствует геометрия. С помощью модельера наши вещи становятся более удобными, стильными и качественными. Его задача изготавливать новые модели одежды, определять общее конструктивное решение, придумывать различные дополнения. Психолог с помощью психогеометрии быстро и точно нарисует психологический портрет испытуемого, узнает, какие черты его характера являются главными, а какие – второстепенными, а также поможет понять, с кем человеку сложнее всего взаимодействовать. А если на минуту представить, что геометрии не существует и ни один человек не подозревает о наличие геометрии, то неужели люди до сих пор жили бы в пещерах, ходили на охоту и одевались в шкуры животных? Изучив литературу, интернет — источники, я сделала вывод, что между геометрией и практической действительностью есть множество точек соприкосновения. Со своим проектом я выступила перед учащимися 7 – 8 классов, большинство учащихся о практическом применении геометрии и не ведало. Поэтому смело можно сделать вывод: если бы люди не стали изучать геометрию и пользоваться ею, то прогресс и множество современных изобретений дались бы человечеству с трудом и возможно гораздо позже.

4.Использованные литература и источники

https://www.nkj.ru/archive/articles/19307/

https://infourok.ru/material.html?mid=137763

https://7lafa.com/pageanswer.php?id=44485

http://obuchonok.ru

https://ru.wikipedia.org/wiki/Геометрия: 

http://interesnik.com/geometriya-v-nashej-zhizni/

Геометрия в нашей жизни

https://www.kakprosto.ru/kak-893421-chem-pomozhet-znanie-geometrii-v-

buduschem#ixzz4zda9DK8v

http://enciklopediya1.ru/index/0-397

Просмотров работы: 7641

«Удивительная наука геометрия»

Удивительная наука

геометрия

Те, кто собирается посвятить свою жизнь науке,

должен представлять,

что наука откроет перед ним сказочные сокровища красоты

« Геометрия является самым могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать»

Г. Галилей.

Мир, в котором мы живем, наполнен геометрией домов, улиц, гор и полей, творениями природы и человека. Лучше ориентироваться в нем, открывать новое, понимать красоту и мудрость окружающего мира поможет нам хорошее знание такого предмета как геометрия.

Геометрия зародилась в глубокой древности. Древние египтяне были замечательными инженерами. Еще в древности они говорили: «Все боится времени, но само время боится пирамид». В Египте существовала такая профессия гарпедонапт или натягиватель веревки.

Натягивателями веревок греки называли Гарпедонаптов — землемеров -геометров. Они должны были восстанавливать границы участков после разлива. И это они успешно делали только с помощью веревки и колышков.

* В Греции геометрия стала математической наукой около 2500 лет назад, но зародилась геометрия в Египте, на плодородных землях Нила. Чтобы собирать налоги, царям требовалось измерять площади. Много знаний требовало и строительство. О серьезности геометрических знаний египтян говорит тот факт, что египетские пирамиды

стоят уже 5 тысяч лет.

Фалес Милетский

Искусны были египетские писцы и гарпедонапты. Но однажды им пришлось устыдиться, потому что пришелец из далекой Греции оказался намного искуснее их. Египтяне задали ему трудную задачу : найти высоту пирамиды. Он нашел простое и красивое решение: воткнул длинную палку вертикально в землю и сказал :

« Когда тень от палки будет равна ее длине, тогда тень от пирамиды будет иметь ту же длину, что и высота пирамиды».

П л а т о н

Черновая работа была выполнена на протяжение многих веков в Вавилоне и Египте. На долю греческих ученых выпало систематизирование материала. Древнегреческий философ Платон , проводивший беседы со своими учениками в роще Академа ( Академ- древнегреческий мифологический герой, которого, по преданию, похоронили в священной роще недалеко от Афин; от его имени произошло слово «Академия») , одним из девизов своей школы провозгласил: «Не знающие геометрии не допускаются».

П и ф а г о р

Это время было особой эпохой не только в Греции, но и почти во всей ойкумене- известном греками обитаемом мире. Как весной, не сговариваясь, сразу зацветают все яблони, точно также в это время возникали новые идеи и учения. В это же время Гомер писал свою поэму «Одиссея»:

Муза, скажи мне о том многоопытном муже который,

Странствуя долго со дня, как святой Илион им разрушен.

Многих людей города посетил и обычаи видел,

Много и сердцем скорбел на морях, о спасенье заботясь»

П и ф а г о р

Ученый ,Пифагор, о котором пишет Гомен, объехав мир, поселился на острове Кротон, где вокруг него образовался

круг преданных ему учеников.

Греки считали за честь учиться математике у Пифагора. Но он требовал от своих учеников выполнения обета, который нашел отражение во фразе «бык на языке» ( «Держи язык за зубами ).

П и ф а г о р

Пифагор верил : чтобы познать суть, меру и связь явлений, надо погасить в себе суетность.

В геометрии его привлекали правильные фигуры и тела.

Сегодня трудно отделить истинные взгляды пифагорейцев от всего наносного, во многом мистического, чем время окутало их учение. Пифагорейцы верили в силу гармонии природы. Они геометризировали концепцию четырех первооснов мира.

Так, например, по их мнению, тетраэдр представлял атом огня, куб – земли, октаэдр – воздуха,

икосаэдр – воды, додекаэдр — вселенная

Теория пяти стихий мироздания вызывает сегодня лишь вежливую улыбку. Но в ней есть мудрость и она удивительно современна. При отборе пяти правильных тел Пифагор руководствовался прежде всего их симметрией.

От симметрии кристаллов до симметрии молекул ДНК «работают» фундаментальные законы, которые управляют всеми процессами физического мира.

Все стремились познать таинства природы.

Город Александрия был основан знаменитым полководцем Александром Македонским около 300 г. до н.э. После его смерти его полководцы разделили империю. Лучший кусок достался Птолемею. Он стал царем Египта. В своей столице он создал одну из крупнейших библиотек того времени. Узнав о сочинении, в котором была изложена геометрия как единая наука, Птолемей, познав автора сочинения, пожелал, чтобы тот обучал его этой науке. На что автор ответил: «В геометрии нет царских путей».

Е в к л и д

В то время знатные и богатые люди обучали своих детей прежде всего философии и литературе, а математике – лишь постольку, поскольку она соприкасается с философией. Знатным не подобало заниматься вычислениями и измерениями.

Одна из легенд рассказывает, что к Евклиду обратился юноша с просьбой взять его в ученики. Юноша спросил, какую пользу он получит, став геометром. Вместо ответа Евклид повелел своему слуге: «Дай этому человеку три обола (древняя монета), он ищет от геометрии пользу».

Е в к л и д

Позднее этот молодой человек досконально изучил «Начала» Евклида. Это про него написаны стихи :

Он чертил задумчивый, не гордый,

Позабыв текущие дела,-

И внезапно непонятной хордой

Тень копья чертеж пересекла.

Но убийц спокойствием пугая,

Он не унижался, не дрожа

Руку протянул, оберегая

Не себя, а знаки чертежа!

А р х и м е д

За свою жизнь Архимед сделал так много, что трудно подробно рассказать. Он с большой точностью определил отношение длины окружности к ее поперечнику.

Великий итальянский ученый Галилео Галилей однажды сказал: «Геометрия является могущественным средством для изощрения наших умственных способностей и дает нам возможность правильно мыслить и рассуждать».

Г а у с с

В первой книге «Начал» Евклид учит строить правильные многоугольники, но вот правильный семиугольник ни Евклид, ни его ученики построить не смогли, а пытались многие, поэтому семиугольная звезда играла определенную роль в астрологии. Однако в 1796 году девятнадцатилетний Гаусс сумел выяснить, какие именно правильные многоугольники могут быть построены с помощью циркуля и линейки. И геттингенцы поставили ему памятник, в пьедестале которого был правильный семнадцатиугольник.

Пятый постулат

Над пятым постулатом из книги «Начала» бились в течение двадцати веков сотни профессиональных геометров и любителей математики.

Лучше остановить Солнце, чем сдвинуть Землю, чем уменьшить сумму углов в треугольнике, свести параллели к схождению.

У Эйнштейна спросили: «Как появляются изобретения, которые переделывают мир?». «Очень просто, — ответил Эйнштейн.- Все знают, что сделать это невозможно. Случайно находится невежда, который это не знает. Он-то и делает изобретения».

Николай ИвановичЛобачевский

Отправным пунктом геометрии Лобачевского послужил V постулат Евклида — аксиома, эквивалентная аксиоме о параллельных. Он входил в список постулатов в «Началах» Евклида. Относительная сложность и неинтуитивность его формулировки вызывала ощущение его вторичности и порождала попытки вывести его как теорему из остальных постулатов Евклида.

Лобачевский в работе «О началах геометрии» (1829), первой его печатной работе по неевклидовой геометрии, ясно заявил, что пятый постулат не может быть доказан на основе других посылок евклидовой геометрии, и что допущение постулата, противоположного постулату Евклида, позволяет построить геометрию столь же содержательную и свободную от противоречий, как и евклидова

Николай Иванович Лобачевский

В итоге Лобачевский выступил как первый наиболее яркий и последовательный пропагандист новой геометрии. Хотя геометрия Лобачевского развивалась как умозрительная теория, и сам Лобачевский называл её «воображаемой геометрией», тем не менее именно он впервые открыто предложил её не как игру ума, а как возможную и полезную теорию пространственных отношений.

Однако доказательство её непротиворечивости было дано позже, когда были указаны её интерпретации (модели).

Медаль имени Лобачевского

«За выдающиеся работы в области геометрии»

Фрактальная геометрия – удивительное чудо

Понятия «фрактальная геометрия» и «фрактал» возникли в конце 70-х гг., а со второй половины 80-х они прочно вошли в словарь программистов, математиков и даже финансовых трейдеров. Сам термин «фрактал» происходит от латинского «fractus» и переводится как «состоящий из фрагментов». Этим словом в 1975 году американский и французский ученый Бенуа Мандельброт обозначил нерегулярные, но самоподобные структуры, которыми он в то время занимался. В 1977 году вышла его книга, которая была полностью посвящена такому уникальному и красивейшему явлению, как фрактальная геометрия природы

Фрактальная геометрия – удивительное чудо

Сам Бенуа Мандельброт был математиком, однако термин «фрактал» не относится к математическим понятиям. Как правило, под ним подразумевают геометрическую фигуру, обладающую одним или несколькими следующими свойствами :

• при увеличении у нее обнаруживается сложная структура;

2) в той или иной степени эта фигура подобна себе самой;

3) ее можно построить с помощью рекурсивных процедур;

4) для нее характерна дробная хаусдорфовая (фрактальная) размерность, превышающая топологическую.

Фрактальная геометрия — это настоящая революция в математическом описании природы. С ее помощью можно описать мир намного понятнее, чем это делает

традиционная математика или физика.

Возьмем, к примеру, броуновское движение.

Невозможные фигуры геометрии

Треугольник Рёло

Невозможный трезубец

Трибар

Бесконечная лестница

Удивительные фигуры в геометрии

П

о

л

и

м

о

н

о

Полиамонд

Фрактал

Лента Мебиуса

Наука геометрия очень важна для человека. Геометрия развивалась за несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции. Большой вклад в развитие геометрии внесли известные учёные: Евклид и его книга под названием «Начала», Архимед, которому принадлежит формула для определения площади треугольника через три его стороны, Менелай, которым были написаны два сочинения

«О вычислении хорд» в 6 книгах и «Сферика» в 3 книгах.

Наука геометрия и сейчас развивается. Мы легко решаем задачи, для которых в древности потребовалось бы много времени и сил.

Разработка урока внеурочной деятельности «Путешествие в страну геометрических фигур»

Логика 5 класс

Тема: «Путешествие в страну геометрических фигур»

Целеполагания:

• познакомить ребят понятием и историей геометрии;

• познакомить обучающихся с элементами геометрии;

• способствовать развитию умений анализировать, сравнивать, обобщать, выделять главное; развивать осознанную математическую речь; развитие познавательного интереса учащихся;

• содействовать воспитанию таких качеств как: самостоятельность, целеустремленность, настойчивость, целенаправленность, трудолюбие, аккуратность, ответственность

Задачи:

— Продолжить формирование навыков контроля результатов деятельности.

— Способствовать развитию коммуникативных навыков. Развивать умение анализировать, обобщать материал, выступать перед аудиторией, развивать интеллектуальные, творческие и исследовательские способности, активизировать интерес к учебным предметам.

— Формирование логического, абстрактного, эвристического, системного мышления.

Оборудование: проектор, экран, компьютер, презентации

План.

1. Организационные моменты.

Сообщение темы и целей урока.

2. Что такое геометрия? История зарождения геометрии.

Очень часто, сами не подозревая того, мы имеем дело с геометрией. Мы вовлекаемся в геометрию, когда работаем с формой и размерами, предметами, их размещением в пространстве. А что такое геометрия? Наука о формах и размерах предметов, а также взаимном размещении фигур называется геометрией. Применение этой науки в жизни встречается очень часто: строительство, ландшафтный дизайн, архитектура и интерьер. И это далеко не полный перечень отраслей, где применяют принципы геометрии.

С чего все начиналось.

С давних времен люди работали на земле. Но, чтобы измерить свои участки, им нужно было проводить математические решения, это и были первые геометрические расчеты. При построении египетских пирамид, также проводились разные расчеты, которые со временем стали основой геометрии. В Египте, в городе Александрия, в 280 году до нашей эры жил ученый Эвклид, он и написал книгу о геометрии. Все, кто имел желание изучать геометрию, более двух тысяч лет пользовались этим учебником. На сегодняшний день эвклидова геометрия признана как несовременная и многие ее тезы ученые откинули. Прошло время, и ученые стали выводить геометрические формулы, теоремы, аксиомы, сформировалось понятие, что изучает геометрия. Сегодня мы с утверждением можем сказать, что это наука о пространстве и отношениях, которые возникают в нем.

Вся геометрия делится на несколько видов. Как пример – классическая геометрия. Она «занимается» точками, плоскостями. В нее входят разделы планиметрии, стереометрии и другие. Познание в системе координат дает нам аналитическая геометрия. Дифференциальные уравнения – это теория и практика дифференциальной геометрии. А итог всем разделам подводит топология, изучающая непрерывность.

Для чего же ты нам нужна, геометрия.

Развитие цивилизации повлекло за собой развитие науки. Геометрией занимались многие ученые, и в результате их научных работ, геометрия нашла себе место на практике. О том, для чего нужна геометрия, можно рассказывать очень много. В первую очередь она связана с такими науками, как инженерия, физика, астрономия, что дает возможность проводить новые открытия и разрабатывать перспективные проекты. Все инженерные расчеты связаны с геометрией, даже, казалось бы, такие мелочные, как, например, установка уличных фонарей. Ведь для этого нужно с высокой точностью просчитать угол падения луча света на землю, чтобы он смог максимально осветить территорию. Также геометрия нужна при расчете перед началом строительства. Архитекторы должны с точностью просчитать все моменты строительства. Законам геометрии подчиняются траектории и габариты транспорта, поэтому водители должны учитывать это для безопасного движения. Можно приводить еще много примеров из жизни, где геометрия занимает не последнюю роль.

Начертательная геометрия

Часто мы слышим о еще одном виде геометрии – начертательной. А что такое начертательная геометрия? Это один из ее многочисленных разделов, который изучает фигуры, которые проецируются на плоскость. Какие задачи стоят перед начертательной геометрией? В первую очередь, это изображение фигур на плоскости и при этом решение метрических задач. Как известно, инженерное творчество требует развития пространственного воображения. Начертательная геометрия, как наука, помогает человеку развивать это пространственное воображение. Для решения задач по начертательной геометрии, в первую очередь, нужен чертеж, на который проецируются фигуры, обозначаются все точки. Строительство, архитектура, искусство – это те сферы деятельности человека, где применяют начертательную геометрию. А еще, благодаря этой науке, сегодня можно показать на плоскости рельеф земли, проектировать дороги, тоннели и каналы. Другие отрасли математики также тесно связаны с начертательной геометрией. Подводя итог, можно без преувеличения сказать, что геометрия – это тот предмет, который можно назвать фундаментом многих наук. 

Геометрия (греческое, от ge — земля и metrein — измерять), наука о пространстве, точнее наука о формах, размерах и границах тех частей пространства, которые в нем занимают вещественные тела. Таково классическое определение геометрии, или, вернее, таково действительное значение классической геометрии. Однако современная геометрия во многих своих дисциплинах выходит далеко за пределы этого определения. Развитее геометрии принесло с собой глубоко идущую эволюцию понятия о пространстве. В том значении, в котором пространство как математический термин широко употребляется современными геометрами, оно уже не может служить первичным понятием, на котором покоится определение геометрии, а, напротив, само находит себе определение в ходе развития геометрических идей. Геометрия даёт общее понятие о геометрической фигуре, под которой понимают не только тело, поверхность, линию или точку, но и любую их совокупность. Геометрия в первоначальном значение есть наука о фигурах, взаимном расположении и размерах их частей, а также о преобразованиях фигур. Это определение вполне согласуется с определением геометрии как науки о пространственных формах и отношениях. Действительно, фигура, как она рассматривается в геометрии, и есть пространственная форма, поэтому в геометрии говорят, например, «шар»,а не «тело шарообразной формы», расположение и размеры определяются пространственными отношениями, наконец , преобразование, как его понимают в геометрии , так же есть некоторое отношение между двумя фигурами — данной и той, в которую она преобразуется.

Где и когда зародилась наука геометрия?

Традиционно считается, что родоначальниками геометрии как систематической науки являются древние греки, перенявшие у египтянремесло землемерия и измерения объёмов тел и превратившие его в строгую научную дисциплину.

Зародилась геометрии в Древнем Египте около 2000 лет до н. э.

Древнегреческий историк Геродот писал: « Сезострис , египетский фараон , разделил землю, дав каждому египтянину участок по жребию и взимал соответствующим образом налог с каждого участка . Случалось , что Нил заливал тот или иной участок, тогда пострадавший обращался к царю , а царь посылал землемеров, чтобы установить , на сколько уменьшился участок , и соответствующим образом уменьшить налог. Так возникла геометрия в Египте, а оттуда перешла в Грецию.

Античные геометры от набора рецептов перешли к установлению общих закономерностей, составили первые систематические и доказательные труды по геометрии.

Начиная с 7 века до н. э. в Древней Греции создаются так называемые философские школы, и приходит постепенный переход, от практической к теоретической геометрии. Всё больше значение в этих школах приобретают рассуждения, при помощи которых удаётся получать новые геометрические свойства, исходя из некоторых положений, принимаемых без доказательств и названных аксиомами. В переводе с греческого слово аксиома означает «принятие положения».

Какая геометрия была?

2000 лет до н. э. В образовании науки геометрии важную роль играли и эстетические потребности людей: желание украсить свои жилища и одежду, рисовать картины окружающей жизни. Все это способствовало формированию и накоплению геометрических сведений. За несколько столетий до нашей эры в Вавилоне, Китае, Египте и Греции уже существовали начальные геометрические знания, которые добывались в основном опытным путем, но они не были еще систематизированы и передавались от поколения к поколению в виде правил и советов, например, правил нахождения площадей фигур, объемов тел, построение прямых углов и т.д. Не было еще доказательств этих правил, и их изложение не представляло собой научной теории.

Какие были великие ученые в области геометрии?

Архимед

Один из известнейших ученых Архимед. Древнегреческий математик, физик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда важных изобретений .

Сведения о жизни Архимеда оставили нам Полибий, Тит Ливий, Цицерон,Плутарх, Витрувий и другие. Почти все они жили на много лет позже описываемых событий, и достоверность этих сведений оценить трудно.

Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений

Главные математические достижения Архимеда касаются проблем, которые сейчас относят к области математического анализа. Греки до Архимеда сумели определить площади многоугольников и круга, объём призмы ицилиндра, пирамиды и конуса. Но только Архимед нашёл гораздо более общий метод вычисления площадей или объёмов. Лучшим своим достижением он считал определение поверхности и объёма шара — задача, которую до него никто решить не мог. Архимед просил выбить на своей могиле шар, вписанный в цилиндр.

Идеи Архимеда почти на два тысячелетия опередили своё время. Только вXVII веке учёные смогли продолжить и развить труды великого греческого математика.

Эвклид

В 3 веке до н. э. жил великий ученый Евкли́д или Эвкли́д 
— древнегреческий математик, автор первых дошедших до нас теоретических трактатов по математике. Биографические сведения о жизни и деятельности Эвклида крайне ограничены. Известно, что он родом из Афин, был учеником Платона. Научная деятельность его протекала в Александрии , где он создал математическую школу. . Евклид — первый математик Александрийской школы. Основное сочинение Евклида называется Начала. Книги с таким же названием, в которых последовательно излагались все основные факты геометрии и теоретической арифметики, составлялись ранее Гиппократом Хиосским, Леонтом и Февдием. Однако Начала Евклида вытеснили все эти сочинения из обихода и в течение более чем двух тысячелетий оставались базовым учебником геометрии. Создавая свой учебник, Евклид включил в него многое из того, что было создано его предшественниками, обработав этот материал и сведя его воедино. Его главная работа содержит ряды вопросов теории чисел; в ней он подвёл итог предшествующему развитию греческой математики и создал фундамент дальнейшего развития математики .

Пифагор

Древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев. Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом».

Самые ранние известные источники об учении Пифагора появились лишь 200 лет спустя после его смерти. Сам Пифагор не оставил сочинений, и все сведения о нём и его учении основываются на трудах его последователей, не всегда беспристрастных.

Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен):

«В день, когда Пифагор открыл свой чертёж знаменитый,
Славную он за него жертву быками воздвиг.»

Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание^[звестное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.

В честь Пифагора назван кратер на Луне

Лобаче́вский

Никола́й Ива́нович Лобаче́вский (20 ноября 1792, Нижний Новгород — 12 февраля 1856, Казань) — русский математик, создатель неевклидовой геометрии, деятель университетского образования и народного просвещения. Известный английский математик Уильям Клиффорд назвал Лобачевского «Коперником геометрии.

Открыл неевклидовую геометрию.

Неевклидовая геометрия, геометрическая теория, основанная на тех же основных посылках, что и обычная евклидова геометрия, за исключением аксиомы о параллельных, которая заменяется на аксиому о параллельных Лобачевского

Однако научные идеи Лобачевского не были поняты современниками.

Не найдя понимания на Родине, Лобачевский попытался найти единомышленников за рубежом.

Но Лобачевский так и умер непризнанным, не дожив до торжества своих идей всего 10-12 лет. Вскоре ситуация в науке коренным образом изменилась. Большую роль в признании трудов Лобачевского сыграли исследования Э. Бельтрами (1868), Ф. Клейна (1871), А. Пуанкаре (1883) и др. Появлениемодели Клейна доказало, что геометрия Лобачевского так же непротиворечива, как и евклидова. Осознание того, что у евклидовой геометрии имеется полноценная альтернатива, произвело огромное впечатление на научный мир и придало импульс другим новаторским идеям в математике и физике.

3. Итоги урока.

Решение логических задач дается всем по-разному, но для учителя важно помочь каждому обучающемуся разобраться в порядке рассуждений и научиться рассуждать логически.

4. Домашнее задание.

Решить задачу 4, 6, 8, 10 в двух вариантах.

Полезная геометрия | Наука и жизнь

В школе мы несколько лет подряд прилежно изучаем геометрию. Но не зря ли мы тратим время? Чем может помочь геометрия в жизни? Измерить расстояние от точки до точки, вычислить площадь или объём предмета и только? Нет, конечно. Законы геометрии применимы буквально на каждом шагу. Просто нужно знать, как ими воспользоваться.

Вешаем зеркало

Вы решили повесить в прихожей зеркало. Тут же возникает вопрос: какой минимальной высоты должно быть зеркало, чтобы человек среднего роста мог видеть себя в нём целиком? И ещё: имеет ли при этом значение размер помещения, где будет висеть зеркало? Решение. Предмет и его отражение симметричны относительно плоскости зеркала. Построим в нём изображение человека (рис. 1): АВ — человек, А₁В₁ — его изображение, точка С — глаз, DE — зеркало. Из рисунка видно, что минимальная высота зеркала приблизительно равна половине роста человека, считая от уровня глаз. При этом высота Е нижнего края зеркала от пола должна быть вдвое меньше расстояния от пола до глаз. Легко понять, что, на каком бы расстоянии от такого зеркала ни находился человек, он сможет увидеть себя в нём с головы до ног, значит, размер помещения значения не имеет.

Завариваем чай

Перед вами стеклянные чайники четырёх моделей одинаковой вместимости (рис. 2). В каком чайнике заваренный чай останется тёплым дольше? Решение. Из курса физики известно, что время охлаждения пропорционально площади поверхности тела. Значит, чем меньше поверхность чайника, тем дольше остывает чай. Самая маленькая площадь поверхности у четвёртого чайника, так как его форма близка к сфере (S = d²).

Выдерживаем прямые углы

Если вы решили склеить коробку, сделать шкатулку или выложить плитку, важно, чтобы все детали были точными прямоугольниками или квадратами. В противном случае всё пойдёт наперекосяк. Как проверить, имеет ли деталь нужную «геометрию»? Решение. Чтобы проверить, у всех ли деталей, с которыми вы работаете, прямые углы и одинаковые линейные размеры, можно использовать строи-тельный угольник (рис. 3), а можно применить знания по геометрии. Убедитесь в том, что противоположные стороны четырёхугольника равны и при этом диагонали тоже имеют одинаковую длину. Как вы и сами знаете, сделать это можно с помощью линейки. Но вот вопрос: обязательно ли проверять и стороны и диагонали? Геометрия утверждает, что да! Например, на рис. 4 диагонали в четырёхугольнике слева равны, но очевидно, что его углы совсем не прямые. А в четырёхугольнике справа противоположные стороны равны, но это тоже не прямоугольник. Для проверки прямоугольности геометрия ещё советует убедиться в равенстве всех четырёх отрезков, на которые разбиваются диагонали в точке их пересечения.

Строим прямой угол на земле

Известен старинный способ постро-ения прямого угла на поверхности земли. Его использовали ещё древние египтяне. Они строили прямой угол с помощью обычной верёвки, на которой через равные расстояния завязаны тринадцать узелков. Чтобы отрезки на верёвке были одинаковые, узелки завязывали вокруг колышков, вбитых в землю на равном расстоянии друг от друга. В чём состоит этот «верёвочный» способ? Решение. В древности при закладке храма такую верёвку с узелками использовали для определения направлений его стен. Концы верёвки на месте крайних узелков связывали, а затем натягивали её на три колышка так, как показано на рис. 5. Стороны при этом имели соотношение 3:4:5. В таком треугольнике один из углов получается прямым. Впоследствии этот факт был доказан в теореме Пифагора. Поэтому первых геометров называли ещё «натягивателями верёвок». Нужно отметить, что таким способом построения прямого угла на местности пользуются и сегодня, например при закладке фундамента небольшого строения.

Проверяем перпендикулярность стен

Как проверить, перпендикулярны ли друг другу соседние стены в комнате, воспользовавшись верёвкой с узелками из предыдущей задачи? Решение. Если предположить, что стены в комнате вертикальны, а пол горизонтален, то проверку проводят так. От точки на полу в углу между стенами откладывают отрезки длиной 3 и 4 единицы (рис. 6). Если стены перпендикулярны, то расстояние между концами отрезков будет равно 5 единицам, так как построенный тре-угольник со сторонами 3, 4, 5 — прямоугольный.

Отмеряем нужный объём

Часто в рецептуре того или иного блюда требуется взять четверть (или половину) стакана жидкости, муки либо какого-либо другого продукта. Как отмерить такой объём с наибольшей точностью, не прибегая к дополнительным измерительным средствам? Решение. Воспользуемся стаканом цилиндрической формы — это важно для точности измерений. Чтобы отмерить четверть стакана жидкости, надо из наполненного стакана вылить столько, чтобы оставшаяся в нём жидкость закрыла половину дна (рис. 7). Она займёт примерно четверть объёма стакана-цилиндра. Аналогично поступаем, если надо отмерить половину стакана. Наклоняем стакан так, чтобы оставшаяся в нём жидкость закрыла всё дно (рис. 8). А можно ли геометрическим способом узнать объём бутылки? Конечно! Для этого надо заполнить бутылку водой чуть меньше чем наполовину (рис. 9, слева) и измерить объём воды, умножив площадь дна бутылки на высоту налитой в неё воды (напомним, что объём цилиндра вычисляется как произведение площади основания на высоту). Затем нужно перевернуть бутылку горлышком вниз так, чтобы вода не вытекла, и измерить объём верхней цилиндрической части бутылки, оставшейся пустой (рис. 9, справа). Полный объём бутылки равен сумме найденных объёмов. Для точности можно учесть толщину стенок бутылки.

Укрепляем калитку

Прямоугольная калитка (рис. 10, слева) со временем расшатывается и становится похожей на параллело-грамм. Этого можно избежать, прибив к ней ещё одну планку. Только надо знать, как это сделать. Решение. Выбор такого положения планки, как показано на рис. 10, справа, основан на свойстве жёсткости треугольника. Оно гласит: существует единственный треугольник с заданными длинами сторон. Планка и есть гипотенуза такого треугольника.

Выбираем табурет

Если вы решили предыдущую задачу, то без труда определите, на какой табурет (рис. 11) можно сесть без риска оказаться на полу. Решение. Безопасный табурет изображён на правой картинке, так как его сиденье и ножки образуют треугольник.

Исправляем ошибку кроя

Предположим, вам нужно вырезать для аппликации два разносторонних треугольника из цветной бумаги — «левый» и «правый». Вы случайно вырезали их одинаковыми — оба «левые». Можно ли, не используя новый кусок бумаги, исправить ошибку? Решение. Для исправления ошибки вы можете разрезать один из треугольников, например так, как показано на рис. 12, а затем сложить из него нужный треугольник.

Находим середину

Как без всяких измерений найти середину негнущегося прута, доски или металлического стержня? Решение. Можно отмерить размеры стержня на шнуре, затем сложить его пополам и отложить полученную длину. А можно воспользоваться геометрическим построением середины отрезка с помощью циркуля и линейки, если, конечно, размеры позволяют это сделать. Ещё более рациональное решение даёт физика. Середину однородного стержня легко найти, используя понятие центра тяжести (рис. 13).

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

Наука и жизнь // Иллюстрации

‹

›

Сферическая геометрия — Википедия

Материал из Википедии — свободной энциклопедии

Большой круг всегда делит сферу на две равные половины. Центр большого круга совпадает с центром сферы Малый круг делит сферу на две неравные части. Центр малого круга не совпадает с центром сферы 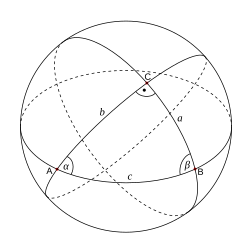Сферический треугольник

Сферическая геометрия — раздел геометрии, изучающий геометрические фигуры на поверхности сферы. Сферическая геометрия возникла в древности в связи с потребностями географии и астрономии.

• Большой круг — это круг, который делит шар (сферу) на две равные половины. Центр большого круга всегда совпадает с центром сферы. На глобусе, к примеру, все меридианы являются большими кругами. А вот из параллелей только экватор является большим кругом. Все остальные параллели — это малые круги.

• Большие круги на поверхности сферы играют роль, аналогичную роли прямых в планиметрии. Кратчайший путь между любыми двумя точками пройдёт по линии большого круга.

• Через любые две точки на поверхности сферы, кроме диаметрально противоположных, можно провести единственный большой круг. Через диаметрально противоположные точки на сфере можно провести сколько угодно больших кругов.

• Любые два больших круга пересекаются по прямой, проходящей через центр сферы, а окружности больших кругов пересекаются в двух диаметрально противоположных точках.

• При пересечении двух больших кругов образуются четыре сферических двуугольника. Площадь двуугольника определяется формулой S=2R2α{\displaystyle S=2R^{2}\alpha }, где R{\displaystyle R} — радиус сферы, а α{\displaystyle \alpha } — угол двуугольника в радианах.

• Три больших круга, не пересекающихся в одной точке, образуют восемь сферических треугольников. Сферический треугольник, все стороны которого меньше половины большого круга, называется эйлеровым. Помимо трёх признаков равенства плоских треугольников, для сферических треугольников имеет место ещё один: два сферических треугольника равны, если их соответствующие углы равны.

Соотношения между элементами сферического треугольника изучает сферическая тригонометрия.

• Алексеевский Д. В., Винберг Э. Б., Солодовников А. С. Геометрия пространств постоянной кривизны. // Итоги науки и техники. Современные проблемы математики. Фундаментальные направления. — М.: ВИНИТИ, 1988. — Т. 29. — С. 1—146.
• Берже М. Геометрия. / Пер. с франц., в 2 т. — М.: Мир, 1984. — Т. II, ч. V: Внутренняя геометрия сферы, гиперболическая геометрия, пространство сфер.
• Степанов Н. Н. Сферическая тригонометрия. — Л.—М., 1948.
• Шафаревич И. Р., Ремизов А. О. Линейная алгебра и геометрия. — М.: Физматлит, 2009.
• Александров А. Д., Нецветаев Н. Ю. Геометрия. — М.: Наука, 1990.
• Александров П. С. Что такое неэвклидова геометрия. — М.: УРСС, 2007.