Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Свойства трапеции
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
Свойства и признаки равнобедренной трапеции
1. В равнобедренной трапеции углы при любом основании равны.
2.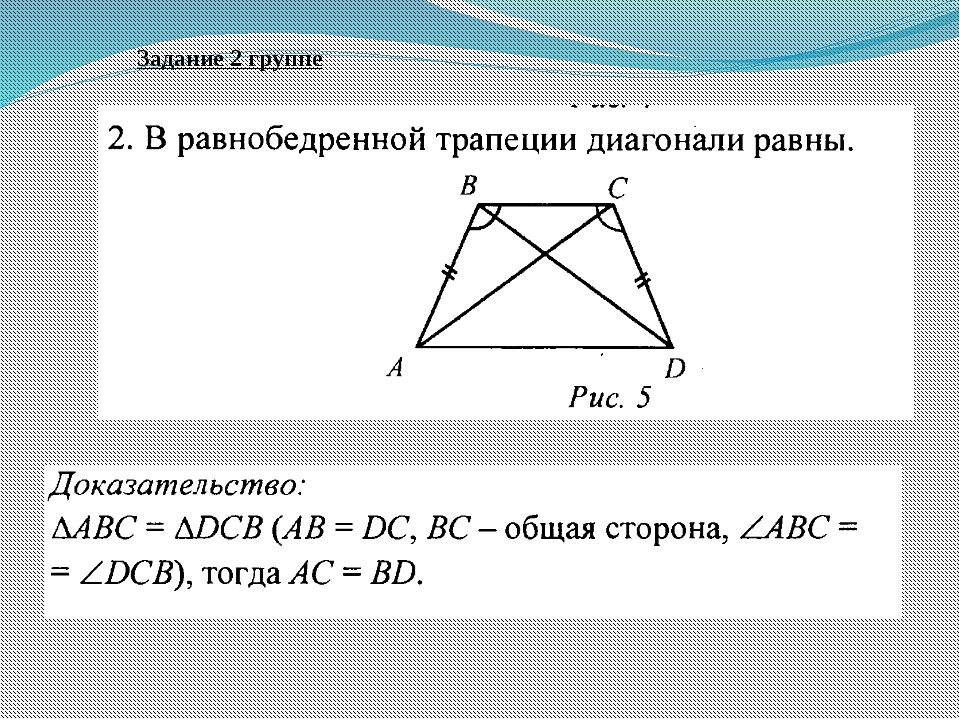 В равнобедренной трапеции длины диагоналей равны.
В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Вписанная окружность
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
Площадь
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
Отношение диагоналей трапеции в точке пересечения. Запоминаем и применяем свойства трапеции. Свойства трапеции, вписанной в окружность
Трапеция — это четырехугольник, имеющий две параллельные стороны, являющиеся основаниями и две не параллельные стороны, являющиеся боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная .
— это трапеция, у которой углы при боковой стороне прямые.
Элементы трапеции
a, b — основания трапеции (a параллельно b ),
m, n — боковые стороны трапеции,
d 1 , d 2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Площадь трапеции
- Через полусумму оснований a, b и высоту h : S = \frac{a + b}{2}\cdot h
- Через среднюю линию MN и высоту h : S = MN\cdot h
- Через диагонали d 1 , d 2 и угол (\sin \varphi ) между ними: S = \frac{d_{1} d_{2} \sin \varphi}{2}
Свойства трапеции
Средняя линия трапеции
Средняя линия
параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции
Сумма углов трапеции , прилежащих к каждой боковой стороне, равна 180^{\circ} :
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликие треугольники трапеции
Равновеликими , то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB
и DOC
, образованные боковыми сторонами. {2}
.
{2}
.
Отношение длин отрезков и оснований
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.

Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции:

Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ).
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ . - А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам:
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.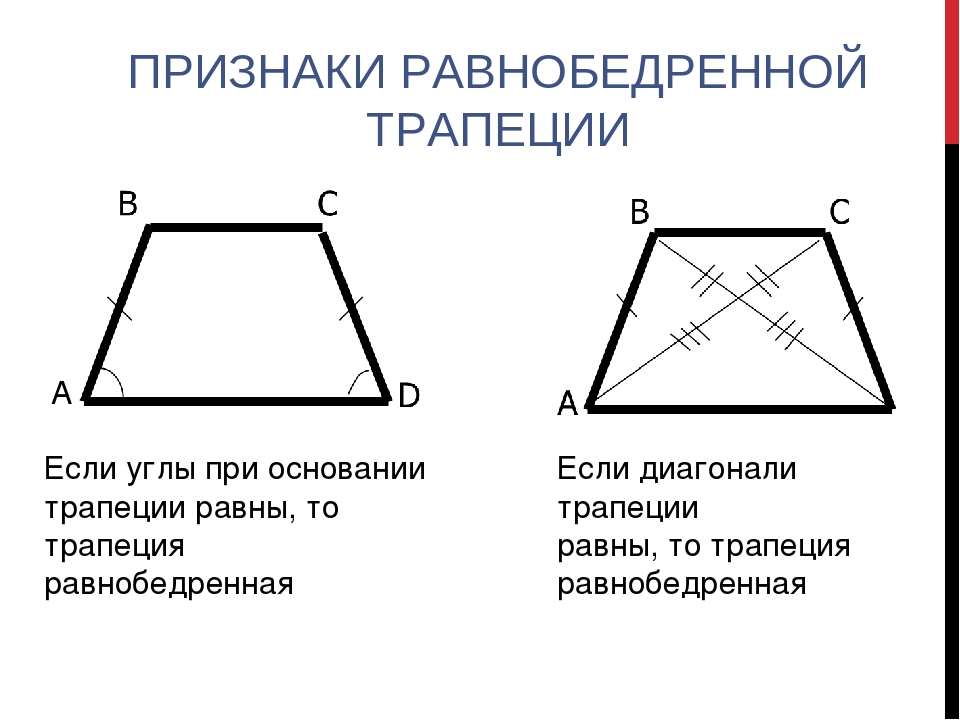
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.

- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка.
 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.

- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие.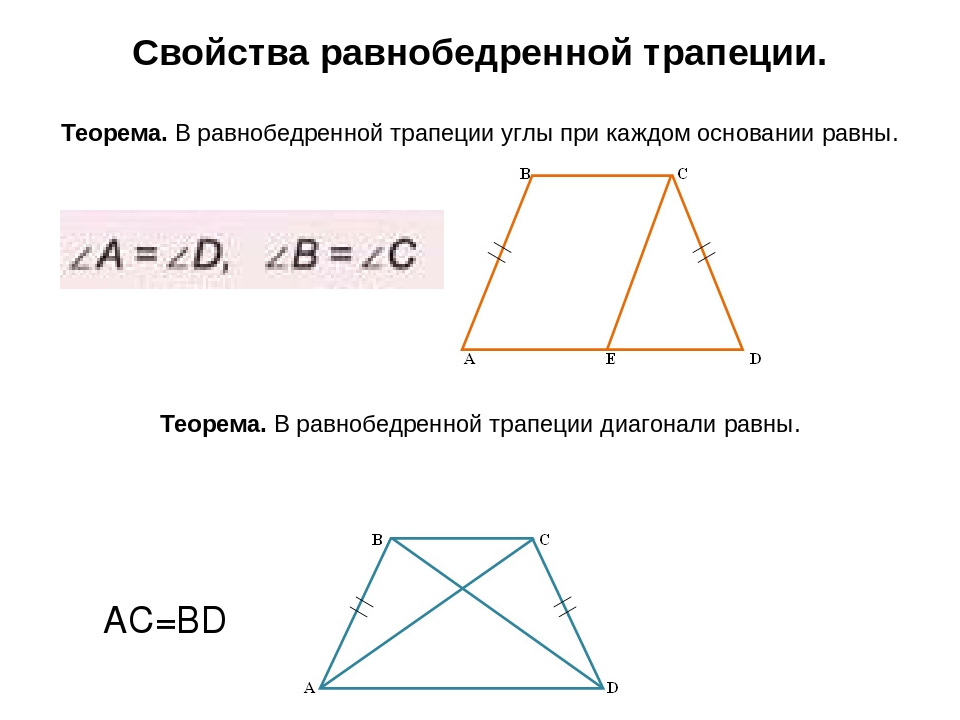 Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.

Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию.
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной.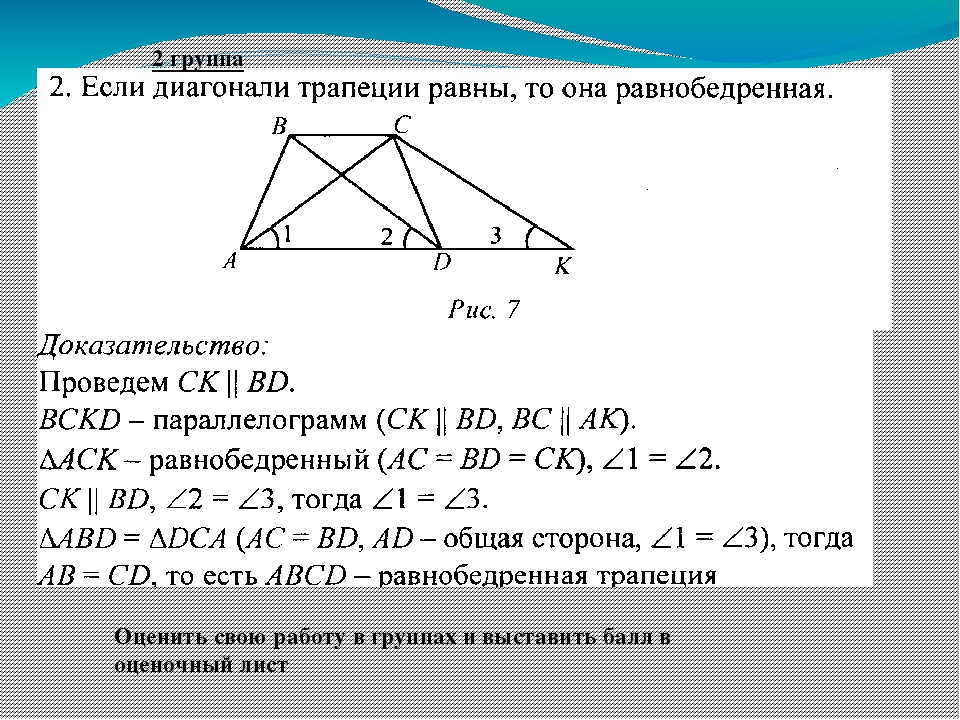 Но вы сами убедились, что разница огромна.
Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .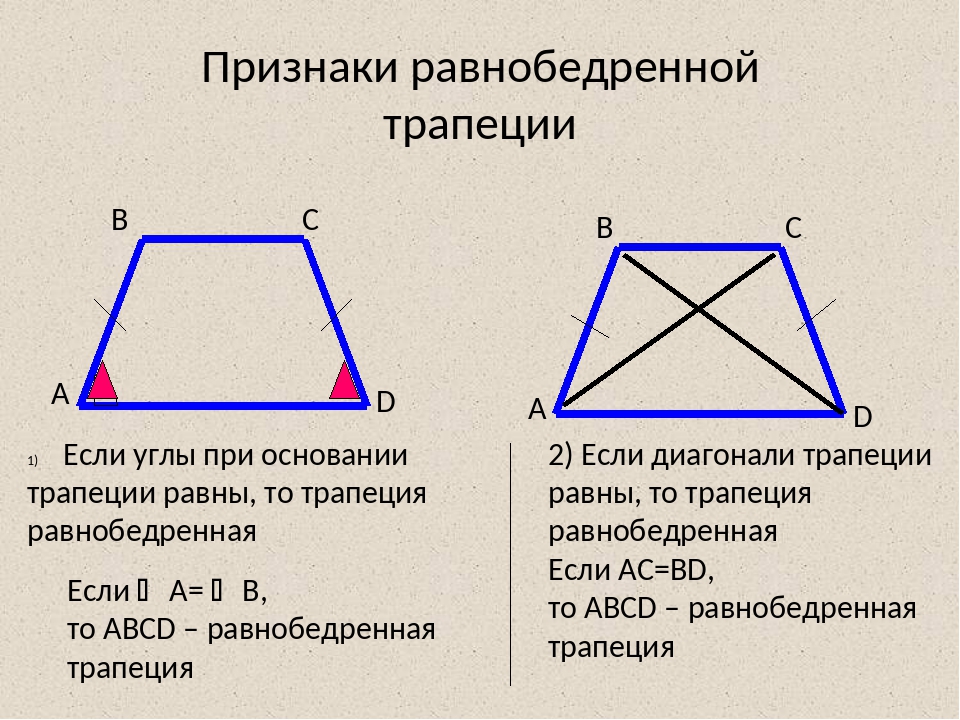
Четырехугольники
Параллелограмм
Параллелограммом называется четырёхугольник, противоположные стороны которого попарно параллельны.
Свойства и признаки параллелограмма
- Диагональ разбивает параллелограмм на два равных треугольника.
- Противоположные стороны параллелограмма попарно равны.
- Противоположные углы параллелограмма попарно равны.
- Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
- Если противоположные стороны четырёхугольника попарно равны, то этот четырёхугольник – параллелограмм.
- Если две противоположные стороны четырёхугольника равны и параллельны, то этот четырёхугольник – параллелограмм.
- Если диагонали четырёхугольника делятся точкой пересечения пополам, то этот четырёхугольник – параллелограмм.
Свойство середин сторон четырёхугольника
Середины сторон любого четырёхугольника являются вершинами параллелограмма, площадь которого равна половине площади четырехугольника.
Прямоугольник
Прямоугольником называется параллелограмм с прямым углом.
Свойства и признаки прямоугольника
- Диагонали прямоугольника равны.
- Если диагонали параллелограмма равны, то этот параллелограмм – прямоугольник.
Квадрат
Квадратом называется прямоугольник, все стороны которого равны.
Ромб
Ромбом называется четырёхугольник, все стороны которого равны.
Свойства и признаки ромба
- Диагонали ромба перпендикулярны.
- Диагонали ромба делят его углы пополам.
- Если диагонали параллелограмма перпендикулярны, то этот параллелограмм – ромб.
- Если диагонали параллелограмма делят его углы пополам, то этот параллелограмм – ромб.
Трапеция
Трапецией называется четырёхугольник, у которого только две противоположные стороны (основания) параллельны.
Средней линией трапеции называется отрезок, соединяющий середины непараллельных сторон (боковых сторон).
Теорема о средней линии трапеции
- Средняя линия трапеции параллельна основаниям и равна их полусумме.
- Отрезок, соединяющий середины диагоналей трапеции, равен полуразности оснований.
Замечательное свойство трапеции
Точка пересечения диагоналей трапеции, точка пересечения продолжений боковых сторон и середины оснований лежат на одной прямой.
Равнобедренная трапеция
Трапеция называется равнобедренной, если ее боковые стороны равны.
Свойства и признаки равнобедренной трапеции
- Углы при основании равнобедренной трапеции равны.
- Диагонали равнобедренной трапеции равны.
- Если углы при основании трапеции равны, то она равнобедренная.

- Если диагонали трапеции равны, то она равнобедренная.
- Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Как доказывать признаки равнобедренной трапеции. Диагонали трапеции. Теоремы: свойства равнобедренной трапеции
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.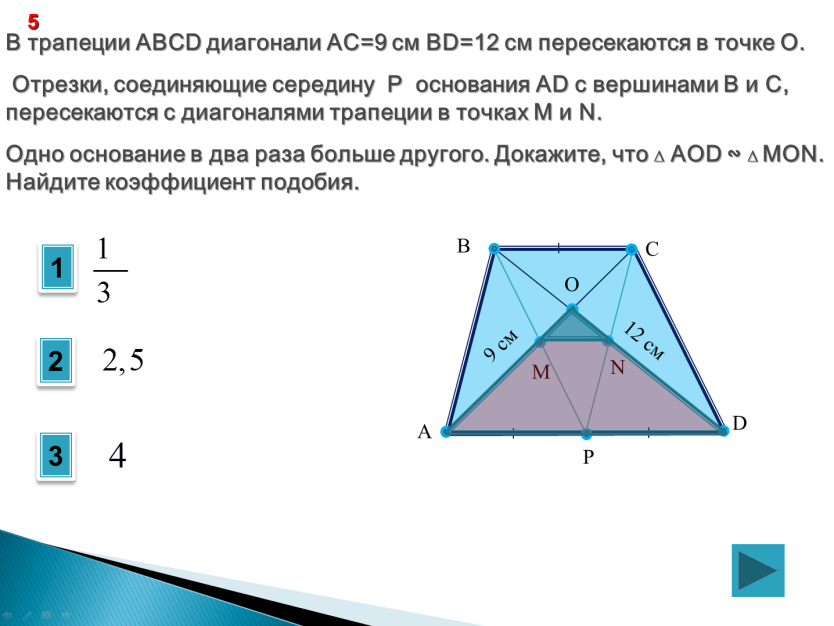
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.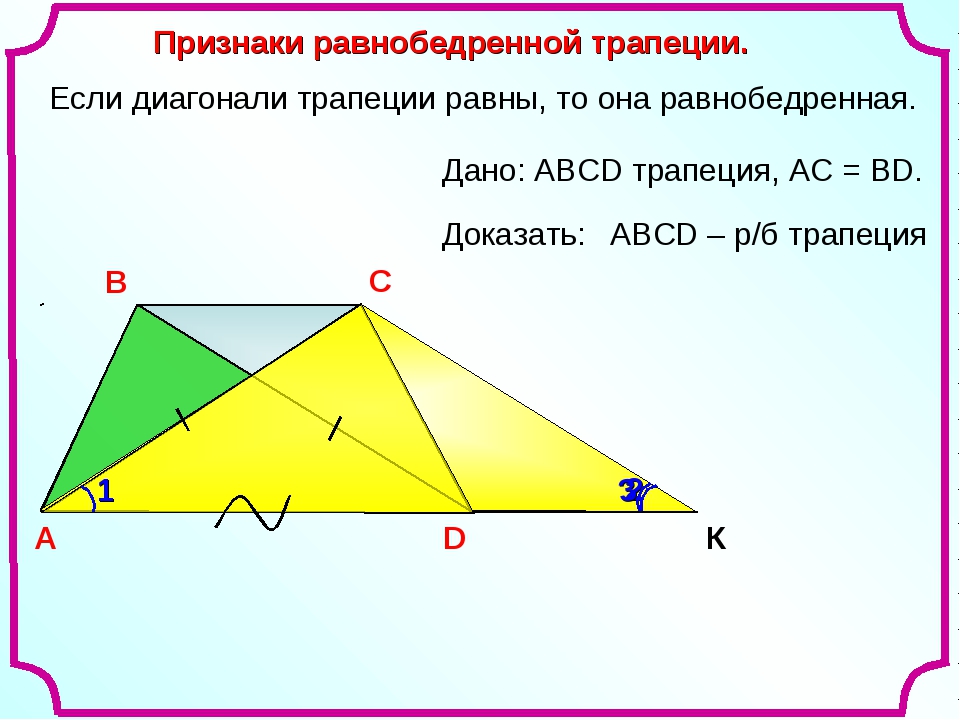
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1.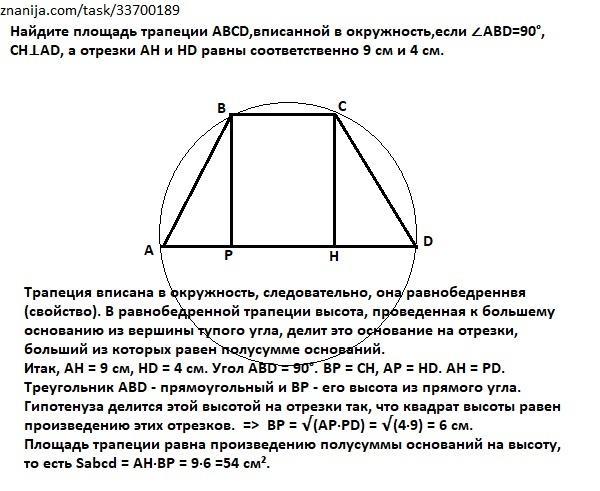 Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований
. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту

Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 . \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\)
, то \(x+kx=y+ky \Rightarrow x=y\)
. Значит \(\triangle AOD\)
– равнобедренный и \(\angle OAD=\angle ODA\)
.
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Поэтому одну из них мы назовем большим , вторую — малым основанием трапеции.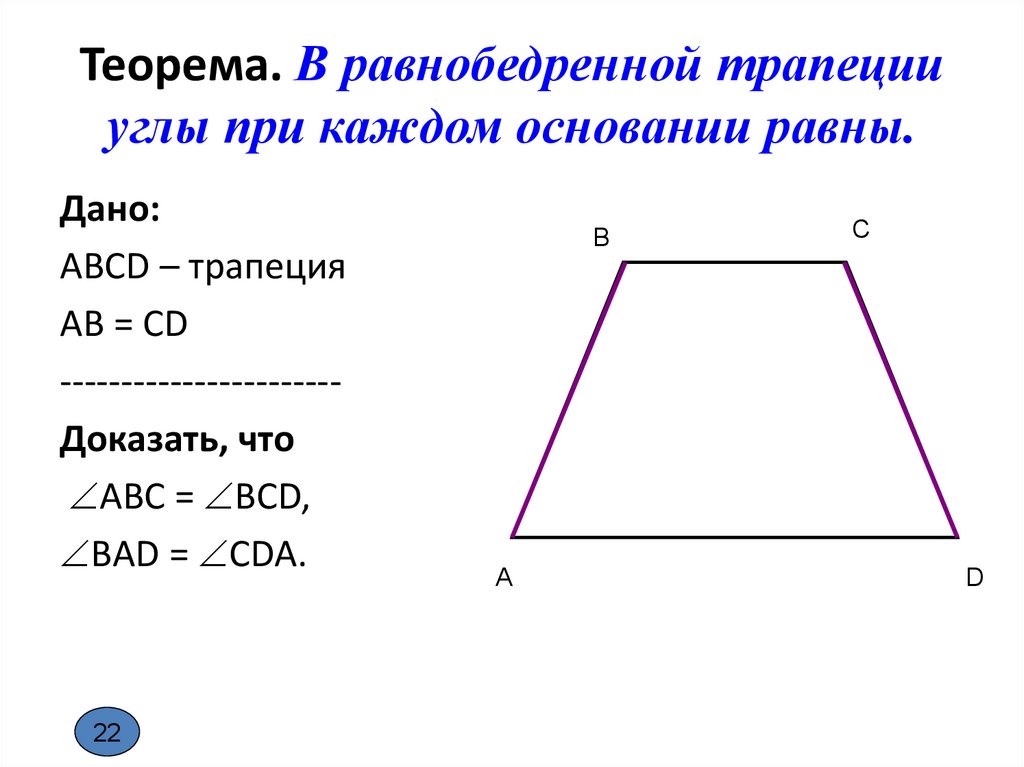 Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8. Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7 . Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8 . Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9. (рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10. (рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11. (рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12. (рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10 . Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11 . Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13 . Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13. Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14 . Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника. Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15 . Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16 . Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17 . Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18 . Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19 . Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.к. односторонние равны. в случае, когда три прямых угла это прямоугольник)
Теорема 20 . Радиус вписанной в трапецию окружности равен половине высоты основания.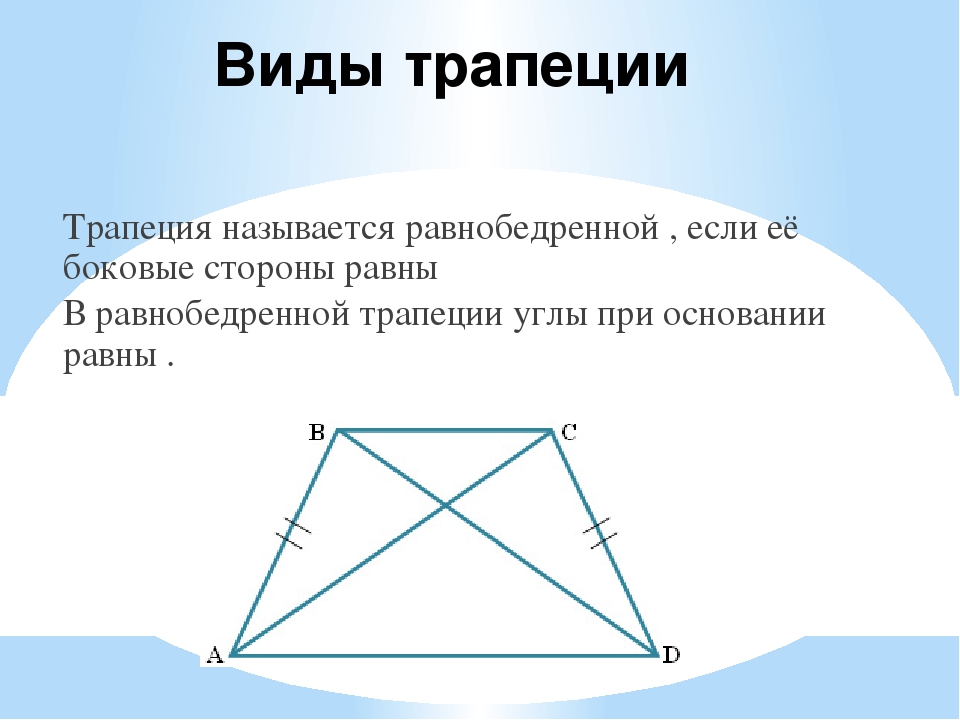 AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21 . Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство: Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.

- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.

- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
В равнобедренной трапеции диагонали перпендикулярны
Если в равнобедренной трапеции диагонали перпендикулярны, при решении задачи будет полезен следующий теоретический материал.
1. Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Если в равнобедренной трапеции диагонали перпендикулярны, высота трапеции равна полусумме оснований.
Проведем через точку C прямую CF, параллельную BD, и продлим прямую AD до пересечения с CF.
Четырехугольник BCFD — параллелограмм ( BC∥DF как основания трапеции, BD∥CF по построению). Значит, CF=BD, DF=BC и AF=AD+BC.
Треугольник ACF прямоугольный (если прямая перпендикулярна одной из двух параллельных прямых, то она перпендикулярна и другой прямой). Поскольку в равнобедренной трапеции диагонали равны, а CF=BD, то CF=AC, то есть треугольник ACF — равнобедренный с основанием AF. Значит, его высота CN является также медианой. А так как медиана прямоугольного треугольника, проведенная к гипотенузе, равна ее половине, то
что в общем виде можно записать как
где h — высота трапеции, a и b — ее основания.
2. Если в равнобедренной трапеции диагонали перпендикулярны, то ее высота равна средней линии.
Так как средняя линия трапеции m равна полусумме оснований, то
3. Если в равнобедренной трапеции диагонали перпендикулярны, то площадь трапеции равна квадрату высоты трапеции (или квадрату полусуммы оснований, или квадрату средней линии).
Так как площадь трапеции находится по формуле
а высота, полусумма оснований и средняя линия равнобокой трапеции с перпендикулярными диагоналями равны между собой:
то
4. Если в равнобедренной трапеции диагонали перпендикулярны, то квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
Так как площадь выпуклого четырехугольника можно найти через его диагонали и угол между ними по формуле
sin 90º =1, и диагонали равнобедренной трапеции равны, то площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна
откуда
Подготовка к ОГЭ и ЕГЭ. «Формулы и свойства трапеции»
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 5
МУНИЦИПАЛЬНОГО ОБРАЗОВАНИЯ город – курорт АНАПА
Рассмотрено и
рекомендовано к использованию
на заседании МО от _______________
Протокол №______
Подготовка к ОГЭ и ЕГЭ.
«Формулы и свойства трапеции»
Методическая разработка
учителя математики
Снегуровой Амины Мугиновны
2018 год.
Оглавление
Введение 3
Определения 4
Частные случаи трапеции 5
Свойства произвольной трапеции 6-7
Свойства равнобедренной трапеции 8-10
Свойства биссектрисы угла трапеции 10-12
Свойства треугольников, образованных диагоналями трапеции 12-13
Формулы нахождения диагоналей трапеции 13-14
Трапеция и окружность 14-17
Дополнительные построения в трапеции 17-23
Для тех, кому интересно. Теоремы. 23-27
Задачи с решениями.27-35
Список используемой литературы.
Введение
Дорогой ученик!
В материалах различных контрольных работ и экзаменов очень часто встречаются задачи на трапецию, решение которых требует от учащихся знаний «непрограммных» свойств трапеции. (Программными считаются свойство средней линии трапеции, свойства диагоналей и углов равнобедренной трапеции.) Свойства, необходимые для решения задач, отсутствуют в учебниках или перенесены в задачи и не воспринимаются как теоретические положения.
Какими же замечательными свойствами обладает трапеция? Как решать геометрические задачи, требующие глубоких знаний? Трапеция обладает рядом интересных и полезных для решения задач свойствами. Если овладеть ими и рассмотреть дополнительные построения в трапеции, то возникает объективная возможность для решения задач повышенной сложности.
В планиметрии существует целый класс таких задач, к которым традиционные методы (метод цепочек равных треугольников, метод геометрических преобразований, векторный метод и др.) либо вовсе не применимы, либо дают сложные и громоздкие решения. Во многих случаях решать такого рода задачи помогает введение в чертеж дополнительных линий – так называемое дополнительное построение. В одних случаях эти построения напрашиваются сами собой, в других они не так очевидны и требуют от решающего достаточно большого опыта, изобретательности, геометрической интуиции.
Так, чертеж данной в задаче фигуры можно достраивать до фигуры другого типа, можно с многоугольной фигурой связывать окружность, а можно целью дополнительного построения ставить выделение на чертеже равных, равновеликих или подобных фигур.
Знание метода дополнительных построений в большинстве случаев позволяет решать, казалось бы, сложные геометрические задачи просто, понятно и красиво.
В этой разработке собраны формулы, свойства и подсказки для решения задач связанных с трапецией. Надеюсь, что ты здесь найдешь для себя много полезной информации.
1.Определения.
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
Параллельные стороны
называются её основаниями, а две другие стороны — боковыми
сторонами.
Высотой трапеции называется расстояние между основаниями.
Kаждый из этих отрезков EF, BM, DK, PQ является высотой трапеции ABCD.
В формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота.
2.Частные случаи трапеции.
Прямоугольной трапецией называется трапециия, в которой одна из боковых сторон перпендикулярна основаниям.
У нее два прямых угла при меньшей боковой стороне.
Эта сторона одновременно является и высотой трапеции.
произвольная
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.
У равнобедренной трапеции так же, как и у равнобедренного треугольника, углы при основании равны.
Трапеция, у которой боковые стороны равны, называется равнобедренной
(равнобокой, равнобочной).
3.Свойства произвольной трапеции.
1. Во всякой трапеции сумма углов , прилежащих к одной ее боковой стороне, равна 1800.
2. Во всякой трапеции средняя линия параллельна ее основаниям, равна полусумме этих оснований и делит диагонали трапеции пополам.
MК =
3.Четыре замечательные точки трапеции:
Во всякой трапеции середины оснований, точка пересечения диагоналей и точка пересечения продолжений боковых сторон лежат на одной прямой.
4. Во всякой трапеции если сумма углов при большем основании равна 900, то боковые стороны лежат на перпендикулярных прямых. Длина отрезка, соединяющего середины оснований, равна полуразности оснований.
5. Свойства отрезка, соединяющего основания трапеции
Отрезок, соединяющий основания всякой трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции.
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношение составляющих его отрезков от стороны основания до точки пересечения диагоналей ( KO/ON ) будет равно соотношению оснований трапеции:
6.Свойства отрезка, параллельного основаниям всякой трапеции.
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
*Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам, то есть КО=ОМ
*Длина отрезка, проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна
KM = .
7.Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему геометрическому оснований, если он делит трапецию на две трапеции, подобные между собой.
8. Во всякой трапеции с основаниями a и b отрезок, параллельный основаниям, концы которого лежат на боковых сторонах, равен среднему квадратичному оснований, если он делит трапецию на две трапеции равной площади (равновеликие).
9.Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований.
d12 + d22 = c2 + d2+ 2ab, d- боковая сторона. d1 и d2 – диагонали.
Свойства равнобедренной трапеции.
Трапеция является равнобедренной тогда и только тогда, когда
*углы, прилежащие к одному основанию, равны
*сумма противолежащих углов 1800;
*диагонали равны;
AC = BD
*отрезки диагоналей, соединяющих точку пересечения с концами одного основания, равны; BO = OC, AO = OD.
*вокруг этой трапеции можно описать окружность.
BC // AD, AB = CD. ABCD – вписанная трапеция.
* высота, проведенная из вершины меньшего основания, разбивает большее основание на отрезки, один из которых равен полуразности оснований, а другой полусумме оснований трапеции, т. е. средней линии трапеции.
*если в равнобедренной трапеции диагонали перпендикулярны, то
1)квадрат ее диагонали равен половине квадрата суммы оснований, а также удвоенному квадрату высоты и удвоенному квадрату средней линии.
2)высота трапеции равна полусумме оснований.
3)ее высота равна средней линии.
4) площадь равнобедренной трапеции, диагонали которой взаимно перпендикулярны, равна квадрату её высоты.
(или квадрату полусуммы оснований, или квадрату средней линии).
*если в равнобокой трапеции высота равна средней линии, то диагонали трапеции взаимно перпендикулярны.
BH = HD = h =.
*высота, проведённая через точку пересечения диагоналей, в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
*в равнобедренной трапеции прямая, проходящая через середины оснований, перпендикулярна им и является осью симметрии трапеции.
*отрезки, последовательно соединяющие середины смежных сторон равнобедренной трапеции, образуют ромб.
MNKE – ромб, то есть
MN=NK=KE= ME.
*в равнобедренной трапеции квадрат диагонали равен квадрату его боковой стороны плюс произведение оснований: d2 = c2 + a b
*площадь равнобедренной трапеции с радиусом вписанной окружности равным r и углом при основании α:
S =
Свойства биссектрисы угла трапеции.
*биссектриса угла отсекает от трапеции равнобедренный треугольник.
*точка пересечения биссектрис тупых углов при основании трапеции принадлежит другому основанию.
*если диагональ трапеции является биссектрисой ее острого угла, то меньшее основание равно боковой стороне трапеции, прилежащей к этому углу.
*биссектриса угла трапеции, пересекающая основание, отсекает от трапеции равнобедренный треугольник.
*биссектрисы углов при боковой стороне трапеции пересекаются под прямым углом.
* точка пересечения биссектрис трапеции, прилежащих к боковой стороне, лежит на средней линии трапеции.
*если биссектриса тупого угла трапеции является диагональю, то боковая сторона равна большему основанию трапеции.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
Если в условии задачи сказано, что основание трапеции равно ее боковой стороне, то отсюда следует, что диагональ трапеции является биссектрисой ее угла.
*если меньшее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне острого угла.
*если большее основание трапеции равно ее боковой стороне, то диагональ трапеции является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если большее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к меньшему основанию.
* если меньшее основание прямоугольной трапеции равно ее меньшей боковой стороне, диагональ является биссектрисой прямого угла, прилежащего к большему основанию.
* если меньшее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне острого угла.
* если большее основание прямоугольной трапеции равно ее большей боковой стороне, диагональ является биссектрисой прилежащего к этой боковой стороне тупого угла.
*если меньшее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой острого угла трапеции.
* если большее основание равнобедренной трапеции равно ее боковой стороне, то диагональ является биссектрисой тупого угла трапеции.
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными.
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом.
*Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
*В подобных треугольниках длины всех линейных элементов пропорциональны, а именно:
отношения периметров, радиусы вписанных окружностей, радиусы описанных окружностей, соответствующих высот, биссектрис, медиан (проведенных из равных углов) подобных треугольников равны отношению соответствующих сторон (лежащих против равных углов) или равны коэффициенту подобия.
*Площади подобных треугольников относятся как квадраты соответствующих сторон или равно квадрату коэффициента подобия.
*Площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
S12= S2 S3
S3: S2 = 2
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны, то есть треугольники являются равновеликими.
Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
Формулы для нахождения диагоналей трапеции
Далее приведены формулы, отображающие зависимость между сторонами, углами трапеции и величиной ее диагоналей. Эти формулы пригодятся для решения задач по геометрии на тему «диагонали трапеции»
Далее, в формулах используются следующие обозначения:
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
h— высота
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Эта группа формул отражает одно из основных свойств диагоналей трапеции:
*Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований. Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
Используем теорему косинусов.
*Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
*Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
4.В прямоугольной трапеции разность квадратов диагоналей равна разности квадратов оснований
d12 — d22 = a2 – b2
*Если диагонали трапеции взаимно перпендикулярны, то длина отрезка, соединяющего середины оснований трапеции равна полусумме оснований.
MH =
BDCE и FAOD прямоугольники, а диагонали прямоугольника равны.
Трапеция и окружность.
1) Если в равнобокую трапецию можно вписать окружность, то средняя линия трапеции равна боковой стороне.
Высота равнобедренной трапеции, в которую можно вписать окружность, является средним геометрическим её оснований
h2 = a ∙ b
2) Если в равнобедренную трапецию вписана окружность, то её боковая сторона равна средней линии. Площадь трапеции определяется произведением средней линии на высоту трапеции.
3. Высота трапеции равна длине диаметра вписанной окружности или двум ее радиусам.
MK — высота трапеции, MK=2r, где r — радиус вписанной в трапецию окружности.
4. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции.
. CF =m, FD =n, OF = r.
∠COD=90º, т.к. ∠ADC+∠BCD=180º — так
как сумма внутренних односторонних углов при параллельных прямых AD и BC и секущей CD равна 1800.
Отсюда радиус вписанной в трапецию окружности выражается через длины отрезков, как которые боковая сторона делится точкой касания, как r = .
А так как высота трапеции равна ее диаметру, то и высоту трапеции можно выразить через длины этих отрезков: h = 2 .
5.Если в трапецию можно вписать окружность и около трапеции можно описать окружность, то проекция диагонали на большее основание, равна боковой стороне и равна средней линии трапеции.
Если в трапецию вписана окружность, в задаче появляется несколько путей, по которым можно повести рассуждение.
1.В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противолежащих сторон равны. Отсюда следует, что если в трапецию вписана окружность, то сумма ее оснований равна сумме боковых сторон.
AB+CD=AD+BC
2. Отрезки касательных, проведенных из одной точки, равны. Отсюда следует, что
AL=AK BL=BM
CM=CF DF=DK
Описанная окружность.
Когда трапецию можно вписать в окружность? Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма его противолежащих углов равна 180º. Отсюда следует, что вписать в окружность можно только равнобокую трапецию.
Радиус окружности, описанной около трапеции, можно найти как радиус окружности, описанной около из одного из двух треугольников, на которые трапецию делит ее диагональ.
Где находится центр окружности, описанной около трапеции? Это зависит от угла между диагональю трапеции и ее боковой стороной.
1)Если диагональ трапеции перпендикулярна ее боковой стороне, то центр окружности, описанной около трапеции, лежит на середине ее большего основания. Радиус описанной около трапеции окружности в этом случае равен половине ее большего основания:
2) Если диагональ трапеции образует с боковой стороной острый угол, центр окружности, описанной около трапеции, лежит внутри трапеции.
3) Если диагональ трапеции образует с боковой стороной тупой угол, центр описанной около трапеции окружности лежит вне трапеции, за большим основанием.
4)Радиус описанной около трапеции окружности можно найти по следствию из теоремы синусов. Из треугольника ACD
Из треугольника ABC
Другой вариант найти радиус описанной окружности —
Синусы угла D и угла CAD можно найти, например, из прямоугольных треугольников CFD и ACF:
При решении задач на трапецию, вписанную в окружность, можно также использовать то, что вписанный угол равен половине соответствующего ему центрального угла. Например,
Использовать углы COD и CAD можно и для нахождения площади трапеции. По формуле нахождения площади четырехугольника через его диагонали
5)Если диагонали вписанной в окружность трапеции (четырехугольника) взаимно перпендикулярны, то сумма квадратов его противоположных сторон равна квадрату диаметра описанной окружности или удвоенному квадрату боковой стороны:
a2 + b2 = 4R2 = 2c2.
6) Если в трапецию вписана окружность, то вершина трапеции, центр вписанной в нее окружности и основание перпендикуляра, опущенного из другой вершины на основание, лежат на одной прямой.
Дополнительные построения как прием при решении задач
Дополнительные построения являются эффективным методом решения геометрических задач. Наиболее часто используются при решении задач:
1. Опускание высот из концов одного основания на другое основание
2. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину
3. Проведение через середину меньшего основания прямых, параллельных боковым сторонам
4. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину .
5. Продолжение боковых сторон до пересечения.
Рассмотрим каждое их них.
При решении задач на отыскание площади дополнительным построением считается построение ее высоты или высот. Если построение высоты не помогает решить задачу, то нужно построить прямую, параллельную одной из ее диагоналей. Потом найти площадь полученного треугольника, который будет равновеликим исходной трапеции.
1. Проведение через вершину трапеции прямой, параллельной диагонали, не содержащей эту вершину.
При дополнительном построении, когда переносится диагональ, образуется треугольник, площадь которого равна площади трапеции.
S1 = S2
Задача.
Найдите площадь трапеции, дмагонали которой равны 8 и 15, а средняя линия равна 8,5.
Решение.
Построим CF // BD и получим SACF = SABCD. Почему?
ABC = CDF, так как DF = BC и эти треугольники имеют одинаковую высоту.
Значит, для того, чтобы найти площадь трапеции нам достаточно найти площадь ACF.
АF = АD + ВС — сумма оснований трапеции. По условию задачи средняя линия трапеции 8,5. Значит сумма оснований АF = 8,52=17.
Рассмотрим ACF. Проверим, является ли он прямоугольным? В этом нам поможет теорема Пифагора:
172 = 82 + 152
289 = 64 + 225.
289 = 289.
ACF – прямоугольный. SACF = AC*CF = 8*15 = 60. SABCD= 60.
Если ACF разносторонний, то его площадь вычислим по формуле Герона.
Ответ:60.
2. Продолжение боковых сторон до пересечения.
Свойства трапеции, достроенной до треугольника
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований.
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
*Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
*Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника.
*Если ABCD равнобедренная трапеция, то KL является биссектрисой, медианой и высотой одновременно.
Это дополнительное построение позволяет перейти от трапеции к треугольнику. Если сумма углов при большем основании равна 900, топродолжив боковые стороны мы получим прямоугольный треугольник.
Задача.
В трапеции ABCD основания АD и ВС равны соответственно 72 и 18, а сумма углов при основании АD равна 900. Найдите радиус окружности, проходящей через точки А и В и касающейся прямой CD, если АВ = 18.
Решение.
Центром О данной окружности будет точка пересечения серединного перпендикуляра к АВ и перпендикуляра, возведенного к стороне CD из точки касания окружности. АВО равнобедренный: АО = ВО. Продлим боковые стороны трапеции и получим прямоугольный треугольник АМD. KMNO – прямоугольник, где KM = MN = NO =КО = R.
BMC AMD.
= , то есть и x = 6. Тогда R = КВ + 6 = 9 + 6 = 15.
Ответ:15.
3. Опускание высот из концов одного основания на другое основание.
Дополнительное построение 1,2 позволяет разбить трапецию на прямоугольник (стороны которого — одно из оснований и высота трапеции) и два прямоугольных треугольника (в которых один из катетов – высота трапеции, а гипотенузы – боковые стороны трапеции)
Построение 1 Построение 2
Задача. Найдите площадь трапеции с основаниями 8 и 13 и боковыми сторонами 3 и 4.
Решение.
Проведем ВН и СM — высоты и получим ABD (египетский треугольник) со сторонами 3,4,5, так как АD – ВС=13 – 8=5.
S= АВ* BD= 6.
Найдем высоту трапеции: h= 2S:5 = 2*6:5= 2,4.
SABCD= 6+2,4*8=25,2. Ответ:25,2.
4. Проведение через середину меньшего основания прямых, параллельных боковым сторонам.
Дополнительное построение 4 делит трапецию на параллелограммы и треугольник. Боковые стороны соединяются в треугольник.
5. Проведение через вершины трапеции прямой, параллельной боковой стороне, не содержащей эту вершину.
Задача. Основания трапеции равны 30см и 15см, а боковые стороны равны 9 см и 12 см. Найдите высоту трапеции.
Решение. Пусть АВСД трапеция, заданная в условии.
Проведем через вершину С прямую, которая параллельна АВ. Пусть эта прямая пересекает АД в точке М.
Тогда АВСМ – параллелограмм и СМ=9, АМ=ДМ=15.
Так как 92+122=152, то, применив обратную теорему Пифагора, приходим к выводу, что СМ перпендикулярна СД.
Заметим, что высота трапеции и треугольника МСД, проведенная из вершины С, совпадают. Для определения искомой высоты применим метод площадей. Пусть искомая высота равна х. Тогда для определения х составим уравнение, дважды вычислив площадь треугольника МСД:
.
Решив это уравнение находим: х=7,2. Ответ: 7,2.
Задача. Боковые стороны AB и CD трапеции ABCD равны 15 и 12 соответственно. Найдите градусную величину угла D, если одно из оснований трапеции на 9 больше другого.
Решение.
Из вершины угла проведем прямую линию, параллельную стороне. Трапеция разделена данной прямой линией на параллелограмм и треугольник. Противоположные стороны параллелограмма равны, значит, длина стороны треугольника равна разности длин оснований трапеции. Данный треугольник определен по трем сторонам. По теореме косинусов определим искомый угол. Вычисления показывают, что боковая сторона перпендикулярна к основанию, искомый угол прямой.
Ответ:
Для тех, кому интересно.
Теорема.
Задачи с решениями.
Пример 1.Найдите площадь равнобедренной трапеции, описанной около окружности с радиусом 4, если известно, что боковая сторона трапеции равна 10.
Решение.
Дано: ABCD — равнобедренная трапеция, r = 4, AB = 10
Найти: SABCD
AB = CD = 10 по условию.
AB + CD = AD + BC по свойству вписанной окружности.
AD + BC = 10 + 10 = 20.
FE = 2r = 2 · 4 = 8.
SABCD=1/2(BC + AD)·FE, SABCD = 1/2 · 20 · 8 = 20/2 · 8 = 10 · 8 = 80.
Пример 2.Основания трапеции равны 10 м и 31 м, а боковые стороны — 20 м и 13 м. Найдите высоту трапеции.
Решение.
Пусть HK = BC = 10 м, BH = CK = x, AH = y, тогда KD = 21 – y
По теореме Пифагора:x2 + y2 = 132x2 + (21 – y)2 = 202x2 + y2 = 169 (1)
x2 + 441 – 42y + y2 = 400 (2)
Вычтем из (2) уравнения (1):441 – 42y = 23142y = 210y = 5AH = 5 м
По теореме Пифагора:BH2 = AB2 – AH2BH2 = 132 – 52BH2 = 169 – 25BH2 = 144
BH = 12
Пример 3.Большее основание трапеции равно 24. Найдите длину меньшего основания, если расстояние между серединами диагоналей равно 4.
Решение.
Пример 4.Диагонали AC и BD трапеции ABCD пересекаются в точке O.
Найдите площадь трапеции, если BC < AD и площади треугольников BOC и ABO равны соответственно равны 2 и 8.
Анализ.
Рассмотреть подобие треугольников.
Квадраты соответствующих сторон относятся как площади треугольников.
Введем параметры треугольников: стороны оснований и высоты треугольников.
Площади трапеции и треугольников определим по известным формулам.
Решение.
Ответ:
Пример 5.В трапеции большее основание равно 10. Диагонали трапеции, равные 8, перпендикулярны боковым сторонам. Найдите площадь трапеции.
Анализ.
Длины диагоналей равны и перпендикулярны боковым сторонам. Имеем равенство прямоугольных треугольников по катету и гипотенузе: ABD = ACD, поэтому трапеция равнобедренная, т.е. АВ = СD.
Применим теорему Пифагора для определения боковой стороны трапеции.
Высоту трапеции определим из равенства площадей.
Проекцию боковой стороны на большее основание легче определить из подобия треугольников, чем по теореме Пифагора.
Длину средней линии в равнобокой трапеции можно определять как разность большего основания и проекции боковой стороны на основание.
Площадь трапеции находим как площадь прямоугольника АМСК, который получим, если достроим трапецию.
Пример 6.Диагонали трапеции взаимно перпендикулярны, а длина ее средней линии равна 9. Найдите длину отрезка, соединяющего середины оснований трапеции.
Анализ.
Задача решается построением.
Достроим прямоугольники и используем свойство прямоугольника: диагонали прямоугольника равны и в точке пересечения делятся пополам.
Длина средней линии равна полусумме длин оснований.
Длина отрезка, соединяющая середины оснований, равна полусумме длин диагоналей двух построенных треугольников.
Пример 7.Длины оснований трапеции равны 1 и 7. Найдите длину отрезка, параллельного основаниям и заключенного между боковыми сторонами, который делит трапецию на две равновеликие части.
Анализ.
Провести из вершины тупого угла трапеции прямую линию, параллельную боковой стороне.
Рассмотреть отношение площадей трапеций.
Определить отношение при подобии треугольников.
Рациональные алгебраические преобразования приведут к результату.
Решение.Ответ:
Пример 11.Равнобедренная трапеция ABCD описана около окружности. Боковая сторона трапеции равна 10, а основания относятся как 1: 4. Найдите площадь трапеции.
Анализ.
Сумма противоположных сторон трапеции равна между собой — свойство описанного четырехугольника.
Трапеция равнобедренная.
Боковая сторона равна длине средней линии.
Применяем теорему Пифагора для нахождения высоты трапеции.
Площадь трапеции определяем по доступной формуле.
Пример 8.Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно вписать окружность, а средняя линия делит ее на части, площади которых относятся как 5: 11. Найдите длину большего основания трапеции.
Анализ.
Трапеция является описанной.
Сумма длин оснований равна сумме боковых сторон.
Средняя линия делит трапецию на две трапеции, высоты которых равны.
Задача сводится к системе уравнений.
Длина средней линии равна половине суммы длин боковых сторон.
Пример 9.Площадь равнобедренной трапеции, описанной около окружности равна 15. Найдите среднюю линию трапеции, если косинус острого угла при ее основании равен 4/5.
Анализ.
Трапеция равнобедренная.
Длина средней линии равна боковой стороне.
Площадь трапеции определяется произведением средней линии на высоту трапеции.
Опустим высоту трапеции из тупого угла. Через заданный косинус угла определим синус угла.
По синусу угла выразим высоту трапеции через боковую сторону.
Пример 10.В прямоугольной трапеции, описанной около окружности, большая боковая сторона равна 13, а средняя линия равна 12,5. Найдите меньшее основание трапеции.
Анализ.
Необходимо использовать свойство сторон четырехугольника, описанной около окружности: сумма длин противоположных сторон равна между собой.
Кроме того, длина средней линии равна полусумме длин сторон оснований.
Проведем из вершины тупого угла высоту трапеции.
Воспользуемся теоремой Пифагора и определим проекцию наклонной боковой стороны на основание.
Пример 11.В равнобедренную трапецию, один из углов которой равен 60°, а площадь равна , вписана окружность. Найдите радиус этой окружности.
Анализ.
Важное положение, что трапеция является равнобедренной и имеет ось симметрии. Тогда длина боковой стороны равна длине средней линии.
Введем параметр боковой стороны, из прямоугольного треугольника по заданному углу определим высоту трапеции, которая является диаметром вписанной окружности. Площадь трапеции определяется как произведение средней линии на высоту трапеции.
.
Пример 12.Найдите площадь равнобедренной трапеции, у которой большее основание равно 13, средняя линия равна 8, а биссектриса тупого угла является диагональю трапеции.
Анализ.
При проведении биссектрисы тупого угла боковая сторона равна большему основанию трапеции. Проекция боковой стороны равнобедренной трапеции равна полуразности длин оснований.
По теореме Пифагора найдем высоту трапеции.
Площадь трапеции находим по формул.
Список используемой литературы
4.
5.
6.
7.
8.
Средняя линяя трапеции. Трапеция. Свойства, признаки, площадь. Средняя линия трапеции
Четырёхугольник, у которого только две стороны параллельны называются трапецией .
Параллельные стороны трапеции называются её основаниями , а те стороны, которые не параллельны, называются боковыми сторонами . Если боковые стороны равны, то такая трапеция является равнобедренной. Расстояние между основаниями называется высотой трапеции.
Средняя Линия Трапеции
Средняя линия — это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям.
Теорема:
Если прямая, пересекающая середину одной боковой стороны, параллельна основаниям трапеции, то она делит пополам вторую боковую сторону трапеции.
Теорема:
Длина средней линии равна среднему арифметическому длин её оснований
MN || AB || DCAM = MD; BN = NC
MN средняя линия, AB и CD — основания, AD и BC — боковые стороны
MN = (AB + DC)/2
Теорема:
Длина средней линии трапеции равна среднему арифметическому длин её оснований.
Основная задача : Доказать, что средняя линия трапеции делит пополам отрезок, концы которого лежат в середине оснований трапеции.
Средняя Линия Треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника. Она параллельна третьей стороне и её длина равна половине длины третьей стороны.
Теорема : Если прямая, пересекающая середину одной стороны треугольника, параллельна другой стороне данного треугольника, то она делит третью сторону пополам.
AM = MC and BN = NC
=>
Применение свойств средней линии треугольника и трапеции
Деление отрезка на определённое количество равных частей.
Задача: Разделить отрезок AB на 5 равных частей.
Решение:
Пусть p это случайный луч, у которого начало это точка А, и который не лежит на прямой AB. Мы последовательно откладываем 5 равных сегментов на p AA 1 = A 1 A 2 = A 2 A 3 = A 3 A 4 = A 4 A 5
Мы соединяем A 5 с B и проводим такие прямые через A 4 , A 3 , A 2 и A 1 , которые параллельны A 5 B. Они пересекают AB соответственно в точках B 4 , B 3 , B 2 и B 1 . Эти точки делят отрезок AB на 5 равных частей. Действительно, из трапеции BB 3 A 3 A 5 мы видим, что BB 4 = B 4 B 3 . Таким же образом, из трапеции B 4 B 2 A 2 A 4 получаем B 4 B 3 = B 3 B 2
В то время как из трапеции B 3 B 1 A 1 A 3 , B 3 B 2 = B 2 B 1 .
Тогда из B 2 AA 2 следует, что B 2 B 1 = B 1 A. В заключении получаем:
AB 1 = B 1 B 2 = B 2 B 3 = B 3 B 4 = B 4 B
Ясно, что для разделения отрезка AB на другое количество равных частей, нам нужно проецировать то же самое количество равных сегментов на луч p. И далее продолжать вышеописанным способом.
В этой статье мы постараемся насколько возможно полно отразить свойства трапеции. В частности, речь пойдет про общие признаки и свойства трапеции, а также про свойства вписанной трапеции и про окружность, вписанную в трапецию. Затронем мы и свойства равнобедренной и прямоугольной трапеции.
Пример решения задачи с использованием рассмотренных свойств поможет вам разложить по местам в голове и лучше запомнить материал.
Трапеция и все-все-все
Для начала коротко вспомним, что такое трапеция и какие еще понятия с ней связаны.
Итак, трапеция – фигура-четырехугольник, две из сторон которой параллельны друг другу (это основания). И две не параллельны – это боковые стороны.
В трапеции может быть опущена высота – перпендикуляр к основаниям. Проведены средняя линия и диагонали. А также из любого угла трапеции возможно провести биссектрису.
Про различные свойства, связанные со всеми эти элементами и их комбинациями, мы сейчас и поговорим.
Свойства диагоналей трапеции
Чтобы было понятнее, пока читаете, набросайте себе на листке трапецию АКМЕ и проведите в ней диагонали.
- Если вы найдете середины каждой из диагоналей (обозначим эти точки Х и Т) и соедините их, получится отрезок. Одно из свойств диагоналей трапеции заключается в том, что отрезок ХТ лежит на средней линии. А его длину можно получив, разделив разность оснований на два: ХТ = (a – b)/2 .
- Перед нами все та же трапеция АКМЕ. Диагонали пересекаются в точке О. Давайте рассмотрим треугольники АОЕ и МОК, образованные отрезками диагоналей вместе с основаниями трапеции. Эти треугольники – подобные. Коэффициент подобия k треугольников выражается через отношение оснований трапеции: k = АЕ/КМ.
Отношение площадей треугольников АОЕ и МОК описывается коэффициентом k 2 . - Все та же трапеция, те же диагонали, пересекающиеся в точке О. Только в этот раз мы будем рассматривать треугольники, которые отрезки диагоналей образовали совместно с боковыми сторонами трапеции. Площади треугольников АКО и ЕМО являются равновеликими – их площади одинаковые.
- Еще одно свойство трапеции включает в себя построение диагоналей. Так, если продолжить боковые стороны АК и МЕ в направлении меньшего основания, то рано или поздно они пересекутся к некоторой точке. Дальше, через середины оснований трапеции проведем прямую. Она пересекает основания в точках Х и Т.
Если мы теперь продлим прямую ХТ, то она соединит вместе точку пересечения диагоналей трапеции О, точку, в которой пересекаются продолжения боковых сторон и середины оснований Х и Т. - Через точку пересечения диагоналей проведем отрезок, который соединит основания трапеции (Т лежит на меньшем основании КМ, Х – на большем АЕ). Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
- А теперь через точку пересечения диагоналей проведем параллельный основаниям трапеции (a и b) отрезок. Точка пересечения разделит его на две равных части. Найти длину отрезка можно по формуле 2ab/(a + b) .
Свойства средней линии трапеции
Среднюю линию проведите в трапеции параллельно ее основаниям.
- Длину средней линии трапеции можно вычислить, если сложить длины оснований и разделить их пополам: m = (a + b)/2 .
- Если провести через оба основания трапецию любой отрезок (высоту, к примеру), средняя линия разделит его на две равных части.
Свойство биссектрисы трапеции
Выберите любой угол трапеции и проведите биссектрису. Возьмем, например, угол КАЕ нашей трапеции АКМЕ. Выполнив построение самостоятельно, вы легко убедитесь – биссектрисой отсекается от основания (или его продолжения на прямой за пределами самой фигуры) отрезок такой же длины, что и боковая сторона.
Свойства углов трапеции
- Какую бы из двух пар прилежащих к боковой стороне углов вы не выбрали, сумма углов в паре всегда составляет 180 0: α + β = 180 0 и γ + δ = 180 0 .
- Соединим середины оснований трапеции отрезком ТХ. Теперь посмотрим на углы при основаниях трапеции. Если сумма углов при любом из них составляет 90 0 , длину отрезка ТХ легко вычислить исходя из разности длин оснований, разделенной пополам: ТХ = (АЕ – КМ)/2 .
- Если через стороны угла трапеции провести параллельные прямые, те разделят стороны угла на пропорциональные отрезки.
Свойства равнобедренной (равнобокой) трапеции
- В равнобедренной трапеции равны углы при любом из оснований.
- Теперь снова постройте трапецию, чтобы проще было представить, о чем речь. Посмотрите внимательно на основание АЕ – вершина противоположного основания М проецируется в некую точку на прямой, которая содержит АЕ. Расстояние от вершины А до точки проекции вершины М и средняя линия равнобедренной трапеции – равны.
- Пару слов о свойстве диагоналей равнобедренной трапеции – их длины равны. А также одинаковы углы наклона этих диагоналей к основанию трапеции.
- Только около равнобедренной трапеции можно описать окружность, поскольку сумма противолежащих углов четырехугольника 180 0 – обязательное условие для этого.
- Из предыдущего пункта следует свойство равнобедренной трапеции – если возле трапеции можно описать окружность, она является равнобедренной.
- Из особенностей равнобедренной трапеции вытекает свойство высоты трапеции: если ее диагонали пересекаются под прямым углом, то длина высоты равна половине суммы оснований: h = (a + b)/2 .
- Снова проведите отрезок ТХ через середины оснований трапеции – в равнобедренной трапеции он является перпендикуляром к основаниям. И одновременно ТХ – ось симметрии равнобедренной трапеции.
- На этот раз опустите на большее основание (обозначим его a) высоту из противолежащей вершины трапеции. Получится два отрезка. Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Свойства трапеции, вписанной в окружность
Раз уже речь зашла о вписанной в окружность трапеции, остановимся на этом вопросе подробней. В частности на том, где находится центр окружности по отношению к трапеции. Тут тоже рекомендуется не полениться взять карандаш в руки и начертить то, о чем пойдет речь ниже. Так и поймете быстрее, и запомните лучше.
- Расположение центра окружности определяется углом наклона диагонали трапеции к ее боковой стороне. Например, диагональ может выходить из вершины трапеции под прямым углом к боковой стороне. В таком случае большее основание пересекает центр описанной окружности точно посередине (R = ½АЕ).
- Диагональ и боковая сторона могут встречаться и под острым углом – тогда центр окружности оказывается внутри трапеции.
- Центр описанной окружности может оказаться вне пределов трапеции, за большим ее основанием, если между диагональю трапеции и боковой стороной – тупой угол.
- Угол, образованный диагональю и большим основанием трапеции АКМЕ (вписанный угол) составляет половину того центрального угла, который ему соответствует:МАЕ = ½МОЕ .
- Коротко про два способа найти радиус описанной окружности. Способ первый: посмотрите внимательно на свой чертеж – что вы видите? Вы без труда заметите, что диагональ разбивает трапецию на два треугольника. Радиус можно найти через отношение стороны треугольника к синусу противолежащего угла, умноженному на два. Например, R = АЕ/2*sinАМЕ . Аналогичным образом формулу можно расписать для любой из сторон обоих треугольников.
- Способ второй: находим радиус описанной окружности через площадь треугольника, образованного диагональю, боковой стороной и основанием трапеции: R = АМ*МЕ*АЕ/4*S АМЕ .
Свойства трапеции, описанной около окружности
Вписать окружность в трапецию можно, если соблюдается одно условие. Подробней о нем ниже. И вместе эта комбинация фигур имеет ряд интересных свойств.
- Если в трапецию вписана окружность, длину ее средней линии можно без труда найти, сложив длины боковых сторон и разделив полученную сумму пополам: m = (c + d)/2 .
- У трапеции АКМЕ, описанной около окружности, сумма длин оснований равна сумме длин боковых сторон: АК + МЕ = КМ + АЕ .
- Из этого свойства оснований трапеции вытекает обратное утверждение: окружность можно вписать в ту трапецию, сумма оснований которой равна сумме боковых сторон.
- Точка касания окружности с радиусом r, вписанной в трапецию, разбивает боковую сторону на два отрезка, назовем их a и b. Радиус окружности можно вычислить по формуле: r = √ab .
- И еще одно свойство. Чтобы не запутаться, этот пример тоже начертите сами. У нас есть старая-добрая трапеция АКМЕ, описанная около окружности. В ней проведены диагонали, пересекающиеся в точке О. Образованные отрезками диагоналей и боковыми сторонами треугольники АОК и ЕОМ – прямоугольные.
Высоты этих треугольников, опущенные на гипотенузы (т.е. боковые стороны трапеции), совпадают с радиусами вписанной окружности. А высота трапеции – совпадает с диаметром вписанной окружности.
Свойства прямоугольной трапеции
Прямоугольной называют трапецию, один из углов которой является прямым. И ее свойства проистекают из этого обстоятельства.
- У прямоугольной трапеции одна из боковых сторон перпендикулярна основаниям.
- Высота и боковая сторона трапеции, прилежащая к прямому углу, равны. Это позволяет вычислять площадь прямоугольной трапеции (общая формула S = (a + b) * h/2 ) не только через высоту, но и через боковую сторону, прилежащую к прямому углу.
- Для прямоугольной трапеции актуальны уже описанные выше общие свойства диагоналей трапеции.
Доказательства некоторых свойств трапеции
Равенство углов при основании равнобедренной трапеции:
- Вы уже наверное и сами догадались, что тут нам снова потребуется трапеция АКМЕ – начертите равнобедренную трапецию. Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Полученный четырехугольник АКМТ – параллелограмм (АК || МТ, КМ || АТ). Поскольку МЕ = КА = МТ, ∆ МТЕ – равнобедренный и МЕТ = МТЕ.
АК || МТ, следовательно МТЕ = КАЕ, МЕТ = МТЕ = КАЕ.
Откуда АКМ = 180 0 — МЕТ = 180 0 — КАЕ = КМЕ.
Что и требовалось доказать.
Теперь на основании свойства равнобедренной трапеции (равенства диагоналей) докажем, что трапеция АКМЕ является равнобедренной :
- Для начала проведем прямую МХ – МХ || КЕ. Получим параллелограмм КМХЕ (основание – МХ || КЕ и КМ || ЕХ).
∆АМХ – равнобедренный, поскольку АМ = КЕ = МХ, а МАХ = МЕА.
МХ || КЕ, КЕА = МХЕ, поэтому МАЕ = МХЕ.
У нас получилось, что треугольники АКЕ и ЕМА равны между собой, т.к АМ = КЕ и АЕ – общая сторона двух треугольников. А также МАЕ = МХЕ. Можем сделать вывод, что АК = МЕ, а отсюда следует и что трапеция АКМЕ – равнобедренная.
Задача для повторения
Основания трапеции АКМЕ равны 9 см и 21 см, боковая сторона КА, равная 8 см, образует угол 150 0 с меньшим основанием. Требуется найти площадь трапеции.
Решение: Из вершины К опустим высоту к большему основанию трапеции. И начнем рассматривать углы трапеции.
Углы АЕМ и КАН являются односторонними. А это значит, в сумме они дают 180 0 . Поэтому КАН = 30 0 (на основании свойства углов трапеции).
Рассмотрим теперь прямоугольный ∆АНК (полагаю, этот момент очевиден читателям без дополнительных доказательств). Из него найдем высоту трапеции КН – в треугольнике она является катетом, который лежит напротив угла в 30 0 . Поэтому КН = ½АВ = 4 см.
Площадь трапеции находим по формуле: S АКМЕ = (КМ + АЕ) * КН/2 = (9 + 21) * 4/2 = 60 см 2 .
Послесловие
Если вы внимательно и вдумчиво изучили эту статью, не поленились с карандашом в руках начертить трапеции для всех приведенных свойств и разобрать их на практике, материал должен был неплохо вами усвоиться.
Конечно, информации тут много, разнообразной и местами даже запутанной: не так уж сложно перепутать свойства описанной трапеции со свойствами вписанной. Но вы сами убедились, что разница огромна.
Теперь у вас есть подробный конспект всех общих свойств трапеции. А также специфических свойств и признаков трапеций равнобедренной и прямоугольной. Им очень удобно пользоваться, чтобы готовиться к контрольным и экзаменам. Попробуйте сами и поделитесь ссылкой с друзьями!
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Средняя линия трапеции, а особенно ее свойства, очень часто используются в геометрии для решения задач и доказательства тех или иных теорем.
– это четырехугольник, у которого только 2 стороны параллельны друг другу. Параллельные стороны называют основаниями (на рисунке 1 — AD и BC ), две другие – боковыми (на рисунке AB и CD ).
Средняя линия трапеции – это отрезок, соединяющий середины ее боковых сторон (на рисунке 1 — KL ).
Свойства средней линии трапеции
Доказательство теоремы о средней линии трапеции
Доказать , что средняя линия трапеции равна полусумме ее оснований и параллельна этим основаниям.
Дана трапеция ABCD со средней линией KL . Для доказательства рассматриваемых свойств требуется провести прямую через точки B и L . На рисунке 2 это прямая BQ . А также продолжить основание AD до пересечения с прямой BQ .
Рассмотрим полученные треугольники LBC и LQD :
- По определению средней линии KL точка L является серединой отрезка CD . Отсюда следует, что отрезки CL и LD равны.
- ∠ BLC = ∠ QLD , так как эти углы вертикальные.
- ∠ BCL = ∠ LDQ , так как эти углы накрест лежащие при параллельных прямых AD и BC и секущей CD .
Из этих 3 равенств следует, что рассмотренные ранее треугольники LBC и LQD равны по 1 стороне и двум прилежащим к ней углам (см. рис. 3). Следовательно, ∠ LBC = ∠ LQD , BC=DQ и самое главное — BL=LQ => KL , являющаяся средней линией трапеции ABCD , также является и средней линией треугольника ABQ . Согласно свойству средней линией треугольника ABQ получаем.
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника
Свойства
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
- Площадь и, соответственно, и объём отсекаемого средней линией треугольника равна 1/4 от площади и, соотвественно, объёму от всего данного треугольника.
Средняя линия четырёхугольника
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма . Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона ;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода . Средние линии второго рода — четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона .
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции
Средняя линия трапеции
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: E F = A D + B C 2 {\displaystyle EF={\frac {AD+BC}{2}}} , где AD и BC — основания трапеции.
В этой статье для вас сделана очередная подборка задач с трапецией. Условия так или иначе связаны с её средней линией. Типы заданий взяты из открытого банка типовых задач. Если есть желание, то можете освежить свои теоретические знания . На блоге уже рассмотрены задачи условия которых связаны с , а также . Кратко о средней линии:
Средняя линия трапеции соединяет середины боковых сторон. Она параллельна основаниям и равна их полусумме.
Перед решением задач давайте рассмотрим теоретический пример.
Дана трапеция ABCD. Диагональ АС пересекаясь со средней линией образует точку К, диагональ BD точку L. Доказать, что отрезок KL равен половине разности оснований.
Давайте сначала отметим тот факт, что средняя линия трапеции делит пополам любой отрезок концы которого лежат на её основаниях. Этот вывод напрашивается сам собой. Представьте отрезок соединяющий две точки оснований, он разобьёт данную трапецию на две других. Получится, что отрезок параллельный основаниям трапеции и проходящий через середину боковой стороны на другой боковой стороне пройдёт через её середину.
Так же это основывается на теореме Фалеса:
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающие вторую прямую, то они отсекут на второй прямой равные отрезки.
То есть в данном случае К середина АС и L середина BD. Следовательно EK есть средняя линия треугольника АВС, LF есть средняя линия треугольника DCB. По свойству средней линии треугольника:
Можем теперь выразить отрезок KL через основания:
Доказано!
Данный пример приведён не просто так. В задачах для самостоятельного решения имеется именно такая задача. Только в ней не сказано, что отрезок соединяющий середины диагоналей лежит на средней линии. Рассмотрим задачи:
27819. Найдите среднюю линию трапеции, если ее основания равны 30 и 16.
Вычисляем по формуле:
27820. Средняя линия трапеции равна 28, а меньшее основание равно 18. Найдите большее основание трапеции.
Выразим большее основание:
Таким образом:
27836. Перпендикуляр, опущенный из вершины тупого угла на большее основание равнобедренной трапеции, делит его на части, имеющие длины 10 и 4. Найдите среднюю линию этой трапеции.
Для того, чтобы найти среднюю линию необходимо знать основания. Основание АВ найти просто: 10+4=14. Найдём DC.
Построим второй перпендикуляр DF:
Отрезки AF, FE и EB будут равны соответственно 4, 6 и 4. Почему?
В равнобедренной трапеции перпендикуляры опущенные к большему основанию разбивают его на три отрезка. Два из них, являющиеся катетами отсекаемых прямоугольных треугольников, равны друг другу. Третий отрезок равен меньшему основанию, так как при построении указанных высот образуется прямоугольник, а в прямоугольнике противолежащие стороны равны. В данной задаче:
Таким образом DC=6. Вычисляем:
27839. Основания трапеции относятся 2:3, а средняя линия равна 5. Найдите меньшее основание.
Введём коэффициент пропорциональности х. Тогда АВ=3х, DC=2х. Можем записать:
Следовательно меньшее основание равно 2∙2=4.
27840. Периметр равнобедренной трапеции равен 80, ее средняя линия равна боковой стороне. Найдите боковую сторону трапеции.
Исходя из условия можем записать:
Если обозначить среднюю линию через величину х, то получится:
Второе уравнение уже можно записать в виде:
27841. Средняя линия трапеции равна 7, а одно из ее оснований больше другого на 4. Найдите большее основание трапеции.
Обозначим меньшее основание (DC) как х, тогда большее (AB) будет равно х+4. Можем записать
Получили, что меньшее основание рано пяти, значит большее равно 9.
27842. Средняя линия трапеции равна 12. Одна из диагоналей делит ее на два отрезка, разность которых равна 2. Найдите большее основание трапеции.
Большее основание трапеции мы без труда найдём если вычислим отрезок ЕО. Он является средней линией в треугольнике ADB, и АВ=2∙ЕО.
Что имеем? Сказано что средняя линия равна 12 и разность отрезков ЕО и ОF равна 2. Можем записать два уравнения и решить систему:
Понятно, что в данном случае подобрать пару чисел можно без вычислений, это 5 и 7. Но, всё-таки, решим систему:
Значит ЕО=12–5=7. Таким образом, большее основание равно АВ=2∙ЕО=14.
27844. В равнобедренной трапеции диагонали перпендикулярны. Высота трапеции равна 12. Найдите ее среднюю линию.
Сразу отметим, что высота проведённая через точку пересечения диагоналей в равнобедренной трапеции лежит на оси симметрии и разбивает трапецию на две равные прямоугольные трапеции, то есть основания этой высотой делятся пополам.
Казалось бы, для вычисления средней линии мы должны найти основания. Тут небольшой тупик возникает… Как зная высоту, в данном случае, вычислить основания? А ни как! Таких трапеций с фиксированной высотой и диагоналями пересекающимися по углом 90 градусов можно построить множество. Как быть?
Посмотрите на формулу средней линии трапеции. Ведь нам необязательно знать сами основания, достаточно узнать их сумму (или полусумму). Это мы сделать можем.
Так как диагонали пересекаются под прямым углом, то высотой EF образуются равнобедренные прямоугольные треугольники:
Из выше сказанного следует, что FO=DF=FC, а OE=AE=EB. Теперь запишем чему равна высота выраженная через отрезки DF и AE:
Таким образом, средняя линия равна 12.
*Вообще это задачка, как вы поняли, для устного счёта. Но, уверен, представленное подробное объяснение необходимо. А так… Если взглянуть на рисунок (при условии, что при построении соблюдён угол между диагоналями), сразу в глаза бросается равенство FO=DF=FC, а OE=AE=EB.
В составе прототипов имеется ещё типы заданий с трапециями. Построена она на листе в клетку и требуется найти среднюю линию, сторона клетки обычно равна 1, но может быть другая величина.
27848. Найдите среднюю линию трапеции ABCD , если стороны квадратных клеток равны 1.
Всё просто, вычисляем основания по клеткам и используем формулу: (2+4)/2=3
Если же основания построены под углом к клеточной сетке, то есть два способа. Например!
Свойства равнобедренных трапеций | Caddell Prep Online
Узнайте о свойствах равнобедренных трапеций, включая отношения между противоположными сторонами, противоположными углами, смежными углами, диагоналями и углами, образованными диагоналями.
Равнобедренная трапеция: Трапеция с одной парой параллельных линий и конгруэнтными непараллельными сторонами.
Равнобедренные трапеции — это особые типы трапеций, у которых пара непараллельных ветвей конгруэнтна друг другу.Это означает, что трапеция кажется симметричной, а диагонали равны по длине.
Подобно равнобедренному треугольнику, равнобедренные трапеции имеют конгруэнтные углы основания. Это означает, что два меньших угла конгруэнтны друг другу, а два больших угла конгруэнтны друг другу.
Когда диагонали нарисованы, они не делят друг друга пополам. Нижняя часть двух диагоналей конгруэнтна друг другу, а верхняя часть двух диагоналей также конгруэнтна друг другу.
Равнобедренная трапеция также имеет два противоположных треугольника, образованных подобными друг другу диагоналями, то есть все их стороны и углы пропорциональны. Два других образованных противоположных треугольника конгруэнтны друг другу по бокам.
Равнобедренные трапеции, углы, стороны, диагонали и другие свойства. Объясняется фотографиями и практическими задачами
- Базовые уголки
- Диагонали
Отличительной чертой этого особого типа трапеции является то, что две непараллельные стороны (XW и YZ ниже) совпадают.
Базовые уголки
Углы основания равнобедренной трапеции совпадают.
Проблема 1
Если вы знаете, что угол BAD равен 44 °, какова мера $$ \ angle ADC $$?
Покажи ответУгол $$ \ angle ADC = 44 ° $$, так как базовые углы совпадают
Проблема 2
$$ \ angle ABC = 130 $$, какой еще угол составляет 130 градусов?
Покажи ответSingle $$ \ angle ADC = 4 ° $$, так как базовые углы совпадают
Проблема 3
Какое значение j в равнобедренной трапеции ниже?
Покажи ответДж = 5
- Базовые уголки
- Диагонали
Диагонали равнобедренной трапеции
Проблема 3
Диагонали равнобедренной трапеции совпадают.Какое значение x ниже? (используйте свои знания о диагоналях!)
Покажи ответХ = 9
назад к четырехугольникам рядом с пареллограммамиРеклама
Равнобедренная трапеция — формула, свойства, определение, примеры
Трапеция — это четырехугольник, у которого параллельна только одна сторона.Равнобедренная трапеция — это трапеция с совпадающими углами при основании и совпадающими непараллельными сторонами. Равнобедренная трапеция обладает множеством интересных свойств, которые делают ее уникальной и помогают нам отличать ее от других четырехугольников. Обсудим их подробнее.
Равнобедренная трапеция, определение
Равнобедренная трапеция может быть определена как трапеция, у которой непараллельные стороны и углы основания имеют одинаковую меру. Другими словами, если две противоположные стороны (основания) трапеции параллельны, а две непараллельные стороны имеют одинаковую длину, то это равнобедренная трапеция.Посмотрите на изображение ниже: стороны c и d равны по длине, а противоположные стороны a и b (основания трапеции) параллельны друг другу.
Свойства равнобедренной трапеции
Ниже приведены свойства равнобедренной трапеции согласно рисунку, приведенному ниже.
- Имеет ось симметрии. Он не имеет вращательной симметрии и одной линии симметрии, соединяющей середину параллельных сторон.
- Одна пара сторон параллельна, и они являются сторонами основания.(AB II DC на данном изображении)
- Остальные стороны, кроме основания, не параллельны и имеют одинаковую длину. (c = d на данном изображении)
- Диагонали одинаковые по длине. (AC = BD)
- Базовые углы такие же. (∠D = ∠C, ∠A = ∠B)
- Сумма противоположных углов составляет 180 ° или дополнительные. (A + ∠C = 180 ° и ∠B + ∠D = 180 °)
- Отрезок, соединяющий середины параллельных сторон, перпендикулярен основаниям. (PQ ⊥ DC)
Формула равнобедренной трапеции
Ниже приведены формулы для расчета площади и периметра равнобедренной трапеции.
Площадь равнобедренной трапеции
Чтобы найти площадь равнобедренной трапеции, нам нужно сложить стороны основания или параллельные стороны и разделить ее на 2, а затем умножить результат на высоту.
Площадь равнобедренной трапеции = (сумма параллельных сторон ÷ 2) × h
Периметр равнобедренной трапеции
Чтобы найти периметр равнобедренной трапеции, мы должны сложить все стороны равнобедренной трапеции.
Периметр равнобедренной трапеции = сумма всех сторон
Статьи по теме о равнобедренной трапеции
Ознакомьтесь с интересными темами, чтобы узнать больше о равнобедренной трапеции.
Часто задаваемые вопросы о равнобедренной трапеции
Каковы характеристики равнобедренной трапеции?
У равнобедренной трапеции четыре стороны. Две противоположные стороны (основания) параллельны друг другу, а две другие стороны равны по длине, но не параллельны друг другу.
Если один базовый угол равнобедренной трапеции равен 30 °. Найдите другой базовый угол.
Согласно свойству равнобедренной трапеции, базовые углы равны, поэтому, если один базовый угол равен 30 °, то другой базовый угол будет равен 30 °.
В чем разница между трапецией и равнобедренной трапецией?
У трапеции каждая сторона имеет разную длину и диагонали не совпадают, тогда как у равнобедренной трапеции непараллельные стороны равны, углы основания равны, диагонали совпадают, а противоположные углы являются дополнительными.
Какова формула площади равнобедренной трапеции?
Формула для вычисления площади равнобедренной трапеции: Площадь = (сумма параллельных сторон ÷ 2) × высота.
Какова формула периметра равнобедренной трапеции?
Формула для расчета периметра равнобедренной трапеции: Периметр = сумма всех сторон равнобедренной трапеции
Равнобедренная трапеция: определение, свойства и формула — видео и стенограмма урока
Определение равнобедренной трапеции
Итак, что же такого особенного в равнобедренной трапеции? Что ж, если вы помните, у равнобедренного треугольника есть два равных угла основания и два равных угла ног.Равнобедренная трапеция получает свои свойства от комбинации этих свойств. Равнобедренная трапеция представляет собой четырехугольник, обладающий следующими свойствами:
- Одна пара параллельных сторон (AB и DC)
- Одна пара конгруэнтных ножек (DA и CB)
- Базовые углы равны (m
- Диагонали совпадают (AC и BD)
- Противоположные углы — дополнительные (их сумма 180 градусов)
Медиана равнобедренной трапеции — это линейный сегмент, образующийся, когда мы соединяем среднюю точку одной ноги со средней точкой другой ноги равнобедренной трапеции.Медиана образует специальную теорему только для равнобедренных трапеций. Длина медианы равна половине суммы двух параллельных сторон. Если мы присвоим переменные a и b измерению параллельных сторон, то длина медианы будет ( a + b ) / 2.
Медиана также параллельна двум параллельным сторонам. стороны. Отрезок MN параллелен обоим отрезкам AB и DC.
Рассмотрим пример:
Если a = 12 см и b = 14 см,
Тогда MN = (12 + 14) / 2
MN = 26/2 = 13 см
Периметр и площадь трапеции
Чтобы найти периметр, сложите все стороны, как и для любого многоугольника.
Чтобы найти площадь, используйте формулу ниже. Сначала найдите среднее значение двух параллельных сторон и умножьте свой ответ на высоту. Другими словами, найдите сумму двух параллельных сторон, разделите свой ответ на два, а затем умножьте свой ответ на высоту. Очень важно отметить, что вы сначала находите сумму, а затем делите на два, а затем умножаете на высоту.
Давайте посмотрим на пример:
Если a = 52 см, b = 130 см и h = 75 см, какова площадь?
A = (52 + 130) / 2 * 75
A = (182/2) * 75
A = 91 * 75
A = 6 825 квадратных см
Краткое содержание урока
A трапеция является a специальный четырехугольник, у которого есть только одна пара параллельных сторон.Ее еще называют трапецией.
Равнобедренная трапеция обладает следующими уникальными свойствами:
- Одна пара параллельных сторон
- Базовые углы совпадают
- Ноги конгруэнтные
- Диагонали совпадают
- Противоположные углы дополнительные
Медиана равнобедренной трапеции — это отрезок линии, образующийся, когда мы соединяем среднюю точку одной ноги с серединой другой ноги равнобедренной трапеции.Периметр определяется сложением всех сторон. Площадь трапеции — это среднее значение двух параллельных сторон, умноженное на высоту.
Как найти длину диагонали трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Докажите, что диагонали равнобедренной трапеции совпадают
Чтобы доказать, что диагонали равнобедренной трапеции совпадают, рассмотрим равнобедренную трапецию, показанную ниже.В этом уроке мы покажем вам два разных способа сделать одно и то же доказательство, используя одну и ту же трапецию.
Первый способ — показать, что треугольник ABC конгруэнтен треугольнику DCB
.Дано : Равнобедренная трапеция ABCD с отрезком AB ≅ сегмент DC
Prove : сегмент AC ≅ сегмент BD
Поскольку трапеция равнобедренная, углы основания совпадают.
Следовательно, ∠CBA ≅ BCD
Кроме того, отрезок BC должен отрезать BC по рефлексивному свойству конгруэнтности.
Согласно постулату SAS, треугольник ABC ≅ треугольник DCB.
Следовательно, сегмент AC ≅ сегмент BD
О чем нужно помнить, когда вы доказываете, что диагонали равнобедренной трапеции совпадают.
Вот некоторые вещи, которые вы должны знать о приведенном выше доказательстве.
- Утверждение , если трапеция равнобедренная, то базовые углы равны , также требует доказательства. Однако мы не будем здесь доказывать.
- У равнобедренной трапеции равные стороны всегда не параллельны.На трапеции выше мы показываем эти стороны красными отметками.
- Рефлексивное свойство относится к числу, которое всегда равно самому себе. Например, 9 = 9 или y = y являются примерами рефлексивного свойства.
- SAS означает «сторона, угол, сторона». Возможно, вам стоит повторить урок о равных треугольниках.
- Чтобы доказать, что диагонали равнобедренной трапеции совпадают, вы также могли бы использовать треугольник ABD и треугольник DCA.
Еще один отличный способ доказать, что диагонали равнобедренной трапеции совпадают. На этот раз мы показываем, что треугольник BAD конгруэнтен треугольнику CDA
.Дано : Равнобедренная трапеция ABCD с отрезком AB ≅ сегмент DC
Prove : сегмент AC ≅ сегмент BD
Поскольку трапеция равнобедренная, базовые углы совпадают
Следовательно, ∠BAD ≅ CDA
Обратите внимание, что на этот раз мы не используем те же базовые углы, что и перед.Базовые углы, которые мы сейчас используем, связаны с основанием на вершине или сегментом AD.
Кроме того, отрезок AD ≅ переходит в отрезок AD по рефлексивному свойству конгруэнтности.Согласно постулату SAS, треугольник BAD ≅ треугольник CDA
Следовательно, сегмент AC ≅ сегмент BD
Формулы равнобедренной трапеции — xGeometry
|
$$ 2p = B + b + 2S $$
Периметр
$$ A = \ frac {\ left (B + b \ right) \ times h} {2} $$
Площадь
$$ B + b = \ frac {2A} {h} $$
Сумма баз
$$ h = \ frac {2A} {B + b} $$
Высота
$$ B + b = 2p — 2S $$
Сумма баз
$$ S = \ frac {2p — B — b} {2} $$
Наклонная сторона
$$ p_ {1} = \ frac {B — b} {2} $$
Косая боковая проекция
$$ B — b = 2 \ times p_ {1} $$
Разница баз
$$ B = b + 2p_ {1} $$
Удлиненное основание
$$ b = B — 2p_ {1} $$
Укороченная база
$$ S = \ sqrt {{p_ {1}} ^ 2 + {h} ^ 2} $$
Сторона (теорема Пифагора)
$$ h = \ sqrt {{S} ^ 2 — {p_ {1}} ^ 2} $$
Высота
$$ p_ {1} = \ sqrt {{S} ^ 2 — {h} ^ 2} $$
Косая боковая проекция
Определение
Равнобедренная трапеция — это трапеция с совпадающими наклонными сторонами.
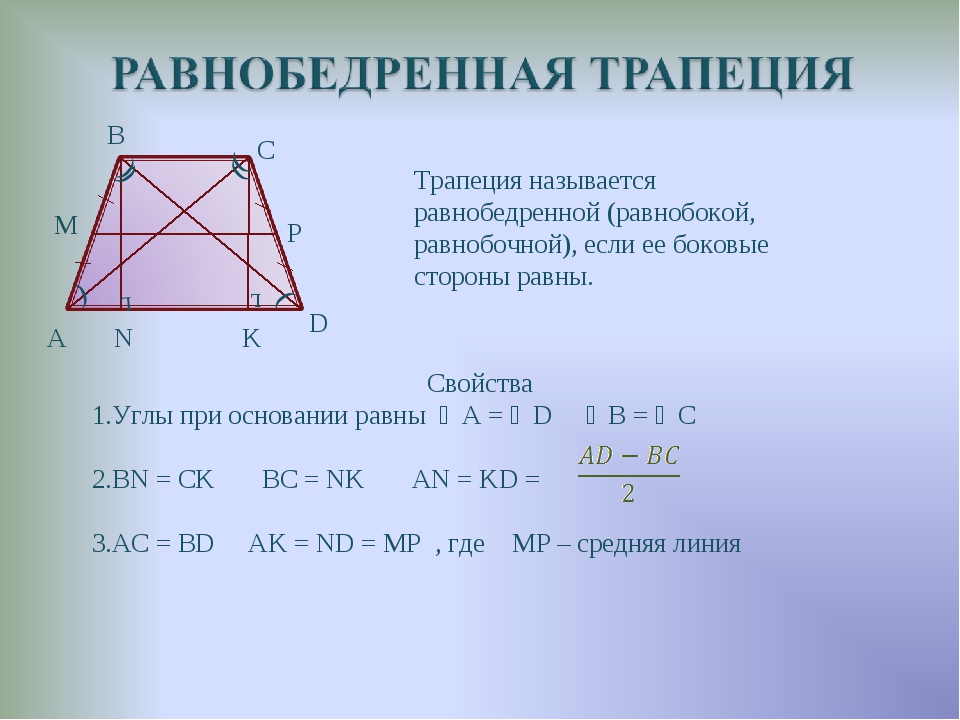
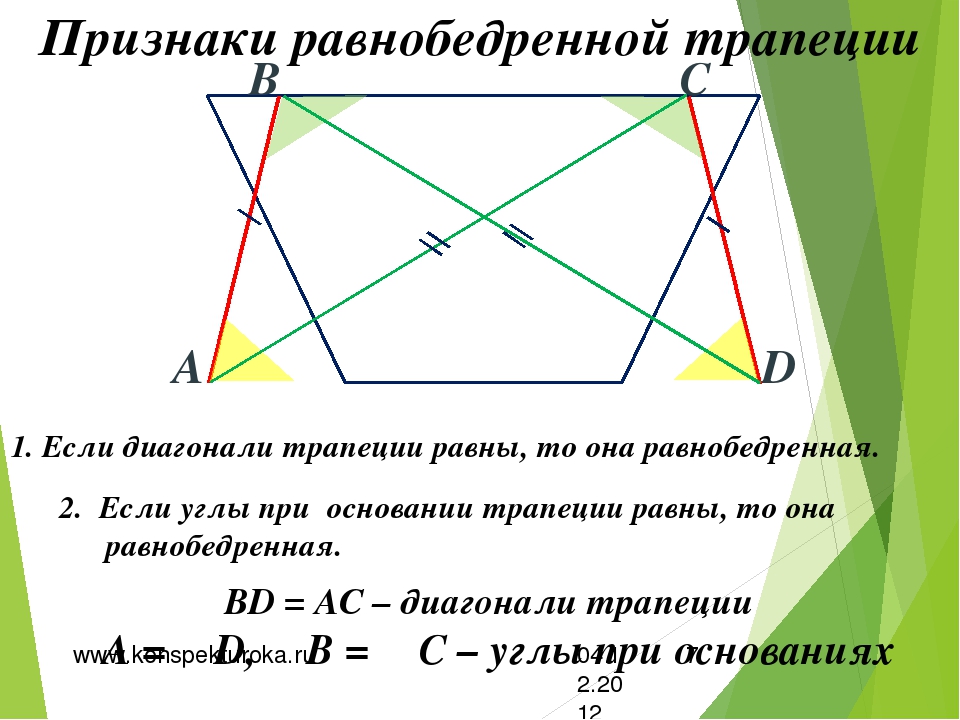
 Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
Точка пересечения диагоналей делит этот отрезок в следующем соотношении: ТО/ОХ = КМ/АЕ .
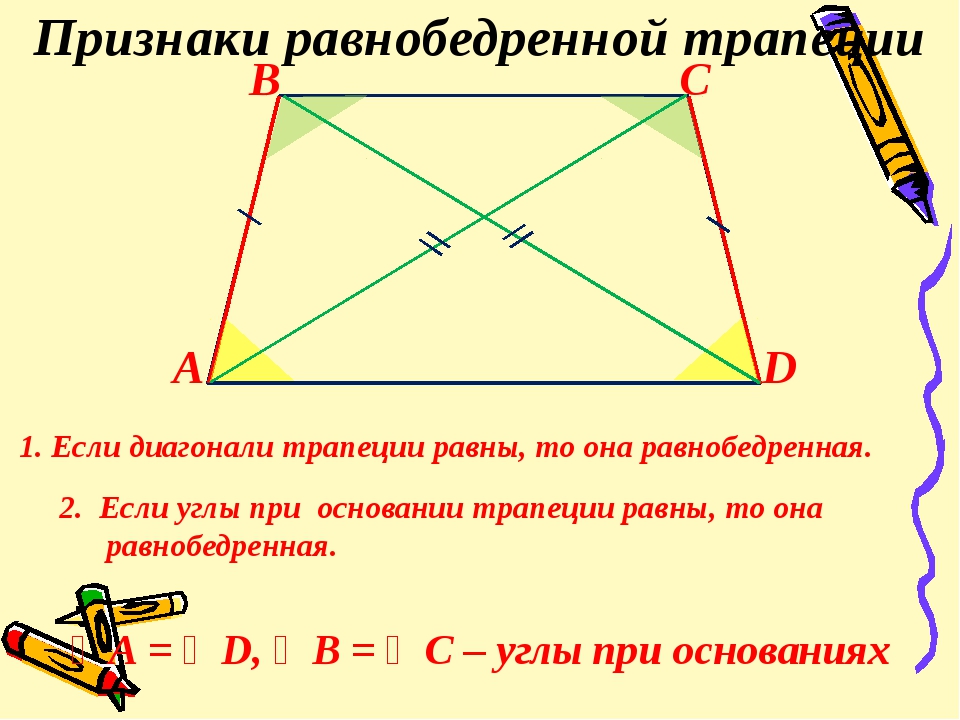 Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .
Длину одного можно найти, если длины оснований сложить и разделить пополам: (a + b)/2 . Второй получим, когда из большего основания вычтем меньшее и полученную разность разделим на два: (a – b)/2 .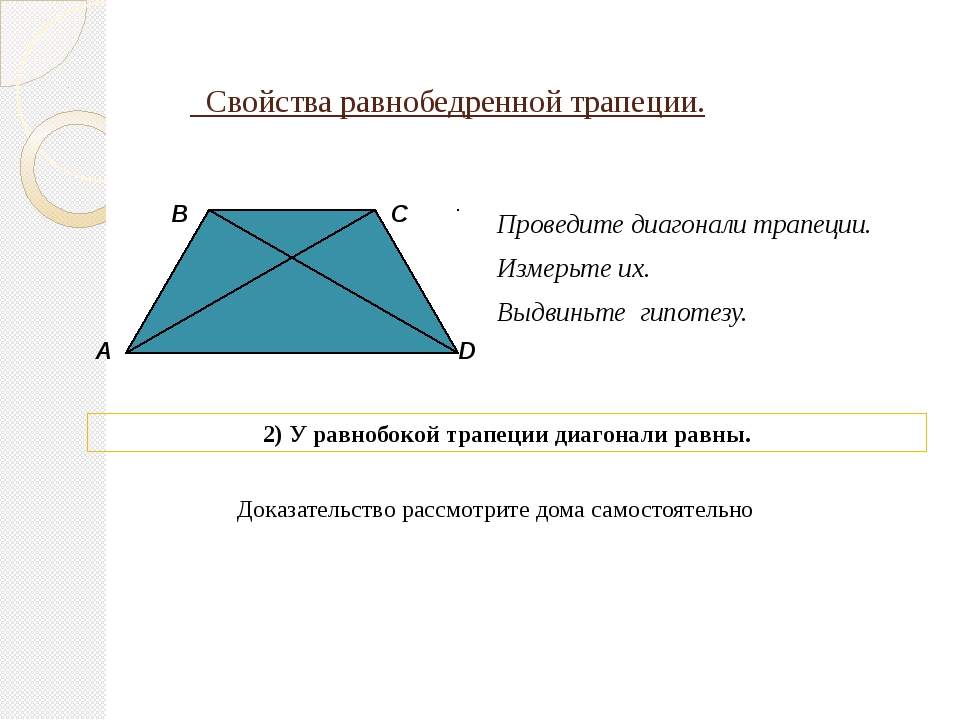
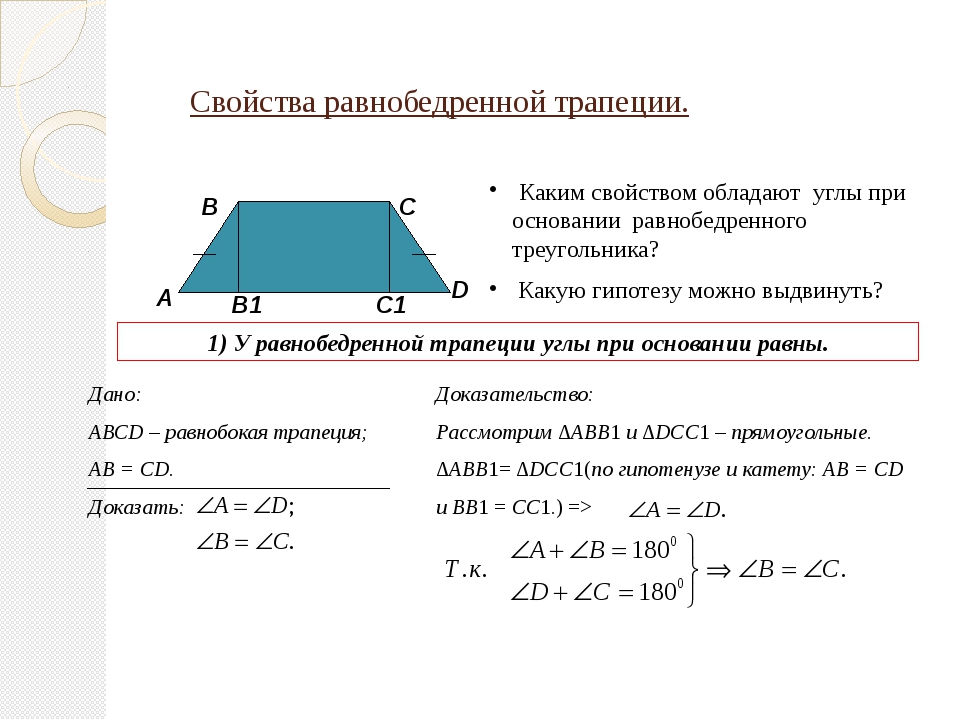
 Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
Проведите из вершины М прямую МТ, параллельную боковой стороне АК (МТ || АК).
 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
