Подготовка школьников к ЕГЭ (Справочник по математике — Элементы математического анализа

Ограниченные и неограниченные функции

      Обозначим буквой   X   некоторое множество чисел, входящих в область определения   D ( f )    функции   y = f (x).

      Определение 1. Функцию   y = f (x)   называют ограниченной сверху на множестве   X ,   если существует такое число   a ,   что для любого   x   из множества   X   выполнено неравенство

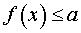
      Определение 2. Функцию   y = f (x)   называют ограниченной снизу на множестве   X ,   если существует такое число   b ,   что для любого   x   из множества   X   выполнено неравенство

      Определение 3. Функцию   y = f (x)   называют ограниченной на множестве   X ,   если существуют такие числа   a    и   b ,   что для любого   x   из множества   X   выполнено неравенство

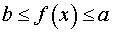
      Определение 4. Функцию   y = f (x)   называют неограниченной сверху на множестве   X ,  если для любого числа   a   существует такой   x   из множества   X ,   для которого выполнено неравенство

      Определение 5. Функцию   y = f (x)   называют неограниченной снизу на множестве   X ,  если для любого числа   b   существует такой   x   из множества   X ,   для которого выполнено неравенство

      Определение 6. Функцию  y = f (x)   называют неограниченной на множестве   X ,  если эта функция или неограничена сверху, или неограничена снизу, или неограничена и сверху, и снизу.

      Проиллюстрируем эти определения следующими примерами.

      Пример 1. Функция   y = x²   (рис. 1) является ограниченной снизу и неограниченной сверху на множестве

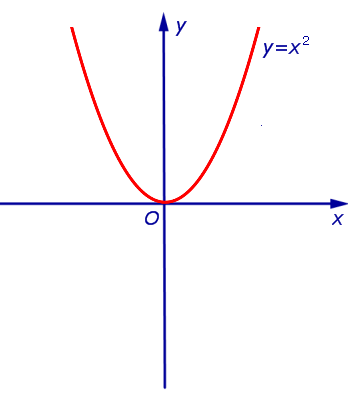
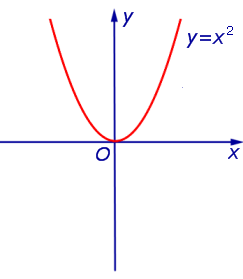
Рис.1

      Пример 2. Функция   y = – x²   (рис. 2) является ограниченной сверху и неограниченной снизу на множестве

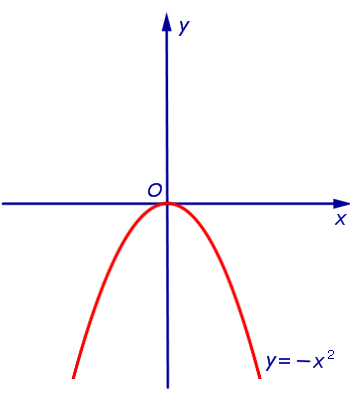
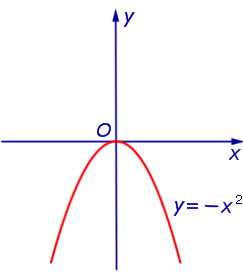
Рис.2

      Пример 3. Функция   y = x   (рис. 3) неограничена сверху и неограничена снизу на множестве

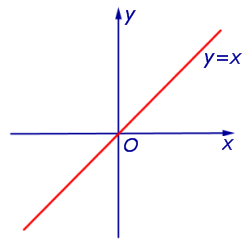
Рис.3

      Пример 4. Функция   y = arctg x   (рис. 4) ограничена на множестве

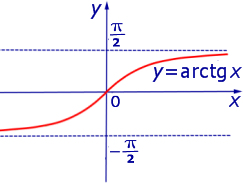
Рис.4

Монотонные и строго монотонные функции

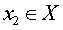      Определение 7. Функцию   y = f (x)   называют возрастающей на множестве   X ,  если для любых чисел и ,   удовлетворяющих неравенству   x₁ < x₂ ,   выполнено неравенство

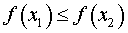
      Замечание 1. Возрастающие функции также называют неубывающими функциями.

      Определение 8. Функцию  y = f (x)   называют убывающей на множестве   X ,  если для любых чисел и 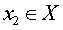,   удовлетворяющих неравенству   x₁ < x₂ ,   выполнено неравенство

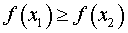
      Замечание 2. Убывающие функции также называют невозрастающими функциями.

      Определение 9. Функцию   y = f (x)   называют строго возрастающей на множестве   X ,  если для любых чисел и 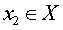,   удовлетворяющих неравенству   x₁ < x₂ ,   выполнено неравенство

f (x₁) < f (x₂)

      Определение 10. Функцию   y = f (x)   называют строго убывающей на множестве   X ,  если для любых чисел и 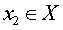,   удовлетворяющих неравенству   x₁ < x₂ ,   выполнено неравенство

f (x₁) > f (x₂)

      Определение 11. Возрастающие и убывающие функции называют монотонными,  строго возрастающие и строго убывающие функции называют строго монотонными.

      Пример 5. Функция   y  = x²   (рис. 1) является строго убывающей функцией на множестве и строго возрастающей на множестве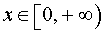

      Пример 6. Функция   y = – x²   (рис. 2) является строго возрастающей функцией на множестве и строго убывающей на множестве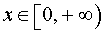

      Пример 7. Функция   y = x   (рис. 3) является строго возрастающей функцией на множестве

      Пример 8. Функция   y = arctg x   (рис. 4) является строго возрастающей на множестве

Четные и нечетные функции

      Определение 12. Функцию   y = f (x) ,   определенную на множестве   X ,  называют четной функцией, если для любого числа   x   из множества   X   число   – x   также принадлежит множеству   X   и выполняется равенство

f (– x) = f (x)

      Определение 13. Функцию   y = f (x) ,   определенную на множестве   X ,   называют нечетной функцией, если для любого числа   x   из множества   X   число   – x   также принадлежит множеству   X   и выполняется равенство

f (– x) = – f (x)

      Пример 9. Функции   y = x²   и   y = – x²   являются четными функциями (рис. 1 и рис. 2), а функции   y = x   и   y = arctg x   являются нечетными функциями (рис. 3 и рис. 4).

      Пример 10. Примерами функций, которые не являются ни четными, ни нечетными функциями, являются показательные и логарифмические функции.

      Утверждение. Любую функцию   y = f (x) ,   определенную на симметричном относительно точки   x = 0   множестве   X ,  можно представить в виде суммы четной и нечетной функций.

      Доказательство. Рассмотрим две функции:

сумма которых равна   f (x) ,   и заметим, что функция   g₁ (x)   является четной функцией, а функция   g₂ (x)   является нечетной функцией. Действительно,

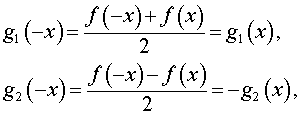
что и завершает доказательство утверждения.

      Замечание 3. Раскладывая функцию   y = e ^x   в сумму четной и нечетной функций, получаем:

      Функцию   g₁ (x)   называют гиперболическим косинусом и обозначают   ch x :

      Функцию   g₂ (x)   называют гиперболическим синусом и обозначают   sh x :

      Таким образом, справедливо равенство

e ^x= sh x + ch x

Периодические и непериодические функции. Период функции

      Определение 14. Число называют периодом функции   y = f (x) ,   если для любого числа   числа   x + T   и   x – T   также принадлежат области определения   D ( f )   и справедливы равенства

f ( x + T ) = f (x) ,    
f ( x – T ) = f (x)

      Определение 15. Если функция имеет период, то ее называют периодической. Если же у функции периода нет, то ее называют непериодической.

      Замечание 4. Если число   T   является периодом некоторой функции, то и число   kT ,   где   k   – любое целое число, отличное от нуля, также является периодом этой функции.

      Пример 11. Функции   y = sin x   и   y = cos x   являются периодическими функциями с периодом   2π , функции   y = tg x   и   y = ctg x   являются периодическими функциями с периодом   π .

      Подробнее об этом можно прочитать в разделе «Свойства тригонометрических функций» → «Периодичность тригонометрических функций. Полупериодичность синуса и косинуса» нашего справочника.

      Пример 12. Показательные, логарифмические и степенные функции являются непериодическими функциями.

График функции. Свойства графиков четных, нечетных, периодических функций

      Рассмотрим плоскость с заданной прямоугольной системой координат   Oxy .

      Определение 16.  Графиком функции   y = f (x)   называют множество всех точек, координаты которых имеют вид  (x; f (x)) , где  .

      Замечание 5. График четной функции симметричен относительно оси ординат   Oy   (см., например, рис. 1 и рис. 2), график нечетной функции симметричен относительно начала координат (см., например, рис. 3 и рис. 4).

      Замечание 6. График периодической функции не изменяется при сдвиге вдоль оси абсцисс   Ox   на период вправо или влево (см., например, раздел «Графики тригонометрических функций» нашего справочника). Поэтому для того, чтобы построить график периодической функции с периодом   T,   достаточно построить график этой функции на любом отрезке оси абсцисс   Ox   длины   T,   а затем сдвигать его влево и вправо на расстояния   nT ,   где   n   – любое натуральное число.

 

      На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ по математике.

www.resolventa.ru

Степенная функция, ее свойства и график

Вы знакомы с функциями y=x, y=x², y=x³, y=1/xи т. д. Все эти функции являются частными случаями степенной функции, т. е. функцииy=x^p, где p — заданное действительное число. Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значенияхx иp имеет смысл степеньx^p. Перейдем к подобному рассмотрению различных случаев в зависимости от показателя степениp.

1. Показатель p=2n -четное натуральное число.

В этом случае степенная функция y=x²ⁿ, гдеn— натуральное число, обладает следующими

свойствами:

• область определения — все действительные числа, т. е. множество R;

• множество значений — неотрицательные числа, т. е. y больше или равно 0;

• функция y=x²ⁿ четная, так какx²ⁿ=(-x)²ⁿ

• функция является убывающей на промежутке x<0 и возрастающей на промежутке x>0.

График функции y=x²ⁿ имеет такой же вид, как например график функцииy=x⁴.

        2. Показатель p=2n-1— нечетное натуральное число В этом случае степенная функцияy=x^2n-1 , где натуральное число, обладает следующими свойствами:

• область определения — множество R;

• множество значений — множество R;

• функция y=x^2n-1нечетная, так как (-x)^2n-1=x^2n-1;

• функция является возрастающей на всей действительной оси.

График функции y=x2n-1имеет такой же вид, как, например, график функцииy=x3.

       3.Показатель p=-2n, гдеn — натуральное число.

В этом случае степенная функция y=x^-2n=1/x²ⁿ обладает следующими свойствами:

• область определения — множество R, кроме x=0;

• множество значений — положительные числа y>0;

• функция  y=1/x²ⁿчетная, так как1/(-x)²ⁿ=1/x

  ²ⁿ;

• функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.

График функции y=1/x²ⁿимеет такой же вид, как, например, график функции y=1/x².

       4.Показатель p=-(2n-1), гдеn— натуральное число. В этом случае степенная функцияy=x^-(2n-1)обладает следующими свойствами:

• область определения — множество R, кроме x=0;

• множество значений — множество R, кроме y=0;

• функция y=x^-(2n-1)нечетная, так как (-x)^-(2n-1)=-x^-(2n-1);

• функция является убывающей на промежутках x<0иx>0.

График функции 

y=x^-(2n-1)имеет такой же вид, как, например, график функцииy=1/x³.

2. Обратные тригонометрические функции, их свойства и графики.

Обратные тригонометрические функции, их свойства и графики.Обра́тные тригонометри́ческие фу́нкции (круговые функции, аркфункции) — математические функции, являющиеся обратными к тригонометрическим функциям.

1. Функция arcsin

График функции .

Арксинусом числа m называется такое значение угла x, для которого 

Функция  непрерывна и ограничена на всей своей числовой прямой. Функция  является строго возрастающей.

1. [Править]Свойства функции arcsin

2. [Править]Получение функции arcsin

Дана функция  На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие  функцией не является. Поэтому мы рассмотрим отрезок, на котором она строго возрастает и принимает все значения 

области значений — . Так как для функции  на интервале каждому значению аргумента соответствует единственное значение функции, то на этом отрезке существует обратная функция  график которой симметричен графику функции  на отрезке  относительно прямой 

studfile.net

Функция и ее свойства

Русская гимназия

КОНСПЕКТ

на тему:

Функция

Выполнил

ученик 10“Ф” класса Бурмистров Сергей

Руководитель

учитель Математики

Юлина О.А.

Нижний Новгород

1997 год

Функция и её свойства

Функция- зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.

Переменная х-

независимая переменная или аргумент.

Переменная у- зависимая переменная

Значение функции- значение у, соответствующее заданному значению х.

Область определения функции- все значения, которые принимает независимая переменная.

Область значений функции (множество значений)- все значения, которые принимает функция.

Функция является четной- если для любого х из области определения функции выполняется равенство f(x)=f(-x)

Функция является нечетной- если для любого х из области определения функции выполняется равенство f(-x)=-f(x)

Возрастающая функция- если для любых х₁и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)<f(х₂)

Убывающая функция- если для любых х₁и

х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)>f(х₂)

Способы задания функции

¨ Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x)-íåêîòîðîå âыðàæåíèå с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

¨ На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента. Примерами табличного задания функции являются таблица квадратов, таблица кубов.

Виды функций и их свойства

1) Постоянная функция- функция, заданная формулой у=b

, где b-некоторое число. Графиком постоянной функции у=b является прямая, параллельная оси абсцисс и проходящая через точку (0;b) на оси ординат

2) Прямая пропорциональность- функция, заданная формулой у=kx, где к¹0. Число kназывается коэффициентом пропорциональности.

Cвойства функции y=kx:

1. Область определения функции- множество всех действительных чисел

2. y=kx — нечетная функция

3. При k>0 функция возрастает, а при k<0 убывает на всей числовой прямой

3)Линейная функция- функция, которая задана формулой y=kx+b, где k иb—действительные числа. Если в частности, k=0, то получаем постоянную функцию y=b; если b=0, то получаем прямую пропорциональность y=kx.

Свойства функции y=kx+b:

1. Область определения- множество всех действительных чисел

2. Функция y=kx+bобщего вида, т.е. ни чётна, ни нечётна.

3. При k>0функция возрастает, а при k<0 убывает на всей числовой прямой

Графиком функции является прямая.

4)Обратная пропорциональность- функция, заданная формулой y=k/х, где k¹0 Число k называют коэффициентом обратной пропорциональности.

Свойства функции y=k/x:

1. Область определения- множество всех действительных чисел кроме нуля

2. y=k/x— нечетная функция

3. Если k>0, то функция убывает на промежутке (0;+¥) и на промежутке (-¥;0). Если k<0, то функция возрастает на промежутке (-¥;0) и на промежутке (0;+¥).

Графиком функции является гипербола.

5)Функция y=x²

Свойства функции y=x²:

1. Область определения- вся числовая прямая

2. y=x²— четная функция

3. На промежутке [0;+¥) функция возрастает

4. На промежутке (-¥;0] функция убывает

Графиком функции является парабола.

6)Функция y=x³

Свойства функции y=x³:

1. Область определения- вся числовая прямая

2. y=x³—нечетная функция

3. Функция возрастает на всей числовой прямой

Графиком функции является кубическая парабола

7)Степенная функция с натуральным показателем- функция, заданная формулой y=xⁿ, где n— натуральное число. При n=1 получаем функцию y=x, ее свойства рассмотрены в п.2. При n=2;3 получаем функции y=x²; y=x³. Их свойства рассмотрены выше.

Пусть n- произвольное четное число, большее двух: 4,6,8… В этом случае функция y=xⁿобладает теми же свойствами, что и функция y=x². График функции напоминает параболу y=x², только ветви графика при |х|>1 тем круче идут вверх, чем больше n, а при |х|<1 тем “теснее прижимаются” к оси Х, чем больше n.

Пусть n- произвольное нечетное число, большее трех: 5,7,9… В этом случае функция y=xⁿобладает теми же свойствами, что и функция y=x³. График функции напоминает кубическую параболу.

8)Степенная функция с целым отрицательным показателем- функция, заданная формулой y=x^-n, где n— натуральное число. При n=1 получаем y=1/х, свойства этой функции рассмотрены в п.4.

Пусть n- нечетное число, большее единицы: 3,5,7… В этом случае функция y=x^-nобладает в основном теми же свойствами, что и функция y=1/х.

Пусть n- четное число, например n=2.

Свойства функции y=x^-2:

1. Функция определена при всех x¹0

2. y=x^-2 — четная функция

3. Функция убывает на (0;+¥) и возрастает на (-¥;0).

Теми же свойствами обладают любые функции при четном n, большем двух.

9)Функция y=Öх

Свойства функции y=Öх:

1. Область определения — луч [0;+¥).

2. Функция y=Öх — общего вида

3. Функция возрастает на луче [0;+¥).

10)Функция y=³Öх

Свойства функции y=³Öх:

1. Область определения- вся числовая прямая

2. Функция y=³Öх нечетна.

3. Функция возрастает на всей числовой прямой.

11)Функция y=ⁿÖх

При четном n функция обладает теми же свойствами, что и функция y=Öх. При нечетном n функция y=ⁿÖх обладает теми же свойствами, что и функция y=³Öх.

12)Степенная функция с положительным дробным показателем- функция, заданная формулой y=x^r, где r— положительная несократимая дробь.

Свойства функции y=x^r:

1. Область определения- луч [0;+¥).

2. Функция общего вида

3. Функция возрастает на [0;+¥).

На рисунке изображен график функции y=x^5/2. Он заключен между графиками функций y=x²и y=x³, заданных на промежутке [0;+¥).Подобный вид имеет любой график функции вида y=x^r, где r>1.

На рисунке изображен график функции y=x^2/3. Подобный вид имеет график любой степенной функции y=x^r , где 0<r<1

13)Степенная функция с отрицательным дробным показателем-функция, заданная формулой y=x^-r, где r— положительная несократимая дробь.

Свойства функции y=x^-r:

1. Обл. определения -промежуток (0;+¥)

2. Функция общего вида

3. Функция убывает на (0;+¥)

14)Обратная функция

Если функция y=f(x) такова, что для любого ее значения y_o уравнениеf(x)=y_o имеет относительно х единственный корень, то говорят, что функция fобратима.

Если функция y=f(x) определена и возрастает (убывает) на промежутке Х и областью ее значений является промежуток Y, то у нее существует обратная функция, причем обратная функция определена и возрастает(убывает) на Y.

Таким образом, чтобы построить график функции, обратной к функции y=f(x), надо график функции y=f(x) подвергнуть преобразованию симметрии относительно прямой y=x.

15)Сложная функция- функция, аргументом которой является другая любая функция.

Возьмем, к примеру, функцию y=x+4. Подставим в аргумент функцию y=x+2. Получается: y(x+2)=x+2+4=x+6. Это и будет являться сложной функцией.

mirznanii.com