Свойства и признаки прямоугольной трапеции 8 класс – Трапеция — что это такое, свойства и виды трапеций (равнобедренная, прямоугольная)

Posted on by alexxlab

Свойства прямоугольной трапеции

В данной статье мы расскажем Вам о свойствах прямоугольной трапеции, как обычной, так и той, в которую вписана окружность.

Для начала напомним некоторые основные определения.

Трапеция – это четырехугольник, имеющий 2 параллельные друг другу стороны, причем 2 другие стороны параллельными не являются.

Прямоугольная трапеция — это такая трапеция, одна из боковых сторон которой перпендикулярна ее основаниям (изображена на рис.).

Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон фигуры (на рис. EF).

Основные свойства прямоугольной трапеции

  1. Средняя линия EF равна половине суммы ее оснований BC и AD.

  2. Средняя линия EF параллельна основаниям трапеции BC и AD.
  3. На одной прямой размещаются:

    • точка пересечения (H) диагоналей прямоугольной трапеции
      AC       и BD;
    • точка пересечения (E) продолжений боковых сторон трапеции AB и CD;
    • середины (F и G) оснований трапеции BC и AD.
    Данным свойством обладает как прямоугольная, так и равносторонняя трапеция.

Свойства прямоугольной трапеции, в которую вписана окружность

  1. Если в прямоугольную трапецию вписана окружность, это значит, что сумма ее оснований и сумма ее боковых сторон равны.
  2. Площадь трапеции ABCD можно найти, перемножив длины ее оснований BC и AD.
    SABCD = BC * AD
  3. Четырехугольник, вершинами которого являются центр вписанной окружности (O), одна из вершин трапеции (A или B), а также точки 2 касания (M и E или M и К), является квадратом.

Узнать подробнее о свойствах трапеции с прямым углом, в которую вписана окружность, а также ознакомиться с доказательствами этих свойств, можно на сайте uznateshe.ru.

Понравилась статья, расскажите о ней друзьям:

Скорее всего, Вам будет интересно:

Тест по геометрии «Свойства и признаки трапеции» (8 класс)

Формулировать и доказывать утверждения о свойствах и признаках трапеции, равнобедренной и прямоугольной трапеции. Решать задачи на вычисление, доказательство и построение трапеции, равнобедренной и прямоугольной трапеции.

(Бондарева Наталья Владимировна, учитель математики)

Базовый уровень.

1.Задание: Отметьте правильный ответ:

Многоугольник, называемый трапецией имеет номер : 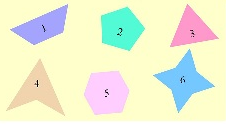hello_html_m350655f5.png

1

2

3

5

2.Задание: Отметьте правильный ответ:

Трапецией является четырёхугольник ABCD, по определению нужно, чтобы:

АВ ∦ CD и ВС АD

АВ CD и ВС АD

АС = ВD

А = D и В = С

3.Задание: Отметьте правильный ответ:

Несправедливое утверждение для равнобедренной трапеции:

Основания равны

Диагонали равны

Углы при основании равны

Основания параллельны

4.Задание: Отметьте правильный ответ:

Утверждение справедливо для любой произвольной трапеции :

Основания параллельны

Боковые стороны равны

Диагонали равны

Углы при основании равны

5.Задание: Отметьте правильный ответ:

Сторона HK прямоугольной трапеции HKLM, если LM = 14 см, а L = 150 равна:

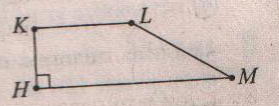
hello_html_53405992.png

7см

14см

6см

8см

6.Задание: Отметьте правильный ответ:

hello_html_m795d9791.png

7.Задание: Отметьте правильный ответ:

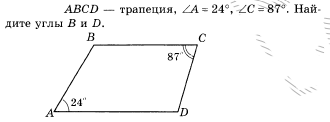
Углы В и D в трапеции ABCD с основаниями AD и BC при А =50, а С= 100:

130; 80

100; 20

10; 140

140; 110

8.Задание: Отметьте правильный ответ:

Разность периметров фигур – в прямоугольной трапеции равна :

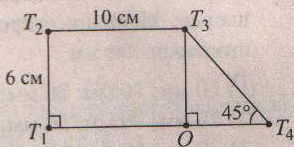
hello_html_m2f15a7e.png

20

6

10

16

9.Задание: Отметьте правильный ответ:

Периметр равнобокой трапеции с основаниями 4 см и 10 см, если диагональ является биссектрисой тупого угла трапеции :

Р = 22

Р = 20

Р = 12

Р = 24

Повышенный уровень

1.Задание: Отметьте правильный ответ:

Вид треугольника АВС, при условии , что диагональ острого угла А в трапеции АВСD является биссектрисой данного угла:

Равнобедренный тупоугольный

Равнобедренный прямоугольный

Равносторонний

разносторонний

2.Задание: Отметьте правильный ответ:

Угол СВЕ в трапеции АВСD, в которой из вершины угла В проведена прямая, параллельная стороне СD и пересекающая сторону АD в точке Е так, что АВЕ = 75, А = 40:

65

75

115

3.Задание: Отметьте правильный ответ:

Углы равнобокой трапеции, в которой разность противолежащих углов

равна :

и

и

и

и 11

4.Задание: Отметьте правильный ответ:

Периметр равнобедренной трапеции, угол при основании которой равен и основания равны 6см и 10см:

24

28

26

20

5.Задание: Отметьте правильный ответ:

Углы равнобокой трапеции, в которой противолежащие углы относятся как 2:7

и

и

и 11

и

6.Задание: Отметьте правильный ответ:

Периметр трапеции ABCD с основаниями AD и BC , при условии, что AD BC , а на стороне AD отмечена точка К так, что КBCD –параллелограмм и DК = 6см, а периметр треугольника АВК равен 25см :

Р = 37см

Р = 27см

Р = 43м

Р = 30см

7.Задание: Отметьте правильный ответ:

Периметр треугольника АВЕ, при условии, что периметр трапеции ABCD с основаниями AD BC равен 32см , а на стороне AD отмечена точка Е так, что ЕBCD –параллелограмм и DЕ = 5см.

= 22см

= 32см

= 42см

= 25см

8.Задание: Отметьте правильный ответ:

Длина меньшей боковой стороны прямоугольной трапеции, при условии, что один из углов равен , средняя линия равна 24см, а основания относятся как 3:5

12см

15см

10см

16см

9.Задание: Дополните:

Длина основания AD в трапеции ABCD , при условии, что диагональ ВD перпендикулярна к стороне АВ и является биссектрисой угла D, периметр трапеции равен 20 см, а А = 60 , будет равна ______

Правильные варианты ответа: 8; 8см.

«Трапеция.Свойства и признаки» — Геометрия

Просмотр содержимого документа
«»Трапеция.Свойства и признаки»»

Трапеция

Трапеция

Трапеция Трапеция –  (от греч. trapezion,  столик). Трапеция   –   четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

Трапеция

Трапеция –  (от греч. trapezion,  столик).

Трапеция   –   четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции .

B C ABCD – трапеция D A BC, AD – основания трапеции, ВС ║ АD AB,CD – боковые стороны Определение: Четырехугольник, у которого только две стороны параллельны, называется трапецией.

B

C

ABCD – трапеция

D

A

BC, AD – основания трапеции, ВС

║ АD

AB,CD – боковые стороны

Определение:

Четырехугольник, у которого только две стороны параллельны, называется трапецией.

Равнобедренная трапеция C B AB=CD ABCD - равнобедренная трапеция A D Определение: Трапеция, у которой боковые стороны равны, называется равнобедренной.

Равнобедренная трапеция

C

B

AB=CD

ABCD — равнобедренная трапеция

A

D

Определение:

Трапеция, у которой боковые стороны равны, называется равнобедренной.

Прямоугольная трапеция B C A = В = 90 0 ABCD - прямоугольная трапеция D A Определение: Трапеция, у которой один из углов прямой, называется прямоугольной.

Прямоугольная трапеция

B

C

A = В = 90 0

ABCD — прямоугольная трапеция

D

A

Определение:

Трапеция, у которой один из углов прямой, называется прямоугольной.

Свойства равнобедренной трапеции В равнобедренной трапеции углы при каждом основании равны. В равнобедренной трапеции диагонали равны.

Свойства равнобедренной трапеции

  • В равнобедренной трапеции углы при каждом основании равны.
  • В равнобедренной трапеции диагонали равны.
Свойства равнобедренной трапеции В равнобедренной трапеции углы при каждом основании равны. В равнобедренной трапеции диагонали равны. Свойства равнобедренной трапеции В равнобедренной трапеции углы при каждом основании равны. В равнобедренной трапеции диагонали равны.
Средняя линия трапеции B C MN - средняя линия трапеции N M D A Определение: Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Средняя линия трапеции

B

C

MN — средняя линия трапеции

N

M

D

A

Определение:

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Свойство средней линии трапеции Средняя линия трапеции параллельна основаниям и равна их полусумме B C MN ║ ВС ║ АD MN = ( BC + AD) / 2 N M D A

Свойство средней линии трапеции

Средняя линия трапеции параллельна основаниям и равна их полусумме

B

C

MN ║ ВС ║ АD

MN = ( BC + AD) / 2

N

M

D

A

Свойство средней линии трапеции Средняя линия трапеции параллельна основаниям и равна их полусумме B C MN ║ ВС ║ АD MN = ( BC + AD) / 2 N M D A

Трапеция. Свойства, признаки трапеции | Подготовка к ЕГЭ по математике

Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).

виды трапеций

Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.
Если боковые стороны равны, трапеция называется равнобедренной.

равнобедренная трапеция

Трапеция,  у которой есть  прямые углы при боковой стороне, называется прямоугольной.

прямоугольная трапеция

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

средняя линия

 

Свойства трапеции

 

1. Средняя линия трапеции параллельна основаниям и равна их полусумме.

свойство средней линии трапеции

2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.

биссектриса в трапеции

3. Треугольники AOD и COB, образованные отрезками диагоналей и основаниями трапеции, подобны.

Коэффициент подобия – k=\frac{AD}{BC}.

Отношение площадей этих треугольников есть k^2.

57

4. Треугольники ABO и DCO, образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.

свойства трапеции, равновеликие треугольники

5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.

окружность, вписанная в трапецию

6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.

qk

 

7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.

е

8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.

трапеция с углами при основании в сумме 90

Свойства и признаки равнобедренной трапеции

 

1. В равнобедренной трапеции углы при любом основании равны.

свойства равнобедренной трапеции

2. В равнобедренной трапеции длины диагоналей равны.

 

3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.

трапеция вписана в окружность

4. Около равнобедренной трапеции можно описать окружность.

5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.

диагонали трапеции перпендикулярны

Вписанная  окружность

 

Если в трапецию вписана окружность с радиусом r  и она делит боковую сторону точкой касания на два отрезка — a и b,  то r=\sqrt{ab}.

4

 

Площадь

 

S=\frac{a+b}{2}\cdot h или S=lh, где  l – средняя линия

площадь трапеции

Смотрите хорошую подборку  задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.

Смотрите также площадь трапеции.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *