Разница между сферой и шаром – Сфера и шар – определение, формула объема и площади с примерами — Детская игровая комната «Волшебный лес»

Posted on 23.08.202016.01.2020 by alexxlab

Содержание

Сфера — Википедия

Сфера (каркасная проекция)

Сфера — поверхность шара

Сфе́ра (др.-греч. σφαῖρα «мяч, шар^[1]») — геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).

Расстояние от точки сферы до её центра называется радиусом сферы. Сфера радиуса 1 называется единичной сферой.

Сфера является поверхностью вращения, образованной при вращении полуокружности вокруг своего диаметра. Площадь сферы в градусной мере с учётом непостоянства значения размеров дуг составляет 41252,96 кв. градусов.

Сфера является частным случаем эллипсоида, у которого все три оси (полуоси, радиусы) равны. Сфера является поверхностью шара. Сфера имеет наименьшую площадь из всех поверхностей, ограничивающих данный объём, также из всех поверхностей с данной площадью сфера ограничивает наибольший объём. Поэтому тела сферической формы встречаются в природе, например, маленькие капли воды при свободном падении приобретают сферическую форму именно из-за минимизации площади поверхности силой поверхностного натяжения.

Объём цилиндра, объём вписанного в него шара, касающегося обоих его оснований, и объём конуса, с вершиной в центре одного основания цилиндра и с основанием, совпадающим с другим основанием цилиндра, находятся в соотношении 3 : 2 : 1^[2].

«Кубок Кеплера»: модель Солнечной системы из пяти правильных многогранников и их вписанных и описанных сфер.

Совершенство сферической формы издавна привлекало внимание мыслителей и учёных, которые с помощью сфер пытались объяснить гармонию окружающего мира. Древнегреческий учёный Пифагор вместе с шарообразной Землёй в центре Вселенной ввёл окружающую Землю удалённую хрустальную сферу, к которой прикреплены звёзды, и семь более близких вращающихся хрустальных сфер, к которым прикреплены Солнце, Луна и пять известных к тому времени планет (исключая Землю). Эта модель впоследствии усложнялась: Евдокс Книдский рассматривал уже 27 подобных сфер, а Аристотель — 55 хрустальных сфер

[3]. Представления о вращающихся небесных сферах господствовали по крайней мере до средних веков и даже вошли в гелиоцентрическую систему мира Николая Коперника, который назвал свой основной труд «О вращении небесных сфер» (лат. De revolutionibus orbium coelestium).

Небесные сферы со времён Древней Греции были частью более общей концепции гармонии сфер о музыкально-астрономическом устройстве мира, куда также входило понятие «музыка сфер». Эта концепция также существовала как минимум до средневековья. У одного из известнейших астрономов, Иоганна Кеплера, сфера занимала центральное место во всей его системе религиозно-мистических представлений, он писал: «Образ триединого бога есть сферическая поверхность, а именно: бог-отец в центре, бог-сын — на поверхности и святой дух — в симметричном отношении между центром и описанной вокруг него сферической поверхностью»

[4]^[5]. Одно из первых значительных сочинений Кеплера, «Тайна мироздания» (лат. Mysterium Cosmographicum), было посвящено параметрам небесных сфер, Кеплер считал, что он открыл замечательную связь между правильными многогранниками, которых только пять, и небесными сферами шести известных к тому времени планет (включая Землю), являвшимися, по Кеплеру, описанными и вписанными сферами этих многогранников. Представления о гармонии сфер сыграли большую роль при открытии Кеплером третьего закона движений небесных тел (во всяком случае, могут рассматриваться как стимул к поиску астрономических соотношений)^[6]. Однако у Кеплера небесные сферы являлись уже чисто математическими объектами, а не физически существующими телами. К тому времени Тихо Браге показал, что движение комет, в частности, Большой кометы 1577 года, несовместимо с существованием твердых небесных сфер^[7]. Как удобная математическая модель, осталась одна небесная сфера, с помощью которой астрономы по сей день представляют видимые положения звезд и планет.

Уравнение сферы в прямоугольной системе координат:

(x−x0)2+(y−y0)2+(z−z0)2=R2,{\displaystyle (x-x_{0})^{2}+(y-y_{0})^{2}+(z-z_{0})^{2}=R^{2},}

где (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})} — координаты центра сферы, R{\displaystyle R} — её радиус.

Параметрическое уравнение сферы с центром в точке (x0,y0,z0){\displaystyle (x_{0},y_{0},z_{0})}:

{x=x0+R⋅sin⁡θ⋅cos⁡ϕ,y=y0+R⋅sin⁡θ⋅sin⁡ϕ,z=z0+R⋅cos⁡θ,{\displaystyle {\begin{cases}x=x_{0}+R\cdot \sin \theta \cdot \cos \phi ,\\y=y_{0}+R\cdot \sin \theta \cdot \sin \phi ,\\z=z_{0}+R\cdot \cos \theta ,\\\end{cases}}}

где θ∈[0,π]{\displaystyle \theta \in [0,\pi ]} и ϕ∈[0,2π).{\displaystyle \phi \in [0,2\pi ).}

Гауссова кривизна сферы постоянна и равна 1/R².

Основные геометрические формулы[править | править код]

Площадь поверхности сферы: S=4πr2=πd2.{\displaystyle S=4\pi r^{2}=\pi d^{2}.}

Объём шара, ограниченного сферой: V=43πr3.{\displaystyle V={\frac {4}{3}}\pi r^{3}.}

Площадь сегмента сферы высоты H{\displaystyle H}: S=2πrH{\displaystyle S=2\pi rH}.

Окружность, лежащая на сфере, центр которой совпадает с центром сферы, называется большим кругом (большой окружностью) сферы. Большие окружности являются геодезическими линиями на сфере; любые две из них пересекаются в двух точках. Иными словами, большие круги сферы являются аналогами прямых на плоскости, расстояние между точками на сфере — длина дуги проходящего через них большого круга. Углу же между прямыми на плоскости соответствует двугранный угол между плоскостями больших кругов. Многие теоремы геометрии на плоскости справедливы и в сферической геометрии, существуют аналоги теоремы синусов, теоремы косинусов для сферических треугольников. В то же время, существует немало отличий, например, в сферическом треугольнике сумма углов всегда больше 180 градусов, к трём признакам равенства треугольников добавляется их равенство по трём углам, у сферического треугольника может быть два и даже три прямых угла — например, у сферического треугольника, образованного экватором и меридианами 0° и 90°.

Расстояние между двумя точками на сфере[править | править код]

Если даны сферические координаты двух точек, то расстояние между ними можно найти так:

L=R⋅arccos⁡(cos⁡θ1⋅cos⁡θ2+sin⁡θ1⋅sin⁡θ2⋅cos⁡(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\cos \theta _{1}\cdot \cos \theta _{2}+\sin \theta _{1}\cdot \sin \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}

Однако, если угол θ{\displaystyle \theta } задан не между осью Z и вектором на точку сферы, а между этим вектором и плоскостью XY (как это принято в земных координатах, заданных широтой и долготой), то формула будет такая:

L=R⋅arccos⁡(sin⁡θ1⋅sin⁡θ2+cos⁡θ1⋅cos⁡θ2⋅cos⁡(ϕ1−ϕ2)).{\displaystyle L=R\cdot \arccos(\sin \theta _{1}\cdot \sin \theta _{2}+\cos \theta _{1}\cdot \cos \theta _{2}\cdot \cos(\phi _{1}-\phi _{2})).}

В этом случае θ1{\displaystyle \theta _{1}} и θ2{\displaystyle \theta _{2}} называются широтами, а ϕ1{\displaystyle \phi _{1}} и ϕ2{\displaystyle \phi _{2}} долготами.

В общем случае уравнение (n−1)-мерной сферы (в n-мерном евклидовом пространстве) имеет вид:

∑i=1n(xi−ai)2=r2,{\displaystyle \sum _{i=1}^{n}(x_{i}-a_{i})^{2}=r^{2},}

где (a1,…,an){\displaystyle (a_{1},…,a_{n})} — центр сферы, а r{\displaystyle r} — радиус.

Пересечением двух n-мерных сфер является (n−1)-мерная сфера, лежащая на радикальной гиперплоскости этих сфер.

В n-мерном пространстве могут попарно касаться друг друга (в разных точках) не более n+1 сфер.

n-мерная инверсия переводит (n−1)-мерную сферу в (n−1)-мерную сферу или гиперплоскость.

С трёхмерной сферой связана одна из задач тысячелетия — гипотеза Пуанкаре, в которой утверждается, что всякое односвязное компактное трёхмерное многообразие без края гомеоморфно такой сфере. Эта гипотеза была доказана Г. Я. Перельманом в начале 2000-х годов на основе результатов Ричарда Гамильтона.

Компактные поверхности и их погружения в трёхмерное пространство
Класс гомеоформности компактной триангулируемой поверхности определяется ориентируемостью, числом компонент границы и эйлеровой характеристикой.
Без границы
С границей
Связанные понятия

Чем отличается круг от шара ?

Круг- фигура плоская, шар — объемная.

Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше] , чем заданное ненулевое. Шар — геометрическое тело, ограниченное поверхностью, все точки которой стоят на равном расстоянии от центра.

КРУГ на листке ту не видишь его с боку или с верху (не обьемный) а ШАР или праавильнее СФЕРА это тот же кург в обьему или как говорят в геометрии СФЕРА ЭТО ВРАЩЯЮЩИЙСЯ КРУГ

Круг — часть плоскости, ограниченная окружностью. А окружность — линия или геометрическое место точек равноудалённых от точки, называемой её центром. Шар, сфера — трёхмерен, объёмен и представляет собой фигуру, ограниченную поверхностью, все точки которой равноудалены от точки, называемой центром шара. Полный телесный угол сферы 4пи стерадиан, а полный угол круга — 2пи радиан.

Сфера и шар / Многогранники / Справочник по геометрии 7-9 класс

Главная
Справочники
Справочник по геометрии 7-9 класс
Многогранники
Сфера и шар

Сфера — поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Центр сферы — данная точка (точка О на рисунке выше).

Радиус сферы — данное расстояние (R на рисунке выше), также это любой отрезок, соединяющий

центр сферы с какой-либо ее точкой.

Диаметр сферы — отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы в два раза больше ее радиуса, т.е. если радиус сферы — R, то ее диаметр — 2R.

Определение

Шар — тело, ограниченное сферой.

Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Шар радиуса R с центром О содержит все точки пространства, расположенные от точки О на расстоянии, не превышающем R (включая и саму точку О

), и не содержит других точек.

Шар также может быть получен вращением полукруга вокруг его диаметра. При этом сфера образуется в результате вращения полуокружности.

Объем шара

Доказательство

Дано: шар радиуса R и объемом V.

Доказать: .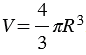

Доказательство:

Воспользуемся принципом Кавальери*. Рассмотрим два тела: половину шара радиуса R и тело Т, представляющее собой цилиндр радиуса R с высотой R, из которого вырезан конус с радиусом основания и высотой R. Представим себе, что оба тела «стоят» на плоскости

(смотри рисунок ниже). Проведем секущую плоскость

, параллельную плоскости

и пересекающую радиус шара ОА, перпендикулярный к плоскости

, в точке А₁, а высоту ВН конуса — в точке В₁.

Сечение половины шара представляет собой круг, по теореме Пифагора радиус этого круга . Поэтому площадь этого круга .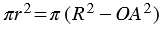

Сечение тела Т представляет собой кольцо, площадь которого равна разности площадей двух кругов: круга радиуса R

и круга радиуса В₁В₂ (смотри рисунок выше), т.е. равна .

ВВ₁В₂ подобен

ВНК по двум углам (

В — общий,

ВВ₁В₂=

ВНК = 90⁰), при этом ВН = НК = R, следовательно, и В₁В₂= ВВ₁, кроме того, ВВ₁ = ОА₁ (т.к. параллельные плоскости отсекают от параллельных прямых равные отрезки), значит, площадь сечения тела Т равна .

Получаем, что площадь сечения половины шара равна площади сечения тела Т. Поэтому и объем половины шара равен объему этого тела. В свою очередь, объем тела Т можно вычислить как разность объемов цилиндра и конуса:

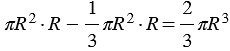Итак, объем половины шара равен 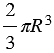, следовательно, объем всего шара 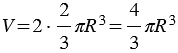. Что и требовалось доказать.

Площадь сферы

Площадь сферы S радиуса R вычисляется по формуле .

Поделись с друзьями в социальных сетях:

Советуем посмотреть:

Предмет стереометрии

Параллельность и перпендикулярность прямых и плоскостей в пространстве

Многогранник

Призма

Параллелепипед

Объём тела

Свойства прямоугольного параллелепипеда

Пирамида

Цилиндр

Конус

Многогранники

Правило встречается в следующих упражнениях:

7 класс

Задание 1225, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1226, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1227, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1230, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 23, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 25, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 26, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1252, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1253, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Задание 1255, Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник

Пользовательское соглашение

Сфера (Шар) [wiki.eduVdom.com]

Шар – это тело, полученное вращением полукруга вокруг диаметра. Поверхность шара называется сферой. Сферу можно рассматривать как тело, полученное вращением полуокружности около её диаметра.

Сфера (Шар) является телом вращения.

Шар (Сфера)
Рис.1
Сравните:
Сфера (сферическая или шаровая поверхность) — называется геометрическое место точек пространства, равноудаленных от одной точки — центра сферы. Тело, ограниченное шаровой (сферической) поверхностью, называется шаром. Шар можно получить, вращая полукруг (или круг) около его диаметра.
Шаром называется тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного (радиуса шара), от данной точки (центра шара).
Центр, диаметр и радиус шара соответствует центру, диаметру и радиусу сферы.
Площадь сферы радиуса R вычисляется по формуле: $$S=4\pi\cdot R^2$$ и равна учетверенной площади большого круга.
Объем шара радиуса R вычисляется по формуле: $$V=\frac{4}{3}\pi\cdot R^3$$ и равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, а высота есть радиус шара.
Объем шара в полтора раза меньше объема описанного вокруг него цилиндра, а площадь поверхности шара — в полтора раза меньше площади полной поверхности того же цилиндра (теорема Архимеда). $$ S=\frac{2}{3}\cdot S_1 \\ V =\frac{2}{3}\cdot V_1 $$ , где S₁ – площадь полной поверхности, V₁ – объем цилиндра. См.Рис.2.
Рис.2
Шаровой сегмент – это часть шара, ограниченная секущей плоскостью. Имеют место формулы: $$ V=\pi h^2 (R-\frac{1}{3}h) \\ S=2\pi\cdot Rh $$ , где V – объем шарового сегмента, S – площадь его поверхности, R – радиус шара, h – высота сегмента. См.Рис.3.
Шаровой сегмент
Рис.3

Шар и сфера — урок. Математика, 6 класс.

Шар — это геометрическое тело.
Предметы, имеющие форму шара, окружают нас очень часто.
Форму шара имеет мяч (футбольный, теннисный, баскетбольный).
Представление о шаре дают арбуз, апельсин, горошина.
Шарообразна и наша планета Земля.

Шар характеризует длина радиуса и диаметра.

Рассмотрим чертёж.
Перед нами изображение шара с центром в точке $O$. Все точки поверхности шара находятся на одинаковом расстоянии от его центра.
Это означает, что если мы выберем на поверхности три любые точки, например, точку $A$, точку $B$ и точку $C$, соединим их с центром шара, то полученные отрезки будут равны ($OA = OB = OC$).

Такие отрезки называют радиусами.

$OA$ — радиус шара, $OB$ — радиус шара и $OC$ — также радиус шара.
Так как центр шара можно соединить с бесконечно многими точками на поверхности шара, то можно провести бесконечно много радиусов.
Радиус шара — это отрезок, который соединяет точку поверхности шара и его центр.
На чертеже отрезок $AB$ соединяет две точки поверхности шара и проходит через его центр.

Отрезок $AB$ — это диаметр шара. Заметим, что отрезок $AB$ состоит из двух отрезков $OA$ и $OB$.
Эти отрезки являются радиусами шара.
Поэтому диаметр шара в два раза больше его радиуса.
Диаметром шара называется отрезок, соединяющий две точки поверхности шара и проходящий через его центр.
Есть название и для поверхности шара. Её называют сферой.

Для шара можно вычислить объём по формуле:
Vшара=43⋅π⋅R3.

Для сферы можно вычислить поверхность по формуле:
Sсферы=4⋅π⋅R2.