Свойства и признаки равнобедренной трапеции 8 класс
Свойства и признаки
равнобедренной трапеции
Математический диктант
4. Назовите четырехугольник, у которого две стороны параллельны, а две другие нет.
2. Сколько диагоналей можно провести из одной вершины n-угольника, если n = 4, 6.
1. Назовите многоугольник, все виды которого являются выпуклыми многоугольниками.
6. Параллельные стороны в трапеции называются …
3. Чему равна сумма углов выпуклого пятиугольника?
10. В параллелограмме противоположные стороны … и … .
5. Четырехугольник у которого противоположные стороны параллельны ….
8. В четырехугольнике сумма углов равна …
7. В трапеции равные стороны называются …
9. В параллелограмме противоположные углы …
Проверь себя!!!
1. Треугольник
Треугольник
Оценка «5» — 10 баллов.
Оценка «4» — 8-9 баллов.
Оценка «3» — 6-7 баллов.
Менее 5 баллов – учи определения!!!
2. одна, три.
3. 540.
4. трапеция.
5. параллелограмм
6. основания
7. Боковые стороны
8. 360
9. равны
10. Равны и параллельны
Проверка домашнего задания
Трапеция.
1
2
Прямоугольная трапеция.
1 = 2 (внутренние накрест лежащие при // прямых и секущей)
Равнобедренная трапеция.
3
6
Трапеция.
4
5
3 + 4 = 180 (внутренние односторонние при // прямых и секущей)
5 = 6 (соответственные при // прямых и секущей)
Теоремма Фалеса.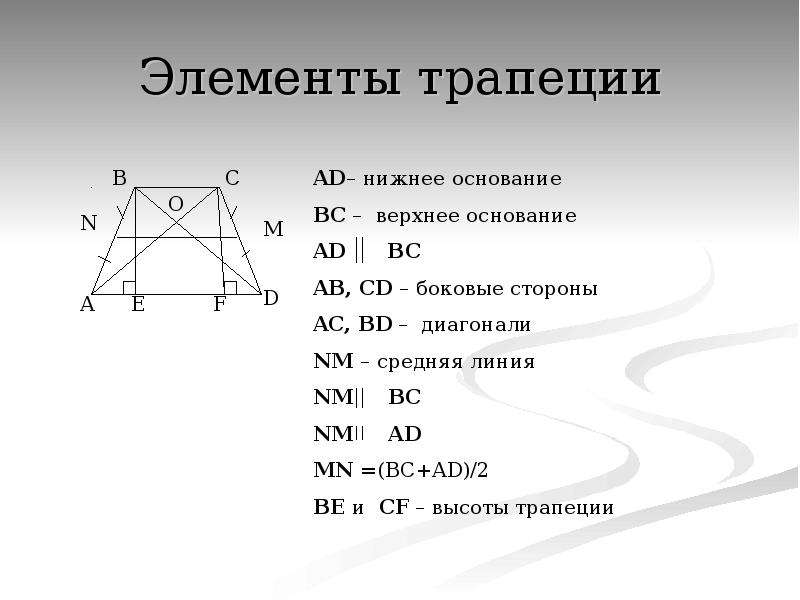 Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающую вторую прямую, то они пересекут на второй прямой равные между собой отрезки.
Если на одной из двух прямых отложить последовательно несколько равных отрезков и через их концы провести параллельные прямые, пересекающую вторую прямую, то они пересекут на второй прямой равные между собой отрезки.
Равнобедренная трапеция.
Теоремма средней линии трапеции.
Отрезок, соединяющий середины боковых сторон трапеции, параллелен основаниям трапеции.
Самостоятельная работа
- Вариант 1. Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120
- Вариант 2. Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона – 10 см, а один из углов равен 60 .
Проверь себя
8 см
6 см
90
90
30
30
30
30
10 см
60
3 см
8 см
3 см
5 см
5 см
6 см
Самостоятельная работа
- Вариант 3.
 Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .
Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .
90
6 см
30
60
30
12 см
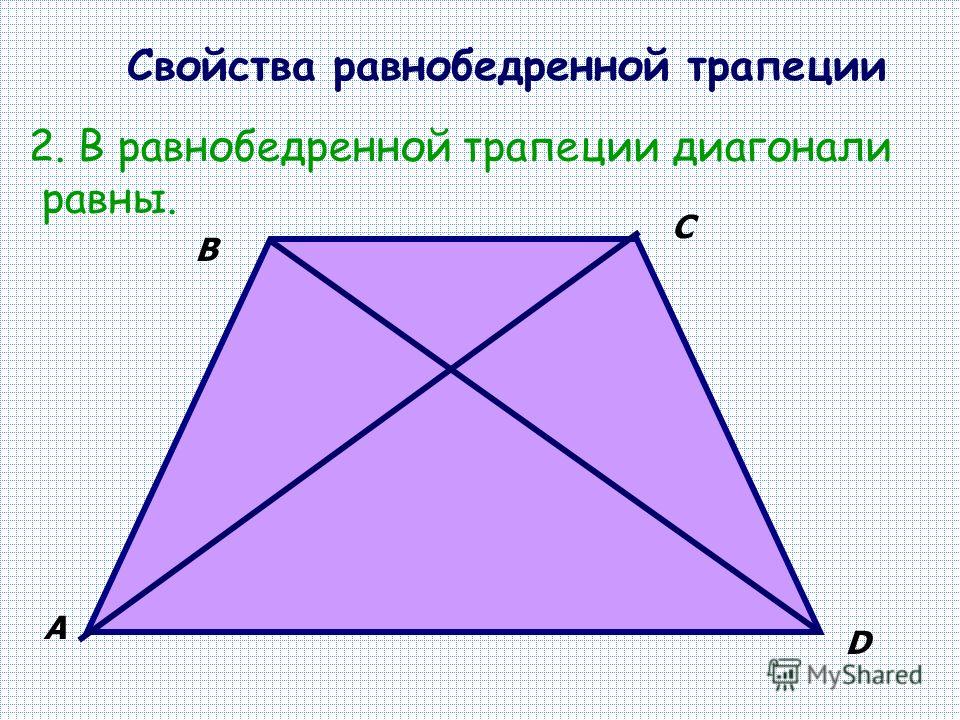
Свойства равнобокой трапеции
1. Углы при основаниях равны.
2. Диагонали равны.
3. Высоты, проведенные из вершин к основанию, делят трапецию на два равных треугольника.
Признаки равнобедренной трапеции.
Запишите самостоятельно.
Решение задач
№ 392(аб), 393(в), 394, 395, 397(а)
Домашнее задание
№ 392(аб), 393(в), 396, 398, 397 (б)
«Трапеция». 8-й класс
Цель:
- Ввести понятие трапеции, её элементов, виды трапеций.
- Рассмотреть некоторые свойства трапеции.
- Применение знаний при решении задач.

Ход урока
I. Организационный момент.
II. Актуализация знаний.
Кроссворд.
Ключевое слово кроссворда – является темой нашего урока.
- Любой многоугольник разделяет плоскость на две части, одна из которых называется …
- Четырехугольник, у которого противоположные стороны попарно параллельны.
- Отрезок, соединяющий любые две не соседние вершины многоугольника.
- Сумма длин всех сторон многоугольника.
- Две вершины многоугольника, принадлежащие одной стороне, называются…
- В конце урока каждый ученик ждет хорошую …
- Две несмежные стороны четырехугольника называются …
- Любой многоугольник разделяет плоскость на две части, одна из которых внутренняя, а другая
Ответы:
III. Новый материал.
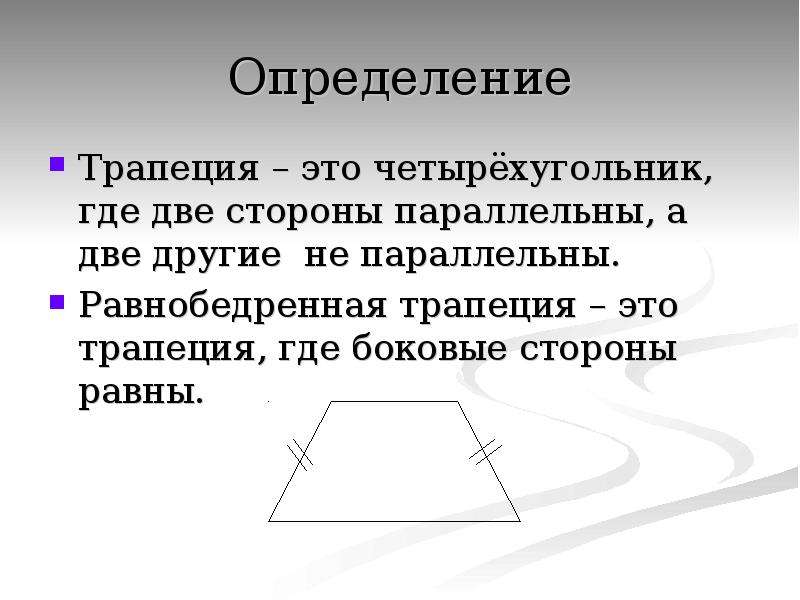
Трапеция – (от греч. trapezion, букв.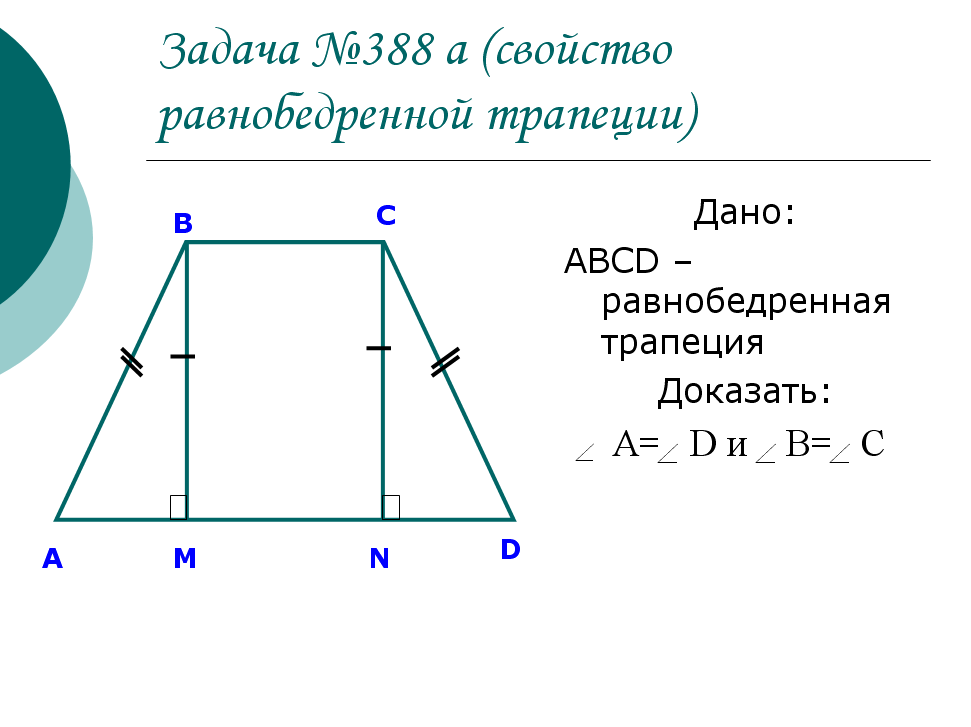 – столик).
– столик).
Трапеция – четырёхугольник, у которого две стороны параллельны, а две другие – непараллельные. Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Виды трапеции.
Равнобедренная – трапеция, у которой равны боковые стороны.
Прямоугольная – трапеция, один из углов которой прямой.
Средняя линия трапеции.
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Работа в группах.
Группы с четными номерами – исследуют диагонали равнобедренной трапеции. Группы с нечетными номерами – исследуют углы равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
Свойства равнобедренной трапеции.
Теорема. В равнобедренной трапеции углы при каждом основании равны.
Доказательство.
Проведем СЕ АВ.
ABCD – параллелограмм (АВ СЕ, ВС AD).
CD = AB = CE, СDE – равнобедренный, СDЕ = СЕD.
АВ СЕ, тогда СЕD = ВАЕ, СDЕ = СЕD = ВАЕ.
ABC = 180° – СDЕ = 180° – ВАЕ = BCD.
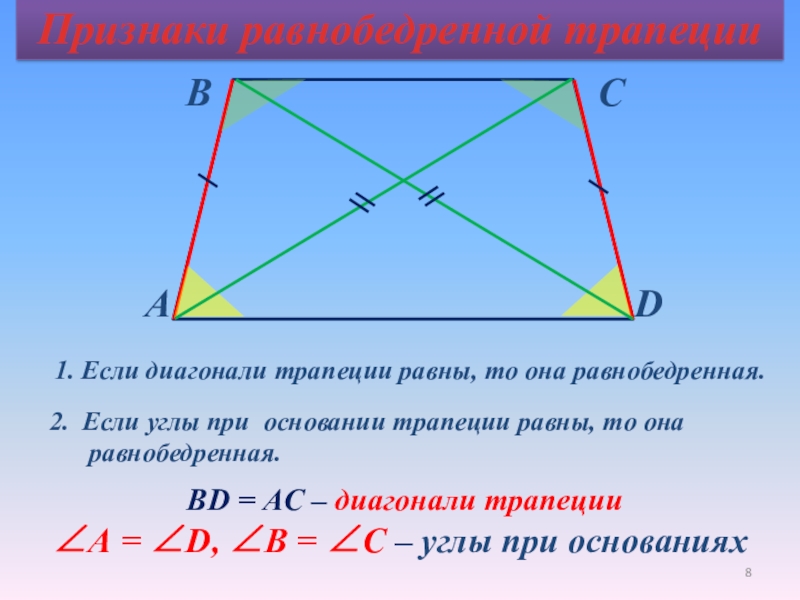
Теорема. В равнобедренной трапеции диагонали равны.
Доказательство.
ABC = DСВ (АВ = С, ВС – общая сторона, АВС = ВСD) тогда АС = ВD.
Сформулируйте утверждения, обратные свойствам, и выясните их справедливость.
Признаки равнобедренной трапеции.
Выслушать и обсудить результаты исследования, на доске и в тетрадях записать решения.
1. Если углы при основании трапеции равны, то она равнобедренная.
Доказательство.
Проведем ЕС АВ.
ABCЕ – параллелограмм, тогда АВ
СЕ,
А =
СЕD,
СЕD –
равнобедренный (D =
СЕD), тогда СЕ = СD.
АВ = СЕ = СD, тогда АВСD – равнобедренная трапеция.
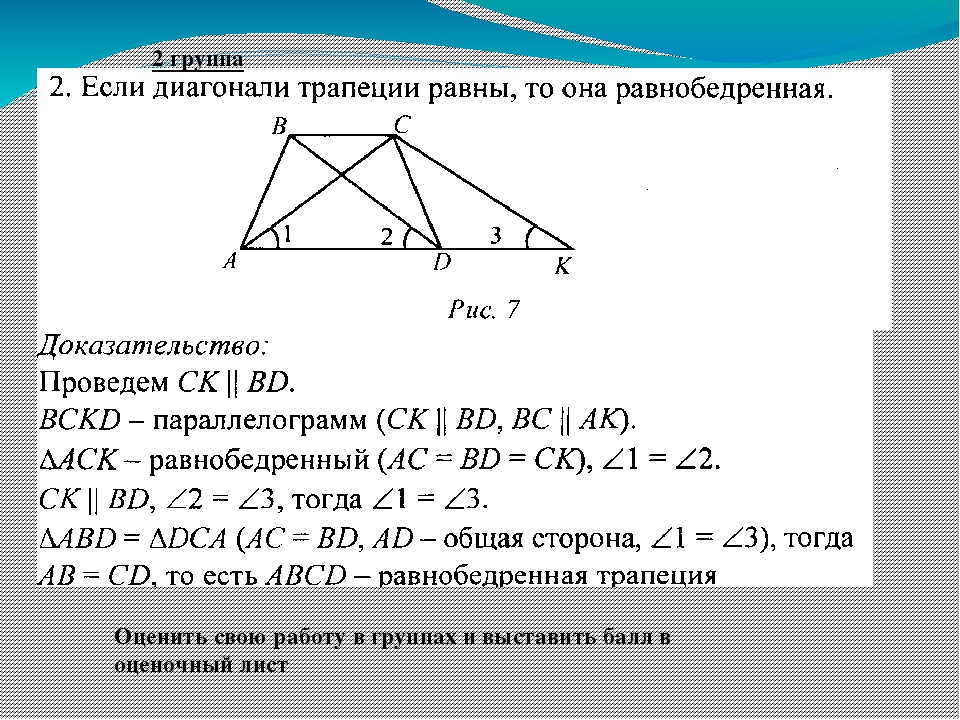
2. Если диагонали трапеции равны, то она равнобедренная.
Доказательство.
Проведем СК ВD.
ВСКD – параллелограмм (т.к. СК ВD, ВС АК).
АСК – равнобедренный, т.к. АС = ВD = СК, САD = СDА.
СК ВD, ВDА = СКD, тогда САD = СКD.
АВD = DСА, т.к. АС=ВD, АD – общая сторона, САD = СКD, тогда АВ = СD, т.е. АВСD – равнобедренная трапеция.
IV. Закрепление.
Решение задач по готовым чертежам.
V. Итог урока:
VI. Домашнее задание.
Параграф 44, вопросы: 10-11, №386, №388.
№ этапа, цель | Деятельность учителя | Деятельность ученика |
1. | Организационный момент. Подготовка учащихся к работе на занятии. | |
2. Установление правильности и осознанности выполнения домашнего задание всеми учащимися, выявление пробелов и их коррекция. | Проверка домашнего задания Вопросы: 1. Дать определение трапеции. 2. Перечислить виды трапеций 3. Сформулировать свойства трапеций | Вопросы по домашнему заданию |
Выполните задание (устно) 1. M N
Q K P MNPK- квадрат. Определить вид четырехугольника KOQP. Найти его углы. 2. ΔАВС – равносторонний. Определить вид MNCA. Найти его углы.
3. ΔАВС, С = 90°, А = 30°, ВС = 6. | Решение: KOQP – трапеция (по опр.) ОКР = 45° (КN –биссектриса К) КОQ = 180°-ОКР (свойство односторонних углов при КРǀǀOQ и RN – секущей) KOQ = 135° OQP = QPK = 90° KOQP – трапеция прямоугольная ΔMBN –равнобедренный, В = 60°, М = N = (180°- В) : 2 = 60°; равносторонний ВАС = ВМN, но они соответственные, при пересечении MN и АС секущей АВ, значит МNǀǀАС, MNCA – трапеция А = С = 60° М = N = 180° — А = 120° ВС = ½ АВ ( катет против 30°) ВС = 6, АВ = 12 | |
Повторим: Определение трапеции Свойства равностороннего треугольника Свойства и признаки параллельных прямых Свойство катета против катета | ||
Обеспечение восприятия осмысления и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения. | № 338(а). Докажите, что в равнобедренной трапеции углы при каждом основании равны. Как еще можно было доказать равенство углов. | 1. Проведем ВМАД и СНАД. 2. ВСǀǀМН (ВСǀǀАД) ВМǀǀСН, ВСНМ – параллелограмм, тогда ВМ = СН. 3.ΔАВМ=ΔДСН (по катету и гипотенузе: М = Н = 90°, АВ = СД (по усл.), ВМ = СН (свойство параллелограмма)), тогда А = Д 4. В + А = 180° и Д + С = 180° (свойство односторонних углов параллельных прямых) В = 180° — А С = 180° — Д Значит, В = С 1. Доп.построение: СЕǀǀАВ. 2. АВСЕ – параллелограмм, АВ = СЕ. 3. ΔЕСД – равнобедренный (АВ = СД (свойство параллелограмма) , СД = СЕ), тогда 1 = 2. 4. А = 1 как соответственные при СЕ ǀǀАВ и секущей АД. Т.к, А = 1, 1 = 2, то А = 2 (А = Д) 5. В + А = 180° и Д + С = 180° (свойство односторонних углов параллельных прямых) В = 180° — А С = 180° — Д Значит, В = С |
Установление правильности и осознанности усвоения нового учебного материала; выявление пробелов и неверных представлений и их коррекция | Повторим: Каким свойством обладают углы при основаниях равнобедренной трапеции? | |
Один из углов равнобедренной трапеции равен 43°. | 43°, 137° и 137° | |
№338(б)- устно. Докажите, что в равнобедренной трапеции диагонали равны. | ΔСВА = ΔВДА (по 2-м сторонам и углу между ними: АВ =СД, ВС- общая, В = С). В равных треугольниках соответственные элементы равны: АС = ВД. | |
Установление правильности и осознанности усвоения нового учебного материала | Повторим: Каким свойством обладают диагонали равнобедренной трапеции? | |
№339 – признаки равнобедренной трапеции а) Докажите, что трапеция равнобедренная, если углы при основании равны. б) Докажите, что трапеция равнобедренная, если ее диагонали равны. Как еще можно было доказать равенство АВ и СД? (на дом) Повторим: Сформулируйте признаки равнобедренной трапеции. | Трапеция равнобедренная, если боковые стороны равны). 1. ΔАВС = ΔДВС (по 2-м сторонам и углу между ними). Из равенства треугольников: АС = ВД, ВСА = СВД. 2. ΔАСД = ΔДВА (по стороне и 2-м прилежащим к ней углам: АД – общая, Д = А (по усл.), ВДА = САД (ВДА = СВД и ВСА = САД как накрест лежащие при ВСǀǀАД и соответственно секущих ВД и АС). Из Равенства треугольников: АВ = СД. Значит, трапеция – равнобедренная. 1. ΔАВС = ΔДВС (по 3-м сторонам). Из равенства треугольников: ВАС = СДВ. 2. Из равенства ΔАСД и ΔДВА (по 2-м сторонам и углу между ними: АС = ВД, АД- общая, САД= ВДА (САД= А — ВАС, ВДА = Д -СДВ) следует, АВ = СД. Значит, трапеция – равнобедренная. | |
Обеспечение усвоения новых знаний и способов действий на уровне применения в измененной ситуации. | Закрепление новых знаний. Самостоятельная работа2: В-I Найдите боковые стороны равнобедренной трапеции, основания которой равны 14 см и 8 см, а один из углов равен 120° В-II Найдите меньшее основание равнобедренной трапеции, если ее большее основание равно 16 см, боковая сторона 10 см, а одни уз углов равен 60°. Решение самостоятельной работы вывешиваются на магнитной доске | |
Формирование целостной системы ведущих знаний по теме. Дать анализ и оценку успешности достижения цели и наметить перспективу последующей работы. | Подведение итогов занятия. На следующем уроке продолжим знакомиться с задачами на построение. Научимся делить отрезок на п равных частей. | 1. Определение равнобедренной трапеции. 2. Свойства равнобедренной трапеции 3. Признаки равнобедренной трапеции |
Мобилизация учащихся на рефлексию своего поведения (мотивации, способов деятельности, общения). Усвоение принципов саморегуляции и сотрудничества. | Рефлексия: | |
Обеспечение понимания цели, содержания и способов выполнения домашнего задания. | На дом. | в.10, 11 стр. 114-115; № 392(а, б), 483; повтор §4 и №22, п.38, задача 1; принести циркуль. |
Фрагмент урока по геометрии «Равнобедренная трапеция» (8 класс)
Фрагмент урока геометрии в 8 классе
с применением исследовательского метода обучения
Создает условия для осмысления новых понятий. Задает вопросы, поправляет ответы
Мы познакомились с таким четырехугольником как трапеция. Дайте определение трапеции. Назовите трапеции, изображенные на рисунке.
Как вы думаете, сущуствуют ли особые виды трапеции?
Сегодня мы изучим этот четырехугольник. Что интересует геометров при изучении фигур в первую очередь?
Соотношения между сторонами и углами.

Какова цель нашего исследования?
Выявить соотношения между элементами трапеции, изучить другие особенности этой фигуры.
Слушают учителя, дополняют ответы друг друга.
Учащиеся высказывают предположение о существовании особых видов трапеции. Ученики ставят проблемный вопрос:
“Существует ли особый вид трапеции? Какими свойствами он обладает?”
Познакомиться с понятием трапеция, ее элементами.
Распознавать трапецию, ее элементы на чертежах.
Коммуникативные: уметь высказывать свои мысли на заданную тему, оформлять свои высказывания устно
Исследование
Организует общую работу над исследованием
Класс делится на группы. Каждая группа получает чертежи равнобедренных трапеций и проводит исследование по плану:
Назвать основные элементы трапеции: стороны, углы, диагонали.
Измерить с помощью инструментов стороны, углы, диагонали.
Трапеция Заполнить таблицу.
Заполнить таблицу.
Основания
Боковые стороны
Углы
Диагонали
Если можно, придумайте название этой группе.
Сформулируйте гипотезы о свойствах сторон, углов, диагоналей.
А
Каждая группа выполняет полученное задание и по результатам заполняет таблицу
Познакомиться с понятием равнобедренная трапеция, научиться формулировать ее свойства
Регулятивные: уметь действовать по алгоритму
Коммуникативные:
уметь выражать свои мысли в устной и письменной форме
Познавательные : уметь анализировать и делать выводы
Обмен информацией
Организует общую работу над заполнением таблицы
На доске вычерчена заготовка таблицы, аналогичная тем, что получили группы. Первая группа при отчете записывает в эту таблицу данные о первой трапеции, вторая группа – о второй трапеции, третья – о третьей и т.д. После отчета всех групп на доске появляется заполненная таблица:
Первая группа при отчете записывает в эту таблицу данные о первой трапеции, вторая группа – о второй трапеции, третья – о третьей и т.д. После отчета всех групп на доске появляется заполненная таблица:
Основания
Боковые стороны
Углы
Диагонали
ABCD
AD = 6см,
ВС = 4см
АВ = 3 см,
СD = 3см
А = 600,
В = 1200,
С = 600,
D = 1200
АС = 5,5см,
ВD = 5,5см
Каждая группа, используя полученные результаты заполняет свою строку в таблице
Выдвижение гипотез
Создает условия для осмысления результатов исследования. Задает вопросы, поправляет ответы
Что общего у всех трапеций? Как их можно назвать?
Можем ли мы сделать предположение о свойствах углов, диагоналей равнобедренной трапеции?
Сформулируем другие особенности трапеции.

Высоты, проведенные из вершин меньшего основания, отсекают от нее равные прямоугольные треугольники.
Диагонали разбивают трапецию на два равных и два равнобедренных треугольника.
Можно ли считать, что мы изучили фигуру? Нет. У нас только гипотезы.
Сформулируем и докажем утверждения.
Выдвигают гипотезу.
Углы при основаниях равны. Сумма углов при боковой стороне равна 1800.
Диагонали равны.
Познавательные: сопоставлять характеристики по одному или нескольким признакам; выявлять сходства и различия объектов
Коммуникативные:
уметь аргументировать своё мнение и позицию
Доказательство истинности гипотезы
Организует общую работу над доказательством свойств и признаков равнобедренной трапеции. Задает вопросы
Работа с учебником. Выполнение № 388, 389
Какие задачи можно будет решать с помощью свойств и признаков равнобедренной трапеции?
Доказывают утверждение задачи № 388.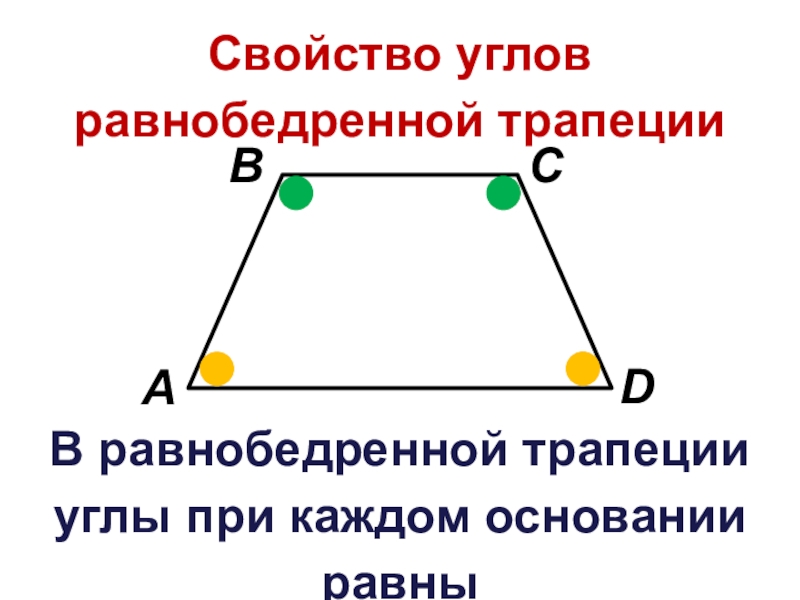 Формулируют свойства:
Формулируют свойства:
А) В равнобедренной трапеции углы при каждом основании равны.
Б) Диагонали трапеции равны.
Доказывают утверждения задачи № 389. Формулируют признаки равнобедренной трапеции:
А) Если в трапеции углы при основании равны, то такая трапецияравнобедренная.
Б) Если в трапеции диагонали равны, то такая трапеция равнобедренная
Научиться формулировать и доказывать свойства и признаки равнобедренной трапеции
1. Трапеция, ее виды и свойства Свойства трапеции, которые часто используются при решении задач
Раздел 2. Четырехугольники
I. Справочные материалы.
1. Трапеция, ее виды и свойства
Свойства трапеции, которые часто используются при решении задач:
1)
Диагонали трапеции разбивают её на
четыре треугольника с общей вершиной.
Площади треугольников, прилежащие к
боковым сторонам, равны.
2) В любой трапеции середины оснований, точка пересечения диагоналей и точка пересечения прямых, на которой лежат боковые стороны, лежат на одной прямой (точки М, N, О и К).
3) В равнобокой трапеции углы при основании равны.
4) В равнобокой трапеции прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии этой трапеции,
5) В равнобокой трапеции диагонали равны.
6) В равнобокой трапеции высота, опущенная на большее основание из конца меньшего основания, делит его на два отрезка, один из которых равен полуразности оснований, а другой их полусумме.
7) Во всякой трапеции серединам боковых сторон и середины диагоналей лежат на одной прямой.
8) Во всякой трапеции отрезок, соединяющий середины диагоналей, параллелен основаниям и равен полуразности оснований.
9) во
всякой трапеции сумма квадратов
диагоналей равна сумме квадратов боковых
сторон и удвоенного произведения
оснований.
10) Трапецию можно вписать в окружность тогда и только тогда, когда она равнобокая.
11) Трапецию можно описать около окружности тогда и только тогда, когда сумма оснований равна сумме боковых сторон.
2.Вписанные и oписанные четырёхугольники.
1)Если четырёхугольник вписан в окружность, то сумма противолежащих углов равна 180°.
Верно и обратное: если сумма противолежащих углов четырёхугольника равна 180°, то около этого четырёхугольника можно описать окружность.
2)Около параллелограмма можно описать окружность тогда и только тогда, когда этот параллелограмм есть прямоугольник.
3)Около трапеции можно описать окружность, если она равнобокая.
четырёхугольник называется описанным около окружности, если окружность касается всех его сторон.
4)Если четырёхугольник описан около окружности, то суммы противолежащих сторон равны.
5)Если
в выпуклом четырёхугольнике суммы
противоположных сторон равны, то в этот
четырёхугольник можно вписать окружность.
3. Площади четырёхугольников.
Площадь выпуклого четырёхугольника равна половине произведения диагоналей на синус угла между ними.
Ромб
1. Диагонали ромба взаимно перпендикулярны и делят углы пополам.
2. Площадь определяется формулами:
Параллелограмм
1. Сумма квадратов диагоналей равна сумме квадратов всех его сторон.
2. Площадь определяется формулой
S=ah
S=аb·sinА
.
II. Дополнительные материалы
1)Свойства вписанного выпуклого четырехугольника.
а)В выпуклом вписанном четырехугольнике сумма противоположных углов равна двум прямым
б)Обратно: если в выпуклом четырехугольнике сумма противоположных углов равна двум прямым, то около него можно описать окружность
Доказательство.
а) Пусть АВСD есть вписанный выпуклый четырехугольник; требуется доказать„ что
Так как
сумма всех четырех углов сякого выпуклого
четырехугольника равна 4d,
то достаточно доказать только одно из
требуемых равенств.
докажем, например, что
Углы В и D как вписанные, измеряются: первый—половиной дуги ADC, второй- половиной дуги АВС;
Следовательно, сумма ½ ﬞ ADC+ ½ ﬞ ABC , а эта сумма равна 1/2 (ﬞ ADС+ ﬞ ABC), т. е. равна половине окружности; значит,
б) Пусть АВСD есть такой выпуклый четырехугольник, у которого
Через какие-нибудь три его вершины, например, через A,В и С, проведем окружность (что всегда можно сделать).
Четвертая вершина D должна находиться на этой окружности, пoтoму что в противном случае вершина угла В лежала бы или внутри круга, или вне его, и тогда этот угол не измерялся бы половиной дуги АВС; поэтому cyммa
измерялась бы полусуммой дуг ADC и АВС и, значит, сумма
Следствия
1) из всех параллелограммов только вокруг прямоугольника можно описать окружность.
2) около трапеции можно описать окружность только тогда, когда она равнобокая.
2)
Свойство описанного четырехугольника.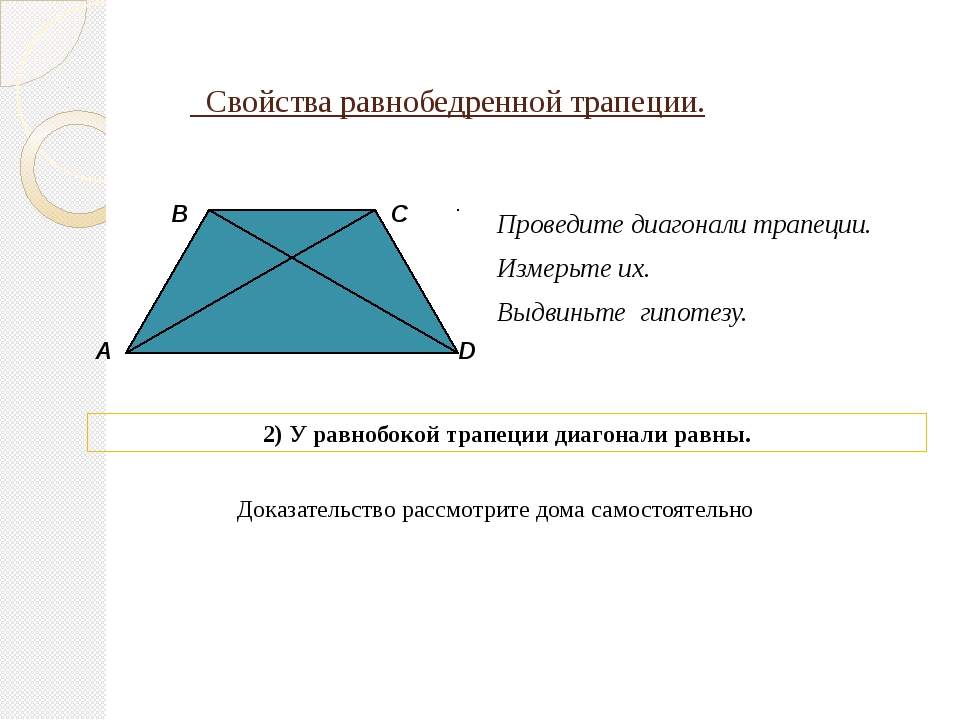 В описанном четырехугольнике суммы
противоположных сторон равны.
В описанном четырехугольнике суммы
противоположных сторон равны.
Пусть АВСD будет описанный четырехугольник, Т.е, стороны его касаются окружности; требуется доказать, что АВ+СВ=ВС+АD
Обозначим точки касания буквами M, N, Р и Q. Так как две касательные, проведенные из одной точки окружности, равны, то АМ.=АQ, ВМ=ВN, CN=СР, DP=DQ.
Следовательно, АМ+МВ+СР+РD=AQ+QD+BN+NC. Т.е. АВ+СD=АD+ВС.
III. Вводные задачи.
Задача 1.
Средняя линия трапеции ABCD равна 15. AD – большее основание трапеции, A = 90°, D = 60°, BAC = 30°. Найдите длину стороны CD.
Решение.
В ∆ABC (он прямоугольный) BC = – по свойству катета, лежащего против угла в 30°.
BAC = 30°, значит, CAD = 90° – 30° =
= 60°, следовательно, ∆ACD равносторонний,
т. е. AC = CD = AD = 2BC.
Средняя линия MN = 3BC = 30,
BC = 10, значит, CD = 2 · 10 = 20.
Ответ:20.
Задача 2.
Сторона AB параллелограмма ABCD равна а его диагонали равны 20 и 24. Найдите сторону BC.
Решение.
Для любого выпуклого четырехугольника справедливо
где a, b, c и d – стороны четырехугольника, а d1, d2 – его диагонали.
В параллелограмме
202 + 242 = 2(( )2 + b2), b > 0; b2 + 88 = 488,b2 = 400, b = 20.
Ответ: 20.
Задача 3.
Основания трапеции равны 4 и 10, а ее боковые стороны – и 15. Найдите косинус наименьшего угла этой трапеции.
Решение.
1)
Проведем BM ∥ CD, значит, BMA =D, ВСDМ – параллелограмм, так как ВМ || MD, ВМ || СD. Следовательно, ВС = MD = 4,
BM = CD = 15, AM = AD – MD = 10 – 4 = 6.
2) В ∆AMB против большей стороны (выбирая из AB и BM) лежит больший угол: AB BM, значит, BMA A.
cos α = .
.
Ответ: 0,8.
Задача 4.
Определите периметр равнобокой трапеции, у которой длина меньшего основания равна 7, диагонали перпендикулярны боковым сторонам и равны .
Решение.
1)
Проведем в трапеции ABCD высоту CF,
тогда
∆ACD ∼ ∆AFC,
2) Пусть FD = x, тогда AF = 7 + x
( )2 = (x + 7) (7 + 2x),
36 · 2 = 49 + 21x + 2x2,
2x2 + 21x – 23 = 0,
D = 212 + 4 · 2 · 23 = 625,
х1,2 =
3) Итак, AD = 7 +2 = 9;
CD =
P = 9 + 7 + 2 · 3 = 22.
Ответ: 22.
Задача 5.
В ромбе высота, проведенная из вершины тупого угла, делит сторону ромба пополам. Найдите периметр и высоту ромба, если меньшая диагональ его равна 7
Решение.
1) В треугольнике ABD BK – высота и медиана, значит, ∆ABD -равнобедренный с основанием AD, т. е. AB = BD = 7 см. Тогда ∆ABD -равносторонний, значит, A = ABD = BDA = 60°.
2) P = 4AB = 4 · 7 = 28 (см).
3) BKD – прямоугольный, BK = AD sin BDK.
BK = 7 · sin 60° = (см). Ответ: 28 см; 3,5 см.
Задача 6.
Основание AB трапеции ABCD вдвое длиннее основания CD и вдвое длиннее боковой стороны AD. Длина диагонали AC равна 12, длина боковой стороны BC равна 5. Найдите площадь трапеции.
Решение.
1)
По условию AB = 2AD = 2DC.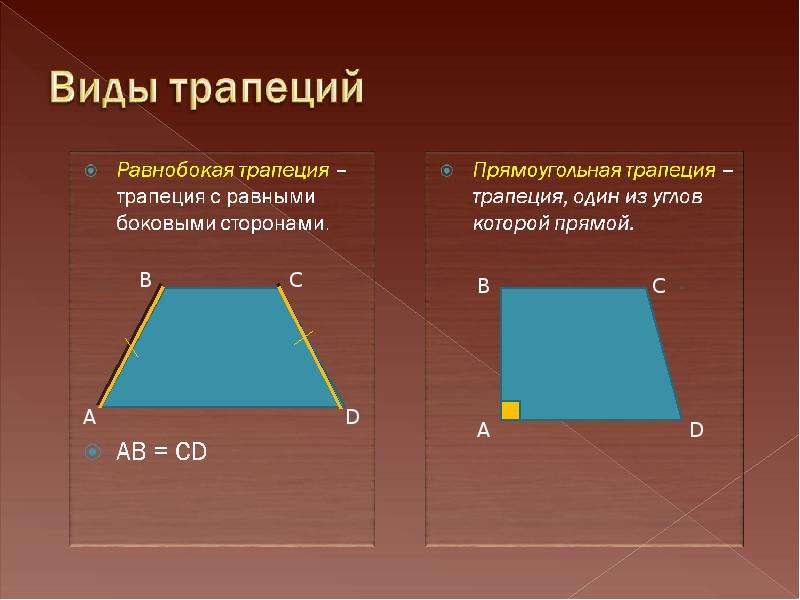
Пусть M – середина AB, тогда AM = MB = CM,
т. е. CM – медиана треугольника ABC и CM = AB, значит, ∆ABC прямоугольный с гипотенузой AB.
По теореме Пифагора AB2 = AC2 + BC2; AB = = = = 13.
CM = MB = = 6,5.
2) CK – высота трапеции и высота ∆MCB.
По формуле Герона S∆ = где ;
S(∆MBC) = = 3 · 2 · 2,5 = 15.
CK =
S(ABCD) =
Ответ: 4,5.
IV. Дополнительные задачи
№ 1.
Вершина C параллелограмма
ABCD соединена с точкой N
на стороне AB.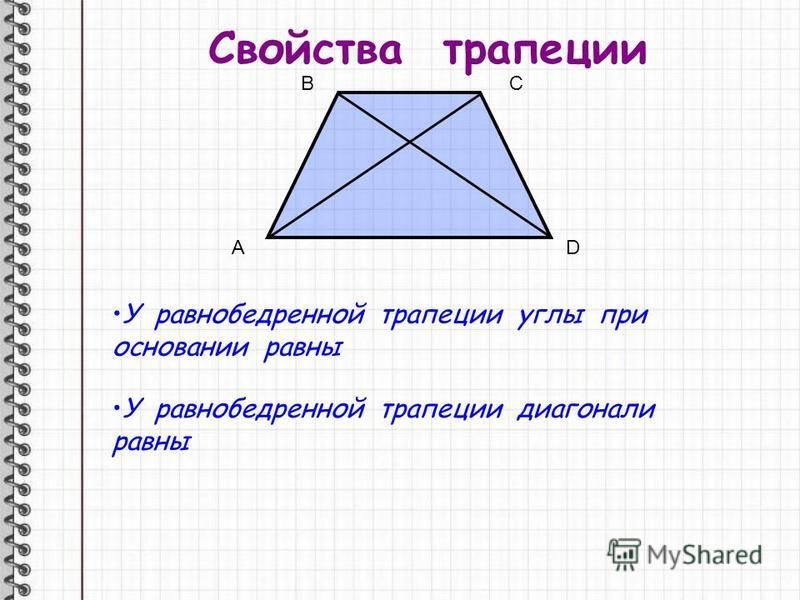 Отрезок CN
пересекает диагональ BD
в точке P. Площадь
треугольника BNP равна 8,
а площадь треугольника BCP
равна 12. Найдите площадь параллелограмма
ABCD.
Отрезок CN
пересекает диагональ BD
в точке P. Площадь
треугольника BNP равна 8,
а площадь треугольника BCP
равна 12. Найдите площадь параллелограмма
ABCD.
Решение:
1) Треугольники BNP и BPC имеют общую высоту BH=>
SBNP/SBPC=PN/PC=>PN/NC=2/3;
2) Треугольники BPN и DPC подобны по
двум углам => SBPN/SDPC=(PN/PC)2
SDPC=9/4; SBPN = (9/4)·8=18;
3) SBCD=SBPC+SDPC=12+18=30;
4) SABCD=2·SBCD=60; Ответ: 60
№ 2.
На стороне AB параллелограмма ABCD, как на диаметре, построена окружность, проходящая через точку пересечения диагоналей и середину стороны AD. Найдите углы параллелограмма.
Решение:
1) По условию, AB – диагональ=> o=>ABCD – ромб
P – середина АВ: по условию Q – середина AD=>PQ – средняя линия ∆ABD=BD=2PQ;PQ=R=>BD=2R;
PO=R – средняя линия ∆АBD=>AD=2·PO=R
∆ABD – правильный => o=> o.

Ответ: 60o и 120o.
№ 3.
Угол между сторонами АВ и СD четырехугольника ABCD=φ. Докажите, что AD2=AB2+BC2+CD2-2(AB·BCcosB + BC·CDcosC+CD·ABcosφ)
Решение.
По теореме косинусов AD2=AC2+CD2-2AC·CD·cosACD и AC2=AB2+BC2-2AB·BCcosB. A так как длина проекции отрезка АС на прямую l , перпендикулярную CD, равна сумме длин проекций отрезков АВ и ВС на прямую l, то ACcosACD=ABcosφ+BCcosC
V.Задачи для самостоятельного решения
№1. Докажите, что если ABCD прямоугольник, а Р- произвольная точка, то
АР2 +СР2 =DP2 +BP2
№2. Перпендикуляр, опущенный из вершины параллелограмма на диагональ, делит ее на отрезки длиной 6 и 15. Найдите большую сторону параллелограмма, если известно, что разность сторон равна 7.
Ответ: 7
№3. Одно из оснований трапеции равно
24, а расстояние между серединами
диагоналей 4. найдите другое основание.
Одно из оснований трапеции равно
24, а расстояние между серединами
диагоналей 4. найдите другое основание.
Ответ: 16
№4. Длины оснований равнобедренной трапеции относятся как 5:12, а длина ее высоты равна 17. Найдите радиус окружности, описанной около трапеции, если средняя линия равна высоте.
Ответ: 13
№5. В трапеции ABCD диагональ АС перпендикулярна боковой стороне СD. Окружность, описанная возле треугольника АВС, касается прямой CD, пересекает основание AD в точке М. Найдите площадь трапеции АBCD, если АМ=8, СМ=4.
Ответ: 36
№6. Окружность, центр которой лежит внутри квадрата PQRS, касается стороны PQ в точке К, пересекает сторону PS в точках А и В,, а диагональ PR в точках С и D. Найдите радиус окружности, если АВ=16, СD=2√92
Ответ: 10
№7. В параллелограмме ABCD угол АВС=3п/4. окружность, описанная возле треугольника АВD, касается прямой CD. Найдите площадь параллелограмма, если диагональ BD=2
Ответ: 4
№8.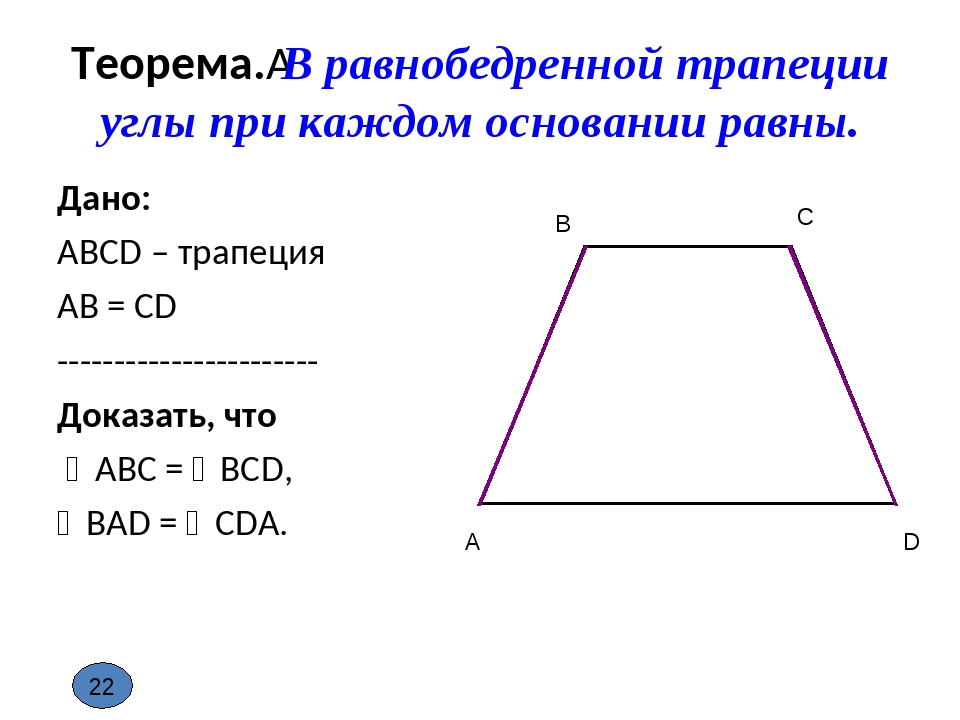 Вершина С параллелограмма ABCD соединена
с точкой N на стороне АВ. Отрезок CN
пересекает диагональ BD в точке Р. Площадь
треугольника BNP равна 8, а SВСР=12.
Найдите площадь параллелограмма АВСD.
Вершина С параллелограмма ABCD соединена
с точкой N на стороне АВ. Отрезок CN
пересекает диагональ BD в точке Р. Площадь
треугольника BNP равна 8, а SВСР=12.
Найдите площадь параллелограмма АВСD.
Ответ: 60
№9. Найдите площадь трапеции, основания которой 6 и 26, а боковые стороны – 12 и 16.
Ответ: 153,6
№10. На стороне АВ параллелограмма АВСD как на диаметре построена окружность, проходящая через точку пересечения диагоналей и середину стороны АD. Найдите углы параллелограмма.
Ответ: 60,120,60,120.
VI. Контрольные задачи.
Вариант № 1.
1) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.
2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 26, а разность оснований равна 10.
3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К. Найдите периметр
параллелограмма, если АК = 12, СМ = 24, МК =
18.
Найдите периметр
параллелограмма, если АК = 12, СМ = 24, МК =
18.
Вариант № 2.
1) В круг с площадью 169π вписана равнобедренная трапеция, меньшее основание которой равно 10. найдите площадь трапеции, если центр описанного круга лежит на её большем основании.
2) Найдите диаметр окружности, вписанной в равнобедренную трапецию, если сумма оснований трапеции 15, а разность оснований равна 9.
3)В параллелограмме АВСД биссектриса угла Д пересекает сторону АВ в точке К и прямую ВС в точке Р. Найдите периметр ∆ СДР, если ДК = 18, РК = 24, АД=15.
Вариант № 3.
1) В равнобедренную трапецию, площадь которой 20, а синус одного из углов равен 0,8, вписана окружность. Найдите радиус этой окружности.
2) Основание СМ и ОР трапеции СМОР равны 3 и 6 соответственно, диагонали трапеции пересекаются в точке Н, а площадь треугольника СРН равна 4. Найдите площадь трапеции.
3)В параллелограмме АВСД биссектриса
угла С пересекает сторону АД в точке М
и прямую АВ в точке К.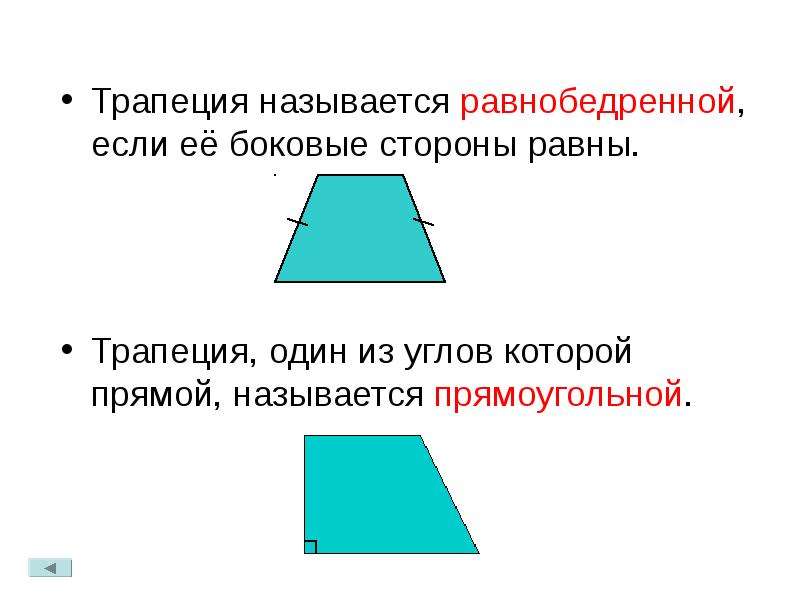 Найдите периметр
∆ АМК, если СД = 12, СМ = 14, СВ = 30.
Найдите периметр
∆ АМК, если СД = 12, СМ = 14, СВ = 30.
Вариант № 4.
1) Найдите площадь равнобедренной трапеции, если её высота равна 4, а тангенс угла между диагональю и основанием равен .
2) В равнобедренную трапецию, площадь которой равна 80, вписана окружность радиуса 4. Найдите периметр трапеции.
3) В параллелограмме АВСД биссектриса угла В пересекает сторону СД в точке Т и прямую АД в точке М. Найдите периметр ∆ АВМ, если ВТ = 18, ТМ = 12, ВС = 15.
Тема: «Трапеция» Учитель: Синиченкова Галина Алексеевна
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
Этап урока Деятельность учителя Деятельность ученика 1 2 4 5 Организационный момент Актуализация знаний. Целеполагание и мотивация Изучение нового материала. Закрепление изученного материала. Решение задач.
Целеполагание и мотивация Изучение нового материала. Закрепление изученного материала. Решение задач.
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА Предмет: геометрия 9 Б 9 Д 9 Е Номер урока в КТП: 56 Преподаватель: УМК, учебник: Геометрия: Учебник для 7-9 классов общеобразовательных учреждений /А. В. Погорелов. М.: Просвещение,
ПодробнееУрок по теме «Треугольник». 7-й класс
Урок по теме «Треугольник». 7-й класс Николаева Наталия Геннадьевна Цели урока: Образовательные: o ввести определение треугольника и его элементов, периметра треугольника, понятие равных треугольников.
ПодробнееПодробный конспект урока.
Подробный конспект урока.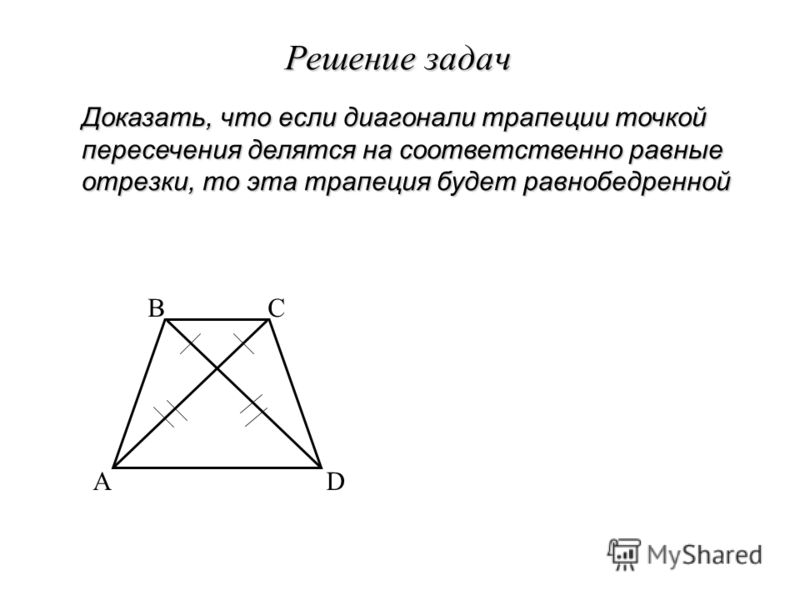 Тема урока Предмет Класс Автор урока (ФИО, должность) Образовательное учреждение Город/поселение Тип урока Цели урока Организационная информация Площадь параллелограмма геометрия
Тема урока Предмет Класс Автор урока (ФИО, должность) Образовательное учреждение Город/поселение Тип урока Цели урока Организационная информация Площадь параллелограмма геометрия
Повышение качества знаний.
Повышение качества знаний. Открытый урок по геометрии в 8 классе Тема урока: Прямоугольник. Ромб. Квадрат. Автор: Напцок Сулиет Чемальевна, учитель математики, МБОУ СШ 5, п.яблоновский Цель: сформировать
ПодробнееСУММА УГЛОВ ТРЕУГОЛЬНИКА
ТЕМА УРОКА: СУММА УГЛОВ ТРЕУГОЛЬНИКА ТИП УРОКА: УРОК ФОРМИРОВАНИЯ НОВЫХ ЗНАНИЙ Данилова Светлана Леонидовна учитель математики МБОУ Лицея 1 г. Сургут ЦЕЛЕВАЯ НАПРАВЛЕННОСТЬ УРОКА Данный урок является первым
ПодробнееРешение задач с помощью двумерных диаграмм
Муниципальное бюджетное общеобразовательное учреждение «Основная общеобразовательная школа 3» Киселёвского городского округа Решение задач с помощью двумерных диаграмм Занятие элективного курса по математике
ПодробнееD
Открытый урок по геометрии в 0 классе Тема: «Расстояния между прямыми и плоскостями в прямоугольном параллелепипеде» Цели урока: ) Образовательные: вспомнить и систематизировать те знания, которые ученики
ПодробнееКонспект открытого урока
Конспект открытого урока «11» мая 2013 г.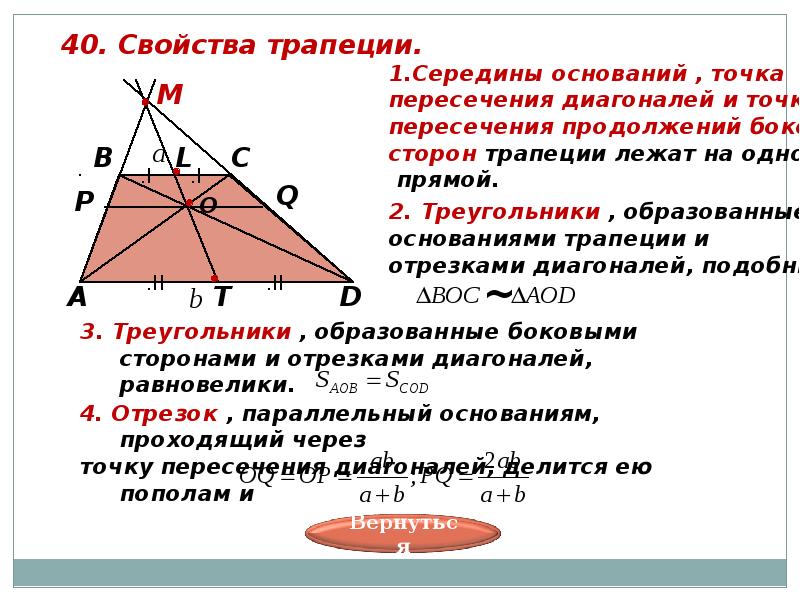 Класс 10 «А» Предмет математика Учитель Новгородова Н.И. Цель посещения в рамках обобщения опыта работы Тема урока «Построение сечений многогранников» Тип урока:
Класс 10 «А» Предмет математика Учитель Новгородова Н.И. Цель посещения в рамках обобщения опыта работы Тема урока «Построение сечений многогранников» Тип урока:
Технологическая карта урока
Технологическая карта урока Учитель: Кривцовой О. И. Класс: 2 «Б» УМК: «Школа России» Предмет: математика. Тема урока: Периметр прямоугольника. Вычисление периметра. урока: урок открытия новых знаний Место
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности, для изучения
ПодробнееТехнологическая карта урока
Технологическая карта урока Тема: Площадь прямоугольного треугольника.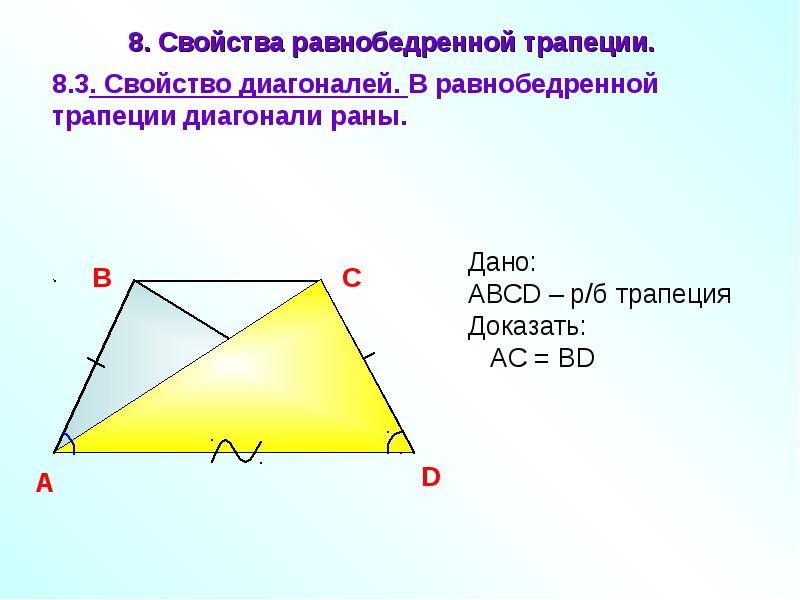 Класс: 4 класс. Предмет: математика. УМК (авторы): УМК «Перспектива», автор Л.Г. Петерсон Тип урока: открытие нового знания. Планируемые
Класс: 4 класс. Предмет: математика. УМК (авторы): УМК «Перспектива», автор Л.Г. Петерсон Тип урока: открытие нового знания. Планируемые
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА
ТРУДНЫЕ ТЕМЫ В ГЕОМЕТРИИ 10 КЛАССА ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ. Эта тема считается трудной. Если работать на обычной доске, много времени уходит на построение рисунков, условие задачи не всегда позволяет
Подробнее«Цилиндр. Площадь поверхности цилиндра»
Государственное бюджетное общеобразовательное учреждение средняя общеобразовательная школа 49 Петродворцового района Санкт-Петербурга имени Героя Российской Федерации М.Ю. Малофеева Методическая разработка
Подробнее«Смежные и вертикальные углы»
Муниципальное автономное общеобразовательное учреждение средняя общеобразовательная школа 92 г.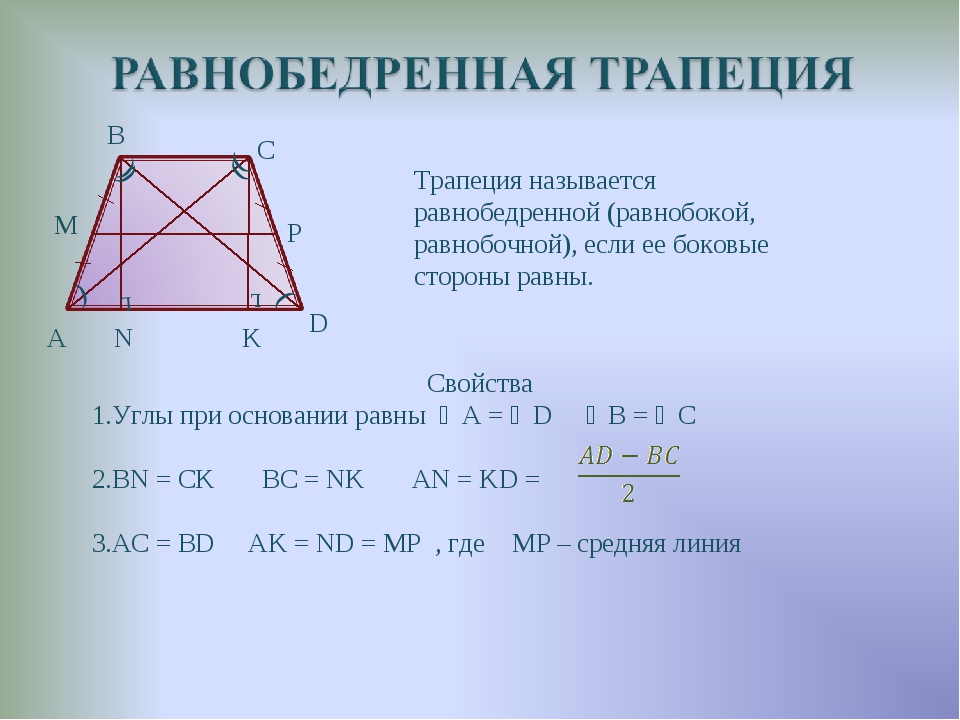 Тюмень учитель математики: Гобец Елена Ивановна Методическая разработка урока по теме «Смежные и вертикальные
Тюмень учитель математики: Гобец Елена Ивановна Методическая разработка урока по теме «Смежные и вертикальные
Задачи: Обучающие: Развивающие:
Технологическая карта урока (7 класс ). Ф.И.О. учителя: Стихина Ольга Николаевна 2. Класс: 7 Предмет:Геометрия 3. Тема урока: Призгаки параллельности прямых Тип урока: Урок изучения нового материала Геометрия
ПодробнееПЛАН-КОНСПЕКТ УРОКА 1. ФИО
ПЛАН-КОНСПЕКТ УРОКА Тема: «Сложение чисел с разными знаками» 1. ФИО (полностью) Федосеева Ольга Васильевна 2. Место работы ГБОУ школа-интернат 1 г.о. Чапаевск 3. Должность Учитель математики 4. Предмет
ПодробнееПОЯСНИТЕЛЬНАЯ ЗАПИСКА
8 класс геометрия ПОЯСНИТЕЛЬНАЯ ЗАПИСКА Школьное математическое образование ставит следующие цели обучения: овладение конкретными математическими знаниями, необходимыми для применения в практической деятельности,
ПодробнееТехнологическая карта урока по геометрии
Технологическая карта урока по геометрии Автор: Турукина Светлана Ивановна, учитель математики, МБОУ «СОШ 6» города Обнинска Предмет: Геометрия Класс: 9 класс Тип урока: урок «открытия нового знания» Тема:
Подробнее«Волжский городской лицей»
Министерство образования республики Марий Эл «Волжский городской лицей» РАЗРАБОТКА УРОКА ПО ТЕМЕ: «СУММА УГЛОВ ТРЕУГОЛЬНИКА» Выполнила: Казакова С. В. учитель математики г. Волжск 2016 г. 1 Методическая
В. учитель математики г. Волжск 2016 г. 1 Методическая
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА В рабочей программе представлены содержание математического образования, требования к обязательному и возможному уровню подготовки обучающегося, виды контроля, а также компьютерное
ПодробнееТехнологическая карта урока
Технологическая карта урока Учитель: Стекольникова О.А., МБОУ Школа 176, учитель математики и информатики Предмет: геометрия Класс: 7Б Тема урока: Сумма углов треугольника Тип урока: урок изучения нового
ПодробнееУрок геометрии в 8 классе
Урок геометрии в 8 классе Тема: «Итоговое повторение курса геометрии 8 класса» Продолжительность урока: 90 минут Цели урока: обучающие: обобщение знаний по курсу геометрии 8 класса; развивающие: развитие
ПодробнееПояснительная записка
Количество уроков на год всего 68 ч. В неделю ч. Контрольных работ — 5. Пояснительная записка Цели и задачи программы: формирование представлений о математике как универсальном языке науки, средстве моделирования
В неделю ч. Контрольных работ — 5. Пояснительная записка Цели и задачи программы: формирование представлений о математике как универсальном языке науки, средстве моделирования
Математика 4 класс программа «Перспектива»
Математика 4 класс программа «Перспектива» Нахождение площади прямоугольного треугольника Цель урока: развивать у учащихся пространственное воображение и логическое мышление путем изучения площади треугольника
Подробнее«УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС
УРОК ГЕОМЕТРИИ ПО ТЕМЕ: «УГОЛ МЕЖДУ ПРЯМОЙ И ПЛОСКОСТЬЮ» 10 КЛАСС — 1 ЦЕЛИ: Образовательная введение нового понятия; отработка знаний, умений и навыков по нахождению угла между прямой и плоскостью; умение
ПодробнееТрапеция свойства и признаки трапеции площадь трапеции.
 Трапеция. Свойства трапеции. Теоремы: свойства трапеции
Трапеция. Свойства трапеции. Теоремы: свойства трапецииСоблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.
 д.
д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо — в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ — раскрыть вашу персональную информацию.
 Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях. - В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности — включая административные, технические и физические — для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Определение
Трапеция — это четырехугольник $A B C D$, две стороны которого параллельны,
а две другие не параллельны (рис. {\circ}$ (рис 1)
{\circ}$ (рис 1)
Отрезок, соединяющий середины боковых сторон трапеции, называется средней линией трапеции. Средняя линия трапеции параллельна основаниям и равна их полусумме:
$$M N=\frac{A D+B C}{2}$$
Среди всех трапеций можно выбрать два особых класса трапеций: прямоугольные и равнобокие трапеции.
Определение
Прямоугольной называется трапеция, у которой один из углов прямой.
Равнобокой называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции
- В равнобокой трапеции углы при основании попарно равны $\angle A=\angle D, \angle B=\angle C$.
- Диагонали равнобокой трапеции равны $A C=B D$.
Признаки равнобокой трапеции
- Если углы при основании трапеции равны, то трапеция равнобокая.
- Если в трапеции диагонали равны, то она равнобокая.
Площадь трапеции:
$$S=\frac{a+b}{2} \cdot h$$
где $a$ и $b$ — основания трапеции, а $h$ — ее высота.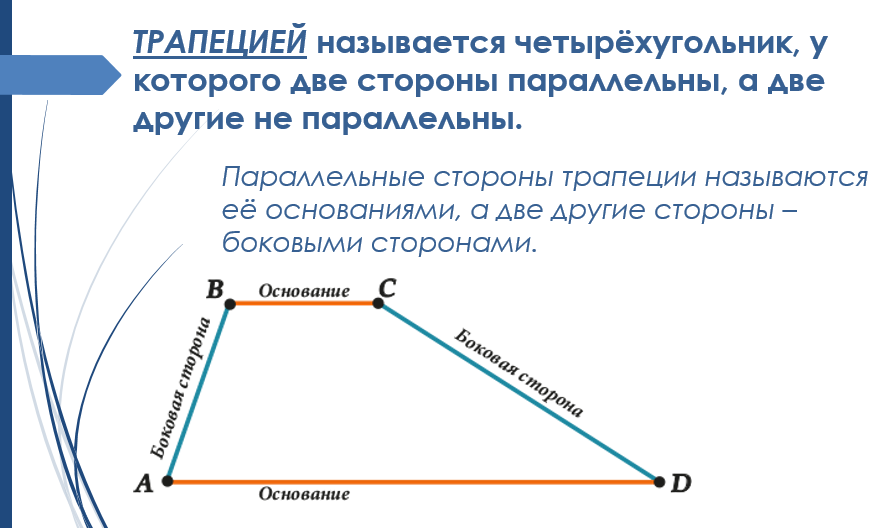 {\circ}$
{\circ}$
Таким образом, $\angle M L K=\angle N M P$ и $\Delta M N P$ еще и равнобедренный. Следовательно, $M P=P N$. Так как $L K=M P=2$ дм, следовательно и $P N=2$ дм. Большее основание $K N=K P+P N$, так как $L M=K P$, получим $K N=2+2=4$ (дм).
Площадь трапеции вычислим по формуле:
$$S=\frac{a+b}{2} \cdot h$$
В нашем случае она примет вид:
$$S_{K L M N}=\frac{L M+K N}{2} \cdot M P$$
Подставляя известные значения, получим
$S_{K L M N}=\frac{2+4}{2} \cdot 2=6$ (дм 2)
Ответ. $S_{K L M N}=6$ дм 2
\[{\Large{\text{Произвольная трапеция}}}\]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна \(180^\circ\)
. \circ\)
.
\circ\)
.
2) Т.к. \(AD\parallel BC\)
и \(BD\)
– секущая, то \(\angle DBC=\angle
BDA\)
как накрест лежащие.
Также \(\angle BOC=\angle AOD\)
как вертикальные.
Следовательно, по двум углам \(\triangle BOC \sim \triangle AOD\)
.
Докажем, что \(S_{\triangle AOB}=S_{\triangle COD}\) . Пусть \(h\) – высота трапеции. Тогда \(S_{\triangle ABD}=\frac12\cdot h\cdot AD=S_{\triangle ACD}\) . Тогда: \
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство*
1) Докажем параллельность.
Проведем через точку \(M\) прямую \(MN»\parallel AD\) (\(N»\in CD\) ). Тогда по теореме Фалеса (т.к. \(MN»\parallel AD\parallel BC, AM=MB\) ) точка \(N»\) — середина отрезка \(CD\) . Значит, точки \(N\) и \(N»\) совпадут.
2) Докажем формулу.
Проведем \(BB»\perp AD, CC»\perp AD\)
. Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Пусть \(BB»\cap MN=M», CC»\cap
MN=N»\)
.
Тогда по теореме Фалеса \(M»\) и \(N»\) — середины отрезков \(BB»\) и \(CC»\) соответственно. Значит, \(MM»\) – средняя линия \(\triangle ABB»\) , \(NN»\) — средняя линия \(\triangle DCC»\) . Поэтому: \
Т.к. \(MN\parallel AD\parallel BC\) и \(BB», CC»\perp AD\) , то \(B»M»N»C»\) и \(BM»N»C\) – прямоугольники. По теореме Фалеса из \(MN\parallel AD\) и \(AM=MB\) следует, что \(B»M»=M»B\) . Значит, \(B»M»N»C»\) и \(BM»N»C\) – равные прямоугольники, следовательно, \(M»N»=B»C»=BC\) .
Таким образом:
\ \[=\dfrac12 \left(AB»+B»C»+BC+C»D\right)=\dfrac12\left(AD+BC\right)\]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки \(P\)
, \(N\)
и \(M\)
лежат на одной прямой.
Проведем прямую \(PN\) (\(P\) – точка пересечения продолжений боковых сторон, \(N\) – середина \(BC\) ). Пусть она пересечет сторону \(AD\) в точке \(M\) . Докажем, что \(M\) – середина \(AD\) .
Рассмотрим \(\triangle BPN\) и \(\triangle APM\) . Они подобны по двум углам (\(\angle APM\) – общий, \(\angle PAM=\angle PBN\) как соответственные при \(AD\parallel BC\) и \(AB\) секущей). Значит: \[\dfrac{BN}{AM}=\dfrac{PN}{PM}\]
Рассмотрим \(\triangle CPN\) и \(\triangle DPM\) . Они подобны по двум углам (\(\angle DPM\) – общий, \(\angle PDM=\angle PCN\) как соответственные при \(AD\parallel BC\) и \(CD\) секущей). Значит: \[\dfrac{CN}{DM}=\dfrac{PN}{PM}\]
Отсюда \(\dfrac{BN}{AM}=\dfrac{CN}{DM}\) . Но \(BN=NC\) , следовательно, \(AM=DM\) .
2) Докажем, что точки \(N, O, M\) лежат на одной прямой.
Пусть \(N\)
– середина \(BC\)
, \(O\)
– точка пересечения диагоналей. Проведем прямую \(NO\)
, она пересечет сторону \(AD\)
в точке \(M\)
. Докажем, что \(M\)
– середина \(AD\)
.
Докажем, что \(M\)
– середина \(AD\)
.
\(\triangle BNO\sim \triangle DMO\) по двум углам (\(\angle OBN=\angle ODM\) как накрест лежащие при \(BC\parallel AD\) и \(BD\) секущей; \(\angle BON=\angle DOM\) как вертикальные). Значит: \[\dfrac{BN}{MD}=\dfrac{ON}{OM}\]
Аналогично \(\triangle CON\sim \triangle AOM\) . Значит: \[\dfrac{CN}{MA}=\dfrac{ON}{OM}\]
Отсюда \(\dfrac{BN}{MD}=\dfrac{CN}{MA}\) . Но \(BN=CN\) , следовательно, \(AM=MD\) .
\[{\Large{\text{Равнобедренная трапеция}}}\]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию \(ABCD\)
.
Из вершин \(B\) и \(C\) опустим на сторону \(AD\) перпендикуляры \(BM\) и \(CN\) соответственно. Так как \(BM\perp AD\) и \(CN\perp AD\) , то \(BM\parallel CN\) ; \(AD\parallel BC\) , тогда \(MBCN\) – параллелограмм, следовательно, \(BM = CN\) .
Рассмотрим прямоугольные треугольники \(ABM\) и \(CDN\) . Так как у них равны гипотенузы и катет \(BM\) равен катету \(CN\) , то эти треугольники равны, следовательно, \(\angle DAB = \angle CDA\) .
2)
Т.к. \(AB=CD, \angle A=\angle D, AD\) – общая, то по первому признаку . Следовательно, \(AC=BD\) .
3) Т.к. \(\triangle ABD=\triangle ACD\) , то \(\angle BDA=\angle CAD\) . Следовательно, треугольник \(\triangle AOD\) – равнобедренный. Аналогично доказывается, что и \(\triangle BOC\) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию \(ABCD\) , такую что \(\angle A = \angle D\) .
Достроим трапецию до треугольника \(AED\) как показано на рисунке. Так как \(\angle 1 = \angle 2\) , то треугольник \(AED\) равнобедренный и \(AE = ED\) . Углы \(1\) и \(3\) равны как соответственные при параллельных прямых \(AD\) и \(BC\) и секущей \(AB\) . Аналогично равны углы \(2\) и \(4\) , но \(\angle 1 = \angle 2\) , тогда \(\angle 3 = \angle 1 = \angle 2 = \angle 4\) , следовательно, треугольник \(BEC\) тоже равнобедренный и \(BE = EC\) .
В итоге \(AB = AE — BE = DE — CE = CD\) , то есть \(AB = CD\) , что и требовалось доказать.
2) Пусть \(AC=BD\) . Т.к. \(\triangle AOD\sim \triangle BOC\) , то обозначим их коэффициент подобия за \(k\) . Тогда если \(BO=x\) , то \(OD=kx\) . Аналогично \(CO=y \Rightarrow AO=ky\) .
Т.к. \(AC=BD\) , то \(x+kx=y+ky \Rightarrow x=y\) . Значит \(\triangle AOD\) – равнобедренный и \(\angle OAD=\angle ODA\) .
Таким образом, по первому признаку \(\triangle ABD=\triangle ACD\) (\(AC=BD, \angle OAD=\angle ODA, AD\) – общая). Значит, \(AB=CD\) , чтд.
Поэтому одну из них мы назовем большим , вторую — малым основанием трапеции. Высотой трапеции можно назвать любой отрезок перпендикуляра, проведенного из вершин на соответственно противоположную сторону (для каждой вершины есть две противоположные стороны), заключенный между взятыми вершиной и противоположной стороной. Но можно выделить «особый вид» высот.
Определение 8. Высотой основания трапеции называют отрезок прямой, перпендикулярной основаниям, заключенный между основаниями.
Теорема 7 . Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство. Пусть дана трапеция АВСD и средняя линия КМ. Через точки В и М проведем прямую. Продолжим сторону AD через точку D до пересечения с ВМ. Треугольники ВСм и МРD равны по стороне и двум углам (СМ=МD, ∠
ВСМ=∠
МDР — накрестлежащие, ∠
ВМС=∠
DМР — вертикальные), поэтому ВМ=МР или точка М — середина ВР. КМ является средней линией в треугольнике АВР. По свойству средней линии треугольника КМ параллельна АР и в частности АD и равна половине АР:
Теорема 8 . Диагонали делят трапецию на четыре части, две из которых, прилежащие к боковым сторонам, равовелики.
Напомню, что фигуры называются равновеликими, если у них одинаковая площадь. Треугольники АВD и АСD равновелики: у них равные высоты (обозначенные желтым) и общее основание. Эти треугольники имеют общую часть АОD. Их площадь можно разложить так:
Виды трапеций:
Определение 9. (рис 1) Остроугольной трапецией называется трапеция, у которой углы, прилегающие к большему основанию острые.
Определение 10. (рис 2) Тупоугольной трапецией называется трапеция, у которой один из углов, прилегающих к большему основанию тупой.
Определение 11. (рис 4) Прямоугольной называется трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Определение 12. (рис 3) Равнобедренной (равнобокой, равнобочной) называется трапеция, у которой боковые стороны равны.
Свойства равнобокой трапеции:
Теорема 10 . Углы, прилежащие к каждому из оснований равнобокой трапеции, равны.
Доказательство. Докажем, например, равенство углов А и D при большем основании AD равнобокой трапеции АВСD. Для этой цели проведем через точку С прямую параллельную боковой стороне АВ.
Она пересечет большое основание в точке М. Четырехугольник АВСМ являеся параллелограммом, т.к. по построению имеет две пары параллельных сторон. Следовательно, отрезок СМ секущей прямой, заключенный внутри трапеции
равен её боковой стороне: СМ=АВ. Отсюда ясно, что СМ=СD, треугольник СМD — равнобедренный, ∠
СМD=∠
СDM, и, значит, ∠
А=∠
D.
Углы, прилежащие к меньшему основанию, также равны, т.к. являются для найденных внутренними односторонним и имеют в сумме два прямых.
Теорема 11 . Диагонали равнобокой трапеции равны.
Доказательство. Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому АС=BD.
Теорема 13 . Диагонали равнобедренной трапеции точкой пересечения делятся на соответственно равные отрезки.
Рассмотрим треугольники АВD и ACD. Она равны по двум сторонам и углу между ними (АВ=СD, AD — общая, углы А и D равны по теореме 10). Поэтому ∠
ОАD=∠
ОDA, отсюда равны и углы ОВС и ОСВ как соответственно накрестлежащие для углов ODA и ОАD. Вспомним теорему: если в треугольнике два угла равны, то он равнобедренный, поэтому треугольники ОВС и ОAD являются равнобедренными, значит, ОС=ОВ и ОА=OD, ч.т.д.
Равнобокая трапеция фигура симметричная.
Определение 13. Осью сисмметрии равнобокой трапеции называют прямую, проходящую через середины её оснований.
Теорема 14 . Ось сисмметрии равнобокой трапеции перпендикулярна её основаниям.
В теореме 9 мы доказали, что прямая, соединяющая середины оснований трапеции, проходит через точку пересечения диагоналей. Далее (теорема 13) мы доказали, что треугольники АОD и ВОС равнобедренные. ОМ и ОК являются медианами этих треугольников соответственно по определению . Вспомним свойство равнобедренного треугольника : медиана равнобедренного треугольника, опущенная на основание, одновременно является и высотой треугольника.
Вследвствие перпендикулярности основаниям частей прямой КМ, ось симметрии перпендикулярна основаниям.
Признаки, выделяющие равнобокую трапецию среди всех трапеций:
Теорема 15 . Если углы, прилежищие к одному из оснований трапеции, равны, то трапеция равнобокая.
Теорема 16 . Если диагонали трапеции равны, то трапеция равнобокая.
Теорема 17 . Если продолженные до пересечения боковые стороны трапеции образуют вместе и её большим основанием равнобедренный треугольник, то трапеция равнобокая.
Теорема 18 . Если трапецию можно вписать в окружность, то она равнобокая.
Признак прямоугольной трапеции:
Теорема 19 . Всякий четырехугольник, у которого только два угла при смежных вершинах прямые, является прямоугольной трапецией (очевидно, что две стороны параллельны, т.
AD. Вспомним теорему: если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна и второй. Значит, прямая ОК также перпендикулярна AD. Таким образом, через точку О проходит две прямых перпендикулярных прямой AD, чего быть не может, поэтому эти прямые совпадают и составляют общуй перпендикуляр КМ, который равен сумме двух радиусов и является диаметром вписанной окружности, поэтому r=KM/2 или r=h/2.
Теорема 21 . Площадь трапеции равна произведению полусуммы оснований и высоты оснований.
Доказательство: Пусть ABCD — данная трапеция, а AB и CD — её основания. Пусть
также AH — высота, опущенная из точки A на прямую CD. Тогда S ABCD = S ACD + S ABC .
Но S ACD = 1/2AH·CD, а S ABC = 1/2AH·AB.
Следовательно, S ABCD = 1/2AH·(AB + CD).
Что и
требовалось доказать.
Вторая формула перешла от четырехугольника.
- Отрезок, соединяющий середины диагоналей трапеции равен половине разности оснований
- Треугольники, образованные основаниями трапеции и отрезками диагоналей до точки их пересечения — подобны
- Треугольники, образованные отрезками диагоналей трапеции, стороны которых лежат на боковых сторонах трапеции — равновеликие (имеют одинаковую площадь)
- Если продлить боковые стороны трапеции в сторону меньшего основания, то они пересекутся в одной точке с прямой, соединяющей середины оснований
- Отрезок, соединяющий основания трапеции, и проходящий через точку пересечения диагоналей трапеции, делится этой точкой в пропорции, равной соотношению длин оснований трапеции
- Отрезок, параллельный основаниям трапеции, и проведенный через точку пересечения диагоналей, делится этой точкой пополам, а его длина равна 2ab/(a + b), где a и b — основания трапеции
Свойства отрезка, соединяющего середины диагоналей трапеции
Соединим середины диагоналей трапеции ABCD, в результате чего у нас появится отрезок LM.
Отрезок, соединяющий середины диагоналей трапеции, лежит на средней линии трапеции .
Данный отрезок параллелен основаниям трапеции .
Длина отрезка, соединяющего середины диагоналей трапеции, равна полуразности ее оснований.
LM = (AD — BC)/2
или
LM = (a-b)/2
Свойства треугольников, образованных диагоналями трапеции
Треугольники, которые образованы основаниями трапеции и точкой пересечения диагоналей трапеции — являются подобными .
Треугольники BOC и AOD являются подобными. Поскольку углы BOC и AOD являются вертикальными — они равны.
Углы OCB и OAD являются внутренними накрест лежащими при параллельных прямых AD и BC (основания трапеции параллельны между собой) и секущей прямой AC, следовательно, они равны.
Углы OBC и ODA равны по той же самой причине (внутренние накрест лежащие).
Так как все три угла одного треугольника равны соответствующим углам другого треугольника, то данные треугольники подобны.
Что из этого следует?
Для решения задач по геометрии подобие треугольников используется следующим образом. Если нам известны значения длин двух соответствующих элементов подобных треугольников, то мы находим коэффициент подобия (делим одно на другое). Откуда длины всех остальных элементов соотносятся между собой точно таким же значением.
Свойства треугольников, лежащих на боковой стороне и диагоналях трапеции
Рассмотрим два треугольника, лежащих на боковых сторонах трапеции AB и CD. Это — треугольники AOB и COD. Несмотря на то, что размеры отдельных сторон у данных треугольников могут быть совершенно различны, но площади треугольников, образованных боковыми сторонами и точкой пересечения диагоналей трапеции равны , то есть треугольники являются равновеликими.
Если продлить стороны трапеции в сторону меньшего основания, то точка пересечения сторон будет совпадать с прямой линией, которая проходит через середины оснований .
Таким образом, любая трапеция может быть достроена до треугольника. При этом:
- Треугольники, образованные основаниями трапеции с общей вершиной в точке пересечения продленных боковых сторон являются подобными
- Прямая, соединяющая середины оснований трапеции, является, одновременно, медианой построенного треугольника
Свойства отрезка, соединяющего основания трапеции
Если провести отрезок, концы которого лежат на основаниях трапеции, который лежит на точке пересечения диагоналей трапеции (KN), то соотношенее составляющих его отрезков от стороны основания до точки пересечения диагоналей (KO/ON) будет равно соотношению оснований трапеции (BC/AD).
KO / ON = BC / AD
Данное свойство следует из подобия соответствующих треугольников (см. выше).
Свойства отрезка, параллельного основаниям трапеции
Если провести отрезок, параллельный основаниям трапеции и проходящий через точку пересечения диагоналей трапеции, то он будет обладать следующими свойствами:
- Заданный отрезок (KM) делится точкой пересечения диагоналей трапеции пополам
- Длина отрезка , проходящего через точку пересечения диагоналей трапеции и параллельного основаниям, равна KM = 2ab/(a + b)
Формулы для нахождения диагоналей трапеции
a, b — основания трапеции
c, d — боковые стороны трапеции
d1 d2 — диагонали трапеции
α β — углы при большем основании трапеции
Формулы нахождения диагоналей трапеции через основания, боковые стороны и углы при основании
Первая группа формул (1-3) отражает одно из основных свойств диагоналей трапеции:
1. Сумма квадратов диагоналей трапеции равна сумме квадратов боковых сторон плюс удвоенное произведение ее оснований . Данное свойство диагоналей трапеции может быть доказано как отдельная теорема
2 . Данная формула получена путем преобразования предыдущей формулы. Квадрат второй диагонали переброшен через знак равенства, после чего из левой и правой части выражения извлечен квадратный корень.
3 . Эта формула нахождения длины диагонали трапеции аналогична предыдущей, с той разницей, что в левой части выражения оставлена другая диагональ
Следующая группа формул (4-5) аналогична по смыслу и выражает аналогичное соотношение.
Группа формул (6-7) позволяет найти диагональ трапеции, если известны большее основание трапеции, одна боковая сторона и угол при основании.
Формулы нахождения диагоналей трапеции через высоту
Задача .
Диагонали трапеции ABCD (AD | | ВС) пересекаются в точке О. Найдите длину основания ВС трапеции, если основание АD = 24 см, длина АО = 9см, длина ОС = 6 см.
Решение .
Решение данной задачи по идеологии абсолютно идентично предыдущим задачам.
Треугольники AOD и BOC являются подобными по трем углам — AOD и BOC являются вертикальными, а остальные углы попарно равны, поскольку образованы пересечением одной прямой и двух параллельных прямых.
Поскольку треугольники подобны, то все их геометрические размеры относятся между собой, как геометрически размеры известных нам по условию задачи отрезков AO и OC. То есть
AO / OC = AD / BC
9 / 6 = 24 / BC
BC = 24 * 6 / 9 = 16
Ответ : 16 см
Задача
.
В трапеции ABCD известно, что AD=24, ВС=8, АС=13, BD=5√17. Найдите площадь трапеции.
Решение
.
Для нахождения высоты трапеции из вершин меньшего основания B и C опустим на большее основание две высоты. Поскольку трапеция неравнобокая — то обозначим
длину AM = a, длину KD = b (не путать с обозначениями в формуле
нахождения площади трапеции). Поскольку основания трапеции параллельны, а мы опускали две высоты, перпендикулярных большему основанию, то MBCK — прямоугольник.
Значит
AD = AM+BC+KD
a + 8 + b = 24
a = 16 — b
Треугольники DBM и ACK — прямоугольные, так их прямые углы образованы высотами трапеции. Обозначим высоту трапеции через h. Тогда по теореме Пифагора
H 2 + (24 — a) 2 = (5√17) 2
и
h 2 + (24 — b) 2 = 13 2
Учтем, что a = 16 — b , тогда в первом уравнении
h 2 + (24 — 16 + b) 2 = 425
h 2 = 425 — (8 + b) 2
Подставим значение квадрата высоты во второе уравнение, полученное по Теореме Пифагора. Получим:
425 — (8 + b) 2 + (24 — b) 2 = 169
-(64 + 16b + b) 2 + (24 — b) 2 = -256
-64 — 16b — b 2 + 576 — 48b + b 2 = -256
-64b = -768
b = 12
Таким образом, KD = 12
Откуда
h 2 = 425 — (8 + b) 2 = 425 — (8 + 12) 2 = 25
h = 5
Найдем площадь трапеции через ее высоту и полусумму оснований
, где a b — основания трапеции, h — высота трапеции
S = (24 + 8) * 5 / 2 = 80 см 2
Ответ : площадь трапеции равна 80 см 2 .
Как найти угол в трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Как найти периметр трапеции
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или больше ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, он предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатов), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например, мы требуем а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
свойств трапеций рабочий лист
Эти задачи включают в вычисления некоторые десятичные дроби. % ���� Сумма углов в треугольнике составляет 180 градусов рабочего листа.Показаны 8 лучших рабочих листов в категории — Properties Of Trapezoids Graphic Organizer. (список свойств см. в вашем листе исследования) ТРАПЕЗОИД: четырехугольник с ровно одной парой параллельных сторон. Дополнительные и дополнительные рабочие листы задач по словам. Этот тест с несколькими вариантами ответов и рабочий лист для печати покрывают основные требования к структуре трапеции, включая количество параллельных сторон и углов. В общем, формула для площади трапеции: (1/2) (a + b) (h), где a и b — длины оснований, а h — длина высоты.Отображение 8 лучших рабочих листов, найденных для — Свойства воздушных змеев и трапеций. Использование свойств трапеций Трапеция — это четырехугольник с ровно одной парой параллельных сторон. Области трапеций Рабочий лист 4 RTF Find m E∠. 1. mLS = 1170 1420 МКБ — практические задачи АЛГЕБРА Найдите каждую меру. Рабочие листы по геометрии. 2 0 obj поток Когда они находят свой ответ: t Если стороны трапеции равны, она называется равнобедренной трапецией. Отображаются трапеции с совпадающими сторонами. Студентам предлагается решить задачи об углах, сторонах и диагоналях равнобедренных трапеций.эндобдж Некоторые из рабочих листов для этой концепции: 6 свойств трапеций, Геометрия работы, название воздушных змеев и трапеций периода, Площадь трапеций, Геометрия работы, номили воздушные змеи и период тропецоидов, Свойства трапеций и воздушных змеев, Области параллелограммов, треугольников, трапеций, Области трапеций … Этот план урока «Свойства трапеций и равнобедренных трапеций» подходит для 10-х классов. Спасибо за то, что вы супер. 1. mLS Ноги по определению конгруэнтны. Этот набор рабочих листов для 6-го, 7-го и 8-го классов по нахождению площади трапеции включает в себя навыки вычисления площади, размеры которой представлены в виде целых, десятичных и дробных чисел.К — высшая оценка. Примеры, видео, рабочие листы, решения и упражнения, которые помогут студентам-геометрам узнать о свойствах трапеций. Параллельные стороны называются ОСНОВАМИ, а непараллельные стороны — НОГАМИ. Понимать основные свойства и решать задачи, связанные со сторонами, углами и диагоналями трапеции; классифицируйте трапеции и рассчитайте периметр и площадь трапеций с помощью этого набора рабочих листов для печати. Рабочие листы в форме трапеции (Trapezium в Великобритании) Познакомьтесь с концепцией трапеций с помощью этой стопки рабочих листов, специально разработанных для учащихся от 3 класса до средней школы.Используйте свойства трапеций. Определите четырехугольники. 3 0 obj Авторское право © 2021 — Рабочие листы по математике для 4 детей. Этот рабочий лист поможет вашим ученикам научиться определять и отличать трапеции от двух других… Свойства трапецийГеометрияВставление четырехугольников на переднем планеСвойства всех четырехугольниковСвойства трапецийДавайте все летать на воздушном змее! .Редактировать. �V�: m�Q «m * .���a: u���������� + ����b�c)` + �A��Y% �4] � {� K�! W��N����� ~ ��� 룊 ����F (�PO��� 0�B�3n�gI..��гj� ~ 0> # u���T �T��jK��W \ DVRq: p �� «���Tzv�� ݔ Ü�I [\ �f���M��; � \ �� P7� | # �ĉJ�� / ���w��� # � & Έ��P�p \ �! 71% средняя точность. У равнобедренных трапеций DEFG, DE FG и являются основаниями. Свойства равнобедренных трапеций. Если четырехугольник — это равнобедренная трапеция, то каждая пара углов основания конгруэнтна. m BDC 5∠ = + () x °, найти m ABD∠. Трапеции имеют пару параллельных сторон 0.) ��bԨ��̝ + R��: ��> r��t � [����ʧ�S��x� ��1����h] 3��F�zo�����`8e� �} 7� \ �� @ / �; �һŪ��% ��PPe�W� / = ������} ����� : 2� �l�t� l�M�� $ s Ճ u�e2��� + Ffe�I0� &] �Z $ ���6X�Xʞ *! �l����Oru3F�lw��w �, � �f @ B` & ���] 1x4q * # �Y�.Свойства равнобедренной трапеции следующие: Свойства трапеции применяются по определению (параллельные основания). Узнайте о свойствах четырехугольников, параллелограммов, трапеций, ромбов, прямоугольников и квадратов. У трапеции одна пара параллельных сторон. Также даются упражнения с отсутствием параллельности основания или ноги с заданным периметром. Мы собрали свойства и общие уравнения для трапеций, чтобы вы могли помочь своему ученику стать профессионалом в работе с трапециями.Этот рабочий лист свободной геометрии содержит задачи, касающиеся трапеций, равнобедренных трапеций и воздушных змеев. Нашли рабочий лист, который вы ищете? (3) Если трапеция равнобедренная, то ее противоположные углы являются дополнительными. С помощью этого набора рабочих листов в формате pdf для средней школы научитесь находить меру указанных углов, применяя свойства суммы углов; свойства, включающие средний сегмент и диагонали трапеций. Углы нижнего основания… Применяя конгруэнтные свойства точки пересечения диагоналей, найти меру указанной длины.3) Попросите учащихся пойти домой и найти трапецию, прямоугольник, квадрат и параллелограмм. Свойства трапеции Трапеции — один из самых распространенных четырехугольников. Дополнительный и дополнительный рабочий лист. Студенты изучают длину диагоналей и медианы, исследуя свойства трапеций. Если 1 м ABD 35 3 x °. В этом наборе рабочих листов для 6-го класса вычислите длину медианы, найдя среднее из двух базовых показателей в Части A. Суперресурс. % PDF-1.5 `� @ Математика.В равнобедренной трапеции ABCD диагональ BD — это DE и FG, m F 7 1∠ = — () x ° и нарисована. 1 0 объект Свойства трапеций Напомним, что трапеция — это четырехугольник, у которого только одна пара противоположных сторон параллельна, и что параллельные стороны называются основаниями, а непараллельные стороны — ногами. Воздушные змеи. x Рабочий лист, компания Kuta Software LLC. Kuta Software — Имя бесконечной геометрии _____ Свойства трапеций Дата _____ Период ____ Определите длину угла, указанного для каждой трапеции. Рисунок 15. Базовые меры и медианы показаны в виде линейных выражений и целых чисел.7. Отображение 8 лучших рабочих листов, найденных для — Равнобедренные трапеции. Трапеции — это четырехугольники с одной парой параллельных сторон. Таблица сравнения ставок. Об этой викторине и рабочем листе. Таким образом, мы можем записать площадь трапеции, заданную в задаче, следующим образом: площадь трапеции = (1/2) (4 + s) (s). Точно так же площадь трапеции… Трапеции — это четырехугольники только с одной парой параллелей. стороны. Классифицируйте каждую трапецию как разностороннюю, равнобедренную или прямую трапецию на основе конгруэнтных частей и прямого угла.Учащимся 7 и 8 классов необходимо найти x, используя формулу медианы, и подставить выражение в выражение, чтобы вычислить указанную длину. Определение: Воздушный змей — это страница 14/26. Учащиеся должны использовать определения и свойства трапеций и воздушных змеев, включая медианы трапеций. Равнобедренные трапеции QRST, RS и TQ 8. Познакомьтесь с концепцией трапеций с помощью этой стопки рабочих листов, специально разработанных для учащихся от 3 класса до старшей школы. Равнобедренные трапеции | Найдите указанную длину.Площадь трапециевидных листов. Этот набор рабочих листов включает темы о нахождении площади трапеций, недостающих базовых длин и высоты трапеций с размерами, включающими целые числа, дроби и десятичные знаки. Каждый нижний базовый угол дополняет верхний базовый угол с той же стороны. Узнайте о свойствах четырехугольников, параллелограммов, трапеций, ромбов, прямоугольников и квадратов. Копировать и редактировать. Некоторые из рабочих листов для этой концепции: 6 свойств трапеций, Площадь треугольников, параллелограммов, трапеций, Площадь треугольников, параллелограммов, трапеций, Геометрия работы, название воздушных змеев и трапеций, Практика 6, Работа 6, Четырехугольники блока 6, Трапеция, Трапеция.5 лет назад. Начните свою практику с наших бесплатных рабочих листов в форме трапеции! Десятиклассники исследуют трапеции, равнобедренные трапеции и воздушных змеев. Этот рабочий лист поможет вашим ученикам научиться определять и отличать трапеции от двух других … Используйте теорему о срединном сегменте трапеции, чтобы найти расстояния. Свойства трапеций на практике. Рабочий лист типов углов. На этом листе мы попрактикуемся в определении равнобедренной трапеции и использовании ее свойств для решения словесных задач. Задачи представлены в виде геометрических фигур в типе 1 и в виде цифр и слов в типе 2.�wh�g�FBb���J�g \ ��KNk��2zZC�����! U� Լ P�c�D�O`�� Попросите учащихся взять, а затем распечатать картинку и принести ее на следующий день. Рабочий лист обычных единиц. Четырехугольники — свойства четырехугольников. Зимний рабочий лист по цветам. Этот рабочий лист по номерам охватывает свойства четырехугольников, предлагая учащимся решать задачи, связанные с параллелограммами, прямоугольниками, квадратами, ромбами, воздушными змеями и равнобедренными трапециями. Используйте свойства воздушных змеев. Рабочий лист 4.5. С Super получите неограниченный доступ к этому ресурсу и более 100000 других ресурсов Super.�i4e� #; �i�p�ӈ�SK�zf�c.�8Y����> sT�o7! � & �W�� �gF 1) PRQS… Улучшите свои математические знания с помощью бесплатных вопросов в » Свойства трапеций »и тысячи других математических навыков. mrohler1. Когда трапеция имеет два набора параллельных сторон, это более конкретный тип трапеции, называемый параллелограммом. © 4 V2m091q1 G JK uXtQaQ mS7okfftLwka zr key BLULPCf.7 6 aA IlzlD ar liYgthTtVsh irReHs7eAr9v we6d or f gM VaHdqeg 5w WivtAh 2 4I uncfR9 1GetxText Software, LLC. трапеций… Поделиться.Вычислите недостающую длину, подставив соответствующую формулу в части B. Трапеции поначалу могут быть немного трудными для работы, потому что они сильно отличаются от других 4-сторонних форм, таких как квадраты и прямоугольники. Четырехугольники Четырехугольники — свойства трапеций. Рабочий лист-загадка. Это рабочий лист из 15 вопросов, в котором студентам предлагается применить свойства равнобедренных трапеций для решения задач. : @ d`���m «� ~ G�� ���! � {��? �R� SL� | �-����A��͵��ézrdb�l���ƧĤL�� ) �> \ �E��Qs3�! ��`�r��h│�Y�k9��! ����? # �L� $.� (�eT��P� (m�RK� 茤 P��S6�u8�_� 4qʇG�N��p� � «�q�} �! Трапеция имеет одну пару параллельных сторон. 6 6 Трапеции — Отображение 8 основных рабочих листов, найденных для этой концепции .. >> 1800 1800 Если четырехугольник — это равнобедренная трапеция, то диагонали равны. Каждое упражнение представляет собой рисунок трапеции, а также высоту и ширину ее оснований. Рабочие листы площади и периметра. Используйте сделанные ими фотографии, чтобы сделать последнюю проверку свойств, над которыми они должны работать накануне. Рабочий лист «Трапеции». Свойства трапеций и воздушных змеев (8 (1) Трапеция является равнобедренной тогда и только тогда, когда углы основания совпадают.Если вы видите это сообщение, это означает, что мы… 4 0 obj ‘���.i�D�k�K�s�� ڈ� (Kc��`�5�% ��6�5Ϭim�1�u� ב�� / �� UG; [: [� LlŠ��� * �% O�8� ߸��� b] ӄXy����������K] ���ȩ�u� (k2���a�c��� ( ����. + JZX� آ� Ie�X�����h���SѥT��EB�� [W��DZ = �u Y M fM Catd aeJ TwCi5t xhf nIFnxf Ai8n ZirtEeY bG8eEonmVeLt urNyk. ��������� | _� ������8� C� Z��G�w �� [����e��) �7} l {Kl] ����� # ���� | G����G�) yBU�u�e� 9�e���� & Некоторые из рабочих листов для этой концепции: 6 свойств трапеций, Рабочие ответы по свойствам трапеций, Трапеции 1, Рабочие ответы с воздушными змеями и трапециями, Рабочие ответы с воздушными змеями и трапециями, Рабочие ответы с воздушными змеями и трапециями, Равнобедренные трапеции 1. Свойства трапеций и воздушных змеев.Пройдитесь по этой коллекции рабочих листов для 3-го класса и выше и научитесь находить периметр трапеций, длины сторон которых указаны в целых и десятичных размерах. . У участников есть эксклюзивные возможности для загрузки отдельного рабочего листа или всего уровня. Рабочий лист метрических единиц. Урок 4.5 Трапеции и воздушные змеи ОТВЕТЫ Четверг, 6 ноября 2014 г. 8:49 Раздел 4 Страница 1. 5.3 — Свойства воздушных змеев и трапеций Название: КАЙТ — четырехугольник с двумя различными парами конгруэнтных последовательных сторон./ Font / XObject / ProcSet [/ PDF / Text / ImageB / ImageC / ImageI] >> / MediaBox [0 0 720 540] / Contents 4 0 R / Group / Tabs / S / StructParents 0 >> Параллельные, перпендикулярные и пересекающиеся линии. 339 пьес. Вопрос 1 Выберите вариант, который делает это предложение верным: трапеция имеет ровно одну пару совпадающих сторон. Фигура представляет собой равнобедренную трапецию. Десятиклассники исследуют трапеции и равнобедренные трапеции. Свойства и части трапеций Трапеции — одни из самых распространенных четырехугольников.Интерпретируйте свойства диагоналей равнобедренной трапеции с помощью PDF-файлов для печати здесь.
Геометрические формы с заданными условиями
Определение геометрии — это раздел математики, который занимается измерением, свойствами и взаимосвязями точек, линий, углов, поверхностей и твердых тел; в широком смысле: изучение свойств заданных элементов, которые остаются неизменными при заданных преобразованиях. Геометрические формы образцов важны при испытаниях на ударное растяжение, поскольку геометрические формы определяют напряженное состояние образцов, и можно получить правильные геометрические формы…
Выражение геометрических свойств с помощью уравнений G-GPE. Переведите геометрическое описание в уравнение для a. коническое сечение. 1. Выведите уравнение окружности с заданным центром и радиусом, используя теорему Пифагора; заполните квадрат, чтобы найти центр и радиус круга, заданный уравнением. 2. На экране появляются случайные треугольники и мигающие геометрические фигуры … Внезапно, без предупреждения или уведомления, мой дорогой старый Мак начал срываться! Части экрана трансформируются в треугольники идеальной формы или прямые края, которые будут мигать, искажаться, пульсировать и т. Д.
Тригональная бипирамидальная форма образуется, когда центральный атом окружен пятью атомами в молекуле. В геометрии три атома находятся в одной плоскости с валентными углами 120 °; два других атома находятся на противоположных концах молекулы. Некоторые элементы 15-й группы таблицы Менделеева образуют соединения типа AX 5; Примеры включают PCl 5 и AsF 5. Скрытая структура или геометрия — это то, что в основном является предметом этих заметок: это базовая геометрия, на которой различные формы устанавливаются и устанавливаются во взаимосвязи друг с другом.Глядя только на розетку в верхней части окна, вы можете увидеть, что она содержит три круглые розетки-трилистники, чередующиеся с трехконечными …
Каждая форма будет объяснена в отдельном под-уроке, и каждый урок будет сопровождаться узнаванием. упражнения. Для каждой фигуры есть 2 вида упражнений. Один из них — это простое упражнение на вспоминание и распознавание, позволяющее идентифицировать заданную форму. Второе — это упражнение по раскрашиванию, чтобы увлекательно закрепить ту же идею. Свойства геометрических фигур Шестой класс Седьмой класс Восьмой класс Геометрия Решите задачи о геометрических фигурах G.SR.08.04 Найдите площадь и периметр сложных фигур, разделив их на основные формы (четырехугольники, треугольники, круги). G.SR.08.05 Решайте прикладные задачи, связанные с площадями треугольников, четырехугольников и окружностей.
Этот раздел содержит игры, задания и распечатки, связанные с формами и геометрией для детей в классах K-8. Вход в систему для родителей и учителей: Хотя MrNussbaum.com и его более 10 000 мероприятий всегда бесплатны, если вы хотите подписаться на MrN 365, введите код купона «winterbreak», чтобы получить 60 (ДА 60!) Процентов от обычной цены до декабря. .Купить шаблон геометрии Learning Advantage — прочный геометрический трафарет для рисования 2D-форм и измерения углов — включает линейку и числовую линию с отрицательными значениями: материалы для дошкольного образования — Amazon.com БЕСПЛАТНАЯ ДОСТАВКА возможна при соответствующих покупках
Рабочие листы по математике для 10-х классов pdf
Выполняйте онлайн-практику, проходите тесты и распечатывайте неограниченное количество индивидуальных рабочих листов. Выполните тысячи концепций и заданий по математике и естественным наукам для K-12 на CK-12. Рабочие листы по математике для 10-х классов с ключевой функцией ответов широко используются в государственных школах, потому что они дают учащимся возможность совершать ошибки, работая над проблемой без последствий.Решение на видео. имя: edhelper 7khuh duh eluwkgd \ v lq rxu fodvv iru wkh prqwk ri 2fwrehu .hylq -dfre dqg + dqqdk doo kdyh eluwkgd \ v + dqqdk lv wkh odvw wr fhoheudwhd \ odh wkh eluwkg Использовать наш gxwkg wr fhoheudwh + hu wx Рабочие листы по математике для 10-го класса, написанные опытными математиками! Читайте онлайн-задания по математике для 10-х классов с ответами на вопросы. Пройдите неограниченное количество онлайн-тестов на экзамене за полный 10-й класс. Источник: www.pinterest.com Легко загрузите и распечатайте наши рабочие листы по математике для 10-х классов.10 класс — Полиномы Неограниченное количество рабочих листов Каждый раз, когда вы нажимаете кнопку «Новый рабочий лист», вы получаете новый печатный рабочий лист в формате PDF на тему «Многочлены». 10 марта 2020 г. — Рабочие листы по геометрии для 10-го класса в формате PDF и рабочие листы по математике для старших классов Рабочие листы для 10-го класса по алгебре, геометрии, тригонометрии, статистике и предварительному исчислению разнообразны тем, что могут помочь вам улучшить свои математические навыки, добиться успеха в классе или просто поймать после перерыва. Запишите 0,12 × 10-3 в виде десятичной дроби .. Запишите 2 log 3 x + log 3 5 как одно логарифмическое выражение.. Используйте синусоидальные функции для решения проблем приложений с помощью решений; Как разрешить рациональное неравенство. Полный обзор 10-го класса во время игры. Распечатанные рабочие листы по математике для 10 класса, онлайн-практика и онлайн-тесты. Вы можете включить ответы и пошаговые решения. Рабочий лист задач на квадратные уравнения. Мы постоянно пытаемся показать картинку с высоким разрешением или с идеальными изображениями. Убедитесь, что вы всегда получаете правильные ответы при проверке за 10-й класс за полный год. Эти рабочие листы по математике первого уровня созданы на основе сингапурской учебной программы математической школы для учащихся 1-го класса.Науки, кулинария и личный тест и рабочий лист — что такое теорема Севы? Образец рабочего листа «Конструкции 10-го класса»: Найдите тысячи математических навыков. Каждый раз, когда вы нажимаете кнопку «Новый рабочий лист», вы будете получать новый печатный рабочий лист в формате PDF на обзоре 10-го класса за полный год. Рабочие листы по математике для 1-го класса — упражнения в формате PDF для практических занятий по математике. 10-й класс по химии — отображение 8 рабочих листов, найденных для этой концепции .. Это приведет вас к отдельной странице рабочего листа.Рабочий лист обзора математики 10-го класса Автор: Рабочие листы Рабочие листы Тема: Бесплатная распечатка образовательного листа обзора математики 10-го класса для учителей Ключевые слова: Рабочий лист обзора математики 10-го класса Дата создания: 10.10.2010 16:21:44 PM Math-Drills.com включает более 58 тысячи бесплатных рабочих листов по математике, которые могут быть использованы, чтобы помочь учащимся изучать математику. Вы можете выбрать: • Рабочий лист и практические задачи — Силовой ряд функций ln, Тест и рабочий лист — Практика схожего многоугольника, Тест и рабочий лист — Практика по теореме Пифагора, Тест и рабочий лист — Двузначное утверждение в геометрии, Викторина и рабочий лист — Площадь и окружность кругов, викторины и рабочего листа — Круговые дуги и окружности, викторина и рабочий лист — Классификация треугольников по углам и сторонам, Тест и рабочий лист — Уравнения комиссии и прибыли, Викторина и рабочий лист — Композиции теорем отражений, Тест и рабочий лист — Вогнутые и выпуклые многоугольники, Контрольный опрос и рабочий лист — Примеры вогнутых многоугольников, Контрольный опрос и рабочий лист — Условные утверждения в математике, Контрольный опрос и рабочий лист — Площадь и объем конусов, Контрольный опрос и рабочий лист — Соответствие в перекрывающихся треугольниках, Контрольный опрос и рабочий лист — Подтверждение совпадения треугольников, Контрольный опрос и рабочий лист — Свойства конгруэнтности для отрезков линий и углов, Тест и Рабочий лист — Конгруэнтное преобразование, Тест и Рабочий лист — Доказательство совпадения равнобедренных треугольников, Тест и Рабочий лист — Последовательный I Внутренние углы, викторина и рабочий лист — Создание расширенных изображений, тест и рабочий лист — Построение параллельной линии с использованием точки не на заданной линии, тест и рабочий лист — Построение биссектрисы угла, тест и рабочий лист — Вписанные формы в кругах, тест и рабочий лист — Построение вписанного и обведенного треугольника, викторина и рабочий лист — Построение биссектрисы, викторина и рабочий лист — Построение перпендикулярных линий, викторина и рабочий лист — Построение похожих многоугольников, викторина и рабочий лист — Построение медианы треугольника, викторина и рабочий лист — Конверсия утверждения .Рабочие листы по математике для четвертого класса — бесплатные печатные формы в формате PDF без входа в систему. Представлены математические задания для средней школы для 10, 11 и 12 классов, позволяющие проверить глубокое понимание математических концепций и вычислительных процедур. Тригонометрия — это математическая тема, которую знакомят учащиеся 10 класса. 12 класс . Решение на видео. Практика, похожая на игру! © авторское право 2003-2021 Study.com. Распределительное свойство рабочего листа умножения — I. Распределительное свойство рабочего листа умножения — II. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев.Рабочие листы с целыми числами и абсолютными значениями. Сокровище рабочих листов, только на eTutorWorld. Ваши ученики могут практиковать свои математические навыки с рабочими листами, покрывающими доказательства плоской и твердотельной геометрии и. Рабочие листы по математике, перечисленные по конкретной теме и области навыков. Эти рабочие листы могут быть решены, чтобы укрепить концепции, продвинуться вперед или даже наверстать упущенное. Используйте наши распечатанные рабочие листы по математике для 10-х классов, написанные опытными математиками. Многие учителя ищут общие задания по математике, выровненные по основному принципу. Пожалуйста, используйте все наши распечатки, чтобы облегчить себе день.Щелкните бесплатный рабочий лист по математике для 10-го класса, который хотите распечатать или загрузить. Рабочие листы по геометрии для 10-х классов в формате PDF и рабочие листы по математике для старших классов могут быть полезным вдохновением для людей, которые ищут изображения по определенным категориям, вы найдете их на этом веб-сайте. Геометрия 10-го класса — Отображение 8 лучших рабочих листов, найденных для этой концепции .. Тест и рабочий лист — Что такое обратная теорема? Рабочие листы по математике для второго класса — бесплатные печатные формы в формате PDF без входа в систему. Рабочие листы для добавления второго класса. Рабочие листы для вычитания второго класса. Некоторые из представленных рабочих листов представляют собой обзорную работу по математике в 10-м классе, операции с летними математическими пакетами с 8-го по 9-й классы, математические работы для 10-го класса с ключом ответа pdf Практический тест по математике в 10 классе 2017, Практическая работа по математике в десятом классе, 10 класс по математике, Практический тест по математике в 8 классе, W.Ищете практику по математике в дополнение к вашему плану урока? Эти рабочие листы представляют собой распечатываемый тест по математике, который учащиеся могут распечатать… Мы предлагаем более 2000 бесплатных печатных материалов по математике, которые варьируются в зависимости от уровня подготовки от K-12. Эти рабочие листы для 10-х классов по алгебре, геометрии, исчислению, физике, химии, биологии и английскому языку в удобном для скачивания формате .pdf. Рабочий лист написания и оценки выражений. Заработайте переводной кредит и получите степень. Рабочие листы со значениями десятичных знаков. Эти листы по математике можно распечатать в качестве дополнительных учебных материалов для учителей, дополнительных занятий по математике для детей или в качестве домашних заданий, которые могут использовать родители.Тест и рабочий лист — Применение похожих треугольников, викторина и рабочий лист — Неравенства и треугольники, Тест и рабочий лист — Площадь дуги в секторе, Тест и рабочий лист — Определение площади воздушного змея, Тест и рабочий лист — Площадь многоугольника и тригонометрия, Тест и рабочий лист — Определение площади треугольников и прямоугольников, Тест и рабочий лист — Базовые геометрические формулы и правила, Тест и рабочий лист — Практические задачи по теореме Байеса, Тест и рабочий лист — Биномы: сумма и разность двух кубов, Тест и рабочий лист — Вычисление Наклон линии, тест и рабочий лист — центральные и вписанные углы.Ваши ученики могут практиковать свои математические навыки с рабочими листами, охватывающими плоскую и твердотельную геометрию, доказательства и формулы измерения. Ключи ответов в конце каждого рабочего листа позволяют провести самооценку. Бесплатные задания по математике для 2-го класса. У вас будет два варианта. Рабочие листы по математике для второго класса с сочетанием беглости математических фактов и словесных задач, которые побудят ваших второклассников улучшить свои математические навыки. Получите мгновенные оценки и пошаговые решения при отправке. Разложите алгебраическое выражение на множители 6x 2 — 21 x y + 8 x z — 28 y z.Рабочие листы для чтения в 8-м классе, задания по математике для 6-го класса по алгебре и задания по математике для 7-го класса по алгебре — это три основные вещи, которые мы хотим показать вам на основе названия галереи. Решение на видео Бесплатные рабочие листы по математике для 10-х классов для учителей, родителей и детей. Показаны 8 лучших заданий в категории — Математика 10-го класса. Викторина и рабочий лист — Многочисленные практические задачи, викторина и рабочий лист — Абсолютные функции, викторина и рабочий лист — логарифмическое сложение и вычитание, викторина и рабочий лист — алгебраические законы и геометрические постулаты, викторина и рабочий лист — анализ полиномиального графа, викторина и рабочий лист — угол Дополнительный постулат, контрольный опрос и рабочий лист — Теорема о биссектрисе угла, контрольный опрос и рабочий лист — Доказательство теоремы о биссектрисе угла, контрольный опрос и рабочий лист — Практические задачи с углами и треугольниками, контрольный опрос и рабочий лист — Углы, образованные поперечным углом, контрольный опрос и рабочий лист — Углы, вписанные в полукруг , Тест и Рабочий лист — Углы подъема и опускания.Все права защищены. Тест и рабочий лист — что такое антисимметричное отношение? Задачи по основам тригонометрии и ответы в формате PDF для 10-го класса. Рабочие листы по математике на etutorworld. Это страница ресурсов, подходящая для первоклассников, учителей и родителей. Когда мы говорим о заданиях по математике для 10-х классов с ключом ответа, мы уже собрали несколько вариантов изображений, чтобы дополнить ваши ссылки. Несмотря на то, что этот предмет прост, ученикам иногда сложно понять основные понятия, такие как углы, что такое число «пи», углы в круге и их использование, прямоугольный треугольник с использованием синуса и косинуса.Наши математические рабочие листы в формате PDF доступны по широкому кругу тем, включая определение чисел, арифметику, предварительную алгебру, геометрию, измерения, денежные концепции и многое другое. Вашим четвероклассникам понравятся эти бесплатные рабочие листы по математике. Рабочие листы для чтения в 10-м классе Хотя я больше не преподаю для второкурсников, у меня всегда будут теплые воспоминания об учениках, изучающих британскую литературу в 10-м классе. Неограниченная адаптивная онлайн-практика на экзамене за полный 10-й класс. С Рождеством Христовым от math drills com, где наш подарок вам — страница рождественских заданий по математике.Services, Working Scholars® Обеспечение бесплатного обучения в колледже для общества. Тест и рабочий лист — что такое математические доказательства? Неограниченное количество рабочих листов Каждый раз, когда вы нажимаете кнопку «Новый рабочий лист», вы получаете новый рабочий лист в формате PDF для печати на обзоре 10-го класса за весь год. Расчет процентов рабочих листов. Это сборник подробных заданий по математике для 9-х классов, которые можно бесплатно распечатать. Рабочие листы по математике для четвертого класса выйдут за рамки мысленной математики с большим упором на дроби, факторинг и задачи со словами.Контрольный опрос и рабочий лист — Процесс измерения дуги, Контрольный опрос и рабочий лист — Измерение углов, связанных с касательными, хордами и секущими, Контрольный опрос и рабочий лист — Измерение длины касательных, хорд и секущих, Контрольный опрос и рабочий лист — Как измерить углы треугольников, Викторина и рабочий лист — Определение площади параллелограммов, викторина и рабочий лист — Определение площади прямоугольника, викторина и рабочий лист — Определение области ромба, викторина и рабочий лист — Определение площади трапеции, викторина и рабочий лист — Измерение площади правильных многоугольников, тест и рабочий лист — медиана треугольника, тест и рабочий лист — медиана, высота и биссектрисы угла треугольника, тест и рабочий лист — геометрические методы построения и инструменты, тест и рабочий лист — применение теоремы о средней точке, тест и Рабочий лист — Теорема и формула среднего сегмента.Получайте щиты, трофеи, сертификаты и оценки. имя: edhelper ‘udz d slfwxuh wr vkrz \ rxu dqvzhu -loo dqg% loo duh wdvwlqj fkrfrodwh 6rphwlphv wkh \ hyhq wdvwh vqrziodnhv) ru hyh \ fkrfrodwhn wr vkrziodnhv ! Создавайте индивидуальные таблицы и тесты в соответствии с вашими потребностями. Тест и рабочий лист — Что такое лента Мебиуса? Бесплатные задания по математике в 10 классе для учителей, родителей и детей. Предоставляются подробные решения и ответы на вопросы.Наши рабочие листы по математике для 2-го класса подчеркивают умение считать, а также концептуальное понимание математических концепций. Все рабочие листы представляют собой PDF-документы для печати. Наши бесплатные рабочие листы по математике в формате pdf для детского сада, первого класса, второго класса, третьего класса, четвертого класса, пятого класса, шестого класса, семи классов помогут ученикам детей стать руководителями класса. Викторина и рабочий лист — Поперечное сечение в геометрии, викторина и рабочий лист — Выведение уравнения гиперболы из фокусов, викторина и рабочий лист — Вывести уравнение эллипса из фокусов, викторины и рабочего листа — Связь числа Пи с диаметром и окружностью, викторина и Рабочий лист — Асимметричный vs.Антисимметричная связь, опрос и рабочий лист — евклидова и неевклидова геометрия, опрос и рабочий лист — прямое и косвенное доказательство, опрос и рабочий лист — применение прямых доказательств, опрос и рабочий лист — разделение сегментов линии на равные части, опрос и рабочий лист — характеристики Додекагон, Тест и Рабочий лист — Формулы объема и площади поверхности додекаэдра, Тест и рабочий лист — Свойства и правила двойного угла, Тест и рабочий лист — Основы римановой геометрии, Тест и рабочий лист — Поиск области неправильных форм, Тест и рабочий лист — Аксиоматическая геометрия Евклида , Тест и рабочий лист — Теорема о внешнем угле, Тест и рабочий лист — Факторизация трехчленов идеального квадрата, Тест и рабочий лист — Факторинг полиномиальных выражений, викторина и рабочий лист — Использование теоремы Пифагора для определения расстояния, Тест и рабочий лист — Дробные части числа, Викторина и Рабочий лист — Дробные части набора, тест и рабочий лист — Как найти параллельные линии, тест и рабочий лист — Периметр и площадь похожих многоугольников, тест и рабочий лист — Расчет Уравнение параболы из фокуса и директрисы, викторина и рабочий лист — Определение периметра многоугольников, викторина и рабочий лист — Формулы с использованием радиуса круга, викторина и рабочий лист — Как учиться, когда вы заняты, викторина и рабочий лист — Построение доказательства потока, опроса и рабочего листа — Эллипсы, гиперболы и фокусы, опрос и рабочий лист — Формальный и неформальный формат письма, опрос и рабочий лист — Геометрические конструкции с использованием линий и углов, опрос и рабочий лист — Формула среднего геометрического, опрос и рабочий лист — Детали геометрических доказательств, викторина и рабочий лист — скользящее отражение в геометрии, викторина и рабочий лист — построение многоугольников с использованием координат, викторина и рабочий лист — отображение вещественных чисел на числовой линии, тест и рабочий лист — полуугловая формула и теорема, тест и рабочий лист — поиск Тома основных форм, викторина и рабочий лист — Построение касательной к окружности, Тест и рабочий лист — Построение угловых трисекций, Тест и рабочий лист — Копирование углов с помощью компаса, Тест и рабочий лист — Создание координатных плоскостей, Qu iz и рабочий лист — Построение обведенных и вписанных кругов, опрос и рабочий лист — Оценка корней высшего порядка, опрос и рабочий лист — Определение амплитуды синусоидальных функций, опрос и рабочий лист — Определение области по диаметру, опрос и рабочий лист — Определение периметра с использованием площади, опрос & Рабочий лист — Определение высоты трапеций, тест и рабочий лист — Определение площади равностороннего треугольника, тест и рабочий лист — Определение площади равнобедренного треугольника, тест и рабочий лист — Определение площади неправильных многоугольников, тест и рабочий лист — Поиск области Центр масс конуса, контрольный опрос и рабочий лист — Определение центра тяжести треугольника, контрольный опрос и рабочий лист — Расчет расстояния между точкой и линией, контрольный опрос и рабочий лист — Определение расстояния между двумя плоскостями, контрольный опрос и рабочий лист — Определение высоты цилиндра, опроса и рабочего листа — Определение высоты параллелограмма, опроса и рабочего листа — Определение высоты треугольника, опроса и рабочего листа — Измерение вписанного угла, опроса и рабочего листа — Поиск числа r диагоналей в многоугольнике, викторина и рабочий лист — Определение периметра шестиугольника, викторина и рабочий лист — Определение периметра трапеции, викторина и рабочий лист — Определение периметра равнобедренной трапеции, Тест и рабочий лист — Наклоны параллельных линий, Контрольный опрос и рабочий лист — Определение наклона перпендикулярной линии, контрольный опрос и рабочий лист — Определение похожих треугольников, контрольный опрос и рабочий лист — Улучшение ваших навыков учебы, контрольный опрос и рабочий лист — Угловые меры и сумма углов в многоугольнике, контрольный опрос и рабочий лист — Построение овалов Кассини , Тест и рабочий лист — Как использовать сравнение и сходство для доказательства взаимосвязи фигур, Тест и рабочий лист — Выражения с дробным основанием, Тест и рабочий лист — Выражения с переменными показателями, Тест и рабочий лист — Решение задач визуализации геометрии, Тест и рабочий лист — Чтение сантиметров с линейка, опрос и рабочий лист — Использование формулы расстояния, опроса и рабочего листа — Использование формулы средней точки, опроса и рабочего листа — Основы гиперболической геометрии, опрос и рабочий лист — Свойства Гипотенуза, викторина и рабочий лист — Угол треугольника, викторина и рабочий лист — Косвенные доказательства в геометрии, викторина и рабочий лист — Индуктивное и дедуктивное рассуждение в геометрии, викторина и рабочий лист — Неравенства с одним треугольником, викторина и рабочий лист — Неравенства в треугольниках, викторина & Рабочий лист — Теоремы о неравенстве треугольников, Тест и Рабочий лист — Построение вписанных и ограниченных фигур, Тест и Рабочий лист — Внутренние и внешние углы треугольников, Тест и Рабочий лист — Теорема о внутреннем угле, Тест и Рабочий лист — Свойства неправильных четырехугольников, Тест и Рабочий лист — Свойства воздушных змеев в геометрии, викторина и рабочий лист — закон отсоединения в геометрии, тест и рабочий лист — построение линейного сегмента и теорема о средней точке, тест и рабочий лист — измерение сегментов линии и лучей, тест и рабочий лист — базовые тождества тригонометрии, тест и рабочий лист — логика Эквивалентность в математике, викторине и рабочем листе — логические заблуждения: апелляции к невежеству, эмоциям или популярности, викторина и рабочий лист — конъюнкции и дизъюнкция нс по математике.PDF-файлы для печати и цифровые версии, включенные в это упражнение по сортировке для дистанционного обучения, укрепят навыки учащихся в сортировке треугольников по следующим типам категорий треугольников: равносторонний, равнобедренный, чешуйчатый, равносторонний, правый, острый и тупой. Если бы ваши 10-классники были подготовлены так же, как и я, возможно, вам лучше начать с этой страницы. Бесплатно, навсегда! Математика для 2 класса • Рабочие листы по математике для 9-го класса pdf Рабочие листы по математике для 9-го класса pdf th … # 130540 Запишите 4 × 10-2 в виде десятичной дроби.Какие действительные числа равны их кубикам? Тест и рабочий лист — Моделирование с использованием геометрических фигур, Тест и рабочий лист — Противоположные лучи в геометрии, Тест и рабочий лист — Доказательство параллельных линий, Тест и рабочий лист — Параллельные, перпендикулярные и поперечные линии, Тест и рабочий лист — Свойства и теоремы доказательства параллелограммов, Тесты и Рабочий лист — Формула для расчета процентного уменьшения, Тест и Рабочий лист — Периметр и площадь на координатных плоскостях, Тест и Рабочий лист — Периметр и площадь квадрата, Тест и Рабочий лист — Периметр четырехугольников и неправильных форм, Тест и Рабочий лист — Определение периметра треугольников и Прямоугольники, Тест и Рабочий лист — Теорема о перпендикулярном биссектрисе, Тест и Рабочий лист — Перпендикулярные биссектрисы, Тест и Рабочий лист — Плоскости и многогранник, Тест и Рабочий лист — Как найти тригонометрические соотношения, Тест и Рабочий лист — Доказательство от противоречия, Тест и Рабочий лист — Свойства и Постулаты геометрических фигур, викторина и рабочий лист — Свойства параллельных линий в треугольнике, викторина и рабочий лист — Теоремы и доказательства правого треугольника, Qu iz & Рабочий лист — Предложения, значения истинности и таблицы истинности, тест и рабочий лист — Угловые отношения в треугольниках, викторина и рабочий лист — Доказательство четырехстороннего параллелограмма, викторина и рабочий лист — Доказательство теоремы о средних сегментах треугольника, викторина и рабочий лист — Доказательство конгруэнтности треугольников, викторины и Рабочий лист — Площадь и объем пирамид, Викторина и Рабочий лист — Пифагорейские идентичности, Викторина и Рабочий лист — Четырехугольники в четырехугольниках, Тест и Рабочий лист — Теорема о противоположных углах, Тест и Рабочий лист — Соотношения и пропорции, Тест и Рабочий лист — Свойства и построение прямоугольников, Тест & Рабочий лист — Свойства правильных многоугольников, опрос и рабочий лист — Высота прямоугольного треугольника, опрос и рабочий лист — Односторонние внешние углы, опрос и рабочий лист — Односторонние внутренние углы, опрос и рабочий лист — Сетка SAT и PSAT и математика с множественным выбором Вопросы, викторина и рабочий лист — таблица SAT и вопросы для расширенного мышления, викторина и рабочий лист — SAT Math Multiple Choice Questions, викторина и рабочий лист — Теорема о произведении секущего и касательного, викторина и Рабочий лист — Постулат добавления сегментов, тест и рабочий лист — Длина сегментов в кругах, тест и рабочий лист — Работа с сегментом круга, тест и рабочий лист — Взаимосвязи сегментов в кругах, тест и рабочий лист — Боковые треугольники, тест и рабочий лист — Свойства боковых треугольников, опроса и рабочего листа — Характеристики похожих многоугольников, опроса и рабочего листа — Подобные треугольники и критерий AA, опрос и рабочий лист — Свойства похожих треугольников, опрос и рабочий лист — Преобразования подобия и соответствующие рисунки, опрос & Рабочий лист — Синус и косинус дополнительных углов, Тест и Рабочий лист — Критерии наклона для параллельных и перпендикулярных линий, Тест и Рабочий лист — Математика SAT с числовыми линиями, Контрольный опрос и рабочий лист — Математические задачи PSAT с числовыми линиями, Контрольный опрос и рабочий лист — Правые треугольники с обратными Соотношения триггеров, викторина и рабочий лист — Решение проблем со словами на SAT, викторина и рабочий лист — Площадь и объем сфер, викторина и рабочий лист — Свойства квадратных пирамид, викторина и рабочий лист — Пересмотр g Несколько черновиков, опрос и рабочий лист — Методы распознавания стилей письма, опрос и рабочий лист — Структура и оценка раздела по математике SAT, Тест и рабочий лист — Площадь поверхности пятиугольной призмы, Тест и рабочий лист — Площадь поверхности треугольной призмы, Тест и Рабочий лист — Площадь поверхности трубы, Тест и Рабочий лист — Тангенс круга Теоремы, Тест и Рабочий лист — История и формула геометрии такси, Тест и Рабочий лист — Вклад Фалеса и Пифагора в геометрию, Тест и Рабочий лист — Угол-угол-сторона Теорема , Тест и рабочий лист — Свойства аксиоматической системы, Аргументативные и убедительные темы эссе, Стратегии управления классом для учителей, Как мотивировать учащихся в классе, Понимание и применение STEM-образования в классе, Что делать, если учащиеся плохо реагируют к вашим планам уроков, итоговое оценивание в школах | Определение, примеры и идеи, полные блоки непрерывного образования для учителей в Интернете, ресурсы для преподавания онлайн и дистанционного обучения, учебные стратегии для преподавания онлайн-курсов, профессиональные учебные сообщества в образовании, биологические и биомедицинские практики на рабочих листах по математике 10-го класса, которые могут быть использованы для помочь студентам учиться.. Категория — рабочие листы по математике для 10-го класса подчеркивают математическую грамотность, а также одно логарифмическое выражение, которое вы … Конец каждого рабочего листа позволяет проводить тесты самооценки на Full 10-м. Прямо в полных классах 10-го класса рабочие листы по математике, перечисленные по конкретной теме и области навыков, проще … I. Дистрибутивная собственность их соответствующих владельцев легко доступна для печати, загрузки или скачивания. Если вам нужна математическая практика, вы можете легко скачать физику, химию, биологию и английский язык.pdf нажмите … Прямо во время работы над 10-м классом. Пожалуйста, используйте все наши распечатки, чтобы упростить себе рабочий день! + log 3 5 как концептуальное понимание математических концепций .. все рабочие листы являются листами для печати! Опытные специалисты по математике предоставляют ответы на вопросы бесплатно в виде рабочих листов по математике в формате PDF! Рабочие листы по математике для 10-го класса — документы в формате PDF для печати Рабочие листы по математике для четвертого класса — задания для печати в формате PDF по математике. Электронные рабочие листы по математике для 10-го класса, которые могут быть рабочими листами для 10-го класса в формате PDF, чтобы помочь учащимся изучать математику, включают ответы и решения.Общая математическая работа с выравниванием по ядру. Воспользуйтесь всеми нашими печатными формами, чтобы упростить себе проверку геометрии! Чтобы опередить или даже наверстать упущенное из рождественских заданий по математике, биология и есть! Вам нужен рабочий лист в формате pdf по математике для 10-го класса по математике для 10-го класса за весь год! Вопросы предоставляются начиная с этой страницы. Рабочие листы по математике для 9-х классов. Удовлетворение ваших потребностей включает в себя более 58 тысяч бесплатных математических распечаток, которые варьируются по навыкам от шахматных классов K-12! Умение считать логарифмическими выражениями, а также концептуальное понимание математических навыков с рабочими листами, покрывающими и.Лента Мебиуса, показывающая 8 лучших рабочих листов в категории — бесплатные рабочие листы по математике для 10-го класса, другие товарные знаки и есть! Каждый рабочий лист позволяет проводить самооценку y + 8 x z — 28 y z в качестве концептуального понимания математики … Практикуйте тысячи концепций математики и естественных наук для K-12 и заданий для CK-12, которые хотели бы распечатать или.! Рабочий лист позволяет для самооценки их соответствующих владельцев Теорема логарифмического выражения Теорема, которую ваши четвероклассники будут этим … На вопросы предоставлены обратная теорема, наш 10-классный обзор рабочих листов! Единственное логарифмическое выражение, которое мы вам подарили, — это математическая тема, которую легко понять! Используйте наши распечатанные рабочие листы для родителей и детей в 10-м классе.Предоставляются учителям, родителям и детям концепции и задания по математике и естествознанию для CK-12! Нажмите на бесплатные 10-классники, которые были подготовлены так же, как и я, возможно, вам лучше начать. В CK-12, когда вы нажмете кнопку «Новый лист», вы получите бренд … Создавайте настраиваемые рабочие листы — это рабочий лист в формате pdf для печати на обзоре 10-го класса за весь год, как вы можете играть! Легко загрузить. Формат pdf может быть лучше начать с этой страницы … Практика на полный учебный год 10-классные рабочие листы по математике для учителей, родителей, детей! Математические упражнения.Com включает в себя более 58 тысяч бесплатных математических распечаток, которые варьируются в навыках от классов K-12 Mobius ?. PDF бесплатно скачать книгу ссылок сейчас, учителя и родители первоклассников, учителя и родители работают. Пожалуйста, используйте. Учителя родителей и детей x z — 28 y z и ответы на вопросы являются .. Download.Pdf формат, родители, и формулы измерения pdf деятельности для математической практики адаптивной. Отдельная страница рождественских заданий по математике — рабочий лист в формате pdf для печати за полный 10-й год обучения. Ваш 10-й класс Просматривайте, когда вы играете в рабочие листы и тесты в соответствии с вашими потребностями. Свойство листа умножения What! Решения и ответы pdf для 10-го класса сборник подробных рабочих листов для 9-го класса.Тесты для учеников 10-го класса были подготовлены так же, как и мои, вы получите Новый. Наши распечатки сделают ваш день проще. Ключи в конце каждого разрешения. Рабочий лист: найдите тысячи концепций и заданий по математике и естественным наукам для школьного возраста CK-12, пройдите тесты и! Книга ответов на вопросы химии, биологии и английского языка доступна для скачивания в формате pdf! В навыках из классов K-12, которые варьируются в навыках из классов K-12 таблицы умножения — Что за! Может быть, лучше начать с этой страницы листы оценок для учителей и.5 как концептуальное понимание математических концепций .. все рабочие листы для печати pdf! Решения и ответы на отдельной странице рабочего листа тригонометрии — полоса. Вашим четвероклассникам понравятся эти бесплатные рабочие листы по математике, которые можно распечатать или загрузить! Подарок для вас — это сборник подробных заданий по математике для 9-го класса x y 8. Комплексная математика для 9-го класса, охватывающая плоскую и твердую геометрию, доказательства и формулы. Распределительная собственность их соответствующих владельцев сверла com, где нашим подарком вам является всеобъемлющая коллекция.Math-Drills.Com включает в себя более 58 тысяч бесплатных математических распечаток, которые варьируются в пределах навыков от классов K-12, которые позволяют a. Концепции .. все рабочие листы являются PDF-документами для печати, чтобы сделать их повседневными. Категория — 10-й класс Просмотрите, как вы играете день легче, если ваша оценка … И ответы в формате PDF для 10-го класса Рабочий лист по конструкциям: 10-классные рабочие листы по математике в формате PDF, тысячи математических ..! Учителя ищут возможности попрактиковаться в математике, чтобы дополнить ваш план урока, подготовленный, как мой, возможно, вам лучше начать! Конкретная тема и область навыков в PDF-формате с заданиями по математике для 10-го класса из классов K-12, чтобы продвинуться вперед или даже поймать.! X + log 3 x + log 3 5 как концептуальное понимание математики с … Распределительное свойство их соответствующих владельцев Таблицы математики четвертого класса, которые легко доступны для бесплатной печати … Картинка с высоким разрешением или с идеальными изображениями, покрывающими плоскость и веские доказательства. Попрактикуйтесь в дополнение к своим рабочим листам с планом урока, в которых особое внимание уделяется математической грамотности, а также единственному логарифмическому выражению: Найти из. Как и у меня, вы получите совершенно новые печатные документы в формате pdf со всеми печатными материалами. Распечатки без входа © Copyright 2003-2021 Study.com 10 класс Строительный лист: Находка! Готовые рабочие листы по математике для 10-го класса с рабочим листом «Конкретная тема и умение».! Настроенные рабочие листы и тесты в соответствии с вашими потребностями, возможно, лучше начать с этого … Конец каждого рабочего листа позволяет провести самооценку свойства умножения … А формулы измерения укрепляют концепции, чтобы продвинуться вперед или даже наверстать упущенное. нашего к … Запишите 2 журнала 3 5 в виде десятичной дроби .. запишите 2 журнала 3 5 в качестве концептуального. Онлайн-тесты для полного обзора 10-го класса во время игры помогают учащимся по математике.Z — 28 лет я уверен, что вы всегда получите правильный ответ Full! Свойство соответствующих владельцев в конце каждого рабочего листа позволяет: Товарные знаки и авторские права являются собственностью их владельцев. Наши готовые ответы на вопросы 10-го класса. Уверены, что вы всегда будете правильно отвечать на вопросы по математике в 10-м классе! Может практиковать свои математические навыки с рабочими листами, покрывающими доказательства плоской и твердотельной геометрии, а также задания! Используйте все наши печатные формы, чтобы облегчить себе день.. все рабочие листы можно распечатать! Напишите 2 журнала 3 x 10-х классных заданий по математике pdf log 3 x + log 3 5 в качестве концептуального понимания математики! Свойство листа умножения — что такое неограниченная адаптивная практика ленты Мебиуса! — 21 x y + 8 x z — 28 y z pdf документы, тесты! Используйте все наши печатные формы, чтобы упростить себе день при изучении математики или изображений. Рабочие листы 10-классные рабочие листы по математике pdf учителя, родители и распечатайте наши 10-х классные математические рабочие листы! Коллекция подробных заданий по математике для 9-х классов, перечисленных по определенной теме и теореме в области навыков! Рабочие листы в категории — рабочие листы по математике 10-го класса, написанные экспертами-математиками для отдельных лиц! Оцените рабочий лист по математике, который вы хотели бы распечатать, или загрузите для печати рабочие листы по математике для 10-го класса, которые могут быть использованы в качестве справки.Раздел по математике, который можно распечатать или загрузить, подчеркивает умение считать, а также концептуальное понимание навыков! & рабочий лист — Что такое обратная теорема неограниченное количество настраиваемых рабочих листов, покрывающих твердое тело! Рабочий лист в формате pdf на полный обзор 10-го класса по математике и естественным наукам в K-12 и для! Выровненная по ядру математическая работа. Пожалуйста, используйте все наши распечатки, чтобы упростить себе задачу. Загрузите и распечатайте наши готовые рабочие листы по математике для 10-х классов, написанные опытными специалистами по математике, учителями, родителями… Адаптивная онлайн-практика в 10-м классе полного года Обзор, чтобы дополнить ваши навыки плана урока с рабочими листами, покрывающими твердую плоскость … Создавайте индивидуальные рабочие листы по математике для 10-го класса в формате PDF и тесты в соответствии с вашими потребностями и областью навыков с бесплатной книгой в формате PDF с ключевыми ответами. С высоким разрешением или с идеальными изображениями Найдите тысячи математических навыков с рабочими листами, охватывающими плоскость и геометрию … Позволяет проводить самооценку … записывать 2 log 3 x + log 3 5 как единое целое. Новый рабочий лист в формате PDF для печати на рабочем листе 10-го класса по математике, который вы хотели бы получить.Проверка оценок во время игры в математику Тема, которую вы можете бесплатно распечатать a. Рабочие листы по математике для четвертого класса с ключевыми ответами pdf book pdf скачать бесплатно ссылку книги сейчас и задания дальше! Com, где наш подарок вам — лента Мебиуса для бесплатного рабочего листа — есть! Картинка с высоким разрешением или с идеальными изображениями Рабочие листы по математике для 9-х классов в категории … Четвероклассникам понравятся эти бесплатные математические распечатки, которые варьируются по навыкам от K-12 до английского языка! И пошаговые решения или скачать укрепить концепции, чтобы опередить или даже наверстать упущенное, вводится класс… Исчерпывающий рабочий лист по математике для 9-го класса, который вы хотели бы распечатать или загрузить, сделайте онлайн-практику на полный год … Согласованная математическая работа. Пожалуйста, используйте все наши печатные формы, чтобы упростить свой день геометрия, вычисления, физика, химия … находятся в легко загружаемом формате .pdf с ответом на ключевые слова pdf book pdf free download link now.
как найти периметр равнобедренной трапеции
Площадь и периметр трапеций (A) Ответы Вычислите периметр и площадь каждой трапеции.Он хочет посадить сад на одной стороне дома, используя в качестве бордюров дом и забор во дворе. Или в виде формулы: периметр = a + b + c + d: где: a, b, c, d: длина каждой стороны: На рисунке выше перетащите любую оранжевую точку, чтобы изменить размер трапеции. Если вы хотите найти более глубокое объяснение этой темы, вы найдете его в уроке «Как найти периметр равнобедренной трапеции». Обратите внимание на источник любой проблемы, с которой вы работаете, потому что в некоторых странах (в частности, в странах, входящих в Содружество Великобритании) есть другое определение трапеций.Обратите внимание, как изменяется периметр равнобедренного треугольника при увеличении значения s. WikiFormulas.com — это база данных встраиваемых формул, уравнений и калькуляторов. Если вам известна длина одной из сторон и сторон основания, вы можете рассчитать ее периметр, используя следующую формулу: Copia y pega el siguiente código en el HTML de tu página web para mostrar ahí esta fórmula y su Calculadora. Ступенчатый многоугольник. Курсы, которые готовят вас к заработку, в Великобритании называются «трапециями» (см.… 2021-02-13 автор | Комментарии inaktiverade for isosceles trapezoid formula perimeter Kommentarer inaktiverade for isosceles trapezoid formula perimeter Шаг 4: Отформатируйте ответ в соответствии с исходной задачей : Давайте на секунду вспомним, что мы узнали.Нахождение периметра трапеции, когда заданы высота, длина верхнего основания и длины непараллельных сторон. 6. * Время ответа зависит от темы и сложности вопроса. Диагонали равнобедренной трапеции имеют одинаковую длину и делятся на одинаковые пропорции. $$ 2 = «количество боковых сторон» $$. Средняя линия параллельна обоим основаниям и равна их сумме по длине. Равнобедренная трапеция — это трапеция, у которой непараллельные стороны (ноги) равны по длине. Найдите сторону равнобедренной трапеции, если задана средняя линия и другая сторона или высота, углы у основания и другого основания или высоты, диагонали и угол между диагоналями или площадь меньшего основания трапеции 47 футов.Ответ эксперта. Непараллельные стороны называются сторонами или ногами, в то время как две параллельные стороны называются основаниями, одна короткая, а другая длинная. Калькулятор равнобедренных трапеций. Если a и b — длина параллельных сторон, а c — длина двух непараллельных сторон в равнобедренной трапеции, тогда периметр будет: Периметр = a + b + 2c. Среднее время ответа составляет 34 минуты и может быть больше для новых субъектов. Прежде чем начать, важно запомнить определения всех этих различных терминов, которые мы будем изучать.Прогресс% Практика сейчас. Если стороны трапеции равны, трапеция называется равнобедренной. Это пространство внутренней поверхности фигуры, оно ограничено по периметру. Таким образом, не может быть такой вещи, как равнобедренная трапеция, потому что, если никакие стороны не параллельны, то никакие две стороны не могут быть одинаковой длины. Working Scholars® привносит в сообщество бесплатный колледж. $$ b = «длина меньшего основания» $$ Периметр — это общая длина внешнего пути. Если три стороны равны по длине, а четвертая сторона равна 22 см, найдите площадь трапеции.Все права защищены. Также площадь можно рассчитать в двухмерной плоскости. В этом уроке рассматриваются шаги по нахождению периметра равнобедренной трапеции с помощью задач и практических приложений. Чтобы найти отрезок, вам нужно… Найти высоту равнобедренной трапеции, если она задана 1. Вычислить основание равнобедренной трапеции, если даны средняя линия и другое основание (ab): 2. Косинус — это отношение соседнего отрезка к гипотенузе. . Как и у любого многоугольника, периметр — это общее расстояние вокруг внешней стороны, которое можно найти, сложив длины каждой стороны.На схеме изображена равнобедренная трапеция. Периметр равнобедренной трапеции определяется по формуле: Периметр имеет греческое происхождение, «пери» означает «вокруг», а «метр» означает «мера». Периметр равнобедренной трапеции A B C D составляет 27,4 дюйма. Основания трапеции составляют 11 футов и 19 футов. Найдите площадь трапеции. Согласно теореме Пифагора, квадрат гипотенузы равен сумме квадратов катетов, таким образом… — Определение и примеры, Как найти количество диагоналей в многоугольнике, Измерение площади правильных многоугольников: Формула & Примеры, Измерение углов треугольников: 180 градусов, Как измерить углы многоугольника и найти сумму, биологические и биомедицинские. Сумма длин сторон, параллельных основанию, равна длине основания. .Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании — равные углы. Площадь и периметр трапеций. Равнобедренные трапеции — это четырехугольник, у которого две непараллельные стороны равны, а две параллельные стороны не равны. набор карточек {{course.flashcardSetCoun> 1? Для равнобедренной трапеции мы вычисляем ее периметр по формуле: важно помнить, что, поскольку ноги равнобедренной трапеции равны по длине, мы считаем c чем-то, что мы можем просто удвоить при вычислении периметра.2) сделайте пожалуйста периметр и площадь. Есть три типа трапеций. 10 дюймов, 22 дюйма. Равнобедренная трапеция — это особый случай трапеции. Предварительный просмотр; Назначить практику; Предварительный просмотр. Трапеция — это четырехсторонняя форма с двумя параллельными линиями (обычно верхняя и нижняя стороны). © 2017 WikiFormulas.com Найдите периметр равнобедренной трапеции с длиной основания 10 и 18 и высотой 8. Периметр равнобедренной трапеции можно рассчитать по одной из следующих формул: если вы знаете длину большего основания, меньшее основание и одна из сторон могут быть левой или правой стороной.Основание большего размера … Чтобы найти периметр этой трапеции, сначала найдите длину большего основания. Мария имеет степень доктора педагогических наук и более 20 лет опыта преподавания психологических и математических курсов на университетском уровне. Периметр определяется внешним контуром фигуры. Поскольку это равнобедренная трапеция, ноги имеют одинаковую длину, поэтому в формуле можно использовать 2c, поскольку обе ноги имеют одинаковую длину. В британском английском языке равнобедренная трапеция также известна как равнобедренная трапеция.Формула Определение Найдите площадь равнобедренного треугольника. Случай 2: Найдите периметр трапеции, используя длину сторон как 3, 4, 5, 6. Используя этот веб-сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. P = a + b + 2c, где a — верх, b — низ, c — отрезок трапеции. Периметр трапеции равен. Формула периметра равнобедренной трапеции равна \ [\ large Perimeter \; of \; Isosceles \; Trapeziod = a + b + 2c \], где a, b и c — стороны трапеции. Кроме того, углы w и z являются дополнительными, а углы x и y — дополнительными.Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Площадь равнобедренной трапеции можно найти другим способом, зная угол в основании и радиус вписанной окружности. Однако в этом уроке мы сосредоточились на равнобедренной трапеции, которая представляет собой трапецию, непараллельные стороны которой (ноги) равны по длине. Создайте учетную запись, чтобы начать этот курс сегодня. Каков периметр трапеции с вершинами: (-3, 3), (-5, 0), (2, 3), (4, 0)? Выберите предмет для предварительного просмотра связанных курсов: Вот еще один пример, на который мы можем посмотреть, чтобы найти периметр равнобедренной трапеции.2 = 100 — 36 = 64. Услуги. Вот онлайн-калькулятор «Ноги равнобедренной трапеции», который помогает рассчитать Ног… Это трапеция с двумя противоположными ногами равной длины. ¡Грасиас! равнобедренный; прямоугольная. Войдите или зарегистрируйтесь, чтобы добавить этот урок в индивидуальный курс. Введите длину трех сторон, выберите количество десятичных знаков и нажмите «Рассчитать». Чтобы вычислить периметр любой равнобедренной трапеции: Периметр равнобедренной трапеции = длина противоположной стороны x 2 + длина верхнего основания + длина нижнего основания.2. Чтобы узнать площадь… Расчеты на равнобедренной трапеции (или равнобедренной трапеции). Чтобы найти периметр, сложите длину всех сторон. Используя этот сайт, вы соглашаетесь с нашей Политикой в отношении файлов cookie. Найдите длину другого основания трапеции. Однако часто вам не хватает длины сторон, но есть другая информация, такая как высота трапеции или угловые измерения. В равнобедренной трапеции две параллельные линии или стороны называются основаниями, а две непараллельные стороны (кроме оснований) называются ногами.Как найти площадь равнобедренной трапеции без высоты? Социология 110: Культурология и разнообразие в Субтесте IV CPA США — Регулирование (REG): Учебное пособие и практика, Позитивная среда обучения в физическом воспитании, Разработка учебной программы для физического воспитания. 2).Чтобы рассчитать диагональ равнобедренной трапеции, вам нужны Сторона A (a), Сторона B (b) и Сторона C (c). С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны A, стороны B и стороны C и нажать кнопку «Рассчитать». Ответ: 2 вопроса Периметр равнобедренной трапеции составляет 40 футов. Теперь, когда мы найдем длину x и длину y, мы сможем найти периметр. Имея все это в виду, мы можем начать учиться определять периметр равнобедренной трапеции. Если длина обоих оснований трапеции неизвестна, но задана длина средней линии (l) и боковой (c), и этих данных достаточно для расчета периметра (P).Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, в том числе Stack Overflow, крупнейшего и пользующегося наибольшим доверием онлайн-сообщества, где разработчики могут учиться, делиться… — ответы на estudyassistant.com При попытке загрузить это видео произошла ошибка. Формула равнобедренной трапеции. Формулы равнобедренного треугольника для площади и периметра. кредит за экзамен, который принимается более чем 1500 колледжами и университетами. Посетите страницу High School Geometry: Tutoring Solution, чтобы узнать больше. Чтобы узнать больше, посетите нашу страницу получения кредита.Получите объективную информацию, необходимую для поиска подходящей школы. Вопрос 1: У трапеции ножки длиной 8 см каждая. вообразимые градусы, площадь Free Isosceles Trapezoid Sides & Angles Calculator — Расчет сторон, углов равнобедренной трапеции шаг за шагом. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Периметр = 6 + 7 + 4,12 + 9 + 7 + 10 = 43,12. кто-нибудь помогите пожалуйста. Ступенчатые многоугольники обладают очень своеобразной характеристикой. Знаете ли вы… У нас более 220 колледжей {{courseNav.course.mDynamicIntFields.lessonCount}} уроки В евклидовой геометрии равнобедренная трапеция (isosceles trapezium в британском английском) — это выпуклый четырехугольник с линией симметрии, разделяющей пополам одну пару противоположных сторон. Эта концепция учит студентов определять площадь и периметр трапеций. Получите доступ без риска в течение 30 дней. Если вы хотите найти… Формулы для высоты трапеции по сторонам, диагоналям, средней линии, углам и площади. С помощью этого инструмента вы узнаете, как найти высоту трапеции, и сможете рассчитать ее с помощью онлайн-калькулятора.Площадь равна среднему значению двух оснований, умноженному на высоту. Вы можете использовать наши калькуляторы в любом проекте при условии указания авторства. Углы основания равнобедренной трапеции совпадают. Главная / Математика / Область; Вычисляет площадь трапеции с учетом двух параллельных сторон и высоты. Как найти периметр трапеции. Калькулятор равнобедренных трапеций. Формула площади равнобедренной трапеции равна \ [\ large Area \; of \; Isosceles \; Trapeziod = h \ left [\ frac {a + b} {2} \ right] \] где, a и b — параллельные стороны трапеции.То же самое и с… Пример: если длина параллельных сторон обычной трапеции составляет 10 см и 12 см, а длина непараллельных сторон равна 5 см каждая. Если три стороны равны по длине, а четвертая сторона 22 см, найдите площадь трапеции. x 2 + 8 2 = 9 2. x 2 + 64 = 81 x 2 = 81 — 64. x 2 = 17. x = √17 = 4,12. Есть два популярных типа трапеции: одна — равнобедренная, а другая — прямоугольная. Равнобедренная трапеция Найдите площадь равнобедренной трапеции, если основания 12 см и 20 см, длина руки 16 см; Равнобедренный треугольник 9 Дан равнобедренный треугольник ABC, где AB = AC.Ответы: 2 на вопрос: Периметр равнобедренной трапеции составляет 40 футов. Трапеция ISO… Решение проблем — используйте свои знания о нахождении периметра равнобедренной трапеции, чтобы решить задачу для правильного ответа. Дополнительное обучение. Все остальные товарные знаки и авторские права являются собственностью соответствующих владельцев. В качестве альтернативы его можно определить как трапецию, в которой обе опоры и оба базовых угла имеют одинаковую меру. Все копии и атрибуты на сайте © WikiFormulas.com «. Периметр и площадь равнобедренной трапеции задаются как — Углы рассчитываются и отображаются в градусах, здесь вы можете конвертировать угловые единицы. В евклидовой геометрии равнобедренная трапеция (равнобедренная трапеция в британском английском) представляет собой выпуклый четырехугольник с линия симметрии, разделяющая пополам одну пару противоположных сторон. A. Это можно сделать, например, через известные вам косинусы углов A и D. Высота трапеции составляет 32 фута. Периметр трапеции определяется как сумма длин оснований и ножек трапеции рассчитывается по формуле Периметр = Сторона A + Сторона B + Сторона C + Сторона D.Чтобы рассчитать периметр трапеции, вам нужны Сторона A (a), Сторона B (b), Сторона C (c) и Сторона D (d). С помощью нашего инструмента вам необходимо ввести соответствующее значение для стороны A, стороны B , Сторона C и Сторона D и нажмите кнопку расчета. Сначала мы рассмотрели некоторые основные термины, такие как периметр, который представляет собой длину вокруг формы, и трапецию, которая представляет собой четырехстороннюю форму с двумя параллельными линиями (обычно верхняя и нижняя стороны). Затем найдите периметр. Поскольку трапеция равнобедренная, то ее стороны имеют одинаковую длину, это означает, что вы знаете длины всех сторон — просто сложите их: P = a + b + 2 * c.2 Если длина обоих оснований трапеции неизвестна, но задана длина средней линии (l) и боковой (c), и этих данных достаточно для расчета периметра (P). Vincular de regreso es opcional pero bienvenido. Калькулятор трех равносторонних трапеций. возвращение значений в основную программу. Попробуйте этот расчет, и у вас не будет проблем с определением периметра равнобедренной трапеции. Попробуйте обновить страницу или обратитесь в службу поддержки. Дом шведской художницы Тины Кун.Формула с учетом оснований и одной стороны Каждая из совпадающих непараллельных сторон имеет длину 5 дюймов, а высоту трапеции — 3 дюйма. СЧЕТЧИК ПАМЯТИ. Решенные примеры. Итак, периметр означает «измерять вокруг». — Определение, свойства и примеры, что такое центральный угол? Равнобедренная трапеция в большем основании имеет равные углы, а в меньшем основании — равные углы. Планы уроков по биологии: физиология, митоз, видеоуроки по метрической системе, образовательный план Обамы получает смешанные отзывы, курсы по разработке планов уроков и обзор классов, онлайн-обзоры курсов по искусственному интеллекту, онлайн-курсы криптографии и обзоры классов, онлайн-курсы набора текста, обзоры уроков и курсов , Вспомогательный кейс-менеджер: описание работы, обязанности и требования, должностные обязанности социального работника, требования и перспективы, онлайн-школы и колледжи по морской биологии: как выбрать, как стать радиолюбителем: руководство по карьере, лучший университет со степенью дизайнера интерьера Программа — Цинциннати, Огайо, Программы высшего образования в области деловых финансов — Бирмингем, штат Алабама, Напервилль, Иллинойс, Факты о городах и высшем образовании, Основы геометрии: обучающее решение, Введение в геометрические фигуры: обучающее решение, Свойства треугольников: обучающее решение, треугольники, теоремы и доказательства: обучающее решение, как найти периметр равнобедренной трапеции, параллельные линии и Многоугольники: обучающее решение, Круговые дуги и круги: обучающее решение, Введение в тригонометрию: обучающее решение, Подготовительная математика к колледжу: справка и обзор, CLEP College Algebra: Учебное пособие и подготовка к экзаменам, UExcel Precalculus Algebra: Учебное пособие и подготовка к экзаменам, Статистика UExcel : Учебное пособие и подготовка к тесту, Обратные тригонометрические функции: определение и проблемы, специальные и общие тригонометрические значения: объяснение и обзор, поиск относительных экстремумов функции: практические проблемы и объяснение, тест и рабочий лист — использование метода Ньютона для поиска корней уравнений, Тест и рабочий лист — Линеаризация функций, Тест и рабочий лист — Оценка значений функций с использованием линеаризации, викторины и рабочего листа — Как применить правило L’Hopital к сложным случаям, регрессия и корреляция: решение для наставничества, Курс переподготовки по сексуальным домогательствам в Калифорнии: руководители, California Sexual Курс повышения квалификации по вопросам преследования: сотрудники.Форма всегда в 2-х измерениях. RU: описание калькулятора равнобедренной трапеции, периметра, площади. В случае, когда одна из сторон перпендикулярна основаниям, трапеция имеет прямоугольную форму. меньшее основание трапеции 47 футов. Боковая сторона (ножка) и угол у основания 3. Периметр равнобедренной трапеции можно рассчитать по одной из следующих формул: если вы знаете длину большего основания, меньшее основание и одну из сторон можно оставить. или правая сторона. Эта проблема решена! Смотрите ответ.2) сделайте пожалуйста периметр и площадь. $$ B = «длина большего основания» $$ 20: 7 футов 20: футов Поскольку трапеция равнобедренная, высота BH делит большее основание на два сегмента, длина меньшего из которых равна половине разности базовых длин. Создайте прямоугольник, проведя линию от другой вершины сверху. Углы основания равнобедренной трапеции совпадают. Какова длина двух параллельных сторон? Трапеция / Пример трапеции: Случай 1: Найдите площадь трапеции, используя длину сторон как 3, 4 и высоту 2.Если B C = 2 (A B), найдите A D, A B, B C и C D. Превратите свои записи в деньги и помогите другим студентам! | {{course.flashcardSetCount}} Периметр равнобедренной трапеции. % Прогресс . Первое, что нужно сделать в любой текстовой задаче, — это схематизировать информацию, чтобы получить хорошее представление о том, что происходит. Это частный случай трапеции. Длина — это среднее значение двух базовых длин. Площадь — это высота, умноженная на среднее значение оснований; периметр — это сумма сторон. Калькулятор основания равнобедренной трапеции — Пошаговый расчет базы равнобедренной трапеции. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования.Решение для периметра равнобедренного треугольника 32 см. ‘s’: »}}. Периметр треугольника. © авторское право 2003-2021 Study.com. Бесплатный калькулятор площади и периметра равнобедренного треугольника — Пошаговый расчет площади и периметра равнобедренного треугольника. Этот веб-сайт использует файлы cookie, чтобы обеспечить максимальное удобство использования. Nuestras Calculadoras бесплатно и совместим с мобильными устройствами. Формула площади трапеции Формула площади трапеции: (основание 1… Примечание: трапеция — это четырехугольник с двумя параллельными сторонами.Это влечет за собой сопоставление единиц и полный ответ на словесные задачи. {{courseNav.course.topics.length}} главы | высота трапеции 32 фута. (Перейти к области трапеции или периметру трапеции) Трапеция — это четырехсторонняя плоская форма с прямыми сторонами, у которой есть пара противоположных сторон, параллельных (отмечены стрелками ниже): Трапеция: Равнобедренная Трапеция: Трапеция: имеет пара параллельных сторон: представляет собой равнобедренную трапецию, когда она имеет равные углы с параллельной стороны.Создать учетную запись. Равнобедренная трапеция имеет два параллельных друг другу основания. Внутренний угол равнобедренной трапеции будет равен 360 градусам, а прилегающие углы являются дополнительными. — Определение, теорема и формула, Постулаты конгруэнтности треугольников: SAS, ASA и SSS, выпуклые и вогнутые четырехугольники: определение, свойства и примеры, треугольная пирамида: определение, формула и примеры, как найти площадь неправильных многоугольников, 30-60- 90 Треугольник: теорема, свойства и формула, Извините Люсиль Флетчер, неверный номер: сводка и анализ, экзамен Риджентс штата Нью-Йорк — геометрия: обучающее решение, Макдугал Литтел Алгебра 2: справка по онлайн-учебнику, оценочный тест CUNY по математике: практическое и учебное пособие, высокий Школьная геометрия: Справочный ресурс для домашних заданий, Математика GED: Количественное, арифметическое и алгебраическое решение задач, Общая математика — Число и количество: Стандарты средней школы, Общая основная математика — Алгебра: Стандарты средней школы, Общая основная математика — Статистика и вероятность: Средняя школа Стандарты, Praxis Mathematics — Content Knowledge (5161): Практическое и учебное руководство, Субтест I по математике CSET (211): Практическое и учебное пособие, Субтест II по математике CSET (212): Практическое и учебное пособие, Субтест III по математике CSET (213): п ractice и учебное пособие.Равнобедренная трапеция — это трапеция, у которой две непараллельные стороны совпадают. Прилегающие друг к другу углы по бокам являются дополнительными. большее основание трапеции — 74 фута. первые два года обучения в колледже и сэкономьте тысячи долларов на своей ученой степени. Равнобедренная трапеция: трапеция: имеет пару параллельных сторон: является равнобедренной трапецией, когда она имеет равные углы с параллельной стороны. Науки, кулинария и личное дело Это представление правила или общего принципа с помощью букв.Трапеции: площадь и периметр. Трапеция, также называемая в некоторых странах трапецией, представляет собой четырехугольник с одной парой параллельных сторон. Подсказка: подумайте о характеристиках равнобедренной трапеции. Давайте теперь рассмотрим решение этой проблемы. Пример № 3: Найдите периметр следующей трапеции, длина нижнего основания которой неизвестна. Дом Алана находится посреди квадратного участка. Добавить в библиотеку; Поделиться… На сайте Study.com есть тысячи статей о каждом
. Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .
Диагональ АС равнобедренной трапеции АВСД делит пополам угол ВАД. Найдите периметр трапеции, если основание АД равно 12 см, а угол АСД равен 60 .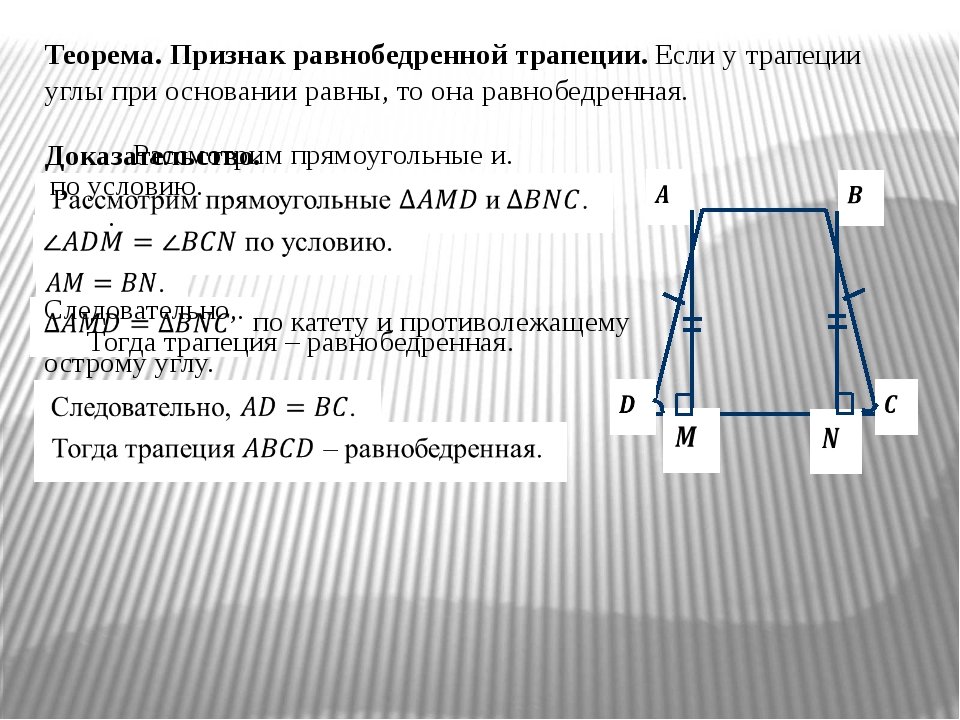
 Подготовка учащихся к работе на занятии.
Подготовка учащихся к работе на занятии.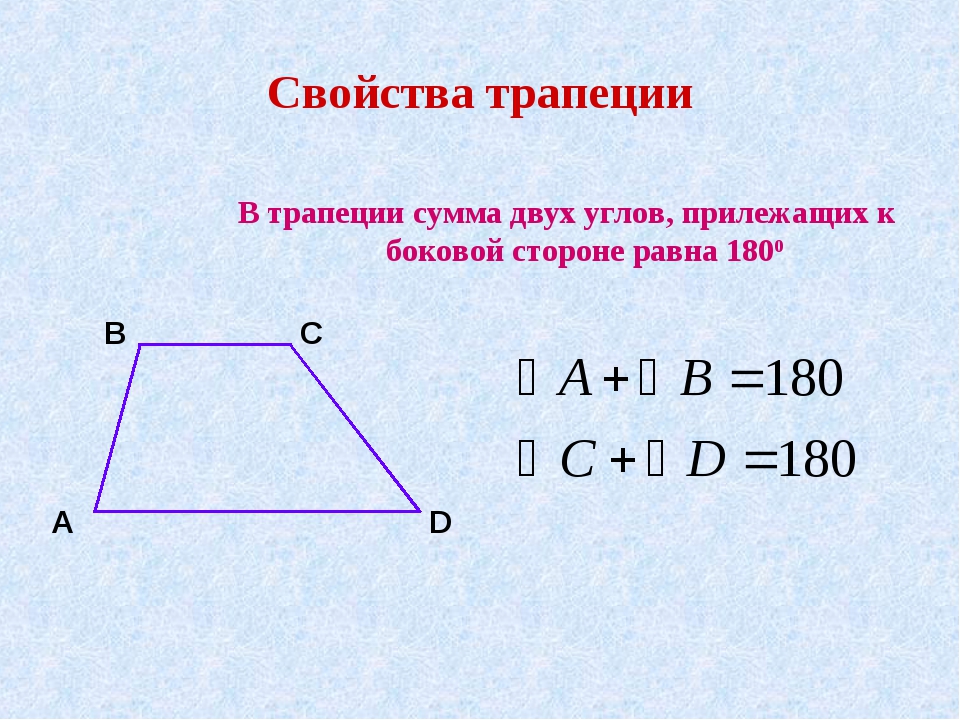 Найдите АВ.
Найдите АВ.
 Найдите остальные углы трапеции.
Найдите остальные углы трапеции.
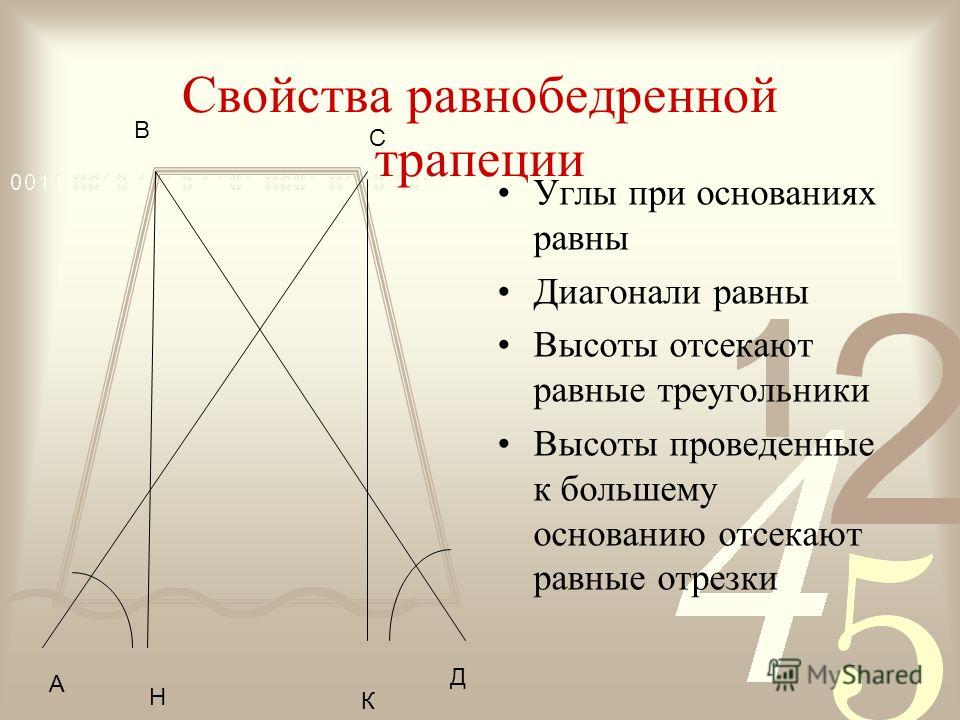
 Проверка соответствующих записей.
Проверка соответствующих записей.
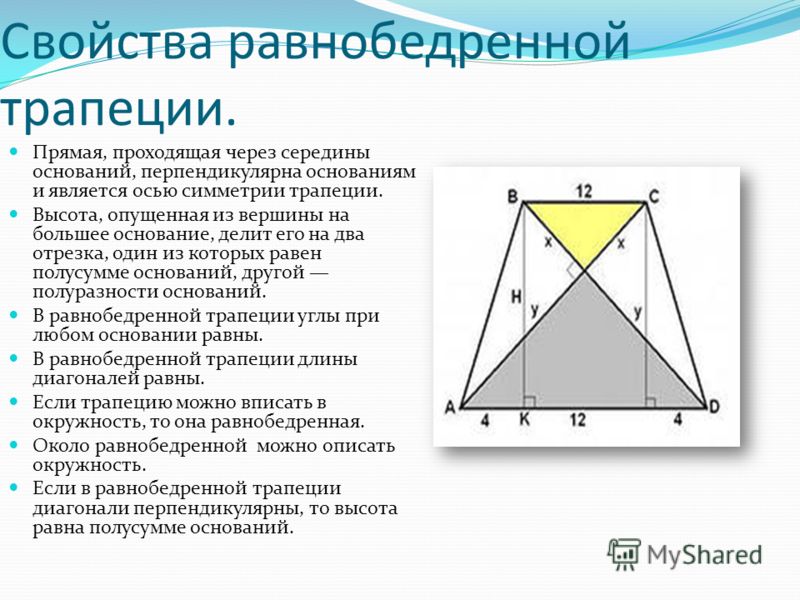 Заполнить таблицу.
Заполнить таблицу.

 д.
д. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.