Доказать с помощью математической индукции онлайн. Метод математической индукции
Лекция 6. Метод математической индукции.
Новые знания в науке и жизни добываются разными способами, но все они (если не углубляться в детали) делятся на два вида – переход от общего к частному и от частного к общему. Первый – это дедукция, второй – индукция. Дедуктивные рассуждения – это то, что в математике обычно называют логическими рассуждениями , и в математической науке дедукция является единственным законным методом исследования. Правила логических рассуждений были сформулированы два с половиной тысячелетия назад древнегреческим учёным Аристотелем. Он создал полный список простейших правильных рассуждений, силлогизмов – «кирпичиков» логики, одновременно указав типичные рассуждения, очень похожие на правильные, однако неправильные (с такими «псевдологическими» рассуждениями мы часто встречаемся в СМИ).
Индукция (induction – по-латыни наведение ) наглядно иллюстрируется известной легендой о том, как Исаак Ньютон сформулировал закон всемирного тяготения после того, как ему на голову упало яблоко. Ещё пример из физики: в таком явлении, как электромагнитная индукция, электрическое поле создает, «наводит» магнитное поле. «Ньютоново яблоко» – типичный пример ситуации, когда один или несколько частных случаев, то есть
Будем вычислять значение трехчлена при некоторых первых значенияхn :
Заметим, что
получаемые в результате вычислений
числа являются простыми. И непосредственно
можно убедиться, что для каждого n от 1 до 39 значение многочлена
является простым числом. Однако приn =40
получаем число 1681=41 2 ,
которое не является простым. Таким
образом, гипотеза, которая здесь могла
возникнуть, то есть гипотеза о том, что
при каждом n число
является простым, оказывается неверной.
Лейбниц в 17 веке
доказал, что при всяком целом положительном n число
делится на 3, число
делится на 5 и т.д. На основании этого он
предположил, что при всяком нечётномk и любом натуральном n число
делится наk ,
но скоро сам заметил, что
не делится на 9.
Рассмотренные примеры позволяют сделать важный вывод: утверждение может быть справедливым в целом ряде частных случаев и в то же время несправедливым вообще. Вопрос о справедливости утверждения в общем случае удается решить посредством применения особого метода рассуждений, называемого
6.1. Принцип математической индукции.
♦ В основе метода математической индукции лежит принцип математической индукции , заключающийся в следующем:
1) проверяется справедливость этого утверждения для n =1 (базис индукции) ,
2) предполагается справедливость этого утверждения для n = k , где k – произвольное натуральное число 1 (предположение индукции) , и с учётом этого предположения устанавливается справедливость его для n = k +1.
Доказательство . Предположим противное, то есть предположим, что утверждение справедливо не для всякого натурального n
. Тогда существует такое натуральное m , что:1) утверждение для n =m несправедливо,
2) для всякого n , меньшего m , утверждение справедливо (иными словами, m есть первое натуральное число, для которого утверждение несправедливо).
Очевидно, что m >1,
т.к. для n =1
утверждение справедливо (условие 1).
Следовательно,
– натуральное число. Выходит, что для
на
dudley.ru
Онлайн урок метод математической индукции.
Давай повторим определения, которые ты уже знаешь и которые мы будем использовать на нашем уроке.
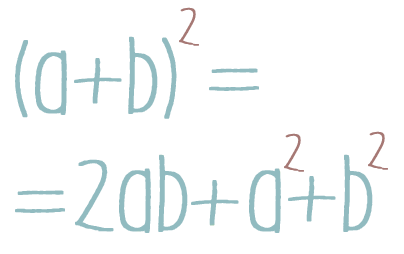
Квадрат суммы двух выражений равен сумме квадратов этих выражений и удвоенного произведения выражений.
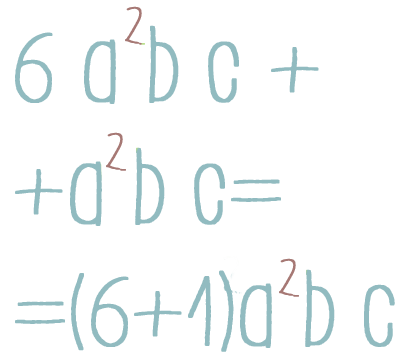
При сложении подобных одночленов, складываются только их коэффициенты, а буквенная часть остается неизменной.
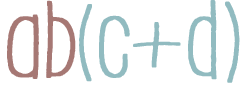
Умножить многочлен на одночлен — это значит каждый член многочлена умножить на этот одночлен и полученные одночлены сложить.
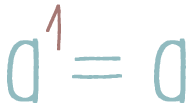
Любое число в первой степени равно самому числу.
Теперь установи соответствие между картинками и определениями, которые мы только что повторили.
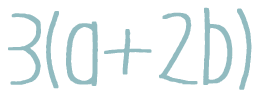
3(a + 2b) = 6a + 3b3(a + 2b) = 3a + 3b3(a + 2b) = 3a + 2b3(a + 2b) = 3a + 6b
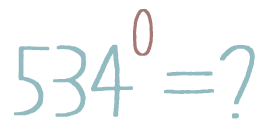
5341 = 05340 = 05340 = 15340 = 534
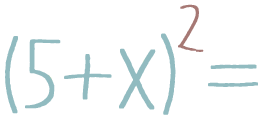
(5 + x)2 = 5 + 10x + x2(5 + x)2 = 25 + 10x + x2(5 + x)2 = 5 + x2(5 + x)2 = 25 + 5x + x2
Прежде чем начнем основную часть урока, перечислю для тебя определения, с которыми мы познакомимся сегодня:
1. Метод математической индукции.
2. База индукции.
3. Шаг индукции.
myalfaschool.ru
Метод математической индукции — ПриМат
Под методом математической индукции понимают следующий способ доказательства: если требуется доказать истинность утверждения то сначала проверяют данное утверждение для некоторого натурально числа , обычно , а потом допускают истинность выражения Далее доказывают истинность утверждения
Упражнение:
Доказательство одноцветности всех лошадей — ошибочное доказательство, что все лошади одного цвета, придуманное венгерским математиком Пойа. Доказательство призвано продемонстрировать ошибки, возникающие при неправильном использовании метода математической индукции.
Доказываемое утверждение: все лошади одного цвета.
Доказательство:
Проведем доказательство по индукции.
База индукции:
Одна лошадь, очевидно, одного (одинакового) цвета.
Шаг индукции:
Пусть доказано, что любые лошадей всегда одного цвета. Рассмотрим каких-то лошадей. Уберем одну лошадь. Оставшиеся лошадей одного цвета по предположению индукции. Возвратим убранную лошадь и уберем какую-то другую. Оставшиеся лошадей снова будут одного цвета. Значит, все лошадей одного цвета.
Отсюда следует, что все лошади одного цвета. Утверждение доказано.
В чем ошибка?
Решение
Спойлер
Опровержение
Противоречие возникает из-за того, что шаг индукции не сообразуется с базой. Он верен лишь при . При (база индукции) получаемые множества оставшихся лошадей не будут пересекаться, и утверждение о равенстве цветов всех лошадей сделать нельзя.
[свернуть]
Пример:
Доказать равенство:
Пусть данное утверждение верно для
Докажем истинность утверждения для
Доказать, что для всех натуральных чисел справедливо неравенство .
Для неравенство принимает вид , т.е. оно справедливо.
Предположим, требуемое неравенство имеет место при некотором и покажем, что оно же справедливо и для .
Сложим предположение индукции с неравенством . Находим , что и требовалось доказать.
Тест «Метод математической индукции»
Лимит времени: 0
Информация
Тестовые вопросы по вышеизложенному материалу.
Вы уже проходили тест ранее. Вы не можете запустить его снова.
Тест загружается…Вы должны войти или зарегистрироваться для того, чтобы начать тест.
Вы должны закончить следующие тесты, чтобы начать этот:
Правильных ответов: 0 из 3
Ваше время:
Время вышло
Вы набрали 0 из 0 баллов (0)
| Средний результат |
|
| Ваш результат |
|
- С ответом
- С отметкой о просмотре
Таблица лучших: Тест «Метод математической индукции»
| Место | Имя | Записано | Баллы | Результат |
|---|---|---|---|---|
| Таблица загружается | ||||
| Нет данных | ||||
Список литературы:
- Лысенко З.М. Конспект лекций по курсу математического анализа.
- В.И.Коляда, А.А.Кореновский «Курс лекций по мат.анализу, часть 1» (Одесса «Астропринт» , 2009г.), стр.4.
Поделиться ссылкой:
Похожее
ib.mazurok.com
Во многих разделах математики приходится доказывать истинность утверждения, зависящего от , т. е. истинность высказывания P(N) Для «NÎN (для любого NÎN P(N) Верно).
Часто это удается доказать Методом математической индукции.
В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение P(N) считается истинным для всех натуральных значений переменной, если выполнены два условия:
1. Предложение P(N) истинно для N = 1.
2. Из предложения, что P(N) истинно для N = K (K — Произвольное натуральное число) следует, что оно истинно для N = K + 1.
Под методом математической индукции понимают следующий способ доказательства
1. Проверяют истинность утверждения для N = 1 – база индукции.
2. Предполагают, что утверждение верно для N = K – Индуктивное предположение.
3. Доказывают, что тогда оно верно и для N = K + 1 индуктивный переход.
Иногда предложение P(N) оказывается верным не для всех натуральных N, а начиная с некоторого для N = N0. В этом случае в базе индукции проверяется истинность P(N) при N = N0.
Пример 1. Пусть . Доказать, что
1. База индукции: при N = 1 по определению S1 = 1 и по формуле получаем один результат. Утверждение верно.
2. Индуктивное предположение. Пусть N = k и .
3. Индуктивный переход. Пусть N = k + 1. Докажем, что .
Действительно, в силу индуктивного предположения
Преобразуем это выражение
Индуктивный переход доказан.
Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!
Пример 2. Доказать
.
1. База индукции. При N = 1, утверждение, очевидно, верно.
2. Индуктивное предположение. Пусть N = K и
3. Индуктивный переход. Пусть N = K + 1. Докажем:
Действительно, возведем правую сторону в квадрат как сумму двух чисел:
Используя индуктивное предположение и формулу суммы арифметической прогрессии: , получим
Пример 3. Доказать неравенство
для .
1. Базой индукции в этом случае является проверка истинности утверждения для , т. е. необходимо проверить неравенство . Для этого достаточно возвести неравенство в квадрат: или 63 < 64 – неравенство верно.
2. Пусть неравенство верно для , т. е.
.
3. Пусть , докажем:
.
Используем предположение индукции
Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть
Остается установить, что лишний множитель не превосходит единицы. Действительно,
.
Пример 4. Доказать, что при любом натуральном число оканчивается цифрой .
1. Наименьшее натуральное , с которого справедливо утверждение, равно . .
2. Пусть при число оканчивается на . Это означает, что это число можно записать в виде , где – какое-то натуральное число. Тогда .
3. Пусть . Докажем, что оканчивается на . Используя полученное представление, получим
Последнее число имеет ровно единиц.
Задачи.
1. Доказать, что при каждом верны равенства
1) .
2) .
3) .
4) .
5) .
6) .
7) .
8) .
9) .
10).
2. Доказать, что при любом .
1) кратно .
2) кратно .
3) кратно .
4) кратно .
5) кратно .
6) кратно 19.
3. Доказать справедливость следующих неравенств для всех натуральных .
1) .
2) .
3) .
4) .
5) .
4. Доказать, что при любом натуральном верно неравенство
1) . 2) .
5. Доказать равенство для любого
1) ,
(в левой части содержится корней).
2) .
6. Пусть – произвольные неотрицательные числа, причем
.
Доказать, что .
7. Доказать неравенство Бернулли
,
8.Пусть – произвольные положительные числа, причем
. Доказать, что .
| < Предыдущая | Следующая > |
|---|
matica.org.ua
Метод математической индукции
Во
многих разделах математики приходится
доказывать истинность утверждения,
зависящего от 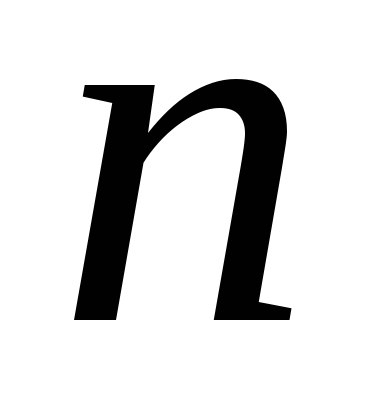 ,
т.е. истинность высказыванияp(n) для nN
(для любого nN p(n) верно).
,
т.е. истинность высказыванияp(n) для nN
(для любого nN p(n) верно).
Часто это удается доказать методом математической индукции.
В основе этого метода лежит принцип математической индукции. Обычно он выбирается в качестве одной из аксиом арифметики и, следовательно, принимается без доказательства. Согласно принципу математической индукции предложение p(n) считается истинным для всех натуральных значений переменной, если выполнены два условия:
1. Предложение p(n) истинно для n = 1.
2. Из предложения, что p(n) истинно для n = k (k — произвольное натуральное число) следует, что оно истинно для n = k + 1.
Под методом математической индукции понимают следующий способ доказательства
1. Проверяют истинность утверждения для n = 1 – база индукции.
2. Предполагают, что утверждение верно для n = k – индуктивное предположение.
3. Доказывают, что тогда оно верно и для n = k + 1 индуктивный переход.
Иногда предложение p(n) оказывается верным не для всех натуральных n, а начиная с некоторого для n = n0. В этом случае в базе индукции проверяется истинность p(n) при n = n0.
Пример
1. Пусть 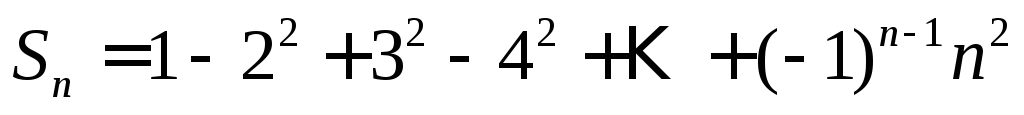 .
Доказать, что
.
Доказать, что

1.
База индукции: при n = 1 по определению S1 = 1 и по формуле 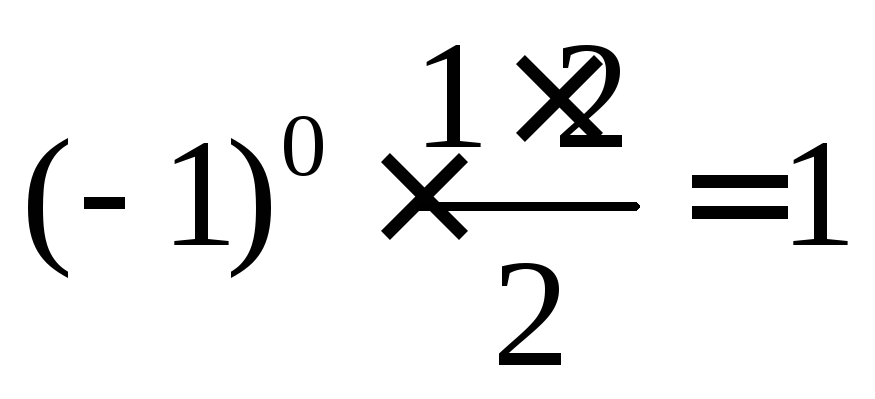 получаем один результат. Утверждение
верно.
получаем один результат. Утверждение
верно.
2.
Индуктивное предположение. Пусть n
= k и 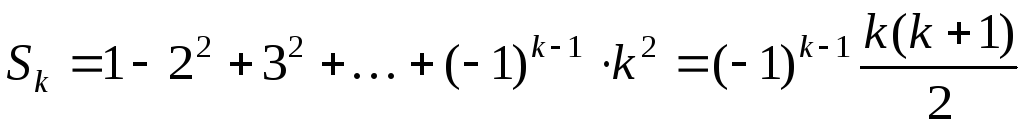 .
.
3.
Индуктивный переход. Пусть n
= k + 1. Докажем,
что 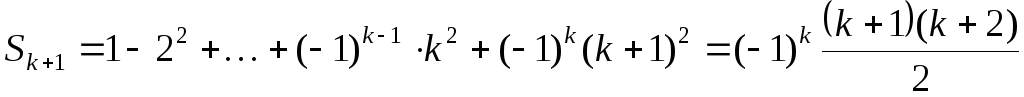 .
.
Действительно, в силу индуктивного предположения
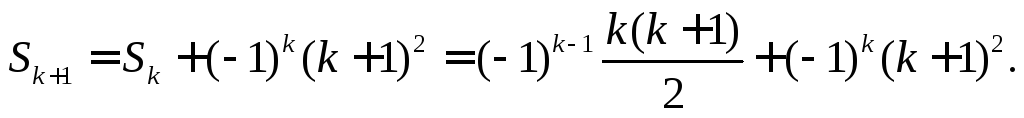
Преобразуем это выражение
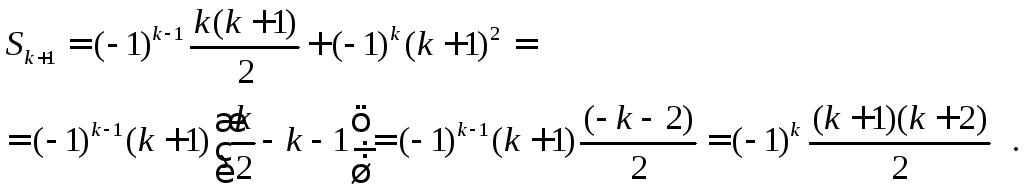
Индуктивный переход доказан.
Замечание. Полезно записать, что дано (индуктивное предположение) и что нужно доказать!
Пример 2. Доказать
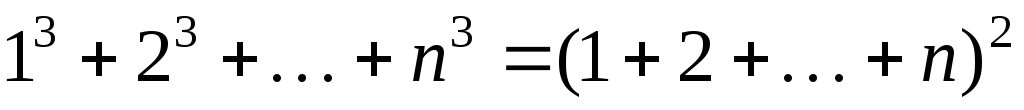 .
.
1. База индукции. При n = 1, утверждение, очевидно, верно.
2. Индуктивное предположение. Пусть n = k и
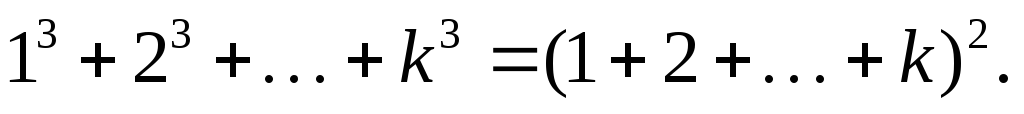
3. Индуктивный переход. Пусть n = k + 1. Докажем:
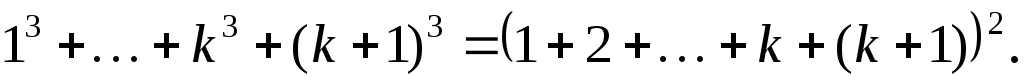
Действительно, возведем правую сторону в квадрат как сумму двух чисел:
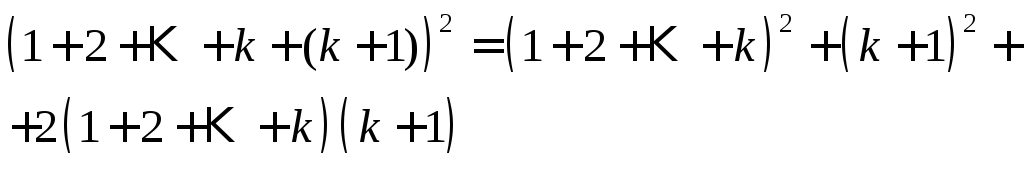
Используя
индуктивное предположение и формулу
суммы арифметической прогрессии: 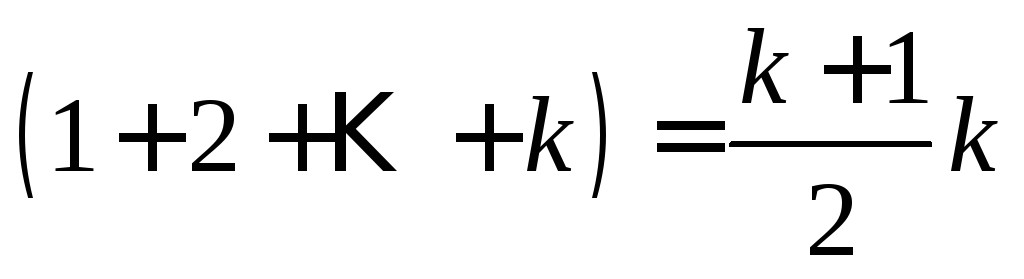 ,
получим
,
получим
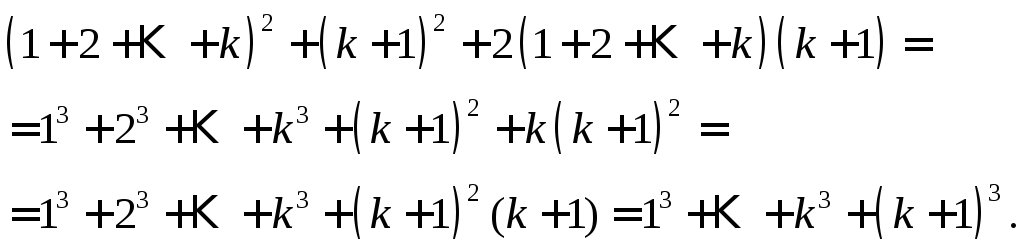
Пример 3. Доказать неравенство
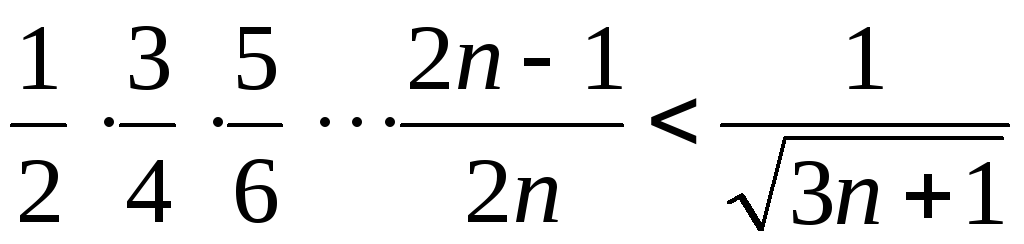 для
для 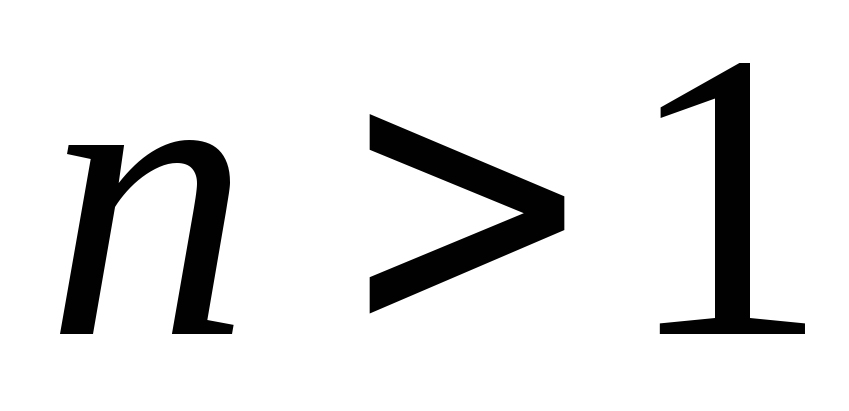 .
.
1.
Базой индукции в этом случае является
проверка истинности утверждения для 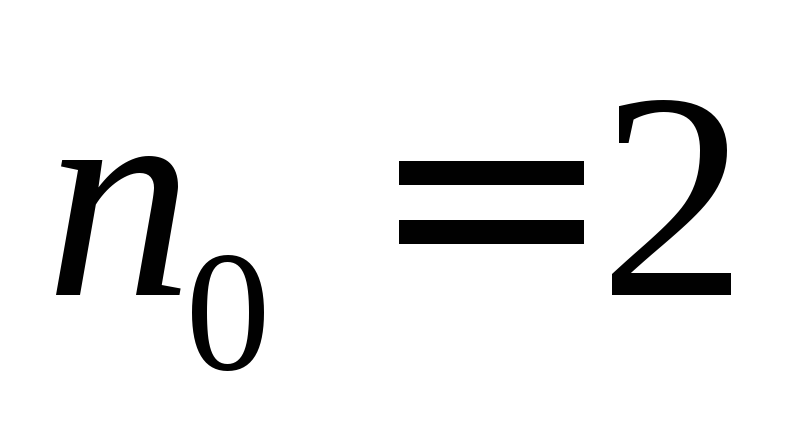 ,
т.е. необходимо проверить неравенство
,
т.е. необходимо проверить неравенство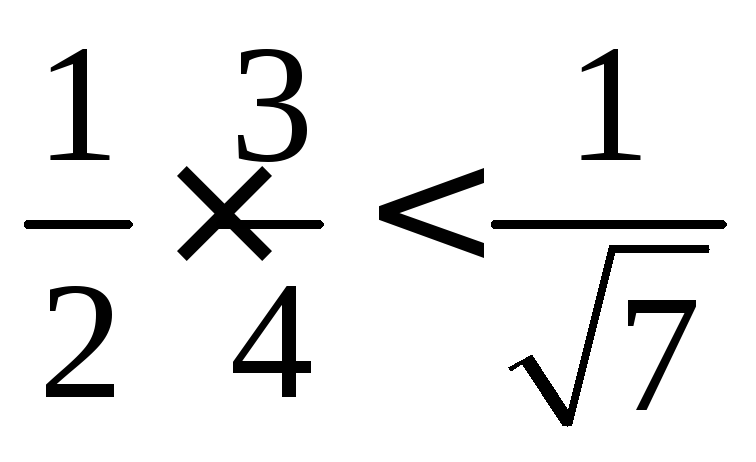 .
Для этого достаточно возвести неравенство
в квадрат:
.
Для этого достаточно возвести неравенство
в квадрат: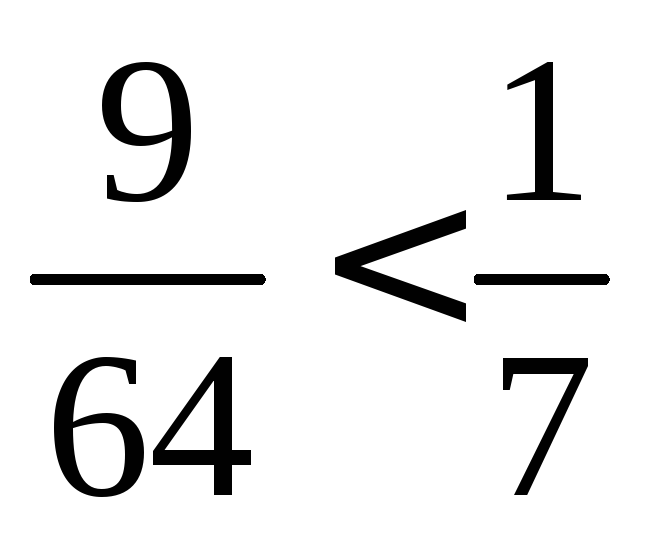 или 63 < 64 – неравенство верно.
или 63 < 64 – неравенство верно.
2.
Пусть неравенство верно для 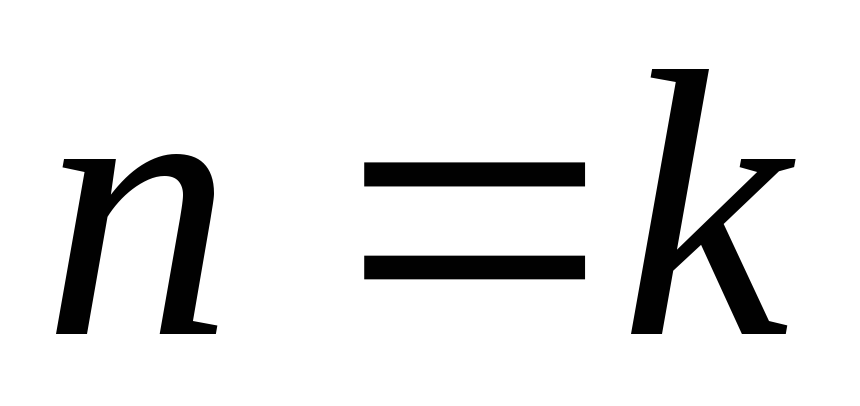 ,
т.е.
,
т.е.
 .
.
3.
Пусть 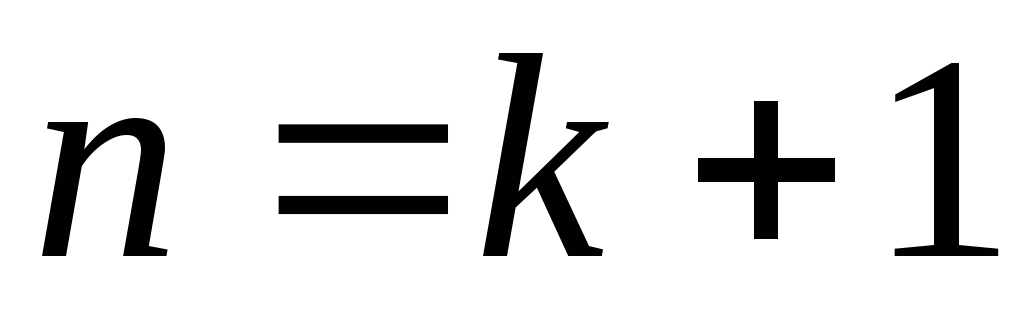 ,
докажем:
,
докажем:
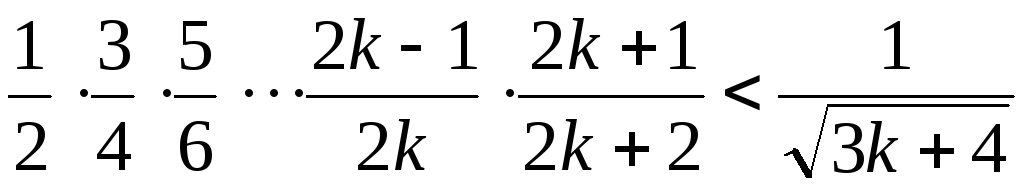 .
.
Используем предположение индукции
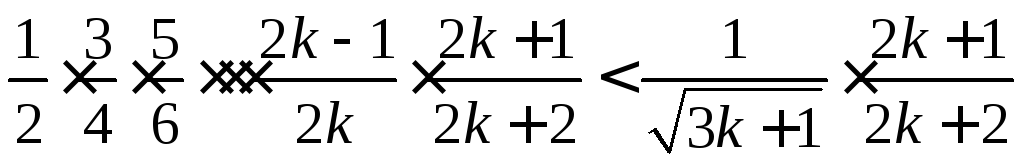
Зная как должна выглядеть правая сторона в доказываемом неравенстве выделим эту часть
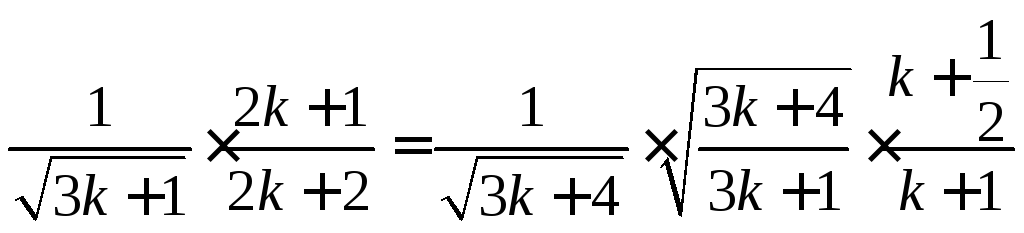
Остается
установить, что лишний множитель 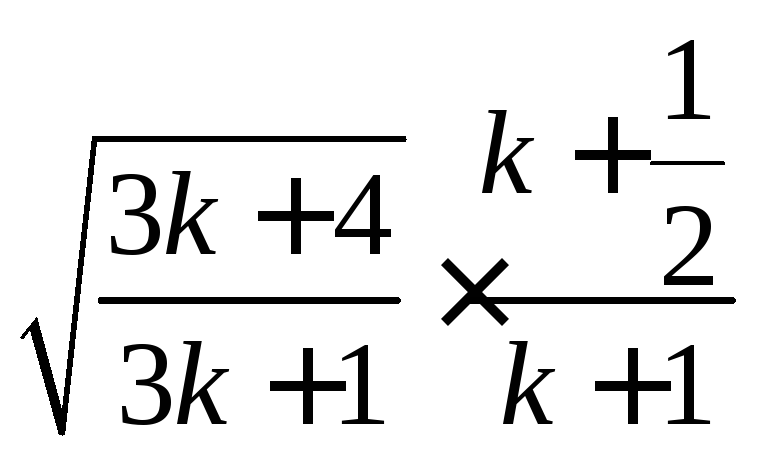 не превосходит единицы. Действительно,
не превосходит единицы. Действительно,
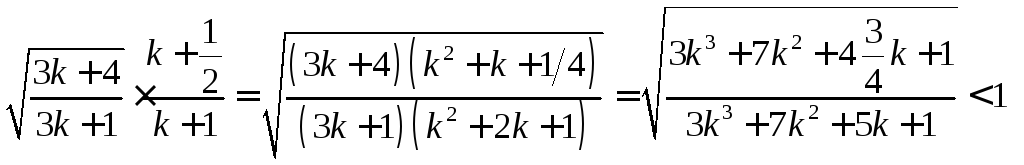 .
.
Пример
4. Доказать,
что при любом натуральном 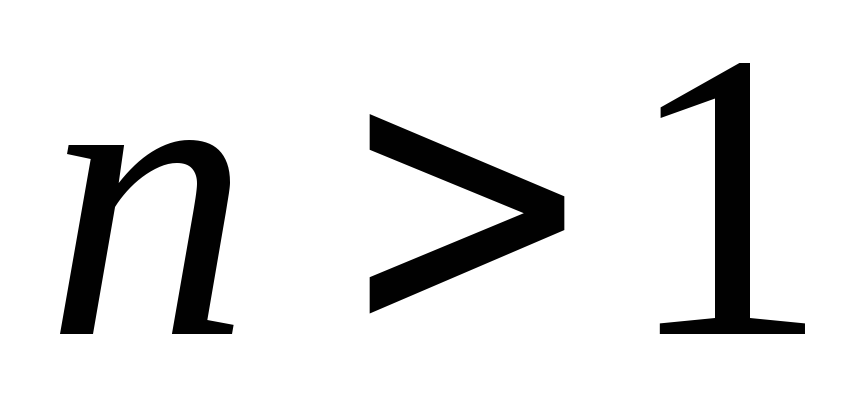 число
число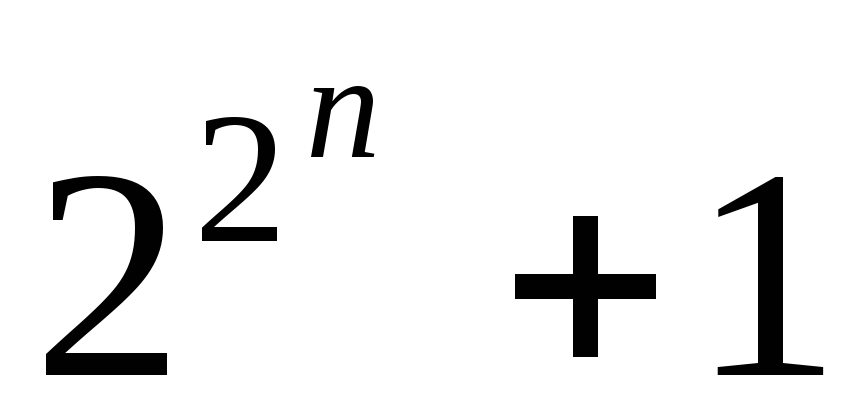 оканчивается цифрой
оканчивается цифрой .
.
1.
Наименьшее натуральное 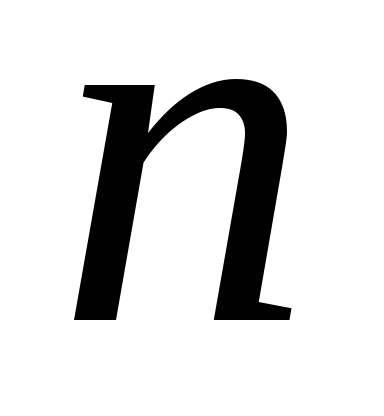 ,
с которого справедливо утверждение,
равно
,
с которого справедливо утверждение,
равно .
.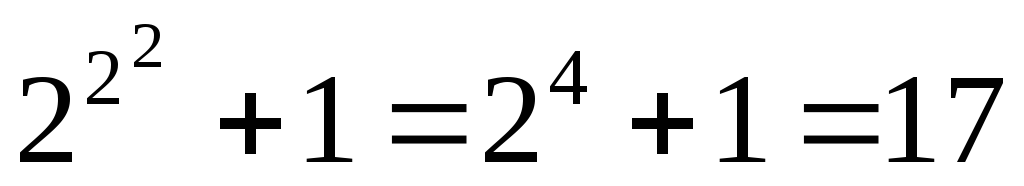 .
.
2.
Пусть при 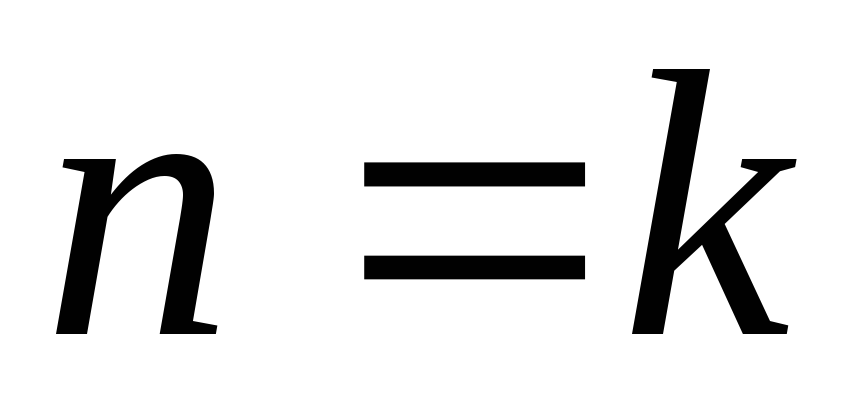 число
число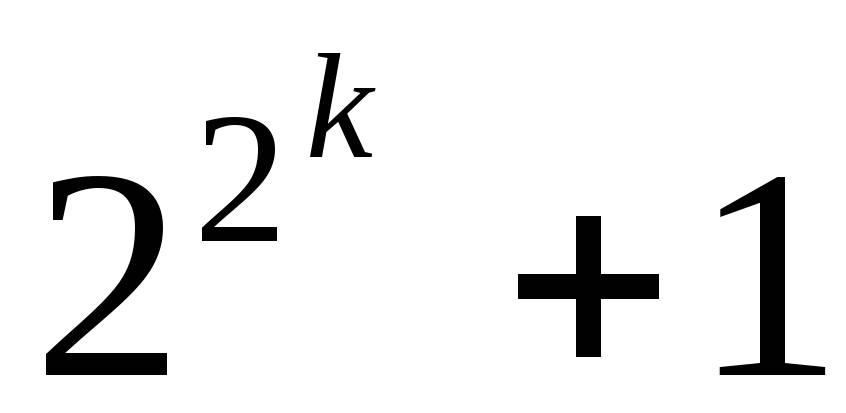 оканчивается на
оканчивается на .
Это означает, что это число можно записать
в виде
.
Это означает, что это число можно записать
в виде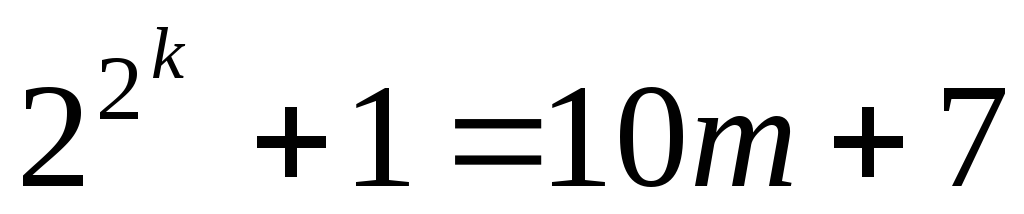 ,
где
,
где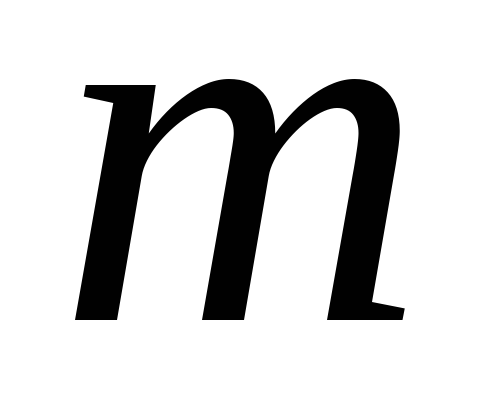 – какое-то натуральное число. Тогда
– какое-то натуральное число. Тогда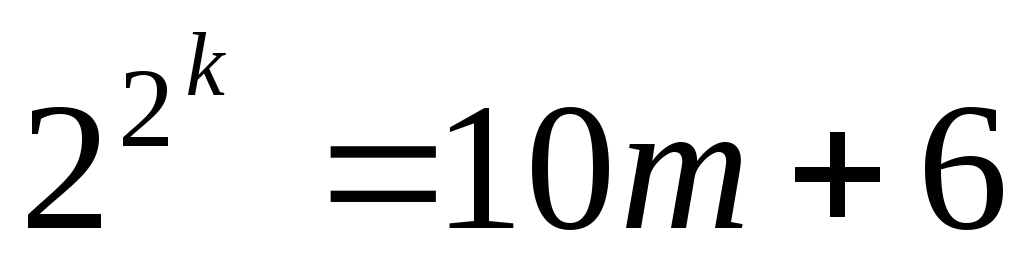 .
.
3.
Пусть 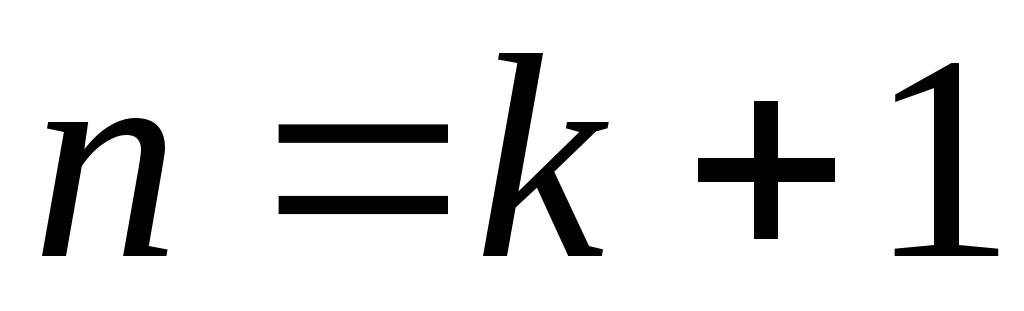 .
Докажем, что
.
Докажем, что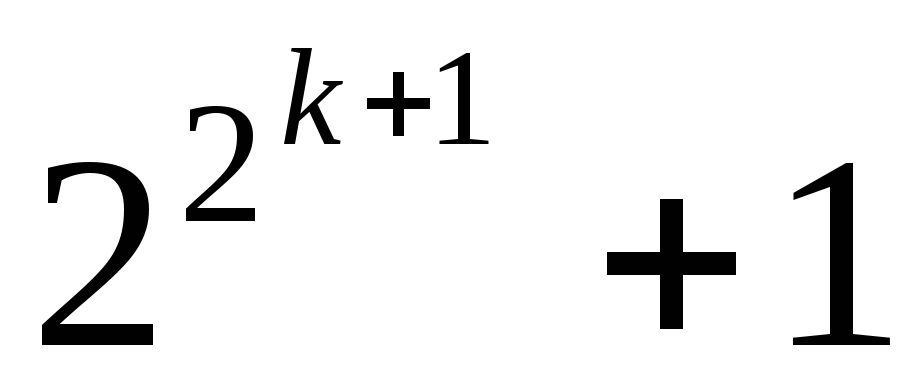 оканчивается на
оканчивается на .
Используя полученное представление,
получим
.
Используя полученное представление,
получим
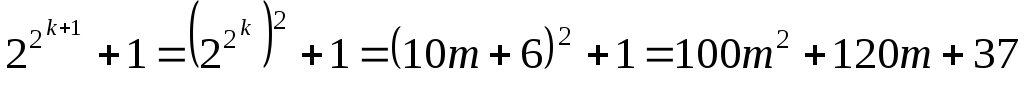
Последнее
число имеет ровно  единиц.
единиц.
Задачи.
1.
Доказать, что при каждом 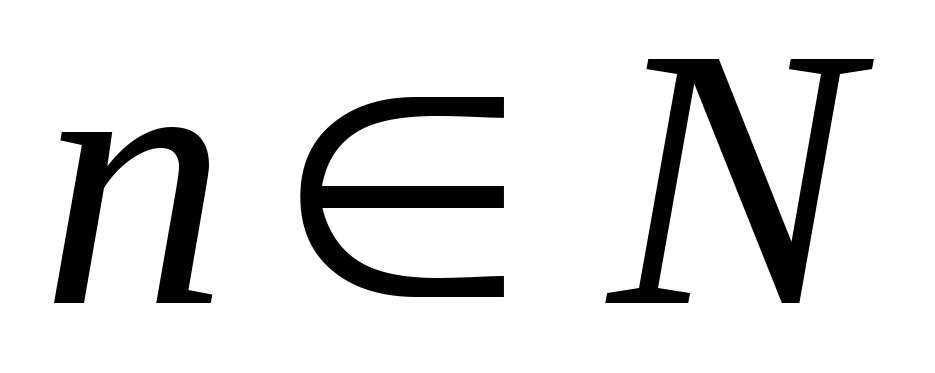 верны равенства
верны равенства
 .
. .
. .
. .
. .
. .
. .
.
8)  .
.
9) 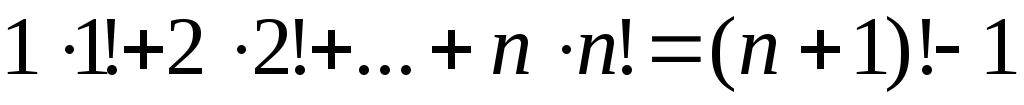 .
.
10)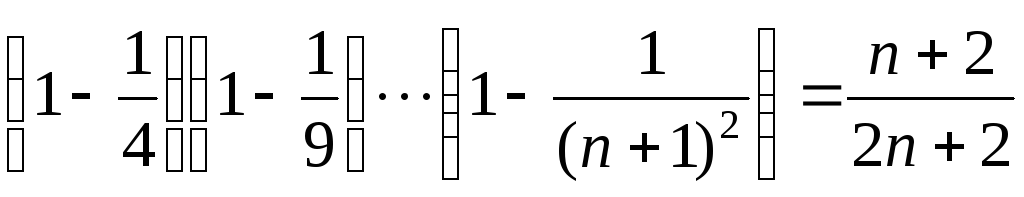 .
.
2.
Доказать, что при любом 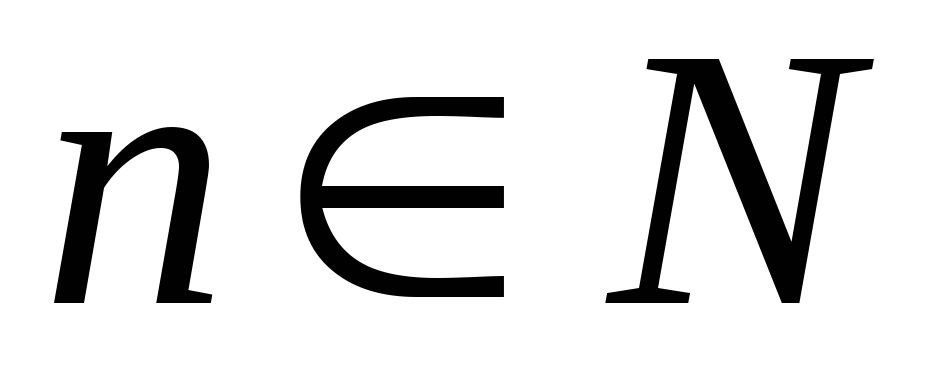 .
.
 кратно
кратно  .
. кратно
кратно  .
. кратно
кратно  .
. кратно
кратно  .
. кратно
кратно  .
. кратно
19.
кратно
19.
3.
Доказать справедливость следующих
неравенств для всех натуральных 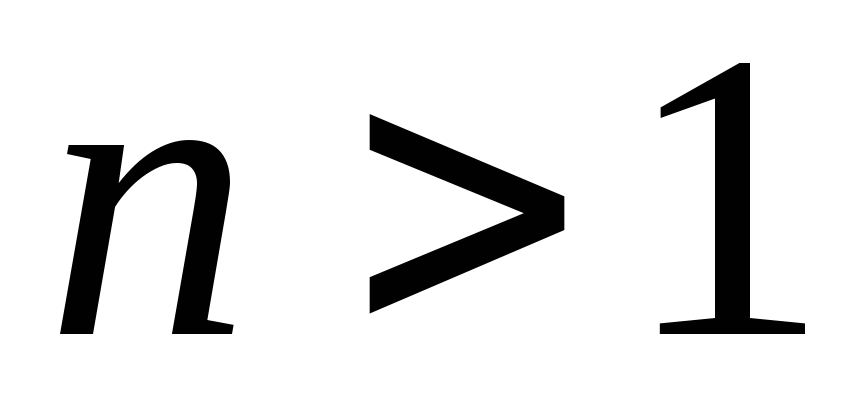 .
.
 .
. .
. .
. .
. .
.
4.
Доказать, что при любом натуральном  верно неравенство
верно неравенство
1) 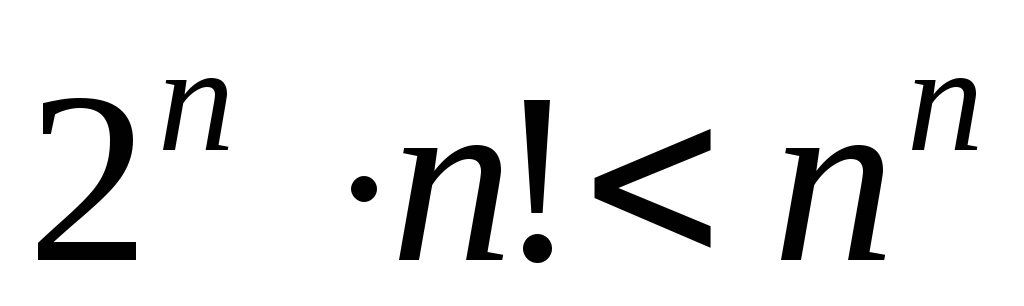 .
2)
.
2)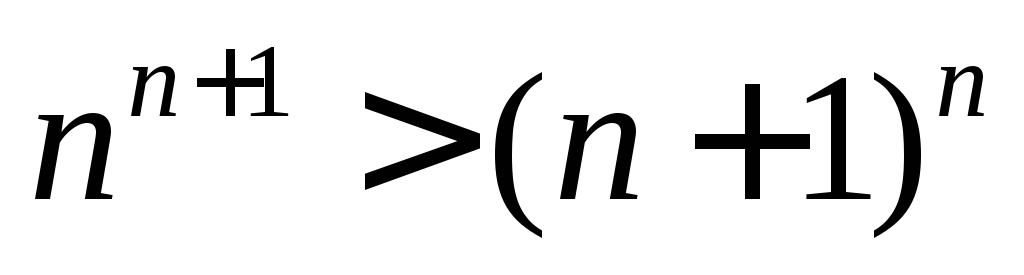 .
.
5.
Доказать равенство для любого 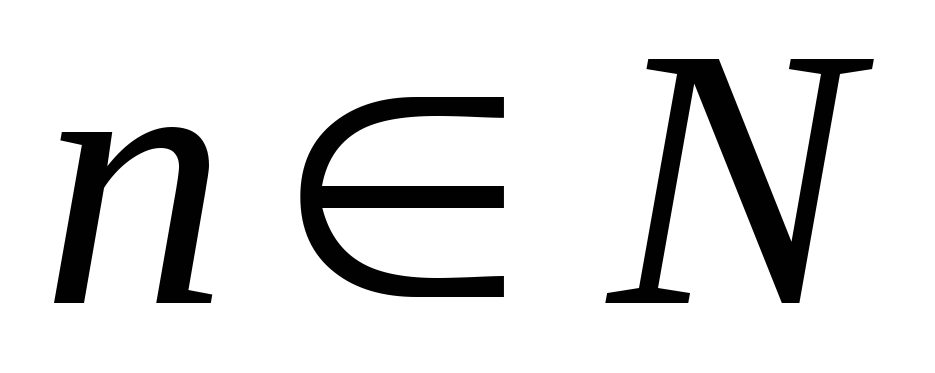
 ,
,
(в
левой части содержится 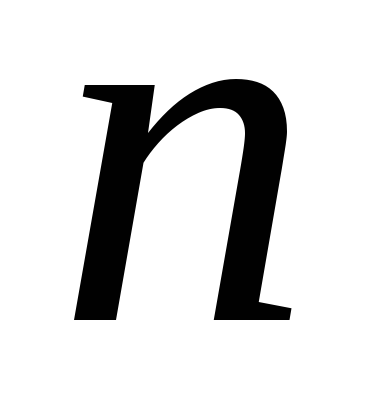 корней).
корней).
 .
.
6.
Пусть 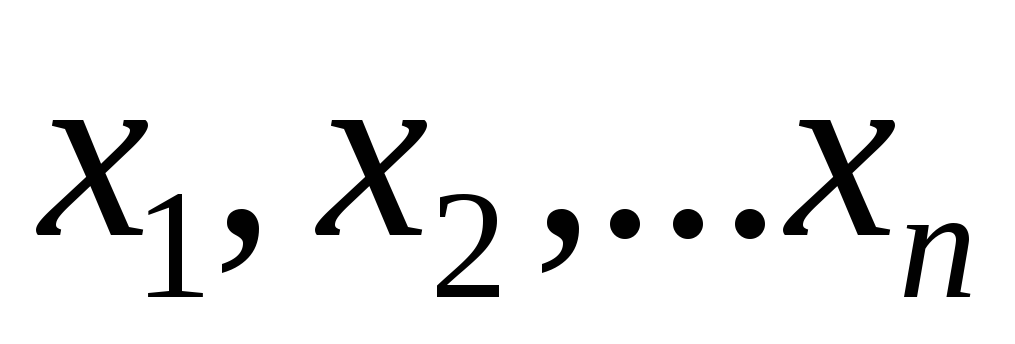 – произвольные неотрицательные числа,
причем
– произвольные неотрицательные числа,
причем
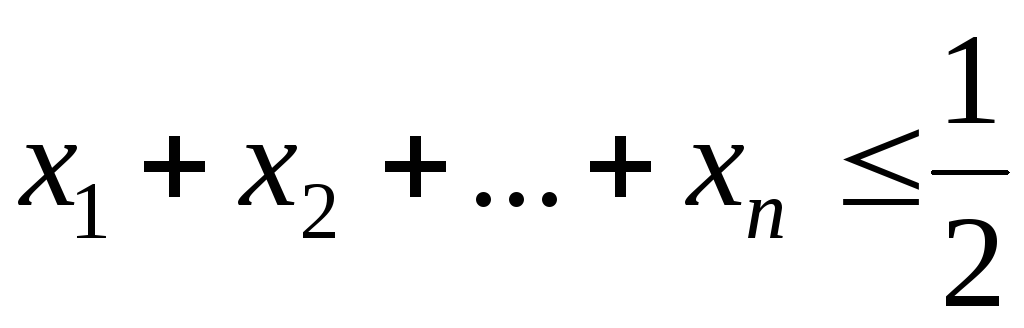 .
.
Доказать,
что 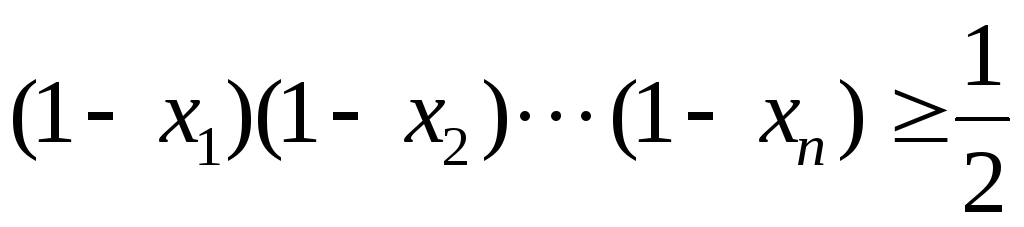 .
.
7. Доказать неравенство Бернулли
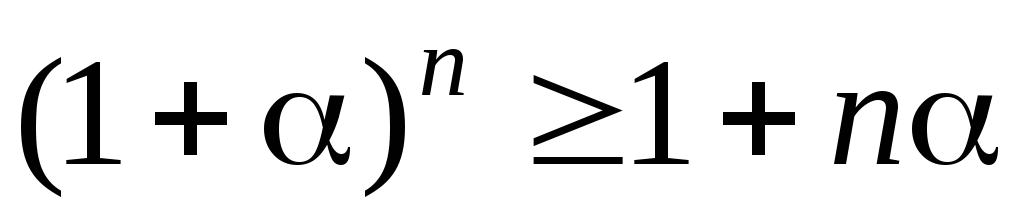 ,
, 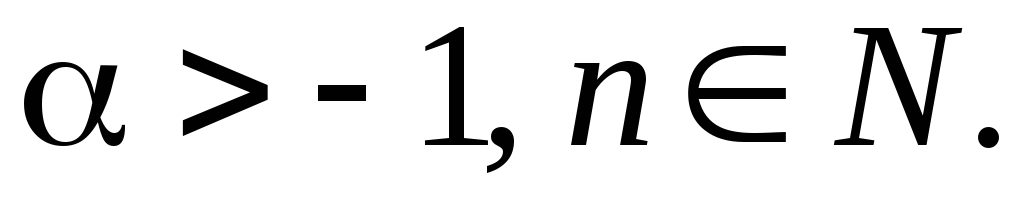
8.Пусть 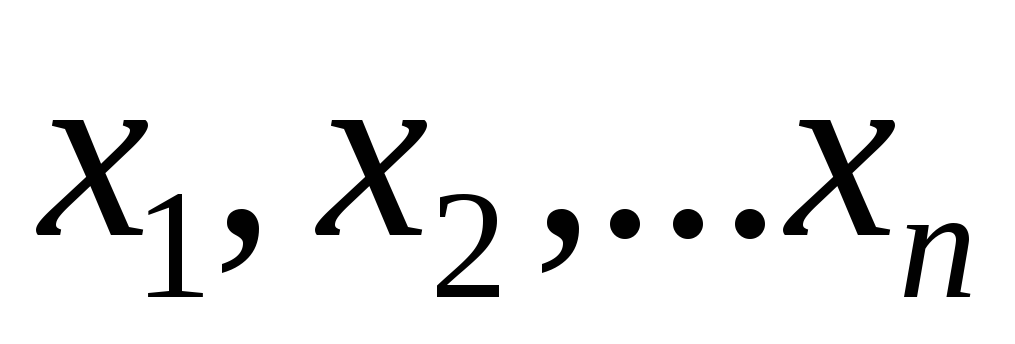 – произвольные положительные числа,
причем
– произвольные положительные числа,
причем
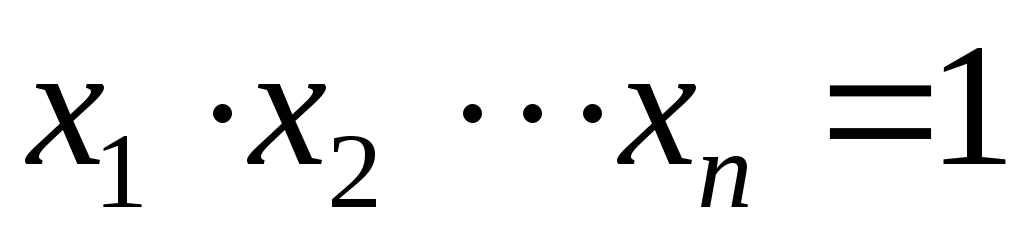 .
Доказать, что
.
Доказать, что 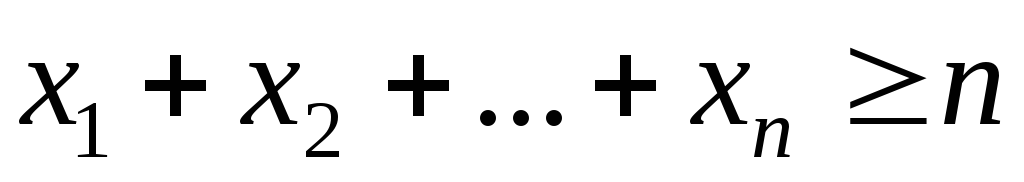 .
.
studfile.net
Метод математической индукции (стр. 1 из 3)
Брянский Городской Лицей №1
Исследовательская работа на тему:
Метод Математической Индукции
Выполнил
Мелешко Константин
ученик 10 физико-математического
Брянского Городского Лицея №1
Проверил
Тюкачева Ольга Ивановна
-2003-
Содержание исследовательской работы
Содержание_ _ _ _ _ _ _ _ _ _ _ _ _ _ 2
Введение_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 3
Основная часть
Полная и неполная индукция_ _ _ _ _ _ _ _ _3-4
Принцип математической индукции_ _ _ _ _4-5
Метод математической индукции_ _ _ _ _ _ 6
Решение Методом Математической Индукции
К задачам на суммирование_ _ _ _ _ _ _ _ _ 7
К задачам на доказательство неравенств_ _8
К задачам на делимость _ _ _ _ _ _ _ _ _ _ _11
К задачам на доказательство тождеств _ _ _12
К другим задачам _ _ _ _ _ _ _ _ _ _ _ _ _ _ 13
Заключение_ _ _ _ _ _ _ _ _ _ _ _ _ _ _ 16
Список использованной литературы _ _ _ _17
Введение
Слово индукцияпо-русски означает наведение, а индуктивными называют выводы, сделанные на основе наблюдений, опытов, т.е. полученные путем заключения от частного к общему.
Роль индуктивных выводов в экспериментальных науках очень велика. Они дают те положения, из которых потом путем дедукции делаются дальнейшие умозаключения. И хотя теоретическая механика основывается на трех законах движения Ньютона, сами эти законы явились результатом глубокого продумывания опытных данных, в частности законов Кеплера движения планет, выведенных им при обработке многолетних наблюдений датского астронома Тихо Браге. Наблюдение, индукция оказываются полезными и в дальнейшем для уточнения сделанных предположений. После опытов Майкельсона по измерению скорости света в движущейся среде оказалось необходимым уточнить законы физики, создать теорию относительности.
В математике роль индукции в значительной степени состоит в том, что она лежит в основе выбираемой аксиоматики. После того как длительная практика показала, что прямой путь всегда короче кривого или ломанного, естественно было сформулировать аксиому: для любых трех точек А, В и С выполняется неравенство
.Лежащее в основе арифметики понятие «следовать за» тоже появилось при наблюдениях за строем солдат, кораблей и другими упорядоченными множествами.
Не следует, однако, думать, что этим исчерпывается роль индукции в математике. Разумеется, мы не должны экспериментально проверять теоремы, логически выведенные из аксиом: если при выводе не было сделано логических ошибок, то они постольку верны, поскольку истинны принятые нами аксиомы. Но из данной системы аксиом можно вывести очень много утверждений. И отбор тех утверждений, которые надо доказывать, вновь подсказывается индукцией. Именно она позволяет отделить полезные теоремы от бесполезных, указывает, какие теоремы могут оказаться верными, и даже помогает наметить путь доказательства.
Суть Математической Индукции
Покажем на примере использование Метода Математической Индукции и в конце сделаем обобщающий вывод.
Пусть требуется установить, что каждое натуральное чётное число nв пределах 44=2+2; 6=3+3; 8=5+3; 10=7+3; 12=7+5;
14=7+7; 16=11+5; 18=13+5; 20=13+7.
Эти девять равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.
Таким образом, полная индукция заключается в том, что общее утверждение доказывается по отдельности в каждом из конечного числа возможных случаев.
Иногда общий результат удаётся предугадать после рассмотрения не всех, а достаточно большого числа частных случаев (так называемая неполная индукция).
Результат, полученный неполной индукцией, остается, однако, лишь гипотезой, пока он не доказан точным математическим рассуждением, охватывающим все частные случаи. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным методом открытия новых истин.
Пусть, например, требуется найти сумму первых n последовательных нечётных чисел. Рассмотрим частные случаи:
1=1=12
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
После рассмотрения этих нескольких частных случаев напрашивается следующий общий вывод:
1+3+5+…+(2n-1)=n2
т.е. сумма n первых последовательных нечётных чисел равна n2
Разумеется, сделанное наблюдение ещё не может служить доказательством справедливости при-
ведённой формулы.
Полная индукция имеет в математике лишь ограниченное применение. Многие интересные математические утверждения охватывают бесконечное число частных случаев, а провести проверку для бесконечного числа случаев мы не в состоянии. Неполная же индукция часто приводит к ошибочным результатам.
Во многих случаях выход из такого рода затруднений заключается в обращении к особому методу рассуждений, называемому методом математической индукции. Он заключается в следующем.
Пусть нужно доказать справедливость некоторого утверждения для любого натурального числаn(например нужно доказать, что сумма первых n нечётных чисел равна n2). Непосредственная проверка этого утверждения для каждого значения nневозможна, поскольку множество натуральных чисел бесконечно. Чтобы доказать это утверждение, проверяют сначала его справедливость для n=1. Затем доказывают, что при любом натуральном значении k из справедливости рассматриваемого утверждения при n=k вытекает его справедливость и при n=k+1.
Тогда утверждение считается доказанным для всех n. В самом деле, утверждение справедливо при n=1. Но тогда оно справедливо и для следующего числа n=1+1=2. Из справедливости утверждения для n=2 вытекает его справедливость для n=2+
+1=3. Отсюда следует справедливость утверждения для n=4 и т.д. Ясно, что, в конце концов, мы дойдём до любого натурального числа n. Значит, утверждение верно для любого n.
Обобщая сказанное, сформулируем следующий общий принцип.
Принцип математической индукции.
Если предложение А(n), зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение А(n) истинно для любого натурального числа n.
В ряде случаев бывает нужно доказать справедливость некоторого утверждения не для всех натуральных чисел, а лишь для n> p, где p-фиксированное натуральное число. В этом случае принципматематической индукции формулируется следующим образом.
Если предложение А(n) истинно при n=p и если А(k)ÞА(k+1) для любого k>p, то предложение А(n) истинно для любого n>p.Доказательство по методу математической индукции проводиться следующим образом. Сначала доказываемое утверждение проверяется для n=1, т.е. устанавливается истинность высказывания А(1). Эту часть доказательства называют базисом индукции. Затем следует часть доказательства, называемая индукционным шагом. В этой части доказывают справедливость утверждения для n=k+1 в предположении справедливости утверждения для n=k (предположение индукции), т.е. доказывают, что А(k)ÞA(k+1).
Применение метода математической индукции в задачах на суммирование
Применение метода математической индукции в задачах на суммирование
Пример:
Доказать, что
1+x2+x3+x4+….+xn=
, где x 1Решение.
, следовательно, при n=1 формула верна.Пусть k- любое натуральное число и пусть формула верна при n=k, т.е.
Докажем тогда
В самом деле ,
.
Значит, по принципу математической индукции формула верна для любого натурального n.
Примеры применения метода математической индукции к доказательству неравенств.
Доказать, что при любом натуральном n>1
.Решение.
Обозначим левую часть неравенства через
. , следовательно, при n=2 неравенство справедливо.Пусть
при некотором k. Докажем, что тогда и . Имеем , .mirznanii.com
Исследовательская работа по теме:» Метод математической индукции»
Понимание и умение применять принцип
математической индукции является хорошим
критерием зрелости, которая совершенно
необходима математику.
А. Н. Колмогоров
Введение
Со времен зарождения жизни человечество стремилось к прогрессу, и свои первые шаги оно начинало с каменного века. Постепенно мир усовершенствовался и изменился. Каменный век перешел в мультимедийный. Даже несколько десятков лет тому назад мы не могли предположить о таких глобальных переменах. Но, несмотря на все изменения, произошедшие за это время, есть вещи, которые не меняются и их ценность со временем не убывает. Всем, например, известно, что Земля круглая, что 2•2=4. К таким ценностям можно отнести и математическую индукцию.
Математическую индукцию можно сравнить с прогрессом. Мы начинаем с низшего, в результате логического мышления приходим к высшему. Человек всегда стремился к прогрессу, к умению развивать свою мысль логически, а значит, сама природа предначертала ему размышлять индуктивно.
Доказательство по индукции наглядно может быть представлено в виде так называемого принципа домино. Пусть какое — угодно число косточек домино выставлено в ряд таким образом, что каждая косточка, падая, обязательно опрокидывает следующую за ней косточку. Тогда, если мы толкнём первую косточку, то все косточки в ряду упадут.
Математической индукцией фактически пользовались еще некоторые древнегреческие ученые. Однако впервые он был явно выражен
Герсонидом в 1321 году. Характеристика
принципа математической индукции
содержится у широко образованного
итальянского математика
ХVI века Ф.Мавролико, переводчика
Архимеда.
В « Трактате об арифметическом треугольнике» Б. Паскаль доказывает закон образования членов этого треугольника методом математической индукции, после чего этот метод начинает постепенно привлекать внимание некоторых ученых,
в частности ,Бернулли. Лишь со второй половины ХIХ века, после трудов Больцано, Коши, Гаусса, Абеля чисто индуктивные
методы доказательств теряют значение
в математике. На первый план выдвигается
дедукция и математическая индукция.
Несомненно, область применения
математической индукции возрастает,
несмотря на это, в школьной программе
ему отводится мало времени. Ну, скажите,
что полезного человеку принесут те два-три урока, за которые он услышит
пять слов теории, решит пять примитивных задач, и, в результате получит пятёрку за то, что он ничего не знает.
А ведь это так важно — уметь размышлять индуктивно.
infourok.ru
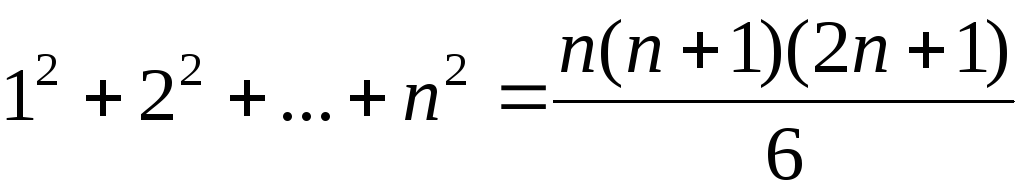 .
.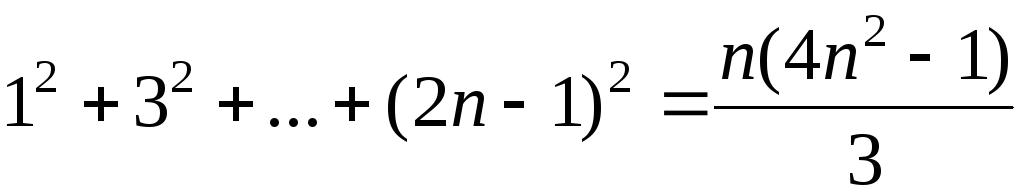 .
.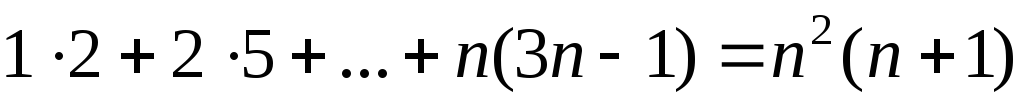 .
.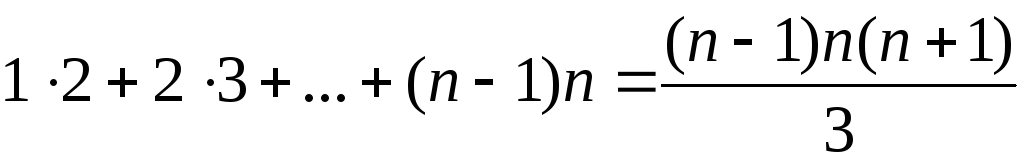 .
.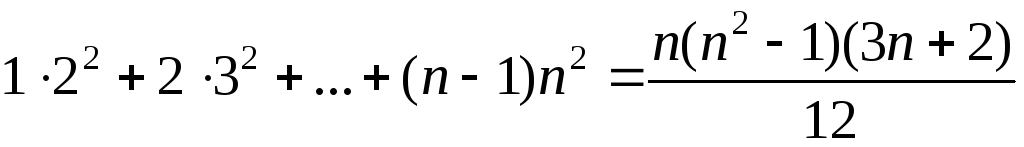 .
.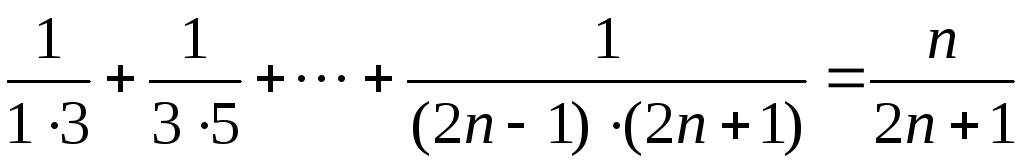 .
.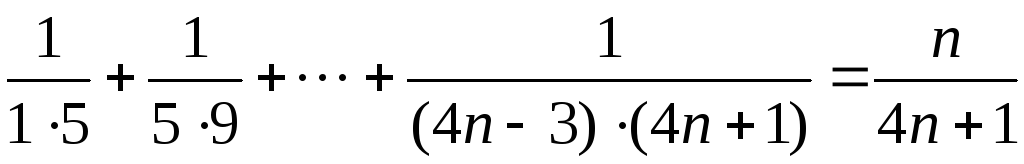 .
.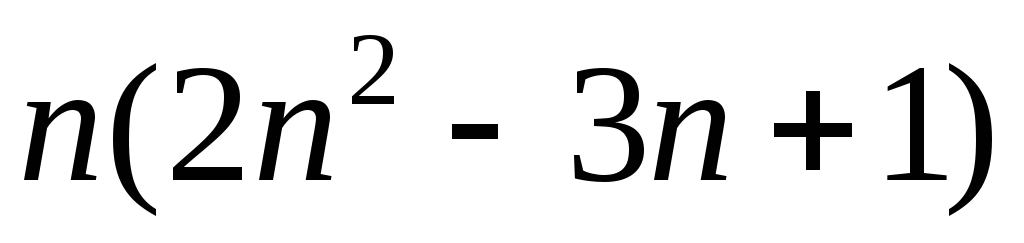 кратно
кратно  .
.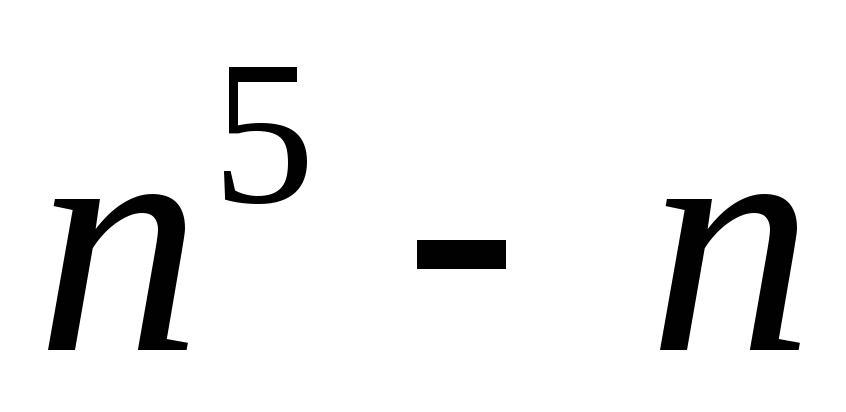 кратно
кратно  .
. кратно
кратно  .
.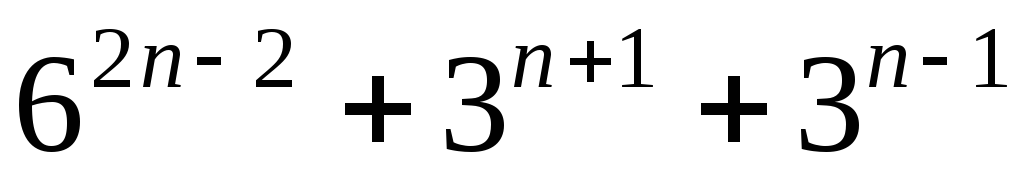 кратно
кратно  .
.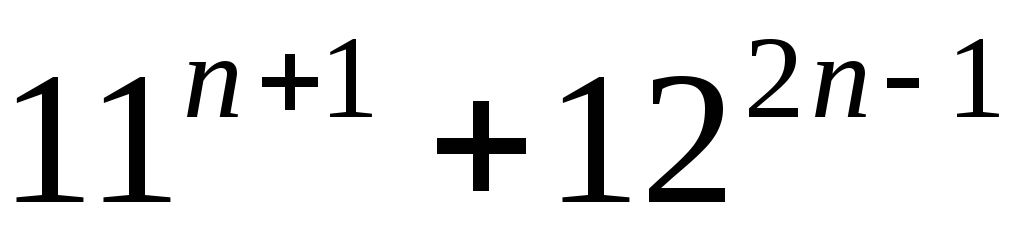 кратно
кратно 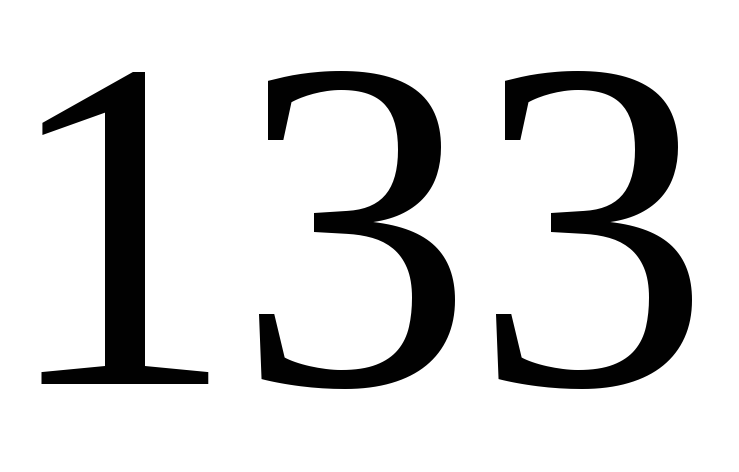 .
.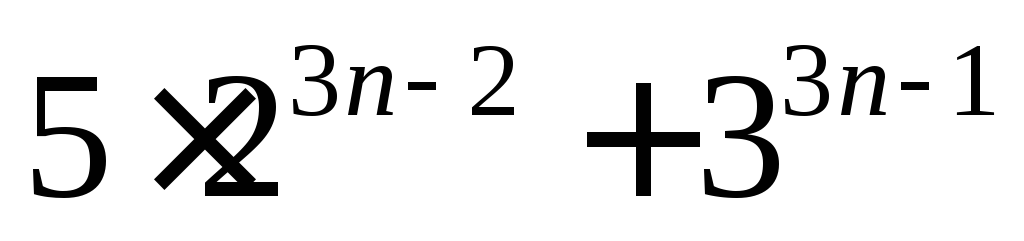 кратно
19.
кратно
19.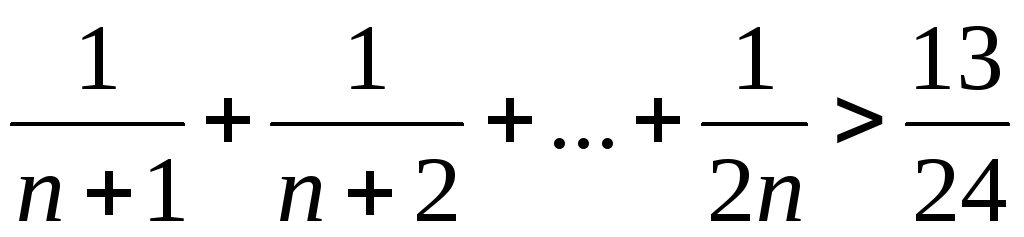 .
.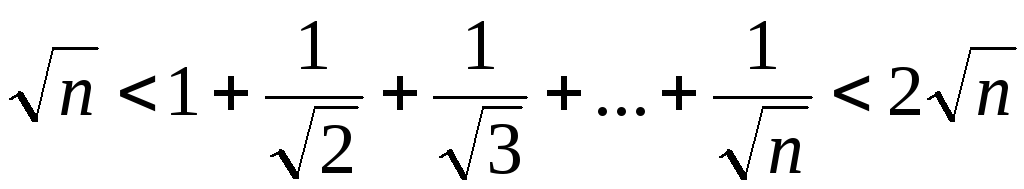 .
.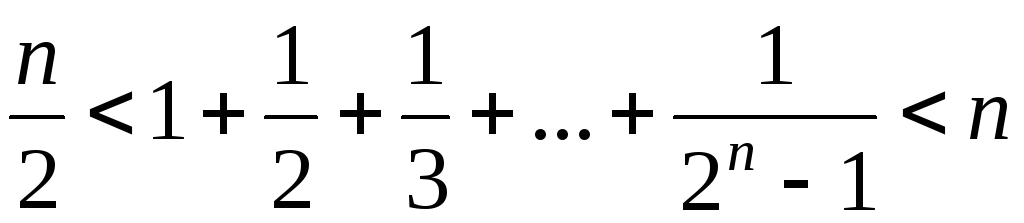 .
.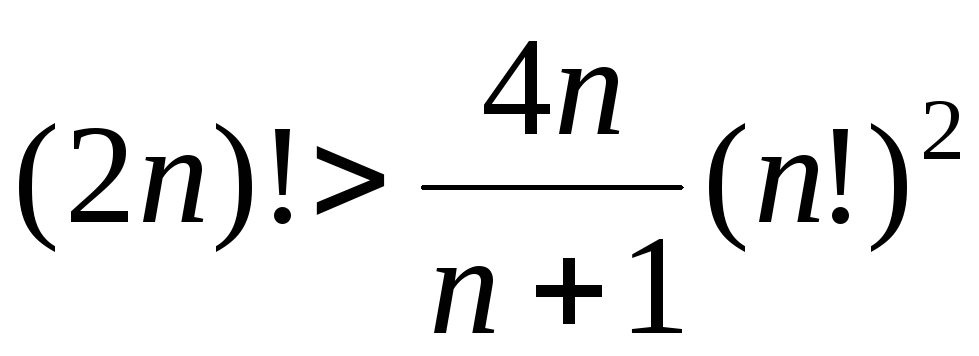 .
.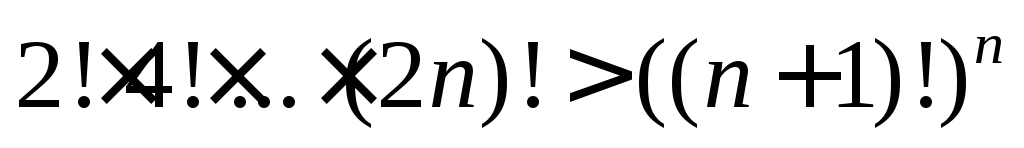 .
.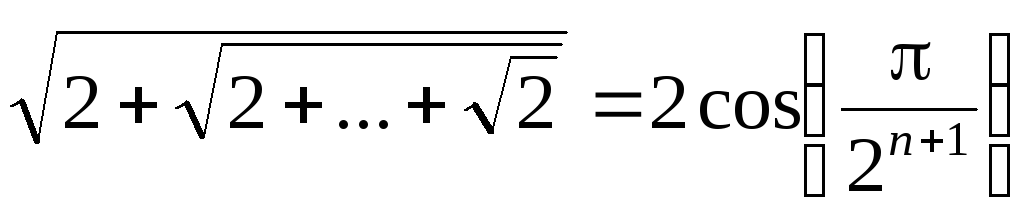 ,
,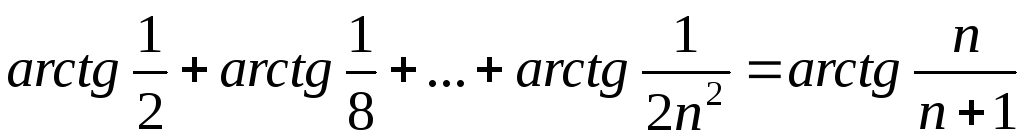 .
.