Что такое окружность как геометрическая фигура: основные свойства и характеристики

Чтобы в общих чертах представить себе, что такое окружность, взгляните на кольцо или обруч. Можно также взять круглый стакан и чашку, поставить вверх дном на лист бумаги и обвести карандашом. При многократном увеличении полученная линия станет толстой и не совсем ровной, и края ее будут размытыми. Окружность как геометрическая фигура не имеет такой характеристики, как толщина.

Окружность: определение и основные средства описания

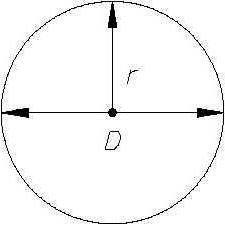
Окружность – это замкнутая кривая, состоящая из множества точек, расположенных в одной плоскости и равноудаленных от центра окружности. При этом центр находится в той же плоскости. Как правило, он обозначается буквой О.

Расстояние от любой из точек окружности до центра называется радиусом и обозначается буквой R.

Если соединить две любые точки окружности, то полученный отрезок будет называться хордой. Хорда, проходящая через центр окружности, — это диаметр, обозначаемый буквой D. Диаметр делит окружность на две равные дуги и по длине вдвое превышает размер радиуса. Таким образом, D = 2R, или R = D/2.

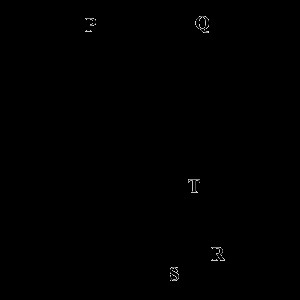
Свойства хорд

1. Если через две любые точки окружности провести хорду, а затем перпендикулярно последней – радиус или диаметр, то этот отрезок разобьет и хорду, и дугу, отсеченную ею, на две равные части. Верно и обратное утверждение: если радиус (диаметр) делит хорду пополам, то он перпендикулярен ей.
2. Если в пределах одной и той же окружности провести две параллельные хорды, то дуги, отсеченные ними, а также заключенные между ними, будут равны.
3. Проведем две хорды PR и QS, пересекающиеся в пределах окружности в точке T. Произведение отрезков одной хорды всегда будет равно произведению отрезков другой хорды, то есть PT х TR = QT х TS.

Длина окружности: общее понятие и основные формулы

Одной из базовых характеристик данной геометрической фигуры является длина окружности. Формула выводится с использованием таких величин, как радиус, диаметр и константа «π», отражающая постоянство отношения длины окружности к ее диаметру.

Таким образом, L = πD, или L = 2πR, где L – это длина окружности, D – диаметр, R – радиус.

Формула длины окружности может рассматриваться как исходная при нахождении радиуса или диаметра по заданной длине окружности: D = L/π, R = L/2π.

Что такое окружность: основные постулаты

1. Прямая и окружность могут располагаться на плоскости следующим образом:

• не иметь общих точек;
• иметь одну общую точку, при этом прямая называется касательной: если провести радиус через центр и точку касания, то он будет перпендикулярен касательной;
• иметь две общие точки, при этом прямая называется секущей.

2. Через три произвольные точки, лежащие в одной плоскости, можно провести не более одной окружности.

3. Две окружности могут соприкасаться только в одной точке, которая расположена на отрезке, соединяющем центры этих окружностей.

4. При любых поворотах относительно центра окружность переходит сама в себя.

5. Что такое окружность с точки зрения симметрии?

• одинаковая кривизна линии в любой из точек;
• центральная симметрия относительно точки О;
• зеркальная симметрия относительно диаметра.

6. Если построить два произвольных вписанных угла, опирающихся на одну и ту же дугу окружности, они будут равны. Угол, опирающийся на дугу, равную половине длины окружности, то есть отсеченную хордой-диаметром, всегда равен 90°.

7. Если сравнивать замкнутые кривые линии одинаковой длины, то получится, что окружность отграничивает участок плоскости наибольшей площади.

Окружность, вписанная в треугольник и описанная около него

Представление о том, что такое окружность, будет неполным без описания особенностей взаимосвязи этой геометрической фигуры с треугольниками.

1. При построении окружности, вписанной в треугольник, ее центр всегда будет совпадать с точкой пересечения биссектрис углов треугольника.
2. Центр окружности, описанной около треугольника, располагается на пересечении срединных перпендикуляров к каждой из сторон треугольника.
3. Если описать окружность около прямоугольного треугольника, то ее центр будет находиться на середине гипотенузы, то есть последняя будет являться диаметром.
4. Центры вписанной и описанной окружностей будут находиться в одной точке, если базой для построения является равносторонний треугольник.

Основные утверждения об окружности и четырехугольниках

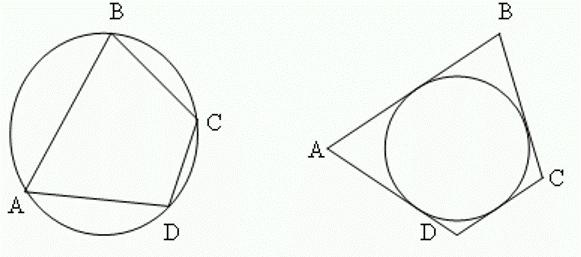
1. Вокруг выпуклого четырехугольника можно описать окружность лишь тогда, когда сумма его противоположных внутренних углов равняется 180°.
2. Построить вписанную в выпуклый четырехугольник окружность можно, если одинакова сумма длин его противоположных сторон.
3. Описать окружность вокруг параллелограмма можно, если его углы прямые.
4. Вписать в параллелограмм окружность можно в том случае, если все его стороны равны, то есть он является ромбом.
5. Построить окружность через углы трапеции можно, только если она равнобедренная. При этом центр описанной окружности будет располагаться на пересечении оси симметрии четырехугольника и срединного перпендикуляра, проведенного к боковой стороне.

fb.ru

Свойства описанной окружности, с примерами

Вокруг любого правильного многоугольника можно описать окружность и только одну.

Центр описанной окружности лежит на пересечении серединных перпендикуляров к сторонам многоугольника.

Площадь многоугольника будет максимальной, если он вписан в окружность.

Свойства окружности, описанной около треугольника

1. Вокруг любого треугольника можно описать окружность, причем только одну.
2. В прямоугольном треугольнике центр описанной окружности лежит на середине гипотенузы.
3. Радиус окружности, описанной около треугольника, равен отношению произведения сторон треугольника к его учетверенной площади:

      

4. Радиус окружности, описанной около треугольника, равен отношению стороны треугольника к удвоенному синусу противолежащего угла

      

Свойства окружности, описанной около четырехугольника

1. Вокруг четырехугольника можно описать окружность, если суммы его противоположных углов равны .
2. Произведение диагоналей вписанного четырёхугольника равно сумме произведений противоположных сторон.
3. Площадь четырёхугольника, вписанного в окружность, можно вычислить по формуле Брахмагупты:

      

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Круг.Свойства круга — математика, уроки

Воспитатель. Покажите левую руку. А теперь, возьмите в левую руку фигуру, которая лежит перед вами, и обведите ее по краю пальчиком правой руки. Нашли уголочки? 

(Нет). У этой фигуры нет уголков, и поэтому ее можно катать. Попробуйте ее прокатить по столу. (Дети катают круги). Эта фигура — называется круг. Как называется эта фигура? (Круг). А что еще похоже на круг? (Мячик, мыльные пузыри). Давайте возьмемся за руки и сделаем большой пузырь.

Игра «Пузырь»

Воспитатель. Сначала наш пузыречек был маленький. (Дети берутся за руки и делают маленький круг). А теперь мы его раздуем, делаем шаги назад. Раздувайся пузырь, (Дети делают большой круг, делая шаги назад)

Раздувайся большой,

Оставайся такой, Да не лопайся.

Воспитатель. Вот какой большой пузырь мы сделали! А как его сделать маленьким? (Идут вперед, сужая круг). Делаем шаги вперед.

Воспитатель. Ребята, давайте подумаем, какие ещё предметы похожи на круг. (Колесо). Послушайте одну историю. Наш друг ослик Иа, из сказки о Вини Пухе, вырастил для нашего детского сада большой урожай овощей и фруктов, а привезти их ему не на чем. Была у него телега, но у нее сломалось одно колесо. Шел он по полю, видит — колесо лежит. Вот здорово, — думает ослик, — поставлю колесо на свою телегу и повезу овощи в детский сад. Покатил он колесо домой и стал ремонтировать телегу. Но колесо оказалось большое. Помогите ослику найти маленькое колесо. У вас на столах лежат «колеса»: большие и маленькие. Найдите маленькое «колесо», чтобы послать ослику. Как это сделать?(Наложить одно колесо на другое). Какое «колесо» меньше? (Красное). Воспитатель. Вот отремонтировал ослик Иа свою телегу и привез овощи и фрукты в наш детский сад.(Воспитатель ставит на стол корзину с овощами

). Выберем овощи и фрукты, похожие на круг. (Дети выбирают).

Воспитатель. Что ты выбрал? На какую фигуру похоже яблоко? (На круг). А помидор? (Тоже на круг). А капуста, какой формы? (Круглая)

Давайте, сделаем компот из яблок. У вас на банке нарисованы круги, нужно положить столько яблок, сколько кружков на банке. (Дети кладут картинки с яблоками на кружки.) На все кружки положили яблоки? (Да). Значит, яблок столько же сколько кружков.

Игра «Две корзины»

Воспитатель. Давайте, поиграем. Стояла корзинка на полке без дела. (Присесть, округлить руки

Скучала, наверно, все лето она. (Наклоны головы, вправо-влево)

Вот осень пришла, и листва пожелтела, (Изобразить ветви деревьев)

Настала пора собирать урожай. (Изобразить срывание фруктов

Корзинка довольна. (Руки округлить перед собой, кивать головой)

Она удивилась, (Развести руки)

Какой уродился в саду урожай! (Подняться на носочки, показать. руками большой круг)Воспитатель. (На столе муляжи или картинки овощей и фруктов). Дети, перед вами фрукты и овощи. Нужно разложить их в две корзины. Положите фрукты и овощи, похожие на круг в одну корзину, а все не похожие на круг — в другую. (Дети выполняют задание).

Игра «Фантазеры».

Воспитатель. Сейчас я дорисую круг до какого-нибудь предмета, а вы назовите, что получилось. (Воспитатель дорисовывает круги, а дети называют, например, апельсин, солнышко, часы и т. д.)

Теперь вы, возьмите карточку с кругом и сами дорисуйте его до какого-нибудь предмета. (Дети выполняют задание). Молодцы, вы нарисовали очень красивые яблоки, помидоры, воздушные шарики.

kopilkaurokov.ru