Окружность и круг | LAMPA

Круг — это множество точек, которые удалены от некоторой точки, называемой центром круга, на расстояние не более чем rrr. rrr называется радиусом круга. Граница круга называется окружностью.

Основные свойства:

• Длина любой не превосходит круга;
• Площадь круга равна S=πr2S=\pi r^2S=πr2;
• Длина окружности равна l=2πrl=2\pi rl=2πr.

Центральный угол

Центральный угол — это угол, вершина которого лежит в центре окружности.

Любые две точки AAA и BBB окружности разбивают ее на две части; каждая из этих частей называется дугой.

Градусная мера дуги — это градусная мера , который опирается на эту дугу.

Вписанный угол

Вписанный угол — это угол, вершина которого лежит на окружности, а стороны пересекают окружность.

Основные свойства:

• Если градусная мера дуги, на которую опирается вписанный угол, равна α\alphaα, то градусная мера вписанного угла равна α2\frac{\alpha }{2}2α​, а градусная мера равна α\alphaα;
• Вписанные углы, опирающиеся на равные дуги, равны;
• Вписанный угол, опирающийся на окружности, равен 90∘90^{\circ}90∘.

Сектор

Сектор — это часть круга, ограниченная двумя радиусами.

Основные свойства:

• Площадь сектора с , имеющим градусную меру α\alphaα, и радиусом RRR равна S=πR2α360∘S=\pi R^2 \frac{\alpha }{360^{\circ}}S=πR2360∘α​. Например, если α=90∘\alpha =90^{\circ}α=90∘, то площадь сектора равна 14πR2\frac{1}{4} \pi R^241​πR2;
• Длина дуги сектора равна l=2πRα360∘l=2\pi R \frac{\alpha }{360^{\circ}}l=2πR360∘α​.

Круг

Круг

Круг — геометрическое место точек плоскости, расстояние от которых до заданной точки, которая называется центром окружности, является постоянной величиной и равна радиуса круга.

Круг с центром в точке О и радиусом r обозначают О (r).

Инструментом для построения окружности есть циркуль — один из основных инструментов геометрии.

1. Терминология

Внутреннюю часть круга, т.е. геометрическое место точек, расстояние которых до центра круга не превышает радиус, называют кругом.

Отрезок прямой, соединяющей две точки окружности называется хордой. Самая длинная из хорд, диаметр, проходящей через центр круга. Диаметр круга равен двум радиусам.

Прямая может не иметь с окружностью общих точек, иметь с кругом одну общую точку (такая прямая называется касательной к окружности) или иметь с ним две общие точки (такая прямая называется секущей к окружности).

Касательная к окружности всегда перпендикулярна к его диаметра, один из концов которого является точкой соприкосновения.

Хорда, секущая, касательная, диаметр.

Дуга, сектор и сегмент

Две точки на окружности разбивают окружность на две дуги. Угол между радиусами, проведенными до двух точек на окружности, называется центральным. Область круга, ограниченная двумя радиусами и дугой называется сектором круга. Область круга, ограниченная хордой и дугой, называется сегментом.

2. Определение круга

2.1. Алгебраическое определение

Круг радиуса r = 1, с центром (a, b) = (1.2, -0.5)

Круг на плоскости, данного радиуса , В определенной выбранной декартовой системе координат и , С центром в точке (a, b) описывается стандартным уравнением

Это уравнение следует из теоремы Пифагора, при ее застовуванни к каждой точке круга, как показано на рисунке справа, где радиус это гипотенуза прямоугольного треугольника, катеты которого x — a и y — b. Если центр окружности находится в начале координат (0, 0), тогда уравнение упрощается до следующего вида:

Общее уравнение окружности:

Если известны координаты трех точек на плоскости и , То уравнение круга, проходящего через эти точки можно записать через определитель :

2.2. Параметрическое определение

Круг на плоскости, данного радиуса , В определенной выбранной декартовой системе координат и Описывается системой уравнений:

где параметр — Пробегает значения от к . С геометрической точки зрения это угол оси x, луча проведенного из начала координат до точки (x, y). Если записать x и y через параметр t, получим:

2.3. Полярные координаты

Уравнение окружности в полярных координатах :

где a — радиус окружности, r ₀ — расстояние от начала координат до центра окружности и φ — угол отложен против часовой стрелки от положительной оси x к линии соединяющей начало координат с центром круга. Для круга, центр которого находится в начале координат r ₀ = _0, это уравнение упрощается до вида r = a. Если r ₀ = a или если начало координат лежит на окружности, тогда получаем уравнение:

.

В общем случае, уравнение можно решить для r:

,

Розвязок со знаком минус перед корнем дает идентичную кривую.

2.4. Комплексная плоскость

Уравнение окружности на комплексной плоскости :

или в параметрическом виде

2.5. Определение Аполлония

Аполлоний из Перги показал, что круг можно задать как множество точек на плоскости, имеющих одинаковое отношение расстояний до двух фокусов A и B. О такой круг иногда говорят, что оно задано двумя точками

3. Свойства

• Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одно.
• Точка касания двух окружностей лежит на прямой, проходящей через их центры.
• Изопериметрические неравенство: Из всех замкнутых кривых данной длины круг ограничивает область максимальной площади.
• Вписанный угол или равен половине центрального угла, опирающегося на его дугу, либо дополняет половину этого угла до 180 .
  • Два вписанных угла, опирающиеся на одну и ту же дугу, равны.
  • Вписанный угол, опирающийся на дугу длиной в половину окружности равна 90 .
• Угол между двумя секущими, проведенными из точки, лежащей вне круга равен пивризници мер дуг, лежащих между секущими.
• Угол между хордами, пересекающимися равен полусумме мер дуги, лежащий в углу и дуги напротив нее.
• Угол между касательной и хордой равен половине градусной меры дуги, взимаемый хордой.
• Отрезки касательных к окружности, проведенных из одной точки, равны и образуют равные углы с прямой, проходящей через эту точку и центр окружности.
• При пересечении двух хорд произведение отрезков, на которые делится одна из них точкой пересечения, равна произведению отрезков на которые делится другая.
• Произведение длин расстояний от выбранной точки до двух точек пересечения окружности и секущей, проходящей через выбранную точку, не зависит от выбора секущей и равна абсолютной величине степени точки относительно окружности.
  • Квадрат длины отрезка касательной равен произведению длин отрезков секущей и равна абсолютной величине степени точки относительно окружности.

4. Длина окружности и площадь круга

Длину дуги окружности с радиусом , Образованного центральным углом , Измеренным в радианах, можно вычислить по формуле

.

Длину окружности с радиусом можно вычислить по формуле

,

где — число пи, которое определяется как отношение длины окружности к ее диаметру.

Площадь ограниченного круга круга равна

,

где — Диаметр.

На протяжении многих веков математиков интересовала задача о квадратуру круга : построение с помощью линейки и циркуля квадрату с площадью, подобной площади круга. Эта задача не имеет решения, поскольку число пи трансцедентне, что доказал в 1882 Фердинанд фон Линдеманн.

5. Круг как конический сечение

Круг проста плоской кривой второго порядка и классифицируется как один из видов конического сечения. В узком смысле круг — отдельный случай эллипса, есть эллипс с одинаковыми полуосями, или другими словами круг является эллипсом с единичным эксцентриситетом.

6. Связанные и нормали

Уравнение касательной к окружности в точке определяется уравнением

,

где A, B и С — коэффициенты в общем уравнении круга.

Уравнение нормали в этой же точке можно записать как

См.. также

Методический материал по теме «Свойства окружности»

«Свойства окружности»

Оглавление

Введение

Свойства касательных к окружности

Окружность, вписанная в произвольный треугольник

Окружность, вписанная в трапецию и описанная около трапеции.

Формула отрезка общей касательной к двум касающимся окружностям

Ведение

В школьном курсе геометрии уделяется немного уроков для изучения темы «Окружность», учащиеся узнают о взаимном расположении окружностей и многоугольников и окружности, получают формулы для нахождения радиуса окружности, вписанной в правильный треугольник, квадрат и правильный шестиугольник, а также формы для радиусов описанных окружностей около квадрата, правильного треугольника и шестиугольника. Но остается открытым вопрос о том, как же находить радиус окружности, вписанной в произвольный треугольник, как связаны отрезки касательных к окружности с радиусом и углами треугольника.

Из школьного курса геометрии известно, где лежит центр окружности, описанной около треугольника, квадрата, правильного шестиугольника, но ведь в окружность можно вписать и трапецию, где в этом случае будет лежать центр этой окружности? Всякую ли трапеции можно вписать в окружность? На эти вопросы поможет ответить данная проектная работа, в которой изложены теоремы и их доказательства, относящиеся к нахождению элементов окружности и многоугольников, как вписанных в окружность, так и описанных около нее. Полученные формулы помогут при решении задач, упростят нахождение радиуса окружности, элементов многоугольника. К тому же в задании ЕГЭ С4 нередко встречаются задачи с вписанными и описанными окружностями. Приведенные факты и формулы помогут сориентироваться учащимся при решении задач на доказательство и нахождение элементов многоугольника из С4.

Предмет проекта:

Окружности, элементы окружностей и многоугольники, вписанные в окружность и описанные около окружности.

Цели

— расширить и систематизировать знания об окружностях и многоугольниках, вписанных в окружность и описанных около окружности.

Задачи:

— изучить и обобщить свойства касательной и секущей к окружности;

— вывести: формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формулу отрезка общей касательной к двум касающимся окружностям;

— изучить особенности окружности, вписанной в трапецию и описанной около нее.

Свойства касательной к окружности

В этом разделе общаются и систематизируются сведения о касательной и секущей к окружности. Приводится доказательство дополнительных свойств, о которых не упоминается в учебнике геометрии, но они могут быть полезны при решении олимпиадных задач и подготовки к экзамену.

Напомним определение касательной и секущей.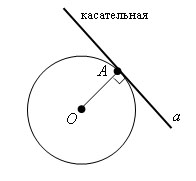

Прямая, имеющая с окружностью только одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Секущей называется прямая, пересекающая окружность.

Основные свойства касательной к окружности

Данные свойства и их доказательства приводят в учебнике геометрии.

• Отрезки касательных к окружности, проведенные из одной точки, равны.

На рисунке изображены две касательные к окружности. AB и AC – отрезки касательных к окружности. AB = AC.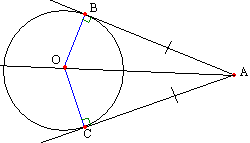

• Углы, образованные касательными, проведенными из одной точки, и прямой, проходящей через центр окружности и эту точку, равны.

На рисунке выше, прямая AO является биссектрисой , значит,

На рисунке касательная проведена к окружности в точке A, тогда прямая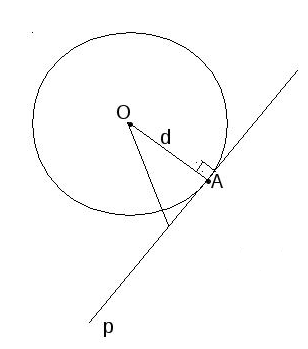

Дополнительные свойства.

Здесь приведем доказательства свойств касательной и секущей к окружности, которые могут быть полезны для вычисления углов и отрезков касательных.

• Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины касательной равен произведению секущей на ее внешнюю часть.

На рисунке МС – касательная, MA – секущая, тогда MC² = MA·MB.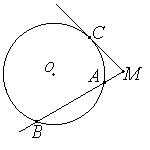

• Если из точки к окружности проведены касательная и секущая, то квадрат отрезка касательной от данной точки до точки касания равен произведению длин отрезков секущей от данной точки до точек её пересечения с окружностью.

На рисунке МА – касательная, МВ – секущая, тогда МА²=МВ·МС

Доказательство: , и следовательно,. У АМС и ВМА угол при вершине М общий, то эти треугольники подобны по двум углам (первый признак подобия треугольников). Из подобия следует: , значит, МА²=МВ·МС.

• Угол между касательными и хордой. Величина угла, образованного касательной и хордой, имеющими общую точку на окружности, равна половине угловой величины дуги, заключенной между его сторонами.

• ∠NAB — угол между касательной MN и хордой AB, имеющих на окружности общую точку A, тогда ∠NAB== (180^о-∠BOC) = ∠АОВ или ∠NAB = .

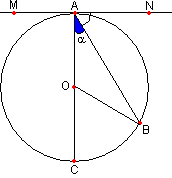
Доказательство: Дополнительное построение. Проводим диаметр АС. Касательная перпендикулярна радиусу, проведенному в точку касания, а, значит, перпендикулярна диаметру АС, тогда ∠CAN=90^о. – вписанный угол, тогда = , ∠NAB=90^о-, получаем ∠NAB== (180^о-∠BOC) = ∠АОВ или ∠NAB = .

Угол между секущими.

• Если точка пересечения двух

  секущих к окружности находится внутри окружности, то угол между секущими равен половине суммы градусных мер дуг, которые они стягивают.

F

M

R

Доказательство: Дополнительное построение. Проведем хорду FR, треугольника FMR получим: Получаем

• Если точка пересечения двух секущих к окружности находится вне окружности, то угол между секущими равен половине разности градусных мер дуг, которые они стягивают.

M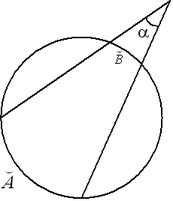

C

D

E

F

Доказательство: Дополнительное построение. Проведем хорду ED, тогда

так как они являются вписанными углами. Из треугольника MED: углами, значит, тогда

Окружность, вписанная в произвольный треугольник

Для выведения формул отрезков касательных к окружности и радиуса окружности, вписанной в треугольник напомним определение окружности, вписанной в треугольник.

Окружность вписана в треугольник, если она касается всех его сторон. Тогда сам треугольник будет описанным вокруг окружности. Расстояние от центра вписанной окружности до каждой из сторон треугольника равно радиусу этой окружности.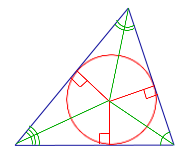

Формулы для отрезков касательных к окружности, вписанной в треугольник

Пусть точки K, M, N – точки касания окружности со сторонами треугольника. Стороны треугольника, описанного около окружности лежат на касательных к этой окружности, тогда отрезки касательных равны, то есть AK=AN, BK=BM, CN=CM. Обозначим их соответственно буквами x, y, z.

р – полупериметр треугольника ABC. .

BC=y+z ; AC=x+z ; AB=x+y, тогда p= = =x+(y+z) =x+BC p=x+BC

Отсюда х= р — BC , т.е. AK=AN=p — BC.

Аналогично y=p — AC ; z=p — AB т.е. BK=BM=

p — AC, CM=CN= p – AB.

Если окружность вписана в треугольник, то отрезки касательных можно вычислить как разность полупериметра и стороны треугольника, на которой данный отрезок касательной не лежит.

В формуле заменим p на a+b+c, где a=BC, b=AC, c=AB, получим:

BK=BM=y

CM=CN=z

В треугольнике со сторонами a, b, c расстояние от вершины А до точек касания вписанной окружности сторон, содержащих эту вершину, равно , расстояние от вершины

B до точек касания вписанной окружности сторон, содержащих эту вершину, равно , расстояние от вершины C до точек касания вписанной окружности сторон, содержащих эту вершину, равно .

Выведем еще одну формулу для вычисления отрезков касательных:

Для доказательства рассмотрим АОN –прямоугольный т.к ONAC (радиус перпендикулярен касательной). AO – отрезок биссектрисы ∠ А => ∠ONA=

ctg ∠ OAN =, тогда

Аналогично и

Окружность, вписанная в трапецию и описанная около трапеции.

Из школьного курса геометрии известно, что в окружность можно вписать любой треугольник, квадрат, правильный шестиугольник. Определим, можно ли в окружность вписать трапецию.

Теорема.

Трапеция вписана в некоторую окружность тогда и только тогда, когда она является равнобедренной.

Доказательство: так как они являются односторонними углами. По теореме Птолемея, если у четырёхугольника суммы величин его противоположных углов равны 180°, то около этого

четырёхугольника можно описать окружность, тогда , значит то есть трапеция должна быть равнобедренной.

Следующая теорема показывает, как можно вычислить радиус окружности, вписанной в трапецию.

Теорема.

Если в трапецию вписана окружность с радиусом r  и она делит боковую сторону точкой касания на два отрезка — a и b,  то B C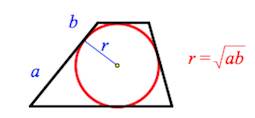

M

O

A D

Доказательство: Если концы боковой стороны соединит с центром окружности, то образуется прямоугольный треугольник ABO, с прямым углом O. Радиус — это высота, опущенная из его прямого угла в точку касания окружности. Из подобия треугольников BOM и AOM, следует что , тогда .

Теорема.

Центр окружности, описанной около трапеции, лежит на пересечении серединных перпендикуляров к сторонам трапеции.

B C

O

A D

Доказательство: Проведем диагональ AC, она делит трапецию на два треугольника, вписанных в окружность, значит отрезки AO, BO, CO равны, так как треугольник ABC является вписанным в окружность. Из школьного курса планиметрии известно, что центром описанной около треугольника окружности является точка пересечения серединных перпендикуляров к сторонам треугольника ABC. Но стороны треугольника ABC являются сторонами трапеции ABCD, значит центр окружности, описанной около трапеции, является точкой пересечения серединных перпендикуляров к сторонам трапеции.

Формула отрезка общей касательной к двум касающимся окружностям

Две окружности имеют различное взаимное расположение относительно друг друга, а именно: окружности могут касаться друг друга, пересекаться, не пересекаться, одна окружность может лежать внутри другой. Рассмотрим случай, когда окружности касаются внешним образом. Они имеют общую точку касания.

Рассмотрим понятие внешней касательной к окружности. Прямую называют внешней касательной к двум окружностям, если она касается каждой из окружностей, а окружности лежат по одну сторону от этой прямой. На рисунке прямая a – внешняя касательная к двум касающимся окружностям.

Теорема.

Отрезок общей внешней касательной к двум касающимся окружностям равен ,где R и r –радиусы окружностей.

Пусть AB – общая касательная к окружностям; O1 и O2 -центры окружностей , тогда

O₁A AB и O₂B AB так как радиус, проведенный в точку касания, перпендикулярен касательной. O₁ABO₂ -прямоугольная трапеция. Проведем высоту O₁Н.

O₁H=AB, O₂H= O₂B-HB= O₂B- O₁A=R-r

По теореме Пифагора O₁O₂ = O₂H+ O₁H

₁H

Решив квадратное уравнение, получаем:

Данная формула применяется для вычисления отрезка общей касательной к двум касающимся окружностям через радиусы этих окружностей. Задачи, в которых присутствует окружность и касательная часто встречаются в С4 ЕГЭ. Применяя эту формулу мы упростим вычисления при решении подобных задач.

Заключение

В ходе работы были изучены основные свойства касательной к окружности, доказаны дополнительные свойства, о которых не упоминается в школьном курсе планиметрии. Произведена систематизация этих свойств. Также были выведены формулы для отрезков касательных к окружности, вписанной в треугольник; формулы радиуса окружности, вписанной в произвольный треугольник; формула отрезка общей касательной к двум касающимся окружностям. Были изучены особенности окружности вписанной и описанной в трапеции. Выведена формула для вычисления радиуса вписанной в трапецию окружности.

Полученные знания станут существенным подспорьем в понимании свойств касательной и секущей к окружности. Будут необходимы при решении как задач курса планиметрии, так и олимпиадных и экзаменационных задач.

Список литературы

1. Учебник по геометрии 7-9 класс, атанасян Л.С. и др.-18-е изд. — М. : «Просвещение», 2008.

2. Геометрия в 7-9 классах. Березина Л. Ю. и др.- 2-е изд., перераб. И доп. – М. : «Экзамен»,2008

3. http://www.alexlarin.narod.ru/ege/2010/C4agk.pdf.

4. http://eek.diary.ru/ сайт по оказанию помощи абитуриентам, студентам,

учителям по математике.

5. Полонский В.Б., Рабинович Е.М., Якир М.С. Учимся решать задачи по геометрии. Учеб.-метод. пособие. – К. «Магистр», 1996.

Круг — ГП Стальмаш

Справочная информация

Круг (круг стальной пруток):
*круг ГОСТ 2590-88 круг стальной горячекатаный,
*круг ГОСТ 7417-75 круг стальной калиброванный,
*круг ГОСТ 14955-77 круг серебрянка, круг со спецотделкой поверхности,
*круг буровой пустотелый ТУ 14-1-681-73.
Круг — геометрическое место точек плоскости, расстояние от которых до данной точки не больше, чем заданное не нулевое (Круг — часть плоскости, ограниченная окружностью).
Круг — это сечение цилиндра плоскостью, перпендикулярной его оси.
Центр круга — точка внутри окружности, имеет равное расстояние до любой точки находящейся на окружности данного круга.
Окружность — граница круга (Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая).
Диаметр круга — отрезок прямой, соединяющий пару наиболее удаленных друг от друга точек окружности, а также длина этого отрезка. Диаметр всегда проходит через центр окружности. Обычно обозначается D или Ø.
Диаметр круга равен удвоенному радиусу окружности: D = 2R, R = D/2.
Радиус круга – расстояние от центра круга до любой точки окружности.
Радиус круга — не только величина расстояния, но и отрезок, соединяющий центр круга с его границей.
Сектор круга — пересечение круга и некоторого его центрального угла, то есть часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга. Сегмент круга — часть круга, ограниченная дугой и стягивающей её хордой.
Свойства круга:
*Круг сохраняется при вращении в плоскости относительно своего центра.
*Круг является выпуклой фигурой.
*Площадь круга радиуса R: S = πR2, где число π = 3.141592… — константа (постоянная величина).
*Периметр круга (длина окружности): L = 2πR.
*Радиус окружности: R = L/2π.
*Диаметр окружности: D = L/π
Отношение длины окружности к её диаметру одинаково для всех окружностей.
Это отношение есть трансцендентное число, обозначаемое греческой буквой пи: π=3,14159…

 

 

http://ооостальмаш.рф