Подготовка школьников к ЕГЭ и ОГЭ (Справочник по математике — Алгебра

Абсолютная величина (модуль) действительного числа
Определение. Абсолютной величиной (модулем) действительного числа a называют неотрицательное число | a | , которое определяется по формуле:


Так, например,
| 5 | = 5, | – 2 | = 2,
| 0 | = 0.
Свойства модуля
Если x и y – действительные числа, то справедливы равенства:
Кроме того, справедливо соотношение:
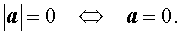
В то же время справедливы неравенства:
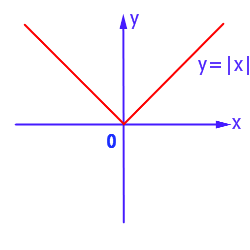
График функции y = | x |
График функции y = | x | имеет следующий вид:
Простейшее уравнение с модулем
Рассмотрим простейшее уравнение с модулем, имеющее вид:
| f (x) | = g(x) .
Поскольку
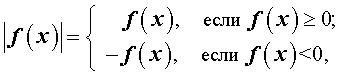

то данное уравнение эквивалентно совокупности двух систем:
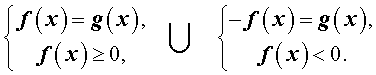

Для решения исходного уравнения остается лишь решить две этих системы и объединить полученные ответы.
Замечание. Решение неравенств с модулями осуществляется аналогично.
Желающим более глубоко освоить тему «Модули», мы рекомендуем изучить наши учебные пособия: «Уравнения и неравенства с модулями» и «Фигуры на координатной плоскости, заданные неравенствами».

На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Модуль вещественного числа и его свойства
Определение. Модуль вещественного числа — это само число , если , и противоположное число , если .
Свойства модуля
1. ,
.
2. .
3. — это расстояние между точками и на числовой оси.
Доказательство.
1. Докажем сначала, что .
Рассмотрим несколько случаев (в этих случаях по-разному раскрываются модули):
Левая часть неравенства получается, если в доказанном неравенстве заменить на , — на , а затем — на , а — на .
2.
Модуль непрерывности — Википедия
Материал из Википедии — свободной энциклопедии
Для любой функции f{\displaystyle f}, определённой на множестве E{\displaystyle E}, можно ввести понятие модуля непрерывности этой функции, обозначаемого ωf(δ){\displaystyle \omega _{f}(\delta )}. Модуль непрерывности — тоже функция, по определению равная
- ωf(δ)=sup{|f(x1)−f(x2)|:(x1,x2∈E)∧|x1−x2|<δ},{\displaystyle \omega _{f}(\delta )=\sup\{|f(x_{1})-f(x_{2})|\colon (x_{1},\;x_{2}\in E)\land |x_{1}-x_{2}|<\delta \},}
или верхней грани колебания функции по всем подотрезкам из E{\displaystyle E} длиной меньше δ{\displaystyle \delta }. Также в литературе встречаются другие обозначения: ω(f,δ){\displaystyle \omega (f,\;\delta )} и (реже) ω(δ,f){\displaystyle \omega (\delta ,\;f)}.
Введённая функция обладает рядом интересных свойств.
- При любом δ{\displaystyle \delta } она неотрицательна.
- Функция не убывает.
- Функция полуаддитивна, если E{\displaystyle E} выпукло:
- ωf(δ1+δ2)⩽ωf(δ1)+ωf(δ2).{\displaystyle \omega _{f}(\delta _{1}+\delta _{2})\leqslant \omega _{f}(\delta _{1})+\omega _{f}(\delta _{2}).}
- По определению в точке 0 модуль непрерывности равен 0:
- ωf(0)=def0.{\displaystyle \omega _{f}(0){\stackrel {\mathrm {def} }{=}}0.}
- Теорема о равномерной непрерывности может быть сформулирована следующим образом. Если функция f{\displaystyle f} определена на отрезке [a,b]{\displaystyle [a,\;b]} и непрерывна на нём, то limδ→0+ωf(δ)=0{\displaystyle \lim _{\delta \to 0+}{\omega _{f}(\delta )}=0}, и наоборот. Данный предел обозначается также ωf(0+){\displaystyle \omega _{f}(0+)}.
- Если f(x){\displaystyle f(x)} непрерывна на [a,b]{\displaystyle [a,\;b]}, то её модуль непрерывности также непрерывная функция на отрезке [0,b−a]{\displaystyle [0,\;b-a]}.
Модуль непрерывности оказался тонким инструментом исследования разнообразных свойств функции, таких как:
Модули непрерывности высших порядков[править | править код]
Нетрудно заметить, что в определении модуля непрерывности используется конечная разность первого порядка от функции f{\displaystyle f}.
- ωf(δ)=sup{|Δh2(f,x)|:(x∈E)∧|h|<δ}.{\displaystyle \omega _{f}(\delta )=\sup\{|\Delta _{h}^{1}(f,\;x)|\colon (x\in E)\land |h|<\delta \}.}
Если вместо конечной разности первого порядка взять конечную разность порядка n{\displaystyle n}, то получим определение модуля непрерывности порядка n{\displaystyle n}. Обычное обозначение для таких модулей — ωn(f,δ){\displaystyle \omega _{n}(f,\;\delta )}.
Свойства[править | править код]
- Если k{\displaystyle k} — целое число, то ωn(f,kδ)⩽knωn(f,δ).{\displaystyle \omega _{n}(f,\;k\delta )\leqslant k^{n}\omega _{n}(f,\;\delta ).}
Неклассические модули непрерывности[править | править код]
Известно много разных обобщений понятия модуля непрерывности. Например, можно заменить оператор конечной разности другим разностным оператором с произвольными коэффициентами. Можно разрешить этим коэффициентам быть непостоянными и меняться в зависимости от точки, где берётся этот разностный оператор. Можно разрешить и шагу, с которым берётся разностный оператор также зависеть от точки. Подобные неклассические модули непрерывности находят своё применение в различных областях современной математики.
Дать определение модуля комплексного числа. Доказать свойства модуля.
Определение.Комплексным числомz=x+iy называется упорядоченная пара действительных чисел 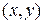 :
: 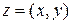 .
.
Действительные числа х и у называются, соответственно, действительной и мнимой частями комплексного числа z и обозначаются: 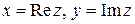
Определение.Вещественное неотрицательное число:

называют модулем комплексного числа 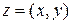 .
.
Теорема. (Об умножении комплексных чисел в тригонометрической форме записи.)
Пусть  , где
, где 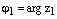 и
и 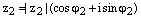 , где
, где 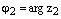 – два произвольных комплексных числа записанных в тригонометрической форме. Тогда
– два произвольных комплексных числа записанных в тригонометрической форме. Тогда
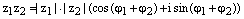 .
.
Теорема. (Свойства модуля комплексного числа.)
Пусть 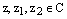 – произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
– произвольные комплексные числа и соответствующие точки на комплексной плоскости. Тогда:
1) 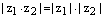 и
и  . Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
. Т.е. модульпроизведения комплексных чисел равен произведению их модулей и модули противоположных чисел равны;
2) расстояниемеждуточками  и
и  комплексной плоскости равно модулю разности соответствующих комплексных чисел:
комплексной плоскости равно модулю разности соответствующих комплексных чисел: 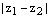
3) 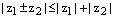 ;
;
4) 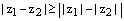 ;
;
Доказательство. 1) По предыдущей теореме имеем:
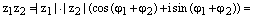
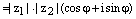 , где
, где 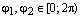 и
и 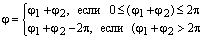 ,
,
т.е.  .
.
Таким образом, равенства 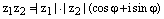
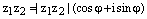 есть тригонометрическаяформа записи числа
есть тригонометрическаяформа записи числа  , следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем
, следовательно, по теореме о равенстве комплексных чисел в тригонометрической форме записи, имеем 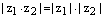 , ч.т.д.
, ч.т.д.Далее, т.к.  , то по только что доказанному свойству
, то по только что доказанному свойству  , ч.т.д.
, ч.т.д.
Заметим, что последнее равенство можно получить и из других соображений.
Противоположные числа на комплекснойплоскости изображаютсяточками симметричными относительно начала координат. Действительно, пусть 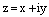
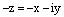 и точки
и точки 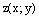 ,
, 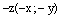 имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.
имеют противоположные декартовые координаты. Значит, в силу симметрии, расстояния от этих точек до начала координат равны, т.е.  , ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.
, ч.т.д. Заметим, также, что такой же результат можно получить с помощью формулы (12) вычисления модуля комплексного числа.2). Пусть 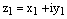 ,
, 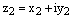 . Тогда
. Тогда 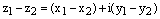
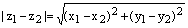 . (14)
. (14)
С другой стороны, рассмотрим числа  и
и  как точки на комплексной плоскости. Тогда точка
как точки на комплексной плоскости. Тогда точка  имеет декартовыекоординаты
имеет декартовыекоординаты 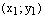 , а
, а 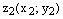 и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
и искомое расстояниемежду ними вычисляется по формуле (14), ч.т.д.
3) Рассмотрим на комплекснойплоскости точки 
 и начало координат О. В общем случае эти три точки являются вершинами треугольника
и начало координат О. В общем случае эти три точки являются вершинами треугольника  :
: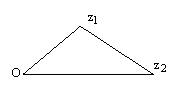
рис.6.
Воспользуемся известным свойством треугольника: длина стороны треугольника не превосходит суммы длин двух его других сторон.
Мы только что доказали, что длина стороны  этого треугольника равна
этого треугольника равна 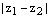 , а длины сторон
, а длины сторон 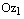 и
и 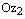
 и
и  :
: 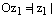 ,
, 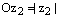 . Отсюда и получаем, что
. Отсюда и получаем, что 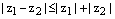 .
.Заменим в последнем неравенстве число  на противоположное число
на противоположное число 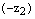 , тогда получаем:
, тогда получаем:
 , ч.т.д.
, ч.т.д.
Заметим, что равенство в этих неравенствах достигается тогда и только тогда, когда  и
и  лежат на одной прямой.
лежат на одной прямой.
4)  , откуда следует
, откуда следует
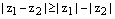 . Поменяв местами
. Поменяв местами  и
и  , получаем
, получаем
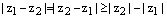 , откуда и следует доказываемое неравенство.
, откуда и следует доказываемое неравенство.
Теорема доказана.