Свойства параболы, с примерами

Парабола является графиком квадратичной функции, которая задается уравнением

   

и обладает следующими свойствами:

– если коэффициент и вершина параболы имеет координаты , то

Область определения – .

Область значений – .

Функция убывает при , возрастает при .

Функция непрерывна и выпукла вниз.

Минимум функции .

– если коэффициент a, а вершина параболы имеет координаты , то

Область определения – .

Область значений – .

Функция убывает при , возрастает при .

Функция непрерывна и выпукла вверх.

Максимум функции .

Примеры решения задач

Понравился сайт? Расскажи друзьям!

ru.solverbook.com

Определение и основные свойства квадратичной функции

Функция вида называется квадратичной функцией.

Квадратичную функцию можно представить в виде

Областью определения этой функции является множество всех действительных чисел.

Область значений лежит в промежутке , если a > 0, и в промежутке 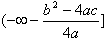, если a < 0.

Графиком квадратичной функции является парабола. Вершина параболы находится в точке

Парабола симметрична относительно прямой . Ветви параболы направлены вверх, если a > 0.

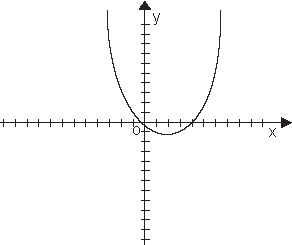
Ветви параболы направлены вниз, если a < 0.

Парабола пересекает ось ОХ в точках x₁ и x₂ , где x₁ и x₂  — корни квадратного уравнения .

 Если квадратное уравнение не имеет корней (дискриминант отрицательный), то парабола лежит выше или ниже оси ОХ, (если a < 0, то ниже; если a > 0, то выше).

Пример: Построить график функции .

Графиком функции является парабола. Ветви параболы направлены вверх. Вершина параболы находится в точке . Осью симметрии параболы будет прямая . Парабола пересекает ось ОХ в точках .

Для точности построения, построим таблицу:

Строим график: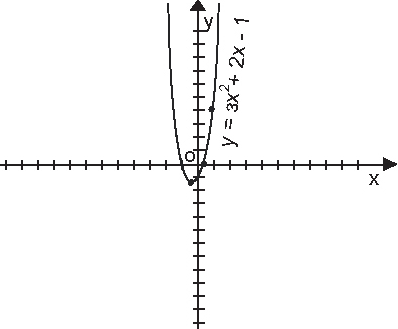

studyport.ru

ВЛИЯНИЕ КОЭФФИЦИЕНТОВ а, b и с НА РАСПОЛОЖЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ

У р о к 15.

Влияние коэффициентов а, b и с на расположение
графика квадратичной функции

Цели: продолжить формирование умения строить график квадратичной функции и перечислять ее свойства; выявить влияние коэффициентов а, b и с на расположение графика квадратичной функции.

Ход урока

I. Организационный момент.

II. Устная работа.

Определите, график какой функции изображен на рисунке:

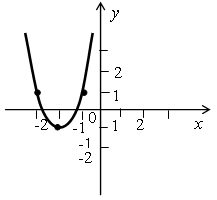
у = х² – 2х – 1;

у = –2х² – 8х;

у = х² – 4х – 1;

у

= 2х² + 8х + 7;

у = 2х² – 1.

б)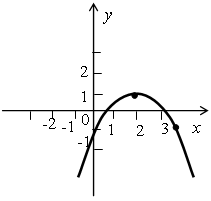

у = х² – 2х;

у = –х² + 4х + 1;

у = –х² – 4х + 1;

у = –х² + 4х – 1;

у = –

х² + 2х – 1.

III. Формирование умений и навыков.

Упражнения:

1. № 127 (а).

2. № 129.

Р е ш е н и е

Прямая у = 6х + b касается параболы у = х² + 8, то есть имеет с ней только одну общую точку в том случае, когда уравнение 6х + b = х² + 8 будет иметь единственное решение.

Это уравнение является квадратным, найдем его дискриминант:

х² – 6х + 8 + b = 0;

D₁ = 9 – (8 – b) = 1 + b;

D₁ = 0, если 1 + b = 0, то есть b = –1.

О т в е т: b = –1.

3. Выявить влияние коэффициентов а, b и

с на расположение графика функции у = ах² + bх + с.

Учащиеся обладают достаточными знаниями, чтобы выполнить это задание самостоятельно. Следует предложить им все полученные выводы занести в тетрадь, при этом выделив «основную» роль каждого из коэффициентов.

1) Коэффициент а влияет на направление ветвей параболы: при а > 0 – ветви направлены вверх, при а < 0 – вниз.

2) Коэффициент b влияет на расположение вершины параболы. При b = 0 вершина лежит на оси оу.

3) Коэффициент с показывает точку пересечения параболы с осью ОУ.

После этого можно привести пример, показывающий, что можно сказать о коэффициентах а, b и с по графику функции.

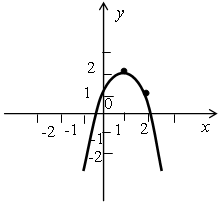
Значение с можно назвать точно: поскольку график пересекает ось ОУ в точке (0; 1), то с = 1.

Коэффициент а можно сравнить с нулем: так как ветви параболы направлены вниз, то а < 0.

Знак коэффициента b можно узнать из формулы, определяющей абсциссу вершины параболы: т = , так как а < 0 и т = 1, то b> 0.

4. Определите, график какой функции изображен на рисунке, опираясь на значение коэффициентов а, b и с.

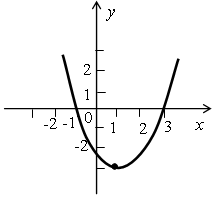
у = –х² + 2х;

у = х² + 2х + 2;

у = 2х² – 3х – 2;

у = х² – 2.

Р е ш е н и е

По изображенному графику делаем следующие выводы о коэффициентах а, b и с:

а > 0, так как ветви параболы направлены вверх;

b ≠ 0, так как вершина параболы не лежит на оси ОУ;

с = –2, так как парабола пересекает ось ординат в точке (0; –2).

Всем этим условиям удовлетворяет только функция у = 2х² – 3х – 2.

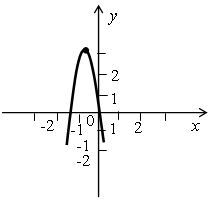
у = х² – 2х;

у = –2х² + х + 3;

у = –3х² – х – 1;

у = –2,7х² – 2х.

Р е ш е н и е

По изображенному графику делаем следующие выводы о коэффициентах а, b и с:

а < 0, так как ветви параболы направлены вниз;

b ≠ 0, так как вершина параболы не лежит на оси ОУ;

с = 0, так как парабола пересекает ось ОУ в точке (0; 0).

Всем этим условиям удовлетворяет только функция у = –2,7х² – 2х.

5. По графику функции у = ах² + bх + с определите знаки коэффициентов

а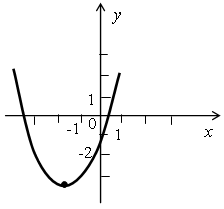, b и с:

а) б)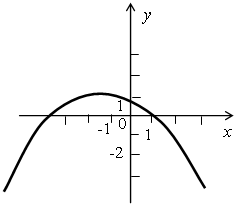

Р е ш е н и е

а) Ветви параболы направлены вверх, поэтому а > 0.

Парабола пересекает ось ординат в нижней полуплоскости, поэтому с < 0. Чтобы узнать знак коэффициента b воспользуемся формулой для нахождения абсциссы вершины параболы: т = . По графику видно, что т < 0, и мы определим, что а > 0. Поэтому b > 0.

б) Аналогично определяем знаки коэффициентов а, b и с:

а < 0, с > 0, b < 0.

Сильным в учебе учащимся можно дать дополнительно выполнить № 247.

Р е ш е н и е

у = х² + рх + q.

а) По теореме Виета, известно, что если х₁ и х₂ – корни уравнения х² +
+ рх + q = 0 (то есть нули данной функции), то х₁ · х₂ = q и х₁ + х₂ = –р. Получаем, что q = 3 · 4 = 12 и р = –(3 + 4) = –7.

б) Точка пересечения параболы с осью ОУ даст значение параметра q, то есть q = 6. Если график функции пересекает ось ОХ в точке (2; 0), то число 2 является корнем уравнения х² + рх + q = 0. Подставляя значение х = 2 в это уравнение, получим, что р = –5.

в) Своего наименьшего значения данная квадратичная функция достигает в вершине параболы, поэтому , откуда р = –12. По условию значение функции у = х² – 12х + q в точке x = 6 равно 24. Подставляя x = 6 и у = 24 в данную функцию, находим, что q = 60.

IV. Проверочная работа.

В а р и а н т 1

1. Постройте график функции у = 2х² + 4х – 6 и найдите, используя график:

а) нули функции;

б) промежутки, в которых у > 0 и y < 0;

в) промежутки возрастания и убывания функции;

г) наименьшее значение функции;

д) область значения функции.

2. Не строя график функции у = –х² + 4х, найдите:

а) нули функции;

б) промежутки возрастания и убывания функции;

в) область значения функции.

3. По графику функции у = ах² + bх + с определите знаки коэффициентов а, b и с:

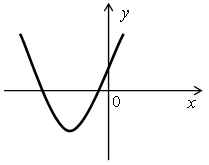
В а р и а н т 2

1. Постройте график функции у = –х² + 2х + 3 и найдите, используя график:

а) нули функции;

б) промежутки, в которых у > 0 и y < 0;

в) промежутки возрастания и убывания функции;

г) наибольшее значение функции;

д) область значения функции.

2. Не строя график функции у = 2х² + 8х, найдите:

а) нули функции;

б) промежутки возрастания и убывания функции;

в) область значения функции.

3. По графику функции у = ах² + bх + с определите знаки коэффициентов а, b и с:

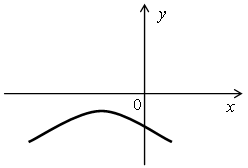
V. Итоги урока.

В о п р о с ы у ч а щ и м с я:

– Опишите алгоритм построения квадратичной функции.

– Перечислите свойства функции у = ах² + bх + с при а > 0 и при а < 0.

– Как влияют коэффициенты а, b и с на расположение графика квадратичной функции?

Домашнее задание: № 127 (б), № 128, № 248.

Д о п о л н и т е л ь н о: № 130.

infourok.ru

«Зачем мне что-то знать о параболе в обычной жизни?» – Яндекс.Знатоки

Парабола — это не просто математическая функция, которую полезно знать для общего развития. У неё есть очень интересные и полезные свойства, которые с успехом применяются и в реальной жизни. Вот пример.

У параболы есть особая точка, называемая фокусом параболы. Крутость этой точки заключается в том, что если на параболу направить пучок параллельных лучей, то отразившись от неё, они все соберутся в фокусе!

Именно поэтому антенны имеют форму параболы. Думаю, вы легко сможете найти на картинке фокус 🙂

Это правило работает и в обратную сторону. Если в фокус поместить источник лучей (например, света или радиоволн), он отразится от параболы и направится параллельно оси её симметрии. Это используется, например, в прожекторах

Крутость математики в том, что изучая абстрактные математические объекты, такие как парабола, мы можем прикладывать их к массе вещей из реального мира. Задумайтесь, как это эффективно: изучив что-то на бумаге, вы можете построить антенну, прожектор, понять движение физических объектов и ещё множество других вещей! Вот ещё пример парабол из реальной жизни:

yandex.ru