Основные единицы СИ — Википедия

Семь основных единиц

Основные единицы Международной системы единиц (СИ) — семь основных единиц измерения основных физических величин СИ. Эти величины — длина, масса, время, сила электрического тока, термодинамическая температура, количество вещества и сила света. Единицы измерения для них — основные единицы СИ — метр, килограмм, секунда, ампер, кельвин, моль и кандела соответственно^[1][2].

Основные единицы СИ определяет Международное бюро мер и весов (МБМВ). Полное официальное описание основных единиц СИ, а также СИ в целом вместе с её толкованием, содержится в действующей редакции Брошюры СИ, опубликованной МБМВ и представленной на его сайте^[3].

В таблице представлены все основные единицы СИ вместе с их определениями, российскими и международными обозначениями, физическими величинами, к которым они относятся, а также с кратким обоснованием их происхождения.

Основные единицы СИ

Единица	Обозначение	Величина	Определение[4]	Историческое происхождение, обоснование
Секунда	с s	Время	Величина секунды устанавливается фиксацией численного значения частоты сверхтонкого расщепления основного состояния атома цезия-133 при температуре 0 К равным в точности 9 192 631 770, когда она выражена единицей СИ с−1, что эквивалентно Гц.	Солнечные сутки разбиваются на 24 часа, каждый час разбивается на 60 минут, каждая минута разбивается на 60 секунд. Секунда — это 1⁄(24 × 60 × 60) часть солнечных суток. Современное определение принято на XIII Генеральной конференции по мерам и весам (ГКМВ) в 1967 году.
Метр	м m	Длина	Величина метра устанавливается фиксацией численного значения скорости света в вакууме равным в точности 299 792 458, когда она выражена единицей СИ м·с−1.	1⁄10 000 000 расстояния от экватора Земли до северного полюса на меридиане Парижа. Современное определение установлено XVII ГКМВ в 1983 г.
Килограмм	кг kg	Масса	Величина килограмма устанавливается фиксацией численного значения постоянной Планка h равным в точности 6,626 070 15 × 10−34, когда она выражена в Дж⋅с.	Масса одного кубического дециметра (литра) чистой воды при температуре 4 °C и стандартном атмосферном давлении на уровне моря. В течение более чем двухсот лет эталоном килограмма служили материальные образцы — Архивный килограмм, затем Международный прототип килограмма.
Ампер	А A	Сила электрического тока	Величина ампера устанавливается фиксацией численного значения элементарного заряда e равным 1,602 176 634 × 10−19, когда он выражен в кулонах.	Предыдущее определение, восходящее к изначальному: ампер есть сила не изменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2⋅10−7ньютонов.
Кельвин	К K	Термодинамическая температура	Величина кельвина устанавливается фиксацией численного значения постоянной Больцмана k равным в точности 1,380 649 × 10−23, когда она выражена в Дж/К.	В 1967—2019 годах определялся как 1/273,16 части термодинамической температуры тройной точки воды [к 1]. Шкала Кельвина использует тот же шаг, что и шкала Цельсия, но 0 кельвинов — это температура абсолютного нуля, а не температура плавления льда. Согласно современному определению ноль шкалы Цельсия установлен таким образом, что температура тройной точки воды равна 0,01 °C. В итоге шкалы Цельсия и Кельвина сдвинуты на 273,15[6]: T [°C] = T [K] − 273,15.
Моль	моль mol	Количество вещества	Один моль содержит ровно 6,022 140 76 × 1023 элементов[к 2]. Это число — фиксированное значение постоянной Авогадро NA, выраженной в единицах моль−1, и называется числом Авогадро.	Атомный вес или молекулярный вес, деленный на постоянную молярной массы, 1 г/моль. В 1971—2019 годах определялся как количество вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде-12 массой 12 г.
Кандела	кд cd	Сила света	Величина канделы устанавливается фиксацией численного значения световой эффективности монохроматического излучения частотой 540·1012 Гц равным в точности 683, когда она выражена единицей СИ м−2·кг−1·с3·кд·ср или кд·ср·Вт−1, что эквивалентно лм·Вт−1.	Сила света (англ. Candlepower, устар. Британская единица силы света), испускаемая горящей свечой. Современное определение установлено XVI ГКМВ в 1979 г.

Наименования и обозначения основных единиц, так же как и всех других единиц СИ, пишутся маленькими буквами (например, метр и его обозначение м). У этого правила есть исключение: обозначения единиц, названных фамилиями учёных, пишутся с заглавной буквы (например, ампер обозначается символом А).

Остальные единицы СИ являются производными и образуются из основных с помощью уравнений, связывающих друг с другом физические величины используемой в СИ Международной системы величин.

Основная единица может использоваться и для производной величины той же размерности. Например, количество осадков определяется как частное от деления объёма на площадь и в СИ выражается в метрах. В этом случае метр используется в качестве когерентной производной единицы^{[2][к 3]}.

Определение СИ через фиксацию констант, вообще говоря, не требует различать основные и производные единицы. Тем не менее, это разделение сохраняется по историческим причинам и для удобства^[7].

С момента принятия Метрической конвенции в 1875 году определения основных единиц измерения несколько раз изменялись. С переопределения метра (1960 год) килограмм остался последней единицей, которая определяется не как свойство природы, а как физический артефакт. Тем не менее, поскольку моль, ампер и кандела были привязаны к килограмму, то и они оказывались привязанными к изготовленному людьми эталону килограмма. Длительное время метрология искала пути для определения килограмма на основе фундаментальных физических констант, так же, как метр определяется через скорость света.

В начале XXI века Международной бюро мер и весов готовило новые определения основных единиц СИ, не привязанные к материальным артефактам (эталонам). Эта работа была окончательно завершена к 2018 году, когда на XXVI Генеральной конференции по мерам и весам были приняты новые определения СИ и её основных единиц. Изменения вступили в силу в 2019 году.

Содержательно изменились определения четырёх основных единиц СИ: килограмма, ампера, кельвина и моля. Новые определения этих единиц основаны на фиксированных численных значениях следующих фундаментальных физических постоянных: постоянной Планка, элементарного электрического заряда, постоянной Больцмана и числа Авогадро, соответственно. Всем этим величинам приписаны точные значения, основанные на результатах наиболее точных измерений, рекомендованных Комитетом по данным для науки и техники (CODATA).

Формально новые определения отменили все предыдущие^[8], однако новые определения метра, секунды и канделы равносильны старым и изменены лишь для поддержания единства стиля. Определения метра и секунды уже были связаны с точными значениями таких постоянных, как скорость света и величина расщепления основного состояния атома цезия. Определение канделы хотя и не привязано к какой-либо фундаментальной постоянной, тем не менее, также может рассматриваться как связанное с точным значением инварианта природы.

Новый облик СИ[править | править код]

Согласно вступившему в силу в 2019 году определению, СИ — это система единиц, в которой^[9]:

• частота сверхтонкого расщепления основного состояния атома цезия-133 в точности равна 9 192 631 770 Гц;
• скорость света в вакууме c в точности равна 299 792 458 м/с;
• постоянная Планка ℎ в точности равна 6,626 070 15⋅10 ⁻³⁴ Дж·с;
• элементарный электрический заряд e в точности равен 1,602 176 634⋅10⁻¹⁹ Кл;
• постоянная Больцмана k в точности равна 1,380 649⋅10⁻²³ Дж/К;
• число Авогадро N_A в точности равно 6,022 140 76⋅10²³ моль⁻¹;
• световая эффективность K_cd монохроматического излучения частотой 540⋅10¹² Гц в точности равна 683 лм/Вт.

1. ↑ В 2005 г. Международный комитет мер и весов установил требования к изотопному составу воды при реализации температуры тройной точки воды: 0,00015576 моля ²H на один моль ¹Н, 0,0003799 моля ¹⁷О на один моль ¹⁶О и 0,0020052 моля ¹⁸О на один моль ¹⁶О^[5]
2. ↑ При применении моля структурные элементы должны быть специфицированы (оговорены) и могут быть атомами, молекулами, ионами, электронами и другими частицами или специфицированными группами частиц.
3. ↑ Когерентные производные единицы — производные единицы, которые образуются по уравнениям, не содержащим коэффициент пропорциональности. Благодаря отсутствию коэффициента при расчётах, если выражать значения всех величин в единицах СИ, в формулы не требуется вводить коэффициенты, зависящие от выбора единиц. БСЭ-3^{[уточните ссылку (уже 239 дней)]}.

1. ↑ Брошюра СИ, 2019, с. 18, 130.
2. ↑ ^{1 2} Международный словарь по метрологии: основные и общие понятия и соответствующие термины / Пер. с англ. и фр.. — 2-е изд., испр. — СПб.: НПО «Профессионал», 2010. — С. 20. — 82 с. — ISBN 978-5-91259-057-3.
3. ↑ Брошюра СИ, 2019.
4. ↑ Брошюра СИ, 2019, с. 18—23, 130—135.
5. ↑ Брошюра СИ, 2019, с. 76, 184.
6. ↑ ГОСТ 8.417—2002. Межгосударственный стандарт. Государственная система обеспечения единства измерений (ГСИ). Единицы величин  (неопр.) (недоступная ссылка). М.: Стандартинформ (2010). — ГОСТ введён в действие с 1 сентября 2003 года. Дата обращения 9 июля 2012. Архивировано 10 ноября 2012 года.
7. ↑ Брошюра СИ, 2019, с. 17, 129.
8. ↑ Брошюра СИ, 2019, с. 93, 198.
9. ↑ Брошюра СИ, 2019, с. 15—16, 127—128.

Размерность физической величины — Википедия

Разме́рность физической величины — выражение, показывающее связь этой величины с основными величинами данной системы физических величин; записывается в виде произведения степеней сомножителей, соответствующих основным величинам, в котором численные коэффициенты опущены^[1][2].

Говоря о размерности, следует различать понятия система физических величин и система единиц.

Система физических величин и система единиц[править | править код]

Под системой физических величин понимается совокупность физических величин вместе с совокупностью уравнений, связывающих эти величины между собой. В свою очередь, система единиц представляет собой набор основных и производных единиц вместе с их кратными и дольными единицами, определенными в соответствии с установленными правилами для данной системы физических величин^[1].

Все величины, входящие в систему физических величин, делят на основные и производные. Под основными понимают величины, условно выбранные в качестве независимых так, что никакая основная величина не может быть выражена через другие основные. Все остальные величины системы определяются через основные величины и называются производными^[1].

Каждой основной величине сопоставляется символ размерности в виде заглавной буквы латинского или греческого алфавита. В различных системах физических величин используются следующие обозначения размерностей^[3]:

Основная величина	Символ для размерности
Длина	L
Масса	M
Время	T
Электрический ток	I
Термодинамическая температура	Θ
Количество вещества	N
Сила света	J

Далее размерности производных величин обозначаются с использованием этих символов.

Символы размерностей используют также для обозначения систем величин^[4]. Так, система величин, основными величинами которой являются длина, масса и время, обозначается как LMT. На её основе были образованы такие системы единиц, как СГС, МКС и МТС. На основе системы LFT, в которой основными величинами являются длина, сила и время, создана система единиц МКГСС^[1].

В Международной системе величин (англ. International System of Quantities, ISQ), на которой базируется Международная система единиц (СИ), в качестве основных величин выбраны длина, масса, время, электрический ток, термодинамическая температура, сила света и количество вещества. Символы их размерностей приведены выше в таблице^[2]. Соответственно Международная система величин обозначается символами LMTIΘNJ.

Для указания размерностей производных величин используют символ dim (от англ. dimension — размер, размерность).

Например, для скорости при равномерном движении выполняется

v=st,{\displaystyle v={\frac {s}{t}},}

где s{\displaystyle s} — длина пути, пройденного телом за время t{\displaystyle t}. Для того, чтобы определить размерность скорости, в данную формулу следует вместо длины пути и времени подставить их размерности:

dim v=LT−1.{\displaystyle \mathrm {dim} ~v=\mathrm {LT^{-1}} .}

Аналогично для размерности ускорения получается

dim a=LT−2.{\displaystyle \mathrm {dim} ~a=\mathrm {LT^{-2}} .}

Из уравнения второго закона Ньютона с учётом размерности ускорения для размерности силы в Международной системе величин и в любой другой системе, где в качестве основных величин используются длина, масса и время, следует:

dim F=LMT−2.{\displaystyle \mathrm {dim} ~F=\mathrm {LMT^{-2}} .}

В общем случае размерность физической величины представляет собой произведение размерностей основных величин, возведённых в различные рациональные степени^[5]. Показатели степеней в этом выражении называют показателями размерности физической величины. Если в размерности величины хотя бы один из показателей размерности не равен нулю, то такую величину называют размерной, если все показатели размерности равны нулю — безразмерной^[1][6].

Как следует из сказанного выше, размерность физической величины зависит от используемой системы величин. Так, например, размерность силы в системе LMT, как указано выше, выражается равенством dim F=LMT^-2, а в системе LFT выполняется dim F=F . Кроме того, безразмерная величина в одной системе величин может стать размерной в другой. Например, в системе LMT электрическая ёмкость имеет размерность L и отношение ёмкости сферического тела к его радиусу — безразмерная величина, тогда как в Международной системе величин (ISQ) это отношение не является безразмерным. Однако многие используемые на практике безразмерные числа (например, критерии подобия, постоянная тонкой структуры в квантовой физике или числа Маха, Рейнольдса, Струхаля и др. в механике сплошных сред) характеризуют относительное влияние тех или иных физических факторов и являются отношением величин с одинаковыми размерностями, поэтому, несмотря на то, что входящие в них величины в разных системах могут иметь разную размерность, сами они всегда будут безразмерными.

В формулах, имеющих физический смысл, только величины, имеющие одинаковую размерность, могут складываться, вычитаться или сравниваться. Например, сложение массы какого-либо предмета с длиной другого предмета не имеет смысла. Также невозможно сказать, что больше: 1 килограмм или 3 секунды. Из этого правила, в частности, следует, что левые и правые части уравнений должны иметь одинаковую размерность.

Кроме того, аргументы экспоненциальных, логарифмических и тригонометрических функций должны быть безразмерными величинами.

Эти правила используются для проверки правильности физических формул. Если в полученном уравнении какое-то из них нарушается, то ясно, что в вычислениях была допущена ошибка.

Анализ размерности — метод, используемый физиками для построения обоснованных гипотез о взаимосвязи различных размерных параметров сложной физической системы. Иногда анализ размерности можно использовать для получения готовых формул (с точностью до безразмерной константы). Суть метода заключается в том, что из параметров, характеризующих систему, составляется выражение, имеющее нужную размерность.

При анализе размерностей формул размерность левой части уравнения должна быть равна размерности правой части уравнения. Отсутствие такого равенства говорит о неверности формулы. Однако наличие такого равенства не даёт стопроцентной гарантии верности формулы.

• Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — 336 c.

1.6. Области и виды измерений

Область измерений – совокупность измерений физических величин, свойственных какой-либо области науки или техники и выделяющихся своей спецификой.

Вид измерений – часть области измерений, имеющая свои особенности и отличающаяся однородностью измеряемых величин.

В метрологии различают следующие области и виды измерений:

1. Измерение геометрических величин: длин, углов, отклонений формы поверхностей.

2. Измерение механических величин: массы, силы, прочности и пластичности, крутящих моментов.

3. Измерение параметров потока, расхода, уровня, объема веществ.

4. Измерение давления: избыточного, атмосферного, абсолютного, вакуума.

5. Физико-химические измерения: вязкости, плотности, концентрации, влажности.

6. Теплофизические и температурные измерения.

7. Измерение времени и частоты.

8. Измерения электрических и магнитных величин на постоянном и переменном токе: силы тока, ЭДС, напряжения, мощности, сопротивления, емкости, индуктивности.

9. Радиоэлектронные измерения: интенсивности сигналов, параметров формы и спектра сигналов.

10. Измерения акустических величин в различных средах (воздушной, твердой, жидкой).

11. Оптические и оптико-физические измерения: оптической плотности, коэффициента пропускания.

12. Измерения ионизирующих излучений и ядерных констант: дозиметрических и спектральных характеристик ионизирующих излучений.

1.6.1. Классификация измерений

Измерения могут быть классифицированы по ряду признаков: по способу получения информации, по характеру изменений измеряемой величины в процессе измерений, по количеству измерительной информации, по отношению к основным единицам.

1) По способу получения информацииизмерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения – измерения, при которых искомое значение величины находят непосредственно из опытных данных (измерения массы на весах, температуры термометром, длины с помощью линейных мер).

Косвенные измерения– измерения, при которых искомое значение находят на основании известной зависимости между этой величиной и величинами, полученными прямыми измерениями (определение плотности однородного тела по его массе и объему, удельного электрического сопротивления проводника по его сопротивлению, длине и площади поперечного сечения).

Совокупные измерения– измерения нескольких однородных величин, при которых искомое значение величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин (измерения, при которых масса отдельных гирь набора находится по известной массе одной из них и по результатам прямых сравнений масс различных сочетаний гирь).

Совместные измерения– одновременные измерения двух или нескольких неодноименных величин для нахождения зависимости между ними (проводимые одновременно измерения приращения длины образца в зависимости от изменений его температуры и определение коэффициента линейного расширения по формуле k=l/(lt)).

В результате измерения должны быть определены 3 величины [9]:

1. Число, выражающее отношение измеряемой физической величины к общепринятой единице измерения ,

где: A – числовое значение измеряемой величины;

X – измеряемая величина;

x – единица измерения.

2. Погрешность результата измерения.

3. Доверительная вероятность допущенной погрешности (при обычных технических измерениях погрешность определяется с вероятностью 95%).

Пример, иллюстрирующий значение доверительной вероятности. Вероятность того, что спектакль в театре состоится, составляет 95%. Люди, купившие билеты на спектакль, обычно не задумываются о небольшой вероятности (῀5%), что спектакль может быть отменен или не состоится по какой-либо причине. Ввиду того, что в этой ситуации вероятность отмены спектакля, равная 5%, является низкой, то зрители не задумываются, покупать билет или нет.

С другой стороны, вероятность того, что (когда вы выходите на улицу), с вами ничего плохого не случится (на голову не упадет кирпич, вы не провалитесь в люк и т.п.), составляет 99,9999%. Вероятность обратного составляет 0,0001%, что ничтожно мало. Поэтому нормальный человек, выходя из дома, не задумывается о том, что с ним что-то может случиться. Но если предположить, что и в этом случае, как и в случае со спектаклем, вероятность благополучного похода на улицу составит 95%, то многие начнут сомневаться, а стоит ли выходить на улицу.

Можно сказать, что доверительная вероятность допущенной погрешности зависит от важности производимых измерений (чем более важны и ответственны измерения, тем более высокая доверительная вероятность допущенной погрешности должна быть задана).

2) По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.

Статистические измерения связаны с определением характеристик случайных процессов, звуковых сигналов, уровня шумов и т.д.

Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

3) По количеству измерительной информации различают однократные и многократные измерения.

Однократные измерения – это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин.

Практическое применение такого вида измерений всегда приводит к большим погрешностям, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин.

Обычно минимальное число измерений больше трех. Преимущество многократных измерений – в значительном снижении влияний случайных факторов на погрешность измерения.

Шаблон:Единица измерения — Википедия

Материал из Википедии — свободной энциклопедии

Перейти к навигации Перейти к поиску

Единица измерения
Тип	основная

Заготовка для копирования

{{Единица измерения
| название    = 
| обозначение = 
| изображение = 
| описание    = 
| величина    = 
| система     = 
| производная = 
| примечание  = 
}}

Пример

{{Единица измерения
| название    = Килограмм
| обозначение = кг, kg
| величина    = [[масса]]
| система     = [[СИ]]
| примечание  = См. [[приставки СИ]]
}}

Параметры

Шаблон-карточка для статей о единицах измерения.

Параметры шаблона

Шаблон использует блочное форматирование параметров.

Параметр		Описание	Тип	Статус
Название	название	Название единицы измерения Пример Килограмм	Неизвестно	необязательный
Обозначение	обозначение	Обозначение единицы измерения Пример кг, kg	Неизвестно	необязательный
Изображение	изображение	Изображение эталона	Имя файла	необязательный
Описание	описание	Описание к изображению	Неизвестно	необязательный
Величина	величина	Величина/параметр Пример [[масса]]	Неизвестно	необязательный
Система	система	Метрическая (СИ, СГС, МКС, МКГСС) или Традиционная (русская система мер английская, французская, китайская, японская), давно устаревшая (древнегреческая, древнеримская, древнеегипетская, древневавилонская, древнееврейская) Пример [[СИ]]	Неизвестно	необязательный
Производная	производная	Если поле не заполнено, величина считается основной, иначе — производной (определяющейся через иные величины данной системы единиц)	Логическое значение	необязательный
Примечание	примечание	Примечания Пример См. [[приставки СИ]]	Неизвестно	необязательный

См. также

Система физических величин — Википедия

Материал из Википедии — свободной энциклопедии

Система физических величин (далее СФВ) — совокупность взаимосвязанных физических величин, образованная по принципу, когда одни физические величины являются независимыми (основными физическими величинами), а другие являются их функциями (производными физическими величинами). СФВ представляет собой структурную схему связей или алгебраическую диаграмму операторов физических величин. Эти связи описываются математическими выражениями, называемыми определяющими уравнениями.^[1][2]

1. Международная система величин (фр. International Système de grandeurs, англ. International System of Quantities, ISQ). Использует размерные электрическую и магнитную постоянные и рационализированную запись формул (в уравнениях Максвелла отсутствует коэффициент 4π).

В качестве основных физических величин в ISQ используются:

Когерентной системой единиц для ISQ является Международная система единиц СИ.

2. Периодическая таблица законов в физике Бартини

Свою гипотезу для отношения между фундаментальными физическими константами Бартини попытался (возможно в шутливой форме^[3]) описать в своей статье.^[4][5]

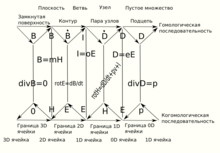Алгебраическая диаграмма уравнений Максвелла для электромагнитного поля (Крон, Рос)

3. Коммутативная диаграмма Крона или СФВ вводит понятие многогранных алгебраических диаграмм и 8 тензоров:

Которые соответствуют физическим величинам из законов Кирхгофа и уравнений Максвела. Он применяет СФВ для метода многогранников (обобщение линейного метода Крона для электрических машин для случая распространения волн через сами машины или пространственные фильтры). Одна стрелка на многогранной диаграмме соответствует тензору c октонионами (многогранной совокупности тензоров).^[2]

СФВ тесно связаны с задачами моделирования и описания физической реальности^[6] на языке Verilog-AMS.

На практике термин «СФВ» применяется редко. Обычно говорят о формулах в системах единиц (СИ, СГС и т. д.), даже если в исследовании единицы измерения и числовые значения величин не используются.

С понятием СФВ тесно связано понятие системы единиц физических величин (СЕФВ). Система единиц называется когерентной для данной системы величин, если единицы измерения производных величин (производные единицы) в системе единиц когерентны, то есть представляют собой произведения степеней единиц основных величин (основных единиц) с коэффициентами пропорциональности, равными единице.

• Г. Крон. Исследование сложных систем по частям — диакоптика. — Москва: Наука, 1972. — 544 с.

Длина — Википедия

Материал из Википедии — свободной энциклопедии

Измерения:
L — длина,
B — ширина,
H — высота, толщина, глубина

Длина — физическая величина, числовая характеристика протяжённости линий.

В большинстве систем измерений единица длины — одна из основных единиц измерения, через которые определяются другие (производные) единицы. В международной системе единиц (СИ) за единицу длины принят метр.

В узком смысле под длиной понимают линейный размер предмета в продольном направлении (обычно это направление наибольшего размера), то есть расстояние между его двумя наиболее удалёнными точками, измеренное горизонтально, в отличие от высоты, которая измеряется в вертикальном направлении, а также ширины или толщины, которые измеряются поперёк объекта (под прямым углом к длине).

В физике термин «длина» обычно используется как синоним «расстояния» и обозначается L{\displaystyle L} или l{\displaystyle l} от нем. länge (длина). Символ размерности длины — dim l = L. В ряду других пространственных величин длина — это величина единичной размерности, тогда как площадь — двухмерная, объём — трёхмерная.

Метрическая система[править | править код]

Метрическая система считается самой удобной из всех придуманных из-за своей простоты. В основе метрической системы лежит единица измерения метр. Все остальные единицы измерения являются кратными степеням десяти от метра (например, километр — это 10³ метров и т. п.), что позволяет облегчить подсчёты. До 1960 года у метра был специальный эталон, ныне хранящийся в Международном бюро мер и весов, расположенном в городе Севр (предместье Парижа, Франция). Сегодня, по определению, метр равен расстоянию, которое проходит свет в вакууме за 1/299 792 458 долю секунды.

Британская/американская система[править | править код]

Исходными английскими мерами длины были миля, ярд, фут и дюйм. Миля пришла в Англию из Древнего Рима, где она определялась как тысяча двойных шагов вооружённого римского воина.

Старорусская система[править | править код]

В Древней Руси мерой длины, веса и т. п. являлся человек. На это указывают названия мер длины: локоть (расстояние от конца вытянутого среднего пальца руки или сжатого кулака до локтевого сгиба), пядь (расстояние между вытянутым большим и указательным пальцами руки), сажень (расстояние от конца пальцев одной руки до конца пальцев другой) и другие^[1].

В частности, аршин был связан с длиной человеческого шага. Однако необходимость унификации систем измерений с британской в связи с развитием международной торговли потребовала введения во времена Петра I так называемого «казённого аршина». Это была мерная линейка с металлическими наконечниками с государственным клеймом. Казённый аршин равнялся 28 английским дюймам и делился на 16 вершков.^[2]

Относительные размеры
объектов, м

-20 —

–

-18 —

–

-16 —

–

-14 —

–

-12 —

–

-10 —

–

-8 —

–

-6 —

–

-4 —

–

-2 —

–

0 —

–

2 —

–

4 —

–

6 —

–

8 —

–

10 —

–

12 —

–

14 —

–

16 —

–

18 —

–

20 —

–

22 —

–

24 —

–

26 —

–

28 —

–

30 —

См. также[править | править код]

Древнегреческая система[править | править код]

Мусульманская система[править | править код]

Типографическая система[править | править код]

Морская система[править | править код]

Морская система измерения длины привязана к размеру планеты Земля. В качестве основной единицы измерения принята морская миля, равная длине одной минуты (1/60 градуса) дуги меридиана земного эллипсоида. Длина морской мили является величиной переменной, зависящей от широты. Её численное значение составляет от 1843 метров на экваторе до 1861,6 метров на полюсах.

Международная морская миля составляет 1852 м, в отличие от морской мили британской системы (1853,184 м). Для измерения меньших размеров применяют кабельтов — 1/10 морской мили, или 185,2 м (округлённо — 185 м)^[4].

Единицы, применяемые в астрономии[править | править код]

Измерительные инструменты и меры[править | править код]

Измерительные приборы[править | править код]

Другие средства[править | править код]

• Большие расстояния в навигации определяются при помощи средств радионавигационных систем или спутниковых систем
• Очень маленькие расстояния измеряются с помощью измерительных микроскопов

Расстояния и размеры объектов, доступных наблюдению[править | править код]

Основной источник: ^[5]

Наблюдаемые объекты	Размер, м
Расстояние от Земли до самого далекого видимого объекта во Вселенной	1,0×1026{\displaystyle 1{,}0\times 10^{26}}
Расстояние от Земли до галактики в созвездии Андромеды	2,0×1022{\displaystyle 2{,}0\times 10^{22}}
Диаметр нашей Галактики	1,0×1021{\displaystyle 1{,}0\times 10^{21}}
Расстояние от Земли до ближайшей звезды в созвездии Центавра	4,0×1016{\displaystyle 4{,}0\times 10^{16}}
Расстояние от Земли до Солнца	1,5×1011{\displaystyle 1{,}5\times 10^{11}}
Диаметр Солнца	1,4×109{\displaystyle 1{,}4\times 10^{9}}
Расстояние от Земли до Луны	3,8×108{\displaystyle 3{,}8\times 10^{8}}
Диаметр Земли	1,3×107{\displaystyle 1{,}3\times 10^{7}}
Самая глубокая впадина на поверхности Земли	1,1×104{\displaystyle 1{,}1\times 10^{4}}
Самая высокая гора на поверхности Земли	9,0×103{\displaystyle 9{,}0\times 10^{3}}
Длина синего кита — самого большого животного на Земле	35{\displaystyle 35}
Рост самого высокого человека	2,85{\displaystyle 2{,}85}
Размеры амебы	5,0×10−4{\displaystyle 5{,}0\times 10^{-4}}
Толщина человеческого волоса	1,0×10−4{\displaystyle 1{,}0\times 10^{-4}}
Диаметр красного кровяного шарика	1,0×10−5{\displaystyle 1{,}0\times 10^{-5}}
Диаметр вируса гриппа	8,0×10−8{\displaystyle 8{,}0\times 10^{-8}}
Длина молекулы гемоглобина	1,5×10−8{\displaystyle 1{,}5\times 10^{-8}}
Расстояние между атомами в твердом теле	1,0×10−10{\displaystyle 1{,}0\times 10^{-10}}
Диаметр ядра атома урана	1,0×10−14{\displaystyle 1{,}0\times 10^{-14}}
Диаметр протона	1,6×10−15{\displaystyle 1{,}6\times 10^{-15}}
Минимальные размеры областей внутри элементарных частиц, доступных экспериментальному изучению с помощью современных ускорителей	1,0×10−17{\displaystyle 1{,}0\times 10^{-17}}

Рациональная система единиц — Википедия

Величина	Формула определения	Значение (система СГС)	Значение (система СИ)
Длина	Комптоновская длина волны электронаℏmc{\displaystyle {\frac {\hbar }{mc}}}	3,862×10−11{\displaystyle 3,862\times 10^{-11}} см	3,862×10−13{\displaystyle 3,862\times 10^{-13}} м
Время	Величина ℏmc2{\displaystyle {\frac {\hbar }{mc^{2}}}}	1,288×10−21{\displaystyle 1,288\times 10^{-21}} с	1,288×10−21{\displaystyle 1,288\times 10^{-21}} с
Масса	Масса электрона m{\displaystyle m}	9,109×10−28{\displaystyle 9,109\times 10^{-28}} г	9,109×10−31{\displaystyle 9,109\times 10^{-31}} кг
Площадь	ℏ2m2c2{\displaystyle {\frac {\hbar ^{2}}{m^{2}c^{2}}}}	1,491×10−21{\displaystyle 1,491\times 10^{-21}} см2	1,491×10−25{\displaystyle 1,491\times 10^{-25}} м2
Энергия	Величина mc2{\displaystyle mc^{2}}	8,187×10−7{\displaystyle 8,187\times 10^{-7}} эрг	8,187×10−14{\displaystyle 8,187\times 10^{-14}} дж
Импульс	Величина mc{\displaystyle mc}	2,731×10−17{\displaystyle 2,731\times 10^{-17}} г*см/с	2,731×10−22{\displaystyle 2,731\times 10^{-22}} кг*м/с
Момент импульса	Постоянная Планка ℏ{\displaystyle \hbar }	1,055×10−27{\displaystyle 1,055\times 10^{-27}} эрг*c	1,055×10−34{\displaystyle 1,055\times 10^{-34}} Дж*c
Электрический заряд	ℏc{\displaystyle {\sqrt {\hbar c}}}	5,623×10−9{\displaystyle 5,623\times 10^{-9}} СГС	1,876×10−18{\displaystyle 1,876\times 10^{-18}} Кл
Скорость	Скорость света c{\displaystyle c}	2,998×1010{\displaystyle 2,998\times 10^{10}} см/с	2,998×108{\displaystyle 2,998\times 10^{8}} м/с
Ускорение	mc3ℏ{\displaystyle {\frac {mc^{3}}{\hbar }}}	2,327×1031{\displaystyle 2,327\times 10^{31}} см/с2	2,327×1029{\displaystyle 2,327\times 10^{29}} м/с2
Сила	Величина m2c3ℏ{\displaystyle {\frac {m^{2}c^{3}}{\hbar }}}	2,120×104{\displaystyle 2,120\times 10^{4}} дин	2,120×10−1{\displaystyle 2,120\times 10^{-1}} Н
Момент силы	mc2{\displaystyle mc^{2}}	8,187×10−7{\displaystyle 8,187\times 10^{-7}} дин*см	8,187×10−14{\displaystyle 8,187\times 10^{-14}} Н*м
Сила тока	mc52ℏ12{\displaystyle {\frac {mc^{\frac {5}{2}}}{\hbar ^{\frac {1}{2}}}}}	4,365×1012{\displaystyle 4,365\times 10^{12}} СГС	1,456×103{\displaystyle 1,456\times 10^{3}} А
Напряжённость электрического поля	m2c52ℏ32{\displaystyle {\frac {m^{2}c^{\frac {5}{2}}}{\hbar ^{\frac {3}{2}}}}}	3,771×1012{\displaystyle 3,771\times 10^{12}} СГС	1,131×1017{\displaystyle 1,131\times 10^{17}} В/м
Потенциал	mc32ℏ12{\displaystyle {\frac {mc^{\frac {3}{2}}}{\hbar ^{\frac {1}{2}}}}}	1,456×102{\displaystyle 1,456\times 10^{2}} СГС	4,366×104{\displaystyle 4,366\times 10^{4}} В