§ 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры FF и F’F^’ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры FF и F’F^’ подобны, то пишется F∼F’F\sim F^’Напомним, что в записи подобия треугольников ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. AA переходит в A1A_1, BB — в B1B_1, CC — в C1C_1. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\angle A=\angle A_1,\;\angle B=\angle B_1,\;\angle C=\angle C_1,\;\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}=\dfrac{AC}{A_1C_1}.
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если MN||ACMN||AC (рис. 5), то
mn=pq=m+pn+q\dfrac mn=\dfrac pq=\frac{m+p}{n+q}
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
mn=m+pn+q\dfrac mn=\dfrac{m+p}{n+q} или mn=pq\dfrac mn=\dfrac pq,
то MNMN параллельна ACAC (доказательство было дано в задании для 9 класса).
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках MM и NN. Найти длину отрезка `MN`, если основания трапеции равны aa и bb.
Пусть OO точка пересечения диагоналей трапеции (рис. 6). Обозначим:
AD=a, BC=b, MO=x, BO=p, OD=q.AD=a,\;BC=b,\;MO=x,\;BO=p,\;OD=q.
$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)
$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$. (2)
Из (1) и (2) следует x=app+q=qp/qp/q+1=aba+bx=a\dfrac p{p+q}=q\dfrac{p/q}{p/q+1}=\dfrac{ab}{a+b}, т. е. MO=aba+b.MO=\dfrac{ab}{a+b}.
Аналогично устанавливаем, что NO=aba+bNO=\dfrac{ab}{a+b}, поэтому MN=2aba+b\boxed{MN=\dfrac{2ab}{a+b}}.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.
 |
| Рис. 6 |
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
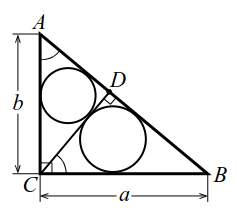
В прямоугольном треугольнике ABCABC из вершины CC прямого угла проведена высота CDCD (рис. 7). Радиусы окружностей, вписанных в треугольники ACDACD и BCDBCD равны соответственно r1r_1 и r2r_2 . Найти радиус окружности, вписанной в треугольник ABCABC.
Обозначим искомый радиус rr, положим AB=cAB=c, AC=bAC=b, BC=aBC=a. Из подобия прямоугольных треугольников ACDACD и ABCABC (у них равные углы при вершине AA) имеем rr1=cb\dfrac r{r_1}=\dfrac cb, откуда b=r1rcb=\dfrac{r_1}rc. Прямоугольные треугольники BCDBCD и BACBAC также подобны, поэтому rr2=ca\dfrac r{r_2}=\dfrac ca, — откуда a=r2rca=\dfrac{r_2}rc. Так как a2+b2=c2a^2+b^2=c^2 то, возводя в квадрат выражения для aa и bb и складывая их, получим r1r2c2+r2r2c2=c2\left(\frac{r_1}r\right)^2c^2+\left(\frac{r_2}r\right)^2c^2=c^2 или r12+r22r2=1\dfrac{r_1^2+r_2^2}{r^2}=1. Находим r=r12+r22r=\sqrt{r_1^2+r_2^2}.
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку MM, лежащую внутри треугольника ABCABC, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны S1S_1, S2S_2 и S3S_3. Найти площадь треугольника ABCABC.
Легко видеть, что треугольники EKMEKM, MQFMQF и PMNPMN подобны треугольнику ABCABC.
Пусть SS -площадь треугольника ABCABC, тогда
S1S=EMAC2; S2S=MFAC2; S3S=PNAC2.\dfrac{S_1}S=\left(\dfrac{EM}{AC}\right)^2;\;\dfrac{S_2}S=\left(\dfrac{MF}{AC}\right)^2;\;\dfrac{S_3}S=\left(\dfrac{PN}{AC}\right)^2.
Откуда находим
EM=S1SAC, MF=S2SAC, PN=S3SAC.EM=\sqrt{\dfrac{S_1}S}AC,\;MF=\sqrt{\dfrac{S_2}S}AC,\;PN=\sqrt{\dfrac{S_3}S}AC.
А так как EM=AP, MF=NCEM=AP,\;MF=NC, то EM+PN+MF=AP+PN+NC=ACEM+PN+MF=AP+PN+NC=AC.
Таким образом, AC=AC·S1S+S2S+S3SAC=AC\cdot\left(\sqrt{\dfrac{S_1}S}+\sqrt{\dfrac{S_2}S}+\sqrt{\dfrac{S_3}S}\right), откуда следует
S=S1+S2+S32S=\left(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}\right)^2.
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна 12SABC\dfrac12S_{ABC}. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть BDBD — медиана треугольника
ABC (BC=a, AC=b, AB=c, BD=ma)ABC\;(BC=a,\;AC=b,\;AB=c,\;BD=m_a), тогда
mc2=a2+b22-c24m_c^2=\dfrac{a^2+b^2}2-\dfrac{c^2}4. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы AA1AA_1 треугольника ABCABC пересекаются в точке OO, AA1=12AA_1=12 и CC1=6CC_1=6 и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника ABCABC.
1. По теореме 1 имеем AO=23AA1=8AO=\dfrac23AA_1=8, CO=23CC1=4CO=\dfrac23CC_1=4.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона ACAC не может равняться `12`, иначе AC=AO+OCAC=AO+OC — нарушено неравенство треугольника. Также не может равняться `12` сторона ABAB, так в этом случае AC1=6AC_1=6 и треугольник AOC1AOC_1 со сторонами `8`, `2`, `6` не существует. Значит, BC=12BC=12 и AC1=6AC_1=6.
2. Площадь треугольника находим по формуле Герона:
p=7, SA1OC=7·1·3·3=37p=7,\;S_{A_1OC}=\sqrt{7\cdot1\cdot3\cdot3}=3\sqrt7.
По теореме 2 площадь треугольника ABCABC в `6` раз больше, находим SABC=187S_{ABC}=18\sqrt7.
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если AA1AA_1 и BB1BB_1 — высоты треугольника ABCABC, то треугольник A1B1CA_1B_1C подобен треугольнику ABCABC с коэффициентом подобия k=A1B1AB=cosCk=\dfrac{A_1B_1}{AB}=\left|\cos C\right|. Можно это утверждение сформулировать так: Если соединить основания двух высот AA1AA_1 и BB1BB_1 треугольника ABCABC, то образуется треугольник, подобный данному: ∆A1B1C~∆ABC\triangle A_1B_1C\sim\triangle ABC.
Из прямоугольных треугольников ACA1ACA_1 следует A1C=AC·cosCA_1C=AC\cdot\cos C или A1C=AC·cos(180°-C)=ACcosCA_1C=AC\cdot \cos(180^\circ-C)=AC\left|\cos C\right| (рис. 11а, б), а из прямоугольных треугольников BCB1BCB_1 следует B1C=BC·cosCB_1C=BC\cdot \cos C или B1C=BC·cos(180°-C)=BCcosCB_1C=BC\cdot \cos(180^\circ-C)=BC\left|\cos C\right|. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты AA1AA_1 и BB1BB_1 (или их продолжения) пересекаются в точке HH, то справедливо равенство AH·HA1=BH·HB1AH\cdot HA_1=BH \cdot HB_1 (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
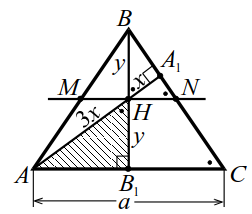
Высоты AA1AA_1 и BB1BB_1 пересекаются в точке HH (рис. 13), при этом AH=3HA1AH=3HA_1 и BH=HB1BH=HB_1. Найти косинус угла ACBACB и площадь треугольника ABCABC, если AC=aAC=a.
Обозначим HA1=x, HB1=yHA_1=x,\;HB_1=y,
1. Точка HH — середина высоты (рис. 13). Если отрезок MHMH проходит через точку HH и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.
2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, MH=HN=a4MH=HN=\dfrac a4 и AB1=B1C=a2AB_1=B_1C=\dfrac a2 Треугольник ABCABC равнобедренный, AB=BCAB=BC.
3. ∠B1BC=90°-∠C\angle B_1BC=90^\circ-\angle C, поэтому ∠BHA1=∠AHB1=∠C\underline{\angle BHA_1=\angle AHB_1=\angle C}, а по второй лемме о высотах AH·HA1=BH·HB1AH\cdot HA_1=BH\cdot HB_1 т. е. 3×2=y2, y=x33x^2=y^2,\;y=x\sqrt3.
Далее, cosC=cos(∠AHB1)=y3x\cos C=\cos (\angle AHB_1)=\dfrac y{3x}, находим cosC=13\cos C=\dfrac1{\sqrt3}.
4. △AHB1: AB12=(3x)2-y2\bigtriangleup AHB_1:\;AB_1^2=(3x)^2-y^2, a24=6×2\dfrac{a^2}4=6x^2, x=a26x=\dfrac a{2\sqrt6}, y=a22y=\dfrac a{2\sqrt2}, тогда
SABC=12AC·BB1=ay=a224S_{ABC}=\dfrac12AC\cdot BB_1=ay=\dfrac{a^2\sqrt2}4.
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если ADAD — биссектриса треугольника ABCABC (рис. 14), то
BDDC=ABAC xy=cb\dfrac{BD}{DC}=\dfrac{AB}{AC}\;\left(\dfrac xy=\dfrac cb\right)
Доказательство легко выполните сами, применяя теорему синусов к треугольникам ADBADB и ADCADC.
Теорема 6. Пусть ADAD — биссектриса треугольника ABCABC (рис. 14), тогда AD=AB·AC-DB·DCAD=\sqrt{AB\cdot AC-DB\cdot DC} (в обозначениях рисунка 14а)
AD=bc-xy\underline{AD=\sqrt{bc-xy}}.
 |
 |
||
| Рис. 14 | Рис. 14а |
Эту теорему докажем. Опишем около треугольника ABCABC окружность, точку пересечения прямой ADAD и окружности обозначим KK (рис. 14а).
Обозначим AD=z, DK=m.△ABD∼∆AKCAD=z,\;DK=m.\bigtriangleup ABD\sim\triangle AKC(∠ABD=∠AKC(\angle ABD=\angle AKC и ∠1=∠2)\angle1=\angle2). Из подобия следует ABAK=ADAC\dfrac{AB}{AK}=\dfrac{AD}{AC}, т. е. cz+m=zb\dfrac c{z+m}=\dfrac zb, откуда z2+zm=bcz^2+zm=bc, z2=bc-zmz^2=bc-zm.
По свойству пересекающихся хорд: AD·DK=BD·CDAD\cdot DK=BD\cdot CD, т. е. z·m=x·yz\cdot m=x\cdot y, тогда z2=bc-xyz^2=bc-xy, z=bc-xyz=\sqrt{bc-xy}.
В треугольнике ABCABC со сторонами AB=5AB=5, AC=3AC=3 биссектриса AD=158AD=\dfrac{15}8. Найти сторону BCBC и радиус вписанной окружности.
По теореме 5 (см. рис. 14) имеем xy=53\dfrac xy=\dfrac53 Обозначим x=5zx=5z, тогда y=3zy=3z. По теореме 6 выполнено равенство 1582=5·3-5z·3z.\left(\dfrac{15}8\right)^2=5\cdot3-5z\cdot3z. Легко находим z=78z=\dfrac78 значит BC=7.BC=7. Радиус вписанной окружности найдём по формуле S=prS=pr (`S` — площадь треугольника, `p` -полупериметр). Имеем p=152p=\dfrac{15}2, по формуле Герона S=152·12·102·92=1532,S=\sqrt{\dfrac{15}2\cdot\dfrac12\cdot\dfrac{10}2\cdot\dfrac92}=\dfrac{15\sqrt3}2, поэтому r=Sp=32.r=\dfrac Sp=\dfrac{\sqrt3}2. ▲
§ 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры FF и F`F` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры FF и F`F` подобны, то пишется F~F`F\sim F`Напомним, что в записи подобия треугольников ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. AA переходит в A1A_1, BB — в B1B_1, CC — в C1C_1. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\angle A=\angle A_1,\;\angle B=\angle B_1,\;\angle C=\angle C_1,\;\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если MN||ACMN||AC (рис. 5), то
mn=pq=m+pn+q\frac mn=\frac pq=\frac{m+p}{n+q}
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
mn=m+pn+q\frac mn=\frac{m+p}{n+q} или mn=pq\frac mn=\frac pq,
то MNMN параллельна ACAC (доказательство было дано в задании для 9 класса).
 |
| Рис. 6 |
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках MM и NN. Найти длину отрезка если основания трапеции равны aa и bb.
Δ Пусть OO точка пересечения диагоналей трапеции (рис. 6). Обозначим:
AD=a, BC=b, MO=x, BO=p, OD=q.AD=a,\;BC=b,\;MO=x,\;BO=p,\;OD=q.
1. BC~AD△BOC~△DOA (по двум углам)⇒ba=pq1.\;\left\{\begin{array}{l}BC\sim AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(по\;двум\;углам)\end{array}\right.\Rightarrow\frac ba=\frac pq
2. MO~AD△MBO~△ABD⇒xa=pp+q2.\;\left\{\begin{array}{l}MO\sim AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right.\Rightarrow\frac xa=\frac p{p+q}
Из (1) и (2) следует x=app+q=qp/qp/q+1=aba+b⇒MO=aba+b.x=a\frac p{p+q}=q\frac{p/q}{p/q+1}=\frac{ab}{a+b}\Rightarrow MO=\frac{ab}{a+b}.
Аналогично устанавливаем, что NO=aba+b⇒MN=2aba+bNO=\frac{ab}{a+b}\Rightarrow MN=\frac{2ab}{a+b}.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить. ▲
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
В прямоугольном треугольнике ABCABC из вершины CC прямого угла проведена высота CDCD (рис. 7). Радиусы окружностей, вписанных в треугольники ACDACD и BCDBCD равны соответственно r1r_1 и r2r_2 . Найти радиус окружности, вписанной в треугольник ABCABC.
Δ Обозначим искомый радиус rr, положим AB=cAB=c, AC=bAC=b, BC=aBC=a. Из подобия прямоугольных треугольников ACDACD и ABCABC (у них равные углы при вершине AA) имеем rr1=cb\frac r{r_1}=\frac cb, откуда b=r1rcb=\frac{r_1}rc. Прямоугольные треугольники BCDBCD и BACBAC также подобны, поэтому rr2=ca\frac r{r_2}=\frac ca, — откуда a=r2rca=\frac{r_2}rc. Так как a2+b2=c2a^2+b^2=c^2 то, возводя в квадрат выражения для aa и bb и складывая их, получим r1r2c2+r2r2c2=c2 ⇒r12+r22r2=1\left(\frac{r_1}r\right)^2c^2+\left(\frac{r_2}r\right)^2c^2=c^2\;\Rightarrow\frac{r_1^2+r_2^2}{r^2}=1. Находим r=r12+r22r=\sqrt{r_1^2+r_2^2} ▲
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку MM, лежащую внутри треугольника ABCABC, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны S1S_1, S2S_2 и S3S_3. Найти площадь треугольника ABCABC.
Легко видеть, что треугольники EKMEKM, MQFMQF и PMNPMN подобны треугольнику ABCABC.
Пусть SS -площадь треугольника ABCABC, тогда
S1S=EMAC2; S2S=MFAC2; S3S=PNAC2.\frac{S_1}S=\left(\frac{EM}{AC}\right)^2;\;\frac{S_2}S=\left(\frac{MF}{AC}\right)^2;\;\frac{S_3}S=\left(\frac{PN}{AC}\right)^2.
Откуда находим
EM=S1SAC, MF=S2SAC, PN=S3SAC.EM=\sqrt{\frac{S_1}S}AC,\;MF=\sqrt{\frac{S_2}S}AC,\;PN=\sqrt{\frac{S_3}S}AC.
А так как EM=AP, MF=NC⇒EM+PN+MF=AP+PN+NC=ACEM=AP,\;MF=NC\Rightarrow EM+PN+MF=AP+PN+NC=AC.
Таким образом, AC=AC*S1S+S2S+S3S⇒S=S1+S2+S32AC=AC\ast\left(\sqrt{\frac{S_1}S}+\sqrt{\frac{S_2}S}+\sqrt{\frac{S_3}S}\right)\Rightarrow S=\left(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}\right)^2. ▲
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении 2 : 1, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на 6 треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из 6 треугольников с вершиной и основанием, равным половине стороны, равна 12SABC\frac12S_{ABC}. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть BDBD — медиана треугольника
ABC (BC=a, AC=b, AB=c, BD=ma)ABC\;(BC=a,\;AC=b,\;AB=c,\;BD=m_a), тогда
mc2=a2+b22-c24m_c^2=\frac{a^2+b^2}2-\frac{c^2}4. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы AA1AA_1 треугольника ABCABC пересекаются в точке OO, AA1=12AA_1=12 и CC1=6CC_1=6 и одна из сторон треугольника равна 12. (рис. 10). Найти площадь треугольника ABCABC.
Δ 1. По теореме 1 имеем AO=23AA1=8, CO=23CC1=4AO=\frac23AA_1=8,\;CO=\frac23CC_1=4.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна 12, сторона ACAC не может равняться 12, иначе AC=AO+OCAC=AO+OC — нарушено неравенство треугольника. Также не может равняться 12 сторона ABAB, так в этом случае AC1=6AC_1=6 и треугольник AOC1AOC_1 со сторонами 8, 2, 6 не существует. Значит, BC=12BC=12 и AC1=6AC_1=6.
2. Площадь треугольника находим по формуле Герона:
p=7, SA1OC=7*1*3*3=37p=7,\;S_{A_1OC}=\sqrt{7\ast1\ast3\ast3}=3\sqrt7.
По теореме 2 площадь треугольника ABCABC в 6 раз больше, находим SABC=187S_{ABC}=18\sqrt7.▲
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если AA1AA_1 и BB1BB_1 — высоты треугольника ABCABC, то треугольник A1B1CA_1B_1C подобен треугольнику ABCABC с коэффициентом подобия k=A1B1AB=cosCk=\frac{A_1B_1}{AB}=\left|\cos C\right|. Можно это утверждение сформулировать так: Если соединить основания двух высот AA1AA_1 и BB1BB_1 треугольника ABCABC, то образуется треугольник, подобный данному: ∆A1B1C~∆ABC\triangle A_1B_1C\sim\triangle ABC.
Из прямоугольных треугольников ACA1ACA_1 следует A1C=AC*cosCA_1C=AC*cosC или A1C=AC*cos(180°-C)=ACcosCA_1C=AC\ast cos(180^\circ-C)=AC\left|\cos C\right| (рис. 11а, б), а из прямоугольных треугольников BCB1BCB_1 следует B1C=BC*cosCB_1C=BC*cosC или B1C=BC*cos(180°-C)=BCcosCB_1C=BC\ast cos(180^\circ-C)=BC\left|\cos C\right|. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты AA1AA_1 и BB1BB_1 (или их продолжения) пересекаются в точке HH, то справедливо равенство AH*HA1=BH*HB1AH*HA_1=BH*HB_1 (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
Высоты AA1AA_1 и BB1BB_1 пересекаются в точке HH (рис. 13), при этом AH=3HA1AH=3HA_1 и BH=HB1BH=HB_1. Найти косинус угла ACBACB и площадь треугольника ABCABC, если AC=aAC=a.
Δ Обозначим HA1=x, HB1=yHA_1=x,\;HB_1=y,
1. Точка HH — середина высоты (рис. 13). Если отрезок MHMH проходит через точку HH и параллелен основаниям, то MN — средняя линия; MN=a/2MN=a/2.
2. ∆HA1N~∆AA1C⇒HNAC=x4x, HN=14a. \triangle HA_1N\sim\triangle AA_1C\Rightarrow\frac{HN}{AC}=\frac x{4x},\;HN=\frac14a.\;Значит, MH=HN=a4MH=HN=\frac a4 и AB1=B1C=a2AB_1=B_1C=\frac a2 Треугольник ABCABC равнобедренный, AB=BCAB=BC.
3. ∠B1BC=90°-∠C⇒∠BHA1=∠AHB1=∠C\angle B_1BC=90^\circ-\angle C\Rightarrow\angle BHA_1=\angle AHB_1=\angle C, а по второй лемме о высотах AH*HA1=BH*HB1AH*HA_1=BH*HB_1 т. е. 3×2=y2, y=x33x^2=y^2,\;y=x\sqrt3.
Далее, cosC=cos(∠AHB1)=y3xcosC=cos(\angle AHB1)=\frac y{3x}, находим cosC=13\cos C=\frac1{\sqrt3}.
4. △AHB1: AB12=(3x)2-y2, a24=6×2, x=a26, y=a22⇒⇒SABC=12AC*BB1=ay=a224\begin{array}{l}\bigtriangleup AHB_1:\;AB_1^2=(3x)^2-y^2,\;\frac{a^2}4=6x^2,\;x=\frac a{2\sqrt6},\;y=\frac a{2\sqrt2}\Rightarrow\\\Rightarrow S_{ABC}=\frac12AC\ast BB_1=ay=\frac{a^2\sqrt2}4\end{array}. ▲
 |
| Рис. 14 |
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если ADAD — биссектриса треугольника ABCABC (рис. 14), то
BDDC=ABAC xy=cb\frac{BD}{DC}=\frac{AB}{AC}\;\left(\frac xy=\frac cb\right)
Доказательство легко выполните сами, применяя теорему синусов к треугольникам ADBADB и ADCADC.
Теорема 6. Пусть ADAD — биссектриса треугольника ABCABC (рис. 14), тогда AD=AB*AC-DB*DCAD=\sqrt{AB\ast AC-DB\ast DC} (в обозначениях рисунка 14а) AD=bc-xyAD=\sqrt{bc-xy}.
 |
| Рис. 14а |
□ Эту теорему докажем. Опишем около треугольника ABCABC окружность, точку пересечения прямой ADAD и окружности обозначим KK (рис. 14а).
Обозначим AD=z, DK=m.△ABD~∆AKC (∠ABD=∠AKC и ∠1=∠2).Из подобия: ABAK=ADAC⇒cz+m=zb⇒⇒z2+zm=bc, z2=bc-zm.\begin{array}{l}AD=z,\;DK=m.\\\bigtriangleup ABD\sim\triangle AKC\;(\angle ABD=\angle AKC\;и\;\\\angle1=\angle2).\\Из\;подобия:\;\\\frac{AB}{AK}=\frac{AD}{AC}\Rightarrow\frac c{z+m}=\frac zb\Rightarrow\\\Rightarrow z^2+zm=bc,\;z^2=bc-zm.\end{array}По свойству пересекающихся хорд:
AD*DK=BD*CD, т.е. z*m=x*y⇒z2=bc-xy, z=bc-xyAD\ast DK=BD\ast CD,\;т.е.\;z\ast m=x\ast y\Rightarrow z^2=bc-xy,\;z=\sqrt{bc-xy}. ■
В треугольнике ABCABC со сторонами AB=5AB=5, AC=3AC=3 биссектриса AD=158AD=\frac{15}8. Найти сторону BCBC и радиус вписанной окружности.
Δ По теореме 5 (см. рис. 14) имеем xy=53\frac xy=\frac53 Обозначим x=5zx=5z, тогда y=3zy=3z. По теореме 6 выполнено равенство 1582=5*3-5z*3z.\left(\frac{15}8\right)^2=5\ast3-5z\ast3z. Легко находим z=78z=\frac78 значит BC=7.BC=7. Радиус вписанной окружности найдём по формуле S=prS=pr (S — площадь треугольника, p -полупериметр). Имеем p=152p=\frac{15}2, по формуле Герона S=152*12*102*92=1532,S=\sqrt{\frac{15}2\ast\frac12\ast\frac{10}2\ast\frac92}=\frac{15\sqrt3}2, поэтому r=Sp=32.r=\frac Sp=\frac{\sqrt3}2. ▲
Планиметрия — § 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры $$ F$$ и $$ {F}^{\text{‘}}$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ {F}^{\text{‘}}$$ подобны, то пишется $$ F\sim {F}^{\text{‘}}$$Напомним, что в записи подобия треугольников $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$ предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. $$ A$$ переходит в $$ {A}_{1}$$, $$ B$$ — в $$ {B}_{1}$$, $$ C$$ — в $$ {C}_{1}$$. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$
$$ \angle A=\angle {A}_{1}, \angle B=\angle {B}_{1}, \angle C=\angle {C}_{1}, {\displaystyle \frac{AB}{{A}_{1}{B}_{1}}}={\displaystyle \frac{BC}{{B}_{1}{C}_{1}}}={\displaystyle \frac{AC}{{A}_{1}{C}_{1}}}$$.
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MN\left|\right|AC$$ (рис. 5), то
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}=\frac{m+p}{n+q}$$
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{m+p}{n+q}}$$ или $$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}$$,
то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.
Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:
$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$
$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)
$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$. (2)
Из (1) и (2) следует $$ x=a{\displaystyle \frac{p}{p+q}}=q{\displaystyle \frac{p/q}{p/q+1}}={\displaystyle \frac{ab}{a+b}}$$, т. е. $$ MO={\displaystyle \frac{ab}{a+b}}.$$
Аналогично устанавливаем, что $$ NO={\displaystyle \frac{ab}{a+b}}$$, поэтому $$ \overline{)MN={\displaystyle \frac{2ab}{a+b}}}$$.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.
 |
| Рис. 6 |
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ {r}_{1}$$ и $$ {r}_{2}$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.
Обозначим искомый радиус $$ r$$, положим $$ AB=c$$, $$ AC=b$$, $$ BC=a$$. Из подобия прямоугольных треугольников $$ ACD$$ и $$ ABC$$ (у них равные углы при вершине $$ A$$) имеем $$ {\displaystyle \frac{r}{{r}_{1}}}={\displaystyle \frac{c}{b}}$$, откуда $$ b={\displaystyle \frac{{r}_{1}}{r}}c$$. Прямоугольные треугольники $$ BCD$$ и $$ BAC$$ также подобны, поэтому $$ {\displaystyle \frac{r}{{r}_{2}}}={\displaystyle \frac{c}{a}}$$, — откуда $$ a={\displaystyle \frac{{r}_{2}}{r}}c$$. Так как $$ {a}^{2}+{b}^{2}={c}^{2}$$ то, возводя в квадрат выражения для $$ a$$ и $$ b$$ и складывая их, получим $$ {\left(\frac{{r}_{1}}{r}\right)}^{2}{c}^{2}+{\left(\frac{{r}_{2}}{r}\right)}^{2}{c}^{2}={c}^{2}$$ или $$ {\displaystyle \frac{{r}_{1}^{2}+{r}_{2}^{2}}{{r}^{2}}}=1$$. Находим $$ r=\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}$$.
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ {S}_{1}$$, $$ {S}_{2}$$ и $$ {S}_{3}$$. Найти площадь треугольника $$ ABC$$.
Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.
Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда
$$ {\displaystyle \frac{{S}_{1}}{S}}={\left({\displaystyle \frac{EM}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{2}}{S}}={\left({\displaystyle \frac{MF}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{3}}{S}}={\left({\displaystyle \frac{PN}{AC}}\right)}^{2}.$$
Откуда находим
$$ EM=\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}AC, MF=\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}AC, PN=\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}AC.$$
А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.
Таким образом, $$ AC=AC·\left(\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}\right)$$, откуда следует
$$ S={\left(\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+\sqrt{{S}_{3}}\right)}^{2}$$.
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ {\displaystyle \frac{1}{2}}{S}_{ABC}$$. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть $$ BD$$ — медиана треугольника
$$ ABC (BC=a, AC=b, AB=c, BD={m}_{a})$$, тогда
$$ {m}_{c}^{2}={\displaystyle \frac{{a}^{2}+{b}^{2}}{2}}-{\displaystyle \frac{{c}^{2}}{4}}$$. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы $$ A{A}_{1}$$ треугольника $$ ABC$$ пересекаются в точке $$ O$$, $$ A{A}_{1}=12$$ и $$ C{C}_{1}=6$$ и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника $$ ABC$$.
1. По теореме 1 имеем $$ AO={\displaystyle \frac{2}{3}}A{A}_{1}=8$$, $$ CO={\displaystyle \frac{2}{3}}C{C}_{1}=4$$.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A{C}_{1}=6$$ и треугольник $$ AO{C}_{1}$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A{C}_{1}=6$$.
2. Площадь треугольника находим по формуле Герона:
$$ p=7, {S}_{{A}_{1}OC}=\sqrt{7·1·3·3}=3\sqrt{7}$$.
По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ {S}_{ABC}=18\sqrt{7}$$.
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если $$ A{A}_{1}$$ и $$ B{B}_{1}$$ — высоты треугольника $$ ABC$$, то треугольник $$ {A}_{1}{B}_{1}C$$ подобен треугольнику $$ ABC$$ с коэффициентом подобия $$ k={\displaystyle \frac{{A}_{1}{B}_{1}}{AB}}=\left|\mathrm{cos}C\right|$$. Можно это утверждение сформулировать так: Если соединить основания двух высот $$ A{A}_{1}$$ и $$ B{B}_{1}$$ треугольника $$ ABC$$, то образуется треугольник, подобный данному: $$ ∆{A}_{1}{B}_{1}C~∆ABC$$.
Из прямоугольных треугольников $$ AC{A}_{1}$$ следует $$ {A}_{1}C=AC·\mathrm{cos}C$$ или $$ {A}_{1}C=AC·\mathrm{cos}(180°-C)=AC\left|\mathrm{cos}C\right|$$ (рис. 11а, б), а из прямоугольных треугольников $$ BC{B}_{1}$$ следует $$ {B}_{1}C=BC·\mathrm{cos}C$$ или $$ {B}_{1}C=BC·\mathrm{cos}(180°-C)=BC\left|\mathrm{cos}C\right|$$. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ (или их продолжения) пересекаются в точке $$ H$$, то справедливо равенство $$ AH·H{A}_{1}=BH·H{B}_{1}$$ (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
Высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ пересекаются в точке $$ H$$ (рис. 13), при этом $$ AH=3H{A}_{1}$$ и $$ BH=H{B}_{1}$$. Найти косинус угла $$ ACB$$ и площадь треугольника $$ ABC$$, если $$ AC=a$$.
Обозначим $$ H{A}_{1}=x, H{B}_{1}=y$$,
1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.
2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, $$ MH=HN={\displaystyle \frac{a}{4}}$$ и $$ A{B}_{1}={B}_{1}C={\displaystyle \frac{a}{2}}$$ Треугольник $$ ABC$$ равнобедренный, $$ AB=BC$$.
3. $$ \angle {B}_{1}BC=90°-\angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H{A}_{1}=BH·H{B}_{1}$$ т. е. $$ 3{x}^{2}={y}^{2}, y=x\sqrt{3}$$.
Далее, $$ \mathrm{cos}C=\mathrm{cos}(\angle AH{B}_{1})={\displaystyle \frac{y}{3x}}$$, находим $$ \mathrm{cos}C={\displaystyle \frac{1}{\sqrt{3}}}$$.
4. $$ △AH{B}_{1}: A{B}_{1}^{2}=(3x{)}^{2}-{y}^{2}$$, $$ {\displaystyle \frac{{a}^{2}}{4}}=6{x}^{2}$$, $$ x={\displaystyle \frac{a}{2\sqrt{6}}}$$, $$ y={\displaystyle \frac{a}{2\sqrt{2}}}$$, тогда
$$ {S}_{ABC}={\displaystyle \frac{1}{2}}AC·B{B}_{1}=ay={\displaystyle \frac{{a}^{2}\sqrt{2}}{4}}$$.
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), то
$$ {\displaystyle \frac{BD}{DC}}={\displaystyle \frac{AB}{AC}} \left({\displaystyle \frac{x}{y}}={\displaystyle \frac{c}{b}}\right)$$
Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.
Теорема 6. Пусть $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=\sqrt{AB·AC-DB·DC}$$ (в обозначениях рисунка 14а)
`ul(AD=sqrt(bc-xy))`.
 |
 |
||
| Рис. 14 | Рис. 14а |
Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).
Обозначим $$ AD=z, DK=m.△ABD\sim ∆AKC$$ $$ (\angle ABD=\angle AKC$$ и $$ \angle 1=\angle 2)$$. Из подобия следует $$ {\displaystyle \frac{AB}{AK}}={\displaystyle \frac{AD}{AC}}$$, т. е. $$ {\displaystyle \frac{c}{z+m}}={\displaystyle \frac{z}{b}}$$, откуда $$ {z}^{2}+zm=bc$$, $$ {z}^{2}=bc-zm$$.
По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ {z}^{2}=bc-xy$$, $$ z=\sqrt{bc-xy}$$.
В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD={\displaystyle \frac{15}{8}}$$. Найти сторону $$ BC$$ и радиус вписанной окружности.
По теореме 5 (см. рис. 14) имеем $$ {\displaystyle \frac{x}{y}}={\displaystyle \frac{5}{3}}$$ Обозначим $$ x=5z$$, тогда $$ y=3z$$. По теореме 6 выполнено равенство $$ {\left({\displaystyle \frac{15}{8}}\right)}^{2}=5·3-5z·3z.$$ Легко находим $$ z={\displaystyle \frac{7}{8}}$$ значит `ul(BC=7)`. Радиус вписанной окружности найдём по формуле $$ S=pr$$ (`S` — площадь треугольника, `p` -полупериметр). Имеем $$ p={\displaystyle \frac{15}{2}}$$, по формуле Герона $$ S=\sqrt{{\displaystyle \frac{15}{2}}·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{10}{2}}·{\displaystyle \frac{9}{2}}}={\displaystyle \frac{15\sqrt{3}}{2}},$$ поэтому $$ r={\displaystyle \frac{S}{p}}={\displaystyle \frac{\sqrt{3}}{2}}.$$
признаки равенства и подобия треугольников, их основные элементы и замечательные точки. Видеоурок. Геометрия 9 Класс
Тема: Итоговое повторение курса геометрии за 7-9 классы
Урок: Треугольники: признаки равенства и подобия треугольников, их основные элементы и замечательные точки
Признаки равенства треугольников.
1 признак: если 2 стороны одного треугольника и угол между ними равны соответственно двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
2 признак: если сторона и 2 прилежащих к ней угла одного треугольника равны соответственно стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
3 признак: если 3 стороны одного треугольника соответственно равны 3м сторонам другого треугольника, то такие треугольники равны.
Свойство: Из равенства треугольников следует равенство всех соответствующих элементов: медианы, радиусы вписанных и описанных окружностей и т.д.
Рассмотрим прямоугольный треугольник.
Для прямоугольных треугольников признак равенства звучит несколько иначе:
Прямоугольные треугольники равны по гипотенузе и катету.
Заметим, что угол 90 градусов одновременно является наибольшим углом в любом прямоугольном треугольнике.
На самом деле, признак равенства прямоугольных треугольников можно сформулировать для произвольного треугольника.
4 признак:
Если 2 стороны и больший угол одного треугольника равны соответственно 2м сторонам и большему углу другого треугольника, то такие треугольники равны.
Доказательство:
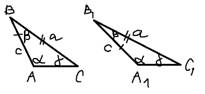
Рассмотрим 2треугольника,  .
.
Дано: 
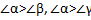 .
.
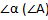 -больший угол.
-больший угол.
Доказать: , 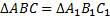 .
.
Доказательство:
Доказательство осуществим точно так же, как доказывается равенство прямоугольных треугольников по катету и гипотенузе, потому как мы находимся в тех же условиях: равны 2 стороны ибольшие углы.
Т.к. 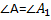 , то
, то  так, что вершина A совместится с вершиной
так, что вершина A совместится с вершиной  .
.
Т.к. 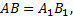 то вершина В совместится в вершиной
то вершина В совместится в вершиной 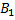 .
.
Но тогда вершины С и 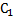 .тоже совместятся. Но как это строго доказать? Докажем от противного:
.тоже совместятся. Но как это строго доказать? Докажем от противного:
Предположим, что точка С совместится с некоторой другой точкой  луча
луча 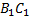 .
.
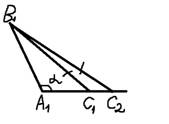
 – равнобедренный, т.е.
– равнобедренный, т.е. 
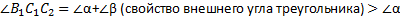
 <
<
Получили противоречие, т.е. вершины С и  тоже совместятся.
тоже совместятся.
Признаки подобия треугольников
1 признак. Если два угла одного треугольника соответственно равны двум углам другого треугольника, то треугольники подобны.
2 признак. Если угол одного треугольника равен углу другого, а стороны, образующие тот угол в одном треугольнике, пропорциональны соответствующим сторонам другого, то такие треугольники подобны.
3 признак. Если три стороны одного треугольника пропорциональны трём сходственным сторонам другого, то треугольники подобны.
Свойства подобных треугольников:
— Отношение периметров и длин биссектрис, медиан, высот и серединных перпендикуляров равно коэффициенту подобия.
— Отношение площадей подобных треугольников равно квадрату коэффициента подобия
Теоремы синусов и косинусов

Теорема косинусов
Для плоского треугольника со сторонами 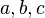 и углом
и углом  , противолежащим стороне
, противолежащим стороне 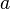
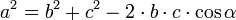 .
.
Заметим, что если треугольник прямоугольный, то 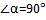 , тогда cos
, тогда cos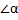 =0 и теорема косинусов трансформируется в основное тригонометрическое тождество.
=0 и теорема косинусов трансформируется в основное тригонометрическое тождество.
Теорема синусов
Для произвольного треугольника
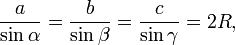
где 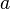
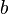 ,
,  — стороны треугольника,
— стороны треугольника,  — соответственно противолежащие им углы, а
— соответственно противолежащие им углы, а 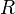 — радиус окружности,описаннойвокруг треугольника.
— радиус окружности,описаннойвокруг треугольника.Основные элементы треугольников
1. Высоты(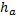 ,
,
В случае, если треугольник тупоугольный, ортоцентр находится вне треугольника.
2. Биссектрисы( ,
, ) треугольника пересекаются в одной точке. Точка пересечения биссектрис – это центр вписанной окружности. Эта точка равноудалена от всех сторон треугольника.
) треугольника пересекаются в одной точке. Точка пересечения биссектрис – это центр вписанной окружности. Эта точка равноудалена от всех сторон треугольника.
3. Медианы(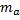 ,
,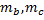 ) треугольника пересекаются в одной точке. Точка пересечения медиан – центр тяжести треугольника. Точкой пересечения медианы делятся в отношении 2:1, считая от вершины.
) треугольника пересекаются в одной точке. Точка пересечения медиан – центр тяжести треугольника. Точкой пересечения медианы делятся в отношении 2:1, считая от вершины.
4. Серединные перпендикуляры треугольника пересекаются в одной точке. Точка пересечения серединных перпендикуляров – это центр описанной окружности.
Список литературы
1. Л.Ф. Атанасян, Геометрия 7-9 (Источник).
2. Б.Г. Зив, В.М.Мейлер, Геометрия. Дидактические материалы, 7 класс (Источник), 8 класс (Источник), 9 класс (Источник).
Домашнее задание
Л.Ф. Атанасян, Геометрия 7-9: №96 (стр. 30), №139 (стр.41), 560 (стр.140)
Планиметрия — § 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры $$ F$$ и $$ {F}^{\text{‘}}$$ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры $$ F$$ и $$ {F}^{\text{‘}}$$ подобны, то пишется $$ F\sim {F}^{\text{‘}}$$Напомним, что в записи подобия треугольников $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$ предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. $$ A$$ переходит в $$ {A}_{1}$$, $$ B$$ — в $$ {B}_{1}$$, $$ C$$ — в $$ {C}_{1}$$. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если $$ ∆ABC~∆{A}_{1}{B}_{1}{C}_{1}$$
$$ \angle A=\angle {A}_{1}, \angle B=\angle {B}_{1}, \angle C=\angle {C}_{1}, {\displaystyle \frac{AB}{{A}_{1}{B}_{1}}}={\displaystyle \frac{BC}{{B}_{1}{C}_{1}}}={\displaystyle \frac{AC}{{A}_{1}{C}_{1}}}$$.
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если $$ MN\left|\right|AC$$ (рис. 5), то
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}=\frac{m+p}{n+q}$$
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
$$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{m+p}{n+q}}$$ или $$ {\displaystyle \frac{m}{n}}={\displaystyle \frac{p}{q}}$$,
то $$ MN$$ параллельна $$ AC$$ (доказательство было дано в задании для 9 класса).
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках $$ M$$ и $$ N$$. Найти длину отрезка `MN`, если основания трапеции равны $$ a$$ и $$ b$$.
Пусть $$ O$$ точка пересечения диагоналей трапеции (рис. 6). Обозначим:
$$ AD=a, BC=b, MO=x, BO=p, OD=q.$$
$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)
$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$. (2)
Из (1) и (2) следует $$ x=a{\displaystyle \frac{p}{p+q}}=q{\displaystyle \frac{p/q}{p/q+1}}={\displaystyle \frac{ab}{a+b}}$$, т. е. $$ MO={\displaystyle \frac{ab}{a+b}}.$$
Аналогично устанавливаем, что $$ NO={\displaystyle \frac{ab}{a+b}}$$, поэтому $$ \overline{)MN={\displaystyle \frac{2ab}{a+b}}}$$.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.
 |
| Рис. 6 |
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
В прямоугольном треугольнике $$ ABC$$ из вершины $$ C$$ прямого угла проведена высота $$ CD$$ (рис. 7). Радиусы окружностей, вписанных в треугольники $$ ACD$$ и $$ BCD$$ равны соответственно $$ {r}_{1}$$ и $$ {r}_{2}$$. Найти радиус окружности, вписанной в треугольник $$ ABC$$.
Обозначим искомый радиус $$ r$$, положим $$ AB=c$$, $$ AC=b$$, $$ BC=a$$. Из подобия прямоугольных треугольников $$ ACD$$ и $$ ABC$$ (у них равные углы при вершине $$ A$$) имеем $$ {\displaystyle \frac{r}{{r}_{1}}}={\displaystyle \frac{c}{b}}$$, откуда $$ b={\displaystyle \frac{{r}_{1}}{r}}c$$. Прямоугольные треугольники $$ BCD$$ и $$ BAC$$ также подобны, поэтому $$ {\displaystyle \frac{r}{{r}_{2}}}={\displaystyle \frac{c}{a}}$$, — откуда $$ a={\displaystyle \frac{{r}_{2}}{r}}c$$. Так как $$ {a}^{2}+{b}^{2}={c}^{2}$$ то, возводя в квадрат выражения для $$ a$$ и $$ b$$ и складывая их, получим $$ {\left(\frac{{r}_{1}}{r}\right)}^{2}{c}^{2}+{\left(\frac{{r}_{2}}{r}\right)}^{2}{c}^{2}={c}^{2}$$ или $$ {\displaystyle \frac{{r}_{1}^{2}+{r}_{2}^{2}}{{r}^{2}}}=1$$. Находим $$ r=\sqrt{{{r}_{1}}^{2}+{{r}_{2}}^{2}}$$.
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку $$ M$$, лежащую внутри треугольника $$ ABC$$, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны $$ {S}_{1}$$, $$ {S}_{2}$$ и $$ {S}_{3}$$. Найти площадь треугольника $$ ABC$$.
Легко видеть, что треугольники $$ EKM$$, $$ MQF$$ и $$ PMN$$ подобны треугольнику $$ ABC$$.
Пусть $$ S$$ -площадь треугольника $$ ABC$$, тогда
$$ {\displaystyle \frac{{S}_{1}}{S}}={\left({\displaystyle \frac{EM}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{2}}{S}}={\left({\displaystyle \frac{MF}{AC}}\right)}^{2}; {\displaystyle \frac{{S}_{3}}{S}}={\left({\displaystyle \frac{PN}{AC}}\right)}^{2}.$$
Откуда находим
$$ EM=\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}AC, MF=\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}AC, PN=\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}AC.$$
А так как $$ EM=AP, MF=NC$$, то $$ EM+PN+MF=AP+PN+NC=AC$$.
Таким образом, $$ AC=AC·\left(\sqrt{{\displaystyle \frac{{S}_{1}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{2}}{S}}}+\sqrt{{\displaystyle \frac{{S}_{3}}{S}}}\right)$$, откуда следует
$$ S={\left(\sqrt{{S}_{1}}+\sqrt{{S}_{2}}+\sqrt{{S}_{3}}\right)}^{2}$$.
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна $$ {\displaystyle \frac{1}{2}}{S}_{ABC}$$. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть $$ BD$$ — медиана треугольника
$$ ABC (BC=a, AC=b, AB=c, BD={m}_{a})$$, тогда
$$ {m}_{c}^{2}={\displaystyle \frac{{a}^{2}+{b}^{2}}{2}}-{\displaystyle \frac{{c}^{2}}{4}}$$. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы $$ A{A}_{1}$$ треугольника $$ ABC$$ пересекаются в точке $$ O$$, $$ A{A}_{1}=12$$ и $$ C{C}_{1}=6$$ и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника $$ ABC$$.
1. По теореме 1 имеем $$ AO={\displaystyle \frac{2}{3}}A{A}_{1}=8$$, $$ CO={\displaystyle \frac{2}{3}}C{C}_{1}=4$$.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона $$ AC$$ не может равняться `12`, иначе $$ AC=AO+OC$$ — нарушено неравенство треугольника. Также не может равняться `12` сторона $$ AB$$, так в этом случае $$ A{C}_{1}=6$$ и треугольник $$ AO{C}_{1}$$ со сторонами `8`, `2`, `6` не существует. Значит, $$ BC=12$$ и $$ A{C}_{1}=6$$.
2. Площадь треугольника находим по формуле Герона:
$$ p=7, {S}_{{A}_{1}OC}=\sqrt{7·1·3·3}=3\sqrt{7}$$.
По теореме 2 площадь треугольника $$ ABC$$ в `6` раз больше, находим $$ {S}_{ABC}=18\sqrt{7}$$.
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если $$ A{A}_{1}$$ и $$ B{B}_{1}$$ — высоты треугольника $$ ABC$$, то треугольник $$ {A}_{1}{B}_{1}C$$ подобен треугольнику $$ ABC$$ с коэффициентом подобия $$ k={\displaystyle \frac{{A}_{1}{B}_{1}}{AB}}=\left|\mathrm{cos}C\right|$$. Можно это утверждение сформулировать так: Если соединить основания двух высот $$ A{A}_{1}$$ и $$ B{B}_{1}$$ треугольника $$ ABC$$, то образуется треугольник, подобный данному: $$ ∆{A}_{1}{B}_{1}C~∆ABC$$.
Из прямоугольных треугольников $$ AC{A}_{1}$$ следует $$ {A}_{1}C=AC·\mathrm{cos}C$$ или $$ {A}_{1}C=AC·\mathrm{cos}(180°-C)=AC\left|\mathrm{cos}C\right|$$ (рис. 11а, б), а из прямоугольных треугольников $$ BC{B}_{1}$$ следует $$ {B}_{1}C=BC·\mathrm{cos}C$$ или $$ {B}_{1}C=BC·\mathrm{cos}(180°-C)=BC\left|\mathrm{cos}C\right|$$. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ (или их продолжения) пересекаются в точке $$ H$$, то справедливо равенство $$ AH·H{A}_{1}=BH·H{B}_{1}$$ (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
Высоты $$ A{A}_{1}$$ и $$ B{B}_{1}$$ пересекаются в точке $$ H$$ (рис. 13), при этом $$ AH=3H{A}_{1}$$ и $$ BH=H{B}_{1}$$. Найти косинус угла $$ ACB$$ и площадь треугольника $$ ABC$$, если $$ AC=a$$.
Обозначим $$ H{A}_{1}=x, H{B}_{1}=y$$,
1. Точка $$ H$$ — середина высоты (рис. 13). Если отрезок $$ MH$$ проходит через точку $$ H$$ и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.
2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, $$ MH=HN={\displaystyle \frac{a}{4}}$$ и $$ A{B}_{1}={B}_{1}C={\displaystyle \frac{a}{2}}$$ Треугольник $$ ABC$$ равнобедренный, $$ AB=BC$$.
3. $$ \angle {B}_{1}BC=90°-\angle C$$, поэтому `ul(/_BHA_1=/_AHB_1=/_C)`, а по второй лемме о высотах $$ AH·H{A}_{1}=BH·H{B}_{1}$$ т. е. $$ 3{x}^{2}={y}^{2}, y=x\sqrt{3}$$.
Далее, $$ \mathrm{cos}C=\mathrm{cos}(\angle AH{B}_{1})={\displaystyle \frac{y}{3x}}$$, находим $$ \mathrm{cos}C={\displaystyle \frac{1}{\sqrt{3}}}$$.
4. $$ △AH{B}_{1}: A{B}_{1}^{2}=(3x{)}^{2}-{y}^{2}$$, $$ {\displaystyle \frac{{a}^{2}}{4}}=6{x}^{2}$$, $$ x={\displaystyle \frac{a}{2\sqrt{6}}}$$, $$ y={\displaystyle \frac{a}{2\sqrt{2}}}$$, тогда
$$ {S}_{ABC}={\displaystyle \frac{1}{2}}AC·B{B}_{1}=ay={\displaystyle \frac{{a}^{2}\sqrt{2}}{4}}$$.
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), то
$$ {\displaystyle \frac{BD}{DC}}={\displaystyle \frac{AB}{AC}} \left({\displaystyle \frac{x}{y}}={\displaystyle \frac{c}{b}}\right)$$
Доказательство легко выполните сами, применяя теорему синусов к треугольникам $$ ADB$$ и $$ ADC$$.
Теорема 6. Пусть $$ AD$$ — биссектриса треугольника $$ ABC$$ (рис. 14), тогда $$ AD=\sqrt{AB·AC-DB·DC}$$ (в обозначениях рисунка 14а)
`ul(AD=sqrt(bc-xy))`.
 |
 |
||
| Рис. 14 | Рис. 14а |
Эту теорему докажем. Опишем около треугольника $$ ABC$$ окружность, точку пересечения прямой $$ AD$$ и окружности обозначим $$ K$$ (рис. 14а).
Обозначим $$ AD=z, DK=m.△ABD\sim ∆AKC$$ $$ (\angle ABD=\angle AKC$$ и $$ \angle 1=\angle 2)$$. Из подобия следует $$ {\displaystyle \frac{AB}{AK}}={\displaystyle \frac{AD}{AC}}$$, т. е. $$ {\displaystyle \frac{c}{z+m}}={\displaystyle \frac{z}{b}}$$, откуда $$ {z}^{2}+zm=bc$$, $$ {z}^{2}=bc-zm$$.
По свойству пересекающихся хорд: $$ AD·DK=BD·CD$$, т. е. $$ z·m=x·y$$, тогда $$ {z}^{2}=bc-xy$$, $$ z=\sqrt{bc-xy}$$.
В треугольнике $$ ABC$$ со сторонами $$ AB=5$$, $$ AC=3$$ биссектриса $$ AD={\displaystyle \frac{15}{8}}$$. Найти сторону $$ BC$$ и радиус вписанной окружности.
По теореме 5 (см. рис. 14) имеем $$ {\displaystyle \frac{x}{y}}={\displaystyle \frac{5}{3}}$$ Обозначим $$ x=5z$$, тогда $$ y=3z$$. По теореме 6 выполнено равенство $$ {\left({\displaystyle \frac{15}{8}}\right)}^{2}=5·3-5z·3z.$$ Легко находим $$ z={\displaystyle \frac{7}{8}}$$ значит `ul(BC=7)`. Радиус вписанной окружности найдём по формуле $$ S=pr$$ (`S` — площадь треугольника, `p` -полупериметр). Имеем $$ p={\displaystyle \frac{15}{2}}$$, по формуле Герона $$ S=\sqrt{{\displaystyle \frac{15}{2}}·{\displaystyle \frac{1}{2}}·{\displaystyle \frac{10}{2}}·{\displaystyle \frac{9}{2}}}={\displaystyle \frac{15\sqrt{3}}{2}},$$ поэтому $$ r={\displaystyle \frac{S}{p}}={\displaystyle \frac{\sqrt{3}}{2}}.$$
Планиметрия — § 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры FF и F`F` называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры FF и F`F` подобны, то пишется F~F`F\sim F`Напомним, что в записи подобия треугольников ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. AA переходит в A1A_1, BB — в B1B_1, CC — в C1C_1. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\angle A=\angle A_1,\;\angle B=\angle B_1,\;\angle C=\angle C_1,\;\frac{AB}{A_1B_1}=\frac{BC}{B_1C_1}=\frac{AC}{A_1C_1}
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если MN||ACMN||AC (рис. 5), то
mn=pq=m+pn+q\frac mn=\frac pq=\frac{m+p}{n+q}
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
mn=m+pn+q\frac mn=\frac{m+p}{n+q} или mn=pq\frac mn=\frac pq,
то MNMN параллельна ACAC (доказательство было дано в задании для 9 класса).
 |
| Рис. 6 |
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках MM и NN. Найти длину отрезка если основания трапеции равны aa и bb.
Δ Пусть OO точка пересечения диагоналей трапеции (рис. 6). Обозначим:
AD=a, BC=b, MO=x, BO=p, OD=q.AD=a,\;BC=b,\;MO=x,\;BO=p,\;OD=q.
1. BC~AD△BOC~△DOA (по двум углам)⇒ba=pq1.\;\left\{\begin{array}{l}BC\sim AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(по\;двум\;углам)\end{array}\right.\Rightarrow\frac ba=\frac pq
2. MO~AD△MBO~△ABD⇒xa=pp+q2.\;\left\{\begin{array}{l}MO\sim AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right.\Rightarrow\frac xa=\frac p{p+q}
Из (1) и (2) следует x=app+q=qp/qp/q+1=aba+b⇒MO=aba+b.x=a\frac p{p+q}=q\frac{p/q}{p/q+1}=\frac{ab}{a+b}\Rightarrow MO=\frac{ab}{a+b}.
Аналогично устанавливаем, что NO=aba+b⇒MN=2aba+bNO=\frac{ab}{a+b}\Rightarrow MN=\frac{2ab}{a+b}.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить. ▲
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
В прямоугольном треугольнике ABCABC из вершины CC прямого угла проведена высота CDCD (рис. 7). Радиусы окружностей, вписанных в треугольники ACDACD и BCDBCD равны соответственно r1r_1 и r2r_2 . Найти радиус окружности, вписанной в треугольник ABCABC.
Δ Обозначим искомый радиус rr, положим AB=cAB=c, AC=bAC=b, BC=aBC=a. Из подобия прямоугольных треугольников ACDACD и ABCABC (у них равные углы при вершине AA) имеем rr1=cb\frac r{r_1}=\frac cb, откуда b=r1rcb=\frac{r_1}rc. Прямоугольные треугольники BCDBCD и BACBAC также подобны, поэтому rr2=ca\frac r{r_2}=\frac ca, — откуда a=r2rca=\frac{r_2}rc. Так как a2+b2=c2a^2+b^2=c^2 то, возводя в квадрат выражения для aa и bb и складывая их, получим r1r2c2+r2r2c2=c2 ⇒r12+r22r2=1\left(\frac{r_1}r\right)^2c^2+\left(\frac{r_2}r\right)^2c^2=c^2\;\Rightarrow\frac{r_1^2+r_2^2}{r^2}=1. Находим r=r12+r22r=\sqrt{r_1^2+r_2^2} ▲
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку MM, лежащую внутри треугольника ABCABC, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны S1S_1, S2S_2 и S3S_3. Найти площадь треугольника ABCABC.
Легко видеть, что треугольники EKMEKM, MQFMQF и PMNPMN подобны треугольнику ABCABC.
Пусть SS -площадь треугольника ABCABC, тогда
S1S=EMAC2; S2S=MFAC2; S3S=PNAC2.\frac{S_1}S=\left(\frac{EM}{AC}\right)^2;\;\frac{S_2}S=\left(\frac{MF}{AC}\right)^2;\;\frac{S_3}S=\left(\frac{PN}{AC}\right)^2.
Откуда находим
EM=S1SAC, MF=S2SAC, PN=S3SAC.EM=\sqrt{\frac{S_1}S}AC,\;MF=\sqrt{\frac{S_2}S}AC,\;PN=\sqrt{\frac{S_3}S}AC.
А так как EM=AP, MF=NC⇒EM+PN+MF=AP+PN+NC=ACEM=AP,\;MF=NC\Rightarrow EM+PN+MF=AP+PN+NC=AC.
Таким образом, AC=AC*S1S+S2S+S3S⇒S=S1+S2+S32AC=AC\ast\left(\sqrt{\frac{S_1}S}+\sqrt{\frac{S_2}S}+\sqrt{\frac{S_3}S}\right)\Rightarrow S=\left(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}\right)^2. ▲
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении 2 : 1, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на 6 треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из 6 треугольников с вершиной и основанием, равным половине стороны, равна 12SABC\frac12S_{ABC}. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть BDBD — медиана треугольника
ABC (BC=a, AC=b, AB=c, BD=ma)ABC\;(BC=a,\;AC=b,\;AB=c,\;BD=m_a), тогда
mc2=a2+b22-c24m_c^2=\frac{a^2+b^2}2-\frac{c^2}4. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы AA1AA_1 треугольника ABCABC пересекаются в точке OO, AA1=12AA_1=12 и CC1=6CC_1=6 и одна из сторон треугольника равна 12. (рис. 10). Найти площадь треугольника ABCABC.
Δ 1. По теореме 1 имеем AO=23AA1=8, CO=23CC1=4AO=\frac23AA_1=8,\;CO=\frac23CC_1=4.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна 12, сторона ACAC не может равняться 12, иначе AC=AO+OCAC=AO+OC — нарушено неравенство треугольника. Также не может равняться 12 сторона ABAB, так в этом случае AC1=6AC_1=6 и треугольник AOC1AOC_1 со сторонами 8, 2, 6 не существует. Значит, BC=12BC=12 и AC1=6AC_1=6.
2. Площадь треугольника находим по формуле Герона:
p=7, SA1OC=7*1*3*3=37p=7,\;S_{A_1OC}=\sqrt{7\ast1\ast3\ast3}=3\sqrt7.
По теореме 2 площадь треугольника ABCABC в 6 раз больше, находим SABC=187S_{ABC}=18\sqrt7.▲
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если AA1AA_1 и BB1BB_1 — высоты треугольника ABCABC, то треугольник A1B1CA_1B_1C подобен треугольнику ABCABC с коэффициентом подобия k=A1B1AB=cosCk=\frac{A_1B_1}{AB}=\left|\cos C\right|. Можно это утверждение сформулировать так: Если соединить основания двух высот AA1AA_1 и BB1BB_1 треугольника ABCABC, то образуется треугольник, подобный данному: ∆A1B1C~∆ABC\triangle A_1B_1C\sim\triangle ABC.
Из прямоугольных треугольников ACA1ACA_1 следует A1C=AC*cosCA_1C=AC*cosC или A1C=AC*cos(180°-C)=ACcosCA_1C=AC\ast cos(180^\circ-C)=AC\left|\cos C\right| (рис. 11а, б), а из прямоугольных треугольников BCB1BCB_1 следует B1C=BC*cosCB_1C=BC*cosC или B1C=BC*cos(180°-C)=BCcosCB_1C=BC\ast cos(180^\circ-C)=BC\left|\cos C\right|. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты AA1AA_1 и BB1BB_1 (или их продолжения) пересекаются в точке HH, то справедливо равенство AH*HA1=BH*HB1AH*HA_1=BH*HB_1 (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
Высоты AA1AA_1 и BB1BB_1 пересекаются в точке HH (рис. 13), при этом AH=3HA1AH=3HA_1 и BH=HB1BH=HB_1. Найти косинус угла ACBACB и площадь треугольника ABCABC, если AC=aAC=a.
Δ Обозначим HA1=x, HB1=yHA_1=x,\;HB_1=y,
1. Точка HH — середина высоты (рис. 13). Если отрезок MHMH проходит через точку HH и параллелен основаниям, то MN — средняя линия; MN=a/2MN=a/2.
2. ∆HA1N~∆AA1C⇒HNAC=x4x, HN=14a. \triangle HA_1N\sim\triangle AA_1C\Rightarrow\frac{HN}{AC}=\frac x{4x},\;HN=\frac14a.\;Значит, MH=HN=a4MH=HN=\frac a4 и AB1=B1C=a2AB_1=B_1C=\frac a2 Треугольник ABCABC равнобедренный, AB=BCAB=BC.
3. ∠B1BC=90°-∠C⇒∠BHA1=∠AHB1=∠C\angle B_1BC=90^\circ-\angle C\Rightarrow\angle BHA_1=\angle AHB_1=\angle C, а по второй лемме о высотах AH*HA1=BH*HB1AH*HA_1=BH*HB_1 т. е. 3×2=y2, y=x33x^2=y^2,\;y=x\sqrt3.
Далее, cosC=cos(∠AHB1)=y3xcosC=cos(\angle AHB1)=\frac y{3x}, находим cosC=13\cos C=\frac1{\sqrt3}.
4. △AHB1: AB12=(3x)2-y2, a24=6×2, x=a26, y=a22⇒⇒SABC=12AC*BB1=ay=a224\begin{array}{l}\bigtriangleup AHB_1:\;AB_1^2=(3x)^2-y^2,\;\frac{a^2}4=6x^2,\;x=\frac a{2\sqrt6},\;y=\frac a{2\sqrt2}\Rightarrow\\\Rightarrow S_{ABC}=\frac12AC\ast BB_1=ay=\frac{a^2\sqrt2}4\end{array}. ▲
 |
| Рис. 14 |
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если ADAD — биссектриса треугольника ABCABC (рис. 14), то
BDDC=ABAC xy=cb\frac{BD}{DC}=\frac{AB}{AC}\;\left(\frac xy=\frac cb\right)
Доказательство легко выполните сами, применяя теорему синусов к треугольникам ADBADB и ADCADC.
Теорема 6. Пусть ADAD — биссектриса треугольника ABCABC (рис. 14), тогда AD=AB*AC-DB*DCAD=\sqrt{AB\ast AC-DB\ast DC} (в обозначениях рисунка 14а) AD=bc-xyAD=\sqrt{bc-xy}.
 |
| Рис. 14а |
□ Эту теорему докажем. Опишем около треугольника ABCABC окружность, точку пересечения прямой ADAD и окружности обозначим KK (рис. 14а).
Обозначим AD=z, DK=m.△ABD~∆AKC (∠ABD=∠AKC и ∠1=∠2).Из подобия: ABAK=ADAC⇒cz+m=zb⇒⇒z2+zm=bc, z2=bc-zm.\begin{array}{l}AD=z,\;DK=m.\\\bigtriangleup ABD\sim\triangle AKC\;(\angle ABD=\angle AKC\;и\;\\\angle1=\angle2).\\Из\;подобия:\;\\\frac{AB}{AK}=\frac{AD}{AC}\Rightarrow\frac c{z+m}=\frac zb\Rightarrow\\\Rightarrow z^2+zm=bc,\;z^2=bc-zm.\end{array}По свойству пересекающихся хорд:
AD*DK=BD*CD, т.е. z*m=x*y⇒z2=bc-xy, z=bc-xyAD\ast DK=BD\ast CD,\;т.е.\;z\ast m=x\ast y\Rightarrow z^2=bc-xy,\;z=\sqrt{bc-xy}. ■
В треугольнике ABCABC со сторонами AB=5AB=5, AC=3AC=3 биссектриса AD=158AD=\frac{15}8. Найти сторону BCBC и радиус вписанной окружности.
Δ По теореме 5 (см. рис. 14) имеем xy=53\frac xy=\frac53 Обозначим x=5zx=5z, тогда y=3zy=3z. По теореме 6 выполнено равенство 1582=5*3-5z*3z.\left(\frac{15}8\right)^2=5\ast3-5z\ast3z. Легко находим z=78z=\frac78 значит BC=7.BC=7. Радиус вписанной окружности найдём по формуле S=prS=pr (S — площадь треугольника, p -полупериметр). Имеем p=152p=\frac{15}2, по формуле Герона S=152*12*102*92=1532,S=\sqrt{\frac{15}2\ast\frac12\ast\frac{10}2\ast\frac92}=\frac{15\sqrt3}2, поэтому r=Sp=32.r=\frac Sp=\frac{\sqrt3}2. ▲
Планиметрия — § 1. Подобие треугольников. Отношение площадей подобных треугольников. Свойства медиан, биссектрис и высот — ЗФТШ, МФТИ
Две фигуры FF и F’F^’ называются подобными, если они переводятся друг в друга преобразованием подобия, т. е. таким преобразованием, при котором расстояния между двумя точками изменяются (увеличиваются или уменьшаются) в одно и то же число раз. Если фигуры FF и F’F^’ подобны, то пишется F∼F’F\sim F^’Напомним, что в записи подобия треугольников ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1предполагается, что вершины, совмещаемые преобразованием подобия, стоят на соответствующих местах, т. е. AA переходит в A1A_1, BB — в B1B_1, CC — в C1C_1. Из свойств преобразования подобия следует, что у подобных фигур соответствующие углы равны, а соответствующие отрезки пропорциональны. В частности, если ∆ABC~∆A1B1C1\triangle ABC\sim\triangle A_1B_1C_1
∠A=∠A1, ∠B=∠B1, ∠C=∠C1, ABA1B1=BCB1C1=ACA1C1\angle A=\angle A_1,\;\angle B=\angle B_1,\;\angle C=\angle C_1,\;\dfrac{AB}{A_1B_1}=\dfrac{BC}{B_1C_1}=\dfrac{AC}{A_1C_1}.
Два треугольника подобны:
- 1) если два угла одного соответственно равны двум углам другого;
- 2) если две стороны одного пропорциональны двум сторонам другого и углы, образованные этими сторонами, равны;
- 3) если три стороны одного треугольника пропорциональны трём сторонам другого.
Из признаков подобия следует утверждения, которые удобно использовать в решении задач:
1°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие в различных точках, отсекает треугольник, подобный данному.
 |
| Рис. 5 |
2°. Прямая, параллельная одной из сторон треугольника и пересекающая две другие стороны, отсекает на них отрезки, пропорциональные данным сторонам, т. е. если MN||ACMN||AC (рис. 5), то
mn=pq=m+pn+q\dfrac mn=\dfrac pq=\frac{m+p}{n+q}
3°. Если прямая пересекает две стороны треугольника и отсекает на них пропорциональные отрезки, то она параллельна третьей стороне, т. е. если (см. рис. 5)
mn=m+pn+q\dfrac mn=\dfrac{m+p}{n+q} или mn=pq\dfrac mn=\dfrac pq,
то MNMN параллельна ACAC (доказательство было дано в задании для 9 класса).
Прямая, проходящая через точку пересечения диагоналей трапеции параллельно её основаниям, пересекает боковые стороны трапеции в точках MM и NN. Найти длину отрезка `MN`, если основания трапеции равны aa и bb.
Пусть OO точка пересечения диагоналей трапеции (рис. 6). Обозначим:
AD=a, BC=b, MO=x, BO=p, OD=q.AD=a,\;BC=b,\;MO=x,\;BO=p,\;OD=q.
$$1.\;\left.\begin{array}{l}BC\parallel AD\\\bigtriangleup BOC\sim\bigtriangleup DOA\;(\mathrm{по}\;\mathrm{двум}\;\mathrm{углам})\end{array}\right|\Rightarrow\dfrac ba=\dfrac pq$$ (1)
$$2.\;\left.\begin{array}{l}MO\parallel AD\\\bigtriangleup MBO\sim\bigtriangleup ABD\end{array}\right|\Rightarrow\dfrac xa=\dfrac p{p+q}$$. (2)
Из (1) и (2) следует x=app+q=qp/qp/q+1=aba+bx=a\dfrac p{p+q}=q\dfrac{p/q}{p/q+1}=\dfrac{ab}{a+b}, т. е. MO=aba+b.MO=\dfrac{ab}{a+b}.
Аналогично устанавливаем, что NO=aba+bNO=\dfrac{ab}{a+b}, поэтому MN=2aba+b\boxed{MN=\dfrac{2ab}{a+b}}.
Результат этой задачи, как утверждение, верное для любой трапеции, следует запомнить.
 |
| Рис. 6 |
Из определения подобия фигур следует, что в подобных фигурах все соответствующие линейные элементы пропорциональны. Так, отношение периметров подобных треугольников равно отношению длин соответствующих сторон. Или, например, в подобных треугольниках отношение радиусов вписанных окружностей (также и описанных окружностей) равно отношению длин соответствующих сторон. Это замечание поможет нам решить следующую задачу.
 |
| Рис. 7 |
В прямоугольном треугольнике ABCABC из вершины CC прямого угла проведена высота CDCD (рис. 7). Радиусы окружностей, вписанных в треугольники ACDACD и BCDBCD равны соответственно r1r_1 и r2r_2 . Найти радиус окружности, вписанной в треугольник ABCABC.
Обозначим искомый радиус rr, положим AB=cAB=c, AC=bAC=b, BC=aBC=a. Из подобия прямоугольных треугольников ACDACD и ABCABC (у них равные углы при вершине AA) имеем rr1=cb\dfrac r{r_1}=\dfrac cb, откуда b=r1rcb=\dfrac{r_1}rc. Прямоугольные треугольники BCDBCD и BACBAC также подобны, поэтому rr2=ca\dfrac r{r_2}=\dfrac ca, — откуда a=r2rca=\dfrac{r_2}rc. Так как a2+b2=c2a^2+b^2=c^2 то, возводя в квадрат выражения для aa и bb и складывая их, получим r1r2c2+r2r2c2=c2\left(\frac{r_1}r\right)^2c^2+\left(\frac{r_2}r\right)^2c^2=c^2 или r12+r22r2=1\dfrac{r_1^2+r_2^2}{r^2}=1. Находим r=r12+r22r=\sqrt{r_1^2+r_2^2}.
Напомним, что площади подобных фигур относятся как квадраты соответствующих линейных элементов. Для треугольников это утверждение можно сформулировать так: площади подобных треугольников относятся как квадраты соответствующих сторон. Рассмотрим характерную задачу на эту тему.
 |
| Рис. 8 |
Через точку MM, лежащую внутри треугольника ABCABC, проведены три прямые, параллельные его сторонам. При этом образовались три треугольника (рис. 8), площади которых равны S1S_1, S2S_2 и S3S_3. Найти площадь треугольника ABCABC.
Легко видеть, что треугольники EKMEKM, MQFMQF и PMNPMN подобны треугольнику ABCABC.
Пусть SS -площадь треугольника ABCABC, тогда
S1S=EMAC2; S2S=MFAC2; S3S=PNAC2.\dfrac{S_1}S=\left(\dfrac{EM}{AC}\right)^2;\;\dfrac{S_2}S=\left(\dfrac{MF}{AC}\right)^2;\;\dfrac{S_3}S=\left(\dfrac{PN}{AC}\right)^2.
Откуда находим
EM=S1SAC, MF=S2SAC, PN=S3SAC.EM=\sqrt{\dfrac{S_1}S}AC,\;MF=\sqrt{\dfrac{S_2}S}AC,\;PN=\sqrt{\dfrac{S_3}S}AC.
А так как EM=AP, MF=NCEM=AP,\;MF=NC, то EM+PN+MF=AP+PN+NC=ACEM+PN+MF=AP+PN+NC=AC.
Таким образом, AC=AC·S1S+S2S+S3SAC=AC\cdot\left(\sqrt{\dfrac{S_1}S}+\sqrt{\dfrac{S_2}S}+\sqrt{\dfrac{S_3}S}\right), откуда следует
S=S1+S2+S32S=\left(\sqrt{S_1}+\sqrt{S_2}+\sqrt{S_3}\right)^2.
Свойства медиан, высот, биссектрис треугольника
В наших заданиях 9-го и 10-го классов здесь повторяемые теоремы и утверждения были доказаны. Для некоторых из них мы напоминаем пути доказательств, доказывая их моменты и давая поясняющие рисунки.
 |
| Рис. 9 |
Теорема 1. Три медианы треугольника пересекаются в одной точке и точкой пересечения каждая медиана делится в отношении `2 : 1`, считая от вершины.
Теорема 2. Три медианы, пересекаясь, разбивают треугольник на `6` треугольников с общей вершиной, площади которых равны между собой.
(На рис. 9 площадь каждого из `6` треугольников с вершиной `M` и основанием, равным половине стороны, равна 12SABC\dfrac12S_{ABC}. Точка пересечения медиан называется центром тяжести треугольника.
Теорема 3. Пусть BDBD — медиана треугольника
ABC (BC=a, AC=b, AB=c, BD=ma)ABC\;(BC=a,\;AC=b,\;AB=c,\;BD=m_a), тогда
mc2=a2+b22-c24m_c^2=\dfrac{a^2+b^2}2-\dfrac{c^2}4. (Доказательство приведено далее в §4 Задания).
 |
| Рис. 10 |
Медианы AA1AA_1 треугольника ABCABC пересекаются в точке OO, AA1=12AA_1=12 и CC1=6CC_1=6 и одна из сторон треугольника равна `12`. (рис. 10). Найти площадь треугольника ABCABC.
1. По теореме 1 имеем AO=23AA1=8AO=\dfrac23AA_1=8, CO=23CC1=4CO=\dfrac23CC_1=4.
Расставим на рисунке 10 длины отрезков медиан. По условию, одна из сторон треугольника равна `12`, сторона ACAC не может равняться `12`, иначе AC=AO+OCAC=AO+OC — нарушено неравенство треугольника. Также не может равняться `12` сторона ABAB, так в этом случае AC1=6AC_1=6 и треугольник AOC1AOC_1 со сторонами `8`, `2`, `6` не существует. Значит, BC=12BC=12 и AC1=6AC_1=6.
2. Площадь треугольника находим по формуле Герона:
p=7, SA1OC=7·1·3·3=37p=7,\;S_{A_1OC}=\sqrt{7\cdot1\cdot3\cdot3}=3\sqrt7.
По теореме 2 площадь треугольника ABCABC в `6` раз больше, находим SABC=187S_{ABC}=18\sqrt7.
Теорема 4. Три высоты треугольника или три прямые, на которых лежат высоты, пересекаются в одной точке. (Эта точка называется ортоцентром треугольника). В остроугольном треугольнике точка пересечения высот лежит внутри треугольника.
Были доказаны также две леммы о высотах
1-ая лемма.
Если AA1AA_1 и BB1BB_1 — высоты треугольника ABCABC, то треугольник A1B1CA_1B_1C подобен треугольнику ABCABC с коэффициентом подобия k=A1B1AB=cosCk=\dfrac{A_1B_1}{AB}=\left|\cos C\right|. Можно это утверждение сформулировать так: Если соединить основания двух высот AA1AA_1 и BB1BB_1 треугольника ABCABC, то образуется треугольник, подобный данному: ∆A1B1C~∆ABC\triangle A_1B_1C\sim\triangle ABC.
Из прямоугольных треугольников ACA1ACA_1 следует A1C=AC·cosCA_1C=AC\cdot\cos C или A1C=AC·cos(180°-C)=ACcosCA_1C=AC\cdot \cos(180^\circ-C)=AC\left|\cos C\right| (рис. 11а, б), а из прямоугольных треугольников BCB1BCB_1 следует B1C=BC·cosCB_1C=BC\cdot \cos C или B1C=BC·cos(180°-C)=BCcosCB_1C=BC\cdot \cos(180^\circ-C)=BC\left|\cos C\right|. Далее рассуждения очевидны.
 |
 |
| Рис. 11a | Рис. 11б |
2-ая лемма.
Если высоты AA1AA_1 и BB1BB_1 (или их продолжения) пересекаются в точке HH, то справедливо равенство AH·HA1=BH·HB1AH\cdot HA_1=BH \cdot HB_1 (рис. 12а, б).
 |
 |
| Рис. 12a | Рис. 12б |
 |
| Рис. 13 |
Высоты AA1AA_1 и BB1BB_1 пересекаются в точке HH (рис. 13), при этом AH=3HA1AH=3HA_1 и BH=HB1BH=HB_1. Найти косинус угла ACBACB и площадь треугольника ABCABC, если AC=aAC=a.
Обозначим HA1=x, HB1=yHA_1=x,\;HB_1=y,
1. Точка HH — середина высоты (рис. 13). Если отрезок MHMH проходит через точку HH и параллелен основаниям, то `MN` — средняя линия; `MN=a/2`.
2. $$\left.\triangle HA_1N\sim\triangle AA_1C\right|\Rightarrow\dfrac{HN}{AC}=\dfrac x{4x},\;HN=\dfrac14a.$$ Значит, MH=HN=a4MH=HN=\dfrac a4 и AB1=B1C=a2AB_1=B_1C=\dfrac a2 Треугольник ABCABC равнобедренный, AB=BCAB=BC.
3. ∠B1BC=90°-∠C\angle B_1BC=90^\circ-\angle C, поэтому ∠BHA1=∠AHB1=∠C\underline{\angle BHA_1=\angle AHB_1=\angle C}, а по второй лемме о высотах AH·HA1=BH·HB1AH\cdot HA_1=BH\cdot HB_1 т. е. 3×2=y2, y=x33x^2=y^2,\;y=x\sqrt3.
Далее, cosC=cos(∠AHB1)=y3x\cos C=\cos (\angle AHB_1)=\dfrac y{3x}, находим cosC=13\cos C=\dfrac1{\sqrt3}.
4. △AHB1: AB12=(3x)2-y2\bigtriangleup AHB_1:\;AB_1^2=(3x)^2-y^2, a24=6×2\dfrac{a^2}4=6x^2, x=a26x=\dfrac a{2\sqrt6}, y=a22y=\dfrac a{2\sqrt2}, тогда
SABC=12AC·BB1=ay=a224S_{ABC}=\dfrac12AC\cdot BB_1=ay=\dfrac{a^2\sqrt2}4.
Теорема 5. Биссектриса угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам, т. е. если ADAD — биссектриса треугольника ABCABC (рис. 14), то
BDDC=ABAC xy=cb\dfrac{BD}{DC}=\dfrac{AB}{AC}\;\left(\dfrac xy=\dfrac cb\right)
Доказательство легко выполните сами, применяя теорему синусов к треугольникам ADBADB и ADCADC.
Теорема 6. Пусть ADAD — биссектриса треугольника ABCABC (рис. 14), тогда AD=AB·AC-DB·DCAD=\sqrt{AB\cdot AC-DB\cdot DC} (в обозначениях рисунка 14а)
AD=bc-xy\underline{AD=\sqrt{bc-xy}}.
 |
 |
||
| Рис. 14 | Рис. 14а |
Эту теорему докажем. Опишем около треугольника ABCABC окружность, точку пересечения прямой ADAD и окружности обозначим KK (рис. 14а).
Обозначим AD=z, DK=m.△ABD∼∆AKCAD=z,\;DK=m.\bigtriangleup ABD\sim\triangle AKC(∠ABD=∠AKC(\angle ABD=\angle AKC и ∠1=∠2)\angle1=\angle2). Из подобия следует ABAK=ADAC\dfrac{AB}{AK}=\dfrac{AD}{AC}, т. е. cz+m=zb\dfrac c{z+m}=\dfrac zb, откуда z2+zm=bcz^2+zm=bc, z2=bc-zmz^2=bc-zm.
По свойству пересекающихся хорд: AD·DK=BD·CDAD\cdot DK=BD\cdot CD, т. е. z·m=x·yz\cdot m=x\cdot y, тогда z2=bc-xyz^2=bc-xy, z=bc-xyz=\sqrt{bc-xy}.
В треугольнике ABCABC со сторонами AB=5AB=5, AC=3AC=3 биссектриса AD=158AD=\dfrac{15}8. Найти сторону BCBC и радиус вписанной окружности.
По теореме 5 (см. рис. 14) имеем xy=53\dfrac xy=\dfrac53 Обозначим x=5zx=5z, тогда y=3zy=3z. По теореме 6 выполнено равенство 1582=5·3-5z·3z.\left(\dfrac{15}8\right)^2=5\cdot3-5z\cdot3z. Легко находим z=78z=\dfrac78 значит BC=7.BC=7. Радиус вписанной окружности найдём по формуле S=prS=pr (`S` — площадь треугольника, `p` -полупериметр). Имеем p=152p=\dfrac{15}2, по формуле Герона S=152·12·102·92=1532,S=\sqrt{\dfrac{15}2\cdot\dfrac12\cdot\dfrac{10}2\cdot\dfrac92}=\dfrac{15\sqrt3}2, поэтому r=Sp=32.r=\dfrac Sp=\dfrac{\sqrt3}2. ▲