Ответ: \(x=\left[-1;0\right]\)
«свойства показательной функции» (10 класс)
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
МБОУ СОШ № 35
Туапсинского района Краснодарского края
СЦЕНАРИЙ УРОКА ПО ПРЕДМЕТУ «АЛГЕБРА И НАЧАЛА АНАЛИЗА»
НА ТЕМУ «СВОЙСТВА ПОКАЗАТЕЛЬНОЙ ФУНКЦИИ» (10 КЛАСС)
Разработан учителями математики МБОУ СОШ № 35
Пгт.Новомихайловский
Туапсинского р-на
Краснодарского края
Колмаковой Валентины Ивановны и Коломиец Надежды Ильиничны.
2013
ОПИСАНИЕ РАБОТЫ
Так как урок является
закрепляющим свойства показательной
функции, то урок
начинается с повторения видов преобразований графиков функций,
учащиеся выполняют преобразования на
интерактивной доске, комментируя их.
Замечание. Главной особенностью данного урока является то, что с помощью использования на уроке различных компьютерных ресурсов (мобильного класса ноут-буков, интерактивной доски и различного программного обеспечения) высвобождается большое количество времени, которое используется для различных целей: повторения, закрепления, обобщения и контроля пройденного материала, подготовки учащихся к восприятию нового учебного материала, подготовки к ЭГЕ, т.е. того, на что зачастую не хватает 40 минут традиционного урока.
После
повторения следует проверка
домашнего задания, выполненного с
помощью компьютера. Учащиеся с помощью
графопостроителя выполнили графики
данных им за неделю до данного урока.
функций, и на уроке должны объяснить, с
помощью какого преобразования они были
выполнены. Таким образом, домашняя
работа не носит традиционный характер,
что увеличивает заинтересованность
учащихся.
На третьем этапе урока учитель предлагает решить два задания из группы В и С, решение которых основано на использовании свойств и преобразований графиков функций.
На четвертом этапе урока закрепляются свойства и преобразование графиков показательной функции с использованием того же оборудования.
Пятый этап: самостоятельная работа учащихся на компьютере с последующей проверкой. Учащиеся на своих ноутбуках отвечают на вопросы теста, затем некоторые ответы проецируются на интерактивную доску и проверяются.
Шестой этап: подведение итогов урока и постановка задач для следующего урока
Обучающие цели:
Обобщение, систематизация и контроль знаний учащихся по теме «Преобразование графиков функций и свойства показательной функции» с использованием мультимедийных и сетевых компьютерных технологий, подготовка учащихся к сдаче экзамена в форме ЕГЭ.

Развивающие цели:
Развитие логического и теоретического мышления, интеллектуальных способностей: умения анализировать, делать выводы.
Воспитательные цели:
Задачи:
повторение знаний основных видов преобразований функций с использованием возможностей работы с интерактивной доской;
обобщение и закрепление знаний и умений производить преобразования графиков функций основных видов;
закрепление знаний свойств показательной функции и преобразований графиков показательной функции;
организация контроля и самоконтроля с помощью выполнения построений графиков функций в среде программы «Графопостроитель»;
формирование положительной мотивации к учению с помощью использования новых компьютерных технологий.
Формы организации учебной деятельности:
фронтальная работа с классом;
индивидуальная тестовая работа за компьютером;
групповая самостоятельная работа за компьютером;
индивидуальная работа с использованием интерактивной доски.

На данном уроке преобладают интерактивные методы
Возрастная группа учеников для данного урока – 10-11 классы. Но использовать описанные выше методы и формы работы, в частности, использование компьютера, интерактивной доски, ноутбуков и соответствующего программного обеспечения можно в 8-10 классах, как при изучении тем, связанных с функцией, так и при изучении других тем, требующих большой наглядности.
В результате проведенной работы можно
отметить высокие результаты написания
плановых ежемесячных контрольных работ
и сдачи ЕГЭ по математике в нашей школе.
Сценарий урока.
Повторение материала и обобщение видов преобразований графиков функций
Повторение материала.(3 мин.)
При повторении изученного материала и обобщении видов преобразований графиков функций проводится фронтальная работа с классом с использованием интерактивной доски, подключенной к компьютеру. На Рабочем столе компьютера двойным щелчком запускается файл, заранее подготовленной в приложении Power Point презентации, имеющей имя Тренажер функции и сохраненной с расширением .pps (Демонстрация презентации).
1-й слайд:
Замечание: Работа с
презентацией, демонстрирующейся с
помощью интерактивной доски отличается
от работы с презентацией с помощью
проектора тем, что все действия, которые
выполняются с помощью щелчков мыши на
компьютере могут выполняться с помощью
прикосновений специальной ручки
непосредственно на интерактивной
доске, не отвлекаясь при этом от беседы
с классом и удерживая внимание учеников
на поставленной задаче.
2-й слайд:
Учитель указывает на любую функцию в левом ряду слайда прикосновением ручки. Надпись с функцией меняет цвет на красный (функция выбирается учителем в любом порядке, так как эта презентация может использоваться на нескольких уроках в качестве устной работы в течение изучения соответствующей темы, набор функций легко изменить, владея
навыками работы с офисными приложениями). Учащиеся должны описать график указанной функции и вид преобразования, после этого учитель нажимает еще раз на ту же надпись и появляется рисунок с графиком этой функции.
Учащиеся устно отвечают на 5-6 вопросов.
1.2. Обобщение видов преобразований на примерах следующих функций(6 мин.)
а) , , ,
б) , , ,
в) , , ,
г) , .
д) Построение графика функции: y=3x—
4 и графика обратной функции
,
получаемого симметрией относительно
прямой (по точкам: (0;-4) и (2;2) для первого графика
и (-4;0) и (2;2) для графика обратной функции).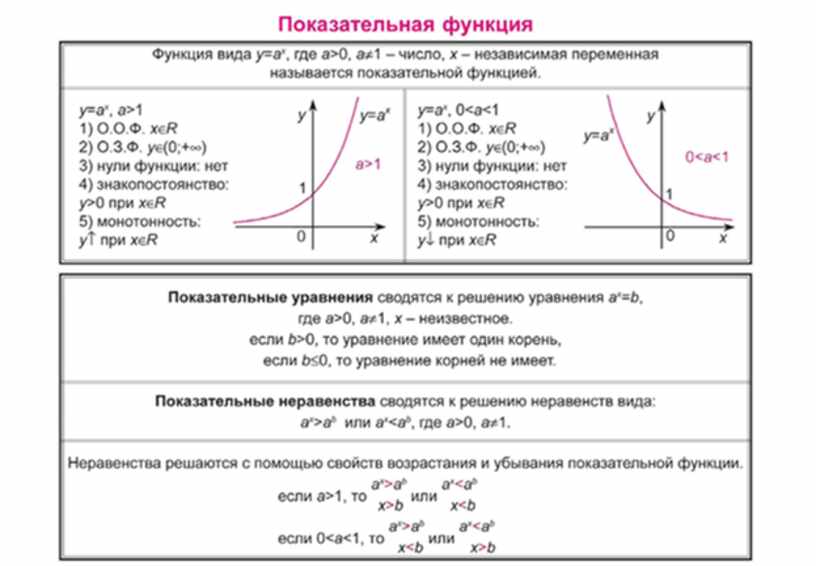
Графики функций строятся учащимися на интерактивной доске с краткими пояснениями. Для этого запускается программа ActivStudioProfessionalEdition. Окно программы представляет собой белый лист с панелью инструментов. Документ называется Флипчартом, состоит из нескольких листов. Все, что было выполнено на листе можно сохранить.
2. Просмотр домашних работ, подготовленных в виде презентаций на компьютерах (примеры преобразований функций).(3 мин)
На
интерактивную доску проецируются
некоторые домашние работы учащихся,
сопровождающиеся краткими объяснениями.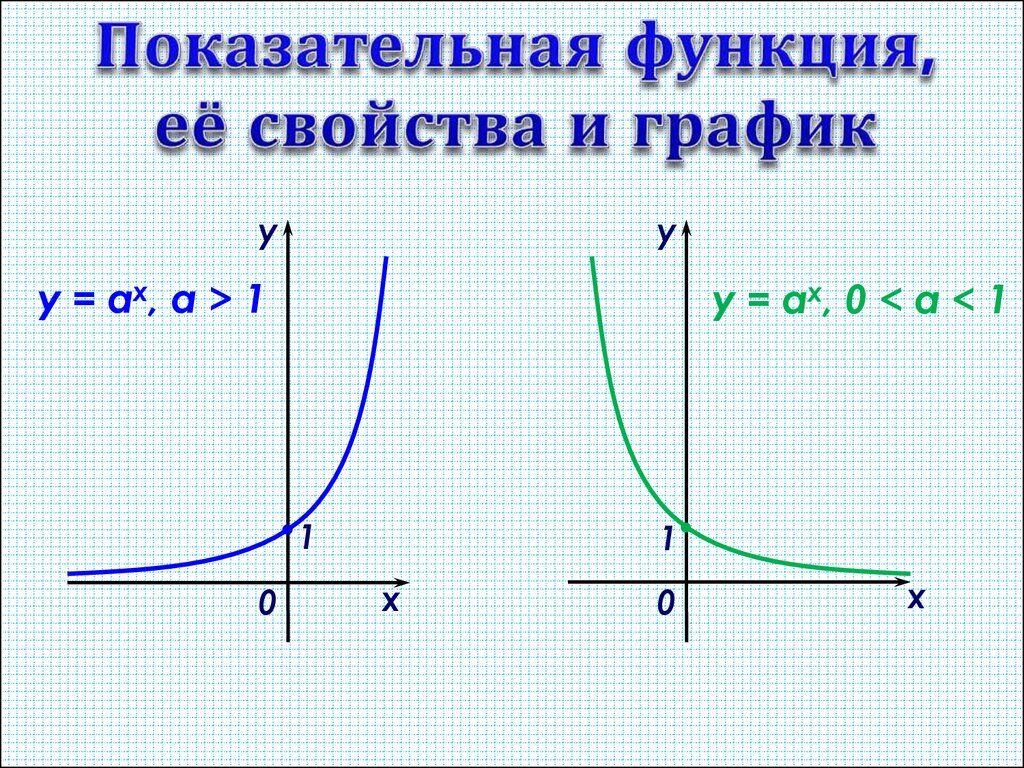 Все работы учитель сохраняет на своем
компьютере с помощью локальной сети
для проверки. Пример домашней работы
см. в приложении № 1.
Все работы учитель сохраняет на своем
компьютере с помощью локальной сети
для проверки. Пример домашней работы
см. в приложении № 1.
3. Решение заданий группы В и С, в которых используются свойства функций или графический способ решения.(6 мин.)
Найдите наибольшее целое число из области значений функции
Объяснение решений заданий группы В и С сопровождается демонстрацией презентаций, в которых решение появляется не сразу, а постепенно (учитель нажимает на слайд для появления решения после прослушивания вариантов ответа учащихся на задаваемые учителем вопросы).
2) При каких система уравнений имеет ровно 2 решения.
Решение:
Систему можно решить графически.
График 1-го уравнения строим так: для строим график функции и отражаем симметрично относительно
оси Ох (заметим, что график не функции,
а уравнения).
Графиком второго уравнения являются концентрические окружности с центром в точке
Из чертежа понятно, что два решения могут быть только, если , .
Ответ: 4
Демонстрация презентации
4. Закрепление свойств показательной функций и преобразование графиков показательной функции ((7 мин.)
Примечание. Учащиеся занимаются построением графиков функций на ноут-буках с использованием компьютерной программы Графопостроитель (Работа с программой Graphwiz).
А) Построение и анализ графиков функций: 1) ; 2) ; 3) ; .
Анализ графиков и повторение свойств показательных функций:
Все графики проходят через точку (0; 1) — D, E;
Графики функций 1) и 2) возрастают, 3) и 4) – убывают;
Чем больше основание (1) и 2) , тем быстрее рост функции (скорость возрастания функции увеличивается).

Б) С помощью программы Графопостроитель каждый ученик на своем ноут-буке выполняет построение графиков функций по индивидуальным карточкам:
1) ; 2) ; 3) ; 4) ; 5) ;
6) ; 7) ; 8) .
После выполненных построений некоторые работы через подключение к локальной сети демонстрируются на интерактивной доске и учащийся (по выбору учителя или по желанию) дает объяснение из какой функции и с помощью каких преобразований был получен график функции.
5.Самостоятельная работа учащихся на компьютере с последующей проверкой(10 мин.)
Учащиеся на ноут-буках выполняют
тест,»свойства показательной функции»
(приложение 2) затем учитель по результатам,
которые появляются у учащихся на экране
после нажатия кнопки Готово выставляет оценки. Используя возможности
локальной сети (результаты отображаются
на компьютере учителя и на интерактивной
доске), некоторые работы проверяются
классом и исправляются ощибки.
6. Подведение итогов урока и постановка задач для следующего урока(5 мин).
На уроке мы проделали следующую работу:
повторили преобразования функций вида ; ; ; ,
рассмотрели два задания группы В и С,
закрепили свойства показательной функции,
повторили построение графиков обратных функций,
провели самостоятельную работу по тесту, контролирующему знания по нахождению множества значений показательной функции.
Оценки за работу на уроке выставляются в журнал и в дневники.
Домашнее задание: прочитать п.38, законспектировать свойства, №499(а, б) по пр.1, №500(б) по пр.3. (учебник под редакцией Колмогорова А.Н.)
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ № 1
Домашняя работа по алгебре и началам анализа
Ученицы 10А класса Лев Марины
1)
2)
3 )
4)
5)
6)
7)
8)
9)
10)
11)
12)
ПРИЛОЖЕНИЕ № 1
Домашняя работа по алгебре и началам анализа
Ученицы
10А класса Шахмильян Анастасии.
13)
14)
15)
16)
17)
18)
19)
ПРИЛОЖЕНИЕ № 2
Тест «Свойства показательной
функции», выполняемый учениками на
уроке
Показательная функция
Основные сведения
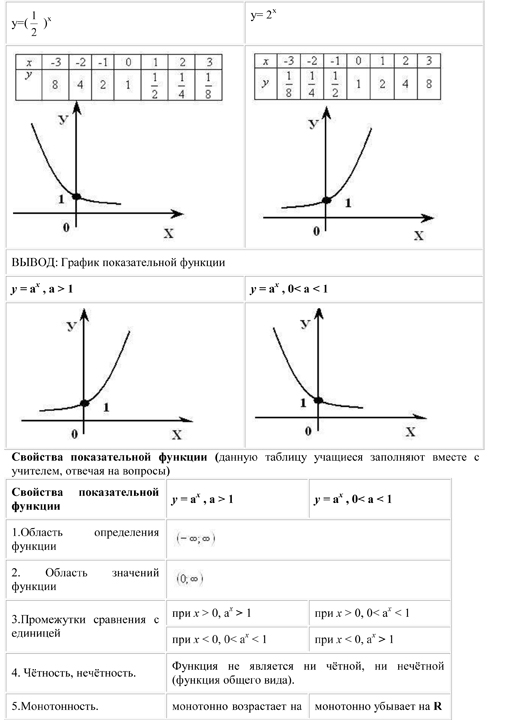
Показательной функцией назыввается функция вида y = ax, где a > 0 и a ≠ 1.
График функции имеет следующий вид:
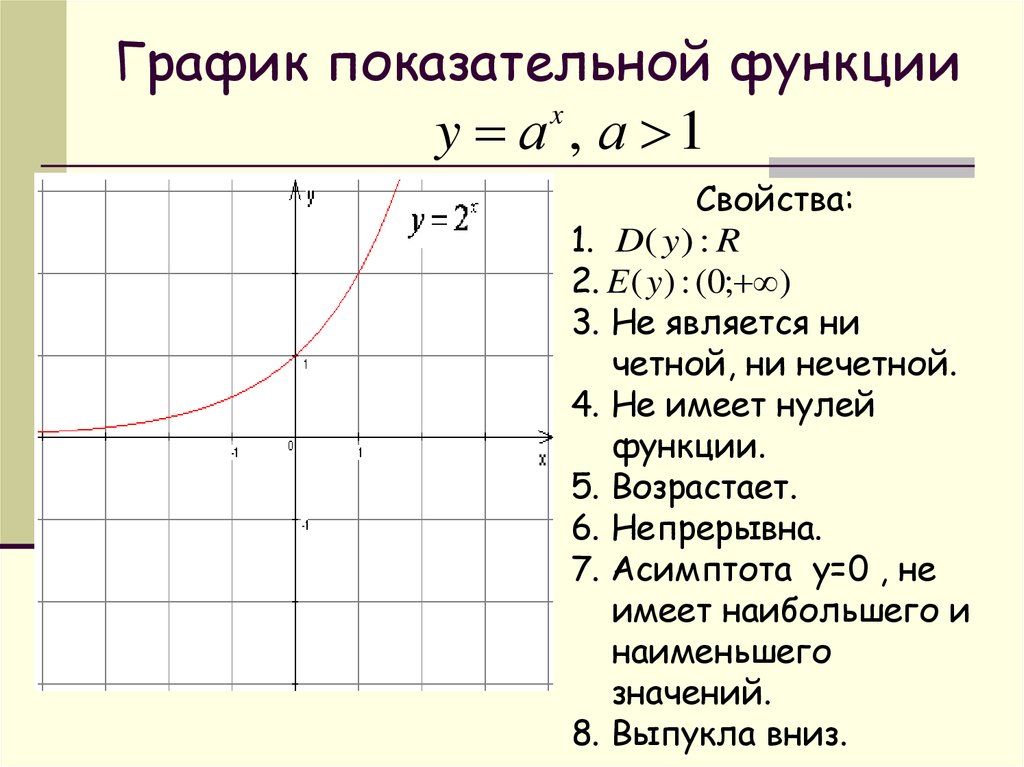
Рассмотрим свойства функции:
- Областью определения функции является множество всех действительных чисел R.
- Множеством значений функции являются все положительные числа, т. е. промежуток E(y): (0; +∞).
- Наименьшего и наибольшего значений функция не имеет.
- Функция не является ни нечетной, ни четной. Имеет общий вид.

- Функция непериодическая.
- График функции пересекает координатную ось Oy в точке (0; 1).
- Функция не имеет нулей.
- при a > 1 функция возрастает на всей числовой прямой; при 0 < a < 1 функция убывает на множестве R.
- Функция принимает положительные значения на всей области определения.
Примеры решения задач
Задача 1.
В одной координатной плоскости построить графики функций:
- y=2x
- y=3x
- y=5x
- y=10x
Решение.
Для начала построим график функции y=2x. Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 1 | 2 | 4 | 8 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует и большее значение функции у. Функция y = 2x возрастает на всей области определения D(y)=R, так как основание функции 2 > 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание a (если a>1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
Задача 2.
В одной координатной плоскости построить графики функций:
Решение.
Для начала построим график функции . Для этого найдем значения функции при x = 0, ±1, ±2, ±3.
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y(x) | 8 | 4 | 2 | 1 |
Отметим полученные точки на координатной плоскости, соединив их плавной линией.
Большему значению аргумента х соответствует меньшее значение функции y. Функция убывает на всей своей области определения: D(y)=R, так как основание функции 0 < < 1.
Подобным образом построим графики остальных функций.
Переменная х может принимать любое значение: D(y)=R, при этом область значений функции: E(y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0 < a < 1) показательной функции y = ax, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Задание 3.
Найти область значений функции:
- y = -2x
- y = +1
- y = 3x+1 — 5
Решение.
1. y = -2x
Область значений показательной функции y = 2x – все положительные числа, т. е. 0 < 2x < +∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем: -∞ < 2x < 0.
Ответ: E(y): (-∞; 0).
2. y = +1
0 < < +∞. Тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0 + 1 < +1 < +∞ + 1
1 < +1 < +∞
Ответ: E(y): (1; +∞).
3. y = 3x+1 — 5.
Запишем функцию ввиде: y = 3·3x — 5, тогда:
0 < 3x < +∞
умножаем все части двойного неравенства на 3:
0·3 < 3x·3 < (+∞)·3
0 < 3x·3 < +∞
из всех частей двойного неравенства вычитаем 5:
0 — 5 < 3x·3 — 5 < +∞ — 5
-5 < 3x·3 — 5 < +∞
Ответ: E(y): (-5; +∞).
Лекция 24. Показательные функции, их свойства. — Студопедия
Показательная функция это функция y(x) = ax, зависящая от показателя степени x, при некотором фиксированном значении основании степени a.
Область определения показательной функции, множество значений
Рассмотрим показательную функцию y(x) = ax
В дальнейшем будем считать, что основание степени a является положительным числом: a > 0. Тогда функция y = ax определена для всех x. Ее область определения: — ∞ < x + ∞. При a ≠ 1 она имеет множество значений: 0 < y < + ∞ При a = 1 показательная функция является постоянной y = 1
График показательной функции
На графике представлены значения показательной функции
y(x) = ax
для четырех значений основания степени: a = 2, a = 8,a = 1/2 и a = 1/8. На графике видно, что при a > 1показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем более сильное убывание.
На графике видно, что при a > 1показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем более сильное убывание.
Свойства показательной функции
Основные формулы
Когда показатель степени x есть натуральное число x = n, выражение an есть произведение n множителей:
| an = | a·a·a· … ·a |
| n раз |
Для произвольного значения x показательная функция определяется так, что обладает всеми свойствами натурального показателя степени.
Частные значения
Пусть y(x) = ax. Тогда
Экстремумы, возрастание, убывание
Показательная функция является монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
Основные ее свойства представлены в таблице.
| y = ax, a > 1 | y = ax, 0 < a < 1 | |
| Область определения | — ∞ < x + ∞ | — ∞ < x + ∞ |
| Область значений | 0 < y < + ∞ | 0 < y < + ∞ |
| Монотонность | монотонно возрастающая | монотонно убывающая |
| Нули, y = 0 | нет | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 | y = 1 |
100 ballov.kz образовательный портал для подготовки к ЕНТ и КТА
В 2021 году казахстанские школьники будут сдавать по-новому Единое национальное тестирование. Помимо того, что главный школьный экзамен будет проходить электронно, выпускникам предоставят возможность испытать свою удачу дважды. Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
Корреспондент zakon.kz побеседовал с вице-министром образования и науки Мирасом Дауленовым и узнал, к чему готовиться будущим абитуриентам.
— О переводе ЕНТ на электронный формат говорилось не раз. И вот, с 2021 года тестирование начнут проводить по-новому. Мирас Мухтарович, расскажите, как это будет?
— По содержанию все остается по-прежнему, но меняется формат. Если раньше школьник садился за парту и ему выдавали бумажный вариант книжки и лист ответа, то теперь тест будут сдавать за компьютером в электронном формате. У каждого выпускника будет свое место, огороженное оргстеклом.
Зарегистрироваться можно будет электронно на сайте Национального центра тестирования. Но, удобство в том, что школьник сам сможет выбрать дату, время и место сдачи тестирования.
Кроме того, в этом году ЕНТ для претендующих на грант будет длиться три месяца, и в течение 100 дней сдать его можно будет два раза.
— Расскажите поподробнее?
— В марте пройдет тестирование для желающих поступить на платной основе, а для претендующих на грант мы ввели новые правила. Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
Школьник, чтобы поступить на грант, по желанию может сдать ЕНТ два раза в апреле, мае или в июне, а наилучший результат отправить на конкурс. Но есть ограничение — два раза в один день сдавать тест нельзя. К примеру, если ты сдал ЕНТ в апреле, то потом повторно можно пересдать его через несколько дней или в мае, июне. Мы рекомендуем все-таки брать небольшой перерыв, чтобы еще лучше подготовиться. Но в любом случае это выбор школьника.
— Система оценивания останется прежней?
— Количество предметов остается прежним — три обязательных предмета и два на выбор. Если в бумажном формате закрашенный вариант ответа уже нельзя было исправить, то в электронном формате школьник сможет вернуться к вопросу и поменять ответ, но до того, как завершил тест.
Самое главное — результаты теста можно будет получить сразу же после нажатия кнопки «завершить тестирование». Раньше уходило очень много времени на проверку ответов, дети и родители переживали, ждали вечера, чтобы узнать результат. Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Сейчас мы все автоматизировали и набранное количество баллов будет выведено на экран сразу же после завершения тестирования.
Максимальное количество баллов остается прежним — 140.
— А апелляция?
— Если сдающий не будет согласен с какими-то вопросами, посчитает их некорректными, то он сразу же на месте сможет подать заявку на апелляцию. Не нужно будет ждать следующего дня, идти в центр тестирования, вуз или школу, все это будет электронно.
— С учетом того, что школьникам не придется вручную закрашивать листы ответов, будет ли изменено время сдачи тестирования?
— Мы решили оставить прежнее время — 240 минут. Но теперь, как вы отметили, школьникам не нужно будет тратить час на то, чтобы правильно закрасить лист ответов, они спокойно смогут использовать это время на решение задач.
— Не секрет, что в некоторых селах и отдаленных населенных пунктах не хватает компьютеров. Как сельские школьники будут сдавать ЕНТ по новому формату?
— Задача в том, чтобы правильно выбрать время и дату тестирования. Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
Центры тестирования есть во всех регионах, в Нур-Султане, Алматы и Шымкенте их несколько. Школьники, проживающие в отдаленных населенных пунктах, как и раньше смогут приехать в город, где есть эти центры, и сдать тестирование.
— На сколько процентов будет обновлена база вопросов?
— База вопросов ежегодно обновляется как минимум на 30%. В этом году мы добавили контекстные задания, то что школьники всегда просили. Мы уделили большое внимание истории Казахстана и всемирной истории — исключили практически все даты. Для нас главное не зазубривание дат, а понимание значения исторических событий. Но по каждому предмету будут контекстные вопросы.
— По вашему мнению система справится с возможными хакерскими атаками, взломами?
— Информационная безопасность — это первостепенный и приоритетный вопрос. Центральный аппарат всей системы находится в Нур-Султане. Связь с региональными центрами сдачи ЕНТ проводится по закрытому VPN-каналу. Коды правильных ответов только в Национальном центре тестирования.
Кроме того, дополнительно через ГТС КНБ (Государственная техническая служба) все тесты проходят проверку на предмет возможного вмешательства. Здесь все не просто, это специальные защищенные каналы связи.
— А что с санитарными требованиями? Нужно ли будет школьникам сдавать ПЦР-тест перед ЕНТ?
— ПЦР-тест сдавать не нужно будет. Требование по маскам будет. При необходимости Центр национального тестирования будет выдавать маски школьникам во время сдачи ЕНТ. И, конечно же, будем измерять температуру. Социальная дистанция будет соблюдаться в каждой аудитории.
— Сколько человек будет сидеть в одной аудитории?
— Участники ЕНТ не за семь дней будут сдавать тестирование, как это было раньше, а в течение трех месяцев. Поэтому по заполняемости аудитории вопросов не будет.
— Будут ли ужесточены требования по дисциплине, запрещенным предметам?
— Мы уделяем большое внимание академической честности. На входе в центры тестирования, как и в предыдущие годы, будут стоять металлоискатели. Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Перечень запрещенных предметов остается прежним — телефоны, шпаргалки и прочее. Но, помимо фронтальной камеры, которая будет транслировать происходящее в аудитории, над каждым столом будет установлена еще одна камера. Она же будет использоваться в качестве идентификации школьника — как Face ID. Сел, зарегистрировался и приступил к заданиям. Мы применеям систему прокторинга.
Понятно, что каждое движение абитуриента нам будет видно. Если во время сдачи ЕНТ обнаружим, что сдающий использовал телефон или шпаргалку, то тестирование автоматически будет прекращено, система отключится.
— А наблюдатели будут присутствовать во время сдачи тестирования?
— Когда в бумажном формате проводили ЕНТ, мы привлекали очень много дежурных. В одной аудитории было по 3-4 человека. При электронной сдаче такого не будет, максимум один наблюдатель, потому что все будет видно по камерам.
— По вашим наблюдениям школьники стали меньше использовать запрещенные предметы, к примеру, пользоваться телефонами?
— Практика показывает, что школьники стали ответственнее относиться к ЕНТ. Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Если в 2019 году на 120 тыс. школьников мы изъяли 120 тыс. запрещенных предметов, по сути у каждого сдающего был телефон. То в прошлом году мы на 120 тыс. школьников обнаружили всего 2,5 тыс. телефонов, и у всех были аннулированы результаты.
Напомню, что в 2020 году мы также начали использовать систему искусственного интеллекта. Это анализ видеозаписей, который проводится после тестирования. Так, в прошлом году 100 абитуриентов лишились грантов за то, что во время сдачи ЕНТ использовали запрещенные предметы.
— Сколько средств выделено на проведение ЕНТ в этом году?
Если раньше на ЕНТ требовалось 1,5 млрд тенге из-за распечатки книжек и листов ответов, то сейчас расходы значительно сокращены за счет перехода на электронный формат. Они будут, но несущественные.
— Все-таки почему именно в 2021 году было принято решение проводить ЕНТ в электронном формате. Это как-то связано с пандемией?
— Это не связано с пандемией. Просто нужно переходить на качественно новый уровень. Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
Мы апробировали данный формат на педагогах школ, вы знаете, что они сдают квалификационный тест, на магистрантах, так почему бы не использовать этот же формат при сдаче ЕНТ. Тем более, что это удобно, и для школьников теперь будет много плюсов.
«Показательная функция, её свойства и график».
тема урока:
Показательная функция, ее свойства и график.
0 , a 1) , называется показательной функцией с основанием а у=а x 0 у=а x a1 х х ГРАФИК — ЭКСПОНЕНТА»Определение
- Функция, заданная формулой у=а x ( где а 0 , a 1) , называется показательной функцией с основанием а
у=а x
0
у=а x
a1
х
х
ГРАФИК — ЭКСПОНЕНТА
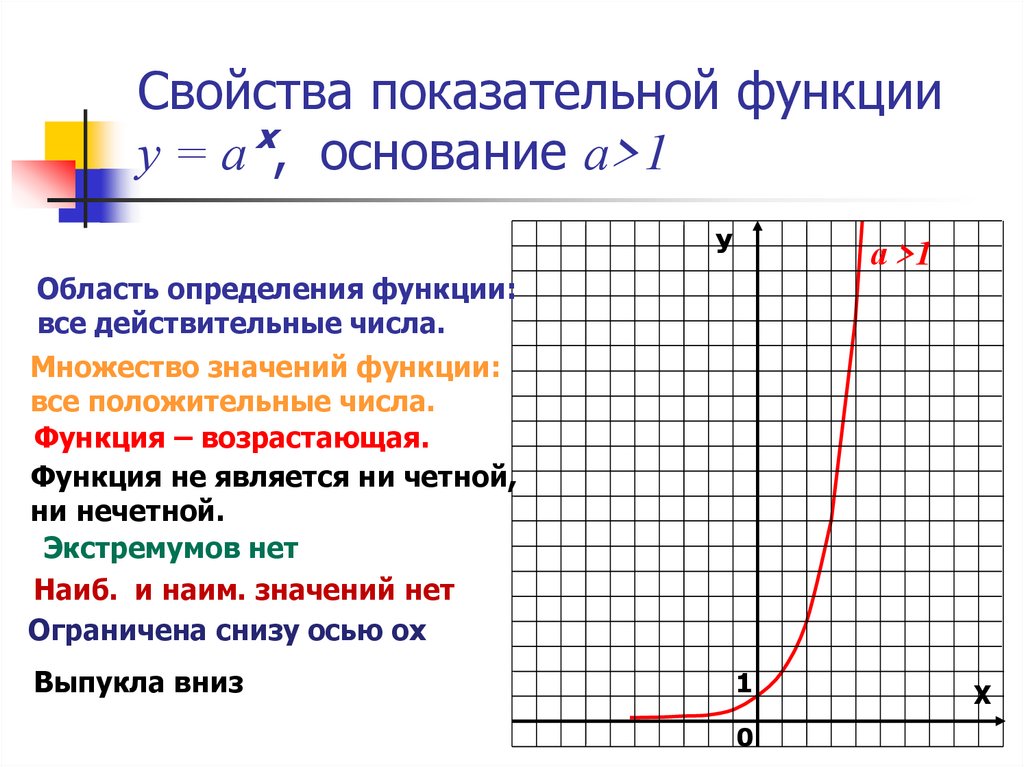
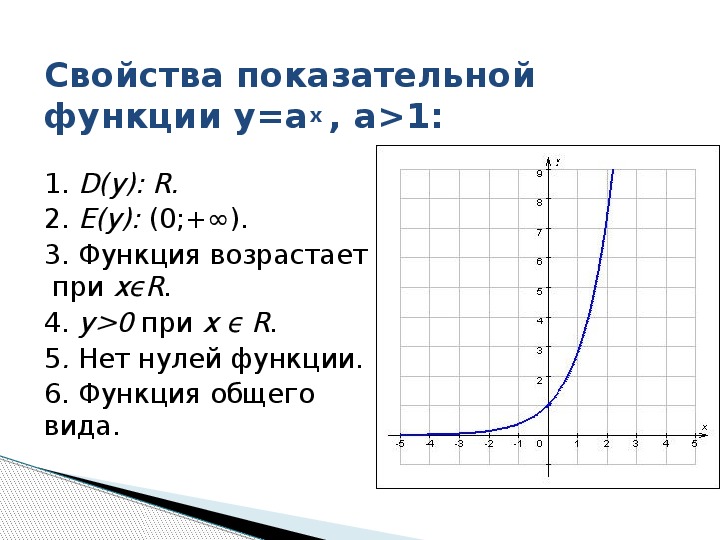
1 Область определения – множество всех действительных чисел D(y) = R ; Ни чётная, ни нечётная; Нет ни наибольшего, ни наименьшего значений; у=а x a1 х ЭКСПОНЕНТА»Свойства показательной функции у=а x при а 1
- Область определения – множество всех действительных чисел D(y) = R ;
- Ни чётная, ни нечётная;
- Нет ни наибольшего, ни наименьшего значений;
у=а x
a1
х
ЭКСПОНЕНТА
1 Область значений – множество всех положительных чисел E( y )= R + ; Ограничена снизу; Непрерывна; у=а x a1 х ЭКСПОНЕНТА»Свойства показательной функции у=а x при а 1
- Область значений – множество всех положительных чисел E( y )= R + ;
- Ограничена снизу;
- Непрерывна;
у=а x
a1
х
ЭКСПОНЕНТА
1 у=а x a1 Функция возрастает на всей области определения; Выпукла вниз; х ЭКСПОНЕНТА»Свойства показательной функции у=а x при а 1
у=а x
a1
- Функция возрастает на всей области определения;
- Выпукла вниз;
х
ЭКСПОНЕНТА
1 у=а x a1 При х =0 значение функции равно 1 х ЭКСПОНЕНТА»Свойства показательной функции у=а x при а 1
у=а x
a1
- При х =0 значение функции равно 1
х
ЭКСПОНЕНТА
Свойства показательной функции у=а x при 0
у=а x
0
- Область определения – множество всех действительных чисел D( y ) = R ;
- Ни чётная, ни нечётная;
- Нет ни наибольшего, ни наименьшего значений;
х
ЭКСПОНЕНТА
Свойства показательной функции у=а x при 0
у=а x
0
- Область значений – множество всех положительных чисел E( y )=R + ;
- Ограничена снизу;
- Непрерывна;
х
ЭКСПОНЕНТА
Свойства показательной функции у=а x при 0
у=а x
0
- Функция убывает на всей области определения;
- Выпукла вниз;
х
ЭКСПОНЕНТА
Свойства показательной функции у=а x при 0
у=а x
0
- При х =0 значение функции равно 1.

х
ЭКСПОНЕНТА
Показательные уравнения
не имеет корней
|
Характеристики графиков экспоненциальных функций
Результаты обучения
- Определите, представляет ли экспоненциальная функция и связанный с ней график рост или спад.
- Нарисуйте график экспоненциальной функции.
Прежде чем мы начнем строить графики, полезно рассмотреть поведение экспоненциального роста. Вспомните таблицу значений для функции вида [латекс] f \ left (x \ right) = {b} ^ {x} [/ latex], основание которой больше единицы. {x} [/ latex] построить график функции
{x} [/ latex] построить график функции
- Создайте таблицу точек.{x} [/ латекс]. Укажите домен, диапазон и асимптоту. Показать решение
Перед построением графика определите поведение и создайте таблицу точек для графика.
- Поскольку b = 0,25 находится между нулем и единицей, мы знаем, что функция убывает. Левый хвост графика будет неограниченно увеличиваться, а правый хвост приблизится к асимптоте y = 0.
- Создайте таблицу баллов.
x –3 –2 –1 0 1 2 3 [латекс] f \ left (x \ right) = {0.{x} [/ латекс] 64 16 4 1 0,25 0,0625 0,015625 - Постройте точку пересечения и [латекс] \ влево (0,1 \ вправо) [/ латекс] вместе с двумя другими точками.
 x [/ latex], где [latex] b> 0 [/ latex] — это функция, которая остается пропорциональной своему исходному значению при увеличении или уменьшении.
x [/ latex], где [latex] b> 0 [/ latex] — это функция, которая остается пропорциональной своему исходному значению при увеличении или уменьшении.Цели обучения
Описать свойства графиков экспоненциальных функций
Основные выводы
Ключевые моменты
- Если основа, [латекс] b [/ латекс], больше, чем [латекс] 1 [/ латекс], то функция экспоненциально возрастает со скоростью роста [латекс] b [/ латекс]. Это известно как экспоненциальный рост.
- Если основа, [латекс] b [/ латекс], меньше [латекс] 1 [/ латекс] (но больше, чем [латекс] 0 [/ латекс]), функция экспоненциально уменьшается со скоростью [латекс] b [/латекс].x [/ latex] принимает только положительные значения и имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты.
Ключевые термины
- экспоненциальный рост : рост стоимости количества, скорость роста которого пропорциональна мгновенному значению количества; например, когда стоимость увеличилась вдвое, скорость увеличения также увеличится вдвое.
 Ставка может быть положительной или отрицательной. Если отрицательный, он также известен как экспоненциальный спад.
Ставка может быть положительной или отрицательной. Если отрицательный, он также известен как экспоненциальный спад. - асимптота : линия, к которой кривая приближается произвольно близко.Асимптота может быть вертикальной, наклонной или горизонтальной. Горизонтальные асимптоты соответствуют значению, к которому кривая приближается, когда [latex] x [/ latex] становится очень большим или очень маленьким.
- экспоненциальная функция : любая функция, в которой независимая переменная представлена в форме экспоненты; они являются обратными функциями логарифмов.
Определения
На самом базовом уровне экспоненциальная функция — это функция, в которой переменная появляется в экспоненте.x [/ latex], когда [latex] b> 1 [/ latex]. Один из способов построить график этой функции — выбрать значения для [latex] x [/ latex] и подставить их в уравнение для генерации значений для [latex] y [/ latex]. При этом мы можем получить следующие баллы:
[латекс] (- 2, \ frac {1} {4}) [/ латекс], [латекс] (- 1, \ frac {1} {2}) [/ латекс], [латекс] (0,1 ) [/ латекс], [латекс] (1,2) [/ латекс] и [латекс] (2,4) [/ латекс]
При соединении точек вы заметите плавную кривую, которая пересекает ось [latex] y [/ latex] в точке [latex] (0,1) [/ latex] и увеличивается как [latex] x [ / latex] принимает все большие и большие значения.
 x [/ latex], когда [latex] 0
x [/ latex], когда [latex] 0 [латекс] (- 2,4) [/ латекс], [латекс] (- 1,2) [/ латекс], [латекс] (0,1) [/ латекс], [латекс] (1, \ frac {1} {2}) [/ latex] и [latex] (2, \ frac {1} {4}) [/ latex]
При соединении точек вы заметите плавную кривую, которая пересекает ось Y в точке [latex] (0,1) [/ latex] и уменьшается по мере того, как [latex] x [/ latex] принимает все больше и больше значения.х [/ латекс]. Поскольку [latex] 1 [/ latex] к любой мощности дает [latex] 1 [/ latex], функция эквивалентна [latex] y = 1 [/ latex], которая представляет собой горизонтальную линию, а не экспоненциальное уравнение.
Если [latex] b [/ latex] отрицательно, то увеличение [latex] b [/ latex] до четной степени приводит к положительному значению для [latex] y [/ latex] при увеличении [latex] b [/ latex] ] в нечетную степень приводит к отрицательному значению [latex] y [/ latex], что делает невозможным соединение полученных точек каким-либо осмысленным способом и, конечно, не таким образом, который генерирует кривую, как в приведенных выше примерах.
 x [/ latex] имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты, потому что кривая всегда будет приближаться к оси [latex] x [/ latex], когда [latex] x [/ latex] приближается к положительному или отрицательная бесконечность, но никогда не пересечет ось, так как никогда не будет равна нулю.
x [/ latex] имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты, потому что кривая всегда будет приближаться к оси [latex] x [/ latex], когда [latex] x [/ latex] приближается к положительному или отрицательная бесконечность, но никогда не пересечет ось, так как никогда не будет равна нулю.Графики логарифмических функций
Логарифмические функции могут быть построены вручную или в электронном виде с точками, обычно определяемыми с помощью калькулятора или таблицы.
Цели обучения
Описать свойства графиков логарифмических функций
Основные выводы
Ключевые моменты
- На графике логарифмическая функция похожа по форме на функцию квадратного корня, но с вертикальной асимптотой, поскольку [latex] x [/ latex] приближается к [latex] 0 [/ latex] справа.
- Точка [latex] (1,0) [/ latex] находится на графике всех логарифмических функций вида [latex] y = log {_b} x [/ latex], где [latex] b [/ latex] положительное действительное число.

- Область логарифмической функции [latex] y = log {_b} x [/ latex], где [latex] b [/ latex] — все положительные действительные числа, представляет собой набор всех положительных действительных чисел, тогда как диапазон эта функция — все действительные числа.
- График логарифмической функции вида [латекс] y = log {_b} x [/ latex] может быть сдвинут по горизонтали и / или вертикали, добавив константу к переменной [latex] x [/ latex] или к [ латекс] и [/ латекс] соответственно.
- Логарифмическая функция вида [latex] y = log {_b} x [/ latex], где [latex] b [/ latex] — положительное вещественное число, может быть построена с помощью калькулятора для определения точек на графике или можно изобразить без калькулятора, используя тот факт, что его обратная функция является экспоненциальной функцией.
Ключевые термины
- логарифмическая функция : Любая функция, в которой независимая переменная отображается в виде логарифма.
 Обратный к логарифмической функции является экспоненциальной функцией и наоборот.
Обратный к логарифмической функции является экспоненциальной функцией и наоборот. - логарифм : Логарифм числа — это показатель степени, на который нужно возвести другое фиксированное значение, основание, чтобы получить это число.
- асимптота : линия, к которой кривая приближается произвольно близко. Асимптоты могут быть горизонтальными, вертикальными или наклонными.
Ниже приведены графики логарифмических функций с основаниями 2, [latex] e [/ latex] и 10.
Логарифмические графики: После [latex] x = 1 [/ latex], где графики пересекают ось [latex] x [/ latex], [latex] \ log_2 (x) [/ latex] красный находится выше [latex] \ log_e (x) [/ latex] зеленого цвета, который выше [latex] \ log_ {10} (x) [/ latex] синего цвета.До этого момента порядок обратный. Все три логарифма имеют ось [latex] y [/ latex] в качестве вертикальной асимптоты и всегда увеличиваются.
Все три логарифмических графика начинаются с крутого подъема после [latex] x = 0 [/ latex], но растягиваются все больше и больше по горизонтали, их наклон уменьшается по мере увеличения [latex] x [/ latex].
 Все они пересекают ось [latex] x [/ latex] в [latex] x = 1 [/ latex].
Все они пересекают ось [latex] x [/ latex] в [latex] x = 1 [/ latex].Свойства графов логарифмических функций
Особые очки
График пересекает ось [latex] x [/ latex] в точке [latex] 1 [/ latex].у = 1 [/ латекс]. Поскольку [latex] b> 0 [/ latex], искомый показатель степени равен [latex] 1 [/ latex] независимо от значения [latex] b [/ latex]. Это означает, что точка [latex] (x, y) = (1,0) [/ latex] всегда будет на логарифмической функции этого типа.
Асимптоты
Ось [latex] y [/ latex] — это вертикальная асимптота графа. Это означает, что кривая приближается к оси [латекс] y [/ латекс], но не пересекает ее.
Давайте посмотрим, что происходит, когда значение [latex] x [/ latex] приближается к нулю справа для уравнения, график которого показан выше.А именно [латекс] y = бревно {_b} x [/ латекс]. Мы можем сделать это, выбрав значения для [latex] x [/ latex], подставив их в уравнение и сгенерировав значения для [latex] y [/ latex].
Предположим, что [latex] b [/ latex] является положительным числом больше, чем [latex] 1 [/ latex], и давайте исследуем значения [latex] x [/ latex] между [latex] 0 [/ latex] ] и [латекс] 1 [/ латекс].
 В этих условиях, если мы допустим [latex] x = \ frac {1} {b} [/ latex], уравнение станет [latex] y = log \ frac {1} {b} [/ latex].
В этих условиях, если мы допустим [latex] x = \ frac {1} {b} [/ latex], уравнение станет [latex] y = log \ frac {1} {b} [/ latex].Таким образом, мы ищем такой показатель степени, что [latex] b [/ latex], возведенный к этому показателю, дает [latex] \ frac {1} {b} [/ latex].{1000}}, — 1000) [/ латекс]
Как видно, чем ближе значение [latex] x [/ latex] к [latex] 0 [/ latex], тем более отрицательным становится график. То есть, когда [latex] x [/ latex] приближается к нулю, график приближается к отрицательной бесконечности. Это означает, что ось [latex] y [/ latex] является вертикальной асимптотой функции.
Домен и диапазон
Область определения функции — все положительные числа. Это означает, что значение функции [latex] x [/ latex] всегда будет положительным.Давайте начнем с рассмотрения, почему значение кривой [latex] x [/ latex] никогда не равно [latex] 0 [/ latex].
Если бы значение [latex] x [/ latex] было равно нулю, функция считала бы [latex] y = log {_b} 0 [/ latex].

Здесь мы ищем такой показатель степени, что [latex] b [/ latex], возведенный в эту экспоненту, равен [latex] 0 [/ latex]. Поскольку [latex] b [/ latex] является положительным числом, не существует показателя, в который мы могли бы возвести [latex] b [/ latex], чтобы получить [latex] 0 [/ latex]. Фактически, поскольку [latex] b [/ latex] положительное значение, возведение его в степень всегда будет давать положительное число.
Диапазон функции — все действительные числа. То есть график может принимать любое действительное число.
Сравнение [latex] y = log {_x} [/ latex] и [latex] y = \ sqrt {x} [/ latex]
На первый взгляд график логарифмической функции легко принять за график функции квадратного корня.
График [latex] y = \ sqrt {x} [/ latex] : График функции квадратного корня напоминает график логарифмической функции, но не имеет вертикальной асимптоты.
Как квадратный корень, так и логарифмические функции имеют домен, ограниченный значениями [latex] x [/ latex] больше, чем [latex] 0 [/ latex].
 Однако у логарифмической функции есть вертикальная асимптота, убывающая в сторону [латекс] — \ infty [/ latex], когда [latex] x [/ latex] приближается к [latex] 0 [/ latex], тогда как квадратный корень достигает минимума [латекс] y [/ latex] -значение [latex] 0 [/ latex]. Диапазон функции квадратного корня — это все неотрицательные действительные числа, тогда как диапазон логарифмической функции — все действительные числа.
Однако у логарифмической функции есть вертикальная асимптота, убывающая в сторону [латекс] — \ infty [/ latex], когда [latex] x [/ latex] приближается к [latex] 0 [/ latex], тогда как квадратный корень достигает минимума [латекс] y [/ latex] -значение [latex] 0 [/ latex]. Диапазон функции квадратного корня — это все неотрицательные действительные числа, тогда как диапазон логарифмической функции — все действительные числа.Графические логарифмические функции
Графические логарифмические функции могут быть выполнены путем определения точек на кривой вручную или с помощью калькулятора.
При построении графиков без калькулятора мы используем тот факт, что обратная логарифмическая функция является экспоненциальной функцией.
При построении графиков с помощью калькулятора мы используем тот факт, что калькулятор может вычислять только десятичные логарифмы (основание — [латекс] 10 [/ latex]), натуральные логарифмы (основание — [латекс] е [/ латекс]) или двоичные логарифмы ( основа [латекс] 2 [/ латекс]).
 y = x [/ латекс]
y = x [/ латекс]Теперь рассмотрим инверсию этой функции.х = у [/ латекс]. Однако, если мы поменяем местами координаты [latex] x [/ latex] и [latex] y [/ latex] каждой точки, мы фактически получим список точек исходной функции.
Это: [латекс] (\ frac {1} {9}, — 2), (\ frac {1} {3}, — 1), (1,0), (3,1), (9, 2) [/ латекс] и [латекс] (27,3) [/ латекс].
Мы строим и соединяем эти точки, чтобы получить график функции [latex] y = log {_3} x [/ latex] ниже.
График [latex] y = log {_3} x [/ latex]: График логарифмической функции с основанием [latex] 3 [/ latex] может быть создан с использованием обратного преобразования функции.Его форма такая же, как и у других логарифмических функций, только в другом масштабе.
Графические логарифмические функции с основаниями между [latex] 0 [/ latex] и [latex] 1 [/ latex]
Итак, мы построили график логарифмических функций, основания которых больше [latex] 1 [/ latex]. Если вместо этого мы рассмотрим логарифмические функции с основанием [latex] b [/ latex], таким, что [latex] 0
Фактически, если [latex] b> 0 [/ latex], график [latex] y = log {_b} x [/ latex] и график [latex] y = log {_ \ frac {1} { b}} x [/ latex] симметричны по оси [latex] x [/ latex].Таким образом, если мы идентифицируем точку [latex] (x, y) [/ latex] на графике [latex] y = log {_b} x [/ latex], мы можем найти соответствующую точку на [latex] y = log {_ \ frac {1} {b}} x [/ latex], изменив знак координаты [latex] y [/ latex]. Соответствующая точка — [латекс] (x, -y) [/ latex].
Вот пример для [latex] b = 2 [/ latex].
Графики [latex] log {_2} x [/ latex] и [latex] log {_ \ frac {1} {2}} x [/ latex] : Графики [latex] log_2 x [/ latex ] И [latex] log {_ \ frac {1} {2}} x [/ latex] симметричны относительно оси x
Решение задач с логарифмическими графами
Некоторые функции с быстро меняющейся формой лучше всего отображать в масштабе, который экспоненциально возрастает, например на логарифмическом графике.
Цели обучения
Преобразуйте задачи в логарифмические масштабы и обсудите преимущества этого
Основные выводы
Ключевые моменты
- В логарифмических графиках используются логарифмические шкалы, в которых значения различаются экспоненциально.
 Например, вместо отметок [латекс] 0,1,2 [/ латекс] и [латекс] 3 [/ латекс], логарифмическая шкала может включать отметки [латекс] 0,1, 1, 10 [/ латекс] и [латекс] 100 [/ латекс], каждый на одинаковом расстоянии от предыдущего и следующего.5 [/ latex] масштабируется для отображения очень широкого диапазона значений [latex] y [/ latex], кривизна около начала координат может быть неразличима на линейных осях. На логарифмических осях это намного яснее.
Например, вместо отметок [латекс] 0,1,2 [/ латекс] и [латекс] 3 [/ латекс], логарифмическая шкала может включать отметки [латекс] 0,1, 1, 10 [/ латекс] и [латекс] 100 [/ латекс], каждый на одинаковом расстоянии от предыдущего и следующего.5 [/ latex] масштабируется для отображения очень широкого диапазона значений [latex] y [/ latex], кривизна около начала координат может быть неразличима на линейных осях. На логарифмических осях это намного яснее.
Ключевые термины
- логарифм : Логарифм числа — это показатель степени, на который нужно увеличить другое фиксированное значение, основание, чтобы получить это число.
- интерполировать : для оценки значения функции между двумя точками, между которыми она табулирована.
Зачем нужна логарифмическая шкала?
Многие математические и физические зависимости функционально зависят от переменных высокого порядка. Это означает, что при небольших изменениях в независимой переменной происходят очень большие изменения в зависимой переменной.
 Таким образом, становится трудно построить график таких функций на стандартной оси.
Таким образом, становится трудно построить график таких функций на стандартной оси.Рассмотрим, например, закон Стефана-Больцмана, который связывает мощность (j * ), излучаемую черным телом, с температурой (T).4 [/ латекс]
На стандартном графике это уравнение может быть довольно громоздким. Зависимость четвертой степени от температуры означает, что мощность увеличивается чрезвычайно быстро. Тот факт, что скорость постоянно увеличивается (и очень круто), означает, что изменение масштаба (масштабирование осей на [латекс] 5 [/ латекс], [латекс] 10 [/ латекс] или даже [латекс] 100 [/ латекс]) ) мало помогает облегчить интерпретацию графика.
Для очень крутых функций можно строить точки более плавно, сохраняя целостность данных: можно использовать график с логарифмической шкалой, где вместо каждого пробела на графике, представляющего постоянное увеличение, он представляет экспоненциальное увеличение .Если нормальный (линейный) график может иметь равные интервалы, идущие от 1, 2, 3, 4, то в логарифмической шкале те же равные интервалы будут представлять 1, 10, 100, 1000.
 x, f (x) = x [/ latex] и [latex] f (x) = \ log x [/ latex] на четырех разные координатные участки.Слева вверху — линейная шкала, справа вверху и слева внизу — полулогарифмические шкалы, а справа внизу — логарифмическая шкала.
x, f (x) = x [/ latex] и [latex] f (x) = \ log x [/ latex] на четырех разные координатные участки.Слева вверху — линейная шкала, справа вверху и слева внизу — полулогарифмические шкалы, а справа внизу — логарифмическая шкала.Как видите, когда обе оси использовали логарифмическую шкалу (внизу справа), график сохранил свойства исходного графика (вверху слева), где обе оси были масштабированы с использованием линейной шкалы. Это означает, что если мы хотим построить график функции, которая является громоздкой в линейном масштабе, мы можем использовать логарифмическую шкалу на каждой оси и сохранить свойства графика, в то же время облегчая построение графика.
В полулогарифмических масштабах функции имеют искаженные формы относительно оригинала. Когда только ось [latex] x [/ latex] имеет логарифмический масштаб, логарифмическая кривая отображается в виде линии, а линейная и экспоненциальная кривые выглядят экспоненциально. Когда только ось [латекс] y [/ латекс] имеет логарифмический масштаб, экспоненциальная кривая отображается как линия, а линейная и логарифмическая кривые выглядят как логарифмические.
 Следует отметить, что примеры на графиках предназначены для иллюстрации точки и что изображенные на графике функции не обязательно были громоздкими на линейно масштабируемом наборе осей.
Следует отметить, что примеры на графиках предназначены для иллюстрации точки и что изображенные на графике функции не обязательно были громоздкими на линейно масштабируемом наборе осей.Преобразование линейной шкалы в логарифмическую
Основное различие между логарифмической и линейной шкалами состоит в том, что, в то время как разница в значениях между линейными точками равного расстояния остается постоянной (то есть, если промежуток от [latex] 0 [/ latex] до [latex] 1 [/ latex] ] по шкале [латекс] 1 [/ латекс] см на странице, расстояние от [латекса] 1 [/ латекса] до [латекса] 2 [/ латекса], от [латекса] 2 [/ латекса] до [латекса ] 3 [/ latex] и т. Д. Будут одинаковыми) разница значений между точками по логарифмической шкале будет меняться экспоненциально.Логарифмическая шкала начинается с определенной степени [латекс] 10 [/ латекс], и с каждой единицей увеличивается на степень [латекс] 10 [/ латекс].
Таким образом, если кто-то хочет преобразовать линейную шкалу (со значениями [latex] 0-5 [/ latex] в логарифмическую шкалу, одним вариантом будет замена [latex] 1,2,3,4 [/ latex] и 5 с [латексом] 0,001,0,01,0,1,1,1,10 [/ латекс] и [латекс] 100 [/ латекс], соответственно.
 Между каждым основным значением на логарифмической шкале хэш-метки становятся все ближе друг к другу с увеличением значения.Например, в пространстве между [latex] 1 [/ latex] и [latex] 10 [/ latex], [latex] 8 [/ latex] и [latex] 9 [/ latex] расположены гораздо ближе друг к другу, чем [ латекс] 2 [/ латекс] и [латекс] 3 [/ латекс].
Между каждым основным значением на логарифмической шкале хэш-метки становятся все ближе друг к другу с увеличением значения.Например, в пространстве между [latex] 1 [/ latex] и [latex] 10 [/ latex], [latex] 8 [/ latex] и [latex] 9 [/ latex] расположены гораздо ближе друг к другу, чем [ латекс] 2 [/ латекс] и [латекс] 3 [/ латекс].Использование логарифмической шкалы имеет два преимущества. Во-первых, это позволяет построить очень большой диапазон данных без потери формы графика. Во-вторых, он позволяет выполнять интерполяцию в любой точке графика, независимо от диапазона графика. Подобные данные в линейном масштабе менее ясны.b = (b) \ log (a) [/ латекс]
Используя вышеизложенное, наше уравнение принимает следующий вид:
[латекс] \ begin {align} \ log j & = 4 \ log {(\ sigma \ tau)} \\ & = 4 \ log {(\ sigma)} + 4 \ log {(\ tau)} \\ & = 4 \ log {(\ tau)} +4 \ log {(\ sigma)} \ end {align} [/ latex]
Решение экспоненциальных уравнений
Экспоненциальные уравнения — это уравнения, в которых переменные встречаются как показатели.

Например, экспоненциальные уравнения имеют вид а Икс знак равно б y .
Чтобы решить экспоненциальные уравнения с той же базой, используйте свойство равенства из экспоненциальные функции .
Если б положительное число, отличное от 1 , тогда б Икс знак равно б y если и только если Икс знак равно y . Другими словами, если основания одинаковые, то экспоненты должны быть одинаковыми.
Пример 1:
Решите уравнение 4 2 Икс — 1 знак равно 64 .
Учтите, что основания не совпадают. Но мы можем переписать 64 в качестве основы 4 .
Мы знаем это, 4 3 знак равно 64 .

Переписать 64 в виде 4 3 так что у каждой стороны одинаковое основание.
4 2 Икс — 1 знак равно 4 3
По свойству равенства экспонент, если основания одинаковые, то показатели должны быть равны.
2 Икс — 1 знак равно 3
Добавлять 1 в каждую сторону.
2 Икс — 1 + 1 знак равно 3 + 1 2 Икс знак равно 4
Разделите каждую сторону на 2 .

2 Икс 2 знак равно 4 2 Икс знак равно 2
Примечание:
Если основания не совпадают, используйте логарифмы для решения экспоненциальных уравнений. Видеть Решение экспоненциальных уравнений с использованием логарифмов .
Экспоненциальных функций
Экспоненциальные функции
Алгебраическое представление
Все экспоненциальные функции являются родственниками этого примитива двухпараметрического семейства . Вариации внутри расширенной семьи — это плавные смены, растяжки и трансформации этого общего запаса.
Параметр a называется точкой пересечения по оси y функции , а параметр b называется базой .
 Вместе они полностью определяют поведение ввода-вывода экспоненциальной функции.
Вместе они полностью определяют поведение ввода-вывода экспоненциальной функции.Обратите внимание, что f (0) = ab 0 = a1 = a: точка пересечения по оси Y — это выход, когда вход равен 0.
Когда a = 0 или b = 0, функция упрощается до y = f (x) = 0 или до тривиальной постоянной функции , выход которой равен 0 для каждого входа. Когда b = 1, функция упрощается до y = f (x) = a1 x = a1 = a, или до постоянной функции, выходом которой является a для каждого входа.
Поскольку многие выражения с отрицательным основанием, например (–1) 1/2 или (–5.3) 7/4 , не имеют алгебраического смысла (они не определяют никаких действительных чисел), и поскольку основание 0 приводит к тривиальной постоянной функции, мы обычно добавляем следующее ограничение для экспоненциальных функций:
Основание b в экспоненциальной функции должно быть положительным.

Поскольку мы работаем только с положительными основаниями, b x всегда положительно.Следовательно, значения f (x) либо всегда положительны, либо всегда отрицательны, в зависимости от знака a. Экспоненциальные функции находятся полностью на одной или другой стороне оси абсцисс. Мы говорим, что у них ограниченный диапазон .
Основание b определяет скорость роста или распада:
- Если 0, функция убывает при увеличении x. (Например, (1/2) 1 > (1/2) 2 > (1/2) 3 .) Меньшие значения b приводят к более быстрому спаду.
- Если b> 1, функция растет на с увеличением x. (Например, (2) 1 (2) 2 (2) 3 .) Большие значения b приводят к более быстрым темпам роста.
Ключевым алгебраическим свойством экспоненциальных функций является следующее:
То есть увеличение любого входа x на постоянный интервал Dx изменяет выход на постоянное кратное b Dx .
 Это свойство экспоненциальных функций легче всего распознать при моделировании.
Это свойство экспоненциальных функций легче всего распознать при моделировании.Есть несколько важных частных случаев вышеупомянутого свойства:
- Когда b> 1 (рост), мы можем выбрать Dx так, чтобы b Dx = 2. Тогда для любого x f (x + Dx) = 2f (x). Мы называем этот входной интервал Dx временем удвоения функции. Каждая растущая экспонента имеет уникальное время удвоения.
- Когда 0 (затухание), мы можем выбрать Dx так, чтобы b Dx = 1 / e, где e = 2.71828 …. Тогда для любого x f (x + Dx) = f (x) / e. Мы называем этот входной интервал Dx критическим временем функции. Каждая убывающая экспонента имеет уникальное критическое время.
Вам может быть интересно узнать о числе e = 2,71828 … , которое используется для определения критического времени убывающей экспоненты. Что это за номер? Его иногда называют естественным основанием экспоненты , и вы узнаете о нем гораздо больше, когда будете изучать математический анализ.
 Если вам сейчас интересно, вы можете узнать больше о числе e, изучив некоторые примеры в следующем всплывающем окне:
Если вам сейчас интересно, вы можете узнать больше о числе e, изучив некоторые примеры в следующем всплывающем окне:Номер e :
Слово «естественный» в «естественном основании экспоненты» предполагает определенную важность. Действительно, в исчислении и во многих приложениях b = e является базой выбора для экспоненциальных функций. Это всегда можно устроить, так как для любого b> 0 мы можем найти k так, чтобы e k = b. Затем мы можем переписать f (x) = ab x как:
То есть любую экспоненциальную функцию можно переписать с натуральным основанием, если мы умножим показатель степени на соответствующий коэффициент k.x`
, где b — основание , а x — показатель степени (или степени ).
Если b больше, чем «1», функция непрерывно увеличивается в значении по мере увеличения x . Особое свойство экспоненциальных функций состоит в том, что наклон функции также непрерывно увеличивается по мере увеличения x .
 x.
x.Уведомление:
- При увеличении x также увеличивается y .
- По мере увеличения x наклон графика также увеличивается.
- Кривая проходит через `(0, 1)`. Все экспоненциальные кривые вида f ( x ) = b x проходят через `(0, 1)`, если `b> 0`.
- Кривая не проходит через ось x . Он становится все ближе и ближе к оси x по мере того, как мы берем все меньшие и меньшие значения x .2 = 9`
В этом случае основание равно «3», а показатель степени равно «2». Мы можем записать это уравнение в виде логарифма (с идентичным значением) следующим образом:
`log_3 9 = 2`
Мы говорим это так: «логарифм« 9 »по основанию« 3 »равен« 2 ». Что мы фактически сделали, так это переместили показатель степени вниз на основную строку.
 Исторически это делалось для упрощения умножения и деления, но логарифмы по-прежнему очень удобны в математике.
Исторически это делалось для упрощения умножения и деления, но логарифмы по-прежнему очень удобны в математике.Логарифмическая функция определяется как:
`f (x) = log_b x`
Основание логарифма составляет b .
Две наиболее распространенные базы, которые мы используем, — это база «10» и база e , которые мы встречаем в логах по базе 10 и естественных логарифмах (база и ) в следующих разделах.
Логарифмическая функция имеет множество реальных приложений в акустике, электронике, анализе землетрясений и прогнозировании населения.(1 «/» 2)) = 1 / sqrt16 = 1 / 4`
В виде логарифма это можно записать как:
`log_16 (1/4) = −1 / 2`
Свойства экспоненциальных и логарифмических функций
EXP1 — Определение экспоненциальной функции : Если f (x) — функция, которую можно записать в форме f (x) = a x , где a> 0, a ≠ 1 и x — любое действительное число, тогда f (x) — экспоненциальная функция, а «a» называется «базой».

Обратите внимание, что функции, являющиеся составной частью экспоненциальной функция и некоторые другие функции также часто упоминаются как экспоненциальные функции. Например, f (x) = 2 ● 3 -2x — 1 будет называться рациональной функцией.
EXP2 — Определение естественного экспоненциального основания : Основание экспоненты «е» равно иррациональному числу. 2.718281828459 … и также определяется как
EXP3 — Горизонтальная асимптота графа базового Графики экспоненциальной функции : Учитывая экспоненциальную функцию f (x) = x , его график будет иметь горизонтальную асимптоту y = 0 для только левая сторона.
EXP4 — Правила сдвига функций, применяемые к экспоненциальному Графики функций : дана экспоненциальная функция f (x) = a x ,
График g (x) = a -x будет отражением f (x) по оси y =.

График h (x) = k ● x будет вертикальным отрезком f (x), но будет иметь такую же общую форму.
График p (x) = -k ● x будет отражением k ● x по оси абсцисс.
EXP5 — Определение логарифмической функции : Учитывая экспоненциальную функцию y = a x , эквивалент Логарифмическая функция имеет вид log a y = x.
Другими словами, вы всегда можете переписать журнал на y = x поскольку y = a x и
, вы всегда можете переписать y = a x как log a y = xEXP6 — Обратное свойство логарифмической функции : Учитывая экспоненциальную функцию f (x) = a x ,
, обратная функция f (x) является логарифмической функцией в виде f -1 (x). = журнал a x.
Также, поскольку (f o f -1 ) (x) = x и (f -1 o f) (x) = x
EXP7 — Свойство журнала — журнал 1 равен 0 : Учитывая логарифмическая функция f (x) = log a x, f (1) = 0.
Другими словами, log a 1 = 0 для любого допустимого экспоненциальное основание a .
EXP8 — Свойство журнала — Журнал a a is 1 : Учитывая логарифмическую функцию f (x) = log a x, f (a) = 1.
Другими словами, log a a = 1 для любого допустимого экспоненциальное основание a .
EXP9 — Правило продукта для журналов : Учитывая логарифмическая функция f (x) = log a x, f (UV) = f (U) + f (V).
Другими словами, log a (UV) = log a U + Log a V для любой допустимой экспоненциальной базы a .

EXP10 — Правило частного для журналов : Учитывая логарифмическая функция f (x) = log a x, f (U / V) = f (U) — f (V).
Другими словами, для любого действительного экспоненциального основания a .
EXP11 — Правило мощности для журналов : Учитывая логарифмическая функция f (x) = log a x, f (x N ) = N ● f (x).
Другими словами, log a (x N ) = N ● log a x.
EXP12 — Изменение основного правила для журналов : Учитывая логарифмическая функция f (x) = log a x, это правда, для любые законные базы a и b , что
Другими словами, мы можем выбрать любую удобную базу b , которая мы хотим (например, base-e или 10), и перепишем наш логарифм как соотношение два бревна base-b.






 Например:
Например:

 Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)—t/t0 , где m0 — первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e—kt, используя данную формулу ученые рассчитали возраст Земли (радий распадается нормально за время равное возрасту Земли).
Этот промежуток времени t0 называется периодом полураспада. Общая формула для этого процесса: m = m0(1/2)—t/t0 , где m0 — первоначальная масса вещества. Чем больше период полураспада, тем медленнее распадается вещество. Это явление используют для определения возраста археологических находок. Радий, например распадается по закону: M = M0e—kt, используя данную формулу ученые рассчитали возраст Земли (радий распадается нормально за время равное возрасту Земли).
 x [/ latex], где [latex] b> 0 [/ latex] — это функция, которая остается пропорциональной своему исходному значению при увеличении или уменьшении.
x [/ latex], где [latex] b> 0 [/ latex] — это функция, которая остается пропорциональной своему исходному значению при увеличении или уменьшении. Ставка может быть положительной или отрицательной. Если отрицательный, он также известен как экспоненциальный спад.
Ставка может быть положительной или отрицательной. Если отрицательный, он также известен как экспоненциальный спад. x [/ latex], когда [latex] 0
x [/ latex], когда [latex] 0  x [/ latex] имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты, потому что кривая всегда будет приближаться к оси [latex] x [/ latex], когда [latex] x [/ latex] приближается к положительному или отрицательная бесконечность, но никогда не пересечет ось, так как никогда не будет равна нулю.
x [/ latex] имеет ось [latex] x [/ latex] в качестве горизонтальной асимптоты, потому что кривая всегда будет приближаться к оси [latex] x [/ latex], когда [latex] x [/ latex] приближается к положительному или отрицательная бесконечность, но никогда не пересечет ось, так как никогда не будет равна нулю.
 Обратный к логарифмической функции является экспоненциальной функцией и наоборот.
Обратный к логарифмической функции является экспоненциальной функцией и наоборот. Все они пересекают ось [latex] x [/ latex] в [latex] x = 1 [/ latex].
Все они пересекают ось [latex] x [/ latex] в [latex] x = 1 [/ latex]. В этих условиях, если мы допустим [latex] x = \ frac {1} {b} [/ latex], уравнение станет [latex] y = log \ frac {1} {b} [/ latex].
В этих условиях, если мы допустим [latex] x = \ frac {1} {b} [/ latex], уравнение станет [latex] y = log \ frac {1} {b} [/ latex].
 Однако у логарифмической функции есть вертикальная асимптота, убывающая в сторону [латекс] — \ infty [/ latex], когда [latex] x [/ latex] приближается к [latex] 0 [/ latex], тогда как квадратный корень достигает минимума [латекс] y [/ latex] -значение [latex] 0 [/ latex]. Диапазон функции квадратного корня — это все неотрицательные действительные числа, тогда как диапазон логарифмической функции — все действительные числа.
Однако у логарифмической функции есть вертикальная асимптота, убывающая в сторону [латекс] — \ infty [/ latex], когда [latex] x [/ latex] приближается к [latex] 0 [/ latex], тогда как квадратный корень достигает минимума [латекс] y [/ latex] -значение [latex] 0 [/ latex]. Диапазон функции квадратного корня — это все неотрицательные действительные числа, тогда как диапазон логарифмической функции — все действительные числа. y = x [/ латекс]
y = x [/ латекс]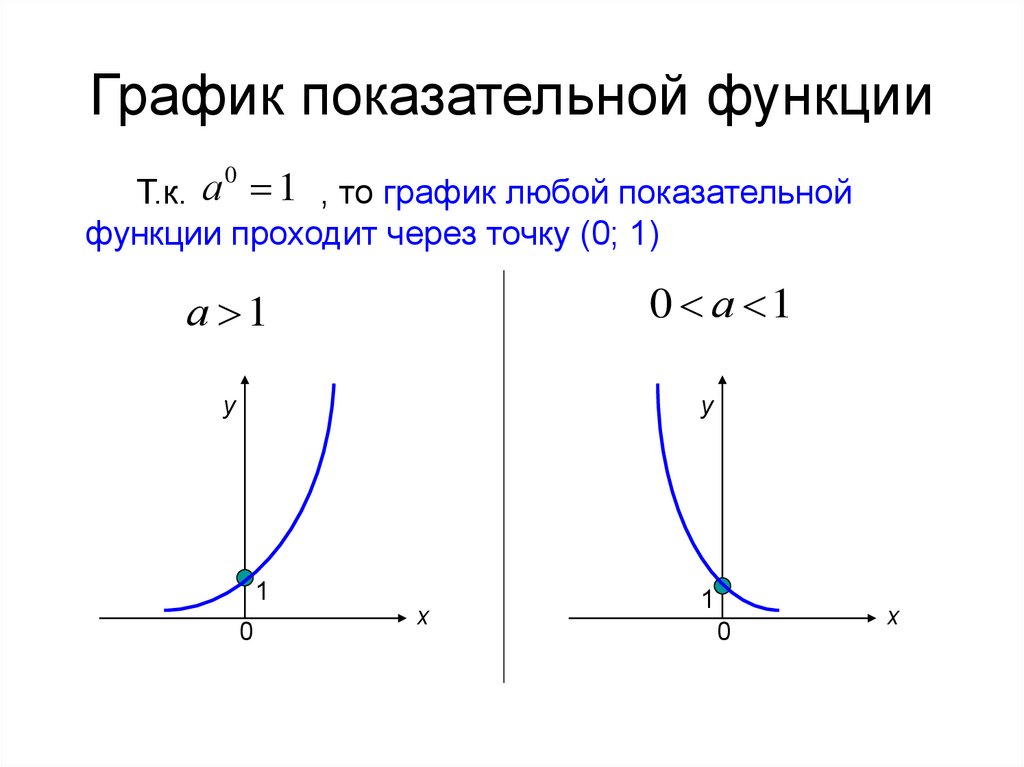 Например, вместо отметок [латекс] 0,1,2 [/ латекс] и [латекс] 3 [/ латекс], логарифмическая шкала может включать отметки [латекс] 0,1, 1, 10 [/ латекс] и [латекс] 100 [/ латекс], каждый на одинаковом расстоянии от предыдущего и следующего.5 [/ latex] масштабируется для отображения очень широкого диапазона значений [latex] y [/ latex], кривизна около начала координат может быть неразличима на линейных осях. На логарифмических осях это намного яснее.
Например, вместо отметок [латекс] 0,1,2 [/ латекс] и [латекс] 3 [/ латекс], логарифмическая шкала может включать отметки [латекс] 0,1, 1, 10 [/ латекс] и [латекс] 100 [/ латекс], каждый на одинаковом расстоянии от предыдущего и следующего.5 [/ latex] масштабируется для отображения очень широкого диапазона значений [latex] y [/ latex], кривизна около начала координат может быть неразличима на линейных осях. На логарифмических осях это намного яснее. Таким образом, становится трудно построить график таких функций на стандартной оси.
Таким образом, становится трудно построить график таких функций на стандартной оси. x, f (x) = x [/ latex] и [latex] f (x) = \ log x [/ latex] на четырех разные координатные участки.Слева вверху — линейная шкала, справа вверху и слева внизу — полулогарифмические шкалы, а справа внизу — логарифмическая шкала.
x, f (x) = x [/ latex] и [latex] f (x) = \ log x [/ latex] на четырех разные координатные участки.Слева вверху — линейная шкала, справа вверху и слева внизу — полулогарифмические шкалы, а справа внизу — логарифмическая шкала. Следует отметить, что примеры на графиках предназначены для иллюстрации точки и что изображенные на графике функции не обязательно были громоздкими на линейно масштабируемом наборе осей.
Следует отметить, что примеры на графиках предназначены для иллюстрации точки и что изображенные на графике функции не обязательно были громоздкими на линейно масштабируемом наборе осей. Между каждым основным значением на логарифмической шкале хэш-метки становятся все ближе друг к другу с увеличением значения.Например, в пространстве между [latex] 1 [/ latex] и [latex] 10 [/ latex], [latex] 8 [/ latex] и [latex] 9 [/ latex] расположены гораздо ближе друг к другу, чем [ латекс] 2 [/ латекс] и [латекс] 3 [/ латекс].
Между каждым основным значением на логарифмической шкале хэш-метки становятся все ближе друг к другу с увеличением значения.Например, в пространстве между [latex] 1 [/ latex] и [latex] 10 [/ latex], [latex] 8 [/ latex] и [latex] 9 [/ latex] расположены гораздо ближе друг к другу, чем [ латекс] 2 [/ латекс] и [латекс] 3 [/ латекс].

 Вместе они полностью определяют поведение ввода-вывода экспоненциальной функции.
Вместе они полностью определяют поведение ввода-вывода экспоненциальной функции.
 Это свойство экспоненциальных функций легче всего распознать при моделировании.
Это свойство экспоненциальных функций легче всего распознать при моделировании. Если вам сейчас интересно, вы можете узнать больше о числе e, изучив некоторые примеры в следующем всплывающем окне:
Если вам сейчас интересно, вы можете узнать больше о числе e, изучив некоторые примеры в следующем всплывающем окне: x.
x. Исторически это делалось для упрощения умножения и деления, но логарифмы по-прежнему очень удобны в математике.
Исторически это делалось для упрощения умножения и деления, но логарифмы по-прежнему очень удобны в математике.