Решение задач на арифметическую и геометрическую прогрессии
Геометрическая прогрессия
Определение геометрической прогрессии
Последовательность 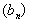 , первый член которой отличен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называется геометрической прогрессией. Число q — знаменатель прогрессии. Таким образом, геометрическая прогрессия есть последовательность, заданная рекуррентно равенством
, первый член которой отличен от нуля и каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же отличное от нуля число q, называется геометрической прогрессией. Число q — знаменатель прогрессии. Таким образом, геометрическая прогрессия есть последовательность, заданная рекуррентно равенством 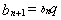 , где
, где 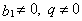 .
.
Отношение любого члена геометрической прогрессии и ему предшествующего члена, равно одному и тому же числу
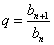
Если
 , то
, то  — монотонна
— монотоннаЕсли
 , то
, то  — постоянна
— постоянна
Последовательность 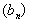
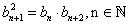 .
.Произведение членов геометрической прогрессии, равностоящих от концов прогрессии, есть величина постоянная.
Формула n-ого члена геометрической прогрессии:
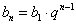 , где
, где 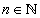
Формулы суммы n членов геометрической прогрессии:


Сумма бесконечной геометрической прогрессии при
 равна
равна 
Решение задач на арифметическую и геометрическую прогрессии
Цель урока: уточнить, обобщить и систематизировать знания по теме «Арифметическая и геометрическая прогрессии» и закрепить умения и навыки в решении задач на прогрессии.
Задачи:
- Вспомнить необходимые правила, научить учащихся применять их при решении различных примеров.
- Развивать математические способности.
- Воспитывать математическую грамотность и прилежность.
Оборудование:
- индивидуальные пластиковые доски у каждого ученика;
- стенд, кодоскоп, экран, конверты с заданиями.
План урока:
- Проверка домашнего задания.
- Повторение теории.
- Устные упражнения.
- Диагностический замер.
- Решение упражнений.
- Домашнее задание.
- Тест.
- Итог урока.
- Дополнительное задание.
Ход урока.
Введение в урок: сообщение целей и задач урока, знакомство с планом.
Проверка домашнего задания.
Учащиеся по образцу проверяют и оценивают свою домашнюю работу (через кодоскоп).
№ 1.
а5 = -3,7; d = -0,6; аn = -9,7; n – ?
а5 = а
an = a1 + d(n – 1)
-9,7 = -1,3 – 0,6(n – 1)
0,6n = 9
n = 15
Ответ: n = 15.
№ 2.
S10
– ?
d = ;
Ответ: .
№ 3.
; ; -?
Ответ: .
Учитель просит сначала поднять руку тех учеников, которые справились со всей работой, затем у кого работа вызвала затруднения.
Повторение теории.
Ученики в парах повторяют теоретический материал.
План ответа:
- Определение.
- Формула n-го члена.
- Формула суммы n-первых членов.
1 вариант отвечает по теме «Арифметическая прогрессия», 2 вариант по теме «Геометрическая прогрессия».
Устные упражнения.
(аn): 4; 9; 16; 25; …
(вn): 32; -16; 8; -4; …
(хn): 1; 8; 27; 64; …
- Какая из данных числовых последовательностей является арифметической прогрессией? (сn)
- Укажите её разность. (3)
- Найдите сумму четырёх первых членов этой прогрессии. (-6)
- Если поменять порядок членов этой прогрессии на обратный, то будет ли полученная последовательность арифметической прогрессией? (Да.)
- Укажите её разность. (-3)
- Какая из данных числовых последовательностей является геометрической прогрессией? (вn)
- Укажите знаменатель этой прогрессии. (-)
- Найдите шестой член данной прогрессии. (-1)
- Сравните в4 и в5. (в4 < в5)
- Если поменять порядок членов этой прогрессии на обратный, то будет ли полученная последовательность геометрической прогрессией? (Да.)
- Укажите знаменатель полученной прогрессии. (-2)
- Найдите сумму четырёх первых членов полученной прогрессии? (20)
Учащиеся записывают ответы на индивидуальных пластиковых досках и показывают учителю.
Диагностический замер.
(an) – арифметическая прогрессия.
- а1 = 17; d = -3; а2 – ?
- а2 = -1; d = 2; а1 – ?
- а3 = 3,2; а4 = 5,6; d – ?
- а1 = -1; d = 2; а5 – ?
- а1 = 19; а5 = -3; S5 – ?
(bn) – геометрическая прогрессия.
- b1 = -7; q = 3; b2 – ?
- b1 = -12; q = ; b3 – ?
- b5 = 6; b6 = 2; q – ?
- 2; b2; 8; 16 … b2 – ?
- b1 = 1; q = -2; S5 – ?
На выполнение этого задания 5 минут. Ученики записывают только ответы. Затем стоя проверяют ответы (учитель показывает через кодоскоп), оценивают свою работу и садятся на свои места. Учитель просит поднять руку, кто выполнил на «5», «4» и т.д.
Ответы: 14; -3; 2,4; 7; 40; -21; -3; 1/3; 4; 11.
10 пр. – «5»; 9, 8, 7 пр. – «4»; 6, 5 пр. – «3»; менее 5 пр. – «2».
Решение упражнений.
Ученики выполняют упражнения, которые оцениваются на экзамене 2 балла и 3 балла (3 ученика у доски, остальные в тетрадях). Группа учеников выполняет индивидуальное задание, которое оценивается 4 балла (после выполнения учащиеся получают лист самоконтроля). Ученики, успешно справившиеся с выполнением задания, приступают к выполнению дополнительного задания.
№ 1. Первый член арифметической прогрессии равен 6, а ее разность равна 4. Начиная с какого номера члены этой прогрессии больше 260?
аn = 6; d = 4; аn
260; n – ?
аn = а1 + d(n – 1)
аn = 6 + 4(n – 1)
6 + 4(n – 1) 260
n 64,5
Т.к. n N, n = 65.
Ответ: начиная с номера 65.
№ 2. Найдите сумму членов арифметической прогрессии с тридцатого по сороковой включительно, если аn = 3n + 5.
аn = 3n + 5; S30-40 – ?
Ответ: 1210.
№ 3. Между числами 3 и 12 вставьте три числа так, чтобы получилась геометрическая прогрессия.
Ответ:
Индивидуальное задание. Сумма первого и пятого членов геометрической прогрессии равна 51, а сумма второго и шестого членов равна 102. Сколько членов этой прогрессии, начиная с первого, нужно сложить, чтобы их сумма была равна 3069?
Ответ: 10.
Домашнее задание:
- Сумма первых трех членов геометрической прогрессии равна 39, знаменатель прогрессии равен -4. Найдите сумму первых четырех членов этой прогрессии.
- Найдите сумму всех натуральных чисел, не превосходящих 200, которые не делятся на 6.
- Найдите сумму первых восьми членов геометрической прогрессии, второй член которой равен 6, а четвертый равен 24.
*В геометрической прогрессии (bn), знаменатель которой – число
отрицательное,
b1 * b2 = -,
b3 * b4 = -8. Найдите эти четыре члена прогрессии.
Тест (на выполнение этого задания 15 минут)(см. Приложение).
Итог урока.
Дополнительное задание*. В арифметической прогрессии среднее арифметическое первых десяти ее членов равно 20. Найдите первый член и разность этой прогрессии, если известно, что они являются числами натуральными (a1 = 11, d = 2; a1 = 2, d = 4).
Прогрессия в геометрических задачах
Пример 1.
Длины сторон AB, BC, AC треугольника ABC образуют в указанном порядке арифметическую прогрессию. Найти во сколько раз высота треугольника ABC, опущенная из вершины A на сторону BC, больше радиуса, вписанной в этот треугольник окружности.
Решение.
Рассмотрим треугольник ABC и проведем в нем высоту AH = h (рис. 1).

Зная, что стороны AB, BC, AC треугольника ABC образуют в указанном порядке арифметическую прогрессию, введем следующие обозначения. Пусть AB = a, тогда BC = a + d, а AC = a + 2d. Здесь d – это разность арифметической прогрессии. Теперь запишем формулы для вычисления площади треугольника.
Итак, во-первых, SABC можно вычислить с помощью высоты, проведенной из вершины A к стороне BC. Имеем:
SABC = 1/2 AH · BC = 1/2 · h · (a + d).
Во-вторых, площадь треугольника можно вычислить с помощью полупериметра и радиуса вписанной в этот треугольник окружности:
SABC = p · r = (AB + BC + CA)/2 · r = (a + a + d + a + 2d)/2 · r = (3a + 3d) · r = = 3(a + d)/2 · r.
Полученные для площади треугольника ABC выражения можно приравнять. Будем иметь:
½ · h · (a + d) = 3(a + d)/2 · r.
Левую и правую части полученного уравнения можно сократить на (a + d) ≠ 0.
1/2 h = 3/2 r. Выразим h:
h = 3 r.
Таким образом, мы получили, что высота треугольника в три раза больше радиуса вписанной в этот треугольник окружности.
Ответ: 3.
Пример 2.
В окружность радиусом √3 вписан правильный треугольник, в треугольник вписана окружность, в окружность снова вписан правильный треугольник и т.д. Найти сумму периметров всех треугольников.
Решение.
1) Так как радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной около этого треугольника окружности, то радиус окружности, описанной коло треугольника A1A2A3 (R1 = √3) в два раза больше радиуса окружности, описанной около треугольника B1B2B3 (R2 = R1/2). Он же, в свою очередь, в два раза больше радиуса окружности, описанной около треугольника C1C2C3 (R3 = R2/2 = R1/4) и т. д. (Rn = R1/2n — 1) (рис. 2).
2) Выразим стороны правильных треугольников через радиусы описанных около них окружностей по формуле a3 = R√3. Тогда имеем:
A1A2 = R1√3;
B1B2 = R2√3 = R1√3/2;
C1C2 = R3√3 = R1√3/4 и т. д.
Периметры соответствующих треугольников равны:
PA1A2A3 = 3R1√3;
PB1B2B3 = 3R1√3/2;
PC1C2C3 = 3R1√3/4 и т. д.
Сумма периметров треугольников (3R1√3 + 3R1√3/2 + 3R1√3/4 + …) представляет собой сумму бесконечно убывающей геометрической прогрессии со знаменателем q = 1/2 и первым членом a1 = 3R1√3 = 3 · √3 · √3 = 9.
С помощью формулы суммы бесконечно убывающей геометрической прогрессии S = a1/(1 – q) находим, что
PA1A2A3 + PB1B2B3 + PC1C2C3 + … = 9/(1 – 1/2) = 18.
Ответ: 18.
К большинству задач по геометрии, а уж тем более к тем из них, в которых необходимо побороться с прогрессией, многие ученики – пользователи нашего сайта – относятся в лучшем случае настороженно. Но когда с помощью наших онлайн репетиторов ученики вдруг начинают понимать ход решения задачи и видеть, какие правила и формулы можно и нужно применять в той или иной ситуации, их чувство самооценки растет и заставляет стремиться к новым свершениям.
Самое главное в решении задач – это научиться не просто, отрешенно вчитываться в текст, а быть настроенным на получение конечного результата. Только тогда решение любой задачи станет приятным и легким делом, не будет ставить в тупик, а будет давать пищу для воображения и ума.
Решение задач – это по-настоящему творческий процесс, и Вы почувствуете это, занимаясь с нами.
Остались вопросы? Не знаете, как решать задачи по геометрии?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru, при полном или частичном копировании материала ссылка на первоисточник обязательна.
Прогрессии: задачи для продвинутых
Прогрессия – благодатная тема. Придумать задач можно великое множество, причем разной сложности, смешать в задаче и арифметическую, и геометрическую прогрессии. Представляю вашему вниманию задачи, которые, по мнению авторов, относятся к уровню В. Но на мой взгляд, задачи довольно сложные – для сильного ученика.
Задача 1. При делении девятого члена арифметической прогрессии на второй ее член в частном получается 7; при делении десятого члена прогрессии на ее пятый член в частном получается 2 и в остатке 5. Найдите двадцатый член этой прогрессии.
Запишем условия:
![Rendered by QuickLaTeX.com \[\frac{a_9}{a_2}=7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-57bd8b6c693f0fa85db830c4f9260807_l3.png)
![Rendered by QuickLaTeX.com \[a_{10}=2a_5+5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-97c11f1d635cd0c68590c95c84ba5851_l3.png)
Теперь распишем члены прогрессии через первый член и разность прогрессии:
![Rendered by QuickLaTeX.com \[a_9=a_1+8d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8ebe582b19e8cfd0812ad5392e1263fc_l3.png)
![Rendered by QuickLaTeX.com \[a_2=a_1+d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f8c8e0b6c869ea1734590a497e9bc374_l3.png)
![Rendered by QuickLaTeX.com \[a_{10}=a_1+9d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-00768c7160f2dfd0eb99fe4831de9134_l3.png)
![Rendered by QuickLaTeX.com \[a_5=a_1+4d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2f1f8647b59dee18ec4f52cea4601ae1_l3.png)
И подставим в наши уравнения:
![Rendered by QuickLaTeX.com \[a_9=7a_7\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fff84560dde90fbc7653b9fa4343bc2d_l3.png)
![Rendered by QuickLaTeX.com \[a_1+8d=7(a_1+d)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-06df5c641c595c822a7686459d9e9e3c_l3.png)
![Rendered by QuickLaTeX.com \[6a_1=d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-465b5ccaac10c19778051a56378f671d_l3.png)
И второе:
![Rendered by QuickLaTeX.com \[a_1+9d=2(a_1+4d)+5\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-958e177de249d602067af14d7437e331_l3.png)
![Rendered by QuickLaTeX.com \[d-5=a_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aed8a1da2fbc6e960341eb06a5ab176d_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[6a_1-5=a_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ab2785716f936c431a6f18a3dd0d8860_l3.png)
![Rendered by QuickLaTeX.com \[a_1=1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4ef7cedaa2233bf1df2a157fdb9978a3_l3.png)
![Rendered by QuickLaTeX.com \[d=6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f939f5e7a2ff1b1efeea2016297611fe_l3.png)
Ответ:  ,
,  .
.
Задача 2. Даны две арифметические прогрессии (11; 15; 19; …), (154; 147; 140; …). Найдите все общие члены этих прогрессий.
Разность первой прогрессии равна 4, второй – 7. Запишем n-ный член для каждой прогрессии:
![Rendered by QuickLaTeX.com \[a_{n1}=7+4n\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2fefd6cf38a0962e67fe8163d2d4fe2a_l3.png)
![Rendered by QuickLaTeX.com \[a_{n2}=161-7m\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bc5010aab338f089a0b5a7132539cf3e_l3.png)
Мы ищем одинаковые члены прогрессий, поэтому приравняем выражения:
![Rendered by QuickLaTeX.com \[7+4n=161-7m\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-26267e8e8c3375c06d41e09a963deeed_l3.png)
![Rendered by QuickLaTeX.com \[m=22-\frac{4}{7}n\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aff8d177a15927113ea8c6bd1446fa87_l3.png)
Таким образом, подберем значения  , кратные 7, чтобы число
, кратные 7, чтобы число  было целым: при
было целым: при  –
–  , при
, при  –
–  , при
, при  –
–  , при
, при  –
–  , при
, при  –
–  .
.
Следовательно, общие члены прогрессий
![Rendered by QuickLaTeX.com \[161-7m=161-7\cdot18=35\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89ad313f152ef8a28ab9ca27e239f14a_l3.png)
![Rendered by QuickLaTeX.com \[161-7m=161-7\cdot14=63\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-41244ad62f7f086f7bfec9d8733c15c5_l3.png)
![Rendered by QuickLaTeX.com \[161-7m=161-7\cdot10=91\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-762d439cde2b33f3ed445655fe12d645_l3.png)
![Rendered by QuickLaTeX.com \[161-7m=161-7\cdot6=119\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-66c0fa5e9bd61c3f69cedd1502b7e18b_l3.png)
![Rendered by QuickLaTeX.com \[161-7m=161-7\cdot2=147\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7c8ae2715b1b966faa5698814df6237e_l3.png)
Ответ: 35, 63, 91, 119, 147.
Задача 3.  – арифметическая прогрессия.
– арифметическая прогрессия.  ,
,  . Найдите
. Найдите  .
.
Сумму можно представить как
![Rendered by QuickLaTeX.com \[a_1+a_3+a_5=a_1+a_1+2d+a_1+4d=3a_1+6d=-12\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8d54df34ed15dee4c1c567484e341864_l3.png)
Разделим на 3:
![Rendered by QuickLaTeX.com \[a_1+2d=-4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b40a88bbbf906d2499e391c2039d1e7a_l3.png)
То есть
![Rendered by QuickLaTeX.com \[a_3=-4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-409153d080937bea1ea08d81492c7e9a_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[a_1+a_5=-8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8ec98a6bef1c4522ab133bfa512f18bd_l3.png)
![Rendered by QuickLaTeX.com \[a_1\cdot a_5=-20\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bfb16febd7d3398f04687f7a29e43ccd_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[a_1(-8-a_1)+20=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d8b2b23b5a4d4837a7de32c627ed3484_l3.png)
![Rendered by QuickLaTeX.com \[a_1^2+8a_1-20=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7c8df9904d7be709e9eb8a38d2d892db_l3.png)
![Rendered by QuickLaTeX.com \[a_1=-10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-023ef41f72b5a82458f08f4e8bd47ef5_l3.png)
Или
![Rendered by QuickLaTeX.com \[a_1=2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c783dfcd770cd886b586170f45ba3e6d_l3.png)
Ответ:  или
или  .
.
Задача 4. Найдите сумму всех чётных трёхзначных чисел, делящихся на 3.
Такие числа обязательно делятся на 6, поэтому образуют арифметическую прогрессию с разностью  . Первый член нашей прогрессии, очевидно, 102 – числа 100 и 101 не делятся на 6. Последний член – 996. Определим его номер:
. Первый член нашей прогрессии, очевидно, 102 – числа 100 и 101 не делятся на 6. Последний член – 996. Определим его номер:
![Rendered by QuickLaTeX.com \[a_n=a_1+d(n-1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aa8f363ee526666e586b2ca63bea6eb0_l3.png)
![Rendered by QuickLaTeX.com \[996=102+6(n-1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9fc4cc17f6541d26bc0a88d85ec6f15b_l3.png)
![Rendered by QuickLaTeX.com \[n=150\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b1def0f33f1cf83a7067a4ebd445b7a2_l3.png)
Теперь можно найти сумму таких чисел:
![Rendered by QuickLaTeX.com \[S_{150}=\frac{2a_1+d(n-1)}{2}n=\frac{204+6(150-1)}{2}\cdot150=82350\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-443d2350c56ea004702d2d104427bfd6_l3.png)
Ответ: 82350.
Задача 5. Сумма бесконечной геометрической прогрессии со знаменателем  равна 4, а сумма кубов её членов равна 192. Найдите первый член и знаменатель прогрессии.
равна 4, а сумма кубов её членов равна 192. Найдите первый член и знаменатель прогрессии.
По условию
![Rendered by QuickLaTeX.com \[S_n=\frac{b_1}{1-q}=4~~~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-38d8360c5121f3760b3a9039b060a235_l3.png)
Также
![Rendered by QuickLaTeX.com \[b_1^3+b_2^3+b_3^3+ \ldots =192\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e9aec26bb6c1318fc30d9b758f909bfd_l3.png)
Запишем последнее так:
![Rendered by QuickLaTeX.com \[b_1^3+b_1^3q^3+b_1^3q^6+\ldots=192\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6e70ebeb9d38f502a5552f2399ff6234_l3.png)
![Rendered by QuickLaTeX.com \[b_1^3 (1+q^3+q^6+\ldots)=192\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d306a81066d5881d51fd3eb5bb33caed_l3.png)
В скобках можно заметить бесконечно убывающую геометрическую прогрессию со знаменателем  , тогда
, тогда
![Rendered by QuickLaTeX.com \[b_1^3\cdot\frac{1}{1-q^3}=192~~~~~~~~~~~~~~~~~~~~(2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9a7724c733696a96fc12a9e018727d3b_l3.png)
А из самого первого уравнения этой задачи следует, что
![Rendered by QuickLaTeX.com \[b_1=4(1-q)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d655c2e2227123d34d696b8af512c50c_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[b_1^3=64(1-q)^3\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e2a0ea152605b68f9a095353d147034f_l3.png)
Подставим это в (2)
![Rendered by QuickLaTeX.com \[64(1-q)^3\frac{1}{1-q^3}=192\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d543f0ce459eb00aa9a8a19d9acdedc3_l3.png)
Откуда, сокращая, получаем
![Rendered by QuickLaTeX.com \[(1-q)^2=3(1+q+q^2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-36be0fed50ce823c37ba40411b75ab92_l3.png)
Получаем квадратное уравнение
![Rendered by QuickLaTeX.com \[2q^2+5q+2=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-38dd0b5448255152621731fd91681a3f_l3.png)
![Rendered by QuickLaTeX.com \[q=-2, q=-\frac{1}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-98a00ea5715ec9521d08c01ed1e21738_l3.png)
Первый корень не подходит по условию, тогда
![Rendered by QuickLaTeX.com \[b_1=4(1-q)=4(1+\frac{1}{2})=6\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b4c81ca5bf0ed02a227d1ea30dafe86d_l3.png)
Ответ:  .
.
Задача 6. Найдите четыре числа, первые три из которых составляют геометрическую прогрессию, а последние три – арифметическую прогрессию. Сумма крайних чисел равна 21; а сума средних равна 18.
Дано: 
![Rendered by QuickLaTeX.com \[a+f=21\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c456d9d24bdfdb3a92d4451187406760_l3.png)
![Rendered by QuickLaTeX.com \[b+c=18\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-53b7245609ff4aef91f922f00a5b1d28_l3.png)
Также известно, что
![Rendered by QuickLaTeX.com \[b=aq\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-53eaa98ace1109859a723d5d288653ca_l3.png)
![Rendered by QuickLaTeX.com \[c=aq^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-97c3d528161c0d8c57d958abff7201ab_l3.png)
![Rendered by QuickLaTeX.com \[c=b+d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-781953f5c1dc257382717401224a9aa7_l3.png)
![Rendered by QuickLaTeX.com \[f=b+2d\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c81611dcd3913eca416bfee47b4481d1_l3.png)
Тогда разность арифметической прогрессии может быть найдена как
![Rendered by QuickLaTeX.com \[d=c-b=aq^2-aq=aq(q-1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2b2463a66c954b20427b1b1fcc7aa083_l3.png)
Сумма средних равна
![Rendered by QuickLaTeX.com \[aq+aq^2=aq(1+q)=18~~~~~~~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-54809cd7585f06385bea1bce0b6b3755_l3.png)
Сумма крайних (с учетом, что  )
)
![Rendered by QuickLaTeX.com \[a+ aq^2+d=21\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c2bebce21ce2883bd0ee06191ea84fd7_l3.png)
Подставим разность  :
:
![Rendered by QuickLaTeX.com \[a+ aq^2+ aq^2-aq =21\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d6decaea105c7c63236b710a446d3851_l3.png)
Имеем:
![Rendered by QuickLaTeX.com \[a(1+2q^2-q)=21~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-10885a2bf0f3d36f5e56f9acc9950f35_l3.png)
Разделим теперь (2) на (1):
![Rendered by QuickLaTeX.com \[\frac{1+2q^2-q }{ q(1+q)}=\frac{7}{6}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-44b4311b8d072b23e83f5ff66798cc0c_l3.png)
Получили квадратное уравнение:
![Rendered by QuickLaTeX.com \[12q^2-13q+6=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f4ae4b7887c8c8ec1256b02c31e116a5_l3.png)
Корни:  или
или  .
.
Если  , то
, то 
Тогда  ,
,  , а
, а  . Следовательно,
. Следовательно,  .
.
Если  , то
, то 
Тогда  ,
,  , а
, а  . Следовательно,
. Следовательно,  .
.
Ответ: 3, 6, 12, 18 или 18,75, 11,25, 6,75, 2,25.
Задача 7. Три числа образуют геометрическую прогрессию. Если второе число увеличить на 2, то прогрессия станет арифметической, а если после этого увеличить последнее число на 9, то прогрессия снова станет геометрической. Найдите эти числа.
Итак,  – образуют геометрическую прогрессию, по ее свойствам
– образуют геометрическую прогрессию, по ее свойствам
![Rendered by QuickLaTeX.com \[b=aq_1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d72f1398c6fea1943c7757c51017c066_l3.png)
![Rendered by QuickLaTeX.com \[c=aq_1^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ebc4c301f2386992a042ca8d370226da_l3.png)
Числа  – образуют арифметическую прогрессию. То есть
– образуют арифметическую прогрессию. То есть
![Rendered by QuickLaTeX.com \[a+d=b+2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b0ca8d1876ad803f4328d4fe346b514d_l3.png)
![Rendered by QuickLaTeX.com \[a+2d=c\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89aece4705ce6fc73e95c2fee3ee2c0c_l3.png)
Числа  снова образуют геометрическую прогрессию, но знаменатель у нее может быть другим:
снова образуют геометрическую прогрессию, но знаменатель у нее может быть другим:
![Rendered by QuickLaTeX.com \[aq_2=b+2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-368752ae0857e2be06eb529247c06361_l3.png)
![Rendered by QuickLaTeX.com \[aq_2^2=c+9\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-375007e027812dff0c29a056aeec70d6_l3.png)
Знаменатель первой геометрической прогрессии
![Rendered by QuickLaTeX.com \[q_1=\frac{c}{b}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-dd2a61816c142a0e1165cd4309ed074b_l3.png)
А второй геометрической
![Rendered by QuickLaTeX.com \[q_2=\frac{c+9}{b+2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-945f9550fae19379c108e34d9a2e5f3c_l3.png)
По свойству геометрической прогрессии можно записать:
![Rendered by QuickLaTeX.com \[b^2=ac\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-62777e95208df12f26fb4c1e45c41bf0_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{b^2}{c}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cce738e4a5812a23f13023fd8c0accfb_l3.png)
Но вторая геометрическая обладает тем же свойством:
![Rendered by QuickLaTeX.com \[(b+2)^2=a(c+9)~~~~~~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9b6226f00e241e0352ee14eddd2e38a3_l3.png)
![Rendered by QuickLaTeX.com \[a=\frac{(b+2)^2}{c+9}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9386ba7c9314bd833f9867cb75539545_l3.png)
Приравниваем  , полученные таким образом из обоих прогрессий:
, полученные таким образом из обоих прогрессий:
![Rendered by QuickLaTeX.com \[\frac{b^2}{c}=\frac{(b+2)^2}{c+9}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a1cb5bc277dc2794d1abd5bbeb9a6b27_l3.png)
Упрощая это, имеем:
![Rendered by QuickLaTeX.com \[b^2(c+9)=(b+2)^2c\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-81237032d0617dfb94ba37e3bc522f7c_l3.png)
![Rendered by QuickLaTeX.com \[9b^2-4bc-4c=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-27ea0a2439049d4ab5d9472e63f7f877_l3.png)
![Rendered by QuickLaTeX.com \[c=\frac{9b^2}{4(b+1)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-39e3c2710acfb9ccc496816a95dcd490_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[a=\frac{b^2}{c}=\frac{b^2}{\frac{9b^2}{4(b+1)}}=\frac{4(b+1)}{9}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c4b1de42fc2d1c1ce02b161c6bdacd3a_l3.png)
Разность арифметической прогрессии
![Rendered by QuickLaTeX.com \[d=b+2-a=b+2-\frac{4(b+1)}{9}=\frac{5b+14}{9}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e6c2e10e181bce9cd2601e9dc0e8675b_l3.png)
Тогда
![Rendered by QuickLaTeX.com \[a+2d=c\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-89aece4705ce6fc73e95c2fee3ee2c0c_l3.png)
![Rendered by QuickLaTeX.com \[\frac{4(b+1)}{9}+\frac{2(5b+14)}{9}=\frac{9b^2}{4(b+1)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3d9ea012d4a2d9fc9dae8e4b6916cc0b_l3.png)
Откуда
![Rendered by QuickLaTeX.com \[4(b+1)+2(5b+14)= \frac{81b^2}{4(b+1)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-73b67af95070e6e0f414d65ad8ba9dd9_l3.png)
![Rendered by QuickLaTeX.com \[4(14b+32)(b+1)=81b^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-80051cd1d0900d1eace1701bd073dc03_l3.png)
![Rendered by QuickLaTeX.com \[25b^2-184b-128=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ea462b3511cbc8e6927286cfaf755f8b_l3.png)
![Rendered by QuickLaTeX.com \[\frac{D}{4}=92^2+128\cdot25=11664=108^2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-39e4c2881f71273debe77128d428f75a_l3.png)
![Rendered by QuickLaTeX.com \[b=\frac{92+108}{25}=8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8f3233f7865cce7dc987eb90feacd7c5_l3.png)
![Rendered by QuickLaTeX.com \[b=\frac{92-108}{25}=-0,64\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7754c2996c8ea6318476dffaceee1414_l3.png)
В случае, если  , то
, то  ,
,  .
.
В случае, если  , то
, то  ,
,  .
.
Ответ: 4, 8, 16 или 0,16, -0,64, 2,56.
Задача 8. Найдите три числа, образующих геометрическую прогрессию, если известно, что их произведение равно 64, а их среднее арифметическое равно  .
.
![Rendered by QuickLaTeX.com \[a\cdot b \cdot c=64\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d65f0a3ca9024d9aedf84ab3163ceddb_l3.png)
![Rendered by QuickLaTeX.com \[\frac{a+b+c}{3}=\frac{14}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-178873d84eca7bb23972c3ea7b4278ab_l3.png)
Или  .
.
По свойству прогрессии
![Rendered by QuickLaTeX.com \[b^2=ac\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-62777e95208df12f26fb4c1e45c41bf0_l3.png)
![Rendered by QuickLaTeX.com \[b^2=\frac{64}{b}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-5af434a0f6f596f03a7aa1c85e65e8c5_l3.png)
Откуда  .
.
Тогда
![Rendered by QuickLaTeX.com \[a \cdot c=16\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-304cd7c667cec72f1330f3a619d5fb6c_l3.png)
![Rendered by QuickLaTeX.com \[a+c=10\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-928e55fe6e3a8d07b127a1d4cedf88d1_l3.png)
Либо  ,
,  , либо наоборот,
, либо наоборот,  ,
,  .
.
Ответ: 2, 4, 8 или 8, 4, 2.
Задача 9. Даны две арифметические прогрессии. Первый и пятый члены первой прогрессии равны соответственно 7 и (-5). У второй прогрессии первый член равен 0, а последний равен 3,5. Найдите сумму членов второй прогрессии, если известно, что третьи члены обеих прогрессий равны между собой.
Так как первый и пятый на одинаковом «расстоянии» от третьего, то выполняется свойство прогрессии:
![Rendered by QuickLaTeX.com \[a_3=\frac{a_1+a_5}{2}=1\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-432091283618f2e17cac1c0ed886653e_l3.png)
Таким образом, у второй прогрессии первый член – 0, а третий – 1, значит, второй – 0,5 и разность тоже 0,5. Следовательно, 3,5 – это восьмой член прогрессии. Осталось сосчитать сумму:
![Rendered by QuickLaTeX.com \[S_8=\frac{2a_1+d(n-1)}{2}n=\frac{0+0,5(8-1)}{2}8=14\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-18b9cd198749ae42a01f8433ad1133d8_l3.png)
Ответ: 14.
Задача 10. Найдите сумму всех трёхзначных чисел, делящихся на 7.
Такие числа обязательно делятся на 7, поэтому образуют арифметическую прогрессию с разностью  . Первый член нашей прогрессии, очевидно, 105 – числа 100, 101, 102, 103 и 104 не делятся на 7. Последний член – 994. Определим его номер:
. Первый член нашей прогрессии, очевидно, 105 – числа 100, 101, 102, 103 и 104 не делятся на 7. Последний член – 994. Определим его номер:
![Rendered by QuickLaTeX.com \[a_n=a_1+d(n-1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aa8f363ee526666e586b2ca63bea6eb0_l3.png)
![Rendered by QuickLaTeX.com \[994=105+7(n-1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ec511796a05384dce59753a7f94f8d24_l3.png)
![Rendered by QuickLaTeX.com \[n=128\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a962dd00ee3714c3bb8f4832ea12fff9_l3.png)
Теперь можно найти сумму таких чисел:
![Rendered by QuickLaTeX.com \[S_{128}=\frac{2a_1+d(n-1)}{2}n=\frac{210+7(128-1)}{2}\cdot128=70336\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-907cf462c8e8026c45804d59210a3c81_l3.png)
Ответ: 70336.
Задача 11. Найдите сумму семи первых членов бесконечной геометрической прогрессии со знаменателем  , если её второй член равен 4, а отношение суммы квадратов членов к сумме членов равна
, если её второй член равен 4, а отношение суммы квадратов членов к сумме членов равна  .
.
![Rendered by QuickLaTeX.com \[b_2=b_1q=4\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-846a526e7756b2216899a70b8e3555a2_l3.png)
![Rendered by QuickLaTeX.com \[\frac{b_1^2+b_2^2+b_3^2+\ldots}{b_1+b_2+b_3+\ldots}=\frac{16}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-46ac5abd5d7a69793686cfdd0f969b46_l3.png)
Преобразуем:
![Rendered by QuickLaTeX.com \[\frac{b_1^2+b_1^2q^2+b_1^2q^4+\ldots}{b_1+b_1q+b_1q^2+\ldots}=\frac{16}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b34cdcb05aa00998dd7188b67a967e4d_l3.png)
![Rendered by QuickLaTeX.com \[\frac{b_1^2(1+q^2+q^4+\ldots)}{b_1(1+q+q^2+\ldots)}=\frac{16}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-106cb77ddbcd743d2c2a958f1850a7de_l3.png)
В скобках имеем в числителе – сумму бесконечно убывающей прогрессии со знаменателем  , а в знаменателе – сумму бесконечно убывающей прогрессии со знаменателем
, а в знаменателе – сумму бесконечно убывающей прогрессии со знаменателем  . Тогда
. Тогда
![Rendered by QuickLaTeX.com \[\frac{b_1\frac{1}{1-q^2}}{\frac{1}{1-q}}=\frac{16}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fac78fb349055f7595fed5d88f157d1f_l3.png)
Или
![Rendered by QuickLaTeX.com \[\frac{b_1}{1+q}=\frac{16}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8c910832ac600ef9f7960a0110f73505_l3.png)
Но  , поэтому
, поэтому
![Rendered by QuickLaTeX.com \[3b_1=16(1+q)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3a9ddf93786807ef9eb4ccf3faf3306b_l3.png)
![Rendered by QuickLaTeX.com \[3\cdot\frac{4}{q}=16(1+q)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-58cbc2f50cdf702f15bf65c3e7d5a432_l3.png)
![Rendered by QuickLaTeX.com \[4q^2+4q-3=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8da826c2580dfeae333c5a83ed587b88_l3.png)
 или
или  , но по условию проходит меньший 1 по модулю знаменатель – то есть
, но по условию проходит меньший 1 по модулю знаменатель – то есть  . Тогда
. Тогда
![Rendered by QuickLaTeX.com \[S_n=\frac{b_1(1-q^n)}{1-q}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c1c3e8387f4a93e351c842a0222254e2_l3.png)
![Rendered by QuickLaTeX.com \[b_1=\frac{4}{q}=8\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f489a07e0e05d96f8ec0198f6024eb7c_l3.png)
![Rendered by QuickLaTeX.com \[S_7=\frac{8(1-0,5^7)}{1-0,5}=\frac{127}{8}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-483d8b5443c65d17640be876ac16055c_l3.png)
Ответ:  .
.
Задача 12. В геометрической прогрессии с отрицательными членами сумма первых шести членов равна (-504) и  . Найдите знаменатель прогрессии.
. Найдите знаменатель прогрессии.
Запишем обе сумы немного по-другому:
![Rendered by QuickLaTeX.com \[b_1+b_1q^3=-24\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-901b75f4e1cccc4cd59fa334bb1a25d6_l3.png)
![Rendered by QuickLaTeX.com \[b_1(1+q^3)=-24~~~~~~~~~~~~~~~~~~~~~~~~~~(1)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-195c45f503f87534783491abcfb8abfc_l3.png)
![Rendered by QuickLaTeX.com \[b_1+b_1q+b_1q^2+b_1q^3+b_1^4+b_1q^5=-504\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ec3dd871697f78018ffd552efaaf85d6_l3.png)
Теперь еще раз преобразуем последнее:
![Rendered by QuickLaTeX.com \[b_1(1+q^3+q^2+q^5+q+q^4)=-504\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8f1576a9648580486e15d3b94c99827b_l3.png)
Или
![Rendered by QuickLaTeX.com \[b_1((1+q^3)+q^2(1+q^3)+q(1+q^3))=-504\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-80a10a4d1715699b079105f39c764132_l3.png)
![Rendered by QuickLaTeX.com \[b_1(1+q^3)(1+q^2+q)=-504~~~~~~~~~~~~~~~~~~~~~~~~~~~(2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3441c5c67fa302f9b12f35d3df450f6d_l3.png)
Разделим (2) на (1)
![Rendered by QuickLaTeX.com \[1+q+q^2=21\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-9d8f528d1476d9ac06cc7e7b3dbb02fe_l3.png)
![Rendered by QuickLaTeX.com \[q^2+q-20=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-46870eb4cba85b08fa7f079187c8dfee_l3.png)
Тогда знаменатель либо  , либо
, либо  .
.
Так как по условию члены прогрессии отрицательны, нам подойдет положительный знаменатель.
Ответ:  .
.
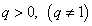 , то
, то 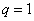 , то
, то 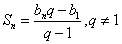
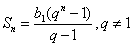
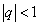 равна
равна