Показательная функция (определение и доказательство свойств)
Определение и свойства
Определение
Показательная функция f(n) = an, с основанием a, от натурального аргумента n – это произведение n множителей, каждый из которых равен a:
.
Здесь .
При она обладает следующими свойствами, вытекающих из правил умножения чисел:
(1.1) a x> 0 при a > 0;
(1.2) строго возрастает при a > 1 и строго убывает при 0 < a < 1;
(1.3) ;
(1.4) ;
(1.5) .
Если положить:
(1.6) ,
(1.7) ,
то показательная функция становится определенной и для целых чисел. При этом свойства (1.1-5) по прежнему выполняются, в которых , . Подробнее ⇓
Если положить:
(1.8) ,
где , то показательная функция становится определенной и для рациональных чисел . При этом выполняются свойства (1.1-7). В них , . Подробнее ⇓
Далее, основываясь на свойствах показательной функции (1.1-8), определенной на множестве рациональных чисел, мы определяем эту функцию на множестве действительных чисел и даем доказательство ее свойств.
Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство ⇓
Определение показательной функции
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Это определение справедливо и в случае, если x является рациональным числом. При этом совпадает со значением показательной функции, определяемом на множестве рациональных чисел. Чтобы убедиться в этом, достаточно в качестве последовательности взять последовательность с постоянными членами .
Заметим, что для доказательства свойств показательной функции, нам достаточно выбрать любую, удобную для нас последовательность рациональных чисел , сходящуюся к x. Действительно, согласно лемме ⇑, значение не зависит от выбора последовательности.
Теорема. Свойства показательной функцииПоказательная функция имеет следующие свойства:
(2.0) определена, при , для всех ; ⇓
(2.1) при a ≠ 1 имеет множество значений ; ⇓
(2.2) строго возрастает при , строго убывает при , является постоянной при ; ⇓
(2.3) ; ⇓
(2.3*) ; ⇓
(2.4) ; ⇓
(2.5) ; ⇓
(2.5*) ; ⇓
(2.6) ; ⇓
(2.7) ; ⇓
(2.8) непрерывна для всех ; ⇓
(2.9) при ;
при . ⇓
Доказательство ⇓
Определение показательной функции на множестве целых чисел
Исследуем вопрос – что будет, если для функции, обладающей свойствами (1.3-5), присвоить отрицательные значения аргумента? Положим
.
Умножим это уравнение на и воспользуемся свойством (1.3):
.
Поскольку , то мы получаем:
.
Отсюда , или
.
В частности, .
Таким образом, свойства (1.3-5) выполняются для отрицательных и нулевого значения n, если положить:
;
.
Тем самым мы определили значения показательной функции для целых чисел. Однако это возможно не для всех значений основания a. Поскольку деление на нуль не возможно, то .
Определение показательной функции на множестве рациональных чисел
Теперь рассмотрим вопрос об определении показательной функции для рациональных значений аргумента. Пусть есть рациональное число. Его можно представить в виде дроби:
,
где – целое, – натуральное.
Возьмем самый простой случай. Пусть . Рассмотрим уравнение:
.
Умножим его левую и правую части на себя n раз. То есть возведем в степень n и применим свойство (1.4):
;
(3.1) .
Таким образом, есть корень степени n из a:
.
Для любого и для , существует единственное решение уравнения (3.1) в области действительных чисел (см. «Доказательство существования и единственности корня степени n»).
Далее мы используем свойства корней:
(3.2) ;
(3.3) .
(3.4) .
В силу свойства (3.2), мы можем определить значения показательной функции для рациональных значений аргумента:
.
Используя свойства (1.3-7) для целых значений аргумента и свойства корней (3.2-4), можно доказать, что (1.3-7) выполняются и для рациональных значений аргумента показательной функции.
Доказательство леммы и свойств показательной функции
Доказательство леммы
Формулировка ⇑ 1. Докажем существование предела
.
Поскольку последовательность сходится, то для нее выполняется условие Коши. Это означает, что имеется такая функция , при которой для любого выполняется неравенство:
(Л.1) при .
Подставим . Тогда
(Л.2) при .
1.1. Пусть .
Докажем, что условие Коши выполняется для последовательности . Применим лемму Бернулли. При имеем:
(Л.3) .
Поскольку последовательность сходится к конечному числу, то она ограничена некоторым числом :
для всех n.
Поскольку показательная функция, определенная на множестве рациональных чисел строго возрастает при a > 1, то
для всех m.
Обозначим . В силу свойства (1.1), . Подставим в (Л.3) и применим условие Коши (Л.1). При имеем:
.
Если положить , то
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
То есть выполняется условие Коши для последовательности . Тогда на основании критерия Коши, эта последовательность сходится.
1.2. Теперь рассмотрим случай . Сведем его к предыдущему. Положим . Тогда , . Мы доказали, что последовательность сходится. Единицу в числителе можно рассматривать как элемент последовательности с постоянными членами, равными 1. Тогда, на основании арифметических свойств, существует предел частного последовательностей .
2. Теперь докажем, что предел не зависит от выбора последовательности .
То есть пусть мы имеем две, сходящиеся к x, последовательности и :
.
Мы доказали, что существуют пределы
и .
Теперь нам нужно доказать, что .
2.1. Пусть .
Рассмотрим разность последовательностей и , то есть последовательность , элементы которой равны разности элементов и . Согласно арифметическим свойствам, существует предел разности, который равен
.
Поскольку последовательности и сходятся к x, то, согласно определению предела последовательности, существуют такие функции и , так что для любого ,
при ,
при .
Положим и пусть . Тогда при имеем:
и ;
;
.
Воспользуемся тем, что конечное число членов последовательности не влияет на существование и величину предела. Отбросим первые членов у последовательностей и . Тогда
.
Применяем лемму Бернулли, аналогично предыдущему:
.
Воспользуемся свойствами пределов последовательностей, связанных неравенствами и вынесем постоянные за знак предела:
.
Применим арифметические свойства пределов:
.
Отсюда .
2.2. Пусть . Тогда ,
.
Предел последовательности не зависит от выбора . Поэтому и предел последовательности также не зависит от выбора .
Лемма доказана.
Доказательство свойств показательной функции
Формулировка ⇑Порядок доказательств свойств показательной функции отличается от порядка, в котором расположены свойства. Это сделано для удобства изложения. Последующие пункты могут использовать свойства, доказанные в первую очередь.
2.А. Сначала докажем, что
(2.А.1) ax> 0.
Согласно определению ⇑,
.
Поскольку последовательность рациональных чисел сходится к конечному числу x, то она ограничена:
.
Поскольку функция , определенная на множестве рациональных чисел монотонна (см. (1.2) ⇑ ), то она достигает своего минимального значения на границе рассматриваемого отрезка. Тогда
(2.А.2) .
Здесь при нужно взять знак “плюс”. При – знак “минус”. При , функция постоянна, . Можно взять любой знак. Выполним в (2.А.2) предельный переход , пользуясь свойствами пределов последовательностей, связанными неравенствами и определением показательной функции ⇑:
;
.
Согласно свойству (1.1) ⇑, . Тогда и
.
2.0. ⇑ Поскольку в определении ⇑, , а аргумент x является произвольным числом и ничем не ограничен, то показательная функция определена при для всех x. Ее областью определения является множество действительных чисел .
2.6. ⇑ . Здесь аргумент является рациональным числом. Мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Мы добавили пункт 2.6, чтобы объединить все свойства вместе.
2.2. ⇑ Докажем строгую монотонность показательной функции при a ≠ 1. То есть, если , то
при ;
при ;
при .
Итак, пусть . Выберем рациональные числа и , удовлетворяющие неравенствам:
.
Возьмем последовательности и , сходящиеся к и :
,
элементы которых удовлетворяют неравенствам:
, .
Тогда
.
2.2.1. Пусть .
Поскольку показательная функция, определенная на множестве рациональных чисел, при , строго возрастает, то
(2.2.1) .
Применим свойства пределов последовательностей, связанных неравенствами и определение показательной функции ⇑:
;
.
Отсюда .
2.2.2. Пусть .
В этом случае, показательная функция, определенная на множестве рациональных чисел, строго убывает. Доказательство такое же, как и в пункте 2.2.1, только начиная с (2.2.1), нужно поменять знаки неравенств:
(2.2.2) ;
;
;
.
2.2.3. Пусть .
Показательная функция , определенная на множестве рациональных чисел , является постоянной . Последовательность является последовательностью из постоянных элементов. Поэтому ее предел также равен единице:
;
для всех x.
2.3. ⇑ Докажем, что
.
Пусть и – произвольные последовательности рациональных чисел, сходящиеся к и :
.
Применим свойство предела суммы для последовательности :
(2.3.1) .
Рассмотрим последовательность . Поскольку, согласно лемме ⇑, и сходятся, то применим свойство предела произведения последовательностей иопределение показательной функции ⇑:
.
С другой стороны, применяя (2.3.1) и свойство (1.3) ⇑ показательной функции от рационального аргумента, имеем:
.
Отсюда
.
2.5. ⇑ Докажем, что
.
Все рассуждения и обозначения такие же, что и при доказательстве свойства (2.3) ⇑. Аналогичным образом, применяя свойство (1.5) ⇑ для рационального аргумента, имеем:
.
2.7. ⇑ Докажем, что
.
Аналогично предыдущему, имеем:
.
Здесь мы учли, что и применили свойство предела частного последовательностей.
2.3*. ⇑ Применяя свойства (2.3) ⇑ и (2.7) ⇑, имеем:
.
2.8. ⇑ Докажем непрерывность показательной функции.
2.8.1. Пусть .
Воспользуемся определением непрерывности функции в терминах приращений. Применяем свойство ax> 0 ⇑ и (2.3) ⇑
.
Поскольку есть сколь угодно малая величина, то считаем, что . Применим лемму Бернулли для действительных чисел:
.
Тогда
.
Применяем свойство пределов функций, связанных неравенством:
;
;
.
2.4. ⇑ Докажем, что
.
2.4.1. Рассмотрим случай .
Пусть – натуральные числа. Тогда
.
Применяя свойство (2.3) ⇑, имеем:
;
(2.4.1) .
Теперь исследуем, что такое . Введем обозначение:
(2.4.2) .
Возведем в n-ю степень. То есть умножим левую и правую части на себя n раз, и применим (2.4.1):
;
.
Поскольку ax> 0 ⇑, то b есть корень степени n из положительного числа :
. Подставляя (2.4.2), имеем:
(2.4.3) .
Применяя свойства (2.4.1) и (2.4.3), для произвольного положительного рационального числа получаем:
;
(2.4.4) .
Пусть есть произвольная последовательность рациональных чисел, сходящаяся к x2:
(2.4.5) .
Применяя (2.4.4), имеем:
.
Рассмотрим последовательность . Учитывая (2.4.5), и применяя арифметические свойства сходящихся последовательностей, получаем, что сходится к :
.
Выше мы доказали, что показательная функция непрерывна ⇑. Используя определение непрерывности функции по Гейне, получаем:
;
.
2.4.2. Рассмотрим случай .
Тогда . Применяя свойство (2.7) ⇑, имеем:
.
2.4.3. Теперь пусть .
Применяем (2.6) ⇑ Тогда .
Поскольку ax1> 0 ⇑, то
;
.
2.5*. ⇑ Докажем, что
.
Применяя свойства (2.7) ⇑, (2.5) ⇑ и (2.4) ⇑, имеем:
.
2.9. ⇑
2.9.1. Пусть .
2.9.1.1. Докажем, что
.
Поскольку функция монотонна ⇑, то согласно теореме о пределе монотонной функции, она имеет конечный или бесконечный предел
.
Поскольку функция имеет предел A, то согласно определению предела функции по Гейне, для любой последовательности , сходящейся к , последовательность сходится к A:
.
Возьмем последовательность натуральных чисел . Она сходится к : . Тогда
.
Для вычисления этого предела, применим неравенство Бернулли:
.
При , правая часть неравенства стремится к . Применяя свойство неравенств бесконечно больших последовательностей, находим, что
.
Отсюда , .
2.9.1.2. Докажем, что
.
Сделаем подстановку . Применим свойство (2.7) ⇑ и свойства бесконечно малых и бесконечно больших функций:
.
2.9.2. Пусть .
Сделаем подстановку . Тогда ,
;
.
2.1. ⇑ Докажем, что при a ≠ 1 показательная функция имеет множество значений .
Рассмотрим функцию на отрезке , где – произвольные числа. Поскольку функция строго монотонна ⇑ и определена для всех x, то она достигает минимума и максимума на концах отрезка – в точках и . Поскольку функция непрерывна ⇑, то согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы ⇑ получаем, что множеством значений показательной функции является множество положительных чисел .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: Изменено:
1cov-edu.ru
Урок 1. Повторение. Показательная функция. Показательные уравнения. Теория
В теоретической части урока мы вспомним свойства степени с натуральным, целым и рациональным показателем. Также мы обсудим показательную функцию и её свойства. Используя эти свойства, выведем правило для решения показательных уравнений.
Подготовка к ЕГЭ по математике
Эксперимент
Урок 1. Повторение. Показательная функция. Показательные уравнения
Теория
Конспект урока
Что такое степень? С этим понятием мы уже сталкивались неоднократно в школьном курсе математики.
Изначально мы говорили про степень с натуральным показателем и вводили следующее определение: выражение 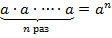 называется степенью. При этом a – называется основанием степени, а n – показателем степени.
называется степенью. При этом a – называется основанием степени, а n – показателем степени.
Фактически, эта запись означала удобное сокращение – вместо того, чтобы каждый раз писать произведение большого количества множителей мы стали использовать удобную и краткую запись.
Исходя из определения степени легко получить свойства степени с натуральным показателем:
1) 
2) 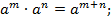
3)  (
(
4) 
5) 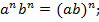
6) 
Однако в математике все понятия рано или поздно обобщаются. Понятие степени оказалось удобно использовать не только в случае натурального показателя. Поэтому впоследствии мы ввели понятие степени с целым показателем.
Чтобы получить выражение  достаточно в третьем свойстве положить:
достаточно в третьем свойстве положить:  и мы получим:
и мы получим: 
Получить выражение для отрицательного показателя степени также несложно. Для этого достаточно взять в третьем свойстве в качестве  Тогда получим:
Тогда получим: 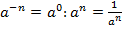 (
(
Несложно убедиться, что при таком определении степени с целым показателем все остальные свойства, уже определённые для степени с натуральным показателем сохраняются (собственно, этого мы и добивались). Таким образом, для степени с целым показателем полный список свойств выглядит так:
1) 
2) 
3)&n
interneturok.ru
Показательная функция, ее свойства и простейшие показательные неравенства
Напомним свойства показательной функции с основанием, большим единицы.
 :
:
х – аргумент, независимая переменная; у – функция, зависимая переменная.

Рис. 1. График показательной функции, основание степени больше единицы
График функции – экспонента (рис. 1).
Основные свойства данного семейства функций:
1. Область определения: 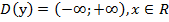 .
.
2. Область значений: 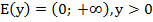 .
.
3. Функция возрастает, т. е. большему значению аргумента соответствует большее значение функции.
4. Если аргумент стремится к минус бесконечности, функция стремится к нулю, если аргумент стремится к плюс бесконечности функция стремится также к плюс бесконечности.
Монотонное возрастание функций данного семейства является ключом к решению показательных неравенств, при условии, что основание степени 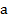 больше единицы.
больше единицы.
Методика решения подобных неравенств:
1. Уравнять основания степеней.
2. Сравнить показатели, сохранив знак неравенства.
Напомним свойства показательной функции с основанием, меньшим единицы, но большим нуля (рис. 2).
 :
:
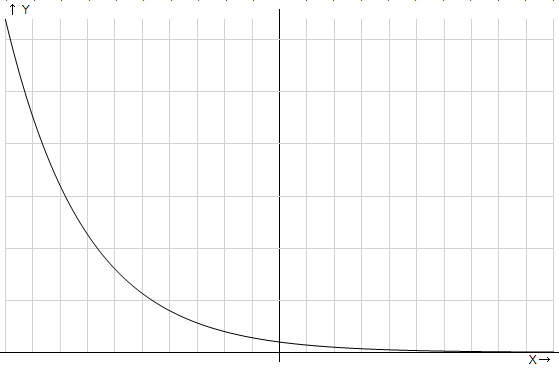
Рис. 2. График показательной функции, основание степени меньше единицы.
Свойства данного семейства функций:
1. Область определения: 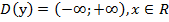 .
.
2. Область значений: 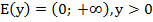
3. Функция убывает, т. е. большему значению аргумента соответствует меньшее значение функции.
4. Если аргумент стремится к мин
interneturok.ru
3. Показательная функция.
Функция
вида  ,
где
,
где называетсяпоказательной функцией.
называетсяпоказательной функцией.
Коэффициент а — положительное число, указывает на возрастание или убывание функции.
Свойства функции:
1. Д(у)=R.
2. Е(у)= 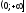
3. Функция возрастает (а>1), убывает (а<1) на всей области определения.
4. График функции пересекает ось ординат в точке (0;1).
5. Функция непрерывна
на всей области определения, дифференцируема
и производная равна  .
.
4. Логарифмическая функция
Логарифмической
функцией называется
функция вида 
Число а определяет расположение графика.
Вместо логарифмической
функции с произвольным основанием
удобно рассматривать функцию вида  .
.
Так как 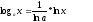 ,
то указанные функции исчерпывают все
логарифмические функции.
,
то указанные функции исчерпывают все
логарифмические функции.
Свойства функции у=ln x.
1. Д(у)= .
.
2. Е(у)=R.
3. Функция принимает нулевое значение при х=1.
4. Функция возрастает на всей области определения.
5. Функция является
непрерывной на всей области определения,
дифференцируема и  .
.
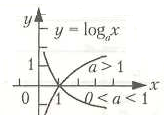 5.
Экспоненциальная функция
5.
Экспоненциальная функция
Функция,
обратная функции 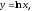 называется экспоненциальной и записывается
уравнением
называется экспоненциальной и записывается
уравнением  .
.
График функции
симметричен графику функции 
Свойства функции: (смотри свойства показательной функции).
6. Степенная функция
Степенной
функцией с
действительным показателем называется
функция вида 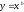 , где b-действительное число, х>0.
, где b-действительное число, х>0.
Примеры степенных
функций:  .
.
Коэффициент b определяет положение графика на координатной плоскости.
Свойства функции.
1. Функция определена для х>0.
2. Е(у)= .
.
3. Функция возрастающая, если b>0 и убывающая, если b<0.
4. Функция непрерывна
на всей области определения, дифференцируемая
и 

Пример использования функций в экономике.
Функции находят широкое применение в экономической теории и практике. Спектр используемых в экономике функций весьма широк: от простейших линейных до функций, получаемых по определенному алгоритму с помощью так называемых рекуррентных соотношений, связывающих состояния изучаемых объектов в разные периоды времени.
Наряду с линейными используются нелинейные функции: дробно-рациональные, степенные (квадратичная, кубическая и т.д.). показательные (экспоненциальные), логарифмические и др. Периодичность, колеблемость ряда экономических процессов позволяет также применять тригонометрические функции.
Наиболее часто в экономике используются следующие функции.
Функция полезности (функция предпочтений) — в широком смысле зависимость полезности, т.е. результата, эффекта некоторого действия от уровня (интенсивности) этого действия.
Производственная функция — зависимость результата производственной деятельности от обусловивших его факторов.
Функция выпуска (частный вид производственной функции) — зависимость объема производства от наличия или потребления ресурсов.
Функция издержек (частный вид производственной функции) — зависимость издержек производства от объема выпуска продукции.
Функции спроса, потребления, предложения — зависимость объема спроса, потребления, предложения на отдельные товары или услуги от различных факторов (например, цены, дохода и т.п.)
20. Предел функции в бесконечности и точке.
Предел функции в бесконечности и точке
С понятием предела числовой последовательности тесно связано понятие предела функции в бесконечности. Если в первом случае переменная n, возрастая, принимает лишь натуральные значения, то во втором случае переменная x, изменяясь, принимает любые значения.
Опр.
Число А называется пределом функции  приx,
стремящемся к бесконечности, если для
любого
существует такое положительное числоS
(зависящее только от
приx,
стремящемся к бесконечности, если для
любого
существует такое положительное числоS
(зависящее только от  ),
что при всех
),
что при всех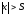 выполняется неравенство
выполняется неравенство
 .
.
Пусть
функция 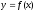 задана в окрестности точкиа,
кроме, быть может, самой точки а.
задана в окрестности точкиа,
кроме, быть может, самой точки а.
Опр.
Число А называется пределом функции 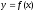 приx,
стремящемся к а,
если для любого
приx,
стремящемся к а,
если для любого  существует такое положительное число
существует такое положительное число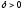 (зависящее только от
(зависящее только от ),
что при всехx,
не равных а и удовлетворяющих условию
),
что при всехx,
не равных а и удовлетворяющих условию  выполняется неравенство
выполняется неравенство
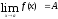 .
.
Замечание 1. Определение предела не требует существования функции в самой точке а.
Замечание
2. Если при стремлении x к а переменная x
принимает лишь значения, меньшие а,
или, наоборот, большие а,
и при этом функция стремится к некоторому
числу А, то говорят об односторонних
пределах функции соответственно слева 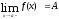 и справа
и справа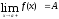 .
.
Функция имеет в точке а предел тогда и только тогда, когда в этой точке существует левый и правый предел и они равны. В таком случае предел функции равен односторонним пределам.
21. Основные теоремы о пределах. Признаки существования пределов.
studfile.net
| 1. |
Значение функции
Сложность: лёгкое |
3 |
| 2. |
Определение показательной функции
Сложность: лёгкое |
1 |
| 3. |
Свойства показательной функции (возрастание функции)
Сложность: лёгкое |
1 |
| 4. |
Умножение степеней с одинаковым основанием
Сложность: лёгкое |
1 |
| 5. |
Деление степеней с одинаковыми основаниями
Сложность: лёгкое |
2 |
| 6. |
Возведение степени в степень
Сложность: лёгкое |
2 |
| 7. |
Значение аргумента
Сложность: среднее |
1 |
| 8. |
Преобразования графика показательной функции
Сложность: среднее |
2 |
| 9. |
Область определения функции (показатель степени — дробь)
Сложность: среднее |
2 |
| 10. |
Свойства показательной функции (возрастание и убывание функции)
Сложность: среднее |
2 |
| 11. |
Свойства степени с рациональным показателем (деление)
Сложность: среднее |
3 |
| 12. |
Свойства степени с рациональным показателем (умножение)
Сложность: среднее |
5 |
| 13. |
График показательной функции, область определения и область значений функции
Сложность: среднее |
3 |
| 14. |
Решение уравнения графически
Сложность: сложное |
4 |
| 15. |
Свойства показательной функции (произведение степеней)
Сложность: сложное |
3 |
www.yaklass.ru
11.3.1. Показательная функция, ее свойства и график математика-повторение
data-ad-client=»ca-pub-8602906481123293″
data-ad-slot=»8834522701″
data-ad-format=»auto»>
- Функцию вида y=ax, где а>0, a≠1, х – любое число, называют показательной функцией.
- Область определения показательной функции: D (y)=R – множество всех действительных чисел.
- Область значений показательной функции: E (y)=R+ — множество всех положительных чисел.
- Показательная функция y=ax возрастает при a>1.
- Показательная функция y=ax убывает при 0<a<1.
Справедливы все свойства степенной функции:
- а0=1 Любое число (кроме нуля) в нулевой степени равно единице.
- а1=а Любое число в первой степени равно самому себе.
- ax∙ay=ax+y При умножении степеней с одинаковыми основаниями основание оставляют прежним, а показатели складывают.
- ax:ay=ax- y При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
- (ax)y=axy При возведении степени в степень основание оставляют прежним, а показатели перемножают
- (a∙b)x=ax∙by При возведении произведения в степень возводят в эту степень каждый из множителей.
- (a/b)x=ax/by При возведении дроби в степень возводят в эту степень и числитель и знаменатель дроби.
- а-х=1/ax
- (a/b)-x=(b/a)x.
Примеры.
1) Построить график функции y=2x. Найдем значения функции
 при х=0, х=±1, х=±2, х=±3.
при х=0, х=±1, х=±2, х=±3.
x=0, y=20=1; Точка А.
x=1, y=21=2; Точка В.
x=2, y=22=4; Точка С.
x=3, y=23=8; Точка D.
x=-1, y=2-1=1/2=0,5; Точка K.
x=-2, y=2-2=1/4=0,25; Точка M.
x=-3, y=2-3=1/8=0,125; Точка N.
Большему значению аргумента х соответствует и большее значение функции у. Функция y=2x возрастает на всей области определения D (y)=R, так как основание функции 2>1.
2) Построить график функции y=(1/2)x. Найдем значения функции
при х=0, х=±1, х=±2, х=±3.
 x=0, y=(½)0=1; Точка A.
x=0, y=(½)0=1; Точка A.
x=1, y=(½)1=½=0,5; Точка B.
x=2, y=(½)2=¼=0,25; Точка C.
x=3, y=(½)3=1/8=0,125; Точка D.
x=-1, y=(½)-1=21=2; Точка K.
x=-2, y=(½)-2=22=4; Точка M.
x=-3, y=(½)-3=23=8; Точка N.
Большему значению аргумента х соответствует меньшее значение функции y. Функция y=(1/2)x убывает на всей своей области определения: D (y)=R, так как основание функции 0<(1/2)<1.
3) В одной координатной плоскости построить графики функций:
y=2x, y=3x, y=5x, y=10x. Сделать выводы.
График функции у=2х мы уже строили, графики остальных функций строим аналогично, причем, достаточно будет найти значения функций при х=0 и при х=±1.
 Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Переменная х может принимать любое значение (D (y)=R), при этом значение у всегда будет больше нуля (E (y)=R+).
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю. Чем больше основание а (если a>1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все данные функции являются возрастающими, так как большему значению аргумента соответствует и большее значение функции.
4) В одной координатной плоскости построить графики функций:
y=(1/2)x, y=(1/3)x, y=(1/5)x, y=(1/10)x. Сделать выводы.
Смотрите построение графика функции y=(1/2)x выше, графики остальных функций строим аналогично, вычислив их значения при х=0 и при х=±1.
 Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Переменная х может принимать любое значение: D (y)=R, при этом область значений функции: E (y)=R+.
Графики всех данных функций пересекают ось Оу в точке (0; 1), так как любое число в нулевой степени равно единице; с осью Ох графики не пересекаются, так как положительное число в любой степени не может быть равным нулю.
Чем меньше основание а (при 0<a<1) показательной функции у=ах, тем ближе расположена кривая к оси Оу.
Все эти функции являются убывающими, так как большему значению аргумента соответствует меньшее значение функции.
Решить графически уравнения:
1) 3x=4-x.
 В одной координатной плоскости построим графики функций: у=3х и у=4-х.
В одной координатной плоскости построим графики функций: у=3х и у=4-х.
Графики пересеклись в точке А(1; 3).
Ответ: 1.
2) 0,5х=х+3.
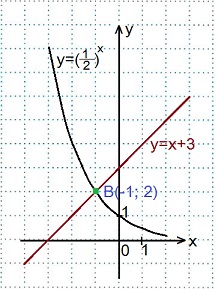
В одной координатной плоскости строим графики функций: у=0,5х
(y=(1/2)x )
и у=х+3.
Графики пересеклись в точке В(-1; 2).
Ответ: -1.
Найти область значений функции: 1) y=-2x; 2) y=(1/3)x+1; 3) y=3x+1-5.
Решение.
1) y=-2x
Область значений показательной функции y=2x – все положительные числа, т.е.
0<2x<+∞. Значит, умножая каждую часть двойного неравенства на (-1), получаем:
— ∞<-2x<0.
Ответ: Е(у)=(-∞; 0).
2) y=(1/3)x+1;
0<(1/3)x<+∞, тогда, прибавляя ко всем частям двойного неравенства число 1, получаем:
0+1<(1/3)x+1<+∞+1;
1<(1/3)x+1<+∞.
Ответ: Е(у)=(1; +∞).
3) y=3x+1-5.
Запишем функцию в виде: у=3х∙3-5.
0<3x<+∞; умножаем все части двойного неравенства на 3:
0∙3<3x∙3<(+∞)∙3;
0<3x∙3<+∞; из всех частей двойного неравенства вычитаем 5:
0-5<3x∙3-5<+∞-5;
— 5<3x∙3-5<+∞.
Ответ: Е(у)=(-5; +∞).
Смотрите Карту сайта, и Вы найдете нужные Вам темы!
Запись имеет метки: Показательная функция
www.mathematics-repetition.com
Степенные функции, их свойства и графики. Степенные функции с рациональным показателем
Напомним свойства и графики степенных функций с целым отрицательным показателем.
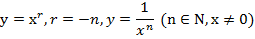
При четных n, 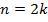 :
:
Пример функции: 
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;1). Особенность функций данного вида – их четность, графики симметричны относительно оси ОУ.

Рис. 1. График функции 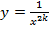
При нечетных n, 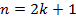 :
:
Пример функции: 
Все графики таких функций проходят через две фиксированные точки: (1;1), (-1;-1). Особенность функций данного вида – их нечетность, графики симметричны относительно начала координат.

Рис. 2. График функции 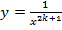
Напомним основное определение.
Степенью неотрицательного числа а с рациональным положительным показателем 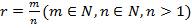 называется число
называется число 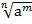 .
.
Степенью положительного числа а с рациональным отрицательным показателем  называется число
называется число  .
.
Для  выполняется равенство:
выполняется равенство:
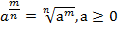

Например: 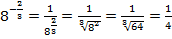 ;
;  – выражение не существует по определению степени с отрицательным рациональным показателем;
– выражение не существует по определению степени с отрицательным рациональным показателем;  существует, т. к. показатель степени целый,
существует, т. к. показатель степени целый,
Перейдем к рассмотрению степенных функций с рациональным отрицательным показателем.

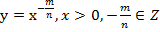
Например:

Для построения графика данной функции можно составить таблицу. Мы поступим иначе: сначала построим и изучим график знаменателя – он нам известен (рисунок 3).

Рис. 3. График функции 
График функции знаменателя проходит через фиксированную точку (1;1). При построении графика исходной функции данная точка остается, при  корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).
корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 4).
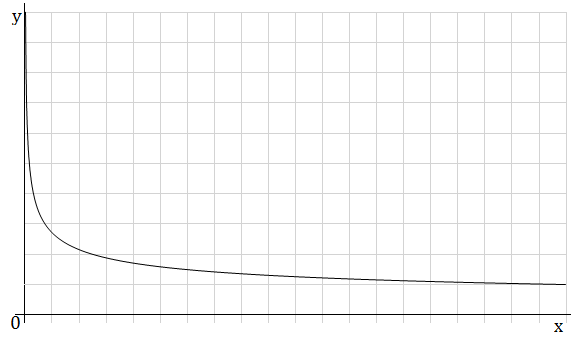
Рис. 4. График функции 
Рассмотрим еще одну функцию из семейства изучаемых функций.

Важно, что  по определению
по определению
Рассмотрим график функции, стоящей в знаменателе: 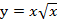 , график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).
, график данной функции нам известен, она возрастает на своей области определения и проходит через точку (1;1) (рисунок 5).

Рис. 5. График функции 
При построении графика исходной функции точка (1;1) остается, при 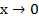 корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).
корень также стремится к нулю, функция стремится к бесконечности. И, наоборот, при стремлении х к бесконечности функция стремится к нулю (рисунок 6).

Рис. 6. График функции 
Рассмотренные примеры помогают понять, каким образом проходит график и каковы свойства изучаемой функции – функции с отрицательным рациональным показателем.
Графики функций данного семейства проходят через точку (1;1), функция убывает на всей области определения.
Область определения функции: 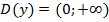
Функция не ограничена сверху, но ограничена снизу. Функция не имеет ни наибольшего, ни наименьшего значения.
Функция непрерывна, принимает все положительные значения от нуля до плюс бесконечности.
Функция выпукла вниз (рисунок 15.7)
На кривой взяты точки А и В, через них проведен отрезок, вся кривая находится ниже отрезка, данное условие выполняется для произвольных двух точек на кривой, следовательно функция выпукла вниз. Рис. 7.

Рис. 7. Выпуклость функции
Важно понять, что функции данного семейства ограничены снизу нулем, но наименьшего значения не имеют.
Пример 1 – найти максимум и минимум функции на интервале [1;8):

вычислим значения функции в концах заданного промежутка:

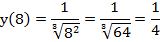
Теперь мы можем выписать ответ на основании того, что функция монотонно убывает.
 , минимального значения нет, так как правая граница не включена в интервал.
, минимального значения нет, так как правая граница не включена в интервал.
Пример 2 – построить и прочесть график функции:

Преобразуем заданную функцию по определению рациональной степени:

Не забудем указать, что по определению 
Строим график функции  , для нас это стандартная кривая, она проходит через точку (1;1), убывает. После этого сдвигаем полученный график на одну единицу вверх, точка (1;1) переходит в точку (1;2) (рисунок 8)
, для нас это стандартная кривая, она проходит через точку (1;1), убывает. После этого сдвигаем полученный график на одну единицу вверх, точка (1;1) переходит в точку (1;2) (рисунок 8)
Читаем полученный график: если аргумент возрастает от нуля (не включая) до бесконечности, функция убывает от бесконечности до единицы (не включая).
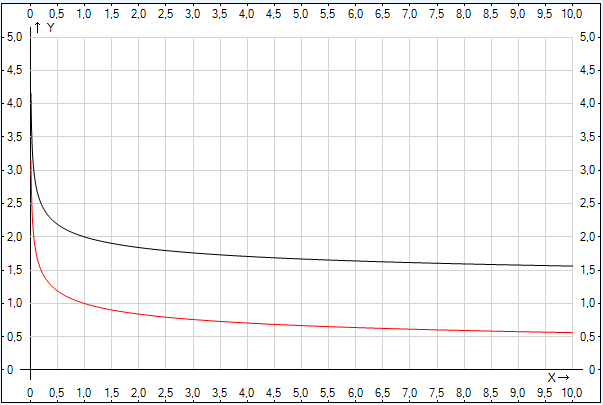
Рис. 8. Построение графика функции 
Пример 3 – построить и прочесть график функции:
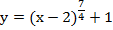
Преобразуем заданную функцию по определению степени с рациональным показателем:
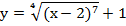
Нам известен график функции  , построим его. Полученная кривая возрастает и проходит через точку (1;1), поскольку показатель степени больше единицы – кривая выпукла вниз. Сдвинем построенную кривую на две единицы вправо (получаем график функции
, построим его. Полученная кривая возрастает и проходит через точку (1;1), поскольку показатель степени больше единицы – кривая выпукла вниз. Сдвинем построенную кривую на две единицы вправо (получаем график функции  ) и на одну единицу вверх – получаем искомый график (рисунок 9)
) и на одну единицу вверх – получаем искомый график (рисунок 9)
Прочтем полученный график:

При возрастании аргумента от двух до бесконечности функция возрастает от единицы до бесконечности.
Пример 4 – построить и прочесть график функции:
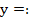

В данном случае функция задана кусочно.
Напомним, что такое модуль, раскроем его по определению:


Итак, строим график функции  . Имеем две ветки:
. Имеем две ветки:  и
и  . После этого строим стандартную кривую
. После этого строим стандартную кривую  на интервале
на интервале  (Рисунок 10)
(Рисунок 10)
Прочтем график построенной функции:
Если аргумент возрастает от минус бесконечности до нуля, функция убывает от бесконечности до нуля. Когда аргумент возрастает от нуля до единицы, функция также возрастает от нуля до единицы. Наконец, когда аргумент возрастает от единицы не включительно до плюс бесконечности, функция убывает от единицы не включительно до нуля не включительно.

Рис. 9. Построение графика функции 

Рис. 10. График кусочно заданной функции
Пример 5 – найти значения параметра, при котором уравнение а) имеет хотя бы одно решение; б) имеет только одно решение:


График заданной функции мы уже построили в предыдущем примере. Теперь рассечем его семейством прямых  и найдем количество точек пересечения для каждого случая.
и найдем количество точек пересечения для каждого случая.
Выполним рассечение (рисунок 11).

Рис. 11. Рассечение графика прямыми 
При  уравнение имеет три решения; при
уравнение имеет три решения; при  уравнение имеет единственное решение
уравнение имеет единственное решение
Ответ: при 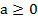 уравнение имеет хотя бы одно решение, при
уравнение имеет хотя бы одно решение, при  уравнение имеет единственное решение.
уравнение имеет единственное решение.
Итак, мы рассмотрели степенные функции, их свойства и графики. На следующем уроке мы перейдем к дифференцированию и интегрированию степенных функций.
Список литературы
- Мордкович А.Г. Алгебра и начала математического анализа. – М.: Мнемозина.
- Муравин Г.К., Муравина О.В. Алгебра и начала математического анализа. – М.: Дрофа.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала математического анализа. – М.: Просвещение.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Uztest.ru (Источник).
- Edu.glavsprav.ru (Источник).
- Pm298.ru (Источник).
Домашнее задание
1. Найдите наибольшее и наименьшее значение функции  на интервале:
на интервале:
а)  ; б)
; б) 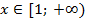 ; в)
; в) 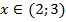 ; г)
; г) 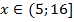
2. Построить и прочесть график функции:
а)  ; б)
; б) ; в)
; в) ; г)
; г) 
3. Решите уравнение с параметром:


interneturok.ru